Guest Post by Willis Eschenbach
I’ve been thinking about thermal lags in the climate system. Everyone is familiar with thermal lag in everyday life. When you put a cast-iron pan on the stove flame, it doesn’t heat up instantly. Instead, the warming process starts instantly, but it takes some amount of time to actually up to a stable heat. And when you turn the heat off, it doesn’t cool down immediately. That’s thermal lag.
Now, Dr. Shaviv claimed that I didn’t understand harmonic analysis and the lag between the sun and what it is heating. I’ll return to that question further down. For now, thermal lag is generally modeled as an “exponential” lag. In an exponential lag, say when you take a hot pan off of the flame, it doesn’t become cold immediately. At first it cools fast. Then as time goes on and it nears room temperature, it cools slower and slower. That “fast at first, slower later” form is characteristic of an exponential process.
In the calculation of an exponential lag, the delay in the response is governed by a time constant called “tau”. The larger the time constant tau, the greater the lag time, and the slower the pan will either heat up or cool down.
With that as prologue, here’s a graph of the heat being turned on and then off under the pan on the stove (black/yellow line), and the temperature response of the pan itself (lines colored blue to red).
 Figure 1. Example graph showing how a pan heats up and cools down. Time is in minutes. The fire is shown by the black/yellow line. The fire goes on under the pan at about time t = 8 minutes, and comes off again five minutes later at about t = 13 minutes or so. The time constant “tau” is measured in whatever the underlying time unit is, in this case minutes. Amplitude in arbitrary units.
Figure 1. Example graph showing how a pan heats up and cools down. Time is in minutes. The fire is shown by the black/yellow line. The fire goes on under the pan at about time t = 8 minutes, and comes off again five minutes later at about t = 13 minutes or so. The time constant “tau” is measured in whatever the underlying time unit is, in this case minutes. Amplitude in arbitrary units.
Figure 1 shows graphically the change in pan temperature, using different colored lines for different values of the time constant tau. The blue lines show small values of tau. A small value for tau would be the situation with say a small thin aluminum frypan, which would rapidly come up to heat and stay at temperature until the fire is turned off. At that point, it cools down quite rapidly. We say that it has small “thermal mass”, so it heats up quickly.
At the other end of the spectrum, the red line shows a large time constant tau of 9 minutes. It would be characteristic of say a big, heavy cast iron cook pot. It would have lots of thermal mass. In the example above, note that the iron pot heats up so slowly that it doesn’t even get up to heat before the fire is turned off.
This illustrates at least three points about this kind of exponential thermal behavior—exponential action, changing shape, and changing size.
First, the action happens exponentially. This means quickly at the start, and then slowing down as time goes on. For example, a hot pan taken off the fire cools rapidly to begin with, but as it approaches room temperature, the cooling slows.
Second, and this is an important point. In general, the shape of the exponential lagged response (the pan temperature) is NOT the same as the shape of the impulse (the on/off of the fire). In the red lines in Figure 1 above, you can see how the square-wave on/off thermal impulse of the flame (black/yellow line) is transformed into a kind of shark-fin shaped thermal response in a heavy cast-iron cookpot.
Third, if the time of the impulse is short enough, the amplitude of the response is smaller than that of the impulse. In other words, in Figure 1 the blue line gets as high as the black/yellow line, but the red line doesn’t get that high before the time comes when it starts dropping again.
There is a special case, however, where the exponentially lagged response has the same shape as the impulse. This is when the impulse has a sinusoidal (sine wave) shape. An example of this would be the solar strength as the earth moves nearer to and further from the sun over the course of the year. Over the course of a year, solar strength varies sinusoidally about 23 W/m2 on a 24/7 global average. It peaks in early January, and bottoms out in early July.
Anyhow, I got to thinking once again about the effect of exponential lag on a sinusoidal input. So I made up a graph like Figure 1, except using a sinusoidal input instead of a square wave input.
 Figure 2. Lagged versions of a sinusoidal input. The input is the black/yellow line in the back of the drawing, which represents a flame under the pot of varying strength. The lagged versions showing temperature variations in the pan are shown in color. Time units are quarter cycles. If the full cycle is one year, tau is in months.
Figure 2. Lagged versions of a sinusoidal input. The input is the black/yellow line in the back of the drawing, which represents a flame under the pot of varying strength. The lagged versions showing temperature variations in the pan are shown in color. Time units are quarter cycles. If the full cycle is one year, tau is in months.
Now, I was very happy when I first saw that result. I was elated because I’d never been able to calculate the thermal lag directly from the observations. Oh, I could fit a lagged curve to the results, but to me that’s unsatisfying. And in this graph, I noticed a very curious thing that I’d not known before.
This is that the peaks of the lagged versions of the input wave fall exactly on the original sinusoidal impulse line (black/yellow). This was important to me, because I’d never been able to figure out how much smaller the lagged response wave was than the size of the original impulse. For example, the peak in the earth’s temperature lags behind the peak in the sun. This makes the thermal response smaller … but how much smaller? The graph gave me hope that I could calculate it, and after much investigation of the various questions, much walking in the forest and lots of headscratching, I’ve figured out a heuristic formula that relates all three variables—the time constant tau, the observable lag in the timing of the peak temperature versus the peak of the input, and the scale factor reflecting the loss of amplitude due to the lag. I’m sure some better mathematician than I can provide the actual functions, but the ones I have are very accurate. I’ve appended the functions at the end.
And there is a lot more to learn from Figure 2.
One thing is that the longer the lag, the smaller the resulting thermal response. Expected, but good to see just how it works.
Another is that the resulting lagged signal is also a sine wave. In this special case, the exponential lag doesn’t change the underlying sinusoidal shape of the input impulse (black/yellow line). An increasing time constant tau just pushes the sine wave further and further back in time after the impulse, and scales that sinusoidal impulse ever smaller with increasing lag.
This has an important corollary. If we are looking for the result of sinusoidally varying forcing, the thermal response will have the same shape as the input forcing, but it will occur later in time.
An important observation is that with increasing tau (blue to red, tau of 1 to 9), the colored lines get closer and closer together. As a result, no matter how big the time constant tau gets, the observable lag will never be greater than a quarter of a cycle. For a yearly varying input like the solar energy, that means that the peak temperatures in the ocean and the land can never lag more than three months behind the peak solar … and if they did they’d have zero amplitude. Figure 3 shows the lags for values of the time constant from one to nine.
 Figure 3. Closeup view of the upper left section of Figure 2. Vertical black lines show the time lags in the peak of the observable response with values of tau varying from one to nine. Time units are quarter cycles. If the full cycle is one year, tau is in months.
Figure 3. Closeup view of the upper left section of Figure 2. Vertical black lines show the time lags in the peak of the observable response with values of tau varying from one to nine. Time units are quarter cycles. If the full cycle is one year, tau is in months.
Notice how the vertical lines bunch up at the right. No matter how large tau gets, the actual lag in the response peak is always less than a quarter cycle.
So now I have have developed the tools do the lag math. I can take a look at the lag between solar input and thermal response, and from that I should be able tell you the time constant tau, as well as the scale factor lambda, which relates the solar input to the change in temperature. Let me put this to a bit of practical use.
I looked for starters at the Northern Hemisphere ocean temperatures, and the corresponding NH sun. I’ll use the data from the CERES satellites. The data is monthly. To increase the accuracy of the calculation of the observable lag, I first fit a spline to both monthly datasets. I spline them at 360 points per year, then I average the points. I do this for both the solar data, and for the ocean temperatures. Then I graph them against each other as follows:
 Figure 4. Scatterplot of the monthly average northern hemisphere solar anomaly versus the monthly average of the northern hemisphere ocean anomaly . Data has been splined before averaging with a resolution of 360 points per year.
Figure 4. Scatterplot of the monthly average northern hemisphere solar anomaly versus the monthly average of the northern hemisphere ocean anomaly . Data has been splined before averaging with a resolution of 360 points per year.
So here’s how the procedure works. Using the splined version shown in Figure 4 allows us to measure the lag between the solar forcing, which has extremes in December and June, and the lagging ocean temperatures with peaks a couple months later, in February and August. This is about two months. Splining it to 360 points puts the measurements in degrees. There is a 61° lag in the summer, and 58 degrees in the winter. So the lag is almost exactly sixty degrees.
Then, using the relationships established above, I find the following:
Observed lag angle: 61° summer, 58° winter
Time constant tau: 3.3 months
Tau-dependent lag scale factor (amplitude reduction from no-lag condition); 0.48
Thermal sensitivity lambda factor (accounting for lag scale factor); 0.067°C per W/m2
I have not mentioned the “lambda” factor in the lagging equations. This is the transfer function or value that converts from the range of solar energy input swings to the range of the resulting temperature swings. Lambda in this case is .067°C per watt per square metre (°C per W/m2). This means that when the solar energy changes by 100 W/m2, the ocean changes temperature by about 7°. Note that this thermal sensitivity (7 degrees per 100 W/m2) is about twice that shown in Figure 4 above. This is because of the lag scale factor—the lagging alone cuts the response about in half, which means that the actual sensitivity is about twice what the observations show.
Now, having calculated those values, I used them to do my test of whether my conversion functions were correct. These were my functions to convert between observed lag, tau, and lag scale factor. Holding my breath and hoping I’d squashed all of the bugs, here’s what I got:
 Figure 5. A comparison of the observed NH ocean temperatures (black lines with circles) with the lagged and scaled solar energy input (red lines).
Figure 5. A comparison of the observed NH ocean temperatures (black lines with circles) with the lagged and scaled solar energy input (red lines).
As you can see, it appears that my method is quite accurate. The values for the time constant tau and the lag scaling factor were calculated directly from the one observation, that of the observed lag between the peaks. It was done without using a fitting process of any kind. This indicates that my functions are, well, functioning well …
Next, let me compare the thermal response of the northern hemisphere land with that of the northern hemisphere ocean.
 Figure 6. As in Figure 5, but also including the land temperature response. Note the different vertical scale from the previous figure.
Figure 6. As in Figure 5, but also including the land temperature response. Note the different vertical scale from the previous figure.
Both the land and the ocean get the same sunlight. As you would expect, the land temperature varies much more than the ocean temperature. Here are the calculated thermal lag parameters for the land, including ocean comparisons.
Observed lag angle: 25° summer, 22° winter (ocean 61° summer, 58° winter)
Time constant tau: 1.0 months (ocean 3.3 months)
Lag scale factor (lagged amplitude divided by no-lag amplitude); 0.91 (ocean 0.48)
Thermal sensitivity factor lambda (accounting for lag scale factor); 0.137 (ocean 0.067°C per W/m2)
Why is the thermal sensitivity factor lambda higher for the land than for the ocean? The answer is, they vary in the thermal mass which is affected by the yearly swings. Curiously, this can be calculated directly from lambda, the thermal transfer function. In a twelve-month dataset, where tau is measured in months, the mass involved in the swings is the mass of a depth of ocean in metres which is 8 times tau. In other words, on land tau = 1 so an amount of mass equal to about 7 metres of ocean is involved in the annual swings. In the ocean, tau = 3.3, meaning the water down to 3.3 * 8 = 26 metres is involved in the annual swings.
Now, I speculated a while back that the lag at the daily level is related to the lag at the annual level. I just realized that I can now answer this question by simply examining a graph of the hourly surface temperature where I live. If my speculation is correct, the time constant for the individual station data should be on the order of that for the entire land mass. That was a tau of 1.0, which is 0.52 radians. I wouldn’t expect too great a fit, because one is a point measurement and the other is a hemispheric average. Anyhow, here’s the Santa Rosa data.
 Figure 7. Hourly surface temperature, Santa Rosa, California.
Figure 7. Hourly surface temperature, Santa Rosa, California.
Now, using the tools I’ve developed I can take just the information visible in this graph, no digitizing, and calculate the time constant tau for that situation. Tau in Santa Rosa for the daily data turns out to be 0.48 radians, compared with 0.52 radians for the monthly values for the entire NH land …
So it does appear that the time constant (in radians) is period-invariant, meaning that it is related to the lag angle and it doesn’t vary with the length of the cycle.
GENERAL CONCLUSIONS
• It is possible to use solely the observed lag between an impulse and the thermally lagged reaction to directly calculate the time constant tau as well as the scale factor resulting from the lagging alone. I’m sure there are mathematicians out there who both knew that and can derive the formulas mathematically.
• Knowing tau and the lag scale factor allows us to calculate the thermal transfer factor lambda.
• In exponential decay the time constant tau is also known as the “e-folding time”. This is similar to the concept of “half-life”. Half-life is the time it takes for something to decay to 0.5 (half) of the original value. Similarly, e-folding time is the time it takes for something to decay to 0.37 (1/e) of the original value.
Let’s see what that means in practice. Over the land, the time constant tau is about one month. That means that after a month, the original signal is down to 0.37 of the original value. So far so good.
So where is the signal after two months? Well, another month has passed, so it is now 0.37 of its value at the start of the month, which is 0.37 times 0.37 = 0.37^2. And so on down the line. This means that it is dropping off fast. In general it falls off as e^(-t/tau). In practice, this means that with a time factor tau which is 2 * pi / 3 or less (a tau of 4 in a twelve-month cycle), any signal will decay to within a percent or two of zero within one cycle.
CLIMATE CONCLUSIONS
Since I’m looking at observational data for the temperatures, the data contains all possible responses to the rhythmic solar forcings. These include but aren’t limited to resonances, reactions, changes in clouds, feedbacks, slow and fast exponential increase and decay from past inputs, regime shifts, variations in water vapor and thus the overall greenhouse effect, the speed of the throughput of the energy, and all of the rest.
Now, what are we measuring with the thermal transfer coefficient lambda? We are measuring what the thermal response of the system would be if there were no thermal lag. But if there were no thermal lag … then it must be an equilibrium thermal transfer coefficient, or quite close to one. This is interesting because this implies that the lambda values for the no-thermal-lag condition must be close to what is called the “equilibrium climate sensitivity”. This is usually expressed as the temperature variation arising from a forcing change of 3.7 W/m2, as this is the calculated change in forcing from a doubling of CO2. For the ocean this gives us a “climate sensitivity” of .07 °C per W/m2 * 3.7 W/m2 = 0.26 degrees per doubling. The land figures are 0.14 °C per W/m2 * 3.7 W/m2 = 0.5 degrees from the forcing change from doubling.
Now, I see this as a measure of the strength of the climate thermal regulation system. The average swing in incoming solar energy in the Northern Hemisphere is two hundred watts per square metre peak to peak. The average swing (weighted ocean/land average) in no-thermal-lag NH temperature is 7°C/.48 lag factor * .7 + 26°C/ .9 lag factor * .3 = 19°C peak-peak. On the other hand, If we figure the blackbody temperature change from that 200 W/m2, if there were no thermal lag that would swing the northern hemisphere’s temperature by 37°C peak to peak … and instead it only swings about half of that, about 19°C. This is from a combination of fixed and variable ground albedo, variable cloud albedo, emergent thermoregulatory phenomena, biosphere variations, and all of the other ways that the climate responds to the changes in forcing. And it’s a good thing we do.
Finally, is there a long-term residual that keeps going for a long time? Possible, to be sure. For example, there could be 11-year cycles from sunspots, or longer cycles from the swings in solar activity. Dr. Shaviv is looking for such longer cycles in the satellite sea level data, and I wish him well. It’s a crazy world out there, and I’ve been surprised before at what people discover. However, given the small size of the thermal time constants, in the range of one to four, it seems such signals would die out for practical purposes in fairly short order
My best regards to everyone, 2:17 am of a foggy night. On the radio, Roger Miller playing through the headphones, “I’m a man of means, by no means … king of the road” … it’s that kind of night for me, and I hope for you as well.
[UPDATE] the always reliable Joe Born writes in the comments:
<blockquote>When you’re talking about a one-pole (“one-box”) system, as Mr. Eschenbach implicitly is (the climate systems isn’t one, but for his purposes we’re assuming it approximates one), the attenuation theoretically is 1/sqrt(1+(tau * omega)^2), and the lag is theoretically arctan(omega * tau)</blockquote>
I’ve used these to re-write my formulas. My old heuristic formula gave the tau of the ocean as 3.27 months … the actual formulas from Joe give a value of 3.30 for the tau of the ocean. So my conclusions are still solid.
I replied to Joe:
Joe, here’re my new formulas based on your equations. They all take native units (e.g. hours, months) for the lag (peak forcing to peak response), tau, and the period. So a function call of lag2tau(2,12) means 2 months lag in a 12-month year, with the result being tau in months.
Attenuation is a decimal from 0 to 1. The empty function calls call the function with the default values, it’s how I test my functions.
tau2lag=function(tau=3.3,period=12) atan(tau*2*pi/period)/(2*pi/period) tau2lag() [1] 1.998003 lag2tau=function(lag=2,period=12) period*tan((2*lag*pi)/period)/(2*pi) lag2tau() [1] 3.307973 tau2atten=function(tau=3.3,period=12) 1/sqrt(1+(tau*2*pi/period)^2) tau2atten() [1] 0.5009052 lag2atten=function(lag=2,period=12) tau2atten(lag2tau(lag,period),period) lag2atten() [1] 0.5 tauconvert=function(tau=3.3,period=12,newperiod=24) tau/period*newperiod tauconvert() [1] 6.6
Note that omega is equal to 2*pi/period, again with the period in native units. Also, since tau is expressed in units of omega it is not conserved when you go between say a 12-month and a 24-hour situation. Use the “tauconvert” function to convert tau between periods. I’ve deleted the old R functions at the end.
w.
My Perennial Request: If you disagree with someone, please have the courtesy to quote the exact words you disagree with. This allows everyone to understand exactly what you object to.
Math Notes: The main equation I use calculates the change in temperature per unit time as
![]()
where the subscript t shows time, T is temperature, F is forcing, tau is the time constant, and lambda is the transfer function or coefficient.
Adopting the terminology that for any variable X, the variable ∆X is defined as:
And making the substitution of alpha for the term involving e
the main equation simplifies to
The first term on the right hand side, involving the forcing change ∆F, is the direct action of the forcing. “Lambda” is the transfer function, which scales the input to the output. The second term on the right, involving the temperature change ∆T, is the lagged action. Incoming forcing is partitioned between the two branches (immediate action and delayed exponential decay action) by the alpha and (1-alpha) terms. As tau gets larger, the immediate direct action decreases and the length of the lagged action increases.
If tau is zero, alpha is zero, and there is no lag. The response is simply the input times lambda, the transfer factor that relates the range of the thermal response to the range of the input forcing.
Tau and lambda are the only parameters in Equation 1. My goal in this investigation was to be able to calculate tau and lambda directly from nothing more than the delay between impulse and response. In that, I’ve been successful.
Dr. Shaviv’s Explanation
I said above that I’d return to Dr. Shaviv’s objections to my previous postings, which I append below:
Eschenbach has no clue on what the meaning of harmonic analysis is. He still thinks I assumed the sea level should be in sync with the forcing…
Suppose the solar forcing is Delta F = F0 exp (i 2 pi t/P)
The heat in the oceans (per unit area) will be (assuming feedback is small)
Q = int Delta F dt = – i P F0 / (2 pi) exp (i 2 pi t / P)
The sea level, if it is only affected by thermal expansion, will then be
Delta h = alpha Q = – i alpha P F0/(2pi) exp (i 2 pi t / P)
thus,
Delta h = alpha Q = – i alpha P/(2pi) Delta F
It seams like an algebraic relation, but in fact, the -i gives a 90° phase shift which describes the integral(!) If one take the real part of the above equation (to get the physical quantities), one finds
Delta F = F0 cos (2 pi t/P)
Delta h = alpha P F0/(2 pi) sin (2 pi t / P ) = alpha P F0/(2 pi) cos (2 pi t / P – pi/2 )
That is, the integral appears in a harmonic analysis as a phase lag of 90°. In real life, this angle is not exactly 90° because of additional processes taking place, which was the whole point of the analysis!
So again, Eschenbach’s analysis, compared the sea level to the solar forcing and found there is a poor fit. It is because the sea level is supposed to lag by 90° after the solar forcing! Eschenbach still does not acknowledge this.
Also, Eschenbach’s claim that I compared to the sea level and not the rate ignores the fact that a harmonic analysis is expected to give a 90° lag if the sea level is the integral of the forcing, and this is exactly the case.
OK. I’ve corrected a couple of Dr. Shaviv’s math typos, in red. I hate math typos, easiest thing to do, and I certainly hope I don’t have any in my math above.
There are two problems in the above explanation. First, Dr. Shaviv is discussing two kinds of lags, without noting the distinction. Second, except for in the math, he uses “forcing” to mean “CHANGE in forcing”.
I’ll start with the question of the two lags, and I’ll use his terminology from his math. The first lag is the 90° lag in a sinusoidal system between the change in forcing Delta F (∆F) and the thermal response Q. The second lag is the thermal lag discussed above. The first sinusoidal lag is a result of the curious fact that the integral of a cosine is a sine, and a cosine is just a sine shifted by 90° … a couple facts that I’ve known since I taught myself calculus in high school.
Note that this lag he is discussing is between ∆F, the change in forcing, and Q, the result. However, in a sinusoidal system the same lag exists between ∆F, the change in forcing, and F, the forcing itself. In other words, although there is a 90° lag between ∆F and Q, there is the same delay between ∆F and F. As a result, there is no lag at all between F and Q.
Now, recall that Dr. Shaviv said above that:
So again, Eschenbach’s analysis compared the sea level to the solar forcing and found there is a poor fit. It is because the sea level is supposed to lag by 90° after the solar forcing!
Here you see the second problem. Dr. Shaviv is incorrectly using the term “forcing” F to mean the CHANGE in forcing ∆F, the quantity which in his equations above he calls “Delta F”. Yes, sea level is supposed to lag Delta F by 90°. But if there were no thermal lag, there would indeed be no lag between sea level and forcing F.
This is a continuing problem with Dr. Shaviv’s claims, which I’ve pointed to before. For example, he also says above:
… a harmonic analysis is expected to give a 90° lag if the sea level is the integral of the forcing, and this is exactly the case.
Not true in the slightest. Look at his own math. In his analysis above, he doesn’t use the integral of the forcing (which would be “int F dt”). His exact statement was:
Q = int Delta F dt
He says that the change in sea level is alpha Q, and he says this sea level change 90° out of sync with the solar forcing F.
But take another look at his equation immediately above … what is the integral of Delta F? … I didn’t see it the first time through myself, but as you might expect the integral of the derivative of the forcing F, which is his int Delta F dt above, is the forcing F itself. That means that Q = F, and it means that in the absence of thermal lags, the sea level changes and the forcing indeed are in sync.
So when Dr. Shaviv’s says that “sea level is the integral of the forcing”, he is simply wrong. His own math shows that sea level is NOT the integral of the forcing F. It is the integral of the change in forcing Delta F ∆F.
The other kind of lag is the lag I discuss above, the lag between the peak forcing F and the peak thermal response. If there is no thermal mass then the thermal response is immediate and the lag is zero. As shown above, the thermal lag can never be more than a quarter cycle, and the thermal lag is a function of a time constant tau.
With those two kinds of lags in mind, consider Dr. Shaviv’s statement:
That is, the integral appears in a harmonic analysis as a phase lag of 90°. In real life, this angle is not exactly 90° because of additional processes taking place, which was the whole point of the analysis!
The phase lag between cos(x) and int (cos(x) is 90°. Always. Exactly. In real life, it is still exactly 90°. It is not changed by “additional processes taking place”. It is a mathematical fact. However, it is not much considered, because in real life the forcings and the responses are NOT 90° out of phase as Dr. Shaviv claims. They are generally in phase, with the response slightly lagging the forcing. If the sun goes stronger and weaker, and the sea level is a function of the sun, we expect the change in sea level to be somewhat thermally lagged behind the forcing … not 90° out of phase plus or minus something.
Let me be clear that I think that Dr. Shaviv knows the difference between the forcing F and the change in forcing ∆F. Otherwise, he couldn’t do the math. I don’t know why he keeps confusing them over and over in his responses.
Finally, I was amused by a commenter on Dr. Shaviv’s quoted passage who said:
I’d rather [Willis] took some math classes. His previous teacher was not up to the task. (He identifies as self-taught). He’s just a few semesters away from a “who knew” moment.
It’s true, I’m self-taught in math. When I was a junior in high school, I finished all the math courses that the school offered. So my math teacher, Mr. Hedgji, bless him, gave me a calculus textbook and said “Go for it”. He helped me when I had questions, and otherwise left me alone to go for it.
So I did, and I never stopped.
I notice that the anonymous commenter couldn’t find any actual math errors of mine to comment on, so he resorted to personal judgements. Meanwhile, I’m the one who puts my math work out here on a regular basis so that folks like the charming commenter can snipe at it, and so that serious mathematicians can point out my flaws. And I’m the one discussing the problems with Dr. Shaviv’s math. Not only that, but I give both the commenter and Dr. Shaviv full opportunity to find any problems with my work and point them out in public. Strange as it may seem, I welcome people finding errors in my work. Folks like Mosher and Nick Stokes and Dan Hughes and too many other commenters to name have saved me literally years of wasted effort running blind alleys by pointing out logical, mathematical, theoretical, or other errors in what I was doing, and my hat’s off to them for their due diligence. It’s no fun at all to have my errors pointed out in public … but it’s far better than the alternative.
So how about an experiment?
For once you can experiment with the climate. What you need to do in order to work out the lag in the system is turn the heating on and off, and watch how the temperature changes in response.
So how do rig up the earth to do the experiment?
Ah yes. At night the heating is turn off, and in the morning its turned on again.
So we can see from the diurnal temperature change how rapidly the atmosphere reacts to changes in any inputs.
That varies from 4C in high humidity tropical areas to 57C in desert areas.
So the lag is very small
All you need to do to get the exponentially lagged response is do a convolution with a suitable exponential decay. Convolution can be easily done, it’s just a kind of weighted running average. In this case the weights are the exponential. You make it as long as is needed to for the values to be too small to worry about.
This is all explained in full detail here where the method was applied to the volacanic forcing of Mt Pinatubo.
https://climategrog.wordpress.com/2015/01/17/on-determination-of-tropical-feedbacks/
This has been posted at Judith Curry’s site and linked here several times.
Well Willis’s computation seems to be a steady state response to a steady state drive signal, by a one pole low pass filter, with a 3 dB cutoff frequency of 1/(2pi.n.tau). where n is Willis’s 1-9.
So no need to do a time domain analysis. But then the question is, why would one assume that the low pass filter is one pole with a single time constant.
But as far as “lags” are concerned, there really isn’t any lag.
Everything happens almost instantaneously, but then there a whole host of things that happen sequentially, and the apparent “lag” is simply all the instants of time involved in handing off the baton to the next process. Each molecule has to bang into its nearest neighbor and so on, and since they have a finite free path velocity, it takes some time to travel the gap to the next molecule to bang into. But each collision is a very short event; all of which can be calculated either by QM or maybe even classical dynamics.
But Mother Gaia is not sitting around asking; “I wonder what value of n.tau Willis is using today ??
That is the whole point with heat. Everything is chaotic and disorganized, but each action, reaction and interaction is happening as fast as it possibly can. Only the limit value of (c) is putting a lid on how fast things can happen.
Now if you really want to do the time response of a transient event, try to feed the single pulse v = Vsin (theta) for (theta = zero to 2pi) into Willis’s single pole n.tau filter.
g
BTW the response does not get “smaller” it just gets more spread out as tau increases.
The area under the graph is always identical.
So, I’ve been doing this with surface data for a handful of years.



 ?w=720
?w=720

This is the day to day change in temp for >23N to <66N lat
Each year is a single plot line.
If you calculate the slope of the lines as they cross zero, you get this.
Next, if you measure the grounds(concrete) temp with an IR thermometer, grass, asphalt, as well as the sky and air temp you can see something like this
Sky is the coldest, then grass, then concrete, finally asphalt, this is the heat of the day, to the following morning. The sloped line on the warmer IR plots is the concrete cooling as a shadow moves down it's length, the distance from the front porch down the walk to the driveway which is asphalt, which is on the south side of the house so it has Sun till later in the afternoon.
Finally Willis's local temp plot
In you notice late in the night (early morning) the rate of cooling drops off a lot, I can explain that as well.
Notice how rel humidity spikes every night? once it get in the 80-90% range the rate of cooling drops off, because while the ground is closer to air temp, the sky is still really cold.
When you look at a longer time frame, you can see the effect of rel humidity maxing out at night.
Willis, consider a pan warmed from above with an IR lamp, but with a really cold surface behind the lamp for the pan to cool to when the lamp is off, and not measuring just the pan, but the air over the pan.
The first 2 plots are duplicates, Oops!
here’s another interesting graph, this is the difference between yesterday’s raising temp, and last nights falling temp.
I was interested in figuring if there had been any loss of cooling at night due to an increase in Co2. First, on a daily clear sky basis, it cools all night until the sun comes up, then if you compare a complete year for many surface stations looking at whether over all that station was warming or cooling. On average it’s cooled more than warmed for 1940-2014 (almost 70 million samples), 50 of the last 74 years are cooling, 30 of the last 34 years cooled.
Also, the warm years (absolute temps) are the years it’s cooled more than warmed. Co2 could not cause this.
Above my pay-grade, but I do hope that by remaining civil we can all learn from this discussion.
Actually, the civil discourse. between Willis and Dr. Shaviv indeed shows how lively debate in science is supposed to happen. Gentlemen, please keep it coming!
With time, you’ll solve the problems of the Universe!…
Willis – great stuff as ever!
It seems to me I can take the 0.067 degrees per W/m^2, multiply by the average peak -trough swing in daily average solar forcing, from memory about 0.3, to give an average trough to peak amplitude of the effect of the solar cycle on ocean temperature of circa 0.022 Degrees. That would be the raw number before reduction due to lags, so perhaps 0.01 degrees.
Quite small to pick out of the noise!
Is that calculation legitimate?
R.
Now that’s the scientific spirit in action. Other people’s views and critiques aren’t a threat but a help.
+100
Yea, thank you Willis. Your generosity of time and effort will advance our knowledge and understanding. You are an example of what “scientist” is supposed to mean. But man, your math leaves me awed. Wish now I had actually become educated.
RE this angle is not exactly 90° because of additional processes taking place, this might be the case if the “additional processes” influenced the period of a sinusoidal forcing, simply because the lagged value would be sometimes be slightly out of phase which the current forcing, but surely using a simple “harmonic component” rather than the actual solar cycle eliminates period variations as a possible source of phase change?
I am reminded of a Feynman comment (from memory) that the most exciting words in science is not “Eureka!” but “That’s funny!”
It’s fascinating to watch the evolution of this investigation, even if all your answers urn out o be wrong. Thanks or sharing.
“Science is a game in which the object is to discover the rules.” -Sylvester Wolfe
typo fix:
…even if all your answers turn out to be wrong. Thanks for sharing.
Usually attributed to Isaac Asimov:
http://quoteinvestigator.com/2015/03/02/eureka-funny/
The older I get, the more I miss-remember. But old jokes are funny again.
Willis,
Here’s a simple electrical analogue – resistor R and capacitor C in parallel to earth, forced with a sinusoidal current I. The voltage (T) across the combined impedance is IR/(1+jωCR), where ω is freq in radians/sec, and j is sqrt(-1). The time constant is RC, and the voltage phase shift is atan(ωRC) – this gives the shift in terms of time constant RC. It’s 0 at low freq, and varies up to 90° with rising frequency, as you say.
Thanks, Nick. I’ll take a long look at that, as it appears to be a close analogue.
All the best,
w.
I’ve seen a motorcycle exhaust system modeled in an analog electrical simulator (SPICE). The math is all the same.
Hi Willis. Thanks again for another wonderful post. You may want to add a note about your use of the word anomaly. Many of the readers will understand you’ve taken, for example, sea surface temperature data in absolute form and then zeroed it to highlight the seasonal component, but some readers might think it was derived from sea surface temperature anomaly data.
Cheers.
The magnitude of the increase in temperature on land compared to the ocean goes a long way toward explaining why the terrestrial modelers are so keen on projecting their land based (adjusted) measurements out over the ocean.
Regarding: “For the ocean this gives us a “climate sensitivity” of .07 °C per W/m2 * 3.7 W/m2 = 0.26 degrees per doubling. The land figures are 0.14 °C per W/m2 * 3.7 W/m2 = 0.5 degrees from the forcing change from doubling.”
This ocean figure is true when the variation is rapid enough (full cycle in one year) for largely only the top few or several meters of ocean to warm up and cool down. The top few or several meters of ocean are having their temperature swings being limited not only by thermal mass, but also by mixing with the ocean underneath. If a thermal forcing is sustained over a longer period of time, so that deeper levels of the ocean can have a corresponding temperature change, then the ocean surface temperature change would be greater. Same for land, whose temperature changes are somewhat limited by exchanging heat with the ocean through the atmosphere.
This would predict temperature change in response to a sudden forcing being non-exponential. The presented data point of tau in radians (for land) being about the same for a daily cycle and an annual one indicates that the time constant (in time units) is not constant, but varies with the duration of a cycle or a pulse of thermal forcing. (The presented data point being the Santa Rosa one, re: “Tau in Santa Rosa for the daily data turns out to be 0.48 radians, compared with 0.52 radians for the monthly values for the entire NH land …
So it does appear that the time constant (in radians) is period-invariant, meaning that it is related to the lag angle and it doesn’t vary with the length of the cycle.”)
You can have a tau that’s orders of magnitude different (e.g. the deep oceans) and not see it in on daily, monthly, or yearly scales. Try applying a huge tau to the periodic or short pulse examples above. You’ll get a flat line. Change the period of the sine wave or length of pulse to 70 years and you’ll see it.
The interesting question is how many taus are in the Earth’s regulatory system.
I’ll also note we simply don’t have enough data to measure the very large taus of the Earth’s regulatory system.
Peter
willis if you crank out this with the lag that’s coupled to the “devries/suess cyclic change of the sun, i think you got a winner….
When you would find the way how the earth as a full mass does behave tpo these cycles of the sun (of which the maunder, wolf and Dalton minima were absolute dips and former optima absolute tops spreaded over a 200 year near sine wave and the 1400 year sine wave of the Bond events i think the actual warming can be explaiend by entirely natural forcing….
something to look into?
Thanks, Frederik. The problem I have with this are is that we have very poor data for the periods in question, either from the solar angle or for the temperatures. So whatever we might do the error bands are going to be floor to ceiling.
w.
We can see the same thing you pointed out on a yearly basis happen on a daily basis. The peak of the sun is somewhere around 1pm but the highest temperature is somewhere from 3-4pm. The coldest time of the day is about 7-8 am after the sun just starts to rise.
Willis, I would like you to do another calculation on top of this study. Please calculate the thermal expansion of the ocean water in the 26 meters that is affected by the up and down in temperature. How much cm or mm can the water rise and fall over the year.
The lags tell you a great deal about what is really going on in the energy system contained in the Earth’s molecules.
The Ocean surface lags behind the solar forcing by about 82 days. In the northern hemisphere, solar energy peaks on June 21 but most of the northern hemisphere ocean surface temperature peaks on September 12.
The Land surface lags behind the annual solar cycle by about 32 days. The lowest solar forcing is December 21, but the lowest Land temperature is January 22.
At 45N, the average mean temperature varies from 20C on July 22 to -10C on January 22. This is equivalent to the land gaining/losing about 0.8 W/m2 per day or about 0.00001 joules/m2/second over the annual cycle.
In the daily cycle. the land air temperature lags behind the Sun by about 3.5 hours. Solar peak at noon, air temperature peak at 3:30 pm.
If one thinks about how much solar energy is coming in at noon on June 21, 960 W/m2 or 960 joules/m2/second (including the average cloudiness), but the actual air temperature is only increasing by about 0.008 joules/m2/second at noon. Almost all of the solar energy, 99.9992% of it, is not going into heating the air, it is immediately being re-emitted back to space and/or is being absorbed into the soil and rock molecules in the surface just as fast as it coming in.
At night time, when there is no solar energy coming in at all, but the air temperature only cools off as if 0.006 joules/m2/second is being emitted out to space. 959.992 joules emitted/lost at noon but only 000.006 joules emitted/lost at night.
On a per second basis, there is a lot going on in the real physical world that is not being captured in climate science. Energy accumulates on a per second basis by extremely minute amounts. The solar cycle only varies by +/- 0.4 W/m2. That is already an extremely small amount so take a extremely small amount and accumulate energy from that variation at even more extreme minute amounts. Over many decades, it could make a difference, but not for a single solar cycle or just a few. It would take 30 or 40 years.
Bill Illis August 24, 2015 at 5:09 am
Thanks, Bill, but you apparently didn’t notice that I just measured those two quantities very accurately. The ocean doesn’t lag by “about 82 days”. From the last 14 years of data, in the summer the ocean lags by 61 days, and in the the winter by 58 days.
Read the post again. I did very accurately, what you are guessing at.
w.
As usual I enjoyed your post. You might consider going to the Electrical Engineering section of your local University’s bookstore and look into “signal processing” and “control systems” texts. A lot of what you have been writing about already has a solid math foundation in those areas.
Greg
Willis, your discussion describes a system that has only one energy storage element. This is very familiar territory to the electronics field, where it would be described as a first-order system. In this case the energy storage element is the mass that is being heated. You could model it as an energy source that feeds a resistor with the output in parallel with a capacitor. (Voltage source+ in series with resistor in series with capacitor returning back to source-, measure the voltage across the capacitor while applying a step to the source). If you can find a free version of Spice you can draw similar graphs and play with the part values – you will see the same relationships you describe.
Of course in the real world there are many energy storage elements besides the mass of the land or sea, and a true working model equivalent in electronic terms would be much more complex. But, since the simple model explains and clarifies the part of the system that is under discussion it is perfectly appropriate to neglect the underlying complexity and focus on the simple broad-stroke relationships. We do this all the time in electronics, deriving a simple relationship that explains the broad strokes then digging into the details when necessary.
Seems to me practically all the heat storage is in the land & ocean. Other heat storage mechanisms would be pretty much negligible — except massive ice-sheets during the glacials.
I would say that at least we should consider more than a single slab ocean model, which what the simple linear model effectively is.
If the deep ocean heat sink can be considered as effectively infinite and of constant temperature and the heat transfer from the mixed layer to deep ocean is typified by eddy diffusion proportional to the temperature gradient, this also simplifies to a linear model with slightly modified feedback.
This was discussed by Paul_K and myself on Willis’ last thread.
Mike says:
Mike, I agree and I wasn’t ignoring the deep oceans. But I’ve pondered the deep ocean below the mixing zone for some time & it has strange characteristics — temperature well below the avg earth temp. Either vast amounts of cold, sinking water are constantly replenishing all of it (unreasonable given the huge volume of the cold water), or it is remarkably thermally insulated (stratification) from the mixing layer above.
Bruce, thanks for the comment. See here for my reply.
w.
Market gyrations today being what they are, I won’t have time to write anything but a drive-by, but I’m sure others will make the point anyway.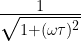 , and the lag is theoretically
, and the lag is theoretically  .
.
When you’re talking about a one-pole (“one-box”) system, as Mr. Eschenbach implicitly is (the climate systems isn’t one, but for his purposes we’re assuming it approximates one), the attenuation theoretically is
Some time ago Mr. Eschenbach wrote about “tautochrones,” and there he observed how different from the response of the lumped-parameter system he uses here the responses of distributed-parameter systems such as heat transfer through the soil are.
As I mentioned in the head post, I was sure that someone wiser than I would know the actual equations. Can’t thank you enough, I’ll make the appropriate changes to my functions to reflect the exact relationships.
All the best,
w.
Glad to help. (I like to think we also serve who only do the sums.)
I wish I could take a little more time with the post, because I’m not sure I correctly understood “Tau in Santa Rosa for the daily data turns out to be 0.48 radians, compared with 0.52 radians for the monthly values for the entire NH land …
“So it does appear that the time constant (in radians) is period-invariant, meaning that it is related to the lag angle and it doesn’t vary with the length of the cycle.”
If I did, my initial impression is that the behavior sounds distinctly non-one-box-like; I would have thought that one-box-system lag at around the 50-radian-lag point would be much more sensitive to a two-and-a-half-decade frequency range–and that lag would increase with frequency, not decrease with it.
As I say, though, I probably didn’t understand that excerpt, and, if I did, I may not yet be analyzing it correctly. Otherwise, I would wonder how much we should base inferences on assuming a one-box approximation.
Joe, here’s my new formulas based on your equations. They all take native units (e.g. hours, months) for the lag (peak forcing to peak response), tau, and the period. So a function call of lag2tau(2,12) means 2 months lag in a 12-month year, with the result being tau in months.
Attenuation is a decimal from 0 to 1. The empty function calls call the function with the default values, it’s how I test my functions.
For comparison, my previous heuristic equation gave me an ocean tau of 3.27 months. The actual formulas above give an ocean tau of 3.30 months … so all of my calculations above are perfectly valid.
I’ll add an update above. I knew someone had the real answer.
w.
This dumb old ox is trying to learn more about the variables associated with climate and I get a cooking lesson!
This is that the peaks of the lagged versions of the input wave fall exactly on the original sinusoidal impulse line (black/yellow). This was important to me, because I’d never been able to figure out how much smaller the lagged response wave was than the size of the original impulse.
This is a classic result and is frequently made use of in correcting for response times of measurement devices (e.g. thermocouples). One way is to simultaneously measure using sensors with different response times, the peaks all lie of the raw data curve which can then be reconstructed.
The reason for this can be easily seen if you look at the differential form of the response equation:
Tg = 𝜏.dTw/dt + Tw
Tg is wire temperature, Tg is gas temperature
At the peak of the measured curve (Tw) dTw/dt=0, therefore Tg = Tw.
If the response time, 𝜏, is known the input curve can be calculated from the measured curve using the above equation.
As the bloke down the pub said, above my paygrade, but I got the jist and failed the math. Sounds interesting WIllis. Keep wandering around the forest scratching your head. Much appreciated.
I would like to see what results when you analyze hourly dew point data at death valley and La Jolla. The transfer of energy through evaporation/condensation is a big factor in the resulting surface temperature,and should be considered in a lag.
Good point I believe.
Thanks, fnhaynie. As I pointed out, the data I used include all such mechanisms. However, quantifying each one is indeed of interest.
w.
I have found that as Rel humidity gets ~>80% or so, the rate of cooling slows, you can see this as the change in cooling rate in Willis’s last graph, and I have a couple graphs near the top of the thread.
It gets interesting when there is more than one lag in the system and even more difficult if you throw in some pure delay. Think heat being carried by ocean currents. Throw in feedbacks and negative feedback becomes positive feedback when the phase shift gets to 180 deg. The response goes from exponential to sine wave. The fact that the oceans have oscillations may indicate 2 or more lags in the system. It’s not an indication of anything being unstable in engineering terms unless the oscillations are growing, closed loop gain at the resonant frequency less than one.
Ltspice is free, good, and has a graphical schematic tool.
Willis,
In Figure 5, there are years where the actual data for the ocean temperature dips lower than or stays higher than the model you developed. Is this the effect of La Nina, El Nino?
Whilst it is interesting to look at the thermal lag in the system in the short term, as I see matters for those that support the view that solar is a major driver in long term climate, one needs to look at the Holocene.
What caused the Holocene Optimum, the Minoan Warm Period, the Roman Warm Period, The Medieval Warm Period, the LIA?
That is what has to be answered. For example, was it:
Planetary procession?
Changes in CO2 (or other so called ghgs)?
Changes in atmospheric aerosols due to volcanos and/or asteroid impact?
Changes in patterns of cloudiness, and if so what drove these changes (was it the sun or perhaps the earth’s magnetic field)?
Changes in the amount of water vapour, and if so what drove those changes?
Was it the sun?
If not one or more of the above, what could it be?
There is a reason why the warmists have been so desperate to flatten the shaft of the hockey stick and to do away with these variations in temperature/climate over the past 12,000 years.
Planetary procession does not explain the periodic warming events, nor does CO2 if it has been essentially stable (as warmists assert) over the last 5,000 to 8,000 years. Volcano eruptions are mere speculation since there is strong evidence of only a few volcano eruptions over this period, and volcanos seem to have only a short term impact on temperature.
Presently, we may not know the answer, and may be we never will know the answer, but most reasonable people can appreciate that solar insolation received by the surface is a strong bet, when considering the possible presently known/contemplated/foreseen candidates. We just do not know the mechanism but with further evidence and understanding we might see the light.
–What caused the Holocene Optimum, the Minoan Warm Period, the Roman Warm Period, The Medieval Warm Period, the LIA?
That is what has to be answered. For example, was it:
Planetary procession?
Changes in CO2 (or other so called ghgs)?
Changes in atmospheric aerosols due to volcanos and/or asteroid impact?
Changes in patterns of cloudiness, and if so what drove these changes (was it the sun or perhaps the earth’s magnetic field)?
Changes in the amount of water vapour, and if so what drove those changes?
Was it the sun?
If not one or more of the above, what could it be? —
Ocean mixing
Ocean surface transparency.
If one could just stir the ocean, it has the largest effect upon global average temperature.
Mixing the ocean causes immediate cooling and long term warming [and rise of sea level due to thermal expansion].
I not going to go into how it’s mixed or how much it is mixed, but just saying if one could thoroughly
mix the ocean, it has huge effect of upon average temperatures. So I think mixing ocean belongs
on the list.
And ocean transparency can effect short term warming which results in longer term cooling- if less
transparent at the surface.
Volcanic eruption can effect this and any fertilization has biological component.
Or just because open oceans currently are very clear and sterile, doesn’t mean this is the constant state of things over the centuries.
But anyhow, what caused the cooling periods appears mostly unresolved.
Obviously it has been cooling ever since the highs of the Holocene Optimum. Since the Optimum, the cooling has been interrupted by a number of warm periods, each one peaking at a slightly lower high, ie., the Holocene Optimum was warmer than the Minoan Warm Period, which in turn was warmer than the Roman Warm Period, which in turn was warmer than the Medieval Warm Period, which in turn was warmer than the late 20th Century warm Period (although we do not know whether the latest warm period has peaked).
Some people ‘believe’ (such as Willis – see his article on radiating the oceans which relies upon circular reasoning for much of what is proposed) that DWLWIR heats the oceans, and the energy absorbed in the top few microns is effectively mixed by the action of waves, swell and ocean overturning. But if that is so, why are the deep oceans so cold? Why is the average temperature of the oceans less than 4 degC?
After all, there has been about 4 billion years of solar plus DWLWIR going into the oceans and if there is effective mixing of the energy being imparted into the oceans, one would expect after all this time for the oceans to be far warmer at least over the top 500 or so metres.
I suspect that when we have better understanding, the only energy in the oceans will be seen to be solar (ignoring the small addition of geothermal), and that DWLWIR does not effectively heat the oceans.
I am of the firm view that it is the oceans that drive the climate but they are in turn driven by the sun and the amount of solar insolation received over time.
During the Holocene, there has been no significant movement of the continental shelves and land masses such that the pattern of oceanic currents (and the general manner in which they distribute energy imparted in the tropical seas pole wards) is likely to be similar to that seen today. Whether the rate of these currents (including the thermohaline circulation) has changed over time is obviously not known, nut if it has, then the most likely candidate for that change is changes in the receipt of solar insolation.
Of course, one might expect there to have been changes in the rate of the thermohaline circulation as ice melts and glaciers recede during the Holocene, but that would be a response not a driver.
–richard verney
August 24, 2015 at 4:36 pm
Obviously it has been cooling ever since the highs of the Holocene Optimum. Since the Optimum, the cooling has been interrupted by a number of warm periods, each one peaking at a slightly lower high, ie., the Holocene Optimum was warmer than the Minoan Warm Period, which in turn was warmer than the Roman Warm Period, which in turn was warmer than the Medieval Warm Period, which in turn was warmer than the late 20th Century warm Period (although we do not know whether the latest warm period has peaked).
Some people ‘believe’ (such as Willis – see his article on radiating the oceans which relies upon circular reasoning for much of what is proposed) that DWLWIR heats the oceans, and the energy absorbed in the top few microns is effectively mixed by the action of waves, swell and ocean overturning. But if that is so, why are the deep oceans so cold? Why is the average temperature of the oceans less than 4 degC? —
I don’t think DWLWIR warms the ocean, but were it to do this, any significant wattage should cause evaporation rather than warming. Or DWLWIR is quite different then SW, which transparent to water.
Or DWLWIR would heat to a depth of about 1 mm, whereas SW warms to meters depth- such differences should be easily measurable/noticeable.
As for cold ocean it’s caused by colder polar temperature and polar sea ice.
As for the slow cooling from the Holocene Optimum, generally it’s due to the orbital variation, I imagine.
How exactly that works, I don’t know. There the issue that in some sense we have yet to recover from the Little Ice Age, perhaps none of the warming periods fully recover. Or the Holocene Optimum is a more complete recovery [from glacial period] and latter recoveries not as complete.
But it seems like good bet that ocean circulation/patterns/mixtures are related to it.
And we return to the question what causes the cooling?
I guess the work of the much-maligned Dr. Evans will eventually be acknowledged and cited as being relevant. “Lag” and “delay” seem to be somewhat similar in nature.
Reminds me of the circuit theory classes taken over 40 years ago. For a linear system, the response to a stimulus is the convolution of the Dirac Delta Function response and the stimulus. Response to a sine wave input will be shifted by about 90 degrees if the inverse of the natural frequency, 1/(2xPixF) is substantially shorter than the time constant of the impulse response. Phase lag will be 45 degrees when the inverse of the natural frequency is equal to the impulse response time constant ASSUMING the impulse response is a simple exponential decay.
Conducive heat transfer happens by diffusion, where the time for heat to diffuse past a surface is proportional to the square of the distance.
Yeah, that’s it. convolution.with the impulse response. Not forgetting to reverse the convolution kernel in this case since it is asymmetric. For FIR filters the kernel is symmetric and reversal is ignored. ie the kernel is a rising exp not a decaying one.
https://climategrog.wordpress.com/2013/03/03/scripts/
This script will do the exp convollution that gives the linear feedback type response.