Guest Post by Willis Eschenbach
Through what in my life is a typical series of misunderstandings and coincidences, I ended up looking at the average model results from the Climate Model Intercomparison Project 5 (CMIP5). I used the model-by-model averages from each of the four scenarios, a total of 38 results. The common period of these results is 1860 to 2100 or some such number. I used the results from 1860 to 2020, so I could see how the models were doing without looking at some imaginary future. The CMIP5 analysis was done a few years ago, so everything up to 2012 they had actual data for. So the 163 years from 1860 to 2012 were a “hindcast” using actual forcing data, and the eight years from 2013 to 2020 were forecasts.
Figure 1. CMIP5 scenario averages by model, plus the overall average.
There were several things I found interesting about Figure 1. First was the large spread. Starting from a common baseline, by 2020 the model results ranged from 1°C of warming to 1.8°C of warming …
Given that horrible inter-model temperature spread in what is a hindcast up to 2012 plus eight years of forecasting, why would anyone trust the models for what will happen by the year 2100?
The other thing that interested me was the yellow line, which reminded me of my post entitled “Life Is Like A Black Box Of Chocolates“. In that post I discussed the idea of a “black box” analysis. The basic concept is that you have a black box with inputs and outputs, and your job is to figure out some procedure, simple or complex, to transform the input into the output. In the present case, the “black box” is a climate model, the inputs are the yearly “radiative forcings” from aerosols and CO2 and volcanoes and the like, and the outputs are the yearly global average temperature values.
That same post also shows that the model outputs can be emulated to an extremely high degree of fidelity by simply lagging and rescaling the inputs. Here’s an example of how well that works, from that post.
Figure 2. Original Caption: “CCSM3 model functional equivalent equation, compared to actual CCSM3 output. The two are almost identical.”
So I got a set of the CMIP5 forcings and used them to emulate the average of the CMIP5 models (links to models and forcings in the Technical Notes at the end). Figure 3 shows that result.
Figure 3. Average of CMIP5 files as in Figure 1, along with black box emulation.
Once again it is a very close match. Having seen that, I wanted to look at some individual results. Here is the first set.
Figure 4. Six scenario averages from different models.
An interesting aspect of this is the variation in the volcano factor. The models seem to handle the forcing from short-term events like volcanoes differently than the gradual increase in overall forcing. And the individual models differ from each other, with the forcing in this group ranging from 0.5 (half the volcanic forcing applied) to 1.8 (eighty percent extra volcanic forcing applied). The correlations are all quite high, ranging from 0.96 to 0.99. Here’s a second group.
Figure 5. Six more scenario averages from different models.
Panel (a) at the top left is interesting, in that it’s obvious that the volcanoes weren’t included in the forcing for that model. As a result, the volcanic forcing factor is zero … and the correlation is still 0.98.
What this shows is that despite their incredible complexity and their thousands and thousands of lines of code and their 20,000 2-D gridcells times 60 layers equals 1.2 million 3-D gridcells … their output can be emulated in one single line of code, viz:
T(n+1) = T(n)+λ ∆F(n+1) *(1-exp( -1 / τ ))+ ΔT(n) exp( -1 / τ )
OK, now lets unpack this equation in English. It looks complex, but it’s not.
T(n) is pronounced “T sub n”. It is the temperature “T” at time “n”. So T sub n plus one, written as T(n+1), is the temperature during the following time period. In this case we’re using years, so it would be the next year’s temperature.
F is the radiative forcing from changes in volcanoes, aerosols, CO2, and other factors, measured in watts per square metre (W/m2). This is the total of all of the forcings under consideration. The same time convention is followed, so F(n) means the forcing “F” in time period “n”.
Delta, or “∆”, means “the change in”. So ∆T(n) is the change in temperature since the previous period, or T(n) minus the previous temperature T(n-1). Correspondingly, ∆F(n) is the change in forcing since the previous time period.
Lambda, or “λ”, is the scale factor. Tau, or “τ”, is the lag time constant. The time constant establishes the amount of the lag in the response of the system to forcing. And finally, “exp (x)” means the number 2.71828 to the power of x.
So in English, this means that the temperature next year, or T(n+1), is equal to the temperature this year, T(n), plus the immediate temperature increase due to the change in forcing, λ F(n+1) *(1-exp( -1 / τ )), plus the lag term, ΔT(n) exp( -1 / τ ) from the previous forcing. This lag term is necessary because the effects of the changes in forcing are not instantaneous.
Curious, no? Millions of gridcells, hundreds of thousands of lines of code, a supercomputer to crunch them … and it turns out that their output is nothing but a lagged (tau) and rescaled (lambda) version of their input.
Having seen that, I thought I’d use the same procedure on the actual temperature record. I’ve used the Berkeley Earth global average surface air temperature record, although the results are very similar using other temperature datasets. Figure 6 shows that result.
Figure 6. The Berkeley Earth temperature record (left panel) including the emulation using the same forcing as in the previous figures. I’ve included Figure 3 as the right panel for comparison.
It turns out that the model average is much more sensitive to the volcanic forcing, and has a shorter time constant tau. And of course, since the earth is a single example and not an average, it contains much more variation and thus a slightly lower correlation with the emulation (0.94 vs 0.99).
So does this show that forcings actually rule the temperature? Well … no, for a simple reason. The forcings have been chosen and refined over the years to give a good fit to the temperature … so the fact that it fits has no probative value at all.
One final thing we can do. IF the temperature is actually a result of the forcings, then we can use the factors above to estimate what the long-term effect of a sudden doubling of CO2 will be. The IPCC says that this will increase the forcing by 3.7 watts per square meter (W/m2). We simply use a step function for the forcing with a jump of 3.7 W/m2 at a given date. Here’s that result, with a jump of 3.7 W/m2 in the model year 1900.
Figure 7. Long-term change in temperature from a doubling of CO2, using 3.7 W/m2 as the increase in forcing and calculated with the lambda and tau values for the Berkeley Earth and CMIP5 Model Average as shown in Figure 6.
Note that with the larger time constant Tau, the real earth (blue line) takes longer to reach equilibrium, on the order of 40 years, than using the CMIP5 model average value. And because the real earth has a larger scale factor Lambda, the end result is slightly larger.
So … is this the mysterious Equilibrium Climate Sensitivity (ECS) we read so much about? Depends. IF the forcing values are accurate and IF forcing roolz temperature … maybe they’re in the ballpark.
Or not. The climate is hugely complex. What I modestly call “Willis’s First Law Of Climate” says:
Everything in the climate is connected with everything else … which in turn is connected with everything else … except when it’s not.
And now, me, I spent the day pressure-washing the deck on the guest house, and my lower back is saying “LIE DOWN, FOOL!” … so I’ll leave you with my best wishes for a wonderful life in this endless universe of mysteries.
w.
My Usual: When you comment please quote the exact words you are discussing. This avoids many of the misunderstandings which are the bane of the intarwebs …
Technical Notes:
I’ve put all of the modeled temperatures and forcing data and a working example of how to do the fitting as an Excel xlsx workbook in my Dropbox here.
Forcings Source: Miller et al.
The forcings are composed of:
- Well mixed greenhouse gases
- Ozone
- Solar
- Land Use
- Snow Albedo & Black Carbon
- Orbital
- Troposphere Aerosols Direct
- Troposphere Aerosols Indirect
- Stratospheric Aerosols (from volcanic eruptions)
Model Results Source: KNMI
Model Scenario Averages Used: (Not all model teams provided averages by scenario)
CanESM2_rcp26
CanESM2_rcp45
CanESM2_rcp85
CCSM4_rcp26
CCSM4_rcp45
CCSM4_rcp60
CCSM4_rcp85
CESM1-CAM5_rcp26
CESM1-CAM5_rcp45
CESM1-CAM5_rcp60
CESM1-CAM5_rcp85
CNRM-CM5_rcp85
CSIRO-Mk3-6-0_rcp26
CSIRO-Mk3-6-0_rcp45
CSIRO-Mk3-6-0_rcp60
CSIRO-Mk3-6-0_rcp85
EC-EARTH_rcp26
EC-EARTH_rcp45
EC-EARTH_rcp85
FIO-ESM_rcp26
FIO-ESM_rcp45
FIO-ESM_rcp60
FIO-ESM_rcp85
HadGEM2-ES_rcp26
HadGEM2-ES_rcp45
HadGEM2-ES_rcp60
HadGEM2-ES_rcp85
IPSL-CM5A-LR_rcp26
IPSL-CM5A-LR_rcp45
IPSL-CM5A-LR_rcp85
MIROC5_rcp26
MIROC5_rcp45
MIROC5_rcp60
MIROC5_rcp85
MPI-ESM-LR_rcp26
MPI-ESM-LR_rcp45
MPI-ESM-LR_rcp85
MPI-ESM-MR_rcp45
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
What is the budget of the CMIP6?
May be you should claim a bit share of it and release supercomputing hours for something more useful.
Have you tried any other variable besides temperature?
I am going to deliberately “misunderstand / misinterpret” your comment (about monetary / funding issues ?), and assume that you are looking for where datasets of RF and GMST “projections” (from 2005 to 2100) can be found for the CMIP6 / SSP set of climate model runs.
NB : The 5 “standard” emission pathways used in AR6 are SSP1-1.9, SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5.
The most frequently “gap fillers”, that I have come across at least, are SSP4-3.4 and SSP4-6.0 (for comparison with CMIP5’s RCP6.0 emission pathway).
1) Go to the IIASA website.
[ URL : https://tntcat.iiasa.ac.at/SspDb/dsd?Action=htmlpage&page=welcome ]
2) Click on the “login as guest” button.
3) Click on the “IAM Scenarios” tab.
4a) In the “(2.) Model/Scenarios” box, de-select the “SSP1 – Baseline”, “SSP2 – Baseline” and “SSP4 – Baseline” options.
NB : “SSP3 – Baseline” = SSP3-7.0 and “SSP5 – Baseline” = SSP5-8.5.
4b) Select the “SSP1 – 1.9”, “SSP1 – 2.6” and “SSP2 – 4.5” [ and “SSP4 – 3.4” and “SSP4 – 6.0” … ] options.
5) In the “(3.) Variable” box, click to open up the “Climate” option, and then the “Concentration”, “Forcing” and “Temperature” sub-options.
6a) Select (sequentially) the variables you are interested in, e.g. “Concentration : CO2”, “Forcing : Total” then “Temperature : Global Mean”.
6b) I found all three “Emissions (harmonized) : CO2” sub-options to be “interesting” as well ..
7) Use the mouse to select (all of !) the data in the “Query Results” table (as a “Guest” the “Output Options : Microsoft Excel” button won’t work), and copy the results to a text file.
8) Once completed for all “interesting” variables, import the final text file(s) into your favourite spreadsheet program.
NB : You only get one datapoint per decade (+ 2005) instead of annual values, but it’s a good start to getting a general feel for the CMIP6 / SSP model run datasets.
Interesting link, I hadn’t come across that set of data before.
I also use KNMI for “ensemble mean” GMST data, but have a personal preference for monthly rather than annual time resolution.
– – – – –
At the risk of being accused of “Look at me !” syndrome, I mostly use the CMIP5 inputs data from Malte Meinshausen’s “RCP Concentration Calculations and Data” page at PIK (the Potsdam Institute) :http://www.pik-potsdam.de/~mmalte/rcps/
Note that they use the standard “Historical Data = up to 2005, use “per-RCP pathway” data from 2006 (even if more up-to-date numbers are available)” assumption, but provide annual data from 1765 (AD / CE) all the way to 2500.
Note also that the “Download all data [files, ASCII and Excel versions ] …” option is a ZIP file only 6MB in size.
Options are available for :
1) “Harmonised” GHG emissions (used as inputs to the full-blown 3-D AOGCM climate models, which then “calculate” atmospheric concentrations as outputs, from which RF values are only a simple algebraic formula away…)
2) “Mixing Ratios”, i.e. atmospheric concentrations / abundances (used as inputs to “models of intermediate complexity”)
3) “Radiative Forcing” numbers (used as inputs to a wide range of “simple” climate models)
For reference, the standard “header” for the RF files includes the following :
COLUMN_DESCRIPTION
1 TOTAL_INCLVOLCANIC_RF Total anthropogenic and natural radiative forcing
2 VOLCANIC_ANNUAL_RF Annual mean volcanic stratospheric aerosol forcing
3 SOLAR_RF Solar irradience forcing
4 TOTAL_ANTHRO_RF Total anthropogenic forcing
5 GHG_RF Total greenhouse gas forcing (CO2, CH4, N2O, HFCs, PFCs, SF6, and Montreal Protocol gases).
6 KYOTOGHG_RF Total forcing from greenhouse gases controlled under the Kyoto Protocol (CO2, CH4, N2O, HFCs, PFCs, SF6).
7 CO2CH4N2O_RF Total forcing from CO2, methan and nitrous oxide.
8 CO2_RF CO2 Forcing
9 CH4_RF Methane Forcing
10 N2O_RF Nitrous Oxide Forcing
11 FGASSUM_RF Total forcing from all flourinated gases controlled under the Kyoto Protocol (HFCs, PFCs, SF6; i.e. columns 13-24)
12 MHALOSUM_RF Total forcing from all gases controlled under the Montreal Protocol (columns 25-40)
13-24 Flourinated gases controlled under the Kyoto Protocol
25-40 Ozone Depleting Substances controlled under the Montreal Protocol
41 TOTAER_DIR_RF Total direct aerosol forcing (aggregating columns 42 to 47)
42 OCI_RF Direct fossil fuel aerosol (organic carbon)
43 BCI_RF Direct fossil fuel aerosol (black carbon)
44 SOXI_RF Direct sulphate aerosol
45 NOXI_RF Direct nitrate aerosol
46 BIOMASSAER_RF Direct biomass burning related aerosol
47 MINERALDUST_RF Direct Forcing from mineral dust aerosol
48 CLOUD_TOT_RF Cloud albedo effect
49 STRATOZ_RF Stratospheric ozone forcing
50 TROPOZ_RF Tropospheric ozone forcing
51 CH4OXSTRATH2O_RF Stratospheric water-vapour from methane oxidisation
52 LANDUSE_RF Landuse albedo
53 BCSNOW_RF Black carbon on snow.
I believe the phrase “horses for courses” is applicable here …
Thanks for the PIK source, hadn’t seen that on.
w.
Epic..
I ignored CO2 forcing. It’s nonsense.
Instead I tweaked ‘Land Use’
I considered land at 45 degress latitude where the average solar input across the whole year, adjusted for 30% cloud Albedo, amounts to 240Watts/sqm
Then I took 1.5E13 square metres of ploughed land to have an albedo of 0.10 at the present time.Going back to 1850 that would have been perennially green grassland with albedo 0.40
I also took another 1.5E13sqm of grazed pasture land to have an albedo of 0.20
Running through the sums there gets an increase across the whole globe of 13.8 Watts/sqm
Putting that into the Total Forcings column, all forcing the same except with WGHG = 0,
I get a temp rise of 3.4 deg Celsius – running it from 1850 to 2021
Just by adjusting the land use for ploughing, tillage and (over) grazing
There are some of us who might say,,,
Well OK, lets go with the 3.5W/sqm for CO2
That is for CO2 working at a wavelength of 15 microns
But, as per OCO2 Sputnik, CO2 absorbs at wavelengths corresponding to 800 Celsius also 400 Celsius
So CO2 re-radiates 3.5Watts coming from the ground (stops it reaching leaving Earth, would it not be fair to say that CO2, working at 400 and 800 Celsius is stopping 7.0 Watts/sqm from reaching the ground
And why not, that is the very signal that OCO2 uses to measure the concentration of the CO2
So lets re-run the spreadsheet with that and get a temp rise of 1.5 Celsius.
In a nutshell, run it with Land Use going from zero up to 13.8 Watts and CO2 going from zero to minus 7 Watts gives a temp rise of 1.5 Celsius from 1850 to present
How does that compare with anything?
Or ignoring all the other forcings, a result of 1.7 Celsius
edit to PS
I should have increased where it adjusts for atmospheric dust. All that tillage has increased that and we know so, it is the root cause of the observed Global Greening – also the ice melt in the Arctic. In no small part the huuuuge amounts of de-icing salt now used on roads in the northern hemisphere.
We know the stuff, it makes the road go white when it dries out and the traffic pummels it down to an incredibly fine powder that could travels 000’s of miles.
Willis Eschenbach reply to Tom.1: “What it proves is that the model outputs are merely a simple transformation of the inputs. Period.”
Musical satirist and Harvard mathematician Tom Lehrer, in his 1958 comedy album, An Evening Wasted with Tom Lehrer, quoted the late Dr. Samuel Gall, inventor of the gall bladder, as saying this:
“Life is like a sewer. What you get out of it depends on what you put in to it.”
Ah yes Tom Lehrer, His “THAT WAS THE YEAR THAT WAS” is also classic Lehrer. “The garbage that we throw into the Bay, they drink at lunch in San Jose.”
Willis,
Thanx for all your posts – they’re always interesting and informative, and get folks thinking, as is obvious from the comments here. I would like to ask the following question: In your equation there is a term involving F[n+1] for calculating T[n+1] – but that implies the forcing for the next period is already known prior to T[n+1] being calculated. That seems a bit non-causal. I’m wondering if F[n+1] could be replaced with F[n] , and still get a good model fit to the data.
We assume because time is everywhere we underatand it. The reality is that time is the least understood physical process. We routinely confuse the effects of time to fool ourselves.
The models are trying to predict the traffic and potholes on the road in the future using averages from today.
The same problem affects all inertial navigation systems. They need mid course corrections based on future data that is not available in the present.
“Pay no attention to the forcings behind the curtain”
Aside from WE’s exposure of the hollowness of the climate models, this focuses on the real issue in how to understand climate: passivity.
Is climate active or passive?
The alarmist mainstream takes an extreme hard-core position of the climate being entirely passive. It only changes from forcing – thus the word “forcing”. It doesn’t want to change and left to itself, never would.
Those that argue that all climate change is solar forced, are of the same passive opinion as the CO2 alarmists. Climate only changes by CO2 / methane / ozone / other atmospheric thing, or climate only changes by solar forcing. The position is the same, only the forcing is different.
These positions have in common that they ignore the ocean, or dismiss it as a passive puddle. It is not.
The climate is in fact active. The atmosphere-ocean system is an excitable medium and a dissipative heat engine. Spontaneous spatiotemporal pattern continually emerges on a wide, fractal range of scales, with the signature log-log distributions. This means that essentially it changes itself. As Richard Lindzen stated, even if the total radiation budget equilibrium at top of atmosphere were to remain in zero balance for a thousand years, the oceans contain enough energy and unstable nonequilibrium dynamic to serve up continual climate change for the whole millenium – and more. I’m happy to go with Lindzen on that one.
“Climate” and “climate change” have exactly the same meaning. Adding “change” to “climate” adds zero meaning, and is a redundant tautology, like “frozen ice” or “wet rain”. It’s possibly the most profoundly stupid phrase in the history of human symbolic language.
I understand that Tau (the number of years taken for forcing to impact on temperatures) is variable, but is much less than ten years. This is consistent with Hansen et al 1988 Scenario C which assumed global emissions were reduced to effectively zero by 2000 and global warming stopped in 2006 or 2007. It is also consistent with Scenario A (emissions growth of 1.5% pa) and Scenario B (roughly constant emissions).
But here is the issue that I have. I might be due to some misunderstanding on my part. If it is then I trust that Willis can put me straight enhancing my understanding and those of others.
The IPCC warming projections in AR4 and SR1.5 were based on Transient Climate Response defined in IPCC TAR 2001 as the temperature change at the time of CO2 doubling. In their example with ECS = 3.5C & CO2 rises at 1% per annum. At this rate CO2 levels will double in 70 years with TCR = 2.0 when ECS = 3.5. 3C of warming is not achieved in even 500 years. On this basis, with ECS = 3.0 and pre-industrial CO2 levels at 280ppm then a CO2 level of 395ppm would eventually lead to 1.5C of warming.
According to Mauna Loa CO2 readings CO2 rose from 316ppm in 1959 to 416ppm in 2021 or less than 32% in 62 years or less than 0.5% pa increase. That implies a doubling of CO2 of >150 years. Methane and Nitrous Oxide have been increasing at lower rates.
If this is true then adding in the forcing from other GHGs effectively the planet is at 445ppm CO2 levels. If ECS = 3.0 then 2.0C of warming will occur in the distant future, or not so distant future depending on your assumptions.
I assume here that a doubling of CO2 is related to an increase in forcing measured in Antony Watts per square metre.
I discussed the apparent difference between Hansen et al 1988 & TCR definition in TAR 2001 in my post below, with relevant graphics.
https://manicbeancounter.com/2021/05/28/hansens-1988-scenario-c-against-tcr-2001/
My background is in computers and programming. I have seen this before – not with climate models but other very complex code, that when I dug in and started sorting out what-did-what found the net sum was a relatively simple function for the gross result and tiny little caveats that amounted to almost nothing for the rest.
It seems each person that inherited the program added their own little parts and then “tunned” until it looked right…never mind if they had actually analyzed what they ended up adding was insignificant (maybe after the tunning).
Programs like this can be very intimidating and convincing, and their owners seldom have any idea how to actually test them in any consistent manner. They just accept the results as meaningful.
One very fast inspection is to look for “bumpers” in the code to keep a *result* from deviating too far from the expected value. When you see these in a model, they are ad-hoc “fixes” for either bad programming or misunderstood physics. It’s like a finding a “divide by zero” when working in quantum mechanics – somethings wrong but you don’t know what, so you “normalize” the result and move on.
What about the clouds?…
For a ‘settled’ science the models show a hilariously large range of predictions. You could argue the hindcast failures are even funnier.
To clarify, are Lambda and Tau simply selected by the modeller to fit the model to the past data, or are they calculable?
Hello Dr. Eschenbach,
very interesting. My point is focused on your e-time τ. IPCC does have 5 different ones in the Bern Model. I made an approximation with the antropogenetic emissions : we have 131ppm against anual emissions of 4.5 ppm gives a τ = 37 years. Taking all CO2 emissions together with 198 GtC by biomass aganist an total biomass reservoir of 600 GtC we will have a τ = 2,5 years. τ is a fundamentel value of IPCC to predict the future scenario. What is the basis of your 4,1 up to 5.7 years?
Thanks, Raimund. First, it’s Mr. E, not Dr. E. I am a 100% autodidact …
Next, I understand that the Bern model has five different e-folding times. I’ve never found anyone who can explain how this works in the physical world.
The basis of the ~ 4 to 5 year value of tau is that that value gives the best fit between the forcings and the model temperatures. If you take a look at the Excel spreadsheet I linked to you can see how the process works.
This is different from the decay time of a pulse of CO2 into the atmosphere. In that case, the pulse will decay back to some pre-pulse value. So there’s no reason to expect the tau of the two processes to be the same.
Hope this helps.
Questions?
Ask’em …
w.
Great work, but I wonder if the post might have benefited from a little more explanation of the model equation’s rationale.
This probably doesn’t matter, because what you’ve is a black-box exercise, and the results are what they are. To me, though, “simply lagging and rescaling the inputs” suggests the following differential equation:
where the dot means time differentiation, so differentiating that equation yields
and the result I get when I solve that equation is a model equation slightly different from yours.
Starting out, I get an integral in
Now, ordinarily I’d have
change linearly throughout the integration interval, but to get a result as close to yours as possible I instead assumed that 
is a constant 
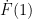in that interval:
When I make the substitutions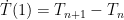
, 
, and 
, though, I get
Instead of being divided by
, that is, 
gets multiplied by 
.
Again, your results are what they are, but I for one got stuck on the model equation.
Rats. You’re correct. It gets multiplied by one minus alpha. I noticed that error early on and I thought I’d changed that.
Good catch. I’ve fixed the head post.
Thanks, Joe, your contributions are always appreciated.
w.
You may want to check the spreadsheet, too.
Done. Thanks again.
w.
Very nice analysis !
A reflection is that if one linearize Stefan Boltzmann´s law (around todays temperature) then the “starting” differential equation can be interpreted as:
Temperature change is proportional to difference between incoming and outgoing energy fluxes
Thanks for the kind words.
And your reflection sounds right. I mean, if we take the rate
of temperature change to be proportional to the radiation imbalance 
:
where
is the radiation imbalance, 
is the effective heat capacity in joules per square meter per kelvin, 
is the albedo, 
is emissivity, 
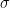is the Stefan-Boltzmann constant, 
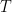is the departure of the global-average surface temperature from a reference value 
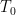, and 
is the greenhouse effect, and if forcing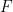 
is what the imbalance would be at the current greenhouse-effect level 
if the departure 
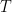from the reference temperature were zero:
then
and
If we assume
, 
, and 
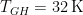, then the equation above gives us 
, which doesn’t differ wildly from the 
that Mr. Eschenbach’s spreadsheet gets for Model 15.
Hi Joe,
Been reading your analysis but I am not sure that I follow you 100%.
My understanding is that you use the “start” differential equation and write T as function of F and R. Then differentiate T with respect to Tgh and set the differential equal to zero (resulting in the expressions for lambda and tau).
I do like your analysis.
A minor thing is that I think you got the unit of labda “upside down”. Should be m2*K / W.
I calculated C just for fun (using Mr Eschenbachs value 5 years). The value I got was about 6*10^8 J/m2/K. This roughly corresponds to 100 meter deep water.
Bottom line seems that a very simple model based on radiation imbalance can reproduce the results from CMIP. I think it is time for IPCC modelers to do something else.
Oops! Yes, I did flub the dimensions.
Anyway, we know that
is the ratio that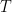 
bears to 
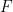when the system is in equilibrium, i.e., when 
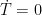. My rationale for using 
was that the change in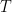 
‘s equilibrium value equals the change in the greenhouse effect 
.
It may help to observe explicitly that my previous comment’s first equation is the differential equation that describes the system’s attempting to reach equilibrium and that its second equation is the algebraic equation that defines forcing
Thanks for your comments.
Yepp, I do follow your analysis (and agree).
I think it is beautiful. One equation (based on fundamental physics) can replace the whole CMIP computer code.