Guest Post by Willis Eschenbach
I’ve been pointing out for some time that the current warming of the globe started about the year 1700, as shown in the following graph from the work of Ljungqvist:
Figure 1. 2,000 years of temperatures in the land areas from 30°N to the North Pole, overlaid with ice core and instrumental CO2 data. Data source: A New Reconstruction Of Temperature Variability In The Extra-Tropical Northern Hemisphere During The Last Two Millennia
However, some folks have been saying things like “Yeah, but that’s not global temperature, it’s just northern hemisphere extratropical temperature”. I hear the same thing whenever someone points out the Medieval Warm Period that peaked around the year 1000 AD. And they’re correct, the Ljungqvist data is just northern hemisphere. Here are the locations of the proxies he used:
Figure 2. Location of all of the proxies used by Ljungqvist to make his 2000-year temperature reconstruction. SOURCE: Op. Cit.
So I thought I’d look to see just how closely related the temperatures in various parts of the globe actually are. For this, I used decadal averages of the Berkeley Earth gridded temperature data, file name “Land_and_Ocean_LatLong1.nc”. I chose decadal averages because that is the time interval of the Ljungqvist data. Here is a graph showing how well various regions of the globe track each other.
Figure 3. Centered decadal average temperatures for the entire globe (red) as well as for various sub-regions of the globe.
As you can see, other than the slope, these all are in extremely good agreement with each other, with correlations as follows:
Figure 4. Correlations between the decadal average global temperatures and the decadal average global temperatures of various subregions. A correlation of “1” means that they move identically in lockstep. Note the excellent correlation of the extratropical northern hemisphere with the entire globe, 0.98.
This extremely good correlation is more visible in a graph like Figure 3 above if we simply adjust the slopes. Figure 5 shows that result.
Figure 5. As in Figure 3, but variance adjusted so that the slopes match
Conclusions? Well, in US elections they used to say “As Maine goes, so goes the nation”. Here, we can say “As the northern hemisphere land 30°N-90°N goes, so goes the globe”.
Simply put, no major part of the globe wanders too far from the global average. And this is particularly true of large land subregions compared to global land temperatures, which is important since the land is where we live.
And this means that since per Ljungqvist the NH 30°N-90°N temperatures peaked in the year 1000 and bottomed out in the year 1700, this would be true for the globe as well.
As I mentioned in my last post, my gorgeous ex-fiancée and I will be wandering around Northern Florida for three weeks starting on Tuesday June 29th, and leaving the kids (our daughter, son-in-law, and 23-month old grandaughter who all live with us full-time) here to enjoy the house without the wrinklies.
So again, if you live in the northern Floridian part of the planet and would like to meet up, drop me a message on the open thread on my blog. Just include in the name of your town, no need to put in your phone or email. I’ll email you if we end up going there. No guarantees, but it’s always fun to talk to WUWT readers in person. I’ll likely be posting periodic updates on our trip on my blog, Skating Under The Ice, for those who are interested.
Best of this wondrous planet to all,
w.
Any claim that global temperatures were being measured in 1850 is in need of some reality.
This post simply demonstrates the consistency of the process known as temperature homogenisation. It is a joke.
Willis,
“…..no major part of the globe wanders too far from the global average.”
I live in a part of the globe which constitutes a fair chunk of SH Land, namely Australia.
Your excellent post brought to mind something that has been troubling me for some time.
According to AR5 (2013) the temperature anomaly by which the world has warmed in the post industrial era,(I assume a baseline of 1850-1900) is 0.85 +/- 0.20C.
In the State of the Climate 2020,for Australia, the CSIRO is stating that the warming of Australia since 1850 displays a temperature anomaly of 1.44C +/- 0.24C.
Allowing for a short difference in timing between the 2 records, something does not compute given the close correlation of the various sub regions in your Figures.
Australia is a hot continent but……
Perhaps there is a simple resolution between the 2 records that I can’t see.
Any thoughts?
One minor correction. The CSIRO figure is from 1910 not 1850 but that should not change the issue much.
First, much as I love Oz, it’s only about 1.5% of the surface area of the planet, so it’s hardly a “major part of the globe” …
Second, land warms faster than the ocean, so in a warming time, land trends will be greater than ocean trends.
Regards,
w.
Why on earth do we all go on and on about CO2 to the EXCLUSION of water which has a far greater influence on the climate?
In fact when water reaches the saturation point in the atmosphere it calls to a halt any CO2 GHE. It also has this ‘joker in the pack’ whereby at evaporation the Planck coefficient of sensitivity is zero; so absorbed energy occurs at constant temperature and is incorporated into Latent Heat. It is buoyant in it’s vapor/gas phase so rises through the atmosphere for dissipation of this latent heat with some to space. To me – fascinating.
None of these things get any mention here in the comments, yet are fundamental to the understanding of the workings of the climate.
If you do delve into these matters as incorporated in the the Hydrocycle you will find that runaway global heating is just not possible in the presence of water.; not that that will get any traction while we all ponder upon the the CO2 molecule and it’s complex effect on the plethora of statistical data flooding out of the computers.
Are we all missing something here?
“They stand upon the CO2 stool…pull it out from underneath and “they’ come tumblin’ down….they have built their house upon the CO2 foundation….no CO2 cause means house comes tumblin’ down. The whole thing is CO2 warms atmosphere – man creates CO2- bad man must stop creating CO2 – “we” are virtuous and we will save the planet from bad man – you must follow our lead and instructions in order to save the planet.
Willis posted, above his Figure 5,: “This extremely good correlation is more visible in a graph like Figure 3 above if we simply adjust the slopes.”
My, oh my! . . . I never thought I see the day that Willis Eschenbach resorts to the same tactics as used by the dark side in climate change discussions 🙂
Miss the point much? I adjusted the slopes to highlight the similarity between the various graphs, NOT to create alarmism about temperature increases. Next time, look at the purpose of what is being done before making a fool of yourself.
w.
My apologies, Willis, if you took my comment seriously. I thought it was obvious that my post was a “tongue in cheek” comment by the fact that I put a “smiley face” at the very end.
Also, in making my post, I was fully aware of your above replies to John Phillips (June 27, 12:27pm) and to Alexander (June 27, 12:30pm) wherein you explained your slope adjustments. I had NO problems with your logic/explanations in those posts.
But thank you for providing a calibration of your sensitivities in this regard . . . this fool will be much more cautious in making future postings directly to you.
My bad, Gordon. Satire and sarcasm translates very poorly to the web. I thought the smiley was to soften the blow of a serious criticism, not to indicate a jocular remark.
I get attacked so often on the web for my faults, both imagined and real, that I’m likely oversensitive …
In any case, thanks for the clarification and my best to you and yours,
w.
I don’t believe Fig.4. I use HadCRUT.4.6.0.0.median 185001 202012.dat.
Anomalies: correlation Globe Land – Globe Land+Ocean 0,94
Anomalies: correlation Globe Ocean – Globe Land+Ocean 0,96
Anomalies: correlation Globe Ocean – Globe Land 0,81
Absolute: correlation Globe Land – Globe Land+Ocean 0,99
Absolute: correlation Globe Ocean – Globe Land+Ocean 0,62
Absolute: correlation Globe Ocean – Globe Land 0,50
First, since as I clearly stated I am using Berkeley Earth data, I fear your numbers have nothing to do with mine.
Second, anomalies have exactly the same correlation as the raw data. Since you are getting different values, you’re doing something wrong.
w.
I believe that there is a paper somewhere showing that the Central England Temperature alone has proved to be an extremely good proxy for temperatures in wider areas and even the world average. This is the longest-running temperature measurement by instrument rather than estimate from proxy, and also shows warming from very early, 18th century or earlier.
Well, since there’s been so much discussion about error and uncertainty, I thought I’d interject some actual science into the question.
Here is “Accuracy vs. Precision, and Error vs. Uncertainty“.
One point of note. Uncertainty is not ± one sigma, or ± two sigma, as some have claimed. As the name states, it is the range within which you are certain that a single measurement will fall.
w.
An excellent primer on accuracy, precision, and uncertainty.
It doesn’t delve deeply into metrology and how errors and uncertainty are propagated but it was never intended to. There are a number of excellent textbooks that a number of scientists and posters here need to study along with the GUM.
The last two sentences are extremely important and follow a recommendation in the GUM.
This should inform folks that the “standard error of the mean” is not considered a scientific indication of accuracy, precision, or uncertainty.
The preceding sentence says “Uncertainties may also be stated along with a probability. In this case the measured value has the stated probability to lie within the confidence interval.” And then goes on to give standard deviation as an example of that. Why do you think that informs us that the standard deviation if the mean isn’t an indication of accuracy?
Did you read the document that WE referenced. The very last statement says:
From the JCGM 2008:
Please note, this has nothing whatsoever to do with SEM (standard error of the mean, sampling, etc. It Is the “dispersion of the value that could reasonably be attributed to the measurand”. That is the definition of the SD (standard deviation). Also note, the SD has nothing to do with the accuracy or precision of the mean.
Read Section 2.3 in its entirety. You’ll see nothing there about SEM or any other statistical parameter defining accuracy or precision. In fact, the following gives a refutation of what you are trying to define uncertainty as meaning.
You questioned variances before. Please note what is defined as a combined standard uncertainty.
Here is another, later definition.
Please read “NOTE 3” closely. Even people who wrote the GUM recognized that many, many people mistake SD (standard deviation) for SEM (standard error of the mean) when discussing uncertainty.
SD and SEM are not the same. Nor does SEM relate in any way to accuracy or precision of the mean.
Your notations a little messed up there.
Note 2 specifically defines the Experimental Standard Deviation of the Mean as
, and says it’s an estimate of the distribution of 
, the sample mean.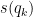 
is the standard deviation of sample.
I think you are completely misinterpreting Note 3. It isn’t saying Standard Deviation of the Mean is a different thing to Standard Error of the Mean. It’s saying calling it the Standard Error rather than the Standard Deviation is wrong. Like a lot of things it’s making a pedantically correct statement, but as I said else where the point of using a different term is to avoid just the sort of confusion I keep seeing here.
The fact that SDM is the same as SEM is obvious from the fact they are both defined using the same equation – see Note 2.
If you think that SDM is different from SEM, explain what that difference is and why it matters.And as I’ve said elsewhere, SDM is used by Taylor to determine accuracy.
As you like Khan Academy, here’s a video that explains standard error of the mean.
https://www.khanacademy.org/math/ap-statistics/sampling-distribution-ap/sampling-distribution-mean/v/standard-error-of-the-mean
That is good video. I particularly like his simulation in which he starts with a distribution that isn’t even remotely normal and yet by taking only N=16 samples the layout of the trials is a normal distribution with its mean centered almost exactly on the population mean with a standard deviation of this mean defined by σ/sqrt(N). In other words, any single trial has a ~68% and ~95% chance of being within 1 and 2 sigma of population mean respectively. That is a powerful result indeed!
The GUM says that the mean is the “best estimate” of a quantity and that the standard error/deviation of the mean equation is the “standard uncertainty” of the estimate of that quantity..
Note that I have the 2008 version of the “Guide to the expression of uncertainty in measurement” so if you have a different version that says something different let me know.
WE,
Thanks for the link. I appreciate it. I would only note that it doesn’t cover how to handle uncertainty itself. The most important factor is that uncertainty associated with independent, random measurements is not a probability distribution and is, therefore, not subject to reduction using statistical analysis methods.
Thanks, Tim. A concept that has helped me understand uncertainty is the idea of “triangular numbers”. A “triangular number” is a set of three numbers. The first one is the smallest value that you think a variable can have. The second number is the most probable value of the variable. The third number is the largest value that you think the variable can have.
Now, this is very closely related to the concept of uncertainty that I quoted above, viz:
The first and last values of the triangular number encompass the range within which you are certain that a single measurement will fall, with the middle value being the most probable value.
Now, someone upstream talked about three boards with their associated uncertainties. The values were 20, 25, and 30, and each value had an associated uncertainty of ±2.
These correspond exactly to the following three triangular numbers. I’m working in the computer language “R”. The “>” indicates a statement, [1] indicates the output of the statement. Here are the three numbers:
Now … what is the sum of these numbers? Well, it won’t be less than the sum of the first value of the three triangular numbers. The most probable answer is the sum of the middle value of the three triangular numbers. And it won’t be more than the sum of the last value of the three triangular numbers. Here’s the calculation.
It won’t be less than 69, the most probable value is 75, and it won’t be more than 81.
Finally, and to the point of the exercise, what is the mean of the three triangular numbers? Well, it’s the sum of the three numbers divided by three, which is:
Note that this is the same as 25 ± 2 … which shows that uncertainty is NOT reduced by taking the mean of the values.
Play with the concept a bit. It’s particularly interesting when the upper and lower extremes are not symmetrical about the most probable value.
Best to all,
w.
Uncertainty of the mean is lower than the uncertainty of the individual elements in the sample. In this case it is 25±1.15. Do a monte carlo simulation and prove this out for yourself. Generate 3 random board sizes and take the mean. Next inject random error with a normal distribution per ± 2 (2σ) and take the mean again. Compare the true mean with the errored mean. Repeat the simulation 1000 times. You will find that ~95% of the time the errored mean falls with in ± 1.15 of the true mean per σ^ =σ/sqrt(N) ; not 2.00.
How many times does it need to be repeated, random error IS NOT uncertainty. True random error when measuring the same thing multiple times with the same device will ultimately result in a Gaussian distribution. A Gaussian distribution is symmetrical around the mean. That is, as many errors below the mean as there is above the mean. A simple average will cancel the random errors out and provide a “true value” based upon the measuring device being used. However, there is no guarantee that the true value is accurate, nor does it allow you to assume more precision than what was actually measured.
You need to answer the simple question about how anomalies with a precision of 1/10th of a degree are created from recorded temperatures that are integers. For example, if the recorded temperature is 77 deg F, how do you get an anomaly of 2.2 deg F?
I’ll bet you you make the 77 integer into a measurement of 77.0 don’t you? Do you realize that is totally and absolutely ignoring the globally accepted Rules of Significant Digits along with ignoring uncertainty. Let’s do the math.
77 – 74.8 = 2.2 (violates significant digit rules by the way)
76.5 – 74.8 = 1.7
77.5 – 74.8 = 2.7
So the anomaly is 2.2 +/- 0.5, i.e. the same uncertainty as with the original recorded measurement. Please note, using significant digits it would be reported as 2 +0.7, -0.3. Nothing wrong with an asymmetric interval for uncertainty by the way.
When I say uncertainty I’m factoring in all kinds of uncertainty including the truncation of digits. It doesn’t matter. And yes, I simulated the truncation of digits too. It raised the standard deviation of the mean from 0.57 (1.15 2σ) to 0.60 (1.20 2σ) for your 3 board example. That is lower the 1.0 uncertainty for each board. BTW…4 boards drops to 0.53 (1.06 2σ) and 5 boards drops to 0.47 (0.94 2σ) and that is with digit truncation uncertainty included. The standard deviation of the mean continues to decline as we add more boards and increase inline with the expectation from σ^ =σ/sqrt(N). If you get a different result let me know.
“How many times does it need to be repeated, random error IS NOT uncertainty.”
Uncertainty is not error, it’s a parameter that indicates the range of likely error. As the sacred text says
It’s that dispersion that is the error. Whether it’s random or not would depend on the reasons for the uncertainty.
“nor does it allow you to assume more precision than what was actually measured.”
You’ve switched to talking about precision from uncertainty. A lack of precision might be a cause of uncertainty but it isn’t the only reason. Are you right to say averaging can never allow you to assume more precision than what was actually measured? Of the top of my head I’d say it depends on the other levels of uncertainty, but where you get it wrong is when you assume that a mean cannot be more precise than any individual measurement.
The example from Taylor that Tim used above shows how it’s possible to measure the length of a sheet of metal and get a more accurate than the measurement. In that case 10 samples are taken to a precision of two decimal places of a mm, but the mean result is give to a precision of three decimal places. I’d say the important point here is that the uncertainty caused by the precision is less than the overall uncertainty.
This becomes much better of instead of measuring the same thing over and over, you measure different things with different sizes well beyond the level of precision in order to find the mean. The uncertainty caused by the the lack of precision becomes insignificant compared to the standard deviation of the population.
“For example, if the recorded temperature is 77 deg F, how do you get an anomaly of 2.2 deg F?”
Because the base is an average. 30 years of 30 daily data = 900 data points, which average to something other than an integer. (Now expect to have to go over the discussion about whether it’s possible to have a mean of 2.4 children per family again)
“Do you realize that is totally and absolutely ignoring the globally accepted Rules of Significant Digits along with ignoring uncertainty.”
There are no “Rules” about significant digits, just standards, and those standards generally allow you to use more digits for intermediate calculations. But most importantly none of this matters if your anomaly based on you antique thermometer is combined with thousands of other entries to produce an average. The difference of a fraction of half a degree C, will vanish in the general CLT mishmash, like all the other sources of uncertainty,
(BTW, what happens when you convert 77F to Celsius?)
Two things.
First, there is a difference between repeated measurements of the same object, and a number of measurements of different objects. If I ask 50 people to measure a cell phone to the nearest mm, I will get a range of measurements. And yes, we can say that the average of those measurements has less uncertainty than that of any single measurement. In general, that kind of uncertainty goes down as the standard deviation of the measurements divided by the square root of the number of measurements.
However, taking this at face value would mean that if we asked a million people to measure the cell phone, the mean would be accurate to the standard deviation of the measurements (~ 0.5mm) divided by sqrt(1000000), or a claimed uncertainty of a thousandth of an mm … which is obviously ludicrous in the real world.
My own personal rule of thumb is that by averaging you can gain one order of magnitude of uncertainty, but no more. So if I’m measuring to the nearest ±0.5 mm, the best I can get is only ± 0.05 mm, even with a million measurements.
Second, this is ONLY for repeated measurements of the same object. Suppose I asked 1,000 people to measure a thousand unique cellphones to the nearest mm … in that situation, averaging doesn’t help one bit. The uncertainty in the final answer is still ± half an mm.
And note that this second condition is what we are looking at when we are averaging temperature readings over time.
Hope this helps,
w.
“Second, this is ONLY for repeated measurements of the same object. Suppose I asked 1,000 people to measure a thousand unique cellphones to the nearest mm … in that situation, averaging doesn’t help one bit. The uncertainty in the final answer is still ± half an mm.”
And this is what I keep asking. Why do people think the rules for the standard error of a mean disappear when you are measuring different things? A quote to that effect from one of the many sources I’m asked to look at would be a start.
The only real difference is that the uncertainty caused by individual measurements are mostly irrelevant given the much bigger standard deviation of the population. If cell phones differ by several cm, an error of a mm or so on each reading will have virtually no impact on the accuracy of the mean. But the idea that the accuracy of the mean cannot be greater than the accuracy of any one measure is demonstrably false. Just look at bdgwx’s simulations, or consider how you can can get an average of 2.4 children when you are only counting to the nearest whole child.
“However, taking this at face value would mean that if we asked a million people to measure the cell phone, the mean would be accurate to the standard deviation of the measurements (~ 0.5mm) divided by sqrt(1000000), or a claimed uncertainty of a thousandth of an mm … which is obviously ludicrous in the real world.”
It may be ludicrous, but that doesn’t make it incorrect.
Out of interest I run a Monte Carlo simulation to estimate pi, but the method of generating random points in a square and seeing what proportion where inside a circle. With a million samples I estimated the standard error of the mean would be 0.0016. The value I got for pi was 3.140588, out by 0.001.
In order to calculate this each point is scored at either 0 or 4, no other option, and the estimate of pi is just the mean of all these 0s and 4s.
Note that this is measuring different things, and you could say there’s no uncertainty in a 0 or 4. So I ran the test again, but in this case added a random number (with uniform distribution) between -1 and +1 to each value, I really though this would cause problems. But the average came out at 3.140954, even closer.
“Second, this is ONLY for repeated measurements of the same object. Suppose I asked 1,000 people to measure a thousand unique cellphones to the nearest mm … in that situation, averaging doesn’t help one bit. The uncertainty in the final answer is still ± half an mm.”
I just simulated this. The simulation creates 1000 unique cell phones of different sizes. Next 1000 people measure each cell phone with ± 0.5 (1σ) of uncertainty. Each person computes a mean of the 1000 cell phones. Each person’s measured mean is compared with the true mean. The standard error of the mean came out to ± 0.0158 which is nearly spot on with the expected value of 0.5/sqrt(1000). The simulation then averaged each person’s mean to arrive at a composite mean. I did the experiment 100 times. The standard error of the composite mean came out to ± 0.0005 which is nearly spot on with the expected value 0.0158/sqrt(1000) or 0.5/sqrt(1000000). At no time did my simulation ever use the formula σ^ =σ/sqrt(N). The uncertainties I report here are natural manifestations of the simulation. If you get something different or if you want me to do a different simulation with truncation uncertainty factored in or with accuracy problems with each person’s instrument let me know.
To summarize…it doesn’t matter if the mean is for the same thing or for different things. The uncertainty is always less than the uncertainty of the individual measurements. I encourage everyone to do their own Monte Carlo simulation and prove this out for themselves.