Guest essay By Christopher Monckton of Brenchley
This series discusses climatology’s recently-discovered grave error in having failed to take due account of the large feedback response to emission temperature. Correct the error and global warming will be small, slow, harmless and net-beneficial. The series continues to attract widespread attention, not only here but elsewhere. The ripples are spreading.
My reply to Roy Spencer’s piece on our discovery at drroyspencer.com has attracted 1400 hits, and the three previous pieces here have attracted 1000+, 350+ and 750+ respectively. Elsewhere, a notoriously irascible skeptical blogger, asked by one of his followers whether he would lead a thread on our result, replied that he did not deign to discuss anything so simple. Simple it is. How could it have been thought the feedback processes in the climate would not respond to the large pre-existing emission temperature to the same degree as they respond to the small enhancement of that temperature caused by adding the non-condensing greenhouse gases to the atmosphere? That is a simple point. But simple does not necessarily mean wrong.
The present article develops the math, which, though not particularly complex, is neither simple nor intuitive. As with previous articles, we shall answer some of the questions raised in comments on the earlier articles. As before, we shall accept ad interim, ad argumentum or ad experimentum all of official climatology except what we can prove to be incorrect.
Let us conduct a simple Gedankenexperiment, running in reverse the model of Lacis et al. (2010), who found that, 50 years after removing all the non-condensing greenhouse gases from the atmosphere, the climate would have settled down to a new equilibrium, giving a slushball or waterbelt Earth with albedo 0.418, implying emission temperature 243.3 K. We shall thus assume ad experimentum that in 1800 there were no greenhouse gases in the atmosphere. For those unfamiliar with the logical modes of argument in scientific discourse, it is not being suggested that there really were no greenhouse gases in 1800.
Lacis found that, only 20 years after removal of the non-condensing greenhouse gases, global mean surface temperature would fall to 253 K. Over the next 30 years it would fall by only 1 K more, to 252 K, or 8.7 K above the emission temperature. Thus, subject to the possibility that the equatorial zone might eventually freeze over, surface temperature in Lacis’ model settled to its new equilibrium after just 50 years.
One question which few opponents in these threads have answered, and none has answered convincingly, is this: What was the source of that additional 8.7 K temperature, given that there were no non-condensing greenhouse gases to drive it? Our answer is that Lacis was implicitly acknowledging the existence of a feedback response to the 243.3 K emission temperature itself – albeit at a value far too small to be realistic. Far too small because, as shown in the previous article, Lacis allocated the 45.1 K difference between the implicit emission temperature of 243.3 K at the specified albedo of 0.418 and today’s global mean surface temperature of 288.4 K (ISCCP, 2018) as follows: Feedback response to emission temperature 252 – 243.3 = 8.7 K; warming directly forced by the naturally-occurring, non-condensing greenhouse gases (288.4 – 252) / 4 = 9.1 K, and, using Lacis’ feedback fraction 0.75, feedback response to warming from the non-condensing greenhouse gases 27.3 K: total 45.1 K. This asymmetric apportionment of the difference between emission temperature and current temperature implies that the 8.7 K feedback response to emission temperature is only 3.6% of 243.3 K, while the 27.3 K feedback response to greenhouse warming is 300% of 9.1 K. Later we shall demonstrate formally that this implausible apportionment is erroneous.
It will be useful to draw a distinction between the pre-industrial position in 1850 (the first year of the HadCRUT series, the earliest global temperature dataset) and the industrial era. We shall assume all global warming before 1850 was natural. That year, surface temperature was about 0.8 K less than today (HadCRUT4) at 287.6 K, or 44.3 K above emission temperature. Lacis’ apportionment of the 44.3 K would thus be 8.7 K, 8.9 K and 26.7 K.
We shall assume that Lacis was right that the directly-forced warming from adding the naturally-occurring, non-condensing greenhouse gases to the air was 8.9 K. Running the experiment in reverse from 1850 allows us to determine the feedback fraction implicit in Lacis’ model after correction to allow for a proper feedback response to emission temperature. Before we do that, let us recall IPCC’s current official list of feedbacks relevant to the derivation of both transient and equilibrium sensitivities:
IPCC’s chosen high-end feedback sum implies Charney sensitivities somewhere between minus infinity and infinity per CO2 doubling. Not a particularly well constrained result after 30 years and hundreds of billions of taxpayers’ dollars. IPCC’s mid-range feedback sum implies a mid-range Charney sensitivity of only 2.2 K, and not the 3.0-3.5 K suggested in previous IPCC reports, nor the 3.3 K in the CMIP3 and CMIP5 ensembles of general-circulation models. No surprise, then, that in 2013, for the first time, IPCC provided no mid-range estimate of Charney sensitivity.
None of the feedbacks listed by IPCC depends for its existence on the presence of any non-condensing greenhouse gas. Therefore, in our world of 1800 without any such gases, all of these feedback processes would be present. To induce a feedback response given the presence of any feedback process, all that is needed is a temperature: i.e., emission temperature. Since feedback processes are present, a feedback response is inevitable.
Emission temperature is dependent on just three quantities: insolation, albedo, and emissivity. Little error arises if emissivity is, as usual, taken as unity. Then, at today’s insolation of 1364.625 Watts per square meter and Lacis’ albedo of 0.418, emission temperature is [1364.625(1 – 0.418) / d / (5.6704 x 10–8)]0.25 = 243.3 K, in accordance with the fundamental equation of radiative transfer, where d, the ratio of the area of the Earth’s spherical surface to that of its great circle, is 4. Likewise, at today’s albedo 0.293, emission temperature would be 255.4 K, the value widely cited in the literature on climate sensitivity.
The reason why official climatology has not hitherto given due weight (or, really, any weight) to the feedback response to emission temperature is that it uses a degenerate form of the zero-dimensional-model equation, ΔTeq = ΔTref / (1 – f ), where equilibrium sensitivity ΔTeq after allowing for feedback is equal to the ratio of reference sensitivity ΔTref to (1 minus the feedback fraction f). The feedback-loop diagram for this equation (below) makes no provision for emission temperature and none, therefore, for any feedback response thereto.
The feedback loop in official climatology’s form of the zero-dimensional-model equation ΔTeq = ΔTref / (1 – f )
Now, this degenerate form of the zero-dimensional-model equation is adequate, if not quite ideal, for deriving equilibrium sensitivities, provided that due allowance has first been made for the feedback response to emission temperature. Yet several commenters find it outrageous that official climatology uses so simple an equation to diagnose the equilibrium sensitivities that the complex general-circulation models might be expected to predict. A few have tried to deny it is used at all. However, Hansen (1984), Schlesinger (1985), IPCC (2007, p. 631 fn.), Roe (2009), Bates (2016) are just a few of the authorities who cite it.
Let us prove by calibration that official climatology’s form of this diagnostic equation, when informed with official inputs, yields the official interval of Charney sensitivities. IPCC (2013, Fig. 9.43) cites Vial et al. (2013) as having diagnosed the CO2 forcing 
, the Planck parameter 
and the feedback sum 
from simulated abrupt 4-fold increases in CO2 concentration in 11 CMIP5 models via the linear-regression method in Gregory (2004). Vial gives the 11 models’ mid-range estimate 
of the feedback sum as 
W m–2 K–1, implying 
, and the 
bounds of 
as 
, i.e. 
.
The implicit CO2 forcing ![clip_image006[1]](http://wattsupwiththat.files.wordpress.com/2018/04/clip_image0061.png "clip_image006[1]"){kind=small}
, in which fast feedbacks were included, was 
W m–2 compared with the 
W m–2 in Andrews (2012). Reference sensitivity 
, taken by Vial as 
, was 
above the CMIP5 models’ mid-range estimate 
. Using these values, official climatology’s version of the zero-dimensional-model equation proves well calibrated, yielding Charney sensitivity 
on 
, near-exactly coextensive with several published official intervals from the CMIP3 and CMIP5 climate models (Table 2).
From this successful calibration it follows that, though the equation assumes feedbacks are linear but some feedbacks are nonlinear, it still correctly apportions equilibrium sensitivities between forced warming and feedback response and, in particular, reproduces the interval of Charney sensitivities projected by the CMIP5 models, which do account for nonlinearities. Calibration does not confirm that the models’ value 
for the feedback fraction or their interval of Charney sensitivities is correct. It does confirm, however, that, at the official values of f, the equation correctly reproduces the official, published Charney-sensitivity predictions from the complex general-circulation models, even though no allowance whatsoever was made for the large feedback response to emission temperature.
Official climatology trains its models by adjusting them until they reproduce past climate. Therefore, the models have been trained to account for the 33 K difference between emission temperature of 255.4 K and today’s surface temperature of 288.4 K. They have assumed that one-quarter to one-third of the 33 K was directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases and the remaining two-thirds to three-quarters was feedback response to that direct warming. Therefore, they have assumed that the feedback fraction was two-thirds to three-quarters of equilibrium sensitivity: i.e., that f was somewhere between 0.67 and 0.75.
As a first step towards making due allowance for the feedback response to emission temperature, official climatology’s version of the zero-dimensional-model equation can be revised to replace the delta input and output signals, indicating mere changes in temperature, with entire or absolute values. Note that the correct form of any equation describing natural occurrences (or any natural law) must be absolute values: the use of deltas is only permissible if the delta-equations are correctly derived from the absolute equation. Accordingly, ΔTeq = ΔTref / (1 – f ) should be Teq = Tref / (1 – f ). The revised feedback loop diagram is below:
After amendment to replace delta inputs and outputs with absolute values, official climatology’s form of the zero-dimensional model equation becomes
Teq = Tref / (1 – f )
To find f where the reference and equilibrium temperatures are known, this revised equation can be rearranged as f = 1 – Tref / Teq. In the reverse Lacis experiment, reference temperature Tref before feedback is the sum of emission temperature TE and the additional temperature ΔTE = 8.9 K that is the direct warming from adding the naturally-occurring, non-condensing greenhouse gases to the air. Thus, Tref = TE + ΔTE = 243.3 + 8.9 = 252.2 K. Equilibrium temperature Teq = 287.6 K is simply the temperature that obtained in 1850, after 50 years of the reverse Lacis experiment. Then f = 1 – Tref / Teq = 1 – 252.2 / 287.6 = 0.123, only a fifth to a sixth of official climatology’s value. The reason for the difference is that, unlike official climatology, we are taking correct account of the feedback response to emission temperature.
Next, how much of the 35.4 K difference between Tref = 252.2 K and Teq = 287.6 K is the feedback response to emission temperature TE = 243.3 K, and how much is the feedback response to the direct greenhouse-gas warming ΔTE = 8.9 K? Simply take the product of each value and f / (1 – f) = 0.14, thus: 243.3 x 0.14 = 34.1 K, and 8.9 x 0.14 = 1.3 K. We prove that this is the correct apportionment by using the standard, mainstream form of the zero-dimensional-model equation that is universal in all dynamical systems except climate. The mainstream equation, unlike the degenerate climate-science form, explicitly separates the input signal (in the climate, the 255.4 K emission temperature) from any amplification (such as the 8.9 K warming from adding the non-condensing greenhouse gases to the atmosphere).
The mainstream zero-dimensional model equation is Teq = Tref μ / (1 – μβ), where Tref is the input signal (here, emission temperature); μ = 1 + ΔTref / Tref is the gain factor representing any amplification of Tref such as that caused by the presence of the naturally-occurring, non-condensing greenhouse gases; β is the feedback fraction; μβ is the feedback factor, equivalent to f in climatology’s current version of the equation; and Teq is equilibrium temperature at re-equilibration of the climate after all feedbacks of sub-decadal duration have acted.
The feedback loop for this corrected form of the zero-dimensional-model equation is below:
The feedback loop diagram for the standard zero-dimensional-model equation
Teq = Tref μ / (1 – μβ)
One advantage of using this mainstream-science form of the zero-dimensional model is that it explicitly and separately accounts for the input signal Tref and for any amplification of it via the gain factor μ in the amplifier, so that it is no longer possible either to ignore or to undervalue either Tref or the feedback response to it that must arise as long as the feedback fraction β is nonzero.
It is proven below that the apportionment of the 35.4 K difference between Tref = 252.2 K and Teq = 287.6 K in 1850 derived earlier in our Gedankenexperiment is in fact the correct apportionment. Starting with the mainstream equation, in due time we introduce the direct or open-loop gain factor μ = 1 + ΔTref / Tref. The feedback factor μβ, the product of the direct or open-loop gain factor μ and the feedback fraction β, has precisely the form that we used in deriving the feedback fraction f as 1 – (243.3 + 8.9) / 287.6 = 0.123, confirming that our apportionment was correct.
Note in passing that in official climatology f is at once the feedback fraction and the feedback factor, since official climatology implicitly (if paradoxically) assumes that the direct or open-loop gain factor μ = 1. In practice, this particular assumption leads official climatology into little error, for the amplification of emission temperature driven by the presence of the non-condensing greenhouse gases is a small fraction of that temperature.
But was it reasonable for us to assume that the 287.6 K temperature in 1850, before Man had exercised any noticeable influence on it, was an equilibrium temperature? Well, yes. We know that in the 168 years since 1850 the world has warmed by only 0.8 K or so, and official climatology attributes all of that warming to Man, not Nature.
Was it reasonable for us to start with Lacis’ implicit emission temperature of 243.3 K, reflecting their specified albedo 0.418 on a waterbelt Earth in the absence of the non-condensing greenhouse gases? Why not start with Pierrehumbert (2011), who said that a snowball Earth would have an albedo 0.6, implying an emission temperature 221.5 K? Let’s do the math. The feedback fraction f = μβ would then be 1 – (221.5 + 8.9) / 287.6 = 0.20.
Thus, from a snowball Earth to 1850, the mean feedback fraction is 0.20; from a waterbelt Earth to 1850, it is 0.12; and at today’s albedo 0.293, implying an emission temperature 255.4 K, it is 1 – (255.4 + 8.9) / 287.6 = 0.08. Which is where we came in at the beginning of this series. For you will notice that, as the great ice sheets melt, the dominance of the surface albedo feedback inexorably diminishes, whereupon the feedback fraction falls over time.
Though the surface albedo feedback may have dominated till now, what about the biggest of all the feedbacks today, the water-vapor feedback? The Clausius-Clapeyron relation implies that the space occupied by the atmosphere may (though not must) carry near-exponentially more water vapor – a greenhouse gas – as it warms. Wentz (2007) found that total column water vapor ought to increase by about 7% per Kelvin of warming. Lacis (2010) allowed for that rate of growth in saying that if one removed the non-condensing greenhouse gases from today’s atmosphere and the temperature fell by 36 K from 288 to 252 K, there would be about 10% of today’s water vapor in the atmosphere: thus, 100% / 1.0736 = 9%.
Specific humidity (g kg–1) at pressure altitudes 300, 6000 and 1000 mb
However, though the increase in column water vapor with warming is thus thought to be exponential, the consequent feedback forcing is approximately logarithmic (just as the direct CO2 forcing is logarithmic). What is more, a substantial fraction of the consequent feedback response is offset by a reduction in the lapse-rate feedback. Accordingly, the water-vapor/lapse-rate feedback response is approximately linear.
Over the period of the NOAA record of specific humidity at three pressure altitudes (above), there was 0.8 K global warming. Therefore, Wentz would have expected an increase of about 5.5% in water vapor. Sure enough, close to the surface, where most of the water vapor is to be found, there was a trend in specific humidity of approximately that value. But the water-vapor feedback response at low altitudes is small because the air is all but saturated already.
However, at altitude, where the air is drier and the only significant warming from additional water vapor might arise, specific humidity actually fell, confirming the non-existence of the predicted tropical mid-troposphere “hot spot” that was supposed to have been driven by increased water vapor. In all, then, there is little evidence to suggest that the temperature response to increased water vapor and correspondingly diminished lapse-rate is non-linear. Other feedbacks are not large enough to make much difference even if they are non-linear.
Our method predicts 0.78 K warming from 1850-2011, and 0.75 K was observed
One commenter here has complained the Planck parameter (the quantity by which a radiative forcing in Watts per square meter is multiplied to convert it to a temperature change) is neither constant nor linear: instead, he says, it is the first derivative of a fourth-power relation, the fundamental equation of radiative transfer. Here, it is necessary to know a little calculus. Adopting the usual harmless simplifying assumption of constant unit emissivity, the first derivative, i.e. the change ΔTref in reference temperature per unit change ΔQ0 in radiative flux density, is simply Tref / (4Q0), which is linear.
A simple approximation to integrate latitudinal variations in the Planck parameter is to take the Schlesinger ratio: i.e., the ratio of surface temperature TS to four times the flux density Q0 = 241.2 Watts per square meter at the emission altitude. At the 255.4 K that would prevail at the surface today without greenhouse gases or feedbacks, the Planck parameter would be 255.4 / (4 x 241.2) = 0.26 Kelvin per Watt per square meter. At today’s 288.4 K surface temperature, the Planck parameter is 288.4 / (4 x 241.2) = 0.30. Not much nonlinearity there.
It is, therefore, reasonable to assume that something like the mean feedback fraction 0.08 derived from the experiment in adding the non-condensing greenhouse gases to the atmosphere will continue to prevail. If so, the equilibrium warming to be expected from the 2.29 Watts per square meter of net industrial-era anthropogenic forcing to 2011 (IPCC, 2013, Fig. SPM.5) will be 2.29 / 3.2 / (1 – 0.08) = 0.78 K. Sure enough, the least-squares linear-regression trend on the HadCRUT4 monthly global mean surface temperature dataset since 1850-2011 (above) shows 0.75 K warming over the period.
But why do the temperature readings from the ARGO bathythermographs indicate a “radiative energy imbalance” suggesting that there is more warming in the pipeline but that the vast heat capacity of the oceans has absorbed it for now?
One possibility is that not all of the global warming since 1850 was anthropogenic. Suppose that the radiative imbalance to 2010 was 0.59 W m–2 (Smith 2015). Warming has thus radiated 2.29 – 0.59 = 1.70 W m–2 (74.2%) to space. Equilibrium warming arising from both anthropogenic and natural forcings to 2011 may thus eventually prove to have been 34.8% greater than the observed 0.75 K industrial-era warming to 2011: i.e., 1.0 K. If 0.78 K of that 1.0 K is anthropogenic, there is nothing to prevent the remaining 0.22 K from having occurred naturally owing to internal variability. This result is actually consistent with the supposed “consensus” proposition that more than half of all recent warming is anthropogenic.
The implication for Charney sensitivity – i.e., equilibrium sensitivity to doubled CO2 concentration – is straightforward. The models find the CO2 forcing to be 3.5 Watts per square meter per doubling. Dividing this by 3.2 to allow for today’s value of the Planck parameter converts that value to a reference sensitivity of 1.1 K. Then Charney sensitivity is 1.1 / (1 – 0.08) = 1.2 K. And that’s the bottom line. Not the 3.3 K mid-range estimate of the CMIP5 models. Not the 11 K imagined by Stern (2006). Just 1.2 K per CO2 doubling. And that is nothing like enough to worry about.
None of the objections raised in response to our result has proven substantial. For instance, Yahoo Answers (even less reliable than Wikipedia) weighed in with the following delightfully fatuous answer to the question “Has Monckton found a fatal error?”
What he does is put forward the following nonsensical argument –
1. If I take the 255.4 K temperature of the earth without greenhouse gases, and I add in the 8K increase with greenhouse gases I get a temperature of 263.4 K.
2. Now, what I’m going to say is say that this total temperature (rather than just the effect of the greenhouse gases) leads to a feedback. And if I use this figure I get a feedback of 1 – (263.4 / 287.6) = 0.08.
And the problem is … how can the temperature of the planet (255.4 K) without greenhouse gases then lead to a feedback? The feedback is due to the gases themselves. You can’t argue that the feedback and hence amplified temperature due to greenhouse gases is actually due to the temperature of the planet without the greenhouse gases! What he’s done is taken the baseline on which the increase and feedback is based, and then circled back to use the baseline as the source of the increase and feedback.
So, I’m afraid it’s total crap …
The error made by Yahoo Answers lies in the false assertion that “the feedback is due to the gases themselves”. No: one must distinguish between the condensing greenhouse gases (a change in the atmospheric burden of water vapor is a feedback process) and the non-condensing greenhouse gases such as CO2 (nearly all changes in the concentration of the non-condensing gases are forcings). All of the feedback processes listed in Table 1 would be present even in the absence of any of the non-condensing greenhouse gases.
Another objection is that perhaps official climatology makes full allowance for the feedback response to emission temperature after all. That objection may be swiftly dealt with. Here is the typically inspissate and obscurantist definition of a “climate feedback” in IPCC (2013):
Climate feedback An interaction in which a perturbation in one climate quantity causes a change in a second, and the change in the second quantity ultimately leads to an additional change in the first. A negative feedback is one in which the initial perturbation is weakened by the changes it causes; a positive feedback is one in which the initial perturbation is enhanced. In this Assessment Report, a somewhat narrower definition is often used in which the climate quantity that is perturbed is the global mean surface temperature, which in turn causes changes in the global radiation budget. In either case, the initial perturbation can either be externally forced or arise as part of internal variability.
IPCC’s definition thus explicitly excludes any possibility of a feedback response to a pre-existing temperature, such as the 255.4 K emission temperature that would prevail at the surface in the absence of any greenhouse gases or feedbacks. It was for this reason that Roy Spencer thought we must be wrong.
Our simple point remains: how can an inanimate feedback process know how to distinguish between the input emission of temperature of 255 K and a further 9 K of temperature arising from the addition of the non-condensing greenhouse gases to the atmospheric mix? How can it know it should react less to the former than to the latter, or (if IPCC’s definition is followed) not at all to the former and extravagantly to the latter? In the end, despite some valiant attempts by true-believers to complicate matters, our point is as simple – and in our submission as unanswerable – as that.
Probably true, Lord Monckton.
The real interesting story is: IPCC doesn’t understand adiabatic process.
I mean, it’s a real scandal that there “scientists” in the 21st century who believe in flat-earth physics and deny gravity. We should focus on shaming them for that.
I’m not sure pointing out their other errors means anything to them. They are conclusion-driven. They label their tales “science” and force the media to repeat their mantras. I’m very sure they are practicing black magic.
Best regards,
Zoe
Zoe, you said ‘IPCC doesn’t understand adiabatic process’. The statement ‘the IPCC is not allowed to understand adiabatic process’ would be more correct, because their charter does not allow them to recognise or take account of any non-anthropogenic causes of ‘climate change’. See here – Principle 2 :https://www.ipcc.ch/pdf/ipcc-principles/ipcc-principles.pdf
It is a pity that the IPCC does not deal more objectively with adaption.
The policy should be targeted adaption where and only where adaption is needed. This works whatever be the cause of any warming, and deals with any problems caused and actually sustained by said warming.
@ Richard Verney the IPCC has no desire to deal with adaption. The UN’s purpose for the IPCC, as various of it’s luminaries have admitted, is:
1. to achieve an unelected world government;
2. to redistribute wealth from the developed nations to the third world; and
3. to fundamentally and permanently change the industrial, economic principles that have stood since the industrial revolution into some form of non-industrial future (at least where the currently developed nations are concerned)
So ‘adaption’ is anathema, it is a non-starter as it would destroy the ‘fear-factor’ that was deliberately chosen (AGW) to terrify the public and achieve the above.
Old England,
2. to redistribute wealth from the developed nations into their own pockets under the illusion of redistribution to the third world; and
There fixed it for you…
In response to Ms Phin, the head posting makes clear that for the sake of argument we are accepting all of official climatology except what we can prove to be erroneous. But the lad from Tottenham is right that IPCC’s mandate is not to investigate whether Man’s influence on Nature is dangerous but to assume that it is and to profit accordingly.
Yeah, I figured out you’re attempting a reductio ad absurdum. Best of luck.
In response to Zoe Phin, we are not attempting a reductio ad absurdum: we are delivering a demonstratio per contradictionem.
Anyone with experience with controls and control theory understands that positive feedback systems are VERY difficult to stabilize and by their nature, run away to their end points with the slightest disturbance. The entire history of Earth’s climate indicates that stability is the norm with the ability to absorb HUGE perturbations without problems. Strongly positive feedback systems simply don’t act this way.
It is like the difference between an acrobat balancing on a high wire, and a marble balanced in the center of a bowl. In one, a slight deviation leads to catastrophe, and in the other, a slight deviation leads to an eventual return to center. I submit that the nature of Earth’s climate is like a marble in a bowl. It always “wants” to return to a balance of energies no matter how much it is disturbed.
Yes, Hoyt. The only (laymen’s) quibble that I have with CM’s treatise is that IMO there are several (if not many) types of feedback operating on different timescales, rather than just one. This raises the question ‘does the model that CM uses exclude water as a GHG’? I presume that it does not, thus allowing for the various types of water-related feedback that our watery planet enables. Has CM assumed that all these different feedbacks can be represented by a single feedback value?
Stability is a human concept. Physical processes just “are”. I Suspect any stability we see is illusionary, caused by not looking in enough detail. The climate is constantly changing as there are constantly varying inputs. The models are gross oversimplifications and so have no way of accurately modelling the climate.
Mr Clagwell’s analogy is apt. The Earth’s climate is strongly resistant to changes in temperature. Therefore, one would expect the climate to respond only a little to our minuscule perturbation of the atmospheric composition. Our current work is intended to demonstrate why it is that the expected response is what is observed.
BoyfromTottenham is concerned about whether we have made sufficient allowance for the different feedbacks. The different feedbacks that IPCC considers relevant to the derivation of equilibrium sensitivity are at Table 1. Our point is that the feedback response – after correction of official climatology’s error – is so small that making a distinction between the precise contributions of the individual feedbacks is of little more value than trying to estimate the number of angels that can dance on the head of a pin.
Or a bowl with two depressions in the bottom and the marble can find its way into one or the other
and every so often be perturbed and then find its way to the other depression. Both a semi-stable warmer climate and a more stable colder climate. (since the ice ages last longer than the interglacials)
I like the analogy of a bowl, but the bowl has a small flat area at the bottom. Every time the marble settles in a different part of the flat area, some group of humans prophesies doomsday and attempts to gain wealth and power from it.
Yes, of course, but apparently this isn’t sufficient enough for far too many people.
Which is why the earth is warming – there is an imbalance of energy between what is being
received by the sun and what is emitted by the earth. Satellites show there is imbalance of a
couple of watts/m^2 and therefore the earth must be warming as long as it is storing energy.
Even if the earth is warming at the rate of 1C per century who cares? In fact here in Canada we would like it warmer. And even if it is warming no one has proved that CO2 has anything to do with it?
Germonio thinks there as a 2 Watt per square meter radiative energy imbalance. Official climatology, however, puts it south of 1 Watt per square meter. The current best estimate is about 0.6. Once the baneful effect of official climatology’s error in overestimating the temperature response to such imbalances is taken into account, this imbalance is of little practical importance.
Everyone agrees that the earth has warmed.
The differences are over how much and what caused it.
Also over whether it is a problem worth worrying about. Much less spending trillions in other people’s money.
Positive feedback is unstable when the closed loop gain becomes negative. The gain equation is,
1/Go = 1/g + f, where Go is the open loop gain, g is the closed look gain and f is the fraction of the output fed back to the input and whose sign indicates positive or negative feedback.
In modern control systems, Go can be considered infinite, thus the stability of 0 = 1/g + f is when (f < 0). In the climate system, Go is approximately 1, thus the stability of 1 = 1/g + f is when (f < 1). Note that this can be rearranged as g = 1/(1 + f), which is the gain equation cited in the Schlesinger paper and which assumes unit open loop gain and which Schlesinger refused to acknowledge.
The scary runaway conditions and tipping points are all predicated on an open loop gain much larger than unity. Note that an open loop gain greater than unity means adding energy to the system and implies an internal source of Joules to power the gain which is also missing from the climate system.
CO2isnotevil is not quite correct. It is not necessary to add energy to a thermodynamic system to warm it: one may also inhibit the rate at which energy is lost by that system to its surroundings. He is quite right, however, to point out the implication of the use of a system-gain factor 1 / (1 – f), where f is the feedback fraction. Such a system gain factor implies a unit open-loop gain, which is of course directly contrary to the notion that enriching the atmosphere with greenhouse gases causes warming.
Christopher,
It’s absolutely necessary to add energy to a thermodynamic system to warm it. Slowing down the cooling is not the same as heating it. As a though experiment, consider doubling the CO2 at night. Will this increase the surface temperature above the starting temperature when the Sun set? Sure, the morning temp will be a little higher then it would have been, but this is not the same as adding heat to the system. This illustrates one of the failures of climate science where slowing down cooling is considered to be the same as warming the system by adding energy. This is how they can arm wave an absurdly high sensitivity factor where 1 W/m^2 of forcing increases surface emissions by 4.3 W/m^2 requiring an impossibly high 3.3 W/m^2 of feedback power.
Regarding the gain. the open loop power gain is indeed 1 (i.e. forcing in, surface emissions out). GHG’s and clouds do not increase the open loop gain, but the illusion of positive feedback from energy being ‘bounced’ back from the atmosphere to the surface makes the closed loop gain seem greater than 1. This is the consequence of the 600 milliwatts/m^2 of ‘feedback’ per W/m^2 of forcing input. The exact feedback fraction can be backed out of this as follows:
1/Go = 1/g + f
1 = 1/1.6 + f
f = 0.375 (37.5% net positive ‘feedback’)
And of course, since the open loop gain is 1, the fact that there appears to be positive feedback does not have the same implications of instability as would be the case with a much larger open loop gain.
Consider an open loop gain of 2. The feedback required to achieve the same closed loop gain of 1.6 becomes,
1/2 = 1/1.6 + f
f = -0.125
Now the system requires 12.5% negative feedback to achieve the same closed loop gain as before. The end result is the same as is the stability criteria. Can you see how feedback and the open loop gain can be traded off against each other to achieve the same closed loop gain without impacting the stability?
Rob,
In your example, the water level will indeed increase without bound by 1 shot glass per iteration since 8 oz are added while 8 oz minus a shot glass is removed. The amount of water (energy) in the system is not remaining the same, thus the equivalent of COE is violated since in each iteration, a shot glass worth of new water is added to the system.
You are not properly accounting for the first law of thermodynamics related to COE and the requirement for work (Joules) to heat something. Your example is illustrating a serious flaw in the consensus logic.
Christopher,
“It is not necessary to add energy to a thermodynamic system to warm it: one may also inhibit the rate at which energy is lost by that system to its surroundings.”
No, the post albedo solar input doesn’t have to increase in order for the system to further warm, but is it logical for the so-called ‘feedback’ response to a perturbation to amplify it beyond what watts forcing the system from the Sun are being amplified?
co2isnotevil,
“It’s absolutely necessary to add energy to a thermodynamic system to warm it. Slowing down the cooling is not the same as heating it.”
If the slowing down of cooling increases the total joules stored in the system in order to achieve balance, why can’t it? Isn’t this the essence of the GHE and how CO2 can theoretically further warm the surface?
Rob,
“Energy is 100% accounted for in my example. Take the initial gallon, the total added from the tap, the total removed down the drain, and the leftover in the bucket, and it is in perfect balance. Not a single ounce unaccounted for.
Except in your example the volume of water is ever increasing, because the amount removed is perpetually less than is added. The GHE from GHGs is not ever increasing the surface temperature. This is because GHGs act to both cool by continuously emitting IR up towards space and warm be re-radiating absorbed upward IR back downwards towards (and not necessarily back to) the surface. The GHE is one of cooling resistance by this underlying mechanism in the ever presence of opposing cooling mechanism via upward emitted IR in conjunction with net upward flow of non-radiant flux from the surface, which acts to accelerate the IR upward cooling push away from the surface in order to achieve pure radiative balance through the TOA. This in essence is why large warming effects from added GHGs don’t make sense, though theoretically they should be providing *some* push in the warming direction.
Rob,
‘The flaw in your example is that if the water represents energy, the system is not in equilibrium. To make your model more representative, you can only add 8 oz minus a shot glass of water in each iteration and the water level (energy in the system) will remain the same. The constraints that you are violating is that the amount of water (energy) entering the system must be equal to the amount of water leaving the system and that as the amount of stored water increases (increasing temperature), the rate at which the water is removed must increase as the volume of water raised to the 4’th power.
Rob,
I’m not really understanding your or co2isnotevil’s arguments here on this.
Rob,
My thought experiment was designed to illustrate the response of the system to specific change in order to distinguish between a change in an actual forcing influence like the Sun and a change to the system, like a change in CO2 concentrations. Without the Sun’s forcing power, a change in CO2 concentrations can’t increase the surface temperature on its own. It’s not a source of new energy, but a redistribution of existing energy. The point being that consensus climate science incorrectly conflates changing CO2 concentrations with new energy arising from increased solar forcing.
It’s crucial to be able to distinguish between a change in actual forcing and a change to the system. When CO2 ‘forcing’ is referenced, it really means how much more solar forcing would be required to have the same effect on the surface temperature while keeping the system (CO2 concentrations) constant.
Relative to your example, it can stop after N iterations if and only if the shot glass is getting exponentially smaller converging close enough to zero after that many iterations. In this example, your shot glass represents IPCC defined ‘forcing’ which being incremental converges to zero in the steady state.
Mathematically, forcing is the dE/dt term in the differential equation, Pi(t) = Po(t) + dE(t)/dt. This is not a first order LTI since while the energy stored by the system (E) is linearly proportional to the surface temperature (T), the emissions of the system (Po) are proportional to T^4. In a first order LTI, like that which describes an RC circuit, Po would be linearly proportional to T. Pi is the legitimate forcing term while Pi minus Po at TOT (or TOA) is the IPCC definition of forcing which is the same as the dE/dt term and represents the rate that energy is added to or removed from the system producing Po. The IPCC considers an instantaneous change in Pi to have the same effect as an instantaneous change in Po which would only be true if Po was independent of E.
Rob,
A more accurate analogy would be to consider the shot class forcing which converge to zero after sufficient iterations. Considering the shot glass Co2 is what’s wrong with your analogy. Co2 is not energy.
This is one of the fundamental errors, and is often made by Willis. One has to be very careful when explaining scientific processes since how systems operate is fundamental to the proper understanding of said system.
For example, I heat an open top pan on a stove to 80 degrees. I take it off the stove, and put a lid on the pan so as to reduce the rate of cooling. The pan never heats above 80 degrees. There is no warming once the lid is placed on top of the pan.
What is happening is that instead of the pan taking say 60 minutes to cool to room temperature, the pan with the lid on takes say 120 minutes to cool to room temperature.
That begs the question in the climate sense. Since contrary to the K&T energy budget cartoon where solar insolation is received 24/7, in the real world solar is not received 24/7 but rather in packages of day and night. Hence since the GHGs inhibit the rate of cooling, the question is whether there are enough hours of darkness (when no solar insolation is received) to allow all the energy that has built up during the course of the day to shed itself to space during the hours of darkness?
Do GHGs delay the cooling of the planet say by 1 second, or 1 minute, or 10 minutes or 1 hour etc. It may be that with increasing amounts of CO2 the coldest period of the night is not reached at say 03:00 hrs but because of the restricting in the rate of cooling, it is reached at say 03:05 hrs. However, as long as the night can cool to its coolest point, before sun up, tit is difficult to envisage that there is a build up of heat brought about by the delay resulting from a reduction in the rate of cooling.
@Rob Bradley
No I do not.
You are dealing with the situation portrayed in the K&T energy budget cartoon where the sun shines 24/7 such that energy is constantly being inputted. If that truly were the real scenario then there could be a build up in temperature as you illustrate.
However, that is not planet Earth. Energy is in effect being inputted only during the day. The question is what happens during the night when energy is no longer being inputted?
One must never overlook that energy is received only on one side of the globe, but energy is being radiated away from the entire surface of the sphere.
Rob Bradley
Yes, at the very specific location of the poles, the sun does shine 24×7, then – six months later – does go dark for an equal six months. Every other location faces either day and night (of varying different lengths and intensity every day), or of continuous sunlight, but each day has less and less lower intensity sunlight. Trenberth-GISS-Hansen’s perfectly insolated, perfectly isolated, perfectly insulated, perfectly average “flat earth” model is valid only near the equinox, only at a latitude of 42-48 degrees.
Any other location, any other dates, and other latitude? Wrong answer.
Rob Bradley
Analogy does not equal Reality.
Analogy does not even simulate Reality. Sometimes, under limited circumstances under simplified examples, Analogy “might” approximate limited parts of Reality.
The shot glass forcing must go to zero because this is how the IPCC defines forcing, as a temporary imbalance that converges to zero as it seeks equilibrium. The stop criteria for the iterations would be when forcing gets close enough to zero.
This illustrates a flaw in the IPCC logic where forcing is defined by Bode to be ALL input received by the system yet the IPCC defines it in this bizarre way that only serves to obfuscate.
Yes, this is exactly what I have been saying for a couple of years..
Please. You are making it simple enough fr people ti understand. That negates the whole point of Moncktons treatise.
Mr Smith’s comment is mere yah-boo. Feedback math is not for wimps: it is counter-intuitive, and quite a lot has to be explained. That is why the head posting is so long, though the algebra deployed is not difficult.
“The entire history of Earth’s climate indicates that stability is the norm with the ability to absorb HUGE perturbations without problems.”
HUGE perturbations, yes. But not a HUGE³ perturbation like, y’know, +100 ppm of CO₂.
Gaia might enjoy a little spanking every now and then, but for God’s sake be reasonable, man.
100ppm delta has needed 63 years since 1955 to get to the 410 level. you would need another 63 years to get to 510. And still is not a doubling from 1880. What in the hell are all of you alarmists worried about? Plants will love the extra CO2.
Begging the question. You assume the answer to prove the answer. The point is to prove that additional CO2 is a huge perturbation, let alone one that feedbacks don’t negate.
Mr Photon says that altering the composition of the atmosphere by 1 part in 10,000 is a huge perturbation. No, it is a very small perturbation. Some 750 million years ago, in the pre-Cambrian, the atmospheric burden of Co2 was 7000 ppmv. Today it is little more than 400. Our work demonstrates that the warming effect of our small perturbation will be far less than had hitherto been imagined.
Re: Alan Tomalty
I think there’s some doubt whether 510 ppm CO2 can be reached in the atmosphere by burning fossil fuel. An increase from 410 to 510 ppm gives ~ 25% increase in CO2 partial pressure. But Henry’s Law says the solubility of CO2 in oceans will increase in proportion to atmospheric partial pressure. The oceans currently store over 7 times the carbon available in fossil fuel reserves. Changes in ocean temperature also change the ocean’s CO2 solubility. Cooling increases solubility; warming reduces.
Plus the greening of the planet is absorbing lots of CO2 into plant material.
(Not to mention the flesh of those creatures that eat plant material)
You say you accept that increasing CO2 will increase temperatures, you attack anyone who doesn’t agree, yet then you throw out a good old meaningless statistic like that. It’s irrelevant what proportion of the atmosphere is CO2; what matters is the relative increase in CO2.
You’re talkiing about a period when there was virtually no advanced life on Earth.
“Bellman” thinks that what matters is the relative rather than absolute increase in CO2 concentration. No: what matters is the proportionate change, or rather the logarithm of the proportionate change. The radiative forcing per CO2 doubling is thus 5.05 ln (2), or 3.5 Watts per square meter (Andrews 2012). Divide this by the Planck parameter 3.2 and one converts the forcing to a direct warming, before accounting for feedback, of 1.1 K. But the CO2 concentration has not yet doubled: indeed, taking into account all anthropogenic influences in the industrial era, the total net forcing is only 2.29 Watts per square meter (IPCC, 2013, fig. SPM.5). Divide that by 3.2 and you get just 0.72 K of direct warming, before accounting for feedback. But only 0.75 K of observed warming has occurred over the period, so that the feedback fraction is just 1 – 0.72 / 0.75, or 0.04. One can bump that up a little, but not much. What it means is that Charney sensitivity is only 1.1 / (1 – 0.04), or 1.15 K.
Yes, that’s what I was saying. What matters is the proportionate change in CO2. A 30% increase in CO2 is a 30% increase irrespective f what proportion of the atmosphere is CO2. Your statement suggested that the increase was a “small perturbation” because it was only “1 part in 10,000” of the atmosphere. But you’d get the same amount of warming if it was 1 part in 100 or 1 part in 10,000,000 – the rest of the atmosphere is irrelevant.
RS is correct: stability is indeed the norm. The climate is in essence thermostatic. The global mean surface temperature, according to the ice cores, has varied by little more than 3 K either side of the 810,000-year mean (Jouzel 2007, adjusted for polar amplification).
Excuse me but isn’t the science settled ? A $Trillion dollars of debt wasted on a math error ?
There better be some splaining . But when you think of it what a graceful way for the con artists and government to walk away from this fraud . Yep those darn scientists steered us wrong .
Oh well ! … Yeah but it’s still warming … just like it’s been doing for over 15,000 years more or less .
Congratulations Mr . Monckton . You popped the hot air balloon .
Many thanks to Amber for her kind words. We think it will prove difficult, if not impossible, for official climatology to go on pretending that the warming effect of our sins of emission will be very large. We are expecting a lot of wriggling and wrestling before a paper by us is eventually accepted for publication in a serious climate journal: but we shall keep trying until either we succeed or it is made clear to us that it is we who are in error.
“Official climatology trains its models by adjusting them until they reproduce past climate. Therefore, the models have been trained to account for the 33 K difference between emission temperature of 255.4 K and today’s surface temperature of 288.4 K. They have assumed that one-quarter to one-third of the 33 K was directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases and the remaining two-thirds to three-quarters was feedback response to that direct warming.”
That makes no sense. Snowball Earth at 255K was not a past climate, so there is no “therefore”. AFAIK, Lacis in 2010 was the first to actually see what happened if you removed non-condensing GHGs in a GCM. They didn’t assume a forced warming fraction – that was the result of their simulation.
Much is said about what “official climatology” says, with very little evidence. The snowball earth calculation is a teaching example – it is not the basis of any grand theory.
Everyone in industry knows CO2 is radiative coolant, so Lacis is obviously wrong. He probably committed fraud.
@ nick , That means that at 280 ppm/v increased the temp by 33 K. We’ve allegedly added 120 ppm/v. So that means at the minimum, 8.48 ppm/v would raise the temp by 1 K. That means the temp on earth should already be 14 K warmer than it is now.
” So that means at the minimum, 8.48 ppm/v would raise the temp by 1 K.”
No, this is fallacious linear reasoning. In fact, it is logarithmic within our range. Extrapolated to zero CO2, that would go to -∞. Obviously, the log stops applying at some stage. The 33K is not based on any linear reasoning, but just a comparison of present state with a case of perfectly clear atmosphere. And it is just a thought experiment to aid thinking. No theory depends on it.
Mr Stokes overlooks the fact that the presence of an emission temperature will induce a feedback response where feedback processes such as surface albedo, cloud albedo and water vapor are present. It is precisely because – as IPCC’s definition of a “climate feedback” shows – theory does not at present take any account of the large feedback response to emission temperature, erroneously misallocating it to the presence of the non-condensing greenhouse gases, that most calculations of both transient and equilibrium sensitivity have hitherto been exaggerations.
” the presence of an emission temperature will induce a feedback response where feedback processes such as surface albedo, cloud albedo and water vapor are present”
Why are those not simply feedback responses to surface albedo, cloud albedo and water vapor? How does emission temperature enter? And if ET can induce a feedback response, why does it need that help?
If ET can induce a feedback response, it must be able to be changed by the output. Otherwise it has no role in a feedback loop.
Nick, as a bystander it appears to me that the argument being made by the Climate Change orthodoxy is that CO2 has a direct effect on the radiative balance of the atmosphere which leads to warming. Then the CO2 driven warming has a feedback effect through a variety of natural mechanisms which leads to additional warming above and beyond the direct effects.
To apply the same logic to past conditions, you can derive the earth’s basal emissivity from first principles, then whatever that temperature happens to be must also trigger feedback through the same natural mechanisms that causes some amount of additional heating to arrive at an actual temperature. The challenge is to determine how the actual temperature of earth in the past was arrived at after accounting for the basal emissivity derived from first principles plus all known natural mechanisms AND the natural feedbacks that much occur due to the 255K contributed from earth’s basal emissivity. The feedback doesn’t change the theoretical temperature of a gray body earth, but it obviously would change the actual temperature.
Snowball Earth was a past climate on at least one, possibly two occasions.
But not one of which GCMs have experience. In fact, a GCM probably couldn’t get there, as Lacis’ run shows.
Mr Stokes says that it would not be possible for a general-circulation model to predict that the temperature prevalent at the surface in the absence of the non-condensing greenhouse gases would be no higher than the emission ttemperature. And what is it that prevents the Earth’s temperature from being 255 K in the presence of clouds, water vapor and ice but in the absence of the non-condensing greenhouse gases? It is, of course, the feedback response to emission temperature itself.
“And what is it that prevents the Earth’s temperature from being 255 K in the presence of clouds, water vapor and ice but in the absence of the non-condensing greenhouse gases? It is, of course, the feedback response to emission temperature itself.”
Suppose you had a dry surface at 255K, emitting 240 W/m2 and then introduced liquid water (or subliming ice). Some would evaporate, wv in the air would radiate back, the surface would warm, , more would evaporate etc. That is classic wv feedback to the forcing, which is the introduction of liquid water. In this case, the response is highly non-linear at first.
I have chosen this interchange as a place to bring a new objection to the party, pointing out an error on the parts of both CM and NS. The quote from Nick Stokes is as good a place to start as any. My observation is related to this: Absent all GHG’s the air temperature above the ground would be well above 288K.
[Emphasis added] NS: “Suppose you had a dry surface at 255K, emitting 240 W/m2 and then introduced liquid water (or subliming ice). Some would evaporate, wv in the air would radiate back, the surface would warm, , more would evaporate etc. That is classic wv feedback to the forcing, which is the introduction of liquid water.”
From CM in his original article, “the native state” refers to what is described in this article as an atmosphere free of non-condensing GHG’s.
It is important to make clear the errors in too much discussion about the effect of GHG’s when added or removed completely. The “33 degrees of warming” often referred to by the IPCC (and hundreds of others) refers to the temperature of the naked moon which has an average temperature of -18C and the current temperature of the atmosphere at 2 metres above the ground of 15C, with the difference being attributed to “the presence of GHG’s”. Gavin Schmidt goes slightly farther calling the ‘native state’ the atmosphere of the Earth, not the same as the naked moon with no atmosphere at all, but the atmosphere without any GHG’s, and further says that the temperature (not of the surface but of the atmosphere) will be -18C in that condition (albedo unchanged).
The IPCC, Gavin, CM and NS should be challenged about this. There is an element missing from all the above equations including the delightful uB in the latest of CM’s explanations.
The temperature of the atmosphere at 2 m elevation, the temperature we experience and measure, is not the same as the temperature of the surface, and it has two contributing elements: convective heating, and radiating heating. I will term the convective heating C and the radiating heating R. It is accepted that all energy leaving the Earth must leave by radiation and that this is emitted from various vertical levels in the system, often simplified to surface emissions and atmospheric emissions.
While one can represent the emissions from the surface and the atmosphere as having a single equivalent radiative elevation and temperature, it is important to remember that the temperature of the atmosphere is a combination of the energy received from C+R, not R alone. The air temperature is not the same as the surface temperature.
I will use Fig 1, Global Energy Flows in Watts/m^2 from Trenberth’s paper
http://www.cgd.ucar.edu/staff/trenbert/trenberth.papers/BAMSmarTrenberth.pdf
The radiation budget for the planet as a whole can be discussed in terms of the radiative transfers in and out, however it is important to remember that the energy in the atmosphere got there by two routes. I do not quibble with the total leaving the system, nor that it is the sum of surface emissions and atmospheric emissions. However, omitting the C from the C+R in stating how the atmosphere got warm in the first place has a major implication for the claim, repeated above, that the “dry surface at 255K, emitting 240 W/m2” represents anything close to reality.
From Trenberth’s Fig 1
Incoming solar radiation 341.3 W/m^2 (units not repeated hereafter)
Absorbed by atmosphere 78 W
Absorbed by the surface 161 W
Absorption by the atmosphere means direct heating, 78 W.
Absorption by the surface leaves not by radiation alone, but by convection [C] to the atmosphere and radiation [R].
Leaving the surface are:
Evapo-transpiration 80 W (delivered to the atmosphere well above the ground)
Thermals 17 W (ditto)
Surface radiation 396 W
Obviously 161 W incoming cannot lead to 396 W outgoing by surface radiation so it is necessary to understand that he has 333 W back-radiation from the atmosphere adding to that absorbed by the surface for a total absorbed of 494 W. Trenberth does not allow that any of the absorbed 333 W is conveyed to the atmosphere by contact, though he does for the 161 W.
So what about the convective heat transfer to the atmosphere of a portion of that 333 W? If receiving 161 W drives (80+17) = 97 W of evapo-transpiration and thermals, then receiving 333 more drives (333/161) * 97 = 201 W of additional convective heat transfer. This is not shown on the drawing, but is instead labelled “Surface radiation”. The 201 W can be apportioned to additional evapo-transpiration 166 W and thermals 35 W.
The [C] term is missing. Why does that matter? Because the surface temperature (2 m above the ground) is the result of that (17+35) = 52 W of direct heating (assuming no condensation of the water vapour).
Further, it means that in a “clear atmosphere” (the term used above) insolation would heat the surface by an additional 42% (161+78). The total heat delivered to the atmosphere would increase because all incoming insolation would reach the ground.
Again I have no quibble with the calculation of the amount of energy leaving the system, but I have a problem accepting that the temperature of the atmosphere from C+R would be 255 K in the absence of all non-condensing GHG’s. The higher surface temperature resulting from the clear atmosphere will definitely increase the value of C and reduce the hitherto assumed value of R (in the presence of condensing GHG’s). Another way of looking at it is, the surface would be cooled by the atmosphere, which we have already agreed has no non-condensing GHG’s so its capacity to radiate energy would be reduced. If it is heated more, and loses the ability to cool radiatively, then the atmosphere at 2m will be warmer. If water vapour is retained as a GHG in this mental experiment, then its back-radiation will warm the surface, and it will again be hotter, and transfer more energy to the air by convection.
Trenberth’s assumption is that in the absence of the 333 W back-radiation there would be nothing emitted by the atmosphere, it would all be emitted by the surface (his 396 W arrow). This is not exactly the same as saying there are no non-condensing GHG’s but I will continue using his Fig.1. He has it as follows:
Incoming radiation absorbed by the surface 161 W
Back-radiation 333 W (no longer present)
Surface radiation 396-333 = 63 W
Evapo-transpiration 80 W
Thermals 17 W
161 – (63+80+17) = 1 W (close enough for government work).
This error, omitting the C term, has been accepted in all discussions of the radiative energy balance. Why does it matter? Because the temperature at 2m above the ground, what we experience and measure, is strongly affected by convective heating, not just surface radiation.
Time of Day
Absent all GHG’s condensing and non-condensing, the surface would warm in the daytime with all 1364 W/m^2 and get very hot, like the moon’s surface, but it would cool dramatically against the atmosphere with the result that the air would heat as if by an electric kettle, per square metre. Such hot air, having no ability to cool by radiation, would simply remain heated, unless it could cool against the surface at night – something that cannot happen on the moon. Thus we can recognize that using an averaged “341 watts” continuous radiation as a model is inappropriate for representing, at all, what happens in real life. From a ‘cold start’ the atmosphere would be convectively heated in the daytime and not cool at night, because it can’t.
A daytime surface receiving all 1364 Watts (clear sky) would dramatically heat the air, not “get hot and radiate it all back to space” as per Trenberth. At night the cold surface would be poorly heated by the air above it because hot air rises and conducts very poorly downwards due to the formation of an inversion layer. The next day, the air would be heated again by the surface which would start from a slightly warmer base temperature due to the heat retained in the transparent atmosphere.
This whole business of comparing a non-GHG atmosphere or a non-condensing GHG atmosphere with the temperature of the naked moon is very misleading, because we are interested in the temperature of the air about 2m above the ground, which has to consider the C term.
Finally, if we assume that there are condensing GHG’s like water and nothing else, accepting therefore that the atmosphere can radiatively cool, it would be something similar to what we have now. The water vapour would cool the atmosphere below the temperature it would otherwise attain in the absence of all GHG’s. Again, absent all GHG’s and in the presence of C, the air temperature would be well above 288K. Absent some GHG’s, why would it cool to 255K? Absent all of them, why would it cool to 243.3K? People are confusing a planet in contact with an atmosphere having a thermal mass, with a naked moon.
Crispin in Waterloo but really … People are confusing a planet in contact with an atmosphere having a thermal mass, with a naked moon.
I liked your post, but why do you omit the evapotranspiration/hydorlogical_cycle that carries latent heat at least as high as the cloud condensation layer of the mid-troposphere? The phase changes of the “condensing” GHGs strikes me as also important. Condensed vs non-condensed H2O is one of the differences between the “surface” and the 2 meter layer.
Whilst, in the past, the extent of the ice caps has varied considerably, it is not known that snowball Earth ever existed.
I find it very difficult to comprehend that it could have existed, since there is so much solar insolation going into the equatorial and tropical oceans, and with ever growing ice caps, it is likely that less oceanic currents will be distributing the energy received in a polewards direction, thereby meaning that more and more of the incoming solar insolation will be retained in the equatorial and tropical oceans themselves.
It is not easy to comprehend how with ever clearer skies developing (due to the water vapour being frozen out and contained in the ice caps) which in turn increases the amount of solar insolation being received that the equatorial and tropical oceans could freeze over.
I consider that snowball Earth is very much a fantasy of incorrect models.
matthewrmarler
I am pretty sure it is not left out: the movement of heat by condensing GHG’s is included in the 87 W as a fraction of the 161 absorbed by the surface. It is very odd that Trenberth has 333 W of back-radiation but no split of that energy striking the surface into multiple components like the 161 W. It is as if the Earth knows that incoming solar radiation has multiple paths out, but back-radiation absorbed by the same surface can only depart by IR radiation.
It is analogous to CM’s observation that the IPCC has no feedbacks until 1850 then suddenly the atmosphere knows that man’s emissions must have lots of feedbacks.
The most important aspect is that the convection of heat from the surface to the atmosphere continues in the complete absence of any GHG’s, whether condensing or not. It is a fundamental error to claim all heat striking the surface will depart by IR or reflection.
It is also a fundamental error to consider an average insolation instead of the full daytime insolation, because an IR-inert atmosphere would heat rapidly and effectively during the day, but have no ability to dispose of the heat save by conduction to the surface, and that hot gas would move rapidly away from the surface.
I was reminded by the Nutty Professor this week that the gases would indeed emit energy – for example nitrogen will emit green light if it is hot enough, so there are limits. The major point is that if a hot, non-GHG atmosphere had a little CO2 added to it, it would cool. Adding more would cool it faster. We had an article presented on WUWT that showed rapid heating of a very cold atmosphere with the addition of a few ppm of CO2, based on the assumption that the surface (and lower atmosphere) would be as cold as the naked moon without any GHG’s.
Painting a hot stove shiny silver reduces IR emissions and drives up the temperature. Painting it black cools it considerably. Even if it had an emissivity of zero, it would still cool by convection. Similarly, an atmosphere with no ability to cool radiatively, would still be heated by the hot surface. All the discussion above overlooks this physical reality.
@Rob Bradley
Nothing of the sort is proven by Venus. We simply do not know how hot Venus would be if say 60% of the CO2 was replaced by say Argon.
What we do know is the the radiative GHE on Venus, if it exists at all, does not operate as it is claimed to operate on planet Earth.
The radiative GHE is said to work here on Earth by the fact that our atmosphere is largely transparent to the wavelength of incoming solar irradiance which solar irradiance is absorbed by the surface and then radiated from the surface at a longer wavelength to which our atmosphere is rather opaque, such that the outgoing emissions are absorbed on the way out and then reradiated from the atmosphere in all directions (some of it downwards).
However, that is not the scenario on Venus. The Venusian atmosphere is almost completely opaque to the wavelength of incoming solar irradiance such that the Russian lander missions meassured incoming solar irradiance at the surface to be only 4 W/m2 !!! Consequently we know that the surface of Venus absorbs almost no incoming solar irradiance because so little of it actually finds its way to the surface to be absorbed, and thence to be radiated from the surface at a different wavelength.
Rob, I would suggest that you should check some basic facts before you make a bare assertion. Venus is simply not well understood, but there are strong arguments that the temperature is simply mass/pressure related.
“Some would evaporate, wv in the air would radiate back, the surface would warm,” ? radiate back? I assume you mean LWR. The amount of “heat” that radiates back can not over come the the total amount of “heat” being sweep away. So the surface would not warm. It would cool down. Think Swamp Cooler effect.
Crispin, mostly quite a convincing critique, thank you. Surely, though, a hot atmosphere’s mass must also radiate hot body LWR. The sun’s atmosphere does. CM of B, of course, doesn’t claim to accept all the rest of concenci theory, but rather accepts it for argument purposes. He should revisit the work with your moon case, convection and a non water GHG case. Finding two major errors in the clime syndicates theory couldn’t hurt.
Ray B
Nothing is shown about a non-radiating atmosphere by looking at Venus.
Gary Pearse
You suggest that a hot atmosphere would radiate – but the point of a non-radiating atmosphere is that it doesn’t – at least not at the temperatures envisaged on Earth. O2 will radiate a little IR, but it is not a meaningful amount.
The postulation is that the ’33 degrees of heating’ comes entirely from GHG’s implying, as Gavin Schmidt and many others do, that a non-radiating atmosphere will be as cold as the surface of a planet with no atmosphere at all. I invite you all to look at the exact wording lest there be any doubt about what is being stated. There are thousands of example so use the IPCC or Gavin.
So in terms of the radiative component of atmospheric heating, they are quite correct – that is how the radiation component works, but they omit the surface heating of that same atmosphere, in the haste to show that it will be as cold as the moon is with no atmosphere at all. This is a very serious error. Sorry to say that CM has also left out this component.
If Venus had a radiatively transparent atmosphere, all solar insolation would strike the surface, heating it to perhaps 400 C initially, which would then heat the atmosphere, which cannot radiate the energy away (by definition, it does not have that capacity). Over time the atmosphere would equilibrate with the surface which would be even hotter, day by day until the hot air cooled against the night surface enough to disposes of what it gained during the day. Perhaps the terminal temperature would be 1000 or 1200 degrees, which as you point out, might radiate from other gases as well (nitrogen in green light and so on).
The impact of adding some CO2 would be to dramatically cool the atmosphere. Adding more and more, it would reach some nadir and start warming again from enhanced feedbacks. What that performance curve looks like I have no idea, but it seems reasonable based on what we know about radiative physics.
Crispin is not correct when he states that I have neglected the feedback response to emission temperature. The whole point of this series is to show that official climatology has neglected that actually large response. Consequently, it has obtained an interval of values for the feedback fraction, and hence for equilibrium sensitivities, that is far too high.
Nor is Crispin correct to imagine that “the naked moon” – which I shall call simply the Moon – has a mean surface temperature of -18 C, or 255 K. The Moon’s mean surface temperature is not stated by the Diviner mission, but it is probably around 190 K, a great deal less than the 271 K naively calculated by NASA using a single global mean calculation based on the fundamental equation of radiative transfer.
The models have to have an equation for climate sensitivity somewhere in the code because they sure as hell cant calculate it from radiative transfer equations according to the bible on “Radiative Heat Transfer” by Dr. Michael Modest. You should read that book Nick before you comment further. Dont worry Nick there are only 4 chapters relevant to gases.
“The models have to have an equation for climate sensitivity somewhere in the code because they sure as hell cant calculate it from radiative transfer equations”
No, they don’t, and yes, they do. Climate models are discretised partial differential equations (with cells). There is nowhere to put an equation for climate sensitivity.
Mr Stokes is right. In the past, models did not give estimates of transient or equilibrium sensitivity directly: they produced outputs from which these sensitivities were diagnosed using the zero-dimensional-model equation. The current generation of models is capable of delivering estimates of climate sensitivity directly. As the head posting shows, those estimates are consistent with the zero-dimensional-model equation in its defective form, and they take no account at all of the feedback response to emission temperature.
Nick, Monckton is not saying the theory started from a snowball earth. He is only using a snowball earth to show that the math changes little. The problem that Monckton is addressing is at some point somebody did devise a grand theory of how earth warmed from (most probably 255k) to present temperature. They then devised models to implement that theory and predict a future based on that theory. Its a great study in scientists as lemmings. . . .accepting the works without question of the guys handing out the checks. I have seen this time and again when science meets politics. The history books are full of it. What Monckton has unveiled could only have happened because “the science was settled” and nobody wanted to debate it. They used to burn people at the stake for doing what Monckton has done or at minimum put them under house arrest. The main takeaway is the treatment of water vapor (approximately linear), the close approximation to warming per Hadcrut, are all “unsettled” but key areas where work needs to be done. I think we all know that this thing has been politicized to such an extent that its actually delaying science in really learning about climate.
“The problem that Monckton is addressing is at some point somebody did devise a grand theory of how earth warmed from (most probably 255k) to present temperature.”
??? Who did that?
Mr Hunter is quite right. The modelers have hitherto assumed, because paper after paper after paper mentions it, that the “natural greenhouse effect” represents the entire 32 K difference between emission temperature and the temperature in 1850 (actually, the papers usually mention the 33 K difference between emission temperature and today’s temperature, but that implies that Man’s sins of emission are part of the natural greenhouse effect). It is in any event self-evident that the models do not take sufficient account (if they take any account at all) of the substantial feedback response to emission temperature – a feedback response that is inevitable given the presence of that temperature and of the feedback processes (listed in table 1 of the head posting) that act upon it.
“The modelers have hitherto assumed, because paper after paper after paper mentions it, that the “natural greenhouse effect” represents the entire 32 K difference between emission temperature and the temperature in 1850”
No quotes, again. Modelers have no need to assume that, and it couldn’t help them anyway. Papers discussing the 32K difference are not so abundant. As Roy Spencer said, the significance of this thought experiment is way over-rated. It is a useful teaching example. It doesn’t help solve the Navier-Stokes equations for the atmosphere.
The last Snowball Earth happened when CO2 was 12,000 ppm.
It happened because super-continent Pannotia was centred over the South Pole.
The Earth’s climate is strictly driven by how much sunlight can be absorbed by molecules on the planet. When you have a bunch of glaciers and sea ice at the poles or lower latitudes, it gets colder. If clouds increase and reflect more sunlight, it gets colder. Put all the continents at the equator and you get no glaciers and very little sea ice and it gets warmer.
This alone results in +15C to -25C temperatures, which is all that the Earth’s temperature has varied by. A simple 100% control then and no role for “non-condensing gas”.
Speaking of that, if there is a Carbon cycle, then CO2 acts as though it is a condensing gas.
Mr Stokes complains that I have provided no references for the repeated statements in climate sensitivity papers that the 33 K difference between emission temperature and today’s temperature is the “natural greenhouse effect”. If he will do me the honor of reading the head posting, he will find several references there.
Lord M,
“Mr Stokes complains that I have provided no references for the repeated statements in climate sensitivity papers”
No. You said
“The modelers have hitherto assumed…”
and give no quotes of modelers assuming that. What you cite (but do not quote) are people diagnosing climate behaviour, for which they find feedback a helpful concept. But it is not assumed by modelers. In fact, GCMs do not (and cannot) use the concept. They solve discretised partial differential equations for momentum, mass and energy exchange between cells.
I repeat, in response to Mr Stokes, that the modelers, in paper after paper after paper, refer to the 33 K difference between emission temperature and today’s temperature as “the natural greenhouse effect”. The models, therefore, are tuned to generate high enough feedback fractions to justify the whole of the 33 K. Of course they do not incorporate the mathematics of feedback explicitly: but the feedback values they imply are diagnosed in papers such as Soden & Held (2006) and Bony (2006) for IPCC (2007), and Vial et al. (2013) for IPCC (2013). It is not difficult to deduce from these diagnoses that the mean CMIP3 and CMIP5 feedback fraction implicit in the models is about 0.67. It is also not difficult to see that that value is high enough, combined with the direct warming from the non-condensing greenhouse gases, to account – on its own – for the entire 33 K that was hitherto imagined to constitute the “natural greenhouse effect”.
However, once proper account is taken of the feedback response to emission temperature, it is inevitable that the mean feedback fraction will be very considerably below 0.67.
Nick rules out Monckton’s hypothetical scenario but nearly everything said by climate alarmists is hypothetical. So climate science often comes down to cherry picking hypotheses.
Mark4asp says that Mr Stokes “rules out my hypothetical scenario”. He certainly does his level best to try, for he has a settled viewpoint on these matters which is much disturbed by our result. However, in the end science comes down to mathematical rigor, and – like it or not – there is a large feedback response to emission temperature, though official climatology attempts to deny that any such response is possible. See, for instance, the definition of a “climate feedback” in IPCC (2013), cited in the head posting. IPCC is simply wrong on this, as is Mr Stokes.
But it does seem intuitive and Occam’s razor comes to mind.
I appreciate what you are doing with this. However, I would be more comfortable if the energy-flux input was providing an energy-flux feedback rather than a temperature feedback. Yes, it can be equivalent imo to to calling an energy-flux feedback a temperature feedback for conductive regimes, but not imo for radiative feedbacks from water vapor for example where the relationship between energy and temp is no longer directly proportional, notwithstanding that gain is also less than 1.0.
Thanks.
I think I have already explained to blueice2hotsea in an earlier thread that, however comfortable he or she may be with energy-flux feedbacks, official climatology performs its sensitivity calculations using temperature feedbacks denominated in Watts per square meter of flux-density change per Kelvin of temperature (or of temperature change). The head posting very plainly states that, for the sake of argument, and for the sake of focusing the discussion on climatology’s central error in misattributing the large feedback response to emission temperature to the non-condensing greenhouse gases, we are accepting all of official climatology except what we can prove to be in error.
“The reason why official climatology has not hitherto given due weight (or, really, any weight) to the feedback response to emission temperature”
The reason is that “emission temperature” is an invariant number, derived just from the emission flux (in turn derived from TSI) and the Stefan Boltzmann equation. It makes no sense to talk of feedback response to an invariant quantity. The reason is that feedback is the result of a feedback loop where, in a system, the input can change the output, which in turn can change the input. That is essential for feedback. If you have an input nothing can change (“emission temperature”) you cannot have a feedback loop.
Actually, the so called ‘feedback response’ is not in response to the emissions temperature, but to the surface temperature. But, not really to the temperature, but to its emissions. For an input forcing expressed in W/m^2, the feedback must also be expressed in W/m^2, otherwise, the two can not be added together, From a technical sense, the surface emissions in excess of the solar forcing are what you can consider to be the ‘feedback’ as the emissions in excess of the forcing must be replenished and the ‘feedback’ is what replenishes it.
From this we can consider that each W/m^2 of solar forcing results in 600 mw/m^2 of feedback so that the surface can emit 1.6 W/m^2 per W/m^2 of solar forcing. This is far less than the 3.3 W/m^2 of feedback required per the IPCC’s claim of a nominal sensitivity of 0.8C per W/m^2 or 4.3 W/m^2 of incremental surface emissions per W/m^2 of forcing.
Now, before you arm wave that the surface/atmosphere boundary is more complicated then this (latent heat, convection, etc), consider what effect these non radiant forms of energy plus their return to the surface (that Trenberth lumps into his ‘back radiation’ term), have on the average temperature and its average emissions other then the effect they are already having on that temperature and its subsequent emissions?
“Actually, the so called ‘feedback response’ is not in response to the emissions temperature, but to the surface temperature.”
That contradicts what Lord M is saying. But perhaps you would like to set out the feedback loop. What is the input that can respond to the output, and what is that output?
The input is forcing from the Sun and the output is the NET radiant emissions by the surface which can be converted to an equivalent temperature using the SB Law. Some fraction of these NET surface emissions are returned to the input as feedback delivered to the surface.
What’s really happening is that the 600 mw of excess surface emissions per W of forcing is replenished by 600 mw coming from the atmosphere. These 600 mw of energy were emitted by the surface in the past and prevented from exiting to space by being absorbed by the atmosphere. It’s not new energy, but surface emissions delayed by GHG’s and clouds. This COE constraint is generally ignored by the consensus.
One thing that may be confusing you is the conversion of doubling CO2 into equivalent forcing and redefining forcing as being ‘incremental’. Only solar energy is a proper forcing influence and all of it forces the system concurrently and each Joule forces equally. Keep in mind that even the IPCC recognizes that doubling CO2 is EQUIVALENT to 3.7 W/m^2 more solar forcing while keeping the system (CO2 concentrations) constant.
In response to Mr Stokes and to co2isnotevil, emission temperature (and this term of art is routinely used in the journals, so it need not be encased in dismissive quote-marks) is the temperature that would prevail at the surface in the absence of any greenhouse gases or of any feedbacks. Mr Stokes imagines that emission temperature is “invariant”: however, even if one assumes that the solar constant is constant, emission temperature varies with the Earth’s albedo. Even if it were invariant, however, it is capable of inducing a feedback response, provided that feedback processes such as those associated with water vapor and clouds are present. The corrected form of the feedback loop (shown in green in the head posting) makes this fact quite clear.
It has come as a shock to many that emission temperature induces a large feedback response: but it is so. The fact that it is so inevitably constrains – and constrains tightly – the magnitude of both transient and equilibrium sensitivities.
Christopher,
My point is that ‘feedback’ (and this does require air quotes), is a DIRECT response to emissions/energy and not temperature. While temperature is a linear way to quantify stored energy, emissions go as temperature raised to the 4’th power which means the hotter something is, the faster it cools and since that in the steady state, total forcing must be equal to total emissions, the relationship between forcing and temperature also goes as T^4. which is far from linear.
I fully understand that you are also trying to frame this in the context of pedantic climate science, however; a bigger part of the problem is that the context and language of climate science is horribly broken, misleading and designed to obfuscate the requirements of physical laws.
CO2isnotevil is entitled to his opinion that feedback is a direct response to emissions or energy and not to temperature. However, official climatology considers that feedbacks are forcings contingent upon the temperatures that induce them, which is why – as correctly shown in table 1 of the head posting – feedbacks are denominated not in Watts per square meter per Watt per square meter but in Watts per square meter per Kelvin. No doubt other conventions might be adopted, but that is the convention that official climatology uses, and, therefore, we use it too.
Yes, consensus climate science does consider this and is one of the reasons they are so incredibly wrong. They presume that the intrinsically non linear relationship between temperature and forcing is approximately linear, which may be true over a narrow range, but is nowhere near true across the range of temperatures found on the planet. From a physical point of view, everything depends on energy fluxes and while this also depends on the temperature by the SB Law, it’s not the linear relationship required for quantifying feedback per Bode’s analysis.
Yes, going back to AR1, the presumption of massive amplification from positive feedback based on the flawed application of Bode to the climate by Hansen and Schlesinger comprised the primary theoretical plausibility for a climate sensitivity large enough to justify the formation of the IPCC/UNFCCC.
“comprised the primary theoretical plausibility for a climate sensitivity large enough”
Not at all. Arrhenius figured a sensitivity of about 4 in 1896. And he wasn’t using Bode.
If there were no ir emissive barrier, e.g. water vapor, that would be true but the starting point here is no non-condensing greenhouse gases, not no water.
AndyHce is quite correct. Climatology draws a useful distinction between the condensing greenhouse gases, chiefly water vapor, which provide various feedback processes, and the non-condensers, such as CO2, which chiefly provide forcings. To work out the feedback fraction correctly, one must remove the non-condensers (as Lacis 2010, 2013 attempted to do) and leave the condensers still present, for without them there would be no feedbacks at all.
In response to Mr Stokes, Arrhenius revisited his calculations in a paper in 1906, substantially reducing his estimate of climate sensitivity. Bode, of course, was not available to him, so he guessed that the water vapor feedback would approximately double the directly-forced warming consequent upon doubling the CO2 concentration.
In the 1920s and 1930s, Harold S Black and his colleagues at Bell Labs, then in New York, developed the theory and mathematics of feedback to assist them in stabilizing long-distance telephone circuits. Now that that theory is available to us, it is possible to improve on Arrhenius’ original estimate. That is what we have attempted to do.
“In response to Mr Stokes, Arrhenius revisited his calculations in a paper in 1906, substantially reducing his estimate of climate sensitivity.”
A common misapprehension. In fact, in that book “Worlds in the Making” (English translation 1908) he said, very explicitly
“If the quantity of carbonic acid [CO2] in the air should sink to one-half its present percentage, the temperature would fall by about 4°; a diminution to one-quarter would reduce the temperature by 8°. On the other hand, any doubling of the percentage of carbon dioxide in the air would raise the temperature of the earth’s surface by 4°; and if the carbon dioxide were increased fourfold, the temperature would rise by 8°. “
IOW, a sensitivity of 4°/doubling – not a substantial reduction. People get excited because he first calculated the sensitivity without water vapor, but then accounted for it, leading to the above.
Nick,
Arrhenius’s calculations in the 1896 paper were very crude, made many assumptions and did not account for quantum mechanical considerations of atmospheric absorption. In fact, the photon had not even been discovered prior to his analysis so he conflated the kinetic temperature of the atmosphere with the radiative temperature of the planet. These two are mostly independent since the temperature arising from molecules in motion has no bearing on the emissions of the planet since ground state molecules in motion do not emit photons under the conditions found within our atmosphere and only photon energy can leave the planet (rockets not withstanding).
Nick Stokes: If you have an input nothing can change (“emission temperature”) you cannot have a feedback loop.
Earth’s climate and weather systems produce clouds and such that can alter the input to the surface of radiant energy from the sun. Whether you want to call them a “feedback loop” or not, they modify the transient temperatures of places on the Earth surface, hence the global mean temperature. They were in operation in the early 1850’s. What was their effect on global mean temperature, compared to their absence, before the industrial revolution produced all this anthropogenic CO2? 0? Surely not.
Mr Marler is right and Mr Stokes wrong. Feedback theory – as encapsulated in the corrected form of the zero-dimensional-model equation – mandates that even an unamplified input signal will induce a feedback response if the feedback fraction fed back from the output node to the input node is nonzero – i.e., if at least one feedback process is present. We have simply followed the standard theory in this respect. Climatology has not.
The solar may be constant, but the earth is rotating so solar input over the whole surface is oscillating. What does this do to the feedback mechanism. Think of the diurnal T swing on the moon. Can one detect with CERES this oscillation.
No, if I understand this correctly, Nick is arguing that there are indeed feedbacks.
He is saying, to give one example, that if you take earth with no GGs, keep the solar input constant, and inject some CO2, the first effect will be to warm the planet slightly by the usual mechanism. This warming will then cause increased water vapor in the atmosphere, and this will then warm some more. So the feedback he is arguing for is increase in CO2, from any level, which then gives rise to further processes that add to the initial warmth caused by the CO2.
I think this is the classic argument of the CAGW tendency. The rise in temperature or forcing effect caused by a doubling of CO2 is usually thought to be 1.2C, and this is supposed to cause increases in atmospheric water vapor which in turn add another 1C to 3C making for the total of somewhere between 2 and 4 degrees total for a doubling. Or maybe more in some accounts of this.
He is saying, at least I think this is it, that you require some forcing of some sort for there to be feedback to it. Christopher seems to be disputing this. I am even less sure what Christopher is saying, but it seems to be something like that the steady state itself gives rise to some warming which can then prompt additional warming…? Don’t know.
This is very difficult to disentangle, but it looks at the moment, seen through a glass darkly, as if logic is on Nick’s side.
Michel is finding it difficult to understand that even an input signal will induce a feedback response provided that at least one nonzero feedback process is present. He should read ch. 3 of Bode (1945) and work through the equations therein, as I did. He will then see that Mr Stokes is simply wrong, and he can then calculate, as I did, that once one has allowed for the actually quite large feedback response to emission temperature the feedback fraction must be considerably smaller than the official value, whereupon all transient and equilibrium sensitivities are about a third of official climatology’s mid-range estimates.
michel,
“The rise in temperature or forcing effect caused by a doubling of CO2 is usually thought to be 1.2C, and this is supposed to cause increases in atmospheric water vapor which in turn add another 1C to 3C making for the total of somewhere between 2 and 4 degrees total for a doubling.”
Examine this from an energy perspective. If 3.7 W/m^2 more solar energy, which is EQUIVALENT to doubling CO2, results in about a 1.2C increase, this increases surface emissions by about 6 W/m^2, or about 1.6 W/m^2 of incremental emissions per W/m^2 of forcing, as does each of the 240 W/m^2 of solar forcing arriving to the planet. If this also resulted in ‘feedback’ that increased the surface temperature by another 2C (per the nominal sensitivity), the surface emissions must increase by about another 10 W/m^2 which is more than the initial forcing. The issue is that the Joules of energy replacing the excess emissions due to ‘feedback’ have no identifiable origin. In fact, if feedback is greater than the forcing, as the IPCC and its self serving consensus claims, the system is unconditionally unstable.
Claiming these come from feedback would mean that each W/m^2 of the 240 W/m^2 of accumulated solar forcing must have also resulted in the same amount of feedback, which would result in emissions corresponding to a surface close to the boiling point of water. Consensus climate has no answer for how can the next W/m^2 of forcing be 3-4 times more powerful on a Joule per Joule basis then each of the 240 W/m^2 of accumulated forcing that preceded.
This excess energy comes from the implicit power supply in the Bode feedback model that is not present in the climate system!
Perpendicular to the point of this article.
No!
He (or she) would not dare to discuss this result because they fear that it is that simple.
If alarmists can’t try to baffle with complexity and obscure with technicalities then they must explain with logic.
Logic and Evidence.
But Logic and Evidence are not the Climatologists’ friends.
The thermodynamics governing the planet are simple and leads to a deterministic sensitivity far less than required to justify the agenda of the IPCC and UNFCCC. The errors that have been made in an effort to override the constraints of the Stefan-Boltzmann LAW, specifically the IMMUTABLE dependency of W/m^2 on T^4, become clear once you tear away the many layers of misdirection and obfuscation. The fact that this insanity has gotten so far indicates that not only do logic and evidence not apply, neither do the laws of physics.
One agrees with Mr Courtney and with CO2isnotevil. The notion that a team led by a layman may have found an elementary and significant error, and that after correction of that error there is no global-warming “crisis”, is bound to horrify some on both sides of the debate. So far, though, I think it is fair to say that no one has landed a blow on our result. In due course, it will gradually become better known. It will eventually appear in the peer-reviewed journals. And, after an unspecified but not indefinite interval, official climatology will be compelled to adjust its calculations accordingly (if we are right).
“One question which few opponents in these threads have answered, and none has answered convincingly, is this: What was the source of that additional 8.7 K temperature, given that there were no non-condensing greenhouse gases to drive it?”
The answer is, condensing greenhouse gases, and clouds, both of which block IR. Lacis traced back to a state where there were no non-condensing GHGs, and the temperature dropped to 252K. The water vapor reduced by 90%; clouds actually increased, and with clouds and ice, albedo increased to about 0.41. If you remove (by fiat) those remaining blockages to IR (but leave the raised albedo at 0.41), the temperature will drop another 8.7K. That isn’t a feedback to anything; it is a fiat. There is no natural process proposed which would cause the water vapor and clouds to disappear.
Also, I suspect that starting from an Earth devoid of water in all forms (liquid, solid, gas), then by fiat and instantly adding solid water and only solid water, would not cause an evolution to the same temperature that Lacis got by approaching from the opposite direction. I very well could be wrong; I’m just guessing.
Such things don’t ‘block’ IR, but temporarily store the energy of its photons and redirect that energy back to the surface or out into space at some later time and by different photons.
In an atmosphere without GHG’s, a photon in the correct frequency domain would head directly away from the earth in a straight line.
In the presence of GHG’s, that photon gets absorbed, then re-emitted in a random direction.
As a result, that photon takes a random walk through the atmosphere until it eventually gets high enough that it is able to escape to space.
The reality is actually more complicated than that. Each time the photon is absorbed by a molecule of some GHG, there is a chance that the energy will be thermalized via a collision with another molecule before re-emission can occur. The energy will stay in this thermalized state until such time as that other molecule collides with a GHG molecule, giving the energy back to the GHG molecule and providing the energy a chance to be emitted as a photon once again.
MarkW,
The idea of thermalization is another of the excess levels of indirection targeted to make the climate seem more complex than it really is.
The most likely path for thermalization is by indirectly energizing uwave (low energy) rotational states. But, this goes both ways as energy converts between a rotational state and a vibrational state. This is Quantum Mechanics and the probability of state energy being ‘converted’ into linear kinetic energy is approximately equal to the probability of linear kinetic energy being ‘converted’ into state energy. The net ‘thermalization’ is then zero.
The only other possibility is when an energized H2O molecule condenses upon an atmospheric water droplet. In this case, the state energy becomes incorporated with the thermal state of the liquid. Of course, we are still talking about LTE and atmospheric water in LTE will absorb the same amount of energy as it emits, thus again, the net transfer is 0.
Not forgetting that if water vapor is reduced by 90% there would greater surface heating, as water vapour absorbs considerable amounts of solar near infrared.
If Yogi Bear is correct that a reduction in water vapor by 90% there would be greater surface heating, then the water vapor feedback response is not an exponential response but a logarithmic response, whereupon the final feedback fraction will be less than 0.08. Indeed, if IPCC is correct that 2.29 Watts per square meter of net anthropogenic forcing has arisen to date, dividing that by 3.2 gives the directly-forced warming, which is 0.72 K. But, over the same period, there has been 0.75 K observed warming. The implicit feedback fraction is then not 0.08 nut 1 – 0.72 / 0.75, or 0.04.
Ah but there would also be greater surface cooling at night with 90% less water vapour.
C.M.
“if IPCC is correct that 2.29 Watts per square meter of net anthropogenic forcing has arisen to date, dividing that by 3.2 gives the directly-forced warming, which is 0.72 K”
An extra 2.29W/m2 at a surface of 288K would raise it by 0.42K.
http://www.spectralcalc.com/blackbody_calculator/blackbody.php
Yogi Bear is confused. The Planck parameter integrates the temperature response to a forcing throughout all layers of the atmosphere. Whether he likes it or not, its value at today’s temperature is approximately 0.3125 Kelvin per Watt per square meter. Therefore, a forcing of 2.29 K will induce a warming of 2.29 * 0.3125 = 2.29 / 3.2 = 0.72 K, exactly as I have said.
I specify surface, you say all layers of the atmosphere. Tomayto tomarto much.
Hurrah! Mr Stokes has finally gotten the point. If one removes the non-condensing greenhouse gases such as CO2 and CH4, water vapor – a condensing gas – remains behind to provide the feedback processes that respond to emission temperature. As the corrected form of the zero-dimensional-model equation in the head posting demonstrates, even if one were to set the direct or open-loop gain factor mu to unity, the output of the feedback loop will differ from the input provided that the feedback fraction beta is nonzero. For feedback responses will occur provided that the conditions precedent to such responses are present: namely, a temperature, and at least one feedback process.
“remains behind to provide the feedback processes that respond to emission temperature”
No, it simply impedes passage of IR and generates a downward flux. It may evaporate more water, by modifying the surface temperature. But it doesn’t modify the emission temperature, which depends on heat flux (240 W/m2) and Stefan-Boltzmann. So no feedback loop involving ET.
In answer to Mr Stokes, no, of course the feedback processes do not alter the emission temperature, which is the input to the feedback loop. Driven by the input temperature, they alter the output temperature. The diagrams in the head posting are surely clear enough.
Mr Stokes is free to call the feedback response to emission temperature a fiat if it pleases him: but, as the corrected version of the zero-dimensional-model equation shows, it is – like it or not – a feedback response. If Mr Stokes would rather not treat the water-dependent feedback processes in the climate as feedback processes, he should address his concerns not to me but to official climatology, whose convention in this respect I have followed.
Mr Stokes now concedes that in the absence of the non-condensing greenhouse gases there would still be the condensing greenhouse gas water vapor in the atmosphere. Climatology treats changes in temperature owing to variations in column water vapor or in specific humidity as a feedback. And, as Mr Stokes now begins to see, that feedback will operate even in the absence of any non-condensing greenhouse gases, for it will respond to emission temperature.
“Climatology treats changes in temperature owing to variations in column water vapor or in specific humidity as a feedback.”
It is a feedback to the change in temperature that evaporated the wv. That is the essential of a loop. The extra wv raises the surface temperature which increase then raises wv etc. But the emission temperature does not change, and cannot be part of such a loop. The loop of changes to surface temp and wv is just conventional wv feedback, as described by “official climatology”.
Mr Stokes is, as usual, incorrect. The emission temperature is derived solely from insolation and albedo. Thereupon, in the presence of feedback processes, a feedback response to emission temperature will arise. That does not alter the emission temperature itself, for the altitude at which the emission temperature obtains rises as the atmosphere warms. But, whether Mr Stokes likes or not, the surface will be warmer than it was at emission temperature after the feedback response to emission temperature has occurred.
“The emission temperature is derived solely from insolation and albedo. Thereupon, in the presence of feedback processes, a feedback response to emission temperature will arise.”
That is pretty funny. How does 255K (-18°C) make water vapour?
N.S.
“The extra wv raises the surface temperature which increase then raises wv etc.”
Extra wv reduces maximum surface temperature because of shortwave absorption, and increases minimum surface temperature because of longwave emission.
Nick wrote: “The answer is, condensing greenhouse gases, and clouds, both of which block IR.”
It might be clearer to say that GHGs and clouds cause the average photon escaping to space to be emitted from higher in the atmosphere, where it is colder than the surface.
Christopher,
I admire you and your team’s effort, but this is awfully complicated and not easy to follow — at least the way you’re laying it out here (and in the other posts). Like I’ve said, it sounds very similar to George White’s simple case and/or argument that it’s not reasonable for watts of GHG forcing to have a 3 times greater ability to warm the surface than watts already forcing the system from the Sun, and that the +0.6 in the surface/TOA ratio of 1.6 (385/240 = 1.6)) is already giving at least a rough measure of the net effect of all physical processes and feedbacks in the system that operate on time scales of decades or less (which certainly includes water vapor and clouds). This would yield sensitivity of about 1.1C for 2xCO2, which is very close to your 1.2C.
Like I’ve said though, I’ll be interested to see the piece in its final form when your team has it ready for submission.
Are you going to make available to us the final form/version you submit for review?
In response to RW, feedback math (particularly where, as here, one need not involve oneself in Fourier transforms or phase changes) is not particularly difficult: but it is heavily counter-intuitive. That is why observers on both sides of the climate question are finding it difficult to grasp the notion that, contrary to the official IPCC definition, a feedback response occurs even where the input temperature remains unamplified. That simple point will eventually be understood by all. But some here have gone to elaborate and not always honest lengths to try to impugn our result. For them, therefore, the head posting provides a more detailed treatment than the earlier postings.
Mr White is entitled to his opinion that the ratio of current surface radiative flux density to the emission flux density is on its own a sufficient measure of the magnitude of the climate response to any perturbation. However, it will only be possible to convince official climatology if a formal proof of its error is provided. That is what we are working towards. We are expecting to face uncommon difficulty in getting our result published, for so many are profiteering by the climate scam that our result proves to be unsoundly founded. So far, however, the attempts here to overthrow our result have been extremely feeble. We are expecting a more compelling challenge from properly-knowledgeable peer reviewers. It may yet turn out that we are wrong. However, the sheer simplicity of our result, and its striking consistency with observation (more than can be said for official climatology’s predictions) point to the possibility that we are right after all. We remain open to the possibility that we are wrong: but the arguments against our idea will need to be a great deal stronger than anything that has been advanced in these threads so far.
Christopher,
“However, it will only be possible to convince official climatology if a formal proof of its error is provided.”
But does your analysis really constitute formal proof of essentially the same error? I’m not sure it does, plus it’s very convoluted and hard to follow (I find at least). There are also a number of fairly loose assumptions, i.e. the results of Lacis 2010 as a baseline starting point and the non-linearity of the system which isn’t sufficiently addressed.
George White’s doesn’t rely on these assumptions, but rather comes from directly measured satellite date; and he can clearly show how the non-linearity of the system works against the incremental response being greater than the absolute response of the system. It’s much easier to follow and understand.
“a feedback response occurs even where the input temperature remains unamplified. ”
I don’t understand this at all. Could you give some further explanation and perhaps another example of it happening?
In reply to RW, the proof of official climatology’s error is actually quite simple. The corrected form of the zero-dimensional-model equation mandates that even an unamplified input signal will induce a feedback response where the feedback fraction is nonzero. Thus: 255 / (1 – 0.08) = 277, not 255. It is really as simple as that. But the extra 22 or 23 K that is the feedback response to emission temperature is currently misallocated so that it stands part of the actually tiny feedback response to the presence of the non-condensing greenhouse gases. This error has the effect of overstating the feedback fraction by an order of magnitude, and the mid-range estimate of Charney sensitivity by triple.
Michel is also having difficulty in understanding that an input signal, even if unamplified, induces a feedback response as long as the feedback fraction is nonzero. The example Michel asks for is to be found in the behavior of the two electronic circuits we built – one on our own and one with the aid of a government laboratory – to simulate the relevant values in the climate. If one were to feed 2.55 volts into the input node, and then return 8% of that from the output node back to the input node, the output of the circuit would be 2.55 / (1 – 0.08) = 2.77 volts. I assure Michel that all of this is absolutely standard feedback theory. All he has to do is read chapter 3 of Bode (1945) and work through the equations in the first few pages. There is absolutely nothing novel or in any way incorrect at this point in our analysis. But, as you will see from some of the hysterical comments here by the usual suspects (some of whom are paid to troll here), they are pretending that our account of the feedback loop is somehow non-standard. No: it is climatology’s version of the feedback loop that is non-standard, and its failure to account for the large feedback response to emission temperature is grave.
Christopher,
“If one were to feed 2.55 volts into the input node, and then return 8% of that from the output node back to the input node, the output of the circuit would be 2.55 / (1 – 0.08) = 2.77 volts.”
While this is true per Bode, the assumption is that the feedback and input are measured to determine how much output to deliver from an infinite, implicit source of Joules (the power supply). The climate system does not represent active gain and instead consumes the input and feedback to produce its output. In your example, the 0.08% of feedback are consumed by the system and no longer available as output, therefore the final output is 2.55*(1 – .08)/(1 – .08) = 2.55. This is the COE constraint ignored by consensus climate science as this was ignored in Hansen’s original feedback paper and has never been corrected.
co2isnotevil April 10, 2018 at 9:09 am said:
“. . . .In your example, the 0.08% of feedback are consumed by the system and no longer available as output, therefore the final output is 2.55*(1 – .08)/(1 – .08) = 2.55. … ”
Likely you are wrong about this, although we do STILL NEED to see Monckton’s actual circuits. In my op-amp Monkton’s circuits, and probably in Monckton’s, the state-variables of the flowgraph are voltages – not currents.
Voltage is an “intensive quantity” (like temperature, pressure, etc.) and distributes; while current, the time derivative of countable charge, is an “extensive quantities” (like energy, mass, etc.) and is subject to conservation (like the zero-sum of Kirchhoff’s law).
And you are 100% correct to insist that the active-or-passive nature of the scheme be addressed.
Mr. Hutchins:
Two things.
First, I think we can pretty much count on Lord Monckton’s circuit being a nothingburger. I’ll be surprised if it’s anything more than one like yours or, more likely, two op amps with respective feedback and input resistors (probably pots) from their output to their inverting input ports to create finite-gain linear forward and feedback amplifiers, and resistances from the resultant forward amplifier’s output port to the resultant feedback amplifier’s input port and vice versa to close the loop with (inverting followed by inverting) positive feedback. (Yes, that configuration’s overall gain has negative, but the guys I’ve seen do this stuff tend to find negative more convenient.)
In other words, all he’ll show is that if you construct a circuit that implements y = (x + fy)g you’ll get—surprise, surprise—y = gx / (1 – fg) for fg < 1. I leave it to you to decide what it says about the guy that he thinks this proves something. (Remember, this is the same guy who thought you could obtain a linear system's response by multiplying its stimulus by its step response.)
Second, my view is that the question of whether the system is active or passive is a red herring. Sure, the amplifiers that make up the analog computer (which is what in essence the circuit would be) are active elements. But that doesn’t mean that the equation they solve needs to describe an active system. (The guys I saw use analog computers were solving differential equations, but I guess there’s nothing that says you can’t use them for algebra if like Lord Monckton you want to frighten the natives.)
Consider a (passive) parallel RLC circuit driven by a sinusoidal current source (source current here being the analog for, say, insolation) whose frequency is near the circuit’s natural frequency. Increasing the parallel resistance (read adding greenhouse gases and thus resistance to radiation escape) will make the voltage (read surface temperature) increase. Yet the system is passive. (Of course, to do positive feedback you’d somehow have to make the resistor responsive to rms voltage, but that’s not inconceivable.)
Bernie,
Voltage is not the same as power. A transformer is a passive circuit that can increase voltage, but the number of Joules that are taken from the secondary is always less than the amount consumed by the primary. The climate system is all about W/m^2 which is a flux of Joules and COE must apply. It’s the Joules of accumulated forcing and feedback that provides the Joules delivered to the surface which causes the surface to heat or cool manifesting a temperature.
The Hansen/Schlesinger climate feedback model is like connecting your turntable output to the audio input and to the power cord. Will you ever get more power out of the amp than is coming from the turntable?
What’s missing is the implicit, infinite source of Joules to power the gain which is the second of only two preconditions for using Bode’s analysis. The other is strict linearity where the absolute gain and incremental gain must be the same. When an amplifier starts to clip and distort, it goes non linear and Bode’s analysis no longer applies. Both of these preconditions were not honored by the feedback model applied by Hansen/Schlesinger and that CM is trying to be consistent with. The real problem is that the model is meaningless to begin with.
https://wattsupwiththat.com/2016/09/07/how-climate-feedback-is-fubar/
To put this in EE terms, a Bode linear feedback amplifier assumes infinite input impedance and zero output impedance. The climate system has the same impedance for its input terminal and for its output.
Thanks Joe –
Somewhere, earlier, I expressed the view that it was very unlikely Monckton’s “labs” could get the circuit wrong. Don’t know however, why it is still TOP SECRET. I did doubt that they did it as efficiently as my $0.81! Bet he overpaid dearly for a “government lab.”
Also, way too much puzzlement about the first-order, resistors only feedback loop; it just a series of gain changes around the loop. If A = 1.5 and f=0.2, for example, and the input is 1, the output of the summer is 10/7, the output of A is 15/7, the output of f is 3/7, and 3/7 + 7/7 = 10/7. Trivial – really isn’t it? It only starts to be interesting at higher orders and with capacitors along with resistors.
The first computer I ever saw advertised was in the Heathkit catalog for $995 (! I didn’t even dream – probably 1959), and the fact that it was an ANALOG computer made no impression. Here is a remarkable YouTube show: https://www.youtube.com/watch?v=iAGGZpgY_H4 . Some years later I was building state-variable filters – two integrators with two feedback paths to a summer. A second-order filter. When someone informed me that it was really an analog computer solving a second-order differential equation, I learned a lot in a mere instant.
I remember your passive RLC from some years back. Always worth using what you already know well.
– Bernie
Bernie,
“In my op-amp Monkton’s circuits, and probably in Monckton’s, the state-variables of the flowgraph are voltages – not currents.”
I don’t see the point of this distinction. In your gain +3 circuit, you specify voltages, but then also write down the corresponding currents, just multiples of the voltage, using Ohm’s law with resistors. I can’t see why you can’t just switch between them as state variables.
And you have to, because as you say, voltage is intensive; current is extensive. You treat the input as a summing junction. But you can’t usefully sum voltages; you have to sum currents at this point.
co1,
“What’s missing is the implicit, infinite source of Joules to power the gain which is the second of only two preconditions for using Bode’s analysis.”
We’ve been through this before, but there is a very obvious source of Joules, which is the flux of 240 W/m2 passing through. As with any electrical circuit, this is not infinite, but is large relative to the fluctuations. It can cause confusion, because heat flux is normally thought of as current, and power supplies as a voltage source. But there is no reason why a power supply can’t be a current source. It’s analogous to a current source applied to a valve or FET channel. The grid/gate voltage modulates the apparent channel resistance, and so the voltage (temperature) across the device fluctuates. Power in is small, especially with FET, since almost no gate current drain. Power out can be large.
Nick,
You can definitely sum voltages and this is what most feedback amplifiers do. The question for you is how can the consensus model add a forcing in W/m^2 to a temperature feedback in degrees K. Yes, they fabricate meaningless dimensional constants to try to fudge this and convert degrees K into W/m^2 of feedback. But all these really do is encapsulate Stefan-Boltzmann to convert K to W/m^2, take a fraction of these converted W/m^2 as feedbacks and add them to the forcing. The sum of these is the output power in W/m^2 which is converted back into a temperature by applying SB in reverse.
Again this goes to the linearity restriction imposed by Bode as a precondition for using his analysis. The input and output dimensionality must be linearly related to each other, all components are strictly linear and the incremental gain (what is called the climate sensitivity) must be equal to the absolute gain (1.6 W/m^2 of surface emissions per W/m^2 of forcing) and which is universally ignored by the IPCC. What they are doing is as ludicrous as starting with a 1000cc of water, adding 1cc of water and claiming that the last cc of water increased the total mass by nearly 4 times more than any of the preceding 1000 cc.
Nick,
You’re not paying attention. I suggest you read Bode’s book, specifically the first two paragraphs. The 240 W/m^2 of power from the Sun is the forcing, not the implicit power supply required by Bode. These two are completely different and the power supply is always implicit and generally not shown. As in my example, this is like connecting your audio source to both the audio input and the power cord. You will never get more power out than goes in as forcing.
Yes, the 240 W/m^2 is power, but the is not in the right place to power the gain as Bode requires. The gain block of the Hansen/Schlesinger model is essentially the atmosphere, which more accurately acts as a mismatched transmission line between surface emissions and planet emissions, where the mismatch causes some power to be reflected back to the surface. A transmission line can accept any amount of power on its input and the output will always be somewhat less owing to losses. If we insert an amplifier we can boost the power and the additional power comes from the implicit power supply.
co2,
” I suggest you read Bode’s book, specifically the first two paragraphs.”
Bode is not the word of God, and does not have a monopoly of knowledge of feedback. And the 240 W/m2 is not the forcing, it is the power supply. The forcing is the 2-3 W/m2 induced by the increase in CO2, and which causes the T response to be figured out. No-one is switching the 240 W/m2 off.
If you do think Bode has something that backs your view, quote it.
Nick,
Bode is the ONLY reference that has anything to do with the theory behind feedback amplifiers and that is cited as a reference in Hansen’s initial paper on climate feedback, Schlesinger’s follow on papers and various rehashes more recently including Roe. The terms forcing, feedback, open loop gain, close loop gain (which the consensus incorrectly calls the sensitivity), sensitivity and others are all defined in Bode’s book and since the feedback model applied to the climate system comes directly from the model of a Bode linear feedback amplifier, Bode’s terminology is the only relevant terminology. The references of the ‘feedback fubar’ article cite specific pages in Bode’s book where these various terms are defined and explained.
You’re claiming that CO2 is a forcing influence. This is incorrect. When the IPCC says that doubling CO2 is 3.7 W/m^2 of forcing, read the fine print. What this means is that doubling CO2 is equivalent to 3.7 W/m^2 more solar forcing while keeping the system (CO2 concentrations) constant. The only forcing, per Bode’s definition of forcing, is the solar energy from the Sun. Changing CO2 concentrations is more like making small changes to a resistor in a feedback amplifier. Per Bode, the sensitivity is a measure of how sensitive the closed loop gain is to some change in a components value, but this is always a dimensionless ratio relating a change in some components value to a proportional change in the closed loop gain. In this context, negative feedback generally reduces the sensitivity of the closed loop gain to variations in component values and is among the reasons we use negative feedback in amplifiers. Such amplifiers typically have open loop gains in the millions or more, while the open loop gain of the climate system is 1.
Hansen incorrectly conflated the closed loop gain with the sensitivity and incorrectly considers that positive feedback amplifies the sensitivity. Making matters worse, Schlesinger applied units of W/m^2 per K to the sensitivity, which even as it’s really the closed loop gain, must also be a dimensionless ratio. You simply can’t amplify incremental forcing in W/m^2 into degrees K. Trying to do so is complete nonsense given the T^4 relationship between temperature and emissions in W/m^2. You can amplify volts into amps, but volts and amps are linearly related to each other and the linearity between the input and output is what’s important.
Nick,
Another point is that feedback is defined as the fraction of the output sent back to the input and is a dimensionless value between -1 and 1. How can you take a fraction of degrees K (incremental or otherwise) call it the feedback and sum it with forcing expressed in W/m^2?
Regarding Bode sensitivity, if a 10% change in a resistor value results in a 1% change in the closed loop gain, the sensitivity related to that resistor is 1%/10% = 0.1
I also may have given Hansen more credit then he deserved, Schlesinger did more of the damage with multiple levels of obfuscation and has even bragged to me that he’s the leading expert on climate system feedback. If he is the expert he claims to be and knew what he was doing, it would have been deviously evil. I’m willing to give him the benefit of the doubt that it was just incompetence reinforced with group think and confirmation bias which has driven much of what passes for science in IPCC reports.
Note that the Hansen and Schlesinger papers were the primary theoretical justification in AR1 for the plausibility of a climate sensitivity large enough to support the formation of the IPCC and UNFCCC. If the feedback errors were purposeful for these ends …
Nick Stokes said at April 10, 2018 at 8:23 pm
“Bernie,
‘In my op-amp [ ] circuits, and probably in Monckton’s, the state-variables of the flowgraph are voltages – not currents.’
I don’t see the point of this distinction. “
Okay the distinction is that an op-amp is a voltage amplifier, not a current amplifier. It amplifies a (tiny, Tiny, TINY) differential input voltage with a very large gain G of about 10^7 to a finite output voltage (zero times infinity, effectively). The output is a voltage source, not a current source.
Please follow this example. In my Fig. 6:
http://electronotes.netfirms.com/EN219Fig6.bmp
I do not specify R so let’s say it is 10k, (so (3/2)R is 15k). The input is 1 volt so 1/10k = 0.1ma is the current through the input resistor. The output is 3 volt. There is no load shown, so let’s put on a load of 1k, and a current of 3/1k = 3ma flows through this added load, to earth. So it looks at first blush like a current gain of 3/(0.1) = 30. (However, no current actually entered the op-amp inputs.)
Now – here is the key point. Suppose I now make the load 2k, up from 1k. If the output WERE a current source of 3ma, the output voltage would have to GO TO 6 volts. (That’s what we MEAN by a current source – variable voltage that adjusts to the load to establish the same current regardless of load.). But it is a voltage source that remains at 3 volts and only 1.5 ma comes out. (With no change except load, the current gain would be just 25 now).The op-amp is not a current amplifier because there is no current into it (except by supply pins) and the output is not a current source.
– Bernie
George
“How can you take a fraction of degrees K (incremental or otherwise) call it the feedback and sum it with forcing expressed in W/m^2?”>/i>
You can’t sum temperatures, just as you can’t usefully sum voltages in feedback. As Bernie says, it’s current that is extensive, conserved, and can be added. And so it is with K and W/m². You have to convert the K to a W/m² for conservative adding.
But this is all ridiculously easy, and doesn’t have to be converted to a Bode framework to work, with all your other nonsense conditions. You just write a balance equation for TOA fluxes:
c0*dT + c1*dT + … = dF
dF is the GHG forcing in W/m². The other terms are the various fluxes that are created by a responding change dT. The units of c0, c1 etc are W/m²/K.
c0 is the Planck flux coef, described by Lord M as 4σT³
c1 could be the wv coef, c2 albedo etc. Units of c’s W/m²/K
Just a conservation equation. Solve for dT:
dT = dF/(c0 + c1 +…) = dF/c0/(1 – f1 – f2 +…) where f1=-c1/c0 etc, unitless
Total feedback is the sum of f’s.
This is all they do. Simple linear algebra. No need for Bode.
Bernie,
Thanks. I think I see why we were at cross purposes earlier. You are using voltage amplifier to mean amplification by a fixed factor, regardless of load. Zero output impedance. By current amplifier, I meant just current increase, even if the amount depends on load.
But I don’t see how zero output impedance fixes what you call state variables. To me, these are just whatever is sufficient to define the state. And you can do that with either V or I (or even a mix). Maybe V is more convenient if V_out is independent of load.
Nick,
The climate system is neither like a voltage amplifier or a current amplifier, The appropriate model is of a power amplifier where power is Joules per second. This imposes COE constraints between the forcing input and surface emissions (surface temperature) output that consensus climate science has proactively ignored for decades largely because when accounted for, the need for the IPCC and UNFCCC disappears.
My point is your constants, c0, c1, … as ‘feedback coefficients’ are complete garbage with no correspondence to anything physical. You can apply as much algebra as you want, but garbage in always means garbage out. Specifically, the proper metric to align with the physics would be W/m^2 per T^4. Why is it that you continue to believe that the feedback is linearly proportional to the 1/T when its physically proportional to 1/T^4? Don’t you believe in first principles physics? Specifically the constraints of SB and COE and the fact that Joules are a measure of work and that it takes work to heat the surface.
What physics do you propose arises from a few trace gases and that turns an intrinsically T^4 relationship between degrees K and W/m^2 into a linear one? Sure, T is proportional to stored energy, but stored energy and forcing are far from the same thing. There’s a fundamental differences between stored Joules manifesting a temperature and the rates of Joules (Watts) arriving to and leaving from a system, Such new physics would overturn everything we know about thermodynamics and Quantum Mechanics and be worthy of a Noble prize and I mean the physics one, not the meaningless political prize that the IPCC and Gore got for promoting climate alarmism.
You are no doubt confused based on what Hansen and Schlesinger did which was to cite Bode as the authoritative reference on feedback, redefine all of Bode’s terms, make a bunch of crap up to fit expectations, shoe horn it into Bode’s analysis and then claim QED. This is among the sloppiest ‘science’ I’ve ever seen and which I consider the core malfeasance that got climate alarmism going as it falsely justified the creation of the IPCC and UNFCCC. The only open question is was this malfeasance purposeful or simply the result of incompetence.
Nick,
Just to reiterate, here’s the question you must answer or the house of cards referred to as consensus climate science collapses.
What law of physics supports the ASSUMPTION that W/m^2 is linear to degrees K?
To Nick at April 11 2:10 AM
Here is perhaps a better notion of an output that IS A CURRENT SOURCE. Take the 3 volt output but instead of bringing it out as an ideal ZERO output impedance bring it out as a very high output impedance, like a 1 Megohm resistor (in series) leading to the load. If I then connect this 1M to earth, 3 microamps flows into a 0 volt load. If I connect this 1M through 100 ohms (very small compared to 1M) to earth, essentially the same 3 microamps flows through the 100 ohms, developing 0.0003 volt across it. So nearly a constant current (3 microamps; or as controlled by Vout) would flow into any small (relative to 1M) resistor load and develop only a tiny load voltage. Perhaps just think of a current source as a very high output impedance, a voltage source as a very low one.
[To be technical, what I just described is NOT a current amplifier but rather a “transconductor” since the current output is proportional to an input voltage. (If you do HAVE a current for input, feed it directly to the first summing node to develop an output voltage.)]
To George at April 10, 7:07 PM
Thanks George – I do remember your “Fubar” comments from the same time frame I was insisting to CM that positive feedback could approach +1. I have nothing to disagree with you about. I am here, as well, defending only the EE issues, not the climate science.
Basically I think your summary is right on:
“The real problem is that the model is meaningless to begin with.”
I think so too. Explaining (or attacking) an issue in terms of a feedback equation (Bode) to represent a contrived feedback scenario relating to a gain in sensitivity that may well not even exist except in a CAGW agenda, is, for sure, doing it the hard way!
Bernie
Bernie
“To be technical, what I just described is NOT a current amplifier but rather a “transconductor” since the current output is proportional to an input voltage.”
It’s also proportional to input current, since the input impedance is R. I don’t understand your insistence that you can only have current amplification if the output impedance is infinite (or very high). Before op amps, amplifying circuits almost always had finite input and output impedance. But we still managed to amplify current and voltage.
George,
“Why is it that you continue to believe that the feedback is linearly proportional to the 1/T when its physically proportional to 1/T^4?”
Because linear feedback analysis has always worked on the basis of linear response to small changes. The thermionic valves of Bode’s day did not provide a linear response to anything. But the analysis still worked.
There is no point in being precious about the T^4 when you are talking about a global average, not a point reading, and a fluctuation of a degree or two in that average.
All I have done above is to point out that the processing of the relations between forcing and temperature dependent feedback is just simple linear algebra, and has no dependence on any Bode requirements.
Nick Stokes April 11, 2018 at 2:10 am
” But I don’t see how zero output impedance fixes what you call state variables.”
I just wanted to make the distinction between a voltage source (or amplifier) [very low output impedance] and a current source (or amplifier) [very high output impedance]. Everyone knows pretty much what a fixed-value voltage source is (the grocery store sells them as batteries). But fixed-value current sources are not available – indeed, you wouldn’t want, for example, a
“flashlight battery” that always delivered 10 amps (that would be a flash indeed).
Op-amps work with voltage for the most part.
co2isnotevil: “The climate system is neither like a voltage amplifier or a current amplifier, The appropriate model is of a power amplifier where power is Joules per second. This imposes COE constraints between the forcing input and surface emissions (surface temperature) output that consensus climate science has proactively ignored for decades largely because when accounted for, the need for the IPCC and UNFCCC disappears.
It may appear as if the law of conservation of energy places limits on amplification of no-feedbacks warming, but this is a fallacy. The sun is, of course, the source of essentially all of the climate system’s energy. The total amount of energy the climate system accumulates from a forcing (say 2XCO2) depends on the size of the imbalance AND how long the imbalance persists. When ECS is high, the imbalance lasts LONGER, explaining why CoE places not limit on warming.
For example, if the planet emits (and reflects) an additional 2 W/m2 to space for every degK increase in Ts (2 W/m2/K), the planet will need to warm 2 K before incoming and outgoing radiation are again in balance. Let’s call this Case A. If the planet emits (and reflects) an additional 1 W/m2 to space for every degK increase in Ts (1 W/m2/K), the planet will need to warm 4 K before incoming and outgoing radiation are again in balance (Case B). If we imagine an instantaneous 4 W/m2 forcing, the initial rate of warming will be the same in both Cases. After 1 K of warming, the imbalance will be down to 2 W/m2 in the Case A, but will still be 3 W/m2 in Case B. After 1.5 K of warming, the imbalance will be only 1 W/m2 in Case A, and 2.5 W/m2 in Case B. The extra energy needed to created more warming doesn’t come directly from the forcing; it comes from an imbalance that persists for longer when ECS is higher.
Nick,5K
” … linear feedback analysis has always worked on the basis of linear response to small changes.”
Congratulations, you have decoded the fundamental error. Now you need to understand why this doesn’t apply. Yes, since AR1, the IPCC has depended on ‘approximate linearity’ to support their case. While they tacitly acknowledge the T^4 relationship between temperature and power density, they say that over a small range of T, it’s approximately linear.
As CM pointed out in a previous post, the slope of the SB relationship changes between about 0.3 and 0.2C per W/m^2 between 255K and the recent average temperature of about 288K. These limits are confirmed by theory and the measured LTE values for the planet and includes the net effects of all feedbacks, positive, negative, known and unknown. These limits are far below the 0.4C per W/m^2 claimed as the low end of the range expected by the IPCC.
A problem that arises when you consider the relationship approximately linear, you end up considering the sensitivity, which is the first derivative of the relationship between temperature and power density, to be a constant, when in fact, it has a 1/T^3 dependency. Furthermore, over the limits of the temperatures found on the surface, the sensitivity varies over more than a +/- 33% range, which is far from even approximately linear.
If you consider the sensitivity a constant, it passes through the origin of the relative relationship between the surface temperature and the surface emissions, as illustrated by the blue line in the following plot which as drawn to scale represents the midpoint of the IPCC expected range. The actual slope, or the sensitivity, is tangent to the relationship between the average surface temperature and the average emitted power density of the planet and because of its non linearity, does not pass through the origin. The actual range is shown by the slopes of the magenta and green lines.
http://www.palisad.com/co2/tp/fig1.png
George
“As CM pointed out in a previous post, the slope of the SB relationship changes between about 0.3 and 0.2C per W/m^2 between 255K and the recent average temperature of about 288K.”
Yes. This comes back to Frank’s point about non-linearity, although the wv story is worse. Scientists don’t attempt to use linear feedback over that range. They use it for climate variations, of a degree or two. The slope going from 287K to 288K changes from 0.1865 to 0.1846 °C/(Wm⁻²).
“you end up considering the sensitivity, which is the first derivative of the relationship between temperature and power density, to be a constant, when in fact, it has a 1/T^3 dependency”
Again, no scientists try to use constant sensitivity over tens of degrees. They use it for possible climate variations in global average temperature. A 5° rise, from 288°C to 293°C, would change that derivative from 0.185 to 0.175 °C/(Wm⁻²). In the context of uncertainty about sensitivity, this is the least of worries.
Your plot, covering the range to zero power out, uses as its lower bound zero heat emitted (or received). This is not a climate variation normally studied.
Nick,
BTW, the assumption of approximate linearity is not a law of physics, but is another assumption, so you still haven’t answered my question. I’ll make it even more general..
What law of physics supports even the most remote plausibility of a linear relationship between degrees K and a power density expressed as W/m^2?
Nick Stokes April 11, 2018 at 2:10 am
Nick – here is a cleaner example of a current amp using an op-amp:
http://electronotes.netfirms.com/CurrentAmp.bmp
The circle with an arrow inside is the standard symbol for a current source. Here the signal current, I_in, is forced through a resistor R1 to produce a voltage I_inR1, which is “followed” or “buffered” by the unity-gain op-amp. (If useful/necessary, add voltage gain at this point with the standard non-inverting amplifier.) No portion of I_in goes into the (+) input. And note that the op-amp is powered from its supply (not shown) and thus CAN produce a larger current at the op-amp output.
Next we assume the op-amp output drives a “low impedance load” (black blob) through a resistor R2 that is much greater than the load, and so the output current is (I_in R1)/R2, so there would be a current gain of R1/R2.
We might see this used if we had a DC current from a sensor (perhaps a thermocouple) and wanted to turn on a transistor. The load would be the base/emitter junction. We suppose we need a bit more current to activate the junction than is available from the sensor itself – hence the current amplifier.
Realistic but rare example – as most op-amps process voltages.
Thanks, Bernie,
You got me tinkering. That impedance is high, but not infinite, because the load adds to R2. I thought another op amp could fix that, as here.
So I_in = (V2-V1)*R0 and I_out = (V2-v1)*R2
so I_out = I_in *(R0/R2) independent of load. R2 does not have to be large.
Bernie, Nick,
An op amp, vacuum tube, transistor or fet has absolutely no correspondence to the ‘gain block’ in the pedantic climate feedback model. Assuming that there’s the least bit of correspondence will lead to the wrong answers about climate ‘feedback’.
The output power delivered by an op-amp is provided by a power supply that’s completely independent of the input (forcing). The climate feedback model gets all of its output power from the input forcing and feedback.
An ideal op-amp has an infinite input impedance and a zero output impedance, while the ‘gain block’ of the climate feedback model has essentially the same impedance on its input and output.
An ideal op-amp has an infinite open loop power gain, while the climate feedback model has unit open loop power gain.
The proportion of the output voltage fed back to the input of an op-amp is still available as output, however, the power consumed by the feedback voltage divided is not. In the climate system, it’s power (Joules) that are being fed back (the physically meaningless cx constants convert temperature to power) which is consumed at the input and is no longer available as output until it passes through the unit power gain block once more.
An op-amp is an absolutely linear amplifier (the absolute gain is always equal to the incremental gain) while the climate mode; ‘gain block’ with W/m^2 in and degrees K out is not even close to being approximately linear.
In fact, the only thing in the climate feedback gain block is the Stefan-Boltzmann Law converting the power output of the ‘amplifier’ into a temperature. To be sure, the T^4 relationship between a temperature and a power density is immutable and no amount of ‘feedback’ can change this.
to co2isnotevil April 12, 2018 at 8:32 am
” Bernie, Nick,. . . . . . An ideal op-amp has an infinite input impedance and a zero output impedance, while the ‘gain block’ of the climate feedback model has essentially the same impedance on its input and output.. . . ”
George – I assume you meant to say “impedance[s] on its input and output [respectively]”. If so I agree with everything you said about op-amps and flowgraphs – or course. I have never said anything different, or at least never intended to.
I comment here on electronics issues, commenting mainly to Nick who seems eager and able to learn more and more electronics. I hope others here find my experience useful.
Bernie
to Nick Stokes April 11, 2018 at 10:20 pm
What you did seems correct. Good. In my example the load is very low impedance so your V2 would approach zero.
If I were using two op-amps, I might just cascade two inverters and drop the input current into the first summing node.
Nick,
“A 5° rise, from 288°C to 293°C, would change that derivative from 0.185 to 0.175 °C/(Wm⁻²). In the context of uncertainty about sensitivity, this is the least of worries.”
The biggest uncertainty is how do they get to a sensitivity of 0.8C per W/m^2 when at 288K, the sensitivity to solar forcing is about 0.18C per W/m^2 and at 277K, it’s only about 0.3C per W/m^2. It’s absolutely absurd to accept that the ‘feedback’ can have 2-3 times the power of the initial forcing which is required to get the the nominal 0.8C per W/m^2 claimed. Anything more than the initial forcing represents an unconditionally unstable system.
If you pay careful attention, the IPCC nominal sensitivity is the average surface temperature divided by the BB emissions at that temperature, or 288/390 which is about 0.75C per W/m^2. Try and plot the sensitivity vs. temperature such that when integrated over forcing, the proper average temperature arises and the sensitivity of the last W/m^2 is as claimed by the IPCC. You will find this to be an impossible task.
“Your plot, covering the range to zero power out, uses as its lower bound zero heat emitted (or received). This is not a climate variation normally studied.”
Once more you hit the nail on the head, too bad you don’t grasp the implications. They don’t study the actual response of the system, for it they did, it would become clear that the entire range of sensitivity claimed is a physical impossibility. FYI, the data in my plot is measured monthly averages of emissions of the planet vs. the temperature of the surface below for constant width slices of latitude.
Here, it is necessary to know a little calculus. Adopting the usual harmless simplifying assumption of constant unit emissivity, the first derivative, i.e. the change ΔTref in reference temperature per unit change ΔQ0 in radiative flux density, is simply Tref / (4Q0), which is linear.
Tref / (4Q0)= Tref/(4σTref^4)= 1/((4σTref^3)
Decidedly nonlinear in terms of T.
Exactly. This dependence, as well as the basic T^4 dependence between temperature and emissions are IMMUTABLE properties of radiating bodies. Even at an emissivity of .0001, the T^4 dependence is still present.
(Max Photon)⁴
The accident-prone “Phil.” does not seem to appreciate how small is the difference between the values of the Planck parameter at 255 and at 288 K. If he were to read the head posting before attempting to comment, he would be better informed – if not necessarily wiser.
Phil. calls the kettle black when he accuses me of sneering. I only give as good as I get, and Phil. is notorious here for his sneering tone. He should learn that if he wants to play alongside the big boys he must bot blub when he gets as good as he gives.
Before he waffles further about calculus, of which he manifestly has a lamentably tenuous grasp, he should understand that T / (4Q) is a linear relation. Let him try plotting T against Q, or T against T / (4Q). In both instances, a straight line results.
Besides, the relevant calculation is set out in the head posting. Phil has done his best to introduce yet another inaccurate and irrelevant distraction, but, owing to his lack of elementary calculus, he has failed.
Monckton of Brenchley April 7, 2018 at 4:06 am
The accident-prone “Phil.” does not seem to appreciate how small is the difference between the values of the Planck parameter at 255 and at 288 K. If he were to read the head posting before attempting to comment, he would be better informed
You are the accident-prone one but as usual try to bluster and insult your way out of it.
As is clear from my post I had read the head posting since i in fact quoted it!
Here it is again with some context:
One commenter here has complained the Planck parameter (the quantity by which a radiative forcing in Watts per square meter is multiplied to convert it to a temperature change) is neither constant nor linear: instead, he says, it is the first derivative of a fourth-power relation, the fundamental equation of radiative transfer. Here, it is necessary to know a little calculus.
Note the attempt to put the commentator down by implying he does not know “a little calculus”.
In fact, as I showed the commenter’s calculus was correct, the first derivative is a cubic.
A correct and non insulting reply would have been ‘the first derivative is indeed non-linear but for such small changes a linear approximation can be used’, but given your usual hubris you couldn’t bring yourself to do it. I even gave you that out when I first remarked on this.
Phil’s knowledge of calculus is severely limited, so let me explain things. The fundamental equation of radiative transfer contains only four terms: temperature, radiative flux density, emissivity and the Stefan-Boltzmann constant. The emissivity is usually taken as constant at unity. In that event, it is permissible to drop the emissivity (and, for the same reason, the Stefan-Boltzmann constant) when obtaining the first derivative of the equation with respect to temperature T and radiative flux density Q, which, as I have previously pointed out, is expressible as T / (4 Q). Like it or not, that is transparently linear. One can, of course, express it also as a cubic relation, but the fact that it can be expressed linearly indicates that – particularly over the limited interval of 33 K that we are concerned with – it will not exercise an extravagantly nonlinear effect.
Indeed, the head posting did all the calculations for you. At the emission temperature of 255 K, the Schlesinger ratio (which gives a respectable approximation to the value of the Planck parameter) is 0.26 Kelvin per Watt per square meter. At today’s temperature, that becomes only 0.30. Not exactly a huge difference, and not worth worrying about. The assertion that the Planck parameter is nonlinear is, therefore, supremely irrelevant – unless one’s purpose is to sow confusion rather than to attain the truth. We here are seekers after truth. Phil, however, is a devotee of a Party Line. Otherwise, he would have conceded this simple point long ago, on being confronted with the evidence that the value of the Planck parameter simply does not vary enough over the interval of interest to make any difference.
“In that event, it is permissible to drop the emissivity (and, for the same reason, the Stefan-Boltzmann constant) when obtaining the first derivative of the equation with respect to temperature T and radiative flux density Q, which, as I have previously pointed out, is expressible as T / (4 Q). Like it or not, that is transparently linear. “
Transparently not. You took the S-B equation
Q = σT⁴ (1)
and differentiated
dQ/dT = 4σT³
Then you seek to revert the derivative as
dT/dQ = 1/(dQ/dT) = T/(4σT⁴) = T/Q
But as Phil. keeps pointing out, this is not linear in T. It is 1/(4σT³). You can’t suddenly claim Q is constant as T changes after having differentiated it wrt T.
= T/Q should be = T/(4Q)
Still not linear.
Monckton of Brenchley April 8, 2018 at 9:00 am
Phil’s knowledge of calculus is severely limited, so let me explain things.
On the contrary my knowledge of calculus is excellent, yours on the other hand, is severely flawed.
I was using calculus while you were still in primary school and used it extensively through my undergraduate, postgraduate and research career to a much higher level than this elementary high school level.
The fundamental equation of radiative transfer contains only four terms: temperature, radiative flux density, emissivity and the Stefan-Boltzmann constant. The emissivity is usually taken as constant at unity. In that event, it is permissible to drop the emissivity (and, for the same reason, the Stefan-Boltzmann constant) when obtaining the first derivative of the equation with respect to temperature T and radiative flux density Q, which, as I have previously pointed out, is expressible as T / (4 Q). Like it or not, that is transparently linear.
Like it or not that is a serious error on your part.
Lumping all the constants as you suggest the S-B equation is as follows:
Q=kT^4 the derivative wrt T is as follows: dQ/dT=4kT^3 clearly nonlinear, substituting for a single variable, T, with a function of two variables which are each functions of each other is nonsense.
One can, of course, express it also as a cubic relation, but the fact that it can be expressed linearly indicates that – particularly over the limited interval of 33 K that we are concerned with – it will not exercise an extravagantly nonlinear effect.
Your expression (T/(4Q)) is not linear wrt T because Q is a quartic function of T, and therefore amounts to T/T^4
Indeed, the head posting did all the calculations for you. At the emission temperature of 255 K, the Schlesinger ratio (which gives a respectable approximation to the value of the Planck parameter) is 0.26 Kelvin per Watt per square meter. At today’s temperature, that becomes only 0.30. Not exactly a huge difference, and not worth worrying about. The assertion that the Planck parameter is nonlinear is, therefore, supremely irrelevant – unless one’s purpose is to sow confusion rather than to attain the truth. We here are seekers after truth. Phil, however, is a devotee of a Party Line.
No I am no devotee of any party line, I do however object to ‘fake science’ especially when delivered in your sneering insulting manner. You’re wrong on the calculus, show some class and admit it.
The accident-prone and calculus-challenged “Phil.” continues to have difficulty with elementary concepts. The Schlesinger ratio is the ratio of surface temperature to four times the emission-altitude radiative flux. That ratio gives an excellent approximation to the official value of the Planck reference-sensitivity parameter. Thus, at emission temperature of 255.4 K, the Schlesinger ratio is 255.4 / 4 / 241.2 = 0.26 Kelvin per Watt per square meter. However, at today’s surface temperature of 288.4 K, the Schlesinger ratio is 288.4 / 4 / 241.2 = 0.30. Since the denominator is constant (assuming that the solar constant is constant), it should be self-evident even to the meanest intellect that plotting the Planck parameter against surface temperature will deliver a straight line. The growth in the Planck parameter is, therefore, ineluctably linear with respect to temperature. All of this is quite elementary.
The calculus-challenged “Phil.” continues to have difficulty in understanding that the Planck parameter varies linearly with respect to surface temperature. The Schlesinger ratio is the ratio of surface temperature to four times the emission-altitude flux, which is constant at 241.2 Watts per square meter. It is inevitable, therefore, that with respect to temperature the Planck parameter will vary linearly.
“The accident-prone and calculus-challenged “Phil.” continues to have difficulty with elementary concepts.”
Phil’s calculus is fine. The head post said
“Here, it is necessary to know a little calculus. Adopting the usual harmless simplifying assumption of constant unit emissivity, the first derivative, i.e. the change ΔTref in reference temperature per unit change ΔQ₀ in radiative flux density, is simply Tref / (4Q₀), which is linear.”
Well, yes, if Q₀ = σ T⁴, then a little calculus gets you dQ₀/dT = 4 σ Tref³ = 4 Q₀/T
inverting
dT/dQ₀ = T/(4Q₀)
So far, so good. And it corresponds to the expression written if T=Tref, and to the re-expression by Lord M here:
“In that event, it is permissible to drop the emissivity (and, for the same reason, the Stefan-Boltzmann constant) when obtaining the first derivative of the equation with respect to temperature T and radiative flux density Q, which, as I have previously pointed out, is expressible as T / (4 Q). Like it or not, that is transparently linear. “
But, as Phil said, this is transparently not linear. It is only after this claim of linearity in the head post that the “Schlesinger ratio” is introduced as an approximation, replacing the numerator by current surface temperature. That does not arise by any calculus.
Mr Stokes is futilely splitting hairs. The head posting provided an explicit calculation of the Planck parameter at 255 K and at 288 K, and the two are not very different. I cannot help it if he had not previously been introduced to the Schlesinger ratio. He is now better informed, if not necessarily wiser. The bottom line is that the Planck parameter grows linearly with temperature.
Monckton of Brenchley April 11, 2018 at 10:06 am
Phil. calls the kettle black when he accuses me of sneering. I only give as good as I get, and Phil. is notorious here for his sneering tone. He should learn that if he wants to play alongside the big boys he must bot blub when he gets as good as he gives.
‘Big boys’ that’s a joke, by the way what is “bot blub”. You’re the one who demeaned another posted for not understanding calculus, and then showed you don’t understand it to even high school level!
Before he waffles further about calculus, of which he manifestly has a lamentably tenuous grasp, he should understand that T / (4Q) is a linear relation. Let him try plotting T against Q, or T against T / (4Q). In both instances, a straight line results.
As I’ve pointed out several times now, T vs Q is a quartic not linear your failure to grasp simple calculus and algebra is stunning. I just plotted T vs Q on XL for fun and get a beautiful curve, as expected, perhaps you should try it?
Besides, the relevant calculation is set out in the head posting. Phil has done his best to introduce yet another inaccurate and irrelevant distraction, but, owing to his lack of elementary calculus, he has failed.
Actually you don’t calculate the Planck parameter, you calculate a linear approximation. For a difference in T from 255 to 288 you’d get a change in the Planck parameter of about 30%.
I’m just trying to correct your faulty maths, any reviewer worth his salt would bounce your paper if it contained such fundamental errors.
So is this basically about oversimplifying a feedback loop that includes high order delays with long time constants?
“this basically about oversimplifying a feedback loop”. Yes mainstream science has oversimplified it by not fully applying it to all forms of surface warming. I am hesitant to call it a math error. Its more of a logic error.
Even NASA can’t lay out a blueprint of the theory. https://climate.nasa.gov/evidence/. The closest they come to a blueprint is work over 100 years old. Originally this site only had item #2 listed until I point out “suggested” was a weak basis for climate alarmism about a year or so ago. Now they have added in some recent observation work in efforts to weakly support the idea like Santer’s 1996 work on recent warming portending sky rocketing warming in the future, a warming that ended in less than 2 years after the paper he wrote. By the time IPCC memorialized it in AR3 (Santer was lead author of the section) the warming was already gone but everybody had their racing blinders on so they didn’t take note.
After that all the work has gone into trying to identify the missing warming, like the warming eating beast only operates part time.
This is the sort of stuff that happens when you fail to carefully blueprint out a theory and everybody and his sister has a different viewpoint on how it all works. The theory that non-condensing greenhouse gases completely control feedbacks is nonsense. Always has been nonsense because less than 30 watt/m2 worth of non-condensing greenhouse gas temperature forcing is a pittance compared to a 1365 watt/m2 sun coming over the horizon every morning.
Thanks! At last with this comment and the one to which you replied I am starting to have the perhaps illusory impression that maybe there is light to be seen through the dense foliage.
Mr Hunter’s clarity is admirable. If we are correct that emission temperature induces a feedback response, then equilibrium sensitivity must be very considerably below current official estimates.
Mr Gutierrez, however, is not correct that this is “basically about oversimplifying a feedback loop that includes high-order delays with long time constants”. As Table 1 makes clear, the timescales for the feedback processes relevant to the derivation of equilibrium sensitivity are short. And every model – including ours – is a simplification. The question for Mr Gutierrez is how to justify the current model, which allows for little or (usually) no feedback response to emission temperature and then, suddenly, a very large feedback response to the small increase in emission temperature accounted for by the directly-forced warming that arises from the presence of the non-condensing greenhouse gases.
One of many mistakes made is to consider the effects of temperature as feedback when they are more properly quantified as the temperature coefficient of a component. Considering that feedback amplifies the sensitivity is another of the many conceptual errors made by many.
Another is that the input to the model developed by Hansen/Schlesinger is a change in total forcing expressed in W/m^2 and not a temperature while the output is a change in temperature expressed in degrees. The linear feedback amplifier analysis developed by Bode only applies when 1) the incremental gain is the same as the absolute gain and 2) the input and output are either in the same units or are in linearly related units. Forcing in W/m^2 is linearly proportional to emissions in W/m^2 which are proportional to T^4 which is not at all linear. As a consequence, the consensus conveniently ignores the 1/T^3 dependence of the sensitivity when expressed as degrees per W/m^2 and ignores the mostly linear relationship where each W/m^2 of solar forcing results in about 1.6 W/m^2 of surface emissions.
(+ emphasis)
Oh you fibber you!
In response to Mr Ross, I am sorry that the head posting did not seem clear. It is long, and it does go into a certain amount of detail, but it uses little more than high-school algebra. That is not its weakness but its strength. Eventually, anyone who is willing to expend a little effort will be able to understand our result.
This is a long winded blog to discredit the IPCC modelling.
A much simpler way to discredit the IPCC and its modelling is the linked image:
http://www.ipcc.ch/report/graphics/images/Assessment%20Reports/AR5%20-%20WG1/Chapter%2002/Fig2-11.jpg
This image has evolved, from black and white to bright colours, through the various report stages over the years but still has the same basic flaw showing huge amounts of heat radiating from a cold atmosphere to a hotter surface. I expect that 99% of the population would know by experience that cold air cannot make a warmer surface hotter. It beggars belief that this diagram still exists in AR5.
NASA realised this nonsense some years ago and has changed its educational material accordingly:
https://pmm.nasa.gov/education/lesson-plans/global-energy-budget
So the 342W/sq.m of so-called back radiation has disappeared here.
IPCC credibility on anything related to science and physics is worthless. Climate models are no more than curve fitting; essentially mathematical constructs that have lost any connection with the physical world in an analytical sense.
The 398 W/m^2 of ‘thermal up surface’ represents an average surface temperature of about 289.5K which is a little high. The older value of 390 W/m^2 corresponded to an average surface temperature of 289K.
Increasing the temperature of either by 0.8C increases the ‘thermal up surface’ emissions by more than 4.3 W/m^2. If this was to arise from 1 W/m^2 of ‘forcing’ as claimed, where are the other 3.3 W/m^2 coming from in order to offset the increased emissions?
Only if the surface is a black body, which is nonsense. Where does the 342W/sq.m back radiation come from. In what universe does a cold object/gas radiate heat to a hotter object. Have you ever had your hand get warmer by being adjacent to a cold air stream! It is pure nonsense and at least NASA now acknowledge that and show a more realistic energy balance.
This is the chart from AR4 WG1:
For some strange reason they believe a farcical 342W/sqm in diagram above is better in 2013 than the previous farcical 324W/sq.m shown here from 2007. That is what happens when you deal with an imaginary world. It can be whatever they want it to be but that does not mean it has any association with the real world – the IPCC reports are fairy tales.
It is sad that Chevron and the other four oil companies defending the Oakland CA v BP public nuisance claim have relied on the IPCC fairy tales; albeit hyping the uncertainty. If they do not get the case dismissed, they could regret that position.
Rick,
The surface itself very close to an ideal BB, much like the surface of the Moon. The atmosphere is what makes the planet (not the surface) deviate from an ideal BB and instead becomes a non ideal BB, also called a gray body, which is a BB with an emissivity < 1. This emissivity is given exactly by (Te/Ts)^4 where Te is the average emission temperature of the planet (about 255K) and Ts is the average surface temperature (about 288K). If Ts is the equivalent temperature of an ideal BB surface, then this becomes an EXACT formulation.
Regarding the 342 W/m^2, the portion of this that returns latent heat and convection energy to the surface is not radiant and is instead energy transported by matter. Some of this is also solar forcing delayed by the water in clouds.
Your second law argument doesn't hold water, as the transfer of energy by photons happens at all temperature and two streams of photons have more warming influence than one stream of photons. Your case of a cold stream of air is energy transported by matter (collisions) which does obey the second law owing to matter to matter contact.
Suppose we had 10 Suns in a small cluster orbiting each other in a volume about the same as the current Sun, where each contributed 34.15 W/m^2 to the solar energy received by Earth for a total of 341.5 W/m^2. Would the Earth's surface temperature be any different then it is today?
Rickwill.
“I expect that 99% of the population would know by experience that cold air cannot make a warmer surface hotter.”
I expect that 99% of the population know to use a blanket to keep warm. The atmosphere is a blanket, with huge quantities of water vapor storing heat and releasing it back to the surface via LWR as it rises and cools.
That part is easy to understand. The harder part is to determine the net effects of a few more molecules of CO2.
sailborder,
“The harder part is to determine the net effects of a few more molecules of CO2.”
Not really, the IPCC makes it seem more complicated than it really is so it can arm wave a sensitivity high enough to justify their existence.
The planet is a relatively simple thermodynamic system, at least at the macroscopic scale and the macroscopic laws of physics can bound it’s behavior quite tightly.
For example, the combined effect of all GHG’s, the clouds, the water cycle and any of the other ‘complexities’ results in only 600 milliwatts of surface emissions above and beyond each W/m^2 of solar forcing.
The next W/m^2 of solar forcing will increase surface emissions by 1 W/m^2 plus the extra 600 milliwatts/m^2 for a total of 1.6 W/m^2. Consider an average surface temp of 288K emitting 390 W/m^2. The new temperature required to increase these emissions by 1.6 W/m^2 is about 288.3K yielding a sensitivity of about 0.3C per W/m^2 and no where near the 0.4-1.2C per W/m^2 claimed by the IPCC and its self serving consensus.
The increase in emissions required to support an 0.8C increase (the IPCC nominal value) is over 4.3 W/m^2 requiring an extra 3.3 W/m^2 of power above and beyond the initial forcing. This requirement is so absurd and such an obvious violation of COE, not only does this provide grounds to eliminate the endangerment finding, it’s sufficient to provide grounds to disband the IPCC and UNFCCC.
Sailwhatever
That’s why all people that live in deserts walk around naked right! Oh wait.
We have had this argument before. This planet is nothing like the moon. This planet is nothing like a blackbody where there is instantaneous response. Heck, even the Lacis paper (which is partly the subject matter of this post) suggests that it would take ages for the oceans to freeze. That is because this planet is nothing like a blackbody.
Richard,
A black body doesn’t requires an instantaneous response, in fact, the relevant mass of the emitting object and its heat capacity determines the time constant for how long it to arrive at a steady state upon some change in forcing.
Once more, the EXACT differential equation governing this is, Pi = Po + dE/dt, where Pi is the arriving power, Po is the emitted power and E is the energy stored by the body that manifests its temperature. dE/dt is the forcing, per the IPCC’s definition and in equilibrium when Pi == Po, dE/dt must be zero.
FYI, it would only take on the order of weeks to months for the top radiating surface of the oceans to freeze if the Sun stopped shining. The evidence of this is how quickly ice builds in polar regions during the darkness of the polar winter.
The boundary between the surface and atmosphere is really no different that the surface of the Moon, even over oceans, and while the effective emissivity may not be exactly 1, this just gets lumped in with the decrease in the planets emissivity arising from the atmosphere relative to the surface temperature.
The data is very clear that the AVERAGE emissions at TOA are linearly proportional to the AVERAGE emissions by the surface. This means that the T^4 relationship between the surface temperature and surface emissions also holds between the surface temperature and emissions by the planet.
http://www.palisad.com/co2/sens/se/po.png
The X axis is surface emissions and the Y axis are the emissions of the planet. Each dot is 1 month of data for a 2.5 degree slice of latitude, where all slices and all months spanning 3 decades are shown.
It’s not really ‘back radiation’, but rather just the total amount of DLR at the surface. Or just the total amount of IR the atmosphere as a whole passes to the surface.
This text is taken from IPCC AR5 WG1 Chapter 2 page 181:
“Since AR4, new estimates for the downward thermal infrared (IR) radiation at the surface have been established that incorporate critical information on cloud base heights from space-borne radar and lidar instruments (L’Ecuyer et al., 2008; Stephens et al., 2012a; Kato et al., 2013). In line with studies based on direct surface radiation measurements (Wild et al., 1998, 2013) these studies propose higher values of global mean downward thermal radiation than presented in previous IPCC assess- ments and typically found in climate models, exceeding 340 W m–2 (Figure 2.11). ”
As you can see they are claiming that a humungous amount of heat is transferred from the cold atmosphere to the warmer surface via some unique form of infrared radiation that manages to defy the second law of thermodynamics. Its a fairy tale. NASA does not even pedal this nonsense anymore.
Rick,
Infrared radiation passed from the atmosphere to the surface is not heat transfer, which involves net flow, and the net flow of energy is away from the surface towards space, satisfying the 2nd law.
That educational model by NASA doesnt make any sense. It shows 100% coming in with 30% reflected and 70% going back out and yet says there is a 15 % deficit in the atmosphere that is made up a little line that says 15% extra radiation absorbed by atmosphere and a water land surplus of 29%. They are trying to imply that the 15% deficit in the atmosphere is LWIR but they try to show it with a little yellow line that supposedly comes from the sun. The problem is that all the suns wattage is already accounted for, so the net result is that this wattage comes from nowhere. The surplus of 29% in the land/water would mean that that heat would have to be absorbed by the oceans as the missing heat. The oceans would soon boil over under that scenario. So they dont even show global warming in the chart because they have 70% insolation with 70% escaping to space.
It is still messed up all the way long.
In the NASA chart surface would emit only 21% of 342W/m2 = 72W/m2. I will strongly advocate the fact that surface emissivity != 1 and (rather 0.92) and henceforth not 288^4 * 5.67e-8 = 390.08W/m2 (side kick @ co2isnotevil) but only 360W/m2. Yet 72W/m2 is simply absurd.
But please take a closer look at what all these models tell on clouds. They reflect 76W/m2 (IPCC), 20% of 342 = 68W/m2 (NASA), 77W/m2 (IPCC again, including Aerosols) or 79W/m2 (NOAA, link at the bottom). Also these charts, if shown, indicate 30W/m2 of upward emissions by clouds.
Accordingly clouds will have a negative forcing of 100W/m2 or higher. Now find their positive forcing, when their net forcing is about -18W/m2 (for instance). And keep in mind, that positive forcing will be part of the GHE, eating into the share that GHGs hold.
Let us take that IPCC model with 398 surface emissions (wrong, just 360W/m2) and 239 TOA. That leaves us with a postulated GHE of 398 – 239 = 159W/m2. We need take away 38W/m2 because of the lower surface emissivity of only 360, which leaves 121W/m2 of the GHE. Then subtract the positive cloud forcing of >100 – 18 = >82. And you are left with only <39W/m2 the remaing GHE. But even that is way too much as I have explained below.
In response to RickWill, the head posting makes it clear that we have accepted for the sake of argument all of official climatology except what we can prove to be erroneous. Our purpose is to prove our result by formal means. That requires going beyond the mere 70-word abstract that summarizes our result, and dealing with all manner of actual and potential objections. The head posting provides some of that proof. Yes, it is long, because I was dealing with several actually baseless objections. But the key idea remains simple. If one accords any reasonable value to the feedback response to emission temperature, then equilibrium sensitivity is bound to be a great deal smaller than official climatology’s current estimates.
Wow I cannot make sense of the nasa kids explanation. I was looking for the new excuse for global warming. To me it looked like 77% of the suns energy goes in and 70% comes out. They didn’t label the values of all the arrows. So there’s the suspicious 15% absorbed by atmosphere but I could not make the numbers add/subtract. If it is a 7% imbalance I guess we burn up before we can do anything about CO2.
Talking of feedbacks.
This year’s March has seen the highest snow cover extent for that month in N America since 1978.
Along with this there has been a record amount of snow mass. So it would be interesting to see if along with this record snowfall there has been also increased amounts of cloud cover as well. A check of the sunshine amounts for the month across N America would be a useful way to find out.
taxed April 6, 2018 at 4:39 pm
Talking of feedbacks.
This year’s March has seen the highest snow cover extent for that month in N America since 1978.
According to Rutgers Snow Lab, since 2011.
https://climate.rutgers.edu/snowcover/chart_anom.php?ui_set=1&ui_region=nhland&ui_month=3
Phil
Yes for the NH as awhole it has been highest since 2011. But for N America its been the highest since 1978.
taxed April 6, 2018 at 5:06 pm
Phil
Yes for the NH as awhole it has been highest since 2011. But for N America its been the highest since 1978.
Yes, you’re right, do you know if that includes Greenland? Elsewhere on their site they differentiate between ‘N America’ and ‘N America (no Greenland)’.
“μ = 1 + ΔTref / Tref is the gain factor representing any amplification of Tref such as that caused by the presence of the naturally-occurring, non-condensing greenhouse gases”
This is where the maths goes wrong. In a gain factor, you need to divide the response ΔTref by whatever change caused it. Then you can get a gain factor which is a reasonably constant property of the system. But here you are just adding an arbitrary amount of GHG. ΔTref might be proportional to the amount added (or not). Then there would be no gain factor that is a property of the system. It is entirely dependent on how much GHG you add, since Tref doesn’t change, or at least not much. It could be as low as 1.
A proper gain would be something like μ = 1 + ΔTref / ΔGHG
There is some chance that that would be an invariant ratio, and hence a system property rather than an input dependent one.
This brings up the issue of linearity that Frank talked about. I think it is minor compared to the general wrongness of trying to talk about feedback to a large invariant temperature. And also minor compared to the fact that, as demonstrated previously, none of this affects the calculation of Charney Sensitivity anyway. But it is true that it is unlikely that a notion of linear gain could be used down to zero GHG. It is a small perturbation notion. Feedback does not have to be linear, so it is perfectly sensible for Lacis to calculate two states and attribute differences to feedback. Linearity only matters if you want to do linear algebra, as with a gain factor.
A proper gain would be something like μ = 1 + ΔTref / ΔGHG
I think the units need to be tuned up a bit.
Yes
” I think it is minor compared to the general wrongness of trying to talk about feedback to a large invariant temperature.”
Why do you ignore the feedback to the large invariant(?) temperature, resulting from the 1850 insolation? How does the the climate feedback mechanism know to ignore that large invariant(?) energy input? Magic?
Mr Stokes appears to believe that the standard representation of a simple gain factor is incorrect. In that event, he should really address himself to the world of elementary mathematics, which – he appears to be suggesting – has been in error on this matter since ancient times.
Mr Stokes also seems to believe that the simple, direct or open-loop gain factor mu is not unitless. Again, he should address himself to the high priests of feedback theory, to whom it is by definition unitless.
Mr Stokes also continues to adhere to his belief that an invariant input signal (assuming ad argumentum that it is invariant) cannot induce a feedback response. Again, he should address himself not to me but to control theory, where it is axiomatic that an input signal, even if unamplified, will necessarily induce a feedback response in the presence of at least one feedback process.
As for linearity vs. nonlinearity, to the extent that the climate system is nonlinear it will be no more nonlinear after correction of official climatology’s error than before. The ineluctable consequence is that equilibrium sensitivity must be well below the current mid-range estimates.
The first para of this destroys your credibility. Nick is obviously saying no such thing. Among Oxford undergraduates 50 or 60 years ago these sort of labored insults were admired and the common currency of Union debate, but those times are long gone.
“Mr Stokes appears to believe that the standard representation of a simple gain factor is incorrect.”
It is not standard, or sensible, to represent a gain factor as a function of the signal supplied. Apart from anything else, it contradicts linearity. And since where linearity is in doubt, the gain factor applies to signals of small amplitude, the expression μ = 1 + ΔTref / Tref says that the gain is 1.
In answer to Mr Stokes, where the input signal is 255 K and the amplification of it owing to the presence of the naturally-occurring, non-condensing greenhouse gases is 9 K, the output signal will be 264 K in the absence of feedback. Now, let us consider the ratio of 264 K to 255 K. It is equal to 1.0353. That is, of course, exactly the same as 1 + 9 / 255. It is known as the simple gain factor or the direct gain factor or the open-loop gain factor or the forward transmission characteristic (there seems to be little in the way of standard feedback terminology). All of this is quite straightforward and entirely standard. Mr Stokes, in questioning this, is not assailing our argument: he is tilting at long-established feedback theory, and on no satisfactory basis that I can discern. If he disagrees with Bode on this, let him write his own textbook and enlighten us all. In the meantime, I shall continue to deploy mainstream science.
“Then Charney sensitivity is 1.1 / (1 – 0.08) = 1.2 K”
Interestingly, if we constrain the sample period to the availability of co2 data by the precision of the keeling method we get empirical sensitivities from hadley and uah data of ECS<2.
Please see
https://ssrn.com/abstract=3157484
CM points out that Hansen et al got their feedback analysis wrong. I think they shouldn’t have applied that analysis in the first place because they didn’t sufficiently justify its use. CM’s very good catch makes that starkly obvious.
The climate system is not LTI. It changes over all time scales. That means the forward and reverse transfer functions change over time. That means you can’t really point to a time when the climate was in equilibrium.
“CM points out that Hansen et al got their feedback analysis wrong.”
But with no specifics and not a single quote. And he didn’t.
In answer to Mr Stokes, I pointed out that Hansen had used the uncorrected form of the zero-dimensional-model equation and had, as a result, not taken account of the large feedback response to emission temperature. That was an error on his part. It has been much copied since. But mere repetition does not sanctify it. Hansen was wrong.
To repeat many previous analyses on this topic, think based on many different lines of evidence that the ‘correct’ ECS value is between 1.45 and 1.65. In any case, no cause for climate arm.
Mine is 1.62 which was aftrer a loooooooooooooooooong calculation based on total volume of gas sizes.
I agree with Mr Istvan and Mr Tomalty that Charney sensitivity is likely to be well below 2 K per CO2 doubling. The literature is moving in that direction too. Our result is a clear indication of the reason why official climatology has hitherto over-predicted future warming.
In response to Germinio (or is it Germonio: there seem to be two, and perhaps the moderators would like to check that the email addresses are genuine), just about any curve may be represented as a Taylor series, especially where that curve models the sum of an infinite series. The corrected form of the zero-dimensional model equation, just like the uncorrected version used in Roe (2009) and many other authorities, can also be expressed as a Taylor-series expansion about whatever equilibrium point seems convenient. However, in view of our finding that the feedback fraction is likely to be very small, there is really no need to go to the bother of carrying out a Taylor-series expansion. The rectangular-hyperbolic shape of the output curve of equilibrium sensitivities is clear enough, and, if we are right, the output falls on the left-hand end of the curve close to the origin, where the slope is near-perfectly linear.
Monckton appears to be confused about what is and is not a Taylor series. The feedback equation in
Roe 2009 *IS* a Taylor series expansion. It does not need to be represented as one since it already is
one. More-over he has presented no justification for his “corrected form” of the feedback equation. It
would appear to be nonsense from both a mathematical and physical point of view and should not be
taken seriously by anyone.
Germonio seems unaware of the distinction between an infinite series and its sum. The zero-dimensional-model equation gives the sum of the infinite series and is not the series itself.
And of course I have presented a justification for the corrected form of the zero-dimensional-model equation. It is to be found in Bode (1945, ch. 3), or in any other standard textbook of feedback theory.
Also, I have had the theory tested in practice, and it works. And I have then compared the predictions of equilibrium sensitivity that the corrected equation suggests with the official predictions, and it is rather obvious that the corrected predictions are far, far closer to reality.
One understands that all of this may come as a terrible shock to Germonio’s belief system, but there it is: science is science, and official climatology is, in the respect explained in this series, gravely awry.
ristvan,
“…the ‘correct’ ECS value is between 1.45 and 1.65.”
Thanks for making your position clear. In the last article Christopher Monckton said these figure were ushing towards the “totalitarian” position.
I appreciate that Monckton thinks that 1.2 is the correct value, and I appreciate that you are both claiming sensitivity is at the lower end of IPCC estimates, but I’m still not sure how two mutually exclusive claims can be interpreted as “game over”.
Bellman appears unaware of the role of uncertainty in science. Our mid-range estimate of Charney sensitivity is 1.2 K. Under various assumptions that we plainly labeled as extreme concessions to the true-believers, one could inrease that to 1.5 K or thereby. But even under those concessions, which we do not consider plausible, reasonable or necessary, Charney sensitivity is only half of the official mid-range estimate.
“Bellman appears unaware of the role of uncertainty in science.”
No, uncertainty is an important part of science. My problem is that you originaly gave a figure for sensitivty that was very certain, 1.2K plus or minus 0.15K. You then quoted ristavan as supporting your position and declared the science settled (game over). Yet ristavan keeps pointing out that your figure is too low, whilst you insist that his figure is implausible and “totalitarian”. I don’t want to help your argument, but I think your claims would be more plausible if you accepted the uncertainty in your position.
It was only a few years ago you were claiming sensitivity was 0.5K, you’ve now more than doubled that figure, and keep showing how making different assumptions can lead to different values, but you never allow the possibility that you might not be correct, that these figures might be uncertain.
In response to Bellman, our best estimate of Charney sensitivity is 1.2 K, but we are here assuming that everything in official climatology is correct except where we can prove the contrary. Professor Happer can prove that the CO2 forcing has been exaggerated by 40%. Professor Harde can prove that it hs been exaggerated by 30%, but for a different reason. Accordingly, the CO2 forcing is really 1.9 Watts per square meter, in which event Charney sensitivity is 0.65 K, and that is before allowing for the exaggerations in various feedbacks found by Lindzen & Choi (2009, 2011) and Spencer & Braswell (2011).
I suspect that Charney sensitivity is not much above 0.5 K, bearing in mind all these researchers’ work. However, what I can myself prove is that official climatology has made a large error in the treatment of feedbacks. Once that large error is corrected, Charney sensitivity falls very substantially, and no amount of wriggling by Bellman will change that.
“I suspect that Charney sensitivity is not much above 0.5 K, bearing in mind all these researchers’ work.”
Yet in your original article and in the legal argument you say that you conducted all sorts of tests that confirmed the 1.2K figure was in the right ballpark, and gave near identical results. Are you now saying you think these tests were flawed?
In response to Bellman, what I think is so and what I can prove to be so are two different things. I am not a totalitarian, so I do not make the totalitarian error of assuming that what I think is so is necessarily so. I have explained patiently to Bellman that I can prove equilibrium sensitivity is of order 1.2 K, and that taking into account the work of others it is likely – though I cannot myself prove it – that equilibrium sensitivity is quite a bit lower than that. Welcome to uncertainty in science.
What can be fairly said is that any equilibbrium sensitivity of less than about 2 K is not enough to be worth worrying about. And, once the error we have identified is taken into account, it cannot exceed 2 K. Game over, so says Mr Istvan. If we are right, then perhaps it is indeed game over.
“In response to Bellman, what I think is so and what I can prove to be so are two different things.”
But you were claiming to have verified the 1.2K figure. I can understand someone disagreeing with the tests of other’s, it just seems strange to be rubbishing your own evidence – especially when you used these tests as arguments in a legal document.
“I have explained patiently to Bellman that I can prove equilibrium sensitivity is of order 1.2 K, and that taking into account the work of others it is likely – though I cannot myself prove it – that equilibrium sensitivity is quite a bit lower than that.”
I think you are using the word “prove” wrongly in that case.
“Welcome to uncertainty in science.”
One of my concerns here is that if you are uncertain about the 1.2K figure, that uncertainty could run in either direction. If it can be much lower it can also be much higher.
“In response to Bellman, our best estimate of Charney sensitivity is 1.2 K”
But just two weeks ago, the “Game over” article started out:
“Skeptics 1, Fanatics 0. That’s the final score.
The corrected mid-range estimate of Charney sensitivity, which is equilibrium sensitivity to doubled CO2 in the air, is less than half of the official mid-range estimates that have prevailed in the past four decades. Transient sensitivity of 1.25 K and Charney sensitivity of 1.45 K are nothing like enough to worry about.”
I’m reminded of our old evening newspaper, which had three editions – Final, Late Final, and Late Final Extra.
As far as I can tell Monckton is either [pruned] or is being deliberately deceitful. The relevant equation in
Roe is:
Delta T = lambda_0 Delta F/(1-f)
This has a clear and simple physical and mathematical meaning – it is the first order Taylor series
expansion for the Temperature of the earth as a function of the forcing starting from some reference
forcing F_0. This tells you that if the initial temperature is T_0 and the forcing is F_0 then linear
approximation to the final temperature is T_0 + Delta T.
What Monckton does is rewrite lambda_0 Delta F as an unphysical Delta T_r giving the equation
Delta T = Delta T_r/(1-f)
and then replaces the changes in temperature with absolute temperatures. This gives his equation
T=T_ref/(1-f).
Now this equation for temperatures makes no physical or mathematical sense and not surprisingly
gives nonsensical results. He can only get away with it because he starts with Delta T_r and not
lambda_0 Delta F. Rather than asking what the feedback results from the emission temperature
Monckton should be asking what is the Delta F that causes this emission temperature since
in the original equation you need a Delta F.
Now you can replace Delta F by F if you like but that is implicitly assuming that you are starting the
Taylor series expansion about a reference system where the forcing is zero, i.e. a system in which
the sun is not shining. Calculating the Taylor series expansion about this point will lead to very different
coefficients than if you calculate the Taylor series expansion about a Temperature of 255K.
[?? .mod]
The preceding public service announcement was brought to you by…
QLav for Men………
it is the first order Taylor series
======?
There is no need for such complexity. Feedback is an infinite geometric series. About the simplest. Infinite series to deal with mathematically.
Unnecessary complexity implies a lack of understanding of the problem. My suspicion is that climatology needed the complexity to shoehorn the mathematics to fit their incomplete treatment of feedback.
“There is no need for such complexity. Feedback is an infinite geometric series.”
An infinite geometric series is unnecessary complexity. The 1/(1-f) comes from solving linear equations. No need to expand.
The status of feedback and gain as derivatives is important, because it says that the ratios of input/output being written have to converge as perturbations get small. Taylor series here just means first order derivative relations.
In response to Mr Stokes, all of the values we are dealing with are small in astronomical terms. But one cannot obtain a correct estimate of the feedback fraction if one ignores the actually quite large feedback response to emission temperature. If the feedback fraction is as small as we find it to be, then there is certainly no need to worry about Taylor-series expansions. As Mr Berple correctly points out, the system-gain factor mu / (1 – mu * beta) is simply the sum of a well-kent infinite geometric series.
Nick, you have simplified the math to the point where you have found the correct answer to the wrong question.
Germinio is entitled to his opinion that replacing delta with absolute input and output values in the zero-dimensional-model equation is incorrect: but he is wrong. He has only to look at the third and most correct form of the feedback-loop equation to realize that the input signal has – like it or not – a large feedback response, even without any non-condensing greenhouse gases to amplify the input signal before it is passed to the output node. He will find the relevant math in Chapter 3 of Bode (1945).
It is, of course, perfectly possible to derive a Taylor series expansion of the correct equation, just as one can for the incorrect equation. But it is really not necessary or at all helpful, for the curve of the output is well known to be a rectangular hyperbola, whichever form of the equation is used. If, as we find, the equilibrium sensitivity lies at the left-hand end of the rectangular hyperbola, close to the origin, the response curve is near-perfectly linear in that region, and it is not at all difficult to work out what the equilibrium sensitivity’s likely interval will be.
Monckton is confused about what is and is not the correct equation. In reality the temperature T is a
complicated function of the forcing F, i.e. T=T(F). The feedback equation in Roe 2009 is then a first
order Taylor series expansion of this unknown function about a reference forcing F_0 and is thus only
valid for small changes in F. Monckton then replaces this first order Taylor series expansion with a second
similar equation for T that has no forcing terms in it at all and claims that since this correct for some
electronic amplifiers with feedback it must be true for the climate. A reference to a textbook on amplifiers
cannot prove that any particular equation is applicable to the climate. He needs to show that his new
equations can be derived from the relevant equations that describe the climate and he has not done this.
A ‘forcing’ is not a real thing; it’s only a shorthand way of adding more independent variables (parameters) to the model parameters rather than go to the extra iterative effort of adding the true dependency. T=T(F) is nonsensical. I guess it was meant to be T=f(F) which is still wrong. All you need is T=f(T)*. It is the f() that contains the forcing effect.
*though from my experience of FEA it is really f(Tout^4-Tin^4)=f(Tout) but I won’t press the point since clearly everyone has simplified that to remove the iterations whether rightly or wrongly.
jasg wrote: “A ‘forcing’ is not a real thing.”
A forcing is a permanent change in the rate at which energy enters and leaves our climate system. An increase in solar irradiation is a real thing. When more radiant energy enters our climate system, the law of conservation of energy demands that the difference be consumed in increasing “internal energy” which is temperature.
Detectors on space craft show that volcanic aerosols reflect more SWR to space as long as they persist in the stratosphere. They produce a forcing – a permanent change in the rate energy enters the planet. The provide a forcing for as long as they last,
If you don’t believe that doubled CO2 would change the rate of radiative cooling to space, they doubling CO2 would not produce a forcing. Based on laboratory experiments, doubling CO2 should reduce the rate of radiative cooling to space by about 1.5%. If these experiments have been correctly done and the data applied to our atmosphere, 2XCO2 represents a forcing. Otherwise no.
As a layman, even with a fair math and science background, I have a lot of difficulty following the argument being made here. Dumb it down for people like me please.
It is simple. The feedback equation is a first order linear Taylor series expansion for the
Temperature as a function of the forcing F. Monckton first calculates the derivative dT/dF
at a forcing value of about 1000 W/m^2 (corresponding to today’s average temperature)
and then uses that coefficient in a similar expansion about a value of F=0. Not surprisingly
he get a nonsensical answer.
dT/dF is not the same as ΔT/ΔF. Calculus doesn’t enter into it and the Taylor series is a total red herring. The whole analysis is straightforward high school algebra.
“Monckton first calculates the derivative dT/dF
at a forcing value of about 1000 W/m^2 (corresponding to today’s average temperature)”
OK, I missed that. Can you specify where exactly he does this?
CommieBob,
You need to read Roe 2009. The equation that Monckton uses is just the first order
Taylor series expansion of T(F). And so
T_0 +Delta T = T(F_0) + dT/dF *Delta F
where dT/dF is evaluated at F_0. This is simple calculus and since it is a first order
approximation it is only valid for small values of Delta F.
sailboarder –
If you read Roe 2009 you see how the feedback equation is derived and hence what it
means. The paper has a whole section about how it is just a Taylor series in disguise.
The term lambda_0/(1-f) is just another way of writing dT/dF evaluated at a particular
value of the forcing. Since he is starting with a reference temperature of about 288K that
is equivalent to using the current forcing from the sun which is about 1000 W/m^2. So
while Monckton does not explicitly calculate dT/dF he is implicitly doing that and hence
it is ridiculous to expect dT/dF evaluated at F=1000 W/m^2 to equal dT/dF evaluated at
any other value of the forcing.
Putting it in other terms:
Mr. Monckton is assuming that f is constant for all values of T, from 0 K to 288 K. I don’t believe that assumption is correct.
“dT/dF is not the same as ΔT/ΔF.”
It had better be close. Calculus is the basis of it. ΔT/ΔF converges to a single number f when the changes are small. If it doesn’t, it is useless. It would mean you had a different gain (or feedback coefficient) for every input.
And that is where Lord M’s maths goes wrong. ΔT/ΔF works as a ratio for small changes, because both tend to zero in proportion. But when he writes μ = 1 + ΔTref / Tref, the numerator tends to 0, but the denominator doesn’t. So the only meaningful value for μ, as gain for small perturbations, is 1, which isn’t interesting.
The whole analysis is straightforward high school algebra.
========
Agreed. Unnecessary mathematical complexity is a sure sign of a lack of understanding and an associated underlying error. Mathematics done correctly should reveal not obscure our understanding.
μ is the gain of the forward element. CM presents three block diagrams. In the first two the forward element is a direct connection. In other words, the forward gain (ie. open loop gain) is unity.
” In the first two the forward element is a direct connection.”
Yes, I commented on that here. Can you make sense of that? It’s like trying to run feedback resistors in parallel with a copper wire.
I can’t see the use of a formulation in which unity is the only possible small amplitude gain.
In response to Mr Mayer, who seems to assume that I am concerned with the purely hypothetical position if the insolation were zero, the temperature feedback processes in the climate system respond to the input signal as it is, not as it might have been if it were not as it is. The input signal, in the absence of any non-condensing greenhouse gases or of any feedback, would be 255.4 K at today’s insolation and albedo. It would not be 0 K. We do not need to know what might have happened if by some mystery the Earth were bathed in no radiance at all – not even the cosmic microwave background. We are dealing with the real Earth, and today’s insolation, and today’s albedo, and, therefore, today’s emission temperature of 255.4 K. To that temperature, like it or not, there is a large feedback response.
Dumb it down for people like me please.
≠==========
Feedback is the sum of an infinite geometric series. Mathematically about the simplest series to deal with. Skip the calculus. Algebra is all you need.
Lord Monckton’s argument is simple. But by leaving open-loop gain (as opposed to just plain loop gain) only implicit he perhaps obscured the degree to which it relies on linearity. So I’ll paraphrase his argument with open-loop gain expressed explicitly.
, i.e., the temperature without back radiation or feedback, is 255 K. If insolation net of albedo is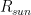 
, that temperature implies an open-loop gain 
. He also read that without feedback the pre-industrial back radiation 
from naturally occurring non-condensing greenhouse gases (“NOGs”) would have added only another 
. Taking the pre-industrial temperature with feedback to be 
, he solves the feedback equation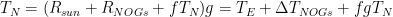 
for loop gain 
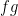(which he calls 
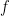) to obtain the modest loop-gain value of 0.08.
above the emission temperature: they instead solved ![T_N=[R_{sun}+R_{NOGs} + f(T_N-T_E)]g](https://s0.wp.com/latex.php?latex=T_N%3D%5BR_%7Bsun%7D%2BR_%7BNOGs%7D+%2B+f%28T_N-T_E%29%5Dg&bg=ffffff&fg=000&s=0&c=20201002)
to arrive at a substantial loop gain of 0.75:
Lord Monckton read that the emission temperature
Although he has sometimes back-pedaled, he contended in his amicus brief that prior to his insight all climatologists had instead computed the feedback relationship by assuming it responded only to the temperature portion
That is, although he pays lip service to nonlinearity, he bases his argument on the system’s being linear.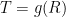
between global average surface temperature 
at equilibrium and the radiation 
that the surface absorbs. Note in particular that 
and 
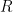represent the entire temperature and radiation values; they are not just departures from some reference levels. Obviously, this representation is a gross simplification;, for example, heat transfer with the surface doesn’t occur only by radiation. But all we’re interested in here is a rough example of what some climate modelers might suppose to be the earth’s behavior.
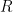includes a quantity 
that depends on the temperature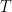 
itself: 
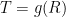becomes 
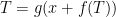, where 
is the radiation’s temperature-independent component. That temperature-independent component may be, say, back radiation caused by carbon dioxide that we’ve placed into the atmosphere by burning fossil fuels.
and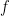 
? I don’t know. But let’s assume some functions that don’t ignore dependence on the entire temperature and observe how that constrains sensitivity. We’d expect temperature to be less dependent on temperature as temperature increases, and modelers who talk about things like tipping points obviously expect back radiation to become increasingly dependent on temperature as temperature increases. So let’s say for the sake of discussion that the functions take the following forms:
, 
, 
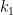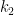are constants.
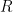is all the radiation, 
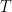is the whole temperature, and 
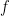responds to that whole temperature.
, 
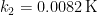, and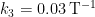 
. If we employ the inverse function 
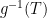of the resultant relationship 
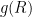on Lord Monckton’s assumed “emission temperature” 
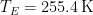, we get a temperature-independent radiation component 
, which we’ll take as our value for insolation after albedo. If we then solve the feedback equation 
for that value we get 
. That is, this model does exhibit a “substantial feedback response” 
to the emission temperature: it exhibits the response that Lord Monckton says the mainstream climate models lack.
of COGS-caused back radiation to the 
of insolation to obtain a higher value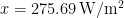 
. Solving the feedback equation 
with this increased temperature-independent radiation component 
gives us Lord Monckton’s pre-industrial temperature 
.
of “forcing.” Forcing is an initial radiation imbalance that would result from suddenly making a given CO2 concentration change. We make an estimate 
of the temperature change needed at the effective emission altitude to cause that radiation change, and we obtain the surface radiation change 
needed to cause the same temperature change at the surface. By solving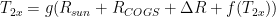 
we obtain a sensitivity 
.
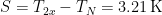If the models instead assume nonlinearity, they can instead arrive at their high sensitivities without ignoring the portion of temperature below some cutoff.
Let’s suppose for purposes of discussion that under the conditions modelers assume in this context the solution to the model equations results in some equilibrium relationship
Let’s also say that the radiation
What is the nature of the functions
and
where
Now, you may think that such relationships are much too simple and imply much greater sensitivity than the evidence supports. I agree; I don’t for a moment think that such relationships are valid. But that’s neither here nor there. What’s important to the present discussion is that they don’t ignore, as Lord Monckton contends that climate models do, the portion of the temperature value that’s less than some “emission temperature”:
Let’s suppose that
Since this model doesn’t lack that response, let’s determine whether recognizing that “substantial feedback response” has caused the model’s equilibrium climate sensitivity to be low. To do that we’ll first add
Equilibrium climate sensitivity is the change in equilibrium temperature caused by a doubling of CO2 concentration, and doubling that concentration is said to result in
By recognizing that the earth isn’t linear, in other words, climatologists are perfectly capable of arriving at a high sensitivity even if they take the entire temperature into account, i.e., even if their models provide “substantial feedback response.”
Of course, that doesn’t make them right. It merely makes Lord Monckton’s argument risible.
“If the models instead assume nonlinearity”
The feedback loop becomes non linear too. The earths remarkable stability says the earth operates in the low, linear portion of the loop gain, ie, CO2 has little effect.
The Born Liar, who seems more interested in doing me down personally and in an arrogant, sneering tone than in trying to attain the objective, scientific truth (perhaps because he is still smarting having been caught out in a malevolent lie on an earlier occasion) here recycles a defective argument that he had made in an earlier thread, but without being honest enough to say so, and without being honest enough to admit that he has now been compelled to tweak the numbers to try to produce a less implausible artificial scenario than his previous artificial scenario, and without being honest enough to admit that I had not derived the 255.4 K emission temperature by “reading” it, as he dishonestly suggests, but by calculating it from officially-published estimates of insolation and albedo, as explicitly set forth in the head posting. The Born Liar is also not honest enough to admit that my value of the emission temperature is not “assumed” but calculated, and not honest enough to admit that the term “emission temperature”, which he puts in pejorative quote-marks, is used frequently in the peer-reviewed literature, which is why I use it too.
So let us look at the Born Liar’s artificial scenario and do the math. He now apportions the 32.2 K difference between the 287.6 K temperature in 1850 and the 255.4 K emission temperature as follows: feedback response to emission temperature 15.2 K, directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases 8.9 K, and 8.1 K feedback response to that directly-forced warming. Using the defective official form of the zero-dimensional-model equation, his implicit feedback fraction, as far as the non-condensing greenhouse gases go, is 1 – 8.9 / (8.9 + 8.1) = 0.48, implying a Charney sensitivity of 2.1 K, right at the bottom end of the official CMIP3 and CMIP5 interval of Charney sensitivities. But he can only push the Charney sensitivity up this far by imagining that his 15.2 K feedback response to emission temperature is only 5.9% of it, while his 8.1 K feedback response to the 8.9 K directly-forced greenhouse warming is 91% of it. In short, he is trying to imply that if one corrects official climatology’s error in either not taking any account of the feedback response to emission temperature (in accordance with IPCC’s definition of a climate feedback) or taking only an inadequate account of it the nonlinearity of the system will be more severe, rather than less severe, than it is now in the uncorrected system. That is the central implausibility of many in his conclusion.
It is now time for the Born Liar to stop being arrogant, stop being vicious, stop being spiteful, stop describing results he does not understand as “risible”, and start doing some real work. Let him begin by finding some concrete examples of models or papers that make explicit and quantified allowance for the feedback response to emission temperature. When he has found them, let him explain why it is that such papers are incompatible with IPCC’s definition of a “climate feedback” as one which arises only in response to a change in temperature, rather than to a pre-existing temperature. Let him explain why it is that his scenario indicates a nonlinearity in the corrected system that is greater rather than less than the nonlinearity in the present system. Let him also justify the reasons for so strong a nonlinearity that the feedback processes in his scenario respond 15 times more enthusiastically to enrichment of the atmosphere with non-condensing greenhouse gases than to emission temperature.
And let him do all this politely, civilly, and in a spirit not of trying to find personal fault with me but of trying to attain the objective truth. If he will learn to behave in a civilized and scientific manner, and if he will cease his campaign of artful misrepresentations and start playing with a straight bat, I shall cease to call him the Born Liar,. Redemption is available to all who repent.
Joe
That is, although he pays lip service to nonlinearity, he bases his argument on the system’s being linear.
If the models instead assume nonlinearity,
You have picked up exactly the wrong end of the stick. But inadvertently you have identified the most interesting aspect of Monckton’s argument. Which simply amounts to a rediscovery of what the climate establishment have been trying to hide – Lorenz’s deterministic nonperiodic flow. Lorenz showed in 1962 that even a simply modeled climate system will never reach equilibrium. That with no change to external inputs the system’s state will always change and can never be characterised by a mean or equilibrium value.
What Monckton has now done is focus attention on the question of, in a climate system, what is equilibrium and stasis and what is perturbation from stasis? And the answer is simple and devastating. Equilibrium and stasis are nonexistent and meaningless concepts in climate. The fault that Monckton has exposed in climate science is far bigger than he realises. He has shown that the whole edifice of back radiation atmospheric modelling and CO2 warming is built on a vacuous foundation – on no foundation at all. At its heart are the impossible, nonexistent and meaningless concepts of equilibrium and stasis. It’s cute for you to be invoking nonlinearity now when talking about a paradigm and narrative built on equilibrium and stasis. These are not features of a dissipative open chaotic-nonlinear system characterised by feedbacks. The climate, that is.
The climate research community thought that they could just ignore Lorenz and he would go away. And it worked – as it always does. He – the person – did go away. But the theory he established didn’t go anywhere except to turn out to be not theory but fact.
Lorenz would have told them if they had listened that the climate is a far from equilibrium system in which stasis can never exist. But instead they built a climate theory on concepts of equilibrium and stasis. Considering the climate as a linear closed system, concepts of thermal balance, equilibrium and stasis are natural and compelling. But they are wrong and the entire theory and paradigm will have to be discarded.
You cant separate a static / equilibrium component and a perturbed / reactive component of the climate. If the system contains positive feedbacks then the whole system is excitable, just as negative feedbacks confer friction to the system. The system is dynamic and can’t be divided into parts where feedback operate and where they don’t. As Lorenz showed, such a system is always changing, in flux. It’s analogous to moving from algebra to Newtonian (OK Leibnitz too) calculus, where the meaningful values are instantaneous changes and rates of change, not static values.
This conclusion is very profound and thus can be arrived at from different directions. Lorenz found one – Monckton has found another.
As usual, Lord Monckton mischaracterizes things. I previously gave an example of how, without ignoring low-temperature feedback, climate modelers might generate high sensitivity and still match Lord Monckton’s numbers. With the head post here Lord Monckton appeared to change his numbers, so I changed the parameters to match the new numbers, just as one would expect climate modelers to tune their models to observations.
Yet, as is his wont, Lord Monckton implies that there’s something sinister in my doing so.
So what? I provided an example of how climatologists might arrive at high sensitivity without ignoring the “emission temperature.” What Lord Monckton basically observed is that I did that by making feedback per degree increase greatly with temperature.
Of course I did. If climatologists are going to get high sensitivity, that’s the only way. I don’t think sensitivity is high, and I don’t think the real-world relationships are what I put in that model. But if climate modelers think evaporation’s net effect (through clouds, greenhouse gases, etc.) is to warm the earth then it wouldn’t be too surprising for them to make this effect per kelvin greater at higher temperatures; that’s the way evaporation works. And the fact that enhanced higher-temperature loop gain would thereby emerge from the modelers’ resultant equations is no evidence that they ignored feedback at lower temperatures. It’s much more likely evidence that they thought, evaporation being what it is, that such feedback is much less in those regimes.
This confuses two things. One is whether the climate models make temperature-affecting things like back radiation, albedo, etc. responsive to temperature throughout the temperature range. To me Lord Monckton’s contentions that they don’t seems nearly inconceivable. The second is whether they call that response feedback. Apparently they don’t, but that’s merely a nomenclature issue; whether they call the response feedback has nothing to do with whether they implement it.
Unfortunately, the two issues keep getting conflated in these threads.
This is the second time Lord Monckton has recently perpetrated that slander at this site. So let me repeat what he calls a “malevolent lie.”
Among other evidence in a previous paperthat Lord Monckton had wandered in over his depth, he provided a “transience fraction” table purportedly derived from the Roe paper but indicating that a Roe-system step response would be lower at 25 years for modest positive feedback than for no feedback at all. Obviously, Roe said no such thing, so I wrote a post directed to some of the reasons why more information was needed about how he chose the transience-fraction values. But Lord Monckton turned down that request by merely repeating that he got them from Roe. What he calls a “malevolent lie” was my saying so.
Someone truly interested in the “objective, scientific truth” would simply show his work rather than whine about my not saying pretty please with sugar and honey on it when I pointed out the omission. But as far as I know he still has given no explanation of how he obtained such implausible values.
philsalmon:
Thanks for you conclusory assertions, but I see no reasoning to back them up.
Have a nice day.
Thanks. Very helpful.
Joe Born
I cited Deterministic Nonperiodic Flow, Lorenz 1962, thinking that the important theory and discovery in this paper regarding chaotic dynamics was common scientific knowledge. That is what citation is for.
https://journals.ametsoc.org/doi/pdf/10.1175/1520-0469(1963)020%3C0130:DNF%3E2.0.CO;2
But in an exercise in collective gaslighting, you and the climate community with you are trying to deny the existence of Ed Lorenz and of DNF 1963. And with good reason.
So I will repeat my arguments in case you missed them the first time:
1. Contrary to your stubborn denial, DNF1963 does exist.
2. The concept of equilibrium in climate dynamics is invalid since Lorenz showed that climate has never and will never attain equilibrium. It possesses the dynamics that it does on the basis of its being a far-from-equilibrium system.
3. The concept of perturbation from a (fictitious) equilibrium is invalid since there is no equilibrium from which to perturb, and in any case the system is endlessly perturbing itself.
4. A Lorenzian model of climate is one that has the fundamental property that it is always changing. Once this is understood, then the term “climate change” is emptied of meaning. “Climate” and “climate change” have the same meaning so “change” is a redundant tautology, the same as saying “the Catholic Pope”.
The use of the term “climate chage” is a statement of denial of or of ignorance of DNF1963 and its inescapable implications.
Phil Salmon
“1. DNF1963 does exist”
Yes, I’ve discussed it here.
“2. The concept of equilibrium in climate dynamics is invalid”
The concept is OK. It may not be attained.
“3.The concept of perturbation from a (fictitious) equilibrium is invalid”
The theory of feedback does not require perturbation from equilibrium, though a stable operating point is conceptually easier. It just describes what happens to perturbations. As to endlessly perturbing, many feedcack amplifiers are constantly responding to signals (eg telecom repeaters). Feedback analysis still works.
“A Lorenzian model of climate is one that has the fundamental property that it is always changing.”
It has the property that it is always evolving according to trajectories that lie on the attractor. But if the attractor shifts, that is something else. AGW moves the attractor.
philsalmon:
My response to you was perhaps too cursory. I don’t deny anything you say about chaotic systems.
I just don’t see how it’s germane to the question before the house, which is whether climate models’ hypersensitivity results from modelers’ failure to recognize various temperature-affecting quantities’ responses to temperatures below the “emission temperature.” The only arguments I’ve seen for that proposition are Lord Monckton’s inept math and irrelevancies such as how feedback is defined.
Yes, yes we can go off on tangents about sensitivity to initial conditions, strange attractors, etc., etc. But what I’m concerned about is that Lord Monckton has horned into that lawsuit with an appalling amicus brief that makes skeptics look like buffoons. Previously he was relatively harmless. Now he has become destructive.
The Born Liar lies again. He now tries to maintain that he made an undeclared alteration to his old argument to take account of some variations in my numbers. That, of course, is nothing but mendacity, for the head posting makes the point that our argument has come full circle, so that we end up with the feedback fraction 0.08 with which we started. Mr Born’s real reason for his undisclosed reworking of his numbers was that he had been humiliated by my pointing out that his earlier attempt had implied a Charney sensitivity not much greater than our own. And, even now, the best he can do is reach a Charney sensitivity of just above 2 K, which is right at the bottom of the models’ range.
He has utterly failed to provide any evidence even to the effect that the net feedback fraction will increase exponentially rather than remaining approximately linear or even declining. He has utterly failed to provide any evidence that – since such small net nonlinearity as may obtain in the feedback process is no less present under the present disposition than under our correction of it – our result will do anything other than greatly reduce equilibrium sensitivities.
All he has done – which did not need to be done – was to devise an artificial scenario bearing little or no relationship to the real climate, and then to show that under that manifestly absurd scenario the temperature feedbacks would somehow know that they should produce 15 times as much response per Kelvin to the presence of the non-condensing greenhouse gases as to the emission temperature. He has offered not a shred of evidence for or explanation of that startling discontinuity, which bears no relation whatsoever to the near-perfectly thermostatic behavior of the climate over the past 810,000 years.
The Born Liar has provided not a shred of evidence that the models take any account of the large feedback to emission temperature. So far, it is only I who have done that – and, even then, the paper I cited did not make any explicit statement that the additional temperature was a feedback response to emission temperature. He has now gone so far as to say he cannot quite believe that the models did not take the feedback response to emission temperature into account, which is perhaps a small step on his part towards the light. But, to everyone but a true-believer sullenly determined to adhere with naive faithfulness to the Party Line, it is surely obvious by now that IPCC’s definition of a “climate feedback”, recited in the head posting, precludes absolutely the assignment of any value to the feedback response to emission temperature; and, now that the Born Liar has had two failed attempts at producing scenarios that correct official climatology’s error, both of which implied Charney sensitivities very considerably below even the mid-range official estimate, and a fortiori still further below the foolish high-end estimates on which policies are based, it must now be apparent even to him that official climatology cannot possibly be giving due weight to the feedback response to emission temperature, for otherwise even its mid-range estimate would be absurdly excessive.
Mr Salmon’s most interesting comment deserves a considered response. I, too, am fascinated by Edward Lorenz’s great paper on deterministic nonperiodic flow – the paper (my edition of it is dated 1963) that founded what would later come to be known as chaos theory, though Lorenz himself did not use the term. Mr Salmon may perhaps also have read the paper by Giorgi (2005) on chaoticity in the climate, and perhaps also the magisterial and also delightful paper by Sir James Lighthill (1998) on chaoticity in the oscillation of a pendulum.
I have seen some arguments to the effect that the climate is not a chaotic object. However, it is plainly an object that behaves chaotically. As Lorenz’s title makes clear, the fact that an object behaves chaotically does not prevent it from behaving deterministically; but chaoticity makes the evolution of the object over time very difficult to predict. My favorite examples of this predictive difficulty are the Mandelbrot set, whose equation is remarkably simple but which constitutes the most complex object in all of mathematics, and the Verhulst population model, which is ordered until the population growth rate exceeds 3 by even the smallest fraction, whereupon its behavior is chaotic.
Mr Salmon is of course quite right that, provided that the index variable or variables is or are within the interval over which chaos reigns, all talk of an “equilibrium” is vain. However, I submit that it is permissible for official climatology to posit actually unobtainable equilibria as the start-point and end-point of a time-series evolution of the chaotic object that is the climate, and then to try to investigate the impact of anthrogenic influences on the closing equilibrium.
The point of our research is simply this: that one must take explicit account of the full feedback response to emission temperature: for it is a large response, accounting for some two-thirds of what is currently and erroneously thought to be the “natural greenhouse effect” caused by the presence of the non-condensing greenhouse gases. However, IPCC’s definition of a “climate feedback” makes no provision for this large feedback response, and, indeed, does its best to exclude it, so that that response can be quietly added to the far smaller feedback response to the presence of the non-condensing gases, thereby greatly inflating equilibrium sensitivity.
A Lorenzian model of climate is one that has the fundamental property that it is always changing. Once this is understood, then the term “climate change” is emptied of meaning.
Nope.
The Lorenz model is actually nothing but a model of Rayleigh-Bénard convection.
https://en.wikipedia.org/wiki/Rayleigh–Bénard_convection
Mathematically it’s a system of 3 coupled non-linear differential equations with 3 variables X,Y, Z and 3 parameters such as the Prandtl number. The parameters are constant quantities related to fluid properties and imposed boundary conditions such as the temperatures held constant on lower and upper plates. In Lorenz calculations they do not change as the dynamic system evolves and representative point (X,Y,Z) follows its trajectory on attractor.
As pointed out by Nick Stokes, the analogy with a specific climate is a specific attractor that corresponds to a specific set of parameters.
Climate change is thus a change in the attractor brought about by a change in the parameters of the non-linear equations. For instance in Lorenz model the imposed boundary temperatures or in climate the sun “constant” or atmospheric CO2 partial pressure.
This is in sharp contrast with a change in variables (X,Y,Z) that is the analogue of weather in a specific climate.
The concept of equilibrium in climate dynamics is invalid
It isn’t invalid.
Climate system is a dissipative structure and “equilibrium” just means that usually a steady state is reached where an essentially constant flow of energy traverses and dissipates in the system. In other words: energy in = energy out, when averaged over some period of time. Energy is just degraded, entropy produced in the system but there is no substantial accumulation or depletion of energy in the system.
Lord Monckton seems unable to refrain from falsehoods. First, he cannot possibly know why I changed the numbers. Second, the “Charney sensitivity” I reported last time was 3.25 K. Third, the value this time to account for his number change was 3.21 K. Moreover, I needed only change parameters if I had wanted even higher sensitivity values.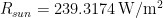
and feedback function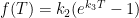 
:
, 
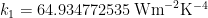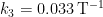
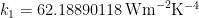, and 
, 
, and 
,
If anyone wants to see for himself who tells the truth, he can reproduce the calculations I described in the comment above. To that end I provide here values pulled directly from the computer, without truncation:
The (after-albedo) radiation absorbed by the surface:
The parameters for the open-loop function
Temperature before naturally occurring greenhouse gases (“NOGs”) or feedback: 255.4 K.
Temperature before NOGs, but with feedback: 255.4 K. + 15.20079 K = 270.60079 K.
Temperature with NOGs, but before feedback to NOGs: 270.60079 K. + 7.8141 K = 278.4149 K.
Temperature with NOGs and feedback: 278.4149 K. + 9.184937 K = 287.599824 K.
Temperature with CO2 doubling but without feedback to CO2 doubling: 287.599824 K + 0.9815485 K = 288.5813721 K.
Temperature with CO2 doubling and feedback: 288.5813721 K + 2.231325 K = 290.812697 K.
“Charney sensitivity,” i.e., the difference between the temperatures with and without CO2 doubling: 290.812697 K – 287.599824 K = 3.212873 K. That is, not Lord Monckton’s “2 K.”
Now the parameters that I used last time in order to produce Lord Monckton’s previous number (244.6 K) for the temperature before NOGs or feedback:
which after somewhat different intermediate values yielded a “Charney sensitivity” of 3.24344 K. (It appears I made a transcription error last time; I reported 3.25 K.)
So, as usual, what Lord Monckton says isn’t even within shouting distance of the truth.
As usual, Lord Monkton spouts irrelevance. I had never contended that I had any evidence for an increasing “feedback fraction.” In fact, I explicitly stated just the opposite:
And I then demonstrated that if modelers thought temperature-affecting quantities’ sensitivity to temperature increased disproportionately with temperature—as they likely believe in light of evaporation’s response to temperature—then, contrary to what Lord Monckton continues to contend, they don’t need to ignore responses to temperatures below the “emission temperature.”
Lord Monckton keeps running from that point by filling these threads with falsehoods, irrelevance, illogic, and sophomoric name-calling. He gives us bombast instead of substance, logorrhea instead of logic, and falsehoods instead of truth.
Nick, Christopher, Joe, gammacrux
I’m grateful for your replies to my amateurish contribution on my favourite chaos theme (I’m a marine biologist turned radiobiologist taking an interest in climate). I probably overstated my case for rhetoric effect.
Nick – I appreciate your acknowledgment of attractors – but I don’t see much of that language in the IPCC and climate literature. I still feel it needs to move more center stage, in many scientific fields not only climate.
Christopher – thanks for the perspective and useful references. “Deterministic” was I guess used by Lorenz in the mathematical sense. That chaos can be represented mathematically makes it deterministic in an ideal Laplacian manner. But the knowledge of initial conditions required for such predictiveness is impossible so in practice deterministic becomes non deterministic. I think the really interesting and important thing about Lorenz’ simulation, on almost the world’s first computer (aside from Turing’s WW2 colossus), is that the system changes by itself without forcing from outside.
Joe
I’m a mere biologist and can’t do complex maths. Chaos literature is full of scary formulas which I ignore entirely and just look at the pictures. (I can just about understand Feigenbaum’s quite simple conditions for chaotic bifurcation.) Monckton’s prose description of his essential case did however seem to make sense. The emission temperature is the “equilibrium” temperature with a warming effect of CO2. Then there is an additional temperature increase caused by a perturbation in the form of an incremental addition of more CO2. The question appeared to be – do feedbacks in the system apply only to the incremental temperature increase from the incremental CO2 addition, or do they apply to all the temperature difference between an “equilibrium” entirely without CO2 and the final temperature with “baseline” and incremental CI2 added. Put in those terms, it seems reasonable that feedbacks should indeed apply to all the temperature elevation caused by CO2. Critics have challenged CM saying “you can’t apply feedbacks to the equilibrium situation, only the incremental”. But even the additional warming from the incremental CO2 still leaves you at an equilibrium. So what indeed is the difference and why discriminate between the two?
(This is how biologists try to verbalise such questions – avoiding maths but still considering ourselves scientists.)
I felt that a chaos perspective would have feedbacks operating instantaneously on the system at all times whatever its state – since the state would always be changing.
gammacrux
The Lorenz model is actually nothing but a model of Rayleigh-Bénard convection.
What’s wrong with that? What is climate other than turbulent flow of water and air?
philsalmon
What’s wrong with that? What is climate other than turbulent flow of water and air?
Nothing is wrong with that. My remark was just to provide the proper context of chaos theory of dynamic systems and emphasize the origin of your misunderstanding, namely the major difference between parameters and variables in that theory.
Yet, that said, climate is actually much more than just a problem of fluid mechanics or evolution of a dynamic chaotic system. It involves a lot of so-called emergent phenomena that definitely cannot simply be inferred, deduced or anticipated from first principles of physics. They must be discovered and studied by observation and experiment.
Biology for instance is clearly involved in cloud formation, for instance with the aerosols produced by marine life and living creatures are precisely the most remarkable emergent phenomena in nature.
So to come back to the concept of “equilibrium”, I can’t see why you dispute the validity of that concept for the climate system while as a biologist you certainnly readily admit it in the case of a living creature such as a grown-up animal. In both case a steady state may eventually be reached where there is nothing but a constant flow of energy that just traverses, degrades and dissipates in the system. No net energy accumulates in or flows out of the system, i. e. the climate doesn’t warm or cool on one hand and the animal neither changes its temperature nor gains or loses weight on the other hand.
The Born Liar provides a Gish gallop of numbers artfully intended to conceal the fact that the equilibrium sensitivity inherent in those numbers depends upon the feedback fraction 1 – 8.9 / 17 = 0.48, giving Charney sensitivity <2,.1 K. And he still provides no explanation of how it is that after correction of official climatology's large error Charney sensitivity remains unaltered at the current official mid-range estimate. Fortunately, very few are paying attention to the Born Liar's expatiations, since he cannot conceal his malevolence. His, therefore is not trustworthy testimony, on grounds of prejudice. It may be disregarded.
Monckton of Brenchley April 7, 2018 at 8:31 am
It is now time for the SNIP Monckton to stop being arrogant, stop being vicious, stop being spiteful, stop describing results he does not understand as “risible”,
And let him do all this politely, civilly, and in a spirit not of trying to find personal fault with me but of trying to attain the objective truth.
Corrected.
Phil. April 10, 2018 at 9:49 am
“Monckton of Brenchley April 7, 2018 at 8:31 am
It is now time for the SNIP Monckton to stop being arrogant, stop being vicious, stop being spiteful, stop describing results he does not understand as “risible”,
And let him do all this politely, civilly, and in a spirit not of trying to find personal fault with me but of trying to attain the objective truth.”
Corrected.
Interesting that my strike-through of Monckton’s insulting remark is deemed worthy of snipping by the Moderator whereas the original insult by Monckton is not and he continues to use it!
Let us conduct a simple Gedankenexperiment, running in reverse the model of Lacis et al. (2010), who found that
I’m a big fan of Christopher Monckton of Brenchley, he’s been a wealth of information and a voice of sanity in this debate. But I question this approach.
The fatal flaw (IMHO) is that we have no way to determine if Lacis et al is accurate. He didn’t test an actual earth, he modeled it. If the model was wrong, then his result, and Christopher’s Gedankenexperiment which is arrived at by running it in reverse, is also wrong, is it not?
I was thinking this as well.
I agree. MB needs to keep it simple, and that whole analysis is just muddying the waters.
Steve Richards is correct and, with respect, David Hoffer has perhaps not understood the limitations of a Gedankenexperiment. I had hoped, in the head posting, to make it clear that I considered Lacis (2010) to be wrong, as my own reverse running of their experiment plainly demonstrated. I had also made it clear that other values of – for instance – albedo and hence of emission temperature might be chosen, though they would not make any difference in the long run.
A Gedankenexperiment is an illustrative example: nothing more. if it doesn’t work for you, no matter: the underltying math still ineluctably requires a substantial feedback response to emission temperature that IPCC’s definition of a “climate feedback” altogether rules out: and, if that response is properly taken into account in its own right rather than being arbitrarily counted as part of the far smaller feedback response to the non-condensing greenhouse gases, equilibrium sensitivity must fall, and fall substantially.
if it doesn’t work for you, no matter
It doesn’t matter if it works for me or not. The alarmist argument has been without merit or evidence for many years. It has been running on emotion and hype for as long as I’ve been paying attention. Finding fault with one paper that may or may not be correct doesn’t persuade the common man.
Mr Richards has it exactly right. Lacis et al. are the nest of vipers at NASA who have been profitably peddling extremism as though it were science. I have taken their paper as an illustration of the error that has been made – but it is only an illustration. It should surely be possible for Mr Hoffer to read the head posting and appreciate that practically nothing in our argument would fall away if we ignored Lacis altogether.
The central question remains – a question that all the true-believing climate fanatics here have been entirely unable to answer in any intelligent fashion. How is it that inanimate feedback processes are capable of distinguishing between emission temperature and the small enhancement of it represented by the direct warming from the presence of the naturally-occurring, non-condensing greenhouse gases, so that they react little if at all to the former but very strongly to the latter?
If Mr Hoffer does not grasp just how fundamental this point is, and just how little it depends on anything in Lacis et al., then my powers of exposition are less than I had hoped.
It should surely be possible for Mr Hoffer to read the head posting and appreciate that practically nothing in our argument would fall away if we ignored Lacis altogether.
Then may I respectfully suggest that you make the argument in just that fashion.
Mr Hoffer need only remove those parts of the head posting that mention Lacis’ paper. The remainder will provide quite enough to chew on.
The whole basis of Moncktons work in this post is to assume that all of ‘official’ climatology is correct and show one major ‘official’ fault with its workings.
If this fault is agreed then it dismantles the climate scare.
No more no less.
Is Lacis et al correct or incorrect? It does not matter other than the fact it is:
a) Is lauded by ‘climatologists’;
b) adopts all current climate theory.
Show the major flaw and the walls fall down.
“At the 255.4 K that would prevail at the surface today without greenhouse gases or feedbacks…”
Without greenhouse gases there would be no cloud albedo. The zero albedo black body figure for the hypothetical uniformly heated globe is 394*0.25^0.25 = 278.6K. For the oceans with a 0.06 albedo that would be reduced to 274.32K or 1.17°C.
“Without greenhouse gases there would be no cloud albedo.”
No you could have water vapour without CO2. The real problem is that the earth started with CO2 and the water came later. the analysis should g o right back to the beginning 4.6 billion years ago. All Monkcton is saying is that there has to be a forcing of water vapour that is always much greater than the forcing of CO2. He rightly points out that the climate models have the sensitivity equation backwards by having a large CO2 forcing at the 1850 year which should have been a large cloud and H2O forcing which then drives the smaller CO2 forcing. Actually Moncktons 1850 bar graph should be (based on his brief submission to the court) 8K for clouds 23.4 K for H2O and 0.8 for CO2. Both Monckton and the climate models attribute a much too large temperature forcing caused by CO2.
Irrelevant to my point.
Yogi Bear appears not to have read the head posting. So let me review the necessary elementary climatology,. First, emission temperature is a function solely of insolation and albedo. If the albedo is today’s 0.293, then the emission temperature will be 255.4 K, and that temperature will obtain at the Earth’s surface. However, there cannot be an albedo as high as 0.293 without clouds and ice, implying the presence of water in various forms, not the least of which is water vapor. Water vapor is a condensing greenhouse gas, and its existence provides the mechanism of a feedback process. That feedback process responds to emission temperature, so that the Earth’s surface temperature will be significantly higher than the emission temperature, even before taking any account of the presence of the non-condensing greenhouse gases.
Monckton appears not to have understood my quote of his, which claimed:
“At the 255.4 K that would prevail at the surface today without greenhouse gases or feedbacks…”
An albedo of 0.293 does naturally imply clouds and water vapour, which is the larger part of the so called greenhouse effect, so the surface temperature would have to higher than 255K without greenhouse gases or feedbacks according to your definition of water vapour being a feedback.
But the water vapour is not a positive feedback to 255K, it’s a thermal reservoir that moderates the diurnal temperature swings like the oceans do. And has enough thermal capacity to enable strong poleward heat transport, as a negative feedback to net changes in total climate forcings.
Yogi Bear is entitled to his opinion about what does and does not constitute a temperature feedback. However, in the head posting we have made it explicit that, for the sake of argument, we have accepted for the sake of argument all of official climatology except what we can prove to be wrong. And, whether Yogi Bear likes it or not, the water-dependent processes in the climate are represented as feedbacks in official climatology. That is precisely how we have represented them, and that is precisely why there is a substantial feedback response to emission temperature – a response that IPCC’s definition of a “climate feedback” does its very best to exclude from the account. In that respect, IPCC is simply wrong.
It’s not a feedback, it’s a longwave clawback from cloud albedo losses, and from near infrared losses by water vapour.
Yogi Bear is entitled to his opinion that the water vapor feedback is not a feedback. But in the head posting I have accepted ad argumentum all of official climatology except what I can prove to be incorrect, and official climatology treats the water vapor feedback as a feedback, denominated in Watts per square meter per Kelvin of the temperature that induced it.
‘Official climatology’ says that Earth’s surface temperature without all greenhouse gases and water vapour is 279K (minus the surface albedo) and not 255K.
“official climatology treats the water vapor feedback as a feedback”
To net changes in surface temperature of course. You cannot legitimately call it a feedback to absolute temperature when it physically substantially reduces maximum daytime land surface temperatures.
Yogi Bear is confused. The water vapor feedback delivers a feedback response to any temperature that is present, whether that temperature be the input signal from the Sun or some amplification thereof forced by the presence of non-condensing greenhouse gases.
“Yogi Bear is confused.”
No you are.
“The water vapor feedback delivers a feedback response to any temperature that is present, whether that temperature be the input signal from the Sun…”
Nonphysical word salad. Water vapour inhibits direct surface heating by the Sun as it absorbs considerable amounts of solar near infrared.
“…or some amplification thereof forced by the presence of non-condensing greenhouse gases.”
You don’t know that a net increase in non-condensing greenhouse gas forcing causes a positive water vapour feedback.
Yogi Bear is even more confused. If the water vapor feedback is negative, as he appears to be suggesting, then our result is demonstrated a fortiori. However, ad argumentum we have accepted all of official climatology except what we can prove to be wrong, and official climatology considers the water vapor feedback to be positive. It does not care whether it is responding to the emission temperature or to the addition to emission temperature caused by adding in the non-condensing greenhouse gases, or to the further temperature increase caused by anthropogenic forcings. It is positive in respect of all of these. However, it is not very strongly positive.
Standard climatology sensibly does not consider water vapour a feedback to emission temperature.
Fourth draft posted. Why?
Write it up, Monckton, submit it for peer review. Quit trying to …what are you trying to do, anyway? Convince more people of this egregious error you go on and on about? If they aren’t convinced yet, why would it work now? How have you dealt with the problem that to have a feedback there has to be initial change? You haven’t, so it’s all a waste of time. Try publishing it and see how far you get, since you’re such a superior scientist. Oh, yeah, you aren’t a scientist. No wonder you don’t get it. Funny how so many skeptics think you have expertise, often the same ones who think that those who went through a decade of post-secondary education and devoted their professional lives to science are so brainless that none of them have thought of looking at natural variation for a explanation for climate change.
And why do you focus on this one paper by Lacis, et al., anyway, if all climate change models by the AGW consensus community suffer from the same error?
You should stuff yourself in a box. According to climatologist orthodoxy your 98.6F body temperature should generate 525+262.5+131.25…=1050 W/m^2 or 204F, and you’ll fry.
That didn’t happen? Lucky you. Then how can you believe climate junk science? Oh yes, you’re a fool, that’s how. You can’t understand the trick played on you by liars who pose as scientists.
Zoe,
That would depend on how well insulated the box was and if you continued to generate heat. If you
were in a box composed of silica aerogel surrounded by a vacuum and had some way of eat then you
would fry.
Germ,
Kristi’s body continually generates heat for days. She can be insulated in solid co2 to emulate extreme co2 atmosphere. WUWT is an infamous source of insight that cooler insulators heat a warmer source, so she should fry, not freeze.
Fortunately, “climatologist orthodoxy” is not nearly as simplistic as you pretend.
” You can’t understand the trick played on you by liars who pose as scientists.” I guess you don’t see the irony in this.
Oh, yeah, you aren’t a scientist
≠========
Drivel. Mathematicians are scientists. Mathematics is the language of science.
As the saying goes: all mathematicians can do science, but not all scientists can do math. Nowhere is this more evident than climate science.
Monckton a mathematician? Does he have a degree I don’t know about, one apart from classics and journalism? Just because someone can do math doesn’t make him a mathematician.
What saying? Mathematicians are not all scientists, although the two fields may collaborate, and climate science is an instance of that. However, mathematicians are not necessarily trained in the methodologies of science.
Fredberple,
It is off topic but Mathematicians are not scientists. Numbers are social constructs and do not
exist in reality but rather follow whatever rules we make up. Some of those roles are amazingly
good models for reality but others aren’t. Some applied mathematicians do science but many others
do amazing research in topics like number theory but they are certainly not doing science.
Germonio appears to think that those of us who study number theory are not doing science. To imagine that pure mathematics is divorced from science is a common and elementary misconception. For instance, the Boolean algebra used in the logic circuits of computers originated in number theory. Even the use of propositional calculus to improve railroad timetabling on busy routes comes from number theory. It was from number theory that many of the fundamental constants of mathematics were derived. And who would have thought that a simple result in probabilistic combinatorics – another branch fo pure math – could be turned into a pair of award-winning, best-selling jigsaw puzzles with million-dollar prizes?
The division between pure and applied math was always to some extent artificial. It is now rapidly disappearing.
Monckton wrote: “Germonio appears to think that those of us who study number theory are not doing science.”
Mathematicians and scientists have different ways of thinking. Scientists start with hypotheses and attempt to DISPROVE them through experiments. Those hypotheses that survive extensive testing become theories. The predictions of well-tested hypotheses can be trusted even if the theory is later revised – when those predictions are within the scope of the theory that has been well tested.
In mathematics, you start with a set of axioms and deduce as much as possible from them. There is little emphasis on testing axioms to see if the deduced mathematics tell us anything useful about the real world. Roe set out some axioms for feedback analysis of climate. You use those axioms to make deductions about amplification of warming. It doesn’t make any difference that Roe requires you to use information from climate models that you don’t believe in. Roe’s axions require a reference state. One version of Roe’s deduction is limited to linear feedbacks, while another version deals with non-linear feedbacks. Unfortunately, you don’t have the data to apply the non-linear version, so linearity becomes one of your axions – not a hypothesis that must be proven to be correct.
A few videos on Youtube show Feynman discussing the difference between mathematicians and physicists.
Frank does not appear to understand that mathematics – which is the language of the sciences – uses all of the methods of applied science and then some. Not the least of the weapons in the arsenal of mathematics is formal logic, in which I have no little training. One of the logical methods of formal demonstration or absolute proof is known as demonstration by contradiction. This method originated with Socratic elenchus, where the great philosopher would take his opponent’s proposition and draw conclusions from it that were agreeable to the opponent. He would then advance a proposition of his own, with which the opponent was likely to agree. When the opponent agreed, Socrates would draw conclusions from the second proposition, and the opponent would agree to them. Then Socrates would point out that one of the conclusions from the second proposition was incompatible with one of the conclusions from the first. If elenchus is deployed correctly, the opponent is left with no choice but to abandon his original proposition,.
Now, control theory contends that even an unamplified input signal will induce a feedback response provided that nonzero feedback processes are present,. This is long and well established, and we tested it empirically at a government laboratory just to make sure.
However, IPCC contends that an unamplified input signal cannot induce a feedback response. Either control theory is correct or IPCC is correct, but not both at the same time.
It is easy to see, using the corrected form of the zero-dimensional-model equation, that IPCC’s definition of a climate feedback is incorrect in that it limits a feedback response only to a perturbation in an original temperature, rather than also to that original temperature itself.
Silber
“How have you dealt with the problem that to have a feedback there has to be initial change?”
All Monckton is saying is that it is the climate models have the forcing built in. He is only ascribing the forcing that the climate models even in 1850 have built in. There has to be some because there was always CO2. There always is a feedback mechanism working. If you were a mathematician Kristi you would have understood that.
“How have you dealt with the problem that to have a feedback there has to be initial change?”
=====!!
Feedback operates on both AC and DC. When the sun warmed the earth from 3 K to 255 K that evaporated water which is the feedback that further warmed the earth. The 255 K temperature today keeps some amount of water in the atmosphere which warms the earth. Itbis this specific warming that has been overlooked in the analysis of climate feedback.
Silver: “How have you dealt with the problem that to have a feedback there has to be initial change?”
Every 24 hours there is a chain temperature. That should be enough to get the ball rolling, no?
*change in”, not “chain”
Of course there are feedback mechanisms. Monckton is not just saying that climate models have the forcing built in, he is changing the math, saying that there is feedback associated with a state, a temperature. Haven’t you been following the argument? Delta T is not the same as T.
Are you a mathematician, Alan? I’d like to have a trained, experienced mathematician explain how this is possible.
Silber says I have “changed the math”. If only it would read ch. 3 of Bode (1945), the standard textbook, it would rapidly discover not only that the corrected form of the zero-dimensional-model equation is what I say it is: it will see a formal proof of exactly how that equation is derived. There is nothing new in our math: what is new is our exposure of the fact that climatology has not made due allowance for the feedback response to emission temperature – a response that can be calculated by using the corrected form of the zero-dimensional-model equation.
Silber whines that there have been four articles in this series. But Silber is not obliged to read any of them, so why whine? If Silber had read the head posting instead of whining about it, Silber would have learned that I have provided a formal demonstration that there must be a feedback response to any temperature in the presence of at least one feedback process.
Silber describes me as a superior scientist and then as not a scientist at all. Perhaps Silber would like to decide upon one or the other viewpoint: they are mutually incompatible.
Silber then perpetrates the argumentum ad verecundiam by imagining that my distinguished co-authors lack the certificates of due Socialist training in climatology that I have at no time pretended to possess.
Finally, Silber asks why I focus on one paper, when I cited several, taking the one paper as the basis for an illustrative Gedankenexperiment. That is a standard method in the philosophy of science, a topic that formed part of my instruction at Cambridge (and I even have a certificate of appropriate Socialist training in Classical architecture, which embodied many ancillary elements such as the philosophy of science as well as the uses of early mathematics).
Silber is perhaps better at Socialist sneering than at science.
Monckton, you have no made any formal demonstration of anything. You have created a whole new
equation
T= T_ref/(1-f)
that superficially looks like Roe’s
Delta T = lambda_0 Delta F/(1-F)
but in fact is completely different and there is no logical way you can derive your equation from the
correct equation in Roe 2009. Simply stating that it is the correct equation is not sufficient.
Whining? That’s a laugh.
I corrected myself – of course you are not a superior scientist, you are no scientist at all. Perhaps you haven’t professed to scientific expertise; why, then, do you feel qualified to say real scientists are unquestionably wrong? Why haven’t you corrected those in the media who have made the mistake of saying you are an expert?
What the eff has this to do with socialism? That’s a classic denier move: attach a political ideology to a scientific theory in order to impugn those who have developed it or believe it. It has nothing to do with the quality of the science, which should never be viewed through the lens of politics. It’s the results of science that are used in policy-making, not policy that determines the science. The latter is an accusation oft made about “consensus” scientists, while the influence of politics on contrarian scientists is conveniently ignored.
Monckton, you are completely wrong about me being a socialist, not that it’s any of your business. The fact that you say such a thing is all the more reason for me to distrust your ability to view climate science from a scientific standpoint, rather than a political one. So much do you desire to “win,” you bring up personal issues that have nothing to do with the subject.
I don’t trust you, Monckton. Can you explain why the House of Lords had to issue an official statement that you never were a member? Why have scientists issued statements saying you misrepresented their work?
(If this is a paper written with co-authors, why aren’t their names in the by-line here? Why do you say “I did…” rather than “we did…”?)
” Most of those who have tried to dismiss our result in these threads know perfectly well that we are in substance right, and no amount of dressing up the actually very simple argument in other clothing would make any difference. These are not people in search of the truth: they are totalitarians wedded to the Party Line for good or ill. In due course we shall find a reasonably serious climate journal to publish our result, which will gradually become well enough known that no one will be able to ignore it, however uncongenial the true-believers may find it.”
Another convenient assertion that is not based on evidence. If argument from reason fails, attack the characters of those you can’t convince. It’s an old propaganda ploy; too bad so many people still fall for it.
(Please refocus onto the topic itself) MOD
Silber now reveals itself as a totalitarian by the use of the contemptible word “denier”. I do not care whether it calls itself a socialist or a marxist or a maoist or a communist or a fascist: it is a totalitarian. For none but a passionate adherent of some rigid Party Line or another would use the deliberately loaded word “denier” of someone who, like me, has stated explicitly in the head posting that he has accepted for the sake of argument all of official climatology except what I can prove to be wrong.
Germonio says that Roe’s form of the zero-dimensional-model is correct. Well, gee, get with the picture. That point is made in the head posting, which says that one can of course use that form of the equation without much error – provided that one has first made due allowance for the large feedback response to the input signal, which, in the climate, is emission temperature. The corrected forms of the equation presented in the head posting made that adjustment.
“Try publishing it and see how far you get, since you’re such a superior scientist.”
Well, he has submitted it to one journal, but the reviewers are giving him a hard time.
Christopher,
Would it help clarity if you replaced your original T with a (T plus delta2T) right from the start, to show that feedbacks are operating even at what some wrongly call an equilibrium?
Then carry this through the algebra you develop above. Hope this helps and does not retard. Geoff
Mr Sherrington makes a constructive suggestion, but I fear it would make little difference. Most of those who have tried to dismiss our result in these threads know perfectly well that we are in substance right, and no amount of dressing up the actually very simple argument in other clothing would make any difference. These are not people in search of the truth: they are totalitarians wedded to the Party Line for good or ill. In due course we shall find a reasonably serious climate journal to publish our result, which will gradually become well enough known that no one will be able to ignore it, however uncongenial the true-believers may find it.
I remain open to a proper argument against our result: but none has thus far been forthcoming.
Off the top of my head I believe you can decompose an infinite geometric series into T + delta T and from there show that the climatology definition of feedback is a special case of the general feedback equation.
In effect decompose the signal into DC and AC and show that the sum of the sum(AC) + sum(DC) = sum(AC+DC).
done as a mathematical proof I don’t believe climatology can prevail.
The series continues to attract widespread attention, not only here but elsewhere. The ripples are spreading.
So funny.
gammacrux is right. It is amusing that the word is spreading so quickly. If our result were laughably wrong, it would not merit anything like the attention it is getting.
The essential issue here is will your paper pass peer review in time to be considered in AR6?
I know that that is out of your hands, but that must be the target.
Sorry Lord Monckton.
I meant “so funny” because your assertion is just wishful thinking.
Ah, it appears that the furtively pseudonymous “gammacrux”, having no scientific point to make, is resorting to mere yah-boo. But the evidence is against “gammacrux”. Just look up Yahoo answers. Now, why would anyone bother to try to trash our result as Yahoo has tried to do, unless our result was a lot more serious than the totalitarian shriekers here have tried to suggest?
Teq = Tref / (1 – f )
============
This is also the formula for the sum of an infinite geometric series, which is the mathematical equivalent of how feedback works physically.
It is hard to argue with this being anything other than the correct description for feedback when it is a simple enough matter to expand this formula into the underlying series, showing each of the iterations of the feedback loop.
Reply below next comment
And again, there is a much bigger mistake, which is much simpler to explain, logically more stringent and it has much more profound consequences.
Clouds make up for most of the albedo, how much exactly can be discussed. Commonly that share would be named to be 2/3s or more of the total albedo, which means something north of 2/3 * 0.31 * 342 = 70.7W/m2. I would confirm that and name the figure to be more like 80W/m2.
While this reflection of solar radiation will doubtlessly lower surface temperatures, clouds will also provide a positive radiative forcing, which then is treated as part of the GHE. As clouds have both, negative and positive effects on surface temperatures, seperating these two effects as if they had nothing to do with each other, is illogical, or straigt forward stupid.
Anyhow, the GHE of clouds is treated as a part of the total GHE, and such they will compete with other GHGs. So the bigger the share of clouds in that role, the smaller the possible contribution of vapour, CO2, methane and so on..
What the IPCC, what the consensus modellers tell us is this: clouds had a negative forcing of somewhere between 13-20W/m2 over all. There would be about +30W/m2 by (re)emission of LWIR and -44 to -50W/m2 be reflection of solar radiation. These +30W/m2 would be their contribution to a total GHE of about 155W/m2.
At that point there are logical mistakes all over the place, which are to be corrected.
1. If clouds emit 30W/m2 downward, they will also emit radiation upward. A fact that is otherwise well acknowledged, just look at the NOAA chart.
2. If clouds emit about 30W/m2 upward as well, both sides of that coin will neutralize each other.
3. The (negative) net forcing will then logically be equal to the albedo effect, which would be either 44-50W/m2, or more realistically, 70-80W/m2. That is as long as we follow the claim clouds would not at all reflect LWIR.
4. A massive negative net forcing of that kind however is not in line with any observations. Indeed, what we see are rather higher temperatures with clouds covers, than without. Ironically that seems specifically true for low clouds in the tropics. (low tropical clouds should have the strongest net negative effect of all, according to the IPCC).
5. Weather data show that temperatures during the night drop by 85% less when there is an overcast sky as compared to a clear sky. So we do know, that clouds stop LWIR from emitting at least as efficient as they block solar radiation by reflection.
6. This effect could not be achieved by merely emitting 30W/m2 of LWIR upward AND downward, which is a neutral thing after all.
7. Rather point 4 and 5 indicate, that clouds must provide a positive forcing that is at least as strong as their total negative forcing. And of course, that positive forcing is competing with other GHGs in that role.
8. As the NOAA chart (correctly!) indicates, total negative cloud forcing amounts to 79W/m2 (reflection of SWR) + 31W/m2 (emission of LWIR) = 110W/m2 (presented as 23% and 9% of 342W/m2).
9. Thus clouds must provide > 110W/m2 to the total GHE of only 155W/m2.
10. The 155W/m2 figure (which is consistent with the infamous 33K GHE) is derived from an assumed 391W/m2 surface emissions (which corresponds to an emissivity of 1 at 288K) and 236W/m2 (=(1-0.31)*342). Real surface emissivity however is not 1, but rather 0.92. Accordingly emissions will only be 360W/m2, dropping the GHE to only 124W/m2.
11. Finally the GHE constituted by all GHGs like CO2, vapour, methane.. can only be 124 – >110 = <14W/m2.
12. So the GHE itself is nothing more, than the logical consequence of deliberately wrong accounting the radiative effects of clouds.
https://de.scribd.com/document/370673949/The-Net-Effect-of-Clouds-on-the-Radiation-Balance-of-Earth-3
“It is hard to argue with this being anything other than the correct description for feedback “
It would be, if there were some system for which Tref is the input and T_eq was the output. But there isn’t.
So if clouds are 110 and total is 124 what is the H2O W/metre 2 and what is the CO2 W/metre2?
As I just wrote, all GHGs together (considering clouds are not definid as GHG), their forcing must be <14W/m2, or less than 3°K with the given numbers.
“However, Hansen (1984), Schlesinger (1985), IPCC (2007, p. 631 fn.), Roe (2009), Bates (2016) are just a few of the authorities who cite it.”
But they are, as always, not quoted. Let’s hear what they actually said.
The first two feedback diagrams are very odd. They show a loop with a feedback function but no amplifier. As an electronic circuit, they would tell you the feedback gain of a length of wire. They are not the “official climatology” model.
T_ref is not an input to a feedback loop. It is the expected output of a reference device without feedback; what would be called open loop gain. Here is Roe’s diagram:
As you’ll see, the feedback model has a change of forcing ΔR as input, and a ΔT as output. It is true that from this can be derived the relation ΔT_eq = ΔT_ref/(1-f). But that isn’t their feedback model. They are not saying that ΔT_ref is a feedback to ΔT_eq. It’s a ratio of two outputs of two different systems.
However, it is explicit that both ΔT’s are proportional to the forcing increment ΔR. That is why the ratio tends to f for small increments. It is a derivative. And why it makes no sense to introduce absolute quantities, which do not tend to zero, into such a ratio. The most you can get is a f value of 1 or -∞.
And so the equation, which first appears I think in the third diagram
ΔT_eq = T_eq -T_ref
is just wrong. ΔT_eq is the response of the feedback circuit to a ΔR. The difference T_eq -T_ref is just the difference between the operating points, possibly incremented, of two different systems. It makes no sense.
What is inside the box called “reference system”? Oh, it is the pre industrial system. So, the climate modellers failed to account for feedback within that box, as MB points out?
No, it is what would happen without feedback. Basically, the Planck sensitivity. You don’t have to worry about feedback within the box. It just has prescribed input/output behaviour. It could be an op amp, which has plenty of feedback within the box. But you just need to know the transfer function.
It is always nice when one does not have to think inside the box, and need only think outside the box!
Outside the box thinking is often wrong!
Mr Stokes finds that Dr Roe’s paper makes no sense. He should take that matter up with Dr Roe. And he seems stubbornly insistent that emission temperature, if unamplified, cannot induce a temperature feedback even where feedback processes are plainly present. In this, he is simply wrong.
“Mr Stokes finds that Dr Roe’s paper makes no sense.”
It makes perfectly good sense. It just has nothing to do with the caricature that you provide. Nor does “official climatology”. That is why analyses like this are useless unless you actually quote the theory that you are attempting to represent.
It is a caricature of feedback, too. In your third fig, you give μ = 1 + ΔT_ref/T_ref. Now in any sensible analysis of feedback or amplifiers, gain is a property of the circuit or device. It is not a function of the perturbation (ΔT_ref) that it may be subject to.
Mr Stokes quibbles about the definition of amplifier gain in a feedback loop. Let me instruct him, then, that his proposed gain factor, which is not unitless, is simply wrong. The gain factor is nothing more nor less than the unitless factor by which the signal from the input node is amplified before being passed to the output node. As in any amplifier, one can either build in or otherwise specify or set a gain factor, and that gain factor is – as a matter of extremely elementary mathematical definition – simply 1 plus the ratio of the change and the input signal.
“As in any amplifier, one can either build in or otherwise specify or set a gain factor, and that gain factor is – as a matter of extremely elementary mathematical definition – simply 1 plus the ratio of the change and the input signal.”
Again, the gain factor is a property of the amplifier. It is the number you use to multiply the input signal to get the output. Gain being a function also of the signal (“ratio of change”) would certainly create a nonlinear response. But more importantly, the gain would no longer simply be a property of the amplifier.
And in this case, if you take out the signal dependent component, the gain is fixed at 1, which is not interesting.
Of course the gain factor is a property of the amplifier. What else could it possibly be? But that does not stop us from specifying what that gain factor is.
“But that does not stop us from specifying what that gain factor is.”
But you haven’t, as a property of the amplifier. Your definition was μ = 1 + ΔT_ref/T_ref. ΔT_ref is the signal. It is not a property of the amplifier. In the limit of small signals, μ = 1. No gain at all.
Nick –
Equations relate dependent and independent variables. It is convention to put the dependent variable (to be calculated) left of the = sign and the independent variables to the right. Thus μ = 1 + ΔT_ref/T_ref is assumed a calculation of μ, perhaps based on an observation of the temperatures signals (if known!) on the right. If solved for ΔT_ref, the very same equation might oblige one to propose a value of μ as a known. Isn’t it anyone’s choice – subject to avoiding confusion – when possible!
Bernie
“is assumed a calculation of μ”
No, it’s the definition, as is explicit in the text above:
” μ = 1 + ΔTref / Tref is the gain factor representing any amplification of Tref”
He even reproves “official climatology” for leaving out the improvement:
“Note in passing that in official climatology f is at once the feedback fraction and the feedback factor, since official climatology implicitly (if paradoxically) assumes that the direct or open-loop gain factor μ = 1.”
“Official climatology” of course does nothing like this. And as usual, no quotes.
Mr Stokes should read the head posting, where he will find plenty of references to papers discussion the zero-dimensional-model equation. If official climatology were to use the corrected form of the equation, then and only then it would accord a value greater than unity to the reference gain factor mu. That factor is dropped from official climatology’s version of the zero-dimensional-model equation because the input signal (emission temperature) is suppressed and replaced by the reference sensitivity. it is in the input that official climatology incorporates what mainstream science treats separately as the reference gain factor mu.
Lord M,
“Mr Stokes should read the head posting, where he will find plenty of references to papers discussion the zero-dimensional-model equation.”
Yes, there are plenty of references. But you never quote what they say. Which is not connected with what you write about.
Mr Stokes’ remark is mere yah-boo.
Nick – you lost me with “….The first two feedback diagrams are very odd. They show a loop with a feedback function but no amplifier. As an electronic circuit, they would tell you the feedback gain of a length of wire. …” Feedback or feedforward???
Mr. Monckton had the same misunderstanding and even quoted you as being in agreement. I am surprised that YOU missed it because you have several times posted my Fig. 6 which had a unity gain amplifier with a feedback of +2/3 around it for a gain of 3.
We assume ideal op-amps to have a VOLTAGE output of ZERO output impedance. When we move this voltage along for later use, we use a wire – same voltage and zero impedance along it. If you prefer, take the output of the first op-amp and put in a voltage-follower op-amp, or 100 of them in series, connecting them with – – – – Wires!
Perhaps more simply, put an amplifier in the feed-forward position and give it a gain of A – any number. Any number includes A = 1.
I would suppose that, in climate models, proposing a feedback mechanism is merely a rational for making a number larger than Nature apparently made it.
Bernie,
“I am surprised that YOU missed it because you have several times posted my Fig. 6 which had a unity gain amplifier with a feedback of +2/3 around it for a gain of 3”
It has a voltage gain of 1. But it has available a very large current gain, and this makes it possible for the circuit to feed back a current which is actually twice the input current, so that the current appearing at the first op amp input node is three times the current supplied; hence the gain. There is no way that a simple wire, which is what Lord M has placed in the corresponding position, could do anything like that.
As I commented, it seems to me that, if implemented as a circuit it would simply be some kind of feedback device (a resistor?) with a short from inlet to outlet. I don’t see how that could yield anything of interest, and it certainly isn’t any kind of “official climatology”.
Mr Stokes has now begun to realize how wrong the official approach to feedback is. For it is rather obvious that the feedback loop diagram in red in the head posting is precisely a representation of the form of the zero-dimensional-model equation that official climatology uses. Now that he can see that diagram, he can at once see how daft it is that the input signal and the gain block have both been suppressed, and the open-loop gain has instead been represented as though it were the input signal. Yes, it is official climatology. And yes, as Mr Stokes says, it is wrong. He has begun to get the point.
Nick – SORRY – you are wrong. Two different things here.
What you refer to as a “feedback diagram” is what an EE calls a “signal-flow-graph” and it represents either voltage (usually) or current (the “nodes” being called “state-variables” or just signals), but NOT an assortment of both; UNLESS some of the paths are not pure numbers (pure meaning “gains” – to include attenuators like 2/3) but are instead, something like a path arrow denoted 1/R (I = V/R) which specifically (mathematically – Ohm’s Law) “converts” a voltage to a current. It would be absurd to claim that a path could have ANY gain A but NOT a gain of A=1.
The circuit of my Fig. 6 is a realization of the flow-graph with voltage nodes. Here once more for convenience:
http://electronotes.netfirms.com/EN219Fig6.bmp
The state-variables (variables of the state of the network) are voltages. The exact currents are not involved (we usually just consider voltage-dividers and currents summing to zero). Op-amps are not current amplifiers, and are capable of supplying only a few milliamps (perhaps 10 ma). [By the way, the feedback gain of -2/3 is positive 2/3 because we allow for the inversion of the first op-amp.] The feedback view is an interpretation of an alternative means of setting a gain of 3. But you don’t need G = 1/(1-f) to analyze the op-amp circuit easily, and correctly.
This is standard electronics and beyond question.
As for climate – I don’t know. But, IF I were a CAGW advocate, and a temperature rise as seen in Nature were too small for my preferred agenda, and I was not able to provide a convincing argument for a direct gain of 3, I might propose an argument for positive feedback (white ice melts to dark water, etc.). But just claiming feedback, arguing over minute details of something undemonstrated, and dragging innocent (and well-established) engineering into it seems like a poor joke.
Bernie,
“it represents either voltage (usually) or current (the “nodes” being called “state-variables” or just signals), but NOT an assortment of both”
My objection is to the complete omission of a device in the forward section. You could have an amplifier of voltage gain 1, say. But ultimately, feedback has to involve feeding back a fraction of the power from the forward stage. So there has to be something there to supply power.
“Op-amps are not current amplifiers, and are capable of supplying only a few milliamps (perhaps 10 ma).”
A device is a current amplifier if it outputs more current than it took in. An op amp may output milliamps, but it should be taking in nanoamps. As a device, your circuit takes in current V_in/R. But it has very low output impedance. If you put a load R from output to earth, the current flowing through it would be 3*V_in/R, after taking in V_in/R. Something has amplified current.
“and dragging innocent (and well-established) engineering into it seems like a poor joke”
But the enthusiast for doing this is Lord M. And there are others at WUWT. You won’t see circuit diagrams in the IPCC reports. And Arrhenius long predated circuits, amplifiers, Bode and all, and still got a sensitivity of 4 K/doubling.
“For it is rather obvious that the feedback loop diagram in red in the head posting is precisely a representation of the form of the zero-dimensional-model equation that official climatology uses.”
It isn’t at all obvious until you quote what “official climatology” actually uses. Not your version, theirs. I showed Roe’s diagram – it was nothing like this. Your red diagram does not represent anything in climatology. It is yours alone.
Nick said (12:02 PM) “…. My objection is to the complete omission of a device in the forward section. You could have an amplifier of voltage gain 1, say. But ultimately, feedback has to involve feeding back a fraction of the power from the forward stage. So there has to be something there to supply power.. . .”
Nope – just supply voltage. First off – there is something there – the first op-amp or the “error amplifier” of the flowgraph. Just as good a voltage source (or an algebraic numerical variable) as any amplifier A (or mu). Keep in mind also that the structure is a LOOP. As you could have multiple feedbacks, you could have multiple input/output points. Feedback for one could be feedforward for another. It just IS what it is and knows not what you call it.
Secondly, it is not “Power” (like Watts) that is fed back, but voltage. This does not require the amplifier to give up anything. If I feed back 1 volt of a 10 volt signal, the amplifier output remains 10 volts and does not go to 9.
Nick also said: “A device is a current amplifier if it outputs more current than it took in. An op amp may output milliamps, but it should be taking in nanoamps.”
Not true – an ideal op-amp TAKES IN ZERO current (typical real input bias is in p-amps) – that’s the basic design principle. The op-amp does require a few ma from its power supply pins for housekeeping and the output supplies or sinks currents (including unbalanced Vin/R types), and may drive a modest current to a later stage. This “collecting-up magic” is through the MASSIVE amounts of negative feedback already considered in all the usual op-amp configurations. But it does NOT amplify current. Current plays the role in an op-amp circuit that currency does in a financial network – balances the books.
[A basic transistor can amplify current – we used to design using the parameter hfe (beta). A special IC called an “operational transconductance amplifier” has a current as an output. But op-amps deal with voltages.]
Nick also said “As a device, your circuit takes in current V_in/R. But it has very low output impedance. If you put a load R from output to earth, the current flowing through it would be 3*V_in/R, after taking in V_in/R. Something has amplified current.”
NOPE again. If you put on a resistor R as a load, true Vout/R could flow as long as it did not (net) exceed the rated current output. If it did, the operating negative feedback would fail.
Perhaps more to the point BTW, I think if one wants to promote or criticize feedback as an electronics/climate comparison one should emphasize the “active” feedback of the electronics case (power supply required) as opposed to the seemingly passive climate case. ( I think Frank and some others suggested this as well.)
Nick also said:
“ But the enthusiast for doing this is Lord M.”
If I understand Monckton correctly this is because he (unwisely?) has chosen to accept all climate doctrine except the limited areas where he chooses to contest. Kind of like a boxing match where you freely allow your opponent to punch you at will except perhaps in the left elbow!
And feedback ideas predate electronics and Bode, etc., like steam engine “governors”. Old engineering counts.
Bernie
“First off – there is something there – the first op-amp or the “error amplifier” of the flowgraph”
Are we looking at the same graph? The top, red one. Do you mean the first junction with the big +? I don’t see any transfer numbers associated with that.
“an ideal op-amp TAKES IN ZERO current”
Ideal. But ideal is the limit of very large current gain. No real device can give a response to a signal of zero power. And if an input signal has finite (non-zero) power, it must input finite current.
“If I feed back 1 volt of a 10 volt signal, the amplifier output remains 10 volts and does not go to 9.”
Well, you actually feed back current. In your case, (2/3)*V_out/R = 2*V_in/R. It’s pretty hard to quantify a voltage that is fed back, since the input is held at 0.
But there is still the mystery of how you can feed back a current larger than the input (V_in/R) if there is no current amplification.
“true Vout/R could flow as long as it did not (net) exceed the rated current output”
That is only three times the input current. There is surely an operating range where that is possible. And then it is an amplified current output.
For Nick Stokes at April 8, 2018 at 11:57 pm
“…Are we looking at the same graph? The top, red one. Do you mean the first junction with the big +? I don’t see any transfer numbers associated with that. …”
That is not a junction or a multiplier– it’s a summer, which is what the + sign is for. Monckton has shown three flowgraphs with three corresponding (completely equivalent) sets of equations, and all six seem exactly right. I think he agrees this is (simple) high-school algebra. Either the flowgraphs OR the equations are sufficient – I prefer the flowgraphs myself.
“… Ideal. But ideal is the limit of very large current gain. No real device can give a response to a signal of zero power. And if an input signal has finite (non-zero) power, it must input finite current…. . . . . . .”
I think I see a MAJOR element of your not understanding. Voltage is an “intensive quantity” that distributes freely (like temperature, pressure, etc.) while current (time derivative of countable charge) is an “extensive quantity” (like mass, energy, etc.) and is subject to conservation (zero-sum, as in Kirchoff’s law).
Non-ideal op-amps are interesting for AC circuits at MHz or above, but for DC circuits (such as we are considering all to be here), op-amps are essentially ideal. They have real open-loop gains of 10^7 (ideally infinite), tiny input bias currents in pa (ideally zero), and output impedances (with negative feedback operating) of perhaps an Ohm (ideally zero). Any current needed to maintain an output voltage Vout into any load RL (that is, Vout/RL) is supplied (ACTIVELY, within ratings) courtesy of the supply pins. Vout adjusts itself (via negative feedback) so that the inputs V(+) and V(-) are equal.
Some additional confusion results from not considering the differences between an op-amp (the infinite gain triangle) and the “configuration” surrounding it which make it useful.
Note that if we INCREASED all the resistors in my Fig. 6 by a factor of 10, all the voltages would remain the SAME, and the currents flowing in the configuration would DIVIDE by 10. STILL, if your proposed load RL did NOT increase, the output current would NOT change in the slightest from Vout/RL.
I know it is helpful here to have been doing this for 45 years!
The opponents seem to be sniping from prepared positions but CMoB and his learned colleagues have bypassed them and are closing on CAGW HQ. When the final redoubt is stormed I hope that something stirring by Jimmy Hendrix with plenty of feedback will be playing. ‘The Anacreontic Song’ would be my choice.
“Voice, Fiddle, and Flute,
“no longer be mute,
“I’ll lend you my Name and inspire you to boot,
“And, besides I’ll instruct you, like me, to intwine
“The Myrtle of Venus with Bacchus’s Vine.”
I hope that Nigel S will sing for us once our result is accepted, published and announced worldwide. We shall of course also welcome a song or two of consolation if we are found to have made a significant error. So far, we do not think that has happened,.
My father (Fifth Indian Division Signals) told me that they came across dead Japanese snipers left behind tied to trees by their retreating comrades as the ‘Forgotten Army’ closed on Rangoon, hence the sniping comment. I look forward to singing lustily!
All Monckton has done is simply pointed out with simple arithmetic that the models were never based on the physics. They were based on a mathematical lie that could never support its own weight. When you start with a false theory and bend over backwards by conspiring to falsify data and call skeptics deniers and make sure that with government money to fund the falsehood with 1000’s of fraudulent climate science papers Dont expect that us skeptics will have any sympathy for anybody involved in this hoax. One lie has inevitably led to a 1000 lies. Criminals soon find out the consequences of that simple mathematical fact of falsehoods.
Mr Tomalty displays just a hint of justifiable anger at the manner in which climate skeptics have been treated by the well-funded totalitarian clique that has dominated climate science until now. We shall continue our own researches until we are confident either that we are wrong, in which case we shall not pursue our argument further, or that we are right, in which case we shall do our best to provide every necessary demonstration. That is how science works – not by the sneering and shrieking of climate fanatics, but by the calm discussion of scientific questions until as much of the truth as is within our power to discern is discerned.
Dr Strangelove is probably not a doctor of anything and certainly not of thermodynamics. Consider the climate at a surface temperature of 255.4 K, the emission temperature. Since there is water, ice, water vapor and cloud cover, the feedback processes caused by the presence of these forms of H2O are in existence. Therefore, at 255.4 K the climate would not be in thermal equilibrium. Therefore the feedback processes would induce a feedback response, and quite a large one. This is really not difficult, provided that one is searching for the objective truth rather than proclaiming some totalitarian Party Line or another.
“Mr Stokes overlooks the fact that the presence of an emission temperature will induce a feedback response where feedback processes such as surface albedo, cloud albedo and water vapor are present.”
How can it do that, when the emission temperature is by definition that pertaining in the absence of GHG’s?
The ET is that radiated by the Earth on receipt of 240 W/m2 at it’s surface via the S-B response.
To do that the Earth must have a transparent atmosphere to terrestrial IR – so NO cloud and WV (and so no albedo from ice).
“Consider the climate at a surface temperature of 255.4 K, the emission temperature. Since there is water, ice, water vapor and cloud cover”
No, there is NOT “water, ice, water vapor and cloud cover” …. except in the model result from Lacis et al (2010) when non-condensing GHG’s are removed by fiat.
http://www.atm.damtp.cam.ac.uk/mcintyre/co2-main-ct-knob-lacis-sci10.pdf
255K is the S-B response to the Sun’s TSI on Earth of 240 W/m2 (which is hypothetically assumed in the Lacis model to have the same albedo as the current Earth). The ET is not a temperature predicated on there being any sort of atmospheric GHG present.
In the Lacis model “water, ice, water vapor and cloud cover” is left over after non-condensing GHG’s have been removed and the system has settled sufficiently.
As Nick has said – a thought experiment.
“the feedback processes caused by the presence of these forms of H2O are in existence” …
As above – only in Lacis et al (2010) – and therefore it cannot be the emission temp as a DeltF is in play to produce it.
The emission T of Earth has an invariant F by definition from an invariant TSI ( practically )
“Therefore, at 255.4 K the climate would not be in thermal equilibrium” ……
Correct, not in the world of Lacis et Al (2010), but that is not a real world as predicated by the S-B response to an unvarying TSI (practically) of 240 W/m2.
“Therefore the feedback processes would induce a feedback response, and quite a large one”
It would – but that is not caused by the ET …. rather, to the feedback of changing forcing due to the remaining condensing GHG (WV and albedo in Lacis). It is changing the 240 W/m2 that has an invariant 255K with no feedback for Earth when the emission temp level is at the surface.
“This is really not difficult, provided that one is searching for the objective truth rather than proclaiming some totalitarian Party Line or another.”
No, it’s not and indeed … that is what scientists since the time of Arrhenius and Tyndall et al have done.
Again for your delectation … My name is Anthony Banton.
In fact your returning to this sceptics’ echo-chamber for your desired confirmation from the majority does not make your “Game over” anything of the sort.
Via some perverse conspiracy ideation as evidenced by “proclaiming some totalitarian Party Line or another.”
Mr Banton, who – now that I have revealed who he is – no longer vainly attempts to lurk behind his furtive pseudonym, is, as usual, hopelessly confused and way out of his depth. So let me explain things in the smallest possible words. We are considering three steps: first, an atmosphere without any greenhouse gases at all, where the emission temperature obtaining at the Earth’s surface would be 255 K; secondly, an atmosphere with all the forms of water now in existence but without any non-condensing greenhouse gases such as CO2, where the temperature at the Earth’s surface would be more like 278 K owing to the large feedback response of the water-based feedback processes to the emission temperature; and thirdly, an atmosphere to which the non-condensing greenhouse gases have been added as well, where the temperature would be today’s 288 K.
At present, however, official climatology – misled by the degenerate form of the zero-dimensional-model equation that it uses, which excludes the emission temperature and therefore any feedback response thereto from the feedback loop – has not appreciated that the emission temperature induces a feedback response even in the absence of the non-condensing greenhouse gases. This is a large, serious and – once it is pointed out – obvious error. Mr Banton will need to raise his game if he is to provide a valid criticism of our result.
“how can an inanimate feedback process know how to distinguish between the input emission of temperature of 255 K and a further 9 K of temperature arising from the addition of the non-condensing greenhouse gases to the atmospheric mix?”
Unlike you, the inanimate feedback process knows it responds to net energy flow and not to absolute temperature.
“IPCC’s definition thus explicitly excludes any possibility of a feedback response to a pre-existing temperature, such as the 255.4 K emission temperature that would prevail at the surface in the absence of any greenhouse gases or feedbacks. It was for this reason that Roy Spencer thought we must be wrong.”
Dr. Spencer knows you are wrong not because of IPCC’s definition but because you believe that a thermodynamic system in thermal equilibrium will induce a feedback unto itself, which is absurd because that means it could change its own temperature without external energy flows.
The feedback magic of The Lord of the Rings
” a thermodynamic system in thermal equilibrium”
Can you explain how the climate system has remained in equilibrium as more CO2 is added? Is there not a response? The IPCC thinks so. If so, why was there not a response to the CO2 that was in the atmosphere prior to 1850?
Why do you think the temperature in 1850 excludes the CO2 greenhouse effect? Or do you think the temperature in 1850 was 255 K?
Dr Strangelove
Why do you think the temperature in 1850 excludes the CO2 greenhouse effect?
Because in CM’s thought experiment CO2 was set to zero in 1850. Read the article.
Then CM’s thought experiment is wrong because obviously there was atmospheric CO2 in 1850. No wonder his conclusion is wrong
Dr Strangelove appears to have no understanding whatsoever of the scientific method. One of its processes is experiment. Running the Lacis model in reverse is one such experiment. The conditions precedent to that experiment are set out with great clarity in the head posting, and it is there expressly stated – precisely in the (vain) hope of avoiding stupidities such as that of Dr Strangelove – that one should not believe that in 1800 there were in reality no non-condensing greenhouse gases in the atmosphere.
“such as the 255.4 K emission temperature that would prevail at the surface in the absence of any greenhouse gases or feedbacks.” Thats a strawman! Nobody is arguing that the 255.4K would not be the emission temperature in the absence of greenhouse gases. What Monckton is arguing is that 255.4 emission temperature would be raised if you introduced water vapor and no CO2. In other words the water would evaporate and create most of the known greenhouse effect from the mean 239w/m2 insolation that created that 255.4k without any greenhouse gases. This runs contrary to the idea that CO2 controls water vapor, CO2 does not, water vapor is controlled by temperature, not just temperature change. We see natural processes changing temperature and feedbacks, not just CO2. Its important to note that Monckton isn’t goring all AGW science. Many are coming up with feedback sensitivities near what Monckton is calculating. The problem is the politics is still trying to sell the old discredited science based upon the argument we know of no other reason why the temperatures in the 80’s and 90’s went up so much other than CO2 and as such adopted large climate sensitivities that do not hold up to scrutiny. Monckton is driving yet another nail in that coffin. The problem is there are trillions of dollars at stake by politicians, scientists, institutions, corporations, and even nations and its hard to keep that in a box.
“The problem is there are trillions of dollars at stake …”
I confess the maths in this is beyond me (though I enjoy trying!). Bill, the one variable you missed from this indictment is the entire environmental philosophy which is at stake. The eco-activists have bet the farm on being able to demonise CO2 as the quickest way to end fossil fuel use and undermine “civilisation as we know it”. If it were otherwise they would not be supporting the environmental destruction that goes with wind and solar “farms” and would be supporting nuclear power for energy with natural gas as a stop-gap. Generally speaking, they aren’t.
Whatever the science, never forget the enviro-political imperative that has got us where we are.
Newminster makes a fair point about the wealth and power of the totalitarian movement that has co-opted environmentalism as its weapon of choice to dismantle the economic hegemony of the West. However, that movement failed when it advanced bogus scientific arguments in its attempt to declare the Jewish race subhuman, and it failed again when it advanced bogus scientific arguments to justify the soaking of seed-corn in water during the winter rather than planting it out in the autumn to toughen in readiness for the spring. As a result of these two totalitarian pseudo-scientific aberrations, some 250 million were killed worldwide. But they failed in the end, for they were anti-scientific, just as global-warming fanaticism will end, for it too is anti-scientific, and now we can prove it.
DrS,
I read it that the thermodynamic system is in equilibrium BECAUSE feedback keeps it that way. Geoff.
Yes if it is in disequilibrium, a feedback can restore it to equilibrium. But 255 K is already in equilibrium without GHG. A feedback will not magically appear unless there is a forcing (energy flux) that disturbs the equilibrium. Dr. Spencer’s analogy is a forcing is a cause, a feedback is an effect. So there is no effect without a cause. Absolute temperature is not a forcing. Change in temperature is a response to a forcing
Mr Hunter is right and “Dr Strangelove” is simply flat-out wrong. Owing to the presence of the feedback processes related to the presence of large amounts of water on Earth, at the emission temperature of 255 K the Earth would not, repeat not, repeat not be in thermal equilibrium. The feedback processes would act to bring the temperature considerably above 255.4 K – even if there were no non-condensing greenhouse gases in the atmosphere at all.
255 K is radiative equilibrium temperature without GHG (water vapor, CO2, others) but including the albedo of clouds (strictly speaking it’s water droplets not water vapor) If you add water vapor, that’s a forcing. Any temperature change is a response to the forcing and not due to 255 K temperature before water vapor was added
Dr Strangelove is entitled to his opinion that the presence of water vapor in the atmosphere constitutes a forcing. However, official climatology considers it to be a feedback. Since we are adopting all of official climatology except what we can demonstrate to be false, we too have taken all water-dependent feedback processes as feedbacks, just as official climatology does. If Dr Strangelove thinks officlal climatology is wrong in this respect, he should not trouble us with his opinions: let him contact secretariat@ipcc.ch.
Nick, further it is no doubt widely true that sensitivity was not determined as suggested by Monckton’s calculations. Instead high sensitivity was invoked by models that attempted to explain short term variations of temperature completely in terms of CO2 using argumentum ignoratium as was essentially stated in AR3.
Argumentum ignoratium is all you need to know to verify that Monckton has a strong point as a layman. That’s true because climate has always changed and we have not done a good job of explaining why.
I have enjoyed your work in this area as at least you have not donned the narrow blinders of the mainstream science that believes the most rapid warming seen is entirely CO2 warming while its clear you are looking more broadly and not putting on the blinders and gone of on a search for the missing warming.
Obviously the only reasonable response countering Monckton’s basic observation and KISS explanation is some more detailed work that ties the greenhouse effect to some overall test of reasonableness, which if not available already puts to mockery the hundreds of billions wasted on this enterprise considering Monckton’s work.
LM says: Lacis’ albedo of 0.418, emission temperature is [1364.625(1 – 0.418) / d / (5.6704 x 10–8)]0.25 = 243.3 K, in accordance with the fundamental equation of radiative transfer, where d, the ratio of the area of the Earth’s spherical surface to that of its great circle, is 4.
I still have huge disagreement with using one side of a disk but the entire surface of the sphere which includes a physical impossibility. The sun cannot shine on the opposite side.
One side absorbs (π2^2) but the whole surface emits (4π2^2) on average input = output.
One side absorbs (πr^2) but the whole surface emits (4πr^2) on average input = output.
Sorry for the typo.
I have some sympathy for Mr Kelly’s position. The derivation of the 255.4 K emission temperature that is standard fare in official climatology leaves a great deal to be desired. it does not account properly for the latitudinal variability in insolation and hence in surface temperature, and it does not account properly for the retention of ocean heat on the nightside. My own calculations suggest that the emission temperature – before allowing for any feedbacks or for the presence of the non-condensing greenhouse gases – is between 265 and 275 K. But I am not yet in a position to prove it, so, as stated in the head posting, I have simply adhered to official climatology’s value for the time being.
That sounds much more likely.
The substantial difference between Earth’s Atmosphere and that of Mars is that Earth’s Atmosphere contains substantial quantities of non GHGs, ie., nitrogen, oxygen and argon. If all the non GHGs in Earth’s Atmosphere were removed we would have an atmosphere very similar to that of the Martian Atmosphere with approximately the same mass, density and pressure.
Mars that has more molecules of GHGs per cubic metre of Martian Atmosphere, than does Earth’s Atmosphere, and is thought to have a GHE of around 1K to 1.5K.
Mars receives less solar insolation so one would expect to see less radiant GHE on Mars. If one corrects for the differences in solar insolation received then one might expect the GHGs in Earth’s Atmosphere to add around 3K of warming.
You do not need to calculate the emission temperature – you can measure it from the emitted
radiation from the top of the atmosphere.
Germonio appears confused about emission temperature. One cannot measure it from the radiation emitted from Earth, because the Earth radiates different amounts at different altitudes. Emission temperature is derived from the incoming solar irradiance and the albedo, and from nothing else.
Monckton wites: “Germonio appears confused about emission temperature. One cannot measure it from the radiation emitted from Earth, because the Earth radiates different amounts at different altitudes. Emission temperature is derived from the incoming solar irradiance and the albedo, and from nothing else.”
In other words, emission temperature is the product of a MODEL involving solar irradiation and albedo. Roe advocates using such a model as a reference state for quantifying feedbacks. However, models aren’t real and feedbacks exist independently from such reference states.
Frank, who seems to be trying to sow deliberate confusion, says that emission temperature is the product of a model. No: it is a product of observation, as he would know if he knew anything of the history of hhe relevant science. The fundamental equation of radiative transfer was derived by Stefan using empirical methods – i.e., observations and measurements. It was then theoretically demonstrated by Ludwig Boltzmann.
It is that equation that tells us the temperature at any point on the dayside of a celestial body once the insolation and albedo are known. The crude average that is represented by the 255.4 K emission temperature that is generally used throughout climatology is probably too low. If so, equiilibrium sensitivity is likely to be even less than we find it to be.
If Frank wants to call the method of arriving at that crude average a “model” he can please himself: but, for our part, as we have made plain in the head posting, we have simply accepted all of official climatology except what we can prove to be erroneous. If Frank thinks the emission temperature should be calculated on some basis other than that which official climatology uses, he should address his concerns not to me but to secretariat@ipcc.ch.
This is one of the fundamental points.
One side of the Earth, which is not a blackbody nor a perfect conductor, absorbs, whilst the entire surface emits. This simple fact cannot be stressed enough.
The problem I see with all such climate feedback models is that they assume the input and output to be separate. In reality the input and output are the same quantity, atmospheric temperature. Which implies that there is a short-circuit across the feedback loop. Input and output are, in fact, a single node.
The situation is somewhat analogous to ‘bootstrapping’ in electronics.
It is hard to see how such an arrangement could provide amplification without being unstable.
It is of course possible to have a stable negative feedback loop under such conditions. Just, not positive.
In response to Mr Macdonald, it is in fact possible to imagine a world without non-condensing greenhouse gases, but with today’s insolation, albedo and water vapor, ice and clouds. In that event, the feedback loop equation (in its corrected form, at any rate) is perfectly capable of giving us a reasonable estimate of the eventual temperature, even before non-condensing gases are added to the mix.
Whenever one encounters a problem of this kind in physics, it is useful to break it down into small pieces placed along a timeline. Following a strict timeline prevents chain-of-causality errors.
Ian
I think this is where Lorenz steps in. The system is indeed unstable and describing constant the “Lorenzian walk” that is not random but chaotic-deterministic. There is no equilibrium. This is a problem for the way this whole question is framed.
Ian,
Climate models have solar radiation as the input and the climate as the output. Or in a feedback model
the input is the change in radiative forcing Delta F and the output is a temperature change Delta T. They
are completely seperate rather than the same quantity.
Germonio has not succeeded in explaining on what rational ground he considers that the corrected form of the feedback-loop equation does not engender a feedback response where the input signal (whether amplified or not) and the feedback fraction are both nonzero. The mathematics is not particularly difficult, and it demonstrates beyond doubt that even in the absence of any amplification there will be a feedback response to emission temperature. Merely reciting the official definition of a feedback, which (perhaps deliberately) falsely attempts to exclude the feedback response to emission temperature does not advance Germonio’s argument one whit.
Do the math. Input signal 255 K. Gain factor 1 (meaning no amplification from non-condensing greenhouse gases). Feedback fraction 0.08 (since feedback processes are present where water vapor is present). Output signal 255 / (1 . 0.08) = 277 K., not 255 K.
Monckton, My rational grounds is that there is no evidence that your “corrected form” of the feedback
loop equation is valid. And you have presented not derivation for this equation from the underlying physics
but have just stated it with no justification.
My question would be in what sense is 255K an input signal? And it is an input signal to what? Once
you change the reference system which you have done then you change the gain and feedback and
as Roe states explicitly you cannot compare feedbacks from difference reference systems.
Germinio should read Bode (1945, ch. 3), where the correct form of the zero-dimensional-model equation is given and proven. That equation is applicable to all dynamical systems on which feedbacks bear. I cited Roe as one of the many papers using the incorrect form of the equation that made no provision for the input signal – in this instance, emission temperature.
Roe’s reference system is that part of the feedback loop that does not incorporate the feedback block on the return path. Properly speaking, it should have the reference temperature (i.e., emission temperature) as the input, and the warming from non-condensing greenhouse gases represented as a direct-gain factor in the mu amplifier block.
Roe, however, made the mistake of not including the reference temperature in his feedback loop. Indeed, he did not use temperature at all, but a change in radiative flux as his input. He then converted that change in flux to a temperature, doing so in that part of the circuit that would normally be occupied by an amplifier block, and then showed the temperature outputting to another radiative flux change. But one cannot go from a temperature to a flux change without a process of conversion – a process absent from Roe’s circuit diagrams.Mr Stokes, in seeking to rely on those diagrams, had not noticed that defect.
Feedbacks are denominated in Watts per square meter per Kelvin of the temperature that induced them. And climatology errs in not including the emission temperature as the input signal.
The whole global warming due to CO2 is a very simple model, just one variable!
I am of the school of adiabatic temperature profiles and I think as we explore the atmospheres of more planets, this will become accepted.
Also, if there were a positive feedback in the atmosphere, an assumption made by the Warmistas, then the planet would have zipped right up to boilibng very quickly. It clearly hasn’t, over 4.5 billion years, therefore I would suggest the assumption is hokam, no matter how frantickly arms are waved.
In response to Robert of Ottawa, we have adopted for the sake of argument all of official climatology except what we can prove to be false. Therefore, we have accepted ad argumentum that greenhouse gases cause a greenhouse effect. Our concern is not with whether such an effect exists (for that has been well established in the laboratory) but with the amplitude of its effect on temperature.
RGHE theory could not exist without the concept of “back” radiation, energy/heat moving from a cold tropospheric “surface” to a hot ground “surface.”
Consider a small heated rod of 0.5 m^2 inside a larger outer tube of 2.0 m^2.
The heated rod is fed 25 watts of electricity for a radiative flux of 50 W/m^2.
The outer tube absorbs that radiation for a radiative flux of 12.5 W/m^2.
RGHE theory says that 50 W/m^2 radiate outwards while 12.5 W/m^2 “back” radiates for a net of 37.5 W/m^2 warming the earth.
A watt is not energy, but power, energy over time: 3.412 Btu per English hour or 3.6 kJ per metric hour.
25 watts is 85.3 Btu/h.
25 W spread over area 1 is 50 W/m^2 moving 85.3 Btu/h.
25 W spread over area 2 is 12.5 W/m^2 also moving 85.3 Btu/h.
Conservation of energy demands that input and output must be equal.
The 25 W, 85.3 Btu/h, that entered as electricity must radiate to the world from surface 2, 25 W or 85.3 Btu/h.
There is exactly ZERO left over to “back” radiate.
In response to Nickreality65, a system subject to incoming and outgoing radiative fluxes, such as the Earth, will gain heat if the incoming flux exceeds the outgoing flux, and its temperature will increase until the outgoing flux again matches the incoming flux. One can heat such a system by increasing the influx (e.g. by greater solar activity), but one can also heat it by inhibiting the efflux.
It seems to me that we agree that RGHE is nonsense.
More net in, warming. Less net in, cooling. Not exactly news.
If more comes in, as it does every perihelion, warming. If less comes in, aphelion, cooling.
Same with the tilt as the poles take turns moving in and out of shadow/sun.
Earth’s albedo, which exists only because of the atmosphere, reflects away 30% of the incoming solar energy. The albedo does not actually cool the earth but makes it less hot which yields the same result.
No atmosphere means hotter earth not colder. See Volokin/Nikolov moon analog papers.
Variations in the albedo play a major, it not the major, role in the state of the climate.
The atmosphere’s thin layer of gases insulate and create a thermal gradient same as the wall of a house per U A dT.
My explanation is based on first principles which even the lay public can understand.
All the S-B BB & QED handwavium just clouds the issue.
Have several papers at WriterBeat, LinkedIn & PSI.
Also the changes in clouds, which directly impacts upon how much incoming solar insolation is reflected or gets through to the surface, whatever be the mechanism that drives the change in patterns of cloudiness, eg., simply chaos, random walks, responses to oceanic conditions, cosmic rays, or other changes in cloud seeding, the response that Willis, from time to time, suggests etc etc..
Different patterns in cloudiness are all part of the natural process, unless man pollutes particulate matter that may promote cloud seeding.
In further response to nickreality, we most certainly do not agree that the radiative greenhouse effect is “nonsense”. As the head posting makes explicit, we have adopted all of official climatology except what we can prove to be falses.
nickreality65 wrote: “Consider a small heated rod of 0.5 m^2 inside a larger outer tube of 2.0 m^2.
The heated rod is fed 25 watts of electricity for a radiative flux of 50 W/m^2.
The outer tube absorbs that radiation for a radiative flux of 12.5 W/m^2”
Unfortunately, this problem is somewhat more complicated than you describe. The inner surface of the outer tube radiates in all directions (not just perpendicular to the surface), so some of that inward radiation is absorbed by the central heated tube and some is absorbed elsewhere by the inner surface. And you need to apply Lambert’s cosine law to correctly calculate how much power is absorbed. These geometric issues are called “viewing angles” and solutions for a variety of common situations can be found on the internet. In the real world, you also need a temperature gradient for conduction to transport heat through the wall of the outer tube.
Imagine a 1 m layer of atmosphere parallel to the surface of the Earth. The atoms in that layer emit equally in all directions. Let’s decompose that emission into three components: 1) A component parallel to the ground. 2) An upward vertical component. 3) An equal downward vertical component. Hopefully you will immediately realize that the horizontal component cancel and don’t contribute anything to radiative heating or cooling of the planet. By cancel, I mean there is no net flux of energy (no heat transfer) in any horizontal direction, not that there is interference. (Interfere requires coherent light sources.) Both the upward and downward components add to the existing fluxes arrive at the layer.
Now we need to consider absorption of the upward and downward fluxes entering the layer. In a thin layer near the edge of space, the downward flux of LWR is extremely weak, so the layer absorbs very little of that flux and contributes more than it absorbs. A thin layer near the surface of the Earth receives 390 W/m2 of upward flux and can absorb more radiation that it emits. So the net result of absorption plus emission in a thin layer of atmosphere might reduce the upward flux and increase the downward flux even though it emits equally in both directions.
Planck showed that thermal radiation in equilibrium with its surroundings has an intensity given by Planck’s Function, B(lambda,T). Equilibrium means as many photons are being emitted as being absorbed. The radiation passing through the atmosphere may not be in such an equilibrium. Upward radiation has been emitted from below, where it is warmer, so more will be absorbed than emitted. The opposite is true for downward radiation. In both cases, the net influence is to bring the local fluxes closer to B(lambda,T). The rate at which those fluxes approach B(lambda,T) depended on the number of absorbing molecules and their absorption coefficient. Photons of strongly absorbed wavelengths may travel only a few meters vertically between emission and absorption and experience neglible change in local temperature. They therefore have B(lambda,T) intensity appropriate for the local temperature. Emission and absorption are equal at these wavelengths. Weakly absorbed photons may travel a kilometer of more between emission and absorption and therefore be out of equilibrium with the local temperature. It is these wavelengths that produce the GHE.
In any layer, the 2LoT is being obeyed. More photons from warmer places are being absorbed than emitted. Fewer photons from cooler places are being absorbed than emitted. Heat flow is the NET flux of radiation from one location to another.
The net result is that the intensity of DLW increase from 0 W/m2 on the cold edge of space to about 333 W/m2 at the warm surface, while OLR starts at 390 W/m2 near the warm surface and has diminished to 240 W/m2 as it finishes passing through the colder upper atmosphere. Note that this wouldn’t happen in an isothermal atmosphere, a temperature gradient is essential. Most of this change takes place in the troposphere, where temperature decreases with altitude.
The 396 W/m^2 upwelling and net 333 W/m^2 GHG energy loop as shown on the K-T power flux balance diagram (Figure 10 Trenberth et al 2011jcli24) is calculated using the S-B equation with an assumed emissivity of 1.0 and an average surface temperature of 16 C, 289 K. Because of the conductive/convective/advective/latent heat participating processes of the atmospheric molecules the actual and correct radiative emissivity is about 0.16, i.e. 63/396.
This GHG energy loop is an inappropriate calculation with zero physical reality.
Without this energy loop the radiative greenhouse effect theory fails.
Without RGHE man-caused climate change does not exist.
It’s called “science.”
Don’t be frightened, spit out the Kool-Aid and give it a try.
Here’s something I posted just now way upthread, where it might get overlooked, so I’m repeating it below:
Silber: “How have you dealt with the problem that to have a feedback there has to be initial change?”
Every 24 hours there is a change in temperature. That should be enough to get the ball rolling, no?
“Every 24 hours there is a change in temperature” – I’m not quite sure what you mean, Roger, by a change in temp every 24 hours, but that’s beside the point. Monckton is not basing his feedback on a change, but on the emission temperature itself.
“As a first step towards making due allowance for the feedback response to emission temperature, official climatology’s version of the zero-dimensional-model equation can be revised to replace the delta input and output signals, indicating mere changes in temperature, with entire or absolute values. Note that the correct form of any equation describing natural occurrences (or any natural law) must be absolute values: the use of deltas is only permissible if the delta-equations are correctly derived from the absolute equation. Accordingly, ΔTeq = ΔTref / (1 – f ) should be Teq = Tref / (1 – f ):”
This makes no sense to me. Although it’s probably the case that my math skills aren’t on par with Moncktons, I don’t see from a physical standpoint how this could be the case, and there are plenty of others who are better qualified and making the same argument. It also seems extraordinarily unlikely to me that all the teams of AGW climate modelers would commit the same error.
That said, I’m not the best person to judge because I’m prejudiced against Monckton, not as a skeptic but as a person. I’ll drop out of this conversation now, but since you asked twice I thought I should answer.
If Silber wishes to understand how it is that the correct version of the zero-dimensional-model equation is derived, try reading ch. 3 of Bode (1945), where everything is explained. The correct version of the zero-dimensional-model equation is Teq = Tref x mu / (1 – mu x beta), where mu is the direct or open-loop gain factor 1 + deltaTref / Tref, beta is the feedback fraction and mu x beta is the feedback factor.
Bode even provides a simple proof that this is the correct equation. And the only remaining question is whether the equation applies as much to the climate as to any other dynamical system (a system that changes its state over time). The answer to that question is that the mathematics of feedback is of universal application to all systems on which feedbacks bear.
Silber should remember that my co-authors include 5 PhDs, three of whom are professors, and one of whom is a professor of applied control theory.
Understanding the matheatics even of the naive feedback loop that is used in official climatology requires study and effort. Read Ch. 3 of Bode before commenting again here.
An excellent debate and well done to CM and those who made genuine challenges and to Anthony for hosting the whole thing. I am no expert, but I support CM’s case, but then I have been waiting a long time for such errors to be found. There are too many indicators that make catastrophic AGW too implausible to be real.
For me, this is also a good use of public review. Proposals either get refined to be stronger or fail miserably when subjected to this level of criticism. But where are the so called experts? Silence is often used to see off challengers. It is also often used when there is no defence. We must be getting close to this challenge requiring some sort of response from the climate establishment. It is a great pity that they will not have the confidence to make their argument here. Also, they will not wish to give this site any legitimacy. This would be a failure of judgement for them.
It would be interesting to hear what CM anticipates as being the next step in this process.
I’ll ‘second’ Schrodingers Cat’s applauding the excellent debate generated by this and CM’s previous posts!
I find I must read with scrupulous attention to detail, to follow the arguments (pro and con) presented here. The algebra is indeed straight forward but the results and implications of the arguments presented require somewhat more ‘digestion’. However the calculated lower value of climate sensitivity to CO2 doubling allies well with the historical records of our planet experiencing geologically extended cold periods of glaciation with only comparatively brief periods of warming. Almost regardless of prior variations in atmospheric CO2 content, the climate record indicates no tendency to ‘runaway’ warmth but does exhibit repeated ‘tipping points’ into brutal periods of glaciation.
Both reality and Monckton’s et.al revised feedback response model/calculations assert CO2 sensitivity must be small and non-hazardous. With acceptance of their revisions, the Catastrophic Anthropogenic Global Warming hypothesis dissipates like a child’s bad dream.
Many thanks both to Schroedinger’s Cat and to J Mac for their kind support. We think our result demonstrates that global warming will be small, slow, harmless and beneficial.
The next step, of course, is peer review, where we are expecting a battle royal. The vested interests ranged against us are many, powerful and wealthy. We are under no illusions to the effect that in this field peer review will be dispassionate and fair. But, in the end, either someone finds a significant error in what we have discovered, or more and more people will find out about it, and the truth will gradually become apparent even if the gatekeepers try to slam the portcullis against us. The truth will find a way.
Anyone ever notice the hilarious fakery of claiming the cold Nitrogen bath Atmosphere is a heater, and that the light-warmed earth is warmer due to the cold nitrogen bath, than if there were no cold nitrogen bath?
This is what brings the people who’ll bark such ludicrous fraud to the point that their “science” is called
“The Sewer of Science.”
But there isn’t
====(
Not correct. 10% feedback can be represented as the infinite sum a/10^0+a/10^1+a/10^2+…
Where a=input.
which gives an output of
a*1.111111…
Which is a*1/.9
Which is out = in * 1/(1-f)
on 255 K in this gives 283.3 out.
Having now adapted the engineers’ modern flow-graph conventions, and having set down the corresponding math (admittedly, just high-school algebra), perhaps one could continue to borrow from EEs and use their “classical sensitivity”.
http://electronotes.netfirms.com/Sensitivity.jpg
This HIGHLY INTUITIVE measure “S” tells us how sensitive a performance parameter; say the area of a rectangular tabletop, is to, perhaps the length (S=1) while the area of a circular table has a sensitivity S=2 to the radius. In a network, we might have a sensitivity of -1/2 of a cutoff frequency to a particular resistor. If S =1, we break even. S=1/2 is a happy result. S=10 might be a disaster – a 5% tolerance error would be a 50% change in performance.
All we are asking is how much of a PERCENTAGE change we expect in (LOCAL) performance (experimental measurement perhaps) if there is an error (like component tolerance) of a certain PERCENTAGE. Exactly what a non-engineer would have gotten around to asking for? Engineers use S to judge general insensitivity of a proposed design and to write down “tuning equations”.
How sensitive is a gain due to feedback (G) to the feedback factor f?
Well, G = A/(1-Af) [ or 1/(1-f) for the case A=1]. Doing the calculation gives S (of G to f) = Gf. This has the happy result that if feedback f is found to be smaller, not ONLY is the gain G smaller, but the sensitivity of G to f is a smaller percentage.
Details and examples from 2016 are here:
http://electronotes.netfirms.com/AN430.pdf
but because you believe that a thermodynamic system in thermal equilibrium will induce a feedback unto itself, which is absurd because that means it could change its own temperature without external energy flows
=======
No. If the forcing is +10 and the feedback is -10, the net force on the system is zero and the system is in equilibrium with a non zero feedback.
this constitutes proof by contradiction that the IPCC is wrong. A system in equilibrium can have non zero feedbacks.
In my mind the issue is the clouds, the clouds, the clouds.
Not just the specific coverage. But at what altitude, what latitude, what time of day and what time of year.
All these factors define the if the cloud acts to warm or cool the earth and by how much. A simple average disc temperature representation of the earth is daft also given the surface temperature of the earth varies every day by at least 100C from place to place, show me how a model can model the cloud and can incorporate a variable such as CO2 changing by 20ppm and can tell us that we will be .2C warmer.
Yeh right as they say in NZ
Mr Treuren is of course right. The behavior of clouds is the largest of all the uncertainties in deriving equilibrium sensitivities. However, in the head posting we are dealing with the certainty that official climatology has at best undervalued and more usually simply overlooked the very large feedback response to emission temperature.
Monckton returns to fantasyland! According to Monckton, the GISS model used by Lacis et al can’t be trusted to predict whether a doubling of CO2 will cause 2 or 4 degC of warming, but the same model can provide useful information about our planet without any condensible GHGs after a cooling of more than 30 degC!
Are any skeptical climate scientists supporting this nonsense?
Frank continues to misunderstand some elementary concepts. Not the least of these is the concept of emission temperature, which is a function solely of insolation and albedo. As noted in the head posting (which Frank should read one day), Pierrehumbert (2011) found that on a snowball Earth the albedo would be 0.6, implying an emission temperature 221.5 K; Lacis (2010) found that on a slushball or waterbelt Earth the albedo would be 0.418, implying an emission temperature 243.3 K, and at today’s albedo of 0.293 the emission temperature is 255.4 K.
As the head posting surely makes explicit, my conclusion is that Lacis et al. have not explicitly acknowledged the existence of the large feedback response to emission temperature, but their paper does state that the temperature in the absence of the non-condensing greenhouse gases would be 252 K, which I said was considerably below the realistic value. In other words, I found that Lacis’ model did not repeat not, provide useful information about our planet without the non-condensing greenhouse gases.
It is Frank, therefore, who, as usual, is spouting nonsense.
Monckton wrotes: “Frank continues to misunderstand some elementary concepts. Not the least of these is the concept of emission temperature, which is a function solely of insolation and albedo”.
What Monckton forgets is that blackbody equivalent emission temperature comes from a MODEL – a blackbody MODEL – that has no physical reality. The most of the photons escaping from Lacis’ hypothetical planet to space (totaling about 200 W/m2) are being emitted from cloud tops (75% clouds), which are colder than the surface. Some are emitted by water vapor in the atmosphere, which is colder than the surface. And some are emitted by the surface, which Lacis’ MODEL says will be 252 K. The total number of photons emitted is equal to a blackbody model at 243 K OR a graybody model at 252 K with emissivity 0.87. Monckton’s speculation is models built upon models built upon models; equations written without bothering to consider whether they represent the underlying physics.
Monckton wrote in this post: “Thus, from a snowball Earth to 1850, the mean feedback fraction is 0.20; from a waterbelt Earth to 1850, it is 0.12; and at today’s albedo 0.293, implying an emission temperature 255.4 K, it is 1 – (255.4 + 8.9) / 287.6 = 0.08. Which is where we came in at the beginning of this series. For you will notice that, as the great ice sheets melt, the dominance of the surface albedo feedback inexorably diminishes, whereupon the feedback fraction falls over time.”
In comments about Monckton’s previous post, I repeatedly pointed out the feedbacks are not linear over more than a few degK. Monckton never admitted that I was correct. Now he has revised his amplification model and found that feedbacks do appear to vary with with temperature. But his ad hoc new models are still based on amplification and control theory. They aren’t based on fundament physics.
Monckton wrote: “As the head posting surely makes explicit, my conclusion is that Lacis et al. have not explicitly acknowledged the existence of the large feedback response to emission temperature, but their paper does state that the temperature in the absence of the non-condensing greenhouse gases would be 252 K, which I said was considerably below the realistic value. In other words, I found that Lacis’ model did not repeat not, provide useful information about our planet without the non-condensing greenhouse gases.”
What Monckton doesn’t realize is that AOGCMs don’t explicitly include feedbacks. Feedback isn’t parameterized; physics occurring inside grid cells is parameterized. Feedbacks are an emergent property of choices made when tuning a model and they are later abstracted from a variety of model experiments. Under these circumstances, it is absurd to say:
“Lacis et al. have not explicitly acknowledged the existence of the large feedback response to emission temperature”
BBeq emission temperature is not a part of Lacis’ model. Feedback is the change in net flux in response to a change in surface temperature. If we don’t trust AOGCMs to predict feedbacks within a few degC of current temperature – and I certainly do not – it is absurd to believe that anything those models say about a 30+ degC colder planet without condensable GHGs can help us predict the effect of 2XCO2. The change in temperature over the past century can tell us something useful about feedbacks, but MONCKTON CONSTANTLY FORGETS THAT WE HAVEN’T REACHED EQUILIBRIUM WARMING. Transient warming needs to be analyzed with EBMs. That has been done by Otto et al 2013 and Lewis and Curry (2015). According to ARGO, today’s forcing of about 2.5 W/m2 has been reached to about 0.7 W/m2 by current warming, meaning that current warming is 40% short of equilibrium warming.
Frank, do you or do you not acknowledge the existence of a large feedback response to the 255K emission temperature? Do you agree that MB identified a fundamental error in the climate models?
Sailboarder asked: Do you or do you not acknowledge the existence of a large feedback response to the 255K emission temperature? Do you agree that MB identified a fundamental error in the climate models?
Sailboarder: What is a “feedback response to an emission temperature”? The simplest way to think of feedback is as a change in the net flux at the TOA in response to a change in surface temperature: λ = dW/dT. Feedback can be divided into two components λ0 for the change in simple thermal emission and λ1 for the sum of all the other feedbacks. The dimensionless feedback factor f = -λ1/λ0). None of these parameters a constants independent of temperature for more than a few degK.
I’m tempted to integrate dW = λ(T)dT from 0 to T so that I can associate a feedback with a temperature, but these thoughts aren’t proving any insight to me.
The simple answer is that Monckton has not identified a fundamental error in “climate models”. Climate scientists make little use of what Monckton calls a zero-dimensional climate model. The climate models they use for most of their work (and to scare the public) are AOGCMs. Monckton’s post tell us nothing about those models. He has simply discovered that linear models give crazy results when applied to non-linear phenomena.
The only thing that matters is the value of λ that will determine our future, If it takes a 1 degK rising in Ts to emit or reflect and addition 1 W/m2 to space (λ = -1 W/m2/K), then it will take 3.7 K of warming to emit an additional 3.7 W/m2 of net radiation and eliminate the imbalance created by a doubling of CO2. When no imbalance exists, the temperature has reached a new steady state. If λ = -2 W/m2/K, then it will only take only 1.75 K of warming and there will be little need for expensive measures to reduce CO2 emissions. This is the crux of the problem. If you insist on converting these simple numbers into dimensionless amplification factors, λ = λ0 + λ1, λ0 = -3.2 W/m2/K and f = -λ1/λ0.
Monckton is telling us that we can learn something about the correct value for λ for the next few degK of warming from AOGCMs. If so, AOGCMs are saying that λ = -1 W/m2/K. Neither of us thinks models are capable of calculating that value correctly. Instead, Monckton wants to use one AOGCM to do a vastly more challenging job, make projections about a planet without any non-condensible GHGs that is 30+ degK colder than today. And somehow avoid the complications from non-linearity. This is somehow supposed to tell us something useful about λ during the next few degK of warming. This makes absolutely no sense to me. Someone who works with electrical circuits and controls systems built from linear components might look at the problem differently. That is why I’m trying to focus everyone’s attention on λ1 and λ0 (which have a physical reality and non-linearity) and not the dimensionless ratio, f, a “Tref” and a “Teq”. Monckton’s presentation has omitted all mention of λ, which the symbol used for feedback in climate science. Temperature isn’t amplifying itself! It is driven by radiation and λ is the factor that converts one into the other.
sailborder:
Yes, there’s substantial feedback at low temperatures, but, no, climate models’ finding high climate sensitivity isn’t evidence that they’ve failed to recognize it. In my comments nearby I set forth an example of nonlinear feedback T = g(R + f(T)) that resulted in the following loop gain:
http://i66.tinypic.com/2641a94.png
As you can see, the loop gain is significant–indeed, at the low end it exceeds unity–yet that model exhibited a climate sensitivity of 3.2 K. Lord Monckton is mucking about in stuff he doesn’t understand.
Frank continues to be more and more confused. Nonlinearity in feedbacks exists whether official climatology’s math or our math is deployed. But if our math is deployed the equilibrium sensitivity will inevitably be less than if the incorrect math is deployed. And our empirical calculation for the industrial era shows a feedback fraction remarkably similar to that which we obtained theoretically for the pre-industrial era.
Frank, in his desperation, resorts to the use of childish capitals. He says I have not allowed for the fact that we are not yet at equilibrium warming. Yet, if only he would actually read the head posting before wasting reams of ill-considered comments on it, he would see that we dealt with that very point, explicitly and in detail. And it didn’t make all that much difference.
Frank also says that emission temperature is “blackbody-equivalent” and says I have forgotten this. No, I haven’t: for the emission temperature is, of course, a graybody temperature, not a blackbody temperature. Frank should really study the fundamental equation of radiative transfer before presuming to lecture me on it.
Finally, Frank has written in a thoroughly arrogant and unpleasant tone throughout. This has been noticed. For, like many commenters from the totalitarian perspective here, Frank has assumed that he is dealing with a mere Classical architect who knows nothing about science or mathematics. He is, however, dealing with a body of competent co-authors who have written a paper that Frank has not yet seen – though that does not prevent him from imagining that we have made no mention of the feedback parameter lambda – and who have, between then, all the relevant qualifications to draw the conclusions we have drawn. His constant and unpleasantly-expressed assumption that I know nothing of what I am talking about, when it is he who – over and over again – has made the most childishly elementary mistakes, reflects ill on him and does us no harm at all,.
The few arrogant totalitarian shriekers here have underestimated the extent to which ordinary readers can tell by the tone of the shriekers’ remarks that they are desperate. And so they should be, for – if we are right – then, scientifically speaking, this is the end of the climate scare.
The Born Liar continues to be vicious and spiteful, saying that I am “mucking about” in matters I do not understand. He has yet to realize that his own knowledge is limited and that, even if it were as great as he pretends, his known animus renders everything he says on this subject suspect.
His contributions here have been as petty and splenetic as usual, and he has merely tried to confuse a simple issue with pointless complications. At my back I have an army of co-authors all of whom are far more knowledgeable than the Born Liar. it doesn’t matter what the Born Liar would like readers here to think of me: the result we have discovered cannot be impugned with mere petty spite.
Lord Monckton, Nick and others following our debate: Some of the confusion in our discussion arises from the horrendous terminology being used by climate scientists. Some of the confusion arises because Roe’s definition of feedback (2008) differs from the the definition used by many others.
The symbol λ is being used to stand for two different quantities, reciprocals as it turns out. Roe (2009) and other sources use λ to stand for the climate sensitivity parameter, which is climate sensitivity expressed in units of K/(W/m2). λ0 is the no-feedbacks climate sensitivity parameter. Multiply by F2x (W/m2/doubling) and you get ECS and NF-ECS (K/doubling). The glossary for AR4 defines the climate sensitivity parameter as being:
“The climate sensitivity parameter (units: °C (W m–2)–1) refers to the equilibrium change in the annual mean global surface temperature following a unit change in radiative forcing.”
https://www.ipcc.ch/publications_and_data/ar4/wg1/en/annex1sglossary-a-d.html
On the other hand, the symbol λ is also used for feedbacks, which are measured in units of W/m2/K. In Table 1 of this post, Monckton reports feedbacks in terms of W/m2/K, but he doesn’t use the symbol λ. In their classic paper on climate feedbacks, Soden and Held (2006) use λ, λ_i for individual feedback_i, and λ for the sum of all feedbacks – the overall climate feedback parameter. The AR4 glossary defines the climate feedback parameter as:
“A way to quantify the radiative response of the climate system to a global surface temperature change induced by a radiative forcing (units: W m–2 °C–1). It varies as the inverse of the effective climate sensitivity. Formally, the Climate Feedback Parameter (Λ) is defined as: Λ = (ΔQ – ΔF) / ΔT, where Q is the global mean radiative forcing, T is the global mean air surface temperature, F is the heat flux into the ocean and Δ represents a change with respect to an unperturbed climate.”
The first sentence is the traditional definition for feedback. Since additional heat lost by the planet is traditionally negative number, the overall climate feedback parameter (λ) is negative. The more formal definition for Λ switches this sign convention. The IPPC’s Table 9.5 cited by Monckton uses BOTH sign conventions. A radiative forcing change ΔQ goes into warming the ocean (ΔF), and the atmosphere (which is negligible), and the TOA radiative imbalance. ΔQ – ΔF and the change in radiative flux across the TOA (ΔR), the “radiative response” in the simpler definition. The more sophisticated definition defines the climate feedback parameter in situations that do not start and end with equilibrium (ΔF = 0).
THERE IS ABSOLUTELY NO DOUBT THAT THE TERM FEEDBACK IN CLIMATE SCIENCE MEANS A QUANTITY MEASURED IN W/m2/K, NOT A DIMENSIONLESS “GAIN”. In Table 1 in this post, Monckton reports feedback in W/m2/K. However, Roe (2009) says:
“In order to quantify the effect of a feedback, a reference system (i.e., a system without the feedback) must be defined.”
The IPCC’s definition of a climate feedback parameter doesn’t require a reference system! THIS IS THE MAIN REASON WHY MONCKTON AND I DISAGREE. If we consider the response to seasonal warming (which can be observed from space every year), we see changes in TOA OLR and reflected SWR. Those feedbacks (responses to a change in Ts) can be quantified in terms of W/m2/K without regard to any reference system. The LWR change is highly linear. Clearly we can and do quantify feedback without regard to a reference system. And if we know the overall climate feedback parameter λ, that is all one needs to know. F_2x / λ = ECS!
If one wants to understand how water vapor feedback contributes to the overall planetary climate feedback parameter OR if one wants to characterize amplification, then Roe and Monckton are right: One needs a reference system without that feedback. The only place we can get a reference system is from an AOGCM. If you don’t trust AOGCMs to produce accurate feedbacks, then you don’t have a system with and without the feedback of interest. IN OTHER WORDS, YOU CAN’T QUANTIFY FEEDBACKS AND A FEEDBACK FRACTION, IF YOU DON’T BELIEVE AOGCMs ARE ACCURATE! (If you do trust AOGCM’s, you already know ECS AND the overall planetary climate feedback parameter.)
IMO, as a skeptic of climate models, Monckton has no business using them to quantify a feedback fraction.
I continued by attempts to settle disagreements by looking into the definition of a zero-dimensional model. Roe doesn’t use this phrase. The first definition I found came from Wikipedia and is a gray-body model. It turns out to be very helpful:
(1-a)*S*(Pi*r^2) = eoT^4*(4*Pi*r^2)
eoT^4 = (1-a)*S/4 at steady state)
If we envision a slow change in Ts (say caused by a change in solar irradiation S) so the system remains in steady-state, and differentiate with respect to Ts (using the chain rule), we get feedbacks:
4eoT^3 + eoT^4*(de/dTs) + (S/4)*da/dTs = 0
4eoT^3 is Planck feedback (λ0)
(S/4)*da/dTs is SWR feedback (the change in albedo/absorptivity with Ts)
eoT^4*(de/dTs) is the change in emissivity with Ts – LWR feedback without Planck feedback.
λF (or λ1) is the sum of second and third terms for a zero-dimensional model.
Why does the emissivity of a planet change with Ts? Most of the photons escaping to space are emitted from well above the Earth’s surface – from cloud tops and GHGs high in the atmosphere. When we treat the planet as a simple gray body – a zero-dimensional model – this means that emissivity must be less than 1. The higher and colder the GHGs emitting radiation to space, the lower the emissivity. With more GHGs in the atmosphere, including water vapor, the average photon escaping to space is emitted from higher (after an instantaneous forcing). (See Lindzen’s “Taking Greenhouse Warming Seriously”). A decrease in the lapse rate due to higher humidity means the upper atmosphere warms more than the surface, increasing emissivity.
Current Earth: T = 288 K, e = 0.615, a (albedo) = 0.30.
Lacis’ Earth without non-condensible GHGs: T = 252 K, e = 0.87, albedo = 0.41
With large changes in Ts, it is easy to see that both absorptivity and emissivity change with Ts. Monckton keeps talking about a [blackbody equivalent] emission temperature, meaning emissivity is 1. However, no planet can have an emissivity approaching 1 if some of the photons escaping to space are emitted from above the surface where it is colder than Ts. If Lacis got rid of clouds and water vapor, then emissivity could approach 1 and wouldn’t change with Ts.
Monckton has asserted that that there is a feedback fraction (not feedback alone) that can be associated with any temperature. In a sense, he is correct. If we start with a blackbody Earth and move to Lacis’ model, albedo and emissivity change and those changes are feedbacks and produce a feedback fraction. If we go from Lacis’s Earth to PI Earth, we start with a changed albedo and an emissivity less than 1 and change both parameters. Those changes produce feedbacks and amplification that have accumulated within today’s planet. And with 2XCO2, there will be further changes in emissivity and absorptivity added on to the existing changes. If your reference state is a blackbody (the ideal reference state according to Roe), then changes due accumulate with rising temperature.
Above I explained how confusing terminology and symbols lead to misunderstanding. Continuing this process with some of the other terminology might help lear up other disagreements.
The AR4 Glossary doesn’t offer a definition for feedback fraction (f), aka gain (g). Monckton doesn’t seem to understand the process for obtaining a feedback fraction f from climate feedback parameters, It is clearly defined by Tsushima and Manabe, PNAS (2013) for both observations (hurrah) and models (hiss). There are few sources more definitive than a paper by Manabe:
“The feedback parameter, λ, may be divided into the feedback parameter of the first kind and that of the second kind, as expressed by
λ=λ0 +λF
The first term, λ0, denotes the change in the TOA flux of the OLR in response to uniform, 1 °C increase in the temperature of the surface–troposphere system. In other words, it denotes the rate of “basic radiative damping” of temperature perturbation that follows approximately the Stefan–Boltzmann law of black- body radiation. Soden and Held (11) estimated λ0 in the CMIP3 models. The average value of λ0 obtained from the models is 3.21 Wm−2·K−1, which is used in the present study. In addition to the primary feedback (i.e., basic radiative damping), there is the feedback of the second kind as described below.
The change in surface temperature induces not only the vertically uniform change in the troposphere but also changes in the vertical lapse rate of temperature, humidity, and cloudiness in the troposphere and in the coverage of snow and sea ice at the Earth’s surface. These changes affect the TOA flux of OLR and that of reflected solar radiation, modifying the strength of radiative feedback as indicated by λF in the right-hand side of Eq. 5. To represent the strength of the feedback of the second kind identified here, Hansen et al. (10) introduced a nondimensional metric called gain factor (g) as expressed by
g = −λF/λ0
Here, the sign of gain factor is chosen such that the feedback of the second kind weakens the overall strength of feedback, thereby enhancing the sensitivity of climate, if gain factor is positive. However, the reverse is the case if the gain factor is negative. Using the gain factor thus defined, the feedback parameter (λ) can be expressed as
λ=λ0*(1−g)”
Manabe’s gain (g) is Monckton’s “feedback fraction” (f). In my comments, I accidentally replaced Manabe’s λF with λ1, but both terms represent the sum of all other feedbacks besides Planck feedback.
Monckton writes: Official climatology trains its models by adjusting them until they reproduce past climate. Therefore, the models have been trained to account for the 33 K difference between emission temperature of 255.4 K and today’s surface temperature of 288.4 K.
This is flat-out wrong. In theory, AOGCMs are tuned so that their output agrees with the climate we observe today. A typical tuning process is described below. Only after a model has been tuned do researchers learn how well it hindcasts historic warming and what its climate sensitivity is.
https://doi.org/10.1029/2012MS000154
During a development stage global climate models have their properties adjusted or tuned in various ways to best match the known state of the Earth’s climate system. These desired properties are observables, such as the radiation balance at the top of the atmosphere, the global mean temperature, sea ice, clouds and wind fields. The tuning is typically performed by adjusting uncertain, or even non‐observable, parameters related to processes not explicitly represented at the model grid resolution. The practice of climate model tuning has seen an increasing level of attention because key model properties, such as climate sensitivity, have been shown to depend on frequently used tuning parameters. Here we provide insights into how climate model tuning is practically done in the case of closing the radiation balance and adjusting the global mean temperature for the Max Planck Institute Earth System Model (MPI‐ESM). We demonstrate that considerable ambiguity exists in the choice of parameters, and present and compare three alternatively tuned, yet plausible configurations of the climate model. The impacts of parameter tuning on climate sensitivity was less than anticipated.
However, experienced researchers have fair idea of what the consequences of the tuning choices they make will be and they can re-tune a model if it predicts too much or too little warming. Isaac Held candidly discusses whether models can be tuned to roughly produce a pre-determined outcome here:
https://www.gfdl.noaa.gov/blog_held/73-tuning-to-the-global-mean-temperature-record/
“This is flat-out wrong”
And no model has been tuned with a history that includes the total absence of CO2.
Frank and Mr Stokes are, as usual, flat-out wrong. Paper after paper after paper states that the “natural greenhouse effect”, the sum of the directly-forced warming from the non-condensing greenhouse gases and the feedback response thereto, is 33 K. As if those numerous papers were not enough, the official definition of a “feedback” explicitly excludes the possibility of a feedback response to emission temperature. The models have been tuned to take these matters into account. And that is why they exaggerate all transient and equilibrium sensitivities.
The central question raised by this series remains: how can inanimate feedback processes decide that they should not respond to emission temperature but should suddenly respond greatly to the very small enhancement of it that arises from the presence of the non-condensing greenhouse gases? For all the flim-flam, no proper answer to that key question has yet been provided by our detractors here. Until they provide one, all that they say will lack credibility.
Monckton says: “Paper after paper after paper states that the “natural greenhouse effect”, the sum of the directly-forced warming from the non-condensing greenhouse gases and the feedback response thereto, is 33 K.”
Many sources say that the greenhouse effect is 33K, but this value is obtained from A MODEL, the blackbody equivalent temperature of 255 K. That MODEL assumes an Earth without GHGs WOULD STILL HAVE TODAY’S ALBEDO (a totally absurd assumption) and that the planet would EMIT LIKE A BLACKBODY (another totally absurd assumption if water vapor and clouds are present). Lacis’ model – which lacks non-condensable GHGs, but includes water vapor and clouds does NOT emit like a blackbody, because many photons escaping directly to space are emitted from cloud tops and water vapor in the atmosphere, both of which are colder than the surface. Does anyone in their right mind think the GISS model correctly reproduces convection and cloud formation when the planet is 30+ degC colder than today?
When climate scientists say that the GHE is 33 K, the public has been FOOLED into thinking that the GHE can be reduced a single, unambiguous number. The calculation requires a MODEL for the Earth without a GHE and the standard model (constant albedo, blackbody emission) isn’t what many expect. The only definite measure of the GHE is the 150 W/m2 difference between mean surface emission (390 W/m2) and mean TOA emission (240 W/m2). The GHE IS 150 W/m2. The enhanced GHE from 2XCO2 IS about 3.5 W/m2. Climate scientists don’t know how to convert changes in radiation (W/m2) into changes in temperature. If they did, WE WOULD ALREADY KNOW ECS.
We don’t know ECS because we don’t know how big feedbacks really are and we can’t trust AOGCMs to properly calculate them! For exactly the same reasons, we can’t trust Lacis’ model for our planet without condensable GHGs to correctly extrapolate feedbacks all the way to 30+ degC colder than today. Therefore anything Monckton derives from Lacis’s and Pierrehumbert’s models is suspect.
Let me make Monckton’s propaganda easier to understand. The GHE is 150 W/m2. If we also accept that the GHE is 33 K, then the climate feedback parameter λ is 4.5 W/m2/K If F_2x is 3.7 W/m2, then ECS is 0.8 K/doubling and f is -0.2. Feedback is modestly negative, trivially different from Monckton’s positive value of 0.08. Amplified global warming therefore must be a hoax. Skip the complicated control theory.
The problem is that feedbacks are not linear. The average value for λ from 255K (or 252K or 240K or ?K) to to the present isn’t relevant to what happens in the future. Feedbacks are highly non-linear. The whole idea is absurd.
Frank continues to maunder on about nonlinearity in feedbacks. But the simple truth is that, insofar as there is any nonlinearity in feedbacks, a) it is not very great; b) it is present in the system whether the corrected or uncorrected math is used; and c) therefore, equilibrium sensitivity will be considerably less using the corrected math than using the uncorrected math, even after the small nonlinearity has been allowed for.
Nibcjtib wrutesL :Frank continues to maunder on about nonlinearity in feedbacks. But the simple truth is that, insofar as there is any nonlinearity in feedbacks, a) it is not very great; b) it is present in the system whether the corrected or uncorrected math is used; and c) therefore, equilibrium sensitivity will be considerably less using the corrected math than using the uncorrected math, even after the small nonlinearity has been allowed for.”
I pointed out that Monckton’s reference (Roe 2008) discusses how to deal with non-linearity. I applied Roe method above and found the correction was large when trying to used data from Lacis’s model for our planet without non-condensible GHGs.
Frank continues to maunder on about nonlinearity in feedbacks. He cites Roe (2009) as an authority on how to handle nonlinear feedbacks. However, he overlooks the fact that Roe makes the same mistake as everyone else in official climatology by failing to accord any value to the large feedback response to emission temperature, and by using a degenerate form of the zero-dimensional-model equation that makes no provision for the emission temperature and, therefore, no provision for any feedback response thereto.
It is precisely because official climatology does not make due allowance for the feedback response to emission temperature that it imagines, quite improperly, that nonlinearity in feedbacks is a big deal. Of course Frank will be able to make nonlinearity look serious if he continues to refuse to use the corrected form of the zero-dimensional-model equation.
Monckton writes: “Let us conduct a simple Gedankenexperiment, running in reverse the model of Lacis et al. (2010), who found that, 50 years after removing all the non-condensing greenhouse gases from the atmosphere, the climate would have settled down to a new equilibrium, giving a slushball or waterbelt Earth with albedo 0.418, implying emission temperature 243.3 K. … Lacis found that, only 20 years after removal of the non-condensing greenhouse gases, global mean surface temperature would fall to 253 K. Over the next 30 years it would fall by only 1 K more, to 252 K, or 8.7 K above the emission temperature…. ”
What does Monckton mean when he says that the “implied emission temperature” is 243.3 K? He is saying that a BLACKBODY at 243. K would emit 199 W/m2 and our planet with an albedo of 0.416 would absorb (1-0.412)*342 = 201 W/m2. Close enough to balance. WHO EVER SAID THE EARTH MUST EMIT LIKE A BLACKBODY? The current Earth emits like a graybody with emissivity 0.615 and temperature 288K. Lacis’ model has more clouds than today. If Lacis’ model has cloud tops at 235 K and a surface at 252K, it would emit about 200 W/m2. And that is before accounting for any reduction in emission due water vapor in the atmosphere.
Monckton continued: “One question which few opponents in these threads have answered, and none has answered convincingly, is this: What was the source of that additional 8.7 K temperature, given that there were no non-condensing greenhouse gases to drive it? Our answer is that Lacis was implicitly acknowledging the existence of a feedback response to the 243.3 K emission temperature itself – albeit at a value far too small to be realistic.”
So low cloud top temperature and water vapor can easily explain why Lacis’ model emitted only about 200 W/m2 of LWR. Just like low cloud top temperature, water vapor and non-condensable GHGs explain why our planet today only emits 240 W/m2 (a blackbody equivalent temperature of 255 K). In both cases we expect the planet to emit like a gray-body, not a blackbody: T = 288K and e = 0.615 gives a graybody emission of 240 W/m2 (like today). T = 252 and e = 0.87 emits 199 W/m2. Mystery explained.
As Frank begins to realize that the Great Cause on which he has wasted so much time is on the brink of outright collapse he becomes ever more hysterical and incoherent. Let me explain to him, yet again, how the fundamental equation of radiative transfer works.
Take a snowball Earth with albedo 0.6. The emission temperature is 221.5 K. Take a waterbelt Earth with albedo 0.418. The emission temperature is 243.3 K. Take today’s Earth, with albedo 0.293. The emission temperature is 0.293 K. None of these temperatures is a blackbody temperature, because the albedos are nonzero. Neither I nor anyone has suggested that the Earth must emit like a blackbody when, given its albedo, it must emit like a graybody.
In this post, Monckton continues to push the idea that feedback can be associated with a temperature, rather than just a temperature change. Does this idea make any sense for climate (not amplifiers or control systems)? The climate feedback parameter λ is the derivative of net radiative balance across the TOA (OLR + reflected SWR) with surface temperature. For changes of a few degK, we can treat λ as a constant, For larger changes, such as those in this post, we can not – emission varies with the FOURTH POWER of temperature. To make this clear, let’s express λ as a function of Ts
dW/dTs = λ(Ts)
dW = λ(Ts)*dTs
This equation can be integrated from T1 to T2, which would define a cumulative feedback for a temperature change from T1 to T2. Or we can imagine an indefinite integral with an unknown constant of integration C. We can evaluate C at absolute zero and find that C = 0.
Now let’s try the same mathematics with amplification, which arises from breaking λ(Ts) up into two components, Planck feedback λ0(Ts) and the sum of all other feedbacks λ1(Ts). f(Ts) = -λ1(Ts)/λ0(Ts)
dW = λ0(Ts)*dTs + λ1(Ts)}*dTs = λ0(Ts)*dTs + -f(Ts)*λ0(Ts)}*dTs
These integrals exist, so we might be able to assign a cumulative value to amplification at any temperature.
Above, I wrote that Lacis’ data fit a graybody model with T = 252, e =0.87, and albedo = 0.412 as well as T =288, e = 0.615 and albedo = 0.30. In other words, but emissivity and absorptivity are changing with temperature when we think of the planet as a gray body.
So, changing the temperature from 3K to 255K won’t induce any feedback effect, but changing the temperature from 255K to 263K will? Makes sense (or not..).
Mr Langlee is right and Frank, as usual, is flat-out wrong. Feedbacks, whether Frank likes it or not, are denominated in Watts per square meter per Kelvin. Being inanimate, they are quite incapable of distinguishing between the input signal (emission temperature) and any amplification thereof. They will simply respond to the input signal, whether amplified or not. The corrected form of the zero-dimensional-model equation makes this quite clear. And, just in case, we built a test rig to check that there is indeed a feedback response to the input signal, and then we got a national laboratory to do the same, We are right about this.
As to Frank’s point about non-linearity, that is the last refuge of a scoundrel. We have shown in the head posting that the variance in the value of the “Planck feedback” is tiny even across 33 K of temperature change. We have shown that the only significant feedback – the water vapor feedback – is approximately linear. In such circumstances, we are fully justified in taking as a working assumption that the feedback fraction is near-invariant.
In any event, to whatever extent the feedback regime in the climate system may be non-linear, correction of the error we have exposed does not have the effect of increasing that non-linearity. Therefore, correction will very substantially diminish both transient and equilibrium sensitivities.
How would Frank explain the very sharp nonlinearity by which the feedback response to emission temperature is either nil or very small, while the feedback response to the modest addition to it represented by the directly-forced warming from the non-condensing greenhouse gases is very large?
“How would Frank explain the very sharp nonlinearity by which the feedback response to emission temperature is either nil or very small, while the feedback response to the modest addition to it represented by the directly-forced warming from the non-condensing greenhouse gases is very large.”
Right — it doesn’t make sense. Moreover, the non-linearity of the system clearly works against the incremental response being greater than the absolute response:
http://www.palisad.com/co2/gf/st_ga.png
http://www.palisad.com/co2/why/pi_gs.png
Plus, each degree of warming requires incrementally more and more power to effect and sustain than the previous degree, which only further works against the incremental response being greater that the absolute response.
The real flaw though in all of this is that there really is no new starting point for the physical processes and feedbacks (mainly water vapor and clouds) since the system is never truly in balance — it perpetually oscillates to maintain an approximate steady-state. The physical processes and feedbacks from water vapor and clouds have no way to distinguish an imbalance from added GHGs from imbalances that occur as a result of the regularly occurring dynamic chaos in the system, and would respond within the same bounds.
The great Cause on which Frank invests his time is Science, not politics. Unlike politicians and attorneys, scientists are expected to tell the truth, the whole truth and nothing but the truth, with all of the ifs ands buts and caveats. However, the vast majority of climate scientists appear to have been attracted to the field to “save the world” and have forgotten their scientific ethics. They live in left-wing ivory towers and have sold out to a political organization (the IPCC) with a charter (consensus) that allegedly requires them to skip over some of the truth and almost all of the caveats. Their reports require unanimous agreement of more than 100 bureaucrats, meaning that their SPMs contain only the convenient part of the truth and none of the caveats, particularly about the fallibility of AOGCMs (their only tool for making projections). Those bureaucrats are advised/controlled by a self-perpetuating group of activist insiders who serve as prosecutor, judge and jury for our fossil-fuel based society. No defense attorneys (nor the press) are allowed to attend, just fanatic environmental organizations ready to pounce if anyone steps out of line. For that reason, it is difficult for any scientist to publicly discuss and publish science that suggests climate sensitivity is low.
Unfortunately, almost all of the science being pushed by politically active skeptics and at this blog is badly flawed. Like this post. And previous posts about the Pause: About the absence of statistically significant warming being evidence that no warming is occurring and that the GHE doesn’t exist. Confusing transient and equilibrium warming. This noise has drowned the growing real evidence that climate sensitivity is near the bottom of the IPCC’ s likely range: EBMs, all AOGCMs show ECS less than 2 when forced with historic SSTs, the weakening evidence for a strong aerosol indirect effect, weakening AR5 claims about the MWP, hurricane intensification. This progress towards a less alarmist future is being ignored because the skeptic position that get the most publicity is that AGW is a hoax. Skeptical (and alarmists) politics is all about “winning”, not uncovering scientific truth. To quote Alice Dreger (a passionate advocate for more unbiased science and research: “Only people like us, with insane amounts of privilege, could ever think it was a good idea to decide what is right before we know what is true”. In her case, the ‘insanely privileged” people she was referring to were her fellow liberal academics. Ms. Dreger’s book is subtitled “Heretics, Activists, and One Scholar’s Search for Justice”. A great read.
Monckton’s Cause is winning.
Frank misrepresents me when he says that I had suggested that the Great Pause in global temperatures indicated that there was no greenhouse effect. On the contrary, in column after column here, as the Paus grew in length to 18 years 9 months before a large el Nino brought it to an end, I made it quite plain that some warming was to be expected and that, therefore, the Pause would not continue indefinitely.
But we seem to be in agreement that equilibrium sensitivity will be well south of 2 K. That is certainly what our result shows.
Frank continues to reveal his ignorance of elementary control theory by pretending that a feedback response cannot arise in the presence of an invariant input signal. The point really is elementary. The corrected version of the zero-dimensional-model equation mandates it. But, because IPCC had attempted to define a feedback as a response only to a change rather than also to an absolute value, we built not one but two simple circuits to make sure that the theoretically-mandated feedback response even to an unamplified input signal actually occurs, and occurs at the expected value. Well, it does. And it’s no good Frank trying to muddy the waters. Control theorists will soon be looking at our result, and they will have no patience with the nonsensical notion that an invariant or unamplified input signal induces no feedback response.
The main criticism of Lord Monckton’s conjecture, if I may call it that, appears to be that one shouldn’t use the equation:
ΔTeq = ΔTref / (1 – f )
for absolute (Kelvin) temperatures i.e. in the form:
Teq = Tref / (1 – f )
But the only reason one can’t use it in this way is if the feedback parameter f were to change as a function of temperature.
If the feedback parameter f is constant across all temperatures from 0°K to 288°K, then Teq = Tref / (1 – f ) is perfectly valid, as demonstrated Monckton’s electrical feedback circuits, and a constant value of f=0.08 is appropriate to explain the single data point that we are considering here, namely that an input temperature of 263°K (the sum of the 255°K emission + 8°K non-condensing GHGs) results in an equilibrium temperature of 288°K.
However… if you make the feedback parameter f a function of temperature, let’s call it f(T), then if course you can’t use a constant value of f on the absolute temperature. Clearly Teq = Tref / (1 – f ) no longer works as it doesn’t capture the changing feedback parameter across large temperature changes. For example, if you used f=0.75 (Lacis et al) and applied it to the full input temperature of 263°K it would imply the earth’s equilibrium temperature is 263°K /(1-0.75) = 1053°K (!). So of course this is absurd.
But the another way to satisfy our single data point, namely that 263°K implies an equilibrium 288°K, is to set the feedback parameter f(T) to zero right the way from 0°K up to 263°K and then jump it up to 0.75 in the region 263°K to 288°K. Then if you would restrict the use of the equations thus:
0°K < T < 263°K ΔTeq = ΔTref / (1 – 0.0 )
263°K < T ΔTeq = ΔTref / (1 – 0.75 )
Then this too satisfies our single data point. So the previous conjecture (Hansen et al) can be thought of this way. Zero feedback until 263°K, followed by a step-change discontinuity in f(T), where it suddenly steps up to 0.75 at the magical 263°K temperature.
Now I'm not familiar with the exponential Clausius-Clapeyron relation w.r.t. temperature, and the logarithmic nature of water vapour feedback (is the end result roughly linear, so a constant feedback parameter?). But my first assumption would definitely not be an f(T) of has this odd square-wave form. What basis is there to assume that? As Lord Monckton eloquently puts it, water vapour is also present in the atmosphere at lower temperatures too, well below 263°K, so how does the mother earth know to provide zero feedback until 263°K and then suddenly crank up the feedback processes at a rate of 0.75 above the magic temperature? Being polite I'd call it: erroneous.
So given we only have one data point, the best we can do is estimate a single value. So a much better starting point would be to assume a constant f = 0.08.
(That's not to say that far more work needs to done to map out f(T) from 0°K up to 288°K, for example when an input ΔT of 2°K is enough to end an ice age and the world might become say 10°K warmer. So in this narrow temperature region f(T) could jump up to 0.8. But it could be zero or negative either side, who knows? So what does this function of f(T) look like? Why don't we know? What have climatologists done with all their funding money, counting polar bears?)
I’m most grateful to Mr Palmes for having really thought hard about our work. He has gotten the point of what we are trying to say, and he has also understood that, though feedback processes are non-linear in the climate system, they are not very non-linear, which is why assuming a single mean feedback fraction is justifiable.
It may assist Mr Palmes to know that we are not dealing with an interval of surface temperature from 0 to 288 K, but from 255 to 288 K. The feedback processes (chiefly the water-vapor and albedo feedbacks) are not concerned with any value less than the emission temperature of 255 K. That is the input temperature to which they would react even in the absence of the non-condensing greenhouse gases. So we are only dealing with an interval of 33 K. Across that interval, nonlinearities in feedbacks tend, if anything, gradually to diminish the feedback fraction rather than to increase it.
In any event, such nonlinearities as may subsist in the feedback processes subsist no less under the present system than under the corrected system. It is inevitable, therefore, that in the corrected system the equilibrium sensitivity will be considerably below its value in the present system. For our corrections do not alter any nonlinearities that may be present.
In reply to Lord Monckton, thank you, that was extremely useful response. I was getting lost down a side alley for no good reason.
In a moment of clarity I suddenly see the elegant simplicity of this. If an input temperature of 263°K (the sum of the 255°K emission + 8°K non-condensing GHGs) results in an equilibrium temperature of 288°K that implies that f=0.08. And then perturbing the input signal by a ΔT of 1.2°K (the direct temperature rise for x2 CO2) this means the input is now 263+1.2 = 264.2. This results in an equilibrium temperature of 264.2 /(1-0.08) = 289.3, which is an equilibrium temperature rise of 1.3°K.
So hang on, isn’t this even better than we thought? We only need to worry about the non-linearity in very close proximity to the current 263°K input signal? Why are we worrying about snowball earth or the feedback parameter near absolute zero. That’s completely irrelevant to the question we’re trying to answer.
I’m not sure why it’s taken me so long to get it, (perhaps led astray by Nick Stokes?)
I am glad that Mr Palmes can now see our result in his mind’s eye. The speed with which he has grasped it is commendable. It took me a great deal longer, with much fumbling around and with publication of several papers raising the questions to which I needed answers before I could finally see the whole picture.
In truth we do not really need to worry about nonlinearity at all. For our separate calculation intended to derive the industrial-era value of the feedback fraction found it to be somewhere between 0.04 and 0.28, depending on how many assumptions unduly favorable to the official position one is prepared to make. That would give an equilibrium sensitivity of 1.2-1.5 K, which is not enough for anyone to worry about.
Harry: The Clausius-Claperyon relationship is not an exponential one. The log of saturation vapor pressure varies with 1/T. 7%/K is a reasonable approximation around 288 K. IIRC, it is closer to 6%/K in the tropics and up to 10%/K around -20 degC. Just another example of Monckton not being familiar with the physics he is using. The real problem, of course, is that our atmosphere is not saturated with water vapor. Relative humidity averages 80% over the ocean and falls with altitude. The assumption that relative humidity will remain the same as the planet cools more than 30 degC is a dubious one.
I think you’ve got the right idea writing f(T) rather than just f (a constant). Don’t forget λ0 also should be written as λ0(T)> It represents simple thermal emission of radiation with varies with T^4. And there is some merit in the idea of integrating.
Frank continues to adopt a childish, hectoring, lecturing tone which is not impressing readers here. He keeps assuming that it is I whom he is having to deal with, rather than a band of expert co-authors with certificates of appropriate Socialist training in the relevant subjects.
And of course, when considering nonlinear functions such as the feedback fraction, one must consider an array of temperature-dependent values. All of that is elementary. However, the central and obvious point is this. Given that the nonlinearities in the system are the same whether one does the math incorrectly, as official climatology does by ignoring the large feedback response to emission temperature, or correctly, as we have done, it is inevitable that, following our correction, Charney sensitivity will be very considerably below what it is currently thought to be.
Y does it seem like all the historic weather data charts on this site end in 2011?? What year is this anyway….I’m conrfused….
In response to Meigs, the most recent IPCC Assessment Report was in 2013, and it gave estimated net anthropogenic forcing from all sources to 2011. For a fair comparison, therefore, one must look at the warming to 2011 as well. Nothing more complicated than that.
Harry: I’ve just been re-scanning the comments on Christopher Monckton’s original “Game Over” and this article. I’m not familiar with the gory detail here (I’m a software consultant, originally trained as a pure mathematician – in fact, I was at Cambridge at the same time as Christopher). But I have a nose for what fits and what doesn’t. On the other thread, commenters called “Frank” and “Nylo” raised this issue, and “Joe Born” weighed in. And here, “Martin Mayer” has stated very concisely the problem that I see with Christopher’s argument.
Then I scrolled to the end of the comments, and found that you had anticipated me – by a couple of hours or so. Yes, the feedback factor can’t possibly be constant at different temperatures!
A thought experiment: Start with an Earth at 3 degrees K, the cosmic background. All greenhouse gases are solid. The molecules can’t vibrate in the modes necessary for the greenhouse effect – or am I wrong? So there’s no feedback at all, at all. Now, turn on the Sun and let the planet warm up to the 255K “emission” temperature. The greenhouse gases, other than water vapour, are now free to do their thing.
Hansen may have assumed that at an average 255K (minus 18C) there was no water vapour. If so, that has to be wrong. Today, we have an average global temperature of 14C, but the highs are around 50C. Those tend to be in dry places, but there surely is water vapour there. So there must have been water vapour, and liquid water too, in our thought experiment when it reached the “magic” 255K. I’m not sure whether, or how much, liquid water can contribute to the greenhouse effect. But ignoring that, as temperature rose towards and beyond 255K in our thought experiment, the water vapour feedback would have increased. So the feedback factor would have changed dramatically as the Earth’s average temperature crossed the line, in terms of average temperature, from water freezing to liquid.
Lacis et al, if I understand right, tried to apportion the greenhouse effect between water vapour and the rest. Christopher is absolutely right to question that apportionment, and what they deduced from it. And my sense of smell tells me that, given the unknowns, it’s odd that the sensitivity answer came out close to the IPCC estimates. But I still don’t buy Christopher’s argument.
“But I still don’t buy Christopher’s argument.”
I do. My Mech Eng control theory was my favorite course. MBs use of an electrical circuit(independently solved) is final proof. The worry about non linearity over such a small temperature range is overreach imo. Less than 3 % likely.
It looks very much to me like à terminology problem. The feedbak term “f” in climatology is delta f in other fields of science. Similar to “forcing” which is delta force in oth34 disciplines.
It is this misuse of terminology that is at the heart of the problem.
Neil Lock seems to think that the interval of interest is from 3 K to 288 K. No, it isn’t: it’s from 255 K to 288 K.
Christopher: But the interval of interest, as you call it, includes the freezing/melting point of water. Around which, we might expect the feedback factor to change significantly. What have I missed?
Oh, and in your earlier essay where you say that the equations are equivalent for delta T and for T, you’re implying that the interval of interest is 0K to 288K.
Neil, you seem to assume that all water on earth would be ice if the earth’s average temperature was -18C, that’s wrong. It’s _average_ temperature, the equator would be above freezing. Now we have an average temperature of 14C, but still there is ice. According to your assumption we should only have liquid water today, since the average temperature is above freezing.
The temperature range of interest is 287K to perhaps 292K, but hopefully less. And you can go back to the LGM if necessary say 282K That is the only range where feedback is relevant and probably a little wide to expect linearity.
In the few billion years, we haven’t had a planet without non-condensible GHGs in the atmosphere. It’s been at least 500 million years since we may have had a snowball Earth, a phenomena that is intensely debated and poorly understood. No one appears to believe that this period was due to the total absence of non-condensible GHGs in the atmosphere.
Peter: No, I suggested that Hansen may have assumed that there is no water vapour when the average temperature is -18C. As you say, that is wrong.
Frank now appears to be admitting that nonlinearity is not much of an issue, after all. If so, he is now correct. But he continues to have difficulty with the concept – well established in the mathematics of dynamical systems – of studying the change of state of the system between two presumed equilibria. One such equilibrium is the Earth’s emission temperature in the absence of greenhouse gases or feedbacks. Another is the Earth’s temperature in the presence of condensing gases and, therefore, of the feedbacks thereto in response to the emission temperature. Another is the Earth’s temperature in the presence of both condensing and non-condensing greenhouse gases, as it stood in 1850 before any anthropogenic perturbation. Another is the temperature following the anthropogenic perturbations to date. Another is the temperature at equilibrium following a doubling of CO2 concentration compared with today. Such stepwise calculations, albeit that several of the steps are artificial, are precisely how official climatology operates. If Frank thinks that it should not do so, he should bring his concerns not to me but to secretariat@ipcc.ch.
A wonderful read Monckton of B. Over 300 responses is an indicator in itself of the importance of your finding, even if all were negative, maybe particularly if all had been negative. A late comment like mine is likely to go unread but I just wanted to say that before this work of yours and amici, I wasted little time on the official math of feedbacks because after climategate and the rest of it, I knew that the official clime syndicate “math” was in some way self serving anyway.
For the first time, I have educated myself on the details, following your straightforward arguments and dare I say simple math (simple like E=Mc^2). You would be a superlative teacher.
The importance of your work is also indicated by the fact that it was raised even by visitors to Yahoo Answers. The Yahoos are, of course, well named.
https://www.merriam-webster.com/dictionary/yahoo
You have poked a huge hole in the clime syndicate hive and I predict that every worker and drone has dropped his other dreary studies to concentrate their venom on your work. Please take care for your security Christopher.
I am most grateful to Mr Pearse for his kind comments. And I am glad that he has not found the rather technical explanation of our result in the head posting too difficult. It is indeed significant that Yahoo Answers has already found it necessary to try – in a remarkably half-baked way – to impugn our result. Now that the matter has been publicly aired, the truth will inexorably spread, however hard the totalitarian profiteers of doom try to stop it. That is the value of true science: in the end, it is unaswerable.
As for my personal security, I am sure that those driving this scam, who have spent large amounts of time and effort on trying and failing to neutralize me, will not be stupid enough to turn me into some sort of martyr. Nothing would be more fatal to their pseudo-moralizing posture than that.
The problem is terminology. What climatology calls “forcing” is a delta force in all other fields. what climatology calls feedback is a delta feedback in all other fields.
The problem is that “f” has been used to represent both feedback and delta feedback which hides the source of the error.
A new term needs to be added to the equations to distinguish the different definitions of the term “feedback”.
Delta feedback may not be precisely correct. But there is a definite difference between how an engineer views feedback as compared to a climatologist.
As such it is an error to use the term “f” to represent two different things. It leads to problems like 1=2. You can prove anything.
In engineering terms, climatology filers out the DC portion of the signal and only applies feedback to the AC portion. So long as you only work in anomalies this is hidden from view.
However, when you convert to absolutes you also need to allow for feedback on the DC portion of the signal.
Climatology T = AC+DC+f(AC)
Engineering T = AC+DC+f(AC+DC)
In reply to Mr Berple, the feedback fraction f is unitless,. It is not, therefore, a delta. The feedback response, in Kelvin, is indeed a delta. It may be helpful if I explain the nomenclature. The input signal (emission temperature), the output signal (equiulibrium temperature) and the feedback response are all denominated in Kelvin. The feedback fraction f, like the open-loop gain factor mu and the feedback factor mu x beta, is unitless. As for f, it does duty in official climatology both as the feedback fraction and as the feedback factor, for mu is assumed to be unity.
Given a surface temperature difference of +/- 42K , Antarctica night (-49°C) vs, Riyadh day (35°C), the emission would be 1.31 times as much in Riyadh and 0.37 times as much in Antarctica, compared to the emission at 288 K average. The departure form linearity is not insignificant over this range, though as your comments imply, the non-linearity would diminish the feedback, ie. it is a negative feedback. I realize that your feedback equation is about a shift in average temperature, thus only a degree or two which is close enough that the non-linearity would be well within the margin of error. Two other comments. Willis, in one of his posts on tropical thunderstorms and temperature feed back, had graphics that indicated a nearly asymptotic limit to temperature of about 34C. Very nonlinear. In regard to water vapor feed back, any heating would result in such feedback, it would be nonsensical to posit that CO2 would be special in this regard. For climate purposes there is an unlimited amount of water available, thus any such feedback should be maximized based on temperature. CO2 would be irrelevant to this, Given the wide variation of temperatures on the surface of the planet currently and in the geologic past, any hypothesis on tipping points or run-away heating should be unequivocally falsified.
“In regard to water vapor feed back, any heating would result in such feedback, it would be nonsensical to posit that CO2 would be special in this regard”
Good point. In addition, if thunderstorms on average start two minutes earlier each day, and finish 2 minutes later, would our measuring systems know? Nope.
Al in Kansas is quite right. If the nonlinearity in feedbacks were anything like as great as it would have to be to impugn our result, global surface temperature would not have varied by as little as 3 K either side of the 810,000-year mean.
May I express my considerable gratitude for the exemplary manner in which Lord Monckton has laid out his argument, and has defended it? And, perhaps, entertained us at the same time? I note the close spacing of the time stamps on his responses to sequential comments here: responses which, despite the short composition time allowed, are pertinent, elegantly constructed, and resolutely informative. And I believe he has not omitted a response to any relevant comment, whether supportive or critical. Rarely has such a complete and competent involvement been recorded in the long history of this great dialogue. I would like to see others follow his example. Perhaps someone from the ‘climate establishment’ would like to join these threads. Or do they think it beneath them?
Now, although I follow the logic of Lord Monckton’s argument, I am not qualified to judge whether the assumptions that he has made – particularly (and this is rather important) whether the error he has claimed to find really is fundamental to basics of the establishment case for CAGW. I am inclined to accept it, for it happens to confirm and explain my own independently derived prejudices upon the subject!
I’d also like to thank – not for the first time – the efforts of Nick Stokes to bring the lord to heel. Nick is a considerable intellect, and he has the knowledge and ammunition to curb the excesses of commenters here, which is much appreciated. However, I’m not sure what Nick actually thinks himself. He’s very good as a devil’s advocate, always probing for error or inconsistency, always challenging, and that’s excellent stuff. But I never ever see him admitting any uncertainties in his own arguments, nor do I hear him making a coherent overall case, nor accepting that others might just have a point. Keep it up, Nick, but it would be good to see you open up a bit yourself.
One point I do take from the argument as a whole. Many here do find it very difficult indeed to accept the central point that Lord M is making – that feedbacks WILL occur – and occur in very much the same manner – on an earth devoid of non-condensing greenhouse gases. Nick seems included in those. Well, that’s something that I have always regarded as self-evident, and if the math describing electrical circuits are a good analogy I’ll take that as a tick of confirmation. I fail to follow the logic of the counter argument at all, and I think it must result from some slavish misinterpretation of the definitions implicit in the forcings/feedback issue. It is a false dichotomy. The real argument should be about how CO2 differs in its effect locally (polar/desert/nocturnal/high altitude) and may therefore reset the thermostat.. Therein is the refuge of the CAGW case, and much is yet be written about it.
Brilliant thread.
Thanks, moth
However, I must say that throughout this thread, and indeed on all threads since the end of March, all my comments (even this one) have gone through moderation, which hampers dialogue considerably. I don’t know why; I have not seen anything said by the mods or Anthony that would explain why this is so.
Happens to me from time to time.
Earmarked as controversial no doubt.
I am most grateful to Mothcatcher for his exceptionally kind comments. I have done my best to answer all relevant points, from whichever direction they came. Our control theorists (two engineers and a professor of applied control theory) are entirely content that even an unamplified input signal in any dynamical system on which nonzero feedback processes bear will induce a feedback response. As Mothcatcher rightly points out, that conclusion is inescapable from the mathematics of the feedback loop – mathematics that applies no less to the climate than to any other dynamical system.
Our point is indeed a simple one, and the only reason why we have had to provide such lengthy and detailed treatments of it is to nail shut the various rat-holes by which official climatology will seek to escape.
I think I am not being unfair when I say that none of the comments in these threads has landed a blow fatal to our result. There has been some nibbling around the edges, but that is all.
The big question now is whether the gatekeepers of the leading climate journals will close the portcullis and try to prevent our paper from being published. If a genuine and material error in our result is found, all well and good – we shall retire gracefully from the field. If, however, no error is found, let it be known to all that the relevant public authorities are now watching carefully how official climatology handles our result. In view of the staggering financial and human cost of global-warming mitigation policies, any dishonest attempt to preserve and protect the profits of those gaining by those policies by improperly refusing to publish our result may occasion a prosecution, not by us but by the public authorities themselves.
Climate scientists are about to find out – the hard way if necessary – that they are subject to just the same law as the rest of us. They are no longer immune. It will come as no surprise to readers of this column that there have been a few instances of outright criminal deception in the peddling of the official climate-change storyline. Such deceptions will no longer be tolerated. It is time for the truth to have its day.
If Lord Monckton is still kindly attending to the many replies, can I ask a question on the importance, or otherwise, of the non-linearity in the feedback parameter at temperatures in the region 255°K to 288°K?
As mentioned above, in my moment of clarity, if an input temperature of 263°K (the sum of the 255°K emission + 8°K non-condensing GHGs) results in an equilibrium temperature of 288°K that implies that f=0.08, using f = 1 – ΔTref / ΔTeq.
Then if we perturb the reference input signal of 263°K. by a ΔT of 1.2°K (the direct temperature rise for doubling CO2) so means the input signal rises to 263+1.2 = 264.2. This results in an equilibrium temperature of Teq = Tref / (1 – f ) = 264.2 /(1-0.08) = 289.3°K, which is an equilibrium temperature rise, ΔTeq, of 1.3°K.
You can also use the ΔTeq = ΔTref / (1 – f ) to arrive at the same result. 1.2°K /(1-0.08) = 1.3°K
So surely, if we can assume that the intricate water vapor and cloud feedbacks are linear in the small interval from 263°K to to 264.2°K then the resulting f = 0.08 will be robust to use for the Charney Sensitivity.
So there’s no need to concern ourselves with non-linearity near absolute zero when our nitrogen atmosphere turns to a super fluid, or snowball earths, or other exciting situations. We are only looking for a robust estimate of the feedback parameter at, or in close neighbourhood (perhaps ±3°K?) to, our single data point, namely the input and equilibrium temperatures in the year 1850 with all the feedback mechanisms that are present in the system at that time.
Is this correct or have I missed something obvious?
Mr Palmes is correct that, once a reasonable value for the feedback fraction has been settled upon, the very small temperature perturbations from now until all oil, coal and gas reserves are exhausted mean that we do not have to worry about nonlinearity in feedbacks.
However, in order to provide a theoretical demonstration of the value of the feedback fraction, it is necessary to examine the interval between two presumed equilibria – the emission temperature of 255 K and the pre-industrial temperature of 287 K that prevailed in 1850. Since the interval is 32 K, nonlinearity in feedbacks might in theory make a difference here. It is easy to establish that the mean feedback fraction, after correction of climatology’s central error, is only 0.08. But the various shriekers here, yelling out the Party Line over and over again, try to pretend that the nonlinearity in the feedback fraction is so great that by 1850 the feedback fraction must have been an order of magnitude greater than the mean value of 0.08.
Trouble is, none of the feedbacks listed in Table 1 contains within it a nonlinearity sufficient – even in the wildest dreams of the totalitarian screamers – to come anywhere close to ten times the 0.08 that we have derived. The water vapor feedback may have increased the atmospheric burden of water vapor tenfold over that 32 K interval, but the feedback response is logarithmic, offsetting to some considerable degree the near-exponential increase in the water vapor content. What is more, the lapse-rate feedback runs directly counter to the water-vapor feedback owing to the imagined (but actually imaginary) tropical mid-troposphere hot-spot that models predict but is not observed in reality except in one or two defective datasets. So there is certainly no tenfold nonlinearity there.
Worse still for the totalitarians, we derived a current value of the feedback fraction from IPCC’s official estimate of 2.29 Watts per square meter of net anthropogenic radiative forcing from 1850-2011 and the observed temperature change of 0.75 K over the period. The feedback fraction thus derived was 0.05. Even after allowing for the “radiative imbalance” in that the oceans are warming, and even on the very generous assumption that none of the warming since 1850 was anthropogenic, the feedback fraction is below 0.3, implying an equilibrium sensitivity of just 1.5 K.
As if that were not enough, our correction to the official math does not in any way alter such nonlinearity as already subsists in the temperature feedbacks. Therefore, doing the calculation correctly will inevitably very greatly reduce equilibrium sensitivity compared with today’s estimates.
The totalitarians are using nonlinearity as the last refuge of the scoundrel: but, bearing in mind all the evidence rather than the very partial selections of it that they have tried to present or misrepresent, it actually makes very little difference to the final numbers. The science is in, the truth is out, Al Gore is through, the game is up, the scam is done and the scare is over.
My thanks to Lord Monckton once again.
But I’m still hoping that any potential non-linearity between 263°K and 288°K will have almost no effect whatsoever.
To borrow some terms from calculus and integration, isn’t what we doing here a kind of ‘integration’ of the feedbacks that occur in the interval between 263°K and 288°K? I know it is not strictly an integration in the mathematic sense, but suspend your mathematical rigor for minute:
Firstly make f a continuous function of T, and then integrate f from 263°K and 288°K with the result equivalent to a constant f 263<T<288 = 0.08, and so the trillion-dollar question is… what happens when we perturbate the interval from 263°K to 264.2°K (a ΔTref, of 1.2°K for 2x CO2)? Will the result be 289.3°K (ΔTeq, of 1.3°K) as expected? Is it valid to carry over our f=0.08 value for this new interval?
In terms of our ‘integral’, we are now integrating our f from 264.2 to 288.3, so over a slightly different interval. But the vast majority of this ‘integral’ is taken over exactly the same range, so this part will yield the same result. We’re just exchanging a small section at the start, with a section added to the end. The middle section of 23.8°K, (or 95% of the total), is common to both calculations.
So to play devil’s advocate and stress test The Monckton Conjecture, why not ask someone to think of the most extreme of non-linear assumptions they can reasonably imagine for f as a function of T in this interval. Then remind them that we are only exchanging the bottom 5% of the interval for a 5% at the top, so how much effect will this have?
I hope the answer would be ‘very little’.
PS We might jest calling this ‘The Monckton Conjecture’, but it may well be useful to name it soon, to help the idea spread. Memes need a name to spread quickly. This is the identification of an egregious error, but this can't be referred to as Monckton's Egregious Error (it’s not your error). Henry Heimlich has his Manoeuvre. The Monckton Manoeuvre maybe? Or The Monckton Supposition? I think you should have the honour of naming your baby.
In response to Mr Palmes, we had of course done some calculations to see whether even the most extreme nonlinearity in the feedback fraction that is plausible after correction of official climatology’s error could make a significant difference to Charney sensitivity. We know that the mean feedback fraction – assuming linearity just for the moment – is 0.081. We have then made a number of assumptions designed to bend the argument rather beyond what is really possible by assuming that the nonlinearity in the feedback fraction is as great as the nonlinear increase of 7% per Kelvin in the column water vapor (actually, we have assumed that at 255 K the increase is 10% per Kelvin, falling gradually to 7% at 287 K). In making this assumption, we have made no reduction for the fact that the water-vapor feedback forcing is approximately logarithmic, offsetting to a large extent the nonlinearity in the column water vapor itself; we have made no reduction for the fact that the interval of interest is not 255 to 287 K but 264 to 287 K; we have made no reduction for the fact that the tropical mid-troposphere hot spot predicted by the models as an inevitable consequence of their excessive estimate of the water vapor feedback is not observed except in one or two defective metadatasets; and we have made no reduction for the fact that, if the hot spot does come into existence, the lapse-rate feedback will become more strongly negative and will countervail to an appreciable extent against the water vapor feedback; and we have made no reduction for the fact that no feedback other than the water vapor feedback has anything like a 7%-per-Kelvin compound acceleration.
In short, we have bent over backwards to accommodate official climatology’s position. And the bottom line is that at 255 K the feedback fraction would be 0.016, while at 287 K it would be about 0.2. The mean feedback fraction would be 0.081. Now, this is a rough-and-ready calculation, of course. But one would be hard put to it to produce a feedback fraction even as high as 0.2 if one made all the reductions that we’d be entitled to make. But let’s call it 0.2. In that event, Charney sensitivity would be less than 1.4 K per CO2 doubling, instead of the 1.2 K per doubling that one gets from assuming the mean feedback fraction of 0.081. The difference made even by the extreme nonlinearity that we have deliberately assumed is less than 0.2 K. Now, if you go back and look at all the waffle that the paid agents of climate fanaticism here have devoted to the nonlinearity issue, you will see what nonsense it all was. Your instinct is quite right: nonlinearity is a non-issue.
Of course, anyone approaching this question with an open mind rather than an open mouth would have seen this as easily as you have. For whatever nonlinearity subsists in the present system will also subsist in our system: but the correction made by our system will inevitably and greatly reduce Charney sensitivity, regardless of the fact that there is nonlinearity. That conclusion isn’t rocket science: it’s common sense. Your instinct, therefore, is amply borne out by the calculations we did.
That’s a nice article, which is actually tackling a problem even bigger: IPCC just doesn’t even have a proper definition of “greenhouse effect”. It use TWO definition concurrently, despite being mutually exclusive, and this shows in Lacis and al. and all related stuff. So, basically, you cannot escape the tangled web of deception
One definition you find page 126 (with figure 1.1) of WG1AR5_ALL_FINAL.pdf.
“The longwave radiation (LWR, also referred to as infrared radiation) emitted from the Earth’s surface is largely absorbed by certain atmospheric constituents—water vapour, carbon dioxide (CO2), methane (CH4), nitrous oxide (N2O) and other greenhouse gases (GHGs); see Annex III for Glossary— and clouds, which themselves emit LWR into all directions. The downward directed component of this LWR adds heat to the lower layers of the atmosphere and to the Earth’s surface (greenhouse effect).”,
The other definition you find in glossary
“Greenhouse effect: The infrared radiative effect of all infrared-absorbing constituents in the atmosphere”
Sound similar? indeed. Is it the same? NO.
For instance, when water condense into clouds and release heat (or just when hot air heated by conduction move upward), this heat is in part lost to space, and in part contributes do “back-radiation”
By the first definition, it is NOT part of the greenhouse effect, as it doesn’t come from LWR emitted from the Earth’s surface
By the second definition it IS part of the greenhouse effect, as it is radiated back thanks to the GHG.
So where does the 8.7K you are talking about? From the fact that at today’s albedo 0.293, emission temperature IS (not just “would be”) 255.4 K,. Just not forget that this is temperature as seen from space, coming from a few kilometers higher that surface. Lapse rate (which doesn’t rely on any GHG, just on some heating from the bottom of atmosphere, to spawn the gradient) ) then makes the difference for surface temperature, making it higher.
If albedo increase in Lacis calculation, I guess this has to do which more clouds, so part of the emission to space would come from clouds (not GHG), and lapse rate would, again, give a somewhat higher temperature at surface than as seen from space.
Said otherwise: these 8.7K would come from back-radiation from clouds, from heat provided by convection
“By the first definition, it is NOT part of the greenhouse effect”
The first is not a definition of GHE. It is a statement about what happens to LWR. It says that some is directed downward, and is then part of the GHE. It does not say that it is the whole of the GHE.
You find no where, before or later in the page, a statement that this is just a contribution, no other contribution is mentioned. I didn’t cut the statement, I reported the whole explanation given. So it is definition, whether you like it or not.
And this first definition is also the very same that gave “greenhouse effect” its name, that is, the way a real greenhouse was (wrongly) assumed to work when the effect was (wrongly) named : interception of LWR going out by a “screen” (of glass in the wrong explanation of real greenhouse, of GHG in atmospheric GHE). Nothing else, no radiation of, say, condensing dew on the glass. Just radiation coming from the bottom, and impeded, net making it lower that it would be without the screen.
So you are wrong.
Besides, please note that from all the heat moved upward in the atmosphere by convective transport, only a fraction is “back-radiated”, so overall the process cools the surface even if it contributes to back-radiation. Meaning, it has negative contribution to surface temperature and you have no reason to include it in a “greenhouse effect”. Which the first definition doesn’t, but the second does.
paqyfelyc: If you want a simple unambiguous and accurate measure of the GHE, use the difference between average surface OLR and average TOA OLR, 150 W/m2. This slow down in radiative cooling to space is caused by GHGs and clouds and certainly must make the Earth warmer than it would be otherwise. However, you need to make a lot of assumptions to calculate how much warmer and that leads to lots of unproductive controversy. (The standard assumption that produces 33 K is that albedo will remain the same, but the planet will emit like a blackbody.) Stick with 150 W/m2.
I first want an unambiguous definition of what we are talking about. Your proposition is legit, provided it is clear what we are talking about. IPCC is not clear in this respect.
And, actually, I think your definition would be fine if lapse rate were zero. But it isn’t.
Paqyfelyc wrote: “actually, I think your definition (GHE = 150 W/m2) would be fine if lapse rate were zero. But it isn’t.”
What would the lapse rate be without GHGs in the atmosphere? (I don’t think there is an unambiguous answer.) However, no GHGs or clouds, the outward LWR flux would be eoTs^4 at the surface and the TOA. Defining the GHE as the difference between these two quantities would make the GHE 0 W/m2 with no GHGs.
As usual, the difficulty is creating a plausible model for the planet without GHGs.
“What would the lapse rate be without GHGs in the atmosphere? ”
basic answer is : “just the same”. This is because calculating lapse rate just depend on gravity and heat capacity (and this, itself, depend on the water content — apply the “dry” lapse rate until condensation occurs, then apply “wet”, corresponding to a higher effective heat capacity, that is, a lower lapse rate ).
Now, I guess GHG DO have some minute effect on lapse rate, through some heating in between instead of all from below as is assumed in basic calculation, which would be equivalent to some variation of heat capacity. Not enough to be even mentioned.
The two “definitions” of GHE are by no means mutually exclusive.
Back radiation of LWR is indeed the essence of the GHE.
Yet it is a common misapprehension to interpret that back radiation just as a part of the upwelling LWR that “comes back” to the surface. Back radiation is the result of an atmosphere with IR active gases radiating IR because it is at appropriate temperature. Local thermodynamic equilibrium and thermalization imply that it is essentially a single parameter, namely temperature T of emitting material in Planck’s law, that determines the amount of emitted radiation at a given wavelength . What sustains the radiation of IR energy of a specific atmospheric layer includes of course its concomitant absorption of LWR from surface or from lower or higher atmospheric layers as well as the latent and sensible heat brought by convective motion of wet air from lower layers or even its absorption of incoming sunlight.
come on, just read yourself.
First sentence you say “The two “definitions” of GHE are by no means mutually exclusive.”
Third sentence you explain that one of these is a “common misapprehension”, that is, wrong.
So make up your mind: are they both legit (and then, exclusive), or one is a “common misapprehension”?
The fact is, the IPCC SPREADS this “common misapprehension”. This part of the report is supposed to be technical, not a simple approximate for commoners not even mentioning that there are other parts weighting 1/5 or more of the effect…
BTW, there is another component, where being a GHG or not doesn’t matter: the simple thermal inertia of atmosphere(*). Is it part part of the greenhouse effect, or is it not? I challenge you to justify the definitionS used by IPCC allows you to unambiguously answer this simple question.
(*) because emission is in 4th power of temperature, a steady 240W result in a higher average temperature than a 120 W and 360 W each half of the time, even-though the emitted power is the same in both case
“It’s a common misapprehension” typical of laymen illiterate in physics…
Nothing more, nothing less.
No serious physicist or scientist would misapprehend it as you do.
Period.
BTW, there is another component, where being a GHG or not doesn’t matter: the simple thermal inertia of atmosphere(*).
And so what ?
This is not at all a “component” of the GHE, It’s just a “component” or feature of the earth’s climate system as is the presence of oceans with even much larger thermal inertia.
And yes the fact is that even without any GHGs or even without any atmosphere at all the average temperature of a rotating non uniformly lit planet is necessarily lower than its emission temperature. Yet this is just a mathematical property namely that: Temission^4 = average of T^4 is always larger than Taverage^4.
BTW the fact that exactly the opposite is true on Earth with Taverage above Temission is precisely the result of an additional phenomenon at work, namely the… GHE of Earth’s atmosphere.
” “It’s a common misapprehension” typical of laymen illiterate in physics… ”
I fairly agree. Too bad it is written, taught and spread by so called “climate scientists”.
Remember, I just thoroughly quoted what IPCC wrote, without omission that would misrepresent their speech. There is simply NO mention of anything else but LWR absorption in this whole page, nor anywhere else IFAIK. No caveat that this is just the main, but not the sole, component of GHE. If that’s misrepresentation, well, don’t put the blame on me. Put it on them, as I do.
And, BTW, no serious physicist or scientist would use such messy definition as “The infrared radiative effect of all infrared-absorbing constituents in the atmosphere”. A simpler “The infrared radiative effect of all constituents in the atmosphere” would be enough, and adding “infrared-absorbing” is just a case for more ambiguity, implying that, may be, the effect is considered only insofar as it come from actual infrared-absorption beforehand (and, then again, after this sentence they AGAIN only mention LWR absorption and nothing else, with no caveat that this is just the main, but not the sole, component of GHE.
No serious physicist or scientist would misapprehend it as THEY do.
I guess this is why you didn’t uphold my challenge: does IPCC definitions allows you to say if the thermal inertia, on which being a GHG or not doesn’t matter, is or is not a contribution to the greenhouse effect?
IPCC doesn’t even have a single definition of GHE
Gammacrux, about your answer of April 10, 2018 at 4:51 am
This wasn’t my question. We are talking about the thermal inertia of atmosphere, not thermal inertia of ocean or the land. It doesn’t really matter if you define this as part of GHE or not part of it. Both are legit, provided we name thing correctly. So, you think it isn’t, Fair enough. This is not the point
My question was : how do you derive this answer out of IPCC definitions of GHE? I expected you to answer “yes it does”, or “yes it does, insofar as it involve some LWR radiation exchange, which it does” , because, thermal inertia works through heat exchange, and radiation is always involved in heat exchange, and part of it would be LWR. You did the opposite. Obviously, the definition you claim is clear and unambiguous allows different and even opposites answer to this simple question.
QED
paqyfelyc
Thermal inertia of atmosphere or anything else is just a matter of its large heat capacity. Period.
By no means is this ever a “part” of the GHE… Again it’s just a feature of the climate system that would actually exist and be of importance even if there were no GHGs at work in it.
So I can’t see why I should ever attempt to derive such a false statement, namely thermal inertia of atmosphere being a “part” of the GHE, out of IPCC definitions of GHE.
gammacrux
When you have a definition, you use it, period. You don’t have the choice to use it or not, and to refrain when the result doesn’t suit you (in your case: includes thermal inertia in GHE while you think a proper definition shouldn’t). If the result is no good, then that’s the definition itself which is no good.
And the fact is, whether you like it or nor, one of the definition of GHE used by IPCC (the one in the glossary) is not clear enough to rule out “thermal inertia of atmosphere being a “part” of the GHE”, as a proper definition should, according to you.
(Besides, it can be argue that GHG effect is nothing more than a part of thermal inertia of atmosphere, not the other way round. But then again, IPCC don’t care to even properly define the thing it is all about, so, who knows…This leave us with no common understanding, for lack of common terminology)
Mr. Monckton:
You have only replied to one of my comments,
not that I care if you reply, but only to criticize
my narrow column formatting — nothing about
the content of my comment. The narrow columns
are needed because I have a vision problem
that can’t be corrected. It’s very difficult for me
to read my own typing with the “normal
wide column format”.
I wish you success with your theory,
and the judge living in California
who was appointed by a Democrat !
If you succeed, then you will be a climate
change skeptic hero — you’re half way there
for trying against a strong, unfriendly “opposition:.
I believe the odds that you, Mr. Monckton,
have discovered “the answer”, are small,
in my opinion.
But even if you have found “the answer”
the odds of ‘selling it’ are also small !
I watched a similar “fan club” build at jonova.com
for a new theory by David Evans, in 2016
… and then fade away,
Of course I believe you most likely are closer to “the truth”,
than the IPCC — the odds that the IPCC has the right
answer are below zero, I believe, after 30 years of wrong
average temperature predictions, they obviously
have the wrong climate physics model as the
foundation for the Global Circulation Models.
.
.
The problem you have is treating the ‘coming
climate change catastrophe’ as if it was
based on real science, and trying to refute it
with real science.
The climate change cult is more like a religion,
based on faith. The believers have their substitute
for traditional religions, also based on faith.
The problem is the coming climate change
catastrophe is based on faith, not science.
CO2 is a greenhouse gas, proven in lab experiments.
CO2 should cause some warming,
but no one knows hoe much.
If there are feedbacks, no one knows
what they are.
If CO2 and feedbacks, if they exist,
caused ALL the warming in the
weather satellite age, since 1979,
then CO2 is harmless.
If CO2 and feedbacks, if they exist,
caused ALL the warming in the
years after 1880,
then CO2 is still harmless.
Evidence that rising CO2 since 1750
has harmed anyone does not exist.
I know that.
You must know that.
The IPCC must know that too.
Leftists want the environment to be
in a “crisis”, so they can come to the
“rescue”, which of course ‘requires’
a stronger, bigger government.
The “crisis” has morphed from DDT
to acid rain. the hole in the ozone layer,
global cooling, and finally global warming
caught on.
But global warming itself did not scare
people much — many of us like to pay big money
to vacation in warmer climates !
So the leftists needed a theory
that would make rising CO2 scary,
and that was the water vapor
positive feedback theory,
(with no proof it exists now, or has
ever been a problem in the past four billion
years, when CO2 levels were higher
than today almost all the time).
What the global warmunists claim is:
(1) 4.5 billion years of natural climate change,
with no obvious disaster from a water vapor
positive feedback, suddenly ended in
the mid-twentieth century, and CO2 ‘took over’
as the “climate controller”, with a new strong
water vapor positive feedback too …
but with no explanation ever given as to how
the climate change process could have
completely changed during the 20th century.
Those beliefs are non-science ( nonsense ),
with no scientific proof — they can’t be
refuted with facts, data and logic, any more
than a traditional religion member could be
convinced there is no god.
Perhaps several consecutive years of
unusually cold weather would disrupt the
climate change cult … but many members
have been brainwashed since the 1980s,
so even that may not change minds !
My climate change blog:
http://www.elOnionBloggle.Blogspot.com
I was wondering why your comments came out as they do. Thanks for explaining. I am also in agreement with your sentiment.
The narrow columns issue
is easily fixed by using narrow window.
The input box will be narrow and will
turn into new line without you having
to bother typing CR/LF
So you would see narrow column you need
while other readers will see normal (for them)
I works, I checked.
Narrow columns are actually
easier to read if they are justified
— that’s why most newspapers
use justified narrow columns,
and so do I with the economics
newsletter I write.
If I type nice justified columns
in my computer, and then
cut and paste, the formatting
changes, and you get what you
see here.
I’ll try your suggestion and hope it
works.
Maybe I need a service dog,
who knows how to type ?
I must apologize to Mr Greene for having called him out on the strange layout of his comments, which does make them less easy to take in. I had no idea that this was owing to his eyesight. A solution to the problem is suggested by a commenter here, and it may be worth Mr Greene’s while to try it.
Mr Greene is, of course, right that even on the very generous assumption that all of the warming since 1850 was anthropogenic the resultant Charney sensitivity will be very low. But what we are hoping to achieve is a formal demonstration that the feedback fraction cannot exceed a maximum value dictated by the behavior of the climate across the 32 K interval from emission temperature, which can be derived with great certainty, and global surface temperature in 1850, which is also relatively well constrained. Once that maximum value has been derived, it can be applied to any future warming. And, on present calculations, it is likely to show a small and harmless Charney sensitivity.
I guess that means we agree:
Co2 is beneficial for green plants,
and any warming from Co2 would be slight,
and mainly at night ( less cooing at night, actually)
primarily in higher, drier latitudes.
The plants want more Co2, not less !
The few people living in higher latitudes
want slightly warmer nights !
Let’s more more Co2 in the air, not less !
Richard Greene wrote, “Leftists want the environment to be in a “crisis”, so they can come to the “rescue”, …”
I suspect the desire to play the role of White Knight is the primary driver behind warmism—it’s psychological, not political.
There’s a line between
wanting to help people and
telling them how to think, and
live … and then hectoring them
when they are skeptical, or disagree.
After this thrashing-out of the issues, CMoB should consider re-authoring his presentation so it anticipates and (mostly—except for a few fuzzy areas) dismisses the objections raised in the comments.
This would also give him an opportunity to incorporate in it some of the good phraseology and new arguments he’s made during these Q-and-A exchanges.
Mr Knights’ constructive reply is very helpful. Our difficulty throughout has been in explaining the idea, so we have thought it best to do things in stages here. We have now revealed enough of the idea to demonstrate that it is robust against various lines of attack – e.g., that the equation we use is linear but the feedback responses are nonlinear, or that we have not taken the Earth’s radiative imbalance into account. We are now working on refining the argument by dealing even more explicitly with the nonlinearity point. Initial calculations indicate that allowing for an extreme nonlinearity such as the 7%-per-Kelvin increase in column water vapor with warming and assuming that this will lead to a 7%-per-Kelvin nonlinear feedback response (it won’t, of course, because the water-vapor feedback forcing is approximately logarithmic and it is additionally compensated for by the lapse-rate feedback), and also assuming that this extreme nonlinearity will apply to all feedback responses, we can show that after 32 K of warming the feedback fraction is little more than 0.2, which gives a Charney sensitivity of less than 1.4 K.
By this method, we hope to be able to complete the proof that Charney sensitivity is below 1.5 K, with not a lot of variance either side of the mid-range estimate 1.2 K. At the moment, we are more concerned with perfecting the argument than with perfecting its presentation. As a result of the exposure that these articles have given to the idea, it is now being studied all over the place and we are getting feedback (if that is the right word) from many quarters. The general feebleness of the climate fanatics’ scientific response to our idea has been noticed. But we remain open to the possibility that we have ourselves made an error, though in the light of the scrutiny the idea has received this is becoming less likely as time passes.
I have at last taken the time to study this feedback criticism in more detail. It appears that it has been around since 2015 so to hear that the authors are still perfecting the argument is a little disappointing after this time. Furthermore it appears to me that the claim it is receiving lots of attention is not borne out by my own experience. Very few articles in mainstream newspapers, nothing seen on the TV in the UK, etc. Maybe I move in the wrong kind of circles or missed it but it looks like it generated some excitement initially and lots of counterpoint criticisms but interest has now died down except for the skeptical blogs.
I think the arguments are generally sound but unfortunately so complicated that they put some people off going through it all. I have a bit of an advantage as I did a lot of this stuff as part of my Elec. Eng. degree course and did actually remember 50% of it despite the 45y time delay.
The arguments could be presented in a much simpler form with very much less mathematics to illustrate the general point without going into the specific numbers too much.( It would no doubt generate a different kind of rebuttal too !). A summarised simpler explanation at the top before going into all the equations would be my recommendation. Set out the Official CAGW Position first – “The consensus view is that the atmosphere works like this….blah,blah.”. Then explain how feedback systems should be correctly used in this application and point out the error.
The criticisms/rebuttals I have seen vary greatly from simple ad hominems (plenty of ’em too), to all sorts of complicated logical shenanigans. Dealing with them all looks relatively pointless. Surely one simply needs to deal with the “official” response but knowing how these things work I expect there isn’t one yet.
Anyway, despite the impression I may have given so far, I do think this is a very useful and impressive piece of work and am hopeful it will get sufficient traction to go a lot further. To CMoB and the team I say “Well done!”.
“The reverend badger” thinks it should not have taken as long as two and a half years for our small, unfunded band of researchers, working in our spare time, to have overthrown a century and more of official climatology. Well, we’re doing our best.
As to presentation, the purpose of the head posting was to deal with certain technical aspects of our discovery. It was not intended for the general reader but for the specialist. We are simply not concerned with presentation at this stage: we are concerned with making sure that we are able to deal with all valid criticisms.
The badger is entitled to his opinion that we should not have bothered to attempt to answer the criticisms that have been put forward. Well, the United Kingdom is a free country, and we chose to exercise our freedom to reply. Welcome to freedom.
That said, we are grateful to Badger for his concluding kind words.
After thinking about this, I’m now doubting the validity of using absolute temperatures.
Looking at the Clausius-Clapeyron relation for water vapour it seems the atmosphere can hold no water vapour at all below -20°C (254°K). So you could convincingly argue that the baseline datum for no feedbacks should be 254°K, not 0°K. And 255°K happens to be the emission temperature we are claiming produces a feedback.
We’d be better to assume the emission temperature of earth of 255°K produces no feedback, (because there is no feedback mechanism present) but if you start increasing the input temperature from there by a ∆T of say 8°K, it starts to create water vapour feedback and the equilibrium temperature of 288°K is seen.
So f = 1-8/32 = 0.75
Bingo.
I wouldn’t have put it that way, because an average temperature of 255 wouldn’t necessarily mean it isn’t, say 280 somewhere. But that’s the big picture: contrary to the conclusion to which Lord Monckton’s naive algebra leads him, the models probably don’t ignore responses to lower temperatures; they probably recognize them but realize they’re very low.
I don’t credit the models, but it’s inconceivable that they suffer the particular “grave error” that Lord Monckton has talked himself into believing he discovered.
255°K is the average. Even on a much colder earth, there would be enough solar radiation at the equator in the day to melt ice and evapourate water locally. I have no idea how cold the earth could be and this process could continue, but a lot colder than 255°K. So, the water vapour feedback mechanism would exist from some much lower temperature allowing changes in albedo and cloud formation.
I think!
Mr Palmes is incorrect on all points. The general-circulation model run by Lacis et al. (2010) found that at 252 K, some 9 K above the 243.3 K emission temperature implicit in their assumption of albedo at 0.418, about 10% of today’s water vapor would be present., for there would be open water in the tropics.
There would, therefore, be a substantial feedback response not only from water vapor but also from the ice albedo, which would progressively melt. The ice albedo feedback would gradually become less important as the climate warmed and there was less ice left to melt, while the water vapor feedback would become progressively more important.
As for the Born Liar’s intervention, he offers absolutely no evidence that the models make any explicit allowance for the feedback response to emission temperature, and he offers absolutely no explanation of how – if they models did make any such explicit allowance – such allowance would be in any way consistent with IPCC’s definition of a feedback as a response only to a perturbation and not also to any pre-existing temperature.
The Born Liar, in his characteristically spiteful manner, describes my algebra as “naive”. Neither he nor anyone else should assume that because an argument is simple it must be either naive or wrong. He has not the slightest interest in the objective truth.
The corrected version of the zero-dimensional-model equation makes it quite clear that there will be a feedback response to emission temperature, provided that feedback processes exist. Since at 255.4 K there would be water vapor and open water in the tropics, the feedback response will occur. And, since the mean feedback response across the 23 K interval between (255 + 9) and 287 K will therefore be 1 – 264 / 287, it will be 0.08 on average. Even assuming a very steep 8%-per-Kelvin nonlinear increase in the feedback fraction from about 0.016 at 255.4 K, the feedback fraction at 287.6 K would be of order 0.2, giving equilibrium sensitivity 3.5 / 3.2 / (1 – 0.2) < 1.4 K.
It is useful that we have a professor of control theory assisting us. It ought to be blindingly obvious that, since such nonlinearity as exists is present in the system whether the math is done correctly or, as now, incorrectly, taking into account the feedback response to emission temperature is bound to reduce the feedback fraction and hence equilibrium sensitivity.
Nor has Lord Monckton offered any evidence that they don’t make such allowance. To see this, consider an equilibrium model that exhibits the following relationship between temperature with and without temperature-affecting quantities’ responses to temperature.
(= 255 K) itself induces a substantial feedback.” That’s because the feedback he’s referring to in that quote is a different animal from the quantity the IPCC defines. So, if climatologists do realize that “emission temperature . . . induces substantial feedback,” that certainly is “consistent with IPCC’s definition of a feedback as a response only to a perturbation and not also to any pre-existing temperature.”
http://i63.tinypic.com/11io3zn.png
I’ll refer to those total responses as “feedback,” although that’s not the same as the IPCC definition. As that graph shows, the consequences of feedback gradually increase with temperature toward the right, but the ratio of temperatures without feedback to those with feedback still remains fairly close to unity: Lord Monckton’s “feedback fraction” remains low. (At the lower end there’s not much feedback, but the open-loop gain in this model is so great that the loop gain exceeds unity until the temperature reaches nearly 40 K.)
Even though the ratio of before- to after-feedback temperatures remains near unity, we can see if we then zoom in on the upper right that from some reference state (in which what I call “feedback” is operative) a small change in before-feedback temperature corresponds to a large change in after-feedback temperature. And the IPCC definition of what it calls “feedback” is based on ratios of such changes. That definition in no way means that the reference state from which the IPCC computes departures lacks temperature-affecting quantities’ responses to any temperatures below some “emission temperature.”
http://i67.tinypic.com/15hd3kg.png
As a matter of substance, that is, the IPCC definition has no bearing on whether, as Lord Monckton contends, “climatologists had made the grave error of not realizing that emission temperature
All this stuff about the IPCC definition is a red herring.
I said “naïve” not because the algebra was simple but because it was performed naïvely.
Despite Lord Monckton’s references to nonlinearity, his comments betray no understanding of nonlinearity’s implications. For a linear system, Lord Monckton’s “feedback fraction” is what in some circles is known as “loop gain,” and loop gain would be independent of temperature if the model were linear. But Lord Monckton applies to nonlinear systems loop-gain results that are valid only for linear systems. For nonlinear systems, moreover, his “feedback fraction” is no longer loop gain. In the nonlinear system I described above, “feedback fraction,” i.e., Lord Monckton’s “f,” has the following relationship to temperature:
http://i64.tinypic.com/1054760.png
As that diagram shows, the “feedback fraction” remains modest for higher temperatures. Lord Monckton erroneously concluded from that fact that the system’s “climate sensitivity” is low. As the previous comment’s diagrams demonstrated, though, it’s not low at all.
The current drawing also depicts the system’s actual loop gain. The large-signal loop gains based on the entire quantities, while the small-signal loop gains are based on departures from respective-temperature states. It is to the latter type of values that the IPCC definitions correspond.
The comments above show that Frank, Germonio, and others have repeatedly attempted to educate Lord Monckton about these distinctions. They have apparently enjoyed no success.
The Born Liar continues to assume that the eminent professor of control theory who is one of our co-authors does not know what he is talking about. Other true-believers in the New Religion have made the same foolish assumption. Sneering at me isn’t going to make any difference to anything.
The Born Liar has produced no evidence that the models make due allowance for the feedback response to emission temperature. He waffles to the effect that the feedback response to emission temperature is not really a feedback response at all as IPCC defines it, but a “different animal”. He really needs to learn som elementary control theory. It is a feedback response, whether Mr Born likes it or not. And if due account is taken of it, there is no way to obtain anything like the absurdly high equilibrium sensitivities posited by IPCC except by assuming a nonlinear feedback response greatly in excess of the theoretical maximum possible nonlinear response – namely, the naive assumption that all feedbacks will respond as nonlinearly to temperature as column water vapor does, making no allowance for the fact that the feedback to changes in column water vapor is logarithmic or for the fact that the tropical mid-troposphere hot spot, without which no significant water vapor feedback can be legitimately or plausibly posited, is not observed in reality except in a couple of defective metadatasets.
The Born Liar also confuses the feedback fraction with what he calls “loop gain”. The usual terminology (insofar as there is any) usually labels the mu gain factor the “open-loop gain factor”. Note, however, that the actual open-loop gain is not a unitless quantity. The “closed-loop gain factor”, or “system gain factor”, takes account of both the mu open-loop gain factor and the feedback fraction, which is simply the fraction of the output signal that is returned to the input node.
Whether the Born Liar likes it or not, the CMIP3 and CMIP5 predicted interval of Charney sensitivity, [2.0, 4.5] K, can be exactly reproduced by the explicitly linear zero-dimensional-model equation that is, again whether he likes it or not, used diagnostically throughout official climatology, provided that one inputs to it the official values of the reference sensitivity and of the feedback-sum interval. Now, how is it that the results of the supposedly nonlinear models can be reproduced with such faithful exactitude by a linear equation that everyone except the Born Liar uses? The answer, of course, is that the feedback response over the 23 K interval of interest is very close to linear.
Besides, one of the most naive errors that true-believers such as the Born Liar are prone to make is to believe that all they need to do to dismiss official climatology’s linear diagnostic equation is to utter the word “nonlinear”. The difficulty they then face is that, though there is only one linear system, which can be shown to approximate the real world very closely, there are infinitely many nonlinear systems, many of which are close enough to linear not to make any real difference. The Born Liar has produced no evidence that the various nonlinear systems with which he has been playing has any particular relevance to the climate. Absent such evidence, all that he says is mere hot air.
Although I will be happy to discuss feedback theory with Lord Monckton’s “eminent professor of control theory” whenever he is able to produce him, I’m not going to respond to the farrago of illogic and irrelevance with which Lord Monckton flees from my demonstration of his error. For the sake of clarity, though, I will define the way in which I used feedback terms, since in my experience there’s little nomenclature unanimity in this field.
to a stimulus 
is given by y = (x + fy)g, where is 
is what I call “open-loop gain” and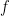 
is the “feedback coefficient” or “feedback gain.” Isolating the response 
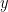gives us 
, and that ratio 
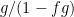of response to stimulus is what I call “closed-loop gain.” The (dimensionless) quantity 
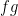, which Lord Monckton calls his “feedback fraction” and has lately been using 
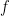to denote, is what I call “loop gain”: the gain encountered to traversing the loop.
For linear feedback the response
It is remarkably difficult to respond to people like the Born Liar and like Frank, who have no interest whatsoever in what is objectively true.
The Born Liar produces reams of meaningless curves, with no data to show how they were generated, and then makes various nonsensical statements about them. He has a purported feedback curve that starts at 0 K. Just one problem with that: there won’t be much in the way of feedback until temperature is high enough to sublimate ice, and not a lot until it’s high enough to melt water at the Equator and then evaporate it.
The feedback processes in the climate were manifestly sufficient to respond to 264.3 K of combined emission temperature and directly-forced warming from the non-condensing greenhouse gases. They did not need to know at what point on the temperature scale they might have begun to operate: for the Sun has been around at least as long as the Earth. They merely reacted to the temperature as they found it – and that was 264. 3 K.
No amount of waffle either from the Born Liar or from Frank can alter this fact.
And I see that the Born Liar agrees with Frank that I have not allowed for the fact that at 255 K the growth in water vapor feedback would be 10% per Kelvin. Well, 255 K is below the freezing point of water. From 273 K to 274 K, i.e. 0-1 C, the column water vapor would increase at 7.5% per Kelvin, not much different from the 7% per Kelvin reported as applicable today based on observation (Wentz et al., 2007).
Let everyone be aware that neither Frank nor the Born Liar has any interest in what is true. But they are wasting their time. Their bad behavior has been noticed, and conclusions have been drawn from it. Now, scientists all over the place are beginning to look at what we have found, and the main reason why some of them have started to look closely is the sheer malevolent stupidity of those who have unfairly and dishonestly tried to find fault here. Very few scientists are dishonest, but they can smell dishonesty on the wind, and they are beginning to dig.
Harry and Joe: Lord Monckton isn’t using the Clausius-Clapeyron itself, he is using an approximation of that equation that only applies near 288 K: 7%/K increase. The correct relationship involves (1/T1 – 1/T2). Another of Monckton’s mistakes.
Yes. I was aware of that. In fact, I had toyed with the idea of putting it in my toy model. Frankly, though, it’s just a magic formula to me, so I was uncomfortable using it before I had gone through its derivation.
But I’ll note in passing that for my toy model the feedback function I assumed (as an aggressive relationship some modelers’ results might exhibit) grows less than 7%/K.
As usual, Frank is wrong. As usual, the Born Liar agrees with Frank because he thinks that is a good way to spite me, and to hell with the truth From 273 to 274 K, the increase in column water vapor is 7.5% per Kelvin, not vastly different from the 7% observed by the satellites today. And what that means, according to Professor Lindzen, is that equlibrium sensitivity cannot ecen rach 1 K per CO2 doubling, because the increase in evaporation keeps the tropics cooler than they would otherwise be. See also Kininmonth (2010). The truth is that the water vapor feedback is not vastly different from linear, as the head posting explains.
Neither the Born Liar nor Frank has offered a shred of hard evidence that such alternative nonlinear models as they favor is any better at predicting global warming than the linear model.
I’m grateful to the good Lord Monckton once again, and would be very pleased if he can convince me that I am wrong about this.
I agree that there will be some small amounts of water vapour present in the atmosphere at temperatures around the 250°K mark, especially in the lower latitudes. My point is that, on average, a temperature around this level would make a not-unreasonable choice of datum from which to measure the ‘input signal’, given that feedbacks are likely to be near zero at or around this datum.
If you think 250°K is a little high, then perhaps 230°K is cold enough for the air to hold no water vapour and for albedo to be high. Trying out 230° as our new datum then, our ‘input temperature’ of 263°K versus the 288 equilibrium is effectively is 34 and 58 °K above our new datum respectively, implying an f = 1- 33/58 = 0.43
So as I see it, this choice of no-feedback datum is really what are talking about here. Let’s put some choices in a table, again using an input signal of 263°K and equilibrium output of 288°K:
Datum Paper ΔTref ΔTeq f ECS
255°K Hansen (1984) 8 33 0.76 4.8°K
243°K Lancis (2013) 20 45 0.56 2.6°K
230°K (example) 33 58 0.43 2.0°K
0°K Monckton (2018) 263 288 0.09 1.3°K
And to me the most appropriate datum would be the temperature at which the feedbacks begin in earnest. They don’t begin at absolute zero. A fair estimate might be the snowball earth with no atmospheric water vapour at perhaps 230°K or thereabouts.
I think you’d may have more traction arguing for a lower datum around this sort of number, rather than requiring the datum to be absolute zero, otherwise it will be too easy for your critics to demonstrate it is higher than that.
In your electronic circuit analogy, design a rig where there is no feedback at all until the input signal reaches the magic value of 230 volts and then a feedback loop circuit kicks in with feedback parameter of 0.43 acting only on the number of volts above 230. So with a 240V input signal the feedback loop acts only on 10 volts to give 10/(1-0.43) = 17 volts giving a total output signal of 257 volts.
Applying an input of 263 volts, the rig would output 288 volts, which is the data point we must satisfy. So this works.
If you can argue that the datum should be 230°K in the table above, (implying an ECS of 2.0°K) that is still a good result.
Mr Palmes really needs to study control theory and also atmospheric physics, One cannot simply charge at this subject like a bull at a gate. It requires considerable knowledge followed by considerable thought.
Whether he likes it or not, the feedback processes in the climate respond to the input signal as they find it, not as it might have been. The input signal relevant to the study of how much impact the non-condensing greenhouse gases have on climate is the temperature that would obtain today at the Earth’s surface without them, and without any feedback response. That temperature is 255.4 K. It is to that signal, and to no lesser signal, that the feedback processes in the climate would respond in the absence of the non-condensing greenhouse gases.
The feedback processes are water-based processes. It is not difficult to do a little spherical geometry and work out that the dayside temperature on a planet with today’s insolation and albedo will be 289 K, which is (coincidentally) the same as the mean whole-Earth surface temperature today. On the dayside at the equator, in the absence of the convective processes now in play, the temperature would be 361.2 Kelvin – very much more than enough to melt ice and start the process of evaporation and convection.
But in practice the non-condensing greenhouse gases are present, so that the mean whole-Earth temperature even before taking account of any feedback will be 264 K. It is to this value, then, that the feedback processes will respond.
The relevant equation, with its loop diagram shown in green, is given in the head posting. That equation does not permit us to assume any lesser value of the input signal than 255.4 K. That input signal is amplified by a further 8.9 K, so that, to first approximation, the feedback processes in the climate will respond to 264.3 K. The equation is entirely clear, and there is simply no scientific basis whatsoever for messing about with it in the manner suggested by Mr Palmes.
As I have already explained to him, even though the feedback processes in operation at a mean planetary temperature of 264 K will be considerable, it is possible to carry out an extreme-nonlinearity calculation by assuming that, though the mean feedback fraction across the 23 K interval of interest is 0.081, the feedback fraction increases exponentially at a rate of about 8% per Kelvin. In practice the exponential increase will be a great deal less than this, but let us push the argument way towards the climate fanatics.
In that event, the feedback fraction at 264 K would be around 0.02, which is actually far smaller than is at all likely, and at 287 K it would be around 0.20. It is of course the latter value that is relevant today, and that would give a Charney sensitivity of less than 1.4 K per CO2 doubling. In practice, since the rate of nonlinearity cannot by any stretch of the most fevered totalitarian imagination exceed 8% per Kelvin (approximately the mean rate of increase in the column water vapor per Kelvin), the final value in the series of values for the feedback fraction will be somewhat less than 0.2. However hard one tries, it is not really possible to push Charney sensitivity much beyond the 1.5 K that is the lower bound of the IPCC’s long-standing interval of predictions.
It is really as simple as that.
“Whether he likes it or not, the feedback processes in the climate respond to the input signal as they find it, not as it might have been. The input signal relevant to the study of how much impact the non-condensing greenhouse gases have on climate is the temperature that would obtain today at the Earth’s surface without them, and without any feedback response.”
How do they find “the temperature that would obtain today at the Earth’s surface without them”?
Mr Stokes is not familiar with the fundamental equation of radiative transfer, so I shall refer him to the head posting – such a good idea to read it before trying to comment on it. There, the calculation to establish the emission temperature in the absence of any non-condensing greenhouse gases and before taking the feedback processes into account is set out, together with several references to IPCC and learned papers where the 255 K value of emission temperature is given. It is quite uncontroversial. but does come as a surprise to those unfamiliar with climate-sensitivity studies.
The corrected equation for the zero dimensional model, also conveniently described in the head posting, makes provision for the emission temperature as its input. The feedback processes arising from the existence of water on our planet in large quantities will act in response to that emission temperature and a feedback response (in Kelvin) will then occur, so that the output signal will be greater than the input signal. Again, all of this is entirely uncontroversial to those with an elementary knowledge of control theory.
Good morning to Lord Monckton, please be assured that I take on board the central point and understand that attributing a zero feedback response to an input temperature of 255°K is not accurate.
However, I was looking forward to a colourful double-page spread in the Sunday Times newspaper demonstrating in simple terms how the climate science had erred, and the ECS is clearly 1.3°C ± not-very-much.
The trouble is the critics can object and ask why you decided the datum should be set at -273°C (0 °K). After all we are not talking about a simple electrical gain circuit. From what I see it is not-unreasonable to assume that an input temperature of say 230°K produces an output temperature of the same 230°K if no appreciable feedback mechanisms are operating at that temperature. Would you agree with this? And if not, how about 220°K or 210°K?
If you agree there are no feedbacks at 210°K, then we need to redesign the test rig so that an input of 210 gives and output of the same 210. Using this rig if you apply the input temperature of 263°K (a world with non-condensing GHGs) we also then need to explain the output equilibrium temperature of 288°K in terms of feedbacks. If you hypothesise that the feedback mechanisms operate in a generally linear fashion above the (rather arbitrary) temperature of 210°K, then we should use an f=0.32:
∆Teq = ∆Tref / (1-f) = (263-210) / (1-0.32) = 53/0.57 ∆Teq = 78
Which yields our equilibrium temperature of 210+78 = 288°K, and implies an ECS of 1.7°K. This is consistent, and attempts to reflect the nature the physical feedback mechanisms at different temperature ranges. If this critique appeared beside your Sunday Times exposé it would hurt its credibility.
However if you can demonstrate that the earth’s feedback mechanisms operate in a roughly linear fashion right down 0°K then I will take on board your choice of 0°K as the datum. Otherwise I think we should set it at a more appropriate value to reflect the nature the atmospheric physics, e.g. the Clausius-Clapeyron result that water vapour feedback does not operate if the (local) air temperature drops below 253°K. Note that I use 210°K in my simple example to allow for warmer-than-average temperatures at midday near the equator, to ensure that even in these locations there will be minimal feedback, even over a long lunch in Riyadh.
Mr Palmes is still not understanding that feedback processes respond to the input temperature signal as it actually is, and not as it might have been without any sunlight. Sunlight is a given. Likewise, the non-condensing greenhouse gases are a given. Therefore, the feedback processes will respond to the 255.4 + 8.9 = 264.3 K mean temperature that would exist before taking feedbacks into account.
It is no good simply making stuff up. The equation is quite clear. Feedback processes do not respond only to that fraction of emission temperature that is above some arbitrary threshold chosen by Mr Palmes. They respond to the emission temperature as it is, plus the direct warming from the non-condensing greenhouse gases.
The Born Liar continues to whine ineffectually about his dimly-remembered conversations with control theorists half a century ago. It is a priori implausible that his half-understood recollections are likely to prove more reliable than the work of an active professor of control theory.
He has produced no sound argument to the effect that taking into account the feedback response to emission temperature will allow the current absurdly high equilibrium sensitivities to be justified. It can be shown that official climatology’s defective form of the zero-dimensional-model equation, which explicitly makes no provision for emission temperature and therefore makes no provision for the feedback response thereto, reproduces exactly the official interval of Charney sensitivities when exactly the official values of the reference sensitivity and the feedback-sum interval are input to it. That is how we know the modelers are making no allowance (or, at best, very little) for the feedback response to emission temperature.
Nope.
The feedback processes just make sense as a part of the response to any perturbation applied to a real initial reference steady state of the system at some temperature Ti, with that perturbation that tends to alter temperature Ti by some amount delta T both directly and indirectly via feedback processes .
If one considers, as Lord M does, that they respond to 264.6 K then the reference initial state of the system is a hypothetical state at 0 K, as rightly pointed out repeatedly by Palmes and many others before. No way out of this.
And this is obviously nothing but plain nonsense ! Since the climate system with incident sunlight can simply never be in a steady state ( with zero radiative TOA imbalance) at 0K.
Period.
The climate sensitivity may well be at the low end of IPCC range. Yet neither good Lord M nor anybody else can tell by now. Predicting that from theory is just definitely out of reach of the science worked out by little homo sapiens sapiens.
Only future observations will eventually be able tell.
Gammacrux has not understood the corrected form of the zero-dimensional-model equation. The reference system consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035 to allow for the directly-forced warming of 8.9 K from the presence of the naturally-occurring, non-condensing greenhouse gases. Since we know the input signal (255.4 K), the direct gain factor (1.035) and the equilibrium temperature or output signal (287.6 K as in 1850), the feedback factor (the product of the direct-gain factor and the feedback fraction) is. as a matter of undeniable fact, (1 – 264.3 / 287.6) or 0.081. Just work through the math in the head posting.
The reference system consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035
No, as your “calculation” ( 255.4 + 8.9) / 255.4 of “open loop gain” unambiguously demonstrates by itself you really do implicitly refer to a hypothetical steady state at 0 K .
Gain only makes sense if it refers to the ratio of changes in temperature observed with and without feedback, temperature changes that take place with respect to some reference steady state system that is perturbed in some way. Perturbation concept BTW implies that the energy involved in the perturbation is fairly small with respect to the total energy of system;
Now your hypothetical 0 K steady reference state may exist only in the absence of sunlight. Consequently what you are actually considering is nothing but the response of that reference system at 0 K to switching on the whole incident sun radiation from scratch. This is by no means just a “perturbation” anymore and any “feedback factor f ” inferred in this way has no reason to be of any relevance to the “f” involved in what happens upon simply doubling atmospheric CO2 with respect to a preindustrial reference state.
Gammacrux should remember to read the head posting before commenting on it. The corrected form of the feedback loop, shown in green in the head posting, makes explicit provision for the input signal. It is a matter of readily-demonstrable fact (a fact that we demonstrated by building two test rigs, one of them at a government laboratory) that, even in the absence of any amplification, the input signal will generate a feedback response provided that nonzero feedback processes are present in the system. An input signal of 255 units will induce a feedback response appropriate to that input signal, regardless of when the feedback processes first became operational. Therefore, the reference system (which consists of the input signal and any amplification thereof) consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035.
In the corrected version of the equation for the feedback loop, there is no statement, explicit or implicit, that there is some hypothetical steady state at 0 K. However, in the erroneous version of the equation used by official climatology (shown in red in the head posting, which is well worth a read), the input signal is erroneously assumed to be zero.
It is no good trying to state, as Gammacrux does, that “Gain only makes sense if it refers to the ratio of changes in temperature observed with and without feedback, temperature changes that take place with respect to some reference steady state system that is perturbed in some way”. Do the math, for Heaven’s sake. Take an input signal of 255.4 units. Set the mu direct-gain factor to 1 (i.e. no amplifier gain). set the beta feedback fraction or return-transmission characteristic to 0.081. And then measure the output signal. There has been no perturbation of the input signal, for the direct-gain factor would exceed unity if there were. And yet the output signal exceeds the input signal. Thus: 255.4 / (1 – 0.081) = 277.9. So, where did the extra 22.5 units in the output signal come from? The answer, of course, is that the extra units came from the amplification of the input signal caused by the nonzero feedback fraction. All of this is elementary control theory. In all sciences but climatology, it is entirely uncontroversial.
Yes, IPCC defines a feedback as responding only to a perturbation. But in that respect IPCC is simply incorrect. That is the error that official climatology has made. It is a serious error. It has led official climatology very greatly to overstate all estimates of equilibrium sensitivity. Correct the error and the warming that will occur is altogether too small to matter.
To answer Gammacrux’s question about how the corrected form of the zero-dimensional-model equation handles doubled CO2, the matter is very simple. The input signal is 255.4 K. The directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases is 8.9 K. The directly-forced warming from the 2.29 Watts per square meter of net anthropogenic forcing in the industrial era to 2011 is 2.29 / 3.2 = 0.72 K. Therefore, the mu direct-gain factor to 2011 is 1+ (8.9 + 0.72) / 255.4 = 1.03767, and the expected temperature for that year is 255.4 x 1.03767 / (1 – 0.081) = 288.4 K, which is indeed the temperature which prevailed that year.
The directly-forced warming from doubled CO2 compared with 2011 is 3.5 / 3.2 = 1.09 K. Therefore, the mu direct-gain factor (also known as the open-loop gain factor) becomes 1 + (8.9 + 0.72 + 1.09) / 255.4 = 1.04193. Then the temperature after doubling CO2 compared with 2011 is 255.4 x 1.04193 / (1 – 0.081) = 289.6 K. Take away the 288.4 K in 2011 and the difference, which is the transient sensitivity to doubled CO2, is 1.2 K.
Note that we could have found the 1.2 K value simply by making 1.09 K the input temperature, just as official climatology does, and then 1.09 / (1 – 0.081) = 1.2 K.
But – and here’s the point – if we have at no earlier point made any allowance for the feedback response to emission temperature itself, we shall be misled – as official climatology was misled – into assuming that the feedback fraction is a great deal higher than 1 – (255.4 + 8.9) / 287.6 = 0.081. The point is that we know with great certainty what the emission temperature would be at today’s insolation and albedo, and we have highish confidence in what the temperature was in 1850. The only other quantity we need is the directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases, and that – as deduced from Lacis (2010) – is 8.9 K. From these values, the feedback fraction of 0.081 is easily derived.
Now, one can argue that owing to nonlinearity in the feedback processes the feedback fraction by 1850 might have been twice the 0.081 that we have thus derived, but certainly no more than that. Thereupon, Charney sensitivity to doubled CO2 would be 1.09 / (1 – 0.16) = 1.3 K. And that is all.
All of this is mainstream control theory. If official climatology wants to borrow from control theory, it must do so correctly. Until now, as IPCC’s definition makes quite plain, it has not done so correctly. It has erred. Remove the effects of the error and global warming becomes a non-problem. It is as simple as that.
As you’ve recognized, what Lord Monckton says here is true:
The resultant back radiation from the air and the clouds, together the resultant lapse rate and albedo, are all quantities that both affect temperature and depend on it: they are feedback mechanisms. But we also know that the climate models implement differential equations that express what the modelers believe are the physics underlying those quantities as well as others. Consider what Lord Monckton’s “grave error” theory implies in light of those facts.
(= 255 K) itself induces a substantial feedback.” That would mean that climate modelers had failed to recognize that below 255 K these quantities depend on temperature and/or that temperature below 255 K depends on them. Does that seem even remotely plausible? Isn’t it much more likely that modelers have simply, as most of us skeptics have long believed, been overestimating the degree to which feedback increases with temperature?
Lord Monckton would have us believe that before his great discovery “climatologists had made the grave error of not realizing that emission temperature
In support of his highly implausible contention, Lord Monckton has been spinning out all these equations he doesn’t really understand and leaps to totally unsupported conclusions. He throws around his “feedback fraction.” But, as I showed here and here, there’s no inconsistency between climatologists’ finding a high “equilibrium climate sensitivity” and their models’ exhibiting a modest “feedback fraction.” Nor is there any inconsistency between a low “feedback fraction” and climatologists’ having, in contrast to Lord Monckton’s assertion, taken into account feedback to temperatures below some “emission temperature.”
Now, Lord Monckton goes on and on about all the experts he consulted. And, look, I make no claim to expertise myself. I’m not a scientist; I earned my daily bread as just a workaday lawyer. But nearly a half century ago I had already spoken about control systems with professors of the discipline, and I had discussed the finer points of feedback with Bell Labs engineers. That didn’t make me an expert, but it did teach me enough to recognize it when someone is blowing smoke.
Lord Monckton is blowing smoke.
The Born Liar continues to be spiteful and silly. He admits – as if the fact were not already self-evident – that he has no scientific expertise: and yet, on the basis of half-remembered and less than half-understood conversations with control theorists a century or so ago, he presumes – in that sneering, arrogant tone that is his specialty – to lecture a professor of control theory and numerous other professors and doctors of science. Let him wait until our paper is published, and then let him write his own paper telling the world that he knows better than all those professors and doctors.
He will have to produce arguments a lot less dishonest and a lot more compelling than the nonsense he has attempted to peddle here. No one is buying.
Gammacrux appears to have the same difficulty with elementary control theory as Mr Palmes, the Born Liar and one or two other true-believers in the New Religion. Feedback processes respond to the temperature that is actually present, not to some lesser temperature. It is of no relevance how the climate might behave with no incident radiation at all. The feedback processes are not confronted with that scenario. They are confronted with 255.4 K of emission temperature plus 8.9 K of directly-forced warming from the non-condensing greenhouse gases: total 264.3 K. It is to that number, and to no lesser number, that they respond. This is entirely elementary, and it is indisputable.
One view from a climate scientist on “feedback”:
******
Why feedback loops are one of the most troubling parts of global warming
They’re vicious circles that will speed up the pace of warming.
Climate change is not simply a matter of cause and effect. It’s more like a vicious circle. Thomas Crowther is a professor at ETH Zürich, a university in Switzerland.
Climate change is not simply a matter of cause and effect. It’s more like a vicious circle.
Click To Tweet
Crowther: “Not only are we directly altering the climate, but that process in itself is kicking off these things that are gonna actually accelerate the damaging impacts over the rest of the century.”
This self-reinforcing cycle is called a feedback loop. For example, warmer temperatures make soil microbes more active. The microbes then release more carbon into the atmosphere – which in turn speeds up global warming, which makes the microbes even more active, and so on.
Crowther: “I just imagine a sort of wheel spiraling out of control.”
Melting sea ice is another example. Because ice is white, it reflects sunlight back to outer space, which reduces the heat absorbed by the earth. But global warming melts the ice, leaving dark ocean water behind. The water then absorbs the sun’s heat, which increases global warming … leading to more melting ice.
Crowther says it’s hard to predict just how much these feedback loops will speed up the pace of global warming, so they represent a worrisome unknown.
Reporting credit: Daisy Simmons/ChavoBart Digital Media.
Photo credit: NASA Goddard Space Flight Center.
Filed under: Diana Madson
https://www.yaleclimateconnections.org/2018/02/why-feedback-loops-are-troubling/
******
The million-dollar researcher
21.02.2018 | News
By: Peter Rüegg | 2 Comments
The ecologist Tom Crowther only recently joined ETH Zurich as assistant professor. Virtually his first achievement was to win a grant offering potential research funding of more than 17 million euros over the next 13 years. So, who is this rising star?
….
https://www.ethz.ch/en/news-and-events/eth-news/news/2018/02/portrait-tom-crowther.html
Tom Crowther gave his inaugural lecture at ETH Zurich on 19 February 2018. The recording “Understanding global-scale ecology in order to combat climate change” can be found here:
https://www.video.ethz.ch/speakers/lecture/bccfbefa-c9b3-419b-90b6-5c50598d31da.html
******
If we are right, Crowther is wrong.
In reply to Lord Monckton, does he not accept that there will be a certain temperature, perhaps not too far below 255°K, where the earth will provide no feedback whatsoever to the input temperature? A temperature where the earth is fully frozen with stable albedo (around 0.6 from your paper) and zero saturation percentage for water vapour held in the atmosphere. I’m not sure if this temperature is 255°K, 230°K or 210°K. For illustrative purposes I chose 230°K based on the snowball earth estimates above.
In reply to “Mr Palmes is still not understanding that feedback processes respond to the input temperature signal as it actually is. “ But at this temperature, no they do respond. That’s is exactly the point. They do not respond at all. 230°K in, 230°K out. No feedbacks. The feedbacks are not in operation at or below this datum temperature. Teq = Tref / (1 -0) 230°K=230°K/1 f=0. The feedbacks are as dormant as the dead parrot in the famous Monty Python sketch.
From 230°K if Tref rises by 1 degree to 231° K and this 1 °K wakes up some hitherto unseen feedback mechanism, then all this feedback ‘knows’ about is the 1°K, not the 231°K. The feedback reacted to 1°K increase above 230°K, not the 230°K itself. Remember 230°K in gives 230°K out.
Where exactly should this datum temperature be set? I’m not qualified to say. But you seem to have chosen 0°K which seems highly improbably to most people. The IPCC and friends seem to have chosen 255°K. At least you can envisage a rationale for that choice.
If I were a betting man and was given the choice of 0°K or 255°K I would choose 255°K, but I suspect the real answer is a little lower than this, because as you say there will be some water vapour around in the warmer climes even at 255°K, hence I put my money around 230°K.
I mean you no ill will and aim to be constructive, but I think we’re barking up the wrong tree here.
If Mr Palmes refuses to understand that feedback processes respond to the temperature that actually exists and not to some lesser value he has plucked out of the air, there is nothing further I can do for him.
The temperature in the absence of feedback amplification, at today’s insolation and albedo, would be 255.4 K plus another 8.9 K directly-forced warming from the non-condensing greenhouse gases. That is 264.3 K. In fact, the pre-feedback temperature is probably quite a bit higher than that, because official climatology underestimates the emission temperature by 5-10 K and, in addition Lacis deliberately chose an artificially low value for the directly-forced warming from the non-condensing greenhouse gases.
Taking 264.3 K as the temperature to which feedback processes respond, and taking 287.6 K as the temperature in 1850 before any sufficient anthropogenic perturbation, the 23 K difference is attributable to the feedback response to the entire 264.3 K temperature, because that is the actual pre-feedback temperature. Now, 264.3 K is not 220 K or 230 K or any other value imagined by Mr Palmes. it is 264.3 K. And the temperature in 1850 was 287.6 K. The difference is represented by the feedback response to that 264.3 K.
How can inanimate feedback processes decide that they would like to do Mr Palmes a favor by refusing to react to the first 255.4 K of temperature and then reacting violently to the next 8.9 K? How can they know, given today’s insolation and albedo, how they might respond at some lesser temperature, and how can they decide not to react to the first 210 or 220 or 230 K? The fact is that they can’t.
Mr Palmes should try building a test rig and inputting not some imaginary value but 255.4 K as the input and a sufficient value for the mu amplification factor to represent the remaining 8.9 K. Then all he has to do is measure the output at various values of the feedback fraction. There would be no point in his inputting, say, 220 K, because that is not the temperature of interest. It matters not that there would be no feedback processes in operation at 220 K, because the baseline temperature is at least 44 K above that value.
The matter really is very simple, though it has eluded official climatology till now.
Finally, Mr Palmes has sneered to the effect that the Sunday Times has not run a double-page spread announcing our discovery. That is not how it works. We must first get our paper through peer review and into a mainstream climate journal. Then, and only then, will we seek publicity.
“…from 230°K if Tref rises by 1 degree to 231°K and this 1°K wakes up some hitherto unseen feedback mechanism, then all this feedback ‘knows’ about is the 1°K, not the 231°K.”
1) It is not the 1°K that “wakes up” such feedback mechanism. It is (Teq + 1°K) that does it. In your scenario, the system is already at 230°K, ‘primed’ for waking the feedback mechanism – so it ‘knows’ about more than just the change of 1°K.
2) I feel that in most of these discussions there is an implicit assumption that increasing Tref by T degrees increases Teq by more than T. That’s positive feedback, and that makes systems unstable, unlike Earth’s climate which seems to be pretty stable. To me that would indicate that sumtotal of all feedbacks that are governing the system, would be negative. In other words, increasing Tref by T degrees results in Teq change smaler than T.
Just my two cents…
“It is (Teq + 1°K) that does it.”
So what would (Teq + 0°K)? Or (Teq + 0.001°K)? IT the response proportional to the (Teq + 0.001°K) or the (0.001°K)? If the latter, how does the Teq enter?
Ive thought more about the implications of this article than any other I have read recently. Thanks for the article. I suspect that the high positive feedback’s of most of climate models, comes from assuming that the feedback is directly related to the 7% water vapor increase per degree C of temperature rise.
Even at 255 Kelvin the amount of water vapor in the atmosphere is still triple that of CO2 at 400 ppm. At 255 water vapor has a saturation pressure of 1.1mmHg. I know this is a bit simplistic but if CO2 contributes 8.9 degrees of warming than should not water vapor also cause more than 8.9 degrees of warming even if there was no CO2 in the atmosphere?
Lowell has grasped the main point. The temperature before feedback is 255.4 K emission temperature plus 8.9 K directly-forced warming from the non-condensing greenhouse gases: total 264.3 K. After feedback, the temperature in 1850 was 287.6 K. The feedback fraction was thus 1 – 264.3 / 287.6 = 0.081.
How could this be so low, given that column water vapor increases at around 7% per Kelvin from 273 K (the freezing point of water) to 287 K? The answer is that the models assume that column water vapor only increases at about 1 to 2% per Kelvin. Therefore, they predict very little increase in evaporation, and they derive a mid-range Charney sensitivity of 2.2-3.4 K. However, at an evaporation rate increasing at the 7% per Kelvin that satellites actually observe, Charney sensitivity falls to 0.9 K. This, as Bill Kininmonth pointed out in an interesting paper in 2010, acts as a powerful constraint on Charney sensitivity. Our top-down method detects this fact by the simple method of comparing the no-feedback temperature of 264.3 K with the after-feedback equilibrium temperature of 287.6 K in 1850.
One or two particularly obtuse commenters here have tried to say that we have failed to take into account the fact that from 273-274 K the increase in column vapour is not 7% but more like 7.5%. Well, gee wow golly gosh, that doesn’t actually make very much difference to anything.
Lowell is quite right: feedback processes, including the water vapor feedback, that respond to the CO2-forced direct warming must also respond to the pre-existing temperature.
In reply to Lord Monckton and Bob K, I cannot accept the proposition to use the full input temperature because it does not match the facts. We need to find an explanation for the following, perhaps easier to put in a table. The Monckton Conjecture (f=0.09 on full input temperature) cannot match a world where there is no water vapour feedback below a certain temperature. We need a rig that can match this:
Input Output
0°K = 0°K (Monckton 0°K – correct)
100°K = 100°K (Monckton 110°K – incorrect)
200°K = 200°K (Monckton 219°K – incorrect)
220°K = 220°K (Monckton 241°K – incorrect)
221°K = 221°K (Monckton 242°K – incorrect)
222°K = 222°K (Monckton 243°K – incorrect)
223°K = 223°K (Monckton 244°K – incorrect)
224°K = 224°K (Monckton 245°K – incorrect)
225°K = 225°K (Monckton 246°K – incorrect)
226°K = 226°K (Monckton 247°K – incorrect)
227°K = 227°K (Monckton 249°K – incorrect)
228°K = 228°K (Monckton 250°K – incorrect)
229°K = 229°K (Monckton 251°K – incorrect)
230°K = 230°K (Monckton 252°K – incorrect)
231°K → 232°K (Monckton 253°K – incorrect)
232°K → 234°K (Monckton 254°K – incorrect)
233°K → 235°K (Monckton 255°K – incorrect)
234°K → 237°K (Monckton 256°K – incorrect)
235°K → 239°K (Monckton 257°K – incorrect)
236°K → 241°K (Monckton 258°K – incorrect)
237°K → 242°K (Monckton 260°K – incorrect)
238°K → 244°K (Monckton 261°K – incorrect)
239°K → 246°K (Monckton 262°K – incorrect)
240°K → 248°K (Monckton 263°K – incorrect)
241°K → 249°K (Monckton 264°K – incorrect)
242°K → 251°K (Monckton 265°K – incorrect)
243°K → 253°K (Monckton 266°K – incorrect)
244°K → 255°K (Monckton 267°K – incorrect)
245°K → 256°K (Monckton 268°K – incorrect)
246°K → 258°K (Monckton 269°K – incorrect)
247°K → 260°K (Monckton 270°K – incorrect)
248°K → 262°K (Monckton 272°K – incorrect)
249°K → 263°K (Monckton 273°K – incorrect)
250°K → 265°K (Monckton 274°K – incorrect)
251°K → 267°K (Monckton 275°K – incorrect)
252°K → 269°K (Monckton 276°K – incorrect)
253°K → 270°K (Monckton 277°K – incorrect)
254°K → 272°K (Monckton 278°K – incorrect)
255°K → 274°K (Monckton 279°K – incorrect)
256°K → 276°K (Monckton 280°K – incorrect)
257°K → 277°K (Monckton 281°K – incorrect)
258°K → 279°K (Monckton 283°K – incorrect)
259°K → 281°K (Monckton 284°K – incorrect)
260°K → 283°K (Monckton 285°K – incorrect)
261°K → 284°K (Monckton 286°K – incorrect)
262°K → 286°K (Monckton 287°K – incorrect)
263°K → 288°K (Monckton 288°K – correct)
The IPCC-style conjecture that feedbacks start at 255°K with f=0.75 is a better fit.
Mr Palmes continues to maintain that somehow the feedback processes that – whether he likes it or not – exist at 264.3 K (for that is why the temperature in 1850 was 287.6 K) should have some method of knowing that they should not respond to some arbitrary lesser temperature dictated by Mr Palmes. I have provided none of the values in that idiotic table: it is Mr Palmes, not I, whose figures are incorrect all the way through.
His childish table, which dishonestly ascribes to me an array of values not one of which is stated or implied or legitimately deducible in anything I have written, can be replaced with the following much simpler position: Emission temperature 255.4 K, plus 8.9 K directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases: total pre-feedback temperature 264.3 K. Equilibrium post-feedback temperature in 1850 was 287.6 K. Feedback fraction thus 1 – 264.3 / 287.6 = 0.081.
For the nth time, this calculation neither states nor implies anything whatsoever about what the position might have been if there had been no sunlight or an albedo other than that which actually obtains today.
There is absolutely no point in speculating on when the feedback processes might first have come into being, for that makes absolutely no difference to the position as it is today. What matters is that, at 264.3 K, the feedback processes are in being, and are influential enough to react to that 264.3 K of temperature by lifting global temperature from 264.3 K to 287.6 K.
But if Mr Palmes does want to speculate, let him consider this: that even assuming a snowball-Earth albedo as high as 0.66, the emission temperature on the dayside at the Equator at noon, even before taking account of any greenhouse-gas forcings or any feedbacks, would be 300 K, much as it is today. The freezing point of water is a little above 273 K. Go figure.
Here is a less inappropriate version of Palmes’ table. And he should note for the future that the symbol “K” is the SI unit for Kelvin, with no degree symbol.
0°K = 0°K (Palmes 0°K – incorrect: fails to allow for cosmic microwave background)
100°K = 100°K (Palmes 110°K – idiotic)
200°K = 200°K (Palmes 219°K – futile)
220°K = 220°K (Palmes 241°K – half-witted)
221°K = 221°K (Palmes 242°K – stupid)
222°K = 222°K (Palmes 243°K – nonsensical)
223°K = 223°K (Palmes 244°K – doltish)
224°K = 224°K (Palmes 245°K – thick)
225°K = 225°K (Palmes 246°K – wrong)
226°K = 226°K (Palmes 247°K – erroneous)
227°K = 227°K (Palmes 249°K – lackwit)
228°K = 228°K (Palmes 250°K – bumbling)
229°K = 229°K (Palmes 251°K – fatuous)
230°K = 230°K (Palmes 252°K – nincompopltious)
231°K → 232°K (Palmes 253°K – asinine)
232°K → 234°K (Palmes 254°K – misguided)
233°K → 235°K (Palmes 255°K – offbeam)
234°K → 237°K (Palmes 256°K – dense)
235°K → 239°K (Palmes 257°K – false)
236°K → 241°K (Palmes 258°K – troglodytic)
237°K → 242°K (Palmes 260°K – ignorant)
238°K → 244°K (Palmes 261°K – imprudent)
239°K → 246°K (Palmes 262°K – unwise)
240°K → 248°K (Palmes 263°K – serpentine)
241°K → 249°K (Palmes 264°K – wicked)
242°K → 251°K (Palmes 265°K – careless)
243°K → 253°K (Palmes 266°K – lacklustre)
244°K → 255°K (Palmes 267°K – barforamic)
245°K → 256°K (Palmes 268°K – witless)
246°K → 258°K (Palmes 269°K – senseless)
247°K → 260°K (Palmes 270°K – vacuous)
248°K → 262°K (Palmes 272°K – empty-headed)
249°K → 263°K (Palmes 273°K – fatheaded)
250°K → 265°K (Palmes 274°K – pointless)
251°K → 267°K (Palmes 275°K – egregious)
252°K → 269°K (Palmes 276°K – inspissate)
253°K → 270°K (Palmes 277°K – duplicitous)
254°K → 272°K (Palmes 278°K – unthinking)
255°K → 274°K (Palmes 279°K – flatulent)
256°K → 276°K (Palmes 280°K – gross)
257°K → 277°K (Palmes 281°K – obscene)
258°K → 279°K (Palmes 283°K – driveling)
259°K → 281°K (Palmes 284°K – sniveling)
260°K → 283°K (Palmes 285°K – barmy)
261°K → 284°K (Palmes 286°K – loony)
262°K → 286°K (Palmes 287°K – mad)
264°K → 288°K (Monckton 288°K – correct)
I’m sorry to annoy Lord Monckton so much, and stand corrected regarding Kelvin. A Kelvin is a Kelvin, not a degree Kelvin.
So can you make clear what you mean when you say the feedback parameter of circa 0.09 acts on the full input signal of 264.3K to output 287.6K?
Surely then it would also act on an input signal of 100K to give an equilibrium temperature of 110K? 100/(1-0.09) = 109.9K
If that is not the case then pleases accept my apologies I’ve misunderstood your conjecture.
If it is what you propose then my simple table is contains your own results so I don’t see why it deserves such derision.
So please confirm the output of your irreducibly simple model for on an input temperature of 100K? Is it 110K or does it take another value?
In response to Mr Palmes, I do not like outright intellectual dishonesty. I have made it repeatedly plain to him that we are not, repeat not, repeat not, repeat not concerned with what might happen in the absence of today’s insolation. The table whose values Mr Palmes falsely ascribed to me was a fiction of his own making, and it was dishonest of him to put my name on value after value after value in his bogus table when he had been repeatedly told that I do not concern myself with values below the sum of emission temperature and the directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases.
For obvious reasons, the feedback regime in the absence of today’s insolation would be markedly different from today’s regime: therefore, Mr Palmes’ naive calculations have absolutely no bearing on our result (or on anything), and do not in any way represent what we are doing. My name should not have been attached to any of those half-baked calculations.
Also, we have not made a “conjecture”: we have provided a demonstration that official climatology has made a substantial error of physics in defining a “climate feedback” in such a way as formally to exclude the actually large feedback response to emission temperature. We have proven that correction of that error greatly reduces all equilibrium sensitivities. In mathematics, the difference between a conjecture and a demonstration is that the former is open to doubt and the latter is proven.
One can nibble at the edges of our result, as some have tried to do here, by saying – for instance – that we have not allowed for nonlinearity in the feedback regime. But what nonlinearity? The two most significant feedbacks – the water vapor feedback and the Planck “feedback” – are net-linear. The most one can legitimately do is suggest that we have assumed a zero slope for the linear feedback response when in fact we should have given it a slope. However, any realistic slope will give a final value of no more than 0.16 for the feedback fraction, and that would imply a Charney sensitivity of 3.5 / 3.2 / (1 – 0.16) = 1.3 K. As Mr Istvan has said, “Game over!”