Jo Nova has a post today about an investigation of climate modeling mathematics by her husband David Evans. Evans believes he has uncovered a significant and perhaps major flaw in the mathematics at the core of the climate models.
She writes:
The climate models, it turns out, have 95% certainty but are based on partial derivatives of dependent variables with 0% certitude, and that’s a No No. Let me explain: effectively climate models model a hypothetical world where all things freeze in a constant state while one factor doubles. But in the real world, many variables are changing simultaneously and the rules are different.
Partial differentials of dependent variables is a wildcard — it may produce an OK estimate sometimes, but other times it produces nonsense, and ominously, there is effectively no way to test. If the climate models predicted the climate, we’d know they got away with it. They didn’t, but we can’t say if they failed because of a partial derivative. It could have been something else. We just know it’s bad practice.
…
The partial derivatives of dependent variables are strictly hypothetical and not empirically verifiable – like the proverbial angels on a pinhead. In climate, you cannot vary just one variable, hold everything else constant, and measure the change in the other variable of interest. Employing partial derivatives in climate therefore incurs unknown approximations – so it is unreliable.
One might argue that the partial derivatives are good approximations, maybe all we’ve got and better than nothing. But this is an unknowable assertion because the partial derivatives are with respect to dependent variables. One might argue that certain climate variables are almost independent, in which case partial derivatives with respect to those variables are only slightly unreliable — and you’d be on more solid ground. But you wouldn’t really know how solid, so any model relying on these partial derivatives would have to be tested against reality — and if the model turned out not to work too well, it may be because the partial derivatives have the wrong values, or it might be because they are conceptually inappropriate, or it could be for some other reason entirely, and you wouldn’t know because said partial derivatives are not empirically verifiable.
It sounds to me as if that estimate is quite a wild card in this case, and perhaps it is this factor that creates such broadly different outcomes in climate models, as seen below:
![CMIP5-90-models-global-Tsfc-vs-obs[1]](https://wattsupwiththat.files.wordpress.com/2013/10/cmip5-90-models-global-tsfc-vs-obs1.jpg?resize=720%2C648)
Evans had previously done some work in this area that held some great promise, but in my opinion he released that work prematurely, and it was heavily refuted.
This looks like a much more concrete issue that will be hard to justify and/or explain away.
UPDATE: (9/29/15) Jo Nova adds this via email, with the request it be included here.
People are quoting us in comments with things we didn’t say, and getting caught by tangential things. It will make the discussion on WUWT more productive.
1. David didn’t say this was a “major error”. To summarize:
The partial derivatives used by the basic model do not,
mathematically, exist, and they are not empirically verifiable —
so they are a poor basis for a model. We use this clue in
later posts of this series to construct a better basic model.
2. This is part 4 of a long series. People need to read the
background to fully understand it. Some inferences are leading
to a pointless discussion. eg: of course partial differentials
can and do work in lots of models. In part 1, David pointed
out that most successful physical models get tested and either
dumped or improved in a short time frame. Climate models,
though, can remain wrong for decades. In parts 2 and 3 David
explains precisely what the basic climate model is.
3. David’s work last year was not refuted. We published one
correction, showing that the notch was suggestive of a delay,
but not mandatory as first thought. The delay (which is what
matters) is still supported by other independent studies of
empirical evidence which we cited. As this series will show,
the big findings from the last round stand up even stronger
than before. Publishing it then was very useful as we got some
useful feedback. The notch is real, it still suggests a delay
of one half a solar cycle, and that fits the data better than
any other explanation. We’ll be going through all that in more
detail.
4. The main point is the disconnect between science and “PR”:
their use of partial derivatives on dependent variables may be
partly right or wholly wrong — yet the IPCC says they are 95%
certain.
Is that 95% have a certainty of being wildly wrong?
Perhaps it’s a 97% certainty?
Of being wildly wrong . . . .
Auto
effectively climate models model a hypothetical world where all things freeze in a constant state while one factor doubles
That may be the case for curve fitting models [like Evan’s], but is certainly NOT the case for physical models that integrate the governing equations forward in time. So, the criticism is barking up the wrong tree.
Integrating forward in time does not deal with changing relationships between parameters.
Your comment betrays that you don’t know how the physical models work.
Evidently the IPCC with known data can’t make the models work in reverse either.
“If I have to explain it to you, you won’t understand it” Bernie. Is that what you’re saying isvalgaard?
“Your comment betrays that you don’t know how the physical models work.”
They DON’T work.
Wrong tree indeed. If this critique were true, computational fluid dynamic models would be fatally flawed instead of being valuable and accurate tools in aerodynamics and elsewhere. Initial value vs boundary value, temporal and spacial grid sizing, and initialization and verification concerns about global climate models running for decades or centuries are better trees to bark up.
If this critique were true, computational fluid dynamic models would be fatally flawed instead of being valuable and accurate tools in aerodynamics and elsewhere
============================================
do computational fluid dynamic models successfully predict how the path of a river will evolve over 50-100 years?
No, and no serious scientists would suggest that they can. What they can show is possible futures. However, no serious scientist would then average these futures and say voila, that is what is going to happen.
But this is exactly what the IPCC and climate models do. They average out a sample of possible futures and claim that this average has some physical meaning as to the future. It doesn’t.
It is the worst kind of fortune telling masquerading as science. one might as well average a coin toss and use this average to plan for the future. It is just a meaningful.
And just why is it, I wonder, that of the endless futures predicted, none have a possibility of cooling?
Linton, your comparison is inapt for at least two reasons. 1. CFD FEA cells for stuff like airplanes are minute (cm) ; the smallest CMIP5 cell is 110km owing to computational constraints. Previous guest post here illustrated the consequences. It is conceivable that on those minute scales PDs are indeed approximately constant. Itbis certain their numeric approximation can be validated experimentally (e.g. Wind tunnels, pipes…). It is inconceivable that themsame constancy is true on large scales; nor is any experimental validation or the parameterized value possible. Both are fatal critiques by Evans.
I do not know were he will come out. I do know from my own academic training in econometrics, 5 years of independent climate research, and halves of two published ebooks that he is correct so far. You might benefit from reading those. Climate Models are covered rather in depth. Evns is discussing a deficiency I had missed, much to my chagrin. But was easy to check and verify he is correct in general. See more detailed comments previously posted below.
I have worked wit h three different teams on CFD modelling and the predictions are STRONGLY influenced by training the model to measurements. In fact the details of the workings are the most useful when working within limits spanned by actual data.
As far as making flow predictions and energy transfers ‘outside the measured boundaries’ they are rapidly hopeless. That’s my experience.
ferdberple
September 28, 2015 at 12:07 pm
“do computational fluid dynamic models successfully predict how the path of a river will evolve over 50-100 years? No, and no serious scientists would suggest that they can.”
Ferd, in your example, one of the biggest variables is not a fluid dynamics one. The substrate for the river has hard parts and soft parts, boulders, gravel lenses, sands and clay layers and lenses from sedimentation during previous positions of the river. I suspect this is also true of climate models, omissions of principal components. Fluid dynamics alone would give you a spaghetti distribution like the climate models.
” CFD FEA cells for stuff like airplanes are minute (cm) ; the smallest CMIP5 cell is 110km owing to computational constraints.”
This is totally unscientific. PDE’s are solved on all scales from electron orbitals to cosmology and astro. There is no number of metres or inches where they become invalid. The grid scale simply limits the resolution, as is well understood.
Evans’ juvenile critique has no reference to scale. He just doesn’t understand how partial derivatives work.
The issue of validation is misunderstood. CFD is also a model. It works out the consequences of model equations (Navier-Stokes etc) where the underlying assumptions apply. The chain of reasoning is mathematical, and needs to be checked mathematically. And that is where Evans’ issue lies. Whether the fluid flows of the atmosphere, or round an aircraft, satisfy the model assumptions is a separate matter that needs to be established for that solution to be used.
Stokes
But, those aircraft FEA approximations WERE NOT “used” for design directly from the N=V equation solutions. The aircraft were flight tested, and the model runs in wind tunnels, AND the (manual, then computer-assisted, then FEA-assisted) equations were run against one another. ONLY after near-continuous CORRECTIONS and retested models and wind tunnel testing lasting from 1985 through 2005, were “model runs” and FEA results allowed to “design” simple airfoils. Even then, the results go back to “flight test” BEFORE passengers are flown.
Even inside the “simple” single flow turbine gas paths for GT and steam power plant engines (which involve NO phase changes nor uncontrolled mixing through thousands of cubic kilometers of unconstrained atmosphere) FEA N-V results are NOT installed until flight testing (thousands of hours of run time are finished.
Curious. Have you bothered to read the 6 parts that he has posted already or are you jumping to conclusions without even giving it a look? Sounds more like the latter than the former. I have always found it amazing how you “experts” attack anything that disagrees with you without even finding out what is said. In case you haven’t bothered to look, the “model” has yet to be presented, only explanation of what it is he is trying to present.
SO, I’ll ask you the same question I usually ask those who tear it apart before you see it – WHERE is YOUR model since you obviously know so much.
David Evans qualifications:
Nick Stokes’ comment:
Who to believe?
“Who to believe?”
That says he’s an electrical engineer who knows about spectral analysis. I don’t see much about partial derivatives there.
I was leader of a computational fluid dynamics group at CSIRO for 15 years. You can see a list of many of my papers here. I wrote a PDE package distributed by NAG, which you can still read about here. I do know about partial derivatives.
Partial derivatives have been used since the eighteenth century – Euler, Laplace. Maxwells equations use them. Einstein’s work is full of them. Yet Evans thinks they won’t work for climate science.
Whoops… I think you misunderstood David Evans. He is not an adherent of the first line you quoted. He is saying that’s what the “basic climate model” assumes. He doesn’t agree with it, he is using the basic model’s assumptions to show it’s inaccuracies.
I don’t know whet you mean by a ‘basic climate model’. The models based of solution of the governing equations do not ‘freeze’ every thing etc. So Evan’s criticism does not apply to them, but certainly to his own model [the ill-fated one with the ‘notch’].
lS, with due respect what you assert is simply wrong, at least with respect to NCAR CAM3. Read the tech notes describing the equation guts. Referenced on this comment thread more than once. i make you the same offer as Willis. Have AW get you my coordinates, I will send you a copy. You certainly will not have a math allergy to that model’s entrails. Its just a long slog.
That’s actually not true. At least, not true as you have stated. Take a very simple physical partial differential equation such as the heat diffusion equation (one of the very simplest indeed). Numerically, there are multiple ways to solve for it, including Euler’s explicit forward method, or average in space/forward in time. However, if one tries say to solve in the incredibly simple 1D heat equation by doing average in time/average in space, a method that -should- work, it fails completely miserably, due to the way the variables interact, leading to a completely absurd results. This is a well known problem in numerical methods.
(As an aside, just because something is a “physical equation” means nothing. It isn’t somehow magically easy to solve, or somehow actually relevant to reality. The solution to any physical partial differential equation may not in any way be actually physically possible).
Even worst, numerical methods are extremely sensitive to step size. A reasonable method for solving a particular partial differential equation may be stable at a certain step size, yet completely devolve to chaos on a very slightly different step size. This sensitivity and range of viable step sizes are also different for each potential solution method. It gets way more complex than this.
And all this time, I haven’t even mentioned a -system of equations-. It is true, you can not hold all variables but one static while doing a system of equations, as that immediately breaks the entire system. So, wheat happens when you have a system of partial differential equations? Considering the difficulty even a single partial differential equation has in being solved, when you have a system of them, it’s even harder to evaluate what one particular equation is actually doing, and making sure it isn’t going into chaos (i.e. reaching positive eigenvalues).
And it gets worst! The solution to any partial differential equation is completely dependent on the starting conditions. That is, all partial differential equations have infinite solutions, until satisfactory starting conditions and/or boundary conditions are set (depending on the equation). However, the behavior of the solution is completely different depending on the initial/boundary conditions, even for the same equation. So, a slight change in the initial conditions or boundaries, and you’ll have a different behavior in time and space, and will not be guaranteed to converge to remotely the same conclusion. And again, that’s just one equation, let alone a system of equations, or systems where the initial and boundary conditions for one equation depends on the output of another.
You can’t really -test- this either, you have to run the simulation and check if it even remotely matches reality. No numerical method ever solve reality, it just approximates it, but ultimately empirical tests are required to verify. This has always been true, in all fields. Heck, the Navier-Stokes equation for fluid dynamics isn’t even actually solved yet, and isn’t applicable to weather because it can’t even remotely be approximated. How can one tell if the chaos of a numerical system converges to the actual chaos of a real, physical system?
Without a way to test the solutions of climate models, they are in no way physically meaningful or reliable for prediction, as we can’t know if they actually are approximating reality or just solutional quirks. Models are sanity checked to make sure they don’t go into the impossible, but that in no way means those that pass that are behaving real, at all.
Anyways, for more reading, this is a very simple primer https://espace.library.uq.edu.au/view/UQ:239427/Lectures_Book.pdf .
All of this may be so, but is really not relevant to Evan’s specific complaints.
“Heck, the Navier-Stokes equation for fluid dynamics isn’t even actually solved yet”.
Professor Pinczewski did in a brilliant thesis: http://primoa.library.unsw.edu.au/primo_library/libweb/action/dlDisplay.do?vid=UNSWS&docId=UNSW_ALMA21127060720001731&fromSitemap=1&afterPDS=true
Brilliant book link, BTW. Added it to my collection of useful stuff to keep accessible via my various kindle book readers. It is short on two topics: a) nonlinear ODEs that lead to chaotic solutions (where I think that there is still a lot of work to do on this subject, in his defense); and b) stiff ODEs (at least I didn’t see much of a discussion on backwards methods etc in my brief perusal, but it WAS a brief one so maybe it is there someplace). Both are relevant to the discussion at hand.
But all in all, I generally agree with everything you’ve said. In a sense, it is surprising that anybody thinks that integrating GCMs, which are basically weather models run out past the point where they are known to be modestly useful by direct comparison with reality, is likely to produce an accurate representation of the global climate fifty years ago in spite of the fact that they can’t do the local weather particularly well fifty hours from now.
rgb
I agree with this discussion. And Evan’s specific complaint has no bearing on the current models.
Ah shoot, I think I completely misread your comment as saying something very different. Sorry about that!
Isvalgaard, in that case, the statement is only slightly modified. You claim all factors aside from the small fraction that you are modeling are either constant or nonexistent, and that none of the unknown factors, which we know exist but don’t know what they are or how they operate, matter.
Sorry, but “physical models” are a joke. Empirical models at least estimate the factors they don’t understand.
lsvalgaard says: September 28, 2015 at 10:47 am
Your comment betrays that you don’t know how the physical models work
—————–
Considering how far off their projections are from the real world observations, It’s obviously they don’t work
So, I take it you bothered to read the 6 parts that have been posted on Evan’s work so far, right? Or is it possible that you still think only in the past? Ah, but your brilliance has surely solved the climate mysteries, so as I like to ask everyone that tears very one else’s work apart. where, exactly is YOUR model that is obviously of superior quality and works perfectly? And could you then tell me what to expect for climate over the next 5 years?
And what is YOURS? Now that you have elevated yourself to be an expert.
One more time. Anthony you should never use that graph of model output without putting a bright vertical line indicating the date of the model so that everyone can see what was hindcasting and what was projection.
So where does the line go on this one?
I agree this is important information.
M. CMIP5 is 1/1/2006.
Thank you!
“M. CMIP5 is 1/1/2006.”
So how many hind castings have there been and what on earth would the projections have looked like with the earlier ones? Might also make a good article.
Also isn’t cheating to just keep updating the hind casts in an attempt to improve the future prognostications?
Agreed because how much higher would the models indicate temperatures should be by now if they did not the double dip created by El Chichon and Pinatubo? The divergence with real world measurements would be off the charts!
…not *have the double dip…
Imbedded within the graph is a caption that says 97% of the models fail — I would like further info on the 3% of the models that did “predict” the applicable temperature “index.” Were the 3% supposing that there was severe curtailment of CO2 emissions or did they have some rational basis that we should put greater resources in to develop further? Curious, open-minded engineers would like to know.
I would suspect that the 3% of models that are in the ball park of the actual temperature extension are there by chance, not because they have all the the important variables properly weighted. Heck, they know that the temperature has to be constrained to be somewhere in a non-fanciful space so they can’t be impossibly wildely out. This means they must have discarded hundreds of models in the development period and maybe even have a factor that limits them in slope.
My major criticism is that there isn’t a much higher percentage than 3% in the ball park. This is, in itself, proof that their equations are trying too hard to imitate an unrealistically warm climate based on their chief control knob, CO2. The distribution of slopes of the predictions are an unwitting measure of the magnitude of their biases. Monckton, et al’s simple hand held calculator model came about because the authors are biased closer to a more realistic reading of climate – that it is not unstable, that it is held in check by feedbacks, not accelerated out of control by them.
Gary says, “I would suspect”…
Yet that is the point is it not? You should not have to suspect, you should know exactly why those runs are different. Yet we never get an answer to that, and we never get an explanation why those runs are ignored and the very wrong “model mean” is used for projections of future harms.
If only 3% of the model outputs were reasonable enough to retain, isn’t that a classic example of ‘Cherry Picking’ to justify the models? It seems to support the claims that initial conditions influence the solution of the PDEs, and the only evidence for the failed solution of an unknown, or multiple unknown PDEs, is what the modeler subjectively decides is an unreasonable end result. I would like to see more congruence in the model outputs and more objectivity in the retained model outputs.
Fair enough, but ristvan says the date was 1/1/2006. But on that date, according to the model outcomes, the temperature varied from 0.8C in one result to 0.2C in another. It cannot possibly be the starting point of the collection of models if the initial statement is different. And it would be truly miraculous if starting there, with hindcasting they all agree on a starting point of zero in 1983. That would be incredible hindcasting – perfect modelling.
I can swallow a starting point for all models, using the same initial conditions, of 1/1/1983. Nothing else with these results.
DH, dead thread observation being checked for different reasons. You are correct. Shows yet again how bad the models are. The CMIP5 ‘experimental protocols’ (essay Models, and elsewhere, Googleable) require initialization 1/12006, or alternatively an average of December 2005. The first mandatory archive result is a 30 year hind cast. So that is how the parameterizations were tuned.
The models do not even get absolute temps right (stuff like freezing, thawing, evaporation). Even on 1/1/2006. See aforesaid essay in my ebook for a graphical illustration drawn from US congressional testimony.
It looks like the journey to Paris, could be very slippery
How I wish that I could agree with you, but the brainwashed minds of out sheeplike leaders are totally closed to any suggestion that beast that they are about to do catastrophically expensive battle with, is a chimera.
Whoops: out=our!
World leaders will joust at windmills. Come hither Paris, we must duel. Our charge is true, upended by reality, we are not. For what breaks on our future doorstep but unbridled heat searing the planet. Yea, though fair Mann rides upon many a story of gloom and doom,….
same argument would apply if actual measurements over past 20 years were far higher than models predicted. In either case, things are happening that the models don’t or can’t capture.
Where exactly are the partial derivatives in question? In the GCMs?
I would have put this differently. The models depend on many parameters. Many of those parameters are not fixed at some definite value by either physics or observation. It is remarkably difficult to estimate the errors in the model output results given an error in the input parameters, moreso when the input parameters are treated as if they are exactly known numbers. It is even more difficult when the output of the model is a chaotic trajectory that is known a priori to not correspond to the actual trajectory of the climate (probability of a good approximation being close to zero). It is impossible altogether when the output of the chaotic model is a set of widely spread model trajectories for a tiny perturbation of the parameters and initial conditions, a spread that will almost certainly widen still further and in unpredictable ways if one samples (with e.g. Monte Carlo) the (say) 95% confidence range for all parameters. And in the end, this still won’t give you a large enough error bar because if there are (say) 14 parameters being sampled out to 95%, it is 50-50 that at least one of them is outside of these bounds (and you won’t know which one(s)).
Finally, a rule of thumb is that error estimates obtained from a direct consideration of Bayesian parametric model uncertainty are almost always empirically too small, especially for an intrinsically nonlinear chaotic model where there is nothing expected to behave in accordance with the central limit theorem.
rgb
rgbatduke:
Yes!
+1
Richard
rgbatduke September 28, 2015 at 10:11 am
– – – – – –
rgbatduke,
Your discussion’s point seems to be somewhat consistent with the discussion by David Evans. Is there a difference fundamentally between Evans and you?
John
If I understand his remarks above, they aren’t really applying to the GCMs because the GCMs, as far as I know, make no use of partial derivatives with respect to parameters. That was the observation I was making. It is different if one is building an N-layer model that has parameters like albedo, emissivity, several absorptivities for atmospheric components. In that case one will get smoothly different answers for different values of parameters in some straightforward way, and error estimates will or should take into account how the output value varies with respect to the uncertain input parameters.
where 
is the global temperature anomaly and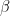 
is the climate sensitivity to CO2 (only) are not smooth functions. In some sense they aren’t functions at all. They are fractal ensembles of possible outcomes where it cannot even be proven that the smoothed/averaged function 
is relevant to any given one of the trajectories produced by the model, or relevant to the actual climate trajectory so that having the ensemble of results might or might not provide one with useful information.
In the case of GCMs, things like
I could be wrong — maybe he is referring to GCMs. But I don’t think so, at least not in any knowledgeable way as I don’t see any place where a partial with respect to parameter is relevant or even well-defined with respect to a GCM.
rgb
Sorry, I’ll try in words:
“…the variation of the temperature anomaly averaged over an ensemble of possible trajectories with respect to a parameter like climate sensitivity is relevant to…”
rgbatduke on September 30, 2015 at 9:19 am
– – – – – –
rgbatduke,
Thank you.
John
I’ve long thought that you could model the global climate as a large collection of analog circuitry, it would just be very hard to tune it. You could make a model of that analog circuit, but all of the partial diff equation in the analog simulators would struggle with something so large.
I also worked in an Mil Aerospace Electronics company that had to do sensitivity analysis, they’d create a transfer function that represented the circuitry, and then do a sensitivity analysis for each node.
I’m surprised I haven’t seen a proposal to make an ASIC for climate modeling.
rgb
I’m just a civilian in all this parameter/partial derivative/yadda yadda yadda stuff; I freely admit I can’t tell up from down.
However, the obvious errors & uncertainty in this tired topic of global warming (aka climate change, etc, etc) is just numbing – especially since it’s claimed this is “settled science”. It’s pretty obvious to this old retired CFO that lots of warmest PhDs aren’t much more informed than I am.
I know how Feynman defined “settled science”; I wonder if Newton’s definition would have differed by so much as a single word. Hell, the warmest can’t even settle on the name of their so-called climate science stuff.
I’m sure the “climate scientists” will find a way to ignore this information just like anything else that contradicts their belief system.
I wish I could edit “there” to “their.”
We knew what you meant.
Jorge
Indeed!
A few years ago, I would have bean critical – but I now realise it is about communication.
Have you communicated to your target audience?
Here that is WUWT’s typical readership/viewers. [Aside and OT: is there a collective noun for those who read something on line? Reader? Viewer? Follower? [not for possible sceptics, I suggest!].
Sharps communicated – and would be understood by, I think >98% of those who read and comment and – a guess, pure arm-waving speculation – >85% of those who just read.
I hope you’ve bean entertained!
Auto
sharps4570 (@sharps_4570) September 28, 2015 at 10:20 am
Fixed.
w.
Auto
collective noun: try audience
Observers is a good one I think.
There are some good discussion points at
http://bishophill.squarespace.com/blog/2015/9/26/great-evans-above.html#comments
John Shade as a couple of “folksy examples” which even non-mathematicians can understand.
Rud Istvan and others also have good comments.
David and Jo are doing more muddying of the waters than shedding light so far, this (to me) non-issue may backfire on them if they get round to producing something of substance.
The models do not work, if they did, they would reflect reality, which they don’t. Not only do they not work for contemporary conditions they don’t work for previous conditions either. The basic hypothesis that CO2 is a major driver of climate is obviously incorrect if we look at FACTS not suppositions, the Medieval and other warm periods happened well before the industrial revolution, we have had CO2 concentrations almost 20 times higher than they currently are in the past, without the planet turning into a cinder. The 18 years and 7 months “pause” was not predicted. looking at the graphs, I think temperatures have peaked and the planet is getting colder.
His approach is mathematically sound so far. The comment criticism that climate models do not actually work with partial derivatives the way his generalization states is easily refuted by the technical notes to NCAR CAM3 (part of CMIP3). CAM3 is particularly interesting because it fairly cleanly separates the dynamical core from the parameterizations; other GCMs don’t. I sent David and Joanne a copy to bolster their work.
The 2015 Mauritsen and Stevens paper adding Lindzen’s adaptive infred iris to a climate model and thereby reducing its sensitivity halfway to observational is a specific axample of the fatal partial derivatives problem, in this case concerning the water vapor feedback. Judith Curry and I did complementary posts on Mauritsen and Stevens on May 26, 2015 at Climate Etc for those interested in digging deeper into this specific example of Evan’s general critique.
It remains to be seen what Evan’s alternative formulation will produce. Hopefully a sensitivity close to the recent observational ones : something around 1.7 using AR5 values (Lewis and Curry 2014), around 1.5 per Nic Lewis most recent 2015 estimate if the newest Stevens aerosol estimates (lower) are included. That was guest posted at Climate Audit and at Climate Etc.
Please indicate where Mauritsen and Stevens refer to “the fatal partial derivatives problem”, I see nothing at all resembling such a reference.
They didn’t. I did. The paper is an example of What happens (lower sensitivity) whennEvans general critique is accounted for in one feedback.
In the context of CAM3, for example equation 3.26 on page 16 deals with this. In it are 6 PDs on the right side describing how partial q/partial t changes. Q is specific humidity, t is temperature. Then read 4.1, the parameterization of deep convection, which includes Lindzens detrainment. Equations 4.16 to 4.20 provide the parameterizations for the sub PDs. All constants. Lindzen’s point is they are not constant. Evens point is such PDs are of dependent variables, a conceptual nono. Another way of generalizing Lindzen’s observation.
It is quite possible than on sufficiently fine scales high resolution, as in CFD, these things are constants. But notmon coarse grid scales.
The adaptive infrared iris hypothesis about tropical convection cell (thunderstorm) feedback on upper troposphere dryness and cirrus is an example of unstable partial derivatives. Adaptive water vapor feedback. Eschenbach makes the same argument focusing on albedo. IMO both UTsH and albedo are at play. My previous guest post here on models explained why such things are computationally constrained, forcing large grids, forcing parameterizations, which are nothing more than guessed constant values of those particular PDs, which are not constants the way the CAM3 math has them. Evans has simply made the point using generalized conceptual math.
Both above paragraphs in this comment simply provide a VERY specific example for you and some of the other negative commenters.
ristvan September 28, 2015 at 10:27 am
Link?? Please cite page number that you are referring to.
Thanks,
w.
Hi Willis. Glad you are here. For NCAR CAM3, see pages 16 and 75-79 of NCAR/TN-464+STN (2004). The official technical notes of the actual guts of CAM3. Warning– do not have math allergies if you want to take a peek atnthose entrails.
As for Evans stuff, his relevant post for my comments here is NS-4 (of the six so far).
Get me your coordinates via AW, I will send you a copy of the CAM3 tech notes. Was referenced extensively in my penultimate examples chapter of The Arts of Truth. Even provided a much simplified feedback equation with partial diffs as lead in to how awful AR4 selection bias got the quantitative estimates wrong, without realizing the bigger underlying problem with the math concept Evans has exposed. My bad. Live and learn.
ristvan September 28, 2015 at 3:34 pm Edit
Thanks, ristvan, but … pass. I asked for a link, not a name. When I’ve followed that kind of clue in the past, far too often I found out it’s not available, or the one I can find is a different edition with different page numbers, or I can’t find it at all.
My rule these days is that I don’t go on a snipe hunt for any man. I don’t have enough days left on this lovely planet to waste my time looking for support for your claim. If you have a copy, post it on the web with a link so anyone can see what you are referring to.
Regards,
w.
Willis, your snipe hunt reference has diminished you greatly in my eyes. If you had bothered to type the exact NCAR doc reference I provided into Google, you would have found it as the first search reference link. i just did. Easy Peasy, albeit a bit old fashioned. Just a reference rather than the lazy hyperlink.
Since you evidently do not know how to hunt snipe, here is the URL for your snipe bag. Make sure to bring along your own special night snipe flashlight. (Ah, the Boy Scout memories…)
http://www.cesm.ucar.edu/models/atm-cam/docs/description/description.pdf
Note further that I even previously offered to send you a copy, to spare you your sniping trouble.
Snipe hunt indeed. Read the document (if you can) and then perhaps apologize. I have cited specific partial diffs by doc equation number, and the pages where they are written out, relevant to the thread comments. And you do not want to hunt snipe?
ristvan September 28, 2015 at 5:17 pm Edit
Ristvan, I learned early on in this game that no matter what I do, no matter what I say, someone will tell me how my action has diminished me in their eyes. Take a number, stand in line, your turn will come when your number is called … I fear that the opinions of random anonymous internet popups regarding my hard-learned life choices are of little interest to me.
I have had that happen … but far more often than not, I’ve gone, looked unsuccessfully, and come back with my blood severely aggravated. Since I can’t guess in advance whether or not it will work, I just play the odds these days.
Oh, I assure you, I know how to hunt snipe … that’s why I don’t go on a snipe hunt for any man.
Will do.
Not interested in the slightest in private off-the-record documents. As I said above (new emphasis mine)
So no … no emails, thanks.
After prodding, you have done the absolute minimum required—provided a link with a page number to give everyone easy and unequivocal access to what you are talking about. You’ve done the absolute minimum, while bitching and moaning about how tough it is to LINK TO YOUR OWN REFERENCE … and now you expect an apology?
Never happen. If you can’t be bothered to post the link, I can’t be bothered to read it. Next time, just post the link, your whining diminishes you in everyone’s eyes.
w.
I read you. Now download the provided link to the technical note on CAM3 that you apparently could not figure out from a precise citation, and then comment on the relevant pages/equations concerning the partial derivatives and their parameterizations.
All else is just stylistic bluster.
Willis, your replies above to this thread say much. But not very much complementary. My golly, you seem stuck in your own skeptical preconsceptions. Me, I just go with the scientific flow. Funny thing is, that flow agrees with much of your speculations about the low latitude troposphere. A dilemma, given your vociferous rejections of what I post, always with additional scientific support.
I don’t know how one avoids this kind of problem. Even if one has one’s work checked by a mathematician it is quite possible that particular mathematician will miss it.
The problem seems similar to the problem of finding software bugs. Any sufficiently complicated software will have bugs and some of those bugs will not be detected before they create a serious problem for the users (eg. heartbleed).
It’s all garbage, the only math that counts is the result. The IPCC made predictions using mathematical models that don’t correspond to reality. Nitpicking over the rightness of these models is useless, unless you are trying to persuade weak minded indiviuals. The math is wrong. And I’ve said so for years now.
Rishrac, sorry to find you think I amongst others have a weak mind. How many books have you written? How many peer reciewed articles have you published? How many issued payents do you have?
But on a separate and much more relevant point, Evans showing rigourously that the GCM models are from first principles of math neither validatable nor verifiable is a bit stronger than just saying they are proven wrong by subsequent observation /projection discepancies.
My opinion, it would be helpful if our side closed ranks rather than exposed flanks. Just sayin as an old Army guy.
Rishrac,
You are correct if you believe we must weight model outputs against empiriclals. The new gold standard has to have some of the actual gold in it or don’t bother. But its also important to critique the roots of GCMs, because though they are merely a simulation, they are valuable long term. We make our critiques to place GCMs in their proper context, as well to improve their function. Can GCMs project with skill? I don’t think they can, and always a good follow up will be “why cant they?”
We have two roads to hoe in understanding our climatic system; A) we can improve our survey methods/tech/coverage/resolution B) we curate and form GCMs which do possess projection skill. As both A and B rely on A to achieve skill, it can be said that we have limited skill at this time
First, let’s talk about the length of time co2 stays in the atmosphere which is included in the models. Second in the co2 series is where the co2 is coming from. Computer models are useful when relevant data and formulas are used. In CAGW, they are not.
The time line for horrible things happening is now not 50 years from now. CAGW started shouting for action 20 years ago. And yes the time line for disaster does matter. Correlation does not make causation. While the incident of co2 may have tracked recent temperature increases, and I use the word MAY HAVE, does not mean that it will continue to do so, and for the last 20 years hasn’t.
Too many people in CAGW have done too many questionable things in a misbegotten belief they are saving the world. Completely contradicting studies have come out that attempt to nullify sound arguments against CAGW.
The very real fact of the matter is that there has been so much tampering done with both the physical evidence, and the psychological mindset, that it is difficult to be objective. The real danger is that in a chaotic system, extreme cold is possible and we will not be prepared for it.
First… co2 time in the atmosphere. Given the amount of co2 released, the rate of rise in co2 ppm should have been anywhere from 8 to 10 ppm rise in any of the last 10 years. The most recorded was 2+ ppm in 1998. Clearly, 50% of current co2 production is being sunk, or the natural output of co2 has diminished , or the sink has increased dramatically over time. Something is happening that trashes the idea that co2 remains in the atmosphere for hundreds of years. In my view 50% is on the low side, I think it is closer to 70 to 80%. Which just the amount of sinking would dwarf the entire output in any year prior to 1960.
Second, where is the co2 coming from. I let that idea stand, although I thought at the time that it was not just a straight line equation to determine what produced co2 based on isotope compounds in co2 in the atmosphere. As time has developed a different understanding of that in conjunction with the amount of sinking that is currently happening. Something is fundamentally wrong with that statement as well, which is also used in the model as a percent of man made versus natural co2.
Which leads to several interesting and disturbing thoughts. If we weren’t producing so much co2, would the amount of co2 be reducing? This is something real, not a computer model, then the balance of co2 is not something that increases and decreases over a long period of time as has been expounded. The disturbing thought is that in less than 100 years most plant life on the planet would die.
This entire subject is bad. You have people calling for criminal penalities, name calling and the like. CAGW is using the analogy of tobacco as a rallying point. This subject differs in that there aren’t hospitals full of people on iron lungs. Additionally, a warming climate is not necessarily a bad thing in every single case as has been made out, or even overall.
I can’t sort out every instance of all the arguments except through math. The math that the IPCC uses to calculate is wrong. No question in my mind. And the physical reality confirms that. That’s the real gold standard. The models can’t foreast correctly forward or backwards, even with known data.
ristvan September 28, 2015 at 4:37 pm
No, no, a thousand times no. That’s great for the army, but very bad for science.That’s what the alarmist side has done, closed ranks and refused to discuss any problems with papers perceived to be on “their side” … and look what that has brought them.
It is our responsibility to try to poke holes in ALL theories, not just the ones we think might oppose our own ideas. If we do not investigate equally and impartially, our credibility will sink to equal theirs … bad outcome.
w.
Hey Willis. Sort of agree when stuff is real. Not when only figments of the imagination. Way too many imagination figments, IMO.
ristvan, I read your “close ranks” comment to mean we should accept disparate VALID criticism of CAGW theory, not as commentary to blindly support all skeptical arguments. Was I correct?
David A, precisely. SkyDragons and such should be loudly and firmly rejected. CO2 is a GHG. Tyndall reported those experiments to the RS in 1859. The big unsolved question is, so what?
Where? The dynamical core does solve partial differential equations, but this is not what he is referring to AFAICT. One has to do a bunch of work in order to define just what you might mean by a partial derivative with respect to a model parameter in a chaotic system or model in the chaotic regime.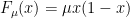
. One can form the partial $\partial F/\partial \mu$, to be certain, but this partial has limited utility in understanding error propagation because the iterated map $F_\mu^n(x)$ has such dramatically distinct behavior depending on where one is with respect to the critical points and the value of 
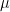itself. Weather/climate is computed in GCMs by solving the PDE at some coarse grained scale (far TOO coarse grained), which essentially means it is a discretely iterated map and in particular is one in which the outcome trajectories are well-known to be already in the strongly chaotic regime. I’m not certain how to begin to define a parametric partial derivative in such a system. It could only have meaning in some ensemble average sense, but I don’t completely see why an ensemble average over trajectories itself has any meaning.
To be more explicit, consider the humble iterated logistic/quadratic map
This is the giant problem swept firmly under the rug by the entire climate modeling community, although it does get pointed out, firmly, now and then by mathematicians that actually work with chaos and nonlinear dynamics. It is even acknowledged by the IPCC (back in AR2?). I used to keep the quote from the report handy, but from memory it was something like “There is no good reason to think that averaging the many chaotic trajectories from a GCM will work, but we’re going to do it anyway.” That’s still the state of the art, and affairs, as of AR5. Only they make it even worse and average the averages over many GCMs, something that is just about as sensible as averaging the average state output from two distinct chaotic iterated maps. That is, no sense at all AFAIK.
rgb
http://wattsupwiththat.com/2015/05/26/the-role-of-sulfur-dioxide-aerosols-in-climate-change/#comment-1946228
We’ve known the warmists’ climate models were false alarmist nonsense for a long time.
As I wrote (above) in 2006:
“I suspect that both the climate computer models and the input assumptions are not only inadequate, but in some cases key data is completely fabricated – for example, the alleged aerosol data that forces models to show cooling from ~1940 to ~1975…. …the modelers simply invented data to force their models to history-match; then they claimed that their models actually reproduced past climate change quite well; and then they claimed they could therefore understand climate systems well enough to confidently predict future catastrophic warming?”,
I suggest that my 2006 suspicion had been validated – see also the following from 2009:
http://wattsupwiththat.com/2009/06/27/new-paper-global-dimming-and-brightening-a-review/#comment-151040
Allan MacRae (03:23:07) 28/06/2009 [excerpt]
Repeating Hoyt : “In none of these studies were any long-term trends found in aerosols, although volcanic events show up quite clearly.”
___________________________
Here is an email just received from Douglas Hoyt [in 2009 – my comments in square brackets]:
It [aerosol numbers used in climate models] comes from the modelling work of Charlson where total aerosol optical depth is modeled as being proportional to industrial activity.
[For example, the 1992 paper in Science by Charlson, Hansen et al]
http://www.sciencemag.org/cgi/content/abstract/255/5043/423
or [the 2000 letter report to James Baker from Hansen and Ramaswamy]
http://74.125.95.132/search?q=cache:DjVCJ3s0PeYJ:www-nacip.ucsd.edu/Ltr-Baker.pdf+%22aerosol+optical+depth%22+time+dependence&cd=4&hl=en&ct=clnk&gl=us
where it says [para 2 of covering letter] “aerosols are not measured with an accuracy that allows determination of even the sign of annual or decadal trends of aerosol climate forcing.”
Let’s turn the question on its head and ask to see the raw measurements of atmospheric transmission that support Charlson.
Hint: There aren’t any, as the statement from the workshop above confirms.
__________________________
IN SUMMARY
There are actual measurements by Hoyt and others that show NO trends in atmospheric aerosols, but volcanic events are clearly evident.
So Charlson, Hansen et al ignored these inconvenient aerosol measurements and “cooked up” (fabricated) aerosol data that forced their climate models to better conform to the global cooling that was observed pre~1975.
Voila! Their models could hindcast (model the past) better using this fabricated aerosol data, and therefore must predict the future with accuracy. (NOT)
That is the evidence of fabrication of the aerosol data used in climate models that (falsely) predict catastrophic humanmade global warming.
And we are going to spend trillions and cripple our Western economies based on this fabrication of false data, this model cooking, this nonsense?
*************************************************
More from Doug Hoyt in 2006:
http://wattsupwiththat.com/2009/03/02/cooler-heads-at-noaa-coming-around-to-natural-variability/#comments
[excerpt]
Answer: Probably no. Please see Douglas Hoyt’s post below. He is the same D.V. Hoyt who authored/co-authored the four papers referenced below.
http://www.climateaudit.org/?p=755
Douglas Hoyt:
July 22nd, 2006 at 5:37 am
Measurements of aerosols did not begin in the 1970s. There were measurements before then, but not so well organized. However, there were a number of pyrheliometric measurements made and it is possible to extract aerosol information from them by the method described in:
Hoyt, D. V., 1979. The apparent atmospheric transmission using the pyrheliometric ratioing techniques. Appl. Optics, 18, 2530-2531.
The pyrheliometric ratioing technique is very insensitive to any changes in calibration of the instruments and very sensitive to aerosol changes.
Here are three papers using the technique:
Hoyt, D. V. and C. Frohlich, 1983. Atmospheric transmission at Davos, Switzerland, 1909-1979. Climatic Change, 5, 61-72.
Hoyt, D. V., C. P. Turner, and R. D. Evans, 1980. Trends in atmospheric transmission at three locations in the United States from 1940 to 1977. Mon. Wea. Rev., 108, 1430-1439.
Hoyt, D. V., 1979. Pyrheliometric and circumsolar sky radiation measurements by the Smithsonian Astrophysical Observatory from 1923 to 1954. Tellus, 31, 217-229.
In none of these studies were any long-term trends found in aerosols, although volcanic events show up quite clearly. There are other studies from Belgium, Ireland, and Hawaii that reach the same conclusions. It is significant that Davos shows no trend whereas the IPCC models show it in the area where the greatest changes in aerosols were occurring.
There are earlier aerosol studies by Hand and in other in Monthly Weather Review going back to the 1880s and these studies also show no trends.
So when MacRae (#321) says: “I suspect that both the climate computer models and the input assumptions are not only inadequate, but in some cases key data is completely fabricated – for example, the alleged aerosol data that forces models to show cooling from ~1940 to ~1975. Isn’t it true that there was little or no quality aerosol data collected during 1940-1975, and the modelers simply invented data to force their models to history-match; then they claimed that their models actually reproduced past climate change quite well; and then they claimed they could therefore understand climate systems well enough to confidently predict future catastrophic warming?”, he close to the truth.
_____________________________________________________________________________
Douglas Hoyt:
July 22nd, 2006 at 10:37 am
Re #328
“Are you the same D.V. Hoyt who wrote the three referenced papers?” Yes.
“Can you please briefly describe the pyrheliometric technique, and how the historic data samples are obtained?”
The technique uses pyrheliometers to look at the sun on clear days. Measurements are made at air mass 5, 4, 3, and 2. The ratios 4/5, 3/4, and 2/3 are found and averaged. The number gives a relative measure of atmospheric transmission and is insensitive to water vapor amount, ozone, solar extraterrestrial irradiance changes, etc. It is also insensitive to any changes in the calibration of the instruments. The ratioing minimizes the spurious responses leaving only the responses to aerosols.
I have data for about 30 locations worldwide going back to the turn of the century. Preliminary analysis shows no trend anywhere, except maybe Japan. There is no funding to do complete checks.
Yes, this is the biggest financial bonanza since the the 19th century North American Gold Rush?
Then there was the South American Gold Rush prior to the above event.
Allen,
” but in some cases key data is completely fabricated – for example, the alleged aerosol data that forces models to show cooling from ~1940 to ~1975…. …the modelers simply invented data to force their models to history-match; then they claimed that their models actually reproduced past climate change quite well;”
Now they cut out the middle-man reason and just adjust the temperatures. Bet the current revision of temperatures looks nothing like back in 2006.
CAGW’s premise that CO2 is climate’s control knob and that all other variables like cloud cover, solar cycle strength, Galactic Cosmic Rays, AMO/PDO 30-yr cycles, ocean current flux, UV FLUX, ENSO, etc., balance out over time is absurd.
Most variables often have some direct or indirect positive and/or negative feedbacks based on their current state and influence other variables to some extent.
I think the empirical evidence is starting show solar cycle strength has more significant Climactic impact than CAGW models account for and certainly more than CO2.
The strongest 63-yr string (1933~1996) of solar cycles in 11,400 obviously had a substantial effect on 20th century warming. When these strong cycles ended in 1996, so did the global warming trend, despite 30% of all manmade CO2 emissions since 1750 being made just since 1996….
BTW, I think the above graph used UAH v.5 and not the new UAH v.6. If that’s the case, I’d like to see the graph using RSS temp data, as RSS and UAH 6.0 are now virtually identical since 1979.
The strongest 63-yr string (1933~1996) of solar cycles in 11,400
That string is not especially strong and not the strongest in 11,400 years,
e.g.
http://www.leif.org/research/GN-Since-1600.png
or
http://www.leif.org/research/Comparison-GSN-14C-Modulation.png
“It is not what you that gets you in trouble, it is what you know that ain’t so”
“It is not what you that gets you in trouble, it is what you know that ain’t so”. I will assume that you mean “It is not what you don’t know that gets you in trouble, it is what you do know that just ain’t so”. Many have a problem with this. Some, for instance, confuse direct observation of gravitational effects of theoretical material called “dark matter” with an observation of an actual factual material itself called dark matter when they are actually observing unexplained gravitational effects.
From what I understand, the clearest linkage between solar activity and earth based events is the effect on shortwave radio propagation due to changes in the electron density of the ionosphere over the 11 year cycle. This is presumably due to increased UV radiation from the faculae around the sunspots and has been shown to correlate well with the 10.7cm flux measurements (especially with a bit of time-averaging).
It is also my understanding that the proposed mechanisms for the coupling of the solar cycle with climate/weather include total solar irradiance, UV flux affecting the upper atmosphere (correlating with the 10.7cm flux) and the solar wind interacting with the cosmic ray flux (correlating with 14C production). The above graph shows that 14C production correlates fairly well but not perfectly with the GSN – I wonder if the discrepancy is due more to measurement error or has basis in physical reality?
The UV, F10.7, etc all vary largely in step with solar activity, so as that vary they all approximately vary.
http://www.leif.org/research/Reconstruction-of-Solar-EUV-Flux-1740-2015.pdf
“The Diurnal Range, rY, of the geomagnetic East component can be determined with confidence from observatory data back to 1840 and estimated with reasonable accuracy a century further back in time. The range rY correlates very strongly with the F10.7 microwave flux and with a range of measures of the EUV-UV flux and thus with the solar magnetic field giving rise to these manifestations of solar activity. The variation of the range also matches closely that of the Sunspot Group Number and the Heliospheric magnetic field…”
Jim, compared to the direct evidence for cosmic inflation, the evidence for dark matter looks positively “robust”.
And what about that dark energy?
I can think of other reasons for the variances seen in Type 1A supernovae that an accelerating expansion of the universe.
Seemed at the time and ever since like thin evidence for such a strong conclusion.
Besides what I can think of, is the perhaps even stronger possibility that the cause is something that no one has any idea about…yet.
Sorry to go OT.
“This looks like a much more concrete issue that will be hard to justify and/or explain away.”
More concrete than the problem that the models do not include PDO, AMO, ENSO, El Nino/La Nina, etc.?
JW, it is an orthogonal critique saying that whatever stuff is in the model still uses faulty math incapable of being verified and validated, from first principles. So even if a model ‘got it right’ there is no way to know whether that was just a fluke, closing the door on conceptual model improvement on computationally constrained grid scales.
Yes in a dynamic chaotic system, when one thing changes everything else in the system changes.
Why this obvious fact doesn’t immediately invalidate the claimed usefulness of models is a mystery. Or maybe not such a mystery due to humanity’s history of falling into periods of stupid
. . .So, in other words…when people drift left and become liberals ??
Perhaps it’s not so much people (individuals) drifting left, as institutions drifting left because of selective hiring. The result is a narrower and narrower academic outlook, unable to deal with the real world in an unbiased and synergistic way.
Or drift right and invade Iraq to stop non-existent WMDs
Either a left or a right drift, if stupidity drives, it arrives back at stupid. Each party at this time is a compromise of reason
Alx
“…Why this obvious fact doesn’t immediately invalidate the claimed usefulness of models is a mystery. Or maybe not such a mystery due to humanity’s history of falling into periods of stupid…”
In response, might I suggest American culture is reaping the rewards of a failing education system. If citizens get out of high school with no more than algebra 1, they have no basis for understanding your quite valid point.
I think you need some good analogies . . and many might understand. It seems something like ecology to me, with interwoven population changes, or players on a basketball court reacting continuously to the other players . . to think one could see into the future of such things with a computer model is kinda funny to me.
My average rate of usage of partial differentials, since exiting academia, has been at about a single digit rate per century, so I have to dust off a lot of cobwebs to grasp the gist of this issue.
But I gather that Evans is saying that when you have a dependant variable, say for example, mean global Temperature; which is a function of several independent variables; perhaps CO2 abundance, atmospheric water content, and TSI value. that the practice is to compute the derivative of the dependent variable (T) WRT each of the independent variables; (CO2), (H2O), and (TSI) while holding all the other independent variables fixed, and then presumably one does some sort of addition of those derivatives, and assumes that gives a valid change for the dependent variable, if all the independent variables are allowed to float free.
This is not an uncommon situation, that arises in many Physics situations.
A perfect example would be ” Ohm’s Law ”
What G. S. Ohm discovered and described as a law, is : ” For certain electrical conductors; mostly pure metals and metallic alloys, the current flowing in a circuit, is directly proportional to the applied voltage, WHEN all the other physical variables are held constant. ”
So we have dI /dV = constant, which we define as resistance, (R)
And we write E = I.R , and call that Ohm’s Law, when Ohm’s Law really says ” R is constant ” Provided of course that all other physical variables are held constant, such as the Temperature of the material, and maybe even the ambient pressure, or the incident EM radiant energy falling on the material.
Well of course that restriction is impossible to achieve in practice, because the dissipation of energy in that resistance is going to convert the electric energy into thermal energy (heat) and the Temperature of the wire or resistor is going to increase.
And since any practical resistance material, such as say Nichrome wire, or Constantan, or any of the other modern resistance materials, has a Temperature coefficient of resistance; which is another partial derivative involved in the problem, it is not possible to exactly satisfy the conditions which Ohm asserted are necessary for his law to hold.
Well in practice, one tries to measure the V / I ratio with such low levels of current, that the amount of heat generated is tiny so the Temperature change is negligible. Using a short pulse of current also reduces the heating, to improve the accuracy, but that introduces its own complexity of accurate measurement of pulsed currents and voltages.
The Tungsten filament of an incandescent light bulb is an example where a perfectly good Ohmic resistance material, is used in an application where the current density level is so high, that the conditions for Ohm’s law aren’t even approximately applicable.
So the light bulb resistance rises dramatically when turned on with the design operating voltage.
The Ohm’s law problem points to the snag that Evans is talking about.
We assume that it is possible to experimentally measure (accurately) each of the partial derivatives involved in the model function, under such conditions that we may take the consequent changes in all of the other independent variables, as being negligible, so that we take them as fixed.
While it is quite possible to measure the Ohmic resistance of a wire under such low current conditions, as to practically satisfy Ohm’s dictate that everything else remains fixed; it is an entirely different kettle of fish to presume that that is even remotely possible in the case of the variables of the climate system, that go into the models.
Well the practitioners of climatology brazenly ignore such dictates, and openly talk about H2O amplification of CO2 induced Temperature changes.
What Evans seems to be pointing out that what is called water feedback amplification of Temperature change due to CO2, is not really a feedback at all. It is simply an example of the impossibility of separating the separate partial derivatives of a dependent variable that is a complex function of many independent variables, none of which can in practice, be constrained to negligibly small values to we can measure any of the partial derivatives correctly.
Well, I’m not going to dig into Evans’ analysis to see exactly what he is presenting; but I think he is certainly raising a red flag of caution.
I can’t even imagine that the independent variables of climate, are not so inextricably intertwined, as to make separation of the variables nigh on impossible.
G
Excellent comment, George. When you think about it, it explains why there are no measurements of AGW.
Anyway, AGW has to be very small because there’s been no global warming.
Very trenchant comment. I did dig in. What Evans has done is about simplest possible generalized version of climate with feedbacks, and shown the generalized case of your Ohm’s Law example problem.
My detailed subcomment above provided another, specific to climate and easy to grasp intuitively without all the math. Although the specific CAM3 math is referenced if somebody wants to dig in deeply. The reason was commenters challenging Evans to provide a specific example of his general mathematical critique. I helped him out a bit since Curry and I wrote companion pieces on Mauritsen and Stevens and the paper was still fresh to mind.
I can provide the math from the IPCC. I can also provide the total net input and net output that was reported.
If the models and numbers were right in the year 2000, I will assure that the only thing anybody on here would be talking about right now would be how to stop the warming. The amount of retained heat since 2000 would be massive. No one would have to go looking for it.
BTW, I don’t have to work for anybody. What I say is factual and the information is easily obtained. Most of the information I refute comes directly from the IPCC. And any other information comes from NOAA or NASA. The rest is physics and math. You can’t fire me, accuse me of being on somebody’s payroll, dishonest, doing something illegal, mentally unstable, have a problem with authority.
So, how about a more specific case of the IPCC using Bode’s formula for feedback amplification in the models the IPCC uses? Ohm’s Law indeed. Somewhere that extra energy just appears? Oh back radiation, that’s it. There are no impendence mismatches in this universe I suppose. We can make fun of people using electrical formulas as an example but lets keep it quite that are models are based on it. I’ve seen better 10th grade science projects than this CAGW. So you are going to lecture me on the second law of thermodynamics? Maybe in some quantum universe where I can run my vehicle without starting it.
(1-r)S(sub I) + eL (sub I) = omega E(T)^4+4+LE +G
incoming 343/w/m^2
outgoing 240 w/m^2
You do the math and tell me how much heat has been retained for every hour for everyday for every meter for the last 20 years. Oh no time frame reference, doesn’t matter, still enormous. No it should be a lot worse than that. The window on total retention should be closing because of the continual release of co2 and the allege buildup of co2. Because of current numbers, from NOAA by the way, of co2 ppm increase per year, I have some questions about the steady increase in co2 over time. Are those numbers going back to the IR right? Are any of the numbers for co2 amounts right? Maybe they will start adjusting those numbers too. I’m sure you’re familiar with the formula.
BTW, that formula states categorically that as of 2008 all of the rise in temps can be attributed to co2 alone. Of course you know that. And you also know that studies have been done for the IPCC , to explain away how run away warming doesn’t seem to be happening, that half of the rise in temps was due to the oceans. The heats hiding in the oceans. Lets bring in thermal expansion of the oceans (forget about the poles melting) . We’re not talking about millimeter rises here. And that would be true, 20 ft on Canal St in NYC. You remember that? You see the problem here? If you don’t your brainwashed or really dumb.
Nothing fits! You are questioning my credentials.? I’m questioning your sanity. How could any sane person believe this mess? Or at the very least have some serious doubts about CAGW
And the dependent variable (CO2?) is looking somewhat more independent lately.
George, perhaps we can extend your analogy further to look at properties of a conductor which might not be deduced from a simple examination of the applicable physical laws.
Say for instance, the skin effect. Now for a given voltage potential difference, a given frequency of alternating current, and a given conductor material, one might suppose that one could increase the carrying capacity of the conductor by simply increasing the cross sectional area. Which one can, up to a point. That point being when the skin effect prevents any increase in carrying capacity, no matter how thick the wire or cable.
Similarly, there seem to be emergent properties particular to the atmosphere that limit how hot the atmosphere can get
The skin effect is caused by eddies created by the varying magnetic field inside the conductor, and was elucidated by experimentation. I wonder if anyone would have ever guessed it would occur based only on first principles?
Might we assume that there are emergent properties of the atmosphere we may not guess, without creating a model of the atmosphere with which to experiment?
A model which would need to be a full scale duplicate of the original?
In other words, something we can never create?
Well Menicholas, I would never endeavor to demonstrate Ohm’s Law with an AC measurement, and certainly never at some high AC frequency.
For starters, any AC circuit is at least going to exhibit an inductance, in the case of the current varying, so immediately the I/V relationship is going to be frequency dependent, and on an instantaneous time basis, the (i/v) ratio will at times range from zero to infinity because of the phase shift, due to the inductive reactance.
Moreover, it is that very inductance which is the cause of the ” skin effect ” , as the phase shift varies as a function of the radius in the wire, so that eventually the current in the central part of the wire is reversed relative to the current at the wire surface. That reversal of the current in the inner parts of the wire results in a lower net current flow, so an apparent increase in the resistance (or real). The whole idea of ” Litz ” wire for RF inductors is to split the wire cross-sectional area up into many finer wires which have a greater surface area per section area, than a single wire, and then the individual wirelets are insulated from each other and intertwined to cancel out a lot of the inductive effects.
AC transcontinental power transmission lines are tightly twisted for the same reason; although at 50 or 60 herz, the wavelength is so long, that the casual observer is not even aware how tightly twisted those transmission lines are. In California, we have many long stretches, where it is easy to observe when they make the occasional 120 degree twist of the three phase wires, maybe at about a km or two spacing. The arms holding the three wires are designed so that by reversing just one of those arms, at a single pole, the three wires can be twisted 120 degrees between that point and the next pole.
Even a straight wire has a finite inductance. As I recall from memory it is about 330 nH / m. You can find those numbers in papers about the series resistance (R), series inductance (L), shunt capacitance (C), and shunt conductance (G) of coaxial cables, from which the characteristic impedance can be calculated from the ratio (L+R)/(C+G). I think it is: sqrt(2pi(L+R)/(C+G)).
And of course the propagation velocity in the cable is sqrt(1/2pi(L+R)(C+G)). That is probably group velocity rather than phase velocity, or maybe the reverse. In any case it can’t exceed (c).
I don’t know why I have to try and remember this stuff. Anybody can giggle it up for themselves.
G
Let’s put some numbers to it …
We measure an incandescent bulb’s resistance with our ohmmeter and get ten ohms.
We calculate the current that will flow when we connect the bulb to 120 volts.
I = E/R = 120 / 10 = 12 amps
We calculate the power that will be dissipated.
P = E I = 120 x 12 = 1440 watts
That’s a problem. The bulb is marked as being 100 watts.
We connect the bulb and measure the current. We calculate the power and get close to 100 watts.
Does this mean Ohm’s Law is wrong? No, it means that we applied it in a situation we did not fully understand. That kind of thing happens a lot. 🙁
Commie, you may get 10 Ohms at 25 deg. C (room Temperature), but when operating, the filament Temperature is more typically 2800 K, so the tungsten resistance is much higher.
So as I said, the conditions under which Ohm’s law is valid are violated in this case.
As a practical matter, most conductive materials apart from metals DO NOT obey Ohm’s law. Semiconductor diodes being a case in point, where the current typically doubles for every 26 mV increase in diode forward voltage (or 60 mV per decade of current increase.) Well that is for silicon. And those numbers too are Temperature dependent, as the effective semiconductor band gap diminishes linearly with absolute Temperature (K), which is well known to anyone who ever designed a Bob Widlar band gap voltage reference on an IC. (I have).
I don’t think we disagree.
I love the incandescent bulb example because it’s easy to demonstrate to students who have no prior circuit theory. My point was always that one is likely to get into trouble if one uses a formula in the wrong situation.
Well when you hurry you make typos or leave out obvious stuff.
The characteristic impedance of a transmission line is calculated from:
Z = sqrt ((R + j.omega.L) / (G + j.omega.C)) I left out the j.omega below.
In practice, R, the series resistance per meter is fairly well known but G the shunt conductance per meter is just a leakage and is likely to be quite unstable, but one assumes that the j.omega.L and j.omega.C terms are dominant in which case the impedance boils down to : Z = sqrt (L / C)
And if R / G = L / C, then the characteristic impedance is quite independent of frequency.
Good luck on satisfying that condition.
g
Not to worry CB we are in sync.
We seldom think about the practical reality that nothing can satisfy Ohm’s law over an indefinite range of current values. Likewise semiconductor diodes don’t satisfy their logarithmic ( or exponential) behavior over an unlimited range of currents. At the low end simple leakage can dominate, while at higher currents the series bulk resistance comes to the fore.
But that is why I abhor the widely believed assumption that Global Temperature strictly follows the logarithm of the CO2 abundance.
It doesn’t, even approximately, for any big enough CO2 range, and is not significantly different from a linear connection over the known data range.
And the theoretical claim from the ” Beer Lambert ” and other imposter laws, is not valid anyway, because that law only applies to the ” absorption ” by the absorber and strictly assumes that the absorbed photons stay dead. They don’t, the energy is either re-radiated via fluorescent type emissions ( and does so isotropically) or is dissipated as heat, which also spreads in three dimensions, so the Beers law assumption does not correctly predict the transmission of the incident radiant energy, which is the only thing that matters in the climate case.
g
The dynamical equations which form the core of the General Circulation Models are derived in Lagrangian co-ordinates by applying Newton’s second law of motion to a single parcel of air which is assumed to maintain its integrity. (e.g. Haltiner and Martin 1957).This means that it does not mix with its surroundings. The resulting equations are then cast in Eulerian co-ordinates and assumed to simultaneously apply to atmospheric motion everywhere on the earth. Such an assumption is clear nonsense.
Partial differential equations are introduced into the equations of motion through the transformation to Eulerian co-ordinates. Given that the basic equations are indefensible why should one be concerned about the values of the partial derivatives?
Reference: Haltiner G. J. and F. L. Martin (1957): Dynamical and Physical Meteorology, McGraw-Hill Book Company Inc. New York, Toronto, London
mod, could you pls. retype
Eurlerian co-ordinates -2
Eulerian co-ordinates
in an interesting comment.
burns 1es eyes.
Fixed.
w.
In the physical world, any mathematical formulation is an approximation. Our problem is to come up with a tolerable approximation.
We know that’s not precisely true. The question is whether it’s true enough.
I’m pretty sure the folks who wrote the model can’t defend the non-mixing approximation with solid numbers. CGMs are built on many unquestioned implicit assumptions and approximations …
I wouldn’t look on the partial derivative issue as a useless exercise. I would look at it as one more nail in the coffin.
I have no quibble with your statement CB, but would clarify, that it is the correspondence of our MODELS of the physical world, which are approximations.
The mathematical description of the behavior of our models maybe highly exact (usually is). Well that’s why we made up all of our mathematics in the first place; since it describes the behavior of our very simplified models.
For example, the differential equation: d^2x / dt^2 = – M.x has solutions of the form:
x = A.cos(omega.t) +B.sin(omega.t) , which exactly describes ” simple harmonic motion ” , BUT that does not mean that any real world case of simple harmonic motion actually exists. (Planetary orbits only approximate SHM form, even in Newtonian form, let alone Einsteinian form.)
The mathematics is all pure fiction, so in that sense it has nothing whatsoever to do with science, which is about actual observations of the real world. And of course, our models of the real world, are also pure fiction; but damn useful anyway.
g
Amen.
Problem for some: What works is so simple http://agwunveiled.blogspot.com It’s not CO2
Argh! I see that illustration is back with CO² where it should read CO₂. Wasn’t that flub formerly fingered, and fixed?
While I’m at it, the thumb in this illustration is very poorly drawn, either in a failed effort to show the end of the digit foreshortened, by lack of knowledge of anatomy, or in a desperate measure to avoid covering up too much of the Joker’s neckware.
Picky³.
Steve,
Or some sort of lame attempt to distract from the horrific spelling.
The real problem is, whatever theoretical games one plays, history is what really counts. We are deep in an Ice Age cycle that is powerful, persistent and a key feature of this ongoing, very cold cycle system is the fact that for some mysterious reason (most likely the sun) things suddenly heats up very, very, very rapidly and this melts most of the glaciers except…another key issue…Antarctica.
This repeat cycle continues today. We are watching powerful people pretend we will all roast to death when this is very highly unlikely. I seriously doubt a tiny increase in CO2 can prevent the next obvious Ice Age.
Emsnews, if we can prevent the next full blown ice age, count me in. I await your action plan
” climate modeling mathematics”
Sceptics should treat with caution such sweeping “refutations” that take out, not just GCM’s, but all the continuum maths that been used in science and engineering for decades. Next time someone tries to tell you that fluid flow can’t be solved, remember that you fly in airplanes designed by people who solve fluid flow computationally.
David Young, like me, has spent much of his working life solving numerically partial differential equations (yes, with partial derivatives). He deals with this nonsense here (and below).
Someone didn’t read the article in its entirety before getting his panties in a wad. There was never a blanket statement made that such a thing is always wrong…just that its validity needs to be tested. I’d say we have enough of a history with airplane flight to know that such computations are accurate in that case. We don’t have that for climate models.
As an aside, can you tell me which products (especially, god forbid, airplanes) are designed based on your computations? Based on the number of fails you’ve had when it comes to discussions here and elsewhere, I want to avoid them. TIA.
Transient Ischemic Attack?
So, how many elements might you break a piston rod into in order to model the stresses? I’m going to guess that it’s close to the same order of magnitude as the number of elements CGM’s use to model the entire earth. Ya think it might make a difference, sport? Not to mention that the fundamental properties of the piston rod material are likely to be very well characterized; global climate elements: not so much.
DJH, precisely. You nailed the fundamental, IMO.
I do not wish to fly with the alarmist “model mean” altimeter.
97% of those damm things have us flying higher then we actually are, so our pilots keep flying those planes into the mountains.
And in the case you mentioned, any other variables involved are likely to be second order effects, so the assumption of stasis for those, while the principle independent variable is varied, is likely to be valid. in climate, I’m not so sure.
g
Yes, Nick Stokes, remember that you fly in airplanes designed by people who solve fluid flow computationally.
lots of that tiny thingings strawn all about vast ocean basins.
australian navy still searching for MH370 / if my memory serves me well /
yes, mod. 2 lazy to look if it was MH370 or another #.
history of technics is a list of desasters, in mekka the Liebherr Kran, in China exploding acid fluids, in GE the ICE in Eschwege…
In Turkey coal mines.
the us has its own table of learning by doing.
That kind feels fit to steer climate.
Smile.
One might surmise, that you actually believe that this story points to equipment failure.
I can’t even conceive of what kind of mechanical equipment failure, would lead to that end result.
g
Actually, many of his posts over there highlight the limitations of climate models, some seemingly going-along with the potential problems identified by David Evans.
Nick,
The fluid flow software models used in designing airplanes and such have been validated and verified. This makes them useful. The GCMs have not, which makes their output untrustworthy and useless for prediction and decision making purposes. You may argue that they are the best we have, but they are still not useful for anyone but a few researchers. As a software engineer, I can assure you they are bug ridden; no fancy math required to dismiss them.
Stokes says:
Stretching the fluid-flow analysis of an airplane to a global atmosphere is like stretching the analysis of a bacterium on an elephant’s back to the whole elephant.
Nick:
Yea, but you can test an airplane fluid flow in a wind tunnel. exactly how are “climate scientists” testing their assumptions?
Before you give me a snarky answer, remember, they claim all this is settled science.
Evans hasn’t tested anything. He’s claiming that:
“The partial derivatives of dependent variables are strictly hypothetical and not empirically verifiable”
“Evans believes he has uncovered a significant and perhaps major flaw in the mathematics at the core of the climate models.”
But GCM’s, like forecasting programs, are standard Computational Fluid Dynamics. If Evans objection to PDs in principle is correct, it applies to all CFD. If CFD works for airplanes, the objection looks dubious. As, mathematically, it is.
It’s right there leading Evan’s second paragraph:
“…Partial differentials of dependent variables is a wildcard — it may produce an OK estimate sometimes, but other times it produces nonsense…”
How does that say or imply that his objection necessarily “applies to all CFD?” It seems pretty clear to me that it doesn’t.
Again, please tell me which products (especially airplanes!) are based on your CFD modeling, because I want to stay well-clear. I think you have an obligation as a human being to tell us all for our own personal safety.
Nick Stokes,
Consider the scales. Consider the materials, and consider the apples not to be oranges
Your specific critique fails on two separate grounds elsewhere already articulated on this thread. You display ignorance of how mathematical models actually work.
I used to build them. Analytically precise calculus, numerical approximation methods, quasicontinuous (numeric methods), fully discrete delta steps…. Once even as an exam question recast the classic partial differential predator prey equations (rabbits and foxes and partial derivatives like breeding rates) as a Markov chain stochastic probability solution equivalent. So know a fair bit about this math modelling stuff and its various permutations. But, nullius in verba. Especially on a mere un peer reviewed blog. So check out the examples and cited references.
Nonsense Nick, he saying the error bars should be way larger then they are.
I do not wish to fly with the alarmist “model mean” altimeter because 97% of those damm things have us flying higher then we actually are, so our pilots keep flying those planes into the mountains.
You make the proper point. Partial differential equation solutions have to be physically tested. They don’t actually “solve” the physical problem completely, but they allow bounds on certainties to be set which then allows testing. If a wing design passes the numerical methods, then awesome, let’s put it in a wind tunnel and see -if it actually works-. But, if it doesn’t pass the computation, then there’s no reason to spend all the time and resources and effort testing it. Numerical methods is an easy way to screen, or diagnose. But, exactly as you say, it all has to be tested in the end as it’s very easy for a numerical method to go very wrong, without any way for one to tell (unless tested against reality).
Now, we’ve gotten comfortable with the computational toolsets scientists worked painstakingly to verify, that it’s easy to forget the history and work that went into something as seemingly simple as the wave motion partial differential.
Models using partial differential equations have to be tested to derive constants for their solutions for very specific and limited bounds… more than just testing for verification. Since you can’t put the earth in a lab and derive these constants the modelers just guess. And anything they can’t even guess at they just assume is constant, like clouds for example.
I assumed each time step in climate model runs got to some sort of numerical “convergence” and then went on to the next time step. I thought this was why they took so long to run. If calcs were based on PDEs holding everything but two variables constant, it seems like they’d run rather quickly.
Michael
I apologize if I’ve grossly misunderstood your comment…however:
I’m not a black-belt mathematician, but I am a fairly decent (retired) CFO – no way is “…numerical convergence…” a substitute for observational evidence.
Of course not. I agree 100%.
If you would glance at my recent illustrated guest post here on models, you would see why they do not. Plus, if you would just glance at all the subcalculations per model cell (this thread, Willis, NCAR CAM3 technical note link) you would have an immediate visceral comprehension of why this is computationally intractable on sufficiently resolved grid scales. Even if you do not grok all the detailed math.
Well, this is unusual … I find myself in agreement with Nick Stokes.
The basic problem that I see with Dr. Evans’ claim is that the numerical methods used in climate models are the same methods used in weather models … and within their known limitations, these weather models work quite well. See here and here for a discussion of how partial differentials of dependent variables are handled in weather models.
My rule of thumb is, scientists are often fools and occasionally crooks but rarely idiots … they didn’t build the weather models without considering the difficulties Dr. Evans mentions, and solving them well enough to give us much better short-term weather predictions than before the advent of numerical computer-model-based forecasting. Short answer? They’ve found ways around the difficulties Dr. Evans sees as insuperable, as is proven by the success of the computer weather forecasting models.
As I see it, the main problem with climate models is that they rest on the claim that if you include the long-term changes in forcing (volcanoes, solar, GHGs, etc) in a weather model, and you run it for 50 model years a whole bunch of times, and you average the whole bunch of results, you’ll know what the climate will be like in 50 years.
I say that’s cargo-cult level nonsense, particularly since most of the active thermally-regulating phenomena are sub-gridcell-size … but hey, that’s just me.
w.
So if people are looking back from 2100 what are they likely to see? What if they can observe that the sun + ocean oscillations+ the moon + other planets+ water vapour+ bacteria +Co2+ undersea and above land volcanoes+ UHIE mistakes + whatever had much more influence on the climate than just Co2? Not to mention constant fiddling with temp data. And according to the HAD 4 data we’ve only had a slight 0.8 C of warming over the last 165 years . That’s after the end of one of the coldest periods of the Holocene. Big deal.
Neville September 28, 2015 at 3:48 pm
I’m gonna go with “One of the greatest misconceptions in the history of science” …
w.
I second that emotion.
Willis, see my reply to this above. On small enough scales, the partials might approach constants. On large scales, there is no way they can. Your own thermostat regulator idea is a very good example. Evans is actually agreeing with you.mwhatnhe has done is state the general analytic calculus case. Please refer to his post 4 eq. 1 for a precise general math statement of what you just asserted–and which is IMO irrefutably true. Your comment looks mostly like violent agreement once the underlying arguments are fully understood. Highest regards.
Might I add that no one is using the weather models as a basis to justify changing modern civilization back to medieval times. Nor are they being used to steal my money to go tilting at windmills.
You miss my point. The weather models prove that the treatment of partial differentials is not the problem … but that assuredly does not mean that we should believe the climate models.
w.
YOU miss the main point that both your criticism ( which is mine also) AND Evans are both valid. BOTH. Why the fight amongst skeptics, other than pride of place? Win the war, not the battle, let alone the skirmisch. Trenberth and Schmidt must be laughing at us all right now. Ridiculous comment thread, especially after I provided this thread the underlying math model support plus a concrete ‘irrefutable’ climate example which some could not bother to lookmup as a ‘snipe hunt’. Shame. Lets all do better at informed science comment/criticism, please. Please.
i have to agree with wayne . the weather models work sometimes. i would imagine there are areas of the world that are far easier to forecast than others. here in the uk it is quite obvious for parameters like wind strength, direction and to a degree rainfall ,the met office record in recent years is not good if you spend a lot of time in and around the sea.
i have a fair few commercial fishing friends ,none use the met office forecasts.
“these weather models work quite well” Hmmm, even within their known limitations, I find it more amazing that they work at all. Yes, it is impressive what they can do with all the modern data inputs and computing power. Nevertheless, I find some room for disagreement with that statement, especially when they forecast.
Someone should do up a nice post on what exactly are the differences between the weather models and the climate models. The weather models probably do not take CO2 into account, not to mention future oceanic circulations. What does happen when you run the best weather models way out into the future? Do they remain stable and still give reasonable weather patterns?
At the most oversimplified level, the climate scare is that if radiation in and radiation out does not balance, the climate will change. CO2 will change radiation out, so global warming happens. (All sides will tell me this is wrong, I know, so don’t bother). My point is that there is an implicit “everything else being equal” in there, and that “everything else held constant” assumption is wrong. Remember, I said this was oversimplified.
The weather models “often” work quite well. But just as often, if you watch carefully, they get the timing wrong, it rains when sun was predicted, the fronts don’t move at the forecast rate, pop up showers occur, down welling winds produce snow when wind was forecast or just the opposite with unanticipated Chinook winds. As a retired farmer and engineer that used weather forecasts for work and determining harvest timing, weather forecasters often do well with generalities, but I would hate to say how many times I cut hay based on a forecast of a week of sunny weather then had to rake and turn the hay because it rained. Regional variation I reckon but sometimes just grossly wrong forecasts. The Jet Stream doesn’t always behave. Even with all the satellite and radar monitoring there is still considerable “error”.
Just personal observations that have affected my income over the years, no mathematics required.
Today it was 16 C in Calgary. Record High was 26. Record low was -9 C. A 35 C variation for this date.
Hard to be a weather forecaster.
“…The basic problem that I see with Dr. Evans’ claim is that the numerical methods used in climate models are the same methods used in weather models … and within their known limitations, these weather models work quite well…”
Well we always hear that “weather is not climate,” that weather is hard to predict short-term but that climate is easy to predict long-term, etc.
And the key phrase you used: “within their known limitations.”
And how do they know the weather models got better. They tried them, I’ll bet many times, with many dead ends until they could predict the weather 5 days out. I doubt very much that the first time they tried to predict the weather from computer calculations that they got anything usable except information that would allow them to try again. So climate predictions of 100 years will probably be fairly good in about 50,000 years or so once they had several thousand iterations to improve their modals. It looks to me, by your links, Willis, that the computations are mainly for velocity’s which may be approximately independent for a short period of time, unlike most other climate parameters. Any variables that are independent will work if they are dependent they will not work in partial differential equations. Notice that they are far far from spot on with 5 day predictions. One reason may be because their assumption or independence of variables is only an approximation.
They also got a bit of help with satellite images and animations of a big storm coming our way, or clear skies at least a week across.
Scott, you and others seem to be missing my point, likely my lack of clarity.
Dr. Evans claims that the climate models’ use of partial differential equations involving dependent variables is a big no-no. He says it invalidates all their results.
My point is that the weather models use partial differential equations of dependent variables, and their forecasts are testably and demonstrably better than the previous non-numerical methods. Why doesn’t it invalidate their results?
So to establish Dr. Evans claim, he (or someone) has to explain why weather models can use “a big no-no” and get the right answer, but it’s lethal for climate models to do the same.
And indeed, it may be explainable—there may be some subtle difference between the weather and climate models that I’m not getting. But if so, it needs to be spelled out to validate his claims.
Please note that I’m not saying that the climate models are right. I think they are worse than useless for long-term predictions of the evolution of the global climate, they are actively misleading. But although there are known problems with the physics, I don’t think that those problems are reason the models are useless. I say they are useless because they leave out or incorrectly parameterize critical sub-grid phenomena like thunderstorms, dust devils, and the like.
All the best,
w.
I suspect that the weather MODELS did not get better. We now have the advantage now of satellite imaging, previously we got oberevers radioing weather, plus the natural effects of Hadley circulation to tell us from which direction the weather would be coming.
Depends what Big Brother wants them to see.
“give us much better short-term weather predictions than before the advent of numerical computer-model-based forecasting.”
Where I live, I’d wouldn’t put the local forecast accuracy (for important weather events) at much better than 50%.
As a non-meteorologist, but end-user of weather forecasts, my impression is that weather forecasts are only marginally better than they were 40 years ago. I attribute that slight improvement to Doppler radar; weather forecasters can see where there are storms and linearly extrapolate their future position. Note that weather forecasters don’t try to forecast out several years. They understand that the extrapolation of their models have limitations. It seems that climate modelers don’t acknowledge similar limitations. Might it be that those PDEs of dependent-variables become divergent after multiple iterations?
For me it isn’t that unusual, because Nick is a smart guy. It’s my objection as well, although I frame it from the other point of view. The GCMs are like weather models because they ARE weather models — run out past their pull-by date. In weather forecasting, that’s the point where the fundamentally chaotic aspect of the system dynamics has caused the manifold small errors and imprecisions in the specification of an initial state and model parameters to grow to where the state produced by the weather forecasting software is no longer going to look at all like the actual weather outside of (perhaps) the sense that it will still be a physically accessible possibility.
Nick points out that in the case of modelling turbulence over airplane wings, the average over the chaos is still useful because one can in some sense do an ensemble average over the turbulence and still be left with a near-stationary “lift” that turns out to be reasonably predictive of the wing’s lift. It might be useful, although this is less certain, at revealing critical instabilities in the design if at least some of the runs end up in a startlingly different part of phase space (which can easily happen in a chaotic system and is what you do NOT want to have happen with airplane wings!)
However, as I’ve pointed out before and no doubt will again, this is not necessarily at all relevant to the problem at hand. For one thing, even if one takes the weather models used to predict things like (to use a contemporary example) hurricane trajectories, running one of the microscopic models many times to produce an ensemble and then averaging over the ensemble of possible hurricane trajectories is not particularly predictive. Literally yesterday Joaquin was predicted by the various types of weather models to remain a tropical storm, dodge around a bit in the Atlantic, and then move off to the north or northwest. There was poor agreement between the ensemble models, the computer models, and the official forecast (which adds considerable human wisdom involving the effect of blocking ridges and so on to the computer efforts).
There is still poor agreement, but now Joaquin is already a hurricane, and forecast to become a major storm. The ensemble models have split sending straight at where I am sitting now and out to see. The computer models favor heading straight at the NC coast at the moment. But the human-mediated forecast is still for it to get pushed somewhat offshore and hit somewhere around Delaware or New York City, not NC per se at all. Even the computer models are split — CFS, HWRF, and NGFDL show me/NC getting smacked soundly by maybe Sunday sometime, possibly as a category 2 or category 3 storm. The rest vote for grazing the NC coast or further out to sea and hitting somewhere to the north. So there could be a category 3 hurricane that hits just before the 10 year record is set this year — there is plenty of heat in the ocean yet and the hurricane would pass right over the Gulf Stream before it came to shore if it heads our way. It would all depend then on shear.
Even as a cat 1 or 2, that could cause much damage — we’ve been raining for over a week and have just flooded at the coast due to the Supermoon + rain last Sunday — huge tides and flooded rivers feeding the sounds. The ground is soaked, and a foot of rain would cause devastating flooding akin to Floyd some years ago.
But that’s not my point — my point is that not even ensemble averages over the chaotic trajectory of one little turbulent whorl (well, not that little) have much predictive value in weather ensembles, and climate models themselves provide substantial evidence that they have little predictive value out twenty or more years. So the assertion that CFD codes work for airline wings does not, as it turns out, mean that they work for either weather (where it is well known that they don’t or the used-after-pull-date GCMs, the climate models.
That doesn’t make Evans observations useful, BTW, it means that I don’t understand them at all. The issue isn’t whether or not climate models solved PDEs — that is cosmically irrelevant to the discussion, of course they do. It is directly addressing the parametric uncertainty, the variation of model output with small variations in the input parameters.
THIS is not something that is meaningful without substantial work being done to define the meaning. For one thing, the GCMs are pretty much always used to produce an ensemble of forecasts from a given starting point, and always perturb the parameters to get the ensemble. So they explicitly are sampling the partial derivatives with respect to the parameters, even in higher dimensions. The problem is that in a chaotic system, the “partial derivatives” are in some sense singular — tiny changes cause trajectories that fill a large phase space of possibilities already. So then one has to define something smooth so that the idea of a derivative itself makes sense, and smoothing an ensemble of chaotic trajectories is not something that necessarily has any meaning at all, so you have to define and specify and cross fingers and hope to be vindicated empirically (which has, in some sense, already not only not happened, it has antihappened and the model ensemble superaverage has been if anything falsified empirically).
And somewhere in there, one does have to face the issue Nick is refusing to face. There exists a coarse grained scale, to be sure, where CFD codes can give useful results. That scale is known empirically and accessible and in some sense verifiable by using adaptive codes. However nobody sane would claim that they give useful results if they are integrated at a scale that is too large, that is, larger than the scale where adaptive codes indicate convergence and the results are validated by e.g. wind tunnel experiments and empirical experience. Not even simple ODEs in linear problems (evaluating two body orbits) are going to give reliable results if you use a huge stepsize, where “huge” is not necessarily known a priori!
There is no reason to think that the CFD codes that make up GCMs are being integrated at that scale. There is excellent reason to think that they are being integrated at scales that are many, many orders of magnitude too coarse. Given that the codes are actively failing to produce a good correspondence with the observed climate only a few decades out from the reference period where they were forced (parametrically tuned) into good agreement at the possible expense of both past and future agreement, there is very little reason to take their predictions seriously enough to bet the bulk of the elective income of the human species for decades to come (if not MORE than that) to fix the problem they are clearly overpredicting, so far.
rgb
“Not even simple ODEs in linear problems (evaluating two body orbits) are going to give reliable results if you use a huge stepsize, where “huge” is not necessarily known a priori!”
Stepsize limitations (time) are known a priori. You work out the process that can propagate fastest, and choose a stepsize so that its effects remain gridwise local over the time. For GCM, that is speed of sound, and gives the CFL condition.
But what you overlook is that a solution of a PDE is just a set of numbers that satisfies it, and if you get a set of numbers, with whatever difficulties, you can check whether it does. More often that is done by checking energy, momentum etc. Then there are issues of uniqueness etc, but you can also check what happens if you perturb. They do a lot of that.
If you tried to solve planetary motions by initial ODE problem, the solar system would pretty soon collapse. But Kepler/Newton could work out planetary motions very well. That is because, in these terms, they treated it as a boundary value problem. Just look for possible solution trajectories. And that is how it goes with GCMs and any large scale CFD (planes and all). You start with a not very well specified initial state. Then you integrate, but with various constraints that keep it stable, turbulence modelling being the most notable. Unphysical energy changes are damped etc. People sometimes think that is cheating, but it isn’t. The requirement of the solution process is just that you find a set of numbers that satisfies the equations, to required accuracy. With the atmosphere, unlike orbits, you can’t do a direct boundary value solution. But you can get the same effect by initial value solution with boundary constraints.
Hmmm, maybe I’m reading different textbooks on nonlinear dynamics than you are. What are the “constraints” on a nonlinear chaotic oscillator? And even the GCMs produces a staggering array of solutions, not to mention the fact that no two GCMs produce the same average solutions.
So how much would you believe your CFD codes for designing a supersonic wing if three different codes gave you three different answers, and each code gave you very different answers every time you ran it?
rgb
GCM’s don’t produce the same solutions at points of time. That is because they don’t preserve initial information – they are not synchronised. You can calculate much about the orbit of the earth without knowing where it is at some particular point in time. You have a manifold of solutions, each valid if everything starts a month later. You can say much about the orbit in a million years time, though you can’t say exactly where in that orbit the Earth will be.
Deviation on average is the real issue, if you’re talking about different models giving different answers on the time-scale we want to know about – climate. They agree reasonably – we’d wish for better. That’s what all the CMIP etc work is about.
Except that if I look at the weather forecast produced by the several different programs, they are often quite different. The occurrence and paths of violent storms or even routine low and high pressure systems are not predicted very well. Even the weather and precipitation from day to day seem to be poorly predicted.
ristvan September 28, 2015 at 3:54 pm
Your reply above discusses airplane wings, assuredly small scale. The part you haven’t dealt with is that computer weather models of large areas (e.g. Europe, see the ECMWF) give better forecasts than we got before such numerical computer weather forecasts were the norm.
So whether or not “the partials might approach constants”, I would strongly dispute your claim that their methods only work on small scales like airplanes, and that there is “no way they can” work for large areas like Europe … the weather models prove that their methods can and do work.
That’s not the problem. The problem is you can’t predict the climate by running a weather model for 50 years … no more than you can predict next years weather by running a weather model for one year.
w.
Propagated error of f(x1,x2,x3…) depends on partial derivatives df/dx1, df/dx2,… when variable x1,x2… are statistically independent. But when the are not covariances come to play. Is this what this note is about? I read all comments and had impression that every body just pretended they knew what the guy was talking about.
Almost everybody. Some of us actually used to know this stuff. Which is why Evan’s reminder is like a big Homer Simpson DUHOO! As embarassing as that is to admit.
Precisely. Or even next month’s weather by running a weather model, or a weather model many times with perturbed initial conditions, out for one whole month. One can do just about as well reading the probable weather from an almanac or assuming that it will be like the weather in that month last year, which is sort of the lowest common denominator seasonal average sort of prediction one can hit without much of a model at all besides the known annual/monthly variations in the weather.
I would say that we might be able to predict the climate by running model 50 years, but that the burden of proof that we can is absolutely upon anyone who would assert otherwise as it isn’t likely to work based on what we have observed from the efforts so far. We are decades to a century of hard work away from where we might be able to.
The latter in my opinion, of course. Who knows for sure? Surprise me.
rgb
Jim G1 –
the script writer tells the story,
the producer determines the end of the story.
Whatever the producer decides –
‘they confuse the observation of an actual factual material
called dark matter when they are actually
observing unexplained gravitational effects.’
is a fascinating summary of the plot.
Thx – Hans
All this is a fancy way of saying they guestimate the unknowns.
In the plot of 90 CMIP5 model projections/predictions, the plot of observed UAH lower troposphere temperatures stops just short of 2013. Of course, the ‘pause’ continues beyond that, albeit that 2015 no doubt will appear warm, and much will depend upon whether a La Nina follows in 2016/7.
But one can see that there are only two models presently tracking below observed UAH lower troposphere temperatures. Perhaps of more significance is what those two models project/predict circa 2018. At around 2018, those two models project/predict rapid warming. If the ‘pause’ continues through to and beyond 2018, those two models will be tracking above UAH lower troposphere observations. By 2020, none of the 90 models will remotely be in line with observations should the ‘pause’ continue through to 2020.
I have often said that 2019 is crunch time for the IPCC and AR6 if the pause continues as it will be impossible to simply ignore the fact that all the models are running warm, the majority very significantly so.
It is obvious that the very warm models are way off target. No one would realistically support their projections, but they are being included because of their impact on averages, ie., the averaged assemble. They permit the averaged assembly to stay on track for circa 2degC warming.
If the warmest running models were ditched, as they should be, the average will come down to a not scary figure and this will end the CAGW scare. How is the IPCC going to treat this? This is why Paris is so significant for the warmists and the proponents of CAGW. It is likely to be their last chance saloon, since if the ‘pause’ continues, mother nature is about to kick them where it really hurts.
if the ‘pause’ continues
And if the ‘pause’ does not continue, what do we say then?
Let me say it now. The pause will definitely not continue but where it goes afterwards is very much up in air, so to speak.
Based on what? Other than wishful thinking…
Shut the door, it’s cold out there ; )
lsvalgaard September 28, 2015 at 7:37 pm
if the ‘pause’ continues
And if the ‘pause’ does not continue, what do we say then?
//////////////////////
We have 90 model projections/predictions all of which show different outcomes. This reminds me of the Dire Straight’s song (Industrial Disease) “…two men say they’re Jesus, one of them must be wrong…” We know as fact that 89 of those 90 models must be wrong, what we do not know is whether one of them is right. If these models was based upon fully known and understood physics, and if the science was truly understood and settled, one would not have 90 different models. One would only have 3 based upon the 3 different future scenarios for CO2, or possibly 9 based upon the 3 different future scenarios for CO2 as altered by the 3 diff3erent scenarios for manmade aerosol emissions. People like making comparison with the aviation industry, and in that industry one does not get 90 different scenarios as to how the plane may fly in usual operation.
I am not making any prediction as to whether the ‘pause’ will or will not continue. Predicting the future makes fools of us all, especially when we know so little and understand even less as to the workings of the Earth’s climate.
What I am pointing out is the trajectory of the two models that are currently running cooler (but close to) the UAH lower troposphere observations in around the year 2018. If the ‘pause’ continues beyond 2018, it will a crunch time for those two models such that all models will be running warm.
If those two models had in 2006 (which I understand to be the date of the model and the date of the forward projection) been zeroed at the then observed UAH lower troposphere temperature, those two models would already be running warm in relation to the UAH lower troposphere observations, but my point is the projected/predicted warming (one of them very rapid warming) post 2018 so we may soon get a chance to look at their projections/predictions and to see what extent they correspond with reality (it always being possible that the UAH lower troposphere will show warming like one of the two models – obviously both models cannot be right since they project/predict different future rates of warming so we know that one of the two is definitely wrong).
I repeat:
if the ‘pause’ does not continue, what do we say then?
PS. When I am suggesting that a model may be right, I merely mean that it is corresponding (for the time being) with reality (ie., real world observations). Of course it may be corresponding with real world observations merely by fluke. It does not necessarily mean that the model has got the science and the maths right. Of course, those that have already diverged significantly, have obviously got something wrong.
lsvalgaard September 28, 2015 at 10:19 pm
I repeat:
if the ‘pause’ does not continue, what do we say then?
//////////////////////////
That depends upon what happens, and whether we are able to identify a possible reason for what has happened.
Say over the next 5 to 8 years, the globe begins to cool at a slightly greater rate than it is presently cooling according to satellite temperature data. That would reinforce the view that the two models were wrong.
If the pause comes to an end, but there is simply a step change in 2015/early 2016 much like the step change in temperatures seen in and around the 1998 Super El Nino, the satellite data will appear flat between say 1979 and the run up to the 1998 Super El Nino, flat from post that event through to the run up to the 2015/6 El Nino, and flat post that even through to say 2023/4. This will suggest that there is zero first order correlation between temperatures and CO2 and that there are two warming episodes to be seen in the satellite data which warming episodes coincide with natural events (El Nino) which do not appear to be driven by CO2. Of course, we might not know what drives Super El Ninos, what causes some El Ninos to release significant energy/heat into the atmosphere which energy/heat is not quickly dissipated.
I accept that we do not know or understand sufficient about the climate and what drives it. The question is whether we can start eliminating things, or whether we can start assessing how much various things influence and drive the climate.
The problem is all down to the quality of data sets and their short period, and the love by some to over extrapolate poor quality data.
I would suggest that unless there is first order correlation between temperatures measured by the satellites and CO2, then all we can say is that the signal to CO” is so small that it cannot be detected by our best measuring devices within the limitation of those devices and their error bounds. That does not mean that there is no signal, merely that it cannot be detected.
Of course, there could be some second order correlation, but to wean that out, one would have to know considerable detail and accuracy on whatever it is that is being claimed to mask the first order correlation. But of course, this is where data sets are hopelessly thin on the ground and of poor quality so one can never address the second order correlation point.
“And if the ‘pause’ does not continue, what do we say then?”
Why just pick the best match in the huge spread of climate model prognostications, yell loudly “See we got it right” and keep drawing the tax funded paychecks.
regarding predictions of future temperature. i stick by the adage (and historical temperatures) that what goes up,must come down.
Jo Nova has a post today about an investigation of climate modeling mathematics by her husband David Evans.
————
Husband? Damn!!! 🙁
“Partial differentials of dependent variables is a wildcard — it may produce an OK estimate sometimes”
I can’t remember exactly but I think I remember Tennekes covered this and how it might affect climate modeling. The basic idea is that it is generally okay to neglect high order terms as long as the spatial and temporal discretization is fine enough. To figure that out one has to reduce the fineness then make it more coarse and compare the results. They should be reaching an asymptotic limit. To improve things, i.e. to use a more course grid or longer time step, some of the more significant HOT’s are included. It’s kind of an art to figure out which ones to keep and which ones to neglect.
Now (again – I think) climate modelers do not do this. Their models have implicit (not solver implicit but just generic English word implicit) self stabilizing mechanisms and they end up not having to make a very fine grid nor taking very find time steps. They then do not check to see if their result is robust to discretization size and hence never really know. As long as they get the “right” answer, everything is good enough.
ristvan September 28, 2015 at 10:27 am
Thanks for the link to your reference. My earlier comment stands. The way that the CAM model handles the physics seems (to my semi-tutored eye) to be the same way that weather models handle the physics, and the weather models get tested every day. However, the devil is in the details …
So for Dr. Evans to show his claim is valid, he’s got to show that the climate models are doing it DIFFERENTLY than the weather models.
Now, it is quite possible that I’m not understanding just how the climate models are doing it differently. But as near as I can tell, Dr. Evans has neither made the claim that the climate models do it differently than the weather models, nor has he explained why weather models work and climate models do not.
Me, I say the reason is not to be found in the physics core, but in the fact that the important emergent thermal regulatory phenomena are sub-grid-scale.
Finally, you say:
How does this show the “fatal partial derivative problem”? This supports my claim, which is that the physics is correct (enough), but some of the basic assumptions are incorrect. If the physics were fatally compromised as Dr. Evans claims, there’s no telling what the addition of the “adaptive iris” would have done. But in the event, it worked just as expected. It greatly reduced climate sensitivity, meaning that the physics is working but reality is not correctly modeled because important aspects are omitted … and that’s only one of the thermal regulatory phenomena that the climate models omit.
Best regards,
w.
I have explained it several times on this thread. Not again. Too boring. Figure it out for yourself.
Show your work. With the linked references to CAM3 you have apparently now managed to find after much criticism and some spoon feeding.
Did you read the above cited CAM3 PDs.? Do you realize their parameterizations are all constants? Do you realize the very real problem that some of those PDs cannot be constants? Again, please show your homework.
ristvan September 28, 2015 at 11:29 pm
ristvan, you have not explained how the weather models can use pd’s and get the right answer, while the climate models cannot. How and where are they different than the climate models, where you claim the error is “fatal”?
Seriously? You’re still sulking because I asked you for a LINK TO YOUR OWN CITATION???
Get real! Giving a link to your own citation is bog-standard everyday practice. For you to moan about being asked to do it is a joke. And for you to insist that everyone who wants to see what you are talking about should waste their time doing a google search and hoping for the best is the height of arrogance. You’re not special. Post a link to your supporting documents like everyone else does, and quit whining about doing it.
w.
“So for Dr. Evans to show his claim is valid, he’s got to show that the climate models are doing it DIFFERENTLY than the weather models.”
Why should the climate models do it differently than weather models to be wrong? As far as I (semi) understand it, the point is that on small scales the errors are unimportant but on larger scales they compound, a point that was made in comments earlier. Scales don’t just mean distances and volumes, they also mean temporal. Over short time scales the weather models might be ok given the initial conditions can be plugged in, but as time goes on the errors compound, making them untenable as models for climate – which is just the long view of weather.
Thanks, agnostic. It’s well known that the weather models cannot see too far into the future because the weather is chaotic. Note that it doesn’t matter how good your computer model is—starting from the same initial conditions, there are many possible future evolutions of the weather, and the further out you go, the wider the spread gets.
So the fact that current weather models can’t predict very far into the future is NOT a reason to assume that they are incorrect.
w.
Hear, hear.
True, the mere fact that partial derivatives can have the shortcoming that Dr. Evans identified does not establish that their shortcoming is significant in the climate-model context. But the arguable success of partial-derivative use in short-term-weather forecasting doesn’t establish that climate models use them accurately.
I look forward to more specificity in Dr. Evans’ argument that they don’t.
Willis Eschenbach says: September 29, 2015 at 1:31 am
So the fact that current weather models can’t predict very far into the future is NOT a reason to assume that they are incorrect.
——————————
I’d say that the fact that current weather models can’t predict very far into the future *is* reason to assume that they are incorrect for anything beyond the short term.
I once knew a mathematician once who proved that there were so many uncertainties in a model that the EPA used for some policy decisions that their results could actually be anywhere on the graph and still be within the goodness of fit.
I don’t understand such things, but the way he described it, they could fiddle with the models to get whatever results they wanted to justify whatever policies they had in mind.
After presenting his paper, he was taken off the workgroup and never invited to participate again, and the modeling continued apace.
Will Eshenbach
“So the fact that current weather models can’t predict very far into the future is NOT a reason to assume that they are incorrect.”
To the contrary. You can get away with incorrect models more easily explaining errors away as chaos.
Thanks, Peter. I see my remark wasn’t clear. Let me try again.
The fact that the weather is chaotic means that even a perfect model could not predict its future state very far into the future.
THEREFORE, the fact that a model cannot predict the weather very far into the future is NOT evidence that the model is flawed.
I hope that’s clearer.
w.
“The fact that the weather is chaotic..”
That is an assumption, and is in fact largely specious.
I note a comparison is being made with weather forecasts, but personally, I do not consider that weather forecasting is particularly good as far as countries which are subject to variable weather conditions.
For example, the UK is particularly fickle. I am unsure whether any forecast given at 11pm gets the next 24 hours right over the entirety of the UK. Do they get the morning, noon, evening night time temperatures right in each county, do they get the patterns of cloudiness right (ie., when the sun will shine through) in each county, do they get the amount of rainfall right in each county, do they get the wind, or patterns of fog or low lying mist right in each county. I bet that there is no day when such a 24 hour weather forecast has been correct for the entirety of the UK.. I certainly can’t remember one. It would be interesting whether the UK Met Office could cite one. And this is now why they say that there is a 10 or 20% or whatever chance of rain etc, so it is difficult to be wrong. What they will, not say is that it will rain in Birmingham at 11:30 for 45 minutes, then it will stop and the rain will onset again at 3.30pm until 10pm when it will stop again and during such time there will be 8 mm of rain.
I accept that weather forecasting has improved these past 40 years, but in the UK, a weather forecast is only good for about 2 days and in general terms only, unless there is particularly benign conditions (a blocking high) when it may extent for a longer period. I emphasise that it is only in general terms that the weather forecast is good, when you look at the detail and what is predicted for each county (the UK is divided into counties much like the US is divided into states, but of course each county is a rather small area), and when you look at each weather component (sun, cloud, rain, wind, mist, fog, temperature etc) for each county, then you quickly appreciate that the forecast is not as sound as the general thrust appears.
I don’t forget that weather computer forecasts are being constantly updated and tuned. The initial parameters are constantly being rechecked and updated and even so, they can’t ‘predict’ with accuracy good regional forecasts, but rather the most general of trends (perhaps splitting the UK up into say 7 areas, Scotland, the boarders, the Midlands, Wales, the South West, the South East, Northern Ireland, and they often have to say that rural areas will be cooler without mentioning what those rural areas will experience).
Personally, I consider that people are getting rosy eyed over the state of weather forecasting and not looking at the detail objectively.
We all know that CGMs do not do regionality well, and yet climate is regional not global, and until regionality can be done well, there is no hope for these models.
Looks to me like the models were built to match the real data for the 80’s/90’s, but do so only because they have been ‘adjusted’ to match, the equations they use bearing no relation to actual climatic input-output relationships.
I’d like to see a model that maps from the IPCC technical reports to the Summary for Policy Makers.
95% of nothing.
jimpoulos- Are you the same person who worked at JND in Atlanta in the 1980’s? Just curious. I knew you then and found it funny that a name from the past would show up so unexpectedly.
Willis said: “However, the devil is in the details …” Exactamente.
We know the limits of weather models — because we check their forecasts against observations.
We also know that climate models are not validated and are running hot. So everybody agrees there is room for improvement, I hope. I hope also that everybody realizes that this is a hard problem, perhaps even impossible, and it is not simple high school physics.
First, you have to get the physics right. No consensus there. Then you have to get the computation right, and this is not trivial. In HPC (high performance computing) there are Grand Challenge problems, i.e. those fundamental problems which would be very useful to solve but which are somewhat beyond our reach at the moment.
Quoting from one top Google hit,
https://en.wikipedia.org/wiki/Grand_Challenges
Everything done so far is not necessarily wrong and not necessarily right. Some details yes, some no. It depends on the details. Not all of the physics is in the climate models and even if the climate models were perfect, it’s still not clear that they could predict, any more than we can predict the stock market.
Exactly …. every single day we see the end of a 5 day forecast and can compare the forecast to reality. That means we’ve had over 20,000 review periods since 1960 when weather modelling began. If you want to limit it to the satellite era then we still have over 13,000 reviews.
If we say 5 decades in a climate forecast is the equivalent of a 5 day weather forecast we’ve had exactly zero since satellite data became available to verify predictions in 1979.
Since the claim as I understand it is we have not validated climate models, I think the comparison to weather models does not help the case.
The atmospheric CO2 level has been above about 150 ppmv (necessary for evolution of life on land as we know it) for at least the entire Phanerozoic eon (the last 542 million or so years). If CO2 was a forcing, its effect on average global temperature (AGT) would be calculated according to its time-integral (or the time-integral of a function thereof) for at least 542 million years. Because there is no way for that calculation to consistently result in the current AGT, CO2 cannot be a forcing.
Variations of this demonstration and identification of what does cause climate change (R^2 > 0.97) are at http://agwunveiled.blogspot.com
it’s funny to see all the allegations made at the start. When you read his article (and the former parts, he is not saying that climate models are useless, they are modeling multiple variables and of which a lot remain unknown in how they “cooperate”
that’s why the models the ipcc use are wrong, they don’t include factors that are yet to be discovered or that are known (AMO and PDO are not included in the IPCC models thus they are already wrong even if the rest is scientifically correctly built).
What i understood from the series is that he does not say the models are useless, but in order to work they need constant training, as such models reuire in order to become reliable and valid. If the models can’t reproduce the known measured past temperature and all other parameters, then you should put it again “at the schoolbanks and train it further” instead of saying that models predict X or Y degrees of warming at a point of time in the future Z.
This is what didn’t happen and still doesn’t happen so that makes these models scientifically incorrect as they are inconsistent with what is being observed. They should retrain them and see what variables do play a role as well together with increasing CO2. Saying that the models are right, while observations show differently is a complete blame to real science, it’s guesswork and i’m sorry then you don’t need models, then i can also say tomorrow the sky “WILL” look purple based on a model and then say it does look purple as my model said so while in fact it’s not the case.
So yes the models need training and maybe in 40 50 years they will have some validity. but now they are useless