Guest Essay by Kip Hansen
“…we should recognise that we are dealing with a coupled nonlinear chaotic system, and therefore that the long-term prediction of future climate states is not possible.”
– IPCC AR4 WG1
Introduction:
The IPCC has long recognized that the climate system is 1) nonlinear and therefore, 2) chaotic. Unfortunately, few of those dealing in climate science – professional and citizen scientists alike – seem to grasp what this really means. I intend to write a short series of essays to clarify the situation regarding the relationship between Climate and Chaos. This will not be a highly technical discussion, but an even-handed basic introduction to the subject to shed some light on just what the IPCC means when it says “we are dealing with a coupled nonlinear chaotic system” and how that should change our understanding of the climate and climate science.
My only qualification for this task is that as a long-term science enthusiast, I have followed the development of Chaos Theory since the late 1960s and during the early 1980s often waited for hours, late into the night, as my Commodore 64 laboriously printed out images of strange attractors on the screen or my old Star 9-pin printer.
PART 1: Linearity
In order to discuss nonlinearity, it is best to start with linearity. We are talking about systems, so let’s look at a definition and a few examples.
Edward Lorenz, the father of Chaos Theory and a meteorologist, in his book “The Essence of Chaos” gives this:
Linear system: A system in which alterations of an initial state will result in proportional alterations in any subsequent state.
In mathematics there are lots of linear systems. The multiplication tables are a good example: x times 2 = y. 2 times 2 = 4. If we double the “x”, we get 4 times 2 = 8. 8 is the double of 4, an exactly proportional result.
When graphing a linear system as we have above, we are marking the whole infinity of results across the entire graphed range. Pick any point on the x-axis, it need not be a whole number, draw a vertically until it intersects the graphed line, the y-axis value at that exact point is the solution to the formula for the x-axis value. We know, and can see, that 2 * 2 = 4 by this method. If we want to know the answer for 2 * 10, we only need to draw a vertical line up from 10 on the x-axis and see that it intersects the line at y-axis value 20. 2 * 20? Up from 20 we see the intersection at 40, voila!
[Aside: It is this feature of linearity that is taught in the modern schools. School children are made to repeat this process of making a graph of a linear formula many times, over and over, and using it to find other values. This is a feature of linear systems, but becomes a bug in our thinking when we attempt to apply it to real world situations, primarily by encouraging this false idea: that linear trend lines predict future values. When we see a straight line, a “trend” line, drawn on a graph, our minds, remembering our school-days drilling with linear graphs, want to extend those lines beyond the data points and believe that they will tell us future, uncalculated, values. This idea is not true in general application, as you shall learn. ]
Not all linear systems are proportional in that way: the ratio between the radius of a circle and its circumference is linear. C =2πR, as we increase the radius, R, we get a proportional increase in Circumference, in a different ratio, due to the presence of the constants in the equation: 2 and π.
In the kitchen, one can have a recipe intended to serve four, and safely double it to create a recipe for 8. Recipes are [mostly] linear. [My wife, who has been a professional cook for a family of 6 and directed an institutional kitchen serving 4 meals a day to 350 people, tells me that a recipe for 4 multiplied by 100 simply creates a mess, not a meal. So recipes are not perfectly linear.]
An automobile accelerator pedal is linear (in theory) – the more you push down, the faster the car goes. It has limits and the proportions change as you change gears.
Because linear equations and relationships are proportional, they make a line when graphed.
A linear spring is one with a linear relationship between force and displacement, meaning the force and displacement are directly proportional to each other. A graph showing force vs. displacement for a linear spring will always be a straight line, with a constant slope.
In electronics, one can change voltage using a potentiometer – turning the knob – in a circuit like this:
In this example, we change the resistance by turning the knob of the potentiometer (an adjustable resistor). As we turn the knob, the voltage increases or decreases in a direct and predictable proportion, following Ohm’s Law, V = IR, where V is the voltage, R the resistance, and I the current flow.
Geometry is full of lovely linear equations – simple relationships that are proportional. Knowing enough side-lengths and angles, one can calculate the lengths of the remaining sides and angles. Because the formulas are linear, if we know the radius of a circle or a sphere, we can find the diameter (by definition), the area or surface area and the circumference.
Aren’t these linear graphs boring? They all have these nice straight lines on them
Richard Gaughan, the author of Accidental Genius: The World’s Greatest By-Chance Discoveries, quips: “One of the paradoxes is that just about every linear system is also a nonlinear system. Thinking you can make one giant cake by quadrupling a recipe will probably not work. …. So most linear systems have a ‘linear regime’ –- a region over which the linear rules apply–- and a ‘nonlinear regime’ –- where they don’t. As long as you’re in the linear regime, the linear equations hold true”.
Linear behavior, in real dynamic systems, is almost always only valid over a small operational range and some models, some dynamic systems, cannot be linearized at all.
How’s that? Well, many of the formulas we use for the processes, dynamical systems, that make civilization possible are ‘almost’ linear, or more accurately, we use the linear versions of them, because the nonlinear version are not easily solvable. For example, Ian Stewart, author of Does God Play Dice?, states:
“…linear equations are usually much easier to solve than nonlinear ones. Find one or two solutions, and you’ve got lots more for free. The equation for the simple harmonic oscillator is linear; the true equation for a pendulum is not. The classic procedure is to linearize the nonlinear by throwing away all the awkward terms in the equation.
….
In classical times, lacking techniques to face up to nonlinearities, the process of linearization was carried out to such extremes that it often occurred while the equations were being set up. Heat flow is a good example: the classical heat equation is linear, even before you try to solve it. But real heat flow isn’t, and according to one expert, Clifford Truesdell, whatever good the classical heat equation has done for mathematics, it did nothing but harm to the physics of heat.”
One homework help site explains this way: “The main idea is to approximate the nonlinear system by using a linear one, hoping that the results of the one will be the same as the other one. This is called linearization of nonlinear systems.” In reality, this is a false hope.
The really important thing to remember is that these linearized formulas of dynamical systems –that are in reality nonlinear – are analogies and, like all analogies, in which one might say “Life is like a game of baseball”, they are not perfect, they are approximations, useful in some cases, maybe helpful for teaching and back-of-an-envelope calculations – but – if your parameters wander out of the system’s ‘linear regime’ your results will not just be a little off, they risk being entirely wrong — entirely wrong because the nature and behavior of nonlinear systems is strikingly different than that of linear systems.
This point bears repeating: The linearized versions of the formulas for dynamic systems used in everyday science, climate science included, are simplified versions of the true phenomena they are meant to describe – simplified to remove the nonlinearities. In the real world, these phenomena, these dynamic systems, behave nonlinearly. Why then do we use these formulas if they do not accurately reflect the real world? Simply because the formulas that do accurately describe the real world are nonlinear and far too difficult to solve – and even when solvable, produce results that are, under many common circumstances, in a word, unpredictable.
Stewart goes on to say:
“Really the whole language in which the discussion is conducted is topsy-turvy. To call a general differential equation ‘nonlinear’ is rather like calling zoology ‘nonpachydermology’.”
Or, as James Gleick reports in CHAOS, Making of a New Science:
“The mathematician Stanislaw Ulam remarked that to call the study of chaos “nonlinear science” was like calling zoology “the study of non-elephant animals.”
Amongst the dynamical systems of nature, nonlinearity is the general rule, and linearity is the rare exception.
Nonlinear system: A system in which alterations of an initial state need not produce proportional alterations in any subsequent states, one that is not linear.
When using linear systems, we expect that the result will be proportional to the input. We turn up the gas on the stove (altering the initial state) and we expect the water to boil faster (increased heating in proportion to the increased heat). Wouldn’t we be surprised though, if one day we turned up the gas and instead of heating, the water froze solid! That’s nonlinearity! (Fortunately, my wife, the once-professional cook, could count on her stoves behaving linearly, and so can you.)
What kinds of real world dynamical systems are nonlinear? Nearly all of them!
Social systems, like economics and the stock market are highly nonlinear, often reacting non-intuitively, non-proportionally, to changes in input – such as news or economic indicators.
Population dynamics; the predator-prey model; voltage and power in a resistor: P = V²2R; the radiant energy emission of a hot object depending on its temperature: R = kT4; the intensity of light transmitted through a thickness of a translucent material; common electronic distortion (think electric guitar solos); amplitude modulation (think AM radios); this list is endless. Even the heating of water, as far as the water is concerned, on a stove has a linear regime and a nonlinear regime, which begins when the water boils instead of heating further. [The temperature at which the system goes nonlinear allowed Sir Richard Burton to determine altitude with a thermometer when searching for the source of the Nile River.] Name a dynamic system and the possibility of it being truly linear is vanishing small. Nonlinearity is the rule.
What does the graph of a nonlinear system look like? Like this:
Here, a simple little formula for Population Dynamics, where the resources limit the population to a certain carrying capacity such as the number of squirrels on an idealized May Island (named for Robert May, who originated this work): xnext = rx(1-x). Some will recognize this equation as the “logistic equation”. Here we have set the carrying capacity of the island as 1 (100%) and express the population – x – in a decimal percentage of that carrying capacity. Each new year we start with the ending population of the previous year as the input for the next. r is the growth rate. So the growth rate times the population times the bit (1-x), which is the amount of the carrying capacity unused. The graph shows the results over 30 years using several different growth rates.
We can see many real life population patterns here:
1) With the relatively low growth rate of 2.7 (blue) the population rises sharply to about 0.6 of the carrying capacity of the island and after a few years, settles down to a steady state at that level.
2) Increasing the growth rate to 3 (orange) creates a situation similar to the above, except the population settles into a saw-tooth pattern which is cyclical with a period of two.
3) At 3.5 (red) we see a more pronounced saw-tooth, with a period of 4.
4) However, at growth rate 4 (green), all bets are off and chaos ensues. The slams up and down finally hitting a [near] extinction in the year 14 – if the vanishing small population survived that at all, it would rapidly increase and start all over again.
5) I have thrown in the purple line which graphs a linear formula of simply adding a little each year to the previous year’s population – xnext = x(1+(0.0005*year)) — slow steady growth of a population maturing in its environment – to contrast the difference between a formula which represents the realities of populations dynamics and a simplified linear versions of them. (Not all linear formulas produce straight lines – some, like this one, are curved, and more difficult to solve.) None of the nonlinear results look anything like the linear one.
Anyone who deals with populations in the wild will be familiar with Robert May’s work on this, it is the classic formula, along with the predator/prey formula, of population dynamics. Dr. May eventually became Princeton University’s Dean for Research. In the next essay, we will get back to looking at this same equation in a different way.
In this example, we changed the growth element of the equation gradually upwards, from 2.7 to 4 and found chaos resulting. Let’s look at one more aspect before we move on.
This image shows the results of xnext = 4x(1-x), the green line in the original, extended out to 200 years. Suppose you were an ecologist who had come to May Island to investigate the squirrel population, and spent a decade there in the period circled in red, say year 65 to 75. You’d measure and record a fairly steady population of around 0.75 of the carrying capacity of the island, with one boom year and one bust year, but otherwise fairly stable. The paper you published based on your data would fly through peer review and be a triumph of ecological science. It would also be entirely wrong. Within ten years the squirrel population would begin to wildly boom-and-bust and possibly go functionally extinct in the 81st or 82nd year. Any “cause” assigned would be a priori wrong. The true cause is the existence of chaos in the real dynamic system of populations under high growth rates.
You may think this a trick of mathematics but I assure you it is not. Ask salmon fishermen in the American Northwest and the sardine fishermen of Steinbeck’s Cannery Row. Natural populations can be steady, they can ebb and flow, and they can be truly chaotic, with wild swings, booms and busts. The chaos is built-in and no external forces are needed. In our May Island example, chaos begins to set in when the squirrels become successful, their growth factor increases above a value of three and their population begins to fluctuate, up and down. When they become too successful, too many surviving squirrel pups each year, a growth factor of 4, disaster follows on the heels of success. For real world scientific confirmation, see this paper: Nonlinear Population Dynamics: Models, Experiments and Data by Cushing et. al. (1998)
Let’s see one more example of nonlinearity. In this one, instead of doing something as obvious as changing a multiplier, we’ll simply change the starting point of a very simple little equation:
At the left of the graph, the orange line overwrites the blue, as they are close to identical. The only thing changed between the blue and orange is that the last digit of the initial value 0.543215 has been rounded up to 2, 0.54322, a change of 1/10000th, or rounded down to 0.54321, depending on the rounding rule, much as your computer, if set to use only 5 decimal places, would do, automatically, without your knowledge. In dynamical sciences, a lot of numbers are rounded up or down. All computers have a limited number of digits that they will carry in any calculation, and have their own built in rounding rules. In our example, the values begin to diverge at day 14, if these are daily results, and by day 19, even the sign of the result is different. Over the period of a month and a half, whole weeks of results are entirely different in numeric values, sign and behavior.
This is the phenomena that Edward Lorenz found in the 1960’s when he programmed the first computational models of the weather, and it shocked him to the core.
This is what I will discuss in the next essay in this series: the attributes and peculiarities of nonlinear systems.
Take Home Messages:
1. Linear systems are tame and predictable – changes in input produce proportional changes in results.
2. Nonlinear systems are not tame – changes in input do not necessarily produce proportional changes in results.
3. Nearly all real world dynamical systems are nonlinear, exceptions are vanishingly rare.
4. Linearized equations for systems that are, in fact, nonlinear, are only approximations and have limited usefulness. The results produced by these linearized equations may not even resemble the real world system results in many common circumstances.
5. Nonlinear systems can shift from orderly, predictable regimes to chaotic regimes under changing conditions.
6. In nonlinear systems, even infinitesimal changes in input can have unexpectedly large changes in the results – in numeric values, sign and behavior.
# # # # #
Author’s Comment Reply Policy:
This is a fascinating subject, with a lot of ground to cover. Let’s try to have comments about just the narrow part of the topic that is presented here in this one essay which tries to introduce readers to linearity and nonlinearity. (What this means to Climate and Climate Science will come in further essays in the series.)
I will try to answer your questions and make clarifications. If I have to repeat the same things too many times, I will post a reading list or give more precise references.
# # # # #
Great stuff, can’t wait for the rest, thanks!
What the IPCC, like many others, has long recognized is false. Linearity and chaos apply to models, not to the real world. Whether models are linear often depends merely on the scale factor applied. A system is linear if f(ax+by) = af(x)+bf(y). Equation do not exist in the real world to apply the definition. Models and equations are strictly manmade.
Chaos does not exist in the real world because the real world has no initial conditions to which it might be sensitive. Only models do. Climatologists and physicists alike often confuse the real world with their models.
+100
Ditto.
I like to paint. If I “paint a tree”, my model of the tree is not the tree.
http://www.maxphoton.com/let-light/
It is mind-blowing how many full-grown, professional adults can’t maintain that separation. In fact, the entire climate catastrophic fiasco hinges on this Tyranny of the Model.
Max Photon:
I was standing gazing at a distant mountain, thinking about how to paint a picture of all those trees with all the contrast and textures.
A friend asked me what I was thinking about.
I replied: ‘I was thinking about how to paint all those trees.’
I realized how ambiguous that statement was and added: ‘It would take a heck of a lot of paint to paint all those trees. There are thousands of them.’
Richard,
All you can do is create symbols (by placing pigment on fiber) that make the viewer’s mind say “tree.”
Max
Or put a coat of paint on each tree. Something about not seeing the painting for the trees.
Reply to Jeff Glassman ==> “Chaos does not exist in the real world” If only it were so. The natural dynamical systems of the world are almost all, exclusively, nonlinear and subject to chaos.
Turbulence in fluid flows of all kinds, including the atmosphere. Heat transfer through and between materials. Everyday population dynamics. Passage of radiant energy through a translucent medium (the atmosphere). All nonlinear dynamical systems, and subject to all the behaviors of nonlinearity.
Stay tuned to the whole series, and see if I can’t convince you of this.
Thanks for reading here.
..if this trend continues
It is so. And what makes it so is logic applied to our definitions of chaos. Many definitions exist, but one essential they all share is system sensitivity to its initial conditions. When Mitchell Feigenbaum (you quoted below; a reference would help) expressed chaos in terms of rapid growth, he was undoubtedly referring to rapid growth from its initial conditions (ICs). Devaney provide a definition that is popular, and several papers use that as a starting point for even more definitions. But I still have an opening in my collection of chaos definitions for one from a scientific field that does not have this IC property.
In Lorentz’s work, his systems were systems of equations. His domain was models of the real world.
One thing is certain. Nothing in the real world has initial conditions. Nor, for that matter, parameters, units, equations, coordinate systems, dimensions, sets, taxonomies, clocks, logic. These are all manmade constructs, expressed in human languages, from what impinges on our senses and instruments from the real world.
Jeff: one feature of nonlinear dynamics is that you can close your eyes and point to any point in time and say “these are my initial conditions.” So that means every chaotic system in the real world has initial conditions. Such systems are sensitively dependent on those initial conditions, so humans can never estimate them accurately enough to insert a model that can predict the future. However as Kip says, knowing that the systems are chaotic means that we understand better why the models don’t work.
Reply to Jeff Glassman ==> It has been some time since I heard someone claim that their own sense of logic trumped the Real World. There are so many real world examples of these chaotic behaviors in natural systems that I find your continuing assertions to the contrary difficult to understand.
Did you read the linked study Nonlinear Population Dynamics: Models, Experiments and Data by Cushing et. al. (1998)? It is a marvelous example of truly exemplary science on this topic.
I can only suggest reading any of the four books listed in the Introduction to Chaos Theory Reading List.
Reading any one of them should manage to bring you around…I hope!
“All nonlinear dynamical systems, and subject to all the behaviors of nonlinearity.”
That doesn’t make them chaotic. You beautifully demonstrate how some population equations behave chaotically, however, do actual populations exhibit such characteristics. Sure they’re complicated and subject to random events (like hurricanes) but that’s not chaos. I’m not going so far as to say there are no real world systems that are chaotic but they seem to be really rare to me. Let’s take squirrel populations for example, to be chaotic in the real world equivalent to the minute changes that significantly alter virtual populations a population of a hundred squirrels would have to be noticeably altered by an oak tree producing 2% less acorns (or the removal of 1 inch of one squirrels tail) a few years after the change. These kind of incredibly small changes don’t seem to be significant in the real world, in other words, the real world population of squirrels is not nearly as sensitive to initial conditions as would be required to consider it chaotic. Oh, and butterflies don’t really set off hurricanes except in virtual worlds. Admittedly, engineers are notorious for only looking at 3 significant digits (often 2, sometimes 1), but really I haven’t ran across many instances in which I really needed more than 2 in 25 years of real world electro-chemical processing which tells me they’re not chaotic even though they are “dynamical” and nonlinear (and sometimes really really complicated in what is certainly a variable rich environment subject to all sorts of random events).
Reply to John West ==> I will try one more time.
Please read any one of the books in the reading list for general understanding, or even just the Wikipedia article on Chaos Theory.
Read the paper I linked on Nonlinear Population Dynamics: Models, Experiments and Data by Cushing et. al. (1998). It is a marvelous example of truly exemplary science on this topic. This paper finds the very odd behaviors of nonlinear population dynamics in actual living populations in tightly controlled lab experiments — not just fooling around with numbers on a computer. Seeing, should be, believing.
As a chemist, try reading this paper Nonlinear Chemical Dynamics: Oscillations, Patterns, and Chaos . The BZ reaction and subsequent discoveries. It is all in there…right in your field.
Good luck.
It is not necessary to get any more complicated than the example a “real world” pendulum (with bearing friction) to demonstrate chaos in most all physical systems. Once released, the best you can do is calculate an envelope outside which the swinging bob CANNOT BE at any given moment in time thereafter, leaving a band of possible “where it is at any given point” in time values.
The bigger and more complex the physical system, the more difficult it becomes to calculate the envelope of possibilities. The 500,000 year record of reconstructed global temperature does a pretty good job of painting such a chaotic envelope for our grandaddy of all earthly non-linear systems. Within that envelope, the system pretty much has life of its own in which specific responses to specific forcing functions are impossible to calculate. Neither episodes of horrific volcanic activity nor cataclysmic meteor strikes has taken global climate outside that cyclic envelope of temperature values.
Mr. Hansen, et.al., I think you and Mr. Glassman are making different arguments, his philosophical and yours physical. In the real world the initial conditions occurred so long ago there is really no way to mentally get from there to the present. Equations, chaos, thought, and all the processes linear or otherwise are all chaotic in the sense that they are unpredictable because it is impossible to describe them in any mathematics accurately enough to match reality. Even the idea of predicting the a solar eclipse hundreds of years from now rests on the idea that no large disturbance in the solar system, say a Jupiter sized planet from far out in the Oort cloud passing between the earth and Venus, will happen. We just don’t know. As Dr. Essex so adroitly shows in several of his presentations, we don’t even know how we could know.
The simplest definition of chaos is unpredictability. Simplest example I can think of is a machine with two buttons, labeled “press a button to start, press a button to stop”. When you press a button the innards do some pseudo random calculation and assigns start and stop to each of the buttons. Every time you press a button the process repeats. When you press a button the machine starts. Press a button and it may stop, or it may not. Every time you press a button it may stop, or not. When it does stop pressing a button may start or maybe not. After an initial button press there is virtually no way to reliably predict what will happen on the next button press, the response is essentially unpredictable and chaotic. It’s also neither linear or non-linear, it’s a simple binary response.
One question- In your graph(7) of xnext = 4x(1-x), after a million or so iterations, is it possible to derive the original equation from the output?
Jeff the natural world certainly had an initial condition if you believe it did not then I am to assume that you do not believe or accept the big bang theory. I personal don’t know if it is truly correct but I am will to admit that is true and if it is that was the initial state of all the chaos that has happen since! Of course it worthless for a climate modeler since all the computing power in the world now or what every will be develop will never be capable of modeling ten years of climate let alone the all the states and chaos since the big bang. Even if you could the model would still not work since the model is not capable of forecasting anything in a chaotic system since chaos cannot not be predicted. I would assume you are with me on the point the people who model climate to the most part are fools on a fools errand.
Jeff
What’s your point – that everything is a cloud of unknowing and only religion can make sense of it. That making an image of nature, let alone God, is forbidden idolatry?
Have you been tasked with evading the implications of ubiquitous chaos and nonlinearity that are uncomfortable for CAGW?
Thanks for trying one more time.
Note in the paper “Nonlinear Chemical Dynamics: Oscillations, Patterns, and Chaos” the authors say “A small but growing number of chemical systems are now known to exhibit chaotic behavior”.
In other words, it’s rare.
They also note: “three fundamental classes of dynamical behavior (stationary, periodic, and chaotic)”.
Hmmm… Exactly how does one differentiate between an amalgamation of coupled complex periodic oscillating systems (with various damping) and a chaotic system? Sensitivity to initial conditions?
Furthermore right in their intro they say “Chemical reactions with nonlinear kinetic behavior can give rise to a remarkable set of spatiotemporal phenomena. These include periodic and chaotic changes …” [bold mine]
So nonlinear (even in the dynamical systems realm) can be something other than chaotic, i.e. periodic.
It seems to me these days we can be too quick to label something chaotic; chaos in the gaps of understanding (or possibly computational ability) if you will. The quintessential question being ‘is weather chaotic?’. Many say it is and while weather simulating models certainly behave chaotically I’m unconvinced that weather is chaotic. Call me a skeptic.
I’ll try to “let it go” for the next two parts and just leave this particular objection (of going from linear to chaotic too quickly) here.
Mr. Glassman’s point is shown in the squirrel population figure where the squirrel population values go to 0 at times. If this really happened just once, there would be no more squirrels on May Island.
I wondered about that too. But it appears one cannot assume that the change in squirrel population is based only on reproduction. Heck, if that were true a population of one squirrel is the same as zero and the population would never recover. So there must be a way for squirrels to arrive from afar, perhaps as stowaways on a visiting supply ship or with a boat of researchers. Of maybe they swim from a neighbouring island, assuming they can swim of course. I guess that’s another part of the chaos.
Reply to DHR and PaulH ==> Couple of points — in the population dynamics graph, it appears that the squirrel population has reached zero — in actuality, it is a very small number. In the real world, this could represent an local extinction event — or it could represent a common ecological case where a plant or animal becomes so locally rare that it appears to have vanished, only to be discovered again in the exact same place some number of years later.
Mr. Glassman seems to be railing against mathematical models in general and incorrectly believes that the chaos is a product of the math — which it is not. The chaotic behaviors are natural phenomena, only recently being discovered to also exist in the very mathematics of the systems described.
Maybe there’s half a squirrel. That’s a start,
100 %
Jeff Glassman
March 15, 2015 at 10:19 am
“Chaos does not exist in the real world because the real world has no initial conditions to which it might be sensitive. Only models do. Climatologists and physicists alike often confuse the real world with their models.”
Any momentary state can count as the initial state of what comes after it, so, you’re wrong. Chaos exists in the real world. It was OBSERVED by Lorenz before the entire branch of chaos mathematics and simulation came into being.
No. You are introducing the man-made element by assigning a point in time. Chaotic progression demonstrable from a point in time is still an arbitrary man-made condition. Chaos exists in the real world only within our context, not nature’s. If we are prepared to describe climate as “non-linear and chaotic”, we are basically saying, that for us, it is unknowable. We attempt to describe it and model it, but we can do so only imperfectly. And since our knowledge is imperfect, our models are even more so. Neither arrives at truth. Schrodinger!
Dirk, I agree. I’m not sure I even understand Jeff Glassman’s point. ALL of our idea’s are simply models of the reality “out there”. Those models may be understood as algorithms. We supply inputs to the algorithms, such as initial or boundary conditions. We turn the crank and produce some prediction for the output.
If the models are good ones and the initial/boundary conditions are chosen appropriately, then the predicted outcomes can be of great value in allowing us to anticipate and thus control, ACTUAL outcomes in the real world.
Consider a man throwing a baseball. If he is good at it (meaning his brain stores an excellent algorithm for the process of throwing the ball), then he can with a high degree of certainty deliver the ball to some precise location at a precise time given inputs such as a visual field (boundary conditions), and the state of play at a given moment (initial conditions). That is the value of the model that is in his head.
Furthermore, this is a highly non-linear system. A change amounting to only fractions of a degree in direction and azimuth can make the difference between a strike or a ball. A Home Run or an Out. Winning the World Series or losing the World Series.
I have chosen an active, participatory example. If that is not to one’s taste we could choose a more passive example. We can use the models (algorithms) of orbital mechanics to predict solar eclipses 100s of years ahead. Newton’s laws plus observations of the sun / earth / moon positions (boundary and initial conditions) permit prediction of a total eclipse on let us say the island of Tahiti beginning at 11:05am on May 5, 2034. That sort of pre-knowledge can also be very useful for controlling outcomes. (Mark Twain provides an interesting fictional instance of that in Connecticut Yankee in King Authur’s Court.)
In what sense is it useful to argue that initial / boundary conditions “don’t exist in the real world”? It makes just as much sense to fuss that MODEL’s “don’t exist” in the real world. True, and so what?
Paul Coppin: If you are trying to say “we don’t know what’s going to happen, but Nature does”, that’s wrong. There is chaos and uncertainty, down to the quantum level. Especially at the quantum level. “Nature” has no idea when an radioactive atom is going to decay. Or exactly where a leaf dropped in a rushing stream will be in 30 seconds, etc., etc.
The Universe is simply not predictable no matter how closely it is measured.
Dear Eustace Cranch,
To be sure you did not miss my apology to you here: http://wattsupwiththat.com/2015/03/12/claim-climate-communication-needs-to-be-less-optimistic-more-climate-disruption/#comment-1881285
here it is!
Take care,
Janice
DirkH,
Look more closely at what Lorenz did. He input what he thought was a previous state (and later discovered it was not) into his model and got something completely unexpected. THIS is what he observed. It was his model which was chaotic. He was in never in a position to claim his model was an accurate description of reality.
In fact, it would be difficult if not impossible to prove any physical system was chaotic unless you could define a model which accurately followed the physical system thus demonstrating it. The difficulty is that chaotic mathematical functions are subject to initial conditions which, in turn, implies that building such a demonstrator is very hard. Regardless, this is a statement about the modeler’s limited knowledge and not the physical system. You can never rule out the possibility that some modulating variable or groups of variables can be found which would simplify the model.
Think about it.
Eustace Cranch,
There is chaos and uncertainty, down to the quantum level. Especially at the quantum level.
There is indeed but only to the observer. The claim that, even if you knew all of the causes and their precise states and STILL get different answers, ultimately means that cause and effect is an illusion. The illusion may BE reality but It is a proposition that is not likely provable as you would be hard pressed to show you know all of the inputs.
Until such a proof comes along, it is better to assume that “random” (even when constrained, i.e., “chaotic”) is a description of modeler limitations and not reality.
Epistemological and not Ontological.
Yes Jeff, but really there is chaos. Chaos, not in the sense of the Physics definition, but in the sense of the state of mind of the proponents of the alarmist theories. They are quite literally in a, “state of extreme confusion and disorder”, that is to say their thinking and indeed subsequent actions, are chaotic.
From a Confucius scholars point of view this sort of malfunction in thinking is inevitable. …….
In the Western tradition, dominated by cosmogonic myth and speculation, in the beginning, at the origin, there is chaos. The transition from religious to philosophic and scientific speculation occurs in terms of the transition from mylhos to logos. In our tradition, because of the dominance of scientific thinking in the last four or five centuries, it is forgotten that, before there was a logos of mythos, there had to be a mythos of chaos; before scientific thinking could rationalize the myths, the myths had to organize chaos. In this view, reasoning is twice removed from the sources of individual and social experience in the primordial chaos at the time of the beginnings.
It is good to see a distinct and culturally different philosophical view expressed here.
Really? Why don’t you try it with physical systems from the real world to see if chaos does not exist in the real world? Do you best to prepare them ‘identically’ and watch them evolve over time.
A lot depends upon how close? What precision do you need. For a circle, pi = Circumference/diameter = C/d and therefore: C=Pi*d and conversely, d = C/pi. Since Pi is not a rational number and is transcendental. Try as you will you can never get an exact value for Pi. Therefore, if you know d exactly then C is always approximate and vice versa if C is known exactly then d is only approximate. In the practical world we can know C and d to our limits of measurements by starting with a good value of Pi with many digits. (Sometimes the constants have relatively large uncertainty in the real world due to measurement error).
Now if know d exactly and approximated C, then used C in n recursive calculations for a large n, number of times, then your final value of F(n,C) will be a function of n and C calculated with m digits of Pi. If your calculations are sensitive to round off error, then at some time for large n F(n,C) would be nonsense. And thus, they would be different depending upon on the initial value of Pi used in the calculations (i.e. the value of m, the number of digits used to estimate Pi).
Sometimes the models can be perfect C=Pi*d but because of our limits in specifying Pi, the calculations will always fail for large n. Now consider a global climate models with a very large number of constants that cannot be measured very well and run it over and over for a 1000 years where each value of the global mean temperature is dependent on the previous years values of global mean temperature and the previous years calculations of all “constants”, then we can see that their long- term predictions can go far astray.
The above discussions refer to cascading errors in the value of approximately known constants. Now introduce many parameters estimated with relatively large errors. Aye Yi Yi,! Now consider the uncertainty of the global climate models.
Wise guys in college used to say,” Constants aren’t and Variables won’t”.
Somebody says, “Really? Why don’t you try it with physical systems from the real world to see if chaos does not exist in the real world? Do you best to prepare them ‘identically’ and watch them evolve over time.”
=======================================================================
Such mathematics are not my area at all. However, philosophically I see the arguments against chaos as having some legs. In some recent debates with Brandon Gates, he kept informing me that all models are wrong. (It did not matter that I told him over and over of course they are, but in the engineering world you learn from your wrong models, the IPCC does not) The question is, why are all models wrong?
The answer is no models are infinitely precise, and all errors propagate. Beyond, and additive to that, not all fundamental forces are absolutely understood on every level including the quantum level.
Take the modeled pool table and classic pool break. The model says this and this will happen, and predicts where all the balls will end up. But it changes every time, despite all attempts to model it. The felt varies against what is known. One ball is slightly out of round. The humidity varies The cue is imperfect, or the cue ball is struck a hemi demi semi bit off. The error in the model vs. reality propagates, and it never gets it right.
Math is a symbol of something. Thus one apple plus one apple equals exactly two apples. As an idea this is perfectly true. But no two apples are exactly alike, therefore the “perfect” answer, is not in truth perfect.
Macroscopically, and microscopically, nothing is know perfectly or infinitely precisely, and errors propagate. Is chaos nothing more then the truth that all models have errors vs. the material reality? . . .
David, mathematical chaos is not necessarily a completely unordered state where not further entropy can occur, which is how the word is used philosophically. If you consider snow flakes, you look at a system that is fully determinant and yet which, except in the broadest of terms, you cannot predict, ever. There are many other natural systems that are governed by fully determinant yet cannot be forecast. All systems following fractals rules are in this case (moutains eroding, trees branching and distributions of leaves on trees).
David A,
Because that’s a ridiculous assertion stated so broadly.
My bottom line in this argument is that if you have little to no faith in models, you should be the first in line arguing for no change. Consistency goes a long way in a debate.
Now from my point of view, I not only want to know why CMIP5 models are wrong, I want them to be fixed. Realizing of course that they’ll never be perfect. Normally I’d then be asking how wrong they can be and still be useful. In this context, I see it as a moot question: they’re the best we’ve got, and I don’t see them getting much better any time soon as much as I wish that were so.
We have an infinitely better idea what CO2 at 280 ppmv looks like, because that era is in the rear-view mirror.
Do you get it yet? No? Very well, keep talking about chaos and unpredictability. Some day yet it may sink in.
Brandon Gates quotes me.
David A,
“In some recent debates with Brandon Gates, he kept informing me that all models are wrong. (It did not matter that I told him over and over of course they are, but in the engineering world you learn from your wrong models, the IPCC does not)
===========================================
Brandon states….”Because that’s a ridiculous assertion stated so broadly”
==========================
Full stop Brandon. My “broad assertion” comment was here. In the thread I gave you several graphics, explained how the IPCC chooses, and then utilized for future projections the “modeled mean” of knowingly wrong in ONE direction models. (They purposefully chose a KNON to be wrong answer to keep their scary stories alive. I also gave you links to detailed analysis of why this is political based post normal science, as opposed to real science.
You answered, with arm flapping detail, mute points about why all models are wrong, continually avoiding the FACT, that the IPCC does CHOOSE to use the mean of the error in one direction wrong models.
If they were building aviation instruments required for doing instrument landings, every one of their planes would crash into the runway because they thought they were higher then they were. (Were yet, they would face murder charges because they KNEW their modeled mean was telling them the planes were higher then they actually were, ad they sold them anyway. Arguing the broad term general about all models have errors”
You did in that post, exactly what you accused me of in this post….”arguing the broad term general about all models have errors” while ignoring the real story, no matter how clearly or how often it was pointed out to you. The rest of you comment follows this pattern.
David A,
You are ascribing motive, which is opinion. The factual statement is demonstrably false; the CMIP5 ensemble results as published in AR5 do not err in ONE direction:
http://1.bp.blogspot.com/-ZY_oL2cq4r4/VQiX3rRH2aI/AAAAAAAAAYo/0VNOKoRIQJw/s1600/CMIP5%2Bvs%2BHADCRUT4%2Btrend%2B1860-2014%2B01.png
Rate of change for all series computed with a least squares linear regression over the interval 1860 through 2014. This plot shows the result of subtracting the HADCRUT4 trend from each individual model trend. As you can see, roughly half of the models in the ensemble understate the observed trend over the entire interval. On balance, the CMIP5 ensemble is hot by 0.07 °C/century, but NOT as you ignorantly claim, because all models the IPCC have chosen are wrong in ONE direction.
All data from KNMI Climate Explorer.
The balance of your post ignores my central point: We have an infinitely better idea what CO2 at 280 ppmv looks like, because that era is in the rear-view mirror.
If you have any ability to be logically consistent, you will realize the import of my point.
Chaos for sure exists in any model of the real world though, and it doesn’t matter what you say, in the end all we have is models of the real world.
That is ultimately the only sane conclusion anyone who studies metaphysics can arrive at. There almost certainly is a real world out there, but we never deal with it directly. We only deal with models of it in our own heads and perceptions.
The game is not to throw models away and deal with reality directly – we can’t – or at least according to the mystics, all you end up with is bliss and no sense of identity 😉 – so we have to be in the business of better models, and in those better models chaos is for sure the best tool we have to describe what happens.
For sure models ain’t reality. That is the first step. The second step is to realise that reality is unattainable and we are stuck with models of it.
Chaos absolutely exists in the real world, Read James Gleick’s book “Chaos: Making A New Science”, if you understand that, and it’s amazingly understandable, you’ll know more about chaos that I’ve seen Climatologists demonstrate.
Paul, so you disagree with this statement…
ferdberple
March 15, 2015 at 12:48 pm
Predictable systems can be thought of as having a single attractor. A planet orbiting a star is predictable. However, when you add a third body the system becomes chaotic, except in the case where all 3 bodies lie in the same plane.
Chaotic doesn’t mean unpredictable, but it does mean unpredictable for all practical purposes. Given infinite precision and infinite time, you can predict a chaotic system.
Reply
======================
Kip Hansen
March 15, 2015 at 1:33 pm
Reply to ferdberple ==> Yes and Yes — think of a child learning to ride a bike — pedaling fast enough to get the bike up to speed, while steering close enough to straight, will get the bike on that stable “Look at me Mom, I’d riding a bike!” point
Nicely formulated Jeff. The map is not the territory. The distinction used to be called a priori/ a posteriori.
I highly recommend the work of Gregory Chaitin. He has continued the work of Goedel and Turing on the efficacy of modeling and meta-modeling. In essence it can be proved that no model can model reality, because the model would have to be more complex and bigger than said reality in order to model it.
Skip, reality may be complex or chaotic in a vulgar usage, but in a technical usage we are just describing reality as complex or chaotic. These theories while useful now will most likely themselves pass in time for more useful theories, at which time Reality will no longer be chaotic 😉
I think my post here, “http://wattsupwiththat.com/2015/03/15/chaos-climate-part-1-linearity/#comment-1884218 is articulating what Fred said below, “Chaotic doesn’t mean unpredictable, but it does mean unpredictable for all practical purposes. Given infinite precision and infinite time, you can predict a chaotic system.”
In this sense a chaotic system does not refer to the physics involved but to our capacity to predict and analyze them. Of course I understand some factor increase in a linear manner, and many are exponential, and in nature, many systems interact. I think however it may be fair to say, nature is not chaotic, but are capacity to predict it is.
Philosophy
The Hindu word for creation is maya, which literally translates as to divide that which is indivisible. In affect from the singularity of infinite energy beyond space and time solutions, comes all relative cause and affect. observations. To focus on one, is to by nature miss the interaction of all. Thus science can know nothing perfectly, as infinite precision and omniscience would be required.. To measure is to see only a part of the whole picture.
Below from a book published in the 1940s.
“The ancient Vedic scriptures declare that the physical world operates under one fundamental law of maya, the principle of relativity and duality. God, the Sole Life, is an Absolute Unity; He cannot appear as the separate and diverse manifestations of a creation except under a false or unreal veil. That cosmic illusion is maya. Every great scientific discovery of modern times has served as a confirmation of this simple pronouncement of the rishis.
Newton’s Law of Motion is a law of maya: “To every action there is always an equal and contrary reaction; the mutual actions of any two bodies are always equal and oppositely directed.” Action and reaction are thus exactly equal. “To have a single force is impossible. There must be, and always is, a pair of forces equal and opposite.”
Fundamental natural activities all betray their mayic origin. Electricity, for example, is a phenomenon of repulsion and attraction; its electrons and protons are electrical opposites. Another example: the atom or final particle of matter is, like the earth itself, a magnet with positive and negative poles. The entire phenomenal world is under the inexorable sway of polarity; no law of physics, chemistry, or any other science is ever found free from inherent opposite or contrasted principles.
Physical science, then, cannot formulate laws outside of maya, the very texture and structure of creation. Nature herself is maya; natural science must perforce deal with her ineluctable quiddity. In her own domain, she is eternal and inexhaustible; future scientists can do no more than probe one aspect after another of her varied infinitude. Science thus remains in a perpetual flux, unable to reach finality; fit indeed to formulate the laws of an already existing and functioning cosmos, but powerless to detect the Law Framer and Sole Operator. The majestic manifestations of gravitation and electricity have become known, but what gravitation and electricity are, no mortal knoweth.”
=========================================
http://www.ananda.org/autobiography/#chap30
.
“Chaos does not exist in the real world because the real world has no initial conditions to which it might be sensitive.”
There is hysteresis, especially in oceanic modes, providing greatly ranging initial conditions. That has though little to do with whether what came before and what follows is actually chaotic or not.
At some point introduce the distinction between nonlinear, and nonlinear dynamic (lagged feedback) systems. A pendulum is the former. Old clocks show pendulums are still well behaved. Squirrels and climate are both the latter. And are not.
Reply to Rud ==> Yes, gently kicked pendulums are wonderfully predictable and constant. However, kick them too hard, or break the pendulum into two sections and they devolve into chaotic behaviors.
I knew about the double pendulum behaviour.
pendulum math gets really messy once you get to the point where sin(x)~=x breaks down.
This needs to be taught in schools, together with physics and calculus. And it should be required that anyone who aspires to have an influence on public policy pass a test at this level of mathematics.
All scientists who study the causes of climate and weather pattern variations need most of their master’s coursework at this level of mathematics.
“This level of mathematics” is stripping the basics down to the bone! I would certainly pray that climate “scientists” know a hell of a lot more mathematics than this!!!
(You’re making me nervous.)
Don’t forget economics.
Very interesting, I look forward to the next part.
@Jeff Glassman: I would offer up one of the hardest physical phenomenon that there is to model, to disprove your assertion – turbulence in fluids. It is inherently chaotic and it dominates so many important aspects of our lives, from the weather to corrosion of pipes to the way our bodies work.
Re: pipe turbulence — good point rxc
–That we have not (and likely cannot) solve the equation describing it,
Dr. Christopher Essex gives as one example of why climate is NOT simulatable:
(from my 2/24/15 comment here: http://wattsupwiththat.com/2015/02/23/inconvenient-study-la-nina-killed-coral-reefs-4100-years-ago-and-lasted-over-two-millenia/#comment-1867617)
“{Essex video here on youtube: https://www.youtube.com/watch?v=19q1i-wAUpY}
{25:17} — Solving the closure problem. {i.e., the “basic physics” equations have not even been SOLVED yet, e.g., the flow of fluids equation “Navier-Stokes Equations” — we still can’t even figure out what the flow of water in a PIPE would be if there were any turbulence.}”
Janice
If this were so then chemical and petrochemical plants requiring thousands of pressure drop flow calculations (and ultimately power consumption calculations ) involving turbulent fluid flow and transfer through pipes could not be designed. If turbulent flow through pipes cannot be figured out then how do these plants get designed, built and operated.
Robert Stevenson
The industries absolutely do “use” turbulent flow approximations all the time. Just like they “use” linear approximations of beam stress-strain and linear approximations of resistance curves. No one at any time can “predict” the exact start of turbulent flow, nor what happens inside the pipe during turbulent flow – All that the designers can do is deliberately select a pump power and valve diameter and pipe diameter sufficient to guarantee that turbulent flow must occur (at some point in the pump discharge path) and that fluid speed and pipe roughness and fluid temperature and pressure are sufficient for that turbulent flow to STAY turbulent all the way through the pipe from end-to-end.
But – to answer the question about “What is the fluid “doing” at any point inside the pipe?” … That we cannot answer.
I agree that turbulent flow in pipes is chaotic but it has been adequately modeled; for turbulent flow in smooth tubes the Blasius equation gives the friction factor accurately for a wide range of Re nos.
f= 0.079/Re^0.25 4000 < Re <10^5
Pipe flow models developed using dimensional analysis give excellent predictions in the turbulent region for velocity and pressure drop. Why in your view cannot models be developed for turbulent flow in the atmosphere to be used to predict the effects of man made global warming and future climate changes?
To invalidate (not disprove; this is about science, not symbolic logic) what I said, you would need to provide a (necessarily new) definition for either linearity or chaos, and then show how turbulent fluid flow is either nonlinear or chaotic according to either definition and without resorting to a model for turbulent flow.
The existence of hard and unsolved problems shows only the limitations of our abilities to model, including poor choices for observations, parameters, or scale factors.
Dear Mr. Glassman,
It would be helpful, I think, so that other commenters could even possibly invalidate or respond precisely to your statements at 10:19am and 11:02am today, if you would define your terms and write more clearly. It appears that you and everyone else (John West, too, perhaps…) are writing past each other here… . And you know what happens when computations start to diverge from reality….. !!!!! 🙂
That is: people are responding to what they THOUGHT you meant,
however,
from your reply, it appears that
what you meant is not what they thought.
#(:))
Janice
Janice, 3/15/15 @ 11:19:
What I believe to be the essentials of the definitions were contained in my opening paragraph. For linearity/nonlinearity, the essence is the equation I gave. For chaos, the key criterion is a heightened sensitivity to initial conditions. If scientific definitions exist without these properties, I hope the posters here will illuminate the dialog.
You might, though, enjoy these related, circular definitions from IPCC, intended for laymen (e.g., Policymakers):
>>Chaos A dynamical system such as the climate system, governed by nonlinear deterministic equations (see Nonlinearity), may exhibit erratic or chaotic behaviour in the sense that very small changes in the initial state of the system in time lead to large and apparently unpredictable changes in its temporal evolution. Such chaotic behaviour may limit the predictability of nonlinear dynamical systems. AR4, Glossary, p. 942.
>>Predictability The extent to which future states of a system may be predicted based on knowledge of current and past states of the system.
>>Since knowledge of the climate system’s past and current states is generally imperfect, as are the models that utilise this knowledge to produce a climate prediction, and since the climate system is inherently nonlinear and chaotic, predictability of the climate system is inherently limited. Even with arbitrarily accurate models and observations, there may still be limits to the predictability of such a nonlinear system (AMS, 2000)
By the way, IPCC’s definition of climate system is a good-enough real world system, but its definition of nonlinearity is a property of simple models sans mathematics.
So in IPCC speak, a real world system is chaotic and unpredictable if the models of it do not produce predictable results. This implies a certain arrogance that climate models are perfect. But more importantly, IPCC blames the failure of its models to predict climate on the climate, not the models.
I think Mr. Glassman is quite clear. He understands the difference between the model and that which is being modeled.
Others should be so clear.
If you by “chaotic” mean “random but constrained” or even plain old “unpredictable” then you are making a statement about your knowledge of the world as expressed in your model. Assuming your model is the world is reification where the models become the reality. In no way does the difficulty in modeling turbulence disprove what Jeff Glassman has said.
.
Glassman: “Chaos does not exist in the real world … .”
rxc: “…– turbulence in fluids. It is inherently chaotic … .”
— This is the crux of the difference that Mr. Glassman needs to clarify. As it is, he has left great ambiguity. What does he mean precisely? Until he clarifies his meaning, we might as well just ignore what he writes. Those who applaud and those who attempt to refute him are equally likely to be mistaken.
You as well, Janice. What could “chaotic” mean and what does it mean to you. So far the best definition would be “random but constrained” but “random” really means “unknown or incalculable”. It can only mean something regarding the extent of one’s knowledge and never about the real world which I think obviously doesn’t suffer from this unknowability.
Glassman: “Chaos does not exist in the real world … .”
Why would anyone think otherwise?
Reply to DAV, Glassman, and janice ==> Perhaps this is my fault, as author, in assuming that my use of the word “chaotic” would be understood in the sense intended when we speak of nonlinearity and ‘chaos theory’.
Amongst the many scholarly definitions of CHAOS is this from Mitchell Feigenbaum:
Edward Lorenz offers this:
Fort readers who think that “chaotic” means the same thing as “entirely random” — see the Wiki article for a brief introduction.
Much of this I hope to make clear in the second and third part of this series.
Dear Mr. Hansen,
Thank you for that very nice definition of terms. That you can explain your position so clearly to a layperson like I shows that you are a master of your subject. It is clear from your writing in your post and your above comment that Glassman and DAV are either: 1. honestly mistaken; or 2. using ambiguity and imprecision deliberately (for what purpose, I will not guess).
Thank you for the great education. Starting a building with the foundation — only way to go!
Janice
Kip, thanks. I hope the future articles make it clear that “chaos” is only an expression of out ability to predict and not something actually present in physical systems. The models are not the reality.
.
Janice,
The fluid is not chaotic. It knows exactly what it is doing at all time.
It only appears chaotic to the observer.
Chaos is in the eye of the modeler, not in what is being modeled.
“It only appears chaotic to the observer.
Science is about observation.
That’s why “chaotic” is the term used to describe that situation.
It is a useful concept. Mr. Glassman is using “chaos” in some obscure, largely unhelpful, way.
Max Photon,
It only appears chaotic to the observer.
An apt description but some people will fail to see that happens only when the observer becomes a modeler and sees chaotic behavior in the model predictions. There is a tendency to see one’s model as being the reality. Climate modelers and the IPCC seem to have fallen into this trap (called reification) as demonstrated, e.g., by their hunt for “missing” heat. “Missing” because it was predicted by the models so it should be present.
As long as the difference between models and reality is maintained or at least commonly understood there isn’t really anything wrong with shortcut descriptions. However, it is quite evident some here can’t see the distinction. From some of Kip Hansen’s comments it seems he may be one of them.
Janice and Mr. Glassman, do my layman thoughts expressed in this post here, “http://wattsupwiththat.com/2015/03/15/chaos-climate-part-1-linearity/#comment-1884218
articulate some of the same thoughts Mr. Glassman is expressing in a more detailed manner?
Missed the link to my comment…
http://wattsupwiththat.com/2015/03/15/chaos-climate-part-1-linearity/#comment-1884218
rxc; Many years ago we were on holiday and I wanted to see if water came out of the shower head in streams, like the single stream from a hosepipe. I turned the shower on and took two photographs through the shower towards the light. The first exposure at about 1/30th second showed streams of water, the second at a wider aperture and 1/1000th second showed droplets all in lines. I reasoned that the turbulence in the shower head prevented a linear egress of the water. I would also hazard a guess that the greater number of holes there are in the shower head, the less chance there would be of predicting how many droplets would come out of each hole.
I will add that I do enjoy swimming, good food, wine and sight-seeing when I go away!!
http://www.sciencealert.com/this-tap-saves-water-by-creating-incredible-patterns
That’s what quantum mechanics is about. You can’t predict the path an individual photon takes but there is an overall ‘order’. From one perspective it is chaotic but from another perspective it is ordered. It’s like Schrodinger’s cat-chaos exists and doesn’t exist at the same time
Alex, chaos and order only exist in the mind of the observer.
Everything is in the eye (or brain) of the modeler. Doesn’t mean there is nothing outside the modeler’s brain for him to model.
E.g., for those who say that evolution (for example) is “only” a theory — they beg the question, a theory of what? In order for there to be a theory at all, there must be something, some phenomenon/a, for the theory to be about. A theory with no real-world referent is like a map that isn’t a map OF anything.
Chaos was observed. Chaos is still observed. Go ahead, draw me a map that doesn’t represent -anything-, not even that weird house-like place you dreamed about the other night.
The model is not the thing modeled. And it can’t exist without the thing modeled.
Chaos was observed
Actually it was only observed in models. If anything it would mean that the models were far from complete.. To say that whatever the model is trying to predict is chaotic because the model predictions are is saying the model is accurate when quite obviously it is not.
Max, you appear to make a novice mistake. Chaos in the mathematical sense is not an absence of order. It is a level of complexity that defies long term precise predictions.
Excellent topic, a very good read. Thank you for taking the time to put this together.
“1) nonlinear and therefore, 2) chaotic” … “Nonlinear systems are not tame – changes in input do not necessarily produce proportional changes in results.”
There are plenty of nonlinear yet “tame” (in that they are completely predictable) systems. Nonlinear includes exponential and logarithmic neither of which are chaotic. This post is oversimplification past the point of absurdity.
I disagree. It is very simplified and could do with more caveats that people can follow up on if they are interested.
But this is an introduction.
It is the level that should be taught to 11 to 13 year olds in schools, but isn’t.
I think this article is useful.
Initial introduction to trigonometry and logarithms are typically taught in 9th-10th grade in US public schools, about 14-15 yr olds. That would be their first real exposure to nonlinear math functions.
“1) nonlinear and therefore, 2) chaotic”
I disagree with this, too. Non-linear and chaotic are quite different and should always be presented as such – even at an introductory level.
joelobryan, That seems a little later than I recall from my schooldays. I’m sure it was long before we started studying for our GCSEs.
Maybe it’s different between the US and England. It would be interesting to know what variation there is in the world’s mathematics teaching.
But I still think these ideas ought to be taught to children of around 11 to 13 years old.
Reply to the “Nonlinear/Chaotic” point ==> I am talking here quite specifically about nonlinear dynamical systems.
Nonlinear mathematical functions are math….not dynamical systems.
For those who are stubbornly holding to “what I learned in college mathematics” — please read any one, or all, of the following books:
Gleick is fun. Explains nonlinear dynamics in context of the people and their discovery process. Stewart is more straightforward technical. Both highly recommended.
There are of course many nonlinear dynamical systems that are not chaotic. It is usually very difficult to prove that a system is chaotic in the mathematical meaning. There are also many well behaved non linear systems that can be easily analyzed and simulated, a car, a robot, celestial motions, a bridge to name a few. There are not many linear systems analyzed in robotics but it is still possibly to get very good results.
The only valid point in your article seems to be that you need to be careful when handling non linear systems but everyone with any knowledge about the subject knows that.
Would you please say what you mean by dynamical systems? What would make a system non-dynamical or partialy dynamical, for instance?
God does not play dice, hirelings do. God owns the Casino!
Reply to Will ==> The Wiki gives:
“A dynamical system is a concept in mathematics where a fixed rule describes how a point in a geometrical space depends on time. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.
At any given time a dynamical system has a state given by a set of real numbers (a vector) that can be represented by a point in an appropriate state space (a geometrical manifold). Small changes in the state of the system create small changes in the numbers. The evolution rule of the dynamical system is a fixed rule that describes what future states follow from the current state. The rule is deterministic; in other words, for a given time interval only one future state follows from the current state.”
(Sorry that is so dense, but you did ask for it).
In plain English a dynamical system is a real world process, a series of events (any continuum is a series of discreet events, one after another) in which the next state of the system depends on the current state. In our population example — squirrels on May Island — the calculation for the number of squirrels next year starts with the ending value of this year. The thing we are measuring is moving through time.
And “In physics and other sciences, a nonlinear [dynamical] system, in contrast to a linear system, is a system which does not satisfy the superposition principle – meaning that the output of a nonlinear system is not directly proportional to the input. …. Nonlinear problems are of interest to engineers, physicists and mathematicians and many other scientists because most systems are inherently nonlinear in nature.”
Kip Hansen, 3/15/2015 @ 12:14 pm
Thinking that I might be able to help you, I found all four of your references available for preview on-line, including the indices and the ability to search the contents. I found some discussions about competing definitions of chaos, but these authors support you: none of you can define the term you pretend to discuss. How easy it is to write volumes about something undefined. Real science articles do not enjoy that luxury.
So too, zero change in inputs can have these results??
Reply to RobRoy ==> Very good question! The answer is “No”. Re-running calculations (re-doing an experiment) with exactly the same inputs gives exactly the same results, assuming you are using the same computer (more on this next time).
I like this definition of chaos.
Kip Hansen
March 15, 2015 at 11:50 am
“Chaos: When the present determines the future, but the approximate present does not approximately determine the future.”
It seems like global climate is the sum of all the regional weather events in a constant chain reaction. It’s never really any one thing at any one time.
Yes RobRoy -That effectively defines a non-linear system. it is the division by zero or where something tangible or measurable happens in zero time or zero space.
Yes, I’m in agreement with Jeff G and John West
We really do have to get our heads around something that is ‘straight-line’ linear Y=Ax+B for instance or something not straight line, such like x-squared, Log(x) or sin(x)
They are still linear functions.
A pendulum is linear no matter what size swing it takes but limiting calculations to small swings is sheer laziness (for lack of a better word) by people who do not want to be bothered to do the actaul calculations. The pendulum is always responding in a linear fashon to whatever forces are applied to it no matter what size swing.
Likewise water in a pipe or swirling in a bucket. Each individual molecule is always responding in a linear fashion to whatever forces are being applied to it at all times.
It is the fact that there are about 36 million million million million molecules in just one liter of water makes the calculation ‘a bit difficult’ Present-day digital technology is not up to the task but that does not make it non-linear system. Basically, its ’rounding error’
Likewise applying the tag ‘chaos’
Each molecule of water knows exactly where its going, where its been and what force is acting on it at all time and responding in a linear fashion – how can it do otherwise? If each molecule is linear, how can the body of water be non-linear?
If we really do want to solve the problem of what a liter of water does in a pipe, simply get a liter of water and a pipe and let the water solve it for you.
Until the digital computer can resolve the forces on each of the 3.6x10e25 water molecules in each litre, in (at a guess) sub-nanosecond timescales – their behaviour will appear chaotic or non-linear.
As skeptics we must not fall into the beguiling trap of thinking (digital) computers are some sort of all powerfull wonder machines -just as the warmists do. Their unquestioning gullibility and naivety is mindblowing sometimes…
Peta in Cumbria ==> Both Gleick and Stewart (see reading list pull quote) insist that the very systems themselves are nonlinear in nature — not just that we have linearized them out of laziness (which is also true). These systems appear nonlinear because they are nonlinear. Nonlinearity is not a trick of lazy mathematicians or physicists.
Read this paper: Nonlinear Population Dynamics: Models, Experiments and Data by Cushing et. al. (1998) and check back in here with your opinion.
P in C, you raise two deep philosophical history of science points, both going back now centuries, amd noth crucialy important. Bravo.
First, is Pascal’s notion that if you knew everything about some state of the universe (the position, momentum, … of every atom, plus all the laws of physics like Newton’s), then the future would be in principle computable and knowable. Also known as LaGrange’s Demon (since the Devil could also do the calculations). Pascal quit math for Christian asceticism shortly after founding probability theory to solve a compulsive Paris gambler friend’s question about how to divide the table stakes if the game stopped short… LaGrange stayed mathematician to the end. This was the deterministic Clockwork Universe idea that Newton inspired.
It eventually foundered on two problems. First, the present state is not precisely knowable (PI has an an infinite number of digits, underlying the Lorentz butterfly effect problem of sensitive dependance on initial conditions, undoubtedly coming in a subsequent installment of this excellent primer). It was Poincare who originally finally laid the celestial clockwork metaphor to rest, by showing that Newton’s three celestial body was not solvable ( because of nonlinear dynamic ‘chaos’ theory, although Henri did have that nomenclature in his time).
Second, Turing computability. Some things are not practically computable (in the digital sense) EVER! See a nice little supplemental reading book, Computability and Unsolvability, by Martin Davis (1958). Which is why GCMs must be parameterized…
The IPCC dogma versus skeptic stuff highlighted by Kip Hansen’s excellent first in his series of posts (if the rest are as good as this one, beyond excellent and worthy of a book) has very deep intellectual roots. ‘Those who do not study history are doomed to repeat it…’ Something like that.
The pendulum starting from “true north” presents special difficulties because of the sensitivity to initial conditions.
PoC, these are deep waters. If you are making the observation that the laws of nature appear to be linear and satisfy the superposition principle at the microscopic classical level, and appear to be strictly reversible at that level, I certainly wouldn’t argue with you, although quantum theory introduces a sort of nonlinearity at the very smallest length/time scales via pair production and vacuum polarization, there is the puzzle of mass (there are nonlinear Higgs models that are still not ruled out as candidates, given that the Higgs boson is not yet really ruled in), and ultimately all of this is empirical probable truth, true so far as we can tell, and we may or may not find some fundamental nonlinearity somewhere.
However, you are also conflating a few things. One of the first things one learns (and subsequently teaches) in physics is that it isn’t laziness that keeps us from treating ever elementary particle in a physical computation. It is that it cannot be done. Not just in the fashion you describe, because there are too many particles to be able to complete the computation of the motion of a pendulum one quark and one electron at a time, not just because we cannot use classical physics to do so and hence must include the vastly greater number of particles in the fields that govern the interaction at all length scales including the ones we currently handle via “renormalization” to avoid the highly nonlinear divergences in the “linear” fields themselves. Because of information theory. We tend to idealize problems — you do it above when you refer to “a pendulum”. If you want to treat the pendulum as a collection of quarks, photons, electrons, gravitons, heavy vector bosons, gluons, and Higgs particles (assuming that there are not other particles such as “darkons” that we cannot yet observe but that play an important role) then you cannot call it a “pendulum” any more. It is simply a very, very long vector of particles, a list that isn’t even stationary in time as you compute. You have to dice spacetime itself up all the way down to the Planck scale, because it is at that scale that vacuum polarization due to pair production and annihilation occur. You have a Heisenproblem — you cannot measure the initial condition of the system at that scale (to do so would be to alter it) so your knowledge of the initial conditions is intrinsically uncertain. Suppose, however, that we pretend that we can, and assign a big, imaginary, pile of particles on a finite space-like sheet of spacetime specific initial conditions.
We still cannot solve the problem for the following reason, and this is one most physicists do not usually think about or fully appreciate. We have now defined a precise knowledge of a system, yes, but it isn’t the right system. There is only one system one can integrate in the way you describe and get the correct answer, because at least two of the interactions have infinite range and one of them directly couples all of the massive particles out to at least ~14 billion light years away. That is the whole thing. The cosmos itself. The “system” you refer to is a strict subsystem of the whole thing. Worse, it is an open subsystem, constantly interacting with the rest. You cannot turn this interaction off, although out of ignorance and/or a certain perversity of the sort used when we present proofs that 1 = 2 (if you divide by zero and don’t tell) we make up “paradoxes” such as Schrodinger’s Cat or the Einstein-Rosen-Podolsky paradox that assume in the one case that the cat is in an adiabatic box that is perfectly decoupled from the physical Universe, and in the other too many things to list, all wrong.
The right way to formulate the problem is then: Write an equation of motion — ideally a quantum, relativistic, equation of motion — for the entire Universe. Fine, I can do that formally easily enough — I simply pretend that I know the density matrix for the entire Universe on a single spacelike sheet that spans the Universe. Note well that this sheet has to represent the precise state of all of the intermediate fields, as those fields from earlier times are by assumption propagating on that sheet and we have to be able to include the effects of e.g. photons en route or molecules in our “pendulum” will spontaneously bounce out of sheer magic when photons from a supernova six billion light years away happen to hit it, introducing error into our pristine computations. Second, I split the Universe into two pieces. One, I will call “the system” (our pendulum). The rest is usually referred to as “the bath”, as it is represented in the simplest cases that can be treated approximately at all a thermal bath with e.g. fixed temperature. The system is now properly an open system, and it interacts with itself via internal interactions at the same time it interacts with everything else (while everything else interacts with itself and with it, the entire systems is coupled).
To solve this system at least approximately in a local differential formulation, one goes through the Nakajima-Zwanzig construction to form a Generalized Master Equation for the “pendulum” — partition, form a projection-valued operator from the bath onto the system, describe the bath semi-classically in terms of probabilities (since we cannot possible know its detailed state) and end up with a non-Markovian set of coupled ODEs for the density matrix of the subsystem with a nontrivial time kernel describing the “memory” of the system for prior states. This does complicate starting the integration, but we are approximate already so we make simple assumptions and do the best we can. We can eliminate the Markov problem by assuming delta-correlated interactions and recover the Langevin equation — which works remarkably well for things like delta-correlated photon interactions in a collection of particles being treated only electromagnetically but is more problematic for gravitation and which does assume a lot of stuff about the bath that may not be true if the “bath” includes your hand as it gives the pendulum a push (ooo, how to predict/compute that).
To solve it exactly, however, is not possible at the human cognitive level because, to put it bluntly, the representation of information in the Universe itself is already maximally parsimonious. It is impossible because of information theory. It is non-computable because one cannot encode the information needed to specify the state of the system, let alone compute it, in a strict subset of the particles of the system being solved, period. The information content of the whole is greater than the information content in any encoding you like of the part. Hence the problem is not computable, period.
It is not laziness. It is that it is a priori impossible for us to integrate any strict subset of the Universe forward in time using a computer that is itself a strict subset of the Universe because for the computation to be exact, the computer has to be able to represent the state of the entire Universe in some encoding (and have room left over for things like the actual computation — normally it would take 2-3 times as much memory to advance a coupled ODE solution) and this is formally, provably, impossible.
The point is this. The entropy of the Universe is zero, because as you note all interactions are reversible. But the entropy of any subset of the Universe, even if you force it to be zero by pretending that you know its initial state exactly when in fact you cannot possibly measure or know it exactly, will not remain zero because the entropy of the rest of the Universe will instantly start to bleed through into the system unless you turn all interactions with the rest of the Universe off or otherwise idealize so that you are no longer solving the same problem, and in any event are not solving the actual problem exactly.
There are then several more things one could note. As my mentor in this sort of thing, Dr. Richard Palmer (ex associate director of the Santa Fe Center for Complex Systems and on the short list to become director until his tragic stroke) once taught me, “more is different”. The physics that best describes quarks interacting with gluons and electrons interacting with quarks is not the physics that best describes an atom. Only a madman would try to solve for the state of an atom in direct terms of quarks, gluons, and electrons. Instead we turn the quarks and gluons into nucleons that have their own rules for interacting with electrons, we turn the nucleons into nuclei that have rules that are again different from those of nucleons, we dress the nucleus with electrons and make an atom, and we have all sorts of rules for the atom that are not at all like the rules for nucleons or nuclei or electrons. When we build molecules we invent an entire science — chemistry — with rules that don’t look much like electromagnetism even though they inherit structure from the atomic rules, the Pauli principle, and so on. Organic chemistry and Biochemistry have new rules once again.
This sort of layering of systems with emergent order and quasiparticles (stable, named structures that become the “nouns” of the new layer, things like “electrons” or “holes” in semiconductor theory) and quasiparticle interactions (e.g. “plasmons”) that have highly nonlinear interactions in many cases. Once again this is not laziness — it is recognizing that the relevant degrees of freedom have self-organized into new structures and new interactions that we name and compute with because the microscopic description is a) not computable; and b) meaningless. This process proceeds at least up to the scale of life and human thought. Yet nobody sane would claim that my thoughts as I type these words are solutions to an initial value problem in physics that can be solved at the level of quarks, gluons, leptons, photons, etc.
Note well that everything you can name that isn’t an elementary particle is a recognizable/nameable spacetime collective quasiparticle. Almost all of these quasiparticles will interact according to nonlinear dynamical schemes, although we spend a lot of time and energy teaching idealized versions of them where “an atom” interacts with other atoms via stately, linearized, means such as “dipole-induced dipole” (Van der Waals) forces, Lennard-Jones potentials, hard sphere models, or as electrostatic ions. Again, this is usually done to make a problem solvable at all in at least an approximate way, one that gives decent agreement with experiment. But there are all too many regimes where really interesting things happen in the sense of the chinese curse — regions of emergent order, critical regions — places where an interaction is trying to make a new quasiparticle but the quasiparticles formed are evanescent and interact so nonlinearly during their brief lifetime that the system isn’t computable using them, but it also has entered a region where the old interaction that is producing the quasiparticles is not computable either.
On top of this is the problem of deterministic chaos. Note well that the problem is shared equally by quantum and classical theories — that’s the point of the Nakajima-Zwanzig equation. Both ways one is simply seeking to integrate a system of coupled differential equations, and in both cases even if the system itself is nominally linear, by the time one partitions and approximates the (far) greater part, one gets crazy stochastic stuff like “wavefunction collapse” in the quasiparticle description of the open system (note well that all processes of measurement are described properly by the Generalized Master Equation as the measuring apparatus is not a part of the system and its state is at best known in an approximate, stochastic semiclassical description, hence our conclusion that the measurement projects out one of the possible quantum states of the system on a purely stochastic basis — we simply don’t know the quantum phases of the measuring system, we don’t know its state, we don’t know the retarded fields, and so we cannot solve the correct problem with is the purely deterministic quantum evolution of system and measuring apparatus and the rest of the Universe all together).
Hope this helps…;-)
rgb
Division by zero is a singularity, a point where an equation or process is not just non-linear but boldly discontinuous. A condition well beyond chaotic that (I hope) has no relevance to climate.
Good article. I wish more people actually had a clue about just how, err, “chaotic” chaos really is and what a joke it is to assume that the last 165 years out of the entire climate record would have been dead solid stable in temperature and flood/drought patterns if only we hadn’t added CO_2 to the atmosphere by burning stuff.
The second problem, of course, is that the GCMs exhibit chaos (if they didn’t NOBODY would take them seriously) and sometimes warm the planet for the next century, sometimes cool it, sometimes do something in between, again from starting values butterfly-effect perturbed to “sample” the phase space of possible outcomes. The resulting trajectories are then averaged per model, and then superaveraged across models without even reweighting the results to reflect the number of perturbed parameter ensemble runs contributing or the non-independence of the CMIP5 models themselves and this “multimodel ensemble mean” is used as the most likely trajectory for the climate.
It is difficult for me to even start on this one. Its stupidity literally takes my breath away. It is not justified by observation. It is not justified by any possible application of statistical science. It is precisely antithetical to the actual climate trajectories produced by the models themselves, which — flawed as they are, with egregiously incorrect autocorrelation times, fluctuation amplitudes, and predictions for things like tropospheric warming, alterations in the frequency or severity of storms, and the patterns of drought and flood — are at least still possible trajectories.
This is something that should be pointed out even more firmly than you do above, with more examples. The average of many chaotic trajectories is not a chaotic trajectory, and is not, in fact, a good predictor for any actual trajectory produced by the nonlinear system.
A final thing to note is that your examples above — Volterra-Lotke, iterated maps — are textbook examples (which is good) in very low dimensionality which is bad. The climate isn’t just nonlinear and chaotic, it is highly multivariate indeed and given that we have no idea what even its present state truly is to any precision at all any attempt to solve a climate system using time-local equations of motion necessarily makes a Markov approximation that cannot possibly be justified in what is a highly non-Markovian dynamical system. Variations well within our uncertainty (not a very difficult hurdle to jump, given that our uncertainty is enormous) in the state of the ocean alone could completely alter the pattern of chaotic attractors and cause the planet’s climate state to jump to almost anything quite independent of what CO_2 is doing. We don’t even have a good grip on the feedbacks involved.
And this is before one gets to the issues with data tampering and the incredible and systematic bias in the pattern of temperature “adjustments” that have been applied to the raw thermometric data to generate what is not presented to the public in the major temperature anomaly estimates. At this point we are building models to chase models built to alter the data so that it fits the models that people are building to fit the data.
It’s very amusing to look at North Carolina’s climate record, “unadjusted”. It is almost completely flat over more than a century. Yet the greenhouse effect should be (by its very nature) warming the planet everywhere, if one uses the linearization argument.
So we have an interesting pair of arguments that are mutually contradictory but are trotted out and presented at will. When we look at the flat, boring climate of NC (indeed of the entire continental US) that is to be expected, because the climate is chaotic and the heating is not uniform, some places are warmed by CO_2 and others are not or may even cool. But when we look at the global temperature anomaly (adjusted or not, for whatever average warming may or may not have occurred over the last 150 years) that we can explain as the linearized response of the climate to more CO_2. Both of these arguments assume that the average climate is stationary. But climate is obviously, empirically, manifestly non-stationary. Not even in NC is it stationary, however flat the overall temperature record is.
rgb
RB, well said,
If today’s public were truly aware of the on-going climate model pseudoscience and temp dataset adjustment fraud being foisted upon them by the Climate change witch-doctors, the CO2 swindle would utterly collapse. At some point in future history of science books, the public and science historians will look back on this IPCC period with a sense of both derision for the climate modellers (for advancing their obviously flawed outputs) and with wonderment at how so mainstream scientists uncritically remained silent and allowed it happen. (pursuit of funding grants and prestige, and fear of grant retribution is the likely human failure IMO).
Reply to Dr. Brown ==> Thank you for weighing in.
In this very introductory — almost kindergarten — essay, I hoped only to familiarize readers with the vaguest of issues surrounding linear vs. nonlinear dynamical systems.
In Part 2, I will introduce readers to some of the most common features of nonlinear dynamical systems, and in Part 3, make some vague, non-technical observations on why this should matter in our understanding of the world at large and in climate science in particular.
I have posted a Chaos Theory Introductory Reading List above (see the pull quote) for those intrigued or incensed by this piece today.
RGB, I concur this is a great article. Climate science was hijacked 25 years ago by space cowboys and computer geeks. They need to stick to data archiving with no adjustments allowed.
If you want a simple introduction to real climate science, which is a biological science, pick up a seed packet from a garden store and look on the back. You should find a map of climate zones something like this
http://planthardiness.ars.usda.gov/PHZMWeb/
By rights climate science is a taxonomy of real live biomes and as such can be mapped in real world terms, not computer guess work. If the real world were some average temperature, the map would be all one color, sillies.
Oh, I’d even allow adjustments, provided that two things were manifestly true when they were made. One is really simple. There is no a priori reason to expect “data adjustments” themselves for any of the usual statistical reasons/methods one might use to adjust data — rejecting some stations, accepting others — to be biased regarding sign. That’s why it is usually best to a) not adjust data except POSSIBLY to reject outliers so far away from the physically reasonable that they are probably errors; b) use random numbers and Monte Carlo as often as possible to ensure a random (iid) sampling. That way one assumes that the unbiased errors will, on average, cancel out when one uses the whole reasonable dataset. This is almost always best practice and is of course the absolute rule in most statistical analyses. If we are computing the mean height of eleven year old males, we don’t “adjust” the data by assuming at all measurements were made rounding up, we assume that the measurers rounded up or down indifferently and hence just use the measurements “as is”. In this case, we cannot even reliably reject most outliers because there are actual eleven year olds who may be much taller or much shorter than everybody else due to e.g. hormonal/glandular disorders. If we throw away a two meter tall eleven year old because that is “impossible”, we may be biasing our result as there might well actually be a two meter tall eleven year old somewhere in the world. There are certainly one meter tall eleven year olds who will never grow larger than 1 meter, even though nearly all eleven year olds are likely around a meter and a half tall. Sifting through the data one record at a time to sort all of this out means ultimately that you are going to apply a heuristic in a statistical computation and if you do it honestly it will cost you just about exactly as much in the precision of your final answer as your final answer would have been imprecise anyway — no real gain, just the impression of your heuristic on the final answer because it fits your preconception of what the answer “should” be.
If we look at adjustments to the temperature record, then, we would expect them to increase warming as often as they increase cooling. We can even compute the p-value for probable bias in the adjustments by applying the binomial distribution to the problem with p = 0.5. If nine adjustments have been made, and all of them produce more warming, that is unlikely in a world where errors are a priori distributed without bias at the level of 1/512, which permits us to reasonably reject the null hypothesis “there is no bias in the corrections being applied”.
The second case is trickier. There can easily be good reasons to think that there are systematic biases in the data record. For example, suppose that the dataset one is using to compute the average height of eleven year olds worldwide has been drawn 90% from U.S. middle school records collected over the last 165 years.
At the beginning of that record, one would be sampling almost exclusively white children, but the diet of those children would have been comparatively poor, the prevalence of childhood diseases (such as polio) that affect growth compartively high, and in those respects it might be unbiased relative to the rest of the world in those respects. The racial mix would still be a problem, as some racial groups are known (know) to have distinct average heights, moreso in the past before much racial mixing occurred.
Over time, however, the diet and healthcare of the children sampled in the record would have improved, and with it (almost certainly) the mean height. Child height is not stationary over 165 years almost anywhere on the planet. At some point black students would start being a substantial part of the record. At a different point hispanic students would become a substantial part of the record. By now the record would be sampling almost every racial group on Earth at some level, and the white/caucasian component would be correspondingly reduced. How can one use the (still mostly US) sample data to “correct” the average obtained both over time as the diet/health of US students diverged from the diet/health of the far more populous Chinese, or Indian or African populations, and for the non-stationary racial balance of global population?
The answer, of course, is that one can’t. Not without information that one simply does not have. If we had an equally reliable set of measurements of (say) the height of eleven year old Indian children, we wouldn’t use it to compute a correction to the US data, we’d use it in the computation. Now the dataset isn’t 90% or more US white kids in 1865. Of course we’d need to know the Chinese data as well. Note that India is not racially homogeneous, and that food and health are not uniformly distributed there either. Ditto China. There are very tall Chinese, and there are very short Chinese. In India the very tall are rather rare (to the best of my recollection). We’d need the African data. Note that collectively there are, and were far more of these children than there were in the US, that the US data only selected a biased fraction of all of the eleven year olds in the US, and that the probable biases compared to the rest of the world change over time.
The solution in real statistics is to take what data one does have, try your best to form e.g. regional averages over time, and develop the world average eleven year old height over the last 165 years with much, much greater error bars in 1850 than one has in 2015. The pristine US data you started with cannot be “corrected” to reflect this. If you have no data at all from China in 1865, you cannot even take modern data on China, compare it to modern US data, compute a “correction” or “scale factor”, and apply that scale factor to the 1865 US data and pretend that it now represents China too, because the mean heights are not stationary and have a time varying racial bias as well!
This is what the temperature records are trying to do, and yet somehow end up doing backwards. For example, we might well examine the US data and find that the non-stationary average height systematically increases from 67 centimeters in 1850 to 74 centimeters in 2015. Let’s call this correction the “Urban Diet Effect”, the combined effects of improving diet and healthcare plus the admixture of new racial groups. We are pretty certain that all the way to the present, this group has a substantially greater, systematically growing height compared to the average height outside of the group. We can sample (for example) the mean heights of all eleven year olds in 2014 with an unbiased sampling and in a truly global way, and find that at the present time the global average including the predominant rural population is only 71 centimeters. We are pretty sure that the US data has been too high across the entire range all the way back to 1850, but that in 1850 the correction is probably small. We can, and in this case probably should, try to build a model for data correction since for whatever reason we are constrained to use the biased, non-stationary, incorrectly localized US data to compute the whole height record.
One would guess that the effect of applying the model would be without question to cool the present relative to the past, systematically, over the entire record. Yet this is the one correction that HadCRUT4 does not make, instead applying a long string of other corrections that always end up with a net warming of the present relative to the past (and generating in the process a near-certainty of systematic bias somewhere, although they would argue that that bias arises from the way temperatures were measured in 1865 compared to the way they are measured today). GISS, IIRC, actually does include a UHI correction and somehow it warms the present as often as it cools the past! The one correction they can apply that almost certainly is actually biased in a monotonic way across the data they apply so that it works out neutral (and hence in “agreement” with HadCRUT4 that ignores it completely, two “independent” routes to the same desired result. Leaves me speechless.
In the end, the comparison of the “corrected” average to the simple average is pretty astounding. Something like half of the observed warming in the record is due to the corrections. In a sane and rational Universe, those corrections would have come with a cost in estimated error almost as large as the correction, because you cannot manufacture information you do not have by means of building a model of it, so building an imperfect model at all to e.g. interpolate, krige, smooth, infill, all comes at a substantial cost in error because one has to make Bayesian assumptions that one cannot usually justify and at the very least these approximations will smooth temperatures and hence cut off temperature extremes. For most of the spring, NC temperatures have been nowhere near their average. If we did not have the real data that revealed that, replacing its temperature with its average would simply have reduced the variance/error of the global temperature estimate at the same time it biased it high, but that reduction would have been entirely artificial.
The most telling symptom of this is in HadCRUT4’s total error estimate. It is just under 0.2 C at the present. It is just under 0.4 C in 1850. And that is absolutely, positively, totally absurd.
I’m very tempted to address the problem with anomalies in this same reply — again using the metaphor of measuring the nonstationary average height of eleven year olds from a biased (not independent, not identically distributed) sampling of eleven year old height data. In particular, consider this. The “anomaly” of this non-stationary distribution is (say) the difference between the true average over the entire record and the average in any given year. We’ve already agreed that the true average is enormously difficult to compute in any year — to put it bluntly, our uncertainty in global temperature today is around 1 C either way, which is actually larger than the 165 year “anomaly” change. Yet they assert that the anomaly is known to 0.2 C today, 0.4 C in 1850!
We are left with a statistical miracle as astounding as that of the loaves and the fishes. We don’t know the temperature of the planet in 1850 to within 1.4 C (being generous!). We don’t know the present temperature to within 1.2 C, which is also probably generous. But we know that it has warmed 0.8 C in the meantime.
Now, I could believe that if people recorded “anomalies” independent of the actual temperature data. This would be the equivalent of making a mark on the schoolhouse wall in 1850, and recording how much above or below that mark the height of eleven year olds were, year to year. We then would end up with no idea what the absolute height of eleven year olds was, but we might — I say might — be able to resolve a statistically significant trend in the timeseries data over 165 years as long as the schoolhouse never burns down, nobody replaces the floor, students don’t start to be measured in their shoes after 1870, etc. We might actually end up knowing the anomaly more accurately than the measurement itself.
However, that is not what we have. We have the actual heights, the actual temperatures. There is no point in forming a local timeseries, fitting a linear trend to it, computing an “anomaly”, and averaging the anomalies on a grid. Just average the damn temperatures on the grid! You cannot do any better than that! If students started wearing shoes halfway, or the schoolhouse floor sagged over the centuries, you aren’t going to magically eliminate that by means of averaging a fit to the data or a delta of the data any more than you would eliminate things by averaging the data itself. The problem isn’t that anomalies are better or worse than the data itself. It is that they inherit almost all of the problems of the data itself no matter what. You are still making an assumption when you elevate the anomaly over the straight average, and unless you allow for the extra error associated with the assumptions you will have the absurdity of knowing the change in height over 165 years more accurately than you know the height itself from the same height data!
rgb
I have recently published a study on this subject.
Adjustments Multiply Warming at US CRN1 Stations
A study of US CRN1 stations, top-rated for their siting quality, shows that GHCN adjusted data produces warming trends several times larger than unadjusted data.
The full text and supporting excel workbooks are available here:
https://rclutz.wordpress.com/
Linearized small changes in a nonlinear system are commonly used where the output control response is rapid and single step..
For example f(x) = sin(x), is of course is a non-linear equation. But over small values of x close to zero,
f(x) ≈ x.
In radians: (0.01 radian = 0.573º)
For example sin(0.01)=0.010000 (six decimal places).
sin(0.02)=0.019999
sin(0.03)=0.029996.
Thus (dx)/(dt) in a system of equations, as long as the deltas are small and the values of x are small, this linearization works quite well for functions of sin.
In control systems, where the angle inputs and deltas can be kept (physically bounded) small, then this approximation works well to linearize the control equations.
The big key CAUTION though is the system control error will rapidly increase if this approximation is iterated several or more times to achieve the output in phase delay. This is 1 big reason why linearized climate models fail, as the small errors propagate rapidly as the system equations are iterated in time, ie. the butterfly wing-flap in Brazil problem.
I would have stated this somewhat differently. For any continuous function of a single variable, say time, one can perform a Taylor series expansion of that function around any given reference time. The most general — if you prefer, “likely” case — in almost any such expansion is that the first order (linear) term will be dominant for sufficiently short times. One can of course generate exceptions or counterexamples, such as fitting a pure quadratic function around its minimum that has no linear term in the Taylor series, but at more general points even a pure quadratic will get the largest contribution from the linear term for sufficiently small steps away.
The problem is unless the system really is a linear system and has no quadratic or higher order dependence, if one keeps going away from the initial point where one linearized, eventually the higher order terms are quite likely to dominate.
This argument is quite general, BTW. I don’t really care what system(s) one is talking about. It is one of the many, many, serious problems with trying to statistically analyze a timeseries so that one can predictively extrapolate it. I’m tempted to just say “it can’t be done”, but that’s not entirely fair as all of human knowledge (including physics itself) is the result of a systematic process of self-consistent statistical extrapolation (inference). However, it is entirely correct to say that it cannot be done without making assumptions that are not, themselves, part of the timeseries data being fit. Assumptions like “the way physics worked yesterday and appears to be working today is going to be pretty much the way it works tomorrow”, which is (if you think about it) impossible to justify by any statistical extrapolation that does not beg the question. One can wait until tomorrow and go “Aha! I was right again!” and use that to strengthen your belief that it will be true for tomorrow again, but it is very difficult to explain why things that appeared to be true yesterday should persist in being true today, without assuming the conclusion. Hume noted this several hundred years ago, and it remains a predominant problem in the philosophy of mathematics and science today.
rgb
Reply to Joel Bryan and Dr. Brown ==> Yes and Yes. As we shall see in the next part of this series, nonlinear dynamical systems often start out quite well behaved, predicable, and offer useable practical solutions.
In the essay above, the squirrel population on May island is wonderfully well behaved, settling down to a steady state slightly above 0.6 of the island’s carrying capacity when the growth rate is below 3. Many, most, nonlinear dynamical systems have this trait — an apparent linear regime and devolving to nonlinear behaviors at some point. Below the point of transition to chaos, we use these functions every day in electronics, audio systems, dynamic fluid flows, etc.
Just an additional comment to the above. Many numerical methods of solving coupled (partial) differential equations work by linearising the problem, so taking small steps in time and space. As Dr Brown points out, this assumes that the higher terms of a Taylor’s expansion of the function in question. One difficulty in this approach is that to reliably linearise climate models, extremely small steps are required in both time and space, which imposes very large grids and very small time steps that is far beyond any computer.
The approach used is the parameterise the space and time meshes to enable a solution that is said to work. This is not necessarily correct because the parameterisation, that is used to compensate for the higher (non-ignorable) terms of Taylor’s series at large steps, is essentially an arbitrary interpolation. This is a real problem in mathematical analysis of cardiac activation and abnormal cardiac rhythms (highly non-linear) where very small changes in parameterisation lead to wildly different results and the meaning of the results in terms of what the heart actually does is questionable.
I had a large book on chaos theory but it was a bit too much for me to get to grips with, I could understand the flight or fight analogy where say a mother animal might back off from a predator then suddenly switch to another state of attack as distance to offspring reduced but I couldn’t see how that applied to air circulation.
I did have a star dot matrix printer tho’ and everytime I printed with it my crickets ( lizard food) would start chirping.
Reply to zemlick ==> Thanks, made me laugh. Chaos Theory is not for the timid…even at an introductory level. In our home, the lizard food always managed to escape and keep us entertained at night with their songs. My boys solved this my releasing a gecko to gobble them up — worked too.
While the gecko was growing up did you ever think to create a linear graph that projected when it would reach Godzilla-like proportions?
Reply to Piper ==> No, but it did eat a lot of escaped crickets! Crickets were easy prey as they couldn’t seem to give up the chirping that gave away their position.
I don’t mean to sound like a jerk, but I have found a lot of “chaos theory” — at least that which has a deterministic basis — to be very accessible, visual, and … well … easy to follow.
For example, the tome titled “Chaos and Fractals: Frontier in Science”, despite its imposing size, is really a rather fast read.
http://www.amazon.com/Chaos-Fractals-New-Frontiers-Science/dp/0387979034/ref=sr_1_2?s=books&ie=UTF8&qid=1426471178&sr=1-2&keywords=chaos+and+fractals
zemlik,
IMO ‘”fight or flight” doesn’t work in animal behaviour, either.
Some rather dubious overlap in physiological phenomena in situations that are far from being similar gives rise to a glib alliteration that seems immediately to make sense to people that, perhaps, have never had to fight nor flee.
To me, it’s like global warming causing cooling.
Fleeing is not a bit like fighting except for the exertion required.
It’s generally described as an immediate excitement of the sympathetic nervous system, but actually, I contend, the initial response to surprise is parasympathetic; the reptilian freeze manoeuvre. It may not last long but it’s the time it takes to realize that what has suddenly appeared before you is not a receptive female but a hairy predator.
Chaos is a good synonym for incomprehensible.
Climate models use non-linearity as a means to an end, averaging them out to produce their projections. Initiating atmospheric-oceanic conditions are randomly varied to simulate the random walk we call weather pattern variations. What they fail to understand is that at most, when fudge factors are removed, only a tiny fraction, if ANY, of their model runs will be the correct ones and will reasonably match observations. The problem with their “chaos runs” now not matching observations is that each and every run has the same fudge factor (a temperature rise “calculation” based on %increase in CO2/water vapor) applied regardless of initiating conditions, thus guaranteeing a rising result for each run. I wish I knew when that fudge factor is applied. Does it enter into the beginning of dynamical calculations or is it tacked on at the end just before the printer springs to life. I am guessing they tried it in the beginning but it either sent the results spiraling past reason or the chaotic nature of the system removed it. To me it seems likely this fudge factor is tacked on at the end to make every stinking one of those runs rise depending on how large the fudge factor is.
No need. The system of equations presumes detailed balance — in the long run, power in has to equal power out. In the dynamics they have terms that represent the greenhouse effect in the radiative transport of heat, attached to assumptions about the time variation of CO_2. As they turn up CO_2, this basically cranks all of the models in a certain (warming) direction along a partial derivative contributing to the overall global temperature. All that they then require is that more models produce (in response to this linearized additional driving) more warming than cooling.
Of course they do get hundred year runs out that produce little or no warming, or that even cool, in spite of the additional forcing. They in fact get a huge envelope of possible future climates, per model. Individual runs warm up far too much, then suddenly cool, then spike back up again. The annual through decadal variance of the individual model runs is many times greater than the observed variance, and fails to exhibit characteristic patterns (like warming in strong ENSO events) simply because the models cannot themselves generate strong or weak ENSO events, or predict any of the multidecadal oscillations, or predict the state of the sun, or predict what humans are really going to do, and of course none of the models is started out at anything like the correct initial conditions because those initial conditions are simply not known. The present conditions are not known, not on the scale needed to initialize the models (which is still far short of what it needs to be for the models to reasonably be expected to be accurate).
The failure of variance and autocorrelation is then hidden by averaging over many trajectories, and then averaging over many models, including models that nobody seriously thinks are right any more because they are seriously out of touch with observed reality — basically they are falsified by the data already but are still included in order to beef up the average warming. The variance of the superaveraged trajectories is still not right, but now it starts to “look like” it produces “realistic” fluctuations.
Nick Stokes recently argued to me that CFD codes work OK even though they don’t compute all the way down to the Kolmogorov scale. However, the counter argument to this is the following. Who in their right mind would ride in an airplane designed using CFD codes that showed in every run that stresses on the airplane would tear it apart, but where the average of those runs stayed solidly within safe tolerances? Who would ride in the airplane when it was easily shown in wind tunnel tests that the airplane design in question doesn’t behave like any of the individual runs or the average over those runs?
You can argue all you want to that CFD code, applied in a sane and rational way to problems that are sufficiently “smooth” and simple, can overcome at least some of the problems associated with meso-scale turbulence without going down all the way to the microscopic scale, but that hardly justifies solving the most difficult CFD problem in the world, an insanely difficult CFD problem, at a scale that doesn’t come close to the scales of many phenomena that are extremely important in its dissipative properties, in a way that no engineering firm would ever accept (for very good and sane reasons!) in the actual engineering of supersonic aircraft where making tiny mistakes in the design can cause the airplane to exhibit sudden, nonlinear, catastrophic failure.
rgb
Hi Kip Hansen – I am glad you are discussing this subject. Here are two of our papers that can contribute to this discussion.
Pielke, R.A., 1998: Climate prediction as an initial value problem. Bull. Amer. Meteor. Soc., 79, 2743-2746. http://pielkeclimatesci.wordpress.com/files/2009/10/r-210.pdf
Rial, J., R.A. Pielke Sr., M. Beniston, M. Claussen, J. Canadell, P. Cox, H. Held, N. de Noblet-Ducoudre, R. Prinn, J. Reynolds, and J.D. Salas, 2004: Nonlinearities, feedbacks and critical thresholds within the Earth’s climate system. Climatic Change, 65, 11-38. http://pielkeclimatesci.wordpress.com/files/2009/10/r-260.pdf
I also recommend searching on my weblog under this topic [https://pielkeclimatesci.wordpress.com/?s=chaos and https://pielkeclimatesci.wordpress.com/?s=nonlinear%5D
Best Regards
Roger Sr.
The second paper, especially, establishes something that I don’t emphasize enough because it is difficult enough to convey the notion of “simple chaos” but have been trying to nudge people on-list to understand at least in principle. The Earth isn’t just chaotic, it is complex. The problem with a term like complex is that it has many meanings (and I don’t want to explain, so I don’t use it in list discussions very often) but the sense in question is complex as in complex (highly multivariate) systems capable of spontaneous self-organization past some critical threshold, along the lines suggested by Nobel Laureate Ilya Prigogene. There is absolutely no doubt that the climate is a complex system, and in fact it may be that its complexity is even more important to understanding and being able to predict is nonlinear dynamics than it chaosity per se. For one thing, we have lots and lots of named self-organized climate structures — ENSO, the PDO, the AMO, the NAO, Hadley circulation, the Gulf Stream (indeed each and every named oceanic current), the jet stream, the monsoon — all of these are recurrent or quasi-stable patterns that participate in the transport of heat from where it is first appears as “new energy” in the Earth’s climate system to where it finally takes off for 3 K outer space.
A tiny variation in just one of these major patterns can have profound global climate effects. It can completely shift the “efficiency” of the system at moving heat from one place to another and hence the distribution of temperatures worldwide. ENSO rather obviously has just such an effect, often a persistent one. Within such a system responses can be completely counterintuitive. Increasing CO_2 could — as it warms the system initially — trigger the system to shift spontaneously to a new, more efficient dissipative pattern that rapidly cools it, quite possibly in a persistent way for timescales of centuries or more (until something shifts it back again). Not only can the system switch between two or more attractors, it can suddenly change the entire landscape of attractors, even without an external forcing change.
I plan to read the paper in some detail, as I did work on optical bistability back in the 80’s and the Earth is manifestly (when viewed at the right timescales:-) an optically bistable, if not multistable, system. Historically, it spontaneously switches regimes (accompanied by rapid warming or cooling), then slowly varies within a regime, then switches again. In even simple systems, the mean field equations exhibit things like hysteresis, dynamical critical phenomena, and much more. In a complex, messy, noisy, chaotic system those same phenomena occur but now resemble the original the way spiders on drugs weave webs that resemble normal spider webs. Unlike a regular web, where seeing one part of the pattern allows at least approximate reconstruction of the whole, the organization deteriorates until (on LSD) it is barely “a web” at all:
http://fractalenlightenment.com/600/chill-out/spiders-weave-better-on-lsd-25
That’s the interesting thing about adding CO_2. Are we adding an anti-psychotic drug to a system that is already crazy, stabilizing it before it might have plunged over the threshold into the next glacial episode, or is it more like LSD, something that destabilizes to where anything could happen — warming, cooling, nothing, both, wild oscillations between the two? According to the best evidence, the climate is already pretty psychotic, as likely to produce 200 to 300 year droughts across the entire Pacific coast as not if you look back over the last 2000 years instead of the last 150 years of comparatively adequate rainfall, and that’s without CO_2. With CO_2 does this become more or less likely?
This is hardly a silly question. Chaotic (simple) systems, chaotic (complex) systems, self-organized systems, have a variety of “critical points” where things can rapidly switch around, but they also have regimes where they do not switch around, where they are comparatively stable. At this point in time we have no idea at all whether adding anthropogenic CO_2 to the atmosphere has been the best possible accident, one that acts like a stabilizing agent so that global climate finally becomes as stable and predictable as climate scientists would have us believe that it would be without it, or is the trigger to a disaster. We don’t even know the sign of the temperature change in the disaster in the event that it turns out to be a disaster. We are decades of very hard work away from being likely to offer even marginally plausible answers to any of these questions — at this point in time we cannot even measure the state of the Earth’s climate system precisely enough to know what a single projection of it (e.g. “global average temperature”) is to within a whole degree Centigrade, and of course we probably don’t know the temperature in our own backyard or in a single cubic kilometer of ocean or atmosphere to that precision either.
rgb
Not a silly question at all – a very good one. Thanks.
Now that video was funny!!!
Explains a lot about why the Obama Admin is so incompetent… the drug-addled have risen to positions of authority in government. I’m just wondering who is the human US political equivalent of the crack spider? Maybe Putin? Maybe the Ayatollah? Maybe the Chinese owning the US national debt?
rgb, I beg to differ in terms of tiny things making big things happen. It takes a lot to scrub out a high pressure blocking system, a LOT of energy. Think jet stream energy. Big strong jet airplanes ride against it like a bucking bronco on speed and just after a hornet stung its nose. Riding with it results in a quick trip from point A to B with quite the jet fuel savings. I think we have been lulled into thinking that a butterfly’s flapping wings in one corner of the world can create a hurricane in another. I don’t think so. We may be missing the real causes by focusing only on tiny things.
Reply to Pamela Gray ==> You are speaking of the infamous butterfly’s flap….
What that is really about is “sensitivity to initial conditions”. One of my examples above speaks to this issue, in a very simple way. The graph is labeled 2×2-1 and shows orange and blue traces.
In this system, the initial input was changed from 0.54321 to 0.54322 — you can see the change in the numeric values and the behavior of the graph over time. Moving the change to the right even further, such as 0.543219876 to 0.5433219877 would only delay the arrival of the chaotic divergent behavior — but arrive it would. It is this feature of nonlinear dynamical systems that is referred to in the so-called Butterfly Effect. In the complex actual world climate, the eruption of a volcano in South America could change the weather in New York a week later.
Reply to Pamela. It is a matter of perspective – big things, little things.
Trying to tie Earth’s entire climate system to just one thing- CO2- is like saying you can predict everything I’m going to do today based on how much caffeine I had this morning.
Reply to Dr. Pielke Sr. ==> Thank you sir, for the compliment and the references.
The subject of “complexity meets chaos” probably is too deep for my 3-part introductory series — but of course, it is at, it may be, the very crux of the Chaos-Climate problem. (I see that Dr. Brown discusses this above).
No a volcano in South America could not change weather in New York a week later. For such a claim to be true there has to be an example of it ever happening.
:@TT
will this do ?
A volcano erupted in southern Chile early Tuesday
morning, spewing ash and lava high into the sky.(2 Mar)
http://www.accuweather.com/en/weather-news/thousands-evacuate-after-explo/43264196
Unusual temperature fluctuations about a week later.
From the graph we see that temperatures were higher than predicted,
http://www.accuweather.com/en/us/new-york-ny/10007/march-weather/349727
It’s an example of the weather in New York changing
about a week after a volcano erupted in South America,
Of course correlation does not prove causation, however
it is interesting nevertheless.
Kip, a very good article, thank you.
Would I be right in saying that anything linear must, by definition be very simple? For example your x2 analogy is a good one, but if it was changed to 2 squared eg 2, 4, 8, 16, 32 etc it would be a curve which is non-linear but still a relatively simple calculation.
Climate has very many variables and I would guess that there are too many to process even in a super- computer to get an accurate assessment. I would think that the mistake that the programmers have made when trying to predict GW is based on one factor (CO2 concentration). Therefore predictions are attempted on probably the most complex non-linear system that exists, with one linear variable (CO2 concentration), logically the models must always be wrong.
Reply to andrewmharding ==> “…anything linear must, by definition be very simple? ” Your “curve” is linear, but not a straight line. You notice at once that no angle is needed, and that every point on the curve is an input/solution pair, and that the whole is proportional. In that sense, it is simple.
I leave talking of climate for a subsequent essay in this series.
Thanks for reading and sharing.
See my essay above on complexity. Actually, there are a couple of them in this thread at this point. The fundamental microscopic interactions that govern all of nature appear to be linear, and “simple”, but in application they are anything but, because when you put many simple objects together, they can self-organize into new structures that are temporally persistent, namable, and that can have all of their properties and interactions given independent of the microscopic rules that give them birth.
More is different.
A fun example of this is Conway’s Game of Life (a computer simulation of a particular kind of iterated map intended to be a crude spatial representation of reproduction in nature). The rules for the game are very simple:
http://en.wikipedia.org/wiki/Conway%27s_Game_of_Life
(which includes a running example of a “glider gun”, BTW, as well as gives the four rules:-). Note that “gliders” are named objects that are commonly seen in the time evolution of many initial states, and that even these simple rules can produces temporally persistent, nameable, complex objects.
Another fun example is “you”. Microscopically your component parts are all, as far as we can tell so far, governed by strictly linear, reversible interactions. Macroscopically you yourself don’t know what you’ll do ten seconds from now, even though the you of ten seconds from now will do it almost without thought (or almost AS the result of a continuous thread of thought that is in no possible way “linear” or “simple”).
rgb
“Would I be right in saying that anything linear must, by definition be very simple?”
Not really, you can have very complicated linear dynamical systems (but I doubt that many people on this thread even know what a linear dynamical system are).
The worst example of “linearizing a non-linear system” must be the entire concept of ECS (Equilibrium Climate Sensitivity)… the temperature change resulting from a doubling of CO2 equivalent.
The natural log is not a linear function, so this simply isn’t true. What you mean to say is that when they idealize the climate system and show that the idealized system will warm (on average) by around 1 C per doubling of CO_2 in a first-principles computation (but one with many idealizing assumptions and neglecting a ton of other stuff going on) that is far from sufficient proof that warming will occur, on average, according to this functional prescription. I agree — it is reasonable, but far from sufficient or proven. Going beyond this and presuming we know the feedbacks from things like water vapor and cloud albedo and plant growth in response to a doubling of CO_2 and using them in an even more idealized model to conclude that we’ll still follow a logarithmic schedule but now warming will be doubled, or tripled, per doubling of CO_2, is to add unverified insult to unverified injury. It is still reasonable, BTW — it’s just that the assertion needs to be taken with a great big grain of error bar salt. A warming of 1 C plus or minus 2 C is more like it. Although how one would reasonably estimate the probable error is not an easy question.
The best statement of this is probably: All things being equal, we expect (for sound reasons) a temperature increase of around 1 to 1.5 C per doubling of CO_2 from the direct effect of the CO_2 on the equilibrium temperature. But since the natural variation of the temperature independent of the CO_2 is not known or computable, since the feedbacks are not well understood or computable, since attempts to compute both are in poor agreement with past observed temperatures or weather patterns, the safest thing to say is that we don’t know any more than this. The actual change in temperature from all factors including ones we do not know or fully understand yet could be bigger, or smaller, or zero, or even negative.
We just don’t know.
But still, the 1 C per doubling is a good and reasonable baseline estimate, one well-justified by physics.
rgb
Well said. That needs to be pointed out incessantly since most people have no clue about the mathematics involved in describing the systems that are used to predict weather. It should also be reiterated on a daily basis that no climate model has any predictive power whatsoever — even when starting from known conditions. Lorenz showed that, but the busybody know-it-alls forever ignore that detail.
What it comes down to is that Green has replaced Red and the color of oppression.
Westerners are particularly liable to this sort of straight-line thinking. SE Asians, and Easterners generally, tend to think that a straight line is likely to run out of steam and return to normal or the mean–or even to morph into a contrary trend. They see reality as cyclic, not progressive. See the book, The Geography of Thought: How Asians and Westerners Think Differently … and Why, here:
http://www.amazon.com/Geography-Thought-Asians-Westerners-Differently/dp/0743255356/ref=sr_1_1?ie=UTF8&qid=1426445166&sr=8-1&keywords=the+geography+of+thought
Reply to rogerknights ==> Thank you for the reading suggestion. I studied Eastern Religions at university and am somewhat aware of the vast difference in basic cognitive approaches in life. Hope my library has a copy!
University of Palembang, Sumatra, Indonesia,
uses this book as part of the Geography coursework
http://v.ht/37nF
The IPCC correctly stated that climate is nonlinear and therefore cannot be predicted. However without telling you, they do assume that the statistical properties of the climate can be predicted by the models. If that weren’t true, the entire program would be worthless. It turns out that a deeper understanding of nonlinear dynamics does make the whole program worthless.
Let’s suppose that I have a mini-climate model that is supposed to predict the climate of Boston. Since it is nonlinear, the results will depend on the initial conditions. If I enter today’s noon temperature as 40 F and run it forward for a year, it might predict 39 F. Since I know there are errors in the temperature measurement, I enter initial temperatures of 39 F and 41 F. The one year predictions for them turn out to 50 F and 27F. This confirms what is known about nonlinear systems, it’s not possible to make good predictions due to sensitive dependence on initial conditions. However, I can run my model for, say, 100,000 model years and collect information on the average temperature, the average high and low, and the maximum high and low. [1] What I will find with the “simple” nonlinear system is that the statistical properties will be the same for any reasonable range of initial temperatures.
Now suppose that I add pressure, wind speed, and several other variables to my model with all their equations and nonlinear couplings to each other in an attempt to improve my model. Since I know that I can’t predict the future with any accuracy I simply plug in 40 F for today’s temperature and crank away for 100,000 model years and extract all the averages and ranges. The results look like Boston weather, more or less. Just to be sure I restart the model with a temperature of 41 F and repeat the process. But instead of getting Boston weather, it looks much more like the weather in Rio de Janeiro. Uh Oh. Try 39 F. This time it’s the South Pole. Double Uh Oh.
This requires further investigation so I restrict the initial temperature to the range 40 +- 0.1 F and choose a bunch of random temperatures in that interval. The same thing happens. Some initial conditions lead to the climate of Boston, but others produce Rio or the South Pole. Try again but with a really tiny range of +- 0.00001 F and the same thing happens again, there are initial conditions in that range that lead to each of the three different climates. It turns out that no matter how small the range is there is no way of telling whether a particular starting point will lead to the climate of Boston, Rio, or the South Pole. After plotting which point leads to a particular climate, it turns out the initial conditions for Boston live on a fractal, as do those for Rio and the South Pole, and the fractals are intertwined.
So I now have a model in which I not only can’t make predictions of the future with any certainty, the model has multiple futures and there is no way of knowing which future will appear when setting the initial conditions because of the fractal structure.[2]
The net result is that there are two kinds of sensitive dependence on initial conditions in nonlinear systems: (1) predictions of the future are uncertain; (2) there may be multiple mutually exclusive futures and which future will appear is unknown.
Current GCMs have many, many variables. It would be stunning if they didn’t exhibit both uncertainty in their predictions and uncertainty in what the stable climate would be in the distant future. It’s not even clear that they have the computational power to investigate this problem by running the climate models for thousands or millions of model years.
[1] The model has to be run for many model years to get rid of transients and arrive at a stable climate. One usually throws out early years, say the first 10,000 to be sure.
[2] This was first discovered about 1985. Google “fractal basin boundaries” and the names Grebogi, Ott, and Yorke for technical papers with lots of pretty pictures that discuss this phenomenon.
What are the statistical properties of a non-linear climate?
I would imagine that to select statistical choices, one needs to know well the function from which you are selecting. We admit we don’t know the function.
I appreciate your model runs and initial condition considerations. Revealing, thanks.
Reply to Paul Linsay ==> Paul, you’ll have to read Dr. Brown’s comments (rgbatduke) if you want a deep discussion of climate models and chaos. That is above my pay scale as they say.
Bubba ==> There are and have been attempts at making predictions based on stochastic systems and data (think, stock market hourly averages) My simple analogy is that making 100 wrong predictions based on the wrong formulas arriving at 100 wrong answers and then averaging the results….you give me the chances of arriving at a correct prediction.
“However without telling you, they do assume that the statistical properties of the climate can be predicted by the models.”
It isn’t the IPCC that isn’t telling you. It is those who pass around the truncated quote that heads this article. It goes on to sat exactly that:
“In sum, a strategy must recognise what is possible. In climate research and modelling, we should recognise that we are dealing with a coupled non-linear chaotic system, and therefore that the long-term prediction of future climate states is not possible. The most we can expect to achieve is the prediction of the probability distribution of the system’s future possible states by the generation of ensembles of model solutions. This reduces climate change to the discernment of significant differences in the statistics of such ensembles.”
Nick, let me be clear. The ‘statistical probability distribution of such ensembles’ that you conjur cannot be determined from AR5’s meager 107 individual runs from 42 distinct models. Especially under nonlinear dynamic conditions. RGBatduke has railed sufficiently against that sort of nonsense on this thread and elsewhere. Take that up with him (pro wrestling tagteam). Now, if your team could produce, say 10000 simulations and make a Monte Carlo arguement, we mighthave a discussion about statistical sufficiency. But you cannot because of Turing imcomputability, even with AR5 inappropriately large grid scales that force parameterization of essential GCM climate processes like convection cells, which inevitably introduces attribution assumptions (ah, which themselves result in the ever growing model/pause discrepancy). The more the rest of us understand this stuff, the more your team ‘loses’. First rule of Army holes: if in one and want out, stop digging.
Nick, the point of my comment is that in a model as complex as a GCM there are many different “climates” possible, each with its own unique statistical properties, and it’s impossible to predict which one is being modeled since initial conditions arbitrarily close together can lead to wildly different “climates”. R.G. Brown mentioned above that the models do exactly that in his comments at 11:46, confirming what I expected. It’s meaningless to average the statistical properties of these various “climates” together since it does not represent the dynamical properties of the system you are studying. It is as if you averaged the properties of all the planets together and claimed that you understood the solar system.
Ishould have referred to my original comment. Does averaging the climates of Boston, Rio, and the South Pole produce anything meaningful? I’d say no.
Nick
Okay, where is the hard work that starts with the full climate system and shows that there is a subset of effective equations that will predict the ensemble of possible states. This is the same question as has been repeatedly raised by RGB. There needs to be some convincing showing that you can integrate out all of the irrelevant chaotic variables and arrive at the properties of the ensemble. Where is that work?
Almost precisely correct. I’d only add a couple of words. Is there a subset of the effective equations (computed at what there is absolutely no good reason to think is an adequate scale — the scale is determined strictly by the fact that it is the finest scale we can afford to compute at all, not because there is some argument that says “Gee, let’s use 100 x 100 x 1 km x 300 second granularity because we know that will work well for problems of this sort because… (list of reasons)”) that will predict the ensemble of final states accurately, in a way that we can have any statistically justified confidence at all?
What would the answer to that question even look like? This isn’t just a one-off problem compared to the rest of computational fluid dynamics. It is so far beyond the capability of ordinary CFD applied to enormously simple geometries that it isn’t in the same computational universe of solutions. It’s eerily similar to the problems of artificial intelligence, where we have to believe that our intelligence arises out of a functioning neural network but where any attempt to make a neural network that does anything but simple classification problems that bear no real resemblance to mentation fail miserably because we have no idea how to design a neural net with the right internal structure to give rise to the complex phenomena of actual intelligence, we can at best get some behavior that “looks intelligent” compared to random chance. People generally do better with AI with deterministic or stochastic rules based systems because we can make some sense of the “quasiparticles”, the persistent structures of decision making and stimulus-response. The planet’s climate is in many ways similar to the “thought” of a living organism and is just as difficult to predict. I’ve often thought about building a planetary neural network and training it to predict the climate, but neural networks suffer from the same problem of extrapolation as any other model — they do well at modelling observed behavior that in any reasonable way interpolates the past training data, and get increasingly unreliable when they are used for inputs far beyond the inputs used to train them. They also look for “easy” solutions that may be wrong at the expense of correct but more complex solutions.
The only way I can think of of validating climate models is by (gasp) comparing them to the real world. Sadly, when we do their output fails in many ways quite aside from their failure to predict anything like a reliable future temperature! Indeed, that’s one of the least of their problems — to be expected in a chaotic turbulent nonlinear highly multivariate dynamical system. It is things like the wrong spectrum of correlation times, the wrong dynamical variance per run that people should be worried about.
It’s always fun to post figure 9.8a of AR5:
http://www.phy.duke.edu/~rgb/Figure9.8.jpg
People miss the forest for the trees when they look at the “spaghetti” in this graph. This spaghetti isn’t even individual runs. They are results from all the CMIP5 models. Note the variance! Let me say that again: NOTE THE VARIANCE! The models are running peak to peak variances around whatever their “mean” behavior is supposed to be that are between two and four times larger than the actual variations of the real climate! There’s one classic example over near 1890 — a red trace that varies by around 1 C over a single year! Down and then right back up!
Say what? this behavior has never been observed in any part of the climate record. It is absurd. No reasonable solution to the climate problem can exhibit behavior like this and be taken seriously. It is badly broken.
Why is this model still in the ensemble?
Yet this behavior is visible in many colors across the entire record. In fact, the only place it isn’t visible is (surprise surprise) in the reference interval where the models magicall see to settle down to having only twice the expected variance and with fewer of the bizarre peaks.
The problem is especially visible post the reference period. The models all vastly overestimated the response to Pinatubo (by roughly a factor of 3). It’s not clear if they are responding at all to the super ENSO of 1997-1998 or if they are just both warming and rebounding from the too-deep dip they gave to Pinatubo. Warming seems most likely because they continue to sweep up at an almost unchanged rate across the entire Pause, where they don’t just get the mean temperature wrong, they are getting the variance wrong by at least a factor of five.
The models in this graph have:
a) Absurd, non-physical variance across almost all of the record. This variance cannot be written off to chaos — these are deterministic local models and if they don’t get the right variance, then from the fluctuation-dissipation theorem they have the wrong dissipative dynamics, end of story (since gettting the dissipative dynamics right is the name of the game here).
b) Absurd, incorrect autocorrelation times. It isn’t just the magnitude of the swings, it is their spectrum, which appears to me to eyeball out just plain wrong compared to the actual climate. Here 165 years is admittedly a short span to be sure as the autocorrelation time of the actual climate appears to range from ballpark 5 years to whatever and obviously getting an accurate spectral decomposition on longer times is increasingly problematic, but it looks to me like there is already a problem from 1 to 10 years for many of the models that is within the resolution of the data.
c) The wrong MME mean over climactically significant parts of the record. This isn’t surprising, as the MME mean has no physically or statistically justifiable meaning, especially when one leaves egregiously incorrect physical models in it contributing on an equal basis with models that are actually getting some of the stuff above much more nearly right.
d) And finally — wait for it — post 2000 it very much appears as though the actual climate is pulling right on out of the ensemble envelope itself. Which in statistical parlance means — since nature isn’t broken, it is nature — that it is very, very unlikely that the statistical ensemble of models is in fact a good representation of the actual dynamics of the climate.
Taken all together, I think that the probability that the CMIP5 models collectively represent the climate in a statistically meaningful way is well under 0.001. If one looks at individual models, one might find that a subset of them — perhaps less than 1/3 of them — are not individually rejectable as having the wrong dynamics via fluctuation dissipation or absurdly incorrect mean behavior. If you redo the average with the successful models, something like 2/3 of the predicted warming will disappear — and we will still have no particularly good reason to think that those models are within a country mile of having the right dynamics, especially dynamics that can be integrated 100 years into the future to give a meaningful answer there.
rgb
RGB: “… If you redo the average with the successful models, something like 2/3 of the predicted warming will disappear — and we will still have no particularly good reason to think that those models are within a country mile of having the right dynamics.”
And thank the roll of the dice that they didn’t by pure accident get a good fit earlier on or we would already have shut down fossil fuels, been taxed to death and they could claim the pause was due to their quick action to save the planet. It would take to the end of most our lifetimes to make the discovery that the projections and the theory are lacking.
It’s sort of maths.
If a person sets off in the morning and walks up a reasonably sized mountain then spends the night at the summit and walks down the same path.
The statement is that he will at some place be at the same place at the same time as he was the day before.
Because send a person walking up the mountain following exactly that person’s footsteps from the day before at some place they will meet and it will be the same time.
The inevitability of that has always bothered me.
I’m not sure if there is anything there. because that is another day, everything has changed.
In concept that might happen, but it won’t because everything has changed 🙂
“…we should recognise that we are dealing with a coupled nonlinear chaotic system, and therefore that the long-term prediction of future climate states is not possible.”
That doesn’t matter if we can predict statistical summaries (functionals of distributions in mathematics) such as mean, variance, median and other quantiles. We can not predict when the next heartbeat will occur, but we can show that mean heart rate is reliably related to drugs, body weight, and exercise routine. No one can predict the exact airflow over a wing and wing tip, but engineers can model realistically and accurately the wing lift and drag as a function of velocity and air density. The Earth mean temperature has increased about 0.9C since about 1880; we do not need to know the exact evolution of wind and temperature in each small region of the Earth, we need to know whether, and if so by how much, that increase has been caused by the accumulation of CO2 in the atmosphere; and whether reducing CO2 will change the future and if so by how much. There is an apparent 950 year period in the global mean temperature over the last 11,500 years; we do not need to know next year’s mean temperature and rainfall in Tallahassee, FL or Karachi, PK, we need to know whether that apparent periodicity is the result of a persistent and reliable physical process that we can study.
One can’t predict statistical summaries of unknown functions, but I take and appreciate your point to be that is all distraction form a focus on the CO2 villain (or champion). Of course, they preselected CO2 to focus upon and I believe it an excellent choice for its additional capacity to distract focus.
Bubba Cow: Consider another example: Romps et al calculated that a 1C increase in global mean temperature would cause a 12% (+/- 5%) increase in the cloud-to-ground lightning strike rate in the US east of the Rockies. Right or wrong, the result does not depend on the ability to predict from a model where and when the lightning strikes will occur.
I disagree. Earth’s climate is not an airplane wing or a human heart. The whole point of this article is that chaotically-coupled systems are not predictable, statistically or otherwise. Read rgbatduke’s comment:
“…the state of the ocean alone could completely alter the pattern of chaotic attractors and cause the planet’s climate state to jump to almost anything quite independent of what CO_2 is doing. We don’t even have a good grip on the feedbacks involved.”
As an electrical engineer, I know that a circuit with multiple positive and negative feedbacks can, and most likely will, respond completely unpredictably to a given input.
Reply to Eustace Cranch ==> Thanks for the Electrical Engineer input. To eliminate this problem, we used to use breadboards 🙂
The human heart analogy is especially interesting, given that many forms of heart failure and death are signalled by period doubling as a route to chaotic defibrillation:
http://www.scholarpedia.org/article/Cardiac_arrhythmia
The heart can beat perfectly normally in a young person with no apparent sign of heart disease, and then go into a malignant rhythm almost without warning because of things that in another “identical” person or even the same person on a different day might not have. Some people, sometimes, react to cocaine that way (see e.g. Len Bias and the cause of his death, even though many people have had just as much cocaine and not had a fatal arrhythmia, quite possibly including Bias himself on earlier occasions — one can hardly argue that he was not enormously cardiovascularly fit but died anyway — from chaos).
As for airplane wings — are you serious? Do you have any idea how delicate and carefully the design of the entire airfoil has to be when one passes certain critical thresholds, such as the speed of sound? But even then planes sometimes just rip apart in midair “for no reason”. Why? Probably because at certain thresholds a malignant period doubling route to chaos exists in the turbulence that kicks it from being spectrally predictable and ignorable to where it creates (suddenly) huge overpressures as certain fluctuations are amplified instead of being damped. In smooth air, those fluctuations are rare and the plane is “safe”. But in the wrong kind of turbulent air, the plane gets positive feedback and those fluctuations can grow and do annoying things like strip a section of your wing or pop your tail off. The whole supersonic transition is even worse — as you approach the speed of sound the character of the dynamics changes and lift changes and drag changes and bluff surfaces facing forward become so unstable that they can easily tear the plane apart in a fraction of a second. Read a book about the quest for supersonic flight and all of the disasters that occurred in world war II as airplanes inadvertently got close to it and discovered that their control surfaces no longer functioned and they could not pull out of a dive, or their tails fell off trying. Supersonic aircraft are shaped the way they are for a carefully computed and empirically verified reason, because I very much doubt that any airplane manufacturer would bet the lives of pilots and passengers on an airplane design that had never had empirical verification in a wind tunnel no matter how brilliant it was on the computer…
rgb
Eustace Cranch: The whole point of this article is that chaotically-coupled systems are not predictable, statistically or otherwise. Read rgbatduke’s comment:
That “whole point” was the very point that I was disputing. Their are lots of examples in dynamical systems theory and its applications in which statistical summaries have been computed. Let me repeat the Romps et al example: they may be right or wrong that a 1C increase in global mean temp will produce a 12% +/-5% increase in lightning frequency, but the chaotic nature of either climate in general or lightning generation in particular is relevant to the argument, and there is no necessity to predict exactly when and where lightning discharges occur.
rgbatduke: Supersonic aircraft are shaped the way they are for a carefully computed and empirically verified reason, because I very much doubt that any airplane manufacturer would bet the lives of pilots and passengers on an airplane design that had never had empirical verification in a wind tunnel no matter how brilliant it was on the computer…
I think you missed my point: much useful information can be acquired about chaotic systems despite the fact that we can not predict their time courses exactly. Of course the “knowledge” must be “tested” before we can refer to it as “knowledge” — did I say different? But the unpredictability of specific trajectories does not imply that useful models of summaries (total lift, effectiveness of heart medication) are impossible. Nothing you wrote in response to my comment supports the main thesis of the leading post.
Sure, but precisely why do you think you can believe the models more than you can believe the simple, actually computable, physical estimate of ~1 C warming per doubling of CO_2?
Also, given the enormous range of results obtained from the models, why do you think that the mean of this range is physically meaningful, even if we could assume (which we cannot) that it is possible to solve the problem at all at the current granularity?
Finally, you assert a 0.9 C increase “since 1890” as a given fact, without (as usual) giving even the acknowledged error bars. In the case of HadCRUT4 the acknowledged error in the vicinity of 1890 is around 0.3 C. In the year 2014 it is around 0.2 C. Ignoring the fact that this is batshit crazy absurd, the 0.9 C you cite is uncertain to at least 0.5 C, and that is the acknowledged possible error, and does not include any UHI correction (which should be a strictly cooling bias that HadCRUT4 does not account for, although they eagerly enough include a whole pile of “corrections” that produce more warming).
Our knowledge of the rise is therefore rather uncertain. Perhaps it is enough to state conclusively that it has gotten warmer, but we don’t know by how much. It is pretty certain that it hasn’t gotten any warmer since 1890 in the state of North Carolina, where I happen to live. The linear temperature trend for well over a century of NC data is flat as a pancake (that is, it goes up, it goes down, but there is zero trend). This is a bit difficult to understand or explain in terms of CO_2, since well-mixed CO_2 should warm the entire planet. It should at the very least be keeping NC winter nights warmer than they otherwise would have been. But there is no trend, certainly nothing like the 0.9 C you assert for the entire planet taken as a whole.
I agree that we “need to know” many of these things, but that my need to know something is no guarantee that it is possible to build a model that will tell me what I need to know, or that data exists that will tell me what I need to know either. A model built to replace the missing data really, truly isn’t guaranteeed to tell me what I need to know. All it will do is tell me whatever the model tells me, not what reality actually was, and without the “reality check” the model could be completely wrong and no matter how badly I need to, I’d never know it.
rgb
Finally, you assert a 0.9 C increase “since 1890″ as a given fact, without (as usual) giving even the acknowledged error bars. In the case of HadCRUT4 the acknowledged error in the vicinity of 1890 is around 0.3 C. In the year 2014 it is around 0.2 C. Ignoring the fact that this is batshit crazy absurd, the 0.9 C you cite is uncertain to at least 0.5 C,
No dispute from me on that score, but one post can not address every issue in sufficient detail for all without being infinite in length. With an uncertainty of 0.5C one accepts that the true value could exceed 1.4C with non-negligible probability. The important thing going forward is that we are now collecting better data for use in future decades. I have criticized what I have called “exaggerated” predictions of future warming elsewhere.
Meanwhile, Next Dec in central Missouri will have a higher mean temp than next July in central Missouri. It would be nice to know whether either mean will increase in response to increased CO2 (or has increased in response to increased CO2), but we do not need to be able to predict the temp at any place, or date, or time in order to have a model adequate to the purpose. We do not now have such an adequate model, but we know enough about mid-Missouri climate to get a car that has a heater (that will sound absurd, but I did once meet a man from Belize who bought a car without a heater, and then drove from NY to CA in March), or carry warm clothing if we plan to take long hikes on December and January Sunday mornings.
mrm: Next Dec in central Missouri will have a higher mean temp than next July in central Missouri.
oops. That was backwards.
To me, the article lacked a certain amount of clarity about the differences between systems that are: linear, non-linear and chaotic.
A linear system obeys the law of superposition and is time invariant. This implies that the transfer characteristic will pass through zero. That is zero in will be zero out. The transfer characteristic will aways be a straight line. This implies that there is more to a linear system than just varying the output in sympathy with the input. Non-linear systems can do that. Basically, the concept of linearity is just a simplification that permits some mathematical analysis.
The guitar distortion referred to can be caused by limiting the possible output range of the system. However, the process is well-defined and repeatable. A chaotic system may be predictable but only if you know all the initial conditions exactly. You may well need to be more exact than most computers can easily simulate and you cannot guarantee to even have a complete list of all the relevant initial conditions.
I would also be stronger about the “vanishingly small” number of linear systems. There are no linear systems in real life. The best we can expect is that a system can be considered linear over a small range.
For instance, the most linear electronic component I can think of is the humble resistor. It follows Ohm’s Law over a small range but there could come a time when you apply too much voltage and the device will fail. At this point, both its linearity and its time invariance will have failed. Even before that point, the resistor will heat up and increase its resistance. The plot of voltage against current, the transfer characteristic, will then become curved.
Reply to graphicconception ==> Yes, that is one of the many definitions for linear systems. We are introducing a topic, and I offer Lorenz’s simple definitions of linear and nonlinear. Lorenz uses the characteristic of proportionality of input to output as his defining point.
“Vanishingly small” covers the chance that someone could come up with a real world natural dynamic system that is linear at all possible values.
“Lorenz uses the characteristic of proportionality of input to output as his defining point.” Superposition is a better basis IMHO. Otherwise you won’t be able to explain how you can input a square wave to an amplifier and not get a square wave out yet the system is still working within its linear range.
If you decompose the input signal into its Fourier components, each component can have its own transfer characteristic slope. They don’t necessarily have the same one.
As for “… linear at all possible values” that list will include infinity. Real world systems cannot cope with that. That is why I say there are none.
@ graphicconception. Its in the details. The essay states that Lorenz used “Linear system: A system in which alterations of an initial state will result in proportional alterations in any subsequent state.” Which of course is a very different statement than Kip uses above.
I believe that that the definition that Lorenz use is kind of correct for a system without inputs. The one that Kip used above is of course completely wrong though.
The superposition principle is probably the best one to use and is the one most often used.
A linear system doesn’t need to be time invariant by the way.
The IPCC has long recognized that the climate system is 1) nonlinear and therefore, 2) chaotic. Unfortunately, few of those dealing in climate science – professional and citizen scientists alike – seem to grasp what this really means
This statement is a lilttle presumptious and probably incorrect. Kip. Damages légérement your argument.
Reply to Stephen Richards ==> Read the comments — you’ll see that my statement is correct. There are a few here that have a good grasp on the subject matter — but not that many.
So you really believe that all non-linear systems are chaotic? I am not sure if anyone here has a good grasp of the subject matter and that includes you.
I agree with the coupled and non-linear aspects of climate, not so sure about whether or not chaos is relevant. Turbulence is chaotic and affects aircraft and plumbing systems, but both are adequately predictable. I’d say it was more the coupled and non-linear aspects that make the climate unpredictable, simply because most of the many variables are unknown functions of many of the other variables.
Reply to climanrecon ==> The very nature of the atmosphere that troubles man, and makes the most differences to our everyday lives, are based on the turbulent, the chaotic — thunderstorms, hurricanes, tornadoes, downdrafts, unexpected sudden shifts in the jet stream…..endless list.
It is the IPCC that says “the long-term prediction of future climate states is not possible.”
climanrecon
March 15, 2015 at 12:28 pm
“Turbulence is chaotic and affects aircraft and plumbing systems, but both are adequately predictable. ”
Parametrized simplifications of known wing geometries can be sufficiently well modeled. The real happenings cannot to this day, otherwise we would have long stopped using real wind channels. Because of the microscopic origins and rapid developments of turbulences (amplifying distortions, which is the essence and origin of chaos).
Great article for the discussion generated. The part of Alan’s blog that’s so refreshing is actual science gets discussed in the comments section. Bravo
The climate seems chaotic, because it depends on changing conditions of space. Many of them can not predict. However DEPENDING exist.
Kip,
I would have said just a little more about linear solution spaces before making the jump to nonlinear ones. The point being that the *solutions themselves* don’t have to look like straight lines for linearity to be present (in the sense we wish to discuss it). For example, suppose that both sin(t) and e^t are solutions to some linear model. Then A sin(t) + B e^t is also a solution, for any values of A and B. I.e. if you saw the system behave like sin(t) in one circumstance, and saw the same system behaving like e^t in another circumstance, you could very easily imagine a new circumstance in which the system would behave a little like both — you could predict the existence of a third circumstance in which it would behave like A sin(t) + B e^t. Your ability to make this kind of linear extrapolation is what goes out the window when your system is nonlinear.
I don’t mean to lecture you, as you are doing a very important service, and I’m sure you know more about nonlinear systems than I do. I only want to make the simple conceptual point that we’re not just talking about *solutions that look like a line.*
Reply to Metric ==> Of course, there are always deeper nuances — linear can be curved as well. Proportionality of outputs to inputs is Lorenz’s key. This is, as explained, a kindergarten introduction 🙂
I bring it up because I can see the following frustrating situation happening. A reader comes away with the impression that “climate modeling is likely to be inaccurate because the modelers are applying a linear model to a nonlinear system.” Then they go and look at a climate model prediction and see something that is definitely not a straight line and think “oh, that criticism must be outdated — they are clearly not just doing linear extrapolations anymore.”
Reply to Metric ==> At some point, we hope that readers can, well….read…. and that giving definitions will help them.
I had trouble finding an example from a homemakers life that would produce a linear, but curved, graph that they would be familiar with.
Thanks for the help.
[Solubility of salt in water, and sugar in water as temperature goes up. .mod]
Thanks again .mod!
Also every harmonic oscillator in existence. A simple harmonic oscillator produces those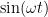
solutions that are so superimposable because the equation of motion is a linear, second order, ordinary differential equation. When things get nasty/chaotic is when you add a nonlinear driving term and/or when you make the ODE itself nonlinear (which just means that it has terms in it that are powers of the solution or derivatives of powers of the solution being sought with the power in question not being “1”).
, 
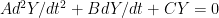
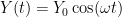
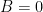, and the right initial conditions. A pure harmonic solution.
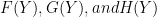are completely general nonlinear functions of 
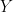. Here one obviously has enormous problems right out of the bat. For one thing, demonstrating that bounded nontrivial solutions exist at all for a given 
combination is a prior chore — there is no reason to think that they will and it is easy to find combinations where they won’t. Indeed, it is probably correct to say that for nearly all combinations they won’t, but this isn’t my own mathematical forte so don’t quote me on that one as an expert.
are themselves nontrivial functions of t and/or Y and not constants. Things get more complicated but are still linear in 2 and 3 D as well — but I’m not going to do an essay on elliptical PDEs at this particular moment. When you put a function of t in place of the 0 on the right you get inhomogeneous versions of the ODEs and a whole new solution methodology is required, searching for particular solutions to the inhomogeneous equation and adding them to solutions to the associatedc homogeneous equation to get a general solution to an initial value problem. The point is that if one takes an equation like:
you will get nice, tame, linearized motion where the oscillator eventually oscillates pretty much at frequency 
. Then you’ll hit a regime where you see a double oscillation in steady state. Tweak and there are four oscillation ampltudes in steady state. Tweak and tweak and the system is suddenly chaotic, unpredictable, aperiodic, where teensy changes in the initial conditions lead you to final states that fill the entire phase space of energetically allowable states after the transients have died out.
is the general second order linear homogeneous ODE. Its general solutions are exponentials. For some ranges of A, B and C those solutions are real exponentials. For others they are complex exponentials. Certain linear combinations of complex exponentials are the trig functions cosine or sine. Hence a solution might look like:
for
A general nonlinear second order homogeneous ODE cannot be written down sensibly as there are an infinite number of them. Something like:
might do it, where
This is the way the mathematics of this stuff looks. Nearly all 1-D equations of motion in physics can be put into a form “like” the first equation where superposition works, even when
which describes a rigid pendulum being driven by harmonic driving torque with an arbitrary amplitude and frequency, for some values of the parameters
There are two or three other “classical” simple chaotic oscillators. I have code written for octave/matlab to demonstrate rigid penduli, or there is the double pendulum that is chaotic all on its own, or there is the “Bender bouncer” — an ordinary harmonically driven linear oscillator but with a nonlinear “‘reflection plane” where the mass “bounces” elastically and instantly reverses its momentum. I used to have code for it, and probably still do. The amazing thing is that even thought the systems are or can be quite different, the advent of chaos is the same. Period doubling to chaos, over and over again. Even in finite difference systems instead of ODE solutions, even in iterated maps. Chaos itself is not unstructured and has namable forms and similarities and patterns, at least until its close cousin complexity gets ahold of it and you have (maybe) chaos in N dimensions where N is not a small number. Hard to know exactly what you have in N dimensions.
rgb
I like your writing style.
Reminds me of reading Martin Gardner.
A question I hope you will answer in the next chapter: in a chaotic climate system like Earth, in which there is a new hypothetical man-made warming component being added to the mix (and that is the only change in conditions from before), then maybe the non-linearity of the system will make it impossible to accurately model, but does that mean it is impossible to even make some general conclusions about what will happen? i.e., can we at least say it is likely that the temperature is going to go up (at some unknown rate)? Or is it possible that the temperature could go down?
And how does the discussion of chaos affect the concept of “tipping points”?
Reply to TBraunlich ==> Thank you for the compliment. Martin’s readers of my generation miss him greatly.
I can not answer your question, neither now nor in the next chapter. Why? We simply do not know enough about how the Earth’s climate system works to make even general conclusions at the scale you ask for — will temperatures go up or down? We do not, for instance, know that “there is a new hypothetical man-made warming component being added to the mix (and that is the only change in conditions from before)”. The sun (responsible for the warmth or the Earth, is also changeable. Land use, forest growth and clearing, row farming or pastures, city building, is changeable. Cosmic rays are changeable and unpredictable. Without knowing the system itself, to some pragmatic level of accuracy, we will not be able to make predictions about the future.
“Tipping Points” are theoretical points at which a system will shift from one regime to another, or from one stable state to another stable state. Ice Ages and Inter-glacials are thought of as semi-stable states of Earth’s climate systems, based on past “experience”. Mostly “tipping points” are being used today as scare tactics in the political debate about atmospheric CO2 concentrations.
Linear behavior, in real dynamic systems, is almost always only valid over a small operational range
============
this is fundamental for bikes, cars, boats, planes. All type of vehicles. They have a stability envelop in which their behavior is near linear. Outside that envelope the behavior is non-linear. Thus, what one must master when learning to drive is to keep the vehicle inside the near linear envelop.
predictable systems can be thought of as having a single attractor. A planet orbiting a star is predictable. However, when you add a third body the system becomes chaotic, except in the case where all 3 bodies lie in the same plane.
Chaotic doesn’t mean unpredictable, but it does mean unpredictable for all practical purposes. Given infinite precision and infinite time, you can predict a chaotic system.
Reply to ferdberple ==> Yes and Yes — think of a child learning to ride a bike — pedaling fast enough to get the bike up to speed, while steering close enough to straight, will get the bike on that stable “Look at me Mom, I’d riding a bike!” point.
Thanks, Kip Hansen.
Excellent essay, I will wait for more.
Good essay, Mr. Hansen. I learned about linear functions way back when some where still trying to disprove Ohm’s Law. (Opppppsss,,,showing my age). As a PS….do you consider logarithmic functions as linear or non-linear, or is this discussed in later parts? As for chaotic….sheesh. Sometimes just waking up is chaotic!
Reply to justthinkin ==> I like the pragmatism of Lorenz’s defintion in which one can count on the output being proportional to changes in the input. As you know, graphing a logarithmic on a log scale is linear — a straight line.
Sadly, not a good answer. Linear refers to the ordinary differential equations being solved (or linearity in the difference equations or iterated map equations). Nonlinear ODEs are everything else. See my discussion, with examples, above.
rgb
Enter entropy into the discussion and see where the reality of the climate models end up.
And to Janice and Pamela….there is nothing more chaotic then a rational, logical mind trying to get a FACT across to a “believer”.
Thanks for that. I didn’t expect to follow it, but it was very clear!
Two trivial points, from my own subject.
Ohms law is not actually relevant to the potentiometer example. It’s just confusing ornamentation here. The current and resistance don’t affect the point you make.
And, P = V²2R? (The “2” should be a / . P is V squared OVER R)!
I thought you’d want to know. Typos easily hide in equations.
Cheers,
Zaphod.
Reply to Zaphod ==> Hmmm — I thought this was my Ohm’s Law quote ” As we turn the knob, the voltage increases or decreases in a direct and predictable proportion, following Ohm’s Law, V = IR, where V is the voltage, R the resistance, and I the current flow.”
Ah, found it, you are referring to “voltage and power in a resistor: P = V²2R” — I think you are right, something in the conversion superscripts and subscripts has fouled me up in this quote.
Let me get it right, you are saying it is correctly Power = Voltage squared over Resistance
Right?
[Current = I = Volts/Resistance
Power = I^2 x Resistance = V^2/R = I x V, but only for DC currents.
For AC currents you have to add in the reactance losses and phase changes.
Those are not imaginary losses, but are calculated using imaginary numbers (sq root of -1) ! .mod]
Thanks .mod!
Does this mean that outputs are usually less and never more than a linear view of the inputs would expect? I assume that waste exists, but not a free lunch.
There are two important implications of Chaos theory for this debate that are missed in this article and elsewhere, yet both were well covered by Lorenz.
The first is that it is the non-linearity of the system that often explains its stability.
This is well explained historically (and by one of the sources to this article, Ian Stewart) in the problem of the stability of the solar system. What if it gets a little bump? What about the complex influence of the other revolving planets? Newton solved the problem with the hand of God. Poincare investigated it with the 3-body problem and therein some of the beginnings of the investigation of non-linear systems. This is not equilibrium, not homeostasis, but stable disequilibrium. We do not require equilibrium for stability – this should be a great relief! Nor do we require predictability. This should be obvious with the common usage of the weather/climate distinction.
Even if the precise condition (weather) of a strange attractor at any time is entirely unpredictable by its condition at a previous time, still it is stable, within its range, against perturbation. Yes, there are tipping points, and the degree of perturbation required to push the system over can vary depending on the condition at the time. But, for the solar system, such a perturbation is very unlikely. And even if we do not fully understand the non-linearity of the system under investigation, the longevity of a system in an environment is empirical evidence of its stability. The solar system has been around for a long time and has taken a lot of knocks. Likewise, the amazing stability of the global atmosphere and the climate in terms of such parameters as temperature.
It is an interesting historical fact of this scare that the ‘tipping point’ is emphasized on the alarmist side (Wallace Broecker has a lot to answer for), but also the ‘untamed’ on the skeptic side (surely this is refuted by the old response that we may not be able to predict what the weather will be like on a particular day next summer, but, eg, with our knowledge of ENSO, we may be able to tell you something about the general climatic trend…due to some predictable linearity in the system). A similar emphasis evolved in the Gaia hypothesis. In the mid-70s Lovelock used it to explain and emphasis the stability of the atmosphere in states of disequilibrium — the hypothesis is biospheric self-regulation of a physical system on the analogy of biological systems (eg a cellular organism).
The other important implication relates to the butterfly effect, and what is seen as its teaching of the ‘sensitivity to initial conditions.’ Actually, this understanding of what is going on is very limited. The root problem is about representation of a continuous system in a discrete system. It has deep philosophical implications to do with the very idea of representation of experience. This is often explained historically with Laplace’s idea that the project of science is to strive to represent the world in a model so as to deliver its perfect predictability. Chaos theory declared Laplace’s project over. The teaching for this scare is this: with the collapse of the empirical science of ‘detection’ in the mid-1990s, and so the resort entirely to theoretical modelling (go look at the transition in the work of Barnett, Wigley, Santer etc), we have entered a realm of SiFi. What is truly remarkable historically is how this SiFi is broadly seen across an educated public as continuous with the empirical science from which it evolved.
Extinctions periods are infrequent on Earth, which proves the stability of the system. Life is fragile.
Reply to berniel ==> Yes, of course, one of the attributes of nonlinear systems is the subject called “strange attractors” or sometimes just “:attractors”. In the kindergarten-level May Island squirrel population example above, we see a nonlinear system that is stable at just above 0.6 of the carrying capacity, As long as we don’t change the growth rate, the system settles down at that value — very stable. In fact, there is a whole range of growth rates that produce stable values near 0.6.
Ordinary biology insists that the squirrel population should grow to approximate the carrying capacity — should grow to or close to 1. It does not in our example, and it does not in the real world.
Thank you for bringing up these points, quite valid, but beyond the introductory level of this essay.
Nice to see the subject introduced to give all a feeling for the insoluble problems that chaotic systems create and to make clear, we’re not talking about something rare. I don’t think nonlinearity is the right term, though. Chaotic systems follow neither linear nor nonlinear functions. For forecasting, there is little help to be gotten from any ‘species’ of math once removed from short term linear (or even nonlinear) approximations. Chaos itself would appear to be in a category all its own.
For climate and I’m sure basically all dynamical systems, we have to go with what we do know for long term changes. We do know that chaotic systems have surprisingly neat geometrical expressions – Kip’s classical paired reflected ‘jelly roll’ pattern with two centres (attractors) which seem to be out of bounds for the mad function of chaos. Moreover, the jellyrolls ‘circles’ are of a dimension, finely spaced, the outermost trace of each seeming to be the outer limit for the trace of the function as far as you take it. The space between coils is probably a function of the error of rounding in a parameter or variable. Finally (?) the traces appear to be confined to two planes in the jellyroll case. This is knowing a lot. It would be fun to see what ‘shapes’ we get in functions by rounding off the value of pi in them as we must with a few million iterations of it . Start with two decimal places and then more. Such studies of chaos are more akin to descriptive studies of biological species behavior.
Now climate’s ‘jellyrolls’ are shaped by two attractors, cold and warm and the outer bounds are +/- 5 degrees C as long as the sun is at least roughly constant. Certainly with presently known orbital dynamics, we have the limits of how much energy is being put in and the there must also be a limit to how much it is possible to “magnify” the surface heat on a water planet or how fast we can remove the heat from the system based on this received energy. The detailed weather is a problem beyond a week or so, but I think we can make somewhat confident prognostications from what we know, that we are more likely heading toward another ice age, hopefully far enough into our future to give us time to adapt or head somewhere else for some of us. We are happily being presented with an excellent opportunity for gathering solid data on the likelihood of runaway climate from CO2. Surely another 10 years of no warming will trim CO2’s effect down to insignificant and we can rely on evidence of net negative feedbacks.
The two centers are not attractors. The object itself is the attractor. And it only has this appearance when looked at from just the right angle. Given the right set of parameters and a starting value ‘close’ to the attractor this shape will result over many iterations. It is infinite in length and non-intersecting, which mean non-repeating. What chaotic means is that if you move the starting point a tiny bit (in any direction), the resulting locations after a few thousand iterations will be far apart, but not predictably far apart. And the same change in a different direction will not lead to a predictable result based on the other change. That is sensitive dependence on initial conditions. It also means that tiny errors can be magnified over time (the butterfly effect). There are patterns in chaotic behavior, but they are unusual – hence ‘strange attractor’ – not a point or group of points, but an infinite line, and the ones I have seen were bounded.
This is the kind of article that makes me keep coming back to WUWT over and over again.
Forgive me for making a comment outside of those constraints and maybe off topic.
One of the great things about WUWT is that there are so many contributors that not only know what they are talking about but they are not attempting to deceive. Honesty is refreshing.
(Carry on.)
The discussion in the article and comments is quite interesting. However, some of it gives the impression that linear systems are always approximate desciptions of the real world and in some sense unimportant. Of course, quantum mechanics and quantum field theory are important and they are, as far as we know, perfectly linear. That said, the implications of non linearity for climate predictions are very important. The modelers seem to acknowledge that they cannot predict weather on the 1 month to 10 year scale. Somehow, they think that they can deduce the basic trends on the 10 to 100 year scale. Why do they believe this? Does it have any justification by for example renormalization theory? Can one lump many of the parameters together on the long term?
“Why do they believe this? ”
Their income depends on it.
Reply to Jim Rose ==> “…quantum mechanics and quantum field theory are important and they are, as far as we know, perfectly linear.”
I’d like some quantum physicists to weight in on this idea. Is Mr. Rose’s statement literally true? Or are the equations for the theories linearized out of necessity or for convenience?
I’m a quantum physicist. Quantum mechanics appears to be perfectly linear. I.E. any sum of valid states results in another valid state. In fact, hypothetical nonlinearities in the state space allow some really crazy stuff to happen that seems like it shouldn’t be possible.
However, the time evolution of certain QFT’s is nonlinear, particularly QCD, causing no end of calculational frustrations when applied at low energy when the nonlinearities are biggest.
Metric thanks for the correction. I guess I am starting to show my age — I was thinking of QED. Its still linear isn’t it?
I suppose I should elaborate on my previous statement just a bit. There are a couple different ways you might think about linearity in QM, and it’s easy to get them confused. Let’s describe the state of 1 particle at position A and 0 particles at position B as |1,0>. Similarly, 0 particles at A and 1 particle at B would be |0,1>, and 1 particle at A and 1 particle at B would be |1,1>. Note that |0,1> + |1,0> IS NOT the same as |1,1> — it has a very different interpretation.
Let the time evolution operator be called U.
Now, when people say “quantum mechanics appears to be ABSOLUTELY linear” they mean the following:
If |0,1> and |1,0> are valid states, then so is A |0,1> + B |1,0>. Also, the time evolution of (A |0,1> + B |1,0>) is U(A |0,1> + B |1,0>) = A U |0,1> + B U|1,0>. This is the part that appears to be completely true, to the best of the knowledge of mankind (with people constantly looking for exceptions that would earn them a Nobel Prize).
However, when people say time evolution is nonlinear, they could mean a few subtly different things: They might mean that U|1,1> cannot be regarded as independent operations on the first particle and the second particle seperately — U has to know about both particles to give the right time evolution. This would be the case, for example, if the two particles are charged and applying forces on one another. They also might mean that the interaction force itself is non-linear — this would correspond to the case (as in QCD) where the force-carrying particles (gluons in QCD) also carry their own charges, and thus the exchange of a single force-mediating particle (representing a single “bump” of force) cannot be treated independently from a bunch of other charge interactions.
To Jim Rose:
You’re absolutely right in the sense described above — the state space is linear for every quantum theory we know of. QED is also said to be “linear” in the sense that the force-mediating particles involved (photons) don’t carry a charge, and thus photons can come and go without adding additional computational nightmares to a system of charges you are trying to understand (though, as you mentioned in your first post, renormalization adds yet another layer to the story). QCD is still linear in the state-space sense of the word, but is no longer linear in the force-interaction sense of the word — the mere act of a force occurring between two particles in QCD means that additional charge is introduced and must be taken into account, leading to an infinite series of equally-important terms that make calculating anything “tricky” to say the least, or “horrendous” to be more blunt.
Why do they believe this?
=================
The arguments that climate is predictable revolve around the central limit theorem, the law of large numbers, and the normal distribution.
Many people are familiar with the law of large numbers, and assume that it holds for climate. While a coin toss isn’t predictable in the short term, in the long term it should even out 50-50. However, this doesn’t work for climate. the law of large numbers works when the system under study has a constant average and deviation. like a coin or a pair of dice. this can be readily shown from the paleo records to be false for climate. the law of large numbers doesn’t apply to climate.
The central limit theorem is a more general case of the law of large numbers, and it tells us that if we sample climate randomly we should get a normal distribution. the normal distribution is quite important, because it allows us to make all sorts of statistical predictions using mathematics developed originally to try and beat the casinos. unfortunately the central limit theorem doesn’t apply for a power series distribution such as climate.
when one looks at climate it becomes apparent that temperature for example is a fractal distribution. When you look at a temperature graph, unless the scale is written underneath, you cannot tell if you are looking at 10’s, hundreds, thousands, or millions of years. When you compare this to a coin toss, you immediately see the difference. The coin toss smooths out the longer the time. Climate doesn’t.
It is the fractal distribution in climate that makes it unpredictable at scale, because we currently lack the mathematics to deal statistically with fractals. Much the same time as chaos theory, they give us a view into infinity we did not suspect existed.
http://en.wikipedia.org/wiki/Benoit_Mandelbrot#/media/File:Mandel_zoom_08_satellite_antenna.jpg
“While in the short term a coin toss isn’t predictable in the long term it should be”. The word “should” is the key word here, because in reality it isn’t. The evidence for this are the many gamblers recording the statistical anomalies on Red, Black, Odd, Even, 1-18 and 19-36 of a roulette table and betting on the option that is at 45% over thousands of spins.
The paradox is that the wheel has no memory of what it did before and the long term trend is meaningless even in this simple “coin toss” scenario. The bank accounts of the people who believe otherwise stand testament to this.
It is of course the number zero that, also paradoxically, does give the house a long term advantage. My understanding of the warmists augment is that the IR absorbtion qualities give their climate models a “house edge”. An extra input that skews the odds in favour of warming over the long term.
Reply to wickedwenchfan ==> In my experience with gamblers, it is their “magical thinking” that gives the House the edge — the “zero” and “double zero” only change the odds. I have a brother who spent years working out a “scientific system” to win at blackjack. It was real and gave him a something <1% advantage — a real statistical advantage but one that could not be taken advantage of — as the gambler can not and will not mechanically follow a system, he always gets and follows a hunch. In the normal course of play, such a small advantage leads to one losing his stake long before his advantage appears as a reality in his pile of chips.
I did know one successful gambler — I was counseling him on personal ethics. I couldn't for the life of me figure out how he managed to not only survive, but get wealthy as a professional poker player in the casinos (not like today's Professional Gambler circuit). I finally got it, "It's simple," he says "I cheat."
This gets a bit beyond my math ability, but if I understand the concept, a non-linear system need not be chaotic, but any two or more coupled non-linear systems cannot be non-chaotic. Like the three body problem. Is that correct?
No. The critical part is that a feedback must amplify distortions, i.e. shift state information to the left over system iterations (when encoding the state vector of the system as a digital representation). You can have nonlinear feedback systems that dampen disturbances, those will not show chaotic behaviour.
Thanks