Guest Post by Willis Eschenbach
Short Post. You can skip this if you understand the tidal force. Some folks seem confused about the nature of tidal forces. Today I saw this gem: “The tide raising force acts in both directions (bulge on each side in the simplistic model)” … the author of that statement may understand the tides, but that isn’t how tidal forces work, they don’t act in different directions.
To clarify the situation, let me give an example. Imagine three one-kilogram masses M1, M2, and M3, connected by a blue rope, that are in free-fall directly into the sun. Figure 1 shows the situation.
Figure 1. Forces on three one-kilogram masses M1—M3, which are in free-fall straight towards the sun, and are connected by the blue rope. The equations at the bottom show the force of gravity on each of the three masses. The “tidal force” is the difference between two gravitational forces on two objects. Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons), and the lunar tidal forces are about twice that, about a micronewton. By comparison, Earth’s gravity exerts a force of about 10 newtons on a 1-kg mass at the surface …
Clearly, the gravitational force on M1 is greater than the force on M2, which in turn is greater than the force on M3. The difference between those two gravitational forces is the tidal force. There are two different tidal forces of interest in the diagram, which are GF1 – GF2, and GF2 – GF3. As a result of these tidal forces, as the three masses fall towards the sun. the near mass M1 moves the furthest, the far mass M3 moves the least, and the blue rope is always under tension.
For tidal forces on a theoretical planet, just imagine that the surface of the planet is the gray dotted line, and that “r” is the radius of the planet. The tidal force is the difference between the force of gravity on the unit mass M2 at the center of the planet, and the forces of gravity on the unit masses M1 and M3 at the points nearest and furthest from the sun.
Calculating the Tidal Forces
As shown in Figure 1, to calculate the tidal force you can just subtract the gravitational force on the unit mass at the center of the planet from the force on the other unit mass, for example GF1 – GF2. So we can use the equations in Figure 1 to calculate the force.
However, when the distance D is much, much larger than the radius r, we can make some simplifying assumptions. First, we can assume that the force between M1 and M2 is the same as the force between M2 and M3. It’s not, as you can see from the equations … but it is not a large error. For tides from the moon, the individual tidal forces are about ±5% different from their average value.
The next simplifying assumption we can make if D is much larger than r is that the average tidal force can be calculated as
Tidal Force = 2 * G * sunmass * r / D^3
This leads to tiny errors with respect to the sun’s average tidal force on the earth, and slightly larger errors with respect to the moon. For the sun we have
Near side true tidal force on earth (GF1 – GF2) = 0.50590 µN
Far side true force (GF2 – GF3) = 0.50583
True average = 0.50587
Approximation = 0.50587
So the approximation of the average tidal force is good to five significant digits …
And for the moon we have:
Near side true tidal force on earth (GF1 – GF2) = 1.1350 µN
Far side true force (GF2 – GF3) = 1.0796
True average = 1.1073
Approximation = 1.1067
For the moon, the approximation of the average is good to four significant digits. For most results, of course, those differences are far too small to be meaningful, and we can use the approximation without concern.
Why Are There Two Tidal Bulges?
Moving on, let’s look at why there are tidal bulges on both the near and far sides. It’s not because the tidal force acts in different directions, because tidal force is always directed towards the sun. So lets look at Figure 1 again, and this time we’ll include a planet and an ocean. As in Figure 1, the planet is simply free-falling into the sun. That result is shown in Figure 2:
Figure 2. Tidal forces elongating the planet and the ocean. Note that the planet is elongated as well, but this is not shown in the diagram because obviously, tides in the solid planet are much smaller than tides in the ocean. NOTE THAT THIS PLANET IS NOT THE EARTH.
As the planet free-falls into the sun, the near side of the ocean is pulled the most. So it moves the most, pulling away from the planet. And the planet, in turn is pulled more than the far side, so it pulls away from the ocean. These relative motions create the “bulges”
In other words, the “bulges” on the two sides of the planet are simply a result of the tidal forces stretching the entire system. Indeed, the atmosphere is subject to the same phenomenon, so there are atmospheric tides as well. In prior centuries, these atmospheric tides were said to affect the weather, although in a cyclical rather than a secular manner. However, such connections, while certainly possible, have proven to be elusive and difficult to establish. One complicating factor is that the atmospheric tides that are caused by the sun occur in combinations with solar heating, which makes the atmosphere swell. Also, the variations in pressure caused by the atmospheric tides are small, on the order of a tenth of a millibar (or of a hectopascal), or a variation of only 0.01% …
Finally, I’ve said that the situation in Figure 2 shows that planet free-falling into the sun. As it gets closer and closer, the tidal forces stretching the system get greater and greater, stretching the system more and more. Eventually, at a distance called the “Roche limit”, the tidal forces can reach such strength that they rip the planet into pieces … dang, to have a ring-side seat right on the Roche limit line for that spectacle would be awesome, even if it were perhaps a bit warm …
My best to all,
w.
PS—As with gravity, every mass in the universe exerts a tidal force on every other mass, so you can personally take credit for raising a tide on the surface of the sun … yeah, it’s a small tide, but it’s real. Just sayin’, I had someone claim the opposite. Lots of tidal misinformation out there.
THE USUAL: If you disagree with me or anyone, please quote exactly what it is you disagree with, and tell us precisely why you disagree. That way, we can understand exactly what it is you object to.
It is amusing to see bright people communicating with such difficulty.
RichardLH says: I can’t see why you didn’t try that route first anyway.
Well I guess that’s just a difference between us. I always try to come up with my own answer first and then look to the answers by others to see if/how my answer compares. Just looking up stuff doesn’t put my brain in gear.
Mike M says:
February 15, 2014 at 6:12 pm
“Well I guess that’s just a difference between us. I always try to come up with my own answer first and then look to the answers by others to see if/how my answer compares. Just looking up stuff doesn’t put my brain in gear.”
I just like to order the stuff I look at I quantitate order first. Tend not to get lost in the minutia then 🙂
RichardLH says:
February 15, 2014 at 3:04 pm
From your link:
“At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.” http://www.lhup.edu/~dsimanek/scenario/Field_tidal.jpg
That’s an interesting geometry, focused at sqrt of 3 Earth radius away from the center.
Mike M says:
February 15, 2014 at 5:55 pm
“Trying to bring in orbital and rotational centripetal force is not required and has insignificant affects.”
I’m pointing to a .0002 m/sec^2 difference in acceleration from a rotational induced difference in sun’s gravitational field which, for a 1 KG mass, is .0002 Newtons. Insignificant?
Ok. but rotational is not tidal. the rotational is uniform and causes an average equatorial bulge in 360 degrees 24/7. without moon or sun then, the net sea level rise is constant . I agree there is probably some small Coriolis effect set up as well… but this is not really the point of the thread. “Pondering tides” was the title.. not, “Would there be ocean currents on a rotating non-orbiting body”
cheers
Mike M says:
February 15, 2014 at 5:31 pm
From the moon, of course.
So if the Earth did not rotate there would be solar tides?
Ulric Lyons says:
February 15, 2014 at 6:18 pm
““At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.” http://www.lhup.edu/~dsimanek/scenario/Field_tidal.jpg
That’s an interesting geometry, focused at sqrt of 3 Earth radius away from the center.”
That’s actually from Wiki as the url notes (and yes it is deliberately exaggerated).
http://en.wikipedia.org/wiki/Tide
Mike M says:
February 15, 2014 at 5:31 pm
From the moon, of course.
So if the Earth did not rotate there would be no solar tides?
Ulric Lyons says:
February 15, 2014 at 6:18 pm
““At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.”
You weren’t suggesting the geometry is wrong are you? The arrows are too long but that is all.
RichardLH says:
February 15, 2014 at 6:39 pm
“You weren’t suggesting the geometry is wrong are you? The arrows are too long but that is all.”
I was remarking upon the described 54.7° angle rather than the diagrammatic representation of it.
It makes a sqrt 2, sqrt 3, sqrt 5 sided triangle.
Ulric Lyons says:
February 15, 2014 at 6:54 pm
correction 1, 2, sqrt 3.
Ulric Lyons says:
February 15, 2014 at 7:08 pm
Third time lucky lol, 1, sqrt 2, sqrt 3.
Mike M says:
February 15, 2014 at 5:55 pm
I’m pointing to a .0002 m/sec^2 difference in acceleration from a rotational induced difference in sun’s gravitational field which, for a 1 KG mass, is .0002 Newtons. Insignificant?
Irrelevant as there is not tidal effect stemming from that as the rotation does not make any difference to the Sun’s gravitational field.
Thought I’d jump in here in case there’s any confusion about Mike M.
Not me.
Gene Selkov says:
February 15, 2014 at 3:55 am
Say what? You post up a cross-section of the moon that looks like it’s drawn by a sixth-grade schoolkid, with no provenance and no supporting data …
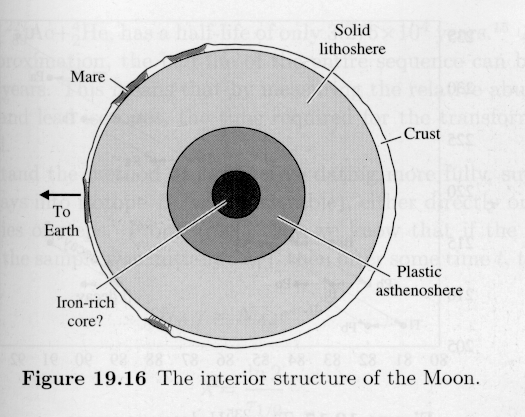
… and you claim that “falsifies” the Roche Limit and tidal elongation, both of which have been understood for centuries? Roche calculated the Roche limit in 1848. Do you think think that your pathetic citation”falsifies” it?
In addition, I find no evidence that either Metis or Pan are orbiting inside the Roche limit, see Wiki, which lists both Metis and Pan as orbiting outside the Roche limit. It also notes that Pan may be close to breaking up …
Absolutely not. However, I made up and used the example shown in Figure 1, because it is very useful for understanding the tidal forces. Plus I had great fun doing the drawings.
.
You are 100% correct. I used to produce and sell tide tables for the Solomon Islands based on my harmonic curve-fitting to generate the tables. Solomons has bizarre tides—for part of the year they have two tides a day, and for part of the year they have one tide per day.
Actually, that’s exactly what it means. How else do you explain two tides a day year after year over most of the planet, when both the sun and the moon only “go round” once a day? There are two tides because the slowly-changing tidal bulges stand still with respect to the much, much faster revolution of the earth. As a result, each part of the ocean goes past one of the bulges every twelve hours.
Or you could look at it the other way around, from an earth-centered point of view. Over a 24-hour period, the sun-moon pair go around the earth once. This drags the two tidal bulges around the planet, with two high tides occurring almost everywhere as a result.
Best regards,
w.
NoAstronomer says:
February 15, 2014 at 8:19 am (Edit)
You are correct. I was speaking of the situation shown in Figs. 1&2, not about the real earth. For the real earth, the total tidal force is the vector sum of the sun force and the moon force. Almost all the time, these are not in line with each other, and the resultant force occurs between them.
w.
Jan Kjetil Andersen says:
February 15, 2014 at 8:37 am
Sorry for the confusion. I thought it would be clear that if I’m describing a planet which is free-falling into the sun, that I was not talking about the earth. I’ve changed the head post to make this clear.
Thanks, Jan,
w.
lsvalgaard says:
February 15, 2014 at 5:04 pm
I know a better one:
Why not buy gold in Mexico City where the gravity acceleration is 9.776 m/s*s and sell it in Anchorage where the gravity acceleration is 9.826 m/s*s.
The difference is 0.5% so you can pocket 0.5 kg each time, not a tiny 0.2 kg.
Alas, the trick will not work for any of us with balance scales, as I think is the preferred method in gold trading.
Perhaps we should concentrate on answering Mike’s concrete question rather than evading to something that some may perceive as quite arrogant.
/ Jan
Kevin Kilty says:
February 15, 2014 at 10:05 am
Thanks, Kevin. As you will note in Figure 1 and Figure 2, the tidal effects do not depend in any sense on centrifugal acceleration. There is no centrifugal acceleration in the Figures, the masses and the planet are falling straight into the sun … and yet we still have tidal forces.
So any explanation that depends on centrifugal acceleration is incorrect.
Finally, it is not true that within a heliocentric frame of reference somehow the forces change direction. The tidal force is the difference between the gravitational forces GF1 and GF2, or GF2 and GF3. These gravitational forces are vectors—they have a strength (magnitude) and they also have a direction (straight towards the sun).
As as result, when you subtract one gravitational force from the other to get the tidal force, the tidal force also has a direction—which is also straight towards the sun.
Now, you can change the frame of reference all that you want … but that doesn’t change the direction of the tidal force vector. It always points towards the sun, no matter what your frame of reference might be.
Regards,
w.
Kirk c says: February 15, 2014 at 6:34 pm “Ok. but rotational is not tidal. ….”
Nothing of what you wrote had anything to do with what I’m asserting. You simply don’t understand. For any given particle orbiting the sun at a given radius from the sun there is an orbital velocity V with an inertial reaction of V^2/R acceleration EXACTLY EQUALING the gravitational pull it experiences from the sun at that orbital radius R. If it suddenly “finds” itself going slower it will be pulled toward the sun. If faster it will move away from the sun.
Such is what a particle sitting on earth’s equator experiences every day. The speed, S, the particle is traveling WRT to earth’s center is simply earth’s equatorial radius times earth’s angular velocity. From ~6am it begins slowing down from V (its component of solar orbital speed, being perpendicular to it rotational velocity spinning around earth at that time of day ), until noon when it reaches the point of maximum decrease, V- S, from solar orbit velocity and then speeds up again until ~6pm when its solar orbital speed is again back to V. Then it continues, now speeding up to V+S at midnight, the amount S more than solar orbital speed V.
When it is going slower than V it is pulled toward the sun by the amount of sun’s gravity which is, at noon, greater than the particle’s now reduced solar orbital inertial reaction (V-S)^2/R . When it is going faster by S at midnight than V it is being flung away from the sun by the increase of solar orbital inertial imbalance (V+S)^2/R which is greater than sun’s gravity.
I calculated the maximum differences in acceleration (V+S)^2/R or (V-S)^2/R versus V^2/R (which are actually slightly different in magnitude but beyond 5 places), as being -.00018 meters/sec^2 offset countering earth’s gravity occurring twice per day, at noon and midnight – two bulges.
For simplification I ignored the difference of R for each by the amount of earth’s radius as well as the sun gravitational field variation that WiIlis addressed which is a much smaller effect.
Is there an seismic instrument, appropriately damped to ignore earthquakes etc. and look only at the difference in gravity occurring over hours? If so it ought to record this effect and see a maximum gravitation pull being reached at 6am and 6pm with a minimum reached at noon and midnight with a difference by about .0002 meters/sec^s.
Clive Best says:
February 15, 2014 at 10:43 am
Well, that force is less than the tidal force by sin(theta). However, you’re missing a term. The problem with your equation is that at the poles in Figure 2, the tidal force is zero. This is because the tidal force depends on the difference in distance to the sun from a given point on the planet, and the distance to the sun from center of the planet. And at the poles, that difference is zero, so the tidal force is zero.
So at the same time that the horizontal force is increasing (by sin(theta)), the tidal force is decreasing (by cos(theta)). As a result, the horizontal component of the tidal force is
2 G m R sin(theta) cos(theta) / r^3
This has a maximum at 45°N and 45°S, which is one reason why the tides are big in those latitudes. However, the maximum is only half of the tidal force [ sin(45) * cos(45) = 0.5 ].
All the best.
w.
Willis,
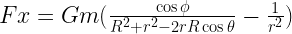
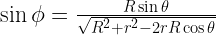
Yes you’re right
The correct equation is more complicated. Taking x as the direction from the centre of the earth to the moon and taking y the vertical axis then the net tidal force has 2 components.
where
and
The tractional force acting along the surface and therefore unaffected by the earth’s gravity is
Fy cos(theta) + Fx sin(theta) . The tractional force is zero at the central bulge and equal and opposite from either side.
Expat says:
February 15, 2014 at 11:28 am
Sorry, Expat, but that’s simply not true. As Figure 2 shows, you get two bulges with no centripetal force at all.
w.
Steve Fitzpatrick says:
February 15, 2014 at 12:48 pm
Steve, neither Leif or I are talking about actual tides on earth. We’re talking about how the tidal forces work on a planet. So whether Clive has it correct or not for the earth is material for a discussion of the actual Earthly tides … it means nothing to this discussion.
Willis Eschenbach says:
February 15, 2014 at 11:30 pm
“This is because the tidal force depends on the difference in distance to the sun from a given point on the planet, and the distance to the sun from center of the planet. And at the poles, that difference is zero, so the tidal force is zero.”
That is valid only 2 days a year for the sun due to earth tilt. All other days of the year is the “Sun tidal zero poles” not at earth geographics poles. Moon inclination will also have large impact on where on earth the “moon tidal force zero poles” are located. And also where on earth the maximum horisontal tide forcing are located. The horisontal forcing that actually move air and water according to Laplace.
That latitude change between 45°N and 45°S +/- 28.36°
In a cyclic way. 18.6 years the most obvious.
Some of the motivation for this article seems to be to dismiss my comment of a couple of days ago: “The tide raising force acts in both directions (bulge on each side in the simplistic model)”
The context of that remark was to explain why Willis’ plot of variation in the magnitude of the tidal force was not correct. He was subtracting the lunar and solar forces at full moon.
His headline graph in that article only peaks once per year , while the tides peak twice per year.
http://wattsupwiththat.com/2014/02/09/time-and-the-tides-wait-for-godot/#comment-1569175
I pointed out the mistakes and provided a modification for his R-code to give the correct addition of forces and a graph that produces the twice per year variations.
So does Willis correct his code and update the graph?
No, he writes another article to insist that he’s right, ridicules my comment and calls me a fool.
The fact that his tidal forces only peak once a year should be a clue to him, but I’m sure there’s a good reason to ignore that too.
As I said above, “You cannot stretch a body with one force” You can accelerate a body with one force. You need to separate the two effects.
http://wattsupwiththat.com/2014/02/14/canute-ponders-the-tides/#comment-1568736
You cannot stretch a body with one force.
In the case above (GF3+GF1)/2 = GF2 will accelerate each of the three tethered weights at the common rate towards the sun.
Two opposing forces (GF3-GF1)/2 will act at each end mass acting to stretch the tethers applying a tensional stress to the ensemble.
The lay reader may wish to decide whether to be guided by Willis or Feynman on this question.
http://www.feynmanlectures.caltech.edu/I_07.html#Ch7-S4
“The result of this imbalance is that the water rises up, away from the center of the earth. On the near side, the attraction from the moon is stronger, and the imbalance is in the opposite direction in space, but again away from the center of the earth. The net result is that we get two tidal bulges.”