Guest Post by Willis Eschenbach
Short Post. You can skip this if you understand the tidal force. Some folks seem confused about the nature of tidal forces. Today I saw this gem: “The tide raising force acts in both directions (bulge on each side in the simplistic model)” … the author of that statement may understand the tides, but that isn’t how tidal forces work, they don’t act in different directions.
To clarify the situation, let me give an example. Imagine three one-kilogram masses M1, M2, and M3, connected by a blue rope, that are in free-fall directly into the sun. Figure 1 shows the situation.
 Figure 1. Forces on three one-kilogram masses M1—M3, which are in free-fall straight towards the sun, and are connected by the blue rope. The equations at the bottom show the force of gravity on each of the three masses. The “tidal force” is the difference between two gravitational forces on two objects. Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons), and the lunar tidal forces are about twice that, about a micronewton. By comparison, Earth’s gravity exerts a force of about 10 newtons on a 1-kg mass at the surface …
Figure 1. Forces on three one-kilogram masses M1—M3, which are in free-fall straight towards the sun, and are connected by the blue rope. The equations at the bottom show the force of gravity on each of the three masses. The “tidal force” is the difference between two gravitational forces on two objects. Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons), and the lunar tidal forces are about twice that, about a micronewton. By comparison, Earth’s gravity exerts a force of about 10 newtons on a 1-kg mass at the surface …
Clearly, the gravitational force on M1 is greater than the force on M2, which in turn is greater than the force on M3. The difference between those two gravitational forces is the tidal force. There are two different tidal forces of interest in the diagram, which are GF1 – GF2, and GF2 – GF3. As a result of these tidal forces, as the three masses fall towards the sun. the near mass M1 moves the furthest, the far mass M3 moves the least, and the blue rope is always under tension.
For tidal forces on a theoretical planet, just imagine that the surface of the planet is the gray dotted line, and that “r” is the radius of the planet. The tidal force is the difference between the force of gravity on the unit mass M2 at the center of the planet, and the forces of gravity on the unit masses M1 and M3 at the points nearest and furthest from the sun.
Calculating the Tidal Forces
As shown in Figure 1, to calculate the tidal force you can just subtract the gravitational force on the unit mass at the center of the planet from the force on the other unit mass, for example GF1 – GF2. So we can use the equations in Figure 1 to calculate the force.
However, when the distance D is much, much larger than the radius r, we can make some simplifying assumptions. First, we can assume that the force between M1 and M2 is the same as the force between M2 and M3. It’s not, as you can see from the equations … but it is not a large error. For tides from the moon, the individual tidal forces are about ±5% different from their average value.
The next simplifying assumption we can make if D is much larger than r is that the average tidal force can be calculated as
Tidal Force = 2 * G * sunmass * r / D^3
This leads to tiny errors with respect to the sun’s average tidal force on the earth, and slightly larger errors with respect to the moon. For the sun we have
Near side true tidal force on earth (GF1 – GF2) = 0.50590 µN
Far side true force (GF2 – GF3) = 0.50583
True average = 0.50587
Approximation = 0.50587
So the approximation of the average tidal force is good to five significant digits …
And for the moon we have:
Near side true tidal force on earth (GF1 – GF2) = 1.1350 µN
Far side true force (GF2 – GF3) = 1.0796
True average = 1.1073
Approximation = 1.1067
For the moon, the approximation of the average is good to four significant digits. For most results, of course, those differences are far too small to be meaningful, and we can use the approximation without concern.
Why Are There Two Tidal Bulges?
Moving on, let’s look at why there are tidal bulges on both the near and far sides. It’s not because the tidal force acts in different directions, because tidal force is always directed towards the sun. So lets look at Figure 1 again, and this time we’ll include a planet and an ocean. As in Figure 1, the planet is simply free-falling into the sun. That result is shown in Figure 2:
 Figure 2. Tidal forces elongating the planet and the ocean. Note that the planet is elongated as well, but this is not shown in the diagram because obviously, tides in the solid planet are much smaller than tides in the ocean. NOTE THAT THIS PLANET IS NOT THE EARTH.
Figure 2. Tidal forces elongating the planet and the ocean. Note that the planet is elongated as well, but this is not shown in the diagram because obviously, tides in the solid planet are much smaller than tides in the ocean. NOTE THAT THIS PLANET IS NOT THE EARTH.
As the planet free-falls into the sun, the near side of the ocean is pulled the most. So it moves the most, pulling away from the planet. And the planet, in turn is pulled more than the far side, so it pulls away from the ocean. These relative motions create the “bulges”
In other words, the “bulges” on the two sides of the planet are simply a result of the tidal forces stretching the entire system. Indeed, the atmosphere is subject to the same phenomenon, so there are atmospheric tides as well. In prior centuries, these atmospheric tides were said to affect the weather, although in a cyclical rather than a secular manner. However, such connections, while certainly possible, have proven to be elusive and difficult to establish. One complicating factor is that the atmospheric tides that are caused by the sun occur in combinations with solar heating, which makes the atmosphere swell. Also, the variations in pressure caused by the atmospheric tides are small, on the order of a tenth of a millibar (or of a hectopascal), or a variation of only 0.01% …
Finally, I’ve said that the situation in Figure 2 shows that planet free-falling into the sun. As it gets closer and closer, the tidal forces stretching the system get greater and greater, stretching the system more and more. Eventually, at a distance called the “Roche limit”, the tidal forces can reach such strength that they rip the planet into pieces … dang, to have a ring-side seat right on the Roche limit line for that spectacle would be awesome, even if it were perhaps a bit warm …
My best to all,
w.
PS—As with gravity, every mass in the universe exerts a tidal force on every other mass, so you can personally take credit for raising a tide on the surface of the sun … yeah, it’s a small tide, but it’s real. Just sayin’, I had someone claim the opposite. Lots of tidal misinformation out there.
THE USUAL: If you disagree with me or anyone, please quote exactly what it is you disagree with, and tell us precisely why you disagree. That way, we can understand exactly what it is you object to.
Just noticed I’d inverted my name to Gerg . LOL, was that what tripped moderation
“DO THE FREAKING MATH, Greg. The two have the same sign. ”
How about reading where I corrected that statement ???
“Not true at all. I have a heliocentric (sun centered) frame of reference, which does NOT rotate about the sun. Neither does the planet in my example. The clue is where I say it is free-falling into the sun …”
OK, I didn’t realise you intended not to rotate anything. So you want to call be a fool for saying something about how planets moons and tides work by comparing to a situation where nothing rotates.
Should still be an interesting exercise.
It’s not clear what the mechanical properiteis of your piece of “string” are so I’ll stick with a steel cable.
As I think we are agreed GF1>GF2>GF3 so the outer mass would accelerate less and get left behind unless it was tethered. Inversely M1 would fall faster. So both cables are under (rougly equal) tension.
You show that we can ignore the asymmetry:
True average = 0.50587
Approximation = 0.50587
So the net force accelerating the three masses is 3GF2 acting 3kg, They experience a common acceleration (since they are tethered) equal to that of the centre mass alone.
But M3 is experiencing less gravitational attraction and has to be pulled by the tether to the tune of GF2-GF3. The tension in the tether is thus that value. Similary the other side which should accelerate more but is held back by the tether.
So at M2 the tensions in the tethers are equal and in opposite directions.
The cables will extent a little due to the tension and both masses will end up a little further away from M2 and continute accelerating as an ensemble. This is the equivalent of the two tideal bugles. The tidal force and the ‘tide’ (stretch in cable) will remain constant until they get significantly closer to the sun and the gravity gradient gets steeper.
All you have done is substituted free-fall acceleration to the sun , without rotation, for a centripetal acceleration towards the sun with rotation.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be lack.
Even a “fool” like me can see that.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be _slack_.
[Mods , you can delete the three posts by “Gerg” 😉 Must have been taken as posting a pseudo form the same email. ]
Willis, I like your rope model, it is very elegant. However, with all due respect, we often formulate dynamical problems from a convenient frame of reference. Pretending that the Earth is an inertial frame of reference is one such convenience. Within this frame of reference the gradient of tide-raising potential appears to act in opposite directions from the center of mass of the Earth-Moon system. The reason for this is the manner in which centrifugal acceleration gets included on the left side of Newton’s equation (The F of F=ma) in the translation from one frame of reference to the other. I don’t see that the view of the matter from this alternative frame of reference is wrong–it does provide correct predictions.
I mean centripetal not centrifugal in my last post.
Kevin Kilty says:
February 15, 2014 at 10:06 am
I mean centripetal not centrifugal in my last post
It doesn’t matter as the tidal effect has nothing to do with rotation or orbital movements.
Willis,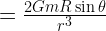
What you write is clear and simple. However the earth is a non-inertial accelerating frame of reference because it is in orbit around the moon-earth barycenter. The mystery of gravity is why the ‘m’ in gravity is the same as the inertial ‘m’ in F=ma. Einstein used this equivalence principal to derive general relativity. The bulge on the opposite side to the moon is not because the centre of the earth feels a stronger gravity than the far side ocean. That only applies to fee falling bodies. It is instead due to the centrifugal acceleration caused by its orbit around the joint barycenter.
The tidal force on the ocean is 10 million times smaller than the earth’s gravity. What moves enormous quantities of water is the tidal component parallel to the surface which is approximately
PS—As with gravity, every mass in the universe exerts a tidal force on every other mass.
No this is not true – An electron does not exert a tidal force on a quark.
lsvalgaard says: “Good that you stop digging your hole deeper and deeper. According to your ‘theory’ a pendulum clock should vary its ticking rate during the day and it does not. ”
Yes, by my theory it does vary! It’s just too small to notice and averages out, cycling every 12 hours. (Like I said, if my numbers are right, the factor is only .002% )
Given that you will not deny that a particle of mass M at the equator is moving faster than earth’s orbital velocity around the sun at midnight and slower than earth’s orbital velocity around the sun at noon – it’s inertial V^2/R reaction (“centrifugal force”) will be greater than its gravitational attraction to the sun (centripetal force) at midnight and less than its gravitational attraction to the sun at noon.
Mike M says:
February 15, 2014 at 11:04 am
Yes, by my theory it does vary! It’s just too small to notice and averages out, cycling every 12 hours. (Like I said, if my numbers are right, the factor is only .002% )
Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.
Gravity by far my most favorite subject to read about and ponder. Semi quantified by Newton and refined by my personal hero [Einstein]. The one thing I can take away from the above comments as well as the bulk of my amateur research is that nobody really has a clue. Experimental data results says the math is very close that we currently use to calculate it but the actual mechanism that produces it still eludes us.
For me the simple fact that something so seemingly mundane as a coin falling to the ground is beyond our understanding is captivating. When i contrast this to the state of ” Climate Science ” which does not even get freaking close to meeting model projections makes me laugh and cry at the same time….
lsvalgaard says: “Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.”
True or false – They ALL have an affect?
You said I was digging a hole and now look who is crawling into one with “measurable”?
The greatest tidal effect if from the moon. The near bulge on earth is from gravitational force. The far side bulge is created by centripetal force. The moon does not rotate around the earth. They both orbit around a common center of mass which is not the center of the earth.
Mike M says:
February 15, 2014 at 11:25 am
lsvalgaard says: “Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.”
True or false – They ALL have an affect?
They have no effect due to rotations or orbital movements. The do have [mostly unmeasurable] tidal effects due to gravity.
FTA: “the author of that statement may understand the tides, but that isn’t how tidal forces work, they don’t act in different directions.”
They do. It’s conceptually a little tricky, but you have made a simple math mistake.
You calculate GF1 – GF2 on the near side. What is this? It is the specific force acting in the direction of the Sun relative to the Earth, i.e., the arrow is starting from the Earth and pointing toward the Sun.
You then calculate GF2 – GF3. This is the specific force acting opposite of the direction of the Sun. The arrow is pointing from the Sun to the Earth.
To get them both in the same direction, you would need to calculate both with respect to the same reference point, GF2.
You see, independently, M1 is experiencing GF1 in the direction of the Sun. M3 is experiencing GF3 with respect to the Sun. With respect to one another, they are experiencing |GF1 – GF3|. This is non-zero, which means the objects are not being pushed in the same direction.
It may help to note that GF2 is actually zero, when you include the centripetal acceleration. Let’s assume we have a circular orbit with angular rate omega = sqrt(mu/D^3). The total specific force acting at the center of the Earth is
GF2 = -mu/D^2 + D*omega^2 = 0
i.e., we are in free fall at the center of the Earth.
The specific force acting on the near side is
GF1 = -mu/(D-r)^2 + (D-r)*omega^2 := (-2*mu/D^3)*r – r*omega^2 = (-3*mu/D^3)*r
The specific force on the far side acting in the direction of the Sun is
GF3 = -mu/(D+r)^2 + (D+r)*omega^2 := (+3*mu/D^3)*r
These specific forces are relative to the Sun. The near one is radially inward toward the Sun, and the far one is radially outward from the Sun. Note that |GF1 – GF3| = (6*mu/D^3)*r, i.e., they are pushing away from each other.
Expat says:
February 15, 2014 at 11:28 am
The greatest tidal effect if from the moon. The near bulge on earth is from gravitational force. The far side bulge is created by centripetal force.
No, very wrong. Both are gravitational. Willis is correct. Rotation and orbital movements have nothing whatsoever to do with the tides.
lsvalgaard says “They have no effect due to rotations or orbital movements.”
FALSE!
Let’s try this again, step by step…
DO YOU DENY that a particle of mass M at the equator is moving faster than earth’s solar orbital velocity around the sun at midnight and slower than earth’s solar orbital velocity around the sun at noon?
“In other words, the “bulges” on the two sides of the Earth are simply a result of the tidal forces stretching the entire system.”
That is a fair desciption. It is the difference in two differenct forces, applied at two different points in the body that exert a tensile stress on the body. You cannot stretch a body with one force. So in the case of two co-linear forces, there will be a net force (the average of the two) actiing to accelerate the body and two opposing components (each half the difference) acting in opposite directions, at the same two points, to stretch the body.
In the case above (GF3+GF1)/2 = GF2 will accelerate each of the three tethered weights at the common rate towards the sun.
Two opposing forces (GF3-GF1)/2 will act at each end mass acting to stretch the tethers applying a tensional stress to the ensemble.
In the case of an orbitting planet, most of the gravitational force is excerted to supply the centrpetal force that produces the centripetal acceleration which ensures the circular orbit. In this experiment it goes to linear acceleration towards the sun.
In both cases there is a residual of two equal and opposing forces that stretch the masses/planat creating the distortions we call “tides”. These are the tide raising forces.
The statement I made yesterday remains valid.
“The tide raising force acts in both directions (bulge on each side in the simplistic model)”
All Willis has done here is to add a large additional force to everything in one direction and then conclude that they all act in the same direction (but with different magnitudes. ). Again, its a question of frame of reference.
It’s a bit like measuring tides as haveing extremes of +/- 2m . Then someone else comes a long , moves the measuring stick and says “no you’re wrong! Here tides are between 8m and 12m , they’re always well above zero”. They then start calling everyone who does not agree with them a “fool”.
Bart says:
February 15, 2014 at 11:34 am
It may help to note that GF2 is actually zero, when you include the centripetal acceleration. Let’s assume we have a circular orbit with angular rate …
Please, Bart. The tidal effects have nothing to do with centripetal accelerations, rotation, orbital movements, etc. Three bodies lined up in the direction of the Sun and falling towards the Sun [[think] of pieces of comet] all are falling under the gravitational force of the Sun directed towards to Sun for all three bodies.
Mike M says:
February 15, 2014 at 11:36 am
DO YOU DENY that a particle of mass M at the equator is moving faster than earth’s solar orbital velocity around the sun at midnight and slower than earth’s solar orbital velocity around the sun at noon?
Whatever you may think of this, such movements have nothing to do with the tidal effects.
lsvalgaard says:
February 15, 2014 at 11:42 am
“The tidal effects have nothing to do with centripetal accelerations…”
Not so. Perhaps you are confusing rotations of the Earth, versus revolution about the Sun. The former has little effect on tides, because it is equally distributed about the Earth. But, the near side of the Earth is indubitably instantaneously accelerating slower with respect to inertial space than the far side.
Bart says:
February 15, 2014 at 11:52 am
But, the near side of the Earth is indubitably instantaneously accelerating slower with respect to inertial space than the far side.
That has nothing to do with the tidal effects. Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit make no reference to rotation or orbital movements, only to the dimensions, masses, and distances of the bodies involved.
lsvalgaard says: Whatever you may think of this, such movements have nothing to do with the tidal effects.
Oh, so now you clam up refusing to recognize even a simple statement of relative motion?
I never said it was THE explanation of ocean tides but I stand by my assertion the force differential is REAL and acts to reduce the net gravitational force at the equator at both midnight and noon which would cause a perfect 12 hour tide period if there was no moon present.
The moon injects another component of variation to screw up the timing but then there is the consistence of highest tides occurring at periods of new and full moon which only amplifies my contention.
lsvalgaard says:
February 15, 2014 at 11:57 am
“Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit…”
You are wrong. Please do not bother me with any more silly stuff like this.
CliveBert
” The bulge on the opposite side to the moon is not because the centre of the earth feels a stronger gravity than the far side ocean. That only applies to fee falling bodies. It is instead due to the centrifugal acceleration caused by its orbit around the joint barycenter.
The tidal force on the ocean is 10 million times smaller than the earth’s gravity. What moves enormous quantities of water is the tidal component parallel to the surface ”
Yes, I think that is what primarily moves the water volume. However, I think it is gravity that sets a limit on how high it can get. As you say its by far the stronger force.
This is the approach the I took the other day in equating the centripetial force to the local value of gravitational attraction. That provides an instananeous equilibrium level to which it would tend.
http://climategrog.wordpress.com/?attachment_id=776
As we all know , the dynamics is a world away from two (or four) bulges.
Mike M says:
February 15, 2014 at 12:00 pm
I never said it was THE explanation of ocean tides but I stand by my assertion the force differential is REAL and acts to reduce the net gravitational force at the equator at both midnight and noon which would cause a perfect 12 hour tide period if there was no moon present.
A force differential is due to gravity, but is not due to rotation or orbital movement.
Bart says:
February 15, 2014 at 12:01 pm
“Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit…”
You are wrong.
The roche limit depends only on the cube root of the ratio of the densities of the bodies [and on the radius of the central body]. As your link says: “we can ignore the centrifugal potential VC and consider only the tidal potential VT”. The centrifugal force being ignored is that of the rotation of a nonspherical body.
Please do not bother me with any more silly stuff like this.
There you go again. A little thought on your part would do you good.
A planet with the dimension and mass as the Earth falling into the Sun from infinity with no centripetal acceleration at all would at the time it distance reached 1 AU experience precisely the same tidal force as the Earth.