Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:

where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that ![]() in stable thermodynamic equilibrium.
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium

In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:

where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.

One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
![]()
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:

where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:

Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
![]()
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Wayne says: “Seems lifting the electrons against gravity in the metal bar from the warm to the cool would cancel if the gradient became -0.0098C/m. ”
Very insightful.
IF the gradient for air and electrons and all other materials were the same 0.0098C/m, THEN maintaining a lapse rate would not lead to a perpetual motion machine.
However, since the lapse rate is given by C_p / g, and since different gases have different values for C_p, then different gases will have different lapse rates. So the premise is indeed wrong, and a stable lapse rate in gases would indeed violate the laws of thermodynamics.
Clearly there are two schools of thought. One school believes that the temperature will be lower at the top due to kinetic energy being changed to gravitational potential energy. The other school believes this will not happen. The GHG controversy rests largely on this point.
No, it doesn’t. There isn’t any controversy. Gravity is incapable of providing net heat to the Earth’s energy budget, and the GHE only deals with the rate at which the Earth loses heat in that budget. Nobody argues that there is a lapse rate in the actual atmosphere. I have just definitively proven above that it is not a feature of static equilibrium, it is a dynamic phenomena caused by differential and irregular time dependent heating and cooling, where the bulk of the heating is at the surface, but where heat loss occurs to some extent very high up in the atmosphere as well.
This has nothing to do with “schools of thought”.
I am troubled on one point. The argument that a continuous flow in a cycle is not equilibrium and thus is some sort of proof favoring one school over the other. Surely dynamic systems can be in “equilibrium” in that there is no net flow into or out of the system, but still allow a cyclical flow within the system.
Surely they cannot, not as long as they are thermally connected at the microscopic scale to allow internal energy transfer within the system. This is precisely the point. Heat never “flows in cycles” in a system in thermal equilibrium. It flows from hot to cold. It never ever spontaneously flows from cold to hot as an steady state thermal process unless one does work on the system. This is what the second law of thermodynamics is all about. The only systems that can “move”, transporting energy around in cycles are ones without mechanisms for energy sharing or dissipation, like planets going around the sun in the limit that you ignore tidal heating and gravity waves and light pressure. In enough time, even those weak effects move energy around and damps periodic motions.
In the case of the gas in the figures above, one could take the silver wire, replace the middle of it with a thermoelectric junction, use the electricity to drive a fan or light a bulb. This, too, would violate the second law — the heat content of the container would systematically lower (as some of the heat in the cycle was converted to work). The net effect would be that all of the energy lost from the container would be converted to work — its temperature would drop as the work appeared in the outside world, quite independent of the temperature out there. This, too, is a direct, textbook case of the violation of the second law of thermodynamics, both the refrigerator statement and the heat engine statement.
At least you are troubled by the right things — you should be troubled by this because your mere common sense tells you that heat, which is basically random motion, cannot remain organized enough to flow around in a circle without something reorganizing it. The microscopic form of the second law says that basically, systems evolve in time from less probable states to more probable states. Take a jar full of identical marbles, some blue and some red, organized with the blue on top and red on the bottom and shake it. You can shake a long, long time before you can expect to see all of the blue on the bottom and the red on top — there are a near-infinity of ways for the marbles to be mixed; only one for them to be cleanly separated red on blue.
That’s the sad thing about this — people don’t understand how much of a law the second law is. Your odds of winning 150 million dollars in the lottery and having the IRS forget to charge you taxes on it due to a clerical error are a gazillion times better than the odds of shaking that jar and getting even a very modest number of mixed-color marbles sorted out by random chance, and that is precisely the reason that heat flows from hot to cold and not the other way around. There are way more states where the energy (per degree of freedom in the system) is approximately equally shared than there are states where it is split up.
Otherwise, your observations about ability to rationalize and so on are well made, but — my advice is don’t bet against the second law. You’ll just lose.
rgb
For 13.7 billion years, …
… Gravity fields have been heating up matter.
That is long enough to be called perpetual.
Just look out at your night sky and see the proof of that. Or maybe even the day-time. The big bright white thing in the sky started shining because of gravity fields heating up matter.
We can extract energy from that we figure out it works exactly. Just like the other ten sources of energy that we didn’t have clue about in times past.
Anyone disputing Jelbrings hypothesis needs to prove that gravity does not provide a minimum heat/energy level in matter when that matter is being held back from falling further through the gravity field by the electro-magnetic and strong forces of the atoms in the rocks at the surface of the planet. The matter is still being pulled through the gravity field, it is just being stopped by the other forces in the atoms of the rocks/liquid.
Has anyone proved that? How could you? We don’t even know how the force of gravity extends its pull. Maybe Higgs bosons increasingly accumulate/stick to matter as it moves into a gravity field and they are attracted to each other. Maybe the Higgs provides heat energy to the matter. If you don’t how it works, you cannot say it has no impact.
George Turner says:
January 24, 2012 at 2:40 pm
George, if you do not know from the context that we are talking about net heat flow through the wire, and not freakin’ brownian movement of electrons, you are not paying enough attention.
w.
If the column of air is not isothermal, that is an emergent phenomenon in the presence of several things:
– A planet
– An active star
– An atmosphere
By this excessive logic, a solar panel can’t possibly be a perpetual motion machine either, so there is no such thing as renewable energy. Especially after the sun fizzles out…
Robert Brown says at 4:36pm:
“The distribution of v at the top (of the atmosphere) and the bottom is identical — the Maxwell-Boltzmann distribution.”
Maxwell-Boltzmann is not applicable in a gravity or electrostatic field. M-B quite clearly limit their derivation of particle velocity to special case of particles with no external forces like no gravity, no electrostatic etc. M-B applies to our famous gas column when it actually is isothermal – in the no gravity case. Caballero 2.2 shows that is the fact and in my view Caballero is correct.
Dewitt Payne: “Please post a calculation of the Velasco lapse rate for a gas column with the surface at STP (101325Pa and 273.15K) and g = 9.81 m/s^2. The number density/cubic meter is ~6E23 molecules/mole/0.0224m^3/mole = 2.7E25.”
I’m a little pressed for time this evening, so I’ll just give you what I have handy, without using your particular values or double-checking. Note that this assumes a monatomic gas. I’ll revise it tomorrow for diatomic (after I read up on rotational degrees of freedom; I’m a layman). As you can see, the lapse rate would be hard to measure experimentally.
f = 3 ; # degrees of freedom
E = 2.2e9; # guesstimate of total energy in a meter-square gas column arbitrarily high
VRW_LapseRate = function(f, E){
k = 1.38e-23; # Boltzmann’s constant
N_0 = 6.023e23; # Avogadro’s number
w_m = 29; # “molecular weight”
m = w_m / N_0 /1000; # molecular mass
g = 9.8; # acceleration of gravity
P_0 = 1.01e5; # atmospheric pressure at sea level
M = P_0 / g; # atmospheric mass per unit earth-surface area
N_m = 1000 * M / w_m; # moles of atmosphere per unit earth-surface area
N = N_m * N_0; # number of molecules per unit earth-surface area
– (2/3) * f * E / (f * N + 2 * N – 2) * m * g / E / k;
}
VRW_LapseRate = function(f, E)
[1] -6.389722e-32
The last line of the function is the result of differentiating Velasco et al’s Equation 8 and converting from kinetic energy to temperature.
As I said, I haven’t double-checked, so there’s likely an error here. You may want to check it yourself.
dlb says:
January 24, 2012 at 3:42 pm
Um … er … well … I must confess, I’m picking my jaw up off the floor.
Here’s the first thing. Nobody is talking about a cubic metre of soil here but you. Why?
Because it has nothing to do with the energy distribution of an ideal gas in a cylinder connected with a piece of silver wire.
I can only shake my head in amazement, dlb. Perhaps if you read the head post again?
w.
A physicist says:
January 24, 2012 at 3:58 pm
Dang. Well, can’t say I’m really surprised. Turn in your PhD at the door, or demonstrate it will flow forever and ever amen, and win the Nobel Prize.
w.
P = T*V helps to understand what’s going on. One must constantly keep in mind that in the gravitationally bound column of gas pressure is constant while temperature and volume are the variables. As its temperature goes up and down its volume goes up and down. Surface pressure is determined by gravitational constant and mass of the gas which do not vary. Temperature is not coupled to pressure therefore pressure is not coupled to temperature. So raising the surface pressure will not cause a rise in equilibrium temperature. It will cause a rise in volume and the gas law wil be satisfied by the change in volume.
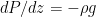
OK, Joules, you’re scaring me. P is absolutely, categorically never equal to V*T. Have you ever heard of “units”? You might look them up some time. Nor is pressure proportional to T*V in an ideal gas (or any gas I can think of). PV = NkT, so P = NkT/V. Nor is pressure constant in a gravitationally bound column of ideal gas. Don’t be absurd — pressure is never constant in any vertical fluid column in a gravitational field. The equation for static force equilibrium is:
Density is (in any situation where this might apply) a strictly positive number, so the pressure must vary with height. I actually derive its isothermal variation with height at the top of this thread. Surface pressures on the Earth vary all of the time, by a few percent. Pressure variations help cause “weather” — that’s why God invented “barometers”, because falling air pressure often warns of a storm, while high pressure usually indicates a fair, sunny day.
Temperature isn’t necessarily “coupled to pressure” — one can certainly have different contains of fluids at any pressure and any temperature — but that doesn’t mean that in various thermodynamic systems:
as a general rule. If you think that, take a soda bottle, screw the lid on good and tight, and put it into some boiling water. Hell, I have a problem just taking those large plastic refillable water bottles back to the store — if you put them into a car with the lids tight you’ll get there with them (often irreversibly) blown up like a balloon. Works the other way too — screw the lid down when it is hot and come back to them partially collapsed.
As for “raising the surface pressure” causing changes in temperature — well, if the surface in question is the cylinder of a gas piston that is being compressed, I beg to differ, especially if it is done rapidly.
Here’s a cute toy that I like to teach my students about:
http://www.practicalsurvivor.com/firepiston
http://www.phy.duke.edu/~rgb/Class/review_53/review_53/node64.html
Lost the figure that went with the problem, sorry, but the pictures in the first one should give you the idea. The point is that whether or not increasing pressure changes the temperature depends on where and how you do it. It certainly can raise the temperature — it depends on the path followed on the P-V curve. Only if you follow an isothermal path does it not change the temperature, but isothermal paths are just one of a myriad of possible paths between a myriad of possible pairs of state points.
I’m also waiting to hear you acknowledge that a static lapse rate in an ideal gas at thermal equilibrium violates the second law of thermodynamics as per the example given above. Since you actually tried to make fun of the textbook physics I’m presenting, it might be appropriate as it sounds like you might be coming to grips with the truth of it.
rgb
The wire suffers from the same loss in gravitational potential energy as it goes higher in the column.
Dear Lord this thread is entertaining. I moved some joules reading through it. Thank you to everyone.
Q. Daniels said @ur momisugly January 24, 2012 at 5:08 pm
I have commenced an extremely empirical experiment what is designed as a empirical disproof of the Second Law of Thermodynamics. This very morning, I mixed 400 ml sterile H2O with 400 ml of the best Italian balsamic vinegar in a bottle and sealed it. Having sealed it with much twisting of the Stelvin seal, I shook it vigorously. Seven times seven times did I shake the Stelvin sealed bottle. When the balsamic vinegar spontaneously separates out from the H2O, verily I shall know that I have violated (desecrated even) the Second Law of Thermodynamics and fully expect to be deported to the US of A for having engaged in a successful conspiracy theory contrary to US law.
t seems to me Robert Brown’s analysis implicitly makes the following claim: if all the greenhouse gases (mainly H20 and C02) were cleansed tonight from earth’s atmosphere, then the atmosphere would evolve toward a more nearly isothermal equilibrium.
Wow, I implicitly said that? Well, imagine that. Who knew? I certainly didn’t.
But let’s try. The problem is difficult because even if there are no GHGs in the atmosphere you still get lateral convection and convective turnover because you are heating the surface more at the equator than at the poles. There would therefore be heat moved from the equator (where the hot air rises) towards the poles (where it cools and becomes less dense) — errr, depending on the shape of the planet. An oblate sphereoid, hmmm, yeah, I think there would likely still be enough surface transport to establish a large scale convective roll with the air rolling north (say) up high, deflecting to spinward as it goes, falling down in a massive spinward spiral, cooling along the ground and being displaced back to the equator. But I’m far from certain about this.
To put it another way, my intuition is that the stratosphere, which currently sits above the greenhouse gases in the troposphere where their is good vertical convection, ought to extend all the way down to the surface. The stratosphere isn’t static — far from it! It just has little vertical shear, and actually warms with height. But the details of the circulation that is established might be difficult to predict (chaotic even). As long as you have day and night and poles and equator, though, you’d have some vertical and lateral convective transport.
This is a good question for a real climate scientist. I’m not even a Sears climate scientist — I’m just a physicist who is trying to keep people from abusing the poor, innocent, second law of thermodynamics in their eagerness to come up with non-GHG surface warming mechanism. It doesn’t really help the anti-CAGW “cause” (Gawd, how I hate that word in the context of climatology post-Mann) if the proposed non-AGW mechanism is nonphysical, especially if it is obviously nonphysical and likely to justly earn the derision of “warmists”. There are plenty of physically plausible places to press them on instead, no need to just make stuff up…
rgb
Joe Born,
After reading the Velasco, et.al. note, it’s quite clear that the authors agree that there is no gravitationally induced lapse rate. For a small number of particles in the control volume, temperature is no longer strictly proportional to the average kinetic energy. But that says precisely nothing about a gravitationally induced lapse rate. In fact the authors specifically state that:
[my emphasis]
Or in short, statement (2) is always wrong, but for different reasons depending on how many molecules are in the control volume. Nowhere in the paper is there a formula for calculating the magnitude of a non-zero lapse rate in the presence of a gravitational field. This has been pointed out to you in one of the previous threads.
Alan Millar says:
January 24, 2012 at 5:22 pm
I couldn’t disagree more. The fact that all sides are welcome to show up at WUWT to advocate for their particular point of view is the strength of the site, not the weakness. Yes, there’s a host of folks out there that believe loop-de-loop stuff. There are even more who are kinda scientific but who could not, right now, give a clear distinction between force, work, and power. There are far too many issuing solemn pronouncements who didn’t even realize that there is a difference between force, work, and power.
But that’s how it is, that’s how the world is. And there are plenty of logical and scientific voices here, including most of those voices who have weight because of their demonstrated understanding of those kinds of distinctions and their willingness to post their views under their own name and history. Not only that, but we’re doing our best to explain this stuff, and discuss it, and debate it.
Finally, the presence here of many believers from the First Church of Gravity is because their Holy Scrolls are being unwound here for everyone to see. In other words, if their claims were being taken apart on Judith Curry’s site, they’d be there screaming as loudly as they are here at the moment. Doesn’t say anything about the site.
It is an issue that I have pushed hard on, however, because the Seekers After Gravity tend to be climate skeptics. I’d like to distinguish that kind of wishful thinking from true skepticism, and make it clear that the latter is very distinct from the former. True skepticism accepts the existence of such controversial and radical new theories as something known as the “Three Laws of Thermodynamics”.
So, I have pushed for and written about the issue here, precisely to see who would say “Don’t be stupid, heat can’t flow indefinitely” and who would say “But you don’t understand, if the force of the adiabatic lapse rate is twice the work, then clearly …”
It’s kind of a modern day scientific shibboleth.
w.
What has Brownian motion got to do with electrons?
And by “net heat”, do you mean the photons from colder to hotter thing?
I thought the compressed gas at the bottom in relation to the less compressed gas at the top simply contained more heat energy/volume even though all molecules in the column would have the same level of excitation.
Precisely. Energy is extensive. Temperature is intensive. Right off of the list:
http://en.wikipedia.org/wiki/Intensive_and_extensive_properties
The one caveat is that a gas does not “contain heat” in the sense that I can say that jar of air at thus and such a pressure and temperature contains so many joules of “heat”. Energy is the proper extensive property, and heat describes a quality of some of the internal energy in a system, namely its availability for doing work.
Good job, keep it up. This sort of thing is all very interesting (and you are pointing out an extremely common error many respondents are making), although I’d have to just turn this thread into an online college thermo course to correct them all. I’m trying to focus on just one thing. No violations of the zeroth or second law of thermodynamics. Oh, hell, people shouldn’t oughta violate the first, either, with their various proposals.
rgb
Joe Born says:
January 24, 2012 at 7:20 pm
But temperature is only strictly proportional to the kinetic energy in the canonical limit and Velasco, et.al. agree that in the canonical limit, the column is isothermal. So you can’t directly convert kinetic energy to temperature for a microcanonical ensemble. Or in other words, your calculation is flawed.
MDR says:
January 24, 2012 at 6:52 pm
I would like to commend and laud this action. He is actually seeking knowledge and understanding. When he finds it, and corrects some prior misunderstanding he had, he not only comes back to say he “identified a flaw” in his reasoning. He explains where he went wrong, and how he got out, so others can avoid the same mistake. I did the same thing in my post “Perpetuum Mobile”.
My thanks to you sir. Your actions represent the best of this site, where people (definitely including myself) can learn something and move the understanding forward.
Warmest regards,
w.
I am not a scientist and never claimed to be so, could someone explain why the gas, or atmosphere in this case, should be colder on top than on the bottom assuming convection works in all cases (cold air falls while hot air rises) Yes, I can figure, as air gets closer to outer space (in really simple terms) it would get mighty cold but, cold air is more dense and as such it should fall more rapidly. Exactly where does gravity enter the picture? It is exerted equally on all temperature states of air, right?
Or should I up my meds? 😉
No, your meds are just fine as they are. It is difficult to explain, impossible in the thread. You need to learn a few things and follow some algebra. The online thermodynamics textbook by Caballero describes the basis for an adiabatic lapse rate, and provides actual graphs of actual soundings of atmospheric temperatures along a vertical column at various locations to show how sometimes the atmosphere follows it, approximately, sometimes it doesn’t, some times (and some places all of the times) it inverts and goes the way you intuitively expect cold below to warm above, and how things like “atmospheric instability” (stormy weather) often depend on local inversions or convective rolls.
The point is that it is actually pretty complicated. To start with, you need to understand what an adiabatic process is, and why lifting, expanding air is expected to expand approximately adiabatically (cooling as it goes) instead of isothermally. Both are possible, mind you, but isothermal expansion requires heat/energy exchange with “something” because the gas does work but its internal energy doesn’t change.
rgb
Robert Brown says at 7:04pm:
“I have just definitively proven above that it is not a feature of static equilibrium…”
If Robert Brown means the top post where he attempts to prove the adiabatic gas column in the presence of gravity is isothermal by ignoring the 0th Law?
No, this is not proven since it is in direct conflict with what Caballero in the link in the Perpetuum Mobile thread proves in Sec. 2-3 – the real world gas column is non-isothermal w/gravity and the device in figure 2 will not run forever with a real non-perfect insulator.
Robert Brown’s disregard for the 0th law means he can use a perfect insulator to prove the column is isothermal in the presence of gravity. This is incorrect theory and cannot be used to disprove EEJ. Ignoring the 0th law means Robert Brown can create a Perpetuum Mobile machine (to sell to Willis’ along with a bridge) with the correct non-isothermal gas column.
Willis said:
Phew … gravity slowing electrons in a wire … thought I’d heard everything.
I’m not sure if I did this right, as it’s not normally the type of electrical calculations I do, but:
One coulombof charge contains 6.24150965e18 electrons, and an electron weighs 9.10938291e−31 kg, so 1 coulomb of electrons weighs 5.68563013e-12 kg. 1 coulomb of electrons 1 kilometer up has a gravitational potential energy of 5.5719175e-8 Joules, and a Volt is defined as 1 Joule/Coulomb, so that would be 0.05571917 microvolts/km, or 17.947 kilometers in height per microvolt. You can do the same calculation in electron volts, with 5.5719175e-8 eV per kilometer..
Robert, it seems that you have completely missed the fact that gravity causes a pressure and density gradient in your air column.
You mean, except for the place where I derived the actual functional form, starting from the gradient required for neutral buoyancy, for the pressure (and by trivial extension, density) of an ideal gas in static, isothermal equilibrium? Missed it except for there?
Funny, I thought that was what most people would have called completely not missed it…
This is a much more complex problem than a quick, partial recitation of a freshman physics text can handle.
No, it’s not. I’ve reduced the whole damn argument to two pictures, and only one counts. It doesn’t involve trying to do statistical mechanics in your head, badly, only pure thermodynamics.
Look at figure 2 above. You explain to me how any supposedly stable thermal lapse rate — I don’t care at all how it is established — in the gas does not violate the second law of thermodynamics when one includes a simple heat conduction pathway between the hot gas at the bottom and the cold gas at the top.
If you agree that the silver will transfer any heat at all between the two reservoirs as long as there is a temperature difference, the only possible way a thermal lapse can be stable is if the perturbation is damped out of the system and the lapse rate restored. This, in turn, requires heat transport down the gas column to restore the lapse rate. This, in turn, causes more heat to be conducted up through the silver wire. Forever, round and round in a cycle.
There is nothing to stop you from cutting the silver wire in the middle and inserting a heat engine instead of conducting pathway, and turn all of the heat energy in the gas into work, violating all of the versions of the second law in the process, or putting the engine inside the gas itself (and inside the adiabatic container) where it will run forever, a PMM2K. A suitably designed (ideal) Dippy Duck placed inside the container is my own personal favorite heat engine — a Perpetually Dippy Ducks run just fine between any two thermal reservoirs at different temperatures, and you assert gravity will create and maintain two such reservoirs spontaneously.
So forget the treatment of pressure, density, and buoyancy. I actually can — and have — treated them, but you obviously haven’t yet made it through that intro physics textbook so that you understand what I’ve done. But you cannot possible be willing to assert that heat will flow in a loop forever, which is a pure consequence of a static, stable, thermal separation in the isolated gas no matter how you think it might come about. You therefore can be certain that no such thing does come about.
rgb
rgb
Heat is Energy is mass by M=E/c^2 so said Einstein.
So what force causes Mass to rise up the silver conductor against gravity ie work has to be done?
The silver conductor is little different from the gas in a column in this respect. The top will be colder than the bottom and heat will not flow up the silver conductor unless a heat source (work) is supplied from the bottom..
Oh, sweet Jesus.
Tell you what. The next time you cook, you be sure to put the food on the bottom of your pan and heat the top. Otherwise, how is all that heat going to manage to make it uphill against gravity?
You can’t seriously be proposing that the silver wire won’t permit heat to flow upwards either.
rgb