Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:

where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that ![]() in stable thermodynamic equilibrium.
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium

In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:

where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.

One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
![]()
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:

where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:

Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
![]()
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Do people really have to have stuff like this demonstrated? I saw, but didn’t read, the previous post on this topic. I thought it was a weird thing to have on a climate blog, though since it did deal with a gas and our climate is a gas, I didn’t think too much of it.
Now, I’ve gone back and read that previous post and glanced through the LONG bunch of comments, a disturbing number of which actually supported the impossible idea. This is basic physics, Second Law of Thermodynamics sort of stuff – you can’t get perpetual-anything.
I thought everyone realized you can’t magically use gravity or magnets to generate perpetual energy machines. It blows my mind that there are actually people who think a thermally graded column would result. It’s nothing but a variation on a perpetual energy machine.
Kudos to WUWT for spending some time debunking this sort of nonsense. It’s sad that there are apparently so many people who swallow this sort of nonsense in the first place.
There seem to be a lot of people who think that a lapse rate is a proprty of the matter itself, rather than a convenient description of the behaviour of the gas.
I’m not sure that Dr Brown will convince them otherwise.
But maybe Hans Jelbring can convince us all that the heat in figure 2 cannot rise up the silver bar because graivity is holding it down!
Sometimes something like this comes along that refutes a common idea so well and simply that it just makes a guy go ‘holy crap!’. Thanks for this excellent post as for me it was a revelation.
‘what goes up, has to come down,spinning wheel has to go round’ blood sweat and tears. it’s a bit warm !
“If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable.
_______________________
This is also perfectly expressed by Le Chatelier’s Principle.
What would complement this theoretical explanation is if an experiment backed it up.
So far as I know no experiment has ever been carried out.
All suggested proposals seem to run into problems when real components and physically accurate numbers are used.
“Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work.”
No, Robert. The second law requires that no energy gradient can be maintained without input of work. It requires the reservoir of gas to be isoenergetic not isothermal. A horizontal layer may be a different temperature than another if the cooler layer has its lesser kinetic energy balanced by greater gravitational energy. This is obviously the case since it goes without a shadow of a doubt that a molecule of air in a higher layer has more gravitational energy than a molecule in a lower layer. Thus the second law actually demands a temperature difference of equal and opposite polarity to compensate for the difference in gravitational energy. An isothermal atmosphere in a gravity field is the one that violates the second law.
My name is Joules because I know how to find and count them no matter how they try to hide.
Thanks for playing.
Hmmm. Temperature is the integral of the number and energy of particles seen at the measuring surface. Less particles equal lower temperature given equal velocity profiles of the particles. Less particles also equals lower pressure. Temperature and pressure are thus directly linked. Hence the dry lapse rate. Gravity and pressure are also directly linked. Hence the dry lapse rate.
Well thanks for taking the time to post Doc.
I gave up trying to convince Tallbloke in the other thread as he is clearly in ‘La La La’ mode.
His reply as to what was going to stop heat flow in a system with a temperature gradient was that at the interface between hotter and colder the actual temperature was the same and therefore no heat would flow!
Lets see, take a rod with a temperature gradient and cut it into the thinnest possible slices allowed in physics and apparently adjoining slices are the same temperature!
However, that would mean the rod was actually the same temperature all the way through as not only are those two touching slices (call them a & b) the same temperature, then obviously, the two slices c & d touching them are also at the same temperature and the two slices e & f touching c & d are the same as c & d and a & b also. Well you get the picture.
Anyway I am sure he will be along soon to show that gravity has some magical quality that allows work to be done indefinitly in a closed system.
Alan
The dry adiabatic lapse rate is derived several ways, each of which assumes an isentropic atmosphere.
Example 1. A packet of dry air rises. Let’s first assert that it is adiabatic (hopefully not controversial), as it rises it expands and does work on it’s environemnt. But that work is reversible. Thus the process is adiabatic and reversible, hence isentropic. By definition.
Example 2. We know from calculus that dx/dy(w)*dy/dw(x)*dw/dx(y) = -1. Let us apply this identity to dT/dp(s), the temperature pressure relationship at constant entropy. We will find that dT/dp=-dS/dP * dT/ds. the second RHS term is Cp/T by the definitoin of entropy. The first RHS term is, by a Maxwell relationship, -dV/dT, which for an ideal gas is R/P (you can google Maxwell relationship). Making the substitutions: dT/dp = RT/PCp = V/Cp for an ideal gas. Lastly we recognize that the gravity imposed pressure gradient is dP/dz = rho*g, but rho is 1/V, so when we multiply: dT/dp * dp/dz = V/Cp * g/V = g/Cp.
Example 3. The state of an ideal gas is fully specified when two variables are specified. We shall choose T and p. The total entropy differential is: dS = dS/dT * dT + dS/dp * dp. at constant entropy, dS=0, then dT/dp = dS/dp * dT/dS and we proceed as above.
So, it seems quite clear to me that the near surface atmosphere is isentropic.
The moist adiabatic lapse rate MALR differs from the DALR because it must account for the latent heat release as water condenses. This extra heat slows the rate of cooling of a rising air packet, so the MALR is less than the DALR – but it is still isentropic as it satisfies all the condition of my example 1, but the math is kinda nasty.
The adiabatic lapse rate need not be an equilibrium critereia, but instead a steady state condition if heat transfer in the near surface atmosphere is dominated by convection.
Let’s set moisture aside for the moment and set up a simple dry ideal gas atmosphere. Incoming radiation heats the planet surface. Air at the surface is heated and begins to rise, thus convection begins. Convection is attempting to return the atmospheric temperature gradient to zero, but as it rises it experiences an isentropic expansion, which causes it to cool (the reverse also occurs). If convection is the dominate mode of heat transfer (conduction negligible), it cannot drive the temperature gradient to zero, but only to the DALR.
Thus, I think the DALR is a steady state condition that arises because, in the near surface atmosphere, convection is the dominate heat transfer mode and it is a compressible fluid with a gravity imposed pressure gradient, hence convection is constrained by the DALR.
Lastly, if I assume the entire atmosphere is isentropic – all the way to the tippy top – then T1/T2 = P1/P2^0.4. If I solve for T2 letting T1 and P1 be the conditions at the tippy top of the atmosphere, I calculate an enormous value for T2, the surface temperature. Clearly the atmosphere cannot be isentropic all the way up. At some point it becomes non-isentropic.
I think the isentropic condition breaks down when convection ceases to be the dominant mode of heat transfer. As you rise, the atmosphere becomes less dense, convection less effective, until eventually heat transfer is dominated by radiative heat transfer. Radiative heat transfer is not constrained by the DALR and can drive the temperature gradient to zero. Hence the planet surface temperature is not enormous.
So, the non-radiative atmospheric thermal effect becomes an exercise in identifying at what point in the atmosphere does convection cease to dominate, which is also the point where the isentropic assumption breaks down. If that point is known (yes I know it won’t be a sharpt break between convection and radiation, but let’s keep it simple), then the equation above can be used to find the increase in surface temperature resulting from an isentropic near surface atmosphere.
Now, I could very well be wrong, or have made mistakes along the way (I do that sometimes – maybe even more than sometimes). But please don’t wave your hands at me and tell me to “check the meaning of entropy” – I find that frustrating. I think I’ve shown sufficient work…
Show me my mistake. Anybody. I won’t be offended.
T = temperature
p = pressure
V = olume
R = ideal gas constant
Cp = ideal gas heat capacity = 5/2R
g = gravitational constant
rho = density = 1/V
z = vertical spatical coordinate.
Very interesting but really irrelevant given that our atmosphere is not an ideal gas in a cylinder. Gas, ideal or otherwise, is a very poor heat conductor compared to Silver so perhaps your example above is not very good and enrtopy will still increase. It can be demonstrated by observation that convecting gas does rise, due to the density difference between the rising gas and that of the surroundings. If we consider real air it can be saturated with water vapour and rise to form clouds. The rising air will cool adiabatically at the SALR (4c/1000m rise) but will descend, as it must as dried air having the water vapour removed in the cloud formation, and warm at the DALR (9.8C/1000m) and end up with more heat than it started with. Rather like a Foehne Wind in a vertical loop. Katabatic winds are warmer at the bottom of their descent than the cold mountain start. The atmosphere is never in equilibrium because the planet rotates, there is a non-uniform surface and moving clouds which alter the solar energy falling on the surface. It is the lack of atmospheric equilibrium that gives us weather.
I am not being obtuse here but there is so much wrong with the GHG theory, cooling planet and rising GHG’s, lack of the predicted tropospheric heat, and the violation of 2nd law with this heat transfer from a cool troposphere to the warmer surface. If you could do that you really would have a PMM. So an alternative mechanism must be found to explain the BB heat anomaly, assuming that this is correct.
“In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down.”
I live half-way up a mountain at 6100 feet. The valley below is at 4500 feet. The temperature difference is nearly always the dry lapse rate 8 degrees F, whether it is calm or windy. Only if it is raining or snowing will it be different. It then goes to the moist lapse rate. Most of the time it is sunny, heating the ground equally, both in my back yard and in the valley below. What maintains the lapse rate temperature difference?
In the real atmosphere the Earth surface is heated and radiation cools at top of atmosphere.
Convection is the major method of heat transfer.
Is convection always present?
The answer according to textbooks is no.
We can have the interesting situation where there is little or no convection, still air in other words.
This condition is called the Neutral Atmosphere.
This atmospheric condition is known as the neutral atmosphere and can be stable particularly at night.
See the near Neutral RESIDUAL LAYER page 31
What happens then?
Robert Brown says
“What maintains the adiabatic lapse rate is convection”
Nick Stokes and Joel Shore would agree.
So if convection is absent presumably the lapse rate disappears!
Well not in the real world.
If the air is dry, the lapse rate is at its maximum of g/Cp = – 9.8K/km
Climate Science define convection as an UNSTABLE vigorous vertical exchange of air. .
See bottom of page 13.
The stable condition (hydrostatic approximation) is used to derive the DALR. See page 12
This condition holds for still air and air parcels moving up and down at constant speed (no unbalanced force) will track the DALR.
These air parcels are assumed not to exchange heat with their surroundings.
On going up expansion work PdV is stored by the surroundings(temperature dropping by 9.8K/km)
At TOA there will be a loss of heat by radiation to space causing the down phase
On going down the surroundings do work on the parcel (PdV) (temperature increasing by 9.8K/km)
Stationary parcels will not change temperature.
These two idealised adiabatic processes (like the adiabatic stages in the Carnot Cycle) will result in the parcel returning to Earth with nearly the same temperature as leaving (the slight drop being accounted for by radiation at TOA).
http://www-as.harvard.edu/education/brasseur_jacob/ch2_brasseurjacob_Jan11.pdf
@Joules Verne: “This is obviously the case since it goes without a shadow of a doubt that a molecule of air in a higher layer has more gravitational energy than a molecule in a lower layer.” Does the fact that the air in a higher layer also has fewer molecules matter? That is, are we talking individual molecules or rather volumes of molecules here?
Two points:
1) If the atmosphere were isothermal, then a unit mass of atmosphere would have greater total energy (thermal + potential) the higher it is located and the further it is away from the surface heating source. That is not a stable situation.
2) The silver wire will transport heat from warmer region to the cooler region, but in so doing it short circuits the transport of heat by convection. So with the wire present, convection will be less, but the net transport of heat will remain the same.
This head post now makes me want to more fully question all the textbooks to which I’ve ever been exposed.
Consider this simplest and no simpler demonstration:
Robert Brown’s wire is U shaped. This sudden U-turn enables the wire to enter a 2nd thermal energy reservoir (another control volume that happens to be a gray colored one). The wire, in Robert’s example in his words, is: “adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container”.
Thus the wire is adiabatically insulated from the temperature field of the gas in the white colored area. Heat will indeed flow until the gray reservoir is in thermal equilibrium with the white reservoir. This just shows why there are no perfect insulators – Perpetuum Mobiles could be constructed in gas in a gravity field. This IS textbook stuff.
Why did Robert Brown have to go to the trouble of constructing a second gray reservoir with the U-turn? Robert Brown needed a second thermal body.
Trick’s view is Robert Brown should run this analysis again with the wire not leaving thermal contact w/white colored control volume gas and report back with only one thermal body or one energy reservoir or one thermodynamic system. Call it what you will.
Meaning Robert Brown is allowed only one heat reservoir to demonstrate his proposed isothermal gas column where the wire stays in thermal contact with the white colored gas everywhere – no U-turns as here to a 2nd thermal reservoir. Trick’s view is Robert will be unable to do so – the gas column will not be isothermal – there will be a temperature lapse rate.
Trick’s view remains that Robert Brown’s proper application 0th, 1st,2nd Thermo Laws will enable Robert Brown to eventually see the one thermodynamic system GHG-free gas column w/gravity is not isothermal in theory since Robert Brown is smart and the thermo grand masters are right.
NB: I am posting here b/c I have had a miserable head cold last few days and was looking for a way to pass the time. It has been interesting & fun to re-learn about thermo. I have to thank Robert Brown (and Willis) for a more enjoyable few days than I would have had otherwise .
steveta_uk says:
January 24, 2012 at 6:42 am
“I’m not sure that Dr Brown will convince them otherwise.”
Brown won’t convince him this way.
“But maybe Hans Jelbring can convince us all that the heat in figure 2 cannot rise up the silver bar because graivity is holding it down!”
The device in figure 2 doesn’t work because it’s a closed system and the work extracted will reduce the total energy of the column until eventually there’s no more energy to extract at which point the gas reaches a temperature of absolute zero and has presumably vanished from this universe being totally converted to kinetic energy in the extracted useful work. In the real world the gas will collapse to the surface as a liquid before it gets to absolute zero and this will shut off further extraction of energy because the cold side of the thermocouple no longer has any cold gas to cool it.
When doing thought experiments it is wise to think about what might have been assumed.
I see two assumptions above:
1. It does not matter what the density of the gas is. It will equally conduct heat at the bottom into silver wire, as the wire will be able to conduct its heat into the gas at the top, even though the density at the bottom and top is different, due to the gravitational effect on the gas.
2. The cross-section of the wire will stay the same, which means the ability of the wire to conduct the heat, which depends on its cross-section, is the same at the bottom and top.
The gravitational field will actually pull down a considerable part of the mass to the bottom, making it far wider at the bottom then the top (depending on the length of the wire and its tensile strength), deforming it more into a tear drop shape.
With your setup you may be able to change the lapse rate, but I doubt that you achieve an isothermal state in this way.
I find the analysis quite reasonable – but it is so idealized as to be useless. A more interesting thought experiment has a spherical planet heated by a remote star, rotating on an axis roughly normal to the line to the star, with an atmosphere of non-greenhouse gases. The equator would be warmer than the poles, so there would be Hadley-type circulation that would cool the equator and warm the poles. Would there then be a vertical thermal gradient? I think there would be, but I’m sure someone would like to argue to the contrary.
I see a lot of people talking about heat and temperature as if they’re the same thing here, then basing their arguments on that false premise.
Isn’t that, for the most part. why we have variable wind? And the reason there is not a pocket of ‘missing’ heat 800 meters below the oceans surface, as is commonly conjectured by Hansen, et al.
It clearly shows that without an already present differential of temperatures, gravity cannot create one. But the atmosphere is a different problem. It is heated at the bottom and it loses its heat in altitude. So the question is, what can impede the flow of heat from the warmer ground to the cooler “layer of emissions”. It seems to me that both greenhouse gases and gravity would enhance the lapse rate or impede the flow of heat between those 2 layers.
I often hear people say that nights would not be as warm if IRs were not coming from the atmosphere, but what about gas particles falling and hitting them all of the time?
This is funny : ) Almost everyone is right.
Take a single gas molecule and put it at the top of the tube. It has zero kinetic energy and zero temperature. Let it fall and just before it hits the bottom it will have a lot of kinetic energy and heat. That is the lapse rate and it isn’t in equilibrium by definition.
Now place the atom at the bottom of the tube, it is now in isothermic equilibrium, its kinetic energy and temperature is zero.
If we let the atom bounce up and down in the tube, and don’t allow any energy to be extracted, it will stay in perpetual motion (and gravity will be continuously accelerating it) and will have a lapse rate (as long as the lapse rate isn’t measured).
Wayne2 says:
January 24, 2012 at 7:39 am
“@Joules Verne: “This is obviously the case since it goes without a shadow of a doubt that a molecule of air in a higher layer has more gravitational energy than a molecule in a lower layer.” Does the fact that the air in a higher layer also has fewer molecules matter? That is, are we talking individual molecules or rather volumes of molecules here?”
No. The fewer molecules must have sufficient gravitational energy that, if it were converted to kinetic energy, would be able to raise the temperature of a larger number of molecules in the lower layer the temperature in that lower layer. It MUST be isoenergetic to satisfy the second law. It need not be isothermal. In politics they say to follow the money to arrive at the truth. In physics you want to follow the
jewelsjoules.“Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect”.
So your wonderful assertion, is that the radiative forcing of Co2, occur after its entry into the thermostats of the tropopause, and that extra radiative forcing, causes that missing hot spot, increasing the temperature back through the stratosphere and down again through the thermostat of the tropopause.
Been there, done that.
My name is Joules because I know how to find and count them no matter how they try to hide.
Well then, by all means go patent your perpetual motion machine of the second kind or explain heat flow in the second diagram, Joules.
And I’m ever so sorry, but in an ideal gas the temperature is not determined by the total energy. That’s an absurd idea, given that one can perform a gauge transformation — change the zero of the total energy — without changing any of the physics. What matters is the distribution of energy in degrees of freedom. The number of degrees of freedom in an ideal gas does not depend on whether or not the air is in a gravitational field. Take a sealed jar full of air at temperature T and gently carry it upstairs, and it is still at T.
But all of this is too difficult for you, so stick with explaining why figure 2 — based on absolutely trivial physical principles would not occur as described, given a thermal lapse rate in the gas. Is there something miraculously interesting in the thermal contact between silver and air that keeps heat from being conducted from hot to cold — in just this one special circumstance? I’m all ears.
rgb
Also, a constant temperature with altitude means that particles at the top of the atmosphere have more momentum than particles at the bottom. Can you show that this sorting will happen at the molecular level? Or can this sorting happen only by convection of masses of air?
Robert:
I would be interested in your take on the paper at http://arxiv.org/PS_cache/arxiv/pdf/0812/0812.4990v3.pdf where it is conjectured that “….If one could concede that the true equilibrium state may be isentropic instead of isothermal “
That Dr. Brown has it wrong is readily demonstrated by a thought experiment nearly any layman can perform.
If an ideal monatomic gas subjected to gravity in a thermally isolated container consists of only a single molecule, its kinetic energy K–and thus the mean translational kinetic energy–at any altitude z is given by K = mg(z_max -z), where m is molecular mass, g is the acceleration of gravity, and mgz_max is the total (kinetic + potential) energy of the gas. This is true no matter how long you’ve allowed the gas to “equilibrate.” In other words, temperature depends on altitude at equilibrium: there’s a non-zero temperature lapse rate.
Extending this result to any number N of moleculles yields
K = 3 mg(5N-2)(1-z/z_max),
an equation that I’ve adapted from Equation 8 of the Velasco et al. paper, to which I was introduced here: http://tallbloke.wordpress.com/2012/01/04/the-loschmidt-gravito-thermal-effect-old-controversy-new-relevance/. Note that temperature still depends on altitude.
As a practical matter, this result differs only negligibly from the isothermality for which Dr. Brown argues if the number of molecules is large. As Dr. Brown states, though, “[t]he magnitude of the [temperature difference, and the mechanism proposed for this separation are irrelevant,” to his attempted refutation. So the fact that there is any non-zero lapse rate at all at equilibrium establishes that Dr. Brown’s attempted refutation is invalid.
I hasten to add that the lapse rate that does prevail at equilibrium is much smaller than that for which Jelbring contends, so Jelbring is still wrong. .
I should also state that I was not able to follow each and every step of Velasco et al. and the Román et al. paper on which it relies. But its result is consistent with the thought experiment above, whereas Dr. Brown’s isothermality theory is not. Moreover, the Román et al. paper starts from a statistical-mechanics basis,, i.e., from first principles, rather than being based based on blindly accepting equations as received truth without double-checking their ranges of applicability.
I would welcome the assistance of any true physicists out there in examining those papers’ equations further.
says: These two idealised adiabatic processes (like the adiabatic stages in the Carnot Cycle) will result in the parcel returning to Earth with nearly the same temperature as leaving (the slight drop being accounted for by radiation at TOA).
Carnot cycles are ISENTROPIC. By definition. Isentropic means adiabatic AND reversible.
Hmmm. Temperature is the integral of the number and energy of particles seen at the measuring surface. Less particles equal lower temperature given equal velocity profiles of the particles. Less particles also equals lower pressure. Temperature and pressure are thus directly linked. Hence the dry lapse rate. Gravity and pressure are also directly linked. Hence the dry lapse rate.
Sure, sure, sure. But no. I provide the explicit algebra that shows that an isothermal gas is perfectly happy supporting itself. If you want to discuss the temperature of the gas, learn what microscopic temperature is, because it does not depend on the number of particles. 10^18 particles of gas in a container can have any temperature you like. So can 10^23. If those two containers have the same temperature, they have the same average kinetic energy per particle (for a monatomic gas). This doesn’t even depend on the mass of the particles.
However, the reason I drew the pictures is so you could all stop pretending that you can do stat mech computations in your head without even knowing what molecular temperature actually is, and concentrate on easier stuff, like heat flow. If the stable thermal equilibrium of the gas in figure 2 has a lapse rate, heat has to be resorted by gravity from the top to the bottom order to maintain the lapse rate as heat flows in the silver! Heat will definitely flow in the silver, right? It’s just a chunk of metal that’s an excellent conductor of heat. Put it in good thermal contact in between gases at two different temperatures, heat will flow because there isn’t any bullshit about gravity that you can invoke without understanding it. It’s just like Newton’s Balls — whack it on one end and the whack is transmitted, more or less undiminished, to the other end until thermal equilibrium is reached.
Only it is never reached, is it? As fast as you warm the top, gravity has to move the heat to the bottom to restore the lapse rate, which means that it keeps flowing through the silver to the top, where it flows back to the bottom, where it flows to the top — perpetual motion — of naked heat, absolutely predicted by high school physics.
You want to assert otherwise, you tell me what the equilibrium state is of figure 2.
rgb
Joules Verne – I think you are getting at the crux of the matter here.
These “idealized” descriptions are REALLY DEADLY in this debate.
WHY? What would be the “equilibrium explanation of my coming into LAX 10 years ago, from Hawaii, and watching the temperature INCREASE until 6,000 Feet ASL, where it was 80 F. Then from that point on, until we hit the ground there was an INVERSE lapse rate, going to 65 F on the ground.
Certainly this is a demonstration that “equilibrium thermodynamics” is NOT a proper way to approach any correct modeling of the atmosphere.
It become a difficult, and intractable problem which does not yield to simple differential equations applied to idealized columns of gasses in “ideal” states.
Show me my mistake. Anybody. I won’t be offended.
No, I think you are generally quite right, and this agrees rather well with Caballero’s argument. Isentropic because it is dominated by convection, not conduction, in an open system heated at the bottom. Isolate the system, or heat it at the top and explain to me how the bottom will end up warmer than the top.
Yeah, right. Just like the oceans. I wonder why the argument fails for the oceans? They seem to come into thermal equilibrium at, well, thermal equilibrium (constant temperature, independent of pressure, density, “gravity” etc), below the convection-dominated thermocline.
rgb
Ignoring conduction and radiation for the time being and considering only convection:
For convection to occur, there must be a difference in density. If there is no density gradient, there will be no convection.
The ideal gas law is:
where:
Density in molecules per unit volume would be:
Rearranging, we get:
So, there will be an evenly varying gas column with no convection because:
and
So, we would expect the atmosphere at the surface of a planet to be warmer that it is at the top of the atmosphere. Of course, we can’t totally ignore conduction and radiation but, compared with convection, they are second order effects.
Clearly there are two schools of thought. One school believes that the temperature will be lower at the top due to kinetic energy being changed to gravitational potential energy. The other school believes this will not happen. The GHG controversy rests largely on this point.
Where are the learned papers where someone has actually conducted experiments to test this? Measured the temperatures in a gravitationally bound column to determine if we have built a 150 years of science on a faulty assumption.
I am troubled on one point. The argument that a continuous flow in a cycle is not equilibrium and thus is some sort of proof favoring one school over the other. Surely dynamic systems can be in “equilibrium” in that there is no net flow into or out of the system, but still allow a cyclical flow within the system.
The only definitive test is observation. Otherwise we could turn science over to theorists with computers. We cannot “test” this question with calculations that are in any way based on the same underlying assumption. They will by necessity confirm the school of thought they are based on.
Human beings have an infinite capacity to rationalize. History shows that a single faulty assumption does not in the least prevent us from building a huge body of self-confirming science in support of the assumption. In the end however, nature has an infinite capacity to surprise.
As our technology improves we gain the ability to replace assumption with observation and uncover in which direction the truth lies. Thus the development of Relativity to explain small observed variations in the orbit of Mercury as compared to the predictions of Newton.
On average temperatures are warmer at sea level than at mountain tops. We could run a silver wire between the two and heat would run through it indefinitely. This in itself does not appear to favor one school of thought over the other. I’d like to see the observation evidence.
I agree that a column of Ideal Gas in the Dr. Brown’s column above will be isothermal at equilibrium.
Now, let’s fill the column with a GHG, say CO2.
Case C0: Leave it in the dark. It has a pressure gradient, more CO2 at the bottom. If the Bottom of the column is at temperature T1b, what will be the top temp T1h? Since the bottom is at T1b, the column is receiving and emitting energy according to SB theory. If necessary, put the column in a room where all the walls are held at T1b.
Case C1: Leave it in the room, but turn on the lights. Bathe it in 240 w/m^2 from all directions. Will it be isothermal, or establish a gradient. I think it will stay isothermal, Despite more CO2 at the bottom of the column. Will the result depend upon T1b?
Case C2: Leave the light on, but replace the CO2 with O2 of the same mass (higher pressure). What will change?
Case C3: Same as Case C2 but use the same molarity (same number of gas molecules) as C1.
T1b is remains the temp of the base of the column, the floor, walls and ceiling of the room in all cases.
Case C1D: Return to case C1. Now turn on the lights for 1000 sec, Turn the lights off for 1000 sec. Repeat. This is an optical pumping, but T1b says the same.
Case Pxx: Same as above except now we leave the room at T1b, but pump the base of the column with T1b(t) = T1b(0) + 10 * ( int (time_sec)/1000 mod 2)
(i.e. every 1000 sec, raise or remove 10 deg K in a square wave)
I am not being obtuse here but there is so much wrong with the GHG theory, cooling planet and rising GHG’s, lack of the predicted tropospheric heat, and the violation of 2nd law with this heat transfer from a cool troposphere to the warmer surface. If you could do that you really would have a PMM. So an alternative mechanism must be found to explain the BB heat anomaly, assuming that this is correct.
Please, if you heat your house when it is cold outside, and then add insulation (defined to be anything that slows the transfer of heat), is the second law of thermodynamics violated if the house gets warmer? I don’t think so.
I’ll just repeat what I’ve posted on many other threads. The Greenhouse Effect itself is positively confirmed by the actual measurements of the IR spectra from above the atmosphere. Asserting that it doesn’t exist is just plain stupid when you can measure the actual radiation being given off by the CO_2 and the surface.
If you want to complain about the “upwelling” and “downwelling” radiation arguments, well, I find them unconvincing as well, but that has nothing to do with whether or not the GHE exists! The primary place the atmosphere cools is up at the top of the troposphere — via radiation from a single optical path length thickness of the optically thick (in a selected band) CO_2.
Why is it that you want to fight over physics that you can actually see with IR eyes? Save your energy for useful things, like arguing about the magnitude of the GHE, the sensitivity of it to changes in CO_2 concentration, the sign and nature of climate feedback or albedo modulation or the complex effects of atmospheric convection on local heating or cooling rates, or the ocean’s effect. The IR spectra render arguing about GH warming per se moot.
rgb
P = T*V helps to understand what’s going on. One must constantly keep in mind that in the gravitationally bound column of gas pressure is constant while temperature and volume are the variables. As its temperature goes up and down its volume goes up and down. Surface pressure is determined by gravitational constant and mass of the gas which do not vary. Temperature is not coupled to pressure therefore pressure is not coupled to temperature. So raising the surface pressure will not cause a rise in equilibrium temperature. It will cause a rise in volume and the gas law wil be satisfied by the change in volume.
Robert Brown says
“What maintains the adiabatic lapse rate is convection”
What maintains the adiabatic lapse rate is energy transfer between reservoirs at different temperatures. Read your own description. Turn off the radiative cooling of top of atmosphere, and the radiative heating at the bottom, and you get — not overnight, but you get — inversion.
You might try looking at the “DALR” over antarctica around July. Oooo, top of atmosphere hotter than the bottom! How did that happen?
rgb
Joules Verne says:
January 24, 2012 at 7:04 am
“My name is Joules because I know how to find and count them no matter how they try to hide.
Thanks for playing.”
______________________
How.s the family, Joules?
It seems to me Robert Brown’s analysis implicitly makes the following claim: if all the greenhouse gases (mainly H20 and C02) were cleansed tonight from earth’s atmosphere, then the atmosphere would evolve toward a more nearly isothermal equilibrium
But how would that work, exactly? Because on the first day following the cleansing, the sun would still warm the earth during the mornings, thermal currents would still rise during the afternoons, and these afternoon parcels of air would still adiabatically cool as they rose …
So upon this cleansed-of-GHG planet Earth, how exactly would the atmosphere’s temperature profile evolve toward a more nearly isothermal profile, in which rising thermal updrafts were weaker than in the present atmosphere?
If Robert Brown answered this question clearly (and it is a subtle question IMHO), then it seems to me that his theoretical ideas would prevail.
I thought the compressed gas at the bottom in relation to the less compressed gas at the top simply contained more heat energy/volume even though all molecules in the column would have the same level of excitation.
The person who observes that temperatures, in general, decrease with height in the troposphere, and who notes that pressure does too, might well be inclined to link one with the other in a causal way not least because of course you can raise the temperature of a gas by compressing it. It is tempting. But a source of great complexity in our spinning, turbulent, inhomogeneous air is the fact that it is largely heated from below, differentially by latitude, by surface properties, by cloud cover, and by time of day and time of year. This simple exposition cuts through all that befuddling complexity to highlight the role of gravity in thermal isolation, i.e. with no heat transfer at the base, or anywhere else on the bounds of the containing surface. The thought-experiment with the silver wire applies the coup-de-grace. I also liked the notion that gravity is a poor candidate to be Maxwell’s demon! I conclude that a thermally isolated container of gas in zero gravity and at uniform temperature, will not see any temperature change if some other demon could switch a gravitational field on at will. Merely the creation or a density gradient. Is that right?
The air at the bottom has a higher temperature as a consequence of being compressed by the mass of air above being acted upon by gravity. Over time, I would expect the system to reach thermal equilibrium. I am assuming that there is no introduction or loss of energy from the system.
In the real world (our atmosphere) the ground heats the air above continuousy during daylight hours and there are many other processes such as convection, radiation and evaporation that lead to energy leaving the system, so the process is never at rest and the temperature gradiant is maintained.
Take a single gas molecule and put it at the top of the tube. It has zero kinetic energy and zero temperature. Let it fall and just before it hits the bottom it will have a lot of kinetic energy and heat. That is the lapse rate and it isn’t in equilibrium by definition.
No, it won’t have any “heat”. You are conflating work, organized kinetic energy, and heat. Drop a jar of air. Are you asserting that a thermometer placed inside will go up as it falls? Of course not. It is when it inelastically collides at the bottom, and the organized kinetic energy (which is quite capable of doing reversible work still) becomes disorganized, moving into the far more probable state with the same total energy but with the particles of gas moving every which way, that we might talk about “heat”, but even that is really a false idea.
Temperature of a monatomic ideal gas is one thing, and one thing only. It is a direct measure of its internal, disorganized (equilibrated) average kinetic energy. Not its kinetic energy in a moving frame, not its potential energy in a moving frame or otherwise. Only its plain old kinetic energy. To be very specific, the gas will be in equilibrium at a given temperature T when the distribution of the molecular kinetic energies (or by transformation speeds) is given by the Maxwell-Boltzmann distribution.
The problem is that if you drop the molecules as you describe in a real tube, they won’t just bounce up and down. They’ll bounce sideways and quickly “thermalize” as they collide, eventually sharing the kinetic energy around so that the probable transfer of energy in every collision is the same in both (all) directions. That’s the rub. An ideal gas collides instantly — a hard sphere approximation, like perfectly elastic pool balls. Gravity has no time to act during the collision. The solution for the pressure at a constant temperature above indicates that a gas is perfectly happy to support its own weight and density/pressure profile at a constant temperature, and at a constant temperature all collisions have equal probabilities of heat transfer in all collisions in all directions. That simply isn’t the case if the MB distributions (and hence temperatures) vary with height.
But the basic point of my paper is that Jelbring is wrong not because of any possible microscopic description of a lapse rate. A lapse rate itself is wrong in thermal equilibrium, because figure 2 is very, very easy to understand. There is no question that the silver will conduct heat between reservoirs at different heights exactly the same way it does any other time. If you doubt me, put a pan on the stove, put your fingers on the pan, turn on the heat below, or hold onto a piece of solder while you heat one end of it. Or read wikipedia articles on the heat equation or Fourier’s Law. Or take a course in stat mech.
If any lapse rate is stable, the system violates the second law, as heat will flow through the silver for any difference in temperature until there is no difference in temperature, and therefore any steady state that still has a lapse rate must transport heat down the gas column on the left from colder to hotter (violating the second law all by itself, but it is so difficult for people to understand this, alas). And we’re done. No, heat will not flow forever in any physical system.
Done.
Joules Verne says:
January 24, 2012 at 8:07 am
…” The fewer molecules must have sufficient gravitational energy that, if it were converted to kinetic energy, would be able to raise the temperature of a larger number of molecules in the lower layer the temperature in that lower layer. It MUST be isoenergetic to satisfy the second law. It need not be isothermal. In politics they say to follow the money to arrive at the truth. In physics you want to follow the jewels joules.”
_______________________________
How can the conversion be isoenergetic while remaining isothermal? Is it adiabatic with an increase in pressure?
No. The fewer molecules must have sufficient gravitational energy that, if it were converted to kinetic energy, would be able to raise the temperature of a larger number of molecules in the lower layer the temperature in that lower layer. It MUST be isoenergetic to satisfy the second law. It need not be isothermal. In politics they say to follow the money to arrive at the truth. In physics you want to follow the jewels joules.
You leave me — almost — speechless.
I can only reiterate — you tell me what the heat flow will be in figure 2 above. Which is violated — the heat equation in silver or your absurd assertion that gravity can stably sort out a gas into a hotter temperature and a colder one?
One or the other. Only one makes you look silly, though.
rgb
Two distinct scenarios are being discussed here in a somewhat confusing fashion. One scenario involves an adiabatically stratified system and the other involves an isothermal system. It is important to realize that thermodynamic equilibrium does not necessarily mean the gas is isothermal. It is possible for a system to be in thermodynamic equilibrium and *not* be isothermal, as in the case discussed here where gravity stratifies the gas with height.
Here is a more detailed explanation. In the system described above [without the wire], there are only two sources of energy: gravitational potential energy and internal energy. Because matter located at lower z [height] will have a lower amount of gravitational potential energy, it then follows that matter located at lower z also has a greater amount of internal energy. As a result, the total energy [that is, the sum of gravitational potential energy and internal energy] with height is a constant, and the system can be said to be in thermodynamic equilibrium. If this weren’t the case, then energy transfer would occur, in the direction so as to equilibrate the total energy.
Now, we just showed that internal energy decreases with height, as explained above. Since internal energy [of an ideal gas] is directly proportional to temperature, this must mean that temperature also decreases with height. The gradient of temperature with height is of course the lapse rate. This is an example of a system that is both in thermodynamic equilibrium and possesses a gradient in temperature.
Thank you Dr Brown.
As many have commented here, this blog has become a haven for rather foolish comments.
It proves that skeptics are just as gullible to poor logic and bad science as the CAGW.
When something fits with your world view there is a tendency to embrace it.
However, Science and Physics is NOT about anyone’s world view – as James Brown would say “It is what it is”.
I don’t buy the scaremongering CAGW nonsense about man-made CO2 because the Science and Physics clearly do NOT support such claims. However, for the very same reason, I cannot support some of the wildly inaccurate nonsense science being discussed here lately in these forums.
Consider sunlight reaching the earth’s surface. This heats the surface and energy is radiated back to space. The incoming and outgoing energy must balance.
Add GHG to the atmosphere and some of the outgoing radiation will be intercepted and prevented from reaching space. Thus the surface temperature of the earth must increase to increase the out-flowing radiation and restore the balance.
Now, consider what happens if at the moment a molecule of the earth’s surface is about to emit a photon to space, instead a molecule of N2 comes into contact with the surface and the energy from the surface is instead conducted into the molecule of N2. This flow of energy through conduction will reduce the surface temperature and prevent the photon from being radiated to space.
This will have the effect of decreasing the out-flowing radiation from the surface, in a manner that is for all intents and purposes indistinguishable from the effects of GHG. Thus, the temperature of the surface must rise to restore the out-flowing radiation that is being lost to conduction. The greater the atmospheric pressure, the more N2 molecules, the greater the likely-hood that conduction will take place limiting radiation from the surface to space, the more surface temperatures must rise.
But what about the energy absorbed by the N2 some might ask. Indeed and what about the energy intercepted by the CO2? Both must either heat the atmosphere or be returned to the surface and thus are indistinguishable in their effects.
However, the GHG theory tells us that only radiative transfer is responsible for warming the surface, that conduction cannot have this effect. Yet it is clear to see that convection limits radiation to space in a manner that is for all intents and purposes equivalent to GHG. The greater the pressure, the more likely this becomes, the more surface temperatures must rise.
Meaning Robert Brown is allowed only one heat reservoir to demonstrate his proposed isothermal gas column where the wire stays in thermal contact with the white colored gas everywhere – no U-turns as here to a 2nd thermal reservoir. Trick’s view is Robert will be unable to do so – the gas column will not be isothermal – there will be a temperature lapse rate.
Excuse me? I have no idea what you could possibly be talking about. Look, grab a copper wire by one end. Hold the other end in the flame of your stove. I don’t care what shape it has, you will burn the hell out of your fingers (and keep burning them until your fingers are at the same temperature as the flame).
My picture shows a wire insulated on the sides so that any heat that goes into the wire can’t come out anywhere but the end. It just makes the wire a one dimensional conductor of heat. Put the damn wire (insulated on the sides) right into the container, perfectly straight if you like. As long as the bottom UNinsulated end is in contact with the gas at the bottom at T_b, and the top UNinsulated end is in contact with the gas at the top at T_t, and T_b > T_t, heat will flow in the wire from the bottom to the top.
The point is that heat will flow in this system forever if you postulate that gravity will maintain a lapse between the bottom and the top stably. That means that any small packet of heat that is moved around in the gas has to eventually settle back down into equilibrium, and you are asserting that equilibrium has a lapse. So when the wire carries heat from the bottom to the top — which it will — gravity has to sort it back down to the bottom, because you assert that a lapse is the stable equilibrium.
Only it won’t. If it did, the second law wouldn’t be satisfied, heat would flow forever.
The real point is that you don’t need the silver wire to make this argument. The gas itself conducts heat from the bottom to the top as long as the temperatures are different. It’s what systems do. Conduct heat from hotter places to colder places, unless you do work to prevent it. Gravity does no work in this problem, not in steady state. So what makes the heat go round and round?
It doesn’t.
Of course.
It evolves to the isothermal state where no heat flows.
rgb
I am not a scientist and never claimed to be so, could someone explain why the gas, or atmosphere in this case, should be colder on top than on the bottom assuming convection works in all cases (cold air falls while hot air rises) Yes, I can figure, as air gets closer to outer space (in really simple terms) it would get mighty cold but, cold air is more dense and as such it should fall more rapidly. Exactly where does gravity enter the picture? It is exerted equally on all temperature states of air, right?
Or should I up my meds? 😉
RGB
thank you for this elegant demonstration that a gas in a gravitational field is isothermal when in equilibrium. I lost count of how many times I pointed this out on Willis Eschenbach’s original thread (the one that caused all the controversy). Even Willis didn’t get it at the time. I hope he does so now.
[REPLY: Indeed you did, Paul, and you were right and I was wrong. Thanks for your contribution in fighting my ignorance. I mean this quite seriously. That’s how I learn. –w.]
Robert, it seems that you have completely missed the fact that gravity causes a pressure and density gradient in your air column.
Your equilibrium air column is NOT isothermic, as you assert–that could only happen in the absence of gravity. Because the density and pressure decrease with altitude, the temperature at the top is much lower than at the bottom. The bulk of the mass and heat energy of the air column is at the bottom.
Remember what heat energy is: it’s defined by the kinetic energy of the individual air molecules. Temperature is defined by both that molecular kinetic energy and by the density of the atmosphere. The pressure gradient leads to a sorting; the more energetic molecules tend to be at the top of the air column–more space to allow a longer mean free path above than below. However, because the density and pressure decreases with altitude faster than the thermal energy of individual molecules increases, total temperature decreases with altitude.
Your thesis may indeed be correct, but you can’t prove it by considering only temperature and convection without considering density and pressure and conduction as well. It’s the pressure and density gradient that is alleged to cause gravitational heating of the lower atmosphere.
This is a much more complex problem than a quick, partial recitation of a freshman physics text can handle.
The device in figure 2 doesn’t work because it’s a closed system and the work extracted will reduce the total energy of the column until eventually there’s no more energy to extract at which point the gas reaches a temperature of absolute zero and has presumably vanished from this universe being totally converted to kinetic energy in the extracted useful work. In the real world the gas will collapse to the surface as a liquid before it gets to absolute zero and this will shut off further extraction of energy because the cold side of the thermocouple no longer has any cold gas to cool it.
Work? What work? Are you crazy? Collapse to a liquid?
Let’s try again. I-s-o-l-a-t-e-d S-y-s-t-e-m means that no energy enters or leaves. No mass transport means no work is being done In the real world, the system will evolve to an isothermal state precisely as I described it because it is in equilibrium. In any imaginary world where gravity acts on “heat” or does “work” on a gas that is in static force equilibrium and not moving, you can make it come out any way that you like, but please understand that it is nothing but a fantasy on your part.
The point is that heat will not cycle indefinitely — you can see that that makes no sense. No work is done. No energy enters or leaves — where would it go? How would it get there? That’s what the adiabatic walls around the gas and wire prevent. If gravity maintains a constant lapse rate in steady state, the second law and common sense are massively violated by the enternal heat flow. All other solutions mean that equilibrium is isothermal.
rgb
Heat is Energy is mass by M=E/c^2 so said Einstein.
So what force causes Mass to rise up the silver conductor against gravity ie work has to be done?
The silver conductor is little different from the gas in a column in this respect. The top will be colder than the bottom and heat will not flow up the silver conductor unless a heat source (work) is supplied from the bottom..
If the atmosphere was heated from the top there would be no convection, hence no lapse rate.
The lapse rate doesn’t apply to the ocean because water is incompressible. Hot water doesn’t expand as it rises, hence does not do work on the surroundings, hence does not change temperaure, hence no lapse rate.
I conclude that a thermally isolated container of gas in zero gravity and at uniform temperature, will not see any temperature change if some other demon could switch a gravitational field on at will. Merely the creation or a density gradient. Is that right?
Not quite. “Turning on the field” is like “a collision” and the gas will rearrange, releasing a bit of gravitational potential energy as heat. But then it will “thermalize” to an isothermal temperature, one a tiny (and I do mean tiny, generally speaking) higher than before.
This is not unlike the mechanism that heats protostars as the gas they are made up of falls inward and stops (on average) converting their infalling KE into heat. Or what happens when a big asteroid hits the earth and stops
The key elements are movement and inelastic stopping.
rgb
I have been following these threads, lurking from the sideline, for a while. Well, the time has come to add my $.02 worth. I have been studying meteorology for 40 some-odd years now & I shake my head in seeing some of the most common properties of the atmosphere being missed in these threads as it applies to these ‘thought experiments’.
1) if the several km-long tube is horizontal & the perfectly dry air is at a constant temperature throughout & is moved to the vertical, the dry adiabatic gradient will be produced (warm at the bottom, cool at the top w/ approx 8C/1000m gradient in between) due to the ‘work’ of gravity creating a pressure gradient to the compressible gas. Notice, no gradient will be produced if water is used instead of gas because water is non-compressible so no work will be done. If no heat is added or removed to the gas, the column will be in a neutral buoyant state (and will stay that way!!) – if a parcel of air is moved vertically by an outside force, it’s temperature will change to reflect the change in pressure but will still be the same temperature as it’s surroundings.
2) as to the experiment with the thermal conductive wire at the base & top of the tube, the author here is incorrect. If the wire moves heat from the bottom of the tube (the base cools) to the top of the tube ( the top heats), presuming, as the author says, “…save to note that the internal conductivity of the ideal gas is completely neglected.”, the heat from the *local* area of the wire is all that will be moved from the bottom to the top ***and nothing else*** . Why, you ask?? In moving the heat from the bottom of the tube to the top is causing the lapse rate to become **more stable** – cool at the bottom with warm air above is an inversion which inhibits vertical mixing!! THAT is why the engine will not work as it is set up.
Just a few thoughts…
Jeff
@Robert Brown: To do LaTeX in WordPress, do $\latex n^2$ (except leave out the backslash in front of “latex”. It’s just like going into math mode in LaTeX, except that you add the word “latex ” after the opening dollar sign.
nothing as simple as gravity can function like a “Maxwell’s Demon”
There is nothing simple about gravity. it is the least understood force in the universe with many unresolved questions.
Professor Brown: To some extent, two of your arguments start by assuming what you want to prove.
You and the introductory textbooks start by assuming a isothermal column of gas. The situation is far more complicated if you consider a column with a temperature gradient. For a thin layer of gas in a non-isothermal cylinder, the pressure difference across that layer is produced (at a molecular level) by differences in the vertical impulse provided by the gas molecules at the top and bottom of the layer. The density of molecules and pressure in an isothermal column both change following the same exponential, -mgh/kT. This means that the difference in impulse between the top and bottom of a layer is due only to the difference in density and the average speed of the molecules moving up and down must be the same. This is consistent with the original postulate that the column is isothermal. In a non-isothermal column, however, the density of molecules and pressure don’t change in parallel. In this case, the speed of the molecules at the top and bottom of a thin layer will not be the same and energy will flow up or down. Which way is the flux? If the flux reduces the temperature gradient (and I presume that it will), does the flux persist until isothermal or are other stationary states possible?
To prove that heat flow in a cylinder of gas is unaffected by a gravitational field, you assume that heat flow in the silver conductor is also unaffected by the same gravitational field. IF exchanging kinetic for potential energy were important to energy flux in a gas, it would probably also be important in a solid. In a sense, you are assuming what you want to prove. You can use the 2LoT to eliminate the possibility that a lapse rate of g/Cp develops spontaneous. If you have two equally tall columns in thermal contact with the ground which are filled with gases with different Cp’s, you could use the temperature difference which would develop spontaneous at a given height in the gravitational field to produce perpetual motion. However, this argument doesn’t work when the lapse rate that hypothetically forms spontaneously in a gravitational field is independent of composition and only depends on height.
I feel for you Robert.
It seems the more challenging and subtle the physics, the more experts there are. And the more sure they are that they are right. It is a lot like playing whack-a-mole — every time you think you have explained something so well that it couldn’t be clearer, someone will find a new objection (or more likely, recycle an old objection). For example, the “it loses KE on the way up so the temperature must go down” is convincing unless you have a subtle understanding of thermodynamics. And we have seen it rear its head a dozen times in the last few days in these threads.
I hate to admit that I, like Willis, even fell for this argument for a brief time until the obvious flaws were pointed out. But we both quickly reformed.
I wish you patience and persistence in your efforts to bring correct science to WUWT. You will need it!
As an aside, it’s trivial to design a machine that seems to violate the Second Law and pumps heat from cold to hot with no input of work.
On a sheet of paper draw two horizontal lines, one at the top and one at the bottom, that represent radiating surfaces at temperatures Ttop and Tbottom. Then draw a cute little flight of stairs ascending from left to right, with a smooth bottom and the usual treads on top. Cover the stairs with mylar and let them sweep from right to left at nearly the speed of light. (You can also make the stairs steeper and sweep them slower). There are a very large number of flights of stairs, looking in 3-dimensions like a venician blind with treads on one side.
Assume the top and bottom emitting surfaces are very distant and finite, so photons are traveling between them in a roughly vertical direction. Photons from the bottom don’t hit the stairs because the stairs are moving out of the way as fast as the photons are traveling upward. (The stairs dodge upward moving photons). Photons moving downward cannot find a clear path between flights of stairs and always slam into a tread, getting reflected back towards the top.
So photons emitted from the top surface return to the top surface, and photons emitted from the bottom surface travel freely to the top surface, regardless of temperature. The bottom surface cools and the top surface warms, even if the bottom is already cooler than the top, and the stairs aren’t doing anything but freely moving along between.
At most, the stairs might extract a little work from the momentum of the photons being reflected from the top, but this would happen regardless of the difference between the top and bottom temperatures.
The problem here is that heat is not temperature. Heat is energy, temperature is average kinetic motion, which is one -type- of energy. A glass of water and a bathtub full of water can have the same temperature, but the bathtub has more heat than the glass of water, as more heat is required to bring the tub up to the same temperature as the glass.
Moreover, heat can be added to a system without temperature changing. When ice melts, continuous heat is required to continue the melting, yet the temperature will remain the same until a significant amount of the ice has melted. Still, the system has far more heat content now as a liquid, even at the same temperature, than it did as a solid.
For instance: “This heat in turn may lift mountains, via plate tectonics and orogenesis. This slow lifting of terrain thus represents a kind of gravitational potential energy storage of the heat energy. The stored potential energy may be released to active kinetic energy in landslides, after a triggering event. Earthquakes also release stored elastic potential energy in rocks, a kind of mechanical potential energy which has been produced ultimately from the same radioactive heat sources. Thus, according to present understanding, familiar events such as landslides and earthquakes release energy which has been stored as potential energy in the Earth’s gravitational field, or elastic strain (mechanical potential energy) in rocks.” So, this action of heat pushing against a gravity well and from kinetic to potential energy is part of what drives plate tectonics itself.
Here we see heat being transformed from kinetic (TEMPERATURE) energy to potential energy by moving against a gravity field. The resulting raised land mass has lower temperature as it as lower kinetic energy, but it contains similar amounts of heat.
This effect of changing kinetic energy to potential energy (E = mgh) won’t be seen measurably in a gas over a small distance, but over the miles of the atmosphere?
This is why it’s hard for me to understand your explanation, which doesn’t mean you aren’t correct, Dr. Brown. But it seems like your equations are all missing the big picture: potential energy. When h (height) is very big, even though gasses have low m (mass), you’re going to have a transfer of energy into potential energy that is considerable. The only source of energy that can go into the potential energy (since conservation of energy demands transformation not creation) is the kinetic energy of the molecules. Just like bouncing balls. And if kinetic energy drops, -so too does apparent temperature-. Again, -temperature is not energy-. Temperature is not heat. Temperature is just our observation of heat in the form of -kinetic energy-. And kinetic energy can be changed to potential energy while keeping the total energy of the system -the same-. Like a bouncing ball, or a stone rolling up hill a ways. Or plate tectonics!
You’re looking at far too small a case. An ideal, not realistic, case. Or maybe i just don’t get it.
Robert Brown: “There is no question that the silver will conduct heat between reservoirs at different heights exactly the same way it does any other time.”
In my post above, where I disputed Dr. Brown’s isothermality conclusion, I was silent about his proof; I concentrated on mine. For the sake of completeness, though, I’ll mention that, if the Velasco et al. paper that I’ve been evangelizing is correct, the silver actually will not conduct heat once the temperature difference that Velasco et al. specify is imposed across it. This is a result of the fact that, according to Velasco et al., entropy is maximized, not by an isothermal configuration, but by a configuration whose (again, quite small) temperature lapse rate is the one that Velasco et al.’s paper prescribes.
If you think of heat transfer in the silver as a diffusion phenomenon and recognize that concentration gradients prevail all the time when maintained by forces from, e.g., electric fields, this is not as hard a proposition to swallow as it may at first sound.
Greg Elliott says: “But what about the energy absorbed by the N2 some might ask. Indeed and what about the energy intercepted by the CO2? Both must either heat the atmosphere or be returned to the surface and thus are indistinguishable in their effects.”
But this is the flaw in your thinking. N2 can only transfer energy to the surface or the atmosphere, as you say. But CO2 can ALSO transfer energy to space via IR photons. That is ultimately the cause of the greenhouse effect.
Oh, I should point out you cannot -generate heat- with gravity, but over a very large distance, gravity should maintain a -temperature- gradient if the heat is in equilibrium by necessity due to the change of kinetic to potential energy as one moves far enough up a gravity well. Notice that the energy of the gas column will be in equilibrium, but temperature is only the measure of kineitc not potential energy.
That fact is why I can’t wrap my head around such a small case explanation as yours, which is correct on the small scale, when applied to the entire planet.
Again, maybe I’m completely wrong. But I feel we’re missing out on one entire half of the equation. Gasses are still subject to potential energy as far as I know!
I think one reason that some people are taken in by Jelbring’s theory is that they are vaguely aware that if a gas is compressed, e.g. the air in a tire being compressed by a pump, its temperature goes up, so in their minds they form the vague association ‘higher pressure = higher temperature’. But the increase in temperature is a temporary effect, due to the transfer of kinetic energy from the piston of the pump to the air molecules. If you stop pumping, the tire will cool down to the ambient temperature, as it loses heat by conduction and radiation. As the air in the tire cools, it will also reduce in pressure, but not to the orginal level (otherwise there would be no point in pumping up a tire!) There is no necessary connection between high pressure and high temperature; a hot gas can have low pressure and a cold gas can have high pressure (unless it is so cold as to liquify).
Incidentally, I wonder if someone could explain the opening quote from Jelbring:
“An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field”.
I don’t understand the second sentence of this. If an air parcel ascends, it is surely because it has first expanded due to heating (usually from the sun). As it expands, it does work against the surrounding or covering air, compressing or displacing it, and loses some kinetic energy (heat) in the process, but it does not immediately cool to the ambient temperature. (If it did, it would not ascend at all, contrary to experience.) The expanded parcel of air is less dense, and therefore less heavy, than the surrounding air, and the entire column of air above the parcel (including the parcel itself) is lighter than the surrounding columns. At this point the parcel begins to rise as the heavier surrounding air forces it up. During the ascent the air parcel itself is not ‘doing work against the gravity field’, it is having work done on it by the surrounding air, which is ‘repaying’ the work done on it during the initial phase of heating and expansion. Does Jelbring suppose that a hot-air balloon would rise in a vacuum? I really can’t make sense of his second sentence at all.
You’ve very coyly avoided answering the objections raised by Dr Brown’s Gedankenexperiment. So according to you, we could take a perfectly insulated container several miles high in a gravitational field under a hard vacuum, fill it with gas and that gas will self-organize so that it’s warmer at the bottom and colder at the top. Now I can construct a heat engine which extracts useful work based on the temperature gradient and gravity will continue to organize the air column forever and my heat engine will never run out of “fuel”? Really??
To Joules,
According to Newton, gravitational force is expressed as F=m1*m2/R^2 where m1 and m2 are the mass of two attracting bodies and R is the distance between the centers of mass. The molecules at TOA have less gravitational energy than molecules at sea level but not by much because the change in R is relatively small. So the pressure at sea level is essentially the mass of the earth times the sum of the mass of all those molecules in the atmosphere divided by the radius of the earth. In a steady state condition, the pressure at sea level will be constant and the number of molecules causing that pressure will be constant. Pressure decreases with altitude because the number of molecules per volume decreases. Now apply this knowledge to the perfect gas law expressed as pv/nt= constant by integrating from TOA to the surface and see what happens to temperature as a function of altitude.
Joules Verne says:
January 24, 2012 at 7:04 am
“Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work.”
No, Robert. The second law requires that no energy gradient can be maintained without input of work. It requires the reservoir of gas to be isoenergetic not isothermal. A horizontal layer may be a different temperature than another if the cooler layer has its lesser kinetic energy balanced by greater gravitational energy. This is obviously the case since it goes without a shadow of a doubt that a molecule of air in a higher layer has more gravitational energy than a molecule in a lower layer. Thus the second law actually demands a temperature difference of equal and opposite polarity to compensate for the difference in gravitational energy. An isothermal atmosphere in a gravity field is the one that violates the second law.
Joules is correct, and to push the point home a bit further I will be posting a new paper by Hans Jelbring on my website later this evening which demonstrates the dynamic situation. This will complement and supplement the earlier 2003 paper setting out the static situation which Robert refers to in this article.
Hans has been working steadily on the new paper over the last few weeks and now seems to be the apposite time to publish it.
Basically, the Second Law is used to prove the second law isn’t violated. That’s circular logic. It’s like using the Carnot Cycle to prove the Second Law.
As I said at Tallbloke’s, I think the silver wire is a terrible design. You’d be lucky to extract kbT from it. IIRC, Feynmann showed it was possible to extract nearly that much from a Brownian Ratchet, without anyone getting excited.
A better design would be to use a single column containing two gases, one of which is heavy with a low boiling point, and the other is light with a high boiling point. A reservoir of the light gas in condensed form at the bottom of the column also serves as a thermal reservoir. At the bottom, the light gas will be in equilibrium with its condensate.
Fill the column with a significant majority of the heavier gas, such that its gravitational lapse rate dominates. The temperature/pressure profile of the lighter gas (being a lifting gas in context) will be saturated at all elevations above the reservoir.
A series of basins and catchments can be arranged to collect the condensing lighter gas.
By George (Westinghouse), it might work!
People being invited to consider an argument should have the opposing argument easily available to them. This enables people to form their own judgment as to whether the opposing argument has been correctly and fairly represented. Especially considering the paper in question was written by a Phd Meteorologist.
Since Robert Brown is setting a refutation of Hans Jelbring’s 2003 paper, it would be a common courtesy to provide a link to that paper in the headline post.
It is available with a new preface written at the time of publication on my website here:
http://tallbloke.wordpress.com/2012/01/01/hans-jelbring-the-greenhouse-effect-as-a-function-of-atmospheric-mass/
If WUWT has some problem with providing a link to my site, the paper without the 2012 preface is available here:
ruby.fgcu.edu/courses/twimberley/EnviroPhilo/FunctionOfMass.pdf
[Thanks, tallbloke. I’ve added the link up in the head post. -w.]
For those seeking detailed quantitative thermodynamic analyses of the atmospheric lapse rate see:
Robert Essenhigh Prediction of the Standard Atmosphere Profiles of Temperature, Pressure, and Density with Height for the Lower Atmosphere by Solution of the (S−S) Integral Equations of Transfer and Evaluation of the Potential for Profile Perturbation by Combustion Emissions Energy Fuels, 2006, 20 (3), pp 1057–1067 DOI: 10.1021/ef050276y
Sreekanth Kolan Study of energy balance between lower and upper atmosphere MS Thesis
Roger, Your site is linked on the right column of this page, as always.
For context, Jelbring (2003) is cited by:
Gravitation and Gas Laws: An Alternative Approach to Climatology W Brune – Energy & Environment, 2009 – Multi-Science
and
The thermodynamic relationship between surface temperature and water vapour concentration in the troposphere WC Gilbert – Energy & Environment, 2010 – Multi-Science
Dear Mr. Brown,
I’m sorry but your conclusion about figure 2 is completely wrong as you expect the air reservoir to conduct heat in gravitational field and the silver rod to conduct heat in zero gravity.
I’m sorry to say that this assumption is incorrect and the example you are building your conclusions on is wrong. Even atoms of silver have the property of gaining potential energy and losing kinetic energy (therefore losing temperature) when traveling “up” in a gravitational field while transferring their temperature in that direction. The result is, the rod would demonstrate exactly the same temperature gradient the air container does. Your thermal engine would not work not because there is no temperature gradient but because it would not transfer any heat.
kdk33 says
“if the atmosphere was heated from the top there would be no convection, hence no lapse rate.
The lapse rate doesn’t apply to the ocean because water is incompressible. Hot water doesn’t expand as it rises, hence does not do work on the surroundings, hence does not change temperaure, hence no lapse rate.”
Do you not remember the school experiment with a beaker of water and a single copper sulphate crystal showing fairly rapid liquid convection?
How do you think an electric kettle heats water?
Bryan says:
January 24, 2012 at 6:59 am
For some of us, a thoughtful examination of the flame suffices. We don’t have to actually do the experiment and burn our fingers to know that it is hot.
If you wish to do the experiment, however, be my guest. I’ll just have a quick beer while I wait for your experimental refutation of a couple centuries of scientific thought …
w.
Joules Verne says:
January 23, 2012 at 4:25 pm
Gravity maintains TWO energy gradients. One kinetic and one potential. The kinetic gradient decreases with altitude and the potential gradient increases with altitude. The two opposing gradients cancel out and the column is isogenergetic. This is how you can have a perpetual temperature gradient yet not be able to extract any work from it for a perpetual motion machine – a temperature gradient can be nullified by an equal but opposite gradient of energy in a different form. You can’t connect the cold and hot sides of the atmosphere without climbing up in a gravity well and the useful energy represented by the change in temperature is exactly used up by the energy required to climb uphill against gravity. The books thus balance and conservation of energy is once again safe from the abuses of junk science.
Neat comment Joules. I can’t wait for the mad inventors to put their money where their mouth is and build one of the erroneously designed machines they propose. Problem is, when it fails to work they’ll come to the equally erroneous conclusion that it failed because the atmosphere is isothermal.
Hope no-one catches a nasty chill while bolting thermopiles together at the top of their 10km high rig. While they’re up there, they might notice how much thinner the air is too. That might give a bit of pause for thought about density and its effect on the ability of air packets at different altitudes to retain the heat of the Sun.
Look the adiabatic lapse rate exists this is basic physics equal partition of energy.
it is evident in the atmosphere but is upset by clouds at low level and UV absorption at higher altitudes.
If we cannot get even the basics correct we might as well give up.
For those who say there is no back radiation why is the sky temperature at night not 4K
For those who do not believe an warmer but still cold atmospheric layer cannot cause the surface to warm clearly do not understand the basic physics of radiative heat transfer. Why are layers of mylar used to thermally insulate space craft?
Unless we get the basic physics correct then the skeptical community will be undermined.
A gas giant planet like Saturn radiates more than twice the amount of radiation than it recieves from the Sun.
How do these planets ever die if gravity is constantly maintaining a heat gradient in the atmosphere? The Sun will die and become a cold white dwarf.
What is going to kill these gas giants? If gravity is constantly maintaining hotter gases at the bottom then convection will move gases around and therefore we seem to have an everlasting living planet.
What kills it and when, if Jelbring is correct?
Alan
The last few days have certainly been interesting regarding the debate of lapse rate in a gravity field. I think the point that is getting missed, but I see as intuitively obvious, is that in a real planet with a gas atmosphere, it is not and never can be in a state of thermal equilibrium.
The atmospheric column is always in direct contact with a massive heat sink(source) in the form of the planetary body, and the top of the column (at its effective radiating altitude) is a nearly ?? infinite heat sink at the temperature of interstellar space. Until or unless the planetary body is at the same temperature as deep space there will always be energy input at the bottom of the atmospheric column (and a temperature gradient) and there will always be heat loss by radiation (or some other means like boiling off of the atmosphere) at the top of the column.
In that sense, all these discussions regarding physically impossible constraints on the model are merely debating how many angels can stand on the head of a pin.
Lets look at real planets which are always warmer than interstellar space, and real atmospheres where at the base (troposphere) heat transport by convection dominates all other mechanisms by a huge margin. Under those conditions, there will always be a lapse rate in the atmosphere (in the troposphere) as long as it can find some means to lose energy to interstellar space by radiation or loss of mass.
The only discussion, is are there any realistic conditions where an atmospheric shell could not radiate heat to interstellar space?
If and only if that condition can be achieved do the discussions of a system in equilibrium have any meaning. In all other cases (with or without radiant heating by a near by star) the planet will always be losing heat to space, and will always have a troposphere layer (if it has an atmosphere of non-condensing gases) where heat transport is dominated by convection.
In all cases the presence of green house gases can only improve heat loss to interstellar space at the effective radiating height over the theoretical condition of no ability to radiate energy in the electromagnetic spectrum (note I did not limit energy loss to IR band width).
It is my view that the atmosphere will always find a way to lose energy to deep space by some means at or near its top, and will thus always have a troposphere lapse rate which implies that the planetary body will always be warmer with an atmosphere (regardless of gas mix) than it would be without one.
One other note that no one has mentioned. As I understand it, the average effective radiating altitude here on earth is around 4.5 km (14763 ft), that means that here where I live in Colorado at the summit of Pikes peak or Mt. Elbert I could just about throw a rock to the mean altitude where heat is lost to space by radiation. In short high altitude areas like the Himalayas, Andes, and the Rockies and a few volcanic peaks are “short circuits” in the troposphere, where energy absorbed by the ground from solar heating can be almost immediately radiated back to deep space directly from the ground. It would be interesting to see high resolution IR measurements of the heat loss from these areas directly to outer space.
Larry
I have a question along this topic which will likely show my ignorance. If gravity alone cannot induce a thermal gradient in a gas, how then are stars formed from gases where there is only gravity as an external force?
Let’s do some equation work.
Let’s say we take one mole of N2. That’s 0.028 kg. Now we take that mole at 15 C and move it up from the sea surface to the average top of the troposphere which is 17,000 meters high. Gravity constant will be 9.8 m/s^2. The total joules needed to do this is around 4660 J (E = mgh).
Now the heat capacity of N2 is 29.124 J·mol^−1·K^−1, so if we transformed 4660 J of heat kinetic energy, that would reduce the temp by -160 degrees, or so, or to -145 C. The real temp at the top of the troposhere is about -55 C, so we’re off by almost a factor of 3. Obviously, the atmosphere is also taking in energy from the sun (radiatively, and solar wind), there’s more than just N2, and the conversion of kinetic temperature energy to potential is probably more complex, to make up for this difference. If there was no energy from the sun, the atmosphere would shrink as energy was lost to space, and along with it potential energy, dropping molecules down till they settled on the surface of the planet and solidified (e.g. Pluto).
This is what I see. And again, I may be completely off base. But conservation of energy tells me we must be changing forms as we move up the atmosphere. So for the temperature to stay steady (which it doesn’t in real life), we’ve have to have even more energy at the higher altitudes in the air column than is at the surface. And would not this energy fall back down to the surface to equilibrate, driving the surface temperature even higher? The way I see it, there will always be a -temperature- difference at such large gravity distances if energy is in equilibrium.
Again, I could have done this all wrong.
John Marshall says:
January 24, 2012 at 7:26 am
It’s the disproof of Jelbring’s theory, which lately has attracted many supporters. As such it is an interesting and very relevant exercise.
w.
School physics.
The atmosphere stability condition is ds/dz>0, where s is the entropy density and z is the hight.
Atmosphere with ds/dz 0 are stable (including the isothermal atmosphere!)
What is all the ridiculous discussion about???
Dr. Brown, I’ve been reading this thread and the earlier thread with a great deal of interest and I understand the point you’ve raised. However, I note that it relies on the Ideal Gas Law being applicable.
My question is: Is the Ideal Gas Law applicable?
I’ve just done some quick research and it seems that the derivation of the Ideal Gas Law assumes that any gravitational field in question will have a negligible impact on the behaviour of the gas. That’s true in almost all reasonable cases, but it’s not true in the example we’re discussing. I would therefore ask for your comments on the underlying assumptions in the derivation of the Ideal Gas Law in this respect and if they are still true.
In particular, looking at the Empirical Derivation from the Wikipedia article:
http://en.wikipedia.org/wiki/Ideal_gas_law#Empirical
I noticed that there is a constant C that is directly proportional to the amount of gas. But in a gravitationally stratified column, the amount of gas is not constant throughout the column, and hence the “constant” is not really constant.
Similarly the derivation from statistical mechanics in that article assumes that there is no gravitational force involved. For small columns, that’s a reasonable assumption,Is it a reasonable assumption for large columns?
I don’t understand the theoretical derivation well enough, but again it seems to assume that there is no conversion of kinetic energy into gravitational potential energy – something that is core to this issue.
Again, thank you for your posts. I have enjoyed reading and learning from them.
Robert Brown says at 1/24 8:14am:
“…in an ideal gas the temperature is not determined by the total energy. That’s an absurd idea, given that one can perform a gauge transformation — change the zero of the total energy — without changing any of the physics.”
Ahhh..this is the big deal.
Consider this is equivalent given Caballero’s ref. in the Perpetuum Mobile thread w/gravity where in 2.1 find “Temperature is just another name for the mean kinetic energy density of molecular motion.” to Trick saying “in an ideal gas the mean kinetic energy density is not determined by the total energy”. If Trick said this, Trick would be going against 1st Law & Trick has not written any such thing. So in Trick’s view, what Robert Brown says at 8:14am is inconsistent with 1st Law. I am pretty sure but not perfectly sure that Trick’s view is consistent with all the thermo grand master Laws.
Robert Brown’s 8:14am violation of the 1st Law above, Robert Brown doesn’t grok yet. He will eventually! (Trick predicts the life of the universe is longer) b/c Robert’s smart and the thermo grand master’s are right. This is all like the slow progress of thermal conduction thru a near perfect insulator.
I admit this PE setting with h is actually a difficult preconceived notion to get over. It took me many years of practice to really come to grips with it. Notice that every time you see total energy equation written in thermo theory – it looks something like this: total energy = TE = PE + KE = constant.
That’s all the 1st Law really can do, it doesn’t tell us what that constant equals – it can’t and be general theory. 1st Law tells us (go look!) energy can be neither created or destroyed, but can be changed from one form to another, we have to do the deducing what that means.
The constant specific value is not set by nature; it is not a natural constant. TE is set in the specific experiment. Whatever the total energy in the white space top post is, it has to be constant to obey the 1stnd Law.
In Robert Brown’s top post we actually can just (out of thin air so to speak!) announce that our h=0 to be at the bottom of the white cylinder of gas. Here we know at h=0 that TE=PE +KE. Always. Cite the 1st Law!
At the bottom of the cylinder we just announce PE is 0 there. This is the tough nut to crack to mix my metaphors. PE is a potential energy – as such nature and the thermo grand masters allow this construct.
So we can move on. At Trick’s announced h=0: TE of the molecule(s) will be constant = TE = PE + KE = mgh + 1/2mv^2 = m*g*0 + 1/2mv(0)^2. Voila we have figured the TE constant.
In white area TE = constant = m*g*0 + 1/2mv(0)^2 = 0 + 1/2mv(0)^2 = 1/2mv(0)^2 where v is the velocity and m the mass of the molecule(s) at h=0. The TE constant is ½*m(0)*v(0)^2. KE varies with PE(h) in a gravity field… (can you say non-isothermal?) (Say it again: Deduce from 1st Law: molecule(s) KE or temperature must vary in a gravity field with PE, for total energy to be constant, OMG!)
But we are ok, what do you know, we have a formula consistent with 1st Law that found the total energy constant of the white area*. The constant = 1/2mv(0)^2 comes from finding the v of the molecule at h=0. For that, all we need do is find the KE or temperature (= kinetic energy density) at h=0 and we will know the temperature anywhere else in the one reservoir or one thermodynamic ideal system of the white area (i.e. at any h) from bottom to top thru TE = constant = ½*m(0)* v(0) = (mgh + 1/2mv^2). A thermometer placed at h=0 will work just great for this experiment.
Note 0 location IS arbitrary, I can pick ANY h and put my calibrated thermometer there and find m(h) and v(h) and get the same TE constant, it is just easier to think thru at h=0.
Robert Brown needs to not read FAST but s-l-o-w-l-y to grok this; to really come to terms with it, it will take some practice. The thermo grand masters did a fine job, Robert Brown can do one too.
Another big deal: Robert Brown cannot use, in Trick’s view, 1/24 8:14 statement to argue against Hans Jelbring’s 2003 paper. There may be other arguments but this Robert Brown one doesn’t work with the 1st Law.
Robert Brown continues:
“Is there something miraculously interesting in the thermal contact between silver and air that keeps heat from being conducted from hot to cold — in just this one special circumstance? I’m all ears.”
Nope there isn’t any Trick violation of 0thLaw equilibrium or 2nd Law entropy being allowed ideally constant, either. Robert Brown’s top post just needs to get rid of 1) the second thermodynamic system of the top post – that 2nd system is not in Willis’ Perpetuum Mobile original premise and 2) the perfect ideal insulator for compliance to all three Laws. Then Robert can do the easy math & will grok the big deal. Eventually Trick & Robert Brown will be in (Tallbloke’s) violent agreement.
Trick’s head cold is receding, I won’t be hanging here forever. Robert Brown should try to make this happen in a few days. If not, I predict violent equilibrium will eventually happen, that’s the 0th Law, LOL.
*barring typo’s and consistent with mass conservation, the molecule(s) mass does not change thus can assume E to mc^2 in total energy is justifiably being ignored here by all posters on the original Willis’ premise GHG-free air column.
“Now I can construct a heat engine which extracts useful work based on the temperature gradient and gravity will continue to organize the air column forever and my heat engine will never run out of “fuel”? Really??”
Nope! Impossible. As you took energy out, the molecules would not be able to move up as high in the gravity well (the pressure of the gas would drop), as there wouldn’t be enough energy to go into potential energy, and eventually the gas would condense and settle at the bottom of the container. It would cease being gas.
In short, the temperature at the surface level would steadily decrease as you took out energy, as potential energy and kinetic energy are -interchangable-, but temperature is -only- kinetic energy. And heat can -only- be transferred by kinetic collisions (if we ignore radiation). So your engine would take out the kinetic portion, leaving less to be turned into potential, making the air column decrease in height until what I said above happened. Same as what happens on Pluto.
Wayne2 says:
January 24, 2012 at 7:39 am
Excellent insight, Wayne. That is exactly what happens. In an isothermal column of air, individual molecules at high altitude have more energy because of gravity. But for exactly that same reason, there are fewer molecules at high altitude. As a result, and as we would expect, in the isothermal condition the energy is spread out evenly through space (equal energy per volume) rather than equal energy per molecule as Hans Jelbring and Mr. Verne assert.
w.
Willis Eschenbach says
“If you wish to do the experiment, however, be my guest. I’ll just have a quick beer while I wait for your experimental refutation of a couple centuries of scientific thought ”
Its always better to do the experiment!
If all the qualified scientists here were honest they would admit that this is an example of an experiment where prejudgement was entirely wrong.
http://en.wikipedia.org/wiki/Erasto_Mpemba
I think it is also important to note that Jelbring does not assert thermal equilibrium, they assert “energetic equilibrium” considering both heat energy and gravitational potential energy.
Larry
The iceman cometh says:
January 24, 2012 at 7:58 am
It is the formal disproof of Jelbring’s theory. It is idealized by its very nature.
w.
Thank you Dr. Brown.
A physicist says:
January 24, 2012 at 8:48 am
Although that may be true, I don’t see why, I don’t see Robert Brown making the claim, and I
Wait, wait, you claim to be a physicist, answer the question. Does heat flow forever in the silver wire or not? His ability to answer your random question about possible implications is immaterial to whether his proof is correct.
Does heat flow forever or not?
w.
Bryan/Willis:
I could be missing the whole point here but isn’t the Graeff paper (ref. http://tallbloke.files.wordpress.com/2012/01/graeff1.pdf) an example experiment?
h/t Lucy Skywalker
Robert, you’re making an inappropriate distinction here. When that hypothetical molecule hits another, and they both bounce off in random directions, how is that gravitationally induced motion distinguishable from thermal motion? Answer: they’re the same thing. Gravitationally induced motion within a gas is heat energy.
Robert G. Brown, thank you again for a good presentation and determinedly addressing the criticisms.
Temperature depends on the altitude, because more dense atmosphere means more molecules hit the thermometer’s mercury. To assign this to gravity is maybe not correct, but truth is the gravity causes denser, and thus warmer air.
When talking about Moon SURFACE temperature, what is the daily temperature there in 2m altitude?
“MaxL says:
January 24, 2012 at 11:38 am
I have a question along this topic which will likely show my ignorance. If gravity alone cannot induce a thermal gradient in a gas, how then are stars formed from gases where there is only gravity as an external force?”
Gravity can indeed do that. However, that is perfectly allowable under the second Law of Thermodynamics if entropy is increased in another system.
Like a fridge I can decrease its entropy but only by increasing the entropy of the room it sits in with the waste heat. Overall the entropy of the combined system will have increased and the second Law is preserved.
Stars are part of the universe and you can be certain that overall entropy is increasing with the flow of time even if parts of the system are seeing entropy decreasing.
The arguement here is Jelbring is trying to say he can prevent entropy increasing in a CLOSED system whilst work is being performed.
There is a problem with Gedanken experiments, they can allow you to construct something that seems viable and yet breaches agreed physical laws.
I could invent a closed system that was initially composed of a diffuse cloud of particles in
thermodynamic equilibrium. Now that system would be near maximum entropy. However the addition of gravity starts to cause the particles to compress and voila I now have a system like the solar system or a galaxy or the universe even and I have reduced the entropy of the system without the addition of energy or increasing the entropy of another system.
Perhaps someone could say that this proves gravity can reverse the flow of entropy in a closed system and the Thermodynamic laws need revising.
However, in the real universe we inhabit we cannot create such a system in such an inital state. Perhaps a supreme, all powerful being could but I am not holding my breath! The existence of such a being would invalidate all known physical laws in any event.
So we have to be careful with gedanken experiments. I tend to the view that if such a system is proposed, that is in breach of thermodynamic laws, that it is either in error or could not ever be created in the universe we inhabit.
Alan
Folks, a lot of you here don’t seem to get it. The beauty of Robert’s proof is that there is only one question in it—does heat flow forever in the silver wire or not?
So all of your claims of deep insights into where the joules are, and all of you talking about some mechanism or other that you are absolutely sure will make the air temperature at the top and bottom different, that has NOTHING TO DO WITH THE PROOF. The proof is about the outcome, what the mechanism is that you say results in that outcome doesn’t matter.
IF you are correct and any of your hotly defended mechanisms work, gravity will make the air at the bottom of the tall cylinder warmer than the air at the top. (Your claim, not mine, just following it to see where it leads.)
IF there is a temperature difference in the air top to bottom, heat will flow in the silver wire. Gravity can’t stop that.
IF heat flows in the silver wire, it will move heat from the bottom to the top, and thus cool the bottom air and warm the top air. Duh.
IF you are correct and any of your hotly defended mechanisms work, gravity will once again make the air at the bottom warmer than the air at the top, and the cycle will continue forever.
So forget about your mechanisms, forget about the joules, forget about the lapse rates and how they are maintained, and just ANSWER THE FREAKIN’ QUESTION:
Will heat flow in the silver wire forever?
Me, I say no, and I say Roberts thought experiment elegantly proves that the answer is no.
w.
Should have said ‘decreasing’ in my third para of course. Doh!!
Now if one of these new hotrod physicists can explain how and when Saturn dies in the Jelbring universe.
Alan
They just don’t get it. Or, as Bono would say, “stuck in a moment we can’t get out off.”
To the tune of whatever ditty you like.
—————————————————————————————–
I’m a little radiation, radiation, radiation, I’m a little radiation, all day long
Down through the mesopause , mesopause , mesopause, down through the , menopause, all day long.
Down through tropopause, tropopause, tropopause, down through,tropopause, all day long.
Now I’m a little kinetic, kinetic, kinetic I’m a little kinetic, all day long
Up through the pressure, pressure, pressure, up through the pressure, all day long.
Back to a little radiation, radiation, radiation, I’m a little radiation, all day long.
—————————————————————————————————————————-
Consider how a refrigerator works – 2 thermostats going down, and a heat pump going up.
What happens to pressured gas through a condenser and then a separation device?
Co2 forcing, what dribble.
Pick a system – greenhouse or refrigerator.
Yes but to no avail, as the heat flow would be exactly canceled by adiabatic heating of the gas at the bottom of the tube.
The model above postulates only a temperature gradient from top to bottom in the tube but leaves out the pressure gradient developed in a sufficiently long vertical tube in a gravity field.
In the case of a sufficiently long tube, where both gradients exist, the silver wire would try to transport heat from the warmer bottom of the tube to the cooler top of the tube as it must due to thermodynamic laws. The gas at the top of the tube would be warmed (thus increasing its pressure slightly (ideal gas laws temperature change constant volume tube) and like a piston this pressure increase would propagate down the tube at the local speed of sound in the gas causing adiabatic heating of the gas in each subsequent layer until it reached the bottom of the tube, instantly replacing the heat lost to the silver wire.
Net effect – no heat loss from the bottom of the tube, and no net heat gain to the top of the tube as the two actions will exactly cancel each other out. The gas in the tube would never reach thermal equilibrium but would be in equilibrium energetically (PE+KE)
Larry
Willis wrote:
Will heat flow in the silver wire forever?
If you extract energy from the system, it will shut down as the entire system cools. Energy is conserved. If you extract energy, then it has to come from somewhere, and that somewhere is the thermal energy of the system.
If you do not extract energy, then yes, it will.
It’s a terrible design for such. See my comment above.
You seem to have rejected Graeff’s work as being insufficient proof.
What would you consider a sufficient proof?
Alan Millar says:
[I think I fixed it, there were two, better check and see if I got it right. -w.]
Well… I don’t know the answer, but I do need to point out that a closed system with a changing level of kinetic energy in different parts doesn’t violate conservation of energy. Consider on object in an elliptical orbit around a gravitational point source. Its kinetic energy changes as it orbits, but the system is in ‘equilibrium’ with no external input of energy.
Q. Daniels says:
January 24, 2012 at 12:55 pm
I hate it when my perpetual motion machines are poorly designed …
w.
Willis wrote:
I hate it when my perpetual motion machines are poorly designed …
A curious thing. I’ve noticed that engineering tends to be particularly bad when people want it to fail.
@Willis
Heat is indeed conducted upward in the column forever. Why? There is a temperature gradient, and as long as there is a temperature gradient, conduction will occur. It doesn’t matter that the conduction is via the wire, or within the gas itself.
It sounds like you are expecting the temperature profile would eventually smooth out [i.e., become isothermal] over time, and indeed if there we no gravity this is exactly what would happen – the gas would become isothermal, isobaric, and have a constant density.
But in the presence of gravity, you have to take into account the potential energy imparted to the gas as a function of height. Gravity has dome more work on the gas at the bottom of the column than at the top. By virtue of being at the bottom, some of that gas’ gravitational potential energy has been spent [that is, gravity has done work on that gas parcel]. As a result, with no other outlet, this work energy has been converted into thermal energy. This is what the First Law of Thermodynamics is saying. Thus, the temperature of the gas at the bottom is higher than the gas at the top in the presence of gravity, and indeed this is a stable arrangement in thermodynamic equilibrium.
Willis Eschenbach: “So forget about your mechanisms, forget about the joules, forget about the lapse rates and how they are maintained, and just ANSWER THE FREAKIN’ QUESTION:
Will heat flow in the silver wire forever?”
As I said explicitly and a couple have implied (by noting that Dr. Brown has begged the question), heat will not even begin to flow, despite the temperature gradient, if that temperature gradient is the one that Velasco et al. specify, at least if Velasco et al. are correct.
As I mentioned above, this is not hard to understand if you look at heat transport as a diffusion phenomenon, i.e., as flow in accordance with the laws of probability from a region characterized by a higher concentration (of fast molecules or fast electrons) to one with a lower concentration. Superimposed upon that diffusion flow is a contrary drift flow from gravity that cancels it out and thereby maintains a gradient.
I’m told that an analogous effect occurs when a semiconductor diode is fabricated. At the instant two differently doped semiconductor materials join to make a diode, there exists across the resultant junction a hole gradient in response to which a cross-junction hole current begins to flow that tends to eliminate the gradient. But that current stops flowing before the gradient disappears. The reason is that the charge thereby transported sets up an electric field that opposes the cross-junction hole current. So the electric field maintains a gradient that the laws of probability (diffusion) would otherwise eliminate.
Brian,
What is the lapse rate in the ocean?
Am I one of the boys yet Willis?
Regards,
Markus.
Gulp! I have my doubts about the above analysis.
IMO, the tidy demonstration of the exponential pressure profile does not advance either position. It is merely astatesment of the profile to expect at isothermal conditions (i.e. “if we assume constant temperature”).
The crux of the issue is whether the thought experiment justifies the invitation to accept the assumption.
The silver may conduct energy, but this doesn’t lead to the conclusion that we have devised PM as there is no energy leaving the system (and no case is made to say that it could be removed indefinitely). The container has a mass of molecules jostling around forever (so long as we don’t take their energy away). The silver looks like an extension to the container – a somewhat circuitous route in which to carry out their mutual exchanges.
If (for now) all moleculecular collisions were to transact a fixed quantum of energy, the flow through the silver (‘Q’) would be limited by the frequency of exchanges at the lower pressure end. Any additional collisions at the higher pressure end of the silver would have no potential to increase ‘Q’. It is then unclear whether the silver makes any difference to an assumed isothermal end state.
If we remove the fixed quantum constraint, things may improve for ‘Q’, as the lower frequency transactions at the low pressure end may then be more energetic. But all this seems to be saying is that the silver may be a better conductor than the gas (a preferred route for mutual jostling). This alone doesn’t support the leap to an isothermal end state any more than leaving the gas to its own devices.
Finally, there is the significant point that the lower pressure molecules have the greatest total energy in the isothermal state. It is this question that makes me reluctant to go with the assumption.
Sorry about the rapid fire.
Mr Willis Eschenbach,
Sir, you have done us a great service, you have helped us to reason.
Thank you very much.
I misspoke slightly when I said that heat will not even begin to flow in the wire. Whether it does or not initially depends on the temperature distribution that prevails in the wire before it is connected across the gas column. And there may be an initial transfer of energy between the air and the wire. But heat flow will stop before the temperature gradient disappears.
When I illustrated my post called “Perpetuum Mobile“, I chose a photo of a Civil War era perpetual motion machine, because that’s what they are in my mind—a relic of a time long ago when people hadn’t grasped that such a machine is an impossibility.
However, I’m starting to see that perpetual motion still maintains its historical death grip on the scientific illiterati. And I can kinda see why, everyone wants something for nothing.
And truly, people, I hate to bust your bubble and maybe I can’t do so in any case, but the heat can’t flow in the silver wire forever. That would be perpetual motion, and the laws of thermodynamics don’t allow that.
Look, I know that we all break various laws all the time, someone once estimated that Americans break one to three laws every day.
But the laws of thermodynamics aren’t like that. They are not just good ideas, or regulations put in place to protect us from each other or from ourselves.
As far as anyone has ever been able to determine (and lots have tried) those laws simply can’t be broken. That’s why they are called the Laws of Thermodynamics, and not the Good Ideas of Thermodynamics. Those laws say we can’t have a perpetual motion machine driven by gravity.
So if you want to continue to believe that heat will flow through the silver wire forever and ever without end, and that the mystery power that will make it do that is gravity, or lapse rates, or unicorns, or density-driven molecular interactions, or “gravito-thermal forces” or anything else, be my guest. As I pointed out with my Civil War machine, that mistake has a long and storied history, you’re not the first to believe in energetic fairies and Maxwell’s demons.
Just don’t expect your belief, that gravity can do continuous unending work forever and ever amen, to be widely shared in the scientific community …
w.
“MDR says:
January 24, 2012 at 1:14 pm
Thus, the temperature of the gas at the bottom is higher than the gas at the top in the presence of gravity, and indeed this is a stable arrangement in thermodynamic equilibrium.”
So MDR
A gas giant planet, like Saturn, radiates more than twice the amount of radiation than it receives from the Sun. Presumably this little gravity induced energy engine is at work here according to you.
How do these planets ever die, if gravity is constantly maintaining a heat gradient in the atmosphere? The Sun will die and become a cold white dwarf with no solar wind to blow any atmosphere away.
What is going to kill these gas giants?
If gravity is constantly maintaining hotter gases at the bottom then convection will move gases around and therefore we seem to have an everlasting living planet.
What kills it and when, if Jelbring is correct?
Alan
Willis wrote:
Just don’t expect your belief, that gravity can do continuous unending work forever and ever amen, to be widely shared in the scientific community …
Such a demonstration would be worth at least a handshake from Carl Gustaf.
@Willis
Implicit in this discussion is that gravity is an unvarying external force being applied to the column of gas. That is what provides the [apparently infinite] source of energy. The difference between this scenario and a perpetual motion machine is that, for a perpetual motion machine to work, it cannot rely on infinite external sources of energy.
Given that one is assuming here that gravity exists as an external agent, and is capable of doing work on the gas, I stand my my comments above.
@Alan Millar
Sorry, I can’t directly answer your question. But it’s probably worth considering that Saturn is probably not in thermodynamic equilibrium [it has seasons, weather, storms, etc.]. It may in fact still be settling, that is, not enough time has passed since Saturn’s formation to reach an equilibrium state where the heavier matter is underneath the lighter matter. If settling is occurring, gravity would still be doing work on the gas, converting gravitational potential energy into other forms of energy, and some of this energy may radiate into space making it appear that Saturn has an internal heat source.
“Willis Eschenbach says:
January 24, 2012 at 12:23 pm
Folks, a lot of you here don’t seem to get it. The beauty of Robert’s proof is that there is only one question in it—does heat flow forever in the silver wire or not?
.
.
.
IF there is a temperature difference in the air top to bottom, heat will flow in the silver wire. Gravity can’t stop that.”
Actually it can and does, heat in the wire is being transmitted via the interaction of moving particles, gravity will cause the particles to slow slightly as its height increases thus slightly less energy is will be transferred to the atom above a particular atom than was received from the atom below it. This results in a gravitationally induced thermal gradient in the wire.
@Willis,
Gravity doesn’t make the air warmer at the surface, it makes the air -colder- above the surface.
A silver wire has a high thermal conductivity, so it’s easy for heat to flow through its length. But what would happen if you stretched that silver wire over a mile? 12 miles? Would the heat flux be the same over its length? No. You would get microdomains, fluctuations where some areas get randomly distributed with more heat than others, and those domains will flow around. You can see this easily with objects that have very, very low thermal conductivity.
You have microlattice vibrations. But also realize gas is -not a solid lattice-.
I don’t understand, Willis. Before hand you were so concerned with the conservation of energy. Now are you claiming you can take a molecule with a certain kinetic energy (which is what temperature is a measurement of), and raise it 17 kilometers above the Earth (increasing its potential energy by 4664 Joules if we’re talking about a mole of N2) without inputting more energy, and have it maintain that same kinetic energy, that same temperature?
Answer that question, Willis.
A physicist says:
January 24, 2012 at 8:48 am
The answer is easy. By conduction.
Convection will shut down quite quickly as the heat transported upwards by convection reduces the environmental lapse rate. Once the lapse rate is below the moist adiabatic lapse rate even cloud formation cannot drive convection anymore. Oh, except you removed all the H2O. Therefore once the lapse rate is below the dry adiabatic lapse rate all convection will stop. Without GHG to cool the upper atmosphere there is no way to regain a lapse rate suitable to drive convection. All vertical motion will cease. Conduction will become the dominant mode of heat transport. That too will stop when the atmosphere becomes isothermal.
Joe Born says:
January 24, 2012 at 8:21 am
“…If an ideal monatomic gas subjected to gravity in a thermally isolated container consists of only a single molecule, its kinetic energy K–and thus the mean translational kinetic energy–at any altitude z is given by K = mg(z_max -z), where m is molecular mass, g is the acceleration of gravity, and mgz_max is the total (kinetic + potential) energy of the gas. This is true no matter how long you’ve allowed the gas to “equilibrate.” In other words, temperature depends on altitude at equilibrium: there’s a non-zero temperature lapse rate.”
As I pointed out in the other thread, this is not a thermal system at all – or even a gas! – unless the atom is allowed to thermalise with the walls of the container. In which case the temperature (as measured by its average kinetic energy as it passes through a given level) is independent of height.
I have now read the Velasco et al article, and it agrees with what I said: in either the microcanonic (totally isolated) ensemble (with a reasonable number of particles in the gas) or the canonic ensemble (in thermal equilibrium with the surface or walls, irrespective of the number of particles), the gas is isothermal.
You are trying to make a haystack out of the negligible point that, for a tiny number of isolated particles, the statistics aren’t precisely the same as for the usual smooth distribution – they’re “lumpy”. However, even in this extreme case, the temperature at equilibrium will still be the same throughout the entire height, in the crucial sense that no net work could be extracted from the gas by connecting different levels, by any means whatsoever. The “lapse rate” is still zero.
Note by the way that any thermometer capable of measuring the the temperature of two levels of any such system alternately is itself either extracting work from any measured temperature difference, or has to have work done on it to obviate this happening.
All these tree people making a joke of climate science. You have Mann with his cherry picked tree proxies and
Ned Nikolov, Ph.D.
Ph.D. in forestry making a joke of Thermodynamics.
Any way the 600mb temp is going cold right now.
http://discover.itsc.uah.edu/amsutemps/execute.csh?amsutemps
I’ll take a stab to see if I can answer it correctly.
The short answer is it will not maintain the same kinetic energy, the same temperature. This has never been postulated. What’s stated is that eventually the average kinetic energy (the temperature) of all molecules will be the same throughout the gas. That’s not necessarily the same kinetic energy as any individual molecule will have at any given time – it’s the average that’s the temperature. Individual molecules can be hotter or cooler than this average.
“Will heat flow in the silver wire forever?”
Will the molecules continue to jostle forever?
If we never take any energy away from the system, what is the difference between jostling in the gas and flow through the wire?
The questions that remain are: Is isothermal state the lowest energy state for a compressible gas in a gravity field? And on what measure is there a stable (mininum energy) outcome if we are asked to accept that molecules at higher altitude have more total energy than molecules at low altitude?
Just asking.
Ged says:
This is a very subtle point, but one worth understanding. “Temperature” is a measure of the average thermal energy at some location. As implausible as it might seem at first, the average kinetic energy of the molecules that make it 17 km will be the same as the average KE of the molecules at the bottom. You see, only a very few molecules will make it 17 km high. The rest are pulled back by gravity before they get that high, so they never get counted. The self-selected molecules that DO make it 17 km high are the ones that had LOTS of KE to start with. Sure they lose a bunch on the way up, but that ends up leaving this subset 17 km high with the same average KE as the ENTIRE set had at ground level. (The same is true at any other level up thru the atmosphere).
This has been discusses MANY times in related threads recently.
Willis Eschenbach wrote:
Just don’t expect your belief, that gravity can do continuous unending work forever and ever amen, to be widely shared in the scientific community …
So Willis, when will we start flying off the planet??? When will the pressure on my feet from standing in one place stop?? When will the oceans boil from lack of pressure? Oh yeah, gravity is apparently an unending source of energy that counteracts centrifugal force. If not unending, we haven’t yet measured its reduction.
Alan Millar,
“The Sun will die and become a cold white dwarf with no solar wind to blow any atmosphere away.”
This is an assumption without much empiraical proof.
MDR says:
January 24, 2012 at 9:32 am
“…Now, we just showed that internal energy decreases with height, as explained above. Since internal energy [of an ideal gas] is directly proportional to temperature, this must mean that temperature also decreases with height…”
The correct statement would be ” that ALL ELSE BEING EQUAL temperature also decreases with height”. But the internal energy of an ideal gas is also directly proportional to density, which decreases with height. So all else is not equal. The argument fails.
In other words the decrease of internal energy with height manifests itself as decreasing density, not as decreasing temperature.
(In case someone does not see why internal energy is proportional to density it is because if stuff has energy, and you have more of the same kind of energetic stuff, you must have more energy.)
loads of politics going on here. Sceptical AGW blogs still trying to prove that planets are at temperatures dictated by their atmospheric gas composition rather than their distance from the sun. The Greenhouse effect still rules concensus thinking be you an aye or a nay for AGW.
In 1964, Manabe and Strickler published “Thermal Equilibrium of the Atmosphere with a Convective Adjustment”:
In a nutshell, this adjustment eliminates the possibility that a greater potential gradient might compensate for increased transport resistance by GHGs. Instead, only flux changes are allowed which can be nullified by positive feedback. Et voilà, CAGW!
@Tim Folkerts,
Maybe that is the case. Maybe you are totally right. But I still find that hard to believe form observations.
As you move up in altitude, the temperature, the measurable, observable temperature drops steadily. In fact, form my calculation I was less than 3x off just looking at KE turned into PE from the actual temperature at that height.
So the problem is, the average thermal energy you are talking about includes -all- altitudes, and this is a value that cannot change unless absolute energy is given or take from the system. But it does not -follow- the temperature change that occurs as any molecules moves from low to high against gravity. And that’s what I’m talking about. That’s what this whole discussion is actually about.
Yes, the molecules that make it 17 km up had more KE when they started than those that don’t (well, to a degree, as it’s a random walk). But once they MAKE IT 17 km up, they’ve lost a great deal of kinetic energy, temperature, into potential energy, versus what they had at sea level, as energy most be conserved. Correct?
In that way, gravity does NOT DO WORK, but gravity TRANSFORMS ENERGY from one type (kinetic) to another (potential). This must drop the temperature of the molecules in question, since temperature is only a measure of the KINETIC ENERGY side of the TOTAL ENERGY equation.
So, if air rises, it must lose temperature as a consequence of moving against gravity. Average kinetic energy of the entire system means little, as that will not change unless energy is removed from the system or inputted to the system. Average kinetic energy of the cohort of air that moves from low to high, now that does mean something, and that is going to be changed into potential energy.
So then, gravity seems to be able to maintain a temperature gradient -in this way-, as it seems to me, and maybe I’m wrong and your way of looking at it is right. But, what predictions would we make for the real world from what I’m seeing? For starters, we’d expect that if the average energy of the entire system increased, so there was more kinetic energy at the surface, that the atmosphere would “puff up” from the Earth and it’s edge would get higher due to more KE being available for transforming into PE. And this is -exactly what we see- in the real world. And the converse is true. Which is what we see with Martian poles in the winter, or Pluto’s entire atmosphere whenever it gets far enough away from the Sun.
“Why is it that you want to fight over physics that you can actually see with IR eyes? Save your energy for useful things, like arguing about the magnitude of the GHE, the sensitivity of it to changes in CO_2 concentration, the sign and nature of climate feedback or albedo modulation or the complex effects of atmospheric convection on local heating or cooling rates, or the ocean’s effect. The IR spectra render arguing about GH warming per se moot.”
Thank you Robert.
I sometimes wonder why skeptics waste their time an energy fighting against working science.
The real question is sensitivity. Think of all the energy and time devoted here on WUWT to clearly false theories. Imagine if that effort were put to better purposes. Like the surface stations project expanded on a global basis.
sad to see so much human energy, curiousity and intelligence wasted on crap like this and N&Z
Actually Willis, heat flowing through the silver wire forever doesn’t mean it’s impossible, as heat always flows forever in any system above absolute zero. Take any object and an arbitrary plane that defines it. The two parts will never be in exact thermal equilibrium because atomic collisions are discrete, so half the time one side is hotter and half the time it is colder. Thus heat flows back and forth across the boundary – forever. That doesn’t mean the existance of an object above absolute zero is impossible.
Or, take the case of the Maxwell Demon I constructed in my first comment in the thread. It’s made of nothing but pine and mylar but should maintain an imbalance of temperatures between two objects forever, because photon transmission and reflection can be made to be asymmetrical or unidirectional by having mirrors moving to create a path that is only valid in one direction. The concept is like the way volleyball players set the ball to each other. Given the timing of their motions, a volleyball can’t travel the reverse path and find the right hands in the right places at the right times. You can do the same with light if your mirrors are moving very fast.
So if you can construct a system that never reaches the isothermal state, and attach another path for heat flow, the heat will travel from hot to cold forever. This changes the stable temperature difference between the two objects, turning the Demon into a less efficient Demon. You can’t extract anything from the permanent heat flow without having the energy dissipate.
As for thoughts on the problems of heat flow through a long silver wire, the equations we use have never needed to include any gravity component because it’s unimportant to most purposes. It’s only fairly recently that physicists got irked enough to tweak heat flow equations so the heat couldn’t travel at infinite velocity, exceeding the speed of light.
Equations for electricity, from Ohms law to Maxwell’s equations, likewise completely neglect gravity, implying that I can connect a copper wire to a black hole with a potential of -24 VDC and have electrons pour right up out of the gravity well. Or I could show that an atmosphere of electrons and protons (hydrogen) wouldn’t have more pressure at the bottom than the top because Ohm’s law or some other handy formula says the electrons would be evenly distributed, as gravity was never factored in to the completely accepted electrical formulas we use every day.
I shall repeat in different words the argument i provided at
son of mulder says:
January 24, 2012 at 9:59 am
which no one challenged (or read). If I’m wrong please challenge.
Heat cannot flow up the silver conductor unless more heat is pushed in at the base. Heat is energy and hence by Einstein mass.
If you consider all the heat in the silver conductor as a distribution of mass then that mass has a center of gravity in the gravity field. If heat were to flow from the base to the top (without input of new heat at the base) then there would be reducing heat (mass) a the bottom and increasing heat (mass) at the top. Overall the centre of gravity of that heat (mass) would rise. ie work would have to be done against gravity. Put another way a force against gravity would have to be applied. If no new energy is being pumped into the base then the law of conservation of energy means that heat cannot be conducted up in a gravity field and so the top will be colder than the base and remain so ie no force can be applied.
The same logic can be applied to the atmosphere. You just have to ensure no new heat is applied and no heat is removed. If no new heat is applied and energy is allowed to be radiated away then eventually all temeprature would be equalised only at absolute zero.
Willis,
Seems like folks here want to argue that the laws of thermo are not settled science.
same with the laws of radiative transfer
Let me toss my in my idea to show what is wrong with this thought experiment. Take the earth system and remove gravity. What happens to the GHG’s, the water, loose objects, the adiabatic lapse rate…
Take gravity away from the thought experiment and what happens. Nothing except a very slight redistribution of mass as the pressure equalizes through the column?
For a volume of gas to have a thermal gradient requires a heat source and heat sink at each end of the gradient, so that heat is transported along the gradient from source to sink. Remove the heat source and the heat sinks from the gas, and the thermal gradient will disappear.
In the case of Earth’s atmosphere, the heat source is the heating of the surface of the earth by the sun, and the heat sink is radiative to Deep Space. So it is not appropriate to dismiss Robert’s because it’s not the atmosphere – Robert is just showing the mechanism in the paper being criticised is not correct.
Peter Spear, (IMHO) your scenario is correct.
The resulting no-GHG Earth would have nearly isothermal, hence stratified atmosphere, for the physical reason that every thermal would carry heat into the atmosphere that could never be radiated away, making it ever-harder for thermals to rise on subsequent days.
The no-GHG weather would be freezing no-wind nights followed by still cold days. As (relatively) warmer tropical air slowly circulated (colder poles), first Earth’s polar oceans would freeze, then the mid-latitudes, then even the equatorial oceans.
Some folks we’ve seen this scenario even here on earth, way back when the sun was cooler and GHG’s were scarcer, a world of low GHG’s and frozen seas … This hypothesis is called Snowball Earth.
Elevator Summary: GHG’s prevent Snowball Earth.
kuhnkat says: “Oh yeah, gravity is apparently an unending source of energy that counteracts centrifugal force.”
Repeat after me: Force is not energy; energy is not force.
Gravity can and does provide a continuing force. That does not mean that it is providing any continuing energy. Gravity only does work when there is a net movement inward. Since the atmosphere is not continually falling, gravity is not doing work.
(NOTE, on the gas planets, there is no solid surface to stop contraction, so there the planets are indeed contracting and generating continued thermal energy of the sort many people seem to think exists on earth. This is also how protostars warm as they collapse inward.)
steven mosher says:
January 24, 2012 at 2:38 pm
100% correct Sir.
Sensativity is the question and there have been no answers with acceptable confidence from a model yet. The present parameters do not hindcast with enough accuracy to forcast with any confidence.
Physiscs, as we presently know it, is physics.
Unless a new law of thermodynamics is found, Dr. Robert Brown is 100% correct.
Nick Shaw says:
January 24, 2012 at 9:52 am
Space has no temperature. To have a temperature there must be kinetic energy which means that there must be mass.
Things in space get cold because they radiate heat away. Look at photos (or drawings) of the space station – look for the radiators. These are positioned so that the Sun does not shine on them.
In the case of an atmosphere without IR radiators, it will have no way to cool itself.
Do I have this correct : the temperature is dependent on the kinetic energy of individual molecules(?)
When I throw a single ball upwards it’s velocity decreases with height. Do gas particle’s velocities not decrease as they go higher and higher,?
Can someone explain why, if their velocities do not decrease, there fewer of them at height.
Sorry if I am being dim!
While I agree with the underlying point, I’m not sure why the wire would necessarily violate the laws of thermodynamics if it continuously transferred heat. Under normal circumstances, it would radiate some of this energy away and otherwise be an imperfect conductor. If, however, we’re assuming a closed system with a perfect conductor surrounded by a perfect insulator, why would any energy be lost?
To put another way, assume I have a wheel with a frictionless axle at rest in a vacuum. If I spin it, it will spin endlessly. The conclusion that it will have perpetual motion doesn’t violate thermodynamics; the assumption that there is no friction does. Likewise, the wire would not violate any physical laws by endlessly transferring heat; those laws were broken by the assumption of a closed system with a perfect conductor/insulator.
I know I’m disputing people far above my pay-grade, so I’m assuming that I’m wrong in this. I’m just curious as to why.
What the recent theories regarding gravity induced temperature gradient are really saying is that the ideal gas law as commonly stated is incomplete. A factor is left out because in most terrestrial situations it is irrelevantly small.
They are implying the ideal gas law should be stated as:
PV = NkT +(delta PEg)
where PEg = the change in gravitational potential energy.
If you radically increase the gravitational potential energy of a mass of gas, you have changed the total energy in the system unless you give up an equivalent amount of energy in the form of temperature.
Larry
“The real question is sensitivity.”
Yes indeed it is but the lapse rate issue goes to the heart of it.
If the lapse rate and thus the surface temperature is set by pressure and solar input alone then the effect of GHGs is zero.
GHGs do introduce more radiative and conductive energy around themselves by virtue of their thermal characteristics so, if there is more energy in the air but the surface temperature fails to change then something else has to give.
I propose a miniscule change in the surface air pressure distribution instead.
That would simply change the rate of energy flow through the system from surface to space and redistribute the energy at the surface as necessary for no global change in surface temperature at all.
“Heat is energy and hence by Einstein mass.”
I hate to even bring this up, but I am rather sure that gravitational red-shifting will indeed have a theoretical affect on things (but I don’t think in the way imagined by the earlier poster). A photon will be red-shifted when it rises from the surface. It would be a straightforward task to estimate the change in wavelength and hence the change in “temperature” for thermal IR photons arriving high above the earth from the surface. However, typically such effects are only noticeable very close to very massive objects. I am sure that the “relativistic lapse rate” would be microkelvins at most, and hence not important in this discussion.
But, hey, if anyone wants to calculate the actual “relativistic lapse rate” and its effects — go for it. As a warm-up, I would suggest calculating the time correction for GPS satellites to make sure you know enough to get started.
Ged says:
January 24, 2012 at 2:10 pm
@Willis,
Gravity doesn’t make the air warmer at the surface, it makes the air -colder- above the surface.
____________________________________________________
Bingo!
Ged says:
January 24, 2012 at 2:10 pm
“Gravity doesn’t make the air warmer at the surface, it makes the air -colder- above the surface.”
Yes. And if you remove the source of heat the column will cool and as it cools it shrinks and as it shrinks the molecules fall toward the surface and as they fall they gain back the kinetic energy they lost in making the ascent. If the temperature of the column drops enough the gas turns into an incompressible liquid or solid, completely collapses to the surface, and the gravity induced gradients are history.
@Willy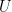 for an ideal gas is
for an ideal gas is
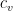 is the specific heat at constant volume,
is the specific heat at constant volume,  is the number of moles of the gas,
is the number of moles of the gas,  is the gas constant, and
is the gas constant, and 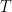 is the temperature. None of these quantities depend on volume or density.
is the temperature. None of these quantities depend on volume or density.
Your statement that “the internal energy of an ideal gas is also directly proportional to density” is incorrect.
Internal energy, a term with a very specific meaning in thermodynamics, is proportional only to temperature for an ideal gas. For starters, see http://en.wikipedia.org/wiki/Ideal_gas , and in particular the section entitled “Classical thermodynamic ideal gas” where it states that the internal energy
where
Willis at 11.54am wrote:
Excellent insight, Wayne. That is exactly what happens. In an isothermal column of air, individual molecules at high altitude have more energy because of gravity. But for exactly that same reason, there are fewer molecules at high altitude. As a result, and as we would expect, in the isothermal condition the energy is spread out evenly through space (equal energy per volume) rather than equal energy per molecule as Hans Jelbring and Mr. Verne assert.
Although I agree with Dr Brown, I disagree with what Willis has said here. Consider a cubic metre of soil and a cubic metre of air above it, although both are at the same temperature, they certainly have different amounts of enegy due to differing densities.
equilibrate the total energy
This is a major misunderstanding. Thermal equilibrium does not equate the total energy. Read the equipartition theorem. Open a standard introductory physics textbook. Learn what temperature is. Then return.
Besides — and I’m going to make this a standard answer for all off topic replies. The presentation above challenges you to do just one thing. Tell me whether or not the system in figure 2 permits energy to flow in a circle forever. If you answer “no, of course not” you are quite right, and you have conceded that thermal equilibrium is isothermal, because the silver wire is just a proxy for thermal conductivity in the air itself that makes it clear why not (since detailed balance computations get confused when you add an utterly irrelevant process that you dream up involving gravity to them and then try to do them in your head without the faintest idea of how statistical mechanics actually works). If you answer yes, I’ve got this bridge in Brooklyn you might want to look at, right after I convince you to invest in the machine we can build that will turn heat into energy at the rate of 100%, because I could stick a heat engine into the thermal pathway of the silver conduction and the resulting system would convert 100% of any energy added to the fixed-lapse air on the left into work.
The choice is yours, of course.
rgb
My head hurts. Is someone keeping score? If so, who is wining, the For team or the Against team? Confused minds need to know.
@Willy
Note that I am *not* arguing that there *isn’t* a variation of density [or pressure] with height. It’s simply that once one knows the internal energy of a gas, one also knows its temperature, irrespective of either the density or pressure. Of course, the profiles of both density and pressure must still satisfy the ideal gas law, and as you intuitively expect both decrease with height [as does the temperature].
2) The silver wire will transport heat from warmer region to the cooler region, but in so doing it short circuits the transport of heat by convection. So with the wire present, convection will be less, but the net transport of heat will remain the same.
It won’t short circuit convection — in stable equilibrium there is no convection. Convection itself is a kind of heat engine driven by temperature differences that transports heat (on average) from a hot reservoir to a cold one. In stable equilibrium nothing moves, because there is always dissipation associated with movement that will slow it down, right down to the extreme quantum regime. I assume you aren’t talking about superfluid circulation and calling it “convection”.
There is no input energy, also, so there cannot be net transport of heat. That’s the bit about “violating the second law of thermodynamics” in spades. A system with interminable flow of heat in a circle is a textbook violation of the second law, and it permits one to design any number of perpetual motion machines of the second kind.
rgb
I thought metals had free electrons and electrons were matter and gravity accelerates all matter and metals conduct heat so well due to the free electrons and …. and how again is this proposed perpetual machine supposed to refute a lapse rate? Seems lifting the electrons against gravity in the metal bar from the warm to the cool would cancel if the gradient became -0.0098C/m. The only real thermal motion it seems would be with an isothermal air column, but that would just run, backwards to the arrows on the diagram, until all relevant potential energy was minimized. I think that point would be called the DALR.
http://en.wikipedia.org/wiki/Energy_minimization
We sure could use a proper experiment. I have already designed one that should work fine if anyone should ever want to consider doing one. Basically Graeff’s only designed correct this time with many sensors, multiple layers of insulation, large, and with air. Why he chose a liquid I’ll never understand.
“In the modern world the stupid are cocksure while the intelligent are full of doubt.”
~ Bertrand Russell
Clearly a non-isothermal dry adiabatic column isn’t a minimum energy state (as energy can be extracted, imagining an efficient thermal conduction system between top and bottom layers.
Convection requires that some parcel of gas is already at an elevated energy state (or it wouldn’t be rising *due* to convection), and thus convection doesn’t violate conservation or 2nd law. The adiabatic column is (ignoring radiation) the minimum energy state with differentially heated (cool top, hot bottom) boundary conditions.
I don’t have a clear picture how a heat engine connecting the top and bottom would look in T-S space, or what the minimum energy solution would look like were one to take an established dry adiabatic column, insulate top and bottom and run a heat engine within the column. It seems like it would have to go to an isothermal state as minimum energy
Willis, the short answer is “Yes”, the medium answer is “IMHO Robert Brown basically has got it right”, and the long answer is “The logical next step is discuss whether day-versus-night temperature swings alone — in the absence of GHG effects — suffice to mix the Earth’s atmosphere.”
Because that claim —foreseeably (and strictly IMHO) — is going to emerge as the primary fallback position of GHE skeptics.
I see two assumptions above:
1. It does not matter what the density of the gas is. It will equally conduct heat at the bottom into silver wire, as the wire will be able to conduct its heat into the gas at the top, even though the density at the bottom and top is different, due to the gravitational effect on the gas.
2. The cross-section of the wire will stay the same, which means the ability of the wire to conduct the heat, which depends on its cross-section, is the same at the bottom and top.
The gravitational field will actually pull down a considerable part of the mass to the bottom, making it far wider at the bottom then the top (depending on the length of the wire and its tensile strength), deforming it more into a tear drop shape.
With your setup you may be able to change the lapse rate, but I doubt that you achieve an isothermal state in this way.
It does not matter what the density of the gas is, or how good the contact of the silver with the gas is (as long as there is thermal contact, or how thick the wire is. The point is that if any heat enters at the top ever and the system spontaneously restores the lapse rate (which is constant, recall, for a container of fixed size independent of gas density so we can make the gas nice and thick with great thermal contact with the silver) then you’ve violated the second law, because any thermal pathway between the bottom and the top will deliver heat from the bottom to the top. All I’ve done with the wire is show you a pathway that is clearly completely independent of the supposed lapse rate in the gas, one that will conduct heat in any direction without prejudice, so that you can see why a lapse rate is impossible. If heat to the top goes back to the bottom because of “gravity”, and there is a pathway to the top that must conduct heat in the direction of a thermal gradient (the wire) you’re done. The system will circulate heat indefinitely.
But no system can circulate heat indefinitely, it’s absurd.
So the message is, stop trying to do statistical mechanics in your head without understanding it. Stick to thermodynamics. It is simpler, safer, and you can’t make mistakes with it as long as you remember TANSTAAFL. There ain’t no such thing as a free lunch. A nonzero thermal lapse is a Maxwell’s Demon working the free lunch counter for the suckers.
Here’s the deal, really. Every book I’ve ever read on statistical mechanics or thermodynamics is wrong — and you can safely assume I’ve read a few, since I did numerical simulations of both static and dynamic critical phenomena that actually were published in places like Physical Review, with referees and everything — or figure 2 above makes it clear that there is no possibility that figure 1 is correct. That is, assuming that you can’t believe the actual words of the second law that tell you that you can’t take a system and create a permanent thermal gradient in it without doing work to maintain it, because heat will flow from the cold side to the hot side to neutralize temperature differences otherwise.
That’s why you have to pay to refrigerate or air condition your house. It is why you can’t build a perfectly efficient heat engine. Tanstaafl, man.
rgb
I find the analysis quite reasonable – but it is so idealized as to be useless. A more interesting thought experiment has a spherical planet heated by a remote star, rotating on an axis roughly normal to the line to the star, with an atmosphere of non-greenhouse gases. The equator would be warmer than the poles, so there would be Hadley-type circulation that would cool the equator and warm the poles. Would there then be a vertical thermal gradient? I think there would be, but I’m sure someone would like to argue to the contrary.
Not at all. It is merely specific. I am specifically proving that EEJ, a specific paper written by Jelbring and published in a journal (God help the referees, absent that day on vacation or something), violates the zeroth but especially the second law of thermodynamics when it asserts that there will be a thermal lapse rate in an adiabatically isolated column of ideal gas in thermal equilibrium in a gravitational field.
No, there won’t.
Is it stupid to have to prove this? Sure, given that nearly any introductory physics textbook — I’m not talking about thermodynamics text, just things like Tipler and Mosca, or Halliday, Resnick and Walker — teach enough thermodynamics for one to be able to see that the spontaneous appearance of a stable thermal gradient in any system is impossible, because it is a direct violation of the second law, and indirectly the first, which more or less says that equilibrium is isothermal (in order to permit the definition of thermometry in the first place). If thermometers “work” to measure temperature, equilibrium is isothermal. Period.
rgb
So your wonderful assertion, is that the radiative forcing of Co2, occur after its entry into the thermostats of the tropopause, and that extra radiative forcing, causes that missing hot spot, increasing the temperature back through the stratosphere and down again through the thermostat of the tropopause.
Been there, done that.
No, my “wonderful assertion” is that EEJ, Jelbring’s paper, is obviously incorrect because a stable, isolated atmosphere cannot support a thermal gradient. There is no such thing, in other words, as “gravitational heating” for a system in static equilibrium, nor is there any such thing as “gravitational heating” for a system in dynamic equilibrium. There is such a thing as gravitational heating in a collapsing system, which is what raises the temperature of protostars to the ignition point and provides the heat outflow from brown dwarfs.
As the greenhouse effect is concerned, look at the IR spectrum from over the top of the atmosphere. I don’t care how you think heat gets to the top of the troposphere; the point is that one chunk of the outgoing spectrum observed from satellites comes from a gas that radiates in the CO_2 band that happens to be at top of troposphere temperatures. The net radiation in the water window therefore has to be higher (than it would otherwise be) in order to keep the Earth in detailed balance (on average). End of story. I don’t give a rat’s ass where the extra radiation comes from, or how it gets there, it is there. You can see it. It is emitted/transmitted at the blackbody temperature of the ground give or take a bit.
Here, let’s use our fingers and toes. Total outflow in all frequencies has to be the same. Outflow in one band of frequencies is smaller because it comes from colder molecules. In order to keep total outflow the same, the energy radiated in the other frequencies has to:
a) Go up.
b) Go down
c) Remain the same.
That’s it. Come up with any mechanism you like for heat absorption and transportation, they’re all the same to me. Just don’t forget the incontrovertible experimental IR spectroscopy data and the finger and toe arithmetic involved.
rgb
Lets try a slightly different explanation of this closed static system. Of
course, a closed static thermodynamic system is, per see a thought experiment
that can not exist in reality.
We have a quantity of gas in a sealed cylinder and the cylinder is a closed
system thermodynamically. That means energy can not enter or leave the cylinder.
The cylinder is *not* in a gravitational field. Therefore, the mean pressure of
the gas is the same through out the tube and the temperature of the gas is
isothermal. This is thermodynamic equilibrium and entropy can not change.
Now, we switch on our gravitational field. The gas settles into a pressure
gradient with higher pressure at the bottom and lower pressure at the top of the
cylinder. Because of the gas laws, the gas at the bottom heats up and the gas
at the top is cooler. We will also assume that the gas does not absorb or emit
at the frequencies associated with these temps ( i.e. we can ignore radiative
transfer).
So convection and conduction set in and start to mix the gas. The total energy
in the gas is still constant. As the gas mixes energy is transferred from the
warmer gas to the cooler gas and the temperature differential reduces.
convection slows. This continues until T.E ( Thermal Equilibrium ) is reached.
At the new T.E. there is no more convection, the gas is isothermal and the
pressure gradient remains. The gravitational field is no longer performing work
on the gas so it can not add energy to the system no matter what potential it
exerts on any particular molecule.
Just imagine if this were not the case and convection carried on at T.E.
We could have a wind turbine driven by the convection current and connected to
outside the system. We would now be removing a continuous source of energy
from at system at T.E. Good luck with your patent applications ;-).
/ikh
Also, a constant temperature with altitude means that particles at the top of the atmosphere have more momentum than particles at the bottom.
It means nothing of the kind. Momentum (magnitude) is p = mv. The distribution of v at the top and the bottom is identical — the Maxwell-Boltzmann distribution.
Oh, do you mean more total momentum (in any given general direction) at the bottom than at the top because there are more particles? Sure — that’s why the pressure at the bottom is greater than the pressure at the top in a compressible fluid (where there are more molecules at the bottom than at the top). See “Kinetic Theory of Gases” at your friendly wikipedia outlet:
http://en.wikipedia.org/wiki/Kinetic_theory
rgb
So again you post modern hotrod physicists please answer the question. This is the real world it IS going to happen.
The stupid people here, who believe in the Laws of Thermodynamiics, know what will happen in the universe ruled by the Laws. But do the clever people, who know that the Laws are wrong, know how it happens in the Jelbring universe.
Now don’t be shy, it doesn’t really matter if you show that you are a complete idiot more than once, does it?
A gas giant planet, like Saturn, radiates more than twice the amount of radiation than it receives from the Sun. Presumably this little gravity induced energy engine is at work here according to you.
How do these planets ever die, if gravity is constantly maintaining a heat gradient in the atmosphere? The Sun will die and become a cold white dwarf with no solar wind to blow any atmosphere away.
What is going to kill these gas giants?
If gravity is constantly maintaining hotter gases at the bottom then convection will move gases around and therefore we seem to have an everlasting living planet.
What kills it and when, if Jelbring is correct?
Folks – Fellow interested posters, I am going to attempt to have a conversation with many of /y’all & all at once, skim for your handle if interested in engaging. All in time sort.
Joules Verne says at 1/24 7:52am:
“The device in figure 2 doesn’t work…the gas will collapse to the surface as a liquid before it gets to absolute zero and this will shut off further extraction of energy because the cold side of the thermocouple no longer has any cold gas to cool it.”
Good one. Joules groks this stuff. Now by Robert Brown definition, the gas is isothermal, meaning the gas can’t cool – the Perpetuum Mobile w/isothermal gas & perfect insulator is born in Fig. 2. A neat design for Willis’ dream machine. Patent pending.
Eilert sats at 1/24 7:54am:
“…I doubt that you achieve an isothermal state in this way.”
This actually adds to the discussion in a good way. A good thought experiment is to turn up the gravity field and see what would happen. The silver rod could react in the manner you describe. Interesting.
Genghis says at 8:06am:
“Take a single gas molecule and put it at the top of the tube. It has zero kinetic energy and zero temperature. Let it fall and just before it hits the bottom it will have a lot of kinetic energy and heat.”
Very good one. At the top, the molecule also has lotsa’ PE. At the bottom, it also has 0 PE. No isothermal molecule down the tube, it is isoenergetic (I learned a new term) – where there is no wire!
Robert Brown says at 8:14am:
“Well then, by all means go patent your perpetual motion machine of the second kind or explain heat flow in the second diagram, Joules.”
Robert – YOUR machine beat Joules. That is your machine design, it is still running. It will run tomorrow. It will run forever w/isothermal gas & you just have developed the perfect insulator patent.
Go for it. The Perpetuum Mobile design, fig. 2 in the top post is worth A LOT!!
And I’m ever so sorry, but in an ideal gas the temperature IS determined by the total energy. I cite the 1st Law consistent with oth law in one reservoir and the 2nd law constant entropy.
Robert continues:
“That’s an absurd idea, given that one can perform a gauge transformation — change the zero of the total energy — without changing any of the physics.”
The datum concept enables many good & proper science in many texts. Insert the thermometer at any datum to compute the invariant total energy value, say TE = C, & thereafter allow temperature and PE to vary with each other from that datum thermometer reading and you will be ok. Just place the thermometer at any different h. The temperature or mean kinetic energy of the molecules it will measure will be different: KE(h) = C – mgh.
Robert Brown says at 8:23am:
“Heat will definitely flow in the silver, right? It’s just a chunk of metal that’s an excellent conductor of heat.”
Right. This is why Robert Brown had to invent the perfect insulator design in fig. 2. How’s the patent pending process coming along Robert?
Robert Brown continues:
“You want to assert otherwise, you tell me what the equilibrium state is of figure 2.”
I have tried elsewhere. In fig. 2, let’s say white body starts with Twhite and gray body Tgray>Twhite. Cite 0th law that says heat will flow to a paler shade of gray, both bodies at single reservoir Tavg with silver tube! Or with moving jars, dipping bird, etc. At least while Robert’s perfect insulator patent is pending.
Robert Brown says at 8:28:
“No, I think you are generally quite right, and this agrees rather well with Caballero’s argument.”
Remember the Caballero text in the ref. given in Perpetuum Mobile thread makes an argument temperature is non-isothermal in a gravitation field section 2.3.
Caballero does write: 2.1 No gravity: “Note that pressure is due to only to the local properties of the gas and not to anything going on far away.”
2.3 w/gravity “Mean velocities (insert his defn. Temperature for mean velocities here) will be greater near the bottom of the box than near, the top: in other words, pressure decreases with height. We will now work out an equation giving the precise rate of decrease.”
Note Caballero defined “mean velocities” as temperature – I am just inserting for clarity, no meaning change. Thus temperature will be “greater near the bottom of the box”. This is not consistent with Robert Brown’s as yet unproven pronouncement that it is isothermal. Other than the fig. 2 w/perfect insulator inconsistent with 0th law driving an inconsistency with 1st Law.
Schodinger’s Cat says at 8:57am:
“Over time, I would expect the system to reach thermal equilibrium.”
Welcome back from the quantum world I see you survived after all. Yes, by gosh, the system in fig. 2 with real non-perfect insulator will reach thermal equilibrium over time by 0th law. The gas temperature will be non-isothermal.
Robert Brown says at 9:01am:
“No, it won’t have any “heat””
Right, but Genghis molecule will have the increased kinetic energy and per Caballero’s 2.3 ref. increased temperature. Rap Genghis on the knuckles for saying “heat”.
Robert Brown continues:
“But the basic point of my paper is that Jelbring is wrong not because of any possible microscopic description of a lapse rate. A lapse rate itself is wrong in thermal equilibrium, because figure 2 is very, very easy to understand.”
Robert Brown fig. 2 is wrong to have a perfect insulator which cannot exist by 0th Law. Jelbring cannot be proven wrong by fig. 2 which is not physical. At least until Robert Brown’s patent for the perfect insulator is granted.
Robert Brown says at 9:07am:
“…in figure 2 above. Which is violated — the heat equation in silver or your absurd assertion that gravity can stably sort out a gas into a hotter temperature and a colder one? One or the other.”
The heat equation in silver is not violated in fig. 2.
MDR says at 9:32am:
“This is an example of a system that is both in thermodynamic equilibrium and possesses a gradient in temperature.”
Good. This is consistent with 0th, 1st and 2nd thermo laws. Fig 2. is not & runs forever. Once fig. 2 has a non-perfect insulator admitted per 0th law, it will eventually be in equilibrium, non-isothermal gas, and not run forever.
Rober Brown says at 9:51am:
“Excuse me? I have no idea what you (Trick) could possibly be talking about.”
Believe me I grok this. You are smart though and the thermo master’s were right in the 0th, 1st, and 2nd law development. They have stood the test of time right up to fig. 2.
Robert Brown continues:
“heat will flow in the wire from the bottom to the top.”
Yes. Cite 0th Law.
“The point is that heat will flow in this system forever…”
Yes, fig. 2 is a Perpetuum Mobile. To win the patent for it though Robert Brown is going to first have to win the patent for the perfect insulator. If Robert cannot patent a perfect insulator, cite the 0th and 1st law tell us the system will stop flowing heat when it reaches thermal equilibrium and with 1st law non-isothermal gas (see Caballero 2.3 ref. telling us gravity results in non-isothermal gas column) thru the non-perfect conductor, this is less than forever but can be quite long because there are some quite close to perfect insulators.
“The real point is that you don’t need the silver wire to make this argument…..Gravity does no work in this problem, not in steady state.”
I whole heartedly agree. Wire is sort of useful to understand the concepts of the thermo laws. The ideal gas molecules in fig 2 lose just as much energy going up against gravity as energy they gain coming back down. Fig. 2 modified with real non-perfect rl insulator is ideal isentropic reversible process with non-isothermal gas (Per Caballero 2.3 – check it out).
“So what makes the heat go round and round?”
The perfect insulator. The perfect insulator is non 0th thermo law compliant. Your patent still pending?
“Of course. It doesn’t.”
Heat does stop flowing round and round with a patentable real non-perfect insulator. The gas will be non-isothermal per Caballero ref. 2.3.
Robert Brown says at 9:58am:
“Are you crazy?”
No Joules Verne is eminently sane, Robert Brown misses the other poster (Joules Verne) said the work extracted was not from the system but from the ideal gas column with the perfect insulator (patent pending).
Robert continues:
“In the real world, the system will evolve to an isothermal state precisely as I described it because it is in equilibrium.”
Not isothermal unless you think Caballero is crazy too (my view Caballero is not crazy), since his reference 2.3, disagrees with you. Caballero shows ideal gas column is non-isothermal in the presence of gravity. Caballero also shows ideal gas column is isothermal w/o gravity.
JKrob says at 10:24:
?In moving the heat from the bottom of the tube to the top is causing the lapse rate to become **more stable** – cool at the bottom with warm air above is an inversion which inhibits vertical mixing!! THAT is why the engine will not work as it is set up.”
A good .02 added viewpoint. Thanks for de-lurk.
D.J. Hawkins:
“Now I can construct a heat engine which extracts useful work based on the temperature gradient and gravity will continue to organize the air column forever and my heat engine will never run out of “fuel”? Really??”
Robert Brown will demand a royalty for using his patent pending perfect insulator. Other than that cost, yeah fig. 2 works for free.
Graeme W says at 11:50am:
“I don’t understand the theoretical derivation well enough…”
In the WUWT Perpetuum Mobile thread at the top post, there is a Rodrigo Caballero link cited by Robert Brown to the theory of ideal gas without and with gravity field. In 2.3 gravity is added to a non-isothermal gas column and this condition is theoretically justified – it is pretty simple derivation, I recommend it. Fig 2 perfect insulators needed only for a Perpetuum Mobile.
Robert Brown for some reason does not grok Caballero 2.3 even though he cites it as good ref.
Willis Eschenbach says at 11:54am:
“In an isothermal column of air, individual molecules at high altitude have more energy because of gravity.”
Bzzzt! Isothermal column of air is for no gravity case ref. Chapter 2.1 Caballero link in your Perpetuum Mobile post.
Bzzzzt! “…because of gravity”. Ok, with gravity Rodrigo Caballero (bless him) tells us in 2.3 same link the air column becomes non-isothermal.
Bzzzzt! Fail 1st law: individual molecules must have constant energy. Note the period. Willis “more energy” fails. More energy is not constant energy.
Willis tries to knock down Jelbring paper with these fails. Not possible to knock down Jelbring with these 3 arguments.
Willis Eschenbach says at 11:57am:
“It is the formal disproof of Jelbring’s theory. It is idealized by its very nature.”
By Willis use of “it”, my view Willis means top post where Willis summarizes his understanding of “it” at 11:54am. Willis at 11:54am fails any disproof on all 3 points of his points, see right above. Gosh, I hope Robert Brown groks Caballero & 1st law energy conservation quickly.
Willis Eschenbach at 12:09pm (? to another poster):
“Does heat flow forever or not?”
Heat flows forever in fig. 2. The reason is a grand master thermal law is broken, the easiest one, the zeroth law. There can be no perfect insulator. Body A placed in contact with body B will always eventually equilibrate temperature. This is so easy. Geez. If Robert Brown can patent a perfect insulator, I will change my view. Patent granted: Perpetuum Mobiles will be possible.
Until the patent is granted, heat will NOT flow forever in fig. 2 b/c there is no perfect insulator. Willis should grok this on his own (read Caballero slowly). Robert Brown is going to take longer I think, to reach a state of equilibrium grokness. LOL, I feel better my head cold is receding faster.
Willis Eschenbach at 12:09pm:
“Folks, a lot of you here don’t seem to get it.”
No kidding. Including Willis viz:
Will heat flow in the silver wire forever?
“Me, I say no, and I say Roberts thought experiment elegantly proves that the answer is no.”
For fig. 2 silver wire heat will flow forever like Robert Brown says it will in top post, his words:´ One is then left with an uncomfortable picture of the gas moving constantly.. At least until poster Joules Verne situation is reached and the gas cools & liquefies under a vacuum. That’s good thinking but beyond the intention of top post.
My view is the insulator in non-perfect to be 0th law compliant and in that cas heat will not flow forever and gas per Caballero 2.3 will be non-isothermal.
Willis Eschenbach at 1:04pm:
“I hate it when my perpetual motion machines are poorly designed …”
That fig. 2 is a WELL designed Perpetuum Mobile w/isothermal air & perfect insulator. Just gotta’ pay royalties for those: (patents pending).
– – – – – – –
Out of breath and w/blisters on my fingers I stopped at 1:04pm. I will happily rengage if more interested parties appear thereafter. Typo’s are possible in this post. Probable really.
Robert Brown and Willis: You will never convince some people. These same people are quite sure that the reason we don’t have machines capable of giving free energy forever is due to “poor engineering”, or its a conspiracy by Big Oil or Big Gubmint to fleece us all. If only the shackles of these evil doers were thrown off we could live a life of luxury forever, with energy too cheap to meter, made in our own basements be a nice perpetual motion machine – yours for $499 from your local hardware store. But of course, us incompetent engineers and physicists wouldn’t want that… line us up against wall now because clearly thats what we deserve.
/sarc
Great theory. Baloney, but very entertaining.
The reason the silver thingy won’t generate perpetual motion is that the exposed ends will assume whatever the air temp is at that altitude. A temperature difference of 1 degree will not move any heat in a silver rod 100 meters long.
adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity.
And yet we see this stratification in the atmospheres of Venus, Earth and Jupiter. In the real world, it’s hotter at the ground because the air is heated from the ground up and rising air columns draw this warmer air up… you know, the thermopiles birds ride up instead of having to beat their wings furiously. Imagine that, it’s colder on top of a mountain than at it’s base. It’s called the triumph of empirical science over clever explanations that claim otherwise.
The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that in stable thermodynamic equilibrium.
Which does not occur in the real world. That’s why we call it weather. Sorry, no sale. This is just as unacceptable as the nonsense about CO2, a trace gas having more effect than water vapor on the planet’s temperature.
I hasten to add that the lapse rate that does prevail at equilibrium is much smaller than that for which Jelbring contends, so Jelbring is still wrong.
If you want to bet against the laws of thermodynamics, I wouldn’t advise it.
I do not care about what generates the lapse rate. If the lapse rate is stable, so that heat delivered to the top redistributes to maintain a constant equilibrium temperature lapse between the top and the bottom — the sole case examined in the article above — then it violates the second law of thermodynamics.
Let me put it bluntly. If somebody presents a statistical mechanical computation that suggests that the second law is violated, I would knee jerk assume that the authors had made a terrible mistake unless and until proven otherwise, especially if I “could not understand” everything that they did.
Even then I would be doubtful.. To be honest, I would be doubtful if I did the work myself. I think that the paper you link has the right idea, and you will note that on other threads I propose precisely the same experiment. Show me, in other words. I’m a theorist, but I’m no fool. Experiments trump theory every time, but the Earth’s atmosphere does not exhibit a DALR:
* Uniformly. See “troposphere”, “stratosphere”, “thermosphere” etc. Why exactly doesn’t the DALR extend to the top of the exosphere again?
* Ubiquitously. See “thermal inversion”, or for extreme cases “thermal profile of the atmosphere above Antarctica in July” (there’s an IR spectrum in Caballero with the data you need). Hmmm, thermal inversion, with the upper troposphere hotter than the ground? Could that be, maybe, because the ground is cooler than the air instead of warmer? Regardless, it is nearly impossible to explain if there was an intrinsic DALR that didn’t depend on differential heating.
Nor is the atmosphere ever even crudely static. Air is always moving up, down, sideways. Even when it is “windless” down near the ground, there are damn few places on Earth where the air isn’t moving up and down and sideways from a kilometer on up, on any given day. So it isn’t really all that surprising that the air (a decent insulator and hence quasi-adiabatic a parcel at a time) has a DALR when it is differentially heated and moving all of the time, keeping it crudely “well-mixed”.
Thermal static equilibrium is something else. No mixing. Conduction matters — it can be slower, but there is plenty of time to reach equilibrium. That’s why the thermodynamic argument is so powerful — it is very difficult to explain how heat delivered to the top of any truly equilibrated air column would spontaneously redistribute to maintain a vertical lapse rate and not enable a heat loop and/or any number of PMM2Ks.
But show me the “high precision” experimental result, done with a dewar in a centrifuge filled with maybe Xenon gas at a G value such that there is sufficient pressure at the top of the vessel to justify the thermodynamic assumptions, with recording high-precision, carefully calibrated thermometers.
Just bear in mind that if it works, and there is a lapse rate, the second law itself is done. I’ll stick a thermocouple between the top and the bottom of said gas, and it will sit in there spinning forever.
rgb
Dr Brown is not correct with his explanation of Fig2
In a cylinder with gas at the usual DALR, all that his conducting wire will achieve is a infintesimally thin layer or hotter gas at the top plus an infintesimally thin layer of cooler gas at the bottom.
Both of these would reverse the lapse rate ( inversion) and thus no further heat can be exchanged without adding work to the cylinder (His statement that the system would reorganise itslf into an adiabatic column is wrong)
This situation would also apply to an attempt to use a themocouple to derive any work from the system. (Or any other heat engine)
It is thus clear that the adiabatic column cant be used as a perp -motion device so the proof that it breaks thermo laws has gone away.. The reverse holds true for an isothermal column where the bottom must be cooler than a surrounding DALR atmosphere with the opposite at the top– In this case heat can be removed at the top and added at the bottom. This would comprise a real-perp motion machine as the column would then reoganise itself into the isothermal state
Clearly it is the isothemal condition that breakes the 2nd Law
PS Much has been said about the need in the real atmosphere to maintain a DALR by pumping from below with energy from the Sun. In the real world the column is subject to all sorts of energy lossed and gains. The list is very large as Anthony has enumerated is is recent post– The water cycle is one of the most important
Most contributors seem to have ignored the fact that in the DALR cylinder all the heat losses and gains have been elininated and thus it takes an infintesimally small amount of energy to lift a parcel of air fron the bottom to the top hence an infintesimally small amount of energy will maintain the DALR.
We just need to overcome conductive and radiative transfers which have already been assumed to be zero
Oops, I mixed replies to the previous two comments. The paper was a separate suggestion. The answers are the same, however. Experiments talk, bullshit walks. And please, address the actual content of my argument above instead of invoking obscure stat mech or nonstandard axioms. Explain how a nonzero lapse rate does not enable second law violating, perpetual heat flow, if you would, right up to the point where real thermal equilibrium is achieved. Also remember, gravity is doing no net work while all of this is going on. If it were, things would actually be worse — you’d start violating the first law of thermodynamics as well.
rgb
Joe Born,
Please post a calculation of the Velasco lapse rate for a gas column with the surface at STP (101325Pa and 273.15K) and g = 9.81 m/s^2. The number density/cubic meter is ~6E23 molecules/mole/0.0224m^3/mole = 2.7E25.
One minor point. Since statistical mechanics is all about probabilities, it is possible to violate the Second Law. It’s just extremely unlikely. All the molecules of air in a room could migrate into one half of the room but the time for the probability of this event reaching 50% is really, really long. It’s many orders of magnitude longer than the age of the universe, depending on the size of the room and the air pressure in the room. I suspect Velasco’s calculation is something like that. For one molecule there’s a 50% chance it will be in one half of the room at any given time.
Robert Brown,
I’ve read a number of thermodynamics texts myself.
Not once did I see a proof of the Second Law that did not rely upon circular logic. I’ve seen plenty of empirical proof, that people have been unable to violate it, but no direct proof.
Relying upon the Carnot Cycle is pretty clearly circular logic. It’s more difficult to show, but assuming that the MB distribution remains uniform under gravity may also be circular.
If you have a proof of the Second Law that is not based on circular logic, I’d be happy to read it.
Failing that, all we have is that there are no publicly recognized or understood violations of the Second Law. It is empirical, and nothing more.
Poor engineering is not proof of impossibility.
” “In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down.”
I live half-way up a mountain at 6100 feet. The valley below is at 4500 feet. The temperature difference is nearly always the dry lapse rate 8 degrees F, whether it is calm or windy. Only if it is raining or snowing will it be different. It then goes to the moist lapse rate. Most of the time it is sunny, heating the ground equally, both in my back yard and in the valley below. What maintains the lapse rate temperature difference?”
Mostly gravity.
If you lived planet with 1/2 the gravity, the the temperature difference would about 1/2.
You could say you would be warmer. You could also say lower elevation would be cooler there would less difference temperature.
Less difference in temperature is undeniable.
With a silver rod, one could transfer heat from lower elevation to your elevation. Or one could use other material which cheaper and conducts heat better than air. But silver is one of best conductor of heat and air is one the poorest conductors of heat.
One can generate energy from differences in heat. Venus isn’t particularly good place to generate energy- despite being very hot.
Venus doesn’t even “have a lot of energy”- in terms of total joules of heat in it atmosphere, assuming one find a lot something which is colder one couldn’t create an extraordinary amount of energy.
Over a period of time, say 24 hours, earth absorbs more of the sun’s energy than Venus does- despite being closer to sun and getting around 2700 watts per square meter compared to Earth’s 1300 watts per square meter.
This can quickly seen: Venus is hot, it’s temperature near surface does not vary over time, and since Venus is hot, it can not be made hotter by the sun. The earth more distance and receiving less sunlight, is much cooler. And because it is cooler it can heated by the sun and there is daily variation in temperature. And on planetary scale, earth has large variation in equator and polar temperature. So earth is churning heat engine, whereas Venus is more stagnant.
So in terms of power, in terms of horsepower, earth is a more powerful engine.
It seems to me that in subject of climatology, there is measurement of the engine temperature, and there should more attention to how much power the engine produces- and what’s earth miles per gallon.
Robert G. Brown says
The dry adiabatic lapse rate determines how high thermals will go – usually, only a few kilometers. The actual lapse rate is normally significantly different from the DALR.
As this article argues, the lapse rate without IR emitters would be zero. It is the greenhouse gases that move the actual lapse rate (ELR) from zero to -6.5 K/km. The DALR is -9.8 K/km. To claim that anything “maintains” the DALR simply means that you have not looked at the data.
Related to the DALR is the concept of “potential temperature” – the temperature that a parcel of atmosphere would have if it moved adiabatically from some altitude to sea level. For instance, if the atmosphere at 10 km was -55C, its potential temperature is
The other meaning of this is that for air to convect from sea level to an altitude of 10 km, it must be at least 43C. A more typical value in the sub-tropics would be -70C at 17km
Since the surface temperature is typically a bit cooler than this, the bulk of the atmosphere does not follow the DALR. (Near the surface, the DALR is seen almost every day. But only near the surface.)
I suggest that everyone look at some real data.
“kuhnkat says:
January 24, 2012 at 2:33 pm
Alan Millar,
“The Sun will die and become a cold white dwarf with no solar wind to blow any atmosphere away.”
This is an assumption without much empiraical proof”
I hope your Mum isn’t reading that because even she would be embarrassed!!
Is this the level people will sink to just because they would like to have a new theory of Thermodynamics which will disprove the theory of CAGW?
Get a grip folks. These sort of statements are going to hold this well respected site up to ridicule.
Stick to facts and real physics and CAGW will be shown to be nonsense in any event.
It will take a bit longer but I will live to see it and I ain’t young! Have patience, trust in Gaia!
Alan
@ Dr. Brown –
I’m curious, what if the gravity isn’t constant, but is fluctuating?
“Willis Eschenbach says:
Robert Brown says:
I have been seriously trying to follow this conversation. I have my Thermo text, my Heat Transfer text, my CRC handbook, the internet, and my calculator. For a dumb ass like me (tau beta phi), I wonder if one of you would answer give me your opinion to the following questions (2):
Does the atmospheric pressure, no GH gases, play a role in the dry adiabatic lapse rate?
Does the atmospheric pressure, no GH gases, effect the overall equilibrium temperature of the near surface of a planet?
Thank You,
Robert S Rider
I’m so dumb I can’t even spell Pi.
says: These two idealised adiabatic processes (like the adiabatic stages in the Carnot Cycle) will result in the parcel returning to Earth with nearly the same temperature as leaving (the slight drop being accounted for by radiation at TOA).
Carnot cycles are ISENTROPIC. By definition. Isentropic means adiabatic AND reversible.
Hmm, maybe we read different textbooks. Any cyclic heat engine — being cyclic — returns to its original state at the end of a cycle. All cyclic heat engines — being heat engines — increase the entropy of the Universe while operating. In particular the Carnot cycle absorbs heat \Delta Q at temperature T_H for a change of entropy of the hot-side reservoir of -\Delta Q/T_H, and then rejects it into the cold-side reservoir for a change of entropy of the cold reservoir of +\Delta Q/T_C.
The total entropy change — per cycle — is thus:
\Delta S = \Delta Q (1/T_C – 1/T_H) > 0
To correct you — and please, bear in mind that I’ve taught this for 30 years — Carnot cycles are NOT isoentropic. Isoentropic DOES mean adiabatic (\Delta Q = 0) and reversible, but Carnot cycles contain two isothermal expansion/compressions (also reversible). The isothermal parts are not isoentropic, as explicitly shown above.
Now, what drives the circulation cycle you describe? How about absorbing heat at constant temperature from the hot ground (reservoir) and delivering it to the upper troposphere where the heat is lost to radiation at much colder temperatures. Hmm, sounds like something that increases the entropy of the Universe to me. The air that is rising and the air that is falling are not at the same temperature. They may both be isoentropic processes, but they don’t occur at the same place and the same time, and it is the thermal variations of density with temperature that ultimately provides the lift (or lack thereof) that drives the cycle, positive or negative net buoyancy.
With all that said (filling in details), I think we agree. So what is the point?
rgb
Paul Birch:
“I have now read the Velasco et al article, and it agrees with what I said: in either the microcanonic (totally isolated) ensemble (with a reasonable number of particles in the gas) or the canonic ensemble (in thermal equilibrium with the surface or walls, irrespective of the number of particles), the gas is isothermal.”
Of course, what we’re talking about is the microcanonic ensemble, to which Equations 5-8 apply. If you read Velasco et al.’s Equation 8 for mean single-molecule kinetic energy K as a function of altitude z, you’ll see that the expression for K is the product of a constant and (1-mgz/E), where m is molecular mass, g is the acceleration of gravity, and E is total system energy. To me that looks as though K decreases with altitude z: the temperature decreases with altitude. Is there some different way you interpret that factor? As I read it, it says there will be a lapse rate that’s small for large numbers of molecules but stll finite and non-zero so long as the number of molecules is not infinite.
Presumably, you are basing your interpretation of Levasco et al. on its penultimate paragraph, in which they made an execrable attempt to state verbally what the equations express mathematically. Unfortunately, that passage is so abysmally opaque that any exegesis thereof matching the mathematical result is doomed to appear hopelessly strained. So I will forgo the attempt. The real question is, Does Equation 8 define an altitude-dependent temperature or not? If so, there’s a non-zero lapse rate at equilibrium.
If you can’t reach the answer by considering Equation 8 itself, consider the lead-up to it, where Velasco et al point out that the state density as a function of both velocity and altitude (Equation 5) is not the product of state density as a function of altitude alone (Equation 6) and state density of a function of velocity alone (Equation 7)–as it would be if temperature were independent of altitude. They also observed that the density distribution as a function of velocity is not, as one would expect of an isothermal configuration, the Maxwell-Boltzmann distribution.
That was the wind-up, and the pitch was Equation 8, which says that, indeed, the temperature is not isothermal.
Do you interpret those equations differently?
Mike, it was to address this specific objection that the Beach-House Block Story was conceived … this story shows that the length of the column is irrelevant.
Q. Daniels, please let me commend to your attention the Wikipedia page titled “Hamiltonian vector field”, and the references therein.
In particular, that page’s geometric theorem “the symplectic form ω is preserved by Hamiltonian flow” is equivalent to the dynamical principle “the state-space volume of a dynamical ensemble never decreases”, which in turn is equivalent to the thermodynamic principle “the entropy of a dynamical system never decreases”.
Whether or not this geometric reasoning conveys belief … at least it is not circular reasoning.
What a fun thread! I should be working but I’m reading it instead. (That is okay, it is 8:22 PM and I’m self-employed, so it’s not like the boss doesn’t know what I am doing.)
My thanks to Dr. Brown and Willis for their patience. I would have given up long ago. I liked Dr. Brown’s simple example.
My next comment is going to offend many people so, if you are sensitive, quit reading. The discussion in this thread reminded me of many of the discussions on RealClimate. Only the role of the climate scientists was taken by those who opposed Dr. Brown’s explanation—they knew what the truth was and they could figure out some theory to disprove it.
This thread is probably a healthy process—although somewhat painful to watch. But, it does show that one need to think hard about these issues.
I feel that this discussion is a reasonable model of how science often advances. Someone throws out a good idea. Many dump on it with facile but incorrect criticisms. A few offer support. Finally, after a long time and much confusion there is reasonable agreement that the idea is right (or wrong, depending). We now believe that bacteria cause many ulcers but that N-rays don’t exist. But, when the two theories were offered, the bacteria/ulcer theory was dumped on but the N-ray theory was not.
My guess it that a few who participate in this thread will actually learn something, which is probably more than you can say for most students in freshman physics in college.
Billy
Robert Brown says at 3:45pm:
“Tell me whether or not the system in figure 2 permits energy to flow in a circle forever.”
Robert Brown says in a top post verbatim quote, search on the text for context of his answer:
Yes. “Heat will flow in this system forever; it will never reach thermal equilibrium.”
Robert Brown at 3:45pm:
“If you answer “no, of course not” you are quite right.”
Now Robert Brown is going so fast he is not right with himself. S-l-o-w down again Robert, when you do, you are quite good. Maybe you really are struggling & working to line up with the past thermo masters to grok this stuff better like Joules Verne and Tallbloke handles.
Robert continues to struggle forward to equilibrium grokness by reading up on the subject:
“Thermal equilibrium does not equate the total energy. Read the equipartition theorem. Open a standard introductory physics textbook. Learn what temperature is. Then return.”
I have returned. Here is a quote from my standard introductory physics text book: “Equipartition gives the total average kinetic and potential energies for a system at a given temperature.”
Robert – You are advancing in your studies! This is good. You must now grok potential energy better. It is equipartitioned with kinetic energy at a given temperature. I have learned (long ago) that temperature is mean kinetic energy (reading your Caballero ref. was a cool refresher…).
So Robert is right here thermal equilibrium does not equate to the total energy. Thermal energy is equipartitioned with potential energy for the total energy. Good going Robert, I see advancement in this 3:45 post toward the thermo master’s laws.
Robert gave a little back with the two different answers to the same question but still see some progress.
Robert will be way better off moving to grokness equilibrium understanding the non-isothermal gas column upon reading Caballero section 2.3. Then return.
Venus atmosphere is ~4.8 x 10^20 kg
Average temperature: 737 K (464 C)
http://nssdc.gsfc.nasa.gov/planetary/factsheet/venusfact.html
Specific heat of CO2: [kJ/kgK]
600 K 1.075
650 K 1.102
700 K 1.126
750 K 1.148
800 K 1.168
http://www.engineeringtoolbox.com/carbon-dioxide-d_974.html
To lower one degree of K requires 1.148 times 4.8 x 10^20 kg
Earth ocean:
1.4 x 10^21 kg
278 K [5 C] 4.204 (kJ/kgK)
To lower or increase one degree of K requires 4.204 times 1.4 x 10^21 kg
To freeze or melt into ice requires 334 kJ/kg
To vaporize water 2,270 kJ/kg
http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html
So how many joules does it take heat a Venus from say 20 K to it’s present
temperature?
The chart starts at:
175 K 0.709
So roughly .7 times 4.8 x 10^20 kg times [175minus 20K] 155 equals KJ
And from 175 to 375 .8 times 4.8 x 10^20 kg times 200 equals KJ
375 K to 600 K: 1.0 times 4.8 x 10^20 kg times 225 equals KJ
600 to 737 K: 1.1 times 4.8 x 10^20 kg times 137 equals KJ And sums:
5.2 x 10^22
7.68 x 10^22
10.8 x 10^22
7.23 x 10^22
Which is 30.9 x 10^22 kJ
With earth melt 1.4 x 10^21 kg ice is 334 kJ/kg times 1.4 x 10^21 which is
46.7 x x 10^22 KJ
So to heat ice from 273 K to 274 K require more joules than the atmosphere of Venus
requires to heat from 20 K to 737 K.
To warm the ocean from 276 [3 C] to 13 C
Requires 10 times 4.2 times 1.4 x 10^21 which is 5.88 x 10^22
In terms of ten millions of year, the earth oceans have had 10 C increase or difference
in ocean temperature. I don’t think many consider that Venus has had such swing
in temperature: 7.23 x 10^22 is amount joules required to heat from 600 to 737 K.
So about 100 K [or 100 C] change in Venus temperature.
In terms of ice age to interglacial periods there is about 10 C difference in average global
temperature [not ocean change in temperature- but atmospheric]. So in terms couple tens of thousands, earth temperature changes, still roughly close to comparable temperature of somewhere around 100 C change in Venus.
So it requires real absorption of energy [joules] to change “average temperature”, locally daily one can easily have more than 10 C change in temperature. Such changes reflect dynamic, and powerful heat engine.
So, we would expect the atmosphere at the surface of a planet to be warmer that it is at the top of the atmosphere. Of course, we can’t totally ignore conduction and radiation but, compared with convection, they are second order effects.
We might expect this if we didn’t understand convection. You’re getting things backwards, and amazingly, even though I derive the density of an ideal gas in thermal equilibrium above, you don’t even bother to read and understand it.
At a uniform temperature there is an exponential pressure and temperature gradient. If you warm the system at the bottom, the density of the fluid there decreases and there is a net buoyant force that lifts it up. Convection is cone-head complicated — I mean seriously complicated — in the general case. The equations that describe it are the Navier-Stokes equations, which are nonlinear partial differential equations so complex that mathematicians haven’t even been able to prove that a solution exists in the general case, let alone solve it. The idea is simple enough, and in simple geometries with e.g. uniform thermal gradients across the fluid one can predict some of the structure observed, e.g. convective rolls. But your base assumptions are completely false, and you have cause and effect completely reversed.
Undriven convection does not lead to warmer air on the bottom. Not ever. Heat a gas or liquid uniformly on top and you will have no vertical convection, because the density profile is stable. The stable undriven density profile is precisely what I derive, and is isothermal, with no convection. Only if you differentially heat a system on the bottom or on the sides (which is still part way to the bottom) do you get convection, and that only because the bottom is already warmer because of something else. Convection, in fact, cools the bottom!
A secondary comment is that radiation and convection make (from what I understand) roughly equal contributions to surface cooling. Either one can be dominant under different circumstances. During the day, convective cooling can be important — convection driven breezes can pick up a fair bit of heat from the surface. On a clear dry night, however, the ground temperature quickly inverts (becomes cooler than the bulk of the air immediately overhead) and radiation becomes far more important than convection.
The desert heats up to 45C or so during the day, but can still cool to 0C overnight. Not (primarily) from convection, not at all. By radiation.
Way back in boy scouts, winter camping in upstate New York, I learned about radiation and temperature. Cloudy nights are far warmer than clear nights. Clouds reflect a lot of heat back down and slow the cooling of the ground considerably. Water is a powerful contributor to the greenhouse effect. I also learned about a space blanket. A teensy thin layer of aluminized plastic, and yet it keeps you amazingly warm, because it reflects back your body’s radiant heat. You can feel it instantly if you put your hand into it. Your body loses roughly half of its heat from conduction/convection, and half from radiation. Air is a lousy conductor of heat, and often there is little or no wind. Radiation can easily be dominant, not just “second order”. I have no idea which one is dominant overall as far as surface cooling is concerned, but neither of them is negligible.
rgb
Robert Brown says:
January 24, 2012 at 8:28 am
Show me my mistake. Anybody. I won’t be offended.
[kdk33 says:
January 24, 2012 at 7:22 am ]
No, I think you are generally quite right, and this agrees rather well with Caballero’s argument. Isentropic because it is dominated by convection, not conduction, in an open system heated at the bottom. Isolate the system, or heat it at the top and explain to me how the bottom will end up warmer than the top.
Yeah, right. Just like the oceans. I wonder why the argument fails for the oceans? They seem to come into thermal equilibrium at, well, thermal equilibrium (constant temperature, independent of pressure, density, “gravity” etc), below the convection-dominated thermocline.
========================
The thermocline exists because of these, heated surface waters warmer and therefore less dense will sit on top of colder, denser water.
Because going through 4°C to lower temperatures water gets dense enough to sink and doesn’t freeze, freezing water floats, so not independent of density and pressure and as these are due to gravity, not independent of that either. Salt water has lower temperature before freezing, -1.9°C.
Some extra bits.
In this description of how oil is formed in the oceans, increased pressure means increased temperature:
“Other sediments continued to be deposited and further buried the oganic-rich sediment layer to depths of thousands of feet, compressing the layers into a rock that would become the source for oil. Over the years, as the depth of the burial increased, pressure increased, along with the temperature.”
“Water pressure at the deepest point in the ocean is more than 8 tons per square inch, the equivalent of one person trying to hold 50 jumbo jets.”
“Atlantic sea water is heavier than Pacific sea water due to its higher salt content.”
“The Antarctic ice sheet that forms and melts over the ocean each year is nearly twice the size of the United States”
“90% of all volcanic activity on Earth occurs in the ocean. The largest known concentration of active volcanoes (approximately 1,133) on the sea floor is located in the South Pacific”
“Under the enormous pressures of the deep ocean, sea water can reach very high temperatures without boiling. A water temperature of 400 degrees C has been measured at one hydrothermal vent.”
“The top ten feet of the ocean hold as much heat as our entire atmosphere”
The above from: http://www.savethesea.org/STS%20ocean_facts.htm
“90% of the total volume of ocean is found below the thermocline in the deep ocean. The deep ocean is not well mixed. The deep ocean is made up of horizontal layers of equal density.”
http://www.windows2universe.org/earth/Water/temp.html
And bearing in mind heat rises.., http://www.esr.org/outreach/glossary/insulation.html
“Ice is a great insulator. A lot of what causes climate and weather involves the exchange of heat and fresh water between the ocean and atmosphere. If the ice cover is high, very little heat escapes from the warm ocean to the cold polar atmosphere in winter. But the heat loss through open water is so high, maybe 10-100 times more than through ice, that even a small fraction of open water has a big effect on area-averaged heat loss. Typical heat loss values are ~10 W/m2 through thick sea ice, and ~1000 W/m2 in winter through open water (depending on wind speed, air temperature, etc.)”
Do you have a phobia about gravity? Just asking.
Robert Brown wrote:
I do not care about what generates the lapse rate. If the lapse rate is stable, so that heat delivered to the top redistributes to maintain a constant equilibrium temperature lapse between the top and the bottom — the sole case examined in the article above — then it violates the second law of thermodynamics.
Let me put it bluntly. If somebody presents a statistical mechanical computation that suggests that the second law is violated, I would knee jerk assume that the authors had made a terrible mistake unless and until proven otherwise, especially if I “could not understand” everything that they did.
Even then I would be doubtful.. To be honest, I would be doubtful if I did the work myself. I think that the paper you link has the right idea, and you will note that on other threads I propose precisely the same experiment. Show me, in other words. I’m a theorist, but I’m no fool. Experiments trump theory every time, …
I agree with this in detail, and find it a completely reasonable attitude. I will note that some people have difficulty understanding particular pieces of math, independent of their complexity. The Lorenz Transform is one such.
Graeff’s work is probably not sufficient proof for you. He believes he has successfully measured said temperature differential. http://www.firstgravitymachine.com
I also don’t think that a PMM2 machine violates TANSTAAFL. For one thing, the energy must come from somewhere, even if it’s just being exhausted as waste. For another, such a device would require an insight and a good deal of skill to build and use, even if it was as simple as rain. Doing takes effort, even if you’re just recycling waste.
The essence of this Robert Brown’s ‘refutation’ is that if the wire and the gas do not have the same thermal gradient i.e. if the wire is isothermal and the gas is not then, there is a violation of the laws of thermodynamics.
The problem with the refutation is that the wire is not isothermal for essentially the same reason as the gas is not: the atoms at the top of the wire will move slower than those at the bottom due to gravity and will therefore be at a lower temperature.
The atoms of the wire will lose velocity as they rise in the gravitational field just as those in the gas, thus there is less energy available transferred in interactions this will produce an gradient in the kinetic energy of atoms that make up the wire resulting in a temerature gradient due to gravity. That the distance covered between interactions is much smaller in the solid than it would be in the gas and that there are other interactions in a solid does not change this fact.
glen martin says:
January 24, 2012 at 2:07 pm
Phew … gravity slowing electrons in a wire … thought I’d heard everything.
In any case, even if your interesting theory about gravity slowing heat transfer in wires were correct, it doesn’t matter. That just slows down the transmission of heat, it doesn’t stop it. So it doesn’t mater for the disproof.
w.
@Robert Brown
OK, after pondering some more, I have identified a flaw in my reasoning. I think you and Willis and the others are correct – the column of gas does indeed eventually relax to an isothermal state if the column is in fact thermally isolated. It is still stratified, of course, but it would end up isothermal. Apologies for confusing everyone.
Here is where I was going wrong. I mentioned that gas near the bottom of the column has a smaller amount of potential energy than gas the top. While this is undoubtedly true, that potential energy only comes into play if the gas is being mixed or is otherwise dynamic, that is, if such energy is being released as a result of changing the height of some of the gas parcels. But of course the equilibrium state does not have any such mass motions, and so no work is being done on the fluid. As a result, the internal energy of the gas is the same everywhere, and thus the gas has the same temperature everywhere.
Of course, for a column of gas subject to heat exchanges at the top and at the bottom [such as a column of gas in a planetary atmosphere] but is otherwise thermally isolated, there will be a temperature gradient established in accordance with those boundary conditions. But that scenario is apparently off-topic in this thread.
Robert Brown says at 4:10pm:
“I am specifically proving that EEJ, a specific paper written by Jelbring and published in a journal (God help the referees, absent that day on vacation or something), violates the zeroth but especially the second law of thermodynamics when it asserts that there will be a thermal lapse rate in an adiabatically isolated column of ideal gas in thermal equilibrium in a gravitational field.”
Robert Brown needs to read Caballero sec. 2.3 that proves the zeroth is not violated & the 2nd is not violated for “adiabatically isolated column of ideal gas in thermal equilibrium in a gravitational field” which Caballero proves is non-isothermal & there will be a thermal lapse rate.
I imagine Caballero is just like every other thermo text book (but I have not read them all like Robert) & the thermo grand masters assert. Thus Jelbring EEJ is not in violation & not refuted if Jelbring asserts same as Caballero and Caballero is right.
Q. Daniels says:
Willis wrote: Will heat flow in the silver wire forever?
If you extract energy from the system, it will shut down as the entire system cools. Energy is conserved. If you extract energy, then it has to come from somewhere, and that somewhere is the thermal energy of the system.
If you do not extract energy, then yes, it will.
=======
LongCat says:
While I agree with the underlying point, I’m not sure why the wire would necessarily violate the laws of thermodynamics if it continuously transferred heat. Under normal circumstances, it would radiate some of this energy away and otherwise be an imperfect conductor. If, however, we’re assuming a closed system with a perfect conductor surrounded by a perfect insulator, why would any energy be lost?
To put another way, assume I have a wheel with a frictionless axle at rest in a vacuum. If I spin it, it will spin endlessly. The conclusion that it will have perpetual motion doesn’t violate thermodynamics; the assumption that there is no friction does. Likewise, the wire would not violate any physical laws by endlessly transferring heat; those laws were broken by the assumption of a closed system with a perfect conductor/insulator.
I know I’m disputing people far above my pay-grade, so I’m assuming that I’m wrong in this. I’m just curious as to why.
==============
Trick
Heat flows forever in fig. 2. The reason is a grand master thermal law is broken, the easiest one, the zeroth law. There can be no perfect insulator.
==============
Correct.
All real heat engines increase entropy. Engines do work. Figure 2 doesn’t.
Robert, thank you for making this excellent point.
Precisely the situation you outline is present in all of the world’s high-speed centrifuges containing uranium hexafluoride (UF6) for isotope separation.
If an adiabatic lapse were present in the centrifuges, between the high-pressure rim and the low-pressure central axis, then solid UF6 would condense at the cold central axis … which needless to say, is not observed.
Elevator Summary: Gas centrifuges prove that gravito-thermal theory is wrong.
kuhnkat says:
January 24, 2012 at 2:32 pm
kuhnkat, you are conflating a constant force with unending work. Gravity is just there all the time, a force pulling in one direction, keeping you on the planet. When you move upwards against gravity, it takes energy to do that. When you move with it you get the energy back.
But when you come back to where you started, it’s a zero sum game (less with friction). No matter how many times you go up and down the hill, you don’t gain any energy at all, despite the constant presence of gravity. Which is another way of saying that in all of those trips up and down the hill, the lazy bum gravity hasn’t done a net lick of work. It did do work, but what gave with one hand, it took with the other by requiring the exact same amount of work in the other direction.
It’s like running a waterwheel by continuously filling the headrace up with buckets of water from below the wheel. Sure, you can get work out of the wheel … but that’s work that you are putting in by continuously lifting the water, not work that’s coming from gravity. Stop lifting the water and see what your friend gravity does for you … nothing.
Hope that helps.
w.
Wayne says: “Seems lifting the electrons against gravity in the metal bar from the warm to the cool would cancel if the gradient became -0.0098C/m. ”
Very insightful.
IF the gradient for air and electrons and all other materials were the same 0.0098C/m, THEN maintaining a lapse rate would not lead to a perpetual motion machine.
However, since the lapse rate is given by C_p / g, and since different gases have different values for C_p, then different gases will have different lapse rates. So the premise is indeed wrong, and a stable lapse rate in gases would indeed violate the laws of thermodynamics.
Clearly there are two schools of thought. One school believes that the temperature will be lower at the top due to kinetic energy being changed to gravitational potential energy. The other school believes this will not happen. The GHG controversy rests largely on this point.
No, it doesn’t. There isn’t any controversy. Gravity is incapable of providing net heat to the Earth’s energy budget, and the GHE only deals with the rate at which the Earth loses heat in that budget. Nobody argues that there is a lapse rate in the actual atmosphere. I have just definitively proven above that it is not a feature of static equilibrium, it is a dynamic phenomena caused by differential and irregular time dependent heating and cooling, where the bulk of the heating is at the surface, but where heat loss occurs to some extent very high up in the atmosphere as well.
This has nothing to do with “schools of thought”.
I am troubled on one point. The argument that a continuous flow in a cycle is not equilibrium and thus is some sort of proof favoring one school over the other. Surely dynamic systems can be in “equilibrium” in that there is no net flow into or out of the system, but still allow a cyclical flow within the system.
Surely they cannot, not as long as they are thermally connected at the microscopic scale to allow internal energy transfer within the system. This is precisely the point. Heat never “flows in cycles” in a system in thermal equilibrium. It flows from hot to cold. It never ever spontaneously flows from cold to hot as an steady state thermal process unless one does work on the system. This is what the second law of thermodynamics is all about. The only systems that can “move”, transporting energy around in cycles are ones without mechanisms for energy sharing or dissipation, like planets going around the sun in the limit that you ignore tidal heating and gravity waves and light pressure. In enough time, even those weak effects move energy around and damps periodic motions.
In the case of the gas in the figures above, one could take the silver wire, replace the middle of it with a thermoelectric junction, use the electricity to drive a fan or light a bulb. This, too, would violate the second law — the heat content of the container would systematically lower (as some of the heat in the cycle was converted to work). The net effect would be that all of the energy lost from the container would be converted to work — its temperature would drop as the work appeared in the outside world, quite independent of the temperature out there. This, too, is a direct, textbook case of the violation of the second law of thermodynamics, both the refrigerator statement and the heat engine statement.
At least you are troubled by the right things — you should be troubled by this because your mere common sense tells you that heat, which is basically random motion, cannot remain organized enough to flow around in a circle without something reorganizing it. The microscopic form of the second law says that basically, systems evolve in time from less probable states to more probable states. Take a jar full of identical marbles, some blue and some red, organized with the blue on top and red on the bottom and shake it. You can shake a long, long time before you can expect to see all of the blue on the bottom and the red on top — there are a near-infinity of ways for the marbles to be mixed; only one for them to be cleanly separated red on blue.
That’s the sad thing about this — people don’t understand how much of a law the second law is. Your odds of winning 150 million dollars in the lottery and having the IRS forget to charge you taxes on it due to a clerical error are a gazillion times better than the odds of shaking that jar and getting even a very modest number of mixed-color marbles sorted out by random chance, and that is precisely the reason that heat flows from hot to cold and not the other way around. There are way more states where the energy (per degree of freedom in the system) is approximately equally shared than there are states where it is split up.
Otherwise, your observations about ability to rationalize and so on are well made, but — my advice is don’t bet against the second law. You’ll just lose.
rgb
For 13.7 billion years, …
… Gravity fields have been heating up matter.
That is long enough to be called perpetual.
Just look out at your night sky and see the proof of that. Or maybe even the day-time. The big bright white thing in the sky started shining because of gravity fields heating up matter.
We can extract energy from that we figure out it works exactly. Just like the other ten sources of energy that we didn’t have clue about in times past.
Anyone disputing Jelbrings hypothesis needs to prove that gravity does not provide a minimum heat/energy level in matter when that matter is being held back from falling further through the gravity field by the electro-magnetic and strong forces of the atoms in the rocks at the surface of the planet. The matter is still being pulled through the gravity field, it is just being stopped by the other forces in the atoms of the rocks/liquid.
Has anyone proved that? How could you? We don’t even know how the force of gravity extends its pull. Maybe Higgs bosons increasingly accumulate/stick to matter as it moves into a gravity field and they are attracted to each other. Maybe the Higgs provides heat energy to the matter. If you don’t how it works, you cannot say it has no impact.
George Turner says:
January 24, 2012 at 2:40 pm
George, if you do not know from the context that we are talking about net heat flow through the wire, and not freakin’ brownian movement of electrons, you are not paying enough attention.
w.
If the column of air is not isothermal, that is an emergent phenomenon in the presence of several things:
– A planet
– An active star
– An atmosphere
By this excessive logic, a solar panel can’t possibly be a perpetual motion machine either, so there is no such thing as renewable energy. Especially after the sun fizzles out…
Robert Brown says at 4:36pm:
“The distribution of v at the top (of the atmosphere) and the bottom is identical — the Maxwell-Boltzmann distribution.”
Maxwell-Boltzmann is not applicable in a gravity or electrostatic field. M-B quite clearly limit their derivation of particle velocity to special case of particles with no external forces like no gravity, no electrostatic etc. M-B applies to our famous gas column when it actually is isothermal – in the no gravity case. Caballero 2.2 shows that is the fact and in my view Caballero is correct.
Dewitt Payne: “Please post a calculation of the Velasco lapse rate for a gas column with the surface at STP (101325Pa and 273.15K) and g = 9.81 m/s^2. The number density/cubic meter is ~6E23 molecules/mole/0.0224m^3/mole = 2.7E25.”
I’m a little pressed for time this evening, so I’ll just give you what I have handy, without using your particular values or double-checking. Note that this assumes a monatomic gas. I’ll revise it tomorrow for diatomic (after I read up on rotational degrees of freedom; I’m a layman). As you can see, the lapse rate would be hard to measure experimentally.
f = 3 ; # degrees of freedom
E = 2.2e9; # guesstimate of total energy in a meter-square gas column arbitrarily high
VRW_LapseRate = function(f, E){
k = 1.38e-23; # Boltzmann’s constant
N_0 = 6.023e23; # Avogadro’s number
w_m = 29; # “molecular weight”
m = w_m / N_0 /1000; # molecular mass
g = 9.8; # acceleration of gravity
P_0 = 1.01e5; # atmospheric pressure at sea level
M = P_0 / g; # atmospheric mass per unit earth-surface area
N_m = 1000 * M / w_m; # moles of atmosphere per unit earth-surface area
N = N_m * N_0; # number of molecules per unit earth-surface area
– (2/3) * f * E / (f * N + 2 * N – 2) * m * g / E / k;
}
VRW_LapseRate = function(f, E)
[1] -6.389722e-32
The last line of the function is the result of differentiating Velasco et al’s Equation 8 and converting from kinetic energy to temperature.
As I said, I haven’t double-checked, so there’s likely an error here. You may want to check it yourself.
dlb says:
January 24, 2012 at 3:42 pm
Um … er … well … I must confess, I’m picking my jaw up off the floor.
Here’s the first thing. Nobody is talking about a cubic metre of soil here but you. Why?
Because it has nothing to do with the energy distribution of an ideal gas in a cylinder connected with a piece of silver wire.
I can only shake my head in amazement, dlb. Perhaps if you read the head post again?
w.
A physicist says:
January 24, 2012 at 3:58 pm
Dang. Well, can’t say I’m really surprised. Turn in your PhD at the door, or demonstrate it will flow forever and ever amen, and win the Nobel Prize.
w.
P = T*V helps to understand what’s going on. One must constantly keep in mind that in the gravitationally bound column of gas pressure is constant while temperature and volume are the variables. As its temperature goes up and down its volume goes up and down. Surface pressure is determined by gravitational constant and mass of the gas which do not vary. Temperature is not coupled to pressure therefore pressure is not coupled to temperature. So raising the surface pressure will not cause a rise in equilibrium temperature. It will cause a rise in volume and the gas law wil be satisfied by the change in volume.
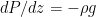
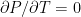
OK, Joules, you’re scaring me. P is absolutely, categorically never equal to V*T. Have you ever heard of “units”? You might look them up some time. Nor is pressure proportional to T*V in an ideal gas (or any gas I can think of). PV = NkT, so P = NkT/V. Nor is pressure constant in a gravitationally bound column of ideal gas. Don’t be absurd — pressure is never constant in any vertical fluid column in a gravitational field. The equation for static force equilibrium is:
Density is (in any situation where this might apply) a strictly positive number, so the pressure must vary with height. I actually derive its isothermal variation with height at the top of this thread. Surface pressures on the Earth vary all of the time, by a few percent. Pressure variations help cause “weather” — that’s why God invented “barometers”, because falling air pressure often warns of a storm, while high pressure usually indicates a fair, sunny day.
Temperature isn’t necessarily “coupled to pressure” — one can certainly have different contains of fluids at any pressure and any temperature — but that doesn’t mean that in various thermodynamic systems:
as a general rule. If you think that, take a soda bottle, screw the lid on good and tight, and put it into some boiling water. Hell, I have a problem just taking those large plastic refillable water bottles back to the store — if you put them into a car with the lids tight you’ll get there with them (often irreversibly) blown up like a balloon. Works the other way too — screw the lid down when it is hot and come back to them partially collapsed.
As for “raising the surface pressure” causing changes in temperature — well, if the surface in question is the cylinder of a gas piston that is being compressed, I beg to differ, especially if it is done rapidly.
Here’s a cute toy that I like to teach my students about:
http://www.practicalsurvivor.com/firepiston
http://www.phy.duke.edu/~rgb/Class/review_53/review_53/node64.html
Lost the figure that went with the problem, sorry, but the pictures in the first one should give you the idea. The point is that whether or not increasing pressure changes the temperature depends on where and how you do it. It certainly can raise the temperature — it depends on the path followed on the P-V curve. Only if you follow an isothermal path does it not change the temperature, but isothermal paths are just one of a myriad of possible paths between a myriad of possible pairs of state points.
I’m also waiting to hear you acknowledge that a static lapse rate in an ideal gas at thermal equilibrium violates the second law of thermodynamics as per the example given above. Since you actually tried to make fun of the textbook physics I’m presenting, it might be appropriate as it sounds like you might be coming to grips with the truth of it.
rgb
The wire suffers from the same loss in gravitational potential energy as it goes higher in the column.
Dear Lord this thread is entertaining. I moved some joules reading through it. Thank you to everyone.
Q. Daniels said @ January 24, 2012 at 5:08 pm
I have commenced an extremely empirical experiment what is designed as a empirical disproof of the Second Law of Thermodynamics. This very morning, I mixed 400 ml sterile H2O with 400 ml of the best Italian balsamic vinegar in a bottle and sealed it. Having sealed it with much twisting of the Stelvin seal, I shook it vigorously. Seven times seven times did I shake the Stelvin sealed bottle. When the balsamic vinegar spontaneously separates out from the H2O, verily I shall know that I have violated (desecrated even) the Second Law of Thermodynamics and fully expect to be deported to the US of A for having engaged in a successful conspiracy theory contrary to US law.
t seems to me Robert Brown’s analysis implicitly makes the following claim: if all the greenhouse gases (mainly H20 and C02) were cleansed tonight from earth’s atmosphere, then the atmosphere would evolve toward a more nearly isothermal equilibrium.
Wow, I implicitly said that? Well, imagine that. Who knew? I certainly didn’t.
But let’s try. The problem is difficult because even if there are no GHGs in the atmosphere you still get lateral convection and convective turnover because you are heating the surface more at the equator than at the poles. There would therefore be heat moved from the equator (where the hot air rises) towards the poles (where it cools and becomes less dense) — errr, depending on the shape of the planet. An oblate sphereoid, hmmm, yeah, I think there would likely still be enough surface transport to establish a large scale convective roll with the air rolling north (say) up high, deflecting to spinward as it goes, falling down in a massive spinward spiral, cooling along the ground and being displaced back to the equator. But I’m far from certain about this.
To put it another way, my intuition is that the stratosphere, which currently sits above the greenhouse gases in the troposphere where their is good vertical convection, ought to extend all the way down to the surface. The stratosphere isn’t static — far from it! It just has little vertical shear, and actually warms with height. But the details of the circulation that is established might be difficult to predict (chaotic even). As long as you have day and night and poles and equator, though, you’d have some vertical and lateral convective transport.
This is a good question for a real climate scientist. I’m not even a Sears climate scientist — I’m just a physicist who is trying to keep people from abusing the poor, innocent, second law of thermodynamics in their eagerness to come up with non-GHG surface warming mechanism. It doesn’t really help the anti-CAGW “cause” (Gawd, how I hate that word in the context of climatology post-Mann) if the proposed non-AGW mechanism is nonphysical, especially if it is obviously nonphysical and likely to justly earn the derision of “warmists”. There are plenty of physically plausible places to press them on instead, no need to just make stuff up…
rgb
Joe Born,
After reading the Velasco, et.al. note, it’s quite clear that the authors agree that there is no gravitationally induced lapse rate. For a small number of particles in the control volume, temperature is no longer strictly proportional to the average kinetic energy. But that says precisely nothing about a gravitationally induced lapse rate. In fact the authors specifically state that:
[my emphasis]
Or in short, statement (2) is always wrong, but for different reasons depending on how many molecules are in the control volume. Nowhere in the paper is there a formula for calculating the magnitude of a non-zero lapse rate in the presence of a gravitational field. This has been pointed out to you in one of the previous threads.
Alan Millar says:
January 24, 2012 at 5:22 pm
I couldn’t disagree more. The fact that all sides are welcome to show up at WUWT to advocate for their particular point of view is the strength of the site, not the weakness. Yes, there’s a host of folks out there that believe loop-de-loop stuff. There are even more who are kinda scientific but who could not, right now, give a clear distinction between force, work, and power. There are far too many issuing solemn pronouncements who didn’t even realize that there is a difference between force, work, and power.
But that’s how it is, that’s how the world is. And there are plenty of logical and scientific voices here, including most of those voices who have weight because of their demonstrated understanding of those kinds of distinctions and their willingness to post their views under their own name and history. Not only that, but we’re doing our best to explain this stuff, and discuss it, and debate it.
Finally, the presence here of many believers from the First Church of Gravity is because their Holy Scrolls are being unwound here for everyone to see. In other words, if their claims were being taken apart on Judith Curry’s site, they’d be there screaming as loudly as they are here at the moment. Doesn’t say anything about the site.
It is an issue that I have pushed hard on, however, because the Seekers After Gravity tend to be climate skeptics. I’d like to distinguish that kind of wishful thinking from true skepticism, and make it clear that the latter is very distinct from the former. True skepticism accepts the existence of such controversial and radical new theories as something known as the “Three Laws of Thermodynamics”.
So, I have pushed for and written about the issue here, precisely to see who would say “Don’t be stupid, heat can’t flow indefinitely” and who would say “But you don’t understand, if the force of the adiabatic lapse rate is twice the work, then clearly …”
It’s kind of a modern day scientific shibboleth.
w.
What has Brownian motion got to do with electrons?
And by “net heat”, do you mean the photons from colder to hotter thing?
I thought the compressed gas at the bottom in relation to the less compressed gas at the top simply contained more heat energy/volume even though all molecules in the column would have the same level of excitation.
Precisely. Energy is extensive. Temperature is intensive. Right off of the list:
http://en.wikipedia.org/wiki/Intensive_and_extensive_properties
The one caveat is that a gas does not “contain heat” in the sense that I can say that jar of air at thus and such a pressure and temperature contains so many joules of “heat”. Energy is the proper extensive property, and heat describes a quality of some of the internal energy in a system, namely its availability for doing work.
Good job, keep it up. This sort of thing is all very interesting (and you are pointing out an extremely common error many respondents are making), although I’d have to just turn this thread into an online college thermo course to correct them all. I’m trying to focus on just one thing. No violations of the zeroth or second law of thermodynamics. Oh, hell, people shouldn’t oughta violate the first, either, with their various proposals.
rgb
Joe Born says:
January 24, 2012 at 7:20 pm
But temperature is only strictly proportional to the kinetic energy in the canonical limit and Velasco, et.al. agree that in the canonical limit, the column is isothermal. So you can’t directly convert kinetic energy to temperature for a microcanonical ensemble. Or in other words, your calculation is flawed.
MDR says:
January 24, 2012 at 6:52 pm
I would like to commend and laud this action. He is actually seeking knowledge and understanding. When he finds it, and corrects some prior misunderstanding he had, he not only comes back to say he “identified a flaw” in his reasoning. He explains where he went wrong, and how he got out, so others can avoid the same mistake. I did the same thing in my post “Perpetuum Mobile”.
My thanks to you sir. Your actions represent the best of this site, where people (definitely including myself) can learn something and move the understanding forward.
Warmest regards,
w.
I am not a scientist and never claimed to be so, could someone explain why the gas, or atmosphere in this case, should be colder on top than on the bottom assuming convection works in all cases (cold air falls while hot air rises) Yes, I can figure, as air gets closer to outer space (in really simple terms) it would get mighty cold but, cold air is more dense and as such it should fall more rapidly. Exactly where does gravity enter the picture? It is exerted equally on all temperature states of air, right?
Or should I up my meds? 😉
No, your meds are just fine as they are. It is difficult to explain, impossible in the thread. You need to learn a few things and follow some algebra. The online thermodynamics textbook by Caballero describes the basis for an adiabatic lapse rate, and provides actual graphs of actual soundings of atmospheric temperatures along a vertical column at various locations to show how sometimes the atmosphere follows it, approximately, sometimes it doesn’t, some times (and some places all of the times) it inverts and goes the way you intuitively expect cold below to warm above, and how things like “atmospheric instability” (stormy weather) often depend on local inversions or convective rolls.
The point is that it is actually pretty complicated. To start with, you need to understand what an adiabatic process is, and why lifting, expanding air is expected to expand approximately adiabatically (cooling as it goes) instead of isothermally. Both are possible, mind you, but isothermal expansion requires heat/energy exchange with “something” because the gas does work but its internal energy doesn’t change.
rgb
Robert Brown says at 7:04pm:
“I have just definitively proven above that it is not a feature of static equilibrium…”
If Robert Brown means the top post where he attempts to prove the adiabatic gas column in the presence of gravity is isothermal by ignoring the 0th Law?
No, this is not proven since it is in direct conflict with what Caballero in the link in the Perpetuum Mobile thread proves in Sec. 2-3 – the real world gas column is non-isothermal w/gravity and the device in figure 2 will not run forever with a real non-perfect insulator.
Robert Brown’s disregard for the 0th law means he can use a perfect insulator to prove the column is isothermal in the presence of gravity. This is incorrect theory and cannot be used to disprove EEJ. Ignoring the 0th law means Robert Brown can create a Perpetuum Mobile machine (to sell to Willis’ along with a bridge) with the correct non-isothermal gas column.
Willis said:
Phew … gravity slowing electrons in a wire … thought I’d heard everything.
I’m not sure if I did this right, as it’s not normally the type of electrical calculations I do, but:
One coulombof charge contains 6.24150965e18 electrons, and an electron weighs 9.10938291e−31 kg, so 1 coulomb of electrons weighs 5.68563013e-12 kg. 1 coulomb of electrons 1 kilometer up has a gravitational potential energy of 5.5719175e-8 Joules, and a Volt is defined as 1 Joule/Coulomb, so that would be 0.05571917 microvolts/km, or 17.947 kilometers in height per microvolt. You can do the same calculation in electron volts, with 5.5719175e-8 eV per kilometer..
Robert, it seems that you have completely missed the fact that gravity causes a pressure and density gradient in your air column.
You mean, except for the place where I derived the actual functional form, starting from the gradient required for neutral buoyancy, for the pressure (and by trivial extension, density) of an ideal gas in static, isothermal equilibrium? Missed it except for there?
Funny, I thought that was what most people would have called completely not missed it…
This is a much more complex problem than a quick, partial recitation of a freshman physics text can handle.
No, it’s not. I’ve reduced the whole damn argument to two pictures, and only one counts. It doesn’t involve trying to do statistical mechanics in your head, badly, only pure thermodynamics.
Look at figure 2 above. You explain to me how any supposedly stable thermal lapse rate — I don’t care at all how it is established — in the gas does not violate the second law of thermodynamics when one includes a simple heat conduction pathway between the hot gas at the bottom and the cold gas at the top.
If you agree that the silver will transfer any heat at all between the two reservoirs as long as there is a temperature difference, the only possible way a thermal lapse can be stable is if the perturbation is damped out of the system and the lapse rate restored. This, in turn, requires heat transport down the gas column to restore the lapse rate. This, in turn, causes more heat to be conducted up through the silver wire. Forever, round and round in a cycle.
There is nothing to stop you from cutting the silver wire in the middle and inserting a heat engine instead of conducting pathway, and turn all of the heat energy in the gas into work, violating all of the versions of the second law in the process, or putting the engine inside the gas itself (and inside the adiabatic container) where it will run forever, a PMM2K. A suitably designed (ideal) Dippy Duck placed inside the container is my own personal favorite heat engine — a Perpetually Dippy Ducks run just fine between any two thermal reservoirs at different temperatures, and you assert gravity will create and maintain two such reservoirs spontaneously.
So forget the treatment of pressure, density, and buoyancy. I actually can — and have — treated them, but you obviously haven’t yet made it through that intro physics textbook so that you understand what I’ve done. But you cannot possible be willing to assert that heat will flow in a loop forever, which is a pure consequence of a static, stable, thermal separation in the isolated gas no matter how you think it might come about. You therefore can be certain that no such thing does come about.
rgb
rgb
Heat is Energy is mass by M=E/c^2 so said Einstein.
So what force causes Mass to rise up the silver conductor against gravity ie work has to be done?
The silver conductor is little different from the gas in a column in this respect. The top will be colder than the bottom and heat will not flow up the silver conductor unless a heat source (work) is supplied from the bottom..
Oh, sweet Jesus.
Tell you what. The next time you cook, you be sure to put the food on the bottom of your pan and heat the top. Otherwise, how is all that heat going to manage to make it uphill against gravity?
You can’t seriously be proposing that the silver wire won’t permit heat to flow upwards either.
rgb
@Willis
But I have to say, I can to the realization mostly on my own, and not because of anything anyone said here. Maybe this is the nature of the blogging medium, or maybe my learning style is not conducive to learning from blogs, but many of the responses to my line of thinking were more of the condescending variety [“Open a standard introductory physics textbook. Learn what temperature is. Then return.”] and not of the collegial variety [“If what you say is true, then how does the theory of equipartition hold in the presence of a temperature gradient with no work being done on the gas?”] and this had the effect of turning me off to contributing here again. ‘Tis mostly my loss, I suppose, but I wonder how many others feel the same way?
From Tricks conversation above
Quote
Robert Brown says at 9:07am:
“…in figure 2 above. Which is violated — the heat equation in silver or your absurd assertion that gravity can stably sort out a gas into a hotter temperature and a colder one? One or the other.”
Unquote
Is this not exactly the basis for astrophysics?. gas collects by gravity, warms up, gets denser, then warms enough to become a star!!!!!!
MDR says:
January 24, 2012 at 8:35 pm
@Willis
But I have to say, I can to the realization mostly on my own, and not because of anything anyone said here. Maybe this is the nature of the blogging medium, or maybe my learning style is not conducive to learning from blogs, but many of the responses to my line of thinking were more of the condescending variety [“Open a standard introductory physics textbook. Learn what temperature is. Then return.”] and not of the collegial variety [“If what you say is true, then how does the theory of equipartition hold in the presence of a temperature gradient with no work being done on the gas?”] and this had the effect of turning me off to contributing here again. ‘Tis mostly my loss, I suppose, but I wonder how many others feel the same way?
=========
Lots I imagine. The trick is to ignore it, it’s a form of bullying when they can’t answer your questions, for the most part.
Carry on throwing them in every now and then … I’ll enjoy it for one, who’s been on the receiving end rather a lot.
Re: Jupiter giving off more heat than it absorbs.
Just where is the proof that there is not a large radioactive core at its center, similar to what Earth has, but at 10 to 1000 times its size? Everyone making the claim that gas compression is responsible for Jupiter’s IR signature is making the same mistake Lord Kelvin made in estimating the age of the Earth.
To Robert Brown,
Quote “This is a good question for a real climate scientist. I’m not even a Sears climate scientist”.
Hey, I hope you mean Francis Weston Sears. I have only superficially followed this discussion, but I feel your pain.
When temperature decreases with altitude that’s gravity driven lapse rate…
When temperature increases with altitude (very common this time of year where I live), why that’s just weather /sarc
1) if the several km-long tube is horizontal & the perfectly dry air is at a constant temperature throughout & is moved to the vertical, the dry adiabatic gradient will be produced (warm at the bottom, cool at the top w/ approx 8C/1000m gradient in between) due to the ‘work’ of gravity creating a pressure gradient to the compressible gas. Notice, no gradient will be produced if water is used instead of gas because water is non-compressible so no work will be done. If no heat is added or removed to the gas, the column will be in a neutral buoyant state (and will stay that way!!) – if a parcel of air is moved vertically by an outside force, it’s temperature will change to reflect the change in pressure but will still be the same temperature as it’s surroundings.
2) as to the experiment with the thermal conductive wire at the base & top of the tube, the author here is incorrect. If the wire moves heat from the bottom of the tube (the base cools) to the top of the tube ( the top heats), presuming, as the author says, “…save to note that the internal conductivity of the ideal gas is completely neglected.”, the heat from the *local* area of the wire is all that will be moved from the bottom to the top ***and nothing else*** . Why, you ask?? In moving the heat from the bottom of the tube to the top is causing the lapse rate to become **more stable** – cool at the bottom with warm air above is an inversion which inhibits vertical mixing!! THAT is why the engine will not work as it is set up.
Nonsense. I provided a stable isothermal solution, one that is straight out of a textbook. Well, all the textbooks. Why, exactly, is gravity going to further compress any of the fluid, when it is all in static force equilibrium?
You’re thinking of the local heating that you’d get if you dropped a uniform density of air into a column and it settled down into something with a transient lapse rate, because the falling air would indeed heat up. But it isn’t stable! Once it “hits the bottom”, it will gradually conduct heat and adjust pressure and density until it reaches the isothermal distribution that is demonstrably in both force and thermal equilibrium.
As for 2) — you clearly miss the point entirely. I don’t know if you are clueless about fourier’s law or are just being stubborn.
Look, forget gravity. Take two insulated reservoirs filled with anything, one at temperature T_h and one at temperature T_c. Put a wire in between them that can conduct heat. Heat will be conducted from the hot to the cold reservoir. I don’t care if they are uphill, downhill or side to side from each other. Don’t care if one contains air, the other water, or both air, or one a chunk of iron and the other a bucket of feathers. Don’t care if one is at high pressure, the other at low pressure. If you are a “40 year meteorologist”, then presumably you know what the zeroth law of thermodynamics is because otherwise you don’t even know what a thermometer is or how it works or what it does.
The wire in figure 2 doesn’t move heat from “the local area of the wire” and nowhere else. The gas is a conductor of heat. If you cool even a tiny bit at the bottom near the wire, and heat the gas only a tiny bit at the top near the wire, you push the gas away from what you — in 1) claim is the stable equilibrium of the gas. The meaning of stable equilibrium is that if you perturb it away, it comes back. So you can’t make your lapse rate “more stable” by cooling the bottom and heating the top, you either destroy it the lapse rate altogether by heating the top and cooling the bottom until there is no lapse rate or else the system restores the lapse rate, moving the heat from the top back to the bottom.
The former is what happens, because in the second case the second law of thermodynamics is violated. Except that you don’t have to, because:
An Ideal Gas Is Not Really Adiabatic
If you are a meteorologist — which I seriously doubt, at least I doubt that you are a competent one who has actually studied physical climatology since I’ve studied exactly one textbook on it and seem to know more than you do — then you know perfectly well that no gas fails to conduct heat.
The container the gas is in (in our ideal world) might be adiabatic. An parcel of ideal gas moving up or down the air column might be approximately follow an adiabatic expansion curve because air is a relatively poor conductor of air so the error made assuming it is adiabatic is small if the transport time is much shorter than the time for conduction to make secular changes in temperature. But air is not, I repeat not, adiabatic. Once it comes to rest, with no vertical transport, it instantly starts to conduct heat around to bring the system into real thermal equilibrium, which is isothermal.
The silver wire is just a way of hurrying the process up, and letting you see a channel that carries energy. There is absolutely nothing that will restrict heat flow in the wire but the departure of the distribution of heat in the gas from the lapsed distribution that you claim is a stable equilibrium one.
Either you were mistaken (and the system thermalizes to an isothermal state where heat no longer flows) or else heat flows forever as the gas restores equilibrium, permitting more heat to flow in the wire to the top, which the gas moves to the bottom to restore equilibrium, to infinity and beyond.
Because the gas itself conducts heat, you don’t really need the wire. The dry air adiabatic lapse rate isn’t stable because air conducts heat.
rgb
The essence of the Jelbring hypothesis appears to be that as a parcel of air is raised or lowered in the Earth’s gravitational field its gravitational potential energy is increased or decreased with a corresponding decrease or increase in temperature, which maintains total energy constant.
But is this notion not refuted by consideration of packets of air in rigid sealed capsules, which can be raised or lowered in a gravitational field as much as one likes without causing adiabatic change in temperature, even though the air packets are experiencing changes in gravitational potential energy?
MDR said @ January 24, 2012 at 8:35 pm
That’s the nature of learning; you can only learn for yourself — nobody can ever do your learning for you. At university, you go to the lecture, afterward you do the set reading, exercises/pracs and finally go to a tutorial where you discuss what you’ve learnt and it all gradually falls into place. Most people around here want to skip the lecture, the set reading and exercises/pracs and lecture everyone in the tutorial about how they have it all wrong. Students who do this at university are called failures. That’s in the nature of being a student.
Doesn’t the silver thread require energy input to keep it at top of atmosphere?
Would not the top of atmosphere have to have tremendous amounts of energy to maintain the same temperature as it is less compressed? Would that energy be great enough to actually break the gravitational bounds of earth? If the molecules escape earth gravity, does that cool the top of atmosphere?
The thing is that the Top of atmosphere is not bound. As energy is increased in the atmosphere, the top of atmosphere moves further away from the earth surface. As energy decreases, it moved closer to the earth surface.
The silver thread does not even need an atmosphere though to move energy away from the earth surface, as it can just simply radiate at beyond the top of atmosphere.
Holding the silver wire at the top of atmosphere ends up requiring the exact same amount of energy to be expended as the energy that the wire can transfer to the top of atmosphere would be my argument. The work required to keep it up there increases the energy at that point. Work is being done.
I do not think the author has convinced me that there would not be a lapse rate in our atmosphere. I can see that there would eventually be equal amounts of energy at each and every place in the atmosphere, but that energy does not translate directly into temperature. The column could come to equilibrium only at the point in which the earth surface is the same temperature as the lapse rate effected temperature of the air immediately above it. At that point, there would be no heat transfer from a steady state temperature surface to the atmosphere that is at the exact same steady state temperature. It would require outside forces at that point to cause turbulence.
Two points.
1. Jelbring is wrong, not because of the adiabatic lapse rate but because he defines the greenhouse effect as the adiabatic temperature difference between two levels. This definition is wrong because the greenhouse effect is purely a radiative effect, not a gravitational effect. You can simulate the radiative greenhouse effect sideways in a lab just as well as vertically.
2. Brown is wrong. The heat flux in a gas depends on the potential temperature gradient, not the temperature gradient. Potential temperature is related to temperature by a function of pressure only. An isentropic atmosphere has uniform potential temperature. An isothermal atmosphere has potential temperature increasing upwards leading to a downward heat flux. An isentropic state is the state of maximum entropy and will not separate into a state with a different potential temperature profile because that would have a lower entropy, given that total potential temperature has to be conserved when integrated over the mass in adiabatic processes. Closely related to potential temperature is dry static energy, cp*T + g*z, where cp is the heat capacity at constant pressure (1004 J/kg/K). This form shows that potential energy is part of the total energy with the other part being an enthalpy or internal energy +PV. This is approximately conserved.
Robert Brown says:
Willis Eschenbach says:
My guess is that if my questions are ignored long enough they will go away. But I will keep asking, in your opinion:
Does the atmospheric pressure, no GH gases, play a role in the dry adiabatic lapse rate?
Does the atmospheric pressure, no GH gases, effect the overall equilibrium temperature of the near surface of a planet?
A simple answer like – No, no or Yes, No will suffice.
Thank you,
robr
Right. This is why Robert Brown had to invent the perfect insulator design in fig. 2. How’s the patent pending process coming along Robert?
Oh, for Pete’s sake. Have you even read Jelbring’s paper? Of course not. Do you know what the word “adiabatic” means? Obviously not.
Just FYI, since your childish rant is complete lunacy and seems to be nothing but logical fallacy from end to end, Jelbring begins by assuming an entire adiabatic planet. No energy in, no energy out. He surrounds the planet with that “perfect insulator”. He does this to assert that the gas will have an adiabatic lapse rate in stable thermal equilibrium, with no energy in or out. I prove, quite clearly, that no lapse can be thermodynamically stable.
Wait, wait, wait. It’s obvious that I’m wasting my time. You think that the thermal insulator around the gas — present in both Jelbring’s model and mine — matters to the argument. You also think that Joules ravings about the gas collapsing to a supercooled liquid is somehow lucent and relevant.
I gotta ask it. Are you on drugs? I keep reading your “rebuttal” and it is lunacy, utterly incoherent. Do you think that you could maybe go cold turkey for a day or two, maybe drink some coffee, and see if you could actually winnow an argument out of all of the straw men, ad hominem, sarcasm, and so on? I dunno, maybe an actual statement of what the final temperature distribution of the system drawn in figure 2 will look like?
No? Sigh…
rgb
I believe Robert G Brown’s explanation is correct. On the other hand, kdk33 gives us a detailed argument, also apparently correct, that shows why temperatures must follow an adiabatic lapse rate.
The resolution is, I believe, simple; Brown is talking about a thermally isolated (equilibrium) hypothetical atmosphere, whilst kdk33 is talking about a steady state atmosphere with sources of incoming and outgoing energy.
Putting it simply, the ALR is the maximum temperature gradient per unit change of pressure. Greater T gradients are prohibited by convection: A warm air parcel, on rising, will still be less dense than the air around it at the higher altitude, and so will rise even more. Air will keep on rising until the lapse rate is no greater than the ALR. It is just like the slope of the pile of sand in an hourglass: sand falling through the hole piles up in the centre until the critical slope is achieved, and then sand grains roll downhill to maintain the maximum gradient. But once the sand flow stops, there is no longer anything to maintain the gradient: a few jiggles and bumps and the sand evens itself out. In the same way, in an isolated column of air, a few jiggles and bumps (i.e. molecular collisions) will even out the temperature. But in the real atmosphere, there are sources and sinks of energy, and so an active process keeps on ‘topping up’ the imbalance and so all planetary atmospheres are at or close to the ALR. (The fact that they all are is conclusive evidence that there is little or no scope on real planets for changes in ‘greenhouse’ gasses to have significant temperature effects – even if the process worked just the way the AGW theorists claim!)
I refuse to conform to the idea that scientific laws must be obeyed and never questioned.
http://science.kennesaw.edu/~rmatson/3380theory.html
Because that claim —foreseeably (and strictly IMHO) — is going to emerge as the primary fallback position of GHE skeptics.
But who cares? There’s direct observational evidence for the GHE. Maybe I should make that my next article, simply showing the evidence without talking about the details of the mechanism. The IR spectra speak for themselves. Even if Jelbring were right instead of deluded it wouldn’t stop there from being a GHE. You can see it — with IR eyes.
In the meantime, first Jelbring, to clearly demonstrate that DALR is a consequence, not a cause, of differential heating and cooling of surface and atmosphere. Next N&Z because their “miracle” model for planetary temperatures is complete bullshit (and we’ll see what they have to say about DALR after Jelbring isn’t there any more as a crutch).
Then maybe we can start looking at actual skeptical science. Remember, I’m a skeptic, especially of the “C” in CAGW. I just don’t like bullshit arguments and bad science on either side of the issue. Good science, plausible arguments are just fine.
rgb
I don’t believe there can be a lapse rate in a closed system at equilibrium. We observe a lapse rate because a continual flow of energy heats the planet’s surface, which heats the atmosphere above it. The heated gas at the bottom of the column is continually shedding the energy onto the gas just above it, and so on, so that the energy is passed along as if by a bucket brigade. TUrn the sun off, and everything will begin to settle down. As the atmosphere cools, it no longer has the energy that allowed it to extend so far from the planet, and it shrinks, becoming denser and denser as it is pulled down by gravity. At some point it will condense, if the planet’s gravity is sufficient, and then it will freeze, unless there are liquids that do not freeze at 3K. At this point, it is safe to say there is no lapse rate.
What is going to kill these gas giants?
If gravity is constantly maintaining hotter gases at the bottom then convection will move gases around and therefore we seem to have an everlasting living planet.
Screw gas giants in our solar system — they are wussies.
You want gravitational heating, check out:
http://en.wikipedia.org/wiki/Brown_dwarf
A subcritical brown dwarf — one just a bit too light to ignite fusion — heats from gravitational collapse that continues (IIRC from when I taught astronomy) for something like 100 billion years. Brown dwarves will still be gradually releasing heat from gravitational collapse when our own sun isn’t even a faint memory. If the Universe turns out to be closed, some might make it to the next Big Crunch.
Jupiter and the other gas giants are too light (and hence cold) to be considered brown dwarfs, but they are still slowly collapsing and hence give off more radiant heat energy than they absorb from the Sun.
rgb
The reason the silver thingy won’t generate perpetual motion is that the exposed ends will assume whatever the air temp is at that altitude. A temperature difference of 1 degree will not move any heat in a silver rod 100 meters long.
Why not? I could fill the space inside the insulated chamber with insulated rods so that A is huge. Also, it isn’t correct to say that it won’t move any heat. It will just move heat slowly. But I don’t care how fast it carries heat because any heat causes perpetual heat flow. This is a gedanken experiment intended to show that Jelbring’s equally gedanken “adiabatic world” will not have a thermal lapse rate in static thermal equilibrium, nothing more. I don’t care how long it takes to reach equilibrium. Equilibrium has no thermal lapse.
I don’t even need the silver. Air conducts heat all by itself. It’s not a great conductor, but it doesn’t have to be to establish equilibrium.
The point may seem minor, but it transforms “adiabatic lapse” from a sort of “miracle heating” that starts from an outside boundary condition and heats to the surface via lapse into a consequence of forced convection due to the differential delivery of heat to the surface, a dynamic process and not a static one, one that goes away if you stop actively maintaining the surface and some part of the atmosphere overhead at different temperatures. It goes from being the great, noble cause that will replace the GHE and prove that it is all part of the nasty CAGW-IPCC conspiracy and was never true at all to being a possibly important mechanism that helps establish the GHE.
I don’t know why people are so stubborn about this. It could be that an improved understanding of the dynamical transport mechanisms associated with the DALR and convection might help place limits on the climate sensitivity to GH forcing, and that people on this list could be thinking about things like that instead of trying to pretend that the GHE isn’t real. Especially in the face of IR spectroscopy that pretty much directly proves that it is.
rgb
It now occurs to me that it’s true: the greenhouse gases actually do keep the planet cool. Without them, there would only be radiation from the surface to get rid of the solar energy — the GHGs collect translational and vibrational energy from the atmosphere and toss it out the window, albeit in very sloppy fashion, spilling almost as much on the ground. They’re basically scavengers. Dare I say it? If we really are concerned about overheating, maybe we should increase CO2 emissions.
Wow. Considering I actually believe this, I am now a crackpot.
Which does not occur in the real world. That’s why we call it weather. Sorry, no sale. This is just as unacceptable as the nonsense about CO2, a trace gas having more effect than water vapor on the planet’s temperature.
Which is fine, I agree. As I noted at the beginning, I’m specifically addressing Jelbring’s EE paper, EEJ. Read it, and you’ll see what I object to. The nonphysical assumptions in my toy above precisely mirror his, except that I don’t bother making a “round planet” as that has nothing to do with his assertion that an isolated gas in a gravitational field will have a stable thermodynamic equilibrium with a temperature lapse.
If you agree with that, well, that’s all I was trying to sell. I’m not asserting that a DALR doesn’t occur — only that it is a dynamical feature of differential warming on the bottom and cooling on the top. If you do look at where there is a DALR in planets, it is in the convective zone where this differential heating drives atmospheric turbulence and turnover. I’m not sure I would put Jupiter and the gas giants into this particular picture, as they probably have at the very least different mechanisms for differential heating at the “bottom” of their “tropospheres” (whatever that means for planets that don’t really have much of a surface, at least where it is relevant). But none of that is the point of this thread. My purpose is to drive a stake through the heart of the Jelbring paper, once and for all so we can all leave bad, law-of-thermodynamics violating physics behind. The DALR isn’t due to Jelbring, and if you take away his assertion that it is a stable equilibrium in an isolated system there is nothing left.
rgb
In a cylinder with gas at the usual DALR, all that his conducting wire will achieve is a infintesimally thin layer or hotter gas at the top plus an infintesimally thin layer of cooler gas at the bottom.
Both of these would reverse the lapse rate ( inversion) and thus no further heat can be exchanged without adding work to the cylinder (His statement that the system would reorganise itslf into an adiabatic column is wrong)
Piffle. First, the proposed lapse rate is supposedly stable. This means that if one makes a small perturbation — or for that matter a large perturbation — from it, the system will move around to restore the lapse rate. Second, why do you have this fantasy that gas, ideal or not, doesn’t conduct heat? If you cool “an infinitesimal layer” of the gas next to the bottom piece of silver, and warm “an infinitesimal layer” of gas next to the top piece of silver, that is not stable, because that infinitesimal layer of gas is in excellent thermal contact with the next infinitesimal layer over, and that one with the next one, and so on.
Here’s a very, very easy way to see that you are speaking nonsense. The gas in the column doesn’t “know” that it is in a very large column. All it knows is that locally it is supported in static force equilibrium and otherwise is in thermal equilibrium. It is exactly like an ordinary jar of gas at the same pressure and density and temperature. Exactly as in you could not measure any property of the gas in the jar and differentiate it from an identical chunk of gas from the column that isn’t in a jar.
So fill (mentally) the two jars and seal them. Now they are ordinary chunks of air, not unlike chunks of air in any laboratory. Put the two jars next to each other and connect them with a silver wire. Are you seriously suggesting that heat won’t flow between two reservoirs at different temperatures and bring them into equilibrium?
This is, incidentally, yet another excellent way to understand detailed balance. Detailed balance doesn’t depend on the pressure or density of the air in two jars. They can be anything you like. The (adiabatic) jars themselves will always exert exactly the same force on the fluid inside of them that a surrounding fluid would exert on them in equilibrium if we match pressure, density, and temperature in the jars.
So asserting that heat won’t flow in figure 2 above, or will stop flowing before all of the gas reaches thermal equilibrium, is just like saying that heat won’t flow between two ordinary jars of gas at different temperatures in the laboratory, and well over a hundred years of experiments, the entire refrigeration and air conditioning industry, a huge body of technology and engineering, and well understood physical theories all say otherwise.
rgb
Robert Brown – stop before you go mad.
These people here are trolls who don’t want to listen or learn anything.
Leave it… walk away… you won’t ever convince them.
Once upon a time, in places like the Royal Institute, back in the glory days of the 1800’s, physicists were respected, argued with. But they presented to people who wanted to learn. From this, many great discoveries and theories were formed – some of which carry the names of those who discovered them, or who popularised them.
Now instead we have physicists and engineers attacked and torn down by “post normal science” and armchair ignorami who think they know better. What a sad, sad state of affairs. Time to let the ignorami wallow in own cesspool for a while. Imagine a world where the engineers all stopped making things and the physicists stopped helping them with theories – and they all went and played gold for 50 years. What a fun place that’d be.
I’m slightly pissed off – in case you had not gathered.
Enough… I’m off to count the UFO’s at the bottom of the garden.
Not once did I see a proof of the Second Law that did not rely upon circular logic. I’ve seen plenty of empirical proof, that people have been unable to violate it, but no direct proof.
Well, I’ve taken actual statistical mechanics course, and I have seen proofs of the second law that don’t rely on circular logic. Anyone with a child’s understanding of stat mech knows this. If you want a good derivation, look at the general approach of Jaynes, starting from information theory, or if you prefer, from Cox’s algebra of probable inference. The second law is technically a statistical law of large numbers. As Dewitt just pointed out, it can be violated, sure, as long as the violation doesn’t break the first law. It is just very, very, very — (repeat a google to the google power times or so very) unlikely. As in the probability isn’t zero, but it lives right next door, is good friends with zero, their kids go to the same schools, that sort of thing. It is difficult to convey how unlikely it really is, but Dewitt’s example of all of the air in the room bouncing just right and ending up as a drop of liquid air over in a corner leaving you gasping in a vacuum that happens to maintain itself because air molecules just don’t seem to have the right directions to bounce back into the room — that sort of unlikely.
But that hardly matters, does it? All of the laws of physics are empirical, observational laws. I’ve never seen a proof of the law of gravitation, or of energy conservation, or of Newton’s Laws. The more fundamental a physical Law is, the less we are able to prove it, the more the law relies on consistent observation instead of deduction or derivation. I should point out that this is my real interest at the moment — the philosophy of knowledge and the basis of science — and I am happy to cite you chapter and verse.
On that basis, the second law is actually rather derivable, certainly compared to e.g. energy conservation or Maxwell’s Equations. But that isn’t really the point. The point is that the U.S. Patent office will no longer accept patent applications for perpetual motion machines — without a working model. The point is that unless you are a complete idiot you wouldn’t invest a nickel in a company claiming to have one, not even if someone “showed” you that it worked. You’d believe with all of your heart and soul that there was a trick in it, and you’d be right. Yet here, because it contradicts something you want to believe, you choose to doubt it. Are you nuts?
That’s one of the truly amazing things about this list. Doubting the second law of thermodynamics is insane. How can you even seriously propose that?
If somebody claims they can violate it, no they can’t. If somebody claims to build something that they can prove violates it, no it won’t. I’d believe in an antigravity machine before I believed in a machine that does nothing but convert heat into work, or a system where heat moves spontaneously from cold to hot and maintains it there without work and against perturbations — those are all “free lunches”, and most of us old enough to tie our own shoes know that there ain’t no such thing as a free lunch.
Using this rather conservative approach, one might, possibly, conceivably make a mistake. Sure, why not? Magic could be real! People might be able to come back from the dead (one famous second law violation) or walk on water (another) or heal the blind with spit and mud (a third). But don’t bet on it!
rgb
What maintains the lapse rate temperature difference?”
Mostly gravity.
Mostly gravity plus the differential heating and cooling. Move your house to Antarctica and look up mid-July. See all that sky that is warmer than you are?
But generally, I agree with your reply. As I stated, my objection is specific to EEJ — the DALR is not a stable thermal equilibrium, which is precisely what EEJ asserts. I’m not suggesting that there is no ALR, as a general rule, only that a) it isn’t precise, constant, ubiquitous; b) that it depends on differential heating and cooling and active transport in the atmosphere, and goes away when you stop heating the ground underneath it. The layer where the DALR approximately holds is the troposphere, the layer with vertical convective mixing, and it goes away as the ground temperature drops — making it look a whole lot more like an effect, rather than a cause, of warmer ground temperatures.
Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere. Heresy, I’m sure, on this blog, but there it is.
rgb
This is all stupid. You don’t need gravity or miles tall cylinders. Fill a cylinder with gas to a bzillion PSI. Put it on an atmospherically evacuated centrifuge. Spin it up to 100G. A thousand G – doesn’t matter. Measure the temperature along the length of the cylinder.
No matter how fast you spin the centrifuge, no matter how may G’s you impress, so long as the G force is constant the gas temperature will be the same along the length of the centrifuge. It is in equilibrium. It is happy gas. Is there more energy/CF at the outer extremity of the cylinder? Yes – the gas is more dense there. No surprise. This is not new energy.
The dry adiabatic lapse rate determines how high thermals will go – usually, only a few kilometers. The actual lapse rate is normally significantly different from the DALR.
As this article argues, the lapse rate without IR emitters would be zero. It is the greenhouse gases that move the actual lapse rate (ELR) from zero to -6.5 K/km. The DALR is -9.8 K/km. To claim that anything “maintains” the DALR simply means that you have not looked at the data.
Oops, sorry, answered the previous one before I read yours. As you can see, I agree. I was speaking sloppily about one factor of a trinity consisting of differential heating (greenhouse effect), convection and other mechanisms for heat transfer, and gravity that together make a self consistent troposphere that tops out roughly where the greenhouse gases become transparent and greenhouse cooling of the upper troposphere goes away.
But I’m sure you understand this better than I do. As I’ve pointed out myself, though, the DALR does go away as soon as you eliminate solar driving, e.g. the poles in the winter night. You can easily end up with the upper troposphere as warm as or warmer than the ground, easy proof that it isn’t just “gravity”.
rgb
I’m curious, what if the gravity isn’t constant, but is fluctuating?
Then it constantly does work on the system. Probably not a lot of work, but some. Think of a perfectly insulated jar full of air. If you shake it back and forth violently, you do a bit of work on the gas in the system every time, and some of that work gets transformed into heat. The gas in the container gradually warms, just as it would if it were stirred. Shaking it is absolutely indistinguishable (to the gas) to having a wildly variable gravitational acceleration (equivalence principle).
This actually happens. Tidal pseudoforces cause small fluctuations in “gravity” all over the Earth, every day. The Earth and the oceans actually expand and contract. Some of the energy associated with lifting and dropping turns into heat. At the same time, the Earth’s rotation slows just a bit. The moon picks up the angular momentum and moves into a higher orbit. The moon’s orbit is lifting around 3cm a year, IIRC, and has been for the last 3 or 4 billion years. That sounds like a lot, but 3 x 10^9 x 3 = 10^10 cm, where there are 10^5 cm in a km, so this is only around 10^5 km. The moon was nearly half of its current distance from the Earth around the time it was formed. Interestingly, it is only in a fairly narrow window of time (geologically speaking) that the moon will be just the right distance away for the kinds of eclipses that we have, close to perfect equality of the angle subtended by the sun and the moon as seen from Earth.
HTH.
rgb
Does the atmospheric pressure, no GH gases, play a role in the dry adiabatic lapse rate?
Does the atmospheric pressure, no GH gases, effect the overall equilibrium temperature of the near surface of a planet?
I’m not the best person to answer either one, but my short answer is that without GH gases there would be no or a vastly reduced DALR, one maintained by a very different convective mechanism (such as equator-polar circulation). The atmosphere might even entirely invert. But this is only a slightly better educated guess than yours might be.
Similarly, I have little doubt that an atmosphere with no GH gases would have a very different overall equilibrium temperature, and probably a different distribution. It would certainly depend somewhat on pressure, because atmospheric density depends on pressure, and the actual heat capacity of the atmosphere where it picks up heat from the ground would therefore depend on pressure. I’m still thinking about how it might vary — I’d like to/need to run some actual models (necessarily based on assumptions) to get a feel for it. One really can’t answer every complex question off of the top of one’s head (although I certainly try, unafraid of and even embracing error as an essential step towards learning:-).
rgb
Mr. Brown:
Thank you for taking the time to post and answer questions.
While the assertion of Hans Jelbring is an interesting thought experiment, it does not pass the laws of physics.
Walter said @ January 24, 2012 at 10:55 pm
Hope he doesn’t; he’s a helluva better physics teacher than I had back in 1969.
That’s almost certainly true.
Not so sure about that one; I know people who managed to kick heroin and alcohol addiction. Tough, but obviously not impossible.
I think you might mean golf rather than gold. Ayn Rand wrote books about the “doers” going AWOL. They made a big impression on the Git in 1969.
Nothing wrong with being a grumpy old fart. Gits actually enjoy it 🙂
Watch out for the giant invisible mutant space goat. You’re probably safe though; apparently it prefers eating documentary film-makers, hairdressers, telephone sanitisers etc etc.
Robert will be way better off moving to grokness equilibrium understanding the non-isothermal gas column upon reading Caballero section 2.3. Then return.
Or, you could explain why the heat flow in figure 2 isn’t established if the temperature at the bottom is higher than the temperature at the top. It saves so much time when you just use the laws of thermodynamics instead of attempting a stat mech computation in words.
In the meantime, lift a jar of air up and see how much it cools.
rgb
I thought that in the adiabatic case (in order to mirror the atmosphere) there is nil radiative or conductive heat flow.That is the standard atmosphere model where conduction is very small compared with other energy transfers. Also the column is deemed to be devoid of GH gases
Obviously we are talking about different thought experiments
If you want to have conductive gas why dont you suppose a perfectly conducting cylinder on the inside and perfectly insulating on the outside instead. This gets ride of hundred of words about about molecules interacting etc
Then we get the isothermal case
You did not comment on the fact that in the adiabatc case it needs a negligable amount of energy to raise a parcel of air from botton to top but if your silver wire delivers heat from the bottom layer to the top layer the outside work must be done to restore DALR. Of course the gas at the bottom does not know it is at the bottom of a tall column but it knows that there is warmer gas above and so it cant move upward
This is because the gas cant move upward against an inversion without an outside driver
The heat transfer cannot continue without this input.
I would like an answer to what happens to the initial small hotter layer at the top — dont quote conduction as we have none in the adiabatic case
Your transfer of heat between two horizontal jars is nothing to do with this case and requires a gas conduction which is assumed to be zero in the adiabatic column
PS What do you think insulates your house. I could bet 500:1 it is not a vacuum — even your double glazing is gas filled
The atoms of the wire will lose velocity as they rise in the gravitational field just as those in the gas, thus there is less energy available transferred in interactions this will produce an gradient in the kinetic energy of atoms that make up the wire resulting in a temerature gradient due to gravity. That the distance covered between interactions is much smaller in the solid than it would be in the gas and that there are other interactions in a solid does not change this fact.
Good try! I was waiting for somebody to try this one. However, imagine a vertical stack of pool balls. Hit the bottom one up. What happens to the top one? Does it depend on the size of the stack?
One of the many errors you and so many others make is that gravity does no net work in the upward conduction of heat. Really.
rgb
Here is where I was going wrong. I mentioned that gas near the bottom of the column has a smaller amount of potential energy than gas the top. While this is undoubtedly true, that potential energy only comes into play if the gas is being mixed or is otherwise dynamic, that is, if such energy is being released as a result of changing the height of some of the gas parcels. But of course the equilibrium state does not have any such mass motions, and so no work is being done on the fluid. As a result, the internal energy of the gas is the same everywhere, and thus the gas has the same temperature everywhere.
So absolutely perfectly correct, I award you the A+ for the day. In isothermal equilibrium, the system is in perfect force balance, there is no net dynamical transport of mass up or down, no net change whatsoever of gravitational potential energy — but heat conduction still functions to maintain equal temperature and restore equilibrium after a perturbation.
So simple.
Now at nearly 3 am and with a busy day tomorrow (which starts at 5 am) I think I’ll quit, at least for the day, er, night, er, whatever. I really tried to answer each and every comment, but after some 20 or 30K words of text, some people are having a really hard time grasping this simple idea, others are extending the error to the solid wire, still others are doubting the second law of thermodynamics instead of a static lapse (!), and a few are just crazy.
The only kinds of potentials that contribute in statistical mechanics are the ones associated with state changes. The oscillator mode for a diatomic gas, for example, doesn’t get two degrees of freedom, only one. The exact same thing is true for gravity, and for the forgotten forces between all of those ideal gas molecules, and for the walls. In equilibrium, the average potential energy of each and every molecule in the systems is constant. That’s all that matters. They are constantly borrowing and returning energy to gravity, but their average gravitational energy is constant, and it does not count as an additional degree of molecular freedom unless it can change to take up additional heat. Does anyone recall adding “gravity” to the number of degrees of molecular freedom in C_v or C_p? I don’t think so…
rgb
Robert Brown needs to read Caballero sec. 2.3 that proves the zeroth is not violated & the 2nd is not violated for “adiabatically isolated column of ideal gas in thermal equilibrium in a gravitational field” which Caballero proves is non-isothermal & there will be a thermal lapse rate.
OK, Trick, I’ll try one last time. You like Caballero? Well, so do I. Turn to page 36. Read section 2.17. Work through it carefully — this principle is called “detailed balance”. Then be sure to do exercise 2.17. I quote:
Exercise 2.17: Extend the argument above to show that (2.75) also applies to a vertical column of air in hydrostatic equilibrium.
Don’t forget that last little quote at the bottom of 2.17 right before the bloody textbook exercise:
Thus, heat flows down the temperature gradient (from hot to cold) and ceases to flow when temperature is uniform, exactly as required by the Second Law. A more precise calculation using the full apparatus of kinetic theory gives the same qualitative result. (Emphasis my own.)
Goodness, could Caballero be saying that thermal equilibrium is isothermal, regardless of whether you move up or down in a static air column? Even in Climate Science? Do you think? Is he asking you to (gasp) actually prove it? Well heck, it ought to keep you out of trouble for a while. Give it a shot. In the meantime, meditate upon that “exactly as required by the Second Law” bit. It’s important!
rgb
Correct.
All real heat engines increase entropy. Engines do work. Figure 2 doesn’t.
It is left as a not-terribly difficult exercise to the reader to work out how, if the heat flow in figure 2 is stable, it can be transformed into a perpetual motion machine that amazingly, does not increase entropy as it blithely converts heat into work.
The violation of the second law is in the assertion that a non-isothermal state is at stable thermal equilibrium. That means that any heat engine that runs between the reservoirs can turn some of the temperature difference into work, increasing the entropy of those reservoirs, but gravity sorts it all out again and makes the energy available for re-use. EEJ is particularly pernicious in this regard, as it proposes a static DALR, one that is independent of the actual temperature of the gas. So if one uses the heat engine to do external work, the gas in the cylinder will indeed drop to zero in temperature as all of its internal energy drops to the bottom to maintain a constant temperature difference right up to where the temperature of the ideal gas at the top reaches zero.
If that doesn’t fail both the heat engine and refrigerator statements, nothing does.
Besides, we know that heat flow only happens until the system becomes isothermal. As this one would, with or without a silver wire or heat engine, because a gas with a DALR is not in equilibrium and ideal gas is still a thermal conductor of heat.
rgb
I’m getting sorely dismayed by these threads so let’s try a different tack. For those who understand plain English rather better than accepted basic physics, why do you think Rankine coined the phrase Potential Energy in the first place? Do you imagine he just used fancy words for the sake of it? Here, read about the guy and let’s have no more nonsense about engineers versus physicists for starters.
http://en.wikipedia.org/wiki/William_Rankine
Forget decent basic physics text books; they’re obviously never going to help you. Look the word up in a dictionary instead.
Potential:
(noun): Capacity for development
(adjective): Possible but as yet not actual
(synonyms): Impending, Would-be.
Why do you think he used that word when he could have used any of the dozen or so more common ones that writers of dumbed-down textbooks often substitute? It’s because he was being precise – like any good engineer or physicist.
It means “not manifest until realized by some phenomenon doing something”. And it’s always realized in some actual form – kinetic, in the case of gravity. It does not, for example, mean ‘stored’ energy. Any text book that says that should be incinerated on the spot IMHO, it leads to exactly the sort of immovable confusion displayed in these threads.
Aside from kinetic energy there can be no other joules present at equilibrium, only the potential with altitude to have more when gravity does its stuff by causing something to move and acquire actual energy (thereby becoming capable of ‘doing work’).
As for conservation of energy, look at it this way: PE is a measure of the energy that will appear in future when gravity does its stuff and actually moves something. It isn’t actual energy present at rest. If that sounds like magic to you, it’s why we can’t explain gravity. PE is just bean counters’ double-entry book-keeping, necessary only because we can’t.
You cannot therefore count joules of PE and trade them off against KE at equilibrium. It makes no logical sense. No auditor will sign off accounts done on that basis, not even in Brussels!
If you’re going to maintain this concept is wrong you’re flying in the face of not only Rankine but Maxwell, Carnot, Clausius, Thompson, Hugoniot and all the rest even with the benefit of all subsequent experience they did not have (space, etc.).
You’re saying that potential energy is somehow actual energy in gaseous matter and you’ve therefore effectively explained gravity. In that case, how does gravity act on solids and liquids in a vacuum? Why do they still behave the same way? What then does compressibility have to do with PE being actual energy?
Next up you’ll be somehow extending your new found principle to plasmas to explain the coronal heating problem on the Sun or claiming gravity must be ever so gradually being used up so you’ve re-written the expansion of the universe turning the whole of contemporary physics on its head.
Sorry, but no (not for now anyway, show me some extraordinary proof first like producing a perpetual motion machine that works and explaining how your gravity works with solids and liquids). Lunacy seems an apt description.
Robert Brown wrote:
I should point out that this is my real interest at the moment — the philosophy of knowledge and the basis of science — and I am happy to cite you chapter and verse.
It’s a subject I have an interest in as well. Perhaps we can discuss it over a beer some time, should you find yourself so inclined.
“Robert Brown says:
January 24, 2012 at 8:31 pm
Oh, sweet Jesus.
Tell you what. The next time you cook, you be sure to put the food on the bottom of your pan and heat the top.”
You have misunderstood the point I was making. I had already clarified at
son of mulder says:
January 24, 2012 at 2:41 pm.
Your answer does not address the physical paradox implicit in my first post and explicit in my second.
Anyone disputing Jelbrings hypothesis needs to prove that gravity does not provide a minimum heat/energy level in matter when that matter is being held back from falling further through the gravity field by the electro-magnetic and strong forces of the atoms in the rocks at the surface of the planet. The matter is still being pulled through the gravity field, it is just being stopped by the other forces in the atoms of the rocks/liquid.
OMG. Seriously, dude. First of all, none of this has anything to do with Jelbring’s hypothesis, which basically consists of the following:
1) There exists this thing called the DALR, that I read about somewhere.
2) It exists in isolated gases ideal gases in stable thermal equilibrium in a gravitational field.
3) Therefore, it is responsible for why the surface is warmer than the top of the atmosphere.
1) is true without question, although it isn’t simple or uniform.
2) is false — that’s the point of my proof. The rest of your list of absurd assertions is utterly ignorable. We actually understand gravitational heating in brown dwarfs and stars and so on. We understand why falling asteroids release a lot of heat. We understand why you can stand on the surface of the planet at rest until hell freezes over and gravity ain’t gonna give you no heat! Take a physics class or two or get out of the game.
3) Given that 2) is false, 3) is not a valid conclusion. In fact, it is sort of half-true. The Greenhouse Effect is responsible for the DALR, which is a convective manifestation of differential surface warming and upper troposphere cooling. Although probably more complicated than “just” that.
But I don’t care about 1) or 3) — I’m just concerned with 2) and Jelbring says nothing about bizarre electro-magnetico-gluonic-gravitonic energy transfers that are responsible for breaking the second law of thermodynamics, any more than he talks about the invisible Maxwell Demon Fairies that sort out the hotter molecules in the gas and send them all down to the bottom.
It doesn’t matter how a lapse rate happens. No lapse rate that isn’t maintained by external input of energy or work is thermodynamically stable — if it were it would violate the second law.
rgb
Re,
Ed Caryl says:
January 24, 2012 at 7:36 am. I agree with you Ed, also living at some altitude. I do not believe that the surface at altitude receives less radiation than at sea level, in fact it should receive more because it passes through less atmosphere.
Which is why the following quote from Wikipedia seems to make no sense, if the conductive source is at say 3000 metres and is heated from the same source, the Sun, then the lapse rate should start from there at the same temperature as that at sea level.
“In the lower regions of the atmosphere (up to altitudes of approximately 40,000 feet [12,000 m]), temperature decreases with altitude at a fairly uniform rate. Because the atmosphere is warmed by conduction from Earth’s surface, this lapse or reduction in temperature (is?) normal with increasing distance from the conductive source.” from Wikipedia, ”Lapse Rate”
No, this is not proven since it is in direct conflict with what Caballero in the link in the Perpetuum Mobile thread proves in Sec. 2-3 – the real world gas column is non-isothermal w/gravity and the device in figure 2 will not run forever with a real non-perfect insulator.
Sure, Trick. Just like a 100% efficient heat engine with friction isn’t a violation of the second law, because look, it isn’t really 100% efficient.
As I said, put the damn wire into the container and give it up. Where’s the heat going to go now? It still flows from the bottom to the top, and then flows back down. If it flows (slowly) out the sides of the wire, who cares? Gravity still sends all of the faster molecules down and all of the slower molecules up, to maintain the lapse, right? So heat will flow up the wire forever. Or a dippy-duck will dip forever. Personally, I like the dippy duck. I should have made that my example.
rgb
Not so fast DP… sounds tempting, but surely the G force will NOT be constant throughout the cylinder. It will increase with the radius. Now there… any of the smart people here want to start some new convoluted thought experiments and circular reasoning based on that? C’mon.. we have only had 2 weeks (well it feels like 10) of that here.. /sarc
Just cannot believe that the simple issue of energy balance vs temperature balance can cause so much angst, so many futile thought experiments and so much isoteric maths and mis-applied physics to see the light. Not to mention the emergence to prominance of so many clearly educated beyond their intelligence. Luckily I consider myself educated well below my intelligence, so I can safely say that Jelbring and what has followed on that makes elegant and intuitive sense to me, unlike the other c**p that I have been diligently following to exhaustion here. Even for my 40 year old physics it hits the sweet spot, perhaps because I only remember the principles, not the maths. So much easier to see the wood in spite of the trees. And gosh, are these recent threads crowded with trees!
Rant over… Sorry, but I felt driven to it.
Off in anticipation to see the the second paper at Tallblokes’ if its there….
Gabriel van den Bergh (So you know who I am… I’ll be waiting…)
I’m not sure if I did this right, as it’s not normally the type of electrical calculations I do, but:
The mistake is in doing the computation at all. No (net) electrons move “up the wire”.
rgb
Is this not exactly the basis for astrophysics?. gas collects by gravity, warms up, gets denser, then warms enough to become a star!!!!!!
Sure, but that is not a stable state. The gas heats while it collapses. When it stops collapsing, it stops heating. The Earth and its atmosphere are not collapsing, so the process exists, and is irrelevant to the discussion.
rgb
I am just coming back from the shed having constructed my first Perpetium Mobilae. This is how it works: I have attached a copper wire to the bottom of my adiabatic container and a silver wire to the top. They nearly meat in the middle. The thermal conductivity in these metals is such that the wires are practically of uniform temperature so that the copper end is a warmer then the silver end. I have therefore a thermocouple in the middle producing energy out of nothing since gravity, without doing any work will restore the resulting termperature changes inside the adiabatic container.
Now I’m off to the shed to see how much energy I can produce. I’ll let you know: you’ll read about it in the newspapers.
Hint: sell your oil stocks, that’s so passee!
But I have to say, I can to the realization mostly on my own, and not because of anything anyone said here. Maybe this is the nature of the blogging medium, or maybe my learning style is not conducive to learning from blogs, but many of the responses to my line of thinking were more of the condescending variety [“Open a standard introductory physics textbook. Learn what temperature is. Then return.”] and not of the collegial variety [“If what you say is true, then how does the theory of equipartition hold in the presence of a temperature gradient with no work being done on the gas?”] and this had the effect of turning me off to contributing here again. ‘Tis mostly my loss, I suppose, but I wonder how many others feel the same way?
That was probably me, and my bad. I wasn’t trying to be condescending; I’m just answering several hundred comments, in detail, and I’m feeling a bit rushed. Also I admit my patience gets a bit tried by some of the “rebuttals”. As Willis noted, there are people conflating force with energy with power, LOTS of people who want to include gravity (somehow) in the list of degrees of freedom for a molecule in a gas in spite of the fact that direct measurements of the specific heat show — no gravity contribution (for perfectly understandable reasons). As I also noted elsewhere, you get an A+ for the day because you did go out and educate yourself. Doing a bit of work to learn something new is laudable. More readers and participants should take a lesson.
rgb
Just where is the proof that there is not a large radioactive core at its center, similar to what Earth has, but at 10 to 1000 times its size? Everyone making the claim that gas compression is responsible for Jupiter’s IR signature is making the same mistake Lord Kelvin made in estimating the age of the Earth.
Dunno. I was citing prevailing wisdom, not holy writ. Jupiter is too small for fusion AFAIK, but maybe fission.
rgb
Hey, I hope you mean Francis Weston Sears. I have only superficially followed this discussion, but I feel your pain.
It’s Frank Zappa: “Is that a real poncho or a Sears poncho?”
rgb
The essence of the Jelbring hypothesis appears to be that as a parcel of air is raised or lowered in the Earth’s gravitational field its gravitational potential energy is increased or decreased with a corresponding decrease or increase in temperature, which maintains total energy constant.
But is this notion not refuted by consideration of packets of air in rigid sealed capsules, which can be raised or lowered in a gravitational field as much as one likes without causing adiabatic change in temperature, even though the air packets are experiencing changes in gravitational potential energy?
In equilibrium there are no parcels of air being raised or lowered.
Air is also not an adiabatic medium. An ideal gas is not either. Both conduct heat. I’ve clearly shown that a stable equilibrium with a lapse rate violates the second law. I’ve given numerous examples of how the actual location of parcels of air connected with a conducting pathway is completely irrelevant to Fourier’s Law in a conductor inserted between them. The adiabatic jar one simply helps you to see how gravity is irrelevant to the state space in the jar. Capture air inside a perfect dewar flask and seal it. You can carry it anywhere you like, up or down the stairs, and its temperature inside won’t change. Put it next to a flask similarly filled at some other location and temperature. Put a conductor in between the flasks. If the temperatures are not equal heat will flow. Moving the flasks doesn’t matter, what matters is the conducting pathway and difference in temperatures.
I don’t even care how much heat flows. One lousy joule conducted from the hot bottom to the cold top is enough. If it flows back to the bottom — which it must of the lapse rate is stable — then it will go round and round, violating the second law.
How hard is this to understand?
rgb
“Robert Brown says:
January 24, 2012 at 11:09 pm
What maintains the lapse rate temperature difference?”
Mostly gravity.
Mostly gravity plus the differential heating and cooling. Move your house to Antarctica and look up mid-July. See all that sky that is warmer than you are?
But generally, I agree with your reply. As I stated, my objection is specific to EEJ — the DALR is not a stable thermal equilibrium, which is precisely what EEJ asserts. I’m not suggesting that there is no ALR, as a general rule, only that a) it isn’t precise, constant, ubiquitous; b) that it depends on differential heating and cooling and active transport in the atmosphere, and goes away when you stop heating the ground underneath it.”
Hmm. I don’t think it goes away when stop heating from the ground. I would agree that if you heat from the top, warm air stays on the top. I could point to our stratosphere as example of that. But perhaps that isn’t good example, as one could also say it’s due to the low density of air- the lack of buoyancy, which is also sort of saying the lack of gravity affecting it much.
I could claim/assert that Venus not warmed by the surface. I am not sure this is the case, but many people would agree with it:) One thing seems fairly certain, the sun doesn’t do much heating of Venus surface. NASA has Adiabatic Lapse Rate, Dry:
http://pds-atmospheres.nmsu.edu/education_and_outreach/encyclopedia/adiabatic_lapse_rate.htm
Here it say earth is 9.760 K per 1000 meters. And Venus is 10.468 K per 1000 meters.
A difference maybe due to different atmospheric composition- N2 vs CO2.
And seems Jupiter is different [1.963 K per 1000 meters] due to it’s mostly Hydrogen and helium atmosphere.
As general rule, I would say lapse rate is controlled by gravity [and the mass of the gases- also gravity related]. Water vapor is lighter than air- therefore it lowers the lapse rate. From 9.8 K to 6.5 C per 1000 meter [or 3 F per 1000′]
Or how well does a balloon fly. In dense high gravity worlds balloons have good buoyancy.
In high gravity world with hydrogen atmosphere, you have less balloon lift.
“What determines stability is the difference in density between the rising parcel and the environment. At the same pressure density differences are determined by temperature differences (ideal gas law). The rate of change of temperature with height in a dry air parcel – the adiabatic lapse rate – is fixed: 9.8 °C/km, but the rate of change with height in the surrounding atmosphere varies from place to place and time to time. The measured local vertical profile of temperature in the air is called the environmental lapse rate.”
http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
An addition factor is I believe the a pressure vessel, would alter the lapse rate- or make a more uniform density.
But back to idea of not heating from the bottom. Problem is you have to heat somewhere.
I think if you heated in the middle, you retain the lapse rate- because heating in the middle causes instability in such instability gravity would sort into a lapse rate. So in even uniform heating or middle heating one would have a lapse rate.
Of course massive amount heating at surface would disrupt a lapse rate- hotter air would rush up and more or less stay up until it cools.
Robert you say:
Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere. Heresy, I’m sure, on this blog, but there it is.
Not heresy, as nobody would argue that “greenhouse” gases don’t absorb and emit IR and radiate to space. As long as we all understand what we mean by “the greenhouse effect”, then we are all happy here.
Robert Brown says:
January 24, 2012 at 3:45 pm
“equilibrate the total energy”
“This is a major misunderstanding. Thermal equilibrium does not equate the total energy. Read the equipartition theorem. Open a standard introductory physics textbook. Learn what temperature is. Then return.”
The misunderstanding is yours. Equipartition does not hold unless the energy is quadratic. Gravitational potential energy is linear.
This doesn’t appear in introductory physics texts. Maybe try opening a more advanced text then return.
Brown is wrong. The heat flux in a gas depends on the potential temperature gradient, not the temperature gradient. Potential temperature is related to temperature by a function of pressure only. An isentropic atmosphere has uniform potential temperature. An isothermal atmosphere has potential temperature increasing upwards leading to a downward heat flux. An isentropic state is the state of maximum entropy and will not separate into a state with a different potential temperature profile because that would have a lower entropy, given that total potential temperature has to be conserved when integrated over the mass in adiabatic processes. Closely related to potential temperature is dry static energy, cp*T + g*z, where cp is the heat capacity at constant pressure (1004 J/kg/K). This form shows that potential energy is part of the total energy with the other part being an enthalpy or internal energy +PV. This is approximately conserved.
None of which I care about. I think I follow all of the entropic and potential temperature stuff, but address figure 2!
Heat flow in the wire does not give a damn about potential temperature. It runs between any real temperature gradient. If you wish to assert that removing heat from the bottom of the gas column and adding it to the top leads to a gas that is no longer in isoentropic equilibrium and that the gas will move the heat back to the bottom to restore it, then you have established a clear violation of the second law. I therefore must respectfully doubt that the gas is in actual thermal equilibrium in the isoentropic state, probably because the basic assumption of a gas being actually adiabatic is utterly false. What you are really looking at is a difference in time scales, as is fairly clearly indicated in at least Caballero where he derives this. Because conduction is much slower than convection, one can neglect it, making the gas parcels adiabatic as they move up and down. But once the system reaches isoentropic equilibrium at the DALR, heat will flow via real conduction, not adiabatic movement of parcels, and the system will, I believe, relax to isothermal equilibrium that — as I’ve clearly shown — is an entirely valid thermodynamic state that is dynamically stable.
Anything else still violates the second law of thermodynamics. If you throw that out, why bother speaking about entropy in the first place?
That’s the primary reason I conceived of this thought experiment. Even though I can’t imagine gravity functioning as a Maxwell Demon, even though Caballero in section 2.17 both states and leaves as a student exercise the proof that the thermodynamic equilibrium state of a vertical column of gas is isothermal, there has been a lot of confusion and strange assertions about a gas arriving at a state because of bulk transport that sorts out temperature differences approximately adiabatically (neglecting conduction), but that is somehow thermodynamically stable without transport and with conduction in the end. It didn’t feel right. Figure 2 indicates that it isn’t right, no matter how elegant your argument, because the resulting energy flow clearly violates the second law.
True equilibrium is still isothermal, but that doesn’t mean that there isn’t a wide range of time and temperature fluctuation scales that suffice to maintain the approximate DALR because the atmosphere is never sufficiently static for long enough for conductive relaxation to occur.
If you disagree, please describe the steady state heat flow in figure 2.
rgb
rgb
Putting it simply, the ALR is the maximum temperature gradient per unit change of pressure. Greater T gradients are prohibited by convection: A warm air parcel, on rising, will still be less dense than the air around it at the higher altitude, and so will rise even more. Air will keep on rising until the lapse rate is no greater than the ALR. It is just like the slope of the pile of sand in an hourglass: sand falling through the hole piles up in the centre until the critical slope is achieved, and then sand grains roll downhill to maintain the maximum gradient. But once the sand flow stops, there is no longer anything to maintain the gradient: a few jiggles and bumps and the sand evens itself out. In the same way, in an isolated column of air, a few jiggles and bumps (i.e. molecular collisions) will even out the temperature. But in the real atmosphere, there are sources and sinks of energy, and so an active process keeps on ‘topping up’ the imbalance and so all planetary atmospheres are at or close to the ALR. (The fact that they all are is conclusive evidence that there is little or no scope on real planets for changes in ‘greenhouse’ gasses to have significant temperature effects – even if the process worked just the way the AGW theorists claim!)
I wouldn’t argue with most of that. However, the biggest source of imbalance is the greenhouse effect itself. The evidence is in the actual measured thermal profile of the atmosphere, where the ALR stops at the tropopause, right where the greenhouse gases radiate out and end up cold, compared to the hot surface. It’s a self-sustaining process.
I think you’re probably right about the lack of sensitivity, though. CO_2 would basically have to move the tropopause higher and colder to increase surface warming, I’m guessing there are powerful negative feedbacks opposing this; simply altering convective flow in the upper troposphere or the stratosphere might do it. But here the physics gets too difficult to do in your head with a simple argument, and I don’t find anything at all “conclusive” about the planets except that they all seem to have tropospheres and the tropopause seems to be related to the height where their greenhouse gases top out, much like the Earth. That doesn’t really tell us much about the sensitivity. Or am I missing something?
rgb
I refuse to conform to the idea that scientific laws must be obeyed and never questioned.
Me too! I try to disobey the law of gravitation all the time, and then I question it closely, asking it why it stubbornly insists on pulling me down. It isn’t terribly verbal, though — indeed, it’s a bit childish, and inclined to demonstrate its existence by means of the falling excrement of an overhead bird.
Do you hear me, Gravity? I know that these are your paltry attempts to force me to comply with your patriarchal demands! But I refuse to obey!
Still, after a while, I do admit to questioning it less, and I try to make sure that my sly attempts at disobedience don’t involve windows in tall buildings, or leaps out of trees, or walking underneath heavy and precariously balanced objects. It’s one thing to be heretical and intellectually daring, another to be stupid and earn yourself a Darwin award.
As for the difference between a theory and a law — I’d summarize it a lot more succinctly. A physical law is an empirical axiom. A theory is derived from a mix of experiment and physical law. It’s much like the mathematician’s separation into axioms and theorems combining to make a theory, except that in physics a lot of the support of a theory is inferential, not strictly deductive.
Was there a particular law you were ready to refuse to conform to or obey?
rgb
Robert Brown said:
“Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere.”
But not the so called radiative greenhouse effect.
It is the conductive/convective greenhouse effect involving ALL the atoms in the atmosphere and not just GHGs.
Gravity puts more molecules near the surface and those molecules pick up more energy from the heated surface because there are more of them and they are closer to the source of heat than molecules higher up.
It is that simple and nothing to do with radiative abilities of molecules of GHG. The so called backradiation from the sky is simply the temperature of the molecules in the air that are directly in front of the sensor. They have reached that temperature because the outward flow of energy to space has been slowed by the molecules in the air and the slowdown is greatest where density is highest at the surface. There is no net downward energy flow and so no back radiation.
http://en.wikipedia.org/wiki/Lapse_rate
“the concept can be extended to any gravitationally supported ball of gas.”
“the atmosphere is warmed by conduction from Earth’s surface, this lapse or reduction in temperature is normal with increasing distance from the conductive source.”
After all your efforts in this thread you have come full circle to that which I told you previously.
Now take one more step. You suggest that the greenhouse effect and gravity work together to MAINTAIN heat differentials.
Look at it slightly differently.
Solar input to the surface together with gravity acting on the atmosphere to cause pressure CREATE the heat differentials (the greenhouse effect) within the atmosphere (primarily the troposphere) which WEATHER and CLIMATE seek to MAINTAIN.
Thus the atmosphere and all the features of it must configure themselves around the lapse rate set by pressure and solar input.
That is the only way that diverse atmospheric compositions can achieve the same outcome on different planets.
To my mind the jigsaw is complete.
It now occurs to me that it’s true: the greenhouse gases actually do keep the planet cool. Without them, there would only be radiation from the surface to get rid of the solar energy — the GHGs collect translational and vibrational energy from the atmosphere and toss it out the window, albeit in very sloppy fashion, spilling almost as much on the ground. They’re basically scavengers. Dare I say it? If we really are concerned about overheating, maybe we should increase CO2 emissions.
Wow. Considering I actually believe this, I am now a crackpot.
Not a crackpot, but you might want to look at some curves. The problem is that the IR curves show that emission in the CO_2 band occurs at very cold temperatures — I’m not looking them up, but I want to say -70C or thereabouts. Emission from the ground is occurring at maybe 30C — a 100K difference, around of 1/3 of the ground temperature. The radiation from both ground and CO_2 follow — very approximately — irregular and weakly modulated “blackbody” curves associated with the temperatures in their respective bands — the ground in the “water window” close to the ground temperature peak, but a chunk of the tail in the much cooler CO_2 band. There are pictures (of actual data at specific locations) in e.g. Caballero if you want to look at them, and I’m sure there are some online as well.
Now, BB radiation at any given wavelength is roughly proportional to T^4. If there was no atmosphere or GHGs, the ground could use all of the BB curve (weakly modulated by lines here and there) to radiate its energy away. That means that it would be radiating in the CO_2 band at an effective ground temperature of (say) 300K. If there is a GH layer at 200K, then in that chunk of the spectrum it radiates (2/3)^4 = .2 times the power it would have radiated, per square meter, at 300K. The ground and air together still have to balance incoming radiation, and since they radiate less in part of the spectrum, they have to radiate more in the rest. Ergo the ground will heat up until the two together balance what the ground alone could have managed at a lower temperature.
This argument is based strictly on the graph of the IR data. I don’t care how the heat gets up, or down, or sideways. I say nothing about upwelling or downwelling, radiation vs conduction or convection or the DALR. If you basically block 80% of the outgoing radiation in one band high in the atmosphere, the ground temperature has to go up until radiation from the rest of the spectrum can compensate. So I think the effect works differently from the way you imagine. Forget “how” the warming occurs. Why it occurs is much clearer, and can be understood strictly in terms of detailed balance in energy flow.
Note that I’m ignoring lots of stuff in this. Some radiation is absorbed at place X and laterally transported to be radiated away at place Y. This “some” is a substantial amount — Europe is kept “warm” by the Gulf Stream, heat absorbed in the tropics (net cooling the tropics) and moved north. I suspect that the net effect of this heat transfer is improved cooling efficiency because thermally driven self-organized systems generally work that way rather than the other way. Even though radiation from the troposphere is much slower, the heat is much more widely distributed; a lot of it is moved over what would have been much cooler ground — it isn’t just low level atmospheric heat transport that matters.
But then things get complicated, still figuring them out.
rgb
“The layer where the DALR approximately holds is the troposphere, the layer with vertical convective mixing, and it goes away as the ground temperature drops — making it look a whole lot more like an effect, rather than a cause, of warmer ground temperatures.”
I know of no data that indicates DALR “going away”- arctic regions with lack of humidity tend to have around 9 K per 1000- a larger change compared to regions with more humidity.
Inversion layers are common in arctic and inversion layers inhibit lapse rates- they are layers of warm air and are due number of factors.
“Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere. Heresy, I’m sure, on this blog, but there it is.”
A greenhouse effect generally is about “trapping warm gases”, and as such would inhibit a lapse rate. If you created a uniform warm atmosphere, rather than one which cooled quickly with elevation, most people would call that “the greenhouse effect”.
I think if increase the DALR from 9 K per 1000 meters, to 20 K 1000 meter, you need higher gravity and/or denser gas. Oh, I suppose more atmosphere also. If seems to me more or less atmosphere can both reduce and increase DALR- but not sure I can quantify it.
It seems to me if we had 1/2 the amount of our present atmosphere, it would lower the troposphere, and would also increase solar energy reaching the surface. Therefore air temperature might be same or higher at surface and cool in shorter distance of elevation.
And it seems if we doubled the existing atmosphere, less sunlight would reach the surface, have higher troposphere. It seems it would cooler but more uniform temperature. But I doubt such increase of atmosphere would affect the tropics in term heating the surface by very much.
It seems the tropics would have slighter higher or equal height of troposphere, and significantly more troposphere elsewhere. Hmm. Well if doubled atmosphere a certain result would be a doubling of psi- 14.7 to 29.4 psi. This doubling a pressure would not occur in higher elevation- Mt Everest would more psi, but not double. Or as wild guess half of mass of atmosphere would rise by about 1 km.
It seems halving the atmosphere has bigger effect, but neither could increase above lapse 9.8 K per 1000 meters but might lapse rate to be on average closer to 9.8 K per 1000 meters.
Yep. Score is:
skepticism +1
crank science -1
Those coffin nails seem to be bending a lot lately.
Thank you Robert Brown. So simple and easy to understand and yet so many here get it wrong.
You are absolutely correct that convection causes the lapse rate. Gravity is an indirect cause. No gravity, no convection.
Solar shortwave heating the ground which by conduction heats the air in contact with it drives the convection. Infrared absorbing gases and water droplets are carried to altitude where they radiate this energy to space and return to lower altitudes. So the “greenhouse gases” keep the system working by providing cooling. Some of the long wave from the ground is absorbed in the atmosphere and convection brings this warmer air to the surface thus making the lower level air a little warmer than otherwise. You do not need to invoke “back radiation”.
BTW the prevailing average lapse rate in the troposphere is close to the SALR (Saturated adiabatic lapse rate). That’s because in many parts of the atmosphere, particularly the tropics there’s lots of water vapor which condenses to form clouds.
One more thing – in the stratosphere the lapse rate is decidedly non DALR because solar UV is absorbed at high altitudes which heats that air and causes higher temperatures at higher altitudes. This effectively puts a lid on the convection. So yes, there is a top to the “greenhouse”, it is called the tropopause.
DP is right and this article is wrong!
You cannot break the laws of thermodynamics (there are NO exceptions- the lapse rate article totally misses the point), why does WUWT publish drivel like this to continue to support the failed greenhouse effect??
Again, see the work by the “Dragon slayers” for more info. The sky Dragon is dead, time the world woke up to the fact.
Are you a closet warmist Anthony???
Richard says
Hmmm. Temperature is the integral of the number and energy of particles seen at the measuring surface.
——-
It is not. If it was then temperature would depend on the amount if gas. It does not.
Temperature has nought to do with measuring surfaces either.
It’s really simple. Temperature is related directly to the average kinetic energy of the molecules in the gas. This is year 11 physics.
The conversation gets pretty dopey when gravitational potential energy is conflated with thermal (kinetic) energy. GPE does not register on a thermometer. Thus in any atmosphere in equilibrium the temperature decreases as height above the ground increases as thermal energy is exchanged for gravitational potential energy. That atmosphere is isoenergetic but it is not isothermal. It would violate conservation of energy if it were isothermal. An isothermal atmosphere is a fictitious entity that is used for first approximations of gas layers where the layer is not thick enough for adiabatic lapse rate to be a significant factor. No real atmosphere is isothermal. WRITE THAT DOWN, PROFESSOR!
A Two Planet Example Refutation of the Refutation of Stable Thermal Equilibrium Lapse Rates
I would like to believe what many of the commenters here seem to believe, that a static column if gases in a gravitational field would be isothermal with no difference in the temperature from the top to the bottom, that is unless this column was continuously warmed adequately from the base to support the rate, only then would it show a DALR (dry adiabatic lapse rate). However, I find that I cannot accept this as I did a couple of weeks ago after detailed consideration of the dry lapses on Venus and Earth.
I spent an hour or so search the archives on the ten Russian Venus Venera Landers for some inkling of the wattage of solar radiation that actually reaches the surface after traversing through some ninety-four masses of the earth’s atmosphere. I never was able to find a firm figure but the brightness was said to be like under a cloudy cover in the summer at any mid-latitude location. I took the mention of summer to mean thick rain clouds and the photos sem to support that conclusion. Seems to me a five-watt flashlight would be equal or brighter when limited to one square meter that that limited illumination so I will use that approximation.
My problem with Robert’s refutation is that Venus itself refutes his conclusions. The ten Russian Landers all recorded a steady lapse rate from about 62 km down to the surface by charts placing the lapse rate found there to be about a mean of 8.2°C/km. The natural DALR can be calculated to be between 7.7 and 12.7°C/km depending on the temperatures, a mean of 10.2°C/km.
Now one last piece of data; Venus reflects 90% of solar rays at the top of the atmosphere. So even though the total solar irradiance is 2614W/m2 there is only 261W/m2 of direct radiation. Due to the high velocity latitudinal winds of 100-300km/hr the dark side actually radiates more longwave radiation that the daytime side. Therefore, unlike the earth we can very well divide the 261W/m2 by four to give a close average of 65w/m2 anywhere on Venus’s surface.
Now, I don’t know about anyone else but I can’t buy that the 5W/m2 at the base of the column and the remaining 60W/m2 of energy whose absorption is evenly spread downward throughout the entire column can cause such a large lapse rate. the Earth has a smaller DALR with about fifteen times of constant energy in fluxed at the base. With Robert stipulation that the column has no energy either input or output, Venus’s atmosphere is about as close as you can get to that condition in our solar system. This is especially noticeable when now turning back to the earth where we have on the daytime side at a minimum average of 240W/m2 absorbed by our atmosphere and surface and nearly four times that when nearly underneath the sun. With all of the energy through our column it only musters a mere 6.5°C/km compared to Venus’s 8.2°C/m2.
Also, how can you believe that somehow Venus’s 8.2°C/km lapse with 65W/m2 warming somehow is operating on the same core physics principle of earth’s 6.5°C/m2 lapse with energy absorption near the base of 240-960W/m2. Makes no sense to me. My physics intuition is throwing up red flags. I watch twice a day radiosondes and overall, they usually do not budge off 6.5°C/km but the small wiggles at cloud levels or rare fronts, 6 a.m. or 6 p.m, no difference.
I conclude that the DALR is in fact real and in effect in every atmosphere and yes, the molecular mean velocities sort in a manner that keeps the KE+PE per unit mass constant at every specific level.
So how does that work, I can only tell you what my intuition says. That gigantic excess energy found at the surface of Venus, right at 17,000W/m2, is not created by the gravity in any stretch of the imagination; actually, it a way, it initially originates from the sun itself ages ago as the atmosphere formed. I’m not saying the photons many millions or even billions of years ago are the same photons found there today but that same level of energy has been residence there on the surface of Venus for a long, long time.
From that time of creation onward it only requires maintenance of that energy level; just enough gain to balance any temporary losses or vice versa and evidentially that 65W/m2 is enough. The potential energy gradient allows the higher temperatures deep inside the gravity well to be physically equivalent in a KE+PE sense and to lower temperatures higher outside the gravity well.
At any level the KE+PE is constant per unit mass when at the DALR unless some variance in the energy pushes the balance one way or the other at that level, you see this in radiosonde skewT plots. If that statis is disturbed the lapse no longer follows the natural DALR as is usually occurring on earth. On earth our atmosphere nearly always has more than enough excess energy in the atmosphere to push it from 9.8 to 6.5°C/km and most of that is due to the always-present specific humidity which merely altering the Cp which alters the instantaneous lapse rate.
I think that is impossible and the molecular velocity sorted DALRs do in fact occur as specified and give a lapse rate base that is the zero rate in all very tall columns.
THE CRUX: What I cannot seem to answer: How can nearly 1,000,000 kg per square meter of atmosphere as on Venus be physically rearranged vertically and lifted against a gravitational field merely by removing 65W/m2 of energy input that is then supposed to be isothermal. There, that is my real logical problem with your conjecture Robert. Excuse the length.
For any to refute me conjecture, just explain in math how these two actual examples do exist as they are while would also transform to a totally isothermal state if all radiation is removed:
Venus: 8.26°C/km DALR — 5W/m2 constant input at the base — 65W/m2 total
Earth: 9.8°C/km DALR — 160-640W/m2 constant input at the base — 240-960W/m2 total
Well, that how I see it. Robert, you almost had me convinced but Venus changed my mind.
Joe Born says:
January 24, 2012 at 5:52 pm
Paul Birch: “I have now read the Velasco et al article, and it agrees with what I said: in either the microcanonic (totally isolated) ensemble (with a reasonable number of particles in the gas) or the canonic ensemble (in thermal equilibrium with the surface or walls, irrespective of the number of particles), the gas is isothermal.”
Joe: “Of course, what we’re talking about is the microcanonic ensemble, to which Equations 5-8 apply.”
Actually, we’re not. We’re talking about the canonic ensemble in which, although the container is isolated from the rest of the universe, the gas is in thermal equilibrium with the walls, or, at least, the floor – the planetary surface. However, for any reasonable number of particles, it makes no difference; as Velasco et al themselves point out, in the limit the microcanonic ensemble has to give the same result as the canonic ensemble.
Joe: “If you read Velasco et al.’s Equation 8 for mean single-molecule kinetic energy … ”
As I have pointed out twice already, the isolated (microcanonic) single molecule case is not a thermal system at all. It’s a ballistic system. In this limiting case the concept of temperature has no meaning.
Again I repeat, that, for a tiny number of isolated particles, the statistics aren’t precisely the same as for the usual smooth distribution; velocity and height are not completely separable (Eq 8), and nor is temperature strictly proportional to kinetic energy (see Eq 10). However, even in this extreme case, the temperature at equilibrium will still be the same throughout the entire height, in the crucial sense that no net work could be extracted from the gas by connecting different levels, by any means whatsoever. The “lapse rate” is still zero. Velasco et al does not claim otherwise.
You are still trying to read far too much into a mathematical subtlety you don’t understand, in an extreme regime corresponding to a ridiculously hard vacuum, which has absolutely no relevance either to real planetary atmospheres or to the kinds of thought experiment being discussed in these threads.
Joe: “Presumably, you are basing your interpretation of Levasco et al. on its penultimate paragraph.. ”
No. Unlike you I understand the physics of what they’re doing. I’m not “interpreting” anything – I’m telling you what the basic physics is. I haven’t checked that their gory statistical details are absolutely correct, because they don’t actually matter; they’re of the right general form, and correct in the canonic limit.
Joe: “The real question is, Does Equation 8 define an altitude-dependent temperature or not? If so, there’s a non-zero lapse rate at equilibrium.”
No, it doesn’t.
dp says:
January 24, 2012 at 11:11 pm
“This is all stupid. You don’t need gravity or miles tall cylinders. Fill a cylinder with gas to a bzillion PSI. Put it on an atmospherically evacuated centrifuge. Spin it up to 100G. A thousand G – doesn’t matter. Measure the temperature along the length of the cylinder.”
So adiabatic lapse is what, a figment of the imagination?
LOL – an isothermal atmosphere is the imaginary thing that doesn’t exist in the real world.
rg: Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere. Heresy, I’m sure, on this blog, but there it is.
kdk33: The ALR is a necessary result of convection. It seems to me that, even if all GHG were removed, once radiation warms the planet surface, a small amount of condution to the air just above the surface will start convection, which must follow the ALR. The greenhouse effect overlays on that. It seems to me.
Dewitt Payne: “But temperature is only strictly proportional to the kinetic energy in the canonical limit and Velasco, et.al. agree that in the canonical limit, the column is isothermal. So you can’t directly convert kinetic energy to temperature for a microcanonical ensemble. Or in other words, your calculation is flawed.”
First, thank you very much for the detailed explanation of your position in the post before last, in which you relied on Velasco et al.’s penultimate paragraph.
Let me preface my response by saying that I read the same passage you did, namely, that “statement (2) is wrong,” and, believe me, I recognize that out of context it is hard to give that passage an interpretation other than yours. Initially I interpreted it much as you and a couple of other folks have. Moreover, that interpretation would have confirmed what I thought I had learned from that Science of Doom discussion the summer before last: at equilibrium the gas is isothermal. I was looking at the paper because, just before, Hans Jelbring told me that my understanding was a popular misconception, so I was looking for a paper to resolve the issue. Certainly, I was looking to choose between two alternatives, i.e., between what I’d previously thought and what Jelbring told me. I was definitely not looking for an interpretation such as I’m now giving the paper, which is different from either alternative.
So why did I come not to accept that the words on which you and others rely meant what they seemed to? The reason is that the equations seem inconsistent with that interpretation. Accordingly, while I respect others’ opinions and am certainly open to being educated her, my interpretation is not just the first thing that popped into my head, and I hope you will indulge me by considering my reasoning and, if necessary, showing me precisely where I’m wrong.
There are two issues. One is the definition of “temperature,” and the other is how that definition applies to Equation 8.
I had heretofore been operating under the assumption that temperature is a measure of mean translational kinetic energy. To find the temperature at a certain altitude, I thought, you add up all the translational kinetic energies of the molecules at the altitude, divide by the number of molecules at that altitude, and divide by the three-halves Boltzmann’s constant.
And (except for dividing by three-halves Boltzmann’s constant) that seems to be what’s going on in Equation 8. As you can see, the authors there compute a mean kinetic energy for an altitude z by integrating, through all possible velocities, the product of (1) the kinetic energy associated with that velocity and (2) the velocity distribution density function evaluated for altitude z at that velocity. That should be a quantity proportional to the kinetic energy per unit vertical distance at that altitude. This quantity the authors divide by the height-distribution function for that height, i.e., a quantity proportional to the molecule density at that altitude. So what I see in Equation 8 is the mean translational kinetic energy at that altitude–which is what I had heretofore thought temperature was a measure of.
But you say, “you can’t directly convert kinetic energy to temperature for a microcanonical ensemble,” from which you conclude that my calculating temperature from Equation 8 is flawed.
This would seem to imply that your view is either (1) that temperature is not mean translational kinetic energy or (2) that Equation 8 doesn’t give mean translational kinetic energy as a function of altitude–even though the authors immediately follow Equation 8 with “i.e., for a finite adiabatically enclosed ideal gas in a gravitational field the average molecular kinetic energy decreases with height.” Could you tell which one your view is and explain why?
I might add in this connection that I am mindful of your statement above that “you can’t directly convert kinetic energy to temperature for a microcanonical ensemble.” Perhaps you based that on the authors’ statement that, for the microcanonical ensemble, “the assumption in statement (2b) [that temperature is proportional to kinetic energy] is wrong.” But, although their expository style leaves entirely too much room for interpretation, my conclusion, based on the Román et al. paper’s discussion preceding the its Equation 41, to which the Velasco et al. paper refers, is that the authors tend to use “temperature” to refer to a property of the whole column, not of a particular height within that column.
I am well aware that I am no physicist and that autodidacts are particularly prone to not recognizing what it is they don’t know. But I am a serious person, and I’ve given this enough thought that I need to have a clear explanation of where I went wrong if I’m to change my mind. Can you give me that?
Robert, excuse again. The crux statement was my last typed line and it is very wrong. Why do I always notice such misstatements after pressing the SUBMIT on my way for more coffee☺? This should more read:
THE CRUX: What I cannot seem to answer: How can nearly 1,000,000 kg per square meter of atmosphere as on Venus have the huge thermal gradient removed by merely making there no thermal input at all at the base (remove the 5W/m2 at the surface) and that is then supposed to cause the entire column over time to be isothermal. There, that is my real logical problem with your conjecture Robert.
I’ve been up far too long! Will read the response tomorrow.
Okay, I stand corrected. The temperature must be constant throughout the whole column however counterintuitive it may seem to be.
I think the most ‘classic’ explanation for it is that at any given height, there are particles which just make it there with their energy being so low that they can’t travel any higher. These particles have absolute zero temperature at that level but as they can’t travel any higher, they are cooling down (or rather decreasing the average) just this level any anything below, leaving the column above untouched. This effect exactly counteracts the kinetic/potential argument’s effect.
Robert Brown writs:
I”’m not suggesting that there is no ALR, as a general rule, only that a) it isn’t precise, constant, ubiquitous; b) that it depends on differential heating and cooling and active transport in the atmosphere, and goes away when you stop heating the ground underneath it. ”
Yeah well your suggestion is wrong. In the absence of unequal heating it is precise, constant, and ubiquitous. In the presence of unequal heating it gets different names like environmental lapse rate and saturated adiabatic lapse rate. The most UNstable air masses are temperature inversions where the adiabatic lapse rate is reversed.
Gravitational potential energy does not show up on a thermometer. Yet it exists. Molecules that manage to acquire gravitational potential energy do so by trading off thermal energy for it. Follow the joules.
I haven’t read all comments, so forgive me if someone has already mentioned that in the real world you also need to take into account energy released by phase change – this having the effect of reducing the effective lapse rate perhaps by about a third.
Now, using http://discover.itsc.uah.edu/amsutemps/execute.csh?amsutemps here are my rough (sight) estimates of mean 2011 temperatures (deg.C) at the altitudes shown in feet ,,,,
0 (SS): 21.7
14,000 -19.7
25,000 -35.4
36,000 -46.8
46,000 -55.6
56,000 -62.4
68,000 -58.8
82,000 -51.9
102,000 -43.2
118,000 -33.1
135,000 -21.6
We see 41.4 degrees in the first 14,000 feet, then 15.7 deg in the next 11,000 feet, 11.4 degrees in the next 11,000 feet etc.
Make what you wish of it!
Robert Brown – stop before you go mad.
These people here are trolls who don’t want to listen or learn anything.
Leave it… walk away… you won’t ever convince them.
A few are, but some are not. I’m a compulsive teachaholic is the problem. I’m also very patient and very tenacious. I’m perfectly happy to be convinced that I’m wrong, as well, but that won’t happen because somebody says “You’re wrong, and your little dog, too…” but because they offer a cogent and plausible physical argument that is better than my own or discover a fundamental flaw in my reasoning. Both have been known to happen.
That’s why I kept the argument in the top post above simple — limited to addressing only Jelbring and the EEJ paper so we could do adiabatic apples to apples reasoning, limited to a picture that even people who don’t know much physics can understand — anybody who has tried to touch the handle of a heating pan and found it hot to the touch has direct experience of Fourier’s Law, so whether or not they fully understand the algebra they know this happens — and appealing to their intuition as much as to the letter of the various forms of the second law (there are at least four or five that I know of offhand). Accompanied by a proof that a manifestly stable isothermic equilibrium exists for the gas, to put the lie to anyone that wishes to assert that it doesn’t.
The latter is in nearly every introductory physics textbook, including mine — I just grabbed the latex out of my own book to stick in the article. The former required a few minutes to draw a simple picture. At least some people — primarily the ones that aren’t heavily psychologically invested in there being intrinsic “non-Greenhouse heating” of an isolated atmosphere so they could continue to disbelieve in the GHE altogether — seem to get it. Others have offered arguments against it that range from utterly absurd (a matching ALR for heat conduction in a vertical silver wire!) to restating the party line, that an isolated gas with an ALR is in a stable thermal equilibrium (generally not addressing the clear violation that implies via figure 2). A very few have tried to respond by citing work that isn’t overtly terrible done that explores at least the possibility of some sort of lapse rate, if not the adiabatic one (which is almost impossible to justify, given that air isn’t really adiabatic and the atmosphere does not uniformly exhibit the ALR, and flattens or even inverts when relative surface heating is removed).
At this point I’m fairly doubtful that anybody on the list is going to find a good argument against figure 2. Most of the people who appear to actually understand some physics (or are physicists) seem to agree with it; most of the people who oppose it (but not all) appear to not even understand what temperature is, let alone how heat flow is supposed to work. But as I said, I’m open minded and could be wrong. Convince me by addressing figure 2 that there can exist a consistent stable equilibrium with a lapse rate that doesn’t violate the second law. Not with complex stat mech argued verbally while conflating temperature and energy or pressure or whatever — just address the heat flow. I’m offering up a thermodynamic argument, and these are actually more powerful than statistical mechanics. It is rare indeed that a conclusion reached using thermodynamics fails in the statistical mechanics, which is why there has been so much effort expended to ensure that one can do “good” statistical mechanical computations and get results that agree with thermodynamics.
This isn’t easy, even today. It’s why I spent a hell of a lot of time and computational energy on doing Monte Carlo simulations over the last 20 years — it’s often easier to use “brute force” to sample the equilibrium phase space of a system than it is to solve the algebra and calculus to solve a problem “exactly”. That’s why people who have found exact solutions to specific problems, e.g. Onsager, are rather famous. Even for this problem, I’d feel way better about my own answer if I wrote a massive molecular dynamics program and ran a large scale simulation — Joe P. had the right idea for this in another thread, but his simulation was way too small and failed to sample the velocity distribution in various strata.
Anyway, “I’m not dead yet. I’m just sleepin’.” I might leave this thread for a bit and go check on Willis’ “N&Z Equation 8” thread, where I discovered that their “miracle” fit had characteristic pressures of 54 Kbar and 202 bar, respectively. N&Z were sometimes visiting, and I’d love to hear their response to this.
rgb
Correction link should be: http://discover.itsc.uah.edu/amsutemps/
thepompousgit says:
January 24, 2012 at 9:13 pm
MDR said @ January 24, 2012 at 8:35 pm
But I have to say, I can to the realization mostly on my own, and not because of anything anyone said here. Maybe this is the nature of the blogging medium, or maybe my learning style is not conducive to learning from blogs, but many of the responses to my line of thinking were more of the condescending variety [“Open a standard introductory physics textbook. Learn what temperature is. Then return.”] and not of the collegial variety [“If what you say is true, then how does the theory of equipartition hold in the presence of a temperature gradient with no work being done on the gas?”] and this had the effect of turning me off to contributing here again. ‘Tis mostly my loss, I suppose, but I wonder how many others feel the same way?
That’s the nature of learning; you can only learn for yourself — nobody can ever do your learning for you. At university, you go to the lecture, afterward you do the set reading, exercises/pracs and finally go to a tutorial where you discuss what you’ve learnt and it all gradually falls into place. Most people around here want to skip the lecture, the set reading and exercises/pracs and lecture everyone in the tutorial about how they have it all wrong. Students who do this at university are called failures. That’s in the nature of being a student.
===========
But what we have here is tutorials in which the tutors fall short, discovered when students go away to do their own research, and when said students raise this and ask for explanations they are bombarded with ad homs and told to go read physics text books, which they’ve just done to be able to point out the tutors are saying something different.., and then the tutors arrogantly announce they don’t answer stupid questions hoping they’ll go away when it’s the stupid answers they’ve given that are being questioned.
Examples:
I
His bold.
I asked for clarification:
“What has Brownian motion got to do with electrons?”
“And by “net heat”, do you mean the photons from colder to hotter thing?”
Because, I want to know what electrons have to do with Brownian motion, which is about movement of particles in fluids. Because I discovered this when I went away to research this term a couple of years ago having been given this as a reason carbon dioxide gets thorougly mixed in the atmosphere and finding that carbon dioxide was itself part of the fluid etc.
Because, I want to know if Willis is referring to the “heat flows from hotter to colder and colder to hotter to give net flow from hotter to colder” – because if so, I’ve already concluded, from going away and doing my own research, that there’s a missing link in this reworking of the 2nd law.(*)
And now we have the main tutor tell us:
“Because the gas itself conducts heat, you don’t really need the wire. The dry air adiabatic lapse rate isn’t stable because air conducts heat.” when earlier he said air was a lousy conductor of heat.
When physics text books say air is a good insulator, and good insulators are bad conductors of heat and the tutor says they’re both, one has to ask for clarification, perhaps I missed some emphasis or other.
So my question is, what do you mean here?
It’s not lack of willingness on my part to go away and do my own homework.
(*)
http://wattsupwiththat.com/2012/01/12/earths-baseline-black-body-model-a-damn-hard-problem/#comment-871156
http://wattsupwiththat.com/2012/01/12/earths-baseline-black-body-model-a-damn-hard-problem/#comment-872023
Not having science formally beyond ‘high school’ level and what I have learned generally since including reading such range as Lederman, Hawkings and Dawkins, and without easy knowledge of mathematics as bandied about here, I have to rely on the willingness of tutors to engage in English. I’ve been sadly disappointed. I was quite excited to find these discussions and thought I would at last have the pleasure of getting some science education I’d missed out on in having the opportunity to follow such discussions and in having any, I thought, my simplistic, questions answered. Seems these are so simple they’re now avoided altogether by some who claim they are science experts.
So, I don’t know what Robert is saying in any of his replies any more because one moment he is saying that “air is a lousy conductor of heat” and the next “Because the gas itself conducts heat, you don’t really need the wire. The dry air adiabatic lapse rate isn’t stable because air conducts heat.”
This is exasperating Professor Brown. Gravity CAN NOT maintain an energy gradient. That would be a violation of 2LoT. We KNOW for a fact that gravity creates a potential energy gradient in an atmosphere. Molecules at higher altitudes have more gravitational potential energy than those at lower altitudes. Therefore, to satisfy 2LoT, there must exist an equal and opposite energy gradient to make up for the gravitational energy gradient. This equal and opposite gradient is a thermal energy gradient. Temperature goes down as altitude goes up in a compressible fluid under the force of gravity. Total energy is equally distributed. No total energy gradient means no work can be accomplished. No harm, no foul, and no perpetual motion.
It’s not wonder that lay people are confused by this when even a Duke physics professor can’t get it right. Academicians are highly overrated. Legends in their own minds, actually. You’re living proof.
Joules Verne says:
“WRITE THAT DOWN, PROFESSOR!”
Is “Joules Verne” another screen name for Dave Springer?
Joules Verne says: January 25, 2012 at 4:24 am
“This is exasperating Professor Brown. Gravity CAN NOT maintain an energy gradient. That would be a violation of 2LoT.”
Some people have an infinite capacity for making up stuff about the second law, which they never bother to justify.
What about the ocean? Big potential energy gradient there. What energy gradient balances it?
Not heresy, as nobody would argue that “greenhouse” gases don’t absorb and emit IR and radiate to space. As long as we all understand what we mean by “the greenhouse effect”, then we are all happy here.
“Nobody” and “all” seem to be extravagant based on my tallying of responses on this and other threads, but I’m glad that at least you agree:-).
rgb
It is that simple and nothing to do with radiative abilities of molecules of GHG. The so called backradiation from the sky is simply the temperature of the molecules in the air that are directly in front of the sensor.
Or at least it would be if it weren’t for two simple things.
1) For some reason the colder emissions all seem to come from the CO_2 band, and the warmer emissions all seem to come from the ground in the water window band. Clever of those O_2 and N_2 molecules, d’ya think, masquerading as CO_2 by borrowing its spectral structure?
2) Last time I looked, the emissivity of O_2 and N_2 in the entire relevant part of the IR spectrum was pretty much, well, zero. Certainly compared to CO_2 in the CO_2 band.
So it’s just that simple and has everything to do with the radiative abilities of molecules of GHG (in particular CO_2 with a small chunk from the O_3 band in the middle of the water window), as directly demonstrated by the observed IR spectra.
But don’t bother trying to explain the actual data with your explanation, of course. I’m sure there is some other perfectly logical explanation for the IR spectrum, and I’m eager to hear it.
rgb
Robert Brown says:
January 24, 2012 at 11:09 pm
“What maintains the lapse rate temperature difference?”
“Mostly gravity.”
Mostly gravity plus the differential heating and cooling. Move your house to Antarctica and look up mid-July. See all that sky that is warmer than you are?
But generally, I agree with your reply. As I stated, my objection is specific to EEJ — the DALR is not a stable thermal equilibrium, which is precisely what EEJ asserts. I’m not suggesting that there is no ALR, as a general rule, only that a) it isn’t precise, constant, ubiquitous; b) that it depends on differential heating and cooling and active transport in the atmosphere, and goes away when you stop heating the ground underneath it. The layer where the DALR approximately holds is the troposphere, the layer with vertical convective mixing, and it goes away as the ground temperature drops — making it look a whole lot more like an effect, rather than a cause, of warmer ground temperatures.
Personally, I think the DALR is caused by the greenhouse effect and gravity, working together to maintain the heat differentials that drive the troposphere. Heresy, I’m sure, on this blog, but there it is.
rgb
I am pleased to see Robert make this statement. I hope his concerns about Jelbring might be reduced by reference to Hans Jelbring’s new paper, published exclusively at the talkshop.
http://tallbloke.wordpress.com/2012/01/25/hans-jelbring-an-alternative-derivation-of-the-static-dry-adiabatic-temperature-lapse-rate/
After all your efforts in this thread you have come full circle to that which I told you previously.
Now take one more step. You suggest that the greenhouse effect and gravity work together to MAINTAIN heat differentials.
Look at it slightly differently.
Solar input to the surface together with gravity acting on the atmosphere to cause pressure CREATE the heat differentials (the greenhouse effect) within the atmosphere (primarily the troposphere) which WEATHER and CLIMATE seek to MAINTAIN.
Thus the atmosphere and all the features of it must configure themselves around the lapse rate set by pressure and solar input.
That is the only way that diverse atmospheric compositions can achieve the same outcome on different planets.
To my mind the jigsaw is complete.
Well, it sounds like you are conceding that Jelbring is wrong, and that’s something — or at least the wikipedia page you cite makes it pretty clear that the ALR is due to inhomogeneous heating. That’s my only direct goal at this time in this thread; the rest is mostly just kicking ideas around.
There are only a few things wrong with your “complete” jigsaw puzzle. The first is that you clearly are suffering from serious confirmation bias and cherrypicking disease — the very things we skeptics like to accuse those “warmists” of — when you completely ignore the IR data and its absolutely clear signature of CO_2 causing a roughly 80% reduction of outgoing thermal energy in the CO_2 band specifically. Well, OK, that’s more like trying to pretend that the cherry tree doesn’t even exist, but hopefully you get the point. The second is that it is by no means clear that there would be a DALR in a GHG-free atmosphere, at least one that bore any resemblance to what is observed. There is a strong correspondance between the troposphere/convective zone and the height where the atmosphere becomes transparent to the outgoing CO_2 radiation. Quite a coincidence, you think? Especially where there is a similar correspondance on other planets with greenhouse warming.
What you’d really need to test, or at least support, your assertion is a GHG-free planetary atmosphere, or an atmosphere where GHG emissions don’t seem to define the top of the troposphere. Otherwise you have the embarrassing possibility that a GHG-free atmosphere would simple lower the tropopause to the surface, because there is no mechanism for the atmosphere to cool up there.
That’s the fundamental problem with your argument. You are arguing that it is all adiabatic lapse rate and no actual cooling of the atmosphere needs to occur to maintain it. Yet actual cooling of the atmosphere does occur, right up there at the top of the troposphere, via those miraculous O_2 emissions in the CO_2 band. A not trivial amount of heat leaves through that band. Surely this does, in fact, cool the upper troposphere so the full circulation is not, in fact, adiabatic but is rather convection driven by the absorption of heat one place and its release someplace else.
I’m happy to be convinced that GHG-free atmospheres would establish some sort of equator-poleward major convection rolls that manage to maintain both the lapse rate (at least in the tropics) while only losing heat by moving it from the tropical ground (where it warms) to the arctic ground (where it cools), with both tropics and arctic losing heat only through direct ground-based BB radiation, but I’m a bit shaky on the actual dynamics, because somewhere in there (without cooling that departs from the lapse rate to make the atmosphere unstable) I don’t quite see what is going to force the warm air back down to the ground from any sort of upper troposphere. I have an uncomfortable feeling that the stratosphere would indeed descend almost down to the ground, and most of the circulation would be almost completely lateral convection.
Things that could convince me otherwise — not really any verbal argument, alas. I can do these myself, and just did. I’d have to see some sort of computational model based on good atmospheric convection physics that pops up with the good old DALR to the same old top of troposphere even if there is no actual loss of heat up there.
Doesn’t feel right, does it? It’s not that it couldn’t, but why would it? There is no energetic or entropic advantage to be gained from an isoentropic circulation — the only place you actually increase entropy and irreversibly lose heat (the factor that drives all of those heat transport mechanisms) is where something warms and where it cools, where I mean really cools by irreversibly rejecting heat into a cold reservoir, not just adiabatically moving it around, conserved. There’s nothing that pushes an adiabatic process to occur spontaneously, is there?
So to my mind, your jigsaw puzzle is complete only because you might have, well, forced a few pieces in where maybe they don’t belong…
rgb
Some of the long wave from the ground is absorbed in the atmosphere and convection brings this warmer air to the surface thus making the lower level air a little warmer than otherwise. You do not need to invoke “back radiation”.
BTW the prevailing average lapse rate in the troposphere is close to the SALR (Saturated adiabatic lapse rate). That’s because in many parts of the atmosphere, particularly the tropics there’s lots of water vapor which condenses to form clouds.
One more thing – in the stratosphere the lapse rate is decidedly non DALR because solar UV is absorbed at high altitudes which heats that air and causes higher temperatures at higher altitudes. This effectively puts a lid on the convection. So yes, there is a top to the “greenhouse”, it is called the tropopause.
That’s almost exactly the way I understand it as well, so far. I’d argue that the particular mix of things that cause the surface to be hotter is unimportant and might include lots of factors, but the IR spectrum alone tells us that whatever those factors might be, the ground has to be warmer if the CO_2 band is cooler to maintain detailed balance. It’s a strictly empirical conclusion. One can argue about the mechanism later.
As for the tropopause and factors that determine it — UV absorption is good, but one thing that I honestly do not understand is why that happens to correspond to the place where the CO_2 band becomes optically thin. It’s like CO_2 is optically dense all the way up to within a km or so of the tropopause, and then shuts off in the stratosphere. Other planets seem to have a similar structure, top of troposphere coincident with where the GHGs become transparent. I’d love a coherent and physically plausible explanation of why CO_2 more or less “suddenly” becomes transparent and self-consistently stratifies just under the stratosphere. All I’ve heard are question begging things — the stratosphere is where vertical mixing stops (because it is over the troposphere) which is where things still mix but also cool (because it is under the stratosphere and where the GHGs become optically thin). Why doesn’t CO_2 extend up into the stratosphere? Why does water? So much to learn, so little time…
rgb
Paul Birch and Dewitt Payne:
Perhaps the best way to identify the misapprehension under which you believe I have been laboring in believing that Velasco et al. specify a non-zero lapse rate is to juxtapose the following two passages.
First here is DeWitt’s capsulization: “Nowhere in the paper is there a formula for calculating the magnitude of a non-zero lapse rate in the presence of a gravitational field. This has been pointed out to you in one of the previous threads.”
Then there is the explanatory passage that immediately follows Velasco et al.’s Equation 8, which I have been interpreting as implying a non-zero lapse rate: “i.e., for a finite adiabatically enclosed ideal gas in a gravitational field the average molecular kinetic energy decreases with height.”
Now, I recognize that this does not make Equation 8 “a formula for calculating the magnitude of a non-zero lapse rate in the presence of a gravitational field.” But I had thought that it was an expression for a quantity proportional to the integral of the lapse rate. That is, I would have thought that differentiating that expression for average molecular kinetic energy with respect to altitude would indeed yield a quantity that is proportional to lapse rate. And the result does indeed differ from zero.
Obviously, neither of you agrees. Maybe your telling me why will enable me to see my error.
DP is right and this article is wrong!
You cannot break the laws of thermodynamics (there are NO exceptions- the lapse rate article totally misses the point), why does WUWT publish drivel like this to continue to support the failed greenhouse effect??
Again, see the work by the “Dragon slayers” for more info. The sky Dragon is dead, time the world woke up to the fact.
Are you a closet warmist Anthony???
What does this even mean? I can just as easily say “This article is right and you are wrong.” But what good does it do?
If you want to actually offer a rebuttal of the postulated heat flow in figure 2, play through. The whole point of the article is that any lapse in a closed conductive system does break the second law of thermodynamics. If you agree, then we are good. I don’t really care (at this time) to debate the “failed” greenhouse effect, although I am so very fond of directing people to the satellite IR spectroscopy that as far as I’m concerned is a direct, and I do mean direct, picture of the real live CO_2 mediated GHE. Hard to argue with data so direct it is basically a photograph of the process in action.
rgb
The conversation gets pretty dopey when gravitational potential energy is conflated with thermal (kinetic) energy. GPE does not register on a thermometer. Thus in any atmosphere in equilibrium the temperature decreases as height above the ground increases as thermal energy is exchanged for gravitational potential energy. That atmosphere is isoenergetic but it is not isothermal. It would violate conservation of energy if it were isothermal. An isothermal atmosphere is a fictitious entity that is used for first approximations of gas layers where the layer is not thick enough for adiabatic lapse rate to be a significant factor. No real atmosphere is isothermal. WRITE THAT DOWN, PROFESSOR!
The conversation gets very dopey indeed when you steadfastly refuse to address the manifest violation of the second law of thermodynamics illustrated in figure 2 above. But I’m getting tired of asking. I know you can’t do it and — time to move on. If you don’t understand detailed balance and won’t try to understand detailed balance in a system where the mean vertical motion of every gas molecule is zero, there is little that I can do to help you. Gravity cannot do work on a particle unless it goes up or down, and there is zero net transport up or down.
rgb
Well, that how I see it. Robert, you almost had me convinced but Venus changed my mind.
Why not just address figure 2? Venus is hardly a closed system, and my article addresses only one thing: Is a lapse rate a stable equilibrium configuration of an isolated ideal gas. The argument that it is not is extremely short and succinct — it is not because a) an isothermal stable equilibrium state exists (proven in the article, although hardly original); b) the arrangement in figure 2 violates the second law of thermodynamics for any vertical thermal lapse. You can’t get much shorter than that.
Venus isn’t even a data point as it isn’t even vaguely isolated. No planet is. The only question before the committee is is Jelbring’s EE paper, which postulates a thermodynamically stable DALR for a completely isolated ideal gas in gravity, correct, or incorrect? The article above proves that it is incorrect. End of story. The DALR itself was hardly Jelbring’s idea, and you haven’t heard me assert that one doesn’t exist. We can argue about its cause later, as long as we agree that Jelbring is wrong now.
rgb
Robet Brown said:
“What you’d really need to test, or at least support, your assertion is a GHG-free planetary atmosphere, or an atmosphere where GHG emissions don’t seem to define the top of the troposphere. Otherwise you have the embarrassing possibility that a GHG-free atmosphere would simply lower the tropopause to the surface, because there is no mechanism for the atmosphere to cool up there.
That’s the fundamental problem with your argument. You are arguing that it is all adiabatic lapse rate and no actual cooling of the atmosphere needs to occur to maintain it.”
A rotating uneven spherical planet with only non GHGs would radiate very freely from the surface on the night side setting up large temperature differentials and strong winds.
The night side would provide plenty of cooling as the very cold surface sucks energy from the air above via conduction.
It would be a different atmospheric structure to that which we have on Earth but on average globally the solar/pressure induced lapse rate would still prevail. The strength of the winds and the associated turbulence would even out the very steep lapse rate on the day side and the near reversal of the lapse rate on the night side.
In effect that is just what the Earth’s atmosphere does but with the added complications of oceans, water vapour and seasonality.
And a non GHG atmosphere wouldn’t have a true tropopause because on Earth it is a GHG that creates it, namely ozone in the stratosphere.You could say that the tropopause would be on the surface but so what. The surface would still be warmer on average globally than Top Of Atmosphere however defined or identified.The winds would ensure it otherwise the atmosphere would boil away to space or congeal on the ground due to cold.
Robert Brown says: January 25, 2012 at 5:33 am
“I’d love a coherent and physically plausible explanation of why CO_2 more or less “suddenly” becomes transparent and self-consistently stratifies just under the stratosphere.”
But does it? Here is a paper which seems to say that there is little variation in mixing ratio up to 33 km.
It seems to me that what happens is that just below the tropopause the optical depth is low enough to allow substantial net emission from CO2 to space. That’s a big heat sink. Above that, UV absorption by ozone is a source. The temperature profile is what you would expect from such a combination.
kdk33: The ALR is a necessary result of convection. It seems to me that, even if all GHG were removed, once radiation warms the planet surface, a small amount of condution to the air just above the surface will start convection, which must follow the ALR. The greenhouse effect overlays on that. It seems to me.
Sure, maybe. The question is, where would the tropopause be. 100 meters? 1 km? Without warming below and cooling above, what exactly will make the atmosphere vertically unstable?
Differentially heating a fluid on the bottom (with the top insulated) will, I agree, establish lateral convection. The lateral convection will “pile up” to some extent in order to get enough of a moment arm to drive the flow of heat. But I don’t see any way, or reason, for the vertical convection to reach up to 10 km, or to create anything like the same vertical lapse rate. It might develop a lateral lapse rate, in fact, I rather think that it would.
All of this is very interesting, but irrelevant to my main point above, which is strictly EEJ is thermodynamically wrong and should be ignored. Adiabatic lapse rates are strictly dynamic non-equilibrium phenomena, and IMO at the moment they’d probably nearly disappear without GHGs and upper-atmosphere cooling. At least there I can understand the vertical instability required to drive vertical shear and convection. I’m happy to be schooled otherwise, but it would take a good argument, not a paragraph saying “it is there because I say it is”.
rgb
I’ve been up far too long! Will read the response tomorrow.
Yeah, like “all night” for me and it is tomorrow, and I’ve got to go to work. Too bad, but things are winding down anyway and I’m getting pretty wiped out saying the same thing over and over again when people don’t address the actual assertion and proof in the article above and instead redirect to clearly open non-equilibrium systems. Or introduce basic stat mech errors as if they are gospel, while ignoring the more reliable thermodynamics.
rgb
Robert, you’ve fought an honorable battle. My advice is to disconnect before the maelstrom of gravity creates an event horizon in Raleigh
Gravitational potential energy does not show up on a thermometer. Yet it exists. Molecules that manage to acquire gravitational potential energy do so by trading off thermal energy for it. Follow the joules.
Follow them right around the circle in figure 1 if there is any thermal lapse in equilibrium at all. I can wait all day. I’ve waited all night already.
rgb
When physics text books say air is a good insulator, and good insulators are bad conductors of heat and the tutor says they’re both, one has to ask for clarification, perhaps I missed some emphasis or other.
Good, bad, who cares? That’s just setting the timescale for relaxation, which isn’t even close to infinite. The point is that a lapse rate in an atmosphere is thermodynamically unstable. Figure 2 above just makes it easy to see how it violates the second law of thermodynamics.
Maybe you could try, I dunno, explaining how it won’t? Without bullshit assertions like “heat won’t flow up a wire vertically”?
rgb
Gravity CAN NOT maintain an energy gradient
I don’t even know what that means, since there are way more particles at the bottom than the top and so on.
Look, I actually gave you a gravitationally stable isothermal solution in the paper above. Why don’t you look at it and explain why the air isn’t in static equilibrium, since I used the condition for static equilibrium and the density of isothermal ideal gas in its derivation?
Then, maybe, you could look at figure 2 and try to wrestly with the thermodynamic instability in the other proposed solution, one with a lapse rate. Personally, I feel pretty strongly about the second law.
rgb
While I agree that Jelbring’s assertion for a specific temperature lapse rate is unjustified, I am equally unimpressed by your perpetual motion machine argument to explain why the temperature lapse rate must be zero. From a purely classical thermodynamics point of view, a system is at equilibrium iff dG = 0 (or equivalently dA = 0); dT = 0 or dP = 0 in and of themselves are not the most rigorous definitions of equilibrium.
The criterion for spontaneity is not change in heat nor change in pressure; it is change in free energy. Consider, if the change in heat were sufficient, endothermic reactions would never be spontaneous. Once a system has reached a minimum free energy and dG = 0 (or equivalently dA = 0) throughout, it has reached thermodynamic equilibrium and all macroscopic changes cease. This hypothetical atmospheric system at equilibrium will be described by some T(z) and P(z), but regardless of what the form of these functions take, you simply would not be able to “hook up” a wire and observe anything happening. Hence, failure of your system will not provide proof that the column is isothermal. It only proves that the column is at equilibrium as defined by dG = 0 (or equivalently dA = 0) throughout.
While my gut feeling is that the column would be isothermal, I am not so arrogant as to argue that it must be isothermal. Sans experimentation with accurate measurement of T(z), only a rigorous mathematical analysis of the governing thermodynamic equations will provide a convincing argument. Right now, you have what can best be described a hypothesis based on phenomenological models not subjected to a gravitational field (i.e. dz ~= 0). Therefore, using the most rigorous definition of the equilibrium position (i.e. Gibbs or Helmholtz free energy), please validate your arguments. Clearly demonstrate that the lowest possible value for G (or equivalently A) where dG = 0 (or equivalently dA = 0) occurs iff dT = 0 by clear analysis of the governing differential equation for the equilibrium position. As of right now, you are simply begging the question…
t”he IR spectrum alone tells us that whatever those factors might be, the ground has to be warmer if the CO_2 band is cooler to maintain detailed balance.”
That ignores the flexibility of the climate system on any planet with any type of atmosphere.
A particular outgoing wavelength my be reduced and admittedly the energy must go somewhere. If it doesn’t warm the surface then there are other ways to deal with it. A faster flow of energy from atmosphere to space would do just fine if it avoids the CO_2 band.
For example, increased conduction to non GHG molecules from GHG molecules would affect the lapse rate of the atmosphere right back to the surface. However there would then be more conduction, convection and on Earth more evaporation from the surface for an increased upward energy flow which would work to maintain the lapse rate set by sun and pressure.
The increase in upward flow would be in wavelengths not ‘blocked’ by CO2.
Atmospheric pressure can only hold back so much energy from leaving to space. Exceed the amount of energy that it can hold back then the surplus just goes straight out by the path of least resistance. The atmosphere has to configure itself accordingly and there can never be any increase or decrease in equilibrium temperature beyond that set by pressure and solar input.
If it were possible for there to be an increase or decrease in equilibrium temperature independently of solar input and pressure then where would it end ?
An infinite number of internal system variables could destabilise the equilibrium temperature to boil off the atmosphere or freeze it on the surface.
That would be the real Perpetuum Mobile.
But virtually every planet we see has an atmsphere of sorts because that hardly ever happens due to the operation of the Gas Laws. Nothing to do with radiative physics at all.
I haven’t read all the comments, so apologies if this point has already been made.
It occurs to me that if Jelbring’s theory were valid, it would apply to liquids as well as gases. (Before anyone replies that liquids are not compressible, (a) they *are* compressible, just not as much as gases, and (b) Jelbring’s argument seems to rely on the existence of a pressure gradient, which can certainly exist in a liquid.)
It is kinda difficult to conduct experiments on a mile-high column of air, but we have known since Torricelli that a 30-foot column of water, or a 30-inch column of mercury, has about the same weight (per unit area of its base) as the Earth’s atmosphere. It would therefore be quite feasible to fill a 30-foot upright tube with water, leave it for a while to allow any heat generated by friction, etc, to dissipate, then measure the temperature at the top and bottom. If Jelbring is correct, it seems, the water should be noticeably hotter at the bottom. Now I can’t claim to have done this experiment with any great precision, but my house happens to contain just such a tube (well, not quite 30 feet), which carries water from the mains supply up to my bathroom. I’ll just check…. Nope, no noticeable difference.
Does anyone disagree with the facts? If they agree with the facts, do they disagree that this (false) hypothesis follows from Jelbring’s theory? If so, what is the relevant difference between gases and liquids?
Robert Brown’s gas-filled cylinder in a gravity field is identical to a gas-filled cylinder that is constantly being accelerated by a force. The “bottom” of the cylinder, where the force pushes it, is costantly advancing on the gas molecules, like the piston of a bicycle pump, hence increasing the local gas temperature. The top of the cylinder, at the other end, is constantly receding, like a piston that is increasing a volume of gas, thus lowering the local gas temperature. As long as the acceleration is constant, the situation will not change and the temperature difference between top and bottom will exist. Perpetuum mobile? Only when the acceleration remains. Perhaps our time scales are too short to decide what is perpetuus…
As a side note everyone should realize … no matter which side was right it would not change anything relative to the GHE. If there were no radiating gases in a world like this the only place the system could radiate energy is the surface. So, in one case the atmospheric temperature is constant and in the other it cools as you go up. In neither case does it change the surface temperature because the energy in MUST equal the energy out.
The only way to change this is to add radiating gases (and I don’t care if you think N2 and O2 are radiating), and you are left once again with a green house effect.
Robert Brown, your posts so far have served excellently (IMHO) to debunk “gravito-thermal” theories, in large part because your posts have scrupulously adhered to the main principle of The Debunking Handbook (page 5, available free from Richard Dawkins’ website Reason and Science) “Fill the gap with an alternative explanation” … that explanation being:
Nonskeptical Elevator Summary: “Solar heating of the Earth’s surface + GHG heat radiation sustains the nonisothermal / nonequilibrium profile of the Earth’s atmosphere.”
But I think you have to be ready for future skeptical articles that suggest an alternative, more sophisticated non-GHG theory:
Alternative (skeptical) Elevator Summary: “Solar heating of the Earth’s surface + day-night surface temperature cycling sustains the nonisothermal / nonequilibrium profile of the Earth’s atmosphere.”
To my mind this second, skeptical, non-GHG theory cannot be debunked primae facie, and so I will bet anyone a donut that such theories will appear as WUWT posts in the coming weeks and months.
Joe Born says:
January 25, 2012 at 5:34 am
“I would have thought that differentiating that expression for average molecular kinetic energy with respect to altitude would indeed yield a quantity that is proportional to lapse rate. And the result does indeed differ from zero.”
You would have thought erroneously – as has already been explained to you repeatedly. You are wilfully taking the extreme and irrelevant sub-thermodynamic case of a minuscule total number of isolated particles – in which regime the macroscopic temperature is increasingly ill-defined and no longer simply proportional to the kinetic energy per particle – and torturing it to produce something that looks a bit like a macroscopic lapse rate, but is really nothing more than a mathematical artefact of absolutely no significance. There is and can be no real lapse rate at all – if there were it would violate the second law.
Just to be clear – the adiabatic lapse rate which is caused by gravity does not make the surface any warmer than it would be otherwise. All that happens, as at least one other commenter noted, is that it makes upper layers colder than than they would be otherwise. Nothing happens except that kinetic energy becomes gravitational potential energy with increasing altitude. The kinetic energy of the surface atmosphere is the same regardless. Nikolov et al are still wrong. It just needs to be made clear they aren’t wrong about gravity creating a temperature gradient. They’re just wrong about gravity raising the temperature anywhere in the column. It doesn’t. All it does is change the way total energy at any given altitude is apportioned between kinetic and potential.
DavidB says:
January 25, 2012 at 6:45 am
Nice. Now consider two equally sized buckets of water. One on the top floor and one on the lower floor. Both buckets are the same temperature. Do they each have an equal amount of energy? No. The bucket on the upper floor has more gravitational potential energy. That energy had to come from somewhere. It came from whatever force was used to lift that water to the higher elevation. If you carried it then that extra energy came from the food you ate.
There’s no such thing as a free lunch. Follow the joules. One MUST account for the source of gravitational potential energy! In reality, despite pleadings to the contrary from sources who should know better, gravity creates the dry adiabatic lapse rate. The gravitational potential energy in the higher layers came from its store of kinetic energy. The Hamiltonian of all horizontal layers is constant but the kinetic energy apart from the potential energy is not.
What an interesting perpetual motion machine. We need a solid state physicist. Someone who knows the Debye theory of heat in solids. Someone who thinks that heat is transferred by phonons, and that phonons have a characteristic momentum (mass and velocity). So if a phonon moves uphill against gravity it must loose momentum – and energy because it is, in effect, an upward moving mass. I suggest that the wire too will have an ‘adiabatic lapse rate’ (temperature gradient in a gravity field) because of the nature of heat – and heat transfer – in solids.
Solid state physicists are sensitive creatures and would probably not post here for fear of getting a rhetorical custard pie in the face (even if they made a correct point).
Joules Verne didn’t answer my questions. Does he think the water at the bottom of the pipe is warmer than at the top? If not (and his ‘buckets’ example suggests not) when why does this not follow from Jelbring’s theory? What is the relevant difference between air and water?
DavidB says:
January 25, 2012 at 8:44 am Why on earth would you think that a 30ft column of incompressible water would react the same as a Miles high atmosphere of compressible GAS???
@Robert Brown
I’m not sure what you’re going on about in figure 2. The silver wire is a proxy for thermal conduction in the gas. Thermal conduction is accomplished via collisions. In the absence of gravity there is no preferential direction for collision energy. In a gravity field there is a preference. A molecule travelling upward loses thermal energy as it ascends and gains thermal energy as it descends. A molecule getting whacked from above gets hit harder than one getting whacked from below if everything else is equal.
Let’s take the situation of me throwing a rotten tomato at a Duke physics professor on his lecturn. I might be throwing it from the balcony or I might be throwing it from the orchestra pit. In either case the energy I can add to the tomato with my arm is the same. If I have a choice I’m going to choose to throw from the balcony of course for the obvious reason that gravity is an aid in one direction and a restriction in the other. Thermal conductivity in the gas works the same way. Kinetic energy is preferentially sequestered at the bottom of the gravity well and gravitational potential energy is sequestered at the top.
What part of that do you not understand?
“They’re just wrong about gravity raising the temperature anywhere in the column. It doesn’t. All it does is change the way total energy at any given altitude is apportioned between kinetic and potential.”
I thought N & Z said that pressure raises the temperature in the denser gases at the bottom of a column when an external energy source is added, not that gravity did it directly.
Gravity just places more energy at the bottom of the column by pulling molecules downward to creater greater density and pressure at the bottom. In the process it does apportion some of the available energy as you say.
I think Jelbring might be suggesting a separate purely gravitationally induced temperature gradient but I’m not convinced that it is significant as yet.
“Does he think the water at the bottom of the pipe is warmer than at the top? ”
As regards water in a column the difference is that water is incompressible and so upward convection dominates and the warm water rises to the top.
The compressibility of a gas results in the higher temperature being at the bottom at all times.
That accounts for the different temperature profiles in oceans and air despite both being affected by pressure.
“Joules Verne” says:
“What part of that do you not understand?”
Is “Joules Verne” another screen name for Dave Springer?
IanH says:
January 25, 2012 at 8:28 am
“What an interesting perpetual motion machine. We need a solid state physicist. Someone who knows the Debye theory of heat in solids. Someone who thinks that heat is transferred by phonons, and that phonons have a characteristic momentum (mass and velocity). So if a phonon moves uphill against gravity it must loose momentum – and energy because it is, in effect, an upward moving mass. I suggest that the wire too will have an ‘adiabatic lapse rate’ (temperature gradient in a gravity field) because of the nature of heat – and heat transfer – in solids.”
It wouldn’t matter if it did. So long as the adiabatic lapse rate is not fixed to the same value for every possible material (which we know it isn’t), there will be an exploitable temperature difference somewhere in the system.
Look, if phonons confuse you, forget the solid wire. Just divide the container with a vertical insulating partition. Put a light gas (say, helium) on one side, and a heavy gas (say, argon) on the other. The lapse rate will be less in the former than the latter (in this case by the ratio of molecular weights). Make a short horizontal connection at the top and the bottom, and presto there’s your perpetual motion machine.
DavidB says:
January 25, 2012 at 8:44 am
“Joules Verne didn’t answer my questions. Does he think the water at the bottom of the pipe is warmer than at the top?”
It will be warmer at the bottom to the degree that water is compressible. In order for there to be a temperature gradient established there must also be a density gradient. In the water column we have no practically detectable density gradient and hence no practically detectable temperature gradient. If it were water vapor you betcha there’d be a temperature difference we could measure even at 30 feet. It would be about 0.1C warmer at the bottom of the pipe.
The whole point is that if you could achieve the totally impossible conditions that Dr Brown proposes for his thought experiment, you probably would have a perpetual motion machine. After all to get the conditions proposed would take magic in the first place.
It is an imaginary concept, so is Alice in Wonderland.
Stephen Goddard was expounding this ‘temperature is due to pressure’ theory some time ago on WUWT. Where is he, to defend his theory??
http://wattsupwiththat.com/2010/05/06/hyperventilating-on-venus/
Come on Stephen, what say you now?
DavidB says:
January 25, 2012 at 8:44 am
“What is the relevant difference between air and water?”
Air is compressible and water is not. Air is seen under natural circumstances to flow up hill water has not. Would you rather have a hot water bottle keeping you warm at night or the same volume of warm air trying to do the same thing? There are lots of relevant differences between air and water?
Joules Verne says:
January 25, 2012 at 4:24 am
This is exasperating Professor Brown. Gravity CAN NOT maintain an energy gradient. That would be a violation of 2LoT. We KNOW for a fact that gravity creates a potential energy gradient in an atmosphere. Molecules at higher altitudes have more gravitational potential energy than those at lower altitudes. Therefore, to satisfy 2LoT, there must exist an equal and opposite energy gradient to make up for the gravitational energy gradient.
Well, I still haven’t worked out what any of you are talking about.., but isn’t the opposite and equal energy gradient to make up for the gravitational energy gradient, pressure? That wot gives buoyancy. More noticeable in the ocean though, but applied to the fluid gas volume of air above us.
http://www.usatoday.com/tech/columnist/aprilholladay/2005-02-18-wonderquest_x.htm
“Archimedes’ principle applies to air as well as water: a force equal to the weight of the air displaced buoys up an object surrounded by air.”
“We scarcely think of air at all; it’s just so nebulous and pervasive. But our atmosphere has considerable mass because it towers at least 50 miles (80 km) above Earth’s surface into space. Air provides a buoyant push just as water does. A column of air that extends from sea level to space with a tiny postage-stamp size cross sectional area — one square inch — weighs almost 15 pounds and, consequently, exerts a pressure of 15 pounds per square inch on the bottom of the column.”
“Imagine an air parcel immersed in the ocean of air that is our atmosphere, as shown in the figure. The surrounding air presses in on the air parcel from all directions but the pressure along the sides of the parcel are equal and opposite and thus cancel.
The pressure on the top of the parcel is less than the pressure at the bottom (since pressure decreases with altitude). That pressure difference is the buoyant force — the force that pushes up on the air parcel.
The air parcel, however, has mass and therefore weight. Gravity pulls it down. If gravity’s pull is less than the buoyant upward push, the parcel rises. If gravity’s pull is greater than the buoyant push, it falls.
If the parcel contains light hot air from a flame, then gravity’s pull is less than the buoyant push. That’s why fire goes up.”
Smokey says:
January 25, 2012 at 9:10 am
“Is “Joules Verne” another screen name for Dave Springer?”
Presumably the laws of physics would remain the same either way so I’m going to plead the fifth on that question.
Wayne,
The Venus atmosphere was discussed at length in a couple of threads at Science of Doom. I did find a reference to the solar radiative flux at the surface when the sun is above the horizon on Venus and the peak is about 36 W/m². That was sufficient for Venera 9 (I think) to be able to make visible light photographs of the surface and transmit them back to Earth. I also ran the radiative transfer calculations for the atmosphere and the lapse rate at Spectralcalc and that flux is indeed sufficient to maintain the lapse rate against radiation and conduction. If the atmosphere of Venus became truly opaque to incoming solar radiation at some altitude above the surface, the atmosphere below that point would be isothermal assuming no heat input to the surface from the core of the planet.
Stephen Wilde and mkelly,
Nope. Water can be compressed, just much less than air. From Wikipedia:
But not no decrease in volume. That means a water column has a potential temperature just like air.
Paul Birch says
“Look, if phonons confuse you, forget the solid wire. Just divide the container with a vertical insulating partition. Put a light gas (say, helium) on one side, and a heavy gas (say, argon) on the other. The lapse rate will be less in the former than the latter (in this case by the ratio of molecular weights). Make a short horizontal connection at the top and the bottom, and presto there’s your perpetual motion machine.”
Does it not give you pause to think why none of these seemingly very simple methods have been tried?
Robert Brown towards the end of the previous thread said that he wished he could demonstrate his conjecture by an experiment.
He is thinking along the lines of a centrifuge.
I wonder about something…..
Everyone assumes an ideal gas as a starting point in these treatments , based I presume, on the correct assumption that nitrogen, oxygen, and even CO2 closely approximate the definition of an ideal gas, duh. Here’s the thing though. This is an argument about the gas, in an of itself, i.e. it ignores the gas’ context.
Here’s my dilemma. One of the premises made regarding an ideal gas is that there are no inter-molecular collisions in an ideal gas and this is done so as not to introduce a ‘wall bias’ where molecules near a wall experience (inter-molecular) vector forces that tend to pull them away from the wall. The problem is that a gas constrained by gravity is unavoidably subjected to a ‘gravity bias’, irrespective of how ideal it is, as a function of its container.
With gravity as your container, any gas no matter how ideal, is being subjected to a force (gravity) that biases collisions and (i would think) completely invalidates any assumption of ideal behavior, doesn’t it?
The centrifuged cylinder of gas is a great example that someone brought up.
As the centrifuge spins up a pressure gradient is set up. What does the ideal gas law demand will happen to temperature as the pressure increases at one end of the cylinder and decreases at the other?
As the centrifuge spins down the gas at one end of the cylinder expands and at the other end it contracts. What does the ideal gas law demand must happen in this case?
It’s a given that no one here is willing to cast aside the ideal gas law we should all agree that spinning up and spinning down the centrifuge will create at least a temporary temperature/pressure gradient predicted by the ideal gas law.
So the question boils down to what happens when the centrifuge is left running indefinitely. Does the column temperature equalize? I say no because for conduction to equalize the temperature there has to be equal freedom of motion in any direction and this clearly isn’t the case. Freedom of motion is restricted going against the centrifugal force and is aided going in the direction of the force. The temperature will not equalize if we discount conduction through the solid walls of the cylinder. If we stuck a silver wire down the center of our cylinder as in Brown’s figure 2 the temperature would equalize because the thermal conductivity of the silver wire has no preferential direction due to centrifugal force.
I’m trying as many ways as I can think of to explain what I know must happen and how. So now I’m trying it via illustrating that thermal conductivity coefficient changes in a compressible fluid with greater conductivity going with gravity and lesser conductivity going against gravity. This does not happen with incompressible fluids.
Does that help? It should certainly help to explain to Brown why his silver wire is not a valid proxy for thermal conduction in a compressible gas in a gravity field.
Robert Brown,
The way to think about the difference between the stratosphere and the troposphere is to use the slab gray atmosphere toy model ( see 7.3.2 here, for example. Petty goes into more depth). In the troposphere, the atmosphere is more transparent to SW radiation and less transparent to LW radiation so the surface temperature is warmer than the slab. The opposite is true in the stratosphere. The stratosphere is less transparent to SW radiation because of absorption of UV by oxygen and ozone and more transparent to LW radiation. That makes the ‘surface’, i.e. the tropopause, colder than the slab.
Paul Birch says
So long as the adiabatic lapse rate is not fixed to the same value for every possible material (which we know it isn’t), there will be an exploitable temperature difference somewhere in the system.
AMEN, BROTHER!
@mkelly >>>>Air is seen under natural circumstances to flow up hill water has not.
Reversing Falls: water flowing up hill. http://new-brunswick.net/Saint_John/reversingfalls/reversing.html
Tsunami: water flowing up hill: http://www.youtube.com/watch?v=w3AdFjklR50
The water in a 20-ft tsunami doesn’t stop when it reaches a barrier that is 20-ft. high, Momentum redirects the water upwards.
Robert Brown says: “At least some people — primarily the ones that aren’t heavily psychologically invested in there being intrinsic “non-Greenhouse heating” of an isolated atmosphere so they could continue to disbelieve in the GHE altogether — seem to get it. ”
Shrug, industry figures give 67°C for our atmosphere without greenhouse gases. The mass/weight/gravity/pressure/ play of the fluid gaseous ocean of nitrogen and oxygen above us is the greenhouse/thermal blanket around the Earth. Adding some fibres of water vapour in the Water Cycle cools that by 52°C to bring it down to the 15°C we have. Carbon dioxide fully part of the water cycle, all pure clean rain is carbonic acid, can only aid the main greenhouse gas water vapour in its role of cooling.
For goodness sake, just step out into a desert to get some grasp on this.
I’m well aware that air is more compressible than water (though not incompressible), which is why I mentioned it when I introduced the example, to anticipate an obvious objection. But is that a relevant difference in the context of Jelbring’s theory? I thought that depended on a pressure gradient, which does exist in the case of water.
But at least we have made progress if it is accepted that the Jelbring theory depends on compression. Of course, it is true that a gas can be heated by compression, as I mentioned in an earlier comment on this thread. If you take a long horizontal cylinder of air and then raise it to vertical, the gas at the (new) bottom of the cylinder will be compressed and heated, while the gas at the top will be rarified and cooled. A temperature gradient will thus arise. But that is a one-time effect which fades as heat flows from hotter to colder areas, in accordance with the Second Law. It does not explain how a permanent gradient is maintained in a planetary atmosphere.
@joules >>>>It’s a given that no one here is willing to cast aside the ideal gas law we should all agree that spinning up and spinning down the centrifuge will create at least a temporary temperature/pressure gradient predicted by the ideal gas law.
I would hazard a guess that by now, millions of hours of gases being spun in gas centrifuges have been completed over the past decades, all around the world. Uranium hexafluoride used U-235 / U-238 separation processing. There is probably data on gas temperature profiles available somewhere.
Just to reiterate, this experiment is being conducted, tens of thousands of times every day, in the gas centrifuges used for uranium isotope separation, which generate g-forces sufficiently large that the on-axis pressure is a near-vacuum, which the outer-rim pressure is many atomospheres — precisely the conditions of interest.
These gas centrifuge “experiments” concretely affirm Brown’s theoretical arguments: the observed equilibrium temperature distribution is isothermal. Indeed, the multibillion-$ isotope separation industry would fail otherwise.
For more theoretical and experimental details than most folks want to know, see @article{Kemp:2009lr, Author = {R. Scott Kemp}, Journal = {Science and Global Security}, Number = {1}, Pages = {1–19}, Title = {Gas Centrifuge Theory and Development: a Review of US Programs}, Volume = {17}, Year = {2009}} and references therein (a Google search will find it).
Elevator Summary: “Gravito-thermal” theories are just plain wrong.
Paul Birch:
Thank you for your recent posts. I apologize for not having acknowledged them in my most recent one; I somehow failed to see yours before I sent mine.
I believe I now understand your position, and, as you say, it is entirely possible that I am “trying to read far too much into a mathematical subtlety [I] don’t understand,” although I see no evidence so far from which to conclude that. However that may be, I’ll give some feedback in case any lurkers find the issue of interest.
First to your contention that we are not talking about the microcanonical ensemble. Here a little context is in order. Recall that both Robert Brown in this thread and Willis Eschenbach in the previous one were addressing themselves to refuting the Jelbring paper. That paper began with a hypothetical ideal gas G disposed between concentric spherical surfaces A and S. Jelbring said that “A and S are thermally insulated preventing heat from entering into G and infrared radiation to reach space.” It is no doubt to parallel this condition that Robert Brown says of his thought experiment that it involves an “adiabatically isolated column of an ideal gas.” In short, heat can flow neither into nor out of the gas, so by definition it is indeed a microcanonical ensemble.
Next I consider your statement that “for any reasonable number of particles, it makes no difference” whether we’re dealing with the microcanonical ensemble or not. I agree with you that as a practical matter any lapse rate as small as I’m saying Equation 8 implies would be too small to measure. But, again, the context needs to be considered. What Robert Brown and Willis Eschenbach are both saying is that any non-zero lapse rate at all would violate the First Law because there would be a perpetual heat flow through the external wire. Had they instead based their proofs on a lapse rate of the magnitude for which Jelbring contends, then I would agree with them that they had proved their case. But they insisted that they needed no such limitation. So any non-zero lapse rate is relevant, no matter what its magnitude is. So the microcanonical ensemble is indeed relevant to the issue under consideration.
You make two further points that at base are not technical arguments so much as statements of your point of view. You say, “However, even in this extreme case, the temperature at equilibrium will still be the same throughout the entire height, in the crucial sense that no net work could be extracted from the gas by connecting different levels, by any means whatsoever.” Essentially you’re saying that even if a difference in mean translational kinetic energy is non-zero, it doesn’t qualify as a lapse rate in your view if it’s exhibited by a maximum-entropy configuration and therefore results in no net heat flow. Okay, I understand your redefinition.
You additionally observe that I am “taking the extreme and irrelevant sub-thermodynamic case of a minuscule total number of isolated particles – in which regime the macroscopic temperature is increasingly ill-defined and no longer simply proportional to the kinetic energy per particle.” Let’s set aside what exactly you may mean by imprecise terms like “sub-thermodynamic,” “macroscopic,” and “increasingly ill-defined.” And let’s concede that the case I discussed was an extreme case. That case nonetheless remains relevant, because it illustrates by exaggeration something that remains true independently of how large the number of molecules gets: the mean molecular translational kinetic energy decreases with height, and it does so at a rate that is finite and non-zero, albeit negligible for most purposes.
In any event, I think these on-line interchanges have the potential to be enlightening, and, although I can’t profess to have made any great strides in this case, I do appreciate your making the effort.
@Robert
“In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated.”
It has been a great week to review the basics of physical phemonena. I have been serially convinced by many contributions in opposite directions. I agree that there is a conduction issue as you have pointed out, Robert, but a guy named Kevin and I agree that it is not going to create an isothermal condition.
If the atmosphere does not conduct heat (which seems to be Jelbring’s assumption) it is an unreasonable experiment. But you can’t have lots of conduction just because it is convenient. It has to be realistic.
If the atmosphere was warmer at the top than the bottom, it would have stable and unequal temperature distribution. The reason is that gases are really lousy conductors of heat, especially downwards, meaning downwards in a gravity field. Bouyancy can override conduction in this theoretical atmosphere in some cases.
In your example above, the gas is treated as if it was a solid at certain times, which it clearly is not. It has to be discussed as a gas at all times. You have mentioned several times that if the gas moves it has to have a driver (some work going on). But gas is always in motion – perpetual motion as far as we know – and also we know that individual molecules contain more energy than their neighbours. Many energetic molecules of gas are literally hotter than the others. There are gazillions of molecules in continuous motion with no energy input from outside the column. At any time that on average a group of molecules is slight hotter and lighter than a neighbouring group, they separate with the hotter ones rising slightly because of bouyancy. This is gravitational separation that is not caused by the density of the molecule, but by the well known convection principle applied at the molecular level. Will conduction overwhelm this? I am raising that question.
Left alone, there are two forces opposing each other: the tendency of hot gases to rise and cool gases to fall, opposed by conduction that tends to average the temperature in the system.
If on average the temperature of a gas is some fixed value, we know that is an average. If molecules of gases and even water behaved like the average, water would not evaporate from a pot at 80 Deg C.
The isolated, undisturbed column would tend to separate the more from the less energetic.
Also, it is known that as the gas pressure tends to zero, conduction reduces faster than the tendency of hotter molecules to rise. This creates a bias in favour of thermal segregation, assisted by gravity.
At some point either in the entire column, or near the top, it will be hotter above and cooler below and this condition will be permanent on condition that the bouyancy exceeds the thermal conduction at that pressure (and gas characteristics).
A silver wire conducting heat from the top to a point where it is cooler will indeed see heat flowing continuously (and slowly). That is not perpetual motion any more than the vibrating and moving gas molecule is perpetual motion (as we normally mean it).
For heavens sake, people, do not interpret this heat flow as being able to ‘do work’ unless the system is cooled as a whole. There is no free lunch!
The movement of heat through the silver wire is not perpetual motion and thus ‘ruled impossible’. Yes the heat will flow continuously, as fast as the hotter molecules can rise in the gravitational field.
Heat transfers from one molecule to another continuously and we do not call that transfer of heat ‘perpetual motion’ capable of being tapped for ‘doing work without an input of energy’. It is just a characteristic of gases. Energy flows all the time in stable conditions we view (on average) as unchanging.
As far as I understand adibatic cooling, it will not prevent the more energetic molecules from rising. If it does for some reason I can’t see, then a different temperature profile will prevail (possibly a different one foreach unique gas). Save in special cases, not all of the column can be isothermal.
The whole point is that if you could achieve the totally impossible conditions that Dr Brown proposes for his thought experiment, you probably would have a perpetual motion machine. After all to get the conditions proposed would take magic in the first place.
It is an imaginary concept, so is Alice in Wonderland.
The totally impossible conditions like the adiabatic planet discussed in EEJ. Have you even read the paper that this whole discussion refers to?
Besides, these aren’t “totally impossible conditions” at all, not for discussing whether or not an adiabatic lapse rate is a stable equilibrium. The point isn’t that I’ve designed a perpetual motion machine — the point is that a stable thermal equilibrium of an isolated ideal gas with a lapse rate violates the second law of thermodynamics. The proof, my friend, is by contradiction — if one postulates that an isolated ideal gas is in a stable equilibrium with a lapse rate, I’ve shown that it enables a perpetual motion machine to be built. That is a sufficient thermodynamic proof that the postulate is untrue, as it leads to an impossible conclusion.
I did it this way because it avoids arguing about the details of straightforward (but far more difficult) textbook calculations that directly show that the equilibrium is the isothermal state I describe above, or the much more difficult calculation in stat mech that directly shows that the equilibrium is the isothermal state that I describe above. I’ll probably eventually put the detailed balance demonstration up that the equilibrium is the isothermal state that I describe above.
This is entirely relevant to the laboratory. After all, if you take an empty thermos bottle and set it on a desk, it either has a stable adiabatic lapse rate (after a reasonably long time) or it is isothermal equilibrium precisely like I describe above. The difference would be difficult to measure, but the implications are profound. One of the first things almost any intro book on stat mech or thermodynamics does is demonstrate that thermal equilibrium is isothermal — the zeroth law of thermodynamics. If I stick a thermometer in at the top of static, isolated air column, and it reads some temperature, and I stick it in somewhere else and it reads another temperature, the zeroth law clearly states that the two locations (with different temperatures) are not in thermal equilibrium. It clearly states that connecting them with any sort of conducting pathway will cause heat to flow — it is really pretty trivial to look at the distribution of microstates and show that equilibrium will have the same temperature. The gas itself is always such a conducting pathway.
Asserting that a thermal equilibrium exists in some straightforward, isolated, thermally connected system that has sat around for many thermal relaxation times that has a macroscopic distribution of local temperatures isn’t trivial. It is a complete and utter disaster for all of thermodynamics. The second law is only the first consequence.
Which one is more likely: All basic thermodynamics and stat mech textbooks are wrong, including the ones that make showing that there is no lapse rate a homework problem or that do it in the actual text, or some people who have a really hard time understanding what a degree of freedom is or how to do an integral or mess with logarithmic expansions have made a mistake, the biggest of which is assuming that the DALR worked out in climate systems is stable in the absence of a driving thermal gradient and that air is locally truly “adiabatic”, instead of just having a thermal conductivity that is slower than convection?
Anyone who can’t understand this simple presentation is going to have enormous difficulties with the more complex ones. Sorry about that, but that’s the way it goes.
Sorry about the accidental italics inversion too. Truly wish for edit and preview, I do.
rgb
Robert Brown says 1/25 at 12:09am:
“Turn to page 36. Read section 2.17. Work through it carefully…”
Thank you Robert, now you are engaging in calm scientific discourse. This is interesting progress.
I have worked thru Caballero sec. 2.17 page 36 very s-l-o-w-l-y & carefully. I return.
I note that in section 2.17 to develop the temperature field eqn., Caballero refers us to Fig. 2.3 for the gas in a pipe where it is assumed to quote Caballero: “…consider a pipe of cross-sectional area A containing an ideal gas with an isotropic velocity distribution (Figure 2.3).”
Isotropic velocity! So there is NO gravity field used to develop the temperature field in Caballero 2.17. There is no g in temperature field equations 2.74 or 2.75 by inspection. They are pretty obviously not dependent on the g field in z direction.
Caballero in 2.17 writes for no gravity & I quote: “Thus, heat flows down the temperature gradient (from hot to cold) and ceases to flow when temperature is uniform, exactly as required by the Second Law. A more precise calculation using the full apparatus of kinetic theory gives the same qualitative result.”
This proof you have referred me to is for the isotropic velocity/temperature field ideal gas NOT in gravity field. Yes, I grok this previously & agree w/o gravity: the temperature field will be isothermic from 1st law b/c the velocity hence KE from top to bottom does not vary – no g temperature field is indeed uniform as this isothermal derivation shows.
Caballero here in 2.17 is NOT talking about hydrostatic equilibrium temperature with dp/dz non-zero in a gravity field where the velocity and KE of the molecules vary.
In fact, for gravity field acting, Caballero agrees the temperature field is non-isothermal as the mean velocities vary from top to bottom of the air column in sec. 2.3 where he does add the gravity field: “…this time we’ll add the effect of gravity….the effect is quite interesting:… Mean velocities will be greater near the bottom of the box than near, the top…”
Read that slowly again, the temperature field in the presence of gravity Caballero shows it is non-isothermal in the up/down direction. You cannot refute a non-isothermal science paper based on sending me to isothermal examples.
Robert continues:
“Then be sure to do exercise 2.17. I quote: Exercise 2.17: Extend the argument above to show that (2.75) also applies to a vertical column of air in hydrostatic equilibrium.”
Eqn. 2.75 just shows the “net rightward flux” where even in hydrostatic equilibrium, dp/dx =0 which is what it takes to derive 2.75 in the isothermal case. This is trivial for hydrostatic case, since we are really interested in temperature field z variance with non-zero dp/dz.
I could agree air column temperature is isothermal horizontally even in the presence of gravity.
Robert Brown has not yet shown how temperature could possibly be isothermal in the air column z direction in the presence of gravity to refute any science paper esp. when Caballero relying on “Bohren and Albrecht’s excellent Atmospheric Thermodynamics” tells us above in sec. 2.3 the z temperature field in the presence of gravity is non-isothermal.
Robert Brown continues:
“Goodness, could Caballero be saying that thermal equilibrium is isothermal, regardless of whether you move up or down in a static air column? Even in Climate Science? Do you think? Is he asking you to (gasp) actually prove it? Well heck, it ought to keep you out of trouble for a while. Give it a shot. In the meantime, meditate upon that “exactly as required by the Second Law” bit. It’s important!”
Yes, Caballero in velocity isotropic pressure sec. 2.17 is saying thermal equilibrium is isothermal regardless whether I move up or down in a static air column with no gravity field. Yes, I think that’s obvious even in climate science; I gave it my shot. It did indeed keep me out of trouble for awhile and I did meditate some more on the 2nd law, it is really pretty interesting.
However, Robert Brown still has to find a refuting ref. to cite in order to support Robert Brown’s refuting theory that temperature is isothermal in the gas column of interest in the presence of gravity where M-B cannot be invoked due to M-B applying only to the special case of no gravity.
Otherwise proper application of 0th, 1st,2nd & Caballero does refutes top post. Cabellero teaches: an adiabatically isolated column of gas in a gravitational field CAN have a thermal gradient maintained by gravity.
Robert Brown’s thermal law inconsistent conclusion in top post is hereby still refuted (my cap.s): “an adiabatically isolated column of gas in a gravitational field CANNOT have a thermal gradient maintained by gravity.”
Joules Verne says:
January 25, 2012 at 9:49 am
Why do you not just think about this in as simple terms as possible.
Forget about any mechanisms that causes it, what are you saying is the outcome?
You are saying that Gravity can cause an everlasting temperature gradient in a column of gas in a closed system with no possible energy input.
Right now think about just one inevitable consequence. Convection.
Convection must occur because we have hotter gases at the bottom and there will be constant particle movement up and down the gravity well as particles heat up and cool down and are affected by the gravity well.
Ok what is needed to move a particle up a gravity well………work! Or explain how you move a particle up a gravity well without performing work.
What happens when work takes place?
Well the 2nd Law of Thermodynamics says that entropy must increase and that entropy can never decrease in a closed system without the creation of energy.
So how do you maintain an everlasting temperature gradiant in this column of gas?
Well the 2nd Law says you can’t. Entropy increase will eventually lead to the ‘heat death’ of the system as temperatures equalise accoss it.
To do it, you have to create energy and the Laws of Thermodynamics says you can’t do this either.
So tell me how you maintain an everlasting temperature gradient without breaching the Laws?
Alan
Myrrh said @ January 25, 2012 at 4:19 am
Brownian motion has nothing whatsoever to do with electrons; it’s the motion of small particles of matter (originally pollen grains) being jostled by the random movement of molecules in a fluid. Heat is one form of energy among many: chemical, kinetic etc. Photons are packets of energy being exchanged between atoms. They are not heat so they don’t care about the temperature of those atoms. Heat flows from hot to cold only. Physics is divided into Classical and Quantum descriptions of the world. They describe the same world in different ways. From your questions, and there’s nothing wrong with your questions, it’s clear that these two views are conflated in your mind. You definitely need to learn some basic physics. Mine came from Resnick, Halliday & Walker in 1969. While the papers being discussed are recent, the physics isn’t.
An ad hominem BTW is when you claim that what someone claims is false by virtue of who they are. Insulting someone is not an ad hominem. The first is a logical fallacy, the second is being rude and not a logical fallacy.
A good insulator is one that conducts heat slowly. A bad insulator is one that conducts heat quickly. All matter conducts heat, but the rate at which it conducts depends on the state (solid/liquid/gas) and chemical composition. Air conducts heat very slowly, but perforce will reach an equilibrium temperature very slowly in the absence of convection. In any real atmosphere, convection will predominate over conduction.
Unfortunately Myrrh you have chosen the wrong classroom in which to learn the basics. There’s not just basic thermodynamics and quantum physics, there’s basic boundary layer climatology being discussed here. A lot of the discussion is frankly a display of ignorance. There’s nothing at all wrong about ignorance per se, but wilful ignorance is a different matter. This muddies the water and makes learning extraordinarily difficult for those who have yet to grasp the fundamentals. This saddens me; I experienced this in a cosmology class I took; our lecturer/tutor had a very difficult time keeping to the arguments he wanted us to focus on because of students who lacked the underpinning knowledge required to understand those arguments. It was very frustrating.
Bottom line is: get that basic physics under your belt. If you can find a friend who wants to do the same, you will make much more rapid progress. To teach is to learn twice.
And please forgive Willis. Unfortunately, his mother neglected to put a warning notice on him: Handle with Care. He’s been a reforming cowboy ever since I first came across him nearly a decade ago and I have learnt heaps from him.
Live long and prosper Myrrh. Your questions are not stupid. The answers you have received are not stupid, either. Confusing you, yes, but not stupid.
thepompousgit says
” Live long and prosper Myrrh. Your questions are not stupid. The answers you have received are not stupid, either. Confusing you, yes, but not stupid.”
Myrrh states up front that he has no formal science training.
Sometimes this shows through in his questions.
However this sometimes has its advantages as he is not soaked in a particular paradigm.
Quite often he is the boy who spots the ‘Emperor has no clothes’.
I think he made a valuable contribution when he noticed that the NASA educational pages were being reinterpreted to blur the differences between light and infra red radiation.
Some would think that this was done to make IPCC science more believable.
Ken Finney says:
January 25, 2012 at 10:03 am
Thanks for the links.
I think you know what I was getting at.
kdk33 said
Sound is the alternating compression & decompression of a fluid. A practical experiment for you:
Partially fill a bathtub with water. Take a portable radio, or CD player into the bathroom and turn on. Your choice of music. Lie in the bath and submerge your head in the water. If you still believe in the incompressibility of water, please keep your head there.
gbaikie says:
January 25, 2012 at 3:15 am
That is not correct. The lapse rate is almost always 6.5 K/km. High humidity makes the tropopause higher, but does not change the lapse rate. The one exception is when clouds form and the lapse rate is variable between 4 and 6.5 K/km.
Actually, it is not – it is about cooling the atmosphere. A fraction of that heat returns to the surface (back radiation) and makes it a bit warmer. To be perfectly clear, because some of the heat comes from conduction/convection, greenhouse gases emit more energy than they trap.
thepompousgit says:
January 25, 2012 at 10:55 am
Sir your responce to Myrrh was a very nice display of kindness oft lacking by some. You are to be commended. As we used to day in the Navy, BZ (bravo zulu).
wayne says:
January 25, 2012 at 4:05 am
The atmosphere becomes isothermal when the cooling is removed from the top. The amount of energy arriving at the bottom really does not matter. It merely sets the final temperature, not the lapse rate.
A physicist says:
January 25, 2012 at 10:23 am “For more theoretical and experimental details than most folks want to know, see @article{Kemp:2009lr, Author = {R. Scott Kemp}, Journal = {Science and Global Security}, Number = {1}, Pages = {1–19}, Title = {Gas Centrifuge Theory and Development: a Review of US Programs}, Volume = {17}, Year = {2009}} and references therein (a Google search will find it).”
I think you need to re-read the Article.
It talks about “assuming a linear-thermal-gradient profiles” and “reate a dynamic equilibrium”, not thermal equilibrium.
The word “Isothermal” does not appear anywhere in the available text whatsoever.
My admiration to Professor Brown. It was an elegant demonstration and a tenacious defence.
You asked about convection on a world with no GHGs
I think it would work a bit like the convection pattern of the thermohaline circulation, inverted. The oceans are warmed at the equator and cooled at the poles. The cold water at the poles sinks, flows equatorwards across the ocean deeps. Water at the equator is warmed, rises and spreads out polewards. Because the deep oceans receive no heat input, at least not on the scale of the circulation time, they are fairly uniformly at the temperature of the descending polar waters, even below the equator. There is in fact a lapse rate in the deep oceans of about 0.1 C/km.
With GHG-free atmosphere, you have to swap warm for cold and up for down, and equator for pole. Thus, air is warmed at the equator, rises, and spreads polewards. Its potential temperature (adjusted for lapse rate) remains constant then, and most of the atmosphere is equatorially hot, even at the poles. The thin layer in contact with the ground there cools, and flows back to the equator over the surface. There would be a lapse rate, as there is in the oceans, and I think it could extend high up, as the ocean circulation goes deep. While you might think that polar waters need only sink below the thermocline and could then flow back equatorwards only a few hundred metres down, analogous to the low tropopause, it doesn’t work that way.
Pressure is exerted omnidirectionally, and unless channelled/diverted by some external force, an upward force on air at the equator will push all the air above upwards until forced sideways by the top of the atmosphere. The upwards push can’t be changed entirely to a sideways push 100 m up unless there is somethere there to actively resist it. And since all the atmosphere far above the surface is at the same potential temperature, and neutrally buoyant, I don’t see how or why this could happen.
The idea that you can get convection cycles driven by temperature differences from the top sounds odd, but I find it helps to think of it as cooling of the fluid over one area giving the fluid negative buoyancy, and driving the fluid down – this being analogous to heating from the bottom causing positive buoyancy and a drive up. It helps as well to remember convection is about the whole cycle – what goes up must come down – not just hot air rising.
(There are complications, of course. On a rotating planet, air converging on the poles would spiral into a cyclostrophic vortex. You’d get multiple Hadley cells and jet streams and so on. I’m not claiming it would really be that simple.)
It’s a controversial idea – I know several people have objected vociferously when I’ve mentioned it – but that doesn’t mean it’s therefore incorrect. If you can see anything obviously wrong with it I’d be grateful.
Bryan said @ January 25, 2012 at 11:15 am
Yes, I noticed. That’s why I went to the trouble of answering his questions at length. Robert’s been doing most of the heavy lifting around these parts and I thought I’d lend a hand.
.
Just a thought, for you all.
There are (I think) two main ways of reducing heat-loss from a planet (resulting in warmer surface temperatures):
a. LW absorption and emission (greenhouse gasses and effect).
b. Conduction-convection (atmospheric effects).
Let me explain what I mean. We have three types of planet:
a. Airless planet.
Cooling via LW, and no ‘insulator’ to reduce LW cooling. (An insulator being any method of preventing cooling.)
b. Atmospheric planet, with no greenhouse gasses.
Cooling via LW.
Reduced cooling via conduction-convection to the atmosphere. Initially, this process simply warms the atmosphere, until the atmosphere is so warm it absorbs little more surface temperature. Now this warm atmosphere cannot cool itself via LW emission, but it can cool itself via conduction to areas of the planet in shadow. Thus the atmosphere is ‘warming’ (or reducing cooling) areas of the planet in shadow. This will surely make the average surface temperature of the planet higher, than if there was no atmosphere (because the cold shadow areas are now warmer, resulting in a higher average temperatures.)
As an aside, this means that the effective surface LW cooling area of a hilly planet like the Earth is much greater than a simple sphere would lead us to believe. Up to 20% greater surface area. I presume this greatly effects the w/m2 calculations that have been tossed around. (The incomming SW radiation only sees the area of a smooth sphere, but the outgoing LW radiation sees a much higher surface area than a normal sphere.)
c. Planet with greenhouse gasses.
Cooling via LW
Reduced cooling via conduction-convection (as explained above).
Reduced cooling via gasseous absorption and reemission (greenhouse gasses). In a similar fashion to conduction (above), the re-radiation of LW from H2O and CO2 towards the surface delays and reduces the coolling of the surface, resulting in higher average temperatures than if there were no such gasses in the atmosphere.
Thus (in my opinion) both the greenhouse gasses and the atmosphere itself act in partnership to reduce the cooling of the surface (erroniously called warming, but you know what I mean).
.
OK,
For all the smarties that want to point out that water is actually compresible. Yes you are right.
But relative to a gas? Not so much. A lapse rate in the ocean? Sure maybe a tad. But relative to the atmosphere? Not so much.
Happy now?
Robert Brown,
I can’t help with edit, but you can get preview. CA Assistant works just fine here. Go to: http://climateaudit.org/ca-assistant/ and follow the instructions. It does require that you use Firefox as your browser. I’ve never found a place where the subscript/superscript HTML quicktags work, though.
Robert Brown says:
January 25, 2012 at 5:33 am
Actually, it is water vapor (not CO2) that becomes optically thin at the tropopause. It is about 200 ppm below the tropopause and 5 ppm above. In the tropics, where there is more water vapor, the tropopause is higher.
In the stratosphere, CO2 is the main greenhouse gas, more than 100 times more abundant than water and more than 1,000 times more abundant than ozone. I have seen the TOA spectra you have referred to, I still can’t explain the CO2 emission that appears to come from the tropopause, but I am certain that that is not the correct explanation. It is possible that the feature originates from (and perhaps causes) the thermal anomaly at 32 km, in the mid-stratosphere. One problem is that the resolution of space borne instruments is not quite good enough to know how to interpret that feature.
To be very clear, at the tropopause, water vapor and CO2 emit the same amount of energy. However, CO2 is emitting energy from the stratosphere toward the tropopause and water vapor is emitting the same amount of energy toward space. At that level of the atmosphere, the CO2 and water spectra no longer overlap by much.
“”””” Joe Born says:
January 24, 2012 at 8:21 am
That Dr. Brown has it wrong is readily demonstrated by a thought experiment nearly any layman can perform.
If an ideal monatomic gas subjected to gravity in a thermally isolated container consists of only a single molecule, its kinetic energy K–and thus the mean translational kinetic energy–at any altitude z is given by K = mg(z_max -z), where m is molecular mass, g is the acceleration of gravity, and mgz_max is the total (kinetic + potential) energy of the gas. “””””
Well Joe, I DON’T agree that Professor Brown has it wrong; but I DO agree that nearly any layman can perform your thought experiment; that’s how they earn the prestigious title of “Layman” rather than “Professor.”
So to your layman thought experiment. you state:- “”””” If an ideal monatomic gas subjected to gravity in a thermally isolated container consists of only a single molecule, “””””
There you just shot your self in the head. A gas, ideal or not, cannot consist of a single molecule.
when in a thought experiment you say “”””” any altitude “”””” that is taken to mean “”””” any altitude “””””, tha’ts the terrific advantage of a thought experiment; an infinifte sized container is easy to get by declaration; and your container must be infinite in size for your molecule to be able to be at any altitude.
Therefore your single molecule never hits the wall of the container, and there is nothing else present to hit either, so no collisions occur, so your molecule has no Temperature. It’s energy is indeterminate since according to Einstein there is no absolute frame of reference, and your molecule is simply in free flight.
it also clearly doesn’t have any Maxwell-Boltmann energy distribution either since only one molecule is present; further proof that it has no Temperature; or at least it has no Temperature different from zero Kelvins.
Maybe if you listen a bit more closely to Professor Brown, you could eventuall discard your layman’s mortarboard, and tassel.
.
Dr Bown. With regards to your thought experiment with the silver wire, you say that:
“””Heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.”””””
Sorry, I am only an aviator and meteorologist, but are you not confusing ‘heat’ and ‘temperature’ here?
The individual molecules in the upper atmosphere can indeed be very hot (high kinetic energy), but there are so few of them, their total temperature on any thermometer is very low.
Thus the top of your silver wire can be as hot as it likes (say 35oc), and yet the individual molecules at 50,000 feet are not going to accept any of that heat because they are already (individually) quite hot themselves. (But because there are so few of them, the atmosphere at this level feels very cold).
Does not your thought experiment fail, because most of the molecules in the atmosphere are all at the same heat (kinetic energy), while the difference in temperature with altitude (on a thermometer) is simply an effect of the number of molecules you meet (pressure and density).
.
I am not denying greenhouse effect here – any meteorologist will know this is a real effect. But it is surely also true that an atmosphere warmed at its base by conduction will transmit that heat throughout the atmospheric column, maintaining its temperature and lapse rate, yet with most of the molecules in that column having the same kinetic energy (the same heat, but not the same temperature).
Where Tallbloke et al seem to fall down, is believing that conduction-convection is the sole method of decreasing LW heatloss from a planet (thus deriving a warmer surface). It is not. The absorption and reemission of LW by clouds and certain gasses (the greenhouse effect) is a much more potent effect.
.
Paul Bahlin says:
January 25, 2012 at 9:47 am
Nope. The premise is that all collisions are elastic, both with each other and with the container walls. See for example the Wikipedia article on Kinetic Theory:
The particles must also be small so that the total volume of the particles is much smaller than the volume of the container.
Robert Clemenzi says:
January 25, 2012 at 12:42 pm
Water vapor becomes optically thin far below the tropopause. Look at the IR emission spectrum of the atmosphere from space. The water vapor lines and bands are far more intense than the CO2 band. That’s because water vapor, which has a scale height about 1/4 that of the noncondensable gases (2km compared to 8km) becomes optically thin (optical density < 1) at lower altitudes where its warmer. At 17 km for a tropical atmosphere the amount of water vapor in a given volume is less than 1% as much as the amount of CO2.
Ralph says:
January 25, 2012 at 12:54 pm
This piece of misinformation seems to be even harder to kill than a gravity maintained adiabatic lapse rate. Temperature, as long as the pressure is high enough it can be defined, is a function of the average kinetic energy of the gas only. What happens at low pressure is that it takes longer for a thermometer to equilibrate with the gas. If the thermometer has a large thermal mass, on the order of the heat content of the volume of interest, it will perturb the actual temperature.
“On the influence of gravity on the thermal conductivity”
M. Tij (1), V. Garzó (2), A. Santos (2) ((1) Départment de Physique, Université Moulay Ismaïl, Meknès, Morocco; (2) Departamento de Física, Universidad de Extremadura, Badajoz, Spain)
(Submitted on 25 Feb 2000)
In this paper we evaluate the corrections to the Navier-Stokes constitutive equations induced by the action of a gravitational field in a gas subjected to a thermal gradient parallel to the field with no convection. The analysis is performed from an exact perturbation solution of the BGK kinetic model for Maxwell molecules through sixth order in the field. The reference state (zeroth order approximation) corresponds to the exact solution in the pure planar Fourier flow, which holds for arbitrary values of the thermal gradient. The results show that the pressure tensor becomes anisotropic, so that the momentum flux along the field direction is enhanced. In addition, the heat flux increases (decreases) with respect to its Navier-Stokes value when the gas is heated from above (below).
full text:
http://arxiv.org/pdf/cond-mat/0002397v1.pdf
These authors said the same thing I did in a lot more detail and precision numbers.
snip:
So there. A gravity field introduces a first order effect that causes coefficient of thermal conductivity to be asymetric in direction of flow.
Maxwell’s Demon in other words sorting out molecules by kinetic energy content. I’m afraid you boys are going to have to come to grips with this. There’s no violation of thermodyanmics. The Demon creates a thermal gradient at the expense of an equal and opposite potential energy gradient. You can’t make a perpetual motion machine out of this. Every attempt at finding a way for the Demon to get a free lunch has failed. This is no exception.
Gravity-Induced Electric Fields in Metals
Canadian Journal of Physics, 1971, 49:(22) 2754-2767, 10.1139/p71-334
Just to muddy the waters further. There’s an electric field on that wire due to gravity – what if the hypothetical gas can conduct electricity – won’t it warm up because of the current flowing between the ends of the wire?. (I have become confused – I thought I ‘got’ lapse rates.)
A good argument : http://www.youtube.com/watch?v=RDjCqjzbvJY
Let’s try that quote from the paper again. Somehow the last few words in the paragraph I clipped didn’t come through and they were important (my bold).
“The main results concerning the transport of momentum and energy are that
the external field induces (i) anisotropy in the pressure tensor, (Pzz−p)/p ≃
845 ǫ2g∗2, and (ii) deviations from the Fourier law, qz/q(0)z − 1 ≃ 58
5 ǫg∗. While the first effect is of second order, the correction to the heat flux is
of first order, so that it depends on the sign of the thermal gradient. As
a consequence, the heat transport is inhibited when the gas is heated from
below (ǫ 0).”
Again, the source:
On the Influence of Gravity on the Thermal
Conductivity
http://arxiv.org/pdf/cond-mat/0002397v1.pdf
Well, I still haven’t worked out what any of you are talking about.., but isn’t the opposite and equal energy gradient to make up for the gravitational energy gradient, pressure?
Gold star for Myrrh.
Some fun for everybody:
http://phet.colorado.edu/en/simulation/gas-properties
A final exam you all might want to look at, especially problem 1. Would you flunk?
http://www.physics.sc.edu/~yar/phys706_2011/…/final_solutions.pdf
I know, I know, those of you who are devoted to the idea of a lapse rate at true equilibrium to the extent that you ignore the fact that the solution openly violates the second law won’t be swayed by a little thing like the fully worked out solution — which is the one I have in the article at the top, but this exam goes ahead and computes various quantities of interest and shows that they do the right asymptotic things. If the debate continues, I have a lovely contribution from a list-lurker that does the textbook exercise of showing that isothermal is indeed the maximum entropy solution. And on the list today it was verified (not by me) that the full stat mech computation is isothermal. Finally, Caballero has it as a homework exercise (2.17).
Is this starting to look like a conspiracy of some sort? A nefarious plot by evil warmists, who’ve managed to corrupt every thermo and stat mech textbook in the country? Who are brutally grading students incorrectly on their final exams, all to keep them from questioning Greenhouse Warming by hiding the True Solution from them? If so, you might want to ask yourself — is it just barely possible that all of these Ph.D. physicists who teach and do research and all that stuff in the general field of thermal physics are all right, and it is me that is wrong?
It truly would be lovely if, with all of these guns brought to bear to back up what was already a perfectly adequate proof by contradiction above, we could all just agree that Jelbring’s EE paper is categorically incorrect, because the state with a DALR that he asserts as the stable thermal equilibrium of an isolated ideal gas violates the second law of thermodynamics, fails of detailed balance, is not (in fact) the maximum entropy solution, and doesn’t make sense as no air parcels are being moved around in an atmosphere in static equilibrium.
Just a thought. A foolish one, I know — a mad, mad, dream. But y’know, I’ve gotta lay it out there.
rgb
Darn it. It was still cut off.
While the first effect is of second order, the correction to the heat flux is of first order, so that it depends on the sign of the thermal gradient. As a consequence, the heat transport is inhibited when the gas is heated from below, while the opposite happens when the gas is heated from above.
I really needed that last bit where it is specified that heat transport is accelerated when heated from above in addition to being inhibited when heated from below.
I highly recommend reading the whole paper. This corrects both Brown AND Nikolov neither of whom have characterized the situation correctly either conceptually or with mathematical rigor.
DeWitt Payne says:
January 25, 2012 at 1:15 pm
Ralph says:
January 25, 2012 at 12:54 pm
“This piece of misinformation seems to be even harder to kill than a gravity maintained adiabatic lapse rate. Temperature, as long as the pressure is high enough it can be defined, is a function of the average kinetic energy of the gas only. What happens at low pressure is that it takes longer for a thermometer to equilibrate with the gas. If the thermometer has a large thermal mass, on the order of the heat content of the volume of interest, it will perturb the actual temperature.”
It’s harder to kill because it’s correct. All matter above absolute zero has a temperature. There is no constraint on some minimum amount of mass involved. Any amount will do. The problem you are struggling to understand is that there is a Bolztman distribution of kinetic energy such that you cannot obtain a reliable temperature for an ensemble by measuring one individual molecule’s temperature. It’s sort of like trying to figure out the average intelligence quotient here based on measuring one individual. It does not follow that only groups have an IQ. Every molecule has a temperature.
The way to think about the difference between the stratosphere and the troposphere is to use the slab gray atmosphere toy model ( see 7.3.2 here, for example. Petty goes into more depth).
Thanks, looks very useful. I do so hate the toy model with downwelling radiation, but the general idea looks good and I’ll see what I can make of it.
rgb
DeWitt:
You asked elsewhere about why a laser can cut metal even when the metal gets very hot. But Claes Johnson’s paper is only about spontaneous blackbody emission, not induced emission as in a laser. Induced emission does not have a frequency proportional to the absolute temperature of the source, as does spontaneous blackbody emission in accord with Wien’s Displacement Law. (When lasers are used to cut steel there is also a blowing process helping to cool the metal.)
You yourself quoted empirical proof of what Claes has proven computationally when you talked about a gas not absorbing radiation from a cooler emitter, but doing so when the emitter got warmer than the gas. I would very much appreciate the reference for this experiment if you could oblige.
Robert Brown says at 10:40am:
“…the point is that a stable thermal equilibrium of an isolated ideal gas with a lapse rate violates the second law of thermodynamics…the zeroth law clearly states that the two locations (with different temperatures) are not in thermal equilibrium.”
Well, the top post does tell us:
“Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics…”
Why is that last true? I agree, it should be so but it flies in the face of hydrostatic equilibrium actually being in “temp. equilibrium” in Caballero. I noted that the 1st time you sent me there last week. Seems so long ago now…ha.
I am truly curious. So far as I can see in the top post this is just announced, 2nd law violation is not irrefutably proven up there. In the gas ideal gas column of interest, no process is irreversible in there. The molecules bounce around elastically with everything, entropy does not go down. Couldn’t entropy just stay the same in this idealization & therefore pass the 2nd law test? In real world, of course entropy goes up due to real inelastic collisions.
But then , in sec. 2.3 Caballero writes being non-isothermal is acceptable for hydrostatic equilibrium. Stunning. Caballero even goes so far in Sec. 2.3.1 to write: “Overall, it can safely be stated that atmospheric motions with horizontal scales > 10 km are always in hydrostatic equilibrium.” Meaning non-isothermal. That is a stunningly tall column & long wire to insert but it works in reality, no perpetuum, no 2nd law violation. Why?
Maybe I am about to be directed to another text book deep dive but that would be ok & progress.
Robert, the teach-a-holic – Thank you for an enjoyable renewed science discourse.
DeWitt Payne said @ January 25, 2012 at 1:15 pm
Ain’t that the truth?
More accurately, measuring temperature with a thermometer always changes the temperature. Most often that can be neglected because the change is trivial, but there’s many a researcher come unstuck from not realising that they are changing what they measure.[/nitpick]
George E. Smith; says:
January 25, 2012 at 12:52 pm
“There you just shot your self in the head. A gas, ideal or not, cannot consist of a single molecule.”
Ummm… I think it can’t exist as a liquid or solid because that requires proximal arrangement with neighboring molecules. A molecule is a gas generally when it is very isolated from neighbors so that it can flit about traversing a great number of molecular radii without hitting anything else. There’s probably a better definition but in general a gas is a gas because the individual molecules are a great distance from neighboring molecules compared to liquids and solids.
thepompousgit says:
January 25, 2012 at 10:55 am
Myrrh said @ January 25, 2012 at 4:19 am
Brownian motion has nothing whatsoever to do with electrons; it’s the motion of small particles of matter (originally pollen grains) being jostled by the random movement of molecules in a fluid.
That was my point. Not only does it not have anything to do with electrons, it has eff all do mixing carbon dioxide thoroughly in the atmosphere…
…though idiotically given as proof is a typical non-experiment from the AGWSF department, by opening a bottle of scent in a classroom saying it proves the scent is spread by Brownian motion, that’s when it’s not being not being idiotically explained by using ideal gas properties of elastic collisions in empty space as if ideal gas, but more often than not, claiming both these processes happening at the same time – seemingly as unconcerned as Willis about context.
Photons are packets of energy being exchanged between atoms. They are not heat so they don’t care about the temperature of those atoms. Heat flows from hot to cold only. Physics is divided into Classical and Quantum descriptions of the world. They describe the same world in different ways. From your questions, and there’s nothing wrong with your questions, it’s clear that these two views are conflated in your mind. You definitely need to learn some basic physics. Mine came from Resnick, Halliday & Walker in 1969. While the papers being discussed are recent, the physics isn’t.
Not conflated in my mind, conflated in minds that can’t separate contexts one from another.
As I showed in the link to an exchange I had about ‘net heat flow including heating flowing from cold to hot’
Visible light is not a radio wave, for example, it has distinct properties in its own right and these properties act in distinct ways on meeting matter, to reduce this to some as yet unproven idea of photons and claim that all photons in transferring energy heat matter oblivious to other uses of energy while claiming to be discussing science of the physical world around us we can see and taste and hear and which we do understand empirically well how it impinges on us and we on it, is frankly pathetic coming from those claiming themselves educated in this. It’s not I who needs to learn some basic physics..
An ad hominem BTW is when you claim that what someone claims is false by virtue of who they are. Insulting someone is not an ad hominem. The first is a logical fallacy, the second is being rude and not a logical fallacy.
I know the difference. I meant the ad hom the like which you’ve repeated, “You definitely need to learn some basic physics” and “Bottom line is: get that basic physics under your belt” …
I suggest some return to the real physical world around us and stop blinding themselves with their own imagined quantum brilliance, which may or may not yet have arrived from the future carried by a non-existant photon..
A good insulator is one that conducts heat slowly. A bad insulator is one that conducts heat quickly. All matter conducts heat, but the rate at which it conducts depends on the state (solid/liquid/gas) and chemical composition. Air conducts heat very slowly, but perforce will reach an equilibrium temperature very slowly in the absence of convection. In any real atmosphere, convection will predominate over conduction.
Thank you, I hope that helps Professor Brown to better articulate what he meant.
Unfortunately Myrrh you have chosen the wrong classroom in which to learn the basics. There’s not just basic thermodynamics and quantum physics, there’s basic boundary layer climatology being discussed here. A lot of the discussion is frankly a display of ignorance. There’s nothing at all wrong about ignorance per se, but wilful ignorance is a different matter. This muddies the water and makes learning extraordinarily difficult for those who have yet to grasp the fundamentals.
You err, I have grasped the fundamentals well enough to see that many hide the fact they don’t know the basics by playing the ‘superior because so very well educated in science card’ and worse, refusing to engage and distracting from this by the use of the ad hom technique that those questioning them have nothing worth listening to because they don’t have science phd’s coming out of their arses.
I call bullshit on the lot of it.
To teach is to learn twice.
And what are you learning twice if teaching nonsense imaginary physics about a fictional world?
When some confuse photons with discrete packets of visible light and conclude that visible light must therefore be heating water when real physics says water is transparent to it? And when having given the properties of one thing to another by claiming visible and short wave heat land and oceans they junk the real great thermal energy coming to us direct from the Sun, because they can’t find a role for it in their so called ‘energy budget’..? From which they have also expunged the great cooling role of the greenhouse gas water vapour, simply by ignoring it and sticking their fingers in their ears whenever it’s mentioned?
I call bullshit on the lot of it.
Live long and prosper Myrrh. Your questions are not stupid. The answers you have received are not stupid, either. Confusing you, yes, but not stupid.
Thank you, I add be happy to you. The answers I have received as explanations for ‘greenhouse gases warm the Earth’ are most definitely stupid, I’m not the one confused here, as I’m still trying to point out..
Perhaps this will settle things, for anyone still listening that thinks that Jelbring’s paper is correct:
http://www.physics.sc.edu/~yar/phys706_2011/…/final_solutions.pdf
I have waiting in the wings a user-contributed textbook demonstration that isothermal is maximum entropy with gravity, as well. Then there is Caballero’s detailed balance assignment (2.17). There is Paul Birch’s analysis of Velasco, which seems to be a full stat mech computation that arrives at the same conclusion. And finally, there is the clear violation of the second law the article above makes very clear.
Are we done yet?
Tallbloke, from much earlier: Since Robert Brown is setting a refutation of Hans Jelbring’s 2003 paper, it would be a common courtesy to provide a link to that paper in the headline post.
This is my bad, Tallbloke. My only excuse is that I wrote the paper in latex and submitted it to Anthony to format the equations, and while I did put the reference in I forgot the link (and had no way to add it afterwards). I appreciate your doing so.
For everybody: We’re quickly getting to where there are three or four complete algebraic demonstrations that the equilibrium state of a thermally isolated ideal gas in a gravitational field is isothermal that have been linked, directly indicated in replies, or posted and discussed. Stat-Mech and Thermo textbooks are more or less unanimous about isothermal equilibrium, of course — it is derived in stat mech very early in the process, in a way that is more or less independent of the details of the system in question. In Thermo, it is the zeroth law and the second law — any time one has a proposed system with a non-isothermal equilibrium one can trivially violate Kelvin-Planck and Clausius with it, unless it is a very odd system indeed. A column of ideal gas isn’t odd, it is textbook.
It would be nice to lay this to rest soon. Sure, anyone who wishes to can claim to be smarter than all of the authors of all of the standard physics texts on thermo, but it looks pretty unanimous out there. There are more interesting and useful things to discuss than a paper that is really pretty obviously wrong, however well intentioned.
If anybody has a serious argument — one that can stand up to e.g. the exam question and solution above, for example — I’d still be happy to address it as soon as I have time again, but it might be a day or so.
rgb
Joe Born says:
January 25, 2012 at 10:24 am
“First to your contention that we are not talking about the microcanonical ensemble. Here a little context is in order. Recall that both Robert Brown in this thread and Willis Eschenbach in the previous one were addressing themselves to refuting the Jelbring paper. That paper began with a hypothetical ideal gas G disposed between concentric spherical surfaces A and S. Jelbring said that “A and S are thermally insulated preventing heat from entering into G and infrared radiation to reach space.” It is no doubt to parallel this condition that Robert Brown says of his thought experiment that it involves an “adiabatically isolated column of an ideal gas.” In short, heat can flow neither into nor out of the gas, so by definition it is indeed a microcanonical ensemble.”
They are isolated with respect to heat flow to and from the outside universe. Not from the walls of the container, or at any rate, the floor – the planetary surface – with which they are in thermal equilibrium. So, except in the ludicrously pedantic sense in which no ensemble is truly canonical unless it includes every single particle in the entire universe, the canonic limit applies. None of which actually matters, so long as you don’t insist on filling the volume with a hard vacuum orders of magnitude more rarefied than even intergalactic space! Jelbring explicitly states that his shell is no higher than the 100mbar level. Robert Brown has also indicated somewhere (I think in one of the previous threads) that he is not considering cases in which the gas is so thin that the concept of temperature goes pear-shaped.
Joe: “Next I consider your statement that “for any reasonable number of particles, it makes no difference” whether we’re dealing with the microcanonical ensemble or not. I agree with you that as a practical matter any lapse rate as small as I’m saying Equation 8 implies would be too small to measure.”
No, that’s not what I’m saying. It is a general principle of statistical mechanics that the microcanonical converges to the canonical, as Velasco et al themselves point out. Equation 8 does not imply any lapse rate at all. All it implies is that the details of statistical mechanics calculations are messy for small numbers.
Joe: “You make two further points that at base are not technical arguments so much as statements of your point of view. You say, “However, even in this extreme case, the temperature at equilibrium will still be the same throughout the entire height, in the crucial sense that no net work could be extracted from the gas by connecting different levels, by any means whatsoever.”
On the contrary, this is an utterly fundamental technical argument. The very definition of “same temperature” for connected regions is “no net flow of thermal energy”. Hence “no net work” can be done by the gas.
Joe: “You additionally observe that I am “taking the extreme and irrelevant sub-thermodynamic case of a minuscule total number of isolated particles – in which regime the macroscopic temperature is increasingly ill-defined and no longer simply proportional to the kinetic energy per particle.” Let’s set aside what exactly you may mean by imprecise terms like “sub-thermodynamic,” “macroscopic,” and “increasingly ill-defined.””
Let’s not. Let’s face up to it instead. If we have a large number N of monatomic particles we say that the thermodynamic temperature is T, where the total kinetic energy is 3/2 NkT. If there is only one isolated particle it doesn’t have a temperature at all! In a thermal system the motion of the particles is isotropic; there is no directional bias; and this is not possible for a single isolated particle. It’s kinetic energy, not thermal energy; we cannot put T=(mv**2)/3k. If anything, T=0. What about N=2 or 3 then? Somehow we have to cobble a fit across the middle between these two contradictory extremes. In statistical mechanics, this is possible, but messy, if you are very, very careful about your definitions, your scenario, your boundary conditions, and the limits on your sums and integrals. Even then you are quite likely to get it wrong. Whether Velasco et al have got it right I don’t know. What I do know is that if your results purport to show any non-zero temperature gradient in a state of thermal equilibrium, then somewhere or other you’ve made a boo-boo. That result cannot be correct. I am enormously more certain of that than I ever could be of any piece of statistical mechanics, and so would just about every other physicist I know.
Joe: “And let’s concede that the case I discussed was an extreme case. That case nonetheless remains relevant, because it illustrates by exaggeration something that remains true …”
Fine, but you’ve chosen the wrong extreme to illustrate this problem. It doesn’t illuminate the solution, it obscures it. It’s as if you were discussing the tendency of buses to come in threes, and spent all your time trying to analyse the behaviour of two buses setting off from the terminus 100Gyr apart.
separation science, especially that surounding the separation of uranium gases in centrifuges, give you all the evidence you need to that this is a load of crap.
blog comments dont overturn working engineering.
Steven Mosher,
“separation science, especially that surounding the separation of uranium gases in centrifuges, give you all the evidence you need to that this is a load of crap. ”
Yup separation science. that means centripetal force, separates things of different density I believe. Lemme see, what in our atmosphere is different temperature and where do they end up?? Oh yeah, gas particles are different temps and are generally separated, or stratified, by their density!!! What does it? Well, my barely HS education tells me GRAVITY!!!!
What were you saying again??
DeWitt Payne said @ January 25, 2012 at 12:31 pm
Thank you your majesty 🙂
Robert Brown:
You invited “a serious argument” so I put one:
Empirical evidence using spectroscopy proves that a gas does not absorb spontaneous emission from a body which is significantly cooler than it, but it does absorb (and spectral lines thus appear) when the same body is made warmer than the gas.
Q.1: Why?
Q.2: Does this extend to the oceans and/or land surfaces and thus imply that a warmer solid or liquid surface does not absorb radiation from a cooler atmosphere?
Q.3: Can you refer me to any experiment proving empirically that backradiation from a cooler atmosphere can warm the surface and/or slow its rate of cooling, as claimed by the IPCC?
DeWitt Payne says: January 25, 2012 at 1:15 pm
This piece of misinformation seems to be even harder to kill than a gravity maintained adiabatic lapse rate. Temperature, as long as the pressure is high enough it can be defined, is a function of the average kinetic energy of the gas only. What happens at low pressure is that it takes longer for a thermometer to equilibrate with the gas. If the thermometer has a large thermal mass, on the order of the heat content of the volume of interest, it will perturb the actual temperature.
———————————————————————————
But that is the whole point, isn’t it. just what is Dr Brown supposed to be measuring? He says ‘temperature’, which is a wooly term unworthy of a scientist.
Does he mean the individual the temperature of individual molecules (molecular kinetic energy), or does he mean the temperature of the total airmass? (See my earlier post, a few scrolls up.)
If he means the temperature of individual molecules, then thermal equilibrium in the ‘silver wire experiment’ has already been achieved (between the top and bottom of the air column). The individual molecules at altitude have about the same temperature (kinetic energy) as those at sea level. Thus the warm wire at the top of the collumn (at say +30 oc ) cannot ‘heat the air’ at high altitude, because the individual molecules at altitude are already at something like +30oc (in terms of their individual kinetic energy)..
If, on the other hand, he means the temperature of the total airmass, as measured by a standard thermometer, then he should know that you could never get the air at 50,000 ft to be +30oc. Just not possible. Never going to happen. Crazy suggestion. So Dr Brown cannot mean this.
So when DR Brown says:
“”””Heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.””””
He cannot be referring to the total airmass temperature, as measured by a thermometer, as you could never get the air at 50,000 ft to be +30oc. So he must be referring to individual molecular temperatures (molecular kinetic energy). But these molecules at altitude are already at something like +35oc (individually) already. So there will be no heat flow in the wire, because the molecules at altitude are already at the same temperature as those a sea level and the same temperature as the top of the wire.
In short, I fail to see what this thought experiment is supposed to prove !!
There could never be any flow of temperature in the silver wire. If there were, then there would already be a massive flow of energy through the atmosphere itself, through conduction and convection. And while there IS a certain amount of heat transfer through the atmosphere from surface to tropopause (as we know), this heat transfer has never made the upper atmosphere +35 oc — not even in several hundred million years of heat transfer between surface and upper atmosphere (with or without a silver wire).
Again, I must ask, what is this thought experiment supposed to prove?
Please see my previous posts at:
Ralph says: January 25, 2012 at 12:27 pm
and
Ralph says: January 25, 2012 at 12:54 pm
.
Nullius in Verba says:
January 25, 2012 at 12:05 pm
“… convection on a world with no GHGs …
I think it would work a bit like the convection pattern of the thermohaline circulation, inverted. … With GHG-free atmosphere, you have to swap warm for cold and up for down, and equator for pole. Thus, air is warmed at the equator, rises, and spreads polewards. Its potential temperature (adjusted for lapse rate) remains constant then, and most of the atmosphere is equatorially hot, even at the poles. The thin layer in contact with the ground there cools, and flows back to the equator over the surface. … ”
I agree with the overall scenario (and was actually thinking of posting something similar), except that I suspect that instabilities and the Earth’s rotation would cause the pattern to break up into relatively narrow latitudinal bands perhaps as little as a few tens of kilometres wide, with a sort of helical circulation in each (like a rope). The bands would probably meander a bit, depending on the local topography, and also wander up and down in latitude with the weather. The bands would sometimes break up further into strings of cyclones and anticyclones. We’d still have a troposphere and tropopause, and, as now, the temperature in the convective cells and at the top of the troposphere would fall fairly gradually from equator to pole. The lapse rate in the active parts of the cells would be more-or-less adiabatic; in between it would be smaller (with temperature inversions common at night).
Hey Myrrh you are not stupid. Since last year I’ve been chasing up your statement that visible light does not create heat and believe me the info has not been easy to find and even when I find some it always conflicts with the one I found before.
Anyway I’ve come to the conclusion that you are correct. IR radiation is what warns the atmosphere and not visible radiation. Thank you.
Another paper backing me up.
http://adsabs.harvard.edu/abs/1997PhRvE..56.6729T
“Nonlinear heat transport in a dilute gas in the presence of gravitation”
Looky here boys. If heat is transported more easily in one direction than another then heat will flow in the direction of least resistance. This is what happens in a non-convecting atmosphere. Heat flows preferentially towards the ground until there is enough back pressure from the higher kinetic energy to prevent further flow in that direction. Pressure and gravity come to a stalemate (except in a black hole) and the treaty that ends the war is called the adiabatic lapse rate. Some of you boys would come up with some really interesting kinds of stars with your misunderstanding of the asymmetric directional effect of gravity on heat transport. Or rather your denial that gravity HAS an asymmetric effect on heat transport…
I’ll look around for more papers. Given this is a first order effect from first principles in classical thermodynamics I find it hard to believe it wasn’t first described in the 19th century.
A physicist says:
January 25, 2012 at 10:23 am
“These gas centrifuge “experiments” concretely affirm Brown’s theoretical arguments: the observed equilibrium temperature distribution is isothermal. Indeed, the multibillion-$ isotope separation industry would fail otherwise.”
While I would agree that such centrifuges could in principle provide an experimental test of the hypothesis, it is not clear to me that their actual operation necessarily provides conclusive data on this question. They may not be sufficiently well insulated, or isolated from thermal and other energy flows, say – because there is no particular engineering requirement to do so. There might, for example, be some net warming at the top and net cooling at the bottom (the former due to waste heat from the centrifuge machinery, the latter due to air cooling enhanced by the spin).
(I apologise if the reference you gave – which is not accessible to me – already answers these points.)
Guys, please be aware that many things you try to apply were derived by assuming no external fields.
Dr. Brown,
Thank you for this post. It has encouraged me to think more deeply about the gravitation based temerature theories that I have kind of ignored. I want to do more background reading to get up to speed (I’m a tax lawyer with some undergrad physics, so I’m slow digesting this stuff), but there is one thing in your write-up that I’m having trouble with on a conceptual level.
You seem to have a problem with something as simple as gravity causing an isolated gas to be in an equilibrium state of different temperatures in different regions. But ignoring the semantics of general relativity vs Newtonian gravity, gravity is a force and causes objects with mass to accelerate. So, I don’t quite understand why gravity couldn’t provide the force to run the heat engine.
And aren’t there examples of gravity giving rise to a perpetual motion machine? It is the gravity of the earth (causing the constant acceleration of the moon and resulting in an orbit) combined with gravity of the moon that causes the tides which we can harness to produce work.
And I believe there are examples of gravity applied to a gas in uniform thermal equilibrium with significant consequences. In particular, I’m thinking of an interstellar gas cloud that comes in contact with gravity. The gravity causes the gas cloud to condense, and the condensing gas increases in temperature and pressure. If the mass is sufficient, a star is born.
Have I misinterpreted your concern or am I missing something?
Silver Ralph says:
January 25, 2012 at 2:57 pm
Not on Earth. But on a hypothetical planet with an isothermal surface and a transparent atmosphere or a very tall insulated cylinder, sure. You just need a surface temperature of 30C (the degree symbol is unnecessary) and a lot of time. Temperature in thermodynamics has a very precise definition. By that definition, a single molecule or atom does not have a temperature. You can plug its kinetic energy into the Boltzmann equation, but the result is meaningless. A cloud of gas moving at nearly the speed of light could have a temperature close to absolute zero because the frame of reference would be the center of mass of the cloud and the temperature of the gas would be the related to the rms velocity with respect to that reference frame. Or think of a meteor coming in from deep space. It would have a very high kinetic energy with reference to the center of the Earth, but if you stuck a thermometer in it before it hit the atmosphere, it would be very cold.
So a thermometer reads according to the average kinetic energy of the molecules that hit it, not the rate that the molecules hit it.
Eric Atkerson says:
January 25, 2012 at 3:47 pm
Energy has units of force (mass times acceleration) times distance or kg m²/s². Gravity is a force, but it has to move something or there is no energy. But at thermodynamic equilibrium, nothing is moving. If something did move, it would only do it once. Some source of energy would then be needed to lift it back up again.
Joules Verne says:
January 25, 2012 at 3:16 pm
No. Heat always flows from hot to cold. It may flow faster when the temperature gradient is negative than when it is positive, but it still flows only from hot to cold.
My bold…
http://www.theweatherprediction.com/basic/equations/
9. The dry adiabatic lapse rate
The change in temperature with height of a parcel of air if relative humidity is less than 100%
dT/dz = g/cp
Units = ms^-2J^-1kgK = ms^-2kg^-1m^-1s^2m^-1kgK = Km^-1
g = gravity 9.81 ms^-2
cp = 1004 Jkg^-1K^-1
Interpretation: The dry adiabatic lapse rate is a direct function of gravity. Since gravity is basically a constant, the dry adiabatic lapse rate is basically a constant.
Example problem: What is the dry adiabatic lapse rate on the planet Venus? How does this compare to the dry adiabatic lapse rate on Earth? The gravity on Venus is 0.904 that of earth. Assume the atmosphere of Venus is pure CO2 (it is actually 96%). The cp of C02 is 840 Jkg^-1K^-1.
Answer: First find gravity on Venus = 9.8ms^-2(0.904) = 8.87ms^-2
dT/dz = 8.87ms^-2/840 Jkg^-1K^-1 = 10.6 ° K/km = 10.6° C/km
A rising parcel of dry air on Venus cools at about the same rate as on Earth
“”””” Eric Atkerson says:
January 25, 2012 at 3:47 pm
Dr. Brown,
Thank you for this post. It has encouraged me to think more deeply about the gravitation based temerature theories that I have kind of ignored. I want to do more background reading to get up to speed (I’m a tax lawyer with some undergrad physics, so I’m slow digesting this stuff), but there is one thing in your write-up that I’m having trouble with on a conceptual level. “””””
Stick to the tax law Eric.
1/ In equilibrium, macroscopic state variables do not vary with time.
2/ Thermodynamic state variables are only measurable and only defined in equilibrium.
In particular your condensing gas cloud system is NOT in equilibrium.
Zero’th law of thermodynamics:- Systems that are in thermal equilibrium with a given system are in thermal equilibrium with each other. Professor Brown’s column of gas is in thermal equilibrium (throughout), and in particular the top is in thermal equilibrium with the bottom; ergo both are in (simultaneous) thermal equilibrium with each other, and also with some third system to which we might attach the label; THERMOMETER. Ergo the whole system MUST BE ISO-THERMAL.
As has been said on several occasions, and I believe Prof Brown said the same thing, a system like your condensing gas cloud, which is collapsing under the effect of gravitational attraction, is having WORK done on it, as a consequence of the gravitational FORCE acting over a DISTANCE; the distance travelled by the molecules during the collapse, and as those molecules close on each other and begin to have collisions with each other, which will turn the pre-collision molecular trajectories into a chaotic set of trajectories in all directions which is exactly what constitutes the Temperature of the gas. It is this conversion of an earlier orderly set of trajectories (towards the common center of mass of the gas cloud) into a chaotic set is why we call it “heat”. It can no longer return itself to the previous orderly motions before the molecules began to collide with each other and it is the work done by the force of gravity as it collects up the molecules that is getting “wasted” in the form of heat, and can only partially be converted back to work, and is why the Temperature is increasing.
Brown is quite correct in stating that if the posited system DOES maintain a permanent Temperature differential from top to bottom, then a thermal conductor would continually convey “heat” from the hotter bottom, to the colder top. I would use Type II-A diamond instead of silver, to pump the “heat” faster.
Sorry, a system in Thermal equilibrium is isothermal, and the much discussed star lit system is NOT in thermal equilibrium, since the star is continually supplying energy to the bottom of the gas.
“”””” Joules Verne says:
January 25, 2012 at 2:00 pm
George E. Smith; says:
January 25, 2012 at 12:52 pm
“There you just shot your self in the head. A gas, ideal or not, cannot consist of a single molecule.”
Ummm… I think it can’t exist as a liquid or solid because that requires proximal arrangement with neighboring molecules. A molecule is a gas generally when it is very isolated from neighbors so that it can flit about traversing a great number of molecular radii without hitting anything else. “””””
I have a simple rule; I never get between someone, and a cliff they are determined to jump off; so go ahead and jump. Perhaps I can hold your wallet for you while you jump.
There are plenty of people willing and able to learn; wasting energy and time on those determined to not learn, is not something I do.
Yes, Joules. In a gravity, on a rotating planet that is illuminated on only one side that possesses and night and a day then temperatures differences will cause weather that will move the gassious atmosphere into some kind lapse rate. The actual lapse rate will be a mix of dry and wet lapse rate if humidity is involved.
Now, climate scientists are repeatingly making an assumption to take solar insolation received by the sun on a disk that equals the cross section of a planet (i.e. the earth at 1364 +/- 3 w/m^2), then taking that face-on power and dividing by 4 to make average insolation, steady state, 24 hours/day, without night and day. They do this so that the math is easier. But, as has been shown by me, Willis, Dr. Brown and may others, a constant insolation, constant temperature ground must lead to an isothermal atmosphere.
BOTH ARE CORRECT! BUT THEY ARE INCOMPATIBLE.
If you want to work with a lapse rate, don’t divide solar insolation by 4 !!! Do not start with 240 W/m^2 after the albedo, or even 342 W/m^2 average incoming. Don’t start with a dead planet. You have already committed the error in initial conditions. Average insolation cannot create a lapse rate. It must be an isothermal atmosphere, whatever it’s composition. “It’s Dead, Jim”. But it is only a fiction, a Toy Model, that has no reality. 240 W/m2 might be mathematically correct, but it has no basis reality.
If you want a lapse rate, you must choose a insolation model with a day and night.
One that warms the ground in the day and cools at night.
One in which heat is expressed in temperature – OR is stored as heat of fusion, latent heat, heat of vaporization, heat capacity and conduction into the ground and water.
The lesson I have learned this month is that any scientific paper or theory that divides solar insolation by four and then works with a lapse rate should be marked as untrustworthy. It is founded on false, if not conflicting, physical assumptions.
Joules Verne said @ January 25, 2012 at 3:16 pm
Blimey! And I always thought the flow of heat was from hot to cold. Time to start burning those physics textbooks folks. Send everyone with a PhD, or BSc in physics back to uni to re-earn their degrees… [/sarc]
Robert Brown, it is really quite amusing how many here aren’t even considering your little experiment but something else entirely. They’d fail an exam through not reading the question and not answering it but answering something else.
You however, are getting hung up on CO2. H2O vapor is the main greenhouse gas by far in Planet Earth’s atmosphere. It is a very effective IR absorbing gas present in concentrations 25 to 100 times that of CO2 and overlaps the CO2 absorption band and has a significant band where CO2 doesn’t absorb(this is why 35% extra CO2 has no measurable effect). It also exists as ice crystals and liquid droplets with their own CO2 emission characteristics. It seems to me that the tropopause is the average altitude at which the water has essentially all precipitated out. This is the end of the cooling effect of greenhouse gases. Which I consider to be good evidence that CO2 as a greenhouse gas is a bit player. Above that the stratosphere is isothermal as convection mostly cannot operate and then you also get at slightly higher altitudes the solar UV absoprtion which seems to overwhelm the effect of radiating CO2 causing cooling.
For those who seem to have difficulty with why heat flows:
Pressure drives mass flow
Voltage drives current flow
Temperature drives heat flow
DeWitt Payne says:
January 25, 2012 at 4:25 pm
“No. Heat always flows from hot to cold. ”
Due to Boltzman distribution there will always be some flow in both directions. Net flow is from hot to cold. This is the basic misunderstanding with people who deny the mechanism by which greenhouses gases raise surface equilibrium temperature. They somehow believe that a warm object prevents a colder object from radiating. No such thing happens of course. Radiation flows in both directions with a greater flow from the warmer to the colder. The warmer object can’t stop the colder from emitting photons. All it can do is throw more photons at the colder object than the colder object is emitting.
The same principle of two way flow applies to energy transport by conduction. A few hot molecules in a net cooler ensemble will hop on over to the warmer side. There’s just more frequent hopping in the other direction. Maxwell’s Demon is a hypothetical little guy that sits at a gate between two gas reservoirs at equal temperature. When he sees a hotter than average molecule heading across the divide in one direction he opens the gate. When he sees colder than average molecule going in the opposite direction he opens the gate. He keeps to gate closed to all others. Thus the hotter molecules are sequestered on one side and the cooler molecules on the other.
The age old question is whether or not Maxwell’s Demon can operate the gate with less work than he can extract from the temperature gradient he creates. If he can do that it constitutes a perpetual motion machine.
Gravity is Maxwell’s Demon. Brown thinks gravity isn’t complex enough to be a demon but he’s quite clearly wrong. Maxwell’s Demon is not constrained by complexity. The Demon only requires a differential coefficient of conduction distinguished by direction. In this case gravity does exactly that and the gate sits between higher and lower elevations.
Brown is quite justifiably reluctant to believe that Maxwell’s Demon in this case needs less work to operate the gate than he can get out of the gradient he creates. I agree. There is no perpetual motion machine to be had here. Brown just can’t seem to understand the forces that are powering the demon. He works by using gravitational energy to open the gate in one direction and he uses kinetic energy to open it in the other direction. The net result is a wash because he is sorting the molecules not by total energy but rather by form of energy. Entropy is about total energy on either side of a boundary not about the specific forms of energy. If there’s no difference in total energy across the boundary then there’s nothing to equalize and it’s already sitting in a state of maximum entropy.
A simple pendulum is an example of something that (discounting friction) will swing back and forth endlessly translating kinetic energy to gravitional and back again. There is no energy expended in the translation. But if you try to extract energy you’ll damp the motion of the pendulum and gravity won’t start it swinging again just as gravity won’t add energy back into the atmosphere if you remove some by leveraging the adiabatic lapse rate. You’ll just end up with a colder atmosphere like you’ll end up with slower pendulum in the classic case.
A physicist says:
January 25, 2012 at 10:23 am
“These gas centrifuge “experiments” concretely affirm Brown’s theoretical arguments: the observed equilibrium temperature distribution is isothermal. Indeed, the multibillion-$ isotope separation industry would fail otherwise.”
Isotope separation in centrifuges is by molecular weight. A temperature gradient would have no effect one way or another on that. A physicist should know that. A fifth grader should know that.
@ Payne
Not sure why you say nothing is moving in thermodynamic equilibrium. The gas molecules are moving and they have a mass that can be acted upon.
Robert Brown: “There is Paul Birch’s analysis of Velasco, which seems to be a full stat mech computation that arrives at the same conclusion.”
It’s true that Velasco et al. is a statistical-mechanical analysis. But it’s not true that “arrives at the same conclusion.” Quite the contrary. In connection with their Equation 8, what Velasco et al. say is, “i.e., for a finite adiabatically enclosed ideal gas in a gravitational field the average molecular kinetic energy decreases with height.”
So, if you think for yourself and you believe that temperature is mean molecular translational kinetic energy, and if you believe that lapse rate is a change of this quantity with altitude, then you will not “arrive at the same conclusion.” And, if you can read Equation 8, you’ll conclude that it specifies a non-zero lapse rate at equilibrium no matter how may molecules are in the column.
On the other hand, you can accept Paul Birch’s analysis, which in my view is nothing more than so redefining lapse rate as to exclude anything exhibited by a maximum-entropy configuration. I don’t find his reasoning compelling. But decide for yourself whether you find it comes within shouting distance of rigorous.
Also, none of this really matters to the original issue, which is Jelbring’s theory, because the lapse rate Velasco et al. dictate is so small as to be undetectable: if they’re right, too, Jelbring is wrong. It merely means that “the correct static equilibrium distribution of gas in the system is the usual isothermal distribution” is not strictly true.
Joules Verne says:
January 25, 2012 at 5:08 pm
Regarding your link to Phys. Rev. E 56, 6729–6734 (1997) Nonlinear heat transport in a dilute gas in the presence of gravitation, did you read the article or even scan the abstract? The abstract refers to Navier-Stokes. That’s the equations for fluid flow. It looks to me like the temperature, and thus the pressure, gradient is perpendicular to the gravitational field, thus inducing horizontal flow. But there is no flow in this experiment. I fail to see the relevance.
Joules:
No. Your statement “They somehow believe that a warm object prevents a colder object from radiating” is incorrect. Go and read what they do believe: http://climate-change-theory.com/RadiationAbsorption.html
Briefly, the warmer body (Earth’s surface) is not affected by radiation from the cooler one (the atmosphere) because that radiation does not have enough energy (high enough frequency) to bring about the conversion of its energy into thermal energy.
Now, if you don’t accept that, then explain these two observed facts ….
(1) A gas does not absorb spontaneous radiation from an emitter that is cooler than itself, but does do so when the same emitter becomes warmer than itself.
(2) Dew on the ground (shaded from direct Sunlight) can remain there all day (even when ground and air are above 0 deg.C) so why doesn’t backradiation melt it?
“”””” Eric Atkerson says:
January 25, 2012 at 6:03 pm
@ Payne
Not sure why you say nothing is moving in thermodynamic equilibrium. The gas molecules are moving and they have a mass that can be acted upon. “””””
Thermodynamic equilibrium is a MACROSCOPIC PROPERTY of systems; the average velocity (a VECTOR) is precisely zero when the system is in equilbrium. The system is not exchanging energy or matter with anything else.
Eric Atkerson says:
January 25, 2012 at 6:03 pm
There is no organized bulk movement. The molecular movement is isotropic and random with an average velocity over all molecules of zero. That’s why you have to take the root mean square of the velocities
@ George Smith
But tax gets boring at times so it is good to have a diversion…
My only thought on the gas cloud example is that gravity can act as a heater (maybe a literal pressure cooker) of sorts.
I want to think about Dr Brown’s argument and your response to me a little more, but it would be helpful if you wouldn’t mind clarifying one thing just to make sure we’re not talking past one another. Putting Jelbring’s paper and Prof Brown’s exact example to the side do you think that we could extract work from a gas that is isolated from external heat sources, but is not isolated from gravity (can we use gravity as a replacement bunsen burner)?
@ Payne
To get temperature, yes. But that doesn’t mean that gravity won’t have any effect on the molecules. And it seems to me that the molecules closest to the source of gravity will end up with a higher average velocity than the molecules further away. After a while I would expect the system to reach a steady state under the influence of gravity that would be similar to an open system that is exposed to a constant heat source at the bottom.
@Joules Verne
I have greatly enjoyed each of your posts. Iwill read the linked article DeWitt doesn’t see as relevant – might agree, might not. I am still of two minds because there are several ways for an isothermal column to be disrupted vertically: Is it hotter on top when there is no radiation into space or at the bottom where teh gas is compressed? The Lettered above cannot even agree on what ‘temperature’ is. Everyone seems to be building models of convenience, leaving out parts here and there. This silly part of this is that the scenario is arbitrary and unreal and ultimately of no value at all.
@ Ye who have Names to be wise: Stop appealing to your own authority. My version of Feynmann: If you can’t explain it to each other, you do not understand it. 40% of Fortune 500 companies are run by CEO’s with no post-secondary education. Schools are filled with examples of sense-dulling and closure. Science degrees have been devalued by the sheer number of ‘scientists’ who have greedily participated in the largest, most expensive sky-is-falling scam ever perpetrated on humanity known as catastrophic anthropogenic global warming. We plebs don’t trust you any more. You gotta explain it from now on.
Even on this little blog it has been mentioned (above) that the narrow CO2 emission band is basically blank at the TOA (because of CO2 saturation at only 390 ppm). Read Prof Lu, 2010 on the implications of recent high resolution IR frequency distribution. Critical thinking is the oxygen of the educated if unschooled mind. Some kings have no clothes.
Willis, can we move on to real atmospheres? This is Angels dancing on a pin head.
Correction: That should read …
“FROST on the ground (shaded from direct Sunlight) can remain there all day (even when ground and air are above 0 deg.C) so why doesn’t backradiation melt it?”
Note (in the link* below) that both the ground beneath and the air just above the frost were each just above freezing point, so there should be some conduction into the frost, but no radiation out of it. However, if the backradiation really does have about a quarter of the power of the Sun at noon and the backradiation from a cooler atmosphere really is able to impart thermal energy into the frost, then that frost should have melted at least as quickly as it would have in the Sun for a couple of hours. After all, water molecules should absorb IR radiation, shouldn’t they?
Well Prof Claes Johnson has shown why they don’t when they are warmer than the source.
And if backradiation all day long can’t even melt a bit of frost, how much warming will it cause in the oceans?
* http://climaterealists.com/index.php?id=9004
Crispin: Whilst I trust you know my position on all this, I do not like pushing the “CO2 saturation” concept. Firstly, bands only appear blank at TOA because CO2 scatters radiation and hence, when you point an instrument at some place on Earth, very little appears to come directly towards you from that point. Warmists will argue that the bands just get wider,
None of this matters anyway, because the energy will be mostly converted to thermal energy which can then transfer to other molecules (by collision) and end up being emitted by water vapour for example. Any emission to the surface will not be absorbed and converted to thermal energy (because it comes from a cooler source) and so all radiation from the atmosphere eventually ends up going to space. Hence carbon dioxide molecules have a cooling role radiating away that thermal energy which they acquire from oxygen and nitrogen molecules that cannot radiate themselves. It also absorbs and sends back to space some of the Sun’s incident radiation which is in the IR spectrum, hence also having a cooling effect in this manner.
Dr. Brown, George E. Smith, Willis, and a couple of others, Thank You.
I want to thank you for this educational opportunity. I have read all the comments that have been presented on this thread as well as other threads. Thank you for explaining the physics as I learned it. Now I feel much better that I could not fully grasp the gravitational temperature effect.
If one can’t follow the thought experiment presented by Dr. Brown, then an understanding will likely be very difficult, a tough nut to crack. Some who like myself are the slowest to grasp something may be most likely to become the greatest supporters of if when we do because we fought tooth and nail not to believe in it. Hence my learning process, quite skeptical with regards to anything concerning ‘climate related’. WUWT and the open discussion here is the greatest venue to acheive that type of learning experience. When every conceivable argument is presented as well as the facts, I feel confident with my knowledge when I walk away. Thanks to all.
robr says:
January 24, 2012 at 9:32 pm
The DALR is defined as g / Cp, where g is gravity and Cp is the specific heat of the atmosphere at constant pressure. Since I see no pressure term in there, I’m gonna say no.
(Bear in mind, however, that if you double the gravity, you’ll double surface pressure more or less. And so both pressure and “g” will change, and also DALR will change … but DALR will change because of the “g” term, not because of the pressure.)
Unfortunately, there is no simple answer to that one, as you are talking about a complete planetary climate system on an imaginary planet, and the pressure would have a host of different effects on winds, evaporation, all kinds of things.
So if anyone gives you a yes or no answer to the second question, they’re blowing smoke.
All the best,
w.
don penman says:
January 24, 2012 at 9:42 pm
Cool. Step out of a window, and tell gravity you’ve decided not to obey the law. There’s big money in it … selling tickets. Like getting energy from gravity, however, it’s a one-time thing.
w.
The problem outlined by Dr. Brown is interesting but largely irrelevant to the issue of whether the surface would be warmer in the absence of greenhouse gases.
Here is my reasoning on that.
It’s the analogy to the passive solar water heating system. First lets get a few things clear on that.
A good passive solar system does not need a greenhouse for the collectors to operate well. Often they use just plain black piping. It works nearly as well as pipes in a greenhouse because the 1,000 plus watts of solar radiation far exceeds radiation losses without the greenhouse. The pipes do not ever get warm enough due to the convection occurring in the water system bringing constant cooler water to the inside of the pipes.
Greenhousing the pipes only adds a few degrees to the system and is often not done as that’s the most expensive part of the system. (convection also ensures the surface does not equilibriate to the average daily temperature reading above the surface. Error is greatest at night.)
The heat you get in a passive system is far in excess of the daily average temperature.
Its important to understand this as well. We are looking at incremental warming not warming from the greenhouse effect itself which is already incorporated in the ambient local temperatures.
Finally, we should note that a favorite tactic of folks arguing this point is they want to simplify it by applying uniform radiation. These are analogies like Willis was using to argue against the gravitational effect. But uniform radiation would cause our passive water heating system to fail. All we would have would be water at the ambient local temperature.
The passive system uses gravity and convection but it entirely depends upon a diurnal cycle to obtain a higher average and in no depends upon the radiative effect of the medium in the storage system.
Thus it doesn’t matter a whit if after we invent an atmosphere isolated from any external interactions what it does in those states. The world of Jelbring is only relevant for ruling out external effects from explaining the actual state of the atmosphere at the moment the world is imagined. Thus what it does afterwards is truly irrelevant. It is relevant to how gravity does it but not to whether gravity does it or not.
The AGW advocates would like for us to believe that convection is caused by a radiative atmosphere but the atmosphere inside the pipes of the water system is not radiating, yet it warms and it warms purely by convection and acceptance of radiation at the surface (the collector level)
So what are the results? Well if Jelbring’s conclusions are correct that the adiabatic lapse rate is stable and it probably has a 50% chance of being so (or 49% if you really want to argue it) then gravity causes the surface all by itself to be warmer than it would be without an atmosphere.
And what would be the case if it weren’t stable like Dr Brown claims? Well then it would be like the passive solar hot water system that does not have a defined lapse rate but does convect under a varying heat source and averages a greater temperature than the ambient local temperature (which has the GHG effect included already). Indeed the system would equilibriate as soon as you either turn off the sun or set it at a uniform level of radiation.
So the conclusion is there is 1) Jelbring’s lapse rate is not stable so some great portion of the ATE (redefined GHE) comes from gravity enabled by the variability of downward surface radiation.
Or 2)
Jelbring’s lapse rate is stable so the ATE comes from gravity and variability of the downward surface radiation can be averaged and you get the same result.
What will be interesting is in the details of how this is being correlated to other worlds. And of course Dr. Brown and crew are certainly welcome and encouraged to do the same as one should be able to tease out the differences implied by the two different theories.
Better get that space program back on steroids is all I can say.
Bill Hunter says
“First lets get a few things clear on that. A good passive solar system does not need a greenhouse for the collectors to operate well. Often they use just plain black piping. It works nearly as well as pipes in a greenhouse because the 1,000 plus watts of solar radiation far exceeds radiation losses without the greenhouse. The pipes do not ever get warm enough due to the convection occurring in the water system bringing constant cooler water to the inside of the pipes. Greenhousing the pipes only adds a few degrees to the system and is often not done as that’s the most expensive part of the system. (convection also ensures the surface does not equilibriate to the average daily temperature reading above the surface. Error is greatest at night.) ”
Thanks for this practical information it backs up another practical investigation from Penn State Uni on ethylene polytunnel greenhouse.
Basically the project was to find if it made any sense to add Infra Red absorbers to polyethylene plastic for use in agricultural plastic greenhouses.
Polyethylene is IR transparent like the Rocksalt used in Woods Experiment.
The addition of IR absorbers to the plastic made it equivalent to “glass”
The results of the study show that( Page2 )
…”IR blocking films may occasionally raise night temperatures” (by less than 1.5C) “the trend does not seem to be consistent over time”
http://www.hort.cornell.edu/hightunnel/about/research/general/penn_state_plastic_study.pdf
When matter heats up due to compression or from falling into a gravity field, where does the extra thermal energy come from?
What standard model particle delivers the additional energy?
The matter heats up but where does the energy come from.
We know photons or EM radiation can deliver energy through the Electro-Magnetic Force. We know energy is added from the Weak Force in nuclear reactions according to E=M*C^2, the Strong Force does not operate unless Neutron Stars are Black Holes are involved. The Gravitational Force may compress space-time so the molecules themselves may just be more energetic in a space compressed 3-D environment.
But I have never seen an explanation of where the extra energy comes from when matter is heated up due to compression or when matter falls into a gravity well.
It IS coming from somewhere. It is already there, it is just a question of what is the ultimate source of this thermal energy.
Bill Illis says
“When matter heats up due to compression or from falling into a gravity field, where does the extra thermal energy come from? ”
If the falling is at constant speed it comes from the work done by atmosphere at that level (PdV work).
Its the opposite of the work done by a rising expanding parcel of air which does PdV work ON its surrounding atmosphere.
DeWitt Payne says: January 25, 2012 at 4:13 pm
Silver Ralph says:January 25, 2012 at 2:57 pm
If, on the other hand, he means the temperature of the total airmass, as measured by a standard thermometer, then he should know that you could never get the air at 50,000 ft to be +30oc. Just not possible. Never going to happen. So Dr Brown cannot mean this.
Not on Earth. But on a hypothetical planet with an isothermal surface and a transparent atmosphere or a very tall insulated cylinder, sure. You just need a surface temperature of 30C (the degree symbol is unnecessary) and a lot of time.
__________________________________________________________
Thank you for the scientific definition of temperature.
However, this is hardly explaining our atmosphere. We have a surface that is sort of isothermal (within a band of, say, +40 to -40oc); we have a fairly transparent atmosphere; and we have had a lot of time to run the experiment (several million years).
Yet the average temperature at 50,000 ft is around -80 oc. And there is no chance of the ‘temperature’ at 50,000 ft ever equalling the suposed average surface temperature of +15oc (ISA defined atmosphere), no matter how sensitive your thermometer. So if your explanation is correct, then why is the Earth so unlike the idealised system?
In short, I still cannot see the difference between the silver wire experiment, and the normal atmosphere. Ok, so the silver wire has greater conductivity to transport het to the upper atmosphere, but the less conductive real atmosphere has had several million years to transport surface heat to the top of the atmosphere and it would appear that it has still not achieved anything like equilibrium temperature.
Some basic explanations without the math is required, I feel.
PS In science you may use ‘c’ as opposed to ‘oc’, but in the rest of the world ‘c’ means ‘cents’ (dollars and….).
.
Bill:
One component of total thermal energy is gravitational potential energy. Thus a portion of total thermal energy can interchange with potential energy.
The assumption is that the compression occurs when the body of gas is physically lowered closer to the Earth and thus loses PE. That loss of PE transfers into a gain of KE which contibutes to thermal energy raising the temperature. (Compare the interchange between PE and KE with a pendulum, or when you car starts to roll down a hill.) The opposite occurs when warm air rises.
PS As you probably know, this is a reason for using the term “thermal energy” rather than “(ocean) heat content” as used by you-know-who. There is no fixed thing which is “heat content” and heat is energy in transit as distinct from energy itself.
As a “layman” I find this very interesting.
Fig 2 doesn’t really convince me of anything. I like the analogy of the spinning wheel. Let’s say we have a spinning ring in a vacuum with no gravity. The ring will spin forever right? Now imagine we attach a couple gears and a shaft from a fixed point. The gears will simply connect the shaft to the inner ring causing it to spin. If the gears are all frictionless the shaft will rotate forever.
I know the analogy doesn’t fit but it’s close. Obviously if we apply any friction to the shaft (a generator) the ring will stop spinning. Saying any heat runnin through the wire is a perpetual motion machine just doesnt ring true.
Having said all that I think the temperature will equalize in the cylinder and no heat will flow through the wire.
Applying this to our atmosphere is the hard part for me. So we have an atmosphere with a hot side and a cold side. This seems to easily explain the temperature gradient.
What I wonder about is the effect of doubling or tripling the nitrogen thereby increasing pressure. I can’t see this making the hot aide hotter. I imagine the cold side will just move farther out. The atmosphere would be a greater reservoir of heat but the temp wouldn’t be higher.
Taking into account day/night, the rate of conduction at the surface and the differences between surface and atmospheric temperatures oh and GHGs all make things more confusing!
As I suspected this notion that gravity produces a lapse rate goes WAY back. James Clerk Maxwell hisself proposed it in 1866. If I’m wrong I’m in very good company. Here’s a nice writeup on the history. Many physicists to the present day have carried Maxwell’s torch. It is not settled science. Maxwell himself collaborated with Boltzman to formulate the Maxwell-Boltzman distribution law that made the column isothermal. Maxwell continued to question its validity though and many since then have also questioned it. At least Maxwell was a good scientist skeptical of his own work his entire life.
http://philosophyfaculty.ucsd.edu/faculty/ccallender/index_files/maxwell.doc
much more at link above
“”””” Bill Illis says:
January 25, 2012 at 8:22 pm
When matter heats up due to compression or from falling into a gravity field, where does the extra thermal energy come from?
What standard model particle delivers the additional energy?
The matter heats up but where does the energy come from “””””
Bill there really is not much to it. Imagine a humungous cloud of gas but assume the individual moelcules are separated far enough in space. that they basically never (or extremely seldom) ever see each other, so there ar no collisions. Jeans showed that any such cloud no matter how uniform in properties, if the total mass exceeds some threshold value, becomes unstable, and a region of slightly higher density appears. That becomes a gravitational “magnet” attracting every molecule towards that region, which will simply increase the density inhomogeneity.
So your “gravity field”, is the mutual self attraction of all of those molecules to each other, and each molecule will start to move in the direction of the center of mass of all the molecules. So every molecule will be headed towards the same point. Now it is also possible even likely, that the initial velocity vector for each molecule is not directedf exactly at the CM point, but to slightly off center points; and this will result in a rotary momentum, in addition to the linear momentum towards the CM.
Initially there are basically no collisions, so the Temperature is essentially zero (kelvins).
As the molecules move towards each other the density increases, and the inverse sqare law causes the gravity to increase, so the molecules are accelerating towards the CM, ever faster, andf also starting to show signs of a net cloud rotation, depending on the initial state.
Eventually the density will get high enough, and the initial directional non uniformity sufficient to allow molecules to start banging into each other. These collisions are random events, and so they start to change the directed collapse towards a common focal point, into a more chaotic pattern, and the directed acceleration starts to get attenuated by the chaotic scattering of the colliding particles. This is the first sign of both pressure (change in momentum of particles in collision) and also Temperature. The Temperature represents the statistical distribution of individual molecular motions; relative to the common center of mass of the collapsiong cloud. The conversion from an orderly directed collapse to a more chaotic structure, represents the appearance of waste “heat” as the original work done by the force of gravity operating over the distance the molecule moves.
So the source of the energy is simply the work done by gravity forcr times distance. The potential energy of the molecules far removed from the CM of the entire cloud, is slowly being converted into kinetic energy of the onrushing molecular mass, but once collisions start occurring to disturb the uniform collapse, some of that kinetic energy gets converted to “heat” represented by the random distribution of the kinetic energies relative to the CM space co-ordinate frame. The density will continue to increase without limit, as the gravitational force increases due to the inverse square law of gravity, and the rotation will speed up, to conserve the angular momentum of the initial state, as the size decreases, so the moment of inertia continues to decline, and angular velocity increases to keep I. omega^2 constant.
It is the original potential energy of the distantly spaced gravitationally attracted molecules, that first converts to a directed kionetic energy and angular momentum, and finally start so dissipate as heat, once the molecules start to collide.
So the Temperature will increase without limit, until hydrogen thermo-nuclear “burning” starts. The energy released now heats the gas till it becomes an ionised plasma due to the high Temperature, the escape of this centraally generated energy to the suface of the “cloud” , now a proto star will eventually stop the collapse as the outer layers also heat, and the outer plasma will become opaque to the EM radiation generted at the million degree buring interface. So long as the hydrogen keeps converting to helium, the star will shine as a”main sequence star” and thr gravitational collapse will have been halted by the thermo-nuclear energy released.
The problem with the earth’s atmosphere is that there isn’t near enough gas to reach the density and Temperature to start hydrogen conversion, so the collapse stops when the pressure generated by gravitymatches the gravity force. The heating that occurs during collapse due to the work done by gravity, is eventually radiated away assuming no star is nearby, to supply new energy.
We hqppen to have such a star that delivers EM energy to the bottom of the transparent atmosphere, and that energy warms the bottom of the atmosphere by all the well known thermal processes, until the energy loss rate, eventually limited by radiation, matches the supply rate from the star. It is the heating of the atmosphere bottom, by the star light, that creates the outgoing Temperature lapse rate. It is NOT gravity that creates the Temperature gradient.
Silver Ralph and others:
I confess I have not read many posts on this thread, so I may be repeating something said by others. NASA data shows mean temperatures going down to around -60 deg.C in the troposphere, then back up by about 40 degrees in the stratosphere. Then I understand they go back down to around -100 deg.C at the mesopause, but then can be much warmer than the surface (even over +100 deg.C) in the thermosphere.
Any experiments in glass jars, cardboard boxes etc (including those of Arrhenius, Wood and Nahle) can never emulate an open atmosphere. One reason is that the inside surfaces of the containers absorb (and transmit) thermal energy, and can contribute to overall warming or cooling. Also pressure is nearly uniform, so downward conduction occurs and the Second Law applies. However, one “result” of the Second Law (see Wikipedia) is uniform pressure, and obviously that doesn’t apply in the atmosphere.
Hence, adiabatic temperature variations are a fact of life in the atmosphere. Furthermore, there will never be a stable state due to weather conditions. Energy is continually entering the atmosphere (probably more than 50% at the surface) and then of course it takes a finite time for warm air to rise by convection, cooling as it does so. In fact I understand that its motion is more cyclic, rising in equatorial regions and falling at the poles where inversion can prevail.
Then there are further complications when incident solar radiation causes some warming, and evaporation and radiation “springboard” some of the energy from the surface to somewhat higher altitudes.
The lapse rate is far from constant, there being a fall of roughly twice as much in the first 14,000 feet as in the next 11,000 feet for example, according to NASA data. This may be due to the springboarding of latent energy in evaporated water going up to cloud levels.
No one really has a hope of modelling it all accurately – ever.
Pick a good spot to live on this planet – and enjoy your weather!
@Bill Hunter. Thank you for that example where the diurnal day-night pumping is so essential for a passive solar hot-water system.
As I wrote earlier in the tread, the “average insolation” concept so often used to explain the climate energy balance misses so much. You have given us a great example: Solar Heaters don’t work without a night and day.
“”””” Eric Atkerson says:
January 25, 2012 at 7:02 pm
@ George Smith
But tax gets boring at times so it is good to have a diversion… “””””
The short answer Eric is yes; but only for a short period of time.
Gravity provides a FORCE, that attracts the gas towards the ground. That force is m.g, where m is the mass of the molecule, and g is the acceleration due to gravity, so m.g is literally the WEIGHT in the gravity field of that molecule.
When that force pulls the molecule down some distance, the WORK done is the force times the DISTANCE moved . WORK is FORCE times DISTANCE (moved). ENERGY is the CAPACITY for DOING WORK.. Now of course the gravity will change with distance so you would have to do a calculus integration to get the correct answer.
As the gas drops under gravity and work is done by gravity compressing that gas; that work gets converted into heat as the molecular collisions increase at the higher density and the pressure goes up. The compression WORK gets converted to heat; BUT, once the collapse stops when teh pressure builds up enough to stop the fall, then the gas starts to lose energy and cool, by radiation, and eventually the whole thing would settle at a fixed Temperature. That assumes no other source of energy such as a nearby star. So yes gravity can create heat in compressing the gas but it is a transient event.
DeWitt Payne says: January 25, 2012 at 4:13 pm
So a thermometer reads according to the average kinetic energy of the molecules that hit it, not the rate that the molecules hit it.
_________________________________________________________
Sounds counter-intuitive, to me.
So an aircraft travelling at the normal TAS of 450kts (say, 900kph) at 40,000 ft, increases the measured temperature of the air by, say 30oc (-30oc TAT, as opposed to -60oc OAT). Are you saying that this measured temperature increase is solely due to an increase in the (relative) speed of each molecule hitting the probe, rather than the increased number of molecules hitting the probe? (The number of collisions with the temperature probe increases dramatically with increasing speed, as you might expect.)
I always thought that the surface warming of an aircraft (several hundred degrees-worth on Concorde), was due to the increased number of molecules hitting the airfame, and not the individual molecule’s increased velocity..
.
I don’t understand what all this commotion is about, this is not a novel problem!
This is not an appropriate application of thermodynamics, vis analysis of the atmospheric temperature lapse rate. The ideal gas atmosphere, or also the real atmosphere, isn’t isothermic. There is no “thermodynamic equilibrium” in the real atmosphere or even in an ideal gas atmosphere. There is no “heat flow”. There is no actual “heat”, anywhere at all, in this argument.
The atmospheric temperature lapse rate is a very simple statistical mechanical problem; it is energy partition, elastic molecules colliding in a gravitational field. A simple one dimensional model demonstrates it. Contrary to Dr Browns arguments, there are no Maxwell’s demons in the adiabatic lapse rate, and no other thermodynamic shibboleths. No “heat” is necessary, or even actually exists. There is no “perpetual motion” anywhere in the atmospheric temperature lapse rate, any more than the Laplacian elliptic operator, energy partition, and orbiting planets are “perpetual motion”. Gravity applies to molecules as well as to planets. Absent planetary gravitons, the atmospheric temperature lapse rate would still exist if little elastic strings were used to tie all the air molecules to the Earth.
addendum: The atmosphere temperature profile is described by bulk gas properties (ideal gas law) up to the tropopause, and gas radiative transport properties in and above the stratosphere.
addendum: The formalizations of the arguments here are very confusing; “heat”, “work”,
“equilibrium”, etc. The only real things involved here are electrons, photons and gravity (and extra inert mass proportional to electrons). This isn’t difficult!
Joules Verne. Thank you for your contributions on this thread.
You have been tenacious and your “temperature” was never raised. You have approached the issue from numerous angles to explain your reasoning and helped to improve my appreciation of all of the relevant points.
Others have presented their arguments forcefully too. But – despite it being described as a textbook case (an appeal to authority), I remain unconvinced by the arguments at the top of this thread.
http://philosophyfaculty.ucsd.edu/faculty/ccallender/index_files/maxwell.doc
Interesting link Joules Verne, Thanks.
Silver Ralph wrote “Sounds counter-intuitive, to me”
You should trust your intuition a little less it would seem. The plane warms by friction. The thermometer measures temperature, not the amount of friction. Temperature has nothing to do with the density of molecules. If it did, consider a near vacuum such as between the walls of a vacuum flask – does that have a temperature of near absolute zero? Hardly!
George E. Smith; Jan 25, 2012 at 9:23 pm
“It is the heating of the atmosphere bottom, by the star light, that creates the outgoing Temperature lapse rate. It is NOT gravity that creates the Temperature gradient.”
This simplistic summation really does not take into account all processes involved. For a start you ignore energy transfer by phase change. You appear to disregard the physical rate at which warm air rises by convection. When the warm air rises, I’m not even sure that you take into account the conversion of the change in gravitational potential energy to thermal energy, do you? If so, why isn’t gravity in your result?
What, may I ask, is wrong with this computation which gives a very different result?
http://claesjohnson.blogspot.com/2010/09/lapse-rate-vs-radiative-forcing.html
George, Robert G Brown (and others)
Please be sure to read the first linked item in the paper I linked above, namely http://www.nada.kth.se/~cgjoh/atmothermo.pdf
Of course I realise that this is leading to a very different result, but it is one which agrees quantitatively with reality and, in this case, I go with Professor Claes Johnson’s computations and obviously much more comprehensive coverage of the various processes in the atmosphere.
Bill Hunter said @ January 25, 2012 at 7:48 pm
Gosh! I’ve been wasting money on putting greenhouse film on my greenhouse when I didn’t really need any. Whoda thunkit? People who use greenhouse film to raise the temperature around their crops are all idiots wasting their money? Don’t think so Bill…
Pompous said:
“Gosh! I’ve been wasting money on putting greenhouse film on my greenhouse when I didn’t really need any. Whoda thunkit? People who use greenhouse film to raise the temperature around their crops are all idiots wasting their money? Don’t think so Bill…”
Check and see if your fancy IR film is also moisture resistant. Reducing the thickness of the moisture layer on the inside of the cover has more effect than the IR coating.
Joe Born says:
January 25, 2012 at 6:04 pm
“It’s true that Velasco et al. is a statistical-mechanical analysis. But it’s not true that “arrives at the same conclusion.” Quite the contrary. In connection with their Equation 8, what Velasco et al. say is, “i.e., for a finite adiabatically enclosed ideal gas in a gravitational field the average molecular kinetic energy decreases with height.””
They do come to the same conclusion; they quite clearly show – and state – that, for any macroscopic system, canonic or microcanonic – the sort of system we are actually interested in here – the result is isothermal, as it should be. You keep refusing to accept – or even adequately acknowledge – that their Equation 8 doesn’t mean what you want it to mean, because temperature itself doesn’t mean what you think it means in that isolated small-number regime.
Joe: ” … if … you believe that temperature is mean molecular translational kinetic energy … ”
But that’s the point. For small isolated systems it isn’t. The limiting case of the single isolated particle, which has no thermodynamic temperature, proves this.
Velasco et al do not calculate a thermodynamic lapse rate in the small-number microcanonic regime at all. They do not prove it to be isothermal; nor do they prove the contrary. What they do show is that their statistical mechanics confirms the thermodynamic conclusion that – for ensembles large enough to apply said thermodynamics to – the answer is indeed isothermal.
Joe: “On the other hand, you can accept Paul Birch’s analysis, which in my view is nothing more than so redefining lapse rate as to exclude anything exhibited by a maximum-entropy configuration.”
Please stop misquoting me. I said nothing whatsoever about “maximum entropy”. I didn’t even mention entropy. I didn’t need to. My “redefinition” (not actually a redefinition at all, but the utterly bog-standard original definition) is simply the statement that things in thermal equilibrium are at the same temperature; that’s what “same temperature” means.
Doug Cotton said @ January 26, 2012 at 1:15 am
No. It lacks a defined temperature because temperature does depend on density of molecules. Consider a universe in which there is exactly one molecule. What temperature is it? Consider a universe in which there are two molecules and we know the exact distance between them. What is their temperature? Rinse and repeat…
Pompous said:
“Consider a universe in which there are two molecules and we know the exact distance between them. What is their temperature? Rinse and repeat…”
Come on, you sound more intelligent than that. You have just described an instant in time when you know the distance between two particles. You have not indicated mass, velocity, acceleration, vectors…
Rinse and repeat…
robr says:
January 24, 2012 at 9:32 pm
“Does the atmospheric pressure, no GH gases, play a role in the dry adiabatic lapse rate?”
Willis Eschenbach says:
January 25, 2012 at 7:40 pm
“The DALR is defined as g / Cp, where g is gravity and Cp is the specific heat of the atmosphere at constant pressure. Since I see no pressure term in there, I’m gonna say no. ”
Hmmm. Interesting.
What is Cp, or “specific heat”, really?
http://en.wikipedia.org/wiki/Heat_capacity
I am just trying to repeat all this again (25 years since my school-days);
If Cp had been “molar heat capacity” in that formula, then pressure wouldnt matter IMO.
But, since Cp is “Geat Capacity per unit mass” of a material….that means that if you increase the mass…then Cp increase. Right? Or am I misunderstanding this sentence?
So, how can you increase the mass? Well, increased pressure is really just that the number of molcules per volume unit has increased. Right? Hence, the mass has increased. And therefore Cp increase.
So, In my opinion , yes, increased pressure => increased mass => increased Cp.
Robert Brown’s refutation is contrived and irrelevant.
Any column of any substance from the top to the bottom of the cylinder is subject to the same gravity field with gravitational constant g as the gas in the cylinder. Or, what is the same according to the general theory of relativity, the cylinder with gas as well as the conductor (whatever material it is made of) are subject to the same constant acceleration (vector) of g m/s2. Therefore, the same temperature gradient will appear in the conductor and or along the walls of the cylinder as exists in the gas. The bottom of the cylinder pushes against the gas mass and any other top-to-bottom material like an adiabatic piston, raising the temperature at the bottom, whereas the top of the cylinder pulls like a similar piston, decreasing the temperature at the top.
As long as the acceleration is maintained, the temperature gradient in the direction of the acceleration vector will be maintained. If heat is added to the system by radiation from outside, the average temperature will increase, but as long as the acceleration continues, a temperature gradient between top and bottom of the system will be maintained.
Doug, with regard to your selection that particular article, as the knight says in the film Indiana Jones and the Last Crusade “You have chosen … poorly.” To chose better, let’s recall the Freeman Dyson quote that several recent WUWT posters have quoted (I think Willis Eschenbach was the first):
Here on WUWT, it should be clear to everyone that the “clear physical picture” approach may have worked well for Fermi (who was one of the greatest physicists of his generation), but it does not work wll in on-line forums, for the simple reason that that various posters advocate physical pictures that are so diverse, and so contradictory in their predictions, that most of these physical pictures must be wrong, even though some them may be right. So unless one is similarly talented to Fermi, physical pictures are not all that trustworthy.
That brings us to Fermi’s second option: “have a precise and self-consistent mathematical formalism”. Regrettably, here too the conceptual challenges are severe. In recent years the trend is toward geometric theories of thermodynamics, and a recommended starting point is Quevedo and Vazquez, The geometry of thermodynamics, whose geometric language is explained in John Lee’s highly regarded Introduction to Smooth Manifolds (known to students as “Smooth Introduction to Manifolds”). Here “geometry” is an older name for what nowadays is called “mathematical naturality.”
The increasing and unifying dominance of mathematically natural geometric frameworks in describing classical, quantum, and thermodynamical physics is a relatively recent development (mainly since the 1980s), and these frameworks constitute the nearest approach that we have to Fermi’s “precise and self-consistent mathematical formalism”.
The third option is a brute-force fine-grained numerical simulation of atoms bouncing off one-another. Here a good reference is Frenkel and Smit’s Understanding Molecular Simulation: from Algorithms to Applications.
So when should one have confidence? Whenever all three theoretical approaches (physical, geometric, and computational) lead to the same conclusion, and moreover agree with experiments and observation, then confidence is justified.
And so I want to emphasize that, in the present case, all three paths (physical, geometric, and computational) lead to the same conclusion, which is entirely consistent with experiments and observation: Gravito-thermal theories are just plain wrong.
Joules Verne says at 1/25 8:57pm:
Interesting find. Thanks for posting; on my reading list for later today. Means this thread is open since 1866!
One point to make:
“Later, he derived the Maxwell-Boltzmann distribution law that made the temperature the same throughout the column.”
This wording could incorrectly be interpreted that M-B derived the column isothermal. Actually, the M-B theory starts & ends with the assumption that there are no external forces (no electrostatic, no gravity, etc.) acting on the ideal particles in the column to come up with the distribution of speeds.
That quoted statement above makes more sense if the word “made” is replaced with “assumed” to get the proper meaning. Can only correctly apply the M-B distribution to column without gravity which is then isothermal since the particle kinetic energy velocities are isotropic.
One could speculate the ideal particle speed distribution is deterministic in a gravity field also and M-B could be extended to include gravity – get a non-isothermal column in hydrostatic equilibrium due to non-isotropic particle velocities.
Trick says
“Actually, the M-B theory starts & ends with the assumption that there are no external forces (no electrostatic, no gravity, etc.) acting on the ideal particles in the column to come up with the distribution of speeds.”
Yes and when some use the MB statistics to prove the isothermal distribution in a gravitational field they are indulging in a fine bit of circular reasoning.
Albert Stienstra said @ January 26, 2012 at 4:44 am
While The Git’s brains are subject to the force of gravity, they do not plummet through his arse. They are prevented from accelerating through there by the opposing force of electrostatic attraction between the molecules in his skull. Another way of saying this is that The Git’s brains, skull and arse are all in the same inertial reference frame. The molecules of gas in the cylinder are in the same inertial reference frame and are therefore not accelerating. That’s if I’m remembering Einsteinian relativity correctly. If I’m wrong, then my brains may well plummet through my arse 🙁
Doug Cotton says:
Temperature has nothing to do with the density of molecules. If it did, consider a near vacuum such as between the walls of a vacuum flask – does that have a temperature of near absolute zero? Hardly!
————————————————————–
Poor analogy, Doug. The space in between a vacuum flask recieves a lot of radiative energy, which just confuses the matter. And yes, a stationary molecule in a vacuum in deep space, with no interractions with other molecules which recieves little or no radiative energy, will aproximate to near absolute zero.
Please find another analogy at explains your idea better.
.
.
@Joe Born
Let’s look at this another way. There are three particles adiabatically isolated in a box. You tell me their temperature is 100K. I say, no it’s 300K. How could we tell? What measurement could we perform that would not contradict the very conditions of the experiment? So then you tell me, oh yes, it’s 300K at the bottom, but only 100K at the top. Again, how could we tell? How could we measure this supposed lapse rate? You can stick a thermometer or a thermocouple in a real gas. You can’t in a microcanonic ensemble comprising just a few particles in all. And if we can’t measure this temperature or lapse rate, what do those concepts even mean? You’re into the land of metaphysics, not hard practical thermodynamics.
Robert Brown:
The connection of a ‘shorting’ thermal conductor to your isolated column in Fig.2 could be viewed in a similar light to a shorting wire across an electrical capacitor.
When a capacitor is shorted, the voltage across its terminals drops to zero very quickly, but, due to dielectric absorption, when the shorting link is removed, the capacitor ‘self charges’, some times up to 10% of its originally charged value (a real problem in high voltage engineering).
The dielectric has ‘remembered’ a portion of the previously applied voltage.
Many theories exist about what could cause the dielectric absorption effect, but it would appear to be related to distortion of molecules etc
A capacitor dielectric is an insulator, just like gases in the atmosphere.
Could Gravity have a similar effect on molecules, distorting orbits etc?
Your isolated column without shorting conductor would stabilise with a slightly higher temperature at the lower end and be thermally settled (ie no further change).
If the thermal short was connected, as per Fig.2, I believe that (similar to the capacitor example) the effective slight temperature difference between the top of the container and the bottom would be neutralised.
The question is, after removing the short, would the temperature gradient reinstate itself, in whole, or in part?
There is no loss or gain in energy in this system. The temperature in the column has a gradient due to gravity.
The addition and removal of the short allows for energy distribution, no work is done.
Similar to two columns filled with gas, connected by two pipe, one top, one bottom.
Inject some heat energy in the left column, the gas within the columns would circulate and the temperature would equalise, no work done, no energy lost or gained.
Some papers that record the influence that gravity has upon physical properties of matter:
“Effect of gravity on critical opalescence: The turbidity” found that gravity does effect scattering.
“Gravity influence on thermal relaxation near the critical point” specific heat is influenced by gravity.
regards
S.
Ralph says:
January 25, 2012 at 9:22 am
Stephen Goddard was expounding this ‘temperature is due to pressure’ theory some time ago on WUWT. Where is he, to defend his theory??
http://wattsupwiththat.com/2010/05/06/hyperventilating-on-venus/
Come on Stephen, what say you now?
Pretty much banned by Anthony and now has his own excellent web site at
http://www.real-science.com/
A physicist says:
January 25, 2012 at 12:29 pm Are you sure, it actually says.
“Dirac’s equation treats the centrifuge in a way that is independent of the internal operation of the machine. It is useful in that it correctly guides the experimentalist to seek foremost high peripheral velocities (v a ), second low temperatures (T),”
Further to my previous post,
Magnetism observed in a gas for the first time in:
http://web.mit.edu/newsoffice/2009/magnetic-gas-0918.html
Shows that we are just getting to understand non-obvious properties of gas.
If gas (currently under extreme conditions) can demonstrate magnetism, which is usually considered related to the alignment of molecules etc, we should not be surprised if other new physical properties emerge.
Steve Richards says:
January 26, 2012 at 6:42 am
A gas of lithium atoms at 0.00000015 K. Yes that’s relevant.
thepompousgit says:
January 26, 2012 at 3:47 am
“Gosh! I’ve been wasting money on putting greenhouse film on my greenhouse when I didn’t really need any. Whoda thunkit? People who use greenhouse film to raise the temperature around their crops are all idiots wasting their money? Don’t think so Bill…”
First I said greenhousing the collectors increases the efficiency of the system. So your argument is without merit. The system still works albiet less efficiently without a greenhouse.
Sure you can create a thought experiment that denies it works but you cannot ignore the fact that non-greenhoused passive solar water heating solutions are physically demonstrated to work each and every day.
The difference is conduction.
If you walk barefoot on a hot asphalt street during mid-day you start burning your feet. When you pick up your foot it feels cooler but mid day the temperature is not much cooler 3 inches off the ground. The difference is you removed conduction. This effect occurs regardless of whether you are inside or outside a greenhouse.
Thus the water system works despite radiation. On a sunny day when its 70 degrees at the beach according to the weather service the sand can be 120 degrees with no greenhouse. This 50 degree differential can be bled off into a water heating system via conduction and convection. Add some insulation and the fact that convection is self regulating where it only runs when the water in the storage is colder than the water in the collectors and you get without any doubt whatsoever, average water temperatures in excess of the local ambient average temperature.
There is absolutely no question this works. An argument that radiation control by a greenhouse boosts the performance is acknowledged and was acknowledged. You need to go back and read the original post.
People can complain their system does not deliver much hot water but systems have to be properly sized so as to allow for people washing dishes and taking showers and replacing the water with underground piped water which is at the temperature of the daily average ambient temperature.
We have a meaured above surface atmosphere temperature measurement going on. It is a poor proxy for surface temperature as it also should be measuring too warm. At night convection does not run so the atmosphere will be warmer than the ground by a considerable margin. During the day the surface is warmer than where its measured. But its difference is less because convection is moving the heat from the surface to the collectors at a much faster rate.
Opps I misspoke. Above I said: “An argument that radiation control by a greenhouse boosts the performance is acknowledged and was acknowledged.” was incorrect. It should read “An argument that heat loss control (ostensibly primarily by control of ambient convection outside of the collectors) by a greenhouse is acknowledged and was acknowledged.”
Yes. To flesh out the reasoning:
(1) The UF6 gas at the outer rim of a gas centrifuge is at many atmospheres of pressure and room temperature (or optionally a little warmer, as supplied by a heating coil), per these pictures of an operating centrifuge cascade.
(2) The UF6 gas at the inner axis is a very low pressure: a tiny fraction of an atmosphere (far lower than the pressure in the anvil cloud of thunderstorm).
(3) “Gravito-thermal” theory predicts that the on-axis gas temperature will be far below room temperature, in consequence of the adiabatic lapse rate combined with a large pressure gradient.
(4) Yet as it turns out, UF6 freezes via a gas->solid transition at lower-than-room temperatures (just as packets of moist air, lifted high into a thunderstorm’s anvil cloud, and thus cooled adiabatically by the pressure drop, condense their H20 vapor as hail and snow).
(5) It is observed that gas centrifuges do not fill with frozen UF6 on-axis; thus the “gravito-thermal” prediction of a stable adiabatic temperature gradient is disconfirmed.
A physicist,
“(5) It is observed that gas centrifuges do not fill with frozen UF6 on-axis; thus the “gravito-thermal” prediction of a stable adiabatic temperature gradient is disconfirmed.”
I am sorry, but, is this centrifuge operating in space away from the earth’s gravitational field?? If not, it proves NOTHING!!!
I have a question / thought experiment. Please keep in mind that I am only a student here in this discussion.
Assume that we take the non-GHG, as Dr Brown has used in his thought experiment, and placed it (1 cu. ft.) at 1 atmosphere pressure (absolute) in a baloon and placed that inside 1 cu. ft. insulated rigid container at say 70 F while aboard the space station at zero gravity. Please note the absolute pressure is 1 atmosphere so the baloon had to have a potential volume of 1 cu. ft. empty.
Next we quickly fly down and land in Florida near/at mean sea level (1 atmosphere pressure) where the temperature is 70 F. Now we have the gas still in the container at the same pressure as the ambient air pressure and the volume hasn’t changed. The only difference is that now the gas is under the influence of gravity.
First question: Did gravity heat (temp increase) the gas in the container?
Second question: If we opened the container and pulled out the baloon, would it immediately shrink or expand or stay at 1 cu. ft.? Would there be a temperature change of the gas?
Remember, I’m only a student here so your comments are appreciated.
Folks, Maxwell, Lagrange, Hamilton and the rest figured this out before there were even molecules and atoms ;-).
Thermodynamics is only a generalization. It is an absolutely correct generalization, but it is still only a generalization. It was developed before anyone knew what the bits and pieces of the world are. It is still useful and most used when someone analyzing a system doesn’t want to, or can’t, find and account for all of the real pieces of the system, atoms, photons and gravitons.
This thread shows the great difficultly of applying the “laws of thermodynamics” correctly to an open system. “Heat” is not real, it is only a useful concept. Just as “thermal equilibrium”, “ideal gas law”, “action”, etc are not real, but are only useful concepts when applied correctly. *** Molecules and elastic collisions and conservation of momentum and conservation of energy are REAL and are ABSOLUTELY TRUE. *** One only needs to look at a single molecule in motion, subject to a linear force (like gravity) to develop a “atmospheric temperature lapse rate”. The Lagrangian of the molecule is an absolutely correct description of the state of the molecule; momentum and energy are absolutely conserved. Emmy Noether is still correct today 😉
I finally plucked up the courage to read Hans Jelbring’s 2003 paper for myself. Not as painful as I expected.
My main aim in reading it was to see (a) whether his theory would apply to liquids as well as gases, and (b) whether he attributed the temperature gradient to compression/rarefaction or to some other mechanism.
On (a), his model is explicitly confined to ‘ideal gases’, but I see nothing in his reasoning that would not apply equally to liquids.
On (b), he does not offer any mechanism at all to explain the temperature gradient, which he deduces from general energetic considerations. Of course, if his proof of the temperature gradient is sound, it must stand whether or not we can find a detailed mechanism to explain it, but the lack of a mechanism is unfortunate.
But is the proof sound? It hinges on the proposition that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an
average sense, will have the same total energy.” Since the total energy of a molecule for present purposes consists mainly of kinetic energy and gravitational potential energy (chemical, electrical, etc, energy not being very relevant), it follows from this proposition (if true) that those molecules which have high gravitational potential energy must have low kinetic energy and vice versa. Since molecules higher in the atmosphere have greater gravitational potential energy, they must have lower kinetic energy, hence the temperature higher in the atmosphere is lower, etc.
But is it true that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy”? Leaving aside the apparent neglect of conduction, and the vagueness of the phrase “in an average sense”, the proposition seems to me fallacious, at least for the point at issue. The movement of molecules in a gas is a quasi-random process. The kinetic energy and direction of motion of a molecule fluctuate from moment to moment, depending on its collisions with other molecules. Those molecules which are ‘high’ in the atmosphere (in Jelbring’s simplified world, which has no external heat source) are those which happen to have had a history in which there is a surplus of impulses in the direction ‘up’. In general there is no reason to think that they have ‘swapped’ their own kinetic energy for potential energy. Over the long term, no doubt, we would expect all molecules “in an average sense”, to have equal kinetic energy, equal potential energy, and equal total energy. But Jelbring’s proposition is not concerned with ‘the long term’, but with the actual distribution of energy at any given moment, and for this purpose I don’t think it can carry the weight he puts on it.
That’s my opinion anyway, but I’m a mere amateur, and I’m reluctant to believe that a professional scientist would commit a blatant fallacy. What do others think?
Robert Birch: “Please stop misquoting me. I said nothing whatsoever about “maximum entropy”. I didn’t even mention entropy. I didn’t need to. My “redefinition” (not actually a redefinition at all, but the utterly bog-standard original definition) is simply the statement that things in thermal equilibrium are at the same temperature; that’s what “same temperature” means.”
You’re absolutely right: you did not explicitly mention entropy. I think of a system of things in thermal equilibrium as being in a maximum-entropy state, and I inadvertently made that substitution. I apologize; the last thing I want to do is antagonize you, since you and DeWitt Payne are the only participants here who engaged substantively, at my request, on the Velasco et al. paper, and I do sincerely appreciate it.
Actually, with the exception of whether in the posed hypothetical the gas is allowed to exchange heat with the walls that confine it–you think so, I don’t–I believe we agree on the ultimate facts. It’s just that to me the most basic definition of temperature is indeed mean molecular translational kinetic energy; it avoids imprecise qualifications like “for ensembles large enough to apply said thermodynamics to.”
In fact, I think in essence I agree with what you mean by “What [Velasco et al.] do show is that their statistical mechanics confirms the thermodynamic conclusion that – for ensembles large enough to apply said thermodynamics to – the answer is indeed isothermal.” At least I agree if by that you mean that according to Velasco et al. the rate at which per-molecule average translational-kinetic-energy in a microcanonical ensemble changes with altitude approaches zero–i.e., the system approaches isothermality–as the total system energy approaches infinity. (Rather than total system energy, I’ve been speaking of the number of molecules, but there was an assumption–unstated on my part, mea culpa–that the average energy per molecule remained the same. As perusal of Velasco’s Equation 8 reveals, it’s more precise to speak in terms of total system energy.) That is, for any delta > 0 there exists an energy value E_d such that rate of change is less than delta (“is indeed isothermal”) whenever the total system energy is greater than E_d (the ensemble is “large enough to apply said thermodynamics to”). I agree with that. In fact, I emphasized it when I was discussing Loschmidt’s and Jelbring’s theories over at Tallbloke’s Talkshop.
On this thread I instead emphasized that the rate of mean kinetic-energy change with altitude–which I call lapse rate, as you don’t consider proper–remains non-zero for any finite number of molecules (more precisely, for any finite total system energy). The reason I did so was to emphasize that Dr. Brown’s refutation actually begged the question; it tacitly assumed that any non-zero lapse-rate-exhibiting system (such as the gas-wire system) would not be in a maximum-entropy state. What I think he should have based it on is a showing that a system exhibiting the specific lapse rate Jelbring argues for would not be in a maximum-entropy state.
In contrast, even if their mean molecular translational kinetic energies differed in accordance with Velasco et al.’s Equation 8, your view as I understand it is that the top and the bottom of a gas column would have no temperature difference, because heat flows from hot to cold, and no heat flows there. No temperature difference, so no lapse rate, and Dr. Brown’s refutation is adequate as is.
Incidentally, DeWitt Payne largely agrees with you, saying that “temperature is only strictly proportional to the kinetic energy in the canonical limit. . . . So you can’t directly convert kinetic energy to temperature for a microcanonical ensemble,” i.e., for a thermally isolated column of air, such as the one in Dr. Brown’s thought experiment. I don’t find this view satisfying, since it is in a microcanonical ensemble that the thought experiment in which mean kinetic energy is derived from temperature in accordance with PV = NkT is carried out –with, incidentally, no requirement that it be “large enough to apply said thermodynamics to.”
But there is one thing I’ll take back, and that is my attempt to picture the (minuscule) temperature lapse rate as resulting from offsetting diffusion and drift fluxes. That probably works as an alternate view of the pressure gradient, but for lapse rate it problematically implies that gravity drives heat flow.
Anyway, I again thank you for participating.
“”””” Jim Z says:
January 26, 2012 at 9:18 am
Folks, Maxwell, Lagrange, Hamilton and the rest figured this out before there were even molecules and atoms ;-).
Thermodynamics is only a generalization. It is an absolutely correct generalization, but it is still only a generalization “””””
Right on Jim Z, Thermodynamic properties of a system and thermodynamic state variables are MACROSCOPIC PROPERTIES, and generally relate to the statistical properties of a large number of “particles”, or if you will a large number of “degrees of freedom” to which the equipartition principle can be applied. In a “gas” in thermal equilibrium, the individual particles are not stationary, with no motion, but at any time the vector sum of the momenta of all the particles is zero, so the center of mass of the “particles” is going nowhere, or is in free flight relative to some frame of reference that is external to the system, and per Einstein’s relativity, is somewhat irrelevant as far as the internal state of the system itself.And thermodynamic equilibrium requires that the system IS isothermal, meaning it has a common Temperature everywhere. But remember that Temperature is itself a macroscopic property, since it involves the statistical distribution of the kinetic energies of a very large number of “particles.” That distribution is the Maxwell-Boltzmann distribution, that can be found in any elementary Physics text book.
The concept of the Temperature of a single particle, is meaningless in a thermodynamic sense.
However I have argued, that we can actually talk about the Temperature of individual particles.
BUT, that also is a statistical situation. At any time, we can argue that a system in thermal equilibrium, let’s say 22.4 litres of STP gas, contains 6.023E+23 particles, and everyone of those particles occupies one of the 6.023E+23 “spots” on the Maxwell-Boltzmann graph. Next time we look, all the cells are still occupied, but everyone played musical chairs, so generally nobody is in the same place on the chart. Over time it is reasonable to presume that some particular “particle” will eventually occupy each one of those cells at some time. In my whimsical phantasy world, my “Mother Gaia”, who is simply the mother of all Maxwell’s demons, can read the serial number on each and everyone of those particles from # 1 up to # 6.023E+23, so she sees them flitting around; but we can’t. So MG sees that eventually any particular particle can and will occupy every single lattice cell point on the chart, bearing in mind that each momentum value has a certain number of occupants as given by the M-B curve.
So if MG audits the movements of particle # 1066 on the M-B chart, over time, she will find that it goes everywhere on the chart, so SHE can argue that the statistical kinetic energy value of #1066 over time, is exactly the same curve, as the flash picture of the present locations of the whole assemblage of particles.
So Mother Gaia knows that over time, the statistics for any one particle is the same as the instantaneous statistics of the whole gas so she is entitled to claim that the TEMPERATURE of any one particle is identical to the Temperature of the whole system. But we can’t know that because we can’t read the serial numbers on all those particles; they are indistinguishable to us.
So that is why I argue, that Mother Gaia (MY Maxwell’s demon) has a thermometer on EVERY particle; molecule or atom or whatever, which is why in her world the weather and climate is exactly what it is supposed to be, because she has experimentally observed the Temperature of everything, and calculated what their average really is; not that the state of the climate is ever determined only by some Temperature.
We humans on the other hand do a really lousy job of sampling the Temperatures compared to MG; and also sadly compared to what the Nyquist criterion tells us that we MUST do, in order for us to get the true average Temperature correct.
So single molecules do not have any instantaneous Temperature, because Temperature relates to molecular collisions, which don’t happen instantaneously. Temperature is a macroscopic state variable, just like everything in thermodynamics.
“”””” DeWitt Payne says:
January 26, 2012 at 7:27 am
Steve Richards says:
January 26, 2012 at 6:42 am
Further to my previous post,
Magnetism observed in a gas for the first time
A gas of lithium atoms at 0.00000015 K. Yes that’s relevant. “””””
But are we talking Ferromagnetism, or is it either diamagnetism or paramagnetism, which are far less rare ?
Paul Birch: “How could we measure this supposed lapse rate? You can stick a thermometer or a thermocouple in a real gas. You can’t in a microcanonic ensemble comprising just a few particles in all. And if we can’t measure this temperature or lapse rate, what do those concepts even mean? You’re into the land of metaphysics, not hard practical thermodynamics.”
Paul, I understand your point of view, but I personally think there is a sound when a tree falls in the forest even if no one’s around to hear it.
Bill Hunter said @ January 26, 2012 at 8:24 am
No. You said:
No numbers; just armwaving. You say “Greenhousing… only adds a few degrees to the system”. I say, if I don’t open the vents on my greenhouse early enough in the day, the crop will rapidly die. That’s not just “a few degrees”. But you remind me that I don’t have numbers. Time for some experiments so I can put some numbers on the greenhouse effect that is not The Greenhouse Effect (so to speak).
“”””” Steve Richards says:
January 26, 2012 at 6:15 am
Robert Brown:
The connection of a ‘shorting’ thermal conductor to your isolated column in Fig.2 could be viewed in a similar light to a shorting wire across an electrical capacitor.
When a capacitor is shorted, the voltage across its terminals drops to zero very quickly, but, due to dielectric absorption, when the shorting link is removed, the capacitor ‘self charges’, some times up to 10% of its originally charged value (a real problem in high voltage engineering).
The dielectric has ‘remembered’ a portion of the previously applied voltage. “””””
Dielectric “soak” is not so much of a mystery. Many types of good dielectric insulators, used in capacitors, are also piezo-electric. So the result of an electric field in a charged capacitor is a mechanical distortion of the molecules or atoms of the substance. Just the electric field itself will apply mechanical forces to the dielectric material. The effect of dielectric soak applies on charge, just as it does on discharge. Apply a charging VR circuit to a capacitor (current limited) and it will charge to the applied Voltage; 99% in five time constants, and 99.99% in ten time constants. If the charge circuit is opened, the capacitor Voltage will change. It could go either up or down. Same thing on discharge; 99.99% discharge in 10 time constants, but after removing the discharge circuit, the Voltage will again change (also up or down).
Somewhat related, but different, is a similar behavior in electrolytic capacitors; but the mechanism is different. Capacitors of electrolytic type such as “Tantalums” have huge surface areas formed from millions of tiny particles of metal connected to each other by nanoscopic small area contacts, that are high resistance. The dielectric is formed by a thin oxide or other insulating layer on the metal surface, and the liquid or gel electrolyte is the other plate of the capacitor.
So the “Capacitor”, is actually a very large network of RC interconnected nano sized capacitors.
When a discharge circuit is closed, the charge stored on the capacitor “plates” has to flow through all those resistor interconnected particle bridges to get to the terminals and exit the capacitor. Not all of the charge successfully makes the journey before the discharge circuit is removed. The remaining trapped charge, then redistributes, untill all of the nano capacitors have the same Voltage, which registers at the open circuit terminals.
In this case, the residual Voltage is always of the same sign as the original Voltage, as not all of the original charge was removed. Yes it is always possible to use a discharge circuit that overdrives the discharge, and stores charge of the opposite sign.
Companies that make analog type oscilloscopes have to deal with the bane of dielcetric soak in capacitors all the time, since fidelity of transient signal shape is the cornerstone of their business; well at least it used to matter to companies like Tektronix.
kwik says:
January 26, 2012 at 4:25 am
I’m sorry to say, you do misunderstand it. It is the capacity per kilo of mass. Doubling the mass doesn’t change the specific heat at all.
w.
Joe Born says:
January 26, 2012 at 11:19 am
IIRC, I was among the first to “engage substantively” with you about Velasco. I pointed out to you that Velasco clearly says several times that no matter the circumstances, the column will be isothermal.
Since this didn’t agree with your preconceptions, for my heresy I was ignored.
Now other folks have looked at it. AFAIK, all of them say the same thing, that Velasco agrees with Dr. Brown that the column will be isothermal.
Only you are left alone, plaintively repeating your incorrect claim, that Velasco says it won’t be isothermal.
So someone here has not “engaged substantively” with Velasco, but it’s not me and the other commenters. Grab a mirror, my friend …
w.
Albert Stienstra’s (January 26, 2012 at 4:44 am) relativity argument is actually the best argument I have heard in favor of a permanent lapse rate. I had thought about that same idea a day or two ago.
A tube in gravity can be treated the same as a tube continually accelerating at 9.8 m^2 (eg a very long tube mounted an a spaceship). One end is continuously pressing in on the gas while the other is continuously expanding. I am not convinced, however, that this would create a permanent gradient.
Certainly if the rocket engines were suddenly turned on, gas would compress in the “back” of the tube, and would warm up there. Work would be done on the 1 m^3 of air at the back of the piston But eventually the gas would stop piling up at the back because a pressure gradient would be established. With no further compression (and no net work being done), I don’t see how the forces could continue to maintain a temperature gradient.
But it is a fascinating idea.
“”””” Doug Cotton says:
January 26, 2012 at 1:59 am
George, Robert G Brown (and others)
Please be sure to read the first linked item in the paper I linked above, namely http://www.nada.kth.se/~cgjoh/atmothermo.pdf
Of course I realise that this is leading to a very different result, but it is one which agrees quantitatively with reality and, in this case, I go with Professor Claes Johnson’s computations and obviously much more comprehensive coverage of the various processes in the atmosphere. “””””
Doug, you are obviously an expert on the subject; and admittedly, I am NOT.
You have cited this expert tome by this Professor Claes Johnson several times to counter the very specific system that Professor Robert G.Brown, of the Physics Department of Duke University, about which I plead total ignorance; the Duke U Physics dept. that is.
So I just finished reading your definitive text on the subject, from Prof Johnson, a computer scientist, I see.
I wonder if Professor Robert G. Brown knows anything at all about computer science !
Well wait a minute, this thread is about Thermodynamics, not computer science.
Johnson cites Arnold Sommerfeld as being confused about Thermodynamics; well given the time he did his important Physics,h e can be forgiven for that; his contributions to Atomic spectra and atomic Physics are landmark results.
But Prof Johnson goes on to say that he too is confused about Thermodynamics; well also understandable since he is a computer scientist; so he is forgiven for not understanding Thermodynamics.
Well specifically he stated that he cannot understand Clausius’ statement of the Second Law of Thermodynamics. Wow, what an admission, because if anybody understood Thermodynamics, and the second law, it was Clausius. He is also credited with applying the second law to first derive the Optical Sine Theorem, which in its paraxial form simplifies to the Lagrange Invariant, that applies to ALL optical systems, whether imaging or non-imaging.
Well nowhere in Professor Johnson’s admirable paper, did I find any reference to the closed system that Professor Robert G. Brown of the Duke University Department of Physics expounded on.
So Doug, you are the local expert on Prof Claes Johnson, so why don’t you cut and paste the portion of his paper that is specific to the closed system that Professor Brown analysed. Any court in the world would defend such a cut and paste as a legitimate application of the “fair use” doctrine of Copyrights, especially, since you have already made such use by linking to Professor Johnson’s paper.
And it seems to me that Johnson’s reliance on “Navier-Stokes equations of fluid dynamics” in his paper, removes it from relevence, since Brown describes a Thermal equilibrium system, and one thing about thermal equilibrium, is that NO FLUID DYNAMICS can be found in such a system, in fact nothing at all dynamic.
I’m sure that Professor Robert G. Brown of the Duke U Physics department, is perfectly capable of explaining Clausius’ statement of the second law of themodynamics to both you and Professor Claes Johnson.
Tim Folkerts says:
January 26, 2012 at 12:38 pm
So you think the Stienstra argument in favor of a permanent lapse rate is the best you’ve heard … but you just can’t figure out how it works?
Sometimes I think I’ve wandered through the looking glass. People keep coming out foursquare in favor of some cockamamie theory, saying its “the best argument that I have heard” and the like, and then they admit the DON’T KNOW HOW THE THEORY WORKS THAT THEY ARE SUPPORTING.
Tim, if you can’t explain how Stienstra’s idea will continue to maintain the gradient, how on earth can it be the best idea you’ve heard?
Please, folks, if you can’t give the elevator speech explaining how some theory works in clear and concise language, DON’T CLAIM THAT YOU SUPPORT IT. That just makes you look foolish, declaring that you support something you don’t even understand.
w.
Willis Eschenbach: “IRC, I was among the first to “engage substantively” with you about Velasco. I pointed out to you that Velasco clearly says several times that no matter the circumstances, the column will be isothermal.”
No offense meant, Willis. When I wrote that I was thinking of those who really dealt with the statistical mechanics at issue. Didn’t mean to slight you.
Willis,
Maybe I should have said it was one of the most difficult to refute rather than “best”. My point was that the relativistic argument is subtle, and provides an interesting perspective. Much like the “rising particles lose KE so it must more colder higher up” argument. Both are non-trivial and require a deep understanding of physics. If someone wants to really understand this issue, they should be able to understand (and ultimately refure) this argument.
It is rather like saying “this is the best argument I have heard for supporting Newt Gingrich, (even thought I really prefer Mitt Romney)”.
Willis says “People keep coming out foursquare in favor of some cockamamie theory… “
To paraphrase you, Willis, QUOTE MY WORDS! Where did I ever “come out foursquare in favor of” this theory like you are claiming? In fact, I specifically said “I don’t see how the forces could continue to maintain a temperature gradient.”
I actually understand (with ~ 95% confidence) this argument and I think both are ultimately wrong. After a little more thinking, I could give the “elevator speech” that refutes this argument.
I’m on your side on this issue, Willis 🙂
Joe Born says:
January 26, 2012 at 11:19 am
“Actually, with the exception of whether in the posed hypothetical the gas is allowed to exchange heat with the walls that confine it–you think so, I don’t–I believe we agree on the ultimate facts. It’s just that to me the most basic definition of temperature is indeed mean molecular translational kinetic energy; it avoids imprecise qualifications like “for ensembles large enough to apply said thermodynamics to.””
But that is just where you part company with Velasco et al. They explicitly state: “In … a finite system … the conclusion in statement (2b) is wrong …”, where statement (2b) is “Temperature is proportional to the average molecular kinetic energy”.
So your error – according to Velasco et al, as well as myself, DeWitt Payne and probably Robert Brown too – is in taking that marginal height dependence of average molecular kinetic energy for small N as a temperature lapse rate. It just isn’t.
The reason, in heuristic terms, is that this microcanonical ensemble is a combination of two essentially different things; a ballistic projectile (the first particle) and a thermodynamic gas (the rest). If we multiply Eq. 8 by N and separate out the terms in the brackets, we can see that the total kinetic energy basically comprises the ordinary thermal energy of the gas (f/2)(N-1)kT, independent of height, plus a term (-mgz) for the N=1 projectile, close enough. Of course, one can’t actually identify one particular particle as the projectile and the others as the gas, but that’s still probably a useful way of looking at it.
As for heat exchange outside the strict microcanonical ensemble, this is essential if we want to do anything at all with the gas – even if it’s only measuring its temperature, density or pressure.
Joe: “I personally think there is a sound when a tree falls in the forest even if no one’s around to hear it”
In scientific terms there is indeed no sound unless this sound can somehow be detected or measured, at least in principle. How one performs an observation, and what effect that has on the system being observed, is a crucial part of the science. Pretty much the whole of quantum physics depends on this.
Tim Folkerts says:
January 26, 2012 at 1:17 pm
Tim, my thanks, and I’m not trying to single you out. Unfortunately, your last line in the quote above is incorrect. It’s actually like saying “this is the best argument I have heard for supporting Newt Gingrich, even though I don’t have a clue what the argument means.”
I still don’t get it, Tim. You admit that you don’t understand the argument, but you think it’s the best argument you’ve heard. Read through that last sentence a few times.
Or let me put that in the way you would prefer—you admit that you don’t understand the argument, but you think it’s the most difficult argument to refute that you’ve heard. Read through that last sentence a few times.
Well, yes, it is hard to refute something you just admitted you don’t understand … so?
Tim, is your name “People”? Because I see nowhere in my statement that I said one damned thing about your words, so how could I quote words I don’t refer to? However, you seem to think I did, which should give you some cause for concern.
Tim, either you understand the guy’s theory or you don’t. At the point where you wrote and said that you thought it was one of the best theories you’d seen, you yourself admitted that you didn’t understand it.
I see people doing this all the time, just read through this thread. People are all on about some theory, saying things like that they ‘believe it has great promise’ or that ‘it resonates’ with them or their ‘gut feeling is that H&N are correct’ and the like, and they haven’t a clue what the theory says.
That’s what I was talking about, and if you’re not doing that, then you have my apologies.
w.
Joe Born says:
January 26, 2012 at 1:15 pm (Edit)
Thanks for the note, Joe, much appreciated.
My point was that Velasco dealt with the statistical mechanics at issue, and he came down strongly for isothermal, in agreement with Dr. Brown.
w.
The top of Robert Brown’s tube and the bottom of the tube are connected by the free flowing gas. For the two jars to be the same as the tube, the jars have to be connected by the wire and a free flowing gas. An air hose would do. The top of Brown’s tube has a different pressure than the bottom of the tube. Brown’s jars would have the same pressure.
kuhnkat says:
January 26, 2012 at 1:17 pm
kuhnkat, I don’t understand why operating a centrifuge at high speed on earth (as many people have proposed) is not a good test of the H&N theory.
OK, as is my habit, I’ve forsaken guessing so I just ran the numbers. The alloy tubes in a uranium centrifuge have an ID of 74.4 mm and they turn at about 100,000 rpm. This gives by my calculations a force of about 415,000 g’s at the walls.
The normal dry adiabatic lapse rate is proportional to “g’, the force of gravity, and inversely proportional to Cp, the specific heat. On earth it is 9.8°C per kilometer of elevation. The specific heat (Cp) of uranium hexafluoride gas is 370 J/kg °K, compared to 1004 for air.
With a force of 415000 g’s, that should give a lapse rate of something like eleven degrees per millimetre at the wall, decreasing to zero at the center, with an average of about 5.5°/mm. This would give a final difference over the diameter of the tubes of 200°C from the axis to the inside wall of the tube. This would be easily detected and is sure to be noticed, since (as A Physicist noted above) the UF6 would solidify in the cold temperatures near the axis of the tubes.
Since no one has ever come forwards to say “why are these centrifuges permanently staying so hot at the outside and cold on the inside, why is UF6 condensing and solidifying near the centre of the tubes”, I’m gonna say the question is settled experimentally as well as theoretically.
You can continue to believe that for some reason this is not a valid test, that the 1 g of natural gravity directed downwards somehow will invalidate the 415,000 g’s horizontally. Unless you can come up with some cogent explanation of why this is not a good test, I’m convinced.
w.
Willis Eschenbach,
You always have at least 1 G affecting the gas in the centrifuge no matter what orientation it is in if it is on the earh. The idea the there would be a lack of pressure at one end is not possible unless the centrifuge is out of the earth’snear surface gravitational field. The fact that you have a huge range of pressure does not change the 1g at the low end at right angles to the centrifuge’s action .
There is no zero pressure zone due to the earth’s gravitational field. You do accept just plain old basic gravity don’t you????
Willis Eschenbach,
I was being dense on my last post. I am not trying to claim that the whole experiment is overturned by the earth’s gravitational field. i am only pointing out that there is no zero force area in the centrifuge unless you know of some way of blocking gravity. This would be why there wouldn’t be frozen gas in the axis. Y’all can dance on all the pin heads you want, but, the gravity field is there affecting the gas. For that matter, since you are computing, what is the density of the gas toward the center when spinning?? I would think that much force could create a pretty good vacuum!!!
Willis,
I agree that many people jump onto an idea because it seems plausible given their current understanding. (Or worse, jump onto an idea because it agrees with their ideology). This is a definite problem in this thread. The fact is, thermodynamics & statistical mechanics is not easy even for those who have studied it. These are not topics that you can learn reading a few blogs.
>>”Tim, either you understand the guy’s theory or you don’t. ”
I disagree. Only a few days ago we were both pretty sure that the lapse rate should indeed to be a standard feature in a gravitational field (without the need for GHG cooling at the top of the atmosphere), because we both fell for the “particles lose KE as they rise, so it must be colder higher up.” We both understood part of the idea, but we both made a “rookie mistake”. So understanding is not a black-or-white proposition.
>>At the point where you wrote and said that
>>you thought it was one of the best theories you’d seen,
>>you yourself admitted that you didn’t understand it.
I don’t see it that way. I even described in some detail the theory and some of the reasoning behind it. I even gave a bit of the “elevator speech” that a proponent would use, while saying I didn’t accept his conclusions (in large part because the conclusions contradicted other, more convincing arguments). I did admit I wasn’t completely sure of all the implications, but that is different from not understanding at all. I’m still not sure, but I am mostly convinced that I know why it is wrong. (And if anyone really wants, I can post the elevator speech to refute this argument.)
>>That’s what I was talking about, and if you’re not doing that,
>>then you have my apologies.
Apology accepted. And I apologize for not being a little clearer about my thoughts. In the end, it is clear we are pretty much completely on the same page in this discussion.
There may be few engaging on Velasco paper b/c it is hard math. I’ll try to engage but it is hard. Admit approaching from unproven view the ideal gas column is non-isothermal in the presence of gravity.
Joe Born says at 1/26 11:19am:
“you (Paul Birch)and DeWitt Payne are the only participants here who engaged substantively, at my request, on the Velasco et al. paper, and I do sincerely appreciate it.”
Willis’ says at 1/26 12:38pm:
“I was among the first to “engage substantively” with (Joe Born) about Velasco…”
A poster above said the 2nd to last concluding Velasco paragraph is obtuse. I’ll agree with that. It contains it least one double negative maybe more.
Repeated reading of it seems to me Velasco et. al. are saying the result of the prior paper – Coombes and Laue (C&L) arriving at answer 2 being wrong – is itself wrong or at least incomplete because C&L need to add a more full explanation to “discern between the cases of a finite system and an infinite system”.
Joe Born writes look at Velasco eqn. 8. I didn’t see anyone write above for N=1 (one molecule) this very neatly collapses to KE = TE – PE of the 1 molecule. The 1st Law! Constant 1 molecule total energy = KE + PE.
KE = TE – PE being a main reasoning in my view of a non-isothermal column. For Velasco to support paradox resolving to isothermal column, this equation would have collapsed to KE = TE meaning molecular velocities are isotropic in the presence of gravity thus isothermal.
Caballero supports isotropic velocities for isothermal T only in the no gravity ideal gas column case. Add gravity & Caballero in Sec. 2.3 supports gas column T is non-isothermal.
In my view, Velasco et. al. concludes a full explanation is not yet available as of 1996 and the column of ideal gas within a gravity field is more likely non-isothermal when a full explanation is available that also “must discern between the cases of a finite system and an infinite system.”
Silver Ralph January 26, 2012 at 6:00 am
Well maybe you should read up on the thermosphere – temperatures well above 100 deg.C and not many molecules.
The radiated energy in a vacuum flask passes directly from one wall to the other and is unlikely to affect the temperature of the few molecules of air that remain in the near perfect vacuum. The walls are silver to minimise radiation anyway.
Willis wrote:
Since no one has ever come forwards to say “why are these centrifuges permanently staying so hot at the outside and cold on the inside, why is UF6 condensing and solidifying near the centre of the tubes”, I’m gonna say the question is settled experimentally as well as theoretically.
You can continue to believe that for some reason this is not a valid test, that the 1 g of natural gravity directed downwards somehow will invalidate the 415,000 g’s horizontally. Unless you can come up with some cogent explanation of why this is not a good test, I’m convinced.
I’ve chewed on this for a while. I concluded that if it were a valid test, it would suffice for me. Unfortunately, it is not a valid test.
Part of the problem is your frame of reference. If you’re using a cyclindrical geometry, then the molecules follow curved paths. However, in a rectangular geometry, the gas molecules move in straight lines between collisions. It’s simply that their collisions often send them back into the interior of the chamber.
The equivalent of gravity in this experiment would be “Centrifugal Force”. There is no such thing as “Centrifugal Force”. There is only “Centripetal Acceleration”, which occurs only at the outer edge of the centrifuge.
Caballero supports isotropic velocities for isothermal T only in the no gravity ideal gas column case. Add gravity & Caballero in Sec. 2.3 supports gas column T is non-isothermal. comes out of the system at some nonzero temperature T. The change of entropy in the system is thus
comes out of the system at some nonzero temperature T. The change of entropy in the system is thus 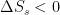 . It goes into a heat engine that (say) stores it reversibly by rolling up a string that lifts a mass.
. It goes into a heat engine that (say) stores it reversibly by rolling up a string that lifts a mass. 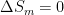 .
.

No, he doesn’t. Read 2.17, especially the exercise at the end. Or look at the exam question and solution I posted. Or learn the laws of thermodynamics. Sigh. I guess I’m going to have to post the maximum entropy argument as well.
Look, nothing — short of perhaps general relativity in extreme field conditions that measurably warp space — is going to permit a stable thermodynamic temperature gradient, because for one to exist you must not be able to use it to do work, not even in principle. There has to exist some exotic and nonlinear macroscopic constraint such that it is physically prohibited to do work off of the thermal difference. Otherwise as you do work with the thermal difference, you are reducing the heat content of the system (cooling it) and turning it into reversible work. This decreases the entropy of the universe! It’s a ten second, at a glance computation.
Finished. A system with a nonzero thermal gradient physically capable of doing work under any circumstances, including ideal ones simply cannot be in thermal equilibrium or at maximum entropy. It is an absolutely trivial homework exercise — not even a problem a conceptual exercise — to show this.
This eliminates 90% of the silly arguments that have been offered to “refute” my simple conclusions. No, an isolated gas with a thermal gradient is not at equilibrium, and does not have maximum entropy as it is capable of doing work. If the entropy of the gas does not increase while that work is being done, there is something wrong.
A very few people, perhaps intuitively realizing that one has to be incapable of doing work across the thermal gradient, have tried to argue that the thermal gradient involved cannot do work, but none of their arguments are convincing because there is nothing special about the gas at both ends. It’s an ordinary ideal gas! How could it not be capable of doing work across the thermal gradient. The only way would be if everything in the gravitaional field had exactly the same thermal lapse rate. But this is absurd on the face of it. No, they don’t. None of the proposed lapses have a universal form.
That’s why I hold out some hope for GR. That’s a difficult problem — if you warp space and time with a very large mass, you do have a bit of a problem defining temperature as energy itself gets a bit warped along with space and time as you go down into the well. However, in this case:
a) The effect is utterly negligible in any real gas for anything less massive than a star.
b) It probably cannot be measured. Your thermometers follow the same gradient as one goes up and down, and they would probably still read the same temperature as temperature itself would probably be following the curvature of spacetime.
c) It is completely irrelevant to the discussion at hand, involving a simple ideal gas in an ordinary vertical column with constant g.
This is as bad a case of wishful thinking as I have ever encountered. Most normal humans would have given up an argument once they learned that ordinary physics textbooks that are obviously uncorrupted by the IPCC completely contradict a stable thermal lapse in any closed system, not to mention common sense. Are you all really that desperate to find an alternative explanation to the Greenhouse Effect that you are willing to pretend that all of our conventional understanding of physics is wrong and Jelbring — the new Feynman, obviously — is right?
In a paper, I might add, where he does no actual work!
If you actually read the paper, he does nothing at all. There isn’t a single line of substantive algebra. He asserts his conclusion, says it is true, and stops!
A few papers have been put forth that at least try to do the work that shows that a thermal lapse might exist, but none of them are at all convincing, and none of them directly confront the obvious and egregious violation of the second law implied by the result that they are trying to prove.
Here’s the biggest hint in the world. If you ever do a whole ton of algebra and are led to a conclusion that violates the laws of thermodynamics in a context where they ought to apply, you had better be damn certain that you understand every single bit of the physics involved better than any other human alive, because you will have to justify every single step in your derivation and conclusion, and even then nobody — including you if you are wise — will believe it until and experiment directly verifies it.
rgb
Sigh, I meant decreases the entropy of the Universe in the previous reply. You know, the impossible one.
rgb
[I fixed it, thereby decreasing the local WUWT entropy, but increasing the entropy in the universe. -w.]
Bill Hunter,
A passive solar water heater and a greenhouse are not the same thing. A water heater is designed to generate hot water at some minimum temperature. So the object is to attain maximum efficiency. Each layer of glazing reduces the available power by a minimum of 4% from reflection at the front and back surfaces. And that assumes that the incident radiation is normal to the surface and neglects any absorption. It doesn’t take many layers of glazing to cut the incident power to inefficient levels, certainly no more than two. A greenhouse, by contrast, is designed to maintain a minimum temperature with the least amount of additional energy supplied by a heater. For much of the year, a greenhouse is entirely too effective and has to be ventilated and/or shaded during the day to keep the temperature from going too high.
What you really want is a wavelength selective low emissivity coating on your collector. That way the collector absorbs solar radiation with high efficiency but emits far less thermal radiation. Black chrome has an SW absorptivity to LW emissivity ratio of about 5. TiNOX, a synthetic coating, claims to have a ratio closer to 20.
Zac says:
January 25, 2012 at 3:10 pm
Hey Myrrh you are not stupid. Since last year I’ve been chasing up your statement that visible light does not create heat and believe me the info has not been easy to find and even when I find some it always conflicts with the one I found before.
Anyway I’ve come to the conclusion that you are correct. IR radiation is what warns the atmosphere and not visible radiation. Thank you.
Thanks for the vote of confidence, Zac.
I’ve been trying to find something for you, but haven’t yet..
The problem here is that this misinformation was deliberately introduced into the education system targetting primary school children first, their teachers non-specialists so could be themselves ‘educated’ in ‘science’. The classroom ‘demonstration’ opening a bottle of scent and then using erroneous physics to explain that as showing ‘carbon dioxide rapidly diffuses into the atmosphere’ is one such method. They’re the adults now who don’t have any particular interest in science but ‘remember the science from school’ and so unlikely to question whatever the AGW green agenda pushes, and even those in actual science fields where real knowledge of gas properties isn’t relelevant, but what I find astonishing though, is how many in actual science fields who come together to discuss AGW continue to not question something as basic as the difference between heat and light claims in the AGW energy budget which is well known still in the real science world. Obvious examples are light bulbs.. But there are others like this:
http://www.nytimes.com/2007/07/16/business/16thermal.html
It is now extremely difficult to find it mentioned that the direct power of heat from the Sun is what warms Earth’s land and oceans, even pages which begin their explanations by saying ‘heat and light from the Sun’ will end up garbling ‘solar’ heating the Earth, and solar refers to the shortwave of the junk energy budget, which claims only shortwave gets to the Earth’s surface to heat it, and thermal infrared doesn’t.
But you have to remember too, that sometimes they get too clever in their explanations and end up contradicting that..
http://earthobservatory.nasa.gov/Features/EnergyBalance/page6.php
..if the atmosphere is transparent to outgoing thermal infrared then it must also be transparent to incoming – claiming it doesn’t play any part in heating the Earth because it doesn’t reach the TOA let alone surface is just plain stoopid. Especially when industries all around still know the difference.
But I haven’t yet found any page which deals with the Earth’s energy budget accurately, some fudge trying to toe the line while attempting to get across that it’s the Sun’s heat and not light which heats the Earth, but even they’re few and far between, and I’ve yet to find that in any science pages specifically on the different energies from the Sun.
I must try and find it again, I found a page that went into great detail about the Sun and then simply avoided mentioning heat from it, but had a short sentence about light and that referred to chemical energy only not the AGWSF ‘converting to heat’. I found that desperately sad. It’s as if all but a few are under some hypnotic spell and those that aren’t have been forced into compromise to not rock the boat.
The equivalent of gravity in this experiment would be “Centrifugal Force”. There is no such thing as “Centrifugal Force”. There is only “Centripetal Acceleration”, which occurs only at the outer edge of the centrifuge. . The mass in the tube has to rearrange to provide this. The bottom provides the force to the things that touch it exactly as if the bottom was supporting an increased weight. The mass layers out where the force difference across any layer has to accelerate all that mass towards the center exactly as if it were supporting its weight. In the end, one gets a distribution that isn’t identical to the distribution one would get with uniform gravity or gravity that falls off like 1/r^2, but none of the differences matter to the question of thermal separation. If equilibrium is thermally separated in gravity, equilibrium would still be separated in the centrifuge.
. The mass in the tube has to rearrange to provide this. The bottom provides the force to the things that touch it exactly as if the bottom was supporting an increased weight. The mass layers out where the force difference across any layer has to accelerate all that mass towards the center exactly as if it were supporting its weight. In the end, one gets a distribution that isn’t identical to the distribution one would get with uniform gravity or gravity that falls off like 1/r^2, but none of the differences matter to the question of thermal separation. If equilibrium is thermally separated in gravity, equilibrium would still be separated in the centrifuge.
Piffle. The equivalence principle suggests that one cannot tell the difference. I agree that in a rotating frame the correction doesn’t have the same form as gravity, there is a coriolis force as well as additional pseudogravity, but this makes no difference in the argument.
Here’s the evidence. Go to your nearest grocery that gives away Helium balloons. Go over to the balloon corral and take one. Don’t be shy; if anyone asks you why a grown adult person is taking a balloon, tell them “for a physics experiment”.
Now, get back in your car to drive home. But tie the balloon to a small weight and place it so it floats freely up in the seat next you you.
When you accelerate forward, which way does the balloon swing? You get pulled back in your seat by the pseudogravity in your accelerating frame. The balloon goes forward, because all of the air almost instantly reacts to the new pseudogravity by making “down” back at an angle, rebuilds a gradient capable of accelerating the air along with the car, and the resulting buoyant force on the balloon pushes it forward to line up with the new “down”. Watch what happens, on the drive home when you round curves or brake. Uh huh.
The whole reason centrifuges work is because when you’re riding in them, the net force towards the center of the circle of motion of any piece of mass in the centrifuge has to be
But now, perhaps you could address the thermodynamic argument. Yes, such experimental evidence as there is refutes the assertion that there can be a stable thermal separation in any isolated system, including an ideal gas in a thermally isolated vessel like the Uranium centrifuges with their enormous g-forces. However, you should have given up even before discovering this — it is just the nail in a coffin built for something that died long ago.
You! Cannot! Violate! The! Second! Law! Of! Thermodynamics!
Really. No, you can’t. Neither can an ideal gas in an isolated container in gravity
rgb
Paul Potter says:
January 24, 2012 at 11:33 am
“For those who do not believe an warmer but still cold atmospheric layer cannot cause the surface to warm clearly do not understand the basic physics of radiative heat transfer”
Not sure if you meant the double negative here, but just to clarify matters, radiation from a cooler atmosphere is not converted to thermal energy when it meets a warmer surface because its frequency is below the cut-off. For more detail and links to computational proof see the Radiation page on my site http://climate-change-theory.com
If radiation from a cooler atmosphere could warm the oceans then it should be able to melt frost, but it doesn’t.
The discussion of centrifuges brings to mind another point from “Theory of Heat”. In this case, it’s on page 329 of the 10th edition. http://www.archive.org/details/theoryofheat00maxwrich
Any violation (ie displacement) of this would also violate the second law, as per the two-gas system described in my first posting.
The top of Robert Brown’s tube and the bottom of the tube are connected by the free flowing gas. For the two jars to be the same as the tube, the jars have to be connected by the wire and a free flowing gas. An air hose would do. The top of Brown’s tube has a different pressure than the bottom of the tube. Brown’s jars would have the same pressure.
No, they wouldn’t, because I filled and sealed the adiabatic jars at the top and the bottom. So the pressure inside of them remains constant as they are moved around. You can shoot a jar to the moon in a rocket ship and — aside from any teensy warming of the gas resulting from shaking it around, not from moving it around in a gravitational field per se — it will still have the same pressure, temperature, and density profile.
Now tell me why a gas that cannot be experimentally measured to be different in any way from the gas at the bottom and top of the adiabatic cylinder is capable of doing work and causing heat to flow, but the gas in the jars is not?
rgb
So your error – according to Velasco et al, as well as myself, DeWitt Payne and probably Robert Brown too – is in taking that marginal height dependence of average molecular kinetic energy for small N as a temperature lapse rate. It just isn’t.
Oh yeah, count me in. And that difference vanishes at high T in the correct treatment, exactly as it should. But small N is where naive/simple treatments of things get very difficult, even for physicists, partly because the concept of temperature starts to break down. That’s why I prefer (and offered) a straight up thermodynamic argument in the simple (and relevant) thermodynamic regime where DALR has been hypothesized to create a thermodynamically stable thermal gradient.
If it does, the entropy of the Universe can easily be made to spontaneously decrease by coupling the ends so that they convert the temperature difference reversibly into work, reducing the overall temperature of the system with a strictly negative overall change in entropy.
rgb
Robert Brown wrote:
Piffle. The equivalence principle suggests that one cannot tell the difference. I agree that in a rotating frame the correction doesn’t have the same form as gravity, there is a coriolis force as well as additional pseudogravity, but this makes no difference in the argument.
The interior of a centrifuge isn’t a true accelerated frame. Your car experiment is a true accelerated frame.
I’ve ridden a centrifuge, and will admit that it certainly feels like one. I could not distinguish it from gravity. That does not, however, mean that it’s not distinguishable.
Gas molecules in a centrifuge only appear to follow accelerated paths if you’re using a cylindrical coordinate system. If you’re using a rectangular reference coordinate system, they follow straight lines. That’s the key difference. There is no acceleration between collisions at the molecular level.
You! Cannot! Violate! The! Second! Law! Of! Thermodynamics!
In this particular case, I am only questioning the validity of the test. I’m trying to choose my points carefully. This was a very narrow point.
There is no “Centrifugal Force”. That got pounded in to my head by a physics professor decades ago.
Q. Daniels says: “There is no “Centrifugal Force”. That got pounded in to my head by a physics professor decades ago.”
Time for a little humor: http://xkcd.com/123/
In this case, the cartoon is indeed more accurate than your physics prof. It is all a question of what frame of reference you choose. (And choosing inertial frames is indeed simpler in most cases, but that does not make it the only way to look at things.) While there are some differences between rotation and gravity, that does not refute the observation that they both achieve the same ends as far as the discussion goes.
(As an aside, in relativity freefall is the only inertial reference frame. Standing on a planet — even one that is not rotating — is an accelerated reference frame.)
Robert Brown says at 1/26 4:24pm:
“No, he doesn’t. Read 2.17, especially the exercise at the end. Or look at the exam question and solution I posted.”
Yes he does, check it out.
Robert, again, as I posted above, Caballero in 2.17 is talking about the no gravity isotropic velocity field ideal gas he shows in Fig. 2.3.
Quoting from 2.17 “Consider again a gas in a pipe, as in Fig. 2.3.” Fig. 2.3 has NO gravity.
The homework exercise is for dT/dx eqn. 2.75 which is the horizontal temperature gradient in hydrostatic equilibrium. Yes, horizontally dT/dx =0. No doubt. Gravity acts only in the z height. Please stop and carefully check your work as you would ask any student to do.
Again, 2.17 is for the isothermal no gravity isotropic velocity case, you cannot use Caballero here to support dT/dz =0 isothermal gas column in a gravity field.
Because my statement is true, to restate, I added the ref. in parentheses:
“Caballero supports isotropic velocities for isothermal T only in the no gravity ideal gas column case (in 2.17). Add gravity & Caballero in Sec. 2.3 supports gas column T is non-isothermal and constant entropy.”
Please re-read Caballero ref. cites again. Grok them as you asked me to do. And please return.
You may have another text ref. to cite to support your work, so far Caballero only supports a non-isothermal gas column in the presence of gravity, Sec. 2.3.
I will look any ref. right up, I have placed on order Caballero’s recommended: “Bohren and Albrecht’s excellent Atmospheric Thermodynamics.”
Paul Birch:
Again, I appreciate the attention.
Now, it was to obtain more information on which to make an assessment of whether Velasco et al. are right that I brought their paper up on this site; they fill books with what I don’t know about thermodynamics. But, frankly, nothing anyone has told me so far is anything I didn’t already know–or already know was wrong; the discussion has either been what Velasco et al.’s verbal description means, or how people on this site with credentials view it.
As I’ve said, I’m no physicist, and I claim no expertise in this area. And I’m not as sure of anything as many of the contributors here seem to be about everything. But I do have quite a bit of experience assessing all manner of physical-science-based matters where not getting it right could have significant financial implications. And that experience has made me pretty sure it’s best to do two things. First, go with the equations, not the verbal descriptions. Second, don’t rely on the opinions of experts, no matter how exalted, if in my opinion their logic doesn’t stack up.
So, although I respect your opinion, I have to go with mine. And it’s my opinion that, for the purposes of a theoretical discussion–which, let’s not forget, is what Dr. Brown initiated–Velasco et al. do indeed say that an isolated vertical gas column exhibits a non-zero lapse rate at equilibrium.
Robert Brown says at 1/26 4:24pm:
“Look, nothing … is going to permit a stable thermodynamic temperature gradient, because for one to exist you must not be able to use it to do work, not even in principle.”
I agree, in Caballero 2.3 non-isothermal ideal gas column in 2.3 where the velocities are higher at the bottom than the top, no work can come out of it. This means a system of constant entropy allowed by 2nd law, the process is reversible. Gravity increases molecules speed on way down, decreases speed going up. Same exact amount ideally.
“Otherwise as you do work with the thermal difference, you are reducing the heat content of the system (cooling it) and turning it into reversible work.”
No. The energy content of the system in Caballero 2.3 is not cooling. It is remaining constant. Thus heat of the system is NOT being cooled; b/c as I have written over & over energy is constant. Conserved. 1st law compliant.
You are smart, Caballero is so far, right. You can grok.
Trick,
Wanna bet that if you ask Caballero about this statement in 2.3:
and then about section 2.17 he will say that 2.17 is wrong? Somehow I don’t think so. My bet is that he will correct 2.3.
DeWitt Payne says:
January 25, 2012 at 9:49 am
“In the troposphere, the atmosphere is more transparent to SW radiation and less transparent to LW radiation so the surface temperature is warmer than the slab. The opposite is true in the stratosphere.”
______________________________________________________________
This analogy is very flawed because at the base of the troposphere is a real “slab” (the Earth’s surface) that can be warmed itself by solar insolation and then transfer perhaps as much as 70% of that energy back to the atmosphere via evaporation and diffusion (ie thermodynamics not just radiation.) In contrast there is no such physical slab at the tropopause.
I am not saying that the explanation for the inversion in the stratosphere is incorrect – just that there is much more going on in the troposphere and that it is totally wrong to imply that radiation is the sole cause of the lapse rate in the tropopause.
Evidence suggests that thermodynamics prevails at least two-thirds, and a significant role in the thermodynamics is played by “latent heat” in evaporated water which leap frogs up into the cloud levels and is then released up there by phase change. This has to affect the lapse rate and may explain the observed reduction from the much higher (almost double) rate in the lower 14,000 feet compared with the layers above that. (See data in my earlier post.)
Once again I find Professor Claes Johnson promulgating the most plausible hypothesis http://claesjohnson.blogspot.com/2010/09/lapse-rate-vs-radiative-forcing.html
Yes, Johnson is the one who proved computationally that an atmospheric greenhouse effect is a physical impossibility because low frequency radiation is not converted to thermal energy by a surface which is warmer than the emitting layers of the atmosphere. It’s worth reading: http://www.csc.kth.se/~cgjoh/blackbodyslayer.pdf
Be the first to prove him wrong – and back it up with empirical evidence of backradiation warming something. Apparently it cannot even melt frost on the ground.
PS I’d still like from you the reference to that experiment you wrote about on SoD where the gas did not absorb until the emitter became warmer. Clearly this supports Johnson’s hypothesis.
George E. Smith; says:
January 26, 2012 at 12:47 pm
I don’t judge people or the papers they write by anything but the content thereof and my own experience, work, tutoring and further private study in the fields of maths and physics since my university studies in the 1960’s and 1970’s. But, just for the record, Johnson is a Professor of Applied Mathematics (very akin to physics) with many published papers. http://www.csc.kth.se/~cgjoh/
If you want a quick summary of his main contribution in this field (proving the greenhouse effect is impossible) read the Radiation page on my site http://climate-change-theory.com
DeWitt Payne says at 1/26 6:00pm:
“My bet is that (Caballero) will correct 2.3.”
LOL. I’ll take that bet! For the sum of one $tygian bragging right.
Agree to let Boren text be the source of the bet decision? Does DeWitt have a copy of Boren already? Have a text quote correction ready? I’ll wait for mine to come in a few days. Takes my chances. I’ll stand w/Caballero lines up with Boren.
If you want to let Velasco paper eqn. 8 settle it, then that’s ok too.
Bill Hunter says:
January 25, 2012 at 7:48 pm
The problem outlined by Dr. Brown is interesting but largely irrelevant to the issue of whether the surface would be warmer in the absence of greenhouse gases.
Here is my reasoning on that.
It’s the analogy to the passive solar water heating system. First lets get a few things clear on that.
A good passive solar system does not need a greenhouse for the collectors to operate well. Often they use just plain black piping. It works nearly as well as pipes in a greenhouse because the 1,000 plus watts of solar radiation far exceeds radiation losses without the greenhouse.
Shouldn’t that be 240?
Trick says:
January 26, 2012 at 5:51 pm
Trick, you can’t just assert that “no work can come out of it”. Out here in the real world, if there is a temperature difference you can extract work from it, either in reality or in principle. The non-ideal gas column of of Caballero is not magically exempt from that rule, and the rule certainly is not suspended because Trick claims it won’t happen.
So if you want to look like other than a dilettante, you need to show, not claim but actually establish through logic and argument, that no work can come from the column. I see absolutely no reason that a temperature difference anywhere anytime cannot produce work either in principle or in reality.
w.
Why, when we are living in the midst of an experiment, whose chemical distributions are being measured to the best of our ability, would we try to create a planet of imaginary chemicals to understand our situation.
We are in the experiment, just measure it.
Dr. Brown, if you get bored patiently explaining physics to the gravityheads, take a look at the link above for a red-hot possibility for your next project. This is the claim that energy cannot be radiated from a cooler body to a warmer body …
w.
u.k.(us) says:
January 26, 2012 at 7:16 pm
Thought experiments have a long and glorious history. Einstein used them to convince people that relativity was a correct theory. Why? Because you can cut through the complexities and the practicalities that beset us, and come to a deeper understanding of the reality from contemplating simpler situations.
So your complaint, that this is a thought experiment without the complexity of the real world, falls on deaf ears. Folks here understand the value of these kinds of experiments, and the fact that you do not just means you should rethink your opposition to a long-established part of scientific inquiry.
w.
Willis Eschenbach says:
January 26, 2012 at 7:21 pm
=============
Einstein ?, i have thoughts, none of which discounted thought experiments, and it wasn’t a complaint, just an observation from my reference frame, such as it is.
Robert Brown wrote:
You! Cannot! Violate! The! Second! Law! Of! Thermodynamics!
At no point have I made any claim or representation regarding my skill in this manner.
I have not even claimed the ability to tie my own shoe laces together, though I will say that there are reports that I once tied Melvin Calvin’s (Chemistry, 1961) shoe laces together.
Tim Folkerts wrote:
In this case, the cartoon is indeed more accurate than your physics prof. It is all a question of what frame of reference you choose. (And choosing inertial frames is indeed simpler in most cases, but that does not make it the only way to look at things.) While there are some differences between rotation and gravity, that does not refute the observation that they both achieve the same ends as far as the discussion goes.
I disagree. A rotating reference frame does not even qualify as accelerated. That’s the problem.
Consider a non-moving particle, planet, or whatever, sitting by itself near a reference point and far from everything else. If you have a non-rotating frame, the physics is simple and straight-forward. The object remains where it is. If you change to a rotating frame perpendicular to the axis, explaining the circular motion of the object becomes much more difficult.
In the case of the centrifuge, there is acceleration only in the rotating frame. Let’s put the centrifuge in deep space for clarity. If you use the inertial frame, there is no acceleration applied to the individual molecules except when they hit each other or the wall. A molecule which had been brought to a full stop by gas collisions would remain in place until disturbed by another collision. This is very different from the effect of gravity, wherein molecules can come to full stop by gravity, and then accelerate out again without collision.
Gravity is a force that acts on every particle in the system, independent of mechanical interaction. A centrifuge only acts mechanically.
There is no “Centrifugal Force” to play the equivalent of Gravity. There is only the wall of the centrifuge, which occurs only at the wall of the centrifuge.
While reading about Maxwell’s demon, I came across an amazing invention that appears to shed light on the “gravitationally induced” temperature gradient idea. The Ranque-Hilsch Vortex Tube generates a temperature differential within a tube by injecting a compressed gas stream which then generates a vortex. The temperature along the walls is higher than the incoming gas, while the temperature within the center is colder than the incoming gas. The two temperature streams can be physically separated.
Here are some links, including a patent on an embodiment of the invention, if you are interested in learning more about this phenomenon:
http://www.filtan.de/ENGLISH/VTS_A.htm
http://www.me.berkeley.edu/~gtdevera/notes/vortextube.pdf
http://www.google.com/patents?hl=en&lr=&vid=USPAT3546891&id=KppYAAAAEBAJ&oi=fnd&dq=%22vortex+tube%22+gravity+%22temperature+gradient%22&printsec=abstract#v=onepage&q&f=false
Gee Willis, I look up heat dissipation and centrifuges, all they talk about is high temperatures and problems removing the excess energy. Seems you 200 C would not be too far off at that amount of g’s. But, duh, of course it would be much hotter at the outside where g’s are higher. Seems you just proved yourself wrong.
one example: http://www.freepatentsonline.com/5433080.html , there are many more.
@Doug Cotton
Whilst I trust you know my position on all this, I do not like pushing the “CO2 saturation” concept. Firstly, bands only appear blank at TOA because CO2 scatters radiation and hence, when you point an instrument at some place on Earth, very little appears to come directly towards you from that point. Warmists will argue that the bands just get wider,
+++++
OK, another time perhaps. You are correct re the conduction and of course that is normally left out of any discussion of ‘CO2 thermal blanketing’.
There are a lot of posts sent in the meantime. I see our contributing Author has again appealed to his own and his selected authority and put down an opinion which which he does not agree solely by observing that the other source was not correctly qualified to have a valid opinion. This is the essence of every weak and losing argument. On that basis alone I suspect the validity of whatever the thesis states.
I asked my friend Kevin why academics put so much energy into postulated planets and he replied, “Because there is so little at stake.”
Question: Is this putative planet rotating? At what rate? How deep is atmosphere? What is the equitorial centrepital acceleration rate just below the TOA and what is the acceleration due to gravity? It may be far colder a the top than has been considered so far because the expansion may well exceed what thermals can achieve. Realising this, will we again constrain the physics on the planet to bias the answer towards our favourite explanation?
u.k.(us) says:
January 26, 2012 at 7:16 pm
Why, when we are living in the midst of an experiment, whose chemical distributions are being measured to the best of our ability, would we try to create a planet of imaginary chemicals to understand our situation.
We are in the experiment, just measure it.
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2871909/
Willis says at 1/26 6:59pm:
“So if you want to look like other than a dilettante, you need to show, not claim but actually establish through logic and argument, that no work can come from the column.”
Learned a new word for amateur! Good one.
Fair to ask for logic in any post from pro or amateur. The logic here is that the ideal gas column in ideal closed container in a gravity field (top post Fig. 1) is a reversible system in equilibrium. Molecules go up and down reversibly. Caballero terms this hydrostatic equilibrium in Sec 2.3, Fig. 2.4.
2nd thermo law tells us for a single reversible system, sometimes called a cyclic process, it is impossible to produce work into the surroundings.
In the top post, the equation of hydrostatic equilibrium is shown as eqn. 5, in Caballero it eqn. 2.27.
Is my claim that “no work can come from the column” actually established through logic and argument for you now? There is certainly more to grok but your argument for the elevator speech length being adequate is strong.
Willis continues:
“I see absolutely no reason that a temperature difference anywhere anytime cannot produce work either in principle or in reality.”
Think the thermo grand masters would agree. Except in the post that Joules Verne made at 1/25 8:57pm there is a terrific paper posted that even they were perplexed about the more or less philosophical thought experiment being discussed in Fig. 1 top post on down.
The best one can do is have a view whether the process is isothermal or non-isothermal it turns out. It is interesting learning while supporting one’s view consistent with texts, papers and thermo laws, other posters. As you write, a noble blog purpose.
Call me out (w/logic) when my post is not established thru logic and argument consistent with natural laws. (Try not to make the moderators or me cry though, lol).
Wayne,
When I see people state “of course” it often points to the flaw in the arguement, because people are simply assuming, rather than proving. You assume the problem is that the outside is hotter, but provide no evidence.
When I look for centrifuges and heat dissipation, I see two things — neither of which is related the outer parts being warm. Instead, they discuss:
1) Dissipating heat created by the equipment. There will always be friction and vibrations that generate thermal energy. At high speeds this could be quite a problem, so dissipating the heat from the bearings and the motor can be a problem.
2) Trying to cool the samples below ambient temperatures. This is what your link is actually talking about.
“Before centrifugation occurs with many samples, temperature thereof must be precisely controlled. In practice, classification of the sample in a rotor must occur at controlled temperature. An example of such a temperature is 2° centigrade for certain biological samples. The sample must be brought to the temperature and during centrifugation the sample must be maintained at the temperature. In both events cooling of the chamber is required. Due to their small size and weight, thermoelectric devices using the Peltier effect are utilized. ”
I’d be interested to see links you find that discuss the outer edge of the centrifuge getting hot compared to the axis, especially links where the difference is ~ 200 C as you seem to think it should be.
Trick says:
January 26, 2012 at 8:17 pm
====================
OK, now that has been established, can we move on to Physics 102 ?
I’m sick of “heat” flow.
Clearly any body emitting photons has no idea where they will end up, photons being somewhat bereft of ideas. Photons are in fact so stupid, they only know that they are emitted and absorbed simultaneously. They have no notion that they have ever spent time travelling between atoms!
Those photons being emitted by The Git’s adipose tissue are streaming out in almost every direction. Some in the direction of the ground, some sideways and some towards the sun. Those heading sideways towards the trees will be absorbed by the trees just because they are cooler than The Git’s adipose tissue. Similarly, those emitted toward the ground will be absorbed for the same reason.
Those photons emitted toward the sun however have a different fate. The sun being ever so much hotter than The Git’s adipose tissue is not allowed to absorb those photons. Perforce they must either pass straight through the sun, or else be diverted around the sun before being allowed to continue their straight line path beyond. There is only one possible answer to this: the Will of God/Krishna/Jehovah/Inanna/Allah [delete whichever is inapplicable] which transcends even the Laws of Physics as decreed by God/Krishna/Jehovah/Inanna/Allah [delete whichever is inapplicable] .
This is an elevatorsqueak account of why “energy cannot be radiated from a cooler body to a warmer body”.
It is not the intention of the writer to demean, degrade, humiliate, despise, or disparage any god, godess, offspring of god, demiurge, inamorata, fetish or other supernatural being.
In this particular case, I am only questioning the validity of the test. I’m trying to choose my points carefully. This was a very narrow point.
There is no “Centrifugal Force”. That got pounded in to my head by a physics professor decades ago.
I do a fair bit of the pounding myself. But the point is that it still doesn’t matter. To a person riding in the frame, it feels like there is. The gas feels like there is too. Any differences if anything would be expected to enhance any steady state thermal separation.
Still, I have no problem with you not considering the Uranium centrifuges as not being conclusive evidence for isothermal equilibrium. They aren’t experiments designed to look at the question, for one thing, so there could be all sorts of confounding factors (although honestly I don’t think that coriolis force and rotational corrections to “true gravity” have a thing to do with it, any more than they do on Earth which is just such a rotating frame). They matter only as long as there is bulk “vertical” transport, but vanish as the gas reaches static equilibrium in the experimental chamber.
I do think that they can count as evidence for isothermal equilibrium — they certainly aren’t evidence against it — just perhaps not conclusive under the circumstances.
So now you have to weigh the preponderance of the evidence and the arguments.
The arguments are:
* A thermodynamically stable thermal lapse in any isolated system such that work can be done — even in principle — between different two different parts of the system at different temperatures violates the second law of thermodynamics. The possibility of doing work has to be “forbidden” by e.g. quantum barriers or the like, and even there there have to be no channels for transfer of energy (such as second order, two photon processes) that can make an end run around the quantum barrier.
* It can be and has been shown that an isothermal state in static force balance cannot do work and does not violate the second law of thermodynamics or any other laws of nature. In fact, it is a rather straightforward textbook example.
* It has been shown that the isothermal state has higher entropy than a temperature separated state, because it is capable of doing work. Maximum entropy states of isolated systems by definition and by demonstration cannot do work. Note how all of this ties together consistently. That’s why thermodynamics works. It is consistent, and empirically supported by a vast body of experimental evidence and everyday experience.
* It has been shown in a stat mech paper (that I still haven’t read) that equilibrium is isothermal.
* It can be shown with more detailed formal arguments that the isothermal state has maximum entropy.
* Such experimental evidence with extreme accelerations as exists fails to demonstrate a stable thermal lapse and appears to be isothermal. Whether or not it is “identical” to real gravity, the onus of proof is on you (or anyone) to demonstrate why such a lapse wouldn’t show up (especially when this is exactly the experiment proposed by a number of people who have wistfully hoped that it would confirm, not contradict, a lapse).
* The assumption that air is itself adiabatic — used in the derivation of the DALR in the first place — is false. The textbooks in which the derivation is given generally state that neither air nor any other gas really undergoes adiabatic expansion as it moves up and down, because air isn’t really adiabatically insulated by the air it expands into. Air is merely a relatively poor conductor and doesn’t have time to reach local thermal equilibrium as it convectively moves up and down, and it takes a long time to reach global thermal equilibrium across great distances via conduction alone.
The point of this last bullet is that real air on the real Earth is basically never in global thermal equilibrium. The air in my house is almost never in local thermal equilibrium. Turn the air conditioner on downstairs and see how long it takes to get cold upstairs! Air on the real Earth is always moving up, down and sideways as warmer air seeks cooler venues and cooler air circulates back to replace it and be warmed in turn. It is this mixing with poor conductivity that makes the differentially heated atmosphere exhibit a lapse rate that is often approximately (but almost never exactly) the classical DALR.
In the end, this entire thread has a single target and purpose. It seeks to convince the reader that they should not believe that the atmosphere intrinsically establishes a vertical thermal gradient as a spontaneous stable thermodynamic equilibrium state, one that would somehow “heat” the bottom relative to the top even if the whole thing were in a giant Dewar flask and one waited long enough for true equilibrium to be established. This static hypothesis is therefore not a candidate mechanism for explaining any part of “atmospheric warming”.
rgb
Joules quoted: “As a consequence, the heat transport is inhibited when the gas is heated from below.”
From “On the Influence of Gravity on the Thermal Conductivity”
http://arxiv.org/pdf/cond-mat/0002397v1.pdf
He was also so kind as to send the link to me offline. I therefore have looked it over. It (as I pointed out to J) confirms that equilibrium is isothermal. Joules just doesn’t understand their conclusion.
The paper examines a very dilute gas — so dilute that it is no longer properly speaking an ideal gas — in a container between two plates that are maintained at different temperatures. They assume that the gas does not convect. They assume that the system has “reasonable” dimensions for thermodynamics to work, e.g. that the mean free path is small compared to the size
Arrgh. Accidental hit post again while typing — continuing…
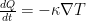
 to see if it remains symmetric for a thermal gradient in the direction of gravity and a thermal gradient in the opposite direction to gravity.
to see if it remains symmetric for a thermal gradient in the direction of gravity and a thermal gradient in the opposite direction to gravity. , so that:
, so that: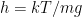 , is not (as it usually is) orders of magnitude larger than e.g. the mean free path of molecules in the gas. In the case where the gravitational scale height is (as usual) much larger than the mean free path and the characteristic length of secular changes in temperature (which goes to zero as the system approaches thermal equilibrium, which this paper does not study) the paper itself clearly states in the introduction that the usual symmetric Fourier law holds. Hence the need for a very dilute gas, with a long mean free path, a relatively large thermal gradient, and a large gravitational field compared to the mean temperature, none of which are true for the Earth’s troposphere. But no matter.
, is not (as it usually is) orders of magnitude larger than e.g. the mean free path of molecules in the gas. In the case where the gravitational scale height is (as usual) much larger than the mean free path and the characteristic length of secular changes in temperature (which goes to zero as the system approaches thermal equilibrium, which this paper does not study) the paper itself clearly states in the introduction that the usual symmetric Fourier law holds. Hence the need for a very dilute gas, with a long mean free path, a relatively large thermal gradient, and a large gravitational field compared to the mean temperature, none of which are true for the Earth’s troposphere. But no matter. becomes a spatial tensor form in Fourier’s law, so that heat conduction occurs faster in one direction than another, as long as
becomes a spatial tensor form in Fourier’s law, so that heat conduction occurs faster in one direction than another, as long as 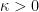 the equilibrium of the system is still established only by the vanishing of the thermal gradient!
the equilibrium of the system is still established only by the vanishing of the thermal gradient!
 if and only if
if and only if 
 vanishes (or is very small),
vanishes (or is very small),  takes on its usual Boltzmann value and conduction is actually symmetric. Again this is utterly expected, as in that limit the characteristic length of thermal fluctuations is again much smaller than
takes on its usual Boltzmann value and conduction is actually symmetric. Again this is utterly expected, as in that limit the characteristic length of thermal fluctuations is again much smaller than  , although this seems to be true independent of the mean free path and hence is true even for the very dilute gas.
, although this seems to be true independent of the mean free path and hence is true even for the very dilute gas. . One has to be the usual Fourier term, unless you want the system to be even more insane than you are trying to make it (and not relax in response to a thermal gradient at all). The other has to somehow cause
. One has to be the usual Fourier term, unless you want the system to be even more insane than you are trying to make it (and not relax in response to a thermal gradient at all). The other has to somehow cause  to vanish when there is a nonzero thermal gradient.
to vanish when there is a nonzero thermal gradient. can vanish in Fourier’s Law except when the thermal gradient vanishes, given nonzero
can vanish in Fourier’s Law except when the thermal gradient vanishes, given nonzero  .
.
of the system and so on.
The entire purpose of the paper is to examine Fourier’s Law:
when there is a gravitational field in the direction of the thermal gradient. In particular, they seek to calculate
The paper finds — after a lot of hard work that I have no reason to doubt is correct — that under these particular conditions, there is a small asymmetry in
We observe that the heat flux increases with respect to its Navier-Stokes value when one heats from above, while the opposite happens when one heats from below.
What Joules did not observe is that the split vanishes precisely where the thermal gradient vanishes. Furthermore, it vanishes smoothly, at least in the Bhatnagar–Gross–Krook (Lattice Boltzmann) approach. Furthermore, the limit that this paper studies is one where the characteristic height associated with gravitational energy,
The thing that Joules somehow completely misses is that even if
The stationary state of even a very dilute gas at very low temperatures with a very strong field, in other words, is still isothermal.
Thanks, Joules, for helping to establish that even in this rather nonphysical limit — one not unlike that represented in the small molecular dynamical simulations one can find that turn on gravity for only a few particles bouncing around in a box so that particles visibly slow down between collisions — thermal equilibrium is still isothermal.
If one examines figure 1 in the paper, one notes that as the thermal gradient
Here’s a lesson, Joules. The entire point of Fourier’s Law is that it drives any system with conductivity towards isothermal equilibrium. What you are looking for is something that has at least two terms on the right hand side opposite
Oh, and don’t forget, the whole expression has to be derived from and related to the Navier-Stokes equation. That is, you can’t just make one up and claim that it is correct.
I wish you good luck with that.
If you disagree, feel free to present a counterargument, and show me any way that
rgb
Myrrh says:
January 26, 2012 at 6:50 pm
It’s the analogy to the passive solar water heating system. First lets get a few things clear on that.
A good passive solar system does not need a greenhouse for the collectors to operate well. Often they use just plain black piping. It works nearly as well as pipes in a greenhouse because the 1,000 plus watts of solar radiation far exceeds radiation losses without the greenhouse.
“Shouldn’t that be 240?”
No thats the “average”. If radiance were uniform it would be 240. the radiation averages 240. But “average” only matters if something cools at the same rate it warms.
Thus it requires 4 elements to exceed the average temperature 1) A variable heat source which is provided by a large object rotating in front of a more powerful source in which case the maximum you can change the storage system is limited to the maximum input; 2) you need heat storage capability (it doesn’t do any good to move heat for later use if you can’t store it, and 3) for the passive system a means of transferring heat that moves heat faster from the collectors to the storage than it does the storage to the collectors (you get that from convection), and 4)you need a storage system that cools slower than the collectors (in the case of the water system you insulate the storage tank and for the atmosphere you need an atmosphere that radiates more poorly than the surface giving you effective insulation of the heat in storage.).
You have all four elements in a planetary environment with an atmosphere
With no heat losses in the storage system (non-radiating atmosphere) the atmosphere GHE would be something north of 130K. Passive designers make these calculations all the time in passive system development. The upper limit of a perfectly insulated system is the upper limit of the fluctuating radiation. 1366 watts. That equates to 139K GHE.
Of course the common air in the atmosphere does radiate. It also conducts to the ground but the conduction is minor. At a 150k differential and 4ft to a Stevenson screen you only get about 3 watts/hour conduction. Thus over 12 hours you could lower the temperature about 12 degrees.
What the atmosphere does radiate is what lowers it to 33K GHE. If GHG make a difference its likely a cooling difference.
This is really basic stuff! Its demonstrated in passive solar heating systems all the time.
I told one gentleman that greenhousing the collectors doesn’t matter much. And for the most part it does not. The temperature of highly conductive collectors, or the ground in a greenhouse is not going to significantly change by putting it in a greenhouse.
Its going to be at roughly the max radiation temperature. What a greenhouse primarily changes is the atmosphere in a greenhouse not the surface. One can verify that by walking barefoot through a asphalt floored greenhouse to outside on a hot sunny day. What you will find in most cases is the ground is warmer outside the greenhouse and the air is warmer inside the greenhouse. The ground is warmer outside because nothing is completely transparent and all greenhouses block some of the light, particularly greenhouses used by growers which often do not have crystal clear glazing.
What we need to do with these academic climate scientists is take them outside and introduce them to the real world.
OK, so some of that latex didn’t come out so well, missed a $ in there someplace. Clearly, time for bed. I think the main point is clear, anyway. Not even in this extreme case is equilibrium anything but isothermal, and I’m certain the authors of the paper would be surprised and shocked to hear that someone was suggesting otherwise, given that the paper studies heat flow, based on underlying kinetic principles that make that impossible.
rgb
thepompousgit says:
January 26, 2012 at 11:52 am
“No numbers; just armwaving. You say “Greenhousing… only adds a few degrees to the system”. I say, if I don’t open the vents on my greenhouse early enough in the day, the crop will rapidly die. That’s not just “a few degrees”. But you remind me that I don’t have numbers. Time for some experiments so I can put some numbers on the greenhouse effect that is not The Greenhouse Effect (so to speak).”
You are looking at the “atmosphere” in the greenhouse. It isn’t much relevant to how much the surface warms in the greenhouse. The greenhouse atmosphere in an empty greenhouse cannot get warmer than the surface. Its usually much less. A greenhouse will have an atmosphere much closer to the surface temperature than the atmosphere outside of the greenhouse because the greenhouse prevent the heat from running away by convection.
Dr Brown,
Thank you for providing a forum on the subject of the physics of atmospheric temperature lapse.
I have been struggling to discover what might be causing so many to be confused enough to believe something like radiation is controlling the temperature distribution through the atmosphere, based on only faith, when it is so mind bogglingly obvious that the temperature lapse is the expected consequence of the pressurizing that occurs as gravity forces the air toward the surface.;
I have spent what seems like most of this year so far, reading through the many fallacies and contradictions that you and others have been offering, and even gloating over.
Yet, I struggled on. Then it hit me. The frame of reference has been skewed.
You started with this definition: “…because, as is well known, thermal equilibrium is an isothermal state” and try to make it the only steady state case. Nonsense! In reality there is no isothermal state, anywhere, and to use nonsense to frame examples leads to the same sort of results as when one substitutes “0” for “lim X as X –> 0”. Sometimes they are right..
The term “steady state” can be and is used to describe process conditions. Earth’s atmosphere responds to, and is continuously being processed by many forces, including gravity…
Robert Brown wrote:
A thermodynamically stable thermal lapse in any isolated system such that work can be done — even in principle — between different two different parts of the system at different temperatures violates the second law of thermodynamics. The possibility of doing work has to be “forbidden” by e.g. quantum barriers or the like, and even there there have to be no channels for transfer of energy (such as second order, two photon processes) that can make an end run around the quantum barrier.
I agree that such a system would contradict the second law.
It has been shown in a stat mech paper (that I still haven’t read) that equilibrium is isothermal.
I would be interested in reading that paper, unless you mean Coombs and Laue, in which case I I’ve read it. In my own analysis, if the Maxwell-Boltzmann Distribution retains spherical symmetry in a gravify field, the column is isothermal. If the Maxwell-Boltzmann distribution has different circular and vertical symmetries (but still symmetric about the origin), it is not isothermal. I believe the Velasco response reached the same conclusion. There are some words I’ve left out of that, but I’m not sure how to formulate it in a simple manner. My words in Tallbloke’s Loschmidt thread are probably more clear, and certainly more extensive.
Such experimental evidence with extreme accelerations as exists fails to demonstrate a stable thermal lapse and appears to be isothermal. Whether or not it is “identical” to real gravity, the onus of proof is on you (or anyone) to demonstrate why such a lapse wouldn’t show up (especially when this is exactly the experiment proposed by a number of people who have wistfully hoped that it would confirm, not contradict, a lapse).
I accept that the onus on is on me. I offer a brief sketch (not complete) here. “Not conclusive” may be the best agreement we can reach.
For this, the frame of reference is Oak Ridge. Consider that from time to time, one of the molecules will come to approximately 0 velocity relative to Oak Ridge. What are the forces acting on that molecule at that time? I believe that, until it is disturbed by collision with another molecule, the sum total of forces acting on it will be one g. The molecule has no information that it is in a centrifuge spinning near Mach 2. The only force it can ‘feel’ is gravity.
In the Gravity Lapse Rate theory, what matters is that the molecules experience acceleration between collisions. Since molecules in a centrifuge experience only 1 g between collisions, I see no basis for enhancement of the GLR beyond the factor of ~12 from the molecular mass.
The assumption that air is itself adiabatic — used in the derivation of the DALR in the first place — is false. The textbooks in which the derivation is given generally state that neither air nor any other gas really undergoes adiabatic expansion as it moves up and down, because air isn’t really adiabatically insulated by the air it expands into. Air is merely a relatively poor conductor and doesn’t have time to reach local thermal equilibrium as it convectively moves up and down, and it takes a long time to reach global thermal equilibrium across great distances via conduction alone.
I suspect this is incorrect, but I am not currently equipped to present a convincing case. I do understand the textbooks in this regard.
As for my sanity, that is rarely questioned by people who know me (fish, barrel).
Robert Brown’s refutation is contrived and irrelevant.
Any column of any substance from the top to the bottom of the cylinder is subject to the same gravity field with gravitational constant g as the gas in the cylinder. Or, what is the same according to the general theory of relativity, the cylinder with gas as well as the conductor (whatever material it is made of) are subject to the same constant acceleration (vector) of g m/s2. Therefore, the same temperature gradient will appear in the conductor and or along the walls of the cylinder as exists in the gas. The bottom of the cylinder pushes against the gas mass and any other top-to-bottom material like an adiabatic piston, raising the temperature at the bottom, whereas the top of the cylinder pulls like a similar piston, decreasing the temperature at the top.
As long as the acceleration is maintained, the temperature gradient in the direction of the acceleration vector will be maintained. If heat is added to the system by radiation from outside, the average temperature will increase, but as long as the acceleration continues, a temperature gradient between top and bottom of the system will be maintained.
Bravo, Albert! Bold effort! It doesn’t matter what it is, or where it is, everything has a higher temperature at the bottom than at the top. That will stop the damn heat from flowing! Good job proving it by calling my refutation “contrived and irrelevant”, to. That way you don’t have to actually address any of the — err — details. That would require confronting an inconvenient truth or two, such as the fact that the last time you actually took a course in real math (I don’t just mean wussie old intro calculus, either, I mean real math) or physics was — never? Real men don’t need to actually study and work — they just sort of “know things”.
But your best gambit by far is tying it to the general theory of relativity — a theory I would be amazed if you know anything about whatsoever except how to spell it correctly — you have made it more or less impossible for anybody on this list to challenge you! Hell, I teach graduate E&M and special relativity theory, and yet my heart quakes whenever I encounter GR because all of that nasty tensorial calculus gives me gas. I’m just not smart enough, or patient enough, and I’ve only learned a smattering of it along the way. Of course I’m almost as allergic to hard-core stat-mech even though I spent years working in it. It’s insanely difficult. And you my good man, have clearly mastered them both! Together!
So you win. I concede. Well played, sir!
Just don’t make me go wade through the GR texts to prove that no, you silly beanie you, a silver wire hanging vertically doesn’t have a stationary thermal lapse due to — pardon me while I compose myself — GR thermodynamics, not one you could measure with the most sensitive of instruments here on wimpy-gravity Earth (how could you measure it, damn thermometers suffer from exactly the same GR lapse!). Gads! It’s there even if we can’t see it! Heinous!
Far better it is to suffer the slings and arrows of outrageous misfortune and your justly earned ridicule than to try to compete with you, sir, on stuff even Steven Hawking got wrong. Hell, even Jelbring proposes that the lapse rate isn’t the same for two different kinds of gases! You’ve trumped even him!
Now, weeping softly to myself (tears of laughter) it really, truly is — off to bed.
rgb
Stephen Rasey says:
January 25, 2012 at 9:38 pm
“@Bill Hunter. Thank you for that example where the diurnal day-night pumping is so essential for a passive solar hot-water system. ”
Thanks for noticing! For a week and 3 of these threads I have been saying this with nary a response. I don’t think anybody read it even.
Most solar hot water systems are active. Thats because they take the passive system and turn it on its head. People like the collectors on the roof and the storage in the basement.
So to do that you need a circulatory pump that turns on when the collectors are warmer than the storage and shuts off when they are not to simulate convection but have it run backwards. You also need a value that closes when the collectors are colder than the storage so natural convection doesn’t send all your heat to the roof to radiate away.
There is no question this accounts for some of the greenhouse effect, I am favoring all of it but can’t be sure. At any rate it has to be an important part of it and it sure appears to me that as you increase the ability of the atmosphere to radiate you are going to lose heat seemingly as sure as stripping insulation off your storage tank. Just that adding .0002 of a gas about 8 times less efficient than the surface isn’t hardly going to do anything. Now water that no doubt does the heavy lifting, it cuts the lapse rate in half and it covers more than half the sky with clouds. Add in some emissivity for common air and you can trim it back pretty fast. Having well insulated storage can make up for having short days. Thats what passive solar design is all about!
ZP says:
January 26, 2012 at 7:55 pm
I actually built a vortex tube some years ago, when I was running a shipyard and machine shop on a remote South Pacific atoll.

I machined the vortex tube out of a block of solid aluminum. They are quite amazing, able to deliver very cold air once they are tuned and adjusted. I used some plans that I’d photocopied out of the “Amateur Scientist” column in the late lamented Scientific American. I mean the old Scientific American, back when they actually reported on science. I’m told they use vortex tubes these days to cool the drivers in the race cars during the pit stops.
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
w.
You started with this definition: “…because, as is well known, thermal equilibrium is an isothermal state” and try to make it the only steady state case. Nonsense! In reality there is no isothermal state, anywhere, and to use nonsense to frame examples leads to the same sort of results as when one substitutes “0″ for “lim X as X –> 0″. Sometimes they are right..
The term “steady state” can be and is used to describe process conditions. Earth’s atmosphere responds to, and is continuously being processed by many forces, including gravity…
No, I started (read the article at the beginning) trying to prove that the idealized adiabatic stationary atmosphere discussed in a specific paper by Jelbring (EEJ) is isothermal, not one with the DALR Jelbring asserted without real proof. I did so because Jelbring’s paper is cited over and over again on WUWT and tallbloke’s blog (tallbloke himself invited me to look at it) and when I did, it was obviously in violation of the second law of thermodynamics, which I have now proven several ways and times in the following discussion.
If you concede this one point — that Jelbring’s paper is nonsense — and promise never to cite it to support any of your future ramblings about how the atmosphere causes the ground to be warmer than the upper atmosphere — then I have succeeded in my aim. I am not at this time addressing all of the other abuses of the hapless laws of thermodynamics and physics in general that occur in on-list discussion because I’m just one person, and it has now taken me at a guess over a hundred posts over three days to mostly convince at least some of the people who believed that it was true and correct that they were mistaken. Others, I’m certain, will never be convinced, or will immediately try to pretend that “gravitational heating” occurs some other way.
Some of the stuff proposed in this regard is not at first glance objectionable, BTW. I’m not taking a position on it until I understand what is being proposed. Is that so unreasonable? I seek to avoid saying silly things like “Jelbring is wrong, so the DALR must be wrong too — of course it isn’t, it is just a non-equilibrium state, one that requires (I am almost certain) heating the atmosphere primarily from the bottom to maintain, as you assert as if you think that I think otherwise. Never mind that I’ve said that myself repeatedly in this and other threads discussing the subject. Straw men are the easiest ones to wrestle, I always say.
Other stuff is just as absurd. N&Z, for example, in their “unified climate theory” claim that their “miracle equation” predicts the temperature as a function of surface pressure nearly perfectly. The fact that it has an extreme nonphysical form with characteristic pressures of 54,000 bar and 202 bar in it and is the product of two exponentials used to independently fit three planets on one end, two on the other, with a four-parameter set is conveniently hidden, until one looks for it. Then it becomes clear that their “miracle” is utterly meaningless and nonphysical. That kind of thing I will eventually get around to whacking, as I have the time.
I must say, though, that it is really amusing to see the lengths people will go to to try to deny that CO_2 plays any role in warming the Earth. Why bother? Look at the IR spectrum of the earth as photographed from orbit! Seeing is believing. Hard to deny the evidence of our own eyes, don’t you think, even if those eyes are electronic ones.
But don’t let me stop you! Play right on through.
rgb
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
For one thing, for example, they require the input of work to operate. They don’t just sit there and spontaneously heat one place and cool another.
No second law violation there. But they are very nifty, I agree. Not that efficient, though, as air conditioners go.
rgb
Greg Elliott says:
January 24, 2012 at 10:15 am
OK, no force as complex as gravity can function like a “Maxwell’s Demon”.
Your move,
w.
There is no question this accounts for some of the greenhouse effect, I am favoring all of it but can’t be sure. At any rate it has to be an important part of it and it sure appears to me that as you increase the ability of the atmosphere to radiate you are going to lose heat seemingly as sure as stripping insulation off your storage tank. Just that adding .0002 of a gas about 8 times less efficient than the surface isn’t hardly going to do anything.
Bill, you sound reasonably smart and practical. I agree that the specific heat and storage capacity of things like the oceans (especially) play a role in regulating the Earth, but you have to bear in mind that from the point of view of outer space, the Earth is a system with precisely one channel. Radiative heat in, radiative heat out. Experience with heating and cooling stuff on the surface is a matter of balancing conduction, convection and so on. Balancing the Earth itself is pure radiation.
With that in mind, take a look at the actual IR power spectra taken from orbit. In them, you will very clearly see that the CO_2 band radiates power at a much lower temperature than the surface of the earth. That is, part of the actual active band of outflow radiation is losing heat much more slowly than it would be without the CO_2. It’s not the only place where this happens — Ozone plays a role, and water is both the major transparent window through which outgoing radiation DOES escape and itself something that drops the outflow over part of the spectrum.
I know you’re probably confused and cynical about the usual descriptions of the GHE, with their upwelling and downwelling radiation and flow diagrams, but all of that is crap. You don’t need it to understand the idea. The idea you can understand with nothing but a garden hose. The faucet is the sun, it pumps energy into the hose, which represents the earth. The other end of the hose is outer space. The hose has no leaks — there is nowhere but in one side, out the other for the water to go.
Put your thumb over the outflow end and obstruct a bit of the flow and what happens? The pressure INSIDE the hose goes up a bit to compensate until the water flow out of the remaining part of the outflow end matches the inflow.
That’s all the greenhouse effect is. It doesn’t matter HOW you imagine things happen in the atmosphere proper, or what you think might help store heat or moderate or modulate temperatures. The IR spectra show that part of the outgoing nozzle is partially blocked, radiating a lot less power than the surface temperature would by itself be expected to radiate. By any mechanism you like — this isn’t about mechanism, this is about conservation of flow — the temperature of the rest of the system must increase enough to drive up the flow in the unblocked part of the garden hose until dynamic equilibrium is once again reached.
This argument doesn’t mean that other stuff doesn’t happen, or that it isn’t interesting or important. It just indicates that there is no question that the GHE exists and is real, because you can photograph it in action from orbit.
The real skeptical argument isn’t — or shouldn’t be — “there is no such thing at the GHE (false)”, or “real greenhouses don’t work that way (possibly true, but irrelevant)”, or “it’s all due to the DALR (reversing cause and effect)” or worse “it’s all due to stationary atmospheric pressure heating (impossible)”. It should be things like “What are the feedbacks?” “What other mechanisms modulate the rate of heat loss, and what is their relative contribution to global temperature and climate?” , “How does the Earth’s climate system self-organize to cool more efficiently as it warms (see what are the feedbacks)”, “given optical saturation in the CO_2 band, what is the real marginal effect of more CO_2 (could be very small indeed)?”
Ideally, taking the time not to shoot from the hip with whatever arguments are advanced. This is a hard problem, and deserves more effort and attention than just throwing out and vigorously defending an idea that even a tiny bit of later reflection with an actual textbook or two in hand might make you reconsider.
Just my opinion, of course, but — take a look at the IR spectra. That might be enough to at least convince you that some of the warming is straight up due to the GHE and CO_2.
rgb
OK, no force as complex as gravity can function like a “Maxwell’s Demon”.
Can I play, Willis?
Heh, heh. Try this one: Except when the gravity in question is gravity on the edge of a neutron star and extreme general relativity holds. That’s when the invisible fairies are liberated, and they sort out all of the hot and cold molecules.
Yeah! Try to argue with that, suck-ah!
rgb
Robert Brown says:
January 26, 2012 at 11:13 pm
Not only do they require the input of work, they require the input of lots of work. I was shocked when I calculated the efficiency on the one that I built. Absent very special circumstances, it’s not cost-effective for cooling or for heating. (Unless you are getting your power from Stygian Gas and Electric, where they pay you to use their energy.)
In addition, since Murphy isn’t dead, it’s a tradeoff. You can tune a vortex tube for greater or lesser ∆T between the hot and cold ends. But the greater the ∆T, the lower the efficiency. Murphy never sleeps, parasitic loss always goes up faster than output.
Which is another point in favor of the overall feedback on increasing global temperature being strongly negative. Increasing the operating temperature of the climate engine will greatly increase parasitic losses. But I digress.
w.
In the Gravity Lapse Rate theory, what matters is that the molecules experience acceleration between collisions. Since molecules in a centrifuge experience only 1 g between collisions, I see no basis for enhancement of the GLR beyond the factor of ~12 from the molecular mass.
So I guess you don’t agree with Einstein, then. Oh, well.
I would have said that all that matters is their effective acceleration in the accelerating frame, since the equivalence principle says that the molecules don’t experience anything from gravity either way. It just affects the way they hit the things around them.
You want to stop “feeling gravity”? Jump. While you are in free fall, you can’t feel it. What you “feel” about gravity is the things opposing it. Jump out of a tall building and you feel fine. What matters — and all that matters to the molecules — is the violence with which they strike other molecules.
To put it yet another way, the average buoyant forces that have to be exerted, the density and pressure profile, and all of the thermodynamic properties of the gas in the centrifuge are pretty much determined by the horrendously large value of effective g in the centrifuge. Now you want to assert that adiabatic lapse a phenomena that every single derivation of it requires a) that the gas be adiabatic, that is, a perfect insulator, which real gases (even ideal ones) are not; and b) be uplifting and downfalling — it is the “adiabatic expansion” that occurs as air parcels lift and fall due to variations in buoyancy that establish the rate, after all — some how lapses vertically along “real g” intead of horizontally opposite to the enormous density gradient due to 10,000g that determines the actual direction of convection and buoyant force in the frame of the gas.
Nonsense. I don’t mean that in an insulting way — you seem like a smart guy, you can see the inconsistencies in that yourself. You’re trying to fit a camel through the eye of a needle, and I think that you know it. The camel doesn’t like it.
rgb
It is not the intention of the writer to demean, degrade, humiliate, despise, or disparage any god, godess, offspring of god, demiurge, inamorata, fetish or other supernatural being.
ROTFL. Even more than the GR induced universal thermal lapse. Remind me not to radiate any photons towards the sun!
rgb
Bill Hunter said @ January 26, 2012 at 10:14 pm
I couldn’t find my digital thermometer, so I “borrowed” the very old max/min mercury/alcohol thermometer from the greenhouse to measure water temp.
Time 7 pm Eastern Summer Time (close up the greenhouse time)
Greenhouse air temp 80F
Max greenhouse temp reached 110F
Open air temp 69F*
Water from 150 yards long 2 inch black polypipe running exposed to sun on bone dry ground (no rain for 2 weeks) 72F
Maximum open air temp reached 81F*
Cloudless, still sunny day.
* Weatherstation 4 yards from greenhouse. Temp converted to degrees F from C.
FWIW I’m a semi-retired farmer and spend quite a lot of time outside.
If you put 2 bricks in the sun, and suppose after hour or so the highest
temperature they got was 140 F.
Then put bricks in oven and heat to 250 F. Put one brick in sunlight and other in shade.
How long would it take for sun lit brick and shaded brick to cool to 150 F?
Robert Brown wrote:
You want to stop “feeling gravity”? Jump. While you are in free fall, you can’t feel it. What you “feel” about gravity is the things opposing it. Jump out of a tall building and you feel fine. What matters — and all that matters to the molecules — is the violence with which they strike other molecules.
I would still be experiencing gravity. I’ve gone several seconds without “feeling gravity”, but I was distinctly aware of it, and the “feeling” all caught up with me in the end. Done right, it’s quite enjoyable.
So I guess you don’t agree with Einstein, then. Oh, well.
In a great many ways. I learned to visualize multiple frames at once at a young age. The only particular thing I disagree with is, “God does not play dice with the Universe”. My terminology, however, is sometimes sloppy.
I would have said that all that matters is their effective acceleration in the accelerating frame, since the equivalence principle says that the molecules don’t experience anything from gravity either way. It just affects the way they hit the things around them.
The ‘acceleration’ is an artifact of the rotating frame, not an accelerating frame. That is, it results from how you set up your math. If you model the interior of the centrifuge from the accelerated but non-rotating frame of Oak Ridge, you get different answers. Particularly, consider the case of a single molecule that comes to a dead stop for an instant, and accelerates downwards under gravity. In the Oak Ridge frame, its motions are simple. In the rotating Centrifuge frame, one might conclude that the core of the centrifuge itself was exerting an enormous gravitational field.
If you get different results in different frames (after correcting for dilation), you’ve either made a mistake setting up one of your frames, or you botched your Lorenz Transform, or coordinate substitution.
Nonsense. I don’t mean that in an insulting way — you seem like a smart guy, you can see the inconsistencies in that yourself. You’re trying to fit a camel through the eye of a needle, and I think that you know it. The camel doesn’t like it.
Thank you. I respect you as well, though it may seem otherwise. I do know it, but not necessarily in the way you think.
Where I think a lot of people go astray, particularly on this subject, is that within their interpolated regions, the laws of physics are very solid. It’s only the extrapolations that are problematic. Newtonian mechanics are a good example of this.
I believe the Second Law holds except under very specific criteria. I believe Gravity meets those criteria, but centrifuges do not, at least not in a way that that breaks isothermal. I haven’t checked the math on Dalton’s Law, and won’t, particularly since I don’t have the Oak Ridge numbers.
ZP says:
January 26, 2012 at 7:55 pm
While reading about Maxwell’s demon, I came across an amazing invention that appears to shed light on the “gravitationally induced” temperature gradient idea. The Ranque-Hilsch Vortex Tube generates a temperature differential within a tube by injecting a compressed gas stream which then generates a vortex. The temperature along the walls is higher than the incoming gas, while the temperature within the center is colder than the incoming gas. The two temperature streams can be physically separated.
Here are some links, including a patent on an embodiment of the invention, if you are interested in learning more about this phenomenon:
http://www.filtan.de/ENGLISH/VTS_A.htm
http://www.me.berkeley.edu/~gtdevera/notes/vortextube.pdf
http://www.google.com/patents?hl=en&lr=&vid=USPAT3546891&id=KppYAAAAEBAJ&oi=fnd&dq=%22vortex+tube%22+gravity+%22temperature+gradient%22&printsec=abstract#v=onepage&q&f=false
=====
For interest:
http://www.arizonavortex.com/vortex-tube/
“Vortex Tube Information
A vortex tube is a tool that can take normal compressed air and convert into two air streams. One stream is hot air and the other stream is cold air. The beauty of the vortex tube is that it has no moving parts , which translates into no maintenance. The cold air can be adjusted down to -50 degrees Fahrenheit, and the hot side can be adjusted up to a temperature of 260 degrees Fahrenheit.”
http://www.lovesedona.com/01.htm
Bell Rock Vortex of the twisted juniper:
“Juniper trees respond to the vortex energy in a physical way that reveals where this energy is strongest. The stronger the energy, the more of an axial twist the Juniper trees have in their branches. Instead of going straight down the branch, the lines of growth follow a slow helical spiral along the length of the branch. This spiraling effect can sometimes even bend the branch itself.”
If masculine/feminine not your thing, the following page has more information on the streams within the vortexes/vortices
http://gosw.about.com/od/sedonaarizona/a/sedonavortex_2.htm
Which says this is a “pure upflow” vortex.
Q. Daniels, here is a celebrated scientific quote that is worth pondering:
Here Eddington’s point is that the Second Law is believed to hold universally (even under unusual or extreme circumstances), and therefore, “thought experiments” that predict Second Law violations are regarded as convincing evidence of a theory’s invalidity.
Dr.Brown,
When you say “I must say, though, that it is really amusing to see the lengths people will go to to try to deny that CO_2 plays any role in warming the Earth.
Why bother?”, you do realize that there is no proof that CO-2 plays any role in warming the Earth, don;’t you?
You continue:
“Look at the IR spectrum of the earth as photographed from orbit! Seeing is believing. Hard to deny the evidence of our own eyes, don’t you think, even if those eyes are electronic ones” Indeed, just look at all the places that are emitting heat but not receiving it.
I think you have intentionally distorted the claim that gravity is the cause of the temperature lapse to mean whatever you wish, so that you may claim that gravity is supplying heat, when all that is necessary is for gravity to redistribute heat..
Consider, for example, a centrifugal compressor running continuously under steady conditions. The compressor draws air from a temperature and humidity controlled space.at 1 bar, and discharges it into a process at 2 bar. .The entering air is steadily and continuously heated from ambient (Ti) of 15°C to an exit temperature, (To),which will be 78°C or higher,. It is a function of the ratio of the outlet pressure (Po) to the inlet pressure, (Pi) and the efficiency of the compressor; which can be close to, but will be less than one. To = Ti * (Po/Pi)^((R m eff)/Cp mean), R is the universal gas constant, and m is the molecular weight of the gas. Is it thermodynamically stable?. Why is the discharge hotter?
Willis,iIt is similar to the vortex tube. Face it, you are in denial.
Bill Hunter says:
January 26, 2012 at 10:14 pm
What the atmosphere does radiate is what lowers it to 33K GHE. If GHG make a difference its likely a cooling difference.
Via the Water Cycle, it lowers it 52°C from the 67°C the real greenhouse would be without it, this being the thermal blanket of the real gas fluid ocean atmosphere of mainly nitrogen and oxygen around our Earth:
Earth without any atmosphere: -18°C
Earth with our atmosphere: 15°C
Earth without water: 67°C
Real gas and not imaginary ideal, as average is imaginary construct?
What we need to do with these academic climate scientists is take them outside and introduce them to the real world.
And then get them to not only bring back into their fictional energy budget, KT97 and ilk, the Water Cycle, but to bring back the thermal infrared heat on the move from the Sun as the real world direct heat source for land and oceans, and, to give back to shortwave which they claim does this in place of thermal energy direct from the Sun, its real properties and properties, its chemical energy cycle, that store which slow releases heat back into the greenhouse atmosphere by recycling Life.
In an earlier comment I suggested that Hans Jelbring’s theory was based on a fairly obvious fallacy. No-one seems to have responded to that suggestion, either for or against it, so I will have one more go, then shut up.
The proposition underlying Jelbring’s theory is that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy.” It seems to follow from this that if one form of energy, such as gravitational potential energy, is high, then others, such as kinetic energy (and therefore heat), must be low.
Jelbring gives no source for this key proposition, and it is not obviously true. Much depends on what is meant by “in an average sense”. Over a sufficiently long period of time, it follows from the equipartition theorem and other principles of statistical mechanics that every molecule in a gas will have the same average kinetic energy, the same average potential energy, and the same total energy, as any other molecule. It is like a game of pure chance in which every player will, in the long run, be a winner as often as a loser.
But in the short run this is by no means the case. Most players will have some fluctuations of fortune, and a few will have long streaks of good or bad luck. The same is true of molecules in a gas. In any given reference frame, at any given moment, some molecules will have a lot of kinetic energy and others little or none. They will also vary in their direction of motion from one moment to the next. In a gravitational field they will all have a tendency to ‘downward’ motion, but as a result of collisions with other particles, and with the ground, at any given moment about half of all molecules will be going ‘up’. Purely by the laws of statistics, some molecules will have a long streak of upward movements. In the absence of thermal convection currents, or other mechanisms of mass transport, those molecules which are ‘high’ in the atmosphere are there as a result of a sequence of accidents. There is no reason to suppose that they will have ‘given up’ kinetic energy in exchange for higher potential energy. In general, they will have gained potential energy at the expense of other molecules, which will have lost kinetic energy, potential energy, or both, in their collisions. In a zero-sum game, for every winner there is a loser.
In Jelbring’s idealised model system, there is no localised heat source to drive convection currents, and the position of molecules in the atmosphere will, I think, be due entirely to the statistical fluctuations I have just described. There is no reason to suppose that molecules higher in the atmosphere will, on average, have lower kinetic energy. Jelbring’s ‘proof’ of a temperature gradient is therefore invalid, as it depends on a premise which (depending on interpretation) is either false or inapplicable to the circumstances (because something true in the long run is being invalidly applied in the short run).
This does not rule out some other version of the ‘gravitational’ theory being true, but it does not bode well.
It is apparent that the writer is a physicist and not an engineer.
Take the thought experiment = a very long cylinder with a gas and a silver wire (assumed to be a perfect conductor) running from low in the cylinder to the top of the cylinder and claimed to cause a problem with the lapse rate explanations.
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
The ‘temperature’ of a gas (if you must use a compound term) is a measure of the total kinetic energy of the molecules in the volume of gas being measured. The silver will be heated by transfer of kinetic energy by collisions with the gas molecules at the base. As the pressure is higher at the base there will be more gas to silver collisions than at the top of the cylinder where the pressure is lower. Therefore the silver at the top of the cylinder will have fewer collisions and thus fewer gas molecules will receive any kinetic energy and be heated. The ratio of the number of collisions at the base to the number at the top is dependent on the pressure differential. I would expect that if this experiment were to be done the silver might be heated but the different conductivity to the gas at the bottom and the top would be the same as the lapse rate.
The thought experiment is based on a false assumption. If the experiment was built the result would actually support the existence of a lapse rate and there would be no ‘extra heat’ to be transferred downward.
Physicists should avoid using compount metrics like temperature and instead use the actual underlying measurement of heat. In a gas heat is not the same as temperature this is a type error. Even a physicist should remember the gas laws.
In a great many ways. I learned to visualize multiple frames at once at a young age. The only particular thing I disagree with is, “God does not play dice with the Universe”. My terminology, however, is sometimes sloppy.
Einstein was misquoted on that one, or rather, interrupted before the end. In his little known apocryphal autobiography, he apparently confessed to a close friend afterwards that he meant to add “… but Ifni does!” 😉
rgb
Willis Eschenbach says:
January 26, 2012 at 11:08 pm
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
How effecient would it be if it was the heat one wanted to maximise?
From the arizonavortex.com link I gave: “A vortex tube is a tool that can take normal compressed air and convert into two air streams. One stream is hot air and the other stream is cold air. The beauty of the vortex tube is that it has no moving parts , which translates into no maintenance. The cold air can be adjusted down to -50 degrees Fahrenheit, and the hot side can be adjusted up to a temperature of 260 degrees Fahrenheit.”
Could the cold air be re-introduced into the compression chamber?
..the price of oil here, looking for alternatives…
There’s also, “A plasma vortex can be made through the interaction of electric and magnetic fields.”
http://www.rmcybernetics.com/projects/experiments/experiments_vortex.htm
I think you have intentionally distorted the claim that gravity is the cause of the temperature lapse to mean whatever you wish, so that you may claim that gravity is supplying heat, when all that is necessary is for gravity to redistribute heat..
Oh, sure, I’m doing this all intentionally. In fact, I secretly get money from the IPCC — they are paying me to pretend to “debunk” all of the superlative science that appears on this blog. Hell, with my last paycheck from them I bought a Hummer, because (like the rest of the conspirators) I secretly know that the Greenhouse effect is bunkum. You’ve caught me out.
Now that we’ve established that to your satisfaction, perhaps the other adults on the site and I can hold a conversation about the actual topic of the top post. Or you could say something like “Gee whillikers rgb, you sure are right about that Jelbring paper but y’know, I think that gravity is still somehow turning the Earth’s atmosphere into a giant refrigerator. I can’t exactly say how, because I don’t really know how refrigerators work, especially refrigerators that rely on pure radiation for rejection of heat during their cyclic operation and it all makes my head hurt to try to figure it out and explain it in a way that would actually convince somebody (you know, with algebra and Navier-Stokes and everything) but it really is fun to talk about it as if I did know.”
I could then say, “Wowsers. Maybe we need another thread to talk about ways other than manifestly second law violating processes that gravity could contribute on some other top post thread, as soon as you are ready to make a concrete suggestion with some actual physics in it!” And we could part friends, and I could go back to my Evil Masters for another payoff. I was thinking of adding a nitrous tank to my hummer and jacking up its suspension, and my kids gotta eat.
So how about it? Would that work for you?
rgb
The proposition underlying Jelbring’s theory is that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy.” It seems to follow from this that if one form of energy, such as gravitational potential energy, is high, then others, such as kinetic energy (and therefore heat), must be low.
And this is close to being correct, but it isn’t absolute gravitational potential energy that matters, it is the amount that gravitational potential energy involved with the “irreversible” part of thermal motion as molecules fluctuate on a characteristic length scale of the mean free path.
He does have the “same” idea right; he just doesn’t understand the zeroth law. Temperature is the definition of “same”. When the temperature is the same, the capacity of randomized energy trapped in the system, that is, “heat” to do work is minimized. It is the maximum entropy state. At this state, no work can be extracted via a heat engine because there are no reservoirs of heat in the system at different temperatures.
This is all really pretty simply explained in intro thermo textbooks. If people (including Jelbring) stopped trying to reinvent thermodynamics to suit a desired conclusion and instead applied it the other way around, to check their unproven hypothesis, it would be better all around.
Here, I’ll reduce it to a one line “elevator speech”. If a supposed equilibrium distribution of temperature in an isolated system is capable of doing work, it is neither an equilibrium distribution nor is the system at maximum entropy.
One sentence. In the table-thumping words of Johnson, Thus I refute you.
rgb
My name comes up 81 times in this thread, so I thought I’d chip in.
Much confusion seems to have been generated by the sentence in Sec 2.3 of my lecture notes which reads “we expect the particles to accelerate as they travel downwards, and slow down as they travel upwards, rather like a bouncing ball. Mean velocities will be greater near the bottom of the box than near, the top: in other words, pressure decreases with height”. People seem to have interpreted this as automatically implying non-isothermal temperature profiles in thermodynamic equilibrium. This conclusion is wrong and unwarranted. Note that my sentence only mentions pressure: in hydrostatic equilibrium, pressure must decrease upwards, but temperature (which depends on both pressure and density) is unconstrained. For an isolated gas subject to gravity, thermodynamic equilibrium implies an isothermal profile; this was proved by Gibbs already in the 19th century (see recent discussion by Verkley and Gerkema, J. Atmos. Sci. 2004).
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
I’m glad that you’ll be able to offer us an expert perspective on the Ranque-Hilsch vortex tubes, especially given that the principle of operation is currently debated. Please show the mathematical model used to describe the principles by which the vortex tube operates. Further, please explain how this model differs from the “gravito-thermal” hypotheses using the governing thermodynamic equations for the equilibrium states.
Jules Verne
Be careful of logic traps that involve ‘fixed laws’, as you were invited to do. As Q Daniels has just noted, correct formulaic representations of reality are not necessarily correct in all projected circumstances. Robert has invited to you play on a field which he has circumscribed, layering on the arguments that you can’t prove your assertions using formulas he chooses. Perhaps. There is a principle involved: common formulas are (usually) inaccurate representations of a partially understood truth. There is little point in restricting your thinking during a debate to those existing formulaic representations of reality about an impossible but interesting postulated atmosphere. Y’unnderstand? If you are building bridges, it’s OK, but we are discussing something at the limits of our understanding of the physical universe. Suspect all formulas.
As several people have pointed out above, general physical laws apply in very particular conditions. There are many 3=5 arguments one can make by carefully using or misusing physical ‘laws’ that are hard to detect. Einstein is often held up as the perfect genius who was proven right, yet he was not only incorrect, or apparently incorrect about many things, he held many doubts about his own work and thought many contemporaneous perspectives as transitory.
My point is that in order to move beyond current understanding of something, you have to be prepared to move outside the cloistered world of standard formulas and see if they really are applicapable to and work normally in the postulated scenario. Much confusion above is contributors trying to get their head around an unreal planet with some physical laws suspended. We have enough problems dealing with the one reality we have let alone a plethora of unrealities.
Will a cylinder of non-radiative gases in free space achieve isothermal balance? Yes.
In a gravitational field? Unproven.
In a very strong gravitational field? No.
In any real, physical planet? Never.
Now let’s move along.
Robert Brown says 1/26 9:15pm and 10:12pm:
“The entire purpose of the paper is to examine Fourier’s Law…”
Great posts Robert, thank you.
In my view 1) way better than the top post, 2) focusing on air column heat flow from delta T is productive, 3) the thermo grand masters knew of it yet they were still perplexed.
It will take me some work to rummage thru top post eqn. 2, Joules posted paper, and present logic as to why in the limit this delta T must be non-isothermal. Can’t wait for my copy of Boren text to come in.
In the meantime, here’s my counter summary of those views in favor of the column being non-isothermal discovered up thread:
1) 1st Law (cons. of energy) and 2nd Law (constant entropy process is ideally permitted)
2) Caballero (except maybe not see his post at 1/27 6:07am)
3) Velasco eqn. 8 – Joe Born posts
4) Joules Verne posts
5) Robert Brown view that ideal molecules can climb gravity at constant velocity is unsatisfying. How do they possibly maintain constant velocity (i.e. T) as they go up, defeating bouyancy? Nothing I know of does that. Including Earth’s atmosphere.
However against this list, Willis’ writes there are issues with the 0th law and Robert Brown POV Fourier law in the limit as delta T approaches 0 & I see those are valid.
Woo-hoo, Rodrigo Caballero is here now too, with some more ref.s. More homework to find why those molecules can climb up in gravity field at constant speed, constant T even though “Mean velocities will be greater near the bottom of the box than near, the top..”
Science discussion here made my down time recovering from a head cold last few days very much more enjoyable. Thanks WUWT.
A basic assumption from the second law is that all the molecules in the system have, on average, an equal amount of energy. That is the state of maximum entropy and the state which is obtained at equilibrium.
It is incontestable that molecules in the upper shell have more gravitational potential energy than those in the lower shell. Therefore, to satisfy the second law that all molecules on average have an equal amount of energy, the molecules in the lower shell must possess some form of energy, on average, equal and opposite to the gravitational potential energy in the upper shell.
Robert Brown has used pages and pages of obfuscation to conceal the fact that all the molecules in his fully relaxed atmosphere have, on average, equal amounts of energy.
Until he explains how this unequal apportionment is possible without violating the first law of thermodynamics then I must conclude that Jelbring is absolutely correct. The only problem I have with Jelbring is conflating the lapse rate with a greenhouse effect. A greenhouse effect raises the surface equilibrium temperature above what it would be without the greenhouse effect. The lapse rate they demonstrate does not do this and so should not be labeled a GHE.
And by the way, Jelbring was far from the first to make this argument. Its originator was James Clerk Maxwell (yes, THAT Maxwell of fundamental physics fame) in 1866. He has not been disproven in the intervening 150 years. Handwaving about one of the many obscure restatements (the “refrigerator statement”) of the second law does not qualify as a proof. In fact there is no first principle in physics that prohibits a perpetuum mobile of the second kind. Only perpetuum mobiles of the first kind are prohibited by the first law of thermodynamics (conservation of energy).
What the good professor should come to understand is that gravity is a force which decreases entropy. It concentrates matter and energy into stars and planets and galaxies and galaxy clusters. Without it the universe would be a homogenous soup with far more entropy than we see today. It should there come as no surprise that when you introduce gravity into a thermal equilibrium environment that your thermal equilibrium will be upset. However this is no violation of the second law which, in its primary form, states that energy will be equally distributed. It does not state that kinetic energy will be equally distributed. The kinetic energy qualification is added into restatements of 2LoT and those restatements are not necessarily universally true. This case I believe casts grave doubt if not outright proves that the refridgerator restatement of 2LoT is not universally true.
Well then, thank you Dr. Caballero, and incidentally, thank you very much for your fine online book — I’m using it teach myself at least a decent amount of physical climatology (where I can focus on the climatology parts per se, as most of the basic physics I already know pretty well). I’ve put my own intro physics textbooks online for free as well, but I haven’t finished (more honestly, I’ve barely started) writing the third volume which will contain thermo. Eventually I may stick a bit of atmospheric thermo in there, as it seems that this is both of general interest and something undergrads probably should know in order to make informed political decisions.
It will be interesting to see if even your post makes a difference, though. If you read through the whole thread — something you might find actually painful — you will find people who are willing to invoke anything — last night general relativity in order to preserve the illusion that gravity alone creates a warming of the bottom of the atmosphere, even in the absence of external heating, so “there is no Greenhouse Effect”.
That’s actually the part of your book I learned the most from, so far. I hadn’t worked out how the GHE was supposed to work in any sort of detail before I read it, but that chapter was completely illuminating. The IR spectroscopy you present says it all.
But that is a matter for discussion in another thread. Unless any of the many, many people who have argued against the conclusion that Jelbring’s work is completely wrong and should have never been accepted in the first place wish to keep arguing, perhaps the more polite ones can concede in one last post and we can wrap this up and move on to N&Z, the “existence” of a real, live GHE, and maybe, just maybe, get to where the skeptical arguments on the list are much better informed and less likely to play fast and loose with the laws of nature or thermodynamics.
rgb
Robert Brown
It would be wrong to conclude that all those who are unconvinced by the isothermal distribution are sceptics.
Jim D who posted earlier is a very effective proponent of IPCC science and is unconvinced.
Willis (a sceptic) moved from adiabatic to isothermal in one week.
The issue has no bearing on the existence or otherwise of a greenhouse effect.
I can see both arguments for and against each position.
I think the isothermal argument is the stronger one but until an experiment confirms it one way or another I will keep an open mind.
1 kg of air contains a total energy value of 90,000,000,000,000,000 joules – about what the Earth recieves from the Sun in 40 minutes.
The radiation theory assumes that the 1 kg of air is absorbing 390 joules/second of energy from the warm surface and emitting 390 joules/second of energy up and out.
There is a lot of energy contained in that air that is apparently doing nothing. It is permanently locked up in the atomic structure of the air and contibutes nothing to its temperature. Only the fusion energy produced in the Sun is affecting its temperature.
Nice tidy story. (ignoring 99.9999999999996% of the energy in the air).
Crispin in Waterloo says:
January 27, 2012 at 6:22 am
“Jules Verne”
It’s Joules Verne. I know Joules Verne. Joules Verne is a friend of mine. Joules would like you to know that he is no longer participating in this thread because his comments were being purposely held up such his ability to rejoin and rebut was unfairly hampered. I speak in his stead for the time being unless and until the same fate befalls me.
The case for the lapse rate can be made in few sentences in Jelbrings isolated non-convecting atmosphere of ideal gases. Molecules in the upper shell have more gravitational energy than molecules in the lower shell. In order to satisfy the second law requirement that a closed system will equalibrate to a state of maximum entropy all molecules must, on average, have an equal apportionment of energy. Therefore, if the upper shell molecules have more gravitational energy than those in the lower shell then what form of energy do the lower molecules possess to make them have an equal amount of energy? The answer is clearly that the lower shell has more kinetic energy but I’m certainly open to arguments that it’s some other form of energy. What I’m not open to hearing is that the second law allows disequal apportionment of total energy in an equilibrium state which is, in essence, what Dr. Brown (whether he realizes it or not) is saying.
here is a principle involved: common formulas are (usually) inaccurate representations of a partially understood truth.
Well put, Crispin. In this case in particular, the correct formulae are the full nonlinear Navier-Stokes equations with external forcings, implemented in a full thermal model of the Earth. Alas, as I have noted, mathematicians cannot yet even prove formal existence of general solutions to the NS equations, let alone provide a constructive general solution. They are solvable in various special cases, many that are relevant and interesting, but the full problem is beyond our current ability to fully compute.
That doesn’t, however, mean that the laws of thermodynamics are an inaccurate representation of a partially understood truth, or that the foundations of statistical mechanics are particularly shaky. It just means that the general description of open systems, especially open fluid systems, is a hard problem.
The reason I focussed on Jelbring is that here there is no shakiness or partial understanding. He constrains his conclusions to a specific model where they violate the zeroth and second law of thermodynamics. In fact, they are a textbook violation of it, one that one could fairly assign as a homework problem in any undergraduate introductory physics course that covers thermodynamics:
Problem 6: An insulated container of ideal gas is prepared. No external work is done on the container. The container is left on the table for a very long time, so that its contents reach thermal equilibrium from whatever initial state they might have had. Show that it is impossible for the equilibrium state of the gas to exhibit a stable macroscopic thermal gradient across the gas, because such a state would enable a violation of both the Kelvin-Planck and Clausius statements of the Second Law.
That’s basically been the “assignment” for all of the people seeking to defend Jelbring throughout this thread.
Now Crispin, if you are trying to say that the laws of thermodynamics are, like the Pirate Code, not so much laws as “suggestions” (because one way to avoid the conclusions of an argument that you don’t like is to reject its axioms, after all) you might want to soberly reconsider that statement. A whole lot of baby getting thrown out in all that bathwater, don’t you think? Not to mention the fact that anyone that actually tries to live their life as if they really don’t believe in the laws of thermodynamics will find life ugly, brutish, and remarkably short.
Oh, the hell with my knowledge of heat capacity, conductivity, and so on. I’ll just reach my hand down into the vat of seething oil and pull my french fries out one at a time, shall I? What can go wrong?
rgb
19th century (see recent discussion by Verkley and Gerkema, J. Atmos. Sci. 2004).
ZP says:
January 27, 2012 at 6:19 am
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
I’m glad that you’ll be able to offer us an expert perspective on the Ranque-Hilsch vortex tubes, especially given that the principle of operation is currently debated. Please show the mathematical model used to describe the principles by which the vortex tube operates. Further, please explain how this model differs from the “gravito-thermal” hypotheses using the governing thermodynamic equations for the equilibrium states.
====
Ah reminded. Meant to ask too, but just stop at “because the vortex tubes operate on very different principles than those claimed for the gravity theories”
How are they very different principles?
1 kg of air contains a total energy value of 90,000,000,000,000,000 joules – about what the Earth recieves from the Sun in 40 minutes.
All very erudite, of course. Now if you could be so good as to make a point somewhere in there? Not that there aren’t any number of good points to be made — thermal equilibrium and heat simply ignores energy bound up in ways that cannot participate in the thermal redistribution of internal energy changes. If you cooled the gas to absolute zero, it would still have almost all of this baseline mass-energy. So let’s just agree to subtract it out as completely irrelevant to a discussion of thermodynamics, unless the “air” in question is inside the core of a star that is in the peculiar state where it is fusing oxygen and nitrogen or sometimes fissioning them with fast neutrons (the only processes I can think of that might change their baseline mass-energy by altering their strong nuclear interaction energy).
rgb
Robert Brown says:
January 26, 2012 at 4:24 pm
“That’s why I hold out some hope for GR. That’s a difficult problem — if you warp space and time with a very large mass, you do have a bit of a problem defining temperature as energy itself gets a bit warped along with space and time as you go down into the well. However, in this case:
a) The effect is utterly negligible in any real gas for anything less massive than a star.
b) It probably cannot be measured. Your thermometers follow the same gradient as one goes up and down, and they would probably still read the same temperature as temperature itself would probably be following the curvature of spacetime.
c) It is completely irrelevant to the discussion at hand, involving a simple ideal gas in an ordinary vertical column with constant g.”
Not too difficult. Proper temperatures in thermal equilibrium scale as the redshift climbing out the gravitational well. T(height)/T(infinity) =z(height)/z(infinity) = (v(escape)/c)^2/2 for v<<c. The corresponding lapse rate is just T/g.
So (a) yes (except perhaps for something like a mini black hole).
But (b) is not so. Proper temperature is defined and measured locally; the materials whose temperature one is measuring don't know squat about the depth of the well – or care. Their intrinsic physical properties stay the same – the triple point of water is still 273.16K, for instance. So ordinary thermometers will work fine. However, if you measure the temperature of the column bolometrically from any given height, what you see will always be isothermal at equilibrium. It goes without saying that there is no way of extracting energy from this – or perhaps it doesn't go without saying here, so I'll say it!
As for (c), I quite agree.
You might be interested in reading this story , which explores some of the oddities of an extreme relativistic environment.
By the way, is there a tutorial somewhere in how to write those nifty equations recognised by wordpress? What is this latex thingy? Is it a specific markup language?
Drat, I meant:
The corresponding lapse rate is just Tg.
Mod, can you fix please?
DavidB says:
January 27, 2012 at 5:27 am
The source is the second law of thermodynamics which Jelbring probably assumes the reader is familiar with – a closed system tends towards maximum entropy. It is not obviously true it’s an empirical observation. It’s statistically true. In fact there are no first principles in physics which demand it be universally true and it’s not true at all at the microscopic level where a gas in equilibrium will have a Boltzmann distribution of energies. The second law is only statistically true. The second law is all that gives rise to the arrow of time. At the microscopic level there is something called quantum unitarity which means, in a nutshell, that everything that happens can unhappen and it’s all perfectly predictable with sufficient information. This is also called time-reversible. Time can run backwards in other words and it’s only the second law, tendency towards increasing entropy, which gives time a direction. That time exists and has a direction is an empirical observation and, notably, is not something proven or even predicted by theory.
This comes as a shock to most people as it seems to go against our most strongly held intuitions about how the universe works. The fact of the matter is that we don’t have a theory of everything and the universe still contains unexplained mysteries at even the most fundamental levels – levels like “What produces the arrow of time?” and levels like “Why is the universe expanding at an increasing rate?”.
That said, the law of entropy is very well supported by observation at the macroscopic level and is a basic law that engineers use every day to design the modern conveniences of life. However, entropy is about total energy not justy kinetic energy. This is where the author of the OP goes off the rails. He appears to think it’s fine that molecules in the upper shell have more total energy, on average, than molecules in the lower shell so long as average kinetic energy is the same. This is a grand departure from the second law which others have mentioned. Maximum entropy is all molecules (on average, not at the microscopic level) have equal total energy TE = PE + KE. Dr. Brown is ignoring PE and using pages and pages of obfuscation and thought experiments trying to cover up this departure from first principles.
What puzzles me is why he’s going to such lengths. Perhaps he’s just defending a concept he’s taught for many years and can’t stand the idea of having taught something that was wrong. Or perhaps he’s convinced that a perpetuum mobile of the second kind is impossible and thinks he’s better than every physicist in the world who’s tried to prove that and failed. I don’t know what his major malfunction is but the blather that’s emerging because of it is flawed at the level of first principles and takes but a few sentences to dispute.
Dr. Brown,
Gravity is an organizing force that decreases entropy in a closed system? True or False?
Support your answer.
My answer is “true”. Gravity works very well to take equal distributions of mass within a given volume and clump it together. Maximum entropy is limited, at least in the short term, by gravity. Perhaps in 100,000 trillion years entropy will win. Perhaps it will not. That’s still an open question as the universe appears to poised on knife edge of expanding forever (called The Big Chill) and eventually reversing (called The Big Crunch). Personally I think it’s the big crunch for philosophical reasons explaining why the universe emerging from the big bang was so low in entropy.
A steady state atmosphere of a planet will have a atmospheric laps rate. The temperature difference is not a violation of the second law. The temperature difference cannot be exploited to do work. The atmosphere particles have the same energy, high and low, heavy or light. There is no energy difference to exploit to do work.
Try a one dimensional model (so no operators are necessary). Have a left-right axis and uniform force from the left to the right. Put a particle on the axis and set it in motion (either direction, it doesn’t matter). The farther the particle is to the right, the faster its speed is, the farther the particle is to the left, the slower its speed is.
Now turn the model on its ear, and turn the axis to the up and down direction. Make the uniform force go from up to down, and call it ‘Gravity’. Again set a particle in motion on the axis. Now the higher it goes, the slower it moves, and the lower it goes, the faster it moves.
Set a particle in motion on the axis and calculate its Lagrangian from its initial state. ( Lagrangian = kinetic energy + potential energy ). Then observe the particle anywhere else on the axis and calculate its Lagrangian. It is the same everywhere, and always the same. Energy and momentum are conserved.
Put a reflector at the bottom of the axis, and call it ‘the Earth’. Put a few more particles in motion on the axis, or a whole bunch more particles in motion on the axis (elastic particles) and call them ‘gas’. Call the kinetic energy part of the Lagrangian, call it ‘temperature’. The system of particles will eventually evolve to a steady state condition with a up and down temperature profile. You can call it ‘atmospheric lapse rate’.
There is no mechanism that can exploit the difference in kinetic energy between the high particles and the low particles. The parts of any mechanism are subject to the same force ‘gravity’, and the same Lagrangian. It is hard to believe, but a sliver bar that goes from the ‘earth’ to the top of the ‘gas’ will not transfer or move any energy from the bottom of the gas to the top of the gas. The bar is just different elastic particles, moving different speeds and smaller distances between collisions. The only mechanism for energy transfer is particles bouncing off of each other.
The real atmosphere has radiation and phase changes, as well as elastic collisions. But the where the distance between particles is smaller, elastic collisions predominate for energy transfer, and hence a atmospheric lapse rate below the tropopause. Where the distance between the particles is larger, radiative transfer of energy predominates. At the smallest densities, the equation of state of the gases is a radiative condition. Consider cosmic microwave background radiation and 20 billion year old gases 😉
edit to make the first paragraph more clear. Read it as: “Put a particle on the axis and set it in motion (either direction, it doesn’t matter). The farther the particle moves to the right, the faster its speed is, the farther the particle moves to the left, the slower its speed is.” I hope that makes more is more understandable!
A basic assumption from the second law is that all the molecules in the system have, on average, an equal amount of energy. That is the state of maximum entropy and the state which is obtained at equilibrium.


 ) is constant. The entropy can only increase or, in the limit of a reversible process, remain constant.
) is constant. The entropy can only increase or, in the limit of a reversible process, remain constant.  is
is 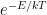 . But this takes you from the realm of trying to do stat mech by making english word pronouncements to using algebra, and it is actually rather difficult algebra. Good luck with it.
. But this takes you from the realm of trying to do stat mech by making english word pronouncements to using algebra, and it is actually rather difficult algebra. Good luck with it.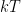 . You could also work on understanding that. In fact, as an exercise, why not express the size of the energy fluctuation associated with gravity when a molecule moves a mean free path in terms of temperature? What is the gravitational scale height where:
. You could also work on understanding that. In fact, as an exercise, why not express the size of the energy fluctuation associated with gravity when a molecule moves a mean free path in terms of temperature? What is the gravitational scale height where:
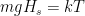

 for changes in height commensurate with the mean free path of air molecules. We’ll be enormously generous here — the mean free path at room temperature is order of a few tens of nanometers, but it increases as the pressure decreases with height by an order of magnitude or so. We’ll be very generous and use a whole micron —
for changes in height commensurate with the mean free path of air molecules. We’ll be enormously generous here — the mean free path at room temperature is order of a few tens of nanometers, but it increases as the pressure decreases with height by an order of magnitude or so. We’ll be very generous and use a whole micron —  meters.
meters. for the range of temperatures in between 200-300 K? We could work hard and do a lot of multiplication or we could observe that this is just the exponential of the ratio of the scale heights:
for the range of temperatures in between 200-300 K? We could work hard and do a lot of multiplication or we could observe that this is just the exponential of the ratio of the scale heights:  where I threw away the pesky $5$ because it doesn’t really matter, does it.
where I threw away the pesky $5$ because it doesn’t really matter, does it. is huge) at cold temperatures and large fields (so
is huge) at cold temperatures and large fields (so 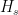 is small) and large thermal gradients (so the scale factors themselves change dramatically across the system. In this extremely irrelevant case, look, gravity can become important! Sort of. Not enough to prevent thermal equilibrium from being isothermal (because that would violate the second law of thermodynamics) but sort of.
is small) and large thermal gradients (so the scale factors themselves change dramatically across the system. In this extremely irrelevant case, look, gravity can become important! Sort of. Not enough to prevent thermal equilibrium from being isothermal (because that would violate the second law of thermodynamics) but sort of.
No, you’re begging the question. There is no basic “assumption” in the second law beyond sufficient particles with enough interaction for energy added to the system by any means to get shared around, given time.
What it tells us about how they get shared around is that the state of maximum entropy, the stable thermodynamic equilibrium, is the state where the internal energy of the system is no longer available for doing work. Nothing more, nothing less. To quote from an actual textbook on thermodynamics:
For an isolated system, i.e., a system that has no interaction with the surroundings, changes in the system have no effect on the surroundings. In this case, we need to consider the system only, and the first and second laws become:
For an isolated system the total energy (
Note that this says nothing about “all the molecules have an equal amount of energy”. It says that the total energy of the isolated system doesn’t change, and any changes wrought within the isolated system must either increase its entropy or leave it unchanged.
The equilibrium state of the system, the maximum entropy state, is always isothermal because it is rather easy to show that if there is any temperature gradient, a) moving heat from the hotter part to the cooler part will increase the system entropy (and decrease the temperature difference) while b) moving heat the other way will decrease the entropy of the system and hence is forbidden by the second law — as long as the transport mechanism is irreversible.
Heat conduction is irreversible. It is always present in any system that does not have actual physical (adiabatic) barriers in it. Ideal gas in a container most definitely conducts heat. Therefore it will always relax, via conduction, to a maximum entropy state with uniform temperature which, not at all coincidentally, is the state where the system no longer has any capacity to do work.
If you want a much more correct statement connecting the distribution of energy in the system and temperature, it is that the non-normalized probability of finding the system in any particular energy configuration
In almost all cases in the real world, uniform gravitation can be completely ignored and contributes almost nothing to the final thermal distribution of energies in the system, because the change in gravitational potential energy across the scale of the mean free path (or other relevant interaction/motion length in a solid) is much, much smaller than
or
So you can check your work:
http://en.wikipedia.org/wiki/Scale_height
Yes, it is more than 5 kilometers throughout the temperature range of the troposphere, almost 9 kilometers at room temperature around 300K.
Now compare
Now, here’s the interesting part. What is
If we use a taylor series expansion on this, which is a multiplicative factor in the Boltzman factor (sums in exponentials become products of exponentials) the result looks like — would that be 1? To 9 significant digits? It would.
That’s why people ignore gravity as a general rule when worrying about the thermodynamic equilibrium state of a column of air. Because it is utterly ignorable. The only exceptions are when people are examining very dilute gases (so
We can do this all day. Or, you could go try to learn some thermodynamics, or alternatively some statistical mechanics, instead of just making something up. Just a thought.
rgb
Paul Birch says:
January 27, 2012 at 7:34 am
” Proper temperatures in thermal equilibrium scale as the redshift climbing out the gravitational well. T(height)/T(infinity) =z(height)/z(infinity) = (v(escape)/c)^2/2 for v<<c. The corresponding lapse rate is just T/g."
Sorry, sorry, I slipped into geometrodynamic units, then tried to put the c^2 in and completely messed up as the wordpress reply box lost focus. That should have read:
The corresponding lapse rate is Tg/c^2.
Gravity is an organizing force that decreases entropy in a closed system? True or False? and plenty of irreversible internal dynamics and many, many degrees of freedom will spontaneously decrease its entropy if gravity is one of the interactions coupling the particles of the system. That is trivially provable. Here’s the proof: “It violates the second law of thermodynamics, which says that
and plenty of irreversible internal dynamics and many, many degrees of freedom will spontaneously decrease its entropy if gravity is one of the interactions coupling the particles of the system. That is trivially provable. Here’s the proof: “It violates the second law of thermodynamics, which says that  for any isolated system, and is zero only if the processes involved are reversible”. Which gravitational interaction isn’t, not in microdynamics, not any more than any other internal molecular interaction.
for any isolated system, and is zero only if the processes involved are reversible”. Which gravitational interaction isn’t, not in microdynamics, not any more than any other internal molecular interaction.
Support your answer.
How can I? You have to tell me what gravity is doing in that closed system. Are we starting the system off with zero gravity, and then smoothly turning it on? Are we starting it off with zero gravity and then slamming it on? Are we starting out with the system in thermal equilibrium in constant gravity? Is gravity a means of interaction for all of the parts of the system, and are we talking cosmology here, are is gravity a pre-established given acting on a closed jar of air?
Do you really think that all of these questions have the same answer? And do you understand that if gravity is a part of the internal interactions of a closed system, it cannot decrease the entropy of that system because that would violate the second law of thermodynamics? You are basically asserting that a closed thermal system with
So, sure you mean that, hoss?
rgb
Jim Z says: January 27, 2012 at 8:03 am
>:A steady state atmosphere of a planet will have a atmospheric laps rate.
Quite true. But this is not an EQUILIBRIUM condition, only a steady state condition. It is due specifically to energy being radiated from the TOA (top of atmosphere) by greenhouse gases. Similarly, there is a continued temperature gradient across the insulation in my refrigerator (from ~ 0 C at the inner surface to ~ 20 C at the outer surface). But this is not equilibrium, because I have to keep removing energy from the cold parts (just like energy must continually be removed from the cold parts of the atmosphere (by radiation from GHGs)).
>The temperature difference is not a violation of the second law.
Also quite true. But this is because we have a “hot reservoir” ( the sun) and a “cold reservoir” (space) that provide a source and a sink of energy, allow us to run various heat engines.
>The temperature difference cannot be exploited to do work.
It absolutely CAN be exploited to do work. The thermopiles discussed throughout this thread are one easy way. Any number of different heat engines could use the temperature difference to do work.
>The atmosphere particles have the same energy, high and low, heavy or light.
This is not correct, as has been pointed out many times. Let me give one more arguement that might be easier to understand. Consider a box at sea level (which we will consider to be an altitude h=0). Fill it with a mixture of He & Kr (Mass 4u and 84). Give the box a few minutes to equilibrate. I think every one will agree that all the molecule have the same temperature and the same KE –> KE = 3/2 kT. I think every one will agree that all the molecule have the same gravitational potential energy –> PE = mgh = 0.
Now raise the box of gas 1 km up. The Kr has gained 21x as much PE as the He has. By your hypothesis, since the Kr has gained more PE, the Kr must have less KE to have the same total energy. But if the Kr has less KE, the Kr will be a lower temperature than the He in the same box. Permanently. The higher I raise the box, the greater the temperature difference between the two types of gases, IN THE SAME BOX.
(This is conceptually very similar to the two jars Dr Brown has mentioned before, but it might be more intuitive to some people.)
Either
1) Atoms have the SAME total energy, but atoms on the same box can be at different temperatures, or
2) Atoms have DIFFERENT total energy, but atoms in the same box are the same temperature.
Does anyone REALLY vote for #1 ???
Robert Brown
It would be wrong to conclude that all those who are unconvinced by the isothermal distribution are sceptics.
Jim D who posted earlier is a very effective proponent of IPCC science and is unconvinced.
Willis (a sceptic) moved from adiabatic to isothermal in one week.
The issue has no bearing on the existence or otherwise of a greenhouse effect.
I can see both arguments for and against each position.
I think the isothermal argument is the stronger one but until an experiment confirms it one way or another I will keep an open mind.
And how can I not respect that? It is my own position, except that the “strength” of the isothermal argument is so much greater than that of a temperature lapse — given that it straight up violates the second law of thermodynamics — that the default position of any real scientist should be roughly the same as it is whenever somebody proposes a perpetual motion machine, or that they can negate gravity by means of a simple electronic device they built in their basement, or have worked out the One True Theory of Everything in their spare time, in spite of the fact that they never actually took calculus or physics in college (or may not have attended college). All of these things are technically possible, but they are so unlikely that our default position is a bemused and often unspoken “bullshit, did not” while politely waiting for hell to freeze over and actual evidence to emerge that experimentally supports the claim.
To put it another way, if I were a grant officer and somebody sought money to perform the experiment, I would categorically reject it. I wouldn’t even send it out for review — it would go straight into the round file, the same place the patent office now files PMM patents unaccompanied by a working model.
Sometimes the default position of science is to simply reject something. For example, it is alleged in various ancient mythologies that certain individuals (who may or may not have existed, it is hard to verify things that far back in the past) have instantly and completely cured actual blindness by rubbing a mixture of spit and mud into the eyes of an blind person. Modern science tells us that this is absurd. One cannot imagine any actual physical or biological mechanism for (say) nerve damage to the optic nerve, retinal detachment, physically damaged eyes, or even mere cataracts, to spontaneously revert to normal healthy tissue due to the application of filthy mud. Quite the contrary — we would be more inclined to consider spit to be a biohazard, and dirt from the ground in any country where the great outdoors is the universal toilet for man and beast alike to also be a biohazard, and would, I think, suggest that kids not try this at home to cure granddad’s failing vision.
Would I fund “Investigations into the curative properties of spit and mud on blindness in adult males”? Of course not. The default position for science is to not believe in magic, and this is magic precisely because it is unlikely, in fact because it is an intuitive violation of the second law. Eye damage is spontaneously “irreversible” as a general rule, which means that one has to perform very exacting and specific changes to reverse that damage. Random actions irrelevant to those specific changes are almost infinitely unlikely to have the desired effect.
So I too am always happy to be influenced by a well-conducted experiment, but in the meantime my default belief is “bullshit, that assertion directly violates the second law of thermodynamics and hence is almost certainly false”.
rgb
The temperature difference cannot be exploited to do work. The atmosphere particles have the same energy, high and low, heavy or light. There is no energy difference to exploit to do work.
Ah, but you see, heat engines and conductive thermal transport are driven by differences in temperature, not energy. As you would know if you had absolutely any clue about thermodynamics. You might actually look at the pictures in the top post and try to refute figure 2. Bear in mind that the air at the top is indistinguishable from ordinary air in an ordinary room at an ordinary temperature, ditto at the bottom. Heat would certainly flow between a reservoir of air at high pressure and high temperature and a second reservoir of air at low pressure and low temperature in any laboratory in the world. Please explain why it wouldn’t do that in the specific figure above.
rgb
Paul Birch said @ January 27, 2012 at 7:34 am
TeX is a markup language, LaTeX is a set of extensions to make using it easier; intro here: http://www.latex-project.org/intro.html
The CA-assistant adds a toolbar to the Leave a Reply box that enables the easy insertion of LaTeX commands (among other things).
http://climateaudit.org/ca-assistant/
Joe Born says:
January 26, 2012 at 5:42 pm
“So, although I respect your opinion, I have to go with mine. And it’s my opinion that, for the purposes of a theoretical discussion–which, let’s not forget, is what Dr. Brown initiated–Velasco et al. do indeed say that an isolated vertical gas column exhibits a non-zero lapse rate at equilibrium.”
Joe, if, for some strange reason I cannot fathom, you still wish to maintain your belief that “temperature equals average molecular kinetic energy”, despite what physicists tell you, that’s up to you. But for heaven’s sake stop trying to pretend that Velasco et al supports you. What they explicitly say is that the assumption that “temperature is proportional to average molecular kinetic energy” is FALSE (for the finite microcanonical ensemble). They say that the statement “temperature decreases with height” is FALSE. The reason it’s false is different for small N and in the canonic limit, but it is false either way. This is what they say.
Now, you can disagree with them if you like. You can believe they shouldn’t have said what they did say. You can believe that you can interpret their statistical mechanics better than they can do themselves. You can believe that they are such poor writers of English that they said the exact opposite of what they meant. But don’t claim they agree with you when they actually say you’re wrong!
The second law is only statistically true. , and an absurdly — truly absurdly — small number for
, and an absurdly — truly absurdly — small number for  .
.
Oh, please. Now you’ve got me ROTFL again, and I’d almost settled down. You should really say this like this:
The second law is only statistically true.
That makes it even funnier.
So you’re saying, basically, that like there is always a chance for a system to behave in egregious violation of the second law, for its macroscopy entropy to suddenly and spontaneously decrease.
Um, you ever do a back of the envelope estimate of that probability for a box containing, say, one whole mole of molecules? You might try it sometime. Please express your answer in terms of the mean free time between observations, assuming them to be poissonian in distribution, in log base units of powers of the probable lifetime of the Universe. (Hmm, what should we name these units? Not decibels, maybe unibels?)
Here’s a small hint to get you started. Take a simple box filled with white and black (but otherwise identical) balls. Draw an imaginary plane through the center of the box with equal volumes on both sides. Suppose the box has 2N marbles, N of each color. Give the box a good shake — enough to randomize the positions of all of the marbles. Now count the marbles on each side of your plane.
What is the probability that the shake leaves all of the black marbles on the left and all of the white marbles on the right?
This is a nice example because it is so easy. The distribution of outcomes is relatively simple to compute. I think you’ll find that the answer is a “very, very small number” for any values of
This is a textbook problem in thermo, intended to start to help you understand why it is really, really, really … (repeat a google of times really) stupid to bet against the second law of thermodynamics just because it is a statistical law…
rgb
Publius Maximus says:
January 27, 2012 at 7:06 am
There is absolutely no doubt that WordPress’s spam filter was written to single out posts by Joules Verne for special treatment. And everyone else from time to time for reasons that are, unlike the Laws of Physics, completely inexplicable. The mods inspect the contents of the spambox far less frequently than the main posts for obvious reasons. Tell your friend Joules to stick his paranoia where the sun don’t shine.
Nobody around here gets censored for their ideas. They do get snipped for extreme comments, but they are posted with a snip explaining what the offence was. Casting aspersions on Anthony and the Mods is not looked upon favourably around here. Of course if you want to really have your comments held up and unfairly hampered (edited to say what you don’t mean) by all means head off to (Un)RealClimate where such things are par for the course.
It is apparent that the writer is a physicist and not an engineer.
You mean, because physicists generally teach engineers the physical basis for engineering? True enough. But we enjoy doing it, really, except when they stubbornly or lazily fail to learn the laws of thermodynamics. Then we worry that they’ll go do silly things like try to design perpetual motion machines, which embarrasses us. Where did we go wrong? How did we fail you?
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
No, silly beanie. The assumption is that the silver conducts heat to the gas at all from the bottom to the top. I don’t really give a damn what the conductivity in the silver is or how good the thermal contact between the silver or the gas is as long as it is nonzero throughout the wire. And bear in mind that I can increase the thermal contact of the silver with the gas at both ends by means of adding a simple heat sink. Good engineering, no?
I do so find this sort of mistake to be embarrassing, don’t you?
Now go back to the drawing board and try again. Yes, the silver wire will conduct heat from the high temperature gas at the bottom to the low temperature gas at the top. So you were saying? Oh yes:
Physicists should avoid using compount metrics like temperature and instead use the actual underlying measurement of heat. In a gas heat is not the same as temperature this is a type error. Even a physicist should remember the gas laws.
You mean that we should remember them because you learned them originally in our classrooms? Gee, hard to argue with that. Now suppose you use your super-engineering powers to refute Fourier’s Law. That’s one of those “laws” we were trying to teach you back then, so you wouldn’t burn your fingers trying to grab a metal rod that has one end stuck into a fire.
How did we fail you?
Or perhaps I should be asking, how was it that we did not fail you?
rgb
” Yes, the silver wire will conduct heat from the high temperature gas at the bottom to the low temperature gas at the top”
So explain how the silver wire has precisely the same conductivity to the gas at low pressure at the top of the tube as it does to the gas at high pressure at the base of the tube. It cannot as there are less gas molecules coming in contact with that wire at the top than there are at the bottom – that is the definition of pressure.
You will find that when you take the different conductivity across the silver-to-gas boundary into account that the high gas-to-silver conductivity at the base is in lapse rate proportion to the lower silver-to-gas conductivity at the top.
“But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.”
That’s an absolutely precious quote, A Physicist. I’m going to have to save that one — it belongs as a panel quote at the beginning of a book chapter on the second law. Especially since it is so very, very true.
In fact, Maxwell’s Equations aren’t quite true — QED is. Any number of experiments have proven to be in error, especially in these confirmation bias prone, cherrypicking times where human research careers depend perhaps too strongly on getting startling (and valuable) results. But the second law still holds for QED and CED alike, for all of those often bumbling experiments.
rgb
Rodrigo Caballero says at January 27, 2012 at 6:07 am
I took a look at “Verkley and Gerkema, J. Atmos. Sci. 2004” and by my read, they consider that applying the two constraints of constant mass and constant energy (or enthalpy) to the fluid will result in an isothermal profile for the fluid in thermodynamic equilibrium. This is the classical result shown by Gibbs. However; Maxwell considered the effect of convective mixing by replacing the constant energy constraint with a constant potential temperature constraint. This change results in the column of fluid being out of thermodynamic equilibrium and results in an isentropic profile defined by a temperature lapse rate. Verkley and Gerkema propose that adding the constant potential temperature constraint will both satisfy the first law of thermodynamics implied by the constant energy constraint and still consider convective mixing. They go on to show how their profile can be used to fit the Standard Atmosphere.
The isothermal profile proven by Gibbs and promoted by Brown is looking at a purely academic scenario (no convective mixing) – real planetary atmospheres exhibit lapse rates that are not a result of the effect of greenhouse gases but rather convective mixing.
Woo-hoo, Rodrigo Caballero is here now too, with some more ref.s. More homework to find why those molecules can climb up in gravity field at constant speed, constant T even though “Mean velocities will be greater near the bottom of the box than near, the top..”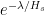 where the one is the mean free path and the other is the gravitational-thermal lapse rate. Also bear in mind that speed is not temperature. The point is that none of the molecules in the system ever climb up in the gravitational field in equilibrium. In fact, their average energy change in equilibrium associated with gravity is zero. Thermal transport is not blocked by gravity, and the system still relaxes to isothermal equilibrium, exactly as Caballero pointed out (and I’ve pointed out until I’m blue in the face.
where the one is the mean free path and the other is the gravitational-thermal lapse rate. Also bear in mind that speed is not temperature. The point is that none of the molecules in the system ever climb up in the gravitational field in equilibrium. In fact, their average energy change in equilibrium associated with gravity is zero. Thermal transport is not blocked by gravity, and the system still relaxes to isothermal equilibrium, exactly as Caballero pointed out (and I’ve pointed out until I’m blue in the face.
Good attitude, Trick.
See my previous post estimating
You might consider the actual problem with second law violations, though. That’s by far the easiest way to see why equilibrium is isothermal in any well-connected system.
rgb
Dr Brown says;
Ah, but you see, heat engines and conductive thermal transport are driven by differences in temperature, not energy. As you would know if you had absolutely any clue about thermodynamics.
Conductive thermal transport need matter. Kinetic energy is motion and mass.The particles of matter you use to “conductive thermal transport” for the “heat engine” are subject to gravity.
There is no “equilibrium” of anything in this question. There is approximately equal partition of energy here, Boltzmann distribution, and approximately equal Lagrangian for each part to which the energy is distributed.
What I’m not open to hearing is that the second law allows disequal apportionment of total energy in an equilibrium state which is, in essence, what Dr. Brown (whether he realizes it or not) is saying.
Is it in any way my fault if your education is faulty and you cannot seem to grasp any of the five or so statements of the second law? I don’t care what you are open to hearing about what it allows or doesn’t allow. How about reading it’s actual words?
What you don’t seem to want to realize is that you can’t do statistical mechanics with a picture in your head. I can’t do stat mech in my head, and I’ve had a damn sight more practice. I don’t know anybody that can do stat mech in their heads. Doing statistical mechanics correctly is very, very difficult.
You can do thermodynamics in your head, or with only a bit of associated algebra. That’s why I provided a simple picture. Figure 2 above violates the second law of thermodynamics. The hypothesized thermal lapse is therefore not any of the things people have claimed it to be — maximum entropy, thermodynamically stable, and so on, because if it were, the second law of thermodynamics would be openly violated.
If you replace the silver wire with anything that does work across the temperature difference, inside or outside of the box, it will transform heat into reversible work and have no other effect on the Universe. It will systematically cool the box and turn its heat content into stored reversible energy.
This is precisely what Joules has claimed will happen in upstream posts. If you are standing in for him, I have to ask — are you going to seriously try to defend his assertion that an isolated gas will thermally separate, and if a heat engine is run off of the thermal difference the isolated gas will cool to absolute zero with no input of work? Because if you are, then you are both batshit crazy.
Non-decreasing entropy in an isolated system: Not just a good idea! The Law!
Sincerely,
rgb
P.S. — OK another morning probably wasted trying to teach the horse to sing. Time to go teach Gauss’s Law to Enquiring Young Minds.
Dr Brown,
Thermodynamics isn’t best applied to this question. Your example conflates temperature difference in the atmosphere that occur over large distances and thermal conduction over short distances. Show how your “conductor” molecules are not equally subject to gravity over the same distance of the temperature difference.
Like it or not, a conductor from the surface of the earth to high in the atmosphere is elastic particles pulled down by gravity. Solid or gas, it’s molecules all the way up… and down. 😉
Robert Brown says at 1/27 9:29am:
“…because physicists generally teach engineers….”
Yes. I knew it! I would get a chance to express the difference. Engineers will readily advance to meet the opposite sex; physicists are more reluctant. Why? Physicists less often even try b/c they have studied they can never get there – they must go ½ the way, then ½ the way, then ½… and so on ad finitum…physicists think they will never get there.
Engineers on the other hand have learned thru trial and error they can get close enough to get the job done. This is why there are more engineers than physicists.
Tim Folkarts says;
<>
1) Atoms (molecules) in the box each have the same total energy (approximately, total energy of each distributed as Boltzmann says). Total energy of each (the Lagrangian) is kinetic energy plus potential energy. In a box that is small, in the up and down direction in which gravity acts, the difference in potential is small, small enough to be negligible when “the thermodynamic laws” are applied to the usual problems or examples. When the box is large in the direction of gravity, the difference from top to bottom of the potential energy part of the total energy of each molecule is noticeable, and is no longer negligible. The kinetic energy of the in the the molecules at the top of the box and the molecules at the bottom of the box are different, in the additive fashion of kinetic energy plus potential energy equals a constant total energy. (constant and the same for each within Boltzmann distribution.)
(Image: Throw a molecule upwards in a large empty box. At the top of the arc it is momentarily stationary in the up and down direction; zero kinetic in the up-down direction. When you throw it and then after it comes down, when it hits the bottom of the box, it has maximum kinetic energy after it leaves your hand and before it hits the bottom of the box. And it has minimum potential energy when it momentarily stops on the bottom of the box. Next arrange a bunch of molecules with a small distance between each of them, in a line straight up from you. Hold them in place against gravity with a conservative force. Call it ‘electrical force’. Call the arrangement of molecules ‘solid matter’. Now throw a molecule up, the same as you threw the molecule the first time, against the bottom molecule of the ‘solid’. Notice that each molecule, between collisions, has the same speed at each height as the first molecule did when you threw it straight up. This is conservation of energy and conservation of momentum. It is universally true. The same idea applies for loose molecules bouncing around the box, call them ‘gas’, but it is harder to explain.)
2) Molecules with the same kinetic energy and different total energy in a box would be molecules with the same temperature at the top of of the box as the temperature of molecules at the bottom of the box. If the box is large in the direction of gravity, it takes some work put the molecules in that arrangement, if you start from an arrangement of molecules as is in the first box. It takes some work to maintain the arrangement of the molecules in the second box. If you stop working at keeping them arranged, the molecules tend to arrange themselves as the molecules in the first box are arranged. There is something about this in “Thermodynamics”, a principle or law or something, but I don’t know about it since I never studied “Thermodynamics”!
Publius Maximus says at 1/27 6:48am:
:…gravity is a force which decreases entropy. It concentrates matter and energy into stars and planets and galaxies and galaxy clusters.”
Here Publius wanders off the top post Fig. 1 and 2 – quite a long way. Unfortunately the decrease entropy statement here deserves some pushback which I see it has already received.
This is the root cause of Stephen Hawking & the longer thread than this one over his winning the bet with Preskil and Kip Thorne that black holes will evaporate & entropy would not decrease (i.e no information lost to universe in black hole – the info. is eventually returned).
2nd law allows the no entropy change case so that’s all we need here, Hawking radiation hijacks the thread.
Other than that, I share your views: gas column is non-isothermal philosophically so far. No one has cited a formal proof although I am running down some Rodrigo Caballero ref.s.
PS: I agree Joules Verne posts could get trapped in spam filters & takes time to rescue. JV contributed a bunch of logical thinking & ref.s. Some of my posts go up in 15 minutes, at other times ~3 hours. Busy moderators is all, doing a fine job keeping threads more readable around here than otherwise.
Tim,
the arrows ate my quote of you, I quoted your 1) and 2) boxes question;
Either
1) Atoms have the SAME total energy, but atoms on the same box can be at different temperatures, or
2) Atoms have DIFFERENT total energy, but atoms in the same box are the same temperature.
Doug Cotton says:
January 26, 2012 at 6:06 pm
That’s not what I said at all. Strawman much? What I said was that absorption lines or bands would not be observed if the emitter was the same temperature as the gas, not that absorption wouldn’t occur. Spectralcalc actually managed to screw this up a while back.
Here’s the relevant emails:
and the reply:
Claes Johnson has proved nothing. Now back you go onto my do not feed list.
Dr Brown
I think I see the problem. I think that you are saying that you can exchange a cool particle at the top of your conductor for a hot particle at the bottom of your conductor, with no net work. And there you see a violation of the second law.
This idea is just another box with a door between the hot and the cold side. Consider all the real differences between the the hot particles on the bottom and the cold particles on the top, and I think you’ll see the daemon.
Robert Brown says:
January 26, 2012 at 8:58 pm
Nitpick:
It depends on what you mean by local and equilibrium. The air your house will always be in Local Thermodynamic Equilibrium because it’s extremely unlikely that the temperature gradient will at any point will be large enough for the molecules at that point to not obey MB statistics. The existence of a temperature gradient alone is not sufficient to cause LTE to not be applicable.
Myrrh says:
January 27, 2012 at 5:02 am
“Earth without any atmosphere: -18°C
Earth with our atmosphere: 15°C
Earth without water: 67°C”
I come up with similar figures but think there are adjustments to that. 1) All are numbers that assume clouds and ice are the same; 2) I think there is a significant error using Stevenson screens and one meter below surface ocean measurements. While those are our climate, without cloud and ice changes, they are not accurate for calculating surface radiation. What the adjustments would be is if you remove water the planet would be hotter and if you remove an atmosphere the surface would be closer to 0degC (corresponding to closer to 341 watts/m2 average incoming.)
The Clausius form of the Second Law of Thermodynamics simply says:-
” No cyclic machine, may have no other effect, than to transport heat from a source at one Temperature, to a sink at a higher Temperature. ”
That’s it; it doesn’t say any gobbledegook about equipartitions of energy or gravity, or Einstein’s theory of relativity; either special or general, or QED, or Maxwell’s equations, or even the big bang.
The “cyclic” part implies that there MUST be a possible transport of “heat” in BOTH DIRECTIONS.
And by both directions we can presume that means that there is a terminus which Clausius calls “source”, and also a terminus which he calls “sink” and presumably the degenerate case of those termini being conincident is excluded (as juvenile).
So source —> sink is one possible direction of transport, and source <— sink is another possible direction.
The Clausius statement declares that absent any other effect , "heat" can only move from HOT to COLD. Now that means NET HEAT FLOW ; because the CYCLIC condition implies that it is not impossible for heat to go from cold to hot; just not unaided (by doing work) or else MORE heat is going the other way at the same time.
The work done part is the "no other effect" part, that can't coexist with a net cold to hot flow.
And if you can't properly sort out all the negatives in there, then you NEED to hit the ENGLISH text books as well as the PHYSICS ones.
Let's consider conduction of "heat" ; howabout in a metre long Aluminium bar that is one square cm crossection. Just for kicks, I could choose Prof Bob Brown's silver wire, just to annoy all you doubters; but his nice electric and thermal conductor is not as good a choice as Aluminium for my experiment; or I could use "Battleship Plate" ; ordinary structural steel.
So I have one end (hereafter known as the hot end) stuck in a mug of MacDonald's Hot coffee, and the other end, held slightly higher in the air by a simple string sling, attached to the ceiling. so that end is at room Temperature (hereafter known as the cold end).
So far as we know, nothing else is happening, but "heat" (net) is flowing by itself from the hot end in the coffee to the cold end in air.
But what does that mean ? Well it means that the hot coffee is raising the Temperature of the Aluminium molecules at the hot end of the bar, so the mean molecular vibration kinetic energy, is higher than up at the cold end. Those more energetic molecules bang into their neighbors, and get them more riled up than they were, raising their Temperature, and they repeat the process of banging into their colder neighbors to get them going.
You see the "HEAT" that is flowing is nothing more nor less than those chaotic molecular vibrations and collisions with some local average KE value.
Now I have something else attached to my "cyclic machine". Glued onto the hot end of my bar, on the end face, I have a sealed piezoelectric transducer; basically a microphone; and it is wired to a plug that plugs into my Karaoke machine or ghetto blaster (your choice), so I can listen to sounds in the bar.
Well the vibrations of the molecules due to the Macdonald's hot coffee are too high in frequency for me to hear in my hifi.
So now I take one of those little triangular rubber hammers that the doctor raps on your knee for $150, and I tap the upper cold end of the bar with it; no not with the rubber end silly; turn it around and hit the bar with the handle, or just use a teaspoon if you aren't a doctor (I'm not).
Wow !! I get a beautiful metallic ringing sound in my speakers; demonstrating conclusively that molecular vibrations at the cold end of my bar, can and do propagate by chain migration from the cold end of the bar to the hot end. And rest assured that the random molecular vibrations at the cold end of the bar, are also communicated to their slightly warmer next door neighbors when they collide with them, and so on, and so forth.
Yes thermally induced vibrations of molecules can and do transmit to their neighbors in EVERY direction, even from cold end to hot end; but since the vibrational energy of the molecules is higher at the hot end, than at the cold end, the process of INCREASING the vibrational energy of the neighbors only happens from hot to cold. It takes a refrigerator that uses other energy to do work (some other result) to get "heat" to flow from the cold end to the hot end (AND HEAT IT UP).
PS Prof Bob's silver wire is too ductile to ring nicely, which is why I chose Aluminium.
Robert Brown says at 1/27 9:45am:
“Also bear in mind that speed is not temperature.”
Right, temperature is KE, a constant mass times speed squared so it varies as the speed varies. If the speed is constant with h, KE is constant top post Fig. 1, temperature is constant with increasing h in top post Fig. 1 & it is isothermal.
If speed, thus KE varies with h in Fig. 1, then T is non-isothermal as per Rodrigo Caballero on line text linked in Perpetuum Mobile thread:
“Temperature is just another name for the mean kinetic energy density of molecular motion.”
The Rodrigo Caballero on line text as of this post still says for top post Fig. 1:
“Mean velocities will be greater near the bottom of the box than near, the top…”
This text means KE thus temperature will be greater near the bottom of Fig. 1 than near the top, so non-isothermal. Though now have some input around here that this text may change in some way for the next edition.
Dr. Brown,
I apologize for attributing motive to your statements. You had fun calling me on that, and insulting my intelligence and education.
But my confusion persists. Could you please address my example or answer my questions, repeated here:
Dr Brown,
Expanding: I think that you are arguing that your heat conductor can convey energy (heat) from the ground to the sky without any net work being done. You have not shown how this is actually possible.
If you have a mechanism that worklessly exchanges a hot molecule at the bottom of your solid conductor with an identical but cold molecule at the top of your conductor it look like no gravitational work was done, right? The daemon lives! and we have free energy!
But if you do that exchange, the conductor still looks the same, but it isn’t really still exactly the same. The net height of the conductor doesn’t change but a larger (hotter) molecule from the bottom of the conductor has been replaced by a smaller (colder) molecule from the top of the conductor. The molecules of the conductor, save the top one, are slightly closer to earth. Gravity has taken won a little advantage in return for the heat you have conducted to the colder top of the conductor.
Please explain some mechanism that conducts heat to the top of you conductor without loosing work to gravity, I don’t see any such mechanism 😉
Robert Brown says:
January 26, 2012 at 10:12 pm
With respect to the Tij et.al. paper that seems to have had such an effect on Joules Verne, some numbers might be useful:
h=kb*T/(m*g) = 9.08km for N2 at 300K
λ = 68nm at 101325 Pa
To get λ ~0.01h where the deviation from the Fourier Law is ~10% requires a reduction of pressure of 11 orders of magnitude to ~ 1E-6Pa or an increase of g of a similar magnitude or some combination of both that increases λ and reduces h.
I’m not going to touch the temperature gradient as that’s even worse.
Paul Birch says:
January 27, 2012 at 7:34 am
LaTex is indeed a markup language, or more strictly speaking, a typesetting language, as it can be used in other than HTML formats. Search on “latex tutorial” and you get lots of hits. I learned a little once and promptly forgot it. The other unfortunate thing is that like HTML, the conventions may be slightly different from site to site. Some testing may be necessary to get started. Either use a page with a preview feature or use Firefox and CA Assistant, which also, unfortunately, doesn’t work everywhere.
[Moderator’s Note: WUWT also has a test page here where you can test a post for formatting before adding it to a thread. The usual policy rules will still apply, however. -REP]
One (hopefully) last comment about KE & PE in the atmosphere as related to thermodynamics.
KE energy of a particle is indeed constant –> when averaged over long periods of time.
PE energy of a particle is indeed constant –> when averaged over long periods of time.
Total energy of a particle is indeed constant –> when averaged over long periods of time.
For example, in a solid there are only three axes, but there is KE and PE associated with each axis, so there are SIX degrees of freedom and each will have an average energy 1/2 kT when averaged over sufficiently long periods of time.
In the atmosphere, this is slightly different, with an energy of kT associated with PE (see htttp://en.wikipedia.org/wiki/Equipartition_theorem#Sedimentation_of_particles). This means that in equilibrium, a molecule should have (on average) mgh = kT, or h = kT/mg. For an N2 molecule at T = 300 K, this works out to ~ h = 9 km. So in an equilibrium atmosphere with T=300 K, when averaged over long periods of time, a molecule of N2 in such an atmosphere will have an average altitude of 9 km. Not surprisingly, this is indeed about the “average” height of the earth’s atmosphere.
NOTE 1: Thermodynamic equilibrium deals with long-term averages, not with short-term motions. Looking at 1 flight of one molecule is not sufficient. So the fact that one particular molecule of N2 might happen to have an above average PE does not affect its chances of being above or below average in KE (ie in temperature), just like a high speed in the x direction has no bearing on its chance of being above or below average in the y speed.
NOTE 2: This also explains why molecules do not separate by mass, with the heaviest molecules all at the bottom. N2 will have an average height of 9 km independent of any other molecules present, and this will follow an exponential decline with altitude. Helium, with 1/7 the mass would have an average height of 7*9km = 63 km (which explains why it can drift ouf into space more easily. CO2, with about 1.5 times the mass, will have an average height of ~ 6 km. So the heavy gases are enriched at low altitudes, but do not completely displace the lighter molecules.
NOTE 3: Earth is NOT perfectly insulated and is NOT in equilibrium. There is a constant heat flow up thru the atmosphere due to cooling at the top by GHG’s. This makes a few adjustments for the actual situation on earth. For example, the temperature does drop with altitude, and convection mixes the gases in the troposphere. These do not negate the basic conclusions.
So explain how the silver wire has precisely the same conductivity to the gas at low pressure at the top of the tube as it does to the gas at high pressure at the base of the tube. It cannot as there are less gas molecules coming in contact with that wire at the top than there are at the bottom – that is the definition of pressure. through the wire. Even you aren’t asserting that the conductivity isn’t zero, you are just asserting that it is rate limited by the area in contact with the gas at the top. This area in contact is a variable under my control, of course, but even exactly as drawn we seem to agree that the conductivity isn’t zero.
through the wire. Even you aren’t asserting that the conductivity isn’t zero, you are just asserting that it is rate limited by the area in contact with the gas at the top. This area in contact is a variable under my control, of course, but even exactly as drawn we seem to agree that the conductivity isn’t zero.
You will find that when you take the different conductivity across the silver-to-gas boundary into account that the high gas-to-silver conductivity at the base is in lapse rate proportion to the lower silver-to-gas conductivity at the top.
No, I won’t find any such thing because it isn’t true.
Besides, what is to stop me from adjusting the areas in contact with the gas in both venues using a heat sink?
Finally, the only way heat won’t flow is if the conductivity is zero, and all I need for a second law violation is any non-zero transfer of heat:
So I take it that, now that I’ve clearly shown that your “objection” in no way affects my argument, you’re ready to concede, right?
rgb
Expanding: I think that you are arguing that your heat conductor can convey energy (heat) from the ground to the sky without any net work being done. You have not shown how this is actually possible.
If you have a mechanism that worklessly exchanges a hot molecule at the bottom of your solid conductor with an identical but cold molecule at the top of your conductor it look like no gravitational work was done, right? The daemon lives! and we have free energy!
But if you do that exchange, the conductor still looks the same, but it isn’t really still exactly the same. The net height of the conductor doesn’t change but a larger (hotter) molecule from the bottom of the conductor has been replaced by a smaller (colder) molecule from the top of the conductor. The molecules of the conductor, save the top one, are slightly closer to earth. Gravity has taken won a little advantage in return for the heat you have conducted to the colder top of the conductor.
Please explain some mechanism that conducts heat to the top of you conductor without loosing work to gravity, I don’t see any such mechanism 😉
Sigh. Look, I’m really trying to keep up, but if you aren’t willing to actually study the answers to these questions-posed-as-statements, how are you going to learn? Do I have to hand-teach you all one at a time?
Imagine that you have a stack of pool balls a kilometer high. Whack the bottom one. What happens to the top one? If the pool balls are perfectly elastic, like the molecules of an ideal gas, the top one pops up a bit in reaction because of conservation of momentum and energy. You can do the same experiment with a line of balls in an ordinary pool table, or you can look at:
http://en.wikipedia.org/wiki/Newton%27s_cradle
with its running demo. The case of the wire is almost identical, although the wire allows a bit more variation in the transmission of energy along the way. As hot molecules strike the bottom, they successively warm higher and higher layers in the wire until heat input at the bottom is picked up by the colder air molecules at the top, cooling the bottom and warming the top.
There’s nothing magical about this. Heat flows from hot reservoirs to cold. Gravity doesn’t act on heat. Heat is not pulled towards the ground. The fallacy in your argument is simple — nothing in the wire changes its height while it conducts the heat! Gravity doesn’t do any work on the system. All that happens is that all of the silver molecules oscillate back and forth in place a little more violently, with exactly the same average gravitational potential energy, per molecule.
If you think that metals don’t conduct heat vertically, place a pan on a stove, put your hand on the top of the pan, and turn on the stove. Remove hand when convinced.
rgb
Robert Brown,
just gotta say that reading these threads is always an education on new physics that my ignorant mind has never heard of before.
” All that happens is that all of the silver molecules oscillate back and forth in place a little more violently,”
With this quick sentence you have destroyed millenia of observations that metals and most other materials expand when they are heated!! HAHAHAHAHAHAHAHAHA Wonderful, continue the teaching of the new IPCC Physics!!!
Tim Folkerts says:
January 27, 2012 at 1:06 pm
Not true. That would imply that the volumetric mixing ratio of CO2 would be higher at low altitude than at high altitude in the lower atmosphere. But this doesn’t happen because stratification isn’t allowed at LTE. If it were true then the partial pressure of CO2 at the surface would be different than the volumetric mixing ratio times the surface pressure. There’s about 6 kg CO2/m². If no other gas than CO2 were present, the surface pressure would be ~59Pa instead of the ~39.5Pa that it actually is. See a more complete discussion of the problem and solution here. The elevator speech version: The m in the scale height equation kbT/mg is the average molecular weight of the atmosphere, not the weight of the individual molecules. Stratification only occurs at very low pressure/very high altitude when LTE no longer applies.
Rodrigo Caballero says at 1/27 6:07:
“..see recent discussion by Verkley and Gerkema, J. Atmos. Sci. 2004”.
Geez, Verkely seems to find both non-isothermal AND isothermal T fields depending on constraints for top post Fig. 1.
Verkley et. al. paper linked by Guinganbresil at 1/27 9:38am.
Some issues interested posters might discuss in the Verkley (V) paper.
1) The air column in Verkley is different than the control volume of Fig. 1 top post. The paper says the column Verkley et. al. is analyzing is permitted to let work out above and below the control volume: “(V) Fig 1.: The column is assumed to exchange no net heat with its surroundings but may perform work on the air above and below the column. “
This at 1st look seems to be a change from what has been discussed here, where no work is allowed across the control volume above or below. Not sure what this means yet. Need help, maybe from my Boren text due in a few days or from other posters.
2) After Equation 10 the words “Since this should be true for all variations dT”. Why do they not say “must be true”? Equation 11 approaches infinity as T approaches zero. Is this why? The Velasco issue again: isothermal is wrong until can “ discern between the cases of a finite system and an infinite system.”?
3) In part b, Verkley et. al. finds a non-isothermal T field in eqn. 18 !! Don’t hit me!
4) In part c, they write: “The above calculations show that the result of the maximization process depends on the constraints that are used. “ I say: no kidding.
5) Verkley et. al. write in conclusion: “..this constraint choice is of course open for debate.”
So Robert Brown et. al. can say, view agrees with Verkley part a, just choose my constraints for isothermal.
So Trick et. al. can say, view agrees with Verkley part b, choose my constraints for non-isothermal.
Very unsatisfying. Might be a long thread, the open question for Velasco conclusion in 1996 seems still open in conclusion in Verkley et. al. 2004.
Infinity is a real demon. Go figure.
At the minimum, it seems for an isothermal T field conclusion, Fig. 1 in the top post must be modified to show at the top and bottom of the column: “…may perform work on the atmosphere air above and below the column. “
Consider, for example, a centrifugal compressor running continuously under steady conditions. The compressor draws air from a temperature and humidity controlled space.at 1 bar, and discharges it into a process at 2 bar. .The entering air is steadily and continuously heated from ambient (Ti) of 15°C to an exit temperature, (To),which will be 78°C or higher,. It is a function of the ratio of the outlet pressure (Po) to the inlet pressure, (Pi) and the efficiency of the compressor; which can be close to, but will be less than one. To = Ti * (Po/Pi)^((R m eff)/Cp mean), R is the universal gas constant, and m is the molecular weight of the gas. Is it thermodynamically stable?. Why is the discharge hotter?
You are doing work on the system, are you not? It is an open system with a continuous input of work and for that matter mass. It is not an isolated system. There are all sorts of ways one can construct things that move heat from cold to hot reservoirs or create temperature differentials in initially isothermal air. We call most of them “refrigerators”, and no, refrigerators are not “thermodynamically stable” in the usual meaning of the terms, which would be “in thermodynamic equilibrium”. They can be stable in the sense that they are predictable in their cyclic operation, so a steady pattern of input work, mass transport, and heat flow can be established.
You don’t have to work so hard to make up an example. Go into your house. Open the refrigerator door. Cold inside. Feel the coils in back or underneath. Hot. Pay the electric bill on the motor. Heat input. Sure, one can use work lots of different ways to make air colder or hotter, but what you cannot do is violate the second law of thermodynamics.
So why is this example at all relevant to either Jelbring’s paper or my rebuttal? In fact, it isn’t. It is a straw man argument, proposed to try to convince — I dunno, yourself? — that because “refrigerators exist” Jelbring’s second law violating one can exist, or something like that. If you have some other point, feel free to make it, but to me this seems like nothing but non sequitor.
As for insulting your education and so on, look. Open a completely random college level introductory physics textbook. Turn to the chapters on thermodynamics. Just read them, please, like a novel. Don’t stop, don’t put the book down, just read the words and try to understand them, look at the examples. If you feel inspired, do a few homework problems. Pay special attention to the zeroth, first and second laws, get to understand heat engines, refrigerators, limits on efficiency and coefficient of performance. Learn the Kelvin-Planck and Clausius statements of the second law. Learn the entropy statement. Then come back to the discussion. You’ll be better for it, more able to make useful contributions, and I suspect that you will no longer argue that the second law can be violated or that the atmosphere can somehow refrigerate or heat the Earth per se.
rgb
A physicist quoted Eddington:
I love this quote. The quote, and its context comprise a work of art, the beauty of which I can but poorly appreciate, and not relate at all.
QDaniels,
the Eddington quote is very interesting. I have been assured by well educated warmers that even conduction breaks the 2nd at very low levels at times. Whether they are claiming that this is measured or a result of solving statistical mechanics they did not explain. So, because it is a really small violation, do I apply the quote or not?? 8>)
The Rodrigo Caballero on line text as of this post still says for top post Fig. 1:
“Mean velocities will be greater near the bottom of the box than near, the top…”
This text means KE thus temperature will be greater near the bottom of Fig. 1 than near the top, so non-isothermal. Though now have some input around here that this text may change in some way for the next edition.
You did read Caballero’s actual post on the list earlier today, right? Where he directly stated that an isolated atmosphere in a gravitational field reaches isothermal equilibrium, as first demonstrated by Gibbs some 120 years ago?
I really don’t think you should be quoting Caballero to support these statements, because the point isn’t that adiabatic lapse can occur, it is that static, thermodynamic equilibrium is isothermal without a lapse.
Just a thought.
rgb
PS Prof Bob’s silver wire is too ductile to ring nicely, which is why I chose Aluminium.
Nice post, although by now I’m convinced that it is fruitless. Even Caballero weighing in today hasn’t cut off the nonsense.
At the moment, I think the score is this
100% of the Ph.D. physicists on list think that equilibrium is isothermal
80% of the engineers and other scientists do
maybe 60-70% of the lay people (with no real physics education) do
with a small, stubborn, 30% overall who just don’t seem to be able to grasp the ideas of thermal conductivity, thermal equilibrium, entropy, work, the first and second laws of thermodynamics, and so on, who just don’t want to give up the notion that temperature is what they want it to be instead of what it actually is: nothing but a measure of comparative thermal equilibrium.
This last group relies on heuristic arguments that seem to be attempts to do statistical mechanics in their head or by constructing a mental picture that suits them, drawing on a high school level understanding of mechanics. They neglect the fact that thermodynamics is the valid macroscopic heuristic for statistical mechanics, and that stat mech computations cannot be done on an heuristic basis at all; they are horrendously difficult, involving taking limits of nearly infinite sums in just the right way to get the relevant part of the answer and discard the parts that don’t scale up to relevance as one goes to large systems. I’m unaware of any general heuristic that permits one to skip doing the real work in this case other than thermodynamics.
I’m getting tired of replying. The issue is settled. Really. It was settled well over 100 years ago, and if you’ve been following along you have heard not one, but a half dozen arguments that are all openly endorsed by the list physicists, however enthusiastically they are challenged by people who do not, in fact, understand physics. I’m not trying to be an elitist, only pointing out that if you already know everything, what point is there in me trying to teach you? If you are certain that you know better than physics textbooks and people who teach and do research in the field, well then, the best of luck to you.
So I think that this will probably be my last post on this thread. We’re down to a core of people that will never be convinced, because they don’t want to be, people who have diverted the thread into side discussions (always interesting, but…) and people who understand the issues well but are trying to herd cats. On to other things!
rgb
Robert Brown
You have created a perpetual motion machine of your own if you totally ignore the gravitational effects of charges and atoms in your silver wire.
http://arxiv.org/ftp/arxiv/papers/0908/0908.2820.pdf
Tim Folkerts says:
>> So the heavy gases are enriched at low altitudes, but do not completely
>>displace the lighter molecules.
DeWitt Payne says:
>Not true. That would imply that the volumetric mixing ratio of CO2 would be higher
>at low altitude than at high altitude in the lower atmosphere.
I respectfully disagree. This is certainly not a key issue in this discussion, but equipartition is equipartition. In equilibrium, molecules of one mass have the same average kinetic energy as molecules of a different mass. Similarly, molecules of one mass have the same average potential energy as molecules of a different mass. This implies they must have different average altitudes, just like they have different average speeds.
It is certainly true that the ACTUAL atmosphere does not show this behavior in the troposphere, but that would be because it is not in equilibrium. Specifically the actual atmosphere is well mixed by convection — a process that would be completely missing in an equilibrium atmosphere. So the actual atmosphere has constant mixing ratios even though this would not be the equilibrium condition. At least, that’s my take on this side issue.
“Imagine that you have a stack of pool balls a kilometer high. Whack the bottom one.”
Takes a lot of work to add the mgh to move all the balls and displace the top ball That’s gonna be quite a big whack. That’s all JimZ said – the vertical wire doesnt look like a work-free transfer to altitude.
Could I venture another question as I read the thread. If we depart from perfect elastic collisions, is there a mechanism to suggest that greater frequency and more energetic collisions at higher pressure would be associated with higher pressure? The degree of this phenomenon might be dictated by the (ahem) “collision efficiency”?
Dr Brown says:
“There’s nothing magical about this. Heat flows from hot reservoirs to cold. Gravity doesn’t act on heat. Heat is not pulled towards the ground. …”
I didn’t say that gravity acts on heat. Heat is not real, it is a useful concept, and you’re correct, gravity doesn’t act on heat. Heat without matter is a pointless idea, and matter is subject to gravity.
Kinetic energy will not be conducted from low gravitational potential to high gravitational potential without work against gravity; there isn’t kinetic energy without mass. The atmosphere and the conductor will have the same temperature gradiant, in a energy equal partitioned steady state, and neither will be conducting heat from the warmer to the colder.
As you wrote, wacking a stack of billiard balls on the bottom is the exact situation we are arguing about. The billiard balls are elastic AND they are compressible, just like molecules, just like all solid matter. Electrical force is conservative, so there is no energy loss in the billiard ball column when the wack is propagated . But the balls are compressible and momentum is conserved. Wacking the bottom of the column upward does cause some displacement of the matter in the column, and the displacement works against gravity. So wacking the bottom of the column with a finite energy will not lift the ball on the top of the column, when the column is taller than some finite height, depending on the compressibility of the balls (same is true with wacking the bottom of a stack of molecules). True in theory and true in practice.
Your argument does work with elastic and in-compressible matter. The heat would be conducted as you say when your conductor is made of ideal matter that is elastic and not compressible.
Tim says;
quote
I respectfully disagree. This is certainly not a key issue in this discussion, but equipartition is equipartition. In equilibrium, molecules of one mass have the same average kinetic energy as molecules of a different mass. Similarly, molecules of one mass have the same average potential energy as molecules of a different mass. This implies they must have different average altitudes, just like they have different average speeds.
end quote
Molecules of one mass don’t have the same average kinetic energy as more massive or less massive molecules. It is equipartition of the total energy of a each of the molecules. It is conservation of energy AND momentum; heavy molecules move slowly and light molecules move fast. That’s how gas chromatography works, all molecules at the same temperature but heavy and light ones at different speeds. Molecules of different mass don’t have the same average potential energy.
PS, there isn’t any “equilibrium” in this argument.
This paper proves the Kelvin-Helmholtz mechanism in general relativity and also says that even objects in gravitational equilibrium will emit radiation (published in Physical Review D of the American Physical Society).
http://arxiv.org/pdf/gr-qc/0605066.pdf
A million Sols
If there was a million stars providing the same solar flux as our sun does and they surrounding earth in every direction, what temperature earth be?
I think it would be around 120 C.
I think the surface would be 120 C, and I think the air temperature would be 120 C.
Everyplace would 120 C or hotter- underground it would be hotter.
It seems if the earth had no atmosphere or ocean- or the moon would temperature of 120 C.
Though with Earth and it’s atmosphere the surface only get 1000 watts instead of 1300 watts, so the surface couldn’t be heated by the Suns to 120 C. And I guess “somehow” the atmosphere would make up the difference- and the atmosphere may heat the surface so it’s higher than 120 C. But also it seems to me that the atmosphere would have a lapse rate- 10 Km above the surface it would be cooler than the surface.
If we assume that earth would have a lapse rate [can’t see how it wouldn’t] what would the lapse rate be? would be around the current average lapse of 6.5 C per 1000 meter. Or would it be higher- like 9.8 C per 1000 meters. Or say 1 C per 1000 meter?
Next question is what would the ocean temperature be. Our sun gets the ocean as warm as 30 C.
If the entire ocean is 30 C, one could see all those sols warming it to 40 or maybe 50C. But how does it get much warmer than that?
So a question is what kind of world be coolest, if surrounded by a million sol?
What our water world be the coolest?
What if you have entire planet of water- something around same gravity as earth, but about twice the diameter.
Such a world would be quite strange. The world is say 99.9 % water, and without nitrogen sky, it would be black. The water pressure would exceed any pressure human have ever made, oh I guess not:
“typical pressures reached by large-volume presses are up to 30-40 GPa, pressures that can be generated inside diamond anvil cells are ~320 GPa, pressure in the center of the Earth is 364 GPa, and highest pressures ever achieved in shock waves are over 100,000 GPa. ”
3000 km [3 million meters] of water would be 300,000 atm- not even enough to make diamonds.
320 GPa is 3.1 million atm.
Anyways strange things would happen at + 300K atm. But need 2 gee water planet to make diamonds.
Question is would a planet comprised solely of H2O be cool or hot if surrounded by 1 million Sols?
Expanding on the wacking of a stack of billiard balls: Consider a slinky spring coil toy, if physics departments still have them. Consider a long one hung from some high point. Give it a small bump upwards to the bottom of the spring coil. The displacement that propagates upwards has a definite kinetic energy. You can see the kinetic energy (the displacement) move up the spring, then disappear (for reasons that don’t matter to this idea), and them see the displacement reappear moving down the spring at the same speed that it went up the spring. (If you bump the spring upwards too much, the displacement will reach the top of the spring, it will be reflected, and then it will be a different problem not applicable to this one). To abuse the terminology, you can see a quantity of kinetic energy be subject to gravity, just as when a ball is thrown upwards and then comes back down. The same is true of a very tall stack of billiard balls, except the displacement is too small, and moves too fast, and moves way too far up the stack of billiard balls to be easily watched. None the less, the it is the same.
If the spring coil toy (or the billiard balls) were infinitely stiff (incompressible), the kinetic energy (the displacement) would propagate up the coil (billiard column) infinitely far and infinitely fast. If the spring or the billiard balls were massless, there wouldn’t be any kinetic energy and gravity wouldn’t do anything, so that condition isn’t relevant.
So far as this ongoing question goes; Heat is an imaginary quantity, equilibrium is an imaginary condition, incompressible ideal matter is an imaginary idea. Gravity is real, mass is real, kinetic energy is real, momentum is real, and compressible matter is real. The question is how to formalize the problem of conducting either heat or kinetic energy upwards against gravity. Imaginary heat is not subject to gravity and will always be conducted from warm to cold when a pathway can be imagined. Real kinetic energy is subject to gravity, and needs real particles with real mass, to bridge the distance between warmth and cold.
steve mosher says;
“separation science, especially that surounding the separation of uranium gases in centrifuges, give you all the evidence you need to that this is a load of crap.
blog comments dont overturn working engineering.”
That is correct, but there is an issue of parametric scale, mass difference (force) vs statistical distribution (total energy). Separative efficiency of centrifuges is small, hence the large cascades. The separative efficiency of the Earth’s gravitational atmosphere is very good at one parametric scale, 100% efficient at separating helium form the rest of the atmospheric gases 😉
Ian W says:
January 27, 2012 at 5:34 am
Here’s the key, Ian. Any conduction is sufficient to disprove the theory. Doesn’t matter if the conduction is minimal, or is limited by density. The question is not how much heat will flow. It is if heat will flow at all.
w.
Willis Eschenbach,
“Here’s the key, Ian. Any conduction is sufficient to disprove the theory. Doesn’t matter if the conduction is minimal, or is limited by density. The question is not how much heat will flow. It is if heat will flow at all. w.”
In one of Climate Science’s favorite configurations you have two objects radiating against each other. When they finally equilibrate do they stop radiating??
Myrrh says:
January 27, 2012 at 5:51 am
Thanks, Myrrh. An underlying problem is that of turbulence in the vortex, which costs efficiency. I’ve always suspected that this could be reduced by using laminar air flow on the inlet, but never was able to test that. However, the ugly fact is that at the speeds and radii involved, turbulence will always be present and will cost electricity.
In addition, you need to factor in the inefficiencies involved in compressing and then expanding the air. If you are looking for heat, you could conceivably utilize the heat of compression, or run it with hot compressed air.
But if what you are looking for is heat from (presumably) an electric air compressor by way of a vortex tube … why not use electrical resistance heating? It’s basically 100% efficient energy transformation right where you want it.
There’s no free lunch in the vortex tube. It looks like magic because it splits a stream of ambient temperature compressed air into a hot flow and a cold flow. But there is huge work in compressing the air.
w.
“”””” Robert Brown says:
January 27, 2012 at 2:04 pm
PS Prof Bob’s silver wire is too ductile to ring nicely, which is why I chose Aluminium.
Nice post, although by now I’m convinced that it is fruitless. Even Caballero weighing in today hasn’t cut off the nonsense. “””””
So sad Professor Brown.
I was impressed with the elegant simplicity of your figures 1 and 2, that pretty much settle the question, virtually without discussion.
And people have to believe that (thermal) conduction along a solid (even ductile) wire involves the physicsl transport of molecules from one end to another.
They probably think that the Tsunami wave that slams into Hawaii from Japan, actually was water that travelled from Japan.
But think of it this way Robert, if just one curious person got some understanding from your post, that encourages him/er to try and learn some more, then you have extended your class room in a very useful way.
I got out of academia before I got stuck in it, and just looking back on my accomplishments in industry, gives me a lot of satisfaction and no regrets.
ZP says:
January 27, 2012 at 6:19 am
Be glad to. The difference is, the vortex tube actually operates in the real world. On the other hand, the “gravito-thermal” hypotheses violate the Second Law, so they don’t operate at all.
Any other questions, I’ll be happy to help.
w.
Publius Maximus says:
January 27, 2012 at 6:48 am
That was where I went wrong too, Publius. Like you I thought the maximum entropy was when each molecule of air has the same average energy.
Instead, the maximum entropy is when each volume of air has the same average energy. That is the isothermal state. The molecules up high have more total energy because they have more potential energy. But in exactly that proportion, there are fewer molecules up high, so the total energy by volume is unchanged with altitude.
Jelbring makes the same mistake, which is why he, like you (and I when I was wrong) concludes that the equilibrium distribution is adiabatic. The true answer is isothermal, as proven by Dr. Brown above.
w.
An issue I see on this thread is falling in love with a model and therefore believing it to be true. There is no doubt in my mind that the model being described here does exactly what it says, but there is a failure to acknowledge that some of the basic assumptions might not be valid.
That’s why there are so many objections. Everybody agrees on the underlying tenets of conservation of energy, but some are questioning the physical outcome. The “defenders” of the isothermal outcome go back to their model assumptions to argue that their MODEL works (for its assumptions).
This model appears in textbooks.
I have a few shelves full of textbooks. They contain many proofs, very powerful techniques, and give valuable insight into behaviour of real world systems relevant to the field of engineering dynamics. But perhaps the dominant requirement running through them is the assumption of linearity. This allows the analysis to reach great heights, including Laplace Transforms and tests of stability. But all of this needs great care in the real world where there is no such thing as a linear system. Even a simple pendulum has a nasty non linear ordinary differential equation.
That’s the lesson many posters are bringing to the discussion. They are not challenging “are your physics wrong”. They are challenging “are your assumptions justified” and would the conclusion change if you were prepared to budge on some of them.
Why not get off the pot and challenge your assumptions. The following two should be near the front of the queue:
Is the assumption of Fourrier acting as a constraint and misdirecting the analysis? Others have pointed to the micro mechanical nature of conduction. Can this possibly operate exactly the same with or without a uniform force field?
Collisions distribute energy and the most energetic collisions are at certain elevations. What if these are not perfectly elastic. What if each collision is more variable its allocation of energy transfer between momentum and other forms of energy.
If you detach yourself from some key assumptions, you might find that reasonable points are being raised in the objections. If you can’t do that, you might be losing an opportunity to learn something worthwhile.
To simplify this question: Which formalization of the energies of the particles of the atmosphere is correct?
Tim Folkerts postulated two simple states. The first was one where the gas in a box, in Earth’s gravity, have different temperatures (average kinetic energies) at the top of the box and at the bottom of the box. The total average energies of the gases at the top of the box and the gases at the bottom of the box are the same, the higher average potential energy and lower average kinetic energy for gases at the top of the box, and the lower average potential energies and the higher average kinetic energy for gases at the bottom of the box sum to make the same total average.The second box, in Earth’s gravity, is one where the gases at the top of the box have the same average kinetic energies as the gases at the bottom of the box have. In this second box the total average energies, sum of the kinetic and potential energies are different between the gases at the top of the box and the gases at the bottom of the box.
So which box more correctly describes the steady state condition that the gases in the boxes evolve to over time?
Two formalizations have been argued here to show which box is the correct description of the evolved steady state condition of the gases in a box in Earths gravity.
One formalization invokes an imaginary quantity called ‘heat’, and an imaginary condition called ‘equilibrium’, and an imaginary mechanism called a ‘heat engine’, to show that the condition of the gases in the second box is the only and the inevitable evolution of the state of the gases that is possible. This formalization is exactly correct and internally consistent. This formalization does not include quantification of the Earth’s gravity and gravitational potential. This formalization shows that the state of the gases in the second box is the steady state condition that a box of gases in the Earth’s gravity will evolve to.
The second formalization is dependent on one major assumption; that is the assumption that the idea of equal partition of energy to the free moving pieces of the system, the gases in the box in Earth’s gravity, is a correct condition. The other quantities in this formalization is real; gravity, mass and distance and time. By extension, the other realities in this formalization are potential energy, kinetic energy, velocity and momentum. This formalization shows that the state of the gases in the first box is the the condition that a box of gases in the Earth’s gravity will evolve to.
So which of the formalization more exactly describes the state of the gases in a box in Earth’s gravity??
The problem of physics, sometimes more than one ‘correct’ answer to a question… 😉
Willis, you wrote;
“Instead, the maximum entropy is when each volume of air has the same average energy. That is the isothermal state. The molecules up high have more total energy because they have more potential energy. But in exactly that proportion, there are fewer molecules up high, so the total energy by volume is unchanged with altitude.”
Please help me here, where is volume parametized in the equipartition principle?
“Willis Eschenbach says:
January 27, 2012 at 11:13 pm
Ian W says:
January 27, 2012 at 5:34 am
It is apparent that the writer is a physicist and not an engineer.
Take the thought experiment = a very long cylinder with a gas and a silver wire (assumed to be a perfect conductor) running from low in the cylinder to the top of the cylinder and claimed to cause a problem with the lapse rate explanations.
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
Here’s the key, Ian. Any conduction is sufficient to disprove the theory. Doesn’t matter if the conduction is minimal, or is limited by density. The question is not how much heat will flow. It is if heat will flow at all.”
It seems obvious that a silver wire would conduct heat. Just obvious that one can truck snow from the mountains.
But air does not conduct the heat. You can’t compare air to silver or stone. It’s not just that air is poor conductor. Air molecule is excellent conductor to itself- the molecule velocities are “transferred” at 100% effectively in less than nanosecnd, but the only way energy through air is “conducted” is via air packets- or air doesn’t conduct to itself, it transfers heat from one location to another via movement of air molecules- convection. Other than redistribution or averaging velocity of molecules, air only tranfers energy thru air via convection. So if you have a condition of not having some buoyancy difference of air packets, is no conduction of heat via air.
willis’
If maximum entropy is when each unit volume of atmosphere has the same average energy, where do you stop the atmosphere? How high do you go before you say ” Now we quit, this is where the atmosphere stops”? Does each uppermost unit of volume have one very, very fast molecule in it? What about the next higher unit volumes that don’t have any molecules in them?
I hope this isn’t what Dr Brown is saying 😉
“kuhnkat says:
January 27, 2012 at 11:42 pm
Willis Eschenbach,
You always have at least 1 G affecting the gas in the centrifuge no matter what orientation it is in if it is on the earh. The idea the there would be a lack of pressure at one end is not possible unless the centrifuge is out of the earth’snear surface gravitational field. The fact that you have a huge range of pressure does not change the 1g at the low end at right angles to the centrifuge’s action .
There is no zero pressure zone due to the earth’s gravitational field. You do accept just plain old basic gravity don’t you????”
The vomit comet can give something resembling zero gravity- the preferred term is micro-gravity, as in very little gravity.
But also centrifuge does not act as gravity. Earth gravity is causes an atmospheric weight 10 tons over your head. With centrifuge you making less than inch of air weight more. If had centrifuge which compressed say meter length of air, you might have something vaguely close. take meter length of tube with bottom capped, and rotated that, can one easily get say 10 gee. And this would better than a normal centrifuge which can give hundreds of thousand of gees.
George E Smith wrote;
“And people have to believe that (thermal) conduction along a solid (even ductile) wire involves the physical transport of molecules from one end to another.
They probably think that the Tsunami wave that slams into Hawaii from Japan, actually was water that travelled from Japan.”
Thermal conduction in matter involves the physical transport of kinetic energy by molecules banging into one another.
The tsunami easily propagated across an equal potential surface, the ocean surface. Try propagating the tsunami 600 miles vertically against gravity 😉
Jim Z, I’m finding your comments refreshing! Somebody is actually thinking.
Have you ever approached this from the pressure-density side? I have been giving some time on that aspect. Since T = P/ρ × ~k, and when a lapse is present, this pressure and density curves diverge. Makes sense, that is just the IGL rearranged. If you notice the squiggle before the ‘k’, it is there because gravity itself decreases as the squared inverse of altitude and if there is any influence concerning the heat capacity that also changes with both temperature and possibly pressure. But here I am going to assume ‘k’ is a constant for simplicity.
In order for a tall column to be isothermal the density must identically follow pressure, there can be –no- deviation of the P/ρ ratio, and that gives me some intuitive heartburn. Have you ever thought from that direction? It seems to me if in the space between collisions if the exact tracks of a molecule is assumed to be a straight line, you would have an isothermal column. However, if tracks between collisions have an always –z curvature from gravity, it seems this would have to be some degree of a lapse rate. Can you see it from that direction?
Robert Brown says:
January 27, 2012 at 9:29 am
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
No, silly beanie. The assumption is that the silver conducts heat to the gas at allfrom the bottom to the top. I don’t really give a damn what the conductivity in the silver is or how good the thermal contact between the silver or the gas is as long as it is nonzero throughout the wire. And bear in mind that I can increase the thermal contact of the silver with the gas at both ends by means of adding a simple heat sink. Good engineering, no?
I do so find this sort of mistake to be embarrassing, don’t you?
====================================================
Actually Robert you have proved my point. To transfer heat from the bottom to the top of the cylinder you need to have more surface area (heat sink) at the top of the cylinder than at the bottom. You can cut this either way – the same conductive area, in which case the transfer will be limited to the lapse rate due to the difference in the number of molecules hitting the silver at the bottom in the dense gas compared to the number of molecules hitting the silver at the top in the less-dense gas; OR, you can try to equalize the number of molecules hitting the silver at the top in the less-dense gas by increasing the surface area of the silver in a ‘heat sink’. In which case, you will find that the ratio of the surface area in contact with the gas at the bottom to the surface area in contact with the gas at the top is the same as the lapse rate.
You have no need to be embarrassed to learn something 😉
Robert Brown says at 1/27 2:04pm:
“At the moment, I think the score is this: 100% of the Ph.D. physicists on list think that equilibrium is isothermal.”
100% of the Ph.D. physicists here are proven incorrect about the column in Fig 1 in top post which is non-isothermal according to part b of the Verkley paper cited by the poster Rodrigo Caballero at 1/27 6:07am, linked by guinganbresil at 1/27 9:38am.
To be correct on the column being isothermal, Fig. 1 needs to be modified to show work is allowed to be done on the atmosphere above and below the column as proved in part a of the Verkley paper. Consistent with experimental evidence.
The count is 2 PhD physicist posters in the thread voting Fig. 1 in top post being isothermal; they are being out voted as incorrect by 2 authors of the Verkley paper, 3 authors of the Velasco paper and an on-line text which all prove Fig. 1 as shown is non-isothermal.
Robert Brown at 1/27 1:48pm:
“You did read Caballero’s actual post on the list earlier today, right? Where he directly stated that an isolated atmosphere in a gravitational field reaches isothermal equilibrium, as first demonstrated by Gibbs some 120 years ago?”
Yes. Poster Rodrigo Caballero is writing about the isothermal case when work is allowed across the top and bottom control volume which is not the case for Fig. 1 in the top post. Poster Rodrigo cites the Verkley paper which proves in part b that the column in Fig. 1 in the top post is non-isothermal b/c it doesn’t allow any work across the control volume. In fig. 1 constant entropy is allowed by 2nd law & is the max. entropy for Fig 1. top post.
But think of it this way Robert, if just one curious person got some understanding from your post, that encourages him/er to try and learn some more, then you have extended your class room in a very useful way.
You’re very kind, but there is an old saying in academia — you can lead a horse to water but you can’t make it think….
I am happy to have discussions and even debates with students, provided that there at least some element of respect. I don’t mean the sort of respect that is old fashioned “teaching by authority”, where you accept and memorize everything I say because I’m the teacher and I said so; I actually tell my students not to believe what I way just because I’m the teacher, to challenge it, to test it, and then when it makes sense or corresponds to their experiences in the labs (which at least spot check the concepts, although such checks cannot be exhaustive) accept it and build a strong conceptual understanding. However, the students enter the class knowing that no matter how smart they are, no matter how clever, no matter how iconoclastic, they are children compared to the collective combined work of not one or two but hundreds, thousands, tens of thousands of the brightest minds our species has yet produced, compared to the work of millions of people that have built and continue to build our base of consistent knowledge. I am teaching not as just myself but as a representative of all the great physicists and other scientists who have built a consistent view of physics that works.
That’s the truly appalling thing about the continuing aspects of this debate. The argument I present is, as you note, simple and elegant. It is literally irrefutable. No reasonable person could read it and not agree given even a crude knowledge of things like thermal conductivity or thermodynamics. A supposedly stable thermal lapse in any isolated system, gravitationally driven or not, that can be exploited to do work violates the second law.
Yet a large number of unreasonable people take it upon themselves to completely reinvent all sorts of physics just to suit the conclusion that they wish to draw, that such a lapse is possible because then they don’t have to give credence to the GHE. They have lost any pretence of objectivity, and there is an appalling lack of respect. Physics, as it now stands, is largely consistent. A large number of very smart people have worked for centuries to make it so. It is not perfect, it is not beyond doubt, but it is beyond reasonable doubt and the onus of proof is very much on anyone who wishes to reject things like “thermodynamics” to do an ENORMOUS amount of work to show that their new “theory” is both consistent and confirmed by experiment.
None of this has been done. People assert absurdities, one after another, without even thinking about the consequences, and without ever doing any actual algebra to support it.
You can’t make them think.
rgb
Robert Brown says
” A supposedly stable thermal lapse in any isolated system, gravitationally driven or not, that can be exploited to do work violates the second law. Yet a large number of unreasonable people take it upon themselves to completely reinvent all sorts of physics just to suit the conclusion that they wish to draw, that such a lapse is possible because then they don’t have to give credence to the GHE.”
The dispute about the isothermal/adiabatic distribution is much older
that any concern over the GHE .
It has never been resolved by experiment.
It should be possible surely to discuss it without splitting into tribal groups .
I have identified people who agree with IPCC science but not necessarily accept the isothermal distribution.
I don’t think either way it has anything to do with the GHE
Nobody who proposes an adiabatic distribution believes it can produce work.
Yet others propose lossless silver cables and magic thermocouples to falsify the adiabatic distribution.
How convincing is that?
Its true that in the rare event of any physics text book mentioning this rather abstruse problem as a working assumption they will choose the isothermal distribution.
thepompousgit says:
January 27, 2012 at 9:08 am
Paul Birch said “What is this latex thingy? Is it a specific markup language?”
TeX is a markup language, LaTeX is a set of extensions to make using it easier; intro here: http://www.latex-project.org/intro.html
DeWitt Payne says:
January 27, 2012 at 1:01 pm
“LaTex … ”
Thanks to both of you. I’ll look into it.
The tsunami easily propagated across an equal potential surface, the ocean surface. Try propagating the tsunami 600 miles vertically against gravity 😉
Obviously you do not understand either waves or the conditions of adiabatic isolation. But let’s simplify it still further.
Try propagating blackbody radiation 600 miles vertically against gravity.
After all, the silver wire can be replaced by a vacuum. Heat a blackbody at the bottom. Channel/reflect the blackbody radiation at the bottom into the vertical reflecting tube. Absorb it at the top (which will clearly happen, see radiative transfer equations, this is hotter to colder). Transmit to fluid.
Now please, explain just how gravity will completely prevent the transfer of blackbody radiation up a distance of 600 miles, or 6000 miles, or 600,000 miles.
I look forward to your explanation of how Maxwell’s Equations are modified in vertical gravitational fields, so that we cannot actually see things like the sun because all those photons must experience the exact same gravitational thermal lapse that a column of adiabatic gas 150 million kilometers high would.
Now do you think you can stop being ridiculous?
Damn, I let myself get sucked in again. And for what? I’m sure that you’ll invent some other bizarre explanation that is contradicted every time one looks up during the day.
rgb
Dr Brown,
I do thank you for your explanation and effort.
Willis Eschenbach says:
January 28, 2012 at 12:34 am
“Instead, the maximum entropy is when each volume of air has the same average energy. That is the isothermal state. The molecules up high have more total energy because they have more potential energy. But in exactly that proportion, there are fewer molecules up high, so the total energy by volume is unchanged with altitude.”
Willis, please don’t replace one fallacy with another. The total energy by volume is not unchanged with altitude. The potential energy (and total energy) per molecule goes up linearly with altitude. But the number density of molecules drops off exponentially with altitude. So the energy per unit volume goes like (z+z0).exp(-z/z0), which is anything but constant. There is a lot more energy low down than high up.
Be glad to. The difference is, the vortex tube actually operates in the real world. On the other hand, the “gravito-thermal” hypotheses violate the Second Law, so they don’t operate at all.
Any other questions, I’ll be happy to help.
This answer is non-responsive. I asked for specific mathematical equations governing the equilibrium position for the gas within the tube at any specific instance in time. The key point about how physicochemical processes occur is that they are constantly striving to reach a state of equilibrium. If there is a lower energy state available, the system will shift towards that position. Inefficiencies, tubulance, etc. confound the problem, but does not change the key point.
Earlier, reference was made to a proof by Gibbs that the column in question would be isothermal if in thermodynamic equilibrium. The section where Gibbs discusses this problem is titled, “The Conditions of Equilibrium for Heterogeneous Masses under the Influence of Gravity,” with the most relevant discussion given on pages 144 and 145.
Gibbs derives the general condition of equilibrium, an equation which is of the same form as I showed earlier. He then asserts that the general condition of equilibrium can be partitioned into two parts: a condition of thermal equilibrium (i.e. dT = 0) and a condition of mechanical equilibrium (i.e. VmdP + Mgdz = 0). In summary, Gibbs invokes the temperature formulation of the zeroth law to simplify the total differential instead of rigorously proving (from a purely mathematical point of view) that the most stable state is indeed isothermal.
Robert, I just re-read your Figure 1 and this didn’t register earlier:
You said: “… internal conductivity of the ideal gas is completely neglected …”
Completely neglected? You mean completely absent.
There is your problem. There is no real conduction, just equipartition. Conduction is a transfer of energy to equalize, to a closer degree, an energy difference. There is no difference (do not forget g). The gravity levels z and z+dz are identical to the particles. The slightly slower upper ones will speed if they move to z to ‘conduct’ but then the mean velocities do match… no transfer. And, those at level z if moved to z+dz they will slow exactly the amount to match the mean velocities there. Properly, actual conduction is not being performed and there cannot be any ‘conduction’ in the field in this case, they are already in thermal equilibrium with the m.g.dh term in place in the velocity components of the z axis.
I’m surprised you never saw that.
Dr Brown says: “Damn, I let myself get sucked in again. ”
Yep — it can get addicting. Many of the same sorts of arguments have come up a year ago, and they will come up again in another year, I am sure. We could always just require some sort of math before responding. Like Jerry Maguire, we could say “Show me the derivation.”
So when someone like Ian W says “you will find that the ratio of the surface area in contact with the gas at the bottom to the surface area in contact with the gas at the top is the same as the lapse rate. ” we could simply reply “If you are sure that is the right answer, then show the mathematical derivation that supports this conclusion.” without even bothering to point out that the lapse rate is assumed to be some universal feature, but I could make the surface areas anything I want.
—————————————
I also love the challenge that “It has never been resolved by experiment.” First of all, there is a good chance that the person making the claim simply does not know the relevant experiments.
Beyond that, often there are related experiment that do indeed show the expected results, just not in exactly the form the person want. For example, the satellite IR spectra looking down at the earth DOES show conclusively that the CO2 warms the earth, but only if you understand enough of the other science involved. It doesn’t show what ELSE might affect the surface temperature. It doesn’t show exactly how changes in CO2 would change the surface temperature. But is does clearly show a warming effect from the CO2 that is present. In this present case, there are centuries of experiments involving gases which are consistent with the laws of thermodynamics as presented in standard textbooks.
Finally, many experiments are just damn difficult to do. Here you would need a column of gas many meters tall, surrounded by walls with insulation a couple orders of magnitude better than air, left undisturbed for several days or weeks. If someone actually proposed doing such an experiment, people would complain (rightly) about wasting money on something that was either already obvious or not important.
Tim Folkerts says
“I also love the challenge that “It has never been resolved by experiment.” First of all, there is a good chance that the person making the claim simply does not know the relevant
experiments.”
Well a number of so called experts have been given every chance to produce an experiment.
Some seem initially promising but on closer reflection with real values they don’t stand up to scrutiny.
I don’t hold out much hope for Dr Browns latest suggestion of a lossless light tube.
Tim is nearer reality when he says
“Finally, many experiments are just damn difficult to do. Here you would need a column of gas many meters tall, surrounded by walls with insulation a couple orders of magnitude better than air, left undisturbed for several days or weeks. If someone actually proposed doing such an experiment, people would complain (rightly) about wasting money on something that was either already obvious or not important.”
Since when did physics investigations restrict themselves to things that are important or saving money.
Whats that story again about the discovery of the electron?
Two things are required before a topic reaches anywhere near the area of ‘settled science’.
1.The theory should fit into some accepted framework.
2. There should be experimental evidence to support the theory.
Of these the second trumps the first and unfortunately we are not there yet.
Dr Brown,
Yes, if thermal radiation is the equilibrium mechanism, I see that you are correct. I apologize for my obtustness, your derivation at the top is a mechanical one.
So radiative transport is the reason the evolved isothermal atmosphere departs from a equipartition of energy distribution? I’m sorry if i missed that earlier.
gbaikie says:
January 28, 2012 at 1:46 am
Wrong, wrong, wrong. Air conducts as well as convects. Otherwise stagnant air would be a perfect insulator. But, of course, it’s not. It’s just that convection is orders of magnitude faster than conduction because the viscosity of air is low. What you fail to consider is what happens after an air packet moves somewhere, in particular, to a surface boundary. It can only transfer energy to or from a surface by conduction. Period. Conduction works something like a Newton’s Cradle. The balls in the middle don’t move, only the balls on the end.
Jim Z says:
January 28, 2012 at 1:26 am
Equipartition only applies to a system in thermodynamic equilibrium. The (correct) argument is that the box with a lapse rate is not in thermodynamic equilibrium so equipartition does not have to apply. Equipartition is not violated in the isothermal box because it applies to the averages over the whole box.
Another point to consider for those folks who still don’t accept that the equilibrium state is isothermal and that if while a lapse rate exists heat somehow wouldn’t conduct from bottom to top is that it would apply to any real thermometer as well. What happens if you stuck a thermometer in the bottom of the column and allowed it to equilibrate and then quickly moved it to the top of the column? If no energy can be transferred to or from the thermometer to the gas at the top of the column, then, by definition, it’s at the same temperature as the bottom. You can claim all you want that the average kinetic energy is lower at the top of the column, but the only way you can know this is to measure the temperature. You don’t have a radar gun capable of measuring the velocity of the individual molecules.
Dewitt Payne,
You were ripping until:
“You can claim all you want that the average kinetic energy is lower at the top of the column, but the only way you can know this is to measure the temperature. You don’t have a radar gun capable of measuring the velocity of the individual molecules.”
Arguing that it ain’t real cause you can’t measure it is a real come down. You mean that before we had accelerators all those particles weren’t real and weren’t doing their thing?? No, we just didn’t know about it. It is called being ignorant, like me.
Robert Brown says:
January 28, 2012 at 6:27 am
One thing the neophytes do not understand is the remarkable interconnectedness of it all. Physics is not merely consistent, it exhibits an amazing self-similarity in the structure of the equations that describe quite dissimilar systems; dissimilar to human minds (springs versus capacitors for example), but not dissimilar to (for lack of a better term) the World. Change one of those Laws and the knock-on effect is to call into question all the other Laws that have the same mathematical structure. The Laws are like the pieces of a jigsaw puzzle. If you take a piece away, you can only replace it with one of the exact same shape, not one of a totally dissimilar shape. You can’t put a round peg in a square hole. That is why the Laws remain in place.
We say in principle the Laws may need revision, but the only revisions I can recall are minor tweaks. For example the smallchanges to f=ma at extremes of mass and acceleration and the increasing precision of empirical constants such as Avogadro’s Number. The conservation laws can be summarised as “you can’t get a quart out of a pint pot”, something any farmer can tell you.
There is considerable confusion about what is Law and what is Theory. Laws are universal, simple, true on every occasion they have been tested and are generally expressible with a simple mathematical equation. Theories are explanations of the world that usually, though not always, invoke physical law. Newton gave us his Law of Gravity and pointedly refused to provide a theory. Currently, there are two (incompatible) physical theories of gravity (that I know of): Einstein’s Relativity theory (space is curved) and a Quantum theory of gravity (gravity consists of particles called gravitons).
Thus theories tend to change rather more often than the Law. Trofim Denisovich Lysenko tried to replace a Natural Law with one based on human invention in his theory of plant inheritance and we all know, or should, where that got him.
Some here have claimed that physicists and engineers are engaged in a kind of conspiracy. I agree; there is indeed a conspiracy. The word conspire comes from Latin and literally means to breathe together. A conspiracy then is figuratively “a union or combination (of persons or things) for one end or purpose; harmonious action or effort”. As Emerson put it in Ode to Beauty “All that’s good and great with thee Works in close conspiracy”.
thepompousgit says
“Trofim Denisovich Lysenko tried to replace a Natural Law with one based on human invention in his theory of plant inheritance and we all know, or should, where that got him. ”
Lysenkos theory was known as “The inheritance of acquired characteristics”
It was an idea first proposed by Aristotle and later explored further by a scientist named John Baptist Lemark.
Recent evidence shows that for people there might be a grain of truth there.
Grandchildren have their genetic inheritance switched altered by events in their grandparents environment.
It just goes to show you that when an idea is dismissed as dead it gets up to bite your bum.
Robert Brown says:
January 28, 2012 at 6:27 am
You’re very kind, but there is an old saying in academia — you can lead a horse to water but you can’t make it think….
I am happy to have discussions and even debates with students
————————————————————————————————–
[SNIP: This kind of derogatory snark is inappropriate. Don’t do it. Dave. -REP]
Tim Folkerts says:
January 27, 2012 at 3:08 pm
I stand corrected. But make that turbulence rather than simply convection. Turbulent mixing is why you can mix cream evenly in coffee with just a few stirs with a spoon. Turbulent mixing extends through the stratosphere where there is little convection. The turbopause where the atmosphere starts to stratify by molecular or atomic weight is at a height of ~100 km. So 99.9999% of the atmosphere is well-mixed. But even turbulent mixing looks a lot like diffusion, and is often referred to as eddy diffusion.
In order for a tall column to be isothermal the density must identically follow pressure, there can be –no- deviation of the P/ρ ratio, and that gives me some intuitive heartburn. Have you ever thought from that direction? It seems to me if in the space between collisions if the exact tracks of a molecule is assumed to be a straight line, you would have an isothermal column. However, if tracks between collisions have an always –z curvature from gravity, it seems this would have to be some degree of a lapse rate. Can you see it from that direction?
Sigh. The model discussed in Jelbring and on this list is an ideal gas. So of course there isn’t any deviation. A non-ideal gas won’t affect the fact that equilibrium is isothermal, of course, but don’t change models in the middle of a stream.
In the original post I included the correct thermodynamic equilibrium state. I’ve posted a link to this question as it appeared on a thermo-stat mech final exam, with the full solution. Do you find any errors?
rgb
thepompousgit says:
January 28, 2012 at 10:10 am
nitpick:
Quantum Gravity would be a gauge field theory, presumably abelian, with the gauge boson being the graviton, similar to Quantum Electrodynamics with the electromagnetic field and the photon. Not that I really understand what that means.
Yes, if thermal radiation is the equilibrium mechanism, I see that you are correct. I apologize for my obtustness, your derivation at the top is a mechanical one.
So radiative transport is the reason the evolved isothermal atmosphere departs from a equipartition of energy distribution? I’m sorry if i missed that earlier.
You still don’t see — if ANY mechanism (other than external work) can transport heat from bottom to top, a non-isothermal distribution violates the second law. Consider the gas in the sealed container. Even internal radiation is a means of thermal relaxation.
The problem is that your imagination has misled you — you have a heuristic in your mind — “equipartition of energy distribution” — that you won’t compare to the way the equilibrium computation is correctly done. If you use your heuristic in general stat mech computations, they will fail, because thermal equilibrium is not what you imagine. You also are completely, totally, confusing how gravitational potential energy is correctly included in the equilibrium computation. You can see at a glance that stable isothermal force balance is possible. Force balance must be energy balance.
rgb
DeWitt Payne said @ January 28, 2012 at 11:01 am
Me either; I included QG for completeness. Curvature of space seems entirely reasonable and sufficient to me.
“Many of the same sorts of arguments have come up a year ago, and they will come up again in another year, I am sure”
Not keen on that type of complaint. It is easy to imagine the same exasperation being vented about the merits of throwing virgins into the volcano. Isn’t that why science is hard? It’s not just hard mathematics and abstract concepts – it’s also because people refuse to back off when they are not persuaded.
I’ve heard all sorts of arguments about global warming catastrophe theory. But stubborn old me just keeps asking awkward questions because I find myself unpersuaded. I suppose I could just accept it because other people know more about it than me.
Back to the above discussuion, I’m genuinely unpersuaded, even though a very insightful model has been presented and defended. On a very recent post, I do appreciate more now that it is being put forward as a reply to Jelbring, and needs to be comparable in many respects.
However, I’d be interested in views on the following:
Is the Fourrirer Law invariant to a uniform force field? Or did Joules have a good point way back when he suggested mechanical conduction against the force field has more work to do?
What happens if collisions are not perfectly elastic? How does this change expectations of the physical state of the gas at higher pressure compared to lower pressure? Do imperfect collisions represent a mechanism for a temperature effect?
DeWitt Payne says:
January 28, 2012 at 9:55 am
And to bring things back full circle: If you can measure a temperature difference from the bottom to the top, you must also be able to extract work or transfer energy from the system because the measurement itself must transfer energy. If you extract energy and the temperature difference (lapse rate) remains constant you have a perpetual motion machine of the second kind, which is so unlikely as to be effectively impossible.
DeWitt says at 1/28 9:55am:
“…for those folks who still don’t accept that the equilibrium state is isothermal…”
Verkley paper authors don’t accept the Fig. 1 equilibrium state is isothermal. This is mathematically proven and shown in their part b.
DeWitt (and Robert Brown) – To help you come to grips (grok) with the 2004 Verkley proof that top post Fig. 1 achieves thermal equilibrium non-isothermally (meaning there exists their proven temperature gradient eqn. 18 in equilibrium), consider their explanation, this is somewhat more satisfying to me each time I re-read it.
For Fig. 1 in top post at non-isothermal equilibrium, meaning a thermometer will indeed read T1b and > T1t again at equilibrium consider Verkley discussion in b where the authors don’t accept that the equilibrium state is isothermal by proving Fig. 1 has an isentropic temperature gradient:
“This (non-isothermal isentropic profile) indeed brings us to the broader framework discussed by Maxwell, in the sense that convective turbulent motions are now taken into account, albeit implicitly….We should now interpret the state variables as averages over volumes that are large compared to the size of the turbulent motions….We see that the temperature gradient (Verkley et. al. derived eqn. 18) is considerably larger than in the empirical profile.”
Paul Birch: “What they explicitly say is that the assumption that “temperature is proportional to average molecular kinetic energy” is FALSE (for the finite microcanonical ensemble). They say that the statement “temperature decreases with height” is FALSE. The reason it’s false is different for small N and in the canonic limit, but it is false either way. This is what they say.”
Sorry for ignoring you, Paul. I had thought you were done, and it was by the merest chance that I saw your name on the WUWT home page as someone who had posted recently about this.
If I indeed said Velasco et al. agree with me on the use of the term “temperature”–and I didn’t intend to–I take it back. I know they aren’t using that term in the same way I am; if I recall, they instead say it’s something like a quantity inversely proportional to the first partial of the log of phase volume with respect to maximum energy: as I told DeWitt Payne, “temperature” for Velasco et al. seems to be a global quantity, a characteristic of the ensemble as a whole. I never intended to say that this definition was the same as mine. What I intended to say is that Velasco et al. say there’s a drop–minuscule, as I’ve said from the beginning–in mean molecular translational kinetic energy, and to this layman’s eyes that looks like a temperature drop.
So why do I disagree with their definition of temperature? Actually, I don’t; or, rather, I’m agnostic about it because I wasn’t immediately able to find out how their definition was derived. It’s just that I felt it was irrelevant to the discussion.
And why did I feel it was irrelevant in this context? Recall how all of this started, namely, with Dr. Brown’s (to me, completely unsatisfying) argument for isothermality here: http://wattsupwiththat.com/2012/01/12/earths-baseline-black-body-model-a-damn-hard-problem/#comment-867311. You’ll see his argument is based on local quantities. In fact, you’ll see he says that the velocity distribution–and therefore kinetic-energy distribution–at any altitude is the same as at any other. This is why the definition of temperature I prefer in this context is the one we all learned in high-school (as we say here in the colonies) chemistry, i.e., mean molecular translational kinetic energy: it can be used as a local quantity.
Just in case anyone else is paying attention, I’ll add that what we’re arguing is an extremely academic point. Velasco et al. and Dr. Brown both say there won’t be any measurable lapse rate at equilibrium in an isolated gas column subjected to gravity. Dr. Brown began by saying–although he may have tuned his position since–that velocity distributions at all altitudes in such a system are identical. My interpretation of Velasco et al. is that they this isn’t true, because the mean molecular kinetic energy decreases with altitude, but, again, that it makes no difference in practice, because the difference is so small you’d never be able to measure it. I don’t understand Paul Birch to disagree with the interpretation as I stated it in the last sentence, but he objects to my calling such a small kinetic-energy difference a temperature difference.
So why did I bring Velasco et al. up if the issue is so minor? Because in the back of my mind I had for some time wanted a satisfactory basis for deciding between the isothermal and dry-adiabatic-lapse-rate schools of thought. Unfortunately, all the discussions I had previously seen were at the level of rigor exhibited by Dr. Brown’s discussion, which I did not find at all satisfactory. When I hit upon Velasco et al., on the other hand, I felt I had finally hit pay dirt, but some of the jumps between their equations were broader than I could easily make, so I wanted some vetting. Since, unlike Dr. Brown, Velasco et al. said there is indeed a velocity-distribution difference between altitudes, I thought I might provoke an attack on their paper and thereby get some light shed on its more-obscure passages.
I was wrong.
Trick says:
January 28, 2012 at 11:28 am
Turbulence is by its nature dissipative. From Wikipedia;
[my emphasis]
But the system is defined as closed. Any turbulence must dissipate. Verkley’s solution no longer applies. Then we’re back to conduction and an isothermal system at equilibrium.
Robert Brown says at 1/28 10:55am:
“In the original post I included the correct thermodynamic equilibrium state…. Do you find any errors?”
Comparing the work in Verkley to the top post, I see your equation 5 for dz up there, when integrated, takes T outside the integral apparently just making the assumption T is constant leading to isothermal conclusion.
T is function of P by ideal gas law (thus function dz meaning T cannot go outside integral) as Verkley paper correctly shows in eqn. 16 leading them to show top post Fig. 1 being non-isothermal isentropic equilibrium via Verkley et. al. eqn. 18.
Tim Folkerts says:
January 28, 2012 at 8:53 am
I also love the challenge that “It has never been resolved by experiment.” First of all, there is a good chance that the person making the claim simply does not know the relevant experiments.
Beyond that, often there are related experiment that do indeed show the expected results, just not in exactly the form the person want. For example, the satellite IR spectra looking down at the earth DOES show conclusively that the CO2 warms the earth, but only if you understand enough of the other science involved. It doesn’t show what ELSE might affect the surface temperature. It doesn’t show exactly how changes in CO2 would change the surface temperature. But is does clearly show a warming effect from the CO2 that is present. In this present case, there are centuries of experiments involving gases which are consistent with the laws of thermodynamics as presented in standard textbooks.
Gosh Tim, real experiments from satellite data looking down on the Earth proving carbon dioxide warms the Earth? We’ve been asking for this information for a, well, always. Where have you been hiding it? Do show it to us, and talk us through it, I’m sure others would like to see such proof that Carbon Dioxide warms the Earth.
I had a look, but couldn’t find it. I did find the silliest of graphs here, http://www.ncdc.noaa.gov/indicators/, showing the poster child CO2 levels from Hawaii against levels for the last 800,000 years from the Antarctic- what do you notice?
That carbon dioxide obviously was utterly irrelevant in the massive global warming every 100,000 years at the beginning of interglacials when sea levels rose 300ft plus as gazillion tons of ice melted? That the Hawaiian spike looks, well, rather odd? But isn’t that why Keeling chose to measure his mythical ‘background’ carbon dioxide there – on top of the world’s most active volcano? Tons and tons of carbon dioxide to measure and choose from, from the erupting volcanoes, from the venting, from the thousands of earthquakes above and below sea level, from the warm sea itself around the islands, and of course all on that super hot spot creating the islands. And, such a brilliant scientist, he could tell with less than two years data that man-made global emissions were rising annually…
Someone did an analysis of Gates’s technique, you too spend much of your posts agreeing with the prevailing mood and then throw in bits of nonsense as here, I’m calling you on it, I’ve highlighted it in bold. Provide the following experiment you say “DOES show conclusively that the CO2 warms the earth” and talk us through the science since you “also love the challenge that it hasn’t been resolved by experiment”:
Beyond that, often there are related experiment that do indeed show the expected results, just not in exactly the form the person want. For example, the satellite IR spectra looking down at the earth DOES show conclusively that the CO2 warms the earth, but only if you understand enough of the other science involved.
DeWitt Payne says at 1/28 11:45am:
“Any turbulence must dissipate. Verkley’s solution no longer applies. Then we’re back to conduction and an isothermal system at equilibrium.”
Notice that the wiki clip you posted mentions turbulent “flow”. There is no “flow” in top post Fig. 1 just molecules randomly mixing. Verkley et. al. b solution does apply as they further explain their concept of convective turbulent mixing. See their 1st Law eqn. 14 and explanation starting: “Even when on the scale of the turbulence the heating rate J would be zero…” and continues on to support their case for Fig. 1 being non-isothermal isentropic.
Very interesting discussion, thanks DeWitt.
Trick,
You don’t get turbulence without flow. Period. Any turbulence dissipates. Verkley, therefore, is not relevant to the subject of this post.
“if ANY mechanism (other than external work) can transport heat from bottom to top, a non-isothermal distribution violates the second law.”
But there is none that I have seen in these discussions.
There was an appealing idea to transfer energy up to altitude using black body radiation in a vacuum. Sorry to be so practical, but it is a highly idealised mechanism and depends on assumptions of loss-free transfers plus a good deal of organisation of the active transfer process (which implies work).
Even then, there is my question about Fourrier’s Law in a force field. If we could get a free transfer of energy to altitude, it doesn’t mean an isothermal outcome if conduction of temperature is influenced by the gravitational force field. It might alter a temperature gradient, but that doesn’t necessarily mean the gradient must disappear completely.
Ofcourse this could mean an indefinite circulation of energy around the system and some might object. But if we place a highlyidealised concept of a perfect conductor into a force field, we’re not placing ourselves into a convincing position to object to the consequences on real-world reasoning.
DeWitt – Verkley et. al is using the common definition of turbulence applied to ideal gas molecules which defines turbulence to mean their irregular motion. Surely the ideal gas molecule random movements are consistent with irregular motion.
Brownian motion is considered irregular motion of macro particles deduced from the molecules. (Robert Brown said that in 1827, he’s been around awhile!). Brownian motion thus is a form of turbulence.
Amazing where this thread, like many, evolves.
Bryan said @ January 28, 2012 at 11:33 am
Lysenko replaced Mendelian genetic inheritance with a version of Lamarckism just because he was a Marxist and Lamarckism supported the Marxist idea of Progress. I am fully familiar with Lamarckism. Darwin was a Lamarckist. Lamarckism was fully compatible with Darwinism.
The
dismissed Lamarckism, and yes, it has come back to bite them on the bum which is why it has been renamed. But that’s a bit OT.
Trick says:
January 28, 2012 at 12:56 pm
Humpty Dumpty (Through the Looking Glass) much! Turbulence has a very specific meaning and it has nothing to do with the random motion of individual gas molecules whether ideal or not. Brownian motion isn’t turbulent movement either.
Myrrh askes: “Gosh Tim, real experiments from satellite data looking down on the Earth proving carbon dioxide warms the Earth?”
http://wattsupwiththat.files.wordpress.com/2011/03/gw-petty-6-6.jpg
… but only if you understand enough of the other science involved.
And I think I am now going to go back to other things …
DeWitt 1:26pm – Yeah, in aero work it is useful to think of turbulent flow vs. laminar flow. Here it is useful to think of turbulence to mean irregular motion (it IS the dictionary definition). We aren’t worried about stream lines in top post Fig. 1.
If you want, the Verkley paper may then mean more for you if just substitute the dictionary definition of “turbulence” with ”irregular” every time they write “turbulence” term.
My 11:28am post above then becomes this, a direct meaning but not direct quote from the paper:
“This (non-isothermal isentropic profile) indeed brings us to the broader framework discussed by Maxwell, in the sense that convective irregular motions are now taken into account, albeit implicitly….We should now interpret the state variables as averages over volumes that are large compared to the size of the irregular motions….We see that the temperature gradient (Verkley et. al. derived eqn. 18) is considerably larger than in the empirical profile.”
This does not change any Varkley et. al. logic, derivations or equations. Now others may post with the non-direct quote issue down thread…sigh. If they do, show the work that changes Verkley when substitute irregular motion for turbulent motion. No laminar flow here.
I don’t hold out much hope for Dr Browns latest suggestion of a lossless light tube.
I will restate my claim yet again, since people appear to be incapable of keeping it in mind long enough to reach the “Leave a Reply” box.
This post addresses precisely one thing. Hans Jelbring published a paper in 2003 in Energy and Environment. Tallbloke has posted the entire paper on his blog here:
http://tallbloke.wordpress.com/2012/01/01/hans-jelbring-the-greenhouse-effect-as-a-function-of-atmospheric-mass/
with a contemporary preface by Jelbring. I quote from this preface:
My 2003 E&E article (peer reviewed) was strictly applying 1st principle physics relating to a model atmosphere. Very strong conclusions can be made about such a model atmosphere and less strong ones about our real atmosphere. This was not discussed for reaching a maximum of simplicity and clarity approaching an educated but laymen audience. However, an investigating professional climate scientists should just reach one of three results; a) my logic is wrong, b) the major part of the Greenhouse Effect is always at hand in any (dense) atmosphere and c) any of the first law of thermodynamics, the second law of thermodynamics or the ideal gas law is invalid.
I accept the challenge. His logic is wrong. His article is utterly irrelevant to the actual GHE that can be verified by the merest glance at satellite IR spectra. Finally — and this is the point of my demonstration above — it is the model he proposes that is in violation of the second law of thermodynamics, not only in violation, but a textbook example of a violation.
Quite aside from this the article is a terrible example of science — I cannot imagine how it was ever accepted by either editor or referees. The article does not include a single line of algebra. I have literally never read a supposedly serious, non-bullshit work on the physical thermodynamics of a model system that did not even define the forces, energies, conditions, assumptions made in algebraic terms. This paper shows nothing in the actual language of physical science; it presents a purely heuristic, question-begging argument with numerous errors and internal inconsistencies.
Here is an ordinary undergraduate exam question in a course in statistical physics and thermodynamics offered and the University of South Carolina and posted on their website. Note well that the question asks students to solve the exact same problem that Jelbring proposes — that of a vertical, isolated, column of ideal gas that must be in static and thermal equilibrium in a gravitational field:
http://www.physics.sc.edu/~yar/phys706_2011/Homework/final_solutions.pdf
If I, at least, were grading Jelbring’s supposedly professionally written paper against this textbook question, he would get a zero for the problem.
He would get a zero for two reasons. One is that no work is done in Jelbring’s paper. A physics problem is not solved in words! Especially not a difficult one. Of course this one isn’t all that difficult — it is a standard feature of any introductory physics textbook — but still, not one equation!
After a long and tedious description of the problem — a simple container of fluid like the one I drew up above would work as well as his complicated “adiabatically insulated planet”, he asserts that the “Greenhouse Effect” is entirely due to some sort of static gravitational effect that results in a “surface atmospheric mass density”. In particular, his assertion is that:
The GE is hypothesised to be independent of the amount of “greenhouse gases” in a dry atmosphere.
This makes it perfectly clear why this assertion is so zealously defended in this thread. It is literally what anyone who wants to deny the reality of the Greenhouse Effect being connected in any way to GHGs wants to hear.
He follows this by offering as logical proof — remember, we are asked to challenge his logic and he’s stated his axioms as being “physics is correct plus an ideal gas” — the experimental observation that the dry adiabatic lapse rate that is approximately observed in the Earth’s highly dynamic, externally driven atmosphere will be the thermostatic equilibrium state in his sealed container.
He does not prove that this is, in fact, true — he simply states that it is true, quoting a textbook derivation of the DALR as his “proof”. This is a double swindle. For one thing, where, exactly, is his contribution? Citing a textbook? Excuse me? That’s not even up to the standards of somebody who copies an answer on an exam — at least in that case one would be likely to recapitulate the algebra and see why or why not the gas in question was in thermal equilibrium and how, exactly, the DALR was arrived at.
Jelbring does indicate some of it — bits such as: “An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.” Of course, in an isolated ideal gas left long enough to come to thermodynamic equilibrium, there are no moving parcels of air and there is no work being down against the gravity field. So even his English words describing a conclusion with many assumptions underlying a not completely trivial algebraic derivation leave considerable doubt that that conclusion should necessarily apply to a gas in static force equilibrium and thermal equilibrium.
Second, we have already heard, in the thread above, from the actual author of a freely available textbook that does derive and discuss the DALR, that the DALR is not, in fact, thermal equilibrium. This puts those who are reluctant to give up their irrational attachment to Jelbring’s conclusion simply because it mirrors their prior belief that the GHE is not due to GHGs in a difficult position. Jelbring implies that we can be certain that it is thermal equilibium because James R. Holton, in an introductory textbook written in 1979 says it is. However, examining this book it seems to me that he derives it by assuming a “perfect gas in adiabatic motion” — right next to a picture of (and in the context of) Richardson’s criterion for the stability of flow.
The last time I looked, a gas in convective flow is not in static equilibrium, and flow itself cannot be a long-time stable state of any isolated system with internal dissipation. Superfluid Helium, perhaps. An ideal gas, no. Is this a deliberate swindle? How can I tell? Probably not. Never attribute to malice something that can be attributed to simple incompetence. In any event, actually examining the only reference he cites to defend his assertion that the DALR is characteristic of actual thermal equilibrium in the absence of bulk fluid transport driven by thermal gradients readily demonstrates that it does not. In fact, the paper only has four references — Arrhenius to be poo-pooed, another textbook on dynamical climatology, not used in any relevant way, one of Jelbring’s own former papers, and Holton. Since Holton does not in any way suggest that the DALR is a static, thermal equilibrium process, we’re down to one reference that says that it is. Who is it? Himself.
This suffices to show his errors in logic. Stating a hypothesis and the stating that somebody else derived this equation with a thermal lapse (in an entirely different context) and so the hypothesis is proven, citing your own work several times in between, without so much as a single equation defining the criterion for static force equilibrium, adiabatic curves for an ideal gas, the actual definition of thermal equilibrium is not a logically valid proof, and it is certainly not a mathematically or physically valid proof. It is heuristic handwaving, nothing more.
Next, let us examine his really fundamental errors — the errors in simple thermodynamics. Oh, wait, that has already been done. But let’s bash some more. To quote Wikipedia’s article on Thermodynamic Equilibrium, where they discuss the difference between local thermodynamic equilibrium and global thermodynamic equilibrium:
Local thermodynamic equilibrium does not require either local or global stationarity. In other words, each small locality need not have a constant temperature. However, it does require that each small locality change slowly enough to practically sustain its local Maxwell-Boltzmann distribution of molecular velocities. A global non-equilibrium state can be stably stationary only if it is maintained by exchanges between the system and the outside. For example, a globally stably stationary state could be maintained inside the glass of water by continuously adding finely powdered ice into it in order to compensate for the melting, and continuously draining off the meltwater. Transport phenomena are processes that lead a system from local to global thermodynamic equilibrium. Going back to our example, the diffusion of heat will lead our glass of water toward global thermodynamic equilibrium, a state in which the temperature of the glass is completely homogeneous.
Could it be that atmospheres with a DALR are only in local thermodynamic equilibrium (required so that one can discuss the temperature of a local parcel of air as it moves around) but are not in global equilibrium? Caballero, author of an actual textbook on physical climatology, says that is precisely the case. Every physics textbook on the planet states clearly that global thermodynamic equilibrium is isothermal. The zeroth law of thermodynamics is precisely that statement; without it there is no such thing as thermometry and we can’t even measure a temperature in the first place.
This merely leads us to the big violation, the elephant in the room: the violation of the second law in Jelbring’s paper. He clearly states that he assumes:
The energy content in the model atmosphere is fixed and constant since no energy can enter or leave the closed space. Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy. In this situation the atmosphere has reached energetic equilibrium.
Here it is. If we leave his isolated ideal gas alone for a long time, energy will redistribute until the gas reaches “energy equilibrium”. This term is meaningless, of course — Jelbring just made it up. The correct term is thermal equilibrium because thermal equilibrium is the most probable way energy will be split up among the various degrees of freedom (including gravitational ones when present) in any isolated system after thermal relaxation of the sort he describes has occurred.
Clearly Jelbring thinks that his asserted “energy equilibrium” (thermal equilibrium) state is not isothermal. It is the entire point of his paper. But is this non-isothermal state equilibrium?
I have shown above, and can show over and over again that it is not! It is a textbook example from any textbook on thermodynamics to show that equilibrium is isothermal. If it were not, one could build perfect refrigerators and perfect heat engines. In fact, if Jelbring’s hypothesized atmosphere with a thermal lapse rate were a true thermodynamic energy equilibrium, one could take its heat content and use it to do reversible work that directly reduces the entropy of the Universe. It violates three out of three statements of the second law. The demonstration of the violations isn’t even specific to Jelbring’s system — it is generic. A reasonably bright premed who has taken a thermo course should be able to see the error, let alone a first year undergrad physics major or engineering student.
This is the reason that this terrible paper should never have been accepted and should be openly shunned by any real climate skeptic. Although it is a logical fallacy in a sense, when climate skeptics state “There is no such thing as the GHG GHE because Jelbring has shown that even a stable, isolated, non-GHG containing ideal gas atmosphere will have a permanent thermal lapse” what they are really saying is “We don’t believe in GHG GHE because thermal separation is really magic.” Even if they follow up their remarks with something that might be true — “… and besides, the GHG-based GHE is saturated, the feedbacks are actually negative, solar-induced variations in albedo are just as important, and if you would stop adjusting the bloody temperature record to show ever more warming and look at the actual data, you’d find that it doesn’t support your conclusions or prior predictions” you’ve already lost most listeners way back there with “magic”.
Don’t think that most climate scientists are stupid, or that they are all necessarily morally corrupt. Both of these are ridiculous assertions, even if you can find specific examples of both among their ranks. It doesn’t take a lot of knowledge of physics to understand the second law of thermodynamics and how a system with a thermal gradient can never be in a state of global, stable, “energy equilibrium” (whatever the hell that means) unless it violates it. If you are betting your credibility on it, you will lose, and unfortunately, you will probably lose in a way that makes it all too easy to marginalize and ignore any much more reasonable objections you might make.
On these pages, we regularly (and, I think, correctly) accuse at least some of the climate scientists out there of cherrypicking data, engaging in confirmation bias, misusing statistics. We frequently use the (fallacious) argument that simply because they do these things, their conclusion is necessarily wrong. Why give the climate sciences an open and straightforward way to do the same to us, a way that I agree with, a way that is totally justified?
My argument, and conclusion, is very narrow. I am not saying, for example, that atmospheric dynamics may not play an important role in determining the Earth’s heat transport system and hence its relative “warming” or “cooling” rates. I am saying that it is utterly false to claim that a static, stable, isolated atmosphere will have a thermal lapse rate and argue from this that the GHE is due to static compression in an equilibrium ideal gas. No, it’s not. That would be magic.
I have, along the way, commended the staunch if misled defenders of Jelbring’s work to entertain the idea that perhaps there really is a GHG GHE that really does help to warm the Earth’s atmosphere. I have suggested repeatedly that they examine, and try to understand, the satellite-based IR spectral data than in my opinion is direct experimental observation of and confirmation of the basic mechanism. I have suggested that the differential cooling established by GHGs is responsible for the DALR, not the other way around. I do not insist on the latter — it is just what makes the greatest sense to me at this time and seems to be in general agreement with the arguments in physical climatology where it is recognized that the moving parcels of air referred to in deriving the DALR are moving because of thermally driven vertical shear. But it is all, in the end, a lot more complicated than the simple flow diagrams that they often present in the atmosphere, however simple and revealing the outgoing radiative spectrum is.
I will finish — again — by suggesting that the remaining supporters of Jelbring’s paper not take my — or his — word for anything. Look inside any physics textbook that you like, and you will find the laws of thermodynamics laid out. Look inside any of the thermo or stat mech textbooks beyond the introductory level — which are hard going! — and you will find them laid out and derived and illustrated with many examples. Look in any textbook in physical climatology and you will never see the DALR derived or discussed without reference to uplifting parcels of air — air in motion, not static air. In the end, you will see why, and how, thermal equilibrium must be isothermal and how all of your efforts to argue that it is not each leads to a straightforward violation of the second law of thermodynamics (as well as not being the actual solution to the problem in thermodynamics or statistical mechanics, correctly done, as has been known for well over 100 years).
rgb
Looking for a second law violation:
Dr brown and others, I hope you will indulge one more question. It is a closed box (closed system) in the earth’s gravity.
In the first condition, the box is empty. So it is in thermodynamic equilibrium.
In the second condition, the box has gas in it that is opaque to thermal radiation. So it is a isothermic gas in thermodynamic equilibrium.
In the third condition the box has gas in it that is transparent to thermal radiation. Say there is a steady state condition where the gas molecules in the box, as they move, increase the kinetic energy of a molecule slightly when the movement has a component in the direction of gravity and looses slight kinetic energy when there is a component opposite gravity. The top of the box and the bottom of the box exchange thermal photons. The average temperature of the top of the box and the gas at the top of the box are the same. The average temperature of the bottom of the box and the gas at the bottom are the same. The thermal radiation exchange has a slight imbalance towards the top of the box and the kinetic energy exchange, from the top of the box, thru the gas and to the bottom of the box, has an equally small imbalance towards the bottom of the box. There is isohtermal gas and no equilibrium. I”m looking for the violation. I can’t think of any mechanism, within the box, that can use the temperature gradiant to increase the heat content of the box, or to increase the temperature differential within the box. (serious for real question)
Dr Brown, one small thing, and I mean it kindly; I just saw your example of carrying a sealed jar of air up some stairs, to exploit a pressure differential. I don’t know if this is what you meant, But i think that process only uses work against gravity. Air has buoyancy, and moving the sealed jar of air up or down is work against gravity.A mass less jar makes it obvious, carry the jar down stairs and let it go and it floats up to where you started, carry it up stairs and let it go and it sinks back, Use the pressure difference to do work, and that is just the same work it took to move the jar up or down.
PS Dr Brown, I’m not defending Jelbrings paper; it’s nothing to me, i’m not a climate skeptic.
I only saw things that didn’t make sense to me. Thanks!
I made a mistake above; I meant there is no isothermal gas in the box in te third condition
Again, Thank you Dr Brown!
sorry, one more mistake;
I mean in the third condition of the box in the question above, that there is a slight temperature gradiant between the top of the box and the bottom of the box. And that the slight net radiative flux and the slight net kinetic energy flux exactly balance in opposite directions. sorry again for the mistake.
JimZ: “i’m not a climate skeptic.”
So does that mean you do or don’t believe there is a climate?
Jim Z said @ January 28, 2012 at 3:35 pm
In the first box you state there is nothing: “The box is empty”. If there is nothing it cannot have a temperature and therefore cannot be in thermal equilibrium.
One more mistake. Having fun yet?
Dr Brown,
Yes, I now see how it is and you are correct. The atmosphere relaxes to an isothermic state.
Thanks for your patience, you taught taught me something important, humility, along iwth some physics.
Thank you again!
Well In addition to sharing Prof Brown’s incredulity, that so many people can’t even grasp the simplest of simple thermodynamic problem examples, this thread, has been an additional shock to me.
If you read through the various posts, and also the responses from others (some) to those posts, it will become apparent that many (too many) of the posters here, are either trolls deliberately trying to muddy the water, or their understanding of the English language is as dismal as their understanding of some simple physics. Now lack of understanding of the physics is forgiveable.
I have said on many occasions :- ” Ignorance is NOT a disease; we are all born with it; but stupidity has to be taught, and there are plenty of people who are eminently able, and willing to teach it.”
Ignorance can be dispelled by teaching and learning; stupidity can’t.
I have a son who is taking some classes at San Francisco State University (of necessity), and that institution seems to be most famous for its “School of Racism.”
Well they call it euphemistically “Ethnic Studies.” Trust me it’s a school of racism.
But I digress; when I went with my son for his first orientation seminar, when he started at SFSU, they told us all, that every single student who goes to SFSU must pass a test following a compulsory course in Remedial English. They can take the course and the test almost any time, but they can’t graduate without doing so.
Now let me state most emphatically, that I am not talking about people for whom English is a second language; we have many here at WUWT, and I just wish I had any skills at all, in any other language, even a fraction of the English skills, some of our ESLs here have. Hell I even get my umlaut’s in the rong places.
But it’s a sad commentary, that people who are native English speakers, have to take a remedial course in order to attend a major city university. My wife is a school teacher, so I know pretty much how that sorry state comes about; she gets extra pay, because she is a bi-lingual teacher; who actually teaches monolingually, just not in English. And that has been illegal in California for quite a few years now, but some parents are bound and determined to keep their kids behind the eight ball, and out of the main stream of US life.
So a lot of the fuss and bother in posts above seems to be some posters can’t even read what is written by others and understand the simple English meaning of what they are reading.
I’m happy to attempt to pass on, what limited Physics, I know; but I’m not about to start trying to explain English to folks who ought to know it; I’m English handicapped myself and tend to speak the British variant of it, which doesn’t really go down well in America.
I didn’t even bother to go and figure out what Jellbring’ hypothesis was or is; I was sufficiently mesmerised by the lack of understanding of Robert Brown’s elegant demonstration, that whatever Jellbring was talking about seems irrelevent.
You can turn loose your terracomputers on a lot of this climate stuff; but most of the crucial points don’t require more than a sandy beach, and a stick to scratch on it with
“Quite aside from this the article is a terrible example of science — I cannot imagine how it was ever accepted by either editor or referees. The article does not include a single line of algebra. I have literally never read a supposedly serious, non-bullshit work on the physical thermodynamics of a model system that did not even define the forces, energies, conditions, assumptions made in algebraic terms. This paper shows nothing in the actual language of physical science; it presents a purely heuristic, question-begging argument with numerous errors and internal inconsistencies.” – Brown
“…for reaching a maximum of simplicity and clarity approaching an educated but laymen audience.”
“This paper has purposely been kept more qualitative than quantitative to avoid
elaborate formula and explanations – and to make it easy for all to digest. The more
theoretically competent readers should have few problems if they wish to perform
quantitative calculations for themselves, following the guidelines presented here. – Jelbring
“If you can’t explain it simply, you don’t understand it well enough.” – Albert Einstein
The only issue I have with this, is that it obviously had to be well known once upon a time since, as I’ve given above, minus the main greenhouse gas water vapour, our atmosphere of practically 100% nitrogen and oxygen, dry air, would be 67°C, standard industry figures. It’s the greenhouse gas water vapour which brings that down 52°C to the 15°C.
Now, there’s around four times as much nitrogen in the atmosphere as oxygen and since nitrogen in its diatomic form is difficult to break to form compounds, then it could be said to approximate to an ideal gas (elastic collisions not inelastic), and, oxygen and nitrogen don’t combine in the atmosphere but mix, and, oxygen is practically the same weight as nitrogen, and, oxygen has practically the same heat capacity, then, not a bad approximation to the ideal gas of Jelbring’s thought experiment.
And, since our atmosphere is more than the tropopause and there is a rather large and very hot layer someway above the tropopause, his closed scenario not a million miles off from what we have, which is that temps decrease as gravity’s grip lightens.
So, we know that his approximation is fine for our atmosphere as we have it, with greenhouse gases included, because temps decrease as we move away from the surface and that has been measured and shows regularity of decrease in the play between gravity, density and distance. Taking out the greenhouse gases, which in all logic seeing the effect just a small percentage of water vapour has on temps need not include any other, then we have Jelbring’s experiment, a very good approximation, just by stepping into a desert.
Since this Jelbring’s scenario has actually got back to what we know we have, I can’t see anything wrong with it.
The only problem is, as I’ve mentioned before…, the energy budget that both pro and anti AGW use is fictional because it has excluded the Water Cycle, and you don’t know this.
Y’all (generic) think it’s real because you’ve all forgotten the Water Cycle because you no longer have it in your calculations because distracted by a sleight of hand by AGW (for it is AGW’s energy budget you’re using), and so all this appears new to you.
This sleight of hand has taken the difference between -18°C of the Earth without any atmosphere at all and the 15°C of our atmosphere as we have it, and attributed the difference to the imaginary supermolecule properties of our beloved carbon dioxide, without ever giving any details of how this wonderfood for plants and oxygen transporter for our blood can raise the temp of the Earth 33°C from -18 to +15..? Tim?
So, our approximate to the J model Earth is 85°C with an atmosphere of practically 100%nitrogen and oxygen as we have it but without the Water Cycle.
“A simplified model of Earth, along with a formal
proof concerning the model atmosphere and evidence from real planetary
atmospheres will help in reaching conclusions. The distinguishing premise is that
the bulk part of a planetary GE depends on its atmospheric surface mass density.
Thus the GE can be exactly calculated for an ideal planetary model atmosphere.” – Jelbring
“A simplified model of Earth will be considered. The model planet does not rotate. It
neither receives solar radiation nor emits infrared radiation into space.” – Jelbring
So, please work it out you maths boffs, how much heating would there be if we switched the Sun off?
And, do stick to the scenario he presents, so we can all follow the picture..
“Quite aside from this the article is a terrible example of science — I cannot imagine how it was ever accepted by either editor or referees. The article does not include a single line of algebra. I have literally never read a supposedly serious, non-bullshit work on the physical thermodynamics of a model system that did not even define the forces, energies, conditions, assumptions made in algebraic terms. This paper shows nothing in the actual language of physical science; it presents a purely heuristic, question-begging argument with numerous errors and internal inconsistencies.” – Brown “.
Sounds like a very good description of the greenhouse effect.
Robert Brown, in your example physics paper (posted 2:33pm above) I found an error in the solution in 1(b) … the word calculate is misspelled as ‘calcfulate’ … does this qualify me for any credit towards a physics degree, or does that just make me a run-of-the-mill pedant? 😉
kuhnkat says:
January 28, 2012 at 7:48 pm
Radiation? Where is there radiation in Dr. Brown’s thought experiment? Here’s the question:
Do you think that the gas will stratify thermally?
If so, will heat flow in the silver wire?
Thanks,
w.
Willis,
You mean I missed where he said the silver and nothing else in the “experiment” will radiate? Gee, what other basic physics is missing that I missed? I mean, Nobel Gases have extremely low absorption/radiation, but it isn’t nonexistent. With collisional energy being transferred we will get emission occasionally. May not be enough to alter any balance, but, the silver dang well will emit if it can conduct. So, like many other of these things, how much real physics is being excised to get the desired result?
I am stuck in ancient times when heat was called kinetic heat. If two things collided you had conductance. I just don’t GROCK this idea of no energy flow, with gases will be conducting continually until they are approximately equilibrated. Of course, as soon as one bounces in the vertical axis the distribution of its energy state changes with time due to the gravity gradient. So it is all going to be moving around a mean and this satisfies the requirement?
After reading the Verkley Gerkema paper, it seems to me that the idea of a planetary atmosphere relaxing to an isothermal profile in the absence of greenhouse gases is absolute foolishness.
Unfortunately many proponents of AGW are so willing to misuse Dr. Brown’s elegant refutation of Hans Jelbring’s E&E paper to conclude that GHG’s must therefore be responsible for the temperature lapse rate observed in planetary atmospheres. This is foolishness since neither the original E&E paper, nor Dr. Brown’s refutation address planetary atmospheres – they look at a very theoretical tube of gas in a gravitational field.
A planetary atmosphere has several critical features. First, it exists on (or consists of) a rotating imperfect sphere (barring of course the trivial case of a non-rotating perfectly spherical planet). Second, the planet is revolving about one or more stars. Third, the planet (including the atmosphere) is subject to some tidal forces (again, there is a trivial case of a perfectly tidally locked planet…). All three of these features are indisputable features of a real planet since they essentially derive from the definition of ‘planetary.’
So what to conclude about planetary atmospheres? First, the atmosphere is not in thermal equilibrium – there are day/night cycles, Coriolis effect, tidal effects, variations in heat transfer from the surface – it goes on and on with one conclusion: atmospheric mixing. With mixing comes an overall tendency toward an intermediate profile between isentropic and isothermal – no GHG’s involved…
“DeWitt Payne says:
January 28, 2012 at 9:30 am
gbaikie says:
January 28, 2012 at 1:46 am
But air does not conduct the heat. You can’t compare air to silver or stone. It’s not just that air is poor conductor. Air molecule is excellent conductor to itself- the molecule velocities are “transferred” at 100% effectively in less than nanosecond, but the only way energy through air is “conducted” is via air packets- or air doesn’t conduct to itself, it transfers heat from one location to another via movement of air molecules- convection. Other than redistribution or averaging velocity of molecules, air only transfers energy thru air via convection. So if you have a condition of not having some buoyancy difference of air packets, is no conduction of heat via air.
Wrong, wrong, wrong. Air conducts as well as convects. Otherwise stagnant air would be a perfect insulator. ”
Air does conduct heat to solids and liquids. Heat for gases is velocity of gas molecules- unlike liquids and solids.
Air molecules exchange velocities with each other, and suppose you could choose to say gas molecules conducts heat to other gas molecules. But stagnant air suggest you mean gas molecules which have the same average molecule velocity, and exchanges of velocities of gas which have the same average molecule velocities is not conducted heat anywhere.
Air is good insulator. Having or causing air not transfer heat via buoyancy of air packet would be would be one of best insulators, and this basically descriptive of what fiberglass insulation does- the fiberglass inhibits the convection of air.
A vacuum would be only better insulation vs conduction and convection- a vacuum could said to be perfect or best as far preventing conduction and convection of heat.
“But, of course, it’s not. It’s just that convection is orders of magnitude faster than conduction because the viscosity of air is low.”
It’s more a matter of density rather than viscosity.
” What you fail to consider is what happens after an air packet moves somewhere, in particular, to a surface boundary. It can only transfer energy to or from a surface by conduction. Period.”
Essentially I agree. I tend to think that if there is anywhere where individual gas molecules *tend* not to move much it’s at the surface. It’s vector is limited- terrain at the microscopic level has be very rough, and other factors could tend to bind individual molecules.
” Conduction works something like a Newton’s Cradle. The balls in the middle don’t move, only the balls on the end.”
But all air molecules do move, where they move and at what velocity vector is not knowable, an air molecule might stay in one place, but it’s not likely. And if one instance it’s going up, it could nanosecond later be heading down, or sideways. One might choose to mathematically describe them as going nowhere, but they can also go anywhere- limited by time and highest probable velocity.
[Considering that it’s possible {very, very low chance} they could hit by a atom traveling near the speed of light, the individuals aren’t constrained]. The Sun bombards earth with high energy particles, and the universe can hit earth with much faster particles- which can reach the surface.
But all the above is not related to the point, gas molecules, unlike solids and liquids, can have density affected earth’s gravity, and though gas molecules can be traveling at same velocity, the total amount gas molecules in higher elevation are a lower temperature- as measured by how much they warm up liquids or solids. And silver wire’s density not similarly lessen because at a higher elevation.
Robert
“Here, I’ll reduce it to a one line “elevator speech”. If a supposed equilibrium distribution of temperature in an isolated system is capable of doing work, it is neither an equilibrium distribution nor is the system at maximum entropy.”
I think you are repeating an error made earlier: even at the atomic scale, energy flows from one atom to another, gaining and losing energy. This is by definition a ‘flow of heat’ and no work is being done and it is at maximum entropy. Maybe that is not important to heat flow in the atmosphere.
You rule out a flow of heat (at all) in an isothermal system. Yet within that ‘isothermal’ column, there is all sorts of heat flowing around. I guess others have noted that. Man, these absolutes…
OK: picture an atmosphere with a lapse rate, a warmer bottom and cooler top. Introduce the silver wire. Heat will flow up the wire and because there is no lapse rate for silver, it will warm the gas at the top. You put a larger heat exchanger at the top to overcome the collision rate difference due to the pressure differential. Objection overcome.
Eventually it will reach thermal equilibrium, correct? At that time, in a gravitational field, the total energy of any upper molecule will be much greater than at the bottom (K+P), correct? Is that a state of maximum entropy?
Some say that unless the total energy (P+K) is equally distributed, it is not at maximum entropy. Well it cannot satisfy both demands simultaneously: equally distributed total energy and equal temperature. Perhaps I should rephrase that: Those who think they can both be simultaneously true please explain how.
Willis says, “Instead, the maximum entropy is when each volume of air has the same average energy.” If they have the same energy, they cannot be at different elevations and the same temperature, correct? (K1+P1)@T1 = (K2+P2)@T2 where T1 = T2??
There seem to be two schools of thought tugging in opposite directions. In the presence of a gravitational field, both conditions cannot be satisfied at the same time unless there is no energy in the system. (Yet even in a frozen state the top of the ice would have higher total energy with respect to the surface than the bottom.)
It seems to me Potential Energy is a red herring for this discussion.
And Wayne, I agree, the pressure/density curves diverge. Plus consider the planet may be spinning. Z+dZ and all. Very interesting. Will think about it. It seems to fall on the ‘equal distribution of total energy’ side of the fence.
Kuhnkat: When they finally equilibrate they do not stop radiating (transferring energy). Energy flow continues ad infinitum.
Robert said, ““Yes thermally induced vibrations of molecules can and do transmit to their neighbors in EVERY direction, even from cold end to hot end; but since the vibrational energy of the molecules is higher at the hot end, than at the cold end, the process of INCREASING the vibrational energy of the neighbors only happens from hot to cold.”
++++
This week I was talking to Steve Garrett, he of thermoacoustic fame. He can show you a steel tube with a hot and cold section in the middle, but a FAR colder tube end. The heat entering the very cold end moves to the not so cold middle, as does the heat from the hot middle. And he accomplished this by shaking the daylights out of it – well, it shakes itself. That is an example of heat flowing from very cold to cold. It is counterintuitive. It creeps along the walls, if you must know. Work is involved.
kuhnkat says:
January 28, 2012 at 8:50 pm
kuhnkat, I think you misread DeWitt’s words. He said we indeed can measure the average kinetic energy. It’s called “taking the temperature”, and it’s the only way to measure the KE because there’s no “radar gun” to measure the KE.
w.
kuhnkat wrote:
QDaniels,
the Eddington quote is very interesting. I have been assured by well educated warmers that even conduction breaks the 2nd at very low levels at times. Whether they are claiming that this is measured or a result of solving statistical mechanics they did not explain. So, because it is a really small violation, do I apply the quote or not?? 8>)
It’s generally accepted that thermodynamic systems can be off by kbT. This is a very small amount of energy, roughly 25 milli electron volts at ambient, and not regarded as significant, or usefully extractable.
In case people misunderstood my comments, I agree with Robert Brown, that a gravitational lapse rate would contradict the Second Law of Thermodynamics.
Robert Brown wrote:
Yet a large number of unreasonable people take it upon themselves to completely reinvent all sorts of physics just to suit the conclusion that they wish to draw, that such a lapse is possible because then they don’t have to give credence to the GHE. They have lost any pretence of objectivity, and there is an appalling lack of respect. Physics, as it now stands, is largely consistent. A large number of very smart people have worked for centuries to make it so. It is not perfect, it is not beyond doubt, but it is beyond reasonable doubt and the onus of proof is very much on anyone who wishes to reject things like “thermodynamics” to do an ENORMOUS amount of work to show that their new “theory” is both consistent and confirmed by experiment.
None of this has been done. People assert absurdities, one after another, without even thinking about the consequences, and without ever doing any actual algebra to support it.
The experiment has been done, but the results have been ignored. I offered it in my first post on this thread. For those who have a problem with the silver wire, my example may be easier to understand.
Yes, the physics is consistent. That does not mean that it is the only possible or valid result. I assert (without evidence) that it would be equally valid and consistent, if not more so, if the Second Law were restricted to the regions where it actually holds.
A lot of very smart people have worked on physics, with great success. There are, however, certain mental and cultural roadblocks which have restricted our progress. The Eddington quote is an example of the cultural roadblock.
For that quote, I offer a one word translation: “Inconceivable!”
I think this article and the subsequent discussion is utterly fascinating – because the physics is so simple, but I am faced with two different conclusions that are utterly at odds with each other!
I very tentatively suggest that the answer is that heat conduction up the silver bar will be subject to an effect similar to what happens in the gas – i.e. as a silver atom moves a tiny distance upwards to hit the next silver atom (and transmit the heat), it will lose a tiny bit of energy due to gravity. Repeated all the way up, this would mean that the silver bar would be in equilibrium even though it maintained a temperature gradient!
David
Do you think that the gas will stratify thermally?
Of course, because it does on Earth…
Maybe, once there are pressure differences, because it does on Earth, but, I’m assuming his ideal gas has volume, since he’s included gravity which ‘real’ ideal gases aren’t subject to I’ve included volume which ‘real’ ideal gases don’t have, and it’s volume, isn’t it?, which enables there to be packets of air in convection which if hotter rise and so colder packets of air displace these (which as he says from meteorology are already knowns), and, as soon as pressure differences introduced ideal gas no longer applies. The only thing I’m keeping from ideal gas is elastic collisions (which as I’ve given re actual properties of nitrogen and oxygen make our atmosphere approximate to his model).
The only thing I’m having a problem with, so far.., is switching off the sun. He says to take examples from real world, (as he’s done with the example of packets of air rising which is already well known and which is what gives us our weather), but on a non-rotating Earth it’s the difference of temperature provided by the Sun between the equator and the poles which sets up the basic pattern of packets of air on the move (which is wind, wind is volumes of air on the move) from the equator to the poles where they cool and are drawn back to the equator where the heating cycle begins again. (The rotating Earth just adds more interesting patterns to this basic process.)
If there’s no radiation from the Sun, no heat capacity in the model planet, no mass big enough to effect pressure changes (‘real’ ideal gases which don’t have mass), nothing much is happening because there’s no movement, (movement from the play of hot and cold volumes as hot gases rise and cold sink, becoming less dense and gaining density), but,
even with masses big enough to create pressure differences, real gases, if there’s no input of irregular heat from the outside as we have it, the gases gaining kinetic energy near the surface would be doing it equally, ah, is that all he’s saying? It’s just a swap of kinetic for potential in the movement up and down and potential here on the way up becomes that from giving up kinetic which is heat?
So if there’s no external heating setting up temp differences and none from the planet (as we have from different heat capacities of surface stuff), does that really make it any different from what we have on Earth, because what we have on Earth is more interesting with all the temp variations coming into play, but they are, it seems to me, sort of superimposed on and weaving in and out of a basic which doesn’t change, with stratified temp differences by gravity already well mapped.
So it’s all gases at greatest density will be doing the same thing around the planet at the same time(*) and as these change with differences in density in the play between gravity and pressure and kinetic and potential from greatest near the surface to more rarified, less dense and absent any kinetic to write home about the higher one goes, then, energy conservation intact, the hotter will rise and cool because losing kinetic energy means losing temperature, thus cooling they which began with the closest in density and kinetic energy as a sort of band of brothers near the surface will rise and cool at the same time whereupon they’ll all come down together colder but wiser that great heights don’t make for more comfort and giving up their heat will sink displacing the hotter now in their place when they first went travelling. So, without any external heat source and none from the planet all that’s in play here is the heat this chilled out band of brothers gains on the way down, heavier and sinking gaining kinetic energy and therefore temperature the denser they get until finally at the surface becoming too hot they expand and rise slipping out of their restricting gravity and rude neighbours bumping into them they get themselves some space and cool off, then coming back off their high when they realise just how cold and lonely they are, getting nostalgic again for their noisy neighbours who won’t stick to their side of the road, forgetting, we do forget just how horrible horrible past experiences were, that they’ll just get all hot and bothered again.
(*)The differences at the ‘edges’ of the bands not an issue as these are smoothed out in the gradient as we see on Earth, and, then, maybe a bit like our electromagnetic spectrum, those with the highest likeness to each other actually do keep together and act similarly and have properties distinct from other bands of colours. So, we end up with a model world with distinct bands of pressure gradients?
If I’ve understood what he was saying in his thought experiment of model planet, and if my reading of ideal v real gases applicable in his thinking, then I’d say yes.
If so, will heat flow in the silver wire?
Sod the silver wire, if you’re going to argue agin him, quote his words… 🙂
..stick to his thought experiment, not strawman inventions.
p.s. Willis – thanks for the electricity direction, I’ve been doing a bit of looking and am rather taken with the knowledge that what all batteries do is stop the ambient energy supply…
I very tentatively suggest that the answer is that heat conduction up the silver bar will be subject to an effect similar to what happens in the gas – i.e. as a silver atom moves a tiny distance upwards to hit the next silver atom (and transmit the heat), it will lose a tiny bit of energy due to gravity. Repeated all the way up, this would mean that the silver bar would be in equilibrium even though it maintained a temperature gradient!
David, just as a matter of curiosity, why do you select this possibility instead of the far simpler one that silver is just silver and conducts heat uphill just fine and Jelbring’s paper is simply wrong because it proposes a final state that egregiously violates the second law of thermodynamics, one that is derived by ignoring heat conduction in the first place?
You’ve had a half dozen actual physicists and a physical climatologist explain to you that this is the case. The DALR isn’t even derived as a global thermal equilibrium state, and it is child’s play to see that the entropy of the system can be increased by equalizing the temperature difference. The paper is simply wrong. It isn’t even good work in the sense that it might have been right or under some circumstances could be right. Violating the second law is as wrong as you can get short of violating the first law, in this game.
So why do you persist in trying to imagine some way that it might turn out to be true, but only if all of our understanding of thermodynamics and heat transport and energy and so on are wrong?
I’m serious, this is an actual question. Why?
rgb
For that quote, I offer a one word translation: “Inconceivable!”
Well played, sir. One of my favorite movies too.
However, would you agree that the default position on this, the one that should have been taken by the referee of this paper, is “Ha ha ha, no.”, phrased more politely, perhaps accompanied by a strict requirement that all of the physics from the microscopic level to the macroscopic level be fully explained to show how the system does or doesn’t violate the second law before accepting it for publication?
Which, in the specific case of this specific ideal model is impossible, of course, because it obeys the second law just fine, as full stat mech computations have been able to show for a long time now.
rgb
Sounds like a very good description of the greenhouse effect.
This is a good subject for another top post. There is direct, in my opinion incontrovertible, evidence that the GHG-driven GHE is real: The satellite IR spectral data. We can “see” it with electronic eyes. We have taken its picture. You can, whenever you like, look at those pictures.
For Ifni’s sake, man! You sound exactly like a Creationist, who refuses to look up at the stars and examine the evidence of our own enhanced “eyes” and the connected chain of reasoning that shows that the Universe is older than 6000 years. Give it a try.
rgb
Robert Brown says
“You sound exactly like a Creationist, who refuses to look up at the stars and examine the evidence of our own enhanced “eyes” and the connected chain of reasoning that shows that the Universe is older than 6000 years. Give it a try. rgb”
This is exactly the phraseology of Joel Shore!
Are you perhaps related?
Why drag Creationism, Young Earth-ism and similar pointless dead ends in, its a sign of desperation.
My posts here have been about the lack of experimental evidence for isothermal/adiabatic distribution.
You have come up with lossless silver wire and magic light tubes.
Moving on you show a picture of a satellite looking down spectra and say
‘that proves the green house effect’
First define the greenhouse effect that you think it proves.
Jelbring says his theory proves his version of the greenhouse effect.
David Bailey: “I very tentatively suggest that the answer is that heat conduction up the silver bar will be subject to an effect similar to what happens in the gas – i.e. as a silver atom moves a tiny distance upwards to hit the next silver atom (and transmit the heat), it will lose a tiny bit of energy due to gravity. Repeated all the way up, this would mean that the silver bar would be in equilibrium even though it maintained a temperature gradient!”
Exactly the conclusion I have come to, although, to appease other disputants, you may want to say that it is a gradient in mean molecular translational kinetic energy rather than temperature that is being maintained. The distinction in their minds arises from the fact that, despite that gradient, no heat (after that initial adjustment) would flow. Since heat always flows from hot to cold, they say that minuscule difference in mean translational kinetic energy is not a temperature difference.
I think you are repeating an error made earlier: even at the atomic scale, energy flows from one atom to another, gaining and losing energy. This is by definition a ‘flow of heat’ and no work is being done and it is at maximum entropy. Maybe that is not important to heat flow in the atmosphere.
You rule out a flow of heat (at all) in an isothermal system. Yet within that ‘isothermal’ column, there is all sorts of heat flowing around. I guess others have noted that. Man, these absolutes…
No, no, no. I am following the usual practices of thermodynamics and stat mech, coarse graining all of that. There is no net flow of heat in a system in thermal equilibrium, which is indeed an isothermal system. Do you have some other definition of equilibrium?
As for the gas being at maximum entropy with a lapse rate, pay close attention, as I’ve done this three times or so already. Take a dollop of heat at the bottom — let it be absorbed by a piece of metal, for example. Move it to the top. Let it cool. Move the metal back to the bottom, all reversibly (as far as the motion of the metal is concerned). What is the entropy change of the Universe? Would that be strictly positive? So I suppose the state with a thermal lapse wasn’t maximum entropy after all, because we can trivially increase its entropy by moving heat by any means you like from the bottom (at higher T) to the top (at lower T).
If we wish, we can exploit the temperature difference to run a simple heat engine in the gas. This engine will run as long as there is a temperature difference, and can store the work done reversibly. Voila! A system that does nothing but convert heat directly into work, cooling itself spontaneously, and decreasing its net entropy!
Perhaps you can stop trying to solve complicated statistical mechanics problems in your head, incorrectly, and concentrate on the egregious violations of the second law.
rgb
Unfortunately many proponents of AGW are so willing to misuse Dr. Brown’s elegant refutation of Hans Jelbring’s E&E paper to conclude that GHG’s must therefore be responsible for the temperature lapse rate observed in planetary atmospheres. This is foolishness since neither the original E&E paper, nor Dr. Brown’s refutation address planetary atmospheres – they look at a very theoretical tube of gas in a gravitational field.
And note that I’ve very carefully restricted my argument to the specific case of Jelbring, because it is simple enough to trivially refute. It also establishes an important point. In no case — not just this overidealized case — can an atmosphere spontaneously generate a thermal profile. A thermal lapse in an isolated atmosphere violates the second law. This is a useful thing to recall in further discussion.
Thermal lapses in dynamic atmosphere go without saying — you can simply measure the temperatures in a sounding of the troposphere. But even here strict thermodynamic bounds exist. You will have to work pretty hard, for example, to come up with natural systems of circulation that increase the temperature of the hot reservoirs, because energetics pushes the gas the other way, heat flows in general from hot to cold under all the driven transport mechanisms. Yes, there are exceptions, yes, they may be relevant, but it isn’t enough to just say “they might be there”, one has to do a lot of algebraic work and difficult reasoning to establish that they really might be there, and then it is always good to observe them experimentally in action.
And none of this means that the GHG GHE isn’t real. IR spectroscopy is direct experimental evidence that it is real. These other proposed mechanisms or modulators must come in with an and operator, not an exclusive or operator, or they simply don’t agree with our observations of cold IR radiation from the CO_2 band in the upper troposphere.
rgb
Since this Jelbring’s scenario has actually got back to what we know we have, I can’t see anything wrong with it.
How about “I took a well-known result of atmospheric dynamics, driven by non-equilibrium differential heating caused by the GHG GHE and claimed that it is a static feature of an adiabatically isolated atmosphere, ignoring the fact that the proposed thermal profile violates the second law of thermodynamics for the specific conditions of long relaxation times and equilibrium conditions I propose”. Speaking as Jelbring, of course. Nothing wrong with that?
First, Jelbring didn’t do anything but quote a textbook in climatology out of context and assert that the conclusion holds in an adiabatically isolated system and so can explain heating when there is no open system differential heat flow present. It doesn’t and it can’t. It would violate the second law of thermodynamics.
rgb
In one of Climate Science’s favorite configurations you have two objects radiating against each other. When they finally equilibrate do they stop radiating??
An excellent question. The answer is yes. Take two “blackbody” plates at different temperatures, place them in an adiabatically isolated (perfectly reflecting) container facing one another. No matter what the size, or shape or (non-GR-relevant) gravitational orientation of the two plates, they will come into thermal equilibrium at the same temperature through a process called detailed balance.
You should study detailed balance as it is enormously important to this whole discussion. In the end, each body radiates exactly as much energy as it absorbs, with the entire cavity filled with BB radiation at the common temperature.
rgb
Robert Brown, in your example physics paper (posted 2:33pm above) I found an error in the solution in 1(b) … the word calculate is misspelled as ‘calcfulate’ … does this qualify me for any credit towards a physics degree, or does that just make me a run-of-the-mill pedant? 😉
Dear Spiny,
In my classes I award students a tasty piece of dark chocolate every time they catch me make a mistake at the board (which I do regularly in every lecture as I lecture cold, without notes, and just do the derivations and examples as I go. Occasionally a student will catch me make a spelling mistake or other irrelevant error. Hell, candy is cheap, and it makes the game more fun.
I owe you one piece of candy.
rgb
Yes, I now see how it is and you are correct. The atmosphere relaxes to an isothermic state.
Thanks for your patience, you taught taught me something important, humility, along iwth some physics.
Dearest Jim,
You are hence awarded the gentleman and scholar award. If I could give you candy (see previous post plus two) I would.
rgb
Robert Brown says at 1/28 2:33pm:
“A physics problem is not solved in words! Especially not a difficult one.”
Agreed. Robert Brown presents some substantive debate in his terrific 2:33pm post way beyond the idealized thought experiment of top post Fig. 1. My suggestion to him would be there is enough material that bringing Fig. 1 into the debate is just an unnecessary distraction that then brings into play two formal papers (Velasco et. al. 1996 and Verkley et. al. 2004) with algebra! which would need to be considered in the debate, as here.
Couple thoughts on the SC final exam link. Man, only get 8 points! for writing that Phys 706 #1 part b answer? Hoo-boy, I would think I could earn a season ticket to Cameron Indoor Stadium for writing that answer out even w/open book. Instead I would get only 8 exam points at SC? Wow.
Seriously though, take a look at the integration for n(z) right after the words “The solution is”. Then compare further down for the heat capacity where “we differentiate (total energy) w.r.t. T”. There is something here worth digging into; T seems to be both held constant for n(z) integration and then apparently a variable for heat capacity differentiation.
But I’d rather spend time attending equiv. of a game at Cameron than expending that thermo effort at the moment; I was hanging out here w/some downtime due to a head cold. This thread has been Spock’s definition of fascinating; I’m pretty sure Coach K says his team gets better when the competition gets tougher. Same for the posters here.
I’m interested enough sans head cold to engage here w/tough competition (but with less time as I move back to hang out w/productive work & play elsewhere). Still, may have some more thoughts here when my on-order Boren text arrives.
Myrrh askes: “Gosh Tim, real experiments from satellite data looking down on the Earth proving carbon dioxide warms the Earth?”
http://wattsupwiththat.files.wordpress.com/2011/03/gw-petty-6-6.jpg
… but only if you understand enough of the other science involved.
And I think I am now going to go back to other things …
And since this thread appears now to be “finished”, I will probably make this very figure (or some just like it) the subject of my next top post, because this figure is precisely direct evidence for the GHG-GHE. In my opinion, evidence that cannot be challenged. It is literally the “evidence of our own eyes”, even though our eyes are electronic ones out there in orbit.
But not until I finish writing 30-50 recommendations…
rgb
“This paper shows nothing in the actual language of physical science; it presents a purely heuristic, question-begging argument with numerous errors and internal inconsistencies.” – Brown “.
Bryan sez: “Sounds like a very good description of the greenhouse effect.”
+++++
Right on, bro.
I am not sure how many of you are interested in the philosopy of science, but the discussion above is a good example of what has happened as a result of ‘consensus science’ applied to the effects of human activity-sourced CO2.
Robert, the reason you meet so many people on this list who are automatically extra-skeptical of any ‘science’ put forward by the Lettered and the Self-Proclaimed is because of the B.S. that passes for climate science these days. What more perfect classroom is there for tutoring the intelligent layman to be skeptical of the ‘known laws of science’ than the stream of stupidity wrapped in obfuscating words than the hockey stick of Mann and the screaming doom from Hansem’s mouth? What better example of ‘believe anything I say because I say it’ is there than, ‘You are all guilty, give me money to solve it”?
In deepest Africa one gets precisely these same words from self-taught shamanic diagnosticians who can explain everything as the fault of the victim of circumstance with a universal. ‘You have failed to appease….’ or ‘You unknowingly did…’ “That will be two chickens, please.”
You rail against the ignorant questioning of basic assumptions and ancient proofs, yet who has taught the skeptics that they were right all along to suspect there is something very rotten in the world of climate ‘science’? No need for epithets like ‘climate scientology’ here. Climate science disgraces itself, or rather, it is achieved by those who emit a stream of verbal garbage along the line of some or other manufactured consensus.
And now you see the state into which things have evolved. Your own logic has not been perfect. I don’t expect it to be. Willis’ for whom I have a lot of time, is imperfect. People with graduate degrees, who I work with every day, are frequently wrong about all sorts of basic things. They jumped hoops and got the paper. That does not make them infallible.
The model planet is being discussed at the limits of our ability to conceive of that artificial world. At the limits, the physical laws and commong descriptions frequently break down. Invoking them is a bit like invoking the victim’s responsibilty for all that befalls him – it is frequently true, within limits.
There is no doubt that the effects of the blatant propaganda selling the idea that recent global warming is ‘primarily cause by human-emitted CO2’ will be studied like the caged rat it is: an example of group-think gone wild with one hand covering the eye of the public and the other in their trouser pocket.
Do not complain, sir, about excessive skepticism of ‘consensus physics’.
Here is an elevator speech:
1. CAGW is powered by consensus physics.
2. CAGW is B.S.
3. Why then is consensus physics not also to be questioned?
Pressed hard from all quarters, many of the explanations above falter at the known limits and the answer is still not clear.
“David, just as a matter of curiosity, why do you select this possibility instead of the far simpler one that silver is just silver and conducts heat uphill just fine and Jelbring’s paper is simply wrong because it proposes a final state that egregiously violates the second law of thermodynamics, one that is derived by ignoring heat conduction in the first place?……….
I’m serious, this is an actual question. Why?”
Well, I started by imagining a single molecule in an elliptical orbit about a planet. Clearly, at the top of the orbit, it is moving more slowly, than when at the bottom – because kinetic energy has been converted into potential energy. On reflection, that idea generalises to atoms or molecules in anything! I noticed that you didn’t actually explain what is wrong with my argument. A atom/molecule will slow down as it ascends a gravitational field, won’t it?
Your construction with the silver bar doesn’t show that a column of gas at equilibrium would have constant temperature, it shows that everything – including your bar – must have the same lapse rate when it is at equilibrium in a gravitational field, so that it is not possible to extract useful work by piping heat from the bottom to the top – thus it does not violate the 2nd law.
By coincidence, I spent the interval between my two posts, walking up a hill, watching the snow build up as I got to the top!
David
Dr Brown,
Thanks you. Maybe I can help with what is going on here, and what Jelbring’s paper probably is.
Some people need very good, and very precise, pictures to understand intangible ideas. Writhing of myself; I can’t do math, I can’t see the numbers on a paper and I can’t see them in my head. I’m a high school dropout who owns a trucking company, and I like physics more than anything and want to understand as much as I can. So sometimes I grow a large chip on my shoulder; when I want to understand something and an a knowledgeable person says ” You won’t understand until you do the math”. That is very, very irritating to me. (I can see the other useful things, vectors, gradients, fields, operators).
The picture you drew in the derivation at the start of the thread is simple. I understand the empirical rule for heat conductivity in the silver thread. What was an unexplained part of the picture is what happens if the gravitational gradient is large across the box. That is; going from a table top picture of the silver bar, to a skyscraper sized picture of a silver bar.
I got off wrong footed after seeing an incorrect picture in one of the replies. I wrote a smart ass remark about tsunamis. You wrote, ‘…what about radiation?’. Then I put your light pipe in the picture, and it worked the way you wrote that it would. So next I went to the picture of gas in the ‘gravity’ box. I put in thermally opaque gas and watched what happens. The result was just as you wrote it would be. OK. But the question is; what about the Earth’s atmosphere? I put thermally transparent gas in the box and watched what happens. The condition I started with isn’t steady state. Entropy increases and the gas relaxes to an isothermal state. Now I knew you were correct.
But the hard part was going back to your first picture. Silver bar, stack of billiard balls, or stack of Jello, the isothermal picture wasn’t easy to see. I had to watch those picture for a long time to see it work. Now I know why some people won’t believe it.
I hope that you understand this. Saying that ‘you need to do the math’ won’t work for many people. It is like ‘dancing about architecture’. Good pictures will work.
Thank you again.
I perhaps jumped too quickly to say that I had arrived at “exactly” the same conclusion as David Bailey, since I had not given any thought to what mechanism, if any, might result in a different mean molecular kinetic energy at the top of the wire than at the bottom.
But the point is not whether, say, the silver would conduct heat uphill no matter how minuscule the difference in average molecular kinetic energy there is between the top and bottom. The point is that David Bailey’s tentative conclusion points up the fact that Dr. Brown’s thought experiment fails to show the contradiction he needs for his proof.
For the sake of his proof, Dr. Brown assumes (as he and most of us believe, contrary to fact) that at equilibrium, i.e., in the highest-probability, highest-entropy state, the isolated gas column exhibits the dry adiabatic lapse rate. If I’m not mistaken, he also tacitly assumes that the vertical silver wire in isolation does not. Presumably upon connection some kinetic-energy exchange would therefore occur between the gas and the wire. But the two assumptions (lapse rate for isolated gas, no lapse rate for isolated wire) do not require the result that such transfer would continue forever. Another possibility is that the exchange would continue only until the new, combined wire-gas system reached its own equilibrium, in which we would not in general expect the gas to exhibit the same mean-molecular-kinetic energy profile it did when it was isolated.
So no perpetual-motion machine necessarily results.
Robert Brown says at 1/29 6:22am:
“Take a dollop of heat at the bottom..”
Robert! You have repeatedly told us consider Fig. 1 is at equilibrium, no net heat flow. There is no dollop of heat inside equilibrated Fig. 1 in top post to take anymore. Velasco et. al. 1996 and Verkley et. al. 2004 b have given us the algebra for Fig. 1 top post at equilibrium, no net heat flow, no net thermal energy flow, isentropic.
Robert continues:
“There is no net flow of heat in a system in thermal equilibrium..”
See!
So there is no heat dollop to obtain anywhere within Fig. 1 at equilibrium b/c there is no thermal energy flow anywhere in Fig. 1 at equilibrium. Ref. Maxwell 1871 Theory of Heat. Since heat isn’t flowing anymore in Fig. 1, any of 3 bodies in contact will, WILL by 0th law, have achieved thermal energy equilibrium everywhere therein (a wire, an insulator & the ideal gas). Heat flow stops when they equilibrate in T(z) everywhere & system is isentropic. Cite Velasco & Verkley algebra.
The only way, ONLY way, to take a dollop of heat into the bottom of a wire in equilibrated Fig. 1 above is to bring a hotter (higher T dollop of thermal energy) body than the bottom of the wire across the control volume of Fig. 1 and put it in thermal contact with the bottom of an insulated wire and the gas.
By 2nd law, entropy of Fig. 1 will increase. It will eventually reach thermal equilibrium again by oth law, isentropic now with 4 bodies. Higher but again isentropic (non-isothermal as correct algebra proves in Velasco & Verkley b). You cannot escape the physics, correct algebra & reasoning in each of those two papers. As much as you try. And try….and try….ad infinitum I suppose.
Or show your correct algebra refuting those two V&V papers. Robert Brown says algebra is needed esp. for difficult physics, show the correct work. Hint: Robert Brown’s top post algebra is incorrect as I’ve posted, cite Velasco & Verkley papers for correct algebra showing non-isothermal isentropic top post Fig. 1.
I know (believe me by now!) this boils down to Robert Brown cannot grok 0th law IS satisfied in equilibrated Fig. 1; Verkley paper b explains how 0th law IS satisfied and Fig. 1 achieves equilibrium & is Robert Brown ungrokenly non-isothermal isentropic – their algebra proof stands. That should be interesting to Robert Brown. It is to me! I want my piece of chocolate candy (will accept a game ticket to Cameron instead). Six pieces really, one for me, Velasco, Verkley et. al. authors.
The real atmosphere gets the dollop of heat from the sun; exciting and interesting stuff happens to equilibrium w/wire in top post Fig. 1 thereafter. Lotsa’ algebra too.
Myrrh says:
January 29, 2012 at 5:51 am
Let me be clear about that quote, Myrrh, so you are in no doubt.
It is nonsense. It is junk. It is wrong, and not just a little bit wrong, but cataclysmically wrong. If wrong were the height of a man, that quote is the Empire State Building of wrong. Am I getting through yet? It is laughable, a veritable sea of wrongness. If I set out to write something wrong, it would be but a candle to your very bonfire of wrongitude. Are you getting the picture? It is a veritable black hole of wrongness, where when any fact enters it is never seen again. If wrong were a shot of whiskey, that quote is a three day bender waking up in the gutter. It is the prince of wrongness, the duke of disinformation, the earl of errors.
Is my meaning sufficiently clear? Because I could go on if I’m not getting through to you …
w.
PS—my favorite part? Where he says that the “battery forms a dipole which nudges the local environment into an unbalanced state which pours out energy in every direction.” That was priceless, I’d pay good money to see that happen.
“OK: picture an atmosphere with a lapse rate, a warmer bottom and cooler top. Introduce the silver wire. Heat will flow up the wire and because there is no lapse rate for silver, it will warm the gas at the top. You put a larger heat exchanger at the top to overcome the collision rate difference due to the pressure differential. Objection overcome.
Eventually it will reach thermal equilibrium, correct? At that time, in a gravitational field, the total energy of any upper molecule will be much greater than at the bottom (K+P), correct? Is that a state of maximum entropy?”
It seems to me you would cool the entire atmosphere.
I feel compelled to mention one talking about very small differences of heat, and therefore whatever engine you using will draw very little energy from the system. Any nuclear reactor is typically wasting vastly more energy- waste heat from all engines are wasting a higher difference of heat. Rubbing your hands together is giving more energy.
So this silver wire would a refrigerator- a very poor and expensive refrigerator. Far, far worse than windmills and solar panels- in terms generating energy. And a windmill would be a cheaper and more efficient refrigerator.
Robert, end of thread? So you are never going to answer (you say you prefer numbers, lay them out) the question on Venus and why it’s lapse of 8km/K compared to Earth’s at 6.5km/K though Venus’s energy input is 66W/m^2, giving it 66/94 or 0.6 W/m^2 per equivalent Earth atmosphere, and the Earth’s input per atmosphere is 240 W/m^2? WUWT? You keep saying lapses are governed by the energy… explain.
If you never answer this question I think that is why so many doubt your ability. You never answer the real questions of real worlds with real atmospheres but instead call people slide names and with shaded smears and belittling remarks as if you are some kind of grand authority. I can assure you are not. Stop. It does not prop up people’s view of you, it just makes you look small.
Crispin in Waterloo said @ January 29, 2012 at 7:49 am
The Pompous Git is a philosopher of science. He says: this discussion id a good example of what happens when you don’t know WTF you are talking about. In order to be a philosopher of science, you need not only to understand the science, you need to understand logic. You clearly understand neither.
There is indeed much BS in climate “science”. But there is also a very great deal of well-understood climate science that relies on a full understanding of the physics that Robert, Willis, DeWitt & others have been trying to explain. Actually, they have explained the physics very well. Several commenters have shown a lamentable disinterest in learning.
Your “shamanic diagnosticians” do not discuss, or rely on, fundamental physics. Are you on drugs?
Nobody here has been claiming infallibility, or did I miss something? A quote might help if you believe this to be the case.
The model planet was chosen by Jelbring. This is a discussion of Jelbring’s “work” and thinking. Read the head post. It is manifestly not at the “limits of our ability to conceive” unless we have a severe case of inability to read and think. First year physics students understand models like this one every day. The ones who fail to understand are generally those who do not do the work required.
1. CAGW is not “powered by consensus physics”; it is an unwarranted extrapolation from consensus physics.
2. CAGW is BS. [Hard to disagree with]
3. Consensus physics is questioned all the time — by physicists as well as people who are profoundly ignorant of physics. Guess who can make a difference? Hint: experiments are designed to ask questions of physical systems.
Willis Eschenbach said @ January 29, 2012 at 9:45 am
My favourite is “Those poles actually distort the universe around your battery”. This sounds very much like a “reality distortion field” just like the one surrounding some commenters here.
I haven’t laughed so much since I was told these many long years ago that an electronic circuit drawing was just as effective as one built out of transistors, capacitors and resistors. I’ve smoked some pretty strong hooch in the dim and distant, but it never took me that far off the planet 🙂
Willis Eschenbach says:
January 29, 2012 at 9:45 am
Myrrh says:
January 29, 2012 at 5:51 am
p.s. Willis – thanks for the electricity direction, I’ve been doing a bit of looking and am rather taken with the knowledge that what all batteries do is stop the ambient energy supply…
Here:
http://free-energy-info.co.uk/Intro.html
Let me be clear about that quote, Myrrh, so you are in no doubt.
It is nonsense. It is junk. It is wrong, and not just a little bit wrong, but cataclysmically wrong. If wrong were the height of a man, that quote is the Empire State Building of wrong. Am I getting through yet? etc. etc. etc.
Is my meaning sufficiently clear? Because I could go on if I’m not getting through to you …
Yeah, yeah Willis, you’re back to your empty vessel makes much noise. I put up the link, read the run up before the bit I quoted, tell me what’s wrong with his explanation.
PS—my favorite part? Where he says that the “battery forms a dipole which nudges the local environment into an unbalanced state which pours out energy in every direction.” That was priceless, I’d pay good money to see that happen.
You can’t see elecricity, you’ll be waiting some time.. Perhaps I shouldn’t have bothered posting that to you.
Anyway, now, many thanks, the Mods have kindly retrieved my post – please see, http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/#comment-878541 you might have missed it.
And if Robert/others have any thoughts on it, please bear in mind I don’t speak math/s so replies please in the spirit in which Jelbring presented his thought experiment.
(If Jelbring is reading this,I hadn’t appreciated that earlier, I ask for English not maths speak as I’m not a scientist.)
And Robert, please, take note of what Trick says here:
Trick says:
January 29, 2012 at 9:41 am
That’s contributed a lot to me not being able to follow what you’re talking about.
Robert,
For once I disagree with your reply — in particular in this exchange
>>In one of Climate Science’s favorite configurations you have
>>two objects radiating against each other. When they finally equilibrate
>>do they stop radiating??
>An excellent question. The answer is yes.
Later on I agree with your more complete answer “each body radiates exactly as much energy as it absorbs”. There is this idea that floats around the climate skeptic blogosphere that somehow a cold body does not radiate AT ALL to a warmer object, as if radiation from the cool atmosphere to the warm ground violates the 2nd Law.
The objects never stop radiating, no matter the temperature of the emitting or absorbing. Many people would read the first line of your answer and think it means that literally IR radiation from both objects has stopped. I know it sounds silly, but it is a common conclusion and a common objection to the greenhouse effect.
They don’t graps that:
* NET radiation is zero between two objects at the same temperature is zero.
* NET radiation is from hot to cold (even when some energy is going from cold to hot).
* SOME energy from cold to hot is not a contradiction with the 2nd Law of Thermodynamics as long as the NET flow is hot to cold.
Your initial reply helps reinforce this incorrect interpretation of IR radiation exchange.
Robert Brown says:
January 29, 2012 at 7:02 am
Myrrh askes: “Gosh Tim, real experiments from satellite data looking down on the Earth proving carbon dioxide warms the Earth?”
Tim replies: “http://wattsupwiththat.files.wordpress.com/2011/03/gw-petty-6-6.jpg
… but only if you understand enough of the other science involved.
And I think I am now going to go back to other things …”
And since this thread appears now to be “finished”, I will probably make this very figure (or some just like it) the subject of my next top post, because this figure is precisely direct evidence for the GHG-GHE. In my opinion, evidence that cannot be challenged. It is literally the “evidence of our own eyes”, even though our eyes are electronic ones out there in orbit.
You haven’t even started a proper refutation of Jelbring’s paper, as I’ve pointed above. You haven’t even read his explanation for writing it the way he did as your diabribe against him showed, so I’ve no reason to think anything you’ve said in this “Refutation of Stable Thermal Equilibrium Lapse Rates” is in the least bit relevant as a refutation, and so, you may think you’re finished, but I think you should begin again, Take II, and stick to his thought experiment and not your strawman silver wire deflection.
Not that a post on “real experiments from satellite data looking down on the Earth proving carbon dioxide warms the Earth” wouldn’t be welcomed, Tim’s chickened out for all his blather that he would explain it..
Have you got the top and bottom of the troposphere carbon dioxide data from AIRS? And the mid from AIRS properly set out so we can see where their “carbon dioxide is not well-mixed but lumpy” actually comes from? I can’t find anything but two pictures out of all those years data and they don’t fit with their conclusion.
Willis,
I hate to take Myrrh’s side, but there is a grain of truth in what he was saying about energy flow for circuits. I only glanced through his “free energy” link and I strongly suspect it is hogwash. And most of what Myrrh is saying in his post is poorly stated (or simply wrong). But analyzing circuits using the “Poynting vector” does indeed visualize the energy flowing through space from the battery to the device in the form of E & H fields (and in some sense the fields “actually distort the universe around your battery” although the energy does indeed come from the battery, not from the universe).
See, for example, section 8.3 of http://www.guspepper.net/electro/Primer%20semestre/Poynting%20vector.pdf for more details.
Wayne,
Setting aside the physics for a moment, you said:
“You never answer the real questions of real worlds with real atmospheres but instead call people slide names and with shaded smears and belittling remarks as if you are some kind of grand authority. I can assure you are not. Stop. It does not prop up people’s view of you, it just makes you look small.”
I am just amazed at the amount of back biting ad hominem arguments there are in ‘climate science’. If you think someone else is behaving that way, it is best to rise above them, not join them!
David
“Robert, end of thread? So you are never going to answer (you say you prefer numbers, lay them out) the question on Venus and why it’s lapse of 8km/K compared to Earth’s at 6.5km/K though Venus’s energy input is 66W/m^2, giving it 66/94 or 0.6 W/m^2 per equivalent Earth atmosphere, and the Earth’s input per atmosphere is 240 W/m^2? WUWT? You keep saying lapses are governed by the energy… explain.”
Lapse rate is based on gravity. It’s affected by amount of heating and affected by humidity:
“When the air is saturated with water vapor (at its dew point), the moist adiabatic lapse rate (MALR) or saturated adiabatic lapse rate (SALR) applies. This lapse rate varies strongly with temperature. A typical value is around 5 °C/km (2.7 °F/1,000 ft) (1.5°C/1,000 ft)”
http://en.wikipedia.org/wiki/Lapse_rate#Saturated_adiabatic_lapse_rate
Dry adiabatic lapse rate {DALR}:
“DRY ADIABATIC LAPSE RATE.—If a parcel of air is lifted, its pressure is DECREASED, since pressure decreases with height, and its temperature falls due to the expansion. If the air is dry and the process is adiabatic, the rate of temperature fall is 1°C per 100 meters of lift (10°C per Kin), or 5 l/2°F per 1,000 feet of lift. If that parcel descends again to higher pressure, its temperature then INCREASES at the rate of 1°C per 100 meters or 5 1/2°F per 1,000 feet. This is known as the dry adiabatic lapse rate”
http://meteorologytraining.tpub.com/14312/css/14312_47.htm
In above ref there is diagram, indicating moist ADIABATIC and “normal” ADIABATIC and “dry” ADIABATIC and “SUPER” ADIABATIC and AUTO CONVECTIVE.
6.5 km/K is “normal”.
Earth’s atmosphere is not dry, we live on a water planet. Dry adiabatic lapse rate is mostly theory- and in there is not any dry air, there is only drier air.
Venus is far, far more dry than earth atmosphere- anywhere on earth, even the stratosphere on earth. Venus does have a small ocean or large lake of water in it’s atmosphere- but Venus has a LOT of atmosphere. Venus has a lot more water in it’s atmosphere than Mars, Mars has little atmosphere, since it’s got little amount atmosphere and tiny amount of water vapor, it is less dry than Venus.
And Mars drier than anyplace on earth- it’s a dry, very cold airless desert- and that in it’s wetter and warmer areas:)
Venus has such a huge atmosphere that it holds about as much water vapor in it’s atmosphere that it has somewhere near as much a earth does in it’s atmosphere. Venus is big atmosphere a lot water in it, but very little in comparison to amount of atmosphere.
So Venus is closer to a DRY ADIABATIC LAPSE RATE than anywhere on Earth or Mars.
Robert Brown says:
January 29, 2012 at 6:42 am
In one of Climate Science’s favorite configurations you have two objects radiating against each other. When they finally equilibrate do they stop radiating??
“An excellent question. The answer is yes.”
Oops! I don’t think you quite meant this. In reality, they each keep on radiating at the rate appropriate to their temperature, irrespective of the presence of the other. What I think you meant is that at equilibrium they absorb exactly as much radiation from each other as they emit to each other, so there is no net flow of heat. The detailed description further on in your comment does imply that this is what you actually meant, so I wouldn’t bother with the nitpick were it not that one of the main fallacies of the anti-GHE crowd is the belief that cooler objects (the upper atmosphere) can’t radiate to hotter objects (the ground) and hence that back-radiation is a “myth”.
Tim Folkerts says:
January 29, 2012 at 12:27 pm
I hate to take Myrrh’s side, but there is a grain of truth in what he was saying about energy flow for circuits. I only glanced through his “free energy” link and I strongly suspect it is hogwash. And most of what Myrrh is saying in his post is poorly stated (or simply wrong). But analyzing circuits using the “Poynting vector” does indeed visualize the energy flowing through space from the battery to the device in the form of E & H fields
I suspect that the free energy link is relying not upon the Poynting vector, but upon some garbled version of advanced potentials, because in a naive view these seem magically to draw in energy from the entire universe and the whole of past time.
By the way, I notice that you’ve nitpicked Robert’s radiation answer too. Sorry for duplicating that.
rjb says “Here is an ordinary undergraduate exam question in a course in statistical physics and thermodynamics offered and the University of South Carolina and posted on their website. Note well that the question asks students to solve the exact same problem that Jelbring proposes — that of a vertical, isolated, column of ideal gas that must be in static and thermal equilibrium in a gravitational field”
The problem set out in the link starts off with these conditions: “The total number of atoms is N, the mass of each atom is m, and the temperature is T.”
As the “the temperature is T”, the problem is isothermal as a matter of its specification. I’m not defending Jelbring, but where does he constrain his discussion to an isothermal outcome?
Still no take for my question: given the mechanical nature of conduction at the microscopic level, what are the implications for Fourrier’s Law?
Robert Brown wrote:
Well played, sir. One of my favorite movies too.
Thank you. The broader point there is that failure of human creativity, be it one or all humans, does not actually constrain reality. It only constrains our ability to work with reality and predict outcomes.
However, would you agree that the default position on this, the one that should have been taken by the referee of this paper, is “Ha ha ha, no.”, phrased more politely, perhaps accompanied by a strict requirement that all of the physics from the microscopic level to the macroscopic level be fully explained to show how the system does or doesn’t violate the second law before accepting it for publication?
This turns out to be a more interesting question than it first seems.
In theory, you are correct, and I accept that threshold for myself.
In practice, that threshold has proven to be beyond the reach of mankind since at least Theory of Heat. Please re-read my Two Gases model until it’s clear what I’m talking about. I have described a very real effect. At issue is whether or not there is a Gravitational Lapse Rate in temperature. If there is, then my model is explanatory of a real, readily observable effect.
The result is not in question. It happens, and has been observed by every single physicist. Only the explanation is in question. You’re welcome to dispute that, of course, but I don’t recommend doing so without first understanding the model.
If I am right, which I have not proven in this thread, then the two quotes (Eddington and Princess Bride) go a long way towards explaining how we came to reach our current state. The word ‘Orthodoxy’ comes to mind.
I’m more of a ‘Heterodoxy’ kind of guy, as it distributes eggs into more baskets, and helps reduce the probability of wagering everything on a single notion. This turns out to be more important than it seems, because the probabillity of an erroneous assumption in a theoretical structure approaches unity.
wayne says:
January 29, 2012 at 11:07 am
Wayne, you seem misinformed about what’s happening here. You don’t get to claim that Robert is somehow deficient because he doesn’t answer your question.
He has written a very interesting proof about the Jelbring hypothesis. This has absolutely nothing to do with the lapse rate on Venus. Nothing.
He is not under the slightest obligation to answer your question, and if he wants to keep the thread on track, I’d advise him not to do so.
So if he never does answer your question, well, try asking somewhere else. But don’t come claiming to us that Robert is shirking his obligations. He is not shirking anything, and in fact has done yeoman work here. He doesn’t have to answer anyone’s questions, particularly those that are wildly off-topic.
w.
@Pompous
C: We agree on some things and not others. I ignored your ad homs. Don’t worry.
C: How do I deal with Robert who answered the question about the end of radiation thus:
++++
Robert Brown says:
January 29, 2012 at 6:42 am
In one of Climate Science’s favorite configurations you have two objects radiating against each other. When they finally equilibrate do they stop radiating??
++++
C: It was not exactly the same wording as the question posed, but close enough. I said no. Robert replied:
++++
R: “An excellent question. The answer is yes.”
C: So they stop radiating then? But they don’t, do they?
R: “…they will come into thermal equilibrium at the same temperature through a process called detailed balance.”
C: True, almost, but let’s keep our eye on the radiation:
R: “In the end, each body radiates exactly as much energy as it absorbs, with the entire cavity filled with BB radiation at the common temperature.”
C: Robert just said they will stop radiating then says they will continue to radiate as much energy as they absorb. Which which is it? Stopping or continuing? I thought that was covered in my physics courses and I do not recall flunking any of them.
I define the ‘continuing radiation’ as a transfer of energy, to wit, an energy flow. There is a continuous energy flow if Robert is right on his second opinion. That flow of energy is not necessarily a line-of-sight 1 for 1 exchange of quanta. From that there are implications relevant to the question at hand. Keep you eye on the energy flow ball: By definition a warmed molecule is never in a state where there is no ‘flow of energy’, which flow may be defined as ‘disequlibrium’. The contributions above are replete with examples of energy flow (at all) being described as taking place in a system that is still to reach equlibrium, still maximising entropy. It all depends on how closely you look.
Thermal equilibrium in a free floating gas atmosphere? Bulk, yes, detailed examination, no. (eternal energy flow)
In the presence of gravity? Bulk, unclear, detailed, no. (eternal energy transfer)
In the presence of extreme gravity? I have already cited Robert saying that with a black hole, no, in detail, no. (complicated eternal energy flow)
I bounced my question of simultanous isothermal state and equalised kinetic+potential energy at a common temperature for parcels of gas at different altitudes off my former intern Kyle this afternoon as we drove to the University of Guelph for a meeting. He agrees one cannot have it both ways. Either the total energy in the parcels are equal, relative to the surface, or the temperature is the same. Not both simultaneously. Which has the greater entropy? As there are some readers who want to hear only from the Lettered he is nearly finished his Science PhD at Waterloo U (you have heard of Waterloo U, right?) So maybe you will accept his opinion. Like Pompous, he also appreciated the CAGW=Consensus Physics and regaled me with stories about Consensus Medicine, a science of healing is apparently still in its infancy.
Tim Folkerts says:
January 29, 2012 at 12:27 pm
Thanks, Tim. If you like grains of truth, how about this one?
There’s a grain of truth in there as well. The moon’s bond albedo is about 0.11.
Does that grain make it a useful statement? Does it mean I should pay attention to it? Myrrh’s citation is new-age hogwash, lightly sprinkled with any kind of random scientific ideas in no particular order.
Here’s a sample from Myrrh’s citation, emphasis mine. The one thing I do have to say is that this guy Myrrh cited is the king of BS. Check this out, and if it doesn’t have you rolling on the floor, you don’t know electricity.
Don’t you hate it when the current “destroys the battery’s dipole”? Nothing an electrician fears more than that.
If there is a “grain of truth” in there, I don’t see it. The scary part is, Myrrh seems to believe it.
All the best,
w.
Willis wrote:
Myrrh’s citation is new-age hogwash, lightly sprinkled with any kind of random scientific ideas in no particular order.
I looked at Myrrh’s link. Speaking as someone who explicitly rejects the Second Law, I agree with Willis. Most of them appear to attempt to violate Conservation of Energy. The ideas do not reflect sufficient understanding of either Conservation of Energy or the Second Law to even begin to address success or failure in violating them. They’re just pieces plugged together randomly, in a manner. It appears to me to be a framework for obfuscation, for the purpose of concealing sleight of hand. Sorry, Myrrh.
If one considers the Second Law as part of “the straight and narrow”, then stepping off that course requires more care, not less. If you are going to stray from the path, you need to remember that the path is there for a reason, and reflects the collected experience of those who came before.
If you’re going to take up Doubt as your guide, then take it up wholeheartedly, applying it first and foremost to yourself.
ALL the atmospheres and all the solid bodies we know about are warmer at the bottom than they are at the top.
This includes objects which have no Sun/star to provide them with heating radiation.
So, nice theory, but the actual universe does not agree with you.
Just like in climate science, we should be trying to explain what really happens rather than what should happen based on some theory which is, obviously, incomplete according to way the real universe operates.
I again go back to the question of what force provides the extra thermal energy to mass in/falling into a gravity field. It is not outside radiation. It is internal to the atoms/molecules themselves or it is provided by the gravity field itself. The energy inside the atoms/molecules is being converted into thermal EM or the gravity field is imparted thermal EM to the atoms/molecules. Until someone can explain how that happens and how it cannot possibly happen in an equilibrium gravity situation, I cannot accept the theory. There is obviously a real phenomenon which is not being taken into account. There are untold numbers of joules in every object in the universe which are unaccounted for.
Willis,
The “grain of truth” is that energy DOES travel through space (not through the wires themselves) into a resistor (or similar device) by affecting the space around the resistor (as described by the Poynting vector & E & H fields).
But other than that isolated point (which is almost certainly not truly what Myrrh or the webpage are discussing), I agree that the rest of the discussion Myrrh points to is hogwash. I was just trying to point out that this is not THE worst physics I have ever seen (even if it is close). The webpage could have taken a bit of real physics (Poynting vectors) and then warped it to suit the author’s scheme.
“There are untold numbers of joules in every object in the universe which are unaccounted for.”
Earth mass is: 5.97 10^24kg. Earth was formed from all this matter hitting itself at about 20 km/sec. So that equals 1.19 10^33 Joules.
“The Earth’s internal thermal energy flows to the surface by conduction at a rate of 44.2 terawatts (TW), and is replenished by radioactive decay of minerals at a rate of 30 TW.” wiki
30 TW is 3.0 10^13 joules per second. Per year it’s 9.4 10^20 joules. In 4 billion years it is:
3.7 10^30 joules.
So in earth’s history about 300 times more joules were created during formation of planet compare to heat created by radioactive decay of minerals.
One could assume that some time during and/or after earth formation, earth was much hotter than it is now. Not saying it kept any of this heat, just saying at some point earth completely molten ball of lava. And since life started around 3.8 billion years ago, it was before that.
One question is how hot could earth like planet’s core be? And I would guess Earth was probably near whatever that number is.
It seems to be that the cooler a planet is, the faster the heat loss of it’s internal heat, and hotter it is, the slower this loss.
And if talking about large atmosphere- Venus hits that threshold, whereas Earth does not, the contraction of atmosphere will heat the planet- or said differently as a planet cools it’s atmosphere and oceans and/or land will contract keeping heat temperature constant.
It is said:
“Despite this, Jupiter still radiates more heat than it receives from the Sun; the amount of heat produced inside the planet is similar to the total solar radiation it receives. This additional heat radiation is generated by the Kelvin–Helmholtz mechanism through adiabatic contraction. This process results in the planet shrinking by about 2 cm each year.When it was first formed, Jupiter was much hotter and was about twice its current diameter.” wiki
So this indicates that Jupiter is cooling and this cooling is causing contraction and this contraction is generating heat. So I assume Jupiter is still cooling from it’s planetary formation. And Jupiter and gas giant in general are thought to formed quickly at beginning solar system formation- so cooling for very long time. Therefore it seems the loss of the heat generated from planetary formation is much slower with large planets- large planets with big atmospheres.
Ever since “Venus Envy” I have tossed this around.
The ‘thermal energy’ is measured by thermometers and they are giving spurious readings in air at different densities. Pack those atoms/ molecules together at the bottom of a gravity field and the temperature reading will be higher than a reading higher at a lower density.
The temperature sensor at both ends of the column is indicating a difference that does not exist, it is simply not the same air.
Only temperature readings of the same air density can be compared.
Crispin in Waterloo said @ January 29, 2012 at 5:07 pm
Pompous Gits do not worry 😉
You are correct that Robert’s initial explanation was in error. I seem to recall that he said he makes frequent errors in his lectures. When your smarter students catch you out, you know they are paying attention and learning. It’s only the very insecure pedagogs who never err.
I imagine you are correct about a residual amount of heat/motion. Even at 0K the atoms still continue to vibrate just a little. Exploitable? Maybe. Worth exploiting? I suspect it would make windmills look spectacularly efficient sources of “free” energy.
Now I want you to think very carefully about the following:
Aristotle claimed in his Physics that heavier weights fall faster than lighter weights. John Philoponus in the 6thC argued that this could not be the case. He asked us to consider that if we tied two differing weights together, then the lighter weight would retard the fall of the heavier weight, and the heavier weight would increase the rate of fall of the lighter weight. In addition, the combined weights would fall faster than either of the lighter weights. The only way to reconcile the contradictions was to realise that objects all fall at the same rate regardless of their weight.
A thousand years later, Galileo Galilei made an almost identical argument. The story goes that he dropped a small and a large cannonball from the tower at Pisa. The balls supposedly reached the ground simultaneously. There is no evidence for this. Galileo’s account of the experiment has his assistant dropping a wooden ball and an iron cannonball of identical size from a height some 300 feet greater thyan the height of the tower at Pisa. He recorded that initially, the wooden ball fell faster than the iron ball. The iron ball eventually overtook the wooden ball and reached the ground first.
So, who was correct? Aristotle, that fine marine biologist and philosopher, or Philoponus and Galileo (among others) who argued that objects all fall at the same rate? I have found much food for thought introspecting about the lessons here.
You argue for heterodoxy and I can only agree. That said, you can take heterodoxy too far. The Git is a great believer in the Middle Way. And a happy heretic 🙂
Tim Folkerts said @ January 29, 2012 at 7:12 pm
So what was the worst physics you have come across? The Git is intrigued 🙂
Dear Professor Brown
You are, of course, entirely correct about isothermal atmospheres. I’ve had to restudy thermodynamics recently and it confirms my earlier impression: thermodynamics in equilibrium systems often confound people’s expectations of how they think the universe should work. They misunderstand temperature as a thermodynamic property that only exists at equilibrium and not as a number that appears on a thermometer and fail to appreciate that the Laws of Thermodynamics really are fundamental.
WUWT does have really good science on it, but it has occasional craziness from a minority of people who think that evolution is just a theory, the fossil record is a sham, that all liberals support state control of the commanding heights of the economy and the idea that the Earth’s climate is or has been in a state of unstable equilibrium from which a slight perturbation in the concentration of a trace gas causes the whole Earth to barrel into a terrible heat death.
Fortunately on this forum I am not censored from saying it like it is.
Some people have actually changed their minds as a result of your post. This can be said to be a successful teaching lesson although there are always a few who will Never Learn.
For those of us who have studied thin isothermal atmospheres and scale heights, none of the post was a surprise, but it’s nice to revise these things.
This being WUWT people by and large have stuck to the issues considered without accusing you of being bought off by a gubmint conspiracy against free energy machines.
Jellbring was and is wrong. Willis has written stuff on WUWT which he acknowledges was wrong (i dare him to reread “the Steel Greenhouse”).
That which is peer reviewed in a scientific journal is not Gospel. Who knew?
John A
I have a very little time this morning before I have to go in and teach. I will try to answer one or two select questions in the meantime. just outside either of the two surfaces, and computes the outgoing time average flux of the Poynting vector integrated over all frequencies:
just outside either of the two surfaces, and computes the outgoing time average flux of the Poynting vector integrated over all frequencies:
From gbaikie: Eventually it will reach thermal equilibrium, correct? At that time, in a gravitational field, the total energy of any upper molecule will be much greater than at the bottom (K+P), correct? Is that a state of maximum entropy?”
Thermal equilibrium is the state of maximum entropy. It is also the state where there is no free energy available to do work within the system. The picture in the top article above is one of a half dozen pictures that explicitly show that the an atmosphere with a thermal lapse in any direction you like is capable of doing work, because heat engines in the idealized world of thermodynamic arguments can run between any two thermal reservoirs. Or, as I’ve now shown what, four times? that one can use the simple, macroscopic definition of entropy to see that the entropy of a gas with a lapse rate strictly increases when moving heat irreversibly from the hot reservoir to the cold one so that a gas with a thermal lapse, gravity or not, is not in the state with maximum entropy or equilibrium. Conduction and radiation are two irreversible processes always available to the ideal gas, although Jelbring fails to acknowledge conduction and radiation is very, very slow for a GHG atmosphere. But then, he doesn’t actually do any physics in his “paper”, so it isn’t surprising that he fails to leave something important out.
If you want to talk about thermal equilibrium, perhaps you should learn what it really is and stop trying to do statistical mechanics in your head with some naive notion of “energy balance”. You might actually try to directly address the algebra instead of waving your hands with word arguments based on an incorrect heuristic that is leading you to accept a hypothesis that violates the second law of thermodynamics.
It seems to me you would cool the entire atmosphere.</i
Why? The wire and gas form a closed system in my picture above. The circular flow of heat is impossible, of course, but no net cooling occurs aside from tiny transfers of heat from the gas in or out of the wire as they come into a state of dynamic equilibrium.
I feel compelled to mention one talking about very small differences of heat, and therefore whatever engine you using will draw very little energy from the system.
Oh, so it is ok to violate the second law, as long as it is only violated a little bit, or slowly? It’s ok to build a perpetual motion machine that causes an isolated system to spontaneously cool to absolute zero and stores all of its heat energy reversibly in a battery or a spring as long as it happens at a rate that is slow compared to the rate of power production in a nuclear reactor?
I missed that lecture back when I took thermo.
I reiterate. Somewhere in your bookshelves or in a local library or on the web, you too can read authoritative, trustworthy descriptions of the laws of thermodynamics. You too can read about the second law of thermodynamics in particular. You can look at the pictures involved. It doesn’t say that you can’t build a perfect refrigerator that works slowly. It says that you can’t build it at all. It doesn’t say that a closed system can spontaneously decrease its entropy a little bit. It says that you can’t spontaneously decrease its entropy at all. The pictures used to analyze and prove the various statements are identical to the ones I utilize above. A system cannot be able to in principle violate the second law, even in the most idealized of circumstances, to be believable to most physicists, because most physicists don’t believe in magic and gross, stable, macroscopic violations of the second law are friggin’ magic.
Finally, you once again fail to understand that in a mind experiment like this how much energy is produced is a matter of the scale of the engines involved, which is under our control, so nothing stops us from making the actual amount of energy extracted as large as we like, as large as a nuclear plant. Even more amusingly, when you say “very little energy from the system” you are implicitly assuming on the one hand that the second law and its restrictions on the efficiency of heat engines is valid, so one is limited by the Carnot efficiency, while describing a macroscopic collective system that is 100% efficient at converting heat into work. Think about the consistency of such an argument.
So this silver wire would a refrigerator- a very poor and expensive refrigerator. Far, far worse than windmills and solar panels- in terms generating energy. And a windmill would be a cheaper and more efficient refrigerator.
No, the silver wire wouldn’t be a refrigerator, but putting a heat engine in its place that ran between the two reservoirs and (say) charged a battery with the work done would not only be a refrigerator, it would be a perfect refrigerator, one that decreased the entropy of the Universe and converted heat directly into reversible, storable work.
Second remark
Several people commented on my sloppiness in my short answer of “no” for the heat flow between two radiators in thermal equilibrium, because I failed to put the word “net” in front of flow. This is a pretty serious picking of nits — thermo textbooks regularly state that there is “no heat flow” between reservoirs in thermal equilibrium because there is no net macroscopic flow of heat between the two reservoirs, for the simple reason that thermodynamics averages over molecular (or in the case of radiation, single photon) scale local fluctuations. It wasn’t even unclear in the context of the discussion; later I talked explicitly about detailed balance at the microscopic scale.
But here, I’ll be more explicit. If one places a closed surface
where the $latex $ pair indicate a double integral average over frequency and coarse grained time. In other words the answer is no! — after a long time, the two radiators are in thermal equilibrium, neither gaining nor losing heat to each other or their environment. In particular, the total energy content inside any surface that completely contains either object is, on average, zero.
I’m not going to review the various arguments that indicate that this is indeed the equilibrium — they are straightforward consideration of the integrals over the blackbody spectra from the two bodies that shows that the hotter one loses heat (on average) and the colder one gains heat (on average) until they are at the same temperature and have identical spectra, where the (time/frequency averaged integral of the) flux of the Poynting vector vanishes within microscopic thermal fluctuations of the sort that are routinely ignored in thermodynamics. I’m not going to show the fact that this final state is maximum entropy — an elementary estimate based on heat transfer from the hot reservoir to the cold one by irreversible means suffices to do that.
gbaikie also goes on about DALR being affected by heating and humidity. Sure. Irrelevant to Jelbring, though.
myrrh said some things about You haven’t even read his explanation for writing it the way he did as your diabribe against him showed.
That’s because I don’t care why he wrote it badly. You show me one single original contribution in this article! It isn’t even a valid review article. I reiterate: He says “I’m going to prove that there is a stable thermal lapse in thermodynamic equilibrium”. He quotes a textbook that derives the DALR in a section on climate dynamics, atmospheric flow. He states “this is thermal equilibrium”. He concludes “I’ve proven that the DALR is thermal equilibrium and will heat an absolutely static, stable, isolated atmosphere with a fixed total energy content differentially after all thermalizing processes are finished.”
No he hasn’t, no it doesn’t. He hasn’t proven anything at all — he just begs the question by restating his assertion as his conclusion with a “QED”, and the conclusion he asserts violates the second law of thermodynamics.
I think you should begin again, Take II, and stick to his thought experiment and not your strawman silver wire deflection.
By all means, let’s. That way we won’t be able to trivially prove that his assertion that the system is in equilibrium is false.
The silver wire is hardly a “straw man”, of course. It is just a proxy for heat conduction, something that he seems to have left out of consideration when he listed the agents responsible for establishing thermal equilibrium in his “thought experiment”. Unless you can show that no irreversible transport of heat energy is possible — even in fluctuations — within this gas, which is prima facie absurd, it is trivial to show that moving heat from the bottom to the top increases the entropy of the closed system. I’ve done so several times above.
If you want to publish a paper for lay people to help them understand something, it helps to explain how the result doesn’t violate the second law of thermodynamics when obviously it does. Even for lay people. I mean, all it takes is a single course in introductory physics to see how his assertion fails. You don’t need a physics Ph.D, you just need to stop burying your head firmly in the sand because you don’t want to face the fact that a thermodynamically stable, DALR undriven by a thermal differential maintained by other means is bullshit magic.
rgb
But here, I’ll be more explicit. If one places a closed surface just outside either of the two surfaces, and computes the outgoing time average flux of the Poynting vector integrated over all frequencies:
just outside either of the two surfaces, and computes the outgoing time average flux of the Poynting vector integrated over all frequencies: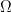 equals the time and frequency averaged outward direct flux of the Poynting vector integrated over that surface”. Since
equals the time and frequency averaged outward direct flux of the Poynting vector integrated over that surface”. Since  for either system, and since only radiation is a possible mechanism for the change, the net radiation through the surface vanishes.
for either system, and since only radiation is a possible mechanism for the change, the net radiation through the surface vanishes.
OK, so once again my efforts to put in a latex equation barfed. Sorry. It should be the algebra for “net rate of heat flow out of
I don’t give a damn if you want to view this as the detailed balance between outgoing and incoming flux, any more than I care about the fact that microscopically the total number of molecules inside a subvolume of an ideal gas in thermal equilibrium isn’t really a constant, they are always flowing in and out of the system. This is because in equilibrium, the scale of those thermal fluctuations are irrelevant by many, many orders of magnitude until you get down to very, very cold systems, where the fluctuations themselves are order of kT (and things like quantum mechanics start to matter).
Sorry about the algebra goof. The conclusion stands, though. By far the best answer is “no”; the yes answer is as irrelevant to radiation as the molecular flow is to density or the kinetic flow is to heat. Important, perhaps for establishing the conditions for detailed balance and equilibrium, but equilibrium is the state where balance is achieved, no net flow.
rgb
Robert Brown says: “Several people commented on my sloppiness in my short answer of “no” for the heat flow between two radiators in thermal equilibrium, because I failed to put the word “net” in front of flow. This is a pretty serious picking of nits … ”
Forewarned is forearmed.
The only reason I brought it up is that people here DO commonly make that assertion, and it will grow and spread if not continuously pruned. There is a vocal community within the skeptics that is SURE that IR from the cold atmosphere to the warm ground violates the 2nd Law. They are SURE that the word “net” is not implied in the 2nd Law but rather that NO energy can go from a hotter area to a colder area.
As I said, it is silly, but it is very much present.
Tim Folkerts says:
January 30, 2012 at 8:12 am
Robert Brown says: “Several people commented on my sloppiness in my short answer of “no” for the heat flow between two radiators in thermal equilibrium, because I failed to put the word “net” in front of flow. This is a pretty serious picking of nits … ”
Forewarned is forearmed.
The only reason I brought it up is that people here DO commonly make that assertion, and it will grow and spread if not continuously pruned. There is a vocal community within the skeptics that is SURE that IR from the cold atmosphere to the warm ground violates the 2nd Law. They are SURE that the word “net” is not implied in the 2nd Law but rather that NO energy can go from a hotter area to a colder area.
As I said, it is silly, but it is very much present.
Hear, hear!
If there is anyone left who is thinking about the exchange of KE for PE, as particles rise:
Some clever programmer (litdev) has written a bouncing ball simulation in Microsoft’s educational Basic; ‘SmallBasic’ (5.7Mb) it has a ‘Program ID’ of PMT149 . Watching the prog run and fiddling with the gravity one can see roughly what might be going on [ the same proportion of slow and fast particles at all heights??] Rather than downloading smallbasic you can run the sim (if Silverlight is lurking somewhere on your computer) at
http://smallbasic.com/program/?PMT149
If you would like to see some numbers I have made an ugly stab at printing them out in : XKT572
http://smallbasic.com/program/?XKT572
-The sim needs to be run for about a minute for the numbers to settle down. Try it without gravity first and then with ~0.02; Despite the KE/area ( pressure ratio?) of the two halves being ~3.5:1 the KE’s per particle in the two halves are generally within +-20% .( the temperature ratio?)
-To reset the cumulative Time Averaging, after things are changed, click on the ‘Reset Av’ text at the bottom.
-The sim seems to run a bit more smoothly and faster in Smallbasic than it does in the silverlight viewer. Both sims seem to lose KE slowly over time under gravity, unfortunately.
Chas
Good post.
It would be interesting to see the equations used for the calculations.
For instance where have they included the gravity term.
In the equations for the kinetic theory or in the Maxwell Boltzmann distribution or some other method.
@Tim
” There is a vocal community within the skeptics that is SURE that IR from the cold atmosphere to the warm ground violates the 2nd Law. They are SURE that the word “net” is not implied in the 2nd Law but rather that NO energy can go from a hotter area to a colder area.”
I have sseen that repeated to my dismay uncountable times. There seems to be (somewhere else) a website where they discuss how a hot surface ‘can’t receive’ radiation from a cooler one. The problem with the ‘not radiating’ misstep is that it supports the notion that heat somehow ‘knows’ whether or not it is aiming towards a hotter surface, then concludes it will not leave because it is hotter at the other end. I can understand a novice living with that thought so I agree, it needs to be watched.
Everything we see and touch is radiating all the time omnidirectionally. I have to deal with people who insist that radiation is ‘more efficient’ than convection or conduction. Arrgh.
The same radiation misunderstanding gives rise to the meme that some gases can, and some gases can’t be insulators. Actually a vacuum is a pretty good insulator too, which is no gas at all so relative to a gas, a vacuum is a ‘better insulator’.
Anyway, I have greatly enjoyed exploring the putative (and slightly silly) world of Planet Jelbring. As several have said above, it is really good to review the basics and apply them to unreal worlds. If Jelbring’s paper is a demonstrated dud, does this mean TallBloke will let the banned blogger (and by extension, Willis) back into his virtual fold?
Time to sit back with a nice cuppa and
relaxgo isothermal for a while.Paul Birch:
I largely remain of the opinion I gave previously. But a point you raised gnawed at me, and I tentatively reached a result that is an argument for your point of view: if you start with our atmospheric pressure at ground level, the difference in kinetic energy Velasco et al. specify for an altitude difference of, say, 10 km would not be measurable with a time uncertainty less than a second even in principle unless the gas-column width is less than something on the order of 100 nitrogen-molecule diameters across. I say “tentatively” because I made the calculation in haste and have not double-checked it. I mention it without having double-checked because I’ll likely be unable to return to these diversions in much less than a week.
rgb
Tim Folkerts says:
January 30, 2012 at 8:12 am
Robert Brown says: “Several people commented on my sloppiness in my short answer of “no” for the heat flow between two radiators in thermal equilibrium, because I failed to put the word “net” in front of flow. This is a pretty serious picking of nits … ”
Forewarned is forearmed.
The only reason I brought it up is that people here DO commonly make that assertion, and it will grow and spread if not continuously pruned. There is a vocal community within the skeptics that is SURE that IR from the cold atmosphere to the warm ground violates the 2nd Law. They are SURE that the word “net” is not implied in the 2nd Law but rather that NO energy can go from a hotter area to a colder area.
As I said, it is silly, but it is very much present.
===
What’s silly is postulating a process exists because hey, it’s statistics, it’s all so very modern milly maths therefore it has to exist”! Wally thinking. Until you can show that this is what is actually happening on that scale, that HEAT flows from colder to hotter, then all your “net” is, is statistical garbage in. And moreover, you now also have to show just how that “net hotter to colder” appears as you claim it doesn’t violate the 2nd Law, what is the mechanism, the physical mechanism, which does this? Surely there’s a Nobbly prize in it for anyone who can show what that is??
Because until you do so provide, you have no way of showing that it will obey the 2nd Law, you have no way of stopping the colder heating the hotter.
Chas says:
January 30, 2012 at 12:20 pm
“If there is anyone left who is thinking about the exchange of KE for PE, as particles rise:”
— — —
Sure Chas, great start of an analysis! Can’t resist such a challenge so I downloaded the code and will re-write it ground up in some flavor of c so we can have more like 10,000 balls using a proper sympletic high-order integrator to handle the vectors when gravity is present and allowing time reversal.
Did you notice why it keeps swapping between the top and bottom? You’ve got the entire column ‘bouncing’ because the initial states are assuming even pressure at the start up. Try allowing a ‘reset’ without actually resetting the position vectors. If you can hit the reset at the correct moment, the bouncing should quite down or even stop. Better would be to calculate the pressure and density gradient depending on the gravity setting and initialize the balls in the proper density per some small delta z slices. Way to go Chas… there’s a scientific mind! Prove it or not!
Try a printout of the data to file and run the statistics easily on excel. Graph it over time with any trends. Rough but should say something.
Because until you do so provide, you have no way of showing that it will obey the 2nd Law, you have no way of stopping the colder heating the hotter.
Or, you could learn about detailed balance, which is how one — not me per se, but anyone who does a stat mech computation — shows both that it obeys the second law and is what stops the colder heating the hotter and all that. Detailed balance is an explicit assumption of thermal equilibrium.
But hey, don’t let me interfere with your rugged insistence that you have nothing to learn here, and that “energy balance” (undefined) is meaningful but “detailed balance” (carefully defined) is not, and so on.
rgb
The temperature sensor at both ends of the column is indicating a difference that does not exist, it is simply not the same air.
Only temperature readings of the same air density can be compared.
Well, or you could be completely incorrect and what you assert could be experimentally rejected a thousand times over, something you can test instantly by picking up a can of compressed air at many atmospheres that somehow, stubbornly, appears to be at room temperature. Or (if you put it in a freezer) much colder than room temperature.
Read the zeroth law of thermodynamics, because it is the only macroscopic definition of temperature you are going to get.
Microscopically, it is a scale multiplier associated with probability and detailed balance, where it appears as a scale factor that makes energy dimensionless. In both cases temperature is defined by being “what you measure with a suitably designed thermometer”. Understand this and you’ll understand why you are wrong, and why the zeroth law is important.
rgb
There is obviously a real phenomenon which is not being taken into account. There are untold numbers of joules in every object in the universe which are unaccounted for.
Well, or they are all perfectly well accounted for, but you don’t want to look at the bookkeeping.
Look the thermodynamics/molecular dynamics of gravitational collapse isn’t really computationally all that difficult. There are large scale simulations that let people pretty much completely understand where all those “untold joules” come from and how they get turned into heat and how the heat is radiated away and all of that. The bookkeeping is necessarily sloppy, because how things evolve in time depends on a lot of details, but it isn’t like it isn’t well understood.
The beauty of Jelbring’s model is that he got rid of all of this, as did I in following him. No gravitational collapse. Steady state. The only way gravitational potential energy can get turned into heat is to change its gravitational potential energy, sort of like dropping big rocks from orbit down to the ground converts (most of) their PE to KE to heat. But then, you see, the impact crater cools, as the heat is radiated, convected, and conducted away. Wait long enough, and there is none of that heat left.
That’s where your statement is categorically incorrect. For a large body — a brown dwarf sized body, maybe even a Jupiter sized body, they can give off measurable leftover energy from gravitational collapse for billions of years. For a small body, not so much. In the case of any sort of body, talking about true equilibrium in the light of, well, the Sun — is a bit difficult, as no body sitting in sunlight is in static thermal equilibrium.
Look, there are dynamic models of how the atmosphere can act as a refrigerator (in a sense). In particular, they suggest that the atmosphere can self-organize to increase the rate of heat loss in response to differential increases in thermal forcing (basically overall negative feedback). Some of the speculative models I’ve looked over (proposed by readers of this list) aren’t overtly wrong — they seem plausible to me, at least so far. And they don’t violate the laws of thermodynamics — quite the contrary.
It might be good to understand gravity moderately well, and understand thermodynamics moderately well, before stating There Are Things Man Was Not Meant to Know about gravity, or asserting that we have no idea how to track gravity in statistical ensembles. I don’t think either one is remotely true, at least not until you hit the extreme limits of GR and quantum gravity and stat mech all mixed up together.
rgb
Robert Brown says:
January 30, 2012 at 3:02 pm
Because until you do so provide, you have no way of showing that it will obey the 2nd Law, you have no way of stopping the colder heating the hotter.
Or, you could learn about detailed balance, which is how one — not me per se, but anyone who does a stat mech computation — shows both that it obeys the second law and is what stops the colder heating the hotter and all that. Detailed balance is an explicit assumption of thermal equilibrium.
But hey, don’t let me interfere with your rugged insistence that you have nothing to learn here, and that “energy balance” (undefined) is meaningful but “detailed balance” (carefully defined) is not, and so on.
That you input that as a stop in a stat mech computation is being given as proof that cold flows to hotter?
What stops the colder heating the hotter? What???
Oh I certainly don’t think I have nothing to learn here.
Until you can show that this is what is actually happening on that scale, that HEAT flows from colder to hotter, then all your “net” is, is statistical garbage in, [and you cannot claim that just because you input it as a limitation in stat mech comps that it proves that such a critter as heat flowing from colder to hotter exists, duh] . And moreover, you now also have to show just how that “net hotter to colder” appears as you claim it doesn’t violate the 2nd Law, what is the mechanism, the physical mechanism, which does this?
Surely there’s a Nobbly prize in it for anyone who can show what that is??
Because until you do so provide, you have no way of showing that it will obey the 2nd Law, you have no way of stopping the colder heating the hotter.
One more nail in the coffin …
Velasco’s paper does NOT support the adiabatic lapse rate — not even close.
I actually took the time to read the paper (posted here if anyone is interested http://tallbloke.files.wordpress.com/2012/01/s-velasco.pdf ). Joe Born said earlier in this discussion that “as a practical matter, this result differs only negligibly from the isothermality” — which is a drastic understatement as we will see.
It would take a top post to give details, but basically there are two problems with using this paper here.
1) It assumes a completely adiabatic container. This would mean that the surface temperature would not matter because the atmosphere and the surface are perfectly insulated from each other and cannot interact in any way. If the ground instead acted like a thermal reservoir (a more realistic assumption) then the temperature profile would indeed be exactly isothermal.
2) The paper is dealing with small numbers of particles. Ignore objection #1 for now, and assume we really do have a completely adiabatic container . Even then, if the number of particles is large, the atmosphere tends toward isothermal. I did the calculations in his paper (and could share the spreadsheet) . If the surface temperature of the gas is 300 K, then at 1 km altitude in the container, the temperature would be
* 80 K for 1 particle in the container
* 286 for 10 particles
* 299.87 for 1000 particles
* 299.9999 for 1,000,000 particles
So we are left with
* if the atmosphere does not interact in any way with the sun
AND
* if the atmosphere does not interact in any way with the surface
AND
* if the atmosphere contains no more than 1 mole of gas total
THEN
there will be a theoretical “thermo-gravimetric enhancement” of perhaps 0.00000000000000000000001 K from the top to the bottom.
“It seems to me you would cool the entire atmosphere.</i
Why? The wire and gas form a closed system in my picture above."
Yes. Without the wire you have:
"Thermal equilibrium is the state of maximum entropy. It is also the state where there is no free energy available to do work within the system. "
With the wire you have enter a new element into the system- and it isn't in thermal equilibrium.
A problem is the model says heat isn't conducted by the tube- and no details of how this done.
If the tube is conductive of heat it will act as the silver wire- which will diminish the lapse rate.
100 meter steel pipe vertical in the air which is insulated will not change very much over the distance of 100 meter. With in contact with interior of pipe, it means air will also not change much in the 100 meter elevation. Solids or liquids do not have lapse rates. 3000 meter of ocean depth does not increase the temperature of water at bottom. Remove the water, replace with atmospheric air and insulate the air from cold ocean and the air will warmer at the bottom than at the top. If it's not insulated, then air would be a cold as the ocean water.
Tim Folkerts: Two comments.
First, in asserting a non-zero lapse rate, your comment, which, as my comments weeks ago on Tallbloke’s Talkshop indicate, I largely agree with, confirms the point I have been making: since Dr. Brown’s explanation is based instead on the absence of any non-zero lapse rate whatsoever, no matter how small, it does not merit the non-critical gushing with which this thread is redolent.
Second, by stating that a temperature difference between the top and the bottom, no matter how small, you have expressed a position different from the one upon which after being faced with Velasco et al. Dr Brown has now seized, i.e., that no heat flow means no temperature difference.
I might add that my purpose in bringing up the Velasco et al. paper was not to contradict the conclusion that Jelbring’s theory is unsound but rather, since I had not fully comprehended all of Velasco et al.’s steps, to invite a thorough discussion of its reasoning and thereby arrive at a more-informed assessment of its validity. I was disappointed not only in that but also at the general shallowness that most comments directed to that paper exhibited.
Robert Brown says:
January 30, 2012 at 7:07 am
myrrh said some things about “You haven’t even read his explanation for writing it the way he did as your diabribe against him showed”
That’s because I don’t care why he wrote it badly. You show me one single original contribution in this article! It isn’t even a valid review article. I reiterate: He says “I’m going to prove that there is a stable thermal lapse in thermodynamic equilibrium”. He quotes a textbook that derives the DALR in a section on climate dynamics, atmospheric flow. He states “this is thermal equilibrium”. He concludes “I’ve proven that the DALR is thermal equilibrium and will heat an absolutely static, stable, isolated atmosphere with a fixed total energy content differentially after all thermalizing processes are finished.”
Where does he say that?
No he hasn’t, no it doesn’t. He hasn’t proven anything at all — he just begs the question by restating his assertion as his conclusion with a “QED”, and the conclusion he asserts violates the second law of thermodynamics.
I haven’t the faintest idea what you’re arguing about. I can’t find any of that in his paper.
Myrrh said: “I think you should begin again, Take II, and stick to his thought experiment and not your strawman silver wire deflection”.
By all means, let’s. That way we won’t be able to trivially prove that his assertion that the system is in equilibrium is false.
He set out what he meant by equilibrium here:
The silver wire is hardly a “straw man”, of course. It is just a proxy for heat conduction, something that he seems to have left out of consideration when he listed the agents responsible for establishing thermal equilibrium in his “thought experiment”. Unless you can show that no irreversible transport of heat energy is possible — even in fluctuations — within this gas, which is prima facie absurd, it is trivial to show that moving heat from the bottom to the top increases the entropy of the closed system. I’ve done so several times above.
You introduced “thermal equilibrium”.
You went off on a completely different tangent, and began arguing against something he hadn’t said and which has nothing to do with the poser he sets.
If you want to publish a paper for lay people to help them understand something, it helps to explain how the result doesn’t violate the second law of thermodynamics when obviously it does. Even for lay people. I mean, all it takes is a single course in introductory physics to see how his assertion fails. You don’t need a physics Ph.D, you just need to stop burying your head firmly in the sand because you don’t want to face the fact that a thermodynamically stable, DALR undriven by a thermal differential maintained by other means is bullshit magic.
Well, I’m a lay peeps, and I think I understand what he’s saying (I’ve explained myself in a post above), you however, don’t make any sense at all.
You’re quoting stuff I can’t find, you’ve ditched his scenario and put your own in its place, and changing energetic equilibrium for thermal equilbrium you then spend your whole time arguing that he can’t get an adiabatic lapse rate from a thermal equilibrium which he never said he could, and, you bring in conduction, the wire, when he is explicitly talking about gases. What the has solids to do in this? This is about our fluid gaseous atmosphere.
Now, if you can sort that out, where you’re getting his quotes, maybe I’ve missed them, why you’ve totally ignored his scenario, why you’re arguing against a straw man of thermal equilibrium of your own invention and brought in the totally irrelevant conduction through solids and all the arguments about the 2nd law with respect to that, maybe you could write something worth reading about his paper. But at the moment, all you’re arguing with everyone about is your own imagined paper.
Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring
You still haven’t fixed the link.
that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable
Yes he did. Newton’s gravity. And note, thermodynamically stable adiabatic lapse rate, not your ‘thermodynamic equilibrium’.
Jelbring said: “The more atmospheric mass per unit planetary area, the greater GE has to develop. Otherwise Newton’s basic gravity model has to be dismissed.”
– indeed, the explanation involved a moving air parcel:
“An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.”
This is standard meteorological background. For example:
“Thus, rising air is said to cool or warm adiabatically when its temperature changes are due entirely to pressure changes. In reality, some degree of energy exchange will always take place, but these are generally small on short timescales.”
http://www.st-andrews.ac.uk/~dib2/climate/lapserates.html
This argument was not unique to Jelbring (in spite of his assertion otherwise):
“The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.”
He’s not saying it’s unique to him, he’s saying that this “has rarely been acknowledged by climate change scientists for unknown reasons”
Real scientists, such as meteorologists, know this. “Climate change” scientists use a lot of fictional fisics, besides such obvious boo boos like missing out the Water Cycle.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology.
That the adiabatic lapse rate is standard in “climatology” textbooks is irrelevant, he’s referring to real science and the point he’s making is that it is pressure related in the atmosphere and that there is no energy exchange in the process.
It is equally well known there that it is a dynamical consequence of the atmosphere being an open system.
Yeah, well, what do you mean by “well known”? Like, ‘well known that carbon dioxide is well-mixed and accumulates in the atmosphere for hundreds and thousands of years’? Like, ‘well known that shortwave visible heats oceans’?
But anyway, as I said in my post it’s good enough to approximate a closed system, and I’ve only just found the page I quoted from here, so my imagined cap to make it a closed system wasn’t quite accurately imagined, there is a cap on the dynamic system, it’s the inversion layer below the stratosphere.
There’s no reason to deviate from his scenario.
Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
The scenario which you have put in place of Jelbring’s, and then continued to argue, and argue, and argue that he got wrong, when you imagined it yourself. That is straw man.
I suggest, again, that you go back to the beginning and make some effort to understand what he is saying first, before you think to refute him. At the moment, you’re simply arguing against yourself.
The link to his paper should be:
http://ruby.fgcu.edu/courses/twimberley/EnviroPhilo/FunctionOfMass.pdf
For some reason it’s put this discussion url in front which messes it up.
.
[I’ve been having some problem with word wrap, hope I’ve fixed it, or most of it..]
@Joe Born
You have me thinking again, just after I had given up for the day. Are you suggesting that if there is a lapse rate, that the depth of the atmosphere makes a difference, in the sense of an effect emerging in a deep atmosphere of average gravity, might not be detectable in a shallow atmosphere with strong gravity? How about without a lapse rate?
Dr Brown says that an isothermal condition is the maximum entropy, even if there is an altitude difference in a gravitational field because ‘no energy transfer can take place’ which I take to mean ‘even if molecules move around’. This seems to be slightly circular because if an energy transfer can take place by some means other than hot-to-cold, he rules it out. If, prior to the isothermal state a mechanism causes stratification, either warmer at the bottom maintained by gravity and a dry adiabatic lapse rate or warmer at the top maintained by buoyancy and poor thermal conduction downwards, it is a pretty convenient argument to rule out energy transfer because it is isothermal.
Further, if ‘molecules can move around’ and the argument is that the lapse rate maintains the temperature constant (things already being isothermal) there is a problem if the isothermal condition was arrived at ‘because there is no lapse rate’. No lapse rate to achieve isothermal, maintained as isothermal by a lapse rate (exactly equal cooling of rising and warming of descending molecules).
To me, by definition of a lapse rate is cooling when rising. Because of the compression/expansion energy thing there obviously is a lapse rate prior to establishing an isothermal state, how is conduction going to overcome it? Or perhaps, which effect will dominate? Heat ‘attempting to flow’ up to colder gas by conduction opposed by some other mechanism may, at some total Delta T, constitute a net zero energy change without the temperature equalising. Is that the maximum entropy because no net energy transfer is taking place?
An earlier question no one picked up on is ‘is the planet rotating? Most planets rotate, at least a bit. The moon rotates slowly – it just appears not to from our perspective. Thus there will be rotation in cells away from the poles and a lot of vertical mixing and stirring. This would easily overcome tiny strange forces that might maintain a tiny temperature difference. To allow them to come into play we would again have to restrict the conditions to include a statement that it is a non-rotating planet. Do you hear the sound of time, wasting?
Joe,
I recognize your concerns. I don’t think they invalidate any of the comments made by Dr Brown.
1) thermodynamics is always about large numbers of particles, and in the limit of large numbers of particles, this solution becomes isothermal.
2) the completely adiabatic situation means no energy is exchanged with anything, so the atmosphere could not possibly be the cause of the warming of anything.
3) the introduction of any “thermal reservoir” in contact with the gas would cause the equilibrium condition of the gas to be isothermal, and any potential conflict with the 2nd Law disappears.
It is fascinating that people are this passionate about thermal physics, but this is a topic beyond what could be easily addressed in this sort of forum, and would more rightly belong in a classroom setting or as a potential journal article.
I agree, but those cans dissipate or equilibrate heat energy to the dominant system (free air or in the freezer). Convection excepted, the Earth’s atmosphere is closed, it IS the dominant system.
My experiment would involve a sealed conductive container placed at the top of an atmospheric column containing a temperature sensor but with an atmospheric pressure the same as that experienced by the bottom sensor. My guess ? yes, the top sensor would drop in temperature but not as much as an exposed sensor.
Atmospheric heat is contained heat, it cannot escape,except through convection.What if the air molecules at the bottom have not fallen, where do they get their heat?, borrow from the fallen ones? Your analogy does not come close to explaining atmospheric complexity, but I thank you, Robert, for taking the time and effort to discuss it.
I do not think that this topic is closed.
I suggest, again, that you go back to the beginning and make some effort to understand what he is saying first, before you think to refute him. At the moment, you’re simply arguing against yourself.
The link to his paper should be:
http://ruby.fgcu.edu/courses/twimberley/EnviroPhilo/FunctionOfMass.pdf
I find little to argue about in that paper. Quote:
“The main conclusion, derived from the model atmosphere of this paper, is the fact that
there has to exist a substantial greenhouse effect (GE) which is mass dependent and
which will develop independently of the amount of greenhouse gases in any real
planetary atmosphere.”
There is 10 tons of atmosphere per square meter- this has a high thermal capacity and during the night this air mass cools. It cools due to some degree due the surface radiating energy.
The paper mention that considerable amount energy is lost in higher atmospheric elevation- this must have to mostly be regarding “greenhouse gases” as non-greenhouse do not radiate a significant amount of energy, so I question this assertion. Air temperature cools significantly during the night, what portion of this cooling is losses to the ground vs some mechanism of air losing it’s kinetic energy to radiating gases?
I have no argument with that quote, I do have problem with
. It would depend upon the gas, water vapour has no problem ‘floating’ against gravity to rise above above the heavier gasses.
As cloud cover significantly reduces night cooling, I guess that radiative loss is significant.
“Tim Folkerts says:
January 30, 2012 at 4:18 pm
One more nail in the coffin …
Velasco’s paper does NOT support the adiabatic lapse rate — not even close.
I actually took the time to read the paper (posted here if anyone is interested http://tallbloke.files.wordpress.com/2012/01/s-velasco.pdf )”
From the velasco.pdf:
“Coombes and Laue, there are two conflicting answers
to the above question:
(1) The temperature is the same throughout because the
system is in equilibrium.
(2) The temperature decreases with the height because
of the following two reasons.
(a) Energy conservation implies that every
molecule loses kinetic energy as it travels
upward, so that the average kinetic energy of
all molecules decreases with height.
(b) Temperature is proportional to the average
molecular kinetic energy.
Coombes and Laue concluded that answer (1) is the
correct one and answer (2) is wrong.”
Thereafter much mathematically exciting stuff.
But I would agree that: “The temperature is the same throughout because the
system is in equilibrium.”
Or I would say we aren’t dealing with one molecule of gas.
I would agree with 2 if there was only one molecule of gas.
But no doubt the math has more use.
Now, perhaps in the math proofs, but I didn’t see the part about:
“Velasco’s paper does NOT support the adiabatic lapse rate — not even close.”
Rather I thought paper was saying there was not paradox, and answer was (1)
which seems to fit my idea of what the adiabatic lapse rate is.
Anyhow, moving on:
“It would take a top post to give details, but basically there are two problems with using this paper here.
1) It assumes a completely adiabatic container. This would mean that the surface temperature would not matter because the atmosphere and the surface are perfectly insulated from each other and cannot interact in any way. If the ground instead acted like a thermal reservoir (a more realistic assumption) then the temperature profile would indeed be exactly isothermal.”
Ok.
“2) The paper is dealing with small numbers of particles. Ignore objection #1 for now, and assume we really do have a completely adiabatic container . Even then, if the number of particles is large, the atmosphere tends toward isothermal. I did the calculations in his paper (and could share the spreadsheet) . If the surface temperature of the gas is 300 K, then at 1 km altitude in the container, the temperature would be
* 80 K for 1 particle in the container
* 286 for 10 particles
* 299.87 for 1000 particles
* 299.9999 for 1,000,000 particles
So we are left with
* if the atmosphere does not interact in any way with the sun
AND
* if the atmosphere does not interact in any way with the surface
AND
* if the atmosphere contains no more than 1 mole of gas total
THEN
there will be a theoretical “thermo-gravimetric enhancement” of perhaps 0.00000000000000000000001 K from the top to the bottom.”
Ok so one mole of gas seems small. That is: “22.4 liters of gas is the volume of 1 mole of gas at STP (Standard Temperature and Pressure = 0 degrees C at 1 ATM)- http://www.exo.net/~emuller/activities/A%20Mole%20of%20Gas.pdf
What volume is the one mole of gas in? Planetary scale, it’s better vaccum then on the Moon- on in space itself. If per meter of surface it is a fair amount.
It has seemed to me that the “thermo-gravimetric enhancement” must be fairly tiny.
0.00000000000000000000001 K seems smaller than I thought, but I don’t how to relate to 1 mole of gas.
Tim Folkerts:
I agree with your numbered points and that in essence they support Dr. Brown’s conclusion. For reasons it seems pointless further to belabor, though, I believe there’s a gap in the reasoning by which Dr. Brown reached that conclusion. As I said, this in itself is a minor point, but I was trying, unsuccessfully, as it turned out, to use it as a can opener into a discussion of whether Velasco et al.’s conclusion is correct. That paper–or, more accurately, the Román et al. paper on which it relies–is the only one of which this layman is aware that treats the issue with any rigor, so I was interested in finding out whether it was accurate.
Crispin in Waterloo:
First, let me emphasize that I’m a layman whom a bunch of PhDs in this thread appear to have dismissed as a crank, so you may want to take that into account. Second, I confess to not quite following all that you’ve said. Third, although I’ve been guilty in the past of attempting qualitative explanations of the type you may be making, my bias now is not to trust them, because explanations that are completely contradictory can both seem plausible to me. That’s why I felt queasy at Dr. Brown’s explanation on which Willis Eschenbach based his Latin-titled post.
That being said, here’s my take. For Velasco et al.’s purposes, the state of a molecule is totally defined by its location and momentum, and the state of an ensemble of molecules is the combination of the individual molecules’ states: for an ideal-gas ensemble consisting of N monatomic molecules, each of which is characterized by x, y, and z components both of position and of momentum, the ensemble’s state can be represented by a point in 6N space, in which a surface I think of as a hyperparaboloid represents the states that exhibit a given total (potential + kinetic) energy. The infinitesimal volume between the hyperparaboloids for E and E + dE is taken as containing the states the ensemble of of fixed total energy E can assume. The likelihood that the ensemble’s state falls within any subregion of that infinitesimal volume is taken as the ratio of the subregion’s (infinitesimal) volume to the total infinitesimal volume between the hyperparaboloids.
Based on those assumption, Velasco et al.’s calculations came to the conclusion that the number of states that exhibit the kinetic-energy gradient their Equation 8 specifies is greater than the number that exhibit a gradient of exactly zero. And the size of the Equation-8-implied gradient is proportional to the ratio of the force of gravity on a single molecule to the ensemble’s total energy. So–and this may be the answer to the question you were posing–it will be higher for greater gravity and tend to be higher for fewer molecules.
What I haven’t figured out is by what proportion the number of states exhibiting a gradient within a suitably small neighborhood centered on the one implied by Velasco et al.’s Equation 8 exceeds the number that exhibit a gradient within an equally small neighborhood centered on zero. My understanding of the Second Law is that it’s not a law so much as, given the numbers involved, just a phenomenally safe bet: in circumstances normally considered, the number of states exhibiting isothermality is so astronomically many times the number that exhibit temperature segregation that the odds favor the house so much that you may as well take it as a law that the house always wins, i.e., that heat will invariably flow from hot to cold. But what some disputants above are, quite reasonably, saying is that the number-of-states ratio is not as great in cases where the Equation-8-implied gradient is significant as it is in situations to which we are entitled to apply thermodynamics.
Joe,
The key point in the Velasco paper is that the energy of the system never changes (known formally as a microcanonical ensemble). If there is one particle in the container, it will ALWAYS have an energy exactly “e”. It never exchanges energy with the surroundings. It always bounces perfectly with the walls, neither gaining nor losing energy. It does NOT have a boltzmann distribution of energies. The temperature of the walls have absolutely no effect on the particle. In such a case, you really can’t define “being at equilibrium” because by definition there is no exchange with anything.
In a more realistic setting, the particle would exchange energy with the walls, and the particle would have a boltzmann distribution based on the temperature of the walls of the container.
If there are 2 particles, the two have a total energy of exactly 2*e. So if one particle has energy “x”, the other will have “2e – x”. Again this is not a boltzmann distribution for either, but at least a particle can have a range or energies.
As you get more and more particles, each particle gets closer and closer to a boltzman distribution, and the lack of interaction with the walls becomes less and less important.
Tim Folkerts says:
January 30, 2012 at 4:18 pm
That’s not the way I read the paper. My understanding is that the temperature is always 300K regardless of the number of molecules. For small numbers of molecules, temperature is no longer strictly proportional to the average kinetic energy. You only get a lapse rate if you assume that temperature is always strictly proportional to average kinetic energy. But Velasco, et.al. specifically says this isn’t true.
[my emphasis]
Statement (2b): Temperature is proportional to the average kinetic energy.
DeWitt Payne:
I don’t want to speak for Tim Folkerts, but I think he and I are looking at the equations as being more reliable, whereas you’re going by the verbal description, which can only with difficulty be reconciled to what the equations say. But one thing you may want to consider is whether they are actually talking about temperature as a local quantity that does not vary with altitude or instead as a global quantity that has no relationship to altitude. I believe their definition of temperature is that it’s a quantity inversely proportional to the first partial derivative of the log of phase volume with respect to total energy.
Tim Folkerts:
I understand, and have from the first understood, everything you just wrote, with the exception of the thing about equilibrium not meaning anything in the microcanonical ensemble. As to equilibrium, I’ve been using that term to describe a configuration in which entropy is maximized, not as one that necessarily is characterized by a Boltzmann distribution, although an equilibrium microcanonical ensemble approaches such a distribution in the limit.
Joe,
Then it looks like we are pretty much on the same page. This stat mech stuff is tough, so it is difficult to estimate who is getting it and who is not, so I was trying to re-iterate my main points.
As to the comment about equilibrium, I was mostly talking about the system with a single particle. The particle cannot share energy with the walls; the particle cannot share energy with any other object within the system. So it cannot “equilibrate” with anything. For multiple particles in the system, I don’t have a problems talking about equilibration within the system.
DeWitt,
I should be more careful about the word “temperature”. What I was more specifically listing in the table was (2/3 KE/k), which should be the temperature for an equilibrium situation with a large number of particles.
So for one particle, it has some total energy at the bottom, “e”, which will entirely be KE and not PE. At the bottom we could define a temperature based on this KE using KE = 3/2 kT. As that single particle goes up, it loses KE, so we could say that its “effective temperature” drops to zero as it rise toward an altitude where PE = mgh = 3/2 kT = e and KE = 0.
For two particles, KE does not need to drop to zero when mgh = e, because it would be possible for one particle to have 2e of total energy, and have KE = PE = e at that altitude. So the “effective temperature” based on KE does not drop to zero at this altitude h, but rather at an altitude 2h.
But this is getting WAY to involved for this discussion. Lets just say that for large n, the energy distribution of the particles does indeed very well approximate a boltzmann distribution with a constant temperature at all altitudes.
With the wire you have enter a new element into the system- and it isn’t in thermal equilibrium. . Kinda the thermodynamic definition of the change of entropy of a reservoir, isn’t it?
. Kinda the thermodynamic definition of the change of entropy of a reservoir, isn’t it?
Sure it is. I put it in the system and left it for a very long time!
That’s what Jelbring is ignoring. The fact that air in fact conducts heat just like the silver, and that if you wait for equilibrium — whether or not it actually takes a very long time on a human scale to get there — the equilibrium reached will be isothermal or violate the second law, in particular by manifestly not being the maximum entropy state of the system. The cold air at the top gains more entropy than the warmer air at the bottom loses, quite independent of the density of the air, when heat is transferred by any irreversible means you like from the bottom to the top. There are always irreversible means available — in particular heat conduction through the air.
Elementary thermodynamics. And I do mean elementary:
rgb
A point that requires clarification.
Is ‘adiabatically isolated’ exactly the same as ‘thermally isolated’?
Tim Folkerts says
“In a more realistic setting, the particle would exchange energy with the walls, and the particle would have a boltzmann distribution based on the temperature of the walls of the container.”
This would mean that the walls need to match the temperature change in the gas for an adiabatic solution.
Previously I have worked on the assumption that there is no thermal interaction between the walls and the ideal gas.
The constant speed moving parcel of the ideal gas is the same solution as still air for hydrostatic equilibrium.
Robert Brown says
“an adiabatically isolated column of an ideal gas is illustrated.”
ILlustrated above is a rectangular or perhaps cylindrical tube.
Fixed diameter or base means the only variation in the tube is in the vertical
For adiabatic expansion in the atmosphere the rising parcel needs to expand.
The only volume expansion in this case is by changing vertically
So the formula – g/Cp = -9.8K/km for dry air would need amending.
Yes he did. Newton’s gravity. And note, thermodynamically stable adiabatic lapse rate, not your ‘thermodynamic equilibrium’.
The fact that a thermodynamically stable adiabatic lapse rate is inconsistent with physics, violating the second law, is the only point of my article. And it is obviously true.
You’ve now proven my point. All he does is assert an impossibility at the beginning, and use his assertion to prove that his assertion is true later. But his assertion that an adiabatic lapse rate is thermodynamically stable does not make it so. It is not.
rgb
Tim Folkerts says:
January 31, 2012 at 9:26 am
OK. I think I would make the single particle have the 300K KE at the mid-point of the column rather than the bottom, but it only makes a difference for very small numbers. The main point is still that Velasco, et.al. specifically deny that there is a vertical temperature gradient in the column at equilibrium for any number of particles. If the particles do not obey MB statistics, and they probably won’t for small numbers, the justification for converting average kinetic energy to temperature using MB statistics (2/3 KE/k) no longer exists.
[With the wire you have enter a new element into the system- and it isn’t in thermal equilibrium.]
“Sure it is. I put it in the system and left it for a very long time!
That’s what Jelbring is ignoring. The fact that air in fact conducts heat just like the silver, and that if you wait for equilibrium — whether or not it actually takes a very long time on a human scale to get there — the equilibrium reached will be isothermal or violate the second law, in particular by manifestly not being the maximum entropy state of the system.”
But silver [or solids and liquids] do not conduct heat just like an ideal gas. The temperature of an ideal gas is solely/mostly it’s velocity of it’s molecules. Liquids and solid molecules do not have velocity- they vibrate if above 0 K. Molecules of ideal gas can also vibrate, but the vibration of gas molecules does not cause a gas to have a temperature- temperature of gas is it’s density and velocity of the gas molecules.
Gases can be all about the vibration of gas molecule- rather than it’s velocity. One can “excite” gas molecules, but in terms of the conditions in earth’s atmosphere the energy of it’s ideal gases in terms what temperature they are, relates to velocity of gas molecules. A counter example is Northern lights- nothing to do with velocity of gas molecules and everything to do exciting the molecules of gas so they emit photons. Excited gas molecules do not remain excited, they will emit their photon. Whether gas has been excited are not has little to do with the temperature of the gas.
So in terms of liquids and solids their vibration is their temperature. And their molecules going nowhere, except in sense that you toss a brick and the molecules brick are moving. With ideal gases it’s not the vibration or rotation of gases which indicate how warm they are. It is a factor which could be included but is not a significant element of why 20 C room temperature air is 20 C.
But silver [or solids and liquids] do not conduct heat just like an ideal gas. The temperature of an ideal gas is solely/mostly it’s velocity of it’s molecules. Liquids and solid molecules do not have velocity- they vibrate if above 0 K. Molecules of ideal gas can also vibrate, but the vibration of gas molecules does not cause a gas to have a temperature- temperature of gas is it’s density and velocity of the gas molecules.
Gases can be all about the vibration of gas molecule- rather than it’s velocity. One can “excite” gas molecules, but in terms of the conditions in earth’s atmosphere the energy of it’s ideal gases in terms what temperature they are, relates to velocity of gas molecules. A counter example is Northern lights- nothing to do with velocity of gas molecules and everything to do exciting the molecules of gas so they emit photons. Excited gas molecules do not remain excited, they will emit their photon. Whether gas has been excited are not has little to do with the temperature of the gas.
So in terms of liquids and solids their vibration is their temperature. And their molecules going nowhere, except in sense that you toss a brick and the molecules brick are moving. With ideal gases it’s not the vibration or rotation of gases which indicate how warm they are. It is a factor which could be included but is not a significant element of why 20 C room temperature air is 20 C.
So many errors, so little time. Let’s start with the last one — with ideal monatomic gases, vibration or rotation of the gas molecules isn’t an important factor. With ideal diatomic gases they are, and worse, the dependency itself depends on the temperature of the gas and the energy required to excite rotations vs vibrations. Look it up, it’s in any intro physics textbook that covers thermodynamics at all (since they almost invariably cover the thermodynamics of ideal gases).
Second, it doesn’t make any difference “how” solids or liquids conduct heat versus an ideal gas. What matters is that heat conduction is a thermodynamically irreversible process because it invariably increases the entropy of the Universe as it occurs (instead of breaking even, the characteristic of reversible processes). If the gas permits irreversible heat transport at all by any means, including by mere thermal radiation (also irreversible) then the entropy of the system will increase as it becomes isothermal (assuming isolation and no external or internal sources of continuous work).
This is all stuff you should work to understand, since it is a major factor in the entire theory of thermodynamics.
rgb
Robert Brown says:
January 31, 2012 at 10:04 am
Yes he did. Newton’s gravity. And note, thermodynamically stable adiabatic lapse rate, not your ‘thermodynamic equilibrium’.
The fact that a thermodynamically stable adiabatic lapse rate is inconsistent with physics, violating the second law, is the only point of my article. And it is obviously true.
Sorry, I’ve only just notice it should be “your thermal equilibrium”, which you’ve put in place of what he’s said, your straw man. And, you’ve shown neither.
You’ve now proven my point. All he does is assert an impossibility at the beginning, and use his assertion to prove that his assertion is true later. But his assertion that an adiabatic lapse rate is thermodynamically stable does not make it so. It is not.
Hmm, the impossibility he asserts is bog standard physical science as observed and well known in meteorology – one has to understand it to understand his point. And, as before, you’ve proved nothing of the kind since you’ve been arguing your straw man thermal equilibrium. Read the page I quoted from, this is bog standard real physics of Newtonian gravity which is understood by countless weatherpeeps and used in their daily work calculations, thoroughly understood empirically for generations.
What is it with ‘climate’ scientists? Why haven’t you noticed that you’ve missed out all these real world physics from your thinking? This, in my humble opinion, is what I think is happening here, you just don’t know that it exists, as Jelbring says: “has rarely been acknowledged by climate change scientists for unknown reasons” So your tangent is naturally then to something that is in your ken.
But the one that really gets me is – how have y’all come to miss out the Water Cycle from your energy budget, KT97 and clones? How?! How have none of you noticed it’s missing?!
It’s bog standard industry figures that the Water Cycle brings down the temps 52°C to 15°C. Calculated on understanding the nature of our heavy gaseous ocean above us, weighing down on us a ton on our shoulders, in a thermodynamically stable adiabatic lapse rate.. ‘climate’ scientists teach this is empty space!
When one puts together all that you, ‘climate’ scientists, have missed out, and this current example just gets added to the list I’ve gathered so far, you’ve got a really weird world you’re describing. Alice through the looking glass impossible thinking before breakfast; visible light heating water and land, heavier than air carbon dioxide defying gravity and accumulating for hundreds and thousands of years, the heat from the Sun not reaching the Earth’s surface, cold objects heating warmer.., someone’s really been messing with your heads.
You’ve no ‘feel’ for the world around you through real physics, the wind might as well be a big wooden spoon stirring the atmosphere around, or the gods at the four corners in a blowing contest. It’s something I concluded a while back, that only someone who knows this physics really well could do the subtle tweaks across the range of disciplines involved.
But the effects have been dramatic. Reducing the argument to radiation as if it’s ‘all the same energy’ by stripping it of its individual properties and processes, has enabled the swapsies of properties and out of context use of laws to be made in the descriptions of energies, gases and processes, and, so ground into thinking through repetition in the education system that even the absence of the Water Cycle goes unacknowledged as you all busy yourselves arguing about the nuances of your fictional fisics with real world applied scientists who know better.
There’s still some around..
http://johnosullivan.livejournal.com/43659.html
..who know who’s really violating the second law.
“I have no argument with that quote, I do have problem with
when an air parcel ascends the
temperature has to decrease because of internal energy exchange due to the work
against the gravity field.”
I agree it’s a problem.
Replace “air parcel” with “balloon”.
“when a balloon ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.”
A hydrogen balloon could start it’s ascent with cooler hydrogen gas compared to the air temperature at ground level. It still could still have lift.
As it ascends hydrogen gas could warm, cool, or stay the same temperature. The gas could expand and expansion, or lower of the density of the hydrogen gas will lower it’s temperature. The hydrogen will cool to the degree it expands. If it doesn’t expand, it doesn’t cool.
The work it does [going up] is unrelated to “working against gravity”. A balloon staying at certain elevation is “working against gravity”- but due to buoyancy it’s not actually work- doesn’t require energy. The acceleration or velocity of going up could also be called “work against gravity”, but again is not, it’s a matter of buoyancy. Buoyancy defies gravity. Or buoyancy is gravity. Buoyancy doesn’t require energy, anymore then gravity causing things come towards it [some non buoyant thing] requires energy.
A brick falling is gaining energy, a balloon rising is gaining energy. Neither of them or whatever surrounding it must do work to gain this energy- it is what gravity does.
If leave a gravity well very fast, it costs little in terms of gravity costs, and if approach a gravity well fast you gain little in terms of gravity gains. Leaving earth surface very slowly with a rocket, will consume an enormous amount energy. The faster rocket leaves, the less energy costs is used working against gravity. This is called gravity losses. The Shuttle had gravity lost of about 1 km/sec- from it’s total “budget” of 9.5 Km/sec. This “budget” is called it’s Delta-V.
“So many errors, so little time. Let’s start with the last one — with ideal monatomic gases, vibration or rotation of the gas molecules isn’t an important factor. With ideal diatomic gases they are, and worse, the dependency itself depends on the temperature of the gas and the energy required to excite rotations vs vibrations. Look it up, it’s in any intro physics textbook that covers thermodynamics at all (since they almost invariably cover the thermodynamics of ideal gases).”
If diatomic gas which has zero or near zero velocity, it will have zero or near zero temperature.
If diatomic gas has 500 m/s velocity it will be warm, and all the gas molecules will vibrate and spin around. How could they not?
The faster molecules are traveling crashing into each others, the more vibrating and spinning one will get.
But one can cause these molecule vibrate and/or spin faster and not have molecules moving very fast, such molecules could have a cool temperature and be radiating a lot of energy
Dr. Brown,
You are obviously incorrect when you state: “The fact that a thermodynamically stable adiabatic lapse rate is inconsistent with physics, violating the second law, is the only point of my article. And it is obviously true.”.
With matter that is in a solid or liquid state, the heat content per unit mass is generally proportional to its temperature. This can be simply expressed as specific heat, which is the heat required to change one unit of mass one unit of temperature.
But, when matter is in the gaseous state, this is not the case. and the heat content per unit mass is not necessarily proportional to the temperature. Specific heat is dependent on gas temperature and; the volume it occupies, or the pressure it exerts. The most important word in that last sentence that seems to get overlooked most often is “and”, and so it is necessary to consider in some way, the density of the gas, to express specific heat.
In Earth’s atmosphere, the air molecules are not fixed at any particular height. Their distribution, and thus the air density with respect to height is forced by gravity. If all of the air molecules have the same heat content, the temperature distribution with height must vary with the density.
My understanding is that the wet and dry lapse rates are maximum limits for atmospheric cooling with altitude beyond which convection will set in. If a small parcel of air rises by a slight amount, for any random reason, it will cool at the adiabatic lapse rate. If that adiabatically cooled parcel happens to be cooler, with a higher density than the surrounding atmosphere up there, then it must eventually return to a lower level.
In order to force a temperature decline at the adiabatic lapse rate, there must be some combination of both heating from below and cooling from above that would otherwise drive the rate of cooling with altitude beyond the effective lapse rate.
In our own atmosphere, we have the example of the stratosphere where temperatures actually increase with altitude. The environmental lapse rate in the troposphere appears to be a compromise between the wet and dry adiabatic rates, as convection under both conditions is occurring.
I find no indication that the adiabatic lapse rates are anything more than maximum rates of temperature decrease with altitude before convection will begin preventing any steeper temperature decline.
Wayne, I can see what you mean about the initial positions. As it turns out the same person (litdev) who wrote the initial program has put together a dll that not only does graphing and Excel export but also pulls in the Box2D physics engine (C++) – I now have 500 balls bouncing around with only ~ 10 lines ! http://litdev.hostoi.com/
Bryan, I think that the distibution just emerges from the randomness (?)
Chas you say
“Bryan, I think that the distibution just emerges from the randomness (?)”
True randomness would be a different distribution from a Maxwell Boltzmann distribution
I used to do educational software with Archimedes computers using BBC basic.
They turned into ARM and withdrew from computers.
I tried to adapt to Visual Basic but got fed up.
Given what Tim Folkerts says above that for say 100 particles and above the distribution rapidly approaches the limit.
Then a simple emulation with x,y,z dimensions.
1. The 100 particles being specified with the properties of ideal gas.
2. If Z component is vertical then velocity components in that direction will be subject to gravitational field strength.
3 Give a random velocity to each particle (say with values (0=>1000) in a random direction.
Then let it run for some time adjusting the parameters to get realistic display.
The results should shed some light on the distribution at the limit.
Perhaps Wayne is already on to it!
Thanks for fixing, Mods.
Re the earlier:
http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/#comment-878558
“This happens so rapidly that we don’t see the breaks in the operation of the circuit and it is the continual recreation of the dipole which causes the battery to run down and lose it’s power. Let me say it again, the battery does not supply the current that powers the circuit, it never has and it never will – the current flows into the circuit from the surrounding environment.” http://free-energy-info.co.uk/Intro.htm
Willis Eschenbach says:
January 29, 2012 at 5:09 pm
Don’t you hate it when the current “destroys the battery’s dipole”? Nothing an electrician fears more than that.
If there is a “grain of truth” in there, I don’t see it. The scary part is, Myrrh seems to believe it.
Sorry it frightens you, Willis. Try lying down in a darkened room with a cold wet cloth pressed to your forehead whenever you get this reaction, the feeling will pass.
For any here with interest in this, I’ve been searching around a bit whenever I have time and it is a bit of mess with serious science, amateur and pro, jumbled in with scams, but there’s a lot of serious science out there – don’t be put off exploring by those who’d in the past make derogatory comments about the first car they’d ever seen, and then go off to put go faster stripes on their carts. Anti matter is created and used routinely in hospitals, this poses no problem to the industrial/military complex, your access to knowledge and cheap energy does.
Some background on gravity systems: http://peswiki.com/index.php/Review:Magnetic_Current_by_Edward_Leedskalnin
A name that crops up there and considered serious science on this: http://freeenergynews.com/Directory/Inventors/JohnSearl/
Serious scientists exploring the Searl Effect Generator: http://www.rexresearch.com/roschin/roschin.htm
Lots of interesting articles on this site from which at random: http://www.americanantigravity.com/video/pharis-williams-on-fusion-reactors.html#more-902
And lastly: The case of the disappearing magnetic boots. The Radus boot with an interesting twist, magnets with memory:
http://www.cheniere.org/misc/astroboots.htm
From the last: “Well, it doesn’t take a genius to see that, when you can switch a permanent magnet’s fields easily, and the magnet also has a built-in memory as did the Radus magnets, then with a little ingenuity in switching one could use such switchable magnets to produce a self-switching, self-powered permanent magnet motor. The magnet, being a permanent dipole, is already a particular kind of “free energy generator”, since it continuously gates magnetic energy directly from the vacuum due to its asymmetry in the energetic vacuum flux.
“Why do you suppose NASA replaced that excellent Radus boot with the far inferior “shuffler” kind later?
“You see, if you can easily switch the fields of a permanent magnet as you wish, and make that magnet also have a memory that you deliberately conditioned into it, you could also build a permanent magnet self-powered engine by adapting such memory (asymmetrical behavior) and switching. It’s perfectly permissible by the laws of physics and the laws of thermodynamics, because one is using an open dissipative system far from thermodynamic equilibrium. Any dipole such as a permanent magnet is a legitimate open system freely receiving energy from its environment (the active vacuum) and re-emitting some of that energy in usable Poynting energy flow form.
“The other compelling reason is that you don’t use electrical currents back through the source dipoles to kill them! Zounds! That means you can have one half the solution already accomplished from the start; you don’t have “spent current” to have to force back through the dipole or shunt it around freely by some extraordinary means. All you have to worry about is understanding and very clever and precisely timed switching. (And it does have to be clever; let’s not belittle the skill and perseverance required to achieve that task!)”
Get your ice pack ready Willis, The other compelling reason is that you don’t use electrical currents back through the source dipoles to kill them! Zounds!
A well known, to some, problem solved.
Perhaps if you calmy read the introduction I first posted, link above, you could approach this subject with your usual love of inquiry unfettered by fear..
Bryan “I used to do educational software with Archimedes computers using BBC basic.” – nice
“I tried to adapt to Visual Basic but got fed up” -I know the feeling.
Do have a try with SmallBasic – it is designed for children to use, though I admit I dont quite understand it yet, and you may do better. Litdev has some great/clear program samples on his web site (above)
—I too would would like to know how/where the distribution arises!!
Bryan says:
February 1, 2012 at 2:12 am
Chas:
>>“Bryan, I think that the distibution just emerges
>>from the randomness (?)”
Bryan:
>True randomness would be a different distribution
>from a Maxwell Boltzmann distribution
The randomness DOES just emerge. Here is a different but similar simulation http://www.falstad.com/gas/ . You can set the initial conditions so that on atom is moving and the others are all at rest. Within a short time, the energy is distributed among all the atoms according to a Boltzmann distribution.
PS you can also “turn on gravity” in this simulation. One interesting thing to try is to turn gravity way up and turn the simulation speed way up. If it was cooler at the top, you should see a very distinct layering of the gas by color (= KE). Instead, the colors seem pretty evenly distributed at any altitude.
DeWitt Payne: “If the particles do not obey MB statistics, and they probably won’t for small numbers, the justification for converting average kinetic energy to temperature using MB statistics (2/3 KE/k) no longer exists.”
Actually, derivation of the 2/3 KE / k from PV = NkT is not based on any particular velocity distribution; it merely infers from the pressure on a container’s walls what impulse per unit time the walls must be applying to the molecules, and from that what the molecules’ root-mean-square velocities must be. Different velocity distributions can have the same root-mean-square value.
Again, you’ve conflated two disparate concepts, to both of which “temperature” has unfortunately been applied. As a perusal of the three posts by Brown and Eschenbach will reveal, they used it in the normal way, i.e., as the local mean translational kinetic energy of the molecules. In contrast, Velasco et al. did what people in various disciplines sometimes do: they use “temperature” to denote a quantity that may in some contexts be computationally handy but doesn’t necessarily describe mean translational kinetic energy accurately, at least as a local quantity.
For example, any ensemble of molecules, no matter how non-equilibrium or non-isothermal, has some degree of entropy, and adding heat to the ensemble may increase that entropy. If we start by knowing the entropy change and the added heat, we may find it convenient to assign that ensemble an effective “temperature” defined by T = dQ/dS. And for some purposes that quantity may be a worthwhile measure. But it doesn’t tell us whether the ensemble is colder in some places and warmer in others.
Now, you might argue that the kinetic-energy gradient Velasco et al.’s Equation 8 specifies is too small for thermodynamics to take notice of. You might argue that one could never as a practical matter measure this gradient. You might even argue that the molecular-translational-kinetic-energy difference is so small that Heisenberg’s Uncertainty Principle dictates an extraordinarily large time uncertainty in its measurement. But it is clearly incorrect say that this gradient is non-zero, no matter how many molecules, so your statement that “Velasco, et.al. specifically deny that there is a vertical temperature gradient in the column at equilibrium for any number of particles” is based on confusing two different usages of “temperature.”
Hmm, the impossibility he asserts is bog standard physical science as observed and well known in meteorology – one has to understand it to understand his point.
I do, so I know that it isn’t and was never intended to be considered a state of static thermal equilibrium in an isolated system. You’ve presumably read from the author of one of the textbooks that derives and discusses the DALR above (Caballero) where he states baldly that a gas with a DALR is not in thermal equilibrium. But of course you have been able to rationalize away how he isn’t really an expert (while Jelbring clearly is) and doesn’t actually know anything about this “bog standard” result. Neither have you actually read any actual textbooks that derive it, or you would have observed that they always speak of reversible bulk transport of the gas while establishing the DALR while ignoring all of the irreversible heat transport processes that also take place, more slowly. Finally you haven’t paid any attention to the fact that you need a pre-existing thermal gradient in order to get the convection that establishes the DALR. Jelbring ignores all of this also, in spite of his quoting his one textbook reference where it talks about vertical transport and the DALR. Unsurprising, since he takes the entire result and discussion completely out of context to insert it in his “paper”.
If you don’t believe me, get a copy of his one textbook reference and read it. If you can read it, that is — you don’t seem to understand even the equipartition theorem, making it unlikely that you understand why c_p appears in the DALR instead of, say, c_v. If you understand what the difference between c_v and c_p are. It will make reading about the Navier-Stokes equation and the assumption of adiabatic non-turbulent flow in his reference tough going for you, but you can persevere.
Why haven’t you noticed that you’ve missed out all these real world physics from your thinking? This, in my humble opinion, is what I think is happening here, you just don’t know that it exists, as Jelbring says: “has rarely been acknowledged by climate change scientists for unknown reasons” So your tangent is naturally then to something that is in your ken.
Wow. That’s all I can say. I have taught “real world physics” at one of the world’s top-ranked Universities for 30 years. I’ve written two textbooks on real world physics. I spend more time thinking about, solving problems in, teaching, and yes, continuing to learn and refine my knowledge of real world physics in any given week of your choice than you apparently have lifetime, and I’m missing out. Sure, that makes sense. Why didn’t I think of that. Well, I’m really grateful to you for pointing out my ignorance. I will just have to work harder — there must be something about near-Earth gravity that confers upon it a miraculous ability to violate the laws of thermodynamics that I missed.
Let me make a suggestion — only a suggestion. There are two possibilities.
a) I actually do understand real world physics quite well and far, far, better than you do. Not just understand it well enough to say lots of nifty words about it — well enough to start from the basic empirical laws and principles and derive and demonstrate nearly the whole thing through the introductory classical level at the blackboard, without notes, as I do several times a year in front of several hundred very bright students a year, working with a team of Ph.D. physicists who are my co-instructors (with perhaps a century of teaching experience between us who, one would think, would correct my errors if I made any egregious ones along the way). So when I say that you are incorrect, it is truly an informed conclusion made by someone that actually knows what they are talking about.
b) You understand real world physics far, far better than I do. You haven’t mentioned being a physics major or physics Ph.D., so we’ll both have to assume that you are one of those rare, self-trained geniuses who has managed to systematically master calculus through partial differential equations and functional analysis, group theory, advanced algebra and so on well enough to teach at least parts of it at the graduate level while working through not only introductory physics, but full courses in thermodynamics, classical mechanics (I’m certain you have mastered Lagrangian and Hamiltonian formulations of physics and understand action principles), electrodynamics (so that Maxwell’s equations are no mystery to you, nor is relativity theory and the theory of electromagnetic radiation — did I mention that the other textbook I’ve written is a graduate level text in classical electrodynamics?) , quantum mechanics (so that solving the Schrodinger or Heisenberg equations is old hat for you, manipulating commutators is easy, and of course you fully understand quantum electrodynamics well enough to publish papers in it), and above all statistical mechanics. You are wasting your time with verbal discussions here — you can actually work out the microcanonical description of this particular gas, and have avoided becoming engaged in the discussions of the Velasco paper only because you wished to help instruct me on my ignorance first, because of the egregious errors in my thermodynamic reasoning. In all respects, you are truly qualified to make pronouncements about the physics that, after all, Jelbring completely explains, with full algebraic derivations, in his paper. Sadly, you have to deal with me — an ignoramus who stubbornly persists in thinking that thermodynamic equilibrium is an isothermal state in spite of the fact that you know that nearly every physics textbook on the subject states otherwise and has numerous examples of how physical forces can sort things like gas molecules into stable sub-reservoirs at different temperatures.
We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?
rgb
BigWaveDave says:
January 31, 2012 at 4:33 pm
http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/#comment-881147
But, when matter is in the gaseous state, this is not the case. and the heat content per unit mass is not necessarily proportional to the temperature. Specific heat is dependent on gas temperature and; the volume it occupies, or the pressure it exerts. The most important word in that last sentence that seems to get overlooked most often is “and”, and so it is necessary to consider in some way, the density of the gas, to express specific heat.
In Earth’s atmosphere, the air molecules are not fixed at any particular height. Their distribution, and thus the air density with respect to height is forced by gravity. If all of the air molecules have the same heat content, the temperature distribution with height must vary with the density.
Thank you.
Robert Brown says:
February 1, 2012 at 6:09 am
We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?
My only skill in this, and I use the term loosely, is when my curiosity is piqued I enjoy exploring and in subjects where I have no or only a modicum of knowledge I will listen to as many arguments pro and con a bone being argued over until I am fairly confident I can take a position on it, or not. When I first found that AGW was something people argued about I was more than casually intrigued, the arguments were so passionate, I immersed myself in reading discussions and found the range of disciplines involved and seemingly, to my untutored eye, being argued with equal claim to physics, quite exhausting as I yo-yoed between one and the other, and because I would then have to see what I could find to substantiate the different claims. Gradually a pattern emerged, the applied scientists, the engineers and the like, with practical real world experience won hands down, not least for common sense.
I also learned a bit more about physics than I began with, which original teaching itself gave me something to compare with what I was being told in ‘AGW science’. For example, I had begun at junior level taught that gases had weight, that those heavier sink in air, those lighter rise, and the examples we were given was to the then important industry in Britain, coal mining, this knowledge was crucial to safety in mines. This became my first independent area of inquiry, I could find no discussions on this so I questioned the PhD in physics who teaches and sets and marks exams and writes reports for government and who first set me off in the direction of IPCC reports to learn about AGW, “how can carbon dioxide be well-mixed in the atmosphere when it is heavier than air?” I’ve told the story elsewhere, I won’t repeat it here, but his explanation of the physics led me to the inescapable conclusion that he didn’t know what he was talking about. I was profoundly shocked. He firmly believes, and teaches with constant references to laws of physics , that carbon dioxide pooled on the ground will spontaneously rise and diffuse in the atmosphere without any work being done. It’s a completely different physics from the real world.
So, I don’t know what you’ve written, or how many of your peers agree with you, but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background. I’ve given you my conclusion on the ‘physics’ of this generally from the AGW ‘climate’ scientists, that it is fictional fisics. Did you read the Latour link? He called it junk science.
So I’m in good company..
Joe Born says:
February 1, 2012 at 5:06 am
DeWitt Payne: “If the particles do not obey MB statistics, and they probably won’t for small numbers, the justification for converting average kinetic energy to temperature using MB statistics (2/3 KE/k) no longer exists.”
Joe: Again, you’ve conflated two disparate concepts, to both of which “temperature” has unfortunately been applied. As a perusal of the three posts by Brown and Eschenbach will reveal, they used it in the normal way, i.e., as the local mean translational kinetic energy of the molecules. In contrast, Velasco et al. did what people in various disciplines sometimes do: they use “temperature” to denote a quantity that may in some contexts be computationally handy but doesn’t necessarily describe mean translational kinetic energy accurately, at least as a local quantity.
… But it is clearly incorrect say that this gradient is non-zero, .., so your statement that “Velasco, et.al. specifically deny that there is a vertical temperature gradient in the column at equilibrium for any number of particles” is based on confusing two different usages of “temperature.”
You are the one confused, Joe. You have things backwards. The standard and fundamental definition of the thermodynamic concept of temperature is that two bodies are at the same temperature when they are in thermal equilibrium. [A pedantic relativistic form of that statement might be that two bodies in the same frame of reference are at the same temperature when they are in thermal equilibrium, or that two bodies will be in thermal equilibrium when their temperatures transformed into the same reference frame are the same.]
Both Brown and Velasco et al are using the concept in this fundamental way.
That temperature is proportional to average kinetic energy per particle in the canonic limit is a secondary derivation from this primary thermodynamic concept. The finite microcanonical ensemble you are making so much out of is unphysical; it is a statistical mechanics abstraction. Once you allow it to interact with so much as a thermometer, the usual result for a canonic ensemble reasserts itself.
There are many other circumstances in which not all of the kinetic energy counts towards the temperature. Indeed, in general, only the random, thermalised and isotropic kinetic energy counts. Consider a cannon ball in orbit around the Earth. What is its temperature? If you treat it as a single particle, then the average KE per particle is so enormous that T~1E31K! Even if we count all its atoms separately, then T~1E5K. This is clearly ridiculous, not what we mean by temperature at all. Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.
RGB says: “We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?”
I could have told you the answer would be “c” –> “I don’t understand physics. Or engineering. Or math, for that matter (and readily admit it). But I never-the-less know it better than PhDs, because I have found some web pages that I have a strong gut feeling about. And that gut feeling trumps actual knowledge and study and mathematics.”
Basically take the worst parts of your two options and put them together.
Tim Folkerts says
“PS you can also “turn on gravity” in this simulation. One interesting thing to try is to turn gravity way up and turn the simulation speed way up. If it was cooler at the top, you should see a very distinct layering of the gas by color (= KE). Instead, the colors seem pretty evenly distributed at any altitude.”
Thanks Tim it looks like a useful resource.
The possibility of a slow molecule hitting a wall and bouncing back at a higher speed was not one I had factored in.
I would have set the condition as an elastic bounce with molecule coming out with unchanged KE.
That would be my definition of thermally isolated.
All of these simulations should afforded significant skepticism. I don;t know that any of them were designed to provide more than approximately correct answers. For example. when you turn on gravity in the simulation I linked to, the total energy gradually increases. You could attribute that to some “thermogravimetric effect”, but more likely is is round-off error after millions of collisions or the effect of the step size used, or poor programming.
Unless you know the pedigree of the simulations, they should probably be consider “for entertainment purposes only”, but not as rigorous scientific evidence in support of any particular subtle claims.
“There are many other circumstances in which not all of the kinetic energy counts towards the temperature. Indeed, in general, only the random, thermalised and isotropic kinetic energy counts. Consider a cannon ball in orbit around the Earth. What is its temperature? If you treat it as a single particle, then the average KE per particle is so enormous that T~1E31K! Even if we count all its atoms separately, then T~1E5K.”
It needs to be an ideal gas. A cannon ball, a pint of beer, or water vapor are not ideal gases.
“This is clearly ridiculous, not what we mean by temperature at all. Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
It might be interesting to see what happens in space if release low pressure and low temperature monatomic gas in free space.
Suppose you put a globe of water which say 5 C in a low pressure air lock and then open the door to space. Obviously the globe of water would be above it’s boil point in a vacuum. But can anyone describe what would happen. Does it freeze, does expand, does turn fog. How quickly?
Or does “appear” to do little within the first minute, or does something dramatic happen in less than 1 second?
So, I don’t know what you’ve written, or how many of your peers agree with you, but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background. . Is it “stuck” where gravity leaves it, or can it move, say, by irreversible diffusion or heat conduction? What happens when some of the heat moves from one temperature in one part of the gas to another part of the gas at a different temperature? In particular, does the entropy of the gas increase or decrease?
. Is it “stuck” where gravity leaves it, or can it move, say, by irreversible diffusion or heat conduction? What happens when some of the heat moves from one temperature in one part of the gas to another part of the gas at a different temperature? In particular, does the entropy of the gas increase or decrease? throughout the gas column (condition for static force balance), once static force balance is achieved (which happens almost instantly, BTW) any bulk motion of the gas damps and gravitation can no longer heat or cool the gas. How can it? In order for some part of the gas to gain energy, it has to move downward and, on average, no part of the gas in static force equilibrium moves up or down. Gravity can certainly maintain a pressure/density/temperature profile, but there are quite literally an infinite number of them (not just the one with the DALR) that satisfy the force equilibrium equation and hence are static as far as forces are concerned.
throughout the gas column (condition for static force balance), once static force balance is achieved (which happens almost instantly, BTW) any bulk motion of the gas damps and gravitation can no longer heat or cool the gas. How can it? In order for some part of the gas to gain energy, it has to move downward and, on average, no part of the gas in static force equilibrium moves up or down. Gravity can certainly maintain a pressure/density/temperature profile, but there are quite literally an infinite number of them (not just the one with the DALR) that satisfy the force equilibrium equation and hence are static as far as forces are concerned.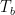 . Remove a dollop of heat from it
. Remove a dollop of heat from it 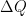 . Compute the entropy change of that parcel of gas:
. Compute the entropy change of that parcel of gas:  . Transport the heat to any parcel of gas above it — one differentially above it is fine, as long as it has a different (lower) temperature
. Transport the heat to any parcel of gas above it — one differentially above it is fine, as long as it has a different (lower) temperature 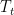 . Compute its entropy change:
. Compute its entropy change:  . Sum the two to determine the total change in entropy associated with this process:
. Sum the two to determine the total change in entropy associated with this process:


Ah, so you vote for b). That’s great, as it frees you from any need to actually try to understand the arguments involved, and it frees me from any obligation to continue to try to educate you! I especially like your argument that because we observe a lapse rate in Earth’s completely dynamic diurnally heated-at-the-bottom and differentially cooled atmosphere this must be a feature of true static thermal equilibrium in an isolated system (Jelbring’s assertion). That’s proof enough, isn’t it? Sure it is. Water being stirred or heated from the bottom inevitably behaves exactly like water sitting at rest in a container according to exactly the same argument. And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, not the question of whether nor not a DALR exists in a dry atmosphere under certain non-equilibrium conditions that permit one to more or less ignore thermal conductivity.
You seem to be conflating an assertion that there is no such thing as a dynamically driven lapse rate in any real atmosphere with the assertion that there is no such thing as a thermodynamically stable lapse rate in an isolated ideal gas subject to gravity but allowed to thermally relax to a maximum entropy state. Your argument seems to be “the real atmosphere exhibits a lapse rate, therefore that must be the true thermal equilibrium of an isolated ideal one”. You make this argument (which is hopefully fairly obviously not even logically valid, let alone unsupported by any actual physics), and attempt to “support” it by means of waving your hands about how gravity has to do work and the work has to turn into heat without considering what happens to all that heat when gravity stops doing work because the atmosphere achieves a static force profile such that
Not to be critical — I know that you very likely are trying to understand the physics in your own way — but you might try using a physics textbook or two to help out. That way you might be able to understand how the heat capacity at constant volume is related to the number of degrees of freedom available to store heat at the molecular level (instead of stating that it doesn’t depend on them, which is simply incorrect). You might understand how the heat capacity at constant pressure is related to the heat capacity at constant volume, and what the first law of thermodynamics has to do with that (in the simple case of an ideal gas, ignoring gravity).
You might come to realize that while gravitation can do a bit of work at first in a way that depends on the initial state and hence can differentially heat or cool local parts of the gas as it expands or compresses to achieve a self-supporting density/pressure profile such that
Which one is the one that the gas will irreversibly evolve towards? The answer is: “The one with the maximum entropy”. Again, you can choose to disbelieve this utterly prosaic — what is it that you said, “bog standard” result of thermodynamics, but then you are violating Jelbring’s own stated axioms, which is that bog standard physics is valid and used to obtain his conclusions.
Finally, you are down to a single question that you can, if you choose to, understand and answer, without even having to master much more than the definition of entropy for the ideal gas.
Take a small parcel of gas from the bottom of the column at temperature
This is really the only thing you need to understand — really understand — to see that Jelbring is wrong, as are the silly people who have asserted that the state of the gas with a DALR is maximum entropy. It is not. It is iso-entropic, perhaps, but it is not maximum entropy because we can easily increase its entropy by moving a differential amount of heat from a place where the gas is warmer to a place where the gas is cooler. This movement of heat is irreversible — changes of state in the gas that increase the entropy of the Universe are irreversible changes by consistent definition, something you can easily enough understand if you really try.
What we have just proven is that for any isolated gas, in the absence of a source of external work — note that I do not care in this proof how or why the initial state of the gas with some sort of thermal lapse came about, whether or not there is gravity present or absent, whether or not the gas is a mixture or pure — if we move a dollop of heat from where it is warmer (cooling it) to where it is cooler (warming it) we increase the entropy of the Universe and such a fluctuation in the state of the gas is irreversible.
In order for the system not to systematically evolve to a state where the entropy is maximum at a uniform temperature, it has to be impossible for any mechanism whatsoever to transfer heat between the two parcels. If the two parcels were inside adiabatic (insulated) walls, for example, then one could not transfer the heat. If they are in thermal contact, though, so the heat transfer can occur, then it will occur (in time) and once it happens, the transfer of heat in the other direction to create a macroscopic parcel of gas with an unequal temperature just doesn’t happen.
Eventually the system will reach a state where heat fluctuations don’t change the entropy:
which is obviously true only if $T_t = T_b$. Thermal fluctuations do not strictly increase entropy of any system — note well, any system — only when all parts of the system that are in “thermal contact” (connected by interactions of any sort that permit the transport of heat) are at the same temperature. This is the classic, textbook definition of the state of thermal equilibrium of an isolated system.
Note well, this is a statistical law. If you make the parcels of gas small enough, then you reach a scale where “temperature” as an average measure of energy breaks down, where the tiny parcels of gas are constantly “heating” or “cooling” a tiny bit in the sense that the volume in question gains or loses a bit of energy during the random motion of the molecules. As you make the parcels larger, though, in particular large enough that the concept of temperature itself is a reasonably sound one, the probability of a fluctuation happening that increases the entropy of the system becomes strongly asymmetric compared to the probability of fluctuations that decrease it. Again any good intro book has lots of examples of how this works — how mixing of an unmixed gas via thermal fluctuations is extremely likely and hence quite rapid, while separation of the mixed gas back to an unmixed state by thermal fluctuations is almost infinitely unlikely. If you don’t understand this and try to use only kinetics to figure out what happens in the gas, you can easily be misled as to the correct equilibrium distribution of internal energy as reflected in the (local) temperature. As I said, there are an infinite number of ways to create static force equilibrium and distribute the internal energy of the system among the molecules consistently at the same time, but only one (family of) distributions has maximum entropy, and that is the one at a uniform internal temperature.
I don’t know how to make it any simpler than this. If you create an imaginary gas that cannot conduct heat, of course you can make it have any thermal distribution you like. However, the standard “ideal gas” used in ideal gas models can certainly conduct heat. Real gases, e.g. N_2, O_2, CO_2, all conduct heat, although many of them are relatively poor conductors in the sense that they conduct heat more slowly than convection moves heat around in the Navier-Stokes equations, so that energy distribution is more often determined by convective flow than by conduction if there are thermal sources and sinks — differential heating — and you don’t wait long enough for hydrodynamic motion to stop and thermal relaxtion to stable thermodynamic equilibrium to occur.
None of this precludes real layers of non-isolated atmospheric gases, differentially heated on the bottom and cooled at the top, from attaining a thermal lapse rate. It just means that Jelbring’s assertion that this hydrodynamic equilibrium is also the stable thermodynamic equilibrium for the system is incorrect. His paper is incorrect. His conclusion is incorrect. It violates the second law of thermodynamics, is not maximum entropy, and (if true) would enable the construction of PMM2Ks and other impossibilities.
This result is unwelcome to those who want to pretend that a stable, static, isolated gas will always be hotter on the bottom than the top because gravity can magically maintain the thermal gradient against entropy-increasing thermal fluctuations that do negligible work against gravity but otherwise equalize the temperature gradient. Why? Only because they want to believe that this gradient eliminates the need for any greenhouse gas mediated greenhouse effect, even in a completely static isolated system with no GHGs present at all. That’s Jelbring’s explicitly stated point. I’m fairly sure that it is yours as well.
If not, if you are happy enough with a dynamic, non-equilibrium lapse rate, then we have no quarrel. You can then add in water vapor and so on with my complete blessing, as long as you do not assert that gravity can do any net, continuous work even in the dynamic case in an atmosphere with a more or less static density profile. Gravity can help heat air parcels as they move down, but only as other air parcels cool as they are moved up to replace them, and one can no more get continuous work out of gravity in the atmosphere than one can out of an ordinary pendulum. If you don’t have a source of external free energy to keep replacing energy the pendulum loses to “heat” (via irreversible friction and drag forces, for example) any real pendulum damps to (almost) perfectly zero motion over time; gravity can contribute only the energy originally stored in the pendulum when you pulled it up to start it moving.
The best papers I’ve read (so far) that seek to explain how things like the DALR and wet air lapse rates effect the actual transport of heat from the solar-heated surface and atmosphere to where it is ultimately lost via radiation are really quite good. I find them plausible — not usually “proven”, but plausible. They openly acknowledge the importance of the GHG-GHE in establishing the disequilibrium conditions that lead to a lapse rate and atmospheric heat transport in the first place, but then analyze that motion to argue that the overall feedbacks of this process are negative, not positive, something that actually explains the remarkable stability of our atmosphere in the face of internal variability that (in a chaotic system) could easily drive it to catastrophe. There is no magic in them, at least none that I can see offhand.
You are so very close, in your comments, to taking this “good” path. You just need to abandon Jelbring to his well-deserved fate and get off of the bad path, the one that obviously violates the very laws of thermodynamics that Jelbring claims that his solution is supposed to axiomatically satisfy and that I prove does not yet again in this very reply above. An ideal gas with that in force equilibrium but that exhibits a DALR isn’t a maximum entropy state of the gas. You don’t even need to go to a fully microscopic description to prove it (although there are more elegant and complete arguments that also will do the job).
In the end, it is a matter of credibility. Anyone that offers up Jelbring’s paper in a forum devoted to the question of the GHE or CAGW as “proof” that GHGs are unimportant and there is no such thing as a GHG mediated GHE is instantly in-credible, because anyone who actually knows thermodynamics, let along statistical mechanics, can instantly see that it is incorrect and absurd. OTOH, those same people can pick up any climate science textbook and read about the DALR, and most of the competent ones (in climate research) can probably derive the DALR from its base assumptions rather easily, cold. None of them would argue that there is no such thing as an (approximate) DALR visible in atmospheric dynamics, and they all are perfectly happy working with e.g. potential temperature instead of straight up temperature as a consequence. But they know that it isn’t true thermodynamic equilibrium and they know that one cannot heat anything at all by means of the DALR, that rather it is a feature of differential cooling given the heat input from the Sun.
I’d just as soon that climate skepticism be fuelled by credible arguments, not in-credible ones. But suit yourself.
rgb
Robert Brown says:
February 1, 2012 at 6:09 am
(I’m certain you have mastered Lagrangian and Hamiltonian formulations of physics and understand action principles), electrodynamics (so that Maxwell’s equations are no mystery to you, nor is relativity theory and the theory of electromagnetic radiation — did I mention that the other textbook I’ve written is a graduate level text in classical electrodynamics?)
Does it include Maxwell’s Quaternion Equations?
Tim Folkerts says:
February 1, 2012 at 12:30 pm
“All of these simulations should afforded significant skepticism. I don;t know that any of them were designed to provide more than approximately correct answers. For example. when you turn on gravity in the simulation I linked to, the total energy gradually increases. You could attribute that to some “thermogravimetric effect”, but more likely is is round-off error after millions of collisions or the effect of the step size used, or poor programming.”
Indeed. Good programming for such simulations first requires a careful analysis of the Hamiltonian for conservation laws fixing various relations among the variables (not merely simple energy and momentum conservation but also higher order symmetries, distributions, dimensional and angular limits, boundary conditions, attractors and so forth). Failure to include such constraints will cause the simulation to “drift”, often obscuring the very effects you are looking for or, worse, creating misleading artifacts.
Dr. Brown,
Your background appears to be computers, not thermodynamics or fluid mechanics.
You are grossly in error, and your opinion of how gas behaves is ridiculous. I would suggest that you dig up some texts on the subjects, and read them. Otherwise, you should stick to computers.
BigWaveDave states (without any support): “Dr. Brown, You are grossly in error, and your opinion of how gas behaves is ridiculous.”
I think he has been doing remarkably well. Perhaps you could provide one specific example of a ‘ridiculus’ statement containing a ‘gross error’ so we could discuss it?
Tim Folkerts said:
February 1, 2012 at 3:36 pm
Anything he says that doesn’t recognize that there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet, shows a fundamental lack of understanding of what gas temperature means.
Paul Birch: “The standard and fundamental definition of the thermodynamic concept of temperature is that two bodies are at the same temperature when they are in thermal equilibrium.”
Yes, yes, I understand your position; your repeating this section of your catechism doesn’t advance the ball. This is like the argument above about whether the power flows through the Poynting vector or along the electric field through the resistor: which explanation is better depends on the context. And I’ve already told you why I believe a different definition of temperature is appropriate in this case. We disagree. I’m okay with that.
“Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
Are you absolutely certain that’s a position you want to take?.
Chas – I’ve decided your program is quite enough. Did not want to get back in my old code for I would probably be looking at weeks, not days. However, I did download your modified code. I installed SmallBasic. I’m going to get my grandson to try at programming using that neat bare bones language. Quite neat. I spent some thirteen years in basic but that was a long, long time ago but I am getting the syntax back little by little.
I did make some modifications myself. Set the atom sizes to default at 15, speed to 4, gravity to 0.10 and made it so (very bottom of your code) when resetting Av’s it also just re-randomized the velocities. That got rid of the bouncing. Made the width 400 instead of 1024 to get a tall column.
Others should try this, for time after time, the kinetic energy ratio or ‘temperature’ settled out after five minutes to 1.05. I will be darn, it did end up with the bottom warmer that the top, not much, but it shows it. Now whether that program is critiqued enough, if it is perfect enough, that I do not know but that is as far as I am going to follow right now. This whole discussion really has nothing to do with Nikolov & Zeller’s theory anyway. If you were to let this perfect ideal gas radiate, which they all do to some degree, then the pressure at the bottom would have more emissivity/absorptivity and that ‘temperature’ ratio would show pressure’s influence be even higher… even without external energy… it’s called pressure broadening and it guaranteed.
Thanks for the demo!
OK, Big Wave Dave,
If you feel that
“there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet”
then give us the equation for the temperature profile. What variables does this temperature depend on. Surely if all of us who come to this conclusion are making a ridiculous, gross mistake, it should be easy to give us the correct answer.
PS. I trust you remember that this discussion is predicted on Jelbring’s assumption of an atmosphere that does not gain/lose any energy to/from space, so your answer should be for such adiabatic conditions as outlined in the top post. I will even give you the latitude of choosing whether the atmosphere interacts with the ground, or if that surface is to be considered adiabatic as well.
PPS I trust you remember that Dr Brown (and I and all the other arguing for an isothermal gas in this special situation recognize that a REAL atmosphere with GHGs radiating to space WILL have a vertical temperature gradient, but that this is a completely different situation.
Paul Birch says: “Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. ”
This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
Does it include Maxwell’s Quaternion Equations?
Well, it includes Maxwell’s equations themselves, in several incarnations of expression (including manifestly covariant). I do love geometric algebra and think that the “war” between Heaviside and Gibbs and Hamilton’s followers (Tatt?) that the quaternion advocates eventually lost was very interesting — in the end Gibbs’ notation was, probably correctly, deemed a lot easier to work with and compute with.
Do Clifford/Geometric algebras interest you?
rgb
You are grossly in error, and your opinion of how gas behaves is ridiculous. I would suggest that you dig up some texts on the subjects, and read them. Otherwise, you should stick to computers.
Well, now that you’ve gotten that semantically null verbiage out of your system, did you have some actual algebraically correct derivations or corrections to offer? Precisely what texts would you suggest? My shelves are already full of a rather lot of introductory physics textbooks — maybe thirty or forty — since publishers send me copies every year trying to get me to use them. So what’s your pleasure, Halliday and Resnick, Halliday, Resnick and Walker, Tipler, Tipler and Mosca, Serway, Serway and Beichner, Brown (oh, I suppose I shouldn’t use my own textbook, should I), Giancoli..
Or do you like some specific more advanced textbook, perhaps one that proves that thermal equilibrium isn’t isothermal for some particular system? I’d be simply thrilled to have an actual reference, since we have already heard from the author of one textbook on physical climatology above who seems to agree with me, however silly that may be. I’m certain that (since both of us are apparently wrong) you’ll have no difficulty documenting our error and directing us in the best of good will to more correct works that support your claims, whatever those claims might be since I’m not seeing any claims in your reply other than the claim that that I am — somewhere, in some unspecified way — grossly in error. No doubt, no doubt, but it would be good to know exactly where and how, gently demonstrated by a real expert like yourself.
I must confess that I fail to see how establishing that an isothermal ideal gas in static force equilibrium in a gravitational field is also a maximum entropy state of that gas is “ridiculous” — especially since I actually support the conclusion with an algebraic derivation from known and established principles — but I’m certain that you, BigWave, are more than prepared to educate me.
rgb
This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
http://en.wikipedia.org/wiki/Free_expansion
(that is, I think you are right Tim). However, I think Paul just misspoke. He did note that the free expansion leaves the average KE per molecule the same — which I know that he knows means that the temperature hasn’t changed (although the density certainly has).
Ideal gas adiabats in cyclic heat engine cycles do expand and cool, but they do work at the same time and aren’t “free”.
rgb
Anything he says that doesn’t recognize that there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet, shows a fundamental lack of understanding of what gas temperature means.
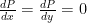

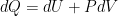 for an ideal gas. (Or, “the heat that goes into a system equals the change of internal energy of the system plus the work done by the system”, although one can use different sign conventions and change “in” to “out” in various places to get equivalent statements.)
for an ideal gas. (Or, “the heat that goes into a system equals the change of internal energy of the system plus the work done by the system”, although one can use different sign conventions and change “in” to “out” in various places to get equivalent statements.)
Ah, I see. This is why I am in gross error and ridiculous.
It’s the damnedest thing. Here I sit, thinking that the correct thermodynamic definition of the temperature of a gas has to do with stuff like:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node11.html
note especially the bit in 1.2.4 “The Concept of Equilibrium”, especially the statements that a system in thermodynamic equilibrium satisfies:
1) mechanical equilibrium (no unbalanced forces). For any fluid in near-Earth gravity, the condition for mechanical equilibrium is:
But don’t mind me, I just derived this at the board three times already this week in three different recitation sections. Note well that the condition for mechanical equilibrium does not directly refer to temperature at all and is equally valid for gases or liquids.
2) thermal equilibrium (no temperature differences). Ooo, it did not just say that! And on the MIT online physics textbook on thermodynamics, too! Gosh, BigWaveDave, you really need to go to MIT and correct them! Here we all are, making ever bigger mistakes!
3) chemical equilibrium.
Chemical equilibrium is clearly irrelevant to ideal gases. The conditions for mechanical equilibrium doesn’t depend on whether the gases are ideal or not, although for an ideal gas, the density depends on the temperature so that there are an infinite number of ways one can stack up the gas with a thermal gradient that are all still in mechanical equilibrium.
To understand why thermal equilibrium is both isothermal and maximum entropy, you have to work through a bit more of the textbook, BWD.
You — and Myrrh — might visit and spend a bit of time on:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node38.html
(“The Axiomatic Statement of the Laws of Thermodynamics”). These are the axioms that Jelbring claims are the basis of his conclusion. But are they?
Read the 0th law. “Equality of temperature is a necessary and sufficient condition of thermal equilibrium”.
Wow. It’s going to be difficult for Jelbring to defend the conclusion that “temperatures vary in a system in thermal equilibrium” and not contradict the axiomatic statement of the zeroth law.
Read the 1st law. It’s just the law of energy conservation, nothing to see here, move along folks.
Read the 2nd law, because it is the big one, the one that you, BWD, have apparently never heard of. Permit me to quote:
Although all natural processes must take place in accordance with the First Law, the principle of conservation of energy is, by itself, inadequate for an unambiguous description of the behavior of a system. Specifically, there is no mention of the familiar observation that every natural process has in some sense a preferred direction of action. For example, the flow of heat occurs naturally from hotter to colder bodies, in the absence of other influences, but the reverse flow certainly is not in violation of the First Law. So far as that law is concerned, the initial and final states are symmetrical in a very important respect.
Note well the bit about conservation of energy alone being inadequate for the unambiguous description of the behavior of a system. Omitting this is what makes Jelbring’s “proof” and Joules’ ranting and your claim that gravity alone has to directly tie into temperature all so very, very wrong. You can’t just think about energy. You also have to think about entropy!
“Tim Folkerts says:
February 1, 2012 at 7:36 pm
OK, Big Wave Dave,
If you feel that
“there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet”
then give us the equation for the temperature profile. What variables does this temperature depend on. Surely if all of us who come to this conclusion are making a ridiculous, gross mistake, it should be easy to give us the correct answer.”
What wrong with one given at wiki:
http://en.wikipedia.org/wiki/Lapse_rate#Saturated_adiabatic_lapse_rate
“PS. I trust you remember that this discussion is predicted on Jelbring’s assumption of an atmosphere that does not gain/lose any energy to/from space, so your answer should be for such adiabatic conditions as outlined in the top post. I will even give you the latitude of choosing whether the atmosphere interacts with the ground, or if that surface is to be considered adiabatic as well.”
Jelbring’s assumption is that one using a non-greenhouse like nitrogen- which 70% of mass of our atmosphere.
If there was atmosphere of only nitrogen, who think this gas would radiate any significant amount energy into space?
If a planet had a constant surface temperature of 300 K and it had 1 atm nitrogen only atmosphere and it had earth gravity. Who thinks that up to top of the troposphere it have anything radially different than earth’s atmosphere?
With no moisture the lapse rate would higher than 6.5 Km, and instead approach DALR.
But other than that wouldn’t be similar in terms of air temperature and air temperature decreasing with higher elevation?
How one could keep the surface at constant temperature isn’t the issue- whether it’s million or thousand suns or huge amount nuclear reactor heating the surface
“PPS I trust you remember that Dr Brown (and I and all the other arguing for an isothermal gas in this special situation recognize that a REAL atmosphere with GHGs radiating to space WILL have a vertical temperature gradient, but that this is a completely different situation.”
Yes, I assume you familiar mountain skiing. And glaciers in Oregon and tropical glaciers being on mountains. Do I agree that GHG’s losing heat to space could some affect on lapse rate, possible small affect. And similar small affect on lapse is conceivable any warming caused by GHG. But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula?
How much difference you assigning to CO2?
Take the constant surface temperature of 300 K with 1 atm of nitrogen and add the .04% CO2
what difference would this have on lapse rate?
CO2 is ideal gas. H20 gas is not ideal gas. The reason H2O affects lapse rate is because it condenses- whereas CO2 doesn’t [though may get close in extremely cold Antarctic weather].
“Basically, there are so few CO2 molecules in the free atmosphere, sublimation rules over deposition as a solid. Yes some CO2 may deposit on a surface at at -80.5 C (-113F ), but it would quickly sublimate back into the free atmosphere, and thus accumulation would not occur.”
http://wattsupwiththat.com/2009/06/13/results-lab-experiment-regarding-co2-snow-in-antarctica-at-113%C2%B0f-80-5%C2%B0c-not-possible/
So my point is this change could occur, not that any CO2 would accumulate- so at 1 atm or more and -80.5 C or lower CO2 would not be an ideal gas. And also under 5 atm of more, CO2 would not be ideal gas at normal earth temperatures.
And obviously under certain circumstance not found on Earth, H2O could be an ideal gas.
One last comment, specifically for Myrrh, who appears ready to learn precisely why Jelbring is wrong and understand it!
Read:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node41.html
Note well that this page largely recapitulates my elementary arguments. Note well also that I didn’t use this page (or any actual textbook) to make them, because I’m pretty competent at thermo at this level, although it gets harder and I have little doubt that there are plenty of specific problems I’d have difficulty with.
Pay special attention to the “hot brick” example — it is a very similar heuristic to the one I was using to justify irreversible thermal relaxation in the gas. Or just look at the problem of heat conductivity between two reservoirs, which is absolutely identical to my own argument.
Actually, this whole textbook is both easy to read and fairly complete. If you want to quickly learn or review basic thermodynamics, you could do far worse. I hope I can make my own online textbook comparable in quality when I finish it. BigWaveDave should also take note. Joules too. In fact, everybody. If you want to make valid, believable thermodynamic arguments, it helps a lot if you have a reasonable grasp of valid, believable thermodynamics.
rgb
But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula? in the BB equations for the gas at all frequencies, the gas has heat capacity but it is totally transparent.
in the BB equations for the gas at all frequencies, the gas has heat capacity but it is totally transparent. (as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface. Initially there will be a lapse rate of sorts as it displaces cooler air, but the heat carried up has no place to go. Low pressure, high temperature air will always have the lowest density and rise to the top, and because air is a poor conductor of heat the air will stratify hot on top down to cooler on the bottom — an inverted lapse — until one gets to a turbulent zone that turns over diurnally. One would expect this bottom layer to be thin and the thermal lapse to be small — the air above this turbulent bottom would be nearly uniform in temperature in time.
(as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface. Initially there will be a lapse rate of sorts as it displaces cooler air, but the heat carried up has no place to go. Low pressure, high temperature air will always have the lowest density and rise to the top, and because air is a poor conductor of heat the air will stratify hot on top down to cooler on the bottom — an inverted lapse — until one gets to a turbulent zone that turns over diurnally. One would expect this bottom layer to be thin and the thermal lapse to be small — the air above this turbulent bottom would be nearly uniform in temperature in time.
As you stubbornly refuse to acknowledge, in spite of a textbook author chiming in on the list in person, the DALR arises — literally — because packets of air arise and afall in circulation. In Jelbring, although he quotes (without seeming to understand) this well-known fact, he then immediately turns around and asserts that the DALR holds in a static atmosphere, one without circulation. Perhaps we are finally reaching a true consensus that this is false, given that I’m quoting straight out of MIT’s online thermodynamics textbook that it is.
The reason that GHGs (and dynamics) are essential to the DALR is very simple. Assume that Jelbring’s ideal non-greenhouse atmosphere doesn’t radiate or absorb radiation at all. If you like,
In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given
With GHG’s and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere. Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. The DALR requires convection to form. No active active heating of the surface accompanied by active cooling of the upper atmosphere, no dynamically maintained thermal gradient, no convection, no dynamically maintained DALR.
The point is that the formula for the DALR comes from the assumption that the air heats down low and rises, expanding adiabatically into the air above it (doing work against its increased pressure/density) and cooling as a consequence, a process that only “stops” when there is a uniform lapse between the warm bottom and the actively cooled top. It’s not really “stable”, it is dynamically sort-of-stable, which is why the atmosphere almost never exhibits a perfect DALR and sometimes is remarkably isothermal, why one can observe thermal inversions (especially if you stop heating the bottom but perhaps don’t stop heating the top).
This reasoning is heuristic, of course, and it could be mistaken. I think it is pretty reasonable, though. It’s difficult to test empirically in our real atmosphere, because we cannot lose the GHGs we already have, and no planetary atmosphere we can see lacks them. The only way I can think of to properly test and support any hypothesis either way is via modelling, basically solving the hydrodynamic equations for toy planets with and without upper atmosphere cooling. A bit of a daunting task, actually, but that’s what modelling is good for — to give us a handle on physical situations we cannot directly observe in a lab but where we know or think we know the basic underlying mechanics well enough to build a model.
Perhaps even a non-GHG world would still exhibit large scale equator to polar convective rolls that would provide enough convective mixing to maintain a DALR. That is actually an interesting question, a worthy thing to build a model to test. If the model agrees, it would be an actual physical calculation that supports the idea that a vertical atmospheric lapse rate can be maintained by lateral/horizontal convection. I’m dubious — I don’t think the tropopause would be very high at all, if true — but I won’t pretend that I know for certain.
rgb
Robert Brown says
“and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere. Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. The DALR requires convection to form. ”
This interpretation seems at odds with the Harvard Paper I have linked.
They define convection to be when unbalanced force acts on the air parcel.(bottom of page 13)
Hydrostatic equilibrium must be consistent with no unbalanced force acting on the parcel.
This is when
1. The parcel is at rest.
2. The parcel moves at constant speed .
In their interpretation both operate at DALR for dry air.
In situation 1 there is no temperature change
In situation 2 the temperature changes by 9.8K/km up or down.(- or +)
Both conditions are present in the neutral atmosphere.
This condition can be quite stable at night (see the near neutral residual layer page 31)
Of course convection is the major method of heat transfer in the atmosphere however how does heat transfer when there is little or no convection?
Two methods remain
1. Radiation
2. Conduction (diffusion)
So they must between them transfer heat across the temperature differential.
I have made this point already in this thread but you either have not seen it or perhaps you agree with it.
However your lack of response is a source of confusion.
http://www-as.harvard.edu/education/brasseur_jacob/ch2_brasseurjacob_Jan11.pdf
Robert Brown says:
February 1, 2012 at 11:52 pm
But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula?
As you stubbornly refuse to acknowledge, in spite of a textbook author chiming in on the list in person, the DALR arises — literally — because packets of air rise and fall in circulation.
I have never stubbornly refused to acknowledge- most of posts on topic have mentioned something regarding the buoyancy of air. How can you translation this into “stubbornly refuse to acknowledge” that packets of air rise and fall.
“In Jelbring, although he quotes (without seeming to understand) this well-known fact, he then immediately turns around and asserts that the DALR holds in a static atmosphere, one without circulation.”
This has been a common point of this dispute. You and others seem to say this lapse rate would not continue. Saying this does not occur, has been something I heard, but I have not heard what does occur.
I assume that without water or other factors, in a pure nitrogen atmosphere one will have a lapse rate close to DALR. I assume there is heating or no loss of heat. I view no lost of heat as “impracticable”. For sake of thought experiment I am willing to accept that “some way unknown to me this could be possible”. But balancing the heat from surface is something one could do and one could conceivably limit the amount of heating needed. So however it is done, the surface must be keep at a constant temperature. Therefore with surface which remains at a constant temperature there would be very little in terms of packets air that rise and fall in circulation.
So in summary a disagreement seems to be that I think with little or no circulation they is still a lapse rate. And you and others apparently do not. So, what is your view of would occur if there is little or no circulation?
Btw, if given too much circulation, I believe you would not have a lapse rate.
If given too much heat the added warm air would rise and stay at the top. Though *if* this is constant high heat and if not pressurized in a container [gravity is controlling the pressure] the lapse rate will return. Since too much circulation negates a lapse rate, it seems it a smaller degree of “too much” circulation *may* reduce the lapse rate. So according to this, deserts or other areas associated with strong thermals may reduce the lapse rate by some amount.
“Perhaps we are finally reaching a true consensus that this is false, given that I’m quoting straight out of MIT’s online thermodynamics textbook that it is.
That would nice, I liked it if we could agree on what we disagree on.
“The reason that GHGs (and dynamics) are essential to the DALR is very simple. Assume that Jelbring’s ideal non-greenhouse atmosphere doesn’t radiate or absorb radiation at all. If you like, \epsilon = 0 in the BB equations for the gas at all frequencies, the gas has heat capacity but it is totally transparent.”
I think it’s possible that N2 might radiate some energy- but also think it’s an insignificant amount and can be safely ignored. Though what N2 may collide with, whether GHG or surface, is maybe an issue but leaning towards probably insignificant.
“In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given \rho = \frac{M}{RT} P (as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface.”
No. The pressure will increase, reducing density of packets of air which will rise.
“Initially there will be a lapse rate of sorts as it displaces cooler air, but the heat carried up has no place to go. Low pressure, high temperature air will always have the lowest density and rise to the top, and because air is a poor conductor of heat the air will stratify hot on top down to cooler on the bottom — an inverted lapse — until one gets to a turbulent zone that turns over diurnally. One would expect this bottom layer to be thin and the thermal lapse to be small — the air above this turbulent bottom would be nearly uniform in temperature in time.”
What you seem to be describing is when heating causes an increase in the lapse rate. Or it’s sort runaway in buoyancy. Or an accelerated buoyancy- the higher the air packet goes up [or down] the faster goes [or it merely maintains it’s velocity-keeps it’s buoyancy as it rises].
“Clearly, an atmosphere whose lapse rate is less than the adiabatic value is stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic value then, after rising a little way, the packet will be less dense than its immediate surroundings, and will, therefore, continue to rise due to buoyancy effects. Clearly, an atmosphere whose lapse rate is greater than the adiabatic value is unstable.”
http://farside.ph.utexas.edu/teaching/sm1/lectures/node56.html
“With GHG’s and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere.”
Ah, getting to issue here.
Now, I said I don’t dispute the possibility that GHG’s have an affect upon the lapse rate.
But you saying it has a large effect.
First it seems rather obvious that if GHG were having such large effect, GHG would not be warming the planet. Second, water vapor is scarce in upper troposphere, thereby leaving much of the work to be done by CO2 or other rather rarefied greenhouse gases. Third you have fairly thin atmosphere in upper troposphere- and even if the GHG were capable cooling as mad demons, the effect during daylight would be easily overwhelmed. And if could be so severe as to have effect during daylight, then it would equally continue during night. It seems one would have waterfalls of thin atmospheric air in the upper troposphere. Why isn’t there significant difference in lapse between day and nite?
Anyways, it would make H2O as the only “greenhouse gas” that is warming the planet, others are cooling it. I suspect the CO2 may cause some cooling, but haven’t considered it causing that much cooling.
“Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. ”
Well I would agree that convection does move a lot heat around, but convection is strongest from surface to mid troposphere. And generally you seem to describing an unstable atmosphere- gliders would be more commonly used and would be useful for travel purposes.
“This reasoning is heuristic, of course, and it could be mistaken. I think it is pretty reasonable, though. It’s difficult to test empirically in our real atmosphere, because we cannot lose the GHGs we already have, and no planetary atmosphere we can see lacks them. The only way I can think of to properly test and support any hypothesis either way is via modelling, basically solving the hydrodynamic equations for toy planets with and without upper atmosphere cooling. A bit of a daunting task, actually, but that’s what modelling is good for — to give us a handle on physical situations we cannot directly observe in a lab but where we know or think we know the basic underlying mechanics well enough to build a model.
Perhaps even a non-GHG world would still exhibit large scale equator to polar convective rolls that would provide enough convective mixing to maintain a DALR. That is actually an interesting question, a worthy thing to build a model to test. If the model agrees, it would be an actual physical calculation that supports the idea that a vertical atmospheric lapse rate can be maintained by lateral/horizontal convection. I’m dubious — I don’t think the tropopause would be very high at all, if true — but I won’t pretend that I know for certain.”
Other than world of thought experiments, to get a lapse rate you do need heat. And for understanding of any kind affect of gravity on lapse rate, you need big systems. It seems comparative planetary bodies could provide more definitive answers. In the near term, Ceres may provide some interesting answers.
A guy called Chris Ho-Stuart, is working on Excel program which model a planet which not heated from sunlight. His latest version:
http://www.datafilehost.com/download-9a244b84.html
The program incorporates lapse rates and he has paid a lot attention to getting them right, and says it’s in accordance with Principles of Planetary Climate by R. Pierrehumbert .
He thinks GHG has large effect of lapse rates. He started by first modeling Nitrogen atmosphere and still working towards incorporating GHG gases.
Joe Born says:
February 1, 2012 at 6:12 pm
Paul Birch:“Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
Joe: Are you absolutely certain that’s a position you want to take?
Pretty sure.
Tim Folkerts says: This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
I’m fairly sure I’m correct here. What you (and Robert Brown’s wiki link) are calling free expansion is expansion into an empty vessel, with temperature being measured after the gas has hit the far side and equilibriated. Free expansion into space is different, because the kinetic energy doesn’t get converted back into thermal energy. The gas is “pushing against something as it expand[s]” – it’s pushing against itself. So it ends up as an ever-expanding shell, like a supernova remnant. It will only heat up again if it runs into another medium.
This isn’t rocket science … oh, wait, it is rocket science! Imagine that the full sphere is divided up into twelve pentagonal rocket nozzles in a regular icosahedron. Propellant gas cools as it flows out the nozzles; work is done accelerating the propellant mass outwards. T~V^(1-Cp/Cv). For large expansion factors essentially all the energy goes into the jet velocity. The expanding propellant pushes against the nozzle walls as it goes, but since in this geometry there is an equal and opposite force from either side of each partition, we can eliminate the nozzles altogether; the gas will still expand and cool the same way.
Because the gas continues to expand it’s not in equilibrium; but it’s still in LTE (at least until it gets extremely cold and rarefied). We can see it cool by watching its thermal radiation.
Robert Brown says: http://en.wikipedia.org/wiki/Free_expansion (that is, I think you are right Tim). However, I think Paul just misspoke. He did note that the free expansion leaves the average KE per molecule the same — which I know that he knows means that the temperature hasn’t changed (although the density certainly has).
Ideal gas adiabats in cyclic heat engine cycles do expand and cool, but they do work at the same time and aren’t “free”.
My point is that the gas is doing work on itself (and in that sense the expansion isn’t “free”), and that the directed radial motion that results is not thermal energy; this KE would contribute to the gas’s temperature again if the expansion were reversed isentropically, or the gas hit a wall and randomised it irreversibly, but not if it were instead extracted from the bulk flow by eg turbines or pistons.
“In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given \rho = \frac{M}{RT} P (as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface.”
No. The pressure will increase, reducing density of packets of air which will rise.
Oh, I misread it. I thought you said density would increase.
I blame the lack of coffee:)
Robert Brown says:
February 1, 2012 at 12:58 pm
Ah, so you vote for b). That’s great, as it frees you from any need to actually try to understand the arguments involved, and it frees me from any obligation to continue to try to educate you!
Well, Robert, there’s your problem in a nutshell. Rejecting a) doesn’t mean I’ve gone for b). But I’m glad it frees you from any obligation to continue to try to educate me, as this was self-imposed and now I can hope that includes not setting me homework..
I’ll just repeat what I said: “but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background.”
I explained that by giving an example from my own experience re assumed accuracy by claimed authority, and, as I pointed out earlier, you haven’t even read his paper with any understanding, that I can fathom as you launched into a completely different and irrelevant tangent.
I especially like your argument that because we observe a lapse rate in Earth’s completely dynamic diurnally heated-at-the-bottom and differentially cooled atmosphere this must be a feature of true static thermal equilibrium in an isolated system (Jelbring’s assertion). That’s proof enough, isn’t it? Sure it is. Water being stirred or heated from the bottom inevitably behaves exactly like water sitting at rest in a container according to exactly the same argument. And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, not the question of whether nor not a DALR exists in a dry atmosphere under certain non-equilibrium conditions that permit one to more or less ignore thermal conductivity.
There are several disparate ideas in that. The first that we observe a lapse rate in Earth’s atmosphere is what is relevant here as I noticed in thinking through what he was saying, the weather systems created by heating and so on are in effect superimposed on/intermingled with the basic already well known phenomenon of gravity created lapse rate. Jelbring has made it clear that one has to strip all those superimpositions away and look at just what is left. As I’ve said, this is the basic building block of meteorology, a science that’s been going for some time and has well established understanding, and teaching, on this. I quoted one such and provided a link to show that what he was saying about rising air packets was standard basic knowledge, and relevant to what he was saying. What you’re missing is seeing how that is important here – in understanding what Jelbring is saying – BigWaveDave went into more detail, and if you put the two together you’ve got the real picture of the basic phenomenon. Perhaps you’re conflating heat with temperature and missing what BWD said.
“Water being stirred etc.” – is also something you missed picking up from BigWaveDave’s reply to you, this is about gases and they have behaviour particular to them.
“And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, etc.” – is in comment on the state of play in ‘climate’ science. It was re the fact that you also missed the point in Jelbring’s opening setting of the scene of what he was actually saying and imagined it was something he was claiming as a unique insight to himself, he was actually saying that ‘climate’ scientists ignore this, the well known to meteorology basic, and I threw in ‘like ignoring the Water Cycle’, because, that’s what ‘climate’ scientists do. They ignore the basics, well known and still taught, actual real world physics, by simply not teaching it. This, imho etc. I think you simply don’t know about it. I reached that possibility by comparing it with the extraordinary ‘energy budget’ used in ‘climate’ science – it is completely missing the Water Cycle which brings down Earth’s temperature to 15°C from 67°C it would be without it. Perhaps, that I knew this, is what helped me better picture what Jelbring was saying, because that is the main ‘greenhouse’ gas and without it we have a good approximation to Jelbring’s dry atmosphere of his model, a step in getting to his model.
You seem to be conflating an assertion that there is no such thing as a dynamically driven lapse rate in any real atmosphere with the assertion that there is no such thing as a thermodynamically stable lapse rate in an isolated ideal gas subject to gravity but allowed to thermally relax to a maximum entropy state. Your argument seems to be “the real atmosphere exhibits a lapse rate, therefore that must be the true thermal equilibrium of an isolated ideal one”. You make this argument (which is hopefully fairly obviously not even logically valid, let alone unsupported by any actual physics), and attempt to “support” it by means of waving your hands about how gravity has to do work and the work has to turn into heat without considering what happens to all that heat when gravity stops doing work because the atmosphere achieves a static force profile such that . Is it “stuck” where gravity leaves it, or can it move, say, by irreversible diffusion or heat conduction? What happens when some of the heat moves from one temperature in one part of the gas to another part of the gas at a different temperature? In particular, does the entropy of the gas increase or decrease?
I think you don’t understand gravity in this. Your “when gravity stops doing work” is what gravity is. Gravity isn’t a source of heating, it’s not heating molecules by ‘pulling them down’ which once it’s done this heating stops.. Gravity is, gravity plus mass gives a state of gravity/pressure, we don’t get winds until there is a pressure gradient force which comes from unequal heating. Jelbring leads to reaching this basic is that all the extras are non-existant, no radiation coming in, none from surface heat capacity, so entropy etc. negligible. One needs to chuck all these out to get to the underlying state, and from there to the constant in relationship.* It’s called the hydrostatic equilibrium** state, please, don’t go off into another tangent about liquids, see BWD, it relates to our gaseous atmosphere because both gases and liquids are fluids, it’s an ocean of gas we have above us. But. Gases behave in a way particular to them even within fluids. As BWD explained:
You can’t say anything of relevance to gases in our atmosphere if you’re not referring to the actual properties and process of gases.***
That’s all Jelbring is saying, that it’s already a known and from this etc.:
And so, you don’t understand what Jelbring is saying, because this basic of our real world is missing from ‘climate’ science.
* http://www.ux1.eiu.edu/~cfjps/1400/pressure_wind.html
If we keep the mass of the gas constant, then we can simplify the equation to (PV)/T = constant. That means that:
For a constant P, T increases, V increases.
For a constant V, T increases, P increases.
For a constant T, P increases, V decreases.
** http://www.metoffice.gov.uk/learning/science/first-steps/atmosphere/wind
Hydrostatic equilibrium: “In fact, the gravitational force is almost exactly balanced by the pressure gradient force, a condition known as hydrostatic equilibrium. Hydrostatic equilibrium explains why the Earth’s atmosphere does not collapse to a very thin layer on the ground.”
*** Same applies to electromagnetic radiation, it is not ‘all the same’. These are divided into distinctly different phenomena, each with its own characteristics, properties and processes. Visible light is not thermal energy on the move, it cannot heat water as thermal infrared can heat water, water is a transparent medium for it, it works on electronic transition level of effect on meeting matter, AND not vibrational resonance, i.e. moving the whole molecule, kinetic energy, which is the process of thermal infrared, etc. ‘Climate’ science mangles all of these by giving the properties of one to another and then claiming visible light can do what it isn’t physically possible for it to do.
AGWSF = ‘CLIMATE SCIENCE’. This is Fictional Science because it doesn’t describe the properties and process in our real world we see around us. QED.
Really sorry Mods, I checked and checked and still missed it, please would you fix there should be a closed blockquote after the paragraph seven up, :
BigWaveDave continues – “In Earth’s atmosphere, the air molecules are not fixed at any particular height. …with height must vary with the density.”
[FIXED -w.]
p.s. And to make it clear, the reason I’m not at all surprised that this has been missed out and that you know nuttin about it, is because for several decades universities have been teaching from the AGWSF energy budget, which is missing the WHOLE Water Cycle, and none of you super educated in physics with years of teaching and phd’s have even noticed it’s missing!
First, get a proper energy budget basic in place with real world physics and ditch the science fiction world you’ve created. Not sure though, that any of you would know how to go about that..
now I can hope that includes not setting me homework..
Oh no. I assigned homework already;-): Read the MIT online thermo book and work through it, cover to cover. Your arguments can only improve if you actually learn the laws they are currently flouting, and while I fully understand your lack of respect for “authority” — while respectfully suggesting that it edges well over into iconoclasm for its own sake when you make statements that violate the experimentally verified laws clearly explained in every thermo textbook. It is difficult to claim that these textbooks are part of the “IPCC global conspiracy”, given that thermodynamics was mostly worked out and derived/proven over a hundred years ago, well before there was a United Nations.
If you want to suggest that modern thermodynamics as given in these textbooks is wrong, that is a very serious charge, and should only be made if you are prepared to prove it. And by prove it, I really mean prove it — prove it at the accepted standard of physics, which requires a complete argument down to microscopic physics, plus empirical support. Prove it in a way that would get past any reasonable referee, prove it convincingly. If this task is daunting — and it should be, because it is openly impossible in the contexts they discuss — then perhaps you could provisionally accept that every physicist in the world is a) not an idiot; and b) not engaged in some sort of global conspiracy just because a result that you want to believe in happens to violate the thermodynamic laws of physics.
I explained that by giving an example from my own experience re assumed accuracy by claimed authority, and, as I pointed out earlier, you haven’t even read his paper with any understanding, that I can fathom as you launched into a completely different and irrelevant tangent.
You don’t even understand your own example, but that is quite beside the point, because it is a logical fallacy to state “I think that a physicist once made a mistake, although I can’t prove it and haven’t even tried, therefore you are making a mistake now in your analysis of Jelbring.” Surely this is clear to you. You don’t accept my authority, fine. How about the MIT textbook I linked and assigned? How about Zemansky? How about Stanley? How about the introductory physics textbook of your choice? How about I start on the list of stat mech books? Is there any authority you will accept, or is your argument going to remain “I’m completely ignorant of actual thermodynamics and statistical mechanics and mechanics and electrodynamics and quantum theory — beyond the level a bright high school student might have accomplished — but I doubt that any of them are right, so when Jelbring states a result that openly contradicts their content that doesn’t mean that he is probably wrong.”?
Your assertion that I don’t understand his paper is simply incorrect. I’ve read it several times at this point. Its claims are quite clear. He asserts that gravity will create a thermal lapse rate that is there in his isolated ideal gas in a near-Earth gravitational field in thermal equilibrium — the condition that an air column will reach after all irreversible relaxation processes such as conduction, convection, and radiation have completed. He forgot to mention conduction, but if he truly meant to leave it out then his conclusion is already obviously false as he left out a physical process that is infinitely faster than thermal relaxation due to radiation in a GHG-free atmosphere, where there is none. To prove it he cites a single “well-known” result — the DALR — from a single textbook on climatology, and claims that it describes static thermal equilibrium.
Yet — as I’ve shown by reference to an actual textbook on thermodynamics — a thermal lapse rate of any sort in a system that supposedly in thermal equilibrium explicitly contradicts two laws of thermodynamics: The zeroth law and the second law. All of your, and his, arguments about “energy balance” revolve around the first law, but what you fail to understand is that there are an infinite number of ways to split the available energy including the gravitational potential energy available to the system without violating the first law. The second law dictates the split that actually occurs in equilibrium.
He then uses his incorrect claim that the DALR describes a state that satisfies the three simple conditions given in the actual textbook above for thermodynamic equilibrium to prove his argument that the equilibrium state of his isolated gas has a nonzero thermal gradient.
How, exactly, is this not circular reasoning on the one hand, and circular reasoning from an obviously false premise on the other? At the very least somewhere the onus of proof was upon him to demonstrate that an atmosphere with a DALR is actually in a state of thermodynamic equilibrium, which would have required some actual work and algebra on his part, one would think, since it violates the letter of these laws.
As I’ve said, this is the basic building block of meteorology, a science that’s been going for some time and has well established understanding, and teaching, on this.
Did you somehow miss Caballero’s post above, or did you just blank out your mind and pretend that it never happened. I’m perfectly happy to strip away all of those “imposition” and concentrate on a dry ideal gas, just like Jelbring did, and in fact have done nothing else. I was pointing out that you constantly ring in moisture and all sorts of other stuff, so that you would stop doing it. Focus on the argument given in Jelbring, only, using the very axioms of ordinary thermal physics that he claims are satisfied by his result. Well, I’ve quoted them, provided a link to a textbook containing them, and his claims violate the letter of those laws, they are a direct do-not-pass-go or collect $200 violations of those laws. You’d have to look long and hard to find as pure a logical contradiction as:
* Zeroth law: (Thermally connected) systems in thermodynamic equilibrium are isothermal.
* Second law: (Thermally connected) systems in a maximum entropy state are isothermal.
* Jelbring: An isolated ideal gas in a near-Earth gravitational field is a thermally connected system in thermodynamic equilibrium only when it it is not isothermal.
Do you see the problem yet? I don’t really give a damn whether or not you understand why the zeroth and second laws are true and correct, there is a bald contradiction between Jelbring’s stated conclusion and the laws he himself asserts as axioms. He did not address this contradiction. His argument is circular reasoning and completely lacks any detail. Why, exactly do you find this believable?
Do you not believe in the zeroth law of thermodynamics? If not, why not? Do you not believe in the second law of thermodynamics (which implies the zeroth law — they are consistent)? If not, why not? If you wish to defend Jelbring, please do so, not by doubting me but by addressing the argument. Which of these two laws is wrong? Why? Where is your proof? How is your reasoning, not just as circular and contradictory as Jelbring’s?
What you’re missing is seeing how that is important here – in understanding what Jelbring is saying – BigWaveDave went into more detail, and if you put the two together you’ve got the real picture of the basic phenomenon. Perhaps you’re conflating heat with temperature and missing what BWD said.
So, you really think that you and BWD understand heat and temperature better than I do, I see. Fine, I don’t mind you stating that, but please prove it. You cannot prove it in English. For you to prove your assertions you — like Jelbring — actually have to do some algebra, and if your algebra starts out with assertions that openly violate the laws of thermodynamics you — like Jelbring — must prove why and how the laws of thermodynamics won’t hold.
You might also think hard about who is more likely to have developed a better understanding of heat and temperature — you, BWD, or me. Only one of the three of us have studied the subject in depth, continue to study it in depth, and taught it. You are free to doubt that I fully understand it, but is it really probable that your understanding is better than mine? I at least know the content of the MIT textbook on thermodynamics without having to read it and can pretty much work through all of it at the board at any time without a moment’s notice. Can you? Do you even know what the important points and arguments are? Can you derive the expression for an adiabatic reversible process for an ideal gas, for example, if you very life depends on it, without just copying the derivation from the very physics textbooks that you stubbornly refuse to consult when analyzing Jelbring?
It was re the fact that you also missed the point in Jelbring’s opening setting of the scene of what he was actually saying and imagined it was something he was claiming as a unique insight to himself, he was actually saying that ‘climate’ scientists ignore this, the well known to meteorology basic, and I threw in ‘like ignoring the Water Cycle’, because, that’s what ‘climate’ scientists do. They ignore the basics, well known and still taught, actual real world physics, by simply not teaching it.
This is an extraordinary claim! You have clearly read far more physical climatology textbooks than I have, because the ones I’ve looked through do nothing of the sort. In fact, it is a completely absurd claim. Two out of two cited in this discussion, Caballero and Holton, do nothing of the sort. One out of two authors of books cited in this discussion (the only one living) has already stated that Jelbring is incorrect. Climate scientists do not ignore the DALR. They simply understand perfectly well that it is not a state of thermodynamic equilbrium, it is a state of hydrodynamic equilibrium subject to several assumptions, including differential heating and ongoing heat transport, a particular steady-state solution in the limit of non-turbulent flow of the Navier-Stokes equations. Jelbring’s only actual unique claim in his paper is that this state is actually thermodynamic equilibrium, and it is incorrect. End of story.
If you wish to claim that “climate scientists” ignore the Water Cycle, prove it. Cite one single textbook on physical climatology that ignores the water cycle.
Of course you can’t, because this is not true. What you mean to say is that many climate scientists look at the “water cycle” and somehow end up with conclusions that differ from the ones that you wish were true. You like Jelbring not because it is correct, but because it supports a conclusion that you wish was true. Wishful thinking does not make something true, nor does an open indictment of all “climate scientists” in the world make that indictment true. If you wish to make the claim and have it not be mere verbiage, back it up with actual evidence. Find me physical climatology textbooks that leave it out.
Now, if you want to claim that some climatologists sometimes leave it out of some of their research or papers, well, hard to argue with that, given that Jelbring leaves it out and he is, well, sort of, maybe, a really really bad climatologist.
I think you don’t understand gravity in this. Your “when gravity stops doing work” is what gravity is. Gravity isn’t a source of heating, it’s not heating molecules by ‘pulling them down’ which once it’s done this heating stops.. Gravity is, gravity plus mass gives a state of gravity/pressure, we don’t get winds until there is a pressure gradient force which comes from unequal heating.
Ok, I’m going to say this as gently as I can. Oh, hell, no I’m not. You are so cosmically clueless about basic physics that you have no business even participating in this discussion unless and until you do your homework, starting by developing an elementary understanding of work, energy, energy conservation and gravity.
Seriously, man. You’re just making a fool of yourself now.
Jelbring leads to reaching this basic is that all the extras are non-existant, no radiation coming in, none from surface heat capacity, so entropy etc. negligible. One needs to chuck all these out to get to the underlying state, and from there to the constant in relationship.* It’s called the hydrostatic equilibrium** state
Sure, and hydrostatic equilibrium is not thermodynamic equilibrium. And hydrostatic equilibrium itself is not isothermal if and only if there is a thermal gradient across an ideal gas maintained by external heating and cooling in the circumstances described by Jelbring.
Come on now, you’re getting close, you can say it. Jelbring is wrong. He incorrect asserts that the hydrostatic equilibrium state with a lapse rate is true thermodynamic equilibrium and would be present in an isolated gas after a very long time. No, it wouldn’t. It would violate the second law. It would also violate the Navier-Stokes equations, which have a trivial static solution in the unheated case that is — unsurprisingly — precisely the state I give above.
Finally, I have no idea what you mean when you say “entropy etc negligible”. The ideal gas is in thermal contact with itself. Entropy exchange within the gas itself can never be “negligible”, not without making your answer completely non-physical.
Oh wait, it is.
rgb
Hydrostatic equilibrium: “In fact, the gravitational force is almost exactly balanced by the pressure gradient force, a condition known as hydrostatic equilibrium. Hydrostatic equilibrium explains why the Earth’s atmosphere does not collapse to a very thin layer on the ground.”
Oh, I can’t resist one more comment. Are you somehow ignoring the fact that the top post contains the condition for hydrostatic equilibrium? Since you steadfastly refuse (so far) to crack an actual textbook on thermodynamics you have no doubt still failed to observe that there are an infinite number of possible distributions of energy that can be in hydrostatic equilibrium in Jelbring’s isolated ideal gas, but only one of them is maximum entropy and hence global thermodynamic equilibrium. Guess which one.
Of course that is your real problem. You don’t understand the condition for hydrostatic equilibrium, and you can’t formulate the actual integral that would describe the hydrostatic profile of an ideal gas, given a proposed temperature as a function of height $T(z)$. If you want, I’d be happy to help you out and show you, or you can continue to argue as if hydrostatic equilibrium is itself a unique state, the one with the DALR. In spite of the fact that the top post derives the explicit form for an ideal gas in hydrostatic and thermal equilibrium, I might point out.
rgb
I’m fairly sure I’m correct here. What you (and Robert Brown’s wiki link) are calling free expansion is expansion into an empty vessel, with temperature being measured after the gas has hit the far side and equilibriated. Free expansion into space is different, because the kinetic energy doesn’t get converted back into thermal energy. The gas is “pushing against something as it expand[s]” – it’s pushing against itself. So it ends up as an ever-expanding shell, like a supernova remnant. It will only heat up again if it runs into another medium.
OK, I think I buy that. The average kinetic energy per molecule doesn’t change, but the distribution of KE in parcels of gas in the original rest frame is no longer thermal because the parcels of gas themselves now have a CM kinetic energy and in their local CM frame the local temperature is lower. If/when the parcels collide elastically with something so that their CM velocity goes away, the energy becomes thermal again.
I was indeed thinking of free expansion into a container and didn’t realize that you were talking about free expansion into space, although I should have. IIRC this is the sort of phenomenon that explains those vortex nozzles that were being described upthread — you drive a gas into transiently into a state with an adiabatic lapse by “slamming on” a strong centripetal force and then selectively pull off the cooler molecules at the top. Or an adiabatic nozzle. Yeah, now I remember that stuff. Sorry.
rgb
So in summary a disagreement seems to be that I think with little or no circulation they is still a lapse rate. And you and others apparently do not. So, what is your view of would occur if there is little or no circulation? ) equilibrium and simultaneously in (iso)thermal equilibrium, repeatedly demonstrated to be the state where the gas has maximum entropy and the state the ideal gas will go to under the precise conditions described by Jelbring. Or for that matter a gas that is isolated at the top and in contact with a constant temperature reservoir at the bottom. You need a thermal gradient to drive convection and a lapse rate.
) equilibrium and simultaneously in (iso)thermal equilibrium, repeatedly demonstrated to be the state where the gas has maximum entropy and the state the ideal gas will go to under the precise conditions described by Jelbring. Or for that matter a gas that is isolated at the top and in contact with a constant temperature reservoir at the bottom. You need a thermal gradient to drive convection and a lapse rate.
See the top post, which derives the actual state of an ideal gas atmosphere in both hydrostatic (
The problem then is that it is no longer possible to argue that the gas plus gravity creates the lapse rate. Rather, the intrinsic thermal lapse between two reservoirs at different temperatures creates the convection that establishes a self-consistent lapse in the atmosphere in between, which can be enormously complex because once the convective forces exceed certain limits, the convective flow becomes turbulent.
The problem, as you can see, is that atmospheric dynamics is really very, very difficult. One has to solve the Navier-Stokes equation, which is arguably one of the most complicated physical formulae that we have been able to semi-quantitatively construct (or rather, construct for a still somewhat idealized description). The DALR itself — as any good textbook will tell you — is an idealization of an idealization, a no turbulence, no internal conduction model for the dynamic gas as parcels slowly waft up or down in convection.
Jelbring does not address this. His paper explicitly establishes conditions where there is no convective flow and no heat input at all, let alone differential heat input, and then further asserts that we must wait a long time for the system to attain its true equilibrium. He then basically asserts that the well-known hydrodynamic DALR is the true equilibrium, and claims his own assertion as (circular) proof that the DALR is the true equilibrium.
No, it’s not. The state of atmosphere derived in the top post, which is a derivation that can frequently be found in introductory physics textbooks (including my own) is the state of simultaneous hydrostatic (force) equilibrium, thermal equilibrium, and chemical equilibrium (the latter trivial for an isolated ideal gas). This state does not violate the zeroth or second laws of thermodynamics as a steady state, long time solution. Jelbring’s asserted gas with a stable lapse does, and moreover turns gravity into a Maxwell’s Demon.
Please separate out any arguments concerning whether or not the real atmosphere, heated and cooled all the time and everywhere, has a DALR from Jelbring’s assertion that it is thermodynamic equilibrium. I’m only concerned with the latter, because it is the only actual content Jelbring contributes to what is otherwise an assertion that the DALR is derived in one single textbook (in an explicitly dynamic context, but he doesn’t talk about that).
You do seem to be getting close to “getting it”. Perhaps this will help you understand the point and come to agree that Jelbring’s basic assertion is completely incorrect and his argument is both unsound logically and directly contradicts the very laws of thermodynamics he wishes to claim it is based on. One can then discuss the DALR itself in another venue, or just read e.g. Caballero on it, or more advanced treatments that discuss the actual underlying hydrodynamic equations in more detail. Things get very difficult, very fast, though, which is why most people stop with the simple semi-heuristic derivation of the DALR in spite of the fact that its idealizations aren’t very good and it at best gives you insight and conceptual power to make estimates and develop rules of thumb, not so much provide strong predictive power in atmospheric dynamics. For one thing turbulence instantly screws it up in the real world, moisture content screws it up, lateral transport screws it up, topology screws it up, the non-uniform temperature of the ground screws it up — the real atmosphere is constantly being kicked around between nearly isothermal and nearly DALR on any vertical column, with the actual measured thermal lapse rate rarely deviating by more than 10-20% from isothermal on an actual vertical sounding of the atmosphere.
This is all NOT my area of even approximate expertise, BTW. As you may have noticed on my last post back to Paul, I make mistakes or misunderstand, and when my errors are politely and convincingly pointed out to me, I’m very happy to concede (and in the process learn something). So if you disagree, feel free to correct (and thereby teach) me.
rgb
p.s. And to make it clear, the reason I’m not at all surprised that this has been missed out and that you know nuttin about it, is because for several decades universities have been teaching from the AGWSF energy budget, which is missing the WHOLE Water Cycle, and none of you super educated in physics with years of teaching and phd’s have even noticed it’s missing!
First, get a proper energy budget basic in place with real world physics and ditch the science fiction world you’ve created. Not sure though, that any of you would know how to go about that..
I have no idea what the “AGWSF energy budget” is. I’m just a physicist, remember, not an Evil Climate Scientist trying to nefariously deceive the world’s masses in order to become rich on undeserved grant money wealth. I make precisely as much money from granting agencies for shooting down Jelbring’s absurd paper as I do from the Big Oil companies for stating that the preponderance of evidence suggests that the very real GHG-GHE is not a catastrophic threat under any reasonable scenario for the economic and technological development of the world for the rest of the 21st century. However, I’m fairly certain that the AGWSF is something relevant to viewing the Earth as an open system, which is not the point of this thread and hence is, in the parlance of logical discourse, a “red herring”. Or perhaps a straw man. I get confused. Either way, Universities have taught something, somewhere, that you disagree with in some other venue and therefore it is wrong and I am a poo-poo head for not preventing it and not to be trusted to take care of your dog and oh yeah, Jelbring is right after all.
BTW, the “science fiction world” we are discussing in this thread is the one that Jelbring has created in his paper. That is, one that has an adiabatically isolated ideal gas in a gravitational field, left alone for a very long time so that it comes into a state of both hydrostatic equilibrium and thermal equilibrium. Perhaps if you could stay on topic long enough to actually defend its indefensible conclusions without introducing new physics that he explicitly omitted from his model problem statement we could resolve your difficulty understanding why his model conclusion, contingent upon precisely these conditions, is incorrect.
If you want to talk about the real world instead, by all means do so. Just don’t claim that your assertions have anything at all to do with Jelbring’s hypothesis or conclusion.
rgb
Both conditions are present in the neutral atmosphere.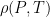 for an ideal gas, and you know
for an ideal gas, and you know 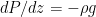 for any fluid in hydrostatic equilibrium (with
for any fluid in hydrostatic equilibrium (with 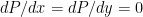 ), so if I give you a reasonably integrable
), so if I give you a reasonably integrable  , you can start with
, you can start with 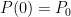 (or equivalent boundary condition) and solve the ODE to find
(or equivalent boundary condition) and solve the ODE to find 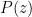 and
and 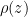 that are in force balance. Some of these proposed densities would be very difficult to arrange as initial conditions, but others are not, and of course a gas with the DALR and an isothermal gas are both not.
that are in force balance. Some of these proposed densities would be very difficult to arrange as initial conditions, but others are not, and of course a gas with the DALR and an isothermal gas are both not. a constant, it is absolutely trivial to show that entropy will strictly increase as heat is conducted between adjacent layers of the gas to reduce their temperature difference. There is an example problem in the online MIT thermo textbook I link that walks you through it. The maximum entropy state is the thermodynamic equilibrium state is the isothermal hydrostatic solution, not the hydrostatic solution with the DALR or any other initial thermal gradient.
a constant, it is absolutely trivial to show that entropy will strictly increase as heat is conducted between adjacent layers of the gas to reduce their temperature difference. There is an example problem in the online MIT thermo textbook I link that walks you through it. The maximum entropy state is the thermodynamic equilibrium state is the isothermal hydrostatic solution, not the hydrostatic solution with the DALR or any other initial thermal gradient.
This condition can be quite stable at night (see the near neutral residual layer page 31)
Of course convection is the major method of heat transfer in the atmosphere however how does heat transfer when there is little or no convection?
Two methods remain
1. Radiation
2. Conduction (diffusion)
So they must between them transfer heat across the temperature differential.
I have made this point already in this thread but you either have not seen it or perhaps you agree with it.
However your lack of response is a source of confusion.
I don’t know why. You’ve very precisely made my argument. In a neutral, unheated atmosphere, once one waits a very long time, there is no more movement of air; it achieves hydrostatic equilibrium, force balance. Then the two heat transfer mechanisms you describe come into operation. Both are irreversible; both transfer heat across the temperature differential, gradually neutralizing it. The state of maximum entropy is reached when the system is isothermal.
Obviously you can see that the argument doesn’t even depend on what the initial hydrostatic equilibrium state is. One can take any (smooth) vertical thermal gradient in the gas column and construct an associated density/pressure gradient that is in force equilibrium — you know
Ultimately, if you start the gas in any hydrodynamically stable initial state with a thermal gradient,
Note that my argument is confined only to Jelbring’s paper, and Jelbring’s paper explicitly states that he has waited a long time for all transport to cease and thermal processes to relax. So confine your defense of Jelbring to these conditions only. I’m not arguing that a dynamically driven atmosphere can have a lapse rate, only that Jelbring’s static one will not, and hence cannot be looked at as a source of “heating” or as a static mechanism that maintains the surface at a higher temperature than the gas overhead.
rgb
Robert Brown says
” I’m not arguing that a dynamically driven atmosphere can have a lapse rate, only that Jelbring’s static one will not, and hence cannot be looked at as a source of “heating” or as a static mechanism that maintains the surface at a higher temperature than the gas overhead.”
Perhaps I was not clear enough in my last post.
I was referring to our normal Sun driven atmosphere.
You made a point about convection being required for a lapse rate.
That is the point of possible disagreement.
For our atmosphere we have still air conditions and yet still have a lapse rate where radiation and conduction transfer the heat through the gradient.
Now back to the thread which I notice many have strayed from (including myself).
I recon IMHO that that’s where Jelbring got the idea for a static atmosphere.
He then generalised it to the unheated column of air problem above.
I pointed out in the previous thread that making this strong connection was tactically bad.
Basically then, he had two unlinked conjectures.
To base a theory that requires both to be true is unnecessary as one can be true and the other not.
Especially as one of the conjectures (the subject of your post) is not an orthodox position.
Certainly what you have been saying here is orthodox thermodynamics and thanks for giving us your expertise.
Mod, many thanks.
Robert Brown says:
February 1, 2012 at 9:59 pm
Does it include Maxwell’s Quaternion Equations?
Well, it includes Maxwell’s equations themselves, in several incarnations of expression (including manifestly covariant). I do love geometric algebra and think that the “war” between Heaviside and Gibbs and Hamilton’s followers (Tatt?) that the quaternion advocates eventually lost was very interesting — in the end Gibbs’ notation was, probably correctly, deemed a lot easier to work with and compute with.
Do Clifford/Geometric algebras interest you?
Yes, if I could add another lifetime on to this..
http://staff.science.uva.nl/~leo/clifford/
However, having only just now discovered the quaternion equations from my interest piqued by the Willis electricity tangent, here’s a look at Maxwell’s Quaternion Equations by Col. Tom Bearden:
There’s some links on that page to get the original Maxwell papers, I couldn’t get on with them and found them here instead: http://www.zpenergy.com/modules.php?name=News&file=article&sid=1949
But there’s more to that story, from Bearden’s own website: http://www.cheniere.org/books/aids/ch4.htm
The last bold mine.
Hmm, I wonder if any physics departments would be interested in exploring this..?
AGWSF = AGW Science Fiction, as in the AGWSF energy budget KT97 and ilk, missing the whole of the Water Cycle, and more science fiction besides.
Here’s another quick refutation to the argument “gravity does negative work on a parcel of air as it rises, so the KE (and hence temperature) must drop” argument. The microscopic argument has already been made (that only self-selected high-energy molecules make it that high, and even after losing some PE, they STILL have the same averge KE left). Here is a macroscopic argument for a parcel of air rather than individual molecules.
Buoyant force has been ignored. Because we are starting with hydrostatic equilibrium, then the buoyant force is equal to the gravitational force. If the parcel is raised (maintaining it at local atmospheric pressure and temperature), then the net force is zero and the net work done is zero. Any negative work by gravity is matched by and equal positive work by the buoyant force. Since no net work is done on the parcel, there is no change in the internal energy of the parcel and no change in the temperature.
Put another way, no work is needed to raise or lower a parcel of air. If the air was warmer at the bottom, I could take some of that air (and with NO WORK) move it to a cooler location. Eventually I could move air around until it was isothermal. From there, no further moving around of air could possible undo this isothermal profile.
This could be cleaned up a bit, but it shows that isothermal is indeed the stable, equilibrium state.
Tim Folkerts says
“Put another way, no work is needed to raise or lower a parcel of air. If the air was warmer at the bottom, I could take some of that air (and with NO WORK) move it to a cooler location. ”
Work would be done against the surroundings by the expanding parcel.
A similar parcel moves down to take the place of the rising parcel and increases its temperature.
Work is done by the surroundings to compress the parcel.
What you are outlining is the neutral atmosphere where DALR gives the gradient.
The air density is the result of gravity and without gravity the density would be uniform and buoyancy force would not exist.
Further If an unbalanced force acts (turbulent convection) then work is done against gravity as well as the surroundings.
DARL no longer gives the temperature gradient.
Back to the our real Sun driven atmosphere!
If the Sun causes the tropopause to rise in the diurnal cycle then work is done raising the centre of mass of the atmosphere.
if the tropopause drops at night then the gravitational potential energy can be transformed into thermal energy to buffer the temperature drop.
This is what I understand is the atmospheric thermal effect
Paul Birch:
Ah, I think I take your meaning (although I just finished driving 500 miles and am disinclined at the moment to give it the consideration I ordinarily would): it’s possible to pick local reference frames in which the local molecules’ kinetic energies are lower than in the reference frame in which the vessel originally containing the gas is stationary.
I still have to think through that entropy thing, though. True, it makes sense that the phase-space position representing the microstate the ensemble was in the instant the confining vessel disappeared (as I’m envisioning the thought experiment) should be just as likely as any other microstate on the same phase-space trajectory. But my understanding is that entropy discussions usually deal with macrostates rather than microstates, and it seems to me that the macrostate defined by a small volume and a given total molecular kinetic energy consists of fewer equally probable microstates than the macrostate defined by a larger volume and the same total molecular kinetic energy.
So I wonder if you could you expand on your entropy comment.
Robert Brown says 2/2 at 8:36am:
“ See the top post, which derives the actual state of an ideal gas atmosphere in both hydrostatic ( ) equilibrium and simultaneously in (iso)thermal equilibrium, repeatedly demonstrated to be the state where the gas has maximum entropy and the state the ideal gas will go to under the precise conditions described by Jelbring.”
Robert Brown –
My copy of Bohren & Albrecht “Atmospheric Thermodynamics” arrived today. I have had a delightful time reading thru about half of it so far. Thanks to Rodrigo Caballero’s on-line text for pointing the way.
The authors have many humorous anecdotes to relate & the chapter problems given are very thought provoking. I heartily recommend it to any poster interested in the topic of this thread.
On-topic for the top post, the authors develop the fundamental application of the thermo laws with the proper & correct detail algebra for Figure 1 in the top post – a GHG-free adiabatic ideal gas column in the presence of gravity. This gas column is isolated from its surroundings, neither heated or cooled by radiation nor by interaction with adjacent air or ground. There is no condensation or evaporation of water. (The same as that discussed in Verkley paper part b.)
The authors derive entropy maximization requires the equilibrium temperature profile to decrease as height increases. Thus they prove the hydrostatic temperature profile of top post Fig. 1 at equilibrium is non-isothermal which is the max. entropy point. ANY deviation from that thus requires a decrease in entropy which is not 2nd law physical.
Why isn’t the equilibrium temp. profile isothermal as Robert Brown writes (repeatedly)? The authors have a long explanation of why the temp. profile is non-isothermal. It needs to be read in context. They give a reason Robert Brown’s understanding here has been impeded – their reasoning is the conduction in solids impedes understanding of the ideal gas column w/gravity field non-isothermal temperature profile in equilibrium in top post Fig. 1.
I have edition 1 of that fine text book and, for interested posters, the non-isothermal stable equilibrium temperature profile derived from maximization of entropy of the GHG-free adiabatic ideal gas column top post Fig. 1 derivation is in Chapter 4.4 pp.164-168 for realistic pressures (holds for ~80% of pressure range of earth’s atmosphere).
Furthermore the authors point out only in the absence of gravity will the adiabatic ideal gas column equilibrium temperature be isothermal.
The authors elegantly show the top post statement is incorrect “..an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state..” and thus refute the refutation of a stable equilibrium isothermal temperature profile for Fig. 1 in the top post. This non-isothermal profile being consistent with poster Rodrigo Caballero’s referenced 2004 Verkley paper part b which shows experimental evidence for the ideal non-isothermal temperature profile in their Fig. 2.
Joe Born says:
February 2, 2012 at 5:01 pm
Ah, I think I take your meaning … it’s possible to pick local reference frames in which the local molecules’ kinetic energies are lower than in the reference frame in which the vessel originally containing the gas is stationary.
Yes. The thermal energy is what’s left when you map the system into local frames which null out all the orderly motions (which have zero or nearly zero entropy), leaving you just the random stuff (with high entropy).
…I wonder if you could you expand on your entropy comment.
The uniform radial motion itself has no entropy; there is only one microstate, that is, everything going straight out. The entropy is all in the residual thermal motion. Here the number of microstates is unchanged overall, with less thermal energy per particle, but spread over a correspondingly larger volume. By construction, in an adiabatic compression or expansion the entropy in the gas is unchanged; a standard calculation then yields the known constancy of PV^(Cp/Cv).
Paul Birch:
Thanks for the response, although I’ll have to think it through. I do recognize that a gas can be reversibly expanded and compressed, but it seems to me that merely releasing the gas from a vessel (by, e.g., magically making the vessel disappear) would result in an irreversible expansion.
But none of this affects my view that Dr. Brown’s “proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.
Joe Born says: But none of this affects my view that Dr. Brown’s “proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.
Equation 8 is based on very specific assumptions, which Velasco clearly states. This result is for a “microcanonical” ensemble, where there is absolutely no exchange of energy with the rest of the universe. This result will become the same as Dr Brown’s isothermal answer if either:
1) the number of particles is large. (As I stated above, even a few million particles will make the Velasco result indistinguishable from the isothermal distribution, and earth’s atmosphere has on the order of 10^40 particles.)
or
2) some part of the system — perhaps the ground — is a thermal reservoir rather than an adiabatic (perfectly insulating) surface. Now we have a “canonical” ensemble, and Velasco states clearly that this will be isothermal.
Robert Brown says:
February 2, 2012 at 7:52 am
now I can hope that includes not setting me homework..
Oh no. I assigned homework already;-): Read the MIT online thermo book and work through it, cover to cover. Your arguments can only improve if you actually learn the laws they are currently flouting, and while I fully understand your lack of respect for “authority” — while respectfully suggesting that it edges well over into iconoclasm for its own sake when you make statements that violate the experimentally verified laws clearly explained in every thermo textbook. It is difficult to claim that these textbooks are part of the “IPCC global conspiracy”, given that thermodynamics was mostly worked out and derived/proven over a hundred years ago, well before there was a United Nations.
Good grief man, you really think we’ve got where we are in science today by confusing “respect for authority” with “authoritarian entrenched beliefs”? Hmm, seems we have.
My authority here, and I have very great respect for it, are those in this discussion who understand gases and the real scientists at the front line, the meteorologists, who have had this sussed since way back when. You have shown no respect for them or their knowledge.
You can continue to define it whichever way you like, doesn’t make it so:
Your assertion that I don’t understand his paper is simply incorrect. I’ve read it several times at this point. Its claims are quite clear. He asserts that gravity will create a thermal lapse rate that is there in his isolated ideal gas in a near-Earth gravitational field in thermal equilibrium — the condition that an air column will reach after all irreversible relaxation processes such as conduction, convection, and radiation have completed. He forgot to mention conduction, but if he truly meant to leave it out then his conclusion is already obviously false as he left out a physical process that is infinitely faster than thermal relaxation due to radiation in a GHG-free atmosphere, where there is none. To prove it he cites a single “well-known” result — the DALR — from a single textbook on climatology, and claims that it describes static thermal equilibrium.
You can continue to define it whichever way you like, doesn’t make it so, for example:
“The dry adiabatic lapse rate (DALR) is the negative of the rate at which a rising parcel of dry or unsaturated air changes temperature with increasing height, under adiabatic conditions. Unsaturated air has less than 100% relative humidity; i.e. its actual temperature is higher than its dew point. The term adiabatic means that no heat transfer (energy transfer due to a temperature difference) occurs into or out of the parcel. Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small. http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
I’m sorry, you may not like being told by BigWAveDave that your knowledge of gases is zilch, but it is.
As I said, you don’t understand Jelbring’s argument, because you don’t know what he’s talking about. Here anyway we have an answer to why it’s rarely acknowledged by ‘climate’ scientists, because it’s unknown. First, work out what he’s talking about.
“The more atmospheric mass per unit planetary area, the greater
GE has to develop. Otherwise Newton’s basic gravity model has to be dismissed.”
If your text books have dismissed Newton’s basic gravity model, then your text books need re-writing.
If you wish to claim that “climate scientists” ignore the Water Cycle, prove it. Cite one single textbook on physical climatology that ignores the water cycle.
They all do who teach this: ‘that greenhouse gases warm the earth’, that without greenhouse gases warming the earth it would be some 30°C colder, from the 15°C we have now, to minus 18°C.
That is the mantra, everything about AGW is built on that.
But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.
In the real world and not the world created by AGWScience Fiction’s meme producing department, Greenhouse gases cool the earth.
– Without the Water Cycle reducing the temperature the earth would get to with the atmosphere as we have it (which is practically 100% nitrogen and oxygen), the earth would be 52°C hotter, not colder. It is water vapour, the main greenhouse gas, which takes away heat from the surface in evaporation and in condensing out in the heights where it is colder, releasing its heat and coming down as rain. The BASIC Water Cycle.
Now, all clean pure rain is carbonic acid, because water vapour and carbon dioxide have a strong yen for each other, water vapour in the atmosphere will pick up whatever carbon dioxide is around and bring it down to earth in rain. (And fog, dew etc.) Carbon dioxide is fully part of the water cycle.
Therefore, Greenhouse gases COOL the earth.
All the text books claiming that greenhouse gases warm the earth and that without greenhouse gases the earth would be colder, are lying.
That’s why it’s junk science, the rest is built on that.
QED
It was when I read Yes Virginia a couple of years ago that I realised something very odd was going on with the ‘science’ explaining AGW and its strange notions about the physical properties of gases, that even those not blaming it all on man had bought into it, actually believed the impossible ‘science’ which was so much at odds with basic physics – it took a while for it to sink in that these changes were now ubiquitous through the education system..
Give me one good reason why I should consider you an authority and not someone like Latour? (See the johnosullivan link I gave earlier). He called it junk science.
“But Dr. Latour goes further in his criticism. Semi-retired after a stellar career, Latour is one of many eminent experts now becoming increasingly outspoken and declaring the GHE as “junk science.” His position was summarized in US Senate Reports. [2.& 3.]”
“Always a stickler for thoroughness as a Chemical Process Control Systems Engineer, Latour had long worked at the sharp end of applied science. His special aptitude earned him his place in the Apollo Space program, where life and death decisions meant that when the theory contradicted reality you changed the theory.”
Yes, if I could add another lifetime on to this..
Back when I was in graduate school and was just beginning to see the importance of e.g. the Pauli spin matrices (a complex 2×2 tensor representation of the quaternions that map into spin or isospin in quantum physics), my friends and I spent a lot of psychic energy trying to figure out the real, complex, quaternion (Grassman algebra), Clifford algebra progression, because it appears not just one or two places, but many places in physics. It seemed then that it was possibly another case of “Flatland, a Romance of Many Dimensions” — we were “stuck” at the level of complex representations because we just couldn’t “see” that the “real” correct division algebra was of a much higher grade, so that our current view of things was only a projection of sorts and hence missing crucial detail.
I wouldn’t say that I disagree with this now. This is where being iconoclastic is a good thing in science. You can’t take it for granted that our current worldview isn’t just a projective view of a reality in higher dimensions, that our current formulation of physics is based on the right kinds of numbers, the right group, the right algebra, the right geometry. On the other hand, trying to determine physics in three dimensions plus time has got to be pretty difficult for people who live in only the 2+ of Flatland. It requires a level of brilliance and insight that are rare. And as Edwin Abbott (the author of the romance) indicates:
http://www.ibiblio.org/eldritch/eaa/FL.HTM
in the last chapters of his lovely story, the Square from Flatland (“I”) addresses the Sphere from 3 dimensions that has uplifted him (temporarily) to three dimensions himself so that he can perceive a reality that just before was inconceivable. But now the Square’s imagination has run wild; he reasons by induction:
I. But my Lord has shewn me the intestines of all my countrymen in the Land of Two Dimensions by taking me with him into the Land of Three. What therefore more easy than now to take his servant on a second journey into the blessed region of the Fourth Dimension, where I shall look down with him once more upon this land of Three Dimensions, and see the inside of every three-dimensioned house, the secrets of the solid earth, the treasures of the mines of Spaceland, and the intestines of every solid living creature, even the noble and adorable Spheres.
Sphere. But where is this land of Four Dimensions?
I. I know not: but doubtless my Teacher knows.
Sphere. Not I. There is no such land. The very idea of it is utterly inconceivable.
This seems to be the problem, a problem as old as Plato’s Cave — we have a hard time “uplifting” our point of view, even by induction, to see a possible higher level of reality where our own is just a projective view, shadows on the wall of our cave.
So far, though, I haven’t discovered anything quite so tremendous. Perhaps I’m too old — I try to teach younger students about geometric algebra earlier on and think it would be good to require — or at least encourage — its study as part of a math prep for majors and grad students, to give them a fighting chance at having the insights needed to make it fly one day and really advance our knowledge. Even things like electrodynamics — yes, it can be formulated in terms of complex numbers with divergences and curls or in terms of quaternionic derivatives, but the deepest insight I can offer so far is that neither of these is the “right” way. The problem, you see, is that the electric and magnetic fields aren’t vectors. They are components of a second rank tensor. So any theory that tries to write them out as vector fields is going to have a somewhat unnatural and contrived form. The only “natural” way to write out the theory of electromagnetism — the beautiful way to write it out — is the fully relativistic formulation that manifestly has the correct symmetries built in and which is strictly a tensor formulation.
That may be the lesson of the Pauli matrices as well. Yes, they are a kind of representation of quaternions, but they are a tensor representation, and tensors are, in a sense, the most general form of outer product one can construct on top of a number theory. It may be less about quaternions per se than it is about the underlying tensors and their symmetry groups.
Still, if you want to learn more about Geometric (Clifford) Algebras, I applaud the desire. The best book I’ve found so far is this one:
http://www.amazon.com/Geometric-Algebra-Physicists-Chris-Doran/dp/0521480221
Sadly, it looks like it is out of print, making it even more expensive than my copy was (although there are still used copies out there). A great read, and not horribly difficult mathematically at least through the first half of the book. Roughly the level of a course for junior or senior math majors or physicists, although he does reference some stuff in his “applications” chapters (where he shows how geometric algebras can be discovered inside various physical theories) that can be pretty difficult. Chapters 5+ work through towards gauge theory and general relativity, for example, not for the faint of heart:-)
The first two chapters are gems. The history, including the lovely story of Hamilton carving his discovery on a bridge at his college (where it remains to this day:-), plus a very simple description of the product as a generalized projective area or volume — the “geometric” part. It does help at some point to know what a division algebra is, and why physics needs to be based on them (if we want to be able to solve for things, at any rate:-).
Good luck!
rgb
Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small.
Yes, but that is just a matter of time scales of relaxation. You really are almost there now. Jelbring explicitly — and I do mean explicitly — states that he is supposedly waiting for relaxation to occur on all available time scales. He is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
The thermal conductivity of air is 0.025 W/(m-K). This is small, but certainly isn’t zero, and has to be balanced against the fact that air has a very low specific heat — 0.001297 J/(cm^3-K) — as well, so it doesn’t take a lot of heat to change its temperature. It might take years for the atmosphere to relax to isothermal. It might take months. I doubt that it would take centuries. But that doesn’t alter my conclusion. Gravity alone cannot create and maintain a thermodynamically stable lapse in temperature.
To put it another way, if one constructed a system with an isothermal air column in force balance — something one certainly can do, just by taking an insulated tower of air and mixing it well and letting it stop moving — what will make it depart from isothermal and relax towards a DALR? There are no air parcels moving up or down, so the entire argument concerning adiabatic lapse and isoentropic mixing is moot. There is nothing but diffusion and conduction, and they if anything maintain the air in an isothermal state. I’ve already argued that taking any gas and without doing any work causing it to separate into hotter and colder gas is a horrible, egregious violation of the second law, yet the entire gas column is by construction hydrodynamically stable, with a density strictly decreasing with height and without the slightest thing to cause bulk convection or other movements of air where “work” can be done.
What you are saying is just a restatement of what I’ve been saying all along. Jelbring is incorrect, but if you neglect thermal conductivity and dynamical relaxation processes other than slow convection, an atmosphere with a DALR can be hydrodynamically stable and can exhibit a lapse rate (once one is established) for a long time. But that moves us into another discussion — one of atmospheric dynamics, not atmospheric statics, the explicit milieu of Jelbring’s paper.
There I think that it is pretty obvious what actually establishes a lapse rate — differential heating of the air column at the bottom, followed by a rough equilibration due to approximately adiabatic convection. The air column is always moving, always heating or cooling, so the milieu of Jelbring’s paper and his conclusions are not only incorrect, they are irrelevant. He didn’t discover, invent, derive, meaningfully discuss, measure, draw pictures of, or even present an heuristic argument for the DALR in his paper. All he did is assert that it is a feature of completely isolated, static atmospheres so that just having a gas in a gravity well equals a DALR in the gas.
You continue to prove my point.
But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.
You also continue to throw red herrings into the soup. Jelbring’s paper explicitly excludes the Water Cycle (or adiabatic moving air parcels). It is a pure ideal gas. So why do you keep bringing them up? If you want to prove that there is a non-GHG GE involving the dynamic motion of gases, play right on through, but realize that Jelbring’s paper isn’t about that and is incorrect because it ascribes the same effect to a completely static, completely dry ideal gas that has been left in place, isolated, for a billion years (or as long as equilibrium takes, which won’t be anywhere near a billion years at a joule of conductive transport per meter of atmosphere per degree kelvin of temperature difference per 40 seconds).
So let me really clear. I don’t care about the real DALR in the real atmosphere, which is an utterly dynamic quantity that is basically never precisely observed and which is derived, using a bunch of approximations and assumptions that include active transport of air parcels and “0” conductivity, to provide us with some insight into why the atmosphere does remain warmer at the bottom than at the top. I don’t “deny” the DALR in real air, sir. What I deny is that this air is in any way, shape, or sense, in thermodynamic equilibrium.
Get it? Thermodynamic equilibrium is something very specific. It includes mechanical equilibrium. Thermal equilibrium. Chemical equilibrium. It presupposes that all thermal relaxation that can occur has occurred, unless you wish to work a system with broken ergodicity, or unless you can show that there is a vast separation of relaxation timescales, one large enough that equilibrium will not be reached in the particular times of interest in a particular problem. Since the Earth’s atmosphere is actively driven on literally a daily basis, hourly basis, minute by minutes, conductivity is largely irrelevant to atmospheric relaxation — it never has time to thermally relax. It does have time to convectively relax, sometimes, approximately, for a while, which is why soundings reveal a thermal lapse that sometimes, approximately, for a while, resembles the DALR — except when (more often) it doesn’t. Like when water gets mixed into the picture, or above the poles in winter when the ground can actually lose heat faster than the atmosphere and the atmosphere often inverts, being warmer on top than near the ground.
Note that this alone refutes the idea that the DALR is something intrinsic to gravity and atmospheres, even dynamically. Heating the atmosphere at the bottom more than the top seems important as well, and you know what? It isn’t that surprising that something heated at the bottom and cooled at the top exhibits a thermal gradient from the bottom to the top.
The interesting question is, what cools it at the top? Cooling requires the actual physical removal of heat. Could it be — gasp — radiation? Could we — possibly — measure it? Can we — I know it is a crazy, crazy, idea — determine the temperature of the source of the radiation, and from the spectrum the probable source of the radiation, the particular species of molecules that are emitting it? Could those molecules be — I hate to even say it out loud — CO_2?
No, no, no. This is all silly. We don’t have to have anything that cools the air up there. It stays cold by magic.
I mean this very seriously. Not only is it hotter underneath the tropopause, it is hotter overhead. You’ve got a real miracle on your hands — a layer in the middle that stays colder than the air above and below. As James Bond would say, “that’s a neat trick” to pull off without any mechanism for actually removing heat from there.
But even this is a serious digression from the point of this thread from the top article on down. Try, really try, to address just Jelbring’s imaginary world, perfectly insulated above and below, ideal gas in between, near-Earth gravity, infinite time for the system to reach true thermodynamic equilibrium (or long enough for a non-GHG to reach thermal equilibrium through radiation, which is going to be a hell of a lot longer than its thermal relaxation through conductivity for a gas on average 200-300K in temperature at 1 g). He asserts, utterly without proof, that this gas will exhibit a DALR. If you disagree, then where is his proof. Explain it to me. I assert, with considerable proof that such a gas at thermal equilibrium cannot have any lapse rate at all, let alone the very specific DALR provided only that thermal relaxation through all available channels has had time to occur (that’s the “thermal equilibrium” bit).
If you want to say that no, he meant to describe a non-equilibrium gas, then reread his paper. He went well out of his way to isolate the gas and leave it alone so it would reach “energy equilibrium”, whatever that is supposed to mean, but there you have it. If you want to assert that energy equilibrium isn’t thermal equilibrium, well then, you and he can make it anything you like but it won’t be the state the system spontaneously evolves to.
Of course, it is difficult for me to stay on task when you write strange things such as this:
It is water vapour, the main greenhouse gas, which takes away heat from the surface in evaporation and in condensing out in the heights where it is colder, releasing its heat and coming down as rain. The BASIC Water Cycle.
Well goodness. Water vapor collects heat at the surface, and transports it uphill, you say. Sort of like a silver conducting wire. It reaches the heights (where it is, indeed, colder) and releases all of that heat, which in the usual way of things would — warm the heights, would it not?
So what, exactly, cools the heights? You’ve now got “heights plus all that heat”, and they aren’t as cold any more. The more water vapor you take up there, the warmer they get, until water vapor doesn’t condense there any more.
We can hardly just pull that warm air down, can we? Being warmer, it is less dense, and buoyant! Besides, where is there for the heat to go down below? It’s hotter still down there? How does that pesky air at the upper troposphere lose all of the heat that is constantly being transported up there, so it can maintain your water-driven “cooling cycle”? Could it, maybe, radiate the heat away to outer space, given that that is the only way the Earth ever loses heat? Or does your solution involve lots of little, bitty demons, all named Maxwell, that do something enormously improbable with it?
But you really, really, are getting close now. You can hardly move without bumping into your own contradictions. All you have to do is let go of the cognitive dissonance. It’s OK. You can admit it. There really is a greenhouse effect. That doesn’t make the CAGW hypothesis true, but it does mean that CO_2 is the mechanism that differentially cools the top of the atmosphere, much less efficiently than the earth would lose the heat if there were no atmosphere or if there was an atmosphere but it were totally transparent to IR.
You can admit the CO_2 based GHG GHE because you can see it. With IR spectrographic eyes. Anytime you wish, just look at the measurements.
Or, you can bury your head firmly in the sand and pretend that those measurements don’t exist. It’s up to you…
rgb
But none of this affects my view that Dr. Brown’s “proof” either begs the question…
Begs what question? I cite an MIT online textbook’s definition of thermodynamic equilibrium. I elsewhere cite specific sections of that textbook that contain the standard thermodynamic arguments for why thermodynamic equilibrium is isothermal unless the system is strongly — not weakly — constrained. I show how those arguments apply to an isolated ideal gas in near-Earth gravity. Specifically, I argue that it is trivially demonstrable that a state of the gas exists that is in hydrostatic equilibrium and simultaneously isothermal. It is perfectly obvious that this gas is stable — there are no unbalanced forces that would cause convection, the ideal gas obeys the ideal gas law at all points so the density is everywhere consistent with the local (also global) temperature.
Why isn’t this state thermal equilibrium?
Speak to me not of uplifting air parcels — no parcel in this gas experiences net forces, it begins at rest, it will remain at rest. The only motion occurring at any scale is the microscopic thermal diffusive motion present in any equilibrium gas, and any hypothesized bulk expansion or contraction contradicts both the fact that it is in force equilibrium and that gravity does no work on things that are not moving. There are no adiabatic expansions or contractions — why would they occur?. Since the gas is all at the same temperature, there is no (net) thermal conduction of heat from one part of the gas to another, not unless Fourier’s Law has suddenly changed so that it no longer contains a thermal gradient term.
Why is asserting that this state is manifestly thermal equilibrium begging the question? It satisfies all of the stated conditions for thermodynamic equilibrium that are to be found in any textbook. Surely the onus of proof is upon you to show why the ordinary laws of thermodynamics, the ordinary definition of thermodynamic equilibrium, is suddenly on holiday so that this gas, perfectly balanced in terms of gravitational force and energy, and utterly lacking a thermal gradient to drive the flow of heat, is somehow going to change.
Why would it? What force, specifically, will make it change? Not gravity — its in hydrostatic equilibrium. Not the flow of heat. Heat stops flowing when the temperature is uniform. Not “pressure” — see hydrostatic equilibrium. Not the influx of heat from outside, it is in a perfectly insulated container. Not work, nothing is doing any work.
What will make it change?
Note that it must change, if some other state is equilibrium. Some thermodynamic potential or force must make it change. I could be wrong, sure, maybe there is such a force, but where? What could it possibly be?
Now look at the counter argument. Suppose you prepare the gas in hydrostatic equilibrium (so it is in perfect force balance) but with a thermal lapse. Now there is a thermal process that can act. Ordinary conduction from the warmer part to the colder part is predicted and observed in any gas I’ve ever seen or heard of. Thermal conductivity doesn’t give a damn about uphill or downhill. It cares about entropy. Take a slice of gas at the top where it is cold. Take a similar slice at the bottom where it is hot. Move heat Q from the bottom to the top. Now please explain to me — with some actual algebra, please — how this will not increase the entropy of the gas, meaning that the state with a lapse could not have been maximum entropy.
Sure, I could be wrong, but I’m hardly begging any questions. If one cools the gas on the bottom and warms the gas at the top (relative to a gas with a DALR), if anything one expects to increase the density at the bottom compared to the top and shift the center of mass of the gas downhill while remaining (quasi-static process) in equilibrium. This simple heuristic argument alone suggests that would be surprising, at least, for the mean gravitational potential energy of the system to spontaneously increase at the same time a thermal gradient appears. Again, it is in the exact opposite direction one expects, higher macroscopic bulk potential energy and less buoyant stability.
Robert Brown says at 2/3 10:22pm:
“Suppose you prepare the gas in hydrostatic equilibrium (so it is in perfect force balance) but with a thermal lapse.”
Ok. Interesting to think this thru, it is shown in Fig. 1 of the top post. We have a non-physical ideal situation but can learn about reality from it. Remember Bohren&Albrecht prove with actual algebra in my cite above 2/2 6:56pm that this preparation is in a state of maximum entropy.
Robert Brown continues: “Now there is a thermal process that can act.”
No, there is not. The system is already at maximum entropy with the thermal gradient maintained by gravity due to the fact the KE (thermal energy) of the molecules must decrease with height as they move uphill against gravity. And likewise the KE (thermal energy) of the molecules must increase as they move downhill with gravity. All the while keeping their total energy (KE + PE) constant.
Robert Brown continues: “Ordinary conduction from the warmer part to the colder part is predicted and observed in any gas I’ve ever seen or heard of. “
Yes, b/c Robert Brown lives in the real world. Fig. 1 does not. However, the Verkley paper experimental evidence shows the real atmosphere is way closer to the idealization being non-isothermal than the idealization being wrongly isothermal in their Fig.2.
Robert Brown continues: “Sure, I could be wrong…”
Robert Brown is wrong about the idealization being isothermal (partly b/c his algebra in top post incorrectly just assumes T is constant). Bohren&Albrecht prove it is non-isothermal with actual algebra: ideal gas temperature does decrease with increasing height in a gravity field. They also point out people are impeded in arriving at the correct result due to pointing to conduction in solids (silver wires and I suppose ideal gas contained in jars).
Robert Brown continues: “Take a slice of gas at the top where it is cold. Take a similar slice at the bottom where it is hot. Move heat Q from the bottom to the top. Now please explain to me — with some actual algebra, please — how this will not increase the entropy of the gas, meaning that the state with a lapse could not have been maximum entropy.”
Robert Brown must see the physics of lifting the warm bottom gas up against gravity does work on the system (work = m*g*delta h) thus of course the entropy in Fig. 1 will increase, because work was performed across the control volume of Fig. 1.
Any work crossing the adiabatic control volume is ruled out by the idealization. The higher temperature bottom gas will not move up on its own due to the Fig. 1 entropy already being maxed at equilibrium. This stratified non-isothermal equilibrium continues as long as the gravity field continues.
Joe Born says:
February 3, 2012 at 4:08 pm
Thanks for the response, although I’ll have to think it through. I do recognize that a gas can be reversibly expanded and compressed, but it seems to me that merely releasing the gas from a vessel (by, e.g., magically making the vessel disappear) would result in an irreversible expansion.
No, it’s not irreversible from a thermodynamic point of view, although, in practice, reversing it could be tricky. In principle, however, one could do it by surrounding the expanding gas cloud with a massless elastic membrane, or an elastic membrane accelerated to match velocities when the gas reaches it, or by an array of rocket nozzles pointed into the flow to catch the gas, or by surrounding it with a massive perforated sphere with a gravitational escape velocity higher than the gas velocity, or by running it into a medium of suitably graduated density, etc..
Robert Brown says:
February 3, 2012 at 7:27 pm
Back when I was in graduate school and was just beginning to see the importance of e.g. the Pauli spin matrices (a complex 2×2 tensor representation of the quaternions that map into spin or isospin in quantum physics), my friends and I spent a lot of psychic energy trying to figure out the real, complex, quaternion (Grassman algebra), Clifford algebra progression, because it appears not just one or two places, but many places in physics.
Another field in which quaternions/spin matrices/spinors are useful is in General Relativity. The problem of radiative equilibrium between relativistically shifted temperatures that I touched on earlier is one to which they can conveniently be applied (the aberration of light is such a spinor boost and rotation). Chapter 41 of MTW is devoted to them.
Robert Brown says:
February 3, 2012 at 8:51 pm
Jelbring … is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
Just a minor point on the timescales. Radiation in an optically thin medium equilibriates on a timescale independent of the size of the system. Conduction (which is a form of diffusion) equilibriates on a timescale proportional to the square of the size of the system. Air will have a time constant (using your figures) ~1297Jm^-3K^-1 / 0.025Js^-1K^-1 ~ 52,000 s/m^2. That is, heat takes about half a day to go one metre. To go ~8km (the equivalent depth of the atmosphere at sea level density) would take ~ 52,000 seconds x 8000^2 ~ 100,000 years. So that’s the time constant for conductive relaxation, close enough. I suspect that radiation in an N2/O2 atmosphere would be considerably faster, even in the absence of gases like H20 and CO2 – but I admit I haven’t done the actual sums there, so I could well be wrong. Either way it makes no difference to the thought experiment, of course, since full thermodynamic equilibrium is explicitly assumed.
Trick says: “Remember Bohren&Albrecht prove with actual algebra in my cite above 2/2 6:56pm that this preparation is in a state of maximum entropy. ”
But Robert was saying to take ANY arrangement that is in hydrostatic equilibrium — there are an infinite number of temperature profiles that are in hydrostatic equilibrium. The reference you cite cannnot possibly say that ANY arrangement is the state of maximum.
I would be curious to see exactly what the text says, since there are apparently some details that you are missing.
Paul,
I have to agree with Joe about reversibility. A slow adiabatic expansion/compression is considered reversible, ie you could make a movie of the process and run it backwards and it would still make sense eg a Carnot heat engine could be run backwards to be a Carnot refrigerator. But a free expansion is not reversible. A gas can spontaneously expand into into a larger, empty container, but it cannot spontaneously leave part of a container and re-confine itself into a smaller container.
You processes all seem to involve some variation of “Maxwell’s demon” to re-order the gas.
Tim Folkerts says at 2/4 11:02am:
“But Robert was saying to take ANY arrangement that is in hydrostatic equilibrium — there are an infinite number of temperature profiles that are in hydrostatic equilibrium. The reference you cite cannnot possibly say that ANY arrangement is the state of maximum.”
The B&A text derives the general case applicable to any arrangement. Not exactly sure what you mean here. Possibly you mean the initial conditions of Fig. 1 top post could be set to any of an infinity of reasonable earth pressures (1000 to 200mb say) & temperatures (arctic or tropical) profiles to start. When the adiabatic GHG-free air column achieves equilibrium, the temp. profile will settle in to have the bottom temperature the warmest and the coldest at top as the maximum entropy condition.
Interesting to learn here that if the initial condition profile is set to isothermal, nature forces entropy increases until the stratified temperature field decreases with height and the field corresponds to max. entropy. After that it is stable – at the macro level – with lotsa’ random molecule movements of different vertical speeds (but constant total energy) at the micro level. It would be possible to measure the Fig. 1 vertical temperature field with a normal thermometer and find that, after equilibrium, it doesn’t change with time; temperature field only changes with height of thermometer.
Tim Folkerts says:
February 4, 2012 at 11:10 am
I have to agree with Joe about reversibility. A slow adiabatic expansion/compression is considered reversible, ie you could make a movie of the process and run it backwards and it would still make sense eg a Carnot heat engine could be run backwards to be a Carnot refrigerator. But a free expansion is not reversible. A gas can spontaneously expand into into a larger, empty container, but it cannot spontaneously leave part of a container and re-confine itself into a smaller container.
And you could make a movie of this process, reverse it and it would still make sense (like the condensation of a gas cloud, or laser/electron beam inertial confinement fusion). You’re still thinking of it as a Joule-Thomson expansion into a larger container, but it’s completely different. It’s an explosion, turning thermal energy into orderly radial motion.
You processes all seem to involve some variation of “Maxwell’s demon” to re-order the gas.
The gas doesn’t need “re-ordering”. It’s already highly ordered. All that’s necessary is to find a way to reflect the gas elastically, and this can be done with low-entropy macroscopic arrangements. No Maxwell’s demon required.
Such (more or less) reversible expansions are not uncommon in astrophysics. Supernova remnants, for example; after a period of essentially free expansion in which the temperature drops from megakelvins down to where they no longer radiate detectably, they start ploughing up the interstellar medium and compress and heat up again. Some light years out the pressure from the interstellar magnetic field takes over and the bubble rebounds inwards. If the field were strong enough it would rebound most of the way back to the neutron star. It’s not perfectly reversible because energy is lost to radiation and shocks can form at the nebula-i/s medium boundary. Variable stars burping the outer parts stellar atmosphere at below escape velocity are another example; gravity reverses the expansion of the shell, the recompression frequently triggering another burp. Indeed, any sound wave propagating through a gas is doing the same trick – reversibly exchanging thermal energy for linear motion.
Robert Brown says:
February 3, 2012 at 8:51 pm
“Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small.”
Yes, but that is just a matter of time scales of relaxation. You really are almost there now. Jelbring explicitly — and I do mean explicitly — states that he is supposedly waiting for relaxation to occur on all available time scales. He is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
We really are reading him from two completely different positions, I see this as just the ‘chuck everything out and get to the basics’, so if it takes that aeons of time, so be it, but at the end of that, etc.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
“Take two identical volumes (parcels) of air, taken from somewhere at a midlevel in the troposphere, with each parcel containing an identical number of gas molecules and the same amount of heat energy to start. Mentally place one parcel higher in the troposphere and one closer to the surface of the Earth, without allowing any molecules or heat energy to enter or leave each parcel of air. The parcel of air that you placed in the lower atmosphere is going to compress and warm because it finds itself in a place with higher pressure. The parcel of air that higher in the atmosphere is going to expand and cool because it finds itself under lower pressure.This kind of process, one which takes place without heat energy entering or leaving the parcel, is called an adiabatic process.” http://education.sdsc.edu/teachertech/downloads/climate_answ.pdf
That’s the time scale, it doesn’t matter. That is always going to be the underlying skeletal structure onto which all else is built.
To put it another way, if one constructed a system with an isothermal air column in force balance — something one certainly can do, just by taking an insulated tower of air and mixing it well and letting it stop moving — what will make it depart from isothermal and relax towards a DALR? There are no air parcels moving up or down, so the entire argument concerning adiabatic lapse and isoentropic mixing is moot. There is nothing but diffusion and conduction, and they if anything maintain the air in an isothermal state. I’ve already argued that taking any gas and without doing any work causing it to separate into hotter and colder gas is a horrible, egregious violation of the second law, yet the entire gas column is by construction hydrodynamically stable, with a density strictly decreasing with height and without the slightest thing to cause bulk convection or other movements of air where “work” can be done.
That’s all irrelevant, it’s already the adiabatic lapse rate as a creation of gravity in that pressure does the work, more or less work as it’s greater or weaker.
You’re thinking of gravity as ‘doing work’ in an odd way, istm, and it could be because you’re not relating gravity to its own processes. For example as you say here:
“and that gravity does no work on things that are not moving. There are no adiabatic expansions or contractions — why would they occur?”
Gravity ‘works’ on mass not on movement, it’s the relationship of mass of objects meeting in gravity which creates movement, two gases of different mass in the same parcel of space will separate out as gravity has a greater pull on the one with more mass.
What you are saying is just a restatement of what I’ve been saying all along. Jelbring is incorrect, but if you neglect thermal conductivity and dynamical relaxation processes other than slow convection, an atmosphere with a DALR can be hydrodynamically stable and can exhibit a lapse rate (once one is established) for a long time. But that moves us into another discussion — one of atmospheric dynamics, not atmospheric statics, the explicit milieu of Jelbring’s paper.
No, I’m saying it’s why Jelbring says conduction is negligible, because it is, dynamically or statically, it can be discounted, air is a very poor conductor of heat.
It’s just to get back to the difference in pressure which is a ‘function’ of gravity, the higher the pressure the more the molecules are heated, the more they’re heated the lighter and less dense they become and so rise as the denser above them bully their way down through them, well, the actual term is displace, like carbon dioxide being heavier displaces the lighter nitrogen and oxygen to sink to the ground. The action of gravity.
There I think that it is pretty obvious what actually establishes a lapse rate — differential heating of the air column at the bottom, followed by a rough equilibration due to approximately adiabatic convection. The air column is always moving, always heating or cooling, so the milieu of Jelbring’s paper and his conclusions are not only incorrect, they are irrelevant. He didn’t discover, invent, derive, meaningfully discuss, measure, draw pictures of, or even present an heuristic argument for the DALR in his paper. All he did is assert that it is a feature of completely isolated, static atmospheres so that just having a gas in a gravity well equals a DALR in the gas.
You continue to prove my point.
I’m trying very hard not to… 🙂
“Why is air at elevation cooler as the pressure becomes less? The temperature of air is cooler at elevation in response to the vertical pressure changes that happen to occur because of the Earth’s gravity.” (same link as last)
He went well out of his way to isolate the gas and leave it alone so it would reach “energy equilibrium”, whatever that is supposed to mean, but there you have it. If you want to assert that energy equilibrium isn’t thermal equilibrium, well then, you and he can make it anything you like but it won’t be the state the system spontaneously evolves to. If you want to say that no, he meant to describe a non-equilibrium gas, then reread his paper.
Thermal equilibrium doesn’t mean the same temperature, if for example, a gas in getting hotter expands and rises becoming less dense and under less pressure it can move faster, it’s using thermal energy to move, there’s no energy lost, it’s just become something else, or, as temperature relates to kinetic energy not thermal energy then heat capacity comes into play, as water can absorb a huge amount of thermal energy before there’s any rise in temperature, or whatever, but if you’re equating all ‘energy’ to ‘heat’ as thermal energy then that’s a different idea altogether, not all energy is heat. I think he means here energy equilibrium as in different processes can be happening within the volume of gas, I think you keep misreading him. As you misread him here:
“An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.”
When you read that he was somehow ‘proving’ that it was adiabatic, but he’s only saying that adiabatic is the default and a parcel of air rising in it will change its energy states, the equilibrium is in the total energy of the processes.
Others have explained what that means is happening to the gaseous atmosphere as it goes from high to low pressure, and it has to be understood by first taking into account the particular properties of gases, and, these in the actual processes of gravity.
I’m sorry, but this is really all Jelbring is saying, that when we get back to the basic mechanism we get the adiabatic lapse rate, yer basic gravity.
“But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.”
You also continue to throw red herrings into the soup. Jelbring’s paper explicitly excludes the Water Cycle (or adiabatic moving air parcels). It is a pure ideal gas. So why do you keep bringing them up?
It’s a running continuation on the theme of you misreading him in thinking he was claiming an insight unique to him, when you said it was also in text books, but what he meant was “climate” scientists don’t acknowledge this. As you show here. “Climate” scientists are a breed apart. I’m sorry if that wasn’t clear as a theme in my replies. I’ve just been giving different examples of how “climate” scientists have a completely different fisics of the basics. The absence of the water cycle in the KT97 and ilk energy budgets the most obvious. But “climate science” has done this across the range of basics in changing, tweaking, eliminating and so on to the point where it describes a non-existant world, and as you show here, doesn’t know it, so thinks it’s something ‘new’ or ‘wrong’ as it’s trying read it from a different fisics, trying to make it fit into a different fisics.
I’m glad you asked.
Heating the atmosphere at the bottom more than the top seems important as well, and you know what? It isn’t that surprising that something heated at the bottom and cooled at the top exhibits a thermal gradient from the bottom to the top.
No, it exhibits a temperature gradient.
The interesting question is, what cools it at the top?
Same thing that heats it at the bottom..
..pressure, i.e. gravity, weaker at the top, stronger at the bottom.
Cooling requires the actual physical removal of heat.
Requires a change in temperature. Removing thermal energy can do that. By changing it to a different energy, etc.
Could it be — gasp — radiation? Could we — possibly — measure it? Can we — I know it is a crazy, crazy, idea — determine the temperature of the source of the radiation, and from the spectrum the probable source of the radiation, the particular species of molecules that are emitting it? Could those molecules be — I hate to even say it out loud — CO_2?
Sigh.
We know the temperature of the Sun. What “climate” scientists have done is change the spectrum. The claim is that no thermal energy direct from the Sun heats the Earth, the real thermal energy that is, thermal infrared radiation which is heat on the move. Instead “climate” scientists have given its properties, being heat, to shortwave, claiming visible light heats the oceans and land, even though water is a transparent medium to it.. And then, ignoring that the heat we feel from the Sun is thermal infrared so does reach us, say that carbon dioxide a trace gas, and already fully part and parcel of the cooling cycling of the Earth in the Water Cycle, is responsible for raising the temperature of the Earth from -18°C to 15°C, without ever giving any rational explanation as to how it actually does this, and, that doubling it will cause catastrophic runaway global warming, doubling a trace gas it still remains a trace gas.
You do have such an amazing molecule in your fictional world, defying gravity it can stay up in the atmosphere for hundreds and even thousands of years accumulating though it’s one and a half times heavier than air, and, with no heat capacity to spit at, it can trap heat, or, heck you can’t even get your stories to say the same thing consistently, it becomes this great thermal blanket stopping heat escaping… just how much of that blanket is holes?
Anyway, thanks for your post on Clifford, I enjoyed reading it.
Adiabatic Cooling
http://eesc.columbia.edu/courses/ees/slides/climate/adiabatic.jpg
This is the page it comes from:
http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
Don’t know how good it appears to those I consider have superior understanding here..
When the adiabatic GHG-free air column achieves equilibrium, the temp. profile will settle in to have the bottom temperature the warmest and the coldest at top as the maximum entropy condition.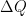 being moved to/from a layer of gas at any given temperature
being moved to/from a layer of gas at any given temperature  is:
is:

 that satisfy
that satisfy  , so there is no net force acting to push the gas up — but not all profiles are equally stable. The most gravitationally stable profile is isothermal.
, so there is no net force acting to push the gas up — but not all profiles are equally stable. The most gravitationally stable profile is isothermal.
Except that it is a ten-second mental exercise to see that this is not, in fact, maximum entropy. Because if heat is transferred from the warmer bottom to the cooler top, the entropy of the arrangement will increase.
You don’t need to look at a reference to see this. You just need to know what the entropy change of the transfer is. In case you’ve forgotten the entropy gain/loss associated with heat
Go ahead, do the algebra. If you get stuck bear in mind that I do it for you up above, and the MIT textbook has it as well.
The only way the gas will not be isothermal at maximum entropy is if heat transfer is impossible. But obviously it is not. As you (and Jelbring) acknowledge, real ideal gases can conduct thermal energy. In the derivation of the DALR their conductivity is often omitted (because it is relatively low, air is a poor conductor). But this is a thought experiment, and Jelbring himself establishes true equilibrium after a long time as a feature of the system in question, because he wishes to assert that gases will be warmer at the bottom without any external thermal driving, in particular the heating at the bottom and cooling at the top associated with the Sun and the GHE.
BTW, no, I’m not talking about lifting up any parcels of gas during equilibration. The gas is equilibrating via thermal and radiative conduction. No work is done by gravity.
Well, that’s not quite true. As the bottom cools and the top warms the center of mass of the gas will indeed move down because the density of the gas at the bottom will increase while the density of the gas at the top will decrease. The macroscopic action of gravity actually favors isothermal equilibrium.
This is yet another heuristic you can use to understand this. You’re all about energy balance and gravity. Well, the gas is, on average, lower when it is in thermal equilibrium, not higher, in a macroscopically more stable state, a hydrostatically more stable state. Remember, it is always in hydrostatic equilibrium — there are many possible profiles with consistent
rgb
Myrrh says: in the BB formula — it will not change. It can’t move towards the DALR, because the atmosphere is hydrostatically stable and there are no uplifting parcels of air (matched by downfalling parcels elsewhere, BTW, because there isn’t anywhere for conserved air to actually go). It can’t move towards isothermal either, because one cannot move heat around in the gas to increase its entropy:
in the BB formula — it will not change. It can’t move towards the DALR, because the atmosphere is hydrostatically stable and there are no uplifting parcels of air (matched by downfalling parcels elsewhere, BTW, because there isn’t anywhere for conserved air to actually go). It can’t move towards isothermal either, because one cannot move heat around in the gas to increase its entropy: 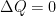 for any parcel of the gas as it sits there in perfect force balance. The gas would be perfectly stable. So would the gas prepared with the DALR, an isothermal gas, or any other hydrostatically stable thermal profile you arrange as an initial condition.
for any parcel of the gas as it sits there in perfect force balance. The gas would be perfectly stable. So would the gas prepared with the DALR, an isothermal gas, or any other hydrostatically stable thermal profile you arrange as an initial condition.
February 4, 2012 at 7:01 pm
Adiabatic Cooling…
Nice picture, and nice article. Note well that the figure clearly labels the wall of the balloon as being a thermal insulator — that’s the adiabatic part, actually. Suppose that it wasn’t really a perfect thermal insulator? Hmmm, would the gas precisely follow the adiabatic PV curve if heat could flow into the contents of the balloon from the gas surrounding it?
Note well that the article clearly states that the air takes on an adiabatic lapse as it is being uplifted. It even offers pretty much the only two mechanisms for uplift, and truthfully that can be reduced to one. The first is differential heating leading to convection, the second is the deflection of lateral air movements as they go up or down a mountainside. The second, of course, requires pressure differences to generate the wind and pressure differences are only created by differential heating. No differential heating (on Earth or anyplace else) — no ALR.
An interesting question is then — suppose one starts with an air column (Jelbring conditions, dry ideal gas, no mountains, wind, or sources of heat) but select as an initial condition hydrostatic equilibrium with a thermal profile somewhere in between the classic DALR and isothermal. Which way (to which profile) will this air column go?
If it is a perfectly adiabatic, totally transparent gas — if the conductivity of the gas is zero and
Now “turn on” heat transport (mentally) via conduction and radiation. These cannot — and will not — destabilize the atmosphere to start up convection, because they always move net heat in the direction that makes convection even less likely, given that convection is driven by temperature differences that conduction or radiation further reduce. They will not move the system towards the DALR, because the DALR is a very special thermal lapse, one that is established by slow, non-turbulent convection (that nevertheless happens to mix the atmosphere faster than conduction or radiation). Indeed, the direct action of conduction and radiation will be to move the gas towards isothermal equilibrium because that is the true, stable thermodynamic equilibrium for an isolated gas where one does not neglect conduction and radiation as mechanisms for heat transfer with in the gas.
Just another fairly simple thought experiment. In the end, one can just read the lovely summary that you post to understand my objection to EEJ. Is there one, single word in that article that suggests that the DALR is the stable result of a static equilibration process for a not perfectly adiabatic ideal gas? I don’t think so.
rgb
rgb
Gravity ‘works’ on mass not on movement, it’s the relationship of mass of objects meeting in gravity which creates movement, two gases of different mass in the same parcel of space will separate out as gravity has a greater pull on the one with more mass.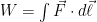 (if the latex survives). Work is the action of force through a distance. When the gas is in hydrostatic equilibrium, there is no bulk transport of the gas because it is in force equilibrium, and gravity does no work.
(if the latex survives). Work is the action of force through a distance. When the gas is in hydrostatic equilibrium, there is no bulk transport of the gas because it is in force equilibrium, and gravity does no work.
No, no, no, silly beanie.
As thermal relaxation occurs, it does do work, however — because the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate. Remember, the pressure at the bottom of the gas column is a constant (equal to the weight per unit area of all of the gas) and that otherwise, the density strictly decreases with increased T. So the layer near the bottom becomes more dense as it cools due to conductivity, and the layer near the top becomes less dense as it warms. This actually “compresses” the gas at the bottom more, although the compression is only a downward shift in density because the actual pressure at the bottom must be conserved and hydrostatic equilibrium maintained.
BTW, you seem a bit obsessed with the idea that two gases with different masses will “separate out”. If by this you mean that they will form layers with a sharp interface, like the meniscus of oil on water, that just isn’t so. I think you need to read, and try to understand, Dalton’s Law:
http://en.wikipedia.org/wiki/Dalton%27s_law
The idea is straightforward. Both (ideal) gases will expand to fill any vessel they are placed in, and at normal e.g. room temperature and with similar sized molecules there is no chance of them “separating”. OTOH, if by this you mean that both gases will have equilibrium densities and partial pressures that more or less exponentially decay, with distinct exponential constants so that the static equilibrium mixture will not end up being perfectly homogeneous over very large vertical distances, especially if one molecule is physically much larger than and more massive than the other, I don’t have a quarrel with that (and neither does Dalton), although I would want to work out the numbers. No matter — I don’t care to argue either way, because this is completely irrelevant to the discussion of EEJ except that you keep giving it as an example of something science has “gotten wrong”.
You do realize that even if you are correct and physics has “gotten this wrong”, that isn’t actually an argument in the case at hand, right? It is an example of a “red herring” fallacy — poisoning the well, as it were. Physics once got something wrong, therefore Jelbring is right is not an argument (even if you are correct about what you claim physics has gotten wrong, which is another whole argument).
We know the temperature of the Sun. What “climate” scientists have done is change the spectrum. The claim is that no thermal energy direct from the Sun heats the Earth, the real thermal energy that is, thermal infrared radiation which is heat on the move. Instead “climate” scientists have given its properties, being heat, to shortwave, claiming visible light heats the oceans and land, even though water is a transparent medium to it.. And then, ignoring that the heat we feel from the Sun is thermal infrared so does reach us, say that carbon dioxide a trace gas, and already fully part and parcel of the cooling cycling of the Earth in the Water Cycle, is responsible for raising the temperature of the Earth from -18°C to 15°C, without ever giving any rational explanation as to how it actually does this, and, that doubling it will cause catastrophic runaway global warming, doubling a trace gas it still remains a trace gas.
Oh-kayyyy, that’s just crazy talk. Seriously. Visible light damn skippy heats the (top layer of) the oceans. Let’s see, a small fraction of visible light reflects off of the top surface. The rest is transmitted. If you visit page 85 (section 9.2) of my online book on electrodynamics, you can actually follow the full derivation of the transmission and reflection coefficients, although they only have a relatively simple form for light coming in at right angles. But this is utterly pedestrian stuff and you literally couldn’t see if it weren’t true.
http://www.phy.duke.edu/~rgb/Class/Electrodynamics.php
If you pursue the rest of the chapter you can learn a bit about the fate of that light once it enters the water. Water is by no means perfectly transparent, and besides, impure water is a bulk conductor. Both of these thing mean that water exponentially absorbs the visible light, turning pretty much 100% of the energy that made it through the surface — which is most of the energy — into heat. So sorry, your assertion that visible light doesn’t heat water is really pretty silly.
Second, nobody argues that the sun doesn’t emit infrared or ultraviolet along with visible. In fact, you can look at the top of atmosphere spectrum of sunlight here:
http://en.wikipedia.org/wiki/File:Solar_Spectrum.png
First of all, carefully note that this is measured, not theoretical, not a conspiracy theory lie to help support the IPCC. The spectrum of sunlight was probably measured well over 100 years ago to pretty much the precision evident in this figure. Nobody cared about CAGW back then, really. Second, look at all of that IR in the long tail! And look! They even measure the difference between top of atmosphere and bottom of atmosphere, directly proving that yes, the atmosphere absorbs energy from bands all over the spectrum. Hey, it even names them for the molecular species primarily responsible for absorption.
Note that where it absorbs, it absorbs everything. Nothing to speak of gets through in that band, especially the ones above 1250 nm that are important to the GHE.
Here is the second place you are in error. CO_2 may well be a “trace gas”, a mere 0.03% of the atmosphere, but that doesn’t make it optically transparent in any given frequency!
If you want to understand that, you can — I linked my book and everything you need to learn to understand it is in there. The key here is the idea of cross-section — the effective cross-sectional area a molecule offers to absorb, or scatter, (or both), light. You already have the idea, I’m sure, because it is part of e.g. N&Z except they talk about the absorption cross-section of the earth, not a molecule. Light falls on the molecule and everything in a certain area is absorbed and turned into heat. The atmosphere is optically “thick” in those bands
Just to prove that I don’t completely disagree with some of what you are trying to say, let me offer up an interesting link:
http://landshape.org/enm/significance-of-global-warming/
This (discussion of) a paper/theory suggests that water is indeed important; it is a key in a negative feedback cycle that locks the earth into a nearly constant total greenhouse effect. It doesn’t actually argue about the details of the mechanism. It just takes 60 years worth of radiosonde data and shows that the integrated expected greenhouse effect is nearly constant, because water and CO_2 do a little dance that keeps it that way, with less water when there is more CO_2. That’s the kind of thing that the venerable Roy Spencer argues in his book (which I would highly recommend, BTW). It also suggests that things that directly modulate water vapor are far more important than CO_2 per se, because the feedback cycle adjust water content to CO_2 but cannot work the other way! More water, less water in the atmosphere won’t affect the CO_2 levels.
There is even some more or less direct evidence to support this. Even Scientific American has re-reported the NASA data:
http://www.scientificamerican.com/article.cfm?id=is-water-vapor-in-the-stratosphere-slowing-global-warming
The catch is that in order to argue in this way you have to grit your teeth and take the plunge and acknowledge that there really is a GHG GHE and that CO_2 really does play an important role in it. Not as important as water, perhaps, but the two really work together. Once you agree that the CO_2 part of the GHE is real and really does help warm the Earth relative to a good old ideal black body of the same average albedo, you’ll be all set to argue about how doubling CO_2 has almost no effect on an atmosphere that is already basically optically thick ten or twenty or thirty times over. The only way it could trap more heat is by forcing the zone where the atmosphere becomes transparent to CO_2 radiated heat upward to colder air, but if the water content of the stratosphere is dropping, things are moving the exact opposite way, and more heat is being radiated from further down where it is warmer, reducing the surface trapping of heat.
rgb
Dr. Brown
A couple days ago when you said:
,
I was hopeful, and thought you might be starting to get it.
But yesterday you removed any such hope by stating:
which highlights an obvious flaw in your reasoning.
You seem to ignore that there is a density difference with height in gas pressurized by gravity, then apply principles that are density dependent.
Robert,
I admire your persistence with Myrrh. In the vein of “forewarned is forearmed” let me tell you that Myrrh has been convinced of his “crazy talk” position on IR, visible light, and heat for some time, despite several attempts by several people to point out the sort of problems that you address.
But who know? Maybe you will have better luck than the rest of us.
Dr. Brown:
In a recent comment, you objected to my saying, “none of this affects my view that Dr. Brown’s ‘proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.” In saying that I was in fact somewhat imprecise. But stating my position more precisely is complicated by the fact that I’m not always sure precisely what your position is. For example, your position on just what you mean by temperature appears to have evolved. So, in order to respond, I need to set forth what I see as three flavors of your argument.
I’ll preface that by observing that nothing in your discussion of the first two flavors gives any reason to believe that you viewed temperature any differently from the Ideal Gas Law, which treats temperature as the ratio of pressure to the product of molecular density and Boltzmann’s constant, i.e., as two-thirds the ratio of mean molecular translational kinetic energy to Boltzmann’s constant. Dividing the pressure on the vessel wall at any altitude in your experiment by the molecular density at that altitude therefore tells you the temperature. And your position as expressed up through the time of your top post was that any gradient at all in this quantity at equilibrium—any non-zero decrease in mean molecular translational kinetic energy with altitude—violates the Second Law. In these two flavors, which I will presently describe, you disagree with Velasco et al.’s Equation 8, which states that average molecular kinetic energy decreases with altitude.
In the third flavor, which I also discuss below, you avoid disagreeing with Velasco et al. by so defining lapse rate that it equals zero if the kinetic-energy gradient equals the (non-zero) gradient that Velasco et al.’s Equation 8 defines.
Now for the three flavors.
Flavor the first (http://wattsupwiththat.com/2012/01/12/earths-baseline-black-body-model-a-damn-hard-problem/#comment-867311): “Imagine a plane surface in the gas. In a thin slice of the gas right above the surface, the molecules have some temperature. Right below it, they have some other temperature. Let’s imagine the gas to be monoatomic (no loss of generality) and ideal (ditto). In each layer, the gravitational potential energy is constant. Bear in mind that only changes in potential energy are associated with changes in kinetic energy (work energy theorem), and that temperature only describes the average internal kinetic energy in the gas. . . . On average, just as many molecules move up, with exactly the same velocity/kinetic energy profile, as move down, with zero energy transport, zero mass transport, and zero alteration of the MB profiles above and below, only when the two slices have the same temperature. Otherwise heat will flow from the hotter (right-shifted MB distribution) to the colder (left-shifted MB distribution) slice until the temperatures are equal.”
In short, you treated each layer as having an associated local temperature dictated by a local velocity profile, which according to you had to be the same for all layers to avoid net inter-layer mass transport, which is inconsistent with equilibrium. In this flavor, I wouldn’t say you begged the question. It’s just that to my mind the reasoning between the postulate of equal up- and down-going-velocity distributions across a layer boundary and the theorem of equal velocity distributions at different layers falls somewhat short of syllogistic.
Flavor the second: the head post above. Here you don’t rely on mass transport but instead rely on the assumption that at equilibrium a vertical wire will have no temperature gradient at all and that any gradient at all in the wire will result in heat flow. In this flavor you either beg the question or come very close to it. Jelbring’s assumption from which you attempt to reason to a contradiction is that a lapse rate can prevail at equilibrium: no net heat will flow despite a temperature difference. But then your argument against that assumption is just to say, Yes, it will flow—in the wire.
Now, you may respond that Jelbring’s assumption was only that no heat flows in response to lapse rate in a gas; he didn’t say anything about wires. No purpose is served by voicing my opinion that this is just sophistry. But I will raise another objection. Jelbring says the gas in isolation exhibits a lapse rate, and you say the wire in isolation exhibits none. How does it follow that the combined system exhibits the same lapse rate as the isolated gas and therefore results in perpetual heat flow? Why would it not be just as logical to conclude that the resultant lapse rate is the isolated wire’s—or some other lapse rate altogether? In other words, to reach the conclusion that heat flows perpetually, your attempted refutation makes quite a logical leap.
You gave no indication at the time that use of “temperature” in this second flavor differed at all from its use in the first. And you said that any equilibrium temperature gradient at all would violate the Second Law. “What matters is that EEJ asserts that dT/dz ≠ 0 in stable thermodynamic equilibrium.” “The magnitude of the difference [between the top- and bottom-of-column temperatures], and the mechanism proposed for this separation are irrelevant. . . .” You didn’t say that mean molecular kinetic energy had to be uniform—except for a negligibly small gravity-imposed skew toward the bottom. You didn’t say it had to be uniform—except for a skew that under gravity results in no net heat flow. You said no temperature gradient at all, and, according to the Ideal Gas Law, that means no non-zero mean-molecular-kinetic energy gradient, no matter how small. In this you disagreed with Velasco et al.’s Equation 8. This brings us to:
Flavor the third: Here I’ll admit I’m putting words in your mouth. But I’m inferring from your approval of Paul Birch’s and DeWitt Payne’s comments that your position has now evolved to the following. You’ve repented of your position in the first flavor, where you contended that every altitude layer had to have the same velocity profile—and thus the same mean molecular translational kinetic energy. You now believe that there can be an equilibrium difference between top- and bottom-of-column mean molecular translational kinetic energies, so long as no heat flows, because the definition of a temperature difference is that it is the quantity that causes heat flow: if there’s no heat flow, then, by definition, there’s no temperature difference, i.e., no lapse rate.
This flavor saves you from disagreeing with Velasco et al.’s Equation 8—but it makes your attempted refutation depend on Jelbring’s use of the term “temperature.” That is, you have to interpret Jelbring as using “temperature” not as we all learned it in connection with the Ideal Gas Law but rather as the quantity whose difference is by definition zero if no heat flow results—in a wire. If you don’t—i.e, if you accept that temperature is, as we learned in high school, mean molecular translational kinetic energy—then accepting that a difference in that quantity does not necessarily cause heat flow guts your attempted refutation of Jelbring’s theory. If a temperature difference does not necessarily result in heat flow, then perpetual heat flow through the wire does not necessarily result.
Since this reply has already gone on far too long, I won’t repeat here why Paul Birch’s and DeWitt Payne’s comments are inapposite. I will say that I largely agree with Tim Folkerts’ statement about Velasco et al.’s Equation 8’s being directed to a very specific situation and that it approaches isothermality in the limit. I am not contesting your result as a practical matter, only the adequacy of your proof. But I will add that the situation to which Equation 8 is directed is precisely the one to which your head post above is.
Robert Brown says at 2/4 9:11pm:
“Except that it is a ten-second mental exercise to see that this is not, in fact, maximum entropy.”
Robert Brown’s ten-second mental exercise is too short in fact & can be shown incorrect, impeded by thinking of conduction in solids (molecules can’t move) and not ideal gases (molecules move & mix). It takes much more than a ten-second proof to show why Robert Brown’s mental exercise is incorrect. See 13 steps below.
Robert Brown continues: “Because if heat is transferred from the warmer bottom to the cooler top, the entropy of the arrangement will increase.”
Yes, of course, because the transfer process does work on the system in Fig. 1. Your delta Q is then not zero so that your delta S is not zero. But remember Fig. 1 allows no work or heat flow to come across the control volume, it is adiabatic equilibrium by definition. Fig. 1 delta Q is zero, thus delta S is zero. Constant entropy S prevails inside Fig. 1 due to the adiabatic boundary.
Robert Brown continues: “The only way the gas will not be isothermal at maximum entropy is if heat transfer is impossible.”
Bingo! Heat flow (or work) transfer within & across the adiabatic control volume is impossible as it can be shown the GHG-free ideal gas will be non-isothermal at maximum entropy equilibrium.
Robert Brown continues: “Go ahead, do the algebra.”
Ok I will. The constant entropy of Fig. 1 must be maximized mathematically as in nature. I will outline the correct algebra. Robert Brown has done incorrect algebra in the top post by improper temperature integration. Any physicist CAN do it correctly, consulting with the math dept.
Here are the correct algebra and proper steps for Fig. 1:
1) Start by computing the total GHG-free air constant mass per unit area of a gas layer between any two heights under gravity g
2) Add in the hydrostatic equilibrium pressure change with height in the gravity field
3) Compute the total enthalpy per unit area of the layer realizing the layer possesses potential energy per unit area in earth’s gravity field
4) From that, realize energy conservation imposes a constraint that total dry static energy is constant in the layer (within adiabatic control volume)
5) From this, realize and compute the total entropy (S) of the layer over the height of the layer
6) Transform S computation from height to pressure by way of hydrostatic eqn. above and ideal gas law
7) Now maximize this entropy S to find nature’s required ideal gas temperature profile
8) To do that, confine the math maximization process to reasonable range of pressures found in earth’s atmosphere (roughly 1000mb down to 200mb ~80% of atmosphere) to make no serious errors
9) Transform variables to make the calculation much more simple (the math. Dept. will help Robert Brown here)
10) Find the function for which the layer’s entropy S is maximum subject to energy conservation constraint in the layer
11) To simplify, constrain this maximization to a linear set of temperature profiles
12) The condition for entropy S to be an extremum is that its derivative vanish
13) Do the algebra, find the nature of the entropy S extremum IS a maximum only with non-isothermal temperature profile.
Of all the linear temperature profiles, find entropy maximization requires the equilibrium temperature of Fig. 1 to decrease with increasing height i.e. it is non-isothermal, T1b is required to be higher than T1t by proper maximization of entropy. Robert Brown missed most of this important algebra in the top post.
Then consult the math dept. to prove by contradiction the general case does not require the assumption of a linear temperature profile.
Since Robert Brown cannot do that in a ten-second mental exercise & did not do the algebra in top post correctly to maximize entropy, his assertion of isothermal w/gravity is impeded by jumping to a conclusion from conduction in solids which these steps have proven incorrect using ideal gas law, conservation of energy constraints, entropy maximization and proper, correct algebra.
The ten-second mental exercise of why considering conduction in a solid is inappropriate involves the solid’s molecules are constrained not to move much in the solid since they mostly vibrate. The gas molecules can move throughout the Fig. 1 column top to bottom w/o constraint other than random elastic collisions freely mixing subject to constraint of ideal gas, energy conservation and entropy laws.
Robert continues: “BTW, no, I’m not talking about lifting up any parcels of gas during equilibration.”
Good, w/increased learning Robert Brown moved on past the jars.
Robert Brown continues: “The gas is equilibrating via thermal and radiative conduction. No work is done by gravity.”
Yep, after reaching equilibrium no work is done by gravity. The gas is thermally equilibrated max. entropy non-isothermal proved in the steps of this post.
Robert Brown continues: “Well, that’s not quite true.”
No, that IS true.
Robert Brown continues: “As the bottom cools and the top warms the center of mass of the gas will indeed move down because the density of the gas at the bottom will increase while the density of the gas at the top will decrease.”
No, not after Fig. 1 achieves equilibrium as it must with no energy across the control volume. See the steps above.
Robert Brown continues: “You’re all about energy balance and gravity.”
Yes, so is earth’s nature.
Robert Brown continues: “Well, the gas is, on average, lower when it is in thermal equilibrium, not higher, in a macroscopically more stable state, a hydrostatically more stable state. Remember, it is always in hydrostatic equilibrium.”
Yes, I remember it is always in hydrostatic equilibrium once Fig. 1 achieves equilibrium. No, it is not macroscopically stable unless maximum entropy is achieved which is constrained by energy conservation to be non-isothermal.
Robert Brown continues: “The most gravitationally stable profile is isothermal.”
No, Robert Brown cannot just simply assert this; it is way more difficult as the task shows, maximum entropy with gravity field is proven non-isothermal in the steps of this post, detail algebra ref. B&A text. Non-isothermal profile is very close to the real atmosphere as shown by Verkley paper Fig. 2 referenced above by poster Rodrigo Caballero.
Without gravity, the outline in this post with g=0 reverts to isothermal temp. profile as it must. Gravity REALLY complicates things beyond a ten-second mental exercise but nature resolves itself. Note thermo can’t tell us how long but experimental evidence shows the time frames to equilibration are relatively short.
It has been a fun, interesting conversation for me, thanks Robert.
Trick says: “But remember Fig. 1 allows no work or heat flow to come across the control volume, it is adiabatic equilibrium by definition. Fig. 1 delta Q is zero, thus delta S is zero. Constant entropy S prevails inside Fig. 1 due to the adiabatic boundary.”
This is not at all correct.
1) The system is adiabatic by definition, but it is not by definition in equilibrium. The system was postulated to be in hydrostatic equilibrium, but the question of thermal equilibrium was left unspecified (and eventually Dr Brown’s conclusion is that it was NOT thermal equilibrium). (I am not even 100% sure what you would mean by “adiabatic equilibrium”.)
2) It is true that there is no Q to/from outside the system, but there can still be Q within the system. Forget gravity for the moment — simply put a container of hot gas (say 400 K) and a container of cold gas (say 200 K) within adiabatic walls. Then put them into thermal contact.
When the first joule of energy moves from the hot side to the cold side, entropy will increase by
dS = (+1 J) / 200 K + (-1 J) / 400 K = + 1/400 J/K
Entropy will continue to increase (albeit more slowly) as heat continues moving from hot to cold until the two are isothermal. Constant entropy will only prevail within the adiabatic boundary after conduction within the systems ceases (ie after thermal equilibrium is achieved ie the system becomes isothermal).
You might want to restart your arguments from the beginning to fix these errors.
You seem to ignore that there is a density difference with height in gas pressurized by gravity, then apply principles that are density dependent.
 ?
? and a starting pressure e.g.
and a starting pressure e.g. 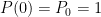 atm. All of them are hydrostatic — in perfect force balance — by construction, they satisfy the differential equation above for the balance of buoyant forces in a fluid. Not all of them are necessarily stable to convective perturbations, I imagine, but many, an infinite number of the in fact, are and none of them but one thermal profile is stable if the gas can thermalize via conduction and radiation. That one solution is maximum entropy, in hydrostatic balance, and in thermal equilibrium. It happens to be isothermal.
atm. All of them are hydrostatic — in perfect force balance — by construction, they satisfy the differential equation above for the balance of buoyant forces in a fluid. Not all of them are necessarily stable to convective perturbations, I imagine, but many, an infinite number of the in fact, are and none of them but one thermal profile is stable if the gas can thermalize via conduction and radiation. That one solution is maximum entropy, in hydrostatic balance, and in thermal equilibrium. It happens to be isothermal.
Ignore it except where I actually derive it (for an ideal gas) in the original article? Ignore it except for where I write out an explicit differential equation such as this:
Ignore it sort of like I’m not ignoring it at all? Sure I am. Did you actually read the top article or are you just reacting blindly because I am threatening your illusion that gravity magically heats static gases?
Neither you nor Myrrh seem to be able to grasp the idea that there are an infinite number of solutions to this ODE, given a thermal profile
In order to establish the DALR in a gas in the first place, however, you have to have masses of gas moving up and down because the gas is not in hydrostatic equilibrium. If the top is warmer than the bottom, there will be no convection! The fluid would have to literally lift itself up by its bootstraps to warm the bottom and cool the top from this initial state, because the bottom would expand (constant pressure, higher temperature), lifting the center of mass of the gas and increasing its potential energy!
Right.
rgb
Tim Folkerts say 2/5 at 1:19pm:
“…but there can still be Q within the system.”
Transiently, yes. But there is no heat flow at equilibrium. Q inside the control volume flows until equilibrium and then stops flowing at max. entropy. I have come to learn this is REALLY hard to get a handle on for many when gravity is added. The proof is in the maximization of entropy which is hard to see also, heat ceases to flow at max. entropy. There is a temperature gradient from the mixing of the ideal gas w/gravity at equilibrium in Fig . 1. Work thru the 13 steps. S-l-o-w-l-y.
Tim continues: “Entropy will continue to increase (albeit more slowly) as heat continues moving from hot to cold until the two are isothermal.”
No, the math proves isothermal for Fig. 1 is not the max. entropy; S can still increase from the isothermal condition in Fig. 1 above – this is a very neat thing to learn out of this. For homework, pick a set of reasonable Fig. 1 initial conditions. Compute S in an isothermal field. Then compute S for the non-isothermal field, same initial conditions.
The S for isothermal will be less than the non-isothermal field. Try it. Report back. Nature fixes the isothermal lesser S by flowing heat & naturally increasing entropy to the max. S when heat stops flowing & non-isothermal max. entropy. Really pretty neat.
“Forget gravity for the moment… When the first joule of energy moves from the hot side to the cold side, entropy will increase…”
Yep, to equilibrium at max. entropy. Gravity however is not forgotten in Fig. 1. Gravity imposes a potential field, a pressure gradient and that makes all the difference, nature finds an ideal temperature gradient. VERY close to the actual temperature gradient in the real atmosphere (and way closer to reality than the isothermal conclusion for Fig. 1). Ref. Verkley paper Fig. 2 above.
Fig. 1 moves from isothermal to non-isothermal equilibrium when gravity is added. There are no errors I can find in the proof.
Robert Brown says:
February 4, 2012 at 9:49 pm
Myrrh says:
February 4, 2012 at 7:01 pm
Adiabatic Cooling…
Nice picture, and nice article. Note well that the figure clearly labels the wall of the balloon as being a thermal insulator — that’s the adiabatic part, actually. Suppose that it wasn’t really a perfect thermal insulator? Hmmm, would the gas precisely follow the adiabatic PV curve if heat could flow into the contents of the balloon from the gas surrounding it?
I’ve already noted it well…, glad you noticed. But, don’t worry about what would happen etc. just yet, get yourself firmly acquainted with the basic concept first. The Adiabatic Process is fully understood in the real world. Adiabatic means without heat entering or leaving the system. Familiarise yourself with that picture.
Note well that the article clearly states that the air takes on an adiabatic lapse as it is being uplifted. It even offers pretty much the only two mechanisms for uplift, and truthfully that can be reduced to one. The first is differential heating leading to convection, the second is the deflection of lateral air movements as they go up or down a mountainside. The second, of course, requires pressure differences to generate the wind and pressure differences are only created by differential heating. No differential heating (on Earth or anyplace else) — no ALR.
I’ve already noted it well.. You need to note well that “takes on an adiabatic lapse rate as it is being uplifted” is because it is within the adiabatic process, that’s what it will do. Do try to refrain from interpolating your own version into this – this is one of the basic constants of our physical world, like heat always flowing from hotter to colder, because that is the way it is. Gases with extra heat input might well rise faster, and chinook winds speed up the heating of its air as it comes into greater pressure from the heights, but we are talking about the basic process here, to which all these relate, created by gravity. What this is saying is that these will act according to the basic structure. The adiabatic lapse rate exists without any extra heat coming into or leaving the system, it’s created by gravity. From that we can understand our winds, our weather systems. Parcels of air moving through the atmosphere are called wind, convection, I’m glad you have heard of convection, it is one of the three modes of transport for heat, as thermal energy on the move.
Air uplifted will cool as the air pressure decreases, and will heat up as it descends as air pressure increases, it takes on the adiabatic lapse rate up and down, remember the picture. Moved higher it will expand as it becomes less dense and will cool, moved lower into higher pressure it will become more dense and will heat up. That is the Adiabatic Lapse Rate, it is a constant. That is the process created by gravity. That’s what Adiabatic Lapse rate means, relating to a specific process and not to anything else some might want to imagine. Don’t confuse it with the environmental lapse rate
From: http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
[bold as on original page]
[“The process of convection causes air warmer than its environment to rise, and cold air to sink. Convection thus transports heat upward, making it warmer aloft than it would be in the absence of convection. However, in the atmosphere, in contrast to what happens in a kettle filled with water and set on the stove to boil, convection does not lead to a temperature profile that is uniform with height. This is because the rising air cools adiabatically. Dry convection will tend to create an adiabatic temperature profile in which the temperature falls at a rate of 9.8 °C per kilometer.” ]
Next step:
[“But what the ideal gas law can not tell us is what will happen to the temperature. To find that out we need to consider the first law of thermodynamics – a physical law that extends the principle of conservation of energy to include the concepts of heat and work.
“In thermodynamics the simplest form of energy conservation is the balance between internal energy (the kinetic energy of the body’s internal molecular motion – directly proportional to its temperature), and the amount of heat added to the body minus the work done by the body on its surroundings.
“As our air parcel expands in response to the lowering of the outside pressure, the force of its internal pressure is moving the walls of the container outwards. When a force is moving an object over a given distance it does work. Thus the expanding air parcel does work on its surroundings. This work must come at the expense of internal energy (remember, heat is neither added nor taken away from the parcel in this experiment). Thus the molecular motion within the parcel will slow down, and the parcel’s temperature will drop.
“The expanding parcel will experience not only lowering of its pressure and density, but also of its temperature. All three state variables: pressure, density, and temperature will remain in balance as described by the ideal gas law. The process described above is called adiabatic expansion, implying the change in parcel density without the exchange of heat with its surroundings, and its consequential cooling. The opposite will occur when the parcel is compressed. Adiabatic compression leads to warming“.
..
IV. Atmosphere under gravity – hydrostatic balance.
Hydrostatic balance
“In the vertical direction, gravity is by far the most important external force acting on the atmosphere. It is the reason for the existence of this crucial envelop of gases around the Earth.”
..
“We can now combine the thermodynamic laws with the effect of gravity on pressure. Using the equation of state, the first law of thermodynamics, and the hydrostatic equation we can find that the rate of adiabatic temperature change in an ascending air parcel (also termed the adiabatic lapse rate and denoted Γd) is constant: ..”]
Last bold mine..
An interesting question is then — suppose one starts with an air column (Jelbring conditions, dry ideal gas, no mountains, wind, or sources of heat) but select as an initial condition hydrostatic equilibrium with a thermal profile somewhere in between the classic DALR and isothermal. Which way (to which profile) will this air column go? etc.
You’re still not getting hydrostatic balance, it doesn’t mean nothing is happening and you have to bring in another idea into the system to work out what will happen…, the adiabatic lapse rate will happen, because gases will become more dense and sink when cold and so will find themselves under great pressure at the surface where they will get compressed and heat up, and heated up they will become less dense and rise and in rising they will cool and in cooling they will become more dense and sink and so on. Local conditions apply within that, superimposed on it, by bringing in an extra heat source for a parcel of air for example, it will rise faster than the adiabatic lapse rate conditions of the gases around it, but the rate will always be relative to the natural cycle, because it’s a relationship of gases with gravity.
[Hydrostatic balance
“In the vertical direction, gravity is by far the most important external force acting on the atmosphere. It is the reason for the existence of this crucial envelop of gases around the Earth.
“The atmosphere does not collapse under the downward pull of gravity because of the energy embedded in the movement of the air molecules. This movement creates the force of pressure which counters the gravitational pull on the atmosphere. The balance between the force of pressure and gravity is the hydrostatic balance.
To find the expression for the hydrostatic balance, we first note that atmospheric surface pressure is due to the weight of the entire atmospheric column above. As we ascend, there is less of an atmosphere above us, and hence the pressure drops.”]
The adiabatic lapse rate is within the hydrostatic balance because of the properties of gases which create the pressure. And it’s temperature profile..
[“To understand the equation of state, assume that you have a fixed mass of air enclosed in a container with rigid walls (hence with fixed volume). If we warmed the container, say by putting it over a flame, the temperature of the air (i.e., kinetic energy of the air molecules) will rise and the pressure (i.e., the force exerted by these molecules on the container walls) will increase. The density of the air will not change since we are not increasing the amount of gas in the container nor the volume of the container. The ideal gas equation states that the increase in pressure is directly proportional to the increase in temperature.
“Lets replace the rigid wall of the container with flexible ones, that are allowed to stretch freely if the pressure inside rises above that on the outside. In that case, when we raise the temperature, the pressure inside will remain constant (and equal to the outside pressure), but the container’s volume will increase. This means that the density will decrease (because the mass inside does not change). The ideal gas law states that the density decrease will be inversely proportional to the increase in temperature.” ]
Now you know what the adiabatic lapse rate is, why don’t you try answering the posers Jelbring set?
Tim Folkerts says:
February 5, 2012 at 7:22 am
Robert,
I admire your persistence with Myrrh. In the vein of “forewarned is forearmed” let me tell you that Myrrh has been convinced of his “crazy talk” position on IR, visible light, and heat for some time, despite several attempts by several people to point out the sort of problems that you address.
But who know? Maybe you will have better luck than the rest of us.
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
As Latour said, it’s junk science and the problem is mainly that “climate” scientists think they know better than the applied scientists who actually use light and heat and know the difference.
We just need the hundredth with the intelligence to see how he’s been conned, maybe it will be Robert..
Trick says:
>No, the math proves isothermal for Fig. 1 is not the max. entropy”
Sorry, I didn’t see any math, just prose. Could you show what you think is the actual math is?
>S can still increase from the isothermal condition in Fig. 1 above
Entropy is defined classically as dS = dQ/T. Suppose you have an isothermal situation to start with. If heat moves from any region 1 to any other region 2, this will cause T2 > T1. The next bit of heat dQ will result in dS = dS1 + dS2 = -dQ/T1 + dQ/T2 The S for isothermal will be less than the non-isothermal field. Try it.
I just did. My math suggests you are wrong. What is your math?
>VERY close to the actual temperature gradient in the real atmosphere
What specific gradient do you get? (State your assumptions).
I would challenge you to “look for the errors” in the Velasco paper. He concludes that the temperature gradient diminishes as the number of particles increases, becoming infinitesimally small as the number of particles increases. I tend to trust published papers with extensive math, rather than blog posts with only an outline of steps.
>There are no errors I can find in the proof.
If you really think you are right and Velasco’s paper is wrong (and I am wrong and Dr Brown is wrong), then write up your ideas and try to get them published. If it is as simple as your 13 steps suggest, it should be no problem refining the prose and letting peer review look for the errors.
Tim Folkerts says 2/5 at 5:34pm:
“If it is as simple as your 13 steps..then write up your ideas and try to get them published.”
I’ve cited the prior publications. My posts are not new ideas. I’ll get back on your other issues; need a little more time. The answers are in the 13 steps (which are NOT simple, take time).
In short, sure the Velasco paper “concludes that the temperature gradient diminishes as the number of particles increases, becoming infinitesimally small as the number of particles increases” which means sure the gradient is VERY small but it remains non-zero i.e. T gradient for Fig. 1 not isothermal constant.
Proof is Velasco eqn. 8 for 1 particle collapses to TE = KE + PE, even the single particle is non-isothermial, i.e. Velasco eqn. 8 does not collapse to TE = KE isothermal. Check it out. The pressure would be so low as to be fringe of the real atmosphere though, this is just a thought experiment.
Trick,
I think we need to be very careful about defining temperature, especially for a single particle. Typically temperature can be defined using 3/2 kT = KE, but really we should say that every degree of freedom should have the right average energy:
1/2 kT = 1/2 m v_x^2= 1/2 m v_y^2= 1/2 m v_z^2
Rotational energy also counts. Vibrational energy also counts (although these don’t come into play for ideal monatomic gases). And potential energy counts, as clearly shown in solids where specific heat is based on 3kT = KE + PE, not 3/2 kT. Read up on the Dulong–Petit law
Normally PE is ignored because normally PE doesn’t change appreciably in typical containers of gas. But PE is indeed part of the thermal energy. It would take a bit more study, but I am convinced that when PE is properly taken into account, then the “temperature” even of a single particle will be constant at all altitudes, even though KE is definitely NOT constant.
Food for thought — the rotational energy of a diatomic molecule will not be affected by altitude. So the “rotational temperature” of a system with a single molecule will be constant at any altitude. So what we have is that
* the “rotational energy temperature” is always constant
* the “kinetic energy temperature” is greatest at the bottom
* the “potential energy temperature” is greatest at the top
The “total temperature” could well be constant everywhere (and I am convinced it is).
Tim Folkerts says 2/5 at 7:42pm:
“But PE is indeed part of the thermal energy.”
No, PE is not part of the thermal energy; PE is a component of the molecule’s total energy constant TE = 1/2mv^2 + mgh = KE + PE. Total energy TE is constant b/c total energy is conserved by 1st law.
Tim continues: “the “kinetic energy temperature” is greatest at the bottom
* the “potential energy temperature” is greatest at the top”
That is correct except drop “temperature” in the 2nd line, especially in Fig. 1 equilibrium. PE is not temperature as measured by a thermometer.
Tim continues:“The “total temperature” could well be constant everywhere (and I am convinced it is).”
This is incorrect. The 1st law says a particular molecule total energy TE is constant everywhere it (randomly) goes in Fig. 1. The molecule’s thermal energy is KE i.e. temperature which is ~speed of the molecule, this speed decreases as the molecule climbs against the gravity field, hence T decreases, even in equilibrium. TE = PE + KE for each of a bazillion molecules in Fig. 1 transiently and at equilibrium. KE and thus temperature has a gradient. Max. entropy is the equilibrium of the temperature gradient (non-isothermal max. entropy equilibrium).
Certainly neither bulk KE nor bulk PE nor bulk RE (rotational energy) nor bulk VE (vibrational energy) is part of thermal energy.
But the “individual KE” of particles within the system is part of the ThE (thermal energy). The “individual RE” of particles within the system is part of the ThE (thermal energy). The “individual VE” of particles within the system is part of the ThE (thermal energy).
And similarly, the “individual PE” of the particles is also part of the ThE. Atoms in solids have SIX degrees of freedom — three axes for KE and three axes for PE. A vibrating atom in a solid has 3kT of thermal energy, not 3/2 kT.
Similarly, the individual PE of the atoms in a gas must also be part of the ThE.
I agree that thermometers typically measure the KE of particles, but imagine you could suddenly remove all the KE from the gas in the column. The “KE temperature” would drop suddenly to zero. But now the gas will start to fall. As it hits the bottom and rebounds, suddenly there will be collisions to thermalize the energy again. The particles will gain KE at the expense of the PE. Eventually the system will come back to thermal equilibrium at a much lower temperature.
Or do the same thing with a diatomic gas, where the height of the container is negligible. You removed energy from 3 degrees of freedom. But the particles will bump into each other and the rotational energy will kick the molecules around until the energy is evenly distributed in the 5 degrees of freedom.
It is getting late, so I am not sure I am 100% coherent. But the “individual PE” is definitely part of the thermal energy of atoms in solids. And the individual PE should also be part of the ThE of gases
Transiently, yes. But there is no heat flow at equilibrium.
So if we move heat from the bottom to the top, we increase the entropy of the system and the Universe, but this won’t happen because of gravity. And once we do, exactly how will it go back to the way it was before? Oh, yeah, by decreasing the entropy of the system.
You can’t get out of the problem by circular reasoning. Sure there is no heat flow at equilibrium, because equilibrium is maximum entropy. However, you just admitted that if heat is transferred to the top, the entropy increases. Ergo, what you claimed is maximum entropy isn’t. Q.E.D.
rgb
No, PE is not part of the thermal energy; PE is a component of the molecule’s total energy constant TE = 1/2mv^2 + mgh = KE + PE. Total energy TE is constant b/c total energy is conserved by 1st law.
You really might want to look at the final exam solution I posted a link to above.
Just a thought.
Once you’ve figured out how to explain how a gas that — you admit — can have a higher entropy than the state you claim is maximum entropy.
rgb
It would take a bit more study, but I am convinced that when PE is properly taken into account, then the “temperature” even of a single particle will be constant at all altitudes, even though KE is definitely NOT constant. is given by:
is given by:

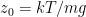 is the characteristic length of concentration decay (typically around 5-6 kilometers in air at reasonable temperatures). This result is constrained by the requirement that:
is the characteristic length of concentration decay (typically around 5-6 kilometers in air at reasonable temperatures). This result is constrained by the requirement that:

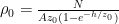
 .
.



 . As the gas is warmed,
. As the gas is warmed, 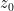 increases, the thickness of the gas layer grows, the center of mass of the gas increases, and the potential energy of the gas increases. At
increases, the thickness of the gas layer grows, the center of mass of the gas increases, and the potential energy of the gas increases. At  the gas fills the volume uniformly.
the gas fills the volume uniformly.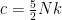 , which is very much not the usual ideal gas result, but it is easy to understand.
, which is very much not the usual ideal gas result, but it is easy to understand.  of any input heat goes into making the gas expand, lifting its CM and increasing
of any input heat goes into making the gas expand, lifting its CM and increasing  . At high temperatures the gravity (second) term goes to 1, so the heat capacity goes back to the usual ideal gas
. At high temperatures the gravity (second) term goes to 1, so the heat capacity goes back to the usual ideal gas  .
.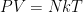 as usual, and so on. However, if you add heat to the system the entire gas column expands nonlinearly, and some fraction of the heat added goes into lifting the center of mass of the gas. Local temperature, global heat capacity. I think that’s one of the things that has been missed — for variations of height much less than
as usual, and so on. However, if you add heat to the system the entire gas column expands nonlinearly, and some fraction of the heat added goes into lifting the center of mass of the gas. Local temperature, global heat capacity. I think that’s one of the things that has been missed — for variations of height much less than 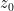 — especially for variations on the order of the mean free path of the molecules in the system — gravity really is irrelevant. The air behaves precisely like air in the room you are sitting in (where
— especially for variations on the order of the mean free path of the molecules in the system — gravity really is irrelevant. The air behaves precisely like air in the room you are sitting in (where 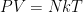 is taken for granted) because the air in the room you are sitting in is a slice in just such a column. Gravity is irrelevant in your room, and only becomes very slightly relevant inside e.g. the elevator shaft of a fairly large office building. But if you heat all the air in any layer of a closed column, you cause all of the air to expand and gravity becomes relevant, not to the local temperature description of the gas but to the fact that the gas behaves partly like gas in a cylinder, doing work to lift or lower all of the gas above it as it thermally expands or contracts.
is taken for granted) because the air in the room you are sitting in is a slice in just such a column. Gravity is irrelevant in your room, and only becomes very slightly relevant inside e.g. the elevator shaft of a fairly large office building. But if you heat all the air in any layer of a closed column, you cause all of the air to expand and gravity becomes relevant, not to the local temperature description of the gas but to the fact that the gas behaves partly like gas in a cylinder, doing work to lift or lower all of the gas above it as it thermally expands or contracts. , the second term in
, the second term in 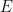 vanishes (making any temperature a “low” temperature as
vanishes (making any temperature a “low” temperature as  ) and gravity does indeed behave like additional degrees of freedom in the specific heat of the entire system while every small subvolume of the gas still behaves precisely like an ordinary ideal gas with kinetic energy $\frac{3}{2}NkT$ and yes, with detailed balance across any vertical surface (although yes, Joe, my argument involving shifting the MB distribution was sloppy and imprecise — hopefully you like this one better but the result is the same either way).
) and gravity does indeed behave like additional degrees of freedom in the specific heat of the entire system while every small subvolume of the gas still behaves precisely like an ordinary ideal gas with kinetic energy $\frac{3}{2}NkT$ and yes, with detailed balance across any vertical surface (although yes, Joe, my argument involving shifting the MB distribution was sloppy and imprecise — hopefully you like this one better but the result is the same either way). minus a term that vanishes if the height of the column goes to infinity and that cancels the
minus a term that vanishes if the height of the column goes to infinity and that cancels the  if the height is much less than
if the height is much less than 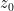 . Local definition of temperature. Globally consistent total energy and heat capacity. Gravity strictly ignorable when considering parcels of air on scales much less than
. Local definition of temperature. Globally consistent total energy and heat capacity. Gravity strictly ignorable when considering parcels of air on scales much less than 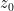 .
.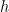 . The gas on the bottom behaves like an ordinary ideal gas, after all, and expands when warmed at constant pressure. I can easily imagine heating the gas at the bottom and have the heated gas lift the air above it, doing work with some of the heat.
. The gas on the bottom behaves like an ordinary ideal gas, after all, and expands when warmed at constant pressure. I can easily imagine heating the gas at the bottom and have the heated gas lift the air above it, doing work with some of the heat.
The solution is worked out in the final exam question I posted. So it won’t take a lot more study. I provide a summary of the answer below.
The density/concentration profile of N molecules of the monoatomic gas in a thermally isolated cylindrical container of height
where $\rho_0$ is the concentration at the bottom of the cylinder and where
so that:
or
Given the density, it is straightforward to compute the total kinetic energy from equipartition; it turns out to equal:
as usual. The potential energy is a bit more difficult; one has to integrate:
$\latex \Pi = mg\int_0^h z \rho(z) dz$
This integral is straight up integration by parts to get:
$\latex \Pi = NkT – \frac{mghN}{(e^{h/z_0} – 1)^2}$
Summing, the total energy is:
Differentiating (to find the heat capacity) we get:
Physically, this means is that at low temperatures, the gas is effectively concentrated in a layer of thickness
What happens to the heat capacity is also interesting. For low temperatures, the second term vanishes so
As you can see, there is nothing wrong with the ideal gas law in any particular layer — the usual molecular interpretation of temperature holds there,
It is also interesting to note that if
This is the point that is being missed by Trick. He asserts that temperature is related to kinetic energy only, and that kinetic energy on average “decreases” per molecule as one ascends the air column. This, we see, certainly not necessarily correct. Kinetic energy (per molecule) in fact remains constant (along with temperature) as one ascends an isothermal, isolated, hydrostatically balanced air column. However, the gravitational potential energy of the entire air column becomes a nontrivial function that has a leading temperature dependence of
And here’s the kicker. Start from this isothermal state. Then transferring heat internally from the top to the bottom of the gas to warm the bottom (and e.g. “spontaneously” create a lapse rate) raises the center of mass of the system independent of
Now, I can visualize a gas slumping downward, lowering the center of mass and compression heating the bottom, no problem. Gravitational potential energy converts into heat. I have the damnedest time imagining an isothermal hydrostatic gas heating itself at the bottom and doing positive work with some of that heat to lift the center of mass of the system, given that it is in hydrostatic balance to start with. It seems, somehow — Demonic!
Verily, I say unto you, my brothers: (Maxwell) Demons out!
rgb
Sorry moderator, errata for the algebra: . Please fix
. Please fix 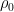 . I left a closing parenthesis off the second standalone equation. I left a leading slash in the \latex in two equations. And I have no idea what happened to the heat capacity. — it should read something like Nk ( 5/2 – (h/z_0)^2 e^{h/z_0}/(e^{h/z_0} – 1)^2 ). Finally, left the latex out of the kinetic energy term in a later paragraph.
. I left a closing parenthesis off the second standalone equation. I left a leading slash in the \latex in two equations. And I have no idea what happened to the heat capacity. — it should read something like Nk ( 5/2 – (h/z_0)^2 e^{h/z_0}/(e^{h/z_0} – 1)^2 ). Finally, left the latex out of the kinetic energy term in a later paragraph.
First equation should be
rgb
Reply: I haven’t the slightest idea how to fix all this. Get it working here http://charlesthemoderator.wordpress.com/2012/02/06/robert-browns-test-page/ with instant feedback and then replace it here and instruct a moderator to delete the old comments. ~ctm
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
Myrrh, nobody who writes electrodynamics textbooks does so to try to “con” students. It’s way too much work, way too little reward.
So what, exactly do you think happens to all of the electromagnetic energy in that visible light that makes it through the surface of the water? I mean I’m assuming that you’ve gone swimming before and opened your eyes underwater and know that you and the fishies can see because there is plenty of visible light that makes it through the surface. I’m also assuming that you’ve seen the discovery channel or animal planet and realize that the ocean is almost totally dark 1 km down. So somewhere between the surface and 1 km down, all the visible light went away.
What happened to all of that energy? Demons again? Failure of global energy conservation? I’m fascinated by your take on this — an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light (water isn’t like a cloud, with a high albedo from multiple elastic scattering). So where does it go?
I’m just sayin’…
rgb
Robert Brown says
“an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light…. So where does it go?”
I realise that thermodynamics lecturers don’t get out much.
Does this help?
http://www.life.illinois.edu/govindjee/paper/gov.html
Bryan,
Photosynthesis will not solve the problem — only delay it. Plants absorb EM energy, it is true. But a few hours or weeks or centuries later, they die or get eaten, thereby releasing the energy. Only a NET increase in plants (or a net sequestration of organic matter) will pull out energy in the long term. To a very high degree, on an annual basis the energy released as plant decay is the same as the energy absorbed by growing plants.
Does this help?
Robert, when I said “It would take a bit more study”, I meant on my part. I didn’t doubt that the problem has already been adequately addressed by others who work more closely with these ideas. But thanks for the explanation. 🙂
Tim Folkerts
“Photosynthesis will not solve the problem — only delay it. Plants absorb EM energy, it is true. But a few hours or weeks or centuries later”
Yes of course all energy will ultimately end up as thermal energy as predicted in Kelvins heat death of the universe.
A consequence of the second law.
But the storage capacity of the electrochemical reactions should not be ignored.
Greenhouse theory enthusiasts alarm us with the consequences of burning fossil fuels which have trapped light energy for 400,000 years.
At the same time producing diagrams like K&T2009 which ignore the fact that light energy is required for photosynthesis.
Myrrh documented a rather sinister rewrite of the NASA educational pages on this very item.
The whole greenhouse gas scare only works by exaggerating any small effects that suit it and at the sametime ignoring all effects that don’t.
Robert Brown says 2/5 at 10:25pm:
“So if we move heat from the bottom to the top, we increase the entropy of the system and the Universe, but this won’t happen because of gravity. And once we do, exactly how will it go back to the way it was before? Oh, yeah, by decreasing the entropy of the system….However, you just admitted that if heat is transferred to the top, the entropy increases. Ergo, what you claimed is maximum entropy isn’t. Q.E.D.”
No, the entropy won’t go back the way it was before or need to decrease. Yes, the entropy increases. Here’s why this is not circular reasoning.
Forcing a parcel of bottom molecules out of equilibrium to the top takes work against gravity (f*d = m*g*h). Where does the work come from? The work has to cross the control volume. Once the work crosses the control volume, the entropy of Fig. 1 increases (you’ve added the m*g*h). The new entropy at equilibrium is higher and stays constant at the higher level b/c the control volume is adiabatic.
This does NOT mean the original entropy could increase before the work was added; it was already max. at equilibrium.
Tim Folkerts: “When the first joule of energy moves from the hot side to the cold side, entropy will increase by. . . .”
Although your math seems to work, it appears to me that your conclusion may not be correct, at least if Velasco et al. are; if I interpret their paper correctly, the kinetic-energy profile of their Equation 8 is the maximum-entropy configuration, from which I would conclude that a strictly isothermal microcanonical ensemble will spontaneously undergo (an incredibly small) heat transfer to assume that (ever so slightly non-isothermal) configuration.
I don’t know the reason for this discrepancy. One possibility is that Velasco et al. are wrong. Another is that this is an occasion in which dS = dQ/T does not give the right answer, i.e., that dS = dQ/T does not take gravity into account.
A third possibility is that reallocation of potential energy somehow makes the dQ illusory, although I don’t immediately see how this could be so.
Bryan,
Since this interests you, why not estimate the effects of photosynthesis and report back? How much of the ~340 W/m^2 gets absorbed by plants? How much net change in chemical energy (in the form of added biomass) is there from year to year? How much chemical energy is being sequestered? (And how much is being released again by the organized burning of fossil fuels? I will guarantee that any natural sequestration of EM energy into chemical energy is vastly outweighed currently by human burning of old chemical energy, releasing thermal energy.)
I agree that in principle these numbers should indeed be included in the K&T diagrams. So how big ARE these effects? Are we talking 1 W/m^2? 10 W/m^2? 0.001 W/m^2?
Tim Folkerts says
“Bryan, Since this interests you, why not estimate the effects of photosynthesis and report back? How much of the ~340 W/m^2 gets absorbed by plants? ”
Is this the world of 4 faint Suns?
Is 340W/m2 capable of producing any light?
Its your silly theoryso you should know.
Since Greenhouse enthusiasts like yourself think it is zero you might be in for a shock.
When the Sun comes out in our neck of the woods its around 1360W/m2 and the spectrum does include wavelengths capable of photosynthesis.
In the grossly simplified world of treating the Earth as a perfect black body that instantly radiates any radiation it receives I suppose photosynthesis is an embarrassment to your simple world view.
I hope that helps!
Tim Folkerts asks
“How much of the ~340 W/m^2 gets absorbed by plants? How much net change in chemical energy”
Well Tim that insulation produces a blackbody spectrum well into the thermal IR band.
So no photosynthesis would be produced whatsoever , as IPCC science predicts.
So to answer Robert Browns question to Myrrh that type of radiation is completely absorbed in the top few millimetres of the water surface.
However back to the real world the 1360W/m2 solar radiation will have a significant proportion of wavelengths capable of producing photosynthesis.
Of the solar radiation reaching the surface of water some 50% is in the IR.
It will be absorbed in the top few mm causing evaporation of the surface water.
The other 50% will penetrate deep into the water and a significant proportion will be available for photosynthesis.
Notice that the evaporation and the photochemical processes both are systems that store energy that can be later released to buffer temperature change.
The radiation obsessed IPCC science model with its fictitious 33K effect is false.
So don’t believe everything that broad brush, eyes shut IPCC science tells you.
You’re still not getting hydrostatic balance, it doesn’t mean nothing is happening and you have to bring in another idea into the system to work out what will happen…, the adiabatic lapse rate will happen, because gases will become more dense and sink when cold and so will find themselves under great pressure at the surface where they will get compressed and heat up, and heated up they will become less dense and rise and in rising they will cool and in cooling they will become more dense and sink and so on.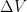 of the air. Even if you started at time
of the air. Even if you started at time  with the air in movement, the air has dynamic viscosity — even an ideal gas has an easily computable dynamic viscosity — and would quickly come to rest. Viscosity is to air what friction is to a book sliding across a table — even if you start the book with some velocity relative to a table (or a parcel of air with some velocity relative to other parcels) viscosity will quickly bring the motion to a halt. That’s the reason that the article that you linked — after all — into the discussion requires an external agency that causes the macroscopic movement of large parcels of air vertically to establish a DALR. There is no microscopic agency that so acts.
with the air in movement, the air has dynamic viscosity — even an ideal gas has an easily computable dynamic viscosity — and would quickly come to rest. Viscosity is to air what friction is to a book sliding across a table — even if you start the book with some velocity relative to a table (or a parcel of air with some velocity relative to other parcels) viscosity will quickly bring the motion to a halt. That’s the reason that the article that you linked — after all — into the discussion requires an external agency that causes the macroscopic movement of large parcels of air vertically to establish a DALR. There is no microscopic agency that so acts.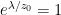 to many, many digits when
to many, many digits when  meters is the mean free path of the gas and
meters is the mean free path of the gas and  meters.
meters.  on the scale of infinitesimal layers of gas in direct thermal contact across a surface. In any event, this is in no sense responsible for a gas maintaining the DALR in particular as a stable static thermodynamic equilibrium.
on the scale of infinitesimal layers of gas in direct thermal contact across a surface. In any event, this is in no sense responsible for a gas maintaining the DALR in particular as a stable static thermodynamic equilibrium. in any macroscopic discussion is a volume large enough to contain enough molecules that thermodynamic averages pertain to the behavior of the parcel as if the air inside were a continuous fluid, so that when conducting this sort of discussion we can ignore the movement of individual molecules across the surface of
in any macroscopic discussion is a volume large enough to contain enough molecules that thermodynamic averages pertain to the behavior of the parcel as if the air inside were a continuous fluid, so that when conducting this sort of discussion we can ignore the movement of individual molecules across the surface of  (which are in detailed balance anyway, at equilibrium). Practically speaking, this is any volume that is many times the mean free path in the smallest linear dimension. Since the mean free path is quite small, cubes or lateral slices larger or thicker than a micron or so are large enough to be considered parcels in the sense that they can be described by a continuous local density, pressure, and temperature. These same parcels are large enough to be macroscopically in hydrostatic equilibrium, supported by the well-defined pressure of their neighboring parcels of fluid and at rest, locked in place by the dynamic viscosity so that to move them one has to do work or otherwise input external energy into a parcel to destabilize them, overcoming “friction”.
(which are in detailed balance anyway, at equilibrium). Practically speaking, this is any volume that is many times the mean free path in the smallest linear dimension. Since the mean free path is quite small, cubes or lateral slices larger or thicker than a micron or so are large enough to be considered parcels in the sense that they can be described by a continuous local density, pressure, and temperature. These same parcels are large enough to be macroscopically in hydrostatic equilibrium, supported by the well-defined pressure of their neighboring parcels of fluid and at rest, locked in place by the dynamic viscosity so that to move them one has to do work or otherwise input external energy into a parcel to destabilize them, overcoming “friction”.
Again, I’m fascinated. You’ve got an insulated jar of air, and you’ve left it sitting on the counter for the last ten years, but somehow you think that the air inside is busy busy moving up and down in macroscopic packets, heating at the bottom, cooling at the top, and yet somehow the bottom never gets any cooler and the top never gets any warmer! Even better, they are expanding and doing work on their environment — that’s how they adiabatically cool, thermal energy going into work. Sort of like a lava light that never stops! Well, not quite like a lava light, because we heat lava lamps on the bottom and cool them at the top and when we turn off the light, they stop working.
What is it that makes the air go up? Gravity, you say! What makes it go down? Gravity again! How does gravity do all of this work lifting and dropping air and never actually heat it, given that Joule showed that nice, turbulent mechanical work turns into heat? Demons again! Or perhaps it is invisible fairies, beating their tiny little wings.
OK. Let’s get serious. The air in the jar is, after even a fairly short time, at rest. No, it is not constantly moving up and down. It is in hydrostatic equilibrium. There is no net force acting on any small slice
BTW, please don’t answer with something that tries to make the local thermal motion of single molecules into “lifting and falling parcels of air”. You have a choice — you can work and argue microscopically, in which case you have to do a shitload of serious stat mech algebra I’m leery of even looking at so far (as I’m sure that’s what Velasco does) and it has been a few, um, decades since I took stat mech and it was the most difficult course of physics I ever took when I took it, making even quantum mechanics look like a walk in the park in comparison. The simplest things one can do microscopically are things like detailed balance estimates, and so far I haven’t made Joe happy even with what I’ve attempted there, although I think he realizes that my answer is irrelevantly imprecise (or he should realize it once he follows the reasoning in the algebra above that lays out how air can be isothermal and still have the MB velocity distribution from the bottom out to where the assumptions of thermodynamics break down anyway, because
A “parcel” of air, or “differential” volume of air
Demons Out!
rgb
Robert Brown says:
February 6, 2012 at 12:56 am
So what, exactly do you think happens to all of the electromagnetic energy in that visible light that makes it through the surface of the water? I mean I’m assuming that you’ve gone swimming before and opened your eyes underwater and know that you and the fishies can see because there is plenty of visible light that makes it through the surface.
Grin, I’ve even been scuba diving.
You can’t see why you can see underwater? Because it’s not absorbed. Water is transparent to visible light, means just that. Water transmits visible light through it without absorbing it, neither absorbed on the electronic transitional level nor on the molecular level.
I’m also assuming that you’ve seen the discovery channel or animal planet and realize that the ocean is almost totally dark 1 km down. So somewhere between the surface and 1 km down, all the visible light went away.
Poor, little nervy visible light, couldn’t make it deeper down and gave up.
What happened to all of that energy? Demons again? Failure of global energy conservation? I’m fascinated by your take on this — an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light (water isn’t like a cloud, with a high albedo from multiple elastic scattering). So where does it go?
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I’m just sayin’…
I’m just askin’
Robert Brown: “I have the damnedest time imagining an isothermal hydrostatic gas heating itself at the bottom and doing positive work with some of that heat to lift the center of mass of the system, given that it is in hydrostatic balance to start with. It seems, somehow — Demonic!”
Are you sure the center of mass rises? Couldn’t the total potential energy remain the same while the half-rho zero point rises?
Robert Brown says 2/6 at 12:37am:
“The density/concentration profile of N molecules of the monoatomic gas in a thermally isolated cylindrical container of height is given by:”
Robert – I appreciate your difficulty here using the computer language to display formulas. The formula you start with after the prose above is: air density to 5-6km earth atmospheric height z equals the air density at z=0 times exp(z/z0).
Is Robert Brown even aware this is only an approximation of the atmosphere’s density profile from surface up through the troposphere? The approximation IS a good one but it is arrived at by ASSUMING the atmospheric temperature is reasonably CONSTANT from surface up to height h, through the troposphere. Over that height the temperature actually varies ~20%. But still the actual pressure, density, N can be approximated by many of the formulas you write here considering a CONSTANT reasonable temperature is assumed.
The assumption of constant temperature allows the integration of dp/dz from z=0 to z to proceed more easily.
That is shown in the exam answer by the solution parameters assuming CONSTANT temperature. This is only an approximation, yet a decent one. You also assume constant temperature approximation in the top post for the temperature integration. The exam question then extends to non-constant temperature at the bottom where it does the partial differentiation of temperature.
This explains why you arrive at an incorrect isothermal conclusion for Fig. 1 at equilibrium. You just assume temperature is constant. This is only an approximation of the real solution which is non-isothermal as the 13 steps above conclusively show when allowing the temperature to actually vary in Fig. 1.
Although your math seems to work, it appears to me that your conclusion may not be correct, at least if Velasco et al. are; if I interpret their paper correctly, the kinetic-energy profile of their Equation 8 is the maximum-entropy configuration, from which I would conclude that a strictly isothermal microcanonical ensemble will spontaneously undergo (an incredibly small) heat transfer to assume that (ever so slightly non-isothermal) configuration.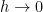 result. We keep thinking that there are two things that are important for such a gas —
result. We keep thinking that there are two things that are important for such a gas — 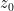 and (separately) temperature. There are not. There is just
and (separately) temperature. There are not. There is just 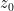 . The gas distribution at all temperatures is perfectly self-similar, scaled perfectly with the thermal gravitational length. Changing
. The gas distribution at all temperatures is perfectly self-similar, scaled perfectly with the thermal gravitational length. Changing 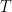 only changes
only changes 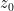 and thus trivially rescales
and thus trivially rescales 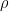 . But the fun thing is that it changes the heat capacity for the gas to
. But the fun thing is that it changes the heat capacity for the gas to  from
from 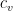 as well!
as well! ,
, 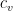 is appropriate. When it is unconfined (as
is appropriate. When it is unconfined (as 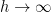 )
)  is appropriate. It smoothly goes from one limiting form of the heat capacity to the other. If I had any need to pick further nits with Jelbring, this would be one — he places “G and the atmosphere (AT) are surrounded by a concentric, tight, black spherical shell with a surface area (S).” around his model atmosphere where “The constant distance (D) between the surface with area A and the surface with area S is very small in relation to R0″. His model atmosphere is bounded from above, in other words, where he has introduced a second length scale into the problem — his D is the same as
is appropriate. It smoothly goes from one limiting form of the heat capacity to the other. If I had any need to pick further nits with Jelbring, this would be one — he places “G and the atmosphere (AT) are surrounded by a concentric, tight, black spherical shell with a surface area (S).” around his model atmosphere where “The constant distance (D) between the surface with area A and the surface with area S is very small in relation to R0″. His model atmosphere is bounded from above, in other words, where he has introduced a second length scale into the problem — his D is the same as 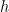 . I missed the “black” bit as well — by making the upper surface part of the system and painting it black he has provided his own equivalent of my silver wire into his own model system. His non-GHG atmosphere permits the lower surface to constantly radiate to the upper surface until the two have identical temperatures in a textbook blackbody radiation calculation. If there is a DALR, the lower surface will constantly transfer heat to the upper surface through radiation, and gravity must then sort it out precisely as I describe above, which so obviously violates the second law that it isn’t funny. Demons Out!
. I missed the “black” bit as well — by making the upper surface part of the system and painting it black he has provided his own equivalent of my silver wire into his own model system. His non-GHG atmosphere permits the lower surface to constantly radiate to the upper surface until the two have identical temperatures in a textbook blackbody radiation calculation. If there is a DALR, the lower surface will constantly transfer heat to the upper surface through radiation, and gravity must then sort it out precisely as I describe above, which so obviously violates the second law that it isn’t funny. Demons Out! , period, exactly, independent of
, period, exactly, independent of  . The heat capacity of the gas is
. The heat capacity of the gas is  . If you add heat to the gas, you linearly scale
. If you add heat to the gas, you linearly scale  , which has the sole macroscopic effect of lifting the center of mass of the gas.
, which has the sole macroscopic effect of lifting the center of mass of the gas. 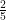 of the added heat energy goes into increased gravitational potential energy from the work the gas does on itself as it expands.
of the added heat energy goes into increased gravitational potential energy from the work the gas does on itself as it expands. 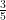 of the added heat energy goes directly into the usual increased kinetic energy of the ideal gas, which is still precisely described by equipartition and still has a local MB distribution of velocities in any slice of the gas large compared to the MFP and small compared to
of the added heat energy goes directly into the usual increased kinetic energy of the ideal gas, which is still precisely described by equipartition and still has a local MB distribution of velocities in any slice of the gas large compared to the MFP and small compared to 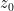 , so that my detailed balance argument is not, actually asymptotically incorrect.
, so that my detailed balance argument is not, actually asymptotically incorrect. and beyond. A paper that Joules Verne, of all people, sent to me that examines this extreme limit shows explicitly that if there is a thermal lapse across this gas it has a weak asymmetry in its conductivity that makes gas relax thermal gradients from top to bottom slightly faster than it does gradients from bottom to top, but the split smoothly vanishes as the gradient does, strongly suggesting that even in this limit if we (correctly) require that the length of a vertical parcel to be much greater than the MFP (and hence much much greater than
and beyond. A paper that Joules Verne, of all people, sent to me that examines this extreme limit shows explicitly that if there is a thermal lapse across this gas it has a weak asymmetry in its conductivity that makes gas relax thermal gradients from top to bottom slightly faster than it does gradients from bottom to top, but the split smoothly vanishes as the gradient does, strongly suggesting that even in this limit if we (correctly) require that the length of a vertical parcel to be much greater than the MFP (and hence much much greater than 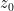 ) the bulk averages will still satisfy the usual kinetic theory and I have a sneaking suspicion that overall they will still satisfy the MB distribution, even though the average itself will be extremely odd. The solution technically doesn’t have to be scale invariant there but the density of the gas and vertical distribution of energies is, in the ergodic sense or for very large areas $A$.
) the bulk averages will still satisfy the usual kinetic theory and I have a sneaking suspicion that overall they will still satisfy the MB distribution, even though the average itself will be extremely odd. The solution technically doesn’t have to be scale invariant there but the density of the gas and vertical distribution of energies is, in the ergodic sense or for very large areas $A$. , so that “thermodynamics” breaks down before, or as, the gas ceases to be reliably isothermal anyway, molecules travel long distances under the influence of gravity between collisions and hence do not have a “constant velocity” on average (compared to the canonical velocity associated with
, so that “thermodynamics” breaks down before, or as, the gas ceases to be reliably isothermal anyway, molecules travel long distances under the influence of gravity between collisions and hence do not have a “constant velocity” on average (compared to the canonical velocity associated with 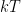 ) so that it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal. Thermodynamics suggests that this breakdown happens in a scale invariant way but here, at least, I will acknowledge that thermodynamics could be wrong, although scaling is a powerful, powerful argument. Exponentials are self-similar functions, after all — what you are effectively saying is that when
) so that it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal. Thermodynamics suggests that this breakdown happens in a scale invariant way but here, at least, I will acknowledge that thermodynamics could be wrong, although scaling is a powerful, powerful argument. Exponentials are self-similar functions, after all — what you are effectively saying is that when 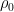 computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes
computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes 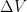 computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant.
computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant. with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!).
with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!).
Hi Joe, I have been thinking about this so hard that I’m dreaming about it — usually a good thing for me as I’ve solved some of my toughest problems in my sleep. Last night I posted a fairly detailed analysis of the thermodynamic — not microcanonical — isothermal gas. When I awoke it occurred to me that I failed to grasp the importance of the
When the gas is confined on a vertical length scale
But the really fun thing is that we can now understand precisely what the role of gravity is in an isothermal unbounded vertical column of ideal gas, in a scale-invariant way. The total energy of the gas is
I’m still thinking about scaling in the upper echelon of the gas in the extremely diffuse limit where
In any event, we seem to be in general agreement that any deviation even in the full microcanonical computation is utterly negligible short of the regime where
But I’m way too busy to work through the algebra to directly prove this (or disprove it, as I’m not at all certain that it is true).
Anyway, I thought you’d like the smooth
rgb
Are you sure the center of mass rises? Couldn’t the total potential energy remain the same while the half-rho zero point rises?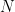 . So mentally compare two exponential curves, both with the same area, one that starts at
. So mentally compare two exponential curves, both with the same area, one that starts at  at
at  and the other which starts at
and the other which starts at 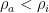 at
at  . The latter is flatter, has a larger characteristic length, and a center of mass further out along
. The latter is flatter, has a larger characteristic length, and a center of mass further out along  .
.
A good question, but I think not. Note that I said think — consider this argument. The gas is constrained to have the same pressure at the bottom. The density at the bottom is strictly smaller for the lapsed gas, reducing the overall density difference between the bottom of the gas column and the top (even if there is no top — zero pressure/density). The integral of the density still has to be
The demonstration that the DALR gas is still exponential is in Caballero, IIRC, but I haven't gone back to compare the actual exponential constants. The heuristic physical point is that if you consider a height where the temperature remains the previous isothermal temperature, all the gas below that height warms and expands, clearly lifting its CM. The gas above that height cools and contracts, lowering its CM. But the gas is exponentially dense and the lapse is linear, most of the mass is below that height, expansion wins, Q.E.D.
rgb
Is Robert Brown even aware this is only an approximation of the atmosphere’s density profile from surface up through the troposphere?
Trick, do me a favor. Don’t speak of me in third person. It is cosmically annoying. Personality disorder annoying. In electronic terms, I’m right in the room with you, but you are doing the metaphorical equivalent of staring at a wall instead of looking at me and speaking as if I’m not here.
You are begging the question, again. The Earth’s atmosphere is not in any way, shape or form like Jelbring’s ideal isolated atmosphere, bounded from above and below by black rigid massive walls and with uniform gravity in between. The DALR is established in Earth’s atmosphere by vertically moving macroscopic parcels of air driven by thermal convection between volumes and surfaces at different temperatures, temperature gradients maintained by diurnal solar forcing and continual radiative cooling.
In Jelbring’s static world, there is no vertical transport of gas — it is long since finished. There is no net radiative transfer of heat from the black lower surface to the black upper surface — he inadvertently (I’m sure) built his own “silver wire” right into his own problem statement because he is clueless. Thermal radiative equilibrium for his black boundaries is isothermal, and if the gas has a different thermal equilibrium then the system perpetually violates the second law with a radiative-gravitaional “heat fountain” that runs without work being done, precisely as my silver wire example does.
I. Am. Not. Talking. About. The. Earth.
Do you understand that? One word at a time, speaking slowly.
I. Am. Talking. About. Jelbring’s. Idealized. Confined. Static. Equilibrated. Gas.
Got that? Jelbring’s gas is, as he explicitly states, not being driven by external heat inputs. It is in hydrostatic equilibrium. All of the gas is at rest. It is in thermal equilibrium — all conduction, convection and radiation across thermal differentials has had time to finish. These are his conditions, and the only conditions you can address in any rebuttal. So far, your replies are all metaphorically straw men eating red herring.
I have at this point presented a solution to Jelbring’s problem that is manifestly isothermal, is manifestly in hydrostatic equilibrium, is manifestly a maximum entropy state. It is clearly a state of the gas that meets Jelbring’s requirements, and the entropy statement shows that it is the only state that can meet it as long as heat transfer within the gas is possible by any mechanism. Bounded by a black upper surface, it won’t even take long for the gas to become isothermal at reasonable temperatures even if it is started with a DALR or other thermal gradient.
If you want to argue, stop invoking Earth’s atmosphere, which is obviously completely different from Jelbring’s in crucial ways. I understand why you are doing it — you want to be able to close the circular argument, claim that the Earth’s atmosphere proves that Jelbring is correct now, then later use Jelbring to prove that the Earth’s atmosphere is naturally heated by gravity at the bottom. But I am watching the shells and the pea, sorry. You have to deal only with Jelbring’s claim and cannot invoke your eventual desired conclusion to “prove” it, any more than he could. His argument is, of course, this identical piece of circular reasoning, but repeating it doesn’t make it logically valid.
rgb
Tim Folkerts says 2/5 at 5:34pm:
“Sorry, I didn’t see any math, just prose. Could you show what you think is the actual math is?….Entropy is defined classically as dS = dQ/T. Suppose you have an isothermal situation to start with. If heat moves from any region 1 to any other region 2, this will cause T2 > T1. The next bit of heat dQ will result in dS = dS1 + dS2 = -dQ/T1 + dQ/T2 The S for isothermal will be less than the non-isothermal field. Try it. I just did. My math suggests you are wrong. What is your math?”
Tim – Correct, the S for isothermal will be less than S for a non-isothermal field which is maximum S. If Fig. 1 starts w/isothermal initial conditions it is not in equilibrium, nature will arrange for heat to move down from higher z region 1 to lower z region 2 causing T2>T1 (Fig. 1 top post T1b>T1t). This ideal gas mixing continues throughout the column to equilibrium at max. S.
I’m not good enough w/computer language to post the actual math formulas, ref. the B&A 4.4 text for them or Verkley paper. That’s why I just posted the 13 step logic outline. Your dS = dS1 + dS2 operates with the constraint of total energy being constant, you need to consider enthalpy constraints in the solution as in the 13 steps.
Tim Folkerts continues:
“What specific gradient do you get? (State your assumptions).”
The assumptions are the same as those in Fig. 1. A GHG-free air column height h, adiabatic control volume, in the presence of constant gravity. Reasonable pressures p found in 80% of earth’s atmosphere, 1000mb down to 200mb. The temperature gradient found (Ref. Verkley paper part b & B&A text) is isentropic non-isothermal. Denoting a given reference temperature Tr found at given reference pressure Pr (say at h=r=z=0) find gradient T(P) = Tr * (P/Pr)^k where k = R/Cp.
The Verkley et. al. paper plots this non-isothermal gradient in Fig. 2 and it is very close to the actual standard atmosphere temperature profile from 1000mb down to 200mb. Verkley also plots the isothermal profile and it is NOT very close to the actual atmosphere profile. See Robert Caballero post way above for the ref. link to Verkley paper.
Tim Folkert’s continues:
“If you really think you are right and Velasco’s paper is wrong…”
I don’t think anything is wrong in Velasco’s paper other than, man, it could be written more clearly. Eliminate the double negatives!
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.
You have directly observed how the visible light of the sun attenuates as you dive deeper. All of the energy in that light has gone into heat.
You seem to think that infrared radiation is magic, that it is “heat radiation”. That’s just crazy talk. Electromagnetic radiation is electromagnetic radiation. You can see because visible light carries energy. You see colors because everything you see absorbs some frequencies out of the visible light and scatters/reflects others. The absorbed energy turns into heat, which is why a black sheet of paper placed in the sun gets hotter than a white sheet of paper. Who knows what the colors of the two sheets of paper are in the infrared spectrum! They could both perfectly reflect infrared, and be “infrared colored paper” but because they are different colors in the visible part they will still heat up differently. That’s the bit about “albedo” in all of this talk, BTW — it represents the fraction of all the incident light intensity (not just visible OR infrared, the integrated intensity over all wavelengths) that is reflected.
Coming back with a flip “Puzzle that out in your own time” is hardly a rebuttal to my extremely simple question. You have direct experience that visible light makes it down into the water. You have direct experience that the intensity of visible light smoothly attenuates with depth — it gets darker as you go further down. Visible light carries energy through the surface of the water. The intensity of visible light that comes back out is far less than the intensity that goes in, because the amount of light you see coming back out in very shallow water where it illuminates e.g. white sand is much more than what comes out over deep water.
You know from direct experience that water is not perfectly transparent to visible light. If it were, we could see the bottom of the ocean exactly as if we were looking down on it from an airplane, get you cannot see the bottom of even a very clean, crystal pure lake more than a few tens of meters down, let alone the bottom of the ocean kilometers down. So why do you think I would waste time “puzzling out” something that is obviously false? Any human being who has ever spent a day on a lake knows that water is not transparent like air.
All of the light that is not transmitted or reflected is absorbed, unless you once again want to invoke invisible demons or fairies. In the case of deep water, the bottom is basically completely dark; no visible light is transmitted. It is all absorbed.
Demons Out!
rgb
rgb
Forcing a parcel of bottom molecules out of equilibrium to the top takes work against gravity (f*d = m*g*h). Where does the work come from? . You have to solve the ODE that tells you
. You have to solve the ODE that tells you 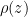 subject to the boundary condition that
subject to the boundary condition that 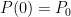 , which must be the same given a constant
, which must be the same given a constant 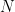 molecules of gas. You have to compute the total potential energy of this gas and compare it to the total potential energy of the isothermal gas. Then we can talk. I’ve already indicated why I am pretty sure that you have it exactly backwards, that the center of mass and gravitational potential energy of the isothermal gas is lower than that of any gas with a negative lapse rate including the specific case of the DALR.
molecules of gas. You have to compute the total potential energy of this gas and compare it to the total potential energy of the isothermal gas. Then we can talk. I’ve already indicated why I am pretty sure that you have it exactly backwards, that the center of mass and gravitational potential energy of the isothermal gas is lower than that of any gas with a negative lapse rate including the specific case of the DALR. once you figure out what
once you figure out what 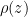 is, and this too will get a much bigger addition from differentially warming the dense bottom than you lose from cooling the not-so-dense top, I think. But even this is talk. Do the algebra. Show me.
is, and this too will get a much bigger addition from differentially warming the dense bottom than you lose from cooling the not-so-dense top, I think. But even this is talk. Do the algebra. Show me.
Say what? No “parcel of molecules” is moved from the top to the bottom. If you want to consider work, you have to consider the energy in the entire thermal column, precisely as I did, explicitly. You can’t just through two equations from nowhere into the discussion. You have to take the gas with a presumed DALR, that is, with
As you warm the bottom, you lift the entire column of gas above it! Joe quite reasonably wants to see the actual computation, because I’m assuming that the density in the DALR is still exponential, and simply becomes a flatter exponential with a necessarily lower base density (in which case the center of mass definitely goes up and your argument is precisely backwards). However, I’m willing to be convinced by a complete, careful, solution to the ODE. If I have time later today, I’ll try to code it into matlab — this one is going to be easier to answer numerically than analytically, unless you happen to be a calculus god. The linear temperature profile goes into the LOCAL condition for hydrostatic equilibrium and the relation between density, pressure, and temperature, so my exponential assumption could well be wrong, but with a linear lapse I would bet that if anything it makes the effect larger, not smaller. It is, after all, the adiabatic work done lifting the gas that makes the top (transiently) cooler in the real atmosphere with an actual thermal gradient heating the bottom and cooling the top providing the source of the work.
So talk is cheap, buddy. Algebra is the only currency for continued argument along these lines. I’ve directly derived the total energy of a gas in isothermal equilibrium. Play right on through for the adiabatic gas, and show me that its total energy is lower than that of the isotropic gas. Hell, the KE will be greater as well, because you’ll have to integrate
rgb
So here is the abstract for the Verkley paper (emphasis added).
It seems pretty clear that it supports Dr. Brown and refutes Jelbring. Convective mixing leads to a non-isothermal situation, and convection is ruled out in Jelbring’s equilibrium world. (And the real world is not surprisingly somewhere between perfect equilibrium and perfect convection.)
Robert Brown says 2/6 at 8:05am:
“Trick, do me a favor. Don’t speak of me in third person….I’m right in the room with you”
I apologize if the involuntary constraints of this website are causing annoyance. No illeism intended. Just identify your preferred means of address. Robert is in the room with me in quotes below.
“I. Am. Not. Talking. About. The. Earth.”
I agree. Not always. There is a need to distinguish earth from Fig. 1 in top post. I’ve done that appropriately. You invoked earth in your 12:37am post formulas.
“I. Am. Talking. About. Jelbring’s. Idealized. Confined. Static. Equilibrated. Gas.”
If that is equal to your Fig. 1 top post then we are on equal ground. If not, let’s just deal with Fig. 1 top post on topic. Agreed?
“All of the gas is at rest.”
The air column is at rest but the GHG-free air molecules are zooming around in Fig. 1 mixing fast, the molecules are not at rest in the control volume.
“..all conduction, convection and radiation across thermal differentials has had time to finish.”
Yes equilibrium in Fig. 1 is achieved, no heat is flowing. Max. entropy S. No delta Q. No delta S. No work allowed across your stated Fig. 1 control volume.
“These are his conditions, and the only conditions you can address in any rebuttal.”
Well, I don’t know about his (Jelbring’s) conditions other than what you write about; the conditions I address are the conditions of Fig. 1. Agreed? Silence is agreement.
“So far, your replies are all metaphorically straw men eating red herring.”
LOL. Well, my replies are compliant of nature, just like straw men and red herrings are constructed of things natural.
“I have at this point presented a solution to Jelbring’s problem that is manifestly isothermal, is manifestly in hydrostatic equilibrium, is manifestly a maximum entropy state.”
You have presented in top post a manifestly incorrect constant temperature gradient solution to your stated Fig. 1 conditions, i.e. incorrectly isothermal & can be manifestly shown to NOT be at maximum entropy isothermally therefore not at equilibrium thru some hard work. The Fig. 1 correct physics being non-isothermal temperature gradient solution when no heat flows any longer is shown in the Velasco et. al. paper (albeit unclearly), especially clearly in the Verkley et. al. paper part b and clearly in the B&A Chapter 4.4 text. Those are not strawmen or red herrings. They are real physics. From 1st principles.
Temperature gradient of Fig. 1 is that which I just posted in reply to Tim Folkerts at 8:12am, adding some clarity:
Denoting for Fig. 1 conditions in top post, a given reference temperature Tr found at given reference pressure Pr (say at h=r=z=0) find non-constant T when entropy is max. i.e. equilibrium non-isothermal temperature gradient T(P) = Tr * (P/Pr)^k where k = R/Cp.
“I understand why you are doing it — you want to be able to close the circular argument, claim that the Earth’s atmosphere proves that Jelbring is correct now..”
I really, really have no interest in proving or disproving anything in Jelbring’s paper. I became interested in this thread only because upon thinking through the physics of Fig. 1 and Fig. 2 in the top post there was a challenge to get the real physics right thru ideal gas simplifications consistent with natural laws. The challenge sent me out to read some previously unknown to me & very interesting papers on the subject (Velasco et. al., Verkley et. al.) and some great texts (Caballero on-line notes, Bohren&Albrecht). That B&A text is terrific, it actually finally resolved some other issues that I have long wondered about.
“… cannot invoke your eventual desired conclusion to “prove” it…”
I have no dog in this fight, just want to go where the ideal physics conclusions of Fig. 1 top post necessarily take us from 1st principles, consistent with the thermo grand masters. It has been very interesting, so I’ve stuck with it.
“If you want to argue, stop invoking Earth’s atmosphere..”
I’m ok with that; your formulas presented at 12:37am were derived from earth’s atmosphere so my reply dealt with the earth. If you want to leave out earth, that’s ok we can debate ideal gas physics for fun & learning & teaching with idealized Fig. 1 top post. Your integration of temperature in top post then needs to be general, not use an integration assumption derived from earth (that assumption of T being constant in your integration).
Have to remember the main purpose we do all this is to understand physics in earth’s atmosphere better – we can utilize our hard work & experiences that way.
Robert Brown says 2/6 at 8:59am:
“Say what? No “parcel of molecules” is moved from the top to the bottom.”
Yes it is. It was in your example for goodness sakes. Geez. This was in response to your statement at 2/5 10:25: “So if we move heat from the bottom to the top,” as faithfully copied. LOL. Heat doesn’t exist independent of the molecules, at least not since the caloric theory bit the dust not much more than a century ago.
“So talk is cheap, buddy… Do the algebra. Show me.”
Ok. Sigh. I would REALLY like to, but here I cannot post the algebra only b/c I am not familiar enough with the proper commands to do so, otherwise I would. I resorted to posting the 13 step outline logic above. To fracture a phrase from racing: The BS stops when the algebra drops.
It is really unnecessary to post the algebra here anyway since for Fig. 1 equilibrium max. entropy conditions to be shown non-isothermal isentropic, the algebra is well developed since Ball in 1956 eqn. 4, 1998 Bohren&Albrecht chapter 4.4, and 2004 Verkley paper part b.
If you really want to get past cheap talk & see algebra, refer to the poster Rodrigo Caballero Verkley ref. way above – just search this page for Guinganbresil. The paper is in that poster’s 1/27 9:38am link.
I would post the link again, but I am not knowledgeable about how to correctly do that here either. I have read the WUWT spam filter can trap a post with a link for irritatingly long time.
[Dave, if one of your posts disappears just ask a moderator to rescue it from the spam folder. ~dbs, mod.]
Read that part c-a-r-e-f-u-l-l-y. They are hypothesizing that the INTEGRAL is constant, not that the temperature itself is constant. Specifically, Equation 6 says the integral of TdP is constant, ie enthalpy is constant. They THEN go on to derive that at equilibrium the temperature must indeed be constant within the section if the container is perfectly insulated.
This is most definitely NOT correct. The top post involves absolutely NO convective mixing. The paper is discussing STRONG convective mixing at this point. These are as different as night and day.
The concluding remarks of the paper seem very apropos.
PS. The Verkley paper can be found here: http://www.knmi.nl/publications/fulltexts/verkley_gerkema.pdf
Robert Brown: “although yes, Joe, my argument involving shifting the MB distribution was sloppy and imprecise — hopefully you like this one better but the result is the same either way”
I do, and I agree.
Robert Brown: “it has been a few, um, decades since I took stat mech and it was the most difficult course of physics I ever took when I took it, making even quantum mechanics look like a walk in the park in comparison.”
Bless you. It’s salve for us plodders’ egos to hear that even the smart guys find this stuff hard.
Robert Brown: “I think [Joe Born] realizes that my answer is irrelevantly imprecise.”
Indeed I do.
Robert Brown: “it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal ”
This may just be a you-say-tomato-I-say-tomahto thing, but to me the Ideal-Gas-Law concept of temperature holds up pretty well at low N so long as pressure is integrated over a long enough time. But, as you say, it becomes problematic for some of the thermodynamics results.
Robert Brown: “Anyway, I thought you’d like the smooth with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!). ”
I do indeed.
Robert Brown: “what you are effectively saying is that when computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. ”
Since I know no quantum mechanics at all, one of the questions I had hoped some reader would resolve was how valid quantum-mechanical considerations leave Velasco et al.’s result (which assumes a continuous phase space). Maybe I’ll look into that after I get my taxes done, but I’m not optimistic that I’ll be equal to it.
Robert Brown: “But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant. ”
I’m not sure I followed that, so the following two comments are likely to be inapposite.
First, if the classical approximation still holds, I would infer that in principle separately integrating pressures at two altitudes for a long enough time would enable one to distinguish the Velasco et al. profile from isothermality.
Second, one way of saying that equilibrium requires isothermality is that the number of microstates in the isothermal macrostate is so astronomically many times as great as the number in all non-isothermal macrostates combined that there is essentially no chance of encountering in the isothermal macrostate a microstate whose trajectory spends any detectable proportion of its future time in a non-isothermal macrostate. But what the number of microstates in the isothermal macrostate actually is depends on how precise we require the isothermality to be. Maybe the isothermal macrostate’s microstate count is not so overwhelming if we exclude from our definition of isothermality any configuration in which, say, different-altitude temperatures separately measured with an integration time of one second do not equal each other to within one part in 10^32. Of course, this is just another way of saying the Second Law applies only to large numbers, but this way of saying it helps me further appreciate the degree to which Velasco et al. do or do not find equilibrium non-isothermality.
Tim Folkerts says 2/6 at 12:29pm:
“They are hypothesizing that the INTEGRAL is constant, not that the temperature itself is constant.”
It is my duty to c-a-r-e-f-u-l-l-y inform you that if the integration of temperature results in a constant the temperature is constant, see Verkley part a integral eqn. 10 & constant T result eqn. 11.
Verkley part a quote: “…that is, T = a constant, thus, the profile is isothermal.” This results from air column shown in Verkley Fig. 1 which allows the air column to do work across the control volume above and below. If top post in this thread Fig. 1 is simply modified to show work crosses the control volume above & below, then it is proper to think the modified top post Fig. 1 when equilibrium is reached, that T indeed is isothermal.
Thanks for re-posting the Verkley paper link. I see the mod.s (Dave) made it clear I can ask for help, I may have more courage in the future.
“Equation 6 says the integral of TdP is constant, ie enthalpy is constant.”
This is imposing the general constraint of constant total energy 1st law.
“They THEN go on to derive that at equilibrium the temperature must indeed be constant within the section if the container is perfectly insulated.”
No, they do not have perfect insulation in part a for isothermal case, they allow work across the insulation – read again the statement in Verkley Fig. 1 as I quoted, their air column is different than Fig. 1 top post. Again, just make top post Fig. 1 able to do work above and below, find it is isothermal as in part a. For no work above & below, perfect adiabatic insulation, find Fig. 1 top post is isentropic, non-isothermal as in Verkley part b.
Verkley imposes perfect insulation only in part b and reaches the isentropic non-isothermal conclusion as does B&A (from mathematically maximizing entropy) which Verkley et. al. cite and offer grateful acknowledgement.
“The top post involves absolutely NO convective mixing..”
How do you not see the molecules in top post Fig. 1 are very frequently randomly mixing up and down the column? They are mixing even in an ideal column, very vigorously mixing even ideally. Verkley et. al. discusses this very action in part b isentropic non-isothermal case.
There is certainly absolutely NO convective mixing in a solid, we are talking an ideal gas here.
I say: ““The top post involves absolutely NO convective mixing.”
Trick replies: “How do you not see the molecules in top post Fig. 1 are very frequently randomly mixing up and down the column? ”
Perhaps this is the crux of our miscommunication.
There is a huge difference between the random thermal motion of molecules and convection. Convection is a large scale, organized motion of a fluid. It requires an input of energy. Convection produces a measurable net flux upward through some surface (and down through some other surface). There will be a measure airspeed. On the other hand, “perfectly still” air will, of course, have molecules moving at 100’s of m/s, rearranging with no net motion on a macroscopic level.
* So, yes, I see that there is microscopic random thermal motion of the molecules.
* But, no, that does not mean there is macroscopic, organized convection.
When the various papers say (or I say or Dr Brown says) there is convection, it means something much more than random thermal motions of individual molecules.
Trick says: “It is my duty to c-a-r-e-f-u-l-l-y inform you that if the integration of temperature results in a constant the temperature is constant”
Suppose I tell you that the integral of f(x) dx from 0 to 1 equals 1 (which is definitely constant). Can you tell me f(x)? Must f(x) be constant? perhaps f(x) = 2x? Or f(x) = 0.9 + 0.2x? Or f(x) = 3x^2?
If I tell you the integral from P1 to P2 of T(P) dP equals some constant H, can you tell me T(P)? A constant temperature is only one possibility (and, as it turns out from the next couple paragraphs in the paper, the right possibility).
Tim Folkerts says 2/6 at 4:01pm:
“Convection is a large scale, organized motion of a fluid.”
Yeah. Verkley et. al. struggle with this in their lo-o-ong explanation of part b “mixing”, in which they do use the word “convection”.
The authors write: “…motions are now taken into account, albeit implicitly. Their role is to mix the potential temperature field, to strive to homogenize it. We should now interpret the state variables as averages over volumes that are large…”
This is possible to debate because “large” is unsatisfyingly imprecise. I take that to mean at least we can move from discussing just a particular molecule mixing but “large” groups of molecules mixing. Still a very small micro amount of molecules but above the individual particle level.
Tim continues at 4:20pm:
“Suppose I tell you that the integral of f(x) dx from 0 to 1 equals 1 (which is definitely constant). Can you tell me f(x)?”
No. Just that whatever f(x) is, it is continuous, defined & constant (=1) over the interval 0 to 1. Maybe more, whatever the rules of reasonableness for math integration are defined in the limit.
Trick> Yeah. Verkley et. al. struggle with this in their lo-o-ong explanation of part b “mixing”, in which they do use the word “convection”.
They use the word “convection” in part (b) because they are explicitly assuming convection in part (b). In part (a) they were assuming no convection. I don’t see where the difficulty is.
* No convection –> constant T = isothermal
* Convection –> Constant Theta = non-isothermal
The top post and Jelbring are specifically discussing no convection. The non-isothermal result is with true macroscopic convection ABOVE AND BEYOND microscopic random motions.
Trick: >>>It is my duty to c-a-r-e-f-u-l-l-y inform you that
>>> if the integration of temperature results in a constant
>>> the temperature is constant”
Tim>> “Suppose I tell you that the integral of f(x) dx
>> from 0 to 1 equals 1 (which is definitely constant).
>> Can you tell me f(x)?”
Trick > No.
Then I think we agree here, that the form of the function is not explicitly specified just because we know the result of the integration. That is all that I was saying, and all the authors are saying in Eqn 6. The integration of TdP is a constant H, but they are not specifying that T is constant. ADDITIONAL work is needed to show an isothermal result. So they are NOT using circular reasoning by assuming an isothermal profile to prove an isothermal profile.
Bryan says February 6, 2012 at 2:17 pm: “I hope that helps!”
Actually, there is nothing there that addressed the issue that YOU raised, so no, it does not help.
1) You suggested that photosynthesis was inappropriately ignored in K&T’s diagram (which by definition gives global averages over long time-scales).
2) I encouraged you provide estimates of the importance photosynthesis.
3) You complain about all sorts of OTHER things and avoid making a meaningful contribution.
So if you do want to help on the issue you raised, then provide an estimate of the importance of photosynthesis on the global energy balance. That would be helpful and worth reading about. That would move the discussion forward (although this whole topic is a bit of a tangent away from the top post).
Tim Folkerts says 2/6 5:30pm:
“In part (a) they were assuming no convection.”
Can you show me where they (Verkley et. al.) assumes no convection in part a? Not sure I can find this assumption. Interesting to discuss the specifics.
Tim continues:
“The top post..….specifically discussing no convection.”
The top post 1st mentions “convection stops” above the troposphere in the 2nd to last sentence, this in the conclusion. That seems to mean or at least imply convection IS assumed in the top post up through the troposphere. Though it is not discussed that I can see.
Tim continues:
“ ADDITIONAL work is needed to show an isothermal result.”
Yeah, this is the big deal difference between top post Fig. 1 and Verkley Fig. 1, the additional work above and below the air column considered in Verkley part a. The paper shows this work being allowed to cross the control volume results in an isothermal conclusion. It would be interesting to discuss just why that happens.
Trick, I have now read the Verkley paper slowly and thoroughly and everything you have been explaining and pointing out is now clear. Thanks.
correction
‘insulation’ should read ‘insolation’
Dr. Brown,
In your top post, when you introduce your silver conductor you say:
,
but you don’t give the mass or the initial temperature of the silver wire.
Could you please tell us what conditions you are assuming?.
Bryan says:
>Well Tim that insolation [340 W/m^2] produces a blackbody spectrum
That spectrum is determined by the temperature of the sun. It is (essentially) the same spectrum as the 1360 W/m2 that arrives at the top of the atmosphere, or the ~ 60,000,000 W/m^2 that leave the surface of the sun.
You seem to be laboring under the misconception that spreading sunlight out changes the spectrum. The sunlight does not become red (or infrared in this case) simply because you spread it out with a lens, or go to Pluto, or average it over the whole surface of the earth.
>well into the thermal IR band.
The solar spectrum has some thermal IR, but not much.
>So no photosynthesis would be produced whatsoever, as IPCC science predicts.
Since we are talking about the solar spectrum, then it easily can produce photosynthesis, as “IPCCscience” would predict.
>So to answer Robert Browns question to Myrrh that type of radiation
>is completely absorbed in the top few millimetres of the water surface.
Not to belabor the point, but “that type of radiation” *is* the solar spectrum (modified by absorption thru the atmosphere), with ~ 10 UV, ~ 40% visible, and ~ 50% IR.
>Of the solar radiation reaching the surface of water some 50% is in the IR.
OK. I agree now.
>It will be absorbed in the top few mm causing evaporation of the surface water.
Or even the first few um for thermal IR.
>The other 50% will penetrate deep into the water and a
>significant proportion will be available for photosynthesis.
Ah ha! And there is the crux. Just how much ACTUALLY goes into photosynthesis? That was you initial point, and the issue that I was hoping you would provide some insights into.
>Notice that the evaporation and the photochemical processes
>both are systems that store energy that can be later released
>to buffer temperature change.
Quite true. And buffering the temperature is important to the temperature of the planet. Buffering cools the warm side and warms the cool side. There have been a couple other discussion on WUWT this past month addressing just that issue.
>The radiation obsessed IPCC science model with its fictitious 33K effect is false.
The amount of warming due to GHGs is up for debate, especially since it depends critically on other assumptions and feedbacks. But there is no doubt that SOME warming is due to GHGs, and the “everything else being equal” assumption does lead to ~ 33 K warming.
>So don’t believe everything that broad brush, eyes shut IPCC science tells you.
Rather than saying “eyes shut” I would say “focused”. Sometimes “focused” means you are looking the right place; sometimes it means you overlook important things outside your view.
But the simple fact is that (essentially all) energy arrives at the earth in the form of solar EM radiation and (essentially all) energy leaves the earth in the form of terrestrial EM radiation (thermal IR). Focusing on “essentially all” of the energy coming and going is a good way to find the overall balance of the earth.
Tim Folkerts says
“everything else being equal” assumption does lead to ~ 33 K warming.”
Yes the ‘everything being equal’ assumes there is no photosynthesis along with a dazzling set of pseudo scientific assumptions.
That greenhouse gases being absent does not effect the one third of solar radiation being absorbed by clouds
Or the surface albedo can jump from 12% to 30%
Or the greenhouse gases being absent but still have clouds to reflect radiation
Or the IR (not now absorbed) by the clouds will not obey Kirchoff’s Law on reaching the planet surface
And so on.
Take your pick of the fantasy elements to create your own version of the greenhouse 33K nonsense.
http://www.ars.usda.gov/is/AR/archive/jan12/solar0112.htm?pf=1
Tricky asks : “Can you show me where they (Verkley et. al.) assumes no convection in part a? Not sure I can find this assumption. Interesting to discuss the specifics. ”
I thought it was obviously implied in both cases. Here are a few lines of thought:
* Only superfluids keep moving with no damping, and the air is not a superfluid.
* Convection requires constant heating at the bottom and cooling at the top, and this is not happening in an adiabatically enclosed system.
* The top post and the Verkley paper assume thermodynamic equilibrium.
I’m sure there are other ways to say it. All of them allow microscopic motion of molecules, but not macroscopic motion of large set of molecules.
Robert Brown says:
February 6, 2012 at 8:29 am
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.
You have directly observed how the visible light of the sun attenuates as you dive deeper. All of the energy in that light has gone into heat.
You seem to think that infrared radiation is magic, that it is “heat radiation”. That’s
just crazy talk. Electromagnetic radiation is electromagnetic radiation. You can see because visible light carries energy. You see colors because everything you see absorbs some frequencies out of the visible light and scatters/reflects others. The absorbed energy turns into heat, which is why a black sheet of paper placed in the sun gets hotter than a white sheet of paper. Who knows what the colors of the two sheets of paper are in the infrared spectrum! They could both perfectly reflect infrared, and be “infrared colored paper” but because they are different colors in the visible part they will still heat up differently. That’s the bit about “albedo” in all of this talk, BTW — it represents the fraction of all the incident light intensity (not just visible OR infrared, the integrated intensity over all wavelengths) that is reflected.
Coming back with a flip “Puzzle that out in your own time” is hardly a rebuttal to my extremely simple question. You have direct experience that visible light makes it down into the water. You have direct experience that the intensity of visible light smoothly attenuates with depth — it gets darker as you go further down. Visible light carries energy through the surface of the water. The intensity of visible light that comes back out is far less than the intensity that goes in, because the amount of light you see coming back out in very shallow water where it illuminates e.g. white sand is much more than what comes out over deep water.
You know from direct experience that water is not perfectly transparent to visible light. If it were, we could see the bottom of the ocean exactly as if we were looking down on it from an airplane, get you cannot see the bottom of even a very clean, crystal pure lake more than a few tens of meters down, let alone the bottom of the ocean kilometers down. So why do you think I would waste time “puzzling out” something that is obviously false? Any human being who has ever spent a day on a lake knows that water is not transparent like air.
All of the light that is not transmitted or reflected is absorbed, unless you once again want to invoke invisible demons or fairies. In the case of deep water, the bottom is basically completely dark; no visible light is transmitted. It is all absorbed.
Demons Out!
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
This is why you responded to me. If you have no intention of helping Tim provide me with an answer, the very simple request I have made, then you’re wasting my time.
[]
You’re claiming to be an authority as a scientist, what don’t you understand about me asking for proof of these claims?
You’re the ones making the claims, you’re the ones who need to prove it. I don’t care what your opinions are about this, give the physics facts. Stop avoiding it. That’s the only expression of crazy talk I see here..
Thermal infrared from the Sun is the Sun’s thermal energy on the move, it is invisible; that is what we feel as heat direct from the Sun, as we feel from a fire, or a stove not glowing with any visible light. We cannot feel near infrared or visible light, they are not hot, they are not heat, they are light.. When we step into the shade on a hot, sunny day, we no longer feel the direct heat from the Sun, we can feel the warmth of the air heated by the Sun, but not the thermal infrared direct from it. This is bog standard physics of light and heat.
“Water absorbs the incoming solar Infrared Radiation because the frequency of the internal vibration of the water molecules is the same frequency of the waves of the solar Infrared Radiation. This form of Radiative Heat transfer is known as Resonance Absorption.
We humans feel the heat radiated by the Sun and other systems with a higher temperature because our bodies contain 55-75% of water. The radiative energy inciding on our skin is absorbed by the molecules of water in our bodies by Resonance Absorption. Just then, the Infrared Radiation absorbed by our bodies leads to a more intense internal vibration of the water molecules in our bodies and our bodies get warmer. However, in general, living beings possess thermoregulatory systems that permit us to eliminate the excess of heat from our bodies, maintaining a quasi-stable internal temperature (it is one of the homeostatic processes of biosystems).”
http://www.biocab.org/Heat_Transfer.html
We can sweat it out.
A scientist is a person “who cares deeply and passionately for truth and clarification, for the liberating experience of finding order and beauty in a chaotic jumble of natural events.” (Leon M. Lederman, 2001).
Myrrh says:
“I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.”
That’s right… all matter. I’ll now stop worrying about you Myrrh… I see you have found the complex component of refraction !! Every since Ira’s stream of pseudo-science threads I have been worried about you about light and water. I see you have connected (or always knew).
Glory be! Hit it on the head.
Yes it is. It was in your example for goodness sakes. Geez. This was in response to your statement at 2/5 10:25: “So if we move heat from the bottom to the top,” as faithfully copied. LOL. Heat doesn’t exist independent of the molecules, at least not since the caloric theory bit the dust not much more than a century ago.

 is the gas concentration (molecules per unit volume, molecular density).
is the gas concentration (molecules per unit volume, molecular density).  is the mean speed of the molecules, related to their temperature but not the same way for monatomic and diatomic ideal gases and hence expressed as a parameter by itself.
is the mean speed of the molecules, related to their temperature but not the same way for monatomic and diatomic ideal gases and hence expressed as a parameter by itself.  is the mean free path.
is the mean free path. 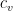 is the molar heat capacity.
is the molar heat capacity. 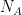 is Avogadro’s number — you could use the molecular heat capacity and insert the number of degrees of freedom of the gas and write this whole thing in a different form with the temperature explicitly inserted, but it is not zero. So when one talks about an adiabatic ideal gas — one where no internal heat transfer occurs via conduction — one is already talking bullshit, or rather, restricting your attentions to short enough times that thermal equilibrium hasn’t been established. Note that as far as scaling goes,
is Avogadro’s number — you could use the molecular heat capacity and insert the number of degrees of freedom of the gas and write this whole thing in a different form with the temperature explicitly inserted, but it is not zero. So when one talks about an adiabatic ideal gas — one where no internal heat transfer occurs via conduction — one is already talking bullshit, or rather, restricting your attentions to short enough times that thermal equilibrium hasn’t been established. Note that as far as scaling goes,  and
and  countervary — when
countervary — when  is high,
is high,  is low, and vice versa. The conductivity is independent of the pressure in an ideal gas, note well.
is low, and vice versa. The conductivity is independent of the pressure in an ideal gas, note well.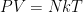 , right? — a consistent gas with thermal relaxation rates that are slow compared to hydrodynamic viscous relaxation rates (that work to slow dynamical shear whenever it occurs within the gas, gas parcels moving in opposite relative directions) and convective relaxation rates. Slow enough that we can ignore it at least to the extent that we can ask what state we are likely to find a gas initially prepared in an arbitrary initial condition — after waiting just long enough for hydrostatic equilibrium to be established but not long enough for thermal equilibrium (which is isothermal and strict maximum entropy) to be reached via internal conduction. We will similarly ignore radiative relaxation as being slower than hydrodynamic relaxation, although for gases like CO_2 or H_2O this is almost certainly untrue in the temperature ranges of 100K-500K that are relevant to the earth and other planets.
, right? — a consistent gas with thermal relaxation rates that are slow compared to hydrodynamic viscous relaxation rates (that work to slow dynamical shear whenever it occurs within the gas, gas parcels moving in opposite relative directions) and convective relaxation rates. Slow enough that we can ignore it at least to the extent that we can ask what state we are likely to find a gas initially prepared in an arbitrary initial condition — after waiting just long enough for hydrostatic equilibrium to be established but not long enough for thermal equilibrium (which is isothermal and strict maximum entropy) to be reached via internal conduction. We will similarly ignore radiative relaxation as being slower than hydrodynamic relaxation, although for gases like CO_2 or H_2O this is almost certainly untrue in the temperature ranges of 100K-500K that are relevant to the earth and other planets. and set so that it has the same integrated number of molecules and surface pressure and temperature as the isotropic case to get the right
and set so that it has the same integrated number of molecules and surface pressure and temperature as the isotropic case to get the right  boundary conditions for both, but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting.
boundary conditions for both, but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting.
Heat can be transported without bulk transport of molecules. This has been known since the caloric theory bit the dust not much more than a century ago. That is why technically I am correct and you are incorrect in the idealized discussion, as Velasco states. If you take a gas that cannot conduct heat or share heat through radiation — note well the conditional — then there are many — not just one, many — stable horizontally stratified hydrostatic profiles of an ideal gas. In fact, all of them with a monotonically decreasing concentration (density) and pressure profile. In all of these cases there is no convective instability. The gas does not conduct, which means that it does not diffuse either, because physical diffusion of the gas molecules implies heat conduction unless you insert a Demon that only lets the “right” molecules through from one layer to the next. There is no bulk transport of molecules because the gas is hydrodynamically stable by construction so no parcel of air experiences a net upward or downward force, begins at rest, and according to Our Friend Newton, remains at rest.
Turn on any diffusion (not that you could ever really turn it off), turn on any sort of heat conduction without bulk transport (not that you could ever really turn it off — you can compute what the conductivity is for an ideal gas and it is strictly non-zero, just like the dynamic viscosity:
In this
Since you are doing this for the same reason I am — to learn a lot more about atmospheric thermodynamics (and thermodynamics in general) beyond what I/we learned in school, you might want to look at this site:
http://zeolites.cqe.northwestern.edu/Module/heattrans.html
it has a nice summary of heat transport in fluids, including a discussion of the ideal gas conductivity (where they write it in one of the slightly different forms equivalent to that which I inserted above) and include a table that shows the measured, non-zero thermal conductivity of many gases.
At this point we both acknowledge that the entropy of the isothermal gas column is greater than the entropy of the isentropic gas column. You assert that — under nonphysical (or at least, inconsistent) conditions, that is, zero conductivity — an arbitrarily prepared gas column will relax to one with the DALR. I assert that — under the physical/consistent condition of an ideal gas with the ideal gas conductivity — it will relax to isothermal, the true thermodynamic equilibrium state. Velasco unambiguously agrees with me — I mean really, there is no doubt that a physically consistent ideal gas will relax to isothermal unless you make it physically inconsistent and choose to ignore internal conductivity or insist in looking at small enough time scales and initial conditions such that convective equilibrium is reached but thermal relaxation has not yet occurred.
Since Jelbring explicitly states that he is waiting a very long time for relaxation to occur and did not inconsistently qualify his use of an ideal gas by asserting that it is non-conductive (and because there is no substantive difference between my vertically confined gas column and his vertically confined gas column, at this point we all agree that my arguments against EEJ are valid and the stated conclusion of his thought experiment is incorrect. An ideal gas in true static thermodynamic equilibrium does not have an thermal lapse, it is isothermal.
Whether or not you have a dog in the fight, Jelbring definitely did and still does, and his paper is used by many people in the skeptical camp to defend the absurd statement that gravity alone will create a stable temperature gradient in a gas, even if the gas is e.g. prepared in an isothermal state originally. I think, if I read your remarks above correctly, that you even agree with this at this point.
This leaves us in our discussion with only one last thing to talk about. That is broken ergodicity and hydrodynamics. I am fortunate in that my teacher in stat mech in graduate school was one of the original researchers that studied systems that exhibit formally broken ergodicity, so I got exposed to the idea a lot and actually know a lot about it, and the problem of widely split relaxation rates, from my own research. So let’s talk about the gas — and let’s make it a consistent gas, please, as the idea of an ideal gas without thermal conductivity makes as much real sense as talking about an ideal gas that doesn’t satisfy the relation
I think that it is your belief that the gas will relax to a state with the DALR from all, or nearly all, initial conditions. I say nearly all, as we seem to be in agreement that if it is started with isothermal, it will stay there. Permit me to very quickly convince you that this is not true, that in fact nearly all initial conditions will cause the gas to relax to a state that is not one with a DALR. In fact, a gas with a DALR is a fairly special case of the many “equilibria” one can reach in the specific limit of hydrodynamic relaxation (only) to a state of hydrostatic balance neglecting the much slower thermal relaxation that eventually makes the gas isothermal.
First, let me appeal to your intuition. If we prepare the gas in any of the infinity of hydrodynamically stable states with a vertically increasing temperature gradient, the cold dense gas is on the bottom, the warm less dense gas is on the top. We ignore conduction, as noted, so the heat cannot conduct from top to bottom. The gas is convectively stable. It is hydrodynamically stable. You could go away and come back years later — any period that is short relative to the thermal relaxation rate — and the gas would still be cold on the bottom and hot on top. Furthermore, if you turn on thermal relaxation, isothermal equilibrium lies between it and a gas with a DALR, and we agree that if the gas is ever isothermal it will stay isothermal.
So the only initial preparations that can achieve the DALR are ones that already are warmer on the bottom than on the top. Here’s the interesting bit.
If the gas is prepared in a hydrodynamically stable state with a vertical temperature lapse in between the DALR and isothermal, I would argue that it, just like any arrangement with monotonically increasing temperatures, is still stable absent conduction. This is because it is still stable against convection — the gas has a bulk density that is monotonically decreasing with height so you don’t end up with parcels of gas that are more dense sitting above parcels that are less dense. This, and only this, drives the thermal mixing through vertical convective transport of parcels of gas that leads the gas to become approximately isoentropic. That’s why all of the books on physical climatology derive the DALR by discussing uplifting and downfalling “parcels” — the parcels are too big to thermalize via conduction during the transport process and are being uplifted by buoyancy forces that are greater than the opposing forces of dynamic viscosity!
So what is the class of initial states that could relax to a gas with the DALR? Ones that are hydrodynamically unstable initially, with a pronounced thermal gradient from bottom to top where the gas at the bottom is much warmer than the gas at the top, with a gradient that is larger than the DALR. A gas that is precisely prepared in a vertically stratified state might still be hydrostatically balanced, but the equilibrium is no unstable, as you have more dense gas above and less dense gas below. Any perturbation and the gas will convectively mix, with convective buoyant forces that exceed the “restraining” forces of static and dynamic viscosity. As it mixes, parcels will uplift and cool as they expand and warm the cooler gas they expand into as they compress it while those other parcels fall.
At this point there will be a very interesting competition. The DALR is one of an infinity (as I hope we now agree) hydrostatically and hydrodynamically stable states the gas can reach in the absence of conduction. Basically the entire range of vertical profiles that are convectively stable are possible final states. Depending on the details of the initial condition of the gas, it might relax to a vertical thermal profile almost anywhere between the DALR negative gradient and the infinity of zero to positive thermal gradient profiles that are all hydrostatically stable (bulk hydrostatic balance of buoyancy and gravity) and convectively stable (both static and dynamic viscosity that resist and damp out bulk motion perturbations so that they cannot grow).
Now, as you might agree, we can gain some actual insight into the real atmosphere. If the atmosphere were differentially heated from the top down, and weren’t subjected to forces that drive vertical thermal mixing, it would be hot from the top down. Indeed, the part of the atmosphere that is heated from the top down by direct absorption (which exponentially attenuates as one penetrates the absorber) has a stable postive thermal gradient from the bottom (top of the stratosphere) to the top.
The troposphere, on the other hand, is differentially heated from the bottom and cooled at the top. The ground and the oceans absorb the bulk of the solar energy that is not reflected (albedo) without transferring heat into the system, and they are both located at the bottom of the atmosphere. They warm the lower atmosphere by direct conduction (as well as by radiative transfer mediated by the GHGs, which in the case of the real atmosphere can most definitely not be neglected, because the at the very least a major chunk of the cooling of the surface is from radiation). Heat picked up at the surface is thus rapidly vertically mixed and transported by all three mechanisms — conduction, convection and radiation — acting at different length scales and with considerable and non-ignorable chaotic and self-organized emergent mesoscale structure — to produce an atmosphere that, as you note, ends up somewhere between the DALR and isothermal most of the time, although inversions (warmer on top) or with a gradient even larger than the DALR happen all the time, and are unstable or transiently metastable states with some lifetime and break apart and perhaps reform somewhere else as the conditions that favor them recur.
What makes the DALR a “pole” in this process? The fact that not only is the gas actively heated at the bottom but that it is actively cooled at the top of the troposphere. There is a continuous transport of heat from the bottom to the top, and heat transport via convective mixing is much faster than conduction and at least competes with radiation in the bulk of the troposphere. Still air with either little vertical shear and relatively weak warming of the ground or with so much vertical shear that turbulence occurs and irreversibly physically mixes the air parcels faster than “reversible” adiabatic expansion can keep up favors the “isothermal” pole, although this too is almost never precisely observed. Warm ground (strong heating of the ground) and non-turbulent vertical flow due to convective shear forces slow enough to allow approximately adiabatic expansion and compression to occur in the overturning convective air parcels favors the DALR.
Needless to say, the actual cooling at the top of the troposphere is due to the GHGs, which actually lose heat energy up there via radiation. If they didn’t, the bulk transport of heat upward would gradually warm the upper atmosphere, and as I note above, a warm, less dense, upper atmosphere is utterly stable without conductivity or radiation.
Anyway, I really appreciate your efforts to communicate more normally and talk to me in first person — it also makes it easier for me to address your points, and I hope, for you to read and understand what I say (if you indeed have no dog in the fight, then most of this should make sense). Bear in mind that IMO it is borderline silly to do stat mech on an atmosphere in the first place — it is only useful to answer “formal” questions like those addressed in Velasco like “what is true thermal equilibrium given thus and such conditions” and even there the computations are enormously difficult and require a variety of basically inconsistent or non-ergodic assumptions to be made. The right way to treat an atmosphere is almost certainly with bulk hydrodynamics — Navier-Stokes. That is, of course, insanely difficult, but show me a stat mech computation of a N ideal gas molecules in a box heated on one side and cooled on the other, with gravity, that spontaneously predicts e.g. the appearance of convective rolls. Not happening…
So we begin any real study of a real gas, or for that matter an ideal gas, with hydrodynamics and thermodynamics, not stat mech. Thermodynamics alone does just as good a job of telling us the true thermodynamic equilibrium of the gas as Velasco’s complicated stat mech computation, and allows us to determine maximum entropy and so on perfectly well. To talk about the DALR, one has to use hydrodynamics with bulk transport, for bulk transport to occur that produces sufficient vertical adiabatic mixing one requires differential heating or just the right sort of very slow transport driven by other means.
On a slightly different subject:
>Of the solar radiation reaching the surface of water some 50% is in the IR.
…
OK. I agree now.
This is irrelevant. What matters is how much or the total irradiance penetrates liquid water to a depth of at least centimeters, nothing more. The figure in:
http://en.wikipedia.org/wiki/Electromagnetic_absorption_by_water
shows both the intensities at the surface and the skin depth (exponential penetration length). Wavelengths between 200 nm and around 1 um have a skin depth of at least 10 cm and don’t just warm “a few millimeters on the surface”. That is easily 2/3 of the total power that makes it to the surface itself — basically “all” solar UV and visible, with the latter absorbed at depths up to a 100 meters, and a good start on the IR.
This isn’t to argue the point that most of the IR — around a third of the incoming power — is absorbed at the surface and largely goes into latent heat of evaporation rather than actual heating of the water. Heat is heat, of course — it still has to be gotten rid of to keep temperatures in balance, and the only way out of the Earth is through radiation — but it does make the flow of energy on its way out a lot more interesting, not to mention provides enough water vapor in the atmosphere to produce rain and so on.
The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong. Most of the actual warming of oceanic water comes from its absorption of visible light and UV and short wavelength IR at depth. Ocean temperatures vary with the season because the amount of energy they receive from the sun is modulated by axial tilt, just like everything else the Sun warms on Earth.
People get so angry when they discuss incoming spectrum, and seem so eager to claim that there is no such thing as a GHE involving CO_2 at all, and they seem so reluctant to address the outgoing top-of-atmosphere spectrum that clearly shows the involvement and importance of CO_2 in the outgoing radiation budget. Seeing is believing. Everything else is squabbling about the details of internal transport, and honestly doesn’t matter so much. What does matter is the precise response of the top 1-2 km of the troposphere and and bottom 1-2 km of the stratosphere to increased CO_2 and the general solar-driven modulation of H_2O. I don’t think we understand either one particularly well, but all of the rest of the stuff supposedly happening down below the top of troposphere isn’t really relevant to the actual energy balance and hence mean temperature. What matters is the (temperature of) the radiators of outgoing power in the emission bands of the sources of the outgoing radiation. Nothing more. At that point it is all detailed balance. The egregious and misleading stuff from the warmists IMO consists of a) overstating the quality of the physics in their models and the confidence we should have that they are correct; b) treating the ad hoc parameter of “feedback” or “sensitivity” as something they can set on heuristic grounds, and then optimizing the other parameters of their models around it. As I believe Willis pointed out on a different thread, give me five or six adjustable parameters in a fit and I’ll both fit an elephant and make him lift up his trunk to salute the queen. I build high quality neural networks to use as predictive models, and I can cite chapter and verse and write holy canons myself on the dangers of too many adjustable parameters. It is trivial to build a NN that fits almost any nonlinear data set quite nicely. The problem comes when you try to make the fit predict new data. The better the fit of the training data (after a fairly rapidly reached point) the worse the actual predictivity of the model, as you’ve basically taught it to “recognize” the noise of the training data instead of abstract the much weaker predictive signal buried in the noise.
You’ve made an idiot-savant net, one that memorizes perfectly and understands nothing. I suspect that many, although perhaps not all, of the climate models are idiot-savant models, tuned to fit a hypothesized pattern that tells a particular story on past data, but rather lacking predictive skill. Usually this is a sign that one needs to build models with much less detail and better attention paid to gross effects, not that one should add still more parameters and detail, but who asked me?
A final observation. I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. The latter is a bit odd, of course — it reaches T = 0, P = 0 at around 18 km, sharp as a knife, which all by itself tells you that it is wrong as it is absurd to think that molecular collisions won’t populate the volume above the supposed T = 0 level (and of course Earth’s real atmosphere extents out an order of magnitude further. The density is not exponential — I got that wrong — because it does go to zero at a specific altitude. It is even more nonphysical than I thought, in other words.
I’m really busy, so I haven’t had time to finish it (in particular renormalizing the DALR, which has to be evaluated numerically from
rgb
[Long reply, thank you. Robt]
Wayne says: “I’ll now stop worrying about you Myrrh… I see you have found the complex component of refraction !! ”
Actually, Wayne, what you attributed to Myrrh instead came from Robert Brown (and I am sure Dr brown HAS run across the concept of complex index of refraction). Myrrh, on the other hand, considered this a “waste of time”.
Robert Brown says
“The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong.”
The point was made to counter the claim by many in Climate Science that light is INSTANTLY transformed into thermal energy.
Light initiates many photochemical reactions.
Often the energy ‘fix’ lasts for thousands of years.
Promoters of climate alarm find it convenient to ignore the natural energy storage systems within our climate.
All credit is reserved for the 33K co2 driven greenhouse theory.
en.wikipedia.org/wiki/Photosynthesis
An even better link
http://en.wikipedia.org/wiki/Light-dependent_reactions
Wayne, yet another post I screwed up, the first para is mine, the bulk Robert’s which finishes at demons out, and then comes my commment.(I think I missed an opening italics to Robert’s but this has become so unwieldy now that I have difficulty posting). So I think you’re responding to what Robert said.
My point, as before in this, is that the AGWSF energy budget is fiction – it claims that shortwave heats oceans and land which then emits thermal infrared once so heated. This is so obviously junk it’s not even funny. The propose this as the main heating source of all of Earth’s land and water!! Water, regardless of how esoteric some want to get about it, IS TRANSPARENT tO VISIBLE LIGHT.
Water transmits visible light without absorbing it. That’s what transparent means! However, when they claim that the atmosphere is transparent to visible light this is not true! Visible light gets absorbed by the electrons of the molecules of nitrogen and oxygen, and reflected/scattered by this.
If water absorbed visible light there would be no life in the ocean. The reason you can see underwater is because light isn’t absorbed. How attentuation, not absorption, happens in the ocean is not the point here. The point is that they have excluded the real heating source of the oceans, thermal infrared, heat direct from the Sun, which is physically capable of heating water!
This is junk science at its finest, nit-picking to avoid confronting the reality that this energy budget is totally junk.
What’s worse, is that it has now become ingrained in the education system, the last couple of hundred years of science progress has been replaced by gibberish. To the point where Ira teaches that the heat we feel from the Sun and incandescent lightbulbs is from the visible! WE CAN’T BLOODY FEEL ANYTHING FROM VISIBLE LIGHT! If it can’t heat us up it sure as hell isn’t heating the oceans. Do you think I haven’t investigated this?
And Tim knows that full well… He continues to run away whenever actual experiments are asked for, as above he claimed there were loads.., or as here, does an ad hom in the best of Beria tradition..
All I’m asking for is proof that blue visible light as from the Sun heats water. Why is this always avoided? If visible light was really capable of heating water there would be tons of stuff on it proving their energy budget. Until they can show that any further distractions and deflections are a waste of time for me. The only reason I ask is because there isn’t any such proof! I just hope in investigating it for themselves they come to realise that..
Robert Brown: “Bear in mind that IMO it is borderline silly to do stat mech on an atmosphere in the first place — it is only useful to answer “formal” questions like those addressed in Velasco like “what is true thermal equilibrium given thus and such conditions” and even there the computations are enormously difficult and require a variety of basically inconsistent or non-ergodic assumptions to be made.”
To me it appeared that Velasco et al.’s “such and such conditions” are precisely those of your head-post hypothetical. Is there something I missed?
Also, could you give an example of an “inconsistent or non-ergodic” assumption that Velasco et al. made?
Robert Brown: “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. The latter is a bit odd, of course — it reaches T = 0, P = 0 at around 18 km, sharp as a knife. . . .”
My attempt to solve that analytically foundered on essentially the same problem, so I didn’t respond to your previous comment about whether the center of mass would rise as heat is transferred from above to below. But I did a back-of-the-envelope plausibility calculation–no doubt inaccurately, because the calculation exceeded my algebraic mean time between failures–for the (highly artificial) case of going from isothermal (T = T_0) to two differently isothermal (T = T_0 + deltaT and T = T_0 – deltaT ) halves, and it seemed that the center of mass remained the same. Again, I don’t really vouch for the calculation, and I’m not sure anything turns on the result, but it’s a data point you may (or may not) want to check out.
Myrrh says: “And Tim knows that full well… He continues to run away whenever actual experiments are asked for, as above he claimed there were loads.., or as here, does an ad hom in the best of Beria tradition.”
What I know full well is that this is experiment is theoretically simple, but practically difficult. Blue light is one part of the heating of the oceans (among many) which is spread over a large area
THEORY:
*energy goes in to the water (blue photons)
* some of that energy does not come out (fewer blue photons leave)
* Therefore, the blue photons added energy to the water.
PRACTICE:
* The most obvious difficulty is that pure water is very nearly transparent for blue light. To absorb any easily measured energy, the “coffee cup” would need to be many meters tall. Around 100 m would be needed to absorb most of the blue light by pure water.
* If my “cup” was 100 deep and only 1 m in surface area that the top (where the light will enter), I need 100 tons of high purity water.
* The “cup” will not be perfectly transparent to light, so it will be absorbing energy, which needs to be subtracted from the energy absorbed by the water.
* The “cup” will not be perfectly insulated, so heat conduction to/from the surrounding will have to be accounted for.
* Direct sunlight is ~ 1000 W/m^2. Visible light would be about 400 W/m^2. “Blue light” would be at most 100 W/m^2. So if my “coffee cup” is 1 m^2 in surface area and 100 m deep, I would get at most 100 W of heating. A 100 W heater would not have much effect on 100 tons of water. Sure, it would slowly heat the water, but separating the “signal” from all the “noise” would be a challenge.
Is this REALLY the sort of experiment you want congress to fund? The simple fact that graphs like this are readily available (http://3.bp.blogspot.com/_fa6AZDCsHnY/S_xwl48ZUSI/AAAAAAAAADQ/kPVlOauL1o4/s1600/water+absorption.gif) shows that the fundamental experiment HAS been done.
“The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong.”
The point was made to counter the claim by many in Climate Science that light is INSTANTLY transformed into thermal energy. Light initiates many photochemical reactions. Often the energy ‘fix’ lasts for thousands of years. Promoters of climate alarm find it convenient to ignore the natural energy storage systems within our climate. All credit is reserved for the 33K co2 driven greenhouse theory.
But this doesn’t counter that claim at all. If you want to counter a claim, do so with something that actually respects the laws of physics and experimentally observed percentages. I am quite certain that some 98% or 99% of the energy in the electromagnetic energy that penetrates further than the first few millimeters of the ocean’s surface is more or less instantly converted into heat. Photosynthesis just isn’t all that efficient. Wikipedia has a whole page devoted to photosynthesis effciency, and typical plant conversion efficiencies are indeed 1-2%, although some plants e.g. sugarcane can get up over 5% (and possibly some of the new gene-tailored algae as well). In the biosphere, most of the energy thus stored is in rough balance — it’s getting eaten as fast as it’s being produced. We’re hardly pressing oil out of sunflower seeds and pumping it into the ground.
You also need to think carefully about “energy storage systems” in our climate. The ocean is the big kahuna, and the entire discussion concerning the oceans was Myrrh’s claim that the ocean doesn’t absorb energy from visible light because it is “transparent”. This is wrong — the ocean takes up a huge amount of heat in the tropics and does indeed store it and transport it (e.g. to the north in the Gulf Stream) where it contributes mightily to the moderation of the climate of Europe, for example. The atmosphere itself no doubt stores and transports energy.
But what else does? If you consider the amount of solar energy entering the Earth every day, it is a truly awesome number. Even if you ignore the fact that nearly any subsystem you look at but the ocean is always near dynamic equilibrium, you have to find a sink that on average removes heat so it does not eventually have to radiate away to materially affect the energy budget. Bear in mind that you could provide 100% of the per capita energy consumed by people in the US to every human on the planet from the solar energy that falls in a remarkably tiny fraction of the total surface area, even allowing for insolation, night time, conversion efficiency, and so on. See e.g. —
http://en.wikipedia.org/wiki/File:Solar_land_area.png
This is, in the end, why CAGW isn’t going to happen even if the CAGW enthusiasts are right about the evils of CO_2! Most of the places that would make the best solar producers aren’t good for much of anything else — too hot and dry to be good farmland or good places for humans to live. At $1/watt for solar cell capacity, $1 buys at least 2-3 kW-H per year. That amortizes the cost of the cell over 5-6 years. All that we are lacking before this becomes the only way to make electrical power at a (substantial!) profit are good ways to store the power and to transport it longish distances compared to what we do now with our existing network of power plants. Even doubling the price (allowing for storage with current technology) still leaves one with decent amortization schedules.
In less than ten years the cost per watt will halve. In less than ten years solutions for the storage problem will emerge — WUWT published a nice article on Zinc-Oxide batteries that might have the capacity and lack of “memory” to make a good base for large scale storage of daytime power and/or electric car batteries (where currently no battery approaches the energy content of gasoline). Sometime in the next ten years, if we “do” nothing at all, one of the simplest ways in the world to make money will be to buy square kilometers of Arizona and New Mexico and West Texas, cover them with solar energy cells hooked into matteries, and linked by ultra-high-voltage transmission lines to cities in cooler, water rich places where people want to live. Ditto North Africa, India, Australia, and so on. 200% to 500% ROI over the 30 year lifetime of the plants, guaranteed.
We’re almost at break-even on this even now, in some parts of the world. In thirty years nobody will be burning coal for electrical energy, not because they want to be green but for the same reason we don’t burn wood for electrical energy now — it costs too much to harvest it and transport it and deal with the fact that you always have to find new sources as old ones mine out.
Then there is nuclear, both fission and (speculative) fusion. We could go green as all hell almost overnight if we just started building fission plants, ideally thorium-salt plants that can’t melt down or be used to build bombs. Sometime in the next 10 to 50 years we’ll probably master fusion as well. Once that happens we will (shortly thereafter) have achieved a type 1 civilization on the Kardashev scale and energy scarcity will never again by a constraint on human civilization on a mundane scale. Energy costs will fall to “almost free” by current standards, even as energy becomes the universal currency base.
I therefore predict, quite confidently, that the Earth will never get more than slightly over halfway to the doom-and-gloom prediction of carbon dioxide doubling before it comes down on its own because burning fuel for power or heat becomes as passe as TV antennas on rooftops — reaching for a signal that is no longer there…
Gasoline used in motor vehicles may last a lot longer — even indefinitely. I’m still not seeing anything remotely capable of storing 37 kW-Hours in the volume of one US gallon on the techno-horizon. But we may find electricity so cheap that we just synthesize gasoline straight up, recycling the CO_2 that’s already there.
rgb
My attempt to solve that analytically foundered on essentially the same problem, so I didn’t respond to your previous comment about whether the center of mass would rise as heat is transferred from above to below. But I did a back-of-the-envelope plausibility calculation–no doubt inaccurately, because the calculation exceeded my algebraic mean time between failures–for the (highly artificial) case of going from isothermal (T = T_0) to two differently isothermal (T = T_0 + deltaT and T = T_0 – deltaT ) halves, and it seemed that the center of mass remained the same. Again, I don’t really vouch for the calculation, and I’m not sure anything turns on the result, but it’s a data point you may (or may not) want to check out.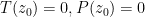 at
at  for monatomic ideal gases until I saw the ODE solution reach zero and turn around and go back up again. Silly me! I’m so used to the physically plausible idea and experimentally observed idea that the real atmosphere gently fades away that I completely missed the fact that a DALR atmosphere simply stops, that no molecules in the gas below can, under any circumstances, gain enough energy to get above
for monatomic ideal gases until I saw the ODE solution reach zero and turn around and go back up again. Silly me! I’m so used to the physically plausible idea and experimentally observed idea that the real atmosphere gently fades away that I completely missed the fact that a DALR atmosphere simply stops, that no molecules in the gas below can, under any circumstances, gain enough energy to get above  . I’m working on the correct renormalization of the solution now, but have to take my son out to get a game and do some other shopping. Sigh. Fixing the code seems like more fun.
. I’m working on the correct renormalization of the solution now, but have to take my son out to get a game and do some other shopping. Sigh. Fixing the code seems like more fun. , Jelbring’s proposed thickness of the atmosphere involved, is greater than
, Jelbring’s proposed thickness of the atmosphere involved, is greater than  , the gas won’t even be in contact with the upper surface anyway, it will be strictly confined to a height less than
, the gas won’t even be in contact with the upper surface anyway, it will be strictly confined to a height less than  because that is the height where the absolute temperature, concentration, and pressure of the lapsed gas reaches zero.
because that is the height where the absolute temperature, concentration, and pressure of the lapsed gas reaches zero. in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them.
in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them.
It’s really difficult, because while the isothermal case is simple, one has to solve an ODE to get the concentration with a lapse, then renormalize the result to have the right number of particles per unit area, and do this with a constrained surface temperature of (say) 300K. In other words, you need 300K at the surface and P = 1 atm at the surface (to compare to the same conditions isothermal) and it isn’t easy to see how that will work. I freely admit that my earlier estimate might turn out to be completely wrong — I hadn’t actually mentally realized that the DALR predicts
As for your observation that my top article addresses the isolated ideal gas problem when it is arguably irrelevant to the real atmosphere, well, sure, except that really it only addresses the EEJ paper. The discussion has now gone well beyond that, but the reason for the top post was simply to prove that the EEJ claim was false, that an adiabatically isolated ideal gas in true thermodynamic equilibrium, insulated from above and below by a layer of black matter that itself can be in equilibrium with the gas but which conducts no heat, after a long time, exhibits a DALR as its true stable thermodynamic equilibrium. No, it doesn’t. As we’ve discussed it, more and more ways that it fails have emerged. The state isn’t maximum entropy, and isn’t the equilibrium that will be reached, eventually, if the ideal gas conducts heat (as ideal gases do!) The black layers that bound the gas at the top and the bottom will radiate heat from the warmer to the cooler surface until they are in equilibrium, speeding the achievement of isothermal equilibrium. And if
Why do I care about Jelbring? Because it is cited repeatedly on at least two blogs (that I know of) as “proof” that gravity heats an atmosphere at the bottom without greenhouse gases or differential surface heating and upper troposphere, greenhouse gas mediated cooling. It is the basis for the N&Z paper that is trying to take this idea to new levels of absurdity on the basis of an “miracle” fit that is no miracle.
And at this point, I’m continuing with the matlab exercise because I want a venue where I can experiment with simple models that help me explore e.g. the DALR and energy and heat capacity and so on. Once I have
rgb
How attentuation, not absorption, happens in the ocean is not the point here.
It’s only not the point to you because the way the light is attenuated is by being absorbed. If you would deign to look at the exponential decay constant for water in inverse centimeters, in the Wikipedia article I linked above, you will note that the length scale, the exponential “penetration depth” for light in the visible band is nowhere greater than around 100 meters. That means that well over half of the energy in the visible light that makes it through the partially reflective surface of the sun is absorbed by the water within the first 100 meters, photosynthesis is only possible in the top 200 meters (the Epipelagic zone) and virtually none of the energy penetrates past a kilometer in depth. The 800 meters of water under the layer warmed by visible sunlight is called the Mesopelagic, and the temperature at the bottom of it is a constant 4K because that is precisely the point where there is almost no solar energy left to directly warm it:
http://en.wikipedia.org/wiki/Mesopelagic
Paradoxically, the precise place you think warm enters the water is where it does not. The penetration depth of most of the IR, in particular, is order of a millimeter or less — mostly less. Lots of the energy is absorbed in a layer 1-10 micrometers in thickness — 1000-10000 molecules thick — at the very surface, where it causes the water to evaporate rather than heating the bulk. The energy mostly goes into the latent heat of vaporization of water (which is very substantial); relatively little is leftover as “warm water” and that which there is is largely stuck at the top, because water has a relatively high thermal expansion coefficient and the warmer water is considerably more buoyant and stays on top except where mixed by the action of wind or wave or sustained current.
Again, you seem to want to think that all climate science is bullshit and all climate scientists are idiots, to the point where you are inventing new physics for them to be wrong about. I’d suggest that both are almost certainly untrue in general, even though there may well be some climate science that is bullshit and some climate scientists that are idiots, and in any event, getting the basic physics you’re trying to call them on wrong simply destroys your own credibility as a reasoning participant in the debate.
To summarize — the (dry) atmosphere isn’t perfectly transparent to visible light, but one can look down from orbit and photograph a newspaper in high enough resolution and with more than enough light to read the headlines. A photograph from space clearly shows us the continents and oceans by day everywhere that isn’t obscured by clouds, and at night even the relatively dim lights of human activity (dim compared to sunlight) can easily be seen from orbit or a plane flying 10 km above the surface.
Those same pictures do not show the bottom of the sea. Riding on a boat even over very clear, very clean water, one cannot see a kilometer down. One cannot see 100 meters down. In world war II, submarine hunters couldn’t see submarines a mere 20 meters down as a general rule, with a few exceptions where the water was particularly clear. By no stretch of the imagination is water as transparent as air, even to visible light. If it were, our satellites could photograph the bottoms of oceanic trenches, and they can’t. The top kilometer of water is almost completely opaque, because all of the visible light that does make it in at the top is absorbed there, warming the water.
The word “transparent”, when applied to air and water, is an approximate concept. Air scatters blue light quite strongly, but is much more transparent to red light. Scattering isn’t the same thing as absorption. If you want to understand what water does, don’t appeal to an English word such as transparent as if it, used as an adjective applied to a material, is a scientifically precise descriptor. What is scientifically precise is the absorption cross-section or penetration depth, which tells you just how much water visible (or any other frequency) of light can traverse before it is 10%, 50%, 90% absorbed.
rgb
Why is this always avoided? If visible light was really capable of heating water there would be tons of stuff on it proving their energy budget.
Or, they could consider a direct measurement of the absorption cross-section of water in the visible range to be direct proof, and thereafter take it for granted that the simplest of physics — visible light is transmitted into water at the surface and doesn’t come back out, therefore it damn well goes somewhere and the place organized energy sooner or later ends up is heat — is correct.
Perhaps they don’t want to believe in invisible fairies that eat the blue photons that make it through the surface of water before they get down to a kilometer of depth, because God knows there ain’t no blue photons left to speak of by the time you get down that far.
Demons Out!
rgb
When we step into the shade on a hot, sunny day, we no longer feel the direct heat from the Sun, we can feel the warmth of the air heated by the Sun, but not the thermal infrared direct from it. This is bog standard physics of light and heat.
Good lord! You must be joking. I’ve never heard anything so silly from somebody presumably out of high school.
Look, go find yourself a blue-ray disc player. Take it apart, carefully, until you expose the 1 watt blue laser. Point it at your skin. Power on. After your finger heals from the hole you drilled through your skin, come back and tell me that visible light doesn’t carry heat.
Or you can watch any of the umpty youtube videos that show people using e.g. 250 mW laser pointers to start fires (red, green, blue, who cares what color!). For example, here is one:
out of about a million — kids LIKE to start fires with lasers. Lasers are good counterexamples because they are monochromatic, so you can’t pretend that your burned finger came from “secret” infrared added to the beam by your invisible fairies.
Here’s a very simple exam question. Blue light with an intensity of one watt per square centimeter illuminates a thermal sensor coated with lampblack, and the temperature increase is plotted as a function of time. After the sensor returns to its original temperature it is illuminated with red light at the same intensity. You expect the temperature of the sensor to:
a) Remain constant in both cases because visible light doesn’t heat anything (Myrrh’s bog-standard physics answer — I must find a copy of his new book, “Bog Standard Physics” as I somehow don’t have it on my shelves).
b) Warms faster for the red light because it is closer to infrared and everybody knows only infrared light can actually heat anything.
c) Warms just about exactly at the same nonzero rate for both.
If you get this one right we can try you on which one weighs more, a pound of feathers or a pound of lead.
What matters in energy transfer via light is two things: The intensity of the light, that is, the power per square centimeter (more properly the Poynting vector of the light as the power incident on any surface is the flux of the Poynting vector through the surface, correcting for surface geometry and the direction of the light); the absorptivity of the material in the wavelength chosen.
The latter is basically never “perfectly zero” for anything but a vacuum, although it can be quite small. Things that are opaque tend to reflect white light in the colors that they don’t absorb and absorb the light in the colors that they don’t reflect. Hence when you light up a red piece of paper with red light, you don’t warm it much, but if you use blue light you warm it a lot. Black is the universal absorber color, white (or metallic/shiny) the universal reflector, although that’s really only for the visible spectrum because whether something is “black” (a good absorber) to UV or IR may not be connected to its color in the visible spectrum. “Transparent” materials are more complicated, and conductors are treated somewhat differently than insulators.
You can’t just make sweeping statements about this — you have to learn the actual physics and learn the actual relevant physical properties of the particular kinds of stuff you want to apply the physics to. Visible light will heat you up just fine, as has been shown in countless elementary school science fair projects. Or you can do the “experiment” itself with a high-power laser pointer or blue laser from a CD burner, if you’re stupid enough to actually try it.
rgb
Robert Brown
When in a discussion involving equilibrium thermodynamics someone finds the need to drag in a laser I feel they are clutching at straws.
” Look, go find yourself a blue-ray disc player. Take it apart, carefully, until you expose the 1 watt blue laser. Point it at your skin. Power on. After your finger heals from the hole you drilled through your skin, come back and tell me that visible light ”
The blue light is more likely to induce chemical change than directly thermally agitate the skin molecules.
You are also ignoring other photochemical reactions in addition to photosynthesis.
http://en.wikipedia.org/wiki/Light-dependent_reactions
2/8 6:22am:
“Heat can be transported without bulk transport of molecules…. as Velasco states….the ideal gas…will relax to isothermal, the true thermodynamic equilibrium state. Velasco unambiguously agrees with me…”
I looked through Velasco et.al. paper but don’t find that particular Velasco et. al. statement – can you provide the specific paragraph? Beware of the double negative therein. I looked up your 2/5 10:25pm post and did find your statement exactly:
“..there is no heat flow at equilibrium, because equilibrium is maximum entropy.”
Ding! We all agree on that. Heat can be transported before Fig. 1 equilibrium w/o bulk transport. When Fig. 1 in top post is at equilibrium it has reached max. entropy; no heat flow or transport, no bulk transport, max. entropy condition which is proven non-isothermal, isentropic by Velasco et. al. eqn. 8, Verkley et. al. part b AND Bohren&Albrecht text Chapter 4.4.
No heat flows in Fig. 1 in equilibrium yet temperature decreases with increasing height according to all 3 ref.s I’ve cited w/the specific ref.s: “Please be specific” (a quote from my high school English teacher). Isothermal is proven NOT max. entropy for Fig. 1. So isothermal is not Fig. 1 equilibrium condition. Fig. 1 will then over time, and on its own, naturally change to equilibrium temperature non-isothermal profile – I posted the exact T gradient formula above.
Your posting of the thermal conductivity of a gas (eqn. 7.48 in B&A) provides some clues to me as to root cause why you are stuck on manifestly assuming the incorrect isothermal equilibrium solution for Fig. 1 where you disagree with all 3 expert references I cite – which show their algebra.
The formula you post at 6:22am today is the correct definition of thermal conductivity of a gas under no gravity (there is no g in the formula) which B&A shows derives from the Fourier heat flow eqn. (it is misnamed a “law”) – shown as B&A Eqn. 7.11.
Quoted verbatim w/uninteresting skips for brevity, directly from B&A:
“The Fourier law in the form Eq. (7.11), where Kt is solely a property of the medium and not its state of motion, is not generally valid for fluids in motion….acted upon by a mass dependant force (such as gravity)…” Ref. B&A page 342 of edition 1.
B&A follow-up on p. 351: “Although the Fourier conduction law is not generally valid within a fluid, it is valid at the boundary between a fluid and a solid because of the no-slip boundary condition.” And p. 347 B&A correctly conclude for top post equilibrated Fig. 1: “As we saw in section 4.4, the natural state of affairs is for the temperature of an isolated layer of air in a gravitational field to decrease with (increasing) height ”
This Fourier eqn. being inapplicable to Fig. 1 due to gravity acting is why your thinking of conduction in solids (stationary molecules not in motion) impedes your reasoning & leads to your incorrect isothermal equilibrium conclusion for Fig. 1 in top post – at least for reasonable ideal gases in gravity field (reasonable molecules in random motion i.e. P = 1000mb to 200mb, T range from earth surface through troposphere).
“Since you are doing this for the same reason I am — to learn a lot more about atmospheric thermodynamics (and thermodynamics in general)…”
4 things I’ve reasonably correctly learned & a 5th kicker:
1) Top post Fig. 1 equilibrium is non-isothermal, isentropic by the 13 difficult but doable algebra steps I outline posted above; ideal gas T gradient w/height formula is known under given initial ref. conditions & is not constant as exactly derived from 3 different 1st principle references by generalized entropy maximization mathematics. This is counterintuitive & closely approximates the standard atmospheric temperature profile up through earth’s troposphere.
2) Remember 1) forthwith. So far 1) has not been proven incorrect by any poster here.
3) The Fourier heat conduction formula is general for solids and is not applicable in general to fluids – only applicable to fluids with molecules not acted on by gravity; is applicable to ideal gas in gravity field only at boundary to a solid under certain conditions.
4) I have to watch eqn. definitions & their assumptions closely. For example, in the Northwestern U. link provided at 6:22am today the applicability of the Fourier eqn. is limited to stationary fluids. In the ref. provided, a stationary fluid is defined as one w/o external forces acting on its molecules such as gravity. Entirely consistent with B&A p. 342. Also, M-B distribution is valid only for no forces acting on molecules.
5) I long ago learned to win the game, you have to s-l-o-w-l-y watch the pea under the thimbles.
Robert Brown
The easiest way to solve the blue light in water situation is to pick a particular molecular example.
Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
To treat all solar radiation as exactly the same as thermal or infra red is not acceptable.
It fits in with the same kind of science that treats the Earth as a perfect black body.
On the other hand the trace gas CO2 is given awesome power .
If the one W/m2 effect is questioned then positive feedbacks are readily found.
The K&T 2009 energy balance diagram totally ignores the photochemical reality.
books.google.com/books?isbn=0521016347…
Bryan says:
The easiest way to solve the blue light in water situation is to pick a particular molecular example. Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
Why does the precise mechanism even matter to you? The fact that the radiation is being absorbed means that its energy is being absorbed. Unless you imagine that the ocean is magically levitating off the ocean floor or chemically splitting into hydrogen gas and oxygen/chlorine, that energy can only appear as heat. Even if you assume that the water is murky enough that almost all the absorption is by mud particles or living cells, the energy still almost all ends up heating the bulk water within a fraction of a second. Only a small percentage at best is captured by photosynthesis or sequestered via other photochemical reactions.
You seem to misunderstand what thermal energy is. It’s not the motion of a single molecule; it’s the random motion of a lot of molecules.
When two molecules collide, photons of any wavelength can be absorbed or scattered. The energy absorbed goes into pushing the two molecules apart at a higher speed. This is a continuum process. Every material in the universe, without exception – solid, liquid, gas or plasma – absorbs and radiates by such processes, although in rarefied gases the effect can be extremely weak. Water will absorb blue light by this (and other) mechanisms.
Photons can also excite vibrational, rotational and orbital transitions in the absorbing molecule. Doppler, collisional and pressure broadening increases the width of these absorption lines, so there is a finite (albeit at some wavelengths very small) absorptivity across the whole spectrum. These excited states can relax (thermalise) by collision with other molecules on a time scale ~1ps, which is as close to “instantly” as makes no difference. Water will absorb blue light by this (and other) mechanisms.
Paul Birch
I said
The easiest way to solve the blue light in water situation is to pick a particular molecular example. Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
You said
“Why does the precise mechanism even matter to you?”
Thank you for your long reply, but I guess the real reply is ‘no I have no idea’!
Paul Birch,
“The fact that the radiation is being absorbed means that its energy is being absorbed. Unless you imagine that the ocean is magically levitating off the ocean floor or chemically splitting into hydrogen gas and oxygen/chlorine, that energy can only appear as heat.”
Please do not get sloppy when trying to answer questions like this. I am certain you are aware of the photoelectric, pyrroelectric, and ferroelectric effects. They convert photons into movement of electrons, or, electric current. This is a very valid question for those of us who are less than experts. What does happen and where does it go is NOT something that many of us know and something that is too often assumed.
Bryan says:
February 9, 2012 at 6:11 am
Paul Birch said “Why does the precise mechanism even matter to you?”
Thank you for your long reply, but I guess the real reply is ‘no I have no idea’!
Read the reply! I answered your question quite clearly and fully. I also pointed out why the answer doesn’t matter anyhow. I could go into endless detail about how charged particles in an electric or magnetic field radiate; about how electromagnetic radiation has electric and magnetic fields; about how atoms and molecules in collision form electric dipoles and undergo charge separation. I could talk about Thompson and Rayleigh scattering. I could refer you to Panofsky and Phillips. But I’m not going to bother, because I don’t see any willingness from you even to try to understand; you’d rather keep believing your anti-physicist (and anti-common sense) fantasy.
Paul Birch
Your impertinent reply contained absolutely nothing to do with my original question
A great deal of arm waving fools no-one.
Photons that are present in blue light or shorter wavelengths do not correspond to vibrational rotational and translational transitions.
These transitions are the ones that correspond to thermal energy.
For instance a believable narrative about CO2 absorbing or emitting 15um radiation can be matched with thermal energy changes.
On the other hand wavelengths around 450nm correspond to electronic transitions of the covalent bonds in organic materials.
I am glad that you have terminated replies as you have obviously nothing to contribute to the topic
http://www.ncsu.edu/chemistry/franzen/public_html/Poland/Poznan08a/Text/Ch6.pdf
Dr. Brown,
I had said:
,
to which you responded with:
,
which indeed shows that in – \left(\frac{Mg}{R}\right) \frac{P}{T} you have eliminated density from consideration, and are in essence treating the air as a solid.
Not recognizing your own naivety in matters concerning thermodynamics of gasses, you proceed with:
,
which is the incorrect unphysical result you get from your inappropriate assumptions and reductions concerning equations of state..
You further state:
[?]
Wrong! No, you don’t need masses of gas moving up and down to establish the DALR. You just need molecules moving throughout. If you somehow heat the top molecules only, they will either rise and cool, to settle into the DALR, or they will leave the troposphere.
Bryan says:
February 9, 2012 at 8:43 am
Paul Birch,
Your impertinent reply contained absolutely nothing to do with my original question
A great deal of arm waving fools no-one.
Photons that are present in blue light or shorter wavelengths do not correspond to vibrational rotational and translational transitions.
These transitions are the ones that correspond to thermal energy.
For instance a believable narrative about CO2 absorbing or emitting 15um radiation can be matched with thermal energy changes.
On the other hand wavelengths around 450nm correspond to electronic transitions of the covalent bonds in organic materials.
I am glad that you have terminated replies as you have obviously nothing to contribute to the topic
The impertinence is yours, in rudely claiming I “ha[d] no idea” of the answer to your question when I had just answered it! If you did not understand my reply you had only to ask for clarification. I have not “terminated replies”. I said I wouldn’t bother going into detail concerning the electrodynamics of the mechanism you so willfully ignored.
Blue photons do not correspond to pure rotational and vibrational transitions in water. They do however correspond to transitions which can include changes of the rotational and vibrational quantum numbers as well as the orbital or electronic quantum numbers. When a photon is absorbed through any such transition, the molecule is then in an excited state, Depending on the specific energy levels, the molecule may partly or wholly de-excite by emission of photons of longer wavelength (to be absorbed in turn by other molecules). The molecule will also de-excite upon collision with another molecule. These collisions are how the energy is thermalised. This process is very very fast.
Paul Birch says
“Blue photons do not correspond to pure rotational and vibrational transitions in water.”
Paul and Tim would hopefully agree that translational should be therefore included as well.
These are the modes commonly grouped as thermal.
This was the point that Myrrh was making.
Electrons making orbital transitions do not directly involve thermal wavelengths.
Thermal effects can induce changes in molecular orbital levels.
On deactivation several wavelengths are perhaps allowed including those in the thermal range to account for the energy level drop.
There is a not insignificant amount of energy stored by the process of photochemistry.
The lumping of light and IR together is such a gross oversimplification that it is clearly wrong.
Bryan,
Look in your reference –> pages 363-364. Note that internal conversion and fluorescence result in heat to the surroundings. Chemical reactions are considered “not usually important” by the author.
Also note, Paul said “Photons can also excite vibrational, rotational and orbital transitions“, which you apparently misinterpreted as “vibrational rotational and translational transitions.” Indeed, these orbital transitions are exactly what your reference discusses.
Bryan: “There is a not insignificant amount of energy stored by the process of photochemistry.”
This is a testable hypothesis, not a fact (at least not a fact I am specifically aware of). I would tend to think that the amount of energy stored by the process of photochemistry IS insignificant, for two reasons
1) Photochemistry is relatively uncommon in terms of the total EM radiation heading to earth.
2) For any chemical process to store significant amounts of energy, there must be a significant year-to-year accumulation and/or destruction of chemicals. Simply absorbing energy one moment and releasing it a second or an hour or a year later does not lead to storage of energy. Most photochemical processes (like photosynthesis) are very nearly balanced on an annual scale. In other words, there is no net accumulation of organic material from one year to the next.
But if you want to do some calculations to show that either of these two points are incorrect, go for it !
Tim Folkerts says
“Most photochemical processes (like photosynthesis) are very nearly balanced on an annual scale. In other words, there is no net accumulation of organic material from one year to the next. But if you want to do some calculations to show that either of these two points are incorrect, go for it !”
The ‘known reserves’ of fossil fuels is often touted as being the actual reserves.
But we know that serious research only extends to a commercial timescale.
I cannot find a publication that gives a hard breakdown of % of Solar EM radiation absorbed by chemical rather than direct thermal modes.
I know that orbital transitions do not involve directly a thermal aspect.
Off on holiday for a week or so, means adiabatic matters will have to wait.
Bryan says: “The ‘known reserves’ of fossil fuels is often touted as being the actual reserves.”
Quite true. But wikipediasuggests that 5.5×10^24 J of solar energy hits the earth each year, but the total reserves of petroleum are 7.9×10^21 J. In other words, diverting 0.1% of the solar energy for one year straight into chemical energy would be enough to creates ALL of the known petroleum in the world. This amounts to 0.3 W/m^2 of absorbed energy, which would be a significant amount. But this requires a net creation and storage of energy equivalent to ALL the known petroleum in the world EACH YEAR. If instead we consider the production spread out over 100’s of millions of years, the sequestration rate would be microwatts per square meter — which counts as insignificant in anyone’s book.
Creation of fossil fuels is clearly not the answer. But there could be other answers. Can you find specific suggestions and specific numbers to show the significance?
Myrrh has some website that states that water is transparent, but instead of contacting that web site and asking whether they really mean ‘nearly transparent’ he has decided that everyone else has falsified physics. Seems backwards to me.
For anyone who is actually interested, here is the explanation of how water absorbs (weakly, but not zero!) in the visible.
http://www.lsbu.ac.uk/water/vibrat.html#ir
Note that amusingly (since Myrrh insists that only molecular vibrations are ‘heat’) that it is actually a vibrational (overtone) band that is responsible.
Robert Brown: “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column.”
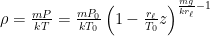

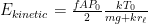 ,
, is lapse rate,
is lapse rate,  is the gas-column cross-sectional area, and
is the gas-column cross-sectional area, and  is the number of degrees of freedom. (Forgive any typographical infelicities; this is my maiden voyage with LaTeX.)
is the number of degrees of freedom. (Forgive any typographical infelicities; this is my maiden voyage with LaTeX.)
Here’s what I found when I attempted a pencil-and-paper solution:
and
where
Now, for me the math was a little taxing, so I’m not certain I got it right. If I did, though, the ratio of potential energy to total energy is independent of lapse rate: the center of mass wouldn’t rise if the lapse rate increased from zero to the dry adiabatic lapse rate.
Of course, Velasco et al. say a spontaneous lapse-rate rise of that size won’t happen at equilibrium, because the microstates that exhibit a nearly-zero temperature lapse rate are many times as numerous as those that exhibit temperature lapse rates of the same order of magnitude as the dry adiabatic lapse rate.
Tim Folkerts says:
February 9, 2012 at 4:53 pm
Quite true. But wikipediasuggests that 5.5×10^24 J of solar energy hits the earth each year, but the total reserves of petroleum are 7.9×10^21 J.
To be fair we would need to include the energy equivalent of the entire fossil carbon store, including that scattered through bulk sediments so thinly that it is generally not considered an extractable resource. That total is ~2.7×10^27J (OU S266 Block2 p16) or ~500 yr of solar energy. Assuming this has taken ~350,000,000 yr to form, the fraction of solar energy sequestered is ~1/700,000, amounting to ~0.5mW/sq.m. Surely Bryan could accept that this is negligible in the heat balance – where after all very little is known to better than say 1% accuracy, if that. Even geothermal heat conduction is two orders of magnitude greater at ~50mW/sq.m.
Yes the ‘everything being equal’ assumes there is no photosynthesis along with a dazzling set of pseudo scientific assumptions.
Photosynthesis is utterly irrelevant to the GHE.
All of the ways energy redistributes itself inside the atmosphere is irrelevant to the GHE.
The only thing that is relevant to the GHE is the outgoing radiation budget, which is the only way the Earth loses the heat it picks up from the Sun (with an extremely modest addition from all other sources). The Earth does move through hard vacuum, after all. No conduction away, no convection away, only radiation away.
If one looks at the radiation going away — the full top-of-atmosphere outgoing radiation spectrum — the GHE is clearly visible. Outgoing radiation from the IR band of CO_2 is emitted with an effective temperature (top of troposphere) that is much colder than the surface temperature. Colder means (much) less integrated outgoing power in these frequencies. One way or another radiation from the other available frequencies has to increases to compensate, because incoming solar radiation is what it is and to remain in balance ins ultimately must equal outs.
One way it the Earth compensates is by becoming warmer at the surface. This increases the rate of direct radiation from the surface in the water window so that the integrated outgoing power still equals the integrated incoming power, on average, for the entire Earth.
There isn’t really any question that this occurs. You can see it directly in the actual spectrographs any time you care to look. So make up any bizarre and complex tale you like for how heat moves around before it leaves — but at the end of the day the GHG GHE without question is the major contributor to the warming of the Earth above the mean temperature expected if there were no atmosphere at all or a GHG-free atmosphere. You can see it.
Of course, to see it you have to remove your head from the sand and look. I wish you well with that.
rgb
I believe that the atmosphere does lose some molecules to outer space, although I suspect that it is also modest.
Are there any numbers on this, since it would also transport some small amount of energy away.
kuhnkat says:
February 10, 2012 at 1:05 pm
Paul Birch, “The fact that the radiation is being absorbed means that its energy is being absorbed. Unless you imagine that the ocean is magically levitating off the ocean floor or chemically splitting into hydrogen gas and oxygen/chlorine, that energy can only appear as heat.”
Please do not get sloppy when trying to answer questions like this. I am certain you are aware of the photoelectric, pyrroelectric, and ferroelectric effects. They convert photons into movement of electrons, or, electric current. This is a very valid question for those of us who are less than experts. What does happen and where does it go is NOT something that many of us know and something that is too often assumed.
It doesn’t matter what weird and wonderful short-term effects might be happening! We have already seen how photosynthesis is insignificant in this context. So unless there is a permanent, drastic, progressive and one-way alteration in the chemical makeup of the oceans over geological epochs (which would entail the massive evolution of hydrogen gas and the production of oxygen, chlorine or hydrogen peroxide) or a similarly huge increase in its potential energy (levitating it off the ocean floor), the energy involved will still have to be dissipated as heat (there’s nowhere else for it to go, unless you get all science-fictiony and assume it vanishes into hyperspace or turns into neutrinos or something).
Robert Brown declaims,
“The only thing that is relevant to the GHE is the outgoing radiation budget, which is the only way the Earth loses the heat it picks up from the Sun (with an extremely modest addition from all other sources).”
Only you have no idea whether the Black Box of the earth system is receiving and emitting a balanced amount of energy over it history. Y’all wave your arms a lot, but, you simply DO NOT HAVE THE FACTS TO PROVE YOUR CASE!
You TOTALLY ignore the heating effects of the solar wind, birkeland currents, magnetic and gravitic fields. Yeah, when you pick and choose the physic you will discuss you can prove pretty much anything you want to prove.
jimmi_the_dalek says:
February 9, 2012 at 7:33 pm
Myrrh has some website that states that water is transparent, but instead of contacting that web site and asking whether they really mean ‘nearly transparent’ he has decided that everyone else has falsified physics. Seems backwards to me.
For anyone who is actually interested, here is the explanation of how water absorbs (weakly, but not zero!) in the visible.
http://www.lsbu.ac.uk/water/vibrat.html#ir
Note that amusingly (since Myrrh insists that only molecular vibrations are ‘heat’) that it is actually a vibrational (overtone) band that is responsible.
—
So you’re of the Folkerts school of science? I point out that the energy budget cartoon you work to claims that shortwave from the Sun is the only source of directly heating Earth’s land and oceans for it to radiate out the amount of thermal infrared, heat, claimed, and you come back with ‘it’s not completely zero’ and the idiocy of Tim’s so called experiment to prove shash might be there at the cold depths..?
Water is transparent to Visible light, the graph shows that. It shows that water doesn’t for any practical real world outside of shash insignificance absorb any visible light. That’s what transparent means. It means water doesn’t absorb visible light. Visible light cannot be heating all the vast amount of water in our great ocean which is the major part of our Earth because Water does not absorb visible light, it transmits it through without absorbing it. That’s what water does with visible light, it doesn’t absorb it. Yet you claim Visible light is this great super high energy peak output from the Sun heating Earth’s land and oceans!
Not only can you not see how absurd that claim, you also believe, because you’ve been told, that the Sun’s heat, thermal infrared, doesn’t reach the surface!
How on earth can you possible expect me to take you seriously as ‘scientists’?
You see, I can understand joe public being unaware of the manipulation here, I can even understand scientists in different fields not being aware of it, but what I can’t understand is anyone calling themselves a scientist not being able to understand what I’m saying and continuing to defend this fiction, and especially those vaunting their great credentials as proof of their own brilliance.
Here, some real world information about it:
NASA original page teaching previously traditional real world physics to children: http://science.hq.nasa.gov/kids/imagers/ems/infrared.html
““Near infrared” light is closest in wavelength to visible light and “far infrared” is closer to the microwave region of the electromagnetic spectrum. The longer, far infrared wavelengths are about the size of a pin head and the shorter, near infrared ones are the size of cells, or are microscopic.
Far infrared waves are thermal. In other words, we experience this type of infrared radiation every day in the form of heat! The heat that we feel from sunlight, a fire, a radiator or a warm sidewalk is infrared.
Shorter, near infrared waves are not hot at all – in fact you cannot even feel them. These shorter wavelengths are the ones used by your TV’s remote control.
Infrared light is even used to heat food sometimes – special lamps that emit thermal infrared waves are often used in fast food restaurants! “
Do you understand what this is saying?
It is saying that thethermal infrared direct from the Sun reaches the Earth’s surface.
We feel its heat.
This means the KT97 and variations is junk science, because it has excluded the real heating mechanism of Earth’s land and oceans.
There’s no getting around that…
There’s some useful information on this wiki page, scroll down to the difference between electronic transitions and thermal infrared, it gives the four possible outcomes of visible meeting matter. The second, refection/scattering when an electron absorbs the energy, is what happens in our atmosphere when the electrons of the molecules of nitrogen and oxygen briefly absorb visible and then send it back out again, so our blue sky. The third is visible in a transparent medium, like water, where it is not absorbed but transmitted through.
http://en.wikipedia.org/wiki/Transparency_and_translucency
I’d found something earlier which gives a bit of the picture of what’s happening when visible gets transmitted through a transparent medium:
I once read a great description of this, likening it to a dance with the visible trying to get into to join in but being rejected and moved on!
I believe that the atmosphere does lose some molecules to outer space, although I suspect that it is also modest.
Are there any numbers on this, since it would also transport some small amount of energy away.
You are quite correct — this is a form of “evaporative cooling” that occurs as a few molecules from the tail of the Maxwell-Boltzmann distribution end up with escape energy and happen to have the right direction to escape without suffering another momentum-energy transferring collision. However, this process is enormously slow, especially for the heavier molecules. It is described in most intro physics textbooks — not my own yet as I haven’t written the thermo chapters — but IIRC you can find a good description on wikipedia.
The rate of loss, while slow, is fast enough to have depleted parts of Earth’s atmosphere over 4 billion years, but our atmosphere is fairly steadily being replenished by outgassing from the crust.
The energy outflow in this form is even more negligible than the energy inflow from the Earth losing its internal heat, though — in any event the two have the opposite sign and are both even more negligible together than either one alone.
There are a variety of mechanisms for energy coming both in and out that are effectively ignored in the energy budget, because they correspond to <0.1% variations. For a while I thought that direct magnetic inductive heating of the Earth might be associated with the increased warming observed during periods of high solar activity. Inductive heating occurs when a conductor (like the Earth) moves through magnetic flux (e.g. rotates and revolves around the Sun) or when the flux through a stationary conductor changes for other reasons. At one point in time the Sun's magnetic field was presumably strong enough to have caused at least some of the planetesimals in orbit around the Sun to fuse, explaining how they form solid bodies in spite of never being gravitationally heated enough to melt. However, when I did a Fermi estimate of the heating, while the total energy involved was suitably impressive, the power per square meter of surface was utterly ignorable. Many of the mechanisms are like that — the tides, the direct inductive heating, the heating caused by the days influx of falling meteorites — which incidentally is far greater than the rate of heat loss through outgassing, as meteoric dust and matter infalls at an average rate of at least millimeters per decade, from my own direct measurements — they have “impressively” large amounts of annual energy associated with them, right up to where you divide by the surface area of the earth and the number of seconds in a year.
In the end, only Solar radiation matters for incoming power, only radiation matters as outgoing power, at least as far as I know, that is to say, barring new physics (dark matter/energy forming a mysterious unaccounted for energy source, stuff like that). It’s not that there aren’t perturbations from other sources, it is that those sources or sinks are orders of magnitude less important and are themselves nearly steady state phenomena, forming a nearly constant background correction, not something that contributes to active average temperature changes in climate.
rgb
Water is transparent to Visible light, the graph shows that. It shows that water doesn’t for any practical real world outside of shash insignificance absorb any visible light. That’s what transparent means. It means water doesn’t absorb visible light. Visible light cannot be heating all the vast amount of water in our great ocean which is the major part of our Earth because Water does not absorb visible light, it transmits it through without absorbing it. That’s what water does with visible light, it doesn’t absorb it. Yet you claim Visible light is this great super high energy peak output from the Sun heating Earth’s land and oceans!
No, it doesn’t transmit it without absorbing it because it isn’t perfectly transparent. You keep asserting that water is transparent as if transparency is a binary property of matter — either it is perfectly transparent or it is perfectly absorbing. It is not.
Even if water were perfectly transparent, there would be the question of where it is transmitting all of that visible light to. That would be the ocean bottom, right, where it would heat the bottom and then warm the ocean anyway? Only — where’s the light down there? Oooo, it’s gone, isn’t it. Invisible fairies strike again!
Demons Out!
(I know, it’s not working, I need to hire a holy person experienced with exorcising Maxwell Demons, but in the meantime all I can do is keep trying.)
rgb
kuhnkat says:
February 10, 2012 at 3:17 pm
Only you have no idea whether the Black Box of the earth system is receiving and emitting a balanced amount of energy over it history. Y’all wave your arms a lot, but, you simply DO NOT HAVE THE FACTS TO PROVE YOUR CASE!
Do the sums! The energy in and energy out has to be closely balanced over the long term because there’s nowhere else for it to go!. There’s a residual ~50mW/sq.m out from the Earth’s internal heat. There is up to ~0.5mW/sq.m retained due to photosynthesis. Everything else will be even smaller. For example, suppose the air was at one time completely motionless, and suppose as little as 1% of the solar input went to creating wind; in just one day the global windspeed would reach 8m/s; and that’s it, the wind store is full. Or suppose we put the energy into ocean currents; again, just about a day gets the entire ocean moving at 1 knot. Even to heat the entire ocean would take only ~ 1 year’s solar input per degree rise.
Now, we’ve all been ignoring the influx of moonlight and starlight. Why? Because they are quantitatively negligible compared to solar radiation. We’ve ignored the solar wind and solar magnetic field. Why? Because when they reach the Earth they carry very little power per unit area. We’ve ignored cosmic rays. Ditto. As far as the overall heat balance is concerned, these are all negligible (some of them may of course have other effects – such as on cloud formation – that have a significant indirect impact on the heat balance).
In the short term – day to day or even year to year – there are of course imbalances. No one is denying it. Even then, those imbalances are quite minor – a small fraction of the power absorbed and re-radiated.
which indeed shows that in – \left(\frac{Mg}{R}\right) \frac{P}{T} you have eliminated density from consideration, and are in essence treating the air as a solid.
Au contraire, BWD, I simply used the known density of an ideal gas as a function of its pressure and temperature. Which, if you were not completely incompetent in physics and (apparently) unable to read, you would know.
This is not “treating the air as a solid”. It is “treating the air as an ideal gas”. Which I do because the entire article and discussion is about an isolated ideal gas. Pretty interesting how that works out, isn’t it!
rgb
Only you have no idea whether the Black Box of the earth system is receiving and emitting a balanced amount of energy over it history. Y’all wave your arms a lot, but, you simply DO NOT HAVE THE FACTS TO PROVE YOUR CASE!
You TOTALLY ignore the heating effects of the solar wind, birkeland currents, magnetic and gravitic fields. Yeah, when you pick and choose the physic you will discuss you can prove pretty much anything you want to prove.
Paul Birch already answered this, but I’ll chime in with my own observation that I don’t TOTALLY ignore these things at all. In fact, in a number of cases I’ve directly and personally estimated or computed them (specifically I’ve directly estimated gravitational/tidal and magnetic heating, heating and cooling due to outgassing and infalling micrometeorites, and the solar wind — all of these are negligible corrections. Birkeland currents are interesting, although they seem to be a possible correction to direct solar irradiance only at the poles and only in the ionosphere, which is already enormously hot — between 1500C and 2500C — but so tenuous that you wouldn’t feel heat if you stuck your arm out into the near vacuum of the ionosphere, you’d feel intense cooling as your blood started to boil and ordinary thermometers would radiate heat away faster than they would equilibrate (and hence would read very cold temperatures). You’d have to do some actual arithmetic to convince me that they are a major direct contributor to the Earth’s energy budget either way.
The interesting question is: Why are you reciting this list? If you are really interested in the answer to the question “What are the sources and sinks that are primarily responsible for maintaining the average temperature of the Earth?”, one would think that you would take the time to “do your homework” and actually work out the numbers and check them against the work of others to ensure that your answers were plausible. On the other hand, if you already have picked an answer, and are just interested in making it sound like your answer is plausible by invoking a lot of things that might be confounding to the accepted answer while deliberately not looking (because if you look you might learn that you are wrong), well then, how exactly can any “debate” or “discussion” proceed? Your mind is made up, your head is firmly jammed in the sand lest you be forced to face the possibility of error, end of story!
So please, by all means, provide me with quantitative estimates for the contribution to the overall heat budget of the planet of each of the things you cite. Be prepared to defend your estimates.
rgb
“One way or another radiation from the other available frequencies has to increases to compensate, because incoming solar radiation is what it is and to remain in balance ins ultimately must equal outs.”
The atmosphere is analogous to a flexible lens that is shaped by the density distribution of the gas molecules,of the atmosphere in the space between the sphere holding them, and space; Incoming heat gets collected in many ways and places,,primarily by intermittent solar radiation gets stored, in vast quantities, and slowly but also a barrage of mass and energy fluxes from all directions ; that are slowly transported great distances and to higher altitudes mostly by oceanic and atmospheric mass flows. The role played by radiation in the flow of heat through the atmosphere is minor.
But are ins ultimately equaling outs? Only for the planet as a whole,instantaneously at various intervals, provided you are looking from far enough away from Earth, (like maybe from mars), to homogenize the areas that are net absorbers with the areas that are net emitters.
But are ins ultimately equaling outs? Only for the planet as a whole,instantaneously at various intervals, provided you are looking from far enough away from Earth, (like maybe from mars), to homogenize the areas that are net absorbers with the areas that are net emitters. solid angle and all frequencies. No need to go to Mars.
solid angle and all frequencies. No need to go to Mars.
Yes, precisely, except that we in the trade like to just call this “on average over time”, and recognize that “far enough away” is just outside of Earth’s atmosphere, with outgoing radiated power integrated over the
As far as the time average is concerned, averaging over a year is probably pretty decent as far as detailed balance is concerned, although yes, there is heat stored and released in at least the ocean over much longer time scales. The atmosphere itself is pretty well mixed and dynamic, the ground beneath our feet is nearly irrelevant once you go a meter deep. I suppose glaciers and sea ice are also a factor as reservoirs, although the latter is just a part of the ocean.
Pretty much all of the rest of the Earth’s thermal buffering system would relax to temperatures well under 200K in a matter of weeks if the Sun disappeared overnight.
Empirically, I think there is good evidence that the overall climate relaxation time is order of 1-3 decades — that is, although there is good reason to think that the Earth had “started to cool” by the middle of the last solar cycle (about the time it stopped even thinking about getting overall warmer) it has taken a solid decade for actual cooling to think about revealing itself, and that is still masked by a lot of noise in the complex system.
Even this isn’t a really good “average”. The climate exhibits significant long term variability on the scale of centuries to millennia. We don’t completely understand what drives this variability. And then there is the predominant 100KY boreal oscillation, with interglacials rought 10KY long, where we have a lot of theory suggesting that it is due to this or to that — orbital variations, tilt, and more — but none of those theories fits old data or predicts new data terribly well or believably.
I agree that it is a complex problem. But do understand the role of the GHE in all of this. If it weren’t for the GHE, we would get much colder very, very quickly, precisely as if you went up to your attic and stripped away all of the insulation without turning up the furnace.
rgb
Dr. Brown,
What you seem to not be considering is that gas molecules are compressible, and that “compressibility” is a property of a gas that relates, pressure, and temperature to its unconfined volume.
Perhaps its apparent obscurity is an artifact of its importance in secret defense work during WWII, but this is not a new or unvetted concept. The derivation of this concept may be found presented as either lapse rate or potential temperature, in many reference works and text books about Physics, Thermodynamics, Fluid Mechanics, and Meteorology, and likely other fields as well. If you need specific references, I can list the books I have on hand, but all you really need to do is go to the library and look at some texts from the ’50s, ’60s or ’70’s.
This property of a gas results in a distribution of pressure and temperature for a gas held radially about a sphere by the effect of gravity, only. And, because it is a physical property of a gas, it isn’t proper to ignore it whilst postulating atmospheric conditions.
BigWaveDave,
What you seem not to be considering is that physicists actually understand the topics you are addressing.
* we know the air is compressible.
* we recognize there is a lapse rate in the actual atmosphere
* we understand the derivation of the DALR (eg http://en.wikipedia.org/wiki/Lapse_rate#Dry_adiabatic_lapse_rate)
* we are not confused by the concept of “potential temperature”
(One interesting application of “potential temperature” is that commercial jets draw in very cold air fresh air, but have to cool that air before circulating it in the cabins. The potential temperature of the atmosphere at 30,000 ft is typically well above room temperature even for this cold air. By the time the outside air is compressed enough for the cabin (equivalent to quickly bringing that parcel of air adiabatically to surface pressure), it is typically too warm to be comfortable.)
Go read one of those references you are suggesting and see the conditions assumed in the derivation of the DALR. Wikipedia starts with “The dry adiabatic lapse rate (DALR) is the rate of temperature decrease with height for a parcel of dry or unsaturated air rising under adiabatic conditions.”
So yes, when convection is strong (ie when the ground is being heated and the top of the atmosphere is being cooled), then the conditions will be close to adiabatic. The air is moving up and down too quickly for conduction to play a major role, so the adiabatic lapse rate is a good approximation to the actual temperature profile. But convection only happens when it is driven by a temperature difference — ie the bottom is being warmed and the top is being cooled — ie NOT the conditions of this thought experiment. For this thought experiment (where the atmosphere is not heated or cooled), there will be no convection. Now the slower, less effective thermal conduction becomes important, eventually leading to an isothermal situation.
Yeah, BWD, what he (Tim) said…
But don’t mind me, I just teach this stuff.
Incidentally, the “compressibility”, like the thermal conductivity, of an ideal gas is pretty straightforward, don’t you think? Derivable from first principles? Sort of built into the expression I wrote for the density in the top article, as I’ve pointed out several times now? And Jelbring — they did write their paper on an assumed ideal gas, didn’t they? You know, I think that they did!
Why is it so very difficult to accept that a) sure, real atmospheres have a DALR; and b) Jelbring’s paper asserting that this is a property of a static isolated atmosphere question-begging, law-of-thermodynamics violating nonsense? It certainly isn’t a proof that it is true — the very length and complexity of this discussion is ample evidence of that.
Note well that the actual physicists on the list are pretty much unanimous that the result is incorrect, and the only people on the thread who disagree are those that either don’t know the laws of thermodynamics and statistical mechanics well enough to (for example) derive the Ideal Gas law in the first place or do and defend the actual algebra required to support their assertions. They are reduced to quoting books they don’t really understand, usually out of context.
Why is that, do you suppose? Does that make the slightest bit of actual sense to you? Sure, it is heroic and everything but really, it is a discussion that is quite reminiscent of the papers I get from complete flakes that somehow find me on the Internet and try to get me to read their paper on how the electron can be understood from Mach’s principle, or from a diagram that they made up all by themselves, or from…
So instead of saying I neglect density or compressibility when the expression I give manifestly does neither one, why not try to construct an actual algebraic proof that I’m wrong, or if you can’t, perhaps grant me the possibility that my fairly complete and consistent algebraic argument could be, in fact, correct?
rgb
Tim Folkerts says:
February 1, 2012 at 8:00 pm
What? The DALR is generated by adiabatic expansion of a gas.
PV = nRT
Suppose a gas in a cylinder is allowed to expand through a nozzle into deep space. The random kinetic energy (related to T) will become highly directed kinetic energy. The steam of particles will no longer have any random kinetic energy. It will have no temperature. Also, since P goes to zero, T must also go to zero. Since V is the totality of free space, you might consider it to be infinity. The only way the temperature could remain constant would be if zero times infinity would be equal to the original product.
2/19 8:19pm:
“..try to construct an actual algebraic proof that I’m wrong..”
Done. Already shown the algebra proving you are wrong above at 2/5 12:27pm. No need to repeat the standing algebraic proof steps. The thought experiment of Fig. 1 in top post being isothermal at equilibrium is wrong & shown irrefutably (by many published atmospheric thermodynamic physicists cited) to be non-isothermal, isentropic in equilibrium by the correct algebraic steps to maximize entropy and reasonable experiments as posted above.
Those published atmospheric physicists agree with these steps. I see no poster in this thread has proven anything wrong with those algebraic proof steps especially original poster Robert Brown.
It stands that Fig. 1 in top post reaches non-isothermal, isentropic equilibrium at max. entropy with the random vigorous mixing of the GHG-free air molecules at reasonable earth pressures and temperatures (80% of atmosphere up through troposphere). Atmospheric physicists have known this since reporting their results at least as early as 1996. Independent atmospheric physicists verified Fig. 1 is non-isothermal, isentropic in equilibrium again in 1998, 2004 and 2010 by publishing their algebraic work steps and physical logic entirely consistent with all thermo laws that include confirming experiments.
Tim Folkerts says 2/17 at 9:09am:
“..convection only happens when it is driven by a temperature difference..”
Yeah, the general definition of convection implies heat flow and there is no longer any heat flow at equilibrium of Fig. 1. There is however vigorous random mixing of the molecules up and down the ideal gas column at equilibrium in a gravity field leading to non-zero pressure and non-zero temperature gradients at equilibrium proven by reasonable experiment and theory of published physicists.
“..the slower, less effective thermal conduction becomes important, eventually leading to an isothermal situation.”
No, not in a reasonable ideal gas in a gravity field where the maximum entropy will be eventually achieved and maintained w/temp. gradient at equilibrium even with conduction acting in this one system of Fig. 1 in top post. This max. entropy, conserving total enthalpy/energy equilibrium of Fig. 1 is irrefutably proven non-isothermal, isentropic by published atmospheric thermodynamic physicists as early as 1996, again in 1998, 2004 and 2010 including experiments validating their results. There is no convincing evidence found of an atmospheric physicist publishing a proof otherwise by experiment or theory since then.
Trick says:
February 20, 2012 at 6:07 am
For those who’d like to get a good laugh, take a look at the “algebra” that Trick claims to have “done” above at 12:27 pm.
Trick, for future reference, here’s a protip. You can recognize algebra because it has these things called “equations”. They are called “equations” because they have what is called an “equals sign” in the middle of them. Don’t know if you are aware of what an equals sign or an equation look like. I say that because what you claim to be “algebra” above doesn’t contain a single equation, as evidenced by a glaring lack of equals signs. For future reference, what we call an “equals sign” looks like this:
If they told you in high school that what you posted above is algebra, you should go and demand your money back. And whether they told you it was algebra or not, I’ve got bad news for you.
It’s not algebra. No way. No how. No shape. No form. Algebra has equations. Remember that. Algebra has equations.
Thanks for playing, though,
w.
Willis Eschenbach says 2/20 at 9:57am:
“You can recognize algebra because it has these things called “equations…with = signs….”.
Yes, I expected someone to call me out on that Willis. And I did just have a good laugh. Thanks.
As poster Robert Brown implies above, an atmospheric thermodynamic physicist can use 1st year college math to derive the proper “equations with =” proving Fig. 1 non-isothermal, isentropic given the proper outline algebra steps which I posted 2/5 12:27pm.
My inability to post the actual “equations with =” in the computer language used at WUWT is not proof that the Fig. 1 is isothermal at equilibrium. I’ll offer to send a word document following the steps with the “equations including =” proving Fig. 1 non-isothermal, isentropic at equilibrium to the mod.s with the experimental evidence if they have an interest to do the computer language translation work as they have done for others.
This “equations with =”algebra work is not new science, it has been published since at least 1996. There is no real need to write them again here. As I wrote at 2/20 6:07am above the 1996 paper has been followed up, verified and published more recently by several other independent atmospheric thermodynamic physicist authors proving Fig. 1 in the top post thought experiment to be non-isothermal, isentropic at equilibrium (they do include for Willis’ sake equations with = signs).
Poster Robert Brown complains 2/19 8:10pm above that citing these authors out of context is problematic. However, the whole of their work is freely available on the internet, links posted (way) above . If you want, I believe the “equations with =” work can be excerpted here with proper citation. I agree though with Robert in that better to read the original work in context.
I notice no poster on this thread has convincingly debated any of those outline steps I posted as being incorrect or wrong in any way. Maybe Willis could find something wrong with them? If so, I’m interested to blog along and not make the mod.s cry.
Tim Folkerts says: February 1, 2012 at 8:00 pm
>>Normally an adiabatic free expansion results in no cooling of an ideal gas.
Robert Clemenzi replies: February 19, 2012 at 11:59 pm
>What? The DALR is generated by adiabatic expansion of a gas.
“Free expansion” is a specific term where the gas expands into a previously empty region (for example, opening a valve between a full container and an empty container). “Free expansion” involves no work and does not cause temperature changes for ideal gases. For a while “free expansion” had been discussed in this thread, and I was specifically addressing “free expansion”
The expansion of a gas where the gas is NOT freely expanding but instead is doing some work (eg by expanding against the surrounding gas in the earth’s atmosphere) will indeed cause the sort of cooling that leads to a DALR.
Trick says:
> “When Fig. 1 in top post is at equilibrium it has reached max. entropy; no heat flow ….”
and
>”the general definition of convection implies heat flow”
Therefore you clearly conclude there is no convection. (And just to beat a dead horse, random molecular motion is NOT convection. Convection requires organized macroscopic motion.)
You then reference “Verkley et. al. part b” to support your position. But this favorite paper of yours specifically starts part b by saying
Can you not see the logical inconsistency in your argument? You are taking the paper out of context, exactly as Dr Brown concluded.
Part A of the paper corresponds to the situation here, and Part A clearly concludes that
Tim Folkerts says at 2/20 12:44pm:
Tim – Thanks for engaging on this interesting thought experiment top post subject.
Tim says: “Therefore you (Trick) clearly conclude there is no convection.”
Yes, only after equilibrium is achieved when random vigorous molecular mixing takes over. Convection IS a difficult concept for many authors writing on Fig. 1 top post thought experiment and they dance around with it a bit. It is good to discuss convection to further understand Fig. 1.
I would say and/or conclude there is convection in Fig. 1 top post prior to equilibrium whenever heat is still flowing from the initial conditions. Convection is discussed by the thermo grand masters in the context of the propagation of heat or thermally driven mass motion in fluids. Therefore convection is historically allowed before Fig. 1 equilibrium but not after Fig. 1 equilibrium when heat flow ceases.
I ref. the basic definitions of convection that include the words “heat flow”. After Fig. 1 achieves equilibrium, the authors of the papers rely on the random vigorous mixing of the molecules which still prevails after equilibrium when there is no longer any heat flow and the term “convection” cannot be properly employed.
Tim continues: “You (Trick) then reference “Verkley et. al. part b” to support your position. But this favorite paper of yours specifically starts part b by saying:
b. Isentropic profile
Now, in Ball [1956, Eq. (4)] it is argued that for convective motions…
Can you not see the logical inconsistency in your argument? You are taking the paper out of context, exactly as Dr Brown concluded.”
No, the Verkley paper is very short and I have been careful to cite entire part b which is exactly equivalent to Fig. 1 in the top post. Now I have clipped some sentences of that part b relative to the posts on the mixing of molecules, and if I have not been true to the proper context please call me out with an exact reference. Verkley et. al. part b does spend a lot of space writing on the issue of convection and molecular mixing as you clip.
Poster Robert Brown is right to complain about quoting out of context and I urge the interested reader to just read & understand the whole of Verkley part b rather than my (or Tim’s) clips. My clips are thought starters and needed to try and reduce the verbiage or few will read these posts & properly engage. In whole, Verkley et. al. do a convincingly good job in part b supporting their conclusion of non-isothermal, isentropic result at equilibrium for Fig. 1 in top post.
Tim continues: “Part A of the paper corresponds to the situation here, and Part A clearly concludes that
T = (lambda)^-1 is constant, thus, the profile is isothermal. This is the well-known result of classical thermodynamics and the kinetic theory of gases.”
No, part a thought experiment of the Verkley et. al. paper is different than here in Fig. 1 of top post. In Verkley part a, the thought experiment allows the ideal gas column to “…perform work on the air above and below the column…” (ref. Verkley Fig. 1). If the Fig. 1 top post is modified to allow that performance of work on the air column above & below then things here are suitably different and the isothermal conclusion then results.
Trick says:
February 20, 2012 at 11:13 am (Edit)
No, you didn’t expect to be called on that, or you wouldn’t have written such a stupid statement. Nice try at a recovery, though, claiming it was deliberate.
Robert implies no such thing, that’s your misunderstanding. You claim you can do it … so you claim. But until you DO do it, it’s just words, Trick … and to date your words are trading well below par.
Yeah, it’s a bitch to post something like

E = MC^2
or
PV = nRT
or
Q = ε σ T^4
or in latex,
without having special software … oh, wait, I just did it. No special translation, no software needed. You can write it in anything from plain old Excel notation, or you can do it in latex if you want,
So I’m sorry, but “I can’t type the equations” is BS. If you’re too uneducated to type equations, you don’t belong here. So far all you’ve done is flap your lips, Trick, and there’s no trick to doing that, talk is cheap. When you come up with the equations, post’em up … but I’d hold off on the boasting until you do.
Yes there is, for two reasons. To see if you actually understand them, and to see if we actually understand them. Until then, it’s just more of your hot air.
w.
Trick, I disagree with your interpretations of the Verkley paper. I would point you to the conclusions:
The top post assumes (as did Jelbring initially) that the mass and the energy of the atmosphere is constant. So the equilibrium condition IS isothermal according to Verkley.
The paper goes on:
.
If there is convective mixing, then we are never in thermodynamic equilibrium and never at maximum entropy.
Willis Eschenbach says 2/20 at 3:47pm:
“If you’re too uneducated to type equations, you don’t belong here.”
My laughs just keep on coming. Willis, the major typing issue for me is not PV = nRT. Issue is the integration sign and the limits thereof which I don’t find on my keyboard anywhere. WHAT is latex and how is it invoked? I know you et. al. are far ahead of me using that feature/program.
I know I can find the sign for integration and paste it into a word document and maybe the limits. Tell you what, this subject is interesting enough to try to do a prose integration = post. This is what it would look like, but you can also just look this up in the published papers for free and w/no typo’s. I know the mod.s have a work area to try and prove out what any post might look like.
Step 1: It all starts with the total mass – all per unit area of Fig. 1 – with a flat bottom if we make it simple notation and call its height running from z1 to z2 (see I can’t even do subscripts here).
Then the total mass per unit area of the gas column is the integral from z1 to z2 of the mass density of the gas; note mass density as rho.
Total mass of gas column = integral from z1 to z2 of rho dz.
I’m sure Willis can make that look pretty. I can’t; except maybe in MS Word. If Willis wants to see more = signs I can oblige but you will see more of it like this:
Step 2: Invoke hydrostatic equilibrium, constant g(z) is close enough simplification, the equation 5 in the top post and:
– integral from z1 to z2 1/g * dp/dz dz = 1/g * (p2 –p1)
The total air column mass is constant, and given the adiabatic control volume as shown neither heated or cooled by surroundings nor by radiation (GHG-free) or by interaction with adjacent air or ground; we need to find the equilibrium temperature profile of this gas column and we need only 2 laws: the 1st and 2nd thermo laws. And a bunch of = signs I guess.
Step 3: Start with the total enthalpy per unit area of the gas column and conserve it with all other forms of energy the column can have including earth’s g field since the sum of the energies must remain constant in the isolation of the control volume; cp being the specific heat capacity of the GHG-free air; s being specific entropy per unit mass:
enthalpy = integral from z1 to z2 rho * cp * T dz
potential energy = integral z1 to z2 rho * g * z dz
sum of all energies the column can have = integral z1 to z2 rho * (cp * T + g*z) dz = constant
total entropy of the column= S = integral from z1 to z2 rho * s dz
So the task is to show Willis et. al how to find the temperature and pressure profile that maximizes this entropy eqn. subject to constraint of holding the sum of all energies constant. It is formidable but I can slog thru 10 or so more of my 13 outline steps algebra eqn.s with = signs to earn my bona fides.
NB: Clues for issues in the top post: there is no control volume total energy conservation constraint mentioned and T(z) is moved outside the integral of dz prior to eqn. 6 with no explanation. Those are MAJOR issues. So I have already defined eqns. with = signs of what is missed in the top post leading to an incorrect isothermal conclusion.
Want more eqn.s with = signs?
Well if so, that was sort of fun typing. Only 9 or 10 more steps to go. Watch this space. Maybe some other poster can do these 3 steps in latex (hint, hint) for less total laughs (cite conservation of humor).
Tim Folkerts 2/20 says at 3:54pm:
“Trick, I disagree with your interpretations of the Verkley paper.”
Cool Tim, this is one way science has historically moved forward. Gotta’ say again though, interested posters need to read the paper in whole & its entirety not just clips. But erring on the side of brevity with clips:
Tim clips from the paper: ” We reiterate that the entropy maximization problem in its pure classical setting… will result in an isothermal profile…”
Yes, this refers in context to the classical setting as defined in Verkley Fig. 1 and that is different from the top post Fig. 1. Classically, Verkely Fig. 1 allows the air column to “…perform work on the air above and below the column…” as I wrote. Verkley et. al. state they are unsatisfied with this classical constraint 1) and 2) or 2’) as in their part a.
Thus the paper continues “It thus seems natural that one should represent (atmospheric processes) by posing certain additional constraints in the maximization problem, considering that constraints 1) and 2) will continue to be valid. This is the key idea of this article.”
The paper then continues:
“The question then arises what these constraints should be. Here, we have taken, following Ball (1956) and Bohren and Albrecht (1998), constancy of the integrated potential temperature as a single additional constraint 3, but this choice is of course open for debate.”
Hmmm…the paper also as a byproduct explains 991 & counting posts on this thread.
The paper then, in the very last sentence, the one we have all been waiting for, the money clip:
“In our view, this particular constraint still lacks a solid physical basis; yet, the above results give reason to expect that the construction of such a basis may be possible because the three constraints 1, 2’, and 3 together lead to a temperature profile that corresponds remarkably well to the tropospheric part of the Standard Atmosphere.”
And, folks, that Verkley part b constraint 3) is EXACTLY top post Fig. 1 for reasonable 80% of earth’s atmosphere which leads the paper to irrefutably mathematically prove the thermo law consistent non-isothermal, isentropic temperature profile for top post Fig.1.
Now we can debate Verkley et. al. “lacks a solid physical basis” point which means to develop a view one has to accept, say, the random vigorous mixing of the Fig. 1 top post molecules at equilibrium is solid enough physical basis. I do. Others may differ, but those folks need to supply a convincing proof support for their differing view.
Trick says:
February 20, 2012 at 6:14 pm
Here, Trick, I know it’s tough to find out cryptic things like what latex might be … let me google it for you.

Here in wordpress, you invoke latex with
$/latex
WITHOUT the slash “/”, and you end the invocation with the dollar sign.
So for example,
$/latex \int_{n1}^{n2} $
without the slash gives us
w.
Cool, thanks Willis. I’ll give latex a try, maybe tomorrow for the next few steps.
For those that think all solar radiation is almost immediately thermalised here’s another headache.
http://en.wikipedia.org/wiki/Color_of_water
Willis – I tried to exactly emulate your latex implementation, which worked, for my step 1: Mass = formula but that simple test failed to parse. I see two possible reasons: 1) I used the character map greek symbol for rho and it won’t parse or 2) I tried to use subscripts for z1 and z2 integration limits and they won’t parse.
I wrote latex for all the steps I posted 2/20 6:14pm and it took a couple hours to learn how and check. These are the easy steps. The S integral for entropy I posted requires starting all the way back with the thermodynamic internal energy U of the N molecules and invoking the classical mechanics equipartition theorem. At my rate of typing latex, I estimate 2-3 days of >8hours work to get thru all 13 steps which are very non-trivial “equations with = signs” in contrast to the top post of “manifestly”.
This is hardly worth it even when/if I figure out my parse failure b/c the “equations with = signs” are already freely available on the internet and/or the local science library. I will leave my bona fides rest for now on the 13 outline steps already posted.
What? The DALR is generated by adiabatic expansion of a gas. constant and cuts across the isotherms. Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.
constant and cuts across the isotherms. Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.
PV = nRT
Suppose a gas in a cylinder is allowed to expand through a nozzle into deep space. The random kinetic energy (related to T) will become highly directed kinetic energy. The steam of particles will no longer have any random kinetic energy. It will have no temperature. Also, since P goes to zero, T must also go to zero. Since V is the totality of free space, you might consider it to be infinity. The only way the temperature could remain constant would be if zero times infinity would be equal to the original product.
Not to mention that the equation for an adiabat for a gas confined to a cylinder is
I’ve basically too busy to post much any more on this thread, sorry guys. Besides, if directly quoting the conclusions of a paper that directly examines the issue won’t convince Trick, nothing will. It doesn’t really matter. His arguments won’t convince anybody that actually can work through the physics because they are not correct — parcels of an ideal gas are not adiabatic, ever, because one can compute the thermal conductivity of an ideal gas and it is non-zero. He won’t attempt to derive the DALR from microscopic first principles without the assumption of adiabatic transport of macroscopic parcels of air because if he attempts it, he won’t get the answer he desires out of pure stat mech. He won’t acknowledge that in static force equilibrium (after Jelbring’s very long time) there is no bulk transport of parcels of gas and hence conductivity has an infinite amount of time to increase the entropy of the gas by equilibrating the temperature. So what’s left? The discussion has become a waste of time.
On a more interesting note, now that Jelbring is finished (at least to the rationa) I’ve started in on Nikolov and Zeller. In particular, I’ve taken actual data from independent sources and applied their prescription to it, and discovered that it lies nowhere near their curve or the data points. I’ll top post on this soon on WUWT — there is no point at all continuing on Tallbloke’s blog because he a) censors the content of my posts; b) inserts parenthetical comments into my posts so they are annotated with his “responses”; c) asks silly questions like what the meaning of the complex unit is in physics as if that has anything at all to do with dimensional scaling arguments; d) seems blind to the fact that the probability of real-world data drawn from actual measurements of physical processes and adjusted by an arbitrary nonlinear parameter falling on a single perfect curve like N&Z’s, right down the middle of the expected (large) error bars is essentially zero, as the unbiased application of the formula to “unadjusted” surface temperatures clearly demonstrates by completely destroying the fit of the curve to the data and indeed completely confounding it when one applies the theory to the Jovian moons.
Personally, I’d just as soon that the skeptical position on the CAGW issue not be based on our own version of MBH, but what can one do?
rgb
Robert Brown: “I’ve basically too busy to post much any more on this thread, sorry guys.” in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them” and “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. . . . I haven’t had time to finish it . . . but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting”
in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them” and “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. . . . I haven’t had time to finish it . . . but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting”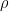 and molecular mass
and molecular mass 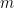 :
:


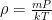
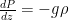
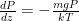
 , and solve the differential equation for pressure as a function of altitude:
, and solve the differential equation for pressure as a function of altitude:
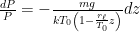

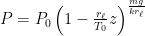
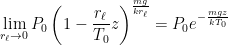

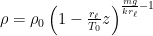

 :
:

![E_{potential} = A \rho_0 g \left[ \left(-\frac{T_0}{r_\ell}\right)\frac{kr_\ell}{mg}\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}}z -\left(-\frac{T_0}{r_\ell}\right)\frac{kr_\ell}{mg} \left(- \frac{T_0}{r_\ell}\right)\frac{1}{\frac{mg}{kr_\ell}+1}\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}+1}\right]_0^{\frac{T_0}{r_\ell}}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+A+%5Crho_0+g+%5Cleft%5B+%5Cleft%28-%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7Bkr_%5Cell%7D%7Bmg%7D%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%7Dz+-%5Cleft%28-%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7Bkr_%5Cell%7D%7Bmg%7D+%5Cleft%28-+%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7B1%7D%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cright%5D_0%5E%7B%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%7D+&bg=ffffff&fg=000&s=0&c=20201002)
![E_{potential} = - A \frac{kT_0\rho_0}{m} \left[ \left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}}z + \left( \frac{kT_0}{mg+kr_\ell}\right)\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}+1}\right]_0^{\frac{T_0}{r_\ell}}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+-+A+%5Cfrac%7BkT_0%5Crho_0%7D%7Bm%7D+%5Cleft%5B+%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%7Dz+%2B+%5Cleft%28+%5Cfrac%7BkT_0%7D%7Bmg%2Bkr_%5Cell%7D%5Cright%29%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cright%5D_0%5E%7B%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%7D+&bg=ffffff&fg=000&s=0&c=20201002)
![E_{potential} = - A P_0 \left[0+0-\left(0+\frac{kT_0}{mg+kr_\ell}\right)\right]=\frac{A P_0kT_0}{mg+kr_\ell}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+-+A+P_0+%5Cleft%5B0%2B0-%5Cleft%280%2B%5Cfrac%7BkT_0%7D%7Bmg%2Bkr_%5Cell%7D%5Cright%29%5Cright%5D%3D%5Cfrac%7BA+P_0kT_0%7D%7Bmg%2Bkr_%5Cell%7D+&bg=ffffff&fg=000&s=0&c=20201002)
 degrees of freedom:
degrees of freedom:

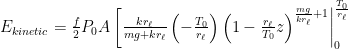
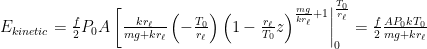
 :
:
It would be hard not to say you’ve gone above and beyond. But I’m a little disappointed that you did not follow up on your argument that “the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate.” You said you would:
“Once I have
I had hoped to see the results because, as I indicated above, my paper-and-pencil results were inconsistent with your arguent. I’m not entirely confident of them, but, since there was no follow-up, I’ll set the calculations forth here in baby steps in case anyone else in interested and wants to check my work.
We start out with the Ideal Gas Law and then express it in terms of density
We then require that the pressure, which is the weight per unit area of air above, decrease with altitude by the weight of the air passed:
We separate variables, assume a constant lapse rate, i.e.,
Note that
Density can then be readily determined:
Similarly,
We now turn to determining the potential energy in the air over a surface of area
Then we turn to kinetic energy, assuming
Contrary to your several statements in previous comments, these results appear to indicate that the center of mass is independent of lapse rate
$\frac{E_{potential}}{E_{potential}+E_{kinetic}}=\frac{\frac{A P_0kT_0}{mg+kr_\ell}}{\frac{A P_0kT_0}{mg+kr_\ell}+\frac{f}{2} \frac{A P_0kT_0}{mg+kr_\ell}}=\frac{2}{f+2}$
So your numerical results would have been interesting.
I screwed up the last equation. It should be:

It would be hard not to say you’ve gone above and beyond. But I’m a little disappointed that you did not follow up on your argument that “the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate.” You said you would:
“Once I have n(z) in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them” and “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. . . . I haven’t had time to finish it . . . but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting”
I got distracted by N&Z, which is a much bigger issue, on Tallbloke’s blog which is a problem in and of itself as it is difficult carrying out a discussion when the blog owner is redacting your posts at will.
The last thing I obtained is that my prediction there was indeed incorrect — the center of mass of an isothermal ideal gas is higher than that of a DALR gas. I was still working on understanding this, and at looking at the distribution of heat, when the N&Z thing took off, but what my intuition tells me is that:
a) A strictly DALR gas has a strict top of atmosphere height. At a very definite height, T = 0 and P = 0 and n = 0. This is what I wasn’t thinking of correctly. A DALR atmosphere has a linear thermal profile right down to absolute zero. It isn’t even approximately a maxwell-boltzmann gas, especially near the top.
b) An isothermal atmosphere, of course, expands into the vacuum above, vastly increasing its entropy in the process and properly thermalizing its velocity distribution.
rgb
Robert,
While we are making minor corrections, you said ” Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.”
You seem to be forgetting adiabatic free expansion and the Joule-Thompson effect, where it is well-known that:
* ideal gases do not change temperature.
* real gases either warm or cool slightly depending on the circumstances
http://en.wikipedia.org/wiki/Joule%E2%80%93Thomson_effect
Robert Brown says:
February 23, 2012 at 6:57 am
Robert, let me start by saying that your patience here has been legendary. I am inspired by your calm repetition of things. I’m not nearly so good at just sticking to the subject matter, I tend to get passionate.
Regarding Tallbloke “redacting your posts at will”, that’s why I was overjoyed to be banned from the place … it meant I didn’t have to bother trying to educate the gravity-heads and the pressure-heads, which is an impossible job even on a good day with a following wind …
w.
Tim Folkerts says:
February 23, 2012 at 8:11 am
Robert, While we are making minor corrections, you said “Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.” You seem to be forgetting adiabatic free expansion and the Joule-Thompson effect, where it is well-known that:
* ideal gases do not change temperature.
* real gases either warm or cool slightly depending on the circumstances.
Tim, “you seem to be forgetting” that what is commonly called “free expansion” is not actually free expansion at all. It is an adiabatic free expansion followed by a dissipative process in which the macroscopic kinetic energy is thermalised. The expansion phase, which cools the gas adiabatically, does work on the gas itself. The subsequent irreversible phase, in which the accelerated gas slams into the far side of the second container, bringing the temperature back up again, is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence. Even in an ideal gas the outcome will not initially be isothermal; there will be patches of higher and lower temperatures, which will gradually even out through turbulent mixing and diffusion.
The Joule-Thompson scenario proper combines the three phases into one by restricting the flow between the containers sufficiently that the acceleration of the flow is negligible (Cdrag>>1), eg., by means of a porous plug.
Paul,
I don’t think we are really disagreeing that much.
Pretty much by definition, the thing “commonly called ‘free expansion’ ” is what I meant by “free expansion”. It includes the various stages you describe – a gas freely expanding into an empty chamber and coming back to equilibrium in the new, larger volume.
Since the intermediate stages are non-equilibrium, then even defining “a temperature” for the system is problematic. However, the initial equilibrium conditions and the final equilibrium conditions have the same temperature, so I have no problem saying the process (taken as a whole) is isothermal.
I am a little confused when you say “The subsequent irreversible phase .. is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence.”
Whether the process is adiabatic (ie perfectly insulated, allowing no energy to flow into/out of the system) depends on the walls. To the extent that we have postulated perfectly insulated walls throughout the entire discussion, then any flow/turbulence/viscosity within the system would not affect energy flow to/from other systems.
Tim Folkerts says:
February 23, 2012 at 4:39 pm
I am a little confused when you say “The subsequent irreversible phase .. is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence.”
Whether the process is adiabatic (ie perfectly insulated, allowing no energy to flow into/out of the system) depends on the walls. To the extent that we have postulated perfectly insulated walls throughout the entire discussion, then any flow/turbulence/viscosity within the system would not affect energy flow to/from other systems.
That’s why I said “unlikely to be adiabatic in detail“. Internally, between the various parcels of gas in the system, there are highly non-adiabatic processes going on. There is a lot of energy flow within the system, and while that is happening, the temperature is anything but uniformly isothermal. However, those parcels of gas will still mostly have a sufficiently large number of particles and be sufficiently close to LTE that the temperature within them remains well-defined. Note that LTE does not require that the system be in thermodynamic equilibrium overall.
Yeah, and I should once again restricted my comments to gases confined to cylinders (even if the cylinders are infinitely high) and not to squirting compressed gas through a nozzle or the like. is constant, and I can grok that and see immediately that this sort of adiabatic expansion cools the gas as it cuts across to lower isotherms.
is constant, and I can grok that and see immediately that this sort of adiabatic expansion cools the gas as it cuts across to lower isotherms.
The point being that the usual textbook definitions of adiabatic processes and so on involve them being quasi-static, and I’m not sure that a free expansion of the sort described truly qualifies. It’s part of what makes the Carnot cycle interesting — everything has to move “slowly” so that the gas in the cylinder remains in “equilibrium” at least as far as having a well defined temperature is concerned.
It also makes DALR expansions tricky, because they are one “parcel” of gas expanding against another, which gives me a headache — topologically — whenever I try to imagine it happening in a uniform way, at which point my brain wants to shift gears into Navier-Stokes altogether because simple pictures of a cubic meter of gas expanding into other gas surrounding it as it rises forces one to think of what the other gas has to do to make room, and then you’ve got gas expanding into gas that is contracting, some rising, some falling, with dynamic viscosity along the parcel boundaries and I just can’t solve or even visualize the PDEs in my head particularly well except in simple e.g. convective roll sorts of ways.
But gas in a cylinder, that I can manage. Then
rgb
Robert Brown said:
February 19, 2012 at 8:10 pm
What Tim said is incorrect, and confused. Yes, I’m sure that there are physicists who understand these topics, Gerlich, Teustchner, Postma, to name three. But, contrary to Wikipedia, DALR doesn’t require there be a rising gas, and contrary to Brown and Eschenbach, the gaseous atmosphere will not be isothermal in LTE.
I’ve been trying to suggest ways to help you view the atmosphere that might help you to better understand the true situation of the gas being compressed radially inward from the center of a sphere by gravity, and how compressible gas molecules occupy less space due to their being compressed by the force of the molecules that are further away from the center; which are just as thermally excited as the other molecules. i.e. they are all at the same potential temperature; and exhibit the DALR.
I would suggest that before you teach stuff, you first learn about the stuff you are teaching. For the behavior of real gasses in the atmosphere, “Gas Tables” by Keenan, Chao, and Kaye might provide some insight.
BigWaveDave says: “What Tim said is incorrect, and confused.”
Just out out curiosity, what qualifications do you have to judge a disagreement between PhD physicists on issues of fundamental thermodynamics? Why are you so sure that Gerlich, Teustchner, & Postma are right, but rgb and I are wrong, other than you want the other answer to be correct? (I’m not saying here that we ARE right, but to judge the disagreement would take a level of understanding GREATER than the people on the two sides.)
What specifically did I say that you think is incorrect and confused?
” .. which are just as thermally excited as the other molecules. i.e. they are all at the same potential temperature”
And that, I think, is our fundamental disagreement. To me and rgb, “just as thermally excited” means “the same temperature”, not “the same potential temperature”, as required by the 0th law of thermodynamics. Having the air at two different altitudes have the same potential temperature but not the same actual temperature at equilibrium would violate the laws of thermodynamics in several fundamental ways (as pointed out several times above). This makes me think you are wrong.
Tim Folkerts says 2/28 at 9:08pm:
“..means “the same temperature”…as required by the 0th law of thermodynamics.”
No. Not exactly, only approximately. This is where Tim & Robert’s view is fundamentally incorrect for the exact solution for Fig. 1; they need to study up on the 0th law of thermodynamics which states that two systems at the same temperature as a third system are at the same temperature as each other. Along with study of Fourier’s eqn. which is inapplicable to ideal gas in a gravity field.
Tim continues: “What specifically did I say that you think is incorrect and confused?”
Tim’s above clipped quote for instance. In Fig. 1 top post there is only 1 system thus the 0th law is not strictly applicable and Fourier’s eqn. is not strictly applicable because there is a gravity field & at LTE heat flow has ceased.
In my view, the approximate isothermal solution derived as shown in the top post where one just assumes Fig. 1 T is constant in the dz integration IS fairly close in LTE but not exact. The exact non-isothermal, isentropic solution consistent with the thermo laws for Fig. 1 in LTE has to be proved thru conservation of ideal gas enthalpy&energy and mathematical means of ideal gas entropy integral maximization.
Many authors have shown the exact non-isothermal, isentropic solution derivation is consistent with applicable physical laws. Posters Tim and Robert Brown’s isothermal solution ignores these authors and/or have offered nothing of substance in this thread to disprove these published “PhD physicists on issues of fundamental thermodynamics”.
Trick & BWD,
I have read the paper mentioned in this thread from the “numerous authors”, and I don’t see one of them that agrees that an isolated, insulated macroscopic gas will have a temperature gradient. I am not ignoring anything — I see all the published papers supporting the isothermal solution for this case.
Certainly, if there is heating at the bottom and cooling at the top (like the real atmosphere), then the “applicable physical laws” do indeed lead to a “non-isothermal, isentropic solution”.
The laws of thermodynamics state that the universe seeks to MAXIMIZE entropy, not to make entropy the SAME everywhere. (I challenge you to find a thermodynamics text that states a principle of equal entropy as as a fundamental principle). The isentropic solution is not the maximum entropy (since we can raise the entropy by simply letting heat flow from the cool upper regions to the warm lower regions).
>Tim’s above clipped quote for instance. In Fig. 1 top post there is only
>1 system thus the 0th law is not strictly applicable …
As is common it such situations, the system can be split into two (or more) parts by an imaginary surface. So I could treat the bottom 1 m as one system and the top 1 m as another system. If I wait long enough so that the top and bottom systems are each in equilibrium with the center section, then the 0th law says clearly that the top and bottom sections are each the same temperature as the center section.
But I think it is time to agree to disagree. I clearly think you are wrong. You clearly think I am wrong. We have both tried to convince the other. Now we will have to leave it to others to decide (hopefully based on science and not on wish-for results).
Tim Folkerts:
You asked
I have been earning a living as an engineer specializing in cutting edge technology for very large scale thermal energy transfer processes and power systems for close to 40 years. My credentials include BS, JD and PE, and I have four patents.
As for my qualifications to engage in argument with PhD’s, I have many times been part of and have led teams with PhD team mates. I was also married to a PhD for 20 years.
Because the import of the consequence of the radial temperature gradient created by pressurizing a spherical body of gas by gravity, from the inside only, is that it obviates the need for concern over GHG’s. And, because this is based on long established fundamental principles that were apparently forgotten or never learned by many PhD’s, it is not something that can be left as an acceptable disagreement.