Guest Post by Willis Eschenbach
Apparently I must be a glutton for punishment, because here I am in the arena once again, discussing the results of my research and preparing for the insults and brickbats.
However, there’s no place I’d rather be—I’m a Teddy Roosevelt man. He famously said:
“It is not the critic who counts; not the man who points out how the strong man stumbles, or where the doer of deeds could have done them better.
The credit belongs to the man who is actually in the arena, whose face is marred by dust and sweat and blood; who strives valiantly; who errs, who comes short again and again, because there is no effort without error and shortcoming; but who does actually strive to do the deeds; who knows great enthusiasms, the great devotions; who spends himself in a worthy cause; who at the best knows in the end the triumph of high achievement, and who at the worst, if he fails, at least fails while daring greatly, so that his place shall never be with those cold and timid souls who neither know victory nor defeat.”
But I digress …
The earth’s climate is an energy flow system that on average is approximately at steady-state. At steady-state, the amount of energy absorbed by each part of the system is equal to the amount of energy lost by that part of the system. If this were not true, the affected parts would be continually either warming or cooling.
And this is true of the earth’s surface. It basically loses as much energy as it gains, and as a result, the earth’s surface temperature over the 20th century was stable to within less than one percent.
Let me start this perambulation with the fact that not all of the energy flux absorbed by the surface is converted to surface temperature and lost to thermal radiation. Some of the energy flux is lost as “sensible” heat, heat we can feel, through conduction to the atmosphere and convection away from the surface. And some is lost from the surface as “latent heat”, meaning it is heat removed by evaporation at the surface. After those losses, the energy that remains heats the surface and is lost as longwave upwelling radiation from the surface.
Figure 1 shows the relative amounts of energy absorbed and lost by the surface.

Figure 1. Energy budget of the surface, showing energy gained (longwave and shortwave) and energy lost (as longwave radiation and as latent/sensible heat.) Since the planet is at a steady state, gains and losses are ~ equal.
Now, suppose that we want to raise the surface temperature of the earth by 1°C. How much additional energy flux will be necessary to maintain that new warmer steady-state?
Well, since at steady-state we need gains to equal losses, we need as much flux as the additional amount of energy flux that will be radiated at the new higher temperature. Using what is known as the “Stefan-Boltzmann Equation”, we can calculate that we need a minimum of an additional 5.5 watts per square meter (W/m2) of energy flux to raise a blackbody at the earth’s temperature by one degree Celsius. (It’s a minimum because the percentage of latent/sensible heat loss increases slightly with increasing temperature, but we can ignore that in this analysis.)
However, we also need to note that from Figure 1, only about 78% of the absorbed energy flux is converted to temperature and lost as radiation. So including latent/sensible heat losses we’ll need 5.5 / .78 ≈ 7 W/m2 of additional total energy flux absorbed by the surface to raise the surface temperature one degree.
Now, consider the mainstream IPCC position, that a doubling of CO2 will increase downwelling longwave at the “top-of-atmosphere” (TOA) by 3.7 W/m2. This means that if you instantaneously double the CO2, the amount of longwave escaping the planet at the top of the atmosphere will be reduced by 3.7 W/m2.
And this additional 3.7 W/m2 of downwelling radiation from the CO2 doubling is claimed by the IPCC to increase the surface temperature by 3°C.
Bottom line? According to the IPCC, it only takes ~ 1.2 W/m2 of additional TOA forcing to increase the surface temperature by 1°C.
So here is the serious question I alluded to in the title …
How does a top-of-atmosphere CO2 forcing of 1.2 W/m2 mysteriously turn into the 7 W/m2 of additional surface energy flux that we need to warm the earth by 1°C?
The IPCC folks wave their hands and vaguely allude to “cloud feedback” and “water vapor feedback” increasing the downwelling IR from the top-of-atmosphere to downwelling IR at the surface.
But this would require that the feedback amplify the original signal by a factor of almost six … and my understanding is that a feedback factor greater than one leads to runaway.
So my question remains:
What mysterious force is changing the 1.2 W/m2 of CO2 TOA forcing, the forcing that the IPCC says will raise the surface temperature by 1°C, into the 7 W/m2 of surface absorbed energy flux that is actually necessary to raise the global temperature by 1°C?
All serious answers welcome.
My best to all,
w.
Footnote: The idea that cloud feedback is positive is quite unlikely. First, Le Chatelier’s Principle says that if a dynamic equilibrium (a steady-state condition like the climate) is disturbed by changing the conditions, the position of equilibrium shifts to counteract the change to reestablish an equilibrium.
Next, the claim of a net positive cloud feedback is contradicted by the CERES data. Here’s net cloud radiative effect (CRE) versus temperature on a gridcell by gridcell basis.

Figure 2. Net cloud radiative effect (CRE). This is the change in downwelling radiation in W/m2 when clouds are present. It includes both the longwave and shortwave effects. Below the horizontal line the net effect is cooling.
The slope of the yellow line indicates the direction of the cloud feedback. If it cools more with increasing temperature (negative feeback), the slope goes down to the right. And if the feedback is positive, if it cools less with increasing temperature, the slope goes up to the right.
In the tropics, about 40% of the planet, the feedback is extremely negative, the slope goes almost vertical. And from -15°C to 15°C, another 33% of the planet, the feedback is also negative.
So it doesn’t seem the answer to my question is “cloud feedback”.
Of Note: As with my previous two posts, I am examining the ramifications and the mathematics of the greenhouse effect. If you think the greenhouse effect violates physical laws, read my two posts, People Living In Glass Planets, and The Steel Greenhouse. And if after reading them, you still think the GH effect doesn’t exist, or that downwelling radiation doesn’t exist, or that radiative energy fluxes don’t add, then please, go away. Don’t go away mad, in fact you are welcome to continue to read the comments … but this is NOT the thread to dispute downwelling radiation or the greenhouse effect. Those subjects tend to totally threadjack the thread to an inane endless discussion that settles nothing, and I’m not interested in that. Please take those and related subjects to some other thread.
I’m interested in a serious answer to my question about how it’s supposed to work, how 1.2 W/m2 at the TOA is converted into 7 W/m2 at the surface, and where that extra energy is allegedly coming from.
MATH: The change in radiation from a 1°C temperature change of some object is given by the differential of the Stefan-Boltzmann equation:
dWdTC = function(c,epsilon=1) 2.27 * 10-7 * epsilon * (c + 273.15)3
where c is the temperature in degrees and epsilon is emissivity. In a steady-state condition where average losses are equal to average gains, this is also the amount of additional energy needed to raise the object’s temperature by 1°C. As is customary in this kind of analysis, and because the emissivity of the earth is somewhere above 0.95, for simplicity I’m using epsilon = 1.
My Usual: Please quote the exact words you are discussing in a comment so we can all follow your train of thought.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
My position, once I started looking into this about 15 years ago or so, and after much reading, was that the Earth’s climate is rather hardy. It has a number of negative feedback mechanisms, rather like the suspension on a car, that allow it to absorb and dissipate “sudden” energy imbalances, rather like potholes.
On this scale, the additional CO2 is barely even noticeable, and its positive effects (the greening of the Earth, slightly reduced temperature gradient between the tropics and poles) far outweigh any negative effects.
Willis
I apologize for being slow to comment but I had to research things to make this point. I think there is a shorting in the list of “major” channels for energy flow. This is your list:
“Let me start this perambulation with the fact that not all of the energy flux absorbed by the surface is converted to surface temperature and lost to thermal radiation. Some of the energy flux is lost as “sensible” heat, heat we can feel, through conduction to the atmosphere and convection away from the surface. And some is lost from the surface as “latent heat”, meaning it is heat removed by evaporation at the surface. After those losses, the energy that remains heats the surface and is lost as longwave upwelling radiation from the surface.”
There is a flow of energy into chemical processes, namely the creation of biomass. To get a grip on the scale of energy that is absorbed in a chemical form (biomass) I looked at the energy and energy efficiency involved. This energy is not thermalized, it is literally absorbed by photosynthesis.
The amount of biomass created by incident insolation is about 200 billions tons per year, with a “standing” mass of 550-560 billion tons. One could view this as a store of energy that is approximately released as fast as it forms, i.e. net zero, however this is not the case. Biomass is forming faster than it is being decayed and burned. The rate of gain is debatable, so I concentrated on the energy per sq m on average to find out if the scale involved is meaningful.
Ignoring the productivity of the oceans, the energy converted to biomass is about 31.5 Watts per sq m over the whole earth. If the oceans are as productive then the energy absorbed is 63 Watts/m^2.
This is a lot of energy compared with other factors people are looking at. For example, if the rate of biomass growth increases at a modest 5%/year it completely offsets the OLR it is claimed will increase by 3 W/m^2 from a doubling of the CO2 concentration – and that is with no deliberate effort to do so. At present, biomass is growing at ~30% faster rate than it did in 1980, directly attributable to a CO2 increase. On balance, this energy channel is significant, in the scientific sense, because the magnitude is 10 to 20 times to grand effects claimed for a CO2 doubling.
Stay well…
Crispin Pemberton-Pigott September 7, 2022 7:38 am
Thanks, Crispin. Actually, that energy is totally thermalized, just not immediately. The energy used in creating plants is released as heat when the plants die and decay. And since this process is going on continually, approximately the same amount of thermal energy is released each year as the amount absorbed in photosynthesis.
w.
This is true only so long as the biomass is not increasing, which it is. It is also true to say that on long term average, the oceans to not retain heat, but it is Trenberth’s claim, for example, that heat gain is hiding in the deep oceans. Given that the total weight of biomass is increasing, and that the rate of gain is rising, and that the quantum of energy involved is 20 times that of CO2 doubling, and estimate of “what is happening” that is not compensated for this energy sequestration is going to be undermined. Putting error bars of 60 W/m^2 on, say, ocean heat gain, renders any claim to have been detected moot.
One problem I see in your calculation that may have already been mentioned is that only a fraction, about 0.6, of the IR energy radiated from the surface reaches space. So if the radiation from the TOA is reduced by 3.7 w/m2 it will require the surface to radiate 3.7/0.6 = 6.2 w/m2 additional radiation to again equilibrium.
That should result in the surface warming by a bit over 1 C. Not 3 C.
Willis: It would help me if you carefully define what you call the “earth’s surface”. In a thermodynamic analysis, surfaces and control volumes are usually defined at the outset.Thanks for an interesting contribution.
Willis: The earth’s climate is an energy flow system that on average is approximately at steady-state. At steady-state, the amount of energy absorbed by each part of the system is equal to the amount of energy lost by that part of the system. If this were not true, the affected parts would be continually either warming or cooling.
And this is true of the earth’s surface. It basically loses as much energy as it gains, and as a result, the earth’s surface temperature over the 20th century was stable to within less than one percent.
Anthony Mills
It would help me if you carefully define what you call the “earth’s surface”
The earth’s surface has many different meanings.
Planets with atmospheres do not have a true surface as opposed to those without an atmosphere.
This leads to the concept of a radiative TOA purely for the concept of where the unimpeded radiation out equals the unimpeded radiation in.
There is also extra earth generated energy that is measured , only 40 TW but never seems to be accounted for in the energy budget.
Willis uses an average energy graph for his earth surface Ceres which does not distinguish between ocean and earth as the SW absorbing layer and accounts for night/day changes by the averaging and does not include the constant but small earth heat contribution.
This enable CERES data to state that the “earth’s [average] surface temperature over the 20th century was stable to within less than one percent.
In reality temperatures, also known as climate, vary considerably between night and day, hilltop dale and sea-bottom, and between summer and winter.
“The earth’s energy flow system that on average is approximately at steady-state.”
Here they do put in the missing word average.
Without the word average the truth is that the affected parts [unaveraged] are continually either warming or cooling.
If energy could be physically stored in a battery by artificial device [not naturally]
Then it would be true that “The earth’s climate is an energy flow system that on average is approximately at steady-state.”
In a mono dimensional averaged non night day world heated only by the sun and only for the atmosphere directly over the disc of the earth.
Since in the real world of physics heat storing capacity to be released at whim does not exist the earth’s surface must release whatever energy comes into it.
If it did not do so it would be unable to be stable as there would be no mechanism for either greater or less heat storage to build up or waste away.
This is a massive point, SB based, that is ignored.
Why should a planet surface equilibrate always at steady state to energy in or out when by activating or deactivating its so called storage methods it could decide to irradiate at twice the incoming flux or warm up by radiating half the incoming flux?
Genuine and unanswerable question.
If I may. I would define two spherical shells, one is that point where you stop falling if you jump out a plane. The other is defined by an optical depth calculated looking down from the TOA. The shell would be located at the point where the optical depth equals one. At that point upwelling radiation leaves the planet.
The optical depth is a function of concentration so doubling the CO2 concentration would raise in altitude the critical OD which would account for the reduced outward radiated energy. Also the OD = 1 is also the mean free path of the photons in the gas.
The transient climate sensitivity (TCS) is 1.8°C per CO2 doubling, according to IPCC AR5 (AR6 has increased this estimate to 2°C). That might be the better value to be used here instead of ECS. The ECS refers to the longer term adjustment which might take couple of hundred years.
Then, the SB law should be applied to the effective emission height, not the surface.
I totally agree that it is highly unlikely that any feedback can be >1 as the climate obviously is self stabilizing and not escalating.
“But this would require that the feedback amplify the original signal by a factor of almost six … and my understanding is that a feedback factor greater than one leads to runaway.”
This statement is false. Basic feedback has the formula 1 + x + x^2 + x^3 + … = 1/(1-x). What does the feedback factor have to be in order for this to equal 6?
1/(1-x) = 6 => x = 5/6
I.e. If 5/6 of the signal is added to the original signal for every feedback cycle, the signal is amplified by a factor of 6. As an iteration equation this can be written as: Xnext =1+X
Iterated this will yield 1 +X + X^2 +X^3 …
340W/m^2 could warm a night time surface to 8°C LOL
500W/m^2 lost, and over half of it returns as longwave to the surface, how does that work?
Ulric, the CERES numbers are a bit different, but here are the required flows. Note that it is at steady-state, meaning that at all levels the gains are equal to the losses.
w.
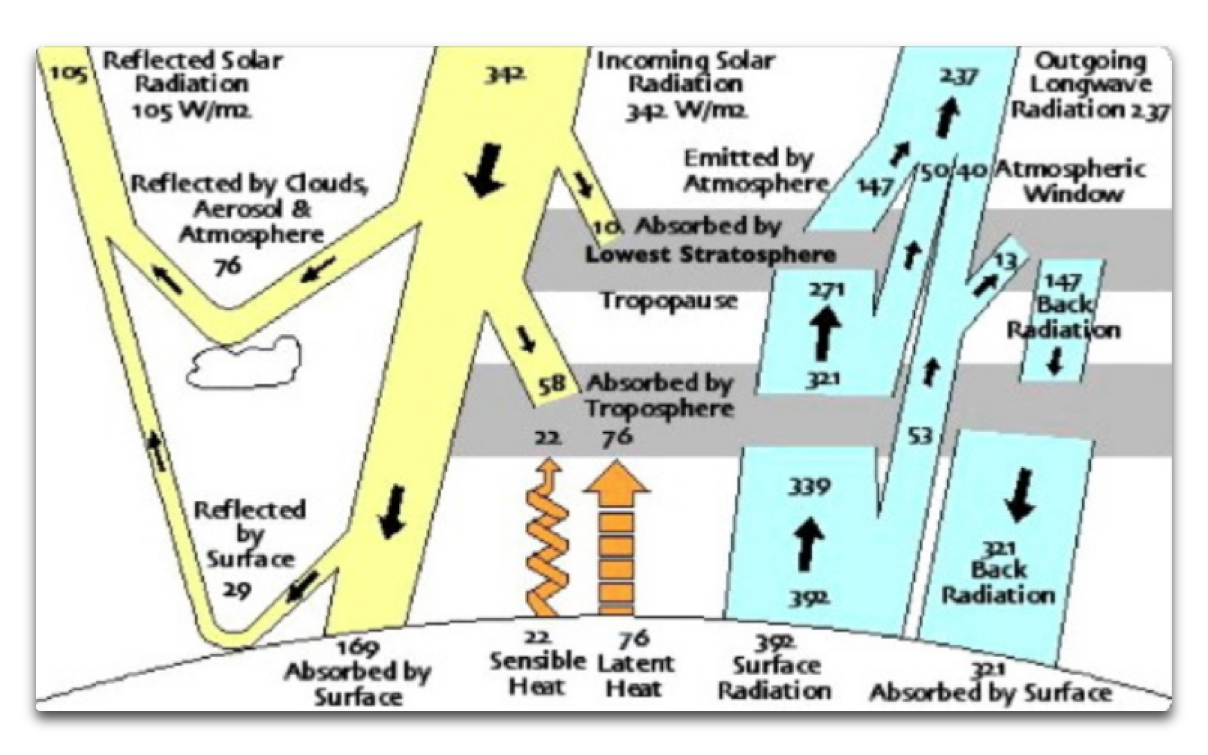
So the troposphere manages to radiate 321 upwards and 321 downwards, that’s clever.