Guest Post by Willis Eschenbach
Lord Monckton has initiated an interesting discussion of the effective radiation level. Such discussions are of value to me because they strike off ideas of things to investigate … so again I go wandering through the data.
Let me define a couple terms I’ll use. “Radiation temperature” is the temperature of a blackbody radiating a given flux of energy. The “effective radiation level” (ERL) of a given area of the earth’s surface is the level in the overlying atmosphere which has the physical temperature corresponding to the radiation temperature of the outgoing longwave radiation of that area.
Now, because the earth is in approximate thermal steady-state, on average the earth radiates the amount of energy that it receives. As an annual average this is about 240 W/m2. This 240 W/m2 corresponds to an effective radiation level (ERL) blackbody temperature of -18.7°C. So on average, the effective radiation level is the altitude where the air temperature is about nineteen below zero Celsius.
However, as with most thing regarding the climate, this average conceals a very complex reality, as shown in Figure 1.
 Figure 1. ERL temperature as calculated by the Stefan-Boltzmann equation.
Figure 1. ERL temperature as calculated by the Stefan-Boltzmann equation.
Note that this effective radiation level (ERL) is not a real physical level in the atmosphere. At any given location, the emitted radiation is a mix of some radiation from the surface plus some more radiation from a variety of levels in the atmosphere. The ERL reflects the average of all of that different radiation. As an average, the ERL is a calculated theoretical construct, rather than being an actual level from which the radiation is physically emitted. It is an “effective” layer, not a real layer.
Now, the Planck parameter is how much the earth’s outgoing radiation increases for a 1°C change in temperature. Previously, I had calculated the Planck parameter using the surface temperature, because that is what is actually of interest. However, this was not correct. What I calculated was a value after feedbacks. But the Planck parameter is a pre-feedback phenomenon.
If I understand him, Lord Monckton says that the proper temperature to use in calculating the Planck parameter is the ERL temperature. And since we’re looking for pre-feedback values, I agree. Now, this is directly calculable from the CERES data. Remember that the ERL is defined as an imaginary layer which calculated using the Stefan-Boltzmann equation. So by definition, the Planck parameter is the derivative of that Stefan-Boltzmann equation with respect to temperature.
This derivative works out to be equal to four times the Stefan-Boltzmann constant time the temperature cubed. Figure 2 shows that value using the temperature of the ERL as the input:
 Figure 2. Planck parameter, calculated as the derivative of the Stefan-Boltzmann equation.
Figure 2. Planck parameter, calculated as the derivative of the Stefan-Boltzmann equation.
Let me note here that up to this point I am agreeing with Lord Monckton, as this is a part of his calculation of what he calls the “reference sensitivity parameter λ0” (which is minus one divided by the Planck parameter). He finds a value of 0.267 °C / W m-2 up to this point. as discussed in Lord Monckton’s earlier post, which is the same as the Planck parameter of -3.75 W/m2 per °C shown in Figure 3.
Now again if I understand both Lord Monckton and the IPCC, for different reasons they both say that the value derived above is NOT the proper value. In both cases they say the raw value is modified by some kind of atmospheric or other process, and that the resulting value is on the order of -3.2 W m-2 / °C . (In passing, let me state I’m not sure exactly what number Lord Monckton endorses as the correct number or why, as he is not finished with his exposition.)
The problem I have with that physically-based explanation is that the ERL is not a real layer. It is a theoretical altitude that is calculated from a single value, the amount of outgoing longwave radiation. So how could that be altered by physical processes? It’s not like a layer of clouds, that can be moved up or down by atmospheric processes. It is a theoretical calculated value derived from observations of outgoing longwave radiation … I can’t see how that would be affected by physical processes.
It seems to me that the derivative of a theoretically calculated value like the ERL temperature can only be the actual mathematical derivative itself, unaffected by any other real-world considerations.
What am I missing here?
w.
My Request: In the unlikely circumstance that you disagree with me or someone else, please quote the exact words you disagree with. Only in that way can we all be clear as to exactly what you object to.
A Bonus Graphic: The CERES data is an amazing dataset. It lets us do things like calculate the nominal altitude of the effective radiation layer all over the planet. I did this by assuming that the lapse rate is a uniform 6.5°C of cooling for every additional kilometre of altitude. This assumption of global uniformity is not true, because the lapse rate varies both by season and by location. Calculated by 10° latitude bands, the lapse rate varies from about three to nine °C cooling per kilometre from pole to pole. However, using 6.5°C / km is good for visualization. To establish the altitude of the ERL, I divided the difference between the surface temperature and the ERL temperature by 6.5 degrees C per km. To that I added the elevation of the underlying surface, which is available as a 1°x1° gridcell digital dataset in the “marelac” package in the R computer language. Figure 3 shows the resulting nominal ERL altitude:
 Figure 3. Nominal altitude of the effective radiation level.
Figure 3. Nominal altitude of the effective radiation level.
The ERL is at its lowest nominal altitude around the South Pole, and is nearly as low at the North Pole, because that’s where the world is coldest. The ERL altitude is highest in the tropics and in temperate mountains.
Please keep in mind that that Figure 3 is a map of the average NOMINAL height of the ERL …
A PERSONAL PS—The gorgeous ex-fiancee and I are back home from salmon fishing, and subsequent salmon feasts with friends along the way, and finally, our daughter’s nuptials. The wedding was a great success. Just family from both sides in the groom’s parents’ lovely backyard, under the pines by Lake Tahoe. The groom was dashingly handsome, our daughter looked radiant in her dress and veil, my beloved older brother officiated, and I wore a tux for the first time in my life.
The wedding feast was lovingly cooked by the bride and groom assisted by various family members, to the accompaniment of much laughter. The bride cooked her famous “Death By Chocolate” cake. She learned to cook it at 13 when we lived in Fiji, and soon she was selling it by the slice at the local coffee shop. So she baked it as the wedding cake, and she and her sister-in-law-to-be decorated it …

Made with so much love it made my eyes water, now that’s a true wedding cake for a joyous wedding. My thanks to all involved.
Funny story. As the parents of the bride, my gorgeous ex-fiancee and I were expected by custom to pay for the wedding, and I had no problem with that. But I didn’t want to be discussing costs and signing checks and trying to rein in a plunging runaway financial chariot. So I called her and told her the plan I’d schemed up one late night. We would give her and her true love a check for X dollars to spend on the wedding … and whatever they didn’t spend, they could spend on the honeymoon. The number of dollars was not outrageous, but it was enough for a lovely wedding.
“No, dad, we couldn’t do that” was the immediate reply. “Give us half of that, it would be plenty!”
“Damn, girl …”, I said, “… you sure do drive a hard bargain!” So we wrote the check for half the amount, and we gave it to her.
Then I created and printed up and gave the graphic below to my gorgeous ex-fiancee …
 … she laughed a warm laugh, the one full of summer sunshine and love for our daughter, stuck it on the refrigerator, and after that we didn’t have a single care in the world. Both the bride and groom have college degrees in Project Management, and they took over and put on a moving and wonderful event. And you can be sure, it was on time and under budget. Dear heavens, I have had immense and arguably undeserved good fortune in my life …
… she laughed a warm laugh, the one full of summer sunshine and love for our daughter, stuck it on the refrigerator, and after that we didn’t have a single care in the world. Both the bride and groom have college degrees in Project Management, and they took over and put on a moving and wonderful event. And you can be sure, it was on time and under budget. Dear heavens, I have had immense and arguably undeserved good fortune in my life …
I’m happy to be back home now from our travels. I do love leaving out on another expedition … I do love traveling with my boon companion … and I do love coming back to my beloved forest in the hills where the silence goes on forever, and where some nights when the wind is right I can hear the Pacific ocean waves breaking on the coast six miles away.
Regards to all, and for each of you I wish friends, relations, inlaws and outlaws of only the most interesting kind …
w.
Moon/Earth Comparison Bulk parameters
Moon Earth Ratio (Moon/Earth)
Mass (1024 kg) 0.07346 5.9724 0.0123
Volume (1010 km3) 2.1968 108.321 0.0203
Equatorial radius (km) 1738.1 6378.1 0.2725
Volumetric mean radius 1737.4 6371.0 0.2727
Mean density (kg/m3) 3344 5514 0.606
Surface gravity (m/s2) 1.62 9.80 0.165
Escape velocity (km/s) 2.38 11.2 0.213
GM (x 106 km3/s2) 0.00490 0.39860 0.0123
Bond albedo 0.11 0.306 0.360
Visual geometric albedo 0.12 0.367 0.330
Visual magnitude V(1,0) +0.21 -3.86 –
Solar irradiance (W/m2) 1361.0 1361.0 1.000
Black-body temperature (K) 270.4 254.0 1.065
Topographic range (km) 13 20 0.650
Moment of inertia (I/MR2) 0.394 0.3308 1.191
Sorry for the data set, but it shows that the earth and moon , which are the same distance from the sun, have quite different radiative temperatures.
The simple explanation for the moon radiating more heat [ technically being a hotter object than earth] is that it has a lower albedo so it is on average hotter than earth at the surface.
Its atmosphere [virtually non existent is presumably quite cold?].
It’s ERL is presumably the surface of the planet.
If the earth ERL is -18.7°C the moon ERL must be -2.4 C.
The Planck parameter of -3.75 W/m2 per °C is presumably correct for the moon surface.
the earth annual average radiation is about 240 W/m2?
I would have thought the earth and the moon receive the same radiation.
Is this worked out from the Solar irradiance (W/m2) 1361.0
In which case albedo may not be being taken into account.
Does the difference between Lord Monckton and the IPCC,[ -3.2 W m-2 / °C ]and yourself [The Planck parameter of -3.75 W/m2 per °C] reflect the fact that the earths higher albedo simply means that the 240W/M2 is not strictly correct, ie that some of the heat is reflected meaning that less than 240 W/M2 actually is absorbed by the earth surface and atmosphere?
In which case one could work backwards I guess and work out the true heat absorption.
Thanks for this. I too would like I to see the premise tested that the Earth’s climate (ie, energy budget) changes more due to changes in reflectivity (albedo) than it does from tiny changes in one mechanism of outgoing long wave radiation.
Mickey Reno:
What do you think of the work of Martin Wild at ETH? Specifically which papers did you read that make you think that albedo changes are not included? What do you think happened to the ~2 W m-2 heating being caused by greenhouse gases?
MieScatter, I guess I was thinking more in terms of geologic time scale changes that could explain glacial and inter-glacial periods, more than just recent AGW time frames. I realize we may not have that many good proxies for such research. But thanks for the pointer to Martin Wild. I just finished a perusal of his 2008 paper “Global Dimming and Brightening, A Review” from the Journal of Geophysical Research (free to download-huzzah). I don’t believe I had read this before. His conclusions are that there exists a real dimming from the early part of the 1900s to the 1980s and a real brightening since then, with some (weak) evidence for a plateau after 2000. Based on my previous understanding of the pan-evaporation experiments or aggregations, the dimming part of this didn’t surprise me. But I’m ignorant of any change to pan-evaporation reality since the 1980s. Have they changed, globally? Another thing to investigate. Anyway, Wild’s conclusions seems to match fairly well the state of AGW conclusions over the past 75 years, if you accept post 1980 warming and a pause following the 1998 El Nino, don’t you think?
Wild clearly believes human activity is central to the brightening (since the 1980s) presumably via particulate air pollution, which he presume are better controlled by developed nations. But I’m not sure this conclusion will hold up globally, given China, India, Africa, and S. American build-out of coal fired electricity after 1980, . It could be that we’ve measured changes in Western behaviors wrt particulate air pollution, rather than globally. And Wild is careful in his language about this, and seems to dislike the term global dimming and global brightening, while accepting that their use is too ubiquitous to change at this point. I’m also happy that Wild means carbon soot, aerosols and hydrocarbons when he says “pollution.” But then he seems to place the blame for most non-volcanic particulates on human beings, which, if true, is a mistake. Nature throws up lots of dust and crud into the atmosphere, and some of it sticks. A simplifying assumption made in order to make ones equations more solvable, ought not be simplified too much. if your goal is to prove that humans matter to the climate, your simplifying assumptions ought never omit the so-called natural state of anything. Wild informs (and I realized this already) that we need a better satellite monitoring system before we can fully understand particulate and cloud reflection of UV. He seems to favor measuring particulates over clouds or water vapor. I would guess, based on his work that he has a simplifying assumption that given aerosols and particulates, clouds will necessarily follow. He takes the water vapor for granted. And speaking of water vapor, Wild, uncharacteristically seems to believe in CO2 as a proxy for all greenhouse gasses. If so, in my opinion that would be a mistake, as I think water vapor should always be presumed as primary GHG when talking about LWIR scattering.
There’s a lot of food for thought. There is still no accurate climate model. It’s still possible that some unknown unknown or complex combination or set of interactions masks the actual results on T from both the IR and UV sides.
340 W/m^2 ISR arrive at the ToA (100 km per NASA), 100 W/m^2 are reflected straight away leaving 240 W/m^2 continuing on to be absorbed by the atmosphere (80 W/m^2) and surface (160 W/m^2). In order to maintain the existing thermal equilibrium and atmospheric temperature (not really required) 240 W/m^2 must leave the ToA. Leaving the surface at 1.5 m (IPCC Glossary) are: thermals, 17 W/m^2; evapotranspiration, 80 W/m^2; LWIR, 63 W/m^2 sub-totaling 160 W/m^2 plus the atmosphere’s 80 W/m^2 making a grand total of 240 W/m^2 OLR at ToA.
When more energy leaves ToA than enters it, the atmosphere will cool down. When less energy leaves the ToA than enters it, the atmosphere will heat up. The GHE theory postulates that GHGs impede/trap/store the flow of heat reducing the amount leaving the ToA and as a consequence the atmosphere will heat up. Actually if the energy moving through to the ToA goes down, say from 240 to 238 W/m^2, the atmosphere will cool per Q/A = U * dT. The same condition could also be due to increased albedo decreasing heat to the atmosphere & surface or ocean absorbing energy.
The S-B ideal BB temperature corresponding to ToA 240 W/m^2 OLR is 255 K or -18 C. This ToA “surface” value is compared to a surface “surface” at 1.5 m temperature of 288 K, 15 C, 390 W/m^2. The 33 C higher 1.5 m temperature is allegedly attributed to/explained by the GHE theory.
BTW the S-B ideal BB radiation equation applies only in a vacuum. For an object to radiate 100% of its energy per S-B there can be no conduction or convection, i.e. no molecules or a vacuum. The upwelling calculation of 15 C, 288 K, 390 W/m^2 only applies/works in vacuum.
Comparing ToA values to 1.5 m values is an incorrect comparison.
The S-B BB ToA “surface” temperature of 255 K should be compared to the ToA observed “surface” temperature of 193 K, -80 C, not the 1.5 m above land “surface” temperature of 288 K, 15 C. The – 62 C difference is explained by the earth’s effective emissivity. The ratio of the ToA observed “surface” temperature (^4) at 100 km to the S-B BB temperature (^4) equals an emissivity of .328. Emissivity is not the same as albedo.
Because the +33 C comparison between ToA “surface” 255 K and 1.5 m “surface” 288 K is invalid the perceived need for a GHE theory/explanation results in an invalid non-solution to a non-problem.
References:
ACS Climate Change Toolkit
Trenberth et. al. 2011 “Atmospheric Moisture Transports …….” Figure 10, IPCC AR5 Annex III
http://earthobservatory.nasa.gov/IOTD/view.php?id=7373
http://principia-scientific.org/the-stefan-boltzmann-law-at-a-non-vacuum-interface-misuse-by-global-warming-alarmists/
I wish I had time to comment on this or even read it in detail , but building the language in which to express the computations and a community building on it trumps all else . ( My friend Morten Kromberg just did a podcast , https://www.functionalgeekery.com/episode-65-morten-kromberg/ , which describes the nature of APL languages the backbone of which I’ve built in an open x86 Forth . )
I will just pose the question of the nature transition from that atmospheric minimum back up the orbital gray body temperature of about 278K ?
Following on from a question I put in comments on one of the earlier threads, I would be pleased if someone can explain the reasoning for flux*(1-albedo) is divided by 4 to get the average temp, when S-B is a T^4 average?
I used 1360 flux, albedo of 0.3:
(a) If you calculate by the divide by 4 method S-B gives an average temperature of -18.6 degC
(b) If you calculate S-B as a double cosine integral over 1 hemisphere and average on T you get -11.0 degC
(c) If you calculate S-B as a double cosine integral over 1 hemisphere and average on T^4 you get +13.3 degC
Still not clear to me why the flux is divided by 4 first…….anyone care to explain, or point me to an explanation?
What am I misunderstanding?
On average, heat leaves Earth at the same total rate Q that it arrives. But it arrives as a parallel beam, so its flux intensity is Q/(disc area=πR²). But it leaves radially, so its average flux intensity is Q/(surface area=4πR²).
Dang … that was nice and clear, and unlike the usual explanations.
w.
ThinkingScientist September 7, 2016 at 6:58 am
“What am I misunderstanding?”
Because it is simple.
1,368 W/m^2 times cross sectional area of earth M^2 with r radius gives watts. The surface of a sphere of radius r is 4 times the surface of a disc of radius r. Divide/spread those watts over the entire ToA spherical surface area for 1,368 / 4 = 342 W/m^2. That’s how they do it. Ask them why.
There is no consideration for day or night, aphelion/perihelion, seasons, etc. It’s just a graphical tool to illustrate where the power flux gozintaz and gosoutaz. And Trenberth et al 2011jcli24 Figure 10 shows 7 out of 8 models, that’s 87.5% of ALL scientists (at least involved in these models) show the atmosphere as cooling, not warming, much to Trenberth’s dismay.
TS, While Nick Stokes answered your question just fine, 4 is the ratio of surface area of a sphere to its projected area, your post brought to my mind other thoughts. First, there is always the issue of weighting these fool averages. If radiant emittance is a function of temperature to the fourth power, then small hot regions with clear, dry sky contribute a disproportionate amount of the outgoing radiation; so, why do we not weight for such influences? Moreover the mean temperature, a single number that is the focus of endless enjoyable argument and scientific employment, is calculated and its uncertainty estimated by assumption that all numbers going into it are IID values–I doubt they are. So, why do we place such significance on this? I doubt that mean earth temperature, in and of itself, has much significance for devining our future.
Finally, climate is experienced locally, climate change as well. So then, someone please tell me what is the usefulness of these blasted zero dimensional models of heat transfer? I am sick of them.
Thanks for letting me rant.
You’re not misunderstanding anything. The divide by 4 method is an over simplification.
Even your (c) won’t work for the real earth. Thanks to Hadley Circulation, heat is transferred from the tropics towards the poles, so the tropics radiate away less heat than they absorb, further poleward, more heat is radiated away than is absorbed directly from the sun.
Willis,
It appears you have the same concerns that I have. Form a post yesterday [ https://wattsupwiththat.com/2016/09/06/feet-of-clay-the-official-errors-that-exaggerated-global-warming-part-3/comment-page-1/#comment-2294128 ] “Ask a good instrumentation engineer all of the things that need to be taken into consideration just to measure the water level in a fifty foot steam generator used at a nuclear power plant where you have cold water on the bottom heated water a few feet up, boiling water above that, saturated steam above that, and then superheated steam above that. All of this affects the delta-P as measured by the level instrument and all of that has to be taken into account in determining the level.”
As a 1°x1° gridcell is used to calculate this, there appears to be an awful lot of averaging going on. Not only are they averaging the conditions for an area that can be about 70 miles by 70 miles at the equator and About 0 by 0 miles at the poles. In Kansas you could have sunny weather and be water skiing on a lake on one side of that grid and have a F4 Tornado on the other side. Been there and seen it.
Similarly, you can place a DP level instrument on the side of a boiler, calibrate it for the specific gravity of H2O at the “average” temperature of the boiler and the average weight of steam above that assumed water level. What you get is a reading that is pure Bull droppings. 75 years ago that is exactly what they did. It was good enough to prevent uncovering the tubes in the boiler and preventing destroying the boiler – after restrictions were placed upon minimum water levels and other operation conditions were established. However, it will not give a true, actual, level of the water in the boiler. A 5° change in inlet water temperature can change the accuracy of the level gauge by more than 10 percent – enough to boil the steam generator dry and the gauge will tell you that you have more than adequate water level as you destroy the boiler.
It is my opinion that they are doing the same thing with “Radiation temperature” and the assumed “Effective Radiation Level.” None of this takes into account the massive differences that can exist in the actual 1°x1° gridcell over the entire height, depth or length of that column. How can they predict exactly what is causing the heat to escape (radiate out) or what is going to trap the heat – clouds, CO2, ice crystals, rain, snow, water vapor, particulates, whatever. Search “earth” images look at the pictures. How are the clouds, all the different types of clouds, factored in. Seems to me from what I read they are just lost in the “averages.” Averages do not work.
Hi Willis!
1. 240 W/m^2 escaping at the TOA is the flux density j needed for energy balance, a physical quantity. However, the theoretical construct comes from calculating a perfect Planck black body (i.e. emissivity = 1) that would emit that 240 W/m^2. Using the Stefan-Boltzmann law, this turns out to be equivalent to a temperature of 255 K. As you note, there is no physical layer in the troposphere (at 4.85 km altitude) that actually emits a 255 K Planck black body spectrum, as any infrared (IR) spectrometer carried by a balloon or aircraft or on the side of a mountain will show. So any “explanation” of the greenhouse effect invoking such a hypothetical layer at 4.85 km altitude is worthless. However, the change in TOA flux on doubling CO2 over a 20 km path length can be calculated quite accurately from molecular constants, for example the 3.39 W/m^2 shown on the MODTRAN spectrum available at https://en.wikipedia.org/wiki/Radiative_forcing . Lambda-zero can be calculated from the formula that the relative change in temperature is 1/4 the relative change in flux density (which I simply call “flux” as I consider 1 m^2, just as one can talk about energy instead of power when one considers 1 second). This factor of 1/4 comes from taking the derivative of the Stefan-Boltzmann law with respect to T, dividing both sides by j, and cross-multiplying.
2. Lambda-zero = (255)/[4(240)] = 0.266. Using 3.7 W/m^2 for delta j, the temperature change for the hypothetical layer would be (0.266)(3.7) = 0.98 K.
Why is this equal to the temperature change at the Earth’s surface, and therefore the climate sensitivity (not including feedbacks)? Temperature profiles of the troposphere at different locations on the Earth, where surface temperatures vary widely, show mostly parallel straight lines with a slope corresponding to the lapse rate of -6.8 K/km. Therefore a temperature change at 4.85 km will be equal to the temperature change at the surface. This is true even if we have modelled the actual troposphere by a single thin hypothetical Planck black body layer that would match both j and delta j at the TOA (which is not at 4.85 km, but at 20 km for the MODTRAN spectrum). This assumes no net absorption or emission between 4.85 and 20 km, and that the inverse square law does not spread out the flux (a valid approximation since 20 km is small compared to the radius of the Earth).
3. Why are the temperature profiles parallel? Because statistical mechanics tells us that the most probable way of adding a finite amount of energy to a finite number of molecules in equal energy states is to add equal amounts to each molecule. Since heat content (enthalpy, H) is heat capacity times temperature, and the heat capacity of linear molecules like N2 and O2 and CO2 is 7k/2 per molecule, where k is Boltzmann’s constant, adding equal amounts of H means delta T is the same for each average molecule. This is true even though density decreases with altitude.
4. Why are the molecules in a column of the troposphere in equal energy states? The dry adiabatic lapse rate can be derived by considering the gravitational potential energy U = mgh for a molecule of mass m at altitude h where g is the acceleration due to gravity, and the enthalpy H = 7kT/2. If there is no heat injected into or sucked from each layer (i.e. for adiabatic conditions), then a gain in altitude by a molecule must come at the expense of a drop in H. I.e. dU/dh = – dH/dh. Using the Chain Rule for derivatives,
dH/dh = (dH/dT).(dT/dh), so d(mgh)/dh = -[d(7kT/2)/dT].dT/dh , so mg = -(7k/2).dT/dh .
Therefore the dry adiabatic lapse rate is dT/dh = -2mg/(7k) which equals -9.8 K/km on substitution of appropriate values for m, g and k.
5. Note that d(U+H)/dh = 0, so U+H is constant, regardless of altitude in the column, and the molecules are in equal energy state. If now equal amounts of heat, delta H, are added to each molecule, U+H will now be greater than for the adiabatic states, but the total U+H for the heated molecules will be equal for each.
6. Schlesinger (1985) assumed a transmission factor of (255/288)^4 = 0.615 would convert j’ , the flux at the 288 K mean surface temperature to the TOA flux, j = 240 W/m^2, emitted by the hypothetical 255 K Planck black body, assuming emissivity 1 for the surface. j’ = sigma.(288)^4 = 390 W/m^2, where sigma = 5.67 x 10^-8 is the Stefan-Boltzmann constant. j = 0.615 j’, so (delta j) = 0.615 (delta j’), and (delta j’) = (delta j)/0.615. Since (delta Tav)/Tav = 1/4 (delta j’)/j’ where Tav is the average temperature of 288 K. Substitution for (delta j’) gives (delta Tav)/288 = 1/4 (delta j)/[ (0.615)(390)]
so that delta Tav = 0.300 (delta j). Why is this value for lambda-zero 0.300/0.266 = 1.13 times larger than the value of Point 2?
7. If we use emissivity 0.98 for the real surface of the Earth, lambda-zero becomes 0.300/0.98 = 0.306, a factor of 0.306/0.266 = 1.15 larger than 0.266. Since 7/6 = 1.166…., this might explain why the factor of 7/6 in front of lambda-zero appears in the formula In the literature cited by Lord Monckton. But this would predict a climate sensitivity of (0.306)( 3.7) = 1.13 K instead of 0.98 K. Why is there a difference of 15% in such a key factor?
8. The short answer is that the TOA flux of 240 W/m^2 escapes from a partially clouded real Earth, whereas Schlesinger’s transmission factor was calculated for a hypothetical cloudless column of the troposphere with a constant lapse rate.
9. Although clouds only partially absorb visible radiation (they are not totally black when we look upward through them during the daytime), they are composed of water droplets or ice crystals that are essentially miniature Planck black bodies that absorb and emit infrared (IR) radiation with emissivity approximately 1.
This absorption will be over all IR frequencies, not just at discrete frequencies corresponding to molecular vibration-rotation bands. Thus the net absorption from the Earth’s surface to the cloud-top will be greater than if there were no clouds. Even if the lapse rate from the cloud-top to 10 km remains at -6.8 K/km, there will be a smaller TOA flux than 240 W/m^2 from the column above clouds. Since clouds cover a non-trivial 62% of the Earth’s surface, the mean flux when both cloud-free and clouded areas are considered will be less than 240 W/m^2. I.e. Schlesinger’s numbers are wrong, since they do not correspond to energy balance. The factor 7/6 is wrong, and must be removed in all future derivations of lambda-zero.
10. Are the numbers in the MODTRAN spectrum also wrong? No, because they predict the correct observed lapse rate of -6.8 K/km. This may be understood by considering what happens when we rise 1 km in the troposphere. The dry adiabatic lapse rate predicts a drop of 9.8 K, and this corresponds to zero injection of heat. Since enthalpy H varies with T, consider the heat needed to bring this drop in temperature to zero. It would be proportional to 9.8 K.
11. Now consider a black body surface with emissivity 1 emitting 390 W/m^2 upward. If 100% of the energy were absorbed within the next 1 km, then by Kirchhoff’s law that a good absorber is a good emitter, 100% of the energy would be emitted upward. We can ignore the back-radiation of 390 W/m^2, because it is simply balanced by another 390 W/m^2 upward emitted by the lower surface; i.e. the emission and back-radiation simply indicate communication between surfaces at thermal equilibrium, with no net change in temperature in either. The process would be repeated in the next 1 km layer, etc. until finally 390 W/m^2 would escape to outer space from the last layer. The result is that the initial opaque surface is simply extended to the surface of the last layer, from which photons are emitted according to the Stefan-Boltzmann law. The temperature change would be zero.
12. The MODTRAN spectrum shows that at 20 km, the TOA flux is 260.12 W/m^2 from a cloud-free 288.2 K Earth’s surface. At emissivity 0.98, the Earth’s surface would emit 383.34 W/m^2, so the transmission factor would be 260.12/383.34 = 0.6786. This is 10% higher than Schlesinger’s estimate of 0.615 in Point 6, explaining most of the difference between the two values of lambda-zero. This higher transmission factor would mean less absorption in the troposphere, and so a smaller value for climate sensitivity.
13. If the transmission factor is 0.6786, then the absorbance is 1 – 0.6786 = 0.3214. If 100% absorption results in a temperature change of 9.8 K from the dry adiabatic change for each km gain in altitude, then 32.14% absorption would produce a temperature change of 0.3214(9.8) = 3.15 K, since equal amounts of added energy per molecule are proportional to equal temperature changes. Therefore the change in temperature would be only -9.8 + 3.15 = -6.65 K for each km rise in altitude. This is close enough to the observed lapse rate of -6.8 K/km that we can claim to have derived it from first principles applied to the numbers in the MODTRAN spectrum, which must be right.
14. The value of lambda-zero using Tav = 288.2 K, j’ = 383.34 W/m^2 and j’ = j/0.6786 (where we have used the correct value for transmission factor that explains the observed lapse rate) is then
(288.2)/[4(0.6786)(383.34)] = 0.277
14. Therefore if we apply the MODTRAN value of 3.39 W/m^2 for the value of (delta j’), the climate sensitivity is 0.277(3.39) = 0.94 K (not including feedbacks). If we use 3.7 W/m^2 for (delta j’), the value would be 1.02 K, a difference of 8%, reflecting the differences in radiative forcing. Since the MODTRAN spectrum is so accurate in predicting/explaining the observed lapse rate, something it was not designed to do, I place more faith in the value of 0.94 K. There are other comments I could make, but I have to leave now for a personal duty.
Except, water transitions through 2 state changes, making it nonlinear, and there’s a lot of it.
Yes, phase transitions are involved in the rate of heat transfer from surface to upper levels in the atmosphere. So are convection currents, radiation transfer between cloud particles and then by collision to the main molecules of the air, and radiation transfer between greenhouse gas molecules and then by collision to the main molecules of the air. At steady state, the energy transferred is stored in N2 and O2 that outnumber CO2 by 2500:1 and water vapour molecules by 60:1 at 15 Celsius. The temperature profiles at steady state are not labelled according to convection, cloud cover, etc. because these, like latent heat transfers are transient things (it cools down when a cloud temporarily blocks the Sun). One exception is the temperature inversion that might occur near the poles during the long night/winter, but this is an indication that steady state is not reached there. The total amount of heat absorbed is proportional to the areas of net absorption in the MODTRAN and experimental spectra, and how that heat is transferred (including by phase changes) is not important if steady state has been achieved. Phase changes, convection, and clouds are confined to the troposphere, and ultimately energy balance is achieved by the photons reflected, and the IR photons that escape to outer space as monitored in the spectrum. Hope this helps.
This is important. Late at night the rate of temperature change slows by at 75% or more, but it happens only as air temps start to near dew points.
All the while the temperature of the sky has not appreciably changed, and the morning breeze also hasn’t started.
For the Stefan-Boltzmann equation’s use, one cannot average radiation. The radiation happens during the day, when it corresponds to the 4th power of the temperature difference between the surface of the Sun and the surface of the Earth, and of course all the issues with angle of incidence. At night, there is no radiation from the Sun.
Averaging radiation is scientifically meaningless, and discussing average radiation with respect to the S-B equation is scientifically meaningless. You have to look at a sphere that is rotating every 24 hours, irradiated with the full power of the Sun half the time, and dark half the time, with varying albedo somewhere around .30-.35, of course with the 23 or so degrees of angle of the Poles, immensely complex.
And of course the ability of the surface of the Earth and the atmosphere of the Earth to radiate to space is affected by the composition of the atmosphere, with water vapor by far the most significant opacity to outgoing infrared. CO2 prevails higher up where there is little water vapor, and the atmosphere is radiating at a temperature to which CO2 is significantly opaque, until you get to the altitude where the molecules of CO2 are so sparse that the atmosphere can radiate freely to Space.
If the Sun irradiated the surface of the Earth 24-7 at half its flux (that is all you have to say, “Flux,” or even “Radiative Flux”), then you could discuss the black-body laws with your averaged radiation. But it doesn’t.
Man, am I glad I am not trying to calculate any of this…
” You have to look at a sphere that is rotating every 24 hours, irradiated with the full power of the Sun half the time, and dark half the time”
No, you have a disc intercepting the radiation 24/24 and you have a sphere radiating 24/24. That is the basis of the 1/4 scaling factor.
However, I will second your reticence about averaging such quantities across the globe when reflectivity and temperature vary so widely both geographically and over 24h.
” At night, there is no radiation from the Sun.”
True but heat from the sun in the earth/sea/atmosphere still radiates out and some extra heat is brought in at the edges by air currents .Agree it is immensely complex.
Ummmmm, haven’t you’all forgotten that the science is settled, no need for this mathy stuff just green-wash politics please?
/sarc
There is also the “actual effective radiation level”.
In reality, there is emission directly from the surface at 0 metres in the atmospheric windows (in the below depiction, this is a hot desert it appears since the temp is very high). There is emission from H2O across many spectrum and at almost all layers of the atmosphere, there is emission from CO2 at 15 um which primarily occurs at -50C high in the stratosphere (CO2 cools off the Earth if you think about it with its large emission spectrum to space in the stratosphere) and we have Ozone emitting near the surface a little but mostly high up in the ozone layer where it is a little warmer than the stratosphere because Ozone also intercepts solar radiation here.
There are in fact, many effective radiation levels and spectra.
http://image.slidesharecdn.com/hollowearthcontrailsglobalwarmingcalculationslecture-100502151329-phpapp02/95/hollow-earth-contrails-global-warming-calculations-lecture-18-728.jpg
And there is a large variation in the actual long-wave emission to space based on the geography and latitude and time of the season etc. In this CERES map from April (a good average month with little seasonal influence) the values are as low as 100 W/m2 in Antarctica to some 300 W/m2 in some place (average is right about 240 W/m2).
Along the same line ot thought
The effective radiation level and corresponding temperature are concepts that are useful to
understand qualitatively the so-called “greenhouse effect”.
However, I believe they are only meaningful and useful if :
1-defined for a given IR wavelength
2-defined for a clear sky condition
3-defined for given local atmospheric conditions
Apologies to those for which the following is well known.
Since the pressure decreases exponentially with altitude z as exp(-z/z0) there is an altitude ERL at
which, for a given wavelength, the CO2 (or other GHG) absorption length equals z0. Any light emitted above z0 will mostly escape to space. Emitted below z0 most of it will be reabsorbed. The simplifying concept is that the TOA radiation at that wavelength is clearly governed by the black body radiation at the temperature occuring at the ERL.
This concept explains the shape of clear sky TOA radiation spectra, such as the one you show:
The CO2 absorption spectrum is between 550 and 800 cm-1. The dotted lines are theoretical black body spectra at various temperatures. The region 620-700 emits like a black body at 218K, except for a sharp peak at the center, which correspond to the CO2 central absorption line. In this wavelength region the ERL is in the tropopause, and the radiation temperature is the tropopause temperature. If CO2 concentration changes, ERL will essentially remain at the tropopause and the radiation will not change appreciably (saturated greenhouse effect). The center line is much more efficient and its ERL is in the stratosphere where the temperature is higher (hence the peak). All the dependence on CO2 concentration comes from the wings below 620 and above 700. There the ERL is in the troposphere and sensitive to CO2 concentration. It is easy to show that the exponential pressure dependence translates for those wavelengths, into the well known logarithmic concentration dependence of the CO2 effect.
One often overlooked issue is that any natural change of the tropopause temperature will modify the 620-700 radiation : a CO2 induced, but essentially CO2 concentration independent, natural change.
Given the above considerations, I do not see much pertinence in averaged URLs and their use with
global S-B radiation laws.
oops, corrected reply.
Along the same line of thoght
The effective radiation level and corresponding temperature are concepts that are useful to
understand qualitatively the so-called “greenhouse effect”.
However, I believe they are only meaningful and useful if :
1-defined for a given IR wavelength
2-defined for a clear sky condition
3-defined for given local atmospheric conditions
Apologies to those for which the following is well known.
Since the pressure decreases exponentially with altitude z as exp(-z/z0) there is an altitude ERL at
which, for a given wavelength, the CO2 (or other GHG) absorption length equals z0. Any light emitted above ERL will mostly escape to space. Emitted below ERL most of it will be reabsorbed. The simplifying concept is that the TOA radiation at that wavelength is clearly governed by the black body radiation at the temperature occuring at the ERL.
This concept explains the shape of clear sky TOA radiation spectra,such as below:
The CO2 absorption spectrum is between 550 and 800 cm-1. The dotted lines are theoretical black body spectra at various temperatures. The region 620-700 emits like a black body at 218K, except for a sharp peak at the center, which correspond to the CO2 central absorption line. In this wavelength region the ERL is in the tropopause, and the radiation temperature is the tropopause temperature. If CO2 concentration changes, ERL will essentially remain at the tropopause and the radiation will not change appreciably (saturated greenhouse effect). The center line is much more efficient and its ERL is in the stratosphere where the temperature is higher (hence the peak). All the dependence on CO2 concentration comes from the wings below 620 and above 700. There the ERL is in the troposphere and sensitive to CO2 concentration. It is easy to show that the exponential pressure dependence translates for those wavelengths, into the well known logarithmic concentration dependence of the CO2 effect.
One often overlooked issue is that any natural change of the tropopause temperature will modify the 620-700 radiation : a CO2 induced, but essentially CO2 concentration independent, natural change.
Given the above considerations, I do not see much pertinence in averaged URLs and their use with
global S-B radiation laws.
What am I missing here?
With utmost and genuine respect Willis, you are missing something fundamental: The understanding that there is no distinction between ‘physical fact’ and ‘model’, that ultimately even what you would call ‘physical fact’ is the output of a model.
All ‘physical facts’ are in the end interpretations of our experience mapped onto a metaphysical model.
WE assume the existence of a ‘physical reality, in a space time ‘dimension’ where everything is interconnected via ‘causality’ and regulated by immutable ‘natural law’.
That the assumptions enable the construction of a coherent and self consistent picture of the world, does not in any sense guarantee that these are in fact fundamental characteristics of the ‘world-as-it-really-is’, as opposed to the ‘world-as-we-see-and-partially-understand-it’, is not denied.
Habitually to deal; with the concepts so derived, as if they were real beguiles us into the comfortable illusion that they are real, not model outputs.
Look at gravity. What is gravity? It is a term, and, post Newton, a mathematically exact term, used to describe a relationship between other model constituents – mass, time, space – that occur in our notion of what is actually generating our experience
We can introduce other less precise terms., like ionosphere, Heavyside layer, troposphere, stratosphere, eco sphere and so on, to describe other relationships.
Do these exist as clearly defined physical entities, with precisely micron less width boundaries? No. Do they physically exist?
Aye, there’s the rub, the $64,000 question.
If you say no, then neither does gravity. If you say yes, then maybe so too do unicorns.
It is a particular conundrum, and elephant in the philosophical and scientific bedroom.
Fortunately, in my case, I was an engineer before I became fascinated by philosophy. WE have a simple adage. “If it works, use it”.
And I am afraid that adage is becoming de rigeur amongst the bleeding edge physical scientists. Is Quantum Theory real? People can’t get their heads round the pictures it puts in their brains. It makes them feel very uncomfortable. In order to physics at this level, scientists simply don’t address the question of the reality or otherwise of the ‘introduced entities’. They simply try to find equations that fit the observable data, couched in terms of meter movements, flashes of fluorescence, and tracks of water vapour….
It works, so we use it, and this computer is living (sic!) proof that the equations of at least some quantum theory, allow predictions to be made that are borne out in practice.
What does it mean in terms of physical reality?
Mate, there is no physical reality Only the experience of one. That is the only way to understand the dilemma and resolve . Physical reality is a way that smart apes can tell each other ‘where’ the ‘best’ ‘banana’ ‘tree’ is. A model of experience, that works.
It shouldn’t be taken so literally.
IN this light the answer to your quandary lies in the misapprehension that there is such a thing as a ‘real world’ that is distinct from a model of it. I wouold say it makes sense to say there is, but with an extreme proviso. It will always lie beyond a later of models we used to represent it. Conscious rational thought itself is a mechanism to map experience into a pre-ordained set of co-ordinates, and the proof of the pudding is never more and never less, than the model output matches experience.
That is as good as it gets, I fear.
We cannot debate the reality or otherwise of concepts. That is either supremely in-decidable, or manifestly wrong. Concepts have no physical reality, but then again, neither does physical reality!
All that matters for the prosecution of accurate rational thought, and that is what science is based on, or rather its philosophical name, natural philosophy, is. And accurate rational thought should take no prisoners, and face up to its ultimate limit. Kant didn’t write ‘a critique of pure reason’ for no reason. It was a warning that in the end, a model is only a model. Not reality. That didn’t stop two centuries of scientists pretending and having success by assuming that in fact their equations WERE reality. Until Quantum physics came along and made the warining all too relevant.
You and I are products of that misapprehension. I just woke up one day and realised that it was a misapprehension. As many philosophers from Occam and onwards have realised.
The real question to ask about ERL is not whether its real or not. It’s whether it is useful. Ultimately does it generate output that agrees with and predicts what you would term ‘data’ ?
If ERL is anything in your model, it’s an ’emergent property’ of what you would call ‘physical processes’ so it can of course move. As that’s what ‘physical objects’ do.
Your confusion seems to stem from a hard assumption that there is a clear distinction between ‘reality’ and ‘theory’, and you know where the border is.
Unfortunately, that is a position that cannot withstand the assault of modern physics: At the bottom, may well be a certain sort of reality. We must assume so, or abandon rational inquiry altogether.
But between us and our notions, and It, I am afraid its ‘models all the way down’.
And it is a long way down.
Willis, thank you for the essay.
Matt, you are welcome. I do the best I can to expose my understandings and my misunderstandings to the harsh glare of the marketplace of ideas. Right or wrong, the learning goes on.
w.
Here’s a conceptual real heat balance approach. These tables display the incoming/outgoing/balance over 24 hours on a horizontal square meter at the equator during the equinox as it rotates beneath the sun. It includes corrections for the oblique incidence where the spherical surface is angled to the incoming TSI. People who design and site solar panels understand this. Just need to repeat for the other 364 days, seasons from solstice to solstice and the other 5.1 E14 square meters minus 1. You will need a bigger computer.
Daylight Incoming Heat
Hour…..angle…..Gain W/m^2
600……….0.0……..0.00
700……..15.0……354.06
800……..30.0……684.00
900……..45.0……967.32
1000……60.0…1,184.72
1100……75.0…1,321.39
1200……90.0…1,368.00
1300……75.0…1,321.39
1400…….60.0..1,184.72
1500…….45.0…1,368.00
1600…….30.0…….684.00
1700…….15.0…….354.06
1800………0.0…………0.00
……Incoming……10,791.7
Heat Loss, 24 hours, Q/A = U * dT, U = 1.5
Hour…….Surface, C……. ToT, C……..Loss W / m^2……Difference
1800………15.56…………(40.00)…………..83.33
1900………14.44…………(40.00)…………..81.67
2000………13.33…………(40.00)…………..80.00
2100………12.22…………(40.00)…………..78.33
2200………11.11…………(40.00)…………..76.67
2300………10.00…………(40.00)…………..75.00
0000………..8.89…………(40.00)…………..73.33
0100………..7.78…………(40.00)…………..71.67
0200………..6.67…………(40.00)…………..70.00
0300………..5.56…………(40.00)…………..68.33
0400………..4.44…………(40.00)…………..66.67
0500………..3.33…………(40.00)…………..65.00 (sub total 890.00)
0600………..3.33…………(40.00)…………..65.00……………. (65.00)
0700………..4.44…………(40.00)…………..66.67…………….287.40
0800………..5.56…………(40.00)…………..68.33…………… 615.67
0900………..6.67…………(40.00)…………..70.00…………….897.32
1000………..7.78…………(40.00)…………..71.67………….1,113.06
1100………..8.89…………(40.00)…………..73.33………….1,248.05
1200………10.00…………(40.00)…………..75.00………….1,293.00
1300………11.11…………(40.00)…………..76.67………….1,244.72
1400………12.22…………(40.00)…………..78.33………….1,106.39
1500………13.33…………(40.00)…………..80.00………….1,288.00
1600………14.44…………(40.00)…………..81.67……………..602.33
1700………15.56…………(40.00)…………..83.33……………..270.73
…………………………………………………….1,780.00…………..9,901.7
……………………Net Balance……………………………10,791.7
This is excellent.
Thanks, I guess.
Well, it’s the same process used to evaluate the furnace needs for a house. Not exactly rocket science – or “climate” science, just basic HVAC,
1500…….45.0…1,368.00
Should be 967.32.
How do they account for the fact that areas of the earth are heated from the light bent around the theoretical flat circular surface disk they calculat with. thus calculations need to be made based upon “apparent” sun rise/set and all of the problems associated with that?
“apparent sunrise/sunset – Due to atmospheric refraction, sunrise occurs shortly before the sun crosses above the horizon. Light from the sun is bent, or refracted, as it enters earth’s atmosphere. See Apparent Sunrise Figure. This effect causes the apparent sunrise to be earlier than the actual sunrise. Similarly, apparent sunset occurs slightly later than actual sunset. The sunrise and sunset times reported in our calculator have been corrected for the approximate effects of atmospheric refraction. However, it should be noted that due to changes in air pressure, relative humidity, and other quantities, we cannot predict the exact effects of atmospheric refraction on sunrise and sunset time. Also note that this possible error increases with higher (closer to the poles) latitudes.”
I see this phenomenon as adding heat, but not being accounted for in their assumed calculations of averages, based upon thumb rules for calculating what various parameters are/should be. Have you ever noticed on a hike in a dry desert how rapidly it gets cold as soon as the visible Sun disappears? It does not get cold at the “actual” (physical) sunset. At times it has felt like I walked into a meat locker when the last sliver disappeared.
Useurbrain,
The phenomenon you present is well known and taught in the Military, I have no idea how it is accounted for if at all:
“Nautical twilight is defined to begin in the morning, and to end in the evening, when the center of the sun is geometrically 12 degrees below the horizon. At the beginning or end of nautical twilight, under good atmospheric conditions and in the absence of other illumination, general outlines of ground objects may be distinguishable, but detailed outdoor operations are not possible. During nautical twilight the illumination level is such that the horizon is still visible even on a Moonless night allowing mariners to take reliable star sights for navigational purposes, hence the name.”
http://aa.usno.navy.mil/faq/docs/RST_defs.php
Where there is light there is energy.
Yes, the rapid cooling near/after Sunset is due to the low water vapour concentration. Since water vapour is the main greenhouse gas overall (twice the absorption as CO2), in desert areas the net outward flux is not balanced by incoming Solar radiation, so the solid surface of the Earth rapidly cools. Near the poles, since the nighttime lasts weeks or months, the loss of heat via radiation of IR photons to outer space is so great that a temperature inversion can occur in the lower km or so of the troposphere. “Back-radiation” from CO2 can then transfer heat stored during the summer/daytime in N2 and O2, but this is slow as it requires transfer from N2 and O2 during collision with CO2 to form excited state CO2 molecules that can emit IR back to the ground. If there is a high water vapour concentration (e.g. near the Equator over the Pacific Ocean), the greenhouse gas H2O vapour can increase the back-radiation, as can liquid water droplets suspended as fog, mist, etc. In addition, condensation or sublimation (to form frost crystals from water vapour, which is a gas, not liquid droplets) transfers heat from the lower troposphere to the ground. Obviously this mechanism is reduced over desert areas at night.
nick, thanks for this. Do you have a link where I can read more about this?
Ron
Don’t really have link. It’s math, algebra, geometry, physics, parameters from the web & astronomy & second year heat transfer class.
Interesting post as usual Willis.




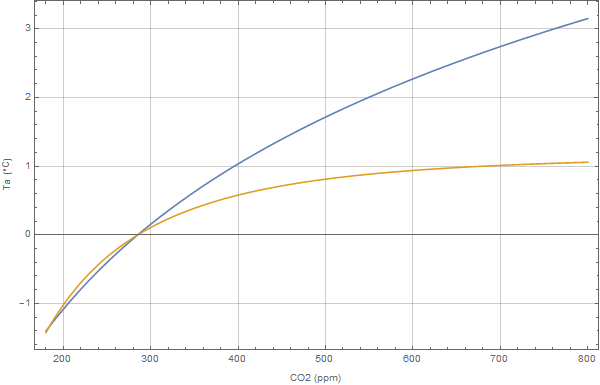


Lately I’ve been doing a Bayesian analysis on the Hadcrut4 vs CO2 concentration. The physical model is a gray-gas atmosphere with the emissivity path-length calculated by integration over the US standard barometric curve. The idea being that averaged over space and time the effective temperature is governed by the atmospheric emissivity which in turn is correlated strongly to the CO2 concentration. Feedbacks are assumed linear over the small anomally ranges and thus only scale the form of the gray-gas model equation. The free parameters are the effective radiation temperature, the exponent of the emissivity vs CO2 concentration, and a temperature offset to model the arbitrary choice of Ta=0. The first plot shows the results of Bayesian parameterization;
The best-fit parameters are Te = 251.3K, e = .454, offs= -48. These values are all close to the expected values. The gray-gas models for CO2/Water vapor mix in the literature have exp ranging from .42 -. 5, and the Te is close to the value Willis determined here. The plot below shows the posterior distributions which are nicely Gaussian except for the temperature distribution. This distribution can be explained by looking at the residual which shows a strong 67 year periodicity which modulates Te.
The equivalent model preferred by the IPCC is the familiar linear transformation of the CO2 forcing which is assumed logarithmic with CO2 concentration. This in turn infers that the emissivity vs path-length curve never saturates. A Bayesian run with the model a*ln(CO2/Co)+b is shown below.
The best-fit parameters are:
a=3.05, Co=278.9 ppm, b= -.502 C
Both models fir the observed data equally well and the variance of the residual is nearly identical.
However, projecting the models out to 800ppm gives drastically different results
The gray-gas model gives a 2xCO2 prediction of 1.7 C versus the non-saturating model’s 2.11
Projecting back to low concentrations is also interesting;
Note that the log model cannot account for the -8 deg anomaly observed in the paleo record at 100 ppm CO2.
I don’t know why I can never seem to get my plots to show up in line here. I was under the impression that WP would figure out an image URL and insert it but that doesn’t seem to work. Any helpful hints would be appreciated.
I can see all but the last one which will not display so I assume there is an error in the link.
See https://wattsupwiththat.com/test/ for more information. The one sentence version is image URLs have to be on their own line and end in an image extension, e.g. .jpg or .png.
Try it – over there, not here.
interesting work Jeff. I’ll look at this in more detail when I have time .
“However, projecting the models out to 800ppm gives drastically different results”
This is good example of why extrapolation way outside the calibration data is unscientific and likely to produce meaningless, misleading results.HoHowever, this comment stands out as being the wrong way to look at things. However, this comment stands out as being the wrong way to look at things. However, this comment stands out as being the wrong way to look at things. However, this comment stands out as being the wrong way to look at things. However, this comment stands out as being the wrong way to look at things.wever, this comment stands out as being the wrong way to look at things.
The whole of IPCC projections are based on models tuned to fit 1960-1990 and then projected to make meaningless speculation about whatever “may” happen in 2100 and beyond.
It is hard to believe that 25000 of the worlds “top scientists” are unaware that this had no scientific validity , so one is obliged to conclude that it is intentionally misleading.
The plot below shows the residual (left red) , a single tone sine fit (left blue) , the power spectral density of the residual (right blue) and the psd after subtracting the sine(right red).

If you’ve ever tried canceling a sine wave in noise this plot should amaze. Getting that level of cancellation over the 170 year period implies the frequency, phase and amplitude were all constant over that period as a mismatch or variance in any of these terms would result in incomplete cancellation which would show up in the PSD plots. Starts to make me believe those who point to an astronomical source of the AMO. Anyway, the point was to show how the AMO modulates Te. Rerunning the Bayesian fit with the sine fit removed from the Ta data makes the Te posterior PDF more Gaussian and reduces the standard error of the parameters.
For what it’s worth, the 2xCo2 projection with the “denoised” data is 1.6C
Corrections to the above:
The offset for the gray gas model = -0.48C not 48 C
fir should be fit
Where in the Paleo record do you find 100 ppm CO2?
My bad. I was trying to post from memory because the plot had been renamed in my archive. I tracked down the plot I was thinking of and it’s more like 190 ppm at the minimum.
I can’t remember where this plot comes from (any help?) but as I recall the temps are either Arctic or Antarctic which would be expected to vary by some multiple (2-3) of the GMST. A purely log CO2 curve can not explain the variance in the paleo record while the GGM does much better.
Many thanks, Willis, for yet another interesting and informative article. However, I have to differ from you on this: “The problem I have with that physically-based explanation is that the ERL is not a real layer. It is a theoretical altitude that is calculated from a single value, the amount of outgoing longwave radiation. So how could that be altered by physical processes? It’s not like a layer of clouds, that can be moved up or down by atmospheric processes. It is a theoretical calculated value derived from observations of outgoing longwave radiation … I can’t see how that would be affected by physical processes.“. (a) At least two values are involved, amount of radiation, and temperature. Maybe others too. (b) Nothing has to move physically for ERL to change, only one of the values involved. So a physical process that affected any of the values involved could easily change the ERL.
Per NASA ERL is 100 km. This is where 240 W/m^ ISR and 240 W/m^2 OLR must balance. It is where molecular density has fallen to the point that conduction/convection/heat/energy concepts fall apart and all that remains is radiation and S-B BB properly applies, where the material gas changes to a photon gas.
“Per NASA ERL is 100 km.”
Hmm, only by NASA definition for a NASA defined ERL.
The chance of any measurement level being exactly 100 of any unit Km, feet , miles , calories etc by chance is astronomical.
They just set an arbitrary easy to calculate measure for their own convenience. True ERL as Willis said is very variable and for the earth averaged depends on the input you assign to the sun. “the ERL is a calculated theoretical construct,”
“This is where 240 W/m^ ISR and 240 W/m^2 OLR must balance. ”
At exactly 100km? I find this hard to believe. Either the distance is wrong or the input is wrong.
http://earthobservatory.nasa.gov/IOTD/view.php?id=7373
340 – 100 albedo = 240. Albedo is out of the equation so 240 ISR and 240 OLR are left to work out the balance.
Thanks Willis for your post.
I apologize if this is off topic, but is this analysis consistent with this from the Climate Change 2007: Working Group I: The Physical Science Basis?
I am surprised that the thermals are so small at 24 W/m^2 especially considering along the sea shore the noticeable on shore cooler winds displacing the rising warmer air.
If you subtract the non radiant component of 24 W/m^2 from thermals and 78 W/m^2 from latent heat from 324 of ‘back radiation’, you are left with 222 W/m^2 which when added to 168 W/m^2 is the 390 W/m^2 of surface radiation corresponding to an average surface temperature of about 288K.
First, the average surface temp per satellite data is closer to 287K and he over-estimates the incident solar power. Second, the return of thermals (what goes up must come down) and latent heat (rain, weather, etc.), neither of which are in the form of photons and can not be properly considered radiation. He also fails to recognize that solar energy absorbed by the atmosphere is primarily by clouds, which are part of the same thermodynamic system as the surface, most of which is ocean which is tightly coupled to the clouds by the hydro cycle, thus separating these components only adds unnecessary wiggle room. For all intents and purposes relative to the equilibrium surface temperature, solar energy absorbed by clouds is equivalent to solar energy absorbed by the oceans (the surface) and this different is not properly lumped in as another back radiation term either.
He also underestimates the size of the transparent window and when asked where he got his value, he says it was an ‘educated guess’. Line by line simulations of the clear sky show the transparency to be about 46% at nominal GHG concentrations. Considering 2/3 of the planet is covered by clouds and traps surface emissions anyway, the resulting transparency is about 1/3 * .46 = .153. Multiplying 390 by .153 results in about 60 W/m^2 as opposed to the 40 W/m^2 claimed. Since clouds are not 100% opaque and about 20% of the surface emissions passes through them, of which 46% passes into space through the transparent window for another 24 W/m^2 is also unaccounted for as passing through the transparent windows in the atmosphere. In total, he underestimates the power passing through the transparent window by about a factor of 2.
So if I understand correctly, you are indicating that the IPCC diagram has many errors? I think it is still widely quoted.
Although I do not have specifics, I tend to think that the system is so complicated and chaotic that anyone could fudge any of the numerous questionable input factors to get whatever answer you want.
co2isnot evil
Thanks for your comments, they are helpful
Catcracking September 7, 2016 at 1:43 pm
Good question, Catcracking, I’ve repeated your graphic here for clarity.


That’s often called the “Kiehl/Trenberth” energy budget, or the “K/T budget”. Curiously, it was the problems with that model that led me to develop my own model of the global energy budget. What I didn’t like about it was that the upward and downward radiation fluxes from the atmospheric layer were different. Unphysical.
Now, this type of model is called a “two-layer model”, with the two layers being the surface and the atmosphere. What I discovered in researching this graphic was that there is no way to use a two-layer model to represent the earth. It needs a minimum of thee layers—the surface plus two atmospheric layers. So I made my own three-layer model, with all of the layers properly balanced. By “balanced” I mean input equals output, and that upwelling radiation is equal to downwelling radiation for the atmospheric layers.
See here for why it needs two atmospheric layers—basically, a greenhouse with only one atmospheric layer can’t account for both the warmth of earth’s surface temperature and the known losses (atmospheric window, latent and sensible heat).
Now, I made that graphic before I knew about the CERES data, which provides actual observations or calculated values for many of those variables. Here is what CERES has to say about those variables which are in its dataset:
I should update my drawing with those values, but it’s quite close, and there are more interesting tasks …
Oh, yeah. I calculated the energy balance with an excel global energy balance spreadsheet I wrote that is available here. It is iterative so you need to set your calculation to “Iteration”.
That should give you a good start …
My best to you,
w.
Hi Willis,
Nice work. Very helpful. A couple of questions. Is it your understanding that the latent heat is transported to the troposphere where it becomes part of the radiation budget at that layer? If so, how do we account for the latent energy released as precipitation? And (this one’s probably stupid), what about the energy required to lift all that water?
Jeff Patterson September 11, 2016 at 9:25 am
Thanks.
Yes, the latent heat is generally transported to the troposphere.
Mmm … I think there may be a misunderstanding. None of the latent energy is released as precipitation. Instead, what happens is that when water vapor precipitates, it releases all of the latent energy in the form of heat.
The only stupid questions on my planet are the questions you (or I) don’t ask … because if i don’t ask, I stay stupid.
Regarding your question, it takes energy (originally from the sun) to evaporate liquid water to make water vapor. Part of this energy is required to break the water to water bonds, but part of it depends on the pressure of the overlying atmosphere. The more pressure, the harder the water molecule must work to break loose.
Adding water vapor to the atmosphere has a curious effect, however, because of a counterintuitive fact—water vapor is only about 2/3 as dense as air. So moist air with lots of water vapor is lighter than dry air with little water vapor.
In addition, further work is done directly by the sunlight warming the surface, which warms the air and expands it. Between the lowered density due to water vapor and the lowered density due to heating, the air (containing the water) rises to the “LCL”, the lifting condensation level. This is where it condenses into clouds.
w.
Catcracking: there are more updated versions of those, with slightly different estimates from different groups. Look for work by Kevin Trenberth, Graeme Stephens and Martin Wild.
This paper summarises the Trenberth results as of 2009, and explains the data sources:
http://www.cgd.ucar.edu/staff/trenbert/trenberth.papers/TFK_bams09.pdf
So by ‘ex-fiancee’ do you mean ‘wife’ Willis?
Whatever, congratulations on your relationship 🙂
Thanks for the good wishes, Jon. The backstory of the gorgeous ex-fiancee is here.
w.
Catcracking
The 390 W/m^2 upwelling is calculated from inserting 15C, 288 K, in the S-B BB equation. This is incorrect.
1) 24 + 78 + (390 – 324) or 66 = 168. All the surface power flux is accounted for, the 324 appears out of nowhere.
2) The downwelling cannot equal the 324 upwelling as that would be 100% efficient perpetual energy motion and can’t happen.
3) The GHGs in the troposphere are at low temperatures, i.e. -20 C to -40 C so their S-B BB output would be about half of the 324, heat can’t flow from cold to hot, and radiating in all directions, not just back to the surface.
4) And the emissivity of CO2 is low, 0.10 or less (Nahle Nasif). There is no way this loop as represented is possible nor is the GHE theory that proposes it.
1) through 4) are violations of basic thermodynamic laws.
Plus this graph originated w/ Trenberth who has an updated version in Trenberth et al 2011jcli24 Figure 10.
Thanks nick
Another peace of the puzzle that you are missing Willis
You might remember the heroic role that newly-invented radar played in the Second World War. People hailed it then as “Our Miracle Ally”. But even in its earliest years, as it was helping win the war, radar proved to be more than an expert enemy locator. Radar technicians, doodling away in their idle moments, found that they could focus a radar beam on a marshmallow and toast it. They also popped popcorn with it. Such was the beginning of microwave cooking. The very same energy that warned the British of the German Luftwaffe invasion and that policemen employ to pinch speeding motorists, is what many of us now have in our kitchens. It’s the same as what carries long distance phone calls and cablevision.
http://www.novelguide.com/reportessay/science/physical-science/microwaves
jmorpuss September 7, 2016 at 5:05 pm
jmorpuss, this is exactly why I ask people to QUOTE THE EXACT WORDS YOU DISAGREE WITH. I have absolutely no idea what you are talking about.
Best regards,
w.
Does it serve any purpose building castles on the loose soil like imaginative numbers? Why not try this with satellite data?
Dr. S. Jeevananda Reddy
The problem with using the slope of SB at the surface is that there is an atmosphere between that surface and the other relevant observables. Relative to the system, a surface emitting 385 W/m^2 of net emissions is resulting in only 240 W/m^2 of output emissions. If instead, you used the slope of SB at T=287 with an emissivity of 0.62 (emissions at 287K = 385 W/m^2 and 385/240 == 1/0.62). Now. the so called ‘zero feedback’ sensitivity has a value of 1/(4 * 0.62 * 5.67E-8 * 287^3) = 0.3. Of course, this is only the zero feedback sensitivity when you consider the open loop gain to be 1/0.62 = 1.61 which is the current steady state closed loop gain with the RELATIVE feedback normalized to zero. Keep in mind that the feedback fraction and open loop gain can be traded off against each other to get whatever closed loop gain is required.
“At any given location, the emitted radiation is a mix of some radiation from the surface plus some more radiation from a variety of levels in the atmosphere.”
Based on modtran investigations I disagree. According to modtran, effectively zero surface radiation makes it to any significant altitude in the atmosphere. The radiation from the surface is absorbed and thermalized for water, CO2 and ozone; the most significant GHG’s.
To be sure, kinetic energy can re emerge as radiation when the conditions are appropriate, but apparently that altitude is 1 km for CO2 and maybe 4.5 km for water. This may seem like quibbling, but there is a huge difference between the speed of light and the speed of…sound?
“the Planck parameter is how much the earth’s outgoing radiation increases for a 1°C change in temperature”
No. the Planck constant is not quantized. It is a sliding scale. We choose 1 degree increments to suit our fancy.
Willis, you are a wonderful person, but you need more physics. The Effective Radiative Level differs for each molecule and each wavelength of light. It further differs for isotopologues. The differences are enormous. You can average them if you wish, but this average will conceal multiple orders of magnitude differences. When we are dealing with a “coupled chaotic system” where the “attractors” are ephemeral pockets of high entropy/low energy, methinks we need to do way better than these averages.
gymnosperm September 7, 2016 at 8:26 pm
Regards, gymnosperm. I fear you’ve overlooked the so-called “infrared window” that lets some surface radiation go straight to space.
When the Planck parameter is expressed as a number it is expressed “per degree C”. This means per one degree C. However, this is specious nitpicking.
Ah, don’t we all, my friend, don’t we all …
Hey, I never would have guessed that averages conceal multiple differences … oh … wait, hang on … now that I think of it, here’s what I ACTUALLY SAID about averages.
You see why I asked you to quote what I said that you object to? You are tilting against imaginary windmills. I’m well aware of the problems with averages, which is WHY I MENTIONED IT!! I’m sorry, you don’t get to give me some paternalistic lecture about things I already am well aware of.
w.
the IR window is affected by clouds, just as other parts of the spectrum.
– http://ipnpr.jpl.nasa.gov/progress_report/42-192/192C.pdf
page 11, fig 11
any water in the system will make a mess of any clearsky calculation as far as i am concerned. eg how can line by line caculations be done without taking into account the emission from water on surrounding water/vapour molecules. when you have all the lines, then you can calculate? well no, because at any given time, a lot of those frequencies that can be absorbed are being absorbed which alter the capacity to absorb the line in question.
Willis, I have read your guest post a while ago, it was quite interesting for me layman.
But here, coming back at this your reply to gymnosperm, I have again the same problem as with many places in guest posts and comments, concerning this wonderful atmospheric window.
Everybody talking about it refers to the corresponding Wikipedia entry, and so you do too.
Though I myself do as well regularly refer to Wiki (en, de, fr) when I want to supply info I guess be valuable, I’m not quite sure wether or not the info stored there concerning this special topic still is really accurate.
A counterexample of Wiki’s explanation we easily can find, e.g.
http://earthobservatory.nasa.gov/Features/RemoteSensing/remote_04.php
(please: don’t tell me “To NASA I never trust”).
Here you may read: The atmosphere is nearly opaque to EM radiation in part of the mid-IR and all of the far-IR regions.
And it is immediately visible on that page that the atmospheric window
http://earthobservatory.nasa.gov/Features/RemoteSensing/Images/atmos_win.gif
indeed appears considerably more restricted than the one presented at Wiki
The german Wiki page concerned with the atmospheric window
https://de.wikipedia.org/wiki/Atmosph%C3%A4risches_Fenster
speaks a little bit different as well
https://upload.wikimedia.org/wikipedia/commons/d/dc/Atmospheric_electromagnetic_opacity-de.svg
Would I use spectralcalc.com every day, I’d obviously obtained from them a license to access their entire panoply, especially
http://spectralcalc.com/atmospheric_paths/paths.php
where I would select “Observer” in the menu, and might upon that obtain, for the range 8-14µ, a nice transmittance plot telling us pretty good how the window looks like today (49US$ for one month).
Fair enough on the lecture.
I have definitely not overlooked the infrared window. The window is actually rather dirty thanks to water, especially in the tropics; and it has a huge “bite” taken out of the middle of it by ozone.
If my work with up and down Modtran is anything but an aberration of the program itself, there is zero lessening of radiation escaping from the surface to space in the water, CO2, or ozone bands until about a kilometer for CO2, 4 km for water and 5 km for ozone.
We are ultimately discussing the greenhouse effect-particularly from CO2-on the ERL. According to Modtran the greenhouse effect begins, not at the surface, but at one kilometer.
Another way of looking at it is that all IR radiation is completely absorbed and thermalized and the atmosphere radiates as a perfect blackbody up to a kilometer.
We could say all the rocks and dirt and the ocean surface and the various “layers” of the atmosphere CAN be averaged up to a km.
Above a km the differences prevail. Co2 radiates continuously from 1 km well into the mesosphere. Water radiates from 4 to 17 km. Ozone radiates from 5 to 40 km.
The putative average ERL at 5.3 km, which your maps show varying considerably from place to place (methinks largely variation in atmospheric pressure), is a porridge of the blackbody radiation below 1 km, and the blackbody radiation less the greenhouse reductions from 1 to 40 km.
The same thing should be what happens on the surface with water vapor when air temp nears dew point temp. All the available receptors at that wavelength are full. What conditions are you setting in modtran for water vapor conditions?
1? I never mess with the defaults.
Bindidon September 11, 2016 at 6:27 am
Thanks, Bindidon. I write for a mythical couple that I call the “literate and interested layman and woman”. So I’m glad to hear that you, who obviously fit that profile, find it both intelligible and interesting.
You might be interested in MODTRAN, which gives the transmittance plot for six regions and thirteen cloud conditions … you can save the data in text form for further analysis.
w.
Willis Eschenbach on September 12, 2016 at 3:17 pm
Thanks / Danke / Merci
If you break the outgoing radiation into the primary sources:
Surface, cloud tops @ur momisugly 2.5 km water vapor @ur momisugly 5 km and CO2 @ur momisugly 10km
Using Trenberth, et al under average cloudy conditions,
The values are 40 30 112 and 53 adding to 235 Wm-2.
Using a lapse rate of 6.5 C / km, the temperatures are in C
15 –1.25 –17.5 and -50
Using Stefan Boltzmann at these temperatures, the changes per C of warming are
0.5584, 0.4440, 1.7640 and 0.9572 adding to 3.724 Wm-2 per C.
The inverse is 0.2685 C/Wm-2 (the temperature sensitivity factor) is close to that of Lord Monckton.
The temperature sensitivity of each source is 0.1846, 0.2197, 0.2644 and 0.3976. The weighted average using their emissions to space is 0.2751.
If one simply uses the 235 total Wm-2 leaving the atmosphere and applies it to a black body, the temperature sensitivity is 0.2699 very close to the above more accurate estimates.
The ERL is a dynamic entity which both causes and responds to convective changes from place to place (including within the vertical column) such that radiative imbalances are neutralised on average over time.
Thus do radiative gases fail to alter the long term thermal equilibrium between energy in from space and energy out to space
The claim that “nobody” doubts the greenhouse theory is false as even a little due diligence research reveals. Spencer Weart points out in his discovery of global warming book how highly controversial and contentious the theory was when first introduced. And for good reason. It was bogus then, it remains bogus now and for the same reasons.
The only way CAGW pseudoscience Frankentheory continues to stumble around is because it powers a progressive world order agenda with all of the attendant wealth redistribution, abuse of power, oppression and misery. How many Bond villains held that same vision and how does it usually turn out?