While some model based claims say that CO2 residence times may be thousands of years, a global experiment in measurable CO2 residence time seems to have already been done for us.
By Christopher Monckton of Brenchley
Is the ~10-year airborne half-life of 14CO2 demonstrated by the bomb-test curve (Fig. 1, and see Professor Gösta Pettersson’s post) the same variable as the IPCC’s residence time of 50-200 years? If so, does its value make any difference over time to the atmospheric concentration of CO2 and hence to any consequent global warming?
Figure 1. The decay curve of atmospheric 14C following the ending of nuclear bomb tests in 1963, assembled from European records by Gösta Pettersson.
The program of nuclear bomb tests that ended in 1963 doubled the atmospheric concentration of 14CO2 compared with its cosmogenic baseline. However, when the tests stopped half the 14C left the atmosphere in ten years. Almost all had gone after 50 years. Why should not the other isotopes of CO2 disappear just as rapidly?
Mr. Born, in comments on my last posting, says the residence time of CO2 has no bearing on its atmospheric concentration: “It’s not an issue of which carbon isotopes we’re talking about. The issue is the difference between CO2 concentration and residence time in the atmosphere of a typical CO2 molecule, of whatever isotope. The bomb tests, which tagged some CO2 molecules, showed us the latter, and I have no reason to believe that the residence time of any other isotope would be much different.”
He goes on to assert that CO2 concentration is independent of the residence time, thus:
The total mass m of airborne CO2 equals the combined mass m12 of 12,13CO2 plus the mass m14 of 14CO2 (1):
Let CO2 be emitted to the atmosphere from all sources at a rate e = e12 + e14 and removed by uptake at a rate u. Then the rate of change in CO2 mass over time is given by
which says the total mass m of CO2, and thus its concentration, varies as the net emission, which is the difference between source e and sink u rates.
For example, if e = u, the total mass m remains unchanged even if few individual molecules remain airborne for long. Also, where e > u, m will rise unless and until u = e. Also, unless thereafter u > e, he thinks the mass m will remain elevated indefinitely. By contrast, he says, the rate of change in 14CO2 mass is given by
which, he says, tells us that, even if e were to remain equal to u, so that total CO2 concentration remained constant, the excess 14CO2 concentration
which is the difference between the (initially elevated) 14CO2 concentration and the prior cosmogenic baseline 14CO2 concentration, would still decay with a time constant m/u, which, therefore, tells us nothing about how long total CO2 concentration would remain at some higher level to which previously-elevated emissions might have raised it. In this scenario, for example, the concentration remains elevated forever even though x decays. Mr. Born concludes that the decay rate of x tells us the turnover rate of CO2 in the air but does not tell us how fast the uptake rate u will adjust to increased emissions.
On the other hand, summarizing Professor Pettersson, reversible reactions tend towards an equilibrium defined by a constant k. Emission into a reservoir perturbs the equilibrium, whereupon relaxation drains the excess x from the reservoir, re-establishing equilibrium over time. Where µ is the rate-constant of decay, which is the reciprocal of the relaxation time, (5) gives the fraction ft of x that remains in the reservoir at any time t, where e, here uniquely, is exp(1):
The IPCC’s current estimates (fig. 2) of the pre-industrial baseline contents of the carbon reservoirs are 600 PgC in the atmosphere, 2000 PgC in the biosphere, and 38,000 PgC in the hydrosphere. Accordingly the equilibrium constant k, equivalent to the baseline pre-industrial ratio of atmospheric to biosphere and hydrosphere carbon reservoirs, is 600 / (2000 + 38,000), or 0.015, so that 1.5% of any excess x that Man or Nature adds to the atmosphere will remain airborne indefinitely.
Empirically, Petterson finds the value of the rate-constant of decay µ to be ~0.07, giving a relaxation time µ–1 of ~14 years and yielding the red curve fitted to the data in Fig. 1. Annual values of the remaining airborne fraction ft of the excess x, determined by me by way of (5), are at Table 1.
Figure 2. The global carbon cycle. Numbers represent reservoir sizes in PgC, and carbon exchange fluxes in PgC yr–1. Dark blue numbers and arrows indicate estimated pre-industrial reservoir sizes and natural fluxes. Red arrows and numbers indicate fluxes averaged over 2000–2009 arising from CO2 emissions from fossil fuel combustion, cement production and land-use change. Red numbers in the reservoirs denote cumulative industrial-era changes from 1750–2011. Source: IPCC (2013), Fig. 6.1.
| t = 1 | .932 | .869 | .810 | .755 | .704 | .657 | .612 | .571 | .533 | .497 |
| 11 | .464 | .433 | .404 | .377 | .362 | .329 | .307 | .287 | .268 | .251 |
| 21 | .235 | .219 | .205 | .192 | .180 | .169 | .158 | .148 | .139 | .130 |
| 31 | .122 | .115 | .108 | .102 | .096 | .090 | .085 | .080 | .076 | .071 |
| 41 | .067 | .064 | .060 | .057 | .054 | .052 | .049 | .047 | .045 | .042 |
| 51 | .041 | .039 | .037 | .036 | .034 | .033 | .032 | .030 | .029 | .028 |
| 61 | .027 | .027 | .026 | .026 | .024 | .024 | .023 | .022 | .022 | .021 |
| 71 | .021 | .021 | .020 | .020 | .019 | .019 | .019 | .019 | .018 | .018 |
| 81 | .018 | .018 | .017 | .017 | .017 | .017 | .017 | .017 | .016 | .016 |
| 91 | .016 | .016 | .016 | .016 | .016 | .016 | .016 | .016 | .016 | .016 |
| 101 | .016 | .015 | .015 | .015 | .015 | .015 | .015 | .015 | .015 | .015 |
| 111 | .015 | .015 | .015 | .015 | .015 | .015 | .015 | .015 | .015 | .015 |
Table 1. Annual fractions ft of the excess x of 14CO2 remaining airborne in a given year t following the bomb-test curve determined via (5), showing the residential half-life of airborne 14C to be ~10 years. As expected, the annual fractions decay after 100 years to a minimum 1.5% above the pre-existing cosmogenic baseline.
Now, it is at once evident that Professor Pettersson’s analysis differs from that of the IPCC, and from that of Mr. Born, in several respects. Who is right?
Mr. Born offers an elegantly-expressed analogy:
“Consider a source emitting 1 L min–1 of a fluid F1 into a reservoir that already contains 15.53 L of F1, while a sink is simultaneously taking up 1 L min–1 of the reservoir’s contents. The contents remain at a steady 15.53 L.
“Now change the source to a different fluid F2, still supplied at 1 L min–1 and miscible ideally with F1 as well as sharing its density and flow characteristics. After 50 minutes, 96% of F1 will have left the reservoir, but the reservoir will still contain 15.53 L.
“Next, instantaneously inject an additional 1 L bolus of F2, raising the reservoir’s contents to 16.53 L. What does that 96% drop in 50 minutes that was previously observed reveal about how rapidly the volume of fluid in the reservoir will change thereafter from 16.53 L? I don’t think it tells us anything. It is the difference between source and sink rates that tells us how fast the volume of fluid in the reservoir will change. The rate, observed above, at which the contents turn over does not tell us that.
“The conceptual problem may arise from the fact that the 14C injection sounds as though it parallels the second operation above: it was, I guess, adding a slug of CO2 over and above pre-existing sources. But – correct me if I’m wrong – that added amount was essentially infinitesimal: it made no detectable change in the CO2 concentration, so in essence it merely changed the isotopic composition of that concentration, not the concentration itself. Therefore, the 14C injection parallels the first step above, while Man’s recent CO2 emissions parallel the second step.”
However, like all analogies, by definition this one breaks down at some point.
Figure 3. Comparison between the decay curves of the remaining airborne fraction ft of the excess x of CO2 across the interval t on [1, 100] years.
As Fig. 3 shows, the equilibrium constant k, the fraction of total excess concentration x that remains airborne indefinitely, has – if it is large enough – a major influence on the rate of decay. At the k = 0.15 determined by Professor Pettersson as the baseline pre-industrial ratio of the contents of the atmospheric to the combined biosphere and hydrosphere carbon reservoirs, the decay curve is close to a standard exponential-decay curve, such that, in (5), k = 0. However, at the 0.217 that is assumed in the Bern climate model, on which all other models rely, the course of the decay curve is markedly altered by the unjustifiably elevated equilibrium constant.
On this ground alone, one would expect CO2 to linger more briefly in the atmosphere than the Bern model and the models dependent upon it assume. To use Mr. Born’s own analogy, if any given quantum of fluid poured into a container remains there for less time than it otherwise would have done (in short, if it finds its way more quickly out of the container than the fixed rate of exit that his analogy implausibly assumes), then, ceteris paribus, there will be less fluid in the container.
Unlike the behavior of the contents of the reservoir described in Mr. Born’s analogy, the fraction of the excess remaining airborne at the end of the decay curve will be independent of the emission rate e and the uptake rate u.
Since the analogy breaks down at the end of the process and, therefore, to some degree throughout it, does it also break down on the question whether the rate of change in the contents of the reservoir is, as Mr. Born maintains in opposition to what Pettersson shows in (5), absolutely described by e – u?
Let us cite Skeptical Science as what the sociologists call a “negative reference group” – an outfit that is trustworthy only in that it is usually wrong about just about everything. The schoolboys at the University of Queensland, which ought really to be ashamed of them, feared Professor Murry Salby’s assertion that temperature change, not Man, is the prime determinant of CO2 concentration change.
They sought to dismiss his idea in their customarily malevolent fashion by sneering that the change in CO2 concentration was equal to the sum of anthropogenic and natural emissions and uptakes. Since there is no anthropogenic uptake to speak of, they contrived the following rinky-dink equationette:
The kiddiwinks say CO2 concentration change is equal to the sum of anthropogenic and natural emissions less the natural uptake. They add that we can measure CO2 concentration growth (equal to net emission) each year, and we can reliably deduce the anthropogenic emission from the global annual fossil-fuel consumption inventories. Rearranging (6):
They say that, since observed ea ≈ 2ΔCO2, the natural world on the left-hand side of (7) is perforce a net CO2 sink, not a net source as they thought Professor Salby had concluded. Yet his case, here as elsewhere, was subtler than they would comprehend.
Professor Salby, having shown by careful cross-correlations on all timescales, even short ones (Fig. 4, left), that CO2 concentration change lags temperature change, demonstrated that in the Mauna Loa record, if one examines it at a higher resolution than what is usually displayed (Fig. 4, right), there is a variation of up to 3 µatm from year to year in the annual CO2 concentration increment (which equals net emission).
Figure 4. Left: CO2 change lags and may be caused by temperature change. Right: The mean annual CO2 increment is 1.5 µatm, but the year-on-year variability is twice that.
The annual changes in anthropogenic CO2 emission are nothing like 3 µatm (Fig. 5, left). However, Professor Salby has detected – and, I think, may have been the first to observe – that the annual fluctuations in the CO2 concentration increment are very closely correlated with annual fluctuations in surface conditions (Fig. 5, right).
Figure 5. Left: global annual anthropogenic CO2 emissions rise near-monotonically and the annual differences are small. Right: an index of surface conditions (blue: 80% temperature change, 20% soil-moisture content) is closely correlated with fluctuations in CO2 concentration (green).
Annual fluctuations of anthropogenic CO2 emissions are small, but those of atmospheric CO2 concentration are very much larger, from which Professor Salby infers that their major cause is not Man but Nature, via changes in temperature. For instance, Henry’s Law holds that a cooler ocean can take up more CO2.
In that thought, perhaps, lies the reconciliation of the Born and Pettersson viewpoints. For the sources and sinks of CO2 are not static, as Mr. Born’s equations (1-4) and analogy assume, but dynamic. Increase the CO2 concentration and the biosphere responds with an observed global increase in net plant productivity. The planet gets greener as trees and plants gobble up the plant food we emit for them.
Similarly, if the weather gets a great deal warmer, as it briefly did during the Great el Niño of 1997/8, outgassing from the ocean will briefly double the annual net CO2 emission. But if it gets a great deal cooler, as it did in 1991/2 following the eruption of Pinatubo, net annual accumulation of CO2 in the atmosphere falls to little more than zero notwithstanding our emissions. It is possible, then, that as the world cools in response to the continuing decline in solar activity the ocean sink may take up more CO2 than we emit, even if we do not reduce our emissions.
Interestingly, several groups are working on demonstrating that, just as Professor Salby can explain recent fluctuations in Co2 concentration as a function of the time-integral of temperature change, in turn temperature change can be explained as a function of the time-integral of variations in solar activity. It’s the Sun, stupid!
It is trivially true that we are adding newly-liberated CO2 to the atmosphere every year, in contrast to the 14C pulse that ended in 1963 with the bomb tests. However, the bomb-test curve does show that just about all CO2 molecules conveniently marked with one or two extra neutrons in their nuclei will nearly all have come out of the atmosphere within 50 years.
To look at it another way, if we stopped adding CO2 to the atmosphere today, the excess remaining in the atmosphere after 100 years would be 1.5% of whatever we have added, and that is all. What is more, that value is not only theoretically derivable as the ratio of the contents of the atmospheric carbon reservoir to those of the combined active reservoirs of the hydrosphere and biosphere but also empirically consistent with the observed bomb-test curve (Fig. 1).
If the IPCC were right, though, the 50-200yr residence time of CO2 that it imagines would imply much-elevated concentrations for another century or two, for otherwise, it would not bother to make such an issue of the residence time. For the residence time of CO2 in the atmosphere does make a difference to future concentration levels.
To do a reductio ad absurdum in the opposite direction, suppose every molecule of CO2 we emitted persisted in the atmosphere only for a fraction of a second, then the influence of anthropogenic CO2 on global temperature would be negligible, and changes in CO2 concentration would be near-entirely dependent upon natural influences.
Atmospheric CO2 concentration is already accumulating in the atmosphere at less than half the rate at which we emit it. Half of all the CO2 we emit does indeed appear to vanish instantly from the atmosphere. This still-unexplained discrepancy, which the IPCC in its less dishonest days used to call the “missing sink”, is more or less exactly accounted for where, as Professor Pettersson suggests, CO2’s atmospheric residence time is indeed as short as the bomb-test curve suggests it is and not as long as the 50-200 years imagined by the IPCC.
And what does IPeCaC have to say about the bomb-test curve? Not a lot:
“Because fossil fuel CO2 is devoid of radiocarbon (14C), reconstructions of the 14C/C isotopic ratio of atmospheric CO2 from tree rings show a declining trend (Levin et al., 2010; Stuiver and Quay, 1981) prior to the massive addition of 14C in the atmosphere by nuclear weapon tests which has been offsetting that declining trend signal.”
And that is just about all They have to say about it.
Has Professor Pettersson provided the mechanism that explains why Professor Salby is right? If the work of these two seekers after truth proves meritorious, then that is the end of the global warming scare.
As Professor Lindzen commented when Professor Salby first told him of his results three years ago, since a given CO2 excess causes only a third of the warming the IPCC imagines, if not much more than half of that excess of CO2 is anthropogenic, and if it spends significantly less time in the atmosphere than the models imagine, there is nowhere for the climate extremists to go. Every component of their contrived theory will have been smashed.
It is because the consequences of this research are so potentially important that I have set out an account of the issue here at some length. It is not for a fumblesome layman such as me to say whether Professor Pettersson and Professor Salby (the latter supported by Professor Lindzen) are right. Or is Mr. Born right?
Quid vobis videtur?
Related articles
- Why and How the IPCC Demonized CO2 with Manufactured Information (wattsupwiththat.com)









Humans are emitting something around 33 billion tons CO2 per year (there are various estimates you know).
Natural processes are absorbing about half of that or 16.5 tons CO2 per year (it might be a little less than half which is were the various estimates start to produce problems).
http://s22.postimg.org/ace9j0jox/CO2_Emit_vs_Absorb_1750_2012.png
The natural process absorption rate appears to be more related to how much Excess CO2 there is in the atmosphere rather than our emission rate. The half is just a fluke. Natural processes have been absorbing about 1.5% of the Excess CO2 above 280 ppm.
http://s24.postimg.org/weyd4smyt/CO2_Absorb_ppm_1750_2012.png
Now the Excess CO2 is something some people might object to. But CO2 appears to reach an equilibrium level around 280 ppm in non-ice-age conditions because it has been right around this level for the past 24 million years ever since C4 plants/grasses evolved. That is where the Earth’s biosphere wants to be at.
If we stopped emitting today, the natural processes would continue to absorb 16.5 tons per year of CO2 out of the atmosphere but the rate would decline over time as the excess CO2 in the atmosphere above the equilibrium level gets lower and lower.
It would take about 130 years to go below 290 ppm and then several decades more to get to 280 ppm.
http://s22.postimg.org/xbbflawmp/CO2_Excess_Residency_Time_150_years.png
Ed_b: “The decaay time for 14C will be shorter as none is being returned from the deep ocean. ”
As someone else today mentioned tagging animals, I’ll use that analogy here. Canadian Geese are born, migrate here, there, and the other place, then end up as supper. Our interest is not the entire lifecycle of a Candadian Goose but only how long it camps out in one location. That is, how long it is a resident for the area we are interested in.
As geese come in we tag some of them with radio collars and note the date. When those tagged geese leave, we note the date. But we don’t care where that geese goes to thereafter. Whether or not they return next year. When they were born, or when they ended up on the menu. And we most certainly don’t care about geese that we don’t tag, that enter our region of interest.
That there is very little 14CO2 being returned from the ocean is the ideal condition. As unlike geese, it’s a real problem attaching radio collars to greenhouse gas. Given that this confounding factor is minimized, we have far less adjustements and other data magic to perform to get an answer in the realm of sensibility.
Ferdinand Engelbeen explains that “what goes into the deep oceans is the 14C/12C ratio of the moment. What comes out of the deep oceans is the composition of ~1000 years ago “. The oceans are emitting CO2 mainly at low latitudes, and absorbing CO2 mainly at high latitudes. The CO2 absorbed at high latitudes is taken down quite quickly into the deep ocean via the Thermohaline Circulation (THC). The CO2 released at low latitudes has taken several hundred years to be transported from the high latitudes through the deep ocean by the THC, so has low 14C. Hence the observed decline rate in atmospheric 14C is faster than for the other isotopes – as per Sisi’s comment.
The absorption of CO2 into the deep ocean is basically a 2-stage process. Ocean-atmosphere CO2 imbalance, such as is caused by man-made CO2 emissions, has a half-life of about 13 years, as any excess atmospheric CO2 is taken up by the ocean surface layer fairly quickly. In this first stage, the CO2 concentration in the surface layer increases, but not by as much as simple arithmetic would suggest because of chemical changes. The second stage is somewhat slower, as CO2 (or C) moves from the surface layer to the deeper ocean.
Jquip – in reply to Ferdinand’s “The ocean surface [..] can not absorb more than ~10% of the change in the atmosphere (due to the buffer/Revelle factor) [..]”, you say “To accept this claim I have to reject that Carbon Dioxide is soluble in water. Alternately, I have to accept that Henry’s Law is invalid and that Carbon bearing molecules exclude Carbon Dioxide from the water.“. By my understanding of the Revelle Factor, it actually increases the amount of CO2 that the ocean can absorb, though Ferdinand has stated the opposite. My understanding is that Revelle found that as CO2 is absorbed into the ocean about 90% of it quite quickly undergoes chemical changes, and hence the increase in CO2 concentration in the ocean is only about a tenth of what might have been expected. Hence the ocean can in fact absorb about 10 times more CO2 than might otherwise have been expected. If Ferdinand is indeed correct, then you must also be correct in arguing that it implies that Carbon bearing molecules exclude Carbon Dioxide from the water. Since that appears to be impossible, I suggest that Ferdinand must be wrong.
Doug Proctor – Much of the stats for man-made CO2 emissions come from reported oil and gas production and consumption. Since production is taxed, there is indeed an incentive to understate it (but no evidence that this happens). Also, OPEC impose production quotas on their members, based on stated reserves. This encourages their members to overstate reserves and understate production. I would expect estimates of man-made CO2 emissions to be roughly in the right ball park.
Pippen Kool – Your comments make no sense to me. You talk about the 14C being “incorporated into the fixed carbon” while the “other isotopes are in equilibrium“. The simple fact is that once the 14C is in the atmosphere, it is just part of the atmospheric CO2 and behaves virtually identically to all CO2 in all respects.
re the 2-stage process – I should clarify that the THC is not the only mechanism by which CO2 or C gets from the surface layer to the deep ocean.
OK, to continue this analogy: but with one change. We DO care about the number of geese that are present (from any cause), but have only tagged a few of those that are present.
If 5000 geese are in the county, one night 25 were sprayed with green paint. A few nights later, 15 were sprayed with orange paint. A week later, 35 were sprayed with yellow paint. The paint wears off at a known rate, but the geese fly in and fly out – also at unknown rates, but presumably at constant rates. The total number of geese appears to be rising over time. Natural deaths of all of the geese present, and death by embarrassment of being painted must also be considered. 8<)
Do you see how the problem is both a little more complicated – and also somewhat simpler than as originally stated? How many painted geese remain at any given time after the first ones were painted?
The bomb tests started in 1945 with only 3 small bombs. They stopped in the early 60's – underground tests since 1960's don't create measurable CO2 in the air.
Ferdinand Engelbeen says:
November 21, 2013 at 5:00 pm
“Except that…”
No exceptions. The CO2 sinks all respond dynamically to increase or decrease in partial pressure.
joeldshore says:
November 21, 2013 at 4:58 pm
Salby observed that CO2 evolves as the time integral of temperature anomaly, not proportional to it. If you have any reference which suggests this was explicitly stated in any notable venue prior to him, please provide it from an un-paywalled source.
Mike Jonas: it implies that Carbon bearing molecules exclude Carbon Dioxide from the water. Since that appears to be impossible”
Rather, I suggest that Ferdinand is correct but that he and I are discussing different things. If we’re talking about the entire life span of a carbon atom bonded only and solely to two oxygen atoms, then I agree with what Ferdinand has put forward. More than that, I suggest that this is the proper sense of what the Bern curve is representing. The lifespan of carbon as carbon dioxide, and not the residency of carbon dioxide in the atmosphere. This not only rectifies the differences in argument, but in the curves, and with the 1/2 buried initial impulse permits that we can explain why the Bern curve still declines under 1/2 total. But then, of course, we don’t care about greenhouse gases not in the atmosphere, if we’re interested in atmospheric effects.
” You talk about the 14C being “incorporated into the fixed carbon” while the “other isotopes are in equilibrium“. ”
What he was attempting to state is that the total CO2 in atmosphere has gone up. So by [dilution], if not corrected for, the Bomb test curve will decline too quickly. On merits that’s correct, and I can’t say whether that correction has been performed or if it is a fresh breath of raw data. But if it is not corrected then, by eyeball, 2000 is at 0.1. And the correction for [dilution] would produce that as [.116] if CO2 had not increased. So that’s fine, but it doesn’t come close to putting the two curves in the same neighborhood.
“And the correction for dillution would produce that as
1.160.116 if CO2 had not increased.”Supposedly I will someday learn to proof read before posting and not after.
Although I’ve read it over several times, I still have not found anything in this post that disproves the point I’ve been trying to make.
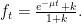
 in Equation (2) above. Specifically, if the mass of
in Equation (2) above. Specifically, if the mass of  injected into the atmosphere is
injected into the atmosphere is  at
at  , the rate of
, the rate of  mass change, which is necessarily the difference
mass change, which is necessarily the difference  between emissions and uptake rates, is given by
between emissions and uptake rates, is given by

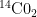 mass changes.
mass changes. concentration, while the other is the concentration of
concentration, while the other is the concentration of 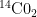 . It’s true, as Lord M. says, that a Pettersson
. It’s true, as Lord M. says, that a Pettersson 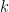 value of 0.015 will yield a terminal value different from the Bern
value of 0.015 will yield a terminal value different from the Bern  value of 0.217, but Fig. 3 shows only the trace of the Bern relationship; it doesn’t give the Petterson relationship, because we have no basis for inferring Pettersson’s
value of 0.217, but Fig. 3 shows only the trace of the Bern relationship; it doesn’t give the Petterson relationship, because we have no basis for inferring Pettersson’s 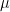 value. The other trace, which depicts the (measured) time constant of the rate of
value. The other trace, which depicts the (measured) time constant of the rate of 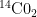 -concentration decay, is a different animal.
-concentration decay, is a different animal.
My point, as Lord Monckton says, is that “the decay rate of [the atmosphere’s carbon-14 content] x tells us the turnover rate of CO2 in the air but does not tell us how fast the uptake rate u will adjust to increased emissions.” My rationale is set forth in Lord M’s discussion of Equations (1)-(4) above.
Now, according to Lord M., Professor Pettersson tells us that the fraction of injected CO2 remaining in the atmosphere at time t is given by:
I don’t profess any expertise on which to base an opinion regarding that equation’s validity, but, if it’s correct, it seems only to give us the value of
But this merely gives a value for the concentration-change quantity in Equation (2) above; it says nothing about Equation (3), which is the rate at which the
Stated another way, Fig. 3 above seems to me to be comparing apples with oranges; one trace is total
In case it proves helpful, I’ll mention that Willis Eschenbach referred to this issue in his Appendix to this post:http://wattsupwiththat.com/2012/05/06/the-bern-model-puzzle/, and the post where I was converted from Lord M’s position to my current one can be found here: http://wattsupwiththat.com/2013/07/01/the-bombtest-curve-and-its-implications-for-atmospheric-carbon-dioxide-residency-time/#comment-1352996.
Equation 3 is not dimensionally correct. e14e has units of ([m]/[t])^2. LHS is in units of [m]/[t]
Well, as much as I admire and esteem the inimitable Lord Moncton, I fear that there is a conflation of two very different things in the head post.
One is the turnover time, and the other is the response or adjustment or e-folding time.
The “turnover time” is how long an average molecule stays in the atmosphere. According to the IPCC:
From both estimations of sources and sinks, and from observational (bomb-test) evidence, the turnover time appears to be on the order of 5 to 8 years. This is not much disputed.
Response or adjustment time, on the other hand, is how long it takes for an emitted pulse of CO2 into the atmosphere to decay to half (or 1/e) of the original value. From the same IPCC source:
These two (response and turnover times) are totally different measurements, which are measuring different things. The turnover time (from bomb tests) is the average time a molecule stays in the atmosphere before being absorbed—5-8 years.
The residence time, on the other hand, is a half-life (or e-folding time). Rather than being an average of actual times like the turnover time, it is the time constant for an exponential decay process. That’s a very different beast than the average of actual lifetimes of molecules in the atmosphere.
I hope that this will illuminate the confusion. There are two times, not one. Turnover is short (~5-8 yrs) Response or e-folding time is longer . Estimates range from about 40 to over 100 years.
Now, as to determining from observations what the e-folding time is, the problem is that we don’t have enough data to determine yet whether there is a long tail or not. The Bern model partitions emissions into four parts of fixed sizes, with three of them having e-folding times of 2.57 years (14%), 18 years (68%), and 171 years (3%), and the fourth (about 15%) hanging around forever … me, I don’t see that as likely, but like I said, to date the difference between the Bern model and a simple single e-folding time of ~40 years is lost in the noise …
Best regards, and Lord Moncton, my thanks to you for all you continue to do.
w.
Ferdinand Engelbeen, please note that CO2/DIC at the surface of the ocean is denuded, with respect to 5m down, due to biotic photosynthesis.
Pretending that the surface is in ‘equilibrium’, with respect to CO2 and O2, is a dumb mistake. just LOOK at the data for the composition of biotic gasses and DIC in actual sea water.
The 14C (as CO2) bomb test is pretty close to a single-turnover experiment, essentially measuring the off rate, that is the rate of exit from the atmosphere. There is a steady state level of production from cosmic rays, that sets the minimum level of 14C. So there is an on rate as expressed in the equations above.
Lets do math.
dC/dt = N – kC (1),
where C is 14C as CO2, N is a fixed rate of 14C formation from cosmic rays, and k is the off rate, that is the rate 14C leaves the atmosphere, not to return. If you can’t get past this part, give up.
This is a non-homogeneous differential equation. Let assume C can be expressed as the product of U and V where U is the solution to the homogeneous equation.
C = U*V (2)
dU/dt + kU = 0 (3).
With solutions
U = A*e^(-kt) (4)
Because dC/dt = dU/dt*V + U*dV/dt, we can substitute (2,3) into (1).
dU/dt*V + U*dV/dt + U*V = N (5)
Rearranging
V*(dU/dt + U) + U*dV/dt = N (6), and because of (3)
U*dV/dt = N (7) and
dV/dt = N / U (8).
Substitute (4) into (8) and
dV/dt = N*A*e^(kt) (9).
Integrating from 0 to t
V = N/Ak * (e^(kt) – 1) (10).
Solutions of C are A1 * U*V + A2 * U, so after some multiplication
C = A1*N/k *(1-e^(-kt) ) + A2 * e ^(-kt) (11)
At t=0, C = A2, and at t = inf, C = A1*N/k. Let A1 = k and A2 = N + Xo, where Xo is the excess 14C we start with at t = 0, then
C = N * (1-e^(-kt)) + (N + Xo)* e^(-kt) (12).
Rearranging we get
C = N*(1 – e^(-kt) + e^(-kt) ) + X * e^(-kt) (13), or finally
C = N + Xo e^(-kt) (14), and since C = N + X, after rearranging
X = Xo e^(-kt) (15).
Clearly, we see the fixed amount N and the decay of the excess X with rate constant k. When I fit the data using this equation, I get a half-life of about 5 years for 14C using ORNL data. My previous attempt failed to subtract N from C first. I just fit the fall, which was a mistake.
Willis, I believe you have missed something very important.
Imagine that the pulse added 1,000 units of 14C to the atmosphere and 14C has a first order rate of disappearance from the atmosphere of a decade.
If the atmospheric reservoir was exactly the same size as the reservoir it is rapidly interacting with then the atmosphere will end up near 500 units after 5 decades.
If the atmospheric reservoir was one third the size as the other reservoir then the atmosphere will end up near 250 units after 5 decades.
If the atmospheric reservoir was one ninth the size as the other reservoir then the atmosphere will end up near 100 units after 5 decades.
If the atmospheric reservoir was one nineteenth the size as the other reservoir then the atmosphere will end up near 50 units after 5 decades.
If the atmospheric reservoir was one thirty ninth the size as the other reservoir then the atmosphere will end up near 25 units after 5 decades.
The END POINT tells you the ratio of the relative size of the interacting reservoirs. It matters not a tinkers cuss what the mechanism of exchange is, what is happening is that the 14C is leaving the atmosphere much more quickly than it is appearing.
There is a quite easy way to model the process. Assume that one third of the 90 GtC that is fixed annually in the ocean falls 50 m before it is oxidized, then half of this falls a further 50 m before being oxidized, , then half of this falls a further 50 m before being oxidized and so on.
What you have is the rapid transport of organic ‘marine snow’ into the depths from the surface, which is of course denuded of CO2/DIC.
This process depends, of course, on the rapid movement of fecal matter and dead organisms. these have been timed as falling at 16–368 m per day.
http://www.int-res.com/articles/ame/27/a027p057.pdf
The moment you stop thinking like a chemist and think like a biochemist, it becomes understandable.
Hoser, don’t forget that the 14C is expressed as 14C:12C ratio and that the total 12CO2 has increased since the bomb tests.
You have to use Anders estimate of annual CO2 release to work out the amount of dilution of 14C, this increases the decay constant to about 7.5 years.
“For the sources and sinks of CO2 are not static, as Mr. Born’s equations (1-4) and analogy assume, but dynamic. Increase the CO2 concentration and the biosphere responds with an observed global increase in net plant productivity. The planet gets greener as trees and plants gobble up the plant food we emit for them.”
The carbon cycle diagram displayed has information on this. They say the plant reservoir has diminished by 15 Gtons C. They aren’t sure that it’s down – the range is -45 to +15. But the key is that the reservoir size is only 350-550 Gt. We’ve burnt about 400 Gt. If the plants had gobbled it, we’d live in a very different world.
“For instance, Henry’s Law holds that a cooler ocean can take up more CO2.”
Yes, but not very much. The ice age transition records tell us, as Ferdinand has often explained, that it’s about 8ppm per °C. Again the diagram says 20 Gtons C gained by the surface ocean, and 135 by the deep. That’s due to the air ppm increase, not cooling.
“Is the ~10-year airborne half-life of 14CO2 demonstrated by the bomb-test curve (Fig. 1, …”
Fig 1 clearly says a 14 yr half-life.
What I’d like to see from Salby and/or fans is their equivalent of that carbon cycle budget diagram. If the CO2 in the air came out of the sea, where did our 400 Gt go?
Ferdinand Engelbeen says:
The problem is in the deep oceans: what goes into the deep oceans is the 14C/12C ratio of the moment. What comes out of the deep oceans is the composition of ~1000 years ago.
I’m not so sure the deep oceans play much of a role WRT to short term C14 decay.
The CO2 exchange between the atmosphere and the hydrosphere all takes place at the interface, not in the deep oceans. Following the sudden increases in atmospheric C14, some of those molecules will quickly be absorbed by the ocean surface. And some of them will be given up again to the atmosphere.
I agree there’s a serious deficit in C14 levels in the deep oceans. But that doesn’t matter. What matters is the C14 deficit in the ocean surface. And that deficit although finite, will be a lot smaller.
I’m VASTLY suspicious of all the “authoritarian proclamations” made about the “influence of ocean acidification” by CO2, having some effect on the rates of absorption and off gassing.
Evidently, these folks are oblivious to the fact that the pH of the ocean, with the Henry’s law, current…absorption of CO2 should be somewhere around 5.7 (well less than 7 and quite “acid” as it would be). Instead, when the oceans are measured, they are actually fairly alkaline, around 7.8, if I recall correctly, and some of the specious claims put the “acidification” in the realm of going from 7.8 to 7.7 (or basic to basic, to be technically correct). The primary reason for this discrepancy, versus PURE WATER, is the “buffer” effect of the vast amount of dissolved species in all ocean water.
Since the exact distribution and pH chemistry is somewhat muddled, hard to track, and can VARY from region to region, we have a situation where:
1. Claims of a truly observable pH shift from 7.8 to 7.7 are DUBIOUS at best.
2. IN a parallel manner, claims that the CO2 absorption and desorption rates are “self influenced” by claimed pH shifts caused by CO2 absorption, also are DUBIOUS claims.
I recall some famous Latin saying that translated loosely means: Ignorance is NOT cured by application of more ignorance to the original problem.
Nick Stokes – The plants seem to be net absorbers – http://www.impactlab.net/2008/06/09/scientists-surprised-to-find-earths-biosphere-booming/ – but we’re looking at 15-16mmt/mth compared with man-made of about 1500mmt/mth. So your main point appears to be correct.
Jquip – My interest is in the take-up rate of CO2 from the atmosphere by the ocean. As I understand it, that is mostly what ChristopherM was getting at with his figures for 14C. My understanding is that the Revelle effect adds greatly to the amount of CO2 that the ocean is able to take up in the short term, compared with a ‘no chemical change’ scenario.
Pippen Kool says:
November 21, 2013 at 2:08 pm
Because you are looking at dilution of the 14C into the fixed carbon; the other isotopes are in equilibrium and won’t diminish.
=================
having got into the fixed carbon, it is no longer in the atmosphere.
Bill Illis says:
November 21, 2013 at 5:26 pm
The half is just a fluke. Natural processes have been absorbing about 1.5% of the Excess CO2 above 280 ppm.
================
it seems unlikely to be a fluke. the absorption has remained constant at 1/2 of human emissions for as long as they have been reporting, while the percentage absorption of CO2 above 280 ppm has not remained constant.
this is one of the unexplained mysteries of CO2 and human emissions, because if the AGW theory is correct, absorption should not be 1/2 of human emissions. Rather it should be a percentage of total CO2. But it isn’t. Which tells us that the theory that the CO2 comes from fossil fuel burning is wrong.
And here is:
Dr. Murry Salby to speak for himself.
Note: In all the many times (and some of you realize that it has been, indeed, many,) I have posted my hero, Dr. Salby’s, lecture on this site, NOT ONCE HAS A SCIENTIST OF WUWT given us his or her detailed comments on the complete content of that lecture. While I have taken notes from it and could post a detailed summary of the video, I have nothing to add.
Has all my posting of Dr. Salby’s lecture been for nought? Has NO ONE watched his lecture? Why–in–the–world haven’t you?
One of the WUWT Science Giants ought to:
1. Watch Dr. Salby’s 2013 Hamburg lecture;
2. Write* a post for WUWT
A. summarizing (with completeness and accuracy) its contents; and
B. Commenting on what Dr. Salby says in that lecture.
*Written so that so non-scientists can understand you — Dr. Salby did it (yes, I understand what he says — just could not ever analyze it for accuracy); i.e., the above scientist-author needs to have: 1) mastered the topic; AND 2) be a good teacher.
Why has NO ONE done this?
I sure wish I could — I would have long ago.
*********************************************
Please forgive my tone above. I just have grown tired over the past 6 months of reading so many lukewarm, tentative, “Well, …. maybe he has a point….. hm…. I just don’t know……. why doesn’t he get it published in a peer reviewed periodical? …….. hm…. …. ,” comments re: Dr. Salby’s work. And then, Ferdinand Englebeen stomps over and bellows that Salby is mixed up …. and NO ONE (that I can recall) but Bart (God bless you, Bart, one of “David’s Mighty Men” of science) defends Salby to any significant degree.
WUWT is about more than being a semi-exclusive club for banter between scientists, isn’t it? It’s about teaching, too, is it not? Teaching is, after all, how we will win the battle for truth.
Thus, THANK YOU, CHRISTOPHER MONCKTON, for twice now getting the word out (at least to some degree) about the content of Dr. Salby’s magnificent work.
And I’ll bet I come back here tomorrow and see that my post was, as usual, completely ignored. That’s okay, v. a v. me and my zany posts, but PAUSE AND CONSIDER THE DISSERVICE YOU ARE DOING TO A GREAT SCIENTIST WHO HAS PUT HIS CAREER ON THE LINE FOR US ALL. — In caps so as you auto-scroll past an “oh, great, a Janice Moore post” (eye roll) you might see this!
#(:))
Is the assumption of homogeneous dispersion accurate?
Being denser, wouldn’t 14CO2 sink faster, and thus be removed faster than 12CO2?
Mike Smith – you say “I’m not so sure the deep oceans play much of a role WRT to short term C14 decay. The CO2 exchange between the atmosphere and the hydrosphere all takes place at the interface, not in the deep oceans.“. I think you are basically correct, but it is important that the absorption by the ocean of CO2 takes place in the higher latitudes and can be followed quite quickly by it sinking to the deeper ocean. Ocean CO2 emissions, on the other hand, take place mainly in the lower latitudes, so do not contain any recently-absorbed 14C. Well, not much.
“Pippen Kool says:” – ad nauseam – various nonsense about CO2 residence times.
You write about “carbon” as though this is something alien to this planet and the life-forms which inhabit it. May I take this opportunity to inform You, that You ARE a Carbon Based Life-form, and ALL the food you ever ate during your life is made from, and based on Carbon. CO2 is the vector gas which make all this possible. The so called residence time, can be as little as ten minutes, or several years, depending on whether there is plant life nearby to absorb the gas, and animals nearby to consume that plant growth. Its all a bit more complex than you imagine, “Pippen Kool”.
Fatuous buffoons who claim that we must reduce the amount of CO2 in the atmosphere are wholly ignorant of the life processes which depend upon this rare gas, and why its concentration varies over time irrespective of the actions of the planet’s inhabitants, and the effects of its concentration at the various levels in the atmosphere over time.