Guest Post by Willis Eschenbach
Although it sounds like the title of an adventure movie like the “Bourne Identity”, the Bern Model is actually a model of the sequestration (removal from the atmosphere) of carbon by natural processes. It allegedly measures how fast CO2 is removed from the atmosphere. The Bern Model is used by the IPCC in their “scenarios” of future CO2 levels. I got to thinking about the Bern Model again after the recent publication of a paper called “Carbon sequestration in wetland dominated coastal systems — a global sink of rapidly diminishing magnitude” (paywalled here ).
 Figure 1. Tidal wetlands. Image Source
Figure 1. Tidal wetlands. Image Source
In the paper they claim that a) wetlands are a large and significant sink for carbon, and b) they are “rapidly diminishing”.
So what does the Bern model say about that?
Y’know, it’s hard to figure out what the Bern model says about anything. This is because, as far as I can see, the Bern model proposes an impossibility. It says that the CO2 in the air is somehow partitioned, and that the different partitions are sequestered at different rates. The details of the model are given here.
For example, in the IPCC Second Assessment Report (SAR), the atmospheric CO2 was divided into six partitions, containing respectively 14%, 13%, 19%, 25%, 21%, and 8% of the atmospheric CO2.
Each of these partitions is said to decay at different rates given by a characteristic time constant “tau” in years. (See Appendix for definitions). The first partition is said to be sequestered immediately. For the SAR, the “tau” time constant values for the five other partitions were taken to be 371.6 years, 55.7 years, 17.01 years, 4.16 years, and 1.33 years respectively.
Now let me stop here to discuss, not the numbers, but the underlying concept. The part of the Bern model that I’ve never understood is, what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?
I don’t get how that is supposed to work. The reference given above says:
CO2 concentration approximation
The CO2 concentration is approximated by a sum of exponentially decaying functions, one for each fraction of the additional concentrations, which should reflect the time scales of different sinks.
So theoretically, the different time constants (ranging from 371.6 years down to 1.33 years) are supposed to represent the different sinks. Here’s a graphic showing those sinks, along with approximations of the storage in each of the sinks as well as the fluxes in and out of the sinks:
Now, I understand that some of those sinks will operate quite quickly, and some will operate much more slowly.
But the Bern model reminds me of the old joke about the thermos bottle (Dewar flask), that poses this question:
The thermos bottle keeps cold things cold, and hot things hot … but how does it know the difference?
So my question is, how do the sinks know the difference? Why don’t the fast-acting sinks just soak up the excess CO2, leaving nothing for the long-term, slow-acting sinks? I mean, if some 13% of the CO2 excess is supposed to hang around in the atmosphere for 371.3 years … how do the fast-acting sinks know to not just absorb it before the slow sinks get to it?
Anyhow, that’s my problem with the Bern model—I can’t figure out how it is supposed to work physically.
Finally, note that there is no experimental evidence that will allow us to distinguish between plain old exponential decay (which is what I would expect) and the complexities of the Bern model. We simply don’t have enough years of accurate data to distinguish between the two.
Nor do we have any kind of evidence to distinguish between the various sets of parameters used in the Bern Model. As I mentioned above, in the IPCC SAR they used five time constants ranging from 1.33 years to 371.6 years (gotta love the accuracy, to six-tenths of a year).
But in the IPCC Third Assessment Report (TAR), they used only three constants, and those ranged from 2.57 years to 171 years.
However, there is nothing that I know of that allows us to establish any of those numbers. Once again, it seems to me that the authors are just picking parameters.
So … does anyone understand how 13% of the atmospheric CO2 is supposed to hang around for 371.6 years without being sequestered by the faster sinks?
All ideas welcome, I have no answers at all for this one. I’ll return to the observational evidence regarding the question of whether the global CO2 sinks are “rapidly diminishing”, and how I calculate the e-folding time of CO2 in a future post.
Best to all,
w.
APPENDIX: Many people confuse two ideas, the residence time of CO2, and the “e-folding time” of a pulse of CO2 emitted to the atmosphere.
The residence time is how long a typical CO2 molecule stays in the atmosphere. We can get an approximate answer from Figure 2. If the atmosphere contains 750 gigatonnes of carbon (GtC), and about 220 GtC are added each year (and removed each year), then the average residence time of a molecule of carbon is something on the order of four years. Of course those numbers are only approximations, but that’s the order of magnitude.
The “e-folding time” of a pulse, on the other hand, which they call “tau” or the time constant, is how long it would take for the atmospheric CO2 levels to drop to 1/e (37%) of the atmospheric CO2 level after the addition of a pulse of CO2. It’s like the “half-life”, the time it takes for something radioactive to decay to half its original value. The e-folding time is what the Bern Model is supposed to calculate. The IPCC, using the Bern Model, says that the e-folding time ranges from 50 to 200 years.
On the other hand, assuming normal exponential decay, I calculate the e-folding time to be about 35 years or so based on the evolution of the atmospheric concentration given the known rates of emission of CO2. Again, this is perforce an approximation because few of the numbers involved in the calculation are known to high accuracy. However, my calculations are generally confirmed by those of Mark Jacobson as published here in the Journal of Geophysical Research.

There’s a massive CO2 sink that resides over Siberia during winter, it is rapidly ‘taken up’ by foliage during Spring and Summer.
We affect the partition in many different ways, on what we plant and harvest and what we do with the harvest. Numerous other biological systems do as well and none are fully understood.
excellent thought post Willis……..
I still can’t figure out how CO2 levels rose to the thousands ppm….
….and crashed to limiting levels
Without man’s help……….
The categories are fixed so that you can see net effects.
Their graph is made in a manner which would make readers not realize how much biomass growth occurs from human CO2 emissions.
Human emissions averaged around 27 billion tons a year of CO2 during the decade of 1999-2009 (on average 7 billion tons annually of carbon), which amounted to about 270 billion tons of CO2 added to the atmosphere. Meanwhile there was a measured increase in atmospheric CO2 levels of 19.4 ppm by volume, 155 billion tons by mass, an amount about 57% of the preceding but only 57% of it.
If one looks at where the other 115 billion tons went, it was a mix of uptake by the oceans and it going into increased growth of biomass (carbon fertilization from higher CO2 levels) / soil.
Approximately 18% (49 billion tons CO2, 13 billion tons carbon) went into accelerated growth of biomass / soil, and about 25% went into the oceans.
To quote TsuBiMo: a biosphere model of the CO2-fertilization effect:
“The observed increase in the CO2 concentration in the atmosphere is lower than the difference between CO2 emission and CO2 dissolution in the ocean. This imbalance, earlier named the ‘missing sink’, comprises up to 1.1 Pg C yr–1, after taking land-use changes into account.” “The simplest explanation for the ‘missing sink’ is CO2 fertilization.”
http://www.int-res.com/articles/cr2002/19/c019p265.pdf
In fact, global net primary productivity as measured by satellites increased by 5% over the past three decades. And, for example, estimated carbon in global vegetation increased from approximately 740 billion tons in 1910 to 780 billion tons in 1990:
http://cdiac.esd.ornl.gov/pns/doers/doer34/doer34.htm
Other observations include those discussed at http://www.co2science.org/subject/f/summaries/forests.php
The categories are fixed so that one can import a sense of order and predictability to a collection of processes that lack both. I can just as easily categorize the residence time of foodstuffs in my refrigerator as beverage, pre-packaged, and leftovers. That doesn’t mean I can predict whether the salsa will become empty within three months or stick around to generate new life forms. It presumes a level of understanding of the “carbon budget” that doesn’t exist. But with such a model I can calculate how much milk will be in my fridge in 2050. Regardless of that result, the dried clump of strawberry jam on the third shelf won’t be inconsistent with my projection.
Turtles, indeed.
Ah! A warmist recently told me that the residence time of CO2 is 2 to 500 years. I replied that that is quite the error bar. He probably had looked up that Bern model and got his information from there. But it really doesn’t make any sense and I would file it under make-work schemes or epicycles. A product of the Warmist Works Progress Administration.
“what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?”
“PV=nRT” basically dashes such a fantastic model on the rocks. A classic example of the modeller’s propensity to assume something corny in order to make the model do their bidding. One school assumes “well mixed” while its class clown decides to countermand the principles behind partial pressures. Hocus-pocus, tiddly-okus, next it’ll be a plague of locusts.
“Calculating” to 4.16 or 1.33 years indicates a remarkable of “accuracy” 3.65 days residence time for “some” CO2. The oceans do NOT absorb CO2 from the atmosphere. The oceans have “vast pools of liquid CO2 on the ocean floors” which keep constant supply of dissolved CO2 and other elemental gases in the water column ready to disperse. See Timothy Casey’s excellent “Volcanic CO2” posted at http://geologist-1011.net While there visit the “Tyndall 1861” actual experiment with Casey’s endnotes and the original translation of Fourier on greenhouse effect. Reality is different than the forced orthodoxy.
The average time molecules remain in the atmophere as a gas is probably a matter of hours. Think how fast a power plant plume vanishes to a global background level. Think about how clouds absorb and transport CO2. It is the different lengths of reservoir changing cycles that is changing the amount of gaseous CO2 we measure in the atmosphere. I have evidence that most of anthropogenic emissions cycle through the environment in about ten years and, at present, contribute less than 10% to atmospheric levels. Click on my name for details.
I’m way out of my depth here, but The Hockey Schtick wrote about The Bern Model with advice from “Dr Tom V. Segalstad, PhD, Associate Professor of Resource and Environmental Geology, The University of Oslo, Norway, who is a world expert on this matter.”
http://hockeyschtick.blogspot.co.uk/2010/03/co2-lifetime-which-do-you-believe.html
Imagine you have three tanks full of water: A, B, and C. A and B are connected with a large pipe. A and C are connected with a narrow pipe. The water levels start off equal.
We dump a load of water into tank A. Quite quickly, the levels in tanks A and B equalise, A falling and B rising. But the level in tank C rises only very slowly. Tank A drops quickly to match B, but then continues to drop far more slowly until it matches C.
Dumping an extra load in A while this is going on would again lead to another fast drop while it matched B again. It ‘knows’ which is which because of the amount in tank B.
I gather the BERN model is more complicated, and the parameters listed are an ansatz obtained by curve-fitting a sum of exponentials to the results of simulation. But I think the choice of a sum of exponentials to represent it is based on the intuition of multiple buffers, like the tanks.
John Daly wrote some stuff about this – I haven’t worked my way through it, so I can’t comment on validity, but I thought you might be interested.
http://www.john-daly.com/dietze/cmodcalc.htm
“Partitioning” is trivial
The simple case of a single exponent corresponds to a first-order linear equiation, but this does not describe the complex nature.
CO2 evolves according to a higher-order linear equation (or a system of first-order linear equations that is the same). Very reasonable. That is where the “partitioning” comes,
You write down these quations and look for eigenmodes. These are the exponents. IPCC effectively claims, there are 6 first order equations or a single 6th order linear equation. OK, no objection, although there can be even more eigenmodes, but let us assume these are the major 6.
Now, the general solution is a sum of these exponents with ARBITRARY pre-factors at each exponent. How to define these pre-factors?
The pre-factors are defined by the initial conditions: the particular CO2-level and 5 (6-1) derivatives (!). IPCC claims, these are 14%, 13%, 19%, 25%, 21%, and 8%. What does it mean?
Effectively IPCC claims to know the 5th derivative of CO2 population down to 1% accuracy level!!!
Sorry, as a physicist I cannot buy such accuracy in derivatives of an experimental value.
Two words… Occam’s Razor
CO2 is determined by climatic factors. Temperature-independent CO2 fluxes into/out of the atmosphere (especially minor ones like the human input) are compensated by the system (oceans).
If we could magically remove 100 ppm of the CO2 from the atmosphere in one day, what would be the transient system response (after 10 days, 1 month, a year…)?
Forgot smth to add.
IPCC claims to Bern model to find out these “prefactors” in simulations with a “CO2-impulse”.
The point is, the linear exponential solutions are valid only in the vicinity of an equilibrium. This means, IPCC must use an infinitesimal CO2-impulse to define the system response.
What does IPCC instead?
They assume the “CO2-impulse” being an instantaneous combustion of ALL POSSIBLE FOSSILE FUELS.
The response is in no way linear then and the results are just crap.
They even introduce some model for “temperature increase” due to higher CO2. The higher temperature means there is less absorption of CO2 by oceans etc…
This is not a science, but a clear misuse of it.
The idea CO2 is partitioned in any way sounds like complete bull to me – CO2 is quickly well mixed in the atmosphere. But its possible some CO2 sinks could be diminishing, that might help explain some of the increase in atmospheric concentration (plus as others have pointed out higher temperatures mean less absorption by the oceans).
I don’t think any discussion of the carbon cycle should be without mention of Salby’s work, if you haven’t seen it:
http://youtu.be/YrI03ts–9I
[REPLY: It was discussed here on April 19. -REP]
The basic assumption of this model seems to be that there is some “perfect” amount of CO2 that the earth tries to return to. Otherwise, if adding CO2 causes it to slowly go away, we should have no CO2 now, right? Thus, they must believe that it does down to this “perfect” amount and just stays there. Why does it stop diminishing? What mechanism could cause it to do so? For that matter, what mechanism would cause it to try and return to some “perfect” amount?
If CO2 goes down to this “perfect” amount and just stays there, CO2 over time should mostly be at that level all throughout history, is it? In fact, it goes up and down all the time, why is that? In fact, even in recent history it has gone up and down, that being the case, how can we even vaguely estimate how fast it will do so, much to the accuracy they claim here. In fact, since we know that CO2 goes up and down, if it does go down over time, we should be able to tell over a long enough time period how fast it goes down on average.Since we do have records of CO2 in the past, we should be able to compare this idea to the real world, and if what they are saying is true, that it goes down steadily over time (despite the actual records that say it does not), should we not be able to check this real world record against this model? Has it been checked? If it has not been checked, is this science? If it has not been checked, this model is fiction.
Also, their idea is that if CO2 increases, it then decreases, well, where does it go? The only place it can go is into the ground as oil, coal, natural gas, etc. This if we burn these, we are merely returning to the atmosphere what came from the atmosphere. This should return to the atmosphere what they claim here is being steadily removed. We need to keep doing this, otherwise we will run completely out of CO2, right? If this is not true, they need to demonstrate that CO2 will go down to this mythical “perfect” amount and just stays there.
Also, if CO2 is decreasing all the time, as they claim, yet it goes up and down over time (and note that the world does not end when it does), then something must be adding it, what, and is it enough to keep us from running out completely? Since we know that in the distant past there was far more CO2 (yet life flourished, go figure), yet now it is near to the level where all life on earth will die, we cannot rely on whatever natural processes add CO2 to bring it back up, since it obviously is not working, CO2 is dangerously low. We need to invent a way to return the CO2 back to the atmosphere. Occording to the IPCC, we have, now they are trying to stop us from doing what this model claims we must do to survive.
Once you understand the logical underlying assumption of this, that there must be a “perfect” level of CO2 that the earth tries to return to, the actual logic is:
The history of the earth shows that there is no perfect amount of CO2 that the earth tries to return to.
We the IPCC however, say that there is.
We say that because we wish it to be so.
We wish it to be so because if it is true, we can tax you and regulate you if it is not perfect.
We are the only authority on when it is perfect.
Ignore that real world behind the curtain!
Peter Huber used to make the controversial claim that North America is a carbon sink, based on a 1998 article in Science. This was based on prevailing winds blowing from West to East, with higher concentrtions of CO2 found on the West coast than the East. Later papers doing carbon inventories have disputed this. Huber responded that there was plenty of ways to miss inventory. Whoever is right, Huber makes a good case that the US does a better job than the rest of the world of replacing farmland with trees.
Isn’t just like a bunch of resistors in parallel? 1/R =1/r1+1/r2+1/r3…..
FTA: “Anyhow, that’s my problem with the Bern model—I can’t figure out how it is supposed to work physically.”
It is because the process of CO2 sequestration is not solved by an ordinary differential equation in time, but by a partial derivative diffusion equation. It has to do with the frequency of CO2 molecules coming into contact with absorbing reservoirs (a.k.a. sinks). If the atmospheric concentration is large, then molecules are snatched from the air frequently. If it is smaller, then it is more likely for an individual molecule to just bob and weave around in the atmosphere for a long time without coming into contact with the surface.
This gives rise to a so-called “fat-tail” response. Such a fat-tail response can be approximated as a sum of exponential responses with discrete time constants.
I am not, of course, advocating the Bern model parameters. The modeling process is reasonable and justifiable, but the parameterization is basically pulled out of a hat.
What we actually see in the data is that CO2 rate of change is effectively modulated by the difference in global temperatures relative to a particular baseline. What is more likely? That CO2 rate of accumulation responds to temperatures, or that temperatures respond to the rate of change of CO2? The latter would require that temperatures be independent of the actual level of CO2, which is clearly not correct. Hence, we must conclude that CO2 is responding to temperature, and not the other way around.
In case anyone misses the point, let me spell the implications out clearly: fat tail or no, the response time for sequestering the majority of anthropogenic CO2 emissions is relatively short, and the system is having no trouble handling it. CO2 levels are being dictated by temperatures, by nature, not by humans.
Interesting Willis. The problem reminds me of pharmacokinetics where the fate of drugs/toxins in the body are studied; wish I knew enough about pk to be more specific unfortunately it was only ancillary to my field of study. Any toxicologists around?
Thanks. I thought I was the only one that didn’t believe this fallacy.
The fast processes will finish with it’s CO2 then go after the next batch !
The alarmists just want an excuse to say CO2 remains in the atmosphere for 100 years which is can’t possibly do.
The different timings are only relevent for the first 376.1 years of the model after that they are totally irrelevant as all sinks will be working. In fact in the real world they will be totally irelevant as all the sinks will be working all of the time. It just padding for the report to make it look more technical.
CO2 works like resistors in parallel.
1/RT=1/R1 + 1/R2+1/R3
So the total resistance can’t be more than the smallest resistor.
for CO2 the 1/2 life of the total can’t be greater than the 1/2 life which is shortest.
The Bern Model needs to introduced to the Law of Entropy (diffusion of any element or compound within a gas or liquid to equal distribution densities). And it should also be introduced to osmosis and other biological mechanisms for absorbing elements and compounds across membranes.
In fact, it seems to need a serious dose of reality
Bart says:
May 6, 2012 at 11:51 am
I want to repeat this part of my post, because people may miss it in with the other stuff, and I think it is important.
What we actually see in the data is that CO2 rate of change is effectively modulated by the difference in global temperatures relative to a particular baseline.
What is more likely? That CO2 rate of accumulation responds to temperatures, or that temperatures respond to the rate of change of CO2? The latter would require that temperatures be independent of the actual level of CO2, which is clearly not correct. Hence, we must conclude that CO2 is responding to temperature, and not the other way around.
In case anyone misses the point, let me spell the implications out clearly: fat tail or no, the response time for sequestering the majority of anthropogenic CO2 emissions is relatively short, and the system is having no trouble handling it. CO2 levels are being dictated by temperatures, by nature, not by humans.
Bart says:
May 6, 2012 at 11:51 am
Thanks, Bart. That all sounds reasonable, but I still don’t understand the physics of it. What you have described is the normal process of exponential decay, where the amount of the decay is proportional to the amount of the imbalance.
What I don’t get is what causes the fast sequestration processes to stop sequestering, and to not sequester anything for the majority of the 371.6 years … and your explanation doesn’t explain that.
w.
Surely they don’t serious use the sum of five or six exponentials, Willis. Nobody could be that dumb. The correct ordinary differential equation for CO_2 concentration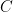 , one that assumes no sources and that the sinks are simple linear sinks that will continue to scavenge CO_2 until it is all gone (so that the “equilibrium concentration” in the absence of sources is zero (neither is true, but it is pretty easy to write a better ODE) is:
, one that assumes no sources and that the sinks are simple linear sinks that will continue to scavenge CO_2 until it is all gone (so that the “equilibrium concentration” in the absence of sources is zero (neither is true, but it is pretty easy to write a better ODE) is:

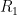 is the rate at which the ocean takes up CO_2. Left to its own devices and with only an oceanic sink, we would have:
is the rate at which the ocean takes up CO_2. Left to its own devices and with only an oceanic sink, we would have:
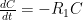
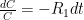
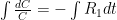
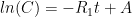
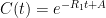
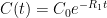
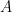 is the constant of integration. I mean, this is first year calculus. I do this in my sleep. The inverse of $R_1$ is the exponential decay constant, the time required for the original CO_2 level to decay to
is the constant of integration. I mean, this is first year calculus. I do this in my sleep. The inverse of $R_1$ is the exponential decay constant, the time required for the original CO_2 level to decay to 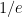 of its original value (for any original value
of its original value (for any original value 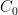 ). If there are two processes running in parallel, the rate for each is independent — if (say) trees remove CO_2 at rate $R_2$, that process doesn’t know anything about the existence of oceans and vice versa, and both remove CO_2 at a rate proportional to the concentration in the actual atmosphere that runs over the sea surface or leaf surface respectively. The same diffusion that causes CO_2 to have the same concentration from the top of the atmosphere to the bottom causes it to have the same concentration over the oceans or over the forests, certainly to within a hair. So both running together result in:
). If there are two processes running in parallel, the rate for each is independent — if (say) trees remove CO_2 at rate $R_2$, that process doesn’t know anything about the existence of oceans and vice versa, and both remove CO_2 at a rate proportional to the concentration in the actual atmosphere that runs over the sea surface or leaf surface respectively. The same diffusion that causes CO_2 to have the same concentration from the top of the atmosphere to the bottom causes it to have the same concentration over the oceans or over the forests, certainly to within a hair. So both running together result in:
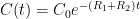
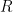 , the exponential time constant is 1/5 of what it would be for one of them alone. This is not rocket science.
, the exponential time constant is 1/5 of what it would be for one of them alone. This is not rocket science.
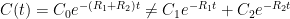
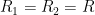 ,
, 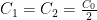 :
:
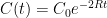
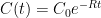
Interpretation: Since CO_2 doesn’t come with a label, EACH process of removal is independent and stochastic and depends only on the net atmospheric CO_2 concentration. Suppose
where
If (say) trees and the ocean both remove CO_2 at the same independent rate, the two together remove it at twice the rate of either alone, so that the exponential time constant is 1/2 what it would have been for either alone. If there are five such independent sinks (where by independent I mean independent chemical processes), all with equal rate constants
This is completely, horribly different from what you describe above. To put it bluntly:
Compare this when
(correct) versus
(incorrect). The latter has exactly twice the correct decay time, and makes no physical sense whatsoever given a global pool of CO_2 without a label. The person that put together such a model for CO_2 — if your description is correct — is a complete and total idiot.
Note that this would not be the case if one were looking at two different processes that operated on two different molecular species. If one had one process that removed CO_2 and one that removed O_3, then the rate at which one lowered the “total concentration of CO_2 + O_3” would be a sum of independent exponentials, because each would act only on the partial pressure/concentration of the one species. However, using a sum of exponentials for independent chemical pathways depleting a shared common resource is simply wrong. Wrong in a way that makes me very seriously doubt the mathematical competence of whoever wrote it. Really, really wrong. Failing introductory calculus wrong. Wrong, wrong, wrong.
(Dear Anthony or moderator — I PRAY that I got all of the latex above right, but it is impossible to change if I didn’t. Please try to fix it for me if it looks bizarre.)
rgb
Nullius in Verba says:
May 6, 2012 at 11:19 am (Edit)
My thanks for your explanation. That was my first thought too, Nullius. But for it to work that way, we have to assume that the sinks become “full”, just like your tank “B” gets full, and thus everything must go to tank “C”.
However, since the various CO2 sinks have continued to operate year after year, and they show no sign of becoming saturated, that’s clearly not the case.
So what we have is more like a tank “A” full of water. It has two pipes coming out the bottom, a large pipe and a narrow pipe.
Now, the flow out of the pipe is a function of the depth of water in the tank, so we get exponential decay, just as with CO2.
But what they are claiming is that not all of the water runs out of the big pipe, only a certain percentage. And after that percentage has run out, the remaining percentage only drains out of the small pipe, over a very long time … and that is the part that seems physically impossible to me.
I’ve searched high and low for the answer to this question, and have found nothing.
w.
What about rain water, which, in its passage through the air dissolves many of the soluble gases e.g. CO2 present in the atmosphere, and which as part of ‘river waters’ eventually makes its way into the oceans?
River and Rain Chemistry
Book: “Biogeochemistry of Inland Waters” – Dissolved Gases
.
“The IPCC, using the Bern Model, says that the e-folding time ranges from 50 to 200 years.”
**********************
Strikes me as a pretty wide ranging estimate. More like a ‘WAG’.
I file this Bern Model under “more BAF (Bovine Academic Flatulence)”.
The physiology of scuba diving divides body tissues into different categories, with different “half-lives”, or nitrogen abosrption rates. Some tissues absorb, and release Nitrogen rapidly, others more slowly; they are given different diffusion coefficients.
Nitrogen absorbed in your tissues in diving is the cause of the bends.
Maybe the Bern Conspiracy is thinking that some absorption mechanisms operate at different rates others. How fast do forests absorb CO2 compared to oceans? etc. Perhaps that is what they are thinking.
mfo says:
May 6, 2012 at 11:19 am
mfo, take a re-read of my appendix above. The author of the hockeyschtick article is conflating the residence time and the e-folding time. As a result, he sees one person saying four years or so for residence time, and another person saying 50 to 200 years for e-folding time, and thinks that there is a contradiction. In fact, they are talking about two totally separate and distinct measurements, residence time and e-folding time.
w.
Willis Eschenbach says:
May 6, 2012 at 12:07 pm
“What I don’t get is what causes the fast sequestration processes to stop sequestering, and to not sequester anything for the majority of the 371.6 years … and your explanation doesn’t explain that.”
The best I can tell you is what I stated:”It has to do with the frequency of CO2 molecules coming into contact with absorbing reservoirs (a.k.a. sinks). If the atmospheric concentration is large, then molecules are snatched from the air frequently. If it is smaller, then it is more likely for an individual molecule to just bob and weave around in the atmosphere for a long time without coming into contact with the surface.” The link I gave explains it from a mathematical viewpoint.
rgbatduke says:
May 6, 2012 at 12:12 pm
“The correct ordinary differential equation…”
It’s a PDE, not an ODE. See comment at May 6, 2012 at 11:51 am.
About 1/2 of the annual human emission are absorbed each year. If they weren’t the growth in CO2 as a % of total would be growing, which it isn’t.
Assuming an exponential rate of uptake, we have a series something like this:
1/2 = 1/4 + 1/8 + /16 + 1/32 ….
With each year absorbing 1/2 of the residual of the previous, to match the rate of the total.
ie: R = R^2 + R^3 + R^4 … R^n , where 0 < R infinity.
What this means is that tau is 2 years. 1/4 + 1/8 = 0.25 + 0.125.= 0.375 = approx 1/e
The mathematical and physical ability of climate scientists appears to be very poor.
The worst case is the assumption by Houghton in 1986 that a gas in Local Thermodynamic Equilibrium is a black body. This in turn implies that the Earth’s surface, in radiative equilibrium, is also a black body, hence the 2009 Trenberth et. al. energy budget claiming 396 W/m^2 IR radiation from the earth when the reality is presumably 63 of which 23 is absorbed by the atmosphere.
The source of this humongous mistake is here: http://books.google.co.uk/books?id=K9wGHim2DXwC&pg=PA11&lpg=PA11&dq=houghton+schwarzschild&source=bl&ots=uf0NxopE_H&sig=8vlpyQINiMyH-IpQrWJF1w21LQU&hl=en&sa=X&ei=6Z2mT7XyO-Od0AWX3LGTBA&ved=0CGMQ6AEwBA#v=onepage&q&f=false
Here is the [good] Wiki write-up: http://en.wikipedia.org/wiki/Thermodynamic_equilibrium
‘In a radiating gas, the photons being emitted and absorbed by the gas need not be in thermodynamic equilibrium with each other or with the massive particles of the gas in order for LTE to exist….. If energies of the molecules located near a given point are observed, they will be distributed according to the Maxwell-Boltzmann distribution for a certain temperature.’
So, the IR absorption in the atmosphere has been exaggerated by 15.5 times. The carbon sequestration part is no surprise; these people are totally out of their depth so haven’t fixed the 4 major scientific errors in the models.
And then they argue that because they measure ‘back radiation’ by pyrgeometers, it’s real They have even cocked this up: a radiometer has a shield behind the detector to stop radiation from the other direction hitting the sensor assembly. So, assuming zero temperature gradient, the signal they measure is an artefact of the instrument because in real life it’s zero. What is measures is temperature convolved with emissivity, and so long as the radiometer points down the temperature gradient, that imaginary radiation cannot do thermodynamic work!
This subject is really the limit of cooperative failure to do science properly. Even the Nobel prize winner has made a Big Mistake!
I’m not sure of the significance of the e-folding time. I presume it must be related to the rate at which a particular sink absorbs CO2, in which case why not use the absorption time? As for the partitions, I just don’t get it. Surely there must be a logical explanation in the text for the various percentages listed.
ferd berple says:
May 6, 2012 at 12:25 pm
“About 1/2 of the annual human emission are absorbed each year.”
In the IPCC framework, that 1/2 dissolves rapidly into the oceans. So, if you include both the oceans and the atmosphere in your modeling, there is no rapid net sequestration.
I agree with the IPCC on the former. But, I do not agree with them that the collective oceans and atmosphere take a long time to send the CO2 to at least semi-permanent sinks.
Bart says:
May 6, 2012 at 12:21 pm
No, the link you gave explains simple exponential decay from a mathematical viewpoint, which tells us nothing about the Bern model.
w.
Willis said: What I don’t get is what causes the fast sequestration processes to stop sequestering, and to not sequester anything for the majority of the 371.6 years … and your explanation doesn’t explain that.
================================
Either there are five different types of CO2…..or CO2 is not well mixed at all……or each “tau” has a low threshold cut off point
The only things that can have a low threshold cutoff point are biology
Cos the other sinks are fully saturated, or already absorbing all they can, so they leave the rest behind for the other longer sinks – then they can claim the natural sinks are saturated and we are evil despite it making no sense. Its all based on the assumption that before 1850 co2 levels were constant and everything lived in a perfect state of equilibirum just on the very the systems absorbtion capacity. Ahhh the world of climate science!
I must step away, so apologies if anyone has a question or challenge to anything I have written. Will check the thread later.
All I’ve got time for today is: Here we go again …
Welcome to the ‘troop’ which denies the measurable EM-nature of bipolar gaseous molecules, e.g. is studied in the field of IR Spectroscopy.
.
The rate of each individual sink is meaningless. What is important is that the total increase each year remains approximately 1/2 of annual emissions. Everything else is simply the good looking girls the magician uses to distract the audience from the sleight of hand.
As Willis points out, the thermos cannot know if the contents are hot or cold. Similarly, the sinks cannot know how long the CO2 has been in the atmosphere, so you cannot have differential rates depending on the age of the CO2 in the atmosphere.
1/2 the increased CO2 is absorbed each year. therefore 1/2 the residue must also be absorbed year to year. The sinks cannot tell if it is new CO2 or old CO2.
What are the mechanisms for removing CO2 from the atmosphere?
1. Asorbsion at the surface of seas and lakes
2, Absorbsion by plants through their leaves
3, Washed out by rain.
Any others?
What is the split in magnitude between these methods because I’d expect some sort of equilibrium for each of 1 & 2 whereas 3 seems to be one way.
Every year this lady named Mother Nature adds a whole lot of CO2 to the atmosphere, and every year she takes out a whole lot. The amount she adds in a given year is only loosely correlated with the amount she takes out, if at all. Year after year we add a little more CO2 to the atmosphere, still only around 4% of the average amount MN does. There is no basis for contending that the amount we add is responsible for what may or may not be an increased concentration with respect to recent history. All we know is that CO2 frozen in ice averages around 280 ppm, but this is definitely an average value as the ice can take hundreds of years to seal off. The only numbers in this entire discussion that have a basis in fact are 220 gT in and out, and an average four year residence time. All else is speculation/conjecture/WAG.
Occam’s Razor rules as always.
Bart says:
May 6, 2012 at 12:32 pm
In the IPCC framework, that 1/2 dissolves rapidly into the oceans.
Nonsense. The oceans cannot tell if that 1/2 comes from this year or last year. If the oceans rapidly absorb 1/2 of the CO2 produced this year, then they must also rapidly absorb 1/2 the remaining CO2 from last year in this year. And so on and so on, for each of the past years.
The ocean cannot tell when the CO2 was produced, so it cannot have a different rate for this years CO2 as compared to CO2 remaining from any other year.
rgbatduke says:
May 6, 2012 at 12:12 pm
Thanks, Robert, your contributions are always welcome. Unfortunately, that is exactly what they do, with the additional (and to my mind completely non-physical) restriction that each of the exponential decays only applies to a certain percentage of the atmospheric CO2. Take a look at the link I gave above, it lays out the math.
Your derivation above is the same one that I use for the normal addition of exponential decays. I collapse them all into the equivalent single decay with the appropriate time constant tau.
But they say that’s not happening. They say each decay operates only and solely on a given percentage of the CO2 … that’s the part that I can’t understand, the part that seems physically impossible.
w.
_Jim says:
May 6, 2012 at 12:35 pm
_Jim and Mydogs, please, this thread is about CO2 sequestration and the Bern Model. Please take the blackbody discussion to some other more appropriate thread.
Thanks,
w.
ferd berple says:
Your comment is awaiting moderation.
May 6, 2012 at 12:39 pm
Bart says:
May 6, 2012 at 12:32 pm
In the IPCC framework, that 1/2 dissolves rapidly into the oceans.
ps: when I said “nonsense” I was referring only to the IPCC framework or any other mechanism that suggests different absorption rates based on the age of the CO2 in the atmosphere.
Willis Eschenbach says:
May 6, 2012 at 12:33 pm
“No, the link you gave explains simple exponential decay from a mathematical viewpoint, which tells us nothing about the Bern model.”
No, that’s not what it explains at all. It is a statistical model in which the probability distribution is exponential, to be used in finding a solution of the Fokker-Planck equation. The “decay” he shows is actually 1/(1+a*sqrt(t)), the reciprocal of 1 plus a constant time the square root of time.
Sorry I cannot explain it better right now. Must go.
son of mulder asks:
“Any others?”
There is overwhelming evidence that the biosphere is expanding due to the increase in CO2. There is no doubt about that. Therefore, it is not in ‘equilibrium’. As ferd berple points out, more of the increase is absorbed every year.
In addition, the oceans contain an enormous quantity of calcium, which is utilized by biological processes to form protective shells for organisms. Those organisms require CO2. With more CO2 available, those organisms rapidly proliferate. When they die, they sink to the ocean floor, thus permanently removing CO2 from the atmosphere.
The planet is greening due to the added CO2, which is completely harmless at current and future concentrations. If CO2 increases from 0.00039 of the atmosphere to 0.00056 of the atmosphere, it is still a very minor trace gas. At such low concentrations plants are the only thing that will notice the change. And any incidental warming will be minor, and welcome.
I am particularly intrigued by the 17.01 year figure, I had no idea climate science was so precise.
son of mulder says:
May 6, 2012 at 12:36 pm
Any others?
================
bacteria…..the entire planet is one big biological filter
They are the most abundant…………..or we wouldn’t be here
Willis Eschenbach – “However, there is nothing that I know of that allows us to establish any of those numbers. Once again, it seems to me that the authors are just picking parameters.”
I would point out a very important part of the link you referenced (http://unfccc.int/resource/brazil/carbon.html):
“All IRFs are obtained by running the Bern model (HILDA and 4-box biosphere) as used in SAR or the Bern CC model (HILDA and LPJ-DGVM) as used in the TAR.” – (IRF’s -> impulse response functions, time factors, and final percentages)
The percentages you quoted are the resulting partial absorptions of various climate compartments resulting from running the Bern model, which is described in Siegenthaler and Joos 1992 (http://tellusb.net/index.php/tellusb/article/viewFile/15441/17291). In short, those percentages are results, not the inputs, of running the Bern model – presented by Joos et al for use by other investigators if they wish to apply the Bern model to their calculations.
Also note the statement that “Parties are free to use a more elaborate carbon cycle model if they choose.” Again – the results of the Bern model were offered as an available computational tool for further work.
I hate to say this, but you give the impression you did not fully read the UN reference (with percentages) that you opened the discussion with…
“My thanks for your explanation. That was my first thought too, Nullius. But for it to work that way, we have to assume that the sinks become “full”, just like your tank “B” gets full, and thus everything must go to tank “C”.”
That’s where I was going with the following paragraph. The buffer ‘tank B’ doesn’t stop absorbing because it’s full, it stops absorbing because the levels equalise. If you keep pouring water into tank A continuously, the water level keeps going up in B continuously. The tanks have infinite capacity, but the ratios of their capacities are much smaller.
The partitioning is the equivalent of the ratio of surface areas in each tank. If A and B are of equal size, then half the water in A flows into B and half stays where it is. If B is a lot bigger than A, then the level in A drops more and the level in B only rises a tiny amount heightwise, although the changes in volume are the same. The atmospheric analogy to surface area is the derivative of buffer content with respect to concentration.
I just went through that post with Salby video (didn’t have time before). Amazing that people still misunderstand the natural CO2-rise argument (like by Salby). Again:
The rise in the atmospheric CO2 is caused by warming climatic factors. The source is anthropogenic CO2, because it’s available in the atmosphere, but the cause is the warmth. Without anthropogenic CO2, oceans would have to release the necessary CO2 to achieve the climatically driven atmospheric CO2.
rgbatduke says:
May 6, 2012 at 12:12 pm
Robert, if I understand you correctly, I can’t tell you how happy I am to see you write this. That was my first response when I read the linked description of the Bern Model, it made my head explode. Unfortunately, I didn’t (and don’t) have your familiarity with the underlying math, so I had to set up some separate sample exponential decay streams in Excel, combine them, and then calculate iteratively the joint time constant … all of which very clumsily lead me to the conclusion that you established with a few lines of math …
Since I did that, which was maybe five years ago, I’ve questioned it and people have given vague handwaving explanations for something that I, like you, consider to be “wrong, wrong, wrong” and without any physical justification.
w.
Willis, with all due respect, that is ALL I had (and have) time for; I have to ‘be somewhere’ shortly. Thanks. I ‘capeesh’/capisce/’savvy’ the expressed desire to stick-to-the-issue-presently-being-debated, too. Good luck with your present efforts, and with that I gotta run … 73’s
.
CO2 started increasing about 1750. Human emissions of CO2 more-or-less started at that time as well. Here is a chart of Human Emissions in CO2 ppm versus the amount of CO2 that actually stayed in the air each year (the airborne fraction – about 50%) since 1750.
http://img163.imageshack.us/img163/9917/co2emissandcon1750.png
Global CO2 levels only increased 1.94 ppm last year (to 390.45 ppm – a little lower than expected) while human emissions continued increasing to about 9.8 billion tonnes Carbon (about 4.6 percentage points of CO2).
The natural sinks of CO2 have been increasing gradually over time so that they are now over 224 billion tons Carbon versus 220 billion tons in 1750. (the actual natural sinks and sources level might be closer to 260 billion tons going by some recent estimates of plant take-up but none-the-less).
http://img233.imageshack.us/img233/1323/carbonnatsinks1750.png
The amount that the natural sinks absorb each year seems to be directly related to the concentration in the atmosphere. There is an equilibrium level of CO2 at about 275 ppm in non-ice-age conditions (this is the level it has been at for the past 24 million years).
So the natural sinks and sources are in equilbrium (give or take) when the CO2 level is 275 ppm or the Carbon level in the atmosphere is 569 billion tonnes.
The rise of the natural sinks over the past 250 years indicate the sinks will absorb down or sequester about 1.0% per year of the excess over this 569 billion tons or 275 ppm.
The last 65 years have been very close to the 1.0% level. It doesn’t matter how much we add each year. The plants and oceans and soils will respond to how much is in the air, not how much we add. And it is about 1.0% of the excess Carbon in the amtosphere each year – Bern model or no.
http://img580.imageshack.us/img580/521/co2absor17502011.png
It will take about 150 years to draw down CO2 to the equilibrium of 275 ppm if we stop adding to the atmosphere each year. Alternatively, we can stabilize the level just by cutting our emissions by 50%.
To attempt to clarify what I wrote in my previous post (http://wattsupwiththat.com/2012/05/06/the-bern-model-puzzle/#comment-978032):
The exponentials, percentages, and time factors in the link Willis Eschenbach provided are approximations that reproduce the results of running the Bern model – much as 3.7 W/m^2 direct forcing per doubling of CO2 is the approximation of running radiative code such as MODTRAN, allowing quick calculations without having to run the model over and over again. I.e., the percentages and time factors are shorthand for the model.
As Joos stated in that link (http://unfccc.int/resource/brazil/carbon.html), the Bern model approximations were offered as a tool for use by others, and “Parties are free to use a more elaborate carbon cycle model if they choose.”
OK, I’ve looked at the model details via the provided link. They are frigging insane. I mean seriously, one should just take the article’s provided advice and ‘use a more complex model’ if we like. I like. Here is a very simple linear model. Still too simple, but at least I can justify its structure:
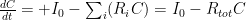
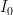 , that is completely independent of the concentration
, that is completely independent of the concentration 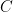 . Because the atmosphere is vast, the percentage of CO_2 in the atmosphere can be considered to be the amount of CO_2 added divided into the total where the latter basically does not vary, hence I don’t need to work harder and write an ODE that saturates at 100% CO_2 — we are in the linear growth regime of a saturating exponential and I can assume assume that the concentration increases linearly at a constant rate independent of how much is already there (true until a significant fraction of the atmosphere is CO_2, utterly true when 400 ppm is CO_2).
. Because the atmosphere is vast, the percentage of CO_2 in the atmosphere can be considered to be the amount of CO_2 added divided into the total where the latter basically does not vary, hence I don’t need to work harder and write an ODE that saturates at 100% CO_2 — we are in the linear growth regime of a saturating exponential and I can assume assume that the concentration increases linearly at a constant rate independent of how much is already there (true until a significant fraction of the atmosphere is CO_2, utterly true when 400 ppm is CO_2).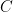 .
. 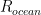 and
and 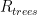 are themselves directly proportional to (or more generally dependent on) other sensible quantities — we might expect the former to be proportional to the total surface area of the ocean for example, or to be related to some function of its area, its local temperature, and the concentration of CO_2 in the water already (which MIGHT vary appreciably geographically, as seawater is not well-mixed and it has its own sources and sinks). We might expect the latter to be dependent on the total surface area of CO_2 scavenging tree leaves, or more simply to total acreage of trees, again leaving open a more complex model that couples in the further modulation by water availability, hours of sunlight, and so on. Still, averaging over these latter probably makes this simple model already pretty reasonable.
are themselves directly proportional to (or more generally dependent on) other sensible quantities — we might expect the former to be proportional to the total surface area of the ocean for example, or to be related to some function of its area, its local temperature, and the concentration of CO_2 in the water already (which MIGHT vary appreciably geographically, as seawater is not well-mixed and it has its own sources and sinks). We might expect the latter to be dependent on the total surface area of CO_2 scavenging tree leaves, or more simply to total acreage of trees, again leaving open a more complex model that couples in the further modulation by water availability, hours of sunlight, and so on. Still, averaging over these latter probably makes this simple model already pretty reasonable.
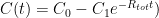
 and where
and where 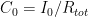 is the steady state concentration one arrives at eventually from any starting concentration, as long as
is the steady state concentration one arrives at eventually from any starting concentration, as long as  (see linearization requirement above).
(see linearization requirement above).  is a constant of integration used to set the initial conditions. If you started from no CO_2 in the air at all, you would make
is a constant of integration used to set the initial conditions. If you started from no CO_2 in the air at all, you would make  so that
so that 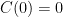 . We don't start from zero, so we have to choose it such that
. We don't start from zero, so we have to choose it such that 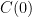 comes out right. At the steady state concentration, the sinks remove CO_2 at the rate
comes out right. At the steady state concentration, the sinks remove CO_2 at the rate 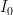 , balancing the sources.
, balancing the sources. and one approaches it exponentially with time constant
and one approaches it exponentially with time constant 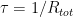 — you can’t get much simpler than that. In fact, if you know
— you can’t get much simpler than that. In fact, if you know 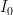 and can measure
and can measure  one can is done, no need for complex integrals over sums of exponential sinks times a source rate (what the hell does that even MEAN).
one can is done, no need for complex integrals over sums of exponential sinks times a source rate (what the hell does that even MEAN).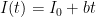 for example, describing source production that is increasing linearly in time, or
for example, describing source production that is increasing linearly in time, or  , a model that assumes source production is itself increasing towards an eventual peak at some rate with exponential time constant
, a model that assumes source production is itself increasing towards an eventual peak at some rate with exponential time constant  . The former suffers from the flaw that it increases without bound. The latter is probably not terrible, but I’m guessing CO_2 sources are bursty and that this equation is a pretty crude approximation of the industrial revolution and eventual saturation of production/sources. Both suffer from the fact that CO_2 production might depend on the concentration
. The former suffers from the flaw that it increases without bound. The latter is probably not terrible, but I’m guessing CO_2 sources are bursty and that this equation is a pretty crude approximation of the industrial revolution and eventual saturation of production/sources. Both suffer from the fact that CO_2 production might depend on the concentration  — although these production mechanisms can probably be handled with negative
— although these production mechanisms can probably be handled with negative  .
. depends on the temperature! A warming ocean can be a CO_2 source (or a heavily reduced sink as its uptake is reduced). A cooling ocean can sequester more CO_2, faster. But even this is too simple because part of the eventual sequestration involves chemistry and biology that depend on temperature, sunlight, animals activity, ocean currents and nutrients… so it is with all of the rates. They themselves might be — indeed, almost certainly are — functions of time!
depends on the temperature! A warming ocean can be a CO_2 source (or a heavily reduced sink as its uptake is reduced). A cooling ocean can sequester more CO_2, faster. But even this is too simple because part of the eventual sequestration involves chemistry and biology that depend on temperature, sunlight, animals activity, ocean currents and nutrients… so it is with all of the rates. They themselves might be — indeed, almost certainly are — functions of time!
Interpretation: We make CO_2 at some rate,
However, CO_2 is removed from the atmosphere by processes that literally have a probability of removing a CO_2 molecule per unit time, given the presence of a molecule to remove. They are all proportional to the concentration. If I double the concentration, I present twice as many molecules per second to the e.g. surface of the sea as candidates for adsorption or to the stoma of a leaf as candidates for respiration and conversion into cellulose or sugar or whatever. They are all independent; if some particular wave removes a molecule of CO_2 at 11:37 today, a leaf on a tree in my back yard doesn’t know about it. The removed CO_2 has no label, and the jostling of molecules in the well-mixed warm air guarantees that one cannot even meaningfully deplete the local concentration of CO_2 by this sort of process, so both remain proportional to the same total concentration
The nice thing about this is that it is a well-known linear first order inhomogeneous ordinary differential equation, and can be directly integrated just as simply as the previous one. The result is (non-calculus people can take my word for it):
where
This simple linear response model shows precisely how one expects the eventual atmospheric concentration of CO_2 to saturate as long as saturation is achieved at low net concentrations of the total atmosphere such that the total relative fractions of N_2 and O_2 were the same and are still much larger than CO_2 taken together. And it is a well known and easily understood one. Equilibrium is
Now as models go this one sucks — it is arguably TOO simple, but it is easy to fix. For example, the ODE is the same if one has a source rate that isn’t constant but is itself a function of time —
A bigger problem is that for the ocean
However, even if we put far more complex differential forms into this ODE, it remains pretty easy to solve without making any sort of formal approximation or decomposition. Matlab lets one program it in and solve it in a matter of minutes, and graph or otherwise present the results at the same time. Writing a parametric form and then fitting the parameters to past data in hope of predicting the future is also possible, although it is a bit dicey as soon as you have a handful of nonlinear parameters because then one is trying to optimize a possibly non-monotonic function on a multidimensional manifold, which is the literal definition of “complex systems” in the Santa Fe institute sense.
Unless you know what you are doing — and few people do — you are likely to start the optimization process out with some set of assumptions and optimize with e.g. a gradient search to find an optimum that “confirms” those assumptions, ignoring the fact that a far better fit is available but is nowhere particularly near your initial guess. In a rough landscape, there might always be local maxima near at hand to get trapped on, and even finding the right neighborhood of the optimal fit can be challenging. Imagine an ant searching for the highest point on the surface of the earth by going up from wherever you drop them. Nearly every point they get dropped on will take them to the top of a grain of sand or a small hill. Only a teensy fraction of the Earth’s surface is mountains, a smaller one big mountains, a handful of mountains the highest peaks in a range, and one range the right range, one mountain the right mountain, one small area of slopes the right SLOPE, ones, that go straight on up to the top without being trapped.
There may be some way to formally justify the Bern model. Offhand I can’t see it — integrating E(t) is fine, but integrating it while multiplying it by that bizarre sum of exponential terms? It doesn’t even look like it has the right asymptotic form, implicit saturation. In other words, although it uses time constants, the time constants aren’t the time constants of a presumed exponential sequestration process that removes CO_2 at a rate proportional to its concentration, they are more like “relaxation times”. The expression looks like an unbounded integral growth in concentration modulated by temporal relaxation times that have nothing to do with concentration but rather describe something else entirely.
Just what is an interesting question, but this is not a sensible sequestration model, which is necessarily at least proportional to concentration. At higher concentrations, plants take up more of it and grow faster. The ocean absorbs more of it (at constant temperature) because more molecules hit the surface per unit time. More of the CO_2 that makes it into the ocean is taken up by algae and bound up, eventually to rain down onto the sea floor, removed from the game for a few hundred million years.
I cannot believe that there isn’t anybody out there in climate-ville that hasn’t worked all this out in a believable model of some sort, something that is a perturbation of the first order linear model I wrote out above. If not, shame on them.
rgb
In relation to sources and sinks, can Willis, or anyone else explain this image of global CO2 concentrations ?
Why don’t warm tropical oceans give high CO2 ?
Why is there a band of high CO2 around the 35S ?
How is the distribution over Africa and S America explained ?
Why does Antarctic ice appear to be such a strong absorber in parts and why such strong striation?
http://www.seos-project.eu/modules/world-of-images/world-of-images-c01-p05.html
Seems this is a mental image issue – like putting the cart in front of the mule. It isn’t the carbon dioxide in the atmosphere that controls the timing. You can buy paints, some are fast-drying. Some dry slowly. Eventually, they all dry. CO2 sinks (hundreds, not 6 or 3) do their thing in their own way, so other things equal (constant CO2 levels), a very slow process might take 371.3 years to sequester a unit of gas, a very fast process might take 1.33 years to do the same. Thus, the numbers (wherever they came from) might have meaning – just not that described. So, one should really call it the Bourne Model insofar as the identity of the processes is a mystery and no one is sure just what is going on.
Well, whatever the Bern model does, it must be correct. After all, once you match the results of 9 GCM models (except one outlier), you have matched them all. CO2 sensitivity was assumed to be 2.5 K to 4.5 K in the models.
” After 80 years, the increase in global average surface temperature is 1.6 K and 2.4 K, respectively. This compares well with the results of nine A/OGCMs (excluding one outlier) which are in the range of 1.5 to 2.7 K”
KR says:
May 6, 2012 at 12:58 pm
Say what?
Look, KR, they used the box model to calculate the IRFs. The part you seem to be missing is that once they have used the box model to calculate the IRFs, then
claiming that the IRFs represent actual physical processes.
Next, you say the IRFs are the “resulting partial absorptions of various climate compartments”. This is similar to what the citation says, that they “reflect the time scales of different sinks”. Both of you are claiming that the IRFs have reflect real-world processes… so could you explain just how it is that the atmosphere is divided into “various climate compartments”, some of which decay quickly and some slowly?
You say ” the results of the Bern model were offered as an available computational tool for further work” … I understand that. What I don’t understand is the physical basis for what they are claiming, which is that e.g. 13% of the airborne CO2 hangs around with an e-folding time of 371.6 years, but is not touched during that time by any of the other sequestration mechanisms.
Perhaps you could explain to us how that works, that certain CO2 molecules are sequestered but some are immune to sequestration for hundreds of years.
I also note that there are no less than four different (and in fact very different) IFTs that have been used by the UN … hardly what one would expect if they actually are the “resulting partial absorptions of various climate compartments”. How are we supposed to pick one of them?
The SAR used five IRFs reflecting, according to you, five “climate compartments”, while the TAR used only three. What happened to two of the “climate compartments” between the SAR and the TAR … the IRFs just disappeared, what happened to the “climate compartments” that you claim they represent? Did they go out of business?
More to the point, why should we believe the model at all? The conclusion of your citation says:
The model calculates CFC-II well, but it misses on CO2. In other words, the model doesn’t work very well, and even the authors don’t understand why their model doesn’t work … not encouraging.
w.
Fascinating stuff, cheers Willis. So instead of trying to capture CO2 underground why not just dump into a high speed sink?
KR says:
May 6, 2012 at 1:19 pm
Both you and the citation I gave have said that the IRFs represent actual physical processes. You said the IRFs represent the “ resulting partial absorptions of various climate compartments”. My citation says that the IRFs “ reflect the time scales of different sinks”
Now you want to claim that this is just a way to approximate the model. Come back when you make up your mind and can explain why the citation is wrong.
w.
PS—See also Robert Brown’s comments above (rgbatduke) …
So … does anyone understand how 13% of the atmospheric CO2 is supposed to hang around for 371.6 years without being sequestered by the faster sinks?
Perhaps you need to look at this the other way around. We have often heard about the 800 year time lag between high temperatures and CO2 concentrations. Is it a coincidence that 371.6 is about half of 800? Is it possible that if the CO2 concentration were to suddenly drop, then various processes would act to raise the CO2? And that the part of the CO2 that is in the deep oceans may take 371.6 years to reach the atmosphere and add 13% to the overall increase in CO2 concentration?
RGB at duke says:
May 6, 2012 at 1:21 pm
…Please try to fix it for me if it looks bizarre.
Here is something bizarre that no one can do much about, let alone fix it.
http://www.vukcevic.talktalk.net/TMC.htm
Dr Burns says:
May 6, 2012 at 1:30 pm
Why does Antarctic ice appear to be such a strong absorber…
Antarctic is simply bizarre, see the link above
They may be discussing on-rate constants only. The concept might be equilibrium and saturation in different reservoirs. The on-rate for a given reservoir is the atmospheric concentration times the rate constant. The off rate is the reservoir concentration times the off-rate constant. If the on-rate equals the off-rate, then the reservoir is at equilibrium. No net uptake would occur.
rate(on) = k(on) * [conc(air)]
rate(of) = k(off) * [conc(res)]
No net uptake occurs when rate(on) = rate(off), that’s equilibrium.
In the real case, you also have a loss rate for CO2 via other routes, e.g. diatom skeletons in the ocean, and leaves or grasses on land. Which means the reservoirs don’t necessarily saturate, and they can continue to take up more CO2. In some cases, the on-rate may depend on the rate of dropout loss in that reservoir since near equilibrium limits the net uptake.
d(CO2 air)/dt = k(off) * [CO2(res)] – k(on) * [CO2(air)]
d(CO2 res)/dt = k(on) * [CO2(air)] – k(off) * [CO2(res)] – k(dropout) * [CO2(res)]
If the reservoir is in dynamic equilibrium, and to a reasonable approximation the reservoir concentration doesn’t change. Then
-k(on) * [CO2(air)] – k(off) * [CO2(res)] = k(dropout) * [CO2(res)] ,
which means both sides of the equation are constant, since CO2(res) doesn’t change.
Since the dropout material doesn’t readily cycle back to the air via the reservoir, it only makes sense when the dropout material can be returned to the atmosphere via another route, e.g. biological digestion, fire, volcanoes, or burning fossil fuel (coal). Returning the dropout material to the atmosphere creates the Carbon cycle we think about.
Partitions in the atmosphere itself make no sense, unless you are silly enough to count flying birds (%P) <- that's an emoticon.
From 1976 to 1997, atmospheric 14CO2 was measured. The levels spiked after due to atmospheric testing of nuclear weapons that ended in the 1960s. These data show the 14CO2 half-life is about 11 years (see raw data here: http://cdiac.ornl.gov/trends/co2/cent-scha.html). In the first approximation, uptake mechanisms won't know the difference between carbon isotopes. It is quite safe to say half of the CO2 in the atmosphere is turned over in about 11.4 years. Five half-lives is about 57 years. That means only about 3% of the CO2 present in the atmosphere 57 years ago is still in the air.
It seems we have an idea of what the dropout rate for CO2 must be, and thus what the replenishment rate must be to keep the atmosphere in roughly steady state. In this simple model, a sudden change in atmospheric CO2 concentration could shift the equilibrium concentration in the reservoirs, and then establish a new constant uptake rate somewhat higher than the old one. If you think about it, perhaps that does make some sense in some cases, such as faster plant growth, or more alkalinty in the ocean (sorry catastrophists, biological action converts carbonic acid to bicarbonate, e.g. by nitrogen fixation).
Yes, models can be misused. It's up to you to decide when they are appropriate.
http://www.seos-project.eu/modules/world-of-images/world-of-images-c01-p05.html
That’s July, two months after annual peak.
Why don’t warm tropical oceans give high CO2 ?
Maybe they do, but you can’t evaluate “vertical” fluxes only on the basis of concentrations in a month (average). The horizontal transport of CO2 in the atmosphere is spatialy and temporarily very dynamic (sesonal). It could also be rain (CO2 scrubbing) in the tropics…
Why is there a band of high CO2 around the 35S ?
High sommer in NH?
How is the distribution over Africa and S America explained ?
Why does Antarctic ice appear to be such a strong absorber in parts and why such strong striation?
Others should speculate. Seasons, moisture, snow, sst, surface altitude, energy budget, mass budget…
Since you like differential equations…
Start with three variables A, B, and C. The volume of flow from A to B is k_AB (A-B), and the volume of flow from A to C is k_AC (A-C).
So
dA/dt = k_AB (B-A) + k_AC (C-A) + E
dB/dt = k_AB (A-B)
dC/dt = k_AC (A-C)
where E is the rate of emission.
Treat L = (A, B, C) as a vector, ignore E for the moment to get dL/dt = ML where M is a matrix of constants. Diagonalise the matrix to get two independent differential equations (the rows of M are not linearly independent), each giving a separate exponential decay with a different time constant. Transforming back to the original variables gives a sum of exponentials.
(I think the two time constants are -k_AB-k_AC +/- Sqrt(k_AB^2-k_AB k_AC +k_AC^2) but I did it quickly.)
Hi _Jim: I did not state that there is no absorption of IR by GHGs. What l add though is that the present IR physics which claims 100% direct thermalisation is wrong and thermalisation is probably indirect at heterogeneous interfaces.
The reason for this is kinetic. Climate Science imagines that the extra quantum of vibrational resonance energy in an excited GHG molecule will decay by dribs and drabs to O2 and N2 over ~1000 collisions so it isn’t re-emitted. This cannot happen: exchange is to another GHG molecule and the principle of Indistinguishability takes over. [See ‘Gibbs’ Paradox’]
This is yet more scientific delusion in that all it needs is the near simultaneous emission of the same energy photon from a an already thermally excited molecule thus restoring LTE. This happens throughout the atmosphere at the speed of light so the GHGs are an energy transfer medium. The conversion to heat probably takes place mainly at clouds.
Frankly I am annoyed because this is the second tome through ignorance you have called me out this way. It’s because i have 40 years’ post PhD experience in applied physics I can show how climate science has been run by amateurs who have completely cocked the subject up. Nothing is right. The modellers are fine though because Manabe and Wetherald were OK, but once Hansen, Trenberth an Houghton took control, the big mistakes happened. it looks deliberate.
Following on from an earlier poster’s comments, the science of decompression diving uses a similar approach to that of the Bern model, to understand the movement of nitrogen into and out of a divers’ body tissues. The approach was pioneered by JS Haldane in 1907. He came up with the idea of using tissue compartments which exchanged nitrogen at different rates. Tissues like blood and nerves were fast, and were able to quickly equilibrate with any changes in the partial pressure of nitrogen. Tissues like muscle and fat were of intermediate speed, while bone was extremely slow. What Haldane did was to come up with a crude multi-compartment (tissue) model, and then carry out very extensive tests to tweak the model so that divers (goats in his initial experiments) did not get decompression sickness (gas bubbles forming in tissue). Over a hundred years on, Haldane-type tissue models are used in most divers’ decompression computers, and they work extremely well.
Some important points about diving science: 1. Haldane, and those who followed, constantly tested and refined their models against experimental data – a process which continues today – over a hundred years on. 2. The models are a crude approximation of a complex system (the human body), but at least the physics is reasonably well understood e.g. the local temperature and pressure gradients and the kinetics of the physical processes – solubility, perfusion and diffusion. 3. In decompression models, only one of the tissue compartments usually controls the behaviour of the model (rate of ascent/decompression stop timing). Therefore, small errors or uncertainties in each compartment are not a major problem.
The application of this approach to climate science is, in my view, highly problematic because: 1. There simply has not been enough time/effort to refine these models against experimental data – a process which can take many decades. 2. The models are a profoundly crude approximation of a bewilderingly complex system (global carbon cycle), about which most of physics/biology/geology/chemistry/vulcanology etc, etc are not well understood. 3 In climate models all of the compartments contribute to the behaviour of the model (CO2 sequestration rate) and so errors and uncertainties in each compartment are cumulative.
Bill Illis says:
May 6, 2012 at 1:16 pm
So the natural sinks and sources are in equilbrium (give or take) when the CO2 level is 275 ppm or the Carbon level in the atmosphere is 569 billion tonnes
====================================
Bill, this is biology…..what you’re calling equilibrium is exactly what happens when a nutrient becomes limiting……..
Bill Illis says:
May 6, 2012 at 1:16 pm
Very interesting charts as always, Bill. Thanks.
[note: the 3rd one has the wrong starting year].
Willis Eschenbach – “You say ” the results of the Bern model were offered as an available computational tool for further work” … I understand that. What I don’t understand is the physical basis for what they are claiming, which is that e.g. 13% of the airborne CO2 hangs around with an e-folding time of 371.6 years, but is not touched during that time by any of the other sequestration mechanisms.”
Then, Willis, I suggest you read the original papers on the Bern model, such as Siegenthaler and Joos 1992.
The percentages you listed are the results of running the Bern model, and as such are a convenient shorthand. The actual physical processes include mixed layer oceanic absorption, eddy currents and thermohaline circulation, etc. The very link you provided states that:
(emphasis added)
Your claim that these are percentages and time constants are the direct processes is a strawman argument – Joos certainly did not make that claim, he stated that these were a useful approximation.
I have to say I find your claims otherwise, and in fact your original post, to be quite disingenuous.
I have been wondering, if there is any reason to expect the rate of carbon exchange between the athmosphere and the ocean ( and other sinks) to be diffrent for diffrent isotopes of C ( CO2 for that matter ) . In other word might it be possible to infere something about the uptake rate of the sinks from the data (its accessible at the CDIAC website ) for the athmospheric dC14 content and the spike caused in it by open air nuclear bomb testing in the last century. I belive the i have somwhere seen a statment claming the “athmospheric half life” calculated from this “experiment” is 5.5 – 6 for the c14 isotope.
It is called a box model. Box models were discarded in the late 70’s, early 80’s, because they cannot describe complex systems.
There is an input into the system, the release of carbon from geologic sources (Vulcanism) and fossil fuels; the influx of carbon into the biosphere.
There is an output from the system, mineralization of carbon into muds, which will become rock; the efflux from the system.
At steady state, influx = efflux. In the previous 800,000 years of pre-industrial times CO2 is between 180-330 ppm. So either we were VERY lucky that influx=efflux due to chance; or the rate of efflux is coupled to the rate of influx. Thus, when CO2 is high, marine animals do well, the ocean biotica grows, more particulate organic matter sinks to the bottom of the ocean, more carbon trapped in mud, more mineralization.
Basic control mechanisms in fact.
It is because the process of CO2 sequestration is not solved by an ordinary differential equation in time, but by a partial derivative diffusion equation. It has to do with the frequency of CO2 molecules coming into contact with absorbing reservoirs (a.k.a. sinks). If the atmospheric concentration is large, then molecules are snatched from the air frequently. If it is smaller, then it is more likely for an individual molecule to just bob and weave around in the atmosphere for a long time without coming into contact with the surface.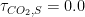 , effectively making the entire sum under the integral zero — this is what you would get if you made carbon dioxide sequestration in these imagined modes instantaneous — then the remainder of the function under the integral is
, effectively making the entire sum under the integral zero — this is what you would get if you made carbon dioxide sequestration in these imagined modes instantaneous — then the remainder of the function under the integral is 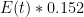 . This will cause CO_2 concentration to grow without bound as long as we are emitting CO_2 at all. Nor will it ever diminish, even if
. This will cause CO_2 concentration to grow without bound as long as we are emitting CO_2 at all. Nor will it ever diminish, even if 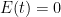 . Worse, all of the terms in the integral I forced to zero by making their time constants absurdly small are themselves non-negative. None of them cause a reduction of
. Worse, all of the terms in the integral I forced to zero by making their time constants absurdly small are themselves non-negative. None of them cause a reduction of 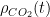 . They only make CO_2 concentration grow faster as one makes their time constants longer as long as
. They only make CO_2 concentration grow faster as one makes their time constants longer as long as  .
. to zero.
to zero.
Dearest Bart,
Piffle. I am talking about the integral in the document Willis linked, which is an integral over time only. If you set all of the
Now, as to your actual assertion that the rate that CO_2 molecules are “snatched from the air” is proportional to the concentration of molecules in the air — absolutely. However, for each mode of removal it is proportional to the total concentration in the air, not the “first fraction, second fraction, third fraction”. The CO_2 molecules don’t come with labels, so that some of them hang out anomalously long because they are “tree removal” molecules instead of “ocean removal” molecules. The ocean and the trees remove molecules at independent rates proportional to the total number of molecules. That is precisely the point of the simple linear response model(s) I wrote down. They actually “do the right thing” and remove CO_2 faster when there is more of it in total, not broken up into fractions that are somehow removed at different rates, as if some CO_2 is “fast decay” CO__2 and comes prelabelled that way and is removed in 2.57 years, but once that fraction is removed none of the rest of the CO_2 can use that fast removal process.
Except that the integral equation for the concentration is absurd — it doesn’t even do that. There is no open hole through which CO_2 can ever drain in this formula — it can do nothing but cause CO_2 to inexorably and monotonicall increase, for any value of the parameters, and CO_2 can never equilibrate unless you set
As I said, piffle. I do teach this sort of thing, and would be happy to expound in much greater depth, but note well that all of this is true before one considers any sort of PDE or multivariate dependence. Those things all modulate the time constants themselves, or make the time deriviative a nonlinear function of the concentration. In general, one can easily handle those things these days by integrating a set of coupled ODEs with a simple e.g. runge-kutta ODE solver in a package like the Gnu Scientific Library or matlab or octave. I tend to use octave or matlab for quick and dirty solutions and the GSL routines (some of which are very slick and very fast) if I need to control error more tightly or solve a “big” problem that needs the speed more than the convenience of programming and plotting.
But one thing one learns when actually working with meaningful equations over a few decades is how to read them and infer meaning or estimate their asymptotics. The “simple carbon cycle model” Willis linked, wherever it came from, is a travesty that quite literally never permits CO_2 concentration to diminish and that purports to break a well-mixed atmosphere into sub-concentrations with different decay rates, which is absurd at the outset because it violates precisely the principle you stated at the top of this response, where removal/sequestration by any reasonable process is proportional to the concentration, not the sub-concentration of “red” versus “blue”, “ocean” vs “tree” CO_2.
rgb
Plankton are a huge consumer of CO2, and they are rate limited by iron in nutrient rich waters and by silicon for diatom shells in others. NOT by CO2. So a significant modulator of CO2 will be volcanism that puts iron and silicon into the biosphere. Precipitation and weathering rates will also modulate those rate limiting nutrients. CO2 is the dependent variable, not the driving one…
http://chiefio.wordpress.com/2012/05/06/of-silicon-iron-and-volcanoes/
The “Bern Model” is broken if it does not address that.
@ Latitude, May 6, 2012 at 10:38 am
“I still can’t figure out how CO2 levels rose to the thousands ppm….
….and crashed to limiting levels
Without man’s help……….”
Perhaps it is because your ( and your teacher’s ) view of the subject is incorrect.
The real question is: “Why is there any CO2 in the atmosphere at all?”
Answer that question and you will have the puzzle solved. CO2 is constantly and irreversibly being sequestered into the formation of insoluble carbonates (organically e.g. Foraminifera and chemically e.g. Calcium carbonate) over millennia.
One possible answer is the concept of a Hydritic Earth. With never ending up dwelling methane being oxidized to CO2.
Dan Kurt
Since you like differential equations… ,
, 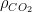 increases, period.
increases, period.
I do, and if you tell me what A, B and C are, and what the equations represent, I'll tell you whether or not I believe the coupled system of equations or the final solution.
But neither one has anything to do with the equation Willis linked. It is an integral equation that has the asymptotic property of monotonic growth of CO_2 concentration completely independent of the parameter values on the domain given. The exponentials aren't the result of solving an ODE even — they are under an integral sign.
That particular integral equation looks like a non-Markovian multi-timescale relaxation equation with a monotonic driver, but whatever it is, it is absurdly wrong before you even begin because it gives utterly nonphysical predictions in some very simple limits. In particular, it never permits CO_2 concentration to decrease, and it never even saturates. If
rgb
[Moderator’s request: it wasn’t just a dollar sign, I guess. Please send the formula again and I will paste it in. -REP]
[Fixed (I think). -w.]
And by the way “The Bern Model” triggered a memory in my head about having read an article by Jarl Ahlbeck some years ago on the John Daly website, where he among other things maintains that the future athmospheric carbon dioxide concentrations the bern model predicts are just a simple minded parabolic fit to to some unrealistic assumptions (not data). I never could really make up my mind if he was right or wrong in that, but for what it is worth the link to the paper is on the line below:
http://www.john-daly.com/ahlbeck/ahlbeck.htm
SNIP: Twice is enough. This is starting to be thread bombing. WUWT also does not encourage tampering with polls. If it has been adjusted to allow only Australians, then foreigners casting votes are simply cheating. -REP
Final comment and then time to do some actual “work”. I do, actually respect the notion that CO_2 concentration should be modelled by a set of coupled ODEs. I also am perfectly happy to believe that some of the absorption mechanisms — e.g. the ocean — are both sources and sinks, or rather are net one or the other but which they are at any given time may well depend on some very complicated, nonlinear, non-Markovian dynamics indeed. In this case trying to write a single trivial integral equation solution for CO_2 concentration (one with a visibly absurd asymptotic behavior) is counterindicated, is it not? In fact, in this case on has to just plain “do the math”.
The point is that one may, actually, be able to write an integrodifferential equation that represents the CO_2 concentration as a function of time. It appears to be the kind of problem for which a master equation can be derived (somebody mentioned Fokker-Planck, although I prefer Langevin, but whatever, a semideterministic set of coupled ODEs with stochastic noise). That is not what the equation given in the link Willis posted is. That equation is just a mistake — all gain terms and no loss terms. Perhaps there is a simple sign error in it, but as it stands it is impossible.
rgb
You are kidding right? Of course there is no actual partition it is a model so you can think through how carbon moves in and out of the atmosphere. You do get that, right? You do understand that to change sinks effects you change what is in each bucket (partition) to model how quickly that sink removes it from the atmosphere, right?
Please tell me you are not this rigid in your thought process – where is your degree from?
E.M.Smith says:
May 6, 2012 at 2:38 pm
Plankton are a huge consumer of CO2, and they are rate limited by iron in nutrient rich waters and by silicon for diatom shells in others. NOT by CO2. So a significant modulator of CO2 will be volcanism that puts iron and silicon into the biosphere.
=========================
Saharan/African dust……….
“I do, and if you tell me what A, B and C are, and what the equations represent, I’ll tell you whether or not I believe the coupled system of equations or the final solution.”
See my previous comments above.
I should perhaps clarify – I don’t consider the BERN model ansatz to be more than a simplistic approximation, and make no comment on its validity or physical significance. I’m just explaining the intuition behind it.
If you have several linked buffers with different rate constants for transfer between them, the system of differential equations generally has a sum-of-exponentials solution. (Or sinusoidal oscillations if some of the eigenvalues are imaginary.) That’s why they used that model to fit the simulation output. It sounds vaguely plausible as a first approximation, but beyond that I make no comment on whether they’re right to do so.
I’m not sure which equation Willis linked you mean.
Dan Kurt says:
May 6, 2012 at 2:48 pm
CO2 is constantly and irreversibly being sequestered into the formation of insoluble carbonates
==================
Gosh Dan, you just explained how denitrification is possible without carbon………….
Nullius,
Thanks for that very effective toy model, and the follow up bit on the effect of the different tank sizes. I’m sure it needs many add ons and caveats, but as a quick and accessable mental model to use as a starting point, for someone who thinks visually, it is a beauty.
Willis,
I have not yet plowed through all the comments so if this is redundant please forgive me. What you have described as the Bern model sounds a lot like a multi-compartment first-order elimination model similar to that of some drugs. A simple one-compartment, first-order elimination model is concentration dependent. That is, you put Drug X into the body and it will be eliminated primarily through one route (usually the kidneys). You have t1/2 elimination constant and about five half-lives later the body has essentially cleared the drug. Some drugs like aminoglycoside antimicrobials have a simple and rather restricted distribution in the human body. Their apparent volume of distribution (a purely theoretical metric derived for the purposes of calculation) is roughly that of the blood volume. Other drugs have very unusual volumes of distribution. An ancient (but good) example is that of digoxin. You can give a few daily doses of 250 µg of digoxin and end up with an observed serum concentration in the ng range much lower than one might anticipate. That drug has gone somewhere else other than the apparent blood volume.
This is where we get into multi-compartment models. A single drug may occupy the blood volume, the serum proteins, adipose tissue, muscle tissue, lung tissue, kidney tissue, lung tissue and brain tissue. Each tissue “compartment” is associated with its own in-and-out elimination constants so a steady state, single elimination constant is virtually impossible to quantify.
I know nothing about the the Bern Model so I can only surmise that maybe this is an elaborate model built on multi-compartment, first-order elimination kinetics. Then again, you have to consider the possibility of zero-order (non-concentration dependent) kinetics. Drugs like ethanol follow this model. If one keep ingesting alcohol at a certain point the liver’s capacity to metabolize alcohol is overwhelmed. We see a real-life “tipping point.” Once those metabolic pathways in the liver become saturated, every additional gram of alcohol ingestion produces a geometrically higher EtOH serum concentration (i.e. blackouts).
I have no idea if any of this is relevant. But what you described bore an amazing resemblance to multi-compartment, first-order kinetics. Still…on a personal level I think it’s BS. Different drugs behave differently in the human body. I have a hard time believing CO2 (a “single drug”) behaves differently in the atmosphere as a whole.
Willis:
I am pleased that you notice some problems with the Bern Model because the IPCC uses only that model of the carbon cycle.
I am especially pleased that you observe the problem of partitioning. In reality, the dynamics of seasonal sequestration indicate that the system can easily absorb ALL the anthropogenic CO2 emission of each year. But CO2 is increasing in the atmosphere.
Importantly, as your question highlights, nobody has a detailed understanding of the carbon cycle and, therefore, it is not possible to define a physical explanation of “partitioning” (as is used in all ‘plumbing’ models such as the Bern Model). Hence, any model that provides a better fit to the empirical data is a superior model to the Bern Model.
I remind that one of our 2005 papers proves any of several models provide better representation of atmospheric CO2 increase than the Bern Model.
(ref. Rorsch A, Courtney RS & Thoenes D, ‘The Interaction of Climate Change and the Carbon Dioxide Cycle’ E&E v16no2 (2005))
Our paper provides six models that each match the empirical data.
We provide three basic models that each assumes a different mechanism dominates the carbon cycle. The first basic model uses a postulated linear relationship of the sink flow and the concentration of CO2 in the atmosphere. The second used uses a power equation that assumes several different processes determine the flow into the sinks. And the third model assumes that the carbon cycle is dominated by biological effects.
For each basic model we assume the anthropogenic emission
(a) is having insignificant effect on the carbon cycle,
and
(b) is affecting the carbon cycle to induce the observed rise in the Mauna Loa data.
Thus, the total of six models is presented.
The six models do not use the ‘5-year-averaging’ to smooth the data that the Bern Model requires for it to match the data. The six modelseach match the empirical data for each year.
However, the six models each provide very different ‘projections’ of future atmospheric carbon dioxide concentration for the same assumed future anthropogenic emission. And other models are also possible.
The ability to model the carbon cycle in such a variety of ways means that according to the available data
(1) the cause of the recent rise in atmospheric carbon dioxide concentration is not known,
(2) the future development of atmospheric carbon dioxide concentration cannot be known, and
(3) any effect of future anthropogenic emissions of carbon dioxide on the atmospheric carbon dioxide concentration cannot be known.
Assertions that isotope ratio changes do not concur with these conclusions are false.
Richard
Oddly enough I read your post whilst in a “Tidal wetland” that I had visited to observe the spring *super moon” tides. Been doing this for more years than I care to remember but the tide was no higher than I’ve seen before (nowhere near), the estuary just as vibrant as ever but the first time I have ever seen a bird surface before me with a wriggling fish in its beak and gobble it down.
KR says:
May 6, 2012 at 2:08 pm
Disingenouus? So you are calling me a liar and a deliberate deceiver, except you are doing it politely?
KR, you can apologize for calling me a liar and we can continue the discussion. Or not.
Your choice.
w.
[Note: logic fixed, the way I wrote it made no sense. Teach me to write when my blood is angrified. -w.]
Wet lands are usually replaced by pasture. Another sink.
Secondly, every previous run up of CO2 has been followed by significant drop. So obviously some other factor9s) may come into play.
Brad says:
May 6, 2012 at 3:14 pm
Haven’t a clue who the “you” is that you are talking about. Me? rgbatduke? KR? Someone else?
Also, rather than saying “you do understand” X, Y, or Z, it would be much more useful if you quote exactly the words you disagree with, and then tell us why you think they are wrong.
Next, please note how what I wrote differs from if I were to have simply asked “You do understand how to respond to a blog post, right?”
Asking that, just like you asking the questions in your post, goes nowhere. You need to point out what you think is wrong, and point out where it is wrong, and tell us how to do it right.
Finally, “where is your degree from?” is a very unpleasant ad hominem. It doesn’t matter where anyone’s degree is from. What matters is, are they right or wrong.
w.
the first thing I noticed is “tau” time calculated to 3 (three!!!) significant figures. A good sign that those involved have NO clue what they are doing. Now let me finish reading…..
“rgbatduke says:
Now, as to your actual assertion that the rate that CO2 molecules are “snatched from the air” is proportional to the concentration of molecules in the air — absolutely. However, for each mode of removal it is proportional to the total concentration in the air, not the “first fraction, second fraction, third fraction”. The CO2 molecules don’t come with labels, so that some of them hang out anomalously long because they are “tree removal” molecules instead of “ocean removal” molecules. ”
This is indeed true, but it presents a problem to the modelers. They know that any saturatable process does not have first order kinetics as it approaches saturation; but if they allow all the first order processes to ‘see’ the whole atmospheric [CO2], then they end up with a rate constant that is the sum of all the rates. They have to artificially add in saturation limits, supported by lots of arm waving, to make their box models spit out the result they want; a saturatable sink.
Take a look at the marine biotica. Total mass 3GtC, annual fixation of carbon, 50GtC. A good fraction of the 50GtC is converted in ‘poop’ and falls to the bottom. If there is oxygen present some is converted to CO2, A lot is encased in mud. The figure of 150 GtC in the sediments is bollocks; that is only the carbon in the surface of the sediment. There is 20,000,000 GtC of Kerogen at the bottom of the oceans; this has been removed from the Wiki figures over the past year. The Kerogen is the true sink of the Carbon Cycle and it can only have come from the biosphere,
The ultimate test of the Bern Box Model is to measure the relative ratios of 14C in the ocean depths. After nuclear testing a large series of 14C were generated and this disappeared from the atmosphere with a t1/2 of about a decade. According to the Bern model, the vast majority of this 14C should be in the upper surface of the ocean, and lower amounts in the ‘saturatable’ sinks.
Look at figure 4
http://www.geo.cornell.edu/geology/classes/eas3030/303_temp/Ocean_14C&_acidification_ppt.pdf
14C is higher at depths less than 2000m than at 2000m; this means the flux of particulate 14C to the bottom is high, then the organic material is partly gasified, CO2/CH4, and rises.
The 14C numbers of the H-bomb tests are not well modeled by the Bern Box models, but they get around it by having a difference in the equilibrium time between surface water and air of CO2, depending on if the isotope is 12C or 14C. Arguing that 12CO2:12CO2 were at equilibrium and 14CO2:14CO2 were not.
right or wrong in that, but for what it is worth the link to the paper is on the line below:
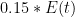 from
from  to the present. I can do this integral in my head for any non-compact function
to the present. I can do this integral in my head for any non-compact function  — it is infinite. Ignoring the
— it is infinite. Ignoring the  and integrating from “a long time ago but not infinity” in such a way that you get the right baseline behavior is obviously wrong in so many ways, if that is what they do.
and integrating from “a long time ago but not infinity” in such a way that you get the right baseline behavior is obviously wrong in so many ways, if that is what they do.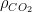 would remain constant for eternity.
would remain constant for eternity. , while 25% of the rest will have diminished by
, while 25% of the rest will have diminished by  and 15% of it will not have changed at all. It might even be correct, but what does this mean? All of the CO_2 molecules in the atmosphere are identical. What one is really describing is some sort of saturation (as you might have noted) of some process that can never take up more than 32% of the atmospheric CO_2, no matter how long you wait, with absolutely no sources at all.
and 15% of it will not have changed at all. It might even be correct, but what does this mean? All of the CO_2 molecules in the atmosphere are identical. What one is really describing is some sort of saturation (as you might have noted) of some process that can never take up more than 32% of the atmospheric CO_2, no matter how long you wait, with absolutely no sources at all.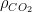 have to change before the assumptions break down? This is a pretty complex model — wouldn’t simpler models work just as well, or even better? Why write the solution as an integral equation at all instead of as a set of coupled ODEs?
have to change before the assumptions break down? This is a pretty complex model — wouldn’t simpler models work just as well, or even better? Why write the solution as an integral equation at all instead of as a set of coupled ODEs? were constant or slowly varying or there was some kernel of meaning to be extracted from converting the ODEs into an integral equation, there might be some point. But when one looks at the leading constant term, presumably added because without it the model is just wrong, it leads to instantly incorrect asymptotic behavior. Surely that is a signal that the rest of the terms cannot be trusted!. The evidence is straightforward — there are times in the past when CO_2 concentration has been much higher. Obviously the monotonic term is fudged over the real historical record or CO_2 now would not be less. But nothing in this equation predicts the asymptotic equilibrium CO_2 concentration if
were constant or slowly varying or there was some kernel of meaning to be extracted from converting the ODEs into an integral equation, there might be some point. But when one looks at the leading constant term, presumably added because without it the model is just wrong, it leads to instantly incorrect asymptotic behavior. Surely that is a signal that the rest of the terms cannot be trusted!. The evidence is straightforward — there are times in the past when CO_2 concentration has been much higher. Obviously the monotonic term is fudged over the real historical record or CO_2 now would not be less. But nothing in this equation predicts the asymptotic equilibrium CO_2 concentration if  is zero. In fact, it creates a completely artificial baseline CO_2 that the decay kernel parts will regress to, one that varies with time to be ever higher now in spite of the fact that one simply didn’t do the integral over all past times and in fact imposed an arbitrary cut-off or something so that it didn’t diverge.
is zero. In fact, it creates a completely artificial baseline CO_2 that the decay kernel parts will regress to, one that varies with time to be ever higher now in spite of the fact that one simply didn’t do the integral over all past times and in fact imposed an arbitrary cut-off or something so that it didn’t diverge. I’m all for it, but be aware that the
I’m all for it, but be aware that the 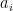 you end up with from an empirical fit are, well, shall we say open to debate in any discussion of physical relevance or meaning, especially one where the mechanisms they supposedly represent can themselves have nontrivial functional dependences.
you end up with from an empirical fit are, well, shall we say open to debate in any discussion of physical relevance or meaning, especially one where the mechanisms they supposedly represent can themselves have nontrivial functional dependences.
http://www.john-daly.com/ahlbeck/ahlbeck.htm
Good paper. Agree or disagree, he is very clear about what he models and the assumptions in it and how he sets his parameters.
You are kidding right? Of course there is no actual partition it is a model so you can think through how carbon moves in and out of the atmosphere. You do get that, right? You do understand that to change sinks effects you change what is in each bucket (partition) to model how quickly that sink removes it from the atmosphere, right?
Please tell me you are not this rigid in your thought process – where is your degree from?
I’m not rigid in my thought process at all. I am looking at the equation Willis linked! Are you? Is there something in that equation that makes you think that it it could possibly be correct? The point I’ve been making is that even if you remove the exponential decaying parts from the kernel entirely, you are left with an integral of
In any event, this integral basically says that 15% of what is added every year is never going to be removed, and in fact is still around from every belch or fart of CO_2 gas since the planet began. The decay kernel then strictly increases this cumulative concentration, it does not decrease it, so that even if we all vanished from the planet tomorrow
This is clearly absurd, as I’ve tried to say so many times now.
We could then go on and address the rest of the kernel, the part that actually might make physical sense, depending on how it is derived. But it is then difficult, actually, to have it make a LOT of sense because the result would almost certainly have a completely incorrect form if $latexE(t)$ were suddenly set to zero. I could be convinced otherwise, but it would certainly take some effort, because then those “buckets” that are basically fairly arbitrary terms in an approximation to a very odd decay function, one that describes a very highly nonexponential process, not a sum of mixed differential processes.
In physics mixed exponential processes are far from unknown. For example, if one activates silver with slow neutrons, two radioactive isotopes are produced with different half-lives. If you try to determine the half lives from the raw count rate, you find that one of the two isotopes decays much more quickly than the other, so that after a suitable time the observed rate is almost all the slow process. One can fit that, then subtract the back-projected result and fit the faster time constant. Or nowadays, of couse, you could use a nonlinear least squares routine to fit the two at the same time and maybe even be able to get the result from a much shorter observation time if you have enough signal.
But note well, two different isotopes. I’m having a very hard time visualizing how, if CO_2 sources all turned off tomorrow, 1/e of 32% of it would have disappeared from the atmosphere within 2.56 years via one channel, but 28% of it will have only gone down by a factor of
At that point I have to say that I become very dubious indeed. First of all, this implies a complete lack of coupling across the “buckets”, which is itself impossible. By the time the fast process has removed 32% of the atmospheric CO_2 — call it ten or fifteen years, depending on how many powers of 1/e you want to call zero, the concentration exposed to the intermediate process has had its baseline concentration dropped by a third or more. This, in turn, destroys the assumptions made in writing out sums of exponentials in the first place, and so its time constant is now meaningless because the CO_2, unlike the silver atoms, has no label! It is quite possible that whatever process was involved in the 18 year exponential decay constant removal has switched sign and become a CO_2 source, because the reason given for not just summing the exponential decay rates of the independent processes is that they are not independent.
Finally, one then has to question the uniqueness of the decomposition of the decay kernel. Why three terms (plus the impossible fourth term)? How “linearized” were the assumptions that went into constructing it, and how far does
The latter is the big question. If
Am I somehow mistaken in this analysis? Is there some way that the baseline CO_2 concentration produced by this model is not strictly increasing from an absolutely arbitrary amount that is whatever value you choose to assign the integral before you really start to do it, say 1710 years in the past (ten of the slowest decay times)?
I’ve done my share of fitting nonlinear multiple exponentials, and you can get all kinds of interesting things if you have three of them and a constant to play with, but there is no good reason to think that the resulting fit is meaningful or extensible.
rgb
P.S. My degree in physics is from Duke. And I’ve published papers on Langevin models in quantum electrodynamics, and spent a decade doing Monte Carlo and finite size scaling analysis that involved fitting exponentially divergent quantities (and made my share of mistakes, and could easily be mistaken here — this is the first few hours I have looked at the equation, after all). But still, wrong/completely nonphysical asymptotic form is not a good sign when looking at a model, as I point out just as emphatically when it is CAGW doubters (like Nikolov and Zeller who propose a model for explaining atmospheric heating that contains utterly nonphysical dimensioned parameters) that come up with it.
And yeah, it disturbs me a lot to talk about “buckets” in a three term exponential decomposition of an integral equation kernel supposed to describe a systems of great underlying complexity with many feedback channels and mechanisms. It’s too many, or too few. Too few to be a good approximation to a laplace transform of the actual integral kernel. Too many to be physically meaningful in a simple linearized model. If you want to write
And in the end, if you have a believable model, why not just integrate the coupled ODEs? That’s what I’d do, every time. If nothing else it can reveal places where your linearization hypotheses are terrible, as you add or tweak detail and the model predictions diverge.
Do you disagree?
[Formatting fixed … I think … -w.]
IMO…until someone can produce evidence that some atmospheric CO2 changes into SUPER CO2 that is time resistant to sequesters…………….
CO2 sequesters are blind to the object [ CO2 ].
The only evidence we have is the variability of the sequester – some do it faster.
rgbatduke: I often read the thread backwards (for various reasons), and I’ve learned to distinguish your comments well before I scroll all the way up to your name. They really stand out. Thanks for participating.
This model doesn’t seem to jive with the idea that the atmosphere is well mixed. It would seem to me that the model would be better characterized by using diffusion models similar to those used in electrochemical systems in soluton.
Freeman Dyson proposed “growing” topsoil (Biomass) as a means to fighting climate change – which he is sceptical of – as this would be more cost effective than reducing emissions and have a positive benefit for agriculture whilst resolving excess CO2.
Why haven’t the greens supported this innovative idea ?
I think it clearly shows the “climate change” debate is about political powerand not much else !
It reads like a weighted average that has not yet been averaged – and perhaps shouldn’t be. If so, then the 1.33 year sink never does fill up, and indeed does keep sequestering, however the size of the “pipe” is only 8% so can not do the whole job in 1.33 years (it would take about 17 years). Meanwhile, while the 1.33 is busy running, so are the slower sinks. So the combined rate would be something less than 17. To go back to the tank of water example, it is like having a single tank with lots of pipes to drain it, let’s say 100. 8 of those pipes are of a size that would empty the tank in 1.33 years if there were 100 of that size. The other 92 pipes on our tank are sized to correspond to the sequestration (drainage) rate of the other partitions. To try a different analogy, it’s like having 100 people drinking from a pitcher of beer the size of a swimming pool. Some are using garden hoses, some are using straws, and others are using fibre optics. The pool eventually empties, everyone gets some beer, just some get a lot more than others.
Willis Eschenbach
You asked: “what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?”
Perhaps the writeup you linked to was just not clear enough, or you interpreted the approximations presented as the model itself – if so, my sincere apologies. It seems quite clear to me what the page (http://unfccc.int/resource/brazil/carbon.html) presented: approximations of the Bern model (http://tellusb.net/index.php/tellusb/article/viewFile/15441/17291) results for how much and how fast CO2 ends up in different partitions, based upon that model of the carbon cycle, as those percentages. Not parameters, not the model itself, but an approximation of the model results. Results presented so that other researchers could use that approximation in their own work, with the stated caveat that “Parties are free to use a more elaborate carbon cycle model if they choose.”
I’m therefore finding quite difficult to see how you arrived at the interpretation you posed when writing the original post – that there is somehow an initial “partitioning”. That’s neither a correct description of the Bern model results nor of the UN page you linked to…
@Latitude says:May 6, 2012 at 3:26 pm
“Gosh Dan, you just explained how denitrification is possible without carbon………….”
So you are a bean farmer!
Dan Kurt
jimboW,
Thanks. It’s appreciated.
rgbatduke,
“However, for each mode of removal it is proportional to the total concentration in the air, not the “first fraction, second fraction, third fraction”. The CO_2 molecules don’t come with labels,”
As I mentioned above, the fractions are not a separation of the atmosphere into labelled portions, but a consequence of the relative sizes of the reservoirs. If water flows from tank A to tank B until levels equalise, and the tanks have equal surface area, they converge on the midpoint and half the water added to tank A stays there. If you add another bucketload to A, they equalise again and half the new bucket goes to B. It’s not some magic form of CO2 that hangs around for longer, it’s just the effect of the level increasing in the destination reservoir.
“In any event, this integral basically says that 15% of what is added every year is never going to be removed, and in fact is still around from every belch or fart of CO_2 gas since the planet began. The decay kernel then strictly increases this cumulative concentration, it does not decrease it, so that even if we all vanished from the planet tomorrow \rho_{CO_2} would remain constant for eternity.”
Ah, right. I’ve figured out what you’re talking about, now.
Yes, that is what the equations says, because it doesn’t include the very long term geological sequestration processes that take place on the order of thousands of years. Those components would have no significant effect – they’d look effectively constant – over the time intervals they ran the simulations for. The first fraction represents all those time constants too big to measure.
CO2 is conserved. If you chuck it into a system with no exits, it will stay there forever.
The integral is a convolution of the emission history with an impulse response function. If you get a pulse of emissions and then nothing, the emission falls further and further behind, t-t’ gets larger and larger, and the impact of the emissions is given a large negative weighting, shrinking it. It does decay.
Hello Willis,
I don’t know anything about this model but I can tell you that there are different physical models which would have similar behaviour.
Consider a thermal model where you have multiple heatsinks with different thermal resistances and heat storage capacity connected to a source of heat via interfaces with different thermal resistances.
A small heatsink connected to your heat source via a low thermal resistance will absorb heat quickly but its temperature will quickly reach equilibrium with the source so it will stop absorbing heat after a short period. At the same time, a large heatsink connected to the heat source via a high thermal resistance will only absorb a small amount of heat but it will take a lot longer to reach equilibrium so it will continue to do so for a long time.
You could come up with a similar electronic model where you have multiple capacitors with different capacities and leakages connected to a node via different value resistors.
I can see how nature could exhibit similar characteristics.
Having said that, their model seems like a clumsy approximation. I don’t know why they don’t use free electronics modeling tools like SPICE which are perfect for examining the response of systems with multiple time constants to perturbations. SPICE has been around for a while and is pretty much perfect for this sort of task. You just have to convert your model into capacitors, resistors and inductors which isn’t very hard. It’s done all the time with thermal modeling.
All modelers are looking towards the next funding round and sensationalism wins the day every time. “Nature”, despite its unwarranted kudos, is not a scientific journal, it is a magazine.
I dont know too much about carbon cycle in the diagram, but I’m very suspicious about the figures concerning the sediments and the sea. As usual, they have forgotten about volcanoes.
The oceans contain mid ocean ridges and other undersea volcanoes that exchange vast amounts of c02 and other elements and minerals with seawater; none of this is represented in the diagram. The mid ocean ridges themselves strech for tens of thousands of kilometres. I know from personal experience that sediments adjacent to underwater voclanoes are enriched in carbonate, as I have drilled though thousands of metres of them. This carbonate exists in a complex arrangement with the heat and c02 sourced from the volanoes, as well as the carbonate in seawater, and I also suspect these undersea volcanoes buffer the acidity of the oceans as a whole-ie if the aicidity of the ocean oes up-more volcanic carbonate is deposited in the sediments-if the ocean acidity goes down-more carbonate is dissolved.
Volcanism has never really been very popular amongst the greens, because they arent very ‘green’ to begin with.
Let’s back away from the problem just a bit and look at some data on carbon. Carbon in the world is located in the following locations/situations:
99.9% is in the sedimentary rocks in the form of limestone and dolomite
.002% is the fossils in the form of crude oil, natural gas, lignite and coal
.06% is in water bodies, primarily the oceans, in the form of CaCO3 and HCO3
.001% is in the atmosphere in the form of CH4, CO2, CO, VOCs and halogens
.005% is in the mineral soil in the form of humus, forest litter, bottom of mires and bogs
.001% is in living organisms, mainly vegetation
The question is then how does carbon dioxide convert -get into- the various forms of carbon storage or sinks? The times for each sink are obviously highly variable with the water bodies being the shortest, vegetation being second and the sedimentary rocks probably being the longest. With data perhaps one could develop relative time intervals. To me, using different times is acceptable for a model, I just don’t like the times and percentages used by the authors. They have made it too simple and precise of a problem.
One has to be careful of pinch points when dealing with something that is only .1% of the whole. In human time frames only water bodies and vegetation are of probable interest. Winds and currents are of the most interest with clearing and replanting of forests and jungles being of important interest as well.
With the CO2 in/out ratio being so constant, I am suspicious of oxidation of limestones and dolomites being undercounted in any material balance calculations. Ninety Nine point nine percent doesn’t have to change very much to sway the other times considerably.
The CO2 uptake can be fitted to give a reasonable match in a number of different ways. My guess is that the Bern model is very wrong because it ignores a dominant process: thermohaline circulation, which leads to absorption of lots of CO2 at high latitudes in cold ocean regions with deep convection. Some of the sinks in the Bern model are real, but almost certainly the model is not an accurate predictor of future CO2 absorption; it suggests far too short a time to “saturate” the system with CO2. Consider a simpler simpler fit to the data: http://wattsupwiththat.com/2009/05/22/a-look-at-human-co2-emissions-vs-ocean-absorption/ Just as good a fit, and more physically reasonable.
The future absorption of CO2 with rising CO2 in the atmosphere will be much higher than the Bern model suggests, and for a very long time (at least several hundred years).
Nicholas says:
May 6, 2012 at 5:42 pm
Thanks, Nicholas. The problem with your model is where you say the sink “will stop absorbing heat”.
The reason it’s a problem is that we know that the sinks have not stopped absorbing CO2. If they were saturated, the airborne fraction (the amount that remains airborne of the amount emitted annually) would be rising. This is just as in your thermal model, when the heatsinks stop absorbing heat, the temperature will rise.
But the airborne fraction has not been rising, which means that the CO2 sinks are not saturating, and so your model fails.
Regarding SPICE, you are right that it would be a good model to use, but to mangle Shakespeare, “The fault, dear Brutus, is not in our models but in ourselves” … a model is only as good as the theory underneath it.
w.
JFD says:
May 6, 2012 at 6:03 pm
I fear you miss the point. The different sinks absorb at different rates, but that doesn’t mean that somehow 13% of the CO2 is immune to sequestration by any but the slowest processes. The faster processes will continue to remove CO2.
w.
To electrical engineers, the impulse response model (the equation) in the link is quite unremarkable – just an ordinary linear system. On our benches, it would look like a bunch of R-C low-pass circuits in parallel (six of them I guess). The partitions (gain constants) and time constants are parameters of the model, and could be derived from rho(t) by deconvolution, if we knew E(t). This assumes the system really is linear (the one on the bench is), and is exactly the sum of six real poles. The theory is straightforward and manipulations such as “Prony’s method” and “Kautz function analysis” are long-established (and quite beautiful ).
That noted, attempting to apply this mathematical procedure to a true CO2 concentration curve is of course, utter nonsense. Likely the CO2 situation is not even linear in the first place, and the measured curves are subject to large systematic and random errors. For a circuit on the bench, we could at least cheat and peek at some of the component values. But for the atmosphere, there are no actual partitions, or separable processes with-defined characteristic times. There are NO discrete components – let alone ones we could identify and measure! It’s just a silly over-beefy model.
For CO2, It is doubtful there would be any usable physical reality to even a single pole model. It’s very very far from being a circuit on a bench.
KR says:
May 6, 2012 at 5:15 pm
No, I asked for an apology before I’d continue the discussion. Or not. Your choice.
In other words, you are saying that IF I was not trying to be deceptive, you apologize …
In other words, no apology at all.
You have accused me, without a shred of evidence, of trying to deceive people. When you are called on it, you say well, if you weren’t trying to deceive people I apologize …
Look, KR, I’m an honest man, and damn proud of it. It seems you may not have had much interaction with my particular breed. I tell the truth as best I know it. I’m sometimes wrong, sure, more often that I’d like to admit … but I admit it nonetheless.
The part you seem to be missing is that to accuse me of trying to deceive people is a nasty, underhanded, slimy tactic.
That’s what you need to apologize for, and it doesn’t depend in the slightest on whether “the writeup I linked to was not clear enough”. Your false allegation is scurrilous, sleazy, untrue, and insulting, whether or not the writeup was clear … and your apology is a joke.
w.
Willis, you are one of the great ones. I very much appreciate your keen mind and the quickness and width of your knowledge and interests. I read your treatises first, always.
I just see that it doesn’t take much exposure to the air of near surface carbonates, arising from landslides, floods, hurricanes, earthquakes; you name it, to introduce enough additional CO2 to the atmosphere to offset the removal by the other sinks. Thus, in human time, there will always be CO2 in the atmosphere no matter what the faster processes do in removing CO2.
I have 99.9% versus .1% in my favor, grin.
JFD
JFD says:
99.9% is in the sedimentary rocks in the form of limestone and dolomite
.002% is the fossils in the form of crude oil, natural gas, lignite and coal
.06% is in water bodies, primarily the oceans, in the form of CaCO3 and HCO3
.001% is in the atmosphere in the form of CH4, CO2, CO, VOCs and halogens
.005% is in the mineral soil in the form of humus, forest litter, bottom of mires and bogs
.001% is in living organisms, mainly vegetation.
No carbon in volcanoes, mid ocean ridge systems? Ever heard of carbonitite volcanoes?
Bill Illis says:
May 6, 2012 at 1:16 pm
“It will take about 150 years to draw down CO2 to the equilibrium of 275 ppm if we stop adding to the atmosphere each year. Alternatively, we can stabilize the level just by cutting our emissions by 50%”
——————————————–
Why would we want to do that?
People upthread have said that I misunderstand the situation. They say he equations that I linked to, with the partitions and the various time constants. are not the model. The actual model, they say, is the computer box-model that generated those partitions and time constants.
I have understood that from the start. What those folks fail to consider is the first line of the linked file, which says:
Parties are free to use a more elaborate carbon cycle model if they choose.
However, a number of the IPCC participants use the simple model given in the linked file. And for those folks, THAT IS THE MODEL THEY ARE USING. They are not using the underlying computer box-model. They are using the simple model given in the linked file.
My point is, as far as I know, that simple model is physically impossible. It doesn’t matter where they get the values for the various parameters (and in fact they use various values).
The problem is, the world simply doesn’t work that way. There is no factual basis for the simple model.
In addition, Robert Brown above shows that not only is the simple model physically impossible, it leads to ludicrous boundary conditions. That’s another, and separate, strike against the model.
In any case, yes, I know that’s not the more complex model. It says that in the first line of the linked file. I do read, you know.
But for the folks using the simple model, that’s the only model they are using. They’re not using the box model, or any even more complex model. They are using the simple model, and that’s the model I’m objecting to.
w.
Sure, I’ve heard of carbonitite volcanoes. They have a high percentage of limestone and dolomite (calcium/magnesium carbonates) in them. They are in the 99.9% of carbon listed first in my post.
_Jim says:
May 6, 2012 at 1:12 pm
73’s back atcha …
H44WE
There was an extensive set of meaurement published in several peer reveiwed papers by by teams of scientists working at Princeton University at the beginning of the 21Century.
Unlike the bovine pasture patties “precise” half-entry, non-debit only, “bookeeping accounting” produced by the EPA, these scientyists measured the CO2 content on the Air blowing in from the Pacific prevailing winds, into North America and they measured what happened to it as it traversed over the continent, and then measured CO2 as it exited on the prevailing winds blowing out over the Atlantic. They discovered it rose over the industrialized Coasts, and the again in industrial midwest, but decreased as it traversed the forests, ranchlands of the West, the breadbaskets of the grasslands and the eastern and southern forests. They also reported the North America continent absorbs much more than it emits by both Man and Nature. The Air blowing out over the Atlantic has much less CO2 the air entering the continent, despite all that the most industrialized country adds.
North America is the biggest Carbon Sink on the Planet and proves there is absolutely no need for America to have any concerns about CO2, even if you concede that CO2 is of any concern at all except to a botanist. If Eurasia produces net CO2, let them remove it. We have already done all we need to do and much more.
“A Large Terrestrial Carbon Sink in North America Implied by Atmospheric and Oceanic Carbon Dioxide Data and Models
S. Fan, M. Gloor, J. Mahlman, S. Pacala, J. Sarmiento, T. Takahashi and P. Tans” Science 16 October 1998:
Vol. 282 no. 5388 pp. 442-446
DOI: 10.1126/science.282.5388.442
, is just typically one of many such papers, that the CAGW Eco-Druids, managed to suppress and/or ignore.
Meanwhile the EPA eco-druids total the reports which estimate the kilo pounds that human industries report emiting; and in their half-assed accounting haven’t found a way to intimidate the mighty Oak and Pine to fill out their bureaucratic forms and to report how many megatons they and their saplings absorb, so don’t bother to include any considerations of that.
ferd berple says:
May 6, 2012 at 12:39 pm
“Nonsense. The oceans cannot tell if that 1/2 comes from this year or last year.”
rgbatduke says:
May 6, 2012 at 2:35 pm
“Dearest Bart, Piffle.”
Guys… if you jump to conclusions and assume your opponents are completely witless without even bothering to understand their reasoning, you are never going to be effective. To get an idea of what they are thinking, consider a simple atmosphere/ocean coupled model of the form
dA/dt = a*O – b*A + H
dO/dt = b*A – a*O – k*(1+a/b)*O
A = atmospheric CO2 concentration
O = oceanic CO2 concentration
H = anthropogenic inputs
a,b,k = coupling constants
The “a” and “b” constants control how quickly CO2 from the atmosphere dissolves into the oceans. The “k” constant determines how quickly the oceans permanently (or, at least, semi-permanently, i.e., sufficiently long as to be of little consequence) sequester CO2.
If you are familiar with Laplace transforms, you can easily show that the transfer function from H to A is
A(s)/H(s)= (s + a + k*(1+(a/b)) / (s^2 + (a + b + k*(1+a/b))*s + k*(a+b) )
Under the assumption that “a” and “b” are much greater than k, this becomes approximately
A(s)/H(s) := (a / (a + b) ) / (s + k)
This approximate transfer function describes a system of the form
dA/dt := -k*A + (a / (a + b) )*H
A similar calculation for O will yield
dO/dt = -k*O + (b / (a+b) )*H
Thus, the fraction a/(a+b) of H accumulates in the atmosphere, and b/(a+b) accumulates in the oceans. The total a/(a+b) + b/(a+b) = 1, so all of it either ends up in the land or in the oceans.
The IPCC effectively says a is approximately equal to b, hence roughly 1/2 ends up in each reservoir in the short term. If this seems unreasonable to you, well, we aren’t done yet, so keep your powder dry. In actual fact, the processes involved are much more complicated than this. Obviously, for one thing, we haven’t included the dynamics of the land reservoir.
And, because the dynamics are governed by diffusion equations, partial differential equations (PDE) which can be cast as an infinite expansion of ordinary differential equations (ODE) (this is a key result of functional analysis), the scalar equations can be expanded into infinite dimensional vector equations, with the components of the vectors summing up to the total. Each component has its own gain and time constant associated with it, and can thereby be considered a partition of the total CO2. It is a mathematical construct, not a physical one, which approximates the physical reality only when it is all summed together.
That is how the Bern model is constructed. I am not saying it is constructed correctly, I am just telling you it is on firm theoretical grounds, and you guys are attacking the castle wall at its most fortified location, instead of just walking around to where they haven’t even laid the first stones.
I’ll acknowledge a personal lack of mathematical virtuosity, but there seem to be two ways of applying mathematics to physical phenomena.
The first is to come up with some ‘cocktail-shaker’ combination of numbers and functions that somehow fits observations and accurately models the past, thus inspiring confidence that it may be useful for predictions. This is essentially ‘hit-and-miss’ with little genuine understanding required, but can be useful for complex, analysis-defying systems.
The second is to accurately quantify and incorporate ALL relevant factors with their correct relationships. This requires a high degree of understanding and becomes progressively more difficult as system complexity increases. Indeed, with something like the weather or CAGW I have to wonder at the claimed reliability of ANY model.
I like to think that mathematicians are gainfully employed but, surely, some phenomena are not readily amenable to mathematical modelling. Will a significant increase in CO2 lead to evolution of more CO2-hungry organisms? Exactly how big a role does the sun play and how do we know what it’s going to do next? What about cosmic rays? I’ve barely scratched the surface here and we’re arguing about the application of high mathematics to poorly-understood phenomena. What’s the weather going to be like next month?
Frankly, I believe that the study of crystal orbs or chicken entrails is just as likely to deliver an understanding of climate as the Bern Model or its rivals.
Surely, fans of this website have noticed that it is a lot easier to poke holes in the asinine pronouncements of the doomsayers than it is to come up with a robust alternative. Think about the reasons for this.
(Wet blanket now hung out to dry.)
I look at the CO2 anual variations of the Hawaii observations due to just the seasonal temperature variations and it is 300% of the annual increase. The ocean’s breath is 3 times the annual increase of the supposed human footpring.
I think David Archer is describing the “Bern” model clearly here.
http://geosci.uchicago.edu/~archer/reprints/archer.2008.tail_implications.pdf
I think they’re arguing that CO2 quickly reaches a balance with sea surface and plants, but is slow to reach balance with the ocean depths. Forr a simple example, if the CO2 ratios in
the oceans’ top layer, in plants,,in the atmosphere, and ocean depths was 2, 1, 1, and 48,
and an additional unit of CO2 was dumped into the system, the balance would quickly reach
2.5, 1.5, and 1.5, but the 48 ocean depth is acting a lot slower, on a scale of about 800 years.
I think the drop in C14 since the nuclear testing spike in the early 1960s is a counter example to the Bern- David Archer model.
http://en.wikipedia.org/wiki/File:Radiocarbon_bomb_spike.svg
Seems to me plants will grab as much CO2 as they can get their grubby leaves on.
Since the CAGW claim is CO2 is “Well Mixed” then the reduction of CO2 in the atmosphere by plants should be governed only by how fast new CO2 can be transported via diffusion or wind into contact with the leaves.
Hydroponic Shop
Given the evidence from the wheat field (C3 plants) that plants will use all the CO2 in their vicinity, coupled with absorption of CO2 by water (rain is a weak acid due to dissolved CO2) I find the residence times over a couple of years very tough to swallow.
As Ian W says:
And of course as the CO2 is brought back to the surface the plants on land and in the ocean gobble it up.
I find myself agreeing with Bart here. And with Nullius, who I think is expressing the right idea, and also with the electrical circuit analogies.
To rephrase Bart (I think) you have a Laplace Transform representation, and you approximate the integrand by a set of poles. Or, if you want to think of it in the real domain, you have the idea that your response can be represented as a weighted average of a whole lot of exponentials (that’s just math), and then you choose a few to be representative.
But you can also see it in electrical terms with resistance-capacitance circuits. Each R-C pair has a time constant, reflecting the timescales in the Bern Model.
And yes, it’s also a multi-box model, and they have difficulties.
I’m glad to see Willis’ appendix – the two different time constants are indeed poorly understood.
The only thing that makes sense to me is the model they are using is assuming saturation of the various processes and assigning a % to that sink. That is, once the fastest sink saturates they assign a value to it, then they look at the 2nd fastest sink and so on. What’s eventually left goes into the slowest sink.
I didn’t read the link but I can’t think of any other way they could generate those percentages.
“CO2 evolves according to a higher-order linear equation (or a system of first-order linear equations that is the same). Very reasonable. That is where the “partitioning” comes,”
NO, NO, NO, NO, NO.
CO2 does not do anything “according to” any equation.
We humans use equations as fair, simlar MODELS of reality. A molecule of ANYTHING never checks some equation to see how to behave. Never.
That is our human imagination that a falling object’s speed “follows” some formula, etc.
This may not seem like a big point, but it makes all the difference in the world. The natural world does not behave according to formulas, with us discovering the formula. The natural world behaves. We develop models that APPROXIIMATE this behavior. If we are lucky.
There seems to be confusion about the integral equation in the link. It is simply a “convolution integral” which says that the output is the input
convolved with the impulse response – very standard stuff. The impulse response, the term in [ ], does (in their formulation) contain a step, but IT is not inside the integral BY ITSELF. It is inside multiplied by E. E in turn can be thought of as a single impulse (or usually as many, possibly an infinite number) of impulses. Thus we may integrate TO a step. This simply means there will be a scaled version of the input in the output. A non-decaying exponential in the impulse response. Overall this corresponds to an exact (actual) circuit configuration.
It seems to me – we should think of CO2 here just like charge on a capacitor. In the circuit, individual (isolated) charges are restricted to their own capacitor (drained by an individual resistor). This is NOT what happens in the atmosphere – obviously. It’s all one capacitor and all the individual sinks are one resistor. Wrong model, and probably a faulty physical understanding.
First thing is, the expression is not the Bern model, it is approximation (regression) of the Bern model. You can understand individual factors as regression coeficients which usually have very limited connection to reality.
Second thing, the categorization of CO2 sinks in SAR has probably nothing to do with categorization of CO2 sinks in TAR – SAR works with five “main sinks”, TAR works with three completely different “main sinks”. In each case real considered CO2 sinks are assigned to five or three groups for simplicity in a way so that differences in each group more or less cancel out to provide consistent behavior of the group.
In order to visualise the expression, divide earth surface to six (SAR) or four (TAR) parts, proportional to coefficients a(0) to a(n). a(0) is part of earth surface which does not act as carbon sink, the rest are carbon sinks with “sinking” effectivity given as tau(n). Also understand that proportion of Earth surface also corresponds to proportion of atmospheric volume above that surface.
The coefficients tau(n) specify effectivity of individual sinks – if tau(1) is 171 and tau(2) is 18 it only means that sink 1 would do with the atmosphere in 171 years what sink 2 would do with it in 18 years, if there was only sink 1, respective sink 2 all over the world.
In the paper they claim that a) wetlands are a large and significant sink for carbon, and b) they are “rapidly diminishing”.
They’re also a large and significant source of methane. As for the “rapidly diminishing” part, I can only assume they believe that any (cue scary music) sea level rise (cut scary music) will cover existing wetlands (aka, “tidal swamps”) without creating new ones…
Bart says:
May 6, 2012 at 7:47 pm
Thanks, Bart. So … where in your derivation do we find the part about the division of the atmosphere into partitions, each of which has a different time constant? That’s the part that seems problematic to me, and I didn’t see anything about that in your math, although I could have overlooked it. What am I missing?
w.
JFD says:
“Sure, I’ve heard of carbonitite volcanoes. They have a high percentage of limestone and dolomite (calcium/magnesium carbonates) in them. They are in the 99.9% of carbon listed first in my post.”
You only mentioned sedimentary rocks, volcanic source rocks are not sedimentary rocks, they source material from the mantle. (as well as recycling material from the crust and from the ocean at plate boundaries). But until there is a mantle cycle ( eg mid ocean ridges) and a subduction cycle (eg largely at plate boundaries) in the carbon cycle diagram, the carbon cycle diagram as shown, is astonishingly incomplete. As I said before, carbonate and volcanoes in the oceans are involved in large scale exchanges, especially along mid ocean ridge systems, and in island arcs. These are not accounted for in the carbon cycle diagram of the IPCC. Carbonitites are another example, contianing >50% carbonate, although the origin of this carbonate is disputed.
As I also mentioned, this is important because I suspect the mid ocean ridges and other volcanoes play a role in e.g. buffering ocean acidity. This is not accounted for by marine biologists, of course.
Bart says:
May 6, 2012 at 7:47 pm
Bart, a question. Why is the rate at which the ocean sequesters CO2 a function of 1 + a/b ? Isn’t it a totally different physical process? Why should it depend on the rate of air/sea exchange?
w.
Nick Stokes says:
May 6, 2012 at 8:22 pm
“But you can also see it in electrical terms with resistance-capacitance circuits. Each R-C pair has a time constant, reflecting the timescales in the Bern Model.”
The characteristics of transmission lines fit this description, and transmission line models are often used to characterize so-called pink noise.
Willis Eschenbach says:
May 6, 2012 at 10:16 pm
“…where in your derivation do we find the part about the division of the atmosphere into partitions, each of which has a different time constant?”
At the part where I said: ” partial differential equations… can be cast as an infinite expansion of ordinary differential equations… Each component has its own gain and time constant… It is a mathematical construct, not a physical one, which approximates the physical reality only when it is all summed together.”
Bart says:
May 6, 2012 at 11:43 pm
Thanks, Bart, but I still don’t see where you get the partitioning. My understanding (which of course may be wrong) is that in an infinite expansion, each term applies to the entire thing, not e.g. 13% of the total for one term and 26% of the total for the second term and the like.
For example, the expansion of Cos(x)/x = 1/x – x/2 + x3/24 – x5/720 + …
But nowhere in there do I find x broken into “13% x / 720 +26% x / 720 …”
Also, normally an infinite expansion has alternating positive and negative terms which decrease in size. This is not true of their expression, where all terms are positive and are of different sizes …
Thanks for your patience in the explanations. As I said at the start, that’s what I’m looking for.
w.
Bart says:
May 6, 2012 at 7:47 pm
Erratum – This sentence should read: “The total a/(a+b) + b/(a+b) = 1, so all of it either ends up in the atmosphere or in the oceans.” The model I demonstrated did not include the land dynamics. Its main purpose was to show how roughly 1/2 of the CO2 could end up rapidly transported from the atmosphere into the oceans without becoming permanently sequestered from the overall system.
As I stated above, I believe this description is moot. That it is mathematically possible is not confirmation that it is the governing process, and the rather strong correlation between CO2 and temperature which I have pointed out indicates that to me that it is an unimportant question. Temperatures are driving CO2 concentration, and not the reverse.
Bart, let me try to explain it a different way. If I understand you, you are saying that the equation that they give in the linked file is an infinite expansion of a transfer function based on the underlying box model.
But if that were the case, why would there be a variety of numbers of terms, along with different coefficients for the terms? If it is an infinite expansion, wouldn’t it have defined coefficients with defined corresponding time constants? They use two forms, for example, one with six terms and the other with four terms. The terms have different coefficients, and apply to different fractions of the whole … how is it possible that that is “an infinite expansion of ordinary differential equations” as you say?
w.
“Another result from this assumption is that IPCC can invoke inappropriate chemical equilibrium equations to give the sequestering of sea water multiple simultaneous time constants, ranging from centuries to thousands in the IPCC reports, and up to 35,000 years in the papers of its key author, oceanographer David Archer, University of Chicago. The assumption is foolishness as shown by its consequences, but it tends to confirm oceanographer Wunsch’s 10,000 year memory claim. The science should have influenced Wunsch to distance himself from IPCC, neither joining with it in the lawsuit, nor identifying himself as a supporter of its conclusion, the existence of AGW”
http://www.rocketscientistsjournal.com/2007/06/on_why_co2_is_known_not_to_hav.html
Willis Eschenbach says:
May 7, 2012 at 12:06 am
‘For example, the expansion of Cos(x)/x = 1/x – x/2 + x3/24 – x5/720 + …
But nowhere in there do I find x broken into “13% x / 720 +26% x / 720 …”’
I assume you mean, if “y = Cos(x)/x”, nowhere do you find y broken into “13% x / 720 +26% x / 720 …”’
But, nothing is stopping you from doing so.
“Also, normally an infinite expansion has alternating positive and negative terms which decrease in size. This is not true of their expression, where all terms are positive and are of different sizes …”
Not generally. For example, exp(x) = 1 + x + x^2/2 + x^3/6 + … The coefficients have to decrease in size or the expansion will not converge. But, the decrease does not have to be monotonic. For example, (1 + x^2)*exp(x) = 1 + x + 1.5*x^2 + 7/6*x^3 + …
Of course, exp(x) is unbounded as a function of x. But, the polynomial base functions are, themselves, unbounded. In the Bern model, the basis functions are decaying exponentials, so this is not a concern. For example, I can expand
(1 + exp(-x)^2)*exp(exp(-x)) = 1 + exp(-x) + 1.5*exp(-2*x) + 7/6*exp(-3*x) + …
Willis Eschenbach says:
May 7, 2012 at 12:16 am
“If it is an infinite expansion, wouldn’t it have defined coefficients with defined corresponding time constants?”
The function is not known a priori, so the coefficients have to be estimated based on observables (my beef being that the observables are not enough to provide a complete description, and not very certain, either). Different estimation techniques and assumptions tend to yield different results.
In addition, practically speaking, you have to truncate the expansion at some point – there generally is not enough information rich data to estimate all the coefficients, and the more coefficients you try to estimate, the more uncertain each estimate becomes. Always, there is a tradeoff between bias and variance. The only question is whether the bias and variance can be small enough for the estimate to be useful.
So, to wrap it up for now, theoretically, the procedure is sound. But, practically speaking, there are plenty of good reasons to be wary, even skeptical (or, downright disbelieving, as I am), of the parameterization.
Dr Burns says:
May 6, 2012 at 1:30 pm
In relation to sources and sinks, can Willis, or anyone else explain this image of global CO2 concentrations ?
Why does Antarctic ice appear to be such a strong absorber in parts and why such strong striation?
http://www.seos-project.eu/modules/world-of-images/world-of-images-c01-p05.html
I think the striations are due to mid-troposphere southward flows of air with relatively high CO2 feeding surface northward katabatic winds.
But I was unable to find a study that supports this, so just a guess on my part.
Haven’t read all the replies, so this point might have been made.
Exponentials are not orthogonal functions like sine waves, and cannot be picked out of a mixture with any accuracy. Noisy data simply exacerbates the problem. Declaring exponential constants to four significant figures is a triumph of optimism.
Mike
“Thanks, Bart. So … where in your derivation do we find the part about the division of the atmosphere into partitions, each of which has a different time constant? That’s the part that seems problematic to me”
Where he says:
“Thus, the fraction a/(a+b) of H accumulates in the atmosphere, and b/(a+b) accumulates in the oceans. The total a/(a+b) + b/(a+b) = 1, so all of it either ends up in the land or in the oceans.”
If a fraction a/(a+b) stays in the air, the time constant for the transfer only applies to the CO2 transferred, which is a proportion b/(a+b) of the total atmosphere.
Some have said that the rate has to be proportional to the total CO2 content of the atmosphere, but this isn’t true. The rate is proportional to the difference in concentrations of the source and destination reservoir, like conductive heat flow is proportional to the difference in temperatures, electrical current is proportional to the difference in voltages, water flow is proportional to the difference in heights, etc.
And the difference between the atmosphere and one sink may be different to the difference between the atmosphere and another sink.
The other thing being assumed is that the CO2 transferred has no effect on the level of CO2 in the sink, that it acts like an infinite void, or an idealised thermodynamic cold sink that can absorb any amount of heat without changing temperature. While there’s no doubt the ocean is a lot bigger than the atmosphere, it’s not infinitely bigger, and to start with only the top layer of the ocean is affected. The level in the sink increases as it absorbs CO2, and the rate of flow is proportional to the difference in levels. So the flow pushes the source to decrease and the sink to rise until they converge on an intermediate level, when flow stops. It’s not because the reservoir is full, or saturated. It’s simply because the levels are equal. If you add more CO2, it will go up again. If you keep adding CO2 it will go up continuously. Stop and the flow will slow and stop, but it decays away exponentially to the intermediate level, not the original level. (A fraction a/(a+b) stays in the air.) This is at some fraction of the difference between them, and that’s where the apparent partitioning comes from.
I’ll try the tanks example with some numbers, in case that helps. Tanks A and B have 1 square metre horizontal cross sections, but are very tall. Tank C has a 98 square metre cross section, and is again tall. The level of water in all three tanks is 3 metres. We now dump a pulse of 3 cubic metres into tank A. Instantaneously the level in that tank doubles to 6 metres. Very quickly, because of the wide pipe connecting them, A drops to 4.5 metres and B rises to 4.5 metres as 1.5 cubic metres of water flows between them. Note that the 3 cubic metres added has been partitioned – half of it has transferred and half stayed. Only 1.5 metres is affected by the rapid exponential decay. Then over a far longer period, the 4.5 metres in A and B equalises with the 3 metres in C. 3 cubic metres (2x(4.5-3)) is spread evenly over 100 square metres, for an equilibrium depth of 3 centimetres. Tanks A and B slowly drop to 3.03 metres, and C even more slowly rises to 3.03 metres. There is 3 cm of permanent rise.
None of the tanks are full. If you dump another three cubic metres into tank A, half of it will still drain into tank B just as rapidly as before. The sink is not saturated, its capacity for absorption not reduced. You could dump 300 cubic metres into it and half would still transfer to B with the same rapid rate constant. But only half.
Willis and others:
I understand the interest in the Bern Model because it is the only carbon cycle model used by e.g. the IPCC. However, the Bern Model is known to be plain wrong because it is based on a false assumption.
A discussion of the physical basis of a model which is known to be plain wrong is a modern-day version of discussing the number of angels which can stand on a pin.
I again point to our 2005 paper which I referenced in my above post at May 6, 2012 at 3:58 pm. As I said in that post, agreement of output of the Bern Model requires 5-year smoothing of the empirical data for output of the Bern Model to match the observed rise in atmospheric CO2 concentration.
The need for 5-year smoothing demonstrates beyond doubt that the Bern Model is plain wrong: the model’s basic assumption is that observed rise of atmospheric CO2 concentration is a direct result of accumulation in the air of the anthropogenic emission of CO2, and the needed smoothing shows that assumption cannot be correct.
(Please note that – as I explain below – the fact that the Bern Model is based on the false assumption does NOT mean the anthropogenic emission cannot be the cause of the observed rise of atmospheric CO2 concentration.)
I explain this as follows.
For each year the annual rise in atmospheric CO2 concentration is the residual of the seasonal variation in atmospheric CO2 concentration. If the observed rise in the concentration is accumulation of the anthropogenic emission then the rise should relate to the emission for each year. However, in some years almost all the anthropogenic CO2 emission seems to be sequestered and in other years almost none. And this mismatch of the hypothesis of anthropogenic accumulation with observations can be overcome by smoothing the data.
2-year smoothing is reasonable because different countries may use different start-dates for their annual accounting periods.
And 3-year smoothing is reasonable because delays in accounting some emissions may result in those emissions being ‘lost’ from a year and ‘added’ to the next year.
But there is no rational reason to smooth the data over more than 3-years.
The IPCC uses 5-year smoothing to obtain agreement between observations and the output of the Bern Model because less smoothing than this fails to obtain the agreement. Simply, the assumption of “accumulation” is disproved by observations.
Furthermore, as I also said in my above post, the observed dynamics of seasonal sequestration indicate that the system can easily absorb ALL the CO2 emission (n.b. both natural and anthropogenic) of each year. But CO2 is increasing in the atmosphere. These observations are explicable as being a result of the entire system of the carbon cycle adjusting to changed conditions (such as increased temperature, and/or addition of the anthropogenic emission, and/or etc.).
The short-term sequestration processes can easily absorb all the emission of each year, but some processes of the system have rate constants of years and decades. Hence, the entire system takes decades to adjust to any change.
And, as our paper shows, the assumption of a slowly adjusting carbon cycle enables the system to be modelled in a variety of ways that each provides a match of model output to observations without any need for any smoothing. This indicates the ‘adjusting carbon cycle’ assumption is plausible but, of course, it does not show it is ‘true’.
In contrast, the need for smoothing of data to get the Bern Model to match ‘model output to observations’ falsifies that model’s basic assumption that observed rise of atmospheric CO2 concentration is a direct result of accumulation in the air of the anthropogenic emission of CO2.
Richard
Willis and others:
I write this as an addendum to my post at May 7, 2012 at 2:09 am.
As several people have noted, the Bern Model is one example of a ‘plumbing model’ of the carbon cycle (personally, I think Engelbeen’s is the ‘best’ of these models).
Adjustment of the carbon cycle is akin to all the tanks and all the pipes varying in size at different and unknown rates. Hence, no ‘plumbing model’ can emulate such adjustment.
And the adjustment will continue until a new equilibrium is attained by the system. But, of course, by then other changes are likely to have happened so more adjustment will occur.
Richard
Bart,
Not sure about the infinite expansion.
I think the number of decaying exponentials is the number of reservoirs minus one.
It’s a system of coupled first-order linear differential equations. If we put the levels in all the n reservoirs into an n dimensional vector L, the homogeneous part is dL/dt = ML for some matrix of constants M. This can be diagonalised dL/dt = (U^-1 D U) L so we can change variables d(UL)/dt = D(UL) and the coupled equations are separated into independent differential equations each in one variable. Once we’ve solved for the variables UL, we can transform back to the original variables.
The matrix is of rank n-1, since we lose one degree of freedom from the conservation of mass. We therefore ought to get n-1 decaying exponentials for n reservoirs.
So if we stop all fossil fuel CO2 the level of CO2 in the atmosphere would drop. There would be a modest fall in global temperature. At what level would the amount of CO2 in the atmosphere stabilise? And as the natural processes of the carbon cycle continue then
1) What is the source of CO2 to maintain stability as the natural sequestering processes would continue as sediments fall below the earth’s surface? Is it essentially just volcanoes?
2) Based on this stable level of atmospheric CO2 what reduction in biogrowth would we expect vs current levels of CO2?
3) What limits would such a fall put on potential global agricultural production vs projected growth in world population?
4) Should we be capturing carbon now so that when carbon fuels run out we can inject CO2 into the atmosphere to maintain agricultural production levels?
Its not clear to me whether the various carbon sinks are acting in series or parallel.
Let’s say the ocean is a fast carbon sink and plankton photosynthesis is a slow carbon sink. The ocean takes up CO2 and then plankton remove it from the water and it sinks to the deep. An initial pulse of CO2 would be reduced quickly, but the ocean would become saturated, then there would be a long tail as the plankton removed it at the same rate as there was further uptake by the ocean.
Is this going in the right direction? Don’t know enough myself.
Thanks Willis for responding to my comment, which was based on a misunderstanding of the link I gave. But what an interesting post, question and comments. I learn something new here every day.
The question, ” what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?” seems to be unanswerable, which perhaps makes the Bern Model wrong and therefore its use by the IPCC wrong.
Particularly as “there is no experimental evidence that will allow us to distinguish between plain old exponential decay (which is what I would expect) and the complexities of the Bern model”.
The Svensmark paper mentioned carbon dioxide being scarce when supernovas were high based on the idea that plants dislike carbon dioxide molecules containing carbon-13, which were then absorbed by the ocean. But this doesn’t seem relevant so apologies if I’m talking through my proverbial.
I look forward to your further posts on sinks and the e-folding time. You have that rare knack for getting straight to the heart of a theory.
son of mulder:
At May 7, 2012 at 2:49 am you ask;
“So if we stop all fossil fuel CO2 the level of CO2 in the atmosphere would drop. There would be a modest fall in global temperature. At what level would the amount of CO2 in the atmosphere stabilise?” etc.
I answer;
Please read my above post at May 6, 2012 at 3:58 pm because it explains why it is not possible for anybody to provide an answer to any of your questions (although some people claim they can).
Richard
Published in January 2008 at
http://icecap.us/images/uploads/CO2vsTMacRae.pdf
Excerpt:
The four parameters ST (surface temperature), LT (lower tropospheric temperature), dCO2/dt (the rate of change of atmsopheric CO2 with time) and CO2 all have a common primary driver, and that driver is not humankind.
Veizer (2005) describes an alternative mechanism (see Figure 1 from Ferguson and Veizer, 2007, included herein). Veizer states that Earth’s climate is primarily caused by natural forces. The Sun (with cosmic rays – ref. Svensmark et al) primarily drives Earth’s water cycle, climate, biosphere and atmospheric CO2.
Veizer’s approach is credible and consistent with the data. The IPCC’s core scientific position is disproved – CO2 lags temperature by ~9 months – the future cannot cause the past.
Faux Science Slayer says
The oceans do NOT absorb CO2 from the atmosphere
——–
The measurements says otherwise.
Allan McRae,
Nice analysis! Temperature variations cause a lagged CO2 response because of the solubility pump’s dependence on temperature. But CO2 change is contributed to by many sources and sinks, and just because one component is caused by temperature doesn’t mean all the others are.
You might find it useful to plot a graph of the correlation coefficient between temperature and lagged CO2 as a function of the lag. That’s the usual way to make lagged relationships clear.
A long time ago I worked on developing an inverse technique for deducing isotope concentrations based on the results of degassing experiments on minerals. It turned out to be mathematically equivalent to a constrained numerical inversion of the Laplace transform. Unfortunately, this is known to be an incredibly ill-conditioned problem. The bottom line is that simultaneously deducing the distribution of amounts AND half-lives from decay data (either radioactive decay or CO2 concentration decay) is incredibly difficult and the uncertainties are enormous because the functions you are using to model the decay (a series of exponentials) are far, far from being orthogonal. Any negative exponential can, to excellent accuracy, be approximated by a sum of other exponentials with different decay rates. You can either deduce decay rate if you know you have a single (or at least very simple but known) combination of reservoirs, or you can deduce the amounts in different reservoirs if you know their decay rates independently. You just can’t to both things simultaneously to any useful degree. I would be quite skeptical of anyone who purported to do both.
I notice that the little cartoon diagram fails to include the sequestration as concrete sets.
Bill Tuttle says:
May 6, 2012 at 10:15 pm
….They’re also a large and significant source of methane. As for the “rapidly diminishing” part, I can only assume they believe that any (cue scary music) sea level rise (cut scary music) will cover existing wetlands (aka, “tidal swamps”) without creating new ones…
________________________________
The “rapidly diminishing” part also sticks in my craw. In the USA swamps are busy forming as the !@#&* beaver dam up streams and creeks. My pretty little creek is now a large multi-acre swamp despite the power company having a guy trap over two hundred beaver in one year. The nearest city, with a drinking water inlet just down stream from the outlet of my creek, now has a Giardia/Beaver Fever problem according to the county Inspections Department guy I asked.
I should also note that the beaver dam raised the water table so high that along with the beaver pond there is now an additional 40 acres that is too soggy to support the lob lolly pine that had been growing and the field beyond the pines is also too wet to plow. That is just on my land. It does not include the addition hundred or so acres belonging to my neighbor.
I should also add about this to the “rapidly diminishing” part.
Running water performs three closely interrelated forms of geologic work:
1. Erosion
2. Transportation
3. Deposition
As rivers erode the river bed the angle of incline becomes lower. In “old age” or where a river/stream dumps into a lake, pond or ocean you get flood plains with low relief across which the water flows meander causing braided channels, deltas and marshes. As the eroded sediment is dumped into lakes and ponds they fill and the later stages are swamps and marshes.
Mankind using dredging can to some extent modify this geologic progression but with “wetlands protection” in many advanced western countries “rapidly diminishing” stopped thirty years ago and has more likely changed to “rapidly advancing” ever since.
In 1971, the international Convention on Wetlands was adopted…The Ramsar List of Wetlands of International Importance includes nearly 2,000 sites, covering all regions of the planet.
In other words this is a recycling of the old “Boogy Man” from the 1960’s for a new generation of ignorant bleeding hearts who are unfamiliar with the complex tangle of international treaties, conventions and accords.
(BTW bleeding hearts is not a derogatory term, it is the con-men using people’s compassion that I have the problem with. Civilization requires EDUCATED bleeding hearts to keep the predators in check. Most people on WUWT fit the category of educated bleeding hearts, or we would not give a darn what happens to future generations.)
The integral is a convolution of the emission history with an impulse response function. If you get a pulse of emissions and then nothing, the emission falls further and further behind, t-t’ gets larger and larger, and the impact of the emissions is given a large negative weighting, shrinking it. It does decay.
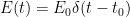
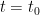 of
of  which we’ll assume was established in the distant past so that it is constant, the concentration will be the following:
which we’ll assume was established in the distant past so that it is constant, the concentration will be the following:
 (1)
(1)
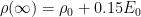
 . That is an absurdity on the face of it — surely there is a natural rate
. That is an absurdity on the face of it — surely there is a natural rate  that would maintain an equilibrium CO_2 concentration, within noise, on all time scales, and equally certainly it won’t take the Earth thousands of years or even hundreds to find that equilibrium. Indeed, I’ve written a very simple linear model for — at least in a linear response model in which exponentials are themselves appropriate — how the equilibrium concentration must depend on the input and total decay rate. My model, gentlemen, will reach follow equilibrium wherever the input might take it. The Bern model, my friends, has no equilibrium —
that would maintain an equilibrium CO_2 concentration, within noise, on all time scales, and equally certainly it won’t take the Earth thousands of years or even hundreds to find that equilibrium. Indeed, I’ve written a very simple linear model for — at least in a linear response model in which exponentials are themselves appropriate — how the equilibrium concentration must depend on the input and total decay rate. My model, gentlemen, will reach follow equilibrium wherever the input might take it. The Bern model, my friends, has no equilibrium — 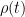 increases without bound for any input at all, and not particularly slowly at that.
increases without bound for any input at all, and not particularly slowly at that.
No, it doesn’t. I understand perfectly well what this model does. If we feed it:
as input — your “emissions pulse” (which we’ll have to assume is uniformly applied, since I imagine that it takes times commensurate with the shortest decay time to mix a bolus through the entire atmosphere) — then it states that — given an initial concentration at
and we are right back where we started, asking why the bolus of CO_2 that was added at time $t_0$ came with four labels and is removed by a sum of exponential processes acting on labelled partial fractions of the whole.
There are two things immediately apparent about this. First, no matter how long you wait, the asymptotic behavior of this is:
It does not decay. This is a monotonically growing model and if it were true we would see CO_2 inexorably increase over the ages because even the 171 year time scale is absurd — it really says that we keep 40% of every delta function “blip”, every breath, the foam from every beer, in the atmosphere, indefinitely. It says that almost 30% of the gasp of breath Albert Einstein exhaled when he first realized that Planck’s quantum hypothesis could explain the photoelectric effect is still with us, not just 30% of the molecules but 30% of the additional concentration that it represented. There is no rate of addition of CO_2 that can lead to equilibrium with this solution but zero.
If this doesn’t strike you as being a blatently political but well-concealed scientific lie, well, you are very forgiving of a certain class of error.
Error, you say? Yes, error. Obvious error. If you will check back to my first post — and Bart’s remarks, if he will take the time to go back and check them, and K.R.’s remarks as he accuses Willis of being less than sincere — it appears that we all agree that there is no way in hell atmospheric CO_2 concentration will decay as a sum of exponentials because this is a horrendous abuse of every principle that leads one to write down exponential functions in the first place. CO_2 does not come with a label, and decay processes act on the total concentration to reduce it until equilibrium is reached. The only conceivable correct local behavior is the product of competing exponentials, never the sum.
Now, it was asserted (by K.R. and perhaps Bart, hard to recall) that the integral presented wasn’t really the sum of exponentials but something way complicated that does in fact arise from unlabelled CO_2 in some math juju magic way. By presenting you with the actual integral of a delta function bolus of CO_2, I refute you. Perhaps K.R. can apologize for his use of “disingenuous” to describe Willis’ stubborn and correct assertion that it did. I have never known Willis to be anything but sincere…;-)
Now, it would be disingenuous to continue without an actual explanation of two things:
a) Why anyone should take seriously a model that cannot — note well cannot — ever produce an equilibrium given a non-zero input function
b) Far up above, I thought that we all agreed that a model that consists of a weighted sum of exponentials acting on partial fractions of the partial pressure was absurd and non-physical, because CO_2 does not come with a label and each process, being stochastic and proportional to the probability of a CO_2 molecule being presented to it, proceeds at a rate proportional to the total CO_2 concentration, not the “tree fraction” of it. I have now conclusively proven that hiding that behavior in a convolution does not eliminate it from the model. What, as they say, is up with that?
The onus is therefore upon any individuals who wish to continue to support the model to start by justifying equation (1) above for a presumed delta function bolus. A derivation would be nice. I want to see precisely how you arrive at a sum of exponential functions each acting on a partial fraction of the additional CO_2, with a “permanent” residual.
rgb
[Formatting fixed … I think. w.]
Some have said that the rate has to be proportional to the total CO2 content of the atmosphere, but this isn’t true. The rate is proportional to the difference in concentrations of the source and destination reservoir, like conductive heat flow is proportional to the difference in temperatures, electrical current is proportional to the difference in voltages, water flow is proportional to the difference in heights, etc.
Yes, but in order for the model to be correct, none of the reservoirs can be in contact with absolute zero, and if the model doesn’t permit the attainment of equilibrium on a reasonable time scale and in a reasonable way, it is just wrong. So why, exactly, will the biosphere adjust its equilibrium upwards? Why won’t the ocean follow the temperature instead of some imagined “fractional difference” leading it to an every higher base equilibrium concentration? Noting well that the total atmospheric CO_2 is just a perturbation of oceanic CO_2 so that for all practical purposes it is an infinite reservoir.
rgb
rgbatduke,
Thanks for the extensive reply. I’ll try to take each of your points systematically. Let me know if I miss anything important.
Your equation (1) contains a number of negative exponentials, which decrease in value over time. That’s what I meant by “decay”.
I already explained why it came with four ‘labels’. Because there are effectively five reservoirs, and five coupled linear ODEs.
Yes, the asymptotic behaviour is that $0.15 E_0$ remains. That’s partly because I think some very slow decay terms are being approximated, and partly because mass is conserved, and if you add CO2 to a system then the total amount of CO2 in the system must increase.
This doesn’t include Einstein’s last breath, though, because that’s part of the exchanges being modelled. The exchange with the biosphere reservoir includes both plants growing and animals eating them. $E_0$ is CO2 added from outside the modelled system.
If you pour water into a container with no exits, the water level increases forever. There is no equilibrium in which the level tails off to a constant, even though you’re still adding more water. Why do you assume there *has* to be an equilibrium?
I try not to assume motive without evidence.
I went through the business about labelling and whether decay is proportional to total concentration or the difference in concentrations previously. If decay is proportional to total concentration, you could only reach equilibrium when total concentration was zero.
I don’t consider anyone here to be disingenuous. Willis asked a sensible question, the answer to which I agree is not at all obvious. And I can quite see where you’re coming from with this.
a) You say “surely there is a natural rate E(t) > 0 that would maintain an equilibrium CO_2 concentration”. Why?
b) I agree CO2 doesn’t come with a label. But I’ve already explained that the partition is a mathematical artefact of the ratio of reservoir sizes, and that a portion does not get transferred because the level rises somewhat in the sink as a result of the transfer.
The case with three or more reservoirs is not intuitively clear, but it seems clear enough with two – that if the buckets are of equal size that only half the water dumped in one ends up in the other. They cannot all return to their previous level – where would the added water go to?
The probability of a CO2 molecule moving from A to B is proportional to the total CO2 concentration in A, but the probability of a molecule moving from B to A is proportional to the total concentration in B. The net flow from one to the other is proportional to the difference in concentrations.
“A derivation would be nice. I want to see precisely how you arrive at a sum of exponential functions each acting on a partial fraction of the additional CO_2, with a “permanent” residual.”
See my comments above regarding the equation dL/dt = ML and diagonalisation. The algebra is messy, but straightforward.
MikeG says:
May 7, 2012 at 1:31 am
“Declaring exponential constants to four significant figures is a triumph of optimism.”
Or, something. Agree completely.
richardscourtney says:
May 7, 2012 at 2:09 am
“This indicates the ‘adjusting carbon cycle’ assumption is plausible but, of course, it does not show it is ‘true’.”
Absolutely. The system is underdetermined and not fully observable. Thus, to get an answer, the analysts have to insert their own biases. The likelihood that they would hit on a faithful model, out of all the possibilities, is vanishingly small.
Nullius in Verba says:
May 7, 2012 at 2:45 am
“The matrix is of rank n-1, since we lose one degree of freedom from the conservation of mass. We therefore ought to get n-1 decaying exponentials for n reservoirs.”
The reservoirs themselves are a continuum. For example, what is the land reservoir? It is trees, grasslands, soil bacteria, rock and sediment formation, mammals, reptiles, amphibians, insects, etc… And, the dynamics of the atmosphere are diffusive. Areas of high and low concentration appear randomly, and the divergence increases near the surface sink. The eigevalues of the Laplacian operator are limitless. So, basically, you are correct, but n tends to infinity.
Gail Combs says:
May 7, 2012 at 6:06 am
My pretty little creek is now a large multi-acre swamp despite the power company having a guy trap over two hundred beaver in one year.
If you had dammed the creek to create a small pond for migrating waterfowl, the EPA would have forced you to tear down your dam (they have the backing of the DoJ) and fined you several thousand dollars for interfering with a watercourse and creating a potential health hazard. Because beavers built the dam, any action you might take (like accidentally dropping a stick of dynamite in the center of the dam) to assist the creek to return to it’s previous state would render you subject to horrendous fines for destroying a Giardia-filled wetland.
Just one more reason to gut the EPA…
[Formatting fixed. -w.]
rgbatduke says:
May 7, 2012 at 8:06 am
“There is no rate of addition of CO_2 that can lead to equilibrium with this solution but zero.”
Yes. As I have been saying, the model is mathematically, theoretically sound. But, they have parameterized it in such a way that it gives the answer they wanted, vastly underestimating the power of the sinks to draw out a substantial fraction of the atmospheric constituents in the near term. There is no data available to establish that the model is correct.
In fact, we know it is incorrect, for the very simple reason that temperature is driving the rate of CO2, and not the other way around. It is obvious in this plot that anthropogenic inputs have, at best, a minor role in establishing the overall concentration. Temperature variation accounts for almost all of it.
Nullius in Verba:
At May 7, 2012 at 9:16 am in relation to a ‘plumbing model’ you ask;
“The case with three or more reservoirs is not intuitively clear, but it seems clear enough with two – that if the buckets are of equal size that only half the water dumped in one ends up in the other. They cannot all return to their previous level – where would the added water go to?”
I answer:
It goes into a change in the volume(s) of the reservoirs.
In other words, the model is misconceived. Please see my above post at May 7, 2012 at 2:09 am and especially its addendum at May 7, 2012 at 2:44 am.
Richard
My Occamized Hypothesis is:
Geology and geogenesis put a sh**-load of CO2 into the early atmosphere. Eventually, life forms (flora) arose able to build themselves and proliferate by using photons to combine H2O and CO2. Shortly, eaters (fauna) evolved to munch on said flora. The flora expanded with little restraint and consumed CO2 until it began to run short. They then evolved to survive on less, but kept going. They are now approaching a lower limit, variously guesstimated to be in the region of 130-260 ppm — famine time. Fauna mass and volume and numbers track this, more or less.
So the “ideal number” is the lower limit, as that’s what the dominant life forms (flora) keep trying to achieve. Warmies are mental vegetables, so they also want to flirt forever with suicide by famine.
Simples!
So
A model valid over decades at this point in history, which is supported by the data, is:
dA/dt = -A/tau + k1*(T-To) + k2*H
A = atmospheric concentration anomaly
tau = time constant (could be operator theoretic, leading to a longer than simple exponential tail)
k1,k2 = proportionality constants (again, could be made operators)
To = equilibrium temperature
H = anthropogenic input
With tau relatively short and k2 not very large, the input from H would be attenuated rapidly. With k1 large, in the near term, the equation then becomes approximately
dA/dt := k1*(T-To)
which is what we see in the data.
richardscourtney says:
May 7, 2012 at 2:09 am
Richard, your paper is paywalled, so I fear I won’t be able to comment. That may be the reason your claims have gotten little traction, because you are referring to an unavailable citation.
All the best,
w.
I could be mistaken, but it seems to me that this Bern Model has appropriated a perfectly good concept of “impulse response” and other ideas of Laplace transform theory encountered by electrical engineers in “Linear Systems Theory.” The theory is of course correct in its EE version. The climate application is highly flawed: first in its inappropriate misapplication, and then in its poor implementation (at least a failure to do it with orthogonal basis functions).
So we are left with comments here pointing out the failings in the climate application. Quite so. But this does not reflect back and invalidate the theory as used in EE. Perhaps you do need to sketch the corresponding circuit (it involves R-C low-pass sections with a common input E (setting time constants), buffered, weighted, and summed (the partitioning lacking in the atmosphere). The equation in the link is correct. The convolution integral does not blow up. Think about electrons on discrete capacitors, not CO2 in the one atmosphere.
Given enough parameters (recall von Neumann’s delicious joke about an elephant modeled with 5 parameters), most mathematical constructions can be made to work locally. A polynomial can model a sinewave locally – but soon runs rapidly to infinity! Wrong choice. Only a fool would try to bake a cake in a refrigerator. But after that failure, should we decide it was not suitable for cooling lemonade?
It does no good to attempt to find fault with established linear systems theory. What seems to be wrong is the inappropriate application attempt, or at least considering it anything more than a local model (no physical meaning).
“a2videodude says:
The bottom line is that simultaneously deducing the distribution of amounts AND half-lives from decay data (either radioactive decay or CO2 concentration decay) is incredibly difficult and the uncertainties are enormous because the functions you are using to model the decay (a series of exponentials) are far, far from being orthogonal. Any negative exponential can, to excellent accuracy, be approximated by a sum of other exponentials with different decay rates. You can either deduce decay rate if you know you have a single (or at least very simple but known) combination of reservoirs, or you can deduce the amounts in different reservoirs if you know their decay rates independently. You just can’t to both things simultaneously to any useful degree.”
Absolutely correct. In a chemical reaction the measured first order rate constant IS the sum of all the first order rate constants, which are individual collisions of molecules of differing energy and colliding on different vectors.
I normally cringe from citing Wikipedia, but there is an interesting plot of carbon-14 concentration since 1945 at en.wikipedia.org/wiki/Carbon-14 that shows an exponential decay (removal of C-14 excess over background levels) consistent with an e-folding time on the order of a decade. The reason for the excess? Atmospheric nuclear testing. A never-to-be-repeated experiment.
Willis:
Thankyou for your comment to me that says;
“Richard, your paper is paywalled, so I fear I won’t be able to comment. That may be the reason your claims have gotten little traction, because you are referring to an unavailable citation.”
OK, I understand that, and I am not arguing that it get “traction”. In this thread I have been pointing out what the paper says so those points can be considered in the context of arguments about the Bern Model.
Also, I have a personal difficulty in that the paper was published in E&E and I am now on the Editorial Board of E&E so I cannot give the paper away. That said, I presented a version of it at the first Heartland Climate Conference and that version is almost completely a ‘cut and paste’ from the paper so I could send you a copy of that if you are interested to read it.
Regards
Richard
Willis Eschenbach
I spent some time re-reading the thread, and you are completely correct. It was entirely inappropriate for me to ascribe ill intent, and I would like to sincerely apologize for doing so in what should be a discussion of the science. Mea culpa, I was wrong. Please – call me on such things if I cross that line again.
—
With respect to the science: I thought it was quite clear that the exponentials and constants in the link you provided (http://unfccc.int/resource/brazil/carbon.html) are not the Bern model itself, which is described in Siegenthaler and Joos 1992 (http://tellusb.net/index.php/tellusb/article/viewFile/15441/17291). That is a multi-box model involving eddys, surface uptake, and the physics of mid-term CO2 absorption, with transport parameters calibrated against carbon-14 distribution measurements – complexities not in that page of exponentials.
Rather, they are approximate exponentials and fractions fitted to the results of running the Bern model, providing other investigators with some tools to estimate mid-term CO2 effects. Along with the caveat that “Parties are free to use a more elaborate carbon cycle model if they choose”. For example, the Bern model does not include CaCO3 chemistry or silicate weathering, long term carbon sinks.
So, as a starting point of discussion on the science:
– Is it clear that those exponentials are not the Bern model?
I am just amazed that nobody has commented on the relationship I have pointed out numerous times, which clearly shows that temperature has been driving CO2 concentration. It is obvious here that there simply is no need to consider human emissions to any significant level. This very simple observation kicks the very foundation out from under the Climate Change imbroglio.
KR says:
May 7, 2012 at 4:47 pm
KR, my thanks to you. It is the mark of an honest man and a gentleman to acknowledge when he has gone over the line. You have my sincere acknowledgement and appreciation.
I thought I had been clear above when I said:
My point is that whether you are using the Bern Model itself, or the simpler model described in the paper that I linked, it needs to be physically plausible and lead to physically plausible results. The problem is that the simple model that I linked to, which emulates the Bern Model, does neither.
My best to you, and again my thanks for your honesty,
w.
Willis Eschenbach – “”…as far as I can see, the Bern model proposes an impossibility. It says that the CO2 in the air is somehow partitioned, and that the different partitions are sequestered at different rates”
I really don’t understand this statement. There are multiple parallel and serial processes occurring in the fairly simple Bern model, and the approximations (constants for weighting and time factor) are just approximations for the various and multiple (parallel and serial) inter-compartment transfer rates. The percentages allow considering different CO2 pulses, and the time factors show how the Bern model inter-compartment movements show up.
There certainly is no initial partitioning of a CO2 input in the Bern model. The complexities of the model, its behavior, are just curve-fitted. Much in the way nuclear reactor fuel decay can be fit with a decaying exponential, regardless of the internal physics – a behavioral description. The exponentials are purely descriptive, behavioral analogs to the Bern model, which was (if I interpret that initial page correctly) provided as one potential resource. The issues raised with compartmentalization are really irrelevant.
I (IMO) don’t believe it’s appropriate to criticize the Bern (or any other model) from that standpoint – two steps back, arguing about the curve-fit to the model behavior. Rather, if you wish to truly critique a model, you need to show where the model itself breaks down. And since there is as far as I can see no discussion here of the assumptions, parameters (fit to among other things the carbon-14 data), and compartmentalization of that model, what is being discussed really isn’t the model at all.
That is not to say that the Bern model is a thing of perfection. It’s 20 years old, does not include long term sequestration such as CaCO3 or rock weathering, a simplistic biosphere compartment, and (as Joos et al note in their paper) has some latitude dependent inaccuracies with replicating C-14 measurements. But to quote George Box, “Essentially, all models are wrong, but some are useful”. A critique of this model needs to show how the model fails to meet observations – something that simply hasn’t been done on this thread.
There has been no demonstration that the model itself isn’t useful – that requires an evaluation against the data. If it fits the data, it’s useful. If it doesn’t, it’s not. I have seen no discussion of the model behavior against observations.
KR says:
May 7, 2012 at 7:53 pm
“A critique of this model needs to show how the model fails to meet observations – something that simply hasn’t been done on this thread.”
Ahem..
Bart
The Bern model is a carbon cycle model, not a temperature model, and the observations used to calibrate the Bern model are carbon-14 distributions in the oceans, also checked against (IIRC) CFC-11 distributions. In regards to the mid-term carbon cycle, the model being discussed is reasonably accurate – it matches those observations.
It would be an error to assume that CO2 is the only forcing WRT temperature, however – methane, CFC’s, aerosols, solar, and the ENSO variations are also in play. All of those affect climate forcings (and hence temperatures) as well. And all of those need to be (and are, in the literature) considered when looking at forcings and climate responses – issues beyond the realm of the carbon-cycle model discussed in this thread.
I am going to repeat what I see as a couple key points, and then add one new thought that may help in pulling them together:
1) As mentioned, the 4 exponential equation is a fit to a more complex model. The fit is statistical, not physical. The underlying model, however, is physical, with diffusive oceans and ecosystems. The first web page I found when googling Bern carbon cycle model has a bit of a description: http://www.climate.unibe.ch/~joos/model_description/model_description.html. Note that even the Bern model is simple compared to the models used by carbon cycle researchers.
2) Nullius’ description of 3 compartments is a decent one for getting the key concept, which is that you have 2 compartments which reach equilibrium with a pulse of emissions (or added water) on one time scale, and a 3rd which reaches equilibrium with the first two on a longer time scale, and some percentage of the added water remains in the original compartment forever.
3) My key additional point, then, is that the Bern cycle approximation is meant to apply to one specific scenario, which is a pulse of carbon emissions in a system which starts at equilibrium. This is why it doesn’t match intuition applied to phenomena like constant airborne fractions, and is only a rough guide to the effect of a stream of emissions over a number of years. Though, as a side note, a constant airborne fraction is a number that depends on the rate of emissions increase, and therefore isn’t a reliable source of information about sink saturation: if next year, human emissions were to drop by a factor of 10, based on my understanding I would predict a reduction in CO2 concentrations (because emissions would be smaller than the sink), so airborne fraction would become negative too. Or if emissions grew by a factor of 10, the airborne fraction would probably grow pretty large, because the sink would not grow nearly as fast. My intuition on sinks is based on the assumption that while there is probably pretty fast equilibration between the very surface ocean and some parts of the ecosystem, the year-to-year changes in sink size will be interactions with the slower moving parts of the system which are driven by the difference between the concentration in the fast-mixing layer and the medium mixing layer.
4) While there is a “permanent” part of the Bern cycle approximation, it isn’t really permanent – carbonate formation does eventually take carbon out of the cycle and back into deep ocean and thence to sedimentary rock (on a greater than ten thousand year timescale), where it will eventually be subsumed, and in millions of years may eventually end up being outgassed by a volcano.
-MMM
KR says:
May 7, 2012 at 8:26 pm
“It would be an error to assume that CO2 is the only forcing WRT temperature…”
Indeed it would. CO2 is not forcing temperature. Temperature is forcing CO2. The fact that the derivative of CO2 is highly correlated with temperature anomaly establishes it. As I related above, the forcing cannot be the other way around without producing absurd consequences.
“In regards to the mid-term carbon cycle, the model being discussed is reasonably accurate – it matches those observations. “
A subjective exercise in curve fitting which cannot gainsay the above.
MMM says:
May 7, 2012 at 8:30 pm
“Note that even the Bern model is simple compared to the models used by carbon cycle researchers.”
I came upon this remarkable relationship between the derivative of CO2 concentration and temperature by accident just last week. It is so blindingly clear that temperature is driving the CO2 concentration that it took me aback. How could this relationship have been missed when researchers have been looking at the problem for decades, and have what are undoubtedly elaborate models into which much time of very smart people has been invested?
The answer: they did not have the observations – the strong correlation has only recently become evident. CO2 has only been reliably sampled since 1958, and a real kink in the rate of change has only come about with the last decade’s lull in temperature rise.
I can only surmise that others who have taken the time to pay attention to what I have put forward here are similarly taken aback, and do not yet know how to respond. Can the solution to the riddle actually be so easy?
Yes, it can.
For those who have not been following along, the way in which CO2 concentration can be insensitive to human inputs while its derivative is effectively proportional to delta-temperature is explained here.
Bart,
Atmospheric concentrations of CO2 are slightly sensitive to anthropogenic emissions; at present, making up less than 10%. http://www.retiredresearcher.wordpress.com.
Willis — A multiple exponential equation is typically the solution to a system of linear differential equations.
To take a simple example, reduce Fig. 2 to three reservoirs — Atmosphere A, Surface Ocean S, and Deep Ocean D. Assume their equilibrium capacities are proportional to the given values, 750, 1020, and 38,100 GtC. If this is an equlibrium, the flows in and out must be equal, so let’s take the averages and say that S to A and back is 91 GtC/yr in and S to D and back is 96 GtC/yr., that these are the instantaneous rates of flow, and that if any reservoir were to change, its outflow(s) would change proportionately.
Then
d/dt A = -(91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)D ,
d/dt D = +(96/1020)S – (96/3810)D.
Setting x equal to the column vector (A, S, D)’, this has the form
d/dt x = B x, where
B = (-91/750 91/1020 0;
91/750 -187/1020 96/38100;
0 96/1020 -96/38100)
The general solution of this system has the form
x = Sum{ c_j exp(d_j t) v_j},
where the column vectors v_j are the right eigenvectors of B and d_j the corresponding eigenvalues.
For this B, the eigenvalues are -.2615, -.0457, 0. Since I assumed for simplicity that all the C is in one of the 3 reservoirs, the changes sum to 0, B is singular, and there is one zero eigenvalue. (If I had included a permanent sink like sediments or biomass, all eigenvalues would be negative and the system would be stationary, but the math works either way.)
The corresponding matrix V of eigenvectors is approximately V =
(-.51 -.44 .02;
.81 -.36 .03;
-.29 .82 .1.00)
The column vector c of weights is determined by the initial condition x_0 = V c, so that
c = V^-1 x_0. For simplicity we may take all variables as deviations from the initial equilibrium. If x_0 = (1, 0, 0)’, so that we are adding 1 GtC to the initial value of A, c will be
c = (-.69, -1.42, .96)’. Over time, A will then be
A = c_1 v_1,1 exp(d_1 t) + c_2 v_1,2 exp(d_2 t) + c_3 v_1,3 exp(d_3 t)
= .35 exp(-.26 t)+ .63 exp(-.05 t) + .02.
The three e-fold times are 3.8, 22, and inf years. The initial unit injection is “partitiioned” into three portions of size .35, .63, .02 with different decay rates, but there in fact is no difference between the gas in the three portions. The sum simply evolves according to this equation.
The same approach can be used to solve more complicated systems, stationary or nonstationary. Does this help?
[Formatting fixed. -w.]
Thanks, Willis!
Bart says: May 7, 2012 at 9:00 pm
“I came upon this remarkable relationship between the derivative of CO2 concentration and temperature by accident just last week.”
Hi Bart – I discovered this dCo2/dt vs T relationship in late December 2007, emailed to a few friends including Roy Spencer, and published in Jan 2008 at
http://icecap.us/images/uploads/CO2vsTMacRae.pdf
Please see my post above at May 7, 2012 at 3:51 am
____________________________
Nullius in Verba says: May 7, 2012 at 4:50 am
“Allan McRae, Nice analysis! Temperature variations cause a lagged CO2 response because of the solubility pump’s dependence on temperature. But CO2 change is contributed to by many sources and sinks, and just because one component is caused by temperature doesn’t mean all the others are.”
Nullius, I don’t think I’ve ever said it’s just about solubility – it’s clearly not. There is a solubility component, and also a huge biological component, and others…. I did say the following in the above 2008 paper:
“Veizer (2005) describes an alternative mechanism (see Figure 1 from Ferguson and Veizer, 2007, included herein). Veizer states that Earth’s climate is primarily caused by natural forces. The Sun (with cosmic rays – ref. Svensmark et al) primarily drives Earth’s water cycle, climate, biosphere and atmospheric CO2.”
See Murry Salby’s more recent work where (I recall) he included both “temperature” AND “soil moisture” as drivers of CO2 and got a somewhat better correlation coefficient. I have not reviewed his work in any detail.
I further think the science is substantially more complicated, with several temperature cycle lengths, each with its associated CO2 lag time.
So – is the current increase in atmospheric CO2 largely natural or manmade?
Please see this 15fps AIRS data animation of global CO2 at
http://svs.gsfc.nasa.gov/vis/a000000/a003500/a003562/carbonDioxideSequence2002_2008_at15fps.mp4
It is difficult to see the impact of humanity in this impressive display of nature’s power.
All I can see is the bountiful impact of Spring, dominated by the Northern Hemisphere with its larger land mass, and some possible ocean sources and sinks.
I’m pretty sure all the data is there to figure this out, and I suspect some already have – perhaps Jan Veizer and colleagues.
Allan MacRae says:
May 7, 2012 at 10:31 pm
Well, Allan, count me an enthusiastic supporter of your position. When you view things the right way, the relationship just comes screaming out at you. Kudos for your writeup.
I knew CO2 and temperatures exhibited seasonal fluctuations which I assumed were correlated in some way, but I never realized there was such a pronounced long term correlation with the derivative and the temperatures. The alleged driving influence of human emissions can now be summed up in the famous words of Laplace: I have no need of that hypothesis.
Bart:
At May 7, 2012 at 9:00 pm you say and ask:
“I came upon this remarkable relationship between the derivative of CO2 concentration and temperature by accident just last week. It is so blindingly clear that temperature is driving the CO2 concentration that it took me aback. How could this relationship have been missed when researchers have been looking at the problem for decades, and have what are undoubtedly elaborate models into which much time of very smart people has been invested?
The relationship is a demonstration of Nigel Calder’s “CO2 Thermometer” which he first proposed in the 1990s. He describes it with honest appraisal of its limitations at
http://calderup.wordpress.com/2010/06/10/co2-thermometer/
And never forget the power of confirmation bias powered by research funding.
In 2005 I gave the final presentation on the on the first day of at a conference in Stockholm. It explained how atmospheric CO2 concentration could be modelled in a variety of ways that were each superior to the Bern Model, and each gave a different development of future atmospheric CO2 concentration for the same input of CO2 to the air.
I then explained what I have repeatedly stated in many places including on WUWT; i.e.
The evidence suggests that the cause of the recent rise in atmospheric CO2 is most probably natural, but it is possible that the cause may have been the anthropogenic emission. Imortantly, the data shows the rise is not accumulation of the anthropogenic emission in the air (as is assumed by e.g. the Bern Model).
A representative of KNMI gave the first presentation of the following morning. He made no reference to my presentation and he said KNMI intended to incorporate the Bern Model into their climate model projections.
So, I conclude that what is knowable is less important than what is useful for climate model development.
Richard
PS Apologies if this is a repost
Thank you Bart for your kind words,
While the dCO2/dt vs Temperature relationship is new information, I suspect that the lag of CO2 after temperature at different time scales (~800 year lag in ice core data, ~9 month in the modern instrument data record) has been long known, and only recently “swept under the rug” by global warming mania. Here are two papers from 1990 and 1995 on the multi-month CO2-after–temperature delay, first brought to my attention as I recall by Richard S Courtney:
Keeling et al (1995)
http://www.nature.com/nature/journal/v375/n6533/abs/375666a0.html
Nature 375, 666 – 670 (22 June 1995); doi:10.1038/375666a0
Interannual extremes in the rate of rise of atmospheric carbon dioxide since 1980
C. D. Keeling*, T. P. Whorf*, M. Wahlen* & J. van der Plichtt†
*Scripps Institution of Oceanography, La Jolla, California 92093-0220, USA
†Center for Isotopic Research, University of Groningen, 9747 AG Groningen, The Netherlands
________
OBSERVATIONS of atmospheric CO2 concentrations at Mauna Loa, Hawaii, and at the South Pole over the past four decades show an approximate proportionality between the rising atmospheric concentrations and industrial CO2 emissions1. This proportionality, which is most apparent during the first 20 years of the records, was disturbed in the 1980s by a disproportionately high rate of rise of atmospheric CO2, followed after 1988 by a pronounced slowing down of the growth rate. To probe the causes of these changes, we examine here the changes expected from the variations in the rates of industrial CO2 emissions over this time, and also from influences of climate such as El Niño events. We use the13C/12C ratio of atmospheric CO2 to distinguish the effects of interannual variations in biospheric and oceanic sources and sinks of carbon. We propose that the recent disproportionate rise and fall in CO2 growth rate were caused mainly by interannual variations in global air temperature (which altered both the terrestrial biospheric and the oceanic carbon sinks), and possibly also by precipitation. We suggest that the anomalous climate-induced rise in CO2 was partially masked by a slowing down in the growth rate of fossil-fuel combustion, and that the latter then exaggerated the subsequent climate-induced fall.
________
Kuo et al (1990)
http://www.nature.com/nature/journal/v343/n6260/abs/343709a0.html
Nature 343, 709 – 714 (22 February 1990); doi:10.1038/343709a0
Coherence established between atmospheric carbon dioxide and global temperature
Cynthia Kuo, Craig Lindberg & David J. Thomson
Mathematical Sciences Research Center, AT&T Bell Labs, Murray Hill, New Jersey 07974, USA
THE hypothesis that the increase in atmospheric carbon dioxide is related to observable changes in the climate is tested using modern methods of time-series analysis. The results confirm that average global temperature is increasing, and that temperature and atmospheric carbon dioxide are significantly correlated over the past thirty years. Changes in carbon dioxide content lag those in temperature by five months.
________
As you can see, Keeling believed that humankind was also causing an increased in atmospheric CO2. I’m not convinced, since human emissions of CO2 are still small compared with natural seasonal flux. I think human CO2 emissions are lost in the noise and are not a significant driver. More likely, the current increase in CO2 is primarily natural. I’ve heard ~all the counter-arguments by now, including the C13/C12 one, and don’t think they hold up.
It is possible that the current increase in atmospheric CO2 is primarily driven by the Medieval Warm Period, ~~800 years ago. The “numerical counter-arguments” rely upon the absolute accuracy of the CO2 data from ice cores. While I think the trends in the ice core data are generally correct, the values of the CO2 concentrations are quite possibly not absolutely accurate, and then the “numerical counter-arguments” fall apart..
Regards, Allan
Hu McCulloch, that would be a reasonable description of the system: including the magic words ‘Assume their equilibrium’. However, the system is not at equilibrium, indeed it is far from equilibrium. There are two zones of high biotic density, the first few meters of the top and the first few centimeters of the bottom. CO2 is a biotic gas and is denuded from the surface layer, as photosynthetic organisms devour it, generating oxygen. CO2 flux from the atmosphere and the lower depths to this area is high. Particulate organic matter rains down from the surface, enriched with14C. Some is intercepted and converted to CO2/CH4, but a reasonable amount reaches the bottom. Look at the numbers once again, slice the ocean into a layer cake of 1m thick layers. The bottom layer has a huge amount of carbon, and also has a higher 14C12C ratio than the bottom 3 kilometers of water. There is a very rapid, y-1, transport of organic matter directly to the bottom of the oceans.
If one wishes to defend the Bern CO2 model, do this experiment. a prior, calculate the equilibrium concentration of molecular oxygen with ocean depth. This should be trivial as 23% atmospheric oxygen gives about 250 micro molar aqueous O2 at the surface.. If the O2 concentration does not follow the physical model of oxygen partition with respect to temperature/pressure, then one must ask why CO2 should.
fhhaynie says:
Thank you for the link.
I would like to see that cross posted to WUWT BTW.
In the article it says
If the atmosphere is “accumulating the lighter CO2 faster” and “the lighter is more from organic origin” would this not indicate the increase in CO2 is more organic in origin and not from burning fossil fuels (inorganic)? (I haven’t had my morning tea yet and may be a bit blurry mentally)
On the other hand I consider coal complete with fossil ferns as “organic”
Gail,
Fossil fuels are of organic origin and have 13CO2 indexes between around -23 and -30.
“It says that the CO2 in the air is somehow partitioned, and that the different partitions are sequestered at different rates. ”
My understanding is that they simulated their “box model” to get its impulse response. They then fitted three or four exponentials, plus a constant, to the resulting impulse response.
As I said I am a bit blurry still. Dr Spencer addressed the “natural” vs “man-made” argument about the C12 – C13 ratio here:
Atmospheric CO2 Increases: Could the Ocean, Rather Than Mankind, Be the Reason?
Spencer Part2: More CO2 Peculiarities – The C13/C12 Isotope Ratio
The fact that these carbon isotope ratios are taken at Mauna Loa, the site of an active volcano that between eruptions, emits variable amounts of carbon dioxide on one hand and a CO2 “active” ocean affected by ENSO on the other does not give me much confidence in the carbon isotope ratio, C13/C12 as the purported signature of anthropogenic CO2.
That is a really small change in signal they are talking about especially given the mythical nature of CO2 as a gas well mixed in the atmosphere.
Further to Bart:
I am still pondering my conclusions in my 2002 paper – as some critics have noted, there are two drivers of CO2 – the humanmade component and the natural component, and both can be having a significant effect – critics suggest the humanmade component is dominant. I suggest the natural component is dominant.
Following my email to him, Roy Spencer also wrote on this subject at
http://wattsupwiththat.com/2008/01/25/double-whammy-friday-roy-spencer-on-how-oceans-are-driving-co2/
One more reference on this subject is by climate statistician William Briggs, at
http://wmbriggs.com/blog/2008/04/21/co2-and-temperature-which-predicts-which/
Prior work, which I became aware of after writing my 2008 paper, includes:
Pieter Tans (Dec 2007)
http://esrl.noaa.gov/gmd/co2conference/agenda.html
Tans noted the [dCO2/dt : Temperature] relationship but did not comment on the ~9 month lag of CO2.
Correction to above
I am still pondering my conclusions in my 2008 paper
Willis, I stumbled over this while looking for something else and thought it had a bit of relevance to your discussion. It is from CO2 Acquittal by Jeffrey A Glassman PhD. He discusses the politics behind partitioning CO2 in one of his responses to a comment.
a) You say “surely there is a natural rate E(t) > 0 that would maintain an equilibrium CO_2 concentration”. Why?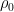 . Furthermore, this equilibrium has a signficant natural variability and probably nonlinear feedback mechanisms — more carbon dioxide in the atmosphere may well increase the rate at which carbon dioxide is removed by the biosphere, for example. There is some evidence that this is already happening, and a well-understood and studied explanation for it (greenhouse studies with CO_2 used to force growth). Trees and plants and algae grow faster and photosynthesize more with more CO_2, not just more proportional to the concentration — that’s per plant — but nonlinearly more, because as the plants grow faster there is more plant. I would argue as well that the ocean is more than just a saturable buffer (although it is a hell of a buffer). In particular, small shifts in the temperature of the ocean can mean big shifts in atmospheric CO_2 concentration, either way.
. Furthermore, this equilibrium has a signficant natural variability and probably nonlinear feedback mechanisms — more carbon dioxide in the atmosphere may well increase the rate at which carbon dioxide is removed by the biosphere, for example. There is some evidence that this is already happening, and a well-understood and studied explanation for it (greenhouse studies with CO_2 used to force growth). Trees and plants and algae grow faster and photosynthesize more with more CO_2, not just more proportional to the concentration — that’s per plant — but nonlinearly more, because as the plants grow faster there is more plant. I would argue as well that the ocean is more than just a saturable buffer (although it is a hell of a buffer). In particular, small shifts in the temperature of the ocean can mean big shifts in atmospheric CO_2 concentration, either way. if its coupled channel dynamics is to be believable, and the long term stability of the solution under various scenarios demonstrated. If you send me or direct me at the actual coupled channel ODEs this integral equation badly represents — the actual ODEs for the channels, mind you — I would be happy to pop them into matlab and crank out some pretty pictures of the results, given some numbers. It isn’t necessary or desireable to write out the solution as an integral equation, especially an integral equation for the “anthropogenic” CO_2 surplus only, when one can simply solve the ODEs linear or not. It isn’t like this is 1960, after all — my laptop is a “supercomputer” by pre-2000 standards. We’re talking a few seconds of computation, a day’s work to generate whole galleries of pictures of solutions for various hypothesized inputs.
if its coupled channel dynamics is to be believable, and the long term stability of the solution under various scenarios demonstrated. If you send me or direct me at the actual coupled channel ODEs this integral equation badly represents — the actual ODEs for the channels, mind you — I would be happy to pop them into matlab and crank out some pretty pictures of the results, given some numbers. It isn’t necessary or desireable to write out the solution as an integral equation, especially an integral equation for the “anthropogenic” CO_2 surplus only, when one can simply solve the ODEs linear or not. It isn’t like this is 1960, after all — my laptop is a “supercomputer” by pre-2000 standards. We’re talking a few seconds of computation, a day’s work to generate whole galleries of pictures of solutions for various hypothesized inputs. contribution from the biosphere that is ignorable in the rate equation, right?
contribution from the biosphere that is ignorable in the rate equation, right?
Because we agree that there is one, you’ve just hidden it. You yourself are using as a baseline “natural emissions”, which presumably maintain an equilibrium, one that is somehow not participatory in this general process because you’ve chopped all of its dynamics out and labelled it
But here is why I doubt this model. Seriously, you cannot exclude the CO_2 produced by the biosphere and volcanic activity and crust outgassing and thermal fluctuations in the ocean in a rate equation, especially one with lots of nonlinear coupling of multiple gain and loss channels. That’s just crazy talk. The question of how the system responds to fluctuations has to include fluctuations from all sources not just “anthropogenic” sources because as I am getting a bit tired of reciting, CO_2 doesn’t come with a label and a volcanic eruption produces a bolus that is indistinguishable at a molecular level from a forest fire or the CO_2 produced by my highly unnatural beer.
Without a natural equilibrium and with your “15% is forever” rule, every burp and belch of natural CO_2 hangs out forever (where forever is a “very long time”. You can’t ascribe gain to just one channel, or argue that you can ignore gain in one channel of a coupled channel system so that it only occurs in the others. That is wrong from the beginning.
I do understand what you are trying to say about adding net carbon to the carbon cycle — one way or another, when one burns lots of carbon that was buried underground, it isn’t buried underground anymore and then participates in the entire carbon cycle. I agree that it will ramp up the equilibrium concentration in the atmosphere. Where we disagree is that I don’t think that we can meaningfully compute how effectively it is buffered and how fast it will decay because of nonlinear feedbacks in the system and because it is a coupled channel system — all it takes is for ONE channel to be bigger than your model thinks it is, for ONE rate to experience nonlinear gain (so that decay isn’t exponential but is faster than exponential) and the model predictions are completely incorrect.
The Earth is for the most part a stable climate system, or at least it was five million years ago. Then something changed, and it gradually cooled until some two and a half million years ago the Pliestocene became bistable with an emerging dominant cold mode. One possible explanation for this — there are several, and the cause could be multifactorial or completely different — is that it could be that CO_2 concentration is pretty much the only thing that sets the Earth’s thermostat, with many (e.g. biological) negative feedbacks that generally prevent overheating but are not so tolerant of cold excursion, which sadly has a positive feedback to CO_2 removal. The carbon content of the crust might well rotate through on hundred million year timescales — “something” releases new CO_2 into the atmosphere at a variable rate (hundred million year episodes of excess volcanism? I still have a hard time buying this, but perhaps). Somehow this surplus CO_2 enters at a rate that is so slightly elevated that the “15% is forever” rule doesn’t cause runaway CO_2 concentration exploding to infinity and beyond — I leave it to your imagination how this could possibly work over several billion years without kicking the Earth into Venus mode if there were any feedback pathway to Venus mode, given an ocean with close to two orders of magnitude more CO_2 dissolved in it than is present in the atmosphere and a very simple relationship between its mean temperature and the dissolved fraction (which I think utterly confounds the simple model above).
In this scenario, the Earth suddenly became less active and the biosphere sink got out in front of the crustal CO_2 sources. At some point glaciation began, the oceans cooled, and as the oceans cooled their CO_2 uptake dramatically increased, sucking the Earth down into a cold phase/ice age where during the worst parts of the glaciation eras, CO_2 levels drop to less than half their current concentration, barely sufficient partial pressure to sustain land based plant growth. Periodically the Earth’s orbit hits just the right conditions to warm the oceans a bit, when they warm they release CO_2, and the released CO_2 feeds back to warm the Earth back up CLOSE to warm phase for a bit before the orbital conditions change enough to permit oceanic cooling that takes up the CO_2 once again.
I disbelieve this scenario for two reasons. The first is that it requires a balance between bursty CO_2 production and CO_2 uptake that is too perfectly tuned to be likely — the system has to be a lot more stable than that which is why your manifestly unstable model is just plain implausible. I respectfully suggest that your model needs to include CO_2 from all sources in
The second is that the data directly refutes it. Disturbed by the fact that studies of e.g. ice core data fairly clearly showed global warming preceded CO_2 increase at the leading edge of the last four or five interglacials, a recent study tried hard to manufacture a picture where CO_2 led temperature at the start of the Holocene. The data are difficult to differentiate, however.
There is no doubt, however, that the CO_2 levels trailed the fall in temperature at the end of the last few interglacials. And thus it is refuted. The whole thing. If high CO_2 levels were responsible for interglacial warming and climate sensitivity is high, it is simply inconceivable that the Earth could slip back into a cooling phase with the high CO_2 levels trailing the temperature not by decades but by centuries. A point that seems to have been missed in the entire CO_2 is the only thermostat discussion, by the way. Obviously whatever it is that makes the Earth cool back down to glacial conditions is perfectly happy to make this happen in spite of supposedly stable high CO_2 levels, and those levels remain high long after the temperature has dropped out beneath them.
Before you argue that this suggests that there ARE long time constants in the carbon cycle, permit me to agree — the data support this. Looking at the CO_2 data, it looks like a time constant of a century or perhaps two might be about right, but of course this relies on a lot of knowledge we don’t have to set correctly.
There are many other puzzles in the CO_2 uptake process. For example, there is a recent paper here:
http://www.sciencemag.org/content/305/5682/367.abstract
that suggests that the ocean alone has taken up 50% of all of the anthropogenic carbon dioxide released since 1800. Curiously, this is with a (presumably)generally warming ocean over this period, and equally interesting, the non-anthropogenic biosphere contributed 20% of the surplus CO_2 to the atmosphere over the same period. So much for a steady state
One of many reasons I don’t like the integral equation we are discussing that I find it very difficult to identify what goes where in it and connect it with papers like this. For example, what that means is that a big chunk of all three exponential terms belong to the ocean, since the ocean alone absorbed more than any of these terms can explain. How can that possibly work? I might buy the ocean as a saturable sink with a variable equilibrium and time constant of 171 years, but not one with a 0.253 fraction. In fact, turning to my trusty calculator, I find that the correct fraction would be 0.58. I see no plausible way for the time constant for the ocean to be somehow “split”. We’re talking simple surface chemistry here, it is the one thing that really does need to be a single aggregate rate because all that ultimately matters is the movement of CO_2 molecules over the air-water interface. Also, even if it were somehow split — perhaps by bands of water at different latitude, which would of course make the entire thing NON-exponential — how in the world could its array of time constants somehow end up being the same as those for soil uptake or land plant uptake?
To be blunt, the evidence from real millennial blasts of CO_2 — the interglacials themselves — suggests a longest exponential damping time on the order of a century. There is absolutely no sign of very long time scale retention. It is very likely that the ocean itself acts as the primary CO_2 reservoir, one that is entirely capable of buffering all of the anthropogenic CO_2 released to date over the course of a few hundred years. If the surplus CO_2 we have released by the end of the 21st century were sufficient to stave off the coming ice age, or even to end the Pliestocene entirely, that would actually be fabulous. If you want climate catastrophe, it is difficult to imagine anything more catastrophic than an average drop in global temperature of 6C, and yet the evidence is overwhelming that this is exactly what the Earth would experience “any century now”, and sadly, the trailing CO_2 evidence from the last several interglacials suggests that whatever mechanism is responsible for the start of fed-back glaciation and a return to cold phase, it laughs at CO_2 and drags it down, probably by cooling the ocean.
In other words, the evidence suggests that it is the temperature of the ocean that sets the equilibrium CO_2 concentration of the atmosphere, not the equilibrium CO_2 concentration of the atmosphere that sets the temperature of the ocean, and that while there is no doubt coupling and feedback between the CO_2 and temperature, it is a secondary modulator compared to some other primary modulator, one that we do not yet understand, that was responsible for the Pliestocene itself.
rgb
The evidence suggests that the cause of the recent rise in atmospheric CO2 is most probably natural, but it is possible that the cause may have been the anthropogenic emission. Importantly, the data shows the rise is not accumulation of the anthropogenic emission in the air (as is assumed by e.g. the Bern Model).
I would agree, especially (as noted above) with the criticism of the Bern Model per se. It is utterly impossible to justify writing down an integral equation that ignores the non-anthropogenic channels (which fluctuate significantly with controls such as temperature and wind and other human activity e.g. changes in land use). It is impossible to justify describing those channels as sinks in the first place — the ocean is both source and sink. So is the soil. So is the biosphere. Whether the ocean is net absorbing or net contributing CO_2 to the atmosphere today involves solving a rather difficult problem, and understanding that difficult problem rather well is necessary before one can couple it with a whole raft of assumptions into a model that pretends that its source/sink fluctuations don’t even exist and that it is, on average a shifting sink only for anthropogenic CO_2.
I’m struck by the metaphor of electrical circuit design when those designs have feedback and noise. You can’t pretend that one part of your amplifier circuit is driven by a feedback current loop to a stable steady state (especially not when there is historical evidence that the fed back current is very noisy) when trying to compute the effect of an additional current added to that fed back current from only one of several external sources. Yet that is precisely what the Bern model does. The same components of the circuit act to damp or amplify the current fluctuations without any regard for whether the fluctuations come from and of the outside sources or the feedback itself.
rgb
I am trying to find references to a major misalignment between the ice core CO2 record and modern atmospheric records of CO2, one that was allegedly “solved” by shifting the ice core record until it matched the modern record.
Can anyone help please?
d/dt A = -(91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)D ,
d/dt D = +(96/1020)S – (96/3810)D.
Finally, some actual differential equations! A model! Now we can play. Now let’s see, A is atmosphere and atmosphere gains and loses CO_2 to the surface from simple surface chemistry. Bravo. S is the surface ocean. D is the deep ocean.
Now, let’s just imagine that I replace this with a model where what you call the deep ocean is the meso ocean M, and where we let D stand for the deep ocean floor. The surface layer S exchanges CO_2 with A and with M, to be sure, but biota in the surface layer S take in CO_2 and photosynthesize it, releasing oxygen and binding up the CO_2 as organic hydrocarbons and sugars, then die, raining down to the bottom. Some fraction of the carbon is released along the way, the rest builds up indefinitely on the sea floor, gradually being subducted at plate boundaries and presumably being recycled, after long enough, as oil, coal, and natural gas reservoirs where “long enough” is a few tens or hundreds of millions of years. As a consequence, CO_2 in this layer is constantly being depleted since the presence of CO_2 is probably the rate limiting factor (perhaps along with the wild card of nutrient circulation cycles and surface temperatures, ignored throughout) on the otherwise unbounded growth potential of the biosphere here.
Carbon is constantly leaving the system from S, in other words, being replaced by crustal carbon cycled in from many channels to A and carbon from M, the vast oceanic sink of dissolved carbon. There is actually very likely a one-way channel of some sort between M and D — carbon dioxide and methane are constantly being bound up there at the ocean floor in situ, forming e.g. clathrates. I very much doubt that this process ever saturates or is in equilibrium. But because I doubt we have even a guesstimate available for this chemistry or the rates involved at 4K and at a few zillion atmospheres of pressure, nor do we have a really clear picture of sea bottom ecology that might contribute, we’ll leave this out. Then we might get:
d/dt A = -(91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
Hmm, things are getting a bit complicated, but look what I did! I proposed an absolutely trivial mechanism that punches a hole out of your detailed balance equation. Furthermore, it is an actual mechanism known to exist. It takes place in a volume of at least 100 meters times the surface area of the entire illuminated ocean. Every plant, every animal that dies in this zone sooner or later contributes a significant fraction of its carbon to the bottom, where it stays.
This is just the ocean and we’ve already found a hole, so to speak, for carbon. Note well that it doesn’t even have to be a big hole — if you bump A you transiently bump S, but S is now damped — it can contribute or pick up CO_2 from M, but all of the while it is removing carbon from the system altogether. Now let’s imagine the other 30% of the earth. In this subsystem we could model it like:
d/dt A = E(t) – (91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
where E(t) is now the sum of all source rates contributing to A that aren’t S. Note well that for this to work, we can’t pretend that there are no contributions from the ground G or the crust (including volcanoes) C as well as humans H and land plants L. Some of these are sources that are not described by detailed balance — they are true sources or sinks. Others have similar (although unknown) chemistry and some sort of equilibrium. At the very least we need to write something like:
d/dt A = H(t) + C(t) – (91/750)A + (91/1020)S – R_{AL} A*L(t) – R_{GA} A + R_{GA} G
d/dt G = +R_{GA} A – R_{AG} G
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
which says that the ground has an equilibrium capacity not unlike the sea surface that takes up and releases CO_2 with some comparative reservoir capacities and exchange rate, humans only contribute at rate H(t), the crust contributes to the atmosphere at some (small) rate C(t) (and contributes to the ocean at some completely unknown rate as well, where I don’t even know where or how to insert the term — possibly a gain term in M — but still, probably small), where land plants net remove CO_2 at some rate that is proportional to both CO_2 concentration and to how many plants there are, which is a function of time whose primary driver at this point is probably human activity.
Are we done? Not at all! We’ve blithely written rate constants into this (that were probably empirically fit since I don’t see how they could possibly be actually measured). Now all of their values will, of course, be entirely wrong. Worse, the rates themselves aren’t constants — they are multivariate functions! They are minimally functional on the temperature — this is chemistry, after all — and as noted are more complicated functions of other stuff as well — rainfall, cloudiness, windiness, past history, state of oceanic currents, state of the earth’s crust. So when solving this, we might want to make all of the rates at the very least functions of time written as constants plus a phenomenological stochastic noise term and investigate entire families of solutions to determine just how sensitive our solutions are to variability in the rates that reasonably matches observed past variability. That’s close to what I did by putting an L(t) term in, but suppose I put a term L into the system instead as representing the carbon bound up in the land plants, and allow for a return (since there no doubt is one, I just buried it in L(t))? Then we have nonlinear cross terms in the system and formally solving it just became a lot more difficult.
Not that it isn’t already pretty difficult. One could, I suppose, still work through the diagonalization process and try to express this as some sort of non-Markovian integral, but it is a lot simpler and more physically meaningful to simply assign A, G, S, M, D initial values, write down guestimates of H(t), L(t), C(t), and give the whole mess to an ODE solver. That way there is no muss, no fuss, no bother, and above all, no bins or buckets. We no longer care about ideas like “fractional lifetime” in some diagonalized linearized solution that ignores a whole ecosystem of underlying natural complexity and chemical and biological activity influenced by large scale macroscopic drivers like ocean currents, decadal oscillations, solar state, weather state — algae growth rates depend on things like thunderstorm rates as lightning binds up nitrogen in a form that can eventually be used by plants — and more, so R_b itself is probably not even approximately a constant and could be better described by whole system of ODEs all by itself, with many channels that dump to D.
The primary advantage of my system compared to the one at the top is that the one at the top does have nowhere for carbon to go. Dump any in via E(t) and A will monotonically increase. Mine depletes to zero if not constantly replenished, because that’s the way it really is! The coal and oil and natural gas we are burning are all carbon that was depleted from the system described above over billions of years. Carbon is constantly being added to the system via C(t) (and possibly other terms we do not know how to describe). A lot of it has ultimately ended up in M. A huge amount of it is in M. There is more in M than anywhere else except maybe C itself (where we aren’t even trying to describe C as a consequence). And the equilibrium carbon content of M is a very delicate function of temperature — delicate only because there is so very much of it that a single degree temperature difference would have an enormous impact on, say, A, where the variations in temperature in S have a relatively small impact.
The point is, that with models and ODEs you get out what you put in. Build a three parameter model with numerically fit constants, you’ll get the best fit that model can produce. It could be a good fit (especially to short term data) and still be horribly wrong for the simple reason that given enough functions with roughly the right shape and enough parameters, you can fit “anything”. Optimizing highly nonlinear multivariate models is my game. It is a difficult game, easy to play badly and get some sort of result, difficult to win. It is also an easy game to skew, to use to lie to yourself with, and I say this as somebody that has done it! It’s not as bad as “hermeneutics” or “exegesis”, but it’s close. If there is some model that you believe badly enough, there is usually some way of making it work, at least if you squint hard enough to blur your eyes to the burn on the toast looks like Jesus.
rgb
To rgbatduke,
To add another complication to your summation of natural cycles. Because of their size and density, decaying phytoplankton will remain near the surface and contribute to the ocean’s out gassing on a relatively short cycle. How long does it take to move from the Arctic to the equator? Another complication is the periodic upwelling off Peru of cold, carbonate saturated bottom water that will outgass as it warms crossing the Pacific near the surface. The inorganic cycle is the major long term player. How long does it take for the ocean’s conveyor belt to make a lap?
Help, Mr. Moderator! Change to before “buckets”.
rgb
[OK, Well, at least seeing the (hidden-by-html-brackets) letters makes the edit make sense … 8<) Robt]
richardscourtney says:
May 8, 2012 at 1:29 am
“He describes it with honest appraisal of its limitations at…”
Thanks, Richard. I think the root of Calder’s angst is that he is trying to satisfy requirements which may be irreconcilable. The CO2 records from ice cores and stomata disagree. Which is right? Perhaps neither. Certainly, if this relationship between temperature and the rate of change of CO2 has held in the past, the former are wrong. But, that does not mean the latter are right.
I am always very wary of claims made of measurements which cannot be directly verified. I have spent enough time in labs testing designs to know that you never really know how things will work in the real world until you have actually put them to the test in a closed loop fashion, with the results used to make corrections until it all works. And that is with components and systems which are designed based on well established principles, and using precision hardware to implement. Nature, as we say, is pernicious. Murphy, of course, proclaimed anything which can go wrong, will. And then, there is Gell-Mann’s variation describing physics: anything which is not forbidden is compulsory. And, Herbert: “Tis many a slip, twixt cup and lip.”
Everyone knows ice cores act as low pass filters with time varying bandwidth, smoothing out the rouch edges increasingly with time. I am not at all convinced, indeed am deeply suspicious, that the degree of smoothing and complexity of the transfer function is underappreciated.
The reliable data we do have, since 1958, says the data is behaving this way over the current timeline, with the derivative of CO2 concentration tracking the temperature. Over a longer timeframe, the relationship likely would change, if temperatures maintained their rise, with CO2 concentration becoming a low pass filtered time series proportional to the temperature anomaly. But, in any case, it is clear that right now, the rate of change in CO2 is governed by temperature.
Allan MacRae says:
May 8, 2012 at 2:48 am
I think the C13/C12 argument is an attempt to construct a simple narrative of a very complex process. An analogy which has come up in various threads is the case of a bucket of water with a hole in the bottom fed by clear mountain spring water. The height of water in the bucket has reached an equilibrium. Then, someone starts injecting 3% extra inflow with blue dyed water. The height of water in the bucket re-stabilizes 3% higher than before, but due to the delay of the color diffusion process, most of the blue dye lingers near the top of the bucket. Even when the spring ice melts, and the clear water inflow increases, adding say 30% more height, the upper levels are bluer than the lower. So, a naive researcher looks at the blue upper waters, and concludes that the dyed water input is responsible for the rise.
fhhaynie says:
May 8, 2012 at 5:19 am
Fred – I have enjoyed your presentations over the years. Not having the time to replicate your research, I have kept it in the bin marked “maybe”. That is why I hoped making the temperature to CO2 rate of change relationship readily accessible to everyone to replicate through this link might help sway people who otherwise would stay on the fence.
Gail Combs –
You may also want to consider Glassman’s post and the Q & A that follows “On why CO2 is known not to have accumulated in the atmosphere & what is happening with CO2 in the modern era.” Very thorough discussion.
http://www.rocketscientistsjournal.com/2007/06/on_why_co2_is_known_not_to_hav.html#more
rgbatduke says:
May 8, 2012 at 9:54 am
Yes, it is substantially guesswork. The value of such equations, IMHO, is substantially qualitative – they can illustrate what kind of dynamics are possible.
It is generally helpful to reduce the order of the model, as I demonstrated above. Model order reduction is a key element of modern control synthesis, e.g., as discussed here.
And, I then showed how we can get a system which will quickly absorb the anthropogenic inputs, yet have CO2 derivative appear to track the temperature anomaly (with respect to a particular baseline) here.
rgbatduke:
Thankyou very much indeed for your comment at May 8, 2012 at 9:54 am and especially for this one of its statements:
“The point is, that with models and ODEs you get out what you put in. Build a three parameter model with numerically fit constants, you’ll get the best fit that model can produce. It could be a good fit (especially to short term data) and still be horribly wrong for the simple reason that given enough functions with roughly the right shape and enough parameters, you can fit “anything”.”
Yes! Oh, yes! I wish I had thought of your phrasing, and I thank you for it.
As I have repeatedly stated above, we proved by demonstration that several very different models each emulates the observed recent rise in atmospheric CO2 concentration better than the Bern Model although each of our models assumes a different mechanism dominates the carbon cycle.
Simply, nobody knows the cause of the observed recent rise in atmospheric CO2 concentration and there is insufficient understanding and quantification of the carbon cycle to enable modelling to indicate the cause.
Richard
richardscourtney says:
May 8, 2012 at 11:12 am
This is the question of observability. For an unobservable system, there exists a non-empty subspace of the possible states which does not affect the output. Thus, you can replicate the output with any observable portion of the state space plus any portion of the unobservable subspace. As the unobservable subspace is typically dense, there are generally an infinite number of possible states which can reproduce the observables.
For observability of stochastic systems, you have the added feature that even theoretically observable states are effectively unobservable because of low S/N.
It is analogous to a system of N equations in which you have greater than N unknowns to solve for. In such an instance, you must constrain your solution space by some means in order to find a unique solution. In the case of climate science, the selection of constraints provides an avenue for confirmation bias.
Bart:
Of course you are right in all you say at May 8, 2012 at 12:03 pm, but I put it to you that the paragraph from rgbatduke (which I quoted in my post at May 8, 2012 at 11:12 am) says the same in words that non-mathematicians can understand.
Also, our point was that it is one thing to know something is theoretically true and it is another to demonstrate it. We demonstrated it; i.e.
the observed rise in atmospheric CO2 can be modelled to have any one or more of several different causes and there is no way to determine which if any of the modeled causes is the right one.
Richard
richardscourtney says:
May 8, 2012 at 1:40 pm
“We demonstrated it; i.e. the observed rise in atmospheric CO2 can be modelled to have any one or more of several different causes and there is no way to determine which if any of the modeled causes is the right one.”
Did your models attempt to reproduce the affine dependence of the derivative of CO2 concentration on temperature? I would expect that to be a discriminator.
In the case of climate science, the selection of constraints provides an avenue for confirmation bias.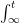 bit. It’s so much simpler to basically solve a Markovian IVP problem than a non-Markovian problem with a multimode decay kernel and an indeterminate initial condition.
bit. It’s so much simpler to basically solve a Markovian IVP problem than a non-Markovian problem with a multimode decay kernel and an indeterminate initial condition.
I couldn’t have said it better myself. We disagree, I think, about numerics vs analytics, but then, I’m a lazy numerical programmer and diagonalizing ODEs to find modes gives me a headache (common as it is in quantum mechanics). The beauty of numerically solving non-stiff ODEs (like this) is that, well, it just works. Really well. Really fast. It’s not like you don’t have to work pretty hard and numerically to evaluate the Bern integral equation anyway, unless you use a particularly simple E(t), and then you have the added complication of just what you’re going to do with that pesky
But as to the rest of it, I think we agree pretty well. It’s a hard problem, and the Bern equation is one, not necessarily particularly plausible, solution proposed that can fit at least some part of the historical data. Is it “right”? Can it extrapolate into the future? Only time, and a fairly considerable AMOUNT of time at that, can tell.
In the meantime, the selection of the model itself is a kind of confirmation bias. 15% of the integral of any positive function you put in for E(t) simply monotonically causes CO_2 to increase. Another 25% decays very slowly on a decadal scale, easy to overwhelm with the integral. It’s carefully selected for maximum scariness, much like the insanely large climate sensitivities.
Or not selected. Scientists who care understand that it is only a model, one of many possible models that might fit the data, can look at it skeptically and decide what to believe, disbelieve, and can actually intelligently compare alternative explanations or debate things like what I put in my previous post that suggest that it would be pretty easy to fit the model and maybe even fit the susceptibility of the model (if that’s what you are claiming that you accomplished) with alternatives that have very different asymptotics and interpretations, or (as Richard has pointed out) with models where anthropogenic CO_2 isn’t even the dominant factor.
What I object to is this being presented to a lay public as the basis for politically and economically expensive policy decisions that direct the entire course of human affairs to the tune of a few trillion dollars over the next couple of decades. If only we could attack things like world hunger, world disease, or world peace with the same fervor (and even a fraction of the same resources). As it is, I think of the billions California is spending to avert a disaster that will quite possibly never occur because it is literally non-physical and impossible, and think of the starving children those billions would feed, or the people who lost their jobs in California when it went bankrupt that that money would employ.
And there is no need to panic. Global temperatures are remarkably stable at the moment. An absolutely trivial model computation suggests that the Earth should be in the process of cooling in the face of CO_2 by as much as 2C at the moment (7% increase in dayside bond albedo over the last 15 years). The cooling won’t happen all at once because the ocean is an enormous buffer of heat as well as CO_2, but it is quite plausible that we will soon see global temperatures actually start to retreat — indeed, it would be surprising if they don’t, given the direct effect of increasing the albedo by that factor.
And in a couple of decades we will (IMO, others on list disagree) on the downhill side of the era when the human race burns carbon to obtain energy anyway, with or without subsidy. There are cheaper ways to get energy that don’t require constant prospecting and tearing up the landscape to get at them. Well, they will be cheaper by then — right now they are marginally less cheap. Human technology marches on, and will solve this problem long before any sort of disaster occurs.
rgb
Yes! Oh, yes! I wish I had thought of your phrasing, and I thank you for it.
Oh, my phrasing isn’t so good — there is far better out there in the annals of other really smart people. Check out this quote from none other that Freeman Dyson, referring to an encounter of his with the even more venerable Enrico Fermi:
http://www.fisica.ufmg.br/~dsoares/fdyson.htm
The punch line:
“In desperation I asked Fermi whether he was not impressed by the agreement between our calculated numbers and his measured numbers. He replied, “How many arbitrary parameters did you use for your calculations?” I thought for a moment about our cut-off procedures and said, “Four.” He said, “I remember my friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
Yeah, John von Neumann was a pretty sharp tool to keep in your shed as well. The Bern model has five free parameters, so it isn’t terribly surprising that it can even make the elephant wiggle his trunk. (Thanks to Willis for pointing this delightful story out on another thread where we were both intent on demolishing an entirely nonphysical theory/multiparameter model of GHG-free warming.)
I feel a lot better about a model when there is some experimental and theoretical grounding that cuts down on the free parameters. “None” is just perfect. One or two is barely tolerable, more so if it isn’t asserted as being “the truth” but is rather being presented as a model calculation for purposes of comparison or insight. Get over two and you’re out there in curve-fitting territory, and by five — well why not just fit meaning-free Legendre polynomials or the like to the function and be done with it?
rgb
Oops, I miscounted. The Bern model has eight free parameters — I forgot the weights of the exponential terms. So wiggle his trunk while whistling Dixie, balanced on a ball. Although perhaps someone might argue that they aren’t really free, I doubt that they are set from theory or measurement.
rgb
Yes the five-parameter elephant.
Above several times I have noted that the integral equation that is at times causing so much worry in these comments is a very basic convolution equation of linear systems theory. Solving it is usually a matter of transforming it into the Laplace transform domain where convolution becomes a multiply operation.
More directly, “by inspection” the impulse response given there (the parallel decaying exponentials) corresponds to a particular configuration of passive R-C circuits. Without further analysis, we recognize exactly what it is and what it can (and can’t) do. It seems quite unlikely it could correspond to CO2 sourcing and sinking to four partitions (electrons to four capacitors in the circuit).
It could only be a “model” in the sense that it can be MADE to fit, given the free parameters. Hence the aptness of von Neumann’s elephant joke – which I also noted above.
Bart:
At May 8, 2012 at 5:03 pm you ask me:
“Did your models attempt to reproduce the affine dependence of the derivative of CO2 concentration on temperature? I would expect that to be a discriminator.”
I answer:
No, that was not their purpose.
Our paper explains;
“It is often suggested that the anthropogenic emission of CO2 is the cause of the rise in atmospheric CO2 concentration that has happened in the recent past (i.e. since 1958 when measurements began), that is happening at present and, therefore, that will happen in the future (1,2,3). But Section 2 of this presentation explained that this suggestion may not be correct and that a likely cause of the rise in atmospheric CO2 concentration that has happened in the recent past is the increased mean temperature that preceded it. A quantitative model of the carbon cycle might resolve this issue but Section 2 also explained that the lack of knowledge of the rate constants of mechanisms operating in the carbon cycle prevents construction of such a model. However, this lack of knowledge does not prevent models from providing useful insights into ways the carbon cycle may be behaving. ‘Attribution studies’ are a possible method to discern mechanisms that are not capable of being the cause of the observed rise of atmospheric CO2 concentration during the twentieth century.
In an attribution study the system is assumed to be behaving in response to suggested mechanism(s) that is modeled, and the behaviour of the model is compared to the empirical data. If the model cannot emulate the empirical data then there is reason to suppose that the suggested mechanism is not the cause (or at least not the sole cause) of the changes recorded in the empirical data.
It is important to note that attribution studies can only be used to reject hypothesis that a mechanism is a cause for an observed effect. Ability to attribute a suggested cause to an effect is not evidence that the suggested cause is the real cause in part or in whole.
Our paper considered three models of the carbon cycle. Each model assumed that a single mechanism is responsible for the rise in atmospheric CO2 concentration that has happened in the recent past (i.e. since 1958 when measurements began). The model was then compared to the empirical data to determine if the modeled mechanism could be rejected as a sole cause of the rise in atmospheric CO2 concentration.”
Richard
Allan MacRae:
I apologise that I overlooked your question at May 8, 2012 at 7:45 am and have only now noticed it.
It asks;
“I am trying to find references to a major misalignment between the ice core CO2 record and modern atmospheric records of CO2, one that was allegedly “solved” by shifting the ice core record until it matched the modern record.
Can anyone help please?”
The earliest explanation of the ‘need’ to adjust the data I know of is in
Siegenthaler U & Oeschger H, ‘Biospheric CO2 emissions during the last 200 years reconstructed by deconvolution of ice core data’, Tellus 39B; 14-154 (1987)
In that paper S&O assert that ice closure time means the data needs to be offset by decades of time because the ‘trapped’ air indicates the atmospheric composition at time of closure. And S&O assert the required offset is indicated by adjusting the data to overlay with the Mauna Loa data.
The earliest paper I know of which adjusts ice core data according to the S&O assertion is
Etheridge DM, Pearman GI & de Silva F, ‘Atmospheric trace-gas variations as revealed by air trapped in an ice core from Law Dome, Antarctica’, Ann. Glaciol. , 10; 28-33 (1988)
(The S&O assertion is clearly daft: there is no known mechanism that would move all the air up through the firn a distance that equates to decades of elapsed time. Indeed, basic physics says atmospheric pressure variations would mix the gases at different elevations while diffusion would tend to reduce high concentrations and increase low concentrations until the ice closed.)
Richard
Hu McCulloch says:
May 7, 2012 at 9:19 pm
Many thanks, Hu, following your explanation I finally see how it could work. The key is that to have it work, we have to have all of the CO2 pass from the atmosphere to one reservoir (the upper ocean in your example), which then passes all the CO2 to a second reservoir (deep ocean) at a different rate. In that way, part of it is absorbed quickly, and the remainder more slowly.
My problem is that to have the five different partitions they describe, you have to have the CO2 absorbed from the atmosphere by one single reservoir, which then transfers it to a second reservoir at a different rate, which then transfers that to a third reservoir at a third rate, which then transfers that to a fourth reservoir at a fourth rate, which then transfers that to a fifth reservoir at a fifth rate.
It also means that there can’t be any other sequestration mechanisms operating, because if there are other sinks, they will continue to absorb the CO2, and will sequester it long before the 371.6 years are up …
So I’m back to my same old problem … I still don’t understand where in the physical world we find such a system. It assumes the one and only sink is the ocean, which is partitioned into 5 sequential sub-sinks … I’m not seeing it.
w.
PS—I am sure that others explained this to me but I didn’t get it until Hu explained it … no telling how the mind works. In any case, my thanks to everyone who tried to explain it, and my apologies for not getting it.
Now I just need to find the five-chambered sequential CO2 sequestering system that corresponds with their math … oh, and also solve the separate and distinct problems pointed out by Robert Brown …
PPS—Someone above suggested modeling it in SPICE as an electrical circuit. What we have is a series C – R – C – R – C – R – C – R – C – R system, with no other path to ground … again, we can model it, but I don’t see the physical system that corresponds to that circuit.
Willis Eschenbach:
Your post at May 9, 2012 at 1:38 am concludes by saying;
“So I’m back to my same old problem … I still don’t understand where in the physical world we find such a system. It assumes the one and only sink is the ocean, which is partitioned into 5 sequential sub-sinks … I’m not seeing it.”
I am pleased that you have grasped the point that the Bern Model does not represent behaviour of the real-world carbon cycle. Perhaps now you can understand my post (above) at May 7, 2012 at 2:09 am which began by saying;
“I understand the interest in the Bern Model because it is the only carbon cycle model used by e.g. the IPCC. However, the Bern Model is known to be plain wrong because it is based on a false assumption.
A discussion of the physical basis of a model which is known to be plain wrong is a modern-day version of discussing the number of angels which can stand on a pin.” etc.
Please note that I am NOT now writing to say, “I told you so” (I am fully aware that one is often forgiven for being wrong but rarely forgiven for being right). I am writing this to make a point which I am certain has great importance but is often missed; viz.
THE CAUSE OF THE RECENT OBSERVED RISE IN ATMOSPHERIC CO2 CONCENTRATION IS NOT KNOWN AND – WITH THE PRESENT STATE OF KNOWLEDGE – IT CANNOT BE KNOWN.
We few who have persistently tried to raise awareness of this point have been subjected to every kind of ridicule and abuse by those who claim to “know” the recent rise in atmospheric CO2 concentration is caused by accumulation of anthropogenic emissions in the air. But whether or not the cause is anthropogenic or natural, that cause is certainly not accumulation of anthropogenic emissions in the air.
And the point is directly pertinent to the AGW-hypothesis which says;
(a) Anthropogenic emissions of GHGs are inducing an increase to atmospheric CO2 concentration;
(b) an increase to atmospheric CO2 concentration raises global temperature
(c) rising global temperature would be net harmful.
At present nobody can know if (a) is true or not, but the existing evidence indicates that if it is true then it is not a direct result of accumulation of anthropogenic emissions in the air. And if (a) is not true then (b) and (c) become irrelevant.
Richard
“My problem is that to have the five different partitions they describe, you have to have the CO2 absorbed from the atmosphere by one single reservoir, which then transfers it to a second reservoir at a different rate, which then…”
It will still work even if all the reservoirs connected, but I’m afraid I can’t think of any clearer explanation as to why than the tanks argument. Sometimes analogies and explanations just don’t catch – there’s some unrealised assumption or preconception that blocks the intuition. The mind’s workings are indeed strange.
It’s sometimes worth persisting with different analogies, but without understanding the reason for the block, it’s a bit hit and miss. Perhaps you can ask again another time, in a few months maybe.
Willis wrote:
“PPS—Someone above suggested modeling it in SPICE as an electrical circuit. What we have is a series C – R – C – R – C – R – C – R – C – R system, with no other path to ground … again, we can model it, but I don’t see the physical system that corresponds to that circuit.”
Actually, it’s a parallel, not a series system, which is evident from the summation sign rather than a product. You don’t need SPICE because it’s so simple. Not that either would have a physical correspondence to what goes on with CO2 in the atmosphere.
Nullius in Verba:
At May 9, 2012 at 11:25 am you say;
“It will still work even if all the reservoirs connected, but I’m afraid I can’t think of any clearer explanation as to why than the tanks argument.”
Hmmm. That depends on what you mean by “work”.
The model can be made to fit the rise in atmospheric CO2 concentration as observed at Mauna Loa since 1958 if the model’s output is given 5-year smoothing. But so what? Many other models which behave very differently can also provide that fit and do not require any smoothing to do it.
If you mean the Bern Model emulates the behaviour of the real carbon cycle then it does not: nothing in that cycle (except possibly the deep ocean) acts like a reservoir with a fixed volume.
Richard
Quinn the Eskimo says:
May 8, 2012 at 10:43 am
Gail Combs –
You may also want to consider Glassman’s post and the Q & A that follows “On why CO2 is known not to have accumulated in the atmosphere & what is happening with CO2 in the modern era.” Very thorough discussion.
http://www.rocketscientistsjournal.com/2007/06/on_why_co2_is_known_not_to_hav.html#more
____________________________________
OH wonderful!
It is so nice to see someone has done a really good rebuttal on the well mixed conjecture. That is a really big nail in the coffin of CO2 warming hype.
BernieH says:
May 9, 2012 at 3:31 pm
Thanks, Bernie. If all of the R/C pairs are in parallel, then your circuit looks like this:

If it’s like that, the quickest path to ground is what rules. Since the claim in the Bern model is that the exponential decay is partitioned, it has to be a series circuit.
w.
Gail Combs says:
May 9, 2012 at 4:18 pm (Edit)
No, Gail and Quinn, it’s not wonderful at all. It’s wildly incorrect. The author of the article is conflating residence time with e-folding time (or half-life). He doesn’t know the difference between the two. As a result, his conclusions are totally incorrect. Re-read my Appendix above.

Finally, is CO2 well-mixed? Well, I suppose it depends on what you call “well-mixed”.
Note that everywhere but the south pole the range is from about 375 – 382 ppmv, or ± 1% … in my book, that’s well mixed. Include the south pole and the range goes to about 368 – 382 ppmv … that’s ± 2%. Again, I call that well-mixed.
In other words, the citation is not a nail in the coffin of anyone but the author.
w.
No, I would use it to begin looking at the change in CO2 concentration with respect to average wind speed and direction with respect to changes in
1. Surface temperature (Cold Japanese current, hotter far west deserts and great basin, slightly cooler eastern US), hotter Gulf Stream off of east coast, colder currents off of Europe, then the central Asian barren highlands and back over the (colder and warmer) Pacific currents.
2. surface mass of growing plants: Great basin across Great plains to farmed Midwest to very tree-covered east coast), then barren areas in central Asia to the very overgrown Indian Peninsula …
3. Lower levels over the Amazon – that extend out over the Atlantic Ocean. But these conflict with the barren Saudi peninsula and Afghanistan and Mongolia that don’t match vegetation, and don’t match human activity to the immediate west. Odd.
4. Amount of human released CO2.
5. Actual direction and speeds of the “average” wind WHEN the measurements of the CO2 were taken.
Highest areas don’t “seem” to track with industrial activity (great basin, mountainous west, but then a high spot over the Atlantic Ocean. If you “translate human activity east” (assuming some west-to-east wind pattern), then where did Europe’s CO2 go? Where did Saudi Arabia and Afghanistan’s CO2 come from? Why is the CO2 high over the entire mountain area out west? There’s nobody west of there other than islands of people at LA and SFO. And nobody west of them for thousands of miles.
Applause, Thank you all for a very interesting discussion !
Hi Willis
What I am doing is less ambitious than what you and others here seem to be attempting.
I am (in the back of my mind) thinking about how CO2 in the atmosphere moves in, out, and about, but I am only working with the
mathematics in the link as what it is – a simple RC network. The integral equation given there is a fundamental convolution relationship between an input signal and the impulse response of a system. Just sophomore-level Laplace transform system theory – no big deal to an EE.
The equation describes the relationship between E (the input) and rho (the concentration). It seems to me that E is an extensive variable (an “amount” or quantity) while rho is an intensive variable (a property, a characteristic number, a concentration, in the same units as C) so we don’t seem to be talking about transfer of anything (such as electrons or CO2 molecules) but only a numerical ratio. So my RC network is a computational device only – it does not represent physical reality.
This “computer” happens to be composed of resistors, capacitors, buffer/multipliers, and a summer. I don’t know how to put a picture in comments here, so I have posted the schematic diagram at:
http://electronotes.netfirms.com/BernModelRC.jpg
Aside from scaling factors (which I would probably get wrong!), the diagram there is the one and only RC network that corresponds to the impulse response in the [ ]. The input is an “inventory” number of all CO2 going in, and rho is a number some “master controller” of all sinks is instructed to maintain. The sinks are NOT a physical analog of the electrons flows in the network – as least as their mathematics shows it.
Much as you and others here have problems with the partitions, so do I. I am not, but if I were considering a true electrical analog (electrons = CO2 molecules and capacitors represent storage of CO2) there is only one atmosphere (one capacitor) and one grand summed source (E) and one net sink. That would be one net resistor – if it’s even linear.
I think they were facing the problem that there does not seem to be a simple (one) exponential decay. Parallel RC’s is one way of handling this (Kautz functions are better). But the parallel RC suggests the partitioning. That’s a problem. Perhaps it was just intended as a computer, not as a physical model.
http://wattsupwiththat.com/2012/05/06/the-bern-model-puzzle/#comment-980201
richardscourtney says: May 9, 2012 at 1:34 am
Allan MacRae asks;
“I am trying to find references to a major misalignment between the ice core CO2 record and modern atmospheric records of CO2, one that was allegedly “solved” by shifting the ice core record until it matched the modern record. Can anyone help please?”
Richard: The earliest explanation of the ‘need’ to adjust the data I know of is in
Siegenthaler U & Oeschger H, ‘Biospheric CO2 emissions during the last 200 years reconstructed by deconvolution of ice core data’, Tellus 39B; 14-154 (1987)
In that paper S&O assert that ice closure time means the data needs to be offset by decades of time because the ‘trapped’ air indicates the atmospheric composition at time of closure. And S&O assert the required offset is indicated by adjusting the data to overlay with the Mauna Loa data.
The earliest paper I know of which adjusts ice core data according to the S&O assertion is
Etheridge DM, Pearman GI & de Silva F, ‘Atmospheric trace-gas variations as revealed by air trapped in an ice core from Law Dome, Antarctica’, Ann. Glaciol. , 10; 28-33 (1988)
(The S&O assertion is clearly daft: there is no known mechanism that would move all the air up through the firn a distance that equates to decades of elapsed time. Indeed, basic physics says atmospheric pressure variations would mix the gases at different elevations while diffusion would tend to reduce high concentrations and increase low concentrations until the ice closed.)
Richard
*********
Thank you very much Richard – I hope you are well. Yes, that is exactly what I was seeking.
Note to Richard, Bart, Willis and others:
This shifting of ice core data to align with Mauna Loa data is just one of several examples of confirmation bias in the current hypothesis that CO2 MUST drive temperature, and the related hypothesis that the primary source of increasing atmospheric CO2 MUST BE humankind.
When one starts to examine this complex subject, similar contradictions become apparent, not the least of which is that atmospheric CO2 lags temperature at all measured time scales (and dCO2/dt changes ~contemporaneously with temperature).
The counterarguments for the observed ~9 month lag of CO2 after temperature are:
A. It is a “feedback effect”.
B. It is clear evidence that time machines really do exist.
Both counterarguments A and B are supported by equally compelling evidence. 🙂
To me, one must start with the evidence, and work back to a logical hypothesis. The CO2-drives-temperature hypothesis and related man-drives-CO2 hypothesis both start with the hypo, and then try (unsuccessfully, imo) to fit the evidence to the hypo. When the evidence fails to fit, the data is “adjusted” and yet another illogical hypo (move-the-air–up-the-ice-firn) is invented, and so on, and so on. The alleged physical system becomes increasingly Byzantine, and increasingly improbable. That, I submit, is the current highly improbable state of “settled” climate science.
I would prefer to start with the evidence, as stated above, and then try to respect fundamental logical concepts such as the Uniformitarian Principle and Occam’s Razor.
Here are some thoughts:
In 2008, I wrote that atmospheric CO2 lagged atmospheric temperature T by ~9 months on a short-time-cycle (~3- 4 years – between major El Nino’s?).
http://icecap.us/images/uploads/CO2vsTMacRae.pdf
I also noted that CO2 lags temperature by ~800 years from ice core data, on a much longer temperature-time cycle..
I have suggested that there could be one or more intermediate cycles where CO2 lags temperature (between 9 months and 800 years).
There should be ample evidence in existing data to develop a much more credible and simpler hypothesis that does not rely for support on data-shifting, “feedback effects” and many other improbable hypotheses.
Regards, Allan
Summary – Multiple Cycles in which CO2 Lags Temperature:
For a mechanism, see Veizer (2005).
I think there are perhaps four cycles in which CO2 lags T:
1. A cycle of thousands of years, in which CO2 lags T by ~~800 years (Vostok ice cores, etc.)
2. A cycle of ~70-90 years (Gleissberg, PDO or similar), in which CO2 lags T by ~5-10 years. This “Beck hypo” is highly contentious – the late Ernst Beck’s direct-measurement CO2 data allegedly supports this possibility, and there is the important question of how much humanmade CO2 affects this and subsequent cycles. Ernst Beck was widely disrespected and his work dismissed by both sides of the CAGW debate – I think this was most unfortunate, and probably was an intellectual and ethical error – there is possibly some merit, particularly in Beck’s data collection work, and many were too quick to dismiss it.
3. The cycle I described in my 2008 icecap.us paper of 3-5 years (El Nino/La Nina), in which CO2 lags T by ~9 months.
4. The seasonal “sawtooth” CO2 cycle, which ranges from ~18 ppm in the North to ~1 ppm at the South Pole.
It is clear that T precedes CO2 in cycles 1, 3 and 4. For possible Cycle 2 we may have inadequate data.
– Allan MacRae, circa 2008
Friends:
OK, it is time to be clear.
The carbon cycle cannot be represented by a ‘plumbing’ or ‘electrical’ circuit because all the ‘tanks’ or ‘resistors’ change with time and their magnitudes, variations and connections are almost completely unknown . Also, the real-world system is very complicated.
The magnitude of the problem is obvious when the processes of the carbon cycle (i.e. the ‘tanks’ or ‘electrical resistors’ and their connections) are considered.
In our paper that I reference above, we considered the most important processes in the carbon cycle to be:
Short-term processes
1. Consumption of CO2 by photosynthesis that takes place in green plants on land. CO2 from the air and water from the soil are coupled to form carbohydrates. Oxygen is liberated. This process takes place mostly in spring and summer. A rough distinction can be made:
1a. The formation of leaves that are short lived (less than a year).
1b. The formation of tree branches and trunks, that are long lived (decades).
2. Production of CO2 by the metabolism of animals, and by the decomposition of vegetable matter by micro-organisms including those in the intestines of animals, whereby oxygen is consumed and water and CO2 (and some carbon monoxide and methane that will eventually be oxidised to CO2) are liberated. Again distinctions can be made:
2a. The decomposition of leaves, that takes place in autumn and continues well into the next winter, spring and summer.
2b. The decomposition of branches, trunks, etc. that typically has a delay of some decades after their formation.
2c. The metabolism of animals that goes on throughout the year.
3. Consumption of CO2 by absorption in cold ocean waters. Part of this is consumed by marine vegetation through photosynthesis.
4. Production of CO2 by desorption from warm ocean waters. Part of this may be the result of decomposition of organic debris.
5. Circulation of ocean waters from warm to cold zones, and vice versa, thus promoting processes 3 and 4.
Longer-term process
6. Formation of peat from dead leaves and branches (eventually leading to lignite and coal).
7. Erosion of silicate rocks, whereby carbonates are formed and silica is liberated.
8. Precipitation of calcium carbonate in the ocean, that sinks to the bottom, together with formation of corals and shells.
Natural processes that add CO2 to the system:
9. Production of CO2 from volcanoes (by eruption and gas leakage).
10. Natural forest fires, coal seam fires and peat fires.
Anthropogenic processes that add CO2 to the system:
11. Production of CO2 by burning of vegetation (“biomass”).
12. Production of CO2 by burning of fossil fuels (and by lime kilns).
Several of these processes are rate dependant and several of them interact.
At higher air temperatures, the rates of processes 1, 2, 4 and 5 will increase and the rate of process 3 will decrease. Process 1 is strongly dependent on temperature, so its rate will vary strongly (maybe by a factor of 10) throughout the changing seasons.
The rates of processes 1, 3 and 4 are dependent on the CO2 concentration in the atmosphere. The rates of processes 1 and 3 will increase with higher CO2 concentration, but the rate of process 4 will decrease.
The rate of process 1 has a complicated dependence on the atmospheric CO2 concentration. At higher concentrations at first there will be an increase that will probably be less than linear (with an “order” <1). But after some time, when more vegetation (more biomass) has been formed, the capacity for photosynthesis will have increased, resulting in a progressive increase of the consumption rate.
Processes 1 to 5 are obviously coupled by mass balances. Our paper assessed the steady-state situation to be an oversimplification because there are two factors that will never be “steady”:
I. The removal of CO2 from the system, or its addition to the system.
II. External factors that are not constant and may influence the process rates, such as varying solar activity.
Modeling this system is a difficult because so little is known concerning the rate equations. However, some things can be stated from the empirical data.
At present the yearly increase of the anthropogenic emissions is conservatively about 0.1 GtC/year. The natural fluctuation of the excess consumption (i.e. consumption processes 1 and 3 minus production processes 2 and 4) is at least 6 ppmv (which corresponds to 12 GtC) in 4 months. This is more than 100 times the yearly increase of human production, which strongly suggests that the dynamics of the natural processes here listed 1-5 can cope easily with the human production of CO2. A serious disruption of the system may be expected when the rate of increase of the anthropogenic emissions becomes larger than the natural variations of CO2. But the above data indicates this is not possible.
The accumulation rate of CO2 in the atmosphere (1.5 ppmv/year which corresponds to 3 GtC/year) is equal to almost half the human emission (6.5 GtC/year). However, this does not mean that half the human emission accumulates in the atmosphere, as is often stated. There are several other and much larger CO2 flows in and out of the atmosphere. The total CO2 flow into the atmosphere is at least 156.5 GtC/year with 150 GtC/year of this being from natural origin and 6.5 GtC/year from human origin. So, on the average, 3/156.5 = 2% of all emissions “accumulate” in the air.
And there are people who think they can make a meaningful simple model of that when nobody knows the rate constants of any of the processes!
Richard
Hi Willis,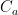 . A current
. A current  is charging it. As it charges, the charge is shared with three other capacitors, labelled
is charging it. As it charges, the charge is shared with three other capacitors, labelled 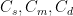 through resistors that limit the current. a is atmosphere, s is sea surface layer, m is the middle ocean beneath that and d is the deep ocean bottom (only), but of course one could add soil, leaf water, and so on. Note well that equilibrium depends on the sizes of the capacitances (relative to
through resistors that limit the current. a is atmosphere, s is sea surface layer, m is the middle ocean beneath that and d is the deep ocean bottom (only), but of course one could add soil, leaf water, and so on. Note well that equilibrium depends on the sizes of the capacitances (relative to 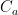 ) and the resistances.
) and the resistances. dumps e.g. a bolus of charge on
dumps e.g. a bolus of charge on 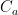 . It bleeds through the surface resistance
. It bleeds through the surface resistance  to try to equilibrate the potential differences across
to try to equilibrate the potential differences across 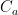 and
and  , but as it does so some of the charge is similarly bled off
, but as it does so some of the charge is similarly bled off  through resistance
through resistance  onto
onto 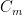 .
. remains in the system, shared between $C_a, C_s, C_m$. How much remains in $C_a$ depends on the relative magnitudes of the other two — in particular, if
remains in the system, shared between $C_a, C_s, C_m$. How much remains in $C_a$ depends on the relative magnitudes of the other two — in particular, if 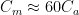 , then less than 1.7 % of the total surplus charge will end up on
, then less than 1.7 % of the total surplus charge will end up on 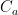 because the ratio of
because the ratio of 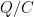 must be the same for all three capacitors.
must be the same for all three capacitors. is “infinite” in size. It is then formally equivalent to ground — indeed the Earth itself IS an enormous capacitor that acts as a ground. If indeed what I label the deep ocean is ground, capable of “permanently” sequestering CO_2 for periods of tens to hundreds of millions of years, requiring an actual turnover of the crust to return it back to the atmosphere, or if it is simply a vast reservoir compared to even
is “infinite” in size. It is then formally equivalent to ground — indeed the Earth itself IS an enormous capacitor that acts as a ground. If indeed what I label the deep ocean is ground, capable of “permanently” sequestering CO_2 for periods of tens to hundreds of millions of years, requiring an actual turnover of the crust to return it back to the atmosphere, or if it is simply a vast reservoir compared to even 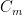 that can hold almost as much carbon as you drop into it without significantly altering the CO_2/charge in
that can hold almost as much carbon as you drop into it without significantly altering the CO_2/charge in 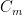 , we can just put a resistor between any reservoir that can directly dump carbon there in our circuit above.
, we can just put a resistor between any reservoir that can directly dump carbon there in our circuit above.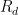 in the figure above with a switch, so one can mentally understand what happens when the switch is closed. Without the pathway (switch open), CO_2/charge builds up indefinitely as there is a nonzero current
in the figure above with a switch, so one can mentally understand what happens when the switch is closed. Without the pathway (switch open), CO_2/charge builds up indefinitely as there is a nonzero current  into the atmosphere
into the atmosphere 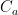 with nowhere to ultimately go to ground. With the switch closed, things are very different indeed. Now charge constantly bleeds off of all three capacitors to ground. The only way to sustain the CO_2 levels in all three is via a nonzero current
with nowhere to ultimately go to ground. With the switch closed, things are very different indeed. Now charge constantly bleeds off of all three capacitors to ground. The only way to sustain the CO_2 levels in all three is via a nonzero current  .
.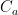 can remain in equilibrium with a nonzero non-anthropogenic current so that only anthropogenic current counts as “charge” in
can remain in equilibrium with a nonzero non-anthropogenic current so that only anthropogenic current counts as “charge” in 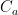 . There are many known non-anthropogenic currents (sources of CO_2) and without a path to either “ground” or a very large reservoir any nonzero current will monotonically boost the charge/CO_2 content of
. There are many known non-anthropogenic currents (sources of CO_2) and without a path to either “ground” or a very large reservoir any nonzero current will monotonically boost the charge/CO_2 content of 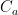 .
.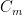 is already more than capable of “grounding”
is already more than capable of “grounding” 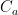 as far as the current discussion is concerned — the ocean contains many, many times more CO_2 in chemical equilibrium than the atmosphere contains, and the “fraction” of any addition that should be permanent in the atmosphere is strictly less than the ratio of their capacitances, all things being equal. So the 0.15 factor in the Bern equation makes little sense to me on strictly physical grounds. If the equilibrium atmosphere contained 15% of all of the carbon in the carbon cycle, that would be the right number. It doesn’t, and it isn’t.
as far as the current discussion is concerned — the ocean contains many, many times more CO_2 in chemical equilibrium than the atmosphere contains, and the “fraction” of any addition that should be permanent in the atmosphere is strictly less than the ratio of their capacitances, all things being equal. So the 0.15 factor in the Bern equation makes little sense to me on strictly physical grounds. If the equilibrium atmosphere contained 15% of all of the carbon in the carbon cycle, that would be the right number. It doesn’t, and it isn’t.


I have to say that I don’t like your RC circuit diagram — you need to put the “atmosphere” in parallel, not in series, and it isn’t really a parallel circuit anyway. Also, you don’t need two resistors in the circuit on either side of the capacitors — one will do since resistors in series add anyway.
I have no way to add a jpg graphic (that I know of) to this — I’ll try doing it in raw html pointing to images I just put onto my own web space, but if Mr. Moderator or anyone with cool super powers can download them and put them inline I would appreciate it.
This is what you were trying to construct, I think. It shows the atmosphere as a capacitor
However, this model is not correct. The atmosphere doesn’t share CO_2 (“charge”) with the deep ocean or middle ocean directly and the rates from surface to middle depend on the differences in “voltage” across the surface capacitor relative to middle, not atmosphere to middle. The first metaphor might work to find equilibrium, when there is no current flowing and the potentials across all the capacitors must be the same, but it won’t work to describe the APPROACH to equilibrium correctly.
I offer a slightly alternative model:
A current
At this point there is no path to ground. All the charge you put in via
Suppose, however, that
I drew such a resistive pathway
I do not suggest that this is an accurate model for the atmosphere, but it is one that at least roughly corresponds to the three processes outlined in the set of coupled ODEs above. Personally, I found the “rocket science journal” discussion of the surface equilibrium exchange a lot more reasonable — it doesn’t try to pretend that
Even
rgb
Figures ADDED by Anthony at the request of RGB:
http://www.phy.duke.edu/~rgb/rc-model.jpg
http://www.phy.duke.edu/~rgb/rc-model2.jpg
OK, it is time to be clear.
The carbon cycle cannot be represented by a ‘plumbing’ or ‘electrical’ circuit because all the ‘tanks’ or ‘resistors’ change with time and their magnitudes, variations and connections are almost completely unknown . Also, the real-world system is very complicated.
Agreed. Please note that I was only correcting Willis’ effort because series was so obviously wrong. In series all of the carbon placed on the lead capacitor just stays there.
However, it actually CAN be so represented. What you are saying is we don’t know how to set the values, and, as you also say, the representation can be wrong. Both are quite true.
I’m reading my way through “The Black Swan”. It should (IMO) be required reading for all scientists. It graphically and precisely illustrates the risk of naive mathematical models, especially those that we have “reduced” to have only a few parameters (usually because that’s all our Platonic little minds can wrap themselves around). It also thoroughly explores the human tendency towards confirmation bias, because we stubbornly continue to try to confirm a theory (which is impossible, usually) instead of disprove it (which is easy, when it works). Feynman says much the same thing — the sad thing about modern science is that we don’t publish null results, and our brains get dopamine-driven satisfaction from “being right”. It is very difficult to say “I don’t know”, or “my favorite hypothesis, when compared to the data, doesn’t quite work right”.
rgb
Any chance (Mr. Moderator) of inserting the figures?
Here they are:
http://www.phy.duke.edu/~rgb/rc-model.jpg
http://www.phy.duke.edu/~rgb/rc-model2.jpg
for those that are wondering why my post above refers to figures and there aren’t any figures.
rgb
REPLY: Done, Anthony
rgbatduke:
At May 10, 2012 at 8:43 am you say to me;
“Please note that I was only correcting Willis’ effort because series was so obviously wrong. In series all of the carbon placed on the lead capacitor just stays there.
However, it actually CAN be so represented. What you are saying is we don’t know how to set the values, and, as you also say, the representation can be wrong. Both are quite true.”
Yes, I knew you were “only correcting Willis’ effort”, and I write to confirm that your understanding of my point is exactly right.
I take this opportunity to thank you for your excellent contributions to the above discussion. I value them.
Richard
richardscourtney says:
May 10, 2012 at 10:19 am
Yeah, as usual Robert Brown has it right … teach me to post late at night without thinking …
w.
richardscourtney says:
May 10, 2012 at 4:32 am
“The carbon cycle cannot be represented by a ‘plumbing’ or ‘electrical’ circuit because all the ‘tanks’ or ‘resistors’ change with time and their magnitudes, variations and connections are almost completely unknown .”
Yes. Which is why I have been saying the value of these models, IMHO, is substantially qualitative.
It is easy to get wrapped around the axle looking at ever more intricate models but, at some point, you gain more insight by stepping back and viewing the forest rather than the trees.
In the model I proffered here, I subsumed all the complexity by allowing the time constant and gains to be operator theoretic. Bounding behavior of the system can be obtained by making these operators constant equal to infinity normed values. It is then apparent that the fundamental properties of the real world system are 1) relatively rapid sequestration of inputs (large norm of the inverse time constant) and 2) temperature sensitivity of sufficient magnitude such that temperature is driving the output.
Aside: Regarding electrical circuit analogies, the case of transmission lines is instructive. These are modeled using parameters such as conductance and capacitance per unit length. Under appropriate circumstances, a distributed element model of discrete components can be used to approximate the behavior. How well the model approximates the true behavior depends on the length of the line, the bandwidth of the signals to which the line will be subjected, and the source and load impedances (boundary conditions). A precise model would be inifinite dimensional, but the number of lumped parameters can be truncated in order to achieve a given degree of fidelity. You generally can get these types of models when you deal with continuum systems which are governed by partial differential equations.
Bart:
Thankyou for your post at May 10, 2012 at 10:39 am.
Before saying why I am responding to your post, I remind of my position which I have stated in many places including WUWT; viz.
I don’t know what has caused the recent rise in atmospheric CO2 concentration, but I want to know.
So, being aware of my stated position, you will surely understand my two responses to your post that I am replying.
Firstly, I thank you for reminding of the simple empirical model which you provided at May 7, 2012 at 10:50 am above. My problem with it is that it fits to a short time series (i.e. 1958 to present) and I fail to see the value of that because – in the absence of a physical basis – extrapolating any such fit is a ‘risky’ thing to do. However, I agree with its assessment that (in the existing data) temperature change is the observable dominant effect on atmospheric CO2; indeed, I have said that in this thread, too.
Secondly, and more importantly, I am very interested in your suggestion that a distributed element model may be helpful to understanding the system. Please note that my background is in materials science so I am very familiar with systems analyses, but I have no knowledge of electrical engineering and, therefore, I am ignorant of distributed element models (i.e. I don’t know what they are, what they do, what they can’t do, and what insights they may provide).
Hence, I write to request an expansion of your suggestion that a distributed element model may be helpful to understanding the system of the carbon cycle. And I ask you to remember my ignorance of electrical engineering so I need an explanation which I can understand (if that is possible).
Richard
Hi RGB –
I am not sure what I(t) in your model2.jpg (which I like fairly well) is exactly. It does not seem to be the “bolus” of CO2 you mention or you would be talking impulse response of the network (which would be a perfectly good way to analyze it). Neither do I think it is merely the current that happens to be flowing in from some other attached driver. So I take it to be an actual “current source” in the sense EE’s us the term.
Try walking into your local Radio Shack and asking for a “current source”. They have only batteries – voltage sources. For anyone this bothers, a good idea of a current source would be a battery with an absurdly large series resistance (say a 1.5 volt battery and 1000 megohms series, which delivers 1.5 na to any ordinary load).
Now, there is of course no switch, so let’s assume our current source is attached, and that it is a constant current Io. Ca begins to charge, and in turn, Cs and Cm, with Rd beginning to draw off current. As you point out, Ca no longer ramps without limit.
I make it that the voltage on Ca becomes Va = Io(Rs+Rd). That is, Io eventually spills through the Rs and Rd series. So Cs becomes charged to Vs=VaRd/(Rs+Rd). And Cm has a voltage Vm = Vs, since no current flows through Rm. This would make Cs and Cm all one “sea” which makes sense.
It would probably be worth looking at the impulse response and/or the decay from constant current charge. What do you think?
I am not sure what I(t) in your model2.jpg (which I like fairly well) is exactly. It does not seem to be the “bolus” of CO2 you mention or you would be talking impulse response of the network (which would be a perfectly good way to analyze it). Neither do I think it is merely the current that happens to be flowing in from some other attached driver. So I take it to be an actual “current source” in the sense EE’s us the term.
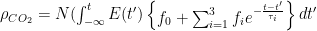
 . Lots of trunk wiggling room.
. Lots of trunk wiggling room. — the charge on a capacitor — is the moral equivalent of
— the charge on a capacitor — is the moral equivalent of 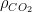 (or more correctly, its volume integral, the total CO_2 in the atmosphere). E(t) in the Bern equation is the “anthropogenic CO_2 current” that is charging up the atmospheric capacitance, which then “drains” at exponential rates $R = 1/\tau$ into reservoirs 1, 2 and 3.
(or more correctly, its volume integral, the total CO_2 in the atmosphere). E(t) in the Bern equation is the “anthropogenic CO_2 current” that is charging up the atmospheric capacitance, which then “drains” at exponential rates $R = 1/\tau$ into reservoirs 1, 2 and 3.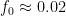 , not
, not 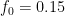 as it is given in the Bern formula. This does depend on the time constants of the various reservoirs, of course.
as it is given in the Bern formula. This does depend on the time constants of the various reservoirs, of course.
I’m assuming it to play precisely the same role as “E(t)” in the Bern equation:
Note the eight parameters:
The point of the metaphor is that
This doesn’t make complete sense to me. It is claimed that the reason for the three terms is (ultimately) detailed balance between three reservoirs and the atmospheric reservoir, perturbing a pre-existing equilibrium with the additional CO_2. In a word, as with the first capacitive model above, any additional CO_2 “charge” delivered to the atmosphere is shared across all connected reservoirs until they all have balanced rates of exchange.
However, it is perfectly obvious that when that is true, the different reservoirs will share the CO_2 in — certainly to first order — the same proportion that they already share it in equilibrium. That is, one would expect roughly 50 parts of any surplus to end up in the ocean (which contains roughly 50 times as much carbon as the air). In the end, that means
But all of this is highly idealized. As Richard Courtney and Bart have pointed out, things are a lot more complicated and unknown than this. For example, every one of the capacitors in the simplified model have variable capacitance and time constants. They vary with respect to many coupled parameters. For example, thinking only of the surface (euphotic zone), things that affect absorption rates include: temperature, wind speed over the surface, frothiness of the surface (related to wind speed), local carbon dioxide content, local nutrient content (oceanic phytoplankton are often growth limited by other nutrients than CO_2), carbon dioxide content above the surface in the atmosphere, presence/absence of sunlight, and details of the thermohaline circulation. Many of these factors are thus themselves functions of both location and past history! — average functions of location, as waters up in Nova Scotia are always a lot colder than they are around Puerto Rico and very likely experience quite different average sustained wind speeds and have different nutrient content and biology. Past history is more complicated — thermohaline circulation operates on a dazzling array of timescales, the longest of which (for complete turnover) are around 1000 years.
That means that the carbon dioxide content of deep oceanic water welling up to the surface — which in part determines how much that water is happy absorbing or releasing once it gets there — was laid down as long as 1000 years ago. It also means that there is a possibility of resonant amplification and positive feedback on an (order of) thousand year loop or any of several shorter loop times in between as thermohaline circulation is chaotic and complex and not just a single coherent flow. Global decadal atmospheric oscillations no doubt play a role as well.
In the end, this means (as Bart suggests, I think) that atmospheric CO_2 content is regulated far more strongly by variations in the capacitance of the soils and the sea than it is by the human “current”.
rgb
[Latex fixed, although you should check it, it seems to be missing a close parenthesis. For the large braces, you need to use \begin{Bmatrix} and \end{Bmatrix}. For large brackets, use \begin{bmatrix} and \end{bmatrix} … w.]
Damn, and I checked it. Likely the wordpress latex doesn’t like \left{ \right} pairs or the like. Sigh. Help Mr. Moderator? I’m really sorry…
rgb
Think rgb meant this:

( Dr. Brown, your were just missing the final “\right}” )
Mods, I’m sorry too. The correct Latex is here. rgb is correct, it was the \left{ or \right} though Latex editors accept it fine. We learn.
http://wattsupwiththat.com/test-2/#comment-982254
[Wayne, see my note above regarding the use of “\begin{Bmatrix}” and “\end{Bmatrix}. w.]
Excerpts from Veizer (GAC 2005):
Pages 14-15: The postulated causation sequence is therefore: brighter sun => enhanced thermal flux + solar wind => muted CRF => less low-level clouds => lower albedo => warmer climate.
Pages 21-22: The hydrologic cycle, in turn, provides us with our climate, including its temperature component. On land, sunlight, temperature, and concomitant availability of water are the dominant controls of biological activity and thus of the rate of photosynthesis and respiration. In the oceans, the rise in temperature results in release of CO2 into air. These two processes together increase the flux of CO2 into the atmosphere. If only short time scales are considered, such a sequence of events would be essentially opposite to that of the IPCC scenario, which drives the models from the bottom up, by assuming that CO2 is the principal climate driver and that variations in celestial input are of subordinate or negligible impact….
… The atmosphere today contains ~ 730 PgC (1 PgC = 1015 g of carbon) as CO2 (Fig. 19). Gross primary productivity (GPP) on land, and the complementary respiration flux of opposite sign, each account annually for ~ 120 Pg. The air/sea exchange flux, in part biologically mediated, accounts for an additional ~90 Pg per year. Biological processes are therefore clearly the most important controls of atmospheric CO2 levels, with an equivalent of the entire atmospheric CO2 budget absorbed and released by the biosphere every few years. The terrestrial biosphere thus appears to have been the dominant interactive reservoir, at least on the annual to decadal time scales, with oceans likely taking over on centennial to millennial time scales.
richardscourtney says:
May 10, 2012 at 11:39 am
“My problem with it is that it fits to a short time series (i.e. 1958 to present) and I fail to see the value of that because…”
It’s 54 years. And, it’s the only reliable data we have.
“Hence, I write to request an expansion of your suggestion that a distributed element model may be helpful to understanding the system of the carbon cycle. “
It was merely an attempt on my part to point out that lumped parameter models, such as in rgbatduke @ May 10, 2012 at 8:32 am, are generally approximations to a continuum model with is defined by partial differential equations.
Again, my main point is that we do not need to wade so deeply into models which cannot be authenticated with present data. It is clear that the broad general outline of the system is that, here and now, and for the past several decades, sinks are more active than supposed so that the sequestration feedback is strong, which attenuates the anthropogenic input markedly, and sensitivity to temperature is high. These conclusions fly directly in the face of the assumption that atmospheric CO2 concentration is being driven by humans.
rgbatduke says:
May 11, 2012 at 3:26 am
‘In the end, this means (as Bart suggests, I think) that atmospheric CO_2 content is regulated far more strongly by variations in the capacitance of the soils and the sea than it is by the human “current”.’
Indeed, he does. More than suggests. Asserts with evidence, that being that the atmospheric CO2 concentration has tracked the integrated temperature anomaly with respect to a particular baseline for the past 54 years, and assuredly into the next several at the very least.
“…for the past 54 years, and assuredly into the next several at the very least.”
I meant my statement to be more forceful than that. I had it in my head that I had described the interval as “decades”. The relationship will almost assuredly hold for the next several decades at the very least.