Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Tim Folkerts says at 2/20 12:44pm:
Tim – Thanks for engaging on this interesting thought experiment top post subject.
Tim says: “Therefore you (Trick) clearly conclude there is no convection.”
Yes, only after equilibrium is achieved when random vigorous molecular mixing takes over. Convection IS a difficult concept for many authors writing on Fig. 1 top post thought experiment and they dance around with it a bit. It is good to discuss convection to further understand Fig. 1.
I would say and/or conclude there is convection in Fig. 1 top post prior to equilibrium whenever heat is still flowing from the initial conditions. Convection is discussed by the thermo grand masters in the context of the propagation of heat or thermally driven mass motion in fluids. Therefore convection is historically allowed before Fig. 1 equilibrium but not after Fig. 1 equilibrium when heat flow ceases.
I ref. the basic definitions of convection that include the words “heat flow”. After Fig. 1 achieves equilibrium, the authors of the papers rely on the random vigorous mixing of the molecules which still prevails after equilibrium when there is no longer any heat flow and the term “convection” cannot be properly employed.
Tim continues: “You (Trick) then reference “Verkley et. al. part b” to support your position. But this favorite paper of yours specifically starts part b by saying:
b. Isentropic profile
Now, in Ball [1956, Eq. (4)] it is argued that for convective motions…
Can you not see the logical inconsistency in your argument? You are taking the paper out of context, exactly as Dr Brown concluded.”
No, the Verkley paper is very short and I have been careful to cite entire part b which is exactly equivalent to Fig. 1 in the top post. Now I have clipped some sentences of that part b relative to the posts on the mixing of molecules, and if I have not been true to the proper context please call me out with an exact reference. Verkley et. al. part b does spend a lot of space writing on the issue of convection and molecular mixing as you clip.
Poster Robert Brown is right to complain about quoting out of context and I urge the interested reader to just read & understand the whole of Verkley part b rather than my (or Tim’s) clips. My clips are thought starters and needed to try and reduce the verbiage or few will read these posts & properly engage. In whole, Verkley et. al. do a convincingly good job in part b supporting their conclusion of non-isothermal, isentropic result at equilibrium for Fig. 1 in top post.
Tim continues: “Part A of the paper corresponds to the situation here, and Part A clearly concludes that
T = (lambda)^-1 is constant, thus, the profile is isothermal. This is the well-known result of classical thermodynamics and the kinetic theory of gases.”
No, part a thought experiment of the Verkley et. al. paper is different than here in Fig. 1 of top post. In Verkley part a, the thought experiment allows the ideal gas column to “…perform work on the air above and below the column…” (ref. Verkley Fig. 1). If the Fig. 1 top post is modified to allow that performance of work on the air column above & below then things here are suitably different and the isothermal conclusion then results.
Trick says:
February 20, 2012 at 11:13 am (Edit)
No, you didn’t expect to be called on that, or you wouldn’t have written such a stupid statement. Nice try at a recovery, though, claiming it was deliberate.
Robert implies no such thing, that’s your misunderstanding. You claim you can do it … so you claim. But until you DO do it, it’s just words, Trick … and to date your words are trading well below par.
Yeah, it’s a bitch to post something like
E = MC^2
or
PV = nRT
or
Q = ε σ T^4
or in latex,
without having special software … oh, wait, I just did it. No special translation, no software needed. You can write it in anything from plain old Excel notation, or you can do it in latex if you want,
So I’m sorry, but “I can’t type the equations” is BS. If you’re too uneducated to type equations, you don’t belong here. So far all you’ve done is flap your lips, Trick, and there’s no trick to doing that, talk is cheap. When you come up with the equations, post’em up … but I’d hold off on the boasting until you do.
Yes there is, for two reasons. To see if you actually understand them, and to see if we actually understand them. Until then, it’s just more of your hot air.
w.
Trick, I disagree with your interpretations of the Verkley paper. I would point you to the conclusions:
The top post assumes (as did Jelbring initially) that the mass and the energy of the atmosphere is constant. So the equilibrium condition IS isothermal according to Verkley.
The paper goes on:
.
If there is convective mixing, then we are never in thermodynamic equilibrium and never at maximum entropy.
Willis Eschenbach says 2/20 at 3:47pm:
“If you’re too uneducated to type equations, you don’t belong here.”
My laughs just keep on coming. Willis, the major typing issue for me is not PV = nRT. Issue is the integration sign and the limits thereof which I don’t find on my keyboard anywhere. WHAT is latex and how is it invoked? I know you et. al. are far ahead of me using that feature/program.
I know I can find the sign for integration and paste it into a word document and maybe the limits. Tell you what, this subject is interesting enough to try to do a prose integration = post. This is what it would look like, but you can also just look this up in the published papers for free and w/no typo’s. I know the mod.s have a work area to try and prove out what any post might look like.
Step 1: It all starts with the total mass – all per unit area of Fig. 1 – with a flat bottom if we make it simple notation and call its height running from z1 to z2 (see I can’t even do subscripts here).
Then the total mass per unit area of the gas column is the integral from z1 to z2 of the mass density of the gas; note mass density as rho.
Total mass of gas column = integral from z1 to z2 of rho dz.
I’m sure Willis can make that look pretty. I can’t; except maybe in MS Word. If Willis wants to see more = signs I can oblige but you will see more of it like this:
Step 2: Invoke hydrostatic equilibrium, constant g(z) is close enough simplification, the equation 5 in the top post and:
– integral from z1 to z2 1/g * dp/dz dz = 1/g * (p2 –p1)
The total air column mass is constant, and given the adiabatic control volume as shown neither heated or cooled by surroundings nor by radiation (GHG-free) or by interaction with adjacent air or ground; we need to find the equilibrium temperature profile of this gas column and we need only 2 laws: the 1st and 2nd thermo laws. And a bunch of = signs I guess.
Step 3: Start with the total enthalpy per unit area of the gas column and conserve it with all other forms of energy the column can have including earth’s g field since the sum of the energies must remain constant in the isolation of the control volume; cp being the specific heat capacity of the GHG-free air; s being specific entropy per unit mass:
enthalpy = integral from z1 to z2 rho * cp * T dz
potential energy = integral z1 to z2 rho * g * z dz
sum of all energies the column can have = integral z1 to z2 rho * (cp * T + g*z) dz = constant
total entropy of the column= S = integral from z1 to z2 rho * s dz
So the task is to show Willis et. al how to find the temperature and pressure profile that maximizes this entropy eqn. subject to constraint of holding the sum of all energies constant. It is formidable but I can slog thru 10 or so more of my 13 outline steps algebra eqn.s with = signs to earn my bona fides.
NB: Clues for issues in the top post: there is no control volume total energy conservation constraint mentioned and T(z) is moved outside the integral of dz prior to eqn. 6 with no explanation. Those are MAJOR issues. So I have already defined eqns. with = signs of what is missed in the top post leading to an incorrect isothermal conclusion.
Want more eqn.s with = signs?
Well if so, that was sort of fun typing. Only 9 or 10 more steps to go. Watch this space. Maybe some other poster can do these 3 steps in latex (hint, hint) for less total laughs (cite conservation of humor).
Tim Folkerts 2/20 says at 3:54pm:
“Trick, I disagree with your interpretations of the Verkley paper.”
Cool Tim, this is one way science has historically moved forward. Gotta’ say again though, interested posters need to read the paper in whole & its entirety not just clips. But erring on the side of brevity with clips:
Tim clips from the paper: ” We reiterate that the entropy maximization problem in its pure classical setting… will result in an isothermal profile…”
Yes, this refers in context to the classical setting as defined in Verkley Fig. 1 and that is different from the top post Fig. 1. Classically, Verkely Fig. 1 allows the air column to “…perform work on the air above and below the column…” as I wrote. Verkley et. al. state they are unsatisfied with this classical constraint 1) and 2) or 2’) as in their part a.
Thus the paper continues “It thus seems natural that one should represent (atmospheric processes) by posing certain additional constraints in the maximization problem, considering that constraints 1) and 2) will continue to be valid. This is the key idea of this article.”
The paper then continues:
“The question then arises what these constraints should be. Here, we have taken, following Ball (1956) and Bohren and Albrecht (1998), constancy of the integrated potential temperature as a single additional constraint 3, but this choice is of course open for debate.”
Hmmm…the paper also as a byproduct explains 991 & counting posts on this thread.
The paper then, in the very last sentence, the one we have all been waiting for, the money clip:
“In our view, this particular constraint still lacks a solid physical basis; yet, the above results give reason to expect that the construction of such a basis may be possible because the three constraints 1, 2’, and 3 together lead to a temperature profile that corresponds remarkably well to the tropospheric part of the Standard Atmosphere.”
And, folks, that Verkley part b constraint 3) is EXACTLY top post Fig. 1 for reasonable 80% of earth’s atmosphere which leads the paper to irrefutably mathematically prove the thermo law consistent non-isothermal, isentropic temperature profile for top post Fig.1.
Now we can debate Verkley et. al. “lacks a solid physical basis” point which means to develop a view one has to accept, say, the random vigorous mixing of the Fig. 1 top post molecules at equilibrium is solid enough physical basis. I do. Others may differ, but those folks need to supply a convincing proof support for their differing view.
Trick says:
February 20, 2012 at 6:14 pm
Here, Trick, I know it’s tough to find out cryptic things like what latex might be … let me google it for you.
Here in wordpress, you invoke latex with
$/latex
WITHOUT the slash “/”, and you end the invocation with the dollar sign.
So for example,
$/latex \int_{n1}^{n2} $
without the slash gives us
w.
Cool, thanks Willis. I’ll give latex a try, maybe tomorrow for the next few steps.
For those that think all solar radiation is almost immediately thermalised here’s another headache.
http://en.wikipedia.org/wiki/Color_of_water
Willis – I tried to exactly emulate your latex implementation, which worked, for my step 1: Mass = formula but that simple test failed to parse. I see two possible reasons: 1) I used the character map greek symbol for rho and it won’t parse or 2) I tried to use subscripts for z1 and z2 integration limits and they won’t parse.
I wrote latex for all the steps I posted 2/20 6:14pm and it took a couple hours to learn how and check. These are the easy steps. The S integral for entropy I posted requires starting all the way back with the thermodynamic internal energy U of the N molecules and invoking the classical mechanics equipartition theorem. At my rate of typing latex, I estimate 2-3 days of >8hours work to get thru all 13 steps which are very non-trivial “equations with = signs” in contrast to the top post of “manifestly”.
This is hardly worth it even when/if I figure out my parse failure b/c the “equations with = signs” are already freely available on the internet and/or the local science library. I will leave my bona fides rest for now on the 13 outline steps already posted.
What? The DALR is generated by adiabatic expansion of a gas.
constant and cuts across the isotherms. Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.
PV = nRT
Suppose a gas in a cylinder is allowed to expand through a nozzle into deep space. The random kinetic energy (related to T) will become highly directed kinetic energy. The steam of particles will no longer have any random kinetic energy. It will have no temperature. Also, since P goes to zero, T must also go to zero. Since V is the totality of free space, you might consider it to be infinity. The only way the temperature could remain constant would be if zero times infinity would be equal to the original product.
Not to mention that the equation for an adiabat for a gas confined to a cylinder is
I’ve basically too busy to post much any more on this thread, sorry guys. Besides, if directly quoting the conclusions of a paper that directly examines the issue won’t convince Trick, nothing will. It doesn’t really matter. His arguments won’t convince anybody that actually can work through the physics because they are not correct — parcels of an ideal gas are not adiabatic, ever, because one can compute the thermal conductivity of an ideal gas and it is non-zero. He won’t attempt to derive the DALR from microscopic first principles without the assumption of adiabatic transport of macroscopic parcels of air because if he attempts it, he won’t get the answer he desires out of pure stat mech. He won’t acknowledge that in static force equilibrium (after Jelbring’s very long time) there is no bulk transport of parcels of gas and hence conductivity has an infinite amount of time to increase the entropy of the gas by equilibrating the temperature. So what’s left? The discussion has become a waste of time.
On a more interesting note, now that Jelbring is finished (at least to the rationa) I’ve started in on Nikolov and Zeller. In particular, I’ve taken actual data from independent sources and applied their prescription to it, and discovered that it lies nowhere near their curve or the data points. I’ll top post on this soon on WUWT — there is no point at all continuing on Tallbloke’s blog because he a) censors the content of my posts; b) inserts parenthetical comments into my posts so they are annotated with his “responses”; c) asks silly questions like what the meaning of the complex unit is in physics as if that has anything at all to do with dimensional scaling arguments; d) seems blind to the fact that the probability of real-world data drawn from actual measurements of physical processes and adjusted by an arbitrary nonlinear parameter falling on a single perfect curve like N&Z’s, right down the middle of the expected (large) error bars is essentially zero, as the unbiased application of the formula to “unadjusted” surface temperatures clearly demonstrates by completely destroying the fit of the curve to the data and indeed completely confounding it when one applies the theory to the Jovian moons.
Personally, I’d just as soon that the skeptical position on the CAGW issue not be based on our own version of MBH, but what can one do?
rgb
Robert Brown: “I’ve basically too busy to post much any more on this thread, sorry guys.”
in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them” and “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. . . . I haven’t had time to finish it . . . but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting”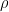
and molecular mass 
:
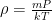
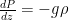
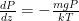
, and solve the differential equation for pressure as a function of altitude:
:
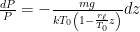
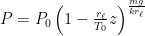
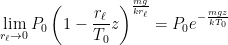
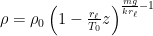
![E_{potential} = A \rho_0 g \left[ \left(-\frac{T_0}{r_\ell}\right)\frac{kr_\ell}{mg}\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}}z -\left(-\frac{T_0}{r_\ell}\right)\frac{kr_\ell}{mg} \left(- \frac{T_0}{r_\ell}\right)\frac{1}{\frac{mg}{kr_\ell}+1}\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}+1}\right]_0^{\frac{T_0}{r_\ell}}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+A+%5Crho_0+g+%5Cleft%5B+%5Cleft%28-%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7Bkr_%5Cell%7D%7Bmg%7D%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%7Dz+-%5Cleft%28-%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7Bkr_%5Cell%7D%7Bmg%7D+%5Cleft%28-+%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%5Cright%29%5Cfrac%7B1%7D%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cright%5D_0%5E%7B%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%7D+&bg=ffffff&fg=000&s=0&c=20201002)
![E_{potential} = - A \frac{kT_0\rho_0}{m} \left[ \left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}}z + \left( \frac{kT_0}{mg+kr_\ell}\right)\left(1-\frac{r_\ell}{T_0}z \right)^{\frac{mg}{kr_\ell}+1}\right]_0^{\frac{T_0}{r_\ell}}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+-+A+%5Cfrac%7BkT_0%5Crho_0%7D%7Bm%7D+%5Cleft%5B+%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%7Dz+%2B+%5Cleft%28+%5Cfrac%7BkT_0%7D%7Bmg%2Bkr_%5Cell%7D%5Cright%29%5Cleft%281-%5Cfrac%7Br_%5Cell%7D%7BT_0%7Dz+%5Cright%29%5E%7B%5Cfrac%7Bmg%7D%7Bkr_%5Cell%7D%2B1%7D%5Cright%5D_0%5E%7B%5Cfrac%7BT_0%7D%7Br_%5Cell%7D%7D+&bg=ffffff&fg=000&s=0&c=20201002)
![E_{potential} = - A P_0 \left[0+0-\left(0+\frac{kT_0}{mg+kr_\ell}\right)\right]=\frac{A P_0kT_0}{mg+kr_\ell}](https://s0.wp.com/latex.php?latex=E_%7Bpotential%7D+%3D+-+A+P_0+%5Cleft%5B0%2B0-%5Cleft%280%2B%5Cfrac%7BkT_0%7D%7Bmg%2Bkr_%5Cell%7D%5Cright%29%5Cright%5D%3D%5Cfrac%7BA+P_0kT_0%7D%7Bmg%2Bkr_%5Cell%7D+&bg=ffffff&fg=000&s=0&c=20201002)
degrees of freedom:
:
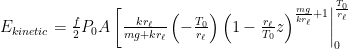
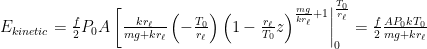
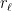It would be hard not to say you’ve gone above and beyond. But I’m a little disappointed that you did not follow up on your argument that “the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate.” You said you would:
“Once I have
I had hoped to see the results because, as I indicated above, my paper-and-pencil results were inconsistent with your arguent. I’m not entirely confident of them, but, since there was no follow-up, I’ll set the calculations forth here in baby steps in case anyone else in interested and wants to check my work.
We start out with the Ideal Gas Law and then express it in terms of density
We then require that the pressure, which is the weight per unit area of air above, decrease with altitude by the weight of the air passed:
We separate variables, assume a constant lapse rate, i.e.,
Note that
Density can then be readily determined:
Similarly,
We now turn to determining the potential energy in the air over a surface of area
Then we turn to kinetic energy, assuming
Contrary to your several statements in previous comments, these results appear to indicate that the center of mass is independent of lapse rate
$\frac{E_{potential}}{E_{potential}+E_{kinetic}}=\frac{\frac{A P_0kT_0}{mg+kr_\ell}}{\frac{A P_0kT_0}{mg+kr_\ell}+\frac{f}{2} \frac{A P_0kT_0}{mg+kr_\ell}}=\frac{2}{f+2}$
So your numerical results would have been interesting.
I screwed up the last equation. It should be:
It would be hard not to say you’ve gone above and beyond. But I’m a little disappointed that you did not follow up on your argument that “the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate.” You said you would:
“Once I have n(z) in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them” and “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. . . . I haven’t had time to finish it . . . but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting”
I got distracted by N&Z, which is a much bigger issue, on Tallbloke’s blog which is a problem in and of itself as it is difficult carrying out a discussion when the blog owner is redacting your posts at will.
The last thing I obtained is that my prediction there was indeed incorrect — the center of mass of an isothermal ideal gas is higher than that of a DALR gas. I was still working on understanding this, and at looking at the distribution of heat, when the N&Z thing took off, but what my intuition tells me is that:
a) A strictly DALR gas has a strict top of atmosphere height. At a very definite height, T = 0 and P = 0 and n = 0. This is what I wasn’t thinking of correctly. A DALR atmosphere has a linear thermal profile right down to absolute zero. It isn’t even approximately a maxwell-boltzmann gas, especially near the top.
b) An isothermal atmosphere, of course, expands into the vacuum above, vastly increasing its entropy in the process and properly thermalizing its velocity distribution.
rgb
Robert,
While we are making minor corrections, you said ” Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.”
You seem to be forgetting adiabatic free expansion and the Joule-Thompson effect, where it is well-known that:
* ideal gases do not change temperature.
* real gases either warm or cool slightly depending on the circumstances
http://en.wikipedia.org/wiki/Joule%E2%80%93Thomson_effect
Robert Brown says:
February 23, 2012 at 6:57 am
Robert, let me start by saying that your patience here has been legendary. I am inspired by your calm repetition of things. I’m not nearly so good at just sticking to the subject matter, I tend to get passionate.
Regarding Tallbloke “redacting your posts at will”, that’s why I was overjoyed to be banned from the place … it meant I didn’t have to bother trying to educate the gravity-heads and the pressure-heads, which is an impossible job even on a good day with a following wind …
w.
Tim Folkerts says:
February 23, 2012 at 8:11 am
Robert, While we are making minor corrections, you said “Adiabatic processes are never isothermal (as far as I can think offhand), because of the first law.” You seem to be forgetting adiabatic free expansion and the Joule-Thompson effect, where it is well-known that:
* ideal gases do not change temperature.
* real gases either warm or cool slightly depending on the circumstances.
Tim, “you seem to be forgetting” that what is commonly called “free expansion” is not actually free expansion at all. It is an adiabatic free expansion followed by a dissipative process in which the macroscopic kinetic energy is thermalised. The expansion phase, which cools the gas adiabatically, does work on the gas itself. The subsequent irreversible phase, in which the accelerated gas slams into the far side of the second container, bringing the temperature back up again, is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence. Even in an ideal gas the outcome will not initially be isothermal; there will be patches of higher and lower temperatures, which will gradually even out through turbulent mixing and diffusion.
The Joule-Thompson scenario proper combines the three phases into one by restricting the flow between the containers sufficiently that the acceleration of the flow is negligible (Cdrag>>1), eg., by means of a porous plug.
Paul,
I don’t think we are really disagreeing that much.
Pretty much by definition, the thing “commonly called ‘free expansion’ ” is what I meant by “free expansion”. It includes the various stages you describe – a gas freely expanding into an empty chamber and coming back to equilibrium in the new, larger volume.
Since the intermediate stages are non-equilibrium, then even defining “a temperature” for the system is problematic. However, the initial equilibrium conditions and the final equilibrium conditions have the same temperature, so I have no problem saying the process (taken as a whole) is isothermal.
I am a little confused when you say “The subsequent irreversible phase .. is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence.”
Whether the process is adiabatic (ie perfectly insulated, allowing no energy to flow into/out of the system) depends on the walls. To the extent that we have postulated perfectly insulated walls throughout the entire discussion, then any flow/turbulence/viscosity within the system would not affect energy flow to/from other systems.
Tim Folkerts says:
February 23, 2012 at 4:39 pm
I am a little confused when you say “The subsequent irreversible phase .. is most unlikely to be adiabatic in detail, because it will involve considerable internal turbulence.”
Whether the process is adiabatic (ie perfectly insulated, allowing no energy to flow into/out of the system) depends on the walls. To the extent that we have postulated perfectly insulated walls throughout the entire discussion, then any flow/turbulence/viscosity within the system would not affect energy flow to/from other systems.
That’s why I said “unlikely to be adiabatic in detail“. Internally, between the various parcels of gas in the system, there are highly non-adiabatic processes going on. There is a lot of energy flow within the system, and while that is happening, the temperature is anything but uniformly isothermal. However, those parcels of gas will still mostly have a sufficiently large number of particles and be sufficiently close to LTE that the temperature within them remains well-defined. Note that LTE does not require that the system be in thermodynamic equilibrium overall.
Yeah, and I should once again restricted my comments to gases confined to cylinders (even if the cylinders are infinitely high) and not to squirting compressed gas through a nozzle or the like.
is constant, and I can grok that and see immediately that this sort of adiabatic expansion cools the gas as it cuts across to lower isotherms.
The point being that the usual textbook definitions of adiabatic processes and so on involve them being quasi-static, and I’m not sure that a free expansion of the sort described truly qualifies. It’s part of what makes the Carnot cycle interesting — everything has to move “slowly” so that the gas in the cylinder remains in “equilibrium” at least as far as having a well defined temperature is concerned.
It also makes DALR expansions tricky, because they are one “parcel” of gas expanding against another, which gives me a headache — topologically — whenever I try to imagine it happening in a uniform way, at which point my brain wants to shift gears into Navier-Stokes altogether because simple pictures of a cubic meter of gas expanding into other gas surrounding it as it rises forces one to think of what the other gas has to do to make room, and then you’ve got gas expanding into gas that is contracting, some rising, some falling, with dynamic viscosity along the parcel boundaries and I just can’t solve or even visualize the PDEs in my head particularly well except in simple e.g. convective roll sorts of ways.
But gas in a cylinder, that I can manage. Then
rgb
Robert Brown said:
February 19, 2012 at 8:10 pm
What Tim said is incorrect, and confused. Yes, I’m sure that there are physicists who understand these topics, Gerlich, Teustchner, Postma, to name three. But, contrary to Wikipedia, DALR doesn’t require there be a rising gas, and contrary to Brown and Eschenbach, the gaseous atmosphere will not be isothermal in LTE.
I’ve been trying to suggest ways to help you view the atmosphere that might help you to better understand the true situation of the gas being compressed radially inward from the center of a sphere by gravity, and how compressible gas molecules occupy less space due to their being compressed by the force of the molecules that are further away from the center; which are just as thermally excited as the other molecules. i.e. they are all at the same potential temperature; and exhibit the DALR.
I would suggest that before you teach stuff, you first learn about the stuff you are teaching. For the behavior of real gasses in the atmosphere, “Gas Tables” by Keenan, Chao, and Kaye might provide some insight.
BigWaveDave says: “What Tim said is incorrect, and confused.”
Just out out curiosity, what qualifications do you have to judge a disagreement between PhD physicists on issues of fundamental thermodynamics? Why are you so sure that Gerlich, Teustchner, & Postma are right, but rgb and I are wrong, other than you want the other answer to be correct? (I’m not saying here that we ARE right, but to judge the disagreement would take a level of understanding GREATER than the people on the two sides.)
What specifically did I say that you think is incorrect and confused?
” .. which are just as thermally excited as the other molecules. i.e. they are all at the same potential temperature”
And that, I think, is our fundamental disagreement. To me and rgb, “just as thermally excited” means “the same temperature”, not “the same potential temperature”, as required by the 0th law of thermodynamics. Having the air at two different altitudes have the same potential temperature but not the same actual temperature at equilibrium would violate the laws of thermodynamics in several fundamental ways (as pointed out several times above). This makes me think you are wrong.
Tim Folkerts says 2/28 at 9:08pm:
“..means “the same temperature”…as required by the 0th law of thermodynamics.”
No. Not exactly, only approximately. This is where Tim & Robert’s view is fundamentally incorrect for the exact solution for Fig. 1; they need to study up on the 0th law of thermodynamics which states that two systems at the same temperature as a third system are at the same temperature as each other. Along with study of Fourier’s eqn. which is inapplicable to ideal gas in a gravity field.
Tim continues: “What specifically did I say that you think is incorrect and confused?”
Tim’s above clipped quote for instance. In Fig. 1 top post there is only 1 system thus the 0th law is not strictly applicable and Fourier’s eqn. is not strictly applicable because there is a gravity field & at LTE heat flow has ceased.
In my view, the approximate isothermal solution derived as shown in the top post where one just assumes Fig. 1 T is constant in the dz integration IS fairly close in LTE but not exact. The exact non-isothermal, isentropic solution consistent with the thermo laws for Fig. 1 in LTE has to be proved thru conservation of ideal gas enthalpy&energy and mathematical means of ideal gas entropy integral maximization.
Many authors have shown the exact non-isothermal, isentropic solution derivation is consistent with applicable physical laws. Posters Tim and Robert Brown’s isothermal solution ignores these authors and/or have offered nothing of substance in this thread to disprove these published “PhD physicists on issues of fundamental thermodynamics”.
Trick & BWD,
I have read the paper mentioned in this thread from the “numerous authors”, and I don’t see one of them that agrees that an isolated, insulated macroscopic gas will have a temperature gradient. I am not ignoring anything — I see all the published papers supporting the isothermal solution for this case.
Certainly, if there is heating at the bottom and cooling at the top (like the real atmosphere), then the “applicable physical laws” do indeed lead to a “non-isothermal, isentropic solution”.
The laws of thermodynamics state that the universe seeks to MAXIMIZE entropy, not to make entropy the SAME everywhere. (I challenge you to find a thermodynamics text that states a principle of equal entropy as as a fundamental principle). The isentropic solution is not the maximum entropy (since we can raise the entropy by simply letting heat flow from the cool upper regions to the warm lower regions).
>Tim’s above clipped quote for instance. In Fig. 1 top post there is only
>1 system thus the 0th law is not strictly applicable …
As is common it such situations, the system can be split into two (or more) parts by an imaginary surface. So I could treat the bottom 1 m as one system and the top 1 m as another system. If I wait long enough so that the top and bottom systems are each in equilibrium with the center section, then the 0th law says clearly that the top and bottom sections are each the same temperature as the center section.
But I think it is time to agree to disagree. I clearly think you are wrong. You clearly think I am wrong. We have both tried to convince the other. Now we will have to leave it to others to decide (hopefully based on science and not on wish-for results).
Tim Folkerts:
You asked
I have been earning a living as an engineer specializing in cutting edge technology for very large scale thermal energy transfer processes and power systems for close to 40 years. My credentials include BS, JD and PE, and I have four patents.
As for my qualifications to engage in argument with PhD’s, I have many times been part of and have led teams with PhD team mates. I was also married to a PhD for 20 years.
Because the import of the consequence of the radial temperature gradient created by pressurizing a spherical body of gas by gravity, from the inside only, is that it obviates the need for concern over GHG’s. And, because this is based on long established fundamental principles that were apparently forgotten or never learned by many PhD’s, it is not something that can be left as an acceptable disagreement.