Guest post by Philip Mulholland and Stephen Wilde
“No government has the right to decide on the truth of scientific principles, nor to prescribe in any way the character of the questions investigated.” Richard P. Feynman.
In this dual scene montage, we see on the left the Earth viewed by the DSCOVR: Deep Space Climate Observatory from its position in solar orbit at the sun side Lagrange Point. In this view we also see the fully illuminated far side of the Moon as it transits the Earth at new moon on the 5th July 2016.
On the right is the iconic image of Earthrise taken on 24th December 1968 as Apollo 8 orbited the Moon. The continent of Antarctica is clearly visible, fully lit as the Earth’s axial tilt presents the south pole towards the sun at the height of the austral summer. The image is displayed here in its original orientation, though it is more commonly viewed with the lunar surface at the bottom of the photo. (Image Caption Credit NASA).
1. Introduction:
The history of Climatology is long and honourable, indeed the very concept of climate goes back to the Greek philosopher Aristotle, who identified the three main climatic zones known to the ancient world. These zones are: –
A. The Torrid Zone – located to the south of Greece in Africa.
B. The Frigid Zone – located to the far north of Greece where lives Boreas, the god of the north wind and winter.
C. The Temperate Zone of Europe, where the four annual seasons occur, and Greece is most favourably located.
Aristotle’s three climate zones can be directly linked to the three main atmospheric circulation cells that we now recognise within the Earth’s atmosphere. These three cells are: –
A. The Hadley cell, which is a thermal cell, driven by solar radiation from space heating the planet’s surface. Two zones of Hadley cells exist in our atmosphere, these are both found in the Tropics and are generally located between the Equator and the Tropic of Cancer in the northern hemisphere and the Tropic of Capricorn in the south. The Hadley cell’s poleward limit is located in the Horse Latitudes; where a zone of descending air exists forming surface high pressure anticyclones. It is the Hadley cell that is the defining atmospheric feature of Aristotle’s Torrid Zone.
B. The Polar cell, which is also a thermal cell, but it is driven by atmospheric circulation caused by radiation cooling from the ground surface directly to space. This radiative cooling produces an atmospheric surface inversion, that is most noticeable in winter. The Polar cell’s equatorward limit is marked by the Polar Front, an oscillating band with an associated strong horizontal surface temperature gradient; above which is found the jet stream of the upper troposphere. The Polar cell is responsible for the formation and surface export towards the equator of cold dense airmasses. It is the Polar cell that is the defining atmospheric feature of Aristotle’s Frigid Zone.
C. The Ferrel cell, which is a mechanical cell, located between the Hadley and Polar cells. It acts as a buffer or cog between the latitudinal limits of the two thermal cells, and has a circulation pattern that abuts and links these two opposing cells. The Ferrel cell forms a zone of mixing and ascending air that is associated with cold cored cyclones. It is the Northern Hemisphere Ferrel cell that accounts for Aristotle’s Temperate Zone, with its annual seasonal changes and varied weather patterns.
This essay completes a four-part series of analysis begun with Calibrating the CERES Image of the Earth’s Radiant Emission to Space, in which using basic meteorological data, a technique to calculate the average temperature of the Earth was demonstrated. The second essay in this series An Analysis of the Earth’s Energy Budget, discussed the mechanism by which the current climate science paradigm, which uses atmospheric power intensity flux recycling in the form of back-radiation accounts for the currently observed average temperature of the Earth. The third essay Modelling the Climate of Noonworld: A New Look at Venus, presented an alternative climate model, using the process of atmospheric circulation on a hypothetical tidally locked planet, to demonstrate that convective atmospheric mass motion recycling can be invoked to explain the greenhouse effect.
In this current essay we use the modelling strategy of Noonworld, and by creating a three-element parallel model constrained to the atmospheric data used in the CERES study, apply this concept of convective atmospheric mass motion flux recycling to study the climate of the Earth.
In formulating this study, we have incorporated into the analysis elements designed to address valid and constructive criticisms made by commentators of the previous essays.
In building a three-element parallel model the primary distinction being studied is between slowly rotating Venus, with its hemisphere encompassing pair of Hadley cells, and rapidly rotating Earth, with its triple cell per hemisphere configuration of Hadley, Ferrel and Polar cells.
The use of a parallel configuration for the model design addresses the concern raised that the primary motion of the Earth’s atmosphere is predominantly zonal and not meridional flow. This design also addresses a feature of tropical climate best summed up as “Nighttime is the winter of the tropics.”
The issue of planetary axial tilt, leading to polar winters dominated by little or no solar flux and summers with no nighttime, was addressed by splitting the polar cell sub-unit in the climate model into two distinctly separate modes of operation. For the summer all convective activity is assumed to recycle the descending air directly back onto a lit arctic surface. By this means the low intensity solar flux inherent at high latitudes is amplified by a process of atmospheric short circuiting during the arctic summer. By contrast during the arctic winter the polar sub-cell unit in the model is assumed to have zero solar influx, and all of the power intensity used to drive the atmospheric circulation arrives by advection from the adjacent Ferrel cell.
Finally, we have adopted a more nuanced approach to the issue of lapse rate, using a wet adiabatic lapse rate for the Hadley cell, an intermediate environmental lapse rate for the Ferrel cell, and a dry adiabatic lapse rate for the Polar cell. This approach is in contrast to the analysis of G.C. Simpson (1928) where he adopted a uniform planetary lapse rate of 6oC/km in his paper “Some Studies in Terrestrial Radiation”.
2. Methodology.
Our modern understanding of the dynamics of the Earth’s planetary climate, and the role that radiant energy has in defining the features of the atmospheric circulation system, has progressed with the formulation of the energy budget diagram used to quantify and rank the importance of the constituent elements of the climate system (Kiehl and Trenberth, 1997). A key metric of the energy budget is the standard Vacuum Planet equation exemplified by Sagan and Chyba (1997). This equation is used in Climate Science to calculate the expected thermal emission temperature Te of an illuminated globe under the average solar irradiance that pertains for a planet’s average orbital distance from the sun, and for that planet’s specific Bond albedo.
From Sagan and Chyba (1997): –
“The equilibrium temperature Te of an airless, rapidly rotating planet is: –
Equation 1: Te ≡ [S π R2(1-A)/4 π R2 ε σ]1/4
where σ is the Stefan-Boltzmann Constant, ε the effective surface emissivity, A the wavelength-integrated Bond albedo, R the planet’s radius (in metres), and S the solar constant (in Watts/m2) at the planet’s average distance from the sun.”
The results of applying this Vacuum Planet equation to the Earth are shown in Table 1:
We are attempting here to analyse the energy flows for the Earth’s three atmospheric circulation cells using the simple Dynamic-Atmosphere Energy-Transport Model (DAET) previously introduced for the study of the climate of Venus. The Earth is modelled as a spherical globe that cuts a circular silhouette, or disk shadow from the beam of the solar irradiance at the planet’s average orbital distance from the Sun. The average fraction of the illumination beam, that the silhouette for each of the three circulation cells intercepts during the course of a year, is latitude dependent.
For the purpose of this analysis it is assumed that the latitudinal reach of the Hadley cell for each hemisphere is from the equator to latitude 30o. The Ferrel cell extends from latitude 30o to the (ant)arctic circle and the Polar cell occupies the remaining latitudes around the pole of rotation. The tropical Hadley cell of energy surplus intercepts 60.90% of the illumination, the temperate mechanical Ferrel cell of energy transport intercepts 36.29%, and the frigid thermal Polar cell of energy deficit intercepts the remaining 2.81% of the Sun’s energy cut out by the disk silhouette (Figure 2).
The Earth has the form of a globe, and because of this spherical shape the surface of the Earth is unevenly illuminated. The location of the maximum possible power intensity at the surface of the Earth occurs at the solar zenith, the unique point on the Earth’s surface where the Sun is directly overhead. At all other locations the slant of the Earth’s surface to the sun’s beam of light lowers the interception intensity. This is a feature of illumination that we observe at both dawn and dusk when our shadows reach their maximum length as the sunlight grazes the surface of the Earth.
The average power intensity at the Earth’s surface is different for each of the three atmospheric cells. The tropical Hadley cells, which occupy 50% of the surface of the Earth, intercept 60.90% of the beam silhouette, and therefore receive the highest radiant beam intensity. The Ferrel cells, which occupy 36.29% of the surface of the Earth, intercept 41.75% of the beam silhouette and therefore receive a lower radiant beam intensity; while the Polar cells, which occupy 8.25% of the surface of the Earth, intercept only 2.81% of the disk silhouette, and therefore receive the lowest average radiant beam power intensity. This quantity of radiant power intensity is defined by the illumination power intensity dilution divisor or “divide by rule” that is specific for each of the three atmospheric cells. This metric is used to constrain the value of the insolation flux used in the modelling process (Figure 3).
The power intensity of the Earth’s average annual irradiance is 1361 W/m2 (Williams, 2019). This flux that arrives at the Top of the Atmosphere (TOA) is then reduced by the Earth’s planetary Bond albedo of 0.306 (Williams, 2019) which acts as a bypass filter diverting radiant solar energy back out to space. It is only the remaining 69.4% of the radiant flux which is absorbed by the planet, and consequently the value of the solar irradiance that drives the Earth’s climate is reduced to a power intensity of 944.53 W/m2 (Figure 4).
It is fundamental to what comes next that the following aspect of power intensity distribution within the Earth’s climate system is appreciated in its full subtlety and implications. In figure 2 we observed that the planet intercepts sunlight as if it is a planar disk. However, because of the attitude (slant) of the surface of a sphere with respect to the parallel rays within the solar beam, the strength of the beam striking the surface decreases from its maximum possible value post-albedo of 944.53 W/m2 at the solar zenith, down to a value of zero at the terminator, the great circle line of dawn and dusk (Figure 4).
Perhaps the most fundamental issue at the heart of climate modelling is the use of the power intensity illumination divisor of integer 4, that is present in the vacuum planet equation (Equation 1). In this special case divisor 4 is used to dilute the insolation to one quarter of the radiant beam intensity. The original, valid and only purpose of the vacuum planet equation is to establish the radiant exhaust temperature of an illuminated planetary body. Planetary bodies of whatever form are only ever illuminated over the surface of a single hemisphere, so the appropriate divisor required to calculate the average insolation power intensity of the fully lit face of a planet is integer 2.
Furthermore, there will exist on every lit planet a unique location, the solar zenith, at which the radiant power intensity at the base of the atmosphere is exactly equal to the value of the solar irradiance at that planet’s orbital distance from the sun. It should again be appreciated that the power intensity illuminating the planet’s atmosphere at the solar zenith is scaled down by the Bond albedo which acts as a bypass filter. The albedo filter acts by removing insolation from the climate system, and returning this discarded portion of the high-frequency radiant flux directly back to space.
Each of the three atmospheric cells that constitute the circulation system of the Earth’s atmosphere has a distinct set of meteorological parameters of areal extent, average insolation power intensity flux, average annual temperature and adiabatic lapse rate. These parameters are listed in Table 2 and have been used to constrain the adiabatic climate modelling process.
In the previous essay Modelling the Climate of Noonworld: A New Look at Venus, an alternative mechanism for energy flux recycling was presented, using the process of atmospheric circulation, to demonstrate that convective atmospheric mass motion can be invoked to explain the planetary greenhouse effect. Atmospheric data for both Venus and also Titan, the tidally locked moon of Saturn, shows that there is little or no thermal contrast between the lit daytime and the dark nighttime hemispheres on these slowly rotating worlds. Our studies indicate that when applied to a slowly rotating planet such as Venus, or indeed Titan, the adiabatic model required only a single energy flux partition ratio, common to both the lit and dark sides of the globe, to achieve an appropriate thermal boost within the atmosphere of these bodies.
However, when a single common energy partition ratio was applied to the process of creating an adiabatic model for the Hadley cell on rapidly rotating Earth, the model failed and created an atmosphere in which the tropopause is higher on the unlit dark side of the globe (Table 5, Attempt 0). Clearly this result is in direct contrast to observed atmospheric data, where we find that the convective process on the lit hemisphere produces a tropopause with a higher elevation during the hours of daylight compared to the nighttime. The solution to this failure of the analysis is to apply two distinct and separate energy partition ratios during the process of inverse modelling, one for each side. On the lit side of energy collection, the partition ratio should be biased in favour of the air. However, on the dark side of energy loss, the partition ratio should be biased in favour of the radiant surface of energy loss to space.
The justification for using two distinct energy partition ratios, for the atmospheric circulation cells on rapidly rotating Earth, is based on observation and deduction. The primary observation is that for the Earth atmospheric convection is predominantly a sunlight driven phenomenon. It creates turbulent air motion at the lit surface boundary of the planet, and in the presence of a gravity field turbulent mixing favours energy retention by the air over direct surface radiant energy loss to space.
Contrastingly at night, in the absence of solar radiant loading, the process of surface radiant cooling predominates as the atmosphere stabilises and develops a surface inversion of cold dense air. This near surface vertical profile results in lateral movement of dense air downslope, away from land surface high elevation points of radiantly efficient emission to space. At these points the overlying air preferentially delivers retained and advected daytime acquired energy down onto the now cooler nighttime surface boundary.
In this essay we use the same algorithm to calculate the average annual surface temperature of the Earth that was used in the first essay Calibrating the CERES Image of the Earth’s Radiant Emission to Space. The key parameters are the global extent of each of the three meteorological cells of Hadley, Ferrel and Polar, and their respective average annual temperatures. By combining these three temperature values using an area weighted average, the average annual temperature of the whole planet can be derived (Table 3).
2.1.Modelling the Earth’s Hadley cell.
The two planetary Hadley cells, present in the tropics of the northern and southern hemispheres, together occupy 50 % of the surface area of the Earth (Table 3), and in total intercept 60.90% of the light that creates the disk silhouette of the planetary beam shadow (Table 2). Because the surface area of the globe’s lit hemisphere is twice the cross-sectional area of the total disk silhouette, it follows that the power intensity illumination divisor for the Hadley cells has a value of (0.5*2)/0.609 = 1.642 (Table 2). This divisor is then applied to the post-albedo dimmed irradiance to create the Hadley cell specific power intensity flux of 575.22 W/m2. This flux is then in turn used to analyse the process of recycling of the captured solar energy by atmospheric mass motion, within the Earth’s Hadley cell using the adiabatic climate model (Table 4).
The objective of the inverse modelling process used in Table 4 is to establish the daytime convection and nighttime advection pair of energy partition ratios for each of the three atmospheric cells. The inverse modelling process is constrained by the two known parameters of annual average temperature and also the average tropopause height for the energy collection (lit side) of each cell. The process of establishing these partition ratios (daytime and nighttime) for the Earth’s Hadley cell involved a sequence of tuning that required a “see-saw” approach of iterative “nudges” (Table 5).
Starting with a neutral nighttime energy partition ratio of 50% radiant loss to space and 50% thermal retention by the air, the inverse modelling process was run with the objective of establishing the lit surface energy partition ratio that creates a daytime tropopause height of 18 km (Table 5, Attempt 1). This first attempt resulted in an adiabatic model of the Hadley cell with an average annual temperature of 33.75oC, which is warmer than the required average temperature of 27.9oC.
In order to reduce the model temperature to the required value of 27.9oC the inverse modelling process was then repeated, but this time adjusting the nighttime energy partition ratio to achieve an increased energy loss to space from the dark side, thereby reducing the average temperature to the required value (Table 5, Attempt 2). This second attempt produced a modelling result in which the daytime tropopause height of 17.8 km is too low.
This undershoot was then corrected by repeating the search for the lit side energy partition ratio that creates a tropopause height of 18 km (Table 5, Attempt 3). This third attempt to tune the model by increasing the retention of flux into the air on the lit side produces an average annual temperature of 28.25oC, which is still too warm.
The fourth attempt, with its increased nighttime radiant loss to space, cools the return flow of air to the lit side sufficiently to successfully achieve both targets of a lit hemisphere tropopause height of 18 km, and an average annual temperature of 27.9oC (Table 5, Attempt 4).
2.2.Modelling the Earth’s Ferrel cell.
The process of establishing the dual component flux partition ratio for the Ferrel cell adopts the same strategy as that established for the Hadley cell described in Section 2.1.
The two planetary Ferrel cells, present in the temperate zones of the northern and southern hemispheres, together occupy 41.75 % of the surface area of the Earth (Table 3) and in total intercept 36.29% of the light that creates the disk silhouette of the planetary beam shadow (Table 2). Because the surface area of the globe’s lit hemisphere is twice the cross-sectional area of the total disk silhouette, it follows that the power intensity illumination divisor for the Ferrel cells has a value of (0.4175*2)/0.3629 = 2.3008 (Table 2). This divisor is then applied to the post-albedo dimmed irradiance to create the Ferrel cell specific power intensity flux of 410.52 W/m2. This flux is then in turn used to analyse the process of recycling of the captured solar energy by atmospheric mass motion, within the Earth’s Ferrel cell using the adiabatic climate model (Table 6).
As with the Hadley cell model the determination of the parameters for the Ferrel cell starts with a neutral nighttime energy partition ratio of 50% radiant loss to space and 50% thermal retention by the air. The inverse modelling process is then run with the objective of establishing the lit surface energy partition ratio that creates a daytime tropopause height of 13 km, for an average annual cell temperature of 6.5oC. As with the analysis of the Hadley cell, a process of “see-saw” iterations were used to achieve the final pair of partition ratios that satisfy both of these data constraints for the Ferrel cell (Table 7).
2.3.Modelling the Earth’s Polar cell.
The two planetary polar cells together occupy 8.25 % of the surface area of the Earth (Table 3) and in total intercept only 2.81% of the light that creates the disk silhouette of the planetary beam shadow (Table 2). As before, because the surface area of the globe’s lit hemisphere is twice the cross-sectional area of the total disk silhouette, it follows that the power intensity illumination divisor for the Polar cells has a value of (0.0825*2)/0.0281 = 5.874 (Table 2). When this divisor is applied to the silhouette of the post-albedo dimmed irradiance it creates the Polar cell specific power intensity flux of 160.81 W/m2.
Modelling tests established that this power intensity can be used to create an average annual Polar cell temperature of minus 20oC (Table 8).
The stable value that results from this initial test, and presented in Table 9 achieves an average annual temperature of minus 20oC for the Polar cell. However, the range of minimum average air temperature from minus 7.6oC for the summer to minus 32.9oC for the winter is actually too small to account for the known winter extrema air temperatures observed in polar regions. For example, air temperatures of lower than minus 50oC for July were recorded during advected katabatic storms at the Little America exploration base, on the ice edge of the Ross Sea in Antarctica (Rubin, 1953; Figure 2).
Modern icecap temperature data recorded for Antarctica regularly reach values of minus 70oC in winter (Figure 5: Dome Argus), and so an alternative modelling strategy was devised to account for these extreme temperature values recorded for winter in polar regions.
The key difference between the polar cells and the two other atmospheric cells present in the Earth’s atmosphere, is that in summer the high latitude polar regions experience months of continuous daylight. The effect of continuous daylight is that any atmospheric convective activity that results in vertical overturning in the Polar cell returns air back onto a lit surface. This return of air onto the illuminated surface effectively short circuits the surface energy partition process, and delivers an energy flux boost directly back to the lit summer Polar cell environment.
By contrast, during their respective winter season, each Polar cell experiences months of continuous darkness and there is no direct input of radiant solar energy. Consequently, all of the energy flux experienced by the cells throughout the months of continuous darkness is a direct result of advected air transported into the polar environment from the abutting Ferrel cell.
In order to address the dichotomy of continuous summer illumination and continuous winter darkness, the design of the adiabatic model of the Polar cell was altered to incorporate the convective feedback process of summer, and also the advected process of winter into two separate modelling streams. For the purposes of this analysis, and as merely a scoping proposal, the average Polar cell summer temperature is assumed to be plus 5oC, and the average winter temperature is assumed to be minus 45oC. These two separate seasonal values combine to create the required average annual temperature for the Polar cell of minus 20oC (Table 10).
We have now completed the individual modelling process for each of the three atmospheric cells. (See Mulholland, 2019a. Earth Adiabatic Parallel Model 20Jun19 Excel Workbook for full details of the Inverse Modelling Workflows).
3. Discussion of the Modelling Results.
The triple cell parallel adiabatic model of Earth’s climate is tuned to produce the expected value of the average annual atmospheric temperature of 288 Kelvin (15oC) using the previously established method of weighted area to determine the average annual temperature of the Earth (Table 3).
The results of the inverse modelling process demonstrate that to achieve a stable average air temperature and also an appropriate cell specific tropopause height, solar energy must be preferentially retained in the climate system by the air over the lit portion of the Earth’s surface (Table 11). Retention in favour of the air occurs because convection at the solar heated surface boundary is a turbulent process. In the presence of a gravity field solar heated air ascends by buoyancy displacement which removes it from contact with the ground. Because the solid ground surface of a planet is the primary low-frequency radiator, ascending air becomes decoupled from this surface and so retains its energy internally as it rises.
Thermal radiant exhaust of energy to space is the primary control on the ambient atmospheric temperature. Even under conditions of reduced atmospheric opacity, the ground surface radiator of the Earth continues to operate through the Infrared Window, first identified as a critical component of atmospheric radiant energy transmission by G.C. Simpson (1928).
Under conditions of zero solar radiant loading, either at night or during the polar winter, the ground surface radiator continues to operate through the atmospheric infrared window. The nighttime is an environment of energy deficit, gasses are poor absorbers and emitters of radiant thermal energy, so they heat most effectively by contact with the sunlit warmed surface during the day, and cool most effectively by contact with the radiatively cooled ground surface by night.
The Antarctic winter temperature inversion profile (Figure 5) is a direct consequence of thermal equilibrium being established and maintained by the process of surface radiative cooling. This cooling is caused by direct radiative energy loss to space through the dry transparent atmosphere above the Antarctic icecap. The radiative process results in the development and maintenance of a surface air temperature inversion. Under these conditions the atmosphere delivers energy to the ground surface radiator, and consequently the energy partition ratio for the winter polar cell is heavily weighted in favour of radiant energy loss to space (Table 11).
3.1 Studying the Effects of Energy Flux Variations within the Adiabatic Model.
In conducting the modelling analysis presented here the key question that must be addressed is this. What is the justification for using energy partition ratio as the basis for determining the average annual temperature of the Earth?
There are three fundamental physical parameters that underpin our modelling process which relate directly to planetary climate, these are: –
1. Global Atmospheric Temperature.
2. Global Atmospheric Pressure.
3. Global Atmospheric Volume.
We have already demonstrated that if we know the areal weighting of the three atmospheric cells, their respective tropopause heights, their TOA temperatures and also respective lapse rates, then the global average temperature of the planetary atmosphere can be calculated. We also know that the average pressure of the atmosphere can be determined by measurement and is common across all three cells, so the remaining issue is the determination of the planetary atmospheric volume.
If we assume that the tropopause is a pressure related phenomenon, and that the 100 mb pressure marks the upper limit of the troposphere (Robinson and Catling, 2014), then the question of applying Boyle’s Law to the total planetary atmosphere potentially has merit and requires investigation. The key objection that the Boyle’s Law relationship relates only to a confined volume of gas assumes that planetary atmospheres are completely unconfined. Clearly this is not strictly true, the total surface area of the Earth does not change, the total mass of the atmosphere, and therefore its pressure is also a fixed quantity.
So, in the presence of a gravity field that binds the atmosphere to the planet it follows that the volume change we observe associated with a change in tropospheric height for each atmospheric cell must be related to the temperature of that cell. Consequently, we can study the planetary atmosphere in total by treating it as a single gravity confined entity with measurable parameters of temperature, pressure and volume.
In order to test the relationship between atmospheric temperature, pressures and volume, a simple single hemisphere adiabatic model was created with an illumination intensity dilution divisor of integer 2. This model is assumed to have simple diabatic radiative cooling from the dark unlit hemisphere, and so a constant partition ratio of 50% radiant energy loss to space and 50% retention by the air was applied to this part of the model (Table 12).
The energy flux within the model was then adjusted by varying the Bond albedo. For each increment of Albedo related radiant power intensity, the inverse modelling process was run to determine the lit surface energy partition ratio that restored the global atmospheric temperature back to a constant value of 15oC.
Because we are now adjusting the Bond albedo, the power intensity flux in our simple model varies from a maximum case of 680.5 W/m2 [1361/2*(1-0.0)] for a totally absorptive Earth (albedo = 0.0), down to a lower limit of 272.2 W/m2, [1361/2*(1-0.60)] for a bright reflective Earth (albedo = 0.60). The power intensity flux lower limit of 272.2 W/m2 occurs because below this value it is impossible for the model Earth to maintain an average annual temperature of 15oC if it becomes any brighter.
The results of these tests are shown in Figure 6.
Using data from the American Vacuum Society (AVS) the temperature and pressure profiles for the average atmosphere are shown in Figures 7 and 8. These data show that for a standard Earth atmosphere and a tropopause defined as occurring at a pressure of 100 mbar (Figure 7) then the average elevation of this pressure is at a height of 16 km (Figure 8).
Starting with a biased surface datum of minus 50 km, the calculated pressure versus height relationship for the Earth’s standard atmosphere (Figure 8) was extended downwards to create a model high pressure atmosphere using an exponential pressure altitude equation (Km versus mbars):-
Equation 2: Pressure =1060.9*EXP(-0.146*C2) mbar
Where C2 is the Datumed Biased Altitude in kilometres.
Equation 2 is constructed to create the standard atmospheric pressure of 1013 mbar at the reference zero altitude of the Earth’s surface under current atmospheric conditions.
For Equation 2 negative altitudes relate to higher than ambient surface pressures, while positive altitudes relate to lower than ambient pressures. The calculated pressures range from a high pressure state for a model atmosphere thickness of 68 km (equation biased altitude of minus 50 km), down to a low pressure state for a model atmosphere thickness of 5.66 km (equation biased altitude of plus 13 km). (See Mulholland, 2019b. Earth Adiabatic PVT Model 20Jun19 Excel Workbook for full details of the Biased Pressure versus Altitude algorithms and tables).
Using a model specific wet adiabatic lapse rate of 3.8 K/km for the lit side of the single cell model, the atmosphere “thickness” records a low of 5.66 km for the high solar energy input case, with a commensurate balancing high radiant energy loss to space. The maximum value of 68 km of atmospheric thickness is achieved for the low solar energy input case, and commensurate balancing low radiant energy loss to space (Figure 6). There is therefore a clear relationship between solar energy input and immediate energy shedding to space by the lit surface. This energy shedding is required to maintain the constant modelled average global temperature of 15oC, and is a pressure dependent effect (Figure 9).
In Figure 9 we see the effective pressure dependent limits under which an Earth with an average planetary temperature of 15oC can exist for a given range of radiant energy loadings at its current orbital distance from the Sun. With the high albedo, (low energy capture) thick atmosphere end-member of the model we are effectively simulating a low temperature version of the atmosphere of the planet Venus.
4. Conclusions and Observations.
1. By creating a dual surface climate model, with one daylit surface of energy surplus and a second dark night surface of energy deficit, we can apply two separate energy partition ratios to these two distinct environments, and study the impacts of these ratios on energy retention and distribution within the model.
2. By assuming that the daytime environment on Earth is dominated by adiabatic convection and has an energy partition ratio weighted in favour of the air, we can account for the process of atmospheric uplift and energy retention by the air.
3. By assuming that the nighttime environment on Earth is dominated by radiative cooling, and has an energy partition ratio weighted in favour of radiant loss to space, we can account for the standard nighttime air temperature profile, and the development of surface temperature inversions in air.
4. By applying a process of inverse modelling, we can establish the values of the energy partition ratio for the Earth’s lit daytime and dark nighttime environments. It is this daytime energy retention in favour of the air that creates the climatic thermal enhancement observed on Earth.
5. By using the appropriate adiabatic lapse rate for each cell, our inverse modelling process can be tuned to replicate the expected tropopause height for the Earth’s tropical Hadley Cell of energy surplus, that of the temperate Ferrel cell, and also the height for the Earth’s Polar Cell of energy deficit.
6. By constructing a simple single lit hemisphere adiabatic model, the range of energy partition ratios required to maintain a constant whole Earth temperature under various solar radiation loadings can be explored. Using an extrapolated pressure altitude equation, the relationship between the energy partition ratio for the lit surface of energy collection and confining atmospheric pressure can be established.
7. Convection efficiency is a pressure related phenomenon. High pressure gaseous environments are more efficient at removing energy from a solar heated surface in the presence of a confining gravity field.
8. Our modelling studies suggest that the opacity of the atmosphere fundamentally controls the height of the radiant emission surface that vents energy to space (as per Robinson and Catling, 2014). However, there is no requirement for opacity to be an atmospheric energy amplifier via radiative feed-back contra Kiehl and Trenberth, (1997).
Our fundamental criticisms of the standard radiative climate model currently used by climate science are as follows: –
First, all materials heat and cool diabatically (laminar exchange of energy through the surface interface), solids do not change position when they heat. Gaseous atmospheres not only heat and cool diabatically, but in addition air also heats adiabatically, which is a turbulent process of energy acquisition, as a critical part of daytime surface heating.
Second, it is physically impossible to lose potential energy by radiant thermal emission. Atmospheric adiabatic energy transport is a meteorological process that delivers energy, without any transport loss, to a distant surface that is itself undergoing diabatic cooling by radiant thermal emission to space.
We have designed our climate model to retain the critical dual surface element of a lit globe, namely night and day. The standard climate model is a single surface model that does not include adiabatic energy transfer, because diabatic thermal equilibrium is assumed at all times (both night and day). When in our model we apply the missing element of adiabatic energy transfer from the lit side, by using distinct and separate energy partition ratios for night and day, then the requirement for back radiation greenhouse gas heating is no longer necessary.
We are able to quantify the degree of adiabatic lit surface energy partition in favour of the air by using the process of inverse modelling, a standard geoscience mathematical technique. The issue of atmospheric opacity then becomes a passive process, and the purported atmospheric action of greenhouse heating by back-radiation can be discounted. We believe that our modelling work presented here should lead to a fundamental reassessment of the atmospheric processes relating to energy partition, retention and flow within the Earth’s climate system.
5. Acknowledgement.
We would like to thank Anthony Watts for allowing us to use the platform of his blog to present our ideas to a wide audience. We believe that science is about exploring ideas and by providing us with this forum we are able to test the validity of our approach to the complex field of climate modelling.
6. References.
American Vacuum Society (AVS) Atmospheric Pressure at Different Altitudes.
Australian Antarctic Division: Dome Argus.
Beal, A., 2011. The Surface Area of a Sphere Between Parallel Planes. Online Blog.
Kiehl, J.T and Trenberth, K.E., 1997. Earth’s Annual Global Mean Energy Budget. Bulletin of the American Meteorological Society, Vol. 78 (2),. pp. 197-208.
Mulholland, P., 2019a. Earth Adiabatic Parallel Model 20Jun19 Excel Workbook.
Mulholland, P., 2019b. Earth Adiabatic PVT Model 20Jun19 Excel Workbook.
Robinson, T.D. and Catling, D.C., 2014. Common 0.1 bar tropopause in thick atmospheres set by pressure-dependent infrared transparency. Nature Geoscience, 7(1), pp. 12-15.
Rubin, M.J., 1953. Seasonal variations of the Antarctic tropopause. Journal of Meteorology, 10(2), pp.127-134.
Sagan, C. and Chyba, C., 1997. The Early Faint Sun Paradox: Organic Shielding of Ultraviolet-Labile Greenhouse Gases. Science, 276(5316), pp. 1217–1221.
Simpson, G.C., 1928. Some Studies in Terrestrial Radiation. Royal Meteorological Society (London) Memoir, Vol II. No. 16, pp. 69-95.
Williams, D.R., 2019. Earth Fact Sheet. NASA NSSDCA, Mail Code 690.1, NASA Goddard Space Flight Center, Greenbelt, MD 20771.
There are three basic arguments in the great climate change/global warming debate.
What it does.
Bickering over the alleged global warming symptoms allegedly caused by mankind’s evil carbon dioxide, i.e. melting ice caps and glaciers, rising sea levels, extreme weather and a plethora of other apocalyptic hallucinations. Refuting these speculative, baseless, fact-free fears with actual observed data proving natural variations fails since these delusions are nothing more than articles of faith, voices in heads and monsters under beds.
How it works.
Unsettled quasi-scientific bickering over details about the mechanism behind the undeniable Radiative GreenHouse Effect, i.e. 1. the atmosphere warms the earth, 2. warming produced by an upwelling/downwelling/”back” perpetual and divinely balanced GHG LWIR energy loop, 3. which is powered by a calculated theoretical “what if” ideal S-B BB LWIR energy upwelling from the surface. Entire RGHE theory is nothing but thermodynamic rubbish!!!
Does it even exist.
Whether the greenhouse effect is even real. By reflecting 30% of the incoming solar radiation the atmosphere actually cools the earth much like that reflective panel behind a car’s windshield. Without an atmosphere the earth would receive 25% to 40% more kJ/h and get warmer becoming much like the barren lunar surface, blazing hot lit side, deep cold dark side, a total refutation of RGHE theory which claims just the opposite.
No greenhouse effect, no greenhouse gases, no man caused climate change or global warming.
“Whether the greenhouse effect is even real. By reflecting 30% of the incoming solar radiation the atmosphere actually cools the earth much like that reflective panel behind a car’s windshield. Without an atmosphere the earth would receive 25% to 40% more kJ/h and get warmer becoming much like the barren lunar surface, blazing hot lit side, deep cold dark side, a total refutation of RGHE theory which claims just the opposite.”
I’m not a scientist by any stretch of the imagination. But it seems you’ve refuted your own claim here. Because the Earth doesn’t get nearly as hot as the Moon on the lit side, and not nearly as cold on the dark side, seems to prove that the atmosphere acts as a blanket, keeping a certain amount of warmth in at all times, and a certain amount out.
But I’m just some guy…
Jeff Alberts
One Lunar Day is about 28 Earth Days, the sun shines for about two Earth weeks, then in the dark for about 2 Earth weeks.
Do you think that if the moon rotated at the same speed as the Earth that it would be the same temperature as the Earth?
The blanket analogy fails, because a blanket controls convection of air, and this is not the greenhouse effect. The greenhouse effect is about radiation. The means by which Earth’s atmosphere regulates temperature is different than a blanket.
But the atmosphere does regulate temperature. Whether a blanket analogy fails or not isn’t the point.
The ocean is the elephant in the room, atmosphere is only his tail.
The weight of the atmosphere determines the amount of energy that the oceans can hold.
And that amount would be 1000 to 1, ocean over atmosphere.
And how much temperature moderation is simply due to the fact that the Earth rotates about 28 times as fast as the moon and there fore any given point on it has that much less time to heat up during the day and similarly less time to cool off at night?
Glad you quote Richard Feynman on this post.
Here is another article which uses his wisdom.
https://rogerfromnewzealand.wordpress.com/2018/05/09/ever-been-told-that-the-science-is-settled-with-global-warming-well-read-this-and-decide-for-yourself/
Cheers
Roger
This essay is #4 in a series on WUWT studying planetary climate modelling.
#1. Calibrating the CERES Image of the Earth’s Radiant Emission to Space, deals with thermal (low frequency) radiant emission to space and shows how to generate an average temperature for the Earth using the meteorological data of areal extent, tropopause height, lapse rate and tropopause temperature for the 3 main atmospheric cells (Hadley, Ferrel and Polar).
#2. An Analysis of the Earth’s Energy Budget, discusses the mechanism by which the current climate science paradigm, which uses atmospheric power intensity flux recycling in the form of back-radiation, accounts for the currently observed average temperature of the Earth.
I show how the Vacuum Planet equation can be replicated using an Excel spreadsheet containing a cascade of descending fractions which tend to a stable value finite limit sum, and that by using a diabatic (50:50) power intensity flux partition ratio there is no atmospheric greenhouse effect.
#3. Modelling the Climate of Noonworld: A New Look at Venus, presented an alternative climate model, using the process of atmospheric circulation on a hypothetical tidally locked planet, to demonstrate that convective atmospheric mass motion recycling can be invoked to explain the greenhouse effect.
The Excel workbooks contain examples of diabatic (50:50) and adiabatic (Lit surface Air Thermal Retention > Lit surface Radiant Emission Loss) climate models which are all based on versions of summing a geometric series of descending fractions.
The diabatic model contains two infinite series (one for each hemisphere).
The geometric series for the lit side energy loss to space is: –
Lit side Series: 1/2 +1/8 + 1/32 + 1/128 …. + 2-n (odd) = 2/3
While the geometric series for the dark side energy loss to space is: –
Dark side Series: 1/4 +1/16 + 1/64 + 1/256 …. + 2-n (even) = 1/3
(Note that the aggregate sum for the limits of both series is 1, and that the gain of this diabatic model is therefore 2). See Figure 3 in the Noonworld essay.
In order to increase the gain in the model (and thereby heat the atmosphere) it is necessary to bias the partition ratio on the lit side in favour of the air. This bias results in a new geometric series which tends to a higher (but still finite) limit.
The concept we are studying is this: –
Forced convection is a pressure related phenomenon. The higher the atmospheric pressure at the ground surface (the place where insolation gets converted into thermal energy) the more energy is captured by the air. This is basic heat engine physics, run your engine at high pressure for high conversion efficiencies.
The Excel spreadsheet is designed to interlink TOA Irradiance, Planetary Bond albedo, atmospheric pressure, adiabatic lapse rate and average temperature.
We are in essence studying a Pressure Volume Temperature relationship for planetary atmospheres.
The Excel spread sheet is built with a cascaded series of interlocking calculations that tend towards the limit sum with increasing precision. The greater the partition ratio in favour of the air, the longer the cycling needs to be in the Excel spreadsheet to establish the finite series limit sum by iteration.
When I first built the spreadsheet, I was amazed to find the incredible power of the Excel Data “What if Analysis” “Goal Seek” Tool. This tool allows me to perform inverse modelling by which the partition ratio (pressure proxy) can be adjusted in the adiabatic model to give the required model gain that creates the required greenhouse temperature effect.
With the “Goal Seek” Tool we can also study how energy input, albedo and pressure combine to produce a stable thermal output (a constant global temperature).
In essence the model allows me to explore numerous planetary scenarios. For example: –
The impact of daily rotation rate on Hadley cell latitudinal reach; e.g. slowly rotating Venus and Titan which both lack a Ferrel cell, versus rapidly rotating Earth and Mars which both have one.
The limits of the solar system Goldilocks’ Zone for different planetary orbits and planet mass.
The model also allows me to study how the Venusian atmosphere changes via out-gassing of carbon dioxide gas from the planet’s mantle with geologic time. The model shows how the early water oceans of Venus boil away into Space as atmospheric pressure rises. With increasing gas pressure Venus converts from a world with a low pressure, water ice albedo and low temperature atmosphere into the modern Venus, with its high pressure, Sulphuric acid ice albedo and high temperature atmosphere.
Compliments on innovative explorations.
Can you model be validated vs others by comparing against accurate surface pressure variations with latitude?
PS For your next iteration, recommend correcting the assumption: “the total mass of the atmosphere, and therefore its pressure is also a fixed quantity”.
The mass varies with H2O and CO2. Mean elevation of the center of mass of the atmosphere varies average temperature and thus with with solar insolation and the solar cycle. Varying this mean elevation – distance to earth’s center – will vary the gravitational attraction and thus the surface pressure. That could be measured with ppm or better accurate pressure sensors.
David,
Thanks for the compliment.
“Can you model be validated vs others by comparing against accurate surface pressure variations with latitude?”
This is a good question and needs accurate data to study this point further.
“The mass varies with H2O and CO2.”
Water yes, but it is a condensing volatile. CO2 not so much, as clearly each molecule of CO2 created by carbon combustion / respiration is replacing a molecule of oxygen, so the gas molecular weight increases by 12 from 32 to 44.
The issue of water mass in the atmosphere is one that puzzles me.
Water with its molecular weight of 18 is a light molecule, hence moist air is buoyant.
Water in the form of rain or snow falling onto a mountain top at high elevation possess potential energy. All of the energy released by descending flowing water drives the planet’s hydrological and sedimentary transport processes.
Rainwater on reaching the surface imposes extra weight onto the ground (landslides triggered by extra soil moisture for example). So, at what point is the extra pressure of the mass of falling water experienced by the ground? Only at the time of impact? If so then this turns water presence into a question of momentum transfer onto the surface at impact, rather than that of static force.
Philip
Good point on effective increase from CO2.
Re H2O. Yes those are challenging counter phenomena with water.
As Richard Feynman summarized “First we guess”. For clues to your questions, how about:
“the change in pressure between the rising versus descending portions of the three cells (compared to their mid points on either side), relative to latitudinal trends”?
Ah, yet people keep forgetting hydrogen bonding …. so water in the atmosphere isn’t just monomers. It is also dimers, trimers, tetramers, etc. all the way up to 100 micron droplets suspended in it.
Then there is the kinetic energy. For gases at Earth surface conditions, they’re moving at approximately 1km/sec (nitrogen) through space. Water monomers would move somewhat faster, dimers a bit slower, comparable to oxygen. The rms difference would be about the square root of the mass ratio. In real life, though, the actual kinetic energy (mostly velocity) of any given atom or molecule can and does vary, so “heavy” carbon dioxide molecule A can be moving faster than water molecule B. The rising/sinking analogy has issues when talking about gases. One of the defining characteristics of gases is that they will fully mix if/when unimpeded.
Philip Mulholland
The Bond albedo is appropriate for a diffuse reflector like the moon. However, 71% of the Earth is covered by water, which reflects specularly, and only provides retro-reflection with the sun at zenith. Therefore, the Bond albedo is a lower bound for the total reflectivity for Earth.
https://wattsupwiththat.com/2016/09/12/why-albedo-is-the-wrong-measure-of-reflectivity-for-modeling-climate/
“Therefore, the Bond albedo is a lower bound for the total reflectivity for Earth”
Clyde,
Thanks for the link to your work. At this point I am trying to match the established modelling process, but the issue of determining albedo is clearly a highly complex specialism.
Albedo is a function of the surface areal distribution of at least the following:-
1. Reflective Clouds
2. Reflective Ice
3. Reflective Land
4. Absorptive Vegetation
5. Absorptive Water
6. Something else I have missed.
The latitudinal distribution of these elements and seasonal changes mean that for the complex dynamic of Earth’s climate a single constant number approach is just the starting point.
Philip,
Truly just a starting point! Nominally diffuse reflectors like vegetation, sand, and snow, actually have a unique bi-directional reflectance distribution function that describes how light is reflected in the upward hemisphere. All of them tend to have a strong forward reflectance lobe. That means, trying to measure just the albedo will miss the light that is scattered or reflected in the forward direction. Because snow is composed of platelets, instead of approximately round grains like sand, it tends to have a strong forward scattering that increases as the snow is compacted. To further complicate things, scattering is dependent on the angle of incidence of sunlight, the complex refractive index, particle size, and the structure of the components . Leaves have a cellulose substrate, internal chemicals such as chlorophyll, a waxy coating, and dew or raindrops on the leaves, and many plants will orient their leaves to either optimize or minimize the solar insolation, depending on the climate and plant. Climatologists are a long way from doing anything more than plugging in a crude approximation to the interaction between plants and sunlight.
Clouds probably come as close to a true Lambertian reflector as anything on Earth. For them, albedo is a good measure. However, for almost everything else albedo is a lower bound.
However, the important point is that the Holy Grail of a single number is probably an underestimate if measurements of the back reflectance are primarily relied upon.
For articles like this, it would be nice to have a link at the top that would take you down to the comments. Especially since every time you post a response, you get taken back to the top of the article.
And then there is the sun: https://www.nature.com/articles/s41598-019-45584-3.pdf
Wow — impressive. But be ready for a massive dissing by “modellers”, because y’all are intruding into their private, sacred bailiwick.
I spent years doing data modeling of Businesses, part of the process for Oracle RDBM migration. The one thing that was a must: A working system to decompose into logical processes, all existing data and processes were validated before a line of code was ever written.
Seems to me that the ‘climate modelers’ are throwing spaghetti at a wall seeing what sticks while getting funding to buy more spaghetti.
Can I get a copy of this from somewhere? Why not post it on SSRN as a work in progress paper? Or ANO?
Brian,
I have published a preprint copy on Research Gate.
https://www.researchgate.net/publication/334067825_Return_to_Earth
What is also odd is that the RSS feed ( https://wattsupwiththat.com/2019/06/27/return-to-earth/feed/ ) displays comments that do not yet appear in the comments section.
So you’re saying that most of the energy in the atmosphere is in the form of kinetic energy, that energy didn’t come from absorbing IR emissions from the surface, and that this kinetic energy feeds back to the surface when the surface is has a lower temperature than the atmosphere. It’s refreshing to see logical science every once in a while.
Robert,
Most of the energy in the atmosphere is in the form of potential energy which cannot be radiated to space.
It comes from transforming KE to PE at the sunlit surface which reduces radiation to space on the lit side and it gets back to the surface as KE under descending columns which is then quickly extracted from the air by the radiatively cooling surface so as to increase radiation to space on the unlit side.
The two processes cancel out within a single convective overturning cycle BUT the delay in radiative emission to space caused by the overturning cycle accumulates additional energy within the system which heats the surface above S-B without any need for greenhouse gases.
Very true, I should have been more specific and stated that most of the energy is KE at the atmosphere-surface boundary – I was just considering the actual thermal flux between surface and atmosphere.
Anyone that disputes this theory needs to explain how an atmosphere with pure N2 would not also heat the planet surface below. I’ve began to suspect that many people here don’t even realize that the “consensus hypothesis” completely ignores many basic physical laws.
http://hyperphysics.phy-astr.gsu.edu/hbase/press.html
https://www.mvsengineering.com/files/Subsurface-Book/MVS-SVE_Chapter02.pdf
Radiative emission influence on surface temperature is less important than the angular momentum of an asteroid. Hint: not very important at all.
A very readable article, which say one thing loudly: the authors understand their subject matter and can explain its salient points with ease. Thank you.
No government has the ability to determine what is good for the people. The people have the right to determine what the government should do to take care of the people and their own interests. Scientific principles are well beyond the understanding of the average politician.
Intersting summary but is this not just a different simplification of the complex climate, earth’s surface, oceans, orbit, and atmosphere which does not allow by itself to explain or predict shifts in local weather changes and trends to the degree C of F or K any more than the established climate models do?
Alexander,
It is not intended to do that though one can use the basic model to calculate the effects of altering one or more climate variables.
The essential point is that the greenhouse effect is caused by atmospheric mass convecting up and down in a gravity field so as to delay loss of some radiation to space and thereby heat the surface above S-B.
It invalidates the radiative theory of the greenhouse effect comprehensively.
Climate modelling requires a completely fresh start.
Yes it’s a different simplification, but the proper starting point for more complex analyses.
Absolutely.
Thank you.
”The essential point is that the greenhouse effect is caused by atmospheric mass convecting up and down in a gravity field so as to delay loss of some radiation to space and thereby heat the surface above S-B.”
That essential “point” is only imaginative, is not observed. Or point to the observation folks. And the surface is NOT above S-B the global surface near surface mean air temperature is equal to S-B & so is the local T, this is easily observed with an inexpensive IR thermometer.
Stephen has always simply imagined rising columns of air being replaced by descending columns. That process is not observed in the actual Earth system, there are no organized descending columns observed.
Hi-lo pressure systems on a global avg. cancel each other for no surface temperature effect. In low pressure local system, the rising air cools due expansion from lowering pressure; lowering air to higher pressure in local systems just as equally warms (this is why it’s called adiabatic process). No net effect on global surface mean T from any global adiabatic process – by definition. The standard atm. lapse rate results from these global equator-to-midlatitude processes being averaged by 1,000s of local soundings.
Observations of convection (lab and in the wild) show rising air (or fluid) columns are replaced laterally at the surface by air/fluid at the same surface temperature flowing in, this is observed in the atm. as laterally windy days (geostrophic windiness). No net effect on global mean surface temperature.
The air that has “risen” mostly stays aloft at its new T and P spreading laterally when observed in the wild (storm cloud tops cauliflower out, they do not roll over and quickly descend to the surface as do Stephen’s imagined columns). They follow the Hadley cell et. al. ambient circulation to distant regions.
As Robert W Turner implied 11:51am, the top post also needs to explain an N2 atmosphere surface temperature or any solar system object or exoplanet atm. with a different surface pressure, grey opacity composition. After reading through it, I doubt this can be done while it is routinely performed with LBLRTM radiative-convective atm. codes.
However, give the authors a chance to show their method can determine Earth global mean surface temperature using the top post methods for say near transparent 100% N2,O2 or more near transparent 100% N2 1bar surface earth atm.
“Stephen has always simply imagined rising columns of air being replaced by descending columns. That process is not observed in the actual Earth system, there are no organized descending columns observed.”
The descending legs of the Hadley, Ferrel and Polar cells in the troposphere and of the Brewer-Dobson circulation in the stratosphere are well documented.
What goes up must come down.
Yes Stephen, what convects up somewhere in a well define observed column is replaced laterally with fluid at same temperature, comes down in no defined column over wide regions somewhere else adiabatically replacing fluid at the local ambient, no global surface mean temperature change from the Hadley Cell et. al similar processes as they do not burn a fuel. These processes occur at local ambient moving existing thermodynamic internal energy around in the system thus neither increasing nor decreasing that energy nor mean surface T which is what is meant by adiabatic.
This is science denial level 11 lol.
No observations of downwelling legs of the global convective cells? Please do yourself a favor and look up “horse latitudes”.
“Please do yourself a favor and look up “horse latitudes”.”
Robert,
Quite so. Cloud Streets are a well-defined atmospheric structure of horizontal rolls of counter-rotating air organised in cells that are oriented approximately parallel to the ground in the 1 to 2 km thick planetary boundary layer.
see Horizontal convective rolls.
Now apply the principle of scale invariance to this organised overturning process and move up to troposphere size using the convective storms of the Intertropical Convergence Zone as the driving mechanism. The descending limb is of this mega-structure, which we call the Hadley cell, are the organised surface anticyclones of the Horse latitudes.
”No observations of downwelling legs of the global convective cells?”
Sure plenty of legs. And descending ambient air regions – deserts for example.
There are no descending columns as Stephen writes though, just ascending convective columns. Watch a video of convection in the atm. or in any fluid. Learn the difference between what Stephen writes imagining what happens and what actually happens in global convective cells and the “horse latitudes”.
“There are no descending columns as Stephen writes though”.
You are engaged in hair splitting there Trick. I suppose you have that to hang on to.
Eric, it is not hair splitting. Stephen relies on his imagined descending local columns to adiabatically heat the surface from the compression to warm air above global Tmean 255K to 288K so that “back radiation greenhouse gas heating is no longer necessary” after his first cycle of the rising of the atm. off the ground.
It’s a real problem for Stephen when the columns are not ever observed doing so in the lab or in the field. The general circulation IS observed and that is observed to occur at ambient.
The rising columns are easily observed & above ambient T as long as they rise, once they equilibrate to surroundings they stop rising and cauliflower out, they do not immediately descend and restart the cycle as Stephen writes. The air at the surface was replaced with ambient air not descending compressed air as in Stephen’s imaginary world. For adiabatic heating of the atm. or any gas you need a piston and cylinder which do not inhabit the atm.
This is all covered in papers of the 1950s (Lorenz) and 1960s radiative-convective atm. reports of Manabe et. al. if you want to learn the basics of meteorology. The field went on to be able to use those principles to reasonably estimate the atm. surface temperature of Venus before it was measured. The field is well established, the top post needs to use the basic principles in the field to be at all relevant in modern times.
Well the top post refers exclusively to the large scale Hadley, Ferrel and Polar cells and not local uplift and descent.
As regards local phenomena it is the case that each discrete area of uplift is surrounded by areas of descent so either way Trick is guilty of a disingenuous attempt to save face.
He is a dishonest Troll who should be ignored.
”As regards local phenomena it is the case that each discrete area of uplift is surrounded by areas of descent”
LARGE areas, now you have better worded it Stephen. Large regions of descending dryer air under which huge deserts are found. That description is what is observed. The Hadley cells et. al. large scale general circulation occurs at ambient so no adiabatic heating is observed, despite years of meteorological observations, the needed pistons and cylinders have never been reported.
This sort of debate is quite obviously painful for Stephen (who lashes out) but it shouldn’t be as it is a necessary part of top post: “We believe that science is about exploring ideas and by providing us with this forum we are able to test the validity of our approach to the complex field of climate modelling.”
It’s remarkable that all three Apollo 8 astronauts are still with us:
https://time.com/5475697/apollo-8-50-years-later/
The trouble with the amplifier concept is that amplifiers conventionally have power supplies. In physics there are explanations of mechanisms that limit energy flow and, conventionally, they don’t invoke feedback or any kind of amplification. Counter EMF is an example. Ohm’s Law is another example. There is also a heat equivalent for Ohm’s Law. link
Amplification and feedback are deeply flawed and unnecessary analogies.
Having supplied an alternative source of surface heating it is legitimate for readers to ask what effect there is from back radiation.
Faster convection lowers the effective emission height whereas slower convection allows it to rise.
The effective emission height is set by the length of time it takes for a single cycle of convective overturning.
One can verify that by noting that if the overturning cycle were instantaneous the emission height would be at the surface as for radiation whereas if convection stopped completely it would be at the top of atmosphere as for a solid.
Everything turns on the speed of convection and nothing else.
So, back radiation adds energy to the surface which accelerates convection which reduces the effective emissions height which causes a planet to radiate from a lower, warmer height which neutralises the surface warming effect of back radiation.
Neat, isn’t it ?
It follows that the denser an atmosphere and the more viscous it becomes, the slower convection runs, the higher and colder the effective emission height becomes and the hotter the surface becomes.
Hence a hot Venus with a high density thick atmosphere with a high effective emission height and a cold Mars with a low density thin atmosphere with a low effective emission height.
Conventionally the back radiation is included with the overall R-Value for the system. example The back radiation is proportional to the forward radiation so the effect on energy flux is linear. ie. the result can be treated the same as straight conduction (or thermal resistance).
It doesn’t work like physical insulation at all.
1. Insulation is a solid. It blocks 100% of IR and visible light.
2. Insulation blocks convection.
3. R-value applies to a stationary 2-D solid surface, convection complicates this.
Does CO2 not have a lower R-value than bulk air? It has a higher emissivity.
The lapse rate(s) determines when convection will kick in. Before that point, we just have radiation and conduction. They can be treated separately but air is a poor conductor so conduction can almost be ignored. The back radiation acts to decrease the net energy radiated from the surface.
Convection moves heat up the atmosphere toward outer space very efficiently so, once it kicks in, the planet sheds a lot more heat. That’s why the first approximation to a rocky planet’s surface temperature is determined by the lapse rate and density of its atmosphere.
Here is an important statement from a paper you should read and understand.
“Of course, it may be that even if the oversimplified picture entertained in IPCC global
climatology is physically incorrect, a thorough discussion may reveal a non-neglible influence of
certain radiative effects (apart from sunlight) on the weather, and hence on its local averages,
the climates, which may be dubbed the CO2 greenhouse effect. But then three key questions
will remain, even if the effect is claimed to serve only as a genuine trigger of a network of
complex reactions:
1. Is there a fundamental CO2 greenhouse effect in physics?
2. If so, what is the fundamental physical principle behind this CO2 greenhouse effect?
3. Is it physically correct to consider radiative heat transfer as the fundamental mechanism
controlling the weather setting thermal conductivity and friction to zero?
The aim of this paper is to give an affirmative negative answer to all of these questions
rendering them rhetoric.”
https://arxiv.org/PS_cache/arxiv/pdf/0707/0707.1161v4.pdf
In my mind, question 3 is the critical one. Once you realize that radiative heat transfer within the atmosphere is a bit player, then questions 1 and 2 are moot. You can’t talk about energy balances and movement of energy within a gas without taking into account Pressure and Volume as well as convection. And you can’t get rid these factors by simply asserting that all the highs and lows (or rising and falling air columns) all “cancel out in average.” Sure they do over long time periods, but changes in such a large volume of gas such as a planetary atmosphere take time, so there is hysteresis in the system and large amounts of energy can and is moved when things are out of balance. You can’t understand this system without taking all this into account because of the amount of energy involved.
Yet we still see the same sophistry, i.e. “The lapse rate(s) determines when convection will kick in.” “Hi-lo pressure systems on a global avg. cancel each other for no surface temperature effect.”, etcetera on every single one of these heat budget posts. They never actually read any of the papers.
Well, in spite of Feynman, it will take an Executive Science Panel under Dr. Happer to sort out this mess.
And a crash program like the Manhatten Project for fusion is urgently required with real government funding.
Going back to the Moon should not be left to private billionaires – I wonder which astronaut will sign up for a Dragon or Blue Orion capsule (one way) trip?
bonbon
If any readers could help to get this onto Dr Happer’s overloaded desk I would be most appreciative.
This is exactly what he needs to validate his existing position on the climate change controversy.
A Manhattan project for fusion is almost guaranteed to fail. Scientific breakthroughs don’t happen on demand, they are mostly serendipitous. link Any attempt to manage the such breakthroughs will actually reduce their likelihood.
Gonna take some time to absorb, re-read, and understand this long post. The biggest problem I see is it is strictly the atmospheric parts of climate. Yet the vast deep cold oceans are where the thermal stability of Earth’s climate lies. The blue-water world space photos at the lead-in of this post demonstrates that nicely. We are land-dwelling inhabitants of a water world, and we seem to forget that frequently with cartoon models depictions of radiant energy fluxes.
As far as throwing cold water on GHG theory, I thought your 2nd post in this series, “An Analysis of the Earth’s Energy Budget”, May 23, 2109, was a clear, but commenter “Frank” had some very good explanations of where the analyses went wrong on physics.
https://wattsupwiththat.com/2019/05/23/an-analysis-of-the-earths-energy-budget/#comment-2709025
and his comments below that one.
I hope “Frank” will comment on this post as well.
========
“Clearly this result is in direct contrast to observed atmospheric data, where we find that the convective process on the lit hemisphere produces a tropopause with a higher elevation during the hours of daylight compared to the nighttime. ”
As an aside, this is why tropical cyclones start rapid intensification phases at night. The lowering tropopause increases the convective heattowers’ teleconnnections between the warm water surface heat and very bottom of the stratosphere.
I think tropical cyclones and their heat engines are an excellent laboratory for many of these ideas. Clearly they are convection driven heat engines and the working fluid is water vapor, and the fuel is latent heat release. The reason I say this is because models of the physics of radiation transfer processes are on much firmer ground than the convective processes (and cloud formation) which a largely just hand-tuned parameters (if not exclusively).
Joel,
I had a look at Frank’s comments but what he doesn’t realise is that faster convection lowers the effective emission height whereas slower convection allows it to rise.
Consequently, his objections are misguided.
I don’t think the Schwarzschild’s equation is very applicable to a convecting atmosphere and it seems grossly misused in atmospheric science.
“According to Schwarzschild’s equation, the rate of fall in outward intensity is proportional to the density of GHGs (n) in the atmosphere and their absorption cross-sections (σλ). Any anthropogenic increase in GHGs will slow down the rate of radiative cooling to space, i.e. produce a radiative forcing.”
That might be true, if all of the energy in the atmosphere were due to radiative absorption in the first place. Of course we know this is laughably not true – pseudoscience. The radiatively absorbing/emitting fraction of the atmosphere is going to radiate IR regardless of whether there is IR absorption from the surface in the first place.
“As an aside, this is why tropical cyclones start rapid intensification phases at night.”
Joel,
An interesting observation and one that was not known to me.
By the same token I assume that temperate latitude cyclones become more intense in winter for the same reason.
Philip Mulholland July 8, 2019 at 1:42 am
A pole receives little or no sunshine in its winter.
=> surface temperatures drop
=> atmosphere shrinks
=> pressure gradient between (thermal) equator and pole increases
=> jetstreams intensify
=> Rosby waves intensify
Classical meteorology has a lot of answers.
I admit to being baffled by this, but I will reread it and perhaps some of it will sink in. Several questions:
First you say
Most of the energy in the atmosphere is internal energy which is some two and one-half times as plentiful as potential energy; but in a practical sense internal and potential energy in the atmosphere are not independent of one another. When air moves vertically its temperature changes simply because parcels in motion do work on the atmosphere or have work done on them by the atmosphere. What exactly consitutes potential energy in your view? Height of tropopause?
Also, why can’t potential energy be radiated away? Especially in view of internal and potential energy being interrelated.
Second, you say
The proportion of energy that is KE in the atmosphere is very small, 0.05% of the total. How can there be an interchange of KE with PE, however you define it, with KE, if the latter is so inconsequential?
Also, is the KE or the PE extracted from the “…air by radiatively cooling the surface…”? And, is being in contact with the surface a necessary part of this?
Third, you say
The impact of delays is interesting to ponder because, as you probably know, delays in systems are responsible for instabilities. However, how do delays lead accumulating additional energy?
Thanks.
Okay so if 0.05% of the energy in the atmosphere is KE and “internal” energies are 2.5 times higher than PE than where is the energy?! I would seriously love to finally see an answer to this because it seems you’re implying that the vast reservoir of energy within the atmosphere is in the intramolecular vibrations or angular momentum.
“However, how do delays lead accumulating additional energy?”
Kevin kilty.
The short answer is Yes.
A slightly longer answer is this. All mass motion processes which disturb an equilibrium create a lag in the system. For example, water lifted from the ocean by evaporation, and then deposited on the top of a mountain in the form of snow forms a stable high-altitude addition of potential energy to the mountain environment. The release of that potential energy, in the form of snow melt creates a delay that can be a seasonal lag, or as in the case of a polar icecap glacier, a millennial timescale lag.
“I admit to being baffled by this”
Let me describe to you the linked chain of logic that I used to arrive at my conclusions in the following way: –
1. Start with the Vacuum Planet equation with its integer 4 divisor of the power intensity flux. This equation was devised by astronomers as a simple way of calculating the thermal radiant emission temperature of a lit planet from external observation data. It is a mathematical trick. I sat in the Environmental Science lecture theatre in Bailrigg in 1972, and that is precisely how I remember it being described (maybe I am remembering with advantages as on St Crispin’s day?). The point is this, no one can ever be in any doubt that in the case of our single sun solar system, all planets are only ever lit on one side. So, the only proper and valid purpose of this trick equation is to calculate the low frequency radiant exhaust flux from a planet.
2. Climate science adopted the Vacuum Planet equation from astronomy, but because it is not calculating the surface temperature of a planet, a mechanism of energy flux recycling was devised to account for the raised surface temperature in the presence of an atmosphere.
3. However, all planets are lit only on one side and collect solar energy as a disk silhouette, but this collected power is distributed over the full surface area of the hemisphere. Hence the illumination divisor of the collection equation for the full area of the lit hemisphere is divide by 2. This is simple spherical geometry and it applies the same logical relationship as the vacuum equation with its integer 4 divisor. However, this time we are applying our illumination dilution divide by 2 process to the sunlight beam on the lit side only, and therefore it is perfectly valid.
4. But how do we link the sunlight daytime hemisphere of warming to the nightside of cooling? If the planet rotates then this is simply a matter of time, but what if the planet is tidally locked? How would the atmosphere respond in this case? To answer this question, we created Noonworld a model of a tidally locked planet with a pure nitrogen atmosphere. In the Noonworld model one side is always being heated and the other is always being cooled, and so we linked the two hemispheres with a single planet-wide Hadley cell.
5. The next modelling question is how do we partition the captured solar energy on the lit side between the two possible exit routes. These are 1. Energy capture by the air and 2. Direct low frequency thermal radiant loss to space. A diabatic partition ratio of 50% to the air and 50% direct loss to space from the lit surface appears to be the most appropriate choice. The model now works by transporting mass and energy to the dark side of Noonworld, where 50% of the power intensity flux is lost to space and 50% is retained. The returning air is therefore carrying energy back to the lit side which is now receiving two sources of energy, the sunlight and the returned air.
6. The Noonworld Hadley cell cycles indefinitely but the recycling process stabilises when the return air carries 1/3 of the retained energy back to the lit side. On the lit side the total budget becomes 1 solar unit plus 1/3 air = 4/3. Of this hemisphere budget 2/3 is lost to space and 2/3 is exported to the dark side. Here 1/3 is lost to space and 1/3 is returned. The Noonworld planetary Hadley cell now forms an endless stable cycle with a system gain of 2.
7. Here is where it starts to get interesting. Our diabatic model of Noonworld, with its 50% : 50% energy partition ratio is in radiative balance, and is an almost exact match to the Vacuum Planet equation. But there is no greenhouse effect, and yet this time we are dealing with a surface system of atmospheric mass movement and energy flux and not a top of the atmosphere equation. So, the question now becomes this. Is a 50%: 50% energy flux partition ratio for the lit side surface correct? In the case of a planet such as Mars with its low-pressure atmosphere and minimal greenhouse effect a 50 :50 ratio is indeed correct for the surface calculation. But what about Earth, Titan and of course Venus, all examples of terrestrial bodies with atmospheres that have greater than 100 mbar surface pressure?
8. On Earth with its 1 bar atmosphere, radiant forced convection on the lit hemisphere and in the presence of a gravity field results in enhanced energy capture by the ascending air. With any flux partition ratio in favour of the air the gain of the Hadley cell increases. For any gain greater than 2 then the surface temperature of the planetary atmosphere will rise, and this is a pressure related effect of solar radiant forced convection. The air temperature will increase and this occurs without any need to invoke radiant blocking by atmospheric opacity, and so the concept of a back-radiation greenhouse effect can be abandoned.
I question the vacuum albedo of 0.3, because that is the existing albedo for the Earth including clouds, that can not exist in vacuum. Please be more specific in the conditions.
I calculate the average surface temperature to be somewhere around 273K if all the atmosphere and clouds was removed
“I question the vacuum albedo of 0.3”
Svend,
The Vacuum Planet equation is a top of atmosphere calculation.
It is being used to measure the situation outside the “black box” of the climate system.
The equation determines the radiant exhaust temperature of the flux going back out into the vacuum of space at the upper edge of the atmosphere.
The albedo filter has already been applied to the insolation and it cuts down the energy inside the climate system. Albedo therefore also controls the power intensity flux leaving the planetary atmosphere.
Joel said:
“Yet the vast deep cold oceans are where the thermal stability of Earth’s climate lies.”
which is absolutely correct but again it comes back to atmospheric pressure bearing down on the ocean surface as per my analysis here:
https://www.newclimatemodel.com/the-setting-and-maintaining-of-earths-equilibrium-temperature/
Second, it is physically impossible to lose potential energy by radiant thermal emission.
========
this to me is the critical issue. The potential energy involved in raising the atmospheric height. This reduces the amount of energy available to radiate to space. And the reduction in radiated energy to space is called the greenhouse effect.
It is my contention that, based on the paleoclimate record and the work done with models, the climate change we have been experienced is caused by the sun and the oceans over which mankind has no control. There is no real evidence that CO2 has any effect on climate and there is plenty of scientific rationale to support the idea that the climate sensitivity of CO2 is zero.
AGW is a conjecture that at first seems to be quite plausible but upon closer inspection, the conjecture is full of holes. The biggest problem is that the AGW conjecture depends upon the existence of a radiant greenhouse effect provided for by trace gases in the Earth’s atmosphere with LWIR absorption bands. The AGW conjecture also seems to assume that all other gases in the Earth’s atmosphere are essentially thermally inert and that all heat transfer from the Earth”s surface to space takes place via LWIR radiation and that all other forms of heat transfer within the Earth’s atmosphere can be ignored. Another assumption is that H2O, the primary greenhouse gas takes its orders from CO2. Something is definitely wrong here.
As it turns out, a real greenhouse does not stay warm because of the presence of heat trapping gases. In fact, the LWIR absorbing gases in the atmosphere do not really trap heat energy because good absorbers are also good radiators and what LWIR energy they absorb, they also radiate away. But the so called greenhouse gases also share energy with surrounding gases and they are heated by neighboring gas molecules and some of that energy they gain from neighboring molecules they radiate away. It is really the non-greenhouse gas molecules that are more apt to trap heat energy because they are such poor radiators to space. A real greenhouse stays warm because the glass decreases cooling by convection. So there is no radiant greenhouse effect that keeps a greenhouse warm. Instead it is entirely a convective greenhouse effect.
So too on Earth where instead of glass, gravity along with the heat capacity of the atmosphere limits cooling by convection. As derived from first principals, the Earth’s convective greenhouse effect keeps the surface on the Earth on average 33 degrees C warmer than it might otherwise be. 33 degrees C is the number derived from first principals and 33 degrees C is what has been measured. Additional warming caused by a radiant greenhouse effect has not been observed on Earth or anywhere else in the solar system for that matter. The radiant greenhouse effect is hence science fiction so hence the AGW conjecture is science fiction as well. If CO2 really affected climate than one would expect that the increase in CO2 over the past 30 years would have caused at least a measurable increase in the dry lapse rate in the troposphere but that has not happened.
What I am saying is definitely not original with me. I believe that the material in this article supports what I am saying. Please let me know where I may be wrong.
Yourself……”As derived from first principals, the Earth’s convective greenhouse effect keeps the surface on the Earth on average 33 degrees C warmer than it might otherwise be. 33 degrees C is the number derived from first principals and 33 degrees C is what has been measured.”
The only extra 33ºC warming that I can see is that of the latent heat of water vapour which reduces the lapse rate to an average of 6.7ºC/km and thereby creates an increase in potential temperature of 3.3ºC/km…which at an average 10km high tropopause gives the 33ºC warming.
If it were possible to instantaneously physically mix that 33ºC of potential temperature increase to that of the adiabatic lapse rate of 10ºC/km , the thermal gradient would pivot around the average to warm the surface by 16.5ºC and cool the tropopause by the same amount.
This warming however is a result of evaporative cooling at the surface …so water in all its forms is a modifier of extremes not an amplifier.
”..but in addition air also heats adiabatically, which is a turbulent process of energy acquisition, as a critical part of daytime surface heating.”
This statement is not well written. Yes, heating is a process of energy acquisition, the gross energy IN ( dayrime SW) is greater than the gross energy OUT (daytime LW). Thus energy IN net of energy OUT positive means energy acquired in a controlled volume. That is plainly a diabatic process & is not “heats adiabatically”. Pistons and cylinders do not inhabit the atm.
”Second, it is physically impossible to lose potential energy by radiant thermal emission. Atmospheric adiabatic energy transport is a meteorological process that delivers energy, without any transport loss.”
This is also not well written. A parcel (higher, same, lower T) than ambient T can cool by emitting radiation, becoming denser than surroundings and sink lower thus losing both total PE and avg. constituent particle KE equal to the emitted radiation by 1LOT until diabatic processes restore equilibrium with surroundings.
“Without any transport loss” implies mass does not radiate when transported which was a problem in the earlier post when radiation was assumed to be ignored so of course did not have any resultant effect.
https://www.ast.cam.ac.uk/~pettini/STARS/Lecture07.pdf
The virial theorem for a system in equilibrium: −2[K] = [U] (7.1)
where K and U are the kinetic and potential energy respectively and the
brackets denote time averages, tells us that:
[E] = [K] + [U] =1/2[U] (7.2)
only half the change in gravitational potential energy is available to be
radiated away as the protostar contracts; the remaining potential energy
supplies the thermal energy that heats the gas.
Robert 11:15am, if you want to learn about an enormous dust cloud in space contracting due the physics of a protostar, this is not the best blog for discussion. If you want to learn about Earth atmosphere available potential energy and the maintenance of the Hadley cell et. al. general circulation the foundational paper you need to learn from is Lorenz 1955, here for example:
https://www.tandfonline.com/doi/pdf/10.3402/tellusa.v7i2.8796
I’ve pointed this paper out to Stephen several times but Stephen is not accomplished enough in meteorology to understand the paper and use its content. The top post discussion of general circulation should use also this paper (and modern successors) from which to build a well-founded discussion on Hadley Cell dynamics of the Earth’s planetary climate or at the very least be consistent with it.
Lorenz 1955 paper opening: “In general the motion of the atmosphere is not adiabatic.” In the top post, go ahead and count the times the word “adiabatic” is employed to describe the motion of the atmosphere. There is an obvious disconnect rather than consistency with the paper.
What Lorenz means in saying that ‘in general the motion of the atmosphere is not adiabatic’ is that it is divergences from the adiabatic condition that generally describe motion within the body of the atmosphere.
He makes that clear in these words:
“Under adiabatic flow the sum of the available potential energy and the kinetic energy is conserved, but large increases in available potential energy are usually accompanied by increases in kinetic energy, and therefore involve nonadiabatic effects.”
Not only does Trick constantly move the goal posts whenever a good point is made but he invariably distorts meanings to suit his preconceived agenda of obfuscation.
In every sense he is a true Troll whose primary purpose is to patronise others and generate a sense of superiority for himself whilst actually getting it all wrong.
He is best ignored.
Stephen, it is decent of you to use Lorenz’ own words. Good job.
Compare Lorenz’ actual words and work to what is found in the top post and show they are consistent with his words, body of paper, and conclusions for: “large increases in available potential energy are usually accompanied by increases in kinetic energy, and therefore involve nonadiabatic effects.”. Show where the authors top post work has progressed beyond the work of Lorenz’ and modern-day successor work in meteorology that built on the foundation he laid.
Top post words:
“adiabatic climate modelling process.”
“the adiabatic model”
“adiabatic climate model (Table 4).”
“adiabatic model of the Hadley cell”
“adiabatic model of the Polar cell”
“adiabatic model of Earth’s climate”
“Single Lit Hemisphere Adiabatic Model.”
So forth. A search for nonadiabatic returned no hits (except 1 for Lorenz’ use) unless a different spelling was used. It appears the authors of the top post have a bit of work to do to reconcile their work with that of Lorenz. Participants in the field of meteorology will not pay attention until that is done.
The top post deals only with the thermal consequences of the initial acquisition and subsequent recycling of the potential energy content of an atmosphere which is exclusively adiabatic and so does not deal with the internal non-adiabatic variations within the bulk flow that Lorenz was referring to.
As usual, your comments are misleading and obfuscatory.
“The top post deals only with the thermal consequences of the initial acquisition and subsequent recycling of the potential energy content of an atmosphere”
Lorenz further down: “Evidently the total potential energy is not a good measure of the amount of energy available for conversion into kinetic energy under adiabatic flow.”
The more I dig in to compare Lorenz words to top post, the larger the task becomes in reconciling the top post with Lorenz’ foundational paper on available PE and the general circulation, just as top post suggests a need for: “we have incorporated into the analysis elements designed to address valid and constructive criticisms made by commentators of the previous essays.”
Temperature on Earth is a function of water, its phases and its distribution.
The vapour pressure of water rises rapidly above 25C:
https://1drv.ms/b/s!Aq1iAj8Yo7jNgzHH3_zoyapHehla
The increase in atmospheric water vapour as the temperature of tropical oceans rise results in. increased cloud formation over tropical and sub-tropical oceans as the air circulates, ultimately reaching the same temperature at the sea ice interface always -1.7C. The increased cloud reflects more sunlight.
Surface temperature of tropical ocean rarely reach 30C while surface temperature of polar oceans is -1.7C. Area averaged ocean surface temperature is 16C; not quite the midpoint of 30C and -1.7C due to the distribution of the water being greater in tropical and sub-tropical zones.
The two very powerful negative feedbacks maintaining temperature control are (a) cloud formation due to increased water vapour reducing the heat input into tropical and sub-tropical oceans and (b) loss of sea ice near the poles due to higher sea surface temperature increasing heat output.
Rising ocean surface temperature results in increased tropical and sub-tropical cloud and reduced sea ice; both contributing to less energy in the climate system and ultimately cooling. Cooling ocean surface results in less tropical and sub-tropical cloud and increased sea ice; both contributing to more energy in the climate systems.
Climate on Earth is controlled by water, its phases and its distribution. Local weather is more complex but it should not be confused with global climate.
The global average temperate of the moon is 197K; nothing like the 254K that is prescribed for an airless rock at Earth’s distance from the sun in the greenhouse gas fairytale.
That 197K is the surface brightness temperature as observed by radiometers on DIVINER that depend on settings for surface emissivity, scattering (albedo) and non-negligible amount of surface particle diffraction. To the extent those settings are off, and diffraction non-negligible, the steady state equilibrium thermometer temperature could be different. But there is no GHCN thermometer data for the moon only very sparse surface instrumental thermometer readings so nobody really knows. For example, the CERES radiometer emissivity settings had to be calibrated with Argo data.
Some work has been done for debate purposes and published showing any eventual GHCN steady state equilibrium near surface thermometer readings would be more like 250K give or take a big margin due all the unknowns. There is no research interest in this currently as no funds available or incented to improve the DIVINER results. Nobody going to live there for long any time soon.
The 197K is a derived value using Diviner data calibrated to surface measurements from Apollo missions – fundamentally the same way CERES data is derived but with a narrower range of surface than with Earth because it does not have to cater for high reflectance clouds:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4447774/
A key point in the paper is Holder’s Inequality that demonstrates the mathematical nonsense of applying Stefan Boltzman equation to an area averaged surface temperature as done in the greenhouse gas fairytale.
The DIVINER project itself did not calibrate a global result to Apollo thermometers Rick; as far as I can find it didn’t publish a global brightness temperature for the moon.
The paper you link modeled the optical properties of the surface: for albedo “The shortwave albedo of regolith was modeled…” and they guessed the regolith emissivity “ε is the average regolith long-wave emissivity; typically 0.95 ≤ ε < 0.99; in this study ε = 0.98…The thermal emissivity of regolith was assumed to be spatially invariant ”. That paper “assumes” the same global surface emissivity as Earth with much larger particle sizes composing the 30% terrain.
The problem with the “assuming” of the regolith emissivity at 0.98 is doesn’t allow for small illuminated particle size diffraction. There is significant diffraction since the moon surface particle size has been significantly pounded to powder with diameter on order of illumination wavelength of interest over 20-25% or more of the surface area. There IS spatial variance.
Taking this issue into account would lead to a higher global brightness temperature result.
The 197K global brightness temperature is at best a guess/assumption until enough thermometers are placed in the surface to then reasonably measure the moon’s global near surface steady state equilibrium thermometer temperature. There is no driver to solve this lack of in situ data or publish improved results by reducing the assumptions so will remain a debate for the foreseeable future.
Btw, Holder’s inequality is an issue with analytical spherical integration so is already taken into account for the actual measurements of the near spherical Earth thus is not an issue with the satellite observations or the GHCN thermometer readings which measure global Teff~255K and global Tsurface~288K.
Holder’s Inequality is not taken into account. The method of deriving the meaningless number 255K then comparing it to an average surface temperature of 288K demonstrates that.
Without thermal inertia, like the vast expanse of surface water on Earth, the area averaged global surface temperature for a non thermally conductive spherical black rock same distance as Earth from the sun would be 160K. The temperature ranges from 398K at midday at 0 latitude to 2.7K for the entirety of the dark side.
The relatively low thermal inertia of the moon; its reflectivity for SWR and emissivity for LWR increases the temperature from the case of the black sphere by 37 degrees K to 197K. Nothing like the meaningless 255K offered in the greenhouse gas fairy tale.
This link will gives you more insight into Holder’s Inequality as applied to averaging Earth’s temperature:
http://www.drroyspencer.com/2016/09/errors-in-estimating-earths-no-atmosphere-average-temperature/
”The method of deriving the meaningless number 255K then comparing it to an average surface temperature of 288K demonstrates that.”
Again, Rick, the 255K is not only “derived”. The 255K is Earth’s multiannual brightness temperature observed from instrumentation on CERES looking down at Earth system.
In the derivation of the 255K, Holder’s inequality is lost in the weeds. Ok, correctly using Holder’s inequality in the derivation analysis you would get 4.003 for the divisor instead of 4. So 254.999K.
And, yes I am aware of Dr. Spencer’s and many others insight that you cannot average intensive properties like temperatures, you have to average extensive properties like energy then convert to temperature.
Yet you still accept the meaningless average brightness temperature of 255K used in the greenhouse gas fairytale.
I accept what the satellites measure (Earth ~255K global steady state equilibrium brightness temperature) since they began observing long enough ago and are well calibrated to surface thermometer temperatures now with data reported over more than 15 annual periods.
As a completely unscientific layman, could one of you more knowledgeable types please explain to me how the atmosphere can hold extra heat if gases expand as they heat up which would cause the atmosphere to expand – and become less dense – thereby increasing the heat loss to space in direct proportion and therefore it would not matter in the co2 concentration were 100 times what it is. Please forgive if this is a stupid question but it explains to me that extra co2 can indeed absorb extra heat but not hold it and not permanently warm the atmosphere. I feel out of my league here!
The idea is that CO2 molecules radiate back down so as to slow down the cooling of the surface.
I have previously explained that if that were to happen then hydrostatic equilibrium would be destroyed, the atmosphere would expand and eventually be lost to space.
Hence my explanation that what actually happens is that any warming of the surface from back radiation results in faster convection which lowers the effective emission height so as to increase radiation to space and neutralise the effect of back radiation.
Mike, the mainstream media talks about global surface warming from added CO2 but does not give the same print or video space to the equal global cooling from added CO2 of the upper regions for nil effect on global atm. internal thermodynamic energy thus nil effect on global atm. expansion.
Trick’s reply is not quite true because the downward portion of radiation from GHGs can still reduce the rate of surface cooling. The upward portion is thus less than would otherwise have gone out from the surface if there were no GHGs.
You have to have a reduction in the effective emission height to neutralise the surface warming effect.
The radiative theory says that GHGs achieve a surface warming effect by raising the effective emission height to a higher colder level so that less radiation gets out but they do not yet realise that enhanced convection drops it back again to neutralise the effect.
“they do not yet realise that enhanced convection drops it back again to neutralise the effect.”
Stephen does not yet realize or understand that convection only moves existing thermodynamic internal energy around within the system of interest, convection does not burn a fuel so cannot raise or lower system internal thermodynamic energy. Convection (windiness) is neutral sum game, what goes up comes down over 4-15 annual periods as observed.
Trick: “convection only moves existing thermodynamic internal energy around within the system of interest, convection does not burn a fuel so cannot raise or lower system internal thermodynamic energy.”
So, you’re saying it’s a perpetual motion machine?
Interesting.
”So, you’re saying it’s a perpetual motion machine?”
No.
Additionally, expanding an atmosphere does not necessarily lead to increased radiation to space because you still have the same number of molecules obstructing the radiative flow from the surface and the same pressure at the surface which is why the gas laws are so important.
What really matters is the length of time needed for convective overturning and in a higher, expanded atmosphere it might take longer which would theoretically heat the surface more.
In reality that can’t happen because of hydrostatic equilibrium whereby the downward force of gravity is balanced by the upward pressure gradient force. If anything permanently upsets that balance the atmospheric cannot be retained.
So, instead, the rate of convection changes so as to alter the effective emission height and stabilise the system.
The effective emission height is the height at which enough radiation exits the system to balance radiation coming in from space.
”Additionally, expanding an atmosphere does not necessarily lead to increased radiation to space because you still have the same number of molecules obstructing the radiative flow from the surface and the same pressure at the surface which is why the gas laws are so important.”
But you would have a greater number on molecules as you add co2 right? And if they are heated they will expand to an equal distance apart. (there is nothing to stop them) So in theory, there would be no increase in density as you add heat because of our open system. And so you would also have a greater number (of radiating co2 molecules) over a wider surface area at the interface with space no? If this is correct, 1000ppm co2 would make no difference.
Adding mass raises temperature but it would require a lot more CO2 than humans could ever emit to make a discernible difference.
Your conclusion is correct but not for the reason you initially proposed.
Where were all the climate scientists for the last 30 years. The Mulholland/Wilde model presented may seem complex. To a degree it is, but not because the math involved is difficult, but because the atmosphere is complex. Partitioning the atmosphere model to match the observable effects- the atmospheric circulation cells- and then adjusting the parameters for energy flow between them to match reality is simple arithmetic, not quantum mechanics(at least directly). Making an Excel spreadsheet do this is complicated and time consuming but it does the job that huge climate computer programs have not.
It also shows how ridiculous trying to boil the climate change down to a single equation, equilibrium climate response, is.
Great Job.
Philo
Thank you.
This is the product of a 6 month’s project with Stephen Wilde and 45 years personal experience as a professional geoscientist with published and confidential modelling work.
And I’ve been a member of the Royal Meteorological Society since 1968 despite being professionally qualified as a lawyer.
I’ve spent over 50 years, incrementally and without realising it, creating my own personal conceptual picture of atmospheric processes which appears to be more accurate than that of the mainstream.
I have really enjoyed this series, but it leaves me with some questions. Thank you for the fine work.
As I understand it, our Moon lacks both an atmosphere and CO2 to help it warm, but it has much higher surface temperatures and lower surface temperatures than we have right next door, right here on Earth. I’m guessing that Earth’s rate of spin allows it to shed heat at night so that it never stores enough heat in a 12 hour heating (daylight) period to begin to compete with the Moon’s high temperatures, even without a Moon ability to store and scatter heat in an atmosphere. Earth’s atmosphere must provide insulation to prevent the warming by the Sun at a rate to match the Moon. Is there a good paper on this topic in the literature that someone can point me to? Seems like there are no GHGs that lead to warming, just gases that provide sunscreen to prevent over warming. Thanks in advance.
“I’m guessing that Earth’s rate of spin allows it to shed heat at night so that it never stores enough heat in a 12 hour heating (daylight) period to begin to compete with the Moon’s high temperatures”
Nicholas,
Thank you for your question, there is a lot to think about in the points you raise and I don’t have a reference for you.
My own opinion is that rate of spin is a critically important feature of planetary climates. For slowly spinning bodies such as Venus and Titan, the atmospheric structure consists of a single hemisphere encompassing Hadley cell. So, for these bodies the only clear exit path to space for deep atmosphere radiant energy is from the polar vortex. For the rapidly spinning Earth the forced descent of air in the Horse latitudes means that there are two additional possible zones (one per hemisphere) where solid surface radiant loss to space can occur. The CERES image shows the effect of forced descent in opening this atmospheric window for energy loss to space.
Of course, none of this is relevant to the Moon which has no atmosphere, so my second thought on this is the roasting spit analogy. Meat burns on a slowly turned spit, whereas the faster turning spit distributes the heat more evenly. This analogy may be more to your taste 😉
Nicholas 7:30pm, perhaps this ref. will suit your needs. It also discusses the difficulty in converting the various DIVINER radiometer channels data to brightness temperatures to estimate surface thermometer (sometimes called kinetic) temperature due to the variation in surface optical properties.
http://luna1.diviner.ucla.edu/~dap/pubs/057.pdf
—–
For the meat with no spin, the energy input would be spread over one hemisphere so integer factor divisor of 2 would be appropriate; for a fast-enough spinning meat energy input would be spread over two hemispheres so factor divisor of 4 would be appropriate – somewhat as discussed in top post.
Nicholas Harding June 28, 2019 at 7:30 pm
Why are you looking at the atmosphere to store heat?
On earth we have oceans where the upper 5-10 m are heated directly by incoming solar.
On a good sunny day in the (sub)tropics ~20 MJ/m^2 solar energy is able to heat the upper 5 m ~1K.
So slowing Earths rotation to that of the moon would allow the upper 5 m to warm ~14K, probably less since energy will be mixed and conducted downward. During the 14 day night this energy will be lost to space again.
The reason for the very high daytime temperatures on the moon is the very poor heat storage capability of the lunar regolith and very poor conductivity as well.
Daytime lunar temperatures are close to radiative balance with incoming solar.
Night time temperatures are ~70-80K above radiative balance.
So yes, spinrate makes a difference, but has to be considered together with heat storage capability.
Actually I am not looking for the atmosphere to store heat; instead it seems to scatter and reflect solar radiation and act as a shield Earth by reflecting some of the solar radiation so that it does not reach Earth (the Moon does not have this feature so it heats to temperatures far in excess of the temperature on Earth and it does this without the benefit of CO2 and AGW. Imagine!). Without atmosphere, spin, and water storage of solar energy I would expect the Earth to have a temperature profile like its nearest neighbor. That its nearest neighbor beats Earth in the high category temperature, hands down, without the benefit of CO2 is instructive.
Nicholas Harding June 29, 2019 at 12:49 pm
Sorry, misunderstood you 😉
If the atmosphere is the reason for the high temperatures on Earth, increasing the spin rate of the moon and adding an Earth like atmosphere should increase the Average Surface Temperature of the moon to the AST of Earth.
Using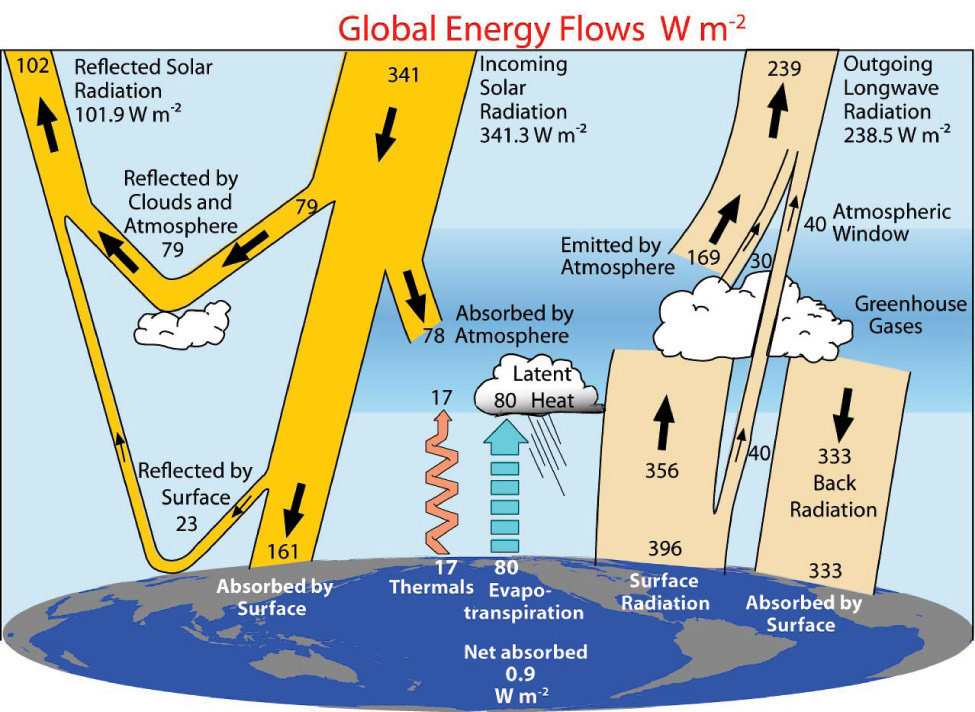
the atmosphere would reflect and absorb ~160 W/m^2, so iso avg ~300 W/m^2 reaching the Lunar surface without atmosphere, with atmosphere this would be just ~160 W/m^2.
Is not going to increase its AST from ~197K to ~290K.
Hi, Ben, Thanks, I notice you continue to misunderstand. We don’t we just leave it there.
Regards,
Messrs Mullholland and Wilde,
Very interesting stuff.
1) Can you explain why you think you can ignore meridonial heat transport across your cell boundaries? I have seen estimates of around 5 PW heat flux across your 30 deg latitude cell boundary. This seems far too large to me to allow one to resolve temperatures within cells by considering solely the radiative flux balance.
2) You have adopted a pressure vs elevation formulation which is appropriate for a constant temperature assumption. It derives from solving dP/dz = -rho x g for an ideal gas with temperature fixed (and z denoting elevation). If this expression is solved (instead) for a constant lapse rate assumption, which seems more appropriate for what you are doing, then the solution has the following form:-
P = Ps x (T/Ts)^[mg/(Rxalpha)]
where T = Ts – alpha*z is the temperature at elevation z and alpha is the lapse rate. All else being equal, substitution of this second formulation changes your estimated elevation at 100mbar by about 3 kms for a moist adiabatic lapse rate. It is still not clear to me exactly what you are doing with this, so I don’t know whether this is a nitpick or not.
“I don’t know whether this is a nitpick or not.”
kribaez
Not a nit-pick at all. The question of meridional versus zonal flow is very profound, and you are the first to question this design point. In the sequence of analysis that led to this post I studied the application of the model to Mars. This is not easy as there is little hard meteorological data to go on for the Martian atmosphere. What I did discover is that on Mars there is little or no meridional flow of air, and of course no flow of water!
Here on Earth it is well acknowledged that the oceans form the primary energy flux transport system for meridional flow, particularly into polar regions (all that floating sea ice melting from below). So, in presenting this model as a purely parallel atmospheric process I am merely trying to get the concepts off the ground (so to speak).
Varying the adiabatic lapse rate varies the emission height but does not of itself vary the temperature difference in the model. I may be over engineering this point and while lapse rate feeds back to partition ratio in the model tuning process, lapse rate is a relatively insensitive variable.
The need to deal properly with seasonal tilt in the arctic is of course another issue. I am more than happy to see this work improved, and your post tells me that people of good faith are looking into this.
Thank you
Philip Mulholland June 29, 2019 at 1:01 am
and in the blog text:
Finally, we have adopted a more nuanced approach to the issue of lapse rate, using a wet adiabatic lapse rate for the Hadley cell, an intermediate environmental lapse rate for the Ferrel cell, and a dry adiabatic lapse rate for the Polar cell.
The WALR and DALR are ONLY valid for the temperature change of rising or sinking volumes of air where the surrounding air is in Hydrostatic Equilibrium.
How do you propose to vary the adiabatic lapse rates??
“How do you propose to vary the adiabatic lapse rates??”
Ben,
I am happy to follow best meteorological practice and to receive good advice when offered from an expert.
I originally started out doing this work with a uniform global lapse rate of 6.5C/km.
Objections were raised elsewhere and so I tried to address these with cell specific lapse rates, WALR for the Hadley cell and DALR for the Polar cell. If this approach is wrong then I am happy to revert back to a uniform planet wide lapse rate of 6.5C/km. I will even adopt the value of 6C/km that Sir George Clarke Simpson, a former head of the Meteorological Office in Edinburgh and past President of the Royal Meteorological Society, used in his 1928 paper “Some Studies in Terrestrial Radiation” if this is deemed to be a better approach.
Philip Mulholland June 29, 2019 at 11:33 am
My point is that using the ALR’s to describe the Environmental Lapse Rate is serious nonsense. The ALR’s do NOT describe a temperature profile of the tropopause.
Afaik the average lapse rate of 6,5 K/km is weighted towards the mid latitudes.
Seems that 6,5 K/km is ok for all latitudes, except perhaps the poles in winter.
In that case the lapse rate is LOWER than 6,5 K/km due to the often massive inversion.
see http://www.pilotfriend.com/av_weather/meteo/hm_temp.htm
especially “Temperature lapse rates in the troposphere”
Ben,
The global average lapse rate is fine for the purpose of our model which is designed only to establish the baseline surface heating arising from convection within a given amount of atmospheric mass at a given strength of gravitational field and a given strength of insolation.
The environmental lapse rate varies wildly from place to place, latitude to latitude and height to height but that makes no difference to the baseline surface temperature enhancement.
In fact it is the sheer amount of variability available that makes the system resistant to destabilising forces.
Stephen Wilde June 30, 2019 at 2:01 pm
Convection (meteorological, like thermals, cumulonimbi etc.) is not heating the surface. Convection is the result of solar heating of the surface, which in turn heats the air just above it. Convection actually removes heated air from the surface.
The general circulation cells (esp. Hadley) are NOT convection.
They are driven by uneven heating at the surface which creates a pressure gradient higher in the atmosphere. This causes air to move from the (thermal) equator towards the poles. The Coriolis effect makes this flow turn eastbound.
The resulting low and high pressure areas AT THE SURFACE drive the backflow (Trade winds etc.)
Ben
All descending air warms as it descends whether it be alongside a cb cloud or in the downward leg of a Hadley cell.
In doing so it reduces the net cooling at the surface.
All up and down movement is convection.
Stephen Wilde July 2, 2019 at 5:04 am
Correct, just as rising air cools while rising. The air moving poleward in the Hadley circulation loses energy to space on its way and slowly sinks, accumulating around 30N creating the high pressure areas. The subsiding air does not reach the surface, it diverges around the level of the subsidence inversion.
Major effect of the subsiding air seems making sure no clouds develop, so the sun can heat the (dry) surface during the day, and let the surface cool massively during the night.
Ben,
At Uni I was taught that “The Horse Latitude Anticyclones occur because of radiative cooling to Space at the Top of the Atmosphere.”
I now know that this is wrong.
Two things: –
1. Slowly rotating Venus does not have a Ferrel cell.
2. On rapidly rotating Earth the decent of mid-latitude air is a forced process due to the Coriolis Effect and not a passive radiative process.
Persson, A.O. (2005). The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885. International Commission on the History of Meteorology 2, 24pp.
This is where my two favourite modelling papers are so important.
Hunt, B.G. (1979). The Influence of the Earth’s Rotation Rate on the General Circulation of the Atmosphere. Journal of the Atmospheric Sciences, Vol. 36 (8), 1392-1408.
Del Genio, A.D. & R. J. Suozzo (1987). A Comparative Study of Rapidly and Slowly Rotating Dynamical Regimes in a Terrestrial General Circulation Model. Journal of the Atmospheric Sciences, Vol. 44 (6), 973-984.
Forced descent of upper atmospheric air on rapidly rotating Earth delivers dry air to the ground, where it can undergo surface radiative cooling (especially at night) creating the semi-permanent anticyclones of Earth’s major desert regions.
Ben,
Very true. But now consider this. The massive cooling at night is a land surface phenomenon.
The situation over the oceans is different, as the graphs you posted show, the mid-latitude oceans are a reservoir of captured sunlight.
Replace our modern world’s meridional orientated Atlantic Oceans with the Cretaceous world’s mid latitude zonal orientated Tethys Ocean. In place of the modern Sahara Desert there were shallow water seas collecting solar energy. The Red Sea located in the Horse Latitudes is the closest modern analogy to these now lost Cretaceous seas.
Baum, S.K. 2001. Glossary of Physical Oceanography Red Sea.
Philip Mulholland July 4, 2019 at 2:25 am
I’ve seen worse, like people claiming that the Hadley circulation is driven by the cb’s that develop at the ITCZ.
Not familiar with the Venus atmosphere, but slow rotation means small Coriolis effect.
Around 30 N/S happens to be the latitude where the pressure gradient force and the Coriolis effect balance on Earth. Poleward moving air is now moving eastbound in the subtropical jet and accumulates at altitude.
The resulting high pressure areas near the surface create oa the tradewinds and the air has to descent the compensate for the outflow.
Philip Mulholland July 4, 2019 at 3:42 am
I’m pretty confident that the high temperatures in the Cretaceous (peak ~85 mya) are caused by major magma eruptions in the oceans. Mainly the Ontong – Java event, but also smaller ones totaling far over 100 million km^3 magma (1 million km^3 magma carries enough energy to warm ALL ocean water 1K)
Just as I’m pretty confident that the high temperatures on Earth are due to our hot deep oceans (~275K ). The atmosphere is a small player in this, just reducing the energy loss to space from average ~400K to average ~240K.
Ben,
The bottom water temperature of the modern Red Sea is 21.7 C and salinity 40.6 psu. (Baum, S.K. 2001)
The Levantine Intermediate Water (LIW) has a temperature of between 15C to 16C. (Baum, S.K. 2001)
In the Strait of Hormuz, the bottom water outflow from the Persian Gulf has a temperature of 22C. This is clearly not a volcanic effect for the shallow waters of the Gulf. (Bower A.S. et al 2000 Plate 6).
In the Cretaceous the Boreal Ocean warm water upwelling kept the arctic climate warm.
(Golovnena L.B. 2000)
Typical Cretaceous open ocean bottom water temperate was 16C. The modern ocean is 4C. The difference is climatic and not volcanic.
Ben Wouters July 5, 2019 at 4:42 am
400K and 240K should be 400 W/m^2 and 240 W/m^2 obviously.
Philip Mulholland July 5, 2019 at 6:50 am
Obviously not. Direct solar heating + mixing reaches down to ~200m or so.
Seasonal variation ensures that solar energy reaches no deeper.
Shallow seas like the Gulf or the Mediterranean are possibly solar heated down to their sea floor.
Outflow water may reach down to ~1500m, but NOT to the deep ocean floor.
If over 100 million km^3 magma erupting in what is now the Pacific had no influence on the ocean temperatures, what did cause the hot water near the ocean floor in the Cretaceous?
see eg https://www.researchgate.net/figure/Comparison-of-key-Late-Cretaceous-bottom-water-and-sea-surface-temperature-records_fig2_263205991
In case you believe CO2 had any influence, Geocarb III shows a steady decline from ~150 mya onward. Temperatures peak 90-80 mya.
Ben,
We are drifting off topic. So, I will close with this: –
One of the key questions in oceanography is why are the bottom waters of the modern oceans so well oxygenated?
Answer, because they are dominated by cold polar sourced surface waters which are themselves well oxygenated.
However warm dense saline tropical sourced bottom waters carry lower oxygen levels and are more prone to anoxia and sapropel formation in isolated basins. E.g. the Mediterranean Sea.
Thermohaline circulation in the modern world is dominated by cold oxygen rich polar sourced bottom waters.
Thermohaline circulation in the Cretaceous world was dominated by warm dense saline oxygen-depleted bottom waters from the tropical Tethys Ocean. These depleted ocean waters led to the formation of sapropel rich lower Cretaceous source rocks in the polar Boreal Ocean.
Have a look at Dr. Eelco J. Rohling The Dark Secret of the Mediterranean for more information on Isopycnal mixing and sapropel formation.
Philip Mulholland July 6, 2019 at 4:08 pm
Ok. Your post.
But the topic of this post and climate discussions in general revolve around the question:
why are the surface temperatures on Earth so high, compared to the Teff, Lunar average temperature or other criteria.
Any answer to that question that does not explain the very high temperatures of our deep oceans (~275K) is bound to be wrong.
I hope nobody is claiming that our cold, low density atmosphere does the heating of water 3-4 km deep
Ben,
No problem.
Your link to the late Cretaceous sea temperature profile (Fig. 3) will be very useful elsewhere.
Thanks.
Philip Mulholland June 29, 2019 at 1:01 am
Would you elaborate on this some more?
My trusted source for anything meteorological says:
Ben,
Everything here is work in progress.
The issue is zonal versus meridional flow
There is no meridional atmospheric flow on Mars.
NASA Mars Atmosphere Model.
Haberle, 2003. Planetary Atmospheres Mars.
Do both Earth and Mars, which are both fast planetary rotators, have radically different atmospheric structures? If so is this difference a pressure issue? I don’t know.
Here is another relevant Oceanography Quote and Links.
“Both of these western boundary currents move significant amounts of warm waters northward and are important in transporting the excess heat the earth receives in the tropics towards the pole”
Introduction to Ocean Gyres
Schmitz and Richardson, 1991 On the sources of the Florida Current.
Philip Mulholland July 2, 2019 at 6:33 am
I have no preference for either division, but it seems important to know what the major energy transport system is.
Very important role of the oceans is carrying daytime solar energy to the nightside.
No flow needed, just the enormous heat capacity of water.
Difference in surface temperature between day and night is just a few degrees.
A good sunny day brings enough energy to warm the upper 5m 1K or so.
see eg
By contrast during the arctic winter the polar sub-cell unit in the model is assumed to have zero solar influx, and all of the power intensity used to drive the atmospheric circulation arrives by advection from the adjacent Ferrel cell…..
So explain the hot spots that pop up in winter in the file AMSRE_SSTAn_M.mov I also wonder why if there is an updated version of this it is so impossible to find?
D Cage,
I wrote
“The polar sub-cell unit in the model is assumed to have zero solar influx”
You write
“So explain the hot spots that pop up in winter in the file AMSRE_SSTAn_M.mov ”
This is not my field of expertise but perhaps it is yours?
If so, please contribute your experience.
If I may assist.
It isn’t just a matter of advection horizontally from the adjacent Ferrell cell.
There is also the matter of downward convection beneath areas of high pressure over unlit polar regions in winter.
The compression warming within them would produce warmer spots at the polar surface.
The head post is a work in progress and refinements are bound to be necessary but the fundamental underlying truth is sound, namely that the greenhouse effect is caused by convection and not radiative gases.
Stephen and Philip,
I admire your efforts to improve the granularity of rotational effects.
However, I am still very puzzled by your conclusion that “the greenhouse effect is caused by convection and not radiative gases”.
In general terms, if there are two conceptual models, call them A and B, and both of them can successfully predict the same observational dataset, then you cannot argue that A is superior to B or vice versa. Only if you can show that Model A predicts additional observations, not explained by Model B, can you argue that it represents a superior conceptual model.
Can you very briefly itemize where you believe that your conceptual model improves explanation of observations?
Thanks in advance.
“However, I am still very puzzled by your conclusion that “the greenhouse effect is caused by convection and not radiative gases””
kribaez
It is all about gain. Both models seek to enhance the surface temperature of a planetary atmosphere by retaining energy within the climate system. Both models do this by power intensity flux recycling. Both models start with the paradox of the Vacuum Planet equation, which is an external measure of thermal radiant flux exhaust to space.
The standard model uses opacity as the mechanism that creates internal power intensity flux recycling within an opaque atmosphere. Our model uses meteorological mass motion processes associated with the formation and maintenance of a Hadley cell, and our model can be applied to a fully transparent atmosphere.
The key point is this: With an equipartition (50% 50%) surface flux our diabatic atmospheric model replicates the result of the Vacuum Planet equation but does so at the base of the atmosphere. The diabatic model has a gain of 2 (it stores internally within the atmosphere a flux reservoir equal to the solar radiant forcing that drives the climate system).
Forced radiant convection in a high-pressure atmosphere (greater than 100mb) is not an equipartition process. Under solar radiant forced convection in a gravity field the partition is weighted in favour of the air. Therefore, the air in the Hadley cell carries more energy over to the dark surface nighttime radiator (deserts get cold at night). As a direct consequence of the uneven distribution of flux, the gain of the Hadley cell rises to a value greater than 2. More gain means more retained flux in the air, which produces higher average planetary air temperatures.
At this point it is clear that a Hadley cell stores flux and so heats the atmosphere, even if that atmosphere is fully transparent.
kribaez,
Our model can predict the way the various parameters interact and those predictions are confirmed by observations on a variety of planets. I will leave Philip to specify them more particularly. but he has found that in particular the behaviour and characteristics of Earth’s Hadley, Ferrell and Polar cells are explained by the convective approach but not the radiative approach.
Since our model works for a fully transparent atmosphere it must follow that back radiation from GHGs cannot be having any thermal effect at the surface.
For my part I was unhappy about the radiative theory because of the need for hydrostatic equilibrium within an atmosphere if it is to be retained long term.
Such equilibrium requires the downward force of gravity to be matched indefinitely by the upward pressure gradient force.
Thus, if you have an component of the atmosphere (such as radiative gases) able to apply a thermal effect out of proportion to its specific gravity so that it can increase surface temperature from a point higher up in the atmosphere then you have a scenario where the upward pressure gradient force permanently exceeds the downward force of gravity.
The atmosphere would expand upwards and the topmost molecules would be lost to space. The weight of the atmosphere would reduce so the excess upward pressure gradient force would expand it further and another top layer would go and so on until the entire atmosphere would have been lost.
For long term retention of an atmosphere any thermal effect at the surface from radiative gases must be neutralised and it is achieved by the fact that faster convection reduces the effective emission height so as to increase radiation to space from a lower warmer location thereby cancelling the effect of radiative gases.
GHGs do have an effect but they serve only to increase the speed of convective overturning to an imperceptible degree.
Faster convection lowers the effective emission height whereas slower convection allows it to rise.
The effective emission height is set by the length of time it takes for a single cycle of convective overturning.
One can verify that by noting that if the overturning cycle were instantaneous the emission height would be at the surface as for radiation whereas if convection stopped completely it would be at the top of atmosphere as for a solid.
Everything turns on the speed of convection and nothing else.
So, back radiation adds energy to the surface which accelerates convection which reduces the effective emissions height which causes a planet to radiate from a lower warmer height which neutralises the surface warming effect of back radiation.
Neat, isn’t it ?
It follows that the denser an atmosphere and the more viscous it becomes, the slower convection runs, the higher and colder the effective emission height becomes and the hotter the surface becomes.
Hence the differences between Venus and Mars, for example.
The convective explanation has a level of completeness and of predictive capability lacking from the radiative theory.
”The standard model uses opacity as the mechanism that creates internal power intensity flux recycling within an opaque atmosphere.“
As does the top post.
Eqn. 1 is for an airless planet, but Table 3 uses not eqn. 1 to partition the area weighted proportion AW%, it uses Earth with its existing full semi-opaque atm. GHE at global thermometer mean ~288K (global emissivity ~0.8 looking up) i.e. NOT an airless Earth eqn. 1.
Table 3 also incorrectly averages intensive property temperature when it should be averaging extensive property energy as pointed out by Dr. Spencer’s link in RickWill’s comment 8:34pm.
You then use an inverse modeling process (sometimes called back calculating, or curve fitting) in Tables 6, 7, 8 to match observed general circulation avg. ambient temperatures (oops, incorrect avg. T again) including Earth’s air w/opacity driven GHE in full effect.
I am puzzled that you never really use Eqn. 1 for an airless planet as far as I can tell to show how “the requirement for back radiation greenhouse gas heating is no longer necessary” since you inverse model with the back radiation (author term) GHE effect fully in place.
This means I am also puzzled as is kribaez as to how you connect the dots inverse modeling to match 15C not with an airless Earth (eqn. 1) but an Earth with atm. It appears you should have inverse modeled to eqn. 1 at about -18C then shown how partitioning the lit side to unlit side raises the global avg. surface energy to mean ~390 for mean global temperature up to 15C from -18C with only the addition of ambient general circulation and NO back radiation (author term) at all in a ~transparent atm. Earth.
Your explanations responding to kribaez in the last two comments do not fully point to the top post methods, it seems the authors instead would rather top post be these last two 5:01am, 5:21am comments where the term diabatic is now used more correctly & a different term “effective emission height” is now used & not found in top post.
In short, the Hadley cell cannot “heat” the transparent atm. as the cell is filled with air at ambient both on lit and unlit sides. When inverse modeled, the cell avg. should match not 15C but that partitioned from global mean -18C with a ~transparent 1bar atm.
1. No, it does not. The atmosphere being modelled is a fully transparent atmosphere of pure nitrogen gas.
2. No, we are using the Vacuum Planet equation in its original intend form as devised by astronomers to measure the thermal radiant exhaust temperature of a planet (with or without an atmosphere) venting radiation into the vacuum of space.
3. Of course it does, these are the surface target conditions that the climate modelling process is trying to replicate.
4. Table 3 comes from meteorological data. These temperature values are the target data for the Earth and are sourced from surface measurements. They are not derived from radiation measurements.
5. No this is the correct average T, so of course it is the target of the inverse modelling process.
6. No the GHE is not yet in place, that is why inverse modelling is required.
7. The Vacuum Planet equation cannot be applied to surface conditions; it was only ever devised to deal with the external thermal view of a planet from space.
8. No again the GHE is not yet in place, that is why inverse modelling is required.
9. Once again the Vacuum planet equation applies to all planets airless or not, it is an astronomer’s equation.
10. Wow! I think you almost got this right. Careful you are slipping. I think I will have to give you a tick for this.
11. Of topic ramble. Nil Points.
12. It is the surface that heats the air, the Hadley cell is an energy reservoir with a gain that is greater than 2 because it involves forced radiant convection in a pressurised atmosphere.
One mark out of 12 – FAIL.
You really need to do better next time and get a full zero score.
Top post: “We believe that science is about exploring ideas and by providing us with this forum we are able to test the validity of our approach to the complex field of climate modelling.” Validity is subject to observational and theoretical proof not prose.
”1. The atmosphere being modelled is a fully transparent atmosphere of pure nitrogen gas.”
No such thing as a fully transparent Earth atm. of pure nitrogen gas Philip. N2 emits and absorbs, though feebly & has been published for Earth STP. See: “The natural greenhouse effect of atmospheric oxygen (O2) and nitrogen (N2)” Hopfner 2012. GEOPHYSICAL RESEARCH LETTERS, VOL. 39, L10706, doi:10.1029/2012GL051409, 2012.
Your Table 3 states: “Calculating the Global Average Temperature of the Earth” shows the existing Earth w/GHE 288K global mean for “Average Annual Global Temperature of the Earth” what it doesn’t state is “Calculating the Global Average Temperature for pure N2 Earth atm. -18C”
You have not inverse modelled Earth with pure N2 atm. global mean ~ -18C with OLR reduction consistent with & as discussed in that paper. You inverse modelled the current atm. at 15C.
For example, you iterated (“4th attempt”) “to successfully achieve” an average annual temperature of 27.9C for Hadley in Table 5 which is shown in Table 3 as the existing natural Hadley “Cell Average Temperature” (again, you don’t properly avg. energy) before area weighting. After iterating & weighting in all cells is applied Table 3 shows 15C (288K) as for the current atm. with existing opacity, not with N2 opacity as shown in the paper I’ve linked.
Again, had you modeled the N2 atm. in your Table 3 and iterations, they would show reduction in OLR due N2 consistent with that paper which means target surface T slightly above 255K (~18C) in Table 3.
If you keep insisting not so, well all you have done is run in a circle of your own. And really don’t care about “exploring ideas…we are able to test the validity of our approach”.
2. Your term “exhaust (brightness) temperature” with any atm. is TOA not the surface temperature & as such does not depend on composition for any planet in ~steady state equilibrium since will be equal to the input energy. For earth that is 240in, 240out no matter the atm. composition whether N2, O2 or as composed today (for OLR brightness temperature 255K).
3. You simply replicate existing conditions at 15C mean & not pure N2 surface mean with the subsequent slight increase above 255K surface temperature due N2 feeble opacity (again, see Hopfner).
4. Table 3 comes from meteorological data properly converted to energy then averaged and that average converted back to verify thermometer temperature at the surface mean 15C. For TOA the energy is direct from radiometers, averaged over multiannual periods then the energy avg. used to compute brightness temperature. Dr. Spencer’s link shows why that process is necessary for temperature.
5. With a pure N2 atm., to be consistent with Hopfner, the correct target is just above 255K for the inverse modeling, all you’ve done is reverse model existing conditions at mean 15C for Hadley cells at existing T. You’ve run in place.
6. Again, you inverse modelled to 15C existing conditions. Not the pure N2 atm. results as shown in the Hopfner paper.
7. The vacuum planet eqn. is Eqn. 1 right? You never use Eqn. 1 again. It’s a distraction.
8. Again, you use existing GHE 15C in Table 1 not Eqn. 1 (no GHE airless) or the pure actual N2 atm. results as in the Hopfner 2012 paper.
9. Eqn. 1 is ONLY for an airless planet. For exoplanets with atm.s, Eqn. 1 is only a starting point. It will have a term added for the opacity of an atm. Robinson & Catling suggest how to do that. For the basic theory of how to do so & which adds in the opacity from today’s atm. at surface 15C w/atm. emissivity 0.8 – see Bohren’s basic analog discussion “Atmosphere Radiation” text p. 33, Eqn. 1.72 where epsilon is the global emissivity of a pure N2, or any composition atm. Eqn. 1.72 works for Earth at emissivity 0.8 as measured, will also show you where Table 3 should have set pure N2 atm. global mean T.
12. At steady state equilibrium 240in., 240out the surface neither heats nor cools the air. The Hadley cell et. al. merely moves existing thermodynamic internal energy around in the control system of interest.
Adiabatic heating is not observed to occur in a planetary atm. because, as long as our atm. has been observed, pistons and cylinders have never been seen to inhabit the atm. Lorenz paper explains why that is – see his horizontal stratification discussion.
Earth atm. is a heat engine not a diesel engine. See Bohren 1998 “Atmosphere Thermodynamics” p. 109. I don’t expect what I write to convince Philip; material other authors in the field write should though if when pointed out Philip really does: “believe that science is about exploring ideas and by providing us with this forum we are able to test the validity of our approach to the complex field of climate modelling.”
Random word salad designed to confuse and distract from the significance of the original post.
Clear denial of the presence of adiabatic heating in descent and the unavoidable thermal consequence of delaying a portion of the radiative throughput in its exit to space.
Trick,
The gain of the equipartition 50% : 50% diabatic model is 2.
This model mimics the Vacuum Planet equation, so no greenhouse effect.
The gain of a forced radiant convection adiabatic model is greater than 2.
It’s all about gain.
Philip, there would be a gain found HAD you used the Vacuum Planet equation but you didn’t, Eqn. 1 is not used. You clearly label Table 3 “Calculating the Global Average Temperature of the Earth” at 15C which you then use to inverse model the general circulation including the existing GHE.
Had Table 3 been setup for: “Calculating the Global Average Temperature” of the Airless Earth using eqn. 1 at “Average Annual Global Temperature” of about -18C, and you then found a gain above -18C from the general circulation you would have something.
Actually, your gain is identically 1. You inverse modeled the existing Earth GHE 15C = 15C.
Trick,
Table 3 is meteorological data – this was discussed in my 1st essay Calibrating the CERES Image of the Earth’s Radiant Emission to Space. It is the target dataset not the starting point.
Equation 1 is the so-called Vacuum Planet equation – this was discussed in my 3rd essay Modelling the Climate of Noonworld: A New Look at Venus. In that essay I also showed how the Diabatic Model is a mimic of the Vacuum Planet equation.
I can now confirm for you that the exact relationship is T Diabatic Model = 0.9891 * Expected T emission. The Diabatic Model temperature is the Vacuum Planet equation temperature scaled by 0.9891. So yes, Equation 1 is being used in my analysis in its directly comparable scaled version, namely the Diabatic Model.
Now I know the gain (internal atmospheric reservoir power intensity boost) of the Diabatic Model is 2, because that is how I built it with the geometric series of halves of halves (Noonworld Essay: Table 4).
Neither the Vacuum Planet equation nor the scale equivalent Diabatic Model predict surface planetary temperatures. Both analytical approaches require a significant boost in retained atmospheric power intensity flux to be able to achieve this required surface temperature rise.
The adiabatic model (unlike the diabatic model) has a flux gain that is greater than 2. It achieves the required power intensity boost by general circulation. So yes, as I am sure you now will kindly affirm, I do have something.
I can’t find the source of .9891 as searches do not show a hit.
In Noonworld, your premise was to ignore atm. radiation:
“This warmed air then rises by convection, and because it is fully transparent, and also because it is no longer in contact with the ground, it retains all of its energy internally.”
So Noonworld is neither airless Eqn. 1 nor a planetary atm. with normal emissivity air as Noonworld has no atm. radiation which is a singularity so you can come up with any answer you like for Noonworld, no one can prove you wrong….or right after a singularity.
”Neither the Vacuum Planet equation nor the scale equivalent Diabatic Model predict surface planetary temperatures.”
Of course not, they both ignore radiation from the atm. at their peril. But if you add global mean atm. emissivity component with all measured input into Eqn. 1 then it shows 288K global surface mean for Earth analog (See Bohren 2006 eqn. 1.72 p. 33). And well-known analog Eqn. 1.72 also computes 255K for a ~transparent (pure N2, only very slight reduction in OLR) Earth atm.
”I know the gain (internal atmospheric reservoir power intensity boost) of the Diabatic Model is 2, because that is how I built it”
And nature built the Earth; nature knows there is no gain from the general circulation above Table 3 as shown 15C = 15C (or pure N2 ~ -18C=-18C). To learn why nature is so observed, start with E. N. Lorenz 1955 paper I already posted.
Your last paragraph contradicts E. N. Lorenz, it creates energy out of nothing, and, no, you do not have something. You have a singularity & you simply show 15C=15C.
You would have something if Table 3 started from -18C, you showed conservation of energy holds in your work for a gain of 33C above that starting point to 15C from the general circulation, and you would then contradict E. N. Lorenz 1955 paper. This would be sensational; you would have found pistons and cylinders inhabit the atm. and, as such, the atm. is not predominantly horizontally stratified in T. You would have to show a ton of observational proof against E. N. Lorenz.
You won’t be able to as Lorenz is observationally generally accepted to be correct with tens of thousands of soundings & since pistons and cylinders have never been seen inhabiting Earth atm. general circulation doing adiabatic heating as found in diesel engines (Bohren 1998 p. 109).
Equation 1 applies to planets with radiative atmospheres and so does not ignore radiation from atmosphere to surface yet it still comes out at ‘only’ 255k.
Table 3 does start at -18c with a 50:50 energy partition and only shows the actual observed temperature when one changes the energy partitions on the lit and unlit sides.
At a specific level of diversion from 50:50 the adiabatic model duly achieves the observed temperature of 15c
For equation 1 the only difference that radiative gases make is the height at which radiation out equals radiation in.
For no radiative capability that would be the surface and for full radiative efficiency it would be top of atmosphere.
Therefore equation 1 does take account of radiation from atmosphere to surface via the variation in emission height.
As regards conduction.the more efficient conduction is the greater the height at which the radiating temperature will be achieved even if all outgoing radiation is from the surface.
In both cases there is radiation to space at 255k so equation 1 applies both with and without radiative gases.
That leaves the issue of the surface temperature increase as due to convection only because of the interplay of conduction and radiation creating a lapse rate slope which controls the speed of convection and thus the length of time that some emission to space is delayed.
The amount of radiation to space delayed by convection is explored in Table 3.
Trick,
I loaded it here last night for you. Look at spreadsheets T1 Sagan and Chyba 1997 for the data and Graph Te vs T Diabatic for the relationship equation.
Mulholland, P 2019 Earth Adiabatic Parallel Model 20Jun19 Research Gate Project: Dynamic-Atmosphere Energy-Transport Climate Model
Stephen 11:43pm: ”Equation 1 applies to planets with radiative atmospheres”
Stephen 12:17am: ”In both cases there is radiation to space at 255k so equation 1 applies both with and without radiative gases.”
Top post disagrees with Stephen: “The equilibrium temperature Te of an airless, rapidly rotating planet is Equation 1”
There is radiation to space in Eqn. 1 but only from the airless planet surface thus per top post Eqn. 1 is NOT “with radiative gases”; Stephen’s imagination is robust, Stephen’s understanding of the basics of meteorology (& even just the top post) not so much.
”Table 3 does start at -18c”
Table 3 & Philip disagrees with Stephen: “By combining these three temperature values using an area weighted average, the average annual temperature of the whole planet can be derived (Table 3) Calculating the Global Average Temperature of the Earth. Average Annual Global Temperature (Celsius) 15.0.”
Philip 11:46am: “Table 3 comes from meteorological data.”
Perhaps Stephen is determined to keep continually rewriting the top post in comments.
—–
Philip 1:28am: I don’t have the Sagan Chyba 1997 paper in inventory, will have to read it first.
Trick,
All planets exist in the Vacuum of Space. The Vacuum Planet equation is a TOA measurement made from the outside in the Vacuum of Space. It does what it says on the tin.
”The Vacuum Planet equation is a TOA measurement made from the outside in the Vacuum of Space. It does what it says on the tin.”
Philip, the tin (top post) reads:
“A key metric of the energy budget is the standard Vacuum Planet equation exemplified by Sagan and Chyba (1997”
From Sagan and Chyba (1997) they are talking about Te at the surface i.e. airless planet compared to Ts at the surface with a radiating atm.:
“The equilibrium temperature Te of an airless, rapidly rotating planet is defined (top post Eqn. 1): Te ≡ [S π R2(1-A)/4 π R2 ε σ]1/4”
Sagan & Chyba for earth today w/radiating atm.& thus at TOA so they write: “For Earth today, Te ~255 K, and the difference deltaT ~33 K between Te and the observed mean surface temperature Ts is due to the mainly H2O-CO2 atmospheric greenhouse effect.”
Contrary to what Trick says the Earth’s Annual Global Mean Energy Budget (Kiehl and Trenberth, 1997 Fig. 7) clearly shows radiative balance at the Top of the Atmosphere.
Solar 235W/m2 in : Thermal 235 W/m2 out.
We can equate this situation to the Vacuum Planet equation because they use divide by 4!
Time to stop responding to Trick. Better things to do.
Philip, far as I can tell for y=mx+b with b=0 and m=0.9891 this is just a check of how well the existing Earth with radiative atm. GHE global surface T 288K spreads out to your general circulation grids, nothing more. Had you done it exact, then m would apparently be 1.
You simply apply your link Sagan and Chyba 1997 writing for current existing Earth Ts=288K: “observed mean surface temperature Ts is due to the mainly H2O-CO2 atmospheric greenhouse effect.” to the general circulation.
Stephen 1:55pm gets it wrong yet again: ”We can equate (K&T TOA) situation to the Vacuum Planet equation because they use divide by 4!”
No. The Vacuum Planet eqn. is “(after Sagan and Chyba, 1997)” for an “airless” planet, in which case only the surface level exists there is no TOA so Stephen’s compare attempt to K&T TOA is incorrect.
For an airless planet at Earth’s orbit & rapid rotation, Sagan and Chyba solve Eqn. 1 to ~255K. What gets Stephen so wound up is that the mean brightness temperature observed at TOA for today’s Earth with today’s atm. is ALSO 255K. Because the rapidly rotating planet is pretty much in steady statement equilibrium with input sunlight 240out,240in (235 for K&T long ago).
Many would expect Stephen should learn but he doesn’t; brightness Tmean 255K at TOA is ONLY due to steady state equilibrium doesn’t depend at all on atm. composition, mass (or even if the planet is airless) after settling down to steady state.
It is Ts (which is why they use s subscript for surface) 288K that depends on atm. composition in S&C97: “observed mean surface temperature Ts is due to the mainly H2O-CO2 atmospheric greenhouse effect.”
Trick relies on an assumption by Sagan and Chyba that the increase in surface temperature is caused by back radiation.
They are wrong for the reasons exhaustively set out in this thread and in the head post.
The radiation field is a product of conduction, convection and the lapse rate. It is not the cause of any of those phenomena.
That appears to be the sole disagreement with Trick who appears to be so solidly attached to the radiative theory that he cannot understand that which is self evident to many others so he resorts to desperately convoluted distortions of the head post and his source material to justify his position.
Far from atmospheric composition being in command of Ts (surface temperature) as per Sagan and Chyba the truth is that composition is irrelevant unless it pertains to total atmospheric mass.
Those two astrophysicists with virtually no knowledge of meteorology or of non-radiative energy transfers in a real atmosphere have a lot to answer for.
Stephen 2:54pm writes I rely on an assumption; this is not correct as I rely on observations and basic principles in meteorology that have stood the test of time & not Stephen’s imagination. Then Stephen complains I resort to “desperately convoluted distortions of the head post” by using verbatim quotes from the head post.
As for Stephen disrespecting Carl Sagan, Stephen should know Prof. Sagan was writing in 1960 about Venus’ 600K atm. near surface observed brightness temperatures (Sagan verbatim quote “which demands a very efficient greenhouse effect”) and 232K “airless” Venus 10 years BEFORE the first thermometer (Venera 7) arrived on the planet surface in 1970.
Stephen and Philip,
Thank you for your responses above. They are not quite giving me what I was asking for. I accept the validity of some of your statements regarding convective balance, but overall I think you are setting up a paradox which is not present in the more conventional explanation – for which I would proably reference as a starting point Ramanathan and Coakley 1978: “Climate Modeling through Radiative-Convective Models” .
Consider three hypothetical planets. Each has a black-body surface with zero albedo and a emissivity of 1.0. Each of them receives 236 W/m2 of SW flux (averaged over area and time during the course of a year). Each of them is in a dynamic steady-state – no net energy loss or gain to the climate system over the course of a year.
Planet A is a “vacuum planet” with no atmosphere.
Planet B is a planet with an 80/20 nitrogen oxygen atmosphere.
Planet C is a planet with an Earth atmosphere, including H2O and CO2, but no albedo-changing clouds.
For each of the three planets, the OLR measurements from outer space yields an average brightness temperature of 254K since, given the assumption of dynamic steady-state, the outgoing OLR is equal to 236W/m2 in all three instances.
Planet A has no lapse rate and the effective emission elevation is the surface of the planet, obviously.
Planet B atmosphere is subject to convective and advective forces and should have a near-surface lapse rate largely determineded by convective physics. The average pressure at surface is determined uniquely by the weight of the atmosphere, and the pressure profile with elevation is determined by dP/dz = -rho x g [ a necessary condition to retain hydrostatic equilibrium]. The vertical temperature profile upto the elevation where convective forces become negligible should approximate the dry adiabatic lapse rate. If this atmosphere were completely transparent to OLR, then the effective emission elevation would be the surface of the planet and the average surface temperature would be 254K – i.e. the same as vacuum Planet A. (It is something of a diversion, but in reality, this N2-O2 atmosphere does have some opacity to OLR because of collision-induced absorption and emission. Its effect should be to elevate surface temperature slightly above 254K with a corresponding shift in the vertical temperature profile. The effective emission height should then be just above the surface of the planet.)
Planet C has almost the same surface pressure as Planet B since, by assumption, it has similar atmospheric mass. However, its average lapse rate is now closer to a moist adiabatic LR. Its observed averaged surface temperature is 288K.
The paradox can be described as follows:-
Planets A and B have average brightness temperatures which correspond to their surface temperature (or near-surface temperature for Planet B). Planet C has a brightness temperature which corresponds to somewhere in the mid-to upper troposphere, if related to average vertical temperature profile, but which in any event is significantly less than the surface temperature.
Since all of our hypothetical planets are by assumption in a dynamic steady-state, any variation of convective and advective heat transport due to diurnal and seasonal fluctuations, cannot change the net energy content of the system over the course of the averaging period. Each planet must gain from solar and lose by OLR exactly 230 watt-years/m2 over the course of the year, resulting in a zero net energy gain.
The surface of Planet C, however, is emitting OLR corresponding to 390 watt-years/m2 of outgoing radiative energy over the same annual period – the consequence of an average surface temperature of 288K. Since the atmosphere cannot accumulate the difference in energy, amounting to 160 watt-years/m2, the atmosphere MUST return this energy to the surface in some manner or form.
There are only two possibilities, then, to explain this return of energy. It is returned EITHER returned as radiative flux – aka back radiation OR it is returned as sensible heat. The problem with the second explanation, and hence the paradox, is that, if you wish to rule out back radiation as an explanation for Planet C, you need to explain why there is a net heat transfer from (cool) atmosphere to the (warmer) surface in Planet C, but no such net heat transfer apparent in Planet B, which also has convective mechanisms in operation. If, on the other hand, you argue that there is indeed a similar transfer of heat from atmosphere to surface in Planet B, you need to explain how and why that does not result in surface heating – in breach of the foundational assumption of dynamic steady-state. (If you allow such heating, then since there is no or little obstacle to the escape of OLR from the surface in Planet B, you have an immediate flux imbalance and hence a contradiction.)
Overall, therefore, it seems impossible to me to replace the “back-radiation model” with a convective heating explanation without introducing a paradox. Evidently, you must disagree with some of my assertions above. Can you perhaps identify how you believe you are avoiding the paradox I describe?
Kribaez,
Planet B would only remain at 254 if it relied only on advection to move energy across the surface. Diabatic energy transfers only would be in operation.
If it has any convection then the surface temperature would rise above 254 in order to provide the additional surface energy required to sustain the necessary ongoing processes of conversion and reconversion between KE and PE. That adds an adiabatic energy transfer to the mix.
It isn’t a case of a cool atmosphere heating a warmer ground.
Descending air heats by compression to its maximum temperature when it reaches the ground. That ground is radiating to space but also draws energy from the air and as it does so that energy is replenished by the flow from above so the net outcome is that the radiating surface does not become as cold as it otherwise would have done.
So , no paradox.
Stephen,
The temperature at any point on the planet’s surface can be thought of as the result of heating or cooling. It is already a resolved quantity in this sense and the system is in dynamic steady-state by assumption. If the average temperature of Planet B rises above 254K “in order to provide the additional surface energy required to sustain the necessary outgoing processes of conversion and reconversion between KE and PE”, then Planet B must start emitting OLR in accordance with this higher average temperature. Since Planet B was exactly in radiative balance at an average surface temp of 254K, AND, by assumption the planet presents little or no resistance to OLR, then this rise in surface temperature must increase OLR and bring the system out of dynamic steady-state – in direct contradiction to the foundational assumption. So, I am really not following your conceptual model here at all.
kribaez.
A surface at a temperature of 288k does not produce OLR at 288k if it is overlain by a convecting atmosphere.
Instead, it emits 255 to space and conducts 33k (in the case of Earth) to the convecting atmosphere.
The same parcel of surface KE cannot be in two places at once or be involved in two processes at once otherwise you breach the law of conservation of energy.
It can be radiated or conducted but not both simultaneously.
Stephen,
Thank you for your last response. At last, I think I understand the reason for the difference in perception. I think unfortunately your explanation would come as a major shock to messrs Stefan and Boltzmann. You are, inadvertently, rewriting the book on a law of physics which has been well-tested for over 100 years. You wrote (with reference to Planet B, a planet with an assumed optically transparent atmosphere):-
“Instead, it emits 255 to space and conducts 33k (in the case of Earth) to the convecting atmosphere.
The same parcel of surface KE cannot be in two places at once or be involved in two processes at once otherwise you breach the law of conservation of energy.
It can be radiated or conducted but not both simultaneously.”
The black body will emit a power flux density corresponding to its temperature in accordance with S-B. ALWAYS. The black body has no mechanism for partitioning its temperature and deciding how much to radiate. The temperature of the body is a measure of its retained energy upto that point in time; it is NOT a measure of the instantaneous fluxes which are acting on it. It is therefore perfectly possible for a black body to be losing energy simultaneously by radiation, convection, conduction and latent heat conversion. If the total flux IN at that moment in time is greater than the total flux OUT, then the body will be gaining heat and its (average) temperature will be rising, and vice versa. The radiative flux emitted by the body at any moment in time will however always be determined by the temperature of the black body at that moment.
So, in the case of our Planet B ( optically transparent atmosphere), for dynamic steady-state the incoming and outgoing fluxes must balance. Once you postulate a surface temperature, that temperature defines the radiative flux leaving the surface. Because of (the assumption of) optical transparancy of the atmosphere, that surface temperature also fixes the OLR actually leaving the planet. Since that OLR must be equal to the incoming SW flux of 236 W/m2, the temperature at the surface must be equal to 254K. We can also infer that for steady-state, there can be no net convective flux between the atmosphere and the surface, once the atmosphere has achieved its steady-state temperature profile. This paradox does not go away so easily.
S B never intended their equation to apply to a surface beneath a converting atmosphere
4:06am: ”S B never intended their equation to apply to a surface beneath a converting atmosphere.”
Stephen doesn’t know what he’s talking about. Stephen makes that up to suit his narrative.
Planck 1912 p.74: “the Stefan-Boltzmann law of radiation can be used for an absolute definition of temperature independent of all substances…the radiation constant has been made the object of as accurate measurements as possible in various places.”
The testing to develop the S-B law* was conducted in lab air along with testing to find the emissivity of each substance; early on it was found a vacuum was unnecessary. Thus S-B works for the moon in vacuum just as well as S-B works at 1bar on Earth surface, the only variables are temperature and frequency to find object radiance in Planck’s Law.
If Stephen would buy an IR thermometer for ~US$30, he could test S-B and find it works outdoors the same on windy days as on still air days. Works the same indoors with a fan blowing on a surface as with no fan.
Stephen just imagines atm. physics; he has little accurate theoretical meteorological knowledge because he can’t read technical papers in the field & no lab experience setting him straight. This a basic reason Stephen can be so wrong about adiabatic heating being found in Earth’s atm., he just makes it up because it suits his narrative.
*Planck 1912: “This law, which states that the volume density and the specific intensity of black radiation are proportional to the fourth power of the absolute temperature, was first established by J. Stefan on a basis of rather rough measurements. It was later deduced by L. Boltzmann on a thermodynamic basis from Maxwell’s radiation pressure and has been more recently confirmed by O. Lummer and E. Pringsheim by exact measurements between 100C and 1300C, the temperature being defined by the gas thermometer.”
The surface may well be radiating at 288k but that radiation never makes to space past a convecting atmosphere.
It is clearly attenuated by convection as it travels upward from the surface to the effective emission height.
The reason is that conduction draws kinetic energy from the upward radiative flux and convection transforms it to potential energy which is not heat and does not radiate.
Otherwise convection could never have been initiated because the energy required for it would have radiated straight out to space in the upward radiative flux.
kribaez July 4, 2019 at 8:48 am
Our moon comes pretty close, average night side temperature ~70-80K, probably due to 40K geothermal “base” temperature plus some carry over heat from the dayside ( very low heat capacity)
”The surface may well be radiating at 288k but that radiation never makes to space past a convecting atmosphere.”
If so, pictures of the surface from space would be impossible as they depend on radiation from the surface. Yet they can read your license plate at avg. 288K from space. Stephen still doesn’t know what he’s discussing, prefers his imagined atm. science over real atm. observation.
Convection is initiated whenever there is a surface warmed from above in a gravity field, Stephen doesn’t know much about convection either.
Pictures from space rely on visible wavelengths and not IR.
Convection occurred as a result of uneven surface heating causing density variations in the horizontal plane.
The variations in density are caused by absorption of energy via conduction and conducted heat cannot have been radiated away simultaneously.
Original Stephen: ”that radiation never makes to space past a convecting atmosphere.”
Next Stephen except for: ”visible wavelengths and not IR”
IR makes it through too Stephen, IR can be seen from space by CERES radiometers! And military satellites. Your imagination has shown to fail again Stephen. Really, you need to get into a modern atm. text to participate correctly in these discussions.
Convection doesn’t occur very much above the tropopause Stephen, yet there is uneven heating causing density variations. Your imagination fails you, yet again.
Conduction AND radiation occur at same time Stephen, kribaez just tried to inform you (yet again) of that fact. They are independent processes.
Stephen, you aren’t worth the trouble with which to respond correct atm. process info., it never “takes”.
Earth radiates to space at 255k. The surface is at 288k.
33k fails to escape the atmosphere.
Convective overturning requires 33k of surface energy to keep it running.
kribaez July 3, 2019 at 11:00 pm
Assuming the 3 planets are receiving energy from only one sun, how do you arrive at the 254K surface temperature for planet A?
Radiative balance temperature for the “sunny” side would be ~330K, night side 0K.
Average surface temperature ~165K
”how do you arrive at the 254K surface temperature for planet A?”
kribaez measured it: ”For each of the three planets, the OLR measurements from outer space yields an average brightness temperature of 254K”
Mean brightness temperature 254K looking down would also be arrived at through analysis using Eqn. 1 in the top post Table 1 “expected Te” “(after Sagan and Chyba, 1997)” for “The equilibrium temperature Te of an airless, rapidly rotating planet”. Conclusion: kribaez’ planet A is rapidly rotating.
Ben,
As Trick suggested, this temperature was the “observed” brightness temperature of a rapidly rotating planet. It represents the spatial and temporal integration of the local temperatures to yield (exactly) an averaged OLR of 236 W/m2 – to match the given incoming averaged SW.
There is no reason to believe that the night side temperature reaches an averaged value of absolute zero. This would imply that the surface itself had zero heat capacity and hence cooled instantaneously to zero absolute as soon as the sun was switched off. For the purpose of the example, we don’t have to know the exact diurnal and seasonal variation of the temperature time series at every point on the planet, or even at every latitude. It is sufficient for illustration purposes to know the resultant.
Trick July 4, 2019 at 6:37 am
kribaez July 4, 2019 at 8:48 am
Zero albedo and 1.0 emissivity suggest an ideal black body (non existant) for which no heat capacity is specified. No heat capacity means no effect from rotation.
I was also wondering about the 236 W/m^2. It is the number often found for incoming solar after albedo. So for planet A and B it is for a different distance from the sun than planet Earth actually is.
The Effective Temperature (Teff) for TSI 1364 W/m^2 are usually given as:
Ideal black body Teff ~278K
Moon Teff ~270K – actual ~197K
Earth Teff ~255K – actual ~288K.
Imo the avg temperature for an idela BB should be ~160K.
Ben, a theoretical black body still has mass so has a specified heat capacity. What is meant by rapidly rotating is fuzzy though, the moon and Venus would be examples of rotating but not rapidly rotating in the meaning of the top post “after Sagan and Chyba”. The Earth is considered rapidly rotating if you read their discussion.
There is a fuzzy transition from the divisor 4 rapidly rotating planet to the divisor 2 for an object tidally locked to its major source of illumination e.g. “Noonworld”.
”Ideal black body Teff ~278K”
The Te in the top post Table 1 is the one being discussed, sure there are other scenarios.
”Moon Teff ~270K – actual ~197K”
Your moon “actual” at 197K is just based on guess work. There is no GHCN for the moon.
Trick July 5, 2019 at 6:12 am
Not sure why a non-existent, theoretical BB should have mass or heat capacity. Being able to make accurate calculations is all that seems to matter.
Interesting (older) article: https://www.pnas.org/content/106/15/6044
A tidally locked BB (1 rotation/orbit) gives the same result, AST ~160K at our distance from our sun.
Introducing an earth-like geothermal flux would bring the night-side from 0K to ~40K, increasing the AST some 20K.
Introducing rotation requires a specification of the heat capacity and conductivity of the object, but even rotation rates like once/second do not even out the difference between poles and equator, so the Effective Temperature of the object will not be reached with rotation alone.
Articles like this don’t give me the impression of being “guess work”:
https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2011JE003987
”Not sure why a non-existent, theoretical BB should have mass or heat capacity.”
Ben, it is commonplace to round up Earth surface emissivity 0.97 to 1.0 for convenience, doing so does not destroy Earth’s heat capacity or mass.
Your Vasavada paper did not compute the 197K global brightness mean for moon. Those who do are guessing.
Trick July 6, 2019 at 9:05 pm
Thankfully not. Earth’s surface temperatures are nowhere near RADIATIVE balance temperatures, reason being the enormous heat capacity of the worlds oceans.
Lunar daytime temperatures are very close to radiative balance temperatures, the night time temperatures are 70-80K above radiative balance.
We can only guess at the reason for that.
But they did publish an average equatorial temperature: 206K.
https://www.diviner.ucla.edu/science
Seems reasonable to assume the average surface temperature of the moon is lower than that.
Vasavada: “Normal albedos are estimated…we restrict local time to 8–10 and 14–16 h…We first estimate…adjust the derived surface temperature…. It models the regolith….We take 0.98 as a representative value…viewed at nadir….approximately 0.98… assuming a normal albedo of 0.1….Given the uncertainties remaining in the reflectance and radiance measurements…the less certain “knobs” in the present work.”
So forth. The website ~206K is only a guess and not found in their actual paper. And what is meant by “surface” is a guess with all the pulverization “occurring within several centimeters of the surface.”
Trick July 7, 2019 at 6:32 am
The daytime temperatures are close to radiative balance temperatures. Imo the197K makes perfect sense given the ~160K AST for an ideal BB with the moons parameters.
The ~270K Teff for the moon is clearly far removed from reality.
Trick June 29, 2019 at 5:40 am
The Teff of ~255K for Earth and the ~270K ARE derived by spreading incoming solar evenly around an entire planet/moon and calculate the average radiation temperature to lose this energy directly to space.
Only inputs are the TSI and albedo.
Teff is a “back of the envelope” calculation to have a first approximation of a planet/moon. No physical process specified.
The brightness temperature must be composed of surface radiation through the atmospheric window plus radiation from various levels of the atmosphere.
This may “look like” a BB radiating at the brightness temperature.
see eg https://www2.bc.edu/jeremy-shakun/Lacis%20et%20al.,%202010,%20Science.pdf
“The difference between the nominal global mean surface temperature (TS = 288 K) and the global mean effective temperature (TE = 255 K) is a common measure of the terrestrial greenhouse effect (GT = TS – TE = 33 K).
Assuming global energy balance, TE is also the Planck radiation equivalent of the 240 W/m2 of global mean solar radiation absorbed by Earth.”
”The ~270K Teff for the moon is clearly far removed from reality.”
Yes, this figure allows for no diffraction from the large amount of moon surface powder with diameters on the illumination wavelength of interest so 270K equilibrium is too high vs. any GHCN moon thermometer field stuck a few cm.s down into the surface. The 197K is too low because the 197K guess for a brightness temperature is from orbital radiometer measurement which would read too low vs. surface thermometers if not corrected for the diffraction in the measurement.
The brightness Teff ~255K for Earth is both reasonably derived from measured data AND measured by satellite radiometers over 4-15 annual periods from surface particle sizes large enough to have no diffraction contamination.
”The daytime temperatures are close to radiative balance temperatures.”
There is no support for this assertion in Vasavada 2012, see Fig. 5 & not even at night. Fig. 7 shows equilibrium temperature achieved a few cm.s below the regolith surface based on some guesses. One of which is no diffraction, which means the equilibrium T in Fig. 5 is too low. That 240K could be bumped up some in reality at the moon equator.
The equilibrium value a moon GHCN thermometer network would achieve is likely below a guess of ~250K and above a guess of ~197K (@ too high emissivity 0.98 not considering diffraction). IMO that’s ~all that can be guessed at the present time. And there is no incentive to narrow the wide range by funding more research.
Well laid out and reasoned scientific concept. In the International Public Movement ALLATRA there is a scientific division ALLATRA SCIENCE, which is engaged in the study of physics, astronomy, climatology, volcanology and others. So they published a report on climate change https://allatra.tv/en/book/on-the-problems-and-consequences-of-global-climate-change in which not only are these changes identified, but also given effective ways to solve these problems. To understand the methodology on the basis of which climate processes are studied, you can still read the Report “Primordial Physics ALLATRA”.
“Nighttime is the winter of the tropics.”. +++ !
Thanks Johann
An old saying but a good one.
For all those confused by Trick’s tricky bafflegab this is the clearest summary of reality :
Equation 1 applies to planets with atmospheres whether they have radiative gases or not but both produce a surface temperature of -18C by relying on diabatic energy transfers only. It makes no difference whether those diabatic energy transfers are via conduction or radiation. In all cases there is an energy split of 50:50 between transfers from surface to air and transfers from air to surface. That is how the standard radiative budget between Earth and space works. All that radiative gases achieve is a change in the emission height whilst surface temperature stays the same. To try to raise that -18C to 15C the radiative theory of AGW proposes that GHGs raise the emission height so as to heat the surface when one extends the lapse rate slope back to the surface. That is not a part of equation 1. In reality, adding GHGs causes faster convection which reduces the emission height so that the planet radiates to space from a lower warmer location and a surface temperature increase is thus prevented. By that mechanism Equation 1 remains valid with a surface temperature at -18C even for planets with GHGs. The solution proposed by the AGW theory would destroy the hydrostatic equilibrium of an atmosphere by causing a scenario whereby the upward pressure gradient force from the raised surface temperature would be permanently in excess of the downward force of gravity. That is impossible to maintain so the radiative solution fails.
Table 3 can also be applied to planets with both radiative and non-radiative atmospheres but in that case we are varying the energy split away from 50:50 on both lit and unlit sides but to an equal and opposite extent on each side. One can only do that by introducing up and down convection which results in adiabatic energy transfers.
As soon as one does that a delay in emission to space of some energy is introduced because of the time required to move the energy surplus on the lit side to the area of energy deficit on the unlit side and the surface temperature rises to 15C from -18C for Earth. That does not upset the balance between the upward pressure gradient force and the downward force of gravity because the extra surface heat is constantly recycled and so cannot push upwards towards space.
The usefulness of Table 3 is that one can calculate the actual observed surface temperature of every planet with an atmosphere simply by varying the proportions of the energy split.
That is not ‘curve fitting’ since it introduces predictive ability which the radiative theory fails to achieve.
The key feature that determines the extent of the observed energy split away from 50:50 for every planet with an atmosphere is atmospheric density at the surface because that controls the efficiency of conduction between surface and air and thus the amount of surface energy transferred in and out of adiabatic processes.
Density is a product solely of atmospheric mass and the strength of the gravitational field.
It follows that the shift of the energy split away from 50:50 is similarly a product solely of atmospheric mass and the strength of the gravitational field.
Therefore, the greenhouse effect is a product solely of atmospheric mass and the strength of the gravitational field.
End of the radiative theory.
Philip’s model proves that it works.
Well said…
the only effect of water vapour on radiative loss by the surface is at night when convection stops, then it can impede the cooling by infrared of the sun-warmed surface.
“Equation 1 applies to planets with atmospheres whether they have radiative gases or not but both produce a surface temperature of -18C by relying on diabatic energy transfers only.”
Equation 1 is a statement of flux balance for a planet in assumed dynamic steady-state; OLR = net received SW. The temperature in Eq 1 is the “brightness temperature” – i.e. the apparent temperature of the planet viewed from space and deduced by the application of S-B to the observed OLR.
If you do not have “radiative gases” in the atmosphere, then this brightness temperature should correspond fairly closely to the actual average temperature of the planet at its surface. If you do have radiative gases, however, this temperature should correspond to some elevation above the surface of the planet, and not to the surface of the planet itself as you seem to indicate here. Earth itself gives a good example of this, does it not? Please see my attempt to state the paradox at 11.00 am July 3.
See my answer to the paradox issue above.
As regards this additional point you aver that radiative gases raise the effective emission height which would be the case if convection did not accelerate.
However, convection does accelerate which restores the original effective emission height so as to eliminate additional surface warming from radiative gases.
We know that must happen because if convection were instantaneous then the emission height would stay at the surface because the process would be as fast as radiation.
If convection were not present at all then the atmosphere would become isothermal and the top of atmosphere would be at the same temperature as the surface so radiation would go from top of atmosphere.
Thus the factor that makes the difference is the speed of (or rather the length of time taken by) convective overturning.
The faster it is the lower and warmer the effective emission height and the slower it is the higher and colder the effective emission height. As the emission height rises the surface warms due to the lapse rate slope.
No convection, no surface temperature enhancement regardless of the radiative characteristics of the atmosphere.
AGW theory omits the non-radiative process of convective overturning which is also capable of altering the emission height but in the opposite direction to the effect of radiative gases.
This is a little off topic from the convection discussions, but I’m intrigued by figure 4. It’s hard to make out because of the poor resolution, but I think it’s basically specifying the same thing as my comment on this other thread (https://wattsupwiththat.com/2019/06/12/earth-as-a-solar-collector/#comment-2723796).
I cheated on that comment some by skipping a few steps–to simplify the math. The differential
should have been a smaller square; that is, instead of specifying the entire ring, I should have divided it up into differential sections. The full double integral is then
I won’t integrate it, but it gives the same answer for the area of a hemisphere. The rings around the solar maximum intensity help simplify the math, but we really need to compute the
s differently.
For example, an individual
moves with the rotation of the Earth along lines of Latitude. Our integral should reflect this motion. A slight change in variables will give us the integral for a lat-long view. If we use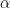 
(alpha) for Latitude angle and 
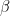(beta) for Longitude angle then we get the following integral for the area of a hemisphere
We need to change from sine to cosine, because a Latitude circumference is maximum at the Equator. I won’t do this integral either, but it gives the same result for the area of a hemisphere. Of course, these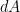
s don’t circle the Sun’s maximum intensity point, so the decrease in intensity needs to be computed with reference to where the Sun’s maximum intensity point is.
It turns out that vector analysis will solve this problem. The math then becomes more complex, because we need to add a time variable into the mix. A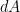
area will enter into the lit side of the Earth (the Earth rotates from west to east) and gains a certain amount of energy. With each 
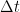, it will gain more energy. It will also radiate this energy. The math is complex enough to require a computer program to handle the difficulties.
Jim
Jim,
Happy to help.
The source tables for Figure 4 are inside the Excel spreadsheet linked in the references in the head post.
Mulholland, P., 2019a. Earth Adiabatic Parallel Model 20Jun19 Excel Workbook.
Philip
So it comes down to a single issue.
Does the S-B equation apply to a surface beneath a convecting atmosphere?
Logic says it cannot, otherwise the same unit of surface heat can be in two places at once namely on its way to space in an upward radiative flux and simultaneously travelling up against gravity in an ascending convective column.
If that unit of energy can only be in one place at a time then one can legitimately partition energy leaving from or returning to the surface in the way proposed in the head post.
Discuss.
I think the answer is that the upward radiative flux from a surface radiating at 288k is incrementally attenuated by conduction and convection until it reaches the effective emission height where 255k escapes to space.
If there were no convection then the atmosphere would become isothermal with the same temperature of 255k from surface top of atmosphere.
The lapse rate slope marks the process of attenuation as the balance between conduction and radiation changes with decreasing density with height.
Density controls the efficiency of conduction so
The greater the density the greater the attenuation and the higher the surface temperature rises.
Stephen,
I get annoyed and sometimes frustrated when climate scientists argue that we should trust climate models because they are founded on “basic physics”, so please do not misunderstand what I am about to say here.
You are challenging basic and very well tested physics.
This is a piece of science that has been tested and used by engineers since the development of Planck’s Law around 1900. In the last forty or fifty years, it has been increasingly common to use non-intrusive temperature measurement in process plant to provide regular online monitoring data to control systems. You may find of some interest the modern literature on the use of measurement of radiative intensity across selected bandwidths to derive and monitor flame or wall temperature in gas-fired furnaces. I choose this as a good example because (a) there is normally ferocious convective activity in the furnace because of the input of air and fuel and evacuation of hot exhaust gases and (b) because the development of soot means that emissivities (especially in the longer wavelengths) approach blackbody behaviour. You will find that despite the presence of convection, Planck’s Law is alive and well – i.e. emitted radiative intensity for any given wavelength is solely dependent on temperature despite the fact that the furnace walls are subjected to a powerful and continuous cooling by convective flux. Of course if Planck’s Law works in the presence of convective cooling, then so does S-B, since it is derivable from Planck by integration across the wavelengths.
Your logic is, I’m afraid, confusing energy and flux.
That example does not work since there is no significant expansion involving work done against gravity which results in a conversion of KE to PE. and no significant recovery of PE from KE in any subsequent descent.
The fact is that where such convective overturning is present the radiative flux at the surface is attenuated with height such that the full amount of radiation at the surface does not escape to space
If you look at the standard K&T diagram you will see evapotranspiration and thermals shown as occurring with the effect of reducing radiation to space so I am not proposing anything novel as regards a partitioning between radiation and conduction at the surface.
Where my account differs is in pointing out that if one takes account of the downward leg of convection as one must then the net effect of convection becomes a surface warming due to the delay in radiating some of the surface energy to space as well described in Philip’s model.
Stephen,
You wrote:- “If you look at the standard K&T diagram you will see evapotranspiration and thermals shown as occurring with the effect of reducing radiation to space so I am not proposing anything novel as regards a partitioning between radiation and conduction at the surface.”
On the contrary, you are proposing something novel and quite patently wrong. The K&T diagram may be inaccurate on several of the flux estimates, but it recognises that the (averaged) radiative emission from the surface is determined by the (averaged) temperature at the surface. Cooling fluxes by evapotranspiration and sensible heat loss are ADDED to the temperature-dependent radiative flux in the K&T diagram, as they clearly must be in accordance with basic physics. You, on the other hand, have claimed several times that you can PARTITION the surface temperature into a part used for radiative emission and another part which supports other cooling fluxes. This is in direct contravention of Planck’s Law, S-B and common sense.
Philip Mulholland, in his previous post, did not make this error, and, indeed, explicitly used S-B to translate between surface temperature and radiative flux emitted from the surface despite the presence of other cooling fluxes. Until you acknowledge this problem, I’m afraid that your explanation for dealing with the paradox arising from your conceptual model has no credibility.
kribaez,
The so-called energy budget diagrams always deal with power intensity flux, as do we in our analysis.
The key issue is to identify the system flux gain.
We know for the equivalence in the relationship between the Vacuum Planet equation and the Diabatic Climate model that the system flux gain is 2 for both sets of basic analysis. Therefore, to achieve surface heating all models and methods of analysis must have a power intensity flux system gain of greater than 2.
In my analysis of the K&T 1997 Fig 7 diagram in my previous post I attempted to open the black box marked Back Radiation 324 W/m^2.
My best attempt resulted in an enhanced Surface Power Intensity budget item of 558 W/m^2 (see Table 4 in previous post). This flux produces a system gain of 2.37 relative to the raw planet Filtered Insolation of 235 W/m^ 2 (divide by 4 rule applied). Have a look at the Energy Lost to Space (Concept) column in Table 3. Note how all of the budget items listed there are required to achieve the balanced exhaust radiation flux to space of 235 W/m^2.
The key point I want to stress is this power output from a system has to include both the radiant flux and also the mass movement fluxes. The K&T 1997 Fig 7. Budget diagram clearly does this but their surface balance of 492 W/m2 produces a system flux gain of 2.09 which I calculate to be too low. This surface balance part of their diagram does not include the 67 W/m^2 of direct insolation absorbed by the air that must also be included in the radiant exhaust to space (Table 3).
”their surface balance of 492…This surface balance part of their diagram does not include the 67 W/m^2 of direct insolation absorbed by the air that must also be included in the radiant exhaust to space (Table 3).”
492=67+24+78+350-165-30-324
That’s from going across KT97 Fig. 7 left to right so this surface balance part of their diagram (492) DOES include the 67 W/m^2 of direct insolation absorbed by the air. Philip apparently incorrectly writes the 67 is not included by KT97.
Opponents will no doubt then argue that the conducted energy in the rising column cools the surface and the conducted energy in the descending column heats the surface for a zero net effect.
What they miss is that once the convective cycle completes its first loop the ascending column no longer needs to take energy from insolation reaching the surface which then returns to 255k at the ambient level of continuing insolation AND both sides are then 33k warmer which takes average surface temperature up to 288k AND there is still only 255k escaping to space.
Philip has modelled the process perfectly correctly.
Energy retained in the system as a result of a delay in the throughput of radiation must warm the surface above S-B.
Some would say…
“The “Greenhouse” theory violates the energy conservation Law DIRECTLY by trying to explain the observed 342 W m-2 IR back radiation with wave-length transformation & re-emission of 240 W m-2 solar radiation absorbed by the climate system!”
and that….
“…. the 33 K Greenhouse effect is physically a MEANINGLESS estimate. It’s a difference between the spherically averaged temperature of present-day Earth and the temperature of an imaginary blackbody disk. The actual “Greenhouse effect” is ~90 K ”
But the 33C of warming can be seen to be provided by the latent heat of water vapour.
A rising column of air passing through the condensation layer will cool at a slower rate due to warming of the air by condensation as it rises to a 10km tropopause.
That slower rate, at say 6.6ºC/km results in an increase in potential temperature of 3.3ºC/km on the descent at the dry adiabatic rate.
A 10km descent at the dry lapse rate results in 33ºC warming…. but only at the expense of cooling by evaporation in the first place.