
Guest post by Kevin Kilty
Introduction
Within the past week or two we have read posts from Dr. Spencer
(6/7/2019), Nick Stokes (6/6/2019), Lord Monckton (6/8/2019), and Willis Eschenbach (6/8/2019) covering a variety of topics involving simple block models; and each one involving, in one way or another, climate feedback. I have had a few thoughts banging around in my mind for a long time which relate to these topics and build on each of these recent works in a series of postings. This one presents a simple block model illustrating the Earth as a thermal solar panel or solar collector. It will have a direct, independent and supportive bearing on Dr. Spencer’s post.
1. Basics of a Collector
Earth bound solar panels are constructed to collect solar irradiance, reduce parasitic heat losses from conduction and convection, and transfer the solar energy they have collected as heat into a working fluid. For the Earth as a whole the only heat loss is outgoing longwave radiation. This makes analyzing the Earth as a solar collector particularly simple. Let’s begin with two important balance equations from thermodynamics.
Energy balance is our primary analytical tool. Stated in words energy balance is:
(1)
Solar energy in = Longwave (IR) energy out + energy being stored
Or symbolically for the Earth this becomes:
(2) ![]()
Where Is represents solar irradiance, αs is solar absorptivity, r is Earth radius, σ is the Stefan-Boltzmann constant (5.67 × 10−8 in S.I. units), e is the effective infra-red (IR) emissivity of the Earth, T is absolute surface temperature, and C represents a capacity for thermal storage. Since the final term representing rate of new storage in Equation 1 is quite small compared to the others, we can ignore it for our purposes, and write energy balance in terms of surface temperature as
(3) 
I have separated out the ratio![]() because it is a common engineering figure of merit for solar collectors used to guide choice of materials.
because it is a common engineering figure of merit for solar collectors used to guide choice of materials.
The second balance equation, one I have mentioned in threads here before, is entropy balance.
(4) Entropy outgoing = Entropy incoming + Entropy generated
We have no particular use for this balance equation at present, but in terms of the operation of a real solar collector we could use it to calculate energy that might have been put to useful work but was wasted by parasitic losses instead. Be assured that global climate models and solar collectors alike have to adhere to both of these balance equations in order to be realistic and provide credible results.
2. Block Model of Our Collector
Let’s stipulate the following. The sun is a black body radiator with a surface temperature of 5900K, and solar irradiance of 1370W/m2 at the orbit of the Earth. Emissivity (e) is a parameter which we will determine from energy balance. Solar absorptivity (αs) equals (1 − A) where A is the Bond Albedo of Earth. We will use a value of 0.3 for A, recognizing that this is uncertain to a degree and varies with time.
Finally, we will use a temperature of 288K for the mean surface, recognizing that this temperature is of the atmosphere at about two meters above the surface. The surface must be, on average, different than 288K in order to allow heat transfer between the surface and the air, but using 288K for the mean surface temperature serves our purposes just fine.
A block model one might derive here is shown in Figure 1. It is much simpler than the block models with feedback loops. In engineering science such a model we refer to simply as a system or possibly as a black box. If this system is linear we can state its operation using an impulse response function, or a transfer function. If the system is non-linear we usually have to get down and dirty and specify the input/output relationship in detail. In control engineering the block is known as a plant, and represents the workings of a facility or machine. It makes good sense to think of Earth as a facility.

In this case of our solar collector the input to the system is solar irradiance, which is, in fact, the only driver of the climate system (CO2 and water vapor feedbacks are internal to the system). The diagram shows that mean temperature is our only observable at present although we could choose to measure others. We use mean surface temperature as a proxy for what is happening in the climate system most of which is hidden from view inside the block. The block appears simple, but may contain great complexity including feedback loops, time constants, delays, and even additional blocks. I plan to address such hidden detail in a subsequent post building on Nick Stokes’ contribution on feedback.
3. Calculating Apparent Emissivity
Let’s put what numbers we can into the model of Equation 3.

In order to make this an equality and produce energy balance emissivity (e) must have a value of about 0.61.
We now arrive at what seems like a paradox. All the materials making up the Earth‘s surface are very black at infrared wavelengths. Pavement, water, soil, plants, skin, snow and ice all have emissivity in the range of 0.9 to 0.96. Yet, energy balance reveals that the effective emissivity is one-third lower. This is a robust result. The resolution of the paradox is that all the dark stuff on the surface is covered by an atmosphere containing infrared active gases. Just as we apply thin coatings to materials to change their radiative properties, the thin coating of atmosphere does the same for the Earth. One cannot use measured temperatures, solar irradiance, and absorptivity, and at the same time balance energy without including the effect of our greenhouse gases.
4. A Note about the Figure of Merit
The ratio ![]() is known as the figure of merit for solar collectors. To make a solar collector that becomes very hot in sunlight, we choose to make it from materials in which
is known as the figure of merit for solar collectors. To make a solar collector that becomes very hot in sunlight, we choose to make it from materials in which ![]() is as large as possible. Think of a chrome alloy tool. Its figure of merit is approximately 6 – It lays in sunlight and…Ouch! On the other hand to fabricate a surface which stays cool in sunlight we seek materials with
is as large as possible. Think of a chrome alloy tool. Its figure of merit is approximately 6 – It lays in sunlight and…Ouch! On the other hand to fabricate a surface which stays cool in sunlight we seek materials with ![]() as small as possible. Some aerospace materials, like aluminum with a thin titanium dioxide coating have a ratio around 0.2. For our Earth solar collector the figure of merit is approximately one.
as small as possible. Some aerospace materials, like aluminum with a thin titanium dioxide coating have a ratio around 0.2. For our Earth solar collector the figure of merit is approximately one.
5. Including Disturbances in the Model
In this model of Earth as a facility we can modify the block diagram to include a separate input that allows for disturbances to the system (Figure 2). It alters the system parameters and changes how the system behaves. If we know enough about the function of the system we can


6. Conclusion
The simple model of Earth as a solar collector shows conclusively that greenhouse gases in the atmosphere lower the effective emissivity of the Earth, which in turn raises the mean temperature of the surface in order to achieve energy balance. We can‘t balance energy using measured values of irradiance, albedo and temperature without a substantial greenhouse effect–A conclusion backing up Dr. Spencer‘s simple diurnal temperature model.
The model of disturbances to the Earth facility presented here is an alternative to block models containing explicit feedback loops. What I find attractive about eliminating feedback loops and making use of disturbance inputs instead, is that we can dispense with the complications which arise from the distinction between top of atmosphere values, and surface values. It also allows us to avoid feedback as an external forcing, which suggests it as a separate source of driving energy, when it is no such thing.
7. Notes:
The discussion about solar collectors and the figure of merit is available from most modern engineering textbooks on heat transport, Heat Transfer by Alan Chapman, MacMillan, 3rd edition, 1974 is an example.
For some discussion about entropy balance, and the engineering calculation of entropy transport and entropy generation, consult any engineering thermodynamics text, even one as old as Obert’s famous text from 1948, Engineering Thermodynamics; or better yet, Zemansky’s Heat and Thermodynamics in any of its eight editions.
Thanks mr. Kilty for an enlightening article.
Your model differs from the Kiehl & Trenberth (K&T) “energy” budget (actually a radiation flux calculation) in that in your budget the sun hits half the earth correctly and radiation out from the whole earth at any time, but K&T averages the incoming radiation over the whole earth all the time, which is unphysical. Thus they must “invent” back radiation in order for the calculation to add up.
You find that there must be an atmospheric effect (aka greenhouse effect) on the emissivity due to IR active elements in the atmosphere, mainly H2O, for your calculation. CO2 is only 400 ppm in the air and only 4 % of this from burning fossil fuels, so the real trillion $ question is; how much influence does this small amount of emission have on global temperature?
Measurements indicates very low influence (ECS).
PetterT
“but K&T averages the incoming radiation over the whole earth all the time, which is unphysical. ”
Could you please exactly show me where this appears in their model?
Check out Dr. Spencer’s article here:
On the Flat Earth Rants of Joe Postma
http://www.drroyspencer.com/2019/06/on-the-flat-earth-rants-of-joe-postma/
“Joe’s claim (as far as I can tell) is that that the solar flux value (often quoted to be around 342 W/m2) is unrealistic because it is for a flat Earth. But as an astrophysicist, he should recognize the division by 4 (“Fs(1-A)/4” and “S/4”) in the upper-left portion of both figures, which takes the solar constant at the distance of the Earth from the sun (about 1,370 W/m2) and spreads it over the spherical shape of the Earth. Thus, the 342 W/m2 value represents a spherical (not flat) Earth. ”
I think Mr. Kilty’s model; energy in over 1/2 earth = energy out over 1/1 earth is correct.
Solar energy in = Longwave (IR) energy out + energy being stored 0/10
You ignored the huge contribution of natural variation. At its simplest level this is the way El Nino causes the temperature to rise. That isn’t in your equation and as such your model does not work.
“That isn’t in your equation and as such your model does not work.”
Balances out to zero.
As NV is moving heat around internal to the climate system, have once been absorbed from the Sun.
That “heat being moved around” can also impact how much LWIR is emitted from the Earth at any point in time as some of that heat becomes available for generating radiation. It’s why a simplistic “energy in = energy out + energy stored” equation is almost useless when it is based on a long term average temperature. It’s why a long term average “global” temperature is useless. It can’t tell you whether days are getting warmer, nights are getting warmer, or if there is a combination of both. Warmer days and warmer nights have a hugely different impact on the environment known as Earth. The long term average is only useful for supporting a political agenda, nothing else.
+ + +
The article states proof that GHG’s lower the effective emissivity of the Earth. Surely there is no proof? The atmosphere lowers the effective emissivity, GHG’s may contribute to the effect but I see no proof that they are the effect.
Assuming a flat Earth (Is*pi*r-squared?)
I don’t think antone denies a greenhouse effect, but it is water-vapour that is responsible. CO2 is piddling.
I might add that we really do lack the precision necessary to detect any CO2 impact.
Hey Kevin,
Nice intro! My understanding is that discussion around subject of feedback was not about mere existence of the greenhouse effect but rather about magnitudes such feedback mechanisms operate. Lord Monckton and his co-authors are convinced that ‘official’ climatology overstates climate sensitivities by misunderstanding how actually feedback works in the context of control theory. I reckon your text does not address directly this issue – but looking forward for next parts!
Kevin Kilty – Thanks for your replies above.
One assumption that all of your calculations are based on is analogous to this argument:
sine(0) = 0
sine(90) = 1
therefore the average sine for 0 thru 90 is .5
But that is wrong. And, since all of your subsequent calculations are built on this wrong assumption how can you claim correctness?
I hope you’ll apply your analytical skills to correct this initial faulty assumption. When attempting to project an evenly distributed two dimensional disk over a hemisphere of the same radius with a gradient result, the equations of area need to be employed and equations of hemisphere segment areas require the use of sine:
________________________________________________________________________________________
Thus the area north of a line of latitude is
A = 2*pi*R^2(1-sin(lat))
The area between two lines of latitude is the difference between the
area north of one latitude and the area north of the other latitude:
A = |2*pi*R^2(1-sin(lat2)) – 2*pi*R^2(1-sin(lat1))|
= 2*pi*R^2 |sin(lat1) – sin(lat2)|
Thomas Homer
“One assumption that all of your calculations are based on is analogous to this argument:
sine(0) = 0
sine(90) = 1
therefore the average sine for 0 thru 90 is .5”
I don’t think that Kevin Kilty does this indeed wrong assumption.
The average incident solar radiation over the sunlit hemisphere is computed by using the square of the cosine of the incident angle (0 ° at the Equator, 90 ° at the Pole).
Integrating cos²(x) from 0 to 1 gives exactly 0.5, and the total incident is therefore obtained by using
pi * R² * flux
Rgds
J.-P. D.
>>
Integrating cos²(x) from 0 to 1 gives exactly 0.5 . . . .
<<
Really? I don’t think that’s right. I’m long past doing integrals from scratch by myself–I use integral tables. On page 420 of the CRC Standard Mathematical Tables is integral number 302 that fits the bill:
If we set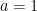 and
and 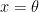 , we have our integral.
, we have our integral.
I’m not sure why you’re integrating from 0 to 1. You should be integrating along the horizontal axis. Instead of degrees, we need to use radians; therefor and
and  .
.
Now we can do the complete integrations:
Jim
Actually you’re right, but the integral should be from -pi/2 to +pi/2. That would give 1/4. But I don’t think cosine squared is the correct function.
Jim
Thanks
Sorry for butting in. I just saw a calculus question and without looking at the context thought I could save someone some time by whipping out the answer.
Obviously, your subsequent calculation below is correct. (Even more obviously, the usual approach dividing the projected circle’s area by the sphere’s area is easier.)
Opps, I left off the differentials. The two integrals should be:
and
Jim
OK
>>
The average incident solar radiation over the sunlit hemisphere is computed by using the square of the cosine of the incident angle (0 ° at the Equator, 90 ° at the Pole).
<<
I was thinking of this problem when I messed up the limits of my integration.
Say the Sun is directly over the Equator. Then the spot on the equator directly underneath the Sun has intensity I. As you move away from that spot or point, the intensity drops off. Here, we are talking about concentric rings centered on that central point. By the time you reach the terminator, the intensity is zero. The logical function describing that drop-off would be , where
, where 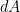 is a differential area that’s a function of
is a differential area that’s a function of 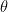 .
.
Now let’s solve for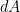 .
. 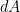 represents one of the concentric rings of infinitesimal width. The length of the ring is
represents one of the concentric rings of infinitesimal width. The length of the ring is 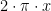 where
where  . We compute the width of the ring from the formula for the length of an arc:
. We compute the width of the ring from the formula for the length of an arc: 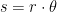 . Notice that when
. Notice that when 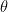 equals a full circle or
equals a full circle or  we have a circumference of a circle of radius
we have a circumference of a circle of radius  . The differential is:
. The differential is:  . Therefore the area of a ring is
. Therefore the area of a ring is  .
.
As a test, if we integrate from to
to  , we should get the area of a hemisphere.
, we should get the area of a hemisphere.
That seems to check, because is one-half the area of a sphere.
is one-half the area of a sphere.
It would be interesting to see what we’d get if we integrate the intensity of the entire hemisphere. That integral is:
If we divide by the area of a sphere, we get
It’s our old divide by 4 process that no one likes.
Jim
Hi Kevin,
You mentioned your reference surface as being TOA, but in equation 2 you used surface temperature. So your effective emissivity just becomes the ratio of OLR to upward surface flux, which is indeed around 0.6.
Your C.dT/dt is a very important number, in the long term it is what drives increased sea temperature, though its absolute instantaneous magnitude may seem small at less than 1 W /m2.
Cheers
“We now arrive at what seems like a paradox. All the materials making up the Earth‘s surface are very black at infrared wavelengths. Pavement, water, soil, plants, skin, snow and ice all have emissivity in the range of 0.9 to 0.96. Yet, energy balance reveals that the effective emissivity is one-third lower. This is a robust result.”
You have neglected the 6% Rayleigh scattering and the roughly 16% of solar shortwave that is absorbed by atmospheric water vapour.
This entire presentation constitutes an attempt to make an ill-founded paradigm fit a few known empirical facts. The standard of proof in rigorous science, however, is that no empirical facts contradict the theory. The clear contradiction here is the putative “effective emissivity” value of 0.61. But in the real world emissivity is almost always nearly equal to the coefficient of absorption, which is much higher in the IR range. As Kilty admits: “Pavement, water, soil, plants, skin, snow and ice all have emissivity in the range of 0.9 to 0.96. Yet, energy balance reveals that the effective emissivity is one-third lower. ”
Far from being “a robust result” readily explained by GHGs, as claimed, the stark discrepancy is due to the conflation of radiative intensity I of blackbody cavity radiation with actual transfer of heat Q by various known mechanisms, of which evaporation is the most important on Earth’s surface. Nowhere is this empirically established fact (see Bowen ratio from a plethora of careful experiments) adequately incorporated in Kilty’s “balance [of] energy,” who mentions entropy without ever dealing with enthalpy. In fact, the only reference to the thermodynamic Q found in this entire thread with well over a hundred comments is in the astute posting by Schroeder on June 12. Even little leaguers have better batting averages!
What exactly is the 30% albedo based upon? It cannot be 30% of the total incident solar irradiance, as around 49% of the solar heating effect is in the near infrared, of which lots will be absorbed rather than reflected.