Guest essay By Christopher Monckton of Brenchley
This series discusses climatology’s recently-discovered grave error in having failed to take due account of the large feedback response to emission temperature. Correct the error and global warming will be small, slow, harmless and net-beneficial. The series continues to attract widespread attention, not only here but elsewhere. The ripples are spreading.
My reply to Roy Spencer’s piece on our discovery at drroyspencer.com has attracted 1400 hits, and the three previous pieces here have attracted 1000+, 350+ and 750+ respectively. Elsewhere, a notoriously irascible skeptical blogger, asked by one of his followers whether he would lead a thread on our result, replied that he did not deign to discuss anything so simple. Simple it is. How could it have been thought the feedback processes in the climate would not respond to the large pre-existing emission temperature to the same degree as they respond to the small enhancement of that temperature caused by adding the non-condensing greenhouse gases to the atmosphere? That is a simple point. But simple does not necessarily mean wrong.
The present article develops the math, which, though not particularly complex, is neither simple nor intuitive. As with previous articles, we shall answer some of the questions raised in comments on the earlier articles. As before, we shall accept ad interim, ad argumentum or ad experimentum all of official climatology except what we can prove to be incorrect.
Let us conduct a simple Gedankenexperiment, running in reverse the model of Lacis et al. (2010), who found that, 50 years after removing all the non-condensing greenhouse gases from the atmosphere, the climate would have settled down to a new equilibrium, giving a slushball or waterbelt Earth with albedo 0.418, implying emission temperature 243.3 K. We shall thus assume ad experimentum that in 1800 there were no greenhouse gases in the atmosphere. For those unfamiliar with the logical modes of argument in scientific discourse, it is not being suggested that there really were no greenhouse gases in 1800.
Lacis found that, only 20 years after removal of the non-condensing greenhouse gases, global mean surface temperature would fall to 253 K. Over the next 30 years it would fall by only 1 K more, to 252 K, or 8.7 K above the emission temperature. Thus, subject to the possibility that the equatorial zone might eventually freeze over, surface temperature in Lacis’ model settled to its new equilibrium after just 50 years.
One question which few opponents in these threads have answered, and none has answered convincingly, is this: What was the source of that additional 8.7 K temperature, given that there were no non-condensing greenhouse gases to drive it? Our answer is that Lacis was implicitly acknowledging the existence of a feedback response to the 243.3 K emission temperature itself – albeit at a value far too small to be realistic. Far too small because, as shown in the previous article, Lacis allocated the 45.1 K difference between the implicit emission temperature of 243.3 K at the specified albedo of 0.418 and today’s global mean surface temperature of 288.4 K (ISCCP, 2018) as follows: Feedback response to emission temperature 252 – 243.3 = 8.7 K; warming directly forced by the naturally-occurring, non-condensing greenhouse gases (288.4 – 252) / 4 = 9.1 K, and, using Lacis’ feedback fraction 0.75, feedback response to warming from the non-condensing greenhouse gases 27.3 K: total 45.1 K. This asymmetric apportionment of the difference between emission temperature and current temperature implies that the 8.7 K feedback response to emission temperature is only 3.6% of 243.3 K, while the 27.3 K feedback response to greenhouse warming is 300% of 9.1 K. Later we shall demonstrate formally that this implausible apportionment is erroneous.
It will be useful to draw a distinction between the pre-industrial position in 1850 (the first year of the HadCRUT series, the earliest global temperature dataset) and the industrial era. We shall assume all global warming before 1850 was natural. That year, surface temperature was about 0.8 K less than today (HadCRUT4) at 287.6 K, or 44.3 K above emission temperature. Lacis’ apportionment of the 44.3 K would thus be 8.7 K, 8.9 K and 26.7 K.
We shall assume that Lacis was right that the directly-forced warming from adding the naturally-occurring, non-condensing greenhouse gases to the air was 8.9 K. Running the experiment in reverse from 1850 allows us to determine the feedback fraction implicit in Lacis’ model after correction to allow for a proper feedback response to emission temperature. Before we do that, let us recall IPCC’s current official list of feedbacks relevant to the derivation of both transient and equilibrium sensitivities:
IPCC’s chosen high-end feedback sum implies Charney sensitivities somewhere between minus infinity and infinity per CO2 doubling. Not a particularly well constrained result after 30 years and hundreds of billions of taxpayers’ dollars. IPCC’s mid-range feedback sum implies a mid-range Charney sensitivity of only 2.2 K, and not the 3.0-3.5 K suggested in previous IPCC reports, nor the 3.3 K in the CMIP3 and CMIP5 ensembles of general-circulation models. No surprise, then, that in 2013, for the first time, IPCC provided no mid-range estimate of Charney sensitivity.
None of the feedbacks listed by IPCC depends for its existence on the presence of any non-condensing greenhouse gas. Therefore, in our world of 1800 without any such gases, all of these feedback processes would be present. To induce a feedback response given the presence of any feedback process, all that is needed is a temperature: i.e., emission temperature. Since feedback processes are present, a feedback response is inevitable.
Emission temperature is dependent on just three quantities: insolation, albedo, and emissivity. Little error arises if emissivity is, as usual, taken as unity. Then, at today’s insolation of 1364.625 Watts per square meter and Lacis’ albedo of 0.418, emission temperature is [1364.625(1 – 0.418) / d / (5.6704 x 10–8)]0.25 = 243.3 K, in accordance with the fundamental equation of radiative transfer, where d, the ratio of the area of the Earth’s spherical surface to that of its great circle, is 4. Likewise, at today’s albedo 0.293, emission temperature would be 255.4 K, the value widely cited in the literature on climate sensitivity.
The reason why official climatology has not hitherto given due weight (or, really, any weight) to the feedback response to emission temperature is that it uses a degenerate form of the zero-dimensional-model equation, ΔTeq = ΔTref / (1 – f ), where equilibrium sensitivity ΔTeq after allowing for feedback is equal to the ratio of reference sensitivity ΔTref to (1 minus the feedback fraction f). The feedback-loop diagram for this equation (below) makes no provision for emission temperature and none, therefore, for any feedback response thereto.
The feedback loop in official climatology’s form of the zero-dimensional-model equation ΔTeq = ΔTref / (1 – f )
Now, this degenerate form of the zero-dimensional-model equation is adequate, if not quite ideal, for deriving equilibrium sensitivities, provided that due allowance has first been made for the feedback response to emission temperature. Yet several commenters find it outrageous that official climatology uses so simple an equation to diagnose the equilibrium sensitivities that the complex general-circulation models might be expected to predict. A few have tried to deny it is used at all. However, Hansen (1984), Schlesinger (1985), IPCC (2007, p. 631 fn.), Roe (2009), Bates (2016) are just a few of the authorities who cite it.
Let us prove by calibration that official climatology’s form of this diagnostic equation, when informed with official inputs, yields the official interval of Charney sensitivities. IPCC (2013, Fig. 9.43) cites Vial et al. (2013) as having diagnosed the CO2 forcing 
, the Planck parameter 
and the feedback sum 
from simulated abrupt 4-fold increases in CO2 concentration in 11 CMIP5 models via the linear-regression method in Gregory (2004). Vial gives the 11 models’ mid-range estimate 
of the feedback sum as 
W m–2 K–1, implying 
, and the 
bounds of 
as 
, i.e. 
.
The implicit CO2 forcing ![clip_image006[1]](http://wattsupwiththat.files.wordpress.com/2018/04/clip_image0061.png?quality=75 "clip_image006[1]"){kind=small}
, in which fast feedbacks were included, was 
W m–2 compared with the 
W m–2 in Andrews (2012). Reference sensitivity 
, taken by Vial as 
, was 
above the CMIP5 models’ mid-range estimate 
. Using these values, official climatology’s version of the zero-dimensional-model equation proves well calibrated, yielding Charney sensitivity 
on 
, near-exactly coextensive with several published official intervals from the CMIP3 and CMIP5 climate models (Table 2).
From this successful calibration it follows that, though the equation assumes feedbacks are linear but some feedbacks are nonlinear, it still correctly apportions equilibrium sensitivities between forced warming and feedback response and, in particular, reproduces the interval of Charney sensitivities projected by the CMIP5 models, which do account for nonlinearities. Calibration does not confirm that the models’ value 
for the feedback fraction or their interval of Charney sensitivities is correct. It does confirm, however, that, at the official values of f, the equation correctly reproduces the official, published Charney-sensitivity predictions from the complex general-circulation models, even though no allowance whatsoever was made for the large feedback response to emission temperature.
Official climatology trains its models by adjusting them until they reproduce past climate. Therefore, the models have been trained to account for the 33 K difference between emission temperature of 255.4 K and today’s surface temperature of 288.4 K. They have assumed that one-quarter to one-third of the 33 K was directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases and the remaining two-thirds to three-quarters was feedback response to that direct warming. Therefore, they have assumed that the feedback fraction was two-thirds to three-quarters of equilibrium sensitivity: i.e., that f was somewhere between 0.67 and 0.75.
As a first step towards making due allowance for the feedback response to emission temperature, official climatology’s version of the zero-dimensional-model equation can be revised to replace the delta input and output signals, indicating mere changes in temperature, with entire or absolute values. Note that the correct form of any equation describing natural occurrences (or any natural law) must be absolute values: the use of deltas is only permissible if the delta-equations are correctly derived from the absolute equation. Accordingly, ΔTeq = ΔTref / (1 – f ) should be Teq = Tref / (1 – f ). The revised feedback loop diagram is below:
After amendment to replace delta inputs and outputs with absolute values, official climatology’s form of the zero-dimensional model equation becomes
Teq = Tref / (1 – f )
To find f where the reference and equilibrium temperatures are known, this revised equation can be rearranged as f = 1 – Tref / Teq. In the reverse Lacis experiment, reference temperature Tref before feedback is the sum of emission temperature TE and the additional temperature ΔTE = 8.9 K that is the direct warming from adding the naturally-occurring, non-condensing greenhouse gases to the air. Thus, Tref = TE + ΔTE = 243.3 + 8.9 = 252.2 K. Equilibrium temperature Teq = 287.6 K is simply the temperature that obtained in 1850, after 50 years of the reverse Lacis experiment. Then f = 1 – Tref / Teq = 1 – 252.2 / 287.6 = 0.123, only a fifth to a sixth of official climatology’s value. The reason for the difference is that, unlike official climatology, we are taking correct account of the feedback response to emission temperature.
Next, how much of the 35.4 K difference between Tref = 252.2 K and Teq = 287.6 K is the feedback response to emission temperature TE = 243.3 K, and how much is the feedback response to the direct greenhouse-gas warming ΔTE = 8.9 K? Simply take the product of each value and f / (1 – f) = 0.14, thus: 243.3 x 0.14 = 34.1 K, and 8.9 x 0.14 = 1.3 K. We prove that this is the correct apportionment by using the standard, mainstream form of the zero-dimensional-model equation that is universal in all dynamical systems except climate. The mainstream equation, unlike the degenerate climate-science form, explicitly separates the input signal (in the climate, the 255.4 K emission temperature) from any amplification (such as the 8.9 K warming from adding the non-condensing greenhouse gases to the atmosphere).
The mainstream zero-dimensional model equation is Teq = Tref μ / (1 – μβ), where Tref is the input signal (here, emission temperature); μ = 1 + ΔTref / Tref is the gain factor representing any amplification of Tref such as that caused by the presence of the naturally-occurring, non-condensing greenhouse gases; β is the feedback fraction; μβ is the feedback factor, equivalent to f in climatology’s current version of the equation; and Teq is equilibrium temperature at re-equilibration of the climate after all feedbacks of sub-decadal duration have acted.
The feedback loop for this corrected form of the zero-dimensional-model equation is below:
The feedback loop diagram for the standard zero-dimensional-model equation
Teq = Tref μ / (1 – μβ)
One advantage of using this mainstream-science form of the zero-dimensional model is that it explicitly and separately accounts for the input signal Tref and for any amplification of it via the gain factor μ in the amplifier, so that it is no longer possible either to ignore or to undervalue either Tref or the feedback response to it that must arise as long as the feedback fraction β is nonzero.
It is proven below that the apportionment of the 35.4 K difference between Tref = 252.2 K and Teq = 287.6 K in 1850 derived earlier in our Gedankenexperiment is in fact the correct apportionment. Starting with the mainstream equation, in due time we introduce the direct or open-loop gain factor μ = 1 + ΔTref / Tref. The feedback factor μβ, the product of the direct or open-loop gain factor μ and the feedback fraction β, has precisely the form that we used in deriving the feedback fraction f as 1 – (243.3 + 8.9) / 287.6 = 0.123, confirming that our apportionment was correct.
Note in passing that in official climatology f is at once the feedback fraction and the feedback factor, since official climatology implicitly (if paradoxically) assumes that the direct or open-loop gain factor μ = 1. In practice, this particular assumption leads official climatology into little error, for the amplification of emission temperature driven by the presence of the non-condensing greenhouse gases is a small fraction of that temperature.
But was it reasonable for us to assume that the 287.6 K temperature in 1850, before Man had exercised any noticeable influence on it, was an equilibrium temperature? Well, yes. We know that in the 168 years since 1850 the world has warmed by only 0.8 K or so, and official climatology attributes all of that warming to Man, not Nature.
Was it reasonable for us to start with Lacis’ implicit emission temperature of 243.3 K, reflecting their specified albedo 0.418 on a waterbelt Earth in the absence of the non-condensing greenhouse gases? Why not start with Pierrehumbert (2011), who said that a snowball Earth would have an albedo 0.6, implying an emission temperature 221.5 K? Let’s do the math. The feedback fraction f = μβ would then be 1 – (221.5 + 8.9) / 287.6 = 0.20.
Thus, from a snowball Earth to 1850, the mean feedback fraction is 0.20; from a waterbelt Earth to 1850, it is 0.12; and at today’s albedo 0.293, implying an emission temperature 255.4 K, it is 1 – (255.4 + 8.9) / 287.6 = 0.08. Which is where we came in at the beginning of this series. For you will notice that, as the great ice sheets melt, the dominance of the surface albedo feedback inexorably diminishes, whereupon the feedback fraction falls over time.
Though the surface albedo feedback may have dominated till now, what about the biggest of all the feedbacks today, the water-vapor feedback? The Clausius-Clapeyron relation implies that the space occupied by the atmosphere may (though not must) carry near-exponentially more water vapor – a greenhouse gas – as it warms. Wentz (2007) found that total column water vapor ought to increase by about 7% per Kelvin of warming. Lacis (2010) allowed for that rate of growth in saying that if one removed the non-condensing greenhouse gases from today’s atmosphere and the temperature fell by 36 K from 288 to 252 K, there would be about 10% of today’s water vapor in the atmosphere: thus, 100% / 1.0736 = 9%.
Specific humidity (g kg–1) at pressure altitudes 300, 6000 and 1000 mb
However, though the increase in column water vapor with warming is thus thought to be exponential, the consequent feedback forcing is approximately logarithmic (just as the direct CO2 forcing is logarithmic). What is more, a substantial fraction of the consequent feedback response is offset by a reduction in the lapse-rate feedback. Accordingly, the water-vapor/lapse-rate feedback response is approximately linear.
Over the period of the NOAA record of specific humidity at three pressure altitudes (above), there was 0.8 K global warming. Therefore, Wentz would have expected an increase of about 5.5% in water vapor. Sure enough, close to the surface, where most of the water vapor is to be found, there was a trend in specific humidity of approximately that value. But the water-vapor feedback response at low altitudes is small because the air is all but saturated already.
However, at altitude, where the air is drier and the only significant warming from additional water vapor might arise, specific humidity actually fell, confirming the non-existence of the predicted tropical mid-troposphere “hot spot” that was supposed to have been driven by increased water vapor. In all, then, there is little evidence to suggest that the temperature response to increased water vapor and correspondingly diminished lapse-rate is non-linear. Other feedbacks are not large enough to make much difference even if they are non-linear.
Our method predicts 0.78 K warming from 1850-2011, and 0.75 K was observed
One commenter here has complained the Planck parameter (the quantity by which a radiative forcing in Watts per square meter is multiplied to convert it to a temperature change) is neither constant nor linear: instead, he says, it is the first derivative of a fourth-power relation, the fundamental equation of radiative transfer. Here, it is necessary to know a little calculus. Adopting the usual harmless simplifying assumption of constant unit emissivity, the first derivative, i.e. the change ΔTref in reference temperature per unit change ΔQ0 in radiative flux density, is simply Tref / (4Q0), which is linear.
A simple approximation to integrate latitudinal variations in the Planck parameter is to take the Schlesinger ratio: i.e., the ratio of surface temperature TS to four times the flux density Q0 = 241.2 Watts per square meter at the emission altitude. At the 255.4 K that would prevail at the surface today without greenhouse gases or feedbacks, the Planck parameter would be 255.4 / (4 x 241.2) = 0.26 Kelvin per Watt per square meter. At today’s 288.4 K surface temperature, the Planck parameter is 288.4 / (4 x 241.2) = 0.30. Not much nonlinearity there.
It is, therefore, reasonable to assume that something like the mean feedback fraction 0.08 derived from the experiment in adding the non-condensing greenhouse gases to the atmosphere will continue to prevail. If so, the equilibrium warming to be expected from the 2.29 Watts per square meter of net industrial-era anthropogenic forcing to 2011 (IPCC, 2013, Fig. SPM.5) will be 2.29 / 3.2 / (1 – 0.08) = 0.78 K. Sure enough, the least-squares linear-regression trend on the HadCRUT4 monthly global mean surface temperature dataset since 1850-2011 (above) shows 0.75 K warming over the period.
But why do the temperature readings from the ARGO bathythermographs indicate a “radiative energy imbalance” suggesting that there is more warming in the pipeline but that the vast heat capacity of the oceans has absorbed it for now?
One possibility is that not all of the global warming since 1850 was anthropogenic. Suppose that the radiative imbalance to 2010 was 0.59 W m–2 (Smith 2015). Warming has thus radiated 2.29 – 0.59 = 1.70 W m–2 (74.2%) to space. Equilibrium warming arising from both anthropogenic and natural forcings to 2011 may thus eventually prove to have been 34.8% greater than the observed 0.75 K industrial-era warming to 2011: i.e., 1.0 K. If 0.78 K of that 1.0 K is anthropogenic, there is nothing to prevent the remaining 0.22 K from having occurred naturally owing to internal variability. This result is actually consistent with the supposed “consensus” proposition that more than half of all recent warming is anthropogenic.
The implication for Charney sensitivity – i.e., equilibrium sensitivity to doubled CO2 concentration – is straightforward. The models find the CO2 forcing to be 3.5 Watts per square meter per doubling. Dividing this by 3.2 to allow for today’s value of the Planck parameter converts that value to a reference sensitivity of 1.1 K. Then Charney sensitivity is 1.1 / (1 – 0.08) = 1.2 K. And that’s the bottom line. Not the 3.3 K mid-range estimate of the CMIP5 models. Not the 11 K imagined by Stern (2006). Just 1.2 K per CO2 doubling. And that is nothing like enough to worry about.
None of the objections raised in response to our result has proven substantial. For instance, Yahoo Answers (even less reliable than Wikipedia) weighed in with the following delightfully fatuous answer to the question “Has Monckton found a fatal error?”
What he does is put forward the following nonsensical argument –
1. If I take the 255.4 K temperature of the earth without greenhouse gases, and I add in the 8K increase with greenhouse gases I get a temperature of 263.4 K.
2. Now, what I’m going to say is say that this total temperature (rather than just the effect of the greenhouse gases) leads to a feedback. And if I use this figure I get a feedback of 1 – (263.4 / 287.6) = 0.08.
And the problem is … how can the temperature of the planet (255.4 K) without greenhouse gases then lead to a feedback? The feedback is due to the gases themselves. You can’t argue that the feedback and hence amplified temperature due to greenhouse gases is actually due to the temperature of the planet without the greenhouse gases! What he’s done is taken the baseline on which the increase and feedback is based, and then circled back to use the baseline as the source of the increase and feedback.
So, I’m afraid it’s total crap …
The error made by Yahoo Answers lies in the false assertion that “the feedback is due to the gases themselves”. No: one must distinguish between the condensing greenhouse gases (a change in the atmospheric burden of water vapor is a feedback process) and the non-condensing greenhouse gases such as CO2 (nearly all changes in the concentration of the non-condensing gases are forcings). All of the feedback processes listed in Table 1 would be present even in the absence of any of the non-condensing greenhouse gases.
Another objection is that perhaps official climatology makes full allowance for the feedback response to emission temperature after all. That objection may be swiftly dealt with. Here is the typically inspissate and obscurantist definition of a “climate feedback” in IPCC (2013):
Climate feedback An interaction in which a perturbation in one climate quantity causes a change in a second, and the change in the second quantity ultimately leads to an additional change in the first. A negative feedback is one in which the initial perturbation is weakened by the changes it causes; a positive feedback is one in which the initial perturbation is enhanced. In this Assessment Report, a somewhat narrower definition is often used in which the climate quantity that is perturbed is the global mean surface temperature, which in turn causes changes in the global radiation budget. In either case, the initial perturbation can either be externally forced or arise as part of internal variability.
IPCC’s definition thus explicitly excludes any possibility of a feedback response to a pre-existing temperature, such as the 255.4 K emission temperature that would prevail at the surface in the absence of any greenhouse gases or feedbacks. It was for this reason that Roy Spencer thought we must be wrong.
Our simple point remains: how can an inanimate feedback process know how to distinguish between the input emission of temperature of 255 K and a further 9 K of temperature arising from the addition of the non-condensing greenhouse gases to the atmospheric mix? How can it know it should react less to the former than to the latter, or (if IPCC’s definition is followed) not at all to the former and extravagantly to the latter? In the end, despite some valiant attempts by true-believers to complicate matters, our point is as simple – and in our submission as unanswerable – as that.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Y does it seem like all the historic weather data charts on this site end in 2011?? What year is this anyway….I’m conrfused….
In response to Meigs, the most recent IPCC Assessment Report was in 2013, and it gave estimated net anthropogenic forcing from all sources to 2011. For a fair comparison, therefore, one must look at the warming to 2011 as well. Nothing more complicated than that.
Harry: I’ve just been re-scanning the comments on Christopher Monckton’s original “Game Over” and this article. I’m not familiar with the gory detail here (I’m a software consultant, originally trained as a pure mathematician – in fact, I was at Cambridge at the same time as Christopher). But I have a nose for what fits and what doesn’t. On the other thread, commenters called “Frank” and “Nylo” raised this issue, and “Joe Born” weighed in. And here, “Martin Mayer” has stated very concisely the problem that I see with Christopher’s argument.
Then I scrolled to the end of the comments, and found that you had anticipated me – by a couple of hours or so. Yes, the feedback factor can’t possibly be constant at different temperatures!
A thought experiment: Start with an Earth at 3 degrees K, the cosmic background. All greenhouse gases are solid. The molecules can’t vibrate in the modes necessary for the greenhouse effect – or am I wrong? So there’s no feedback at all, at all. Now, turn on the Sun and let the planet warm up to the 255K “emission” temperature. The greenhouse gases, other than water vapour, are now free to do their thing.
Hansen may have assumed that at an average 255K (minus 18C) there was no water vapour. If so, that has to be wrong. Today, we have an average global temperature of 14C, but the highs are around 50C. Those tend to be in dry places, but there surely is water vapour there. So there must have been water vapour, and liquid water too, in our thought experiment when it reached the “magic” 255K. I’m not sure whether, or how much, liquid water can contribute to the greenhouse effect. But ignoring that, as temperature rose towards and beyond 255K in our thought experiment, the water vapour feedback would have increased. So the feedback factor would have changed dramatically as the Earth’s average temperature crossed the line, in terms of average temperature, from water freezing to liquid.
Lacis et al, if I understand right, tried to apportion the greenhouse effect between water vapour and the rest. Christopher is absolutely right to question that apportionment, and what they deduced from it. And my sense of smell tells me that, given the unknowns, it’s odd that the sensitivity answer came out close to the IPCC estimates. But I still don’t buy Christopher’s argument.
“But I still don’t buy Christopher’s argument.”
I do. My Mech Eng control theory was my favorite course. MBs use of an electrical circuit(independently solved) is final proof. The worry about non linearity over such a small temperature range is overreach imo. Less than 3 % likely.
It looks very much to me like à terminology problem. The feedbak term “f” in climatology is delta f in other fields of science. Similar to “forcing” which is delta force in oth34 disciplines.
It is this misuse of terminology that is at the heart of the problem.
Neil Lock seems to think that the interval of interest is from 3 K to 288 K. No, it isn’t: it’s from 255 K to 288 K.
Christopher: But the interval of interest, as you call it, includes the freezing/melting point of water. Around which, we might expect the feedback factor to change significantly. What have I missed?
Oh, and in your earlier essay where you say that the equations are equivalent for delta T and for T, you’re implying that the interval of interest is 0K to 288K.
Neil, you seem to assume that all water on earth would be ice if the earth’s average temperature was -18C, that’s wrong. It’s _average_ temperature, the equator would be above freezing. Now we have an average temperature of 14C, but still there is ice. According to your assumption we should only have liquid water today, since the average temperature is above freezing.
The temperature range of interest is 287K to perhaps 292K, but hopefully less. And you can go back to the LGM if necessary say 282K That is the only range where feedback is relevant and probably a little wide to expect linearity.
In the few billion years, we haven’t had a planet without non-condensible GHGs in the atmosphere. It’s been at least 500 million years since we may have had a snowball Earth, a phenomena that is intensely debated and poorly understood. No one appears to believe that this period was due to the total absence of non-condensible GHGs in the atmosphere.
Peter: No, I suggested that Hansen may have assumed that there is no water vapour when the average temperature is -18C. As you say, that is wrong.
Frank now appears to be admitting that nonlinearity is not much of an issue, after all. If so, he is now correct. But he continues to have difficulty with the concept – well established in the mathematics of dynamical systems – of studying the change of state of the system between two presumed equilibria. One such equilibrium is the Earth’s emission temperature in the absence of greenhouse gases or feedbacks. Another is the Earth’s temperature in the presence of condensing gases and, therefore, of the feedbacks thereto in response to the emission temperature. Another is the Earth’s temperature in the presence of both condensing and non-condensing greenhouse gases, as it stood in 1850 before any anthropogenic perturbation. Another is the temperature following the anthropogenic perturbations to date. Another is the temperature at equilibrium following a doubling of CO2 concentration compared with today. Such stepwise calculations, albeit that several of the steps are artificial, are precisely how official climatology operates. If Frank thinks that it should not do so, he should bring his concerns not to me but to secretariat@ipcc.ch.
A wonderful read Monckton of B. Over 300 responses is an indicator in itself of the importance of your finding, even if all were negative, maybe particularly if all had been negative. A late comment like mine is likely to go unread but I just wanted to say that before this work of yours and amici, I wasted little time on the official math of feedbacks because after climategate and the rest of it, I knew that the official clime syndicate “math” was in some way self serving anyway.
For the first time, I have educated myself on the details, following your straightforward arguments and dare I say simple math (simple like E=Mc^2). You would be a superlative teacher.
The importance of your work is also indicated by the fact that it was raised even by visitors to Yahoo Answers. The Yahoos are, of course, well named.
https://www.merriam-webster.com/dictionary/yahoo
You have poked a huge hole in the clime syndicate hive and I predict that every worker and drone has dropped his other dreary studies to concentrate their venom on your work. Please take care for your security Christopher.
I am most grateful to Mr Pearse for his kind comments. And I am glad that he has not found the rather technical explanation of our result in the head posting too difficult. It is indeed significant that Yahoo Answers has already found it necessary to try – in a remarkably half-baked way – to impugn our result. Now that the matter has been publicly aired, the truth will inexorably spread, however hard the totalitarian profiteers of doom try to stop it. That is the value of true science: in the end, it is unaswerable.
As for my personal security, I am sure that those driving this scam, who have spent large amounts of time and effort on trying and failing to neutralize me, will not be stupid enough to turn me into some sort of martyr. Nothing would be more fatal to their pseudo-moralizing posture than that.
The problem is terminology. What climatology calls “forcing” is a delta force in all other fields. what climatology calls feedback is a delta feedback in all other fields.
The problem is that “f” has been used to represent both feedback and delta feedback which hides the source of the error.
A new term needs to be added to the equations to distinguish the different definitions of the term “feedback”.
Delta feedback may not be precisely correct. But there is a definite difference between how an engineer views feedback as compared to a climatologist.
As such it is an error to use the term “f” to represent two different things. It leads to problems like 1=2. You can prove anything.
In engineering terms, climatology filers out the DC portion of the signal and only applies feedback to the AC portion. So long as you only work in anomalies this is hidden from view.
However, when you convert to absolutes you also need to allow for feedback on the DC portion of the signal.
Climatology T = AC+DC+f(AC)
Engineering T = AC+DC+f(AC+DC)
In reply to Mr Berple, the feedback fraction f is unitless,. It is not, therefore, a delta. The feedback response, in Kelvin, is indeed a delta. It may be helpful if I explain the nomenclature. The input signal (emission temperature), the output signal (equiulibrium temperature) and the feedback response are all denominated in Kelvin. The feedback fraction f, like the open-loop gain factor mu and the feedback factor mu x beta, is unitless. As for f, it does duty in official climatology both as the feedback fraction and as the feedback factor, for mu is assumed to be unity.
Given a surface temperature difference of +/- 42K , Antarctica night (-49°C) vs, Riyadh day (35°C), the emission would be 1.31 times as much in Riyadh and 0.37 times as much in Antarctica, compared to the emission at 288 K average. The departure form linearity is not insignificant over this range, though as your comments imply, the non-linearity would diminish the feedback, ie. it is a negative feedback. I realize that your feedback equation is about a shift in average temperature, thus only a degree or two which is close enough that the non-linearity would be well within the margin of error. Two other comments. Willis, in one of his posts on tropical thunderstorms and temperature feed back, had graphics that indicated a nearly asymptotic limit to temperature of about 34C. Very nonlinear. In regard to water vapor feed back, any heating would result in such feedback, it would be nonsensical to posit that CO2 would be special in this regard. For climate purposes there is an unlimited amount of water available, thus any such feedback should be maximized based on temperature. CO2 would be irrelevant to this, Given the wide variation of temperatures on the surface of the planet currently and in the geologic past, any hypothesis on tipping points or run-away heating should be unequivocally falsified.
“In regard to water vapor feed back, any heating would result in such feedback, it would be nonsensical to posit that CO2 would be special in this regard”
Good point. In addition, if thunderstorms on average start two minutes earlier each day, and finish 2 minutes later, would our measuring systems know? Nope.
Al in Kansas is quite right. If the nonlinearity in feedbacks were anything like as great as it would have to be to impugn our result, global surface temperature would not have varied by as little as 3 K either side of the 810,000-year mean.
May I express my considerable gratitude for the exemplary manner in which Lord Monckton has laid out his argument, and has defended it? And, perhaps, entertained us at the same time? I note the close spacing of the time stamps on his responses to sequential comments here: responses which, despite the short composition time allowed, are pertinent, elegantly constructed, and resolutely informative. And I believe he has not omitted a response to any relevant comment, whether supportive or critical. Rarely has such a complete and competent involvement been recorded in the long history of this great dialogue. I would like to see others follow his example. Perhaps someone from the ‘climate establishment’ would like to join these threads. Or do they think it beneath them?
Now, although I follow the logic of Lord Monckton’s argument, I am not qualified to judge whether the assumptions that he has made – particularly (and this is rather important) whether the error he has claimed to find really is fundamental to basics of the establishment case for CAGW. I am inclined to accept it, for it happens to confirm and explain my own independently derived prejudices upon the subject!
I’d also like to thank – not for the first time – the efforts of Nick Stokes to bring the lord to heel. Nick is a considerable intellect, and he has the knowledge and ammunition to curb the excesses of commenters here, which is much appreciated. However, I’m not sure what Nick actually thinks himself. He’s very good as a devil’s advocate, always probing for error or inconsistency, always challenging, and that’s excellent stuff. But I never ever see him admitting any uncertainties in his own arguments, nor do I hear him making a coherent overall case, nor accepting that others might just have a point. Keep it up, Nick, but it would be good to see you open up a bit yourself.
One point I do take from the argument as a whole. Many here do find it very difficult indeed to accept the central point that Lord M is making – that feedbacks WILL occur – and occur in very much the same manner – on an earth devoid of non-condensing greenhouse gases. Nick seems included in those. Well, that’s something that I have always regarded as self-evident, and if the math describing electrical circuits are a good analogy I’ll take that as a tick of confirmation. I fail to follow the logic of the counter argument at all, and I think it must result from some slavish misinterpretation of the definitions implicit in the forcings/feedback issue. It is a false dichotomy. The real argument should be about how CO2 differs in its effect locally (polar/desert/nocturnal/high altitude) and may therefore reset the thermostat.. Therein is the refuge of the CAGW case, and much is yet be written about it.
Brilliant thread.
Thanks, moth
However, I must say that throughout this thread, and indeed on all threads since the end of March, all my comments (even this one) have gone through moderation, which hampers dialogue considerably. I don’t know why; I have not seen anything said by the mods or Anthony that would explain why this is so.
Happens to me from time to time.
Earmarked as controversial no doubt.
I am most grateful to Mothcatcher for his exceptionally kind comments. I have done my best to answer all relevant points, from whichever direction they came. Our control theorists (two engineers and a professor of applied control theory) are entirely content that even an unamplified input signal in any dynamical system on which nonzero feedback processes bear will induce a feedback response. As Mothcatcher rightly points out, that conclusion is inescapable from the mathematics of the feedback loop – mathematics that applies no less to the climate than to any other dynamical system.
Our point is indeed a simple one, and the only reason why we have had to provide such lengthy and detailed treatments of it is to nail shut the various rat-holes by which official climatology will seek to escape.
I think I am not being unfair when I say that none of the comments in these threads has landed a blow fatal to our result. There has been some nibbling around the edges, but that is all.
The big question now is whether the gatekeepers of the leading climate journals will close the portcullis and try to prevent our paper from being published. If a genuine and material error in our result is found, all well and good – we shall retire gracefully from the field. If, however, no error is found, let it be known to all that the relevant public authorities are now watching carefully how official climatology handles our result. In view of the staggering financial and human cost of global-warming mitigation policies, any dishonest attempt to preserve and protect the profits of those gaining by those policies by improperly refusing to publish our result may occasion a prosecution, not by us but by the public authorities themselves.
Climate scientists are about to find out – the hard way if necessary – that they are subject to just the same law as the rest of us. They are no longer immune. It will come as no surprise to readers of this column that there have been a few instances of outright criminal deception in the peddling of the official climate-change storyline. Such deceptions will no longer be tolerated. It is time for the truth to have its day.
If Lord Monckton is still kindly attending to the many replies, can I ask a question on the importance, or otherwise, of the non-linearity in the feedback parameter at temperatures in the region 255°K to 288°K?
As mentioned above, in my moment of clarity, if an input temperature of 263°K (the sum of the 255°K emission + 8°K non-condensing GHGs) results in an equilibrium temperature of 288°K that implies that f=0.08, using f = 1 – ΔTref / ΔTeq.
Then if we perturb the reference input signal of 263°K. by a ΔT of 1.2°K (the direct temperature rise for doubling CO2) so means the input signal rises to 263+1.2 = 264.2. This results in an equilibrium temperature of Teq = Tref / (1 – f ) = 264.2 /(1-0.08) = 289.3°K, which is an equilibrium temperature rise, ΔTeq, of 1.3°K.
You can also use the ΔTeq = ΔTref / (1 – f ) to arrive at the same result. 1.2°K /(1-0.08) = 1.3°K
So surely, if we can assume that the intricate water vapor and cloud feedbacks are linear in the small interval from 263°K to to 264.2°K then the resulting f = 0.08 will be robust to use for the Charney Sensitivity.
So there’s no need to concern ourselves with non-linearity near absolute zero when our nitrogen atmosphere turns to a super fluid, or snowball earths, or other exciting situations. We are only looking for a robust estimate of the feedback parameter at, or in close neighbourhood (perhaps ±3°K?) to, our single data point, namely the input and equilibrium temperatures in the year 1850 with all the feedback mechanisms that are present in the system at that time.
Is this correct or have I missed something obvious?
Mr Palmes is correct that, once a reasonable value for the feedback fraction has been settled upon, the very small temperature perturbations from now until all oil, coal and gas reserves are exhausted mean that we do not have to worry about nonlinearity in feedbacks.
However, in order to provide a theoretical demonstration of the value of the feedback fraction, it is necessary to examine the interval between two presumed equilibria – the emission temperature of 255 K and the pre-industrial temperature of 287 K that prevailed in 1850. Since the interval is 32 K, nonlinearity in feedbacks might in theory make a difference here. It is easy to establish that the mean feedback fraction, after correction of climatology’s central error, is only 0.08. But the various shriekers here, yelling out the Party Line over and over again, try to pretend that the nonlinearity in the feedback fraction is so great that by 1850 the feedback fraction must have been an order of magnitude greater than the mean value of 0.08.
Trouble is, none of the feedbacks listed in Table 1 contains within it a nonlinearity sufficient – even in the wildest dreams of the totalitarian screamers – to come anywhere close to ten times the 0.08 that we have derived. The water vapor feedback may have increased the atmospheric burden of water vapor tenfold over that 32 K interval, but the feedback response is logarithmic, offsetting to some considerable degree the near-exponential increase in the water vapor content. What is more, the lapse-rate feedback runs directly counter to the water-vapor feedback owing to the imagined (but actually imaginary) tropical mid-troposphere hot-spot that models predict but is not observed in reality except in one or two defective datasets. So there is certainly no tenfold nonlinearity there.
Worse still for the totalitarians, we derived a current value of the feedback fraction from IPCC’s official estimate of 2.29 Watts per square meter of net anthropogenic radiative forcing from 1850-2011 and the observed temperature change of 0.75 K over the period. The feedback fraction thus derived was 0.05. Even after allowing for the “radiative imbalance” in that the oceans are warming, and even on the very generous assumption that none of the warming since 1850 was anthropogenic, the feedback fraction is below 0.3, implying an equilibrium sensitivity of just 1.5 K.
As if that were not enough, our correction to the official math does not in any way alter such nonlinearity as already subsists in the temperature feedbacks. Therefore, doing the calculation correctly will inevitably very greatly reduce equilibrium sensitivity compared with today’s estimates.
The totalitarians are using nonlinearity as the last refuge of the scoundrel: but, bearing in mind all the evidence rather than the very partial selections of it that they have tried to present or misrepresent, it actually makes very little difference to the final numbers. The science is in, the truth is out, Al Gore is through, the game is up, the scam is done and the scare is over.
My thanks to Lord Monckton once again.
But I’m still hoping that any potential non-linearity between 263°K and 288°K will have almost no effect whatsoever.
To borrow some terms from calculus and integration, isn’t what we doing here a kind of ‘integration’ of the feedbacks that occur in the interval between 263°K and 288°K? I know it is not strictly an integration in the mathematic sense, but suspend your mathematical rigor for minute:
Firstly make f a continuous function of T, and then integrate f from 263°K and 288°K with the result equivalent to a constant f 263<T<288 = 0.08, and so the trillion-dollar question is… what happens when we perturbate the interval from 263°K to 264.2°K (a ΔTref, of 1.2°K for 2x CO2)? Will the result be 289.3°K (ΔTeq, of 1.3°K) as expected? Is it valid to carry over our f=0.08 value for this new interval?
In terms of our ‘integral’, we are now integrating our f from 264.2 to 288.3, so over a slightly different interval. But the vast majority of this ‘integral’ is taken over exactly the same range, so this part will yield the same result. We’re just exchanging a small section at the start, with a section added to the end. The middle section of 23.8°K, (or 95% of the total), is common to both calculations.
So to play devil’s advocate and stress test The Monckton Conjecture, why not ask someone to think of the most extreme of non-linear assumptions they can reasonably imagine for f as a function of T in this interval. Then remind them that we are only exchanging the bottom 5% of the interval for a 5% at the top, so how much effect will this have?
I hope the answer would be ‘very little’.
PS We might jest calling this ‘The Monckton Conjecture’, but it may well be useful to name it soon, to help the idea spread. Memes need a name to spread quickly. This is the identification of an egregious error, but this can't be referred to as Monckton's Egregious Error (it’s not your error). Henry Heimlich has his Manoeuvre. The Monckton Manoeuvre maybe? Or The Monckton Supposition? I think you should have the honour of naming your baby.
In response to Mr Palmes, we had of course done some calculations to see whether even the most extreme nonlinearity in the feedback fraction that is plausible after correction of official climatology’s error could make a significant difference to Charney sensitivity. We know that the mean feedback fraction – assuming linearity just for the moment – is 0.081. We have then made a number of assumptions designed to bend the argument rather beyond what is really possible by assuming that the nonlinearity in the feedback fraction is as great as the nonlinear increase of 7% per Kelvin in the column water vapor (actually, we have assumed that at 255 K the increase is 10% per Kelvin, falling gradually to 7% at 287 K). In making this assumption, we have made no reduction for the fact that the water-vapor feedback forcing is approximately logarithmic, offsetting to a large extent the nonlinearity in the column water vapor itself; we have made no reduction for the fact that the interval of interest is not 255 to 287 K but 264 to 287 K; we have made no reduction for the fact that the tropical mid-troposphere hot spot predicted by the models as an inevitable consequence of their excessive estimate of the water vapor feedback is not observed except in one or two defective metadatasets; and we have made no reduction for the fact that, if the hot spot does come into existence, the lapse-rate feedback will become more strongly negative and will countervail to an appreciable extent against the water vapor feedback; and we have made no reduction for the fact that no feedback other than the water vapor feedback has anything like a 7%-per-Kelvin compound acceleration.
In short, we have bent over backwards to accommodate official climatology’s position. And the bottom line is that at 255 K the feedback fraction would be 0.016, while at 287 K it would be about 0.2. The mean feedback fraction would be 0.081. Now, this is a rough-and-ready calculation, of course. But one would be hard put to it to produce a feedback fraction even as high as 0.2 if one made all the reductions that we’d be entitled to make. But let’s call it 0.2. In that event, Charney sensitivity would be less than 1.4 K per CO2 doubling, instead of the 1.2 K per doubling that one gets from assuming the mean feedback fraction of 0.081. The difference made even by the extreme nonlinearity that we have deliberately assumed is less than 0.2 K. Now, if you go back and look at all the waffle that the paid agents of climate fanaticism here have devoted to the nonlinearity issue, you will see what nonsense it all was. Your instinct is quite right: nonlinearity is a non-issue.
Of course, anyone approaching this question with an open mind rather than an open mouth would have seen this as easily as you have. For whatever nonlinearity subsists in the present system will also subsist in our system: but the correction made by our system will inevitably and greatly reduce Charney sensitivity, regardless of the fact that there is nonlinearity. That conclusion isn’t rocket science: it’s common sense. Your instinct, therefore, is amply borne out by the calculations we did.
That’s a nice article, which is actually tackling a problem even bigger: IPCC just doesn’t even have a proper definition of “greenhouse effect”. It use TWO definition concurrently, despite being mutually exclusive, and this shows in Lacis and al. and all related stuff. So, basically, you cannot escape the tangled web of deception
One definition you find page 126 (with figure 1.1) of WG1AR5_ALL_FINAL.pdf.
“The longwave radiation (LWR, also referred to as infrared radiation) emitted from the Earth’s surface is largely absorbed by certain atmospheric constituents—water vapour, carbon dioxide (CO2), methane (CH4), nitrous oxide (N2O) and other greenhouse gases (GHGs); see Annex III for Glossary— and clouds, which themselves emit LWR into all directions. The downward directed component of this LWR adds heat to the lower layers of the atmosphere and to the Earth’s surface (greenhouse effect).”,
The other definition you find in glossary
“Greenhouse effect: The infrared radiative effect of all infrared-absorbing constituents in the atmosphere”
Sound similar? indeed. Is it the same? NO.
For instance, when water condense into clouds and release heat (or just when hot air heated by conduction move upward), this heat is in part lost to space, and in part contributes do “back-radiation”
By the first definition, it is NOT part of the greenhouse effect, as it doesn’t come from LWR emitted from the Earth’s surface
By the second definition it IS part of the greenhouse effect, as it is radiated back thanks to the GHG.
So where does the 8.7K you are talking about? From the fact that at today’s albedo 0.293, emission temperature IS (not just “would be”) 255.4 K,. Just not forget that this is temperature as seen from space, coming from a few kilometers higher that surface. Lapse rate (which doesn’t rely on any GHG, just on some heating from the bottom of atmosphere, to spawn the gradient) ) then makes the difference for surface temperature, making it higher.
If albedo increase in Lacis calculation, I guess this has to do which more clouds, so part of the emission to space would come from clouds (not GHG), and lapse rate would, again, give a somewhat higher temperature at surface than as seen from space.
Said otherwise: these 8.7K would come from back-radiation from clouds, from heat provided by convection
“By the first definition, it is NOT part of the greenhouse effect”
The first is not a definition of GHE. It is a statement about what happens to LWR. It says that some is directed downward, and is then part of the GHE. It does not say that it is the whole of the GHE.
You find no where, before or later in the page, a statement that this is just a contribution, no other contribution is mentioned. I didn’t cut the statement, I reported the whole explanation given. So it is definition, whether you like it or not.
And this first definition is also the very same that gave “greenhouse effect” its name, that is, the way a real greenhouse was (wrongly) assumed to work when the effect was (wrongly) named : interception of LWR going out by a “screen” (of glass in the wrong explanation of real greenhouse, of GHG in atmospheric GHE). Nothing else, no radiation of, say, condensing dew on the glass. Just radiation coming from the bottom, and impeded, net making it lower that it would be without the screen.
So you are wrong.
Besides, please note that from all the heat moved upward in the atmosphere by convective transport, only a fraction is “back-radiated”, so overall the process cools the surface even if it contributes to back-radiation. Meaning, it has negative contribution to surface temperature and you have no reason to include it in a “greenhouse effect”. Which the first definition doesn’t, but the second does.
paqyfelyc: If you want a simple unambiguous and accurate measure of the GHE, use the difference between average surface OLR and average TOA OLR, 150 W/m2. This slow down in radiative cooling to space is caused by GHGs and clouds and certainly must make the Earth warmer than it would be otherwise. However, you need to make a lot of assumptions to calculate how much warmer and that leads to lots of unproductive controversy. (The standard assumption that produces 33 K is that albedo will remain the same, but the planet will emit like a blackbody.) Stick with 150 W/m2.
I first want an unambiguous definition of what we are talking about. Your proposition is legit, provided it is clear what we are talking about. IPCC is not clear in this respect.
And, actually, I think your definition would be fine if lapse rate were zero. But it isn’t.
Paqyfelyc wrote: “actually, I think your definition (GHE = 150 W/m2) would be fine if lapse rate were zero. But it isn’t.”
What would the lapse rate be without GHGs in the atmosphere? (I don’t think there is an unambiguous answer.) However, no GHGs or clouds, the outward LWR flux would be eoTs^4 at the surface and the TOA. Defining the GHE as the difference between these two quantities would make the GHE 0 W/m2 with no GHGs.
As usual, the difficulty is creating a plausible model for the planet without GHGs.
“What would the lapse rate be without GHGs in the atmosphere? ”
basic answer is : “just the same”. This is because calculating lapse rate just depend on gravity and heat capacity (and this, itself, depend on the water content — apply the “dry” lapse rate until condensation occurs, then apply “wet”, corresponding to a higher effective heat capacity, that is, a lower lapse rate ).
Now, I guess GHG DO have some minute effect on lapse rate, through some heating in between instead of all from below as is assumed in basic calculation, which would be equivalent to some variation of heat capacity. Not enough to be even mentioned.
The two “definitions” of GHE are by no means mutually exclusive.
Back radiation of LWR is indeed the essence of the GHE.
Yet it is a common misapprehension to interpret that back radiation just as a part of the upwelling LWR that “comes back” to the surface. Back radiation is the result of an atmosphere with IR active gases radiating IR because it is at appropriate temperature. Local thermodynamic equilibrium and thermalization imply that it is essentially a single parameter, namely temperature T of emitting material in Planck’s law, that determines the amount of emitted radiation at a given wavelength . What sustains the radiation of IR energy of a specific atmospheric layer includes of course its concomitant absorption of LWR from surface or from lower or higher atmospheric layers as well as the latent and sensible heat brought by convective motion of wet air from lower layers or even its absorption of incoming sunlight.
come on, just read yourself.
First sentence you say “The two “definitions” of GHE are by no means mutually exclusive.”
Third sentence you explain that one of these is a “common misapprehension”, that is, wrong.
So make up your mind: are they both legit (and then, exclusive), or one is a “common misapprehension”?
The fact is, the IPCC SPREADS this “common misapprehension”. This part of the report is supposed to be technical, not a simple approximate for commoners not even mentioning that there are other parts weighting 1/5 or more of the effect…
BTW, there is another component, where being a GHG or not doesn’t matter: the simple thermal inertia of atmosphere(*). Is it part part of the greenhouse effect, or is it not? I challenge you to justify the definitionS used by IPCC allows you to unambiguously answer this simple question.
(*) because emission is in 4th power of temperature, a steady 240W result in a higher average temperature than a 120 W and 360 W each half of the time, even-though the emitted power is the same in both case
“It’s a common misapprehension” typical of laymen illiterate in physics…
Nothing more, nothing less.
No serious physicist or scientist would misapprehend it as you do.
Period.
BTW, there is another component, where being a GHG or not doesn’t matter: the simple thermal inertia of atmosphere(*).
And so what ?
This is not at all a “component” of the GHE, It’s just a “component” or feature of the earth’s climate system as is the presence of oceans with even much larger thermal inertia.
And yes the fact is that even without any GHGs or even without any atmosphere at all the average temperature of a rotating non uniformly lit planet is necessarily lower than its emission temperature. Yet this is just a mathematical property namely that: Temission^4 = average of T^4 is always larger than Taverage^4.
BTW the fact that exactly the opposite is true on Earth with Taverage above Temission is precisely the result of an additional phenomenon at work, namely the… GHE of Earth’s atmosphere.
” “It’s a common misapprehension” typical of laymen illiterate in physics… ”
I fairly agree. Too bad it is written, taught and spread by so called “climate scientists”.
Remember, I just thoroughly quoted what IPCC wrote, without omission that would misrepresent their speech. There is simply NO mention of anything else but LWR absorption in this whole page, nor anywhere else IFAIK. No caveat that this is just the main, but not the sole, component of GHE. If that’s misrepresentation, well, don’t put the blame on me. Put it on them, as I do.
And, BTW, no serious physicist or scientist would use such messy definition as “The infrared radiative effect of all infrared-absorbing constituents in the atmosphere”. A simpler “The infrared radiative effect of all constituents in the atmosphere” would be enough, and adding “infrared-absorbing” is just a case for more ambiguity, implying that, may be, the effect is considered only insofar as it come from actual infrared-absorption beforehand (and, then again, after this sentence they AGAIN only mention LWR absorption and nothing else, with no caveat that this is just the main, but not the sole, component of GHE.
No serious physicist or scientist would misapprehend it as THEY do.
I guess this is why you didn’t uphold my challenge: does IPCC definitions allows you to say if the thermal inertia, on which being a GHG or not doesn’t matter, is or is not a contribution to the greenhouse effect?
IPCC doesn’t even have a single definition of GHE
Gammacrux, about your answer of April 10, 2018 at 4:51 am
This wasn’t my question. We are talking about the thermal inertia of atmosphere, not thermal inertia of ocean or the land. It doesn’t really matter if you define this as part of GHE or not part of it. Both are legit, provided we name thing correctly. So, you think it isn’t, Fair enough. This is not the point
My question was : how do you derive this answer out of IPCC definitions of GHE? I expected you to answer “yes it does”, or “yes it does, insofar as it involve some LWR radiation exchange, which it does” , because, thermal inertia works through heat exchange, and radiation is always involved in heat exchange, and part of it would be LWR. You did the opposite. Obviously, the definition you claim is clear and unambiguous allows different and even opposites answer to this simple question.
QED
paqyfelyc
Thermal inertia of atmosphere or anything else is just a matter of its large heat capacity. Period.
By no means is this ever a “part” of the GHE… Again it’s just a feature of the climate system that would actually exist and be of importance even if there were no GHGs at work in it.
So I can’t see why I should ever attempt to derive such a false statement, namely thermal inertia of atmosphere being a “part” of the GHE, out of IPCC definitions of GHE.
gammacrux
When you have a definition, you use it, period. You don’t have the choice to use it or not, and to refrain when the result doesn’t suit you (in your case: includes thermal inertia in GHE while you think a proper definition shouldn’t). If the result is no good, then that’s the definition itself which is no good.
And the fact is, whether you like it or nor, one of the definition of GHE used by IPCC (the one in the glossary) is not clear enough to rule out “thermal inertia of atmosphere being a “part” of the GHE”, as a proper definition should, according to you.
(Besides, it can be argue that GHG effect is nothing more than a part of thermal inertia of atmosphere, not the other way round. But then again, IPCC don’t care to even properly define the thing it is all about, so, who knows…This leave us with no common understanding, for lack of common terminology)
Mr. Monckton:
You have only replied to one of my comments,
not that I care if you reply, but only to criticize
my narrow column formatting — nothing about
the content of my comment. The narrow columns
are needed because I have a vision problem
that can’t be corrected. It’s very difficult for me
to read my own typing with the “normal
wide column format”.
I wish you success with your theory,
and the judge living in California
who was appointed by a Democrat !
If you succeed, then you will be a climate
change skeptic hero — you’re half way there
for trying against a strong, unfriendly “opposition:.
I believe the odds that you, Mr. Monckton,
have discovered “the answer”, are small,
in my opinion.
But even if you have found “the answer”
the odds of ‘selling it’ are also small !
I watched a similar “fan club” build at jonova.com
for a new theory by David Evans, in 2016
… and then fade away,
Of course I believe you most likely are closer to “the truth”,
than the IPCC — the odds that the IPCC has the right
answer are below zero, I believe, after 30 years of wrong
average temperature predictions, they obviously
have the wrong climate physics model as the
foundation for the Global Circulation Models.
.
.
The problem you have is treating the ‘coming
climate change catastrophe’ as if it was
based on real science, and trying to refute it
with real science.
The climate change cult is more like a religion,
based on faith. The believers have their substitute
for traditional religions, also based on faith.
The problem is the coming climate change
catastrophe is based on faith, not science.
CO2 is a greenhouse gas, proven in lab experiments.
CO2 should cause some warming,
but no one knows hoe much.
If there are feedbacks, no one knows
what they are.
If CO2 and feedbacks, if they exist,
caused ALL the warming in the
weather satellite age, since 1979,
then CO2 is harmless.
If CO2 and feedbacks, if they exist,
caused ALL the warming in the
years after 1880,
then CO2 is still harmless.
Evidence that rising CO2 since 1750
has harmed anyone does not exist.
I know that.
You must know that.
The IPCC must know that too.
Leftists want the environment to be
in a “crisis”, so they can come to the
“rescue”, which of course ‘requires’
a stronger, bigger government.
The “crisis” has morphed from DDT
to acid rain. the hole in the ozone layer,
global cooling, and finally global warming
caught on.
But global warming itself did not scare
people much — many of us like to pay big money
to vacation in warmer climates !
So the leftists needed a theory
that would make rising CO2 scary,
and that was the water vapor
positive feedback theory,
(with no proof it exists now, or has
ever been a problem in the past four billion
years, when CO2 levels were higher
than today almost all the time).
What the global warmunists claim is:
(1) 4.5 billion years of natural climate change,
with no obvious disaster from a water vapor
positive feedback, suddenly ended in
the mid-twentieth century, and CO2 ‘took over’
as the “climate controller”, with a new strong
water vapor positive feedback too …
but with no explanation ever given as to how
the climate change process could have
completely changed during the 20th century.
Those beliefs are non-science ( nonsense ),
with no scientific proof — they can’t be
refuted with facts, data and logic, any more
than a traditional religion member could be
convinced there is no god.
Perhaps several consecutive years of
unusually cold weather would disrupt the
climate change cult … but many members
have been brainwashed since the 1980s,
so even that may not change minds !
My climate change blog:
http://www.elOnionBloggle.Blogspot.com
I was wondering why your comments came out as they do. Thanks for explaining. I am also in agreement with your sentiment.
The narrow columns issue
is easily fixed by using narrow window.
The input box will be narrow and will
turn into new line without you having
to bother typing CR/LF
So you would see narrow column you need
while other readers will see normal (for them)
I works, I checked.
Narrow columns are actually
easier to read if they are justified
— that’s why most newspapers
use justified narrow columns,
and so do I with the economics
newsletter I write.
If I type nice justified columns
in my computer, and then
cut and paste, the formatting
changes, and you get what you
see here.
I’ll try your suggestion and hope it
works.
Maybe I need a service dog,
who knows how to type ?
I must apologize to Mr Greene for having called him out on the strange layout of his comments, which does make them less easy to take in. I had no idea that this was owing to his eyesight. A solution to the problem is suggested by a commenter here, and it may be worth Mr Greene’s while to try it.
Mr Greene is, of course, right that even on the very generous assumption that all of the warming since 1850 was anthropogenic the resultant Charney sensitivity will be very low. But what we are hoping to achieve is a formal demonstration that the feedback fraction cannot exceed a maximum value dictated by the behavior of the climate across the 32 K interval from emission temperature, which can be derived with great certainty, and global surface temperature in 1850, which is also relatively well constrained. Once that maximum value has been derived, it can be applied to any future warming. And, on present calculations, it is likely to show a small and harmless Charney sensitivity.
I guess that means we agree:
Co2 is beneficial for green plants,
and any warming from Co2 would be slight,
and mainly at night ( less cooing at night, actually)
primarily in higher, drier latitudes.
The plants want more Co2, not less !
The few people living in higher latitudes
want slightly warmer nights !
Let’s more more Co2 in the air, not less !
Richard Greene wrote, “Leftists want the environment to be in a “crisis”, so they can come to the “rescue”, …”
I suspect the desire to play the role of White Knight is the primary driver behind warmism—it’s psychological, not political.
There’s a line between
wanting to help people and
telling them how to think, and
live … and then hectoring them
when they are skeptical, or disagree.
After this thrashing-out of the issues, CMoB should consider re-authoring his presentation so it anticipates and (mostly—except for a few fuzzy areas) dismisses the objections raised in the comments.
This would also give him an opportunity to incorporate in it some of the good phraseology and new arguments he’s made during these Q-and-A exchanges.
Mr Knights’ constructive reply is very helpful. Our difficulty throughout has been in explaining the idea, so we have thought it best to do things in stages here. We have now revealed enough of the idea to demonstrate that it is robust against various lines of attack – e.g., that the equation we use is linear but the feedback responses are nonlinear, or that we have not taken the Earth’s radiative imbalance into account. We are now working on refining the argument by dealing even more explicitly with the nonlinearity point. Initial calculations indicate that allowing for an extreme nonlinearity such as the 7%-per-Kelvin increase in column water vapor with warming and assuming that this will lead to a 7%-per-Kelvin nonlinear feedback response (it won’t, of course, because the water-vapor feedback forcing is approximately logarithmic and it is additionally compensated for by the lapse-rate feedback), and also assuming that this extreme nonlinearity will apply to all feedback responses, we can show that after 32 K of warming the feedback fraction is little more than 0.2, which gives a Charney sensitivity of less than 1.4 K.
By this method, we hope to be able to complete the proof that Charney sensitivity is below 1.5 K, with not a lot of variance either side of the mid-range estimate 1.2 K. At the moment, we are more concerned with perfecting the argument than with perfecting its presentation. As a result of the exposure that these articles have given to the idea, it is now being studied all over the place and we are getting feedback (if that is the right word) from many quarters. The general feebleness of the climate fanatics’ scientific response to our idea has been noticed. But we remain open to the possibility that we have ourselves made an error, though in the light of the scrutiny the idea has received this is becoming less likely as time passes.
I have at last taken the time to study this feedback criticism in more detail. It appears that it has been around since 2015 so to hear that the authors are still perfecting the argument is a little disappointing after this time. Furthermore it appears to me that the claim it is receiving lots of attention is not borne out by my own experience. Very few articles in mainstream newspapers, nothing seen on the TV in the UK, etc. Maybe I move in the wrong kind of circles or missed it but it looks like it generated some excitement initially and lots of counterpoint criticisms but interest has now died down except for the skeptical blogs.
I think the arguments are generally sound but unfortunately so complicated that they put some people off going through it all. I have a bit of an advantage as I did a lot of this stuff as part of my Elec. Eng. degree course and did actually remember 50% of it despite the 45y time delay.
The arguments could be presented in a much simpler form with very much less mathematics to illustrate the general point without going into the specific numbers too much.( It would no doubt generate a different kind of rebuttal too !). A summarised simpler explanation at the top before going into all the equations would be my recommendation. Set out the Official CAGW Position first – “The consensus view is that the atmosphere works like this….blah,blah.”. Then explain how feedback systems should be correctly used in this application and point out the error.
The criticisms/rebuttals I have seen vary greatly from simple ad hominems (plenty of ’em too), to all sorts of complicated logical shenanigans. Dealing with them all looks relatively pointless. Surely one simply needs to deal with the “official” response but knowing how these things work I expect there isn’t one yet.
Anyway, despite the impression I may have given so far, I do think this is a very useful and impressive piece of work and am hopeful it will get sufficient traction to go a lot further. To CMoB and the team I say “Well done!”.
“The reverend badger” thinks it should not have taken as long as two and a half years for our small, unfunded band of researchers, working in our spare time, to have overthrown a century and more of official climatology. Well, we’re doing our best.
As to presentation, the purpose of the head posting was to deal with certain technical aspects of our discovery. It was not intended for the general reader but for the specialist. We are simply not concerned with presentation at this stage: we are concerned with making sure that we are able to deal with all valid criticisms.
The badger is entitled to his opinion that we should not have bothered to attempt to answer the criticisms that have been put forward. Well, the United Kingdom is a free country, and we chose to exercise our freedom to reply. Welcome to freedom.
That said, we are grateful to Badger for his concluding kind words.
After thinking about this, I’m now doubting the validity of using absolute temperatures.
Looking at the Clausius-Clapeyron relation for water vapour it seems the atmosphere can hold no water vapour at all below -20°C (254°K). So you could convincingly argue that the baseline datum for no feedbacks should be 254°K, not 0°K. And 255°K happens to be the emission temperature we are claiming produces a feedback.
We’d be better to assume the emission temperature of earth of 255°K produces no feedback, (because there is no feedback mechanism present) but if you start increasing the input temperature from there by a ∆T of say 8°K, it starts to create water vapour feedback and the equilibrium temperature of 288°K is seen.
So f = 1-8/32 = 0.75
Bingo.
I wouldn’t have put it that way, because an average temperature of 255 wouldn’t necessarily mean it isn’t, say 280 somewhere. But that’s the big picture: contrary to the conclusion to which Lord Monckton’s naive algebra leads him, the models probably don’t ignore responses to lower temperatures; they probably recognize them but realize they’re very low.
I don’t credit the models, but it’s inconceivable that they suffer the particular “grave error” that Lord Monckton has talked himself into believing he discovered.
255°K is the average. Even on a much colder earth, there would be enough solar radiation at the equator in the day to melt ice and evapourate water locally. I have no idea how cold the earth could be and this process could continue, but a lot colder than 255°K. So, the water vapour feedback mechanism would exist from some much lower temperature allowing changes in albedo and cloud formation.
I think!
Mr Palmes is incorrect on all points. The general-circulation model run by Lacis et al. (2010) found that at 252 K, some 9 K above the 243.3 K emission temperature implicit in their assumption of albedo at 0.418, about 10% of today’s water vapor would be present., for there would be open water in the tropics.
There would, therefore, be a substantial feedback response not only from water vapor but also from the ice albedo, which would progressively melt. The ice albedo feedback would gradually become less important as the climate warmed and there was less ice left to melt, while the water vapor feedback would become progressively more important.
As for the Born Liar’s intervention, he offers absolutely no evidence that the models make any explicit allowance for the feedback response to emission temperature, and he offers absolutely no explanation of how – if they models did make any such explicit allowance – such allowance would be in any way consistent with IPCC’s definition of a feedback as a response only to a perturbation and not also to any pre-existing temperature.
The Born Liar, in his characteristically spiteful manner, describes my algebra as “naive”. Neither he nor anyone else should assume that because an argument is simple it must be either naive or wrong. He has not the slightest interest in the objective truth.
The corrected version of the zero-dimensional-model equation makes it quite clear that there will be a feedback response to emission temperature, provided that feedback processes exist. Since at 255.4 K there would be water vapor and open water in the tropics, the feedback response will occur. And, since the mean feedback response across the 23 K interval between (255 + 9) and 287 K will therefore be 1 – 264 / 287, it will be 0.08 on average. Even assuming a very steep 8%-per-Kelvin nonlinear increase in the feedback fraction from about 0.016 at 255.4 K, the feedback fraction at 287.6 K would be of order 0.2, giving equilibrium sensitivity 3.5 / 3.2 / (1 – 0.2) < 1.4 K.
It is useful that we have a professor of control theory assisting us. It ought to be blindingly obvious that, since such nonlinearity as exists is present in the system whether the math is done correctly or, as now, incorrectly, taking into account the feedback response to emission temperature is bound to reduce the feedback fraction and hence equilibrium sensitivity.
Nor has Lord Monckton offered any evidence that they don’t make such allowance. To see this, consider an equilibrium model that exhibits the following relationship between temperature with and without temperature-affecting quantities’ responses to temperature.
(= 255 K) itself induces a substantial feedback.” That’s because the feedback he’s referring to in that quote is a different animal from the quantity the IPCC defines. So, if climatologists do realize that “emission temperature . . . induces substantial feedback,” that certainly is “consistent with IPCC’s definition of a feedback as a response only to a perturbation and not also to any pre-existing temperature.”
http://i63.tinypic.com/11io3zn.png
I’ll refer to those total responses as “feedback,” although that’s not the same as the IPCC definition. As that graph shows, the consequences of feedback gradually increase with temperature toward the right, but the ratio of temperatures without feedback to those with feedback still remains fairly close to unity: Lord Monckton’s “feedback fraction” remains low. (At the lower end there’s not much feedback, but the open-loop gain in this model is so great that the loop gain exceeds unity until the temperature reaches nearly 40 K.)
Even though the ratio of before- to after-feedback temperatures remains near unity, we can see if we then zoom in on the upper right that from some reference state (in which what I call “feedback” is operative) a small change in before-feedback temperature corresponds to a large change in after-feedback temperature. And the IPCC definition of what it calls “feedback” is based on ratios of such changes. That definition in no way means that the reference state from which the IPCC computes departures lacks temperature-affecting quantities’ responses to any temperatures below some “emission temperature.”
http://i67.tinypic.com/15hd3kg.png
As a matter of substance, that is, the IPCC definition has no bearing on whether, as Lord Monckton contends, “climatologists had made the grave error of not realizing that emission temperature
All this stuff about the IPCC definition is a red herring.
I said “naïve” not because the algebra was simple but because it was performed naïvely.
Despite Lord Monckton’s references to nonlinearity, his comments betray no understanding of nonlinearity’s implications. For a linear system, Lord Monckton’s “feedback fraction” is what in some circles is known as “loop gain,” and loop gain would be independent of temperature if the model were linear. But Lord Monckton applies to nonlinear systems loop-gain results that are valid only for linear systems. For nonlinear systems, moreover, his “feedback fraction” is no longer loop gain. In the nonlinear system I described above, “feedback fraction,” i.e., Lord Monckton’s “f,” has the following relationship to temperature:
http://i64.tinypic.com/1054760.png
As that diagram shows, the “feedback fraction” remains modest for higher temperatures. Lord Monckton erroneously concluded from that fact that the system’s “climate sensitivity” is low. As the previous comment’s diagrams demonstrated, though, it’s not low at all.
The current drawing also depicts the system’s actual loop gain. The large-signal loop gains based on the entire quantities, while the small-signal loop gains are based on departures from respective-temperature states. It is to the latter type of values that the IPCC definitions correspond.
The comments above show that Frank, Germonio, and others have repeatedly attempted to educate Lord Monckton about these distinctions. They have apparently enjoyed no success.
The Born Liar continues to assume that the eminent professor of control theory who is one of our co-authors does not know what he is talking about. Other true-believers in the New Religion have made the same foolish assumption. Sneering at me isn’t going to make any difference to anything.
The Born Liar has produced no evidence that the models make due allowance for the feedback response to emission temperature. He waffles to the effect that the feedback response to emission temperature is not really a feedback response at all as IPCC defines it, but a “different animal”. He really needs to learn som elementary control theory. It is a feedback response, whether Mr Born likes it or not. And if due account is taken of it, there is no way to obtain anything like the absurdly high equilibrium sensitivities posited by IPCC except by assuming a nonlinear feedback response greatly in excess of the theoretical maximum possible nonlinear response – namely, the naive assumption that all feedbacks will respond as nonlinearly to temperature as column water vapor does, making no allowance for the fact that the feedback to changes in column water vapor is logarithmic or for the fact that the tropical mid-troposphere hot spot, without which no significant water vapor feedback can be legitimately or plausibly posited, is not observed in reality except in a couple of defective metadatasets.
The Born Liar also confuses the feedback fraction with what he calls “loop gain”. The usual terminology (insofar as there is any) usually labels the mu gain factor the “open-loop gain factor”. Note, however, that the actual open-loop gain is not a unitless quantity. The “closed-loop gain factor”, or “system gain factor”, takes account of both the mu open-loop gain factor and the feedback fraction, which is simply the fraction of the output signal that is returned to the input node.
Whether the Born Liar likes it or not, the CMIP3 and CMIP5 predicted interval of Charney sensitivity, [2.0, 4.5] K, can be exactly reproduced by the explicitly linear zero-dimensional-model equation that is, again whether he likes it or not, used diagnostically throughout official climatology, provided that one inputs to it the official values of the reference sensitivity and of the feedback-sum interval. Now, how is it that the results of the supposedly nonlinear models can be reproduced with such faithful exactitude by a linear equation that everyone except the Born Liar uses? The answer, of course, is that the feedback response over the 23 K interval of interest is very close to linear.
Besides, one of the most naive errors that true-believers such as the Born Liar are prone to make is to believe that all they need to do to dismiss official climatology’s linear diagnostic equation is to utter the word “nonlinear”. The difficulty they then face is that, though there is only one linear system, which can be shown to approximate the real world very closely, there are infinitely many nonlinear systems, many of which are close enough to linear not to make any real difference. The Born Liar has produced no evidence that the various nonlinear systems with which he has been playing has any particular relevance to the climate. Absent such evidence, all that he says is mere hot air.
Although I will be happy to discuss feedback theory with Lord Monckton’s “eminent professor of control theory” whenever he is able to produce him, I’m not going to respond to the farrago of illogic and irrelevance with which Lord Monckton flees from my demonstration of his error. For the sake of clarity, though, I will define the way in which I used feedback terms, since in my experience there’s little nomenclature unanimity in this field.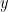
to a stimulus 
is given by y = (x + fy)g, where is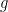 
is what I call “open-loop gain” and 
is the “feedback coefficient” or “feedback gain.” Isolating the response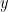 
gives us 
, and that ratio 
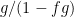of response to stimulus is what I call “closed-loop gain.” The (dimensionless) quantity 
, which Lord Monckton calls his “feedback fraction” and has lately been using 
to denote, is what I call “loop gain”: the gain encountered to traversing the loop.
For linear feedback the response
It is remarkably difficult to respond to people like the Born Liar and like Frank, who have no interest whatsoever in what is objectively true.
The Born Liar produces reams of meaningless curves, with no data to show how they were generated, and then makes various nonsensical statements about them. He has a purported feedback curve that starts at 0 K. Just one problem with that: there won’t be much in the way of feedback until temperature is high enough to sublimate ice, and not a lot until it’s high enough to melt water at the Equator and then evaporate it.
The feedback processes in the climate were manifestly sufficient to respond to 264.3 K of combined emission temperature and directly-forced warming from the non-condensing greenhouse gases. They did not need to know at what point on the temperature scale they might have begun to operate: for the Sun has been around at least as long as the Earth. They merely reacted to the temperature as they found it – and that was 264. 3 K.
No amount of waffle either from the Born Liar or from Frank can alter this fact.
And I see that the Born Liar agrees with Frank that I have not allowed for the fact that at 255 K the growth in water vapor feedback would be 10% per Kelvin. Well, 255 K is below the freezing point of water. From 273 K to 274 K, i.e. 0-1 C, the column water vapor would increase at 7.5% per Kelvin, not much different from the 7% per Kelvin reported as applicable today based on observation (Wentz et al., 2007).
Let everyone be aware that neither Frank nor the Born Liar has any interest in what is true. But they are wasting their time. Their bad behavior has been noticed, and conclusions have been drawn from it. Now, scientists all over the place are beginning to look at what we have found, and the main reason why some of them have started to look closely is the sheer malevolent stupidity of those who have unfairly and dishonestly tried to find fault here. Very few scientists are dishonest, but they can smell dishonesty on the wind, and they are beginning to dig.
Harry and Joe: Lord Monckton isn’t using the Clausius-Clapeyron itself, he is using an approximation of that equation that only applies near 288 K: 7%/K increase. The correct relationship involves (1/T1 – 1/T2). Another of Monckton’s mistakes.
Yes. I was aware of that. In fact, I had toyed with the idea of putting it in my toy model. Frankly, though, it’s just a magic formula to me, so I was uncomfortable using it before I had gone through its derivation.
But I’ll note in passing that for my toy model the feedback function I assumed (as an aggressive relationship some modelers’ results might exhibit) grows less than 7%/K.
As usual, Frank is wrong. As usual, the Born Liar agrees with Frank because he thinks that is a good way to spite me, and to hell with the truth From 273 to 274 K, the increase in column water vapor is 7.5% per Kelvin, not vastly different from the 7% observed by the satellites today. And what that means, according to Professor Lindzen, is that equlibrium sensitivity cannot ecen rach 1 K per CO2 doubling, because the increase in evaporation keeps the tropics cooler than they would otherwise be. See also Kininmonth (2010). The truth is that the water vapor feedback is not vastly different from linear, as the head posting explains.
Neither the Born Liar nor Frank has offered a shred of hard evidence that such alternative nonlinear models as they favor is any better at predicting global warming than the linear model.
I’m grateful to the good Lord Monckton once again, and would be very pleased if he can convince me that I am wrong about this.
I agree that there will be some small amounts of water vapour present in the atmosphere at temperatures around the 250°K mark, especially in the lower latitudes. My point is that, on average, a temperature around this level would make a not-unreasonable choice of datum from which to measure the ‘input signal’, given that feedbacks are likely to be near zero at or around this datum.
If you think 250°K is a little high, then perhaps 230°K is cold enough for the air to hold no water vapour and for albedo to be high. Trying out 230° as our new datum then, our ‘input temperature’ of 263°K versus the 288 equilibrium is effectively is 34 and 58 °K above our new datum respectively, implying an f = 1- 33/58 = 0.43
So as I see it, this choice of no-feedback datum is really what are talking about here. Let’s put some choices in a table, again using an input signal of 263°K and equilibrium output of 288°K:
Datum Paper ΔTref ΔTeq f ECS
255°K Hansen (1984) 8 33 0.76 4.8°K
243°K Lancis (2013) 20 45 0.56 2.6°K
230°K (example) 33 58 0.43 2.0°K
0°K Monckton (2018) 263 288 0.09 1.3°K
And to me the most appropriate datum would be the temperature at which the feedbacks begin in earnest. They don’t begin at absolute zero. A fair estimate might be the snowball earth with no atmospheric water vapour at perhaps 230°K or thereabouts.
I think you’d may have more traction arguing for a lower datum around this sort of number, rather than requiring the datum to be absolute zero, otherwise it will be too easy for your critics to demonstrate it is higher than that.
In your electronic circuit analogy, design a rig where there is no feedback at all until the input signal reaches the magic value of 230 volts and then a feedback loop circuit kicks in with feedback parameter of 0.43 acting only on the number of volts above 230. So with a 240V input signal the feedback loop acts only on 10 volts to give 10/(1-0.43) = 17 volts giving a total output signal of 257 volts.
Applying an input of 263 volts, the rig would output 288 volts, which is the data point we must satisfy. So this works.
If you can argue that the datum should be 230°K in the table above, (implying an ECS of 2.0°K) that is still a good result.
Mr Palmes really needs to study control theory and also atmospheric physics, One cannot simply charge at this subject like a bull at a gate. It requires considerable knowledge followed by considerable thought.
Whether he likes it or not, the feedback processes in the climate respond to the input signal as they find it, not as it might have been. The input signal relevant to the study of how much impact the non-condensing greenhouse gases have on climate is the temperature that would obtain today at the Earth’s surface without them, and without any feedback response. That temperature is 255.4 K. It is to that signal, and to no lesser signal, that the feedback processes in the climate would respond in the absence of the non-condensing greenhouse gases.
The feedback processes are water-based processes. It is not difficult to do a little spherical geometry and work out that the dayside temperature on a planet with today’s insolation and albedo will be 289 K, which is (coincidentally) the same as the mean whole-Earth surface temperature today. On the dayside at the equator, in the absence of the convective processes now in play, the temperature would be 361.2 Kelvin – very much more than enough to melt ice and start the process of evaporation and convection.
But in practice the non-condensing greenhouse gases are present, so that the mean whole-Earth temperature even before taking account of any feedback will be 264 K. It is to this value, then, that the feedback processes will respond.
The relevant equation, with its loop diagram shown in green, is given in the head posting. That equation does not permit us to assume any lesser value of the input signal than 255.4 K. That input signal is amplified by a further 8.9 K, so that, to first approximation, the feedback processes in the climate will respond to 264.3 K. The equation is entirely clear, and there is simply no scientific basis whatsoever for messing about with it in the manner suggested by Mr Palmes.
As I have already explained to him, even though the feedback processes in operation at a mean planetary temperature of 264 K will be considerable, it is possible to carry out an extreme-nonlinearity calculation by assuming that, though the mean feedback fraction across the 23 K interval of interest is 0.081, the feedback fraction increases exponentially at a rate of about 8% per Kelvin. In practice the exponential increase will be a great deal less than this, but let us push the argument way towards the climate fanatics.
In that event, the feedback fraction at 264 K would be around 0.02, which is actually far smaller than is at all likely, and at 287 K it would be around 0.20. It is of course the latter value that is relevant today, and that would give a Charney sensitivity of less than 1.4 K per CO2 doubling. In practice, since the rate of nonlinearity cannot by any stretch of the most fevered totalitarian imagination exceed 8% per Kelvin (approximately the mean rate of increase in the column water vapor per Kelvin), the final value in the series of values for the feedback fraction will be somewhat less than 0.2. However hard one tries, it is not really possible to push Charney sensitivity much beyond the 1.5 K that is the lower bound of the IPCC’s long-standing interval of predictions.
It is really as simple as that.
“Whether he likes it or not, the feedback processes in the climate respond to the input signal as they find it, not as it might have been. The input signal relevant to the study of how much impact the non-condensing greenhouse gases have on climate is the temperature that would obtain today at the Earth’s surface without them, and without any feedback response.”
How do they find “the temperature that would obtain today at the Earth’s surface without them”?
Mr Stokes is not familiar with the fundamental equation of radiative transfer, so I shall refer him to the head posting – such a good idea to read it before trying to comment on it. There, the calculation to establish the emission temperature in the absence of any non-condensing greenhouse gases and before taking the feedback processes into account is set out, together with several references to IPCC and learned papers where the 255 K value of emission temperature is given. It is quite uncontroversial. but does come as a surprise to those unfamiliar with climate-sensitivity studies.
The corrected equation for the zero dimensional model, also conveniently described in the head posting, makes provision for the emission temperature as its input. The feedback processes arising from the existence of water on our planet in large quantities will act in response to that emission temperature and a feedback response (in Kelvin) will then occur, so that the output signal will be greater than the input signal. Again, all of this is entirely uncontroversial to those with an elementary knowledge of control theory.
Good morning to Lord Monckton, please be assured that I take on board the central point and understand that attributing a zero feedback response to an input temperature of 255°K is not accurate.
However, I was looking forward to a colourful double-page spread in the Sunday Times newspaper demonstrating in simple terms how the climate science had erred, and the ECS is clearly 1.3°C ± not-very-much.
The trouble is the critics can object and ask why you decided the datum should be set at -273°C (0 °K). After all we are not talking about a simple electrical gain circuit. From what I see it is not-unreasonable to assume that an input temperature of say 230°K produces an output temperature of the same 230°K if no appreciable feedback mechanisms are operating at that temperature. Would you agree with this? And if not, how about 220°K or 210°K?
If you agree there are no feedbacks at 210°K, then we need to redesign the test rig so that an input of 210 gives and output of the same 210. Using this rig if you apply the input temperature of 263°K (a world with non-condensing GHGs) we also then need to explain the output equilibrium temperature of 288°K in terms of feedbacks. If you hypothesise that the feedback mechanisms operate in a generally linear fashion above the (rather arbitrary) temperature of 210°K, then we should use an f=0.32:
∆Teq = ∆Tref / (1-f) = (263-210) / (1-0.32) = 53/0.57 ∆Teq = 78
Which yields our equilibrium temperature of 210+78 = 288°K, and implies an ECS of 1.7°K. This is consistent, and attempts to reflect the nature the physical feedback mechanisms at different temperature ranges. If this critique appeared beside your Sunday Times exposé it would hurt its credibility.
However if you can demonstrate that the earth’s feedback mechanisms operate in a roughly linear fashion right down 0°K then I will take on board your choice of 0°K as the datum. Otherwise I think we should set it at a more appropriate value to reflect the nature the atmospheric physics, e.g. the Clausius-Clapeyron result that water vapour feedback does not operate if the (local) air temperature drops below 253°K. Note that I use 210°K in my simple example to allow for warmer-than-average temperatures at midday near the equator, to ensure that even in these locations there will be minimal feedback, even over a long lunch in Riyadh.
Mr Palmes is still not understanding that feedback processes respond to the input temperature signal as it actually is, and not as it might have been without any sunlight. Sunlight is a given. Likewise, the non-condensing greenhouse gases are a given. Therefore, the feedback processes will respond to the 255.4 + 8.9 = 264.3 K mean temperature that would exist before taking feedbacks into account.
It is no good simply making stuff up. The equation is quite clear. Feedback processes do not respond only to that fraction of emission temperature that is above some arbitrary threshold chosen by Mr Palmes. They respond to the emission temperature as it is, plus the direct warming from the non-condensing greenhouse gases.
The Born Liar continues to whine ineffectually about his dimly-remembered conversations with control theorists half a century ago. It is a priori implausible that his half-understood recollections are likely to prove more reliable than the work of an active professor of control theory.
He has produced no sound argument to the effect that taking into account the feedback response to emission temperature will allow the current absurdly high equilibrium sensitivities to be justified. It can be shown that official climatology’s defective form of the zero-dimensional-model equation, which explicitly makes no provision for emission temperature and therefore makes no provision for the feedback response thereto, reproduces exactly the official interval of Charney sensitivities when exactly the official values of the reference sensitivity and the feedback-sum interval are input to it. That is how we know the modelers are making no allowance (or, at best, very little) for the feedback response to emission temperature.
Nope.
The feedback processes just make sense as a part of the response to any perturbation applied to a real initial reference steady state of the system at some temperature Ti, with that perturbation that tends to alter temperature Ti by some amount delta T both directly and indirectly via feedback processes .
If one considers, as Lord M does, that they respond to 264.6 K then the reference initial state of the system is a hypothetical state at 0 K, as rightly pointed out repeatedly by Palmes and many others before. No way out of this.
And this is obviously nothing but plain nonsense ! Since the climate system with incident sunlight can simply never be in a steady state ( with zero radiative TOA imbalance) at 0K.
Period.
The climate sensitivity may well be at the low end of IPCC range. Yet neither good Lord M nor anybody else can tell by now. Predicting that from theory is just definitely out of reach of the science worked out by little homo sapiens sapiens.
Only future observations will eventually be able tell.
Gammacrux has not understood the corrected form of the zero-dimensional-model equation. The reference system consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035 to allow for the directly-forced warming of 8.9 K from the presence of the naturally-occurring, non-condensing greenhouse gases. Since we know the input signal (255.4 K), the direct gain factor (1.035) and the equilibrium temperature or output signal (287.6 K as in 1850), the feedback factor (the product of the direct-gain factor and the feedback fraction) is. as a matter of undeniable fact, (1 – 264.3 / 287.6) or 0.081. Just work through the math in the head posting.
The reference system consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035
No, as your “calculation” ( 255.4 + 8.9) / 255.4 of “open loop gain” unambiguously demonstrates by itself you really do implicitly refer to a hypothetical steady state at 0 K .
Gain only makes sense if it refers to the ratio of changes in temperature observed with and without feedback, temperature changes that take place with respect to some reference steady state system that is perturbed in some way. Perturbation concept BTW implies that the energy involved in the perturbation is fairly small with respect to the total energy of system;
Now your hypothetical 0 K steady reference state may exist only in the absence of sunlight. Consequently what you are actually considering is nothing but the response of that reference system at 0 K to switching on the whole incident sun radiation from scratch. This is by no means just a “perturbation” anymore and any “feedback factor f ” inferred in this way has no reason to be of any relevance to the “f” involved in what happens upon simply doubling atmospheric CO2 with respect to a preindustrial reference state.
Gammacrux should remember to read the head posting before commenting on it. The corrected form of the feedback loop, shown in green in the head posting, makes explicit provision for the input signal. It is a matter of readily-demonstrable fact (a fact that we demonstrated by building two test rigs, one of them at a government laboratory) that, even in the absence of any amplification, the input signal will generate a feedback response provided that nonzero feedback processes are present in the system. An input signal of 255 units will induce a feedback response appropriate to that input signal, regardless of when the feedback processes first became operational. Therefore, the reference system (which consists of the input signal and any amplification thereof) consists of emission temperature 255.4 K – not 0 K – and a direct or open-loop gain factor 1 + 8.9 / 255.4 = 1.035.
In the corrected version of the equation for the feedback loop, there is no statement, explicit or implicit, that there is some hypothetical steady state at 0 K. However, in the erroneous version of the equation used by official climatology (shown in red in the head posting, which is well worth a read), the input signal is erroneously assumed to be zero.
It is no good trying to state, as Gammacrux does, that “Gain only makes sense if it refers to the ratio of changes in temperature observed with and without feedback, temperature changes that take place with respect to some reference steady state system that is perturbed in some way”. Do the math, for Heaven’s sake. Take an input signal of 255.4 units. Set the mu direct-gain factor to 1 (i.e. no amplifier gain). set the beta feedback fraction or return-transmission characteristic to 0.081. And then measure the output signal. There has been no perturbation of the input signal, for the direct-gain factor would exceed unity if there were. And yet the output signal exceeds the input signal. Thus: 255.4 / (1 – 0.081) = 277.9. So, where did the extra 22.5 units in the output signal come from? The answer, of course, is that the extra units came from the amplification of the input signal caused by the nonzero feedback fraction. All of this is elementary control theory. In all sciences but climatology, it is entirely uncontroversial.
Yes, IPCC defines a feedback as responding only to a perturbation. But in that respect IPCC is simply incorrect. That is the error that official climatology has made. It is a serious error. It has led official climatology very greatly to overstate all estimates of equilibrium sensitivity. Correct the error and the warming that will occur is altogether too small to matter.
To answer Gammacrux’s question about how the corrected form of the zero-dimensional-model equation handles doubled CO2, the matter is very simple. The input signal is 255.4 K. The directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases is 8.9 K. The directly-forced warming from the 2.29 Watts per square meter of net anthropogenic forcing in the industrial era to 2011 is 2.29 / 3.2 = 0.72 K. Therefore, the mu direct-gain factor to 2011 is 1+ (8.9 + 0.72) / 255.4 = 1.03767, and the expected temperature for that year is 255.4 x 1.03767 / (1 – 0.081) = 288.4 K, which is indeed the temperature which prevailed that year.
The directly-forced warming from doubled CO2 compared with 2011 is 3.5 / 3.2 = 1.09 K. Therefore, the mu direct-gain factor (also known as the open-loop gain factor) becomes 1 + (8.9 + 0.72 + 1.09) / 255.4 = 1.04193. Then the temperature after doubling CO2 compared with 2011 is 255.4 x 1.04193 / (1 – 0.081) = 289.6 K. Take away the 288.4 K in 2011 and the difference, which is the transient sensitivity to doubled CO2, is 1.2 K.
Note that we could have found the 1.2 K value simply by making 1.09 K the input temperature, just as official climatology does, and then 1.09 / (1 – 0.081) = 1.2 K.
But – and here’s the point – if we have at no earlier point made any allowance for the feedback response to emission temperature itself, we shall be misled – as official climatology was misled – into assuming that the feedback fraction is a great deal higher than 1 – (255.4 + 8.9) / 287.6 = 0.081. The point is that we know with great certainty what the emission temperature would be at today’s insolation and albedo, and we have highish confidence in what the temperature was in 1850. The only other quantity we need is the directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases, and that – as deduced from Lacis (2010) – is 8.9 K. From these values, the feedback fraction of 0.081 is easily derived.
Now, one can argue that owing to nonlinearity in the feedback processes the feedback fraction by 1850 might have been twice the 0.081 that we have thus derived, but certainly no more than that. Thereupon, Charney sensitivity to doubled CO2 would be 1.09 / (1 – 0.16) = 1.3 K. And that is all.
All of this is mainstream control theory. If official climatology wants to borrow from control theory, it must do so correctly. Until now, as IPCC’s definition makes quite plain, it has not done so correctly. It has erred. Remove the effects of the error and global warming becomes a non-problem. It is as simple as that.
As you’ve recognized, what Lord Monckton says here is true:
The resultant back radiation from the air and the clouds, together the resultant lapse rate and albedo, are all quantities that both affect temperature and depend on it: they are feedback mechanisms. But we also know that the climate models implement differential equations that express what the modelers believe are the physics underlying those quantities as well as others. Consider what Lord Monckton’s “grave error” theory implies in light of those facts.
(= 255 K) itself induces a substantial feedback.” That would mean that climate modelers had failed to recognize that below 255 K these quantities depend on temperature and/or that temperature below 255 K depends on them. Does that seem even remotely plausible? Isn’t it much more likely that modelers have simply, as most of us skeptics have long believed, been overestimating the degree to which feedback increases with temperature?
Lord Monckton would have us believe that before his great discovery “climatologists had made the grave error of not realizing that emission temperature
In support of his highly implausible contention, Lord Monckton has been spinning out all these equations he doesn’t really understand and leaps to totally unsupported conclusions. He throws around his “feedback fraction.” But, as I showed here and here, there’s no inconsistency between climatologists’ finding a high “equilibrium climate sensitivity” and their models’ exhibiting a modest “feedback fraction.” Nor is there any inconsistency between a low “feedback fraction” and climatologists’ having, in contrast to Lord Monckton’s assertion, taken into account feedback to temperatures below some “emission temperature.”
Now, Lord Monckton goes on and on about all the experts he consulted. And, look, I make no claim to expertise myself. I’m not a scientist; I earned my daily bread as just a workaday lawyer. But nearly a half century ago I had already spoken about control systems with professors of the discipline, and I had discussed the finer points of feedback with Bell Labs engineers. That didn’t make me an expert, but it did teach me enough to recognize it when someone is blowing smoke.
Lord Monckton is blowing smoke.
The Born Liar continues to be spiteful and silly. He admits – as if the fact were not already self-evident – that he has no scientific expertise: and yet, on the basis of half-remembered and less than half-understood conversations with control theorists a century or so ago, he presumes – in that sneering, arrogant tone that is his specialty – to lecture a professor of control theory and numerous other professors and doctors of science. Let him wait until our paper is published, and then let him write his own paper telling the world that he knows better than all those professors and doctors.
He will have to produce arguments a lot less dishonest and a lot more compelling than the nonsense he has attempted to peddle here. No one is buying.
Gammacrux appears to have the same difficulty with elementary control theory as Mr Palmes, the Born Liar and one or two other true-believers in the New Religion. Feedback processes respond to the temperature that is actually present, not to some lesser temperature. It is of no relevance how the climate might behave with no incident radiation at all. The feedback processes are not confronted with that scenario. They are confronted with 255.4 K of emission temperature plus 8.9 K of directly-forced warming from the non-condensing greenhouse gases: total 264.3 K. It is to that number, and to no lesser number, that they respond. This is entirely elementary, and it is indisputable.
One view from a climate scientist on “feedback”:
******
Why feedback loops are one of the most troubling parts of global warming
They’re vicious circles that will speed up the pace of warming.
Climate change is not simply a matter of cause and effect. It’s more like a vicious circle. Thomas Crowther is a professor at ETH Zürich, a university in Switzerland.
Climate change is not simply a matter of cause and effect. It’s more like a vicious circle.
Click To Tweet
Crowther: “Not only are we directly altering the climate, but that process in itself is kicking off these things that are gonna actually accelerate the damaging impacts over the rest of the century.”
This self-reinforcing cycle is called a feedback loop. For example, warmer temperatures make soil microbes more active. The microbes then release more carbon into the atmosphere – which in turn speeds up global warming, which makes the microbes even more active, and so on.
Crowther: “I just imagine a sort of wheel spiraling out of control.”
Melting sea ice is another example. Because ice is white, it reflects sunlight back to outer space, which reduces the heat absorbed by the earth. But global warming melts the ice, leaving dark ocean water behind. The water then absorbs the sun’s heat, which increases global warming … leading to more melting ice.
Crowther says it’s hard to predict just how much these feedback loops will speed up the pace of global warming, so they represent a worrisome unknown.
Reporting credit: Daisy Simmons/ChavoBart Digital Media.
Photo credit: NASA Goddard Space Flight Center.
Filed under: Diana Madson
https://www.yaleclimateconnections.org/2018/02/why-feedback-loops-are-troubling/
******
The million-dollar researcher
21.02.2018 | News
By: Peter Rüegg | 2 Comments
The ecologist Tom Crowther only recently joined ETH Zurich as assistant professor. Virtually his first achievement was to win a grant offering potential research funding of more than 17 million euros over the next 13 years. So, who is this rising star?
….
https://www.ethz.ch/en/news-and-events/eth-news/news/2018/02/portrait-tom-crowther.html
Tom Crowther gave his inaugural lecture at ETH Zurich on 19 February 2018. The recording “Understanding global-scale ecology in order to combat climate change” can be found here:
https://www.video.ethz.ch/speakers/lecture/bccfbefa-c9b3-419b-90b6-5c50598d31da.html
******
If we are right, Crowther is wrong.
In reply to Lord Monckton, does he not accept that there will be a certain temperature, perhaps not too far below 255°K, where the earth will provide no feedback whatsoever to the input temperature? A temperature where the earth is fully frozen with stable albedo (around 0.6 from your paper) and zero saturation percentage for water vapour held in the atmosphere. I’m not sure if this temperature is 255°K, 230°K or 210°K. For illustrative purposes I chose 230°K based on the snowball earth estimates above.
In reply to “Mr Palmes is still not understanding that feedback processes respond to the input temperature signal as it actually is. “ But at this temperature, no they do respond. That’s is exactly the point. They do not respond at all. 230°K in, 230°K out. No feedbacks. The feedbacks are not in operation at or below this datum temperature. Teq = Tref / (1 -0) 230°K=230°K/1 f=0. The feedbacks are as dormant as the dead parrot in the famous Monty Python sketch.
From 230°K if Tref rises by 1 degree to 231° K and this 1 °K wakes up some hitherto unseen feedback mechanism, then all this feedback ‘knows’ about is the 1°K, not the 231°K. The feedback reacted to 1°K increase above 230°K, not the 230°K itself. Remember 230°K in gives 230°K out.
Where exactly should this datum temperature be set? I’m not qualified to say. But you seem to have chosen 0°K which seems highly improbably to most people. The IPCC and friends seem to have chosen 255°K. At least you can envisage a rationale for that choice.
If I were a betting man and was given the choice of 0°K or 255°K I would choose 255°K, but I suspect the real answer is a little lower than this, because as you say there will be some water vapour around in the warmer climes even at 255°K, hence I put my money around 230°K.
I mean you no ill will and aim to be constructive, but I think we’re barking up the wrong tree here.
If Mr Palmes refuses to understand that feedback processes respond to the temperature that actually exists and not to some lesser value he has plucked out of the air, there is nothing further I can do for him.
The temperature in the absence of feedback amplification, at today’s insolation and albedo, would be 255.4 K plus another 8.9 K directly-forced warming from the non-condensing greenhouse gases. That is 264.3 K. In fact, the pre-feedback temperature is probably quite a bit higher than that, because official climatology underestimates the emission temperature by 5-10 K and, in addition Lacis deliberately chose an artificially low value for the directly-forced warming from the non-condensing greenhouse gases.
Taking 264.3 K as the temperature to which feedback processes respond, and taking 287.6 K as the temperature in 1850 before any sufficient anthropogenic perturbation, the 23 K difference is attributable to the feedback response to the entire 264.3 K temperature, because that is the actual pre-feedback temperature. Now, 264.3 K is not 220 K or 230 K or any other value imagined by Mr Palmes. it is 264.3 K. And the temperature in 1850 was 287.6 K. The difference is represented by the feedback response to that 264.3 K.
How can inanimate feedback processes decide that they would like to do Mr Palmes a favor by refusing to react to the first 255.4 K of temperature and then reacting violently to the next 8.9 K? How can they know, given today’s insolation and albedo, how they might respond at some lesser temperature, and how can they decide not to react to the first 210 or 220 or 230 K? The fact is that they can’t.
Mr Palmes should try building a test rig and inputting not some imaginary value but 255.4 K as the input and a sufficient value for the mu amplification factor to represent the remaining 8.9 K. Then all he has to do is measure the output at various values of the feedback fraction. There would be no point in his inputting, say, 220 K, because that is not the temperature of interest. It matters not that there would be no feedback processes in operation at 220 K, because the baseline temperature is at least 44 K above that value.
The matter really is very simple, though it has eluded official climatology till now.
Finally, Mr Palmes has sneered to the effect that the Sunday Times has not run a double-page spread announcing our discovery. That is not how it works. We must first get our paper through peer review and into a mainstream climate journal. Then, and only then, will we seek publicity.
“…from 230°K if Tref rises by 1 degree to 231°K and this 1°K wakes up some hitherto unseen feedback mechanism, then all this feedback ‘knows’ about is the 1°K, not the 231°K.”
1) It is not the 1°K that “wakes up” such feedback mechanism. It is (Teq + 1°K) that does it. In your scenario, the system is already at 230°K, ‘primed’ for waking the feedback mechanism – so it ‘knows’ about more than just the change of 1°K.
2) I feel that in most of these discussions there is an implicit assumption that increasing Tref by T degrees increases Teq by more than T. That’s positive feedback, and that makes systems unstable, unlike Earth’s climate which seems to be pretty stable. To me that would indicate that sumtotal of all feedbacks that are governing the system, would be negative. In other words, increasing Tref by T degrees results in Teq change smaler than T.
Just my two cents…
“It is (Teq + 1°K) that does it.”
So what would (Teq + 0°K)? Or (Teq + 0.001°K)? IT the response proportional to the (Teq + 0.001°K) or the (0.001°K)? If the latter, how does the Teq enter?
Ive thought more about the implications of this article than any other I have read recently. Thanks for the article. I suspect that the high positive feedback’s of most of climate models, comes from assuming that the feedback is directly related to the 7% water vapor increase per degree C of temperature rise.
Even at 255 Kelvin the amount of water vapor in the atmosphere is still triple that of CO2 at 400 ppm. At 255 water vapor has a saturation pressure of 1.1mmHg. I know this is a bit simplistic but if CO2 contributes 8.9 degrees of warming than should not water vapor also cause more than 8.9 degrees of warming even if there was no CO2 in the atmosphere?
Lowell has grasped the main point. The temperature before feedback is 255.4 K emission temperature plus 8.9 K directly-forced warming from the non-condensing greenhouse gases: total 264.3 K. After feedback, the temperature in 1850 was 287.6 K. The feedback fraction was thus 1 – 264.3 / 287.6 = 0.081.
How could this be so low, given that column water vapor increases at around 7% per Kelvin from 273 K (the freezing point of water) to 287 K? The answer is that the models assume that column water vapor only increases at about 1 to 2% per Kelvin. Therefore, they predict very little increase in evaporation, and they derive a mid-range Charney sensitivity of 2.2-3.4 K. However, at an evaporation rate increasing at the 7% per Kelvin that satellites actually observe, Charney sensitivity falls to 0.9 K. This, as Bill Kininmonth pointed out in an interesting paper in 2010, acts as a powerful constraint on Charney sensitivity. Our top-down method detects this fact by the simple method of comparing the no-feedback temperature of 264.3 K with the after-feedback equilibrium temperature of 287.6 K in 1850.
One or two particularly obtuse commenters here have tried to say that we have failed to take into account the fact that from 273-274 K the increase in column vapour is not 7% but more like 7.5%. Well, gee wow golly gosh, that doesn’t actually make very much difference to anything.
Lowell is quite right: feedback processes, including the water vapor feedback, that respond to the CO2-forced direct warming must also respond to the pre-existing temperature.
In reply to Lord Monckton and Bob K, I cannot accept the proposition to use the full input temperature because it does not match the facts. We need to find an explanation for the following, perhaps easier to put in a table. The Monckton Conjecture (f=0.09 on full input temperature) cannot match a world where there is no water vapour feedback below a certain temperature. We need a rig that can match this:
Input Output
0°K = 0°K (Monckton 0°K – correct)
100°K = 100°K (Monckton 110°K – incorrect)
200°K = 200°K (Monckton 219°K – incorrect)
220°K = 220°K (Monckton 241°K – incorrect)
221°K = 221°K (Monckton 242°K – incorrect)
222°K = 222°K (Monckton 243°K – incorrect)
223°K = 223°K (Monckton 244°K – incorrect)
224°K = 224°K (Monckton 245°K – incorrect)
225°K = 225°K (Monckton 246°K – incorrect)
226°K = 226°K (Monckton 247°K – incorrect)
227°K = 227°K (Monckton 249°K – incorrect)
228°K = 228°K (Monckton 250°K – incorrect)
229°K = 229°K (Monckton 251°K – incorrect)
230°K = 230°K (Monckton 252°K – incorrect)
231°K → 232°K (Monckton 253°K – incorrect)
232°K → 234°K (Monckton 254°K – incorrect)
233°K → 235°K (Monckton 255°K – incorrect)
234°K → 237°K (Monckton 256°K – incorrect)
235°K → 239°K (Monckton 257°K – incorrect)
236°K → 241°K (Monckton 258°K – incorrect)
237°K → 242°K (Monckton 260°K – incorrect)
238°K → 244°K (Monckton 261°K – incorrect)
239°K → 246°K (Monckton 262°K – incorrect)
240°K → 248°K (Monckton 263°K – incorrect)
241°K → 249°K (Monckton 264°K – incorrect)
242°K → 251°K (Monckton 265°K – incorrect)
243°K → 253°K (Monckton 266°K – incorrect)
244°K → 255°K (Monckton 267°K – incorrect)
245°K → 256°K (Monckton 268°K – incorrect)
246°K → 258°K (Monckton 269°K – incorrect)
247°K → 260°K (Monckton 270°K – incorrect)
248°K → 262°K (Monckton 272°K – incorrect)
249°K → 263°K (Monckton 273°K – incorrect)
250°K → 265°K (Monckton 274°K – incorrect)
251°K → 267°K (Monckton 275°K – incorrect)
252°K → 269°K (Monckton 276°K – incorrect)
253°K → 270°K (Monckton 277°K – incorrect)
254°K → 272°K (Monckton 278°K – incorrect)
255°K → 274°K (Monckton 279°K – incorrect)
256°K → 276°K (Monckton 280°K – incorrect)
257°K → 277°K (Monckton 281°K – incorrect)
258°K → 279°K (Monckton 283°K – incorrect)
259°K → 281°K (Monckton 284°K – incorrect)
260°K → 283°K (Monckton 285°K – incorrect)
261°K → 284°K (Monckton 286°K – incorrect)
262°K → 286°K (Monckton 287°K – incorrect)
263°K → 288°K (Monckton 288°K – correct)
The IPCC-style conjecture that feedbacks start at 255°K with f=0.75 is a better fit.
Mr Palmes continues to maintain that somehow the feedback processes that – whether he likes it or not – exist at 264.3 K (for that is why the temperature in 1850 was 287.6 K) should have some method of knowing that they should not respond to some arbitrary lesser temperature dictated by Mr Palmes. I have provided none of the values in that idiotic table: it is Mr Palmes, not I, whose figures are incorrect all the way through.
His childish table, which dishonestly ascribes to me an array of values not one of which is stated or implied or legitimately deducible in anything I have written, can be replaced with the following much simpler position: Emission temperature 255.4 K, plus 8.9 K directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases: total pre-feedback temperature 264.3 K. Equilibrium post-feedback temperature in 1850 was 287.6 K. Feedback fraction thus 1 – 264.3 / 287.6 = 0.081.
For the nth time, this calculation neither states nor implies anything whatsoever about what the position might have been if there had been no sunlight or an albedo other than that which actually obtains today.
There is absolutely no point in speculating on when the feedback processes might first have come into being, for that makes absolutely no difference to the position as it is today. What matters is that, at 264.3 K, the feedback processes are in being, and are influential enough to react to that 264.3 K of temperature by lifting global temperature from 264.3 K to 287.6 K.
But if Mr Palmes does want to speculate, let him consider this: that even assuming a snowball-Earth albedo as high as 0.66, the emission temperature on the dayside at the Equator at noon, even before taking account of any greenhouse-gas forcings or any feedbacks, would be 300 K, much as it is today. The freezing point of water is a little above 273 K. Go figure.
Here is a less inappropriate version of Palmes’ table. And he should note for the future that the symbol “K” is the SI unit for Kelvin, with no degree symbol.
0°K = 0°K (Palmes 0°K – incorrect: fails to allow for cosmic microwave background)
100°K = 100°K (Palmes 110°K – idiotic)
200°K = 200°K (Palmes 219°K – futile)
220°K = 220°K (Palmes 241°K – half-witted)
221°K = 221°K (Palmes 242°K – stupid)
222°K = 222°K (Palmes 243°K – nonsensical)
223°K = 223°K (Palmes 244°K – doltish)
224°K = 224°K (Palmes 245°K – thick)
225°K = 225°K (Palmes 246°K – wrong)
226°K = 226°K (Palmes 247°K – erroneous)
227°K = 227°K (Palmes 249°K – lackwit)
228°K = 228°K (Palmes 250°K – bumbling)
229°K = 229°K (Palmes 251°K – fatuous)
230°K = 230°K (Palmes 252°K – nincompopltious)
231°K → 232°K (Palmes 253°K – asinine)
232°K → 234°K (Palmes 254°K – misguided)
233°K → 235°K (Palmes 255°K – offbeam)
234°K → 237°K (Palmes 256°K – dense)
235°K → 239°K (Palmes 257°K – false)
236°K → 241°K (Palmes 258°K – troglodytic)
237°K → 242°K (Palmes 260°K – ignorant)
238°K → 244°K (Palmes 261°K – imprudent)
239°K → 246°K (Palmes 262°K – unwise)
240°K → 248°K (Palmes 263°K – serpentine)
241°K → 249°K (Palmes 264°K – wicked)
242°K → 251°K (Palmes 265°K – careless)
243°K → 253°K (Palmes 266°K – lacklustre)
244°K → 255°K (Palmes 267°K – barforamic)
245°K → 256°K (Palmes 268°K – witless)
246°K → 258°K (Palmes 269°K – senseless)
247°K → 260°K (Palmes 270°K – vacuous)
248°K → 262°K (Palmes 272°K – empty-headed)
249°K → 263°K (Palmes 273°K – fatheaded)
250°K → 265°K (Palmes 274°K – pointless)
251°K → 267°K (Palmes 275°K – egregious)
252°K → 269°K (Palmes 276°K – inspissate)
253°K → 270°K (Palmes 277°K – duplicitous)
254°K → 272°K (Palmes 278°K – unthinking)
255°K → 274°K (Palmes 279°K – flatulent)
256°K → 276°K (Palmes 280°K – gross)
257°K → 277°K (Palmes 281°K – obscene)
258°K → 279°K (Palmes 283°K – driveling)
259°K → 281°K (Palmes 284°K – sniveling)
260°K → 283°K (Palmes 285°K – barmy)
261°K → 284°K (Palmes 286°K – loony)
262°K → 286°K (Palmes 287°K – mad)
264°K → 288°K (Monckton 288°K – correct)
I’m sorry to annoy Lord Monckton so much, and stand corrected regarding Kelvin. A Kelvin is a Kelvin, not a degree Kelvin.
So can you make clear what you mean when you say the feedback parameter of circa 0.09 acts on the full input signal of 264.3K to output 287.6K?
Surely then it would also act on an input signal of 100K to give an equilibrium temperature of 110K? 100/(1-0.09) = 109.9K
If that is not the case then pleases accept my apologies I’ve misunderstood your conjecture.
If it is what you propose then my simple table is contains your own results so I don’t see why it deserves such derision.
So please confirm the output of your irreducibly simple model for on an input temperature of 100K? Is it 110K or does it take another value?
In response to Mr Palmes, I do not like outright intellectual dishonesty. I have made it repeatedly plain to him that we are not, repeat not, repeat not, repeat not concerned with what might happen in the absence of today’s insolation. The table whose values Mr Palmes falsely ascribed to me was a fiction of his own making, and it was dishonest of him to put my name on value after value after value in his bogus table when he had been repeatedly told that I do not concern myself with values below the sum of emission temperature and the directly-forced warming from the presence of the naturally-occurring, non-condensing greenhouse gases.
For obvious reasons, the feedback regime in the absence of today’s insolation would be markedly different from today’s regime: therefore, Mr Palmes’ naive calculations have absolutely no bearing on our result (or on anything), and do not in any way represent what we are doing. My name should not have been attached to any of those half-baked calculations.
Also, we have not made a “conjecture”: we have provided a demonstration that official climatology has made a substantial error of physics in defining a “climate feedback” in such a way as formally to exclude the actually large feedback response to emission temperature. We have proven that correction of that error greatly reduces all equilibrium sensitivities. In mathematics, the difference between a conjecture and a demonstration is that the former is open to doubt and the latter is proven.
One can nibble at the edges of our result, as some have tried to do here, by saying – for instance – that we have not allowed for nonlinearity in the feedback regime. But what nonlinearity? The two most significant feedbacks – the water vapor feedback and the Planck “feedback” – are net-linear. The most one can legitimately do is suggest that we have assumed a zero slope for the linear feedback response when in fact we should have given it a slope. However, any realistic slope will give a final value of no more than 0.16 for the feedback fraction, and that would imply a Charney sensitivity of 3.5 / 3.2 / (1 – 0.16) = 1.3 K. As Mr Istvan has said, “Game over!”