Guest Post by Willis Eschenbach
While investigating the question of cycles in climate datasets (Part 1, Part 2), I invented a method I called “sinusoidal periodicity”. What I did was to fit a sine wave of various periods to the data, and record the amplitude of the best fit. I figured it had been invented before, so I asked people what I was doing and what its name was. I also asked if there was a faster way to do it, as my method does a lot of optimization (fitting) and thus is slow. An alert reader, Michael Gordon, pointed out that I was doing a type Fast Fourier Transform (FFT) … and provided a link to Nick Stokes’ R code to verify that indeed, my results are identical to the periodogram of his Fast Fourier Transform. So, it turns out that what I’ve invented can be best described as the “Slow Fourier Transform”, since it does exactly what the FFT does, only much slower … which sounds like bad news.
My great thanks to Michael, however, because actually I’m stoked to find out that I’m doing a Fourier transform. First, I greatly enjoy coming up with new ideas on my own and then finding out people have thought of them before me. Some folks might see that as a loss, finding out that someone thought of my invention or innovation before I did. But to me, that just means that my self-education is on the right track, and I’m coming up with valuable stuff. And in this case it also means that my results are a recognized quantity, a periodogram of the data. This is good news because people already understand what it is I’m showing.
 Figure 1. Slow Fourier transform periodograms of four long-term surface air temperature datasets. Values are the peak-to-peak amplitude of the best-fit sine wave at each cycle length. The longest period shown in each panel is half the full length of the dataset. Top panel is Armagh Observatory in Ireland. The second panel is the Central England Temperature (CET), which is an average of three stations in central England. Third panel is the Berkeley Earth global temperature dataset. The fourth panel shows the HadCRUT4 global temperature dataset. Note that the units are in degrees C, and represent the peak-to-peak swings in temperature at each given cycle length. Data in color are significant after adjustment for autocorrelation at the 90% level. Significance is calculated after removing the monthly seasonal average variations.
Figure 1. Slow Fourier transform periodograms of four long-term surface air temperature datasets. Values are the peak-to-peak amplitude of the best-fit sine wave at each cycle length. The longest period shown in each panel is half the full length of the dataset. Top panel is Armagh Observatory in Ireland. The second panel is the Central England Temperature (CET), which is an average of three stations in central England. Third panel is the Berkeley Earth global temperature dataset. The fourth panel shows the HadCRUT4 global temperature dataset. Note that the units are in degrees C, and represent the peak-to-peak swings in temperature at each given cycle length. Data in color are significant after adjustment for autocorrelation at the 90% level. Significance is calculated after removing the monthly seasonal average variations.
I’m also overjoyed that my method gives identical results to its much speedier cousin, the Fast Fourier transform (FFT), because the Slow Fourier Transform (SFT) has a number of very significant advantages over the FFT. These advantages are particularly important in climate science.
The first big advantage is that the SFT is insensitive to gaps in the data. For example, the Brest tide data goes back to 1807, but there are some missing sections, e.g. from 1836-1846 and 1857-1860. As far as I know, the FFT cannot analyze the full length of the Brest data in one block, but that makes no difference to the SFT. It can utilize all of the data. As you can imagine, in climate science this is a very common issue, so this will allow people to greatly extend the usage of the Fourier transform.
The second big advantage is that the SFT can be used on an irregularly spaced time series. The FFT requires data that is uniformly spaced in time. But there’s a lot of valuable irregularly spaced climate data out there. The slow Fourier transform allows us to calculate the periodogram of the cycles in that irregular data, regardless of the timing of the observations. Even if all you have are observations scattered at various times throughout the year, with entire years missing and some years only having two observations while other years have two hundred observations … no matter. All that affects is the error of the results, it doesn’t prevent the calculation as it does with the FFT.
The third advantage is that the slow Fourier transform is explainable in layman’s terms. If you tell folks that you are transforming data from the time domain to the frequency domain, people’s eyes glaze over. But everyone understands the idea of e.g. a slow six-inch (150 mm) decade-long swing in the sea level, and that is what I am measuring directly and experimentally. Which me leads to …
… the fourth advantage, which is that the results are in the same units as the data. This means that a slow Fourier transform of tidal data gives answers in mm, and an SFT of temperature data (as in Figure 1) gives answers in °C. This allows for an intuitive understanding of the meaning of the results.
The final and largest advantage, however, is that the SFT method allows the calculation of the actual statistical significance of the results for each individual cycle length. The SFT involves fitting a sine wave to some time data. Once the phase and amplitude are optimized (fit) to the best value, we can use a standard least squares linear model to determine the p-value of the relationship between that sine wave and the data. In other words, this is not a theoretical calculation of the significance of the result. It is the actual p-value of the actual sine wave vis-a-vis the actual data at that particular cycle length. As a result, it automatically adjusts for the fact that some of the data may be missing. Note that I have adjusted for autocorrelation using the method of Nychka. In Figure 1 above, results that are significant at the 90% threshold are shown in color. See the note at the end for further discussion regarding significance.
Finally, before moving on, let me emphasize that I doubt if I’m the first person to come up with this method. All I claim is that I came up with it independently. If anyone knows of an earlier reference to the technique, please let me know.
So with that as prologue, let’s take a look at Figure 1, which I repeat here for ease of reference.
There are some interesting things and curious oddities about these results. First, note that we have three spatial scales involved. Armagh is a single station. The CET is a three-station average taken to be representative of the country. And the Berkeley Earth and HadCRUT4 data are global averages. Despite that, however, the cyclical swings in all four cases are on the order of 0.3 to 0.4°C … I’m pretty sure I don’t understand why that might be. Although I must say, it does have a certain pleasing fractal quality to it. It’s curious, however, that the cycles in an individual station should have the same amplitude as cycles as the global average data … but we have to follow the facts wherever they many lead us.
The next thing that I noticed about this graphic was the close correlation between the Armagh and the CET records. While these two areas are physically not all that far apart, they are on different islands, and one is a three-station average. Despite that, they both show peaks at 3, 7.8, 8.2, 11, 13, 14, 21, 24, 28, 34, and 42 years. The valleys between the peaks are also correlated. At about 50 years, however, they begin to diverge. Possibly this is random fluctuations, although the CET dropping to zero at 65 years would seem to rule that out.
I do note, however, that neither the Armagh nor the CET show the reputed 60-year period. In fact, none of the datasets show significant cycles at 60 years … go figure. Two of the four show peaks at 55 years … but both of them have larger peaks, one at 75 and one at 85 years. The other two (Armagh and HadCRUT) show nothing around 60 years.
If anything, this data would argue for something like an 80-year cycle. However … lets not be hasty. There’s more to come.
Here’s the next oddity. As mentioned above, the Armagh and CET periodograms have neatly aligned peaks and valleys over much of their lengths. And the Berkeley Earth periodogram looks at first blush to be quite similar as well. But Figure 2 reveals the oddity:
 Figure 2. As in Figure 1 (without significance information). Black lines connect the peaks and valleys of the Berkeley Earth and CET periodograms. As above, the length of each periodogram is half the length of the dataset.
Figure 2. As in Figure 1 (without significance information). Black lines connect the peaks and valleys of the Berkeley Earth and CET periodograms. As above, the length of each periodogram is half the length of the dataset.
The peaks and valleys of CET and Armagh line up one right above the other. But that’s not true about CET and Berkeley Earth. They fan out. Again, I’m pretty sure I don’t know why. It may be a subtle effect of the Berkeley Earth processing algorithm, I don’t know.
However, despite that, I’m quite impressed by the similarity between the station, local area, and global periodograms. The HadCRUT dataset is clearly the odd man out.
Next, I looked at the differences between the first and second halves of the individual datasets. Figure 3 shows that result for the Armagh dataset. As a well-documented single-station record, presumably this is the cleanest and most internally consistent dataset of the four.
 Figure 3. The periodogram of the full Armagh dataset, as well as of the first and second halves of that dataset.
Figure 3. The periodogram of the full Armagh dataset, as well as of the first and second halves of that dataset.
This is a perfect example of why I pay little attention to purported cycles in the climate datasets. In the first half of the Armagh data, which covers a hundred years, there are strong cycles centered on 23 and 38 years, and almost no power at 28 years.
In the second half of the data, both the strong cycles disappear, as does the lack of power at 28 years. They are replaced by a pair of much smaller peaks at 21 and 29 years, with a minimum at 35 years … go figure.
And remember, the 24 and 38 year periods persisted for about four and about three full periods respectively in the 104-year half-datasets … they persisted for 100 years, and then disappeared. How can one say anything about long-term cycles in a system like that?
Of course, having seen that odd result, I had to look at the same analysis for the CET data. Figure 4 shows those periodograms.
 Figure 4. The periodogram of the full CET dataset, and the first and second halves of that dataset.
Figure 4. The periodogram of the full CET dataset, and the first and second halves of that dataset.
Again, this supports my contention that looking for regular cycles in climate data is a fools errand. Compare the first half of the CET data with the first half of the Armagh data. Both contain significant peaks at 23 and 38 years, with a pronounced v-shaped valley between.
Now look at the second half of each dataset. Each has four very small peaks, at 11, 13, 21, and 27 years, followed by a rising section to the end. The similarity in the cycles of both the full and half datasets from Armagh and the CET, which are two totally independent records, indicates that the cycles which are appearing and disappearing synchronously are real. They are not just random fluctuations in the aether. In that part of the planet, the green and lovely British Isles, in the 19th century there was a strong ~22 year cycle. A hundred years, that’s about five full periods at 22 years per cycle. You’d think after that amount of time you could depend on that … but nooo, in the next hundred years there’s no sign of the pesky 22-year period. It has sunk back into the depths of the fractal ocean without a trace …
One other two-hundred year dataset is shown in Figure 1. Here’s the same analysis using that data, from Berkeley Earth. I have trimmed it to the 1796-2002 common period of the CET and Armagh.
 Figure 5. The SFT periodogram of the full Berkeley Earth dataset, and the first and second halves of that dataset.
Figure 5. The SFT periodogram of the full Berkeley Earth dataset, and the first and second halves of that dataset.
Dang, would you look at that? That’s nothing but pretty. In the first half of the data, once again we see the same two peaks, this time at 24 and 36 years. And just like the CET, there is no sign of the 24-year peak in the second hundred years. It has vanished, just like in the individual datasets. In Figure 6 I summarize the first and second halves of the three datasets shown in Figs. 3-5, so you can see what I mean about the similarities in the timing of the peaks and valleys:
 Figure 6. SFT Periodograms of the first and second halves of the three 208-year datasets. Top row is Berkeley Earth, middle row is CET, and bottom row is Armagh Observatory.
Figure 6. SFT Periodograms of the first and second halves of the three 208-year datasets. Top row is Berkeley Earth, middle row is CET, and bottom row is Armagh Observatory.
So this is an even further confirmation of both the reality of the ~23-year cycle in the first half of the data … as well as the reality of the total disappearance of the ~23-year cycle in the last half of the data. The similarity of these three datasets is a bit of a shock to me, as they range from an individual station to a global average.
So that’s the story of the SFT, the slow Fourier transform. The conclusion is not hard to draw. Don’t bother trying to capture temperature cycles in the wild, those jokers have been taking lessons from the Cheshire Cat. You can watch a strong cycle go up and down for a hundred years. Then just when you think you’ve caught it and corralled it and identified it, and you have it all caged and fenced about with numbers and causes and explanation, you turn your back for a few seconds, and when you turn round again, it has faded out completely, and some other cycle has taken its place.
Despite that, I do believe that this tool, the slow Fourier transform, should provide me with many hours of entertainment …
My best wishes to all,
w.
As Usual, Gotta Say It: Please, if you disagree with me (and yes, unbelievably, that has actually happened in the past), I ask you to have the courtesy to quote the exact words that you disagree with. It lets us all understand just what you think is wrong.
Statistical Significance: As I stated above, I used a 90% level of significance in coloring the significant data. This was for a simple reason. If I use a 95% significance threshold, almost none of the cycles are statistically significant. However, as the above graphs show, the agreement not only between the three independent datasets but between the individual halves of the datasets is strong evidence that we are dealing with real cycles … well, real disappearing cycles, but when they are present they are undoubtedly real. As a result, I reduced the significance threshold to 90% to indicate at least a relative level of statistical significance. Since I maintained that same threshold throughout, it allows us to make distinctions of relative significance based on a uniform metric.
Alternatively, you could argue for the higher 95% significance threshold, and say that this shows that there are almost no significant cycles in the temperature data … I’m easy with either one.
Data and Code: All the data and code used to do the analysis and make these graphics is in a 1.5 Mb zipped folder called “Slow Fourier Transform“. If you change your R directory to that folder it should all work. The file “sea level cycles.R” is the main file. It contains piles of code for this and the last two posts on tidal cycles. The section on temperature (this post) starts at about line 450. Some code on this planet is user-friendly. This code is user-aggressive. Things are not necessarily in order. It’s not designed to be run top to bottom. Persevere, I’ll answer questions.
The nomenclature that I have always understood as the standard:
DFT = discrete Fourier transform – relationship between (x0,….xN-1) complex values (time domain) and (X0,…XN-1) complex values (frequency domain).
FFT = algorithm for efficiently computing the DFT ie using the order of N logN operations, rather than N^2 operations.
I can’t wait for the flood of papers, in the newly ressucitated Pattern Recognition in Physics, using your method of SFT.
The Fourier Transform goes back to 1822. It takes the form:
F(ω) = ∫ f(t) cos(ωt+b) dt
where b is a phase. You can drop b; it’s enough to calculate a version with sin and cos to cover all phases (just use the sum formula for cos).
It’s an infinite integral, and works as a function. Supply any ω, and you can get F(ω). Nothing about a regular array. Numerically, though, you have to approximate. You can only have a finite interval, and evaluate f at a finite number of points. They don’t have to be equally spaced, but you need a good quadrature formula.
That’s basically what you are calling the SFT. In the continuum version, all trig functions are orthogonal, which means you can calculate parts of the spectrum independently. On a finite interval, generally only harmonics of the fundamental, with period equal to the length, are orthogonal to each other. And even then, only approximately, because of the inexact quadrature.
If you restrict to those harmonics, you have a Fourier series. If you use a quadrature with equally spaced intervals, the harmonics become orthogonal again (re summation), up to a number equal to the number of points. That is the Discrete Fourier Transform.
The Fast Fourier Transform is just an efficient way of doing the DFT arithmetic. It isn’t calculating something else. If you want to get a different set of frequencies from the DFT, you can use a longer interval, with padding. You’ll start from a lower fundamental, with the same HF limit, so the divisions are finer. With zero padding, you’re evaluating the same integrals, but the harmonics are orthogonal on the new interval, not the old. You’ll get artefacts from the cut-off to padding.
People use the FFT with padding because it quickly gives you a lot of finely spaced points, even if they’re not the ones you would ideally have chosen. It’s evaluating the same integrals as you are. You can interpolate the data for missing values – there is nothing better. You would do better to interpolate with the SFT too.
“the SFT method allows the calculation of the actual statistical significance of the results for each individual cycle length.”
Any of these methods gives an output which is just a weighted sum of the data. the significance test is the same for all.
BTW, I wrote the R code that you linked to.
Intriguing. The way the cycles of a given frequency fade up and down over time reminds me of nothing so much as when you listen carefully to a bell as the sound dies away. The individual frequencies (pitches) there also come and go as the energy surges from one mode of oscillation to another and back again. Given that the frequency components of the sound of a bell aren’t a neat series of exact number harmonics either, the analogy seems pretty good – although since the Earth’s climate has an external energy source to keep it “ringing”, perhaps a closer match would be a cross between a bell and a Chladni plate. A comparison with the Stadium Wave diagram might prove interesting, too.
Thank you Willis.
I think your results supports the idea of climate as a chaotic system, and that the behavior does not disappear when looking at global mean temperatures.
My favorite is the chaos pendulum that is 100% deterministic but still has a chaotic motion that is unpredictable even if we know the energy content.
So even if we exactly knew the energy balance of the earth we could not predict the temperature in the atmosphere.
I agree with Nick Stokes on this one. An FT is an FT and the FFT is just a fast algorithm for achieving the result.
Otherwise, still a very interesting article as usual.
Meta-cycles? Cycles of cycles, the way they come and go?
First, the “Fast” fourier transform is just one of a number of methods to achieve a transform from time-space to fequency-space. The FFT works, because the transform is a bit like a matrix – lots of well defined and related transforms which can be dramatically simplified. However in principle it is just a discrete fourier transform – which is a fourier transform with regular data on a “comb” pattern.
Willis, what you are dealing with is a discrete fourier transform on an irregular pattern. I would suggest being very careful, because the properties of a regular transform whilst not easy to understand, are at least predictable by the expert. In contrast, when you start having missing data and even irregularly spaced data, it gets increasingly complex to understand how much of what is seen is due to the way the data is presented and how much is an artefact of the actual original continuous signal before it was transformed to a discrete set of data points.
Every such transform adds its own signature to the final signal. (At least when viewed in the entirety of frequency space).
When you take random noise and restrict the frequency components by e.g. averaging, or having a limited set of data, you are very likely to get some form of “ringing”.
Ringing looks like some form of periodicity. And for information, the first paper to mention global warming was a paper trying to explain why the “camp century cycles” of temperature that had been spotted in the camp century ice cores had not predicted global cooling as the climate community expected.
The rise in CO2 was seen as a way to explain why the predictions based on – I think it was something like 128 year cycles had not occurred. That of course led to a new vogue of predicting the end of the world from CO2 — and the camp century cycle predictions of global cooling were hidden and many even deny such predictions were made.
The statistics of frequency-phase space
Your post raises a very interesting question which is this: how does one apply statistics to signals views in frequency-phase space. For a single frequency, the method I was taught was to look at the background profile of the noise – work out the signal to noise ratio and then use some statistics.
I therefore assume the probability of a signal not being noise (or random variation) for a signal with more than one frequency, is the average of the summation of this probability for all frequencies and phases.
Can anyone tell me if this is correct and/or what this kind of statistics is called so that I might finally find something someone else has written on it and know if I’m barking up the wrong tree.
In past I’ve done some work with the CET data. It is correct that it doesn’t show the 60 year periodicity. Analysing annual composite doesn’t revel anything particularly interesting, but analysing (from the 350 year record) two months around summer (June & July) and winter (December & January) solstices, the rest is just transition, it is found that they have distinct spectra.
Further more, it becomes obvious where and why the ’60 year’ (AMO) confusion arises, as shown
HERE
i.e the AMO spectrum (which clearly shows 60 year periodicity) is the envelope of 2 or 3 components clearly shown in the summer CET. Proximity of the CET to the AMO area would favour commonality of trends in the two.
“I’m also overjoyed that my method gives identical results to its much speedier cousin, the Fast Fourier transform (FFT), because the Slow Fourier Transform (SFT) has a number of very significant advantages over the FFT. These advantages are particularly important in climate science.”
……………………………
Should one really point to your own poor math education that explicitely?
Your “SFT” is known as DFT.
FFT does exactly the same thing DFT, just faster. There is no difference in the result.
Your “gaps” in data cannot be treated appropriately by any Fourier transform because of the Gibbs effect (look around what it is).
The right thing you might apply in this case might be wavelets.
Anyway a good idea would be to learn the basic math BEFORE you “publish” smth.
Even if it is just WUWT.
Just a nitpick but the CET record is not an average of the same three stations over the time period you are analyzing. It was compiled originally from multiple records:
“Manley1953) published a time series of monthly mean temperatures representative of central England for 1698-1952, followed (Manley 1974) by an extended and revised series for 1659-1973. Up to 1814 his data are based mainly on overlapping sequences of observations from a variety of carefully chosen and documented locations. Up to 1722, available instrumental records fail to overlap and Manley needs to use non-instrumental series for Utrecht compiled by Labrijn (1945), in order to mate the monthly central England temperature (CET) series complete.Between 1723 and the 1760s there are no gaps in the composite instrumental record, but the observations generally were taken in unheated rooms rather than with a truly outdoor exposure….”
Since 1879 it has been made up from a selection of stations that have changed over time.CET is also is a combination of records from different UK climate areas from wet and humid (Lancashire) to hotter and dry (Cambridgeshire). Up to 1974 the monthly CET values were based on Oxford and seven stations in the NW (Lancashire etc) but then, until 2004, they switched to Rothamsted, Malvern plis 0.5 of Ringway and Squires Gate – also included in the earlier seven. Then in 2004 they switched again to Rothamsted, Malvern and Stonyhurst equally weighted – Oxford? In 2007 they switched Pershore for Malvern. CET in the late 20th century does not agree with the official Meteo records for that area.
http://www.metoffice.gov.uk/hadobs/hadcet/ParkerHorton_CET_IJOC_2005.pdf
You criticized such compilations in your 2011 paper short-long-splice so what makes CET acceptable in your current paper and what impact does the splicing have?
http://wattsupwiththat.com/2011/11/11/short-splice-long-splice/#more-51027
Also, those who consider cycles to be present in the temperature record consider them to be a combination of multiple cycles with frequencies ranging from the 11 year solar cycle to the 1500 year (1300 to 1800 year) Bond cycle – how does this affect your results? Just asking!
Alex:
Please read Nick Stokes comment high above, he says the same but so much nicer.
Also, as i can’t see you show any errors in the post, why so unpleasant?
I think looking for normal variability is important and having read Eisenbachs contribution I look forward to yours.
A few random thoughts:
1. I think, don’t actually know, that the magic in the FFT is that it is very lightweight computationally and therefore can be done in real time. That’s useful in a lot of situations that have no relevance whatsoever to what you are doing. Your method should be fine for your purposes?
2. If I understand Mssr Fourier’s ideas correctly, any time series can be approximated as the sum of a bunch of sine waves with an appropriate amplitude, perod, and phase. Which suggests (to me at least) that any set of data can be analyzed and cycles found. The test is not whether cycles can be found. They WILL be. But whether they predict usefully outside the interval analyzed.
3. Because random noise will have a Fourier transform, and random noise could go anywhere in the next interval with each possible “future” having its own unique transform, that suggests to me that there are possibly multiple valid solutions for the Fourier transform of the current interval. I’ve always meant to look into that. If I’m right about that, then your solutions might not be correct, but not unique. THAT might be worth keeping in mind. Of course I could be fantasizing.
Anyway, good luck. Keep us posted.
“FFT does exactly the same thing DFT, just faster. There is no difference in the result.”
That is true. The difference is in finding out that you calculate the same values more than once, and avoiding it.
Willis, if you fit a sinewave and a cosine wave (both of zero phase) then you do not have to search for phase. The best fit phase is a linear combination of the sine and cosine fits.
I think that a simple sum of the square of the amplitudes will give you what you want. To get back to the same unit take the square root i.e. Result = sqrt( C^2 + S^2), C and S being the amplitudes of the best fit.
It should speed up you SFT if you don’t have to search for phase.
@Scottish Sceptic.
If the noise is Gaussian, then the distribution of the power spectrum is a chi squared distribution and each harmonic has a chi squared distribution with 2 degrees of freedom, i.e.: a negative exponential. This allows significance of spectral components to be tested. In non gausian signals, the diostribution of the power spectrum can often be calculated via the characteristic function of the distribution.
I’m not sure how you are “fitting” a sine/cosine. If you are simply calculating the intgral if the product of a function with a specific sine/cosine wave, then you are simply calculating a DFT.
However, you refer to “optimisation”, which, strictly, implies fitting a sine wave according to an objective function, i.e.:least squares or some other criterion. If you are doing this then you are definitely not calculating Fourier components because the processes are not mathematically equivalent.
I agree with Alex about gaps in the data. A sampled signal is created by multiplying a continuous signal by a set of Dirac functions. In the frequency domain this is a convolution between the spectrum of the sampling process and the signal spectrum. If the sampling is irregular, you will NOT calculate the the true spectrum of the signal.
See Oppenheim and Schafer: Digital signal processing, chapter 1.
Willis: “Again, this supports my contention that looking for regular cycles in climate data is a fools errand. ”
Indeed, anyone thinking that they will find stable, constant amplitude signals resulting from the multiple interacting systems that make up climate is a fool.
FFT, SFT, PA , whatever kind of way you do it you will only find CONSTANT AMPLITUDE signal this way because that’s all you are trying to fit.
That does not mean it’s useless but it needs some more skill to interpret what is shown.
Once again we need the trig identity:
cos(A)+cos(B) = 2*cos((B+A)/2)*cos((B-A)/2) eqn 1
(where cos(A) means cos (2*pi*t/A) if we want to talk in periods not frequency.)
With a little basic algebra this can expressed the other way around
cos(C)*cos(D) = cos((C+D))+cos((C-D)) eqn 2
That is also a special case where the amplitudes of each component are equal. It is more likely that the modulation will be moderate rather than totally going down to zero at some point (which is the RHS as it is shown above). The result is a triplet of peaks that are symmetrically placed in terms of frequency as I explain here:
http://climategrog.wordpress.com/2013/09/08/amplitude-modulation-triplets/
If the physical reality is the RHS , what you will find by frequency analysis is the LHS. It’s not wrong, it is mathematically identical. What can go wrong is in the conclusions that are drawn if this equivalence is not understood, and the fact the freq analysis cannot direct show amplitude varying signals is not realised.
Now if we look at figure 3 where the Armagh dataset is split into first and second halves, in the top panel (full) we see a small peak at what looks like 28 years, that is missing in the middle panel (first half).
In “full” there are two pairs of peaks either side of 28 that appear (as well as can be guessed from these graphs) to the modulation triplets I’ve described, both centred on 28y.
Also the side peaks in red in middle panel look like they overlay the the left and right pairs in “full”. This may be a due to lesser resolution from using an earlier period, or just sampling a different part of the modulation series.
The red peaks appear to be 23 and 36, by eqn 1 that gives a modulation period of 120y that will produce “beat” envelop of 60 years. None of which will show directly in the freq analysis unless there is strong non-linearity or some secondary effects in climate causing an additional signal.
Now looking at the triplets in “full” and calculating the average _freq_ of the outer peaks:
21 and 41 => 27.7y 86y
24 and 34 => 28y 163y
Symmetrical as I suggested and centred on the same value: that of the centre peak. Again using eqn 1 we find the modulation periods causing these triplets to be 86y and 163y. A higher resolution spectrum would give a better indication of the symmetry (which is an important safeguard against seeing spurious triplets everywhere).
in the lower panel (2nd half) we see again 21 and 28 and the suggestion of something that could be third peak seen in “full” that is not resolved from a strong rise at the end.
So instead of throwing up your hands and saying “go figure” like it is some kind of result maybe you need to “go figure” what is in the spectrum and how to interpret it.
I will try to take a closer, higher resolution look at the Armagh record later , it looks interesting.
And the Berkeley Earth and HadCRUT4 data are global averages.
According to your Fig.1, Berkeley Earth has global average temperatures starting from 1752… Sorry, but suspension of disbelief goes only so far.
I’m not sure about this process. I have ‘played’ with ‘sound’ and fourier transform. Try 3 minutes of music (continuous) and then try the same 3 minutes with 10 seconds chopped out of every minute. Compare your results then get back to us. I may be wrong.
Interesting read. I too like to start from scratch (first principles) when deriving methods and “data fits”. There are advantages to that path. Like you, I’m “tickled” when my approach turns out to be one already in use by folks “who should know”. At rare times, I’ve proved the “accepted method” was inapplicable to a specific problem (usually due to incorrect assumptions “hidden” in the “accepted method”). In those rare cases, my “thinking” was seriously challenged by “entrenched professionals”, at first. FWIW to someone who seems to derive similar pleasure from a similar activity.
Ah, Ive just noticed that both CET and Armagh have a peak about 85y ( hard to be more precise on this scale. This abviously ties in with the modulation triplets I noted and suggests some physically separate variation or strong non linear effect is present.
anyway it seems to corroborate the ( 21 28, 41 ) triplet as being correctly interpreted as 27.7y modulated by 86y.
RS ” If the sampling is irregular, you will NOT calculate the the true spectrum of the signal.”
That is strictly true. However, as long as this is recognised, I think it’s a useful means of bridging gaps in the data. Some awareness of the distortion caused and not doing it over very broken data would seem prudent but I think it’s a useful alternative to zero padded FFT and similar techniques that have strict continuity requirements.
A SFT of the NAO would be interesting.
Willis. More nice work and you get people thinking. A few comments/thoughts:
1. Nick Stokes’ comment is well worth reading.
2. FFTs are limited to values of 2^n (16, 32, 64, 128 …).
3. People often pad the time series with zeros to get finer detail in the frequency domain.
4. While regular sampling is implied in the FFT you could just jam irregular data through it as it only takes the time series as input and not the sample times. The result would not be reliable.
5. FFTs are not approximations. They are an exact band-limited representation of a time series. This is why you can transform to frequency and back to time and recover the original data set.
6. FFT frequency profiles are normally shown as a power spectrum from low to high frequency (the reverse of your plots).
7. Gaps in a time series are easily interpolated with little effect on the frequency content. Large gaps can be worked around by splitting the time series at the gap and applying an FFT separately to both sections.
8. Units are “real” and “preserved” in a FFT. Time becomes frequency, for example (secs > Hz or 1/secs). Upon the reverse FFT you always go back to your original units.
9. The early Berkley dataset shows well-behaved higher frequency content (Figure 5) that is not present in the other datasets. This makes me wonder if it is more heavily filtered, or outliers removed.
10. If I was researching the frequency content of a time series and obtained power spectra similar to your periodicity diagrams I would cry. Based on the large variation in frequency content one can only conclude that many of the climate “cycles” we read about are not periodic in the temperature data, or fall well below natural variation. This is probably what makes climate scientists so “valuable”.
Thanks Willis. Good explorations.
You said “Looking for regular cycles in climate data is a fools errand.”
But the imprints of the 24 hrs, seasonal and orbital annual cycles will be there. Also the Sun will mark the record with its “around” 11-years cycle. ENSO and PDO will mark it.
Having a cyclic nature is not the same as having a regular cyclic nature.
Nick Stokes says:
The Fourier Transform goes back to 1822. It takes the form:
F(ω) = ∫ f(t) cos(ωt+b) dt
where b is a phase. You can drop b; it’s enough to calculate a version with sin and cos to cover all phases (just use the sum formula for cos).
===
That’s a cosine transformation, the full fourier is
F(ω) = ∫ f(t) exp(iωt) dt ; i or j in E eng world is srqt(-1)
exp(iωt) = i.cos(ωt)+ sin(ωt)
FT ( or FFT ) is a complex spectrum containing both “cos” and “sin” terms which thus contains the phase information .
atan2(Re/Im) ; atan2 being arctan that knows the difference between the +ve and -ve quadrants.
BTW Nick, nice confirmation of the equivalence of SFT and padded FFT. Shows the results are a useful estimation of the spectrum for broken data.
I’m ultimately more comfortable with several short periods (with gaps) rather than one long period that has been smoothed. The short periods are real, the long period is unreal.
Tweaking numbers smacks of ‘climate science’. Inevitably you end up with results you want to see.
Science battles should be over apodization, not sampling of Internet polls.
There is a FFT algorithm called FOURG that allows for any N number of input points as long as N is non-prime. I’ve used N LOG N for so long I forgot. I think FOURG is also known as the Cooley – Tukey algorithm. I have it somewhere in FORTRAN IV so Gavin would be proud.
Greg says: May 4, 2014 at 5:11 am
“That’s a cosine transformation, “
Not with the arbitrary phase term. Try with b=π/2.
That’s my point there. Expand the cos and you get a lin comb of sin and cos transform. The latter are all you need.
Willis re figure 5: “Dang, would you look at that? That’s nothing but pretty. In the first half of the data, once again we see the same two peaks, this time at 24 and 36 years. And just like the CET, there is no sign of the 24-year peak in the second hundred years.”
Again you insert your interpretation in place of what the data shows. It does not show “no sign of” it shows a reduced amplitude at 24…25 years.
freq ave(20 33) = 24.9
modulation = 101.5y.
Now since your data sample for 2nd half is 102, there may be some data processing reason for this apparent modulation, or it maybe physical. In either case it is incorrect to conclude there is “no sign” of it. You are just not reading the signs correctly.
The combined amplitude of those three peaks is about the same at “first half” and “full”.
Doesn’t all this analysis show that Mannipulated temperature series strips out natural cycles? Do we have anything close to raw data to work with anymore?
It may be fun playing with software etc. but that is how Mann found a hockey stick. Please point my nose towards something real, like a temperature or something. Like something in these cycles that relate to real life.
@Greg.
I agree that you can approximate the spectrum using irregularly sampled data by quadrature or padding. The problem is that if you express the FFT in matrix form, its eigenvectors are orthogonal. When irregularly sampled, this is no longer true. The problem arises (in my experience) when you try to use the spectrum for Fourier interpolation. This has occurred quite often in my area where I sampled a “signal” spatially and the sampling depends on the geometry of the signal in question.
I’m still worried because I don’t understand what has been done here. There is reference to “fitting” and “optimisation”, which is not the case in a DFT which is essentially a correlation. If there has been “optimisation” of some objective function, then I suspect that what is being discussed is not a DFT (as is well known, least squares fit of co/sin waves by least sqares does not give the correct result).
Steve from Rockwood says:
“2. FFTs are limited to values of 2^n (16, 32, 64, 128 …).”
This is a commonly held belief but its not true. FFT’s can be computed using any prime numbers. The ultimate performance in this respect would be the MIT fftw code (which is what my company uses, under licence, for very large 3D fft)
And as I said in the previous post, what Willis doing is a Fourier analysis but by fitting each sine wave one at a time in the time domain. Its not new or original and its very inefficient.
I’ll ask a question by first summarizing what various folks have pointed out above. (which has an average
(which has an average 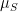 ) and minimizing the quantity
) and minimizing the quantity ![\sum\limits_{n}^{}\left[ S_n - \mu_S - r_k \sin(2\pi t_n /T_k + \phi_k)\right] ^2](https://s0.wp.com/latex.php?latex=%5Csum%5Climits_%7Bn%7D%5E%7B%7D%5Cleft%5B+S_n+-+%5Cmu_S+-+r_k+%5Csin%282%5Cpi++t_n+%2FT_k+%2B+%5Cphi_k%29%5Cright%5D+%5E2&bg=ffffff&fg=000&s=0&c=20201002) for various sine frequencies
for various sine frequencies  by finding optimal values of
by finding optimal values of  and
and  . You see as among this approach’s advantages that
. You see as among this approach’s advantages that  has the same units of measure as the data
has the same units of measure as the data  .
. , with all frequencies
, with all frequencies 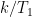 so chosen that the sinusoids (
so chosen that the sinusoids ( ) have respective integer numbers of periods over the
) have respective integer numbers of periods over the  record and are thus orthogonal: to the extent that the discrete Fourier Transform approximates the continuous Fourier Transform, adding them together reduces the error.
record and are thus orthogonal: to the extent that the discrete Fourier Transform approximates the continuous Fourier Transform, adding them together reduces the error.![\int\limits_{0}^{T_1}\left[ a(t)-\mu_a - r\left[ b(t)-\mu_b\right] \right]^2dt](https://s0.wp.com/latex.php?latex=%5Cint%5Climits_%7B0%7D%5E%7BT_1%7D%5Cleft%5B+a%28t%29-%5Cmu_a+-+r%5Cleft%5B+b%28t%29-%5Cmu_b%5Cright%5D+%5Cright%5D%5E2dt&bg=ffffff&fg=000&s=0&c=20201002) , one sets to zero the derivative of that quantity with respect to
, one sets to zero the derivative of that quantity with respect to  and solves for
and solves for  , resulting in
, resulting in  . So correlation is just a short cut to error minimization. And
. So correlation is just a short cut to error minimization. And  ‘s units are the same as
‘s units are the same as  ‘s if
‘s if 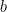 is dimensionless, so, despite the fact that folks are wont to distinguish between the time and frequency domains, I don’t see why you couldn’t assign the Fourier coefficients the input data’s units of measure.
is dimensionless, so, despite the fact that folks are wont to distinguish between the time and frequency domains, I don’t see why you couldn’t assign the Fourier coefficients the input data’s units of measure. and the sinusoidal component
and the sinusoidal component  ?
?
Although I didn’t have the patience to run down all the R functions you use, my guess is that you’re taking the (detrended) data
In apparent contrast, a DFT (which the FFT is an algorithm for computing efficiently) works by correlation
With the possible exception of the orthogonality constraint and your ignoring the errors that omitted data impose, though, these are actually the same things. To minimize
That was the wind-up. Here’s the pitch: In this scheme, what is the mathematical expression for the confidence interval? Can that be expressed in terms of the data
to Thinking Scientist:
I thought you could use any number, not just a prime one. The series of numbers you referred to are not prime
Willis,
Climate cycles don’t have clockwork periodicity. Even if the primary driver is some sort of astrophysical cycle with a stable periodicity, the Earth’s climate doesn’t react exactly the same way each time. On top of that, there are many convolved cycles with different periods and amplitudes. Atmosphere and oceanic circulations are very stochastic processes. In the HadCRUT series, the nominal 60-yr cycle can range from about 50 to 80 years.
If you are looking for highly regular cycles, you won’t see them. If you are looking for coherent patterns of quasi periodic fluctuations, they are hard to miss.
Have you tried your SFT on the GISP 2 ice core d18O series? It would be interesting to see how that compares to Davis & Bohling.
RS says: May 4, 2014 at 5:59 am
“If there has been “optimisation” of some objective function, then I suspect that what is being discussed is not a DFT (as is well known, least squares fit of co/sin waves by least sqares does not give the correct result).”
He’s fitting each sinusoid to the objective function of minimum sum squares deviation (pointwise), varying amplitude and phase. I showed here how that is equivalent to FT (mod of complex form). It gets more complicated if you don’t have orthogonality, as you say (ie not DFT). But the objective function itself is just a quadratic, so you can differentiate and get it in one shot.
I’ve run Willis’ code with test sinusoids. It works quite well – as well as other FTs. I would say that it is quite robust to missing data and not much affected by non-periodicity over the interval, as long as you stick to periods less than 1/3 total, as he does. It’s slow – about 20 secs on my PC for 200 yrs; FFT is sub-second.
You’d expect all that. FT’s with orthogonality do minimise that sum squares. And above the third harmonic, deviation from orthogonality due to ends isn’t too bad.
sorry Nick
that all sounded like IPCC talk with the if, buts and maybes. I designed an electronic system based on that and it didn’t do shit. I won’t design anything unless I have zero error bars or less than .001%
For all the people who know things about FFT, how well does it work for heteroscedastic data?
It’s easy to see that the errors in the data sets change with time, as seen in this image that I made a while back. [The image has some smoothing and fits that can be ignored. I made it back when I thought Lovejoy was saying that error as a function of time was constant and small, and I wanted to double-check that for myself.]
Regression can get around that by assuming that the error has the same distribution type, even if the parameters of that change over time. It will screw up any error estimates, but the coefficients should be fine. I have no idea what this means for FFT, though, which is why I ask. Thanks!
to Indpndt:
I’m not much of an expert on FFT, just generally familiar with it’s principles. Essentially you take a curve/line and you can break it down to sine waves of various properties. What u decide based on those sine waves is up to you. You should be able to ‘reassemble’ those sine waves to the original curve/line. The points on your original diagram are not much use in this. Use the blue line.
Thanks, David Middleton. Good observation.
“the Earth’s climate doesn’t react exactly the same way each time.”
That, I think, is because our planet responds to the few regular cycles from ever changing points in its unfolding history.
A new winter starts after a new fall, so even if the astronomical conditions are the same, the response will be new.
So, climate is not theoretical-clockwork cyclical, maybe a clock with a loosely fitting mechanism that at times gains, at other times looses. And when El Niño winds it up real tight it shifts to a new regime that only later La Niñas will relax.
alex says:
May 4, 2014 at 1:25 am
Well … no. My SFT gives the same result as a DFT … but by an entirely different method.
Yes, and so does the SFT, only slower. There is no difference in the result. However, there is a large difference in the method.
So you claim. However, when I’ve actually tested my method by removing data and then putting it back it, I find it works quite well. I think it may relate to the fact that I’m NOT transforming the data from the time space to the frequency space and back again as is done by a Fourier transform. I arrive at the same point, but by a different method that as far as I can tell from my testing is NOT subject to the Gibbs effect. So what did you find when you actually tested my method? Oh … right …
Come back when you’ve actually used my method and you know what you are talking about. Right now, you’re just revealing your own poor math education by making claims about a mathematical method that you have never tested in your life.
w.
RS says:
May 4, 2014 at 3:56 am
Thanks, RS. I am indeed optimizing, meaning that I adjust the phase and the amplitude of the sine wave to get the best fit.
And whether I am “calculating Fourier components” or not is of little interest, because I arrive at the same endpoint. Go figure …
w.
Hi Willis
There seem to be two alexs on this site . I’m Alex with a capital A – I’m the nice one. I don’t denigrate, I just ask questions or make statements politely.
Seeing different cycle lengths at different times brings to mind what you see in a negative-feedback process control environment when trying to regulate an output under changing conditions. My experience is with PID tuning for regulating pressures/flows in a natural gas pipeline. It’s very easy to come up with control parameters for any given situation, but it can be very tricky to handle any and all conditions you are likely to encounter, especially as they change. Obviously, you must when safety and reliability are at stake.
In any particular set of conditions, there will always be an oscillation and its cycle length and amplitude will be fairly uniform. Change any condition that affects the system (upstream pressure, downstream pressure, downstream demand, varying set-points), and the system will stabilize with an oscillation with a different amplitude and/or cycle length. In my situation, things changed all the time based on temperature, time-of-day, season, etc.
What brought this to mind was Willis’s earth-thermostat hypothesis. Assuming that there is such a thing, if whatever affects climate never changes then you wouldn’t expect to see the length or amplitude of the resulting cycles change over time. The apparent fact that they did change implies that something, probably several things, did change and, in my mind, likely changes all the time.
In my closed-system environment, it was a bitch to come up with control algorithms that adequately handled the limited range of conditions likely to be encountered. I can’t even imagine what it would take to understand what’s happening with our planet – certainly not today’s global climate models. But in all cases, I would expect to see cycles like the ones Willis found and to see the length and amplitude change over time as well. With so many unpredictable inputs (volcanoes, cosmic rays, whatever), I don’t think you would ever be able to predict these, only see them after the fact.
RS says:
May 4, 2014 at 3:56 am
Thanks, RS. Since I’m not wandering into the frequency domain, I’m not sure why this would apply. Once again, all of you guys are making claims based on what the Fourier transform does. I’m doing something different and arriving at the same endpoint.

And yes, if you remove any data from a complete dataset, you will NOT calculate the true spectrum of the signal … the question is, how resilient is the method to gaps in the data. The standard Fourier transform is not resilient at all. The slow Fourier transform is surprisingly resilient.
Please, folks, test my method before making claims, no matter how theoretically correct you might think that they are. Yes, if there are gaps in the data the results will be different, in part simply because we have less data. But here’s an example of what I’m talking about. This shows the Armagh periodogram, along with a periodogram of the Armagh data with a full 5% of it removed at random, and also a periodogram of the Armagh data with a five-year chuck of it cut out from 1900-1905:
Can you do that with a standard Fourier transform?
You guys are making claims based on the traditional method of creating the periodogram. I’m not using that method.
w.
Nick Stokes says:
May 4, 2014 at 12:36 am
Sorry, Nick, I didn’t see your name on the post so I didn’t credit you. I’ve changed the head post to reflect your contribution, much appreciated.
w.
Alex says:
May 4, 2014 at 7:33 am
Thanks, Capital A Alex, noted.
w.
But Willis, you are wandering into the frequency domain. You are calculating the amplitude and phase of various components in the signal and you are making an implicit assumption about the structure of the signal in the frequency domain. In this case, one has to understand the relationship between sampling statistics and computation of the Fourier Integral.
This is a fundamental property of the signal and it doesn’t matter how you try to estimate the frequency (or period) and phase, one is dealing with a signal that is corrupted by irregular sampling. For example, when you have established the Fourier coefficients, using these for interpolation will give errors.
The problem with non-periodic sampling is that it forces corelation between components that are othogonal. If you express the the DFT in matrix form, it has orthogonal eigenvectors. When the sampling is irregular, the eigenvectors are non-orthogonal. To put this another way, when one reconstructs (interpolates) a signal that is regularly sampled, one can treat the process as a convolution with sin(wt)/t. This has the property in regular sampling of being zero at each sample and so the original signal is unaffected and the interpolated samples are a weighted sum of, in principle, the infinite sequence of samples in the signal. This cannot be done for an irregular signal as one cannot assign a frequency,w, to the interpolating function.
This is a bit of an arm waving explanation but the point I am making is that there exists an underlying theory to relate irregular sampling an its spectrum.
The other question is why not perform the calculation using simple quadrature, i.e.: direct integration of Fourier integral?.
Don’t bother trying to capture temperature cycles in the wild, those jokers have been taking lessons from the Cheshire Cat.
=========================
This shows how cycles can imitate the Cheshire Cat:
http://www.animations.physics.unsw.edu.au/jw/beats.htm
In performing a Fourier analysis to look for periodicities, like you are doing, it is best to first detrend the data. A trend can be viewed as either non-periodic or a periodic term that has a period longer than the duration of the data time series. Without removal of a trend, you will end up mapping a (possibly messy) continuum of Fourier power into the power of the periodic ingredients that might actually be present in the data. Also, I would call the discrete fitting of individual Fourier terms to a data time series a “periodogram”.
@Nick Stokes
You are of course correct. I didn’t express myself very well. What I was getting at was that irregular sampling biases a minimisation method. (Consider an irregularly sampled square wave). The errors will obviously depend on the structure of the signal and, I would guess, become more pronounced at higher frequencies.
A more general point is whether FT methods are the best for spectral estimation. While one thinks of the DFT as generating a spectrum, which it does with some limitations, its importance is in manipulation, via convolution etc, rather than spectral estimation per se. I would imagine that other methods of spectral estimation, such as minimum entropy or eigenvector decomposition of the auto-correlation matrix might be more stable with this sort of data.
Perhaps, I don’t have much to offer here but a while ago I tried a different tact. I analyzed the Hadcrut4 data and simply tried a curve fitting procedure that I used to characterize magnetic properties (BH curves). The model equation I used in those cases was a high order polynomial divided by another high order polynomial. It worked quite well.


In this instance I used the fit equation of multiple sinusoids:
I got the following results.
https://onedrive.live.com/redir?resid=A14244340288E543!4393&authkey=!AKZvfIj0HHrcjMw&ithint=folder%2c
With only roughly half of a cycle I will not vouch for the validity of the cycle with the long period. However, I clearly think that there is an approximate 60 year cycle. To me it passes the eyeball test. At one time I was showing a 10.7 year cycle but when I read Willis’s earlier post about the solar cycle I had to agree its magnitude was negligible. I then tried to find a second long period cycle that might work. It is there but the magnitude is also negligible.
Nick Stokes says:
That’s my point there. Expand the cos and you get a lin comb of sin and cos transform. The latter are all you need.
Indeed, if there is both phase and amplitude param in the cosine at each freq , it is entirely equivalent to the full FT. I beg your pardon.
It’s clearly “I agree with Nick” day — again, his observations are dead on, with a hat tip to Greg as well for correctly giving the equation of a Fourier transform (within normalization). To reiterate, given any function latex \~f(\omega) = \frac{1}{\sqrt{2}} \int_{-\infty}^{\infty) f(x) e^{-i\omega x} dx$
latex \~f(\omega) = \frac{1}{\sqrt{2}} \int_{-\infty}^{\infty) f(x) e^{-i\omega x} dx$

and:
Sine and cosine transforms are just the imaginary and/or real parts of this.
The FT has many interesting properties other than orthogonality (note the forward and backward transformation are symmetric) and the relation of that orthogonality to the Dirac delta function, which is not really a function but the limit of a distribution. One of them is what the transform of a function with compact support — even a pure sinusoidal harmonic function produces a finite width around the single frequency represented if you FT it on a finite interval, and on another thread I pointed out that what is called “pressure broadening” produces a Lorentzian line shape in radiation physics because collisions randomly interrupt the phase of the emitted wave, effectively doing the same thing but with many possible data intervals smeared out over a range.
If anybody cares about the kinds of “ringing” artifacts caused by domain truncation, Wikipedia has a whole article on them with numerous links:
http://en.wikipedia.org/wiki/Ringing_artifacts
They are relevant to lots and lots of things — measureable physical phenomena arise because waves in material are like harmonic waves in some cases and so interesting things happen at sharp boundaries. There are connections between this and the Heisenberg uncertainty principle — a single frequency spatial wave must have non-compact support, and the shorter you make its support relative to its wavelength, the broader its fourier transform, which is basically saying that the more you localize it, the less certain is its momentum in QM. There are connections to data compression (especially JPEG image compression). There are connections to data processing. And as Nick said, even with a long train of data, one still has to deal with the numerical issues of doing the integral if one isn’t integrating an analytic function that can be done with a piece of paper and pen. Quadrature is subtle, in part because quadrature itself always is fitting a smooth function to data and evaluating the integral of the smooth function, and there is no way to know if the functional relationship that the data is sampling is actually smooth and interpolable in between. One can always find functions that fool any give quadrature program, and in the end if one has pure data without any other knowledge (so one cannot hand wave an expectation of smoothness at some level) one is basically crossing one’s fingers and hoping when one applies a quadrature algorithm to evaluate its integral. Many of these problems are apropos the long-running discussion of evaluating global average of any sort from sparse data.
You might also want to look into wavelet transforms:
http://en.wikipedia.org/wiki/Wavelet_transform
and links therein. Wavelets are one of several approaches to dealing with FT artifacts for datasets with compact support. Basically (if I understand correct, which I may not:-) they do something “like” a FT but within a form-factor “window” of some finite width to effectively remove artifacts like ringing from the result within encapsulated frequency ranges. Note well the connection to the ‘uncertainty principle’ associated with FTs — FTs contain an intrinsic no-free-lunch behavior between the frequency and time domain and wavelets are an attempt to get a “minimum collective uncertainty” decomposition rather than one that minimizes one kind of uncertainty at the expense of the other. Lots of other good links here too.
rgb
@ Alex says:
May 4, 2014 at 7:33 am
So, then you are not the alex who can’t spell “explicitly”. Good.
OK, so screw me, once again WordPress ate my (equation) homework. Sigh. Instead of trying to fix it I’ll just post:
http://en.wikipedia.org/wiki/Fourier_transform#Other_conventions
Again, a wealth of information. Tons of really good books on the subject, too.
The Fourier Transform goes back to 1822.
And, IIRC, the FFT goes back to Gauss’ Theory of the motion of the heavenly bodies moving about the sun in conic sections, published in 1809, which is even earliar 😉 I think he was using it to fit trigonometric series. Gauss was a very, very, very smart guy.
Re: missing points or unevenly spaced samples. There are various methods out there, including interpolating between sample points. I don’t know what is best practice these days.
This would be a good time to review a couple of my WUWT favorites with 2,500 year records from tree rings, see
http://wattsupwiththat.com/2011/12/07/in-china-there-are-no-hockey-sticks/ which shows the big cycles are 110, 199, 800, 1324 years long. It does show others, e.g. 18 (Saros cycle?), 24 (close to your 20s), 30, and 37.
http://wattsupwiththat.com/2012/06/17/manns-hockey-stick-refuted-10-years-before-it-was-published/ which stays in the time domain.
The Chinese paper claims the record is long enough for forecasting, and then forecasts cooling though 2068. I’d like to see that work replicated….
As David and Andres point out, above, the real world system does not always have ‘pure’ cycles with a consistent wavelength that the Fourier transform would highlight.
If a cycle has a period of 50 years one time, then 65 years, then 60 years, it will not appear in the frequency spectrum as a strong peak.
For example, while one can see in the temperature data alternating periods of roughly three decades of warming and cooling superimposed on the data, periods that appear to be connected to the PDO and the changing dominance of nino-over-nina conditions versus nina-over-nino, that does not recur at precisely sixty year intervals.
So I’m not sure that the FT method is of great value in ascertaining what cyclicity exists or does not exist in the real world.
Willis – re the difference between half-data sets – what would be fascinating to see (but lots more work) would be the equivalent of a spectrogram plot (with your cycle length x-axis rotated to be vertical, amplitude represented by color/intensity) and process sequential 104-year blocks stepped in time by 1 year increments to obtain an x-axis. This would reveal whether any particular cycle length tends to appear, disappear, reappear over time. Generally easy to do with regular sampled data series & FFT, but may be just too painful using “SFT”…
The Fourier Transform goes back to 1822.
And the FFT to 1805, Carl Friedrich Gauss, “Theoria interpolationis methodo nova tractata”, which is even earlier 😉
Gunnar Strandell says:
May 4, 2014 at 12:55 am
My favorite is the chaos pendulum that is 100% deterministic but still has a chaotic motion that is unpredictable even if we know the energy content.
===============
very interesting result. like temperature. the motion is bounded, but impossible to calculate where it will be in the future. might be high, might be low, without any change in forcings. at infinity the average is perhaps meaningful, but along the way it is the variance that rules the results.
http://www.myphysicslab.com/dbl_pendulum.html
“According to your Fig.1, Berkeley Earth has global average temperatures starting from 1752… Sorry, but suspension of disbelief goes only so far.”
one can, and we do, calculate our expectation for the entire field given the observations at that time.
Its pretty simple. However the errors bars are large. That said, one can predict, and we do, what the average temperature would be for all unsampled locations at that time. This estimate uses all the data
available, and assumes that the correlation structure is constant over time.
More gas to the fire! Has anyone tried Prony’s method (1795!) for this problem?
You are trying to fit data to a form:
x(t) = Sum over k { Bk e^(-sigmak t) cos (omegak t + thetak) }
thus just a sum of decaying sinusoidal waveforms (much like human speech). It at first appears that one only needs 4 data points for each k (four equations in 4 unknowns: B, sigma, omega, and fi). [Sigma=0 if no decay.] Two problems: (1) these are NOT linear equations and (2) noisy samples CAN spoil everything.
I have never discovered what Prony was doing with discrete series in 1795, but he transformed the non-linear problem to one of first finding the poles (the frequency and decay constants) in terms of a LINEAR DIFFERENCE equations (discrete-time resonator), to which initial conditions could then be applied, much as we learned to solve differential equations in Calculus 101 (general and particular parts to the problem).
With Prony, you only need tiny amounts of data. Four consecutive points DO give you one sinusoidal component. And it is then trivial to compute (and compare) the rest of the series. The result of course does NOT necessarily mean anything. It is quite possible that your initial assumptions that the signal being analyzed is composed of sinusoidal waveforms and/or that you guessed the right order, is wrong. Does your series represent the data outside the training? Often (usually?) not.
Noise is the second problem, but it can be attacked. I recently wrote up some comments on this:
http://electronotes.netfirms.com/EN221.pdf
and the first references there may be a better introduction. Things like solving a very large overdetermined set of equations (least squares pseudoinverse) and autocorrelation (Yule-Walker) are very useful.
Fun to try. Any connection to reality is, or course, tenuous!
Good review of Fourier stuff on this thread, and wavelets always should be considered.
Given the data are taken from nature and that feedbacks (positive and negative) exist in nature, an FT analysis may not tell one what they may think. The global biome, for example, responds immediately to Krakatoa-scale volcanic activity. Also – I’m not sure why Willis thinks he’s not working in both the time and frequency domains, but that is what [SF]FT does. When I read the first few paragraphs I knew I was looking at an FT analysis, and it also reminded me of early work with Lissajous and spectrum analysis work I did with swept filters and noise/wave generators back when things were analog.
Anyway – another very interesting article that sheds light on the complexities of climate analysis.
RS says:
May 4, 2014 at 9:03 am
Thanks, RS. That’s helpful. I think the difference might best be understood by considering what I’m doing at a given cycle length. Let’s take 60 years as an example.

I have a chunk of data. It may or may not be either periodic or complete. I use an iterative fitting procedure to determine the phase and amplitude of the best fit of a sine wave with a period of sixty years.
Now, forget about our friend Joe Fourier for a moment. All I’m doing is determining the amplitude of the best fit.
So let’s suppose for a moment that our chunk of data is a 60-year sine wave with a bunch of random normal error added to it.
Now consider how much effect the removal of a portion of that 60-year signal plus error will have on the amplitude of the fitted sine wave … not much. The chopping out of chunks of the signal doesn’t affect the fit a whole lot.
Now, if the missing data is regular in nature, like you chopped out every 13th year of the signal, that will definitely affect the results. But in general, my algorithm is remarkably resistant to missing data.
That’s what I meant when I said that I’m not transforming a time-domain signal into the frequency domain and then back out again. I’m just looking at how well a sine wave matches the data.
Here’s an example showing what I mean. I’ve taken a 180-year signal which is a sine wave with a period of 30 years, plus gaussian noise with a standard deviation of 0.5. Then I altered that data in two ways. In one, I randomly removed 20% of the data. In the other, I removed all of the data for 1900 to 1902, as well as the data for 1917. Then I ran the slow Fourier algorithm on all three. Here are the results:
As you can see, even with 20% of the data missing, or with a couple of year-long sections missing entirely, there is little effect on the results,
Thanks. Yes, I understand that. However, I’m not trying to reconstruct a signal from a set of orthogonal (or non-orthogonal) components.
As my example above shows, i can knock out 20% of a signal and still get essentially the same periodogram. I’d be interested in what your underlying theory would say about that.
I’d love to, but I don’t see how to do what you propose. Perhaps you could explain in a bit more detail.
w.
Willis, you may like this.
Where sea ice is will affect ocean currents and ocean currents will affect where sea ice grows and shrinks.
The way I envision the system is that harmonic circulation patterns will form in some ice conditions and be destroyed in others.
Jeffrey says:
May 4, 2014 at 9:23 am
Thanks, Jeffrey. As the code shows, but also as I forgot to mention, all data series are detrended before analysis.
w.
“Jeffrey says:
May 4, 2014 at 9:23 am
In performing a Fourier analysis to look for periodicities, like you are doing, it is best to first detrend the data.”
YUP!
This is one of the tricks that folks can use to manufacture 60 year cycles.
How?
Well first off to “detrend” the data one is asserting that there is a ‘trend’ in the data. Well, the data
have no trend. The data are just the data. A trend comes about by a DECISION to apply a model to the
data. For example, one asserts that there is a linear trend and then that trend is removed.
But we know that many trends can be found in the data. we could fit a quadratic, we could fit a spline.
we can find many models that “fit” the data and ‘remove” the trend terms from the data. But the data as the data have no trend. Trend is a property of a model used to explain the data.
If you fiddle about there is no doubt that one can remove a “trend” and find a cycle in what’s left.
The trick is removing a well chosen ‘trend”. That is, if you cherry pick a different trend to ‘remove’
you can engineer out a 60 year cycle.
This is how scaffetta gets his 60 year cycle.
Say what? yes, the trick is in the detrend step. remember you can detrend with a linear trend or you
can pick some other trend to remove. The data have no trend, the model you fit to data has the trend term.
http://www.skepticalscience.com/Astronomical_cycles.html
##### key paragraph
“The data has been detrended assuming an underlying parabolic trend. The main 60 year cycle, due to the alignment of Jupiter and Saturn, shows up very clear, but there are more. In particular, he identifies a total of 10 cycles due to combination of planets motion and one due to the moon (fig. 6B in the paper). Of those cycles, only two more are considered significant, namely those with periods of 20 and 30 years.
Fascinating. But then, a few pages later, Scafetta writes:
“However, the meaning of the quadratic fit forecast should not be mistaken: indeed, alternative fitting functions can be adopted, they would equally well fit the data from 1850 to 2009 but may diverge during the 21st century.”
His warning is on the problem of extrapolation of the trend in the future, which he nonetheless shows. But this sentence made me think that it’s true, once we put physics aside, we’re free to use the trend we like; so why parabolic? I decided to take a closer look, and this turns out to be the beginning of the end.
#############
Bottom line.
You can produce the magical 60 year cycle by cherry picking the trend you choose to remove.
next, to do cycle analysis properly the “trend” has to be removed.
but, removal of the trend IS UNDERDETERMINED. That means nothing in the data tells you
what the underlying data generating process really is. Many models can fit the data.
Next most models ( Im talking statistical models) fit to climate data are NON PHYSICAL. that is
their functional form is wrong from a physics standpoint ( temperature cannot increase linearly over all time).
Cycle analysis after trend removal is pretty much doomed to failure unless one can show that the trend removed is in fact a unique feature of the data generating process or at best the cycle analysis is only true if the assumptions about the trend removal are valid. That is all the statistical tests are subject to a methodological uncertainty that is typically not calculated.
1. Assume the trend is linear ( back up this assumption with a statistical test)
2. adjust the data by removing it
3. find a cycle
4. Assert the existence of the cycle with 95% confidence
5. Dont tell people that step 1 has its own uncertainty. Dont tell people that you had a choice of
trends ( data generating models) to remove and that the methodological uncertainty is substantial.
Having said that it’s not “wrong” to remove a linear trend. Its an assumption. Its just a tool, a choice. There are other choices and so ones understanding is conditioned by that choice. And that choice is open. It is an assumption about the underlying process. It is applying a theory to the data to produce adjusted data. The other path to understanding is to create models of the underlying process. That would be a GCM.
RS says:
May 4, 2014 at 9:26 am
Thanks, RS. I love the web, your comments point me to further investigations. OK, let’s consider an irregularly sampled square wave. I’ve taken a 180-years series composed of six 30-year square waves. Then I randomly knocked out a full 40% of the data. Forty percent gone. Here are the results:

I’m not seeing the degradation of the results that you seem to be implying …
w.
Alex says “to Thinking Scientist:
I thought you could use any number, not just a prime one. The series of numbers you referred to are not prime”
You may be correct about any number, but I thought it was only primes. As for the numbers, I didn’t refer to the numbers, they were from the linked quote. They are all powers of the prime 2. An fft can be efficiently solved for any prime, the genius of the fftw code from MIT is that it decomposes the dimensions of the problem into prime factors. It also works in 2D or 3D. If you give it datasets for which the number of samples in each coordinate are already powers of primes, it is astonishingly fast.
The most effiecient appear to be powers of 3, 5 and 7. It can perform fft up to prime factors of 13 as I recall.
Willis Eschenbach: “I’d love to [directly compute the Fourier integral], but I don’t see how to do what you propose. Perhaps you could explain in a bit more detail.”
I’m not positive, but he may have meant something along this line:
DFTtrunc = function(x){
# x is the raw data whose first and last values are not missing
# This function computes half the DFT and omits the DC term
N = length(x);
K = floor(N / 2); # Frequency-bin count; only half a full DFT
X = complex(K); # Receives the DFT
dt = 2 * pi / N;
t = (0:(N-1)) * dt;
# Starting k at 0 eliminates the DC term:
for(k in 1:K) X[k] = sum(x * exp(1i * k * t), na.rm = TRUE) / length(x[-is.na(x)]);
list(mag = abs(X), phase = Arg(X)) ; # Magnitude and phase
}
I haven’t actually run the code above, but the point, as I mentioned in my previous comment, is that correlation (which Fourier Transformation does) is equivalent to error minimization, and you may thereby skip a lot of computer cycles.
An FFT is possible for any NON-prime (called “composite”) length. For example, there are FFTs for length 64 (2^6), for 100 (2*2*5*5), for 99 (3*3*11) but not for 97 or 101. In a language such as Matlab, you ask for an FFT of any length. If the number is prime (e.g., 101) Mallab apparently does the DFT.
The FFT and the DFT or a sequence should be identical to many many decimal places. The FFT is just a fast algorithm for calculating the DFT (a formula). In terms of numerical results, the two terms are largely used interchangeably.
To see the difference in computation time, one can measure flops for different length for an amusing plot such as:
http://electronotes.netfirms.com/AN387.pdf
Here you see an N^2 curve for the prime numbers and what I found to be 3.3 N Log2 N for the powers of 2. Lengths that are neither prime nor powers of 2 are in between. The most composite are faster. For lengths that have only two factors (e.g., 3 and a prime factor) we see a corresponding quadratic trend.
You need to window your finite time series. Note that the Fourier transform function goes from negative infinity to positive infinity. You don’t have that much data. Mathematically, the DFT treats a finite series as infinitely repeating the same series. This means for example if you start with a temperature of 10deGc and end with a temperature of 12deGC you end up with a step function of 2deGC in your infinite time series, which ends up as a sinx/x noise in the frequency domain. It looks to me like I could draw a sinx/x kind of envelope around your data in some cases, so I’d be worried about that.
SOP for inventing any new time of signal analysis is to put various standard signals in and see that you get out what you would expect. For example, pink noise, red noise, white noise, sine wave of various frequencies phase shifted various amounts, triangle wave. There are tons of texts that show you what the output should ideally look like for ideal signals.
Another point – in general you need about 4 periods to get any interesting data on the low frequency side. You have about 206 years of data, which means any signal slower than 50 years is going to be pretty fuzzy. (yes in theory you could do this with 2 cycles, but with noisy data it’s much harder). Think of this as Nyquist limit on its head. It’s not much discussed unfortunately, all the texts talk about Nyquist on the high frequency side, but it applies on the low frequency side as well.
In the end, the big problem with CAGW is – there simply isn’t enough data to support any conclusions in either direction. We just have to wait for the data.
Joe Born says:
May 4, 2014 at 12:24 pm
Joe, as always good to hear from you. Actually, I found a faster method, which may have been what he meant. This is to use a linear model fitting sine and cosine terms of the form
value = a sin(w t) + b cos(w t)
where w is 1/period, t is time, and a and b are the variables to be fitted.
I use a linear model lm() to give me the values for a and b. The amplitude I’m looking for is the range of the fitted curve. No optimization.
Regards,
w.
Peter Sable says:
May 4, 2014 at 12:51 pm
Thanks, Peter. I agree completely. My rule of thumb is nothing longer than a third of the dataset. That’s the reason for the yellow lines up above, a danger zone. I probably should put the yellow line at a quarter of the dataset length as you propose, and a red line at a third of the length.
And yes, I discuss this a lot. Folks keep trying to squeeze 60-year cycles out of 7-year datasets and the like … can’t be done.
Actually, we’re getting to the point where that is less of an issue, although it will always be an issue in the field. Things like the satellite measurements of temperature and ice coverage are in their fourth decade or so. And the Argo buoys have greatly increased our understanding of the ocean.
However, for understanding the long-term effects, you are 100% correct, we need centuries of data.
In addition, even when we have a number of repetitions to confirm our results, say five cycles of the ~22-year signal in the early halves of the three datasets, that satisfies the statistical requirements … but the son of a gun disappears in the later halves of the datasets. Go figure.
w.
http://mathworld.wolfram.com/DiscreteFourierTransform.html
Explore
rgb says: “I pointed out that what is called “pressure broadening” produces a Lorentzian line shape in radiation physics because collisions randomly interrupt the phase of the emitted wave, effectively doing the same thing but with many possible data intervals smeared out over a range.”
Thanks, I missed that one last time around. I knew it was a Lorentzian profile but it’s interesting to see that explanation of why.
Do you know anything about correcting for instrument defects by deconvolution, by any chance?
Sorry, by “instruments” I meant diffraction spectrometers. In particular I’m trying to wring a bit more resolution out of an ‘echelle’ spectrometer.
@Willis Eschenbach
Considering a square wave: In your example, this would be insensitive. I think the “spectra” you have shown are interesting because, using an FFT you would get the the well known series (assuming the series is symmetric about zero) of
cos(wt)+cos(3wt)+ cos(5wt)……
Your example shows this but, as expected the higher frequencies are degraded in the decimated version. If you were to use a shorter period or a higher frequency, this effect would be more pronounced. In other words, it sort of works for your example but you cannot assume that this is always true.
What is striking, however, is that there are marked side-lobes at the fundamental frequency/period, at about 20% of the peak amplitude. These should definitely not be present and are an artefact of the processing, which in the regularly sampled data should be, according to your thesis, exact. The shape is of the form sinc(w) which suggests that there is an artifactual windowing problem.
As regards quadrature: This is reasonably straight forward provided the sampling decimation is not too severe. In principle, one interpolates the signal between samples and evaluates
integral[A(x).f(x)]dx between xn and xn+1, where A(x) is a harmonic and f(x) is the signal. There are a number of schemes for doing this but they all have problems. Any data with discontinuities (by which I mean the derivatives are discontinuous) may cause problems, although these are handled exactly in the regularly spaced DFT.. See Froberg(1970) Introduction to Numerical analysis, chapter 10.
Very common sort of thing in exploration seismic processing, where countless variations of what you have described are used for interpolation and noise suppression. One such variation is known as the anti-leakage Fourier transform.
Willis, I enjoyed seeing your work and description,. I often think that “multiple independent invention” of new concepts is common in science, as there may be thousands of scientists coming to similar analysis & conclusions at the same time, but only one, the “first past the publishing post”, gets the credit when that is a very artificial criteria, but one that : [is at least verifiable, can have a big influence on careers and status, often ignores subtleties and important advantages of the “also ran” analysis]. One of very many historical examples, if I remember correctly, is the derivation of Force = 1/2 * mass * acceleration by an Italian contemporary (and fan of) Isaac Newton, whose later formula did not of course have the 1/2 factor. Re-inventing the wheel IS an important process as well – we need at least some people to pursue independent tinking, as this helps highlight failures and weaknesses in the mainstream consensus scientific religions.
It would be nice to see the same results if you were to tackle wavelet and Hilbert transforms (as per rgbatduke’s interesting comments of May 4, 2014 at 9:50 am). I am lost with the latter, but it has become a line of pursuit by at least one scientist, Walter Freeman, for the “meso-scale” analysis of brain signals (EEG, between the microscale neuron assembly scale and the “macro-scale” level of brain regions or whole brian analysis) – this is an interesting practical aaplication of a technique that apparently is linear in a sense. Of particular interest are analysis for “discontinuities” including non-stationary transitions.
Willis Eschenbach: “Actually, I found a faster method, which may have been what he meant. This is to use a linear model fitting sine and cosine terms of the form. . . .”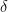 of x.” Or “There’s less than a 5% chance that the outcome we’ve observed would result if the situation we’ve assumed for the sake of argument really prevailed.” But I can’t map either of those meanings to this context. Can you or someone else here explain that usage?
of x.” Or “There’s less than a 5% chance that the outcome we’ve observed would result if the situation we’ve assumed for the sake of argument really prevailed.” But I can’t map either of those meanings to this context. Can you or someone else here explain that usage?
Yes, that’s faster as a practical matter for the R user. Since you probably used “lm” rather than “nlm,” though, it probably actually does use essentially the correlation approach internally that I’ve suggested, but (at least if I had optimized the operation order) I’m guessing that from the computer’s point of view “lm” requires the extra step of solving two linear equations simultaneously; “lm” wouldn’t know initially that the two model functions are orthogonal and thereby finesse around that step.
By the way, for those of us who are allergic to statistics, I wonder if you could explain what you mean by “significance” in “used a 90% level of significance in coloring the significant data.” I’m guessing that you’re comparing something to, say, 1.65 standard deviations of the untrended data, but I don’t know what that something is.
Specifically, my statistics-bereft view of “significance” is that it means, “If the process works in such and such a fashion, (i.e. if a certain model applies), then (e.g.) 95% of the time its outcome will be within
I make my living largely off the FFT. One can represent any shape at all with it. But the technique is NOT predictive. One can’t use it to predict the future. I support what you do with climate skepticism but I am a big skeptic of using Fourier transforms to predict the future. Discrete FT’s are repetitive, periodic and repeat their shapes exactly over time.
Glenn Morton says:
May 4, 2014 at 4:06 pm
Couldn’t agree more, Glenn.
w.
Does Willis give money to Watts?
Watts up is the greatest Skeptic site ever. Except for the Willis stuff.
People come to this site. And it’s brilliant! But Willis posts. And it’s stupid!
Why does Watt post Willis stuff?
RS says:
May 4, 2014 at 2:34 pm
Thanks, RS. I don’t assume that it is always true. It’s hard for me to assume much, as I am I was just taking a look at the square wave at your suggestion, because you seemed to assume that the problem of missing data would be bad there … however, I didn’t find that to be the case. Even a lot of missing data didn’t change the shape of the resulting periodogram.
I don’t recall stating that my sampling would be “exact”. To the contrary, I said:
So I’m not unaware that there are limitations, and that different kinds of problems with the data will have different effects on the results. No surprise, my method is subject to the usual constraints and caveats that any mathematical method has, user discretion is advised, void where prohibited or taxed, do not insert square peg into round hole … that’s true of mathematical procedure from addition on up.
.
But it works very well for my purposes, in that I can determine where the most powerful cycles are in a dataset with gaps in it. I have been investigating purported cycles in the various climate datasets, many of which have gaps in them, and for that it is a very useful tool.
My thanks for all your assistance and comments, much appreciated,
w.
Blue Sky,
Willis posts lots of interesting stuff. Some just can’t appreciate it I guess.
@Joe Born
Your comment about statistics of cycles is well taken.
If the noise is gaussian (or nearly so) the power spectrum is a chi squared distribution and the power in each harmonic is chi-squared with two degrees of freedom, i.e.: a negative exponential distribution. Knowing the total power in the signal allows one to calculate whether a particular harmonic is “significantly” above the noise.
Lokking at WE’s plot of the spectrum or periodogram of a square wave above in response to my comments about an irregularly sampled square wave, there are obvious artefacts with side-lobes around the fundamental which are comparable in magnitude to the 3rd harmonic. I guess that any simple statistical test on the basis of power distribution would regard these as significant harmonics.
Looking more closely at these plots, there is a problem because the higher harmonics do not have the same amplitude, which they should for a square wave. This may be because the test function is not even and this is basically a cosine transform. If phase is calculated, then the results strike me as wrong.
Also, there should be no no leakage in the spectrum for a simple case such as this. It looks as though the spectrum has been convolved with a sinc(w) function, which in the normal way of looking at spectra, would imply a window in the time domain.
I don;’t know what the explanation of this is, but there seems to be something seriously wrong with the computation. I would suggest that this methodology needs to be thoroughly tested on cases where there known solutions.
Blue Sky (!) Perhaps choose a more appropriate screen name to accompany your vitriolic comment. Or withdraw the comment. Or use your real name.
RS says: May 4, 2014 at 5:11 pm
“Looking more closely at these plots, there is a problem because the higher harmonics do not have the same amplitude, which they should for a square wave.”
No, there should be odd harmonics diminishing as 1/n, and that looks right.
Blue Sky says:
May 4, 2014 at 4:24 pm
###
If more people took the same approach as Willis in getting from zero knowledge to working understanding, we would not be in the mess we are in right now. One can learn a lot from the methodology he employs. He shows us all that anyone with the will, the guts and the curiosity to push oneself in the pursuit of knowledge, can understand anything.
ThinkingScientist “Its not new or original and its very inefficient.”
But it is easy to understand. Not everyone is a mathematician. I am not. I can struggle with calculus but since this problem is to be solved numerically anyway, which by its nature is discrete/finite, it isn’t an exact representation of the integral anyway.
RS: “why not perform the calculation using simple quadrature, i.e.: direct integration of Fourier integral?.”
Because I don’t know how to do that? Naturally if the data were itself continuous — not sampled into data points but *continuous*, and expressable as a function, then you could use math functions directly and the output would be a transformed continuous function.
But that’s not how computers work. The data is finite and sampled at discrete, sometimes irregular intervals. Calculus just isn’t going to work for *implementation* but is a good way to express the problem IF your readers understand the math (I probably won’t without a lot more work than I’m likely to have time to invest).
GlynnMhor “If a cycle has a period of 50 years one time, then 65 years, then 60 years, it will not appear in the frequency spectrum as a strong peak.”
Agreed — BUT if the cycles are not sinusoidal a complex family of sine and cosine periods will be found that, when reconstituted, reproduce the observation. As a diagnostic tool, this result is evidence only of complexity of the input data although it has been argued that with enough patience you can analyse these peaks and discern the period modulating signal that might itself not be apparent or visible in the data.
As others have pointed out, many of these phenomenon exist in audio and radio engineering.
What about missing data:
If you simply remove the missing data and abut the next series of points, the step discontinuity will cause ringing (as several readers have identified) but viewed as a process what happens is the abrupt change in phase causes failure to cancel noise at nearly all wavelengths and a small loss of amplitude of discovered peaks, depending on how many good cycles were found compared to the gap. You still get your period detection with slightly smaller amplitude because some of that amplitude has been diverted to “sidebands” in the spectrum.
A family of regularly-spaced sidebands reveals a step discontinuity and the spacing will itself be an artifact of the size of the discontinuity. It is essentially identical to radio “phase modulation” because the missing data causes a phase shift, or modulation, which creates sidebands.
One solution to the problem is to pad the gap with zeros — don’t interpolate (IMO) — such that when the data resumes it is still in phase. If your data is daily and you skip 30 days, insert 30 zeros. What will happen is these zeros will then multiply by your testing sine wave and will neither add to, nor subtract from, the energy of the particular wavelength you are testing at that moment. You’ll still get discontinuity harmonics and a bit less noise cancellation but at least you won’t get a phase shift and sidebands.
Highly discontinuous data shouldn’t use the row number as the divisor for the sine generating function. Rather, you should map the row number to a time function, and then insert that time function into your sine generating function. It will work fine and give good results.
The idea can be expressed by imagining RANDOM sampling of a sine wave while keeping track of the time each sample was made. When analyzed, you use the time stamps as the multiplier of where you are on the cycle:
For each data point with timestamp and value: Sum ( sin(datapoint_timestamp/slicesize) * datapoint_value )
The “slicesize” is incremented on each pass and determines the wavelength of the sine wave (the period being sought).
Do this all in floating point for great flexibility and precision. The SFT we’ve been looking at is basically the same but presumes a regular timestamp increment. If it isn’t regular then it ought to be specified.
With a long enough integration time (many samples), white noise should cancel completely in any DFT/FFT. But since all real-world samplings start and end, these endpoints introduce a period and artifacts.
I very much like the fact the Willis doesn’t always “know” what some of those who were formally trained may “think they know”. Every once in a blue moon, what they think they know isn’t true. Takes a considerable pair to head off into the academic deep grass without the standard-issue map those who inhabit that grass carry in their breast pockets. Great fun to watch!
Few people had commented on issues related to windowing of the data. I think it would be important to point out that Fourier transform of any kind is not necessarily appropriate method for analysis of climate data, at least not without applying carefully chosen window.
The issue here is that Fourier transform assumes that data that is being transformed is periodic and infinitely repeats itself – for example, if you use 200 years of global temperatures, the previous 200 years are exact copy of it and following 200 years are exact copy of it, and so on ad infinitum.
This assumptions is of course wrong – as we all know, climate is always changing so it does not repeat itself, no matter what interval it is.
To illustrate the problems that could be expected from such an assumption, consider Fourier Transform of simple sinusoidal. It should be a single spectral line in frequency domain. But depending which data set is used for transform, results could be very surprising. When doing FT of whole period (or any number of whole periods) of that sinusoidal, the result is correct, a single spectral line of that frequency. But try to imagine what would happen if you take, for example, 1.5 periods of such sin wave and append it to the end of another 1.5 periods. This would not look like original sinusoidal at all. This is, however, what FT assumes is being transformed, and output of FT would be the spectrum of such curve, not the simple sinusoidal that was used.
This problem is well known in DFT processing, and it is dealt with by applying window function, which tapers endpoints of data set to 0 in a specific fashion, that depends on particular window function.
What is interesting about SFT is that it could be made immune to this problem, given proper selection of optimization function and proper constraints on the way it finds its solution. In case of my example of 1.5 period of sin wave, optimization algorithm would probably find proper single sinusoidal rather then set of different frequencies and phases.
I can also see how it can be much more robust dealing with missing data.
So, subject of more serious verification, I’d say this method should be much more appropriate than FFT for analysis of climate data.
FYI, In general, similar methods are pretty common in noise cancelation algorithms where noise is non-random.
I, for example, used it to find appropriate amplitude and phase of 60Hz noise source in very weak signal (similar to EEG and EKG noise cancellation).
Best
Dan in Nevada says:
May 4, 2014 at 7:51 am
“Seeing different cycle lengths at different times brings to mind what you see in a negative-feedback process control environment when trying to regulate an output under changing conditions. My experience is with PID tuning for regulating pressures/flows in a natural gas pipeline.”
I can imagine in a long pipeline, apart from variations in pressure and temperature induced by operation of transmission equipment, superimposed variations in volume/density of the oil plus changes in the dimensions of the pipe by ambient temperature and atmospheric pressure, changes in the slopes of the pipe, nearby traffic vibrations etc….that one could expect occasional, unpredictable coincidence of oscillation peaks would cause a serious problem.
Earth’s climate with global/celestial/geological/biological factors, all the oscillations of the sea and atmosphere, irregular contributions from volcanoes, earthquakes, hurricanes, tornadoes,…. yeah modelling and control are out of the question at the current state of knowledge.
In Willis’s work, looking at some of the comments of Greg and others, it seems to me the longer “rough” periods have the biggest effect on temperature over time and much of the short term ones are closer to something like noise saddled on these durable ones. Maybe 50 to 80 years is how grainy the significant oscillating signals are and the in between ones should not be seen as having disappeared.
A very good review of basics of Fourier Transform can be found in Numerical Recipes The Art of Scientific Computing.. This is an excellent text for many digital analysis techniques. The subroutines have been written in many different computer languages and are available. Care must be taken when using FFT that the data are treated properly, usually the endpoints of the raw data are tapered and care must be utilized to not alias data by using too crude sampling.
Consider the little “valley” between the 21 year and 24 year peaks in figure 4, top chart. Notice also that a little peak fills the valley just to the right at 28.
Whereas the chart just below it shows a nice peak at 22 and a nice null to the right at 28, also a peak at 8.
This spectrum is typical of frequency (or phase) modulation in radio engineering in a non-linear mixer. Normally radio waves ignore each other, just as ocean waves normally ignore each other.
But where a nonlinearity exists, these waves won’t ignore each other, each modifies the other, producing artifacts that reveal the nature of the nonlinearity and what went into it.
This nonlinearity can exist in the data itself and isn’t a natural phenomenon. If you simply close the gap of missing data, you have introduced a nonlinearity that will mimic phase or frequency modulation, splitting peaks into two (or more) components and creating sidebands that fill nulls.
In nature a big non-linearity is freezing water — a phase change of water but it also forces a phase shift in the temperature signal. As energy continues to dwindle, temperature dwindles until it starts forming ice — Central England is the name of the chart. In this case splitting peaks suggests a possible natural nonlinearity.
Therefore it is likely that a real 22 year phenomenon exists but is being modulated in a phase-shifting (frequency modulating) way to produce energy peaks at 21 and 24. Notice the peak at 8 is also split by what appears to be a proportionally similar amount. If your data is continuous then this is a natural nonlinearity; but if your data is NOT continuous then what you see is an artifact of missing — or ALTERED — data.
By the way, the technique can be used to discover edited photographs, where one photo has been spliced onto another. If the seams are blended their frequency (or period) spectrum will differ substantially at the seam where the two photos were blended; also, if different cameras were used or at different resolutions the DFT of the lateral image frequencies will differ in the pasted portion of the image. This itself can be imaged by assigning a color or brightness to the highest frequency found in any small range of pixels (such as JPEG’s 16×16 blocks). Interestingly, JPEG has already done the DCT (discrete cosine transform) and directly encodes the highest frequency found.
“But where a nonlinearity exists, these waves won’t ignore each other”
That’s good point to remember, FT et al are all built on the assumption of a linear system where a signal can be chopped up at will any group of components can be added to make a reconstruction of the signal. That does not mean the system has to be linear in it’s operation but at least the variable being analysed has to be linearly additive.
This was one of my problems with the Steucker and Timmerman paper last year based on spectral analysis of trade wind speeds. Wind speeds are not linearly additive and thus not susceptible to spectral analysis.
Since the kinetic energy of the wind is proportional to wind speed squared, this may be a better choice.
http://climategrog.wordpress.com/?attachment_id=283
Michael Gordon says: “This spectrum is typical of frequency (or phase) modulation in radio engineering in a non-linear mixer. Normally radio waves ignore each other, just as ocean waves normally ignore each other”.
Can you be more specific about that splitting and how it applies to those peaks. I noted those five peaks fitted rather well to being read as amplitude modulation.
http://wattsupwiththat.com/2014/05/03/the-slow-fourier-transform-sft/#comment-1628239
Now looking at the triplets in “full” panel of the graph and calculating the average _freq_ of the outer peaks:
21 and 41 => 27.7y 86y
24 and 34 => 28y 163y
Udar says: “This problem is well known in DFT processing, and it is dealt with by applying window function, which tapers endpoints of data set to 0 in a specific fashion, that depends on particular window function.
What is interesting about SFT is that it could be made immune to this problem, given proper selection of optimization function and proper constraints on the way it finds its solution.”
===
This may be a significant advantage of SFT for longer periodicities which are one of the main points of interest in climate.
Usually Fourier spectral analysis requires a tapering window fn which is quite destructive and distorting to the longer periods but gives more accurate results of the high frequency end. In electronics and audio this is often not a problem since the periods being examined are orders of magnitude shorter than the available samples. Sadly not so in climate.
I generally use an extended cosine window fn that is flat over 80% and just tapers the last 10% at each end. This usually works quite well once the autocorrelation has been removed with a diff, but it’s still a compromise.
Could you more specific about what you consider to be “proper selection” and “proper constraints”?
re:
21 and 41 => 27.7y 86y
24 and 34 => 28y 163y
What would be interesting is to find the phase of the implied 86 and 163 periodicities and get more accuracy than the crude nearest year values for 21,41 and 24,34. With more precise calculations, it should be clearer whether those longer periods harmonics since they will have large uncertainty as they stand.
There is a possibility a whole series of harmonics there : 21,42,84,168. Now there’s nothing magic about that but it would simply be the Fourier components of non-harmonic circa 168y form. Now in a 200y record there’s no reason to see that as a repetitive cycle on it own, it’s just the long term record.
What is interesting is it’s apparent interaction with the circa 28y periodicity. It seems that this long term variation is modulating the 28 y periodicity
It is interesting that I also found a circa 28y modulation in Pacific trade wind data linked above.
A.M. side-bands: 28.6583 4.4450 -28.3212
One thing that comes out of longer records, like BEST and these individual series is that 18th and 19th century showed much larger variability in temp than 20th c.
Now is the current reduction due to a damping of more CO2 radiative “blanket” effect or just a long term modulation? If it’s the former we should be glad of our atmospheric CO2, if not we can we expect the larger variability to return (irrespective of CO2) and with it more “extreme weather”?
I’ve no idea what the 28y period is about but if it’s in Armagh air temps and Pacfic trade winds , it gets interesting.
Martin Gordon says:
“But it is easy to understand. Not everyone is a mathematician. I am not. I can struggle with calculus but since this problem is to be solved numerically anyway, which by its nature is discrete/finite, it isn’t an exact representation of the integral anyway.”
Fair enough if this and the previous article were written as ” how to understand fourier transforms by simple time domain examples”. But they are not, they are written as though some new method of analysis were invented. And when I pointed out to Willis that this was effectively calculating the ft in the time domain he did not understand.
ThinkingScientist says:
May 5, 2014 at 12:18 am
Hogwash. I knew some unpleasant person would come along with this lame accusation, which is one of the reasons why I wrote:
So no, your claim just reveals that your animosity exceeds your ability to read.
w.
The normal way to do FFT on irregular data is to do sine or cubic interpolation to caret an ‘analogue’ time series which is then ‘resampled’ to get a times series to feed to the FFT.
What this SFT is, is exactly the same as using sine interpolations.
And I am afraid to say a cursory inspection of the other ‘differences’ doesn’t hold water either.
I am not decrying the fact that the results are indeed extremely interesting, but merely pointing out that reinventing a wheel doesn’t make it any the less round, in the end 😉
If I had the time I’d code up an algo to do sine interpolations and FFT with a choice of how the results are displayed for any arbitrary time/amplitude series.
RS:
I appreciate your response, but it explains no better than Mr. Eschenbach has been able to what he means by “significance.” Knowing my limitations in statistics, I’m perfectly willing to accept that everyone but me understands perfectly well what he meant. Still, I’ve seen no evidence that even he does.
As to his method generally, it is in my view no less valid in identifying a frequency component in a signal than a DFT is. There’s nothing holy about the particular selection of sinusoids that DFT uses if all you want to do is find a given sinusoidal component in a signal, and, outside of the sinusoid selection, his approach is exactly the same as the DFT: it essentially uses correlation.
The reason for the DFT’s particular sinusoid selection is that it’s more appropriate for analyzing a linear system’s response to a signal. Since a linear system’s response to a sinusoid is a sinusoid of the same frequency and (often) readily determined phase and amplitude, and since adding the DFT-determined components together reconstitutes the original signal, and since a linear system’s response to a sum of components is the sum of its responses to the individual components, the DFT can be used to compute a linear system’s response. To the extent that Mr. Eschenbach’s approach uses a sinusoid selection different from the DFT’s, it can’t be used in that way–but he never contended that it could.
So, while there’s no doubt plenty of truth among the various disputants’ statements, I personally see nothing further of interest other than what Mr. Eschenbach means by “significance.” And the prospect of seeing that clarified seem increasingly remote.
Joe Born says: May 5, 2014 at 2:53 am
‘I appreciate your response, but it explains no better than Mr. Eschenbach has been able to what he means by “significance.”’
In his recent version that he described to you, using lm(), the R regression reports standard error for the coefficients a and b. I think that might be what is meant. It involves assumptions of independence; the residuals after fitting are assumed to be iid. Their variance is estimated by the sample variance, and the variance of a and b just follow from the fact that they are a linear combination of the data. Since Willis end up with sqrt(a^2+b^2) there is a bit of extra calculation there.
The residuals are probably autocorrelated, not iid, so the confidence interval range will be understated.
The primitive wheel reinvented here is equivalent to arbitrarily limiting wavelet extent to a single value and deliberately ignoring every other possible value from across the entire extent spectrum for every single grain.
Why would someone artificially impose such infinitely vision-narrowing blinders?
3 dark possibilities:
1. ignorance
2. deception
3. ignorance & deception
Nick Stokes:![\sqrt{a^2 + b^2}\cos[t + \arctan(b/a)]](https://s0.wp.com/latex.php?latex=%5Csqrt%7Ba%5E2+%2B+b%5E2%7D%5Ccos%5Bt+%2B+%5Carctan%28b%2Fa%29%5D&bg=ffffff&fg=000&s=0&c=20201002) , exactly what does the fact that the resultant standard error is a certain multiple of the determined sinusoidal-component magnitude tell us about how “significant” our result is if the signal consists exclusively of, say, five equal-amplitude frequency components?
, exactly what does the fact that the resultant standard error is a certain multiple of the determined sinusoidal-component magnitude tell us about how “significant” our result is if the signal consists exclusively of, say, five equal-amplitude frequency components?
Thanks for the response. It was helpful, but my ignorance of statistics compels me to take some time, which I probably won’t have any more of today, to explain to myself in simple terms what it really means .
That is, if we eliminate the independence issue by, say, correlating with a single sequence
I’m not arguing here; I’m just thinking on “paper.”
Fourier transform is a fancy name for a Fourier series which was in the A level maths syllabus and I subsequently used them in heat transfer calculations involving time temperature distributioin..
Joe Born says: May 5, 2014 at 4:57 am
I think you’re right. If you fit one component, the residuals contain the effect of the noise plus the other components. But the other components would be included in the estimate of variance as if they were noise.
If you fitted the five components jointly, you’d get a much lower estimate. But in general you don’t have that information.
chemengrls says: Fourier transform is a fancy name for a Fourier series
No Fourier transform is a fancy name for a Fourier transform . It’s a mathematical operation which converts from the time domain representation to frequency domain representation .
Fourier series is a fancy name for a Fourier series, a theoretically infinite series of harmonic terms, with individual coefficients.
Go back a read your A level maths, and pay attention this time.
You might also pick up an old copy of the Dover Books Classic “The Measurement of Power Spectra”, by Blackman & Tukey.
It’s been my companion for over 50 years.
Greg says:
“Could you more specific about what you consider to be “proper selection” and “proper constraints”?”
Those were of course weasel way of saying it’s probably going to work but I am not sure how yet.
The problem is that optimization algorithms could produce unexpected results and should be approached carefully. There is always a danger of them finding wrong solution.
That said, after thinking about it a bit more, I think the way Willis does it will work fines is.
To be sure, I’d have to do some testing on it (and by “I” I mean someone else – as I do not, unfortunately, have time to do it myself 🙁 )
But right now, my thinking is that SFT would not assume periodicity of the dataset and would be completely immune to edge issues add that as one more advantage of this method vs regular FFT or DFTs
Joe Born says:
May 4, 2014 at 3:45 pm
I’m using the lm() function in R. The R linear model function reports the statistics of the fit as a p-value. When I say a 90% threshold, I mean a p-value of less than 0.1 for the linear model fit after correcting for autocorrelation. Sorry for the confusion.
w.
Well, “pressure broadening” and its “pathological” distribution could be killing the Cheshire cats, from time to time.
I’m late to this party and don’t have time to slog through all the other comments. So I’ll apologize if anyone else has said this before.
1: You might want to to try visualizing your data as a “waterfall”. Where you take smaller overlapping lengths of time and watch the peaks move in time.
2: This looks very similar to Modal analysis from mechanical engineering. The only problem with this is the “Unit Under Test” and input forcing function is not constant. So it is much harder to compare different locations with a linear transform function. (matching peaks).
Leo Smith says:
May 5, 2014 at 2:35 am
Thanks, Leo. What do you mean by using an interpolation to “caret” an “analogue” time series? How do you decide the frequency of the sinusoidal interpolation function? How do you decide if the sinusoidal curve should go up or down? What does a sinusoidal interpretation of a square wave that is missing 40% of its data look like? And in the square wave case, shouldn’t we be using linear interpolation? These questions and more …
A google search on either “caret” or “sine interpolation” finds little of assistance. I do find things on sinc interpolation [ sine(x)/x ], however, such as this:
Is sinc interpolation what you were referring to? Or did you actually mean sine interpolation?


Also, that paper says that when the data is “clumped”, the sinc interpolation is unsatisfactory. And unfortunately, climate data is often “clumped”, with long stretches missing entirely.
Let me offer up an example. The data for this example is here as a small CSV file. It’s 180 years of an 18-year squarewave, plus the same square wave with about a third of the data points missing. I’ve taken out both long stretches of years, as well as deleting a number of individual months of data. This is the data.
Top panel is the square wave, middle panel is the square wave with the data chopped out of it, and the bottom panel shows what data was removed, since the scale is too large to see a missing data point in the middle panel.
My problem is that your method involves an “interpolation” of that middle panel … and I’m having a hard time conceptualizing what that “interpolation” might look like.
In any case, here’s what the SFT does with the two datasets:
Upper panel is the slow Fourier transform periodogram of an 18-year square wave with the same number of data points as in the lower panel. I wanted to compare two datasets of the same length.
Lower panel is the periodogram of the chopped-up square wave. Given that a third of the data missing, I’d say that the slow Fourier transform is doing a respectable job …
I’d be curious to see what your sine [sinc?] interpolation would do with that data.
Never claimed it did … I pointed out what I said were advantages over the FFT. You seem to be agreeing that at least some of those advantages are real. You say the SFT is equivalent to using an FFT on a sine interpolation of the data. Perhaps so.
I pointed out that I didn’t think that I’d invented the method. You are agreeing with that also, although it remains to be seen if your proposed equivalence is correct. I always get nervous when someone says “a cursory inspection” … for example, my method certainly has the advantage of being easier to explain.
I’d be interested in your response to what I said in bold was the largest advantage of the SFT, which was that the SFT method provides an accurate measure of the statistical significance of each cycle length, based not on theory but on the actual data involved, including the size and nature of the gaps in the data.
Thanks for that, Leo. Perhaps you could at least run your analysis on the square wave CSV data I linked to above and show your results.
Or perhaps you could point me to a simple explanation of the method of “sine interpolation”. I’m having a hard time believing that my output will be the same as the output of the sine interpolation, inter alia in the matter of the statistics of the results. My method, since it doesn’t interpolate, will have a much lower “N” (number of data points) than any analysis of interpolated data. How does sine interpolation handle that issue?
My method gives me a standard and well understood way to calculate the actual statistical significance of the various individual frequencies. So for example, if the missing data has a pattern, say every 10th data point is missing, then that will affect some frequencies more than others. My method allows the determination of exactly how the pattern of the missing data affects the results.
Does sine interpolation of a “resampled” series do the same? I don’t know.
Also, suppose we have a totally irregular array of data points, which have no common sampling frequency smaller than their least common multiplier. Using my method, I do the analysis on those actual points.
Using your method, as I understand it, not one of those actual points will be sampled. Instead, a series of arbitrary regularly spaced points will be created using sine interpolation, and then the calculated values at those arbitrary points will be used for the FFT.
Is my understanding correct? And if so … well, I’m not seeing how doing an FFT on an entire string of interpolated points will give exactly the same answer as me using the SFT on the actual points. It just seems like the extra step of the sine [sinc?] interpolation would have to increase the error of the results. Might not happen, I’ve been surprised before … but I’m not understanding how it would work.
I know your time is short, but any assistance would be appreciated. And my thanks for further discussion of what it is that the SFT might be doing. You say the SFT is exactly equivalent to a standard Fourier transform of the sine (sinc?) interpolation of the data. I’m very interested to see if that is the case.
Regards,
w.
Nick Stokes says:
May 5, 2014 at 3:55 am
Thanks, Nick. To avoid the extra calculation, I just took the “fitted values” from the lm() function.
Then I used lm() again comparing the fitted values themselves to the data. This gives me the statistics for the final combination of the sine and cosine terms.
I think there is a more accurate way, however, that will help avoid false positives. More on that if it works out.
Since I said twice in the head post that I had adjusted for autocorrelation, I’m not sure what this means.
Your contributions appreciated,
w.
Blue Sky says:
May 4, 2014 at 4:24 pm
Thanks, Blue. From the head post:
I’ve been wrong more than once. You’ll have to point out which time you are referring to.
Regards,
w.
For everyone complaining that Willis has not discovered anything new here, or criticizing him for his lack of mathematics education… consider this…
Although many of you already knew about Fourier Transforms, I pretty much guarantee that none of you stumbled across them and developed them on your own, without having had them taught to you. Willis just did exactly that.
So yes, Willis may be behind in formal education compared to you complainers, but he’s clearly shown that he’s just flat-out smarter than you.
So… please keep your criticisms to yourselves. Most of us just don’t want to hear it.
Willis
SFT
Or Fourier Series? After the recent discussion on your previous post this will no doubt prove to be very useful in my own work.
But with regard to your own work here it’s all rather immaterial as the results seem pretty good.
For what it’s worth, I’ll probably do a similar “Fourier Series” approach later today. But I’ll probably do it via multilinear regression this needs to be fast and at least as fast as a simple DFT with similar “dimensions”. With an efficient method (R has got some) for solving large systems of linear equations your approach could be fast/faster. Anyways, you might have done this already in which case ignore.
Anton
… please keep your criticisms to yourselves. Most of us just don’t want to hear it.
Calm down, calm down…
I don’t think anyone is having a go. It seems like quite a courteous exchange to me. And it is a blog where nobody learns anything if we all just pat each other on the back.
Anton Eagle says:
May 5, 2014 at 2:49 pm
For everyone complaining that Willis has not discovered anything new here, or criticizing him for his lack of mathematics education… consider this…
Although many of you already knew about Fourier Transforms, I pretty much guarantee that none of you stumbled across them and developed them on your own, without having had them taught to you. Willis just did exactly that.
So yes, Willis may be behind in formal education compared to you complainers, but he’s clearly shown that he’s just flat-out smarter than you.
So… please keep your criticisms to yourselves. Most of us just don’t want to hear it.
Leave a Reply
Enter your comment here…
I didn’t know that – thought Willis had a PhD in physics, chemistry or mechanical engineering.
Anyway I suspect Fourier invented his series solution to help him * solve transient heat transfer
problems in conduction (see Fourier’s general equation).
* Certainly others such as Schack, H P Gurney and J Lurie applied Fourier series to this end.
chemengrls says:
May 6, 2014 at 2:29 am
Man, I wish. I’ve taken exactly two college science classes, Physics 101 and Chemistry 101. Oh, and calculus. I learned about Fourier from the Encyclopedia Britannica.
w.
I tell you the mods round here are a useful bunch…cheers for correcting my last comment.
Willis Eschenbach: “I’m using the lm() function in R. The R linear model function reports the statistics of the fit as a p-value. ”
Thanks for the response. I’m still looking for that output of lm() in my distribution of R, but I’m sure that some day some errant combination of keystrokes will overcome R’s inscrutable documentation and reveal that my version has had it all the time.
Willis,
With this comment:
“I knew some unpleasant person would come along with this lame accusation”
you seem to be acting hyper-sensitive to what was fairly mild criticism. I would also politely remind you that you may think my words unpleasant, which is your perogative, but as you don’t know me personally then to suggest I am an unpleasant person is not reasonable. Especially as I went to some trouble to write you several paragraphs on interesting places to visit in Southern England, including Salisbury Cathedral, a little while back.
Joe Born (May 6, 2014 at 4:47 am)
Try running the function summary() on the output of the lm() function.
As well, the function confint() can provide confidence intervals for all of the estimated coefficients.
E.g.:
reg = lm(y~x)
summary(reg)
confint(reg)
cd says:
May 6, 2014 at 4:20 am
That was me, I try to make folks’ contributions look right.
w.
Joe Born says:
May 6, 2014 at 4:47 am
Ah, my bad, sorry. You need to look at the summary of the lm results, like so:
summary(lm())
Use the “names” function to reveal the named arguments, comme ça ..
names(summary(lm()))
w.
RomanM and Willis Eschenbach:
Thanks a lot for the pointers. They worked for me.
ThinkingScientist says:
May 6, 2014 at 5:45 am
First, ThinkingScientist, let me say that you are right. The fact that you have acted in an unpleasant manner doesn’t make you an unpleasant person. That was a bridge too far. My apologies. As to your taking the trouble to write regarding Salisbury, thanks for that as well. I fear that with the literally hundreds of people I interact with on the web, who said what six months ago is often a blur.
To the topic at hand. You had said:
You made a most unpleasant accusation—that I was trying to take credit for something invented by another man. This is called “scientific plagiarism”, presenting a new method of analysis as if it were one’s own when someone else came up with the idea.
Now, that’s not a nice thing to accuse a scientist of, even on a good day.
But this is not my first rodeo. I’ve had warm, intelligent, sensitive folks like you try this particular unpleasantness before. So knowing what was likely coming. I specifically said in the head post that it was likely NOT a new method of analysis, and that while I came up with it independently I was likely NOT the first person to come up with the idea. (Although to date no one has come up with any prior art.)
To accuse me of plagiarism after reading my specific disclaimer is not just unpleasant. It is negligent as well.
Now, am I “hyper-sensitive to what was fairly mild criticism”? First off, an accusation of scientific plagiarism is hardly “fairly mild criticism” on my planet.
Second, I just had Dr. Roy Spencer unsuccessfully try to accuse me of the same thing. Fortunately, the web never forgets. I had to do with him what I’ve done with you, specifically object and use the web record to show conclusively that he was wrong. Tends to put one’s nerves on edge, though.
Third, I come into this battle armed with nothing but my reputation and my honor. I don’t have a PhD. I don’t have a string of publications as long as your arm. I don’t have colleagues and graduate students and co-workers. I don’t have awards from John Kerry’s wife like Hansen, or a No-Bull prize like Mann. I’m not the head of a department or a school. I work building houses.
I enlisted in the climate wars equipped with my honor and my insatiable curiosity and my cranial horsepower and little more. As a result, I’ve had to fight hard for every inch that I’ve gained. And yes, that’s made me sensitive when people try to impugn my honor as you did.
I never try to take credit for what another man has done, I want to give credit where credit is due. Look at this post. Nick Stokes pointed out that he’d written a post I referred to … so I went back in and edited this post to give him that credit. More to the point, I knew someone likely had invented the idea before, and I specifically stated that, and I asked people to name the names of whoever did invent this method. Accusing me of plagiarism after that is … well, unpleasant.
Finally, ThinkingScientist, I have a simple rule. I don’t accept moral or ethical instruction from someone who is unwilling to sign their own name to their own words. Call me crazy, but I won’t do it. I’m perfectly happy to take scientific instruction from such a person. Science is about the ideas and whether they are right or wrong.
But taking scientific instruction is the limit. If you want me to listen to your advice on more serious matters, you’ll have to sign your words. See, I have to defend the things that I said on the web, whether I said them last year or ten years ago.
But you? You can give me crappy advice, accuse me of plagiarism, get upset when I call you on it … and then change your name to GamerBabe37 and never have to take any responsibility for what you’ve said in the slightest.
So I’m sorry, ThinkingScientist, but I won’t take advice and admonition on ethics and honor from some random internet popup who is unwilling to take responsibility for his own words.
Note that I’m not saying that anonymity is bad. There are valid reasons for it. It’s a choice that people make, for a whole variety of different reasons.
It’s just that when you make that choice, when you slip on that mask, there are things that you give up. One of them is the right to lecture folks on their behavior. If you won’t take responsibility for your own behavior, why should others pay the slightest attention to your advice in that matter?
Best regards,
w.
Comments on this thread suggest that there is still much confusion about the various “Fourier Performers” in the arena. Not surprising as there are (at least) seven of them.
http://electronotes.netfirms.com/FourierMap.jpg
There are the two transforms that address systems more than signals (Laplace Transform and z-Transform). Then there is the very familiar Fourier Series – FS, and it’s “parent” the (continuous time) Fourier Transform – CTFT. (That’s four.) The FS has a “dual” that is often overlooked, the Discrete-Time Fourier Transform of DTFT. The DTFT is merely a FS with the roles of time and freq reversed. It relates a discrete time series (dual to discrete “harmonics” in the FS) to a corresponding now-periodic spectrum (AKA “aliasing”). The DTFT makes five, and the DTFT (note well the extra T) is DIFFERENT from the Discrete Fourier Transform (DFT) and the fast FFT where both time and frequency are both discrete and periodic (that’s all seven).
The “Fourier Map” in the link above summarizes multiple notions and relationships, and I have used it for 20 years.
Few of these transforms yield to closed form solutions. When computing from actual data, we usually need to trick the FFT into yielding a satisfactory approximation.
Perhaps visitors to the Fourier arena claiming to be new relatives need to be vetted against this family already there. I personally haven’t figured it all out.
I posted a comment earlier but after further consideration I realize I did not furnish enough background on my perspective and what I was trying to achieve.
I spent several decades trying to resolve issues with rotating equipment. In the earlier days we collected data and analyzed with swept frequency analysis making use of filters. The results were somewhat useful and also very noisy.
To me the introduction of the desktop FFT analyzer was roughly equivalent to the introduction of the HP 35 calculator (which cost approximately 1/2 months take home pay at the time). The FFT made visible to me the things that needed to be worked on with the objective to reduce vibration and make the equipment more reliable.
We had the luxury of acquiring raw data over an extended period of time so we did not suffer from having insufficient data. In these days we were simply doing detective work to find out what needed worked on. There was no such thing as a general computer model of the equipment. Rather, we were simply trying to find out what might need to be considered.
I did not perform the FFT analysis of the analogue tapes. My job was to make use of the analyzed data to look for explanations that would lead to remedies.
There are many comments on this article and I would be in the camp that there is insufficient data. That means plan B.
I have used the technique before but my approach to the detective work was simply to try and find an equation that might just fit the data. The validity of the results can be judged later but I simply was trying to detect natural cycles that might be present. The model equation consisted of 5 sinusoids.
Many readers may be way ahead of me and were already aware of what might be present. I was not so what I did was consistent with the approach I have used for years and that was simply to do some detective work so that I could understand what I was dealing with. It will be up to you to determine if anything I have done here is useful or insightful.
I inspected Hadcrut4 data on both a monthly basis and a yearly basis.
For the monthly data fitting the model equation to the data yielded the following:
I wish I knew how to make the graph available but I don’t. I judge it to be a good fit.
I did the same with the Hadcrut4 data on a yearly basis instead of the monthly basis. The results were:
Char Guess bmin bmax b Period
‘Amp 0.373928293335057 -1000 1000 0.456756591908584
‘Freq 0.00288184438040346 -1000 1000 0.0028356804964 352.649038298718
“Phase ” 1.65015934150811 -1000 1000 2.88817321720208
‘Amp 0.121904543009585 -1000 1000 0.112106012502226
‘Freq 0.0166666666666667 -1000 1000 0.0147134718840 67.9649241104327
“Phase ” 1 -1000 1000 23.1091565760669
‘Amp -0.0159596662864541 -1000 1000 0.0962192542383451
‘Freq 0.0061 -1000 1000 0.004934103435 202.671065392359
“Phase ” 1 -1000 1000 12.8395859438275
‘Amp 0.1 -1000 1000 -0.0253860619362965
‘Freq 0.25 -1000 1000 0.239294052343 4.17895885922845
“Phase ” 1 -1000 1000 91.0841625820464
‘Amp 0.1 -1000 1000 0.0475776733567028
‘Freq 0.04 -1000 1000 0.046203369505 21.6434431232757
“Phase ” 1 -1000 1000 -71.9060344118493
It took 681 iterations. The SSE was 44.037. The correlation coefficient was .861
The results for Hadcrut4 on a yearly basis.
Char Guess bmin bmax b Period
‘Amp 0.373928293335057 -1000 1000 0.5590459822568
‘Freq 0.00288184438040 -1000 1000 0.00287618100569 347.683264029118
‘Phase 1.65015934150811 -1000 1000 2.53417606588117
‘Amp 0.121904543009585 -1000 1000 0.111200199537111
‘Freq 0.0166666666666667 -1000 1000 0.014688221188 68.0817634172082
‘Phase 0.1 -1000 1000 23.4628856990436
‘Amp 0.01 -1000 1000 -0.202734098630665
‘Freq 0.0049 -1000 1000 0.004071935205 245.583475568171
‘Phase 1 -1000 1000 7.49413657611414
‘Amp 0.02 -1000 1000 0.0229749619103338
‘Freq 0.25 -1000 1000 0.239142083456 4.18161448435935
‘Phase -5 -1000 1000 191.081913392333
‘Amp 0.1 -1000 1000 0.0462677041430509
‘Freq 0.04 -1000 1000 0.0461238862996 21.6807402894059
‘Phase 1 -1000 1000 -70.7912168132773
It required 654 iterations. The resulting SSE was 1.35 and the correlation coefficient was 0.94.
I wish I knew how to include the graphs. I will learn that eventually.
There is some things in common between the two evaluations. There is a long period cycle of approximately 350 years. Is that real? It could also be a 1000 year cycle identified not too long ago from ice cores. In that same article I believe they identified something around 334 years. Could it be the same? I do not know.
Instead of a 60 year cycle both analyses show something in the mid 60s. There are also similarities in the 4 year and 21 year cycles. The one that appears different are the two in the 200 year time frame.
In the end all I have done is do something based upon my experience and it is an effort to get around the lack of a longer time record of temperatures. This is nothing more than initial detective work. I am just trying to figure out what I might be dealing with and have to explain.
Climate knowledge is a little out of my realm but if I think I can contribute something useful I will try. I am hard to embarrass and am willing to suffer embarrassment. You can learn from that too without getting hard feelings.
For the most part for the decades I worked on rotating equipment most of the innovations came from the insight we gained from test data. To me test data are gold. We are still trying to get a robust computer model so we won’t have to rely so much on test. Sort of reminds one of today’s computer climate models.
I wrote three sentences in my last post. The first was to frame my response and suggest you were (in my view) over-reacting. The second sentence was to suggest that if you felt my words were unpleasant, it was unfair to then suggest I was also unpleasant. You have responded by apologising and accepting it was a step too far. You did not need to apologise, but thank you anyway. Finally, I used an example where I had previously tried to help you.
But then you seem to have gone on to develop an argument spread over something like 14 paragraphs, developing a theme where you are saying I have accused you of plagiarism and then delivering what appears to be a moralising sermon, partly focussing on my anonymous moniker (which has remained unchanged for about 8 years or so).
Just for the record, I have not accused you of plagiarism and certainly did not intend anything of the sort. But I stand by my points that you are being hyper-sensitive to criticism and over-reacting and I think your response to my simple 3 sentences shows this.
But hey ho, if it makes you feel better to get it off your chest, fine.
Apologies, the post above was intended for Willis. I omitted to address it correctly.
ThinkingScientist says:
May 6, 2014 at 1:07 pm
I accept and am glad to hear that you did not intend to accuse me of plagiarism. Thank you for clarifying that.
However, you assuredly accused me of plagiarism when you said:
Despite not intending to do so, you have made a clear accusation—that I am implying that I invented something I didn’t invent. That is an accusation of scientific plagiarism. And yes, I’m damn sensitive to that, especially from someone unwilling to stand behind his own words.
In fact, I’m sensitive enough to specifically deny a couple times in the head post and my previous post that I was the first person to come up with the idea. When I first described the idea I wrote:
And in the head post I said:
Now, after I’ve specifically disowned the idea that I’m the inventor a couple times, you accuse me of writing “as though some new method of analysis were invented”?
And when I protest, you get all huffy and say it wasn’t an accusation of plagiarism? You accuse me of taking credit for some other man’s invention. Howe is that not an accusation of plagiarism?
And I stand by what I said. I don’t take advice on ethics, morality, or whether I’m “hyper-sensitive” from anonymous internet popups. I thought I’d made that clear.
w.
PS—You keep repeating that you only wrote “three simple sentences” inexculpation, as though it is not possible to make untrue accusations in that short a paragraph … despite having just proven that it is quite possible to do so.
I do not understand R-Code anywhere near well enough to tell if the SFT is a variation on, or even perhaps identical to something familiar in the Fourier arena. I do understand the standard Fourier ploys fairly well. As I suggested in a comment above, we do understand the Fourier Series, the Fourier Transform, and the FFT. The FFT exploits the even spacings in both time and frequency, which results in a periodicity in the exponential factors (colorfully called “twiddle factors”) such that an efficient algorithm can be run. Otherwise the relationship is N equations in N unknowns (slow – but usually speed is not important).
Moreover, the FS has a much-neglected dual cousin the Discrete-Time Fourier Transform (DTFT), rarely used except to find the frequency response of a filter from its impulse response, but which describes a periodic function of frequency in terms of discrete time samples. This is the DTFT, NOT the DFT=FFT. It can (being a frequency response) be solved for any frequency, equally spaced or clustered. Likewise, the FS of course gives time values for any choices of time. These calculations can be inverted easily but not fast. Once solved for arbitrary spacings in time and/or frequency, it of course gives the FFT answer for equal spacings.
I am guessing, and very possibly not helping any. I need to see equations, or Matlab.
Thanks, Bernie. Here’s what I’m doing.
For each cycle length, say 43 months, I fit a 43-month sine wave to the data. I note down the peak to peak amplitude of the resulting best-fit sine wave.
That’s it. That’s all I’m doing. Fitting a sine wave of each possible cycle length from 2 to datalength/2 to the data, and recording the amplitude. That’s what I’m calling the slow Fourier transform.
This may indeed be the same as the Discrete Time Fourier Transform. Sounds possible. I’ll need to do more research, which I do love to do. Thanks for the direction.
Hope that helps,
w.
Willis

I read your post where you were going to singularly look at how a frequency with a period of 43 months was applied.
I know I have more to learn more about posting comments here. In my last one I thought the message would be clear but it came out like garbage. So I shall try again.
In earlier postings you noted the lack of data and I would certainly agree. This is why I tried a curve fitting procedure that I have used since the mid 80s that was available with the DOS version of TKsolver. I tried to fit both the monthly and the yearly Hadcrut4 data with a curve that is composed of 5 sinusoids.
First the monthly data. I make an initial guess for amplitude, frequency and phase for each of the sine waves. The resulting answer is given in the b column.
Monthly
Char Guess b Period
‘Amp 0.3739 0.4568
‘Freq 0.0029 0.0028 352.6490
“Phase 1.6502 2.8882
‘Amp 0.1219 0.1121
‘Freq 0.0167 0.0147 67.9649
“Phase 1.0000 23.1092
‘Amp -0.0160 0.0962
‘Freq 0.0061 0.0049 202.6711
“Phase 1.0000 12.8396
‘Amp 0.1000 -0.0254
‘Freq 0.2500 0.2393 4.1790
“Phase 1.0000 91.0842
‘Amp 0.1000 0.0476
‘Freq 0.0400 0.0462 21.6434
“Phase 1.0000 -71.906
It took 681 iterations to come up with the above results.
The correlation coefficient was 0.8605
When I did the same for the yearly averaged data I got the following:
.Yearly
Char Guess b Period
‘Amp 0.3739 0.5590
‘Freq 0.0029 0.0029 347.6833
‘Phase 1.6502 2.5342
‘Amp 0.1219 0.1112
‘Freq 0.0167 0.0147 68.0818
‘Phase 0.1000 23.4629
‘Amp 0.0100 -0.2027
‘Freq 0.0049 0.0041 245.5835
‘Phase 1.0000 7.4941
‘Amp 0.0200 0.0230
‘Freq 0.2500 0.2391 4.1816
‘Phase -5.0000 191.0819
‘Amp 0.1000 0.0463
‘Freq 0.0400 0.0461 21.6807
‘Phase 1.0000 -70.7912
It took 654 iterations to come up with the above results.
The correlation coefficient was 0.942
I apologize that my last post was useless. Maybe this one will fall into the same category for different reasons. I was just doing detective work and trying to figure out if there were cycles in the raw data.
I wish I knew how to enter a figure but the first link is to the monthly figure and the second is to the yearly figure.
I think both figures pass the eyeball test. Both sets of data gave roughly the same result except for a wide difference between 202 years and 245. The cycle with the long period of around 350 might be similar to the 334 year cycle that was identified in the ice cores in an article published not long abo. In another post a bit further back a 350 year solar cycle seemed to show up.
In any case, I am trying to be helpful and not a bother.
My experience is rotating equipment not science and all I did here was what I would have done if I had minimal data to work with.
Thanks Willis –
That helps immensely. It appears to me that what you are doing is less of a Fourier transform of any flavor and more like a sweeping bandpass filter (a classical frequency-analysis method), or perhaps a “bank” of bandpass filters for which you then look for channels with significant responses (which is or can be similar to a DFT=FFT). I have to think more about the DTFT, but it does describe frequency responses of digital filters, so is relevant to any filter approach – or so it seems to me.
Further above I suggested “Prony’s Method” (1795!) which can be described as: “Here is some data – find the poles (resonances)”. Prony is not particular about having equally spaced data without gaps. It is really N equations in N unknowns (linear difference equations replacing non-linear trig equations). This could shorten a search for frequencies. But Prony doesn’t do well with noise. I just recently reviewed this:
http://electronotes.netfirms.com/EN221.pdf
If you look at this, the items in the references, 1b and 1c are a lot more basic.
Of course, many of these things do pretty much the same things, and are valid.
We are all still having fun – are we not? I enjoy all your posts.
Bernie
The pride of blog-lions gathered here seems to be blind to certain basics,
duly explicated in introductory texts on signal/system analysis, but often
neglected in DSP texts. Here is a brief “Idiot’s Guide” to them:
1. The FFT is a finite Fourier-series transform whose harmonic
analysis frequencies are set by the record length and the Nyquist frequency
is set by the signal sampling rate. Its line-spectrum output consists of
finite-amplitude sinusoids that orthogonally decompose the data series
EXACTLY, but always under the tacit ASSUMPTION that the N-point data series
d(n)is strictly N-periodic. In other words, it can be extended indefinitely
by the relationship f(n+kN)= d(n), for all integer k, to produce an
entirely predictable infinite data series f(m), where m = n + kN.
2. Even in the case of strictly periodic signals, whenever the
record-length is NOT equal to an integer multiple of the TRUE period the
FFT fails to identify the cardinal harmonics, smearing them into adjoining
frequencies. This has nothing to do with any physical phenomenon, such as
“line broadening,” being entirely an ARTIFACT of record length.
3. Zero-padding the data series merely changes the COMPUTATIONAL resolution
of the FFT, but adds not one bit of INFORMATION about the signal outside the
time-range of the record. Only in the case of time-limited signals, such as
the weights of an FIR filter, does such padding preserve without any
distortion whatever information is present in the data series. In all
other cases, it introduces a larger set of NEW sinusoidal components, such
that they all add up to the data series and whatever zeros were padded.
This is clearly a wholly unrealistic representation of usually aperiodic
geophysical signals that continue indefinitely before and after the
available record. Especially strongly distorted are the lowest frequencies,
corresponding to periods a large fraction of the record length.
4. The Fourier Integral has bilaterally infinite limits and an integrand
NECESSARILY incorporating BOTH cosine and sine terms. It converges,
however, ONLY in the case of transient signals, the integral of whose
ABSOLUTE VALUES is finite over the infinite time interval. That’s why
signal analysis relies upon the convergence factor of the Laplace Transform
for analytic specification of non-decaying CONTINUING signals that are
aperiodic. In either case, the transform is no longer discrete, but a
CONTINUUM of INFINITESIMAL sinusoids, which are mutually orthogonal ONLY
because the signal is specified over an infinite time interval.
5. The auto-correlation function (acf) of signals usually found in
nature provides a vital means to distinguish between periodic and random
FTA:
“You’d think after that amount of time you could depend on that … but nooo, in the next hundred years there’s no sign of the pesky 22-year period. It has sunk back into the depths of the fractal ocean without a trace …”
Willis, try this. Generate a series w(k) of “white” noise using your favorite random number generator. Feed it into a system model of the form
y(k) = 1.995*y(k-1) – 0.999*y(k-2) + w(k)
Plot y(k). What do you see? Something qualitatively like this?
If you are interested, I will be glad to discuss this further with you, and the implications for your question above.
Bart –
Am I missing something? It seems you just have a sharp 2nd-order bandpass with peak at frequency 0.01 so what you got is exactly what we expect. Isn’t it just ordinary bandpass filtered white noise?
http://electronotes.netfirms.com/Res.jpg
1sky1 –
I agree with points 1. to 4., AND with 5. except you need to say how you set a detection threshold for an autocorrelation peak. Obviously it has to be less than 100% of the zero delay value. I think you have to try different values (90%, 50%. etc.) and then argue your choice.
Bart says:
May 9, 2014 at 6:20 pm
What you’ve shown is a depth-2 autoregressive model which is right on the edge of instability. You can model and plot it in one line in R like this:
And indeed, the results are indistinguishable from yours.
However, if you modify the parameters even slightly, the series becomes unstable:
What you are showing in your linked file is an oddity that occurs when ar1 is almost 2 and ar2 is almost -1. The procedure is operating right on the edge of instability. If the parameters change even slightly, you get runaway positive feedback. And just below that runaway feedback threshold, you get the kind of cyclical behavior shown in your link.
As a result, it is extremely unlikely that this situation exists in nature. Nature doesn’t run that near to positive feedback. If it did, it would have gone off the charts long ago.
And in fact, if we analyze e.g. the CET as a depth-2 AR model, we get this:
Call: arima(x = CET, order = c(2, 0, 0)) Coefficients: ar1 ar2 intercept 1.2980 -0.5924 9.2213 s.e. 0.0123 0.0123 0.1163Note that ar1 is nowhere near 2, and ar2 is nowhere near -1. So it is far from instability, and therefore it doesn’t give results that look anything like what you show. Instead the results from such a model are somewhat lifelike.
However, pure AR models do poorly at replicating natural datasets. I generally use ARMA models of depth 2, which usually give much more lifelike results than pure AR models of any depth.
As you say, if you are interested, I will be glad to discuss this further with you …
w.
1sky1 says:
May 9, 2014 at 5:28 pm
I sure hope you don’t think this kind of egregious boasting improves your traction here … when a man comes on strong like that, from then on his stock tends to sell at a deep discount. There are people reading this blog who are both smarter and better educated regarding Fourier analysis than either you or I. I doubt that they are “blind to” the “certain basics” you go on to list.
I don’t think I’m blind to them either, but then I was born yesterday, que se yo? Well, except for the autocorrelation question. You say:
Here’s the ACF of the CET data …

Not sure how that is a vital means to distinguish between periodic and random signals. Your comments appreciated.
w.
Willis Eschenbach says:
May 10, 2014 at 12:52 am
“As a result, it is extremely unlikely that this situation exists in nature.”
You couldn’t be farther from the truth. This is exactly how nature works. Ring a bell. Slosh a cup of coffee. Drive over a pothole. Throw a rock in a pond. Twang a guitar string. How long the oscillations last depends on how pure the metal, how viscous the fluid, how old your shock absorbers, how big your rock and deep and wide the pond, how good your strings and stiff your guitar neck.
Nature abounds with such examples. Resonances are ubiquitous. Excite them with a persistent broadband input, and they will vary chaotically in amplitude and phase. But, there is structure. And, that structure can be used for estimation, prediction, and control.
Nature is stable because energy is conserved. But, it does not have to dissipate rapidly. And, the rate of dissipation is what determines how long oscillations which are excited will persist, and how pure they will appear over a given timeline.
I’m not going to argue this with you. I know very well it is true. I deal with it every goddammed day. So, if you want to be an ass about it, go ahead. I’m done.
Bart says:
May 10, 2014 at 2:36 am
It appears you totally missed my point, likely my lack of clarity. My reference to “this situation” meant an AR system such as you described, which is running right on the edge of positive feedback.
Yes, nature has resonances and feedback and damping systems and all the stuff you talk about.
But what nature doesn’t have are systems running on the edge of runaway positive feedback. If it did, such systems would have run away long ago. Since they haven’t, we can assume they don’t exist.
Oh, I see now. You’re right. And you know it very well. So obviously, there is no use in discussing it, you’re done …
Is that what’s called the “scientific method” on your planet? Is that what’s called a “conversation”?
Look, Bart, you set out to school me with some non-representative, non-realistic equation with odd properties that you thought I wouldn’t understand.
Instead of that happening, I pointed out that your equation was a simple two-lag AR model. Not only that, I pointed out that if you change the parameters by a few parts in a thousand, your example goes into runaway feedback. I noted that the only reason it had such variations in amplitude was that it was delicately balanced right on the edge of runaway, and that as such, it doesn’t represent a natural system. I added that such 2-lag AR models don’t look very lifelike in any case.
And now, rather than deal with the fact that you set out to school me and you got schooled instead, now you say you’re “done”. You want to stop the discussion, claim you are 100% right and by golly you know it, so you’re gonna take your ball and go home?
We should all be so lucky.
I could only wish it were true that you are “done”, Bart. But sadly, I’m sure you’ll be back to try your tricks again ..
w.
Bart –
It’s not that the specific resonator you proposed is “wrong”, (although as I tried to gently suggest, above, it is a schoolboy exercise) but that such a high-Q does NOT generally exist in nature. It CAN mathematically exist, and CAN exist digitally (numerically) but not if built of springs, capacitors, biological tissues, etc. A few accidental, small-scale, high-Q resonators (perhaps a cave as a Helmholtz resonator) might be noted.
As Willis suggested correctly, a continuous time resonator of that Q would wander into oscillation. Eighty years ago people had “regenerative” radio receivers that added a positive feedback component. In attempting to “pull in” a weak station, the user set the regeneration (“‘tickler coil”) so high that it not only drifted into a local squeal, but broadcast to the neighborhood!
Willis Eschenbach says:
May 10, 2014 at 3:32 am
“But what nature doesn’t have are systems running on the edge of runaway positive feedback.”
Surely, you jest. What do you think a resonance is? You don’t get any runaway condition because energy is not spontaneously created. But, natural systems can store energy with low losses, and does quite frequently, resulting in sustained oscillations. Drive that resonance with persistent inputs whose bandwidth extends across that resonance, and you get persistent wobbles.
“Look, Bart, you set out to school me with some non-representative, non-realistic equation with odd properties that you thought I wouldn’t understand.”
No, Willis. You’re being paranoid. I set out to explain to you why apparent oscillations seem to come and go in terms you would understand.
Bernie Hutchins says:
May 10, 2014 at 9:37 am
I wasn’t proposing any specific resonator, just attempting to demonstrate a concept. But I assure you, high-Q systems abound in nature.
I’d go into more depth, but why play to a hostile audience? I really don’t know what burr Willis has gotten under his saddle with me, but this I don’t need.
One last thing – you think the Q of the system I gave you is unreasonably high? It had 1% damping, which is higher than we generally assume for worst case structural modes. How about this one?
y(k) = 1.608*y(k-1) – 0.9875*y(k-2) + w(k)
Better? it’s essentially the same system. It has a different gain, hence RMS, but its poles are mapped from the same continuous transfer function poles, just sampled at a slower rate.
Perspective. It matters a lot when you are dealing with a massive system like the Earth with very slow dynamics.
Bart said:
“I wasn’t proposing any specific resonator, just attempting to demonstrate a concept. But I assure you, high-Q systems abound in nature.
I’d go into more depth, but why play to a hostile audience?”
Bart – I already suggested a cave as a possible Helmholtz resonator. But if such high-Q systems “abound” why not mention a few to humor us? I can’t, offhand, imagine any others aside from possible biologically-guided ones. I am not hostile – just honestly inquisitive.
Bart also said:
“How about this one? y(k) = 1.608*y(k-1) – 0.9875*y(k-2) + w(k) Better? it’s essentially the same system. It has a different gain, hence RMS, but its poles are mapped from the same continuous transfer function poles, just sampled at a slower rate.”
Bart – this is just changing the peak from 0.01 times the sampling frequency to 0.1 times the sampling frequency. Isn’t that all? You didn’t say previously that you were “mapping” a continuous function. What is your map? What is the analog prototype? In particular, what is the Q of the prototype? No zeros so it looks like it might be impulse invariant ? But I miss the significance of the change.
Bernie Hutchins says:
May 10, 2014 at 11:19 am
“…why not mention a few to humor us…”
I did. You seem to be laboring under the assumption that I am proposing cesium oscillator type Q-factors. Hardly. The Q factor of the system I gave as an example is about 50. It didn’t even need to be that high. Just high enough that oscillations can be self-sustained for maybe a cycle or two.
How high does that need to be? For a continuous system with characteristic function s^2 + (wn/Q)*s + wn^2, the time constant is tau = 2*Q/wn = Q*Tn/pi, so the ratio of the time constant to the period is tau/Tn = Q/pi. Let tau be, say, 5 cycles. Then, Q = 5*pi = a little over 15.
“…this is just changing the peak from 0.01 times the sampling frequency to 0.1 times the sampling frequency.”
Yes. The sample frequency went from 1 time unit to 10 of them. It is a zero order hold equivalent, z = exp(s*T), where T is the sample period. It’s not precise, because I rounded the coefficients, but close enough. The frequency was wn = 2*pi*0.01 rad/time-unit. The damping ratio was zeta = 0.01, hence Q = 50.
To Willis:
I am well aware that you are having quite a time with people making nit-picky arguments against you on other threads right now, and you are huddled in a defensive crouch. But, my input here is meant to be constructive, not condescending or supercilious, and possibly open up other avenues you might like to explore when you have the time.
And yes, Bernie, the actual zero-order hold equivalent has a zero. I didn’t bother with that – I just wanted to demonstrate a simple recursion which would produce lightly damped oscillations.
For comparison, a cesium fountain has a Q of about 10 to the 10th power. We’re not talking especially, or even moderately, high Q’s here.
… relative to that.
Bart gave these examples:
“This is exactly how nature works. Ring a bell. Slosh a cup of coffee. Drive over a pothole. Throw a rock in a pond. Twang a guitar string. How long the oscillations last depends on how pure the metal, how viscous the fluid, how old your shock absorbers, how big your rock and deep and wide the pond, how good your strings and stiff your guitar neck.”
Bart – Thanks, I saw those but did not suppose they were intended as examples any more than the digital resonator you gave. The bell, the suspension system, and the guitar string are not found in Nature, which is why I said examples with “biologic guidance” (even engineers are biological!) were possible. (Are you confusing Natural with Physical? I thought this was more about climate sort of things.) I am not sure of the rock in the pond – is that really a resonance (?) – or a radial wave phenomenon. Coffee cup – not too sure but the Q is probably 2-3 at most – my experiment using log-decrement. Possibly you should accept my Helmholst-Cave and seek similar if there are any.
Your analog/digital system transformation seems “non-standard” but I still don’t have any idea why you needed to offer the filtered noise example.
Bernie Hutchins says:
May 10, 2014 at 12:33 pm
Bernie, this is silly. For crying out loud, bang on a hollow log instead of a bell. Twang a twig instead of a guitar string. Is the rock in the pond exciting a resonance? Certainly. The motion is the superposition of the excited normal modes of oscillation with characteristic viscous damping.
The Q factor is roughly the number of cycles you will see after application of impulsive forcing before they damp out. Let’s see, I’ve got a coffee cup right here. Tap the side… so. 1, 2, 3… 14, 15…20, 21… I get at least 30 oscillations before I can’t see them anymore.
Nonstandard? Say what?
Why did I offer it? Because this is how nature works. Resonances abound. Excite them persistently, and oscillations will grow and fade over time. Sometimes they will be evident, and sometimes not. But, that does not mean that they do not have a physical cause which can be modeled to project, at least into the near future, how they will evolve over time.
Willis was suggesting that the oscillations he observed were a fluke with no physical significance, because they were not sustained over time. But, the conclusion of no physical significance does not follow from the observation.
Everything driving the climate is subject to these kinds of dynamics. The oceans oscillate in their basins. Kelvin waves propagate through the atmosphere. The tides are a manifestation of particularly high Q oscillations of the Moon about the Earth, and the Earth about the Sun, with the damping displayed in the orbital recessions.
The Sun, itself, displays such behavior. See, for example, here and the three other previous pictures (click on the left arrow at the side of the picture to navigate backward).
WordPress seems to have truncated my comment here. The missing part is reproduced below. I’ll try to answer any substantive questions that may arise next week, but all ad hominem comments will be summarily ignored.
5. The auto-correlation function (acf) of signals usually found in
nature provides a vital means to distinguish between periodic and random
signal components. In the former case, the acf is likewise periodic; in
the latter case, it decays with lag, i.e., is transient. Unlike periodic
signals, random signals are far from being perfectly predictable. It is
the rate of decay of acf, which is inversely proportional to signal
bandwith in the frequency domain, that determines the time-horizon over
which useful predictions can be made by optimal prediction filters. The
cornerstone of random signal analysis is NOT the FFT, but is provided by
the Wiener-Kintchine theorem, which defines the power density spectrum as
the F. integral of the decaying acf. Decimation (in time or in frequency)
algorithms must be employed to make periodograms provided by FFT analysis
approximate the power spectrum.
6. Sinusoidal regression is a least-squares curve-fitting method that is
legitimate ONLY in the case of truly period signals. It can be used very
effectively to determine the amplitude and phase when the period is known A
PRIORI–even in noisy records shorter than a single cycle (as described by
Munk in “Super-resolution of the tides”). The periodicity need not be
commensurable with the data sampling interval. However, even in
principle, it cannot provide a VARIANCE-PRESERVING decomposition of a more
general, random-signal data record, or when the signal period is unknown,
because it provides no set of ORTHOGONAL basis functions. When added up, the
discrete sinusoids thus identified generally do NOT add up to the data
series, as with the FFT.
The “Willisgram” simply sweeps a LS curve-fitting routine through
a comb of periods dictated by the sampling rate under the mistaken
assumption that the maximum amplitude obtained identifies the most
prominent periodicity. It doesn’t even identify the (perhaps
incommensurable) sinusoid which minimizes the residual in the data series.
Nor does the absence of a large amplitude sinusoid in such analysis of
short records prove the absence of irregular, quasi-periodic oscillations
commonly found in nature. The only “advantage” it offers is that of
satisfying naive presuppositions of what geophysical signals are composed.
This merely perpetuates the long tradition in the dismal field of “climate
science” of tinkering up quaint, ad hoc data analysis methods without
credible analytic foundations.
(1) Bart Said:
“Bernie, this is silly. For crying out loud, bang on a hollow log instead of a bell. Twang a twig instead of a guitar string. Is the rock in the pond exciting a resonance? Certainly. The motion is the superposition of the excited normal modes of oscillation with characteristic viscous damping.”
Bart –
Well I think the pebble in the pond is a different problem – as I recall – probably because of the lack of boundary conditions as we would have in, for example, your plucked string. The log and the twig are biologically guided. Still – my Helmholtz cave seems the best example. No matter – I need your “natural” log in a moment.
(2) Bart also said:
“The Q factor is roughly the number of cycles you will see after application of impulsive forcing before they damp out. Let’s see, I’ve got a coffee cup right here. Tap the side… so. 1, 2, 3… 14, 15…20, 21… I get at least 30 oscillations before I can’t see them anymore.”
Bart –
Not much of a way to do science! One method of measuring Q is to measure the “ring time”, tr, (to 1/e or about 37%). Then Q=pi*fo*tr. So if we went to about (1/e)^3 or about 5%, 3*tr, Q would be about the number of oscillations – which is where your rule of thumb apparently comes from. Good luck stopping at 5%. Is 5% “observable” or not. Depends. At what point did you stop? More to the point use instead Q = -pi/Ln(d) where Ln(d) is the “natural log” (see it was handy) of the decrement (the change in amplitude from one cycle to the next). This is what I used with the coffee cup. Mine died very quickly. I don’t see how you could have possibly seen 30 oscillations! But I did find that there are at least three resonant modes you can get – so this is a bad example.
(3) Bart also said:
Nonstandard? Say what?
Bart –
Nonstandard because people don’t use the direct map z=exp(sT) because it doesn’t guarantee anything (preserve anything from the analog response). Mostly Bilinear-z and IIV are used, occasionally forward and/or backward difference, but not the matched z. That was out, or should have been, about 40 years ago. Not that it matters since you were just making things up as an example.
(4) Bart –
Yes this is silly. What we need to get to is the fact that you can’t name and/or give evidence for any CLIMATE parameter that has a record suggesting a Q of 50 – by your own rule of thumb – 50 observations, decaying. Surface temperature, ocean heat, ice cover, tornadoes, sea level? No reason to expect simplicity.
1sky1 –
I read through your addendum to your earlier post. Likely you will agree that even a moderate-length text-posting such as yours is not an adequate substitute for a complete technical presentation with equations and figures, including well-defined test examples. Of course, that would be a week’s work or so.
One simple thing that is not clear to me is what you mean by:
“ The “Willisgram” simply sweeps a LS curve-fitting routine through
a comb of periods dictated by the sampling rate under the mistaken
assumption that the maximum amplitude obtained identifies the most
prominent periodicity. It doesn’t even identify the (perhaps
incommensurable) sinusoid which minimizes the residual in the data series.
Nor does the absence of a large amplitude sinusoid in such analysis of
short records prove the absence of irregular, quasi-periodic oscillations
commonly found in nature.”
The question is: Does it not “identify” the sinusoidal because it is totally wrong in concept, or is it just imprecise; perhaps even being forced to select from widely spaced choices with a “real” answer in between?
Thanks
Bernie Hutchins says:
May 10, 2014 at 5:57 pm
Wow. Sorry, no. No. No. No. No. Not much point in continuing this dialogue.
Bart said, May 11, 2014 at 10:58 am
“Wow. Sorry, no. No. No. No. No. Not much point in continuing this dialogue.”
Bart –
You are of course free to discontinue. It might show a bit more class (and increase your credibility) if you FIRST responded to my comments, in line with whatever ability you have, and THEN asked to stop. Otherwise it could just be a cop-out!
Your linking to Wikipedia probably was an indication of your level of experience that I should have noted, rather than gotten more technical, and I apologize for that.
Sincere best wishes and thanks for your time.
Bernie
Bernie Hutchins:
The figure of merit in “sinusoidal regression,” as in any LS curve-fitting
scheme, is NOT the amplitude of the fitted sinusoid, but the variance of
the residual. The “Willisgram” shows the former for a PRE-SELECTED discrete
set of periods coinciding with INTEGER multiples of the data-sampling
interval, but fails to show the latter. This leaves unresolved the SINGLE
sinusoid amongst all periods, possibly INCOMMENSURABLE with the sampling
interval, that best fits the available data in the LS sense.
But more importantly, even that best-fitting sinusoid is not necessarily a
good–or even reasonable–representation of the continuous-time signal that
gave rise to the data. Only in cases where the signal actually contains
strictly periodic components, such as the annual cycle, can sinusoidal
regression be expected to provide meaningful results. In all other cases,
it leads to badly mistaken expectations, as the prognosticators of solar
sunspots rudely discovered with SC24. That is the consequence of mistaking
a narrow-band random process (with strong structural similarities to that
of shoaling swell) for a periodic signal suitable for analysis by repeated
sinusoidal regression. [BTW, for those interested in distinguishing the
difference between truly periodic and narrow-band processes, I can e-mail
the estimated acfs of the monthly S.F. sea-level and of the yearly Zurich
SSN data to any address.]
It needs to be recognized that, because of frequency entanglement in
non-orthogonal decompositions (particularly of long periods in short
records), a wide range of linearly incremented periods will show large
amplitudes that would NOT be there in much longer records. That is the
irretrievable failure of the conception behind the “Willisgram.”
Undoubtedly, the brief sketch of the landscape of proper signal analysis
methods I provided here is wholly inadequate to the task of elucidating a
complex subject to analytic novices. But that’s what a plethora of
introductory texts written since the 1960s undertake. A popular one is
Oppenheim & Shafer’s “Discrete-time Signal Processing.” It’s dismaying that
basic concepts covered there continue to elude so many who feature
themselves “climate scientists.” And it’s disturbing that the ANNUAL
cycle, which is HIGHLY prominent in both sea-level and temperature data, is
nowhere displayed in any results on this and previous related threads.
1sky1 –
Thanks for the reply.
I understand what you are saying. But I think my most fundamental doubt is that there is enough “Fourier” signal in the climate data that any “detection” means much. I think this is your view too?
But it does seem to me that you can get the frequency pretty accurately using Prony’s method (or similar) combined with some least square manipulations to handle the noise that Prony can’t tolerate directly, and when the system has a dominant (not necessarily high-Q) pole pair. This likely works even when an FFT lies through its teeth! NOT saying that it helps with climate data.
I first learned DSP using a 1972 mimeograph version of O&S! I co-taught with the “Halloween” (black/orange covers) versions, and later versions. I didn’t think the students liked it very much, and I never used any text when teaching by myself. Certainly I don’t think you were suggesting that that text was very useful for what you have been saying? Not to say that some very BASIC misunderstandings are not common in the comments. The basic one hurt. The more subtle ones get all of us from time to time (i.e., every day!)
Bernie Hutchins:
To be sure, detection and proper identification of oscillations in the multi-decadal to centennial range from climate records seldom much longer than a century is a real challenge. That challenge is scarcely helped by applying data analysis methods ill-suited to the intrinsic character of the underlying signal. Sadly, confusion between periodic and aperiodic signals is rampant in “climate science,” whose mind-set is rooted in the data = mean + trend + cycle + i.i.d. noise paradigm of classical statistics, with understanding of stochastic processes imprisoned in simple Markov chains. My purpose here was to draw a sharp distinction between periodic, transient, and far more complex random signals encountered in geophysics and to indicate suitable analysis frameworks for each.
It strikes me that Prony’s method is applicable only to transient (finite energy) signals, but not to continuing (finite power) signals, periodic or random. In the latter case, when there no strictly periodic components, the very idea of using LS curve-fitting methods on two or three wave-forms is foolish prima facie. Even “surfer dudes” recognize that no two waves are alike in height and apparent “period.” Few in “climate science” manifest such wisdom. We are truly at the threshold of reliable, meaningful characterization of long-period oscillations. Nevertheless, unlike curve-fitiing routines, sound signal analysis methods provide the best glimpse available of those signal characteristics.
You’re entirely correct that O&S’ latest opus was not my reference nor my recommendation. It is simply a cheaply available text that covers some of bare basics. At least the authors had learned enough from their sabbatical at WHOI to avoid the lapses that made their earlier “Halloween” opus indeed frightful. I wrote the commnent off the top of my head, deliberately refraining from recommending “Signal Analysis” by Papoulis, which is intended for a more advanced audience. BTW, I began hands-on learning as a summer undergraduate apprentice to one of Wiener’s students, who had his own copy of the “yellow peril,” and in loaded up in grad school on “Statistical Theory of Communication” along with geophysical course-work. Always nice to meet someone who has solid grasp of the subject.
1sky1 –
I myself have a detailed and complete understanding of the earth’s climate system; which curiously has an exact counterpart detailed and complete understanding of my vegetable garden: “Sometimes things grow, and sometimes they don’t”.
In a similar vein, I tend to have to discover things for myself. I am not offering that necessarily as a virtue, but as the easiest and perhaps only way I myself can learn. And I’m not too good at learning something until I really need it. Give me someone’s basic idea (or a notion of my own) and let me play with Matlab writing my own code. “The purpose of computation is insight, not numbers.” – Richard Hamming
Prony’s method works for any decay constant, including no decay. If you take four samples like [0, 0.5 sqrt(3)/2, 1] Prony happily tells you the frequency is 1/12 if you specify that it is 2nd order and there is no noise. The FFT lies, and never heard of a frequency 1/12 anyway. Prony is just as happy with a frequency 1/12.123, for example. And it is linear. A perhaps limited, but a valuable tool. I’m still trying to see what it can do. I learned Prony from Tom Parks who remarked that “people are always re-inventing Prony’s method”. At that time, I noted that the methods was coming up on 200 years old (invented in 1795).
Yes I love all the signal analysis and modeling stuff. But many years ago in a senior physics lab I fit some data to every possible math function I could imagine, and plotted every possible graph. My professor, Herb Mahr, praised my industry in doing so, and ever so gently (bless his heart) told me that it didn’t really MEAN anything.
Nothing new under the sun.
Bernie
Bernie:
There indeed is little new under the sun–except in the minds of the “way
cool” ME-generation that treats what isn’t presented on the Web as de facto
non-existent. This, of course, leaves the field wide open for puerile
claims of “invention,” which you’re mature enough to see through.
It turns out that Pony’s method has been tried out on transient geophysical
signals found in seismograms and sea-level disturbances by tsunamis (see:
http://www.reproducibility.org/RSF/book/tccs/nar/paper.pdf and
http://oos.soest.hawaii.edu/pacioos/about/documents/technicalreports/TechRep_PacIOOS_SL_Forecast_07-17-2012.pdf).
If I read correctly (with only ~1/2hr available in my schedule for Web
browsing), in effect it fits an ARIMA model to the data, reminiscent of EOF
decomposition in “singular” spectrum analysis, or fitting a purely AR model
to the sample acf in Burg’s “maximum entropy” spectral estimation algorithm,
thereby extending it to longer lags than the short data record can
robustly estimate. I.e., it’s an attempt to replace genuine empirical
information with a presumptive model.
What many decades of experience in empirically-based research has taught me
is that all attempts to find free lunch ultimately leave the serious
scientific appetite hungry. When the rubber of preconception meets the
hard road of reality, it’s the rubber that usually breaks. But that is rare
in “climate science,” where data are much too often manufactured, or
presented, to conform to preconception. An example of this is the sample
acf of the exceptionally noisy monthly CET, shown by Willis on a
LOGARITHMIC scale and only for lags of 2yrs and longer–a transparent
attempt to induce the naive conclusion that long-term temperature series
conform to the exponential decay of a “red noise” process. That’s how weeds
from the garden, masterfully promoted on the Web, get sold as roses.