Statistical failure of A Population-Based Case–Control Study of Extreme Summer Temperature and Birth
Guest Post by Willis Eschenbach
The story of how global warming causes congenital cataracts in newborns babies has been getting wide media attention. So I thought I’d take a look at the study itself. It’s called A Population-Based Case–Control Study of Extreme Summer Temperature and Birth Defects, and it is available from the usually-scientific National Institutes of Health here.
Figure 1. Dice with various numbers of sides. SOURCE
.jpg/250px-Dice_(typical_role_playing_game_dice).jpg){kind=link}
I have to confess, I laughed out loud when I read the study. Here’s what I found so funny.
When doing statistics, one thing you have to be careful about is whether your result happened by pure random chance. Maybe you just got lucky. Or maybe that result you got happens by chance a lot.
Statisticians use the “p-value” to estimate how likely it is that the result occurred by random chance. A small p-value means it is unlikely that it occurred by chance. The p-value is the odds (as a percentage) that your result occurred by random chance. So a p-value less than say 0.05 means that there is less than 5% odds of that occurring by random chance.
This 5% level is commonly taken to be a level indicating what is called “statistical significance”. If the p-value is below 0.05, the result is deemed to be statistically significant. However, there’s nothing magical about 5%, some scientific fields more commonly use a stricter criteria of 1% for statistical significance. But in this study, the significance level was chosen as a p-value less than 0.05.
Another way of stating this same thing is that a p-value of 0.05 means that one time in twenty (1.0 / 0.05), the result you are looking for will occur by random chance. Once in twenty you’ll get what is called a “false positive”—the bell rings, but it is not actually significant, it occurred randomly.
Here’s the problem. If I have a one in twenty chance of a false positive when looking at one single association (say heat with cataracts), what are my odds of finding a false positive if I look at say five associations (heat with spina bifida, heat with hypoplasia, heat with cataracts, etc.)? Because obviously, the more cases I look at, the greater my chances are of hitting a false positive.
To calculate that, the formula that gives the odds of finding at least one false positive is
FP = 1 – (1 – p)N
where FP is the odds of finding a false positive, p is the p-value (in this case 0.05), and N is the number of trials. For my example of five trials, that gives us
FP = 1 – (1 – 0.05)5 = 0.22
So about one time in five (22%) you’ll find a false positive using a p-value of 0.05 and five trials.
How does this apply to the cataract study?
Well, to find the one correlation that was significant at the 0.05 level, they compared temperature to no less than 28 different variables. As they describe it (emphasis mine):
Outcome assessment. Using International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM; Centers for Disease Control and Prevention 2011a) diagnoses codes from the CMR records, birth defect cases were classified into the 45 birth defects categories that meet the reporting standards of the National Birth Defects Prevention Network (NBDPN 2010). Of these, we selected the 28 groups of major birth defects within the six body systems with prior animal or human studies suggesting an association with heat: central nervous system (e.g., neural-tube defects, microcephaly), eye (e.g., microphthalmia, congenital cataracts), cardiovascular, craniofacial, renal, and musculoskeletal defects (e.g., abdominal wall defects, limb defects).
So they are looking at the relationship between temperature and no less than 28 independent variables.
Using the formula above, if we look at the case of N = 28 different variables, we will get a false positive about three times out of four (76%).
So it is absolutely unsurprising, and totally lacking in statistical significance, that in a comparison with 28 variables, someone would find that temperature is correlated with one of them at a p-value of 0.05. In fact, it is more likely than not that they would find one with a p-value equal to 0.05.
They thought they found something rare, something to beat skeptics over the head with, but it happens three times out of four. That’s what I found so funny.
Next, a simple reality check. The authors say:
Among 6,422 cases and 59,328 controls that shared at least 1 week of the critical period in summer, a 5-degree [F] increase in mean daily minimum UAT was significantly associated with congenital cataracts (aOR = 1.51; 95% CI: 1.14, 1.99).
A 5°F (2.75°C) increase in summer temperature is significantly associated with congenital cataracts? Really? Now, think about that for a minute.
This study was done in New York. There’s about a 20°F difference in summer temperature between New York and Phoenix. That’s four times the 5°F they claim causes cataracts in the study group. So by their claim that if you heat up your kids will be born blind, we should be seeing lots of congenital cataracts, not only in Phoenix, but in Florida and in Cairo and in tropical areas, deserts, and hot zones all around the world … not happening, as far as I can tell.
Like I said, reality check. Sadly, this is another case where the Venn diagram of the intersection of the climate science fraternity and the statistical fraternity gives us the empty set …
w.
UPDATE: Statistician William Briggs weighs in on this train wreck of a paper.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Not been on this before, but what a great range of comments in this thread. One of the really nice things was the humility of rgbatduke – someone who clearly is comfortable with the use of statistics, remarking on what he does not know. It’s sad to note though that folks who don’t come anywhere near his level of expertise are able to pass themselves off as statistical experts, and so our society is being shaped in so many ways by those who abuse their level of knowledge – the AGW scam, passive smoking, efficacy of drugs, you name it, our society is being shaped by those who are abusing their knowledge in some way. I’ve gone through university in the UK – did various degree courses (biochemistry, public health engineering) in which statistics was always a part. But I never paid any attention to the stats part of the courses, simply because in my final exams, stats would usually get maybe one question out of 8, and I could rely on my choice being reduced to answering 5 out of 7. So I always ignored stats – until I did an MBA, there was no getting past it, I finally had to knuckle down. What I remember from that is enough to know that usually I don’t know – so I’d like to think I’m in the group who know enough to know what I know but more importantly, know what I don’t know. As the general population is made up of people who don’t know that they don’t know stats can be abused without fear of comment. And our society is very much poorer for it. Environmental groups can frighten folks with claims that are simply preposterous – and few ever question them. They are the new gods of information, held in high esteem by the general population all over the world, yet they are mainly charlatans, selling quack medicines. With the dumbing down of education here in the UK, things will only get worse. I cannot see any change at all – not until university courses are organised so that stats is an integral part of every question – no escape; and basic stats is taught as a “must do” subject in every school. Probably will never happen. So good luck guys, in your quest as the voices of reason and truth, but I fear you are both literally and figuratively tilting at windmills.
It’s seems a strange conclusion, even without dredging the data for correlations. These were *unborn* kids supposedly affected. During their gestation, where they were was thermostatted far more precisely than any conventional environmental control system. That’s the advantage of being internally gestating homeotherms.
Or are there Burroughs’ Martians among us?
Monty’s not opening the doors randomly. He’s opening them because he knows they don’t contain the zillion samolians. Each empty door he opens gives you a little more information than you had when you made your original choice. If he were opening them randomly, your gut would be right.
And Bayes theorem and information theory are one and the same thing, in the end. Information is the key. Monty can actually open any of the doors that (he knows) do not contain the prize randomly (if there are more than two), it won’t matter. But he cannot open a random door out of the set of unchosen doors, because then it might contain the prize. We learn a bit more of what Monty knows with every door he opens, and it shifts our odds if we use the information. But this is hard to understand, so let’s work it out. It’s not too difficult.
Here’s a very simple parsing of the chances. When you chose between the 3 doors originally, you had a 1 in 3 chance of guessing the right door. Each of the other doors also had a 1 in 3 chance of being right, so 2 out of 3 times you guessed wrong. Monty opens a door and reveals it to contain a year’s supply of dogfood — and a dog — not the two week vacation in Tahiti. The door you selected has a 33% chance of being right, but the other door has a 100% chance (now) of being right — 67% of the time.
Better to switch, don’t you think? Unless you cherish the barbecue grill and year’s supply of steaks that is the other “junk” prize.
The key thing is to realize that the second “trial” is not independent of the first, so you have to deal with conditional and joint probabilities, which is what Bayes theorem is all about.
Note well that this is defeated if Monty is permitted to choose whether or not to open a door. For example, he could open a door only if you’ve chosen the actual prize to entice you to switch — this is actually not crazy, maybe the company likes to conserve valuable prizes. So if he knows you have chosen correctly, he opens a door to entice you to re-choose (assuming that you are a good statistician and know that you “should” double your chances by doing so, but if you have chosen incorrectly he always goes ahead and reveals the dogfood you’ve chosen. Ouch. You win only if you always stick, 1/3 of the time, and even less if you are enticed into switching — you win 0% of the time if you always switch.
This opens up a whole range of games Monty can play by rarely opening a door when the prize is on his side even if you’ve lost, so that you learn that there is some chance of winning. Most of those games (if played perfectly) would increase your optimum yield from 1/3, but now we’re well on the way to inventing rock-paper-scissors games, where the optimum strategy is to guess completely randomly (and win on average half the time) but where humans can often nevertheless exploit information theory and beat the hell out of their opponents when neither side chooses randomly. Humans have a hard time CHOOSING randomly without using dice or coin flips — what we intuitively think of as being a “random” sequence almost never is.
rgb
You will always have better odds switching, the greater N is the greater the advantage to switching.
Well, not quite. Your original choice was 1/N. The chances that it was behind one of the other doors is (N-1)/N. One door on the right is opened. If you choose from the remaining unopened doors, the chances are now 1/(N-2) of winning if you reselect from that side AND the prize is there. The chance of winning is thus the product: p(switch and rechoose) = (N-1)/N-2) * 1/N (for N>2 for this to make any sense). For N=3 p(s&r) = 2/1 * 1/3 = 2/3, double your original chance.
For N =4 p(s&r) = 3/2 * 1/4 = 3/8, or 1.5 times your original chance.
For N = 5 p = 4/3 * 1/5, or 1.33 tiems your original chance.
For N=1000, p = 999/998 * 1/1000, hardly worth it to switch.
So the MAXIMUM advantage to switching is exactly N=3.
rgb
It’s seems a strange conclusion, even without dredging the data for correlations. These were *unborn* kids supposedly affected. During their gestation, where they were was thermostatted far more precisely than any conventional environmental control system. That’s the advantage of being internally gestating homeotherms.
Or are there Burroughs’ Martians among us?
It isn’t that simple. There is substantial, convincing evidence with p much smaller than 0.05 that fevers during critical periods are correlated with the defect, where it is more likely the fever per se that is the cause and not the virus or other cause of fever because it is positively associated with the fever caused by MANY diseases, not just one or two.
It is also certainly a true fact that prolonged exposure to very high outside temperatures with inadequate shade, water, and/or too much humidity so sweating doesn’t work to keep you cool can lead to hyperthermia, where your internal body temperature creeps up over its “normal” set point because you literally cannot throw off heat fast enough. When the temperature outside is 100F, for example, you are trying to cool into an environment hotter than you are, which REQUIRES sweating profusely. One can literally overwhelm one’s natural thermostat, leading to heat exhaustion and heat stroke as your body’s internal temperature rises to 102F and then to 104-105 F, where your brain basically malfunctions and you have strong odds of straight up dying.
It is therefore a reasonable hypothesis that environmental hyperthermia during pregnancy could lead to birth defects, this particular one among others. As I pointed out, neural tube defects are the most likely ones to first observe as they are most strongly correlated with fever-induced hyperthermia.
However, this is a long ways away from showing that pregnant women have a high enough chance of experiencing actual internal hyperthermia to affect birth defect rates by increasing them by 50%. That is, in fact, close to absurd. It takes time and a certain amount of abuse or stupidity to experience hyperthermia, as we naturally seek cooler environments and cool drinks when it is hot out. One needs MOST of the women in question to have spent long times outdoors, not drinking, and consequently overheating to the point of having the equivalent of a low grade fever. Maybe, but I doubt it, and if so why weren’t neural tube defects spiked first?
Bayesian analysis of neural tube defects and other disorders related to fevers suggest that the hypothesis is probably false, and in any event is marginal on the data, especially when it is a dredged conclusion.
rgb
Mr Briggs has just swatted this piece of trash into the round file….:
http://wmbriggs.com/blog/?p=6870
The most common cause of cataracts in infants is being kissed on the eyes by a parent with a herpes outbreak or “cold sore” on their lips. Source: “Herpes: What to do when you have it” by Dr Oscar Gillespie
E.M.Smith says:
Another case of “Climate Science” done by folks who took one Stats class, then forgot most of it.
Possibly they had a similar level of education in biology. Or are just unable to think through the logic of humans being placental mammals.
One nit — The 75% chance is for any study that has 28 different data dredges going on. There is not a 3/4 chance that any one of them will be.
If 10 different studies of this sort were done, 3 out of 4 would get a positive result.
Another NIT– The problem with these studies in general is that they study the dead and ignore the living. Instead of looking at the percent dead, look at the percent living.
(You have to be able to equate dead with ‘having cataracts’ and living with ‘not having cataracts’)
Studies like this focus on the small numbers on the dead end of the spectrum and fail to consider how it is that so many people manage to avoid getting cataracts having been exposed to the same conditions.
Smokers have 25-40x risk of getting lung cancer because they smoke. This also means that there is a 92% chance that in 60 years of smoking they won’t get lung cancer. There are a few rational epidemiologists out there. Unfortunately epidemiologists are sort of like lawyers, we have way more of them than we need.
To stay employed though, they need to do work. Hence we get this stuff.
The great irony of epidemiology is that the valuable work the do is not in the positive correlations they find. It is in the negative. All the results that say “no correlation” are the ones that are meaningful. (There are a few rare exceptions, smoking/lung cancer, oral sex/Oral cancer[caused by HPV]).
“I have to confess, I laughed out loud when I read the study.”
As I did with your title. Knew exactly who wrote it before looking.
Was getting a bit worried of late that Willis hasn’t posted for a while – welcome back. I always enjoy a good read.
michaelozanne says:
December 21, 2012 at 10:08 am
“Mr Briggs has just swatted this piece of trash into the round file….:”
Hmm. Briggs talks about “…presence or absence of 84 different birth defects…” and also “…for a couple of the 84 birth defects….”
There were 84 comparisons, but for 28 birth defects, with three indices of heat as causes. One of these could be a typo, but when he repeats it, this raises a question about how carefully he read the paper.
In a sort of similar vein: in the paper, they stated: “We found positive and consistent associations with congenital cataracts of multiple ambient heat exposure indicators, including 5-degree increases in the mean daily UAT (minimum, mean, and maximum), a heat wave episode, the number of heat waves, and the number of days above the 90th percentile of UAT.”
Now, I don’t think it useful to go calculating the probability of hitting on all three indicators by chance, since the three indicators should be highly correlated.. But it does seem to indicate that dividing the 5% criterion by 84 may be too conservative. If you pick any one of the indicators, the cataracts come out statistically significant. Perhaps it might be more realistic, in this case, to divide bu 28 instead. The presumed high degree of correlation among heat indicators would actually support this, since it means they weren’t really doing 84 independent correlations. I suspect that there must be some way of dealing with this, although the authors may not have known about it.
They mention cataracts being associated with the number of heat waves and the number of days above 90th percentile of UAT, That actually looks to me like a dose-response relationship, which is definitly stronger evidence than a simple statistical significance for incidence. But they give no details so it’s hard to tell. If they really saw a dose-response relationship, it would seem strange that they didn’t mention it.
rgbatduke says:
December 21, 2012 at 8:15 am
Or perhaps the rate is actually higher among women more exposed to heat, but the study was diluted by women who didn’t get overheated Perhaps some were better adapted to heat due to genetic background. Perhaps only a few women worked outside or inside without air conditioning, didn’t have it at home, and were constitutionally less able to withstand these conditions.
From the paper:
So, at least they considered some explanations for the lack of neural tube defects showing up.
So, quick google scholar search on animal studies for neural tube defects:
http://content.karger.com/ProdukteDB/produkte.asp?Aktion=ShowAbstractBuch&ArtikelNr=242767&ProduktNr=247786
http://onlinelibrary.wiley.com/doi/10.1002/tera.1420290313/abstract
http://onlinelibrary.wiley.com/doi/10.1002/tera.1420310212/abstract
These first three abstracts I got back (articles paywalled) showed one that counted prenatal death, one that considered it, and one that didn’t mention it (although the paper could have). So, perhaps the fact that they couldn’t track prenatal deaths might have some bearing on the question neural tube defects.
Another point: these mouse studies looked at severe temperature elevations, perhaps as much as 5-6 deg. C, which would stand a good chance of killing a human. Then again, there may be birth defects in mice with milder heating, but at a rate difficult to see without an enormous study.
Also, the lens of the eye is a strange beast. It is the only human organ for which occupational exposure to radiation is known to have deterministic rather than stochastic effects. Get enough radiation exposure, and you WILL get cataracts, whereas you MIGHT get cancer (and your chances of that, as a radiation worker working within the occupational limits are pretty low).
Articles on this are harder to find but this one
http://onlinelibrary.wiley.com/doi/10.1111/j.1741-4520.1996.tb00316.x/abstract
mentions finding changes in the lens of fetal guinea pigs subjected to hyperthermia, that could show up later in life as cataracts, and also induction of cataracts at different stages of pregnancy (though most strongly in early pregnancy, when the eyes would be forming).
Given this, it’s plausible that pregnant women exposed to mild hyperthermia for days on end (slowly building up tissue damage) might have offspring with more cataracts than neural tube defects, whereas for more acute exposures such as fevers, this would be reversed. This would be because the lens can accumulate subtle damage over time, at least for radiation. The neural tube closes, or it doesn’t, over a relatively brief time.
All of this together doesn’t make the paper believable. I think it tilts the odds in that direction a bit. If there turns out to be something going on here, it’s good to know for a few reasons. MRI scans used to be contraindicated for pregnant women, since the effects of the slight heating from the RF (I think about 1 deg..C) were unknown. Extra knowledge is always helpful. Still, there are a lot of reasons why waving this paperaround in relation to global warming is pretty silly: the results are uncertain, to say the least; they indicate, if anything, something that’s probably a rare problem, and people who get frightened from something like this won’t be considering things like adaptation to a warmer environment. Maybe they will eventually start giving stronger warnings to pregnant women to avoid overheating. I somehow sense that they are already doing this themselves.
http://imgs.xkcd.com/comics/depth_perception.png
JazzyT, you say:
JazzyT, you are wrong. The cataracts are not statistically significant, because they were found as the result of a data dredge. It doesn’t matter whether you look at it as finding 5 “significant” results out of 84, or 1 or 2 “significant” results out of 28 makes no difference. For N=84, we expect 4 false positives, about what we got. For 28, we also expect about what we got., 1 or 2.
In other words, the results are EXACTLY AS EXPECTED FROM RANDOM CHANCE. This means it is incorrect to say that “the cataracts come out statistically significant”. They do not.
You go on to say:
You’re missing the point. We don’t have a scrap of evidence that any of the women overheated at all. It would be surprising to me if they did, at least if my wife’s behavior when pregnant is any guide. She was sensitive to heat, and wouldn’t go out in it unless she had to.
Note that we’re not talking about simply getting hot. For their theory to work the women would have to have suffered hyperthermia, where the body temperature actually rises … and we have no evidence that they did that.
But without actual evidence, they are just blowing smoke. Without actual evidence, speculating about whether “some were better adapted to heat” goes nowhere. Without actual evidence, we know nothing. Without actual evidence, their study is meaningless.
Plausible? For it to be “plausible”, you’d have to have pregnant women being “exposed to mild hyperthermia for days on end”. How on earth is that supposed to happen? Our bodies are exquisitely tuned to keep the body temperature within a very narrow range no matter the environmental temperature. You are describing pregnant women running a 1° or so fever for days and days … how is that “plausible”? Sounds highly improbable to me.
You close by saying in part:
Sorry to be so blunt, but the paper is trash. It has no evidence, it is a data-dredge between the temperature at the nearest airport and birth defects. There has been no physically plausible mechanism suggested whereby a “heat wave” would raise the temperature of the fetus. In fact, there is no evidence that the women have even experienced excessive heat at all.
As a result, I have no idea what could “tip the odds” in favor of the paper being believable. It is evidence-free and statistically ludicrous, no matter how you tip it …
w.
I’d say that a statistical study on statistics would probably show that, as a statistical average, people are not very good at statistics.
Mero, you wrote, “I’d say that a statistical study on statistics would probably show that, as a statistical average, people are not very good at statistics.” Yep. 9 out of 10 are definitely below average…
;>
MJM
Merovign says:
December 22, 2012 at 2:32 pm
One of the tragedies of the world is that if you ask someone how intelligent they are, most folks will say “a little above average”. It’s almost magical how there is a perfect inverse relationship between actual intelligence and the self-estimation process, with the balance so exact that everyone ends up a little above average.
Unfortunately, if you ask a climate scientist how good a statistician they are, there’s a good chance you’ll get the same answer.
I am by no means a journeyman statistician, my knowledge is wider than it is deep, I defer to Dr. Brown from Duke University (posting as rgbatduke) for that, heck, someone corrected a couple of my statistical errors upstream … but I am smart enough to recognize a data dredge when I see one.
w.
OK, first, I’m not actually trying to save this paper, I don’t think that much of it. But, I’m not absolutely certain that it was a waste of (probably public) money, either, especially since reporting weak or negative results lets other researchers decide whether they might want to follow on or not. But any publicity that this paper gets regarding global warming is just silly, and reflects, among other thins, a slow news day in the warm zone.
Having said that, I do like learning new stuff, and I do tend to try to avoid being to certain about things–such as “this paper is useless”–until I’m justified in being sure about it.;
Willis Eschenbach says:
December 21, 2012 at 11:54 pm
My bad. I gave the argument and neglected to say what the real point was. I’d like to quit posting right around sleepytime, but that’s when I can grab some free time.
I was talking specifically about applying the Bonferroni adjustment, mentioned in the paper and also above:
Lance Wallace says:
December 20, 2012 at 1:04 am
I hadn’t actually picked up on Lance going with 28 comparisons instead of 84. As he said, we want to look at 28 different comparison, but with only a 5% chance of even one of them being a spurious correlation. We’ll use the equation you started with:
FP = 1 – (1 – p)^N
If you want to avoid even one false positive at the “p” level, you divide p by N, for
FP = 1 – (1 – p/N)^N
Rather than write this out in all its gory glory, we’ll just give the answers for N=28 and N=84.
For p=0.5 and N=28, the false positive rate FP = (1-001786)^28 = 0.9512
For N= 84 we get p = 0.9512 again.
You end up with a chance that’s actually slight less than 5%, though only very slightly, that even one correlation is a false alarm I’d never heard of it before this conversation. But yes, it’s actually possible to go data-dredging and get meaningful results, as long as it’s done properly. (It helps if you have meaningful background information.)
It”m not sure whether the usual terminology for the data dredge without Bonferrroni corrrecton would be “not statistically significant” or “statistically significant, but meaningless.”
Welcome to epidemiology! Without a huge amount of resources, you can’t do things like track down individual women and ask them if they remember hypotherma during a years-distant pregnancy. Some unkonwn percentage of those who didn’t actually collapse might not remember anyway. A (much more expensive) prospective study would give better info by letting pregnant women keep journals, or something, but at a much higher cost.
You don’t spend a lot of money on a big study until little studies like this one tell you whether it’s worth doing. So instead of implanting a radio-telemetry thermometer in each of 10,000 pregnant women, or even something far less preposterous but still expensive, you make do with whatever you can get. When you don’t have data, you use proxies–like the temperature at the nearest airport. If that tells you something interesting, then you go for the big-money studies.
A sample size of one…but, I’m glad she had the sense to come in out of the heat. Not all women have that option. When I was a teenager, I worked on a farm during a couple of summers. (I was too young for other full-time work.) Our crew took on a family with parents, young kids, and a very visibly pregnant teen daughter. She didn’t do much work–always complained about the heat. about her husband being in prison, and kept saying, “Mama, I wanna go lay down…” She did what she could to avoid heat stress, and Mama did let her lie down in the shade sometimes, but none of us were really able to get out of the heat of a Southern (US) farm in summer.
Another sample size of one, but your wife, and that poor girl (her family was very poor) represent two ways things can go. In a lot of places I’ve lived, when there’s a heat wave, they put out warnings on the radio and TV to go check on neighbors or others you know, and I’m very used to hearing a small death toll for the really severe ones. Even in some hot areas, not everyone even has air conditioning. In the cities, people have been known to sleep on the fire escape, and they put sprinklers on fire hydrants for the kids, but there’s only so much you can do.
Welcome to epidemiology…when you can’t yet afford direct data, ya gotta use proxies, with all their limitations. We don’t know how many women suffered heat exhaustion or heat stroke, but with a sample size of 6,400 (and a control group o 59,000) it probably wasn’t zero. I’m sure the authors had access to data on incidence rates.
Just for fun, I started fooling around with the confidence intervals on the congenital cataract data.I applied Bonferroni adjustment for N=28, on the theory that max, min, and mean temperature on really hot days ought to be correlated. They mentioned that with the Bonferroni adjustment for N-84, they would not be statistically significant at the 95% level. For N=28, they were not either, though they would have come closer. For one dataset, (minimum daily UAT) actually looked at the p-value required to hit 1.0 for the lower bound on the confidence interval for the odds ratio. For a two-tailed test, p=0.964, so it fails a two-tailed test at 95%, but would have passed a one-tailed test. I suspect that this would be true of the others as well.
All this was done with the assumption that the logarithm of the odds ratio would follow a normal distribution, as is, well, normal, and looking up cumulative probabilities for various Z values, rescaling things as necessary. I can post more details if anyone REALLY wants them.
All of this doesn’t make me like the paper. But I used to date an epidemiologist, and I gained a lot of respect for a field that was much more complicated, capable, and important than I’d ever known. She wasn’t doing cataracts and heat, she was doing causation studies and clinical trials for cancer and AIDS. She was quite skeptical of some of the science she saw. From her, I found out just enough about things that looked good and weren’t, or looked bad but weren’t, that in order to pass final judgement on a paper like this, I’d want run it past a trusted expert, like her.
And again–it’s just silly that a nebulous piece like this, that is at best preliminary, should be touted as showing adverse health effects of global warming–without noting that the paper is uncertain at best, and even the results panned out with a bigger study, that people can and do adapt to temperature changes, and that, in the end, surgery to correct cataracts exists, and is mild in comparison to fixing, say, spina bifida.
On the other hand, now I know a couple of things about stats that I didn’t know before, and I’m definitely good with that.
Well, the people in India have the highest cataract in the world. Due to radioactive exposure one assumes from the slide of India into Asia releasing deep gases from the interior like radon.
Did you notice that even tho the UN experiment with high Vit A supplement going bad ( the children got cancer) the push for added Vit A to rice is back?
You end up with a chance that’s actually slight less than 5%, though only very slightly, that even one correlation is a false alarm I’d never heard of it before this conversation. But yes, it’s actually possible to go data-dredging and get meaningful results, as long as it’s done properly. (It helps if you have meaningful background information.)
C, or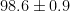 
F. There is an entire wikipedia article on it. It is typically lowest around 4 a.m. and highest around 4 p.m. A temperature of 99.1 F might be considered evidence of a fever in the early morning but not in the mid to late afternoon. These temperatures also vary with activity, e.g. exercise. In fact, the wikipedia article:
JT, I largely agree with your modified comments above — and made many of the same points. There is a “proven” association between fevers, at least, and a variety of birth defects. It is perfectly reasonable to ask the question: “Is environmentally induced hyperthermia a plausible cause of some of the birth defects known to be plausibly caused by fevers?”
However, you still miss one of Willis’ (and my) main points. This is not what they investigated. They investigated — data dredge style — whether or not there was any correlation between airport temperatures in the general vicinity and not one but a vast array of possible defects. Now, what do you think you would observe if you had a thermometer embedded inside your gut over the course of a day?
The answer is that the thermometer would read — under normal circumstances —
http://en.wikipedia.org/wiki/Human_body_temperature
lists not one but many factors that affect body temperature. Food, drink, tobacco, clothing, exercise, sleep cycle, psychological stress, and alcohol consumption all affect body core temperature. Sleeping under an electric blanket is known to raise nighttime core temperatures as well. Pregnancy was not listed as a risk factor for hyperthermia. That isn’t to say that it isn’t — indeed, the following article:
http://www.ncbi.nlm.nih.gov/pubmed/16933304
suggests that “an episode of hyperthermia is not uncommon during pregnancy” from all causes already and yes, this article does directly study the consequences, with neural defects prominently leading the way (not just one, but many, and in humans, not just animal models). It also specifically looks at episodes of hyperthermia (as well as fever) in pregnant women, not at “heat waves” at a nearby airport.
Medical hyperthermia occurs when the body produces more heat than it can dissipate. This can happen by increasing production — exercise, eating, drinking warm or stimulating liquids — or by interfering with the body’s heat loss mechanisms e.g. wearing sweatsuits to exercise in, spending a long time in very hot/humid conditions without drinking plenty of fluids and sweating. It leads to what we consider “heat exhaustion” — headache, confusion, fatigue — associated with a 1-2F increase in body temperature (about the same as a mild fever of 101-102 F). If left untreated, it can progress to heat stroke when body temperatures elevate to 104-105 F (about the same sort of fever one gets from serious diseases, e.g. malaria). Malaria used to be one of the few known cures for syphilis as the high fever it produced was fatal to the syphilis spirochete. Of course, you had to survive the malaria…
All of these factors are profound and unconsidered confounders in this data-dredge study. Consider — are birth defects rates correlated with keeping your household thermostat set high? Sleeping under an electric blanket if pregnant? Exercising during pregnancy (which would be by far the biggest risk factor, right)? Working outside picking cotton or harvesting fruits and vegetables in midsummer while pregnant? Living in Florida? Being fat (because fat is a good insulator and ready source of energy and requires more metabolic core expenditure to move around)? Because I would bet that there are plenty of fat female migrant workers who live in Florida and pick vegetables in midsummer while pregnant or who live in tent camps or non-air-conditioned trailers while their husbands work — are they an undetected epidemic of birth defects, and if so could we distinguish the defects caused by heat from those caused by exposure to e.g. toxic pesticides?
In order for this study to even think of having meaning, one would have to prove an association between airport temperatures and specific episodes of hyperthermia in pregnant women. It does not even try to assert a specific relationship between outside temperatures and episodes of hyperthermia in pregnant women. It leaves it to the imagination!
Is this science? It is not. B is known to be correlated with C (hyperthermia with birth defects) in a certain spectrum. A is hypothesized to be correlated with B (high airport temperatures cause hyperthermia in pregnant women). Instead of studying the relationship between A and B, study the relationship between A and C (assuming there is a relationship between A and B, as it were). Even then, observe precisely the distribution of correlations between A and C that one would expect from random chance (see the xkcd comic I posted up above, seriously — it says it all, screw “corrections”). Pick the most extreme of these, claim a possible causal relationship.
What have they proven? That high airport temperatures cause hyperthermia in pregnant women? Surely there are easier and more direct ways to prove that, and this is the only plausible causal connection between high airport temperatures and hyperthermia-induced birth defects!
In fact, given actual knowledge of the connection between hyperthermia and fever episodes and birth defects, one has only to study the incidence of episodes of clinical hyperthermia with outside temperature to be able to predict the expected increases in birth defects, is that not correct?
This was not done, and it was the first thing that should have been done. Then they could go further and try to associate specific episodes of hyperthermia that are actually caused by the heat wave with specific birth defects and maybe — just maybe — they’d get an association. But not with only 60,000 samples. That’s too small to get good numbers with a 0.0004 baseline prevalence. If they had 250,000 samples, all randomly drawn (we can talk about bias another time) then they’d expect to get around 100 of these particular birth defects “normally”. They then might be able to resolve the effect of specific episodes of hyperthermia on the birth defect, and would be left only having to prove a bump in the rate of episodes of hyperthermia during heat waves that corresponded accurately with the bump in this birth defect, and explain why all of the other defects studied had a null result!
Why was it only the green jellybeans that caused acne? Why not the blue, purple, mauve… ones?
There is a lovely book that you should all buy and read, called “How to Lie With Statistics”. It was written in 1952 by Darrell Huff. It is not heavy math — it is easy to read and very short. It walks one through how even well-meaning people with an axe to grind mispresent statistics in countless ways to deliberately or accidentally mislead their audience towards a desired conclusion.
These methods are in common use in climate science today, starting almost on page one — confusion of the three types of “averages” that can be presented as an average. In climate science this issue is enormously apropos as it is all but impossible to cleanly define or measure the mean enthalpy content of the Earth as a function of time. The Earth’s mean temperature is presented to two decimal places — another way of misleading discussed in the book (and used by e.g. Karl Marx with great effect). The “Gee-Whiz Graph”, however, is one of the major weapons. For example, leaving out the base and plotting only the variance (a.k.a. “the anomaly”) on a scale that arbitrarily distorts the size of the variation compared to the actual total value, on a range that happens to be the range that allows one to argue for the conclusions one wishes everybody to accept. The Darkening Shadow (map manipulation) is commonplace — painting Antarctica red. And of course, Post Hoc Rides Again (these are chapter titles), as in this study — he doesn’t explicitly describe data dredging, but he does point out that correlation is not causality.
This study is a pure data dredge. It doesn’t even study the right relationship, the one that actually would establish the right correlation from which the inference could reasonably be made, and it obtains a result precisely as meaningful as the green jellybeans cause acne example, right down to the headline at the end! The media loves to statisculate (term defined in book) because boring null statistics don’t sell the news. Two newspapermen caused an entire crime wave back in Theodore Roosevelt’s day, just by reporting every crime that occurred, no matter how small. The actual crime rate hadn’t changed — only the attention of the media — but people went in fear of their life and property.
How to Lie With Statistics should be mandatory reading in every intro stats class. It is actually more valuable to read it, for the ordinary human, than learning all about means and standard deviations and Student’s T and so on. Of course, a lot of people have a good feel for it as part of their sheer common sense. Joe the Cab Driver in Taleb’s equally awesome book, The Black Swan, understands this. Joe is a natural Bayesian.
BTW, your computation of 5% being “barely” wrong is incorrect. It is way off. This result is completely insignificant when viewed globally, precisely as is the case with green jellybeans.
rgb
rgbatduke says: @ur momisugly December 23, 2012 at 6:40 am
….There is a lovely book that you should all buy and read, called “How to Lie With Statistics”. It was written in 1952 by Darrell Huff…
>>>>>>>>>>>>>>>>>>>>>>>>>>
I will second that suggestion.
After reading that book you will never look at a poll splashed all over the newspapers or a ‘Scientific study’ quite the same way again and you do not have to be a math wiz to understand the book.
It should be a must give to every high School student on your shopping list.
JazzyT, you discuss the Bonferroni correction. Your conclusion is as follows:
As I said, I’m not a journeyman statistician. And I, like you, had never heard of the Bonferroni correction, but I think that you have the stick by the wrong end.
The Bonferroni correction is an approximation. It is a correction such that
1- (1 – p/N)N ≈ p
for small values of p, regardless of the value of N
For example, for p = 0.05, you get 0.05 with N =1, and with p = 0.05 and N = 100 you get 0.049.
This doesn’t mean what you think it means, though. You think it means that in the data dredge, the cataract result at p=0.05 is significant. The correction works the opposite way.
It means that if you are looking at 28 results, in order to consider your data dredge as a whole to have yielded significant results at the p = 0.05 level, you need to find an individual result that is significant at the level of p divided by N, which is 0.05 / 28 = .003. As far as I know, the authors did not find anything approaching that level of significance.
As I mentioned, the Bonferroni correction is an approximation. It is a lovely and very accurate one for our normal range of interest, say from p = 0.05 and smaller. At p = 0.05, the error even with N = 100 is quite small, about 0.001.
At p = 0.5, on the other hand, the error with N=100 is about 0.1, not bad I suppose. The good news is that we never do probability calcs in that range of p-values, so it doesn’t matter. The Bonferroni calculation is a neat trick to approximate the p-value that you would need to declare a data dredge successful … I’ll remember that one.
A huge problem is that the data dredge is often invisible, because it is not all done at once. It may occur over some months. It is then dismissed as something like “the understandably long process of looking for a small signal that is difficult to find and isolate”.
Fair enough. But after someone has looked for the infamous “anthropological fingerprint” in enough obscure corners of the climate, they can’t just declare success because the results for the positive correlation they finally found have a p-value of 0.05 …
This is particularly epidemic among people looking for astronomical correlations with the weather. They search for relationship between the global temperature or some other climate variable with things like the synodic period of Jupiter and Saturn or the intervals between the nearest approach of the moon to the earth. Far too often, someone spends months looks through literally dozens and dozens of these correlations, and then finally finds a result with p = 0.045, and declares that it is significant.
This is one reason I very much dislike the significance level being taken as p = 0.05. That means you’ll find a false positive one time in twenty. If you look at as few as a dozen possible correlations in search of the real one, you have nearly a 50/50 chance of having a false positive.
If you take P = 0.01 as being significant, on the other hand, with a dozen possible correlations you have only a 11% chance of a false positive. So you are better insulated from the data dredge, with a dozen possible correlations you have an 11% chance of a false positive.
w.
Couple of things:
1) I’d add Joel Best’s “Damned Lies and Statistics” to the “How to Lie…” book recommendation. And if you get his sequel, “More Damned Lies and Statistics” you’ll even find an example about rabbits and Antismokers I’d recommended to him in an email! 🙂
2) RG, you said, “Now, what do you think you would observe if you had a thermometer embedded inside your gut over the course of a day?” Back when I was young and hypochondriaciacal (Ok, ok, not a word, but it works.) I went through a period of worrying that I would die in the wee hours when I’d take my temp and find it down around 96 degrees. :> Guess I’m just a cold-blooded guy.
:>
MJM
At p = 0.5, on the other hand, the error with N=100 is about 0.1, not bad I suppose. The good news is that we never do probability calcs in that range of p-values, so it doesn’t matter. The Bonferroni calculation is a neat trick to approximate the p-value that you would need to declare a data dredge successful … I’ll remember that one.
Also consider actually looking at the distribution of p. This gives you some very useful information. For p to have any meaning in the first place, the “mean results” one is studying have to be Gaussian, that is, the central limit theorem has to have kicked in. In that case, if the null hypothesis is true, the distribution of p should be uniform — your experiment is a very odd kind of a random number generator, because it is a projection of the two-sided complementary error function, the inverse of the gaussian distribution. This is a function that is one when the value occurs at the centroid of the gaussian around the (null hypothesis) expected value and decreases to zero when one reaches the wings. It is this kind of thing one is implicitly referring to when one talks of 0.05 in the fist place — it just means that the result is two standard deviations from the mean, and has enough data that you have “confidence” in it.
But are the results normal? Is p distributed uniformly? Can one distinguish p from a uniform distribution with e.g. a Kolmogorov-Smirnov test? A histogram of p-values from the study could be very revealing. If it were egregiously non-flat it would suggest that either their hypothesis concerning “confidence” is false, that there really isn’t enough data in the study to have much confidence in it (something I suspect is the case) or that the null hypothesis is false and there are correlations on a broad scale. However, figuring out which would be difficult without simply making the study four or five times as large and fixing the flaws.
rgb
Back when I was young and hypochondriaciacal (Ok, ok, not a word, but it works.) I went through a period of worrying that I would die in the wee hours when I’d take my temp and find it down around 96 degrees. :> Guess I’m just a cold-blooded guy.
96 is probably a bit on the low side, but there is considerable variation depending on where and how you measured your temperature, the precision of your instruments, and from person to person. That’s another kicker. We haven’t even touched drugs or foods that can affect body temperature, how your cardiovascular health affects your body temperature, how much natural variation there is in body temperature. For example, 98.6 plus or minus 0.9 degrees — what exactly does that 0.9 degrees stand for? A Gaussian standard deviation? An absolute range with or without some skew? Somewhere somebody may have had people swallow button recording thermometers, or stuck them up their butts or fastened them inside a cervical cap and had them wear them for weeks and then read off the results, and somewhere out there in the Universe of data one can probably find real time temperature vs time for 1000 people over twelve months and some variation in conditions. This is the sort of thing that is needed as a Bayesian prior for this study.
There are some very nifty recording thermometers available at this point — I looked into them extensively a decade ago when trying to think about clever ways of monitoring computers in server rooms. One really could attach a button device to the end of a tampon and measure not only core temperature, but core temperature right next to the womb in pregnant women, if you could find somebody willing to risk doing ANYTHING with pregnant women that COULD cause a miscarriage or whatever. That would give you some seriously useful information.
rgb
For applyinh the Bonferroni correction with 28 correlations,
Willis Eschenbach says:
December 23, 2012 at 5:02 pm
As far as I know, the authors did not find anything approaching that level of significance.
(5/28 = 0.018, but no matter here…)
Actually, what I’m saying is that they did get close to that level of significance, but they don’t seem to have realized this. It takes a few derivations to find out. Essentially, you move the ends of their confidence intervals from the p=0.05 level out to the p=0.05/28 level.
So, some about this article, but more about such studies in general:
It’s true that to draw really believable conclusions about about heat waves causing birth defects, you need to connect the dots to find out who was exposed to hot temperatures. Finding out who actually had an episode of hyperthermia may or may not be of interest depending on the study, since population effects of environmental stressors actually is a valid thing to study., Looking at the individual establishes the causal chain more rigorously, and that’s a different, but important study if you’re looking at important effects.
It looks like this was a pilot study, aimed at getting preliminary data for a grant proposal. All the data used were available as relatively simple records: airport temperatures, and various birth defect stats. For hypothermia episodes, these probably would have no record at all if there were no hospital admissions–heat stroke would show up, but not heat exhaustion. Even then, making correlations requires matching up birth defects with heat stroke for individuals using personally identifiable information, rather than summary statistics. This can require permission from the patients, which can get expensive. So instead, people settle for proxies for the real data, like airport temperature for local temperature, (The latter would itself require tracking individuals and the expense thereof.) Limitations, such as neural tube defects that aren’t always documented, or airport temps as proxies for local temps, just have to be accepted, at least until there’s more money. Cataracts, which show up more easily, could act as a proxy to suggest (not show) birth defects. (Sometimes we have no choice but to use proxies, ever: our best data on the effects of radiation on humans comes from survivors of the Nagasaki and Hiroshima bombings. Since they weren’t wearing dosimeters, and we don’t want to repeat the experiment, all we have to represent their radiation dose is their location at the time of the blast.)
That this was a pilot study is, perhaps, suggested in the abstract:
If a pilot study shows interesting results, it can support an application to fund a larger study, that starts to take care of these problems, and make more direct measurements–To do the science “right.” The early results are still science, but their limitations must be ackowleged. For grant finding, statistical significance is not necessary if there’s good reason to believe that a larger sample size would give them. A result that fails to give significance can still be used to estimate statistical power (how likely you are to get a true positive if it’s there). Insufficient statistical power, often from too small a sample, can sink an NIH grant application.
Pilot studies can give data worthy of publication. This one didn’t seem to, though it’s not up to me to set editorial policy at a journal in a field I don’t work in. In any event, the data must be presented coherently and honestly, and competently, which didn’t happen here. Probably dull-witted authors and lax reviewers, probably, although crazy reviewers insisting on bizarre edits is always possible.
So the study, at least, can’t have been intended to draw really firm conclusions, and it didn’t. Reporting any such, much less as a connection to climate change is one more indicator of the demise of that undervalued, but valuable asset: the competent science reporter.
(For my procedure of translating the confidence intervals from p=0.05 to p=(0.05/28), I wanted to re-check my derivations and comment, but I’m too tired right now–hopefully in the next few days.)