Statistical failure of A Population-Based Case–Control Study of Extreme Summer Temperature and Birth
Guest Post by Willis Eschenbach
The story of how global warming causes congenital cataracts in newborns babies has been getting wide media attention. So I thought I’d take a look at the study itself. It’s called A Population-Based Case–Control Study of Extreme Summer Temperature and Birth Defects, and it is available from the usually-scientific National Institutes of Health here.
Figure 1. Dice with various numbers of sides. SOURCE
.jpg/250px-Dice_(typical_role_playing_game_dice).jpg){kind=link}
I have to confess, I laughed out loud when I read the study. Here’s what I found so funny.
When doing statistics, one thing you have to be careful about is whether your result happened by pure random chance. Maybe you just got lucky. Or maybe that result you got happens by chance a lot.
Statisticians use the “p-value” to estimate how likely it is that the result occurred by random chance. A small p-value means it is unlikely that it occurred by chance. The p-value is the odds (as a percentage) that your result occurred by random chance. So a p-value less than say 0.05 means that there is less than 5% odds of that occurring by random chance.
This 5% level is commonly taken to be a level indicating what is called “statistical significance”. If the p-value is below 0.05, the result is deemed to be statistically significant. However, there’s nothing magical about 5%, some scientific fields more commonly use a stricter criteria of 1% for statistical significance. But in this study, the significance level was chosen as a p-value less than 0.05.
Another way of stating this same thing is that a p-value of 0.05 means that one time in twenty (1.0 / 0.05), the result you are looking for will occur by random chance. Once in twenty you’ll get what is called a “false positive”—the bell rings, but it is not actually significant, it occurred randomly.
Here’s the problem. If I have a one in twenty chance of a false positive when looking at one single association (say heat with cataracts), what are my odds of finding a false positive if I look at say five associations (heat with spina bifida, heat with hypoplasia, heat with cataracts, etc.)? Because obviously, the more cases I look at, the greater my chances are of hitting a false positive.
To calculate that, the formula that gives the odds of finding at least one false positive is
FP = 1 – (1 – p)N
where FP is the odds of finding a false positive, p is the p-value (in this case 0.05), and N is the number of trials. For my example of five trials, that gives us
FP = 1 – (1 – 0.05)5 = 0.22
So about one time in five (22%) you’ll find a false positive using a p-value of 0.05 and five trials.
How does this apply to the cataract study?
Well, to find the one correlation that was significant at the 0.05 level, they compared temperature to no less than 28 different variables. As they describe it (emphasis mine):
Outcome assessment. Using International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM; Centers for Disease Control and Prevention 2011a) diagnoses codes from the CMR records, birth defect cases were classified into the 45 birth defects categories that meet the reporting standards of the National Birth Defects Prevention Network (NBDPN 2010). Of these, we selected the 28 groups of major birth defects within the six body systems with prior animal or human studies suggesting an association with heat: central nervous system (e.g., neural-tube defects, microcephaly), eye (e.g., microphthalmia, congenital cataracts), cardiovascular, craniofacial, renal, and musculoskeletal defects (e.g., abdominal wall defects, limb defects).
So they are looking at the relationship between temperature and no less than 28 independent variables.
Using the formula above, if we look at the case of N = 28 different variables, we will get a false positive about three times out of four (76%).
So it is absolutely unsurprising, and totally lacking in statistical significance, that in a comparison with 28 variables, someone would find that temperature is correlated with one of them at a p-value of 0.05. In fact, it is more likely than not that they would find one with a p-value equal to 0.05.
They thought they found something rare, something to beat skeptics over the head with, but it happens three times out of four. That’s what I found so funny.
Next, a simple reality check. The authors say:
Among 6,422 cases and 59,328 controls that shared at least 1 week of the critical period in summer, a 5-degree [F] increase in mean daily minimum UAT was significantly associated with congenital cataracts (aOR = 1.51; 95% CI: 1.14, 1.99).
A 5°F (2.75°C) increase in summer temperature is significantly associated with congenital cataracts? Really? Now, think about that for a minute.
This study was done in New York. There’s about a 20°F difference in summer temperature between New York and Phoenix. That’s four times the 5°F they claim causes cataracts in the study group. So by their claim that if you heat up your kids will be born blind, we should be seeing lots of congenital cataracts, not only in Phoenix, but in Florida and in Cairo and in tropical areas, deserts, and hot zones all around the world … not happening, as far as I can tell.
Like I said, reality check. Sadly, this is another case where the Venn diagram of the intersection of the climate science fraternity and the statistical fraternity gives us the empty set …
w.
UPDATE: Statistician William Briggs weighs in on this train wreck of a paper.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Cataracts are a common problem in Nepal, but this is due to the high altitude, and therefore thin atmosphere, allowing in more uv. Perhaps they could find a link to climate change there. http://www.cureblindness.org/
Without a lot of statistics behind me I tend to agree with Willis Eschenbach.
This study seeks significance at a very weak level, the sort that would be attempted in a student physiology t test.Were the groups randomly selected to eliminate bias from nutrition, housing demography genetics and culture? Was there an out of contact control group? As another commentator pointed out cataracts don’t seem to be a feature in hot climates, so when does a heat wave become climate change?
What is outstanding about these results is the lack of any significant damage in any subject, under the perceived conditions of heat, in the vast majority of heat sensitive embryological defects, in a study so open to random effects.
Further, quoting animal studies, it should be remembered that congenital cataract formation is a feature of some lines of dogs, especially in the cocker spaniel and has a strong genetic component.
If such is the case in man, then this study must lead to funding to genetically test parents so that their affected children may be identified and treated early to prevent further disability.
This is the appropriate public health response.
Excellent summary of the p-value! It’s odd they used a p-value of 0.05 as health fields typically require testing to 0.01 to reduce the odds of false positives .
By thecway, is there anything bad that global warming won’t cause?
Whoever reviewed this paper made a terrible brainless job. It is usual standard in biomedical epidemiological research to apply Bonferroni correction for multiple comparisons. Thus , agreed, the methodology is a nonsense. I personally review papers for top ranked medical journal (e.g. NEJM and JAMA) and I can assure everybody that a paper like this has no chance to be published in those journals.
Most importantly, statistics means nothing if there is no reasonable pathophysiological hypothesis to explain the finding (which actually should be the reason to perform a study).
BUT there is even more fun in this paper. According to table 3 there appear to be a protective effect of temperatures for the onset of anophthalmia/microphthalmia (OR 0.70 CI 0.52-0.93). So, if you heat a pregnant woman you have more chance of cataract but less eye gross developmental problems. Since cataract is curable and anophthalmia is not……. voting is open.
Not sure why you need to explain this, Willis – what they’re doing is little more than an infinite number of monkeys, and even Bob Newhart knew about those:
Now we just need to wait for the gazornanplat……
Hi Willy,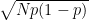
for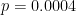 
) 5. Two sigma is 10. Sigma is commensurate with the expectation value — the worst possible case for drawing reliable conclusions.
Your argument is dead on the money. It’s simplest to just look at p itself — given 28 throws of a 20 sided die, one expects 1 (FP) to come up. Slightly more than one FP to come up, in fact. But this is not all.
In order to properly assess the impact of FPs, one has to use Bayes’ Theorem. The problem is that a broad population analysis of this sort requires one to know a lot about the prevalence of the diseases in question — both rate and details of distribution. So what, exactly, is the prevalence of congenital cataracts? Google to the rescue. In at least one study I just grabbed from the UK, prevalence was reported to be somewhere between 2.5 and 3.5 births per 10,000, depending on how long one waited to make the diagnosis. This distribution is not flat — as one article I found puts it: Congenital ocular anomalies are major contributors to childhood visual morbidity. Congenital cataract is one of the few of these visually handicapping disorders that is amenable to primary prevention—for example, through a rubella immunization program…
In other words, there are problems beyond applying a 0.05 “significance” test to a shotgun blast of studies. The disease has a fairly low prevalence and it has at least one significant confounding factor (whether or not rubella is prevalent in the community). Are there other confounding factors? From another study (all of them available unpaywalled online, thankfully): In southern India, the prevalence of congenital cataract is estimated to be 1 to 4 cases per 10,000 children examined.4 A major portion of these is hereditary, or genetic, in origin.
We see that the disorder is not only associated with whether or not the parents and community have been adequately immunized against diseases — something that for better or worse is unevenly distributed worldwide with temperate zone nations having a much higher degree of immunization coverage than tropical ones — but that the prevalence in southern India is almost exactly that observed in the UK. Now, I lived in northern India (New Delhi) for seven years in the 60s, right across that “Ice Age Cometh” dip in temperatures that had people worried going into the 70s, and it went down to freezing precisely three times in seven years. In southern India it didn’t get close — it is hot (even compared to northern India). New Delhi is easily 5F warmer than any point in the UK, on average — Bangalore is probably 10F warmer than the UK.
We also have the fact that, of the cases reported, at the very least many of them are hereditary — not caused by the heat but caused by inherited genetic factors that run in families. In fact the second article was looking at: The authors focus attention on congenital lamellar cataract, which is associated with the R168W mutation in γC-crystallin, and congenital zonular pulverulent cataract, which is associated with a 5-bp insertion in the γC-crystallin gene. — specific mutations. This is real science, of course, not shotgun-blast population studies.
I could continue to search, but I think it is already pretty clear that two things are true. First, prevalence is not particularly accurately known. In the UK, with first world medicine, they fail to diagnose 1/3 of the cases observed before the individual is 15 years old (hence the rise in prevalence with the age at first diagnosis). The prevalence there is slightly less than 4 in 10,000. In India the prevalence — which is likely to be reported less efficiently early on, but one presumes that even in India blindness is blindness and by age 15 a diagnosis is likely — is given as 1 to 4 in 10,000, which sounds like the final prevalence is almost exactly the same as it is in the UK!
Now let’s think about this: 6,422 cases and 59,328 controls. What exactly does this mean? In 60,000 iid samples, one would expect to get 24 cases of congenital cataracts. Sigma for this is (
To put it another way, suppose that only 15 people got congenital cataracts in this control group. Would that justify the conclusion that the prevalence in the general population is really around 2 in 10,000, not 4, just because it is only a 5% likely occurrence? Don’t make me laugh. Similarly, a prevalence as high as three sigma would be no particular cause for alarm, especially if the group were truly randomly selected so that the samples were reliably iid (it never is, but that’s another story).
Now consider the “case” group. 6000*0.0004 means that 2.4 individuals are expected to get cataracts in this group! Sigma is now almost 2. There is almost no rate at which this group could get cataracts that would be worthy of attention. Statistics just doesn’t work for small populations with a low prevalence.
This may not be the structure of the study — they could be trying something even sketchier than this — but one can, as you note, take great comfort in the large scale numbers between people who live all the time in hot South India versus the people who live all of the time in the cold UK. The prevalence in the two populations is more or less the same, with millions of individuals contributing to the prevalence numbers in both cases. End of story.
One is reminded of a famous study involving cancer rates of people living near high voltage transmission lines that was conducted in just this fashion, and got precisely this kind of result — examine a small population (compared to incidence rates of cancer) for all kinds of cancer. Some forms of cancer will (in the small population) always happen less frequently than expected, some about the expected rate, some more than expected. Look at 20 to fifty cancers, and at least one or two are going to be at rates unlikely at the 0.05 level. Publish, generate lots of alarm, and it takes years to get fear of living near a power line out of the collective minds of the people. Or what they are doing now with cell phones, ditto. Big, expensive, careful studies refute this kind of bullshit statistics but it takes years.
We should talk about p in random number generator testing sometime. dieharder, my test suite, generates a list of some 80 or 90 test pvalues. One cannot use anything as puerile as 0.05 rejection, because one expects four or five tests to fail at this level every run with a perfect random number generator! In fact, if this many tests did not fail, on average, one would be certain that the generator was not random!
Statistics is a two-edged sword!
rgb
Nah … that’s why there are biostatisticians.
This study indeed seems like a classic example of the “Data dredge”, well described by John Brignell: http://www.numberwatch.co.uk/data_dredge.htm
Yeah. Deserves further study. My bet is there is nothing there, but who knows.
Incidentally, one of the more interesting climate related illnesses is MS. It is far less prevalent in Queensland than it is in Tasmania.
A good explanation of data dredging. Anyone interested in this further might enjoy numberwatch.com
“Figures don’t lie, but liars can figure” attribution forgotten.
Another excellent piece, Willis. Keep up the good work. Will you ask the publisher for a retraction and to stop using the “experts” who reviewed this 3rd grade level paper?
Bill
“one-in-a-million chances crop up nine times out of ten” (Terry Pratchett, “Equal Rites”)
Also http://tvtropes.org/pmwiki/pmwiki.php/Main/MillionToOneChance (warning: seriously addictive site)
Psychologists, doctors, sociologists take the Stats 101 course and get away from the subject as quickly as decently possible. I remember (no link) a report in, I think, Discovery Magazine a few decades ago of a report on stress caused by air pollution and auto accidents on the California freeways. The study involved measurements of CO, particulates, etc taken along a major highway and they found that when these were high, there was a statistically significant correlation with highway accident deaths! I kid you not! Organizations like CDC, of course, employ statisticians in their studies because of the importance of keeping doctors away from the subject.
Why should we worry when global warming should be felt mostly in winter? Uhi on the other hand is something else.
John Ionnides (http://en.wikipedia.org/wiki/John_P._A._Ioannidis )has led the fight against this statistical nonsense in the field of medical research. Alas NIH does not seem to be listening or reading.
.
So if the paper is proven to be cr@p, and the paper was funded by the government – can we get our money back?
And if they resist such a proposal, can we sue? I would happily give $50 to a fund to sue the ass of these guys.
.
All this tells us is that the AGW ‘research’ bucket is still deep and well filled .
How much quality research has gone undone becasue the researchers have been unwilling or unable to link it to ‘the cause ‘ no matter how slightly and therefore been unable to get funding . Is a good question and one ,the answer to which, we may all come to regret.
Actually, what they missed in this report, is that congenital cataracts are caused by coffee. Our own assessment of this data has demonstrated that the mother of every effected child drank coffee during the pregnancy. Q.E.D.
Details of where to send the government grants, is available on application. Six figure sums only, please.
Willis,
I disagree that the result regarding cataract isn’t statistically significant. The hypothesis that was tested against the null hypothesis wasn’t that at least one (or even four) among the 28 possible associations would turn out to be significant to the 95% level. If that had been the hypothesis, then the fact that at least one such association would be significant wouldn’t itself be significant to the 95% level. This is something the authors clearly acknowledge. But rather, the study aims at testing several independent hypotheses. It could just as well have been 28 completely independent studies some of which would have produced significant results and some not. That among such a large number of studies, about 4 of them could have been expected to produce false positives isn’t disputed. It is in the very nature of results that are significant to the 95% level that 1 in 20 such result, on average, will be occur by chance — provided the null hypothesis is always true. But the individual studies that produce positive results still would have produces significant results. You can’t nullify the significance of the result of one single study simply by considering it in the context of a group of similar studies that test *independent* associations. That the researchers tested 28 independent hypotheses at once rather than publishing 28 different papers is irrelevant to the significance of the individual results since they are, indeed, independent.
I initially misread Willis’s reply to Pierre-Normand.
Willis is quite right that claiming significance in this case is deceptive. He was not claiming, as I originally wrongly thought, that we should not publish work that shows no statistical significance. To fail to do so is to commit the anti-science error known as the file drawer problem.
I fear that the file drawer problem is endemic in climate science. I cannot prove it, of course, since the evidence is not published; but I point out that the conditions of groupthink, ‘consensus’, activism and the widespread (fallacious) meme of being under siege by well funded hostile anti-science groups are precisely those conditions that would be most likely to exacerbate this problem.
Oh, and I’m sorry I didn’t get to refer to XKCD’s 882 first; as Willis notes, ‘he did it without calculations… nice.’
The “paper”is statistical junk. I have had a thing about medical research and the abuse of statistics going back to the ‘fifties. I devour these papers (which have become much less difficult to get hold of since the advent of the internet) simply because of the naivety of the statistical thinking which is a wonder to behold. This “paper” is not at all unusual in this respect – virtually all medical research papers are as bad or worse. The ones produced by good well meaning people I am talking about, not the ones produced by outright statistical rogues like the late Professor Doll (smoking) or the late Ancel Keys (dietary fats). It is my long held personal suspicion that those who are attracted to medical research are congenitally innumerate. They beat the AGW crowd into a cocked hat.
Sounds like vitamin D deficiency to me… Fixing it is no different than fixing Spina bifida with folic acid at the right dosage.,
http://www.thelancet.com/journals/lancet/article/PIIS0140-6736(96)91331-8/fulltext
Based on this study, pregnant mothers do much better at the daily dosage of 4,000 IU vs what is recommended 600IU which isn’t even enough to push us into optimal range of vitamin D level. No wonder why we get sick with cold or flu or infection easily during the cold months…
http://grassrootshealth.net/index.php/press/92-press-20100430
One could easily say that this disease happens more often in NY than AZ is because of long winter forcing us to stay in the house and not see sun much compared to AZ where winter is short and sun (specifically UVB sunlight) is more intense to help skin produce vitamin D… All you have to do is conduct vitamin D study. Very simple study.
Anyone even aware that during the midday with clean air in the summer in bathing suit without sunblock gives you 20,000 IU of vitamin D after 20-30 minutes (for Caucasian people)? The darker your skin gets, the longer it takes to reach 20,000 IU. It can be 10x longer for people with darkest skin color. The recommendation of 600 IU a day makes no sense. Someone made that recommendation on faulty science a long time ago. It used to be 200 IU a day 20,30 years ago. We paid the price…
While the statistics errors are bad – the lack of sensible checks against birth defect numbers in areas with high temperatures, or with the rate of birth defects in the cooler seasons are showing their medical ignorance. These would be extremely easy checks to make but of course the result would not get them the further research funding that they are actually fishing for. So the lack of sensible validation checks make the paper a waste of money. They might just as well state that having an air conditioning failure in summer causes congenital birth defects.
If they really want to motivate action, they should have released a study, whose results would indicate AGW causes a reduction in penis and breast sizes. With society’s fixation on this parameter, there would be an instant demand for a new LIA.
We really are a strange and predictable people. GK
Yes, that’s the fallacy behind clinical test batteries in check-ups. If you do 30 tests at least one comes abnormal and you can treat a patient for nothing but a false positive. When performing multiple tests the confidence level must be increased dramatically.