Guest Post by Willis Eschenbach
In my previous post, A Longer Look at Climate Sensitivity, I showed that the match between lagged net sunshine (the solar energy remaining after albedo reflections) and the observational temperature record is quite good. However, there was still a discrepancy between the trends, with the observational trends being slightly larger than the calculated results. For the NH, the difference was about 0.1°C per decade, and for the SH, it was about 0 05°C per decade.
I got to thinking about the “exponential decay” function that I had used to calculate the lag in warming and cooling. When the incoming radiation increases or decreases, it takes a while for the earth to warm up or to cool down. In my calculations shown in my previous post, this lag was represented by a gradual exponential decay.
But nature often doesn’t follow quite that kind of exponential decay. Instead, it quite often follows what is called a “fat-tailed”, “heavy-tailed”, or “long-tailed” exponential decay. Figure 1 shows the difference between two examples of a standard exponential decay, and a fat-tailed exponential decay (golden line).
Figure 1. Exponential and fat-tailed exponential decay, for values of “t” from 1 to 30 months. Lines show the fraction of the original amount that remains after time “t”. The “fatness” of the tail is controlled by the variable “c”. Line with circles shows the standard exponential decay, from t=1 to t=20. Golden line shows a fat-tailed exponential decay. Black line shows a standard exponential decay, with a longer time constant “tau”. The “fatness” of the tail is controlled by the variable “c”.
Note that at longer times “t”, a fat-tailed decay function gives the same result as a standard exponential decay function with a longer time constant. For example, in Figure 1 at “t” equal to 12 months, a standard exponential decay with a time constant “tau” of 6.2 months (black line) gives the same result as the fat-tailed decay (golden line).
So what difference does it make when I use a fat-tailed exponential decay function, rather than a standard exponential decay function, in my previous analysis? Figure 2 shows the results:
Figure 2. Observations and calculated values, Northern and Southern Hemisphere temperatures. Note that the observations are almost hidden by the calculation.
While this is quite similar to my previous result, there is one major difference. The trends fit better. The difference in the trends in my previous results is just barely visible. But when I use a fat-tailed exponential decay function, the difference in trend can no longer be seen. The trend in the NH is about three times as large as the trend in the SH (0.3°C vs 0.1°C per decade). Despite that, using solely the variations in net sunshine we are able to replicate each hemisphere exactly.
Now, before I go any further, I acknowledge that I am using three tuned parameters. The parameters are lambda, the climate sensitivity; tau, the time constant; and c, the variable that controls the fatness of the tail of the exponential decay.
Parameter fitting is a procedure that I’m usually chary of. However, in this case each of the parameters has a clear physical meaning, a meaning which is consistent with our understanding of how the system actually works. In addition, there are two findings that increase my confidence that these are accurate representations of physical reality.
The first is that when I went from a regular to a fat-tailed distribution, the climate sensitivity did not change for either the NH or the SH. If they had changed radically, I would have been suspicious of the introduction of the variable “c”.
The second is that, although the calculations for the NH and the SH are entirely separate, the fitting process produced the same “c” value for the “fatness” of the tail, c = 0.6. This indicates that this value is not varying just to match the situation, but that there is a real physical meaning for the value.
Here are the results using the regular exponential decay calculations
SH NH lambda 0.05 0.10°C per W/m2 tau 2.4 1.9 months RMS residual error 0.17 0.26 °C trend error 0.05 ± 0.04 0.11 ± 0.08, °C / decade (95% confidence interval)
As you can see, the error in the trends, although small, is statistically different from zero in both cases. However, when I use the fat-tailed exponential decay function, I get the following results.
SH NH lambda 0.04 0.09°C per W/m2 tau 2.2 1.5 months c 0.59 0.61 RMS residual error 0.16 0.26 °C trend error -0.03 ± 0.04 0.03 ± 0.08, °C / decade (95% confidence interval)
In this case, the error in the trends is not different from zero in either the SH or the NH. So my calculations show that the value of the net sun (solar radiation minus albedo reflections) is quite sufficient to explain both the annual and decadal temperature variations, in both the Northern and Southern Hemispheres, from 1984 to 1997. This is particularly significant because this is the period of the large recent warming that people claim is due to CO2.
Now, bear in mind that my calculations do not include any forcing from CO2. Could CO2 explain the 0.03°C per decade of error that remains in the NH trend? We can run the numbers to find out.
At the start of the analysis in 1984 the CO2 level was 344 ppmv, and at the end of 1997 it was 363 ppmv. If we take the IPCC value of 3.7 W/m2, this is a change in forcing of log(363/344,2) * 3.7 = 0.28 W/m2 per decade. If we assume the sensitivity determined in my analysis (0.08°C per W/m2 for the NH), that gives us a trend of 0.02°C per decade from CO2. This is smaller than the trend error for either the NH or the SH.
So it is clearly possible that CO2 is in the mix, which would not surprise me … but only if the climate sensitivity is as low as my calculations indicate. There’s just no room for CO2 if the sensitivity is as high as the IPCC claims, because almost every bit of the variation in temperature is already adequately explained by the net sun.
Best to all,
w.
PS: Let me request that if you disagree with something I’ve said, QUOTE MY WORDS. I’m happy to either defend, or to admit to the errors in, what I have said. But I can’t and won’t defend your interpretation of what I said. If you quote my words, it makes all of the communication much clearer.
MATH NOTES: The standard exponential decay after a time “t” is given by:
e^(-1 * t/tau) [ or as written in Excel notation, exp(-1 * t/tau) ]
where “tau” is the time constant and e is the base of the natural logarithms, ≈ 2.718. The time constant tau and the variable t are in whatever units you are using (months, years, etc). The time constant tau is a measure that is like a half-life. However, instead of being the time it takes for something to decay to half its starting value, tau is the time it takes for something to decay exponentially to 1/e ≈ 1/2.7 ≈ 37% of its starting value. This can be verified by noting that when t equals tau, the equation reduces to e^-1 = 1/e.
For the fat-tailed distribution, I used a very similar form by replacing t/tau with (t/tau)^c. This makes the full equation
e^(-1 * (t/tau)^c) [ or in Excel notation exp(-1 * (t/tau)^c) ].
The variable “c’ varies between zero and one to control how fat the tail is, with smaller values giving a fatter tail.
[UPDATE: My thanks to Paul_K, who pointed out in the previous thread that my formula was slightly wrong. In that thread I was using
∆T(k) = λ ∆F(k)/τ + ∆T(k-1) * exp(-1 / τ)
when I should have been using
∆T(k) = λ ∆F(k)(1 – exp(-1/ τ) + ∆T(k-1) * exp(-1 / τ)
The result of the error is that I have underestimated the sensitivity slightly, while everything else remains the same. Instead of the sensitivities for the SH and the NH being 0.04°C per W/m2 and 0.08°C per W/m2 respectively in the both the current calculations, the correct sensitivities for this fat-tailed analysis should have been 0.04°C per W/m2 and 0.09°C per W/m2. The error was slightly larger in the previous thread, increasing them to 0.05 and 0.10 respectively. I have updated the tables above accordingly.
w.]
[ERROR UPDATE: The headings (NH and SH) were switched in the two blocks of text in the center of the post. I have fixed them.
I used R which is the gas constant which varies from gas to gas.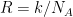
where 
is Avogadro’s number. There is no difference between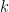 
and 
— they just express the ideal gas law in different units — moles vs molecules. NEITHER of them expresses it in terms of molar mass — if you want to turn it into a formula for mass density you have to scale it by molecular weight. And it doesn’t vary from gas to gas — rather either a gas behaves approximately like an ideal gas in a given pressure/temperature range or it doesn’t, and whether or not it does depends on details of intermolecular interaction (and e.g. whether or not one is near a phase transition).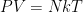
completely break down). But dry air for the most part is reasonably ideal. Humid air all bets are off, however. Water vapour isn’t even vaguely, approximately, ideal in its behavior at typical Earth temperatures and humidities.
Say what?
All of this stuff is fairly clearly laid out in any decent textbook on thermodynamics or stat mech. Sadly, some of the math is pretty complicated, especially the math associated with phase transitions (which are highly nonlinear phenomena where things like
rgb
Joe,
OK, I managed to grab a few minutes off from toting barges and lifting bales to have a look at your work. You have come as close as I have seen to developing a meaningful physical underpinning for a response function with multiple superposed timeframes, but you are not there yet. Please do not be put off by the critique I make here. I think you have a great chance of finding a credible solution, but this isn’t it. All I am trying to do here is to make clear to you the broad constraints you need to consider for such a solution. I certainly don’t want to discourage you from carrying on the search.
I took your three starting equations to confirm that they do yield the differential equation you derive. I saw immediately that you have a typo in your equation. There should be a T1 term (rather than a constant) on the LHS, as you noted, but you should also note that its coefficient should be (r1r2 – ab). This is sufficiently close to what you wrote that I am sure it is a typo rather than any conceptual difference.
I then solved the equation for T1 to verify the solution form, and to match up the constants and coefficients.
The big problem stems from your three starting assumptions and their interpretation. As a general rule, the energy balance equations (actually flux balance) start with a Top of Atmosphere (TOA) balance. The basic idea is that after a flux perturbation (i.e. a forcing) the net flux difference has to “go somewhere”. If we ignore orbital kinetics, it is the only externally sourced energy to change the heat content of the planet. The assumption is that you can move heat around internally or store it – which might affect surface temperature – but you can’t add system energy outside of the TOA net flux balance.
A commonly made assumption is that the total energy over time (the integral of the net flux term) should be approximately equal to the total heat gain in the ocean, because of the ocean’s huge heat capacity, relative to other options. There is nothing at all to stop you from asserting that the net energy gain should be partitioned (instead) between the ocean and the atmosphere, which is what I think you are trying to do here. You do need to be aware however that given the relative heat capacities, your term C2 dT2/dt is likely to be very small and unlikely to be the main reason for needing a multi-period response function to explain observations! Most of the explanations for multi-time response of temperature in the time domain are based on slow deep ocean response, and this requires a connection via heat flux, not radiative flux. Atmospheric heat gain is small beer by comparison.
However, let’s continue to consider your solution under the assumption that energy associated with the total net flux imbalance is exhaustively partitioned between the atmosphere and the ocean – your two heat capacities. Your three equations do not reflect this partitioning. Your first equation looks remarkably similar to a typical TOA radiative balance for a single capacity system. However, when we get to your third equation – it becomes clear that you are treating FsubT as the total radiation the surface receives. You declare F to be the radiative flux from space, but note that this IS NOT equal to the TOA forcing and has a very complex relationship with the TOA forcing. It IS possible to express the energy balance at the surface, but you cannot do it with just radiative terms. Both your first and third equations would have to include latent heat and sensible heat gains/losses to make any sense if they are expressed at the surface. For a full description of what this looks like, there is a paper written by Ramanathan in 1981 which is still the best I have seen. I will dig out the reference.
In summary, there is no conservation of radiative energy within the system, which is perhaps what you are assuming (?). You are trying to express an energy balance in terms of a radiative balance at surface. This is a no, no.
Quite seriously, please don’t stop trying.
Joe,
Trying again, the Ramanathan paper is downloadable from here:
http://journals.ametsoc.org/doi/abs/10.1175/1520-0469%281981%29038%3C0918%3ATROOAI%3E2.0.CO%3B2
Paul
The equation PV = nRT describes interlinked relationships and can be used to predict the system outcome from changes in individual variables.
describes a hard-sphere (non-interacting) gas in thermal equilibrium. It has absolutely nothing to do with “interlinked relationships”. It can predict system outcome, provided that the system is a closed system in thermal equilibrium or a slowly varying “quasi-static” system that is always approximately in thermal equilibrium. It can be heuristically useful somewhat past that regime, as long as one no longer says predict but rather understand some aspects of.
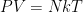in the real world (as opposed to idealized cylinders of an ideal gas in an idealized physics textbook that is clearly the only thing you’ve ever looked at to try to understand thermodynamics).
In so far as Earths atmosphere is composed of non ideal gases the air circulation adjusts appropriately so that the equation is preserved overall.
You do realize that this is complete nonsense, right?
The Earth’s atmosphere is primarily composed of gases that in fact are for all practical purposes ideal — N_2 and O_2 liquefy at temperatures well below the lowest temperatures (or pressures well above the highest pressures) found on the surface of the Earth — and CO_2 and O_3 and H_2 and He and Argon and the other trace gases ditto. The sole wild card is water vapor, which is constantly moving huge chunks of heat into and out of the surrounding air as it evaporates and condenses. Finally, as for “adjusting” so that the equation is “preserved overall” — what in the world does this even mean? The Earth’s atmospheric pressure and temperature vary wildly in all directions, all the time. It is safer to say that it is never in equilibrium than it is always in equilibrium. It is an open thermal system with energy coming in and going out in a very inhomogeneous way everywhere, all the time.
Finally, even in the very simplest studies of thermodynamics — first year into physics level stuff involving “ideal gases” (used simply because we can write down a reasonably simple equation of state that most undergrads can manage algebraically, not because it is particularly correct or universally applicable) — one usually learns about the First Law of Thermodynamics:
In words: The heat added in to a system plus the work done on a system equals the change of the internal energy of a system. Of these, only the latter (the enthalpy) is related to temperature per se.
There exist isothermal quasi-static processes — e.g. isothermal expansion of an ideal gas — for which the right hand side is zero. There exist adiabatic processes — e.g. adiabatic expansion or compression of an ideal gas without input or loss of heat. There exist processes where the gas is sealed in a container at constant volume so no work is done on or by the gas, where heating the gas directly increases the temperature. But most generally, all three happen at once — parcels of gas in an actual atmosphere are compressed or expand (work) while gaining or losing heat (conductivity, radiation) while changing their temperature, often in air that is saturated with humidity so that instead of changing temperature of the air water is pushed into or out of its liquid state, gobbling up or contributing a latent heat of vaporization along the way.
It is almost insulting to pretend that one can gain insight into atmospheric dynamics and actually predict global average climate on the basis of the ideal gas law. Piffle. The problem is a hard problem. Making the smallest assertion concerning the average behavior of the system can only be rationally done after doing some serious mathematics, not just waving your hands and saying that all of the underlying dynamics in this open system just happens to come out so that the ideal gas law — of all things — is true “on average” after all.
And then (when you’ve managed the First Law) we can try working on the Second Law of Thermodynamics, which also conspires against the “prettiness” of
rgb
Sigh. I meant decrease of albedo in the 80’s and 90’s and increase in the albedo by 7% from the late 90’s to the present.
The bottom line being that the heating of the 80’s and 90’s can be proximately attributed solely to decreased albedo for unknown reasons, and the lack of additional heating and possible advent of weak cooling since then can also be tentatively attributed to increased albedo for equally unknown reasons. Yes, there are hypotheses for why albedo has varied. No, IMO they are not proven yet.
And it isn’t just albedo. The water vapor content of the stratosphere has dropped by 10% over a similar time frame.
Sadly, climate scientists are for the most part so distracted by CO_2 that they are ignoring albedo and stratospheric water vapor. If they weren’t they’d be mousy quiet about further heating, because the connection between both and global temperature ain’t rocket science, and without knowing the proximate cause of the albedo change they cannot say when, or if, or how, albedo will shift again.
rgb
More errata:
so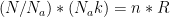 
. Algebraic lydexsia strickes again…:-)
But seriously, I do know this stuff, somewhere, deep down inside;-)
rgb
Robert said in relation to the ideal gas law:
“It can predict system outcome, provided that the system is a closed system in thermal equilibrium or a slowly varying “quasi-static” system that is always approximately in thermal equilibrium”.
That is exactly what a planet with an atmosphere is.
In order not to lose the atmosphere the system has to be in thermal equilibrium or a slowly varying quasi-static system for so long as an atmosphere is present. If it were not, the atmosphere would boil off or freeze to the surface.
The only way that can be achieved is for radiation in to equal radiation out for most of the time and so it does as per observations. The only thing that changes is the height at which that balance occurs and the relevant variable is the volume of the atmosphere.
Thus, by your own admission the ideal gas law can predict system outcome for a planet with an atmosphere.
The system does it by altering the atmospheric circulation to always respond negatively to anything that tries to disturb the equilibrium.
If some internal factor causes incoming to exceed outgoing then the circulation changes to accelerate energy flow through the system so that equilibrium or quasi equilibrium is maintained.
Likewise if some internal factor causes outgoing to exceed incoming then the circulation changes to decelerate energy flow through the system.
Only increased top of atmosphere energy input or an increase in atmospheric mass will raise the equilibrium temperature as well as increasing the volume of the atmosphere.
What happens on Earth happens on all the other planets or moons with atmospheres too but we do not appear to have enough data about the way the other atmospheres reconfigure themselves over time to maintain their top of atmosphere energy balances.
At least N & Z are making a start.
You also said this:
“The bottom line being that the heating of the 80′s and 90′s can be proximately attributed solely to decreased albedo for unknown reasons, and the lack of additional heating and possible advent of weak cooling since then can also be tentatively attributed to increased albedo for equally unknown reasons.”
With which I absolutely agree but I am giving you a reason. And at the heart of it is atmospheric pressure at the surface and the ability of an atmosphere to change volume to counter destabilising influences and in the process reconfigure the surface distribution of pressure which alters albedo via clouds or aerosols or anything else that might affect the optical depth of the atmosphere.
The daft thing is that I agree with your conclusions about many things relating to climate and I agree with Willis generally about his thermostat hypothesis but neither of you will accept what seems obvious to me, namely that the behaviour of gases restrained by gravity and subjected to insolation as described in the ideal gas law and as observed in the Standard Atmosphere does indeed supply the answer that you both need.
Paul_K: “You do need to be aware however that given the relative heat capacities, your term C2 dT2/dt is likely to be very small and unlikely to be the main reason for needing a multi-period response function to explain observations! Most of the explanations for multi-time response of temperature in the time domain are based on slow deep ocean response, and this requires a connection via heat flux, not radiative flux. Atmospheric heat gain is small beer by comparison.”
First, let me make sure that I have not unintentionally flown false colors here. I’m not a scientist–I don’t even play one on TV:-) I’m just a retired lawyer attempting to separate the climate-debate wheat from the chaff, the latter of which seems greatly to outweigh the former, So I wouldn’t dream of attempting to write the actual equations for climate system. I just whipped off some equations to show that physical systems could indeed result in “multiple-pole” behavior (as guys who know this stuff tell me they refer to it.) I emphatically was not “trying to express an energy balance in terms of a radiative balance at surface,” and, although I’m a rank layman, I am aware that latent heat, conduction, convection, etc. would all go into the mix.
Be that as it may, I completely agree with your other statement I quoted above, and in fact I think I made an observation to that general effect in one of my previous comments in this thread. I even thought of using the oceans instead of the atmosphere for my matching equations and including conduction. But, as I say, I’m a layman, and all this math gives me a headache.
So I hope you’ll understand if I decline your invitation to keep trying. I got into this only because my bluster detector went off when Mr. Eschenbach claimed his approach would have detected a greater error if there were additionally longer time constants. (And, by the way, although I agree with you that it doesn’t matter much, I have demonstrated to myself that the time constants he gets for a single-pole system are indeed about half a period (half a month) too great.)
Joe Born says:
June 9, 2012 at 3:53 pm
Thanks, Joe. Bluster? I was stating a fact, Joe, which is that despite trying a whole range of possible configurations, I haven’t been able to fit a pair of time constants, one longer and one shorter, to the actual data. I can’t make it converge to that kind of arrangement no matter what I’ve tried.
Nor, as near as I can tell, have you been able to fit something like that to the actual data, or at least you haven’t reported the results. Nor has Paul_K. You’ve come up with very interesting formulas, but no actual results that fit the observations.
So that’s why I said that the error increases when I added a second, longer time constant to the setup. It was not bluster, it was simply a report of what I found. Might be right, might be wrong, I just report them as I find them.
Now it’s entirely possible that someone can come up with a way to do so. I couldn’t, and so far neither has anyone else, but absence of evidence is not evidence of absence.
Finally, I see no reason why the instantaneous sensitivity would be so small if there is a much larger sensitivity hiding out somewhere. What would make the sensitivity go from the short-term sensitivity of ~ 0.3° per doubling of CO2, which I’ve calculated above, to ten times that in the long term as the IPCC claims? I can’t see physically how that might happen.
In any case, I’m looking now at the CERES albedo dataset, which is gridded. With that I should be able to distinguish between the sensitivity and time constant of the ocean and the land separately.
However, given that I already have NH and SH figures for lambda and tau, and I know that the SH is 82% ocean and the NH is 62% ocean, I can at least estimate the values for land and ocean separately. Setting up the equations, with “x” being the value for the ocean and “y” being the value for the land, I get:
In[7]:= eqn1 = .62 x + .38 y == 1.9
eqn2 = .82 x + .18 y == 2.4
Solve[{eqn1, eqn2}, {x, y}]
Out[9]= {{x -> 2.85, y -> 0.35}}
As expected, this gives a longer time constant for the ocean (2.8 months) and a shorter time constant for the land (a third of a month).
Regarding the climate sensitivity, I find the following
In[10]:= eqn3 = .62 x + .38 y == .1
eqn4 = .82 x + .18 y == .05
Solve[{eqn3, eqn4}, {x, y}]
Out[12]= {{x -> 0.005, y -> 0.255}}
Again as expected, we find the sensitivity for the ocean to be small (0.005°C per W/m2) and that of the land to be significantly larger (0.25° per W/m2).
However, these are just estimates and certainly may be in error. I should be able to give you better results after I crunch the CERES data.
w.
Paul_K says:
June 9, 2012 at 12:26 pm
Likely my fault, but I didn’t understand this one, Paul. Most of the heating of the ocean is from direct penetration of the solar flux into the “photic zone”, the top one or two hundred metres or so of the ocean. The heat is retained in the ocean by the absorption of the longwave radiation in the surface layer, which slows the cooling rate of the ocean.
But heat flux from the atmosphere? That doesn’t do a whole lot, for the reason that you point out, which is that the relative heat capacities of the ocean and atmosphere are so different. There’s just not enough heat in the atmospheric boundary layer to do a whole lot of oceanic heating.
The combination of all that is why I am perplexed by your claim that the deep ocean response “requires a connection by heat flux, not radiative flux”.
w.
Willis Eschenbach: “I was stating a fact, Joe, which is that despite trying a whole range of possible configurations, I haven’t been able to fit a pair of time constants, one longer and one shorter, to the actual data. I can’t make it converge to that kind of arrangement no matter what I’ve tried.”
If indeed you applied your data to a double-pole model–a premise for which I had missed any evidence in this thread–then perhaps a no-long-time-constant conclusion is indeed warranted. But your post seemed to indicate–because you gave the actual equation–that you applied the data only to a single-pole model. If that’s the case, then what I’ve seen, as I explain below, is that you are not justified in concluding the negative implied by “If there is a long slow response, why would it not show up in the fourteen years of data that I have, particularly since it is among the fastest-warming periods in the 20th century?”
Willis Eschenbach: “Nor, as near as I can tell, have you been able to fit something like that to the actual data, or at least you haven’t reported the results.”
That’s true; I haven’t fit the data to a two-pole model.. To be candid, I haven’t even tried. This despite the fact that I (I think I) have written such a model. Indeed, the reason I haven’t tried is that in truth I doubt I’d find a two-pole fit; i.e., I’m not arguing that I really think there’s a significant long-time constant response to insolation.
My argument is directed only to whether your single-pole model would find the longer time constant if it were there. On that score, I believe I do have “actual results.” Specifically, I applied a sine wave, and the steady-state response of a two-pole system to a sine wave, to your (single-pole) model, and what I found is that it concluded, with very small error, that the sensitivity was less than what the two-pole system’s actually is and that the time constant was nearer to the short time constant than to the long time constant. (I don’t recall how great the errors were when I additionally added a trend, i.e., added a ramp to the sine wave; perhaps there’s some ammunition for you there.)
If indeed you have applied your data to a two-pole model, then my reservations my not be so serious. But I’d be grateful if you could confirm that, preferably by giving the model equations explicitly, as you did for your single-pole model.
On the other hand, here are findings that tend to support Mr. Eschenbach’s conclusion.
Having recognized during our colloquy that I really should have applied his radiation data to a two-time-constant model myself rather than just invite him to do so, I went through that exercise, varying the time constants and sensitivities as he did. (This is in distinction to what I had previously done, which was determine whether his one-time-constant model would detect a significant long-time-constant component if there were one. In that case, I concluded that such a component could escape undetected, at least in some circumstances.) Although I found as a result of this new exercise that both hemispheres’ data provide a better fit to models that (at least nominally) exhibit two time constants, the improvement was minuscule.
In the case of the Northern Hemisphere, in fact, even this faint contention is an overstatement, since the sensitivity of the two-time-constant model’s longer-time-constant (17.2-month) component was less than 0.1% of its (1.2-month) shorter-time-constant component’s: what appeared as a second time constant is readily written off as noise.
In the case of the Southern Hemisphere, the data do match a model having 1.3- and 12.9-month time constants marginally better than they do the best (1.5-month) single-time-constant model I found, but that two-time-constant model’s longer-time-constant component exhibited a sensitivity barely more than 10% the shorter-time-constant component’s. (I should note here that my time-constant values differ from Mr. Eschenbach’s because I use different model equations. Although I prefer mine, the distinction is not important.) As far as the ultimate question before the house is concerned, this time constant is not significant, either.
So, although I remain convinced that Mr. Eschenbach’s one-pole-model approach could miss a significant second time constant if one existed, my two-time-constant-model approach turned up no evidence of one, either.
A caveat: as Mr. Eschenbach did, I searched for best-match models by using Excel’s “Solver” facility. In the case of the two-pole model, though, that facility was faced with six parameters (a sensitivity and time constant for each of the poles, and two initial-condition values) to vary. This makes the question rather a poser, so “Solver” required a certain amount of hand-holding. A consequence is that I’m not entirely confident that I didn’t miss a better local optimum somewhere. Additionally, since I didn’t really expect to find a significant sensitivity with a long time constant, there’s always the danger of confirmation bias.
Thanks for that, Joe. You’ve run up against the problem I found. When I looked at the “two-box model” solution, utilizing a second longer time constant, I got a minuscule sensitivity. Similar to your finding, it is on the order of a tenth of the first sensitivity that I found above in the head post.
I took another run at it this morning, using a slightly different technique I thought of last night while falling asleep (get the residuals and try to model them with a longer time constant). I had no success with that one either, same result, longer time constant but tiny sensitivity.
Let me say again that absence of evidence is definitely not evidence of absence, so the fact I’ve not been able to find such a relationship doesn’t mean that it doesn’t exist. I continue to look, and as I mentioned above, I’m now looking at the CERES data. As usual I’ll report my findings as soon as I have some …
w.
Willis:
I’m not sure where you’re going with your series of articles on the climate sensitivity. As you develop an argument, I urge you to avoid building the fallacy that is known as “base-rate neglect” into this argument. It is a logical error that people tend to make when they assign numerical values to the conditional probabilities of the outcomes of events. This error is committed, for example, when it is assumed that the best estimate of this year’s batting average for a specified baseball player is the previous batting average for the same player. Actually, the best estimate lies between his previous average and the league average; the league average is the base-rate. To assume that the best estimate is his previous average is to a) neglect the base-rate and b) fabricate information Skeptics and warmers alike are extremely prone to fabricating information in this way.
When information is fabricated, this “crime” is discovered if and when the model is statistically tested and the observed relative frequency of a outcome is found to lie closer to the base-rate than predicted by the model. A requirement for statistical testing is the existence of the underlying statistical population. IPCC climatologistists make it impossible for their “crime” to be detected by refusing to identify the statistical population for their study of global warming. Thus far, you’ve not defined the population for your study either.
Re:Willis Eschenbach says:
June 9, 2012 at 11:38 pm
Likely my fault, but I didn’t understand this one, Paul. Most of the heating of the ocean is from direct penetration of the solar flux into the “photic zone”, the top one or two hundred metres or so of the ocean. The heat is retained in the ocean by the absorption of the longwave radiation in the surface layer, which slows the cooling rate of the ocean.
Wills,
No argument from me. The heat flux I was referring to was heat flux from deep ocean to the mixed layer.
Terry Oldberg says:
June 10, 2012 at 2:10 pm
Thanks, Terry, but I haven’t a clue what you are referring to when you say “fabricating information”. I’m not fabricating anything, as far as I know.
As to “where [I’m] going with [my] series of articles on the climate sensitivity”, I’m not going anywhere. I am attempting to estimate the climate sensitivity based on observations of the planet.
Now, I understand that you don’t think that “climate sensitivity” is measurable because, as you say:
I fear that despite your prior explanation, I still don’t understand what that means. Suppose you have a thermometer in your yard, enclosed in a Stevenson Screen so it is out of the sun. Surely you will find that when the sun is stronger, your thermometer will indicate a warmer temperature … so why, in your opinion, is the average magnitude of that change not quantifiable, either for one thermometer or the average of a hundred thermometers? Why are the records of the temperatures and the isolation in your yard for say thirty days not a sample?
Also, you say that there are no “events, statistical population, or sample” involved. Why are e.g. the average monthly albedos or the average monthly solar insolation not a statistical population from which I have taken a sample from 1984 to 1997? What am I missing?
All the best,
w.
Willis:
Thank you for taking the time to reply. When you say “Why are the records of the temperatures and the isolation in your yard for say thirty days not a sample?” it sounds as though you are conflating the idea that is referenced by the term “sample” with the idea that is referenced by the term “time series.” A record of the temperatures in one’s yard is an example of a time series. A record of the insolation in one’s yard is a different example of a time series.
The term “event” is synonymous with the term “happening.” In the game of baseball, an example of an event is an at bat. A statistical population is comprised of statistically independent events. A subset of these events in which the events have been observed is a “sample.”
Like every event, an at bat can be described by a pair of states of nature. One of these states is a condition on the associated model’s dependent variables and is called an “outcome.” The other state is a condition on this model’s independent variables and is called a “condition.” For an event that is an at bat, an example of an outcome is a hit and an example of a condition is the batter’s identity.
Prior to the publication, circa 1960, of papers by Stein and James of Stanford University, statisticians thought that the best estimator of a baseball player’s batting average for the following season was this player’s batting average in preceeding seasons. In using this estimator, they inadvertently fabricated information. Stein and James showed that a better estimator of a player’s batting average for the following season lies between his own past batting average and the batting average for the league. The latter estimator claims possession of less information about the player’s batting average.
The batting average for the league is an example of a “base-rate.” One can avoid fabricating information by factoring the base-rate into one’s estimates of the relative frequencies of future outcomes.Today, cognitive psychologists rate one’s thinking as illogical if it neglects or underweights the base-rate. The error of neglecting the base rate plays a role in the thinking of modern day climatologists. For them, there is no statistical population and hence no base-rate.
Willis,
You wrote:
“Finally, I see no reason why the instantaneous sensitivity would be so small if there is a much larger sensitivity hiding out somewhere. What would make the sensitivity go from the short-term sensitivity of ~ 0.3° per doubling of CO2, which I’ve calculated above, to ten times that in the long term as the IPCC claims? I can’t see physically how that might happen.”
I don’t think you have taken on board what I was trying to explain in one of my previous comments (Paul_K says:
June 5, 2012 at 2:15 am).
You cannot make a direct comparison between your 0.3° per doubling and the IPCC’s 3° per doubling, because you are comparing apples and bananas. You are not considering the conventional input forcings and you are not considering the conventional feedback terms which go into the IPCC number. As I tried to explain earlier, you would need to back them out if you want to try to make a valid comparison.
To illustrate the point, suppose for a minute that 90% of the variation in (your) net received SW is due to fluctuations in sea ice albedo plus clouds, and that they are fluctuating because they really are temperature-dependent feedbacks. Then only some 10% of what you are calling input forcing would conventionally be considered a forcing, so you would be overestimating your feedback coefficient (1/lambda) by a factor of 10 for the same temperature sensitivity. In fact the true situation is a bit more complicated than this, but you need to get the basic idea that your sensitivity cannot be directly compared with IPCC’s climate sensitivity.
I know I’m repeating myself, but your finding is much more important in the context of attribution than it is for climate sensitivity.
Paul_K says:
June 10, 2012 at 6:14 pm
Paul, the IPCC does not “back out” the feedbacks. They explicitly include them in their calculation of the overall sensitivity, which is how they get from a blackbody change in temperature (~ 0.7°C per doubling of CO2) to the 3°C per doubling that they claim. The only difference is that they claim the net feedbacks are overwhelmingly positive, while the observations say they are net negative.
Since they don’t remove the feedback terms, neither have I, in that regard it’s apples to apples … what am I missing? I could easily be wrong, I just don’t understand where.
Now, I do understand that I have not included the change in upwelling longwave radiation, but I have estimated it above, and I am currently working on the CERES dataset which includes ULR. Once I include that, however, I don’t see why other feedbacks (which are all included in the IPCC numbers) should be backed out.
My best to you, and thanks for all of the assistance, it is much appreciated,
w.
PS—I just finished the preliminary analysis of the CERES data. It is a 1° gridded dataset showing downwelling and upwelling solar radiation, along with upwelling longwave radiation. The CERES data shows that as a global average,
∆ULR = 0.16 ∆NSR + .006 , with a p-value less than 2E-16
where ∆ULR is the change in upwelling longwave radiation and ∆NSR is the change in net solar radiation (downwelling minus upwelling), and both ULR and NSR are taken as positive numbers.
So instead of having a change in net solar forcing of e.g. 1 W/m2, we have a net solar forcing of 0.84 W/m2. This means that my sensitivity is underestimated by 1/0.84, or about 20%. This is actually a smaller difference than my estimate from above, where I thought it was more like 40%.
Please note that this calculation is direct, without area-averaging. I don’t think that makes a difference, because what we are looking at is basically ∆ULR / ∆NSR, with the constant term approximately zero (0.006), and both variables are affected equally by the area of the cell. However, I’m happy to be convinced otherwise.
Hi again, Willis,
You wrote:-
“Paul, the IPCC does not “back out” the feedbacks. They explicitly include them in their calculation of the overall sensitivity, which is how they get from a blackbody change in temperature (~ 0.7°C per doubling of CO2) to the 3°C per doubling that they claim. The only difference is that they claim the net feedbacks are overwhelmingly positive, while the observations say they are net negative.
Since they don’t remove the feedback terms, neither have I, in that regard it’s apples to apples … what am I missing? I could easily be wrong, I just don’t understand where.”
You can write the TOA balance as:-
Net flux imbalance = F – feedback * ∆T (Equation 1)
Your climate sensitivity term expressed in deg C/watts/m2 is equal to 1/(feedback). This scales by the magnitude of F, since the equilibrium temperature as net flux goes to zero is given by
∆T = F/(feedback) .
In equation (1), the net flux imbalance is the total SW and LW imbalance. The F value and the value of (feedback) are the sum of the SW and LW constituent components.
Now let’s split up the forcings and feedback terms into their constituents. We can write:-
Net flux imbalance = (F1 + F2 + F3 + ) – (feedback1 + feedback2 + feedback3+…) * ∆T
Now consider what happens if you take one of the feedback terms, say cloud SW response, and redefine it as a forcing. Your “new” forcing may look like this:
F = (F1 + F2 + F3 +…- feedback1* ∆T )
and your new feedback term looks like this:-
(feedback) = ( feedback2 + feedback3+…) * ∆T
You still balance the equation, but when you calculate your feedback term, it is not the same as the feedback term you would calculate from Equation (1), because you have re-labelled part of the IPCC feedback as a forcing. Do you see it now?
Robert Brown,
you mentioned the massive variation in albedo of around 1990 and commented on it being an all time high (and later corrected it to all time low). I think your use of ‘all time’, while correct is a bit misleading. I’ve only found about 30 yrs worth of albedo data total. “all time” implies over history, not just over the history of 30 years of data. Have you found an actual source of albedo data that is better coverage than I described?
Have you noticed that many of the older albedo estimates for Earth also tend to give higher values than we have been measuring over recent years, more in the 0.35 to 0.40 realm as compared to the nominal 0.30 range?
Are you familiar with Palle’ and Goode and their Earthshine project?
We don’t really even have good data over the satellite era and yet there’s all these people trying to figure out (or claiming to have figured out) climate sensitivities and precision power balance without taking albedo into account. BTW, essentially all of them assume constant albedo.
Terry Oldberg says:
June 11, 2012 at 9:00 am
Thanks, Terry, but I still don’t see the difference. Why is the measurement of temperature every day a “time series” but a measurement of someone’s success at batting every day is not a time series? Why is the daily measurement of temperature not an “event” while the daily measurement of batting success is an event?
I don’t get it. I don’t see the different you are pointing at. Suppose I have a machine that rolls the dice once a minute. Once every day at 3:00 I record one roll of the dice, and at the same time I record one temperature … is one of these an “event” and the other not an “event”, and if so, why?
w.
Willis:
It’s not the measurement of temperature which is a time series but rather is the record of the temperatures that were measured which is a time series.
Also, while the measurement of a quantity is a type of event, this type of event is not the best for didactic purposes. For these purposes, an at bat works better. This is, in fact, the event that was featured in a Scientific American article on the topic I am addressing. If you’d like me to teach you, lets stick with the at bat for the time being.
Terry
Terry Oldberg says:
June 12, 2012 at 7:42 am
Terry, I would like to learn from anyone, but I’m getting very frustrated, because your vague hand-waving doesn’t teach anything. I asked a simple question. You gave me … well … nothing. I still still have no clue why a series of measurements of temperature is different from a series of measurements of batting skill. I still have no idea what distinguishes an “event” in your lexicon from something which is not an “event”. I asked a clear and specific question, viz:
You come back to tell me what is the best for didactic purposes …
w.
Willis:
Thank you for taking the time to respond. The presentation which you characterize as “vague hand waving” is a presentation of terms and concepts of mathematical statistics which you evidently do not know. While you do not know them, I cannot inform you of important shortcomings in the methodology of the IPCC inquiry into anthropogenic global warming. These same shortcomings are a feature of your own works.
I can teach you about these terms and concepts but only if you move your point of view from the lofty position of debater to the humble position of student. While in the position of debater, I find, you are prone to veering off the topic that I have introduced for didactic purposes in ways that preserve your own ignorance and that serve to preserve the misimpression that your own works are flawless..
Terry Oldberg says:
June 12, 2012 at 10:35 am
I am under no illusions that my works are flawless, I’ve been on the earth far too long to hold such a childish claim. I have publicly acknowledged a number of errors in my work in the past, so I fear that you are off in fantasy about my “misimpressions”.
All I asked for was simple answers to simple questions, viz:
and
and
and
So far, you have not answered a single one of my questions. Since you are obviously unwilling to answer questions, and instead you want to lecture me about my shortcomings, I fear you’ll never get any traction for whatever ideas you are pushing.
I am interested in learning from you, but if you want to teach someone, Terry, you likely need to answer questions. The Sufis say “Some say that a teacher needs to be this way, and some say a teacher should be that way. But all a teacher needs is to be what the student needs …” In other words, trying to force your favorite teaching style on someone doesn’t work. You need to adapt your style to be what the student needs … and it appears that you are far too arrogant and proud to do that. You think you have the right teaching style and you are unwilling to change that … I have no problem with that, that’s your prerogative, but it doesn’t work for me.
So I fear that your teaching style is not at all what I need. What I need is someone willing to answer questions, not someone who wants to make mysterious undefined distinctions between an “event” and a non-event, and then refuse to explain the difference while at the same time insulting me …
In other words, sorry, not interested in the slightest. Take your teaching style to someone who cares for it and for whom it works.
w.
Willis:
Thanks for the response. I’ll hold my opinion on the decorum that is required of a student for another occasion. Your questions and my answers follow:
Q1: Suppose you have a thermometer in your yard, enclosed in a Stevenson Screen so it is out of the sun. Surely you will find that when the sun is stronger, your thermometer will indicate a warmer temperature … so why, in your opinion, is the average magnitude of that change not quantifiable, either for one thermometer or the average of a hundred thermometers?
A1: The premise that “when the sun is stronger, your thermometer will indicate a warmer temperature” is incorrect.
Q2: Why are the records of the temperatures and the isolation in your yard for say thirty days not a sample?
A2: They are not a sample but rather are a time series.
Q3: Why are e.g. the average monthly albedos or the average monthly solar insolation not a statistical population from which I have taken a sample from 1984 to 1997? What am I missing?
A3: The average monthly albedos or average monthly insolations are not statistical populations because neither an average monthly albedo nor an average monthly insolation is a statistical event. Possibly, the two quantities are variables belonging to a model.
Q4: Suppose I have a machine that rolls the dice once a minute. Once every day at 3:00 I record one roll of the dice, and at the same time I record one temperature … is one of these an “event” and the other not an “event”, and if so, why?
A4: Whether or not the outcome of an event is recorded is immaterial to the definition of an “event.” Also, in the context of a study of anthropogenic global warming, the definition of an event must reference a state of nature that is additional to its outcome. For the purpose of setting policy on CO2 emissions, one needs a predictive model. A prediction from such a model is an extrapolation from an observed condition on the model’s independent variables to an unobserved but observable condition on the model’s dependent variables. The former condition is called a “condition.” The latter condition is called an “outcome.” The conditions and outcomes are states of the climate. Each event in the associated population is describable by: a) its condition b) the time at which this condition is observable c) the outcome and d) the time at which the outcome is observable. The two times define a time period; for the statistical independence of the various events, their periods do not overlap. An event in which both conditions have been observed is said to be an “observed event”; A “sample” is a collection of observed events.
Terry Oldberg says:
June 12, 2012 at 12:43 pm
Dude, if you think my decorum is inadequate, you have already lost the plot. You seem to be looking for someone willing to kiss your ring, and that’s not me. Your overweening arrogance has now successfully cost you the whole game. The tragedy is, I actually thought you might be on to something and be able to teach it. You’ll have to find someone else to impress, because frankly, Terry, I don’t give a damn. Here’s a quarter, call someone who cares.
w.
PS: As an explanation of why I don’t give a damn, this interaction sums up the problem nicely:
You have already made that claim, more than once … but what you haven’t done is ANSWER THE FREAKING QUESTION. But despite not answering the question time after time, you want to lecture me on decorum … sorry, my friend, but it doesn’t work that way.
Willis:
i answered that question. See A2.
Terry Oldberg,
“i answered that question. See A2.”
Great response. Bwahhaha.
You remind me a bit of the character played by Jack Nicholson in the movie “Anger Management”. If your intention is to drive Willis up the wall, then you are doing a highly successful job. If your intention is to convince Willis, and indeed any other readers, of the need for rigorous canonical form from a frequentist philosophy, alas, I fear you are doing a job of the same quality as Peter Gleick on the subject of how to better communicate the need for ethics in science.
Strangely enough, I agree with quite a lot of what you are saying; lack of attention to basic precepts and their handmaiden, canonical form, has led to a loss, or in some cases, a complete absence of statistical rigour in climate science. (And by the way I don’t think we support the same football club – I’m more a Bayesian pragmatist – but if you will accept a little advice from this not-so-humble student, you need to talk into the listening. It would be better to explain what you are trying to do about getting mainstream scientists to accept the need for statistical rigour and why clarity on basic definitions is important. After that, you might gently suggest that we should all consider the implications for our own self-challenge.
It really is a bit much when you are going after the mote in Willis’s eye and not clearly explaining the beams in the IPCC literature, at least in context for Willis.
Also stop answering questions about meaning with another definition, and explain why the distinction MATTERS.