Guest Post by Willis Eschenbach
In my previous post, A Longer Look at Climate Sensitivity, I showed that the match between lagged net sunshine (the solar energy remaining after albedo reflections) and the observational temperature record is quite good. However, there was still a discrepancy between the trends, with the observational trends being slightly larger than the calculated results. For the NH, the difference was about 0.1°C per decade, and for the SH, it was about 0 05°C per decade.
I got to thinking about the “exponential decay” function that I had used to calculate the lag in warming and cooling. When the incoming radiation increases or decreases, it takes a while for the earth to warm up or to cool down. In my calculations shown in my previous post, this lag was represented by a gradual exponential decay.
But nature often doesn’t follow quite that kind of exponential decay. Instead, it quite often follows what is called a “fat-tailed”, “heavy-tailed”, or “long-tailed” exponential decay. Figure 1 shows the difference between two examples of a standard exponential decay, and a fat-tailed exponential decay (golden line).
Figure 1. Exponential and fat-tailed exponential decay, for values of “t” from 1 to 30 months. Lines show the fraction of the original amount that remains after time “t”. The “fatness” of the tail is controlled by the variable “c”. Line with circles shows the standard exponential decay, from t=1 to t=20. Golden line shows a fat-tailed exponential decay. Black line shows a standard exponential decay, with a longer time constant “tau”. The “fatness” of the tail is controlled by the variable “c”.
Note that at longer times “t”, a fat-tailed decay function gives the same result as a standard exponential decay function with a longer time constant. For example, in Figure 1 at “t” equal to 12 months, a standard exponential decay with a time constant “tau” of 6.2 months (black line) gives the same result as the fat-tailed decay (golden line).
So what difference does it make when I use a fat-tailed exponential decay function, rather than a standard exponential decay function, in my previous analysis? Figure 2 shows the results:
Figure 2. Observations and calculated values, Northern and Southern Hemisphere temperatures. Note that the observations are almost hidden by the calculation.
While this is quite similar to my previous result, there is one major difference. The trends fit better. The difference in the trends in my previous results is just barely visible. But when I use a fat-tailed exponential decay function, the difference in trend can no longer be seen. The trend in the NH is about three times as large as the trend in the SH (0.3°C vs 0.1°C per decade). Despite that, using solely the variations in net sunshine we are able to replicate each hemisphere exactly.
Now, before I go any further, I acknowledge that I am using three tuned parameters. The parameters are lambda, the climate sensitivity; tau, the time constant; and c, the variable that controls the fatness of the tail of the exponential decay.
Parameter fitting is a procedure that I’m usually chary of. However, in this case each of the parameters has a clear physical meaning, a meaning which is consistent with our understanding of how the system actually works. In addition, there are two findings that increase my confidence that these are accurate representations of physical reality.
The first is that when I went from a regular to a fat-tailed distribution, the climate sensitivity did not change for either the NH or the SH. If they had changed radically, I would have been suspicious of the introduction of the variable “c”.
The second is that, although the calculations for the NH and the SH are entirely separate, the fitting process produced the same “c” value for the “fatness” of the tail, c = 0.6. This indicates that this value is not varying just to match the situation, but that there is a real physical meaning for the value.
Here are the results using the regular exponential decay calculations
SH NH lambda 0.05 0.10°C per W/m2 tau 2.4 1.9 months RMS residual error 0.17 0.26 °C trend error 0.05 ± 0.04 0.11 ± 0.08, °C / decade (95% confidence interval)
As you can see, the error in the trends, although small, is statistically different from zero in both cases. However, when I use the fat-tailed exponential decay function, I get the following results.
SH NH lambda 0.04 0.09°C per W/m2 tau 2.2 1.5 months c 0.59 0.61 RMS residual error 0.16 0.26 °C trend error -0.03 ± 0.04 0.03 ± 0.08, °C / decade (95% confidence interval)
In this case, the error in the trends is not different from zero in either the SH or the NH. So my calculations show that the value of the net sun (solar radiation minus albedo reflections) is quite sufficient to explain both the annual and decadal temperature variations, in both the Northern and Southern Hemispheres, from 1984 to 1997. This is particularly significant because this is the period of the large recent warming that people claim is due to CO2.
Now, bear in mind that my calculations do not include any forcing from CO2. Could CO2 explain the 0.03°C per decade of error that remains in the NH trend? We can run the numbers to find out.
At the start of the analysis in 1984 the CO2 level was 344 ppmv, and at the end of 1997 it was 363 ppmv. If we take the IPCC value of 3.7 W/m2, this is a change in forcing of log(363/344,2) * 3.7 = 0.28 W/m2 per decade. If we assume the sensitivity determined in my analysis (0.08°C per W/m2 for the NH), that gives us a trend of 0.02°C per decade from CO2. This is smaller than the trend error for either the NH or the SH.
So it is clearly possible that CO2 is in the mix, which would not surprise me … but only if the climate sensitivity is as low as my calculations indicate. There’s just no room for CO2 if the sensitivity is as high as the IPCC claims, because almost every bit of the variation in temperature is already adequately explained by the net sun.
Best to all,
w.
PS: Let me request that if you disagree with something I’ve said, QUOTE MY WORDS. I’m happy to either defend, or to admit to the errors in, what I have said. But I can’t and won’t defend your interpretation of what I said. If you quote my words, it makes all of the communication much clearer.
MATH NOTES: The standard exponential decay after a time “t” is given by:
e^(-1 * t/tau) [ or as written in Excel notation, exp(-1 * t/tau) ]
where “tau” is the time constant and e is the base of the natural logarithms, ≈ 2.718. The time constant tau and the variable t are in whatever units you are using (months, years, etc). The time constant tau is a measure that is like a half-life. However, instead of being the time it takes for something to decay to half its starting value, tau is the time it takes for something to decay exponentially to 1/e ≈ 1/2.7 ≈ 37% of its starting value. This can be verified by noting that when t equals tau, the equation reduces to e^-1 = 1/e.
For the fat-tailed distribution, I used a very similar form by replacing t/tau with (t/tau)^c. This makes the full equation
e^(-1 * (t/tau)^c) [ or in Excel notation exp(-1 * (t/tau)^c) ].
The variable “c’ varies between zero and one to control how fat the tail is, with smaller values giving a fatter tail.
[UPDATE: My thanks to Paul_K, who pointed out in the previous thread that my formula was slightly wrong. In that thread I was using
∆T(k) = λ ∆F(k)/τ + ∆T(k-1) * exp(-1 / τ)
when I should have been using
∆T(k) = λ ∆F(k)(1 – exp(-1/ τ) + ∆T(k-1) * exp(-1 / τ)
The result of the error is that I have underestimated the sensitivity slightly, while everything else remains the same. Instead of the sensitivities for the SH and the NH being 0.04°C per W/m2 and 0.08°C per W/m2 respectively in the both the current calculations, the correct sensitivities for this fat-tailed analysis should have been 0.04°C per W/m2 and 0.09°C per W/m2. The error was slightly larger in the previous thread, increasing them to 0.05 and 0.10 respectively. I have updated the tables above accordingly.
w.]
[ERROR UPDATE: The headings (NH and SH) were switched in the two blocks of text in the center of the post. I have fixed them.
Why do people keep traipsing out the “ideal gas law” in regard to the earth atmosphere where it has no applicability at all. It is an idealized formula for a sytem that is in static equilibrium. Earth atmosphere is never in any kind of equilibrium.
, that describe local variations in molar density (or, with a conversion factor for moles to mass, mass density). Those relations are useful (and often used) to derive various relations in climate science. But one derives those relations. One doesn’t wave one’s hands and pretend that the words correctly describe a complex mathematical system.
You took the words right out of my — uh, keyboard. It is not correct to say that it has “no applicability at all”, though. It has some local validity for “parcels” of air in a coarse grained description of the atmosphere. That is, if I take a chunk of air the size of a breadbox in between my two hands, it has a roughly uniform pressure, temperature, volume, and mass, and is “pretty well” described by PV = NkT. If you take too small a parcel it isn’t (and it gets to be too hard to solve the PDEs that describe the global system. If you take too big a parcel, as you note, the pressure in the parcel differs significantly from top to bottom, the temperature varies across or up and down the parcel, the parcel is differentially moving, there is turbulence in the parcel, etc.
The best that can be said for the ideal gas law is that you can form a set of partial differential equations from it, things like
rgb
Oops, I needed an “R”, not a “k” in the PDE in the previous reply. I was thinking moles, but I’m used to working with molecules. Sorry — scale one or the other by Avogadro’s number…
rgb
[Fixed -w.]
When a gas expands its temperature drops.
The troposphere expands vertically when more energy is added.
Unless the additional energy represents an increase in total system energy content the temperature at the surface will not rise.
Total system energy content only increases if one increases top of atmosphere insolation OR total atmospheric mass.The more massive an atmosphere the higher the surface temperature.
If the energy content of the troposphere increases from any other cause then that represents only a redistribution of available energy within the system and so there need be no increase in surface temperature.
In practice some areas of the surface warm but others cool and the net effect on average global surface temperature is near zero.
As far as I am aware that is all well established science relating to non radiative energy transfers.
Robert Brown asked:
“What on earth does “greater atmospheric mass” have to do with anything, aside from providing more matter to help carry this heat from place to place?”
You answered your own question. Think it through.
If there is more matter carrying more heat from place to place then the surface temperature will get higher before that heat is finally released to space because the shifting from place to place takes longer and more energy accumulates in the system.
Absolutely bog standard basic physics and at base what N & Z are saying. It is also as per the Ideal Gas Law which describes the dynamic relationship etween the 5 parameters of Pressure, Volume, Temperature, molecular density and the gas constant R.
When a gas expands its temperature drops.
Maybe you should learn the first law of thermodynamics sometime.
I’m just saying.
rgb
If there is more matter carrying more heat from place to place then the surface temperature will get higher before that heat is finally released to space because the shifting from place to place takes longer and more energy accumulates in the system.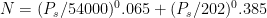
where 
is the dimensionless scaled relative-to-greybody warming computed relative to the moon as the “ideal” representative greybody and 
is surface pressure in bar, as a universal law that works perfectly — and I do mean perfectly — for Mercury, the Moon, Triton, Titan, Europa, Mars, Earth and Venus, which is true if one uses their special sauce to evaluate 
, and which results in a very imperfect fit (some would cruelly be tempted to call it no fit at all) if one leaves out the sauce and uses published numbers with error bars, and an even more contrary fit if one includes the Jovian moons besides Europa (and, I’m sure, other moons of the other gas giants or the gas giants themselves, provided one could actually get data on their “surface” pressure and temperature in the first place).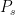
and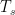 
are large (and completely unacknowledged in their miracle fit — where exactly is that pesky 
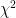that should accompany any such fit?).
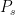(and countervaries with distance from Jupiter so your assertion that “Jupiter warms them” is irrelevant if true — it doesn’t warm them enough, does it?).
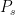only used to “predict” a relative surface temperature. Yet no such variation is observed in N&Z’s “miracle curve”, is it? Not even in planets in their list with enormously different albedos, where if you plotted the albedos of the planets or moons against their surface pressure you would get no correlation whatsoever. Again we see this in just three Jovian moons — albedos of 0.2, 0.4, and over 0.6 where in all cases the atmospheric surface pressure is basically “hard vacuum” (
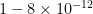bar — picobar).
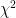for the number of degrees of freedom and a p-value for the null hypothesis of “this is unbiased measured data that just happened to fit exactly on this curve” that is most correctly interpreted as “the null hypothesis is almost certainly false” quite independent of the curve in question and its merits. What the source of bias is, well, I personally think that is pretty clear, especially after I plot the data myself and land nowhere near their curve with any small body but the Moon, Mars, Earth and Venus when I omit the secret sauce.
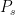and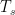 
for the moons we used to fit this curve and ignored the rest, forgetting that the inclusion of error bars or independent checking of our numbers would reveal what we did to anyone that actually looked”. But of course that isn’t plausible. Is it?
Granting that there is some truth to this, it has nothing to do with the ideal gas law. Nor is it even vaguely, remotely, original to N&Z — adiabatic lapse rates are derived (subject to various assumptions) in over-the-counter climate physics textbooks.
Finally, it is not “at base what they are saying”. They are saying that
There is other stuff N&Z do that isn’t terrible. I appreciate their desire to improve the computation of average surface temperature, since that sucks even on the Earth (with huge numbers of sampling stations and methods) and is almost laughable when one attempts to determine a mean temperature for the other planets from a teensy handful of observations, but ultimately that simply means that the error bars on both
But the paper in question is awful. Seriously, seriously awful. It is completely stupid to try to make the “base” albedo of all planetoids match that of the moon. Europa is covered in ice, Ganymede very definitely is not, and this is “reflected” in their bond albedos — 0.43 for Ganymede, 0.67 for Europa. But the real wild card is Callisto — a bond albedo of ~0.2, farthest from Jupiter (and hence least susceptible to all forms of warming from Jupiter).
If you compare Europa (included by N&Z) and Callisto (not included for obvious reasons) the whole argument is over. The mean surface temperature of Callisto is considerably higher than that of Europa. Of course it is, its albedo is around a third as large. It’s dark and absorbs lots of sunlight where Europa reflects it before it has any chance to warm it. It is farther from Jupiter (so if Jupiter is a source of radiant heat, it should be cooler). It is farther from Jupiter (so if Jupiter is a source of tidal heating, it should be cooler). It’s mean insolation is, of course, on average the same as Europa and the variations there cannot possibly be used to explain the fact that Callisto is over 20% warmer than Europa!
By every standard, if “moon-referenced greybody atmospheric heating” is a valid concept for moon-sized objects with atmospheres, Europa should be warmer than Callisto. It is not. Ganymede, farther from Jupiter, with the same atmospheric pressure as Callisto but an intermediate albedo (between Europa and Callisto) has — wait for it — a temperature that it intermediate between Europa and Callisto.
The temperature differences at near-constant insolation of all three Jovian moons is easily explained by something else — the albedo — completely independent of
The albedo therefore should (and, of course, does) modulate an unpredictable error/difference/anomaly compared to any function of
A bit of a puzzle, isn’t it? All of these moons, yet the one included is the one that (after suitable and occult secret sauce adjustments) fits square on their curve. A clearly necessary anomaly is omitted, a correction relative to a pressure only model based on albedo where the latter is completely decorrelated from surface pressure and where one of the snippets of physics we are pretty certain of is that actual surface insolation contributing to heating is TOA insolation minus the reflected fraction which is directly dependent on the albedo, not the surface pressure. And yet damn, they all fit square onto a horribly nonlinear curve with impossibly nonphysical reference pressures and absurd exponents, even though the error bars in our knowledge of their surface pressures and temperatures — quite aside from the albedo-based corrections — are in some cases almost as large as the quantities themselves. Which leads to a miniscule
One is tempted to interpret their miracle as “we fit the moon, mars, the Earth and Venus with a four parameter nonlinear function, and then tweaked our estimate of
rgb
Paul_K: “Can you reparse the equation so that it is tied to, say, a heat balance for a multiple capacity system with some assumptions?”
Yes, I can, but I’ll need to get back to you tomorrow; I’m just responding now so you won’t think I’m ignoring you.
http://www.qrg.northwestern.edu/projects/vss/docs/thermal/3-how-could-expanding-gas-cause-heat-loss.html
“When gas expands, the decrease in pressure causes the molecules to slow down. This makes the gas cold.”
Thus if one adds energy to a gaseous atmosphere open to space, which then expands, the two processes offset one another if there is no additional input from an external energy source such as a sun and no increase in atmospheric mass.
“Granting that there is some truth to this:
“If there is more matter carrying more heat from place to place then the surface temperature will get higher before that heat is finally released to space because the shifting from place to place takes longer and more energy accumulates in the system.”
it has nothing to do with the ideal gas law”
The Ideal Gas Law describes the relationships between pressure, volume, molecular density, temperature and the gas constant R.
Therefore it has everything to do with the temperature that will develop within an atmosphere of a given mass at a given pressure and subjected to insolation.
Increase the mass then all other things remaining equal temperature will rise.
It is the Ideal Gas Law governing non radiative energy transfers which adjusts the internal system energy flows to ensure that radiative energy in always matches radiative energy out at a given atmospheric mass subjected to a given level of solar input.
Oh No! It’s worse than we thought…
the obvious cause of albedo variation is cloud cover fraction which does affect both incoming and outgoing. It’s not the only cause of albedo variation. Evidently, one can vary the reflectivity of clouds by varying the size of the nucleation particles. Use smaller particles and you get higher reflectivity out of the same patch of clouds and that doesn’t have an effect on LWR like increased cloud cover fraction.
As I recall, Lindzen has an Iris effect theory using this sort of albedo variation.
For the whole Earth average, balance for incoming and outgoing power happens at about 239 W/m^2 coming in and going out. Radiation leaving the Earth’s surface at the average T value, 288K, results in an escape rate of around 270 W/m^2 for power leaving the troposphere which means that about 70% of the surface emission escapes or is replaced by atmospheric emission on the way out. With about 70% of surface radiation escaping one can see that to reduce 270W/m^2 down to 239 W/m^2 would require a reduced output from the surface of around 43W/m^2, dropping 390 down to 347 W/m^2 which is equivalent to a radiating temperature average of around 280K. That would mean the surface T would be down around 280K or a mere 7 deg C about freezing.
What is happening here is that around 60% of the Earth has clouds and 40% is clear sky. Clear skies contribute around 270W/m^2 and the overall average is around 239. Working through a weighted average (60/40), one can determine an average emission for cloudy skies. This comes out to around 218 W/m^2 of radiated power coming from cloud tops that needs to escape the atmosphere. This corresponds to around 249 K or -24 deg C. That’s the atmospheric temperature about halfway to the tropopause.
Consequently, while losing cloud cover, one increases the radiated power leaving the Earth as well as reducing albedo and allowing more incoming solar power. If one assumed we totally lost all cloud cover and wound up with an Earth albedo of 0.08 (due to all that of water on the surface), we’d only have 313 W/m^2 coming in to be absorbed and to be balanced. If we assume the same fraction of surface emissions make it through the atmosphere (70% for clear skies), then the surface would have to heat up enough to radiate 450 w/m^2 and that corresponds to a T average of 298K, only 10 degrees warmer than the 288k mean.
anyone here starting to see how lunatic claims of 6 deg C rise due to a somewhat minor increase of a trace gas like co2?
Robert, you said this:
“one of the snippets of physics we are pretty certain of is that actual surface insolation contributing to heating is TOA insolation minus the reflected fraction which is directly dependent on the albedo, not the surface pressure.”N & Z have only made a tentative start by
Do you not realise that surface pressure sets both the surface temperature at a given level of insolation AND the amount and shape of atmospheric circulation required to produce a given albedo ?
For any given planet with an atmosphere the air circulation must reconfigure itself until radiation in equals radiation out.
In the process it influences albedo.
If the air circulation were to fail in its task then there could be no atmosphere because it would be congealed on the surface or boiled off to space.
The equation of the Ideal Gas Law ultimately determines how the energy flows through the atmosphere must be configured in order for stability to be maintained and for an atmosphere to be retained and remain gaseous.
I suspect that when we know more about the atmospheric circulations of the moons of Jupiter and the various phase changes of materials that can occur within them then we will see how and why they have differing temperatures and / or fail to fit the curve noted by N & Z.
Note the fit of the easiest examples to the curve. Nothing in nature is perfect and so it will never be as neat as you seem to expect. As regards examples that do not fit I am sure that the reasons will be found within the particular air circulations and compositional variations of those examples.
Given the huge differences between Venus, Earth, Mars and the Moon the mere fact that they fit anywhere near each other on any curve is quite a surprise and highly likely to be of more general significance.
Let it ride for a few years before sounding off witrh such certainty 🙂
“N & Z have only made a tentative start by”
Mods, could you remove the above words from para 1 of my last post please.
[Done. -w.]
Paul_K: “Can you reparse the equation so that it is tied to, say, a heat balance for a multiple capacity system with some assumptions?”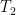
responds to the surface temperature and also loses heat by re-radiation, it behaves similarly:
the surface receives is made up of radiation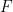 
from space 
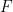and some re-radiation from the atmosphere proportional to the atmosphere’s temperature, we have
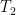results in:
,
If, say, the atmospheric temperature
Now let’s say that the total radiation
Plugging that in above and re-arranging to eliminate
Paul_K: “Can you reparse the equation so that it is tied to, say, a heat balance for a multiple capacity system with some assumptions?”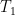
rises in response to total received radiation 
and cools as it re-radiates, its temperature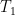 
behaves thus:
.
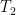responds to the surface temperature and also loses heat by re-radiation, it behaves similarly:
.
the surface receives is made up of radiation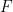 
from space and some re-radiation from the atmosphere proportional to the atmosphere’s temperature:
.
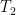results in:
,
,
and whose time constants are 
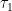and 
.
Sorry my last response was obscure; haste makes waste. Let me try again:
If the earth’s surface temperature
If, say, the atmospheric temperature
Now let’s say that the total radiation
Plugging that in above and re-arranging to eliminate
which is of the same form as
namely, the equation, whose form I gave the other day, for the two-pole system whose sensitivity is
Robert and Willis may find this new article informative
http://tallbloke.wordpress.com/2012/06/08/pressure-induced-changes-in-surface-temperature-of-titan-neptunes-largest-moon/
Thanks Tallbloke.
There are some pretty amazing gaps in the general scientific knowledge of some highly qualified and experienced but apparently overly specialised scientists.
Stephen Wilde says:
June 7, 2012 at 1:39 am
Now one could argue that the atmosphere not being an ideal gas the Law is capable of being invalidated but if one were to say that then you have to show exactly how and to what extent the non ideal nature of the gas causes a divergence from what the Law predicts.
Oh but the atmosphere is an ideal gas, Stephen – according to the fisics created to promote AGW. That’s why they don’t have convection, or gravity..
They don’t have anything between the vacuum of space and Earth, their atmosphere is empty space; hence only radiation applicable.
They can’t follow your arguments because they can’t relate the ideal gas laws to real gases (which no real gas obeys), they really think the atmosphere is comprised of ideal gas molecules, except water vapour, which travel at high speed through empty space bouncing off each other, and the container,without attraction. By which they get carbon dioxide thoroughly mixed because as per ideal gas description it will spontaneously rise from the ground and diffuse at great speed through the atmosphere, which for them is empty space. That’s why it can stay up hundreds and even thousands of years accumulating, because it is ideal gas it doesn’t have any weight, is not subject to gravity.
Their ideal gas world has it that gases aren’t buoyant in air – how can they be since they have no air?
They have no way of producing clouds, even though they say water vapour isn’t an ideal gas, clouds just magikly appear. They don’t have rain because in their ideal gas world there is no attraction, carbon dioxide just goes bouncy bouncy all over the empty space accumulating.
Don’t look for internal consistency in their arguments for this, they will in the same paragraph describe ideal gas diffusion in empty space as the reason carbon dioxide becomes thoroughly mixed in no time at all and then say it’s because it’s being bounced around in Brownian motion and that’s the reason scent wafts across the room when the bottle is opened..
But empty space is what they have as a concept of the atmosphere around them between their ears..
…they have no sound in their AGW Science Fiction world, they can’t hear this.
They don’t get the joke.
See my post here where I tell the story of how I discovered they think this is real physics and so why arguments between those who still live in the real world where gases have volume subject to gravity, who have a real fluid gas atmosphere with weight around them, and those who live through the looking glass with Al where impossible physics is the norm where gases are hard imaginary ideal gas dots bouncing off each other and the walls of a container, talk past each other.
http://wattsupwiththat.com/2012/06/02/what-can-we-learn-from-the-mauna-loa-co2-curve-2/#comment-1003183
Do you not realise that surface pressure sets both the surface temperature at a given level of insolation AND the amount and shape of atmospheric circulation required to produce a given albedo ?
Do you not realize that the actual data on albedo makes it clear that this statement is completely, utterly, cosmically false, untrue, not the case, absurd?
It isn’t even particularly true for the last three planets on the list — Mars, Earth and Venus — if you want to find a “trend”. Nor is it true just for the Earth. The Earth’s albedo has varied 7% over the last 15 years. Are you trying to assert that the mean surface pressure has varied at all over that time as a causal factor? If so, data please.
Look, plot albedo against surface pressure. Then come talk.
rgb
Re:Joe Born says:
June 7, 2012 at 4:52 pm
Wow. Seriously brilliant, Joe.
This is again a “watch this space” post since I have literally only just picked up your post. I need to play with it for a while before getting back to you. I may need a day because “she indoors” is on my back at the moment.
“The Earth’s albedo has varied 7% over the last 15 years. Are you trying to assert that the mean surface pressure has varied at all over that time as a causal factor? If so, data please.”
Mean surface pressure ?
That doesn’t vary except over geological timescales.
What does vary is the surface distribution of pressure and, indeed, cloudiness and albedo has varied.
However it is result of a reconfiguration of the surface pressure patterns. In the case of Earth albedo declined when the jets were more zonal and is now increasing with more meridional jets.
So, to make it clearer.
Mean surface pressure sets the surface temperature.
Changes in the regional distribution of surface pressure reconfigure the atmospheric circulation to ensure that radiation out equals radiation in and part of the process is changing cloudiness and albedo.
Plot albedo against the changing surface pressure distribution and apply some thought.
Paul_K says, June 5, 2012 at 2:15 am: As before, Willis, please take this as a constructive critique of your work. I am not trying to do a hatchet job, I promise you.
Unlike Willis who never ceases to do that in the case of Nikolov & Zeller…
“””””” …….Stephen Wilde says:
June 7, 2012 at 1:39 am
George.
K is the alternative term that Robert used for R.
The equation is based on the assumption that every one of those five factors is interlinked and will respond predictably to changes in the others.You accept that the value of R (or K) is a physical constant so knowing that is the key…….””””””
Stephen,
The ideal gas law, and indeed any of the other equations of state such as the Van der Waals equation, apply ONLY to systems, where the values of p, v, T are absolutely constant everywhere in the system, and that the amount of material (n) also is fixed.
R is the ideal gas constant, so it is NOT K which represents Temperature, or k, which is Boltzman’s constant. One cannot go throwing around universal symbols willy nilly, as knowledgeable readers, are expecting standard physical terms to use accepted standard symbols.
In earth’s atmosphere, none of the p, v, T trio is even vaguely constant everywhere in the atmosphere. Nothing useful is learned by applying an equation to a system which simply does not conform to the set of restrictions for which that equation is valid.
George.
Robert used K instead of R. He later acknowledged that as an error. I just referred to it in passing by way of covering my back because I thought he knew something I didn’t.
I used R which is the gas constant which varies from gas to gas.
In Earth’s atmosphere P (pressure) is a constant if taken globally at less than geological timescales.
Likewise T being a measure of solar input is also nearly a constant because raw TSI varies so little.
n is also fixed because there are only so many gas molecules in the atmosphere (ignoring phase changes).
V is variable as seen from the rising and falling of the tropopause and the expansion and contraction of the upper atmosphere in response to solar variability.
So, if something internal to the system such as GHGs try to increase temperature in the atmosphere the variability of V provides a mechanism for offsetting the thermal effect of the GHGs.
The equation PV = nRT describes interlinked relationships and can be used to predict the system outcome from changes in individual variables.
In so far as Earths atmosphere is composed of non ideal gases the air circulation adjusts appropriately so that the equation is preserved overall.
Paul_K:
.
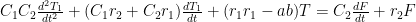Just in case you were tempted to rely on my algebra, I’ll mention that a factor is missing from one of my last missive’s equations. That equation should have read:
What does vary is the surface distribution of pressure and, indeed, cloudiness and albedo has varied.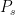
in N&Z — and albedo, that works across all of the bodies in the solar system. Be sure to include the gas giants, as soon as you figure out what their “surface pressure” and “surface temperature” is, compared to their albedo. Surely that is no crazier than including Venus — a wild card in the solar system — in the same plot as Europa, Mars, the Earth, and Mercury.
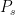that describes or predicts planetoid albedo!
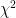for their fit.
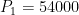bar and 
bar respectively and raised to the power of 
and $\nu_2 = 0.385$ respectively. Show me where that rule comes from, or what it has to do with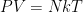 
, albedo, the DALR, or anything else in the known universe. Explain to me how a reference pressure that could only be found at the bottom of a water column 540,000 meters deep appears in an expression predicting surface temperatures on airless moons (while those same expressions completely ignore albedo).
Are we talking in the same solar system? Nikolov and Zeller isn’t about the Earth. It makes egregious claims for the planetary bodies of the solar system. Show me a plot of correlation between mean surface pressure on planetary objects —
As for the Earth — again I remind you that we are talking about Nikolov and Zeller, not just “the Earth”, and N&Z include the mean surface temperature of the Earth plotted against mean surface pressure. So while of course, sure, cloudiness and hence albedo varies with surface air pressure (for complex reasons) on Earth, this neither explains (by providing a causal factor) the increase in albedo in the 80s and 90s to all-time (recorded) highs and its subsequent decrease by 7% afterwards. Nobody knows why either one happened, in the sense that they predicted either event or can predict when the current albedo will shift again or in what direction. All that we know is that all things being equal increased mean albedo means decreased mean global temperature because it directly modulates insolation (primary heat source) by reflecting sunlight away with almost no air or surface warming and only indirectly and inconsistently modulates heat loss — cloudy days being consistently cooler than sunny days, most times and places.
So please, if you want to argue don’t change the topic of the argument in mid-stream. I assert that N&Z’s work is both incorrect and indefensible even as a hypothesis or wild assertion. By this I don’t mean to say that air pressure is completely irrelevant to e.g. the DALR, nor do I mean to say that the ideal gas law is completely inapplicable to atmospheric air, so don’t put words in my mouth or raise red herrings or straw men in the argument. I will say it again — albedo is visibly almost completely decorrelated with surface atmospheric pressure in planetary objects. It varies by a factor of three or more in planetary objects with no or almost no atmosphere — simply the color of their surface rock is different for different airless bodies. It varies by a factor of 5 (or even six) across the observable ranges. Some of the planetary objects with the highest albedo have almost no atmosphere. Some have atmospheres so thick and deep we don’t even know how thick and deep they are because we can’t see through them to the bottom. Atmospheric chemistry varies wildly. Temperature varies wildly. There is no simple physical rule based on
There is a simple rule predicting how planetoid greybody temperature should vary based on albedo, however. The physics in this rule is pretty elementary and has long since been verified. It is used (for better or worse) in climate science (including by N&Z) for the baseline temperature from which the GHE proceeds. Yet N&Z’s plot of the planets utterly fails to respect this rule — Europa, Titan and Triton have no business being on their “miracle curve” because all of three have somewhat anomalous albedos compared to their atmospheric pressure. Of course they aren’t on their curve — if you plot them using over the counter data rather than data processed with their secret sauce — and they aren’t believably on their curve under any circumstances (even with the sauce) if one plots the error bars for the data and uses them to compute an actual Pearson’s
So let’s stay on topic. We’re not discussing the weather — the tendency for rain on the Earth when the barometer drops, fair weather when the barometer is high — we’re not even talking about climate on the Earth, we’re talking about the scaled, dimensionless relative surface temperature of a list of planetoid objects compared to the moon, as a function of mean, dimensionless surface pressure scaled by
rgb