Guest Post by Willis Eschenbach
In my previous post, A Longer Look at Climate Sensitivity, I showed that the match between lagged net sunshine (the solar energy remaining after albedo reflections) and the observational temperature record is quite good. However, there was still a discrepancy between the trends, with the observational trends being slightly larger than the calculated results. For the NH, the difference was about 0.1°C per decade, and for the SH, it was about 0 05°C per decade.
I got to thinking about the “exponential decay” function that I had used to calculate the lag in warming and cooling. When the incoming radiation increases or decreases, it takes a while for the earth to warm up or to cool down. In my calculations shown in my previous post, this lag was represented by a gradual exponential decay.
But nature often doesn’t follow quite that kind of exponential decay. Instead, it quite often follows what is called a “fat-tailed”, “heavy-tailed”, or “long-tailed” exponential decay. Figure 1 shows the difference between two examples of a standard exponential decay, and a fat-tailed exponential decay (golden line).
Figure 1. Exponential and fat-tailed exponential decay, for values of “t” from 1 to 30 months. Lines show the fraction of the original amount that remains after time “t”. The “fatness” of the tail is controlled by the variable “c”. Line with circles shows the standard exponential decay, from t=1 to t=20. Golden line shows a fat-tailed exponential decay. Black line shows a standard exponential decay, with a longer time constant “tau”. The “fatness” of the tail is controlled by the variable “c”.
Note that at longer times “t”, a fat-tailed decay function gives the same result as a standard exponential decay function with a longer time constant. For example, in Figure 1 at “t” equal to 12 months, a standard exponential decay with a time constant “tau” of 6.2 months (black line) gives the same result as the fat-tailed decay (golden line).
So what difference does it make when I use a fat-tailed exponential decay function, rather than a standard exponential decay function, in my previous analysis? Figure 2 shows the results:
Figure 2. Observations and calculated values, Northern and Southern Hemisphere temperatures. Note that the observations are almost hidden by the calculation.
While this is quite similar to my previous result, there is one major difference. The trends fit better. The difference in the trends in my previous results is just barely visible. But when I use a fat-tailed exponential decay function, the difference in trend can no longer be seen. The trend in the NH is about three times as large as the trend in the SH (0.3°C vs 0.1°C per decade). Despite that, using solely the variations in net sunshine we are able to replicate each hemisphere exactly.
Now, before I go any further, I acknowledge that I am using three tuned parameters. The parameters are lambda, the climate sensitivity; tau, the time constant; and c, the variable that controls the fatness of the tail of the exponential decay.
Parameter fitting is a procedure that I’m usually chary of. However, in this case each of the parameters has a clear physical meaning, a meaning which is consistent with our understanding of how the system actually works. In addition, there are two findings that increase my confidence that these are accurate representations of physical reality.
The first is that when I went from a regular to a fat-tailed distribution, the climate sensitivity did not change for either the NH or the SH. If they had changed radically, I would have been suspicious of the introduction of the variable “c”.
The second is that, although the calculations for the NH and the SH are entirely separate, the fitting process produced the same “c” value for the “fatness” of the tail, c = 0.6. This indicates that this value is not varying just to match the situation, but that there is a real physical meaning for the value.
Here are the results using the regular exponential decay calculations
SH NH lambda 0.05 0.10°C per W/m2 tau 2.4 1.9 months RMS residual error 0.17 0.26 °C trend error 0.05 ± 0.04 0.11 ± 0.08, °C / decade (95% confidence interval)
As you can see, the error in the trends, although small, is statistically different from zero in both cases. However, when I use the fat-tailed exponential decay function, I get the following results.
SH NH lambda 0.04 0.09°C per W/m2 tau 2.2 1.5 months c 0.59 0.61 RMS residual error 0.16 0.26 °C trend error -0.03 ± 0.04 0.03 ± 0.08, °C / decade (95% confidence interval)
In this case, the error in the trends is not different from zero in either the SH or the NH. So my calculations show that the value of the net sun (solar radiation minus albedo reflections) is quite sufficient to explain both the annual and decadal temperature variations, in both the Northern and Southern Hemispheres, from 1984 to 1997. This is particularly significant because this is the period of the large recent warming that people claim is due to CO2.
Now, bear in mind that my calculations do not include any forcing from CO2. Could CO2 explain the 0.03°C per decade of error that remains in the NH trend? We can run the numbers to find out.
At the start of the analysis in 1984 the CO2 level was 344 ppmv, and at the end of 1997 it was 363 ppmv. If we take the IPCC value of 3.7 W/m2, this is a change in forcing of log(363/344,2) * 3.7 = 0.28 W/m2 per decade. If we assume the sensitivity determined in my analysis (0.08°C per W/m2 for the NH), that gives us a trend of 0.02°C per decade from CO2. This is smaller than the trend error for either the NH or the SH.
So it is clearly possible that CO2 is in the mix, which would not surprise me … but only if the climate sensitivity is as low as my calculations indicate. There’s just no room for CO2 if the sensitivity is as high as the IPCC claims, because almost every bit of the variation in temperature is already adequately explained by the net sun.
Best to all,
w.
PS: Let me request that if you disagree with something I’ve said, QUOTE MY WORDS. I’m happy to either defend, or to admit to the errors in, what I have said. But I can’t and won’t defend your interpretation of what I said. If you quote my words, it makes all of the communication much clearer.
MATH NOTES: The standard exponential decay after a time “t” is given by:
e^(-1 * t/tau) [ or as written in Excel notation, exp(-1 * t/tau) ]
where “tau” is the time constant and e is the base of the natural logarithms, ≈ 2.718. The time constant tau and the variable t are in whatever units you are using (months, years, etc). The time constant tau is a measure that is like a half-life. However, instead of being the time it takes for something to decay to half its starting value, tau is the time it takes for something to decay exponentially to 1/e ≈ 1/2.7 ≈ 37% of its starting value. This can be verified by noting that when t equals tau, the equation reduces to e^-1 = 1/e.
For the fat-tailed distribution, I used a very similar form by replacing t/tau with (t/tau)^c. This makes the full equation
e^(-1 * (t/tau)^c) [ or in Excel notation exp(-1 * (t/tau)^c) ].
The variable “c’ varies between zero and one to control how fat the tail is, with smaller values giving a fatter tail.
[UPDATE: My thanks to Paul_K, who pointed out in the previous thread that my formula was slightly wrong. In that thread I was using
∆T(k) = λ ∆F(k)/τ + ∆T(k-1) * exp(-1 / τ)
when I should have been using
∆T(k) = λ ∆F(k)(1 – exp(-1/ τ) + ∆T(k-1) * exp(-1 / τ)
The result of the error is that I have underestimated the sensitivity slightly, while everything else remains the same. Instead of the sensitivities for the SH and the NH being 0.04°C per W/m2 and 0.08°C per W/m2 respectively in the both the current calculations, the correct sensitivities for this fat-tailed analysis should have been 0.04°C per W/m2 and 0.09°C per W/m2. The error was slightly larger in the previous thread, increasing them to 0.05 and 0.10 respectively. I have updated the tables above accordingly.
w.]
[ERROR UPDATE: The headings (NH and SH) were switched in the two blocks of text in the center of the post. I have fixed them.
Instead of the sensitivities for the SH and the NH being 0.04°C per W/m2 and 0.08°C per W/m2 respectively in the both the current calculations, the correct sensitivities for this fat-tailed analysis should have been 0.04°C per W/m2 and 0.09°C per W/m2.
Are the tables mislabeled? It seems that either here or in the tables you have interchanged “NH” and “SH”.
Stephen Wilde, according to this theory, if cloud cover returned to 1984 levels, so would temperature. Is that what you would say? Since you say cloud cover has increased in the last decade, how much more increase is left to get back to 1984 levels. Also, why is the cloud cover going up and down like this, if it is not responding to temperature change. And how can a negative feedback be consistent with increasing temperatures, while already above average, going with decreasing cloud cover as happened during most of the 1990’s? Surely this is a positive feedback effect, if anything.
Robert Brown says:
June 5, 2012 at 5:23 pm
In brief, the Moon’s albedo is the albedo the other bodies would have if they had no atmosphere or ice.
Except that it’s not. I suggest that you look up the actual data on the Jovian moons.
Hi Robert: We have to bear in mind that Jupiter kicks out more energy than arrives at it from the Sun, and that its moons are in some cases tidally locked in ways that introduces a squeezing effect which warms them. It’s still early days for N&Z’s work; I am defending a space for them to expand it in where they can get feedback and ideas from the community. I am not blind to the difficulties with their theory, and have made my own criticisms and offered possible alternative interpretations of data. They are currently taking their time to assimilate criticism (including yours) and work on the issues raised. That is a reasonable way to do science.
Shooting them down in flames, heaping ad hominem abuse on them and misrepresenting how their equations fit together as Willis did is not.
Now, can you explain to me the physical basis for squaring the speed of light in the equation E=mc^2. Nothing can go faster than light, so this is obviously a meaningless unphysical concept isn’t it? 😉
Cheers
TB.
Jim D.
You will need to read my various articles to get answers to your questions. I don’t want to derail this thread with all the detail.
Robert Brown said:
“I really, truly don’t understand why you continue to defend the work of Nikolov and Zeller. Being skeptical of badly done climate science is one thing — endorsing junk science based on cherrypicked and possibly “adjusted” data just because it supports the implausible hypothesis that there is no such thing as a greenhouse effect, especially when one can DIRECTLY OBSERVE the CO_2 hole in TOA IR emissions, seems to me, at least, to be unwise.”
I’m puzzled as to why someone as experienced and knowledgeable as Robert gets so emphatic and emotional. I was intending to avoid discussion of N & Z here but this thread is nearly done and I can’t let Robert’s assertions pass.
As I’ve pointed out before, the N & Z findings are pretty much as one would expect from application of the well established and accepted Ideal Gas Law applied to planetary atmospheres.
Pointing to the moons of Jupiter as a suitable example to set against the other planets is misleading for the reasons that tallbloke points out. For those moons Jupiter itself is a secondary energy source so they are not comparable to the free standing planets used by N & Z.
The CO2 spectral ‘hole’ is an inappropriate distraction because the albedo response of the system as a whole takes that feature into account.
N & Z do not hypothesise that there is no greenhouse effect. They simply say that the phenomenon usually described as the greenhouse effect is a consequence of atmospheric density interacting with insolation at the surface so that temperature is highest at the surface where density is greatest.
That is how Wikipaedia and most science textbooks describe how the observed atmospheric temperature lapse rate arises. Surface temperature in a largely non GHG atmosphere is derived from surface heating plus conduction and convection rather than radiative processes.
GHGs (especially water vapour) actually aid the convective process and so stabilise rather than destabilising the system. The presence of GHGs means that the system can shift energy faster vertically to space than without them so the air circulation need be less violent horizontally in order to achieve in / out radiative balance.
The fact is that the atmospheric circulation of ANY planet reconfigures that circulation as necessary until radiative energy in equals radiative energy out and the surface temperature is set by atmospheric mass plus insolation at top of atmosphere.
If anything other than top of atmosphere insolation or atmospheric mass tries to change the surface temperature then the air circulation changes accordingly to negate the effect.
It really is that simple.
Shooting them down in flames, heaping ad hominem abuse on them and misrepresenting how their equations fit together as Willis did is not.
being only one of them, and zero predictions that are egregiously violated. Finally, the entire theory makes sense — it can be derived from simple principles of invariance and ultimately it is difficult to imagine it not being (very probably, at least approximately) true.
Now, can you explain to me the physical basis for squaring the speed of light in the equation E=mc^2. Nothing can go faster than light, so this is obviously a meaningless unphysical concept isn’t it? 😉
Actually, shooting them down in flames is absolutely the right thing to do when their work merits it, except that the truly correct thing all around is for them to shoot themselves down in flames and follow the recommendations of Feynman and present confounding as well as confirmatory data, and quite possibly refrain from publication altogether (or at the very least publish as a very speculative paper that is utterly honest about the problems/weaknesses) if the confounding parts exceed the confirmatory parts by some margin or the theory makes no physical sense.
IIRC the original study publication on your blog, nobody engaged in ad hominem (including Willis) at the beginning — I personally was impressed, although puzzled, by the perfection of the curve they obtained. People weren’t even “suspicious” at first, although a few people may have had their spidey-bullshit sense activated by e.g. that very (impossible) perfection. The problem evolved, as it always does, when some absolutely appropriate criticisms emerged (from Willis, from me, from several other physics people and people who work a lot with curve fitting) and the discussion polarized into defensive on one side and increasingly (but appropriately strident on the other side. When something is wrong (and it is your baby) it hurts, but science is cruel. I’ve been wrong in exactly that way. You get over it.
Regarding the speed of light — I’ve written a textbook on graduate level classical electrodynamics. Do you really want to go there and have me explain precisely why, dimensionally, this is exactly how one would naively expect energy to scale, why c is indeed a nearly universal scale parameter in classical relativistic and quantum relativistic physics (and above all, in electrodynamics and the tightly coupled theory of special relativity)? I’d say “read a few textbooks, possibly including mine” as an answer to a grad student, but the math (and conceptual basis) is tough going if you don’t work your way there over a few years of study. The first pass through special relativity for undergrad physics majors causes their brains to explode and recoalesce, better and smarter, six weeks later…
That’s why N&Z’s miracle equation does not work. I can point to something absolutely ubiquitous — light (and the general propagation of all massless fields) that has c as its/their speed. I can point to an entire geometric manifold — spacetime — that appears to have the speed of light quite literally built in to its invariances and coordinate transformation properties. I can point to a dozen physically observable consequences of that inertial coordinate invariance,
Point to one single point in any planetary atmosphere where a pressure of what was it — 54000 bar? — occurs. Or show me how a reference pressure of 200 bar (again, IIRC without looking it up in my own code/directory where I studied this) is relevant in any way to pressures on Mars, Europa. Show one could reason for including SOME but not ALL of the moons of Jupiter — there is absolutely no reason to exclude e.g. Ganymede except that if you plot it using their formula, it falls far from their curve. Of course if you plot Europa using the accepted data without using their special sauce, it falls far from their curve too.
Finally, as I’ve pointed out before and will again — the p-value of their absurdly nonlinear curve with its nonphysical parameters, for almost any reasonable error bars, is something like 0.99, or even higher. Although I didn’t really twig to that on the first pass through their work, that is as far as I’m concerned almost certain proof that they fit the data to the curve somehow, not the curve to the data. I do hypothesis testing with random distributions — dieharder is one big harness for generating p-values — and p = 0.99 is just as suspicious as p = 0.01. In particular, it is good justification for rejecting the null hypothesis “This is an unbiased work and it just happened to come out this way”. Throwing Ganymede in, replotting Europa, they merely further confirm what one already is almost certain is true.
I have no problem at all giving them a bully pulpit of sorts where they can be heard. Free speech is a valuable privilege in modern society. I do have a problem with sheltering them from equally free criticism or even by implication providing them with an “endorsement” of any sort while these enormous problems remain with their theory and the data.
The “right thing to do” is absolutely to withdraw the paper voluntarily and go back to the drawing board, and only come back when the theory makes sense. IMO that will be “never”, I’m sorry to say, because this is a senseless theory. It ignores far too much physics, and postulates absurd replacements to fit bent data across completely disparate regimes. But we have been through all of this, and I’m quite certain that nothing I say has the slightest impact. That alone is the mark of junk science. Not that they disrespect me — I could care less — but that they disrespect everybody who has pointed out these problems (and ignore those problems), and leave their paper out there, attracting flies.
rgb
Re:Willis Eschenbach says:
June 5, 2012 at 10:22 am
Hi again Willis,
Thanks for the thoughtful response.
You wrote:-
“Next, you say that a standard exponential decay is somehow theoretically more solidly based than a “fat-tailed” exponential decay. I fear I don’t see why, given that fat-tailed distributions are as common in nature as their standard exponential counterparts. You see this as using “evermore complicated response functions”, but I think that there is more physical justification for using a fat-tailed response than there is for using a standard response.”
The “standard exponential decay” function is not haphazardly chosen. It is THE UNIQUE solution to the heat balance equation for a single capacity system under the assumption that the Earth has a linear radiative response to temperature.
As soon as you postulate an arbitrary response function, you disconnect your results from a physically meaningful conceptual model, where the assumptions can be clearly stated and tested. I would have no problem with your re-stating the heat balance equation under a different set of testable assumptions and then fitting the new temperature solution to your data. That way, you have a story. But fitting an arbitrary functional form which cannot be tied back to a physical system looks like curve-fitting.
You also wrote:-
“This is one of the more enduring myths of the GCMs, that they somehow “exhibit non-linear behavior”. The two that I have tested, the CCSM3 and theGISSE models, are strictly and definitely linear. I have no reason to assume that the other models are different.”
The following article explains how the GCMs can exhibit linear behaviour over the instrumental period, and yet have a declared climate sensitivity much larger than would be expected if the linear behaviour were to continue into the higher temperature range. (Section E of the article also includes a derivation of the linear feedback equation and its solution. )
http://rankexploits.com/musings/2011/equilibrium-climate-sensitivity-and-mathturbation-part-2/
This second article below provides direct evidence that the GCMs really do exhibit a nonlinear radiative response – nearly every one of them – and makes use of the fact that you CAN fit a linear model to the GCM results over the instrument period.
http://rankexploits.com/musings/2012/the-arbitrariness-of-the-ipcc-feedback-calculations/
Evidently, the nonlinearity in the GCM’s is not a myth. However, it’s a completely separate question whether this feature is solely a property of the GCM’s or whether it is also a real world feature, since it only manifests itself in future projections.
So I would stand by my recommendations:- (a) that you continue to tie your response function to a physically meaningful model and (b) that you focus on attribution rather than long-term climate sensitivity. Just saying.
Re:Joe Born says:
June 5, 2012 at 4:40 pm
Joe,
You need to learn not to take on intellectual giants!
Thanks for your response re the second order linear ODE in support of your response function. It works in the sense of yielding your two-pole solution, But, at the risk of sounding like I am moving the goalposts, this wasn’t what I meant when I spoke of a “physically meaningful” governing equation.
Can you reparse the equation so that it is tied to, say, a heat balance for a multiple capacity system with some assumptions?
Paul
Re:Willis Eschenbach says:
June 5, 2012 at 10:22 am
My second attempt to post this. The first disappeared into cyberspace.
Hi Willis,
You wrote:-
“Next, you say that a standard exponential decay is somehow theoretically more solidly based than a “fat-tailed” exponential decay. I fear I don’t see why, given that fat-tailed distributions are as common in nature as their standard exponential counterparts. You see this as using “evermore complicated response functions”, but I think that there is more physical justification for using a fat-tailed response than there is for using a standard response.”
The “standard exponential decay” function is not haphazardly chosen. It is the UNIQUE solution to the heat balance equation for a single capacity system under the assumption that the Earth has a linear radiative response to temperature.
As soon as you postulate an arbitrary response function, you disconnect your results from a physically meaningful conceptual model, where the assumptions can be clearly stated and tested. I would have no problem with your re-stating the heat balance equation under a different set of testable assumptions and then fitting the new solution form to your data. That way, you have a story. But fitting an arbitrary solution form which cannot be tied back to a physical system looks like curve-fitting.
You also wrote:-
“This is one of the more enduring myths of the GCMs, that they somehow “exhibit non-linear behavior”. The two that I have tested, the CCSM3 and theGISSE models, are strictly and definitely linear. I have no reason to assume that the other models are different.”
The following article explains how the GCMs can exhibit linear behaviour over the instrumental period, and yet have a declared climate sensitivity much larger than would be expected if the linear behaviour were to continue into the higher temperature range. (Section E of the article also includes a derivation of the linear feedback equation and its solution. )
http://rankexploits.com/musings/2011/equilibrium-climate-sensitivity-and-mathturbation-part-2/
This second article below provides direct evidence that the GCMs really do exhibit a nonlinear radiative response – nearly every one of them – and makes use of the fact that you CAN fit a linear model to the GCM results over the instrument period.
http://rankexploits.com/musings/2012/the-arbitrariness-of-the-ipcc-feedback-calculations/
The nonlinearity in the GCM’s is not a myth. However, it’s a completely separate question whether this feature is solely a property of the models or whether it is also a real world feature, since it manifests itself in future projections.
So I would stand by my recommendations:- (a) that you tie your response function to a physically meaningful model (you choose and defend the model) and (b) that you focus on attribution rather than long-term climate sensitivity. Just saying.
tallbloke says:
After more than 5 months, they have shown no evidence of “assimilat[ing] criticism”. They have yet to admit one thing wrong in their original paper (and their subsequent “Part 1” response to critics) even though those things contain huge errors that show complete ignorance on very basic things like how one correctly adds convection into a model of the atmosphere and how one applies conservation of energy to a system that is not isolated. Until they are willing and able to correct such basic nonsense, they are rightfully dismissed.
This is just a bizarre question. Squaring c doesn’t produce something faster than the speed of light. It produces something of different dimensions. You can’t compare c and c^2 when c is dimensional… It is comparing apples to tofurky. (If you think c^2 is “larger” than c, try writing c in, say, astronomical units (AU) per second and square it and see what you get!)
Stephen Wilde says:
It has nothing to do with the ideal gas law. It has to do with people who don’t understand laws that have more than two variables in them. And, by the way, for someone who touts the ideal gas law, you ought to at least learn what the terms in it mean; Over at tallbloke’s in a post a few months ago you seemed to think that in the form pV = nRT, n is some sort of (number?) density; it is not. It is a number of moles. (If you divided n by V then you would have a molar density.) I can understand having this confusion at some level since n is sometimes used as a number density in, say, solid state physics (e.g. semiconductor devices); however, it is a pretty weird mistake for someone who claims to understand the implications of the ideal gas law better than scientists do.
Wikipedia and most science textbooks, unlike you, understand that while one might say that the lapse rate in the troposphere itself is mainly determined by convective processes, the vitally important boundary conditions on the temperature structure are provided by radiative processes. Please don’t project your own ignorance onto others…You are unjustly maligning them by claiming that they agree with your misconceptions.
Only for those who don’t understand basic physics.
joeldshore said:
“you seemed to think that in the form pV = nRT, n is some sort of (number?) density; it is not”
The definition of ‘n’ is as follows:
“n is the amount of substance of gas (also known as number of moles), ”
The more such substance in a given volume (V) the greater the density.
and joeldshore said
“the vitally important boundary conditions on the temperature structure are provided by radiative processes”
radiative processes are vitally important only in that radiative energy in must equal radiative energy out. It is the non radiative processes that adjust to ensure that that is achieved WITHOUT needing system energy content to rise.
More energy in the troposphere for whatever reason other than top of atmosphere insolation or atmospheric mass is simply dealt with by a change in tropospheric volume in accordance with pV = nRT.
If one increases insolation or atmospheric mass then the increase in volume will be accompanied by a temperature rise at the surface. Otherwise not.
“””””……Now, can you explain to me the physical basis for squaring the speed of light in the equation E=mc^2. Nothing can go faster than light, so this is obviously a meaningless unphysical concept isn’t it? ;-).
Cheers
TB……….”””””
Not so fast TB, in the expression, E = mc^2 , E is energy; not velocity, and because the equation must dimensionally balance, then mc^2, must also represent an energy; not a velocity; so it is simply no problem.
Everybody understands that in the non-relativistic world, the kinetic energy of a mass moving at a velocity v in some co-ordinate frame, is given by E = 1/2mv^2 .
But remember that E = mc^2 represents the energy that would be obtained by converting the entire mass m into energy, so that a mass balance would show the loss of some mass.
Particle Physicists, such as our friend Anna V even use a set of units where c = hbar =1, so that Einstein’s relation equates energy and mass as essentially the same thing. Interestingly the second term, hbar = 1 also equates energy with frequency (of photons; which just happen to travel at the speed of light) via the Planck/Einstein relation; E =hf , but in this case f is radians per second, and not Hertz.
In electomagnetism, it is the group velocity which can’t exceed c, and information propagates at the group velocity. The phase velocity is not so restricted.
If you point a flashlight up in the air and snap it rapidly in an arc, at some radial distance the spot of light is going faster than c. Just watch a wave arriving on a beach at a slight angle off normal, and you will see the contact point run along the beach must faster than the group velocity of the wave.
Stephen Wilde says:
There is absolutely no scientific reason to believe this. It contradicts a century of understanding of radiative transfer. It contradicts the actual results from including convective processes in a model correctly, whether it be a full-scale climate model or the simplest model for the greenhouse effect (such as the one that N&Z added convection to in a clearly incorrect manner by doing it so that it drove the atmosphere to be isothermal rather than having a lapse rate). Furthermore, nobody has succeeded in showing that it can obey conservation of energy, again at any level of mathematical modeling of the system.
It is simply a religious belief.
By the way, a change to a two time constant exponential model for Willis’curve fit, does not really introduce an extra parameter. The curve “shape” is defined by three variables, not four; two time constants, and the fraction of the starting value that represents one of the components. The other component then is by default the difference from 1 in amplitude
joeldshore said:
“It is simply a religious belief.”
Ok, got that.
The Ideal Gas Law is a religious belief 🙂
Yeah, Stephen, what they said. And more — N&Z already use Jovian moons in their plot. They just pick the moons. They already use Saturnian moons in their plot. They just pick the moons.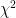
for the curve is probably less than 1, for 8 points fit. If you understand statistics, you realize that this is extremely unlikely. It’s up there along with rolling double sixes 8 times in a row (or rather, since one is fitting eight points with “4” parameters, 4 times in a row). Sure, it happens. And sure, it doesn’t happen very often, and if you’re not a sucker and it happens the first time somebody picks up the dice, you check to see if the dice aren’t loaded.
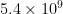Newtons per square meter. There is no physical process involving gases, especially not ideal gases, where this scale pressure has or could have the slightest bit of meaning, in part because no gas would remain gas at this pressure at planetary temperatures. 54,000 atmospheres is as far divorced from the ideal gas law (or any gas law) as it is possible to be — atoms would be jammed so close together that their valence and maybe even inner shell electrons would be interpenetrating and pure Pauli would be holding them apart. Nor is there any reasonable interpretation of an exponent like 0.065 applied to this term. It has nothing to do with dimension of simple e.g. bulk volume or surface or even possible fractal dimensions that might be relevant to gases. If you disagree, feel free to play through and refute me — show me how you get to an exponent of 0.065 from the ideal gas law or the more reasonable Vanderwaals gas, or a still more reasonable real gas with nontrivial interactions that can actually undergo phase changes (an ideal gas can’t).
of the fit (with their numbers only) and with my replacements of their numbers when I got bored with being censored and commented out inline in my own replies on TB’s blog and quit working on it, but that would be very easy to do. Then you can look at the distribution of Pearson’s chi-squared for the fit and decide for yourself if it is even conceivable that a fit of honestly noisy and uncertain data could be so perfect. It does show the Jovian moons and Mercury — plotted with readily available data — falling nowhere near their curve, including Europa, but the moon (reference, can’t miss), Titan (their numbers), Mars, the Earth, and Venus are still perfectly fit.
I repeat — I have personally attempted to reproduce their results with data I personally pulled. Lacking their secret sauce, the numbers I got were scattered — actually somewhat believably — all over the place, not on their miracle curve. Their curve basically “fit” the moon — no choice because they built that in — and at the far end, Mars, Earth and Venus. If you break things down, the last three are fit primarily with one of the two power laws, the first five with the other, if you use the specific values they used which happen to fit on the curve. This slightly oversimplifies, as the combination does bend things a bit on the middle of the Mars and smaller sequence where the forms both contribute, but it is a decent enough heuristic description.
I also recommend that you imagine their curve plotted with honest error bars on each point, which for some of the points are almost as large as the points themselves. Their curve goes almost perfectly through the points in the centers of the error bars.
Finally, I do teach intro thermodynamics, and have started to write a textbook embracing the subject. I can derive PV = NkT from first principles using both elementary arguments (good for intro physics) and using actual stat mech. I can, among other things, prove that the equilibrium state of an isolated atmosphere is isothermal in spite of having a pressure gradient. So saying that their result is “simple” because it depends somehow on PV = NkT is both incorrect — they advance no theoretical argument or derivation whatsoever of their strictly numerical result — and misleading, because PV = NkT actually scales in a very physically reasonable and observable way — the Boltzmann (or molar equivalent Ideal Gas) constant sets the scale just right so that the law works remarkably well for things like Oxygen at 1 atmosphere of pressure at roughly 300 K.
This is what their empirical fit does not do. I posted and showed in considerable detail way back then that their four parameter fit could be (indeed must be, to make sense of it) put in dimensionless form. In dimensionless form, each term is represented by two numbers — a dimensionless exponent and a physical constant. In fact, it is basically the following function:
The 54000 and 202 are pressures expressed in atmospheres. Note well, 1 atmosphere is roughly one bar or 100,000 Pascals (Newtons per square meter). There is no place in the atmosphere of any planet in the solar system that has a pressure vaguely near 54,000 atmospheres, or
The second term (which is largely what fits the last three planets, Mars through Venus), although on the surface more reasonable — at least pressures like 202 atmospheres are found in fluids on the surface of the Earth, such as 2000 or so meters beneath the surface of the sea, and one could imagine an exponent of 1/3 or some renormalized variant thereof, it is still pretty far divorced from actual gas atmospheric pressures even on Venus, so far divorced that it is very difficult indeed to see how such a pressure could possibly be relevant to e.g. Mars with its surface pressure of 0.0064 bar (yes, that is 202/0.0064 = 31560 times less than the reference pressure).
To put this in understandable terms, finding these scale pressures is analogous to discovering that we cannot describe the motion of a baseball accurately without using in an irreducible way a scale length a million times the size of the baseball, raised to the 17th power. It is saying that something that happens when atoms are jammed together so tightly that their electronic shells have deeply interpenetrated is somehow relevant to the physics of motion of those same atoms when they are so far separated, so diffuse, and so cold, that they almost never interact at all with long mean free paths and little kinetic energy. It is so obviously wrong that any physicist who sees N&Z’s results placed in dimensionless form will instantly say “this can’t possibly be right, it makes no sense at all”.
No, Stephen, 54,000 atmospheres cannot possibly be a scale constant that describes the atmosphere of Europa in some physically reasonable way. It is cosmic debris of pure nonlinear curve fitting, with enough parameters to fit an elephant once you don’t even bother to restrict the form of the fit on physical grounds.
I have the actual matlab code that replicates N&Z’s results with the rest of Jupiter’s moons thrown in! and with over the counter numbers used for most of the other planetary bodies, if you or anybody else wants to play. I was getting ready to actually compute a reasonable guestimate of the
You can then believe what you like about their result. I believe the evidence, especially when I’ve checked it personally against their theory myself.
rgb
But
Stephen says:
No…It is the magical way you think it operates that is a religious belief. E.g., how things magically change to make the surface temperature remain constant when you want it to and to change when you want it to.
Well Robert, I wasn’t trying to justify the N & Z work in detail because I think it is just a version of the Ideal Gas Law and the Standard Atmosphere. I told Ned that much myself and I await hearing how he proposes to distinguish those concepts from his idea of the so called Atmospheric Thermal Enhancement.
Anyway to my mind the important fact is that ANY two or more planets even get close to any sort of curve in the first place given the diversity of planetary conditions.
N & Z may have chosen just the Jupiter moons that suited them but personally I would discount ALL Jupiter’s moons because Jupiter is a secondary heat source.
Of more relevance here would be for you to explain to me and any others still reading why the Ideal Gas Law and the Standard Atmosphere do not or cannot explain how the atmospheric volume could change to negate any surface heating that would otherwise arise from causes other than greater atmospheric mass or more top of atmosphere insolation.
We see from observational evidence that the tropopause rises when the troposphere gets warmer. Given the expansion of volume evidenced by that observation why would the surface need to warm up at all ?
According to the Ideal Gas Law the available energy is spread through a larger volume which means there need be no more energy at the surface than before.
If there were no volume increase then yes the surface would get warmer but there is a volume increase and it is proportionate to the degree of warming.
So you can have more energy in a larger volume of air but instead of a higher surface temperature you just get a change in the air circulation pattern which serves to remove energy from the surface faster than before for a zero effect on surface temperature except regionally whilst energy is transported faster from surface to space and equator to poles.
Basic meteorology tells us that for every warm wind flowing poleward there is a cold wind flowing equatorward so the system remains in balance except for periods when the adjustment process is in progress.
In practice that means cyclical warming and cooling as the rate of energy throughput constantly changes as necessary to maintain system equilibrium despite attempts to disrupt that equilibrium from internal system characteristics other than atmospheric mass or external forcings such as a change in insolation.
All one will see from more GHGs is a shift in the air circulation with no change in average global system energy content. In so far as GHGs slow down outgoing radiation from the surface they facilitate a faster water cycle plus more conduction and convection which offsets the effect and the evidence for that faster or larger water cycle and more vigorous convection is the rise in the height of the tropopause with resultant latitudinal climate zone shifting.
But the sun and oceans already do that naturally to such an extent that the effect of our emissions will be unmeasurable.
All that is a natural application of the Ideal Gas Laws and if you aver that it doesn’t work like that then please say why not.
In particular you need to explain how an expanded atmospheric volume could fail to prevent surface warming when there is no increase in atmospheric mass or in energy from the sun.
Are you able to break the formula pV = nR (orK) T such that the atmosphere does not expand enough to eliminate the surface warming effect that would otherwise occur ?
What could prevent the atmosphere from expanding enough ?
There is no constraining force around the Earth apart from gravity and that stays constant for present purposes.
“””””…..Stephen Wilde says:
June 6, 2012 at 3:54 pm
Well Robert, I wasn’t trying to justify the N & Z work in detail because I think it is just a version of the Ideal Gas Law and the Standard Atmosphere………..pV = nR (orK) T………”””””
Your formula, contains p, V, n, R, T, or maybe K whatever that be.
The equation is based on an assumption; namely, that EVERY one of those five factors is absolutely constant over the “system” space. It has NO applicability to a system, where four out of those five terms may vary over the space occupied by the system. Fortunately the other one; R, is a physical constant.
Why do people keep traipsing out the “ideal gas law” in regard to the earth atmosphere where it has no applicability at all. It is an idealized formula for a sytem that is in static equilibrium. Earth atmosphere is never in any kind of equilibrium.
George.
K is the alternative term that Robert used for R.
The equation is based on the assumption that every one of those five factors is interlinked and will respond predictably to changes in the others.You accept that the value of R (or K) is a physical constant so knowing that is the key.
Thus the equation is capable of describing how the system equilibrium is maintained. Change any one or more of the terms and one or more of the others changes to restore equilibrium and confirm the validity of the Ideal Gas Law.
Now one could argue that the atmosphere not being an ideal gas the Law is capable of being invalidated but if one were to say that then you have to show exactly how and to what extent the non ideal nature of the gas causes a divergence from what the Law predicts.
As far as I am aware the differences are negligible in practice hence the regular use of the concept of a Standard Atmosphere.
So it comes down to the fact that there is an increase in volume when there is greater energy content in the troposphere. Can you demonstrate that that expansion is not sufficient to offset the surface warming that would have occurred in the absence of that expansion ?
I should add that Willis’s findings highlighted by this thread, if correct, could only be explained by a process such as the one described by the terms of the Ideal Gas Law.
If it were not for the Ideal Gas Law then clouds and sunshine would not be sufficient to explain observations.
The link between clouds, and the Ideal Gas Law is that changes in the volume of the atmosphere as predicted by the Ideal Gas Law are what change the vertical heights, the surface air pressure distribution beneath the tropopause and ultimately the amount of cloud globally.
In effect Willis is here proving the point though I know that as yet he doesn’t accept the link to surface pressure and cloudiness via the Ideal Gas Laws.
It pretty much removes the need for Svensmark’s cosmic ray hypothesis too. All one needs to change albedo is shifts in the surface air pressure distribution and those shifts occur as a result of the processes implicit in the Ideal Gas Law.
There is increase of both pressure and temperature at the surface; what else pushes the TOA up? It requires real force to do so.
Brian H asked:
“There is increase of both pressure and temperature at the surface; what else pushes the TOA up?”
Taking the globe as a whole there is no increase in pressure despite the increased energy content of the troposphere.To increase pressure globally you need greater atmospheric mass or a stronger gravitational field.
There is however, a redistribution of surface pressure regionally which is what changes cloudiness and albedo as per Willis’s findings.
In the absence of a change in pressure globally the rise in the tropopause is due to increased buoyancy within the troposphere. It is not necessary for the surface temperature to rise other than regionally and since what goes up must come down and what flows poleward must flow back equatorward the regional changes balance out.
An example:
During the late 20th century warming spell the more zonal circulation allowed the equatorial air masses to expand and the air flowing poleward across the mid latitudes became a fraction warmer.
However the more zonal jets reduced inflows of warm air to the polar regions which actually became colder. It is known that zonal jets tend to cut off and isolate the polar air masses.
The net effect was pretty much zero globally and the reverse applies when the jets become more meridional. Then the polar regions warm due to more incursions of warm air and the mid latitudes cool due to more polar air flows across them
There is a complicating factor in the Arctic because warm ocean water can flow into the Arctic ocean below the ice and melt it from beneath but the global air circulation and albedo simply changes accordingly to accommodate that feature too.
There is a case for arguing that the observed warming is simply an artifact of our non satellite temperature measuring system which failed to give appropriate relative weights to polar, equatorial and mid latitude temperature readings.
Hence the satellites showing much less variability.
∆T(k) = λ ∆F(k)(1 – exp(-1/ τ) + ∆T(k-1) * exp(-1 / τ)
Willis, I’m not sure how this is supposed to read but the number of brackets does not match here. Please check. However, I’d agree with others that it would be better to stick to a simple exp unless you can give a positive reason for doing otherwise (eg land and sea responses or different ocean depths 200m).
The other thing about different responses on different time scales. There must be a strong negative feedback on short time scales otherwise we would not be here to discuss it. I think this is what Linzen and Choi 2011 (On the Observational Determination of Climate Sensitivity and Its Implications) was picking up and why their feedback was a lot stronger than other studies.
They deliberately picked out sections of the record showing significant (deseasonalised) change.
These are, by choice, the parts of the record with the fastest change, hence the greatest radiative imbalance. Thus they are informative but probably not a measure of “the” feedback value (or the implied sensitivity) but that of short term response to imbalance.
They used actual data from ERBE and CERES TOA , this may be good alternative to the model TOA you used here and may provide a better test for you hypothesis.
Equally your choice of looking at the annual cycle during a period with a large decadal warming trend will reveal the annual time-scale response by the shape of the Lissajous figures and the decadal scale from the change of the figures over time.
I like this Lissajous approach as I think this kind of overall system analysis can tell us more about how it behaves than dubious home rolled statistics.
Equally I don’t think you can look for just for one time constant. I think there are different depths of ocean (primarily) involved that will have hugely different time constants. For a simple analogy think of paralleled capacitors : short term response being nF decadal uF and centennial scale mF ; deep ocean in farad !
The overall long term feedback must be negative as is witnessed by the last 4.5 billion years.
Somewhere in the middle is a positive feedback that gives rise to the bistable glacial-interglacial climate flip-flop. We are already at the hot state of the bistable, there is 4.5 Ga of data showing sufficient negative feedback for the system to be solidly constrained and not susceptible to “tipping points” .despite huge changes in “forcing”.
I suggest you look at the Lindzen and Choi paper, it looks at the tropics specifically as I suggested you could do in the earlier thread. They will probably point you to relevant data that you said you were unable to get for the albedo paper.
Your initial result still has value despite not accounting for LW. The fact that the model worked as well as it did indicates you should be able to make the gross approximation that LW is affected in a similar way to SW.
While there are a number of reasons why this is technically not accurate, it has to be said that your model is probably the most accurate of anything I have seen in the last 5 years of looking at a whole range areas of climate related studies.
Despite the naivety of the approach, I think that makes it a remarkable achievement.
/best.
Of more relevance here would be for you to explain to me and any others still reading why the Ideal Gas Law and the Standard Atmosphere do not or cannot explain how the atmospheric volume could change to negate any surface heating that would otherwise arise from causes other than greater atmospheric mass or more top of atmosphere insolation.
What, exactly, is it about the ideal Gas law that you are fond of? It is utterly free of dynamics. It describes one specific thing — a gas in a container in a gravity-free idealized environment, where the molecules of gas are basically non-interacting or are trivially (hard sphere) interacting, so it cannot describe phase changes.
If you want to understand atmospheric dynamics, you can start by looking at the Navier-Stokes equations — nonlinear partial differential equations so fiendishly difficult that mathematicians cannot even prove that general solutions exist, let alone find them in any but the simplest cases. Of course this isn’t enough — the Earth is a set of coupled Navier-Stokes systems (at least one for atmosphere and another for the oceans), and in the ocean, density is driven by salinity, evaporation, turnover, temperature, land runoff, ice melt, surface winds and weather — over 1 to 1000 year timescales (so some fraction of what the ocean and climate are doing now depends on what the ocean and climate did during the dark ages). In other words, too complex for humans to be able to solve. Still, if you want to understand, for example, the adiabatic lapse rate and why a lower atmosphere is warmer than the upper atmosphere even though gravity does no net work heating the system then Navier-Stokes is the right place to start, although one can make heuristic arguments that help you with the general idea without it.
The ideal gas law per se is (obviously) isothermal, and as soon as you start to let one parcel of gas expand into another (even in those heuristic arguments) you have to take a staggering amount of stuff into account — buoyancy, turbulence, compressibility, conductivity, non-Markovian past history so that even describing the parcel itself according to the ideal gas law with a strictly local temperature requires the full use of the first law of thermodynamics (work done by or on the parcel, heat flow in and out of the parcel, total enthalpy of the parcel) and then there is always the water in the air, which isn’t even approximately describable by an ideal gas law. Water is a polar molecule! It is always strongly interacting at a molecular level, and it has startlingly nonlinear radiative properties as well. So I don’t really “get” your fixation on the ideal gas law as an explanation for Nikolov and Zeller’s “miracle”.
On top of this, I don’t understand what you are asking me to do. Explain how the atmospheric volume would change to negate any surface heating that would otherwise arise from causes other than greater atmospheric mass? Greater atmospheric mass doesn’t cause any surface heating. What changes in atmospheric volume? And what about albedo? TOA insolation matters, sure, but the fraction of that which reaches the ground is determined in large part by straight up albedo, and the albedos of the planets on N&Z’s list are staggeringly different. I don’t even understand what this sentence means — its referents make no sense. Volume doesn’t have anything to do with surface heating. Surface heating is pretty much caused by insolation first, winds blown in from places where insolation caused surface heating second, and winds blown in from still more delayed reservoirs (e.g. the ocean) carrying heat delivered by insolation in some mix of air temperature and latent heat (humidity). What on earth does “greater atmospheric mass” have to do with anything, aside from providing more matter to help carry this heat from place to place?
rgb