Guest Post by Willis Eschenbach
After I published my previous post, “An Observational Estimate of Climate Sensitivity“, a number of people objected that I was just looking at the average annual cycle. On a time scale of decades, they said, things are very different, and the climate sensitivity is much larger. So I decided to repeat my analysis without using the annual averages that I used in my last post. Figure 1 shows that result for the Northern Hemisphere (NH) and the Southern Hemisphere (SH):
 Figure 1. Temperatures calculated using solely the variations in solar input (net solar energy after albedo reflections). The observations are so well matched by the calculations that you cannot see the lines showing the observations, because they are hidden by the lines showing the calculations. The two hemispheres have different time constants (tau) and climate sensitivities (lambda). For the NH, the time constant is 1.9 months, and the climate sensitivity is 0.30°C for a doubling of CO2. The corresponding figures for the SH are 2.4 months and 0.14°C for a doubling of CO2.
Figure 1. Temperatures calculated using solely the variations in solar input (net solar energy after albedo reflections). The observations are so well matched by the calculations that you cannot see the lines showing the observations, because they are hidden by the lines showing the calculations. The two hemispheres have different time constants (tau) and climate sensitivities (lambda). For the NH, the time constant is 1.9 months, and the climate sensitivity is 0.30°C for a doubling of CO2. The corresponding figures for the SH are 2.4 months and 0.14°C for a doubling of CO2.
I did this using the same lagged model as in my previous post, but applied to the actual data rather than the averages. Please see that post and the associated spreadsheet for the calculation details. Now, there are a number of interesting things about this graph.
First, despite the nay-sayers, the climate sensitivities I used in my previous post do an excellent job of calculating the temperature changes over a decade and a half. Over the period of record the NH temperature rose by 0.4°C, and the model calculated that quite exactly. In the SH, there was almost no rise at all, and the model calculated that very accurately as well.
Second, the sun plus the albedo were all that were necessary to make these calculations. I did not use aerosols, volcanic forcing, methane, CO2, black carbon, aerosol indirect effect, land use, snow and ice albedo, or any of the other things that the modelers claim to rule the temperature. Sunlight and albedo seem to be necessary and sufficient variables to explain the temperature changes over that time period.
Third, the greenhouse gases are generally considered to be “well-mixed”, so a variety of explanations have been put forward to explain the differences in hemispherical temperature trends … when in fact, the albedo and the sun explain the different trends very well.
Fourth, there is no statistically significant trend in the residuals (calculated minus observations) for either the NH or the SH.
Fifth, I have been saying for many years now that the climate responds to disturbances and changes in the forcing by counteracting them. For example, I have held that the effect of volcanoes on the climate is wildly overestimated in the climate models, because the albedo changes to balance things back out.
We are fortunate in that this dataset encompasses one of the largest volcanic eruptions in modern times, that of Pinatubo … can you pick it out in the record shown in Figure 1? I can’t, and I say that the reason is that the clouds respond immediately to such a disturbance in a thermostatic fashion.
Sixth, if there were actually a longer time constant (tau), or a larger climate sensitivity (lambda) over decade-long periods, then it would show up in the NH residuals but not the SH residuals. This is because there is a trend in the NH and basically no trend in the SH. But the calculations using the given time constants and sensitivities were able to capture both hemispheres very accurately. The RMS error of the residuals is only a couple tenths of a degree.
OK, folks, there it is, tear it apart … but please remember that this is science, and that the game is to attack the science, not the person doing the science.
Also, note that it is meaningless to say my results are a “joke” or are “nonsense”. The results fit the observations extremely well. If you don’t like that, well, you need to find, identify, and point out the errors in my data, my logic, or my mathematics.
All the best,
w.
PS—I’ve been told many times, as though it settled the argument, that nobody has ever produced a model that explains the temperature rise without including anthropogenic contributions from CO2 and the like … well, the model above explains a 0.5°C/decade rise in the ’80s and ’90s, the very rise people are worried about, without any anthropogenic contribution at all.
[UPDATE: My thanks to Stephen Rasey who alertly noted below that my calculation of the trend was being thrown off slightly by end-point effects. I have corrected the graphic and related references to the trend. It makes no difference to the calculations or my conclusions. -w.]
[UPDATE: My thanks to Paul_K, who pointed out that my formula was slightly wrong. I was using
∆T(k) = λ ∆F(k)/τ + ∆T(k-1) * exp(-1 / τ)
∆T(k) = λ ∆F(k)(1 – exp(-1/ τ)) + ∆T(k-1) * exp(-1 / τ)
The result of the error is that I have underestimated the sensitivity slightly, while everything else remains the same. Instead of the sensitivities for the SH and the NH being 0.04°C per W/m2 and 0.08°C per W/m2 respectively, the correct sensitivities should have been 0.05°C per W/m2 and 0.10°C per W/m2.
-w.]
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
There has been several comments with link to various versions of a relative humidity graph showing declining relative humidity in the upper atmosphere. I created the graphs. It is in the “Water Vapour Feedback” section of my “Climate Change Science essay at
http://www.friendsofscience.org/assets/documents/FOS%20Essay/Climate_Change_Science.html#Water_vapour
A link to the NOAA data source is given just above the graph. To recreate the graph use Variable “Relative Humidity”, select “Seasonal average”, First month of season “Jan”, second month “Dec”. Select “Area weight grids”. You can select “analysis level” from 1000 mb to 300 mb.
This is a very large dataset of radiosonde data. It is not cherry picked. The second graph shows specific humidity (g/kg air) at 400 mbar pressure level has declined by 13.5% (best fit line) from 1948 to 2011. Also, satellite data can now measure humidity in the upper troposphere. The third chart shows declining humidity from satellite data in the 300 mb to 500 mb range.
A constant RH in the topical troposphere would cause an enhanced warming at about 8 km, but no such warming is found in any dataset, radiosonde or satellite, thus confirming the declining humidity found by the radiosonde data. Increasing humidity and temperatures in the tropical troposphere would have caused increased hurricane energy, but in fact, global hurricane activity has decreased to the lowest level in 32 years.
Further down in the water vapour feedback section of the essay you will find a graph of specific humidity (g/kg) versus CO2 concentration. It shows water vapour specific humidity declining in the topics 0.11 g/kg, or 13%, from 1960 to 2011. Note the very high R2 correlation of 0.713. The graph is here:
http://www.friendsofscience.org/assets/documents/FOS%20Essay/SH400TropicsVsCO2.jpg
This is important because a line-by-line radiative code shows that an absolute change in the quantity of water vapour in a layer 300 to 400 mb pressure level has 30 times the effect on out-going radiation as the same change near the surface. (The specific humidity vapour at 300 to 400 mb is 5.2% of that near the surface.) It matters where in the atmosphere the humidity changes. Increasing humidity near the surface has very little radiative effect on temperatures.
RichardCourtney, well there isn’t anything to address as you still fail to grasp the concept of freqency response of a low pass filter.
Now who is silly here.
George E. Smith Let me make this clear, I am a luke warmer.
Looking at a high frequency response is like looking at the response of a tree when you shake it vigourously: It won’t bend a lot. However, if you push it slowly, repeatedly, you can get it into a swing with a so big amplitude that it breaks.
The concept here is eigenfrequency.
Now we can observe a lot of those eigenfrequency harmonics in climate: eg the multidecadal oscillation, the Dangaard-oescher cycle and the ice age cycle. Now if one of those natural cycles tunes in with an external forcing, you get a major climatic effect. The ice age cyclicity is an obvious example.
Unfortunately the annual cycle is not one of those natural climate harmonics, and that is the reason why the response is so low as Willis discovered, and Douglas Hoyt before him.
I inadvertently submitted the following comment on the previous post rather than here. Basically it appears, contrary to what I would have thought, that Mr. Eschenbach’s approach is likely to understate sensitivity significantly.
Specifically, I applied Mr. Eschenbach’s approach to synthetic data I generated from a system whose step response is 0.2 * [1 – exp(-t/2)] + 0.4 * [1 – exp(-t/50)], i.e., to a system in which lambda is 0.6. At least if I did the math right, Mr. Eschenbach’s approach instead infers a sensitivity of 0.34. The stimulus I applied was a 600-sample record of a sinusoid whose period was 120. (All those dimensionless time values can, for instance, be months.) A similar result was produced from a period-12 sinusoid. The rms error in each case was less than 10^(-6)
I’m not sure what all the conclusions one might draw from this are. But, if I did it right, it seems at a minimum we can conclude that inferring low sensitivity from this experiment, elegant as it was, may not be warranted.
I would be greatly interested in hearing from anyone who has tried something similar; it could be that I just did the math wrong.
I can’t say I have fully followed Willis’ argument, in these two postings, the first using annualized data for TSI solar energy input, and the second; following criticism of that approach; using the continuous and trivially calculated orbital variations in TSI throughout the year, because of the known earth orbital parameters. Willis then seems to be saying that coupling that with available albedo, and Temperature data over a 14 year period, he was able to completely explain the Temperature data with just the albedo data, and the observed Temperature (anomalies) data for that period, with no call for CO2 data input at all.
I should comment here that “albedo” isn’t just a four syllable fancy word for reflectance…. Albedo specifically refers to the reflectance/scattering OF INCOMING SOLAR SPECTRUM ENERGY, back into space. If the externally detected radiation coming from earth is NOT solar spectrum radiation, such as LWIR from the surface, it ISNOT a part of earth’s albedo.
Albedo includes a 2-3% Fresnel reflection from water surfaces; given approximately by
((N-1)/(N+1))^2, where N is the refractive index (1.333) for water. It includes Mie scattering by water droplets in clouds, which is simply ordinary geometrical optical refraction of mostly light, by water droplets.. It’s easy to show that a single water drop, focusses light into an almost 2 pi cone of light exiting from the far side of the drop. A handful of such encounters, and the light is scattered into an isotropic distribution with no preferred direction. For smaller droplets, optical diffraction theory, rather than geometrical (ray ) optics has to be invoked, but the net result of diffraction, is an even more scattered oupput from the droplet. In any case this diffuse brightness of cloouds is NOT optical reflectance, it is scattering, and it is not water absorption, followed by LWIR emission The original wavelength (frequency) of the sunlight is preserved or it isn’t part of albedo. Snow and ice also contribute to albedo. In the case of ice that has melted so it isn’t still snow crystals, the reflectance isn’t much, still pretty much the same 2-3% as for water. And just so nobody raises it, I will say here, that at glancing angles, ice reflectance increases rapidly above the 2% normal incidence value. specifically, R remains almost constant up to the Brewster angle, arct tan(N), at which the reflected beam is completely plane polarized, and then it increases above that that ahppens at about 53 deg (from normal) for water or ice. For snaow, the apparent reflectance is much higher (for fresh snow), but it too is more a scatteing like clouds, rather than reflectance. Snow a few hours old that has had sun on it, has much lower reflectance because of micro surface melting, and refreezing.
So water is a big player in albedo reflectance. Surprisingly many plants such as grasses and such have quite high solar relfectances, as do a lot of rock materials.
So Willis is more or less suggesting that variations in the amount of sunlight reflected back to space largely by water, alters the captured component of solar spectrum energy, in such a fashion as to completely explain the observed Temperature changes at least over that 14 year period.
His analysis, is a more detailed example of a couple of extreme mind experiments I have suggested several times from many years ago.
I suspect that Richard S. Courtney is aware of those posted at other locations, in the past.
I call these two experiments, the “Birdseye” experiment, and the “Venus” experiment. The first is named after the chap (Birdseye) who invented quick frozen foods; legend has it as a result of ice fishing, where the catch was quick frozen right out of the water.
So the aim of the birdseye experiment, is to quick freeze the earth, as an aid to removing all water from the atmosphere; that is every single molecule of water to be removed; even if you have to use tweezers to get the last few.
So the experiment which is done on your X-Box, or Teracomputer, calls for turning off the sun, and lowering earth surface Temperature to zero deg C, unless it is already colder than that, in which case it retains its lower Temperature. Atmospheric water all precipitates out, either as liquid or solid depending on where it is. At zero deg surface Temperature, the oceans do not freeze, because of the saltiness, Now according to legend, if it were not for CO2, the earth would be a frozen ice ball at 255 K, but we will leave all CO2 and other non H2O GHGs intact.
So now we turn the sun back on, and restore all the laws of physics.
Now in the absence of positive water feedback to CO2 global warming, we are all supposed to eventually freeze to death, absent the greenhouse warming of H2O vapor in the atmosphere.
I believe that Peter Humbug actually did this experiment, at least the water removal aspect of it on his tera Playstation, and he said he got all the water back in just 3 months.
So what happened ? Well with no water in the atmosphere, there are no clouds, and no water vapor absorption of any incomingsolar energy, so the albedo, isn’t anything like 0.35, or whatever it usually is, so with TSI at an annual average of 1362 W/m^2, and not much atmospheric reflection and absorption, we have the mother of all global warming forcings, and the surface level solar irradiance is way higher than normal; maybe by 20% or so, some 270 W/m^2 of positive forcing, and since the ocean immediately below the surface is still warm, we now get massibe evaporation from all water bodies in sunlight, and H2O starts to repopulate the atmosphere. The surface Temperatures may go up substantially rather than drop, and that just means more evaporation and more water vapor in the atmosphere. So now the water vapor starts to attenuate some of that incoming sunlight, and the atmospheric warming starts massive convection of warm moist air to higher altitudes, where after sundown, eventually clouds will start to form, and now the albedo of earth starts to creep up again, which will lower the solar energy reaching the ground and the ocean, and moderate the heating.
Well eventually you can see where this is heading; more water in the atmosphere, more clouds more albedo, reduced surface sunlight, as well as of course more water vapor induced greenhouse warming of the atmosphere by surface LWIR captured by H2O, with a trifle of assistance from the pre-existing CO2. Eventually the TSI is cut down to size, and an energy balance is reached at some Temperature which I call the Bridseye Temperature (and state).
I have no idea where the BE Temperature is relative to today’s Temperatures.
So how about that other extreme, the “Venus” experiment.
Well we do the opposite. We crank up the sun, and we raise the whole earth up to say 120 F, and we fill the atmosphere from pole to pole and from the ground to say 50,000 ft with water vapor and clouds, so no blue sky is showing anywhere. Then we set the sun back to normal..
Well we already know that with water saturated clouds from the ground up, there is virtually no sunlight reaching the ground at all, day or night.
So now it is going to get bloody cold on the ground, with no sunlight at all, and it is going to start precipitating; rain, hail, sleet, snow, frogs, whatever. It will rain for 40 days, and 40 nights, until enough water has precipitated out of those all sky clouds, that a little sunlight shows through, and you can start to tell whether it is day or night.
With some sunlight starting to filter through the clouds,it will actually stop cooling, in some places, and as more water precipitates out, the daylight will increase, and it will get a little warmer, and the torrential rains and snow storms will moderate, and the Temperature on the surface will slowly warm p, and more sunlight get through, and clouds break up giving some clear skies. Eventually the sunlight reaching the earth will match the LWIR radiation losses to space, and the Temperature will settle down to some Temperature I call the Venus Temperature. I have no idea where the Venus Temperature is, compared to today’s Temperatures. In particular, I have no idea where the Venus Temperature is relative to the Birdseye Temperature.
One is a steady state Temperature established from a frozen iceball exteme condition, while the other is a steady state Temperature established from a thermal runaway extreme condition.
If the Birdseye Temperature, and the Venus Temperature are different, we can be sure that the condition between those two Temperatures, is unstable, and if the earth climate were located between Birdseye, and Venus, then the system would be driven to one or other of those steady state stable Temperatures; it cannot remain in the unstable regime between them.
So who can provide a rational Physical explanation, for why the earth climate would have two stable states; or even more. There could be several pairs of temperatures, with unstasble regions between the members of the pair, and stable conditions between pairs.
Well I personally don’t know of an explanation for any difference between the Venus Temperature and the Birdseye Temperature. Now remember that we are talking about the earth orbital system as it exists today. We believe from Milankovitch, that major changes in earth orbital parameters would change the system, and crete new states. But with the way things are today, it seems that we are sitting in a feedback regulated stable steady state, where TSI and albedo, regulate the earth Temperature.
Leif S has told us many times, that the sun does not control the earth climate. Well I believe to some extent that is true. If we once had a weak sun, we likely had a different albedo too. And if we fiddle with the CO2, I believe that all we do is shift the albedo, in Willis’ model to some other value. but Temperature wisw, nothing much happens.
It is the direct H2O interplay with TSI through albedo, that regulates earth’s Temperature, and if we had no CO2 in the atmospere, well we would just have a slightly different albedo, but a 255 K ice earth, we would not have.
As for Hans E’s objection to Willis’ model. It is certainly true, that a system, with a hundred year or thousand year or million year resonance, such as thre ice cycles he mentions, will not be significantly driven by an annual cyclic forcing signal, such as Willis used in his analysis; driving a resonant system, that far off frequency will certainly produce small responses.
But Willis, was looking at responses over just 14 years, from data for the actual Temperature and albedo data he has. Wh cares about a quite unrelated response that is clearly due to some other more cataclysmic system change, than elliptical orbital change in instantaneous TSI.
Willis,
I’ve only just picked up this thread unfortunately. Otherwise I would have commented much earlier on this and your earlier thread.
I think you have drifted off the rails somewhere. You may still have an important finding buried here concerning the relative strength of shortwave variation as a control on the temperature response – but your argument is incoherent mathematically.
The main problem is that the temperature formula you are using here is NOT a solution to the linear feedback equation. It seems clear from your comments about the meaning of lambda and tau, together with your references back to the original matching of the linear feedback equation to the GISS-E results, that you think that it is. Well, it just ain’t.
If you want to apply a single formula for temperature, which DOES represent the solution to the linear feedback equation, you need, using your definition of lambda:-
T(k) = Fk*α *λ + (1-α) * T(k-1)
where Fk is the cumulative forcing at the kth time step,
α = 1 – exp(-DELT/τ)
DELT is the timestep size in years, in your case (1/12). The e-folding time, τ, also has units of years.
You can obtain the above by analytic superposition. (A slightly different, and slightly less accurate form, can be obtained from the convolution integral using a response to a unit step forcing of
T = λ *(1 – exp(-t/τ)) . To understand the difference, check out a series expansion of the exponential term.)
You need to rework your results and see whether (a) you still obtain a great fit and (b) what values of λ and τ you come up with.
Hans Erren says:
June 2, 2012 at 1:17 pm
Hi, Hans, thanks for your comment. It appears you have failed to notice that my analysis also fits the decadal trends of both the NH and the SH. If your claim were true, my method couldn’t possibly do that … and yet it does.
w.
Paul_K says:
June 3, 2012 at 11:30 pm
Riiiiight, it’s “incoherent mathematically”, and yet despite that it correctly calculates both the annual and the decadal temperature variations in both the NH and the SH …
I would say you have a different definition of “incoherent”. I did what I did. You may not like it, or think I have not described it correctly, or something, I’m not sure what. But in fact, what I have done works.
Now, what I have used is
∆T(k) = λ ∆F(k) / τ + ∆T(k-1) * exp(-t / τ)
where lambda is climate sensitivity and tau is the time constant.
If that is incorrect in your view, and it certainly could be, then please give me what you think is the correct formula for ∆T(k).
Many thanks, I await your formula,
w.
I like the general idea, which is determining the feedbacks empirically from the the annual cycle.
This will indeed capture all effects which work on this timescale, e.g. water-vapor-, cloud- and snow-albedo-feedback and give a good estimate of the local climate sensitivity.
It gets complicated by (ocean and atmospheric) heat capacity and heat transfers. The implicit assumption seems to be that there’s no net heat transfer between southern and northern hemisphere. To the degree that’s not true, the temperature response and climate sensitivity is underestimated. The results also suggest that the heat capacity is not totally accounted for, because the final climate sensitivity is just the magnitude of the annual cycle. If we locked the earth on SH summer (+100W), would it eventually just get ~5°C warmer? I don’t think so…
Hans Erren:
I am replying to your post addressed to me at June 3, 2012 at 2:54 pm. It says;
I answer you are “silly here”.
I do “grasp the concept of frequency response of a low pass filter” while you don’t. Willis’ model matches annual and decadal effects. This indicates that any longer frequencies filtered from the model must be of centennial or longer length. Such long frequencies are not relevant to anthropogenic effects (i.e. the purpose of present climatological investigation).
You are using your ignorance (which may be real or feigned) of “the concept of frequency response of a low pass filter” as an excuse to not address my points.
Please address my points or go away. I remind that they are as I stated at June 2, 2012 at 2:41 pm.
Richard
If we set a = λ/τ and b = exp(-1/ τ), the formula can be simplified to:
T(n+1) = a*F(n+1) + b*T(n)
Now it’s a little more obvious that you’re calculating an exponential moving average of the flux F.
The equilibrium temperature to a constant flux F, i.e., the climate sensitivity, is then:
T = a/(1-b) * F
It’s kind of estimating the heat capacity and then using it to extrapolate the equilibrium, but it’s not using the physical formulas, e.g. cooling should actually be a function of T^4, etc.
The main result, that the lower SH warming correspondents approximately to its smaller annual cycle is probably a coincidence.
Paul_K: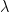 significantly for some multiple-pole systems. Also, although it does capture trends, the Northern- and Southern Hemisphere trends it captured in his example look to me to be off by 20% and 50% respectively.
significantly for some multiple-pole systems. Also, although it does capture trends, the Northern- and Southern Hemisphere trends it captured in his example look to me to be off by 20% and 50% respectively.
I, too, found Mr. Eschenbach’s formula puzzling. The way I eventually explained it to myself is given at http://wattsupwiththat.com/2012/05/29/an-observational-estimate-of-climate-sensitivity/#comment-995842. (I note that a LaTeX infelicity crept into the Dirac-delta-function definition, but presumably that won’t detain you.)
My sense is that in a simple single-pole system his approach overstates the lag by half a sample period but is otherwise reasonably effective. But it seems to underestimate the long-term sensitivity
Um… All EXTREMELY interesting, but has anyone done any calculations on the cumulative thermal effect of burning all the oil/coal/wood/ethanol/-fry-oil/witches that define our industrial civilisation? It seems to me that all this burning of stuff must heat up the atmosphere,and as NASA tells us the amout of radiated heat hasn’t changed (sorry… don’t ask me for a reference… I don’t remember where I read that), then all that heat must have had an effect.
Just a thought.
Willis,
Jeez,what a grouchy response! And I was only trying to help.
“If that is incorrect in your view, and it certainly could be, then please give me what you think is the correct formula for ∆T(k).”
I gave you the precise formula already in terms of temperature change from time zero. Your deltaT’s are between timesteps. So, to go from my formula to yours, you only need to write the formula for Tk-1 and take the difference. In your format, your formula should then become:-
∆T(k) = λ ∆F(k)(1 – exp(-DELT/ τ)) + ∆T(k-1) * exp(-DELT / τ)
If you want to work in months for tau, then you can continue to set DELT to unity (but I don’t really like it).
The difference between the above formula and your formula then is that the lambda value and the tau values in the above REALLY DO REFLECT the climate sensitivity and e-folding time ( = heat capacity * lambda) as generally derived from the linear feedback equation. If you equate the two versions, you will see that your version of lambda is actually equal to the climate sensitivity times tau times (1 – exp(-1/τ)).
lambda(Willis) = lambda(corrected version) * τ * (1 – exp(-1/τ))
This is why “your” climate sensitivity times a forcing of 3.7 does not give you the same answer as your spreadsheet calculation.
I tested the cumulative version and the incremental version of the above formulas on your spreadsheet and they yield the same result as you obtained in terms of the value of tau but with a revised value of climate sensitivity. Since YOUR version of climate sensitivity and MY version of climate sensitivity are only different by a constant factor for the same value of tau, the modeled (predicted) values of temperature are identical to the values that you obtained.
So this doesn’t change your main conclusions, but does improve mathematical coherence.
Stop grouching and put the check in the mail.
Paul
joeldshore says:June 3, 2012 at 9:01 am
Steve Keohane says:
Wrong again, Joel, the charts are not accrued by concordance with a belief system, they are the only ones I have seen. No picking at all, just the only ones to come along. You certainly spend a lot of energy constructing fantasies.
Fine…So, you personally didn’t cherrypick the data. You just visited places where those who presented the graphs cherrypicked them. So, you are blissfully unaware of scientific data that goes against what you want to believe because you hang out in places that present only cherrypicked data to support your preconceptions.
Interesting you left out that it is THE NOAA dataset, in total. Your line“So, you are blissfully unaware of scientific data that goes against what you want to believe because you hang out in places that present only cherrypicked data to support your preconceptions.”
must then apply to yourself.
Joe Born,
Nice analysis. You got there the hard way, I think.
See my previous post for an explanation of the difference between the short and long-term estimate of climate sensitivity.
Ken Gregory says: June 3, 2012 at 2:53 pm
Thanks for your post and link. I think RH% is the unspoken elephant in the room. If RH% had been constant, then rising temperature over the past century would indicate warming. Without running the numbers, there could still be a bit of warming. I have been helping a friend with a greenhouse building company, who build in what they call ‘climate batteries’ or heat storage chambers. Basically they are the subsoil, isolated by insulation, with the greenhouse air pumped through, storing heat for the winter and cooling in the summer. I came up with formulas so they could calculate the size of the ‘battery’ needed for the size of the greenhouse. It seems to work empirically. I will try to apply this to the atmosphere to see if the mass change due to RH% Δ overrides the temperature increase insofar as total heat content is concerned.
“Second, the sun plus the albedo were all that were necessary to make these calculations. I did not use aerosols, volcanic forcing, methane, CO2, black carbon, aerosol indirect effect, land use, snow and ice albedo, or any of the other things that the modelers claim to rule the temperature. Sunlight and albedo seem to be necessary and sufficient variables to explain the temperature changes over that time period.”
If you perform multiple regressions with limited independent variables (leaving out relevant forcings, for example, things we know affect climate energies), you will over-fit the variables you have included. After that, it will be completely unsurprising that you seem not to need any other contributions. And – it will be incorrect.
Paul_K says:
June 4, 2012 at 7:02 am
Paul, calling my work wrong is a simple statement. Calling it “mathematically incoherent” is an insulting attack. You seem surprised that when you attack someone, they bite back.
Moving on to the substantive point, you give the formula:
I see that you are correct. The difference is quite small, however, and when I re-run the analysis it doesn’t affect the fit. All it affects is the value of lambda. Instead of the climate sensitivities for the SH and the NH being 0.04 and 0.08 °C per W/m2 as I calculated, they are 0.05 and 0.10 °C per W/m2.
Thank you for the correction, Paul. I apologize for grouching at you, but having my work called “incoherent” is a slap in the face. I’ve posted a correction in the head post.
All the best,
w.
Paul_K:
Thanks for your input on the modeling equation. I had actually wanted to add yet another refinement so that the results would not be off a half period, as I think they tend to be, but my eyes tend to glaze over when I do that stuff, and I doubt that it matters much. .
Anyway, I applied your equation to synthetic data for a system whose step response is 0.2[1-exp(-k/2)] + 0.4[1-exp(k/48)], i.e., to one in which “lambda” should be 0.2 + 0.4 = 0.6, and, as Mr. Eschenbach’s approach did, yours appeared to underestimate the sensitivity significantly. I don’t see this as a problem with the math; to me it suggests that those folks who were cautioning us about latent sensitivity may not be completely off base, at least theoretically.
Since I was using Excel, I generated the output analytically rather than by numerical convolution, and it’s always dangerous for us laymen thus to work without a net, so you may want to go through that exercise yourself.
Willis,
If I had wanted to insult you, I might have described YOU as incoherent. Or I might be politely describing you as drunk. If I want to say that your argument lacks mathematical coherence then I might describe your ARGUMENT as, well, mathematically incoherent.
These are not fighting words where I come from, merely a description of the problem and an invitation to consider an alternative mathematical proposition – which might turn out to be more, er, coherent, or not as the case may be.
Anyway, I promise you I was not trying to raise your hackles, but that is often the problem with the written word – it lacks a smile.
Paul
Re:Joe Born says:
June 4, 2012 at 2:42 pm
Hi again, Joe,
I too can’t get interested in the half-timestep problem, it is ultimately (solely) a definitional issue related to the input forcings.
It does not does not surprise me that the solution to a well-defined linear ODE (as proposed by Willis, and which I sought to modify) does not fit your response function (a solution in temperature in this instance) that comes from a different, probably nonlinear system. My guess is that you cannot derive a physically meaningful governing equation which has the response function you propose. But I know your engineering maths is really good from your previous postings, so to cover my bases or as**s, my second guess is that, if you CAN define a meaningful governing equation, then it is an ODE which is non-linear in temperature. (Incidentally if you want to rise to this challenge, I would love to see your answer!)
Well, I have the technology to deal with that, as they say. A two layer ocean model (highly nonlinear) is highly versatile and would yield an excellent approximation to your response function. See Section F here for a description:-
http://rankexploits.com/musings/2011/equilibrium-climate-sensitivity-and-mathturbation-part-2/
But I am not sure that it is necessary or desirable in this instance. One of the strengths of Willis’s argument here lies in the fact that over the historic period a match of the forcings to temperature in the GCMs – at least in those tested so far – can be effected very accurately under the assumption of a simple one-box linear feedback equation. This covers all of the forcings with no unaccounted for flux or temperature differences. This does not mean that one can infer the non-existence of some slow secondary heat flux term (your 24-factor tau term) or even multiple terms, but you can conclude that these terms are not highly relevant to the performance over the shorter timeframes. If then, over the critical shorter period in the same time interval , you can show that behaviour is largely controlled by SW effects (sun and albedo), why would you want to dilute the impact by considering the existence of the far more complicated slow response terms?
Well the answer may be that the focus is on equilibrium climate sensitivity, in which case I am going to take it up with Willis, because this is a non-starter. The focus needs to be on the relative importance of the SW effects vs the LW effects, because this speaks directly and loudly to the ATTRIBUTION argument. It is here that Willis’s findings may be really important.
In summary, I am sure you are right. Neither I nor Willis can approximate your summed exponentials with a two parameter model. It does not matter because Willis can duplicate GCM performance (for several GCMs) over the entire instrumental history with a two-parameter linear feedback model. He can therefore show using the same simple model which emulates GCM performance that most of the temperature rise can be explained by the variation in TSI and albedo over the critical period. For me this is the strength of what he has uncovered here.
“Ian Biner says:
June 4, 2012 at 3:33 am
Um… All EXTREMELY interesting, but has anyone done any calculations on the cumulative thermal effect of burning all the oil/coal/wood/ethanol/-fry-oil/witches that define our industrial civilisation? It seems to me that all this burning of stuff must heat up the atmosphere,and as NASA tells us the amout of radiated heat hasn’t changed (sorry… don’t ask me for a reference… I don’t remember where I read that), then all that heat must have had an effect.
Just a thought.
”
The energy contained in the oil coal wood… being burned is quite small compared to just how much energy comes in every second to the Earth. Think about it. All the stuff we burn is organic material like wood which was synthesized in plants by solar energy at some time or another. One of the problems with our modern society is the ability to measure practically anything, regardless of how small or insignificant it is. One can always make a case and throw numbers around about how devastating something is. How about the catastrophic increase in power being created (or would be created) by a universal world wide health exercise plan. Or how about the added extra eating required to supply the energy for all that exercise. Apply those numbers out of context and you can make what sounds like a devastating case. In context of the real world they would qualify as being not relevant to anything climate related.
That is why people have only concerned themselves with co2 emissions which have been grossly hyped. co2 does offer a straightforward calculation of how much effect it might have and it offers a tremendous political club capable of destroying or conquering nations. If there is too much burning going on at there (that is too much consuming going on for the planet to handle) then the totally inferior approaches to government and society which are incapable ultimately of even feeding their people can be hyped as being superior and that must be implemented to “save” the Earth from those evilllll human beans who, left to their own devices will continue to consume the whole planet, buying car after car after car until there’s no more places to store the old ones. (and lots and lots of other such rubbish)
Paul_K: .
.
Actually, the system I suggesting generating synthetic data from is indeed linear and can readily be imagined as two simple feedback systems mutually coupled, such as the earth’s surface and a lumped-parameter representation of the greenhouse-gas atmosphere (although I find a four-year lag in such a system hard to imagine). Without taking time to get the constants right, I’ll just say its (again, linear) differential equation is of the form
I’ll agree with you that the response-to-insolation demonstration is important. To the extent that it is intended to establish sensitivity limits, though, it’s far from bullet-proof. That was my point in bringing up the two-(real-) pole system: Mr. Eschenbach’s technique could be very wide of the mark on that score.
174 petawatts vs. 13 terrawatts. Anthro is about 0.007% of natural. Still worried?
http://en.wikipedia.org/wiki/Earth's_energy_budget
Never worried. It was just a random thought so I turned to all the greater minds here for clarification. Thanks.