Guest Post by Willis Eschenbach
Although it sounds like the title of an adventure movie like the “Bourne Identity”, the Bern Model is actually a model of the sequestration (removal from the atmosphere) of carbon by natural processes. It allegedly measures how fast CO2 is removed from the atmosphere. The Bern Model is used by the IPCC in their “scenarios” of future CO2 levels. I got to thinking about the Bern Model again after the recent publication of a paper called “Carbon sequestration in wetland dominated coastal systems — a global sink of rapidly diminishing magnitude” (paywalled here ).
Figure 1. Tidal wetlands. Image Source
In the paper they claim that a) wetlands are a large and significant sink for carbon, and b) they are “rapidly diminishing”.
So what does the Bern model say about that?
Y’know, it’s hard to figure out what the Bern model says about anything. This is because, as far as I can see, the Bern model proposes an impossibility. It says that the CO2 in the air is somehow partitioned, and that the different partitions are sequestered at different rates. The details of the model are given here.
For example, in the IPCC Second Assessment Report (SAR), the atmospheric CO2 was divided into six partitions, containing respectively 14%, 13%, 19%, 25%, 21%, and 8% of the atmospheric CO2.
Each of these partitions is said to decay at different rates given by a characteristic time constant “tau” in years. (See Appendix for definitions). The first partition is said to be sequestered immediately. For the SAR, the “tau” time constant values for the five other partitions were taken to be 371.6 years, 55.7 years, 17.01 years, 4.16 years, and 1.33 years respectively.
Now let me stop here to discuss, not the numbers, but the underlying concept. The part of the Bern model that I’ve never understood is, what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?
I don’t get how that is supposed to work. The reference given above says:
CO2 concentration approximation
The CO2 concentration is approximated by a sum of exponentially decaying functions, one for each fraction of the additional concentrations, which should reflect the time scales of different sinks.
So theoretically, the different time constants (ranging from 371.6 years down to 1.33 years) are supposed to represent the different sinks. Here’s a graphic showing those sinks, along with approximations of the storage in each of the sinks as well as the fluxes in and out of the sinks:
Figure 2. Carbon cycle.
Now, I understand that some of those sinks will operate quite quickly, and some will operate much more slowly.
But the Bern model reminds me of the old joke about the thermos bottle (Dewar flask), that poses this question:
The thermos bottle keeps cold things cold, and hot things hot … but how does it know the difference?
So my question is, how do the sinks know the difference? Why don’t the fast-acting sinks just soak up the excess CO2, leaving nothing for the long-term, slow-acting sinks? I mean, if some 13% of the CO2 excess is supposed to hang around in the atmosphere for 371.3 years … how do the fast-acting sinks know to not just absorb it before the slow sinks get to it?
Anyhow, that’s my problem with the Bern model—I can’t figure out how it is supposed to work physically.
Finally, note that there is no experimental evidence that will allow us to distinguish between plain old exponential decay (which is what I would expect) and the complexities of the Bern model. We simply don’t have enough years of accurate data to distinguish between the two.
Nor do we have any kind of evidence to distinguish between the various sets of parameters used in the Bern Model. As I mentioned above, in the IPCC SAR they used five time constants ranging from 1.33 years to 371.6 years (gotta love the accuracy, to six-tenths of a year).
But in the IPCC Third Assessment Report (TAR), they used only three constants, and those ranged from 2.57 years to 171 years.
However, there is nothing that I know of that allows us to establish any of those numbers. Once again, it seems to me that the authors are just picking parameters.
So … does anyone understand how 13% of the atmospheric CO2 is supposed to hang around for 371.6 years without being sequestered by the faster sinks?
All ideas welcome, I have no answers at all for this one. I’ll return to the observational evidence regarding the question of whether the global CO2 sinks are “rapidly diminishing”, and how I calculate the e-folding time of CO2 in a future post.
Best to all,
w.
APPENDIX: Many people confuse two ideas, the residence time of CO2, and the “e-folding time” of a pulse of CO2 emitted to the atmosphere.
The residence time is how long a typical CO2 molecule stays in the atmosphere. We can get an approximate answer from Figure 2. If the atmosphere contains 750 gigatonnes of carbon (GtC), and about 220 GtC are added each year (and removed each year), then the average residence time of a molecule of carbon is something on the order of four years. Of course those numbers are only approximations, but that’s the order of magnitude.
The “e-folding time” of a pulse, on the other hand, which they call “tau” or the time constant, is how long it would take for the atmospheric CO2 levels to drop to 1/e (37%) of the atmospheric CO2 level after the addition of a pulse of CO2. It’s like the “half-life”, the time it takes for something radioactive to decay to half its original value. The e-folding time is what the Bern Model is supposed to calculate. The IPCC, using the Bern Model, says that the e-folding time ranges from 50 to 200 years.
On the other hand, assuming normal exponential decay, I calculate the e-folding time to be about 35 years or so based on the evolution of the atmospheric concentration given the known rates of emission of CO2. Again, this is perforce an approximation because few of the numbers involved in the calculation are known to high accuracy. However, my calculations are generally confirmed by those of Mark Jacobson as published here in the Journal of Geophysical Research.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Correction to above
I am still pondering my conclusions in my 2008 paper
Willis, I stumbled over this while looking for something else and thought it had a bit of relevance to your discussion. It is from CO2 Acquittal by Jeffrey A Glassman PhD. He discusses the politics behind partitioning CO2 in one of his responses to a comment.
a) You say “surely there is a natural rate E(t) > 0 that would maintain an equilibrium CO_2 concentration”. Why?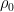
. Furthermore, this equilibrium has a signficant natural variability and probably nonlinear feedback mechanisms — more carbon dioxide in the atmosphere may well increase the rate at which carbon dioxide is removed by the biosphere, for example. There is some evidence that this is already happening, and a well-understood and studied explanation for it (greenhouse studies with CO_2 used to force growth). Trees and plants and algae grow faster and photosynthesize more with more CO_2, not just more proportional to the concentration — that’s per plant — but nonlinearly more, because as the plants grow faster there is more plant. I would argue as well that the ocean is more than just a saturable buffer (although it is a hell of a buffer). In particular, small shifts in the temperature of the ocean can mean big shifts in atmospheric CO_2 concentration, either way.
if its coupled channel dynamics is to be believable, and the long term stability of the solution under various scenarios demonstrated. If you send me or direct me at the actual coupled channel ODEs this integral equation badly represents — the actual ODEs for the channels, mind you — I would be happy to pop them into matlab and crank out some pretty pictures of the results, given some numbers. It isn’t necessary or desireable to write out the solution as an integral equation, especially an integral equation for the “anthropogenic” CO_2 surplus only, when one can simply solve the ODEs linear or not. It isn’t like this is 1960, after all — my laptop is a “supercomputer” by pre-2000 standards. We’re talking a few seconds of computation, a day’s work to generate whole galleries of pictures of solutions for various hypothesized inputs.
contribution from the biosphere that is ignorable in the rate equation, right?
Because we agree that there is one, you’ve just hidden it. You yourself are using as a baseline “natural emissions”, which presumably maintain an equilibrium, one that is somehow not participatory in this general process because you’ve chopped all of its dynamics out and labelled it
But here is why I doubt this model. Seriously, you cannot exclude the CO_2 produced by the biosphere and volcanic activity and crust outgassing and thermal fluctuations in the ocean in a rate equation, especially one with lots of nonlinear coupling of multiple gain and loss channels. That’s just crazy talk. The question of how the system responds to fluctuations has to include fluctuations from all sources not just “anthropogenic” sources because as I am getting a bit tired of reciting, CO_2 doesn’t come with a label and a volcanic eruption produces a bolus that is indistinguishable at a molecular level from a forest fire or the CO_2 produced by my highly unnatural beer.
Without a natural equilibrium and with your “15% is forever” rule, every burp and belch of natural CO_2 hangs out forever (where forever is a “very long time”. You can’t ascribe gain to just one channel, or argue that you can ignore gain in one channel of a coupled channel system so that it only occurs in the others. That is wrong from the beginning.
I do understand what you are trying to say about adding net carbon to the carbon cycle — one way or another, when one burns lots of carbon that was buried underground, it isn’t buried underground anymore and then participates in the entire carbon cycle. I agree that it will ramp up the equilibrium concentration in the atmosphere. Where we disagree is that I don’t think that we can meaningfully compute how effectively it is buffered and how fast it will decay because of nonlinear feedbacks in the system and because it is a coupled channel system — all it takes is for ONE channel to be bigger than your model thinks it is, for ONE rate to experience nonlinear gain (so that decay isn’t exponential but is faster than exponential) and the model predictions are completely incorrect.
The Earth is for the most part a stable climate system, or at least it was five million years ago. Then something changed, and it gradually cooled until some two and a half million years ago the Pliestocene became bistable with an emerging dominant cold mode. One possible explanation for this — there are several, and the cause could be multifactorial or completely different — is that it could be that CO_2 concentration is pretty much the only thing that sets the Earth’s thermostat, with many (e.g. biological) negative feedbacks that generally prevent overheating but are not so tolerant of cold excursion, which sadly has a positive feedback to CO_2 removal. The carbon content of the crust might well rotate through on hundred million year timescales — “something” releases new CO_2 into the atmosphere at a variable rate (hundred million year episodes of excess volcanism? I still have a hard time buying this, but perhaps). Somehow this surplus CO_2 enters at a rate that is so slightly elevated that the “15% is forever” rule doesn’t cause runaway CO_2 concentration exploding to infinity and beyond — I leave it to your imagination how this could possibly work over several billion years without kicking the Earth into Venus mode if there were any feedback pathway to Venus mode, given an ocean with close to two orders of magnitude more CO_2 dissolved in it than is present in the atmosphere and a very simple relationship between its mean temperature and the dissolved fraction (which I think utterly confounds the simple model above).
In this scenario, the Earth suddenly became less active and the biosphere sink got out in front of the crustal CO_2 sources. At some point glaciation began, the oceans cooled, and as the oceans cooled their CO_2 uptake dramatically increased, sucking the Earth down into a cold phase/ice age where during the worst parts of the glaciation eras, CO_2 levels drop to less than half their current concentration, barely sufficient partial pressure to sustain land based plant growth. Periodically the Earth’s orbit hits just the right conditions to warm the oceans a bit, when they warm they release CO_2, and the released CO_2 feeds back to warm the Earth back up CLOSE to warm phase for a bit before the orbital conditions change enough to permit oceanic cooling that takes up the CO_2 once again.
I disbelieve this scenario for two reasons. The first is that it requires a balance between bursty CO_2 production and CO_2 uptake that is too perfectly tuned to be likely — the system has to be a lot more stable than that which is why your manifestly unstable model is just plain implausible. I respectfully suggest that your model needs to include CO_2 from all sources in
The second is that the data directly refutes it. Disturbed by the fact that studies of e.g. ice core data fairly clearly showed global warming preceded CO_2 increase at the leading edge of the last four or five interglacials, a recent study tried hard to manufacture a picture where CO_2 led temperature at the start of the Holocene. The data are difficult to differentiate, however.
There is no doubt, however, that the CO_2 levels trailed the fall in temperature at the end of the last few interglacials. And thus it is refuted. The whole thing. If high CO_2 levels were responsible for interglacial warming and climate sensitivity is high, it is simply inconceivable that the Earth could slip back into a cooling phase with the high CO_2 levels trailing the temperature not by decades but by centuries. A point that seems to have been missed in the entire CO_2 is the only thermostat discussion, by the way. Obviously whatever it is that makes the Earth cool back down to glacial conditions is perfectly happy to make this happen in spite of supposedly stable high CO_2 levels, and those levels remain high long after the temperature has dropped out beneath them.
Before you argue that this suggests that there ARE long time constants in the carbon cycle, permit me to agree — the data support this. Looking at the CO_2 data, it looks like a time constant of a century or perhaps two might be about right, but of course this relies on a lot of knowledge we don’t have to set correctly.
There are many other puzzles in the CO_2 uptake process. For example, there is a recent paper here:
http://www.sciencemag.org/content/305/5682/367.abstract
that suggests that the ocean alone has taken up 50% of all of the anthropogenic carbon dioxide released since 1800. Curiously, this is with a (presumably)generally warming ocean over this period, and equally interesting, the non-anthropogenic biosphere contributed 20% of the surplus CO_2 to the atmosphere over the same period. So much for a steady state
One of many reasons I don’t like the integral equation we are discussing that I find it very difficult to identify what goes where in it and connect it with papers like this. For example, what that means is that a big chunk of all three exponential terms belong to the ocean, since the ocean alone absorbed more than any of these terms can explain. How can that possibly work? I might buy the ocean as a saturable sink with a variable equilibrium and time constant of 171 years, but not one with a 0.253 fraction. In fact, turning to my trusty calculator, I find that the correct fraction would be 0.58. I see no plausible way for the time constant for the ocean to be somehow “split”. We’re talking simple surface chemistry here, it is the one thing that really does need to be a single aggregate rate because all that ultimately matters is the movement of CO_2 molecules over the air-water interface. Also, even if it were somehow split — perhaps by bands of water at different latitude, which would of course make the entire thing NON-exponential — how in the world could its array of time constants somehow end up being the same as those for soil uptake or land plant uptake?
To be blunt, the evidence from real millennial blasts of CO_2 — the interglacials themselves — suggests a longest exponential damping time on the order of a century. There is absolutely no sign of very long time scale retention. It is very likely that the ocean itself acts as the primary CO_2 reservoir, one that is entirely capable of buffering all of the anthropogenic CO_2 released to date over the course of a few hundred years. If the surplus CO_2 we have released by the end of the 21st century were sufficient to stave off the coming ice age, or even to end the Pliestocene entirely, that would actually be fabulous. If you want climate catastrophe, it is difficult to imagine anything more catastrophic than an average drop in global temperature of 6C, and yet the evidence is overwhelming that this is exactly what the Earth would experience “any century now”, and sadly, the trailing CO_2 evidence from the last several interglacials suggests that whatever mechanism is responsible for the start of fed-back glaciation and a return to cold phase, it laughs at CO_2 and drags it down, probably by cooling the ocean.
In other words, the evidence suggests that it is the temperature of the ocean that sets the equilibrium CO_2 concentration of the atmosphere, not the equilibrium CO_2 concentration of the atmosphere that sets the temperature of the ocean, and that while there is no doubt coupling and feedback between the CO_2 and temperature, it is a secondary modulator compared to some other primary modulator, one that we do not yet understand, that was responsible for the Pliestocene itself.
rgb
The evidence suggests that the cause of the recent rise in atmospheric CO2 is most probably natural, but it is possible that the cause may have been the anthropogenic emission. Importantly, the data shows the rise is not accumulation of the anthropogenic emission in the air (as is assumed by e.g. the Bern Model).
I would agree, especially (as noted above) with the criticism of the Bern Model per se. It is utterly impossible to justify writing down an integral equation that ignores the non-anthropogenic channels (which fluctuate significantly with controls such as temperature and wind and other human activity e.g. changes in land use). It is impossible to justify describing those channels as sinks in the first place — the ocean is both source and sink. So is the soil. So is the biosphere. Whether the ocean is net absorbing or net contributing CO_2 to the atmosphere today involves solving a rather difficult problem, and understanding that difficult problem rather well is necessary before one can couple it with a whole raft of assumptions into a model that pretends that its source/sink fluctuations don’t even exist and that it is, on average a shifting sink only for anthropogenic CO_2.
I’m struck by the metaphor of electrical circuit design when those designs have feedback and noise. You can’t pretend that one part of your amplifier circuit is driven by a feedback current loop to a stable steady state (especially not when there is historical evidence that the fed back current is very noisy) when trying to compute the effect of an additional current added to that fed back current from only one of several external sources. Yet that is precisely what the Bern model does. The same components of the circuit act to damp or amplify the current fluctuations without any regard for whether the fluctuations come from and of the outside sources or the feedback itself.
rgb
I am trying to find references to a major misalignment between the ice core CO2 record and modern atmospheric records of CO2, one that was allegedly “solved” by shifting the ice core record until it matched the modern record.
Can anyone help please?
d/dt A = -(91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)D ,
d/dt D = +(96/1020)S – (96/3810)D.
Finally, some actual differential equations! A model! Now we can play. Now let’s see, A is atmosphere and atmosphere gains and loses CO_2 to the surface from simple surface chemistry. Bravo. S is the surface ocean. D is the deep ocean.
Now, let’s just imagine that I replace this with a model where what you call the deep ocean is the meso ocean M, and where we let D stand for the deep ocean floor. The surface layer S exchanges CO_2 with A and with M, to be sure, but biota in the surface layer S take in CO_2 and photosynthesize it, releasing oxygen and binding up the CO_2 as organic hydrocarbons and sugars, then die, raining down to the bottom. Some fraction of the carbon is released along the way, the rest builds up indefinitely on the sea floor, gradually being subducted at plate boundaries and presumably being recycled, after long enough, as oil, coal, and natural gas reservoirs where “long enough” is a few tens or hundreds of millions of years. As a consequence, CO_2 in this layer is constantly being depleted since the presence of CO_2 is probably the rate limiting factor (perhaps along with the wild card of nutrient circulation cycles and surface temperatures, ignored throughout) on the otherwise unbounded growth potential of the biosphere here.
Carbon is constantly leaving the system from S, in other words, being replaced by crustal carbon cycled in from many channels to A and carbon from M, the vast oceanic sink of dissolved carbon. There is actually very likely a one-way channel of some sort between M and D — carbon dioxide and methane are constantly being bound up there at the ocean floor in situ, forming e.g. clathrates. I very much doubt that this process ever saturates or is in equilibrium. But because I doubt we have even a guesstimate available for this chemistry or the rates involved at 4K and at a few zillion atmospheres of pressure, nor do we have a really clear picture of sea bottom ecology that might contribute, we’ll leave this out. Then we might get:
d/dt A = -(91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
Hmm, things are getting a bit complicated, but look what I did! I proposed an absolutely trivial mechanism that punches a hole out of your detailed balance equation. Furthermore, it is an actual mechanism known to exist. It takes place in a volume of at least 100 meters times the surface area of the entire illuminated ocean. Every plant, every animal that dies in this zone sooner or later contributes a significant fraction of its carbon to the bottom, where it stays.
This is just the ocean and we’ve already found a hole, so to speak, for carbon. Note well that it doesn’t even have to be a big hole — if you bump A you transiently bump S, but S is now damped — it can contribute or pick up CO_2 from M, but all of the while it is removing carbon from the system altogether. Now let’s imagine the other 30% of the earth. In this subsystem we could model it like:
d/dt A = E(t) – (91/750)A + (91/1020)S,
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
where E(t) is now the sum of all source rates contributing to A that aren’t S. Note well that for this to work, we can’t pretend that there are no contributions from the ground G or the crust (including volcanoes) C as well as humans H and land plants L. Some of these are sources that are not described by detailed balance — they are true sources or sinks. Others have similar (although unknown) chemistry and some sort of equilibrium. At the very least we need to write something like:
d/dt A = H(t) + C(t) – (91/750)A + (91/1020)S – R_{AL} A*L(t) – R_{GA} A + R_{GA} G
d/dt G = +R_{GA} A – R_{AG} G
d/dt S = +(91/750)A – (91/1020)S – (96/1020)S + (96/38100)M – R_b S ,
d/dt M = +(96/38100) S – (96/38100) M
d/dt D = + R_b S
which says that the ground has an equilibrium capacity not unlike the sea surface that takes up and releases CO_2 with some comparative reservoir capacities and exchange rate, humans only contribute at rate H(t), the crust contributes to the atmosphere at some (small) rate C(t) (and contributes to the ocean at some completely unknown rate as well, where I don’t even know where or how to insert the term — possibly a gain term in M — but still, probably small), where land plants net remove CO_2 at some rate that is proportional to both CO_2 concentration and to how many plants there are, which is a function of time whose primary driver at this point is probably human activity.
Are we done? Not at all! We’ve blithely written rate constants into this (that were probably empirically fit since I don’t see how they could possibly be actually measured). Now all of their values will, of course, be entirely wrong. Worse, the rates themselves aren’t constants — they are multivariate functions! They are minimally functional on the temperature — this is chemistry, after all — and as noted are more complicated functions of other stuff as well — rainfall, cloudiness, windiness, past history, state of oceanic currents, state of the earth’s crust. So when solving this, we might want to make all of the rates at the very least functions of time written as constants plus a phenomenological stochastic noise term and investigate entire families of solutions to determine just how sensitive our solutions are to variability in the rates that reasonably matches observed past variability. That’s close to what I did by putting an L(t) term in, but suppose I put a term L into the system instead as representing the carbon bound up in the land plants, and allow for a return (since there no doubt is one, I just buried it in L(t))? Then we have nonlinear cross terms in the system and formally solving it just became a lot more difficult.
Not that it isn’t already pretty difficult. One could, I suppose, still work through the diagonalization process and try to express this as some sort of non-Markovian integral, but it is a lot simpler and more physically meaningful to simply assign A, G, S, M, D initial values, write down guestimates of H(t), L(t), C(t), and give the whole mess to an ODE solver. That way there is no muss, no fuss, no bother, and above all, no bins or buckets. We no longer care about ideas like “fractional lifetime” in some diagonalized linearized solution that ignores a whole ecosystem of underlying natural complexity and chemical and biological activity influenced by large scale macroscopic drivers like ocean currents, decadal oscillations, solar state, weather state — algae growth rates depend on things like thunderstorm rates as lightning binds up nitrogen in a form that can eventually be used by plants — and more, so R_b itself is probably not even approximately a constant and could be better described by whole system of ODEs all by itself, with many channels that dump to D.
The primary advantage of my system compared to the one at the top is that the one at the top does have nowhere for carbon to go. Dump any in via E(t) and A will monotonically increase. Mine depletes to zero if not constantly replenished, because that’s the way it really is! The coal and oil and natural gas we are burning are all carbon that was depleted from the system described above over billions of years. Carbon is constantly being added to the system via C(t) (and possibly other terms we do not know how to describe). A lot of it has ultimately ended up in M. A huge amount of it is in M. There is more in M than anywhere else except maybe C itself (where we aren’t even trying to describe C as a consequence). And the equilibrium carbon content of M is a very delicate function of temperature — delicate only because there is so very much of it that a single degree temperature difference would have an enormous impact on, say, A, where the variations in temperature in S have a relatively small impact.
The point is, that with models and ODEs you get out what you put in. Build a three parameter model with numerically fit constants, you’ll get the best fit that model can produce. It could be a good fit (especially to short term data) and still be horribly wrong for the simple reason that given enough functions with roughly the right shape and enough parameters, you can fit “anything”. Optimizing highly nonlinear multivariate models is my game. It is a difficult game, easy to play badly and get some sort of result, difficult to win. It is also an easy game to skew, to use to lie to yourself with, and I say this as somebody that has done it! It’s not as bad as “hermeneutics” or “exegesis”, but it’s close. If there is some model that you believe badly enough, there is usually some way of making it work, at least if you squint hard enough to blur your eyes to the burn on the toast looks like Jesus.
rgb
To rgbatduke,
To add another complication to your summation of natural cycles. Because of their size and density, decaying phytoplankton will remain near the surface and contribute to the ocean’s out gassing on a relatively short cycle. How long does it take to move from the Arctic to the equator? Another complication is the periodic upwelling off Peru of cold, carbonate saturated bottom water that will outgass as it warms crossing the Pacific near the surface. The inorganic cycle is the major long term player. How long does it take for the ocean’s conveyor belt to make a lap?
Help, Mr. Moderator! Change to before “buckets”.
rgb
[OK, Well, at least seeing the (hidden-by-html-brackets) letters makes the edit make sense … 8<) Robt]
richardscourtney says:
May 8, 2012 at 1:29 am
“He describes it with honest appraisal of its limitations at…”
Thanks, Richard. I think the root of Calder’s angst is that he is trying to satisfy requirements which may be irreconcilable. The CO2 records from ice cores and stomata disagree. Which is right? Perhaps neither. Certainly, if this relationship between temperature and the rate of change of CO2 has held in the past, the former are wrong. But, that does not mean the latter are right.
I am always very wary of claims made of measurements which cannot be directly verified. I have spent enough time in labs testing designs to know that you never really know how things will work in the real world until you have actually put them to the test in a closed loop fashion, with the results used to make corrections until it all works. And that is with components and systems which are designed based on well established principles, and using precision hardware to implement. Nature, as we say, is pernicious. Murphy, of course, proclaimed anything which can go wrong, will. And then, there is Gell-Mann’s variation describing physics: anything which is not forbidden is compulsory. And, Herbert: “Tis many a slip, twixt cup and lip.”
Everyone knows ice cores act as low pass filters with time varying bandwidth, smoothing out the rouch edges increasingly with time. I am not at all convinced, indeed am deeply suspicious, that the degree of smoothing and complexity of the transfer function is underappreciated.
The reliable data we do have, since 1958, says the data is behaving this way over the current timeline, with the derivative of CO2 concentration tracking the temperature. Over a longer timeframe, the relationship likely would change, if temperatures maintained their rise, with CO2 concentration becoming a low pass filtered time series proportional to the temperature anomaly. But, in any case, it is clear that right now, the rate of change in CO2 is governed by temperature.
Allan MacRae says:
May 8, 2012 at 2:48 am
I think the C13/C12 argument is an attempt to construct a simple narrative of a very complex process. An analogy which has come up in various threads is the case of a bucket of water with a hole in the bottom fed by clear mountain spring water. The height of water in the bucket has reached an equilibrium. Then, someone starts injecting 3% extra inflow with blue dyed water. The height of water in the bucket re-stabilizes 3% higher than before, but due to the delay of the color diffusion process, most of the blue dye lingers near the top of the bucket. Even when the spring ice melts, and the clear water inflow increases, adding say 30% more height, the upper levels are bluer than the lower. So, a naive researcher looks at the blue upper waters, and concludes that the dyed water input is responsible for the rise.
fhhaynie says:
May 8, 2012 at 5:19 am
Fred – I have enjoyed your presentations over the years. Not having the time to replicate your research, I have kept it in the bin marked “maybe”. That is why I hoped making the temperature to CO2 rate of change relationship readily accessible to everyone to replicate through this link might help sway people who otherwise would stay on the fence.
Gail Combs –
You may also want to consider Glassman’s post and the Q & A that follows “On why CO2 is known not to have accumulated in the atmosphere & what is happening with CO2 in the modern era.” Very thorough discussion.
http://www.rocketscientistsjournal.com/2007/06/on_why_co2_is_known_not_to_hav.html#more
rgbatduke says:
May 8, 2012 at 9:54 am
Yes, it is substantially guesswork. The value of such equations, IMHO, is substantially qualitative – they can illustrate what kind of dynamics are possible.
It is generally helpful to reduce the order of the model, as I demonstrated above. Model order reduction is a key element of modern control synthesis, e.g., as discussed here.
And, I then showed how we can get a system which will quickly absorb the anthropogenic inputs, yet have CO2 derivative appear to track the temperature anomaly (with respect to a particular baseline) here.
rgbatduke:
Thankyou very much indeed for your comment at May 8, 2012 at 9:54 am and especially for this one of its statements:
“The point is, that with models and ODEs you get out what you put in. Build a three parameter model with numerically fit constants, you’ll get the best fit that model can produce. It could be a good fit (especially to short term data) and still be horribly wrong for the simple reason that given enough functions with roughly the right shape and enough parameters, you can fit “anything”.”
Yes! Oh, yes! I wish I had thought of your phrasing, and I thank you for it.
As I have repeatedly stated above, we proved by demonstration that several very different models each emulates the observed recent rise in atmospheric CO2 concentration better than the Bern Model although each of our models assumes a different mechanism dominates the carbon cycle.
Simply, nobody knows the cause of the observed recent rise in atmospheric CO2 concentration and there is insufficient understanding and quantification of the carbon cycle to enable modelling to indicate the cause.
Richard
richardscourtney says:
May 8, 2012 at 11:12 am
This is the question of observability. For an unobservable system, there exists a non-empty subspace of the possible states which does not affect the output. Thus, you can replicate the output with any observable portion of the state space plus any portion of the unobservable subspace. As the unobservable subspace is typically dense, there are generally an infinite number of possible states which can reproduce the observables.
For observability of stochastic systems, you have the added feature that even theoretically observable states are effectively unobservable because of low S/N.
It is analogous to a system of N equations in which you have greater than N unknowns to solve for. In such an instance, you must constrain your solution space by some means in order to find a unique solution. In the case of climate science, the selection of constraints provides an avenue for confirmation bias.
Bart:
Of course you are right in all you say at May 8, 2012 at 12:03 pm, but I put it to you that the paragraph from rgbatduke (which I quoted in my post at May 8, 2012 at 11:12 am) says the same in words that non-mathematicians can understand.
Also, our point was that it is one thing to know something is theoretically true and it is another to demonstrate it. We demonstrated it; i.e.
the observed rise in atmospheric CO2 can be modelled to have any one or more of several different causes and there is no way to determine which if any of the modeled causes is the right one.
Richard
richardscourtney says:
May 8, 2012 at 1:40 pm
“We demonstrated it; i.e. the observed rise in atmospheric CO2 can be modelled to have any one or more of several different causes and there is no way to determine which if any of the modeled causes is the right one.”
Did your models attempt to reproduce the affine dependence of the derivative of CO2 concentration on temperature? I would expect that to be a discriminator.
In the case of climate science, the selection of constraints provides an avenue for confirmation bias.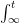
bit. It’s so much simpler to basically solve a Markovian IVP problem than a non-Markovian problem with a multimode decay kernel and an indeterminate initial condition.
I couldn’t have said it better myself. We disagree, I think, about numerics vs analytics, but then, I’m a lazy numerical programmer and diagonalizing ODEs to find modes gives me a headache (common as it is in quantum mechanics). The beauty of numerically solving non-stiff ODEs (like this) is that, well, it just works. Really well. Really fast. It’s not like you don’t have to work pretty hard and numerically to evaluate the Bern integral equation anyway, unless you use a particularly simple E(t), and then you have the added complication of just what you’re going to do with that pesky
But as to the rest of it, I think we agree pretty well. It’s a hard problem, and the Bern equation is one, not necessarily particularly plausible, solution proposed that can fit at least some part of the historical data. Is it “right”? Can it extrapolate into the future? Only time, and a fairly considerable AMOUNT of time at that, can tell.
In the meantime, the selection of the model itself is a kind of confirmation bias. 15% of the integral of any positive function you put in for E(t) simply monotonically causes CO_2 to increase. Another 25% decays very slowly on a decadal scale, easy to overwhelm with the integral. It’s carefully selected for maximum scariness, much like the insanely large climate sensitivities.
Or not selected. Scientists who care understand that it is only a model, one of many possible models that might fit the data, can look at it skeptically and decide what to believe, disbelieve, and can actually intelligently compare alternative explanations or debate things like what I put in my previous post that suggest that it would be pretty easy to fit the model and maybe even fit the susceptibility of the model (if that’s what you are claiming that you accomplished) with alternatives that have very different asymptotics and interpretations, or (as Richard has pointed out) with models where anthropogenic CO_2 isn’t even the dominant factor.
What I object to is this being presented to a lay public as the basis for politically and economically expensive policy decisions that direct the entire course of human affairs to the tune of a few trillion dollars over the next couple of decades. If only we could attack things like world hunger, world disease, or world peace with the same fervor (and even a fraction of the same resources). As it is, I think of the billions California is spending to avert a disaster that will quite possibly never occur because it is literally non-physical and impossible, and think of the starving children those billions would feed, or the people who lost their jobs in California when it went bankrupt that that money would employ.
And there is no need to panic. Global temperatures are remarkably stable at the moment. An absolutely trivial model computation suggests that the Earth should be in the process of cooling in the face of CO_2 by as much as 2C at the moment (7% increase in dayside bond albedo over the last 15 years). The cooling won’t happen all at once because the ocean is an enormous buffer of heat as well as CO_2, but it is quite plausible that we will soon see global temperatures actually start to retreat — indeed, it would be surprising if they don’t, given the direct effect of increasing the albedo by that factor.
And in a couple of decades we will (IMO, others on list disagree) on the downhill side of the era when the human race burns carbon to obtain energy anyway, with or without subsidy. There are cheaper ways to get energy that don’t require constant prospecting and tearing up the landscape to get at them. Well, they will be cheaper by then — right now they are marginally less cheap. Human technology marches on, and will solve this problem long before any sort of disaster occurs.
rgb
Yes! Oh, yes! I wish I had thought of your phrasing, and I thank you for it.
Oh, my phrasing isn’t so good — there is far better out there in the annals of other really smart people. Check out this quote from none other that Freeman Dyson, referring to an encounter of his with the even more venerable Enrico Fermi:
http://www.fisica.ufmg.br/~dsoares/fdyson.htm
The punch line:
“In desperation I asked Fermi whether he was not impressed by the agreement between our calculated numbers and his measured numbers. He replied, “How many arbitrary parameters did you use for your calculations?” I thought for a moment about our cut-off procedures and said, “Four.” He said, “I remember my friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
Yeah, John von Neumann was a pretty sharp tool to keep in your shed as well. The Bern model has five free parameters, so it isn’t terribly surprising that it can even make the elephant wiggle his trunk. (Thanks to Willis for pointing this delightful story out on another thread where we were both intent on demolishing an entirely nonphysical theory/multiparameter model of GHG-free warming.)
I feel a lot better about a model when there is some experimental and theoretical grounding that cuts down on the free parameters. “None” is just perfect. One or two is barely tolerable, more so if it isn’t asserted as being “the truth” but is rather being presented as a model calculation for purposes of comparison or insight. Get over two and you’re out there in curve-fitting territory, and by five — well why not just fit meaning-free Legendre polynomials or the like to the function and be done with it?
rgb
Oops, I miscounted. The Bern model has eight free parameters — I forgot the weights of the exponential terms. So wiggle his trunk while whistling Dixie, balanced on a ball. Although perhaps someone might argue that they aren’t really free, I doubt that they are set from theory or measurement.
rgb
Yes the five-parameter elephant.
Above several times I have noted that the integral equation that is at times causing so much worry in these comments is a very basic convolution equation of linear systems theory. Solving it is usually a matter of transforming it into the Laplace transform domain where convolution becomes a multiply operation.
More directly, “by inspection” the impulse response given there (the parallel decaying exponentials) corresponds to a particular configuration of passive R-C circuits. Without further analysis, we recognize exactly what it is and what it can (and can’t) do. It seems quite unlikely it could correspond to CO2 sourcing and sinking to four partitions (electrons to four capacitors in the circuit).
It could only be a “model” in the sense that it can be MADE to fit, given the free parameters. Hence the aptness of von Neumann’s elephant joke – which I also noted above.
Bart:
At May 8, 2012 at 5:03 pm you ask me:
“Did your models attempt to reproduce the affine dependence of the derivative of CO2 concentration on temperature? I would expect that to be a discriminator.”
I answer:
No, that was not their purpose.
Our paper explains;
“It is often suggested that the anthropogenic emission of CO2 is the cause of the rise in atmospheric CO2 concentration that has happened in the recent past (i.e. since 1958 when measurements began), that is happening at present and, therefore, that will happen in the future (1,2,3). But Section 2 of this presentation explained that this suggestion may not be correct and that a likely cause of the rise in atmospheric CO2 concentration that has happened in the recent past is the increased mean temperature that preceded it. A quantitative model of the carbon cycle might resolve this issue but Section 2 also explained that the lack of knowledge of the rate constants of mechanisms operating in the carbon cycle prevents construction of such a model. However, this lack of knowledge does not prevent models from providing useful insights into ways the carbon cycle may be behaving. ‘Attribution studies’ are a possible method to discern mechanisms that are not capable of being the cause of the observed rise of atmospheric CO2 concentration during the twentieth century.
In an attribution study the system is assumed to be behaving in response to suggested mechanism(s) that is modeled, and the behaviour of the model is compared to the empirical data. If the model cannot emulate the empirical data then there is reason to suppose that the suggested mechanism is not the cause (or at least not the sole cause) of the changes recorded in the empirical data.
It is important to note that attribution studies can only be used to reject hypothesis that a mechanism is a cause for an observed effect. Ability to attribute a suggested cause to an effect is not evidence that the suggested cause is the real cause in part or in whole.
Our paper considered three models of the carbon cycle. Each model assumed that a single mechanism is responsible for the rise in atmospheric CO2 concentration that has happened in the recent past (i.e. since 1958 when measurements began). The model was then compared to the empirical data to determine if the modeled mechanism could be rejected as a sole cause of the rise in atmospheric CO2 concentration.”
Richard
Allan MacRae:
I apologise that I overlooked your question at May 8, 2012 at 7:45 am and have only now noticed it.
It asks;
“I am trying to find references to a major misalignment between the ice core CO2 record and modern atmospheric records of CO2, one that was allegedly “solved” by shifting the ice core record until it matched the modern record.
Can anyone help please?”
The earliest explanation of the ‘need’ to adjust the data I know of is in
Siegenthaler U & Oeschger H, ‘Biospheric CO2 emissions during the last 200 years reconstructed by deconvolution of ice core data’, Tellus 39B; 14-154 (1987)
In that paper S&O assert that ice closure time means the data needs to be offset by decades of time because the ‘trapped’ air indicates the atmospheric composition at time of closure. And S&O assert the required offset is indicated by adjusting the data to overlay with the Mauna Loa data.
The earliest paper I know of which adjusts ice core data according to the S&O assertion is
Etheridge DM, Pearman GI & de Silva F, ‘Atmospheric trace-gas variations as revealed by air trapped in an ice core from Law Dome, Antarctica’, Ann. Glaciol. , 10; 28-33 (1988)
(The S&O assertion is clearly daft: there is no known mechanism that would move all the air up through the firn a distance that equates to decades of elapsed time. Indeed, basic physics says atmospheric pressure variations would mix the gases at different elevations while diffusion would tend to reduce high concentrations and increase low concentrations until the ice closed.)
Richard
Hu McCulloch says:
May 7, 2012 at 9:19 pm
Many thanks, Hu, following your explanation I finally see how it could work. The key is that to have it work, we have to have all of the CO2 pass from the atmosphere to one reservoir (the upper ocean in your example), which then passes all the CO2 to a second reservoir (deep ocean) at a different rate. In that way, part of it is absorbed quickly, and the remainder more slowly.
My problem is that to have the five different partitions they describe, you have to have the CO2 absorbed from the atmosphere by one single reservoir, which then transfers it to a second reservoir at a different rate, which then transfers that to a third reservoir at a third rate, which then transfers that to a fourth reservoir at a fourth rate, which then transfers that to a fifth reservoir at a fifth rate.
It also means that there can’t be any other sequestration mechanisms operating, because if there are other sinks, they will continue to absorb the CO2, and will sequester it long before the 371.6 years are up …
So I’m back to my same old problem … I still don’t understand where in the physical world we find such a system. It assumes the one and only sink is the ocean, which is partitioned into 5 sequential sub-sinks … I’m not seeing it.
w.
PS—I am sure that others explained this to me but I didn’t get it until Hu explained it … no telling how the mind works. In any case, my thanks to everyone who tried to explain it, and my apologies for not getting it.
Now I just need to find the five-chambered sequential CO2 sequestering system that corresponds with their math … oh, and also solve the separate and distinct problems pointed out by Robert Brown …
PPS—Someone above suggested modeling it in SPICE as an electrical circuit. What we have is a series C – R – C – R – C – R – C – R – C – R system, with no other path to ground … again, we can model it, but I don’t see the physical system that corresponds to that circuit.
Willis Eschenbach:
Your post at May 9, 2012 at 1:38 am concludes by saying;
“So I’m back to my same old problem … I still don’t understand where in the physical world we find such a system. It assumes the one and only sink is the ocean, which is partitioned into 5 sequential sub-sinks … I’m not seeing it.”
I am pleased that you have grasped the point that the Bern Model does not represent behaviour of the real-world carbon cycle. Perhaps now you can understand my post (above) at May 7, 2012 at 2:09 am which began by saying;
“I understand the interest in the Bern Model because it is the only carbon cycle model used by e.g. the IPCC. However, the Bern Model is known to be plain wrong because it is based on a false assumption.
A discussion of the physical basis of a model which is known to be plain wrong is a modern-day version of discussing the number of angels which can stand on a pin.” etc.
Please note that I am NOT now writing to say, “I told you so” (I am fully aware that one is often forgiven for being wrong but rarely forgiven for being right). I am writing this to make a point which I am certain has great importance but is often missed; viz.
THE CAUSE OF THE RECENT OBSERVED RISE IN ATMOSPHERIC CO2 CONCENTRATION IS NOT KNOWN AND – WITH THE PRESENT STATE OF KNOWLEDGE – IT CANNOT BE KNOWN.
We few who have persistently tried to raise awareness of this point have been subjected to every kind of ridicule and abuse by those who claim to “know” the recent rise in atmospheric CO2 concentration is caused by accumulation of anthropogenic emissions in the air. But whether or not the cause is anthropogenic or natural, that cause is certainly not accumulation of anthropogenic emissions in the air.
And the point is directly pertinent to the AGW-hypothesis which says;
(a) Anthropogenic emissions of GHGs are inducing an increase to atmospheric CO2 concentration;
(b) an increase to atmospheric CO2 concentration raises global temperature
(c) rising global temperature would be net harmful.
At present nobody can know if (a) is true or not, but the existing evidence indicates that if it is true then it is not a direct result of accumulation of anthropogenic emissions in the air. And if (a) is not true then (b) and (c) become irrelevant.
Richard
“My problem is that to have the five different partitions they describe, you have to have the CO2 absorbed from the atmosphere by one single reservoir, which then transfers it to a second reservoir at a different rate, which then…”
It will still work even if all the reservoirs connected, but I’m afraid I can’t think of any clearer explanation as to why than the tanks argument. Sometimes analogies and explanations just don’t catch – there’s some unrealised assumption or preconception that blocks the intuition. The mind’s workings are indeed strange.
It’s sometimes worth persisting with different analogies, but without understanding the reason for the block, it’s a bit hit and miss. Perhaps you can ask again another time, in a few months maybe.
Willis wrote:
“PPS—Someone above suggested modeling it in SPICE as an electrical circuit. What we have is a series C – R – C – R – C – R – C – R – C – R system, with no other path to ground … again, we can model it, but I don’t see the physical system that corresponds to that circuit.”
Actually, it’s a parallel, not a series system, which is evident from the summation sign rather than a product. You don’t need SPICE because it’s so simple. Not that either would have a physical correspondence to what goes on with CO2 in the atmosphere.
Nullius in Verba:
At May 9, 2012 at 11:25 am you say;
“It will still work even if all the reservoirs connected, but I’m afraid I can’t think of any clearer explanation as to why than the tanks argument.”
Hmmm. That depends on what you mean by “work”.
The model can be made to fit the rise in atmospheric CO2 concentration as observed at Mauna Loa since 1958 if the model’s output is given 5-year smoothing. But so what? Many other models which behave very differently can also provide that fit and do not require any smoothing to do it.
If you mean the Bern Model emulates the behaviour of the real carbon cycle then it does not: nothing in that cycle (except possibly the deep ocean) acts like a reservoir with a fixed volume.
Richard