Guest Post by Willis Eschenbach
Although it sounds like the title of an adventure movie like the “Bourne Identity”, the Bern Model is actually a model of the sequestration (removal from the atmosphere) of carbon by natural processes. It allegedly measures how fast CO2 is removed from the atmosphere. The Bern Model is used by the IPCC in their “scenarios” of future CO2 levels. I got to thinking about the Bern Model again after the recent publication of a paper called “Carbon sequestration in wetland dominated coastal systems — a global sink of rapidly diminishing magnitude” (paywalled here ).
 Figure 1. Tidal wetlands. Image Source
Figure 1. Tidal wetlands. Image Source
In the paper they claim that a) wetlands are a large and significant sink for carbon, and b) they are “rapidly diminishing”.
So what does the Bern model say about that?
Y’know, it’s hard to figure out what the Bern model says about anything. This is because, as far as I can see, the Bern model proposes an impossibility. It says that the CO2 in the air is somehow partitioned, and that the different partitions are sequestered at different rates. The details of the model are given here.
For example, in the IPCC Second Assessment Report (SAR), the atmospheric CO2 was divided into six partitions, containing respectively 14%, 13%, 19%, 25%, 21%, and 8% of the atmospheric CO2.
Each of these partitions is said to decay at different rates given by a characteristic time constant “tau” in years. (See Appendix for definitions). The first partition is said to be sequestered immediately. For the SAR, the “tau” time constant values for the five other partitions were taken to be 371.6 years, 55.7 years, 17.01 years, 4.16 years, and 1.33 years respectively.
Now let me stop here to discuss, not the numbers, but the underlying concept. The part of the Bern model that I’ve never understood is, what is the physical mechanism that is partitioning the CO2 so that some of it is sequestered quickly, and some is sequestered slowly?
I don’t get how that is supposed to work. The reference given above says:
CO2 concentration approximation
The CO2 concentration is approximated by a sum of exponentially decaying functions, one for each fraction of the additional concentrations, which should reflect the time scales of different sinks.
So theoretically, the different time constants (ranging from 371.6 years down to 1.33 years) are supposed to represent the different sinks. Here’s a graphic showing those sinks, along with approximations of the storage in each of the sinks as well as the fluxes in and out of the sinks:
Now, I understand that some of those sinks will operate quite quickly, and some will operate much more slowly.
But the Bern model reminds me of the old joke about the thermos bottle (Dewar flask), that poses this question:
The thermos bottle keeps cold things cold, and hot things hot … but how does it know the difference?
So my question is, how do the sinks know the difference? Why don’t the fast-acting sinks just soak up the excess CO2, leaving nothing for the long-term, slow-acting sinks? I mean, if some 13% of the CO2 excess is supposed to hang around in the atmosphere for 371.3 years … how do the fast-acting sinks know to not just absorb it before the slow sinks get to it?
Anyhow, that’s my problem with the Bern model—I can’t figure out how it is supposed to work physically.
Finally, note that there is no experimental evidence that will allow us to distinguish between plain old exponential decay (which is what I would expect) and the complexities of the Bern model. We simply don’t have enough years of accurate data to distinguish between the two.
Nor do we have any kind of evidence to distinguish between the various sets of parameters used in the Bern Model. As I mentioned above, in the IPCC SAR they used five time constants ranging from 1.33 years to 371.6 years (gotta love the accuracy, to six-tenths of a year).
But in the IPCC Third Assessment Report (TAR), they used only three constants, and those ranged from 2.57 years to 171 years.
However, there is nothing that I know of that allows us to establish any of those numbers. Once again, it seems to me that the authors are just picking parameters.
So … does anyone understand how 13% of the atmospheric CO2 is supposed to hang around for 371.6 years without being sequestered by the faster sinks?
All ideas welcome, I have no answers at all for this one. I’ll return to the observational evidence regarding the question of whether the global CO2 sinks are “rapidly diminishing”, and how I calculate the e-folding time of CO2 in a future post.
Best to all,
w.
APPENDIX: Many people confuse two ideas, the residence time of CO2, and the “e-folding time” of a pulse of CO2 emitted to the atmosphere.
The residence time is how long a typical CO2 molecule stays in the atmosphere. We can get an approximate answer from Figure 2. If the atmosphere contains 750 gigatonnes of carbon (GtC), and about 220 GtC are added each year (and removed each year), then the average residence time of a molecule of carbon is something on the order of four years. Of course those numbers are only approximations, but that’s the order of magnitude.
The “e-folding time” of a pulse, on the other hand, which they call “tau” or the time constant, is how long it would take for the atmospheric CO2 levels to drop to 1/e (37%) of the atmospheric CO2 level after the addition of a pulse of CO2. It’s like the “half-life”, the time it takes for something radioactive to decay to half its original value. The e-folding time is what the Bern Model is supposed to calculate. The IPCC, using the Bern Model, says that the e-folding time ranges from 50 to 200 years.
On the other hand, assuming normal exponential decay, I calculate the e-folding time to be about 35 years or so based on the evolution of the atmospheric concentration given the known rates of emission of CO2. Again, this is perforce an approximation because few of the numbers involved in the calculation are known to high accuracy. However, my calculations are generally confirmed by those of Mark Jacobson as published here in the Journal of Geophysical Research.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.

Hi _Jim: I did not state that there is no absorption of IR by GHGs. What l add though is that the present IR physics which claims 100% direct thermalisation is wrong and thermalisation is probably indirect at heterogeneous interfaces.
The reason for this is kinetic. Climate Science imagines that the extra quantum of vibrational resonance energy in an excited GHG molecule will decay by dribs and drabs to O2 and N2 over ~1000 collisions so it isn’t re-emitted. This cannot happen: exchange is to another GHG molecule and the principle of Indistinguishability takes over. [See ‘Gibbs’ Paradox’]
This is yet more scientific delusion in that all it needs is the near simultaneous emission of the same energy photon from a an already thermally excited molecule thus restoring LTE. This happens throughout the atmosphere at the speed of light so the GHGs are an energy transfer medium. The conversion to heat probably takes place mainly at clouds.
Frankly I am annoyed because this is the second tome through ignorance you have called me out this way. It’s because i have 40 years’ post PhD experience in applied physics I can show how climate science has been run by amateurs who have completely cocked the subject up. Nothing is right. The modellers are fine though because Manabe and Wetherald were OK, but once Hansen, Trenberth an Houghton took control, the big mistakes happened. it looks deliberate.
Following on from an earlier poster’s comments, the science of decompression diving uses a similar approach to that of the Bern model, to understand the movement of nitrogen into and out of a divers’ body tissues. The approach was pioneered by JS Haldane in 1907. He came up with the idea of using tissue compartments which exchanged nitrogen at different rates. Tissues like blood and nerves were fast, and were able to quickly equilibrate with any changes in the partial pressure of nitrogen. Tissues like muscle and fat were of intermediate speed, while bone was extremely slow. What Haldane did was to come up with a crude multi-compartment (tissue) model, and then carry out very extensive tests to tweak the model so that divers (goats in his initial experiments) did not get decompression sickness (gas bubbles forming in tissue). Over a hundred years on, Haldane-type tissue models are used in most divers’ decompression computers, and they work extremely well.
Some important points about diving science: 1. Haldane, and those who followed, constantly tested and refined their models against experimental data – a process which continues today – over a hundred years on. 2. The models are a crude approximation of a complex system (the human body), but at least the physics is reasonably well understood e.g. the local temperature and pressure gradients and the kinetics of the physical processes – solubility, perfusion and diffusion. 3. In decompression models, only one of the tissue compartments usually controls the behaviour of the model (rate of ascent/decompression stop timing). Therefore, small errors or uncertainties in each compartment are not a major problem.
The application of this approach to climate science is, in my view, highly problematic because: 1. There simply has not been enough time/effort to refine these models against experimental data – a process which can take many decades. 2. The models are a profoundly crude approximation of a bewilderingly complex system (global carbon cycle), about which most of physics/biology/geology/chemistry/vulcanology etc, etc are not well understood. 3 In climate models all of the compartments contribute to the behaviour of the model (CO2 sequestration rate) and so errors and uncertainties in each compartment are cumulative.
Bill Illis says:
May 6, 2012 at 1:16 pm
So the natural sinks and sources are in equilbrium (give or take) when the CO2 level is 275 ppm or the Carbon level in the atmosphere is 569 billion tonnes
====================================
Bill, this is biology…..what you’re calling equilibrium is exactly what happens when a nutrient becomes limiting……..
Bill Illis says:
May 6, 2012 at 1:16 pm
Very interesting charts as always, Bill. Thanks.
[note: the 3rd one has the wrong starting year].
Willis Eschenbach – “You say ” the results of the Bern model were offered as an available computational tool for further work” … I understand that. What I don’t understand is the physical basis for what they are claiming, which is that e.g. 13% of the airborne CO2 hangs around with an e-folding time of 371.6 years, but is not touched during that time by any of the other sequestration mechanisms.”
Then, Willis, I suggest you read the original papers on the Bern model, such as Siegenthaler and Joos 1992.
The percentages you listed are the results of running the Bern model, and as such are a convenient shorthand. The actual physical processes include mixed layer oceanic absorption, eddy currents and thermohaline circulation, etc. The very link you provided states that:
(emphasis added)
Your claim that these are percentages and time constants are the direct processes is a strawman argument – Joos certainly did not make that claim, he stated that these were a useful approximation.
I have to say I find your claims otherwise, and in fact your original post, to be quite disingenuous.
I have been wondering, if there is any reason to expect the rate of carbon exchange between the athmosphere and the ocean ( and other sinks) to be diffrent for diffrent isotopes of C ( CO2 for that matter ) . In other word might it be possible to infere something about the uptake rate of the sinks from the data (its accessible at the CDIAC website ) for the athmospheric dC14 content and the spike caused in it by open air nuclear bomb testing in the last century. I belive the i have somwhere seen a statment claming the “athmospheric half life” calculated from this “experiment” is 5.5 – 6 for the c14 isotope.
It is called a box model. Box models were discarded in the late 70’s, early 80’s, because they cannot describe complex systems.
There is an input into the system, the release of carbon from geologic sources (Vulcanism) and fossil fuels; the influx of carbon into the biosphere.
There is an output from the system, mineralization of carbon into muds, which will become rock; the efflux from the system.
At steady state, influx = efflux. In the previous 800,000 years of pre-industrial times CO2 is between 180-330 ppm. So either we were VERY lucky that influx=efflux due to chance; or the rate of efflux is coupled to the rate of influx. Thus, when CO2 is high, marine animals do well, the ocean biotica grows, more particulate organic matter sinks to the bottom of the ocean, more carbon trapped in mud, more mineralization.
Basic control mechanisms in fact.
It is because the process of CO2 sequestration is not solved by an ordinary differential equation in time, but by a partial derivative diffusion equation. It has to do with the frequency of CO2 molecules coming into contact with absorbing reservoirs (a.k.a. sinks). If the atmospheric concentration is large, then molecules are snatched from the air frequently. If it is smaller, then it is more likely for an individual molecule to just bob and weave around in the atmosphere for a long time without coming into contact with the surface.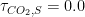 , effectively making the entire sum under the integral zero — this is what you would get if you made carbon dioxide sequestration in these imagined modes instantaneous — then the remainder of the function under the integral is
, effectively making the entire sum under the integral zero — this is what you would get if you made carbon dioxide sequestration in these imagined modes instantaneous — then the remainder of the function under the integral is 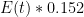 . This will cause CO_2 concentration to grow without bound as long as we are emitting CO_2 at all. Nor will it ever diminish, even if
. This will cause CO_2 concentration to grow without bound as long as we are emitting CO_2 at all. Nor will it ever diminish, even if 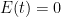 . Worse, all of the terms in the integral I forced to zero by making their time constants absurdly small are themselves non-negative. None of them cause a reduction of
. Worse, all of the terms in the integral I forced to zero by making their time constants absurdly small are themselves non-negative. None of them cause a reduction of 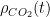 . They only make CO_2 concentration grow faster as one makes their time constants longer as long as
. They only make CO_2 concentration grow faster as one makes their time constants longer as long as  .
. to zero.
to zero.
Dearest Bart,
Piffle. I am talking about the integral in the document Willis linked, which is an integral over time only. If you set all of the
Now, as to your actual assertion that the rate that CO_2 molecules are “snatched from the air” is proportional to the concentration of molecules in the air — absolutely. However, for each mode of removal it is proportional to the total concentration in the air, not the “first fraction, second fraction, third fraction”. The CO_2 molecules don’t come with labels, so that some of them hang out anomalously long because they are “tree removal” molecules instead of “ocean removal” molecules. The ocean and the trees remove molecules at independent rates proportional to the total number of molecules. That is precisely the point of the simple linear response model(s) I wrote down. They actually “do the right thing” and remove CO_2 faster when there is more of it in total, not broken up into fractions that are somehow removed at different rates, as if some CO_2 is “fast decay” CO__2 and comes prelabelled that way and is removed in 2.57 years, but once that fraction is removed none of the rest of the CO_2 can use that fast removal process.
Except that the integral equation for the concentration is absurd — it doesn’t even do that. There is no open hole through which CO_2 can ever drain in this formula — it can do nothing but cause CO_2 to inexorably and monotonicall increase, for any value of the parameters, and CO_2 can never equilibrate unless you set
As I said, piffle. I do teach this sort of thing, and would be happy to expound in much greater depth, but note well that all of this is true before one considers any sort of PDE or multivariate dependence. Those things all modulate the time constants themselves, or make the time deriviative a nonlinear function of the concentration. In general, one can easily handle those things these days by integrating a set of coupled ODEs with a simple e.g. runge-kutta ODE solver in a package like the Gnu Scientific Library or matlab or octave. I tend to use octave or matlab for quick and dirty solutions and the GSL routines (some of which are very slick and very fast) if I need to control error more tightly or solve a “big” problem that needs the speed more than the convenience of programming and plotting.
But one thing one learns when actually working with meaningful equations over a few decades is how to read them and infer meaning or estimate their asymptotics. The “simple carbon cycle model” Willis linked, wherever it came from, is a travesty that quite literally never permits CO_2 concentration to diminish and that purports to break a well-mixed atmosphere into sub-concentrations with different decay rates, which is absurd at the outset because it violates precisely the principle you stated at the top of this response, where removal/sequestration by any reasonable process is proportional to the concentration, not the sub-concentration of “red” versus “blue”, “ocean” vs “tree” CO_2.
rgb
Plankton are a huge consumer of CO2, and they are rate limited by iron in nutrient rich waters and by silicon for diatom shells in others. NOT by CO2. So a significant modulator of CO2 will be volcanism that puts iron and silicon into the biosphere. Precipitation and weathering rates will also modulate those rate limiting nutrients. CO2 is the dependent variable, not the driving one…
http://chiefio.wordpress.com/2012/05/06/of-silicon-iron-and-volcanoes/
The “Bern Model” is broken if it does not address that.
@ur momisugly Latitude, May 6, 2012 at 10:38 am
“I still can’t figure out how CO2 levels rose to the thousands ppm….
….and crashed to limiting levels
Without man’s help……….”
Perhaps it is because your ( and your teacher’s ) view of the subject is incorrect.
The real question is: “Why is there any CO2 in the atmosphere at all?”
Answer that question and you will have the puzzle solved. CO2 is constantly and irreversibly being sequestered into the formation of insoluble carbonates (organically e.g. Foraminifera and chemically e.g. Calcium carbonate) over millennia.
One possible answer is the concept of a Hydritic Earth. With never ending up dwelling methane being oxidized to CO2.
Dan Kurt
Since you like differential equations… ,
, 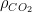 increases, period.
increases, period.
I do, and if you tell me what A, B and C are, and what the equations represent, I'll tell you whether or not I believe the coupled system of equations or the final solution.
But neither one has anything to do with the equation Willis linked. It is an integral equation that has the asymptotic property of monotonic growth of CO_2 concentration completely independent of the parameter values on the domain given. The exponentials aren't the result of solving an ODE even — they are under an integral sign.
That particular integral equation looks like a non-Markovian multi-timescale relaxation equation with a monotonic driver, but whatever it is, it is absurdly wrong before you even begin because it gives utterly nonphysical predictions in some very simple limits. In particular, it never permits CO_2 concentration to decrease, and it never even saturates. If
rgb
[Moderator’s request: it wasn’t just a dollar sign, I guess. Please send the formula again and I will paste it in. -REP]
[Fixed (I think). -w.]
And by the way “The Bern Model” triggered a memory in my head about having read an article by Jarl Ahlbeck some years ago on the John Daly website, where he among other things maintains that the future athmospheric carbon dioxide concentrations the bern model predicts are just a simple minded parabolic fit to to some unrealistic assumptions (not data). I never could really make up my mind if he was right or wrong in that, but for what it is worth the link to the paper is on the line below:
http://www.john-daly.com/ahlbeck/ahlbeck.htm
SNIP: Twice is enough. This is starting to be thread bombing. WUWT also does not encourage tampering with polls. If it has been adjusted to allow only Australians, then foreigners casting votes are simply cheating. -REP
Final comment and then time to do some actual “work”. I do, actually respect the notion that CO_2 concentration should be modelled by a set of coupled ODEs. I also am perfectly happy to believe that some of the absorption mechanisms — e.g. the ocean — are both sources and sinks, or rather are net one or the other but which they are at any given time may well depend on some very complicated, nonlinear, non-Markovian dynamics indeed. In this case trying to write a single trivial integral equation solution for CO_2 concentration (one with a visibly absurd asymptotic behavior) is counterindicated, is it not? In fact, in this case on has to just plain “do the math”.
The point is that one may, actually, be able to write an integrodifferential equation that represents the CO_2 concentration as a function of time. It appears to be the kind of problem for which a master equation can be derived (somebody mentioned Fokker-Planck, although I prefer Langevin, but whatever, a semideterministic set of coupled ODEs with stochastic noise). That is not what the equation given in the link Willis posted is. That equation is just a mistake — all gain terms and no loss terms. Perhaps there is a simple sign error in it, but as it stands it is impossible.
rgb
You are kidding right? Of course there is no actual partition it is a model so you can think through how carbon moves in and out of the atmosphere. You do get that, right? You do understand that to change sinks effects you change what is in each bucket (partition) to model how quickly that sink removes it from the atmosphere, right?
Please tell me you are not this rigid in your thought process – where is your degree from?
E.M.Smith says:
May 6, 2012 at 2:38 pm
Plankton are a huge consumer of CO2, and they are rate limited by iron in nutrient rich waters and by silicon for diatom shells in others. NOT by CO2. So a significant modulator of CO2 will be volcanism that puts iron and silicon into the biosphere.
=========================
Saharan/African dust……….
“I do, and if you tell me what A, B and C are, and what the equations represent, I’ll tell you whether or not I believe the coupled system of equations or the final solution.”
See my previous comments above.
I should perhaps clarify – I don’t consider the BERN model ansatz to be more than a simplistic approximation, and make no comment on its validity or physical significance. I’m just explaining the intuition behind it.
If you have several linked buffers with different rate constants for transfer between them, the system of differential equations generally has a sum-of-exponentials solution. (Or sinusoidal oscillations if some of the eigenvalues are imaginary.) That’s why they used that model to fit the simulation output. It sounds vaguely plausible as a first approximation, but beyond that I make no comment on whether they’re right to do so.
I’m not sure which equation Willis linked you mean.
Dan Kurt says:
May 6, 2012 at 2:48 pm
CO2 is constantly and irreversibly being sequestered into the formation of insoluble carbonates
==================
Gosh Dan, you just explained how denitrification is possible without carbon………….
Nullius,
Thanks for that very effective toy model, and the follow up bit on the effect of the different tank sizes. I’m sure it needs many add ons and caveats, but as a quick and accessable mental model to use as a starting point, for someone who thinks visually, it is a beauty.
Willis,
I have not yet plowed through all the comments so if this is redundant please forgive me. What you have described as the Bern model sounds a lot like a multi-compartment first-order elimination model similar to that of some drugs. A simple one-compartment, first-order elimination model is concentration dependent. That is, you put Drug X into the body and it will be eliminated primarily through one route (usually the kidneys). You have t1/2 elimination constant and about five half-lives later the body has essentially cleared the drug. Some drugs like aminoglycoside antimicrobials have a simple and rather restricted distribution in the human body. Their apparent volume of distribution (a purely theoretical metric derived for the purposes of calculation) is roughly that of the blood volume. Other drugs have very unusual volumes of distribution. An ancient (but good) example is that of digoxin. You can give a few daily doses of 250 µg of digoxin and end up with an observed serum concentration in the ng range much lower than one might anticipate. That drug has gone somewhere else other than the apparent blood volume.
This is where we get into multi-compartment models. A single drug may occupy the blood volume, the serum proteins, adipose tissue, muscle tissue, lung tissue, kidney tissue, lung tissue and brain tissue. Each tissue “compartment” is associated with its own in-and-out elimination constants so a steady state, single elimination constant is virtually impossible to quantify.
I know nothing about the the Bern Model so I can only surmise that maybe this is an elaborate model built on multi-compartment, first-order elimination kinetics. Then again, you have to consider the possibility of zero-order (non-concentration dependent) kinetics. Drugs like ethanol follow this model. If one keep ingesting alcohol at a certain point the liver’s capacity to metabolize alcohol is overwhelmed. We see a real-life “tipping point.” Once those metabolic pathways in the liver become saturated, every additional gram of alcohol ingestion produces a geometrically higher EtOH serum concentration (i.e. blackouts).
I have no idea if any of this is relevant. But what you described bore an amazing resemblance to multi-compartment, first-order kinetics. Still…on a personal level I think it’s BS. Different drugs behave differently in the human body. I have a hard time believing CO2 (a “single drug”) behaves differently in the atmosphere as a whole.
Willis:
I am pleased that you notice some problems with the Bern Model because the IPCC uses only that model of the carbon cycle.
I am especially pleased that you observe the problem of partitioning. In reality, the dynamics of seasonal sequestration indicate that the system can easily absorb ALL the anthropogenic CO2 emission of each year. But CO2 is increasing in the atmosphere.
Importantly, as your question highlights, nobody has a detailed understanding of the carbon cycle and, therefore, it is not possible to define a physical explanation of “partitioning” (as is used in all ‘plumbing’ models such as the Bern Model). Hence, any model that provides a better fit to the empirical data is a superior model to the Bern Model.
I remind that one of our 2005 papers proves any of several models provide better representation of atmospheric CO2 increase than the Bern Model.
(ref. Rorsch A, Courtney RS & Thoenes D, ‘The Interaction of Climate Change and the Carbon Dioxide Cycle’ E&E v16no2 (2005))
Our paper provides six models that each match the empirical data.
We provide three basic models that each assumes a different mechanism dominates the carbon cycle. The first basic model uses a postulated linear relationship of the sink flow and the concentration of CO2 in the atmosphere. The second used uses a power equation that assumes several different processes determine the flow into the sinks. And the third model assumes that the carbon cycle is dominated by biological effects.
For each basic model we assume the anthropogenic emission
(a) is having insignificant effect on the carbon cycle,
and
(b) is affecting the carbon cycle to induce the observed rise in the Mauna Loa data.
Thus, the total of six models is presented.
The six models do not use the ‘5-year-averaging’ to smooth the data that the Bern Model requires for it to match the data. The six modelseach match the empirical data for each year.
However, the six models each provide very different ‘projections’ of future atmospheric carbon dioxide concentration for the same assumed future anthropogenic emission. And other models are also possible.
The ability to model the carbon cycle in such a variety of ways means that according to the available data
(1) the cause of the recent rise in atmospheric carbon dioxide concentration is not known,
(2) the future development of atmospheric carbon dioxide concentration cannot be known, and
(3) any effect of future anthropogenic emissions of carbon dioxide on the atmospheric carbon dioxide concentration cannot be known.
Assertions that isotope ratio changes do not concur with these conclusions are false.
Richard
Oddly enough I read your post whilst in a “Tidal wetland” that I had visited to observe the spring *super moon” tides. Been doing this for more years than I care to remember but the tide was no higher than I’ve seen before (nowhere near), the estuary just as vibrant as ever but the first time I have ever seen a bird surface before me with a wriggling fish in its beak and gobble it down.
KR says:
May 6, 2012 at 2:08 pm
Disingenouus? So you are calling me a liar and a deliberate deceiver, except you are doing it politely?
KR, you can apologize for calling me a liar and we can continue the discussion. Or not.
Your choice.
w.
[Note: logic fixed, the way I wrote it made no sense. Teach me to write when my blood is angrified. -w.]
Wet lands are usually replaced by pasture. Another sink.
Secondly, every previous run up of CO2 has been followed by significant drop. So obviously some other factor9s) may come into play.
Brad says:
May 6, 2012 at 3:14 pm
Haven’t a clue who the “you” is that you are talking about. Me? rgbatduke? KR? Someone else?
Also, rather than saying “you do understand” X, Y, or Z, it would be much more useful if you quote exactly the words you disagree with, and then tell us why you think they are wrong.
Next, please note how what I wrote differs from if I were to have simply asked “You do understand how to respond to a blog post, right?”
Asking that, just like you asking the questions in your post, goes nowhere. You need to point out what you think is wrong, and point out where it is wrong, and tell us how to do it right.
Finally, “where is your degree from?” is a very unpleasant ad hominem. It doesn’t matter where anyone’s degree is from. What matters is, are they right or wrong.
w.