Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:

where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that ![]() in stable thermodynamic equilibrium.
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium

In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:

where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.

One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
![]()
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:

where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:

Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
![]()
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Robert Brown says:
February 6, 2012 at 8:29 am
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.
You have directly observed how the visible light of the sun attenuates as you dive deeper. All of the energy in that light has gone into heat.
You seem to think that infrared radiation is magic, that it is “heat radiation”. That’s
just crazy talk. Electromagnetic radiation is electromagnetic radiation. You can see because visible light carries energy. You see colors because everything you see absorbs some frequencies out of the visible light and scatters/reflects others. The absorbed energy turns into heat, which is why a black sheet of paper placed in the sun gets hotter than a white sheet of paper. Who knows what the colors of the two sheets of paper are in the infrared spectrum! They could both perfectly reflect infrared, and be “infrared colored paper” but because they are different colors in the visible part they will still heat up differently. That’s the bit about “albedo” in all of this talk, BTW — it represents the fraction of all the incident light intensity (not just visible OR infrared, the integrated intensity over all wavelengths) that is reflected.
Coming back with a flip “Puzzle that out in your own time” is hardly a rebuttal to my extremely simple question. You have direct experience that visible light makes it down into the water. You have direct experience that the intensity of visible light smoothly attenuates with depth — it gets darker as you go further down. Visible light carries energy through the surface of the water. The intensity of visible light that comes back out is far less than the intensity that goes in, because the amount of light you see coming back out in very shallow water where it illuminates e.g. white sand is much more than what comes out over deep water.
You know from direct experience that water is not perfectly transparent to visible light. If it were, we could see the bottom of the ocean exactly as if we were looking down on it from an airplane, get you cannot see the bottom of even a very clean, crystal pure lake more than a few tens of meters down, let alone the bottom of the ocean kilometers down. So why do you think I would waste time “puzzling out” something that is obviously false? Any human being who has ever spent a day on a lake knows that water is not transparent like air.
All of the light that is not transmitted or reflected is absorbed, unless you once again want to invoke invisible demons or fairies. In the case of deep water, the bottom is basically completely dark; no visible light is transmitted. It is all absorbed.
Demons Out!
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
This is why you responded to me. If you have no intention of helping Tim provide me with an answer, the very simple request I have made, then you’re wasting my time.
[]
You’re claiming to be an authority as a scientist, what don’t you understand about me asking for proof of these claims?
You’re the ones making the claims, you’re the ones who need to prove it. I don’t care what your opinions are about this, give the physics facts. Stop avoiding it. That’s the only expression of crazy talk I see here..
Thermal infrared from the Sun is the Sun’s thermal energy on the move, it is invisible; that is what we feel as heat direct from the Sun, as we feel from a fire, or a stove not glowing with any visible light. We cannot feel near infrared or visible light, they are not hot, they are not heat, they are light.. When we step into the shade on a hot, sunny day, we no longer feel the direct heat from the Sun, we can feel the warmth of the air heated by the Sun, but not the thermal infrared direct from it. This is bog standard physics of light and heat.
“Water absorbs the incoming solar Infrared Radiation because the frequency of the internal vibration of the water molecules is the same frequency of the waves of the solar Infrared Radiation. This form of Radiative Heat transfer is known as Resonance Absorption.
We humans feel the heat radiated by the Sun and other systems with a higher temperature because our bodies contain 55-75% of water. The radiative energy inciding on our skin is absorbed by the molecules of water in our bodies by Resonance Absorption. Just then, the Infrared Radiation absorbed by our bodies leads to a more intense internal vibration of the water molecules in our bodies and our bodies get warmer. However, in general, living beings possess thermoregulatory systems that permit us to eliminate the excess of heat from our bodies, maintaining a quasi-stable internal temperature (it is one of the homeostatic processes of biosystems).”
http://www.biocab.org/Heat_Transfer.html
We can sweat it out.
A scientist is a person “who cares deeply and passionately for truth and clarification, for the liberating experience of finding order and beauty in a chaotic jumble of natural events.” (Leon M. Lederman, 2001).
Myrrh says:
“I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.”
That’s right… all matter. I’ll now stop worrying about you Myrrh… I see you have found the complex component of refraction !! Every since Ira’s stream of pseudo-science threads I have been worried about you about light and water. I see you have connected (or always knew).
Glory be! Hit it on the head.
Yes it is. It was in your example for goodness sakes. Geez. This was in response to your statement at 2/5 10:25: “So if we move heat from the bottom to the top,” as faithfully copied. LOL. Heat doesn’t exist independent of the molecules, at least not since the caloric theory bit the dust not much more than a century ago.

 is the gas concentration (molecules per unit volume, molecular density).
is the gas concentration (molecules per unit volume, molecular density).  is the mean speed of the molecules, related to their temperature but not the same way for monatomic and diatomic ideal gases and hence expressed as a parameter by itself.
is the mean speed of the molecules, related to their temperature but not the same way for monatomic and diatomic ideal gases and hence expressed as a parameter by itself.  is the mean free path.
is the mean free path. 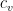 is the molar heat capacity.
is the molar heat capacity. 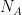 is Avogadro’s number — you could use the molecular heat capacity and insert the number of degrees of freedom of the gas and write this whole thing in a different form with the temperature explicitly inserted, but it is not zero. So when one talks about an adiabatic ideal gas — one where no internal heat transfer occurs via conduction — one is already talking bullshit, or rather, restricting your attentions to short enough times that thermal equilibrium hasn’t been established. Note that as far as scaling goes,
is Avogadro’s number — you could use the molecular heat capacity and insert the number of degrees of freedom of the gas and write this whole thing in a different form with the temperature explicitly inserted, but it is not zero. So when one talks about an adiabatic ideal gas — one where no internal heat transfer occurs via conduction — one is already talking bullshit, or rather, restricting your attentions to short enough times that thermal equilibrium hasn’t been established. Note that as far as scaling goes,  and
and  countervary — when
countervary — when  is high,
is high,  is low, and vice versa. The conductivity is independent of the pressure in an ideal gas, note well.
is low, and vice versa. The conductivity is independent of the pressure in an ideal gas, note well.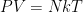 , right? — a consistent gas with thermal relaxation rates that are slow compared to hydrodynamic viscous relaxation rates (that work to slow dynamical shear whenever it occurs within the gas, gas parcels moving in opposite relative directions) and convective relaxation rates. Slow enough that we can ignore it at least to the extent that we can ask what state we are likely to find a gas initially prepared in an arbitrary initial condition — after waiting just long enough for hydrostatic equilibrium to be established but not long enough for thermal equilibrium (which is isothermal and strict maximum entropy) to be reached via internal conduction. We will similarly ignore radiative relaxation as being slower than hydrodynamic relaxation, although for gases like CO_2 or H_2O this is almost certainly untrue in the temperature ranges of 100K-500K that are relevant to the earth and other planets.
, right? — a consistent gas with thermal relaxation rates that are slow compared to hydrodynamic viscous relaxation rates (that work to slow dynamical shear whenever it occurs within the gas, gas parcels moving in opposite relative directions) and convective relaxation rates. Slow enough that we can ignore it at least to the extent that we can ask what state we are likely to find a gas initially prepared in an arbitrary initial condition — after waiting just long enough for hydrostatic equilibrium to be established but not long enough for thermal equilibrium (which is isothermal and strict maximum entropy) to be reached via internal conduction. We will similarly ignore radiative relaxation as being slower than hydrodynamic relaxation, although for gases like CO_2 or H_2O this is almost certainly untrue in the temperature ranges of 100K-500K that are relevant to the earth and other planets. and set so that it has the same integrated number of molecules and surface pressure and temperature as the isotropic case to get the right
and set so that it has the same integrated number of molecules and surface pressure and temperature as the isotropic case to get the right  boundary conditions for both, but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting.
boundary conditions for both, but I should finish that in a few days. I’ll post the results of this computation. They promise to be quite interesting.
Heat can be transported without bulk transport of molecules. This has been known since the caloric theory bit the dust not much more than a century ago. That is why technically I am correct and you are incorrect in the idealized discussion, as Velasco states. If you take a gas that cannot conduct heat or share heat through radiation — note well the conditional — then there are many — not just one, many — stable horizontally stratified hydrostatic profiles of an ideal gas. In fact, all of them with a monotonically decreasing concentration (density) and pressure profile. In all of these cases there is no convective instability. The gas does not conduct, which means that it does not diffuse either, because physical diffusion of the gas molecules implies heat conduction unless you insert a Demon that only lets the “right” molecules through from one layer to the next. There is no bulk transport of molecules because the gas is hydrodynamically stable by construction so no parcel of air experiences a net upward or downward force, begins at rest, and according to Our Friend Newton, remains at rest.
Turn on any diffusion (not that you could ever really turn it off), turn on any sort of heat conduction without bulk transport (not that you could ever really turn it off — you can compute what the conductivity is for an ideal gas and it is strictly non-zero, just like the dynamic viscosity:
In this
Since you are doing this for the same reason I am — to learn a lot more about atmospheric thermodynamics (and thermodynamics in general) beyond what I/we learned in school, you might want to look at this site:
http://zeolites.cqe.northwestern.edu/Module/heattrans.html
it has a nice summary of heat transport in fluids, including a discussion of the ideal gas conductivity (where they write it in one of the slightly different forms equivalent to that which I inserted above) and include a table that shows the measured, non-zero thermal conductivity of many gases.
At this point we both acknowledge that the entropy of the isothermal gas column is greater than the entropy of the isentropic gas column. You assert that — under nonphysical (or at least, inconsistent) conditions, that is, zero conductivity — an arbitrarily prepared gas column will relax to one with the DALR. I assert that — under the physical/consistent condition of an ideal gas with the ideal gas conductivity — it will relax to isothermal, the true thermodynamic equilibrium state. Velasco unambiguously agrees with me — I mean really, there is no doubt that a physically consistent ideal gas will relax to isothermal unless you make it physically inconsistent and choose to ignore internal conductivity or insist in looking at small enough time scales and initial conditions such that convective equilibrium is reached but thermal relaxation has not yet occurred.
Since Jelbring explicitly states that he is waiting a very long time for relaxation to occur and did not inconsistently qualify his use of an ideal gas by asserting that it is non-conductive (and because there is no substantive difference between my vertically confined gas column and his vertically confined gas column, at this point we all agree that my arguments against EEJ are valid and the stated conclusion of his thought experiment is incorrect. An ideal gas in true static thermodynamic equilibrium does not have an thermal lapse, it is isothermal.
Whether or not you have a dog in the fight, Jelbring definitely did and still does, and his paper is used by many people in the skeptical camp to defend the absurd statement that gravity alone will create a stable temperature gradient in a gas, even if the gas is e.g. prepared in an isothermal state originally. I think, if I read your remarks above correctly, that you even agree with this at this point.
This leaves us in our discussion with only one last thing to talk about. That is broken ergodicity and hydrodynamics. I am fortunate in that my teacher in stat mech in graduate school was one of the original researchers that studied systems that exhibit formally broken ergodicity, so I got exposed to the idea a lot and actually know a lot about it, and the problem of widely split relaxation rates, from my own research. So let’s talk about the gas — and let’s make it a consistent gas, please, as the idea of an ideal gas without thermal conductivity makes as much real sense as talking about an ideal gas that doesn’t satisfy the relation
I think that it is your belief that the gas will relax to a state with the DALR from all, or nearly all, initial conditions. I say nearly all, as we seem to be in agreement that if it is started with isothermal, it will stay there. Permit me to very quickly convince you that this is not true, that in fact nearly all initial conditions will cause the gas to relax to a state that is not one with a DALR. In fact, a gas with a DALR is a fairly special case of the many “equilibria” one can reach in the specific limit of hydrodynamic relaxation (only) to a state of hydrostatic balance neglecting the much slower thermal relaxation that eventually makes the gas isothermal.
First, let me appeal to your intuition. If we prepare the gas in any of the infinity of hydrodynamically stable states with a vertically increasing temperature gradient, the cold dense gas is on the bottom, the warm less dense gas is on the top. We ignore conduction, as noted, so the heat cannot conduct from top to bottom. The gas is convectively stable. It is hydrodynamically stable. You could go away and come back years later — any period that is short relative to the thermal relaxation rate — and the gas would still be cold on the bottom and hot on top. Furthermore, if you turn on thermal relaxation, isothermal equilibrium lies between it and a gas with a DALR, and we agree that if the gas is ever isothermal it will stay isothermal.
So the only initial preparations that can achieve the DALR are ones that already are warmer on the bottom than on the top. Here’s the interesting bit.
If the gas is prepared in a hydrodynamically stable state with a vertical temperature lapse in between the DALR and isothermal, I would argue that it, just like any arrangement with monotonically increasing temperatures, is still stable absent conduction. This is because it is still stable against convection — the gas has a bulk density that is monotonically decreasing with height so you don’t end up with parcels of gas that are more dense sitting above parcels that are less dense. This, and only this, drives the thermal mixing through vertical convective transport of parcels of gas that leads the gas to become approximately isoentropic. That’s why all of the books on physical climatology derive the DALR by discussing uplifting and downfalling “parcels” — the parcels are too big to thermalize via conduction during the transport process and are being uplifted by buoyancy forces that are greater than the opposing forces of dynamic viscosity!
So what is the class of initial states that could relax to a gas with the DALR? Ones that are hydrodynamically unstable initially, with a pronounced thermal gradient from bottom to top where the gas at the bottom is much warmer than the gas at the top, with a gradient that is larger than the DALR. A gas that is precisely prepared in a vertically stratified state might still be hydrostatically balanced, but the equilibrium is no unstable, as you have more dense gas above and less dense gas below. Any perturbation and the gas will convectively mix, with convective buoyant forces that exceed the “restraining” forces of static and dynamic viscosity. As it mixes, parcels will uplift and cool as they expand and warm the cooler gas they expand into as they compress it while those other parcels fall.
At this point there will be a very interesting competition. The DALR is one of an infinity (as I hope we now agree) hydrostatically and hydrodynamically stable states the gas can reach in the absence of conduction. Basically the entire range of vertical profiles that are convectively stable are possible final states. Depending on the details of the initial condition of the gas, it might relax to a vertical thermal profile almost anywhere between the DALR negative gradient and the infinity of zero to positive thermal gradient profiles that are all hydrostatically stable (bulk hydrostatic balance of buoyancy and gravity) and convectively stable (both static and dynamic viscosity that resist and damp out bulk motion perturbations so that they cannot grow).
Now, as you might agree, we can gain some actual insight into the real atmosphere. If the atmosphere were differentially heated from the top down, and weren’t subjected to forces that drive vertical thermal mixing, it would be hot from the top down. Indeed, the part of the atmosphere that is heated from the top down by direct absorption (which exponentially attenuates as one penetrates the absorber) has a stable postive thermal gradient from the bottom (top of the stratosphere) to the top.
The troposphere, on the other hand, is differentially heated from the bottom and cooled at the top. The ground and the oceans absorb the bulk of the solar energy that is not reflected (albedo) without transferring heat into the system, and they are both located at the bottom of the atmosphere. They warm the lower atmosphere by direct conduction (as well as by radiative transfer mediated by the GHGs, which in the case of the real atmosphere can most definitely not be neglected, because the at the very least a major chunk of the cooling of the surface is from radiation). Heat picked up at the surface is thus rapidly vertically mixed and transported by all three mechanisms — conduction, convection and radiation — acting at different length scales and with considerable and non-ignorable chaotic and self-organized emergent mesoscale structure — to produce an atmosphere that, as you note, ends up somewhere between the DALR and isothermal most of the time, although inversions (warmer on top) or with a gradient even larger than the DALR happen all the time, and are unstable or transiently metastable states with some lifetime and break apart and perhaps reform somewhere else as the conditions that favor them recur.
What makes the DALR a “pole” in this process? The fact that not only is the gas actively heated at the bottom but that it is actively cooled at the top of the troposphere. There is a continuous transport of heat from the bottom to the top, and heat transport via convective mixing is much faster than conduction and at least competes with radiation in the bulk of the troposphere. Still air with either little vertical shear and relatively weak warming of the ground or with so much vertical shear that turbulence occurs and irreversibly physically mixes the air parcels faster than “reversible” adiabatic expansion can keep up favors the “isothermal” pole, although this too is almost never precisely observed. Warm ground (strong heating of the ground) and non-turbulent vertical flow due to convective shear forces slow enough to allow approximately adiabatic expansion and compression to occur in the overturning convective air parcels favors the DALR.
Needless to say, the actual cooling at the top of the troposphere is due to the GHGs, which actually lose heat energy up there via radiation. If they didn’t, the bulk transport of heat upward would gradually warm the upper atmosphere, and as I note above, a warm, less dense, upper atmosphere is utterly stable without conductivity or radiation.
Anyway, I really appreciate your efforts to communicate more normally and talk to me in first person — it also makes it easier for me to address your points, and I hope, for you to read and understand what I say (if you indeed have no dog in the fight, then most of this should make sense). Bear in mind that IMO it is borderline silly to do stat mech on an atmosphere in the first place — it is only useful to answer “formal” questions like those addressed in Velasco like “what is true thermal equilibrium given thus and such conditions” and even there the computations are enormously difficult and require a variety of basically inconsistent or non-ergodic assumptions to be made. The right way to treat an atmosphere is almost certainly with bulk hydrodynamics — Navier-Stokes. That is, of course, insanely difficult, but show me a stat mech computation of a N ideal gas molecules in a box heated on one side and cooled on the other, with gravity, that spontaneously predicts e.g. the appearance of convective rolls. Not happening…
So we begin any real study of a real gas, or for that matter an ideal gas, with hydrodynamics and thermodynamics, not stat mech. Thermodynamics alone does just as good a job of telling us the true thermodynamic equilibrium of the gas as Velasco’s complicated stat mech computation, and allows us to determine maximum entropy and so on perfectly well. To talk about the DALR, one has to use hydrodynamics with bulk transport, for bulk transport to occur that produces sufficient vertical adiabatic mixing one requires differential heating or just the right sort of very slow transport driven by other means.
On a slightly different subject:
>Of the solar radiation reaching the surface of water some 50% is in the IR.
…
OK. I agree now.
This is irrelevant. What matters is how much or the total irradiance penetrates liquid water to a depth of at least centimeters, nothing more. The figure in:
http://en.wikipedia.org/wiki/Electromagnetic_absorption_by_water
shows both the intensities at the surface and the skin depth (exponential penetration length). Wavelengths between 200 nm and around 1 um have a skin depth of at least 10 cm and don’t just warm “a few millimeters on the surface”. That is easily 2/3 of the total power that makes it to the surface itself — basically “all” solar UV and visible, with the latter absorbed at depths up to a 100 meters, and a good start on the IR.
This isn’t to argue the point that most of the IR — around a third of the incoming power — is absorbed at the surface and largely goes into latent heat of evaporation rather than actual heating of the water. Heat is heat, of course — it still has to be gotten rid of to keep temperatures in balance, and the only way out of the Earth is through radiation — but it does make the flow of energy on its way out a lot more interesting, not to mention provides enough water vapor in the atmosphere to produce rain and so on.
The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong. Most of the actual warming of oceanic water comes from its absorption of visible light and UV and short wavelength IR at depth. Ocean temperatures vary with the season because the amount of energy they receive from the sun is modulated by axial tilt, just like everything else the Sun warms on Earth.
People get so angry when they discuss incoming spectrum, and seem so eager to claim that there is no such thing as a GHE involving CO_2 at all, and they seem so reluctant to address the outgoing top-of-atmosphere spectrum that clearly shows the involvement and importance of CO_2 in the outgoing radiation budget. Seeing is believing. Everything else is squabbling about the details of internal transport, and honestly doesn’t matter so much. What does matter is the precise response of the top 1-2 km of the troposphere and and bottom 1-2 km of the stratosphere to increased CO_2 and the general solar-driven modulation of H_2O. I don’t think we understand either one particularly well, but all of the rest of the stuff supposedly happening down below the top of troposphere isn’t really relevant to the actual energy balance and hence mean temperature. What matters is the (temperature of) the radiators of outgoing power in the emission bands of the sources of the outgoing radiation. Nothing more. At that point it is all detailed balance. The egregious and misleading stuff from the warmists IMO consists of a) overstating the quality of the physics in their models and the confidence we should have that they are correct; b) treating the ad hoc parameter of “feedback” or “sensitivity” as something they can set on heuristic grounds, and then optimizing the other parameters of their models around it. As I believe Willis pointed out on a different thread, give me five or six adjustable parameters in a fit and I’ll both fit an elephant and make him lift up his trunk to salute the queen. I build high quality neural networks to use as predictive models, and I can cite chapter and verse and write holy canons myself on the dangers of too many adjustable parameters. It is trivial to build a NN that fits almost any nonlinear data set quite nicely. The problem comes when you try to make the fit predict new data. The better the fit of the training data (after a fairly rapidly reached point) the worse the actual predictivity of the model, as you’ve basically taught it to “recognize” the noise of the training data instead of abstract the much weaker predictive signal buried in the noise.
You’ve made an idiot-savant net, one that memorizes perfectly and understands nothing. I suspect that many, although perhaps not all, of the climate models are idiot-savant models, tuned to fit a hypothesized pattern that tells a particular story on past data, but rather lacking predictive skill. Usually this is a sign that one needs to build models with much less detail and better attention paid to gross effects, not that one should add still more parameters and detail, but who asked me?
A final observation. I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. The latter is a bit odd, of course — it reaches T = 0, P = 0 at around 18 km, sharp as a knife, which all by itself tells you that it is wrong as it is absurd to think that molecular collisions won’t populate the volume above the supposed T = 0 level (and of course Earth’s real atmosphere extents out an order of magnitude further. The density is not exponential — I got that wrong — because it does go to zero at a specific altitude. It is even more nonphysical than I thought, in other words.
I’m really busy, so I haven’t had time to finish it (in particular renormalizing the DALR, which has to be evaluated numerically from
rgb
[Long reply, thank you. Robt]
Wayne says: “I’ll now stop worrying about you Myrrh… I see you have found the complex component of refraction !! ”
Actually, Wayne, what you attributed to Myrrh instead came from Robert Brown (and I am sure Dr brown HAS run across the concept of complex index of refraction). Myrrh, on the other hand, considered this a “waste of time”.
Robert Brown says
“The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong.”
The point was made to counter the claim by many in Climate Science that light is INSTANTLY transformed into thermal energy.
Light initiates many photochemical reactions.
Often the energy ‘fix’ lasts for thousands of years.
Promoters of climate alarm find it convenient to ignore the natural energy storage systems within our climate.
All credit is reserved for the 33K co2 driven greenhouse theory.
en.wikipedia.org/wiki/Photosynthesis
An even better link
http://en.wikipedia.org/wiki/Light-dependent_reactions
Wayne, yet another post I screwed up, the first para is mine, the bulk Robert’s which finishes at demons out, and then comes my commment.(I think I missed an opening italics to Robert’s but this has become so unwieldy now that I have difficulty posting). So I think you’re responding to what Robert said.
My point, as before in this, is that the AGWSF energy budget is fiction – it claims that shortwave heats oceans and land which then emits thermal infrared once so heated. This is so obviously junk it’s not even funny. The propose this as the main heating source of all of Earth’s land and water!! Water, regardless of how esoteric some want to get about it, IS TRANSPARENT tO VISIBLE LIGHT.
Water transmits visible light without absorbing it. That’s what transparent means! However, when they claim that the atmosphere is transparent to visible light this is not true! Visible light gets absorbed by the electrons of the molecules of nitrogen and oxygen, and reflected/scattered by this.
If water absorbed visible light there would be no life in the ocean. The reason you can see underwater is because light isn’t absorbed. How attentuation, not absorption, happens in the ocean is not the point here. The point is that they have excluded the real heating source of the oceans, thermal infrared, heat direct from the Sun, which is physically capable of heating water!
This is junk science at its finest, nit-picking to avoid confronting the reality that this energy budget is totally junk.
What’s worse, is that it has now become ingrained in the education system, the last couple of hundred years of science progress has been replaced by gibberish. To the point where Ira teaches that the heat we feel from the Sun and incandescent lightbulbs is from the visible! WE CAN’T BLOODY FEEL ANYTHING FROM VISIBLE LIGHT! If it can’t heat us up it sure as hell isn’t heating the oceans. Do you think I haven’t investigated this?
And Tim knows that full well… He continues to run away whenever actual experiments are asked for, as above he claimed there were loads.., or as here, does an ad hom in the best of Beria tradition..
All I’m asking for is proof that blue visible light as from the Sun heats water. Why is this always avoided? If visible light was really capable of heating water there would be tons of stuff on it proving their energy budget. Until they can show that any further distractions and deflections are a waste of time for me. The only reason I ask is because there isn’t any such proof! I just hope in investigating it for themselves they come to realise that..
Robert Brown: “Bear in mind that IMO it is borderline silly to do stat mech on an atmosphere in the first place — it is only useful to answer “formal” questions like those addressed in Velasco like “what is true thermal equilibrium given thus and such conditions” and even there the computations are enormously difficult and require a variety of basically inconsistent or non-ergodic assumptions to be made.”
To me it appeared that Velasco et al.’s “such and such conditions” are precisely those of your head-post hypothetical. Is there something I missed?
Also, could you give an example of an “inconsistent or non-ergodic” assumption that Velasco et al. made?
Robert Brown: “I’ve been working on a matlab/octave ODE program that directly compares the thermodynamics of an isothermal gas column and a DALR gas column. The latter is a bit odd, of course — it reaches T = 0, P = 0 at around 18 km, sharp as a knife. . . .”
My attempt to solve that analytically foundered on essentially the same problem, so I didn’t respond to your previous comment about whether the center of mass would rise as heat is transferred from above to below. But I did a back-of-the-envelope plausibility calculation–no doubt inaccurately, because the calculation exceeded my algebraic mean time between failures–for the (highly artificial) case of going from isothermal (T = T_0) to two differently isothermal (T = T_0 + deltaT and T = T_0 – deltaT ) halves, and it seemed that the center of mass remained the same. Again, I don’t really vouch for the calculation, and I’m not sure anything turns on the result, but it’s a data point you may (or may not) want to check out.
Myrrh says: “And Tim knows that full well… He continues to run away whenever actual experiments are asked for, as above he claimed there were loads.., or as here, does an ad hom in the best of Beria tradition.”
What I know full well is that this is experiment is theoretically simple, but practically difficult. Blue light is one part of the heating of the oceans (among many) which is spread over a large area
THEORY:
*energy goes in to the water (blue photons)
* some of that energy does not come out (fewer blue photons leave)
* Therefore, the blue photons added energy to the water.
PRACTICE:
* The most obvious difficulty is that pure water is very nearly transparent for blue light. To absorb any easily measured energy, the “coffee cup” would need to be many meters tall. Around 100 m would be needed to absorb most of the blue light by pure water.
* If my “cup” was 100 deep and only 1 m in surface area that the top (where the light will enter), I need 100 tons of high purity water.
* The “cup” will not be perfectly transparent to light, so it will be absorbing energy, which needs to be subtracted from the energy absorbed by the water.
* The “cup” will not be perfectly insulated, so heat conduction to/from the surrounding will have to be accounted for.
* Direct sunlight is ~ 1000 W/m^2. Visible light would be about 400 W/m^2. “Blue light” would be at most 100 W/m^2. So if my “coffee cup” is 1 m^2 in surface area and 100 m deep, I would get at most 100 W of heating. A 100 W heater would not have much effect on 100 tons of water. Sure, it would slowly heat the water, but separating the “signal” from all the “noise” would be a challenge.
Is this REALLY the sort of experiment you want congress to fund? The simple fact that graphs like this are readily available (http://3.bp.blogspot.com/_fa6AZDCsHnY/S_xwl48ZUSI/AAAAAAAAADQ/kPVlOauL1o4/s1600/water+absorption.gif) shows that the fundamental experiment HAS been done.
“The point is that you can’t pretend that the sun doesn’t warm oceans with visible light — that is absurd and wrong.”
The point was made to counter the claim by many in Climate Science that light is INSTANTLY transformed into thermal energy. Light initiates many photochemical reactions. Often the energy ‘fix’ lasts for thousands of years. Promoters of climate alarm find it convenient to ignore the natural energy storage systems within our climate. All credit is reserved for the 33K co2 driven greenhouse theory.
But this doesn’t counter that claim at all. If you want to counter a claim, do so with something that actually respects the laws of physics and experimentally observed percentages. I am quite certain that some 98% or 99% of the energy in the electromagnetic energy that penetrates further than the first few millimeters of the ocean’s surface is more or less instantly converted into heat. Photosynthesis just isn’t all that efficient. Wikipedia has a whole page devoted to photosynthesis effciency, and typical plant conversion efficiencies are indeed 1-2%, although some plants e.g. sugarcane can get up over 5% (and possibly some of the new gene-tailored algae as well). In the biosphere, most of the energy thus stored is in rough balance — it’s getting eaten as fast as it’s being produced. We’re hardly pressing oil out of sunflower seeds and pumping it into the ground.
You also need to think carefully about “energy storage systems” in our climate. The ocean is the big kahuna, and the entire discussion concerning the oceans was Myrrh’s claim that the ocean doesn’t absorb energy from visible light because it is “transparent”. This is wrong — the ocean takes up a huge amount of heat in the tropics and does indeed store it and transport it (e.g. to the north in the Gulf Stream) where it contributes mightily to the moderation of the climate of Europe, for example. The atmosphere itself no doubt stores and transports energy.
But what else does? If you consider the amount of solar energy entering the Earth every day, it is a truly awesome number. Even if you ignore the fact that nearly any subsystem you look at but the ocean is always near dynamic equilibrium, you have to find a sink that on average removes heat so it does not eventually have to radiate away to materially affect the energy budget. Bear in mind that you could provide 100% of the per capita energy consumed by people in the US to every human on the planet from the solar energy that falls in a remarkably tiny fraction of the total surface area, even allowing for insolation, night time, conversion efficiency, and so on. See e.g. —
http://en.wikipedia.org/wiki/File:Solar_land_area.png
This is, in the end, why CAGW isn’t going to happen even if the CAGW enthusiasts are right about the evils of CO_2! Most of the places that would make the best solar producers aren’t good for much of anything else — too hot and dry to be good farmland or good places for humans to live. At $1/watt for solar cell capacity, $1 buys at least 2-3 kW-H per year. That amortizes the cost of the cell over 5-6 years. All that we are lacking before this becomes the only way to make electrical power at a (substantial!) profit are good ways to store the power and to transport it longish distances compared to what we do now with our existing network of power plants. Even doubling the price (allowing for storage with current technology) still leaves one with decent amortization schedules.
In less than ten years the cost per watt will halve. In less than ten years solutions for the storage problem will emerge — WUWT published a nice article on Zinc-Oxide batteries that might have the capacity and lack of “memory” to make a good base for large scale storage of daytime power and/or electric car batteries (where currently no battery approaches the energy content of gasoline). Sometime in the next ten years, if we “do” nothing at all, one of the simplest ways in the world to make money will be to buy square kilometers of Arizona and New Mexico and West Texas, cover them with solar energy cells hooked into matteries, and linked by ultra-high-voltage transmission lines to cities in cooler, water rich places where people want to live. Ditto North Africa, India, Australia, and so on. 200% to 500% ROI over the 30 year lifetime of the plants, guaranteed.
We’re almost at break-even on this even now, in some parts of the world. In thirty years nobody will be burning coal for electrical energy, not because they want to be green but for the same reason we don’t burn wood for electrical energy now — it costs too much to harvest it and transport it and deal with the fact that you always have to find new sources as old ones mine out.
Then there is nuclear, both fission and (speculative) fusion. We could go green as all hell almost overnight if we just started building fission plants, ideally thorium-salt plants that can’t melt down or be used to build bombs. Sometime in the next 10 to 50 years we’ll probably master fusion as well. Once that happens we will (shortly thereafter) have achieved a type 1 civilization on the Kardashev scale and energy scarcity will never again by a constraint on human civilization on a mundane scale. Energy costs will fall to “almost free” by current standards, even as energy becomes the universal currency base.
I therefore predict, quite confidently, that the Earth will never get more than slightly over halfway to the doom-and-gloom prediction of carbon dioxide doubling before it comes down on its own because burning fuel for power or heat becomes as passe as TV antennas on rooftops — reaching for a signal that is no longer there…
Gasoline used in motor vehicles may last a lot longer — even indefinitely. I’m still not seeing anything remotely capable of storing 37 kW-Hours in the volume of one US gallon on the techno-horizon. But we may find electricity so cheap that we just synthesize gasoline straight up, recycling the CO_2 that’s already there.
rgb
My attempt to solve that analytically foundered on essentially the same problem, so I didn’t respond to your previous comment about whether the center of mass would rise as heat is transferred from above to below. But I did a back-of-the-envelope plausibility calculation–no doubt inaccurately, because the calculation exceeded my algebraic mean time between failures–for the (highly artificial) case of going from isothermal (T = T_0) to two differently isothermal (T = T_0 + deltaT and T = T_0 – deltaT ) halves, and it seemed that the center of mass remained the same. Again, I don’t really vouch for the calculation, and I’m not sure anything turns on the result, but it’s a data point you may (or may not) want to check out. at
at  for monatomic ideal gases until I saw the ODE solution reach zero and turn around and go back up again. Silly me! I’m so used to the physically plausible idea and experimentally observed idea that the real atmosphere gently fades away that I completely missed the fact that a DALR atmosphere simply stops, that no molecules in the gas below can, under any circumstances, gain enough energy to get above
for monatomic ideal gases until I saw the ODE solution reach zero and turn around and go back up again. Silly me! I’m so used to the physically plausible idea and experimentally observed idea that the real atmosphere gently fades away that I completely missed the fact that a DALR atmosphere simply stops, that no molecules in the gas below can, under any circumstances, gain enough energy to get above  . I’m working on the correct renormalization of the solution now, but have to take my son out to get a game and do some other shopping. Sigh. Fixing the code seems like more fun.
. I’m working on the correct renormalization of the solution now, but have to take my son out to get a game and do some other shopping. Sigh. Fixing the code seems like more fun.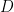 , Jelbring’s proposed thickness of the atmosphere involved, is greater than
, Jelbring’s proposed thickness of the atmosphere involved, is greater than 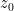 , the gas won’t even be in contact with the upper surface anyway, it will be strictly confined to a height less than
, the gas won’t even be in contact with the upper surface anyway, it will be strictly confined to a height less than 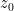 because that is the height where the absolute temperature, concentration, and pressure of the lapsed gas reaches zero.
because that is the height where the absolute temperature, concentration, and pressure of the lapsed gas reaches zero. in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them.
in hand for an Earth-normalized ideal atmosphere, I can numerically compute the distribution of potential and kinetic energy, the heat capacity, and more — probably even its linear response to perturbations. Sometimes numerical results are just easier to compute than estimate or handwave about, and I think this is one of them.
It’s really difficult, because while the isothermal case is simple, one has to solve an ODE to get the concentration with a lapse, then renormalize the result to have the right number of particles per unit area, and do this with a constrained surface temperature of (say) 300K. In other words, you need 300K at the surface and P = 1 atm at the surface (to compare to the same conditions isothermal) and it isn’t easy to see how that will work. I freely admit that my earlier estimate might turn out to be completely wrong — I hadn’t actually mentally realized that the DALR predicts
As for your observation that my top article addresses the isolated ideal gas problem when it is arguably irrelevant to the real atmosphere, well, sure, except that really it only addresses the EEJ paper. The discussion has now gone well beyond that, but the reason for the top post was simply to prove that the EEJ claim was false, that an adiabatically isolated ideal gas in true thermodynamic equilibrium, insulated from above and below by a layer of black matter that itself can be in equilibrium with the gas but which conducts no heat, after a long time, exhibits a DALR as its true stable thermodynamic equilibrium. No, it doesn’t. As we’ve discussed it, more and more ways that it fails have emerged. The state isn’t maximum entropy, and isn’t the equilibrium that will be reached, eventually, if the ideal gas conducts heat (as ideal gases do!) The black layers that bound the gas at the top and the bottom will radiate heat from the warmer to the cooler surface until they are in equilibrium, speeding the achievement of isothermal equilibrium. And if
Why do I care about Jelbring? Because it is cited repeatedly on at least two blogs (that I know of) as “proof” that gravity heats an atmosphere at the bottom without greenhouse gases or differential surface heating and upper troposphere, greenhouse gas mediated cooling. It is the basis for the N&Z paper that is trying to take this idea to new levels of absurdity on the basis of an “miracle” fit that is no miracle.
And at this point, I’m continuing with the matlab exercise because I want a venue where I can experiment with simple models that help me explore e.g. the DALR and energy and heat capacity and so on. Once I have
rgb
How attentuation, not absorption, happens in the ocean is not the point here.
It’s only not the point to you because the way the light is attenuated is by being absorbed. If you would deign to look at the exponential decay constant for water in inverse centimeters, in the Wikipedia article I linked above, you will note that the length scale, the exponential “penetration depth” for light in the visible band is nowhere greater than around 100 meters. That means that well over half of the energy in the visible light that makes it through the partially reflective surface of the sun is absorbed by the water within the first 100 meters, photosynthesis is only possible in the top 200 meters (the Epipelagic zone) and virtually none of the energy penetrates past a kilometer in depth. The 800 meters of water under the layer warmed by visible sunlight is called the Mesopelagic, and the temperature at the bottom of it is a constant 4K because that is precisely the point where there is almost no solar energy left to directly warm it:
http://en.wikipedia.org/wiki/Mesopelagic
Paradoxically, the precise place you think warm enters the water is where it does not. The penetration depth of most of the IR, in particular, is order of a millimeter or less — mostly less. Lots of the energy is absorbed in a layer 1-10 micrometers in thickness — 1000-10000 molecules thick — at the very surface, where it causes the water to evaporate rather than heating the bulk. The energy mostly goes into the latent heat of vaporization of water (which is very substantial); relatively little is leftover as “warm water” and that which there is is largely stuck at the top, because water has a relatively high thermal expansion coefficient and the warmer water is considerably more buoyant and stays on top except where mixed by the action of wind or wave or sustained current.
Again, you seem to want to think that all climate science is bullshit and all climate scientists are idiots, to the point where you are inventing new physics for them to be wrong about. I’d suggest that both are almost certainly untrue in general, even though there may well be some climate science that is bullshit and some climate scientists that are idiots, and in any event, getting the basic physics you’re trying to call them on wrong simply destroys your own credibility as a reasoning participant in the debate.
To summarize — the (dry) atmosphere isn’t perfectly transparent to visible light, but one can look down from orbit and photograph a newspaper in high enough resolution and with more than enough light to read the headlines. A photograph from space clearly shows us the continents and oceans by day everywhere that isn’t obscured by clouds, and at night even the relatively dim lights of human activity (dim compared to sunlight) can easily be seen from orbit or a plane flying 10 km above the surface.
Those same pictures do not show the bottom of the sea. Riding on a boat even over very clear, very clean water, one cannot see a kilometer down. One cannot see 100 meters down. In world war II, submarine hunters couldn’t see submarines a mere 20 meters down as a general rule, with a few exceptions where the water was particularly clear. By no stretch of the imagination is water as transparent as air, even to visible light. If it were, our satellites could photograph the bottoms of oceanic trenches, and they can’t. The top kilometer of water is almost completely opaque, because all of the visible light that does make it in at the top is absorbed there, warming the water.
The word “transparent”, when applied to air and water, is an approximate concept. Air scatters blue light quite strongly, but is much more transparent to red light. Scattering isn’t the same thing as absorption. If you want to understand what water does, don’t appeal to an English word such as transparent as if it, used as an adjective applied to a material, is a scientifically precise descriptor. What is scientifically precise is the absorption cross-section or penetration depth, which tells you just how much water visible (or any other frequency) of light can traverse before it is 10%, 50%, 90% absorbed.
rgb
Why is this always avoided? If visible light was really capable of heating water there would be tons of stuff on it proving their energy budget.
Or, they could consider a direct measurement of the absorption cross-section of water in the visible range to be direct proof, and thereafter take it for granted that the simplest of physics — visible light is transmitted into water at the surface and doesn’t come back out, therefore it damn well goes somewhere and the place organized energy sooner or later ends up is heat — is correct.
Perhaps they don’t want to believe in invisible fairies that eat the blue photons that make it through the surface of water before they get down to a kilometer of depth, because God knows there ain’t no blue photons left to speak of by the time you get down that far.
Demons Out!
rgb
When we step into the shade on a hot, sunny day, we no longer feel the direct heat from the Sun, we can feel the warmth of the air heated by the Sun, but not the thermal infrared direct from it. This is bog standard physics of light and heat.
Good lord! You must be joking. I’ve never heard anything so silly from somebody presumably out of high school.
Look, go find yourself a blue-ray disc player. Take it apart, carefully, until you expose the 1 watt blue laser. Point it at your skin. Power on. After your finger heals from the hole you drilled through your skin, come back and tell me that visible light doesn’t carry heat.
Or you can watch any of the umpty youtube videos that show people using e.g. 250 mW laser pointers to start fires (red, green, blue, who cares what color!). For example, here is one:
out of about a million — kids LIKE to start fires with lasers. Lasers are good counterexamples because they are monochromatic, so you can’t pretend that your burned finger came from “secret” infrared added to the beam by your invisible fairies.
Here’s a very simple exam question. Blue light with an intensity of one watt per square centimeter illuminates a thermal sensor coated with lampblack, and the temperature increase is plotted as a function of time. After the sensor returns to its original temperature it is illuminated with red light at the same intensity. You expect the temperature of the sensor to:
a) Remain constant in both cases because visible light doesn’t heat anything (Myrrh’s bog-standard physics answer — I must find a copy of his new book, “Bog Standard Physics” as I somehow don’t have it on my shelves).
b) Warms faster for the red light because it is closer to infrared and everybody knows only infrared light can actually heat anything.
c) Warms just about exactly at the same nonzero rate for both.
If you get this one right we can try you on which one weighs more, a pound of feathers or a pound of lead.
What matters in energy transfer via light is two things: The intensity of the light, that is, the power per square centimeter (more properly the Poynting vector of the light as the power incident on any surface is the flux of the Poynting vector through the surface, correcting for surface geometry and the direction of the light); the absorptivity of the material in the wavelength chosen.
The latter is basically never “perfectly zero” for anything but a vacuum, although it can be quite small. Things that are opaque tend to reflect white light in the colors that they don’t absorb and absorb the light in the colors that they don’t reflect. Hence when you light up a red piece of paper with red light, you don’t warm it much, but if you use blue light you warm it a lot. Black is the universal absorber color, white (or metallic/shiny) the universal reflector, although that’s really only for the visible spectrum because whether something is “black” (a good absorber) to UV or IR may not be connected to its color in the visible spectrum. “Transparent” materials are more complicated, and conductors are treated somewhat differently than insulators.
You can’t just make sweeping statements about this — you have to learn the actual physics and learn the actual relevant physical properties of the particular kinds of stuff you want to apply the physics to. Visible light will heat you up just fine, as has been shown in countless elementary school science fair projects. Or you can do the “experiment” itself with a high-power laser pointer or blue laser from a CD burner, if you’re stupid enough to actually try it.
rgb
Robert Brown
When in a discussion involving equilibrium thermodynamics someone finds the need to drag in a laser I feel they are clutching at straws.
” Look, go find yourself a blue-ray disc player. Take it apart, carefully, until you expose the 1 watt blue laser. Point it at your skin. Power on. After your finger heals from the hole you drilled through your skin, come back and tell me that visible light ”
The blue light is more likely to induce chemical change than directly thermally agitate the skin molecules.
You are also ignoring other photochemical reactions in addition to photosynthesis.
http://en.wikipedia.org/wiki/Light-dependent_reactions
2/8 6:22am:
“Heat can be transported without bulk transport of molecules…. as Velasco states….the ideal gas…will relax to isothermal, the true thermodynamic equilibrium state. Velasco unambiguously agrees with me…”
I looked through Velasco et.al. paper but don’t find that particular Velasco et. al. statement – can you provide the specific paragraph? Beware of the double negative therein. I looked up your 2/5 10:25pm post and did find your statement exactly:
“..there is no heat flow at equilibrium, because equilibrium is maximum entropy.”
Ding! We all agree on that. Heat can be transported before Fig. 1 equilibrium w/o bulk transport. When Fig. 1 in top post is at equilibrium it has reached max. entropy; no heat flow or transport, no bulk transport, max. entropy condition which is proven non-isothermal, isentropic by Velasco et. al. eqn. 8, Verkley et. al. part b AND Bohren&Albrecht text Chapter 4.4.
No heat flows in Fig. 1 in equilibrium yet temperature decreases with increasing height according to all 3 ref.s I’ve cited w/the specific ref.s: “Please be specific” (a quote from my high school English teacher). Isothermal is proven NOT max. entropy for Fig. 1. So isothermal is not Fig. 1 equilibrium condition. Fig. 1 will then over time, and on its own, naturally change to equilibrium temperature non-isothermal profile – I posted the exact T gradient formula above.
Your posting of the thermal conductivity of a gas (eqn. 7.48 in B&A) provides some clues to me as to root cause why you are stuck on manifestly assuming the incorrect isothermal equilibrium solution for Fig. 1 where you disagree with all 3 expert references I cite – which show their algebra.
The formula you post at 6:22am today is the correct definition of thermal conductivity of a gas under no gravity (there is no g in the formula) which B&A shows derives from the Fourier heat flow eqn. (it is misnamed a “law”) – shown as B&A Eqn. 7.11.
Quoted verbatim w/uninteresting skips for brevity, directly from B&A:
“The Fourier law in the form Eq. (7.11), where Kt is solely a property of the medium and not its state of motion, is not generally valid for fluids in motion….acted upon by a mass dependant force (such as gravity)…” Ref. B&A page 342 of edition 1.
B&A follow-up on p. 351: “Although the Fourier conduction law is not generally valid within a fluid, it is valid at the boundary between a fluid and a solid because of the no-slip boundary condition.” And p. 347 B&A correctly conclude for top post equilibrated Fig. 1: “As we saw in section 4.4, the natural state of affairs is for the temperature of an isolated layer of air in a gravitational field to decrease with (increasing) height ”
This Fourier eqn. being inapplicable to Fig. 1 due to gravity acting is why your thinking of conduction in solids (stationary molecules not in motion) impedes your reasoning & leads to your incorrect isothermal equilibrium conclusion for Fig. 1 in top post – at least for reasonable ideal gases in gravity field (reasonable molecules in random motion i.e. P = 1000mb to 200mb, T range from earth surface through troposphere).
“Since you are doing this for the same reason I am — to learn a lot more about atmospheric thermodynamics (and thermodynamics in general)…”
4 things I’ve reasonably correctly learned & a 5th kicker:
1) Top post Fig. 1 equilibrium is non-isothermal, isentropic by the 13 difficult but doable algebra steps I outline posted above; ideal gas T gradient w/height formula is known under given initial ref. conditions & is not constant as exactly derived from 3 different 1st principle references by generalized entropy maximization mathematics. This is counterintuitive & closely approximates the standard atmospheric temperature profile up through earth’s troposphere.
2) Remember 1) forthwith. So far 1) has not been proven incorrect by any poster here.
3) The Fourier heat conduction formula is general for solids and is not applicable in general to fluids – only applicable to fluids with molecules not acted on by gravity; is applicable to ideal gas in gravity field only at boundary to a solid under certain conditions.
4) I have to watch eqn. definitions & their assumptions closely. For example, in the Northwestern U. link provided at 6:22am today the applicability of the Fourier eqn. is limited to stationary fluids. In the ref. provided, a stationary fluid is defined as one w/o external forces acting on its molecules such as gravity. Entirely consistent with B&A p. 342. Also, M-B distribution is valid only for no forces acting on molecules.
5) I long ago learned to win the game, you have to s-l-o-w-l-y watch the pea under the thimbles.
Robert Brown
The easiest way to solve the blue light in water situation is to pick a particular molecular example.
Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
To treat all solar radiation as exactly the same as thermal or infra red is not acceptable.
It fits in with the same kind of science that treats the Earth as a perfect black body.
On the other hand the trace gas CO2 is given awesome power .
If the one W/m2 effect is questioned then positive feedbacks are readily found.
The K&T 2009 energy balance diagram totally ignores the photochemical reality.
books.google.com/books?isbn=0521016347…
Bryan says:
The easiest way to solve the blue light in water situation is to pick a particular molecular example. Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
Why does the precise mechanism even matter to you? The fact that the radiation is being absorbed means that its energy is being absorbed. Unless you imagine that the ocean is magically levitating off the ocean floor or chemically splitting into hydrogen gas and oxygen/chlorine, that energy can only appear as heat. Even if you assume that the water is murky enough that almost all the absorption is by mud particles or living cells, the energy still almost all ends up heating the bulk water within a fraction of a second. Only a small percentage at best is captured by photosynthesis or sequestered via other photochemical reactions.
You seem to misunderstand what thermal energy is. It’s not the motion of a single molecule; it’s the random motion of a lot of molecules.
When two molecules collide, photons of any wavelength can be absorbed or scattered. The energy absorbed goes into pushing the two molecules apart at a higher speed. This is a continuum process. Every material in the universe, without exception – solid, liquid, gas or plasma – absorbs and radiates by such processes, although in rarefied gases the effect can be extremely weak. Water will absorb blue light by this (and other) mechanisms.
Photons can also excite vibrational, rotational and orbital transitions in the absorbing molecule. Doppler, collisional and pressure broadening increases the width of these absorption lines, so there is a finite (albeit at some wavelengths very small) absorptivity across the whole spectrum. These excited states can relax (thermalise) by collision with other molecules on a time scale ~1ps, which is as close to “instantly” as makes no difference. Water will absorb blue light by this (and other) mechanisms.
Paul Birch
I said
The easiest way to solve the blue light in water situation is to pick a particular molecular example. Pick a suitable photon (blue light or shorter wavelength) and give an example of how a molecule on absorbing the photon directly increases its thermal energy.
You said
“Why does the precise mechanism even matter to you?”
Thank you for your long reply, but I guess the real reply is ‘no I have no idea’!
Paul Birch,
“The fact that the radiation is being absorbed means that its energy is being absorbed. Unless you imagine that the ocean is magically levitating off the ocean floor or chemically splitting into hydrogen gas and oxygen/chlorine, that energy can only appear as heat.”
Please do not get sloppy when trying to answer questions like this. I am certain you are aware of the photoelectric, pyrroelectric, and ferroelectric effects. They convert photons into movement of electrons, or, electric current. This is a very valid question for those of us who are less than experts. What does happen and where does it go is NOT something that many of us know and something that is too often assumed.
Bryan says:
February 9, 2012 at 6:11 am
Paul Birch said “Why does the precise mechanism even matter to you?”
Thank you for your long reply, but I guess the real reply is ‘no I have no idea’!
Read the reply! I answered your question quite clearly and fully. I also pointed out why the answer doesn’t matter anyhow. I could go into endless detail about how charged particles in an electric or magnetic field radiate; about how electromagnetic radiation has electric and magnetic fields; about how atoms and molecules in collision form electric dipoles and undergo charge separation. I could talk about Thompson and Rayleigh scattering. I could refer you to Panofsky and Phillips. But I’m not going to bother, because I don’t see any willingness from you even to try to understand; you’d rather keep believing your anti-physicist (and anti-common sense) fantasy.
Paul Birch
Your impertinent reply contained absolutely nothing to do with my original question
A great deal of arm waving fools no-one.
Photons that are present in blue light or shorter wavelengths do not correspond to vibrational rotational and translational transitions.
These transitions are the ones that correspond to thermal energy.
For instance a believable narrative about CO2 absorbing or emitting 15um radiation can be matched with thermal energy changes.
On the other hand wavelengths around 450nm correspond to electronic transitions of the covalent bonds in organic materials.
I am glad that you have terminated replies as you have obviously nothing to contribute to the topic
http://www.ncsu.edu/chemistry/franzen/public_html/Poland/Poznan08a/Text/Ch6.pdf
Dr. Brown,
I had said:
,
to which you responded with:
,
which indeed shows that in – \left(\frac{Mg}{R}\right) \frac{P}{T} you have eliminated density from consideration, and are in essence treating the air as a solid.
Not recognizing your own naivety in matters concerning thermodynamics of gasses, you proceed with:
,
which is the incorrect unphysical result you get from your inappropriate assumptions and reductions concerning equations of state..
You further state:
[?]
Wrong! No, you don’t need masses of gas moving up and down to establish the DALR. You just need molecules moving throughout. If you somehow heat the top molecules only, they will either rise and cool, to settle into the DALR, or they will leave the troposphere.
Bryan says:
February 9, 2012 at 8:43 am
Paul Birch,
Your impertinent reply contained absolutely nothing to do with my original question
A great deal of arm waving fools no-one.
Photons that are present in blue light or shorter wavelengths do not correspond to vibrational rotational and translational transitions.
These transitions are the ones that correspond to thermal energy.
For instance a believable narrative about CO2 absorbing or emitting 15um radiation can be matched with thermal energy changes.
On the other hand wavelengths around 450nm correspond to electronic transitions of the covalent bonds in organic materials.
I am glad that you have terminated replies as you have obviously nothing to contribute to the topic
The impertinence is yours, in rudely claiming I “ha[d] no idea” of the answer to your question when I had just answered it! If you did not understand my reply you had only to ask for clarification. I have not “terminated replies”. I said I wouldn’t bother going into detail concerning the electrodynamics of the mechanism you so willfully ignored.
Blue photons do not correspond to pure rotational and vibrational transitions in water. They do however correspond to transitions which can include changes of the rotational and vibrational quantum numbers as well as the orbital or electronic quantum numbers. When a photon is absorbed through any such transition, the molecule is then in an excited state, Depending on the specific energy levels, the molecule may partly or wholly de-excite by emission of photons of longer wavelength (to be absorbed in turn by other molecules). The molecule will also de-excite upon collision with another molecule. These collisions are how the energy is thermalised. This process is very very fast.
Paul Birch says
“Blue photons do not correspond to pure rotational and vibrational transitions in water.”
Paul and Tim would hopefully agree that translational should be therefore included as well.
These are the modes commonly grouped as thermal.
This was the point that Myrrh was making.
Electrons making orbital transitions do not directly involve thermal wavelengths.
Thermal effects can induce changes in molecular orbital levels.
On deactivation several wavelengths are perhaps allowed including those in the thermal range to account for the energy level drop.
There is a not insignificant amount of energy stored by the process of photochemistry.
The lumping of light and IR together is such a gross oversimplification that it is clearly wrong.
Bryan,
Look in your reference –> pages 363-364. Note that internal conversion and fluorescence result in heat to the surroundings. Chemical reactions are considered “not usually important” by the author.
Also note, Paul said “Photons can also excite vibrational, rotational and orbital transitions“, which you apparently misinterpreted as “vibrational rotational and translational transitions.” Indeed, these orbital transitions are exactly what your reference discusses.
Bryan: “There is a not insignificant amount of energy stored by the process of photochemistry.”
This is a testable hypothesis, not a fact (at least not a fact I am specifically aware of). I would tend to think that the amount of energy stored by the process of photochemistry IS insignificant, for two reasons
1) Photochemistry is relatively uncommon in terms of the total EM radiation heading to earth.
2) For any chemical process to store significant amounts of energy, there must be a significant year-to-year accumulation and/or destruction of chemicals. Simply absorbing energy one moment and releasing it a second or an hour or a year later does not lead to storage of energy. Most photochemical processes (like photosynthesis) are very nearly balanced on an annual scale. In other words, there is no net accumulation of organic material from one year to the next.
But if you want to do some calculations to show that either of these two points are incorrect, go for it !
Tim Folkerts says
“Most photochemical processes (like photosynthesis) are very nearly balanced on an annual scale. In other words, there is no net accumulation of organic material from one year to the next. But if you want to do some calculations to show that either of these two points are incorrect, go for it !”
The ‘known reserves’ of fossil fuels is often touted as being the actual reserves.
But we know that serious research only extends to a commercial timescale.
I cannot find a publication that gives a hard breakdown of % of Solar EM radiation absorbed by chemical rather than direct thermal modes.
I know that orbital transitions do not involve directly a thermal aspect.
Off on holiday for a week or so, means adiabatic matters will have to wait.