Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:

where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that ![]() in stable thermodynamic equilibrium.
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium

In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:

where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.

One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
![]()
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:

where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:

Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
![]()
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Robert Brown says 2/6 at 12:37am:
“The density/concentration profile of N molecules of the monoatomic gas in a thermally isolated cylindrical container of height is given by:”
Robert – I appreciate your difficulty here using the computer language to display formulas. The formula you start with after the prose above is: air density to 5-6km earth atmospheric height z equals the air density at z=0 times exp(z/z0).
Is Robert Brown even aware this is only an approximation of the atmosphere’s density profile from surface up through the troposphere? The approximation IS a good one but it is arrived at by ASSUMING the atmospheric temperature is reasonably CONSTANT from surface up to height h, through the troposphere. Over that height the temperature actually varies ~20%. But still the actual pressure, density, N can be approximated by many of the formulas you write here considering a CONSTANT reasonable temperature is assumed.
The assumption of constant temperature allows the integration of dp/dz from z=0 to z to proceed more easily.
That is shown in the exam answer by the solution parameters assuming CONSTANT temperature. This is only an approximation, yet a decent one. You also assume constant temperature approximation in the top post for the temperature integration. The exam question then extends to non-constant temperature at the bottom where it does the partial differentiation of temperature.
This explains why you arrive at an incorrect isothermal conclusion for Fig. 1 at equilibrium. You just assume temperature is constant. This is only an approximation of the real solution which is non-isothermal as the 13 steps above conclusively show when allowing the temperature to actually vary in Fig. 1.
Although your math seems to work, it appears to me that your conclusion may not be correct, at least if Velasco et al. are; if I interpret their paper correctly, the kinetic-energy profile of their Equation 8 is the maximum-entropy configuration, from which I would conclude that a strictly isothermal microcanonical ensemble will spontaneously undergo (an incredibly small) heat transfer to assume that (ever so slightly non-isothermal) configuration.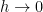 result. We keep thinking that there are two things that are important for such a gas —
result. We keep thinking that there are two things that are important for such a gas — 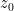 and (separately) temperature. There are not. There is just
and (separately) temperature. There are not. There is just 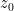 . The gas distribution at all temperatures is perfectly self-similar, scaled perfectly with the thermal gravitational length. Changing
. The gas distribution at all temperatures is perfectly self-similar, scaled perfectly with the thermal gravitational length. Changing 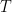 only changes
only changes 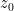 and thus trivially rescales
and thus trivially rescales 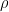 . But the fun thing is that it changes the heat capacity for the gas to
. But the fun thing is that it changes the heat capacity for the gas to  from
from 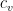 as well!
as well! ,
, 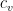 is appropriate. When it is unconfined (as
is appropriate. When it is unconfined (as 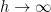 )
)  is appropriate. It smoothly goes from one limiting form of the heat capacity to the other. If I had any need to pick further nits with Jelbring, this would be one — he places “G and the atmosphere (AT) are surrounded by a concentric, tight, black spherical shell with a surface area (S).” around his model atmosphere where “The constant distance (D) between the surface with area A and the surface with area S is very small in relation to R0″. His model atmosphere is bounded from above, in other words, where he has introduced a second length scale into the problem — his D is the same as
is appropriate. It smoothly goes from one limiting form of the heat capacity to the other. If I had any need to pick further nits with Jelbring, this would be one — he places “G and the atmosphere (AT) are surrounded by a concentric, tight, black spherical shell with a surface area (S).” around his model atmosphere where “The constant distance (D) between the surface with area A and the surface with area S is very small in relation to R0″. His model atmosphere is bounded from above, in other words, where he has introduced a second length scale into the problem — his D is the same as 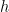 . I missed the “black” bit as well — by making the upper surface part of the system and painting it black he has provided his own equivalent of my silver wire into his own model system. His non-GHG atmosphere permits the lower surface to constantly radiate to the upper surface until the two have identical temperatures in a textbook blackbody radiation calculation. If there is a DALR, the lower surface will constantly transfer heat to the upper surface through radiation, and gravity must then sort it out precisely as I describe above, which so obviously violates the second law that it isn’t funny. Demons Out!
. I missed the “black” bit as well — by making the upper surface part of the system and painting it black he has provided his own equivalent of my silver wire into his own model system. His non-GHG atmosphere permits the lower surface to constantly radiate to the upper surface until the two have identical temperatures in a textbook blackbody radiation calculation. If there is a DALR, the lower surface will constantly transfer heat to the upper surface through radiation, and gravity must then sort it out precisely as I describe above, which so obviously violates the second law that it isn’t funny. Demons Out! , period, exactly, independent of
, period, exactly, independent of 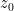 . The heat capacity of the gas is
. The heat capacity of the gas is  . If you add heat to the gas, you linearly scale
. If you add heat to the gas, you linearly scale 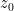 , which has the sole macroscopic effect of lifting the center of mass of the gas.
, which has the sole macroscopic effect of lifting the center of mass of the gas. 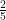 of the added heat energy goes into increased gravitational potential energy from the work the gas does on itself as it expands.
of the added heat energy goes into increased gravitational potential energy from the work the gas does on itself as it expands. 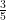 of the added heat energy goes directly into the usual increased kinetic energy of the ideal gas, which is still precisely described by equipartition and still has a local MB distribution of velocities in any slice of the gas large compared to the MFP and small compared to
of the added heat energy goes directly into the usual increased kinetic energy of the ideal gas, which is still precisely described by equipartition and still has a local MB distribution of velocities in any slice of the gas large compared to the MFP and small compared to 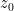 , so that my detailed balance argument is not, actually asymptotically incorrect.
, so that my detailed balance argument is not, actually asymptotically incorrect. and beyond. A paper that Joules Verne, of all people, sent to me that examines this extreme limit shows explicitly that if there is a thermal lapse across this gas it has a weak asymmetry in its conductivity that makes gas relax thermal gradients from top to bottom slightly faster than it does gradients from bottom to top, but the split smoothly vanishes as the gradient does, strongly suggesting that even in this limit if we (correctly) require that the length of a vertical parcel to be much greater than the MFP (and hence much much greater than
and beyond. A paper that Joules Verne, of all people, sent to me that examines this extreme limit shows explicitly that if there is a thermal lapse across this gas it has a weak asymmetry in its conductivity that makes gas relax thermal gradients from top to bottom slightly faster than it does gradients from bottom to top, but the split smoothly vanishes as the gradient does, strongly suggesting that even in this limit if we (correctly) require that the length of a vertical parcel to be much greater than the MFP (and hence much much greater than 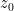 ) the bulk averages will still satisfy the usual kinetic theory and I have a sneaking suspicion that overall they will still satisfy the MB distribution, even though the average itself will be extremely odd. The solution technically doesn’t have to be scale invariant there but the density of the gas and vertical distribution of energies is, in the ergodic sense or for very large areas $A$.
) the bulk averages will still satisfy the usual kinetic theory and I have a sneaking suspicion that overall they will still satisfy the MB distribution, even though the average itself will be extremely odd. The solution technically doesn’t have to be scale invariant there but the density of the gas and vertical distribution of energies is, in the ergodic sense or for very large areas $A$. , so that “thermodynamics” breaks down before, or as, the gas ceases to be reliably isothermal anyway, molecules travel long distances under the influence of gravity between collisions and hence do not have a “constant velocity” on average (compared to the canonical velocity associated with
, so that “thermodynamics” breaks down before, or as, the gas ceases to be reliably isothermal anyway, molecules travel long distances under the influence of gravity between collisions and hence do not have a “constant velocity” on average (compared to the canonical velocity associated with 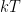 ) so that it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal. Thermodynamics suggests that this breakdown happens in a scale invariant way but here, at least, I will acknowledge that thermodynamics could be wrong, although scaling is a powerful, powerful argument. Exponentials are self-similar functions, after all — what you are effectively saying is that when
) so that it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal. Thermodynamics suggests that this breakdown happens in a scale invariant way but here, at least, I will acknowledge that thermodynamics could be wrong, although scaling is a powerful, powerful argument. Exponentials are self-similar functions, after all — what you are effectively saying is that when 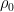 computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes
computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes 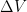 computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant.
computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant. with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!).
with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!).
Hi Joe, I have been thinking about this so hard that I’m dreaming about it — usually a good thing for me as I’ve solved some of my toughest problems in my sleep. Last night I posted a fairly detailed analysis of the thermodynamic — not microcanonical — isothermal gas. When I awoke it occurred to me that I failed to grasp the importance of the
When the gas is confined on a vertical length scale
But the really fun thing is that we can now understand precisely what the role of gravity is in an isothermal unbounded vertical column of ideal gas, in a scale-invariant way. The total energy of the gas is
I’m still thinking about scaling in the upper echelon of the gas in the extremely diffuse limit where
In any event, we seem to be in general agreement that any deviation even in the full microcanonical computation is utterly negligible short of the regime where
But I’m way too busy to work through the algebra to directly prove this (or disprove it, as I’m not at all certain that it is true).
Anyway, I thought you’d like the smooth
rgb
Are you sure the center of mass rises? Couldn’t the total potential energy remain the same while the half-rho zero point rises?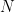 . So mentally compare two exponential curves, both with the same area, one that starts at
. So mentally compare two exponential curves, both with the same area, one that starts at  at
at  and the other which starts at
and the other which starts at 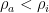 at
at  . The latter is flatter, has a larger characteristic length, and a center of mass further out along
. The latter is flatter, has a larger characteristic length, and a center of mass further out along  .
.
A good question, but I think not. Note that I said think — consider this argument. The gas is constrained to have the same pressure at the bottom. The density at the bottom is strictly smaller for the lapsed gas, reducing the overall density difference between the bottom of the gas column and the top (even if there is no top — zero pressure/density). The integral of the density still has to be
The demonstration that the DALR gas is still exponential is in Caballero, IIRC, but I haven't gone back to compare the actual exponential constants. The heuristic physical point is that if you consider a height where the temperature remains the previous isothermal temperature, all the gas below that height warms and expands, clearly lifting its CM. The gas above that height cools and contracts, lowering its CM. But the gas is exponentially dense and the lapse is linear, most of the mass is below that height, expansion wins, Q.E.D.
rgb
Is Robert Brown even aware this is only an approximation of the atmosphere’s density profile from surface up through the troposphere?
Trick, do me a favor. Don’t speak of me in third person. It is cosmically annoying. Personality disorder annoying. In electronic terms, I’m right in the room with you, but you are doing the metaphorical equivalent of staring at a wall instead of looking at me and speaking as if I’m not here.
You are begging the question, again. The Earth’s atmosphere is not in any way, shape or form like Jelbring’s ideal isolated atmosphere, bounded from above and below by black rigid massive walls and with uniform gravity in between. The DALR is established in Earth’s atmosphere by vertically moving macroscopic parcels of air driven by thermal convection between volumes and surfaces at different temperatures, temperature gradients maintained by diurnal solar forcing and continual radiative cooling.
In Jelbring’s static world, there is no vertical transport of gas — it is long since finished. There is no net radiative transfer of heat from the black lower surface to the black upper surface — he inadvertently (I’m sure) built his own “silver wire” right into his own problem statement because he is clueless. Thermal radiative equilibrium for his black boundaries is isothermal, and if the gas has a different thermal equilibrium then the system perpetually violates the second law with a radiative-gravitaional “heat fountain” that runs without work being done, precisely as my silver wire example does.
I. Am. Not. Talking. About. The. Earth.
Do you understand that? One word at a time, speaking slowly.
I. Am. Talking. About. Jelbring’s. Idealized. Confined. Static. Equilibrated. Gas.
Got that? Jelbring’s gas is, as he explicitly states, not being driven by external heat inputs. It is in hydrostatic equilibrium. All of the gas is at rest. It is in thermal equilibrium — all conduction, convection and radiation across thermal differentials has had time to finish. These are his conditions, and the only conditions you can address in any rebuttal. So far, your replies are all metaphorically straw men eating red herring.
I have at this point presented a solution to Jelbring’s problem that is manifestly isothermal, is manifestly in hydrostatic equilibrium, is manifestly a maximum entropy state. It is clearly a state of the gas that meets Jelbring’s requirements, and the entropy statement shows that it is the only state that can meet it as long as heat transfer within the gas is possible by any mechanism. Bounded by a black upper surface, it won’t even take long for the gas to become isothermal at reasonable temperatures even if it is started with a DALR or other thermal gradient.
If you want to argue, stop invoking Earth’s atmosphere, which is obviously completely different from Jelbring’s in crucial ways. I understand why you are doing it — you want to be able to close the circular argument, claim that the Earth’s atmosphere proves that Jelbring is correct now, then later use Jelbring to prove that the Earth’s atmosphere is naturally heated by gravity at the bottom. But I am watching the shells and the pea, sorry. You have to deal only with Jelbring’s claim and cannot invoke your eventual desired conclusion to “prove” it, any more than he could. His argument is, of course, this identical piece of circular reasoning, but repeating it doesn’t make it logically valid.
rgb
Tim Folkerts says 2/5 at 5:34pm:
“Sorry, I didn’t see any math, just prose. Could you show what you think is the actual math is?….Entropy is defined classically as dS = dQ/T. Suppose you have an isothermal situation to start with. If heat moves from any region 1 to any other region 2, this will cause T2 > T1. The next bit of heat dQ will result in dS = dS1 + dS2 = -dQ/T1 + dQ/T2 The S for isothermal will be less than the non-isothermal field. Try it. I just did. My math suggests you are wrong. What is your math?”
Tim – Correct, the S for isothermal will be less than S for a non-isothermal field which is maximum S. If Fig. 1 starts w/isothermal initial conditions it is not in equilibrium, nature will arrange for heat to move down from higher z region 1 to lower z region 2 causing T2>T1 (Fig. 1 top post T1b>T1t). This ideal gas mixing continues throughout the column to equilibrium at max. S.
I’m not good enough w/computer language to post the actual math formulas, ref. the B&A 4.4 text for them or Verkley paper. That’s why I just posted the 13 step logic outline. Your dS = dS1 + dS2 operates with the constraint of total energy being constant, you need to consider enthalpy constraints in the solution as in the 13 steps.
Tim Folkerts continues:
“What specific gradient do you get? (State your assumptions).”
The assumptions are the same as those in Fig. 1. A GHG-free air column height h, adiabatic control volume, in the presence of constant gravity. Reasonable pressures p found in 80% of earth’s atmosphere, 1000mb down to 200mb. The temperature gradient found (Ref. Verkley paper part b & B&A text) is isentropic non-isothermal. Denoting a given reference temperature Tr found at given reference pressure Pr (say at h=r=z=0) find gradient T(P) = Tr * (P/Pr)^k where k = R/Cp.
The Verkley et. al. paper plots this non-isothermal gradient in Fig. 2 and it is very close to the actual standard atmosphere temperature profile from 1000mb down to 200mb. Verkley also plots the isothermal profile and it is NOT very close to the actual atmosphere profile. See Robert Caballero post way above for the ref. link to Verkley paper.
Tim Folkert’s continues:
“If you really think you are right and Velasco’s paper is wrong…”
I don’t think anything is wrong in Velasco’s paper other than, man, it could be written more clearly. Eliminate the double negatives!
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I see why Tim has gotten frustrated. I had thought that you were serious in wanting to understand the physics, and that you would take the time to look at things like the physics of absorption and scattering of light in dispersive media.
You skin dive. As you go deeper, it gets darker, because water is not completely transparent to visible light! Any more than glass is, or air is, or anything but vacuum is. If you move electromagnetic energy through matter made up of charge with a complex dispersion — and all physical matter has a complex dispersion, even if the complex part is small — then some of its energy is absorbed and turned into heat. It doesn’t matter what non-zero frequency the radiation has, or what the specific details are of the matter — physical matter isn’t perfectly transparent to electromagnetic radiation, period.
You have directly observed how the visible light of the sun attenuates as you dive deeper. All of the energy in that light has gone into heat.
You seem to think that infrared radiation is magic, that it is “heat radiation”. That’s just crazy talk. Electromagnetic radiation is electromagnetic radiation. You can see because visible light carries energy. You see colors because everything you see absorbs some frequencies out of the visible light and scatters/reflects others. The absorbed energy turns into heat, which is why a black sheet of paper placed in the sun gets hotter than a white sheet of paper. Who knows what the colors of the two sheets of paper are in the infrared spectrum! They could both perfectly reflect infrared, and be “infrared colored paper” but because they are different colors in the visible part they will still heat up differently. That’s the bit about “albedo” in all of this talk, BTW — it represents the fraction of all the incident light intensity (not just visible OR infrared, the integrated intensity over all wavelengths) that is reflected.
Coming back with a flip “Puzzle that out in your own time” is hardly a rebuttal to my extremely simple question. You have direct experience that visible light makes it down into the water. You have direct experience that the intensity of visible light smoothly attenuates with depth — it gets darker as you go further down. Visible light carries energy through the surface of the water. The intensity of visible light that comes back out is far less than the intensity that goes in, because the amount of light you see coming back out in very shallow water where it illuminates e.g. white sand is much more than what comes out over deep water.
You know from direct experience that water is not perfectly transparent to visible light. If it were, we could see the bottom of the ocean exactly as if we were looking down on it from an airplane, get you cannot see the bottom of even a very clean, crystal pure lake more than a few tens of meters down, let alone the bottom of the ocean kilometers down. So why do you think I would waste time “puzzling out” something that is obviously false? Any human being who has ever spent a day on a lake knows that water is not transparent like air.
All of the light that is not transmitted or reflected is absorbed, unless you once again want to invoke invisible demons or fairies. In the case of deep water, the bottom is basically completely dark; no visible light is transmitted. It is all absorbed.
Demons Out!
rgb
rgb
Forcing a parcel of bottom molecules out of equilibrium to the top takes work against gravity (f*d = m*g*h). Where does the work come from? . You have to solve the ODE that tells you
. You have to solve the ODE that tells you 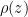 subject to the boundary condition that
subject to the boundary condition that 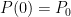 , which must be the same given a constant
, which must be the same given a constant 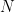 molecules of gas. You have to compute the total potential energy of this gas and compare it to the total potential energy of the isothermal gas. Then we can talk. I’ve already indicated why I am pretty sure that you have it exactly backwards, that the center of mass and gravitational potential energy of the isothermal gas is lower than that of any gas with a negative lapse rate including the specific case of the DALR.
molecules of gas. You have to compute the total potential energy of this gas and compare it to the total potential energy of the isothermal gas. Then we can talk. I’ve already indicated why I am pretty sure that you have it exactly backwards, that the center of mass and gravitational potential energy of the isothermal gas is lower than that of any gas with a negative lapse rate including the specific case of the DALR. once you figure out what
once you figure out what 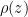 is, and this too will get a much bigger addition from differentially warming the dense bottom than you lose from cooling the not-so-dense top, I think. But even this is talk. Do the algebra. Show me.
is, and this too will get a much bigger addition from differentially warming the dense bottom than you lose from cooling the not-so-dense top, I think. But even this is talk. Do the algebra. Show me.
Say what? No “parcel of molecules” is moved from the top to the bottom. If you want to consider work, you have to consider the energy in the entire thermal column, precisely as I did, explicitly. You can’t just through two equations from nowhere into the discussion. You have to take the gas with a presumed DALR, that is, with
As you warm the bottom, you lift the entire column of gas above it! Joe quite reasonably wants to see the actual computation, because I’m assuming that the density in the DALR is still exponential, and simply becomes a flatter exponential with a necessarily lower base density (in which case the center of mass definitely goes up and your argument is precisely backwards). However, I’m willing to be convinced by a complete, careful, solution to the ODE. If I have time later today, I’ll try to code it into matlab — this one is going to be easier to answer numerically than analytically, unless you happen to be a calculus god. The linear temperature profile goes into the LOCAL condition for hydrostatic equilibrium and the relation between density, pressure, and temperature, so my exponential assumption could well be wrong, but with a linear lapse I would bet that if anything it makes the effect larger, not smaller. It is, after all, the adiabatic work done lifting the gas that makes the top (transiently) cooler in the real atmosphere with an actual thermal gradient heating the bottom and cooling the top providing the source of the work.
So talk is cheap, buddy. Algebra is the only currency for continued argument along these lines. I’ve directly derived the total energy of a gas in isothermal equilibrium. Play right on through for the adiabatic gas, and show me that its total energy is lower than that of the isotropic gas. Hell, the KE will be greater as well, because you’ll have to integrate
rgb
So here is the abstract for the Verkley paper (emphasis added).
It seems pretty clear that it supports Dr. Brown and refutes Jelbring. Convective mixing leads to a non-isothermal situation, and convection is ruled out in Jelbring’s equilibrium world. (And the real world is not surprisingly somewhere between perfect equilibrium and perfect convection.)
Robert Brown says 2/6 at 8:05am:
“Trick, do me a favor. Don’t speak of me in third person….I’m right in the room with you”
I apologize if the involuntary constraints of this website are causing annoyance. No illeism intended. Just identify your preferred means of address. Robert is in the room with me in quotes below.
“I. Am. Not. Talking. About. The. Earth.”
I agree. Not always. There is a need to distinguish earth from Fig. 1 in top post. I’ve done that appropriately. You invoked earth in your 12:37am post formulas.
“I. Am. Talking. About. Jelbring’s. Idealized. Confined. Static. Equilibrated. Gas.”
If that is equal to your Fig. 1 top post then we are on equal ground. If not, let’s just deal with Fig. 1 top post on topic. Agreed?
“All of the gas is at rest.”
The air column is at rest but the GHG-free air molecules are zooming around in Fig. 1 mixing fast, the molecules are not at rest in the control volume.
“..all conduction, convection and radiation across thermal differentials has had time to finish.”
Yes equilibrium in Fig. 1 is achieved, no heat is flowing. Max. entropy S. No delta Q. No delta S. No work allowed across your stated Fig. 1 control volume.
“These are his conditions, and the only conditions you can address in any rebuttal.”
Well, I don’t know about his (Jelbring’s) conditions other than what you write about; the conditions I address are the conditions of Fig. 1. Agreed? Silence is agreement.
“So far, your replies are all metaphorically straw men eating red herring.”
LOL. Well, my replies are compliant of nature, just like straw men and red herrings are constructed of things natural.
“I have at this point presented a solution to Jelbring’s problem that is manifestly isothermal, is manifestly in hydrostatic equilibrium, is manifestly a maximum entropy state.”
You have presented in top post a manifestly incorrect constant temperature gradient solution to your stated Fig. 1 conditions, i.e. incorrectly isothermal & can be manifestly shown to NOT be at maximum entropy isothermally therefore not at equilibrium thru some hard work. The Fig. 1 correct physics being non-isothermal temperature gradient solution when no heat flows any longer is shown in the Velasco et. al. paper (albeit unclearly), especially clearly in the Verkley et. al. paper part b and clearly in the B&A Chapter 4.4 text. Those are not strawmen or red herrings. They are real physics. From 1st principles.
Temperature gradient of Fig. 1 is that which I just posted in reply to Tim Folkerts at 8:12am, adding some clarity:
Denoting for Fig. 1 conditions in top post, a given reference temperature Tr found at given reference pressure Pr (say at h=r=z=0) find non-constant T when entropy is max. i.e. equilibrium non-isothermal temperature gradient T(P) = Tr * (P/Pr)^k where k = R/Cp.
“I understand why you are doing it — you want to be able to close the circular argument, claim that the Earth’s atmosphere proves that Jelbring is correct now..”
I really, really have no interest in proving or disproving anything in Jelbring’s paper. I became interested in this thread only because upon thinking through the physics of Fig. 1 and Fig. 2 in the top post there was a challenge to get the real physics right thru ideal gas simplifications consistent with natural laws. The challenge sent me out to read some previously unknown to me & very interesting papers on the subject (Velasco et. al., Verkley et. al.) and some great texts (Caballero on-line notes, Bohren&Albrecht). That B&A text is terrific, it actually finally resolved some other issues that I have long wondered about.
“… cannot invoke your eventual desired conclusion to “prove” it…”
I have no dog in this fight, just want to go where the ideal physics conclusions of Fig. 1 top post necessarily take us from 1st principles, consistent with the thermo grand masters. It has been very interesting, so I’ve stuck with it.
“If you want to argue, stop invoking Earth’s atmosphere..”
I’m ok with that; your formulas presented at 12:37am were derived from earth’s atmosphere so my reply dealt with the earth. If you want to leave out earth, that’s ok we can debate ideal gas physics for fun & learning & teaching with idealized Fig. 1 top post. Your integration of temperature in top post then needs to be general, not use an integration assumption derived from earth (that assumption of T being constant in your integration).
Have to remember the main purpose we do all this is to understand physics in earth’s atmosphere better – we can utilize our hard work & experiences that way.
Robert Brown says 2/6 at 8:59am:
“Say what? No “parcel of molecules” is moved from the top to the bottom.”
Yes it is. It was in your example for goodness sakes. Geez. This was in response to your statement at 2/5 10:25: “So if we move heat from the bottom to the top,” as faithfully copied. LOL. Heat doesn’t exist independent of the molecules, at least not since the caloric theory bit the dust not much more than a century ago.
“So talk is cheap, buddy… Do the algebra. Show me.”
Ok. Sigh. I would REALLY like to, but here I cannot post the algebra only b/c I am not familiar enough with the proper commands to do so, otherwise I would. I resorted to posting the 13 step outline logic above. To fracture a phrase from racing: The BS stops when the algebra drops.
It is really unnecessary to post the algebra here anyway since for Fig. 1 equilibrium max. entropy conditions to be shown non-isothermal isentropic, the algebra is well developed since Ball in 1956 eqn. 4, 1998 Bohren&Albrecht chapter 4.4, and 2004 Verkley paper part b.
If you really want to get past cheap talk & see algebra, refer to the poster Rodrigo Caballero Verkley ref. way above – just search this page for Guinganbresil. The paper is in that poster’s 1/27 9:38am link.
I would post the link again, but I am not knowledgeable about how to correctly do that here either. I have read the WUWT spam filter can trap a post with a link for irritatingly long time.
[Dave, if one of your posts disappears just ask a moderator to rescue it from the spam folder. ~dbs, mod.]
Read that part c-a-r-e-f-u-l-l-y. They are hypothesizing that the INTEGRAL is constant, not that the temperature itself is constant. Specifically, Equation 6 says the integral of TdP is constant, ie enthalpy is constant. They THEN go on to derive that at equilibrium the temperature must indeed be constant within the section if the container is perfectly insulated.
This is most definitely NOT correct. The top post involves absolutely NO convective mixing. The paper is discussing STRONG convective mixing at this point. These are as different as night and day.
The concluding remarks of the paper seem very apropos.
PS. The Verkley paper can be found here: http://www.knmi.nl/publications/fulltexts/verkley_gerkema.pdf
Robert Brown: “although yes, Joe, my argument involving shifting the MB distribution was sloppy and imprecise — hopefully you like this one better but the result is the same either way”
I do, and I agree.
Robert Brown: “it has been a few, um, decades since I took stat mech and it was the most difficult course of physics I ever took when I took it, making even quantum mechanics look like a walk in the park in comparison.”
Bless you. It’s salve for us plodders’ egos to hear that even the smart guys find this stuff hard.
Robert Brown: “I think [Joe Born] realizes that my answer is irrelevantly imprecise.”
Indeed I do.
Robert Brown: “it would be more correct to say that the gas no longer has a temperature than to say that it is no longer isothermal ”
This may just be a you-say-tomato-I-say-tomahto thing, but to me the Ideal-Gas-Law concept of temperature holds up pretty well at low N so long as pressure is integrated over a long enough time. But, as you say, it becomes problematic for some of the thermodynamics results.
Robert Brown: “Anyway, I thought you’d like the smooth with the extra energy going directly and scalably into lifting the CM of the expanding gas (work!). ”
I do indeed.
Robert Brown: “what you are effectively saying is that when computed for the gas at some scale height is no longer even approximately smooth on the scale of parcel volumes computing averages as if it is continuous becomes problematic. So does computing thermodynamics as if mechanics is classical, for that matter. ”
Since I know no quantum mechanics at all, one of the questions I had hoped some reader would resolve was how valid quantum-mechanical considerations leave Velasco et al.’s result (which assumes a continuous phase space). Maybe I’ll look into that after I get my taxes done, but I’m not optimistic that I’ll be equal to it.
Robert Brown: “But ergodicity is still expected, and the thermodynamics suggest that the functional shape of the phase space sampled by the molecules of even the very dilute gas high up in the vertical column is scale invariant, so that a true ergodic average will be similarly invariant. ”
I’m not sure I followed that, so the following two comments are likely to be inapposite.
First, if the classical approximation still holds, I would infer that in principle separately integrating pressures at two altitudes for a long enough time would enable one to distinguish the Velasco et al. profile from isothermality.
Second, one way of saying that equilibrium requires isothermality is that the number of microstates in the isothermal macrostate is so astronomically many times as great as the number in all non-isothermal macrostates combined that there is essentially no chance of encountering in the isothermal macrostate a microstate whose trajectory spends any detectable proportion of its future time in a non-isothermal macrostate. But what the number of microstates in the isothermal macrostate actually is depends on how precise we require the isothermality to be. Maybe the isothermal macrostate’s microstate count is not so overwhelming if we exclude from our definition of isothermality any configuration in which, say, different-altitude temperatures separately measured with an integration time of one second do not equal each other to within one part in 10^32. Of course, this is just another way of saying the Second Law applies only to large numbers, but this way of saying it helps me further appreciate the degree to which Velasco et al. do or do not find equilibrium non-isothermality.
Tim Folkerts says 2/6 at 12:29pm:
“They are hypothesizing that the INTEGRAL is constant, not that the temperature itself is constant.”
It is my duty to c-a-r-e-f-u-l-l-y inform you that if the integration of temperature results in a constant the temperature is constant, see Verkley part a integral eqn. 10 & constant T result eqn. 11.
Verkley part a quote: “…that is, T = a constant, thus, the profile is isothermal.” This results from air column shown in Verkley Fig. 1 which allows the air column to do work across the control volume above and below. If top post in this thread Fig. 1 is simply modified to show work crosses the control volume above & below, then it is proper to think the modified top post Fig. 1 when equilibrium is reached, that T indeed is isothermal.
Thanks for re-posting the Verkley paper link. I see the mod.s (Dave) made it clear I can ask for help, I may have more courage in the future.
“Equation 6 says the integral of TdP is constant, ie enthalpy is constant.”
This is imposing the general constraint of constant total energy 1st law.
“They THEN go on to derive that at equilibrium the temperature must indeed be constant within the section if the container is perfectly insulated.”
No, they do not have perfect insulation in part a for isothermal case, they allow work across the insulation – read again the statement in Verkley Fig. 1 as I quoted, their air column is different than Fig. 1 top post. Again, just make top post Fig. 1 able to do work above and below, find it is isothermal as in part a. For no work above & below, perfect adiabatic insulation, find Fig. 1 top post is isentropic, non-isothermal as in Verkley part b.
Verkley imposes perfect insulation only in part b and reaches the isentropic non-isothermal conclusion as does B&A (from mathematically maximizing entropy) which Verkley et. al. cite and offer grateful acknowledgement.
“The top post involves absolutely NO convective mixing..”
How do you not see the molecules in top post Fig. 1 are very frequently randomly mixing up and down the column? They are mixing even in an ideal column, very vigorously mixing even ideally. Verkley et. al. discusses this very action in part b isentropic non-isothermal case.
There is certainly absolutely NO convective mixing in a solid, we are talking an ideal gas here.
I say: ““The top post involves absolutely NO convective mixing.”
Trick replies: “How do you not see the molecules in top post Fig. 1 are very frequently randomly mixing up and down the column? ”
Perhaps this is the crux of our miscommunication.
There is a huge difference between the random thermal motion of molecules and convection. Convection is a large scale, organized motion of a fluid. It requires an input of energy. Convection produces a measurable net flux upward through some surface (and down through some other surface). There will be a measure airspeed. On the other hand, “perfectly still” air will, of course, have molecules moving at 100’s of m/s, rearranging with no net motion on a macroscopic level.
* So, yes, I see that there is microscopic random thermal motion of the molecules.
* But, no, that does not mean there is macroscopic, organized convection.
When the various papers say (or I say or Dr Brown says) there is convection, it means something much more than random thermal motions of individual molecules.
Trick says: “It is my duty to c-a-r-e-f-u-l-l-y inform you that if the integration of temperature results in a constant the temperature is constant”
Suppose I tell you that the integral of f(x) dx from 0 to 1 equals 1 (which is definitely constant). Can you tell me f(x)? Must f(x) be constant? perhaps f(x) = 2x? Or f(x) = 0.9 + 0.2x? Or f(x) = 3x^2?
If I tell you the integral from P1 to P2 of T(P) dP equals some constant H, can you tell me T(P)? A constant temperature is only one possibility (and, as it turns out from the next couple paragraphs in the paper, the right possibility).
Tim Folkerts says 2/6 at 4:01pm:
“Convection is a large scale, organized motion of a fluid.”
Yeah. Verkley et. al. struggle with this in their lo-o-ong explanation of part b “mixing”, in which they do use the word “convection”.
The authors write: “…motions are now taken into account, albeit implicitly. Their role is to mix the potential temperature field, to strive to homogenize it. We should now interpret the state variables as averages over volumes that are large…”
This is possible to debate because “large” is unsatisfyingly imprecise. I take that to mean at least we can move from discussing just a particular molecule mixing but “large” groups of molecules mixing. Still a very small micro amount of molecules but above the individual particle level.
Tim continues at 4:20pm:
“Suppose I tell you that the integral of f(x) dx from 0 to 1 equals 1 (which is definitely constant). Can you tell me f(x)?”
No. Just that whatever f(x) is, it is continuous, defined & constant (=1) over the interval 0 to 1. Maybe more, whatever the rules of reasonableness for math integration are defined in the limit.
Trick> Yeah. Verkley et. al. struggle with this in their lo-o-ong explanation of part b “mixing”, in which they do use the word “convection”.
They use the word “convection” in part (b) because they are explicitly assuming convection in part (b). In part (a) they were assuming no convection. I don’t see where the difficulty is.
* No convection –> constant T = isothermal
* Convection –> Constant Theta = non-isothermal
The top post and Jelbring are specifically discussing no convection. The non-isothermal result is with true macroscopic convection ABOVE AND BEYOND microscopic random motions.
Trick: >>>It is my duty to c-a-r-e-f-u-l-l-y inform you that
>>> if the integration of temperature results in a constant
>>> the temperature is constant”
Tim>> “Suppose I tell you that the integral of f(x) dx
>> from 0 to 1 equals 1 (which is definitely constant).
>> Can you tell me f(x)?”
Trick > No.
Then I think we agree here, that the form of the function is not explicitly specified just because we know the result of the integration. That is all that I was saying, and all the authors are saying in Eqn 6. The integration of TdP is a constant H, but they are not specifying that T is constant. ADDITIONAL work is needed to show an isothermal result. So they are NOT using circular reasoning by assuming an isothermal profile to prove an isothermal profile.
Bryan says February 6, 2012 at 2:17 pm: “I hope that helps!”
Actually, there is nothing there that addressed the issue that YOU raised, so no, it does not help.
1) You suggested that photosynthesis was inappropriately ignored in K&T’s diagram (which by definition gives global averages over long time-scales).
2) I encouraged you provide estimates of the importance photosynthesis.
3) You complain about all sorts of OTHER things and avoid making a meaningful contribution.
So if you do want to help on the issue you raised, then provide an estimate of the importance of photosynthesis on the global energy balance. That would be helpful and worth reading about. That would move the discussion forward (although this whole topic is a bit of a tangent away from the top post).
Tim Folkerts says 2/6 5:30pm:
“In part (a) they were assuming no convection.”
Can you show me where they (Verkley et. al.) assumes no convection in part a? Not sure I can find this assumption. Interesting to discuss the specifics.
Tim continues:
“The top post..….specifically discussing no convection.”
The top post 1st mentions “convection stops” above the troposphere in the 2nd to last sentence, this in the conclusion. That seems to mean or at least imply convection IS assumed in the top post up through the troposphere. Though it is not discussed that I can see.
Tim continues:
“ ADDITIONAL work is needed to show an isothermal result.”
Yeah, this is the big deal difference between top post Fig. 1 and Verkley Fig. 1, the additional work above and below the air column considered in Verkley part a. The paper shows this work being allowed to cross the control volume results in an isothermal conclusion. It would be interesting to discuss just why that happens.
Trick, I have now read the Verkley paper slowly and thoroughly and everything you have been explaining and pointing out is now clear. Thanks.
correction
‘insulation’ should read ‘insolation’
Dr. Brown,
In your top post, when you introduce your silver conductor you say:
,
but you don’t give the mass or the initial temperature of the silver wire.
Could you please tell us what conditions you are assuming?.
Bryan says:
>Well Tim that insolation [340 W/m^2] produces a blackbody spectrum
That spectrum is determined by the temperature of the sun. It is (essentially) the same spectrum as the 1360 W/m2 that arrives at the top of the atmosphere, or the ~ 60,000,000 W/m^2 that leave the surface of the sun.
You seem to be laboring under the misconception that spreading sunlight out changes the spectrum. The sunlight does not become red (or infrared in this case) simply because you spread it out with a lens, or go to Pluto, or average it over the whole surface of the earth.
>well into the thermal IR band.
The solar spectrum has some thermal IR, but not much.
>So no photosynthesis would be produced whatsoever, as IPCC science predicts.
Since we are talking about the solar spectrum, then it easily can produce photosynthesis, as “IPCCscience” would predict.
>So to answer Robert Browns question to Myrrh that type of radiation
>is completely absorbed in the top few millimetres of the water surface.
Not to belabor the point, but “that type of radiation” *is* the solar spectrum (modified by absorption thru the atmosphere), with ~ 10 UV, ~ 40% visible, and ~ 50% IR.
>Of the solar radiation reaching the surface of water some 50% is in the IR.
OK. I agree now.
>It will be absorbed in the top few mm causing evaporation of the surface water.
Or even the first few um for thermal IR.
>The other 50% will penetrate deep into the water and a
>significant proportion will be available for photosynthesis.
Ah ha! And there is the crux. Just how much ACTUALLY goes into photosynthesis? That was you initial point, and the issue that I was hoping you would provide some insights into.
>Notice that the evaporation and the photochemical processes
>both are systems that store energy that can be later released
>to buffer temperature change.
Quite true. And buffering the temperature is important to the temperature of the planet. Buffering cools the warm side and warms the cool side. There have been a couple other discussion on WUWT this past month addressing just that issue.
>The radiation obsessed IPCC science model with its fictitious 33K effect is false.
The amount of warming due to GHGs is up for debate, especially since it depends critically on other assumptions and feedbacks. But there is no doubt that SOME warming is due to GHGs, and the “everything else being equal” assumption does lead to ~ 33 K warming.
>So don’t believe everything that broad brush, eyes shut IPCC science tells you.
Rather than saying “eyes shut” I would say “focused”. Sometimes “focused” means you are looking the right place; sometimes it means you overlook important things outside your view.
But the simple fact is that (essentially all) energy arrives at the earth in the form of solar EM radiation and (essentially all) energy leaves the earth in the form of terrestrial EM radiation (thermal IR). Focusing on “essentially all” of the energy coming and going is a good way to find the overall balance of the earth.
Tim Folkerts says
“everything else being equal” assumption does lead to ~ 33 K warming.”
Yes the ‘everything being equal’ assumes there is no photosynthesis along with a dazzling set of pseudo scientific assumptions.
That greenhouse gases being absent does not effect the one third of solar radiation being absorbed by clouds
Or the surface albedo can jump from 12% to 30%
Or the greenhouse gases being absent but still have clouds to reflect radiation
Or the IR (not now absorbed) by the clouds will not obey Kirchoff’s Law on reaching the planet surface
And so on.
Take your pick of the fantasy elements to create your own version of the greenhouse 33K nonsense.
http://www.ars.usda.gov/is/AR/archive/jan12/solar0112.htm?pf=1
Tricky asks : “Can you show me where they (Verkley et. al.) assumes no convection in part a? Not sure I can find this assumption. Interesting to discuss the specifics. ”
I thought it was obviously implied in both cases. Here are a few lines of thought:
* Only superfluids keep moving with no damping, and the air is not a superfluid.
* Convection requires constant heating at the bottom and cooling at the top, and this is not happening in an adiabatically enclosed system.
* The top post and the Verkley paper assume thermodynamic equilibrium.
I’m sure there are other ways to say it. All of them allow microscopic motion of molecules, but not macroscopic motion of large set of molecules.