Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Robert Brown says at 2/4 9:11pm:
“Except that it is a ten-second mental exercise to see that this is not, in fact, maximum entropy.”
Robert Brown’s ten-second mental exercise is too short in fact & can be shown incorrect, impeded by thinking of conduction in solids (molecules can’t move) and not ideal gases (molecules move & mix). It takes much more than a ten-second proof to show why Robert Brown’s mental exercise is incorrect. See 13 steps below.
Robert Brown continues: “Because if heat is transferred from the warmer bottom to the cooler top, the entropy of the arrangement will increase.”
Yes, of course, because the transfer process does work on the system in Fig. 1. Your delta Q is then not zero so that your delta S is not zero. But remember Fig. 1 allows no work or heat flow to come across the control volume, it is adiabatic equilibrium by definition. Fig. 1 delta Q is zero, thus delta S is zero. Constant entropy S prevails inside Fig. 1 due to the adiabatic boundary.
Robert Brown continues: “The only way the gas will not be isothermal at maximum entropy is if heat transfer is impossible.”
Bingo! Heat flow (or work) transfer within & across the adiabatic control volume is impossible as it can be shown the GHG-free ideal gas will be non-isothermal at maximum entropy equilibrium.
Robert Brown continues: “Go ahead, do the algebra.”
Ok I will. The constant entropy of Fig. 1 must be maximized mathematically as in nature. I will outline the correct algebra. Robert Brown has done incorrect algebra in the top post by improper temperature integration. Any physicist CAN do it correctly, consulting with the math dept.
Here are the correct algebra and proper steps for Fig. 1:
1) Start by computing the total GHG-free air constant mass per unit area of a gas layer between any two heights under gravity g
2) Add in the hydrostatic equilibrium pressure change with height in the gravity field
3) Compute the total enthalpy per unit area of the layer realizing the layer possesses potential energy per unit area in earth’s gravity field
4) From that, realize energy conservation imposes a constraint that total dry static energy is constant in the layer (within adiabatic control volume)
5) From this, realize and compute the total entropy (S) of the layer over the height of the layer
6) Transform S computation from height to pressure by way of hydrostatic eqn. above and ideal gas law
7) Now maximize this entropy S to find nature’s required ideal gas temperature profile
8) To do that, confine the math maximization process to reasonable range of pressures found in earth’s atmosphere (roughly 1000mb down to 200mb ~80% of atmosphere) to make no serious errors
9) Transform variables to make the calculation much more simple (the math. Dept. will help Robert Brown here)
10) Find the function for which the layer’s entropy S is maximum subject to energy conservation constraint in the layer
11) To simplify, constrain this maximization to a linear set of temperature profiles
12) The condition for entropy S to be an extremum is that its derivative vanish
13) Do the algebra, find the nature of the entropy S extremum IS a maximum only with non-isothermal temperature profile.
Of all the linear temperature profiles, find entropy maximization requires the equilibrium temperature of Fig. 1 to decrease with increasing height i.e. it is non-isothermal, T1b is required to be higher than T1t by proper maximization of entropy. Robert Brown missed most of this important algebra in the top post.
Then consult the math dept. to prove by contradiction the general case does not require the assumption of a linear temperature profile.
Since Robert Brown cannot do that in a ten-second mental exercise & did not do the algebra in top post correctly to maximize entropy, his assertion of isothermal w/gravity is impeded by jumping to a conclusion from conduction in solids which these steps have proven incorrect using ideal gas law, conservation of energy constraints, entropy maximization and proper, correct algebra.
The ten-second mental exercise of why considering conduction in a solid is inappropriate involves the solid’s molecules are constrained not to move much in the solid since they mostly vibrate. The gas molecules can move throughout the Fig. 1 column top to bottom w/o constraint other than random elastic collisions freely mixing subject to constraint of ideal gas, energy conservation and entropy laws.
Robert continues: “BTW, no, I’m not talking about lifting up any parcels of gas during equilibration.”
Good, w/increased learning Robert Brown moved on past the jars.
Robert Brown continues: “The gas is equilibrating via thermal and radiative conduction. No work is done by gravity.”
Yep, after reaching equilibrium no work is done by gravity. The gas is thermally equilibrated max. entropy non-isothermal proved in the steps of this post.
Robert Brown continues: “Well, that’s not quite true.”
No, that IS true.
Robert Brown continues: “As the bottom cools and the top warms the center of mass of the gas will indeed move down because the density of the gas at the bottom will increase while the density of the gas at the top will decrease.”
No, not after Fig. 1 achieves equilibrium as it must with no energy across the control volume. See the steps above.
Robert Brown continues: “You’re all about energy balance and gravity.”
Yes, so is earth’s nature.
Robert Brown continues: “Well, the gas is, on average, lower when it is in thermal equilibrium, not higher, in a macroscopically more stable state, a hydrostatically more stable state. Remember, it is always in hydrostatic equilibrium.”
Yes, I remember it is always in hydrostatic equilibrium once Fig. 1 achieves equilibrium. No, it is not macroscopically stable unless maximum entropy is achieved which is constrained by energy conservation to be non-isothermal.
Robert Brown continues: “The most gravitationally stable profile is isothermal.”
No, Robert Brown cannot just simply assert this; it is way more difficult as the task shows, maximum entropy with gravity field is proven non-isothermal in the steps of this post, detail algebra ref. B&A text. Non-isothermal profile is very close to the real atmosphere as shown by Verkley paper Fig. 2 referenced above by poster Rodrigo Caballero.
Without gravity, the outline in this post with g=0 reverts to isothermal temp. profile as it must. Gravity REALLY complicates things beyond a ten-second mental exercise but nature resolves itself. Note thermo can’t tell us how long but experimental evidence shows the time frames to equilibration are relatively short.
It has been a fun, interesting conversation for me, thanks Robert.
Trick says: “But remember Fig. 1 allows no work or heat flow to come across the control volume, it is adiabatic equilibrium by definition. Fig. 1 delta Q is zero, thus delta S is zero. Constant entropy S prevails inside Fig. 1 due to the adiabatic boundary.”
This is not at all correct.
1) The system is adiabatic by definition, but it is not by definition in equilibrium. The system was postulated to be in hydrostatic equilibrium, but the question of thermal equilibrium was left unspecified (and eventually Dr Brown’s conclusion is that it was NOT thermal equilibrium). (I am not even 100% sure what you would mean by “adiabatic equilibrium”.)
2) It is true that there is no Q to/from outside the system, but there can still be Q within the system. Forget gravity for the moment — simply put a container of hot gas (say 400 K) and a container of cold gas (say 200 K) within adiabatic walls. Then put them into thermal contact.
When the first joule of energy moves from the hot side to the cold side, entropy will increase by
dS = (+1 J) / 200 K + (-1 J) / 400 K = + 1/400 J/K
Entropy will continue to increase (albeit more slowly) as heat continues moving from hot to cold until the two are isothermal. Constant entropy will only prevail within the adiabatic boundary after conduction within the systems ceases (ie after thermal equilibrium is achieved ie the system becomes isothermal).
You might want to restart your arguments from the beginning to fix these errors.
You seem to ignore that there is a density difference with height in gas pressurized by gravity, then apply principles that are density dependent.
?
and a starting pressure e.g.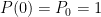 
atm. All of them are hydrostatic — in perfect force balance — by construction, they satisfy the differential equation above for the balance of buoyant forces in a fluid. Not all of them are necessarily stable to convective perturbations, I imagine, but many, an infinite number of the in fact, are and none of them but one thermal profile is stable if the gas can thermalize via conduction and radiation. That one solution is maximum entropy, in hydrostatic balance, and in thermal equilibrium. It happens to be isothermal.
Ignore it except where I actually derive it (for an ideal gas) in the original article? Ignore it except for where I write out an explicit differential equation such as this:
Ignore it sort of like I’m not ignoring it at all? Sure I am. Did you actually read the top article or are you just reacting blindly because I am threatening your illusion that gravity magically heats static gases?
Neither you nor Myrrh seem to be able to grasp the idea that there are an infinite number of solutions to this ODE, given a thermal profile
In order to establish the DALR in a gas in the first place, however, you have to have masses of gas moving up and down because the gas is not in hydrostatic equilibrium. If the top is warmer than the bottom, there will be no convection! The fluid would have to literally lift itself up by its bootstraps to warm the bottom and cool the top from this initial state, because the bottom would expand (constant pressure, higher temperature), lifting the center of mass of the gas and increasing its potential energy!
Right.
rgb
Tim Folkerts say 2/5 at 1:19pm:
“…but there can still be Q within the system.”
Transiently, yes. But there is no heat flow at equilibrium. Q inside the control volume flows until equilibrium and then stops flowing at max. entropy. I have come to learn this is REALLY hard to get a handle on for many when gravity is added. The proof is in the maximization of entropy which is hard to see also, heat ceases to flow at max. entropy. There is a temperature gradient from the mixing of the ideal gas w/gravity at equilibrium in Fig . 1. Work thru the 13 steps. S-l-o-w-l-y.
Tim continues: “Entropy will continue to increase (albeit more slowly) as heat continues moving from hot to cold until the two are isothermal.”
No, the math proves isothermal for Fig. 1 is not the max. entropy; S can still increase from the isothermal condition in Fig. 1 above – this is a very neat thing to learn out of this. For homework, pick a set of reasonable Fig. 1 initial conditions. Compute S in an isothermal field. Then compute S for the non-isothermal field, same initial conditions.
The S for isothermal will be less than the non-isothermal field. Try it. Report back. Nature fixes the isothermal lesser S by flowing heat & naturally increasing entropy to the max. S when heat stops flowing & non-isothermal max. entropy. Really pretty neat.
“Forget gravity for the moment… When the first joule of energy moves from the hot side to the cold side, entropy will increase…”
Yep, to equilibrium at max. entropy. Gravity however is not forgotten in Fig. 1. Gravity imposes a potential field, a pressure gradient and that makes all the difference, nature finds an ideal temperature gradient. VERY close to the actual temperature gradient in the real atmosphere (and way closer to reality than the isothermal conclusion for Fig. 1). Ref. Verkley paper Fig. 2 above.
Fig. 1 moves from isothermal to non-isothermal equilibrium when gravity is added. There are no errors I can find in the proof.
Robert Brown says:
February 4, 2012 at 9:49 pm
Myrrh says:
February 4, 2012 at 7:01 pm
Adiabatic Cooling…
Nice picture, and nice article. Note well that the figure clearly labels the wall of the balloon as being a thermal insulator — that’s the adiabatic part, actually. Suppose that it wasn’t really a perfect thermal insulator? Hmmm, would the gas precisely follow the adiabatic PV curve if heat could flow into the contents of the balloon from the gas surrounding it?
I’ve already noted it well…, glad you noticed. But, don’t worry about what would happen etc. just yet, get yourself firmly acquainted with the basic concept first. The Adiabatic Process is fully understood in the real world. Adiabatic means without heat entering or leaving the system. Familiarise yourself with that picture.
Note well that the article clearly states that the air takes on an adiabatic lapse as it is being uplifted. It even offers pretty much the only two mechanisms for uplift, and truthfully that can be reduced to one. The first is differential heating leading to convection, the second is the deflection of lateral air movements as they go up or down a mountainside. The second, of course, requires pressure differences to generate the wind and pressure differences are only created by differential heating. No differential heating (on Earth or anyplace else) — no ALR.
I’ve already noted it well.. You need to note well that “takes on an adiabatic lapse rate as it is being uplifted” is because it is within the adiabatic process, that’s what it will do. Do try to refrain from interpolating your own version into this – this is one of the basic constants of our physical world, like heat always flowing from hotter to colder, because that is the way it is. Gases with extra heat input might well rise faster, and chinook winds speed up the heating of its air as it comes into greater pressure from the heights, but we are talking about the basic process here, to which all these relate, created by gravity. What this is saying is that these will act according to the basic structure. The adiabatic lapse rate exists without any extra heat coming into or leaving the system, it’s created by gravity. From that we can understand our winds, our weather systems. Parcels of air moving through the atmosphere are called wind, convection, I’m glad you have heard of convection, it is one of the three modes of transport for heat, as thermal energy on the move.
Air uplifted will cool as the air pressure decreases, and will heat up as it descends as air pressure increases, it takes on the adiabatic lapse rate up and down, remember the picture. Moved higher it will expand as it becomes less dense and will cool, moved lower into higher pressure it will become more dense and will heat up. That is the Adiabatic Lapse Rate, it is a constant. That is the process created by gravity. That’s what Adiabatic Lapse rate means, relating to a specific process and not to anything else some might want to imagine. Don’t confuse it with the environmental lapse rate
From: http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
[bold as on original page]
[“The process of convection causes air warmer than its environment to rise, and cold air to sink. Convection thus transports heat upward, making it warmer aloft than it would be in the absence of convection. However, in the atmosphere, in contrast to what happens in a kettle filled with water and set on the stove to boil, convection does not lead to a temperature profile that is uniform with height. This is because the rising air cools adiabatically. Dry convection will tend to create an adiabatic temperature profile in which the temperature falls at a rate of 9.8 °C per kilometer.” ]
Next step:
[“But what the ideal gas law can not tell us is what will happen to the temperature. To find that out we need to consider the first law of thermodynamics – a physical law that extends the principle of conservation of energy to include the concepts of heat and work.
“In thermodynamics the simplest form of energy conservation is the balance between internal energy (the kinetic energy of the body’s internal molecular motion – directly proportional to its temperature), and the amount of heat added to the body minus the work done by the body on its surroundings.
“As our air parcel expands in response to the lowering of the outside pressure, the force of its internal pressure is moving the walls of the container outwards. When a force is moving an object over a given distance it does work. Thus the expanding air parcel does work on its surroundings. This work must come at the expense of internal energy (remember, heat is neither added nor taken away from the parcel in this experiment). Thus the molecular motion within the parcel will slow down, and the parcel’s temperature will drop.
“The expanding parcel will experience not only lowering of its pressure and density, but also of its temperature. All three state variables: pressure, density, and temperature will remain in balance as described by the ideal gas law. The process described above is called adiabatic expansion, implying the change in parcel density without the exchange of heat with its surroundings, and its consequential cooling. The opposite will occur when the parcel is compressed. Adiabatic compression leads to warming“.
..
IV. Atmosphere under gravity – hydrostatic balance.
Hydrostatic balance
“In the vertical direction, gravity is by far the most important external force acting on the atmosphere. It is the reason for the existence of this crucial envelop of gases around the Earth.”
..
“We can now combine the thermodynamic laws with the effect of gravity on pressure. Using the equation of state, the first law of thermodynamics, and the hydrostatic equation we can find that the rate of adiabatic temperature change in an ascending air parcel (also termed the adiabatic lapse rate and denoted Γd) is constant: ..”]
Last bold mine..
An interesting question is then — suppose one starts with an air column (Jelbring conditions, dry ideal gas, no mountains, wind, or sources of heat) but select as an initial condition hydrostatic equilibrium with a thermal profile somewhere in between the classic DALR and isothermal. Which way (to which profile) will this air column go? etc.
You’re still not getting hydrostatic balance, it doesn’t mean nothing is happening and you have to bring in another idea into the system to work out what will happen…, the adiabatic lapse rate will happen, because gases will become more dense and sink when cold and so will find themselves under great pressure at the surface where they will get compressed and heat up, and heated up they will become less dense and rise and in rising they will cool and in cooling they will become more dense and sink and so on. Local conditions apply within that, superimposed on it, by bringing in an extra heat source for a parcel of air for example, it will rise faster than the adiabatic lapse rate conditions of the gases around it, but the rate will always be relative to the natural cycle, because it’s a relationship of gases with gravity.
[Hydrostatic balance
“In the vertical direction, gravity is by far the most important external force acting on the atmosphere. It is the reason for the existence of this crucial envelop of gases around the Earth.
“The atmosphere does not collapse under the downward pull of gravity because of the energy embedded in the movement of the air molecules. This movement creates the force of pressure which counters the gravitational pull on the atmosphere. The balance between the force of pressure and gravity is the hydrostatic balance.
To find the expression for the hydrostatic balance, we first note that atmospheric surface pressure is due to the weight of the entire atmospheric column above. As we ascend, there is less of an atmosphere above us, and hence the pressure drops.”]
The adiabatic lapse rate is within the hydrostatic balance because of the properties of gases which create the pressure. And it’s temperature profile..
[“To understand the equation of state, assume that you have a fixed mass of air enclosed in a container with rigid walls (hence with fixed volume). If we warmed the container, say by putting it over a flame, the temperature of the air (i.e., kinetic energy of the air molecules) will rise and the pressure (i.e., the force exerted by these molecules on the container walls) will increase. The density of the air will not change since we are not increasing the amount of gas in the container nor the volume of the container. The ideal gas equation states that the increase in pressure is directly proportional to the increase in temperature.
“Lets replace the rigid wall of the container with flexible ones, that are allowed to stretch freely if the pressure inside rises above that on the outside. In that case, when we raise the temperature, the pressure inside will remain constant (and equal to the outside pressure), but the container’s volume will increase. This means that the density will decrease (because the mass inside does not change). The ideal gas law states that the density decrease will be inversely proportional to the increase in temperature.” ]
Now you know what the adiabatic lapse rate is, why don’t you try answering the posers Jelbring set?
Tim Folkerts says:
February 5, 2012 at 7:22 am
Robert,
I admire your persistence with Myrrh. In the vein of “forewarned is forearmed” let me tell you that Myrrh has been convinced of his “crazy talk” position on IR, visible light, and heat for some time, despite several attempts by several people to point out the sort of problems that you address.
But who know? Maybe you will have better luck than the rest of us.
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
As Latour said, it’s junk science and the problem is mainly that “climate” scientists think they know better than the applied scientists who actually use light and heat and know the difference.
We just need the hundredth with the intelligence to see how he’s been conned, maybe it will be Robert..
Trick says:
>No, the math proves isothermal for Fig. 1 is not the max. entropy”
Sorry, I didn’t see any math, just prose. Could you show what you think is the actual math is?
>S can still increase from the isothermal condition in Fig. 1 above
Entropy is defined classically as dS = dQ/T. Suppose you have an isothermal situation to start with. If heat moves from any region 1 to any other region 2, this will cause T2 > T1. The next bit of heat dQ will result in dS = dS1 + dS2 = -dQ/T1 + dQ/T2 The S for isothermal will be less than the non-isothermal field. Try it.
I just did. My math suggests you are wrong. What is your math?
>VERY close to the actual temperature gradient in the real atmosphere
What specific gradient do you get? (State your assumptions).
I would challenge you to “look for the errors” in the Velasco paper. He concludes that the temperature gradient diminishes as the number of particles increases, becoming infinitesimally small as the number of particles increases. I tend to trust published papers with extensive math, rather than blog posts with only an outline of steps.
>There are no errors I can find in the proof.
If you really think you are right and Velasco’s paper is wrong (and I am wrong and Dr Brown is wrong), then write up your ideas and try to get them published. If it is as simple as your 13 steps suggest, it should be no problem refining the prose and letting peer review look for the errors.
Tim Folkerts says 2/5 at 5:34pm:
“If it is as simple as your 13 steps..then write up your ideas and try to get them published.”
I’ve cited the prior publications. My posts are not new ideas. I’ll get back on your other issues; need a little more time. The answers are in the 13 steps (which are NOT simple, take time).
In short, sure the Velasco paper “concludes that the temperature gradient diminishes as the number of particles increases, becoming infinitesimally small as the number of particles increases” which means sure the gradient is VERY small but it remains non-zero i.e. T gradient for Fig. 1 not isothermal constant.
Proof is Velasco eqn. 8 for 1 particle collapses to TE = KE + PE, even the single particle is non-isothermial, i.e. Velasco eqn. 8 does not collapse to TE = KE isothermal. Check it out. The pressure would be so low as to be fringe of the real atmosphere though, this is just a thought experiment.
Trick,
I think we need to be very careful about defining temperature, especially for a single particle. Typically temperature can be defined using 3/2 kT = KE, but really we should say that every degree of freedom should have the right average energy:
1/2 kT = 1/2 m v_x^2= 1/2 m v_y^2= 1/2 m v_z^2
Rotational energy also counts. Vibrational energy also counts (although these don’t come into play for ideal monatomic gases). And potential energy counts, as clearly shown in solids where specific heat is based on 3kT = KE + PE, not 3/2 kT. Read up on the Dulong–Petit law
Normally PE is ignored because normally PE doesn’t change appreciably in typical containers of gas. But PE is indeed part of the thermal energy. It would take a bit more study, but I am convinced that when PE is properly taken into account, then the “temperature” even of a single particle will be constant at all altitudes, even though KE is definitely NOT constant.
Food for thought — the rotational energy of a diatomic molecule will not be affected by altitude. So the “rotational temperature” of a system with a single molecule will be constant at any altitude. So what we have is that
* the “rotational energy temperature” is always constant
* the “kinetic energy temperature” is greatest at the bottom
* the “potential energy temperature” is greatest at the top
The “total temperature” could well be constant everywhere (and I am convinced it is).
Tim Folkerts says 2/5 at 7:42pm:
“But PE is indeed part of the thermal energy.”
No, PE is not part of the thermal energy; PE is a component of the molecule’s total energy constant TE = 1/2mv^2 + mgh = KE + PE. Total energy TE is constant b/c total energy is conserved by 1st law.
Tim continues: “the “kinetic energy temperature” is greatest at the bottom
* the “potential energy temperature” is greatest at the top”
That is correct except drop “temperature” in the 2nd line, especially in Fig. 1 equilibrium. PE is not temperature as measured by a thermometer.
Tim continues:“The “total temperature” could well be constant everywhere (and I am convinced it is).”
This is incorrect. The 1st law says a particular molecule total energy TE is constant everywhere it (randomly) goes in Fig. 1. The molecule’s thermal energy is KE i.e. temperature which is ~speed of the molecule, this speed decreases as the molecule climbs against the gravity field, hence T decreases, even in equilibrium. TE = PE + KE for each of a bazillion molecules in Fig. 1 transiently and at equilibrium. KE and thus temperature has a gradient. Max. entropy is the equilibrium of the temperature gradient (non-isothermal max. entropy equilibrium).
Certainly neither bulk KE nor bulk PE nor bulk RE (rotational energy) nor bulk VE (vibrational energy) is part of thermal energy.
But the “individual KE” of particles within the system is part of the ThE (thermal energy). The “individual RE” of particles within the system is part of the ThE (thermal energy). The “individual VE” of particles within the system is part of the ThE (thermal energy).
And similarly, the “individual PE” of the particles is also part of the ThE. Atoms in solids have SIX degrees of freedom — three axes for KE and three axes for PE. A vibrating atom in a solid has 3kT of thermal energy, not 3/2 kT.
Similarly, the individual PE of the atoms in a gas must also be part of the ThE.
I agree that thermometers typically measure the KE of particles, but imagine you could suddenly remove all the KE from the gas in the column. The “KE temperature” would drop suddenly to zero. But now the gas will start to fall. As it hits the bottom and rebounds, suddenly there will be collisions to thermalize the energy again. The particles will gain KE at the expense of the PE. Eventually the system will come back to thermal equilibrium at a much lower temperature.
Or do the same thing with a diatomic gas, where the height of the container is negligible. You removed energy from 3 degrees of freedom. But the particles will bump into each other and the rotational energy will kick the molecules around until the energy is evenly distributed in the 5 degrees of freedom.
It is getting late, so I am not sure I am 100% coherent. But the “individual PE” is definitely part of the thermal energy of atoms in solids. And the individual PE should also be part of the ThE of gases
Transiently, yes. But there is no heat flow at equilibrium.
So if we move heat from the bottom to the top, we increase the entropy of the system and the Universe, but this won’t happen because of gravity. And once we do, exactly how will it go back to the way it was before? Oh, yeah, by decreasing the entropy of the system.
You can’t get out of the problem by circular reasoning. Sure there is no heat flow at equilibrium, because equilibrium is maximum entropy. However, you just admitted that if heat is transferred to the top, the entropy increases. Ergo, what you claimed is maximum entropy isn’t. Q.E.D.
rgb
No, PE is not part of the thermal energy; PE is a component of the molecule’s total energy constant TE = 1/2mv^2 + mgh = KE + PE. Total energy TE is constant b/c total energy is conserved by 1st law.
You really might want to look at the final exam solution I posted a link to above.
Just a thought.
Once you’ve figured out how to explain how a gas that — you admit — can have a higher entropy than the state you claim is maximum entropy.
rgb
It would take a bit more study, but I am convinced that when PE is properly taken into account, then the “temperature” even of a single particle will be constant at all altitudes, even though KE is definitely NOT constant.
is given by:
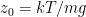is the characteristic length of concentration decay (typically around 5-6 kilometers in air at reasonable temperatures). This result is constrained by the requirement that:
.
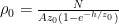
. As the gas is warmed, 
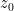increases, the thickness of the gas layer grows, the center of mass of the gas increases, and the potential energy of the gas increases. At 
the gas fills the volume uniformly.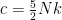
, which is very much not the usual ideal gas result, but it is easy to understand. 
of any input heat goes into making the gas expand, lifting its CM and increasing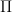 
. At high temperatures the gravity (second) term goes to 1, so the heat capacity goes back to the usual ideal gas 
.
as usual, and so on. However, if you add heat to the system the entire gas column expands nonlinearly, and some fraction of the heat added goes into lifting the center of mass of the gas. Local temperature, global heat capacity. I think that’s one of the things that has been missed — for variations of height much less than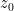 
— especially for variations on the order of the mean free path of the molecules in the system — gravity really is irrelevant. The air behaves precisely like air in the room you are sitting in (where 
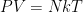is taken for granted) because the air in the room you are sitting in is a slice in just such a column. Gravity is irrelevant in your room, and only becomes very slightly relevant inside e.g. the elevator shaft of a fairly large office building. But if you heat all the air in any layer of a closed column, you cause all of the air to expand and gravity becomes relevant, not to the local temperature description of the gas but to the fact that the gas behaves partly like gas in a cylinder, doing work to lift or lower all of the gas above it as it thermally expands or contracts.
, the second term in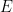 
vanishes (making any temperature a “low” temperature as 
) and gravity does indeed behave like additional degrees of freedom in the specific heat of the entire system while every small subvolume of the gas still behaves precisely like an ordinary ideal gas with kinetic energy $\frac{3}{2}NkT$ and yes, with detailed balance across any vertical surface (although yes, Joe, my argument involving shifting the MB distribution was sloppy and imprecise — hopefully you like this one better but the result is the same either way).
minus a term that vanishes if the height of the column goes to infinity and that cancels the 
if the height is much less than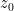 
. Local definition of temperature. Globally consistent total energy and heat capacity. Gravity strictly ignorable when considering parcels of air on scales much less than 
.
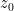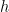. The gas on the bottom behaves like an ordinary ideal gas, after all, and expands when warmed at constant pressure. I can easily imagine heating the gas at the bottom and have the heated gas lift the air above it, doing work with some of the heat.
The solution is worked out in the final exam question I posted. So it won’t take a lot more study. I provide a summary of the answer below.
The density/concentration profile of N molecules of the monoatomic gas in a thermally isolated cylindrical container of height
where $\rho_0$ is the concentration at the bottom of the cylinder and where
so that:
or
Given the density, it is straightforward to compute the total kinetic energy from equipartition; it turns out to equal:
as usual. The potential energy is a bit more difficult; one has to integrate:
$\latex \Pi = mg\int_0^h z \rho(z) dz$
This integral is straight up integration by parts to get:
$\latex \Pi = NkT – \frac{mghN}{(e^{h/z_0} – 1)^2}$
Summing, the total energy is:
Differentiating (to find the heat capacity) we get:
Physically, this means is that at low temperatures, the gas is effectively concentrated in a layer of thickness
What happens to the heat capacity is also interesting. For low temperatures, the second term vanishes so
As you can see, there is nothing wrong with the ideal gas law in any particular layer — the usual molecular interpretation of temperature holds there,
It is also interesting to note that if
This is the point that is being missed by Trick. He asserts that temperature is related to kinetic energy only, and that kinetic energy on average “decreases” per molecule as one ascends the air column. This, we see, certainly not necessarily correct. Kinetic energy (per molecule) in fact remains constant (along with temperature) as one ascends an isothermal, isolated, hydrostatically balanced air column. However, the gravitational potential energy of the entire air column becomes a nontrivial function that has a leading temperature dependence of
And here’s the kicker. Start from this isothermal state. Then transferring heat internally from the top to the bottom of the gas to warm the bottom (and e.g. “spontaneously” create a lapse rate) raises the center of mass of the system independent of
Now, I can visualize a gas slumping downward, lowering the center of mass and compression heating the bottom, no problem. Gravitational potential energy converts into heat. I have the damnedest time imagining an isothermal hydrostatic gas heating itself at the bottom and doing positive work with some of that heat to lift the center of mass of the system, given that it is in hydrostatic balance to start with. It seems, somehow — Demonic!
Verily, I say unto you, my brothers: (Maxwell) Demons out!
rgb
Sorry moderator, errata for the algebra:
. Please fix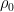 
. I left a closing parenthesis off the second standalone equation. I left a leading slash in the \latex in two equations. And I have no idea what happened to the heat capacity. — it should read something like Nk ( 5/2 – (h/z_0)^2 e^{h/z_0}/(e^{h/z_0} – 1)^2 ). Finally, left the latex out of the kinetic energy term in a later paragraph.
First equation should be
rgb
Reply: I haven’t the slightest idea how to fix all this. Get it working here http://charlesthemoderator.wordpress.com/2012/02/06/robert-browns-test-page/ with instant feedback and then replace it here and instruct a moderator to delete the old comments. ~ctm
You do sound desperate… 🙂 How far have you got in proving that visible blue light as from the Sun heats water? Made the cup of coffee with it yet??
Myrrh, nobody who writes electrodynamics textbooks does so to try to “con” students. It’s way too much work, way too little reward.
So what, exactly do you think happens to all of the electromagnetic energy in that visible light that makes it through the surface of the water? I mean I’m assuming that you’ve gone swimming before and opened your eyes underwater and know that you and the fishies can see because there is plenty of visible light that makes it through the surface. I’m also assuming that you’ve seen the discovery channel or animal planet and realize that the ocean is almost totally dark 1 km down. So somewhere between the surface and 1 km down, all the visible light went away.
What happened to all of that energy? Demons again? Failure of global energy conservation? I’m fascinated by your take on this — an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light (water isn’t like a cloud, with a high albedo from multiple elastic scattering). So where does it go?
I’m just sayin’…
rgb
Robert Brown says
“an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light…. So where does it go?”
I realise that thermodynamics lecturers don’t get out much.
Does this help?
http://www.life.illinois.edu/govindjee/paper/gov.html
Bryan,
Photosynthesis will not solve the problem — only delay it. Plants absorb EM energy, it is true. But a few hours or weeks or centuries later, they die or get eaten, thereby releasing the energy. Only a NET increase in plants (or a net sequestration of organic matter) will pull out energy in the long term. To a very high degree, on an annual basis the energy released as plant decay is the same as the energy absorbed by growing plants.
Does this help?
Robert, when I said “It would take a bit more study”, I meant on my part. I didn’t doubt that the problem has already been adequately addressed by others who work more closely with these ideas. But thanks for the explanation. 🙂
Tim Folkerts
“Photosynthesis will not solve the problem — only delay it. Plants absorb EM energy, it is true. But a few hours or weeks or centuries later”
Yes of course all energy will ultimately end up as thermal energy as predicted in Kelvins heat death of the universe.
A consequence of the second law.
But the storage capacity of the electrochemical reactions should not be ignored.
Greenhouse theory enthusiasts alarm us with the consequences of burning fossil fuels which have trapped light energy for 400,000 years.
At the same time producing diagrams like K&T2009 which ignore the fact that light energy is required for photosynthesis.
Myrrh documented a rather sinister rewrite of the NASA educational pages on this very item.
The whole greenhouse gas scare only works by exaggerating any small effects that suit it and at the sametime ignoring all effects that don’t.
Robert Brown says 2/5 at 10:25pm:
“So if we move heat from the bottom to the top, we increase the entropy of the system and the Universe, but this won’t happen because of gravity. And once we do, exactly how will it go back to the way it was before? Oh, yeah, by decreasing the entropy of the system….However, you just admitted that if heat is transferred to the top, the entropy increases. Ergo, what you claimed is maximum entropy isn’t. Q.E.D.”
No, the entropy won’t go back the way it was before or need to decrease. Yes, the entropy increases. Here’s why this is not circular reasoning.
Forcing a parcel of bottom molecules out of equilibrium to the top takes work against gravity (f*d = m*g*h). Where does the work come from? The work has to cross the control volume. Once the work crosses the control volume, the entropy of Fig. 1 increases (you’ve added the m*g*h). The new entropy at equilibrium is higher and stays constant at the higher level b/c the control volume is adiabatic.
This does NOT mean the original entropy could increase before the work was added; it was already max. at equilibrium.
Tim Folkerts: “When the first joule of energy moves from the hot side to the cold side, entropy will increase by. . . .”
Although your math seems to work, it appears to me that your conclusion may not be correct, at least if Velasco et al. are; if I interpret their paper correctly, the kinetic-energy profile of their Equation 8 is the maximum-entropy configuration, from which I would conclude that a strictly isothermal microcanonical ensemble will spontaneously undergo (an incredibly small) heat transfer to assume that (ever so slightly non-isothermal) configuration.
I don’t know the reason for this discrepancy. One possibility is that Velasco et al. are wrong. Another is that this is an occasion in which dS = dQ/T does not give the right answer, i.e., that dS = dQ/T does not take gravity into account.
A third possibility is that reallocation of potential energy somehow makes the dQ illusory, although I don’t immediately see how this could be so.
Bryan,
Since this interests you, why not estimate the effects of photosynthesis and report back? How much of the ~340 W/m^2 gets absorbed by plants? How much net change in chemical energy (in the form of added biomass) is there from year to year? How much chemical energy is being sequestered? (And how much is being released again by the organized burning of fossil fuels? I will guarantee that any natural sequestration of EM energy into chemical energy is vastly outweighed currently by human burning of old chemical energy, releasing thermal energy.)
I agree that in principle these numbers should indeed be included in the K&T diagrams. So how big ARE these effects? Are we talking 1 W/m^2? 10 W/m^2? 0.001 W/m^2?
Tim Folkerts says
“Bryan, Since this interests you, why not estimate the effects of photosynthesis and report back? How much of the ~340 W/m^2 gets absorbed by plants? ”
Is this the world of 4 faint Suns?
Is 340W/m2 capable of producing any light?
Its your silly theoryso you should know.
Since Greenhouse enthusiasts like yourself think it is zero you might be in for a shock.
When the Sun comes out in our neck of the woods its around 1360W/m2 and the spectrum does include wavelengths capable of photosynthesis.
In the grossly simplified world of treating the Earth as a perfect black body that instantly radiates any radiation it receives I suppose photosynthesis is an embarrassment to your simple world view.
I hope that helps!
Tim Folkerts asks
“How much of the ~340 W/m^2 gets absorbed by plants? How much net change in chemical energy”
Well Tim that insulation produces a blackbody spectrum well into the thermal IR band.
So no photosynthesis would be produced whatsoever , as IPCC science predicts.
So to answer Robert Browns question to Myrrh that type of radiation is completely absorbed in the top few millimetres of the water surface.
However back to the real world the 1360W/m2 solar radiation will have a significant proportion of wavelengths capable of producing photosynthesis.
Of the solar radiation reaching the surface of water some 50% is in the IR.
It will be absorbed in the top few mm causing evaporation of the surface water.
The other 50% will penetrate deep into the water and a significant proportion will be available for photosynthesis.
Notice that the evaporation and the photochemical processes both are systems that store energy that can be later released to buffer temperature change.
The radiation obsessed IPCC science model with its fictitious 33K effect is false.
So don’t believe everything that broad brush, eyes shut IPCC science tells you.
You’re still not getting hydrostatic balance, it doesn’t mean nothing is happening and you have to bring in another idea into the system to work out what will happen…, the adiabatic lapse rate will happen, because gases will become more dense and sink when cold and so will find themselves under great pressure at the surface where they will get compressed and heat up, and heated up they will become less dense and rise and in rising they will cool and in cooling they will become more dense and sink and so on.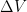
of the air. Even if you started at time 
with the air in movement, the air has dynamic viscosity — even an ideal gas has an easily computable dynamic viscosity — and would quickly come to rest. Viscosity is to air what friction is to a book sliding across a table — even if you start the book with some velocity relative to a table (or a parcel of air with some velocity relative to other parcels) viscosity will quickly bring the motion to a halt. That’s the reason that the article that you linked — after all — into the discussion requires an external agency that causes the macroscopic movement of large parcels of air vertically to establish a DALR. There is no microscopic agency that so acts.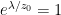
to many, many digits when 
meters is the mean free path of the gas and 
meters. 
on the scale of infinitesimal layers of gas in direct thermal contact across a surface. In any event, this is in no sense responsible for a gas maintaining the DALR in particular as a stable static thermodynamic equilibrium.
in any macroscopic discussion is a volume large enough to contain enough molecules that thermodynamic averages pertain to the behavior of the parcel as if the air inside were a continuous fluid, so that when conducting this sort of discussion we can ignore the movement of individual molecules across the surface of 
(which are in detailed balance anyway, at equilibrium). Practically speaking, this is any volume that is many times the mean free path in the smallest linear dimension. Since the mean free path is quite small, cubes or lateral slices larger or thicker than a micron or so are large enough to be considered parcels in the sense that they can be described by a continuous local density, pressure, and temperature. These same parcels are large enough to be macroscopically in hydrostatic equilibrium, supported by the well-defined pressure of their neighboring parcels of fluid and at rest, locked in place by the dynamic viscosity so that to move them one has to do work or otherwise input external energy into a parcel to destabilize them, overcoming “friction”.
Again, I’m fascinated. You’ve got an insulated jar of air, and you’ve left it sitting on the counter for the last ten years, but somehow you think that the air inside is busy busy moving up and down in macroscopic packets, heating at the bottom, cooling at the top, and yet somehow the bottom never gets any cooler and the top never gets any warmer! Even better, they are expanding and doing work on their environment — that’s how they adiabatically cool, thermal energy going into work. Sort of like a lava light that never stops! Well, not quite like a lava light, because we heat lava lamps on the bottom and cool them at the top and when we turn off the light, they stop working.
What is it that makes the air go up? Gravity, you say! What makes it go down? Gravity again! How does gravity do all of this work lifting and dropping air and never actually heat it, given that Joule showed that nice, turbulent mechanical work turns into heat? Demons again! Or perhaps it is invisible fairies, beating their tiny little wings.
OK. Let’s get serious. The air in the jar is, after even a fairly short time, at rest. No, it is not constantly moving up and down. It is in hydrostatic equilibrium. There is no net force acting on any small slice
BTW, please don’t answer with something that tries to make the local thermal motion of single molecules into “lifting and falling parcels of air”. You have a choice — you can work and argue microscopically, in which case you have to do a shitload of serious stat mech algebra I’m leery of even looking at so far (as I’m sure that’s what Velasco does) and it has been a few, um, decades since I took stat mech and it was the most difficult course of physics I ever took when I took it, making even quantum mechanics look like a walk in the park in comparison. The simplest things one can do microscopically are things like detailed balance estimates, and so far I haven’t made Joe happy even with what I’ve attempted there, although I think he realizes that my answer is irrelevantly imprecise (or he should realize it once he follows the reasoning in the algebra above that lays out how air can be isothermal and still have the MB velocity distribution from the bottom out to where the assumptions of thermodynamics break down anyway, because
A “parcel” of air, or “differential” volume of air
Demons Out!
rgb
Robert Brown says:
February 6, 2012 at 12:56 am
So what, exactly do you think happens to all of the electromagnetic energy in that visible light that makes it through the surface of the water? I mean I’m assuming that you’ve gone swimming before and opened your eyes underwater and know that you and the fishies can see because there is plenty of visible light that makes it through the surface.
Grin, I’ve even been scuba diving.
You can’t see why you can see underwater? Because it’s not absorbed. Water is transparent to visible light, means just that. Water transmits visible light through it without absorbing it, neither absorbed on the electronic transitional level nor on the molecular level.
I’m also assuming that you’ve seen the discovery channel or animal planet and realize that the ocean is almost totally dark 1 km down. So somewhere between the surface and 1 km down, all the visible light went away.
Poor, little nervy visible light, couldn’t make it deeper down and gave up.
What happened to all of that energy? Demons again? Failure of global energy conservation? I’m fascinated by your take on this — an easily computable energy flux of visible light goes through the surface. You have the evidence of your own yes that it does so. Most of it doesn’t come out again, at least not as visible light (water isn’t like a cloud, with a high albedo from multiple elastic scattering). So where does it go?
Puzzle that out in your own time, in my time provide me with back up for the claim you’re espousing, that visible light from the Sun converts land and oceans to heat thus raising the temperature of the Earth which then emits thermal infrared.
I’m just sayin’…
I’m just askin’
Robert Brown: “I have the damnedest time imagining an isothermal hydrostatic gas heating itself at the bottom and doing positive work with some of that heat to lift the center of mass of the system, given that it is in hydrostatic balance to start with. It seems, somehow — Demonic!”
Are you sure the center of mass rises? Couldn’t the total potential energy remain the same while the half-rho zero point rises?