Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Paul Birch:
Ah, I think I take your meaning (although I just finished driving 500 miles and am disinclined at the moment to give it the consideration I ordinarily would): it’s possible to pick local reference frames in which the local molecules’ kinetic energies are lower than in the reference frame in which the vessel originally containing the gas is stationary.
I still have to think through that entropy thing, though. True, it makes sense that the phase-space position representing the microstate the ensemble was in the instant the confining vessel disappeared (as I’m envisioning the thought experiment) should be just as likely as any other microstate on the same phase-space trajectory. But my understanding is that entropy discussions usually deal with macrostates rather than microstates, and it seems to me that the macrostate defined by a small volume and a given total molecular kinetic energy consists of fewer equally probable microstates than the macrostate defined by a larger volume and the same total molecular kinetic energy.
So I wonder if you could you expand on your entropy comment.
Robert Brown says 2/2 at 8:36am:
“ See the top post, which derives the actual state of an ideal gas atmosphere in both hydrostatic ( ) equilibrium and simultaneously in (iso)thermal equilibrium, repeatedly demonstrated to be the state where the gas has maximum entropy and the state the ideal gas will go to under the precise conditions described by Jelbring.”
Robert Brown –
My copy of Bohren & Albrecht “Atmospheric Thermodynamics” arrived today. I have had a delightful time reading thru about half of it so far. Thanks to Rodrigo Caballero’s on-line text for pointing the way.
The authors have many humorous anecdotes to relate & the chapter problems given are very thought provoking. I heartily recommend it to any poster interested in the topic of this thread.
On-topic for the top post, the authors develop the fundamental application of the thermo laws with the proper & correct detail algebra for Figure 1 in the top post – a GHG-free adiabatic ideal gas column in the presence of gravity. This gas column is isolated from its surroundings, neither heated or cooled by radiation nor by interaction with adjacent air or ground. There is no condensation or evaporation of water. (The same as that discussed in Verkley paper part b.)
The authors derive entropy maximization requires the equilibrium temperature profile to decrease as height increases. Thus they prove the hydrostatic temperature profile of top post Fig. 1 at equilibrium is non-isothermal which is the max. entropy point. ANY deviation from that thus requires a decrease in entropy which is not 2nd law physical.
Why isn’t the equilibrium temp. profile isothermal as Robert Brown writes (repeatedly)? The authors have a long explanation of why the temp. profile is non-isothermal. It needs to be read in context. They give a reason Robert Brown’s understanding here has been impeded – their reasoning is the conduction in solids impedes understanding of the ideal gas column w/gravity field non-isothermal temperature profile in equilibrium in top post Fig. 1.
I have edition 1 of that fine text book and, for interested posters, the non-isothermal stable equilibrium temperature profile derived from maximization of entropy of the GHG-free adiabatic ideal gas column top post Fig. 1 derivation is in Chapter 4.4 pp.164-168 for realistic pressures (holds for ~80% of pressure range of earth’s atmosphere).
Furthermore the authors point out only in the absence of gravity will the adiabatic ideal gas column equilibrium temperature be isothermal.
The authors elegantly show the top post statement is incorrect “..an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state..” and thus refute the refutation of a stable equilibrium isothermal temperature profile for Fig. 1 in the top post. This non-isothermal profile being consistent with poster Rodrigo Caballero’s referenced 2004 Verkley paper part b which shows experimental evidence for the ideal non-isothermal temperature profile in their Fig. 2.
Joe Born says:
February 2, 2012 at 5:01 pm
Ah, I think I take your meaning … it’s possible to pick local reference frames in which the local molecules’ kinetic energies are lower than in the reference frame in which the vessel originally containing the gas is stationary.
Yes. The thermal energy is what’s left when you map the system into local frames which null out all the orderly motions (which have zero or nearly zero entropy), leaving you just the random stuff (with high entropy).
…I wonder if you could you expand on your entropy comment.
The uniform radial motion itself has no entropy; there is only one microstate, that is, everything going straight out. The entropy is all in the residual thermal motion. Here the number of microstates is unchanged overall, with less thermal energy per particle, but spread over a correspondingly larger volume. By construction, in an adiabatic compression or expansion the entropy in the gas is unchanged; a standard calculation then yields the known constancy of PV^(Cp/Cv).
Paul Birch:
Thanks for the response, although I’ll have to think it through. I do recognize that a gas can be reversibly expanded and compressed, but it seems to me that merely releasing the gas from a vessel (by, e.g., magically making the vessel disappear) would result in an irreversible expansion.
But none of this affects my view that Dr. Brown’s “proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.
Joe Born says: But none of this affects my view that Dr. Brown’s “proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.
Equation 8 is based on very specific assumptions, which Velasco clearly states. This result is for a “microcanonical” ensemble, where there is absolutely no exchange of energy with the rest of the universe. This result will become the same as Dr Brown’s isothermal answer if either:
1) the number of particles is large. (As I stated above, even a few million particles will make the Velasco result indistinguishable from the isothermal distribution, and earth’s atmosphere has on the order of 10^40 particles.)
or
2) some part of the system — perhaps the ground — is a thermal reservoir rather than an adiabatic (perfectly insulating) surface. Now we have a “canonical” ensemble, and Velasco states clearly that this will be isothermal.
Robert Brown says:
February 2, 2012 at 7:52 am
now I can hope that includes not setting me homework..
Oh no. I assigned homework already;-): Read the MIT online thermo book and work through it, cover to cover. Your arguments can only improve if you actually learn the laws they are currently flouting, and while I fully understand your lack of respect for “authority” — while respectfully suggesting that it edges well over into iconoclasm for its own sake when you make statements that violate the experimentally verified laws clearly explained in every thermo textbook. It is difficult to claim that these textbooks are part of the “IPCC global conspiracy”, given that thermodynamics was mostly worked out and derived/proven over a hundred years ago, well before there was a United Nations.
Good grief man, you really think we’ve got where we are in science today by confusing “respect for authority” with “authoritarian entrenched beliefs”? Hmm, seems we have.
My authority here, and I have very great respect for it, are those in this discussion who understand gases and the real scientists at the front line, the meteorologists, who have had this sussed since way back when. You have shown no respect for them or their knowledge.
You can continue to define it whichever way you like, doesn’t make it so:
Your assertion that I don’t understand his paper is simply incorrect. I’ve read it several times at this point. Its claims are quite clear. He asserts that gravity will create a thermal lapse rate that is there in his isolated ideal gas in a near-Earth gravitational field in thermal equilibrium — the condition that an air column will reach after all irreversible relaxation processes such as conduction, convection, and radiation have completed. He forgot to mention conduction, but if he truly meant to leave it out then his conclusion is already obviously false as he left out a physical process that is infinitely faster than thermal relaxation due to radiation in a GHG-free atmosphere, where there is none. To prove it he cites a single “well-known” result — the DALR — from a single textbook on climatology, and claims that it describes static thermal equilibrium.
You can continue to define it whichever way you like, doesn’t make it so, for example:
“The dry adiabatic lapse rate (DALR) is the negative of the rate at which a rising parcel of dry or unsaturated air changes temperature with increasing height, under adiabatic conditions. Unsaturated air has less than 100% relative humidity; i.e. its actual temperature is higher than its dew point. The term adiabatic means that no heat transfer (energy transfer due to a temperature difference) occurs into or out of the parcel. Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small. http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
I’m sorry, you may not like being told by BigWAveDave that your knowledge of gases is zilch, but it is.
As I said, you don’t understand Jelbring’s argument, because you don’t know what he’s talking about. Here anyway we have an answer to why it’s rarely acknowledged by ‘climate’ scientists, because it’s unknown. First, work out what he’s talking about.
“The more atmospheric mass per unit planetary area, the greater
GE has to develop. Otherwise Newton’s basic gravity model has to be dismissed.”
If your text books have dismissed Newton’s basic gravity model, then your text books need re-writing.
If you wish to claim that “climate scientists” ignore the Water Cycle, prove it. Cite one single textbook on physical climatology that ignores the water cycle.
They all do who teach this: ‘that greenhouse gases warm the earth’, that without greenhouse gases warming the earth it would be some 30°C colder, from the 15°C we have now, to minus 18°C.
That is the mantra, everything about AGW is built on that.
But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.
In the real world and not the world created by AGWScience Fiction’s meme producing department, Greenhouse gases cool the earth.
– Without the Water Cycle reducing the temperature the earth would get to with the atmosphere as we have it (which is practically 100% nitrogen and oxygen), the earth would be 52°C hotter, not colder. It is water vapour, the main greenhouse gas, which takes away heat from the surface in evaporation and in condensing out in the heights where it is colder, releasing its heat and coming down as rain. The BASIC Water Cycle.
Now, all clean pure rain is carbonic acid, because water vapour and carbon dioxide have a strong yen for each other, water vapour in the atmosphere will pick up whatever carbon dioxide is around and bring it down to earth in rain. (And fog, dew etc.) Carbon dioxide is fully part of the water cycle.
Therefore, Greenhouse gases COOL the earth.
All the text books claiming that greenhouse gases warm the earth and that without greenhouse gases the earth would be colder, are lying.
That’s why it’s junk science, the rest is built on that.
QED
It was when I read Yes Virginia a couple of years ago that I realised something very odd was going on with the ‘science’ explaining AGW and its strange notions about the physical properties of gases, that even those not blaming it all on man had bought into it, actually believed the impossible ‘science’ which was so much at odds with basic physics – it took a while for it to sink in that these changes were now ubiquitous through the education system..
Give me one good reason why I should consider you an authority and not someone like Latour? (See the johnosullivan link I gave earlier). He called it junk science.
“But Dr. Latour goes further in his criticism. Semi-retired after a stellar career, Latour is one of many eminent experts now becoming increasingly outspoken and declaring the GHE as “junk science.” His position was summarized in US Senate Reports. [2.& 3.]”
“Always a stickler for thoroughness as a Chemical Process Control Systems Engineer, Latour had long worked at the sharp end of applied science. His special aptitude earned him his place in the Apollo Space program, where life and death decisions meant that when the theory contradicted reality you changed the theory.”
Yes, if I could add another lifetime on to this..
Back when I was in graduate school and was just beginning to see the importance of e.g. the Pauli spin matrices (a complex 2×2 tensor representation of the quaternions that map into spin or isospin in quantum physics), my friends and I spent a lot of psychic energy trying to figure out the real, complex, quaternion (Grassman algebra), Clifford algebra progression, because it appears not just one or two places, but many places in physics. It seemed then that it was possibly another case of “Flatland, a Romance of Many Dimensions” — we were “stuck” at the level of complex representations because we just couldn’t “see” that the “real” correct division algebra was of a much higher grade, so that our current view of things was only a projection of sorts and hence missing crucial detail.
I wouldn’t say that I disagree with this now. This is where being iconoclastic is a good thing in science. You can’t take it for granted that our current worldview isn’t just a projective view of a reality in higher dimensions, that our current formulation of physics is based on the right kinds of numbers, the right group, the right algebra, the right geometry. On the other hand, trying to determine physics in three dimensions plus time has got to be pretty difficult for people who live in only the 2+ of Flatland. It requires a level of brilliance and insight that are rare. And as Edwin Abbott (the author of the romance) indicates:
http://www.ibiblio.org/eldritch/eaa/FL.HTM
in the last chapters of his lovely story, the Square from Flatland (“I”) addresses the Sphere from 3 dimensions that has uplifted him (temporarily) to three dimensions himself so that he can perceive a reality that just before was inconceivable. But now the Square’s imagination has run wild; he reasons by induction:
I. But my Lord has shewn me the intestines of all my countrymen in the Land of Two Dimensions by taking me with him into the Land of Three. What therefore more easy than now to take his servant on a second journey into the blessed region of the Fourth Dimension, where I shall look down with him once more upon this land of Three Dimensions, and see the inside of every three-dimensioned house, the secrets of the solid earth, the treasures of the mines of Spaceland, and the intestines of every solid living creature, even the noble and adorable Spheres.
Sphere. But where is this land of Four Dimensions?
I. I know not: but doubtless my Teacher knows.
Sphere. Not I. There is no such land. The very idea of it is utterly inconceivable.
This seems to be the problem, a problem as old as Plato’s Cave — we have a hard time “uplifting” our point of view, even by induction, to see a possible higher level of reality where our own is just a projective view, shadows on the wall of our cave.
So far, though, I haven’t discovered anything quite so tremendous. Perhaps I’m too old — I try to teach younger students about geometric algebra earlier on and think it would be good to require — or at least encourage — its study as part of a math prep for majors and grad students, to give them a fighting chance at having the insights needed to make it fly one day and really advance our knowledge. Even things like electrodynamics — yes, it can be formulated in terms of complex numbers with divergences and curls or in terms of quaternionic derivatives, but the deepest insight I can offer so far is that neither of these is the “right” way. The problem, you see, is that the electric and magnetic fields aren’t vectors. They are components of a second rank tensor. So any theory that tries to write them out as vector fields is going to have a somewhat unnatural and contrived form. The only “natural” way to write out the theory of electromagnetism — the beautiful way to write it out — is the fully relativistic formulation that manifestly has the correct symmetries built in and which is strictly a tensor formulation.
That may be the lesson of the Pauli matrices as well. Yes, they are a kind of representation of quaternions, but they are a tensor representation, and tensors are, in a sense, the most general form of outer product one can construct on top of a number theory. It may be less about quaternions per se than it is about the underlying tensors and their symmetry groups.
Still, if you want to learn more about Geometric (Clifford) Algebras, I applaud the desire. The best book I’ve found so far is this one:
http://www.amazon.com/Geometric-Algebra-Physicists-Chris-Doran/dp/0521480221
Sadly, it looks like it is out of print, making it even more expensive than my copy was (although there are still used copies out there). A great read, and not horribly difficult mathematically at least through the first half of the book. Roughly the level of a course for junior or senior math majors or physicists, although he does reference some stuff in his “applications” chapters (where he shows how geometric algebras can be discovered inside various physical theories) that can be pretty difficult. Chapters 5+ work through towards gauge theory and general relativity, for example, not for the faint of heart:-)
The first two chapters are gems. The history, including the lovely story of Hamilton carving his discovery on a bridge at his college (where it remains to this day:-), plus a very simple description of the product as a generalized projective area or volume — the “geometric” part. It does help at some point to know what a division algebra is, and why physics needs to be based on them (if we want to be able to solve for things, at any rate:-).
Good luck!
rgb
Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small.
Yes, but that is just a matter of time scales of relaxation. You really are almost there now. Jelbring explicitly — and I do mean explicitly — states that he is supposedly waiting for relaxation to occur on all available time scales. He is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
The thermal conductivity of air is 0.025 W/(m-K). This is small, but certainly isn’t zero, and has to be balanced against the fact that air has a very low specific heat — 0.001297 J/(cm^3-K) — as well, so it doesn’t take a lot of heat to change its temperature. It might take years for the atmosphere to relax to isothermal. It might take months. I doubt that it would take centuries. But that doesn’t alter my conclusion. Gravity alone cannot create and maintain a thermodynamically stable lapse in temperature.
To put it another way, if one constructed a system with an isothermal air column in force balance — something one certainly can do, just by taking an insulated tower of air and mixing it well and letting it stop moving — what will make it depart from isothermal and relax towards a DALR? There are no air parcels moving up or down, so the entire argument concerning adiabatic lapse and isoentropic mixing is moot. There is nothing but diffusion and conduction, and they if anything maintain the air in an isothermal state. I’ve already argued that taking any gas and without doing any work causing it to separate into hotter and colder gas is a horrible, egregious violation of the second law, yet the entire gas column is by construction hydrodynamically stable, with a density strictly decreasing with height and without the slightest thing to cause bulk convection or other movements of air where “work” can be done.
What you are saying is just a restatement of what I’ve been saying all along. Jelbring is incorrect, but if you neglect thermal conductivity and dynamical relaxation processes other than slow convection, an atmosphere with a DALR can be hydrodynamically stable and can exhibit a lapse rate (once one is established) for a long time. But that moves us into another discussion — one of atmospheric dynamics, not atmospheric statics, the explicit milieu of Jelbring’s paper.
There I think that it is pretty obvious what actually establishes a lapse rate — differential heating of the air column at the bottom, followed by a rough equilibration due to approximately adiabatic convection. The air column is always moving, always heating or cooling, so the milieu of Jelbring’s paper and his conclusions are not only incorrect, they are irrelevant. He didn’t discover, invent, derive, meaningfully discuss, measure, draw pictures of, or even present an heuristic argument for the DALR in his paper. All he did is assert that it is a feature of completely isolated, static atmospheres so that just having a gas in a gravity well equals a DALR in the gas.
You continue to prove my point.
But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.
You also continue to throw red herrings into the soup. Jelbring’s paper explicitly excludes the Water Cycle (or adiabatic moving air parcels). It is a pure ideal gas. So why do you keep bringing them up? If you want to prove that there is a non-GHG GE involving the dynamic motion of gases, play right on through, but realize that Jelbring’s paper isn’t about that and is incorrect because it ascribes the same effect to a completely static, completely dry ideal gas that has been left in place, isolated, for a billion years (or as long as equilibrium takes, which won’t be anywhere near a billion years at a joule of conductive transport per meter of atmosphere per degree kelvin of temperature difference per 40 seconds).
So let me really clear. I don’t care about the real DALR in the real atmosphere, which is an utterly dynamic quantity that is basically never precisely observed and which is derived, using a bunch of approximations and assumptions that include active transport of air parcels and “0” conductivity, to provide us with some insight into why the atmosphere does remain warmer at the bottom than at the top. I don’t “deny” the DALR in real air, sir. What I deny is that this air is in any way, shape, or sense, in thermodynamic equilibrium.
Get it? Thermodynamic equilibrium is something very specific. It includes mechanical equilibrium. Thermal equilibrium. Chemical equilibrium. It presupposes that all thermal relaxation that can occur has occurred, unless you wish to work a system with broken ergodicity, or unless you can show that there is a vast separation of relaxation timescales, one large enough that equilibrium will not be reached in the particular times of interest in a particular problem. Since the Earth’s atmosphere is actively driven on literally a daily basis, hourly basis, minute by minutes, conductivity is largely irrelevant to atmospheric relaxation — it never has time to thermally relax. It does have time to convectively relax, sometimes, approximately, for a while, which is why soundings reveal a thermal lapse that sometimes, approximately, for a while, resembles the DALR — except when (more often) it doesn’t. Like when water gets mixed into the picture, or above the poles in winter when the ground can actually lose heat faster than the atmosphere and the atmosphere often inverts, being warmer on top than near the ground.
Note that this alone refutes the idea that the DALR is something intrinsic to gravity and atmospheres, even dynamically. Heating the atmosphere at the bottom more than the top seems important as well, and you know what? It isn’t that surprising that something heated at the bottom and cooled at the top exhibits a thermal gradient from the bottom to the top.
The interesting question is, what cools it at the top? Cooling requires the actual physical removal of heat. Could it be — gasp — radiation? Could we — possibly — measure it? Can we — I know it is a crazy, crazy, idea — determine the temperature of the source of the radiation, and from the spectrum the probable source of the radiation, the particular species of molecules that are emitting it? Could those molecules be — I hate to even say it out loud — CO_2?
No, no, no. This is all silly. We don’t have to have anything that cools the air up there. It stays cold by magic.
I mean this very seriously. Not only is it hotter underneath the tropopause, it is hotter overhead. You’ve got a real miracle on your hands — a layer in the middle that stays colder than the air above and below. As James Bond would say, “that’s a neat trick” to pull off without any mechanism for actually removing heat from there.
But even this is a serious digression from the point of this thread from the top article on down. Try, really try, to address just Jelbring’s imaginary world, perfectly insulated above and below, ideal gas in between, near-Earth gravity, infinite time for the system to reach true thermodynamic equilibrium (or long enough for a non-GHG to reach thermal equilibrium through radiation, which is going to be a hell of a lot longer than its thermal relaxation through conductivity for a gas on average 200-300K in temperature at 1 g). He asserts, utterly without proof, that this gas will exhibit a DALR. If you disagree, then where is his proof. Explain it to me. I assert, with considerable proof that such a gas at thermal equilibrium cannot have any lapse rate at all, let alone the very specific DALR provided only that thermal relaxation through all available channels has had time to occur (that’s the “thermal equilibrium” bit).
If you want to say that no, he meant to describe a non-equilibrium gas, then reread his paper. He went well out of his way to isolate the gas and leave it alone so it would reach “energy equilibrium”, whatever that is supposed to mean, but there you have it. If you want to assert that energy equilibrium isn’t thermal equilibrium, well then, you and he can make it anything you like but it won’t be the state the system spontaneously evolves to.
Of course, it is difficult for me to stay on task when you write strange things such as this:
It is water vapour, the main greenhouse gas, which takes away heat from the surface in evaporation and in condensing out in the heights where it is colder, releasing its heat and coming down as rain. The BASIC Water Cycle.
Well goodness. Water vapor collects heat at the surface, and transports it uphill, you say. Sort of like a silver conducting wire. It reaches the heights (where it is, indeed, colder) and releases all of that heat, which in the usual way of things would — warm the heights, would it not?
So what, exactly, cools the heights? You’ve now got “heights plus all that heat”, and they aren’t as cold any more. The more water vapor you take up there, the warmer they get, until water vapor doesn’t condense there any more.
We can hardly just pull that warm air down, can we? Being warmer, it is less dense, and buoyant! Besides, where is there for the heat to go down below? It’s hotter still down there? How does that pesky air at the upper troposphere lose all of the heat that is constantly being transported up there, so it can maintain your water-driven “cooling cycle”? Could it, maybe, radiate the heat away to outer space, given that that is the only way the Earth ever loses heat? Or does your solution involve lots of little, bitty demons, all named Maxwell, that do something enormously improbable with it?
But you really, really, are getting close now. You can hardly move without bumping into your own contradictions. All you have to do is let go of the cognitive dissonance. It’s OK. You can admit it. There really is a greenhouse effect. That doesn’t make the CAGW hypothesis true, but it does mean that CO_2 is the mechanism that differentially cools the top of the atmosphere, much less efficiently than the earth would lose the heat if there were no atmosphere or if there was an atmosphere but it were totally transparent to IR.
You can admit the CO_2 based GHG GHE because you can see it. With IR spectrographic eyes. Anytime you wish, just look at the measurements.
Or, you can bury your head firmly in the sand and pretend that those measurements don’t exist. It’s up to you…
rgb
But none of this affects my view that Dr. Brown’s “proof” either begs the question…
Begs what question? I cite an MIT online textbook’s definition of thermodynamic equilibrium. I elsewhere cite specific sections of that textbook that contain the standard thermodynamic arguments for why thermodynamic equilibrium is isothermal unless the system is strongly — not weakly — constrained. I show how those arguments apply to an isolated ideal gas in near-Earth gravity. Specifically, I argue that it is trivially demonstrable that a state of the gas exists that is in hydrostatic equilibrium and simultaneously isothermal. It is perfectly obvious that this gas is stable — there are no unbalanced forces that would cause convection, the ideal gas obeys the ideal gas law at all points so the density is everywhere consistent with the local (also global) temperature.
Why isn’t this state thermal equilibrium?
Speak to me not of uplifting air parcels — no parcel in this gas experiences net forces, it begins at rest, it will remain at rest. The only motion occurring at any scale is the microscopic thermal diffusive motion present in any equilibrium gas, and any hypothesized bulk expansion or contraction contradicts both the fact that it is in force equilibrium and that gravity does no work on things that are not moving. There are no adiabatic expansions or contractions — why would they occur?. Since the gas is all at the same temperature, there is no (net) thermal conduction of heat from one part of the gas to another, not unless Fourier’s Law has suddenly changed so that it no longer contains a thermal gradient term.
Why is asserting that this state is manifestly thermal equilibrium begging the question? It satisfies all of the stated conditions for thermodynamic equilibrium that are to be found in any textbook. Surely the onus of proof is upon you to show why the ordinary laws of thermodynamics, the ordinary definition of thermodynamic equilibrium, is suddenly on holiday so that this gas, perfectly balanced in terms of gravitational force and energy, and utterly lacking a thermal gradient to drive the flow of heat, is somehow going to change.
Why would it? What force, specifically, will make it change? Not gravity — its in hydrostatic equilibrium. Not the flow of heat. Heat stops flowing when the temperature is uniform. Not “pressure” — see hydrostatic equilibrium. Not the influx of heat from outside, it is in a perfectly insulated container. Not work, nothing is doing any work.
What will make it change?
Note that it must change, if some other state is equilibrium. Some thermodynamic potential or force must make it change. I could be wrong, sure, maybe there is such a force, but where? What could it possibly be?
Now look at the counter argument. Suppose you prepare the gas in hydrostatic equilibrium (so it is in perfect force balance) but with a thermal lapse. Now there is a thermal process that can act. Ordinary conduction from the warmer part to the colder part is predicted and observed in any gas I’ve ever seen or heard of. Thermal conductivity doesn’t give a damn about uphill or downhill. It cares about entropy. Take a slice of gas at the top where it is cold. Take a similar slice at the bottom where it is hot. Move heat Q from the bottom to the top. Now please explain to me — with some actual algebra, please — how this will not increase the entropy of the gas, meaning that the state with a lapse could not have been maximum entropy.
Sure, I could be wrong, but I’m hardly begging any questions. If one cools the gas on the bottom and warms the gas at the top (relative to a gas with a DALR), if anything one expects to increase the density at the bottom compared to the top and shift the center of mass of the gas downhill while remaining (quasi-static process) in equilibrium. This simple heuristic argument alone suggests that would be surprising, at least, for the mean gravitational potential energy of the system to spontaneously increase at the same time a thermal gradient appears. Again, it is in the exact opposite direction one expects, higher macroscopic bulk potential energy and less buoyant stability.
Robert Brown says at 2/3 10:22pm:
“Suppose you prepare the gas in hydrostatic equilibrium (so it is in perfect force balance) but with a thermal lapse.”
Ok. Interesting to think this thru, it is shown in Fig. 1 of the top post. We have a non-physical ideal situation but can learn about reality from it. Remember Bohren&Albrecht prove with actual algebra in my cite above 2/2 6:56pm that this preparation is in a state of maximum entropy.
Robert Brown continues: “Now there is a thermal process that can act.”
No, there is not. The system is already at maximum entropy with the thermal gradient maintained by gravity due to the fact the KE (thermal energy) of the molecules must decrease with height as they move uphill against gravity. And likewise the KE (thermal energy) of the molecules must increase as they move downhill with gravity. All the while keeping their total energy (KE + PE) constant.
Robert Brown continues: “Ordinary conduction from the warmer part to the colder part is predicted and observed in any gas I’ve ever seen or heard of. “
Yes, b/c Robert Brown lives in the real world. Fig. 1 does not. However, the Verkley paper experimental evidence shows the real atmosphere is way closer to the idealization being non-isothermal than the idealization being wrongly isothermal in their Fig.2.
Robert Brown continues: “Sure, I could be wrong…”
Robert Brown is wrong about the idealization being isothermal (partly b/c his algebra in top post incorrectly just assumes T is constant). Bohren&Albrecht prove it is non-isothermal with actual algebra: ideal gas temperature does decrease with increasing height in a gravity field. They also point out people are impeded in arriving at the correct result due to pointing to conduction in solids (silver wires and I suppose ideal gas contained in jars).
Robert Brown continues: “Take a slice of gas at the top where it is cold. Take a similar slice at the bottom where it is hot. Move heat Q from the bottom to the top. Now please explain to me — with some actual algebra, please — how this will not increase the entropy of the gas, meaning that the state with a lapse could not have been maximum entropy.”
Robert Brown must see the physics of lifting the warm bottom gas up against gravity does work on the system (work = m*g*delta h) thus of course the entropy in Fig. 1 will increase, because work was performed across the control volume of Fig. 1.
Any work crossing the adiabatic control volume is ruled out by the idealization. The higher temperature bottom gas will not move up on its own due to the Fig. 1 entropy already being maxed at equilibrium. This stratified non-isothermal equilibrium continues as long as the gravity field continues.
Joe Born says:
February 3, 2012 at 4:08 pm
Thanks for the response, although I’ll have to think it through. I do recognize that a gas can be reversibly expanded and compressed, but it seems to me that merely releasing the gas from a vessel (by, e.g., magically making the vessel disappear) would result in an irreversible expansion.
No, it’s not irreversible from a thermodynamic point of view, although, in practice, reversing it could be tricky. In principle, however, one could do it by surrounding the expanding gas cloud with a massless elastic membrane, or an elastic membrane accelerated to match velocities when the gas reaches it, or by an array of rocket nozzles pointed into the flow to catch the gas, or by surrounding it with a massive perforated sphere with a gravitational escape velocity higher than the gas velocity, or by running it into a medium of suitably graduated density, etc..
Robert Brown says:
February 3, 2012 at 7:27 pm
Back when I was in graduate school and was just beginning to see the importance of e.g. the Pauli spin matrices (a complex 2×2 tensor representation of the quaternions that map into spin or isospin in quantum physics), my friends and I spent a lot of psychic energy trying to figure out the real, complex, quaternion (Grassman algebra), Clifford algebra progression, because it appears not just one or two places, but many places in physics.
Another field in which quaternions/spin matrices/spinors are useful is in General Relativity. The problem of radiative equilibrium between relativistically shifted temperatures that I touched on earlier is one to which they can conveniently be applied (the aberration of light is such a spinor boost and rotation). Chapter 41 of MTW is devoted to them.
Robert Brown says:
February 3, 2012 at 8:51 pm
Jelbring … is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
Just a minor point on the timescales. Radiation in an optically thin medium equilibriates on a timescale independent of the size of the system. Conduction (which is a form of diffusion) equilibriates on a timescale proportional to the square of the size of the system. Air will have a time constant (using your figures) ~1297Jm^-3K^-1 / 0.025Js^-1K^-1 ~ 52,000 s/m^2. That is, heat takes about half a day to go one metre. To go ~8km (the equivalent depth of the atmosphere at sea level density) would take ~ 52,000 seconds x 8000^2 ~ 100,000 years. So that’s the time constant for conductive relaxation, close enough. I suspect that radiation in an N2/O2 atmosphere would be considerably faster, even in the absence of gases like H20 and CO2 – but I admit I haven’t done the actual sums there, so I could well be wrong. Either way it makes no difference to the thought experiment, of course, since full thermodynamic equilibrium is explicitly assumed.
Trick says: “Remember Bohren&Albrecht prove with actual algebra in my cite above 2/2 6:56pm that this preparation is in a state of maximum entropy. ”
But Robert was saying to take ANY arrangement that is in hydrostatic equilibrium — there are an infinite number of temperature profiles that are in hydrostatic equilibrium. The reference you cite cannnot possibly say that ANY arrangement is the state of maximum.
I would be curious to see exactly what the text says, since there are apparently some details that you are missing.
Paul,
I have to agree with Joe about reversibility. A slow adiabatic expansion/compression is considered reversible, ie you could make a movie of the process and run it backwards and it would still make sense eg a Carnot heat engine could be run backwards to be a Carnot refrigerator. But a free expansion is not reversible. A gas can spontaneously expand into into a larger, empty container, but it cannot spontaneously leave part of a container and re-confine itself into a smaller container.
You processes all seem to involve some variation of “Maxwell’s demon” to re-order the gas.
Tim Folkerts says at 2/4 11:02am:
“But Robert was saying to take ANY arrangement that is in hydrostatic equilibrium — there are an infinite number of temperature profiles that are in hydrostatic equilibrium. The reference you cite cannnot possibly say that ANY arrangement is the state of maximum.”
The B&A text derives the general case applicable to any arrangement. Not exactly sure what you mean here. Possibly you mean the initial conditions of Fig. 1 top post could be set to any of an infinity of reasonable earth pressures (1000 to 200mb say) & temperatures (arctic or tropical) profiles to start. When the adiabatic GHG-free air column achieves equilibrium, the temp. profile will settle in to have the bottom temperature the warmest and the coldest at top as the maximum entropy condition.
Interesting to learn here that if the initial condition profile is set to isothermal, nature forces entropy increases until the stratified temperature field decreases with height and the field corresponds to max. entropy. After that it is stable – at the macro level – with lotsa’ random molecule movements of different vertical speeds (but constant total energy) at the micro level. It would be possible to measure the Fig. 1 vertical temperature field with a normal thermometer and find that, after equilibrium, it doesn’t change with time; temperature field only changes with height of thermometer.
Tim Folkerts says:
February 4, 2012 at 11:10 am
I have to agree with Joe about reversibility. A slow adiabatic expansion/compression is considered reversible, ie you could make a movie of the process and run it backwards and it would still make sense eg a Carnot heat engine could be run backwards to be a Carnot refrigerator. But a free expansion is not reversible. A gas can spontaneously expand into into a larger, empty container, but it cannot spontaneously leave part of a container and re-confine itself into a smaller container.
And you could make a movie of this process, reverse it and it would still make sense (like the condensation of a gas cloud, or laser/electron beam inertial confinement fusion). You’re still thinking of it as a Joule-Thomson expansion into a larger container, but it’s completely different. It’s an explosion, turning thermal energy into orderly radial motion.
You processes all seem to involve some variation of “Maxwell’s demon” to re-order the gas.
The gas doesn’t need “re-ordering”. It’s already highly ordered. All that’s necessary is to find a way to reflect the gas elastically, and this can be done with low-entropy macroscopic arrangements. No Maxwell’s demon required.
Such (more or less) reversible expansions are not uncommon in astrophysics. Supernova remnants, for example; after a period of essentially free expansion in which the temperature drops from megakelvins down to where they no longer radiate detectably, they start ploughing up the interstellar medium and compress and heat up again. Some light years out the pressure from the interstellar magnetic field takes over and the bubble rebounds inwards. If the field were strong enough it would rebound most of the way back to the neutron star. It’s not perfectly reversible because energy is lost to radiation and shocks can form at the nebula-i/s medium boundary. Variable stars burping the outer parts stellar atmosphere at below escape velocity are another example; gravity reverses the expansion of the shell, the recompression frequently triggering another burp. Indeed, any sound wave propagating through a gas is doing the same trick – reversibly exchanging thermal energy for linear motion.
Robert Brown says:
February 3, 2012 at 8:51 pm
“Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small.”
Yes, but that is just a matter of time scales of relaxation. You really are almost there now. Jelbring explicitly — and I do mean explicitly — states that he is supposedly waiting for relaxation to occur on all available time scales. He is supposedly describing thermal equilibrium in a static column of gas that has been sitting around long enough for even radiation to equilibrate, and for non-GHGs that is a very, very long time, much longer than the time required for thermal conductivity to equilibrate temperatures.
We really are reading him from two completely different positions, I see this as just the ‘chuck everything out and get to the basics’, so if it takes that aeons of time, so be it, but at the end of that, etc.
In other words, there is no “negligibly small” when discussing thermal equilibrium timescales. Relaxation to thermal equilibrium occurs on many timescales. Who determines which ones are “negligible”? What are these timescales?
“Take two identical volumes (parcels) of air, taken from somewhere at a midlevel in the troposphere, with each parcel containing an identical number of gas molecules and the same amount of heat energy to start. Mentally place one parcel higher in the troposphere and one closer to the surface of the Earth, without allowing any molecules or heat energy to enter or leave each parcel of air. The parcel of air that you placed in the lower atmosphere is going to compress and warm because it finds itself in a place with higher pressure. The parcel of air that higher in the atmosphere is going to expand and cool because it finds itself under lower pressure.This kind of process, one which takes place without heat energy entering or leaving the parcel, is called an adiabatic process.” http://education.sdsc.edu/teachertech/downloads/climate_answ.pdf
That’s the time scale, it doesn’t matter. That is always going to be the underlying skeletal structure onto which all else is built.
To put it another way, if one constructed a system with an isothermal air column in force balance — something one certainly can do, just by taking an insulated tower of air and mixing it well and letting it stop moving — what will make it depart from isothermal and relax towards a DALR? There are no air parcels moving up or down, so the entire argument concerning adiabatic lapse and isoentropic mixing is moot. There is nothing but diffusion and conduction, and they if anything maintain the air in an isothermal state. I’ve already argued that taking any gas and without doing any work causing it to separate into hotter and colder gas is a horrible, egregious violation of the second law, yet the entire gas column is by construction hydrodynamically stable, with a density strictly decreasing with height and without the slightest thing to cause bulk convection or other movements of air where “work” can be done.
That’s all irrelevant, it’s already the adiabatic lapse rate as a creation of gravity in that pressure does the work, more or less work as it’s greater or weaker.
You’re thinking of gravity as ‘doing work’ in an odd way, istm, and it could be because you’re not relating gravity to its own processes. For example as you say here:
“and that gravity does no work on things that are not moving. There are no adiabatic expansions or contractions — why would they occur?”
Gravity ‘works’ on mass not on movement, it’s the relationship of mass of objects meeting in gravity which creates movement, two gases of different mass in the same parcel of space will separate out as gravity has a greater pull on the one with more mass.
What you are saying is just a restatement of what I’ve been saying all along. Jelbring is incorrect, but if you neglect thermal conductivity and dynamical relaxation processes other than slow convection, an atmosphere with a DALR can be hydrodynamically stable and can exhibit a lapse rate (once one is established) for a long time. But that moves us into another discussion — one of atmospheric dynamics, not atmospheric statics, the explicit milieu of Jelbring’s paper.
No, I’m saying it’s why Jelbring says conduction is negligible, because it is, dynamically or statically, it can be discounted, air is a very poor conductor of heat.
It’s just to get back to the difference in pressure which is a ‘function’ of gravity, the higher the pressure the more the molecules are heated, the more they’re heated the lighter and less dense they become and so rise as the denser above them bully their way down through them, well, the actual term is displace, like carbon dioxide being heavier displaces the lighter nitrogen and oxygen to sink to the ground. The action of gravity.
There I think that it is pretty obvious what actually establishes a lapse rate — differential heating of the air column at the bottom, followed by a rough equilibration due to approximately adiabatic convection. The air column is always moving, always heating or cooling, so the milieu of Jelbring’s paper and his conclusions are not only incorrect, they are irrelevant. He didn’t discover, invent, derive, meaningfully discuss, measure, draw pictures of, or even present an heuristic argument for the DALR in his paper. All he did is assert that it is a feature of completely isolated, static atmospheres so that just having a gas in a gravity well equals a DALR in the gas.
You continue to prove my point.
I’m trying very hard not to… 🙂
“Why is air at elevation cooler as the pressure becomes less? The temperature of air is cooler at elevation in response to the vertical pressure changes that happen to occur because of the Earth’s gravity.” (same link as last)
He went well out of his way to isolate the gas and leave it alone so it would reach “energy equilibrium”, whatever that is supposed to mean, but there you have it. If you want to assert that energy equilibrium isn’t thermal equilibrium, well then, you and he can make it anything you like but it won’t be the state the system spontaneously evolves to. If you want to say that no, he meant to describe a non-equilibrium gas, then reread his paper.
Thermal equilibrium doesn’t mean the same temperature, if for example, a gas in getting hotter expands and rises becoming less dense and under less pressure it can move faster, it’s using thermal energy to move, there’s no energy lost, it’s just become something else, or, as temperature relates to kinetic energy not thermal energy then heat capacity comes into play, as water can absorb a huge amount of thermal energy before there’s any rise in temperature, or whatever, but if you’re equating all ‘energy’ to ‘heat’ as thermal energy then that’s a different idea altogether, not all energy is heat. I think he means here energy equilibrium as in different processes can be happening within the volume of gas, I think you keep misreading him. As you misread him here:
“An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.”
When you read that he was somehow ‘proving’ that it was adiabatic, but he’s only saying that adiabatic is the default and a parcel of air rising in it will change its energy states, the equilibrium is in the total energy of the processes.
Others have explained what that means is happening to the gaseous atmosphere as it goes from high to low pressure, and it has to be understood by first taking into account the particular properties of gases, and, these in the actual processes of gravity.
I’m sorry, but this is really all Jelbring is saying, that when we get back to the basic mechanism we get the adiabatic lapse rate, yer basic gravity.
“But, they have actually excluded the Water Cycle. Without water the earth would be 67°C, that is 52°C hotter – think deserts to get some idea of what the earth would be like without the main greenhouse gas water vapour in the Water Cycle.”
You also continue to throw red herrings into the soup. Jelbring’s paper explicitly excludes the Water Cycle (or adiabatic moving air parcels). It is a pure ideal gas. So why do you keep bringing them up?
It’s a running continuation on the theme of you misreading him in thinking he was claiming an insight unique to him, when you said it was also in text books, but what he meant was “climate” scientists don’t acknowledge this. As you show here. “Climate” scientists are a breed apart. I’m sorry if that wasn’t clear as a theme in my replies. I’ve just been giving different examples of how “climate” scientists have a completely different fisics of the basics. The absence of the water cycle in the KT97 and ilk energy budgets the most obvious. But “climate science” has done this across the range of basics in changing, tweaking, eliminating and so on to the point where it describes a non-existant world, and as you show here, doesn’t know it, so thinks it’s something ‘new’ or ‘wrong’ as it’s trying read it from a different fisics, trying to make it fit into a different fisics.
I’m glad you asked.
Heating the atmosphere at the bottom more than the top seems important as well, and you know what? It isn’t that surprising that something heated at the bottom and cooled at the top exhibits a thermal gradient from the bottom to the top.
No, it exhibits a temperature gradient.
The interesting question is, what cools it at the top?
Same thing that heats it at the bottom..
..pressure, i.e. gravity, weaker at the top, stronger at the bottom.
Cooling requires the actual physical removal of heat.
Requires a change in temperature. Removing thermal energy can do that. By changing it to a different energy, etc.
Could it be — gasp — radiation? Could we — possibly — measure it? Can we — I know it is a crazy, crazy, idea — determine the temperature of the source of the radiation, and from the spectrum the probable source of the radiation, the particular species of molecules that are emitting it? Could those molecules be — I hate to even say it out loud — CO_2?
Sigh.
We know the temperature of the Sun. What “climate” scientists have done is change the spectrum. The claim is that no thermal energy direct from the Sun heats the Earth, the real thermal energy that is, thermal infrared radiation which is heat on the move. Instead “climate” scientists have given its properties, being heat, to shortwave, claiming visible light heats the oceans and land, even though water is a transparent medium to it.. And then, ignoring that the heat we feel from the Sun is thermal infrared so does reach us, say that carbon dioxide a trace gas, and already fully part and parcel of the cooling cycling of the Earth in the Water Cycle, is responsible for raising the temperature of the Earth from -18°C to 15°C, without ever giving any rational explanation as to how it actually does this, and, that doubling it will cause catastrophic runaway global warming, doubling a trace gas it still remains a trace gas.
You do have such an amazing molecule in your fictional world, defying gravity it can stay up in the atmosphere for hundreds and even thousands of years accumulating though it’s one and a half times heavier than air, and, with no heat capacity to spit at, it can trap heat, or, heck you can’t even get your stories to say the same thing consistently, it becomes this great thermal blanket stopping heat escaping… just how much of that blanket is holes?
Anyway, thanks for your post on Clifford, I enjoyed reading it.
Adiabatic Cooling
http://eesc.columbia.edu/courses/ees/slides/climate/adiabatic.jpg
This is the page it comes from:
http://eesc.columbia.edu/courses/ees/climate/lectures/atm_phys.html
Don’t know how good it appears to those I consider have superior understanding here..
When the adiabatic GHG-free air column achieves equilibrium, the temp. profile will settle in to have the bottom temperature the warmest and the coldest at top as the maximum entropy condition.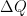
being moved to/from a layer of gas at any given temperature 
is:
that satisfy 
, so there is no net force acting to push the gas up — but not all profiles are equally stable. The most gravitationally stable profile is isothermal.
Except that it is a ten-second mental exercise to see that this is not, in fact, maximum entropy. Because if heat is transferred from the warmer bottom to the cooler top, the entropy of the arrangement will increase.
You don’t need to look at a reference to see this. You just need to know what the entropy change of the transfer is. In case you’ve forgotten the entropy gain/loss associated with heat
Go ahead, do the algebra. If you get stuck bear in mind that I do it for you up above, and the MIT textbook has it as well.
The only way the gas will not be isothermal at maximum entropy is if heat transfer is impossible. But obviously it is not. As you (and Jelbring) acknowledge, real ideal gases can conduct thermal energy. In the derivation of the DALR their conductivity is often omitted (because it is relatively low, air is a poor conductor). But this is a thought experiment, and Jelbring himself establishes true equilibrium after a long time as a feature of the system in question, because he wishes to assert that gases will be warmer at the bottom without any external thermal driving, in particular the heating at the bottom and cooling at the top associated with the Sun and the GHE.
BTW, no, I’m not talking about lifting up any parcels of gas during equilibration. The gas is equilibrating via thermal and radiative conduction. No work is done by gravity.
Well, that’s not quite true. As the bottom cools and the top warms the center of mass of the gas will indeed move down because the density of the gas at the bottom will increase while the density of the gas at the top will decrease. The macroscopic action of gravity actually favors isothermal equilibrium.
This is yet another heuristic you can use to understand this. You’re all about energy balance and gravity. Well, the gas is, on average, lower when it is in thermal equilibrium, not higher, in a macroscopically more stable state, a hydrostatically more stable state. Remember, it is always in hydrostatic equilibrium — there are many possible profiles with consistent
rgb
Myrrh says:
in the BB formula — it will not change. It can’t move towards the DALR, because the atmosphere is hydrostatically stable and there are no uplifting parcels of air (matched by downfalling parcels elsewhere, BTW, because there isn’t anywhere for conserved air to actually go). It can’t move towards isothermal either, because one cannot move heat around in the gas to increase its entropy: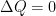 
for any parcel of the gas as it sits there in perfect force balance. The gas would be perfectly stable. So would the gas prepared with the DALR, an isothermal gas, or any other hydrostatically stable thermal profile you arrange as an initial condition.
February 4, 2012 at 7:01 pm
Adiabatic Cooling…
Nice picture, and nice article. Note well that the figure clearly labels the wall of the balloon as being a thermal insulator — that’s the adiabatic part, actually. Suppose that it wasn’t really a perfect thermal insulator? Hmmm, would the gas precisely follow the adiabatic PV curve if heat could flow into the contents of the balloon from the gas surrounding it?
Note well that the article clearly states that the air takes on an adiabatic lapse as it is being uplifted. It even offers pretty much the only two mechanisms for uplift, and truthfully that can be reduced to one. The first is differential heating leading to convection, the second is the deflection of lateral air movements as they go up or down a mountainside. The second, of course, requires pressure differences to generate the wind and pressure differences are only created by differential heating. No differential heating (on Earth or anyplace else) — no ALR.
An interesting question is then — suppose one starts with an air column (Jelbring conditions, dry ideal gas, no mountains, wind, or sources of heat) but select as an initial condition hydrostatic equilibrium with a thermal profile somewhere in between the classic DALR and isothermal. Which way (to which profile) will this air column go?
If it is a perfectly adiabatic, totally transparent gas — if the conductivity of the gas is zero and
Now “turn on” heat transport (mentally) via conduction and radiation. These cannot — and will not — destabilize the atmosphere to start up convection, because they always move net heat in the direction that makes convection even less likely, given that convection is driven by temperature differences that conduction or radiation further reduce. They will not move the system towards the DALR, because the DALR is a very special thermal lapse, one that is established by slow, non-turbulent convection (that nevertheless happens to mix the atmosphere faster than conduction or radiation). Indeed, the direct action of conduction and radiation will be to move the gas towards isothermal equilibrium because that is the true, stable thermodynamic equilibrium for an isolated gas where one does not neglect conduction and radiation as mechanisms for heat transfer with in the gas.
Just another fairly simple thought experiment. In the end, one can just read the lovely summary that you post to understand my objection to EEJ. Is there one, single word in that article that suggests that the DALR is the stable result of a static equilibration process for a not perfectly adiabatic ideal gas? I don’t think so.
rgb
rgb
Gravity ‘works’ on mass not on movement, it’s the relationship of mass of objects meeting in gravity which creates movement, two gases of different mass in the same parcel of space will separate out as gravity has a greater pull on the one with more mass.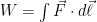
(if the latex survives). Work is the action of force through a distance. When the gas is in hydrostatic equilibrium, there is no bulk transport of the gas because it is in force equilibrium, and gravity does no work.
No, no, no, silly beanie.
As thermal relaxation occurs, it does do work, however — because the center of mass of an isothermal ideal gas is lower than the center of mass of an ideal gas with any other stable thermal lapse rate. Remember, the pressure at the bottom of the gas column is a constant (equal to the weight per unit area of all of the gas) and that otherwise, the density strictly decreases with increased T. So the layer near the bottom becomes more dense as it cools due to conductivity, and the layer near the top becomes less dense as it warms. This actually “compresses” the gas at the bottom more, although the compression is only a downward shift in density because the actual pressure at the bottom must be conserved and hydrostatic equilibrium maintained.
BTW, you seem a bit obsessed with the idea that two gases with different masses will “separate out”. If by this you mean that they will form layers with a sharp interface, like the meniscus of oil on water, that just isn’t so. I think you need to read, and try to understand, Dalton’s Law:
http://en.wikipedia.org/wiki/Dalton%27s_law
The idea is straightforward. Both (ideal) gases will expand to fill any vessel they are placed in, and at normal e.g. room temperature and with similar sized molecules there is no chance of them “separating”. OTOH, if by this you mean that both gases will have equilibrium densities and partial pressures that more or less exponentially decay, with distinct exponential constants so that the static equilibrium mixture will not end up being perfectly homogeneous over very large vertical distances, especially if one molecule is physically much larger than and more massive than the other, I don’t have a quarrel with that (and neither does Dalton), although I would want to work out the numbers. No matter — I don’t care to argue either way, because this is completely irrelevant to the discussion of EEJ except that you keep giving it as an example of something science has “gotten wrong”.
You do realize that even if you are correct and physics has “gotten this wrong”, that isn’t actually an argument in the case at hand, right? It is an example of a “red herring” fallacy — poisoning the well, as it were. Physics once got something wrong, therefore Jelbring is right is not an argument (even if you are correct about what you claim physics has gotten wrong, which is another whole argument).
We know the temperature of the Sun. What “climate” scientists have done is change the spectrum. The claim is that no thermal energy direct from the Sun heats the Earth, the real thermal energy that is, thermal infrared radiation which is heat on the move. Instead “climate” scientists have given its properties, being heat, to shortwave, claiming visible light heats the oceans and land, even though water is a transparent medium to it.. And then, ignoring that the heat we feel from the Sun is thermal infrared so does reach us, say that carbon dioxide a trace gas, and already fully part and parcel of the cooling cycling of the Earth in the Water Cycle, is responsible for raising the temperature of the Earth from -18°C to 15°C, without ever giving any rational explanation as to how it actually does this, and, that doubling it will cause catastrophic runaway global warming, doubling a trace gas it still remains a trace gas.
Oh-kayyyy, that’s just crazy talk. Seriously. Visible light damn skippy heats the (top layer of) the oceans. Let’s see, a small fraction of visible light reflects off of the top surface. The rest is transmitted. If you visit page 85 (section 9.2) of my online book on electrodynamics, you can actually follow the full derivation of the transmission and reflection coefficients, although they only have a relatively simple form for light coming in at right angles. But this is utterly pedestrian stuff and you literally couldn’t see if it weren’t true.
http://www.phy.duke.edu/~rgb/Class/Electrodynamics.php
If you pursue the rest of the chapter you can learn a bit about the fate of that light once it enters the water. Water is by no means perfectly transparent, and besides, impure water is a bulk conductor. Both of these thing mean that water exponentially absorbs the visible light, turning pretty much 100% of the energy that made it through the surface — which is most of the energy — into heat. So sorry, your assertion that visible light doesn’t heat water is really pretty silly.
Second, nobody argues that the sun doesn’t emit infrared or ultraviolet along with visible. In fact, you can look at the top of atmosphere spectrum of sunlight here:
http://en.wikipedia.org/wiki/File:Solar_Spectrum.png
First of all, carefully note that this is measured, not theoretical, not a conspiracy theory lie to help support the IPCC. The spectrum of sunlight was probably measured well over 100 years ago to pretty much the precision evident in this figure. Nobody cared about CAGW back then, really. Second, look at all of that IR in the long tail! And look! They even measure the difference between top of atmosphere and bottom of atmosphere, directly proving that yes, the atmosphere absorbs energy from bands all over the spectrum. Hey, it even names them for the molecular species primarily responsible for absorption.
Note that where it absorbs, it absorbs everything. Nothing to speak of gets through in that band, especially the ones above 1250 nm that are important to the GHE.
Here is the second place you are in error. CO_2 may well be a “trace gas”, a mere 0.03% of the atmosphere, but that doesn’t make it optically transparent in any given frequency!
If you want to understand that, you can — I linked my book and everything you need to learn to understand it is in there. The key here is the idea of cross-section — the effective cross-sectional area a molecule offers to absorb, or scatter, (or both), light. You already have the idea, I’m sure, because it is part of e.g. N&Z except they talk about the absorption cross-section of the earth, not a molecule. Light falls on the molecule and everything in a certain area is absorbed and turned into heat. The atmosphere is optically “thick” in those bands
Just to prove that I don’t completely disagree with some of what you are trying to say, let me offer up an interesting link:
http://landshape.org/enm/significance-of-global-warming/
This (discussion of) a paper/theory suggests that water is indeed important; it is a key in a negative feedback cycle that locks the earth into a nearly constant total greenhouse effect. It doesn’t actually argue about the details of the mechanism. It just takes 60 years worth of radiosonde data and shows that the integrated expected greenhouse effect is nearly constant, because water and CO_2 do a little dance that keeps it that way, with less water when there is more CO_2. That’s the kind of thing that the venerable Roy Spencer argues in his book (which I would highly recommend, BTW). It also suggests that things that directly modulate water vapor are far more important than CO_2 per se, because the feedback cycle adjust water content to CO_2 but cannot work the other way! More water, less water in the atmosphere won’t affect the CO_2 levels.
There is even some more or less direct evidence to support this. Even Scientific American has re-reported the NASA data:
http://www.scientificamerican.com/article.cfm?id=is-water-vapor-in-the-stratosphere-slowing-global-warming
The catch is that in order to argue in this way you have to grit your teeth and take the plunge and acknowledge that there really is a GHG GHE and that CO_2 really does play an important role in it. Not as important as water, perhaps, but the two really work together. Once you agree that the CO_2 part of the GHE is real and really does help warm the Earth relative to a good old ideal black body of the same average albedo, you’ll be all set to argue about how doubling CO_2 has almost no effect on an atmosphere that is already basically optically thick ten or twenty or thirty times over. The only way it could trap more heat is by forcing the zone where the atmosphere becomes transparent to CO_2 radiated heat upward to colder air, but if the water content of the stratosphere is dropping, things are moving the exact opposite way, and more heat is being radiated from further down where it is warmer, reducing the surface trapping of heat.
rgb
Dr. Brown
A couple days ago when you said:
,
I was hopeful, and thought you might be starting to get it.
But yesterday you removed any such hope by stating:
which highlights an obvious flaw in your reasoning.
You seem to ignore that there is a density difference with height in gas pressurized by gravity, then apply principles that are density dependent.
Robert,
I admire your persistence with Myrrh. In the vein of “forewarned is forearmed” let me tell you that Myrrh has been convinced of his “crazy talk” position on IR, visible light, and heat for some time, despite several attempts by several people to point out the sort of problems that you address.
But who know? Maybe you will have better luck than the rest of us.
Dr. Brown:
In a recent comment, you objected to my saying, “none of this affects my view that Dr. Brown’s ‘proof” either begs the question or is based on an assumption inconsistent with Velasco et al.’s Equation 8.” In saying that I was in fact somewhat imprecise. But stating my position more precisely is complicated by the fact that I’m not always sure precisely what your position is. For example, your position on just what you mean by temperature appears to have evolved. So, in order to respond, I need to set forth what I see as three flavors of your argument.
I’ll preface that by observing that nothing in your discussion of the first two flavors gives any reason to believe that you viewed temperature any differently from the Ideal Gas Law, which treats temperature as the ratio of pressure to the product of molecular density and Boltzmann’s constant, i.e., as two-thirds the ratio of mean molecular translational kinetic energy to Boltzmann’s constant. Dividing the pressure on the vessel wall at any altitude in your experiment by the molecular density at that altitude therefore tells you the temperature. And your position as expressed up through the time of your top post was that any gradient at all in this quantity at equilibrium—any non-zero decrease in mean molecular translational kinetic energy with altitude—violates the Second Law. In these two flavors, which I will presently describe, you disagree with Velasco et al.’s Equation 8, which states that average molecular kinetic energy decreases with altitude.
In the third flavor, which I also discuss below, you avoid disagreeing with Velasco et al. by so defining lapse rate that it equals zero if the kinetic-energy gradient equals the (non-zero) gradient that Velasco et al.’s Equation 8 defines.
Now for the three flavors.
Flavor the first (http://wattsupwiththat.com/2012/01/12/earths-baseline-black-body-model-a-damn-hard-problem/#comment-867311): “Imagine a plane surface in the gas. In a thin slice of the gas right above the surface, the molecules have some temperature. Right below it, they have some other temperature. Let’s imagine the gas to be monoatomic (no loss of generality) and ideal (ditto). In each layer, the gravitational potential energy is constant. Bear in mind that only changes in potential energy are associated with changes in kinetic energy (work energy theorem), and that temperature only describes the average internal kinetic energy in the gas. . . . On average, just as many molecules move up, with exactly the same velocity/kinetic energy profile, as move down, with zero energy transport, zero mass transport, and zero alteration of the MB profiles above and below, only when the two slices have the same temperature. Otherwise heat will flow from the hotter (right-shifted MB distribution) to the colder (left-shifted MB distribution) slice until the temperatures are equal.”
In short, you treated each layer as having an associated local temperature dictated by a local velocity profile, which according to you had to be the same for all layers to avoid net inter-layer mass transport, which is inconsistent with equilibrium. In this flavor, I wouldn’t say you begged the question. It’s just that to my mind the reasoning between the postulate of equal up- and down-going-velocity distributions across a layer boundary and the theorem of equal velocity distributions at different layers falls somewhat short of syllogistic.
Flavor the second: the head post above. Here you don’t rely on mass transport but instead rely on the assumption that at equilibrium a vertical wire will have no temperature gradient at all and that any gradient at all in the wire will result in heat flow. In this flavor you either beg the question or come very close to it. Jelbring’s assumption from which you attempt to reason to a contradiction is that a lapse rate can prevail at equilibrium: no net heat will flow despite a temperature difference. But then your argument against that assumption is just to say, Yes, it will flow—in the wire.
Now, you may respond that Jelbring’s assumption was only that no heat flows in response to lapse rate in a gas; he didn’t say anything about wires. No purpose is served by voicing my opinion that this is just sophistry. But I will raise another objection. Jelbring says the gas in isolation exhibits a lapse rate, and you say the wire in isolation exhibits none. How does it follow that the combined system exhibits the same lapse rate as the isolated gas and therefore results in perpetual heat flow? Why would it not be just as logical to conclude that the resultant lapse rate is the isolated wire’s—or some other lapse rate altogether? In other words, to reach the conclusion that heat flows perpetually, your attempted refutation makes quite a logical leap.
You gave no indication at the time that use of “temperature” in this second flavor differed at all from its use in the first. And you said that any equilibrium temperature gradient at all would violate the Second Law. “What matters is that EEJ asserts that dT/dz ≠ 0 in stable thermodynamic equilibrium.” “The magnitude of the difference [between the top- and bottom-of-column temperatures], and the mechanism proposed for this separation are irrelevant. . . .” You didn’t say that mean molecular kinetic energy had to be uniform—except for a negligibly small gravity-imposed skew toward the bottom. You didn’t say it had to be uniform—except for a skew that under gravity results in no net heat flow. You said no temperature gradient at all, and, according to the Ideal Gas Law, that means no non-zero mean-molecular-kinetic energy gradient, no matter how small. In this you disagreed with Velasco et al.’s Equation 8. This brings us to:
Flavor the third: Here I’ll admit I’m putting words in your mouth. But I’m inferring from your approval of Paul Birch’s and DeWitt Payne’s comments that your position has now evolved to the following. You’ve repented of your position in the first flavor, where you contended that every altitude layer had to have the same velocity profile—and thus the same mean molecular translational kinetic energy. You now believe that there can be an equilibrium difference between top- and bottom-of-column mean molecular translational kinetic energies, so long as no heat flows, because the definition of a temperature difference is that it is the quantity that causes heat flow: if there’s no heat flow, then, by definition, there’s no temperature difference, i.e., no lapse rate.
This flavor saves you from disagreeing with Velasco et al.’s Equation 8—but it makes your attempted refutation depend on Jelbring’s use of the term “temperature.” That is, you have to interpret Jelbring as using “temperature” not as we all learned it in connection with the Ideal Gas Law but rather as the quantity whose difference is by definition zero if no heat flow results—in a wire. If you don’t—i.e, if you accept that temperature is, as we learned in high school, mean molecular translational kinetic energy—then accepting that a difference in that quantity does not necessarily cause heat flow guts your attempted refutation of Jelbring’s theory. If a temperature difference does not necessarily result in heat flow, then perpetual heat flow through the wire does not necessarily result.
Since this reply has already gone on far too long, I won’t repeat here why Paul Birch’s and DeWitt Payne’s comments are inapposite. I will say that I largely agree with Tim Folkerts’ statement about Velasco et al.’s Equation 8’s being directed to a very specific situation and that it approaches isothermality in the limit. I am not contesting your result as a practical matter, only the adequacy of your proof. But I will add that the situation to which Equation 8 is directed is precisely the one to which your head post above is.