Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Chas – I’ve decided your program is quite enough. Did not want to get back in my old code for I would probably be looking at weeks, not days. However, I did download your modified code. I installed SmallBasic. I’m going to get my grandson to try at programming using that neat bare bones language. Quite neat. I spent some thirteen years in basic but that was a long, long time ago but I am getting the syntax back little by little.
I did make some modifications myself. Set the atom sizes to default at 15, speed to 4, gravity to 0.10 and made it so (very bottom of your code) when resetting Av’s it also just re-randomized the velocities. That got rid of the bouncing. Made the width 400 instead of 1024 to get a tall column.
Others should try this, for time after time, the kinetic energy ratio or ‘temperature’ settled out after five minutes to 1.05. I will be darn, it did end up with the bottom warmer that the top, not much, but it shows it. Now whether that program is critiqued enough, if it is perfect enough, that I do not know but that is as far as I am going to follow right now. This whole discussion really has nothing to do with Nikolov & Zeller’s theory anyway. If you were to let this perfect ideal gas radiate, which they all do to some degree, then the pressure at the bottom would have more emissivity/absorptivity and that ‘temperature’ ratio would show pressure’s influence be even higher… even without external energy… it’s called pressure broadening and it guaranteed.
Thanks for the demo!
OK, Big Wave Dave,
If you feel that
“there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet”
then give us the equation for the temperature profile. What variables does this temperature depend on. Surely if all of us who come to this conclusion are making a ridiculous, gross mistake, it should be easy to give us the correct answer.
PS. I trust you remember that this discussion is predicted on Jelbring’s assumption of an atmosphere that does not gain/lose any energy to/from space, so your answer should be for such adiabatic conditions as outlined in the top post. I will even give you the latitude of choosing whether the atmosphere interacts with the ground, or if that surface is to be considered adiabatic as well.
PPS I trust you remember that Dr Brown (and I and all the other arguing for an isothermal gas in this special situation recognize that a REAL atmosphere with GHGs radiating to space WILL have a vertical temperature gradient, but that this is a completely different situation.
Paul Birch says: “Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. ”
This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
Does it include Maxwell’s Quaternion Equations?
Well, it includes Maxwell’s equations themselves, in several incarnations of expression (including manifestly covariant). I do love geometric algebra and think that the “war” between Heaviside and Gibbs and Hamilton’s followers (Tatt?) that the quaternion advocates eventually lost was very interesting — in the end Gibbs’ notation was, probably correctly, deemed a lot easier to work with and compute with.
Do Clifford/Geometric algebras interest you?
rgb
You are grossly in error, and your opinion of how gas behaves is ridiculous. I would suggest that you dig up some texts on the subjects, and read them. Otherwise, you should stick to computers.
Well, now that you’ve gotten that semantically null verbiage out of your system, did you have some actual algebraically correct derivations or corrections to offer? Precisely what texts would you suggest? My shelves are already full of a rather lot of introductory physics textbooks — maybe thirty or forty — since publishers send me copies every year trying to get me to use them. So what’s your pleasure, Halliday and Resnick, Halliday, Resnick and Walker, Tipler, Tipler and Mosca, Serway, Serway and Beichner, Brown (oh, I suppose I shouldn’t use my own textbook, should I), Giancoli..
Or do you like some specific more advanced textbook, perhaps one that proves that thermal equilibrium isn’t isothermal for some particular system? I’d be simply thrilled to have an actual reference, since we have already heard from the author of one textbook on physical climatology above who seems to agree with me, however silly that may be. I’m certain that (since both of us are apparently wrong) you’ll have no difficulty documenting our error and directing us in the best of good will to more correct works that support your claims, whatever those claims might be since I’m not seeing any claims in your reply other than the claim that that I am — somewhere, in some unspecified way — grossly in error. No doubt, no doubt, but it would be good to know exactly where and how, gently demonstrated by a real expert like yourself.
I must confess that I fail to see how establishing that an isothermal ideal gas in static force equilibrium in a gravitational field is also a maximum entropy state of that gas is “ridiculous” — especially since I actually support the conclusion with an algebraic derivation from known and established principles — but I’m certain that you, BigWave, are more than prepared to educate me.
rgb
This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
http://en.wikipedia.org/wiki/Free_expansion
(that is, I think you are right Tim). However, I think Paul just misspoke. He did note that the free expansion leaves the average KE per molecule the same — which I know that he knows means that the temperature hasn’t changed (although the density certainly has).
Ideal gas adiabats in cyclic heat engine cycles do expand and cool, but they do work at the same time and aren’t “free”.
rgb
Anything he says that doesn’t recognize that there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet, shows a fundamental lack of understanding of what gas temperature means.
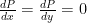
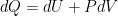for an ideal gas. (Or, “the heat that goes into a system equals the change of internal energy of the system plus the work done by the system”, although one can use different sign conventions and change “in” to “out” in various places to get equivalent statements.)
Ah, I see. This is why I am in gross error and ridiculous.
It’s the damnedest thing. Here I sit, thinking that the correct thermodynamic definition of the temperature of a gas has to do with stuff like:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node11.html
note especially the bit in 1.2.4 “The Concept of Equilibrium”, especially the statements that a system in thermodynamic equilibrium satisfies:
1) mechanical equilibrium (no unbalanced forces). For any fluid in near-Earth gravity, the condition for mechanical equilibrium is:
But don’t mind me, I just derived this at the board three times already this week in three different recitation sections. Note well that the condition for mechanical equilibrium does not directly refer to temperature at all and is equally valid for gases or liquids.
2) thermal equilibrium (no temperature differences). Ooo, it did not just say that! And on the MIT online physics textbook on thermodynamics, too! Gosh, BigWaveDave, you really need to go to MIT and correct them! Here we all are, making ever bigger mistakes!
3) chemical equilibrium.
Chemical equilibrium is clearly irrelevant to ideal gases. The conditions for mechanical equilibrium doesn’t depend on whether the gases are ideal or not, although for an ideal gas, the density depends on the temperature so that there are an infinite number of ways one can stack up the gas with a thermal gradient that are all still in mechanical equilibrium.
To understand why thermal equilibrium is both isothermal and maximum entropy, you have to work through a bit more of the textbook, BWD.
You — and Myrrh — might visit and spend a bit of time on:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node38.html
(“The Axiomatic Statement of the Laws of Thermodynamics”). These are the axioms that Jelbring claims are the basis of his conclusion. But are they?
Read the 0th law. “Equality of temperature is a necessary and sufficient condition of thermal equilibrium”.
Wow. It’s going to be difficult for Jelbring to defend the conclusion that “temperatures vary in a system in thermal equilibrium” and not contradict the axiomatic statement of the zeroth law.
Read the 1st law. It’s just the law of energy conservation, nothing to see here, move along folks.
Read the 2nd law, because it is the big one, the one that you, BWD, have apparently never heard of. Permit me to quote:
Although all natural processes must take place in accordance with the First Law, the principle of conservation of energy is, by itself, inadequate for an unambiguous description of the behavior of a system. Specifically, there is no mention of the familiar observation that every natural process has in some sense a preferred direction of action. For example, the flow of heat occurs naturally from hotter to colder bodies, in the absence of other influences, but the reverse flow certainly is not in violation of the First Law. So far as that law is concerned, the initial and final states are symmetrical in a very important respect.
Note well the bit about conservation of energy alone being inadequate for the unambiguous description of the behavior of a system. Omitting this is what makes Jelbring’s “proof” and Joules’ ranting and your claim that gravity alone has to directly tie into temperature all so very, very wrong. You can’t just think about energy. You also have to think about entropy!
“Tim Folkerts says:
February 1, 2012 at 7:36 pm
OK, Big Wave Dave,
If you feel that
“there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet”
then give us the equation for the temperature profile. What variables does this temperature depend on. Surely if all of us who come to this conclusion are making a ridiculous, gross mistake, it should be easy to give us the correct answer.”
What wrong with one given at wiki:
http://en.wikipedia.org/wiki/Lapse_rate#Saturated_adiabatic_lapse_rate
“PS. I trust you remember that this discussion is predicted on Jelbring’s assumption of an atmosphere that does not gain/lose any energy to/from space, so your answer should be for such adiabatic conditions as outlined in the top post. I will even give you the latitude of choosing whether the atmosphere interacts with the ground, or if that surface is to be considered adiabatic as well.”
Jelbring’s assumption is that one using a non-greenhouse like nitrogen- which 70% of mass of our atmosphere.
If there was atmosphere of only nitrogen, who think this gas would radiate any significant amount energy into space?
If a planet had a constant surface temperature of 300 K and it had 1 atm nitrogen only atmosphere and it had earth gravity. Who thinks that up to top of the troposphere it have anything radially different than earth’s atmosphere?
With no moisture the lapse rate would higher than 6.5 Km, and instead approach DALR.
But other than that wouldn’t be similar in terms of air temperature and air temperature decreasing with higher elevation?
How one could keep the surface at constant temperature isn’t the issue- whether it’s million or thousand suns or huge amount nuclear reactor heating the surface
“PPS I trust you remember that Dr Brown (and I and all the other arguing for an isothermal gas in this special situation recognize that a REAL atmosphere with GHGs radiating to space WILL have a vertical temperature gradient, but that this is a completely different situation.”
Yes, I assume you familiar mountain skiing. And glaciers in Oregon and tropical glaciers being on mountains. Do I agree that GHG’s losing heat to space could some affect on lapse rate, possible small affect. And similar small affect on lapse is conceivable any warming caused by GHG. But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula?
How much difference you assigning to CO2?
Take the constant surface temperature of 300 K with 1 atm of nitrogen and add the .04% CO2
what difference would this have on lapse rate?
CO2 is ideal gas. H20 gas is not ideal gas. The reason H2O affects lapse rate is because it condenses- whereas CO2 doesn’t [though may get close in extremely cold Antarctic weather].
“Basically, there are so few CO2 molecules in the free atmosphere, sublimation rules over deposition as a solid. Yes some CO2 may deposit on a surface at at -80.5 C (-113F ), but it would quickly sublimate back into the free atmosphere, and thus accumulation would not occur.”
http://wattsupwiththat.com/2009/06/13/results-lab-experiment-regarding-co2-snow-in-antarctica-at-113%C2%B0f-80-5%C2%B0c-not-possible/
So my point is this change could occur, not that any CO2 would accumulate- so at 1 atm or more and -80.5 C or lower CO2 would not be an ideal gas. And also under 5 atm of more, CO2 would not be ideal gas at normal earth temperatures.
And obviously under certain circumstance not found on Earth, H2O could be an ideal gas.
One last comment, specifically for Myrrh, who appears ready to learn precisely why Jelbring is wrong and understand it!
Read:
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node41.html
Note well that this page largely recapitulates my elementary arguments. Note well also that I didn’t use this page (or any actual textbook) to make them, because I’m pretty competent at thermo at this level, although it gets harder and I have little doubt that there are plenty of specific problems I’d have difficulty with.
Pay special attention to the “hot brick” example — it is a very similar heuristic to the one I was using to justify irreversible thermal relaxation in the gas. Or just look at the problem of heat conductivity between two reservoirs, which is absolutely identical to my own argument.
Actually, this whole textbook is both easy to read and fairly complete. If you want to quickly learn or review basic thermodynamics, you could do far worse. I hope I can make my own online textbook comparable in quality when I finish it. BigWaveDave should also take note. Joules too. In fact, everybody. If you want to make valid, believable thermodynamic arguments, it helps a lot if you have a reasonable grasp of valid, believable thermodynamics.
rgb
But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula?
in the BB equations for the gas at all frequencies, the gas has heat capacity but it is totally transparent.
(as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface. Initially there will be a lapse rate of sorts as it displaces cooler air, but the heat carried up has no place to go. Low pressure, high temperature air will always have the lowest density and rise to the top, and because air is a poor conductor of heat the air will stratify hot on top down to cooler on the bottom — an inverted lapse — until one gets to a turbulent zone that turns over diurnally. One would expect this bottom layer to be thin and the thermal lapse to be small — the air above this turbulent bottom would be nearly uniform in temperature in time.
As you stubbornly refuse to acknowledge, in spite of a textbook author chiming in on the list in person, the DALR arises — literally — because packets of air arise and afall in circulation. In Jelbring, although he quotes (without seeming to understand) this well-known fact, he then immediately turns around and asserts that the DALR holds in a static atmosphere, one without circulation. Perhaps we are finally reaching a true consensus that this is false, given that I’m quoting straight out of MIT’s online thermodynamics textbook that it is.
The reason that GHGs (and dynamics) are essential to the DALR is very simple. Assume that Jelbring’s ideal non-greenhouse atmosphere doesn’t radiate or absorb radiation at all. If you like,
In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given
With GHG’s and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere. Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. The DALR requires convection to form. No active active heating of the surface accompanied by active cooling of the upper atmosphere, no dynamically maintained thermal gradient, no convection, no dynamically maintained DALR.
The point is that the formula for the DALR comes from the assumption that the air heats down low and rises, expanding adiabatically into the air above it (doing work against its increased pressure/density) and cooling as a consequence, a process that only “stops” when there is a uniform lapse between the warm bottom and the actively cooled top. It’s not really “stable”, it is dynamically sort-of-stable, which is why the atmosphere almost never exhibits a perfect DALR and sometimes is remarkably isothermal, why one can observe thermal inversions (especially if you stop heating the bottom but perhaps don’t stop heating the top).
This reasoning is heuristic, of course, and it could be mistaken. I think it is pretty reasonable, though. It’s difficult to test empirically in our real atmosphere, because we cannot lose the GHGs we already have, and no planetary atmosphere we can see lacks them. The only way I can think of to properly test and support any hypothesis either way is via modelling, basically solving the hydrodynamic equations for toy planets with and without upper atmosphere cooling. A bit of a daunting task, actually, but that’s what modelling is good for — to give us a handle on physical situations we cannot directly observe in a lab but where we know or think we know the basic underlying mechanics well enough to build a model.
Perhaps even a non-GHG world would still exhibit large scale equator to polar convective rolls that would provide enough convective mixing to maintain a DALR. That is actually an interesting question, a worthy thing to build a model to test. If the model agrees, it would be an actual physical calculation that supports the idea that a vertical atmospheric lapse rate can be maintained by lateral/horizontal convection. I’m dubious — I don’t think the tropopause would be very high at all, if true — but I won’t pretend that I know for certain.
rgb
Robert Brown says
“and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere. Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. The DALR requires convection to form. ”
This interpretation seems at odds with the Harvard Paper I have linked.
They define convection to be when unbalanced force acts on the air parcel.(bottom of page 13)
Hydrostatic equilibrium must be consistent with no unbalanced force acting on the parcel.
This is when
1. The parcel is at rest.
2. The parcel moves at constant speed .
In their interpretation both operate at DALR for dry air.
In situation 1 there is no temperature change
In situation 2 the temperature changes by 9.8K/km up or down.(- or +)
Both conditions are present in the neutral atmosphere.
This condition can be quite stable at night (see the near neutral residual layer page 31)
Of course convection is the major method of heat transfer in the atmosphere however how does heat transfer when there is little or no convection?
Two methods remain
1. Radiation
2. Conduction (diffusion)
So they must between them transfer heat across the temperature differential.
I have made this point already in this thread but you either have not seen it or perhaps you agree with it.
However your lack of response is a source of confusion.
http://www-as.harvard.edu/education/brasseur_jacob/ch2_brasseurjacob_Jan11.pdf
Robert Brown says:
February 1, 2012 at 11:52 pm
But you seem to suggest that GHG are some dominate factor in regards to lapse rate, where is this formula?
As you stubbornly refuse to acknowledge, in spite of a textbook author chiming in on the list in person, the DALR arises — literally — because packets of air rise and fall in circulation.
I have never stubbornly refused to acknowledge- most of posts on topic have mentioned something regarding the buoyancy of air. How can you translation this into “stubbornly refuse to acknowledge” that packets of air rise and fall.
“In Jelbring, although he quotes (without seeming to understand) this well-known fact, he then immediately turns around and asserts that the DALR holds in a static atmosphere, one without circulation.”
This has been a common point of this dispute. You and others seem to say this lapse rate would not continue. Saying this does not occur, has been something I heard, but I have not heard what does occur.
I assume that without water or other factors, in a pure nitrogen atmosphere one will have a lapse rate close to DALR. I assume there is heating or no loss of heat. I view no lost of heat as “impracticable”. For sake of thought experiment I am willing to accept that “some way unknown to me this could be possible”. But balancing the heat from surface is something one could do and one could conceivably limit the amount of heating needed. So however it is done, the surface must be keep at a constant temperature. Therefore with surface which remains at a constant temperature there would be very little in terms of packets air that rise and fall in circulation.
So in summary a disagreement seems to be that I think with little or no circulation they is still a lapse rate. And you and others apparently do not. So, what is your view of would occur if there is little or no circulation?
Btw, if given too much circulation, I believe you would not have a lapse rate.
If given too much heat the added warm air would rise and stay at the top. Though *if* this is constant high heat and if not pressurized in a container [gravity is controlling the pressure] the lapse rate will return. Since too much circulation negates a lapse rate, it seems it a smaller degree of “too much” circulation *may* reduce the lapse rate. So according to this, deserts or other areas associated with strong thermals may reduce the lapse rate by some amount.
“Perhaps we are finally reaching a true consensus that this is false, given that I’m quoting straight out of MIT’s online thermodynamics textbook that it is.
That would nice, I liked it if we could agree on what we disagree on.
“The reason that GHGs (and dynamics) are essential to the DALR is very simple. Assume that Jelbring’s ideal non-greenhouse atmosphere doesn’t radiate or absorb radiation at all. If you like, \epsilon = 0 in the BB equations for the gas at all frequencies, the gas has heat capacity but it is totally transparent.”
I think it’s possible that N2 might radiate some energy- but also think it’s an insignificant amount and can be safely ignored. Though what N2 may collide with, whether GHG or surface, is maybe an issue but leaning towards probably insignificant.
“In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given \rho = \frac{M}{RT} P (as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface.”
No. The pressure will increase, reducing density of packets of air which will rise.
“Initially there will be a lapse rate of sorts as it displaces cooler air, but the heat carried up has no place to go. Low pressure, high temperature air will always have the lowest density and rise to the top, and because air is a poor conductor of heat the air will stratify hot on top down to cooler on the bottom — an inverted lapse — until one gets to a turbulent zone that turns over diurnally. One would expect this bottom layer to be thin and the thermal lapse to be small — the air above this turbulent bottom would be nearly uniform in temperature in time.”
What you seem to be describing is when heating causes an increase in the lapse rate. Or it’s sort runaway in buoyancy. Or an accelerated buoyancy- the higher the air packet goes up [or down] the faster goes [or it merely maintains it’s velocity-keeps it’s buoyancy as it rises].
“Clearly, an atmosphere whose lapse rate is less than the adiabatic value is stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic value then, after rising a little way, the packet will be less dense than its immediate surroundings, and will, therefore, continue to rise due to buoyancy effects. Clearly, an atmosphere whose lapse rate is greater than the adiabatic value is unstable.”
http://farside.ph.utexas.edu/teaching/sm1/lectures/node56.html
“With GHG’s and a GHE, the upper troposphere cools via radiation. This creates a thermal gradient in the atmosphere.”
Ah, getting to issue here.
Now, I said I don’t dispute the possibility that GHG’s have an affect upon the lapse rate.
But you saying it has a large effect.
First it seems rather obvious that if GHG were having such large effect, GHG would not be warming the planet. Second, water vapor is scarce in upper troposphere, thereby leaving much of the work to be done by CO2 or other rather rarefied greenhouse gases. Third you have fairly thin atmosphere in upper troposphere- and even if the GHG were capable cooling as mad demons, the effect during daylight would be easily overwhelmed. And if could be so severe as to have effect during daylight, then it would equally continue during night. It seems one would have waterfalls of thin atmospheric air in the upper troposphere. Why isn’t there significant difference in lapse between day and nite?
Anyways, it would make H2O as the only “greenhouse gas” that is warming the planet, others are cooling it. I suspect the CO2 may cause some cooling, but haven’t considered it causing that much cooling.
“Vertical gravity-driven convection requires a thermal gradient — picking up heat at the bottom, lowering of density and rising, cooling at top, increasing density and falling. ”
Well I would agree that convection does move a lot heat around, but convection is strongest from surface to mid troposphere. And generally you seem to describing an unstable atmosphere- gliders would be more commonly used and would be useful for travel purposes.
“This reasoning is heuristic, of course, and it could be mistaken. I think it is pretty reasonable, though. It’s difficult to test empirically in our real atmosphere, because we cannot lose the GHGs we already have, and no planetary atmosphere we can see lacks them. The only way I can think of to properly test and support any hypothesis either way is via modelling, basically solving the hydrodynamic equations for toy planets with and without upper atmosphere cooling. A bit of a daunting task, actually, but that’s what modelling is good for — to give us a handle on physical situations we cannot directly observe in a lab but where we know or think we know the basic underlying mechanics well enough to build a model.
Perhaps even a non-GHG world would still exhibit large scale equator to polar convective rolls that would provide enough convective mixing to maintain a DALR. That is actually an interesting question, a worthy thing to build a model to test. If the model agrees, it would be an actual physical calculation that supports the idea that a vertical atmospheric lapse rate can be maintained by lateral/horizontal convection. I’m dubious — I don’t think the tropopause would be very high at all, if true — but I won’t pretend that I know for certain.”
Other than world of thought experiments, to get a lapse rate you do need heat. And for understanding of any kind affect of gravity on lapse rate, you need big systems. It seems comparative planetary bodies could provide more definitive answers. In the near term, Ceres may provide some interesting answers.
A guy called Chris Ho-Stuart, is working on Excel program which model a planet which not heated from sunlight. His latest version:
http://www.datafilehost.com/download-9a244b84.html
The program incorporates lapse rates and he has paid a lot attention to getting them right, and says it’s in accordance with Principles of Planetary Climate by R. Pierrehumbert .
He thinks GHG has large effect of lapse rates. He started by first modeling Nitrogen atmosphere and still working towards incorporating GHG gases.
Joe Born says:
February 1, 2012 at 6:12 pm
Paul Birch:“Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
Joe: Are you absolutely certain that’s a position you want to take?
Pretty sure.
Tim Folkerts says: This seems like an odd interpretation. Normally an adiabatic free expansion results in no cooling of an ideal gas. And I would consider “rushing out into free space” as a free expansion. If the gas were pushing against something as it expanded, then it would cool, but I don’t see that in your hypothetical situation.
I’m fairly sure I’m correct here. What you (and Robert Brown’s wiki link) are calling free expansion is expansion into an empty vessel, with temperature being measured after the gas has hit the far side and equilibriated. Free expansion into space is different, because the kinetic energy doesn’t get converted back into thermal energy. The gas is “pushing against something as it expand[s]” – it’s pushing against itself. So it ends up as an ever-expanding shell, like a supernova remnant. It will only heat up again if it runs into another medium.
This isn’t rocket science … oh, wait, it is rocket science! Imagine that the full sphere is divided up into twelve pentagonal rocket nozzles in a regular icosahedron. Propellant gas cools as it flows out the nozzles; work is done accelerating the propellant mass outwards. T~V^(1-Cp/Cv). For large expansion factors essentially all the energy goes into the jet velocity. The expanding propellant pushes against the nozzle walls as it goes, but since in this geometry there is an equal and opposite force from either side of each partition, we can eliminate the nozzles altogether; the gas will still expand and cool the same way.
Because the gas continues to expand it’s not in equilibrium; but it’s still in LTE (at least until it gets extremely cold and rarefied). We can see it cool by watching its thermal radiation.
Robert Brown says: http://en.wikipedia.org/wiki/Free_expansion (that is, I think you are right Tim). However, I think Paul just misspoke. He did note that the free expansion leaves the average KE per molecule the same — which I know that he knows means that the temperature hasn’t changed (although the density certainly has).
Ideal gas adiabats in cyclic heat engine cycles do expand and cool, but they do work at the same time and aren’t “free”.
My point is that the gas is doing work on itself (and in that sense the expansion isn’t “free”), and that the directed radial motion that results is not thermal energy; this KE would contribute to the gas’s temperature again if the expansion were reversed isentropically, or the gas hit a wall and randomised it irreversibly, but not if it were instead extracted from the bulk flow by eg turbines or pistons.
“In that case it can be warmed by the surface and cooled by the surface but only by the surface. For an ideal gas, the density of the gas is given \rho = \frac{M}{RT} P (as shown in the top article). At the surface, this means that when the surface is heated, the air in contact with the surface will be heated, its density will decrease, and it will rise, carrying away some of the heat from the surface.”
No. The pressure will increase, reducing density of packets of air which will rise.
Oh, I misread it. I thought you said density would increase.
I blame the lack of coffee:)
Robert Brown says:
February 1, 2012 at 12:58 pm
Ah, so you vote for b). That’s great, as it frees you from any need to actually try to understand the arguments involved, and it frees me from any obligation to continue to try to educate you!
Well, Robert, there’s your problem in a nutshell. Rejecting a) doesn’t mean I’ve gone for b). But I’m glad it frees you from any obligation to continue to try to educate me, as this was self-imposed and now I can hope that includes not setting me homework..
I’ll just repeat what I said: “but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background.”
I explained that by giving an example from my own experience re assumed accuracy by claimed authority, and, as I pointed out earlier, you haven’t even read his paper with any understanding, that I can fathom as you launched into a completely different and irrelevant tangent.
I especially like your argument that because we observe a lapse rate in Earth’s completely dynamic diurnally heated-at-the-bottom and differentially cooled atmosphere this must be a feature of true static thermal equilibrium in an isolated system (Jelbring’s assertion). That’s proof enough, isn’t it? Sure it is. Water being stirred or heated from the bottom inevitably behaves exactly like water sitting at rest in a container according to exactly the same argument. And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, not the question of whether nor not a DALR exists in a dry atmosphere under certain non-equilibrium conditions that permit one to more or less ignore thermal conductivity.
There are several disparate ideas in that. The first that we observe a lapse rate in Earth’s atmosphere is what is relevant here as I noticed in thinking through what he was saying, the weather systems created by heating and so on are in effect superimposed on/intermingled with the basic already well known phenomenon of gravity created lapse rate. Jelbring has made it clear that one has to strip all those superimpositions away and look at just what is left. As I’ve said, this is the basic building block of meteorology, a science that’s been going for some time and has well established understanding, and teaching, on this. I quoted one such and provided a link to show that what he was saying about rising air packets was standard basic knowledge, and relevant to what he was saying. What you’re missing is seeing how that is important here – in understanding what Jelbring is saying – BigWaveDave went into more detail, and if you put the two together you’ve got the real picture of the basic phenomenon. Perhaps you’re conflating heat with temperature and missing what BWD said.
“Water being stirred etc.” – is also something you missed picking up from BigWaveDave’s reply to you, this is about gases and they have behaviour particular to them.
“And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, etc.” – is in comment on the state of play in ‘climate’ science. It was re the fact that you also missed the point in Jelbring’s opening setting of the scene of what he was actually saying and imagined it was something he was claiming as a unique insight to himself, he was actually saying that ‘climate’ scientists ignore this, the well known to meteorology basic, and I threw in ‘like ignoring the Water Cycle’, because, that’s what ‘climate’ scientists do. They ignore the basics, well known and still taught, actual real world physics, by simply not teaching it. This, imho etc. I think you simply don’t know about it. I reached that possibility by comparing it with the extraordinary ‘energy budget’ used in ‘climate’ science – it is completely missing the Water Cycle which brings down Earth’s temperature to 15°C from 67°C it would be without it. Perhaps, that I knew this, is what helped me better picture what Jelbring was saying, because that is the main ‘greenhouse’ gas and without it we have a good approximation to Jelbring’s dry atmosphere of his model, a step in getting to his model.
You seem to be conflating an assertion that there is no such thing as a dynamically driven lapse rate in any real atmosphere with the assertion that there is no such thing as a thermodynamically stable lapse rate in an isolated ideal gas subject to gravity but allowed to thermally relax to a maximum entropy state. Your argument seems to be “the real atmosphere exhibits a lapse rate, therefore that must be the true thermal equilibrium of an isolated ideal one”. You make this argument (which is hopefully fairly obviously not even logically valid, let alone unsupported by any actual physics), and attempt to “support” it by means of waving your hands about how gravity has to do work and the work has to turn into heat without considering what happens to all that heat when gravity stops doing work because the atmosphere achieves a static force profile such that . Is it “stuck” where gravity leaves it, or can it move, say, by irreversible diffusion or heat conduction? What happens when some of the heat moves from one temperature in one part of the gas to another part of the gas at a different temperature? In particular, does the entropy of the gas increase or decrease?
I think you don’t understand gravity in this. Your “when gravity stops doing work” is what gravity is. Gravity isn’t a source of heating, it’s not heating molecules by ‘pulling them down’ which once it’s done this heating stops.. Gravity is, gravity plus mass gives a state of gravity/pressure, we don’t get winds until there is a pressure gradient force which comes from unequal heating. Jelbring leads to reaching this basic is that all the extras are non-existant, no radiation coming in, none from surface heat capacity, so entropy etc. negligible. One needs to chuck all these out to get to the underlying state, and from there to the constant in relationship.* It’s called the hydrostatic equilibrium** state, please, don’t go off into another tangent about liquids, see BWD, it relates to our gaseous atmosphere because both gases and liquids are fluids, it’s an ocean of gas we have above us. But. Gases behave in a way particular to them even within fluids. As BWD explained:
You can’t say anything of relevance to gases in our atmosphere if you’re not referring to the actual properties and process of gases.***
That’s all Jelbring is saying, that it’s already a known and from this etc.:
And so, you don’t understand what Jelbring is saying, because this basic of our real world is missing from ‘climate’ science.
* http://www.ux1.eiu.edu/~cfjps/1400/pressure_wind.html
If we keep the mass of the gas constant, then we can simplify the equation to (PV)/T = constant. That means that:
For a constant P, T increases, V increases.
For a constant V, T increases, P increases.
For a constant T, P increases, V decreases.
** http://www.metoffice.gov.uk/learning/science/first-steps/atmosphere/wind
Hydrostatic equilibrium: “In fact, the gravitational force is almost exactly balanced by the pressure gradient force, a condition known as hydrostatic equilibrium. Hydrostatic equilibrium explains why the Earth’s atmosphere does not collapse to a very thin layer on the ground.”
*** Same applies to electromagnetic radiation, it is not ‘all the same’. These are divided into distinctly different phenomena, each with its own characteristics, properties and processes. Visible light is not thermal energy on the move, it cannot heat water as thermal infrared can heat water, water is a transparent medium for it, it works on electronic transition level of effect on meeting matter, AND not vibrational resonance, i.e. moving the whole molecule, kinetic energy, which is the process of thermal infrared, etc. ‘Climate’ science mangles all of these by giving the properties of one to another and then claiming visible light can do what it isn’t physically possible for it to do.
AGWSF = ‘CLIMATE SCIENCE’. This is Fictional Science because it doesn’t describe the properties and process in our real world we see around us. QED.
Really sorry Mods, I checked and checked and still missed it, please would you fix there should be a closed blockquote after the paragraph seven up, :
BigWaveDave continues – “In Earth’s atmosphere, the air molecules are not fixed at any particular height. …with height must vary with the density.”
[FIXED -w.]
p.s. And to make it clear, the reason I’m not at all surprised that this has been missed out and that you know nuttin about it, is because for several decades universities have been teaching from the AGWSF energy budget, which is missing the WHOLE Water Cycle, and none of you super educated in physics with years of teaching and phd’s have even noticed it’s missing!
First, get a proper energy budget basic in place with real world physics and ditch the science fiction world you’ve created. Not sure though, that any of you would know how to go about that..
now I can hope that includes not setting me homework..
Oh no. I assigned homework already;-): Read the MIT online thermo book and work through it, cover to cover. Your arguments can only improve if you actually learn the laws they are currently flouting, and while I fully understand your lack of respect for “authority” — while respectfully suggesting that it edges well over into iconoclasm for its own sake when you make statements that violate the experimentally verified laws clearly explained in every thermo textbook. It is difficult to claim that these textbooks are part of the “IPCC global conspiracy”, given that thermodynamics was mostly worked out and derived/proven over a hundred years ago, well before there was a United Nations.
If you want to suggest that modern thermodynamics as given in these textbooks is wrong, that is a very serious charge, and should only be made if you are prepared to prove it. And by prove it, I really mean prove it — prove it at the accepted standard of physics, which requires a complete argument down to microscopic physics, plus empirical support. Prove it in a way that would get past any reasonable referee, prove it convincingly. If this task is daunting — and it should be, because it is openly impossible in the contexts they discuss — then perhaps you could provisionally accept that every physicist in the world is a) not an idiot; and b) not engaged in some sort of global conspiracy just because a result that you want to believe in happens to violate the thermodynamic laws of physics.
I explained that by giving an example from my own experience re assumed accuracy by claimed authority, and, as I pointed out earlier, you haven’t even read his paper with any understanding, that I can fathom as you launched into a completely different and irrelevant tangent.
You don’t even understand your own example, but that is quite beside the point, because it is a logical fallacy to state “I think that a physicist once made a mistake, although I can’t prove it and haven’t even tried, therefore you are making a mistake now in your analysis of Jelbring.” Surely this is clear to you. You don’t accept my authority, fine. How about the MIT textbook I linked and assigned? How about Zemansky? How about Stanley? How about the introductory physics textbook of your choice? How about I start on the list of stat mech books? Is there any authority you will accept, or is your argument going to remain “I’m completely ignorant of actual thermodynamics and statistical mechanics and mechanics and electrodynamics and quantum theory — beyond the level a bright high school student might have accomplished — but I doubt that any of them are right, so when Jelbring states a result that openly contradicts their content that doesn’t mean that he is probably wrong.”?
Your assertion that I don’t understand his paper is simply incorrect. I’ve read it several times at this point. Its claims are quite clear. He asserts that gravity will create a thermal lapse rate that is there in his isolated ideal gas in a near-Earth gravitational field in thermal equilibrium — the condition that an air column will reach after all irreversible relaxation processes such as conduction, convection, and radiation have completed. He forgot to mention conduction, but if he truly meant to leave it out then his conclusion is already obviously false as he left out a physical process that is infinitely faster than thermal relaxation due to radiation in a GHG-free atmosphere, where there is none. To prove it he cites a single “well-known” result — the DALR — from a single textbook on climatology, and claims that it describes static thermal equilibrium.
Yet — as I’ve shown by reference to an actual textbook on thermodynamics — a thermal lapse rate of any sort in a system that supposedly in thermal equilibrium explicitly contradicts two laws of thermodynamics: The zeroth law and the second law. All of your, and his, arguments about “energy balance” revolve around the first law, but what you fail to understand is that there are an infinite number of ways to split the available energy including the gravitational potential energy available to the system without violating the first law. The second law dictates the split that actually occurs in equilibrium.
He then uses his incorrect claim that the DALR describes a state that satisfies the three simple conditions given in the actual textbook above for thermodynamic equilibrium to prove his argument that the equilibrium state of his isolated gas has a nonzero thermal gradient.
How, exactly, is this not circular reasoning on the one hand, and circular reasoning from an obviously false premise on the other? At the very least somewhere the onus of proof was upon him to demonstrate that an atmosphere with a DALR is actually in a state of thermodynamic equilibrium, which would have required some actual work and algebra on his part, one would think, since it violates the letter of these laws.
As I’ve said, this is the basic building block of meteorology, a science that’s been going for some time and has well established understanding, and teaching, on this.
Did you somehow miss Caballero’s post above, or did you just blank out your mind and pretend that it never happened. I’m perfectly happy to strip away all of those “imposition” and concentrate on a dry ideal gas, just like Jelbring did, and in fact have done nothing else. I was pointing out that you constantly ring in moisture and all sorts of other stuff, so that you would stop doing it. Focus on the argument given in Jelbring, only, using the very axioms of ordinary thermal physics that he claims are satisfied by his result. Well, I’ve quoted them, provided a link to a textbook containing them, and his claims violate the letter of those laws, they are a direct do-not-pass-go or collect $200 violations of those laws. You’d have to look long and hard to find as pure a logical contradiction as:
* Zeroth law: (Thermally connected) systems in thermodynamic equilibrium are isothermal.
* Second law: (Thermally connected) systems in a maximum entropy state are isothermal.
* Jelbring: An isolated ideal gas in a near-Earth gravitational field is a thermally connected system in thermodynamic equilibrium only when it it is not isothermal.
Do you see the problem yet? I don’t really give a damn whether or not you understand why the zeroth and second laws are true and correct, there is a bald contradiction between Jelbring’s stated conclusion and the laws he himself asserts as axioms. He did not address this contradiction. His argument is circular reasoning and completely lacks any detail. Why, exactly do you find this believable?
Do you not believe in the zeroth law of thermodynamics? If not, why not? Do you not believe in the second law of thermodynamics (which implies the zeroth law — they are consistent)? If not, why not? If you wish to defend Jelbring, please do so, not by doubting me but by addressing the argument. Which of these two laws is wrong? Why? Where is your proof? How is your reasoning, not just as circular and contradictory as Jelbring’s?
What you’re missing is seeing how that is important here – in understanding what Jelbring is saying – BigWaveDave went into more detail, and if you put the two together you’ve got the real picture of the basic phenomenon. Perhaps you’re conflating heat with temperature and missing what BWD said.
So, you really think that you and BWD understand heat and temperature better than I do, I see. Fine, I don’t mind you stating that, but please prove it. You cannot prove it in English. For you to prove your assertions you — like Jelbring — actually have to do some algebra, and if your algebra starts out with assertions that openly violate the laws of thermodynamics you — like Jelbring — must prove why and how the laws of thermodynamics won’t hold.
You might also think hard about who is more likely to have developed a better understanding of heat and temperature — you, BWD, or me. Only one of the three of us have studied the subject in depth, continue to study it in depth, and taught it. You are free to doubt that I fully understand it, but is it really probable that your understanding is better than mine? I at least know the content of the MIT textbook on thermodynamics without having to read it and can pretty much work through all of it at the board at any time without a moment’s notice. Can you? Do you even know what the important points and arguments are? Can you derive the expression for an adiabatic reversible process for an ideal gas, for example, if you very life depends on it, without just copying the derivation from the very physics textbooks that you stubbornly refuse to consult when analyzing Jelbring?
It was re the fact that you also missed the point in Jelbring’s opening setting of the scene of what he was actually saying and imagined it was something he was claiming as a unique insight to himself, he was actually saying that ‘climate’ scientists ignore this, the well known to meteorology basic, and I threw in ‘like ignoring the Water Cycle’, because, that’s what ‘climate’ scientists do. They ignore the basics, well known and still taught, actual real world physics, by simply not teaching it.
This is an extraordinary claim! You have clearly read far more physical climatology textbooks than I have, because the ones I’ve looked through do nothing of the sort. In fact, it is a completely absurd claim. Two out of two cited in this discussion, Caballero and Holton, do nothing of the sort. One out of two authors of books cited in this discussion (the only one living) has already stated that Jelbring is incorrect. Climate scientists do not ignore the DALR. They simply understand perfectly well that it is not a state of thermodynamic equilbrium, it is a state of hydrodynamic equilibrium subject to several assumptions, including differential heating and ongoing heat transport, a particular steady-state solution in the limit of non-turbulent flow of the Navier-Stokes equations. Jelbring’s only actual unique claim in his paper is that this state is actually thermodynamic equilibrium, and it is incorrect. End of story.
If you wish to claim that “climate scientists” ignore the Water Cycle, prove it. Cite one single textbook on physical climatology that ignores the water cycle.
Of course you can’t, because this is not true. What you mean to say is that many climate scientists look at the “water cycle” and somehow end up with conclusions that differ from the ones that you wish were true. You like Jelbring not because it is correct, but because it supports a conclusion that you wish was true. Wishful thinking does not make something true, nor does an open indictment of all “climate scientists” in the world make that indictment true. If you wish to make the claim and have it not be mere verbiage, back it up with actual evidence. Find me physical climatology textbooks that leave it out.
Now, if you want to claim that some climatologists sometimes leave it out of some of their research or papers, well, hard to argue with that, given that Jelbring leaves it out and he is, well, sort of, maybe, a really really bad climatologist.
I think you don’t understand gravity in this. Your “when gravity stops doing work” is what gravity is. Gravity isn’t a source of heating, it’s not heating molecules by ‘pulling them down’ which once it’s done this heating stops.. Gravity is, gravity plus mass gives a state of gravity/pressure, we don’t get winds until there is a pressure gradient force which comes from unequal heating.
Ok, I’m going to say this as gently as I can. Oh, hell, no I’m not. You are so cosmically clueless about basic physics that you have no business even participating in this discussion unless and until you do your homework, starting by developing an elementary understanding of work, energy, energy conservation and gravity.
Seriously, man. You’re just making a fool of yourself now.
Jelbring leads to reaching this basic is that all the extras are non-existant, no radiation coming in, none from surface heat capacity, so entropy etc. negligible. One needs to chuck all these out to get to the underlying state, and from there to the constant in relationship.* It’s called the hydrostatic equilibrium** state
Sure, and hydrostatic equilibrium is not thermodynamic equilibrium. And hydrostatic equilibrium itself is not isothermal if and only if there is a thermal gradient across an ideal gas maintained by external heating and cooling in the circumstances described by Jelbring.
Come on now, you’re getting close, you can say it. Jelbring is wrong. He incorrect asserts that the hydrostatic equilibrium state with a lapse rate is true thermodynamic equilibrium and would be present in an isolated gas after a very long time. No, it wouldn’t. It would violate the second law. It would also violate the Navier-Stokes equations, which have a trivial static solution in the unheated case that is — unsurprisingly — precisely the state I give above.
Finally, I have no idea what you mean when you say “entropy etc negligible”. The ideal gas is in thermal contact with itself. Entropy exchange within the gas itself can never be “negligible”, not without making your answer completely non-physical.
Oh wait, it is.
rgb
Hydrostatic equilibrium: “In fact, the gravitational force is almost exactly balanced by the pressure gradient force, a condition known as hydrostatic equilibrium. Hydrostatic equilibrium explains why the Earth’s atmosphere does not collapse to a very thin layer on the ground.”
Oh, I can’t resist one more comment. Are you somehow ignoring the fact that the top post contains the condition for hydrostatic equilibrium? Since you steadfastly refuse (so far) to crack an actual textbook on thermodynamics you have no doubt still failed to observe that there are an infinite number of possible distributions of energy that can be in hydrostatic equilibrium in Jelbring’s isolated ideal gas, but only one of them is maximum entropy and hence global thermodynamic equilibrium. Guess which one.
Of course that is your real problem. You don’t understand the condition for hydrostatic equilibrium, and you can’t formulate the actual integral that would describe the hydrostatic profile of an ideal gas, given a proposed temperature as a function of height $T(z)$. If you want, I’d be happy to help you out and show you, or you can continue to argue as if hydrostatic equilibrium is itself a unique state, the one with the DALR. In spite of the fact that the top post derives the explicit form for an ideal gas in hydrostatic and thermal equilibrium, I might point out.
rgb
I’m fairly sure I’m correct here. What you (and Robert Brown’s wiki link) are calling free expansion is expansion into an empty vessel, with temperature being measured after the gas has hit the far side and equilibriated. Free expansion into space is different, because the kinetic energy doesn’t get converted back into thermal energy. The gas is “pushing against something as it expand[s]” – it’s pushing against itself. So it ends up as an ever-expanding shell, like a supernova remnant. It will only heat up again if it runs into another medium.
OK, I think I buy that. The average kinetic energy per molecule doesn’t change, but the distribution of KE in parcels of gas in the original rest frame is no longer thermal because the parcels of gas themselves now have a CM kinetic energy and in their local CM frame the local temperature is lower. If/when the parcels collide elastically with something so that their CM velocity goes away, the energy becomes thermal again.
I was indeed thinking of free expansion into a container and didn’t realize that you were talking about free expansion into space, although I should have. IIRC this is the sort of phenomenon that explains those vortex nozzles that were being described upthread — you drive a gas into transiently into a state with an adiabatic lapse by “slamming on” a strong centripetal force and then selectively pull off the cooler molecules at the top. Or an adiabatic nozzle. Yeah, now I remember that stuff. Sorry.
rgb
So in summary a disagreement seems to be that I think with little or no circulation they is still a lapse rate. And you and others apparently do not. So, what is your view of would occur if there is little or no circulation?
) equilibrium and simultaneously in (iso)thermal equilibrium, repeatedly demonstrated to be the state where the gas has maximum entropy and the state the ideal gas will go to under the precise conditions described by Jelbring. Or for that matter a gas that is isolated at the top and in contact with a constant temperature reservoir at the bottom. You need a thermal gradient to drive convection and a lapse rate.
See the top post, which derives the actual state of an ideal gas atmosphere in both hydrostatic (
The problem then is that it is no longer possible to argue that the gas plus gravity creates the lapse rate. Rather, the intrinsic thermal lapse between two reservoirs at different temperatures creates the convection that establishes a self-consistent lapse in the atmosphere in between, which can be enormously complex because once the convective forces exceed certain limits, the convective flow becomes turbulent.
The problem, as you can see, is that atmospheric dynamics is really very, very difficult. One has to solve the Navier-Stokes equation, which is arguably one of the most complicated physical formulae that we have been able to semi-quantitatively construct (or rather, construct for a still somewhat idealized description). The DALR itself — as any good textbook will tell you — is an idealization of an idealization, a no turbulence, no internal conduction model for the dynamic gas as parcels slowly waft up or down in convection.
Jelbring does not address this. His paper explicitly establishes conditions where there is no convective flow and no heat input at all, let alone differential heat input, and then further asserts that we must wait a long time for the system to attain its true equilibrium. He then basically asserts that the well-known hydrodynamic DALR is the true equilibrium, and claims his own assertion as (circular) proof that the DALR is the true equilibrium.
No, it’s not. The state of atmosphere derived in the top post, which is a derivation that can frequently be found in introductory physics textbooks (including my own) is the state of simultaneous hydrostatic (force) equilibrium, thermal equilibrium, and chemical equilibrium (the latter trivial for an isolated ideal gas). This state does not violate the zeroth or second laws of thermodynamics as a steady state, long time solution. Jelbring’s asserted gas with a stable lapse does, and moreover turns gravity into a Maxwell’s Demon.
Please separate out any arguments concerning whether or not the real atmosphere, heated and cooled all the time and everywhere, has a DALR from Jelbring’s assertion that it is thermodynamic equilibrium. I’m only concerned with the latter, because it is the only actual content Jelbring contributes to what is otherwise an assertion that the DALR is derived in one single textbook (in an explicitly dynamic context, but he doesn’t talk about that).
You do seem to be getting close to “getting it”. Perhaps this will help you understand the point and come to agree that Jelbring’s basic assertion is completely incorrect and his argument is both unsound logically and directly contradicts the very laws of thermodynamics he wishes to claim it is based on. One can then discuss the DALR itself in another venue, or just read e.g. Caballero on it, or more advanced treatments that discuss the actual underlying hydrodynamic equations in more detail. Things get very difficult, very fast, though, which is why most people stop with the simple semi-heuristic derivation of the DALR in spite of the fact that its idealizations aren’t very good and it at best gives you insight and conceptual power to make estimates and develop rules of thumb, not so much provide strong predictive power in atmospheric dynamics. For one thing turbulence instantly screws it up in the real world, moisture content screws it up, lateral transport screws it up, topology screws it up, the non-uniform temperature of the ground screws it up — the real atmosphere is constantly being kicked around between nearly isothermal and nearly DALR on any vertical column, with the actual measured thermal lapse rate rarely deviating by more than 10-20% from isothermal on an actual vertical sounding of the atmosphere.
This is all NOT my area of even approximate expertise, BTW. As you may have noticed on my last post back to Paul, I make mistakes or misunderstand, and when my errors are politely and convincingly pointed out to me, I’m very happy to concede (and in the process learn something). So if you disagree, feel free to correct (and thereby teach) me.
rgb
p.s. And to make it clear, the reason I’m not at all surprised that this has been missed out and that you know nuttin about it, is because for several decades universities have been teaching from the AGWSF energy budget, which is missing the WHOLE Water Cycle, and none of you super educated in physics with years of teaching and phd’s have even noticed it’s missing!
First, get a proper energy budget basic in place with real world physics and ditch the science fiction world you’ve created. Not sure though, that any of you would know how to go about that..
I have no idea what the “AGWSF energy budget” is. I’m just a physicist, remember, not an Evil Climate Scientist trying to nefariously deceive the world’s masses in order to become rich on undeserved grant money wealth. I make precisely as much money from granting agencies for shooting down Jelbring’s absurd paper as I do from the Big Oil companies for stating that the preponderance of evidence suggests that the very real GHG-GHE is not a catastrophic threat under any reasonable scenario for the economic and technological development of the world for the rest of the 21st century. However, I’m fairly certain that the AGWSF is something relevant to viewing the Earth as an open system, which is not the point of this thread and hence is, in the parlance of logical discourse, a “red herring”. Or perhaps a straw man. I get confused. Either way, Universities have taught something, somewhere, that you disagree with in some other venue and therefore it is wrong and I am a poo-poo head for not preventing it and not to be trusted to take care of your dog and oh yeah, Jelbring is right after all.
BTW, the “science fiction world” we are discussing in this thread is the one that Jelbring has created in his paper. That is, one that has an adiabatically isolated ideal gas in a gravitational field, left alone for a very long time so that it comes into a state of both hydrostatic equilibrium and thermal equilibrium. Perhaps if you could stay on topic long enough to actually defend its indefensible conclusions without introducing new physics that he explicitly omitted from his model problem statement we could resolve your difficulty understanding why his model conclusion, contingent upon precisely these conditions, is incorrect.
If you want to talk about the real world instead, by all means do so. Just don’t claim that your assertions have anything at all to do with Jelbring’s hypothesis or conclusion.
rgb
Both conditions are present in the neutral atmosphere.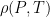
for an ideal gas, and you know 
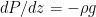for any fluid in hydrostatic equilibrium (with 
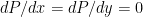), so if I give you a reasonably integrable 
, you can start with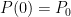 
(or equivalent boundary condition) and solve the ODE to fi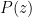nd 
and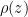 
that are in force balance. Some of these proposed densities would be very difficult to arrange as initial conditions, but others are not, and of course a gas with the DALR and an isothermal gas are both not.
a constant, it is absolutely trivial to show that entropy will strictly increase as heat is conducted between adjacent layers of the gas to reduce their temperature difference. There is an example problem in the online MIT thermo textbook I link that walks you through it. The maximum entropy state is the thermodynamic equilibrium state is the isothermal hydrostatic solution, not the hydrostatic solution with the DALR or any other initial thermal gradient.
This condition can be quite stable at night (see the near neutral residual layer page 31)
Of course convection is the major method of heat transfer in the atmosphere however how does heat transfer when there is little or no convection?
Two methods remain
1. Radiation
2. Conduction (diffusion)
So they must between them transfer heat across the temperature differential.
I have made this point already in this thread but you either have not seen it or perhaps you agree with it.
However your lack of response is a source of confusion.
I don’t know why. You’ve very precisely made my argument. In a neutral, unheated atmosphere, once one waits a very long time, there is no more movement of air; it achieves hydrostatic equilibrium, force balance. Then the two heat transfer mechanisms you describe come into operation. Both are irreversible; both transfer heat across the temperature differential, gradually neutralizing it. The state of maximum entropy is reached when the system is isothermal.
Obviously you can see that the argument doesn’t even depend on what the initial hydrostatic equilibrium state is. One can take any (smooth) vertical thermal gradient in the gas column and construct an associated density/pressure gradient that is in force equilibrium — you know
Ultimately, if you start the gas in any hydrodynamically stable initial state with a thermal gradient,
Note that my argument is confined only to Jelbring’s paper, and Jelbring’s paper explicitly states that he has waited a long time for all transport to cease and thermal processes to relax. So confine your defense of Jelbring to these conditions only. I’m not arguing that a dynamically driven atmosphere can have a lapse rate, only that Jelbring’s static one will not, and hence cannot be looked at as a source of “heating” or as a static mechanism that maintains the surface at a higher temperature than the gas overhead.
rgb
Robert Brown says
” I’m not arguing that a dynamically driven atmosphere can have a lapse rate, only that Jelbring’s static one will not, and hence cannot be looked at as a source of “heating” or as a static mechanism that maintains the surface at a higher temperature than the gas overhead.”
Perhaps I was not clear enough in my last post.
I was referring to our normal Sun driven atmosphere.
You made a point about convection being required for a lapse rate.
That is the point of possible disagreement.
For our atmosphere we have still air conditions and yet still have a lapse rate where radiation and conduction transfer the heat through the gradient.
Now back to the thread which I notice many have strayed from (including myself).
I recon IMHO that that’s where Jelbring got the idea for a static atmosphere.
He then generalised it to the unheated column of air problem above.
I pointed out in the previous thread that making this strong connection was tactically bad.
Basically then, he had two unlinked conjectures.
To base a theory that requires both to be true is unnecessary as one can be true and the other not.
Especially as one of the conjectures (the subject of your post) is not an orthodox position.
Certainly what you have been saying here is orthodox thermodynamics and thanks for giving us your expertise.
Mod, many thanks.
Robert Brown says:
February 1, 2012 at 9:59 pm
Does it include Maxwell’s Quaternion Equations?
Well, it includes Maxwell’s equations themselves, in several incarnations of expression (including manifestly covariant). I do love geometric algebra and think that the “war” between Heaviside and Gibbs and Hamilton’s followers (Tatt?) that the quaternion advocates eventually lost was very interesting — in the end Gibbs’ notation was, probably correctly, deemed a lot easier to work with and compute with.
Do Clifford/Geometric algebras interest you?
Yes, if I could add another lifetime on to this..
http://staff.science.uva.nl/~leo/clifford/
However, having only just now discovered the quaternion equations from my interest piqued by the Willis electricity tangent, here’s a look at Maxwell’s Quaternion Equations by Col. Tom Bearden:
There’s some links on that page to get the original Maxwell papers, I couldn’t get on with them and found them here instead: http://www.zpenergy.com/modules.php?name=News&file=article&sid=1949
But there’s more to that story, from Bearden’s own website: http://www.cheniere.org/books/aids/ch4.htm
The last bold mine.
Hmm, I wonder if any physics departments would be interested in exploring this..?
AGWSF = AGW Science Fiction, as in the AGWSF energy budget KT97 and ilk, missing the whole of the Water Cycle, and more science fiction besides.
Here’s another quick refutation to the argument “gravity does negative work on a parcel of air as it rises, so the KE (and hence temperature) must drop” argument. The microscopic argument has already been made (that only self-selected high-energy molecules make it that high, and even after losing some PE, they STILL have the same averge KE left). Here is a macroscopic argument for a parcel of air rather than individual molecules.
Buoyant force has been ignored. Because we are starting with hydrostatic equilibrium, then the buoyant force is equal to the gravitational force. If the parcel is raised (maintaining it at local atmospheric pressure and temperature), then the net force is zero and the net work done is zero. Any negative work by gravity is matched by and equal positive work by the buoyant force. Since no net work is done on the parcel, there is no change in the internal energy of the parcel and no change in the temperature.
Put another way, no work is needed to raise or lower a parcel of air. If the air was warmer at the bottom, I could take some of that air (and with NO WORK) move it to a cooler location. Eventually I could move air around until it was isothermal. From there, no further moving around of air could possible undo this isothermal profile.
This could be cleaned up a bit, but it shows that isothermal is indeed the stable, equilibrium state.
Tim Folkerts says
“Put another way, no work is needed to raise or lower a parcel of air. If the air was warmer at the bottom, I could take some of that air (and with NO WORK) move it to a cooler location. ”
Work would be done against the surroundings by the expanding parcel.
A similar parcel moves down to take the place of the rising parcel and increases its temperature.
Work is done by the surroundings to compress the parcel.
What you are outlining is the neutral atmosphere where DALR gives the gradient.
The air density is the result of gravity and without gravity the density would be uniform and buoyancy force would not exist.
Further If an unbalanced force acts (turbulent convection) then work is done against gravity as well as the surroundings.
DARL no longer gives the temperature gradient.
Back to the our real Sun driven atmosphere!
If the Sun causes the tropopause to rise in the diurnal cycle then work is done raising the centre of mass of the atmosphere.
if the tropopause drops at night then the gravitational potential energy can be transformed into thermal energy to buffer the temperature drop.
This is what I understand is the atmospheric thermal effect