Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
“I have no argument with that quote, I do have problem with
when an air parcel ascends the
temperature has to decrease because of internal energy exchange due to the work
against the gravity field.”
I agree it’s a problem.
Replace “air parcel” with “balloon”.
“when a balloon ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.”
A hydrogen balloon could start it’s ascent with cooler hydrogen gas compared to the air temperature at ground level. It still could still have lift.
As it ascends hydrogen gas could warm, cool, or stay the same temperature. The gas could expand and expansion, or lower of the density of the hydrogen gas will lower it’s temperature. The hydrogen will cool to the degree it expands. If it doesn’t expand, it doesn’t cool.
The work it does [going up] is unrelated to “working against gravity”. A balloon staying at certain elevation is “working against gravity”- but due to buoyancy it’s not actually work- doesn’t require energy. The acceleration or velocity of going up could also be called “work against gravity”, but again is not, it’s a matter of buoyancy. Buoyancy defies gravity. Or buoyancy is gravity. Buoyancy doesn’t require energy, anymore then gravity causing things come towards it [some non buoyant thing] requires energy.
A brick falling is gaining energy, a balloon rising is gaining energy. Neither of them or whatever surrounding it must do work to gain this energy- it is what gravity does.
If leave a gravity well very fast, it costs little in terms of gravity costs, and if approach a gravity well fast you gain little in terms of gravity gains. Leaving earth surface very slowly with a rocket, will consume an enormous amount energy. The faster rocket leaves, the less energy costs is used working against gravity. This is called gravity losses. The Shuttle had gravity lost of about 1 km/sec- from it’s total “budget” of 9.5 Km/sec. This “budget” is called it’s Delta-V.
“So many errors, so little time. Let’s start with the last one — with ideal monatomic gases, vibration or rotation of the gas molecules isn’t an important factor. With ideal diatomic gases they are, and worse, the dependency itself depends on the temperature of the gas and the energy required to excite rotations vs vibrations. Look it up, it’s in any intro physics textbook that covers thermodynamics at all (since they almost invariably cover the thermodynamics of ideal gases).”
If diatomic gas which has zero or near zero velocity, it will have zero or near zero temperature.
If diatomic gas has 500 m/s velocity it will be warm, and all the gas molecules will vibrate and spin around. How could they not?
The faster molecules are traveling crashing into each others, the more vibrating and spinning one will get.
But one can cause these molecule vibrate and/or spin faster and not have molecules moving very fast, such molecules could have a cool temperature and be radiating a lot of energy
Dr. Brown,
You are obviously incorrect when you state: “The fact that a thermodynamically stable adiabatic lapse rate is inconsistent with physics, violating the second law, is the only point of my article. And it is obviously true.”.
With matter that is in a solid or liquid state, the heat content per unit mass is generally proportional to its temperature. This can be simply expressed as specific heat, which is the heat required to change one unit of mass one unit of temperature.
But, when matter is in the gaseous state, this is not the case. and the heat content per unit mass is not necessarily proportional to the temperature. Specific heat is dependent on gas temperature and; the volume it occupies, or the pressure it exerts. The most important word in that last sentence that seems to get overlooked most often is “and”, and so it is necessary to consider in some way, the density of the gas, to express specific heat.
In Earth’s atmosphere, the air molecules are not fixed at any particular height. Their distribution, and thus the air density with respect to height is forced by gravity. If all of the air molecules have the same heat content, the temperature distribution with height must vary with the density.
My understanding is that the wet and dry lapse rates are maximum limits for atmospheric cooling with altitude beyond which convection will set in. If a small parcel of air rises by a slight amount, for any random reason, it will cool at the adiabatic lapse rate. If that adiabatically cooled parcel happens to be cooler, with a higher density than the surrounding atmosphere up there, then it must eventually return to a lower level.
In order to force a temperature decline at the adiabatic lapse rate, there must be some combination of both heating from below and cooling from above that would otherwise drive the rate of cooling with altitude beyond the effective lapse rate.
In our own atmosphere, we have the example of the stratosphere where temperatures actually increase with altitude. The environmental lapse rate in the troposphere appears to be a compromise between the wet and dry adiabatic rates, as convection under both conditions is occurring.
I find no indication that the adiabatic lapse rates are anything more than maximum rates of temperature decrease with altitude before convection will begin preventing any steeper temperature decline.
Wayne, I can see what you mean about the initial positions. As it turns out the same person (litdev) who wrote the initial program has put together a dll that not only does graphing and Excel export but also pulls in the Box2D physics engine (C++) – I now have 500 balls bouncing around with only ~ 10 lines ! http://litdev.hostoi.com/
Bryan, I think that the distibution just emerges from the randomness (?)
Chas you say
“Bryan, I think that the distibution just emerges from the randomness (?)”
True randomness would be a different distribution from a Maxwell Boltzmann distribution
I used to do educational software with Archimedes computers using BBC basic.
They turned into ARM and withdrew from computers.
I tried to adapt to Visual Basic but got fed up.
Given what Tim Folkerts says above that for say 100 particles and above the distribution rapidly approaches the limit.
Then a simple emulation with x,y,z dimensions.
1. The 100 particles being specified with the properties of ideal gas.
2. If Z component is vertical then velocity components in that direction will be subject to gravitational field strength.
3 Give a random velocity to each particle (say with values (0=>1000) in a random direction.
Then let it run for some time adjusting the parameters to get realistic display.
The results should shed some light on the distribution at the limit.
Perhaps Wayne is already on to it!
Thanks for fixing, Mods.
Re the earlier:
http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/#comment-878558
“This happens so rapidly that we don’t see the breaks in the operation of the circuit and it is the continual recreation of the dipole which causes the battery to run down and lose it’s power. Let me say it again, the battery does not supply the current that powers the circuit, it never has and it never will – the current flows into the circuit from the surrounding environment.” http://free-energy-info.co.uk/Intro.htm
Willis Eschenbach says:
January 29, 2012 at 5:09 pm
Don’t you hate it when the current “destroys the battery’s dipole”? Nothing an electrician fears more than that.
If there is a “grain of truth” in there, I don’t see it. The scary part is, Myrrh seems to believe it.
Sorry it frightens you, Willis. Try lying down in a darkened room with a cold wet cloth pressed to your forehead whenever you get this reaction, the feeling will pass.
For any here with interest in this, I’ve been searching around a bit whenever I have time and it is a bit of mess with serious science, amateur and pro, jumbled in with scams, but there’s a lot of serious science out there – don’t be put off exploring by those who’d in the past make derogatory comments about the first car they’d ever seen, and then go off to put go faster stripes on their carts. Anti matter is created and used routinely in hospitals, this poses no problem to the industrial/military complex, your access to knowledge and cheap energy does.
Some background on gravity systems: http://peswiki.com/index.php/Review:Magnetic_Current_by_Edward_Leedskalnin
A name that crops up there and considered serious science on this: http://freeenergynews.com/Directory/Inventors/JohnSearl/
Serious scientists exploring the Searl Effect Generator: http://www.rexresearch.com/roschin/roschin.htm
Lots of interesting articles on this site from which at random: http://www.americanantigravity.com/video/pharis-williams-on-fusion-reactors.html#more-902
And lastly: The case of the disappearing magnetic boots. The Radus boot with an interesting twist, magnets with memory:
http://www.cheniere.org/misc/astroboots.htm
From the last: “Well, it doesn’t take a genius to see that, when you can switch a permanent magnet’s fields easily, and the magnet also has a built-in memory as did the Radus magnets, then with a little ingenuity in switching one could use such switchable magnets to produce a self-switching, self-powered permanent magnet motor. The magnet, being a permanent dipole, is already a particular kind of “free energy generator”, since it continuously gates magnetic energy directly from the vacuum due to its asymmetry in the energetic vacuum flux.
“Why do you suppose NASA replaced that excellent Radus boot with the far inferior “shuffler” kind later?
“You see, if you can easily switch the fields of a permanent magnet as you wish, and make that magnet also have a memory that you deliberately conditioned into it, you could also build a permanent magnet self-powered engine by adapting such memory (asymmetrical behavior) and switching. It’s perfectly permissible by the laws of physics and the laws of thermodynamics, because one is using an open dissipative system far from thermodynamic equilibrium. Any dipole such as a permanent magnet is a legitimate open system freely receiving energy from its environment (the active vacuum) and re-emitting some of that energy in usable Poynting energy flow form.
“The other compelling reason is that you don’t use electrical currents back through the source dipoles to kill them! Zounds! That means you can have one half the solution already accomplished from the start; you don’t have “spent current” to have to force back through the dipole or shunt it around freely by some extraordinary means. All you have to worry about is understanding and very clever and precisely timed switching. (And it does have to be clever; let’s not belittle the skill and perseverance required to achieve that task!)”
Get your ice pack ready Willis, The other compelling reason is that you don’t use electrical currents back through the source dipoles to kill them! Zounds!
A well known, to some, problem solved.
Perhaps if you calmy read the introduction I first posted, link above, you could approach this subject with your usual love of inquiry unfettered by fear..
Bryan “I used to do educational software with Archimedes computers using BBC basic.” – nice
“I tried to adapt to Visual Basic but got fed up” -I know the feeling.
Do have a try with SmallBasic – it is designed for children to use, though I admit I dont quite understand it yet, and you may do better. Litdev has some great/clear program samples on his web site (above)
—I too would would like to know how/where the distribution arises!!
Bryan says:
February 1, 2012 at 2:12 am
Chas:
>>“Bryan, I think that the distibution just emerges
>>from the randomness (?)”
Bryan:
>True randomness would be a different distribution
>from a Maxwell Boltzmann distribution
The randomness DOES just emerge. Here is a different but similar simulation http://www.falstad.com/gas/ . You can set the initial conditions so that on atom is moving and the others are all at rest. Within a short time, the energy is distributed among all the atoms according to a Boltzmann distribution.
PS you can also “turn on gravity” in this simulation. One interesting thing to try is to turn gravity way up and turn the simulation speed way up. If it was cooler at the top, you should see a very distinct layering of the gas by color (= KE). Instead, the colors seem pretty evenly distributed at any altitude.
DeWitt Payne: “If the particles do not obey MB statistics, and they probably won’t for small numbers, the justification for converting average kinetic energy to temperature using MB statistics (2/3 KE/k) no longer exists.”
Actually, derivation of the 2/3 KE / k from PV = NkT is not based on any particular velocity distribution; it merely infers from the pressure on a container’s walls what impulse per unit time the walls must be applying to the molecules, and from that what the molecules’ root-mean-square velocities must be. Different velocity distributions can have the same root-mean-square value.
Again, you’ve conflated two disparate concepts, to both of which “temperature” has unfortunately been applied. As a perusal of the three posts by Brown and Eschenbach will reveal, they used it in the normal way, i.e., as the local mean translational kinetic energy of the molecules. In contrast, Velasco et al. did what people in various disciplines sometimes do: they use “temperature” to denote a quantity that may in some contexts be computationally handy but doesn’t necessarily describe mean translational kinetic energy accurately, at least as a local quantity.
For example, any ensemble of molecules, no matter how non-equilibrium or non-isothermal, has some degree of entropy, and adding heat to the ensemble may increase that entropy. If we start by knowing the entropy change and the added heat, we may find it convenient to assign that ensemble an effective “temperature” defined by T = dQ/dS. And for some purposes that quantity may be a worthwhile measure. But it doesn’t tell us whether the ensemble is colder in some places and warmer in others.
Now, you might argue that the kinetic-energy gradient Velasco et al.’s Equation 8 specifies is too small for thermodynamics to take notice of. You might argue that one could never as a practical matter measure this gradient. You might even argue that the molecular-translational-kinetic-energy difference is so small that Heisenberg’s Uncertainty Principle dictates an extraordinarily large time uncertainty in its measurement. But it is clearly incorrect say that this gradient is non-zero, no matter how many molecules, so your statement that “Velasco, et.al. specifically deny that there is a vertical temperature gradient in the column at equilibrium for any number of particles” is based on confusing two different usages of “temperature.”
Hmm, the impossibility he asserts is bog standard physical science as observed and well known in meteorology – one has to understand it to understand his point.
I do, so I know that it isn’t and was never intended to be considered a state of static thermal equilibrium in an isolated system. You’ve presumably read from the author of one of the textbooks that derives and discusses the DALR above (Caballero) where he states baldly that a gas with a DALR is not in thermal equilibrium. But of course you have been able to rationalize away how he isn’t really an expert (while Jelbring clearly is) and doesn’t actually know anything about this “bog standard” result. Neither have you actually read any actual textbooks that derive it, or you would have observed that they always speak of reversible bulk transport of the gas while establishing the DALR while ignoring all of the irreversible heat transport processes that also take place, more slowly. Finally you haven’t paid any attention to the fact that you need a pre-existing thermal gradient in order to get the convection that establishes the DALR. Jelbring ignores all of this also, in spite of his quoting his one textbook reference where it talks about vertical transport and the DALR. Unsurprising, since he takes the entire result and discussion completely out of context to insert it in his “paper”.
If you don’t believe me, get a copy of his one textbook reference and read it. If you can read it, that is — you don’t seem to understand even the equipartition theorem, making it unlikely that you understand why c_p appears in the DALR instead of, say, c_v. If you understand what the difference between c_v and c_p are. It will make reading about the Navier-Stokes equation and the assumption of adiabatic non-turbulent flow in his reference tough going for you, but you can persevere.
Why haven’t you noticed that you’ve missed out all these real world physics from your thinking? This, in my humble opinion, is what I think is happening here, you just don’t know that it exists, as Jelbring says: “has rarely been acknowledged by climate change scientists for unknown reasons” So your tangent is naturally then to something that is in your ken.
Wow. That’s all I can say. I have taught “real world physics” at one of the world’s top-ranked Universities for 30 years. I’ve written two textbooks on real world physics. I spend more time thinking about, solving problems in, teaching, and yes, continuing to learn and refine my knowledge of real world physics in any given week of your choice than you apparently have lifetime, and I’m missing out. Sure, that makes sense. Why didn’t I think of that. Well, I’m really grateful to you for pointing out my ignorance. I will just have to work harder — there must be something about near-Earth gravity that confers upon it a miraculous ability to violate the laws of thermodynamics that I missed.
Let me make a suggestion — only a suggestion. There are two possibilities.
a) I actually do understand real world physics quite well and far, far, better than you do. Not just understand it well enough to say lots of nifty words about it — well enough to start from the basic empirical laws and principles and derive and demonstrate nearly the whole thing through the introductory classical level at the blackboard, without notes, as I do several times a year in front of several hundred very bright students a year, working with a team of Ph.D. physicists who are my co-instructors (with perhaps a century of teaching experience between us who, one would think, would correct my errors if I made any egregious ones along the way). So when I say that you are incorrect, it is truly an informed conclusion made by someone that actually knows what they are talking about.
b) You understand real world physics far, far better than I do. You haven’t mentioned being a physics major or physics Ph.D., so we’ll both have to assume that you are one of those rare, self-trained geniuses who has managed to systematically master calculus through partial differential equations and functional analysis, group theory, advanced algebra and so on well enough to teach at least parts of it at the graduate level while working through not only introductory physics, but full courses in thermodynamics, classical mechanics (I’m certain you have mastered Lagrangian and Hamiltonian formulations of physics and understand action principles), electrodynamics (so that Maxwell’s equations are no mystery to you, nor is relativity theory and the theory of electromagnetic radiation — did I mention that the other textbook I’ve written is a graduate level text in classical electrodynamics?) , quantum mechanics (so that solving the Schrodinger or Heisenberg equations is old hat for you, manipulating commutators is easy, and of course you fully understand quantum electrodynamics well enough to publish papers in it), and above all statistical mechanics. You are wasting your time with verbal discussions here — you can actually work out the microcanonical description of this particular gas, and have avoided becoming engaged in the discussions of the Velasco paper only because you wished to help instruct me on my ignorance first, because of the egregious errors in my thermodynamic reasoning. In all respects, you are truly qualified to make pronouncements about the physics that, after all, Jelbring completely explains, with full algebraic derivations, in his paper. Sadly, you have to deal with me — an ignoramus who stubbornly persists in thinking that thermodynamic equilibrium is an isothermal state in spite of the fact that you know that nearly every physics textbook on the subject states otherwise and has numerous examples of how physical forces can sort things like gas molecules into stable sub-reservoirs at different temperatures.
We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?
rgb
BigWaveDave says:
January 31, 2012 at 4:33 pm
http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/#comment-881147
But, when matter is in the gaseous state, this is not the case. and the heat content per unit mass is not necessarily proportional to the temperature. Specific heat is dependent on gas temperature and; the volume it occupies, or the pressure it exerts. The most important word in that last sentence that seems to get overlooked most often is “and”, and so it is necessary to consider in some way, the density of the gas, to express specific heat.
In Earth’s atmosphere, the air molecules are not fixed at any particular height. Their distribution, and thus the air density with respect to height is forced by gravity. If all of the air molecules have the same heat content, the temperature distribution with height must vary with the density.
Thank you.
Robert Brown says:
February 1, 2012 at 6:09 am
We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?
My only skill in this, and I use the term loosely, is when my curiosity is piqued I enjoy exploring and in subjects where I have no or only a modicum of knowledge I will listen to as many arguments pro and con a bone being argued over until I am fairly confident I can take a position on it, or not. When I first found that AGW was something people argued about I was more than casually intrigued, the arguments were so passionate, I immersed myself in reading discussions and found the range of disciplines involved and seemingly, to my untutored eye, being argued with equal claim to physics, quite exhausting as I yo-yoed between one and the other, and because I would then have to see what I could find to substantiate the different claims. Gradually a pattern emerged, the applied scientists, the engineers and the like, with practical real world experience won hands down, not least for common sense.
I also learned a bit more about physics than I began with, which original teaching itself gave me something to compare with what I was being told in ‘AGW science’. For example, I had begun at junior level taught that gases had weight, that those heavier sink in air, those lighter rise, and the examples we were given was to the then important industry in Britain, coal mining, this knowledge was crucial to safety in mines. This became my first independent area of inquiry, I could find no discussions on this so I questioned the PhD in physics who teaches and sets and marks exams and writes reports for government and who first set me off in the direction of IPCC reports to learn about AGW, “how can carbon dioxide be well-mixed in the atmosphere when it is heavier than air?” I’ve told the story elsewhere, I won’t repeat it here, but his explanation of the physics led me to the inescapable conclusion that he didn’t know what he was talking about. I was profoundly shocked. He firmly believes, and teaches with constant references to laws of physics , that carbon dioxide pooled on the ground will spontaneously rise and diffuse in the atmosphere without any work being done. It’s a completely different physics from the real world.
So, I don’t know what you’ve written, or how many of your peers agree with you, but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background. I’ve given you my conclusion on the ‘physics’ of this generally from the AGW ‘climate’ scientists, that it is fictional fisics. Did you read the Latour link? He called it junk science.
So I’m in good company..
Joe Born says:
February 1, 2012 at 5:06 am
DeWitt Payne: “If the particles do not obey MB statistics, and they probably won’t for small numbers, the justification for converting average kinetic energy to temperature using MB statistics (2/3 KE/k) no longer exists.”
Joe: Again, you’ve conflated two disparate concepts, to both of which “temperature” has unfortunately been applied. As a perusal of the three posts by Brown and Eschenbach will reveal, they used it in the normal way, i.e., as the local mean translational kinetic energy of the molecules. In contrast, Velasco et al. did what people in various disciplines sometimes do: they use “temperature” to denote a quantity that may in some contexts be computationally handy but doesn’t necessarily describe mean translational kinetic energy accurately, at least as a local quantity.
… But it is clearly incorrect say that this gradient is non-zero, .., so your statement that “Velasco, et.al. specifically deny that there is a vertical temperature gradient in the column at equilibrium for any number of particles” is based on confusing two different usages of “temperature.”
You are the one confused, Joe. You have things backwards. The standard and fundamental definition of the thermodynamic concept of temperature is that two bodies are at the same temperature when they are in thermal equilibrium. [A pedantic relativistic form of that statement might be that two bodies in the same frame of reference are at the same temperature when they are in thermal equilibrium, or that two bodies will be in thermal equilibrium when their temperatures transformed into the same reference frame are the same.]
Both Brown and Velasco et al are using the concept in this fundamental way.
That temperature is proportional to average kinetic energy per particle in the canonic limit is a secondary derivation from this primary thermodynamic concept. The finite microcanonical ensemble you are making so much out of is unphysical; it is a statistical mechanics abstraction. Once you allow it to interact with so much as a thermometer, the usual result for a canonic ensemble reasserts itself.
There are many other circumstances in which not all of the kinetic energy counts towards the temperature. Indeed, in general, only the random, thermalised and isotropic kinetic energy counts. Consider a cannon ball in orbit around the Earth. What is its temperature? If you treat it as a single particle, then the average KE per particle is so enormous that T~1E31K! Even if we count all its atoms separately, then T~1E5K. This is clearly ridiculous, not what we mean by temperature at all. Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.
RGB says: “We’ll see just how arrogant and crazy you are. Do you chose a), sir, or b)?”
I could have told you the answer would be “c” –> “I don’t understand physics. Or engineering. Or math, for that matter (and readily admit it). But I never-the-less know it better than PhDs, because I have found some web pages that I have a strong gut feeling about. And that gut feeling trumps actual knowledge and study and mathematics.”
Basically take the worst parts of your two options and put them together.
Tim Folkerts says
“PS you can also “turn on gravity” in this simulation. One interesting thing to try is to turn gravity way up and turn the simulation speed way up. If it was cooler at the top, you should see a very distinct layering of the gas by color (= KE). Instead, the colors seem pretty evenly distributed at any altitude.”
Thanks Tim it looks like a useful resource.
The possibility of a slow molecule hitting a wall and bouncing back at a higher speed was not one I had factored in.
I would have set the condition as an elastic bounce with molecule coming out with unchanged KE.
That would be my definition of thermally isolated.
All of these simulations should afforded significant skepticism. I don;t know that any of them were designed to provide more than approximately correct answers. For example. when you turn on gravity in the simulation I linked to, the total energy gradually increases. You could attribute that to some “thermogravimetric effect”, but more likely is is round-off error after millions of collisions or the effect of the step size used, or poor programming.
Unless you know the pedigree of the simulations, they should probably be consider “for entertainment purposes only”, but not as rigorous scientific evidence in support of any particular subtle claims.
“There are many other circumstances in which not all of the kinetic energy counts towards the temperature. Indeed, in general, only the random, thermalised and isotropic kinetic energy counts. Consider a cannon ball in orbit around the Earth. What is its temperature? If you treat it as a single particle, then the average KE per particle is so enormous that T~1E31K! Even if we count all its atoms separately, then T~1E5K.”
It needs to be an ideal gas. A cannon ball, a pint of beer, or water vapor are not ideal gases.
“This is clearly ridiculous, not what we mean by temperature at all. Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
It might be interesting to see what happens in space if release low pressure and low temperature monatomic gas in free space.
Suppose you put a globe of water which say 5 C in a low pressure air lock and then open the door to space. Obviously the globe of water would be above it’s boil point in a vacuum. But can anyone describe what would happen. Does it freeze, does expand, does turn fog. How quickly?
Or does “appear” to do little within the first minute, or does something dramatic happen in less than 1 second?
So, I don’t know what you’ve written, or how many of your peers agree with you, but I have absolutely no confidence that you are accurate in your assessment of Jelbring because of your education and professional background.
. Is it “stuck” where gravity leaves it, or can it move, say, by irreversible diffusion or heat conduction? What happens when some of the heat moves from one temperature in one part of the gas to another part of the gas at a different temperature? In particular, does the entropy of the gas increase or decrease?
throughout the gas column (condition for static force balance), once static force balance is achieved (which happens almost instantly, BTW) any bulk motion of the gas damps and gravitation can no longer heat or cool the gas. How can it? In order for some part of the gas to gain energy, it has to move downward and, on average, no part of the gas in static force equilibrium moves up or down. Gravity can certainly maintain a pressure/density/temperature profile, but there are quite literally an infinite number of them (not just the one with the DALR) that satisfy the force equilibrium equation and hence are static as far as forces are concerned.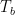
. Remove a dollop of heat from it 
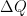. Compute the entropy change of that parcel of gas: 
. Transport the heat to any parcel of gas above it — one differentially above it is fine, as long as it has a different (lower) temperature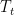 
. Compute its entropy change: 
. Sum the two to determine the total change in entropy associated with this process:
Ah, so you vote for b). That’s great, as it frees you from any need to actually try to understand the arguments involved, and it frees me from any obligation to continue to try to educate you! I especially like your argument that because we observe a lapse rate in Earth’s completely dynamic diurnally heated-at-the-bottom and differentially cooled atmosphere this must be a feature of true static thermal equilibrium in an isolated system (Jelbring’s assertion). That’s proof enough, isn’t it? Sure it is. Water being stirred or heated from the bottom inevitably behaves exactly like water sitting at rest in a container according to exactly the same argument. And constantly inserting distractors like “what about water vapor” into your arguments is also very useful given that we are discussing the validity of Jelbring, not the question of whether nor not a DALR exists in a dry atmosphere under certain non-equilibrium conditions that permit one to more or less ignore thermal conductivity.
You seem to be conflating an assertion that there is no such thing as a dynamically driven lapse rate in any real atmosphere with the assertion that there is no such thing as a thermodynamically stable lapse rate in an isolated ideal gas subject to gravity but allowed to thermally relax to a maximum entropy state. Your argument seems to be “the real atmosphere exhibits a lapse rate, therefore that must be the true thermal equilibrium of an isolated ideal one”. You make this argument (which is hopefully fairly obviously not even logically valid, let alone unsupported by any actual physics), and attempt to “support” it by means of waving your hands about how gravity has to do work and the work has to turn into heat without considering what happens to all that heat when gravity stops doing work because the atmosphere achieves a static force profile such that
Not to be critical — I know that you very likely are trying to understand the physics in your own way — but you might try using a physics textbook or two to help out. That way you might be able to understand how the heat capacity at constant volume is related to the number of degrees of freedom available to store heat at the molecular level (instead of stating that it doesn’t depend on them, which is simply incorrect). You might understand how the heat capacity at constant pressure is related to the heat capacity at constant volume, and what the first law of thermodynamics has to do with that (in the simple case of an ideal gas, ignoring gravity).
You might come to realize that while gravitation can do a bit of work at first in a way that depends on the initial state and hence can differentially heat or cool local parts of the gas as it expands or compresses to achieve a self-supporting density/pressure profile such that
Which one is the one that the gas will irreversibly evolve towards? The answer is: “The one with the maximum entropy”. Again, you can choose to disbelieve this utterly prosaic — what is it that you said, “bog standard” result of thermodynamics, but then you are violating Jelbring’s own stated axioms, which is that bog standard physics is valid and used to obtain his conclusions.
Finally, you are down to a single question that you can, if you choose to, understand and answer, without even having to master much more than the definition of entropy for the ideal gas.
Take a small parcel of gas from the bottom of the column at temperature
This is really the only thing you need to understand — really understand — to see that Jelbring is wrong, as are the silly people who have asserted that the state of the gas with a DALR is maximum entropy. It is not. It is iso-entropic, perhaps, but it is not maximum entropy because we can easily increase its entropy by moving a differential amount of heat from a place where the gas is warmer to a place where the gas is cooler. This movement of heat is irreversible — changes of state in the gas that increase the entropy of the Universe are irreversible changes by consistent definition, something you can easily enough understand if you really try.
What we have just proven is that for any isolated gas, in the absence of a source of external work — note that I do not care in this proof how or why the initial state of the gas with some sort of thermal lapse came about, whether or not there is gravity present or absent, whether or not the gas is a mixture or pure — if we move a dollop of heat from where it is warmer (cooling it) to where it is cooler (warming it) we increase the entropy of the Universe and such a fluctuation in the state of the gas is irreversible.
In order for the system not to systematically evolve to a state where the entropy is maximum at a uniform temperature, it has to be impossible for any mechanism whatsoever to transfer heat between the two parcels. If the two parcels were inside adiabatic (insulated) walls, for example, then one could not transfer the heat. If they are in thermal contact, though, so the heat transfer can occur, then it will occur (in time) and once it happens, the transfer of heat in the other direction to create a macroscopic parcel of gas with an unequal temperature just doesn’t happen.
Eventually the system will reach a state where heat fluctuations don’t change the entropy:
which is obviously true only if $T_t = T_b$. Thermal fluctuations do not strictly increase entropy of any system — note well, any system — only when all parts of the system that are in “thermal contact” (connected by interactions of any sort that permit the transport of heat) are at the same temperature. This is the classic, textbook definition of the state of thermal equilibrium of an isolated system.
Note well, this is a statistical law. If you make the parcels of gas small enough, then you reach a scale where “temperature” as an average measure of energy breaks down, where the tiny parcels of gas are constantly “heating” or “cooling” a tiny bit in the sense that the volume in question gains or loses a bit of energy during the random motion of the molecules. As you make the parcels larger, though, in particular large enough that the concept of temperature itself is a reasonably sound one, the probability of a fluctuation happening that increases the entropy of the system becomes strongly asymmetric compared to the probability of fluctuations that decrease it. Again any good intro book has lots of examples of how this works — how mixing of an unmixed gas via thermal fluctuations is extremely likely and hence quite rapid, while separation of the mixed gas back to an unmixed state by thermal fluctuations is almost infinitely unlikely. If you don’t understand this and try to use only kinetics to figure out what happens in the gas, you can easily be misled as to the correct equilibrium distribution of internal energy as reflected in the (local) temperature. As I said, there are an infinite number of ways to create static force equilibrium and distribute the internal energy of the system among the molecules consistently at the same time, but only one (family of) distributions has maximum entropy, and that is the one at a uniform internal temperature.
I don’t know how to make it any simpler than this. If you create an imaginary gas that cannot conduct heat, of course you can make it have any thermal distribution you like. However, the standard “ideal gas” used in ideal gas models can certainly conduct heat. Real gases, e.g. N_2, O_2, CO_2, all conduct heat, although many of them are relatively poor conductors in the sense that they conduct heat more slowly than convection moves heat around in the Navier-Stokes equations, so that energy distribution is more often determined by convective flow than by conduction if there are thermal sources and sinks — differential heating — and you don’t wait long enough for hydrodynamic motion to stop and thermal relaxtion to stable thermodynamic equilibrium to occur.
None of this precludes real layers of non-isolated atmospheric gases, differentially heated on the bottom and cooled at the top, from attaining a thermal lapse rate. It just means that Jelbring’s assertion that this hydrodynamic equilibrium is also the stable thermodynamic equilibrium for the system is incorrect. His paper is incorrect. His conclusion is incorrect. It violates the second law of thermodynamics, is not maximum entropy, and (if true) would enable the construction of PMM2Ks and other impossibilities.
This result is unwelcome to those who want to pretend that a stable, static, isolated gas will always be hotter on the bottom than the top because gravity can magically maintain the thermal gradient against entropy-increasing thermal fluctuations that do negligible work against gravity but otherwise equalize the temperature gradient. Why? Only because they want to believe that this gradient eliminates the need for any greenhouse gas mediated greenhouse effect, even in a completely static isolated system with no GHGs present at all. That’s Jelbring’s explicitly stated point. I’m fairly sure that it is yours as well.
If not, if you are happy enough with a dynamic, non-equilibrium lapse rate, then we have no quarrel. You can then add in water vapor and so on with my complete blessing, as long as you do not assert that gravity can do any net, continuous work even in the dynamic case in an atmosphere with a more or less static density profile. Gravity can help heat air parcels as they move down, but only as other air parcels cool as they are moved up to replace them, and one can no more get continuous work out of gravity in the atmosphere than one can out of an ordinary pendulum. If you don’t have a source of external free energy to keep replacing energy the pendulum loses to “heat” (via irreversible friction and drag forces, for example) any real pendulum damps to (almost) perfectly zero motion over time; gravity can contribute only the energy originally stored in the pendulum when you pulled it up to start it moving.
The best papers I’ve read (so far) that seek to explain how things like the DALR and wet air lapse rates effect the actual transport of heat from the solar-heated surface and atmosphere to where it is ultimately lost via radiation are really quite good. I find them plausible — not usually “proven”, but plausible. They openly acknowledge the importance of the GHG-GHE in establishing the disequilibrium conditions that lead to a lapse rate and atmospheric heat transport in the first place, but then analyze that motion to argue that the overall feedbacks of this process are negative, not positive, something that actually explains the remarkable stability of our atmosphere in the face of internal variability that (in a chaotic system) could easily drive it to catastrophe. There is no magic in them, at least none that I can see offhand.
You are so very close, in your comments, to taking this “good” path. You just need to abandon Jelbring to his well-deserved fate and get off of the bad path, the one that obviously violates the very laws of thermodynamics that Jelbring claims that his solution is supposed to axiomatically satisfy and that I prove does not yet again in this very reply above. An ideal gas with that in force equilibrium but that exhibits a DALR isn’t a maximum entropy state of the gas. You don’t even need to go to a fully microscopic description to prove it (although there are more elegant and complete arguments that also will do the job).
In the end, it is a matter of credibility. Anyone that offers up Jelbring’s paper in a forum devoted to the question of the GHE or CAGW as “proof” that GHGs are unimportant and there is no such thing as a GHG mediated GHE is instantly in-credible, because anyone who actually knows thermodynamics, let along statistical mechanics, can instantly see that it is incorrect and absurd. OTOH, those same people can pick up any climate science textbook and read about the DALR, and most of the competent ones (in climate research) can probably derive the DALR from its base assumptions rather easily, cold. None of them would argue that there is no such thing as an (approximate) DALR visible in atmospheric dynamics, and they all are perfectly happy working with e.g. potential temperature instead of straight up temperature as a consequence. But they know that it isn’t true thermodynamic equilibrium and they know that one cannot heat anything at all by means of the DALR, that rather it is a feature of differential cooling given the heat input from the Sun.
I’d just as soon that climate skepticism be fuelled by credible arguments, not in-credible ones. But suit yourself.
rgb
Robert Brown says:
February 1, 2012 at 6:09 am
(I’m certain you have mastered Lagrangian and Hamiltonian formulations of physics and understand action principles), electrodynamics (so that Maxwell’s equations are no mystery to you, nor is relativity theory and the theory of electromagnetic radiation — did I mention that the other textbook I’ve written is a graduate level text in classical electrodynamics?)
Does it include Maxwell’s Quaternion Equations?
Tim Folkerts says:
February 1, 2012 at 12:30 pm
“All of these simulations should afforded significant skepticism. I don;t know that any of them were designed to provide more than approximately correct answers. For example. when you turn on gravity in the simulation I linked to, the total energy gradually increases. You could attribute that to some “thermogravimetric effect”, but more likely is is round-off error after millions of collisions or the effect of the step size used, or poor programming.”
Indeed. Good programming for such simulations first requires a careful analysis of the Hamiltonian for conservation laws fixing various relations among the variables (not merely simple energy and momentum conservation but also higher order symmetries, distributions, dimensional and angular limits, boundary conditions, attractors and so forth). Failure to include such constraints will cause the simulation to “drift”, often obscuring the very effects you are looking for or, worse, creating misleading artifacts.
Dr. Brown,
Your background appears to be computers, not thermodynamics or fluid mechanics.
You are grossly in error, and your opinion of how gas behaves is ridiculous. I would suggest that you dig up some texts on the subjects, and read them. Otherwise, you should stick to computers.
BigWaveDave states (without any support): “Dr. Brown, You are grossly in error, and your opinion of how gas behaves is ridiculous.”
I think he has been doing remarkably well. Perhaps you could provide one specific example of a ‘ridiculus’ statement containing a ‘gross error’ so we could discuss it?
Tim Folkerts said:
February 1, 2012 at 3:36 pm
Anything he says that doesn’t recognize that there is a vertical temperature gradient implicit in the situation where a sufficient quantity of gas is being held by the gravity of a planet, shows a fundamental lack of understanding of what gas temperature means.
Paul Birch: “The standard and fundamental definition of the thermodynamic concept of temperature is that two bodies are at the same temperature when they are in thermal equilibrium.”
Yes, yes, I understand your position; your repeating this section of your catechism doesn’t advance the ball. This is like the argument above about whether the power flows through the Poynting vector or along the electric field through the resistor: which explanation is better depends on the context. And I’ve already told you why I believe a different definition of temperature is appropriate in this case. We disagree. I’m okay with that.
“Or consider a quantity of monatomic gas in free space, which we allow to expand adiabatically. The gas rushes out in all directions, cooling as it does so to a very low temperature. Yet the kinetic energy per particle stays exactly the same! (So does the entropy.) What has happened is that the gas has done work on itself, converting thermal energy to ballistic kinetic energy.”
Are you absolutely certain that’s a position you want to take?.