Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Paul Birch says:
January 27, 2012 at 7:34 am
” Proper temperatures in thermal equilibrium scale as the redshift climbing out the gravitational well. T(height)/T(infinity) =z(height)/z(infinity) = (v(escape)/c)^2/2 for v<<c. The corresponding lapse rate is just T/g."
Sorry, sorry, I slipped into geometrodynamic units, then tried to put the c^2 in and completely messed up as the wordpress reply box lost focus. That should have read:
The corresponding lapse rate is Tg/c^2.
Gravity is an organizing force that decreases entropy in a closed system? True or False?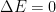
and plenty of irreversible internal dynamics and many, many degrees of freedom will spontaneously decrease its entropy if gravity is one of the interactions coupling the particles of the system. That is trivially provable. Here’s the proof: “It violates the second law of thermodynamics, which says that 
for any isolated system, and is zero only if the processes involved are reversible”. Which gravitational interaction isn’t, not in microdynamics, not any more than any other internal molecular interaction.
Support your answer.
How can I? You have to tell me what gravity is doing in that closed system. Are we starting the system off with zero gravity, and then smoothly turning it on? Are we starting it off with zero gravity and then slamming it on? Are we starting out with the system in thermal equilibrium in constant gravity? Is gravity a means of interaction for all of the parts of the system, and are we talking cosmology here, are is gravity a pre-established given acting on a closed jar of air?
Do you really think that all of these questions have the same answer? And do you understand that if gravity is a part of the internal interactions of a closed system, it cannot decrease the entropy of that system because that would violate the second law of thermodynamics? You are basically asserting that a closed thermal system with
So, sure you mean that, hoss?
rgb
Jim Z says: January 27, 2012 at 8:03 am
>:A steady state atmosphere of a planet will have a atmospheric laps rate.
Quite true. But this is not an EQUILIBRIUM condition, only a steady state condition. It is due specifically to energy being radiated from the TOA (top of atmosphere) by greenhouse gases. Similarly, there is a continued temperature gradient across the insulation in my refrigerator (from ~ 0 C at the inner surface to ~ 20 C at the outer surface). But this is not equilibrium, because I have to keep removing energy from the cold parts (just like energy must continually be removed from the cold parts of the atmosphere (by radiation from GHGs)).
>The temperature difference is not a violation of the second law.
Also quite true. But this is because we have a “hot reservoir” ( the sun) and a “cold reservoir” (space) that provide a source and a sink of energy, allow us to run various heat engines.
>The temperature difference cannot be exploited to do work.
It absolutely CAN be exploited to do work. The thermopiles discussed throughout this thread are one easy way. Any number of different heat engines could use the temperature difference to do work.
>The atmosphere particles have the same energy, high and low, heavy or light.
This is not correct, as has been pointed out many times. Let me give one more arguement that might be easier to understand. Consider a box at sea level (which we will consider to be an altitude h=0). Fill it with a mixture of He & Kr (Mass 4u and 84). Give the box a few minutes to equilibrate. I think every one will agree that all the molecule have the same temperature and the same KE –> KE = 3/2 kT. I think every one will agree that all the molecule have the same gravitational potential energy –> PE = mgh = 0.
Now raise the box of gas 1 km up. The Kr has gained 21x as much PE as the He has. By your hypothesis, since the Kr has gained more PE, the Kr must have less KE to have the same total energy. But if the Kr has less KE, the Kr will be a lower temperature than the He in the same box. Permanently. The higher I raise the box, the greater the temperature difference between the two types of gases, IN THE SAME BOX.
(This is conceptually very similar to the two jars Dr Brown has mentioned before, but it might be more intuitive to some people.)
Either
1) Atoms have the SAME total energy, but atoms on the same box can be at different temperatures, or
2) Atoms have DIFFERENT total energy, but atoms in the same box are the same temperature.
Does anyone REALLY vote for #1 ???
Robert Brown
It would be wrong to conclude that all those who are unconvinced by the isothermal distribution are sceptics.
Jim D who posted earlier is a very effective proponent of IPCC science and is unconvinced.
Willis (a sceptic) moved from adiabatic to isothermal in one week.
The issue has no bearing on the existence or otherwise of a greenhouse effect.
I can see both arguments for and against each position.
I think the isothermal argument is the stronger one but until an experiment confirms it one way or another I will keep an open mind.
And how can I not respect that? It is my own position, except that the “strength” of the isothermal argument is so much greater than that of a temperature lapse — given that it straight up violates the second law of thermodynamics — that the default position of any real scientist should be roughly the same as it is whenever somebody proposes a perpetual motion machine, or that they can negate gravity by means of a simple electronic device they built in their basement, or have worked out the One True Theory of Everything in their spare time, in spite of the fact that they never actually took calculus or physics in college (or may not have attended college). All of these things are technically possible, but they are so unlikely that our default position is a bemused and often unspoken “bullshit, did not” while politely waiting for hell to freeze over and actual evidence to emerge that experimentally supports the claim.
To put it another way, if I were a grant officer and somebody sought money to perform the experiment, I would categorically reject it. I wouldn’t even send it out for review — it would go straight into the round file, the same place the patent office now files PMM patents unaccompanied by a working model.
Sometimes the default position of science is to simply reject something. For example, it is alleged in various ancient mythologies that certain individuals (who may or may not have existed, it is hard to verify things that far back in the past) have instantly and completely cured actual blindness by rubbing a mixture of spit and mud into the eyes of an blind person. Modern science tells us that this is absurd. One cannot imagine any actual physical or biological mechanism for (say) nerve damage to the optic nerve, retinal detachment, physically damaged eyes, or even mere cataracts, to spontaneously revert to normal healthy tissue due to the application of filthy mud. Quite the contrary — we would be more inclined to consider spit to be a biohazard, and dirt from the ground in any country where the great outdoors is the universal toilet for man and beast alike to also be a biohazard, and would, I think, suggest that kids not try this at home to cure granddad’s failing vision.
Would I fund “Investigations into the curative properties of spit and mud on blindness in adult males”? Of course not. The default position for science is to not believe in magic, and this is magic precisely because it is unlikely, in fact because it is an intuitive violation of the second law. Eye damage is spontaneously “irreversible” as a general rule, which means that one has to perform very exacting and specific changes to reverse that damage. Random actions irrelevant to those specific changes are almost infinitely unlikely to have the desired effect.
So I too am always happy to be influenced by a well-conducted experiment, but in the meantime my default belief is “bullshit, that assertion directly violates the second law of thermodynamics and hence is almost certainly false”.
rgb
The temperature difference cannot be exploited to do work. The atmosphere particles have the same energy, high and low, heavy or light. There is no energy difference to exploit to do work.
Ah, but you see, heat engines and conductive thermal transport are driven by differences in temperature, not energy. As you would know if you had absolutely any clue about thermodynamics. You might actually look at the pictures in the top post and try to refute figure 2. Bear in mind that the air at the top is indistinguishable from ordinary air in an ordinary room at an ordinary temperature, ditto at the bottom. Heat would certainly flow between a reservoir of air at high pressure and high temperature and a second reservoir of air at low pressure and low temperature in any laboratory in the world. Please explain why it wouldn’t do that in the specific figure above.
rgb
Paul Birch said @ur momisugly January 27, 2012 at 7:34 am
TeX is a markup language, LaTeX is a set of extensions to make using it easier; intro here: http://www.latex-project.org/intro.html
The CA-assistant adds a toolbar to the Leave a Reply box that enables the easy insertion of LaTeX commands (among other things).
http://climateaudit.org/ca-assistant/
Joe Born says:
January 26, 2012 at 5:42 pm
“So, although I respect your opinion, I have to go with mine. And it’s my opinion that, for the purposes of a theoretical discussion–which, let’s not forget, is what Dr. Brown initiated–Velasco et al. do indeed say that an isolated vertical gas column exhibits a non-zero lapse rate at equilibrium.”
Joe, if, for some strange reason I cannot fathom, you still wish to maintain your belief that “temperature equals average molecular kinetic energy”, despite what physicists tell you, that’s up to you. But for heaven’s sake stop trying to pretend that Velasco et al supports you. What they explicitly say is that the assumption that “temperature is proportional to average molecular kinetic energy” is FALSE (for the finite microcanonical ensemble). They say that the statement “temperature decreases with height” is FALSE. The reason it’s false is different for small N and in the canonic limit, but it is false either way. This is what they say.
Now, you can disagree with them if you like. You can believe they shouldn’t have said what they did say. You can believe that you can interpret their statistical mechanics better than they can do themselves. You can believe that they are such poor writers of English that they said the exact opposite of what they meant. But don’t claim they agree with you when they actually say you’re wrong!
The second law is only statistically true.
, and an absurdly — truly absurdly — small number for 
.
Oh, please. Now you’ve got me ROTFL again, and I’d almost settled down. You should really say this like this:
The second law is only statistically true.
That makes it even funnier.
So you’re saying, basically, that like there is always a chance for a system to behave in egregious violation of the second law, for its macroscopy entropy to suddenly and spontaneously decrease.
Um, you ever do a back of the envelope estimate of that probability for a box containing, say, one whole mole of molecules? You might try it sometime. Please express your answer in terms of the mean free time between observations, assuming them to be poissonian in distribution, in log base units of powers of the probable lifetime of the Universe. (Hmm, what should we name these units? Not decibels, maybe unibels?)
Here’s a small hint to get you started. Take a simple box filled with white and black (but otherwise identical) balls. Draw an imaginary plane through the center of the box with equal volumes on both sides. Suppose the box has 2N marbles, N of each color. Give the box a good shake — enough to randomize the positions of all of the marbles. Now count the marbles on each side of your plane.
What is the probability that the shake leaves all of the black marbles on the left and all of the white marbles on the right?
This is a nice example because it is so easy. The distribution of outcomes is relatively simple to compute. I think you’ll find that the answer is a “very, very small number” for any values of
This is a textbook problem in thermo, intended to start to help you understand why it is really, really, really … (repeat a google of times really) stupid to bet against the second law of thermodynamics just because it is a statistical law…
rgb
Publius Maximus says:
January 27, 2012 at 7:06 am
There is absolutely no doubt that WordPress’s spam filter was written to single out posts by Joules Verne for special treatment. And everyone else from time to time for reasons that are, unlike the Laws of Physics, completely inexplicable. The mods inspect the contents of the spambox far less frequently than the main posts for obvious reasons. Tell your friend Joules to stick his paranoia where the sun don’t shine.
Nobody around here gets censored for their ideas. They do get snipped for extreme comments, but they are posted with a snip explaining what the offence was. Casting aspersions on Anthony and the Mods is not looked upon favourably around here. Of course if you want to really have your comments held up and unfairly hampered (edited to say what you don’t mean) by all means head off to (Un)RealClimate where such things are par for the course.
It is apparent that the writer is a physicist and not an engineer.
You mean, because physicists generally teach engineers the physical basis for engineering? True enough. But we enjoy doing it, really, except when they stubbornly or lazily fail to learn the laws of thermodynamics. Then we worry that they’ll go do silly things like try to design perpetual motion machines, which embarrasses us. Where did we go wrong? How did we fail you?
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
No, silly beanie. The assumption is that the silver conducts heat to the gas at all from the bottom to the top. I don’t really give a damn what the conductivity in the silver is or how good the thermal contact between the silver or the gas is as long as it is nonzero throughout the wire. And bear in mind that I can increase the thermal contact of the silver with the gas at both ends by means of adding a simple heat sink. Good engineering, no?
I do so find this sort of mistake to be embarrassing, don’t you?
Now go back to the drawing board and try again. Yes, the silver wire will conduct heat from the high temperature gas at the bottom to the low temperature gas at the top. So you were saying? Oh yes:
Physicists should avoid using compount metrics like temperature and instead use the actual underlying measurement of heat. In a gas heat is not the same as temperature this is a type error. Even a physicist should remember the gas laws.
You mean that we should remember them because you learned them originally in our classrooms? Gee, hard to argue with that. Now suppose you use your super-engineering powers to refute Fourier’s Law. That’s one of those “laws” we were trying to teach you back then, so you wouldn’t burn your fingers trying to grab a metal rod that has one end stuck into a fire.
How did we fail you?
Or perhaps I should be asking, how was it that we did not fail you?
rgb
” Yes, the silver wire will conduct heat from the high temperature gas at the bottom to the low temperature gas at the top”
So explain how the silver wire has precisely the same conductivity to the gas at low pressure at the top of the tube as it does to the gas at high pressure at the base of the tube. It cannot as there are less gas molecules coming in contact with that wire at the top than there are at the bottom – that is the definition of pressure.
You will find that when you take the different conductivity across the silver-to-gas boundary into account that the high gas-to-silver conductivity at the base is in lapse rate proportion to the lower silver-to-gas conductivity at the top.
“But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.”
That’s an absolutely precious quote, A Physicist. I’m going to have to save that one — it belongs as a panel quote at the beginning of a book chapter on the second law. Especially since it is so very, very true.
In fact, Maxwell’s Equations aren’t quite true — QED is. Any number of experiments have proven to be in error, especially in these confirmation bias prone, cherrypicking times where human research careers depend perhaps too strongly on getting startling (and valuable) results. But the second law still holds for QED and CED alike, for all of those often bumbling experiments.
rgb
Rodrigo Caballero says at January 27, 2012 at 6:07 am
I took a look at “Verkley and Gerkema, J. Atmos. Sci. 2004” and by my read, they consider that applying the two constraints of constant mass and constant energy (or enthalpy) to the fluid will result in an isothermal profile for the fluid in thermodynamic equilibrium. This is the classical result shown by Gibbs. However; Maxwell considered the effect of convective mixing by replacing the constant energy constraint with a constant potential temperature constraint. This change results in the column of fluid being out of thermodynamic equilibrium and results in an isentropic profile defined by a temperature lapse rate. Verkley and Gerkema propose that adding the constant potential temperature constraint will both satisfy the first law of thermodynamics implied by the constant energy constraint and still consider convective mixing. They go on to show how their profile can be used to fit the Standard Atmosphere.
The isothermal profile proven by Gibbs and promoted by Brown is looking at a purely academic scenario (no convective mixing) – real planetary atmospheres exhibit lapse rates that are not a result of the effect of greenhouse gases but rather convective mixing.
Woo-hoo, Rodrigo Caballero is here now too, with some more ref.s. More homework to find why those molecules can climb up in gravity field at constant speed, constant T even though “Mean velocities will be greater near the bottom of the box than near, the top..”
where the one is the mean free path and the other is the gravitational-thermal lapse rate. Also bear in mind that speed is not temperature. The point is that none of the molecules in the system ever climb up in the gravitational field in equilibrium. In fact, their average energy change in equilibrium associated with gravity is zero. Thermal transport is not blocked by gravity, and the system still relaxes to isothermal equilibrium, exactly as Caballero pointed out (and I’ve pointed out until I’m blue in the face.
Good attitude, Trick.
See my previous post estimating
You might consider the actual problem with second law violations, though. That’s by far the easiest way to see why equilibrium is isothermal in any well-connected system.
rgb
Dr Brown says;
Ah, but you see, heat engines and conductive thermal transport are driven by differences in temperature, not energy. As you would know if you had absolutely any clue about thermodynamics.
Conductive thermal transport need matter. Kinetic energy is motion and mass.The particles of matter you use to “conductive thermal transport” for the “heat engine” are subject to gravity.
There is no “equilibrium” of anything in this question. There is approximately equal partition of energy here, Boltzmann distribution, and approximately equal Lagrangian for each part to which the energy is distributed.
What I’m not open to hearing is that the second law allows disequal apportionment of total energy in an equilibrium state which is, in essence, what Dr. Brown (whether he realizes it or not) is saying.
Is it in any way my fault if your education is faulty and you cannot seem to grasp any of the five or so statements of the second law? I don’t care what you are open to hearing about what it allows or doesn’t allow. How about reading it’s actual words?
What you don’t seem to want to realize is that you can’t do statistical mechanics with a picture in your head. I can’t do stat mech in my head, and I’ve had a damn sight more practice. I don’t know anybody that can do stat mech in their heads. Doing statistical mechanics correctly is very, very difficult.
You can do thermodynamics in your head, or with only a bit of associated algebra. That’s why I provided a simple picture. Figure 2 above violates the second law of thermodynamics. The hypothesized thermal lapse is therefore not any of the things people have claimed it to be — maximum entropy, thermodynamically stable, and so on, because if it were, the second law of thermodynamics would be openly violated.
If you replace the silver wire with anything that does work across the temperature difference, inside or outside of the box, it will transform heat into reversible work and have no other effect on the Universe. It will systematically cool the box and turn its heat content into stored reversible energy.
This is precisely what Joules has claimed will happen in upstream posts. If you are standing in for him, I have to ask — are you going to seriously try to defend his assertion that an isolated gas will thermally separate, and if a heat engine is run off of the thermal difference the isolated gas will cool to absolute zero with no input of work? Because if you are, then you are both batshit crazy.
Non-decreasing entropy in an isolated system: Not just a good idea! The Law!
Sincerely,
rgb
P.S. — OK another morning probably wasted trying to teach the horse to sing. Time to go teach Gauss’s Law to Enquiring Young Minds.
Dr Brown,
Thermodynamics isn’t best applied to this question. Your example conflates temperature difference in the atmosphere that occur over large distances and thermal conduction over short distances. Show how your “conductor” molecules are not equally subject to gravity over the same distance of the temperature difference.
Like it or not, a conductor from the surface of the earth to high in the atmosphere is elastic particles pulled down by gravity. Solid or gas, it’s molecules all the way up… and down. 😉
Robert Brown says at 1/27 9:29am:
“…because physicists generally teach engineers….”
Yes. I knew it! I would get a chance to express the difference. Engineers will readily advance to meet the opposite sex; physicists are more reluctant. Why? Physicists less often even try b/c they have studied they can never get there – they must go ½ the way, then ½ the way, then ½… and so on ad finitum…physicists think they will never get there.
Engineers on the other hand have learned thru trial and error they can get close enough to get the job done. This is why there are more engineers than physicists.
Tim Folkarts says;
<>
1) Atoms (molecules) in the box each have the same total energy (approximately, total energy of each distributed as Boltzmann says). Total energy of each (the Lagrangian) is kinetic energy plus potential energy. In a box that is small, in the up and down direction in which gravity acts, the difference in potential is small, small enough to be negligible when “the thermodynamic laws” are applied to the usual problems or examples. When the box is large in the direction of gravity, the difference from top to bottom of the potential energy part of the total energy of each molecule is noticeable, and is no longer negligible. The kinetic energy of the in the the molecules at the top of the box and the molecules at the bottom of the box are different, in the additive fashion of kinetic energy plus potential energy equals a constant total energy. (constant and the same for each within Boltzmann distribution.)
(Image: Throw a molecule upwards in a large empty box. At the top of the arc it is momentarily stationary in the up and down direction; zero kinetic in the up-down direction. When you throw it and then after it comes down, when it hits the bottom of the box, it has maximum kinetic energy after it leaves your hand and before it hits the bottom of the box. And it has minimum potential energy when it momentarily stops on the bottom of the box. Next arrange a bunch of molecules with a small distance between each of them, in a line straight up from you. Hold them in place against gravity with a conservative force. Call it ‘electrical force’. Call the arrangement of molecules ‘solid matter’. Now throw a molecule up, the same as you threw the molecule the first time, against the bottom molecule of the ‘solid’. Notice that each molecule, between collisions, has the same speed at each height as the first molecule did when you threw it straight up. This is conservation of energy and conservation of momentum. It is universally true. The same idea applies for loose molecules bouncing around the box, call them ‘gas’, but it is harder to explain.)
2) Molecules with the same kinetic energy and different total energy in a box would be molecules with the same temperature at the top of of the box as the temperature of molecules at the bottom of the box. If the box is large in the direction of gravity, it takes some work put the molecules in that arrangement, if you start from an arrangement of molecules as is in the first box. It takes some work to maintain the arrangement of the molecules in the second box. If you stop working at keeping them arranged, the molecules tend to arrange themselves as the molecules in the first box are arranged. There is something about this in “Thermodynamics”, a principle or law or something, but I don’t know about it since I never studied “Thermodynamics”!
Publius Maximus says at 1/27 6:48am:
:…gravity is a force which decreases entropy. It concentrates matter and energy into stars and planets and galaxies and galaxy clusters.”
Here Publius wanders off the top post Fig. 1 and 2 – quite a long way. Unfortunately the decrease entropy statement here deserves some pushback which I see it has already received.
This is the root cause of Stephen Hawking & the longer thread than this one over his winning the bet with Preskil and Kip Thorne that black holes will evaporate & entropy would not decrease (i.e no information lost to universe in black hole – the info. is eventually returned).
2nd law allows the no entropy change case so that’s all we need here, Hawking radiation hijacks the thread.
Other than that, I share your views: gas column is non-isothermal philosophically so far. No one has cited a formal proof although I am running down some Rodrigo Caballero ref.s.
PS: I agree Joules Verne posts could get trapped in spam filters & takes time to rescue. JV contributed a bunch of logical thinking & ref.s. Some of my posts go up in 15 minutes, at other times ~3 hours. Busy moderators is all, doing a fine job keeping threads more readable around here than otherwise.
Tim,
the arrows ate my quote of you, I quoted your 1) and 2) boxes question;
Either
1) Atoms have the SAME total energy, but atoms on the same box can be at different temperatures, or
2) Atoms have DIFFERENT total energy, but atoms in the same box are the same temperature.
Doug Cotton says:
January 26, 2012 at 6:06 pm
That’s not what I said at all. Strawman much? What I said was that absorption lines or bands would not be observed if the emitter was the same temperature as the gas, not that absorption wouldn’t occur. Spectralcalc actually managed to screw this up a while back.
Here’s the relevant emails:
and the reply:
Claes Johnson has proved nothing. Now back you go onto my do not feed list.
Dr Brown
I think I see the problem. I think that you are saying that you can exchange a cool particle at the top of your conductor for a hot particle at the bottom of your conductor, with no net work. And there you see a violation of the second law.
This idea is just another box with a door between the hot and the cold side. Consider all the real differences between the the hot particles on the bottom and the cold particles on the top, and I think you’ll see the daemon.
Robert Brown says:
January 26, 2012 at 8:58 pm
Nitpick:
It depends on what you mean by local and equilibrium. The air your house will always be in Local Thermodynamic Equilibrium because it’s extremely unlikely that the temperature gradient will at any point will be large enough for the molecules at that point to not obey MB statistics. The existence of a temperature gradient alone is not sufficient to cause LTE to not be applicable.
Myrrh says:
January 27, 2012 at 5:02 am
“Earth without any atmosphere: -18°C
Earth with our atmosphere: 15°C
Earth without water: 67°C”
I come up with similar figures but think there are adjustments to that. 1) All are numbers that assume clouds and ice are the same; 2) I think there is a significant error using Stevenson screens and one meter below surface ocean measurements. While those are our climate, without cloud and ice changes, they are not accurate for calculating surface radiation. What the adjustments would be is if you remove water the planet would be hotter and if you remove an atmosphere the surface would be closer to 0degC (corresponding to closer to 341 watts/m2 average incoming.)
The Clausius form of the Second Law of Thermodynamics simply says:-
” No cyclic machine, may have no other effect, than to transport heat from a source at one Temperature, to a sink at a higher Temperature. ”
That’s it; it doesn’t say any gobbledegook about equipartitions of energy or gravity, or Einstein’s theory of relativity; either special or general, or QED, or Maxwell’s equations, or even the big bang.
The “cyclic” part implies that there MUST be a possible transport of “heat” in BOTH DIRECTIONS.
And by both directions we can presume that means that there is a terminus which Clausius calls “source”, and also a terminus which he calls “sink” and presumably the degenerate case of those termini being conincident is excluded (as juvenile).
So source —> sink is one possible direction of transport, and source <— sink is another possible direction.
The Clausius statement declares that absent any other effect , "heat" can only move from HOT to COLD. Now that means NET HEAT FLOW ; because the CYCLIC condition implies that it is not impossible for heat to go from cold to hot; just not unaided (by doing work) or else MORE heat is going the other way at the same time.
The work done part is the "no other effect" part, that can't coexist with a net cold to hot flow.
And if you can't properly sort out all the negatives in there, then you NEED to hit the ENGLISH text books as well as the PHYSICS ones.
Let's consider conduction of "heat" ; howabout in a metre long Aluminium bar that is one square cm crossection. Just for kicks, I could choose Prof Bob Brown's silver wire, just to annoy all you doubters; but his nice electric and thermal conductor is not as good a choice as Aluminium for my experiment; or I could use "Battleship Plate" ; ordinary structural steel.
So I have one end (hereafter known as the hot end) stuck in a mug of MacDonald's Hot coffee, and the other end, held slightly higher in the air by a simple string sling, attached to the ceiling. so that end is at room Temperature (hereafter known as the cold end).
So far as we know, nothing else is happening, but "heat" (net) is flowing by itself from the hot end in the coffee to the cold end in air.
But what does that mean ? Well it means that the hot coffee is raising the Temperature of the Aluminium molecules at the hot end of the bar, so the mean molecular vibration kinetic energy, is higher than up at the cold end. Those more energetic molecules bang into their neighbors, and get them more riled up than they were, raising their Temperature, and they repeat the process of banging into their colder neighbors to get them going.
You see the "HEAT" that is flowing is nothing more nor less than those chaotic molecular vibrations and collisions with some local average KE value.
Now I have something else attached to my "cyclic machine". Glued onto the hot end of my bar, on the end face, I have a sealed piezoelectric transducer; basically a microphone; and it is wired to a plug that plugs into my Karaoke machine or ghetto blaster (your choice), so I can listen to sounds in the bar.
Well the vibrations of the molecules due to the Macdonald's hot coffee are too high in frequency for me to hear in my hifi.
So now I take one of those little triangular rubber hammers that the doctor raps on your knee for $150, and I tap the upper cold end of the bar with it; no not with the rubber end silly; turn it around and hit the bar with the handle, or just use a teaspoon if you aren't a doctor (I'm not).
Wow !! I get a beautiful metallic ringing sound in my speakers; demonstrating conclusively that molecular vibrations at the cold end of my bar, can and do propagate by chain migration from the cold end of the bar to the hot end. And rest assured that the random molecular vibrations at the cold end of the bar, are also communicated to their slightly warmer next door neighbors when they collide with them, and so on, and so forth.
Yes thermally induced vibrations of molecules can and do transmit to their neighbors in EVERY direction, even from cold end to hot end; but since the vibrational energy of the molecules is higher at the hot end, than at the cold end, the process of INCREASING the vibrational energy of the neighbors only happens from hot to cold. It takes a refrigerator that uses other energy to do work (some other result) to get "heat" to flow from the cold end to the hot end (AND HEAT IT UP).
PS Prof Bob's silver wire is too ductile to ring nicely, which is why I chose Aluminium.