Guest post by Robert G. Brown
Duke University Physics Department
The Problem
In 2003 a paper was published in Energy & Environment by Hans Jelbring that asserted that a gravitationally bound, adiabatically isolated shell of ideal gas would exhibit a thermodynamically stable adiabatic lapse rate. No plausible explanation was offered for this state being thermodynamically stable – indeed, the explanation involved a moving air parcel:
An adiabatically moving air parcel has no energy loss or gain to the surroundings. For example, when an air parcel ascends the temperature has to decrease because of internal energy exchange due to the work against the gravity field.
This argument was not unique to Jelbring (in spite of his assertion otherwise):
The theoretically deducible influence of gravity on GE has rarely been acknowledged by climate change scientists for unknown reasons.
The adiabatic lapse rate was and is a standard feature in nearly every textbook on physical climatology. It is equally well known there that it is a dynamical consequence of the atmosphere being an open system. Those same textbooks carefully demonstrate that there is no lapse rate in an ideal gas in a gravitational field in thermal equilibrium because, as is well known, thermal equilibrium is an isothermal state; nothing as simple as gravity can function like a “Maxwell’s Demon” to cause the spontaneous stable equilibrium separation of gas molecules into hotter and colder reservoirs.
Spontaneous separation of a reservoir of gas into stable sub-reservoirs at different temperatures violates the second law of thermodynamics. It is a direct, literal violation of the refrigerator statement of the second law of thermodynamics as it causes and maintains such a separation without the input of external work. As is usually the case, violation of the refrigeration statement allows heat engines to be constructed that do nothing but convert heat into work – violating the “no perfectly efficient heat engine” statement as well.
The proposed adiabatic thermal lapse rate in EEJ is:
where g is the gravitational acceleration (presumed approximately constant throughout the spherical shell) and cp is the heat capacity per kilogram of the particular “ideal” gas at constant pressure. The details of the arguments for an adiabatic lapse rate in open systems is unimportant, nor does it matter what cp is as long as it is not zero or infinity.
What matters is that EEJ asserts that 
in stable thermodynamic equilibrium.
The purpose of this short paper is to demonstrate that such a system is not, in fact, in thermal equilibrium and that the correct static equilibrium distribution of gas in the system is the usual isothermal distribution.
The Failure of Equilibrium
In figure 1 above, an adiabatically isolated column of an ideal gas is illustrated. According to EEJ, this gas spontaneously equilibrates into a state where the temperature at the bottom of the column Tb is strictly greater than the temperature Tt at the top of the column. The magnitude of the difference, and the mechanism proposed for this separation are irrelevant, save to note that the internal conductivity of the ideal gas is completely neglected. It is assumed that the only mechanism for achieving equilibrium is physical (adiabatic) mixing of the air, mixing that in some fundamental sense does not allow for the fact that even an ideal gas conducts heat.
Note well the implication of stability. If additional heat is added to or removed from this container, it will always distribute itself in such a way as to maintain the lapse rate, which is a constant independent of absolute temperature. If the distribution of energy in the container is changed, then gravity will cause a flow of heat that will return the distribution of energy to one with Tb > Tt . For an ideal gas in an adiabatic container in a gravitational field, one will always observe the gas in this state once equilibrium is established, and while the time required to achieve equilibrium is not given in EEJ, it is presumably commensurate with convective mixing times of ordinary gases within the container and hence not terribly long.
Now imagine that the bottom of the container and top of the container are connected with a solid conductive material, e.g. a silver wire (adiabatically insulated except where it is in good thermal contact with the gas at the top and bottom of the container) of length L . Such a wire admits the thermally driven conduction of heat according to Fourier’s Law:
where λ is the thermal conductivity of silver, A is the cross-sectional area of the wire, and ΔT=Tb–Tt . This is an empirical law, and in no way depends on whether or not the wire is oriented horizontally or vertically (although there is a small correction for the bends in the wire above if one actually solves the heat equation for the particular geometry – this correction is completely irrelevant to the argument, however).
As one can see in figure 2, there can be no question that heat will flow in this silver wire. Its two ends are maintained at different temperatures. It will therefore systematically transfer heat energy from the bottom of the air column to the top via thermal conduction through the silver as long as the temperature difference is maintained.
One now has a choice:
- If EEJ is correct, the heat added to the top will redistribute itself to maintain the adiabatic lapse rate. How rapidly it does so compared to the rate of heat flow through the silver is irrelevant. The inescapable point is that in order to do so, there has to be net heat transfer from the top of the gas column to the bottom whenever the temperature of the top and bottom deviate from the adiabatic lapse rate if it is indeed a thermal equilibrium state.
- Otherwise, heat will flow from the bottom to the top until they are at the same temperature. At this point the top and the bottom are indeed in thermal equilibrium.
It is hopefully clear that the first of these statements is impossible. Heat will flow in this system forever; it will never reach thermal equilibrium. Thermal equilibrium for the silver no longer means the same thing as thermal equilibrium for the gas – heat only fails to flow in the silver when it is isothermal, but heat only fails to flow in the gas when it exhibits an adiabatic lapse in temperature that leaves it explicitly not isothermal. The combined system can literally never reach thermal equilibrium.
Of course this is nonsense. Any such system would quickly reach thermal equilibrium – one where the top and bottom of the gas are at an equal temperature. Nor does one require a silver wire to accomplish this. The gas is perfectly capable of conducting heat from the bottom of the container to the top all by itself!
One is then left with an uncomfortable picture of the gas moving constantly – heat must be adiabatically convected downward to the bottom of the container in figure 1 in ongoing opposition to the upward directed flow of heat due to the fact that Fourier’s Law applies to the ideal gas in such a way that equilibrium is never reached!
Of course, this will not happen. The gas in the container will quickly reach equilibrium. What will that equilibrium look like? The answer is contained in almost any introductory physics textbook. Take an ideal gas in thermal equilibrium:
where N is the number of molecules in the volume V, k is Boltzmann’s constant, and T is the temperature in degrees Kelvin. n is the number of moles of gas in question and R is the ideal gas constant. If we assume a constant temperature in the adiabatically isolated container, one gets the following formula for the density of an ideal gas:
where M is the molar mass, the number of kilograms of the gas per mole.
The formula for that describes the static equilibrium of a fluid is unchanged by the compressibility (or lack thereof) of the fluid – for the fluid to be in force balance the variation of the pressure must be:
(so that the pressure decreases with height, assuming a non-negative density). If we multiply both sides by dz and integrate, now we get:
Exponentiating both sides of this expression, we get the usual exponential isothermal lapse in the pressure, and by extension the density:
where P0 is the pressure at z=0 (the bottom of the container).
This describes a gas that is manifestly:
- In static force equilibrium. There is no bulk transport of the gas as buoyancy and gravity are in perfect balance throughout.
- In thermal equilibrium. There is no thermal gradient in the gas to drive the conduction of heat.
If this system is perturbed away from equilibrium, it will quickly return to this combination of static and thermal equilibrium, as both are stable. Even in the case of a gas with an adiabatic lapse rate (e.g. the atmosphere) remarkably small deviations are observed from the predicted P(z) one gets treating the atmosphere as an ideal gas. An adiabatically isolated gas initially prepared in a state with an adiabatic lapse rate will thermally equilibrate due to the internal conduction of heat within the gas by all mechanisms and relax to precisely this state.
Conclusion
As we can see, it is an introductory physics textbook exercise to demonstrate that an adiabatically isolated column of gas in a gravitational field cannot have a thermal gradient maintained by gravity. The same can readily be demonstrated by correctly using thermodynamics at a higher level or by using statistical mechanics, but it is not really necessary. The elementary argument already suffices to show violation of both the zeroth and second laws of thermodynamics by the assertion itself.
In nature, the dry adiabatic lapse rate of air in the atmosphere is maintained because the system is differentially heated from below causing parcels of air to constantly move up and down. Reverse that to a cooling, like those observed during the winter in the air above Antarctica, and the lapse rate readily inverts. Follow the air column up above the troposphere and the lapse rate fails to be observed in the stratosphere, precisely where vertical convection stops dominating heat transport. The EEJ assertion, that the dry adiabatic lapse rate alone explains the bulk of so-called “greenhouse warming” of the atmosphere as a stable feature of a bulk equilibrium gas, is incorrect.
Bill Hunter says:
January 26, 2012 at 10:14 pm
What the atmosphere does radiate is what lowers it to 33K GHE. If GHG make a difference its likely a cooling difference.
Via the Water Cycle, it lowers it 52°C from the 67°C the real greenhouse would be without it, this being the thermal blanket of the real gas fluid ocean atmosphere of mainly nitrogen and oxygen around our Earth:
Earth without any atmosphere: -18°C
Earth with our atmosphere: 15°C
Earth without water: 67°C
Real gas and not imaginary ideal, as average is imaginary construct?
What we need to do with these academic climate scientists is take them outside and introduce them to the real world.
And then get them to not only bring back into their fictional energy budget, KT97 and ilk, the Water Cycle, but to bring back the thermal infrared heat on the move from the Sun as the real world direct heat source for land and oceans, and, to give back to shortwave which they claim does this in place of thermal energy direct from the Sun, its real properties and properties, its chemical energy cycle, that store which slow releases heat back into the greenhouse atmosphere by recycling Life.
In an earlier comment I suggested that Hans Jelbring’s theory was based on a fairly obvious fallacy. No-one seems to have responded to that suggestion, either for or against it, so I will have one more go, then shut up.
The proposition underlying Jelbring’s theory is that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy.” It seems to follow from this that if one form of energy, such as gravitational potential energy, is high, then others, such as kinetic energy (and therefore heat), must be low.
Jelbring gives no source for this key proposition, and it is not obviously true. Much depends on what is meant by “in an average sense”. Over a sufficiently long period of time, it follows from the equipartition theorem and other principles of statistical mechanics that every molecule in a gas will have the same average kinetic energy, the same average potential energy, and the same total energy, as any other molecule. It is like a game of pure chance in which every player will, in the long run, be a winner as often as a loser.
But in the short run this is by no means the case. Most players will have some fluctuations of fortune, and a few will have long streaks of good or bad luck. The same is true of molecules in a gas. In any given reference frame, at any given moment, some molecules will have a lot of kinetic energy and others little or none. They will also vary in their direction of motion from one moment to the next. In a gravitational field they will all have a tendency to ‘downward’ motion, but as a result of collisions with other particles, and with the ground, at any given moment about half of all molecules will be going ‘up’. Purely by the laws of statistics, some molecules will have a long streak of upward movements. In the absence of thermal convection currents, or other mechanisms of mass transport, those molecules which are ‘high’ in the atmosphere are there as a result of a sequence of accidents. There is no reason to suppose that they will have ‘given up’ kinetic energy in exchange for higher potential energy. In general, they will have gained potential energy at the expense of other molecules, which will have lost kinetic energy, potential energy, or both, in their collisions. In a zero-sum game, for every winner there is a loser.
In Jelbring’s idealised model system, there is no localised heat source to drive convection currents, and the position of molecules in the atmosphere will, I think, be due entirely to the statistical fluctuations I have just described. There is no reason to suppose that molecules higher in the atmosphere will, on average, have lower kinetic energy. Jelbring’s ‘proof’ of a temperature gradient is therefore invalid, as it depends on a premise which (depending on interpretation) is either false or inapplicable to the circumstances (because something true in the long run is being invalidly applied in the short run).
This does not rule out some other version of the ‘gravitational’ theory being true, but it does not bode well.
It is apparent that the writer is a physicist and not an engineer.
Take the thought experiment = a very long cylinder with a gas and a silver wire (assumed to be a perfect conductor) running from low in the cylinder to the top of the cylinder and claimed to cause a problem with the lapse rate explanations.
The assumption that is false in this ‘experiment’ is that the silver to gas heat conductivity at the top of the cylinder is the same as that as at the base of the cylinder. This is an error and the assumption is false.
The ‘temperature’ of a gas (if you must use a compound term) is a measure of the total kinetic energy of the molecules in the volume of gas being measured. The silver will be heated by transfer of kinetic energy by collisions with the gas molecules at the base. As the pressure is higher at the base there will be more gas to silver collisions than at the top of the cylinder where the pressure is lower. Therefore the silver at the top of the cylinder will have fewer collisions and thus fewer gas molecules will receive any kinetic energy and be heated. The ratio of the number of collisions at the base to the number at the top is dependent on the pressure differential. I would expect that if this experiment were to be done the silver might be heated but the different conductivity to the gas at the bottom and the top would be the same as the lapse rate.
The thought experiment is based on a false assumption. If the experiment was built the result would actually support the existence of a lapse rate and there would be no ‘extra heat’ to be transferred downward.
Physicists should avoid using compount metrics like temperature and instead use the actual underlying measurement of heat. In a gas heat is not the same as temperature this is a type error. Even a physicist should remember the gas laws.
In a great many ways. I learned to visualize multiple frames at once at a young age. The only particular thing I disagree with is, “God does not play dice with the Universe”. My terminology, however, is sometimes sloppy.
Einstein was misquoted on that one, or rather, interrupted before the end. In his little known apocryphal autobiography, he apparently confessed to a close friend afterwards that he meant to add “… but Ifni does!” 😉
rgb
Willis Eschenbach says:
January 26, 2012 at 11:08 pm
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
How effecient would it be if it was the heat one wanted to maximise?
From the arizonavortex.com link I gave: “A vortex tube is a tool that can take normal compressed air and convert into two air streams. One stream is hot air and the other stream is cold air. The beauty of the vortex tube is that it has no moving parts , which translates into no maintenance. The cold air can be adjusted down to -50 degrees Fahrenheit, and the hot side can be adjusted up to a temperature of 260 degrees Fahrenheit.”
Could the cold air be re-introduced into the compression chamber?
..the price of oil here, looking for alternatives…
There’s also, “A plasma vortex can be made through the interaction of electric and magnetic fields.”
http://www.rmcybernetics.com/projects/experiments/experiments_vortex.htm
I think you have intentionally distorted the claim that gravity is the cause of the temperature lapse to mean whatever you wish, so that you may claim that gravity is supplying heat, when all that is necessary is for gravity to redistribute heat..
Oh, sure, I’m doing this all intentionally. In fact, I secretly get money from the IPCC — they are paying me to pretend to “debunk” all of the superlative science that appears on this blog. Hell, with my last paycheck from them I bought a Hummer, because (like the rest of the conspirators) I secretly know that the Greenhouse effect is bunkum. You’ve caught me out.
Now that we’ve established that to your satisfaction, perhaps the other adults on the site and I can hold a conversation about the actual topic of the top post. Or you could say something like “Gee whillikers rgb, you sure are right about that Jelbring paper but y’know, I think that gravity is still somehow turning the Earth’s atmosphere into a giant refrigerator. I can’t exactly say how, because I don’t really know how refrigerators work, especially refrigerators that rely on pure radiation for rejection of heat during their cyclic operation and it all makes my head hurt to try to figure it out and explain it in a way that would actually convince somebody (you know, with algebra and Navier-Stokes and everything) but it really is fun to talk about it as if I did know.”
I could then say, “Wowsers. Maybe we need another thread to talk about ways other than manifestly second law violating processes that gravity could contribute on some other top post thread, as soon as you are ready to make a concrete suggestion with some actual physics in it!” And we could part friends, and I could go back to my Evil Masters for another payoff. I was thinking of adding a nitrous tank to my hummer and jacking up its suspension, and my kids gotta eat.
So how about it? Would that work for you?
rgb
The proposition underlying Jelbring’s theory is that “Nature will redistribute the contained atmospheric energy (using both convective and radiative processes) until each molecule, in an average sense, will have the same total energy.” It seems to follow from this that if one form of energy, such as gravitational potential energy, is high, then others, such as kinetic energy (and therefore heat), must be low.
And this is close to being correct, but it isn’t absolute gravitational potential energy that matters, it is the amount that gravitational potential energy involved with the “irreversible” part of thermal motion as molecules fluctuate on a characteristic length scale of the mean free path.
He does have the “same” idea right; he just doesn’t understand the zeroth law. Temperature is the definition of “same”. When the temperature is the same, the capacity of randomized energy trapped in the system, that is, “heat” to do work is minimized. It is the maximum entropy state. At this state, no work can be extracted via a heat engine because there are no reservoirs of heat in the system at different temperatures.
This is all really pretty simply explained in intro thermo textbooks. If people (including Jelbring) stopped trying to reinvent thermodynamics to suit a desired conclusion and instead applied it the other way around, to check their unproven hypothesis, it would be better all around.
Here, I’ll reduce it to a one line “elevator speech”. If a supposed equilibrium distribution of temperature in an isolated system is capable of doing work, it is neither an equilibrium distribution nor is the system at maximum entropy.
One sentence. In the table-thumping words of Johnson, Thus I refute you.
rgb
My name comes up 81 times in this thread, so I thought I’d chip in.
Much confusion seems to have been generated by the sentence in Sec 2.3 of my lecture notes which reads “we expect the particles to accelerate as they travel downwards, and slow down as they travel upwards, rather like a bouncing ball. Mean velocities will be greater near the bottom of the box than near, the top: in other words, pressure decreases with height”. People seem to have interpreted this as automatically implying non-isothermal temperature profiles in thermodynamic equilibrium. This conclusion is wrong and unwarranted. Note that my sentence only mentions pressure: in hydrostatic equilibrium, pressure must decrease upwards, but temperature (which depends on both pressure and density) is unconstrained. For an isolated gas subject to gravity, thermodynamic equilibrium implies an isothermal profile; this was proved by Gibbs already in the 19th century (see recent discussion by Verkley and Gerkema, J. Atmos. Sci. 2004).
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
I’m glad that you’ll be able to offer us an expert perspective on the Ranque-Hilsch vortex tubes, especially given that the principle of operation is currently debated. Please show the mathematical model used to describe the principles by which the vortex tube operates. Further, please explain how this model differs from the “gravito-thermal” hypotheses using the governing thermodynamic equations for the equilibrium states.
Jules Verne
Be careful of logic traps that involve ‘fixed laws’, as you were invited to do. As Q Daniels has just noted, correct formulaic representations of reality are not necessarily correct in all projected circumstances. Robert has invited to you play on a field which he has circumscribed, layering on the arguments that you can’t prove your assertions using formulas he chooses. Perhaps. There is a principle involved: common formulas are (usually) inaccurate representations of a partially understood truth. There is little point in restricting your thinking during a debate to those existing formulaic representations of reality about an impossible but interesting postulated atmosphere. Y’unnderstand? If you are building bridges, it’s OK, but we are discussing something at the limits of our understanding of the physical universe. Suspect all formulas.
As several people have pointed out above, general physical laws apply in very particular conditions. There are many 3=5 arguments one can make by carefully using or misusing physical ‘laws’ that are hard to detect. Einstein is often held up as the perfect genius who was proven right, yet he was not only incorrect, or apparently incorrect about many things, he held many doubts about his own work and thought many contemporaneous perspectives as transitory.
My point is that in order to move beyond current understanding of something, you have to be prepared to move outside the cloistered world of standard formulas and see if they really are applicapable to and work normally in the postulated scenario. Much confusion above is contributors trying to get their head around an unreal planet with some physical laws suspended. We have enough problems dealing with the one reality we have let alone a plethora of unrealities.
Will a cylinder of non-radiative gases in free space achieve isothermal balance? Yes.
In a gravitational field? Unproven.
In a very strong gravitational field? No.
In any real, physical planet? Never.
Now let’s move along.
Robert Brown says 1/26 9:15pm and 10:12pm:
“The entire purpose of the paper is to examine Fourier’s Law…”
Great posts Robert, thank you.
In my view 1) way better than the top post, 2) focusing on air column heat flow from delta T is productive, 3) the thermo grand masters knew of it yet they were still perplexed.
It will take me some work to rummage thru top post eqn. 2, Joules posted paper, and present logic as to why in the limit this delta T must be non-isothermal. Can’t wait for my copy of Boren text to come in.
In the meantime, here’s my counter summary of those views in favor of the column being non-isothermal discovered up thread:
1) 1st Law (cons. of energy) and 2nd Law (constant entropy process is ideally permitted)
2) Caballero (except maybe not see his post at 1/27 6:07am)
3) Velasco eqn. 8 – Joe Born posts
4) Joules Verne posts
5) Robert Brown view that ideal molecules can climb gravity at constant velocity is unsatisfying. How do they possibly maintain constant velocity (i.e. T) as they go up, defeating bouyancy? Nothing I know of does that. Including Earth’s atmosphere.
However against this list, Willis’ writes there are issues with the 0th law and Robert Brown POV Fourier law in the limit as delta T approaches 0 & I see those are valid.
Woo-hoo, Rodrigo Caballero is here now too, with some more ref.s. More homework to find why those molecules can climb up in gravity field at constant speed, constant T even though “Mean velocities will be greater near the bottom of the box than near, the top..”
Science discussion here made my down time recovering from a head cold last few days very much more enjoyable. Thanks WUWT.
A basic assumption from the second law is that all the molecules in the system have, on average, an equal amount of energy. That is the state of maximum entropy and the state which is obtained at equilibrium.
It is incontestable that molecules in the upper shell have more gravitational potential energy than those in the lower shell. Therefore, to satisfy the second law that all molecules on average have an equal amount of energy, the molecules in the lower shell must possess some form of energy, on average, equal and opposite to the gravitational potential energy in the upper shell.
Robert Brown has used pages and pages of obfuscation to conceal the fact that all the molecules in his fully relaxed atmosphere have, on average, equal amounts of energy.
Until he explains how this unequal apportionment is possible without violating the first law of thermodynamics then I must conclude that Jelbring is absolutely correct. The only problem I have with Jelbring is conflating the lapse rate with a greenhouse effect. A greenhouse effect raises the surface equilibrium temperature above what it would be without the greenhouse effect. The lapse rate they demonstrate does not do this and so should not be labeled a GHE.
And by the way, Jelbring was far from the first to make this argument. Its originator was James Clerk Maxwell (yes, THAT Maxwell of fundamental physics fame) in 1866. He has not been disproven in the intervening 150 years. Handwaving about one of the many obscure restatements (the “refrigerator statement”) of the second law does not qualify as a proof. In fact there is no first principle in physics that prohibits a perpetuum mobile of the second kind. Only perpetuum mobiles of the first kind are prohibited by the first law of thermodynamics (conservation of energy).
What the good professor should come to understand is that gravity is a force which decreases entropy. It concentrates matter and energy into stars and planets and galaxies and galaxy clusters. Without it the universe would be a homogenous soup with far more entropy than we see today. It should there come as no surprise that when you introduce gravity into a thermal equilibrium environment that your thermal equilibrium will be upset. However this is no violation of the second law which, in its primary form, states that energy will be equally distributed. It does not state that kinetic energy will be equally distributed. The kinetic energy qualification is added into restatements of 2LoT and those restatements are not necessarily universally true. This case I believe casts grave doubt if not outright proves that the refridgerator restatement of 2LoT is not universally true.
Well then, thank you Dr. Caballero, and incidentally, thank you very much for your fine online book — I’m using it teach myself at least a decent amount of physical climatology (where I can focus on the climatology parts per se, as most of the basic physics I already know pretty well). I’ve put my own intro physics textbooks online for free as well, but I haven’t finished (more honestly, I’ve barely started) writing the third volume which will contain thermo. Eventually I may stick a bit of atmospheric thermo in there, as it seems that this is both of general interest and something undergrads probably should know in order to make informed political decisions.
It will be interesting to see if even your post makes a difference, though. If you read through the whole thread — something you might find actually painful — you will find people who are willing to invoke anything — last night general relativity in order to preserve the illusion that gravity alone creates a warming of the bottom of the atmosphere, even in the absence of external heating, so “there is no Greenhouse Effect”.
That’s actually the part of your book I learned the most from, so far. I hadn’t worked out how the GHE was supposed to work in any sort of detail before I read it, but that chapter was completely illuminating. The IR spectroscopy you present says it all.
But that is a matter for discussion in another thread. Unless any of the many, many people who have argued against the conclusion that Jelbring’s work is completely wrong and should have never been accepted in the first place wish to keep arguing, perhaps the more polite ones can concede in one last post and we can wrap this up and move on to N&Z, the “existence” of a real, live GHE, and maybe, just maybe, get to where the skeptical arguments on the list are much better informed and less likely to play fast and loose with the laws of nature or thermodynamics.
rgb
Robert Brown
It would be wrong to conclude that all those who are unconvinced by the isothermal distribution are sceptics.
Jim D who posted earlier is a very effective proponent of IPCC science and is unconvinced.
Willis (a sceptic) moved from adiabatic to isothermal in one week.
The issue has no bearing on the existence or otherwise of a greenhouse effect.
I can see both arguments for and against each position.
I think the isothermal argument is the stronger one but until an experiment confirms it one way or another I will keep an open mind.
1 kg of air contains a total energy value of 90,000,000,000,000,000 joules – about what the Earth recieves from the Sun in 40 minutes.
The radiation theory assumes that the 1 kg of air is absorbing 390 joules/second of energy from the warm surface and emitting 390 joules/second of energy up and out.
There is a lot of energy contained in that air that is apparently doing nothing. It is permanently locked up in the atomic structure of the air and contibutes nothing to its temperature. Only the fusion energy produced in the Sun is affecting its temperature.
Nice tidy story. (ignoring 99.9999999999996% of the energy in the air).
Crispin in Waterloo says:
January 27, 2012 at 6:22 am
“Jules Verne”
It’s Joules Verne. I know Joules Verne. Joules Verne is a friend of mine. Joules would like you to know that he is no longer participating in this thread because his comments were being purposely held up such his ability to rejoin and rebut was unfairly hampered. I speak in his stead for the time being unless and until the same fate befalls me.
The case for the lapse rate can be made in few sentences in Jelbrings isolated non-convecting atmosphere of ideal gases. Molecules in the upper shell have more gravitational energy than molecules in the lower shell. In order to satisfy the second law requirement that a closed system will equalibrate to a state of maximum entropy all molecules must, on average, have an equal apportionment of energy. Therefore, if the upper shell molecules have more gravitational energy than those in the lower shell then what form of energy do the lower molecules possess to make them have an equal amount of energy? The answer is clearly that the lower shell has more kinetic energy but I’m certainly open to arguments that it’s some other form of energy. What I’m not open to hearing is that the second law allows disequal apportionment of total energy in an equilibrium state which is, in essence, what Dr. Brown (whether he realizes it or not) is saying.
here is a principle involved: common formulas are (usually) inaccurate representations of a partially understood truth.
Well put, Crispin. In this case in particular, the correct formulae are the full nonlinear Navier-Stokes equations with external forcings, implemented in a full thermal model of the Earth. Alas, as I have noted, mathematicians cannot yet even prove formal existence of general solutions to the NS equations, let alone provide a constructive general solution. They are solvable in various special cases, many that are relevant and interesting, but the full problem is beyond our current ability to fully compute.
That doesn’t, however, mean that the laws of thermodynamics are an inaccurate representation of a partially understood truth, or that the foundations of statistical mechanics are particularly shaky. It just means that the general description of open systems, especially open fluid systems, is a hard problem.
The reason I focussed on Jelbring is that here there is no shakiness or partial understanding. He constrains his conclusions to a specific model where they violate the zeroth and second law of thermodynamics. In fact, they are a textbook violation of it, one that one could fairly assign as a homework problem in any undergraduate introductory physics course that covers thermodynamics:
Problem 6: An insulated container of ideal gas is prepared. No external work is done on the container. The container is left on the table for a very long time, so that its contents reach thermal equilibrium from whatever initial state they might have had. Show that it is impossible for the equilibrium state of the gas to exhibit a stable macroscopic thermal gradient across the gas, because such a state would enable a violation of both the Kelvin-Planck and Clausius statements of the Second Law.
That’s basically been the “assignment” for all of the people seeking to defend Jelbring throughout this thread.
Now Crispin, if you are trying to say that the laws of thermodynamics are, like the Pirate Code, not so much laws as “suggestions” (because one way to avoid the conclusions of an argument that you don’t like is to reject its axioms, after all) you might want to soberly reconsider that statement. A whole lot of baby getting thrown out in all that bathwater, don’t you think? Not to mention the fact that anyone that actually tries to live their life as if they really don’t believe in the laws of thermodynamics will find life ugly, brutish, and remarkably short.
Oh, the hell with my knowledge of heat capacity, conductivity, and so on. I’ll just reach my hand down into the vat of seething oil and pull my french fries out one at a time, shall I? What can go wrong?
rgb
19th century (see recent discussion by Verkley and Gerkema, J. Atmos. Sci. 2004).
ZP says:
January 27, 2012 at 6:19 am
As one of the few people who have personally built, tested, modified, measured, played around with and experimented with the Ranque-Hilsch vortex tube, I can say from personal experience that they don’t shed any light on the various “gravito-thermal” hypotheses, because the vortex tubes operate on very different principles than those claimed for the gravity theories.
I’m glad that you’ll be able to offer us an expert perspective on the Ranque-Hilsch vortex tubes, especially given that the principle of operation is currently debated. Please show the mathematical model used to describe the principles by which the vortex tube operates. Further, please explain how this model differs from the “gravito-thermal” hypotheses using the governing thermodynamic equations for the equilibrium states.
====
Ah reminded. Meant to ask too, but just stop at “because the vortex tubes operate on very different principles than those claimed for the gravity theories”
How are they very different principles?
1 kg of air contains a total energy value of 90,000,000,000,000,000 joules – about what the Earth recieves from the Sun in 40 minutes.
All very erudite, of course. Now if you could be so good as to make a point somewhere in there? Not that there aren’t any number of good points to be made — thermal equilibrium and heat simply ignores energy bound up in ways that cannot participate in the thermal redistribution of internal energy changes. If you cooled the gas to absolute zero, it would still have almost all of this baseline mass-energy. So let’s just agree to subtract it out as completely irrelevant to a discussion of thermodynamics, unless the “air” in question is inside the core of a star that is in the peculiar state where it is fusing oxygen and nitrogen or sometimes fissioning them with fast neutrons (the only processes I can think of that might change their baseline mass-energy by altering their strong nuclear interaction energy).
rgb
Robert Brown says:
January 26, 2012 at 4:24 pm
“That’s why I hold out some hope for GR. That’s a difficult problem — if you warp space and time with a very large mass, you do have a bit of a problem defining temperature as energy itself gets a bit warped along with space and time as you go down into the well. However, in this case:
a) The effect is utterly negligible in any real gas for anything less massive than a star.
b) It probably cannot be measured. Your thermometers follow the same gradient as one goes up and down, and they would probably still read the same temperature as temperature itself would probably be following the curvature of spacetime.
c) It is completely irrelevant to the discussion at hand, involving a simple ideal gas in an ordinary vertical column with constant g.”
Not too difficult. Proper temperatures in thermal equilibrium scale as the redshift climbing out the gravitational well. T(height)/T(infinity) =z(height)/z(infinity) = (v(escape)/c)^2/2 for v<<c. The corresponding lapse rate is just T/g.
So (a) yes (except perhaps for something like a mini black hole).
But (b) is not so. Proper temperature is defined and measured locally; the materials whose temperature one is measuring don't know squat about the depth of the well – or care. Their intrinsic physical properties stay the same – the triple point of water is still 273.16K, for instance. So ordinary thermometers will work fine. However, if you measure the temperature of the column bolometrically from any given height, what you see will always be isothermal at equilibrium. It goes without saying that there is no way of extracting energy from this – or perhaps it doesn't go without saying here, so I'll say it!
As for (c), I quite agree.
You might be interested in reading this story , which explores some of the oddities of an extreme relativistic environment.
By the way, is there a tutorial somewhere in how to write those nifty equations recognised by wordpress? What is this latex thingy? Is it a specific markup language?
Drat, I meant:
The corresponding lapse rate is just Tg.
Mod, can you fix please?
DavidB says:
January 27, 2012 at 5:27 am
The source is the second law of thermodynamics which Jelbring probably assumes the reader is familiar with – a closed system tends towards maximum entropy. It is not obviously true it’s an empirical observation. It’s statistically true. In fact there are no first principles in physics which demand it be universally true and it’s not true at all at the microscopic level where a gas in equilibrium will have a Boltzmann distribution of energies. The second law is only statistically true. The second law is all that gives rise to the arrow of time. At the microscopic level there is something called quantum unitarity which means, in a nutshell, that everything that happens can unhappen and it’s all perfectly predictable with sufficient information. This is also called time-reversible. Time can run backwards in other words and it’s only the second law, tendency towards increasing entropy, which gives time a direction. That time exists and has a direction is an empirical observation and, notably, is not something proven or even predicted by theory.
This comes as a shock to most people as it seems to go against our most strongly held intuitions about how the universe works. The fact of the matter is that we don’t have a theory of everything and the universe still contains unexplained mysteries at even the most fundamental levels – levels like “What produces the arrow of time?” and levels like “Why is the universe expanding at an increasing rate?”.
That said, the law of entropy is very well supported by observation at the macroscopic level and is a basic law that engineers use every day to design the modern conveniences of life. However, entropy is about total energy not justy kinetic energy. This is where the author of the OP goes off the rails. He appears to think it’s fine that molecules in the upper shell have more total energy, on average, than molecules in the lower shell so long as average kinetic energy is the same. This is a grand departure from the second law which others have mentioned. Maximum entropy is all molecules (on average, not at the microscopic level) have equal total energy TE = PE + KE. Dr. Brown is ignoring PE and using pages and pages of obfuscation and thought experiments trying to cover up this departure from first principles.
What puzzles me is why he’s going to such lengths. Perhaps he’s just defending a concept he’s taught for many years and can’t stand the idea of having taught something that was wrong. Or perhaps he’s convinced that a perpetuum mobile of the second kind is impossible and thinks he’s better than every physicist in the world who’s tried to prove that and failed. I don’t know what his major malfunction is but the blather that’s emerging because of it is flawed at the level of first principles and takes but a few sentences to dispute.
Dr. Brown,
Gravity is an organizing force that decreases entropy in a closed system? True or False?
Support your answer.
My answer is “true”. Gravity works very well to take equal distributions of mass within a given volume and clump it together. Maximum entropy is limited, at least in the short term, by gravity. Perhaps in 100,000 trillion years entropy will win. Perhaps it will not. That’s still an open question as the universe appears to poised on knife edge of expanding forever (called The Big Chill) and eventually reversing (called The Big Crunch). Personally I think it’s the big crunch for philosophical reasons explaining why the universe emerging from the big bang was so low in entropy.
A steady state atmosphere of a planet will have a atmospheric laps rate. The temperature difference is not a violation of the second law. The temperature difference cannot be exploited to do work. The atmosphere particles have the same energy, high and low, heavy or light. There is no energy difference to exploit to do work.
Try a one dimensional model (so no operators are necessary). Have a left-right axis and uniform force from the left to the right. Put a particle on the axis and set it in motion (either direction, it doesn’t matter). The farther the particle is to the right, the faster its speed is, the farther the particle is to the left, the slower its speed is.
Now turn the model on its ear, and turn the axis to the up and down direction. Make the uniform force go from up to down, and call it ‘Gravity’. Again set a particle in motion on the axis. Now the higher it goes, the slower it moves, and the lower it goes, the faster it moves.
Set a particle in motion on the axis and calculate its Lagrangian from its initial state. ( Lagrangian = kinetic energy + potential energy ). Then observe the particle anywhere else on the axis and calculate its Lagrangian. It is the same everywhere, and always the same. Energy and momentum are conserved.
Put a reflector at the bottom of the axis, and call it ‘the Earth’. Put a few more particles in motion on the axis, or a whole bunch more particles in motion on the axis (elastic particles) and call them ‘gas’. Call the kinetic energy part of the Lagrangian, call it ‘temperature’. The system of particles will eventually evolve to a steady state condition with a up and down temperature profile. You can call it ‘atmospheric lapse rate’.
There is no mechanism that can exploit the difference in kinetic energy between the high particles and the low particles. The parts of any mechanism are subject to the same force ‘gravity’, and the same Lagrangian. It is hard to believe, but a sliver bar that goes from the ‘earth’ to the top of the ‘gas’ will not transfer or move any energy from the bottom of the gas to the top of the gas. The bar is just different elastic particles, moving different speeds and smaller distances between collisions. The only mechanism for energy transfer is particles bouncing off of each other.
The real atmosphere has radiation and phase changes, as well as elastic collisions. But the where the distance between particles is smaller, elastic collisions predominate for energy transfer, and hence a atmospheric lapse rate below the tropopause. Where the distance between the particles is larger, radiative transfer of energy predominates. At the smallest densities, the equation of state of the gases is a radiative condition. Consider cosmic microwave background radiation and 20 billion year old gases 😉
edit to make the first paragraph more clear. Read it as: “Put a particle on the axis and set it in motion (either direction, it doesn’t matter). The farther the particle moves to the right, the faster its speed is, the farther the particle moves to the left, the slower its speed is.” I hope that makes more is more understandable!
A basic assumption from the second law is that all the molecules in the system have, on average, an equal amount of energy. That is the state of maximum entropy and the state which is obtained at equilibrium.
) is constant. The entropy can only increase or, in the limit of a reversible process, remain constant. 
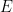is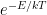 
. But this takes you from the realm of trying to do stat mech by making english word pronouncements to using algebra, and it is actually rather difficult algebra. Good luck with it.
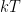. You could also work on understanding that. In fact, as an exercise, why not express the size of the energy fluctuation associated with gravity when a molecule moves a mean free path in terms of temperature? What is the gravitational scale height where:
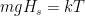
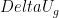for changes in height commensurate with the mean free path of air molecules. We’ll be enormously generous here — the mean free path at room temperature is order of a few tens of nanometers, but it increases as the pressure decreases with height by an order of magnitude or so. We’ll be very generous and use a whole micron — 
meters.
for the range of temperatures in between 200-300 K? We could work hard and do a lot of multiplication or we could observe that this is just the exponential of the ratio of the scale heights: 
where I threw away the pesky $5$ because it doesn’t really matter, does it.
is huge) at cold temperatures and large fields (so 
is small) and large thermal gradients (so the scale factors themselves change dramatically across the system. In this extremely irrelevant case, look, gravity can become important! Sort of. Not enough to prevent thermal equilibrium from being isothermal (because that would violate the second law of thermodynamics) but sort of.
No, you’re begging the question. There is no basic “assumption” in the second law beyond sufficient particles with enough interaction for energy added to the system by any means to get shared around, given time.
What it tells us about how they get shared around is that the state of maximum entropy, the stable thermodynamic equilibrium, is the state where the internal energy of the system is no longer available for doing work. Nothing more, nothing less. To quote from an actual textbook on thermodynamics:
For an isolated system, i.e., a system that has no interaction with the surroundings, changes in the system have no effect on the surroundings. In this case, we need to consider the system only, and the first and second laws become:
For an isolated system the total energy (
Note that this says nothing about “all the molecules have an equal amount of energy”. It says that the total energy of the isolated system doesn’t change, and any changes wrought within the isolated system must either increase its entropy or leave it unchanged.
The equilibrium state of the system, the maximum entropy state, is always isothermal because it is rather easy to show that if there is any temperature gradient, a) moving heat from the hotter part to the cooler part will increase the system entropy (and decrease the temperature difference) while b) moving heat the other way will decrease the entropy of the system and hence is forbidden by the second law — as long as the transport mechanism is irreversible.
Heat conduction is irreversible. It is always present in any system that does not have actual physical (adiabatic) barriers in it. Ideal gas in a container most definitely conducts heat. Therefore it will always relax, via conduction, to a maximum entropy state with uniform temperature which, not at all coincidentally, is the state where the system no longer has any capacity to do work.
If you want a much more correct statement connecting the distribution of energy in the system and temperature, it is that the non-normalized probability of finding the system in any particular energy configuration
In almost all cases in the real world, uniform gravitation can be completely ignored and contributes almost nothing to the final thermal distribution of energies in the system, because the change in gravitational potential energy across the scale of the mean free path (or other relevant interaction/motion length in a solid) is much, much smaller than
or
So you can check your work:
http://en.wikipedia.org/wiki/Scale_height
Yes, it is more than 5 kilometers throughout the temperature range of the troposphere, almost 9 kilometers at room temperature around 300K.
Now compare
Now, here’s the interesting part. What is
If we use a taylor series expansion on this, which is a multiplicative factor in the Boltzman factor (sums in exponentials become products of exponentials) the result looks like — would that be 1? To 9 significant digits? It would.
That’s why people ignore gravity as a general rule when worrying about the thermodynamic equilibrium state of a column of air. Because it is utterly ignorable. The only exceptions are when people are examining very dilute gases (so
We can do this all day. Or, you could go try to learn some thermodynamics, or alternatively some statistical mechanics, instead of just making something up. Just a thought.
rgb