Last month we introduced you to the new reference site EverythingClimate.org
We would like to take advantage of the brain trust in our audience to refine and harden the articles on the site, one article at a time.
We want input to improve and tighten up both the Pro and Con sections, (Calling on Nick Stokes, etc.)
We will start with one article at at time and if this works well, it will become a regular feature.
So here’s the first one. Please give us your input. If you wish to email marked up word or PDF documents, use the information on this page to submit.
Measuring the Earth’s Global Average Temperature is a Scientific and Objective Process
Pro: Surface Temperature Measurements are Accurate
A new assessment of NASA’s record of global temperatures revealed that the agency’s estimate of Earth’s long-term temperature rise in recent decades is accurate to within less than a tenth of a degree Fahrenheit, providing confidence that past and future research is correctly capturing rising surface temperatures.
….
Another recent study evaluated US NASA Goddard’s Global Surface Temperature Analysis, (GISTEMP) in a different way that also added confidence to its estimate of long-term warming. A paper published in March 2019, led by Joel Susskind of NASA’s Goddard Space Flight Center, compared GISTEMP data with that of the Atmospheric Infrared Sounder (AIRS), onboard NASA’s Aqua satellite.
GISTEMP uses air temperature recorded with thermometers slightly above the ground or sea, while AIRS uses infrared sensing to measure the temperature right at the Earth’s surface (or “skin temperature”) from space. The AIRS record of temperature change since 2003 (which begins when Aqua launched) closely matched the GISTEMP record.
Comparing two measurements that were similar but recorded in very different ways ensured that they were independent of each other, Schmidt said. One difference was that AIRS showed more warming in the northernmost latitudes.
“The Arctic is one of the places we already detected was warming the most. The AIRS data suggests that it’s warming even faster than we thought,” said Schmidt, who was also a co-author on the Susskind paper.
Taken together, Schmidt said, the two studies help establish GISTEMP as a reliable index for current and future climate research.
“Each of those is a way in which you can try and provide evidence that what you’re doing is real,” Schmidt said. “We’re testing the robustness of the method itself, the robustness of the assumptions, and of the final result against a totally independent data set.”
https://climate.nasa.gov/news/2876/new-studies-increase-confidence-in-nasas-measure-of-earths-temperature/
Con: Surface Temperature Records are Distorted
Global warming is made artificially warmer by manufacturing climate data where there isn’t any.
The following quotes are from the [peer reviewed] research, A Critical Review of Global Surface Temperature Data, published in Social Science Research Network (SSRN) by Ross McKitrick, Ph.D. Professor of Economics at the University of Guelph, Guelph Ontario Canada.
“There are three main global temperature histories: the United Kingdom’s University of East Anglia’s Climate Research Unit (CRU-Hadley record (HADCRU), the US NASA Goddard’s Global Surface Temperature Analysis (GISTEMP) record, and the US National Oceanic and Atmospheric Administration (NOAA) record. All three global averages depend on the same underlying land data archive, the US Global Historical Climatology Network (GHCN). CRU and GISS supplement it with a small amount of additional data. Because of this reliance on GHCN, its quality deficiencies will constrain the quality of all derived products.”
As you can imagine, there were very few air temperature monitoring stations around the world in 1880. In fact, prior to 1950, the US had by far the most comprehensive set of temperature stations. Europe, Southern Canada, the coast of China, the coast of Australia and Southern Canada had a considerable number of stations prior to 1950. Vast land regions of the world had virtually no air temperature stations. To this day, Antarctica, Greenland, Siberia, Sahara, Amazon, Northern Canada, the Himalayas have extremely sparce if not virtually non-existent air temperature stations and records.
“While GHCN v2 has at least some data from most places in the world, continuous coverage for the whole of the 20th century is largely limited to the US, southern Canada, Europe and a few other locations.”
Top panel: locations with at least partial mean temperature records in GHCN v2 available in 2010.
Bottom panel: locations with a mean temperature record available in 1900.
With respect to the oceans, seas and lakes of the world, covering 71% of the surface area of the globe, there are only inconsistent and poor-quality air temperature and sea surface temperature (SST) data collected as ships plied mostly established sea lanes across all the oceans, seas and lakes of the world. These temperature readings were made at differing times of day, using disparate equipment and methods. Air temperature measurements were taken at inconsistent altitudes above sea level and SSTs were taken at varying depths. GHCN uses SSTs to extrapolate air temperatures. Scientist literally must make millions of adjustments to this data to calibrate all of these records so that they can be combined and used to determine the GHCN data set. These records and adjustments cannot possibly provide the quality of measurements needed to determine an accurate historical record of average global temperature. The potential errors in interpreting this data far exceed the amount of temperature variance.
“Oceanic data are based on sea surface temperature (SST) rather than marine air temperature (MAT). All three global products rely on SST series derived from the International Comprehensive Ocean-Atmosphere Data Set (ICOADS) archive, though the Hadley Centre switched to a real time network source after 1998, which may have caused a jump in that series. ICOADS observations were primarily obtained from ships that voluntarily monitored sea surface temperatures (SST). Prior to the post-war era, coverage of the southern oceans and polar regions was very thin.”
“The shipping data upon which ICOADS relied exclusively until the late 1970s, and continues to use for about 10 percent of its observations, are bedeviled by the fact that two different types of data are mixed together. The older method for measuring SST was to draw a bucket of water from the sea surface to the deck of the ship and insert a thermometer. Different kinds of buckets (wooden or Met Office-issued canvas buckets, for instance) could generate different readings, and were often biased cool relative to the actual temperature (Thompson et al. 2008).”
“Beginning in the 20th century, as wind-propulsion gave way to engines, readings began to come from sensors monitoring the temperature of water drawn into the engine cooling system. These readings typically have a warm bias compared to the actual SST (Thompson et al. 2008). US vessels are believed to have switched to engine intake readings fairly quickly, whereas UK ships retained the bucket approach much longer. More recently some ships have reported temperatures using hull sensors. In addition, changing ship size introduced artificial trends into ICOADS data (Kent et al. 2007).”
More recently, the temperature stations comprising the set of stations providing measurements used in the GHCN have undergone dramatic changes.
“The number of weather stations providing data to GHCN plunged in 1990 and again in 2005. The sample size has fallen by over 75% from its peak in the early 1970s, and is now smaller than at any time since 1919. The collapse in sample size has not been spatially uniform. It has increased the relative fraction of data coming from airports to about 50 percent (up from about 30 percent in the 1970s). It has also reduced the average latitude of source data and removed relatively more high-altitude monitoring sites. GHCN applies adjustments to try and correct for sampling discontinuities. These have tended to increase the warming trend over the 20th century. After 1990 the magnitude of the adjustments (positive and negative) gets implausibly large. CRU has stated that about 98 percent of its input data are from GHCN. GISS also relies on GHCN with some additional US data from the USHCN network, and some additional Antarctic data sources. NOAA relies entirely on the GHCN network.”
To compensate for this tremendous lack of air temperature data, in order to get a global temperature average, scientists interpolate data from surrounding areas that have data. When such interpolation is done, the measured global temperature actually increases.
NASA Goddard Institute for Space Studies (GISS) is the world’s authority on climate change data. Yet, much of their warming signal is manufactured in statistical methods visible on their own website, as illustrated by how data smoothing creates a warming signal where there isn’t any temperature data.
When station data is used to extrapolate over distance, any errors in the source data will get magnified and spread over a large area2. For example, in Africa there is very little climate data. Say the nearest active data station from the center of the African Savannah is 400 miles (644km) away, at an airport in a city. But, to cover that area without data, they use that city temperature data to extrapolate for the African Savannah. In doing so They are adding the Urban Heat Island of the city to a wide area of the Savanah through the interpolation process, and in turn that raises the global temperature average.
As an illustration, NASA GISS published a July 2019 temperature map with 250 KM ‘smoothing radius’ and also one with 1200 KM ‘smoothing radius.3’ The first map does not extrapolate temperature data over the Savanah (where no real data exists) and results in a global temperature anomaly of 0.88 C. The second, which extends over the Savanah results in a warmer global temperature anomaly of 0.92 C.
This kind of statistically induced warming is not real.
References:
- Systematic Error in Climate Measurements: The surface air temperature record. Pat Frank, April 19, 2016. https://wattsupwiththat.com/2016/04/19/systematic-error-in-climate-measurements-the-surface-air-temperature-record/
- A Critical Review of Global Surface Temperature Data, published in Social Science Research Network (SSRN) by Ross McKitrick, Ph.D. Professor of Economics at the University of Guelph, Guelph Ontario Canada. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1653928
- NASA GISS Surface Temperature Analysis (v4) – Global Maps https://data.giss.nasa.gov/gistemp/maps/index_v4.html
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
LaMagna, C. (2018). A Comparison of Daily Temperature-Averaging Methods: Spatial Variability and Recent Change for the CONUS, Journal of Climate, 31(3), 979-996. Retrieved Feb 25, 2021, from https://journals.ametsoc.org/view/journals/clim/31/3/jcli-d-17-0089.1.xml
A paper less than 3 years old.
Its not just that hoping that averaging will cancel out random variations, even if there were no changes to sites that were spread evenly around the globe, is amateurish. They essentially reconstruct an ideal record from a proxy for an intensive property using a method borrowed from mining that is meant for a real intensive property.
Its not just that mean of min/max is randomly, but not perfectly randomly, different from a mean of continuous measurements by a range larger than warming during the past 100 years, even the latter is the result of the effects of not only changing sunlight but moving air. The minimum temperature is of a packet of air long gone by the time the maximum is reached. Its not an intensive property. Your thermometers need to move with the air for that. So the mean of min/max or hourly readings are proxies.
I would expect a good record, ie no site changes and an even spread around the globe, to give a useful average for how the global climate has changed, but barely better than qualitative.
15 years ago, sceptics argued that global temperatures warmed 0.6 degrees in 100 years and most was before 1940. Adjustments of few tenths of a degree and its no longer an issue?
I think AR4 had a line about consensus that at least half the warming since 1950 was due to human emissions. That’s 0.3°C out of a degree since the start of the IR, give or take a few tenths.
“A paper less than 3 years old.”
I posted such an analysis nearly 7 years ago here
https://moyhu.blogspot.com/2014/07/tobs-pictured.html
There is a considerable difference, but mainly it depends on the time of day the min/max is read. It can be higher or lower than the continuous measurement.
The fact is, of course, that most of the data we have available is min/max.
“The fact is, of course, that most of the data we have available is min/max.”
Woah! Another whopper!
There are all kinds of stations around the world that have multiple temperature readings per day clear back to 2020, ranging from 1 minute intervals to 5 minute intervals!
Since climate is dependent on the *entire* temperature profile, an integral of the daily temperature profile at each station would give significantly better indications of the actual climate at each station. This is commonly known as a degree-day.
Since this data *is* available and is a far better metric than max/min why aren’t the so-called climate scientists using it?
They failed second-year calculus?
I suspect that most of them are not physical scientists but applied mathematicians and computer programmers. They don’t even know the right questions to ask let alone to put in their models.
If the best data available is not fit for purpose, then it isn’t fit for purpose.
Using ever more fanciful algorithms to tease the answer you want from poor data isn’t science.
Needed to be done in 1989.
Berkley Earth already examined tens of thousands of surface temp readings and demonstrated that there is no UHI effect biasing the trend.
any article which chooses not to include Berkley results would be dishonest.
I would agree, and I’ve seen plenty of other studies showing a large impact of UHI on surface temp readings.
I can’t remember where it was, but I really liked the study where someone mounted a thermometer to the top of their car and drove through a city. I recall that the temperature climbed about 3-5 degC, peaking in the center of the city, and then dropped to the baseline on the other side of the city. Quite a striking example of UHI.
G’day GregB,
Could well have been about 50 years ago, late 60’s early 70’s. Forrest Mims III in one of the “Archer” booklets sold by Radio Shack. He was investigating the use of thermistors for measuring temperature. He drove his daughter to and from school daily.
[Back in the days of the 741 Op Amp, discrete transistors, and the digital wonderland of the 7400 series of DIP chips. (Dual Inline Plastic)]
And of course Anthony, our ‘get out and test it’ host, did something similar – with modern equipment – in Reno if I remember correctly.
Not again, griff, are you really not able to learn your lessons you get here ?
No, Berkley Earth demonstrated nothing at all.
any article which chooses not to include Berkley results would be dishonest.
When griff gets hold of a good lie, he never lets go.
Berkley Earth’s analysis has been shredded to the point where only a true believer would still quote them.
There are two credible and reliable long term measures of temperature. The first is the Central England Temperature series which is a proxy for global temperature … a far far far better proxy for global temperature than some tree-ring. This not only indicates the long term trend, but also the scale of variability and unless you discuss long term variation, there is no point talking about temperature.
The second less reliable record is the yearly maximum (or minimum) temperature from the very few permanent min/max thermometers situated in areas which have not changed their vegetative cover. The reason it needs to be yearly, is that the yearly max temperature (or min if taking a year as summer to summer) cannot be double counted so there is no reason to apply any adjustment nor any debate about adjustments.
And on the other side … no temperature measurement relying on NASA is credible.
For my part the there are two major issues at stake here:
1) For a trend to have any validity the data collection methods and recording must be CONSTANT over the period which has proved to be not the case in practical terms where the climate is concerned, since changes in the technology, locations and volume of deployment have regularly occurred. The statistical assumptions and manipulations of variable measurements should therefore be treated with a good deal of scepticism.
2) Temperature is but one of many factors of State which influence the enthalpy of a system. It gives no information on that aspect unless the other factors are accounted for. As an example: Two parcels of air of equal mass could have the same enthalpy but if one of the parcels is moving then it will have a lower temperature. Hence whereas the enthalpy remains constant the temperature changes. It is the enthalpy that determines the climate not necessarily the temperature which is merely an indicator.
IMO the concept of a global mean temperature is just that:— a concept with little value in practical terms; but will leave that to others to argue about.
One aspect of temperature readings that is being absolutely overlooked is this:
There is a latency with liquid in glass (LIG) thermometers versus thermistor temperature sensors (TTS).
A transient spike in temperature from a passing hot wind (say from over asphalt) will quickly register with a TTS (well under a minute), while there’s a latency with LIQ (well over a minute). One will record “record setting temperatures” while the other will not.
This alone can explain modern versus historical temperature discrepancies.
In 1920 that “record setting temperature” needed to be sustained long enough for the LIG to register. Not so much for a TTS sensor in 2014.
There are more things that can cause brief warm excursions than can cause cold excursions.
Up to and including jet exhausts.
The main problem is average.temperature. It is well known that nighttime temps have been coming up but daytime high temps have been going down, so the average can be increasing, but only becasue of the increased nighttime temps- all because of increased water vapor as well as urban heat effect. This February at my home in Maine, there were 18 days of below average daytime highs but on those same days, there were 10 days of above average nighttime highs.
“Last month we introduced you to the new reference site EverythingClimate.org”
Even now, it’s pretty good. It can of course be improved but I suggest the focus should be on making it readable to the average person who is never going to dig into the issues deeply. It should be, I think, a “Climate science for Dummies”.
Look at the following: https://www.amazon.com/Cranky-Uncle-vs-Climate-Change/dp/0806540273/
John Cook has made a cartoon book making fun of climate “deniers”. How about a cartoon book making fun of climate alarmists? Or- having “EverythingClimate” do that? I know that some will think that’s not professional and won’t change the minds of alarmists. I doubt anything will- so why try to do it with serious writing when cartoons catch the attention of “the masses”. Just a thought- probably a bad idea. But if I were wealthy- I’d pay someone to do the cartoon book of climate alarmists. Some of the cartoons would be of Cook!
“I know that some will think that’s not professional and won’t change the minds of alarmists.”
I don’t think we should focus on dedicated alarmists. Rather, focus on the undecided, which would probably be made up of a lot of younger people, not set in their ways yet, and open to taking in information.
The “lack of science evidence” is on the skeptics side. I think it has to be very effective to challenge an alarmist to produce evidence and then no evidence is produced. Sensible people can put two and two together.
“John Cook has made a cartoon book making fun of climate “deniers”. How about a cartoon book making fun of climate alarmists?”
The skill sets to do so successfully just aren’t there. You laugh at each other’s non jokes, but they fall flat in superterranea. It’s why “Conservative Comedy” is an oxymoron….
Sorry, ‘cept for P.J. O’Rourke. Where did he go? I had to look on my book shelf to even remember his name….
Assume I’m a skeptical persuer after truth, and searching on the internet for answers I happen to find Everything Climate. At first glance I might think this is going to be a good source of information, but I don’t think it would take me long to get suspicous, not least by the complete anonymity of the place. There’s no indication of who any of the articles are by and the About page leaves me none the wiser. But being skeptical it does start of alarm bells – “EC is a website covering both sides of the climate debate – factually”. This is exactly what someone want’s me to think so I’m going to assume the opposite. Maybe this is a fanatical green organization, maybe big oil, who knows? But my initial assumption is that anyone claiming to represent both sides of a supposed debate, and insisting they will be only using facts, almost certainly won’t be.
Taking this article as an example, it starts by making the statement “Measuring the Earth’s Global Average Temperature is a Scientific and Objective Process”, which already feels like a loaded question. This is followed by what I assume is meant to be “both sides” of the “debate”. But neither are addressing the head-line statement. The question really seems to be “how accurate are global temperature sets?”.
At this point it soon becomes clear that the it’s not exactly covering both sides equally. On the Pro side, a few paragraphs from a NASA press release, with no link to the paper they are referring to. On the Con side a much more extensive set of quotes from what we are assured is a peer reviewed paper.
But reading through the Con part, I get increasing confused as to how much is from the McKitrick paper, and how much is the personal opinion of the anonymous blog post writer. It starts, sure enough, with a blockquote, and there a few other passages in quotes, but much of it is not quoted and doesn’t appear to come from the paper at all. This includes the claim that “Global warming is made artificially warmer by manufacturing climate data where there isn’t any.” and conclusion “This kind of statistically induced warming is not real.” Either these are quotes from the McKitrick paper, or are someones interpretation of the claims, or are original research.
In a world in which disagreeing with a progressive can and often does get one fired. Demanding that actual names be used is no different from a demand that only the government approved opinions be allowed.
Then use pseudonyms. I’m not asking that everyone uses their real names – that would be hypocritical. What I’m saying is that it looks fishy if something claiming to be offering objective non-partisan analysis, has zero indication of whose behind the website. How do I know they really are being objective and are not a cover for some organization or individual with an agenda to prove.
You make excellent points- however, if the logic is solid, it makes no difference who wrote it or who paid for it.
Just two rules of analyzing data in physical science is needed to refute current climate science estimates of climate science.
The last significant digit in any stated answer should usually be of the same order of magnitude (in the same decimal position) as the uncertainty (Richard Taylor, “An Introduction to Error Analysis, 2nd Ed)
The uncertainty of independent, non-correlated data points increases as they are added together in root sum square.
Since the recognized uncertainty for land stations recognized by the federal government is +/- 0.6C the stated value then any temperature stated value from such a station should show no more than an entry in the tenth digit. Any average calculated from multiple such measurements should show nothing past the tenth digit. Thus trying to identify differences in the hundredths digit to show warming is a violation of physical science tenets.
If you add 100 independent, non-correlated temperature values together to calculate an average and each value has an uncertainty of +/- 0.5C then the resulting uncertainty is [ +/- 0.5 x sqrt(100)] = +/- 0.5 x 10 = +/- 5C.
Thus your average becomes useless in trying to identify differences in the tenths or hundredths digit.
Far too many so-called climate scientists want to view these independent, non-correlated temperatures as a common population that can be lumped together in a data set, assumed to be part of a normal probability distribution which is then subject to statistical analysis – i.e. the uncertainty of the total goes down as the number of items in the data set goes up.
That is just a flat-out violation of the tenets of physical science.
Which means the uncertainty in the average is ±0.05°C.
BZZZZT. Try again.
OK, 5 / 100 = 0.05. Do you want me to try yet again or do you want to explain why I’m wrong.
Granted, I’m sure that’s not the exact formula, but the general principle is that as you average more data the uncertainties reduce, rather than increase.
See: https://wattsupwiththat.com/2021/02/24/crowd-sourcing-a-crucible/#comment-3193219
I’m more confused than ever now. According to Tim Gorman the problem is the data is Independent and non-correlated, but your link says the problem is the data is correlated. Of course, if the noise isn’t random you cannot simply divide by √N, but your link only says that at most you are left with the same amount of uncertainty as you would have for an individual station, not as is being claimed that it ALWAYS goes up.
Tell me how temp data in Thailand can be correlated with temp data in Niger?
I don’t agree with Climate Detective about correlation, even for stations only 1 mile apart. Clouds, rain, etc can cause the temp data even for such stations to be vastly different. Depending on terrain they may even be a quite different altitudes.
Temperature data is highly correlated to the angle of the sun in the sky, both north-south and east-west, and to seasonal variation. It is not nearly as correlated with distance. For some stations there may be a high correlation with close stations, for other stations the correlation may be almost zero. And this doesn’t even include the station calibration or the stations uncertainty. The readings from a newly calibrated station may be different than the readings from a similar station located only feet away, let alone miles away.
Unless you can quantify *all* those various factors among all the stations in your “average” that impact correlation, it is far better to assume no correlation.
Think about it, how correlated are the temp measurements taken in the middle of a 3 acre asphalt parking lot compared to a rural station ten miles upwind in a pristine environment? Can you venture a correlation factor at all?
Nobody is saying Thailand is correlated with Niger. They are over 3000 km apart so the correlation is zero. But Washington DC is strongly correlated with Baltimore.
The way to test correlation is to measure it. I have here.
https://climatescienceinvestigations.blogspot.com/2020/06/11-correlation-between-station.html
If you disagree then go and measure the correlations yourself, and remember, these are the correlations between anomalies not actual raw temperature readings. The correlations between raw readings are even higher due to the dominance of seasonal variations.
“Think about it, how correlated are the temp measurements taken in the middle of a 3 acre asphalt parking lot compared to a rural station ten miles upwind in a pristine environment?”
You clearly don’t understand correlations. They measure the synchronous movement of two datasets. They do not compare the means or the relative sizes. The rural and urban stations can have different means but if they are close their weather will be the same, so when the temperature of one goes up, so will the temperature of the other. Even if the amounts are different the correlation will be strong.
Is Pikes Peak temperatures correlated with Denver temperatures? They are only 100km apart. Is the temperature in Valley Falls, KS correlated with the temperature in Berryton, KS? They are on opposite sides of the Kansas River Valley and have significant differences in their weather and temperatures. Or how about San Diego and Romana, CA? They are only 30 miles apart and have vastly different temperatures throughout the year.
Correlation in anomalies is meaningless. The anomalies on Pikes Peak are vastly different than those in Denver. Same with Valley Falls and Berryton. San Diego can be at 65F while Ramona is at 100F, far above the baseline temperature for that area of CA.
Any two geographical points that are far enough apart that sunrise and sunset occurs at different times of the day simply cannot have either their temperatures or anomalies moving in sync. It’s impossible.
What you are trying to do is ignore the time factor that the temperatures are truly correlated to. You can certainly overlay the temperature curve for one location on top of the temperature curve for another location by ignoring the time factor and make them look like they are in sync – but its a false correlation. They simply do not go up and down at the same time. Plot them on a time axis and you will find that one will start up while the other is still going down. Then you will find that one starts down before the other one.
It’s like saying two sine waves that are out-of-phase are correlated. The correlation factor is less than one. Depending on terrain, altitude, and humidity the correlation may be significantly less than one.
Do you understand anomalies? They are calculated relative to each monthly mean of that particular temperature record, not some baseline for the region.
Your point about the time difference is irrelevant because the time scale for the correlation is months not hours or minutes. So there is no time difference.
So what? Anomalies carry a greater uncertainty than either the individual absolute temperature or the calculated mean. The uncertainty of the absolute temp and the baseline temp add by root sum square.
Months? Really? The monthly figures are not made up from daily temperatures? Where do you go to measure a “monthly” temperature?
Correlation has to go all the way down or its no good!
Even the daily mean is derived from Tmin and Tmax. These are time independent. They are not measured at the same time or relative time everywhere so the time lag between two stations is irrelevant.
OMG!
Let’s split your statement up.
“They are not measured at the same time or relative time everywhere”
True!
” so the time lag between two stations is irrelevant.”
Wrong!
You measure the correlation between two data sets by taking their dot product. The temperature profile at a station is close to being a sine wave. You determine the correlation between two sine waves by taking their dot product.
Asin(x) * Bsin(x+p) where p is the phase difference between the two. They are only perfectly correlated when p = 0. when p = 1.57 radians the correlation is zero.
You simply cannot ignore this basic physical fact.
And this is only *time* dependence on correlation.It doesn’t even begin to address geography and terrain dependence on correlation.
But ignoring seems to be a major meme in climate scientists today – ignore uncertainty, ignore how to properly handle time series, ignore that individual temperature measurements are independent and not part of the probability distribution of a random variable, ignore the fact that the earth is not a billard ball!
It’s willful ignorance from the top to the bottom!
“The temperature profile at a station is close to being a sine wave. “
Over what time period?
24 hours? Yes.
365 days? Yes.
Time differences of a few minutes matter for the first set of 24 hour data but not for the second set which is recorded daily. The problem is all the actual historical data was recorded daily not by the second. So it is the 365 day periodicity that matters and the small time difference between neighbouring stations doesn’t. It has no measurable impact.
I’m sorry. I missed this.
“So it is the 365 day periodicity that matters and the small time difference between neighbouring stations doesn’t. It has no measurable impact.”
If it is a time series at the start then it is a time series all the way through. Daily temps are a time series. They get grouped into monthly temps as a time series. Those monthly temps get grouped into an annual temp which becomes part of an annual time series.
So what? The issue is, does the difference in longitude affect correlations? The answer is no because all daily max and min temperature measurements are made relative to local time (i.e the position of the Sun) not GMT.
More properly, what you are calling a mean (which is also the median) should be called the “mid-range” value resulting from Tmin and Tmax.
Agreed. But these values are all we have for most station data before 2000.
However, you can only potentially get a correlation of 1.00 if the values of the two variables have a 1:1 correspondence in value.
And for temperature, if they have a 1:1 correspondence in time.
No.
Two sine waves with the same period and phase difference will have a correlation coefficient of 1.00 even if their amplitudes are completely different, e.g. even if one amplitude is a factor of 1000 greater than the other.
“same period and phase difference”
NO KIDDING? But time differences *ARE* phase differences. Two temperature sine waves with a time difference are OUT OF PHASE!
I don’t think that you are right because the formula for the correlation coefficient has xy co-variance in the numerator and the product of the x standard deviation and y standard deviation in the denominator, and those will differ by a factor of the square root of 1,000.
Basically, a correlation coefficient of 1.00 means that the independent variable is a perfect predictor of the dependent variable. That is, they are equal! They can’t be equal if one is different by a factor of 1,000.
Tim
There can be weak correlation for stations in the same hemisphere and at the same longitude, declining as the difference in longitude increases, until one achieves anti-correlation on opposite sides of the world. There can also be short-term auto-correlation in a time series because of thermal mass, although it is not a given. Trying to untangle that would try the patience of a saint.
Oh, I agree. but *weak* correlation means that has to be accounted for. And it doesn’t appear to be so in climate science.
Untangling things is supposed to be the reason for science. Ignoring factors because it is too hard to untangle them just leads to incorrect science.
This only applies when you have multiple measurements of the SAME THING using the SAME DEVICE. This allows you to build a probability distribution for the results which can be statistically analyzed.
It is a far different thing when you have single measurements of different things by different devices, i.e. independent populations of size one.
I would also point out that the uncertainty of the mean is what is usually calculated statistically. That is based on the assumption that the mean is the true value of a Gaussian distribution. But if the distribution deviates from Gaussian in any way, e.g. the mean and median are not the same, then that assumption may not apply.
Bellman
You mistakenly claimed, “… as you average more data the uncertainties reduce, rather than increase.”
The reduction of the standard error of the mean only applies to random errors. To be sure that one is only dealing with random errors, the property being measured must be time-invariant, it must be measured with the same instrument, and if recorded by a human, by the same observer. Different observers are liable to introduce systematic errors. Therefore, while the precision may be improved by many observers, they will introduce systematic errors that reduce the accuracy, which isn’t the case with a single observer.
It you try to average measurements that vary with time, you are averaging the trend as well as the error resulting from random error. If the trend is increasing strongly, the apparent error will increase over time. If you use different instruments with different calibrations, you can actually increase the error because you are adding systematic changes and not just random changes. There are many caveats that have to be observed to be able to legitimately claim that the precision is improved with multiple measurement.
Now why would you freely admit that you don’t think you provided the correct formula, and yet be so adamant that you understand the “general principle?” Think about it!
I’m assuming any errors are random, but even if they are not and all go in the same direction the uncertainty of the average cannot be greater than the individual uncertainties.
That doesn’t follow at all. If you use the same instrument or observer you are more likely to get a systematic error. What if your instrument is badly calibrated or your observer always rounds up when they should be rounding down.
Again, no idea why you’d think that. A single person is more likely to introduce systematic errors than multiple observers.
We haven’t got on to time series, at present I’m just talking about the uncertainties of averaging 100 independent thermometers.
Doesn’t follow, unless the uncertainty is a percentage, which we are assuming isn’t the case.
Yes, it’s always possible that all errors go the same way, but what I’m trying to establish is why some here think the uncertainties inevitably increase with multiple independent measurements.
Because I didn’t want to get too hung up on the exact formula, because I tend to doubt myself, and because I know how many factors might impact on the formula. And because I wanted to be open to the idea that someone might explain something I hadn’t previously known. General principles are more likely to be correct than abstract formulae, but I like to give people the chance to demonstrate why I might be wrong – remembering the adage about you being the easiest person to fool.
Bellman,
Yes, an observer will almost always create a systematic error from things such as parallax, and a different mental model for rounding off. That will affect the accuracy, but should provide for the highest precision because they will be consistent. However, with multiple observers, the various systematic errors characteristic of the observer may result in some cancellation of accuracy errors, but will result in less precision. It becomes a trade-off. However, without some standard to compare to, it is problematic that the accuracy can be assessed properly. The trick is to be sure that the instrument is calibrated carefully and correctly. Offhand, I’d expect that instrument calibration is going to be done more carefully in advanced countries than in Third-World countries.
OK, I assume it was just an error in your original comment, when you said:
I will stand by my recent statement,
“I’m assuming any errors are random, but even if they are not and all go in the same direction the uncertainty of the average cannot be greater than the individual uncertainties.”
I gave you the answer to this before. Did you not bother to read it? You measure three sticks using three different devices, each with a different uncertainty specification. Say you come up with 8′ +/- u1, 16′ +/- u2, and 24′ +/- u3 where u1<u2<u3. Now you glue them end to end.
What is the overall uncertainty of the overall length with them glued together? u1? u2? u3? u1+u2+u3? root sum square of u1/u2/u3? (u1+u2+u3)/3?
I am assuming you would say u3, the largest. Right?
“That doesn’t follow at all. If you use the same instrument or observer you are more likely to get a systematic error. What if your instrument is badly calibrated or your observer always rounds up when they should be rounding down.”
Every instrument has systematic error. It can’t be avoided. There is no such thing as perfect accuracy with infinite precision. If someone is doing it wrong then you correct the process and redo the measurements. But you see that only works for time-invariant mesurands. How do you go back and remeasure temperature? With temperature you get the uncertainty you get at that point in time and you must do the best you can to identify what that uncertainty is.
“Again, no idea why you’d think that. A single person is more likely to introduce systematic errors than multiple observers.”
You are a mathematician, right? Did you ever take chemistry lab or physics lab or any kind of an engineering lab? If you had you would understand this. Everyone is different and everyone reads and interprets measurements differently. Some have better eyesight or reflexes, some have worse. Some will scootch to the left to read a figure under a meter needle, some to the right – and each gets a slightly different reading, even if a parallax mirror is provided. Some will tighten down a connection screw more tightly than others,changing the resistance between measurand and the measuring device. This is *especially* true when using micrometers where “how tight to screw it down” is a purely subjective decision.
If the same person does the same process over and over all these subjective things will be at least consistent. Some may implement the process better than others but if one person does it then it will still be consistent. It will be far easier for someone else to replicate the measurement consistently even if the difference in measurement is consistently different for each person.
“We haven’t got on to time series, at present I’m just talking about the uncertainties of averaging 100 independent thermometers.”
Every temperature is part of a time series. Why would you think otherwise. What do you think time zones are for? If those 100 independent thermometers are located apart then they are measuring different things at different times! Not only that but each individual station is building a time series when it takes multiple measurements, e.g. Tmax and Tmin occur at different times.
“Doesn’t follow, unless the uncertainty is a percentage, which we are assuming isn’t the case.”
Again, you don’t live in the material world much do you? What happens when you are using a sensor to measure the diameter of a wire being pulled through a die? What happens to that sensor as miles of wire are pulled through it? The apparent error will increase (the wire will appear to narrow) over time as the sensor wears away.
“Yes, it’s always possible that all errors go the same way, but what I’m trying to establish is why some here think the uncertainties inevitably increase with multiple independent measurements.”
For one thing, you have your definition wrong. It’s multiple independent measurements of DIFFERENT THINGS!
After all this time and debate you still haven’t even gotten the definitions correct. You are stubbornly clinging to the idea that all measurements generate random errors that create a probability distribution around a mean – whether it is measurements of the same thing or different things.
“General principles are more likely to be correct than abstract formulae, but I like to give people the chance to demonstrate why I might be wrong – remembering the adage about you being the easiest person to fool.”
General principles are most likely explained correctly by formulas. Like Gauss’ Law. Or Newton’s Law of Gravity. Or the General Equation for the Propagation of Uncertainty.
I keep reading your answers and they keep avoiding the issue. We are discussing the mean not the sum, hence your example of measuring three different sticks is only relevant if we want to know the combined length of the three sticks, not if you want to know the uncertainty in the mean length of the stick.
Because it’s possible to take a single reading? Of course, we are talking about time series to see how temperatures are changing, but at any point we are only interested in the average on a specific day, or time. My point was that the issue we are discussing is how uncertain a specific single average, and don’t want to add needless complications. That’s why it’s better to see how this argument works with heights or other static data.
Yes, but the point I was questioning was the claim that if a series is increasing rapidly the errors would increase.
Firstly, I’m not sure how it’s possible not to have a probability distribution, regardless of what you are measuring. Secondly, I’m not claiming anything about what the distribution is. As a thought experiment, I can assume that all errors are positive and equal to the full uncertainty. The average cannot be bigger than the maximum uncertainty, and this doesn’t matter if you are measuring the same thing with the same instrument, or completely different things with different instruments.
“We are discussing the mean not the sum,”
How do you calculate the mean if you don’t know the length? And if the length has an uncertainty then the mean will also! And remember, like temperatures, you only get one shot at measuring.
“Because it’s possible to take a single reading? ”
And if you take a reading at t0, t1, t2, t3 ….. that doesn’t define a time series?
“but at any point we are only interested in the average on a specific day, or time”
If each measurement is a single reading at a point in time then how do you take its average? The average would be the reading!
You can certainly average all the values over time by integrating the entire temperature profile – but that is not the mid-range of Tmax and Tmin. For the positive part of the curve it is .637Tmax and for the bottom part it is .637Tmin. And I don’t think anyone in climate science is doing that integration.
“My point was that the issue we are discussing is how uncertain a specific single average,”
The uncertainty of a single average with independent components is the combined uncertainty of its components as root sum square.
“Yes, but the point I was questioning was the claim that if a series is increasing rapidly the errors would increase.”
The series is the readings of the sensor. The more time moves on the errors it produces get larger as the sensor wears away. How rapidly the errors grow depends on how fast the sensor wears away. The problem with time series like temperatures is how fast *are* the variances and uncertainties growing over time. Mapping the averages of time separated readings won’t tell you that. The averages hide the variances. That’s why linear regression on time series, especially those concoted from averages are so misleading most of the time.
“Firstly, I’m not sure how it’s possible not to have a probability distribution, regardless of what you are measuring.”
And this is why you don’t understand uncertainty. How did you get a physics PhD without understanding this?
“ As a thought experiment, I can assume that all errors are positive”
And you continue to show your total lack of understanding concerning error and uncertainty. They are not the same!
“The average cannot be bigger than the maximum uncertainty, and this doesn’t matter if you are measuring the same thing with the same instrument, or completely different things with different instruments.”
The average of *what*?
One more time: If I take a thousand readings of a crankshaft journal with a micrometer then some readings will occur more often that others. That means there is a probability distribution associated with those readings. The one that happens most often, if the probability distribution is Gaussian,is most likely the true value. In this case the uncertainties *can* be minimized by statistics, not eliminated mind you, but minimized. No matter how many measurements you take and how carefully you calculate the standard deviation of the mean, that standard deviation will never go to zero.
Now, if one thousand of us take a single, independent reading of one thousand crankshaft journals using different devices and someone asks me what the size of a crankshaft journal is what do I tell them? I don’t even know if all the crankshafts were from the same type of engine. There is no guarantee that the average of all those readings is the true value or even if there is a true value.
The best I can do is to take an average along with the uncertainty estimate for each measurement and tell them that the average size of the journals that were measured is such and such. And the uncertainty in that average is the root sum square of sum of the uncertainties. (the more journals I measure the greater the uncertainty gets because the measurements are not of the same thing).
Now, for an iterative CGM. We assume that the output of the CGM has some kind of relationship with its inputs. So if we do multiple runs of that CGM it should provide a set of outputs that can be averaged to get a more certain output.
The problem is that if the CGM has an uncertainty in iteration 0 then that uncertainty gets put into iteration 1 and it gets larger. So after 100 runs the uncertainty of the final output can actually be bigger than the average of the outputs. And that is the problem with the CGM’s today.
Yes, and I say the uncertainty of the mean is equal to the uncertainty of the length divided by the sample size.
This is getting increasingly weird. Yes of course if you make a time series you have a time series.
I’m really not sure if you are not getting this or just pretending at this point. The average we are talking about is the average of the 100 thermometers.
Agreed. But that’s not what I’m doing in this thought experiment. I have 100 thermometers giving me a single reading, each with an uncertainty of ±0.5°C. I’m adding up all the readings and dividing by 100 and I expect the uncertainty of the average to be less than ±0.5°C, whilst you think it will be ±5°C. I don’t care if each thermometer is recording the temperature at the exact same time, or if they are giving me the max or min or mid point value. I’m just interested in what you think happens when you average anything.
Except your own equations suggest you are wrong.
I didn’t. I think you’re confusing me with Climate Detective. But could you explain how it’s possible to measure anything and not have a probability distribution? You might not know what the distribution is, but it has to exist.
I take uncertainty to mean the bounds of probable errors. I’m not saying errors are the same as uncertainties, but it’s possible to imagine the worst case where every error equals its bounds.
The average of the measurements.
This is a straw man argument. I’ve never said the uncertainties will go to zero.
Which I’m sure is true of crankshaft journals. But nobody is saying the average of 100 thermometer readings tell us what any individual thermometer reads. The average is the goal. It’s what we are trying to estimate by averaging.
This still seems absurd. What if you were measuring millions of the same type of but different crankshafts,each with an uncertainty of 1mm? You cannot tell me the average to within a meter, but if you only averaged 100, you could tell me to within 10mm?
It would help with the rest of the comment if I knew what a CGM was. Maybe you mean GCM, but if so it has nothing to do with this discussion.
“Yes, and I say the uncertainty of the mean is equal to the uncertainty of the length divided by the sample size.”
You only have one sample. The measurements you took. You can’t go back and remeasure a temperature nor can you make multiple measurements of it. You’ve got one chance at it and no more.
So what is your sample size? (hint: 1)
“This is getting increasingly weird. Yes of course if you make a time series you have a time series.”
It isn’t weird. Taking temperatures *have* to be a time series. You can stop time so taking sequential measurements mean you are creating a time series. What’s weird about that?
“I’m really not sure if you are not getting this or just pretending at this point. The average we are talking about is the average of the 100 thermometers.”
Each one of those 100 thermometers are measuring different things at different times. Each one is creating its own time series with sequential measurements of different things. Again, you can’t stop time and measure the same temperature multiple times. Nor can two different stations measure the same thing, you can’t transport the atmosphere being measured at one to another one.
The correct average would be one that uses the temperature at each 100 stations AT THE SAME PRECISE TIME. If they are offset in time then when one is at Tmax the other one won’t be. So the true average will be something less than Tmax. It will be Tmax_1 + (Tmax_2 – x) where x>0. If you use Tmax at both locations, disregarding the time differential then the average temp indicates a higher average than it should if it is trying to represent the condition of the atmosphere at a specific time.
“ I expect the uncertainty of the average to be less than ±0.5°C,:”
You expect the uncertainty to be less than +/- 0.5C because you look at the temperatures as a probability distribution, typically Gaussian, where you can use the standard deviation of the mean to get the mean more accurately – which implies that the mean is the true value and the more accurately you can calculate the mean the more you decrease the uncertainty of what you are measuring. Going along with that is that the measurand must be the same for all measurements and therefore you are building a probability distribution around that measurand.
If the measurand is *not* the same thing then the temperatures do *not* describe a probability distribution. If they don’t describe a probability distribution then the standard deviation of the mean is not applicable. When you combine all of the elements garnered from measuring different things you must use a different method to combine the uncertainties. That method is the root sum square of the uncertainties. And that does not include dividing by the number of measurements – that is used with a probability distribution.
“Except your own equations suggest you are wrong.”
No, they do not. The documentation on the internet is legion about how to do this. Taylor’s “An Introduction to Error Analysis” goes into it in detail. So does Bevington’s “Data Reduction and Error Analysis”. When you say *I* am doing things wrong you are saying *they* are doing things wrong. My equations are right out of their books.
“I didn’t. I think you’re confusing me with Climate Detective. But could you explain how it’s possible to measure anything and not have a probability distribution? You might not know what the distribution is, but it has to exist.”
How can different things generate a probability distribution? We aren’t talking about multiple measurements of different things, we are talking about single, independent measurements of different things. How does that generate a probability distribution? The value at one station is not dependent on the value at another station. You aren’t studying a random variable.
“I take uncertainty to mean the bounds of probable errors. I”
You are still stuck on believing that uncertainty is error. It isn’t. An uncertainty interval has no probability. It doesn’t give you any indication of where the true value actually is, only where it may be. A probability distribution *will* give you an indication of where the true value might be. They are two different things.
“The average of the measurements.”
What does an average of the measurements of different things tell you? When you are looking for an average you are looking for a metric that will tell you something. You can certainly calculate an average of the measurements of different things but that doesn’t mean that average will tell you anything. Think about it. One temperature is 72F and the other is 32F. The average is 52F. So exactly what does that tell you about anything? It doesn’t tell you anything about the 72F temp or the 32F temp. It doesn’t even tell you anything about the climate in between!
“This is a straw man argument. I’ve never said the uncertainties will go to zero.”
You keep talking about the standard deviation of the mean and that is what that process is meant to do. Of course it would require an infinite number of measurements so it’s improbable but that doesn’t have anything to do with the intent.
”
Which I’m sure is true of crankshaft journals. But nobody is saying the average of 100 thermometer readings tell us what any individual thermometer reads. The average is the goal. It’s what we are trying to estimate by averaging”
Again, what does the average tell you? Does it tell you anything about the temperature at each individual station? Does it tell you anything about the temperature at *any* station. You are putting some kind of faith in the average because you view the temps as a probability distribution. But the uncertainty of measurements taken from different things at different times doesn’t create a probability distribution. The average doesn’t tell you that it is the most likely temperature you will encounter.
“This still seems absurd. What if you were measuring millions of the same type ” (bolding mine).
The operative word is *SAME*. But temperatures at different stations are *not* measurements of the SAME temperature, not even the same type of temperature, especially if you are doing a global average. In the case of the same type you can build a probability distribution — IF that same type is made in the same production run. Change the cast, the milling machine, or the milling head and you won’t be measuring the same thing.
Sorry about the acronym mixup, senior moment Of course I am talking about GCM’s. But the GCM’s *are* built to calculate a global average. And they are supposed to be validated against measurements of the global average. But the global average is so uncertain that its wasted effort. Throw a dart against a board loaded with temperatures and you would probably get closer than the global average being measured today.
No I’m saying I suspect you are misinterpreting what they say.
I think we are talking about different things here. When I say a measurement has a probability distribution, I mean there exists an implied distribution, from which the measurement will be taken. You are talking about how you can use multiple measurements to estimate the distribution.
Obviously if you only have one value and no other information it will be impossible to know what the PDF is but it still exists.
And it really doesn’t matter for this argument what the PDF of the uncertainty is. It’s sufficient to know it’s a bound on the error. If it isn’t a reasonable bound and you don’t know the PDF than I’m not sure how useful the concept of an uncertainty measure is. Why say the uncertainty is ±0.5°C, if there’s an unknown chance that the true value could be way outside the uncertainty bound?
Yet for all your formulae saying the global average is meaningless, and the uncertainty could be tens of degrees out, all the actual global estimates show very consistent values. If it was actually nothing more than a random set of averages, why do monthly temperatures never change by 5°C in a single month?
Tim
I have a copy of Taylor’s An Introduction to Error Analysis, which I have been re-reading.
That is an excellent beginning text on uncertainty. It is important to keep in mind the difference between error and uncertainty. The GUM is certainly NOT light reading but it is also enlightening.
I wish I knew where the mistaken assumption originated that the error of the mean defines the precision of the mean (average). It really defines an interval where the mean may lie and that is all. Somehow that interval has become translated into the definition of the precision of the value.
From Bevington and Robinson’s Data Reduction and Error Analysis for the Physical Sciences.
Also, from Taylor’s Introduction to Error Analysis.
You are wrong because when you have INDEPENDENT, NON-CORRELATED data you do *NOT* divide by N to calculate uncertainty.
When combining independent, non-correlated data, each with an uncertainty interval, the uncertainty *ALWAYS* goes up, never down.
You only divide by N when you have dependent, correlated data that forms a probability distribution. Independent, non-correlated data does not represent a probability distribution.
I’m always prepared to accept I might be wrong so could you point me to an explanation of this. Because at first glance it seems obviously wrong. Why does being NON-CORRELATED mean uncertainty will increase as sample size increases? Are you really saying that if I take 100 measurements with independent temperature readings, each with an independent error of ±0.5°C, the average could be out by 5°C?
Maybe I’m just misunderstanding what you are trying to say, but even if every measurement was out by the same amount in the same direction, the average would only be out by the same amount.
That is EXACTLY what I am saying.
First, uncertainty is not error, especially not random error that can cancel. Uncertainty has no probability distribution.
If you have one ruler with an uncertainty to measure one board and a second ruler with a different uncertainty to measure a second board which uncertainty would you use to describe the uncertainty of their sum? Why would you expect the uncertainty to go *down* when you add the the two measurement results together? In fact, the total uncertainty will be some kind of sum of the two separate uncertainties.
Because of the recognition that some of the uncertainties in a large number of independent measurements of different things may cancel, the uncertainties are usually added as root sum square instead of directly added. If you have a situation where you believe this condition to not be true then direct addition of the uncertainties is certainly legitimate.
If you must think of it statistical terms then ask yourself why variances add as root sum square.Just remember that uncertainties don’t have a probability distribution so they don’t have a variance or standard deviation. This is merely an analogy.
Say you have a function f = a + b. let k = partial derivative of f with respect to a. let m = the partial derivative of f with respect to b. let u_a be the uncertainty for a and u_b be the uncertainty for b.
The standard formula for propagation of error is
u_total^^2 = (k)(u_a^^2) + (m)(u_b^^2) + (k)(m)(u_a)(u_b)(r_ab)
where r_ab is the correlation between a and b.
If a and b are truly independent then r_ab = 0, there is no correlation between them. And the partial derivative of with respect to a and b are both one.
Thus the formula is reduced to u_total = sqrt( u_a^^2 + u_b^^2).
And you can extend that out to however many measurements you have. Thus, if u_a = u_b = …. u_n you wind up with:
u_total = (+/-u) (sqrt(n) and for n=100 u_total = +/- 10u.
if u is +/- 0,5C then for 100 stations your final uncertainty is
+/- 5C.
QED.
But everything you are saying there is about summing the data. I’m talking about what happens when you take the average.
Umm, the average is the sum, divided by a constant.
Yes and the difference between me and Tim Gorman, and I assume you, is that I think you also have to divide the uncertainty by a constant. Gorman seems to think that the uncertainty of the total sum will also be the uncertainty of the average. This makes no sense to me and I think is easily refuted.
In Gorman’s example 100 non-corrolated thermometers, each with an uncertainty ±0.5°C are added together to give a combined uncertainty of ±5°C, which is correct, but then he wants to divide the result by 100 to get an average, whilst saying the uncertainty of the average is still ±5°C. The absurdity of this can be seen if instead of 100 thermometers, you had 1,000,000. This would result in an uncertainty on the average of ±500°C. It’s claiming that it’s possible the average of the million thermometers could be much bigger than any individual thermometer reading.
Wow! You just hit the jackpot for why the “global average temperature” is so meaningless.
As you add more and more stations the uncertainty keeps growing. I gave you the standard equation for the propagation of uncertainty. Unless you can show mathematically how that equation is wrong then you are just whining.
Remember, the uncertainty only gives you the interval in which the true value could lie. It doesn’t tell you the true value. If the interval becomes wider than the result you are looking for then you need to redesign your experimental process, there is something wrong with it.
You may not like that but it *is* the truth. It’s the way physical science works.
Can you even quote the standard equation for propagation of uncertainty?
If you have q = Ab where A is a constant, e.g. your number of stations, then the uncertainty terms include the partial derivative of each member on the right side with respect to q.
The partial derivative of a constant is ZERO. So the contribution of the constant to the uncertainty is ZERO.
Why is this so hard to understand?
“Why is this so hard to understand?”
Because it is wrong!
q = Ab
So ∆q = A.∆b + b.∆A
∆A = 0
So ∆q = A.∆b
If A = N (number of stations) and b is the mean of q, then the uncertainty in the mean is N times less than the uncertainty in the sum of the readings q.
So the constant A scales the uncertainty.
QED!
Go look up how to propagate uncertainty of a product.
if f = Ab then you can either use fractional uncertainty or the standard equation for propagation of error.
Let’s do fractional uncertainty.
(∆f/f)^^2 = (∆b/b)^^2 + (∆A/A)^^2
Since (as you admit) ∆A = 0
the ∆A element disappears leaving:
∆f/f = (∆b/b)
You will get the same result using the standard equation for uncertainty since the partial derivative of f with respect to A is zero, the derivative of a constant is zero.
b is a variable, not a constant. Assuming it is a mean leads to b being a constant. The ∆ of a constant is zero. This would lead to the result that f has zero uncertainty – an obvious fallacy.
You *need* to keep your definitions constant throughout your math.
“b is a variable, not a constant.”
Yes!
“Assuming it is a mean leads to b being a constant.”
NO!!! It is a set of means, one for each month. Each one is the sum of N different measurement from N different stations. It is still a variable (or vector); one that is derived from adding other variables (or vectors).
Let’s set A=N and b = m.
f = Nm
m is a variable for the mean temperature each month.
f is a variable for the total of the temperature readings from N different sites each month.
N is a constant.
So the uncertainty in f is
∆f = N.∆m + m.∆N
∆N = 0 because it is a constant.
So ∆f = N.∆m
This means that the uncertainty (and standard deviation) in the set of mean values in a temperature trend is N times less than the uncertainty ∆f in the sum of the individual records f used to calculate the mean value each month. This is because the mean values are all N times less than the f values. In other words the ratios of error to variable are equal for f and m.
∆f/f = (∆m/m)
Well at least you got that bit right!
This means that the uncertainty in each mean value is N times less than the uncertainty in the sum of the values used to calculate the mean, just as the mean m is N times less than f.
But the uncertainty in the sum is √N times more than the uncertainty in a typical data value in the sum because the variances of these datasets add, not the standard deviations. So the uncertainty in the mean will be √N times LESS than the uncertainty in any one of the variables used to calculate the mean (assuming those individual uncertainties are all approximately of the same magnitude) – unless of course the original datasets used in the mean are correlated.
“NO!!! It is a set of means, one for each month. Each one is the sum of N different measurement from N different stations. “
You have (N1 +/- u1, N2 +/- u2, ……, N12+/- u12)
When you sum N1 thru N12 you add the uncertainties by root sum square. N is *not* a probability distribtion. It is 12 independent, uncorrelated data sets of population 1. N1 is not dependent on and does not drive N2, and on through N12, so they *are* independent. Single *values* have no correlation. N1 = {72} is not correlated with N12 = {30}. The covariance between two values is zero – no correlation.
Let me repeat, N1->N12 do *not* represent a probability distribution. They are twelve separate, individual, independent data values taken from separate, individual, independent populations of temperatures. Each has its own uncertainty interval. They are each separate in time. Each population has its own variance and represent independent time series.
Your equations are wrong.
Exactly what does the mean of month 12 (N) multiplied by 12 (the month) supposed to represent anyway?
When you sum the means to find an average mean you get
f = N1 + N2 +…. +N12
What you have are 12 uncertainties associated with those means, u1 to u12. When you sum those root sum square:
∆f = sqrt(u1^^2 + u2^^2 + …. + u12^^2)
—————————–
∆f = N.∆m + m.∆N
∆N = 0 because it is a constant.
So ∆f = N.∆m
——————————-
There is no uncertainty with m, the number of the month! There is no ∆m. There *is* an uncertainty with a calculated mean derived from values with uncertainties.
Nor does the number of the month times the uncertainty in each mean have any meaning, i.e. m∆N. It is a meaningless value.
“∆f/f = (∆m/m)
Another meaningless equation. There is no uncertainty in the number of the month.
Bottom line? Your math skills seem to be atrocious. You can’t even frame the problem correctly let alone assuming that the number of a month has an uncertainty.
Give it up, man. You are losing it.
You got yourself confused again.
Each regional monthly mean is the sum of N measurements for that month, one from each of N stations. The time series for a station is the set of all monthly readings for that station – up to several thousand values from 1701 onwards, not just 12.
The N readings each month are partially correlated. They are NOT independent. They are a population. They are not a normal distribution, but then nothing is. The more data you have the closer you will get to a normal distribution.
Together the N readings describe the temperature of the region – that is the population at time t. The more stations you have and the closer they are together, the more accurately you can determine the mean temperature of the region at time t (the law of large numbers). The same argument applies globally.
You can then apply regression analysis to see how the regional mean temperature evolves over time by comparing the regional means from month to month.
The variance of the sum of all temperatures from the N stations in month i is the sum of the variances for each station temperature. The uncertainty (denoted by ∆f) in that sum (denoted by f) of those N readings is the square root of the sum of variances . The uncertainty in the mean for month i (denoted ∆m) is the uncertainty of the sum (∆f) divided by N because the mean for month i (m) is the sum of the readings (f) divided by N. The two ratios must be the same.
∆f/f = (∆m/m)
“2) You get 12 monthly means no matter how many components are involved. “
If a temperature record is 50 years long and the data is expressed as the mean temperature each month, then there are 600 entries not 12. So every one of the 600 months has its own mean.
“3) Your conventions are confusing. Is N the number of stations or the number of measurements or the number of means?”
No. I tried to make it as clear as possible. N is the number of stations. If you haven’t grasped that everything else you wrote is pointless.
I believe that climate projection is done an an annual basis, not a monthly basis.
But it doesn’t matter. You still malformed your equations. Since each is an independent value you will have a root sum square for the uncertainty of the conglomeration.
So you can’t actually *show* where it is wrong. All you can do is use the argumentative fallacy of Argument by Dismissal.
Not surprising. That’s the typical tactic of those supporting the non-scientific climate science today.
No. Can you point me to an example which is applicable to uncertainty in averages.
I’m really not that interested in the details of approximation theory or the distinction between physical and climate science. What I am interested in is how said theory can result in more uncertainty the bigger the sample size.
I’m prepared to accept I’m wrong if you could explain or show some reference to this paradox, but in the meantime it defies logic. How can the uncertainty of an average of a million thermometers be a thousand times greater than that of any individual reading? How is it possible that averaging a million thermometers could give you a result 500°C warmer than any individual reading?
You keep talking about sample size. Sample size only applies if you are using a common measurand. Then you can take multiple measurements of the same thing and build up a probability distribution. You can then take samples from that probability distribution and calculate a value called the standard deviation of the mean. With multiple samples you can narrow that standard deviation and get a more accurate mean. Be aware, however, that this only works properly if you have a Gaussian distribution. If the mean and median are different then you have a non-Gaussian distribution and other rules apply.
But comparing temperatures at different stations is measuring different things. Each measurement does *not* become a member of a random variable defining a probability distribution. You have multiple data sets of population size ONE.
One situation is: multiple measurements of the same thing.
The other is : single measurements of different things.
If you can’t discern the difference between the two then you would seem to be willfully ignorant.
The uncertainty does *NOT* tell you what the true value (temperature) will be. It only tells you the interval within which the true value (temperature) can lie. Once that uncertainty interval exceeds the quantity you are trying to identify then you may as well stop. E.g. trying to identify a 0.16C difference when the uncertainty interval is +/- 0.5C. The actual true value can lie anywhere in that interval. How do you *know* that the true value is thus 0.16C? Even identifying temperature values in the hundredths digit violates the use of data in physical science. If your temperatures go out to the tenths digit then how do you even identify a temp of 0.16C?
Climate science does it by ignoring uncertainty and its impact on the significant digit in the stated value. They calculate averages and anomalies out to however many digits they need when they should only be calculated out to the tenths digit.
If you don’t care about uncertainty theory and approximation theory then how do you know if you are being led down a primrose path or not?
Never twice the same temperature! You only get one chance to make a good first impression or measure the temperature at a particular instant in time.
Have you read this:
https://wattsupwiththat.com/2017/04/23/the-meaning-and-utility-of-averages-as-it-applies-to-climate/
If the graphics are not showing, left-click on the blank space.
This is Stats 101: you are not averaging multiple independent samplings of the same quantity that have a normal distribution, therefore the standard deviation is not reduced by 1/sqrt(N).
Again, according to the post I was responding to we are averaging independent samplings.
Independent samplings of DIFFERENT THINGS. The air at station A is independent of the air at station B. You aren’t measuring the same thing!
Therefore you cannot build a probability distribution from those measurements.
Nor are you using the same device. This is like saying I can reduce the uncertainty of measuring one thing with two devices and the uncertainty would be reduced by a factor of two.
You keep saying that the statistics change if you are averaging different things, but I fail to see how. You said that all the thermometers have the same uncertainty, why would it make a difference if you are averaging different temperatures with different thermometers, rather than the same thing with the same thermometer.
You have two situations:
The first one can be considered to build up a probability distribution. The measurements become a random variable where the generated values are correlated and can be analyzed using standard statistics for probability distributions.
The second one builds up multiple data sets with a population of ONE size of one. The mean of the population is the measured value. The standard deviation of each population is zero.They are *not* members of a random variable described by a probability distribution.
I only assumed that the thermometers all have the same uncertainty. That is *not* a requirement. It only simplifies calculations. Many thermometers have different uncertainties but most are in the range of +/- 0.5C or greater. For example, the Federal Meteorological Handbook No. 1 only requires an uncertainty of +/- 0.6C for its measurement stations. Even the Argo floats, using thermistor sensors that have a .001C precision, have an uncertainty of +/- 0.5C, since the sensor uncertainty does not define the uncertainty of the overall measuring structure.
Think about it. You have three boards of different lengths. For whatever reason you use three different measurement devices with different uncertainty specifications to measure their lengths. You then glue them together. What is the uncertainty for the overall length? Is it the lowest value of uncertainty? Is it the highest value of uncertainty? Is it the sum of the three uncertainties? Or is it a something like a root sum square of the three uncertainties since some of the uncertainties overlap? Or is the total uncertainty *less* than all three uncertainties summed in some manner?
“The second one builds up multiple data sets with a population of ONE size of one. The mean of the population is the measured value. The standard deviation of each population is zero.They are *not* members of a random variable described by a probability distribution.”
Wrong! If you measure the height of every person in the world you get a probability distribution. Even if you use a different ruler.
When you add all the single, independent measured values, with their attached uncertainties, together you still increase the uncertainty of the mean you calculate. Calculating that mean more and more accurately using the stated values while ignoring the uncertainty that results is only fooling yourself. The stated values are not 100% accurate. So when you calculate the mean from those stated values the resulting mean is not 100% accurate either. You may have calculated the mean more and more accurately but that doesn’t mean the mean itself is more accurate.
That is why it is so important to design such an experiment very, very carefully to minimize the uncertainty associated with each element of the experiment. E.g. measure each person multiple times using the same device so that you can minimize the uncertainty via calculating the mean of the resulting Gaussian distribution for each person. Only then combine the values for each person into a probability distribution with a much smaller uncertainty interval.
“Wrong! If you measure the height of every person in the world you get a probability distribution. Even if you use a different ruler.”
The height of people can be used to build a probability distribution. You *can* analyze this in the statistical manner you wish. I would caution you that what you find for a mean is probably useless because you have mixed incongruous populations. If you were to try and buy coats for the entire world population they would probably only fit a small proportion. Measure all the pygmies and all the Watusis and calculate the mean – what would it actually tell you?
Temperatures are not humans. There is no probability distributions you can build from temperatures. As I said, each location is a a data set of population size one. The mean temperature of two different locations, say Point Barrow and Miami do not tell you anything about the probability of that same temperature appearing anywhere except at those two locations. And the temperature curve at those two locations are time separated so they mean even less! They are not correlated in time at all.
Uncertainty is NOT error; instead it is an indication of the state of knowledge about a numerical result.
Read the GUM.
Uncertainty is an estimate of the likely range of error. I don’t see how that distinction helps in trying to assess the uncertainty in an average. The overall uncertainty in the average cannot be greater than the largest uncertainty in any of the individual measurements because the combined error cannot be greater than any individual error.
Uncertainty is not error. Get that into your head.
Uncertainty is only an interval in which the true value can lie.
And the overall uncertainty of a sum of stated values *DOES* grow!
“the largest uncertainty in any of the individual measurements because the combined error cannot be greater than any individual error.”
See? You are still equating uncertainty with the probability distribution associated with multiple measurements of the same thing.
Uncertainty is *NOT* a probability distribution. There is no probability associated with *any* point in the uncertainty interval.
So the uncertainty of combined measurements can *certainly* be larger than the uncertainty of any individual component!
Which is what I was saying. It’s the range of likely errors.
And we are not talking about sums but averages. But you keep ignoring that distinction.
Then “uncertainty” has no meaning. If uncertainty is “an interval in which the true values can lie”, but you can derive an uncertainty interval that is much bigger than what the true value can lie you clearly have a contradiction, or at least not a serous attempt to determine the best uncertainty bounds. Saying the average height of a person is say 2m, but with an uncertainty interval of ±5m, might be technically correct, but isn’t very useful.
Which is what I was saying. It’s the range of likely errors.
———————————————–
ROFL! You agree uncertainty is not error then turn right round and call uncertainty ERROR!
Did you actually read this before you posted it?
———————————————
And we are not talking about sums but averages. But you keep ignoring that distinction.
———————————————-
Again, ROFL!!!! An average *is a SUM of values divided by the number of values!
I repeat: did you actually read this before you posted it?
“Then “uncertainty” has no meaning.”
Of course it does!!! The fact that you can’t understand it doesn’t imply it has no meaning. It has no meaning *for you* because you refuse to listen!
“but you can derive an uncertainty interval that is much bigger than what the true value can lie”
The uncertainty interval, by definition, is the interval in which the true value can lie. If it’s bigger than what you think the true value could possibly be then that is nothing buy YOUR OPINION! You need to look at what you are doing and figure out why it is wrong! The wrong thing to do is just dismiss the uncertainty analysis!
“Saying the average height of a person is say 2m, but with an uncertainty interval of ±5m, might be technically correct, but isn’t very useful.”
Why isn’t it useful? It tells you that you need to look at the definition of the population you defined and see what is wrong with it. If you make your population 100 pygmies and 100 Watusis you will come up with an average that is meaningless. You can’t use it for anything, like buying coats for the population. You need to look to your population definition! It also means you need to look to your experimental process to see if your measurement process can be improved!
What you are trying to do is rationalize to yourself that the entire global climate determination is *not* filled with statistical error, that the uncertainty of its results is not so wide as to invalidate the outputs. You are trying to tell yourself that your religious faith in CAGW *has* to be right, it can’t possibly be wrong. And so you just deny any evidence that might actually show your religious belief is right.
You admitted you don’t understand propagation of uncertainty. How then can you say it is wrong?
No, I said it was a range of the potential error. Probably could have used more precise language. As you say “Uncertainty is only an interval in which the true value can lie.” If we measure something as having value 10 but we know the uncertainty is ±1, the true value can be between 9 and 11 – the extent by which the true value value differs from our measured value is the error, hence for an uncertainty value of 1, the error is at most 1. Would that be a suitable was of expressing it?
Yes, that’s exactly what I mean by an average – mean to be more precise. And again it all comes down to why you feel you don’t have to divide the uncertainty of the sum by the number of values.
Yes, it’s my opinion that the true temperature of the earth cannot be over 500°C and cannot increase just because you add more measurements.
How many times have I been told that if the data doesn’t agree with the theory you must dismiss the theory.
“why isn’t it useful to know the true average height of a person might be between -3m and 7m, is that the question you are asking?
You seem to be saying that it’s useful as it tells you the averaging process was a fault (as opposed to your propagation equations). You illustrate this with the example of averaging a group of short and tall people, and saying the mean is meaningless. But the problem is your uncertainty calculations apply just as well if all the people are the same height, so if it’s meaningless to average Pygmies and Watusis it’s equally wrong to average any group, and the more people you measure the wronger the result is.
But how exactly is anyone supposed to do that if uncertainties inevitably increase the larger the sample size, either you need to use measurements with zero uncertainty, or make sure your sample size is a small as possible.
I suspect your interpretation of it is wrong, because it produces results that don’t agree with reality.
It isn’t that hard. Take two numbers 10 +/- 1 and 10 +/- 2. What are the low/high values?
11 + 12 = 23
9 + 8 = 17
That is a range of 5 that the sum could lay within. Another way to state that is 10 +/- 2.5.
Which by the way is about the same as the sqrt (1^2 + 2^2) = 2.2 when using RSS.
Not too hard. Although your range should be 6, and sums 20 ± 3.0.
Now what happens when you take the average of those two values?
(11 + 12) / 22 = 11.5
(9 + 8) / 2 = 8.5
Which is another way of saying 10 ± 1.5.
Therefore at most the uncertainty of the average is equal to the average of the uncertainties, and usually less.
This is not how uncertainties work! I’ve given you the standard equation for the propagation of error before! Apparently you are unable to comprehend it.
q = (a + b)/v
let k = partial derivative of q with respect to a
let m = partial derivative of q with respect to b
let n = partial derivative of q with respect to v
let r = covariance of a and b
let s = covariance of a and v
let t = covariance of b and v
Assume a, b, and v are independent so r, s, and t equal 0
(q_u)^^2 = k^^2(u_a)^^2 + m^^2(u_b)^^2 + n^^2(u_v)^^2
Now assume that v is a constant, in this case 2. What is the partial of a constant? ZERO. So n = 0. The third term drops out.
The partial derivatives of k and m = 1.
So the final equation is
( q_u)^^2 = (u_a)^^2 + (u_b) ^^2.
This is the standard way of propagating uncertainty. Go here:
http://physics.gmu.edu/~jcressma/Phys246/PropUncertExample.pdf
It gives a very simple way of calculating uncertainty that you might understand. In case you refuse to understand this example the summary is for the density of a block of material. You have three length measurements with an uncertainty of 3% for each, and one mass measurement with an uncertainty of 1.3%. The uncertainty in the density is sqrt_ (1.3%)^^2 + (3 x 3%)^^2 ] = 9%.
This is such a common process in physics and engineering that it just amazes me every single day that those associated with studying the climate have absolutely no understanding of this principle. It’s like every single person in climate science is an applied mathematician that has never studied physical science at all. How did these people skip Physics 101 in college?
I assume you mean propagation of uncertainties.
You obviously know more about the theory than I do – I am not a physicist, or for that matter a climate scientist. I’m just a layman with a slight interest in statistics. But I still think you must be misapplying the theory, because you are giving my results that do not reflect and cannot reflect reality.
If these results are so obvious in the world of physics, why can you not provide me with a single example explaining how it applies to averaging?
The question is really simple, if you have a sum of a hundred observations with an uncertainty on that sum, why would you not divide the uncertainty by 100 when you divide the sum by 100? Common sense say you should, and the formulae say you should. e.g.
Function
gives 
https://chem.libretexts.org/Under_Construction/Purgatory/Book%3A_Analytical_Chemistry_2.0_(Harvey)/04_Evaluating_Analytical_Data/4.3%3A_Propagation_of_Uncertainty
Bellman, fortunately I am a physicist. And I can tell you that you are 100% correct. I have made the same point below.
https://wattsupwiththat.com/2021/02/24/crowd-sourcing-a-crucible/#comment-3194492
The uncertainty in CGM’s is so high because they carry their iterations out beyond the point that the output becomes more uncertain than what they are outputting. If they stopped at that point the uncertainty probably wouldn’t look so bad to you. It’s not the uncertainty that is bad, it is the model and carrying its results out past where the outputs are reasonable.
I’ve given you the general formula for propagation of uncertainty at least twice. IT DOES APPLY TO AVERAGES! And I’ve demonstrated how to apply it to averages. And why the uncertainty is not divided by N.
Once again, N is a constant. The partial derivative of a constant is zero. It doesn’t matter if N is in the denominator of numerator of the function, it is still an additive to the overall root sum square. Since it goes to zero, it drops out of the equation.
Again,
Let f(a,b, c) = (a + b)/c
(I am going to use “P” for partial because I don’t know how to get the actual char)
∆f = sqrt( Pf/Pa)u_a^^2 + (Pf/Pb)u_b^^2 + (Pf/Pc)u_c^^2)
Pf/Pc, where c is a constant )the number of terms in the average) then equals zero.
So all you are left with is the first two terms for a and b.
From Taylor: Let q = Bx
The fractional uncertainty in q = Bx is the sum of the fractional uncertainties in B and x. Because the uncertainty in B is zero, this implies that
∆q/q = ∆x/x. The constant falls out of the uncertainty. (bolding mine, tpg)
It doesn’t matter if B = 1/2 or 2 or anything. If it is a constant with no uncertainty then it doesn’t affect the uncertainty in any way.
Think about it. If I have a board that is 12″ +/- .25″ and I cut it in half, how does that lessen the uncertainty I have for each piece? Did I cut it 100% accurately at the half point? If I measure each board with the same device the uncertainty will still be +/- .25″. The uncertainty isn’t cut in half because the board was cut in half.
Now I glue the boards back together. Each has been measured to be 6″ +/- .25″. How certain am I of the overall length without remeasuring the overall board (remember you can’t remeasure temperatures)? It certainly won’t be within .25″. It’s got to be something greater than that! In something simple like that you can probably directly add the uncertainties and be pretty close to the total uncertainty. Or you can use the root sum square and get +/- 0.35.
Read your linked site a little closer=>
It says for R = A/B that
u_r/r = sqrt( (u_A/A)^^2 + (u_B/B) )
Now u_B is a constant so u_B = 0.
And you are left with u_r/r = sqrt( (u_A/A)^^2 )
You can keep repeating your equations all you like, I’ve come to the conclusion you are an unreliable witness and will have to give me some independent evidence to convince me otherwise.
It seems to me the uncertainty should reduce if you reduce the size of the board. What happens if you cut it into 100 pieces? Each board is approximately 0.12″, if you are going to suggest each piece still has an uncertainty of ±0.25″ you’d have to assume very imprecise cutting.
What! That’s insane. You’ve just cut a board in half and glued it back together, and you are now less certain of how long it is? How thick is your glue?
I think you mean B is a constant. And so as you say, you are left with
So, as
It follows that
Exactly the same as with the first equation. And so confirming my point that to get the uncertainty for the average you must divide the uncertainty of the sum, buy the sample size. Was this the point you were trying to make?
“You can keep repeating your equations all you like, I’ve come to the conclusion you are an unreliable witness and will have to give me some independent evidence to convince me otherwise.”
I’ve given you references from Taylor and Bevington and even provided quotes from their textbooks. If you don’t consider those to be independent evidence then you are just continuing to be willfully ignorant — and I can’t fix that no matter what I do.
“It seems to me the uncertainty should reduce if you reduce the size of the board. What happens if you cut it into 100 pieces? Each board is approximately 0.12″, if you are going to suggest each piece still has an uncertainty of ±0.25″ you’d have to assume very imprecise cutting.”
Why would you assume that the uncertainty would get less as you cut more pieces? What happens to the saw blade? Does it wear at all? If you have something smaller than you can measure then you are certainly uncertain about it!
“What! That’s insane. You’ve just cut a board in half and glued it back together, and you are now less certain of how long it is? How thick is your glue?”
Again, how thick is your saw blade?
“Exactly the same as with the first equation.”
Can you not even work the equation you were given? There is no u_a/B.
The equation from your link says:
u_r/r = sqrt( (u_A/A)^^2 + (u_B/b)^^2) )
So how does it follow that u_r = u_A/B?
Where in Pete’s name did you get that one from?
I think you need a nap!
Did any of them mention averages?
The uncertainty of each piece reduces.
It’s an imaginary saw.
I probably do need a nap, but I thought the algebra was simple enough.
The function is
Where here B is a constant equal to the number of measures, A is the sum of the measures, and R is the average of the measures. Am I OK so far?
Now the document says the uncertainty is given by
But as
, this simplifies to
Now
, so substituting for R gives
Dividing through by A we have
or
“Did any of them mention averages?”
Of course. In relation to the mean of a random variable and its probability distribution.
“The uncertainty of each piece reduces.”
Why? How do you allow for the width of the saw blade? How do you allow for the operator following the cut line? If your measuring device is only accurate to +/- .25 it doesn’t matter how long of a piece or how short of a piece you are measuring, the uncertainty of each measurement will still be +/- .25. And when you stack the pieces end to end the uncertainties will add – root sum square.
B * u_r = u_A
Your substitution is invalid. You are substituting from the function equation into the uncertainty equation. u_R/ R is a percentage of R and is an uncertainty. You can’t substitute a non-uncertainty into the equation.
Relative uncertainty is only one way to calculate the uncertainty. You can also use the general equation for propagating uncertainty. In that equation the percentage uncertainty does appear. Yet you get the same result – u_R = sqrt ( (u_A)^^2) )
Be careful with your substitutions. It isn’t just plain algebra. You have to be using common terms.
Yet it gave me exactly the same result as the first equation which you’ve ignored.
You introduced this equation. You implied it meant something with regard to averaging. The formula is saying if you have a quantity R derived by dividing one measurement A by another measurement B, the uncertainty of R as a ratio of R will be given by that particular formula using the uncertainties in A and B.
The only reason to bring this up regarding averaging is to say that A is a sum of measurements, B the number of measurements, and hence, R is the mean. As you said the uncertainty of B is zero, so we know that the ratio of the uncertainty of R to R is the same as the ratio of the uncertainty of A to A. The only logical conclusion is that if R is less than A, than the uncertainty of R is less than the uncertainty of A.
This is equivalent to the first equation
which is saying if you derive a quantity by scaling a measurement, the uncertainty of the quantity can be derived by scaling the uncertainty of the measurement.
Why do you keep avoiding simplifying that equation? All you are saying is
But if this is meant to apply to the
case, it’s clearly wrong if it gives a different result to the one we are discussing.
“The only reason to bring this up regarding averaging is to say that A is a sum of measurements, B the number of measurements, and hence, R is the mean.”
In the equation there is *nothing* that says A is a sum of measurements or that B is the number of measurements. That’s an assumption you are making.
If you have a more than one measurement then the equation becomes
R = (A1 + A2 + A3 …. + An)/B where B may or may not equal the n.
So the uncertainty becomes:
((
R)/R )^^2= (
A1/A1)^^2 + …. + 
An/An)^^2 + (
B/B)^^2
A could be any measure with a known uncertainty. I assume that’s the point of having multiple versions of the formula, so you can calculate more complex situations from basic building blocks. I assumed you meant A to be a sum, becasue I couldn’t think of any other reason you’d use that specific equation.
Either your new equation ends up being the same as the other two, or there’s a mistake somewhere.
And I think the mistake is where you claim that the uncertainty for R = (A1 + A2 + A3 …. + An)/B is
(I’ve dropped the final term as it is zero.)
Where does this come from? It looks like the formula for multiplying or dividing two quantities, but you are not multiplying or dividing A1, A2 …, you are adding them.
I’m sorrry to be so late in replying. My computer got farkled and I just got back on line. I’m still working on restoring everything.
The equation above is for calculating RELATIVE uncertainty instead of direct uncertainty.
If you will check dimensions on one side of your substituted equation you have a direct uncertainty and on the other you have a relative uncertainty (w/B). What you have done is created an inequality. You have to treat percentage uncertainty as a value of its own.
I’m looking for the part where they explain that uncertainties of an average increase as sample size increases.
I think we agree that uncertainty decreases when you make multiple measurements of the same thing. I’m interested in confirmation that it works the other way round when you average different things.
Taylor’s Introduction to Error Analysis Section 3.4
For example, if we measure the thickness T of 200 sheets of paper and get the answer T = 1.3 ± 0.1 inches, it immediately follows that the thickness t of a single sheet is
+1000
Only if a number of conditions are met.
The most important of which is that each measurement must be by the same instrument measuring the same thing.
None of these conditions are met by the climate data.
Reasonable if you are only using data as the final stated answer, but you want to retain more significant figures when using the data for calculations. Global temperature data is usually being used as the basis of calculations, such as long term averages, trends etc.
*INTERMEDIATE* calculations may use *one* more significant digit to prevent rounding error. That extra significant digit should be dropped in the final result of the last calculation, either by truncation or rounding.
The temperature data used to calculate things like long term averages should have its last significant digit of the same magnitude as the uncertainty, i.e. the tenths digit.
When you *add* all these together the magnitude of the last significant digit of hte result should be no more than the magnitude of the last significant digit in any component data – if you get an answer in the hundredths digit from adding data with only figures in the tenths digit then you need to check your manual addition, your calculator, or your computer program. Something terrible went wrong.
When you divide by the number of data points you will probably wind up with more digits than the tenths digit. Since that quotient is the final calculation then it should be either truncated to the tenths digit or rounded to the tenths digit.
Using inaccurate data makes calculations more precise?
The data is only accurate to 0.6C. It doesn’t matter how many digits past that point are recorded.
It can do, depending on the reasons for the inaccuracy. At the least it won’t do any harm. The more precise value represents a mid-point of the inaccuracy, rounding up or down loses some information.
NO! NO!
You cannot artificially increase precision. Doing so does *NOT* increase accuracy or decrease inaccuracy. Midpoints are no more a true value than any other point! You simply do not understand uncertainty at all!
You are a perfect example of what R. Feynman described in this quote:
“The first principle is that you must not fool yourself and you are the easiest person to fool.”
You are fooling yourself thinking you can increase or decrease accuracy by artificially increasing precision through calculation results.
Yes, always important to consider how easy it is to fool yourself.
Words to live by:
Defining the Terms Used to Discuss Significant Figures
http://www.chemistry.wustl.edu/~coursedev/Online%20tutorials/SigFigs.htm
I wasn’t talking about “expressing a number”, but about using it.
But what does “beyond the place to which we have actually measured” mean? Let alone “and therefore are certain of”? This whole discussion has been about uncertainty.
Tim Gorman
“If you add 100 independent, non-correlated temperature values together to calculate an average and each value has an uncertainty of +/- 0.5C then the resulting uncertainty is [ +/- 0.5 x sqrt(100)] = +/- 0.5 x 10 = +/- 5C.”
True, But when you take the mean you then divide both readings (the sum and the total uncertainty) by 100. So the uncertainty in the mean is ±0.05 °C.
That is basic error analysis in physics. That is why you average multiple readings to improve accuracy.
“Far too many so-called climate scientists want to view these independent, non-correlated temperatures as a common population that can be lumped together in a data set, assumed to be part of a normal probability distribution which is then subject to statistical analysis”
That is not what is happening. The issues of independence and normal distributions are irrelevant. They are taking multiple measurements at the same time at different points across the region in order to find the mean temperature for the region. There is nothing wrong there, just your understanding or errors and means.
No, you do *NOT* divide the uncertainty, not for independent, non-correlated data sets of size one.
You, and so many others on here, think temperatures (and this applies to anomalies as well) can be combined into one population that makes up some kind of a probability distribution that can then be analyzed in the same manner as multiple measurements of the same thing using the same device!
Measurements of different things using different devices are do not represent a random variable with a probability distribution. The uncertainties associated with such measurements do not cancel, which is what you do when you are calculating the standard deviation of the mean by dividing by the number of data points.
“They are taking multiple measurements at the same time at different points across the region “
THEY ARE TAKING MULTIPLE MEASUREMENTS OF DIFFERENT THINGS! They are *not* taking multiple measurements of the same thing! If you don’t have the same measurand then the multiple measurements become independent and uncorrelated. They do not become part of a random variable with a probability distribution.
There is *nothing* wrong with my understanding of this!
If you have one ruler with an uncertainty specification and use that to measure one board and then you take a ruler with a different uncertainty to measure a second board, then what is the uncertainty of the two measurement values added together.
According to you the uncertainty (which one I have no idea) would have to be divided by two. But the logical conclusion is that the overall uncertainty would GROW, not decline. And root sum square is used to allow for the fact that the total uncertainty may not be a direct sum of the individual uncertainties (although in this case they would be!).
This is all standard in physical science – but not in climate science apparently!
For instance from: https://chem.libretexts.org/Courses/Providence_College/CHM_331_Advanced_Analytical_Chemistry_1/03%3A_Evaluating_Analytical_Data/3.03%3A_Propagation_of_Uncertainty
Uncertainty When Adding or SubtractingWhen we add or subtract measurements we propagate their absolute uncertainties. For example, if the result is given by the equation
R=A+B−C
the the absolute uncertainty in R is
u_R = sqrt( u_a^^2 + u_b^^2 + u_c^^2)
——————————————
I could point you to a plethora of further examples on the internet. Or you can use google yourself.
If you think the data is correlated than all you have to do is add a third term addressing the covariance.
let f = a + b (like you are preparing to calculate an average.
let k = partial of f with respect to a
let m = partial of f with respect to b
let r_ab^^2 be the covariance between a and b..
Then the standard error propagation formula is:
u_t^^2 = (u_a^^2)k^^2 + (u_b^^2)m^^2 + (2)km(r_ab^^2)
Now, let’s talk about the first mid-range value. The two values t_max and t_min are used to calculate the mid-range. The correlation of these two can be evaluated two ways. The derivative of the temperature curve at points t_max and t_min are zero, meaning there is no direction which can be compared to determine correlation. Or you can calculate the
covariance = sum from i to n (t_max – mean_tmax)(t_min -mean_tmin) / N, where N is the population size (= 1). Since t_max – mean_tmax = 0 and the same for t_min the covariance is zero. cov = 0 implies independence. This makes sense, t_max has no relationship to t_min. The driving force behind these is today’s WEATHER.
So we know the third term above is zero.
This leaves us with u_total^^2 = u_tmax^^2 + u_tmin^^2
Thus if the uncertainty of t_max and t_min is +/- 0.5 the midrange will have an uncertainty of +/- 0.7, an increased uncertainty.
The same thing happens as you add different mid-ranges to get a global average.
I simply don’t know why so many people in climate science are unaware of how to propagate uncertainty. They always assume that all temp data is correlated and describes a probability distribution. I guess most of them are straight math majors and not physical scientists.
And, I made the case here: https://wattsupwiththat.com/2017/04/23/the-meaning-and-utility-of-averages-as-it-applies-to-climate/
that the probability distribution of Earth’s annual temperatures is skewed.
Of course it’s screwed. I like your post.
By lumping Tmax from *everywhere* all together it makes it sound like the earth is much hotter than it actually is. Even mid-range temps vary by time around the earth. The mid-range value in Topeka happens at a different time that in NYC. When you add them both together it makes it look like the entire area between Topeka and NYC are the same at the same time and the heat content of the earth is thus “hotter” than it really is.
You simply cannot ignore the fact that temperature records are time series. The temp changes with time.
And the exact same thing happens in infilling and homogenizing. If you don’t account for the time differences then you overestimate or underestimate the actual heat content.
There’s a problem right in the title: “the Earth’s Global Average Temperature”
What’s available and widely discussed is not the mean *temperature*, but the mean temperature *anomaly*. This is a very different thing, though also much easier to estimate for surfaces. But by focusing solely on long-term trend in anomalies, we obscure how small and slow anomaly trends are compared to natural and seasonal variation in actual temperature — and also obscures the wide range in actual temperature estimates are between models.
A valid complaint about a mean average surface temperature is that it is physically meaningless. This is completely true, but is true of temperature anomolies as well. Actual things on earth interact with actual temperatures.
I ran into a problem the other day. I have a trusty old yard stick that came from Solana Beach Hardware down by La Jolla, CA, It’s at least 50 years old. It has been aroundalmost longer than Climate Change. The printing is clear. The wood is strong and straight. Every once in a while I stretch my modern Stanley Leaverlock 16′ tape along it to see if it is still in calibration. Of course I always allow for moisture content, direction of grain, wood species temperature coefficient of expansion. I actually worked out an algorithm to speed up the process. I am glad to report that through the years and many relocations it seems pretty consistent, winter and summer. But I have a problem. The other day I was boring a 2.935″ diameter hole for a 2-15/16″ OD bushing. I was going for a .0025″ interference fit. Pretty standard stuff and well within the capabilities of my lathe. As they say measure twice and cut once which I did several times and took the average, the mean and calibrated with the algorithm but but the bushing just slides thru the bore. What went wrong?
Did you measure the bushing? Or just take it for granted?
The bushing size was fully inspected by several scientists and 97% of them agreed that the size was settled.
As others have already noted, the first major flaw in the climate science argument is that the climate scientists can measure temperatures, either locally or globally, to an accuracy of 0.1 °C. They cannot. The biggest problem is measurement error which is far greater than climate scientists acknowledge.
The second problem is correlation which also results in larger errors to average regional temperatures than most people generally expect.
The third problem is chaotic self-similarity in the temperature record which means that noise persists longer over time.
First let’s consider measurement accuracy. We can test this by looking at temperature records from the Netherlands.
What is interesting and useful about the Netherlands is that there are at least 9 pairs of weather stations where each pair is less than one mile apart. So you might think these should give virtually identical results, but they don’t, and they shouldn’t.
Error analysis suggests that even if you can measure daily temperatures at a given location to an accuracy of ±0.5 °C, the error in the daily mean will be ±0.7 °C, and the error in the monthly mean will be √30 times less. This will be the error in both station’s data, but the error in their difference will be √2 times greater. So the error in the temperature difference will be ±0.18 °C. For a temperature time series this equates to a standard deviation for the temperature difference over time of about ±0.25 °C. And guess what? That is exactly what the data shows.
See https://climatescienceinvestigations.blogspot.com/2020/12/43-reliability-of-individual.html
You are describing the “error of the mean”. First, this is not uncertainty is calculated. Second, you can only reduce error by the √N if the errors are random errors generated by multiple readings of the same thing by the same device. What you are doing in this process is combining the means of two different populations. The variance will increase when this is done and will in turn increase the standard deviation.
Lastly, read up on metrology and how lab equipment is certified. You simply can not reduce error by “averaging” the readings from two different devices. It simply is not allowed. Would you allow this to be done to determine the altitude of the plane you are flying in? How about getting results from a DUI test.
You may show they both have the same readings but that is no guarantee of any accuracy what so ever. Neither is it a guarantee that they are both reading the same thing, which is why you are not allowed to certify measurements by using multiple devices to obtain an average.
Next consider correlation. Most people assume that if you average 100 sets of data, then the noise in the mean will be √100 or 10 times less than the noise in the individual datasets. But this is only true if the datasets are all independent and the noise is random. Temperature records are not independent: they are highly correlated over distances of up to 500 km.
See https://climatescienceinvestigations.blogspot.com/2020/06/11-correlation-between-station.html
This means that when you average all the data for Texas, the standard deviation of the noise is virtually the same as it is for an individual record like Brenham.
This means that there is always a huge amount of uncertainty even in the temperature trend for an entire country or region.
For example the Texas average is shown here https://climatescienceinvestigations.blogspot.com/2021/02/52-texas-temperature-trends.html
Note there is no warming in Texas!!!
The “noise” you are describing is actually “the signal”. Noise is extraneous information not associated with the signal you are analyzing. The “average” you describe is a method to smooth a continuous signal. You do lose information when you do this. Variance is one of the big items that gets wiped away. Variance is actually what we are looking for in temperature variations.
What you are trying to do with averaging is obtain information that you can use a regression on to show growth. The problem with this is that we are dealing with a time series. Regressions on a time series can generate spurious signals.
Here is a discussion about time series and using regression from Duke University.
Stationarity and differencing of time series data (duke.edu)
CD
You said, “… they are highly correlated over distances of up to 500 km.”
I think that it would be more accurate to say that they may be highly correlated. I have previously provided the example of a cold front moving across the continent. There will be little if any correlation between temperatures on either side of the front. Similarly, with a temperature inversion, if one moves up a mountain and crosses the boundary with the inversion there will be no correlation. Any attempt at linear interpolation between a station below the inversion and above will insure that only the two end-point stations will be correct. Lastly, there may be microclimate pockets, particularly near large lakes, where there is little correlation with the changes in temperature (or precipitation) at distance. Indeed, the correlation can be expected to decrease rapidly as one moves up wind, and less rapidly as one moves downwind.
“I think that it would be more accurate to say that they may be highly correlated.”
I think may is too weak. They are generally but not always highly correlated. Look at the data here in Fig. 45.1a for New Zealand.
https://climatescienceinvestigations.blogspot.com/2020/12/45-review-of-year-2020.html
Almost all stations within 100 km have correlations of over +0.8. For under 500 km separations they are almost all correlated to better than +0.6.
Your argument about weather fronts is not really valid. We are talking about correlations in the monthly average temperatures. Weather fronts move across continents in a couple of days. So in a single month all locations will experience roughly similar amounts of time on either side of the front. So the mean monthly temperatures will still be similar for almost all adjacent stations.
As for microclimates, there may be some differences, but even here it is the change from their average that is relevant, not the fact that their average is different.
There are at least two confounding factors for the correlation to be strong.
Both of these can have a negative impact on correlation. And this is in addition to the negative correlation that time has on separated locations.
The biggest factor temperature is correlated to is time-of-day and season.
Correlation is meant to describe the relationship between two variables. Just because two variables are highly correlated to something doesn’t mean they are highly correlated to each other. Your example in the Netherlands simply doesn’t describe the entire population of temperatures. The relationship between the north side of the Kansas River Valley and the south side of the Kansas River valley is a constant one, being exactly the same is the exception, not the rule. The same applies to Pikes Peak and Denver. The temps in all these locations go up and down with the sun be they are all different from each other. it’s that way *everywhere*! The temperature in Roaring River is vastly different than that in Cassville, AR, minimums, maximums, and variances. Yet they are only a few miles apart.
The earth is not a cue ball!
CD
You said,
That means that only 64% of the variance is explained or predicted by the independent variable. I wouldn’t consider that all that good.
Finally, there is chaos and fractal behaviour. The effect of this is to massively reduce the extent to which time averaging your data will reduce the noise. The point here is that the fluctuations in the temperature data are not like white noise. If they were then the noise in data averaged over 100 years would be 10 times less that that averaged over one year. Instead it is only about 3 times less. The result is that climate scientists underestimate the amount of natural variation over time that there is in temperature data.
See https://climatescienceinvestigations.blogspot.com/2020/05/9-fooled-by-randomness.html
And https://climatescienceinvestigations.blogspot.com/2020/07/17-noise-fractals-and-scaling-revisited.html
And https://climatescienceinvestigations.blogspot.com/2020/12/42-study-of-fractal-self-similarity-and.html
I propose a follow up article titled: Measuring the Rainbow’s Global Average Color is a Scientific and Objective Process
We could follow that with: Measuring the Global Average Number of Trees in a Monarchy is a Scientific and Objective Process.
Or how about an article explaining how one can objectively apply science to things in a way that produces nothing meaningful? Or you could have an article explaining why averaging things strips the meaning and usefulness out of individual pieces of data?
We could find the mean wavelength, which I suspect would be close to the peak of the solar spectrum, perhaps minus the blue scattering.
SIGNIFICANT FIGURES
The first thing in addressing the Global Average Temperature (GAT) is to go back to basic physical measurement as taught to generations of people but so very often forgotten because of the prevalence of Spreadsheet Software. The first thing I learned was how to use significant figures and the rules for determining them. The following from Washington University at St. Louis describes the value and care that should be taken with scientific measurements.
Significant Figures: The number of digits used to express a measured or calculated quantity.
“By using significant figures, we can show how precise a number is. If we express a number beyond the place to which we have actually measured (and are therefore certain of), we compromise the integrity of what this number is representing. It is important after learning and understanding significant figures to use them properly throughout your scientific career.”
http://www.chemistry.wustl.edu/~coursedev/Online%20tutorials/SigFigs.htm
Doing calculations with temps prior to about 1980 involve temp recordings of integer numbers. No chemistry or physics professor would let you take 3 or or even 30 integer measurements of anything and average them to a decimal value. What happens when you get a repeating decimal? Who or what decides where to stop adding decimal places and why? Is the number with two decimal places expressing a number beyond the place to which we have actually measured?
Subtracting a base year average that happens to include temps recorded to 1/10th of degree from integer temps should result in integer values. Even my high school chemistry/physics teacher would have given me a failing grade for doing what climate scientists do when determining anomaly values.
In order to NOT “compromise the integrity of what this number is representing”, any mathematical manipulation of temps recorded at integers should result in integers! To do otherwise compromises the integrity of GAT to where it means nothing.
When I see temperature anomaly graphs that have what is obviously 1/100ths of a degree from the 18th century up to about 1980 I cringe. There are no statistics in the world that let you modify integer values to something like 76.00. Not the Law of Large Numbers or the Central Limit Theory or Sampling Theory allows people to do this. The number is simply 76 .
These kinds of “mistakes” are exactly what Washington University is defining. The anomalies are compromising the integrity of what the precision of the original measurement was.
This makes GAT anomalies unfit for purpose from the start.
Jim,
You said, “Subtracting a base year average that happens to include temps recorded to 1/10th of degree from integer temps should result in integer values.”
Fundamentally, I agree that subtracting an integer from a decimal number should be represented as an integer result when dealing with real measurements.
However, there is really nothing special about the baseline. It is simply an arbitrary bench mark to show how much change has occurred since a given 30-year period of time, usually starting with a year ending in a one, most likely as part of the attempt to scare people. Changing calendars would result in different decades. One could define the baseline as being an exact integer or a decimal number with as many significant figures as desired. It is all really smoke and mirrors. If the attempt is to demonstrate modern warming, then an agreed-to standard baseline approximating the 30-year period prior to the Industrial Revolution would be the most reasonable baseline, and being fixed, rather than shifted every decade, it would be easier to compare various calculations. If the purpose is to characterize and compare the records from nearby stations for purposes of ‘homogenization,’ again any baseline could be used, which might be the starting 30-year period for the most recent station being included in the anomaly calculations. In conclusion, under the best of circumstances, the number of significant figures to the right of the decimal point should not be greater than the number in the original temperature measurements, else one could not calculate daily, weekly, or even monthly standard deviations. It would take more than three-months of readings to justify adding another significant figure even for stations that met the criteria of only random variations.
Generally speaking, the historical time-series should represent the precision of the least precise measurement(s) that contribute to calculating an average or standard deviation. I suppose one could use weighting to handle less precise measurements for a 30-year or decadal period. However, that complicates the calculations and may provide for the introduction of subjective bias.
Exactly. Using the “error of the mean” as a way to increase the precision of a measurement or average is misusing what that statistical parameter actually depicts.
As I said, my high school chemistry/physics teacher would have had a coronary if I took 3 measurements to the nearest gram and then concluded that the “true value” was accurate to two or more decimal places.
“Subtracting a base year average that happens to include temps recorded to 1/10th of degree from integer temps should result in integer values. Even my high school chemistry/physics teacher would have given me a failing grade for doing what climate scientists do when determining anomaly values.”
That is not what climate scientists do. They subtract the monthly reference temperature, which has an error of about ±0.023 °C, from the monthly mean temperatures, which have an error of about ±0.128 °C, and get a time series for the temperature anomaly which has a standard deviation of over 2 °C. None of that is inconsistent with quoting monthly mean temperature anomaly records to an accuracy of ±0.05 °C or so. Nor does it justify rounding all the anomalies to integer values.
See https://climatescienceinvestigations.blogspot.com/2021/02/47-calculating-monthly-anomalies-using.html
https://wattsupwiththat.com/2017/04/12/are-claimed-global-record-temperatures-valid/
Until the most recent change in baseline, the baseline included temps that were recorded as integers, this means the final calculation should have been rounded to an integer also. The newest baseline should include temps recorded to the nearest 1/10th which means final calculations should be rounded to the nearest 1/10th also. That is, if traditional scientific procedure is used to calculate significant digits.
A monthly “error” of ±0.023 C is obviously an error of the mean calculation. This is not an indication of precision of the value. At the very least, the standard deviation of the population should be reported and not standard error. Read the GUM for an explanation. Available here:
BIPM – Guide to the Expression of Uncertainty in Measurement (GUM)
Now, let me add these are “errors”, not uncertainties. The uncertainty of an integer temp recorded in 1901 as an integer is ±0.5. You can’t change that. In fact, I believe the Weather Bureau states the uncertainty as ±2 degrees for this time, but I’ll assume the standard ±0.5 deg. Since it is an integer, Significant Digit rules require the value of any add/subtract calculation to contain no more decimal digits than the LEAST precise measurement. (So, for example: 70 – 68.1543 = 1.8457 -> 2)
As you can see, anomalies that follow standard scientific practice of using Significant Digits should only be calculated with 0 decimal digits when using integer recorded temps. If standard values of error are included the ±2 deg would be shown as the error bars for this time period which means statistically it is entirely possible no warming has happened since these temps were recorded.
That is the issue no one wants to deal with. However, it is a real problem when comparing newer, more precise and accurate temps to older, less precise and accurate data. You can not simply wave your hands and wish it away or cover it up. You certainly can not motor onward and end up making older information look more precise and accurate than it really is. That IS NOT good scientific practice.
If you are interested in family size, and only count to the nearest whole child, would it be wrong to say the average family had 2.4 children?
Actually it is. That why you see most people who discuss family size say that there are predominately two children families. The item you seldom see is the variance that is associated with that mean. A mean (average) has no meaning without an associated variance.
It is also a perfect scenario that people use to show how incomplete statistics mislead people. Like this: On average everyone has one ovary and one testicle.
I’m all in favor of quoting the variance. But what good is that if you’ve deliberately changed the quoted mean? You can always quote the modal if you want as well, but saying the mean is 2 when it’s actually 2.4 could make a lot of difference.
There is a reason for significant digits. Like it or not, the data you are looking at for children is in integers. The mean must be rounded to an integer to make any sense. You are confusing simple mathematics of numbers on a number line with real, physical measurements.
If the figure was going to be used in an interim calculation to determine some other value, of course 2.4 could be used.
If the figure is used to quote the number of children in a family you must use the rounded number.
Would you be in favor of stating that you have only one testicle? Statistics are a tool. You can’t make that tool fit every purpose. I am sure you’ve heard the adage that if all you have is a hammer for a tool, everything looks like a nail.
I think you’re confusing significant figures with decimal places here. If I count 242 children in 100 families I have 3 significant figures. If I say the mean is 2.42 I still have 3 significant figures.
It makes sense to truncate the digits for a lot of reasons, but I also think there’s a danger in over applying prescriptive rules. If the rule is that you can only describe averages to the nearest integer, then it’s a silly and potentially dangerous rule.
But how do you know when a mean value will be used in some other interim calculation. I’m not sure what the point of publishing an average would be if you didn’t expect it to be used in some way. An obvious example of family size would be to determine if size was changing over time. Knowing that the average number of children was 2 fifty years ago and is 2 today isn’t helpful if the actual numbers where 2.4 and 1.5. Nor is it helpful to see the size suddenly drop from 2 to 1, if that was a change between 1.5 and 1.4.
But the figure is quoting the number of children in a family, it’s the average number of children across all families.
No I am basically saying that variance also enters into the equation but too many people ignore that statistical parameter. You should state the variance. Ex: 2 +/- 2
As I said above, by all means state the variance, or preferably the standard deviation, but do so with the correct mean.
“I think you’re confusing significant figures with decimal places here.”
Here is the rule Taylor states:
“The last significant figure in any stated answer should usually be of the same order of magnitude (in the same decimal position) as the uncertainty.”
“If I say the mean is 2.42 I still have 3 significant figures.”
This implies a precision beyond what your measurements provide. It’s what a mathematician might consider to be ok but not a scientist or engineer.
“But how do you know when a mean value will be used in some other interim calculation.”
The mean *is* the final computation of an interim calculation. Any other *new* calculation should use the final calculation of the mean as it is stated (i.e. the last significant digit should be of the same magnitude of the uncertainty). There is no other “interim” calculation, only *new* calculations.
There’s pretty much zero uncertainty in counting children and in dividing one number by another. Hence if you divide an integer by 100 the answer is certain to 2dp.
100 is a constant so it doesn’t affect significant digits. Therefore, whatever the numerator is controls the number of signifiant digits. Example, 126 / 100 = 1.26. The numerator has 3 sig figs so the answer can also. Example 126 / 37 = 3.405. This number must be rounded to 3.41.
The first real problem is when you get averages out to 3 or 4 decimal places when temp integers generally have only two sig fig. When you get an average of 75.123 from all integer temps with two sig figs, your average can only have two sig figs.
This applies to base line calculation also. If you use any integers with only two digits, then you may have only two sig figs in the answer. If you use temps with two digits and one decimal place, you can only have averages to two+one decimal (3 total).
Averaging different things does not allow you to portray measurements to more precision than that to which they were measured. I’ll repeat this instruction from Washington Univ @ur momisugly St. Louis:
“Significant Figures: The number of digits used to express a measured or calculated quantity.
By using significant figures, we can show how precise a number is. If we express a number beyond the place to which we have actually measured (and are therefore certain of), we compromise the integrity of what this number is representing. It is important after learning and understanding significant figures to use them properly throughout your scientific career.”
The second big problem is subtracting temps with decimal points, such as a base line average, from integer temps. You simply may not increase the decimal digits beyond the number with the least number of decimals. That means for integer temps, subtracting baseline numbers with several decimals, one must round the answer to the nearest integer.
That is why when I see temps in the 1800’s and early 1900’s showing anomalies out to the 1/100ths place, I know immediately that the significant digit rules have not been applied properly. What is being displayed expresses the temp beyond the place to which it was measured.
Which is what I was saying and you disagreed with.
And now you’re contradicting your first statement. I only need to measure to the nearest child in order to have an average that is a fraction.
Firstly I’m not keen on the pedantry. How many places you represent a number to is style not an absolute rule.
More importantly, the number you are measuring in an average is the average. The individual measures are just the intermediate calculations. If I count 242 children and divide by 100, I’ve measure the average to 2dp or 3sf.
I should add, after all this, I’m not against reporting uncertainty. On the contrary, much of my postings here are criticizing people for ignoring uncertainty, whether it’s Monckton’s 5 year 7 month pause, or Spencer’s extrapolations to population zero.
My point is that in statistics, the uncertainty of measurements are mostly irrelevant. It’s the uncertainty caused by sampling that’s calculated. Any uncertainty of measurements are counted for implicitly in the variability of the data.
“My point is that in statistics, the uncertainty of measurements are mostly irrelevant. It’s the uncertainty caused by sampling that’s calculated. Any uncertainty of measurements are counted for implicitly in the variability of the data.”
You *still* don’t get it. There is no variability in a data set of size one. The uncertainty is all you have. You can’t lump a quantity of populations of size one together and now say you have a population of 1000 and you can calculate a mean of that 1000 and that becomes the uncertainty.
Doing so assumes that you have created a probability distribution whose values describe random error associated with measurements of the same measurand. You haven’t done that!
So the uncertainty of each individual measurement remains important to the overall result.
At least one of us still doesn’t get it, or even know what “it” is?
We do not have a data set of size one, we have a data set of as many samples as we have. We are not trying to establish how good each individual measurement is, we are trying to determine how good the average of the samples is, i.e. how close it is to the true population average. You don’t need to know what the pdf of the uncertainty of any individual measurement is.
If all your measurements are equal the uncertainty of each measurement will be the distribution of the sample and will be roughly equal to the uncertainty of an individual measurement divided by the square root of the sample size. If the measurements vary a lot compared with the uncertainties of individual measurements then those uncertainties will have little effect on the uncertainty of the average, but it doesn’t matter because any uncertainties will be present in the distribution of the samples; large uncertainties will increase the variance which will increase the uncertainty of the average.
“The first real problem is when you get averages out to 3 or 4 decimal places when temp integers generally have only two sig fig. When you get an average of 75.123 from all integer temps with two sig figs, your average can only have two sig figs.”
No. The average will have greater accuracy than the original individual measurements because the individual measurement errors are independent. If your original measurements are accurate to ±0.5 °C, and you average 30 (or 31 or occasionally 28 or 29) readings in a month to get the monthly mean then the monthly mean temperature will be accurate to ±0.5/√30 or ± 0.09 °C. In the station data sets the monthly mean temperatures are generally only quoted to one decimal place (see Berkeley Earth).
When you calculate the 12 reference temperatures, one for each month of the year, you are averaging around 900 readings. The uncertainty in this reading is now ±0.5/√900 or ± 0.017 °C and so this should be quoted to two decimal places.
“The second big problem is subtracting temps with decimal points, such as a base line average, from integer temps. You simply may not increase the decimal digits beyond the number with the least number of decimals. That means for integer temps, subtracting baseline numbers with several decimals, one must round the answer to the nearest integer.”
Your general point is correct.
When subtracting temperatures with differing numbers of decimal places, the accuracy of the answer should be determined by the number with smallest number of verified decimal places, in this case ±0.1 °C. Not doing this rounding means that the calculated value of all your anomalies will differ by the rounding error (or about ±0.02 °C) from the value they should express.
But the rounding error is just an offset in your final result because you are subtracting the same number from every monthly reading. So this offset is constant over the whole length of your temperature time series. It is also at least two orders of magnitude (i.e. a factor of 100) less than the standard deviation in the anomaly over time for a given time series. Climate scientists aren’t interested in the absolute value of either the temperature or its anomaly, only in its change over time. But as the offset is constant over time, when calculating the trend or temperature change over time it cancels, and so it does not influence the trend. And this will also remain true when you average time series to derive a regional time series.
So the error of about 0.02 °C between the published values for the anomalies and what you believe their correct values should be is not remotely significant, and so has no detrimental impact on the data analysis.
“If your original measurements are accurate to ±0.5 °C, and you average 30 (or 31 or occasionally 28 or 29) readings in a month to get the monthly mean then the monthly mean temperature will be accurate to ±0.5/√30 or ± 0.09 °C.”
Nope. This is no different than sticking 30 boards end-to-end (i.e. a sum) and saying that the uncertainty of the total is less than the uncertainty associated with each. It fails the common sense test!
The total relative uncertainty of a quotient t = X/Y is:
(delta_t/t)^^2 = (delta_X/X)^^2 + (delta_Y/Y)^^2
Since Y is a constant if follows that delta_Y = 0 and the second term falls out. The total uncertainty is that associated with X, and since X is a sum of independent measurements delta_X is the root sum square of the individual, independent measurements. If the uncertainty of each of the independent measurements is +/- 0.5C then the total uncertainty, delta_X, is +/- 5C. To get the relative uncertainty divide 5 by the sum of the temperatures and you get a PERCENTAGE uncertainty, not an absolute uncertainty. Just as a for instance, let’s assume each individual daily mid-range temp is 20C for a sum of 20 x 30 = 600. So your overall RELATIVE uncertainty becomes +/- 5/600 or +/- 0.8%.
Using anomalies only changes the scale. It’s like using Kelvin instead of Celcius. Since the absolute numbers are bigger the percentages look smaller and therefore less significant. But that is exactly like making your car speedometer have a max reading of 500mph. The difference between 60mph and 80mph looks very small and insignificant on your speedometer – but it isn’t insignificant. Just ask the Highway Patrolman who stops you for speeding. Anomalies *hide* the significance of what you are measuring, and that’s a *bad* thing in physical science. If you actually calculate the uncertainty in your baseline you’ll find that the anomalies disappear into the uncertainty band around the baseline!
Relative uncertainty makes little sense when you are using a Celcius scale, as I pointed out to you before. 21°C is not 5% warmer than 20°C.
As I’ve also pointed out to you in these comments, if
Then it follows that the uncertainty of t is less than the uncertainty of X, in the same proportion as t is to X. It follows that if
is the uncertainty of the sum of 100 values, then as t = X / 100,
Hence, to get the uncertainty of the sum of n samples, multiply the individual uncertainty by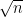
, to get the uncertainty of the average divide the individual uncertainty by 
.
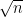“Nope. This is no different than sticking 30 boards end-to-end (i.e. a sum) and saying that the uncertainty of the total is less than the uncertainty associated with each. It fails the common sense test!”
Oh dear. That is why the “common sense” test is not generally used in maths and physics. We physicists and mathematicians prefer logic.
Suppose you have 30 boards all of length between 100 mm and say 300 mm (the values don’t really matter). Suppose you measure each one with a metre rule to a precision of ±0.5 mm and the sum of these measurements then comes to let’s say 6234 mm. So the average length of the boards is 6234/30 = 207.8 mm.
Now suppose you stick the 30 different boards together and measure the total length. Will it be 6234 mm exactly? Unlikely. Because the values you measured each have an error of ±0.5 mm. So how close will the measured length of the stuck-together boards be to the sum of the readings, 6234 mm?
Well, there are 30 boards so the error between the sum of the individual readings and the length of the boards when stuck together must be AT MOST 30×0.5mm or ±15 mm. So your comment appears to imply that the sum of the lengths will be 6234 ± 15 mm. Which means the mean length will be 207.8 ± 0.5 mm (dividing both sum and total error by 30). So the error in the mean is the same as in the individual measurements. But this is wrong!
The reason is because the errors from the 30 boards do not all add. This is because some of the individual recorded measurements will be the result of rounding up, and some will be from rounding down. That means that their errors will partially cancel. This is because all the measurements are independent. Therefore their errors will be independent. Some errors will be positive (where the rounded/recorded value is greater than the true value); some will be negative (the rounded/recorded value is less than the true value).
So you need to add the 30 errors by summing their squares otherwise you will overestimate the error in the sum. In which case the total error in the sum will be √(0.5^2 x 30) = √(0.25 x 30) = √7.5 = ±2.7 mm and NOT ±15 mm. Then when you find the mean you again divide by 30 to get 207.80 ± 0.09 mm.
So, if your measurements are INDEPENDENT, the error in the mean (±0.09 mm) is less than the error in the individual measurements (±0.5 mm).
But as I pointed out here
https://wattsupwiththat.com/2021/02/24/crowd-sourcing-a-crucible/#comment-3196169
if you just repeat the same measurement on the same board 30 times, the errors repeat with the same sign and there is no reduction after averaging. This is because, if the rounded/recorded measured value is greater than the true value for one measurement, it will probably be greater for the remaining 29 measurements as well.
The rest of what you wrote makes no sense to me, partly because you seem to have confused % errors with mean errors.
Bellman, the key criterion when discussing errors is the independence of the measurements. It is not about correlation, or causality or normal distributions – it about independence.
Consider this example.
Suppose you have a plank of wood that is 555.1111111 mm long exactly and you try to measure its length using a one metre rule with a precision of ±0.5 mm. If you measure the length of the plank once your answer will be 555.0 ± 0.5 mm.
Now suppose you measure the length of the plank one million times with the same ruler at the same point on the plank and take the mean. Does your accuracy of measurement improve by a factor of 1000 to 555.1111±0.0005 mm because you repeated your measurement one million times?
The answer is no. Your final calculated answer (call it answer 2) will probably be 555.0000 ± 0.0005 mm. But the problem here is that the difference between answer 2 and the true value of 555.1111111 mm is now greater than the new uncertainty in answer 2 (i.e. 0.1111111 mm versus 0.0005 mm) whereas when your answer for a single measurement was 555.0 ± 0.5 mm the uncertainty was greater than the difference, as it should be. So the new uncertainty cannot be right.
The solution is that if your measurements are not independent then you must add the uncertainties when you sum the readings, not determine the square root of the sum of the squares (SSR) of the uncertainties. Repeating the same measurement one million times then gives an uncertainty of ±0.5 km in the total of all the one million readings (instead of 0.5 m), where the total of all one million readings is likely to be approximately 555 km. So the average measurement is the total divided by one million, which is 555.0 ± 0.5 mm : the same as for a single reading. So we have consistency.
However, when measurements are independent, and you sum the results, the total uncertainty would be the square root of the sum of the squares (SSR) of the uncertainties for each measurement. When you take the mean you still divide both the total and the total uncertainty by the number of readings. So when you measure the minimum and maximum temperature at a given location on Monday, those two measurements are independent. When you repeat the measurements on Tuesday, those results are not only independent of each but are also independent of Monday’s readings.
So if the precision of the thermometers used to measure site temperatures is ±0.5 °C, then the uncertainty in the daily mean will be ±0.7 °C (i.e. √2 greater than 0.5 °C). The precision of the monthly mean will be √28 or √29 or √30 or √31 less than ±0.7 °C and so it will be about ±0.13 °C. This is also much greater than the precision of the monthly reference temperatures for each month which are 0.024 °C = ±0.13/√30. This is because the January reference temperature is the average of all January mean daily temperatures over a 30 year interval (so 31×30 readings in total). The reference temperatures are subtracted from the monthly mean temperatures to produce the anomalies. Thus the precision of the anomalies will be more or less the same as that of the monthly mean, i.e. ±0.13 °C.
It has also been suggested by some that the anomaly data (and temperature data in general) does not conform to a normal distribution. Well actually it does. I have measured it. See Fig. 17.3 here
https://climatescienceinvestigations.blogspot.com/2020/07/17-noise-fractals-and-scaling-revisited.html
and Fig. 27.1 here
https://climatescienceinvestigations.blogspot.com/2020/07/27-scaling-of-temperature-anomalies-for.html
You have shown the frequency distribution for anomalies.
Show us the frequency distributions for the absolute temps you used to get the anomalies.
I’ll guarantee they are not Gaussian distributions. That would mean that doing anomalies does affect drastically the statistical parameters that the raw data actually has.
You must then translate your anomaly averages back into absolute temps that show the same original distribution in order to have any real world significance.
Here is an analysis I did for several cities around the U.S. The one called Total Avg is actually a plot of a small set of samples of size N=6 on data from each station for July and August 2019.
As you can see, the sample means distribution looks nothing like any of the individual stations. Nor does it allow you to reverse and retrieve any of the components. It is only useful for finding the approximate mean of the original population and the variance of the original population.
If the anomalies for a single station are Gaussian then the anomalies for each month at that station will probably be Gaussian.
If the anomalies at a single station (in say the month of May) are Gaussian then the raw data for May at that station must be Gaussian. The difference between the two is a constant – the monthly mean reference temperature (MRT). Adding a constant to a Gaussian gives a Gaussian – one that is just offset from zero.
If you look at the MRTs of all the stations in a large enough sample (say 1000 stations, so 12000 data values), the distribution of the MRTs will be Gaussian. So the distribution of raw temperatures from all those stations will be the convolution of a Gaussian with a Gaussian, which is just another Gaussian.
The problem with your data is that there is just not enough of it. Each city looks like it is the sum of up to twelve offset Gaussians (they aren’t – you just don’t have enough data): you can see that clearly with Northgate, Charlottesville and Tulsa. Each Gaussian has a width of about 1 °C, but if the range of your monthly means (MRTs) is more than 12 °C (which it is for Northgate, Charlottesville and Tulsa) then the Gaussians for the monthly or seasonal temperatures don’t overlap sufficiently. Your data then looks lumpy. Even then the average distribution TOT_AVG is close to a Gaussian. Yes it is slightly skewed, but that is because your sample of 6 stations is not homogeneous. It is skewed. Just use more data.
So it is true that raw temperatures at a given station may not be Gaussian in distribution. You may get two (or more) overlapping peaks, one for summer, one for winter. These may have different heights and widths, but the deviation from the mean temperatures will still be Gaussian. That is why we use anomalies. Your problem is lack of sample size and local inhomogeneities at certain stations.
You know enough to be dangerous. What sampling and presumably your method does is derive a pseudo-distribution that lets you estimate the mean and variance of the population. However you can not use this pseudo-distribution to develop further calculation because it is not a description of the real population.
BTW, you have been sounding like you think N as in “sqrt N” is the number of data points you have. It is not. It is the size of the samples you take from the population. You can take multiple samples each the size of N.
This link will give you a variety of refreshers on sampling.
Sampling distribution of the sample mean | Probability and Statistics | Khan Academy
Before you question it, that is why there is a requirement for measuring the same thing multiple times and for the errors being randomly distributed (Gaussian distribution). When these are met, you can treat each measurement as a sample and can divide by sqrt N to get the standard error of the mean.
After watching the videos you should understand why the standard error of the mean doesn’t define the precision of the mean . It only defines the interval in which the mean may lie. The value of the mean is determined by the significant digits used in the measurement.
You keep talking about samples and populations. So what do you consider to be the original population and what are the samples? And remember, the sample needs to be a random selection of data from that population.
By averaging days into months and months into years by station then calculating an anomaly base for each station individually, you are predetermining each individual station to be its own population. The data points you have are not random samples of the entire temperature database, they are unique to each station. That is hardly IID.
To do it properly, you would take all of the stations for a single day, sample them, find the sample means and variance. You could then calculate the population variance by multiplying the sample means distribution by the sqrt of the sample size.
Here is the kicker, you can get the mean by simply finding the mean of all the temps for that day, then calculate the variance directly. You don’t need to sample. Why? Because you have all the data points you will ever have to begin with. Is there uncertainty? You bet, that’s what some of us have been saying. The available temps are not good distributions around the earth. That is one reason to advocate for more regional/local data study. You can have much more accurate data projections. I think you have already seen that.
That is daily data for July and August for each of the stations. Basically 360 data points. Sample size was 6 and I took 60 samples. I can tell you the mean of the sample means was within 3 decimal point of the mean of all 360 data points all summed together and divided by sixty. So basically the CLT was confirmed.
The problem I had and I haven’t ever had a chance to determine why, is that it is obvious that the variance of the whole is pretty high. Yet multiplying the variance of the sample means distribution by sqrt 6 doesn’t indicate that.
“If the anomalies for a single station are Gaussian then the anomalies for each month at that station will probably be Gaussian.”
The temperature profile for any location is a sine wave. A sine wave is not a Gaussian probability distribution. If the temperature profile is not a Gaussian probability distribution then how can the anomalies be a Gaussian?
If the daily temperature profiles are not Gaussian then how can their monthly values be a Gaussian probability distribution?
VARIANCE
Variance in the Global Average Temperature (GAT) is never discussed or published. This reference says:
https://www.calculator.net/standard-deviation-calculator.html?numberinputs=76%2C80%2C81%2C80%2C89%2C87%2C80%2C82%2C82%2C80%2C78%2C80%2C81%2C79%2C80%2C79%2C78%2C79%2C72%2C71%2C73%2C71%2C70%2C83%2C86%2C84%2C87%2C80%2C70%2C75%2C80&ctype=p&x=56&y=17
“Standard deviation in statistics, typically denoted by σ, is a measure of variation or dispersion (refers to a distribution’s extent of stretching or squeezing) between values in a set of data.”
“The population standard deviation, the standard definition of σ, is used when an entire population can be measured, and is the square root of the variance of a given data set. ”
“Standard deviation is also used in weather to determine differences in regional climate. Imagine two cities, one on the coast and one deep inland, that have the same mean temperature of 75°F. While this may prompt the belief that the temperatures of these two cities are virtually the same, the reality could be masked if only the mean is addressed and the standard deviation ignored. Coastal cities tend to have far more stable temperatures due to regulation by large bodies of water, since water has a higher heat capacity than land; essentially, this makes water far less susceptible to changes in temperature, and coastal areas remain warmer in winter, and cooler in summer due to the amount of energy required to change the temperature of water. Hence, while the coastal city may have temperature ranges between 60°F and 85°F over a given period of time to result in a mean of 75°F, an inland city could have temperatures ranging from 30°F to 110°F to result in the same mean.”
One must make some definitions as to what the populations making up GAT actually are. You can hear all kinds of definitions from CAGW adherents but they basically say it is all the points on the earth and the stations are just a sample. This can’t be because in sampling theory, the samples must have some randomness to what what is chosen. The simple description is that each sample should be representative of the population which requires that each sample have somewhat the same distribution as the whole population.
So now let’s discuss what is actually used for populations. We can do that by discerning what is used to calculate anomalies. Each station has a base temperature determined by averaging that stations temperatures either daily, monthly, or annually. Then the base is subtracted from each of the data points. THIS ESTABLISHES EACH STATION AS A STAND ALONE POPULATION. It will have its own mean (average) and variance.
Thus when combining multiple operation one can not assume that the variances are equal nor do they reduce. Variances add when combining populations. For those familiar with statistics, this is NOT pooled variance because the variance of each population is not equal. The following explains it well.
https://apcentral.collegeboard.org/courses/ap-statistics/classroom-resources/why-variances-add-and-why-it-matters
The basic takeaway is:
“Okay, how about the second most important theorem? I say it’s the fact that for the sum or difference of independent random variables, variances add:
For independent random variables X and Y,
Var( X +/- Y) = Var(X) + Var(Y)”
As you can see the variances add when combining the means of numerous independent populations. Why is this important? Because this variance should also carry over to anomalies. This means you can end up with anomalies that have a standard deviation of 0.2 +/- 2 degrees (example).
This makes current temperature growth statistically insignificant. The organizations promoting a GAT calculation should be required to publish their analysis of variance including the math to obtain it.
You are talking about mean temperatures and not mean anomalies. The biggest influence on the standard deviation (SD) of mean temperatures outside the tropics are seasonal fluctuations. These get worse the closer you get to the poles. But if you use temperature anomalies, the seasonal fluctuations are removed and so the SD is reduced. Typical SDs for anomalies range from about 1 °C to 2 °C.
Variances do not add when you add populations, only when you add corresponding readings from different populations. The variance of a random sample from a population is the same as the variance of the whole population. The SD of the first 30 years of data in a temperature record is about the same as the SD of the last 30 years of data. Look at a graph of temperature anomalies: the data spread is constant over time.
Example: http://berkeleyearth.lbl.gov/stations/13013
When you take the mean of different temperature records, however, you would expect the SD to decrease. Suppose you calculate the set of mean values from adding dataset X and dataset Y. It is then true that if you add X to Y to get Z, then
Var(Z) = Var( X + Y) = Var(X) + Var(Y)
But only if X and Y are uncorrelated.
But Z is not the mean. and neither is X+Y : the term (X+Y)/2 is the mean. So the variance about the mean of X+Y is
Var[( X + Y)/2] = [Var(X) + Var(Y) ]/2
So if Var(X) = Var(Y) the SD reduces by a factor of √2 or 1.414.
Except this does not happen either for regional temperature data because the fluctuations of the temperature anomalies from neighbouring station ARE highly correlated.
For example, check out the data from Poland:
https://climatescienceinvestigations.blogspot.com/2021/02/50-poland-temperature-trends.html
Compare the data spread in Fig. 50.1 for Warsaw with that in Fig. 50.3 for the whole of Poland. They are virtually the same even though the Poland mean temperature trend in Fig. 50.3 is the average of over 50 different datasets from 1950 onwards.
“You are talking about mean temperatures and not mean anomalies. The biggest influence on the standard deviation (SD) of mean temperatures outside the tropics are seasonal fluctuations.”
Did you not read what Jim wrote at ALL?
Jim: “Hence, while the coastal city may have temperature ranges between 60°F and 85°F over a given period of time to result in a mean of 75°F, an inland city could have temperatures ranging from 30°F to 110°F to result in the same mean.””
No anomaly will properly address the variance in each population. Why is that so hard to understand?
I can give you two other locations to look at. San Diego and Ramona. The variance of these two areas, only 25miles apart is wide, very wide.
“Variances do not add when you add populations, only when you add corresponding readings from different populations.”
If you have different variances then you have different populations!
“The variance of a random sample from a population is the same as the variance of the whole population. “
If your sample doesn’t have the same standard deviation and variance as the overall population then you have a bad sample.
How many stations have the same variance?
If you are using two independent values, (X+Y)/2 implies just two values, with a population size of one then the covariance by definition is zero. Meaning they *are* uncorrelated. cov = (Y-Y_mean)(X-X_mean) divided by 2. For a population of size one the value and the mean are the same meaning (Y-Y_mean) = (X – X_mean) = 0.
Thus the two values are uncorrelated.
“Except this does not happen either for regional temperature data because the fluctuations of the temperature anomalies from neighbouring station ARE highly correlated.”
Again, you didn’t read Jim’s message. Are stations 25miles apart automatically correlated? I can assure you that San Diego and Ramona temperatures are not correlated.
Most of the stations around the globe are *NOT* correlated to most others. The numbers they might be correlated with is miniscule. So how do you justify they are *all* correlated?
Remember, these are *time series*. All temperature profiles are time series. The further apart in time (think sunrise/sunset offsets based on geographical distance) the series are the less and less correlated they are. I.e. the series are not stationery. Analyzing non-stationery data is much more complicated than what the climate scientists are doing. Anomalies don’t fix this problem. Does the term “first difference” mean anything to you?
“The numbers they might be correlated with is miniscule. So how do you justify they are *all* correlated?”
I didn’t say they were all correlated. I showed that correlation is often very strong when stations are close (up to 95% when less than 100 km apart), but declines with distance. I gave you a link. Here it is again.
https://climatescienceinvestigations.blogspot.com/2020/06/11-correlation-between-station.html
Read it!
The implication is that stations within 500 km are generally (but not always) strongly correlated. That means the variance of the mean does not decrease compared to the variance of the individual variables X and Y as it normally would.
If Z = X + Y (where X and Y are different data dataset) and M is a dataset of the mean of the respective elements of X and Y, M = Z/2.
If X and Y are uncorrelated, Var(Z) = Var(X) + Var(Y)
and Var(M) = Var(Z)/4 (slight correction to earlier comment when I divided by 2 not 4).
So if Var(X) = Var(Y) then Var(M) = VAR(X)/2 and SD(M) = SD(X)/√2
So the standard deviation (SD) of the mean should be less than the mean standard deviation of the different various datasets in the mean by about 1.4.
But this does not happen because the datasets are correlated to various degrees as I showed here
https://climatescienceinvestigations.blogspot.com/2021/02/50-poland-temperature-trends.html
Compare the SD of Warsaw (2.31 °C see Fig. 50.1) and Poland (2.15 °C see Fig. 50.3).
Remember: statistical independence of X and Y requires the the covariance of X and Y to be zero. But that is the same condition for zero correlation.
“I can give you two other locations to look at. San Diego and Ramona. The variance of these two areas, only 25miles apart is wide, very wide.”
The difference in variance is not the issue. The issue is, are they correlated? The answer is YES. The correlation coefficient for their monthly average temperatures is +0.93. The correlation for their monthly anomalies is +0.59.
Ramona Fire Dept data
San Diego North Island data
“ didn’t say they were all correlated. I showed that correlation is often very strong when stations are close (up to 95% when less than 100 km apart)”
And I gave you two examples, one 25miles apart and the other 100km, where the temperatures are not correlated at all. They are *not* outliers either!
I notice you use the term “often”. Often is not always. Which ones do you not consider correlated when infilling data?
“The implication is that stations within 500 km are generally (but not always) strongly correlated.”
Now it is an implication and “not always”? Which ones do you exclude? Or do you just include all stations?
“So the standard deviation (SD) of the mean”
And *NOW* we are back to assuming that all temperatures are members of a random variable with a Gaussian probability distribution.
An assumption that is *NOT* supported by you at all!
The covariance of two data sets with a population of one, i.e. temperature A at station A and temperature B at station B is zero. The mean of a single value data set is the value in the data set. Covariance is calculated (A – Amean)(B-Bmean) divided by the population size of one. Since A = Amean the and B=Bmean the covariance is zero. A zero covariance means they are independent. You cannot combine independent data values into a supposed probability distribution of a random variable.
Tell me what the slope of the trend is for temp = 71F? What is the slope of the temp = 25F? When you are calculating correlation you are finding out if the slope of the data sets is equal. So give me your answer!
“The correlation coefficient for their monthly average temperatures is +0.93. The correlation for their monthly anomalies is +0.59.”
The correlation is to time of day/season, not temperature. There is no relationship between the temperatures at each location. One is driven by coastal winds and humidity (wetter) and the other by desert factors.
Coastal winds keep one cool while the other exists in a desert climate with higher temps in the day and lower temps at night, think difference in cloud cover.
What you have identified is called a “coincidental correlation” due to confounding factors. It’s like saying there is a correlation between the stock prices of Tesla and Amazon. it’s pure coincidence. In this case it is physically wrong to say that. It’s also wrong to use the correlation based on time-of-day/season to imply a relationship between the temperatures in the two locations. Especially to prove that you could use the temperatures in Ramona to infill temperatures up the coast from San Diego. Yet that is what *you* are trying to do.
So far you refuse to admit that time lessens the correlation of two physically separated data sets and that confounding factors can cause coincidental correlation.
A common malady for climate science. Ignore anything that analysis of reality harder than assuming temperatures widely spread over the globe make up a probability distribution for a random variable *and* that the probability distribution is Gaussian.
Wow, just wow!
Not worth replying to.
CD —> “Variances do not add when you add populations, only when you add corresponding readings from different populations.”
You need to show a reference that verifies this. Otherwise you are making an unsupported assertion.
I gave one reference that includes the math that proves this statement wrong. I can give you others if you need them. Please show the reference that supports your assertion.
CD —>. “The variance of a random sample from a population is the same as variance of the whole population.”
You are simply stating a requirement for meeting sampling. You have not proved that a daily, monthly, or annual average from a station has the same variance as the whole “population” you are claiming.
As I have stated elsewhere, you need to decide if you are using populations or samples. Samples don’t apply unless you meet certain criteria such as each sample being representative of the statistical attributes of the whole. Taking a station from the Southern Hemisphere and one from the northern hemisphere will quickly show you that their statistical parameters are not similar.
The fact that you create anomalies by station belies the claim that you are using samples because you use individual station base averages to calculate them. That means each station is a stand alone population.
CD —> “But if you use temperature anomalies, the seasonal fluctuations are removed and so the SD is reduced.”
Thank you for admitting that anomalies are a cheap trick to derive a number that reduces the perceived standard deviation. You are obviously a mathematician and not someone who deals with physical requirements.
This would be equivalent to an engineer responsible for a bridge saying I’m going to use anomalies to calculate average deflection of the steel beams. That way the standard deviations are reduced and will show less wear and tear on the steel and we won’t need to replace them as quickly.
You do realize that anomaly calculations DO NOT affect the real variation (standard deviation) of absolute temperatures. If it was real science you could reverse the process all the way back to the original stations individual readings.
We are fast approaching the time when local/and regional entities are going to need temperature and other climate information (sea levels, rainfall, droughts) pertinent to their specific mitigation plans. A single, global temperature is not going to suffice. When they start seeing info that doesn’t show CAGW I suspect something will hit the fan. You don’t want to be part of the something. Beware of promoting “tricks” that give you what you want.
“Variances do not add when you add populations, only when you add corresponding readings from different populations.”
This is badly worded. It should read:
“Variances do not add when you combine samples from the same population, only when you add corresponding readings from different populations.”
“You have not proved that a daily, monthly, or annual average from a station has the same variance as the whole “population” you are claiming.”
This does not make any sense.
All I do is look at the data and report it. The data shows that the variance of the regional temperature time-series derived from averaging the anomalies from multiple station time-series is often only slightly less than the variance of those individual station time-series. I showed that here
https://climatescienceinvestigations.blogspot.com/2021/02/50-poland-temperature-trends.html
The SD of Warsaw is 2.31 °C (see Fig. 50.1) and for Poland it is 2.15 °C (see Fig. 50.3) despite the mean trend for Poland being derived from over 50 different datasets each with a SD of about 2 °C. That is fact. It also is a recurring phenomenon. I have also showed it elsewhere in other countries. If you dispute this, where is your evidence to the contrary?
“Taking a station from the Southern Hemisphere and one from the northern hemisphere will quickly show you that their statistical parameters are not similar.”
So what? Just because two samples have different statistical parameters does not mean they are not part of the same population. Two samples will only have identical statistical parameters when both are so large they are the same as the entire population. Nor does a population need to be homogeneous. Nor does each sample need to be a perfect random sample of the population with a normal distribution. If the samples themselves constitute a normal distribution, or one that represents the statistical properties of the whole population, that is sufficient.
“The fact that you create anomalies by station belies the claim that you are using samples because you use individual station base averages to calculate them. That means each station is a stand alone population.”
No it isn’t. Each station is a sample. The population is the ensemble of all the global temperature data. Converting to anomalies does not alter this.
“Thank you for admitting that anomalies are a cheap trick…”
No they are not. How they are often used and abused can be a cheap trick, but there is nothing wrong with using anomalies per se. As a way or renormalizing or offsetting the data so that you are just looking at the change in temperatures they make a lot of sense. It is no different to removing the dc bias from an electronic signal so that you can just look at the ac component.
“You are obviously a mathematician and not someone who deals with physical requirements.”
No I am a physicist with a PhD – as stated on my blog.
“You do realize that anomaly calculations DO NOT affect the real variation (standard deviation) of absolute temperatures.”
Most of the real variation (standard deviation) is due to seasonal variation. This does not change with time (i.e. decade to decade). What we want to look at is the bit that is time-dependent. That is why we use anomalies. See here
https://climatescienceinvestigations.blogspot.com/2020/05/combining-temperature-records-into.html
The SD of the monthly reference temperatures (MRTs) as irrelevant.
https://climatescienceinvestigations.blogspot.com/2021/02/47-calculating-monthly-anomalies-using.html
Just because they vary with location is not a problem. Remember
GAT = E(T) = E(A+M) = E(A) + E(M)
where E(A) is the expectation (mean) of the anomalies and E(M) is the expectation of the MRT. E(M) is fixed (time-independent) so the GAT only depends on the anomalies.
CD –>
“No it isn’t. Each station is a sample. The population is the ensemble of all the global temperature data. Converting to anomalies does not alter this.”
Again you appear to be saying individual station temp trends are “samples” of the overall population of world wide temperatures. If you wish to do this, then one of the basic requirements is that each member of the population has an equal chance of being chosen in each sample. This would mean with 1000 stations, and 365 temps per year, you would need to insure your sample size is large enough to insure you have included a representative sample each variation in temperature (that is what you are sampling). You would have 365,000 members in your population. You need a very large sample size to guarantee each member has an equal chance of being sampled.
You should be able to see how using each station as a “sample” does not come close to satisfying this fundamental requirement of sampling theory. There are many resources on the internet to explain this. Here is one:
Sampling (yale.edu)
“Variances do not add when you combine samples from the same population, only when you add corresponding readings from different populations.”
Variances of individual samples don’t necessarily add, but that is not where variance comes into play if you want to continue with your “entire population” theory. Sampling is done in order to obtain a distribution that can show one what the the two main statistical parameters of the population looks like. The procedure is to find the mean of each sample, then plot the “sample means”, that is the mean of each sample. The Central Limit Theory predicts that when done properly you will end up with a normal (Gaussian) distribution where the mean of all the sample means is close to the mean of the population. You also can infer that the variance of the sample means distribution can be used to determine the variance of the population. This lets one multiply the sample means variance by (√N).
See the following:
Sample Means (yale.edu)
A corollary of this is that all 365,000 members is the entire population for each year. You can do it by month which multiplies the number of data points by 12.
I’m sure you can visualize what the variance would be by including the entire global temperature readings into one population. You are talking summer and winter temps all being included together. The variance will be huge.
The upshot of this is that to determine anomalies you must use the data points you have calculated. For a century, you have 100 data points, thirty of which will be used to determine the base. Not a lot of data. Of course, you could expand that to monthly data which would give you 1200 data points for a century and 360 for a base.
As above, the way you structure data defines each station as a stand alone finite population distribution. When you combine them to calculate a GAT, the variances all add.
In the end, I stand by my statement that stations are stand alone populations because of the way they are treated in the calculations. The variances of combined populations DO ADD.
I showed you a reference with the math. You need to respect this by also including at least one reference supporting your assertion that they don’t add.
=======================================
CD –> “ It is no different to removing the dc bias from an electronic signal so that you can just look at the ac component.”
It is nothing like removing a DC offset from a simple sine wave. What you are doing with anomalies is scaling the values associated with the signal. That includes both the absolute value and the variance.
This would be like finding the entire average value (varying plus DC offset) of a sine wave and subtracting it from the original signal. What you have done is scaled both the absolute value and the variance to a smaller amount. By combining this new value with others you are weighting those with a larger variance more than those with smaller variances.
What happens is that a 0.1 to 0.2 anomaly increase looks like a 100% increase rather than what it is. I tutor high school math and science. Believe me, there are lots of students and teachers and parents that believe the 100% increase because that is all that is presented to them. If GAT was able to be rescaled to the actual absolute values and presented that way, you would see much less of a concern about CAGW.
The fact that you have scaled both quantities by a different amount (i.e. the baseline value of each station) means you can no longer assume that either the value of the anomaly or the variance can be added directly.
What is another problem? You can never tell any locality or region how their temperature is changing. Why do you think every study and paper you read automatically assumes the GAT applies to what they are studying? In other words, the temperature everywhere is changing by the same amount! By the very fact that there is a gradient from the equator to the poles belies that fact. It makes the GAT a TERRIBLE parameter to make mitigation plans from. You end up with the whole world doing the same thing for perhaps the wrong reason. Is sea level going to change the same EVERYWHERE? Is EVERYWHERE going to see the same amount of temperature rise? Are farmers EVERYWHERE going to start planting drought and heat resistant crops? Are farmers EVERYWHERE going to experience longer growing degree days due to the temperature rise.
======================================
CD –>
“Most of the real variation (standard deviation) is due to seasonal variation. This does not change with time (i.e. decade to decade). What we want to look at is the bit that is time-dependent. That is why we use anomalies. “
Anomalies are no more time-dependent than the values used to create them. If an anomaly is time-dependent so is the absolute temperature.
I don’t disagree however with the need for time dependent studies. This IS what temperature data series are – time series. All of the statistical gyrations such as determining a GAT is a waste of time. It is only done so simple regression algorithms can be applied in spreadsheet software. I have been advocating for serious time series analysis recently.
Anomalies do not detrend temperature data so you can begin to see what cycles there are and begin to compare what/when other atmospheric conditions drive certain things.
A friend has been working on this and it is beginning to appear that TSI, sunspots, and ENSO have very serious components in the changing temperatures. It also shows rather convincingly that not everywhere (or even most) regions are seeing anything like what GAT and GCM’s are showing.
This may be the explanation for why the Empirical Rule in statistics suggests that the standard deviation for the annual surface-temperature probability distribution should be several tens of degrees, rather than hundredths of a degree.
One fundamental scientific issue which is ignored by all these guardians of global datasets is that you cannot meaningfully “average” temperatures of different physical media: eg air and water, with very different physical properties.
Technically, temperature ( unlike energy ) is NOT an “extensive” property: if you mix two buckets of water at 10 deg C you do not get water at 20deg C. What you should do is add or average thermal energy content.
Now so long as you have the same medium ( eg sea water: of the same salinity ) you can make use of the fact that thermal energy is directly proportional to temperature and use temperature as a proxy for energy.
However, this all falls apart rapidly if you are mixing measurements of air and water which have specific heat capacities ( joule/kelvin/kg ) which vary by a factor of four. The temperature is no longer a valid proxy. Air temps change four times as quickly for the same change in energy. Thus any “average” temperatures of a mix of air and SST will be biased by a factor of four towards the changes in the air record.
An average is an abstract statistic. That does not imply that is physically meaningful how ever carefully you calculate your “average temperature”.
If you want to compare “average temperatures” of holiday resorts in different countries that may be near enough to chose your package tour.
If you are attempting to assess changes in the energy balance of a system and compare it to energy input in the form of accumulated radiative “forcing” you have got your “basic physics” totally wrong.
Examining rate of change of land and sea temperature records shows that land-based SAT changes about twice as fast as SST. That means that averaging SAT and SST will bais towards the more rapid changes in land records.
Even if you had reliable, self-consistent, well sampled land and sea records, when you start calculating the average it becomes physically meaningless.
It may be possible to practice some kind of 50% weighting of the land record, though I am unaware of this ever being discussed, let alone being put in to practice by our data guardians.
https://judithcurry.com/2016/02/10/are-land-sea-temperature-averages-meaningful/
Land itself varies enormously between swamp and marshlands to arid, dry sand or bare rock or ice covered terrain.
That these supposed “global average temperatures” have become the de facto metric by which we assess change and the need to take “climate action”, simply underlines the fundamentally non scientific nature of the exercise.
Like the even more arbitrary “2 degree limit” this is more about a pseudo-scientific dressing for a political agenda.
Just a thought.
I know sometimes an article is “pinned” to the top.
Perhaps “pin” this and future such for a day or two, then “pin” it again for a day or two?
You’re looking for thoughtful Editing of the article (the Pro part and the Con part), not necessarily comments ABOUT the article.
Right?
An occasional reminder to contribute would be nice.
Con: Surface Temperature Records are DistortedGlobal warming is made artificially warmer by manufacturing climate data where there isn’t any.
One way to check and analyse the temperature records is to calculate the temperature trend for a region by averaging the original data anomalies for that region, and compare the result with official climate group results. Most of these groups use various combinations of homogenization, gridding and breakpoint adjustments. So far I have looked at most of the Southern Hemisphere and parts of Europe. In many cases there are significant differences when compared to the official results.
For a summary see https://climatescienceinvestigations.blogspot.com/2020/12/45-review-of-year-2020.html
I also recently looked at Texas. The result, based on the raw data, was no warming since records began in 1849. Again, this is very different to the official version.
See https://climatescienceinvestigations.blogspot.com/2021/02/52-texas-temperature-trends.html
I also found a sudden jump in the temperature data in Europe of about 1 °C that seems to have occurred almost everywhere in central Europe around about 1988.
See https://climatescienceinvestigations.blogspot.com/2020/12/44-europe-temperature-trends-since-1700.html
The same feature is seen in trends for Belgium, Netherlands, Denmark, Germany, Poland and the Baltic States. I have yet to check the rest of Europe.
There is one other point I would make that I think is not fully appreciated: the urban heat island (UHI) effect. I think there is a misunderstanding that this is just due to trapping of hot air by tall buildings or changes to the surface albedo from tarmac and concrete. There is actually a bigger issue: waste heat output. It only takes 2.25 W/m2 of additional surface heat to raise the surface temperature by 1 °C. And remember all energy generated by humans must end up as heat.
See https://climatescienceinvestigations.blogspot.com/2020/06/14-surface-heating.html
On this basis, the energy usage of Germany probably heats the entire country by 0.6 °C. This has nothing to do with CO2. Renewables would have the same effect. For Belgium the temperature rise should be nearly 1 °C. For Greater London it should be more than 4 °C.
Stop reporting only anomalies. The average temperature of the earth is about 16 degrees C, and it may have warmed by about 1 degree since the little ice age. Yet we are supposed to believe that further warming of 0.5 degrees will be catastrophic?
You should believe in following the money. Using anomalies engenders the ability to raise alarm and therefore generate more money.
Re: “Measuring the Earth’s Global Average Temperature is a Scientific and Objective Process”
Yes it can be, but it isn’t now.
The problems start with the lack of a clear definition: what is a global average temperature?
Here’s one: the global average temperature is a measure of the total energy content of the troposphere. Notice that this is incomplete (e.g. surface and subsurface energy change is not considered) but it has the advantage that rough measures for it exist: radiosonde data goes back, in some cases, to 1905. It’s quite rough, but it’s a starting point. (oh, and the data shows that <a href=https://winface.com/node/13> global warming is not happening</a> ..)
Here’s another: global average temperature is a measure of the average energy absorbed by the earth facing sides of six black bodies in appropriately distributed stationary orbits over a 24 hour period. Just picture the world with a thermometer shoved into the atmosphere.. This one has no current data, isn’t terribly useful for forecasting, but is easy (easy, not cheap) to set-up and would be fun to derive stuff from.
Bottom line: the question only makes sense in the context of the necessary definitions and a use case or two… but, given those, Yes: it can be an objective process.
Temperatures in northern Canada vary.
The southern Yukon gets quite cold – Whitehorse for example.
One day loading of a 737 airliner had to be expedited as temperature was dropping toward the authorized limit for takeoff, roughly -50 IIRC (I forget if C or F as it was around the time Canada changed to metric).
The weather station at Alert in the High Arctic – for a while NASA’s only station north of 60 – is subject to Foehn winds, so readings can vary quickly. (A modest effect I gather, unlike Dawson Creek and Calgary and places in Colorado.)
That title deserves a long wet raspberry.
Unmentioned are the history behind the temperature measurement stations and oceanic sea surface measurements: