Sarah Knapton, Science Editor
24 August 2017 • 7:00pm

A 3,700-year-old clay tablet has proven that the Babylonians developed trigonometry 1,500 years before the Greeks and were using a sophisticated method of mathematics which could change how we calculate today.
The tablet, known as Plimpton 332, was discovered in the early 1900s in Southern Iraq by the American archaeologist and diplomat Edgar Banks, who was the inspiration for Indiana Jones.
The true meaning of the tablet has eluded experts until now but new research by the University of New South Wales, Australia, has shown it is the world’s oldest and most accurate trigonometric table, which was probably used by ancient architects to construct temples, palaces and canals.
However unlike today’s trigonometry, Babylonian mathematics used a base 60, or sexagesimal system, rather than the 10 which is used today. Because 60 is far easier to divide by three, experts studying the tablet, found that the calculations are far more accurate.

“Our research reveals that Plimpton 322 describes the shapes of right-angle triangles using a novel kind of trigonometry based on ratios, not angles and circles,” said Dr Daniel Mansfield of the School of Mathematics and Statistics in the UNSW Faculty of Science.
“It is a fascinating mathematical work that demonstrates undoubted genius. The tablet not only contains the world’s oldest trigonometric table; it is also the only completely accurate trigonometric table, because of the very different Babylonian approach to arithmetic and geometry.
“This means it has great relevance for our modern world. Babylonian mathematics may have been out of fashion for more than 3000 years, but it has possible practical applications in surveying, computer graphics and education.
“This is a rare example of the ancient world teaching us something new.”
The Greek astronomer Hipparchus, who lived around 120BC, has long been regarded as the father of trigonometry, with his ‘table of chords’ on a circle considered the oldest trigonometric table.
A trigonometric table allows a user to determine two unknown ratios of a right-angled triangle using just one known ratio. But the tablet is far older than Hipparchus, demonstrating that the Babylonians were already well advanced in complex mathematics far earlier.

The tablet, which is thought to have come from the ancient Sumerian city of Larsa, has been dated to between 1822 and 1762 BC. It is now in the Rare Book and Manuscript Library at Columbia University in New York.
“Plimpton 322 predates Hipparchus by more than 1000 years,” says Dr Wildberger.
“It opens up new possibilities not just for modern mathematics research, but also for mathematics education. With Plimpton 322 we see a simpler, more accurate trigonometry that has clear advantages over our own.
“A treasure-trove of Babylonian tablets exists, but only a fraction of them have been studied yet. The mathematical world is only waking up to the fact that this ancient but very sophisticated mathematical culture has much to teach us.”
HT/TA
how cool!
how cool ? Good question, since they don’t ACTUALLY tell us anything about it.
What are these “clear advantages” precisely ?
So the BIG discovery is that if you have 60 different symbols for individual digits you can represent a greater accuracy is a given number of digits?
Well aren’t we lucky that we have some loony-toon archaeologist in silly glasses and a blue jacket to explain that to us. We would never have known.
Fortunately for we Greg, this ”..loony-toon archaeologist in silly glasses and a blue jacket” is balanced out by your own erudite self (And could you please not include my own dear self under your blanket of ”We”? There still remain people in this world who have some respect for me).
One of the advantages of the Babylonian Trig is:
Well the Babbelonians didn’t bother to tell us anything about it did they ?
But when I was in school, I used a book of seven figure tables of logs and trig function, and even logs of trig functions, so don’t babble on and tell me that a brick beats out my bible sized book of trig tables.
G
All same, I am amazed by what they apparently did. And 60 is not divisible by seven, so it really isn’t all that useful. Did you know that 60 is also divisible by 10, and also by 12, so dozen that tell you something ?? We use both of those bases.
This is big and very fascinating. Hope I don’t have to learn base 60 numeracy. I am too old for that now.
You sort of already have.
1 hour = 60 min’s. 1 min = 60 sec’s.
Not quite the same is it. Base 60 would require unique symbols for the numbers 10-59, just as the letters A-F are the symbols for 10-15 in Hexadecimal.
John,

The sexagesimal Babylonian system was positional, using only two cuneiform symbols to count units and tens to notate the 59 non-zero digits. I’ll see if I can copy them here:
In lieu of extra appendages or repurposing other paired body parts, they had the abacus.
Or the fingers and toes of three people.
thanks for the explanation Gloateus
So you needed 5=9=14 cuniform marks to represent the integer number 59. How is that “better” or “more accurate” than binary, decimal or hex ?
Greg,
It isn’t easier to write, obviously. IMO the authors believe that not the writing system but the counting system produces simpler fractions. Or something. It’s unclear, but pretty plain that they are referring to any Base 60 system rather than the method of writing the numbers.
so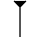 is hex 1 ; and
is hex 1 ; and is hex A
is hex A
59 is represented as (AAAAA) ( 111111111 ) . Pretty clever of them in 1800 BC but hardly going revolutionise “accuracty” of modern calculations , is it?
I have used these “surveyor’s units” when dealing with property maps and locations on them. They’re terrible. I can’t wait to put them into AutoCAD, or some other system that converts them to base 10″ Christian Units”. I then do all my work in base 10, and only convert them back in the final print in order to torment future users.
Using binary, 10 fingers can go up to 1023.
John S
August 25, 2017 at 12:29 pm
John….
I think SasjaL seems quite correct also as correct as you, I do not see a problem there..
According to Gloateus below table, the counting system there is a base 10 one that does not go as far as our one up to 99 by only up to 59……..
Will be interesting to know how their number 100 immediately after the 59 would be represented in their counting system!
It is amazing, it seems the quantity for their number 1.000.000 (as per our digits, not our counting system ) in their table will be represented by the 150 (cuneiform of 1 followed by the cuneiform of 50) according to their cuneiforms, where 100 will be represented by the 110 ( cuneiform of 1 followed by the cuneiform of 10), and the 100 billion by the 5050. An interesting view point……..Only ten cuneiform for the 100 billion……
Maybe this could address Greg’s concern below.
cheers
Sorry, seems more like the 5050 stands for 1 Trillion instead of a 100 Billion, and 4040 seems like the 100 Billion.
Only 8 cuneiforms for 100 Billion and 10 for a Trillion, if I have got it right….this time around…. 🙂
Whiten,
They didn’t have a “decilmal” point, so had to infer order of magnitude from context.
Gloateus
August 25, 2017 at 4:16 pm
Whiten,
They didn’t have a “decilmal” point, so had to infer order of magnitude from context.
———–
I get what you say, but all counting system have got what we call the decimal point,,,, the counting system in question here, we referring to does not have the “zero”, what makes it complicated if we try to distinguish it as a base 9 or a base 10 counting system, according to our point of reference.
But considering it as a base 9 counting system will be wrong from my point of view, and make it much difficult to understand.
As far as I can tell a system is not a counting system without the decimal point.
In a binary system made up of the 0 and 1 digit the decimal point is the 10. and in a base 3 system, with 0,1,2 representing digits the decimal point is 10 and also followed respectively by the 20….
cheers
Whiten,
As you may know, the technical, generic term is radix point.
The Babylonian system lacked a symbol to serve the function of radix point, so the place of the units had to be inferred from context. Hence, a Babylonian numeral for 59 or less could have represented xx or xx×60 or xx×60×60 or xx/60, etc.
We inherited our time system and angle system (degrees) from the Babylonians. In advanced math, you generally use radians instead of degrees. It’s interesting that the Babylonians had no concept of “zero,” but they did have a way of representing a zero digit in their number system. It was more like a non-number or a special character to hold the place of a zero position.
>>
whiten
August 25, 2017 at 4:42 pm
As far as I can tell a system is not a counting system without the decimal point.
In a binary system made up of the 0 and 1 digit the decimal point is the 10. and in a base 3 system, with 0,1,2 representing digits the decimal point is 10 and also followed respectively by the 20….
<<
A “decimal point” refers to base ten numbers. The general term is “base point.” In binary, it’s called a “binary point.” In base sixteen, it’s called a “hexadecimal point.” In base eight, it’s called an “octal point.”
In an integer based, positional number system, the base is always 10–read as “one-zero” (unless you’re referring to decimal numbers, and then it’s called “ten”).
I really don’t understand your comment. The standard is the base point is just to the right of the unit’s position. What follows “10” is “11”–even in binary.
Jim
Jim Masterson
August 26, 2017 at 1:59 pm
Thanks Jim.
First any counting system is a base 10 counting system by its own point of view.
So for example,what we consider a base 3 counting system by our point of view in reference to our counting system, is a base 10 counting system from the point of view of that counting system.
So if we used what we consider a base 3 counting system, that one will be the base 10 counting system to us by our point of view according to that reference.
I know this is a difficult and messy way, but that how it seems to be.
Again, my position in this thread is that regardless of the above, the Babilonian counting system is a base 10 counting system from our 10 base reference point.
That is the most important thing to consider to understand that system, even when it does not have a “Zero”, which actually is even more important to understand.
The table of cueniforms above is very easy to memorize.
Actually even the system generating the whole possible numbers from that table is easy in principle, and very harmonious, only it requires to acknowledge that numbers from 60 to 99 do not exist in any scale required.
And the number after 59 is 100, which I tried to explain it above.
As I do not have a keyboard accommodating or allowing for queniform typing I use our numbers to represent the queniform.
Anyway, if you read this:
“Gloateus
August 25, 2017 at 4:16 pm
Whiten,
They didn’t have a “decilmal” point, so had to infer order of magnitude from context.”
——–
you have to consider that it is very essential.
My comment just above it addresses this particular important issue.
The 5050 holds two values outside the context.
A specific one and a non specific one.
Specific one is 5050 = 50.5, a number with decimal point, with no need for Babilonians to actually have a sign needed for the decimal point.
The unspecific one is 5050 = a Trillion.
The 15050 it will be the specific value for trillion, 15050 = 1 Trillion.
Example of order of magnitude through context:
1- I am 5050 years old – I am 50.5 years old.
2- The Earth is 5050 km way from the Sun – the Earth is a Trillion km from the Sun.
3- According to observations, it is estimated there is 5050 Galaxies in our universe – According to our observations, it is estimated there is 50.5 Galaxies in our universe.
Regardless of the number being to small or strange in this case, the context above has a very lose scale range and not specific enough, so by default the specific value of the number will considered, which is 50.5.
The number of galaxies for that statement, according to the specifics can be considered as 1 Trillion only in the form of its specific value Trillion as 15050.
The system of unraveling and generating the numbers from the basic cueniform table above is easy and can be easy memorized, but the problem is that the numbers have meaning only under specific context or specific tables, and there is triple and double values for the numbers, but only one of the values will be specific out of context and reference tables.
The basic simple benefit is that a number like 56 50 50 50 = 56 Billion Trillion, can be recorded and checked for errors very quickly and take very little space, saving space and time.
Try to write that number in full digits in our counting system, and see how much space and time it takes..
And that is the most basic profit……
Now that may be wrong, but I can not see how, as everything there is so easy and harmonious if the system understood and applied, as from my point of view…..but hay you never know,…I may have to consider being wrong and in the same time being inventing a brand new counting system…:)
Hopefully this makes some sense..
thanks.
>> =
=  and
and  =
=  . Numbers
. Numbers  to
to 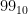 are
are  to
to 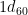 . So numbers
. So numbers  to
to 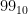 do exist in base 60. The number after
do exist in base 60. The number after  is
is  .
.
only it requires to acknowledge that numbers from 60 to 99 do not exist in any scale required.
And the number after 59 is 100, which I tried to explain it above.
<<
I think you’re confusing our imperfect representation of a base 60 number system by using our base 10 number system. A true base 60 number system would require 60 different digits We have digits 0-9 and then we’ve run out. If we add our alphabet, we get another 26 or 0-9A-Z, which is still not enough. However, if we add the lower case letters, then we only need 24 more or 0-9A-Za-x (digits y and z are not required). Here,
>>
The 5050 holds two values . . . .
<<
I’m sorry, but you’ve lost me during this whole discussion.
Jim
Jim Masterson
August 26, 2017 at 10:31 pm
Thank you again Jim
You say:
‘I think you’re confusing our imperfect representation of a base 60 number system by using our base 10 number system. A true base 60 number system would require 60 different digits We have digits 0-9 and then we’ve run out.’
—————-
I think you are confused Jim. 🙂
You see Jim, There is only two basic cuneiform characters that the table uses.
Moving in counting from the first to second it takes exactly ten fingers.
Also the repeating “decimal point” for the second character in that table is base 10, as per both point of views, ours and Babilinians math.
The quantity that queniforms represent in that table, from first to last are the same correspondingly as per the quantities that will be represented from our numbers from 1 to 59.
It is shouting from the outset that it is basically a same base 10 system as ours.
The only difference is that it cuts out at 59 instead of 99. and does not recognize the ‘zero’ as a calculus or number property.
Of course refusing to consider and address it this way it makes it impossible to understand it.
The system there is very easy to access.
Let me try again.
Let say we try to turn our counting system similar to theirs by dropping the “zero”.
Without the zero we have to make for the number hundred that comes after 99.
The only way to do that is as Babilonians seem to have done it, which means for us we have to be putting number 1 in front of number 10.
110 = hundred, 1101= 1hundred1, 91099 = 999 and than from hundred as according to base ten moving to next scale thousands, 120 = 1 thousands, this is very easy identified as per cuneiforms table.
And keep going this way we get, 130 = 10 thousands, 140 = 100 thousands, 150 = 1 Million, and jumping back,
110 150 = 100 Million, but the actual number will be 11050 for the merit of the essentials of such a system, and so forth so on up 15050 = 1 Trillion, which will not be a problem to, and according to tables and context, can be used as 5050 in a non specific form, 5050 = a Trillion. That will be in the main”spirit” of the system, saving time and space.
Many whole numbers in this system have many possible holding quantity values. especially in queniform format than our number format.
So the actual 1 Trillion is 15050, so specifically 5050 is a whole number that can only represent a non whole quantity, like in the case of our non whole number 50.5, and in some cases used as representing the non specific value for Trillion, a trillion.
Further with the point of multiple values and the context\’s order of magnitude:
The specific form of 100 million is 110150, but this very rarely may be used in this form, only when no good enough specification in the context or tables.
usually it will be used in the form of 11050.
11050 = hundred 50, also
11050 = hundred Million, also
11050= 1.15
So again a whole number representing a non whole quantity also.
What value that number actually will be referring to or hold it will be wholly dependent in specifics of context and tables used in.
Apart from the saving of time and space the other superiority of such a mathematical system is that it does not have or need to have non whole numbers to represent non whole quantities, (note the examples given in my previous comment).
Very, very tidy system at that point.
Another more difficult to understand superiority of such mathematical system is that for it to actually work, it has to be a mending construct of calculus and conceptual logical, in it’s core, some thing that are maths completely lack.
This kind of mathematical construct is completely blocked in it’s core to take a reasoning or rationale position from a separation point, by default.
A rationale separation point is like in your case, when you even refuse to consider that the Babilonian math is a 10 base math, from the outset and face value, without trying to figure it out, because of the biases of separation position instilled by the authority’s position already taken in this case….:)
Any way, to me still it seems easy to conclude that the cueniforms represent clearly a base 10 system from our and their point of view…
You:
“The 5050 holds two values . . . .
<<
I’m sorry, but you’ve lost me during this whole discussion.
Jim"
————–
Hopefully this is of some help….
Thanks Jim.
If you read this please do not mind to reply, if feel up to.
Still interested in other people's and commenters opinion in this one.
cheers
>> using my number system from above.
using my number system from above.
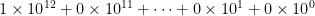 .
.
It is shouting from the outset that it is basically a same base 10 system as ours.
<<
No, it’s not. The first sixty characters are formed from an additive type system–not a positional system. It’s similar to Roman numerals, and no one is claiming Roman numerals are a base-ten system. (Roman numerals are both an additive and subtractive system. That makes doing calculations extremely difficult. Try multiplying two large numbers in Roman numerals where you have both additive parts and subtractive parts in both numbers.) For example, our twenty in base ten is two-zero. The Babylonian twenty is ten + ten. Our thirty is three-zero; their thirty is ten + ten + ten and so on. After fifty-nine, their system is positional.
Apparently they used a space to represent an empty position initially and later inserted a placeholder character to serve this purpose. Their “sixty” character looks like a one-space which would be like
>>
Hopefully this is of some help….
<<
Not really. You’re mixing bases in the same sequence, and it’s extremely confusing to me. What exactly does 5050 represent? Saying 5050 = 1 trillion doesn’t explain it. You see, our (US) 1 trillion is:
Doing something like that would be more clear to me.
Jim
Jim Masterson
August 27, 2017 at 12:00 pm
Our thirty is three-zero; their thirty is ten + ten + ten and so on. After fifty-nine, their system is positional.
————–
Hello again.
Thanks again.
Unless you let that “Zero” go, free, you would not understand what I was trying a say.
Regardless of Romans, the Babilonian system does not have a zero, has only two base characters, and any other character including these two still according to their table holds the same quantity value to the corresponding of our numbers from 1 to 59.
There is nothing different in their table, apart from not having a zero and cutting at 59 instead of 99.
If we do the same thing to our system the only difference in between will be that our system will have 10 basic characters and still will be a base 10 system as before. which in reality (the number of basic characters being more than two) will not allow our system to properly convert, in a workable way, in to the Babilonian system….the main problem in our system if the zero dropped…..
I tried to show a way how numbers or quantities work in the Babilonian system according to their queniform table, and it works well if you try to follow the method even when using our numbers instead of queniforms.
I can not be inventing a new brand mathematical system!
If a method works well when it considers that the system is actually base 10, then the system is a base ten, unless some one shows a better method that makes the system in question better understood and make work it better.
Did you spot any problems with the method I offered for translating the Babilonian queniforms?
To me it seems good enough to generate all possible numbers and make a easy translation. If I was wrong about the base 10, then it would not work.
It also explains why there is no any non whole numbers, as no any needed or required to represent or hold non whole quantity values, which it makes that system highly superior to ours.
Do you have any other better method to offer? I am all ears here. Eager to learn!
I think you may get it if you try to exercise a little with that mathematical system, by really getting off the calculus conceptual value of the zero…..let it go wholly lose… 🙂
Any way again, still looking that something else can tell more and clearly if there is any errors or wrong in this approach of mine…..
Still your argument, with all its value, does not yet cut it for me…….
thanks again
cheers
OOOPS
Jim, you say:
“Saying 5050 = 1 trillion doesn’t explain it.”
————–
You see Jim, I never said that to you in my replies to you.
I think I did not say that at all in this thread.
Actually, I tried to explain it, in a way, that it makes it wrong if put as above…..
No much room, for errors there….
Try to get over of that mental “bug” that gets you to claim that I did say something that actually I did not….
Maybe my point made will be clear then…
cheers
60 for a base is no where near as smart as 2. Yes or no, on or off, zero or one.
Back in the days when logic elements were expensive, a lot of effort was spent on systems other than one. How about -1, 0, +1 for a base three system. Hey! isn’t three divisible by three what is this BS about 60 being divisible by 3. So is 12.
Actually base 3 uses less circuit elements than binary, assuming you need three devices (valves or transistors, and with 3N devices, you can count to 3^N, which is more than the 2^N you can count with 2N devices.
if you get serious and ask which base is the most efficient, it isn’t 2 and it isn’t 3. Using the same premise that with BN devices you can count to B^N, you get the highest count for a given number of devices if B = e 2.718….
Whoopee that’s really useful to know; what does 0.718… of a transistor look like.
But it does indicate why base 3 is more efficient than base 2.
G
So Jim with the Roman additive/subtractive system, we write 8 as VIII.
So why don’t we write it as IIX which is fewer characters.
Many many years ago I purchased myself some Jo blocks (Johannson Blocks).
A standard full set had I believe 81 blocks.
0.1000, 0.1001,2,3,4,5,6,7,8,9,0.1010,20,3040,50,60 70, 80, 90 etc you get the picture Ten blocks incrementing by 0.0001, or 0.001, 0.01, 0.1 and so on with a base thickness of 0.1.
so you could sack 0.1001+0.1040+0.1300+0.7000 to get a total of 1.0341 inches, so hard to make a short stack.
One Japanese manufacturer started making blocks with a base thickness of 0.0500 instead of 0.1000. So you could make a shorter stack.
I still couldn’t afford an 81 piece set, so I invented my own set using the 50 mil blocks, in a BCD set.
I could buy a 0.0501, 0.0502, 0.0504, 0.0508 set of four to make any value.
But I found a better way. I bought a 0,1,2,4,7 set so five, block per decade, but never more than two blocks for the 0-9 instead of ten blocks per decade..
So I could make any value that a standard 100 mil Johannson 81 piece set could with no greater base thickness.
The company that sold me the selected blocks actually gave me a real 81 piece Johannson box with a crack in it, to put my custom set in. When they figured out what I was up to they sent me a note saying they should offer such a set for sale. But mine was the only one in the world.
Somebody stole it in a burglary, so if you see one in a real cracked Johannson box, you will know it is mine.
G
>>
george e. smith
August 27, 2017 at 9:03 pm
60 for a base is no where near as smart as 2. Yes or no, on or off, zero or one.
. . .
But it does indicate why base 3 is more efficient than base 2.
>>
If you want to take advantage of an abundant number system, we only need to go to base twelve. There’s no need to go all the way to sixty. And I’m not sure what you mean by efficiency. If we use base ten circuits, then there’s no need to convert our numbers to binary and back. I think the main reason why we use binary circuits (besides the simplicity), is that they are more immune to noise.
As for simplicity, how long did it take you to learn your addition and multiplication tables? In binary there are only two, and they are only two-by-two in size. They can be mastered in a few minutes. The binary multiplication table is easier than the binary addition table as there is no carry involved.
Jim
>>
george e. smith
August 27, 2017 at 9:30 pm
So Jim with the Roman additive/subtractive system, we write 8 as VIII.
So why don’t we write it as IIX which is fewer characters.
<<
Why do some clocks use four I’s instead of IV? I think you can use IIX for eight or VIIII for nine. The Romans probably did. The “only-three rule” is a more modern implementation of Roman numerals.
There are many possible reasons for clocks using four I’s instead of IV. Symmetry is one. I like the one where Jupiter’s name starts with IV. Maybe the Romans didn’t like invoking their god’s name on their clocks.
Jim
Jim Masterson
August 28, 2017 at 7:59 am
” ……… I like the one where Jupiter’s name starts with IV. Maybe the Romans didn’t like invoking their god’s name on their clocks.”
——————
Maybe so……..but then also maybe not…..Strange their God’s name to be IV (four)….strange indeed and interesting, mathematics and religion mixed ! 😉
cheers
>>
whiten
August 28, 2017 at 3:57 pm
Strange their God’s name to be IV (four)
<<
It’s not. The Latin word for Jupiter is JUPPITER (“father Jove”). But the Romans used “I” for their “J” and “V” for their “U.” The Latin spelling of Jupiter is IVPPITER. “IV” is the beginning of their god’s name. Of course, there were no clocks back then, but it’s thought that clock makers just continued this ancient aversion that uses four I’s instead of “IV.”
Jim
Jim Masterson
August 28, 2017 at 4:25 pm
>>
whiten
August 28, 2017 at 3:57 pm
Strange their God’s name to be IV (four)
<<
It’s not. The Latin word for Jupiter is JUPPITER (“father Jove”). But the Romans used “I” for their “J” and “V” for their “U.” The Latin spelling of Jupiter is IVPPITER.
———————————————————————————————
Hello again Jim, if you read this, of course 🙂
I tried not to get `involved with the Roman numbers, but, as it stand I have no choice but to go a little further in this subject.
The Latin spelling of Jupiter is very interesting and tempting.to me. 🙂
Ok, let me try to do a Roman table for a non zero mathematical system. (Please do not lough if I get all this wrong)
I am not claiming other than the table will use Roman numbers supposedly for a Non zero system as the Babilonian one. Simply to show that according to such a system maybe number IV is not four and IX is not nine.
And also supposedly maybe getting to explain the need of the space or another symbol in such a counting system. Hopefully the try would not be that bad 🙂
Consider this as simply an exercise.
A possible table for a non Zero Roman mathematical system:
——————————————————————————————————————————
I ONE N Forty
V FIVE M Fifty (all this basic symbols made by possible combinations of only one
X TEN single symbol of a segment)
—————–
I 1 XI 11 XXI 21 XXXI 31 NI 41 MI 51
II 2 XII 12 XXII 22 XXXII 32 NII 42 MII 52
III 3 XIII 13 XXIII 23 XXXIII 33 NIII 43 MIII 53
IIII 4 XIIII 14 XXIIII 24 XXXIIII 34 NIIII 44 MIIII 54
V 5 XV 15 XXV 25 XXXV 35 NV 45 MV 55
VI 6 XVI 16 XXVI 26 XXXVI 36 NVI 46 MVI 56
VII 7 XVII 17 XXVII 27 XXXVII 37 NVII 47 MVII 57
VIII 8 XVIII 18 XXVIII 28 XXXVIII 38 NVIII 48 MVIII 58
VIIII 9 XVIIII 19 XXVIIII 29 XXXVIIII 39 NVIIII 49 MVIIII 59
X TEN XX Twenty XXX Thirty N Forty M Fifty
IX IXX IXXX IN IM
1hundred 1Thousand TEN 1Hundred 1Million
thousand thousand
IXIM or then IXM IMM
1 hundred Million 1Trillion
——————————————————————————————————————————
This is only for the purpose of an exercise where the only thing to be considered is the point of a Non zero system, (note no need about arguing if it is base 60 or base 10).
One thing in such a system I think will be the need some times for the use of number "closing", like the number for a ratio a metric or a non adjustable or non variable number, like in a metric, ratio or parametric table.
When needed as in a metric table, I think the space or a special symbol is used.
For example:
" If Roman number XV needs to be entered in a metric a ratio or parameter table.
In this case it may be simple. Adding a X and turn it in XVX, means that the XV (15 ) is a closed number, as XVX will not have any other possible meaning. Or something like adding a P may turn and do similar, XVP,,,, or as for example in the case of the number IV adding a P is the only way to make the number invariable, IVP …… supposedly if P considered as a symbol to do that, of course."
In queniform Babilonian math a space or a symbol may have being used in such cases.
For example like for the 5050 as mentioned in my previous replies.
If 5050 = 50.5 and that has to enter in a non variable status as per above, a space or another symbol may be used like 50 50 or 50P50 or 50#50, or whatever one may chose.
The table above, before me posting it looks ok and tidy, hopefully stays that way after I post.
Thanks Jim…
cheers
Oh, the whole table got F#ckd….
really sorry/
>>
whiten
August 29, 2017 at 5:44 pm
Oh, the whole table got F#ckd….
really sorry/
<<
I’ve tried to post tables on WordPress before, and they looked worse than yours.
You do know that there are standard Roman numerals covering the numbers you’re trying to represent?
For example:
one = I
five = V
ten = X
fifty = L
one hundred = C
five hundred = D
one thousand = M
So forty is XL, fifty is L, eighty is LXXX, ninety is XC, and so on. The system doesn’t lead to unique representations, because forty-five can be XLV or VL.
It’s interesting that Roman fractions are in a duodecimal system (based 12).
Jim
Jim
—————
You do know that there are standard Roman numerals covering the numbers you’re trying to represent?
For example:
one = I
five = V
ten = X
fifty = L
one hundred = C
five hundred = D
one thousand = M
So forty is XL, fifty is L, eighty is LXXX, ninety is XC, and so on. The system doesn’t lead to unique representations, because forty-five can be XLV or VL.
It’s interesting that Roman fractions are in a duodecimal system (based 12).
——————————————————————————————————————————
Hello Jim.
I know now because of you what the guess of the standard Roman numerals may be representing.
I do not see a table there, and am not asking for one, but you see, if referring to what you have posted, you see, the:
“one hundred = C
five hundred = D
one thousand = M”
do not enter, or can not be part of a table.
So, what left of with for a numeral table are:
“one = I
five = V
ten = X
fifty = L”
Which from the outset show that even in that way the numerals in that table will be cut at 59, as in my table above, and where Forty= XXXX.
But the main point Jim is that there is no any standard number or symbol for “Zero|”, which makes the system a non zero system.
From where I stand, and as I will try to explain it further, such a non zero system is a very strict one,
So considering my previous table and your offered standard, I think a swap of the “N” there for “L”, will be a good correction, where Forty = L instead of = “N”, and where other numeral standards like “C” or “D” do not actually hold any quantity value them self but are simply helpers like the “space” or “P” as I tried to explain it in my early comment, and M = 50.
The “C” and “D” do not even apply to the segment rule, which needed…..per the easiness of memorizing the table.
The “L” before “, M”, works better than “N” before “M”, like 40 before 50. 🙂
You will not be able to have a Roman numeral table for a non zero system otherwise, it seems impossible. (to bend the spoon)
The IV can not be four and the IX can not be nine in a non zero system, as the system will break and make no sense…
Let me explain, why the non zero system, from my point of view can not be cut anywhere else than 59,
or as per Roman numerals MVIIII.
From a previous comment of mine:
56505050 = Billion Trillion.
In this one there is two error, one in counting and one logical.
Following the method I offered here as per the Babilonian math, the supposed correct representing will be:
56505050 = Million Trillion = 5650 5050.
But still there is a logical error. when for a colloquial purpose that still may stand as no problem, but for the math purpose instead neither Billion Trillion or Million Trillion are proper correct mathematical numbers, and never can be proper mathematical number scales.
Same as Hundred ten Thousand, or Hundred hundred Thousand, or Hundred Ten Trillion.
So, the only places that a non zero system to continue by a jump back, are at 20 or 50 or 80.
Meaning the system will cut respectively at 29 or 59 or 89, no any where else.
For example with our system cutting at 99, the jump back point will be 90, where 190 the jump point back = 10 Trillion and the jump back will result in a Hundred 10 Trillion scale, a fake one mathematically.
If you follow my earlier examples you will see this to hold true as per my explanation.
At 80 where 180 = 1Trillion the jump back will be for a scale 1Hundred Trillion,
at 50 where 150 = 1Million, the jump back will produce a 1Hundred Trillion,
and at 20 where 120 = 1Thousand the jump back will produce a 1Hundred Thousands, which in Roman may look like 1XXX.
Now Cutting at 29 as per a 120 point of jump, soon enough the system will have to run in long string of Xes in Roman and long strings of 10 or a long string of a mixture of 10 and 20 as per our system…….no good at all. and the cutting at 89 as per a 180 jump back point will end up to be very heavy and imbalanced as it will require more symbols and a lot of heavy translation of numbers where at some point it will be impossible to handle and counterproductive, not balanced at all.
The cut at 59 as per the 150 jump back point is heavy, but manageable and very balanced and symmetrical.
So from this angle, a non zero mathematical system is forced to cut at 59, either in cueniform or Roman, no any other way there as far as I can tell…….
That will be my explanation why the Babilonian cueniform non zero mathematical system cuts at 59, and why any workable non zero system is forced to cur at 59.
I do not think any table will work unless it is cut at 59 or MVIIII in Roman.
Roman numerals suggest to me that the Mathematical system was not a Roman one, but only learned, transferred and adapted by the Romans.
The introduction of the V makes the numerals and the table seem cleaner and tidier but still more difficult than cueniform Babilonian one, therefor the Romans must have needed more helping symbols like “C”, “D” or “P” to pass through obstacles at the thick application of the system.
For example, according to my table, when “N” swapped for “L”, XL= only 1050, which only it can represent a non whole quantity, which will be 10.5 in our counting system,
and 1XL will be 1Hundred Thousands.
Hopefully this clarifies more my point made to you.
There is no way that a Roman numeral table that works can be constructed if standards interpreted the way you have put them………As far as I can tell at this point, you may try but never get anywhere that way with a non zero system, and without a proper table there is no way to be sure what the Roman numerals may actually mean, will be any ones guess, and the most correct will be the “Authority” that decides about such as…
This went to long, hope you will not mind….. 🙂
Still is in a terms of exercise, and supposition of a possible explanation, there may be many other things that I may not know or be aware, which may turn this exercise in a very funny one..
Thank you Jim, you been rally kind
cheers
growing the extra digits would tax my system……
Or did they re-purpose teeth, ears, etc.?
You never know.
Auto
Gloateus
August 25, 2017 at 4:47 pm
Sorry Gloateus, I am only referring to your table above.
As per that table the counting system there as put out does definitely not have a “zero”, and does not recognize it.
Strange enough it also does not have a “60” also, and it does not recognize such a number at all, regardless of our reference point.
Again I am referring to your table above…..
There was a symbol for 60. Unlike our 10, it had its own numeral:
http://www.internetlooks.com/babyloniannumbers.jpg
Gloateus
August 25, 2017 at 5:38 pm
Thank you for keeping up with this. I have not being after this kind of thing before.
Just tried to play with the first table you had above.
Now, as I am getting a bit confused here, where, in this second table I can not distinguish between the number one and sixty, or the number 2 and 120, let me ask…..is this second table simply just a proper one or just kinda of exercise developed table for the purpose of trying to explain this cuneiform numerical system in accordance to some expert’s believe or understanding……as from where I stand it does not seem very harmonious with the basics and the principle of the first table format.
Just asking……for further info…
Whiten,
Yes. The symbols for one and sixty are the same, ie a single stylus impression in the clay.
Which is why I said that the value of a numeral has to be inferred from context. Recall that the Babylonian system is, like Base 10, a positional system.
Gloateus
August 25, 2017 at 6:10 pm
Thanks again Gloateus.
I see now, the first table must have confused me because I really thought that the base of the cuneiform numrercal were only two as shown first in your table, when actually there are three, the third one a result of as you say it ” a single stylus impression in the clay.”.
If you have got that third one there “the single stylus impression ‘ wold have being more clarifying.
Anyway, thanks for the help….very interesting numericals….probably got to cheek it closely….
cheers
My bad for shoddy numeral “communication”, as they say in the CACA sc@m.
No body else there to help me with further understanding of the Babilonian cuneiform counting system, apart from Gloateus.
No body even trying to correct me with my superficial understanding in my simple attempt of translating the cuneiform numbers as per my try in the previous comments…..A little disappointing to me… 🙂
I thought I will be grilled in this one..:)
Whiten,
At the time of this tablet, they left a space to indicate a place without value, similar to the modern zero. Babylonians later devised a sign to represent this empty place, but, as noted above, continued to lack a symbol to serve the function of radix point, so the place of the units had to be inferred from context.
Gloateus
Still they do not have a calculus zero.
To them it seems the concept was in the term of absence, still very powerful in their system.
It is more in the conceptual logic of its “value” than in a calculus concept…….hard to bend the mind around it in that way when the zero holds a calculus value as in our system.
What I was trying a show is what I see from my point of view….a mathematical construct that works in the principle of calculus mended and infused with logical in the core of the system, where the concept of absence is very important and flexible, but not crystallized as in our mathematical system.
What do you think about the way of my approach at this point, in this silly attempt of mine to get to a translation method for cuneiforms math?
Does it make any sense at all ?
Okay, since this ‘new’ old trig is easier I want my grades in trig to be ‘adjusted’ upwards. It’s not my fault they forced me to learn a harder version of trig.
If the climate alarmists can ‘adjust’ why can’t I?
Netflix has a documentary “The story of Maths” covering maths from ancient times to today. It is very interesting. Also includes the invention of 0, base 60, etc.
This doesn’t mean the Greeks didn’t invent Trigonometry, they invented it using a different method. They just weren’t the first to invent it.
Good point. And the author misuses “developed,” here. The Greeks certainly “developed” trigonometry, even if they did not invent it (which, as you said, they likely did — independent genius, as recognized in modern patent law).
More accurately, the Greeks invented one form of Trigonometry and the Babylonians a different form of Trigonometry. This takes nothing away from the Greek’s achievements, and their form is what has been used thoughout history, not the Babylonian’s, which apparently died off.
332 322
330.32 31022!!
Sorry but this article reeks of same bad science reporting we know so well, e.g., “It is also the only completely accurate trigonometric table”.
Don’t know the details but it seems implausible that using base 60 could simplify calculations in any way that could be considered significant today (where everything is done in base 2). Base is a simple transformation. I can see it making a difference for manual calculation of some key quantities, but there is nothing deep about choice of base.
Maybe they just mean that the system yields fewer repeating decimals than Base 10, hence less rounding off.
Apparently, the numbers on the tablet were exact.
https://en.wikipedia.org/wiki/Plimpton_322
Best to see what else comes of this news.
exact once five “errors” in 15 lines were “corrected” ??
Well this is WonkyPedia , so expect to have to rewrite the article before it makes sense.
When you divide the circumference of a circle into 360 equal arcs – a base 60 table is completely accurate.
When you divide it into 400 equal arcs (the gradian system, from the French Revolution “rationalization” of measures, still used in some fields) – not. Base 10 representations are then completely accurate.
Calculate using radians (the “irrational” base pi), and you are also accurate, so long as you stay in base pi.
Conversions between “incompatible” bases is what leads to repeating, or irrational representations. Just the reality of the abstract symbol systems called “mathematics.”
The Classic Greeks imposed their “modern” decimal system (quotes there, not modern to us, but to them) on the “legacy” Babylonian base 60 system of circular measure – so, of course, their tables are not accurate.
We’ve got a lot to learn, don’t we. A lot to learn about history, and a lot to learn about the Earth’s climate, among other things.
Science is *so* exciting! You never know what you are going to get next!
Does this mean that the Babylonians had more fingers than us?
No, but they wore sandals, and always did math in groups of three people 😉
Very cool. I wonder why it took 100 years to decode this tablet and discover the new/old trigonometry.
It didn’t. It was translated soon after discovery, but there is controversy over whether it represents what would be called trig today:
https://en.wikipedia.org/wiki/Plimpton_322
The new study argues that the tables do reflect trig.
Oddly, their superior knowledge of trig didn’t help them in the Greco-Persian Wars.
(I know that the Persian empire was not the Babylonian empire but presumably they had inherited the trig, and who knows, maybe it did help, but not enough. Were their archers more accurate because of this superior trig? Is that why the Greeks didn’t use archers; because Hipparchus hadn’t figured out trig yet?)
The Greeks did use archers and other missile-armed light infantry and cavalry. Alexander’s foot archers were both native Macedonians and mercs from Crete:
https://en.wikipedia.org/wiki/Ancient_Macedonian_army#Archers
He raised a horse archer unit after defeating Darius:
https://en.wikipedia.org/wiki/Ancient_Macedonian_army#Horse_archers
Alexander’s army evolved, but even at the outset was a sophisticated, combined arms force, consisting of light and heavy infantry, light and heavy cavalry and field and siege artillery, with an extensive logistical mule train and navy. It wasn’t all sarissa-armed heavy infantry phalanx, plus his Companion heavy cavalry.
And of course, Odysseus slaying the suitors of Penelope, after shooting through the ax heads.
Slings had more firepower but took longer to master than bows, and often enough barbarian slingers were hired as mercenaries. Only legend made David a hero in killing Goliath: if the account is true, he cheated. The situation would be comparable to Indiana Jones shooting the swordsman. –AGF
Ideally, an ancient army included all forms of missile-armed light infantry, ie archers, slingers and javelineers, plus horse archers, ie one type of light cavalry.
Balearic slingers were the best, since they practiced from childhood, like English longbowmen.
Roman legionaries were “medium infantry”, since they carried two pila (javelins) as well as their brutal close combat weapon, the gladius (Spanish short sword), for when fighting as heavy infantry. However, Roman legions were always accompanied by auxiliary troops, who were mainly light infantry and cavalry, although also cheaper versions of the standard legionary. Among the attached light infantry were Balearic slingers and Cretan archers.
Thus a legion was not just the 5000-odd Roman troops, but a similar number of auxiliaries, for a division-sized formation of around 10,000 fighting men.
Spanish conquistadors claimed that Inca slingshot struck like arquebus balls, but I doubt that. Slingshot in the ancient armies was made of standarized, elongated lead lozenges.
http://www.ancientresource.com/images/roman/spears_arrowheads/slingshot-7594.jpg
and if he ran out of lead shot, the slinger could always fall back on a pile of nicely rounded stones and still be quite effective. Imagine a stone just a bit smaller than a modern baseball, coming in at a speed comparable to what a major league pitcher can do with it. (from the sling) That would not be something I would want to get hit with.
WWS,
Yes, an experienced slinger could make the needed adjustments for a different mass and maybe even shape, and still be accurate enough for government work. But standard shot clearly had such great advantages that it was adopted universally in the ancient world. Dunno about Incas, though.
A combined arms force would want all three types of missile-armed light infantry, since each has strengths and weaknesses.
Alexander was always adapting Macedonian tactics to new situations. When he died, he was planning a campaign into Arabia. His innovation for that war was to replace the innermost pikemen in a sarissa square with archers. It’s a great tragedy for humanity that he died before conquering Arabia. Had he done so, the region would have been brought into the Hellenistic world, and we all would have been spared the abomination of Isl@m.
He then probably would have returned to North Africa to subdue Carthage, then on to Spain and probably to southern Gaul and Italy, making the Mediterranean a Greek lake. He might have nipped Rome in the bud.
Gloateus. Would not the archer have been using a thumbdraw with that short bow?
Bruce,
Quite possibly, but on period art, I’ve only ever seen the draw as on the black and red ware above.
It’s pretty clear that the ancients knew a lot more then we give them credit for, especially based on the design of ancient structures. It wouldn’t surprise me that a lot of ‘recent’ knowledge of math, astronomy and other sciences could have been known in the past, but just got lost owing to the small number of people who had that knowledge. At the time, few people were even educated enough to read and write, much less to understand anything about math and science.
Now that it has been shown that the Greeks were cultural appropriators and supremacists, I hope we can get on with the important work of smashing all extant Greek statues.
Since we (still) measure time and to some extent navigation with base 6 or modified base 6 numbers, there’s some application for this, in those areas – assuming people making navigation computers haven’t been doing this for decades and the reporter just never checked.
But the article is terrible and, sadly, quite representative of “science news.”
I have an hypothesis that it was not base 6 but base 12 – “duodecimal” that the ancients used. There are still remnants of this in the imperial system. 12 inches in a foot for example and there are others such as a dozen or a gross. I would argue that this was the system used in ancient times and was lost by the time of the Greeks and then Romans using the decimal system.
Think about how easy it is to do mental multiplication and division by 1, 5 and 10 in the decimal system. This applies also to evens and odds – in other words the digit 2.
If you train yourself to use duodecimal (which I did when I was younger with twelve different symbols than what we use for the decimal system because that can be confusing) then all of sudden the same ease of calculation applies to the digits 1, 2, 3, 4, 6, 8, 9 and 12. Adding another symbol for the decimal number 60 incorporates the magic number 5 into the system. This leaves 7 and 11 as the only numbers less than the base that can not easily be manipulated mentally to do arithmetic. Mythology gives special magical properties to these two numbers (7 and 11) possibly because they were intractable to mental manipulation.
Training myself to use duodecimal did me no good because I couldn’t convince anyone else to use it :-(. Converting back and forth from decimal to duodecimal strains the brain!
Having looked at the supposed symbols used by the Babylonians I was never convinced that the archaeologists had them correct. Never having easy access to the original source material nor the time I never pursued this hypothesis… maybe someone younger might do this. Sure there’s a PhD in there somewhere!
There is abundant archaeological documentary evidence for the Babylonian numeral system. Might as well say that we have the Roman numeral system wrong. Or the Mayan.
Yes Gloateus just like there is abundant evidence for CO2 as a potent greenhouse gas that causes all kinds of mischief (or not)…. I did say it was an hypothesis not a theory ;-). Where is your curiosity?
My curiosity is satisfied at every possible point by the fact of translating cuneiform.
Comparing the fact of translating cuneiform with the hypothesis of AGW is idiotic. Sorry, but that’s the reality.
The paper can be found for open access here:
http://ac.els-cdn.com/S0315086017300691/1-s2.0-S0315086017300691-main.pdf?_tid=65a420d8-89c6-11e7-bc72-00000aab0f02&acdnat=1503687266_d9e1cf256cea4a07f15e348c430472dd
Or follow your nose from here if you encounter problems:
https://www.journals.elsevier.com/historia-mathematica/
I thought the paper quite interesting. It’s nice that it’s available: http://www.sciencedirect.com/science/article/pii/S0315086017300691
“The true meaning of the tablet has eluded experts until now but new research by the University of New South Wales, Australia, has shown it is the world’s oldest and most accurate trigonometric table, which was probably used by ancient architects to construct temples, palaces and canals.
However unlike today’s trigonometry, Babylonian mathematics used a base 60, or sexagesimal system, rather than the 10 which is used today. Because 60 is far easier to divide by three, experts studying the tablet, found that the calculations are far more accurate.”
As an engineer that used a lot of trig in various calculations but not a math geek, I really don’t understand the above comments. I am impressed that these guys were so intelligent many years ago just as I am impressed as to the capability of our older engineers to design huge structures including complex bridges before the current tools were available; however, I don’t understand the comments like “60 is easier to divide by 3”.
60/3 = 20.
10/3 = 3.333333333333333333333333333333333333333333333333333333333333333333, etc.
But the statement in the article is about as stupid as saying 20 is more precise than 3 1/3. It doesn’t make sense. 3 1/3 is perfectly precise.
And the table’s accuracy is irrelevant when it comes to actually measuring and/or building something that is 20 units long, as opposed to something that is 3 1/3 units long, which depends on the construction methods and tools available.
Correct.
It’s only more accurate if you try to decimalize it rather than leaving the remainder as a fraction expressed in decimals.
“Because 60 is far easier to divide by three …”
Makes no sense to me either.
If anyone wants to know the real reason, start from scratch and do it again. You will figure out why they used a base 6 (and 60). Divide by three has really got nothing to do with it.
A common theory is that 60, a superior highly composite number (the previous and next in the series being 12 and 120), was chosen due to its prime factorization: 2×2×3×5, which makes it divisible by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30. Integers and fractions were represented identically — a radix point was not written but rather made clear by context.
https://en.wikipedia.org/wiki/Babylonian_numerals
Besides the prime number theory which Gloateus had mentioned. don’t forget how religion was so deeply interwoven with everything the ancients thought and did. They had observed from time immemorial that a year around the sun had 360 days, plus 5 feast days; therefore it would have been obvious to them that the series 6 x 6 x 10 had been ordained by the Gods, and was a vital part of the nature of the universe. For that reason they built not just their maths, but their entire cosmology around those holy numbers.
https://youtu.be/i9-ZPGp1AJE
WWS,
Yes, the sexagesimal system was apparently based upon astronomical observation rather than number of digits, although the Babylonian version included ten as well as 60, as you note.
Recall also that the Six Day creation myth also comes from Mesopotamia. Sixty six-day weeks in twelve thirty-day months of five weeks each, corresponding roughly to the lunar cycle, with some days left over, is a system found around the world.
[wws] “They had observed from time immemorial that a year around the sun had 360 days, plus 5 feast days”
Since we have enslaved carbon and harnessed the might of wealth redistribution and government assistance, this ratio has reversed. I count 5 ‘fasting days’ of diligent effort to complete one government-year of paperwork, and 360 glorious feasting days. 360 contains a wealth of integer divisors that allow accurate allocation and combination of feast ingredients. It is no coincidence that 360 single portion small food items approximates the limit an adult can carry, making bribes easier to calculate and accomplish. It is why we say things like, “An apple a day keeps the teacher away.”
Using sexagesimal number systems has been shown to result in more sex, but it also offers a solution to one of the most disturbing and shameful aspects of modern civilization, decimal portions of children. By mapping a system of polygamy and polyandry to the feasting-year, comprising whole factors of the 60 with the same verve as combining feast ingredients… any desired population replacement rate can be achieved, with wholesome integral children.
wonder if this was precursor/related to the 360 deg in circle and subsequent navigational aids that developed.
pretty cool no matter.
Yes, we owe the 360 degree system, the minute and seconds of latitude and time, etc. to the Babylonian sexigesimal system and its Sumerian precursor.
Make that sexagesimal.
Actually, the use is nowhere near as clearly defined as this writer claims. The missing part of the tile would establish whether this is actually logarithms or not … but then it is missing …
From another article:
C’mon, guys … don’t believe something because it is new and just out of the box without listening to opposing views. Remind you of climate science much?
w.
As noted above.
Gloateus August 25, 2017 at 11:40 am
WE, I was about to post a similar comment after reading the paper and other scholars reactions to it. You beat me to it.
Friberg wrote a paper on it in 1981:
http://ac.els-cdn.com/0315086081900690/1-s2.0-0315086081900690-main.pdf?_tid=d5049dd8-89c4-11e7-b6b2-00000aab0f6b&acdnat=1503686593_9ff15ff132598e173099aed886414b04
Yes, this slick UNSW marketing campaign just happens to coincide with undergraduate university application time.
Call me cynical.
Color you realistic.
Not sure what color that is.
This is nothing new . I mentioned it in http://cosy.com/views/pythag.htm back on SUN.JUN,970608 .
A quick google shows it’s been known since at least 1922 .
The Egyptians were first.
The Great Pyramid is a 2 x Pi pyramid, the formula for a circle. Height 280 cubits, perimeter 1760 cubits. …. The Second Pyramid is a 3-4-5 pyramid. ….. The Red Pyramid is a 21-22-29 pythagorean pyramid – with cubit measurements to multiples of those dimensions.
You need some serious math, to derive the 21-22-29 triangle.
P.S. The 1760 cubit perimeter of the Great Pyramid is the same units as the Imperial Mile, and it was done for the same reason – it is a Pi measurement system.
1760 mile … 220 furlong … 22 chain … 5.5 rod. It is all Pi based.
R
https://en.wikipedia.org/wiki/History_of_trigonometry#Early_trigonometry
Footnotes citing sources deleted:
“The ancient Egyptians and Babylonians had known of theorems on the ratios of the sides of similar triangles for many centuries. However, as pre-Hellenic societies lacked the concept of an angle measure, they were limited to studying the sides of triangles instead.
“The Babylonian astronomers kept detailed records on the rising and setting of stars, the motion of the planets, and the solar and lunar eclipses, all of which required familiarity with angular distances measured on the celestial sphere. Based on one interpretation of the Plimpton 322 cuneiform tablet (c. 1900 BC), some have even asserted that the ancient Babylonians had a table of secants. There is, however, much debate as to whether it is a table of Pythagorean triples, a solution of quadratic equations, or a trigonometric table.
“The Egyptians, on the other hand, used a primitive form of trigonometry for building pyramids in the 2nd millennium BC. The Rhind Mathematical Papyrus, written by the Egyptian scribe Ahmes (c. 1680–1620 BC), contains the following problem related to trigonometry:
“If a pyramid is 250 cubits high and the side of its base 360 cubits long, what is its seked?”
“Ahmes’ solution to the problem is the ratio of half the side of the base of the pyramid to its height, or the run-to-rise ratio of its face. In other words, the quantity he found for the seked is the cotangent of the angle to the base of the pyramid and its face.”
ralfellis August 25, 2017 at 12:32 pm
Huh? Where is “2 x Pi” in that? In addition, we only GUESS that the height was originally 280 cubits, that’s not known. Current height is much lower than that.
Dear heavens, EVERY pyramid can be expressed in such a fashion … so freakin’ what? I just built a pyramid of bricks. It is a 5-7-8.6 pyramid. Do I get some kind of prize?
Nope … you need to be a serious numerologist who finds meaning in every meaningless number. Look at all the ink wasted on the lines drawn inside the Great Pyramid—everyone has a theory, every theory is different.
What is a “pi measurement system”? And in any case:
and
So … 1760 cubits could be anything from 921.36 to 931.39 metres. An “Imperial Mile”, on the other hand, is 1,609.34 metres. So I have no clue what you are talking about.
“1760 mile”? What does that mean? And a furlong is an eighth of a mile … what does that have to do with Pi? Finally, a furlong is 10 chains or 40 rods, so where did you get “5.5 rods”???
That is numerology, my friend, not science in any form.
w.
“Finally, a furlong is 10 chains or 40 rods, so where did you get “5.5 rods”???”
1 mile = 1760 yards = 8 furlongs = 80 chain = 320 rods . Easy as pi.
It is all Pi based. 😉
The Great Pyramid was originally faced with smooth stones and a cap, which made it higher than now, with only its core stones intact. There are still some facing stones around the base, presumably too big to plunder whole.
A rod, pole or perch is 5 1/2 yards. There are 4 to a chain.
Ralf Ellis is merely reporting the speculation of others over the Giza pyramid:
https://en.wikipedia.org/wiki/Great_Pyramid_of_Giza
albeit I think his speculation about the imperial measurement system is rather more his own.
I have tried to make a reply, but it just disappears.
Does this mean it is in moderation?
R
Willis, looks like you have a problem here.….
The Pi used is 22 / 7, the fractional equivalent, because that gives whole numbers for both the height and perimeter length of the pyramid. Two times Pi is 44 / 7. 40 times that is 1760 / 280. And 1760 and 280 are the dimensions of the Great Pyramid.
Ralph
Not really. F.linders P.etrie found the original corners, and two sides of the p.yramid still have original casing stones, and the others have erosion marks on the foundation blocks where they were stolen. Plus we have the angle of the pyramid from the very accurate casing blocks in situ. Plus we have an average depth of casing blocks, that can be applied to the rest of the structure, thus deriving the angle of the original face. The height of the p.yramid is not necessary, as it can be calculated.
R
My mistake, I should have said 20-21-29 (trying to do it from memory). But I did say pythagorean, Willis, so I think you should have twigged my mistake, as this is only the 5th pythagorean up from the 3-4-5. Surely you know all the small pythagorean triangles – no?? I think your views have clouded your reasoning.
–
Yes, you do need some math to derive the 20-21-29 pythagorean triangle. There are only 16 pythagoreans, with sides less that 100 units, and you cannot simply guess the 20-21-29 triangle.
–
Do you think that the people who created the largest monument in the world were Neanderthals, who knew no math? Really? Why do you think the ancients were less intelligent than yourself, eh??
–
It is a measurement system based upon the Pi numerator 22. Again, the simple Pi fraction of 22/7 was used, to enable whole numbers on both sides of the fraction.
–
Yeah, we know that. The same Egyptian royal cubit was also the cubit used for the TempIe of SoIomon. So what?
–
Who said cubits, Willis?? Your views are clouding your judgement again. Read my post again. It is the metrological ratios that are the same, not the exact cubit length. The mile and furlong are quite obviously measured in yards, not cubits. And the yard is a different length.
–
Measuring a mile in meters is not very sensible. It is almost as bad as those who measure the pyramids in meters, and then cannot see the mathematical reasoning behind pyramid design. Do you think there was no design for the pyramids? That they were just piling stones on top of each other at random?
–
You are not familiar with Imperial measures, are you?
1760 yards = 1 mile
220 yards = 1 furlong
22 yards = 1 chain
5.5 yards = 1 rod
And all of those units are based upon the Pi numerator of 22. (The fractional Pi equivalent.). I think you can see that. The very foundations of this metrological system is therefore based upon Pi.
–
No, it is ancient mathematics.
But the wisdom of the ancients went right over your head.
Ralph
.
The reply would not post because the system did not like the name F.linders P.etrie.
Most strange.
R
Greg August 25, 2017 at 1:56 pm Edit
I’m sorry, but you haven’t answered the question—where did you get “5.5 rods”?
w.
Did I say “5.5 rods” ? I don’t think I did. I said “5.5 rod”
… … … (ie: shorthand for 5.5 yards to the rod.)
Sorry I thought I was talking to Americans here, who are still wedded to the Imperial system. Perhaps not. Anyway, as I said before, the ratios that form Imperial measures are based upon the fractional Pi numerator of 22.
And a quarter of 22 is 5.5. … Which is one rod.
So the Imperial ratios are:
1760 yards = 1 mile
220 yards = 1 furlong … divisor 8
22 yards = 1 chain … divisor 10
5.5 yards = 1 rod … divisor 4
Ralph
Hi Willis.
The pyramid builders used a distance measuring wheel with a radius of 1 cubit. 1 cubit up and 1 rotation along puts a ratio of 1 up to 2Pi along in their measurements without them having any understanding of Pi.
ralfellis August 25, 2017 at 3:29 pm
and
Oh, piss off with your arrogance. I’ve done land surveying, which is the only place where these curious measurements are used, so I know Imperial measures both in theory and in practice. You have no clue what I know, please stop pretending you do.
You STILL have not explained what five and a half rods are, or why you are mentioning them. And you still haven’t noticed that you are NOT using pi, you are using 22/7 instead. It would have been easier if you’d told the truth from the start, which was that you were not discussing Pi …
And “5.5 rods” still doesn’t a damn thing. IF you meant 5.5 yards = 1 rod, then you should have said that.
Finally, one mile is 8 furlongs, one furlong is 10 chains, and one chain is four rods. Oh, and you left out the smallest measure, one rod is 25 links … you sure you understand Imperial measurements? In any case, please explain what on earth any of that has to do with Pi.
w.
PS—Your insistence on using 22/7 for Pi reminds me of the Indiana Pi Bill, viz:
You really have an ego, Willis, and a problem with anger management.
The original posing was to all WUWT, not toyourself. And WUWT happens to be an American site where Imperial measures should be readily understood.
.
What do you always say, Willis?
*** QUOTE MY EXACT WORDS ***
I will reiterate that I NEVER said ‘5.5 rods’. And if you cannot twig that there are 5.5 yards in a rod, as a surveyor, then there is no hope for you.
P.S. I was also a surveyor.
Ralph
I think you mean a 20-21-29 triangle.
sure do.
Yeah, it was a 20-21-29 pyramid.
But my answers to Willis all disappear into the aether.
R
20-21-29 triangle etc is not so hard. Once you have noted a few easy ones like 3-4-5 ie you know how to multiply numbers already, you just write out a nice cuniform table of all square numbers up to 30, this will need two small blocks of wet mud.
You then test some combos higher than the basic 3,4 and see whether the result is in your table of squares. You then make some more mud tablets and write all the ones which work up to 29^2
4000 years later someone with a nasty blue jacket and silly glasses will come along and ….
But, but, but – I thought that the ancients were knuckIe-draggers who could only grunt and scream.
To derive pythagorean triangles, you need to know that certain triangles might be special, otherwise you would never look for them. This implies a certain amount of mathematical inquiry as a prerequisite. You then need to understand squares and square roots, and set out a table with several thousand cells, to calculate each possibility.
How many possibilities are there? 1 to 30 for three sides, minus some duplicates…. I’ll let you calculate that.
R
“The Great Pyramid.. Height 280 cubits, perimeter 1760 cubits”
Close, but those whole numbers don’t yield the observed side angle.
English feet fits better, 612ft from the from the base to the virtual apex up the middle of one side, and from the middle of that side to dead center, 378ft, yields a height to a virtual apex of 481.31ft, and much closer to the observed side angle of 51deg 51min etc.
612 is 4*153, 153 is the 17th triangular number.
378 is the 27th triangular number.
612+378 = 990, the 44th triangular number.
990*16 = 15840ft, = 3 Imperial Miles.
That would be the Pythagorean perspective.
Pi, try 3927 / 1250 = 3.1416. Why 3927? it’s 17*231 and also 7*561, the 21st and 33rd triangular numbers. There are 125.0 megalithic yard (340 feet) circles at Avebury, using that figure the error from true Pi would be three hundredths of an inch on the circumference. For interest, look on google maps and see how close the center of Avebury main ring is to one seventh of 360° north of the equator.
Base 60 will get you more non-extended fractions and probably more practical accuracy, but if you look at an old book of trigonometric tables you’ll find plenty of precision. A modern computer will undoubtedly produce even more precision.
by choosing to write down a subset of rations which all correspond to rational numbers you can remain totally accurate. That is not something of which were unaware until this Aussie genius in New-southo popped his head up.
See how far you get trying to predict and eclipse only using rational numbers.
Very interesting. Makes you wonder if science and maths is sometimes temporarily forgotten, perhaps due to war but is then rediscovered. We see it with the Greeks use of algebra which was forgotten until rediscovered by the Arabs a thousand years later.
Speaking of Greeks I have always been fascinated by what is often described as the worlds first computer, used to predict planetary movement over 2000 years ago. It was rediscovered at the bottom of the ocean and reconstructed
https://www.livescience.com/1166-scientists-unravel-mystery-ancient-greek-machine.html
Tonyb
Arabs didn’t rediscover algebra, but kept its memory alive. They knew it from Greek texts lost in the West and from Indian math.
And of course it never was lost in Byzantium. After the Turks conquered Constantinople, fleeing Greek savants brought much of the original ancient math and science West. Copernicus benefited from this new source of ancient knowledge.
That was really my point, the knowledge was lost to the west, kept alive elsewhere
“We see it with the Greeks use of algebra which was forgotten until rediscovered by the Arabs a thousand years later.”
Ah yes, now I re-read it , I realise that is exactly what you were suggesting 😉
climatereason August 25, 2017 at 2:28 pm
Except that the Arabs didn’t rediscover algebra a thousand years later. For starters, they didn’t rediscover it at all, but learned it from ancient Greek and Indian texts, in the cities of the advanced civilizations which they conquered. Second, Rome fell in AD 476. The Arabs didn’t suddenly invent algebra in 1476. By that time, the original Greek texts had already returned to the West from the Byzantine Diaspora, not the bastardized translations from Greek to Latin to Arabic and back to Latin.
I got a bit intrigued by all this.
Let’s assume that Babylonians had a notion of square root, than Pythagoras’s theorem is a peace of cake.
In our decimal system, whole numbers square roots (1, 2, 3,4, etc) the radicands (1,4,9,16,25 etc to 144) are separated by sequence of odd numbers and grouped in blocks of 5 (half of base 10)
1….11….21
3….13….23
5….15….etc
7….17
9….19
Now let’s assume that the Babylonians used as base not 10, not 60, but simply 6
So what is base 6, sequence of above numbers written in Arabic numbers when regrouped in blocks of 3 (half of base6)
1……11……21……31…….etc
3……13……23……33
5……15……25……35
If zero was not known than the first number (1 shown in bold) is simply dropped.
Knowing this simple relationship of differences between radicands that give whole number sq. root then calculating hypotenuse from two catets or any other combination becomes an easy task.
Whether this holds for base 6 three digits blocks series (radicand more than 10,000+ in decimal system) more research required, grant money run out.
(assuming all this is correct and makes sense to any of you)
‘then’
you don’t need a notion of sqrt to do that, just a square, which is rather obvious.
difference of two squares: x^2-y^2 = (x-y)*(x+y) ; (x-y)=1
so the column method will hold for all even based number systems , as far as you wish to go.
In decimal system yes, but what I had in mind is in the base 6 system
If first 3 digits is 100 yes, but if it is 111 then maybe not when shown in Arabic.
However if 6 symbols for 6 numbers are say: ■ ♦ ▲►▼◄ only god only knows.
The algebra is independent of number base and the symbols used for the digits. The only condition is that the number base is even, for the columns to repeat.
As you noted you need the concept of zero and 0^2=0 to get the initial 1
There seems to be an attitude among people that all those old dudes were “stupid” because we know more now. Yet, we’re just now learning what they already found out.
Kind of like a teenager mistaking the lack of knowing how to “twitter” for a lack of wisdom.
Well, on the face of it, it seems a refreshing discovery although it could have been even better if they explained just what it was. Today’s scientists are loathe to reveal any data. This is the post normal world and maybe the geometry is just unknown to University of NSW.
They still have an anachronistic center of exultance in climate science – originator of the Ship of Climate Fools – and they seem unaware that Donald Trump cancelled global warming science. Reminds me of lost platoons of Japanese soldiers sighted over a couple of decades after the war was over, dashing around in the jungles of Indonesia unaware of the armistice.
20 minuye video with two of the authors that goes into more detail
I’m suspicious of any putative “science” with the acronym BEST.
here’s another video by the same folks
1+24/60.+51/360.+10/360./60. = 1.54212962962963
root 2 ??
Thanks for the video links. I learned quite a bit from the explanations.
ralfellis August 25, 2017 at 3:24 pm
So there is no “2 X Pi” in that at all … just something that kinda sorta approximates Pi? Why didn’t you just say so?
I’m sorry, Ralph, but 22/7 is NOT Pi, no matter how you want it to be.
In addition, as far as is known, the approximation 22/7 was NOT used by the Egyptians, it was used by Archimedes. See here and here for more.
w.
It is not what I wanted, it is what the designer of the pyramid wanted.
If you read “Complete Pyramids” by Lehner, the Great Pyramid is 2 x 22 / 7 (ie: 2 x Pi).
(The height is 7 units. The circumference 2 x 22 units.)
(Using the fractional Pi, and scaled up by a factor of 40).
Engineered to the nearest 4 cms – in a building over 146 m tall and 230 m base length.
And using the Rind papyrus for evidence of the Pi fractional used is not entirely relevant, as this is a Hyksos document dating from the 17th century BC. The pyramid was 800 years before this time – if you believe the dating and the attribution to Khufu.**
And yes, information and knowledge was being lost over the centuries, rather than gained, as the increasingly smaller and poorly built ‘pyramids’ of later dynasties attest. Some hardly deserve to be called pyramids. The megalithic pyramids stand apart as being something quite unique. And since they are uninscribed, they were not tombs. No burial has been found in a pyramid. They are better described as cathedrals, perhaps, but certainly not tombs. We have many fine cathedrals in Europe, but they were not built as tombs. And every Christian cathedral contains an empty tomb, the same as the pyramids do. Do you know where it is?
** Khufu does not exist. His name on the Abydos king-list is Ufura. But Howard Vyse misspelled the hieroglyphs.
Ralph
ralfellis August 25, 2017 at 4:31 pm
Awesome! What was the designer’s name, and how do you know what he wanted?
w.
Willis,
https://en.wikipedia.org/wiki/Hemiunu
Among the evidence for the GP’s use as a tomb is this sarcophagus in the “King’s Chamber”:
Gloateus August 25, 2017 at 4:50 pm
He is BELIEVED to be the architect … meaning that he’s the likeliest suspect. I find:
… “is considered to be the architect” …
And I’m still waiting for Ralph’s answer as to how Ralph knows that Hemiunu wanted Pi to be 22/7 as he claimed …
w.
Willis , you are being very picky. He did show you can get a ratio of 2*pi . All values of pi are approximations and 22/7 was well known and often given when I was at school before the age of electronic calculators.
pi -22/7 / pi = 0.000402 or 402 ppm
That is certainly good enough for an engineering project like a pyramid.
You pedantic carry on after that looks rather dishonest.
Whether that ratio shows they had knowledge of the ratio pi, seems less clear but is interesting.
Thanks for the clarification Ralph.
Sorry, Willis, you are becoming tiresome here.
If the largest building in the world is demonstrably made to 2 x 22 / 7 (formula for circle) and the building next door is made to a 3-4-5 (pythagorean triangle), I think we can rightly assume that the architect was embodying items of mathematics for future generations. Or simply showing off.
But the evidence from history suggests the former. Josephus Flavius says that two pillars (pyramids) were made to record the wisdom of the ancients, one of brick and one of stone. (The Egyptian and Sumerian pyramids, of stone and brick.) So we have an ancient tradition that says the same thing – that wisdom was being encoded into architecture.
Look, if we measure the Pantheon, and find that the hemisphere of the dome has the same radius as its height above the ground, I think we are rightly justified in saying that the architect was designing a giant sphere. And since the heavens above were seen as a hemisphere, and it was already known in this era that the Earth was a sphere, I think we can also assume that the architect was encoding this knowledge into his or her design. See Architecture and Mathematics from Antiquity to the Future by Kim Williams, 6-83.
.
As I said before, every church and cathedral contains an empty sarcophagus – it is called an altar (covered by a cloth that is symbolic of the winding sheet of Jesus). This is because an empty sarcophagus is the foundation for this creed. Masonry is likewise based upon the symbolism of an empty sarcophagus (of Hiram Abif). This is because an empty sarcophagus is the foundation for this creed.
An empty sarcophagus in the Great Pyramid is more likely to be evidence for a resurrection cult, like Christianity and Masonry. And since every Masonic temple is supposed to have a double-square floorplan, the same as the King’s Chamber has, there are yet more similarities.
And no self respecting pharaoh would EVER be buried in an uninscribed tomb that did not glorify his name. It is unthinkable. Witness the 18th dynasty tombs in the Valley of the Kings. But if these were pyramidal cathedrals, dedicated to whole dynasties of pharaohs, this would explain the lack of inscriptions. Westminster Abbey may contain some royal burials (which pyramids do not), but you would still not call Westminster Abbey a tomb.
Ralph
The Pantheon:
https://sites.math.washington.edu/~greenber/PiPyr.html
http://egypt.hitchins.net/pyramid-myths/khufus-pyramid-does-not.html
And it gives a nice symmetry too, so the perimeter of the G.P. can be 1760 cu and the height 280 cu. And which architect does not like symmetry?
And the 280 and 7 measurements were embodied into the cubit sub-units. The cubit was subdivided into 7 hands and 28 fingers, which is symbolic of the 22 / 7 Pi fractional, and the 280 height of the pyramid. While the 22 numerator formed the basis of the ‘pyramid mile’ and the imperial mile (just multiply by a factor of 40 and by the 2 in the formula for a circle). And of course 1/4 of 22 is that famous 5.5 rod, that Willis is continually stumbling over (there is evidence that 5.5 cubits was used in the G.P.)
And do remember that this was the sacred cubit. The profane cubit only had 6 hands and 24 fingers, which did not embody anything. But the priesthood had 7 hands and 28 fingers, because they knew what the fractional approximation of Pi was. And since knowledge is power, they were keeping this to themselves…..
R
“An empty sarcophagus in the Great Pyramid is more likely to be evidence for a resurrection cult”
With a constant 68°F in the Kings chamber, that could well be a brewing vat for ale. The salt deposits in the Queens chamber would be the barrel sterilization room, and the barrels get rolled down the grand gallery and put into the subterranean chamber to mature. 😉
ralfellis August 26, 2017 at 2:54 am
I get tiresome when someone doesn’t answer my questions. You claimed that some off the wall ratio was “what [the designer of the Great Pyramid] wanted”.
I asked how you knew what he wanted … and you’ve responded with bafflegab.
How about you admit you don’t know what he wanted, nobody does? Read Mosher’s link and second link below. You’re just repeating 19th century numerology, and poor numerology at that.
w.
ralfellis August 26, 2017 at 2:54 am
My reply didn’t post, perhaps because it too included the apparently banned name of P.e.t.r.i.e.
The short version is that the sarcophagus is empty because all the pyramids were looted. Tomb raiders took virtually everything, and anything they might have left rotted.
On pyramids as tombs:
https://www.quora.com/What-was-the-purpose-of-the-pyramids-of-Giza
And as launching pads for souls to Sirius, Orion and other stars, with shafts aimed toward their positions at time of construction:
https://www.theguardian.com/world/2001/may/14/humanities.highereducation
But that is not really true, is it.
The entrances to the Second and Third Pyramids at Giza are obvious, so everyone knew where they were. Which is not secure for a tomb. But it is fine for a cathedral. The entrance to the Great Pyramid was also open, as Strabo desribes it, and the stone door that closed it.
However, there were hidden chambers in the Great Pyramid. Possibly with mummies and treasures??? But these were first discovered by Caliph al Mamoun in the 14th century (?), but history appears to record that the chambers were empty, and Mamoun went away empty handed.
Ralph
Mosher.
That table of pyramid angles is uninformed.
Firstly, they should be looking for 22/7, not pure Pi. And the GP is accrurate to about five decimal places when using 22/7. There is no point making a monument to fractional measurements, as it is almost impossible for the architects to follow the plans, and almost impossible for anyone to work out what measurements are ‘meaningfull’. A nice whole 1760 cubits and 280 cubits related to 22 / 7 is much more meaningfull that decimal places.
And then he goes on to comparing the 5th to 7th dynasty pyramids, without realising that these are not megalithic, and not made to the same standards whatsoever. The only pyramids worth investigating are those at Giza and Dahshur.
R
ralfellis August 27, 2017 at 12:21 pm
Gosh, Ralph, you mean that if you throw out all the pyramids that do NOT fit your goofy theories, the remainder show that you are 100% correct?
There’s a job for you in the tree-ring scam, that’s for sure.
w.
ralfellis August 27, 2017 at 12:21 pm
Despite requests, you have NOT shown the slightest scrap of evidence that the ancient Egyptians used 22/7 as an estimate of Pi. Provide a link, or your claims are busted … because your unsupported word is worthless.
w.
PS—As is my unsupported word, for that matter …
The Babylonians may also have created rudimentary batteries and used them to experiment with electrolysis, based on artifacts consisting of small urns with metal rods and chemical traces inside.
Those jars most likely used as batteries were Parthian or Sassanian, ie from long after the Babylonians.
However, some copper vessels found in Sumerian remains, ie from before the Babylonians, show signs of having been plated, whether electrically or not.
But archaeologists today doubt that the artifacts are indeed batteries.
https://en.wikipedia.org/wiki/Baghdad_Battery
Thanks for clarification.
I saw this in the comments over at The Independent on this same story:
“I learned on my 1979 Open University History of Mathematics course from a 1930’s book on Babylonian mathematics that the sexagesimal base 60 also had Place Notation for numbers less than one, the first column being, sixtieths, the second column being three thousand six hundredths and the third column being two hundred and sixteen thousandths. A fourth column would be accurate to 1.29 millionths, all written with just two symbols, a wedge at one end of a stylus and a round circle from the other end of the same circle, arrange in tight patterns, rather like dots on a dice, being easy to read,which is pretty economical.
Not only that, but kids learned their sine, cosine and tangent tables to rhyming verse, so could solve any triangle knowing one side and an angle. They also used lines, squares and cubes like Leggo sticks, squares and cubes to solve quadratic and cubic equations, posed as a verbal question. Obvious square roots and cube roots were easy to them and there is a well known tablet around giving the square root of two to about fourteen sexagesimal places…”
That’s pretty cool if true
And AFAIK, we’ve yet to recreate exactly some well-known historical materials, like “Roman concrete” (could set and cure underwater, used among other things for bridge-building) and “Greek fire” (oily liquid that ignited on contact with water, used as a fearsome naval weapon by the Byzantines).
The properties of Roman have been attributed to including volcanic ash in the mixture, and using larger aggregate than normal in modern concrete, so large in fact as to amount to rubble. Hence, Roman concrete was laid rather than poured. The dome of the Pantheon is remarkable for its use of pottery shards as “aggregate”.
It is being copied today by adding fly ash in lieu of volcanic “ash”.
You’re right that the precise composition of Greek fire remains unknown. Remarkable that the Byzantine state could keep a secret for over 1300 years. But then the price of bread remained the same there for a millennium.
The secret to Roman concrete was discovered recently. It was seawater
All concrete can set and cure underwater. Concrete curing is a hydration reaction.
Lime mortar requires CO2 which is where this whole thing got started I guess. Concrete made with lime mortar won’t set under water (unless you’ve used broken bricks or tiles as the aggregate which act as a pozzolan to form a crude cement mortar). Confusion between ‘cement’ and ‘concrete’ is common. US calls concrete blocks ‘cement’ blocks for instance. Cement is like the flour in a fruit cake and concrete the cake.
‘Roman Cement’ reinvented by Rev. James Parker (patent 1796) after picking up some Septaria on a walk along the beach on Isle of Sheppey (Kent, UK). This is close enough for now https://en.wikipedia.org/wiki/James_Parker_(cement_maker)
For those interested in the history of structural engineering Sheppey also has the world’s first modern framed building built in 1860 by Royal Navy at Sheerness dockyard.
http://www.tandfonline.com/doi/abs/10.1179/tns.1959.005?journalCode=yhet19
In the middle column, fourth row down, the third decimal place is wrong. No wonder Babylon fell…
Perhaps it was their invention of EVs …
If the tablet was found near Larsa and dates from ~1700 BC then strictly I’m not sure it can be described as “Babylonian” implying from Semitic-speaking origin.
The southern Euphrates plain was still occupied by Sumerians, thought to be from a different ‘West Asian’ language group maybe proto-Indo-European.
Pretty sure that the table is Semitic, although the Babylonians appropriated and improved the Sumerian Base 60 system.
Transition from Sumerian to Babylonian is usually given as c. 1900 BC.
Very interesting stuff, and, yes, we do often underestimate the knowledge and skills of the ancients. That is why theories about ancient accomplishments being done by extra-terrestrials are so popular. However, I am quite skeptical about the article’s conclusions.
First, for all we know, this “trigonometry” may have been invented/discovered by a few very bright chaps who used it only rarely for the benefit of the ruling class, and it was then forgotten. Today, largely thanks to the Greeks, every high school sophomore is “supposed to” understand trigonometry, how many Sumerian teenagers understood it or its applications (granted, probably more than American teenagers, but that is another issue)? Besides, how good is technology if it is lost for 3,000 years only to be discovered later by a society smart enough to interpret it? At least what the Greeks created they preserved.
Second, I am always skeptical about predictions. The article opines that we could learn soooo much from this discovery, that we can lern soooo much from an ancient, non-Western society. Really? Aren’t these the people who promised us flying cars?
Well, I’m a life long fan of base 12! I wish we used it as I’d like the base to be divisible by 2 and 3 exactly! Actually, the oldest “abacus” is the human hand. The thumb is used to count the division on each finger, three on each of the four fingers. The other hand is used to keep the total, starting with thumb symbolising 1 dozen, followed by each of the five fingers giving a total of 60; naturally! 😉
Should be: “The thumb is used to count the divisions on each finger, three on each of the four fingers. “
Ancient Egyptians and Babylonians ‘invented’ plane geometry and trigonometry. They used it for practical purposes of land area measurements and astronomy and astrology to predict seasons for agriculture and future events. The ancient Greeks developed these crude knowledge into formal theories. It’s like Egyptians and Babylonians were great auto mechanics. The Greeks invented mechanical engineering.
‘the calculations are far more accurate’. Hm, the representation of fractions in base 60 is more precise. Trigonometry is trigonometry, whatever base is used. We use base 2 in calculators. The sine of 30 degrees is still 0.5.
I think the ancient Greeks developed a sort of worship for logic, which, though it took them a long way, failed them once they discovered irrational numbers. The concept of complex numbers involving calculations using the square root of negative one would have been quite beyond them, requiring more “can-do” thinkers. I also believe this conceptual failure is the main reason Greek maths stagnated, with the inevitable knock-on effect on further scientific and technological progress.
However the Greeks did bring about that logical mathematical machinery involving theorems, proofs and so on, which far surpassed the achievements of other civilizations, which only had collections of useful algorithms at best.
Harking back to earlier comments regarding Roman concrete; and moving off on a tangent…..
As a consequence of a recent discussion in my local pub, I understand that the ancient Egyptians had developed an aggregate of crushed granite and quartz, with some kind of binder, to make “artificial” granite.
This granite was then poured into forms, or shaped like pottery.
Once it cured, it was/is indistinguishable from “real” granite.
Does anyone know anything about this? Or was it just the cheap liquor talking?
I don’t know, William. But, you get a clink of the (rootbeer) stein for moving off on a tangent.
#(:))
It’s a French materials scientist and amateur archaeology theorist talking. This guy argued that the blocks of the Great Pyramid were cast on site from a concrete or cement-like mixture, not cut and hauled there from a quarry. This has been shown false by Eocene fossils in the limestone, among other evidence.
https://en.wikipedia.org/wiki/Joseph_Davidovits
However, the Egyptians did use a cement-like mixture between some of the blocks, in which Davidovits claimed to have found a hair. This story morphed into his having found hairs inside the rock blocks.
Fossils in Egyptian stone monuments:
http://www.abc.net.au/science/articles/2008/04/28/2229383.htm
Gloateus: thanks for the links; they made for interesting reading.
If the guy’s theory were correct, it would certainly answer a lot of questions!
Back to the pub…… (for more tangents)
Hmmm…. This sounds like ancient cultural appropriation to me.
/wink
ralfellis August 26, 2017 at 2:05 am Edit
Ralph, what you said was what I quoted:
That was said, not to “all WUWT”, but to me. So once again, piss off. You have no clue what I am or am not familiar with.
IDID quote your words. I’ll quote them again. You said:
And as I said above, if you meant 5.5 yards in a rod, then you should say so … but you didn’t say a word about yards.
Congratulations. Your momma must be proud.
w.
This entire subject of “inventor of trigonometry” needs a closer look. Does it mean anything?
Trigonometric functions had to wait for series approximation techniques us to really understand and use them. Is that the “real” trigonometry? “Functions” of a variable don’t exist for these ancient blokes either, or for anyone else until the 17th C. A.D. so far as anyone can tell. Much of ancient geometry from Eudoxus (4th C. B.C.) revolves around triangles. What distinguishes “trigonometry” from general geometry?
Pythagorean triples, i.e. the A, B, & C of standard right triangles, are ancient, and they find them everywhere completely devoid of the method used to derive them. Nobody knows whether they were calculated or physically measured using ropes. Pythagoras, the man we associate with this right triangle theorem, was trained in Egypt. Thus, the contest for inventor of math has never been between the Greeks and Mesopotamians, it’s always between the Egyptians, Mesopotamians, Pre-Vedics, Pre-Druids, Yellow River civilization, and the civilizations that are currently underwater due to the end of the last ice age.
This Telegraph article is a puff piece.
look at the remainders of the hypotenuse first minus the long side, and second minus the short side.
Row 1:
169 – 120 = 7^2.
169 – 119 = 2 x 5^2.
Row 2:
4825 – 3456 = 37^2.
4825 – 3367 = 2 x 27^2.
Row 3:
6649 – 4800 = 43^2.
6649 – 4601 = 2 x 32^2.
Row 4:
18541 – 13500 = 71^2.
18541 – 12709 = 2 x 54^2.
Row 5:
97 – 72 = 5^2.
97 – 65 = 2 x 4^2.
Row 6:
481 – 360 = 11^2.
481 – 319 = 2 x 9^2.
Row 7:
3541 – 2700 = 29^2.
3541 – 2291 = 2 x 25^2.
Row 8:
1249 – 960 = 17^2.
1249 – 799 = 2 x 15^2.
Row 9:
769 – 600 = 13^2.
769 – 481 = 2 x 12^2.
Row 10:
8161 – 6480 = 41^2.
8161 – 4961 = 2 x 40^2.
Row 11:
75 – 60 = 15. {no square]
75 – 45 = 30. {no square]
Row 12:
2929 – 2400 = 23^2.
2929 – 1679 = 2 x 25^2.
Row 13:
289 – 240 = 7^2.
289 – 161 = 2 x 8^2.
Row 14:
3229 – 2700 = 23^2.
3229 – 1771 = 2 x 27^2.
Row 15:
106 – 90 = 4^2.
106 – 56 = 2 x 5^2.
To calculate the hypotenuse, example Row 4:
Add the short side and the long side:
13500 + 12709 = 26209,
minus the product of the square roots and the two:
(71 x 54 x 2) = 7668:
26209 – 7668 = 18541.
And it then follows that the hypotenuse plus the short side, then divided by two, is a square, and the hypotenuse minus the short side, then divided by two, is also a square.
Also in each case, the hypotenuse plus the long side, is also a squared number.
e.g. 18541+13500 = 179^2.
So the short side is the product of the square root of the hypotenuse plus the long side, and the square root of the hypotenuse minus the long side.
71 x 179 in Row 4.
The apparent values in the first column on the tablet are the short side divided by the long side, then squared, I don’t get see the relevance of them yet though.
Further, each short side is divisible by the square root of the remainder of the hypotenuse minus the long side, e.g. Row 4; 12709 / 71 = 179.
oops sorry about the chaotic comment nesting!
Apparently this is not new at all. Mario Livio in oneof his books referred to this already.
It begs the question, from whom did the babylonians learn this information?
“The largest number that always divides abc is 60”
https://en.wikipedia.org/wiki/Pythagorean_triple#General_properties
ralfellis August 27, 2017 at 12:21 pm
What about the famous “Bent Pyramid”? How does that fit into your Egyptian numerology? The side has two slopes, 54° and 43° …
I mean, you’ve already claimed (but failed to back up) that the builder of the Great Pyramid wanted to make the ratio of the circumference to the height equal to 2 * Pi.
Given your arcane inside knowledge of the inner thoughts of ancient Egyptians, what did the designer of the Bent Pyramid want to do regarding Pi?
w.
Gloateus said: “Or the fingers and toes of 2 people”
I’m sure in those situations, other parts of anatomy were also of interest.