Guest Post by Willis Eschenbach (NOTE UPDATE AT END)
There’s a recent and good post here at WUWT by Larry Kummer about sea level rise. However, I disagree with a couple of his comments, viz:
(b) There are some tentative signs that the rate of increase is already accelerating, rather than just fluctuating. But the data is noisy (lots of natural variation) and the (tentative) acceleration is small — near the resolving power of these systems (hence the significance of the frequent revisions).
(c) Graph E in paper (5) is the key. As the world continues to warm, the rate of sea level rise will accelerate (probably slowly).
This question all revolves around whether the rate of sea level rise is relatively steady, or whether it is accelerating … so how do we tell the difference?
Well, how I do it is to fit two models to the data and see which one works better. The first is a straight-line model (a linear fit), and the other is an accelerating model (a “quadratic” fit). Figure 1 shows an example of some pseudo-tidal data which in fact has an accelerating rate of sea level rise. I’ve created it by simply adding an accelerating trend to an actual tidal record.
Figure 1. Artificial pseudodata of a tidal gauge recording an accelerating rate of sea level rise.
As you can see, the blue line showing an accelerating (quadratic) fit matches the data much better than the linear fit (red). How much better? Well, that’s measured by something called “R-squared” (R^2). This is a value between zero and one which measures how well the given line explains the dataset.
The R^2 for the blue line (0.88 ± 0.02) is much larger than the R^2 for the red line (0.77 ± 0.02). And since the difference between the two values is greater than the sum of the standard errors of the two values, we can say that the difference between them is statistically significant. In other words, in the Figure 1 case, we can say that there is a statistically significant acceleration in the dataset.
So that is what I planned to look at—whether the difference between the R^2 for the linear and the quadratic fits is greater than the sum of their standard errors.
With that as prologue, let me discuss my methods. I took the full tidal dataset from the Permanent Service for Mean Sea Level. It has 1,505 tide station records in it. However, as with most historical datasets, there are lots of gaps and stations with short or spotty records.
So I had to use a subset of the data. Because the long lunar tidal cycle is just over fifty years, you need at least that much data to get a serious estimate of the rate of sea level rise. And we are interested in any recent acceleration. So I limited my analysis to tidal stations with data starting before 1950 and ending after 2015. This cuts the list down to 171 stations which cover the period of interest.
However, some of these are missing a lot of data, some with over half of the data gone. I wanted enough data to have faith in the analysis, so I further limited the dataset to those stations having 95% or more of the data during 1950-2015. This further reduced the number of tidal stations to 63. Figure 2 shows a sample of 10 of these.
Figure 2. Typical records which fit the criteria of the ex-ante data selection process (95% data coverage from 1950-2017)
Now, my Mark 1 Eyeball says that if there is acceleration there, it is minor … but let’s look at the numbers. Here is a scatterplot of the R^2 values of the linear fit versus the R^2 values of the quadratic fit:
Figure 3. Scatterplot, R^2 of the linear fit vs. the R^2 of the accelerating (quadratic) fit. Dots above the diagonal line are stations where the R^2 of the accelerating (quadratic) fit is larger than the R^2 of the linear fit.
As you can see, in almost all cases the gain in the goodness of fit when we go from linear to quadratic fits is trivially small, invisible at this scale. And when I examined the gain in R^2 versus the standard errors for each of the 63 stations, in every single case the accelerating fit was NOT statistically better than the linear fit.
In other words, not one of these datasets shows statistically significant acceleration.
And that is why at the top I said that I disagree with the following statement from the other post, viz:
There are some tentative signs that the rate of increase is already accelerating …
Simply not true. Figure 3 shows clearly that the tidal gauges contain no such “tentative signs”. NOT ONE of these 63 full tidal datasets shows statistically significant acceleration, and more to the point, most of them show only a trivially small difference between acceleration and a simple linear fit.
The other statement I disagreed with was:
As the world continues to warm, the rate of sea level rise will accelerate (probably slowly) …
Look, this is just the same nonsense that the alarmists have been peddling for the last thirty years, that in the future the sea level rise will accelerate, that New York will be underwater, and the like … but it has been thirty years since the first bogus prognostication was made, and there is still no evidence that the sea level rise is accelerating.
Look, I’m all in favor of taking care about the future … however, call me crazy but I need EVIDENCE before I start hyperventilating about Miami sinking into the ocean.
5 PM, the dreaded global warming has cooled down now. Me, I’m going to post this and then go outside to lay some pavers in the new level space I just made with my own sweat. Plus a rented backhoe. I could have hired someone, but why should illegal immigrants have all the fun? I like living in the hills … but this is the first and only flat spot on my land, so I’m making it nice.
What a universe!
Best to everyone,
w.
PS—The Usual: When you comment, please QUOTE THE EXACT WORDS YOU ARE DISCUSSING, so that we can all be clear about your precise subject.
DATA—I’ve put the 63-station data here, as a CSV file so that anyone can use it in Excel or any other program.
[UPDATE] Over at Tamino’s website, where since about 2009 I’m barred from commenting because I was asking inconvenient questions, he points out that there is a simpler and more accurate method for finding out if a dataset contains acceleration. This is to see if the squared term in the quadratic equation is statistically significant after correction for autocorrelation, duh … he is correct.
My thanks to him for pointing this out, although I do have to deduct points for his repeated ad hominem attacks on me in his post … haters gonna hate, I guess.
Using his method I identified seven of the sixty-three stations as having statistically significant acceleration and three stations with statistically significant deceleration. However, the average value of their acceleration is 0.015 ± 0.012 mm/yr2 … which is not statistically different from zero. Here are the stations and their accelerations:
VLISSINGEN BALTIMORE SMOGEN KEY WEST KETCHIKAN
0.0605 0.0542 0.0676 0.0477 -0.0543
WEST-TERSCHELLING SANDY HOOK JUNEAU SITKA KWAJALEIN
0.0979 0.0510 -0.1052 -0.0573 0.1258
I note that one station he says has significant acceleration doesn’t appear in this list (Boston). I find that the p-value of the acceleration term for Boston is 0.08, not significant. I suspect the difference is in how we account for autocorrelation. I use the method of Koutsoyiannis, detailed here. I don’t know how Tamino does it.
I would also note that the average acceleration of the entire 63-station dataset is 0.014 ± 0.008, still not statistically significant. And if this turns out to be the long-term acceleration, currently the rate of rise is on the order of a couple of mm/yr, or 166 mm (about 7 inches) by the year 2100. IF this increases at 0.014 mm/yr2, this will make a difference of 48 mm (under two inches) this century.
Curiously, in the previous fifty-year period 1900-1950 there are only three sites with significant acceleration out of 38 datasets covering the period, and none are in the first list:
NEW YORK (THE BATTERY) HARLINGEN SEATTLE
0.0976 -0.1182 0.0959
Whatever any future sea level acceleration turns out to be, it is very unlikely to put the Statue of Liberty underwater anytime soon …
Man, I love writing for the web. All my errors get exposed in the burning glare of the public marketplace of ideas, I get to learn new things, what’s not to like?
Your more likely to see the water control systems break down and South Florida return to Everglades before the sea swamps Miami
Willis
Typo?
data starting before 1950 and ending after 1915.
Thanks, Ian, fixed.
w.
The Jevrejeva data derived from tide gauges was discussed in a post by David Middleton a few days ago. That data goes back to 1820 and also reports an acceleration.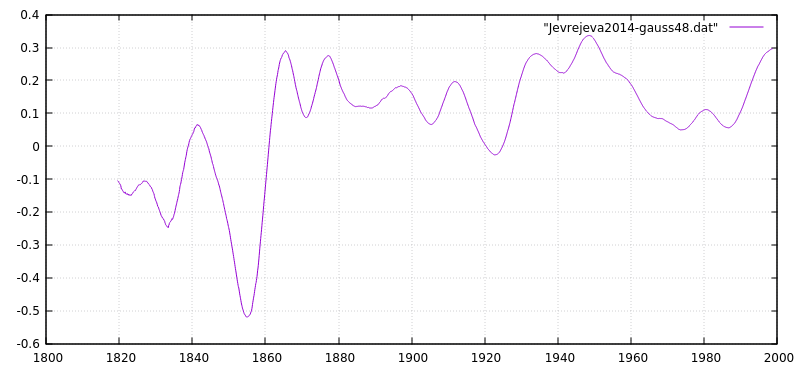
I used a 48 month gaussian filter on the rate of change of mean sea level to remove the short term fuzz.
As Jevrejeva 2014 reports there is an acceleration but it happened BEFORE 1900 and thus had nothing to do with human CO2 etc. In fact, it was almost a step change from decreaseing sea level ( negative change ) to rising sea levels which occurred around 1860.
Jevrejeva 2014 confirms that there is NO acceleration in the 20th century.
So looking at that data we see that if you blinker the analysis suitably ( eg. post 1950 because you are looking human attributable effect, and don’t want to to find anything contrary to that idea, as IPCC does with global temps ) you will find evidence of acceleration.
However, it is abundantly clear that this is no more that the preceding wiggles which can only be attributed to natural causes.
There was a notable ( natural ) acceleration around 1860 but the last 150y has basically being hovering around the same steady rate of rise, oblivious to the alleged effects of AGW, GHE etc.
If we chose to study 1920 – 1950 we can find a deceleration which is probably a little stronger than the later acceleration. There are no grounds for suggesting the later variability is due to human causes.
Since attempts to explain the lack of catastrophic global warming over the last two decades seems to centre on the idea that all the heat is hiding in the oceans, it is BIG problem that the oceans don’t seem to have noticed yet.
This is sea level week (-:
There’s been a flurry of “sea level is accelerating” stories in the “Popular Press” in the last week or so, most cite that the rate of sea level rise has doubled or more since 1970 or thereabouts. Prior history seems to be ignored. So what do long running tide gauges say about the rate for the last several decades?
http://oi66.tinypic.com/1zv7rwg.jpg
The median value shows a tiny increase compared to 1950.
Thanks, Steve, but only seven tide gauges? Put some error bars on the average and you’ll see the problem.
w.
Good job, Mr. Eschenbach. But Steve Case got to the heart of the matter. Yes, you can find acceleration if you take the right interval and the right data set.
But, as Mr. Case recognized, you could have found that much acceleration half a century ago, too–and it was followed by deceleration. In other words, the question isn’t whether there’s been some acceleration. Of course there has been, if you pick the right interval and time scale. The question is whether that acceleration gives us much insight into the future, which is what we’re really concerned with. The answer is no.
‘Twas ever thus. As Mark Twain said over a hundred years ago:
Love the Twain quote, Joe. Thanks! The ‘money’ line: “One gets such wholesale returns of conjecture out of such a trifling investment of fact.” That describes man-made climate change science to a ‘T’.
Despite the obvious flaws, probably still a better rough temperature proxy there than GISS models, too.
What a quandary! Do I side with Willis or Larry?
I’m gonna lean towards not accelerating…
And, it wouldn’t matter if it was…
David these are purportedly from a Liverpool University study, please could you show us the graph from the original paper, as you did in 2008 , The abstract of this 2014 paper stated that the sea level acceleration was calculated to be small 0.02 mm /yr^2.
Also the dip at 1860 does not appear in the Liverpool , Stockholm or Amsterdam data, nor in the data from Jevrejeva in 2008
Your dip states that the sea behaved differently in northern Europe to the rest of the data.Yet you in a post earlier lauded Liverpool as one of the best tidal study group in the world.
Ref SJevrejeva st al Global and Planetary Change vol113, p11 (2014)
“Liverpool” has nothing to do with anything. You keep asking why individual tide gauge stations don’t look like a eustatic sea level reconstruction. That’s like asking why a 2×4 doesn’t look like a house.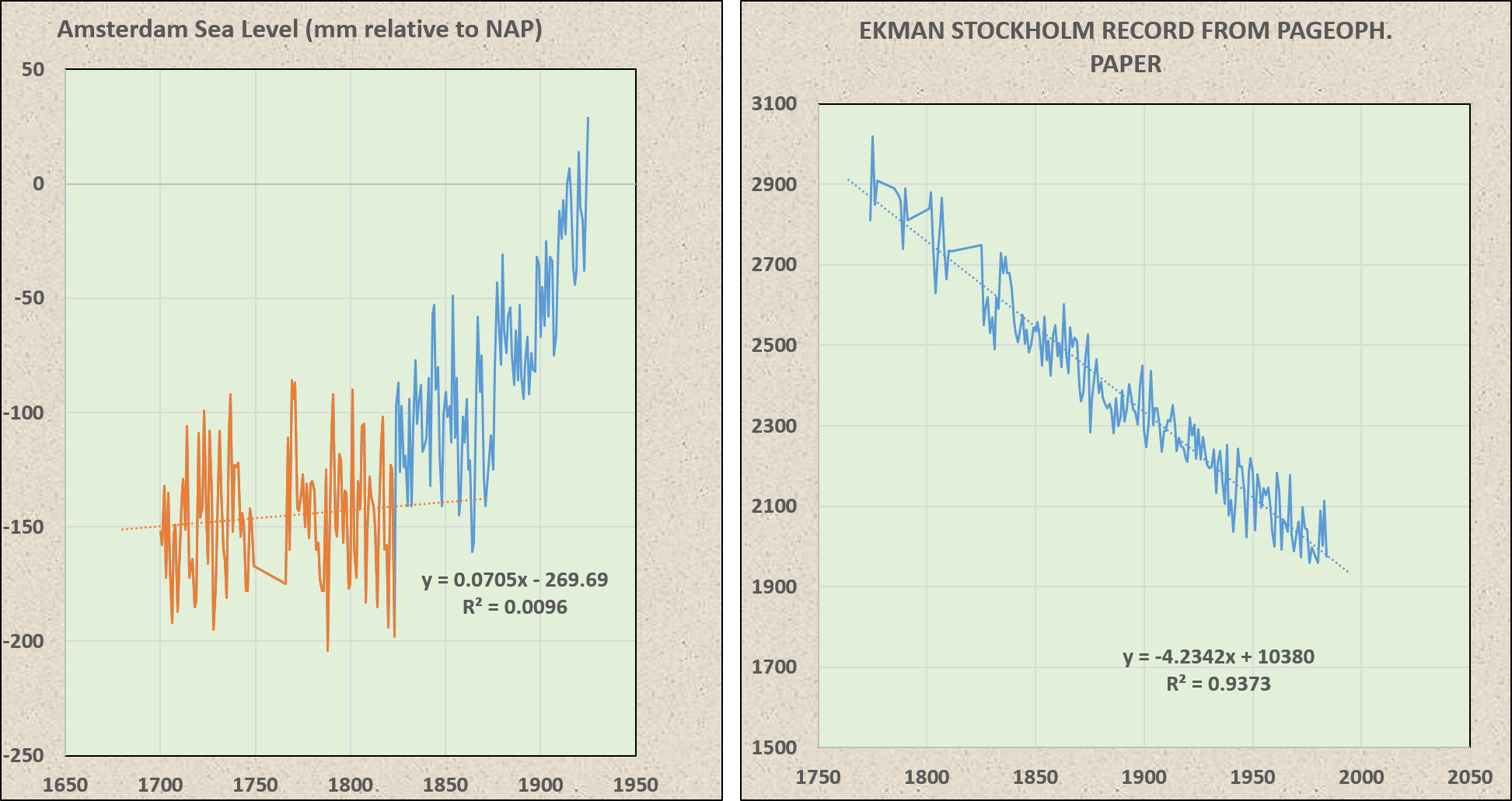
Tide gauges reflect eustatic (water moving up and down) and isostatic (land moving up and down) sea level changes.
A reconstruction of global eustatic sea level is an average of many tide gauges after the isostatic component has been removed.
The tide gauge at Amsterdam shows no sea level trend before 1823, a step-shift up, and then no trend until 1875. Stockholm exhibits a steady 4 mm/yr drop in sea level.
Jevrejeva 2008 looks like this…
http://www.psmsl.org/products/reconstructions/figure1.gif
http://www.psmsl.org/products/reconstructions/jevrejevaetal2008.php
Jevrejeva 2014 looks like this…
http://www.psmsl.org/products/reconstructions/jevrejevaetal2014.php
It’s not *MY* dip. The “dip” is in the reconstruction…
http://nora.nerc.ac.uk/504181/1/1-s2.0-S0921818113002750-main.pdf
Here’s an animated comparison of Jevrejeva 08 and 14…
The pre-1850 error range is large in both reconstructions. The error ranges generally overlap. The difference appears to be in the data selection pre-1850.
If you go to this PSMSL page
http://www.psmsl.org/products/reconstructions/gslGPChange2014.txt
and plot out column “D” from 1861.29 the trend is flat, no acceleration.
Quick & dirty – Here’s what that looks like:
http://oi66.tinypic.com/iz1g2g.jpg
Yep.
Spot on Willis, but that’s not surprising since you usually are !!
Sea levels rose sharply some 12,000 years ago as we
came out of the last ice agebegan using trendy SUV’s. It seems the only way to solve this catastrophic dilemma is to have millions of wind-powered snow making machines create another mile-high glacier over Canada (sorry).Gotta keep the SUV’s though.. Station wagon’s are just so yesterday.
Since the manipulate the land based temperature records, why have they not started manipulating and adjusting the tide gauge records? With terrestrial temperature readings they “adjust” the station data but leave the satellites alone. With sea level measurements they now adjust the satellite measurements but leave the tide gauges alone. It won’t be long before they control all of the data and there will be no sanity check.
The ever upward adjustment of their data is in correlation to their bank accounts.
Having done quite a bit of stats in my time as a undergrad psych, I found two things, guilt is a strong motivator for behaviour change (and I sat through a number of lectures about how guilt could be used to get people to be ‘more green’) and that stats can be massaged to produce a result. Even if you don’t get a statistically significant result, you can always throw in the line that the data is “trending towards significance” and that’ll probably be good enough for people with an agenda to push. Nice to see some numbers here reflecting some cold math and not bias
Forrest, I don’t see the issue. Perhaps you’d see the question clearer if you take a tide station which is decreasing, and you add acceleration to it … you’d get a quadratic curve, but it wouldn’t look like Figure 1.
w.
Forrest Gardener July 20, 2017 at 8:02 pm
No, it’s not “fine”. It means you haven’t explained your point well enough for the other person in the discussion to understand it.
I know that. But once again, I don’t see your point.
Thanks,
w.
Forrest Gardener July 20, 2017 at 8:02 pm
A further note. Forrest, I’m sorry, but an exponential function will not work at all in this application. Inappropriate choice. Think about it. If you can’t say why it won’t work, just ask.
w.
Not everyone thinks so (-:
Paleoclimate Implications for Human-Made Climate Change
James E. Hansen and Makiko Sato
http://www.mahurangi.org.nz/wp/wp-content/uploads/2014/12/Figure-7-v2.jpg
Fig. 7. Five-meter sea level change in 21st century under assumption of linear change (Alley, 2010) and exponential change (Hansen, 2007), the latter with a 10-year doubling time.
Steve Case July 21, 2017 at 3:56 am
The difference is that Hansen is looking at models for global sea level rise, which is known to be increasing. I’m looking at individual tidal records, some of which are decreasing …
w.
Excellent post.
Thanks Willis.
So Willis, you did some sailing. Probably using charts surveyed well over 100 years ago. More likely 200+. So in all that time did you ever see a chart datum corrected for sea level rise? Did you ever see any chart that was obviously wrong due to what you now recognize as sea level rise?
Ferd, interesting question. However, we have a couple of difficulties. First off, older charts are often in fathoms (6 feet, 1.8m) and half fathoms … so if sea level has gone up by 8″ (200 mm) in a century, the general average over the last hundred years, you couldn’t see it on the chart. Lost in the noise.
The second problem is that the old navigators had no exact idea where the zero point of the tide is at their particular location … or where “mean lower low water” (MLLW) is, which is the current zero point. This adds another couple of feet to the uncertainty.
Finally, NOBODY trusts a chart to anything like a fathom. You’d be mad to do so. If the boat draws three feet and the charts say there’s a fathom of water … well, you damn well better keep your eyes open.
So no, I don’t think there has been enough change to invalidate the old charts.
w.
Hi Willis, fathom charts were drawn to the nearest foot for water less than one fathom. It has been my experience they were drawn to a level of accuracy few could duplicate today. Bligh’s charts of Tonga are astounding accurate, drawn in the 1773? While aboard the Bounty.
But what really interested me was drying and awash rocks as we sailed, which are of course extremely dangerous so you pay attention to any errors. The problem is there were none. which suggests sea level rise is a non event.
Thanks, Ferd. Different charts from different countries used different minimum measures. And IF someone stays in one harbor for some months as Bligh did in Tonga, you can take a reasonable guess at MLLW.
But in many instances that was not the case. If you sail into a harbor and you only spend a few days there taking depths, you do NOT know MLLW with any kind of accuracy.
However, I’m still not following the story. Bligh went to Tonga in 1773. We do NOT know what the sea level was then. The PSMSL graph shows a steady decrease in sea level from 1807 to 1860 … is this accurate? We don’t know. What did sea level do from 1773 to 1807? If sea level fell as it fell in the following half century, it would have been about at the level it is today.
But the fact that the sea level in 1773 MIGHT be about the same as it is today does NOT mean that the sea level currently is not rising …
Finally, the idea that Admiralty charts are not adjusted vertically is not correct. With each new printing, they MAY be adjusted to a more accurate datum. Here’s what the Brits say (from a giant PDF not worth downloading):
My point is that we know a lot less than people think about these questions.
w.
I’ve worked one particular field in the Gulf of Mexico for 4 different companies since 1988. Neither the water depth of the platform nor any of the wells drilled from it has changed. Of course, we only measure to the nearest foot… So Gorebal Warming-related sea level rise is below our resolution… 😉
I would expect sailors 200+ years ago could tell you within a foot MLLW. Anything your life depends on you tend to get very good at (those that don’t die). And this applied in spades for those sailors that charted the earth. I expect every sailor appreciates what it is like sailing uncharted waters. The level of skill involved. Even back 15 years, after 20 afloat I routinely predict the change in weather better than our local weather service, without even thinking about it.
ferdberple July 20, 2017 at 7:46 pm
As a lifelong swabbie and a blue-water sailor, I find that doubtful. The problem is that the tide varies radically around the planet. For example, most places have two high tides and two low tides per day.
Then there are other spots with one high and one low tide per day.
And in the Solomon Islands, there are two high and low tides per day for half the year and one high and low tide per day for the other half of the year. Go figure.
This doesn’t even include the question of the “amphidromic points” …
Finally, tidal analysis in Britain didn’t even begin as a formal study until 1867.
So no, with all of that, if you sailed into an unknown port, your errors will not be small. Remember, it’s not just as simple as determining MLLW. You then need to reduce your observations to MLLW … which means that you need the height of the tide at each of your soundings …
Best regards, stay safe on the big ocean,
w.
Also, Forrest, I run by Occams Razor, “Don’t multiply causes unnecessarily”. A cubic equation has one more parameter than a quadratic, which in turn has one more than a linear regress.
THEREFORE, we need to show a SIGNIFICANT difference at each step in complexity to justify taking that step.
And looking at the data, I’m guessing that a cubic equation would NOT meet that test.
w.
I’ll take adjusted r-squared for $1000, Alex.
“With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” – John von Neumann
“String Theory is just power fitting the Universe.” – Tsk Tsk
Tsk Tsk
+6.022 X 10^^23 & Supersymmetry died at CERN
Forrest Gardener July 20, 2017 at 8:03 pm
Again, yes, but so what?
w.
Forrest Gardener July 20, 2017 at 10:33 pm
Since I’m only interested in the domain that I’m fitting … so what?
I always enjoy it when someone runs out of answers and starts thinking up excuses for not answering. The variety of excuses provided is always good for a laugh …
w.
Forrest, one other comment.
If you think an exponential is a better function to use than a quadratic, how about you ACTUALLY USE IT ON THE DATA THAT I GAVE YOU and post your results here. That way we can see if you actually have a point.
You talk the talk … but can you walk the walk? So far, you’re all hat and no cattle.
And before you start the project, you might consider the difficulty in fitting an exponential curve to the record for Juneau in Figure 2 …
w.
I have thought that an exponential function is the best choice for acceleration. It`s like putting money in the bank and let it grow (with constant interest). Most scientists talk about exponential growth when it comes to acceleration. So I cannot see why it will not work.
nobodysknowledge July 21, 2017 at 2:12 am
Nobodys, thank for the question. Take a look at the Juneau record in Figure 2, and consider fitting an exponential to that …
w.
Forrest,
Willis said; “If you think an exponential is a better function to use than a quadratic, how about you ACTUALLY USE IT ON THE DATA THAT I GAVE YOU and post your results here. That way we can see if you actually have a point.”
The data is available so show us how an exponential, a cubic, or whatever function you choose has a better fit. Otherwise, what is your point?
So the world authority on sea level rise is in Colorado, about as far from the sea as any place on earth. Pretty much describes the results they generate.
Hmm, have you read this per chance …
“Is the detection of accelerated sea level rise imminent?” doi:10.1038/srep31245
https://www.nature.com/articles/srep31245
Since using their own numbers the mean acceleration is currently negative (and utterly meaningless anyway given the noise) we can presumably safely assume the answer is emphatically no.
I guess we’ll just have to rely on rulers and numerological barking dogs for an opinionated coin flip having first deducted the odd volcano, etc. here and there by whatever dubious means. Meanwhile the world keeps on turning and churning, just as it did yesterday.
http://www.realclimate.org/images//sea_level_rise_vs_temperature.png
The rate of sea level rise is tied to the surface temperature above an equilibrium state temperature. Seeing how global temps have paused, the rate of sea level rise has also paused. The future largely depends on the success of AGW theory. (don’t bet the beach front house on that)…
So what is the quantitative rise or fall in sea level for a temperature change of 1 deg C?
For the 3 cases when that 1 deg C is from satellite microwave, from surface air temperature and from sea temperature.
Why can there not be a simple equation linking rise/ fall to temperature somewhere?
Why cannot the oceans emulate a liquid in glass thermometer?
Geoff
Fonz, the data from the PSMSL disagrees entirely with your graph. It looks like this:
w.
Hi, Willis, graphs like rahmstorf are dime a dozen. Here’s another one albeit much more crude. (rahmstorf is highly smoothed to get what they got) Remember, these are derivative plots, the RATE of sea level rise, not the accumulation there of. i can at least see the rate of accumulation speeding up and slowing down and then up again in your graph. Is that particular data set available in a derivative plot?
Let me know, if possible, where you think rahmstorf (and the rest) might be going wrong here. Thanx…
Thanks, Afonz. The problem is that you get very different answers depending on when and how much you smooth.
Best regards,
w.
Geoff,
That’s a bit difficult to work out.
The oceans are a bit more complicated than liquid in a thermometer.
Varying depths, currents, bits of land that poke out into them, how long it takes to warm up…
First how much ocean are you warming by 1 degree C ..a column of 1 metre, 10metres, 100 metres, 1000 metres, 6000 metres?
It’d take a while to warm up 6000 metres of water by 1 degree C
Here’s a go at it…page 6 is the immediately relevant bit but includes lots of assumptions
[The author admits it’s a very simplistic approach but it gives you an idea of what’s involved]
The calculations suggest a 17cm rise if temperature increases 3 degrees.
http://cosmo.nyu.edu/Shoshana_Sommer.pdf
Greg K
Thanks for he references, though I note I did a Google months ago and found some of same.
Fundamentally, when a photon enters the sea it will change the energy of the sea almost instaneously. In this state, it expand or contracts. If you select a vertical column of water from a larger region of systematic change, that should emulate a LIG thermometer. Mixing, stratification, density, salinity should not really influence this emulation. Therefore, it should be possible to derive said equation linking sea level and temperature changes.
I would have thought this a fundamental equation for oceanography, but despite several searches I have not been able to find that equation. Most papers go straight to Their change with time. I want time out of the equation like it is when you stick a thermometer under your tongue. You do not have to wait hours to your tongue to equilibrate.
The oceans do not have temporary energy storage buffers where the effect of a photon can be stored, hidden, until the ocean works out what to dobwith it.
BTW, I have similar lack of success when I try to find out if oceans cool at night, how fast, and by what mechanism: and the reverse case in daytime.
Geoff
The red curve in Fonz’s graph from Rahmstorf 2007 is based on Church & White (2006), a PSMSL reconstruction… I don’t think any two PSMSL reconstructions have looked alike. Jeverejeva et at, 2014 does indicate local variations in the rate of SLR which could be due to fluctuations in the rate of warming…
The long-term rate since ~1860 has been about 1.9 mm/yr. There have been alternating 20-40 year sequences of ~3 mm/yr and ~1 mm/yr.
Geoff Sherrington July 21, 2017, at 5:31 am
Regarding your question, viz: “So what is the quantitative rise or fall in sea level for a temperature change of 1 deg C?” and your further comment:
Good question, Geoff. Well, yes, the info is there … but it’s a 75-term equation with variables of salinity, temperature, and pressure. See here and here for further details and further links. Since these variables change from the surface downwards, analyzing a water column is not a simple task.
It also explains why the results change over time. Heating goes on at the surface. As the heat spreads and mixes downwards, it sequentially affects waters of different temperature, salinity, and pressure … which have different coefficients of expansion than did the original heated surface water.
Nor is this a difference that makes no difference. Here’s the coefficient of expansion with salinity = 35 PSU, temperature = 35°C, and pressure = 0 dbar (surface).
> gsw_alpha(SA = 35,CT = 35,p = 0)
[1] 0.000367
And here is the same, but with salinity = 34 PSU, temperature = 4°C, and pressure = 100 dbar (about 100m depth).
> gsw_alpha(SA = 34,CT = 4,p = 100)
[1] 0.000101
The coefficient of expansion differs by a factor of three between the two situations.
Sorry, but there’s no simple answer.
Regards,
w.
PS—This is why I program in the computer language R … because there are packages for just about everything. This package is called “gsw”. It provides an interface to the TEOS-10 / GSW (Gibbs Sea Water) library. This contains functions to calculate a whole host of oceanic properties (e.g. enthalpy, freezing temperature, density, latent heat of evaporation) from the underlying variables.
Geoff Sherrington July 20, 2017 at 8:06 pm
If (a big If) MSL has in fact risen 350 mm since 1850, and if (an even bigger If) average global temperature has indeed increased 1.0 degree C since then, then the answer to your question should be about 350 mm.
However the effect is probably not a direct linear relationship, so who knows? Sea level was higher in the past when it was warmer during the Holocene and previous interglacials, with the continents in about their present arrangement, and if prior epochs, periods, eras and eons, when the continents were arranged differently, so there is at least a general relationship.
The high sea level of the Cretaceous however owed to thermal expansion and ridge growth due to rapid sea floor spreading, as well as to the hot and equable climate of that period.
Sea level rise from the depths of the last glacial until the present interglacial is about 130 meters(!) Being generous, if we divide that number by 5C (thought to be the maximum global temperature difference from the last glacial to this interglacial) we get about 25 meters per degree celsius. That means it takes a long time for everything to equilibrate with a change in surface temps…
The world ocean is all connected, and so sea level change in one place is propagated to every other location over some period of time, but how fast does this occur?
At the same time this is occurring, currents are moving water around, as are the tides. And the wind is doing so as well. And all three are doing so in a separate and different and complicated manner, which is constantly changing for every point on Earth and for every second of every day (take a look at a detailed representation of the eddies and curlicues of the Gulf Stream, frinstince).
On top of this, going on at the same time, the Sun is shining on some areas of the ocean, some places brightly and at a direct angle, some places not so brightly and not as direct an angle, and this changes constantly due to clouds and the turning of the Earth, and varies as well by latitude, and the effect of latitude is constantly varying as the Earth proceeds in it’s orbit.
Near Antarctica this time of year, little Sun is hitting the southern ocean, and it is being swept by roaring winds of a cold temperature and varying humidity, which is sucking varying amounts of heat from the water from conduction and evaporation.
Near the Tropic of Cancer, the Sun is shining directly down and strongly warming the Ocean.
So the water is all the time contracting in some places, expanding in others, moving around, mixing up, and swirling hither and yon…and each of this changes is causing the volume and the level of the water to change, and these changes are being propagated outward at some speed or another…which speed probably varies as well.
So…you want an amount of rise or fall of the ocean for a certain change in temp?
Which temp is that?
Is that the average global surface temp?
The one which does not measure enthalpy but just a thermometer reading? Which takes no account of wind? Or anything else. And this temp…is it the fiddled with temp, or the straight reading?
Is there a “true” global average temp, which we would know if we were smarter and less smarmily political and had more thermometers and read them more accurately…or is the entire concept of global temp hokum, as some say it is?
Or are we comparing some local temp with some local sea level?
Plainly, given the above motions and variations, doing such locally would be a fools errand to try and measure.
Theoretically speaking, and all else being equal…is that the basis of the question (How much does the ocean height vary with a certain change in temp?)?
All else is not equal, and never will be on a round planet which is spinning and rotating and warmed on one side and cooled on the other and subject to all manner of jostling and pushing and pulling.
The dance may be too complicated to ever make into a diagram that can be eyeballed and reckoned with at a glance.
http://3.bp.blogspot.com/-euS8dNkoD7g/Uv3LDkxy2TI/AAAAAAAAAso/ObWFGy7BHBI/s1600/DanceSteps.jpg
“Sea level rise from the depths of the last glacial until the present interglacial is about 130 meters(!) Being generous, if we divide that number by 5C (thought to be the maximum global temperature difference from the last glacial to this interglacial) we get about 25 meters per degree Celsius. That means it takes a long time for everything to equilibrate with a change in surface temps…”
There is no equivalence between global average temp and sea level.
At some points in time, water from the oceans is accumulating on land and the ocean falls, and at other points in time, the water frozen onto land is melting, on average, and the volume of the ocean is increasing and presumably sea level is rising.
But wait a second there…we can look at temp reconstructions and see that at some certain “global temperature”, the Earth may be heading towards a glacial maximum and ice is increasing, or heading into and interglacial and ice is melting.
I think that trying to picture the Earth as an idealized cartoon diagram and drawing sweeping conclusions is silly, personally. Too many things are going on in too many places which may or may not be directly correlated or not, and the degree or lack thereof may be changing over time.
Besides…do we actually know if Antarctica and/or Greenland are gaining or losing ice?
Are there some years yes and some years no?
Ya gotta be crazy to think the people who purport to be studying this and telling everyone “the facts” are even able to know, let alone credible enough to believe.
Great analysis
Thanks
I would hazard that the Alarums, are more interested in issues of belief and spirituality than issues of measurement and the portrait of measurement by graph [Chart] (a method of René Descartes [Latin, Renatus Cartesius])!
“(c) Graph E in paper (5) is the key. As the world continues to warm, the rate of sea level rise will accelerate (probably slowly).”
Indeed! And Not! In this statement there is the presumption given without evidence or proof, “As the world continues to warm”.
Evidence shows this presumption false!
Only the Believers and Spiritualist will ignore evidence (i.e. measurement) because their God does not communicate Truth by measurement or Observation. For them “Truth” is revealed! … late at night … in a closet … sitting on a toilet … having sexual intercourse with a same-sex partner … watching a re-run of “Seinfeld” at 04:30 GMT (their way of getting instructions from God before the sun rise)!
But is not … TOPEX POSEIDON … measurement? … the monk cries.
Ah Ha! The “adjustments” … “the adjustments” … to confirm the desired … belief! Belief Must Rule! and Belief will be fed … to appease … Belief!
Belief
JBom –
I would politely ask that you rethink what you’ve said, ’cause a lot of truth has been discerned over the years while sitting on a toilet.
/grin
When a trend is essentially linear as Willis’s analysis indicates, fitting higher order polynomials will produce equations with very small coefficients for the higher order terms (x^2, x^3, …). Often these coefficients will be on the order of 10^-5 or -6. The result is essentially to approximate a simple linear fit.
Forest
Quaint Forest? What an old-fashioned word to use.
A little upset you didn’t pass the Willis test?
Forrest Gardener July 20, 2017, at 8:07 pm
Forrest, it was not obvious from what you wrote that you did understand this issue, and Rick is not a mind reader.
In addition, I and others often write for the lurkers, so I explain things in simpler terms than if it were just you and I discussing the issue. Don’t like it? Well, after your hissy fit … who cares?
TL;DR version? Get a grip, you are currently ruining what up to now was your decent reputation.
w.
Actually, sea level rise is very similar to global warming. Just like temperature, the daily change in sea level height due to orbital mechanics is much greater than any observed effect that might be due to humans.
It is only by removing mathematically the daily and seasonal variations in temperature and sea levels that one can claim that what remains is in any way significant. Otherwise it would be too small to notice.
If a single tree can prove “global” warming, why not a single tide gauge?
http://www.psmsl.org/data/obtaining/rlr.monthly.plots/145.png
Jevrejeva reported in her 2014 article an average rise of 1.9 mm/year/, with an acceleration of 0.002 mmyear/year, using a quadratic equation to get the acceleration. I took her data and verified the 1.9 mm/year, as well as the 0.002 mm/year/year acceleration. (I used a different method, not a quadratic equation but a fit to the first differences, which should give the same answer.) However, the uncertainty of the fit to the first differences was more than half of the value, meaning the acceleration was not significantly different from zero.
https://dl.dropboxusercontent.com/u/75831381/Jevrejeva%20sea%20level%20change.xlsx
I took ALL the tide gauges in the PMSL database and how each individual one changed each year from 1909 to 2009 (recognizing that they come and go.) 30,966 individual annual measurements
What you see is that there GROUPS which are either dropping fast, or rising fast or staying stable. This is glacial isostatic adjustment. Some tide gauges are rising at 12 mms per year and at least one is falling at 12 mms/year (and then some which have eroneous readings and vary too much to be valid).
This means that by simply cherrypicking which tide gauges to use, you can get ANY number you want and any acceleration value you want.
This is what Church and White have always done (a large number of gauges but picked in just the right way and never the same from study to study). The best method is to adjust each individual one for GPS land movement (which appears to be fairly stable) and then use as many as you can and use the same gauges over as long a time as possible.
That is why the only correct sample is the subset of PSMSL that is both long record (>60 years) and diff GPS corrected for vertical land motion. There are about 70 such tide gauges out of about 148 with diff GPS. NH bias, but no reason to think that matters to global SLR given the bathtub effect. They show 2.1-2.2mm/year and most definitely no acceleration.
Use Australia for the SH component. Little to no postglacial land adjustment there, thanks to so little glaciation during the last “ice age”.
“…0.002 mm/year/year acceleration.”
“…meaning the acceleration was not significantly different from zero.”
0.002 millimeters is 2 micro meters. 2 millionths of a meter.
Per year.
Or zero.
Hmmm…
Well just how big is two micrometers?
Can we think of some familiar objects of this size?
Well, a red blood cell is about 2 to 4 times this size…too big.
One wavelength of visible light is between about 1/3 and 2/3s of a micrometer…too small.
A human hair? Varies…are we talking blonds or brunettes? But at an average of 80 micrometers, we are way off anyways.
In any case, a micrometer is a distance too small to see.
Which means it might as well be zero for all the effect it will have on anything real.
But what gets me is this…someone trying to claim, with a straight face, that the body of water pictured below and extending clear around the never still Earth, the change in height of this, over a year, can be discerned to a level comparable to lining up ten virus particles in a row?
http://archive.sailingscuttlebutt.com/photos/04/bigwaves/1.jpg
This is actually pretty funny.
I wonder if it was an intentional joke?
https://youtu.be/i7WWrGxv1eg
Let’s see … if the annual 2 mm rise continues consistent with the last 150 years of data, and the top of the Statue of Liberty is 326 feet above water or 99,365 mm, then best calculation is that it will be under water in 49,683 years if you extrapolate current conditions.
Only problem is that we will be halfway into the next ice age by then with a mile of ice above where Chicago is now, so do not see from where the water could come being locked on land. Maybe you could walk in the cold from Manhattan to Statue of Liberty which would be on a big hill, but also enough time for another species of humans to evolve.
http://lh3.ggpht.com/-xi4vhYwxuGE/UJAZrxRnYHI/AAAAAAAABVI/isS6k-W6Qrk/NewImage.png
And of course the world is not going to continue warming steadily for tens of thousands of years. There will be ups and downs, then descent into the next glacial epoch.
“Killer AGW” activists claim we have defeated the glacial – interglacial oscillation. Endless interglacial. That’s what they purport.
““Killer AGW” activists claim we have defeated the glacial – interglacial oscillation.”
Sounds like UK Chancellor of the Exchequer Gordon Brown’s 2003 claim that he had eliminated ‘Boom and Bust’.
That ended badly…
I always think back to Akasofu’s 2010 temperature graph – if you have an oscillation superimposed on a linear trend – there will be times when it appears that there is acceleration and times that there appears to be a deceleration. The underlying trend is linear, ie not accelerating and sinusoidal, ie not accelerating.
As far as I see – this apears to be the same here, with the sea level data. 75-80 year oscillation superimposed on linear trend.
You would need to extract both those trends to see if there is a significant divergence.
Perhaps it’s at least partly cyclical, so likely not going logarithmic.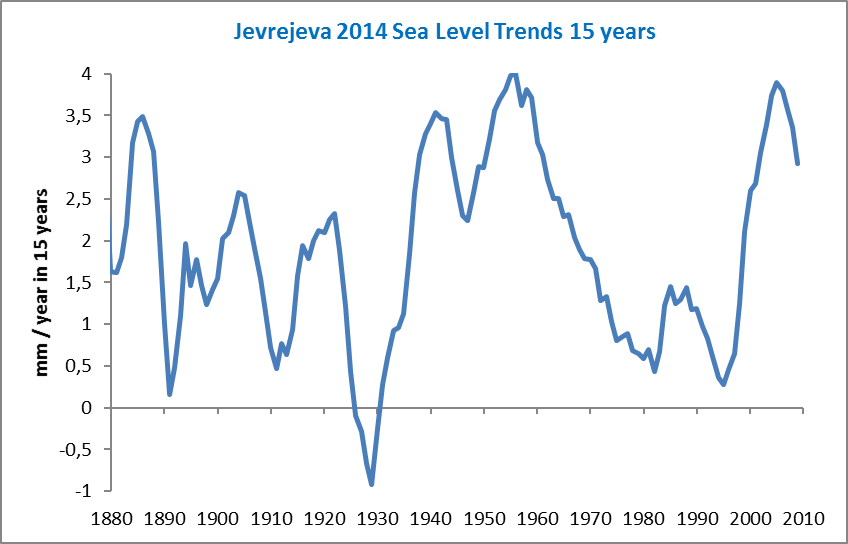
[/img]
[img
how do I add an image/graph to my post?
I’ll have to spell it out because if I use all the bits and parts WordPress tries to make it an image …
I use
img src=”IMAGE_URL” width = “640”
with a “<" at the start of the line and a ” />” at the end of the line. Replace IMAGE_URL with the actual URL of the image.
w.
Mydrrin’s graph …
Also, there is a link to a “Test” page in the bar under the image at the top of every page, where you can test this stuff. It contains info on how to do bold, italic, quotes, and all the rest.
Thank-you.
Sliding averages are a kind of running mean and bear all the same defects: a lot of noise shorter than filter period gets through ( look at all those spikes ) ; spurious peaks and troughs because of on inverted lobes in the filter frequency response.
If you want to filter that data you get a better result with a 48 month guassian. Compare.
Willis quotes
I dont understand how they come to this conclusion as it simply doesn’t follow. Increased rate of sea level rise is dependent on the energy flow increasing but the temperature is dependent on the energy accumulating. Totally different and one doesn’t imply the other.
Sailing from San Diego to Auckland New Zealand, anyone telling me that sea levels are increasing 1.3mm a year needs a head Doctor !
(water, water everywhere and all the boards did shrink )
Willis
The aspect that i find difficult is that the sea level rise shows an abrupt change in 1850 and then a linear increase. The oceans are a large body of water. I cannot envisage a forcing that would generate such a response. I would expect the forcing to be sinusoidal. That would not generate such a response.
A (stupid?) question: Have your data been corrected for ‘uplift/subsidence’ (where the gauges stand) ??
In Denmark, where I live, such vertical movements are substantial – see example here:
http://www.fotoagent.dk/single_picture/10852/25/mega/Figur_4.JPG
(scale in mm per year)
I suppose there are similar movements where ‘your’ (63) gauges are located(?).
Good question, Hans. It’s the reason I used the method I did. You see, the uplift/subsidence is slow and steady, only changing slowly. That means that the in the comparison I used between linear and quadratic for each site, the uplift/subsidence cancels out.
w.
Juneau is rising at ~14mm/yr due to isostatic rebound.
On the site of the Dutch Government local sealevel rise is depicted linear at a rate of 1,9 mm/year(1890-2014) and includes a statement of no acceleration. A footnote on global sealevel mentioned acceleration.
Willis – thank you for your interesting post. I work in coastal engineering based in the UK, obliged to apply SLR scenarios that reflect the accelerating SLR hypothesis to scheme design. Compliant but sceptical, I point colleagues to the UC global mean SL satellite data record (’93 – ) which eyeballs no acceleration trend. Is this dataset too short to apply your statistical approach to, or did you simply go for the longest dataset(s) available?
Thanks, Prolefed. I just went for the longest available. However, there’s only 24 years * 12 months = 288 data points in the satellite dataset. This means that the errors will be correspondingly larger than in the datasets I used, by about 50% …
It’s 2 AM here, I’ll look at it tomorrow, but I’d be stunned if there is any statically significant acceleration.
w.
Thank you Willis – I wasn’t expecting a reply so soon – get some rest!
And here’s me thinking I was the only one that had problems with that post and by the sound of it probably the least schooled .
Thank you for your work Willis and stellar job on the retaining wall , hope you put drainage in for the forthcoming Armageddon.
I must say I find fitting relatively simple matehematical formulae to long term data of what is implicitly a very, very complex mechanism’s outcome is a bit reckless. In the example given we have the quadratic fit used to postulate that the trend for sea level rise on the out years ahead is ‘accelerating’ whereas a quick glance says that in about 1963 it had just stopped falling. Longer period data tells as this is nonsense so on what basis is the quadratic a meaningful ‘model’.
The worst, the dumbest, the most moronic example of this sort of frogshite ‘science’ was in apeper on sea evel rise where that tracked the western Pacific MSL over a reasonable time and loa and behold there was a periodic variation they attributed ( quite logically and correctly it seems) to the Pacific DEcadal Oscillation. Then the wheels fell off. They fitted a line to the data and got an uptrend! DOOM, we’ll all be droended etc. The trouble was the oscilating pattern clearly started on a trough and finished (after several cycles) on a peak so the ‘uptrend’ was just a conbstruct of that bit of idiocy. They would have got the same result if the data conformed to a pure sine wave which must have zero uptrend by definition.
Anyway whenever I see linear fits I just turn the page these days. Now a Fourier series I can come at but even that is dependent on getting a long enough data set.
Units and terminology please?
……………..
Sea level rise is a distance. A distance between a measured point and a reference point. A convenient unit is millimeters, mm.
This distance is not constant over time. The first derivative of distance with respect to time is velocity. Convenient units might be mm per year.
This velocity is not constant over time. The first derivative of velocity, being the second derivative of distance, with respect to time is acceleration. Units here are mm per year per year.
(Please excuse the lack of formal scientific notation for the units, a bit complicated for Word Press).
……………
There is no reason to mention the word “rate” because its use is confusing. I wonder what Larry Kummer really means by “the rate of sea level rise will accelerate”. Likewise with you Willis, “an accelerating rate of sea level rise”. Are we moving to the third derivative of distance? Heavens, no, do not go there. It is named the “jerk”.
I am being more than pedantic. For example, “rate” by itself has to be qualified to have meaning, like rate with respect to time, rate with respect to weight, rate w.r.t wavelength and so on through the physics library.
………………
The full meaning of sea level changes can be captured by the proper, basic, scientific variables of distance, velocity and acceleration, so why not use them and only them?
…………..
Also, a minor disagreement about choice of a quadratic to fit a non-linear response curve. Some recent papers have proposed that the global sea level curve is sigmoidal, with a velocity v1 from say 1900-60, a lower or even negative velocity v2 1960-90 or whenever, followed by a return to the original velocity v1 1990-today. There is no “one curve fits all different hypotheses”, but the quadratic is one of the worst fits for such a sigmoid.
………….
Never mind, Willis makes the point that no acceleration is seen in tide gauge data from goodness of fit studies over multi-decade terms like these. That is what is important.
Geoff
Geoff, I don’t understand your point. You say:
Geoff, the word “rate” here is used as a common synonym for “velocity”. It is, as you point out, the first derivative of the sea level with respect to time, and has units typically of mm/year.
So I can never say “I was doing a hundred around the corner when the car came unstuck”? In many applications the units are obvious from the context. If you think that the rate of the sea level rise is with respect to weight … well, I don’t know what to say.
Now, as to whether the rate is “accelerating”, it would likely be more accurate to say that the rate of sea level rise is “increasing over time” … but do you truly think anyone misundersands what is being said? If so, they haven’t mentioned it.
Why not? Because words become “terms of art”. “Terms of art” are words that have a special meaning in a certain context. For sea level rise, people use “rate” for “velocity”. Is this exact? No … but that’s the way she is spoken.
For data on that, Google finds 410,000 examples for the exact term “rate of sea level rise”. But when you search for “velocity of sea level rise” Google only finds …
… four measly examples. Four.
You can rail against that all night long, but that’s how she is spoken. We say “Things were going along at a rate of knots” because in common parlance, “rate” is a substitute for “velocity”. That’s why we don’t say “the velocity of inflation” … the English language, even in science, is far from logical. You have two choices about that fact … dig it or complain about it. Because you sure aren’t going to change it.
While that may be true for the globe, let’s start from our start, the data we’re using. Here’s Figure 2 again, sample data.
Those look like sigmoids to you?
Thanks, Geoff.
w.
“Never mind, Willis makes the point that no acceleration is seen in tide gauge data from goodness of fit studies over multi-decade terms like these. That is what is important.
Geoff”
This thread and umpteen more like it demonstrate very well the principle that it takes far longer to debunk a load of BS than it does to spew it.
The ocean is right where it has always been, and although it acts up occasionally, it always goes back into it holding pen eventually.
The average position varies slightly over time, but it changes every day by far more than the average has changed over the lifetime of me, you, our parents, grandparents, great grandparents, and who knows who else.
But people who are good at making crap up and convincing others it is true, can run circles around dry facts like “Where is the ocean”?
Same as it ever was.
https://youtu.be/I1wg1DNHbNU
a comprehensive analysis of selection bias in tide gauge measurements between 1807-2010 indicated that (a) sea levels are only rising at a rate of about 1 mm/yr (as of 2010), and (b) a total of 65% of the world’s tide gauges have recorded stable to falling sea levels.
http://notrickszone.com/2017/06/05/sea-levels-are-stable-to-falling-at-about-half-of-the-worlds-tide-gauges/#sthash.ZzzcusEg.dpbs
Another long term view:
http://climate.mr-int.ch/images/graphs/sea_level.png
Note the steep rise-rate around 1800, and the multi-decadal rise-rate oscillations (over an increasing trend).
Willis, what do you think what is the reason that the recent years are a bit warmer, say less than a degree C than what the temps were when our great-grandparents were born, but that the seas rise so linearly as they do?
I think it is odd to see how linear the sea level change is. Freaking odd! I don’t see any good reason behind it.
I come up with two explanations. The land-based temps have little to do with ocean heat uptake and glacier melt. And of course, the linearity can be accidental, since it will not be linear forever. But assuming land-based air temp at 2m has been risen, is that just something that does not correlate with sea level rise?
Great analysis, but a pity that it seems to be episodic. By that I mean that it takes significant human work to do and isn’t likely to be done on an ongoing basis in an affordable manner. Isn’t this something that would better be done every month automatically with summaries for the general population that could be absorbed within a few seconds at most and ideally in the sub-second time frame?
And yes, I’m actually interested in setting up something like that. Contact me if you’re interested.
Yes, we need month to month updates for something which has not changed appreciably in a hundred and fifty years.
Yes, you do, because if you do that in an automated way, when somebody claims otherwise *as alarmists are claiming right now* they won’t be taken seriously.
The cheaper computing power gets, the more these sorts of calculations need to be done. Anything done once when it’s expensive should be done regularly when the task becomes trivially cheap because of reduced computing costs.
Church & White along with other studies show a rapid acceleration of the rate of sea level rise.
The tide gauges have gone from approx 1mm per year circa 1880’s to 2.0mm circa today. While the satelite measurements have gone from 3.0mm to approx 3.2-3.3mm circa today. Both the tide gauges and the satelite measures show a doubling of the rate of approx 100-150 years.
The acceleration is cited in the numberous studies appears to be mostly from the switch from tide gauges to satelite measurements. The remaining acceleration appears to be from the short term cyclical changes.
Actually they don’t. The two Church and White papers I have studied used bith different time frames and different subsets of tide gauges. Apples to oranges. See my recent guest post on SLR and closure for more details.
Houston, J. R. and Dean, R. G., “Sea Level Acceleration Based of U.S. Tide Gauges and Extensions of previous global-gauge analyses,” J. of Coastal Research, Vol. 27, No. 3, pp 409 – 417 (May, 2011).
They used 57 U.S. tide gauge records from PSMSL with lengths of 60 – 156 years. They found a small deceleration from 1930 – 2010.
For global extent, they extended Douglas (1992) by 25 years, and analyzed revised data of Church and White (2006) from 1930 – 2007 and obtained small decelerations similar to the U.S. records.
Acceleration: -0.012 mm/yr^2 for U.S. or Global.
the notion of accurately measuring millimetres of sea level rise never mind thousandths of millimetres no matter what equipment is used is to me a nonsense.as usual a great expose of the numbers by willis ,but i fear the numbers at the outset bear no relation to reality,a consistent trend in climate science i believe.
bitchilly July 21, 2017 at 4:50 pm Edit
Depends on your equipment. The Australian SEAFRAME tide stations combine a stilling well and a sonic measuring apparatus. It measures the sea level every six minutes, accurate to 1mm …
w.
How many tide gages and for how long use such a method?
The scatter plot is interesting, but I think it would be more definitive to plot linear vs linear+quadratic. N’est Pas?
Most interestingly, they have just found the missing sea level acceleration
https://www.scientificamerican.com/article/satellite-snafu-masked-true-sea-level-rise-for-decades/?utm_source=pdb&utm_medium=email&utm_campaign=07202017&variable=a553eadb90dd3b52fbf8d01481e04811
obviously if the data don’t match your dogma, you torture them, until they confess.
Hi Willis. I think this analysis shows that your analysis is incorrect. Can you comment?
http://tamino.wordpress.com/2017/07/21/sea-level-rise-is-accelerating/#more-9358
Tamino throws in a red herring by declaring acceleration in Boston and deceleration in Juneau is evidence that Willis’s analysis is incorrect. But the claimed deceleration at Juneau is claimed to be caused by the reduced glacier mass attracting less ocean water. This case has been presented a number of times, always without reference. However, if you calculate from Newton’s law F=Gm1m2/r^2 for an estimate of the glacier melt and it’s average distance from shore, and apply some hydrostatics, you will find this claim to be highly exaggerated. Like most warmunist stuff, a small investment in truth yields a major return in catastrophic predictions, plus a major return in donations to the website.
Doug: Gravitational effects of melting ice on local sea levels now is well established. An easy way to enter the literature is to search for peer reviewed papers by Jerry Mitrovica. Here is a brief lay explanation: http://nautil.us/issue/33/attraction/why-our-intuition-about-sea_level-rise-is-wrong
Tom Dayton, that was some painful reading. I always hurt mentally when I read a journalist’s interpretation of a discussion with a scientist. That was a lot of generalization and not a lot of detail and it, as usual, raises more questions than it answers.
How does this specifically have to do with Juneau? Is there an exceptionally large glacier nearby? Is it melting fast enough to show a true gravitational effect? Is the shape of the land nearby sufficient to justify this explanation? If this was all due to gravitational effects from local glaciers does that mean that only gauges near a glacier are showing this phenomenon? Are there any gauges in the tropics showing this downward slope? What’s the excuse for those?
Andrew, my suggestion was for you to search for the peer reviewed literature, which has details. Instead of complaining about the lack of detail in the brief lay explanation I was nice enough to point you to, why don’t you read the actual literature?
Tom, you make my exact point…referring to articles with no calcs….maybe you should study Mitrovica’s calcs yourself before you start sending me “lay information”. I did similar calcs for university physics assignments 40 years ago. And gravity, despite being “real physics” doesn’t explain the amount of Juneau deceleration. Try again.
Thanks, Martin. I’m including an update on this in the head post. Short answer is that I had slightly overestimated the error. By Tamino’s method, there are seven stations with significant acceleration and three stations with significant deceleration. My thanks to Tamino.
w.
Thanks Willis. Are you sure you used Tamino’s method? He doesn’t include it in his post. What method did you use to correct for autocorrelation?
Thanks.
Sorry, I didn’t see your update. Thanks.
i am sure willis can/has commented,though i fear it would be a waste of time with the individual concerned.
Willis is mistaken—sea level rise is accelerating. See this post from Tamino: https://tamino.wordpress.com/2017/07/21/sea-level-rise-is-accelerating/
I decided to follow the click bait, although I try to not do that very often. What followed was an interesting bit of “Willis is ‘insert insult here’ ” followed up with a discussion in statistical analysis. The p- value is then trotted out along with comments about how that is used to determine that sea level rise is accelerating.
How about this. Why don’t you show your full design of experiments. If you are going to trot out the p-value, you need to make sure you define the H0 and H1. Why? Because the p-value only is important if it allows us to reject the H0 or Null Hypothesis. I may be wrong but Willis’ H0 appears to be that it is a linear fit only. That means that the H1 would be that it is either statistically the same or the quadratic fits. That means the very low p-value would support the H1, which might be why Willis used the R^2 instead of the p-value.
Of course I could be wrong……..but if I am it is because no one has taken the time to express what their H0 or H1 might be. Don’t play around with p-values unless you plainly express your H0 and H1 values.
Tamino is a mistake himself.
Global Absolute Sea Level can not be determined from uncorrected Tide Gauge data. Tide Gauge data relates only and exclusively to Local Relative Sea Level. The relationship between each local Relative Sea Level and Global Absolute Sea Level is unknown without a great deal of additional data.
All Tide Gauge data, to be used outside of its proper place — determining local Relative Sea Level — must be first corrected with reliable precise information on the vertical movement (up and down) of the land to which the gauge is attached. The only truly reliable data on this comes from the NOAA CORS system.
Even when corrected, Tide Gauge data only speaks to the question of what the sea level is doing locally. Global Eustatic Average Sea Level ( “eustatic” refers to global changes in sea level relative to a fixed point, such as the centre of the earth) can not be determined from Tide Gauge data — nor can rates or rise or fall of global sea level.
Tide Gauge measurements are in effect measuring from a moving platform — the land — which moves up and down on its own, independent of the sea surface. The sea surface also moves up and down on short term cycles (tides) and long-term changes. The local long term changes are not linearly connected to Global Sea Level rise or fall. Local sea level may fall while global levels rise, and vice versa.
That said, all human related sea level problems are LOCAL. It only matters where the sea touches the land. New York cares not what the sea level is doing in Hong Kong, no NY subway is flooded by sea level rising in Hong Kong. If local sea levels are rising and it is a problem for that locality then whether or not Global Sea level is going up or down is irrelevant.
“That said, all human related sea level problems are LOCAL.”
Which is why all of the forecasts concerning sea level that have come out of decades of climate research have thus far have been of nearly zero practical use.
Why are so many of your R^2s in Figure 3 less than 0.5? Doesn’t this analysis similarly indicate that the linear trends are not statistically better than pure intercept models?
Good point !
Forrest Gardener July 21, 2017 at 2:48 am
You misunderstand my purpose in fitting the model. It is NOT to provide an accurate model for the last two hundred years of data. Instead, it is simply to determine whether a given short section of the data is better fitted by a straight line or an accelerating curve of some type.
So you are right that “There is nothing about sea level rises which suggests a quadratic relationship with time” … but I’m not trying to show that. Heck, you propose using an exponential function … are you claiming that that suggests sea level has an exponential relationship with time? I see nothing to suggest that either.
I don’t see that at all, nor did I say it. How do you get that result? Remember, Figure 1 is pseudodata …
Hey, you were the one heading for the door after I asked you to fit an exponential curve to the Juneau record shown in Figure 2, not me. Whether you’ve “run out of answers” or not, I still don’t have an answer to that question …
If you don’t want to put your money where your mouth is, that’s up to you. However, the proposal YOU make to use e.g. some exponential function or other is YOUR proposed analysis, not mine.
You don’t get to wave your hands and say it’s better to do it some other way and then expect me to prove or disprove YOUR claim for you. If you think it’s better to do it some other way then please show us.
I gave up doing that kind of snipe hunt long ago. I used to go and, for example, use some exponential analysis or other. Then I’d return and tell the person my results, and they’d say “Oh, that’s not the kind of exponential analysis I was referring to …”
You see the problem. After doing that a few times, I just gave it up. If you think it can be done better, I invite you to show us how. I say this because I’m not a mind reader, so I DON’T KNOW HOW YOU PLAN TO DO IT and I’m damned if I’m gonna guess just so you can tell me I’m wrong.
The same to you, and thanks for your willingness to continue the discussion
w.
Sea level is still lower than it was during the Medieval, Roman and Minoan Warm Periods and Holocene Climate Optimum.
Eemian interglacial sea level in the continental US, without benefit of a Neanderthal industrial age in Eurasia:
http://www.tobiasbuckell.com/wordpress/images/2013/01/NewImage3.png
Don’t know where that image came from, but it is mistaken. Maximum sea levels were 5 to 7 meters above those of today. Image shows all of Florida submerged. But look at an elevation map of Florida: http://ete.cet.edu/gcc/style/images/uploads/Sea%20level%20risk-FL.png
More than half the state is higher than 10 meters above sea level, and some 40-50 meters above sea level. Florida was not all under water during the Eemian.
That map shows a tongue of water extending up almost all the way to Illinois, past places that are 300 feet above sea level.
Although it also shows Philadelphia, at about 40 feet, not under water.
I guess one thing I have never heard people talk about is how we are draining ground water, that used to never be used. We pull millions of acre feet of water out of the ground every year that finds its way to the oceans. This water used to not be on the surface! I have a well from an aquifer that is essentially not refilling and has enough water for our little area for about 50-100 years.
The effects of ground water irrigation on sea level has been discussed on this blog fairly often.
Hmm. You seem to be unaware that simply comparing R^2 values is no way to compare how well two models characterize the process that generates a set of data. That should be pretty obvious from just LOOKING at your Figure 1.
Patrick wrote
in response to Willis’ article where Willis wrote
So Willis wasn’t even trying to characterize the process generating the data. That wasn’t even his aim. He even said he was fitting the data.
Willis: I think the “standard method” for detecting acceleration in SLR is to perform a fit to
h = at^2 + bt + c
and then look at the confidence interval for a. And that requires correcting for autocorrelation (in the residuals). I’ve tried this with the satellite altimetry record (before the recent correction) and found a small acceleration with zero barely within in the 95% ci. In that case, the R2 for the linear and quadratic fits were essentially the same (0.97 and 0.98).
More importantly, currently SLR is about 1″/decade and we need to experience an acceleration of 1 inch/decade/decade to reach about 1 m of SLR by the end of the century. Even the high end of the 95% ci was well below this value.
Willis, thank you for your essay.
Ok. Though this is a statistical methods argument this truck driver has a more direct question.
Where the hell is the water coming from? Most of the Antarctic is gaining SMB. Though Greenland ice sheet SMB was decreasing a little it is now gaining. Neither can account for the amount of SLR it seems to me.
Thermal expansion and ground water are accounting for the bulk of the rise?
Thermal expansion and creative accounting are apparently the two main drivers of SLR… 😉
Thermal expansion, ground water pumping, and melting of high altitude glaciers are all contributors. There probably is some net accumulation of ice in the Antartic, but I think Grace data continues to indicate net loss in Greenland. That said, claims of more than a meter sea level rise before 2100 are utterly bonkers…. more likely is somewhere under 50 cm by 2100. The Statue of Liberty is safe…. though the liberty the Statue celebrates is truly threatened by those who insist people must “fundamentally change” how they live their lives to ‘avoid catastrophe’. It’s just science being subverted and corrupted to advance green/left policies..
Thank you to those that responded.
GRACE data on ice masses overlaying areas like some in Greenland which have ongoing active geological/ Geothermal processes seems to have been less than optimal.
Afonzarelli.
Your chart runs to 2014 but there has been more than one paper published since then which has indicated the SMB of Antarctica is actually growing slightly. That would indicate that the contribution from Antarctica would be negative.
As for the Steric contribution that would correlate with the higher SSTS.
I guess over all one should expect that if that chart ran to the present the total would be somewhat less?
Forrest,
It’s not clear that you understand what Willis is doing. You are correct that a linear model might not be the best model for sea-level rise, but Willis isn’t trying to model sea-level rise. He is looking for evidence of acceleration.
As you may or may not know, any finite and continuous function can be represented by a power series. So whatever the correct model for sea level is, it can be represented by the series d(t) = a0 + a1*t + a2*t^2 + …. a0 would be a constant sea level, a1 is a constant change in level, a2 is a constant acceleration, etc. If there is any acceleration in the data, it will show up as a nonzero a2, no matter what the correct model is. That’s why the linear vs. quadratic fit is the right test to do.
It’s true that such a fit would not work prior to 1950, but it does allow Willis to conclude–correctly–that there is no evidence of acceleration between 1950 and 2015. That’s all his post is about and he did the test the way it should be done.
Forrest,
I can see that you don’t understand what I’m talking about. I am not presenting some “ideas.” I am stating basic mathematical facts, known to anyone with a decent knowledge of calculus.
If sea level can be calculated at all (which you are assuming when you speak of a model), it is certainly a continuous and finite function of time. If sea level is definable at all (such as the average of sea-level gauges around the world), it is calculable for every moment in time. Since it is nonphysical for the sea to suddenly be, say, three inches higher without going through intermediate heights (such as 1 inch, 2 inches, etc.), it is certainly continuous. And since it is also nonphysical for the sea level to be infinitely high, it is also finite. Any accurate model of sea level, then, would also be continuous and finite. Again, these are not ideas, just simple facts based on common sense and basic calculus.
So why is Willis justified in stopping at the quadratic term? Because he’s only looking for evidence of acceleration. Suppose the actual model is more than quadratic. The we could rewrite the series as
d(t) = a0 + a1*t + (a2 + a3*t + a4*t^2+..)*t^2.
The third “constant” (the part in parentheses), which now depends on time, is the true acceleration. For Willis’s best fit, it will be calculated as a single number, basically the average acceleration over the chosen time interval. But it will be nonzero if there is any acceleration at all. If it is zero, then all true constant terms (a2, a3, a4, …) must be zero also.
Take a look at Willis’s update based on Tamino’s criticism. The direct approach is to see if the term in parentheses is actually zero. It is. But what Willis did originally is still correct, if less direct.
Your analysis seems to show that an accelerating fit is perhaps marginaly better than a linear fit (a few more points above the line than below it), but essentially both are just as good. It seems that this simplistic analysis is unable to differentiate between linear and rising, and it is not possible to distinguish between them using this method.
Thus an accereraing sea level is just as likely as a linear one, from this analysis.
This seems to show that this is not a good way to distinguish between linear and rising rates.
Those interested in a professional view of what Walter Munk calls the “enigma’ of sea level should read: http://www.pnas.org/content/99/10/6550.full
Those seriously interested in the question of accelerating SLR on a global scale will recognize that a sparse sampling of tide gauge records examined only via regressional methods applied on a time-scale dictated solely by data availability doesn’t provide a scientifically satisfactory answer.
On a Friday afternoon, I can’t take the time to replicate a longer comment explicating these two issues, which totally disappeared, because WUWT was “not responding” to my submission.
1sky1, they’ll eventually show up… (it’s been happening to everybody of late)
I’ll believe it when I see it. Another comment disappeared on this thread early this afternoon.
Willis is an a-hole.
…
There is no such thing as a” lunar tidal cycle is just over fifty years”
…
No wonder he can’t get anything published. he’s an idiot.
The Metonic cycle is 19 years.
Willis may be a lot of things, but one thing he ain’t is an idiot. (watch your manners steve)…
Steve Heins July 22, 2017 at 10:25 am
Steve Heins July 21, 2017 at 7:05 pm
Good heavens, you are such a charming fellow. Do you talk to your momma with that mouth?
Moving on from your pathetic boorishness, on the point of the lunar cycles, none of the longer lunar cycles repeat exactly. There’s a cycle at about 18 years, which is called the “Saros Cycle” It returns fairly close, but not exactly, to the same point where it started.
In addition, there is a cycle which is three of the 18-year cycles, so it’s just over fifty years (54 years 34 days, if you’re interested). It returns even more closely to where it started.
And as a result, you need about fifty years of data so that you can remove the tidal effects from the data to determine the true sea level.
If you actually would like to learn about this and not just persist in your ignorance, I wrote an entire post on it here.
Finally, as to whether I “can’t get anything published”, a quick google search would have disabused you of that stupidity. In addition to a short “Communications Arising” in Nature magazine, I have five other articles in the scientific journals … and there are over sixty citations to these articles in the journals.
Nice try, though, Steve. See Vanna White on the way out, she’ll tell you what gifts we have for failed contestants …
w.
The “here” link does not seem to work.
Thanks, Menicholas, fixed.
w.
Willis fails again….
“In addition, there is a cycle which is three of the 18-year cycles, so it’s just over fifty years (54 years 34 days, if you’re interested).”
…
The Nodal tide cycle is 18.6 years, so please try multiplying 18.6 by three. The answer is 55.8.
..
http://geology.geoscienceworld.org/content/1/3/141
..
But seriously, there is no 50/54 year cycle. Three revolutions the minute hand on a clock is not one minute, it’s THREE.
“a short “Communications Arising” in Nature magazine?”
…
Congratulations on getting a comment published.
…
Maybe if you try real hard, you can get an article published.
Whoof…tough crowd.
Rob and Steve must be great fun at parties.
Keith Sketchley July 22, 2017 at 6:00 pm
It is clear that, like many people, you don’t know the difference in Nature magazine between a Brief Communications Arising, a Letter to the Editor, and a Comment. And why should you? You’ve likely never needed to know.
What’s not clear is why you wanted to reveal that fact to us. In future, you might want to consider Mark Twain’s advice, “It is better to keep your mouth closed and let people think you are a fool than to open it and remove all doubt.”
Moving on to the issue at hand:
A Letter to the Editor has to be very short, and is not peer reviewed. From their guidelines:
Note the difference …
A “Brief Communications Arising” is longer, up to 500 words, and is allowed one graphic. More importantly, it is PEER REVIEWED.
Finally, a “Comment“, contrary to your naive view, is written and commissioned by the magazine’s Editors. So no … I didn’t write a Comment.
If you are interested in attacking your ignorance regarding Brief Communications Arising in Nature, see here … or not …
Regarding your charming and wildly incorrect statement that “Maybe if you try real hard, you can get an article published.”, I have over 60 scientific citations to the analyses that I have published in the scientific journals …
Regards,
w.
PS—You might want to reconsider this kind of ugly ad hominem attacks. They do a couple of things you might not have noticed.
First, they show that you don’t have any relevant scientific objections. Or as I put it, when a man starts throwing mud, you can be sure he’s out of real ammunition..
Second, they damage your reputation. This is particularly true as in this case, where you had your facts on backwards. If you are simply wrong about something, everyone understands that. We’ve all been wrong.
But when you get all nasty, and you crank up the personal attacks … and then you get your head handed to you because you didn’t understand what you were talking about … well, you can bet that folks in the peanut gallery are pointing and laughing.
Thank you Willis for your link to Communications Arising.
..
I especially like this sentence: “Critical comments on recent Nature papers may, after peer review, be published online as Brief Communications Arising”
…
Please note I highlighted the most important word in the description for you. A “comment” is a “comment” even if it is “peer reviewed”
Keith Sketchley July 23, 2017 at 12:02 pm
That’s it? That’s your brilliant insight???
Let me try to explain this one more time.
I think we can both agree that if I say “Hi, Keith, you’re looking good today”, that is a comment. So with that as my starting point, let me highlight the difference between me and you.
Me, I once read an article in Nature that seemed erroneous. I went out and researched the subject. Then I developed a hypothesis. I collected the data to support it. I put the data into the form of a graphic. I wrote up my claims and submitted them to Nature magazine. It was read by three peer reviewers, two of whom wanted further changes to the manuscript.
I made some of the changes. Then I resubmitted it, and after further discussion, I made one further change and convinced them that one change wasn’t necessary.
After all of that, it was published.
So that’s what I did.
And what did you do?
You claimed that what I had produced and gotten published was nothing more than a “comment”, and since in your world all comments seem to be equal, you are claiming that what I did was no more valuable or impressive than to say “Hi, Keith, you’re looking good today”, because they are both comments … riiiiight …
There are two parts in this play. I’m playing the guy who actually did the hard yards and persevered through opposition and accomplished something.
You’re playing the guy who turns himself inside out and defies logic to try to diminish my accomplishments in other peoples’ eyes.
I know which part I prefer to play … what I don’t understand is the nasty spiteful nature of your attack. What do you get out of trying to bite my ankles? Surely you must know it makes you look petty, like a child defacing a painting because he can’t paint himself.
Up to you, amigo. I’m gonna let you have the last word … but I promise I’ll answer you as soon as you notify me that you have had something published in Nature.
And on that mythical day what would I do?
Call me crazy, but I would hope to congratulate you on the achievement because I know that getting published in Nature is never easy.
Until that distant day, my best regards to you and yours,
w
PS: For years there was no citation of my Brief Communications Arising. In it, I’d said that the change in the Lake Tanganyika fisheries was NOT due to climate change. Anyhow, a year or so ago it got cited … in a full article in Nature which said that the change in the Lake Tanganyika fisheries was NOT due to climate change. I was quite proud to have seen that a full decade before.
And meanwhile, you’re tying yourself in knots vainly trying to prove that what I did was meaningless … like I said, I know which part in this play I prefer …
Wow, so your comment got cited?
…
It’s still just a comment. That’s what the link says……”Communications Arising” are peer reviewed comments.
PS, if it took you all that time effort and energy to get a simple comment published, can you imagine how many YEARS it would take you to get a real research article published in Nature?
Rising sea vs. water pump. Pump won. Dutch drained the sea in Flevoland (1,419 sq. km.)
King Canute at work. Who’s laughing now?
I suspect the difference is in how we account for autocorrelation. I use the method of Koutsoyiannis, detailed here. I don’t know how Tamino does it.
I think Tamino models the autocorrelation as ARIMA(1,1) noise.
https://www.researchgate.net/publication/265467321_Time_and_tide_analysis_of_sea_level_time_series
Thanks, Phil, that’s a clear explanation of the autocorrelation method.
However, my repeated tests have shown me that I get much more accurate results using the method of Koutsoyiannis, as I described here. This is because the Koutsoyiannis actually measures the effect in the particular dataset, while the ad-hoc method uses the value of the autocorrelation to estimate the effect.
In short, the method I use is theoretically developed a priori, while Tamino (if he’s using the method you’ve cited) is using an ad-hoc adjustment.
Regards,
w.
After modeling the sample autocorrelation as an ARIMA(1,1) process, Tamino proceeds with the quaint notion that geophysical power spectra need to be compensated for autocorrelation, akin to the compensation of confidence intervals for linear regression. Since the power density of a random signal is defined by the Wiener-Khintchine theorem as the Fourier transform of its acf, his ensuing chain of calculations and conclusions is inane.
Koutsoyannis fares scarcely better, because he posits an AR(1) process a priori as characterizing the acf, thus making it totally dependent upon the sampled value at lag one. This greatly oversimplifies most geophysical data, especially when wave motion is involved.
Acceleration is intrinsically a high-frequency phenomenon, since it is determined by the second derivative in the case of analytic functions. In the practical case of discretely sampled signals, its power transfer function is distinctly high-pass, being proportional to sin^2 in the baseband interval 0 to pi/2. If we are to discuss acceleration of SLR scientifically, an objective choice needs to be made for any smoothing to be applied to best display the salient signal characteristics. The smoothing supplied by linear regression over the length of available data does not meet that requirement.
Oh, the “dazzle them with bullsh!t” approach, is it now?
No matter how you slice it, or how many times you pass your high dollar value word salad through the vegematic slicer dicer, the Mark 1 eyeball still shows the truth, plain as daylight.
No acceleration is evident.
Sorry that should be ARMA(1,1).
See the smoothed 15-yr rate of change of sea level:
If there were no accelerations and decelerations, the plot would be nearly flat.
To rank amateurs, most scientific descriptions are just “high dollar value word salad.”
Reposted from a comment to the Larry Kummer article from 20 July:
Perhaps the author(s) are unaware of the Gregory et al. assessment from a few years ago:
http://journals.ametsoc.org/doi/abs/10.1175/JCLI-D-12-00319.1
Abstract
Confidence in projections of global-mean sea level rise (GMSLR) depends on an ability to account for GMSLR during the twentieth century. There are contributions from ocean thermal expansion, mass loss from glaciers and ice sheets, groundwater extraction, and reservoir impoundment. Progress has been made toward solving the “enigma” of twentieth-century GMSLR, which is that the observed GMSLR has previously been found to exceed the sum of estimated contributions, especially for the earlier decades. The authors propose the following: thermal expansion simulated by climate models may previously have been underestimated because of their not including volcanic forcing in their control state; the rate of glacier mass loss was larger than previously estimated and was not smaller in the first half than in the second half of the century; the Greenland ice sheet could have made a positive contribution throughout the century; and groundwater depletion and reservoir impoundment, which are of opposite sign, may have been approximately equal in magnitude. It is possible to reconstruct the time series of GMSLR from the quantified contributions, apart from a constant residual term, which is small enough to be explained as a long-term contribution from the Antarctic ice sheet. The reconstructions account for the observation that the rate of GMSLR was not much larger during the last 50 years than during the twentieth century as a whole, despite the increasing anthropogenic forcing. Semiempirical methods for projecting GMSLR depend on the existence of a relationship between global climate change and the rate of GMSLR, but the implication of the authors’ closure of the budget is that such a relationship is weak or absent during the twentieth century.
Notice the final sentence. Such honesty is rare these days.
I’ve been having a running debate on this on Twitter with those who think there is acceleration. When I posted that not one surface station shows acceleration, the rebuttal from some is GLOBALLY together they show acceleration. So, 300 cars with a speed of 50kph collectively show an acceleration to 100kph, even though not one speedometer shows anything but 50kph. Got it.
Another demanded I show all stations to see there is no acceleration. I post a handful from around the world and state categorically that’s all I need to do to show not one station shows acceleration. That for there to be acceleration at some stations and not others would mean those with no acceleration are some how defying gravity.
Yep, in the world of AGW alarmists the laws of physics dont apply.
They also look for ANY acceleration at all, as if even a tiny little temporary acceleration is proof there will be a 2 meter rise by 2100. Again, this shows their complete lack of understanding and their desperation for anything to grasp.
To get to 2 meters by 2100 would require an acceleration (compound growth) of 3.7% per year. The least understood concept is compound growth. All compound growth has a doubling period. Each doubling period is the same as all previous doubling periods combined. This means that by 2099 sea level would have to be rising 8cm in that one year alone. Impossible.
Lastly, if you look at their graphs they show a rate of 1.7mm per year until 1990, then suddenly in that year, the rate of rise DOUBLED (100% acceleration) to a stable 3.3mm per year. No explanation how that could happen.
(I’d like to post some graphics, but have no idea how to do that, can someone post how, pls?)
If you have a link that is a jpeg from a host website, just copy the web address on a separate line where you want the graphic.
You cannot post graphs you have saved on your computer…they have to be in the form of links to a website.
Or so I believe.
Up top, just below the site name, there is a row of tabs…one is to a test page…use it to test out what you want to do to see if it will work.
I am no eggspurt, but I know those few things.
As for sea level rise…the amount they claim is ludicrous…not based on evidence, just makin’ stuff up.
Many predict rates of rise that would rival meltwater pulse 1A.
Personally, I have mostly given up on arguing with people I do not know on social media sites.
It is truly pointless.
But sites like this and a few others are different…they are places that people can go for non-fake news, and false statements should not go unchallenged.
Even at congressional hearings run by guys like Ted Cruz, or news network programs like Tucker Carlson…many false statements go unchallenged, just slide on by, perpetuating all matter of *insert your favorite phrase for crap that aint true*.
Thanks, lets see if that works.
It does so here is another. This is what surface stations should look like if the rate doubled in 1990:
This graphic is common showing sea level rate accelerating instantly in 1990. With some comments I’ve added.
Oh I get it…you hate children.
Why do you hate children?
/sarc off
I have perhaps a stupid question. Could not plate tectonics contribute to sea level variation?
It does, which is why Alaska’s land is rising (sea level falling).
And what about those ever growing mid oceanic ridges?
There are spreading centers, but also subduction zones.
Some seem to think Earth is expanding.
What it comes down to is, the total change in the level of the ocean over the past 150 years would not be even detectable if all you went by was pictures or where the beaches are.
Except for places where land has been displaced vertically by geologic forces, and where erosion has taken place…there is no place in the world where anyone could live in 1867 that they cannot live now because the ocean is too high. No one’s house has been flooded due to gradually rising oceans.
Storms…different story.
Has anyone applied ‘Tamino’s method’ to the UC satellite data record?
Whatever any future sea level acceleration turns out to be, it is very unlikely to put the Statue of Liberty underwater anytime soon …
As long as we don’t get any storms. Sandy closed Liberty Island for 8 months (75% 0f the island was flooded) and much of the infrastructure was destroyed. Here’s the dock before and after.
We will get storms. No matter what.
Did you have an idea that events which have always occurred can be stopped by political decree or virtue signaling obeisance?
Menicholas July 22, 2017 at 1:21 pm
We will get storms. No matter what.
Did you have an idea that events which have always occurred can be stopped by political decree or virtue signaling obeisance?
Flooding of Ellis Island and Liberty Island haven’t ‘always occurred’. Perhaps the rise in sea level there of a foot or so over the last century had something to do with it?
You could use the Holgate-9 series of stations, as those stations are well known and spread around the globe.
Thanks, Svend. I’ve looked for a list of those stations in the past. Do you have a link?
w.
The best i can do is ask you to look at http://climate4you.com/
And specifically sea level and this one: http://climate4you.com/images/Holgate-9_Since1900-NEW.gif
It is mentioned which stations are used.
I belive it is the same stations all the time, so even if the rate could be a little different from other compilations, the change of rate must be usefull and valid.
Thanks, Svend, I can get the names from there. However, I was surprised that there is only one southern hemisphere series ..
w.
Rob Bradley July 22, 2017, at 3:24 pm
Fails again? You haven’t established that I failed before.
Sorry for my lack of clarity. What I meant was that the longer cycle is about three of the 18-year cycles. It’s not exactly three because we’re dealing with a solar system, not a clock.
..
But seriously there is no Nodal tide cycle. By that I mean it’s only approximate, it doesn’t return to the exact same point, although it’s close. And the 54+ year cycle returns even more closely to the same point. So both are more properly termed pseudocycles … and both are entirely different from the sweep of a minute hand on a clock. That’s a simple sine wave. These are not.
Did you bother to read the post I linked to? In that post I described all of this in detail. I also overlaid a series of 54+ year cycles to show that they are indeed real.
w.
PS-Let me suggest that you lose the ‘tude, it doesn’t look good when you’re spouting nonsense.
You don’t get it. I’ve spent hundreds and hundreds of hours studying the moon cycles. I had to because back in the 90’s I ran a shipyard on a remote atoll in the Solomon Islands. When you have a slipway you need tide tables. The SI Government produced tide tables … but usually only printed them in September or something.
So I had to make my own. I took the previous year of tidal data and entered it by hand in my ancient Mac. Then I spent a couple months crunching the data and learning about lunar cycles … from my Encyclopedia Britannica, a necessity on a remote island.
And at the end of that I was able to produce a set of tide tables for each year of the time I worked there … and I published it and sold it in the capital city of Honiara as well.
Now, at some point in the future when you have amassed enough knowledge to take a years of past tide tables and create this year’s tide tables on them … well, you’ll have earned the right to use some ‘tude on folks as innocent as you are today … but not on me.
1) ” that the longer cycle is about three of the 18-year cycles.”
2) “there is no Nodal tide cycle.”
…
Therefore there is no 54/55 year cycle
…
(basic logic Willie) …
…
PS, Google is your friend, I suggest browse the 1660 results you get for a search on “Nodal tidal cycle”
…
PPS, the solar system is darn good clock. We have things called “days,” and “years” based upon the clock like precision of the movements of the planets. The orbit of the moon is quite predictable.
Rob, if you read the post and the actual words Willis used, you will see he referred to the saros cycle, which is a period of 223 synodic months.
This cycles has been known since ancient times, and was what allowed certain cultures and not certain others to be able to predict eclipses.
Willis did not refer to the somewhat longer period known as the nodal tidal cycle. You seem to have translated one into the other inside your own head…those words are yours, not his.
BTW…223 synodic months is an interval known to great accuracy.
It is “approximately 6585.3211 days”.
Or, more simply, 18 years, 11 days, and 8 hours.
Three times that gives an even number of days.
And that three saros cycle period is exactly the number Willis cited.
I do not even have to break out my mark one pencil to do that multiplication.
Although I did do something you seemed unable or unwilling to do…I looked up stuff before I decided i was remembering correctly and criticized anyone.
You should try it sometime.
https://en.wikipedia.org/wiki/Saros_(astronomy)
https://en.wikipedia.org/wiki/Lunar_standstill
Menicholas: re-read the post, and focus on this: “Because the long lunar tidal cycle is just over fifty years”
…
See the word “tidal?”
…
You claim “if you read the post and the actual words Willis used, you will see he referred to the saros cycle”
….
Nope, he mentions that in a comment, but not in the post. Do you know the difference between the post, and the comments?
Ba-zing!
Ooh, you got me there!
I think it is worth noting that your rude comment was attached to his comment (did i use the right word…um, yup, I think so this time), not to the headline post.
Notice when you make a comment on a post, or on another comment…just what the little oblong button thingy says that you hit in order to …um…POST IT…says?
That one right down there on the bottom right as you POST your next rude-ass COMMENT to me.
See it?
What does it say?
If I had known this was grammar N@zi day, I would have peer reviewed each word of the comment I um…posted.
My bad.
So, your rude ass comment you posted in which you pulled the phrase no one else had mentioned out of your, uh, hat and attributed it to someone who had not said that…that was a reference to the top article?
But the words you quoted were not from up top.
So, like all warmistas…you just make crap up all day long.
It is like a reflex with you guys, aint it?
If you have a point, could you please make it?
…
There’s not much point in talking about sea level, which is measured with tidal gauges, and confusing it with an eclipse(s) that follows a saros cycle. Maybe you should direct your ire at Willis, since his sloppy writing and confusion about different cycles would best be solved with your help.
Just admit it…you did not know the difference between saros and nodal tide cycles. Or that there was one.
You conflated them and made a false attribution.
It is right there in black and white for all time.
If it will make you happy Menicholas, I will admit that Willis did confuse the two.
“And the 54+ year cycle returns even more closely to the same point.”
I love this graphic animation, which illustrates the variation between one eclipse and the next one in that saros series:
http://eclipse.gsfc.nasa.gov/SEsaros/SEsaros136.html
Turns out NASA is still good for something.
A few somethings…just not anything related to climate.
Oh, wrong link.
This is the one:
Link broken …
I do not know why it is that little square, but when I click on it I get the GIF from a wiki article.
it is the progression over one saros series of the path of each eclipse n the series.
Interesting pattern.
I wonder if each saros has a similar pattern?
Do you not see the GIF if you click the link?
Huh … works now.
Interesting graphic …
w.
Willis, to get the acceleration, did you remember to multiply the quadratic coefficient by 2?
Yes, and thanks for checking.
w.
Willis, it looks like you have simply assumed that the 50+ year cycle you refer to has a significant effect on tides. I don’t think you have justified that assumption, so it looks like you have simply declared it so that you can ignore 95% of the 1,505 tide stations. Is there a paper that shows the effect of this cycle on tides?
Martin, you come here and without a scrap of evidence you’ve accused me of bad faith, of trying to rig the game so I can ignore some station. You can stuff that false accusation where the sun don’t shine.
As to the substance, it is well known in the study of the tides that we need about 50 years of data in order to get mm level accuracy regarding sea level rise. Hang on … OK, there’s a good exposition of this in the section of this paper called “Asymptotic Trend Evaluation”. See also the graphic of the same name at the end of the paper.
And next time you want to ask a scientific question, just leave out the nasty untrue assumptions about my motives, OK? You have no clue what my motives are, they are irrelevant in any case, and it demeans you to be making such accusations. Stick to the science …
w.
I apologize for giving you that impression, Willis, but I was careful not to accuse you of anything. If you reread my comment, you will see that I did not accuse you. I said that your blog post “looks like” you are trying to ignore most of the data because you did not include the justification which you have just now provided. However, the word “lunar” does not appear in the paper you provided. The word “moon” does appear exactly once, and it does appear in the context of an 18.6 year cycle, but there is no mention at all of a 50+ year cycle, so you still have not justified your claim that this 50+ year lunar tide cycle is of significance. I’m afraid it still looks like you are trying to ignore most of the data. I’m not accusing you; it “looks” that way to me because I can’t see that you have justified your assumption.
But you are certainly wrong about your readers not having a clue what your motives are. We have all your blog posts.
Martin Smith July 24, 2017 at 11:26 am
Oh, I get it now. So if I were to say “It looks like Martin Smith spends most of his time ignoring the truth and spreading lies”, I’m not actually accusing you of doing anything wrong, because I put some weasel words in the sentence? …
Maybe that worked with your mom or your sister or someone. Won’t work here in the real world.
Dude, half the time neither you nor I know what ourown motives are. The idea that you can determine my motives from my writings, when I cannot clearly delineate them from this side of my eyeballs, doesn’t even pass the laugh test.
w.
From reading only two comments from me, do you really think you can reasonably make this claim?: “It looks like Martin Smith spends most of his time ignoring the truth and spreading lies”
You actually have not justified your claim that there is a 50+ year lunar tide cycle that has a significant effect on sea level rise. You haven’t done that, but your argument depends on it.
Martin Smith July 24, 2017 at 11:51 am
I didn’t say you were a liar. To use your excuse, I didn’t say you are spreading lies. I said it “looks like” you’re spreading lies … hey, if you can deny responsibility on such a bogus pretext, why can’t I?
You don’t get it. It would be a damaging insult if I were to say
and if I were to say that, which I wouldn’t, I also wouldn’t get to deny responsibility by claiming “Hey, I didn’t say you WERE a child molester … I just said it’s POSSIBLE, which is clearly, obviously, and demostrably true …”
Did you read the citation that I posted? Obviously not, since it said you need fifty years of data to get mmm accuracy:
They say you need fifty years in order to get accurate estimates of “the tidal amplitudes and phases” … which is WHY I SELECTED THE FIFTY YEAR DATA LENGTH.
w.
>They say you need fifty years in order to get accurate estimates of “the tidal amplitudes and phases”
No they don’t.
I accept that you will not address the point I raised, so I will conclude by stating my understanding of your analysis: You throw out almost all the SLR data, and then you conclude from the remaining small fraction of the data that the SLR data do not show a statistically significant acceleration in SLR.
Martin Smith July 24, 2017 at 1:10 pm Edit
Martin, they not only state you need fifty years of data to get mm accuracy as I quoted above, they give a clear explanation of why, plus a graphic showing the relationship between length of tidal data and accuracy. The apparent fact that you are unable to understand that does not mean that the rest of us are.
Not address the point you made? I want some of what you’re smoking. I’ve answered repeatedly, in detail, with citations. I’ve also pointed you to my analysis of the actual tidal forces which clearly shows the longer tidal cycles.
I do note that you’ve gone back to attacking my motives, claiming cherry-picking without a scrap of actual evidence. What is it you want? Hey, you can use all of the 1500 or so datasets … are you arguing for that?
Because if not, that means that you need to make some ex-ante choices about which tide stations to use. I made my ex-ante choice (stations with 95% data over the last 50 years), which is totally justifiable given our knowledge of the relationship between tide data length and accuracy.
However, making such an ex-ante choice IS NOT CHERRY-PICKING AS YOU FOOLISHLY ASSERT. Unless we are going to use a dataset with only a few years of data, like some among the 1500 candidates, we have to set up a standard of which to use.
Don’t like my choice? No worries. You get to make your own choices. I’ve given you the link to the data source in the head post. I await your analysis of this data.
I also note that you are returning to your baseless ad hominem attacks. When you have a scientific argument, please come back and we can discuss it.
Why do I think that despite all of your whining about my analysis, we’re never going to see your analysis of this data? …
w.
Willis, here again is my understanding of your analysis:
You throw out almost all the SLR data, and then you conclude from analyzing the remaining small fraction of the data that the SLR data do not show a statistically significant acceleration in SLR.
You did throw out almost all the SLR data. That’s a fact. Did you conclude from analyzing the remaining small fraction of the SLR data that the SLR data do not show a statistically significant acceleration in SLR? Is that your conclusion, based on the data you analyzed?
For those actually interested in the question of tidal data length and accuracy, which by all accounts doesn’t include Martin Smith, see here.
Best to all,
w.
I’ve got an interesting debate going on at your friend’s site. Seems they dont like the fact that sat data shows a doubling of sea level in the 1990-1993 period and flat since. https://tamino.wordpress.com/2017/07/24/boston-sea-level/#comment-99191
Too bad you’re banned. Guess I will be too soon.
J, why don’t you prove your claim (I think you mean doubling of sea level rise rate, not doubling of sea level) instead of just declaring it?
The doubling of the rate of rise, from 1.7mm up to 1990 to 3.4mm afterwards comes from the sat data. Surface station data shows no doubling. The sats are wrong.
No it doesn’t, J. Tamino has explained where and why your claim is wrong. I won’t repost Tamino’s work here, but you now know why your claims are wrong, so it is really disingenuous to make the same claims here.
No he has not. He’s trying to shoehorn an acceleration curve onto a clear straight line data set. It is his OPINION that fits better than a straight line.
?itok=amqLr7zW
Here is the sat data, again. How you dont see a straight line is beyond me. Interesting how your side has turned into the deniers.
J, the straight line you see is computed by simple linear regression. It always computes a straight line through any set of data. The straight line is the trend. There is always a straight trend line through the data. It is the trend. It always exists, but it says nothing about whether sea level rise is accelerating.
Re: “the sats are wrong”
local sea rise from local gauges is contaminated by local changes in land height, which can be significant. sats are clearly superior.
If they are superior, how come a calibration went unnoticed for 20 years? Sat data is rot with a lot of uncertainty and noise.
“In addition, the amplitude of the residual trend pattern is significantly lower than the expected error in trend patterns from satellite altimetry (in the order of 2 mm/yr to 3 mm/yr) and therefore suggests that satellite altimetry measurement is still not accurate enough to detect the anthropogenic signal in the 20 year tropical Pacific sea level trends. ”
https://tel.archives-ouvertes.fr/tel-01317607/document
“Sat data is rot with a lot of uncertainty and noise.”
Remember that, next time you tout satellite data as the best temperature data we have.
I’ve never relied on sat temp data. The only measurements I accept are the direct ones on the ground.
Good for you. Then you know there was no “pause” or “hiatus” in global average temperature rise, and you know the global average temperature rise is accelerating.
And what is the rate of this acceleration? Do we expect the earth’s temp to double in the next few decades?
No, I dont see temps “accelerating” anywhere on the planet. If anything Tmax is down or flat:
I don’t know what your graph represents, J, because you don’t provide any links or citations. Clearly, it is not the global average temperature, which is what you and I are talking about. Apparently your graph shows the summer maximum temperature for somewhere. It says nothing about the global average temperature, which, again, is what you and I are talking about. Here is the complete explanation you are missing. It shows the global average temperature is rising, and the rise is accelerating. But no, I have not done the statistical analysis Tamino has done. The data are also available for each graph:
http://data.giss.nasa.gov/gistemp/graphs_v3/
And here is the statistical analysis by Tamino:
http://tamino.wordpress.com/2017/01/18/global-temperature-the-big-3/
So I say to you again: Good for you. Then you know there was no “pause” or “hiatus” in global average temperature rise, and you know the global average temperature rise is accelerating.
Willis, won’t you answer my question? Here is my understanding of your analysis:
You throw out almost all the SLR data, and then you conclude from analyzing the remaining small fraction of the data that the SLR data do not show a statistically significant acceleration in SLR.
You did throw out almost all the SLR data. That’s a fact. Did you conclude from analyzing the remaining small fraction of the SLR data that the SLR data do not show a statistically significant acceleration in SLR? Is that your conclusion, based on the data you analyzed?
You have to throw out incomplete data, or records of too short a period. You cant include them because it incorrectly skews the results.
I think we should allow Willis to answer for himself, J.