Guest Post By Willis Eschenbach
Often I start off by looking at one thing, and I wind up getting side-tractored merrily down some indistinct overgrown jungle path. I was thinking about the difference in the strength of the sunshine between the apogee aphelion, which is when the Earth is furthest from the sun in July, and the perigee perihelion in January, when the Earth and the sun are nearest. On a global 24/7 average value, there is a peak-to-peak aphelion to perihelion swing of about twenty-two watts per square metre (22 W/m2). I note in passing that this is the same change in downwelling radiation that we’d theoretically get if starting in July the CO2 concentration went from its current level of 400 ppmv up to the dizzying heights of 24,700 ppmv by January, and then went back down again to 400 ppmv by the following July … but I digress.
Now, because the Earth and sun are nearest in January when the southern hemisphere is tilted towards the sun, there is a larger swing in the solar strength in the southern hemisphere than in the northern.
While I was investigating this, I got to looking at the corresponding swings of the ocean surface temperature. I split them up by hemisphere, and I noticed a most curious thing. Here’s the graph of the annual cycle of solar input and sea surface temperature for the two hemispheres:
Figure 1. Scatterplot, top-of-atmosphere (TOA) solar input anomaly versus ocean surface temperature. Northern hemisphere shown in violet, southern hemisphere shown in blue. Monthly data has been splined with a cubic spline. Data from the CERES satellite dataset.
So … what is the oddity? The oddity is that although the swings in incoming solar energy are significantly larger in the southern hemisphere, the swings in ocean temperature are larger in the northern hemisphere. Why should that be?
The difference is impressive. As a raw measure, the northern hemisphere ocean surface temperature changes about seven degrees C from peak to peak, and the TOA solar varies by 216 W/m2 peak to peak. This gives a change of 0.032°C per W/m2 change in solar input.
In the southern hemisphere, on the other hand, the ocean surface temperature only swings 4.7°C, while the solar input varies by 287 W/m2 peak to peak. This gives a change of .0162°C per W/m2, about half the change of the northern hemisphere.
So that’s today’s puzzle—why should the ocean in the northern hemisphere warm twice as much as the southern hemisphere ocean for a given change in solar forcing?
Part of the answer may lie in the depth of the ocean’s mixed layer. This is the layer at the top of the ocean that is mixed regularly by a combination of wind, waves, currents, tides, and nocturnal overturning. As a result, in any given location the mixed layer all has about the same annual average temperature. (However, monthly changes are still largest and the surface and decrease with increasing depth.) This mixed layer worldwide averages about 60 metres in depth. But the mixed layer is deeper in the southern hemisphere, averaging about 68 metres in the southern hemisphere versus about 47 metres in the northern.
However, two things argue against that conclusion. One is that the mixed layer in the southern hemisphere is about 45% deeper than in the northern … but the northern hemisphere sensitivity of temperature to incoming solar is double, not 40% larger.
The other thing that argues against the mixed layer difference is that the thermal lags in the two hemispheres are very similar, with peak temperatures in each hemisphere occurring almost exactly two months after peak solar. In a previous post entitled “Lags and Leads” I discussed how we can use the difference in time between the peaks of solar power and temperature shown in the scatterplot in Figure 1 to calculate the time constant “tau” of the system. This two month lag is equivalent to a time constant tau in both hemispheres of 3.3 months.
Then, using that time constant tau we can calculate the equivalent depth of seawater needed to create a thermal lag of that duration. A time constant tau of 3.3 months works out to be equivalent to 25 metres of seawater with all parts equally and fully involved in the monthly temperature changes (or a deeper mixed layer with monthly temperature swings decreasing with depth).
But since the time constant “tau” is the same for both hemispheres, this means that the equivalent depth of water that is actually involved in the annual cycle is the same in both hemispheres.
Or in other words, the more of the ocean that is involved in monthly temperature swings, the greater the lag there will be between solar and temperature peaks. But in this case, the thermal lags are the same in both hemispheres, meaning the equivalent depth of ocean involved is the same.
Then, I thought “Well, maybe it’s because one pole is underwater and the other pole is on land”. So I repeated the calculation of the temperature and solar swings using just the range from 60° North to 60° South, in order to eliminate the effect of the poles and the ice … no difference. The northern hemisphere non-polar ocean warms twice as much for a given change in solar energy as does the southern non-polar ocean. The difference is not at the poles.
So my question remains … why is the northern hemisphere ocean surface temperature twice as sensitive to a change in solar input as is the southern hemisphere ocean temperature?
My best to all. Here, we have had a rare June rain, most welcome in this dry land, so for all of you today, I wish you the weather of your choosing in the fields of your dreams …
w.
My Usual Request: Misunderstandings can be minimized by specificity. If you disagree with me or anyone, please quote the exact words you disagree with, so we can all understand the exact nature of your objections. I can defend my own words. I cannot defend someone else’s interpretation of some unidentified words of mine.
My Other Request: If you believe that e.g. I’m using the wrong method or the wrong dataset, please educate me and others by demonstrating the proper use of the right method or the right dataset. Simply claiming I’m wrong about methods or data doesn’t advance the discussion unless you can point us to the right way to do it.
UPDATE: Here are two maps of the same data, which is the change in ocean temperature per 0ne watt/metre squared (W/m2) change in top of atmosphere (TOA) solar radiation …
The gray contour lines show the global average value of 0.02 °C per W/m2.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Somewhat related article, involving changes in earth’s wobble.
Though they never mention that Earth’s rotation speed has been increasing since the mid 90’s and more so in the time period used for this study. hmm still could be solar related…
NASA Study Solves Two Mysteries About Wobbling Earth
APRIL 8, 2016
http://www.jpl.nasa.gov/news/news.php?feature=6332
…A Sharp Turn to the East
Around the year 2000, Earth’s spin axis took an abrupt turn toward the east and is now drifting almost twice as fast as before, at a rate of almost 7 inches (17 centimeters) a year. “It’s no longer moving toward Hudson Bay, but instead toward the British Isles,” said Adhikari. “That’s a massive swing.” Adhikari and Ivins set out to explain this unexpected change.
…The researchers found the answer in Eurasia. “The bulk of the answer is a deficit of water in Eurasia: the Indian subcontinent and the Caspian Sea area,” Adhikari said.
The finding was a surprise. This region has lost water mass due to depletion of aquifers and drought, but the loss is nowhere near as great as the change in the ice sheets.
…So why did the smaller loss have such a strong effect? The researchers say it’s because the spin axis is very sensitive to changes occurring around 45 degrees latitude, both north and south. “This is well explained in the theory of rotating objects,” Adhikari explained. “That’s why changes in the Indian subcontinent, for example, are so important.”
New Insight on an Old Wobble
In the process of solving this recent mystery, the researchers unexpectedly came up with a promising new solution to a very old problem, as well. One particular wobble in Earth’s rotation has perplexed scientists since observations began in 1899. Every six to 14 years, the spin axis wobbles about 20 to 60 inches (0.5 to 1.5 meters) either east or west of its general direction of drift.
…When the researchers input the GRACE observations on changes in land water mass from April 2002 to March 2015 into classic physics equations that predict pole positions, they found that the results matched the observed east-west wobble very closely. “This is much more than a simple correlation,” coauthor Ivins said. “We have isolated the cause.”
The discovery raises the possibility that the 115-year record of east-west wobbles in Earth’s spin axis may, in fact, be a remarkably good record of changes in land water storage. “That could tell us something about past climate — whether the intensity of drought or wetness has amplified over time, and in which locations,” said Adhikari….
Carla, very interesting! Any thoughts on how this would affect sea level and its measurement?
Barclay E MacDonald June 18, 2016 at 9:00 pm
—————————————————————–
First off Mr. MacDonald, I found the article to be, well, misleading.
Blaming it on glowball warming/climate change.
Do I think that polar motion, gravity anomalys, melting ice, growing ice, land water usage, drought etc could and does affect sea level rise, yes.
But……….in the technical doc, there is a disclaimer of sorts that actually states that they did not use Length of Day (LOD), changes in Earth’s rotation rate.
How can a study on polar motion and the Earth’s various wobbles over a period from 2003-2015 and include rising and falling of sea levels at different locations around the planet and not include rotation rate ie LOD?
Now the different locations of the rising and falling of sea levels may be quite interesting for us, but one of the main mechanisms is missing.
Can’t always through the baby out with the bath water, Carla. Yea, sometimes the water is pretty dirty though.
The technical article:
Climate-driven polar motion: 2003–2015
http://advances.sciencemag.org/content/2/4/e1501693.full
Surendra Adhikari* and Erik R. Ivins
Just a little polar motion to excite our day..
http://aiuws.unibe.ch/code/erp_new.jpg
http://www.aiub.unibe.ch/research/code___analysis_center/gps_derived_earth_rotation_parameters/index_eng.html
Willis asks: “why is the northern hemisphere ocean surface temperature twice as sensitive to a change in solar input as is the southern hemisphere ocean temperature?
1) Solar input is normally expressed in terms of what units?
2) Temperature is expressed in what units?
3) What do you need to know to convert the units in the answer to question 1) to the units for questions 2)?
Your post answered part of the question: Peak temperature occurs two months after peak insolation.
Hope you don’t mind the questions. I’ve “lectured” on some aspects of this problem before. Perhaps the Socratic method will work.
Willis, what time span does your sea surface temperature cover?
I like ristvan’s current idea but cloud cover could also be an answer. Is there anyway to check cloud cover? If so, it could be good support for your cloud-thermostat hypothesis.
Thomas, the data covers March 2000 to February 2015.
w.
There is a typo in this sentence-
“On a global 24/7 average value, there is a peak-to-peak apogee to perigee swing of about twenty-two watts per square metre (22 W/m2).”
Should be about 250 W/m^2 p-p?
Thanks, Chris. The aphelion-perigelion change is indeed 22 W/m2. The rest of the change is from the changing tilt of the earth with respect to the sun.
w.
Willis-
OK. I missed the important ‘global 24/7’ in your sentence.
Thanks.
Is the Mediterranean Sea included in NH oceans?
A minor but important point. The “gee” in apogee and perigee refer to earth orbiting objects. The correct terms are aphelion and perihelion for a sun orbiting object.
Thanks, Bill, fixed.
w.
As usual, a thought-provoking marshaling of data. I have no idea what the explanation is. But a somewhat tangential comment follows.
As Mr. Eschenbach’s “Leads and Lags” post did, this one relies on a lumped-parameter, “one-box” model as an approximation. (Otherwise the “tau” parameter’s meaning is problematic.) But the period invariance Mr. Eschenbach mentioned in that previous post tends to militate against relying on such an approximation.
Period invariance is instead characteristic of what one might call an “infinite-number-of-boxes” model, or, more typically, a distributed-parameter, diffusion model. As one might conclude from comments to the post I wrote about that some years ago, there is reason to suspect that a hybrid of lumped- and distributed-parameter models may be superior to both.
Again, this is somewhat tangential, but Mr. Eschenbach’s reference above to inferring “tau” from lag suggested it might be worth reminding readers that the theoretical basis for that inference is questionable.
Thanks, Joe, always good to hear from you. My point was simple. If the lag in both hemispheres is the same, which it demonstrably and measurably is, then it is unlikely that the amount of ocean mass involved is radically different.
As to using the simplest model that fits the data, I plead guilty … as I showed in the previous post, such a model emulates the observed ocean temperature to a very high degree of fidelity (see Figure 5).. Given that accuracy, what would be the justification for unnecessarily multiplying entities in violation of Occam’s Razor?
w.
I apologize for going off on a tangent. I wasn’t attempting to dispute the overall point that the mass being heated is unlikely to provide the entire explanation for the gain difference. My comment was meant only as an aside, directed to those of a more-mathematical bent, who would recognize that the relationship between phase and time constant prevails only for one-box models and that for a one-box model the gain difference upon which you remarked admits of only one explanation.
, where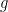 
is equilibrium gain, 
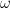is 
, 
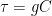is the time constant, and 
is heat capacity, while phase is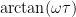 
. That is, there are only two parameters: heat capacity and equilibrium gain, sometimes called the “Planck sensitvity” at this site. So, if the yearly-variation gain really does differ between hemispheres that exhibit the same phase, the equilibrium gain does, too: the Southern Hemisphere’s radiation-emission change for a given change in temperature exceeds that of the Northern Hemisphere.
Specifically, the yearly-variation gain for a one-box model is
As I say, for those of a more-mathematical bent, that would be the only possible conclusion if one were to stick with a one-box model and truly believe the observed gain difference. Again, though, this is only tangential to the questions your observation raised.
Joe: One doesn’t need a very sophisticated model to understand why seasonal warming is twice as great in NH than SH oceans. 80% of the SH is ocean, 60% of the NH is ocean. The mixed layer in the NH is 47 m deep in the NH and 68 m deep in the SH. That means the heat capacity of the SH is roughly double that in the HN.
The concept of climate sensitivity (K/(W/m2)) makes skeptics think that every forcing can be converted into a temperature change without considering: 1) heat capacity 2) the time required for temperature to change, 3) how Planck feedback (or more accurately the climate feedback parameter) gradually negates the radiative imbalance associated with a forcing. 4) how quickly heat penetrates below the mixed layer (which is defined by seasonal change). Every time I comment on some aspect of this (real) physics, I get no response, Do you understand this phenomena?
It is trivial to calculate that a +1 W/m2 radiative imbalance is capable of warming the planet at an INITIAL RATE of 0.2 K/yr (assuming that all the change occurs within a 50 m deep mixed layer). This is a good place to start thinking about Pinatubo. A +100 W/m2 imbalance can warm at an initial rate of 1.7 K/month. Or, if we use the numbers above, 1.07 K/month in the SH and 2.0 K/month in the NH.) This would a reasonable place to start thinking about seasonal warming – if surface temperature were in equilibrium with incoming radiation. Starting with climate sensitivity is hopeless.
Total heat capacity of the Northern hemisphere is less than the Soithern; more land in the North. So other things being equal, the North should have greater seasonality than the South, and it does. The influence of land temps on water temps is tempered, of course, but greater seasonality in the ocean in the north is a reasonable consequence of lower total heat capacit in the north.
At the end of the day it must be about the earth’s preferred energy configuration.
As per the observation that the two hemispheres have the same albedo, and in line with to the second law of thermodynamics, the earth strives to be as thermally homogeneous as it can be within the constraints the earth imposes. (ie spherical, rotating, with ocean currents and land masses as well as composition and density of its atmosphere to name a few) The earth’s climate system at a large scale over long time periods achieves that and one of the mechanisms that can change is cloud cover.
So…with less surface area, the Northern hemisphere oceans need to be warmer to get the “right” amount of cloud to make all that happen. Having said that, it could also be about the right amount of cloud cover to get to the preferred configuration if we’re out of whack currently…
Willis, if you can, you should map the interrelationships.
Cheers.
“So that’s today’s puzzle—why should the ocean in the northern hemisphere warm twice as much as the southern hemisphere ocean for a given change in solar forcing?”
WR: suggestion for tomorrow’s puzzle: why should the ocean in the northern hemisphere cool twice as much as the southern hemisphere ocean for a given change in solar forcing?
My idea: energy flows from warm to cold. The average temperature of the sea is higher than the average temperature of the land. So sea warms the land. The NH has relatively more land and less sea than the SH. So on the NH less sea has to warm more land. Therefore NH oceans will cool faster than the oceans on the SH.
Except in NH Summer the land is a higher temperature than the sea.
If so, in summer time NH land masses will warm the sea. And in NH winter time very cold land masses will cool the sea strongly. Resulting in a large NH sea temperature swing.
Doesn’t worK.
The reason land temps have a larger swing is because they have a lower specific heat capacity. So to the same degree as they warm more, they have less capacity to warm anything else. They are not creating energy. There is no means for land to add more heat than would be falling on the same area if it were ocean.
Plus land can only affect sea via the air and the degree to which the atmosphere can heat the ocean is limited. There is some horizontal heat transfer which is how oceans stabilise land temp swings. To the extent that land summer temps warm the air above, most of that heat is going to go up not down.
Greg, it is about averages. It will be interesting to see the yearly facts. Land temperatures in the NH in wintertime are far down: land can absorb a lot of energy from the sea.
There is a [huge] horizontal and vertical energy transport. Compare for example the high surface winter temperatures in Western Europe (with a lot of oceanic westerlies) with the winter temperatures in East Asia at the same latitude to see the effect of the horizontal energy transport. Vertically, the energy in the air brought upwards by low pressure systems at sea lowers down in high pressure areas at land.
Land masses are losing a lot of energy in wintertime. Where does the energy come from? Without the sun, Earth would only have a temperature around 3K or so. What keeps the high latitudes in Siberia in wintertime at temperatures of around 240K? The high latitude land area’s lack sun energy and there is nearly no energy available in the subsurface: it radiates quickly outward. Only the sea is containing enough energy to keep Siberia relatively (!) ‘warm’ in wintertime. In doing so, the oceans at the NH cool down strongly.
So the story is about ‘losing heat’. And about the total heat content of the subsurface of the NH and the SH in which the sea plays an overwhelming role.
I think that specific heat content is a worthless concept things do not contain heat , if enough energy was put into the ocean it would boil away but the solid part of the earth would still be there absorbing that energy. I think that the solid part of the earth heats up faster than the oceans because all energy is absorbed at surface level and there is no deep penetration as there is in the oceans
There is very little contract between land and sea. The interaction sea -> air ; air -> land. The amount of air in contact with the surface does not contain much sensible heat.
If you want a link between winter temps on land and sea I would suggest it is to do with cloud cover.
Also remember when talking about “land temperatures” we are usually measuring land, near surface air temperature not the temperature of the land. So a lot of this will be warmer marine air blowing over land, not transferring heat to the land.
The warm ocean air radiates the heat to space more easily when the atmosphere is cold and dry above Greg
Sarah Kang in he linked paper below agrees with you Wim Rost
Surely the answer lies in the largely landlocked ocean basins of the N pacific and indian oceans. The southern parts of these two are regularly flushed out by the vigorous circumpolar westerlies and the southern ocean west to east current. Northern ocean basins do not have this and are largely recycling water in trapped gyres with little direct access to colder polar water.
Willis, I’m true to my little rhyme:
Climate changes with the sun,
The ways oceans run
And clouds, so complexly begun.
That’s my story and I’m stickin’ tuit.
Sarah Kang and Richard Seager had an interesting paper that revisits a paper from James Croll done in 1870. Croll is the founder of astronomical theory of ice ages. They hypothesize that ocean transport of heat from the SH across the equator to the NH is responsible for the temp difference between the hemispheres already noted in 1870 before added CO2 could be the cause.
“”Croll!s arguments for how currents accomplish this transport was stated as follows:
Since there is a constant flow of water from the southern hemisphere to the
northern in the form of surface currents, it must be compensated by undercurrents
of equal magnitude from the northern hemisphere to the southern. The
currents, however, which cross the equator are far higher in temperature than
their compensating undercurrents; consequently there is constant transference of
heat from the southern hemisphere to the northern.
“”
http://ocp.ldeo.columbia.edu/res/div/ocp/pub/seager/Kang_Seager_subm.pdf
Ocean heat transport could be moderating the SH temperature delta T and exacerbating the NH delta T.
In my opinion this is part of the explanation, if not the most significant part of the explanation. I made a point similar to this in Willis’ old article Radiating the Oceans. Ocean heat transport is a key component of understanding climate on this water world of ours.
Ozone?
Production/destruction processes are constant in the atmosphere and their rates are effected in a big way by both angle of incidence and intensity of UV rays from the sun. So in January, the SH is turned more directly toward the sun AND it is getting a higher dosage due to being at perihelion. From there, it gets real complicated fast as you’ve got a lot of different processes going on, including ozone being a GHG, mopping up other GHG’s like methane through chemical reactions, and as the Dobson units increase, direct absorption of incoming UV at altitude instead of lower down in the atmosphere or even at surface.
My expectation is that the real explanation will be the sum of several different process. But I thought I would through this one out there for cosideration.
agreed. it is the amount of UV allowed through the atmosphere that heats the oceans the most. But it is not only ozone being formed TOA; there are peroxides and nitrogenous oxides as well being formed by the most energetic particles released from the sun. They do the same thing: restrict more UV coming through. (e.g. compare spectra of H2O2 with ozone).
[perhaps off topic: there never was a ozone hole in the SH. Peroxide is formed preferentially to ozone if more OH radicals are available.]
HenryP, you might find this article of interest regarding solar spectrum ocean heating.
http://journals.ametsoc.org/doi/pdf/10.1175/1520-0485(1994)024%3C1652:HRWTUO%3E2.0.CO%3B2
Turning the question round the other way then why does the southern hemisphere ocean respond less to solar radiation than the northern hemisphere ocean. My answer to this question would be that the southern hemisphere has a lot more sea ice than the northern hemisphere at a higher latitude which makes the water colder when it melts.
sea ice as thermal ballast damping excursions makes sense to me
Willis wrote: “”Why is the northern hemisphere ocean surface temperature twice as sensitive to a change in solar input as is the southern hemisphere ocean temperature?
Answer (to a first approximation): The heat capacity of the SH is twice as big as the heat capacity of the NH, so the same seasonal change in insolation produces half as much warming in the SH as in the NH.
60% of the NH is covered by ocean with a mixed layer averaging 47 m deep. 80% of the SH is covered by ocean with a mixed layer 68 m deep. Ignoring the heat capacity of land and atmosphere, the ratio is 1.93:1.
Due to the eccentricity (3.5%) of the earth’s orbit, the SH receives 17 W/m2 (7%) more during its summer than the NH. The rest of the 22 W/m2 is due seasonal snow cover in the NH which increases the earth’s surface albedo during winter in the NH. These two factors oppose each other, so the difference is 12 W/m2. The seasonal change in radiation is about 250 W/m2. So the seasonal change in insolation is about 5% bigger in the SH.
To a second approximation, the ratio of warming should be about 1.84:1, which is still within reasonable agreement with observation. This ratio will drop a little if we account for the heat capacity of the land and atmosphere. We may also need to accounted for any different in seasonal changes in cloud cover between the NH and the SH.
The difference between climate sensitivity and ordinary heat transfer causes massive confusion. When discussing climate change, we convert a forcing usually measured in terms of W/m2 into a temperature change usually measured in degK. If you do dimensional analysis of these units, you will find that these units are incompatible: In ordinary heat transfer, Watts is energy/time, W/m2 is energy/time/area, temperature proportional to energy/VOLUME (or energy/mass). Heat capacity is the factor used to convert energy to temperature. The depth of the mixed layer connects the area of the material being heated (the ocean) with the volume of the material being heated by a change in insolation. The warming of the NH and SH are problems of ordinary heat transfer.
Equilibrium climate sensitivity is not an ordinary heat transfer problem. As the planet warms, it radiates more heat to space and any radiative imbalance at the TOA gradually drops to zero – assuming a constant forcing. For an instantaneous doubling of CO2, we have an immediate radiative imbalance of 4 W/m2 that gradually drops to zero, mostly in the first decade. That energy (power * time = energy) goes into warming the ocean – but the depth of ocean (heat capacity) being warmed is far greater than the seasonal mixed layer. ECS allows us to convert a forcing (W/m2) into warming only after a long period of time (decades to centuries) and the depth of the mixed layer is irrelevant to this process. TCR allow us to convert a gradually increasing forcing to warming over one or more decades -which only gets us part way to equilibrium, which is why TCR is about 2/3 of ECS.
The concepts of climate sensitivity (ECS and TCR) can NEVER be applied to seasonal change. Seasonal temperature change has nothing to do with reaching or approaching equilibrium! By the time peak warming is reached in August in the NH, peak insolation is long past. NH SST is 1 K warmer in September at the equinox than in June at maximum insolation! Due to the high heat capacity of the ocean, the temperature of the ocean lags far behind changes in insolation.
The importance of heat capacity can also be seen by looking at local temperature. Away from the coastal areas, land temperature in the NH usual peaks in July. In the Arctic, minimum sea ice occurs in mid-September (a week or two before the equinox), because heat need to melt 1 meter of ice is equivalent to that needed to raise the temperature of a 40 m mixed layer by 1 K. .
The cooling observed after volcanic eruptions is somewhat less than expected from climate sensitivity for similar reasons – the planet hasn’t had time to reach or approach a new equilibrium temperature before the radiative forcing from volcanic aerosols begins to diminish.
Frank, you are full of assertions with nothing to back it up.
After Mt. Pinatubo, radiative forcing peaked in less than six months, yet the cooling continued for 3 or 4 years.
Sensitivity to volcanoes is much less than “expected” since climate is less sensitive than those expectations. It’ s the expactations which are wrong, nothing else.
https://judithcurry.com/2015/02/06/on-determination-of-tropical-feedbacks/
The time constant I derived from ERBE data was about 8mo.
I also showed that the volcanic forcing was constiderably stronger than more recent values used by modellers, thus the climate sensitivity is much less. My value was very similar to calculations done by the same climatologists in 1990 before they went off the rails distorting everything to back up AGW.
Of course, if CS is less for volcanic forcing it is very likely to be less to GHG. Distorint both values is why they are running hot since 2000, a period with no major volcanoes to counter their exaggerated AGW.
Greg: I wrote a long discussion about the 2X larger seasonal warming in the NH. Then I commented that the same principles apply to volcanos. Maximum cooling occurred 1.5 years after Pinatubo (not 3-4 years). Warming over years 1.5 to 3.5 restored pre-eruption temperature. The data is noisy. IMO, the best analysis of Pinatubo was done by Paul_K at Lucia’s.
http://rankexploits.com/musings/2012/pinatubo-climate-sensitivity-and-two-dogs-that-didnt-bark-in-the-night/
Perhaps your comments apply to seasonal temperature change as. Well as Pinatubo. If you understand the factor-method for doing scientific calculations, we can have an intelligent conversation about how to calculate the temperature change produced by a radiative imbalance. If you believe that a radiative imbalance can be simply converted to a temperature using climate sensitivity, ask yourself how long a forcing must be applied before the resulting temperature change is complete? One day? One week? One month? One year? One decade? One century? Justify your choice. Climate sensitivity controls the amount of temperature change after equilibrium is reached. Heat capacity controls the RATE at which equilibrium is approached. Equilibrium requires no radiative imbalance. Read Paul_K.
Well done and thought provoking as usual. Just to prove that I actually read it, in the eighth paragraph “(However, monthly changes are still largest and the surface and decrease with increasing depth.) “, I’m pretty sure the first “and” should be “at”
No difference when you exclude 60 N/S – 90 N/S? That’s a bit of a surprise. Would it be worth taking a shot at excluding 40 N/S – 90 N/S to eliminate the Southern Circumpolar flow? Or more generally, in what 10 or 15 degree latitude bands does the difference show up?
Look at the globe . There is a circulation in the southern ocean that cant be repeated in the Northern.
This gives a better distribution of ocean heat.
Roaring 40s and screaming 50s.
That is my guess.
The graph is extremely smoots for a scatterplot, of course it must be some sort of hemispheric smoothed average. Do you have a real scatterplot of all temperature vs insolation?
It is clearly each point being the average of each month across the years of the data.
The spatial distribution of ocean regions and continents is unevenly arranged across the Earth’s surface. In the Northern Hemisphere, the ratio of land to ocean is about 1 to 1.5. The ratio of land to ocean in the Southern Hemisphere is 1 to 4. This greater abundance of ocean surface has some fascinating effects on the environment of the southern half of our planet. For example, climate of Southern Hemisphere locations is often more moderate when compared to similar places in the Northern Hemisphere. This fact is primarily due to the presence of large amounts of heat energy stored in the oceans.
It seems to me that the differences between total volumes of water in the two hemispheres would have a major impact on the amount of solar heating measured, as might the temp of the winds blowing from the landmasses in the northern hemisphere. I know that water has quite a (relatively) high specific heat (1), and if the total volume of water in the southern hemisphere is significantly higher than the northern hemisphere – assuming other factors such as mixing, overall depth, currents etc being roughly equal – then that greater volume of water in the southern hemisphere would take that solar heat and “divide” it into a much greater volume of water, which would mean overall lower temps.
Yes, the direct solar heating of the seawater per unit of surface area would vary by the total watts/m2 available from the sun, but the (possible) additional heat blown by the trade winds coming from the land might be am uncalculated but important factor?
There are no inductive inferences.
Karl Popper.
“However, two things argue against that conclusion. One is that the mixed layer in the southern hemisphere is about 45% deeper than in the northern … but the northern hemisphere sensitivity of temperature to incoming solar is double, not 40% larger.”
Would the relationship be linear? I doubt it.
“The other thing that argues against the mixed layer difference is that the thermal lags in the two hemispheres are very similar, with peak temperatures in each hemisphere occurring almost exactly two months after peak solar.”
That’s dominated by the timing of seasonal northerly and southerly displacement of atmospheric circulation.
Fig. 12
Evolution with UT and season of the maximum absolute value of the primary current function Ψ1 in the Northern ( ΨN ) and Southern ( ΨS ) hemispheres. ΨN and ΨS represent the total currents (in kA) flowing in the dayside vortex for each hemisphere. F10.7=100 SFU