Guest Post by Willis Eschenbach
I’ve been looking again into the satellite rainfall measurements from the Tropical Rainfall Measurement Mission (TRMM). I discussed my first look at this rainfall data in a post called Cooling and Warming, Clouds and Thunderstorms. There I showed that the cooling from thunderstorm-driven evaporation is a major heat-regulating mechanism in the tropics. This is another piece of evidence for my hypothesis that the global temperature is regulated by emergent phenomena, including tropical thunderstorms. This regulation keeps the temperature within a very narrow range (e.g. ± 0.3°C over the entire 20th century).
In that post, I looked at averages over the period of record. For this post, instead of averages over time I’ve looked at the changes in rainfall amounts over time. To begin the temporal investigation, Figure 1 shows the month-by-month variations in the average rainfall.
Figure 1. Movie loop of the monthly averages of the tropical rainfall, Dec 1997 – Mar 2015. The coverage of the mission only extends from 40°N to 40°S. Note that this covers about two-thirds of the surface of the planet. Units are mm/month.
Note how the rainfall amounts clearly delineate the Inter-Tropical Convergence Zone (ITCZ) that runs along and generally just above the Equator. As the name implies, the winds of both the northern and southern tropics converge near the equator. Where the winds meet there is intense rainfall, along with the deep thunderstorm convection that drives the global atmospheric circulation.
It is interesting to see the waves of precipitation wash over places like India. It’s like the earth breathing—in the summer when India gets hot, the hot air rises. When the air rises, it draws in the moist air from off of the Indian Ocean, which pours down as the monsoon rain.
Brazil, on the other hand, was a surprise in that I never knew that all of Brazil but the far north has a long dry period from July to January or so. And when it rains, the rain comes down from the north. Always more to learn.
Now, when I look at a timeseries record, I want to be able to separate out the regular seasonal changes from the rest of the data. Figure 2 shows the month-by-month rainfall averages for the area 40°N to 40°S, decomposed into the seasonal and residual components.
Figure 2. Decomposition of the monthly rainfall record (red line, top panel) into two components—a repeating seasonal component (blue line, middle panel) and a residual component (bottom panel) which is the data minus the seasonal component. The p-value is adjusted for autocorrelation by using the Hurst exponent to calculate the effective degrees of freedom. See here for details of the adjustment.
The main thing that stands out for me in this record are the two biggest El Nino/La Nina episodes, one in 1997-1998, and one in 2009-2010. We can see that during these episodes the tropical rainfall went up. There is also an overall trend, but it is not statistically significant.
Now, we can convert the rainfall data into evaporative cooling data. To do so, we utilize the rule that what comes down must go up. So if a half meter of rain falls in a month, a half meter of water must have been evaporated during the month.
And we know that it takes about 75 watt-years of energy to evaporate one cubic meter of seawater. This lets us convert the rainfall data to evaporative cooling data. Figure 3 shows that result. Of course it is identical in shape to the rainfall data, only the units are changed.
Figure 3. As in Figure 2, showing the decomposition of the monthly evaporative cooling record (red line, top panel) into two components—a repeating seasonal component (blue line, middle panel) and a residual component (bottom panel) which is the data minus the seasonal component.
As mentioned above, I’ve shown that as the temperature goes up, so does the thunderstorm-driven evaporative cooling. In other words, the variations in thunderstorm evaporative cooling are a response to the temperature variations.
Note the size of the variations in cooling, which can change by up to eight watts per square metre in a single month. This can be compared with the estimated changes in CO2 which are expected to be about four watts per square metre in a century …
This dependence of thunderstorm evaporative cooling on temperature be seen more clearly by looking at the deep tropics, what are sometimes called the “wet tropics”. The graph below shows the area from 10°N to 10°S. You can see in the bottom panel that the evaporative cooling was high during the 1997/8, the 2002/3, the 2006/7, and the 2009/10 El Nino/La Nina episodes, and decreased during the subsequent La Nina episodes
Figure 4. As in Figure 1, but for the deep tropics from 10°N to 10°S. This shows the decomposition of the monthly thunderstorm evaporative cooling record (red line, top panel) into two components—a repeating seasonal component (blue line, middle panel) and a residual component (bottom panel) which is the data minus the seasonal component.
The first thing that caught my eye is that at 120 watts per square metre, the evaporative cooling in the deep tropics is about 50% stronger than in the full TRMM 40°N/S dataset.
You can also see the El Nino/La Nina pump in operation. The “La Nina” portion of the El Nino/La Nina pump is much clearer in this deep tropical data. We can also see the smaller El Ninos of 2002/3 and 2007/8 along with the subsequent La Ninas.
Now, here is the interesting part. I wanted to compare the evaporation with the surface temperature. To start with, I used the HadCRUT4 surface temperature for the deep tropics. Figure 5 shows the two datasets, one of temperature, and the other of evaporative cooling.
Figure 5. Temperature and evaporation in the deep tropics 10°N to 10°S latitude. The upper panel shows the HadCRUT4 surface temperature data. The lower panel shows the evaporative cooling calculated from the TRMM rainfall data.
As you can see, the two datasets follow each other very closely. To demonstrate that, Figure 6 below shows the evaporation, along with the linear estimate of the evaporation based solely on the surface temperature:
Figure 6. Evaporation in the deep tropics 10°N to 10°S latitude (black), along with estimated evaporation based on temperature (red).
Note that this covers the entire deep tropics from 10°N to 10°S. This is not just the El Nino region in the Pacific, but also the other oceans and the land as well. And as you can see, in the deep tropics the temperature and the evaporative cooling are quite intimately related around the globe.
Now this correlation of temperature and evaporation should be no surprise. Common experience tells us that the warmer a wet object is, the quicker it dries by evaporation. So we’d expect evaporation to increase and decrease in parallel with temperature.
The surprising part of this analysis from my perspective was the size of the variation in evaporative cooling. We get a very large variation in evaporative cooling given a small change in temperature. Evaporative cooling rises by 27 W/m2 of increased cooling for each one degree C of surface warming.
I wasn’t all that convinced that big a number was correct, so I decided to check it against the CERES surface temperature data. It turns out that the CERES data gives us about the same answer. CERES data for the deep tropics says there’s an average of a 23 W/m2 increase in evaporative cooling per degree of surface warming for the deep tropics (10°N/S). Here’s the larger picture from the CERES data:
Figure 7. Trends in evaporative cooling per degree C of warming, for each 1°x1° gridcell from 40° North to 40° S.
As noted above, the TRMM data covers about two-thirds of the surface area of the Earth. From appearances, unlike in the tropics, the correlation of evaporation and temperature is negative in the unsurveyed areas of both the northern and southern extratropics. The grey line at about 30°N/S shows where the relationship goes negative. This is no surprise. In the extratropics, rain is associated with cold fronts instead of being associated with thermally driven tropical thunderstorms. As a result, although the overall average change in cooling shown in Fig. 6 is 11.7 W/m2 per degree of warming, I suspect this be largely offset once we have precipitation data for the currently unsurveyed areas.
Regardless of the unknown global average, however, in the tropics (and particularly the deep tropics) evaporative cooling generally goes up, and sometimes very rapidly, with increasing temperature. To take another look at it, Figure 8 shows deep tropical evaporation as a function of the CERES temperature data (note that the CERES data doesn’t cover the end of the 1997/8 El Nino-La Nina episode.
Figure 8. Evaporation in the deep tropics 10°N to 10°S latitude (black), along with estimated evaporation based on the CERES satellite-measured surface temperature (red).
So I got to thinking … if there were no thunderstorms, how large would we expect the change in evaporation to be for a one degree change in temperature? We expect the evaporation to go up with increasing temperature … but how fast?
To answer this, I turned to the literature. Evaporation can only be approximated, and there is more than one way to do it. I used the formula given here (Equation 5) for evaporation over the ocean, as well as the formula in the R package EcoHydRology. The two methods gave somewhat different answers for the change in evaporative cooling per degree of warming (see “Math Notes” below). One says that assuming tropical conditions gives us about 4 W/m2 per degree warming in the deep tropics. The other says about 6-7 W/m2 per degree. And no matter how I play with the variables of wind and temperature and relative humidity, I can’t fit the data with anything more than about 7-9 W/m2 increase in evaporative cooling per degree of surface warming.
On the other hand, the answer that we’ve gotten from a couple of sets of observations (HadCRUT4 and CERES) gives a value of around 25 W/m2 of increased evaporative cooling per degree of warming for the deep tropics. And the trends of individual gridcells in Figure 6 shows evaporative cooling of more than three times that per degree of warming.
To put the contrast starkly, at the average temperature of the deep tropics (~27°C), from theoretical considerations we’d expect a 1°C rise in temperature to increase evaporation by somewhat less than ten W/m2 depending on your assumptions … but the observed average increase is 23-27 W/m2, much more than the theoretical increase in evaporation from temperature alone. I hold that this is because of the thermally controlled nature of thunderstorms.
I think that the causative chain runs as follows:
Increased surface temperature ==> earlier and more daily thunderstorms ==> increased evaporation ==> increased cooling
However, I’m happy to entertain alternative hypotheses.
To recap: the unexpected finding is NOT that evaporation increases with temperature. We’d expect that. The unexpected part is that the evaporation increases by 27 W/m2 per degree C of warming, while the theoretical increase in evaporation per degree of warming is much less than that, under ten W/m2 per degree C.
How is this increase in evaporation accomplished? Well, therein lies the story of one of the under-appreciated abilities of the thunderstorm. A thunderstorm is a dual-fuel heat engine. It runs on either temperature or water vapor. And beyond that, it can create its own fuel as it runs.
Thunderstorms run off of low-density air. The low-density air rises, bearing water vapor upwards to the level where the water vapor condenses. The heat of condensation then powers the deep convection up the tower of the thunderstorm.
Now, there are two ways to get low-density air. One way is to heat the air, so it expands and rises. The other way is to increase the relative humidity of the air, because counterintuitively, water vapor is lighter than the air. So when evaporation increases, the air gets lighter and rises.
And here’s the beauty part. The thunderstorm doesn’t just depend on the existing evaporation. Instead, it generates its own increased evaporation (and thus increased evaporative cooling) in several ways.
First, once the thunderstorm forms it generates strong surface winds in front of and underneath the storm. Evaporation is a linear function of the wind speed, with a coefficient of about 0.7. So if wind speed increases from say 2 m/sec (4.4 mph) up to 10 m/sec (22 mph), you get about three and a half times the evaporation.
The next way that thunderstorms increase evaporation is that they are surrounded by dry descending air. Thunderstorms condense the water out of the air as it is lifted high into the troposphere. As a result, when the air exits from the top of the thunderstorm, it contains very little water. From there it descends, providing a constant source of dry air to the surface. If there is 120 W/m2 evaporative cooling in the deep tropics and the air dries from a relative humidity of 0.75 to 0.65, the evaporative cooling increases by about a third, to about 160 W/m2. So this provision of dry air is quite a large factor in the increased evaporation.
The final way that thunderstorms increase evaporation is by increasing the evaporating surface area of the water. Over the ocean, which is 83% of the deep tropics, wind-driven waves increase the oceanic surface area. Wind-driven short-period waves of say 1/2 metre height and 30 metre wavelength increase the ocean surface area by about 1%. But when those waves start to break, or when the storm winds blow the water off of the tree leaves and the grass, sending fine spray into the air, surface area increase from the spray droplets can be 5% or more.
So once the thunderstorm gets started, it manufactures low-density air that keeps it going by generating strong winds at the base, by lowering the relative humidity of the surrounding air, and by increasing the evaporating surface area. This lets the thunderstorm cool the surface to a temperature well below the thunderstorm initiation temperature.
I highlight this because it is a crucial and often overlooked fact, one than distinguishes thunderstorms from simple linear feedback. Once the thunderstorm is initiated, it operates in the exact same manner as manmade refrigerators. It uses evaporation to remove heat from the area to be cooled. And because it is generating its own fuel (low density moist air) it can continue to cool the surface to below the temperature at which it started. And this “overshoot” in turn means that it can keep a “steady state” temperature that only varies within a narrow range. When the temperature gets too high, it gets pushed down below the thunderstorm initiation temperature. Then the temperature starts to rise again, and when it does, a new thunderstorm forms, and it pushes the temperature down below initiation temperature. The cycle repeats endlessly, and the temperature of the system varies little.
And this is the reason for the large variation of evaporation with temperature. Tropical thunderstorms are a threshold-based emergent phenomena. This means that they emerge spontaneously once a certain threshold is surpassed. In the case of tropical thunderstorms, the threshold is mainly temperature-based. As a result, the evaporative cooling due to tropical thunderstorms is a function of the surface temperature.
In closing let me add this final movie. It shows the entire history of the TRMM tropical rainfall observations, month by month. To me, there’s nothing as fascinating as observational data.
My best wishes to you all,
w.
My Usual Request: If you disagree with me or anyone, please quote the exact words you disagree with. I can defend my own words. I cannot defend someone’s interpretation of my words.
My New Request: If you think that e.g. I’m using the wrong method on the wrong dataset, please educate me and others by demonstrating the proper use of the right method on the right dataset. Simply claiming I’m wrong doesn’t advance the discussion.
Math Notes: I’ve used the R package EcoHydRology to estimate the evaporative heat flows from a wet surface. Most (83%) of the deep tropics is ocean, and the rest is usually wet, so it is a reasonable approximation. The function I used is called “EvapHeat”. The package documentation says
EvapHeat : Evaporative heat exchange between a wet surface and the surrounding air
Description
Evaporative heat exchange between a surface and the surrounding air [ kJ m-2 d-1 ]. This function is only intended for wet surfaces, i.e., it assumes the vapor density at the surface is the saturation vapor density
Usage
EvapHeat(surftemp, airtemp, relativehumidity=NULL, Tn=NULL, wind=2)
Arguments
surftemp : surface temperature [C]
airtemp : average daily air temperature [C]
relativehumidity : relative humidity, 0-1 [-]
Tn : minimum dailiy air temperature, assumed to be dew point temperature if relativehumidity unknown [C]
wind : average daily windspeed [m/s]
This function gives the answer in curious units, kilojoules/m2 per day. So I convert it to watts continuous by multiplying by 1000 joules per kilojoule and dividing by 86,400 seconds per day. This is joules/second/m2, which is the same as watts/m2. I used this function with reasonable numbers for the variables in the deep tropics (surftemp ≈ 27°C, airtemp ≈ surftemp – 0.5°C, relative humidity ≈ 0.85, wind ≈ 2 m/sec.) The values for the surface and air temperatures are from the TAO buoy data.
The second way that I determined the increase in evaporation with temperature was using the formula shown here at the bottom of page 6. It gives smaller values for the increase in evaporation with a 1°C increase in surface temperature.
After much experimentation I found that regardless of the exact values chosen for the variables (surface temperature, etc.), the change in evaporative cooling per degree of surface warming is far below the ~ 25 W/m2 of evaporative cooling shown by the TRMM data. In all cases I investigated, any combination of values that gave a total evaporative cooling of ~ 120 W/m2 also gave a change in cooling of less than ten W/m2 of additional cooling for a 1° surface temperature change.
Thanks Willis, I believe there is a paper here. It should be published.
I second that. Given all the data from all the posts on this subject, there is definitely enough to fill a science journal paper.
Seconded (thirded?). Brilliant.
Lindzen?
Yes. Two things at a casual skim strike me. First how massive is the effect of thunderstorms and secondly how extremely non linear and difficult to ‘parameterise’, they are.
This could be the face saving way out for climate scientists “We were right about CO2, but we missed the thunderstorms” would allow them to accept the reality of the situation.
Absolutely sounds like a paper for the journals.
I’d add that this leads directly to a solution for warming. Increase ocean evaporation. Giant misting devices off the coast of California, Northern Africa, and Western Australia would cool the planet and provide much needed rain to desert areas.
Willis, you’re really getting this hammered down…congratulations
“It is interesting to see the waves of precipitation… It’s like the earth breathing…”
What’s also fascinating is the areas without. I first noticed it in Southern California, and then went looking for it in the Sahara, but you can see the pulsing of moisture approach from the south, and not quite make it, and then as that retreats the pulse from the north that doesn’t quite make it…
There’s an interesting dynamic there, almost like high ground in a sea of moisture, keeping those areas dry.
Daniel, you are noticing something important. When the earth warms enough, about another two degrees as it was prior to 6600 BC, those waves will ‘break through’ and the Sahara turns green once again.
[Note: “Kent Pitman” is a sockpuppet name used by a banned commenter. ~mod.]
Nope, because the system is bounded. He’s discovered an unstable equilibrium point (talking phase plane dynamics here), that then goes to chaos when it runs into the boundary condition of the system (i.e. the thunderstorm can only get so big before it interferes with itself due to hitting the cap of the troposphere). Due to the fact that thunderstorms build up energy (evaporation) and then discharge energy (lightning/rain), it’s likely the equilibrium point is best described as an unstable spiral. Once enough power is drained from the thunderstorm (hitting land, wind sheer, other dynamics), the system dynamics moves towards the stable equilibrium node until it gets captured on the eigenvector and the storm dies.
Be interesting to know what bifurcation mechanism controls thunderstorm development and die down.
Phase plane analysis is fun and useful. For reference so that this is not a mystery to you (as claiming perpetual motion if not in jest suggests you have not heard about nonlinear dynamics like this), see http://www.math.psu.edu/tseng/class/Math251/Notes-PhasePlane.pdf
Ged
Well said.
Nonlinear pattern structures such as thunderstorms export entropy, since emergent structure reduce the level of disorder or entropy. However the second law of thermodynamics demands that systems overall increase in entropy. Thus such pattern systems balance the books entropically by providing heat to their surroundings. Since the surroundings of a thunderstorm include the upper atmosphere and space, this is why, if I’m not wrong, thunderstorms are mandated by Thermodynamics 2 to export heat to space. This is also a role of thunderstorms that Willis has proposed.
I agree with Anthony, a paper here.
Fascinating to watch the Earth breathing like that.
Also how there are areas of ocean that get very little rain compared to others.
Australia doesn’t get much either.
“Earth breathing”.
Just what I thought.
Oldseadog,
The “breathing earth” analogy applies to polar ice, too:
http://www.thisiscolossal.com/wp-content/uploads/2013/08/BreathingEarth.gif
(Notice that Greenland never really melts)
Great movie, dbstealy. If we had a comparable Antarctic movie, we’d see how less variable conditoins are over total ocean. Temp variations are greater over land because of the greater thermal inertia of a huge mass of water.
It’s not breathing, it’s weeping, pining for the fjords. (Resists posting Parrot sketch yet again).
Robert,
I was between sips of Sancerre, so I don’t have to stick you for a screen.
Priceless.
Plus a pile!
Auto
I never knew that water vapour is lighter than air.
This fits with the fact that it is always hot and humid in Sydney’s West before a cooling thunderstorm.
Also clouds are usually high, not fog, so the area involved is saturated with water vapour.
Water vapor is also invisible, clouds and visible steam are condensed from vapor to water droplets.
It makes sense though if you look at it, O2 is 32 and N2 is 28 mix them and wagging the ratios makes an average mass of about 29. Water vapor is 18 so as the proportion of water goes up, the mass of the column goes down. I think I have seen Doctor Brown do it a little more precisely in a post not too long ago.
Lewis,
That’s why home runs are easier to hit in warm, humid air than cold, dry air. 🙂
Unless that cold, dry air is at 5280 feet (Coors Field)?
roks
Not Mile High Stadium? Or is that hockey, rather than baseball?
The altitude seems enticingly accurate, I must say.
Auto
Thanks. A wonderful post. Even before reading your text I had the same impression from the animation – that I was watching the Earth inhale and exhale. Your insights from personal experience and very capable analysis deserve much wider exposure. I also wonder from this and your other posts about emergent phenomena and tropical thunderstorms, what the calculations are for the potential and kinetic energy transfers from elevating massive amounts of water into the atmosphere (increased potential energy) and then returning it to the surface (conversion back to kinetic and/or mechanical energy) where an enormous amount if work is done to reshape Earth’s surface. I presume these are largely in addition to and mostly separate from the thermal energy transfers.
Thanks. Very interesting. The water vapour cycle is thus an effective global heat pump.
Willis – The next way that thunderstorms increase evaporation is that they are surrounded by dry descending air. Thunderstorms condense the water out of the air as it is lifted high into the troposphere.
Don’t leave out the PE / KE conversion.
Potential Energy Equations Calculator – http://www.ajdesigner.com/phppotentialenergy/potential_energy_equation_z.php
So for your M^3 of water (1000 KG) @ 3000 meters elevation (9800 FT) you get a potential energy of 29,400,000 joules
But rain, due to friction, has a terminal velocity of under 9 m/s or Kinetic Energy – http://www.ajdesigner.com/phpenergykenetic/kenetic_energy_equation.php#ajscroll
for the 1000 KG = 40,500 joules.
My senior engineering professor taught that friction converts to heat.
So the condensed rain heats up, after less than 10 meters falling, and re-evaporates multiple times until the 29,359,500 joules are used up heating the air.
With an average rain fall of 1m around the globe per year, it comes out to 0.9W/m2.
I was expecting it to be a lot smaller.
It is interesting to see how observational data departs from values expected by theory.
Even the climate models have increased evaporative cooling as the climate system warms (as evidenced by their increased precipitation, they go hand-in-hand). That’s not the models’ shortcoming.
It is one of the models’ shortcomings. The models have too little evaporation (2-3% per deg C when it should be ~7%), hence their ECS is too high.
[ECS – Equilibrium Climate Sensitivity – the climate’s sensitivity to CO2]
Thanks, Dr. Roy. You are indeed correct that the models show increased cooling as the climate system warms. The problem is, they have it in the wrong places at the wrong times. My next post will be a brief look at that oddity.
w.
To Roy Spencer:
However, the climate models show only about 3%/C increase in evaporation. Using a typical value of 80 W/m^2 gives only about 2.5 W/m^2 per C of warming. Using simple physics for constant wind speed and wave action one gets: For constant relative humidity (RH) about 6.6%/C and for constant specific humidity about two times this. Using 80 W/m2 for a global average this gives about 5.3 and 10.6 W/m^2/C. The tropics might run 1.5 times the global average, up to about 16 W/m^2 if the specific humidity can’t increase fast enough to get constant RH, but still much below Willis’ data of about 27 W/m^2. The increase in wind speed and drop in humidity during a thunderstorm as Willis suggests could be the difference.
Incidentally only at 6.6%/C or 5.3 W/m^2/C the negative feedback from evaporation is more than the IPCC values for positive feedback from water vapor feedback. About -0.74 C/C vs. about +0.54 C/C for water vapor. If Willis is correct, this could be a major factor with much stronger negative feedbacks. It reminds me of Lindzen and Choi’s famous paper showing a strong increase in outgoing radiation with surface temperature. The tops of thunderclouds with little water vapor above look at an infrared atmospheric window of about 75%, vs. only about 25% from the surface, and thus radiate efficiently to space.
See my papers on evaporation:
http://wattsupwiththat.com/2014/04/15/major-errors-apparent-in-climate-model- evaporation-estimates/
http://edberry.com/blog/climate-clash/g90-climate-sensitivity/improved-simple-climate-sensitivity-model/
Bingo! for the IR windows at the tops of Tropical thunder clouds in my view.
The tops of thunderclouds with little water vapor above look at an infrared atmospheric window of about 75%, vs. only about 25% from the surface, and thus radiate efficiently to space.
That is a very salient fact. if indeed it is true. I had suspected as much but never found a reference to the value..
If the radiation is happening beyond most of the CO2, it makes the existing radiation calculations complete nonsense.
Richard, Roy and Willis: Issac Held discusses why climate models predict less than a 7%/K increase in precipitation at the link below. Basically, the models predict an increase in relative humidity over the ocean to suppress evaporation.
http://www.gfdl.noaa.gov/blog/isaac-held/2014/06/26/47-relative-humidity-over-the-oceans/
A 7%/K increase in precipitation translates into an increase in convection of latent heat of 5.5 W/m2/K. OLR increases by 5.4 W/m2/K (at 288 K). DLR increases 4.9 W/m2/K (at 277 K, the temperature that produces DLR of 333 W/m2 assuming an emissivity of 1). Combined this gives a response of 5.0 W/m2/K at the surface. This is much greater than the change in energy flux at the TOA: 3.7 W/m2/K for a simple blackbody at 255 degK, 3.2 W/m2/K for Planck feedback in climate models and 1.2 W/m2/K for a planet with a climate sensitivity of 3 K/2XCO2.
Our planet can’t experience a 5 W/m2/K increase in outward energy flux at the surface and a 1.2 W/m2/K increase at the TOA. For ECS to be 3, the increase in latent heat flux needs to be 0.7 W/m2/K, which translates into a 1%/K increase in precipitation – assuming constant wind and no change in albedo. If Willis is correct that evaporative cooling in the deep tropics increases 27 W/m2/K, this is big enough to influence ECS for the whole planet! And climate models must produce huge errors in precipitation in the deep tropics.
Willis, this is an excellent presentation. Serious consideration to peer reviewed publication is in order.
I have followed your many posts here @ WUWT and I’m convinced you are on to CAGW busting theory/hypothesis. I haven’t read a convincing argument against it. And it becomes more solid with every additional post you offer. Please keep up the good work.
To Frank regarding the models predicting less evaporation increase than about 6 to 7% and only 1 to 3%. Yes, and the models are wrong. The only way to explain this low rate of increase is a reduction in wind speed (which they do not do) or an increase in relative humidity (RH) above that to maintain constant RH. However much data over many locations and years show that RH drops a little with rising temperature. The complex computer model people keep thinking that their results are the same as real data. So if their results show less evaporation increases than expected for constant RH, than that “proves” that RH must increase with temperature.
And they all still make a large error in thinking energy constraints limit evaporation. The energy for evaporation comes from the temperature of the water reduced by the partial water vapor pressure of the atmosphere. What happens is that the evaporation cooling reduces the temperature rise less than they estimate (from CO2 warming) and there is no energy constraint, energy balance is just fine. Do they also think that a bar of steel will not expand when warming by 1 C as expected because they do not know where the energy comes from. Well then do not claim it warms so much.
Richard wrote: “The only way to explain this low rate of increase is a reduction in wind speed (which they do not do) or an increase in relative humidity (RH) above that to maintain constant RH. However much data over many locations and years show that RH drops a little with rising temperature.”
According to Isaac, the future rise in relative humidity in climate models develops only over the ocean. The relative humidity over land decreases. Do you have a reference that shows relative humidity over the ocean decreases with warming?
Richard also wrote: “The complex computer model people keep thinking that their results are the same as real data.”
Actually, model data is superior to real data (observations), especially when you are looking for changes that take place over decades. Observations are always incomplete and contain measurement error of various kinds. If the observations come from re-analysis data, that can also introduce distortions. With models, you can do repeat experiments or conduct well-controlled experiments where only one variable is changed at a time. Finally, if anyone does find a disagreement between model data and observations, someone can always cherry-pick “homogenized” observations that do agree with model data. Working with observations is a waste of time. [/sarcasm]
So back a few millions of years ago, before the ice age, when temperatures were much warmer than today, can we predict from this what the tropics were like? The poles were ice free. I’m thinking some seriously bad thunderstorm activity plus….?
Just to pick a nit: That seems decidedly nonlinear to me. Maybe something like evaporation = k * speed ^ 0.78?
Hey, Joe, good to hear from you. In the example, wind speed has gone up five times. Evaporation has gone up 0.7 * 5 = 3.5 times. Linear.
Thanks,
w.
I see. You’re assuming a non-zero intercept:
If the evaporation E = 1 ml/m^2/sec for wind speed v = 2 m/sec and E = 3.5 ml/m^2/sec for v = 10 m/sec, then the linear relationship is E = 3/8 ml/m^2/sec + 5/16 ml/m^3 * v.
Linear (black) vs. nonlinear (red):
v = seq(0, 12, 0.01);
plot(NA, xlim = c(0, 12), xlab = “Wind Speed”, ylim = c(0, 4), ylab = “Evaporation Rate”);
abline(3/8, 5/16, lwd = 2);
abline(h = c(1, 3.5), v = c(2, 10), lty = 2);
a = log(3.5) / log(5);
k = 2 ^ (-a);
lines(v, k * v ^ a, col = 2, lwd = 2);
The relationship is linear, but at zero wind speed, there is still evaporation. There is a speed value where it doubles (I can’t recall the value).
Richard wrote: “The relationship is linear, but at zero wind speed, there is still evaporation. There is a speed value where it doubles (I can’t recall the value).”
If there is no wind, any water vapor immediately above the surface of the ocean can travel upward only by molecular diffusion, which is ridiculously slow. In practice, there is always a thin layer of air above water that is saturated with water vapor, and convection is required to transport it anywhere else in a sensible period of time. Wind blowing at 1 m/s over the surface of the ocean has a Reynolds number for turbulent flow in less than 1 m. This turbulence is the rate limiting step in vertical transport of water from the ocean and the saturated thin layer of air immediately above. This is why the rate of evaporation depends on wind speed (far more than it depends on temperature).
Richard Petschauer:
Thanks. That sounds plausible; i.e., I am not knowledgeable enough to be able to tell whether it’s true or not, but it’s certainly consistent with, e.g., http://www.engineeringtoolbox.com/evaporation-water-surface-d_690.html.
I made the comment about linearity only because Mr. Eschenbach seemed to be saying that the evaporation rate is multiplied by 3.5 whenever the wind speed quintuples. That defines a logarithmic relationship, of course, not the linear one that you and the above-mentioned site specify. But I infer from Mr. Eschenbach’s response that this point is too subtle to make it likely that further attempts at explanation would prove fruitful.
Incidentally, I had attempted to digest your “Major Errors” post, but you left too many questions unanswered for me to persist.
I just noticed there’s still activity in this thread, so I’ll take the time to clean up after myself.
I erroneously said:
The relationship defined by evaporation rate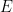
‘s being multiplied by 3.5 every time the wind speed 
quintuples isn’t logarithmic. It’s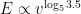 
, as I’d previously suggested.
As Mr. Petschauer observed, though, it appears that the evaporation rate is not actually multiplied by 3.5 every time the wind speed quintuples but instead bears the linear relationship to wind speed that the link in my previous comment sets forth.
The movies are hypnotic in a good way. What surprised me is the very high rainfall in the relatively small areas of the oceans. Maybe this can be used to collect fresh water in the future.
“Envisions wind powered ships with BIG funnels collecting the rainwater.*
Frank says:
“If there is no wind, any water vapor immediately above the surface of the ocean can travel upward only by molecular diffusion, which is ridiculously slow.”
I have seen equations by ASHRAE (Society off Heating, Refrigeration and AC Engineer) based on data on indoor swimming pools that show evaporation based on water and air temp and RH that shows evaporation with no wind. I also have seen data on evaporation from outdoor swimming pools that also include wind speed. Extrapolating the curve to zero wind speed still shows some evaporation.
At the water air interface, water vapor is lighter than air so it rises refreshing the interface to some extent. The surface water cools and sinks doing a similar thing. But whatever happens for constant wind speed and wave action for a change in water temperature, the same conditions will occur before and after the warming. Evaporation will increase as a function of the differences in the water vapor pressure of saturated air at the water temperature and the water vapor pressure of the air that depends on its temperature and relative humidity. Water vapor pressure increases from about 6 to 7% per C depending on the actual temperature in the ranges of interest on the surface and lower atmosphere.
Joe Born said to Richard Petschauer
“Incidentally, I had attempted to digest your “Major Errors” post, but you left too many questions unanswered for me to persist”
Joe is referring to:
http://wattsupwiththat.com/2014/04/15/major-errors-apparent-in-climate-model- evaporation-estimates/
Sorry Joe I did not make it more clear. Maybe I should rewrite it.
The gist of the paper is: The climate model people (including Trenberth in an Email to me) attempt to justify their very low increases in evaporation by saying that there is “not enough energy” to support the expected increased in evaporation. The problem is that they assume the water temperature rise is predetermined by their calculations and hence its outward longwave radiation is fixed and in order to retain the total energy leaving the surface and match the incoming energy, latent heat leaving the surface from evaporation is constrained. They ignore the fact that evaporation cools the surface and reduces the longwave outward radiation so that more can come from latent heat. But they cannot admit the surface warms less than the models show. The equations I used for energy balance at the surface, atmosphere and at the planet level solves this problem.
The real reason it seems the climate models underestimate evaporation (I think they use the correct equations) is that they over estimate surface relative humidity (RH) and have it increase more than enough to maintain constant RH. They claim it is nearly constant. But a slight change makes a large difference. They also underestimate precipitation, that is very hard to estimate, which reduces humidity and increases evaporation (and thunderstorms more as Willis suggests). Globally evaporation and precipitation must be nearly equal. It is interesting to note that evaporation is easier to estimate but hard to measure (except from a closed container), while the reverse is true for precipitation.
I appreciate the reply. I hope, but doubt, that I’ll get time to revisit that post.
Great graphics. One nit is your equating precip with evaporative cooling locally, the ITCZ gathers moisture from the north and south boundaries of the Hadley circulation.
“the ITCZ gathers moisture from the north and south boundaries of the Hadley circulation”
I was wondering if anyone would note this.
To continue your thought Steve:…and deposits the dry air emerging at the top, not in the vicinity of the ITCZ, but centered around 30 degrees North and South…the B climate zone desert belts…thousands of miles away.
As noted by Willis, this is the primary circulation pattern of the Earth.
That is true of the big picture, but the whole system has bit of a fractal feel. As you peer down at individual systems you see the same patterns emerge at smaller scales until you get to the individual thunder cell where it stops (or at least becomes way less defined – there may be smaller columns within a cell, just because I’ve never heard of it doesn’t mean it isn’t there.) Air around a line of thunderstorms throws dry air up to contribute to the ITCZ pattern but some returns around the storm locally as well due to dry air being denser and the air below being swept into the thunderstorm at its base. This is observed with individual cells within the line as well. The cumulative effect is as you have stated, but much more complex when looked at closely.
i agree, but there is the larger scale contribution. Consider, are the continents a net source or sink of atmospheric water? Insofar as their rivers flow into the ocean they are a sink.
Thanks for this massive effort, Willis. This would make a paper of real interest to Science. Compared to this we see a lot of substandard stuff published these days.
Fascinating (and crystal clear) read! Even more fascinating Earth “respiration”!
So, reversely, historical average precipitation data for the tropics could be a proxy for historical (world) temperatures?
The Earth sweats to cool off, sort of like we do. Interesting.
‘Always more to learn.’
I say that constantly when I argue climate change…. and the alarmists sneer in ignorance.
So, if global temperatures ‘tried’ to go up, the Earth would respond with more rainfall? Is what happened to North Africa / Sahara a consequence of Earths cooling in the past? Less heat, less rain?
Is what happened to North Africa / Sahara a consequence of Earths cooling in the past?
WR: Could be yes. The famous rock paintings of Tassili n’Ajjer in the south of Algeria with large wild animals and crocodiles, now somewhere in the middle of the Sahara, seem to date from at most 9-10 millennia ago (Wikipedia). The Neolithic Subpluvial wet period was the period from about 9500 – 5000 BP (yes, in the warm Holocene Climatic Optimum)
Present warmer temperatures in combination with better drought resistance of plants due to extra CO2 in combination with a higher growth rate because of the same CO2 could change back the Sahel (and other semi arid parts of the world like parts of Australia) to greener times. This map shows it’s already happening: http://www.drroyspencer.com/wp-content/uploads/co2_growth.jpg
As I say, a warm planet is a happy planet.
No. The African Humid Periods are a recurrent phenomena about every 23,000 years linked to the precession cycle, modulated by the eccentricity cycle (Milankovitch) and reflected in the Mediterranean sediments sapropels (dark organic layers). They are caused by the northern migration of the Inter-Tropical Convergence Zone (ITCZ) due to the high latitudes receiving more insolation.
http://www.nature.com/scitable/content/ne0000/ne0000/ne0000/ne0000/74570127/1_2.png
Each dark layer corresponds to an African Humid Period and their grouping reflects the interaction between the precessional and eccentricity cycles.
http://www.nature.com/scitable/knowledge/library/green-sahara-african-humid-periods-paced-by-82884405
We now happen to be near a minimum in the precession cycle (bottom in about 1000 years). In about 8,000 years the Sahara will be green again. Some predictions about future climate can be done with high confidence.
No question this is brilliant analysis, Willis and, in keeping with your posts in general, you always find the unexpected. I think of the CAGW theory now of missing these ‘unexpecteds’, largely because you can’t many of these with deterministic models. I join the many others here in pushing you to publish this. You have also grown a body of ideas through teasing out empirical data to support them- I would say a book on the planet’s heat engine would be an enormous contribution to climate science.
“…cooling shown in Fig. 6 is 11.7 W/m2 per degree of warming, I suspect this be largely offset once we have precipitation data for the currently unsurveyed areas.”
Of course, minus the ‘heat’ radiated to space from the evap/thunderstorm activity. It would be interesting to also compare this cooling to the radiant energy exiting the TOA.
Hi Willis. I enjoy your articles.
You said “And we know that it takes about 75 watt-years per square metre to evaporate one cubic meter of seawater per year.”
The units are muddled up.
watt * year * m^-2 = m^3 * year^-1 * specific heat of water
watt * second * m^-2 = m^3 * second^-1 * specific heat of water
watt * second * m^-2 = m^3 * second^-1 * Joules * m^-3
watt * second * m^-2 = second^-1 * Joules
Joules * m^-2 = second^-1 * Joules
m^-2 = second^-1
m^2 = second ??????
“watt-years per square metre” Is an amount of energy per square metre.
The evaporation of 1 cubic metre of water is an amount of energy.
So the evaporation of 1 cubic metre of water per square metre is an amount of energy per square metre.
But 1 cubic metre of water per square metre means a depth of 1 metre.
I think what you meant is:
“it takes about 75 watt-years per square metre to evaporate one meter depth of seawater”
Or, to make it clearer:
“it takes about 75 watts per square metre to evaporate one meter depth of seawater per year.”
Checking the units
“it takes about 75 watts per square metre to evaporate one meter depth of seawater per year.”
watt * m^-2 = m * specific heat of water * year^-1
watt * m^-2 = m * Joules * m^-3 * second^-1
watt * second * m^-2 = m * Joules * m^-3
Joules * m^-2 = m * Joules * m^-3
Joules * m^-2 = Joules * m^-2
That agrees
Willis, Many thanks for an interesting and extremely well illustrated post on this important subject.
If I’ve interpreted Figures 2 and 5 correctly, they suggest a 1 C change in surface temperature is associated with a circa 10% change in precipitation over 40S-40N (if the temperature change was similar in the deep tropics to 40S-40N)? That is much higher than the 1-2% per C precipitation change in CMIP3 GCMs (Vechi and Soden 2007), which seems too low. The change is higher, 2-3.3 % per C, in CMIP5 GCMs (Mauritzen and Stevens 2015), increasing to 3.5-4% per C when including a LW IRIS effect. However, your findings are quite close to an estimate for the observed increase in global precitptation over 1987-2006 of 7.4% per C (Wentz et al 2007). Whilst Lambert et al (2008) argue that Wentz’s finding was not representative of longer term changes under greeenhouse gas warming, and that it did not imply GCMs were wrong on this, I do not find their reasoning very convincing.
Nic: It is worth noting that evaporation is directly linked to ECS. If ECS is 3, then the energy flux leaving the planet increases at only 1.2 W/m2/K. If evaporation increases 7%/K, that is 5.5 W/m2/K. OLR increases 5.4 W/m2/K (at 288 K), but is nearly cancelled by the increase in DLR of 4.9 W/m2/K (at 277 K). We can’t have a response of 6 W/m2/K at the surface at 1.2 W/m2/K at the TOA. Climate models must contain a mechanism for dramatically suppressing the expected 7%/K increase in evaporation. See:
http://www.gfdl.noaa.gov/blog/isaac-held/2014/06/26/47-relative-humidity-over-the-oceans/
Love the movie representation. Would be interesting to see the wave function plotted so some study could reveal changes in amplitude and frequency. Even subtle central deviations from equator. This is important for the other two thirds of planet where the apparent consistency of the equatorial tropics causes extremes at the edges. This is most noticable when the wave-like slop hits me in Australia. Hits and misses may be mis-interpreted as climate change when nothing more than a random tropical slop event. ….. Not sure I have described this clearly, but I am keen on seeing the movie as a sort of maths sine wave. Changes in amplitude or periodicy could be weather predictors fot non equatorial regions…. Maybe?
Oops…..other third of planet.
This excellent analysis carries with it two second order effects that further explain low sensitivity to GHG forcings via the mechanism Willis demonstrates. First is Lindzen’s adaptive infrared iris. He focused on reduced cirrus as the diagnostic, from bigger/taller convection cells (Tstorms) producing more precipitation, leaving less moisture for detrainment into cirrus. But the idea can be broadend to include thermoregulation of upper troposphere specific humidity, which lessens the water vapor feedback. Second is the simple idea that tall thunderstorms carry the latent heat of evaporation released by condensation with temperature lapse rate higher into the troposphere, lessening the efficacy of the CO2 ‘GHG insulating blanket’. Depending on Tstorm and CO2 concentration, it is like ‘conceptually’ punching holes in the insulation through which the Tstorm concentrated heat more easily escapes to space.
Seperate onservation. Climate models cannot simulte Tstorms because of the latge size of their computationally constrained grid cells. Willis’ work suggests some of the ways the forced resulting parameterizations are wrong. For example, the models produce about half the tropical precipitation that is actually observed.
“punching holes in the insulation“. Nice description.
“Climate models cannot simulate Tstorms because of the large size of their computationally constrained grid cells.“. Keep saying it, it needs to be much more widely understood. [Typos fixed in the quote]
-or- “Punching Holes in the Greenhouse Ceiling” would make a good title for the paper.
“Can thunderstorms break through the (greenhouse) gas ceiling?”
+1
Really good T storms regularly dome into the stratosphere.
Yes, this is precisely the prediction from Dr. Bill Gray. The increased water vapor along with some low level warming enhances convection driving the water vapor higher in the atmosphere. This condenses out more water (and latent heat) which leaves less water vapor. This reduces the GHE where it has one of the strongest effects. Also, the air is cooled more which helps cool of the surface when it descends.
Interestingly this process is a brilliant design. As we increase CO2 we get a small amount of warming and a small increase in precipitation. These are the 3 ingredients for plant growth. All 3 rise in tandem.
Fantastic science article Willis. Well done WUWT more of this type of thing please!
Willis Enjoy your stories which are entertaining and well written, and you papers on science and logic are the same. Very understandable. The thought occurred to me that it might have something to do with being truthful. Someone that claims to have and answer and doesn’t puts fills there paper with unintelligible verbiage, full of might and maybe, and yes a Dr degree from somewhere. Your logic is actually believable.
We are blessed to have you posting your thoughts and your trips.
Thanks
The major disagreement is that the heat that is released during a thunderstorm or any storm because of the increased co2 retains that heat and continues in a never ending cycle. I’ve argued the same. It comes down to whether the heat is retained or released.
Most thunderstorms can reach much higher than 9800 feet. And it is fairly cold up there. I think that the heat is released at that point. There is something wrong with the calculations of the IPCC. Hence, the big o debate about the second law of thermodynamics and it’s application in this case.
The IPCC in support of the retained heat sernario, commissioned a study on the total incoming and outgoing heat on a planet wide bases. Since the first one, I have not seen or heard of a second. Over 15 years with the additional co2, those numbers have to be in favor of the retained heat if the math is correct. The amount of incoming has to have remained constant ( the suns output doesn’t change. IPCC), while the total released should have been reduced.
I think they already know. The suns output changes, and the heat released from earth is variable. Short term changes in the output of the sun keeps the temperature from falling or rising too fast. Long term changes in output, result in long term temperature changes. The current level, and for the foreseeable future, of co2 is too small to have much of an impact.
CO2 cant retain heat……maybe just poor choice of words.
The problem is convincing the CAGW crowd. I am only assuming that part of their analysis is correct for the sake of argument. It’s endless if I didn’t start somewhere. And they will argue, still are, the second law of thermodynamics.
My concern was to put this research in context of what the IPCC believes. Tropical thunderstorms or not, the heat is retained per the IPCC. (Not me) If the heat is released from more thunderstorm activity, CAGW doesn’t have much of a case. If the suns output varies, they also don’t have a case. More co2 or not.
“Short term changes in the output of the sun keeps the temperature from falling or rising too fast. ”
I agree with this completely rishrac. As a daily observer of global water vapor images as well as solar activity indices for several years, I’ve seen the oceans explode with evaporation during higher solar (TSI) days, and the opposite during low TSI solar periods. Getting all that into the form like Willis has is another story however.
Willis .Superb post!
See section 1.3.2 at
http://climatesense-norpag.blogspot.com/2014/07/climate-forecasting-methods-and-cooling.html
“The IPCC climate models are further incorrectly structured because they are based on three irrational and false assumptions. First, that CO2 is the main climate driver. Second, that in calculating climate sensitivity, the GHE due to water vapor should be added to that of CO2 as a positive feed back effect. Third, that the GHE of water vapor is always positive. As to the last point, the feedbacks cannot be always positive otherwise we wouldn’t be here to talk about it. For example, an important negative feed back related to Tropical Cyclones has recently been investigated by Trenberth, see:
http://www.cpc.ncep.noaa.gov/products/outreach/proceedings/cdw31_proceedings/S6_05_Kevin_Trenberth_NCAR.ppt”
He says in Fig 2.
http://3.bp.blogspot.com/-ZBGetxdt0Xw/U8QyoqRJsWI/AAAAAAAAASM/ewt1U0mXdfA/s1600/TrenPPT.pn
The evaporative peak at about 2003 in your Fig 8 is probably the important millennial RSS temperature peak. http://2.bp.blogspot.com/-zZLVnsvgYTw/Vj0GEDv2q7I/AAAAAAAAAag/eumhxpS9ciE/s1600/trend11615.png
Because of the thermal inertia of the oceans the corresponding peak in the solar driver is at about 1991
http://3.bp.blogspot.com/-QoRTLG14Siw/VdOUiiFaI5I/AAAAAAAAAYM/NxQVb2LMefk/s1600/oulu20158.gif
For further discussion see
http://climatesense-norpag.blogspot.com/2015/04/climate-and-co2-exchange-with-freeman.html
Willis, a nice article. However, I have my doubts of a quality of the EcoHydRology package.The description of a function EvapHeat rings an alarm bell for me. It uses an average temperature and an average wind speed, to compute something that is highly nonlinear in both a temperature and a wind speed. As a surface temperature of a tropical ocean does not vary much in one place, using an average temperature is probably OK. But when the wind starts blowing off tops of waves, the evaporation increases dramatically. In addition, the conversion of an evaporation rate to a heat looks rather simplistic – a latent heat of evaporation depends on temperature, and I wonder how good a result all constants hardcoded in the package yield at 30 degrees C.
During the August 29, 2015 storm that hit Washington State, I was in the Puget Sound area and observed 60 to 70 mph winds with gusts up in the 80s blow the tops off of white-capped waves. This airborne moisture quickly became atomized forming a humid haze in the atmosphere.
Curious George November 11, 2015 at 3:09 pm
Thanks, George. To quote myself:
If you know a better way, bring it on. I’ve looked at the literature, and what I find are all variations on what is called “Dalton’s formula”. It says that evaporation is some function of the wind times the difference in vapor pressure ocean to air. So far I’ve tried three different variants, and none of the three show anything like the observed 23-27 W/m2 change in evaporation per degree C of surface temperature change.
Regards,
w.
Willis, You are focusing too much on thunderstorms and not enough on evaporation^^ Not saying you are wrong, just saying.
You seem to be missing two things, one is that the top of the thunderstorms is cooler for a given altitude. If you look at the thermal images you can see that the top of the storms are colder. If the heat from condensation was being carried higher the IR images would be warmer.
Second the surface (skin temperature) is much more consistent than the measurements indicate and it is the surface which evaporates.
What controls the temperature is cloud coverage, less cloud coverage equals higher temps and higher cloud coverage equals lower temps.
http://www.climate4you.com/images/HadCRUT3%20and%20TropicalCloudCoverISCCP.gif
Are you suggesting that OLWR is only from the top of the storm cloud? How about the OLWR from a point well below the top of the storm passing through (upwards) from a point where the water vapor has been precipitated? Think about it before you reply. Then consider the OLWR being released to ‘space’ as the dry air descends outside the storm. Does it not emit to space at this point?
eyesonu, yes the OLWR is what is measured by the IR. And yes the energy gets transported poleward before becoming OLWR.
Radiation energy varies with the fourth power of temperature. Colder air, different spectrum, less intensity.
jinghis said:
***FINALLY*** someone who speaks he truth!! Yes, there is the ‘heat of condensation’ (latent heat release) *BUT* it only adds about 3 F of heating to the 5.5 F cooling process every 1000′ so the rising air is still cooling…just not as fast. The BIG thing missed is that when that air that has risen begins to sink to maintain hydrostatic balance, it will WARM @5.5F/1000′ (dry adiabatic) because most of the moisture has been ‘wrung out’. So, as the air returns to it’s original level, it is warmer than when it began & this is where the Trade Wind Inversion is created from & stabilizes the atmosphere suppressing convection.
Think about it…works every time!
Interesting. Playing this out, if I understand this correctly, back at the surface, some of the now warmer descending air locally–but more so in advance of the direction of movement of the thunderstorm–gets recycled into the thunderstorm. Since these winds are warmer, wouldn’t this would be a fourth way (adding to Willis’ first three) in which thunderstorms increase evaporation.
Doesn’t this “wrung out” air at altitude become the source of the Hadley cells? When most of this dry air descends, it is near 30 degrees north and south. Thus the high temps in the Sahara, etc.
I suggest these desert zones that circle the Earth form a second heat radiating mechanism. The low humidity allows heat to freely radiate to space at night.
SR
This is not quite correct.
When air rises in a thunderstorm, the latent heat release from condensing water warms the air within the thunderstorm compared to the air surrounding the thunderstorm so it is ‘warmer’ than for a given altitude. What you describe as being colder at the thunderstorm cloud tops is another process where by the white cloud tops reflect sunlight and radiate heat rapidly effectively giving a skin temperature colder than the surrounding air.which is picked up by satellites.
Outflow from thunderstorms and hurricanes for that matter at the cloud tops is caused by higher air pressure compared to its surrounding air. Why is that? Because the layer of air in the thunderstorm/hurricane core is warmer than its surroundings which expands that layer of air and thus raising the pressure height level at the top of the layer. High pressure air moves to the surrounding low pressure air and hence the outflow at the top of thunderstorms and hurricanes.
Yes the air will warm when lowering back down to the surface following the dry adiabat but this will only be warmer than the surrounding air because it was warmed from latent heat release in the first place withing the thunderstorm. You can not create energy from nothing there has to be a process involved to change air parcel heat and this case it is the latent heat release.
Having said all of that, then if thunderstorms act as a negative feedback and thermostat against GHG warming then increased thunderstorm activity should in theory result in more warm moisture laden air to rise in the atmosphere and warm the upper troposphere I would have thought unless something offsets this somehow. More cloud would mean less solar reaching the ground so perhaps this is the equilibrium process.
Why do you suppose tropical cloud cover shows no response to the 1997 nino? Hell, stratospheric water vapor and tropospheric precipitable show a very clear spikes.
jinghis November 11, 2015 at 3:11 pm
Thanks, jinghis. First, since you didn’t quote a word I said, it’s unclear what you are objecting to. I asked you to quote what you disagree with, and I did so for an important reason. Without it, I haven’t a clue what difference whatever you think I’m “missing” might make. How would what I’m “missing” change my conclusions, and which ones would it change?
Next, you seem to think that the thermal images show that the top of the thunderstorms is cooler than the surrounding air. Not true. What you are comparing in the thermal images is the temperature of the thunderstorm tops to the temperature of either the lower clouds or the temperature of the surface, depending on conditions. You are not comparing the thunderstorm top temperature to the surrounding air at “a given altitude” as you seem to think. We know this because if the thunderstorm tower top were actually colder than the surrounding air, it would sink … and since it doesn’t, we have to know that the top of the tower is at the same temperature as the surrounding air.
(Note that this description above is for a mature thunderstorm. When the tower is boiling skyward as the thunderstorm forms, the tower top is most definitely warmer than the surrounding air. The vertical tower development continues until the tower top is at the same temperature as the surrounding air, at which point it levels off and ceases vertical growth.)
I’m sorry, but this makes no sense. First, the temperature of the ocean skin is more variable than the underlying water temperature, not more consistent. It warms and cools with each gust of wind.
Second, I don’t understand what difference it makes.
You say:
While I would generally agree, there is no one single thing that controls temperature. Instead, the temperature is regulated by an interlocking system of clouds, thunderstorms, dust devils, El Nino/La Ninas, waterspouts, and other emergent phenomena.
I am interested in your graph, however. It says “climate4you graph” but when I went there I couldn’t find any cloud datasets at all. Do you have a link to the data, or at least to the graph?
And while I’m one the subject, PLEASE DON’T POST UN-CITED GRAPHS. Sorry for shouting, but this one angrifies my blood. I generally just glance at uncited graphs and then ignore them. Without context and a link to the DATA (not a link to the graph but a link to the data itself), they are worse than meaningless, as they can be actively misleading. I’m not accusing you of bad intent or trying to mislead, you understand. I’m just saying that graphs without data are not science, they’re just an advertisement.
Many thanks,
w.
Here is the part of EcoHydRology that gives me shivers:
EvapHeat <- function (surftemp, airtemp, relativehumidity=NULL, Tn=NULL, wind=2) {
## surftemp: Temperature of surface [degrees C]
## airtemp: Temperature of air [degrees C]
## relativehumidity: between 0 – 1 [-]
## Tn minimum dailiy air temperature, assumed to be the dewpoint temperature [C]
## surftemp: Temperature of surface [degrees C]
## wind average daily windspeed [m/s]
windfunction = 0 & relativehumidity <= 1) {
airvapordensity <- relativehumidity * SatVaporDensity(airtemp)
}
else {
airvapordensity <- SatVaporDensity(Tn)
}
surfacevapordensity <- SatVaporDensity(surftemp)
return(round(86400 * windfunction * (surfacevapordensity – airvapordensity)))
}
SatVaporDensity <- function(T_C){
# T_C = Temperature [C]
VP <- SatVaporPressure(T_C)
return(round(VP/(0.462 * (T_C+273.15)), 4))
}
SatVaporPressure <- function(T_C){
# saturated vapor pressure at a given temperature (kPa)
#T_C: temperature [C]
return(0.611 * exp((17.3*T_C)/(237.2+T_C)))
}
Large mountain ranges cause rain shadows and deserts behind them in a lot of areas like the Sahara/ Gobi, but I always wonder how fast some of these mountains happened, Driving through the Rockies I see some really amazing rock formations that just do not seem to have happened with slow speed of tectonic plates (5-10 cm/year). They appear to have been way more violent which may be why some of our glacial periods happened so quickly?
Thanks Willis, good work. For anyone who has been in the tropics for some time, or at different times of the year, this is almost intuitive, obvious. But you have to explain it to the Warmistas, almost all of who do not live in the tropics, but rather the temperate regions of the planet.
I get the idea many warmistas never go outside, and rarely even look out a window.
They are, in general, not the outdoorsy and observant type.
I think of Willis’ work as being the other end of the stick: A study of the negative feedback mechanism that keep the “global temperature” as stable. Others, such as Svenmark, are trying to understand what drives the changes, which is more difficult due to multiple factors, while the Warmistas deny anything other than CO2.
Superb Willis,
TRMM is a very nice dataset. Glad to see someone put it to good use.
A couple of notes.
1. It’s nice to see CERES and Hadcrut4 both agree.
2. nic Lewis comment gave me an idea
comparing to GCM would be cool
Except they don’t agree. CERES shows less warming. Could this be due to incorrect adjustments to the hadcrut4 data? It would be a nice exercise to see what the hadcrut4 data would look like if one adjusted it to show 23 w/m2. One could then compare that to the UAH or RSS satellite data to see if that removed the 21st century divergence.
IPCC AR5 admits in TS.6 they don’t understand the water cycle and in FAQ 8.1 IPCC dismisses water vapor because A) they can’t explain or model, B) it’s a natural force and violates IPCC’s mandate of man caused only.
BTW IPCC assigns clouds an RF of -20 W/m^2 (watt is power not energy) which is cooling and lots of it.
If you work the numbers on IPCC AR5 Figure 6.1 you will discover that anthro C is partitioned 57/43 between natural sequestration and atmospheric retention. (555 – 240 = 315 PgC & 240/555) IMO this arbitrary partition was “assumed” in order to “prove” (i.e. make the numbers work) that anthro C was solely/90% responsible for the 112 ppmv atmos CO2 increase between 1750 – 2011. C is not CO2.
PgC * 3.67 = PgCO2 * 0.1291 = ppmv atmospheric CO2
IPCC AR5 Figure 6.1
……………………………….PgC/y……ppmv/y
FF & Land Use Source…….8.9……….4.22
Ocean & Land Sink…………4.9……… 2.32
Net Source.……….………..4.0……….1.90
If the anthro 8.9 Pg C/y (4.2 ppmv CO2/y) suddenly vanishes the natural cycle that remains would be a constant sink of 2.3 ppmv CO2/y. Reverse extrapolation (GCMs & RCPs apply forward extrapolation) calculates that 121 years in the past (278 ppmv CO2/2.3 ppmv CO2) or the year 1629 (1750-121) atmos CO2 would have been 0, zero, nadda, zip, nowhere to be found.
Oh, what a tangled web we weave!
The 8.9 Pg/y of anthro C simply vanishes in earth’s 45,000 plus Pg C cauldron of stores and fluxes. Mankind’s egoistic, egocentric, conceit means less than nothing to the earth, the solar system and the universe.
Thunderstorms lead me to the question of the effect and causation of hurricanes. Essentially, as I understand it, they’re basically super thunderstorms (or tightly associated with them). Would more thunderstorms cause more or less hurricane formation? By that I mean that more thunderstorms spread out over a wider area would dissipate the energy the hurricanes would need to feed themselves. I seem to remember Dr. Curry wrote a paper predicting global warming would cause more intense hurricanes, though the opposite seems to be happening.
Hurricanes cannot form and sustain if wind shear exists.
It is not a simple matter of more thunderstorms or warmer water.
If you note what happened in 2004 and 2005, just prior to the sudden formation of hurricane after hurricane, wind shear dropped off over the formation zones.
Thunderstorms don’t spin.
If you take a weather reporting station on land, look at the daily time variation of temperature over many years then go mildly multivariate and include daily rainfall, you will commonly find that at least 30% of the temperature variability can be explained, statistically before mechanistically, by rainfall.
Put simply, rain cools.
What is more, rain cools without mention of carbon carbon dioxide, greenhouse gases ….
With the current search for record this and that, extreme climate and so on, remember that a high temperature might or might not be unprecedented simply because the rain fell mainly in another paddock nearby.
The fickle finger of fate makes global headlines come and go like thunderstorms ….
It is all so contrived by those more interested in headlines than data.
Willis,
In this and other pictorial representations, such as some covering El Nino events, the eye is drawn to a lot of activity around the Indonesian islands. At times they look like the start point for repeating processes but this is just a strong pictorial effect. In the world of real data and observation, have others theorised if Indo does have a key role and if so, why?
Could it be a focus on the ring of fire with a permanent (for now) high geothermal gradient seeding processes like you describe here?
Hi Geoff
More likely the Asian and Australasian land masses blocking ocean currents (and to a lesser extent winds) on the western side of a large ocean basin. Heat and moisture accumulate near Indonesia- more to the north of the equator because there is more ocean to the north- Australia and New Guinea are further to the East. Which is why the ENSO cycle is in phase with NH seasons- building up in NH summer/autumn when the larger north Pacific is more directly exposed to the sun, peaking in NH winter, and hard to predict in NH spring. What interests me is the way the rainfall appears to circulate anti clockwise about Jakarta as the monsoon ebbs and flows.
Please see my studies relating Northeast Brazil:
1. Climatic fluctuations and homogenization of Northeast Brazil using precipitation data, Pesq. Agropec. bras., Brasilia, 19:529-543, 1984 — homogeneous zones, I- above 4-5 deg. S. lat,; II – between 4-5 and 8-10 degress S. lat. and III – below 8-10 deg S. Lat. Fortaleza data has very long precipitation series. This showed 52 year cycle [similar to onset dates over Kerala Coat in India] with submultiples of 26, 13 & 6.5 years with stronger amplitudes in 26 &13 year cycles. — 2013 was dry year, soalso the case with Durban.
2. A simple method for the estimation of global solar radiation over northeast Brazil, Pesq. Agropec. bras., Brasilia, 19:391-405, 1984 — The input in to this model is precipitation [cube root of precipitation]
3. A method for the estimation of potential evapotranspiration and/or open pan evaporation over Brazil. Pesq. Agropec. bras., Brasilia, 19:247-267, 1984 — The input is precipitation [cube root of precipitation]
Dr. S. Jeevananda Reddy
The GIF movies that show the “earth breathing” are just spectacular.
Love this site and contributors!
There is also the fact that less than ten percent of water droplets in clouds make it down to ground level, the rest evaporates mid air, close to the cloud base. That’s how clouds stay afloat.
So there is a lot more evaporative cooling going on, than calculated from net precipitation. True, it is not cooling at the surface itself, but some way above it, still, it gives a large contribution to vertical heat transport to the upper troposphere, where absolute humidity gets so low, that water vapor no longer acts as a greenhouse gas, letting radiative cooling to space kick in.
Rain that evaporates before reaching the ground is called virga.
You can see it with the naked eye. Very common in deserts. As BP points out, it amounts to multiple rounds of evaporative cooling.
http://www.weather.gov.sg/climate-past-climate-trends/
These climate trends from the link above from Singapore which is 1 deg North of the equator and remains in a semi permanent tropical weather pattern all year round show some interesting results. Firstly that there has been an increase temps and precip from the mid 70s to mid 90s then it has leveled off very much like the global Satellite temperature records suggest. To me this implies a new equilibrium has been reached where perhaps temps rose and increased evaporation, but only to a point where increase precipitation now overrides the warmer signal from GHG warming. This would add weight to Willis’s theory I think.
Willis,
Very nice post. Clear and informative. The most interesting thing is the ‘self-sustaining’ nature of convective storms, where wind from the storm increases evaporation and so drives total cooling far beyond what you might expect. The persistence of convective cells is quite amazing over open water; you can watch them for hours.
Nature’s heat pipe. Huacane does the same thing. Moves a ton of heat with little delta T
Willis,
Buried tonight and long since down with the convective cooling thing, but the crazy thing about your animation is that the Indian ocean completely has its own program. The Atlantic and Pacific oceans follow the trade winds and the Hadley circulation. Why doesn’t the Indian ocean follow suit? Check out Bob Tisdale’s animation of the 1997 nino SST’s. That telegraphs across the Indian ocean and bounces off Africa very sensibly as one would expect the rainfall to do.
Nope. The rainfall in your graphic trends SW to NE and stacks up in the crook of Indonesia and the west side of the horn of India. Almost like the Hadley were displaced half a tropic to the south by the landmass of Eurasia.
Wind-driven short-period waves of say 1/2 metre height and 30 metre wavelength increase the ocean surface area by about 1%. But when those waves start to break, or when the storm winds blow the water off of the tree leaves and the grass, sending fine spray into the air, surface area increase from the spray droplets can be 5% or more.
======================================
those figures seem low to me.
Fascinating post Willis. A very clear and persuasive description of the mechanism whereby thunderstorms extract heat from the oceans.
That said, it seems to be only half the story. I get that the heat goes into the evaporating and rising water vapor, but what happens at the other end of the pipe when the water vapor condenses back into liquid water and releases that same heat?
In order for there to be a net cooling effect on the planet, would there not have to be a mechanism whereby the heat gets released (radiated?) to space?
I am not saying there isn’t such a mechanism, but I’m curious as to what you think it is. How does it work?
I think you can get a better picture from this article.
https://stevengoddard.wordpress.com/2015/05/09/dr-bill-gray-explains-why-climate-models-dont-work/
Thank you, Richard. The citation is right on point and very illuminating.
After your animation, thunderstorms seems to be moving or circulating counter clockwise which make sense since there is more sea surface in the southern hemisphere. I wonder if, at times, if it circulates in a clockwise fashion? I doubt it.
Late to the party, but does anyone else see that it seems not to want to rain in the Pacific along the exact Equator? As in, to the point of “hopping” over it altogether before beginning to rain on the southern side?
Any thoughts as to why it would do this? Seems pretty counter-intuitive to me; I bet you can’t even see that line if you were out there sailing across it, let alone feel the difference, so why should the ITCZ care?
Figure 6 has me concerned. That fit is ridiculously good. How is the monthly rainfall calculated?
Climate models show decreasing thunderstorm activity in a warming world, but greater intensity.
This appears to be unsupported by Willis’s own analysis, though is global rather than regional – tropical.
http://link.springer.com/chapter/10.1007%2F978-1-4020-9079-0_24#page-2
Very good.
Great post Willis!
Here’s what retired Australian meteorologist Bill Kininmonth had to say on this topic in The Australian newspaper on April 29th 2009:
Cold facts dispel theories on warming
http://www.theaustralian.com.au/opinion/cold-facts-dispel-theories-on-warming/story-e6frg6zo-1225704690711
“Seventy per cent of the Earth’s surface is made up of ocean and much of the remaining surface is transpiring vegetation.
Evaporation and the exchange of latent energy from the surface is a strong constraint to surface temperature rise.
It is not rocket science that water from a canvas bag is cool even on the hottest days.
Furthermore, the surface temperatures of the warmest tropical oceans seldom exceed 30 C and for millions of years the underlying cold sub-surface waters have provided a powerful thermal buffer to warming.
The suggestion of anthropogenic global warming exceeding a tipping point and leading to runaway or irreversible global warming is a violation of conservation of energy principles.
Computer models are the essential tool for prediction of future climate. Since the IPCC fourth assessment, several independent analyses of the characteristics of the various models have been published in the scientific literature. These analyses reveal serious defects.
As the Earth warmed during the 1980s and ’90s, it was observed that the convective overturning of the tropics (the Hadley circulation) increased. In contrast, the overturning of the computer models is portrayed to decrease as increasing carbon dioxide generates global warming.
Separately it is found that the computer models under specify (by a factor of three) the important rate of increase of evaporation with projected temperature rise, meaning that the models under specify rainfall increase and exaggerate the risk of drought.
The same evaporation problem causes an exaggeration of the temperature response to carbon dioxide, but the exaggeration is a model failure and not reality.
The greenhouse effect is real, as is the enhancement due to increasing carbon dioxide concentration.
However, the likely extent of global temperature rise from a doubling of carbon dioxide is less than 1C.”
Very interesting, as usual. Thanks for that.
A few problems here.
1. The rain in -10/10N is not a result of evaporation within -10/10N. Vapor is transported from outside.
2. Evaporation is determined by temp AND wind.
3. Most of the energy is returned to the surface as DWLW.
“3. Most of the energy is returned to the surface as DWLW.”
How could that possibly add up? It can’t even be half. It might be a short distance before much is absorbed by water vapour before it can reach space but the emission from water liquid is almost continuous and its many discrete bands with water vapour. Meanwhile in the downward direction, there is cloud!
WE
“This is another piece of evidence for my hypothesis that the global temperature is regulated by emergent phenomena, including tropical thunderstorms. This regulation keeps the temperature within a very narrow range (e.g. ± 0.3°C over the entire 20th century)”
Ok so .you get the heat higher in the atmosphere (13km limit?) but then how is the heat going to escape. At the height the mean free path is of the order of 1 metre so not all heat will make it to background space. So does the temperature at which radiation escapes increase? or does the temperature remain the same?
Convection may move the heat upwards but only radiation will cool the earth
The free path upward is longer than the free path downward due to the difference in density. The energy flows outward through multiple absorption – emissions steps.
Willis previously indicated that the thunderstorms would start earlier in the day, and maybe stop a bit later. Say 5 minutes both ways.(can this be measured?) The Troposphere temperature does not change. The refrigerator simply runs a bit longer. That is how the man made effects are overwhelmed.
Willis you are really SCARING ME now! At the beginning of the week, as I was doing a “mentally non challenging” set of tasks, I was mulling this though: “Every lbm or Kg of water coming out of the sky, in the long run represents 1100 BTU of heat, that ultimately was discharged to space by “radiation”….SO what is the net effect of rainfall on the energy balance of the atmosphere. THIS IS REALLY SPOOKY, I’m now thinking things, and Willis is working them out, shortly after I think about them. AND, by the way, I’m delighted with this work.
Thanks-but where are the ocean currents? They have some impact I guess.
And now you know why we look for climate change at the poles.
it doesnt really matter if the tropics are regulated…
And are we finding warming at the poles? I think not yet. With some luck we will warm back up to:
“before the Little Ice Age, Norwegian Vikings sailed as far north and west as Ellesmere Island, Skraeling Island and Ruin Island for hunting expeditions and trading with the Inuit and people of the Dorset culture who already inhabited the region.[16] Between the end of the 15th century and the 20th century, colonial powers from Europe dispatched explorers in an attempt to discover a commercial sea route north and west around North America. The Northwest Passage represented a new route to the established trading nations of Asia”
Quote from Wikipedia
Seems a bit of a ‘sweep the problem under the carpet statement to me’. The tropics are the heat engine of the earth’s weather and climate. If the extra warming from GHG in the tropics is offset somehow by convection processes then a large part of the warming of the Earth from GHG could be overestimated. Polar regions only see the sun for 6 months of the year so warmth here is transient and largely advected in from warmer latitudes. If those warmer latitudes are not much warmer from AGW and potentially less than GCMs suggest then the tropics DO matter.
Of course the equatorial and tropical regions are of the utmost importance since this is where the real power in the heat pump lies. We live on a water world, and we need to get to grips with how this water world works understanding the oceans and in particular the equatorial and tropical oceans, ocean currents and the water cycle is the key. Unfortunately, this appears to escape Mosher who prefers computer models to investigating and understanding physical processes..
Anything happening at the poles is inconsequential in nature, given the lack of solar energy and the floating nature of the ice. There is no prospect that land ice in Antarctica (or for that matter in central Greenland) will melt before the present inter glacial comes to an end, and the planet falls back into the deep clutches of the ice age in which it is presently in.
Further if the poles were of importance, we would have numerous unmanned temperature monitoring stations far away from any Arctic, or Antarctic base, so that we can see what is happening. Instead of that, temperatures at the poles, particularly the Arctic, is mainly made up by extrapolating data from stations up to 1200km away. How can one look for warming when the data is for the main part simply made up?
““And we know that it takes about 75 watt-years per square metre to evaporate one cubic meter of seawater per year”
I don’t know who “we” is. Apparently some of “us” (read: you) can’t balance units. It takes about 75 watt-years to evaporate one cubic meter of seawater. No “square metre” or “per year” is required. By they way, I noticed the spelling of “metre.” Have you moved to France? If so thank goodness for small blessings.
Seriously, if you can’t even balance units then you have no business commenting on the Bubkingham-Pi theorem.
Please. Just stop.
Why stop? This is brilliant work. Your nit picking is what should be stopped.
Aaaaaaand this is the problem with Willis’s work. People who ride the short bus are encouraged to join the debate as if it is a debate over feelings and not physics.
Dinostratus November 13, 2015 at 4:31 am
Indeed it’s a problem, but no matter what I do, you just keep jumping off the short bus and joining the debate as if you had something to offer …
w.
I offer that the heat of vaporization for water is ~2570 KJ/kg. No area nor the reciprocal of time is required to boil water. Also I do not habitually breathe through my mouth, drag my knuckles nor ride a short bus.
Dinostratus November 12, 2015 at 12:12 pm
Others understood what I meant without any problem. However, to humor you, I’ve fixed it.
Happy now?
Oh, big surprise, you’re still not happy. Now you’ve joined the grammar Nazis, have you? Out of things to complain about, so you complain about my spelling? Sorry, pal, you’ll just have to get used to it. I spell metre that way deliberately to distinguish it from the other kind of meter. It is my deliberate (and of course futile) attempt to make the English language make more sense.
The bizarre part to me, Dino, is why you continue to read what I write when all you ever do is whine and bitch about how I’m doing it all wrong. If you don’t like how I write, stop reading what I write … is that too complex for you?
w.
“The bizarre part to me, Dino, is why you continue to read what I write when all you ever do is whine and bitch about how I’m doing it all wrong. If you don’t like how I write, stop reading what I write … is that too complex for you?”
It is because you beclown the skeptical argument.
Thinking about it though, making fun of you is similar to making fun of the warmists. They are arrogant blowhards all too eager to find validation in public pronouncements despite being repeatedly wrong. Just simply wrong. But at least they get their units right. At least they understand that only single sided FFT’s are used to investigate IVP’s. At least they understand the Buckingham-Pi theorem. At least they know there is more than one lyapunov exponent in a system with a dimensionality greater than two. You do not.
So go hang out with those who insist on being persistently wrong. We have no need for you.
Thunderstorms run off of low-density air. The low-density air rises, bearing water vapor upwards to the level where the water vapor condenses. The heat of condensation then powers the deep convection up the tower of the thunderstorm.
So, where does the heat eventually go?
(1) into the stratosphere? Should be able to see it with balloons, RSS, etc…. right?
(2) Off into space. Should also be able to see this somehow. Measurements?
(3) Energy translated into wind? This energy dissipates into… the ocean? Warming that?
I mean, the energy ends up somewhere… where does it eventually reside? What’s the pathway?
Peter
Radiates to space. There is much less CO2 to prevent the heat rapidly radiating to space.
Radiates to space. There is much less CO2 to prevent the heat rapidly radiating to space.
Okay, that’s one of the hypothesis, but where’s the data to support this? What data would falsify this hypothesis?
Also, does that imply the extra heat from the extra thunderstorms radiate MORE heat to space than before C02 increases surface temperature? If so, where’s the data?
Peter, good question. Why don’t you do like Willis and find it and post it?
The average rain is around 1000mm (2.7mm/day), and that should give 75W/m2 alone in evaporation.
Some of the rain has gone to ice before it falls out giving som exstra and as usual half the power is lost to space and half back to ground, so a good guess is that one mm/day of rain gives 15 to 20W/m2 lost to space. Tropical oceans are hot and evaporate the most, like they got most sun.
Another weird thing is the feed from the southeast to the northwest in the southern Pacific that joins the ITC at the Indonesian warm pool. In the north Pacific the Kuroshio current is the diametric opposite of a mirror image. I have seen this in Navier-Stokes eddies in SST’s before, but the rainfall makes it crystal clear. This only makes sense as a Ferrell cell direction of flow, but that would mean the Hadley circulation isn’t pushing back all the way to the equator, all the while there is an opposite seeminglysouth shunted Hadley flow stacking rain up against the other side of Indonesia from the Indian Ocean.
Willis,
“Note the size of the variations in cooling, which can change by up to eight watts per square metre in a single month. This can be compared with the estimated changes in CO2 which are expected to be about four watts per square metre in a century …”
The change in average solar radiation reaching the Earth between perihelion and apehelion is 74 watts per sq m., sun at zenith, (wiki), or about 18 times the effect of a CO2 doubling. How does this relate to the cooling of 8 watts per sq m in a month, that you describe?
Tony November 13, 2015 at 1:13 am
Thanks, Tony. You’ve got the idea right but not the numbers. The difference between January sun at perihelion and July sun at aphelion is about 88.8 W/m2 instantaneous (CERES data). However, all the rest of the numbers I discussed are 24/7 averages, so we need to divide the instantaneous solar changes by 4. This gives us a difference over the year of 22.2 W/m2 as a global 24/7 average.
However, nothing in climate is simple. When the earth is nearer the sun, the instantaneous insolation goes up … but the planet also speeds up, so it spends less time in the area of higher insolation. And the reverse is true as well. When the planet is further away from the sun, it receives less insolation, but it is there for a longer time.
And because both insolation and speed are governed by an inverse square law, they exactly cancel each other out. Physics is amazing, there’s no free lunch.
As a result, while the instantaneous insolation goes up and down, the total insolation doesn’t change at all. For example, despite the southern hemisphere being pointed towards the sun in January when the sun is strongest, it gets exactly the same total amount of insolation over the year as does the northern hemisphere.
Crazy, huh? Here’s another oddity. Do you know what place on earth gets the most hours of daylight per year? Gotta figure the Equator, right?
It’s a trick question. Every place on earth gets the same number of hours of daylight per year, an average of twelve per day.
Hope this helps, if not ask again.
w.
One important process that keeps the pressure in thunderstorms low and maintains its stability for a while is that condensation itself lowers the pressure. At 5000m elevation 10kg of water dislocate 25 m^3 of air. At twice the elevation, it’s twice as much. This condensation at high altitude, decreases the pressure high up, encouraging further convection, until the convected air humidity is below the dew point of the heated column, at which point the storm dies.
Mihail A November 13, 2015 at 9:04 am
Thanks for that, Mihail. The idea of condensation-driven wind is the work of a Russian woman whose name escapes me at the moment. It’s a fascinating idea, although I haven’t looked at it in detail.
I’m not sure how you are calculating your values, but to me they don’t tell the whole story. I don’t usually conceptualize it in terms of pressure, I think in terms of density. So let me explain it that way.
When we add water vapor to dry air, the density goes down because the atomic weight of water is 18, and that of air is around 29. As a result, the mixture of air and water vapor is lighter than the surrounding dry air, and thus it has buoyancy and tends to rise.
On the other hand, if we remove water vapor from moist air, it becomes more dense, and thus it is heavier than the surrounding moist air and it tends to sink. That’s half the story. Here’s the other half.
While it is true that condensation by itself would increase the density and thus cause the air parcel to lose buoyancy, the condensation also releases a large amount of heat. And of course, since PV = nRT, the heat reduces the density.
And when I think about it, the density decrease from the amount of heat released must be greater than the density increase due to the condensation. I say this because it is the heat that is liberated in the lower condensing areas of a thunderstorm cloud that drives the vertical expansion and maintenance of the thunderstorm tower … so it must perforce be more buoyant after condensation than before condensation.
All the best to you,
w.
Thank you for your quick reply Willis. I totally agree with the 2 points you make in your reply and they are real. Humid air is less dense than dry air and condensation makes air more dense. At the same time condensation releases a lot of latent heat in the system. What I was talking here about is a different phenomenon than these 2. As you said, pV = nRT. This phenomenon involves the decrease in n, as the water gas molecules leave the gas system as a result of condensation (the density of the liquid is orders of magnitude higher than the gas). V stays constant, for the purpose of this phenomenon, we make abstraction of T (which we can analyze separately), so p must decrease as a result of condensation. This effect is even stronger in downpours and at the time of thunderhead formation, when huge amuonts of water condense very fast on the convective column. Evaporation in the absence of thunderstorms is never as fast, as it’s the result of the steady-state process of insolation, so the opposite process of pressure increase from evaporation is never really as dramatic.
Yes Wilis, and if patient a person can watch clouds top grow slowly upward because of the latent heat released from condensation. And this warming increases the radiation to space – the other part of negative feedback from increased surface evaporation, the first being surface cooling. Nature’s air conditioning system – all powered by free solar energy!
That’s good. Thank you again.
I think that it is worth writing up for publication, like others above, but then I frequently do.
Thanks Willis. I didn’t know what averaging needed to be applied to the 74/88.8 Watts per sq m peak figure.
My point was that if a change of 22.2 Watts/sq m every 6 months had a significant impact, it should bring about a measurable change in average temperatures every 6 months, either at the equator or as a global average. From what I can see, it has no effect at all on temperature? If 22.2 W/sq m has no effect, what hope has a CO2’s doubling of a measly 4 W/sq m?