Guest Post by Willis Eschenbach [note new Update at the end, and new Figs. 4-6]
In climate science, linearity is the order of the day. The global climate models are all based around the idea that in the long run, when we calculate the global temperature everything else averages out, and we’re left with the claim that the change in temperature is equal to the climate sensitivity times the change in forcing. Mathematically, this is:
∆T = lambda ∆F
where T is global average surface temperature, F is the net top-of-atmosphere (TOA) forcing (radiation imbalance), and lambda is called the “climate sensitivity”.
In other words, the idea is that the change in temperature is a linear function of the change in TOA forcing. I doubt it greatly myself, I don’t think the world is that simple, but assuming linearity makes the calculations so simple that people can’t seem to break away from it.
Now, of course people know it’s not really linear … but when I point that out, often the claim is made that it’s close enough to linear over the range of interest that we can assume linearity with little error.
So to see if the relationships really are linear, I thought I’d use the CERES satellite data to compare the surface temperature T and the TOA forcing F. Figure 1 shows that graph:
 Figure 1. Land only, forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude. Note that there is little land from 50S to 65S. Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. Click graphics to enlarge.
Figure 1. Land only, forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude. Note that there is little land from 50S to 65S. Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. Click graphics to enlarge.
As you can see, far from being linear, the relationship between TOA forcing and surface temperature is all over the place. At the lowest temperatures, they are inversely correlated. In the middle there’s a clear trend … but then at the highest temperatures, they decouple from each other, and there is little correlation of any kind.
The situation is somewhat simpler over the ocean, although even there we find large variations:
 Figure 2. Ocean only, net forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude.
Figure 2. Ocean only, net forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude.
While the changes are not as extreme as those on land, the relationship is still far from linear. In particular, note how the top part of the data slopes further and further to the right with increasing forcing. This is a clear indication that as the temperature rises, the climate sensitivity decreases. It takes more and more energy to gain another degree of temperature, and so at the upper right the curve levels off.
At the warmest end, there is a pretty hard limit to the surface temperature of the ocean at just over 30°C. (In passing, I note that there also appears to be a pretty hard limit on the land surface air temperature, at about the same level, around 30°C. Curiously, this land temperature is achieved at annual average TOA radiation imbalances ranging from -50 W/m2 up to 50 W/m2.)
Now, what I’ve shown above are the annual average values. In addition to those, however, we are interested in lambda, the climate sensitivity which those figures don’t show. According to the IPCC, the equilibrium climate sensitivity (ECS) is somewhere in the range of 1.5 to 4.5 °C for each doubling of CO2. Now, there are a several kinds of sensitivities, among them monthly, decadal, and equilibrium climate sensitivities.
Monthly sensitivity
Monthly climate sensitivity is what happens when the TOA forcing imbalance in a given 1°x1° gridcell goes from say plus fifty W/m2 one month (adding energy), to minus fifty W/m2 the next month (losing energy). Of course this causes a corresponding difference in the temperature of the two months. The monthly climate sensitivity is how much the temperature changes for a given change in the TOA forcing.
But the land and the oceans can’t change temperature immediately. There is a lag in the process. So monthly climate sensitivity is the smallest of the three, because the temperatures haven’t had time to change. Figure 3 shows the monthly climate sensitivities based on the CERES monthly data.
 Figure 3. The monthly climate sensitivity.
Figure 3. The monthly climate sensitivity.
As you might expect, the ocean temperatures change less from a given change in forcing than do the land temperatures. This is because of the ocean’s greater thermal mass which is in play at all timescales, along with the higher specific heat of water versus soil, as well as the greater evaporation over the ocean.
Decadal Sensitivity
Decadal sensitivity, also called transient climate response (TCR), is the response we see on the scale of decades. Of course, it is larger than the monthly sensitivity. If the system could respond instantaneously to forcing changes, the decadal sensitivity would be the same as the monthly sensitivity. But because of the lag, the monthly sensitivity is smaller. Since the larger the lag, the smaller the temperature change, we can use the amount of the lag to calculate the TCR from the monthly climate response. The lag over the land averages 0.85 months, and over the ocean it is longer at 2.0 months. For the land, the TCR averages about 1.6 times the monthly climate sensitivity. The ocean adjustment for TCR is larger, of course, since the lag is longer. Ocean TCR is averages about 2.8 times the monthly ocean climate sensitivity. See the Notes below for the calculation method.
Figure 4 shows what happens when we put the lag information together with the monthly climate sensitivity. It shows, for each gridcell, the decadal climate sensitivity, or transient climate response (TCR). It is expressed in degrees C per doubling of CO2 (which is the same as degrees per a forcing increase of 3.7 W/m2). The TCR shown in Figure 4 includes the adjustment for the lag, on a gridcell-by-gridcell basis.
 Figure 4. Transient climate response (TCR). This is calculated by taking the monthly climate sensitivity for each gridcell, and multiplying it by the lag factor calculated for that gridcell. [NOTE: This Figure, and the values derived from it, are now updated from the original post. The effect of the change is to reduce the estimated transient and equilibrium sensitivity. See the Update at the end of the post for details.]
Figure 4. Transient climate response (TCR). This is calculated by taking the monthly climate sensitivity for each gridcell, and multiplying it by the lag factor calculated for that gridcell. [NOTE: This Figure, and the values derived from it, are now updated from the original post. The effect of the change is to reduce the estimated transient and equilibrium sensitivity. See the Update at the end of the post for details.]
Now, there are a variety of interesting things about Figure 3. One is that once the lag is taken into account, some of the difference between the climate sensitivity of the ocean and the land disappears, and some is changed. This is particularly evident in the southern hemisphere, compare Southern Africa or Australia in Figures 3 and 4.
Also, you can see, water once again rules. Once we remove the effect of the lags, the drier areas are clearly defined, and they are the places with the greatest sensitivity to changes in TOA radiative forcing. This makes sense because there is little water to evaporate, so most of the energy goes into heating the system. Wetter tropical areas, on the other hand, respond much more like the ocean, with less sensitivity to a given change in TOA forcing.
Equilibrium Sensitivity
Equilibrium sensitivity (ECS), the longest-term kind of sensitivity, is what would theoretically happen once all of the various heat reservoirs reach their equilibrium temperature. According to the study by Otto using actual observations, for the past 50 years the ECR has stayed steady at about 130% of the TCR. The study by Forster, on the other hand, showed that the 19 climate models studied gave an ECR which ranged from 110% to 240% of the TCR, with an average of 180% … go figure.
This lets us calculate global average sensitivity. If we use the model percentages to estimate the equilibrium climate sensitivity (ECS) from the TCR, that gives an ECS of from 0.14 * 1.1 to 0.14 *2.4. This implies an equilibrium climate sensitivity in the range of 0.2°C to 0.3°C per doubling of CO2, with a most likely value (per the models) of 0.25°C per doubling. If we use the 130% estimate from the Otto study, we get a very similar result, .14 * 1.3 = 0.2°C per doubling. (NOTE: these values are reduced from the original calculations. See the Update at the end of the post for details.]
This is small enough to be lost in the noise of our particularly noisy climate system.
A final comment on linearity. Remember that we started out with the following claim, that the change in temperature is equal to the change in forcing times a constant called the “climate sensitivity”. Mathematically that is
∆T = lambda ∆F
I have long held that this is a totally inadequate representation, in part because I say that lambda itself, the climate sensitivity, is not a constant. Instead, it is a function of T. However, as usual … we cannot assume linearity in any form. Figure 5 shows a scatterplot of the TCR (the decadal climate sensitivity) versus surface temperature.
 Figure 5. Transient climate response versus the average annual temperature, land only. Note that the TCR only rarely goes below zero. The greatest response is in Antarctica (dark red).
Figure 5. Transient climate response versus the average annual temperature, land only. Note that the TCR only rarely goes below zero. The greatest response is in Antarctica (dark red).
Here, we see the decoupling of the temperature and the TCR at the highest temperatures. Note also how few gridcells are warmer than 30°C. As you can see, while there is clearly a drop in the TCR (sensitivity) with increasing temperature, the relationship is far from linear. And looking at the ocean data is even more curious. Figure 6 shows the same relationship as Figure 5. Note the different scales in both the X and Y directions.
 Figure 6. As in Figure 5, except for the ocean instead of the land. Note the scales differ from those of Figure 5.
Figure 6. As in Figure 5, except for the ocean instead of the land. Note the scales differ from those of Figure 5.
Gotta love the climate system, endlessly complex. The ocean shows a totally different pattern than that of the land. First, by and large the transient climate response of the global ocean is less than a tenth of a degree C per doubling of CO2 (global mean = 0.08°C/2xCO2). And contrary to my expectations, below about 20°C, there is very little sign of any drop in the TCR with temperature as we see in the land in Figure 5. And above about 25°C there is a clear and fast dropoff, with a number of areas (including the “Pacific Warm Pool”) showing negative climate responses.
I also see in passing that the 30°C limit on the temperatures observed in the open ocean occurs at the point where the TCR=0 …
What do I conclude from all of this? Well, I’m not sure what it all means. A few things are clear. My first conclusion is that the idea that the temperature is a linear function of the forcing is not supported by the observations. The relationship is far from linear, and cannot be simply approximated.
Next, the estimates of the ECS arising from this observational study range from 0.2°C to 0.5°C per doubling of CO2. This is well below the estimate of the Intergovernmental Panel on Climate Change … but then what do you expect from government work?
Finally, the decoupling of the variables at the warm end of the spectrum of gridcells is a clear sign of the active temperature regulation system at work.
Bottom line? The climate isn’t linear, never was … and succumbing to the fatal lure of assumed linearity has set the field of climate science back by decades.
Anyhow, I’ve been looking at this stuff for too long. I’m gonna post it, my eyeballs are glazing over. My best regards to everyone,
w.
NOTES
LAG CALCULATIONS
I used the Lissajous figures of the interaction between the monthly averages of the TOA forcing and the surface temperature response to determine the lag.
 Figure N1. Formula for calculating the phase angle from the Lissajous figure.
Figure N1. Formula for calculating the phase angle from the Lissajous figure.
This lets me calculate the phase angle between forcing and temperature. I always work in degrees, old habit. I then calculate the multiplier, which is:
Multiplier = 1/exp(phase_angle°/360°/-.159)
The derivation of this formula is given in my post here. [NOTE: per the update at the end, I’m no longer using this formula.]
To investigate the shape of the response of the surface temperature to the TOA forcing imbalance, I use what I call “scribble plots”. I use random colors, and I draw the Lissajous figures for each gridcell along a given line of latitude. For example, here are the scribble plots for the land for every ten degrees from eighty north down to the equator.
Figure N2. Scribble plots for the northern hemisphere, TOA forcing vs surface temperature.
And here are the scribble plots from 20°N to 20°S:
Figure N3. Scribble plots for the tropics, TOA forcing vs surface temperature.
As you can see, the areas near the equator have a much smaller response to a given change in forcing than do the extratropical and polar areas.
DATA AND CODE
Land temperatures from here.
CERES datafile requisition site
CERES datafile (zip, 58 MByte)
sea temperatures from here.
R code is here … you may need eyebeach, it’s not pretty.
All data in one 156 Mb file here, in R format (saved using the R instruction “save()”)
[UPDATE] Part of the beauty of writing for the web is that my errors don’t last long. From the comments, Joe Born identifies a problem:
Joe Born says:
December 19, 2013 at 5:37 am
My last question may have been a little obscure. I guess what I’m really asking is what model you’re using to obtain your multiplier.
Joe, you always ask the best questions. Upon investigation, I see that my previous analysis of the effect of the lags was incorrect.
What I did to check my previous results was what I should have done, to drive a standard lagging incremental formula with a sinusoidal forcing:
R[t] = R[t-1] + (F[t] – F[t-1]) * (1 – timefactor) + (R[t-1] – R[t-2]) * timefactor
where t is time, F is some sinusoidal forcing, R is response, timefactor = e ^ (-1/tau), and tau is the time constant.
Then I measured the actual drop in amplitude and plotted it against the phase angle of the lag. By examination, this was found to be an extremely good fit to
Amplitude as % of original = 1 – e ^ (-.189/phi)
where phi is the phase angle of the lag, from 0 to 1. (The phase angle is the lag divided by the cycle length.)
The spreadsheet showing my calculations is here.
My thanks to Joe for the identification of the error. I’ve replaced the erroneous figures, Figure 4-6. For Figs. 5 and 6 the changes were not very visible. They were a bit more visible in Figure 4, so I’ve retained the original version of Figure 4 below.
NOTE: THE FIGURE BELOW CONTAINS AN ERROR AND IS RETAINED FOR COMPARISON VALUE ONLY!! 
NOTE: THE FIGURE ABOVE CONTAINS AN ERROR AND IS RETAINED FOR COMPARISON VALUE ONLY!!
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.


” Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. ”
My understanding is that the error in satellite measurement of these two quantities is too great to permit their difference to be calculated meaningfully. So, presumably some Climate Science “forcing” results were used here, rather than genuine data. Is that a fair assumption?
This once again goes to demonstrate the time proven adage of “nature always abhors a straight line”.
I was so impressed by the logic of this article that I was really hoping for some alarmist criticism to see if anyone could try and undermine Willis’ logic. There has been none so far.
As it stands, and assuming the conclusions are correct, then it is one of the most important articles ever written on climate science, totally destroying the foundations of climate alarmism.
The temperature sensitivity of 0.2°C to 0.5°C for a doubling of CO2 levels is, as you say, lies within the boundaries of statistical noise.
So if we could return to the year 1900 and could somehow strip out the effects of natural climate cycles, UHI, agriculture, irrigation, plus cherry picking and homogenisation of historical data, by how much would the Earth’s temperature have risen today?
The answer: Not a lot and much less than the usually quoted figure of 0.7°C.
The cost of climate alarmism is apparently approaching $1.0 billion per day, so you can rely on the fact the contents of Willis’ article will be ignored and/or condemned and/or ridiculed by the Climate Establishment. Nothing can be allowed to derail the Global Waming Gravy Train.
Beautiful pics !
A few thoughts. Neg slope tails in land record may not be too important in total energy if area is considered.
I’m surprised there’s not more change in slope in oceans near tropics but by eye it’s a least a factor of 3 or 4 which is huge. Fitting central area, poles and tropics to get relative figures may be useful.
If I wanted Lissajous figures I’d be interested in the NH oceans. There is a whole ‘tube’ of loops that look very regular there like a tunnel of breaking surf, it would be interesting to isolate them and see what the storey is.
Not too convinced by the lag formula approach based on a pure harmonic. I’d suggest lag regression plots or just plotting different lags and see how flat you can get the loops. They are not round by you can compromise.
See examples I posted on Euan Mearns’ site:
http://euanmearns.com/uk-temperatures-since-1956-physical-models-and-interpretation-of-temperature-change/#comment-266
http://climategrog.wordpress.com/?attachment_id=638
regards.
I agree with Lord Monkton. The IPCC has never claimed linearity. They have always said that the “forcing” (hate that term – there’s no “force” involved) is itself dependent on the concentration of CO2 in the atmosphere. At some point the levels of CO2 in the atmosphere reach a saturation point and have no further impact. Some scientists have claimed that the 17 year pause might indicate we have already reached the effective saturation point of CO2 in the atmosphere.
The models are effectively “piecewise linear” with the linear equation only being relevent to the concentration we have at any given time (normally the present).
As you know, I dispute the models entirely. I claim that the theory of CO2 based warming supposes that an IR emitter can add energy to another IR emitter and normally we would never model a system that way since it would allow a system to “pull itself up by its own bootstraps” to a higher level of overall energy in direct contradiction of the law of conservation of energy. That is to say, in its simplest form the greenhouse gas theory implies a greenhouse gas would make a planet warmer, causing it to emit more energy, making the greenhouse gas more energetic, causing it to emit more energy, making the planet more energetic so on ad infinitum. This is not possible. We avoid the same difficulty in radio frequency calculations by assuming the radio transmitter does not receive any energy from nearby radio transmitters, even though in principle you would expect that a radio transmitter would indeed receive energy from other radio transmitters.
We always have to ignore the possibility that two emitters of energy can absorb energy from each other, not matter how tempting it might be to speculate that this is what must be happening, because it will always lead us to a model that contradcits the conservation of energy law.
A fair bit of this is above my pay rate but if you fire heated gas from a paint stripping gun at the surface of water, the water temperature will not rise indicating that surface tension blocks physical heat. Water accepts radiation but not “heat”. Would that have anything to do with it.
The problem is that the only bit of surface IR energy comprising OLR is in the ‘atmospheric window’. The H2O IR (defined as its spectral temperature) comes from -1.5 deg C, about 2.6 km in temperate zones, and the CO2 IR mainly comes from the lower stratosphere.
This is because for equal surface and local air temperature, there is zero net surface IR emission in self-absorbed GHG bands, standard radiative physics.
The concept of surface forcing is unscientific and irrelevant: for Climate Alchemy to become a Science, it has to junk forcing.
I like this work by Willis and in the end I think we are all going to find that the limiting factor for ocean heat content at a given level of insolation (after accounting for internal ocean circulations) is atmospheric pressure on the ocean surface.
And ocean heat content controls air heat content on a watery world.
Of course, that brings us full circle back to atmospheric mass and gravity leaving the radiative characteristics of GHGs nowhere in comparison.
In my comment above change the first sentence to ‘The problem is that the only bit of surfaceIR energy’
[Fixed – w.]
stephen wilde says:
December 19, 2013 at 2:23 am
Its feedbacks like that which give rise to the nonlinearity.
“The lag over the land averages 0.85 months, and over the ocean it is longer at 2.0 months.”
Yes, so you are still dealing with annual sensitivity, not decadal.
First temperature can only be accurately taken when a body is in thermal equilibrium. The earth never is!!!!!!!!! So how can we accurately find an average temperature???
Secondly the assumed TOA solar input is assumed to be 340W/m2 by the IPCC. With this poor energy input the water cycle would not work!!! Actual solar input is 1370W/m2 which averages to 500W/m2 onto the SUNLIT hemisphere which is enough to have a water cycle. This is reality not some model built to suit a crappy theory.
As always I stand in awe of your ability to visualize the mountains of data.
There’s a detail I don’t understand, though. The formula for the multiplier comes from diffusion through a depth. In particular, it uses the relative amplitude at the depth that gives the phase lag you observed. I’m having trouble understanding why that quantity is relevant in this context. A particular difficulty is that in diffusion the phase lag can exceed 2 pi, whereas I don’t see how that would happen for the radiation / surface-temperature relationship.
Could you elaborate a little on how the one relationship is relevant to the other?
Aw come on. Take that first diagram, invert it a la Mickey Mann, twist it around in the best tradition of the Global Warmmongering twisters and behold! A hockey stick.
Very interesting, presentation, looking at the numbers in different ways. I certainly like how clearly the oceans limit at 32C. I actually dove in water that warm in Darwin Bay, Australia. Now I’m off to shovel the snow of the driveway.
I find this very convincing.
Why? Because it is based on real data, reflects more accurately what we are actually seeing, is much closer to what basics physics says should happen, and Willis doesn’t get another grant or academic posting based on slanting the results and hiding the data.
“We always have to ignore the possibility that two emitters of energy can absorb energy from each other, not matter how tempting it might be to speculate that this is what must be happening, because it will always lead us to a model that contradcits the conservation of energy law.”
Not quite. Two RF emitters near each other will indeed absorb energy from each other and output energy on a new frequency. This is called inter-modulation and is a big problem at some locations. Now, is the total RF energy changed? I strongly doubt it, but I don’t know for sure.
Figure 1. reminds me on HR diagram, see :
http://en.wikipedia.org/wiki/H-R_Diagram
Can you please plot logT- LogF graph?
You can call it than Eschenbach- Štritof (to much sch or Š) or Willis- Nikki diagram. 🙂
Willis says: So to see if the relationships really are linear, I thought I’d use the CERES satellite data …
Unfortunately, that first graph doesn’t tell you anything about the linearity of sensitivity. What it tells you is that convection carries lots of energy from the equator to the poles.
Consider Antarctica – the red dots. There is a net negative radiation imbalance, so more radiative energy is leaving than arriving each year. On an annual basis, this means that roughly equal amounts of OTHER energy must be arriving, which would be air and water currents. Similarly, the areas near the equator have a positive value, meaning large amounts of energy are being carried away by convection.
The “hook” in the red data does NOT tell us that as the forcing increases, the temperature will decrease in that region. It simply tells us that convection carries a lot of energy to the coasts of Antarctica but not so much to the interior.
Without digging into the details of your calculations, I wonder if convection may be confounding some of your other calculations.
My last question may have been a little obscure. I guess what I’m really asking is what model you’re using to obtain your multiplier.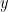 is related to the stimulus
is related to the stimulus  as follows:
as follows:

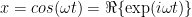 ,
,
 .
.



 . It isn’t, of course. You seem instead to have chosen a model in which the response is that of a semi-infinite slab at some depth. Since I don’t see why you base responses at the surface to responses at various depths, though, I suspect that not all is as it seems.
. It isn’t, of course. You seem instead to have chosen a model in which the response is that of a semi-infinite slab at some depth. Since I don’t see why you base responses at the surface to responses at various depths, though, I suspect that not all is as it seems.
Suppose, for example, that according to your model the response
and the stimulus is sinusoidal:
then, since the system is (gasp) linear, we know that the response is given by
Plugging that into the system equation gives:
So your multiplier would have been
I know I’ve just gotten hung up on a detail, but I’ll appreciate any answer you have time for.
Willis: “But the land and the oceans can’t change temperature immediately. There is a lag in the process. So monthly climate sensitivity is the smallest of the three, because the temperatures haven’t had time to change.”
No, it would be more appropriate to compare delta_d/dt(SST) to delta_Rad , the fast response is mostly orthogonal ie rate of change.
The response to the ‘lambda’ relaxation equation is neither purely in-phase nor orthogonal but a sliding mix of the two which varies with frequency, so you really can’t just plot SST-Rad and start drawing simplistic conclusions. and defining “monthly” sensitivities.
http://climategrog.wordpress.com/?attachment_id=399
However, if you can estimate the lag for a particular frequency range, or the ratio of in-phase and orthogonal components that make up the temp response , that could give an estimation of tau and hence lambda.
Do that separately for tropics and temperate zones and it put numbers on the degree of regulation provided by your governor.
Just an idea.
Joe, you seem familiar with this stuff. Do you see any flaws in what I linked there?
http://climategrog.wordpress.com/?attachment_id=399
Thanks Willis, for this inspiring approach – I wish I had your graphing capabilities!
and to reply to Martin A – yes, you are right to finger the TOA imbalance ‘data’…..its resolution is about 5 watts per square metre with a consistent excess of that value over zero…..and the modellers are looking for 0.5 to 1 watt excess as their expectation. So – the ‘data’ is ‘constrained’ to use NASA’s phrase, by the ocean heat content data. As Bob Tisdale will tell you, the OHC data is not accurate either and – guess what? It is adjusted in ‘re-analysis’ to reflect the expected excess from the TOA!!!! I think this is what is called a circular argument! It doesn’t seem to worry the modellers at all.
If the IPCC don’t claim linearity how do they justify simple scalar number (3) as their feedback multiplier, when this multiplier is clearly inversely related to temperature. Surely the question must then be, how quickly does gain fall as temperature rises, as this will have a critical effect on ultimate equilibrium temperature rise for a doubling of CO2
Thanks Willis; A superb post!
Your illustrations make clear lambda is a chimera at best. Again proof that it is not possible to model Earth’s climate with the little physical knowledge that we have now.
And then to conduct “experiments” where these models supply the “data” is criminal.
My guess is that if you looked at two slabs of ocean at plus and minus 60 degrees latitude over the course of years you would see a pair of race track ‘8’s, where you have to pump more energy into the ocean in spring and less in the fall, to achieve the same temperature.