Alternative title: “Standing on the shoulders of Giant Bob”
Guest post by Phil Salmon
Introduction
One of the themes to emerge from the climate debate here on WUWT, concerns “chaos” and nonlinear system dynamics and pattern. Anyone acquainted at all with the nature of dynamical chaos and nonlinear / non-equilibrium pattern formation, and who also has an interest in the scientific questions about climate, cannot fail to sense that dynamical chaos has to be an important player in climate. Simply on account of the huge complexity of climate over the expanse of earth’s surface and deep time, and also the obvious impossibility of equilibrium in a rotating system with continuous substantial imbalances of heat and kinetic energy.
However, a “sense” is hardly adequate scientifically; it is necessary to go further than this and forge some kind of physical and mathematical model or hypothesis which can be tested. But here one runs into the problem of chaotic systems being .. well, chaotic and unpredictable; indeed for some the movement of a system into the chaotic region represents falling off the edge of the world of scientific testability and orthodox Popperian experimental investigation. Is it a contradiction in terms to imagine that you can study chaos scientifically and mathematically? The scientific community at large – not only climate science – while giving lip service to chaotic pattern formation as a real phenomenon, generally shrinks back from serious engagement with it, back into the comfortable regions of tidy linear and equilibrium equations.
However there does exist a well-established science of physical and mathematical study of chaotic, nonlinear systems, in which a wide range of nonlinear pattern forming systems are well understood and characterized. But owing to the human tendency to associate in closed communities – nowhere more in evidence than in the multi-faceted scientific world, there is in my view too little engagement between the chaos and nonlinear dynamics experts and scientists in a wide range of natural sciences whose studied systems are – unknown to both sides – accurately and usefully characterized by well-researched nonlinear pattern systems.
It is the purpose of this article to propose a well-known experimental “nonlinear oscillator”, namely the Belousov-Zhabotinsky chemical reaction, as an analogy – in terms of its dynamics and spatio-temporal pattern – for the El Nino Southern Oscillation (ENSO) system in the equatorial Pacific Ocean. This would characterize and alternation between El Nino and La Nina as a nonlinear oscillator. The definitive work of Bob Tisdale on the ENSO is used to liken the alternating multi-decadal periods of eE Nino and La Nina dominance (the PDO) as the two wings of the Lorenz butterfly attractor.
The term “chaos”, while a common shorthand for a class of phenomena and systems, is not a very accurate or helpful one. Chaos itself, strictly speaking, is truly chaotic and not a very fruitful area of mathmatic investigation. A system passes from the region of linear dynamics through “fringes” or borderlands of mathematical bifurcation before reaching full blown chaos, and it is in these marginal and transitional borderlands where the interesting phenomena of strange attractors and spontaneous pattern formation arise. But it is hard to find a convenient single word that takes its place – it is easier to say “chaos” than “nonlinear pattern formation in far-from-equilibrium dissipative systems”.
Even “nonlinear”, while better than “chaos”, is still inadequate: there are plenty of physical and mathematical systems which are clearly not “linear” but not related to non-equilibrium emergent pattern formation. A relative of mine – a TV weatherman in Monterrey, California for many years before his retirement – pointed this out to me, that it is not necessary to invoke nonlinear pattern formation to account for acute sensitivity to initial conditions – a simple high power relationship is sufficient for this. Acute sensitivity to initial conditions does indeed characterize many nonlinear systems – indeed, one popular metaphor for chaotic systems is the “butterfly wing” effect – namely that a butterfly wing’s disturbance of the air in one place can result in massive changes in weather systems a continent away. The butterfly wing analogy was coined by Edward Lorenz – a pioneer in mathematical study of non-equilibrium pattern system and also a meteorologist – we will return to Lorenz later. However this sensitivity does not uniquely define the type of system we are considering. (The “butterfly wing” metaphor is now inseparable from the actor Jeff Goldblum and his rather inane use of the phrase in the Jurassic Park films.)
If I had to propose an alternative to “chaotic” as a general short term for such systems with spontaneous nonlinear pattern dynamics, I would go for something like “non-equilibrium pattern” systems.
One of the most helpful references I have found on the subject of non-equilibrium pattern systems is the PhD thesis of a chemical engineer Matthias Bertram, entitled “controlling turbulence and pattern formation in chemical reactions” – previously posted on his web site but now reposted on Google docs:
Matthias uses the term “pattern formation in dissipative systems”. To quote from the introduction of this thesis:
“The concepts of self-organization and dissipative structures go back to Schrodinger and Prigogine [1–3]. The spontaneous formation of spatio-temporal patterns can occur when a stationary state far from thermodynamic equilibrium is maintained through the dissipation of energy that is continuously fed into the system. While for closed systems the second law of thermodynamics requires relaxation to a state of maximal entropy, open systems are able to interchange matter and energy with their environment. By taking up energy of higher value (low entropy) and delivering energy of lower value (high entropy) they are able to export entropy, and thus to spontaneously develop structures characterized by a higher degree of order than present in the environment.”
The author goes on to analyze several experimental non-equilibrium pattern systems, including the Belousov-Zhabotinsky reaction. He outlines the essential conditions for the operation of a nonlinear oscillator such as a far from equilibrium state, and an “excitable medium”, that is, a medium within which localized positive feedbacks can be initiated and run their course according to their associated refractory period. We will return to these parameters when we consider the ENSO.
The Belousov-Zhabotinsky reaction
There is a helpful short introduction to the Belousov-Zhabotinsky (“BZ”) reaction on Wikipedia:
http://en.wikipedia.org/wiki/Belousov%E2%80%93Zhabotinsky_reaction
Have a look at this youtube video shown in figure 1:
Figure 1A. A video of the BZ nonlinear oscillation in a stirred beaker.
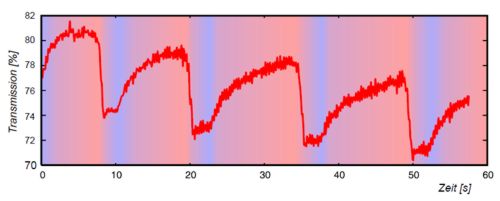
Figure 1B. A graph of light transmissivity over time, illustrating the BZ reaction (from Wikipedia DE)
What you are looking at is the Belousov-Zhabotinsky (BZ) reaction in a stirred beaker. It is striking in that the beaker’s liquid contents oscillate between a dark blue colour and clear transparency, for multiple cycles. Most of us can recall school chemistry lessons from the (more or less) distant past, where we saw reactions such as the titration of potassium permanganate with hydrogen peroxide, causing a beaker or tube full of liquid to change from dark purple color to clear, or vice versa. But not many of us probably saw the oscillating BZ reaction with a tube of liquid oscillating between the two starkly contrasting states. The BZ reaction “involves several reagents and various intermediate species; the central reaction step is the oxidation of malonic acid by bromate, catalyzed by metal ions” (Matthias Bertram 2002). The system is jumping between two states looking for equilibrium but finding it in neither.
This is intriguing to watch but what is going on here, and what significance does it have to climate, to the behavior of atmospheres and oceans?
The BZ reaction is a gateway to a whole branch of science which is, to repeat, still very incompletely explored and whose significance is under-appreciated. The two individuals, Boris Belousov and Anatol Zhabotinsky, who established their eponymous reaction, have an interesting history which has some resonance with the politics of climate science. Boris Belousov accidentally came across the oscillating reaction in Soviet Russia during the early 1950’s (one of the important and long undiscovered Soviet scientific discoveries that also included the “Ilissarov frame” orthopedic method for making new bone by gradual movement apart of fractured bone ends). Belousov’s attempts to publish this finding were rejected repeatedly, on the grounds of the familiar “where’s the mechanism?” argumentum ad ignorantium. In 1961 a graduate student Anatol Zhabotinsky took up and ran with the discovery, but it was not until an international conference in Prague in 1969 that the reaction became widely known, two decades after its inception.
The BZ reaction is a “reaction-diffusion system”. It is a non-equilibrium pattern phenomenon known as a nonlinear oscillator; there are certain prerequisites for such a system to develop:
- The system is far from equilibrium
- It is an open system with a flow through of energy (dissipative)
- The system has an “excitable” medium
The BZ reaction meets these requirements sufficiently to set off nonlinear oscillation. Note that condition 2 is only partly and temporarily met – a tube of chemicals is not really open; however the availability of reagents makes the system for a limited time behave like an open system until the reagents become exhausted.
The BZ reaction in a thin film
There are many types and flavours of the BZ reaction. In the first example we saw the reaction in a beaker: however when the reaction is carried out in a thin film, a new element arises: instead of the solution changing colour en-masse, the colour changes are associated with intricate evolving patterns such as radiating ripples and spirals.
You can search for “BZ reaction” on youtube and find many examples of attractive moving patterns, some with musical accompaniment. One of these is given in the link below:
Figure 2. Three animations of the BZ reaction in a thin film, showing evolving spatiotemporal waves and patterns and alternations of dominant colour phase.
This link presents three BZ thin film animations. In the first, regions of orange and pale blue colour repeatedly expand and contract, encroaching on each-other reciprocally, such that looking at the dish as a whole, the predominant colour alternates between orange and pale blue. The second animation is one where typical BZ fringe and spiral patterns in dark and light purple radiate from various centers. If you look in the bottom left corner, a tongue of darker purple periodically grows and recedes. The third animation is a slower moving version of the first – if you have the patience to watch all of it, again there is an overall pattern of alternation between orange and pale blue as the predominant colour.
Another youtube video of a thin film BZ reaction is given in the link below; while it is tediously slow and would have benefited from acceleration, it shows nicely the radiating BZ patterns characterized by alternation between orange and pale blue as the predominant color.
http://www.youtube.com/watch?v=S20Jsfu9rkQ
Figure 3. Another animation of the BZ reaction in a thin film showing travelling patterns and alternating phases.
During some parts of these BZ sequences, especially of the first animation, you have the feeling that you could be watching one of Bob Tisdale’s animations of the temporal evolution of sea surface temperatures (SSTs), such as that occurring in the equatorial Pacific with alternating el Nino and La Nina cycles: such an animation is given (By Bob) in the link below:
Figure 4. An animation of sea surface temperature anomalies in the Pacific during the transition from el Nino to La Nina systems during 1997 – 1999 (from Bob Tisdale’s blogspot), from web page: http://bobtisdale.blogspot.com/2010/12/enso-related-variations-in-kuroshio.html
If one focuses on the south eastern Pacific off the Peruvian coast, where the alternating tongues of warm and cool surface water characterize respectively the alternating en Nino and La Nina, the analogy to the BZ reaction is particularly compelling.
The ENSO as a nonlinear oscillator?
However beyond an intriguing qualitative visual similarity, what basis is there for proposing that the ENSO could constitute the same type of nonlinear oscillator as the BZ reaction? Please note that I am not proposing that chemical reactions play a role in the ENSO – no, chemical potentials in the BZ reactor are matched by thermodynamic potentials in the atmosphere-ocean system. Specifically we can return to the question of the essential pre-requisites that the BZ system meets to operate as a nonlinear oscillator; how would the ENSO system also meet these pre-requisites?
1. A system far from equilibrium
At least this one is a no-brainer. Solar energy input is very unequally distributed on the earth’s surface, maximally at the equator and minimally at the poles. Add to this the rotation of the earth and associated day-night cycle, and oblique axis rotation causing reciprocal summer and winter in north and south hemispheres, and ocean circulation, and it soon becomes clear that equilibrium is never remotely approached. (In fact, a world with atmosphere, ocean and heat flux in equilibrium is a nightmare to contemplate, with stagnant anoxic seas and stale motionless air.)
2. An open, dissipative system
The global climate system is open, as it receives heat input from the sun which (Leif Svalgaard notwithstanding ) is subject to minor periodic fluctuation. Heat is also radiated out to space. Heat energy enters and leaves the system; thus it is dissipative.
3. A system with an excitable medium
This is perhaps the most critical requirement. “Excitable” implies that an induced change at one location sets in motion a positive feedback which results in local amplification and propagation of the induced change – for instance taking the form of a travelling wave in the BZ reaction. This is not a wave in the sense of an energy wave through water or air that merely transmits energy, but a wave in which a spreading reaction is stimulated generating new local energy with the propagating wave. A cascade of chemical reactions in the BZ reaction constitutes this excitability. This positive feedback is limited and runs its course – characterised by a refractory period – but its operation is sufficient to drive and sustain the nonlinear oscillation, and in some cases to generate complex spatiotemporal patterns.
How could such excitability exist in the equatorial Pacific where the ENSO takes place? To discuss this question I need to refer to an exchange I had a few months ago with Bob Tisdale on a thread here at WUWT. The topic was one of these chicken-and-egg discussions of what drives the ENSO, either top-down by trade winds for instance, or bottom up by variation in deep upwelling. I posed the question to (who better?) Bob Tisdale, suggesting that the spread of both the el Nino and the La Nina, could involve a time-limited positive feedback. The nature of these positive feedbacks is indicated in the two diagrams below.
Figure 5. The La Nina positive feedback: enhanced Peruvian cold upwelling sharpens the equatorial Pacific east-west pressure gradient, driving stronger trade winds which propel further upwelling.
Figure 6. The el Nino positive feedback: decreased upwelling weakens the trade winds which propel the upwelling.
Please note that in the schematic systems in figures 5 and 6 it is not really relevant which comes first – changes in the trade winds or in upwelling. They are linked in a feedback loop. The analogy that I had in mind was of the on-shore and off-shore breezes that occur in summer in temperate coastal locations such as the British Isles. Here, in the day, increasing land temperature warms the surface air, causing it to decrease in density and rise, drawing in on-shore winds from the sea. Conversely at night, the land temperature quickly cools, increasing surface air density such that the wind is reversed to an off-shore breeze. (By contrast the air temperature over the sea is relatively constant). It was this essential mechanism that I suggested for the equatorial Pacific ENSO system, that the upwelling off Peru associated with the start of a La Nina cycle, in cooling the east Pacific surface layer air, creates a higher air pressure or density to the east that acts to drive east-to-west (easterly) trade winds (of the type that propelled Thor Heyerdahl and his companions on their epic Peru to Indonesia crossing of the Pacific on their “Kon Tiki” balsa wood raft, recapitulating the voyages millennia earlier of Polynesian mariners and ocean island settlers). These energised trade winds will push Pacific surface equatorial water westwards, adding impetus to the Peruvian upwelling by drawing eastern Pacific deep water toward the surface in a conveyer-belt like fashion. Thus the full cycle of a positive feedback illustrated in figure 5.
Conversely, during an el Nino cycle, upwelling is slowed or interrupted, resulting proximally in increased solar heating of more static, less mixed surface water in the Pacific east. This will decrease the temperature and pressure east-west difference, sapping force from the trades and resulting in doldrum conditions of decreased winds. The weakened trades will then slow the upwelling conveyor, connecting a feedback cycle that moves toward interrupted upwelling and a rapid spread of warm surface water from the east Pacific (figure 6).
It was a big moment for me when Bob Tisdale replied to the affirmative, agreeing that a time-limited positive feedback did indeed drive the onset of el Nino and La Nina, until both ran their course, reaching, to quote the term Bob used, “saturation”. Of course the whole system involves more complexity than this idealised system – there are periods of neither el Nino nor La Nina, or of modified, “Modoki” el Nino systems. However for me Bob’s positive reply was very important because the final piece of the jigsaw for this BZ-reaction analogy fell into place. Now I had my excitable or reactive medium. So it began to become clearer that the ENSO can indeed be characterised as a nonlinear oscillator, analogous to the BZ reaction-diffusion system.
3. The attractors and longer term pattern of ENSO (the PDO)
A feature of non-equilibrium pattern systems and their spatio-temporal evolution is an attractor. An attractor is a subset of the (often multidimensional) phase space that characterises a system, towards which the evolving system state converges. When an attractor takes on a complex fractal form it becomes a “strange attractor”. The strangeness of attractors does not however mean that they are not well understood – on the contrary, many different classes of attractor have been identified and studied mathematically.
A somewhat dry and technical description of attractors is given in wikipedia:
http://en.wikipedia.org/wiki/Attractor
In the context of our analogy of the ENSO as a nonlinear oscillator, a particularly interesting type of nonlinear attractor is the Lorenz attractor. Figure 7 below shows the time plot of phase space displacement of a Roessler and a Lorenz attractor. In figure 8, the phase space trajectory plot is given for the two corresponding attractors. The Lorenz attractor displays phase space “tearing” into two separate domains, while the Roessler attractor is characterised by phase space folding. The bilaterally torn attractor is sometimes referred to as the Lorenz “butterfly”.
(The chaos butterfly is rehabilitated! Providing one understands that one is referring to the Lorenz butterfly attractor, not the spurious “butterfly wing” effect.)
Of course, the Lorenz and Roessler attractors are simple classic types of nonlinear attractor. The Lorenz attractor exhibits oscillation of a fractal nature on more than one scale: the fine scale oscillation itself oscillates over a longer time period between higher and lower values of the phase space parameter on the y axis. More complex versions of both attractors exist – and many further types also. Figure 9 shows two examples, a Roessler attractor which shows tearing like a Lorenz attractor, and a folded chaotic BZ reactor attractor which kind of looks like a cross between a Roessler and a Lorenz.
 Figure 7. The time plot of phase space displacement of a Roessler and a Lorenz attractor.
Figure 7. The time plot of phase space displacement of a Roessler and a Lorenz attractor.
Figure 8A. The phase space trajectory plot of the Roessler attractor (folding)
 Figure 8B the Lorenz attractor (tearing).
Figure 8B the Lorenz attractor (tearing).
 Figure 9A. A half inverted torn chaos solution to a Roessler attractor
Figure 9A. A half inverted torn chaos solution to a Roessler attractor
 Figure 9B. a folded chaotic BZ attractor.
Figure 9B. a folded chaotic BZ attractor.
A note on reading the literature on chaos and non-equilibrium pattern dynamics. Only pay minimal attention to the text and even less to the maths. Just look at the pictures. It is the spatiotemporal multidimensional patterns that are the unifying and compelling feature, and it is pattern analogies between disparate systems which reveal the unifying pattern processes at work. In the above figures I have not defined the parameters in the x and y axis – they don’t really matter.
The Lorenz attractor and the ENSO
Does the time plot of the Lorenz attractor in figure 7 (b), with its higher and lower frequency components, remind you of anything? The wavetrain appears to spend alternating periods oscillating in a higher and a lower region of the y axis. Here again our discussion turns to the definitive work by Bob Tisdale on the ENSO. Bob’s recent posting on WUWT (reposted from his own blogspot) entitled “Integrating ENSO: multidecadal changes in sea surface temperature” had the subtitle “Do multidecadal changes in the strength and frequency of el Nino and La Nina events cause global sea surface temperature anomalies to rise and fall over multidecadal periods?”. A link to this article (pdf) is:
This tour-de-force of the ENSO and its controlling influence on global SSTs demonstrated how, over the past century, there have been alternating periods of about three decades duration during which the el Nino and La Nina systems are reciprocally dominant. Two plots from Bob’s article are shown below in figure 10.
Figure 10a shows the ENSO oscillations exhibiting alternating periods of higher and lower elevation on the y axis (Nino SST 3.4 anomalies), although with far more noise than the tidier level-switching oscillation of the Lorenz attractor. The Nino 3.4 plot thus resembles a very untidy or chaotic Lorenz attractor time plot of the type shown in figure 7b. The alternating periods dominated by the el Nino (1910-1944, 1976-2009) and by La Nina (1945-1975) represent the two wings of the Lorenz butterfly. Thus this period-alternation between a generally warming el Nino dominated phase and a cooling La Nina dominated phase, fits in with the description of the ENSO system as a nonlinear oscillator, of the BZ reaction type, and characterised by a torn attractor of the Lorenz – or possibly modified torn Roessler – variety. It is also known as the Pacific decadal oscillation, or PDO.
Figure 10A. The Nino 3.4 SST anomalies from 1910 to the present, averaged into roughly 30 year periods by Bob Tisdale.
Figure 10B. Global SST compared to period-averaged Nino 3.4 anomaly. Both from “Multidecadal changes in sea surface temperature” by Bob Tisdale.
Is the PDO the Lorenz butterfly attractor of the ENSO?
Closely linked to the ENSO is the PDO – indeed Bob Tisdale asserts that the PDO is an epiphenomenon of the ENSO. His recent posting on multidecadal variation in SSTs elucidates this relationship, showing the PDO to essentially comprise alternating periods of el Nino and La Nina dominance. On the basis of the proposal presented here that the ENSO is a nonlinear oscillator, we can suggest further that the alternating “PDO” phases are the paired “butterfly wings” of a Lorenz attractor characterising the ENSO.
Figure 11. Could the Pacific Decadal Oscillation (PDO) represent the operation of a Lorenz “butterfly” torn attractor on the ENSO?
Periodic forcing of the ENSO nonlinear oscillator
At this point, some of you may be saying “hold on a moment – I’m not convinced by this BZ reaction analogy. Most of the BZ reactions (e.g. shown on youtube) show spiral and fringe patterns that are not at all persuasive analogies to the shifting regional patterns of ocean surface temperatures”. You would have a point. However it is necessary at this stage to introduce another class of nonlinear oscillators – the periodically forced nonlinear oscillator. The BZ reactions that were referred to above, and shown in the attached movies, are all unforced examples. These unforced BZ reactions oscillate and their own natural frequency, and are indeed often characterised by such radiating spiral and fringe patterns. But the spatiotemporal patterns can change profoundly when the BZ reaction is subject to periodic forcing. Figure 12, provided by Matthias Bertram’s PhD thesis, shows a series of spatial patterns from a BZ reaction which is catalysed by a light sensitive metal catalyst, then subject to various regimes of periodic forcing by light pulses. The first case (a) is unforced and looks like many of the youtube BZ reaction animations. However a wide range of different patterns is observed (b-g) when different periodic forcings are applied.
Figure 12. A BZ reaction with a light-sensitive metal catalyst, showing spatially extended nonlinear oscillator patterns. Case (a) is unforced; all the remaining are subject to different amplitudes and frequencies of light pulse periodic forcing. Taken from the PhD thesis of Matthias Bertram.
Anna Lin et al. (2004) looked further at the role of periodic forcing in the light-sensitive BZ reaction. The BZ system in the absence of forcing oscillates at its natural frequency. When forcing was applied by periodic light flashes, they found a difference in the kind of response depending on whether the forcing was strong or weak. To quote the authors:
“The entrainment to the forcing can take place even when the oscillator is detuned from an exact resonance [refs]. In this case, a periodic force with a frequency f(f) shifts the oscillator from its natural frequency, f(0), to a new frequency, f(r), such that f(f) / f(r) is a rational number m:n. When the forcing amplitude is too weak this frequency adjustment or locking does not occur; the ratio f(f) / f(r) is irrational and the oscillations are quasi-periodic. In dissipative systems frequency locking is the major signature of resonant response.”
So with strong forcing, “frequency locking” occurs and there is a clear relationship between the frequencies of the periodic forcing and of the BZ systems responsive forced oscillation. However when the forcing is weak, the reaction’s responsive frequency shows a much more complex relation to the forcing frequency, and its resultant oscillations can be described as “quasi-periodic”.
Returning to the ENSO, how could the equatorial Pacific nonlinear oscillator be periodically forced? Periodic forcing of the oceans and of climate in general is a frequent topic of posts at WUWT. There are many such known and potential sources of periodic forcing over a wide range of time-scales. The Milankovich orbital related cycles operate over periods of 105 years to decades and centuries (in the case of resonant harmonics of orbital oscillations). Then there is oscillation in solar output from the 11 year sunspot cycles to the longer periodicities such as the Gleissburg cycles. One persuasive source of PDO forcing is solar-barycentric, as outlined by Sidorenko et al. (2010), the movement of the solar system barycenter around the sub-Jupiter point (center of gravity of a solar system containing only the sun and Jupiter):
This periodic asymmetry in the solar orbit has shown a wavelength and inflection points similar to the PDO cycle in the last two centuries.
Turning to the oceans and the thermo-haline circulation of deep ocean currents, it is well known that the strength of cold water downwelling at the key sites such as the Norwegian sea is subject to significant variation – indeed after a period of a few decades of relative weakness, Norwegian sea downwelling has recently strengthened (Nature, 29 November 2008, doi:10.1038/news.2008.1262 – link in references). Once could go on. There is no shortage of potential sources of periodic forcing of the atmosphere-ocean system, either of the equatorial Pacific or indeed globally.
If the PDO represents the operation of the ENSO Lorenz attractor, then the periodicity of the PDO should tell us if the system is unforced or forced and frequency locked – in which cases it would have regular periodicity, or if it is weakly periodically forced, in which case an irregular wavelength might be expected. Jacoby et al. 2004 traced the PDO oscillations over the last 400 years, using oak tree rings on the Russian Kurille Islands:
http://www.wsl.ch/info/mitarbeitende//frank/publications_EN/Jacoby_etal_PPP_2004.pdf
A PDO wavetrain is clearly discernible but the wavelength varies from 30-60 years. The PDO thus appears to be a real multidecadal oscillation but it is not frequency locked, showing frequency variation. This points to the PDO arising from a weakly periodically forced ENSO. Mantua et al. (2002) also review data on palaeo-records of the PDO, concluding that its wavelength varies from 50-70 years. They concluded that the causes of the PDO are unknown.
http://www.atmos.washington.edu/~mantua/REPORTS/PDO/JO%20Pacific%20Decadal%20Oscillation%20rev.pdf
Thus the PDO seems to be almost but not quite regular – apparently aiming for a 60 year cycle but fluctuating from it. This could be evidence of periodic forcing of the ENSO system that close to the boundary between “weak” and “strong” forcing. Of course, these suggestions about sources of periodic forcing of the ENSO and PDO are speculative. If, as set out by Lin et al. (2004), in the case of a weak periodic forcing of a nonlinear oscillator such as the BZ reactor, the relation between a putative forcing frequency f(f) and the responsive frequency f(r) is irrational, this complicates the search for conclusive proof of such a link. However the PDO’s apparently limited departure from 60 year periodicity might suggest a forcing near the boundary of strong and weak, and therefore an intermittent frequency locking.
Conclusions
- Owing to the far-from-equilibrium state of the earth’s atmosphere and ocean climate system, the a priori case for the operation of non-equilibrium/nonlinear pattern dynamics is strong.
- The Belousov-Zhabotinsky reaction-diffusion system in a thin film is a compelling model of a nonlinear oscillation arising spontaneously in a far-from-equilibrium spatially-extended system, with apparent similarities to the ENSO sea surface temperature spatio-temporal oscillation in the equatorial Pacific.
- The apparent positive feedbacks (spatio-temporally limited) associated with the initiation of both el Nino and La Nina systems, linking Peruvian coast deep upwelling with equatorial trade winds, qualify the equatorial Pacific as an excitable medium, a key pre-requisite of an oscillating reaction-diffusion system such as the BZ reaction. The open and dissipative nature of the climate and ocean meet another such requirement.
- Of the class of known attractors of nonlinear oscillatory systems, the Lorenz and possibly Roessler attractors bear similarities to the attractor likely responsible for the alternating phases of La Nina and el Nino dominance that characterise the ENSO and constitute the PDO.
- It is possible that the ENSO / PDO system might be periodically forced; the significant but limited variation of the time-period of the PDO evidenced in the palaeo-record of the last few centuries suggests a forcing strength close to the threshold required for frequency locking.
- If the ENSO and PDO can be characterised as a nonlinear oscillator with a Lorenz type attractor, one might speculatively extend the analogy more widely to the earth’s climate as a whole, and such features as the alternation between glacial and interglacial states (during a glacial epoch such as the present one).
- It is hoped that scientists and mathematicians with expertise in non-equilibrium pattern systems, such as reaction-diffusion oscillatory systems, might bring their analytical techniques to bear on the study of the earth’s atmosphere, oceans and climate. In this way the hypotheses presented here could be confirmed or refuted, and perhaps the nature and identity of the significant drivers of climate could be found.
Postscript
What implications does this paper have for anthropogenic global warming (AGW), if any? It was not written primarily to address the AGW issue. CO2 is not mentioned. However there are some indirect implications. The finding that Bob Tisdale’s observation of alternating periods of el Nino and La Nina dominance – in other words the PDO – is well described by a nonlinear oscillator driven by a torn Lorenz (or Lorenz-Roessler) attractor, give Bob’s conclusions greater “real-world” plausibility. (Nonlinear attractors are a common feature of the real world.) It is also a riposte to those who argue against the reality of the PDO or AMO (Pacific decadal oscillation, Atlantic multidecadal oscillation) on the grounds that a credible mechanism does not exist. It does!
One important mathematical aspect of a nonlinear oscillator with an attractor is its “Lyapunov stability”. Alexander Lyapunov, from Yaroslavl, Russia, established a century ago the maths of stability of both linear and nonlinear systems, such that a nonlinear system such as an oscillator is characterised by a “Lyapunov exponent”. The full works on this are given here:
http://cobweb.ecn.purdue.edu/~zak/ECE_675/Lyapunov_tutorial.pdf
The maths here is all way over my head – I’m a “mere” biologist! Essentially the Lyapunov exponent assesses how strong or “attractive” the attractor is – i.e. how strong a perturbation of the system is needed to move it – unwillingly – away from its attractor. More expert mathematic analysis of the ENSO as nonlinear oscillator would include derivation of the Lyapunov exponents. This would tell us the stability of the system and its resistance to change due to any outside influences.
The global circulation models (GCMs) are essentially linear. That presumably is why they generally fail to reproduce the ENSO and PDO. (If they show any nonlinear behaviour it is probably more by accident than design.) It remains to be seen whether climate and ocean modelling – of the ENSO or of larger parts of the global climate, which used a nonlinear oscillator as a starting point, would be more effective.
Post-postscript
Mathematical / computer modelling of a nonlinear oscillator such as the BZ reaction is not too difficult (for people into that kind of thing) and well established. The “Brusselator” – so named for being invented at the Free University of Brussels (VUB) is a good example:
http://en.wikipedia.org/wiki/Brusselator
References
Controlling turbulence and pattern formation in chemical reactions. Matthias Bertram, PhD thesis, Berlin, 2002. https://docs.google.com/leaf?id=0B9p_cojT-pflY2Y2MmZmMWQtOWQ0Mi00MzJkLTkyYmQtMWQ5Y2ExOTQ3ZDdm&hl=en_GB
G. Nicolis and I. Prigogine, Self-organization in Nonequilibrium Systems (Wiley, New York, 1977).
E. Schroedinger, What is Life ? (Cambridge Univ. Press, 1944).
P. Glandsdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations (Wiley, New York, 1971).
The ENSO-Related Variations In Kuroshio-Oyashio Extension (KOE) SST Anomalies And Their Impact On Northern Hemisphere Temperatures. Bo Tisdale, from the web page: http://bobtisdale.blogspot.com/2010/12/enso-related-variations-in-kuroshio.html
Integrating ENSO: Mutidecadal variation in sea surface temperature. Bob Tisdale.
Pdf of this article: https://docs.google.com/leaf?id=0B9p_cojT-pflYjYyMTdkYzItMDMwOS00MjFjLWJmYTAtMzdjYjM1YjhhMmFj&hl=en_GB
Resonance tongues and patterns in periodically forced reaction-diffusion systems. Anna Lin et al., DOI: 10.1103/PhysRevE.69.066217, Cite as: arXiv:nlin/0401031v1 [nlin.PS].
Nature, 29 November 2008, doi:10.1038/news.2008.1262.
http://www.nature.com/news/2008/081129/full/news.2008.1262.html
G. Jacoby, O. Solomina,1, D. Frank, N. Eremenko, R. D’Arrigo (2004) Kunashir (Kuriles) Oak 400-year reconstruction of temperature and relation to the Pacific Decadal Oscillation. Palaeogeography, Palaeoclimatology, Palaeoecology 209 (2004) 303–311.
http://www.wsl.ch/info/mitarbeitende//frank/publications_EN/Jacoby_etal_PPP_2004.pdf
Mantua et al. (2002)
http://www.atmos.washington.edu/~mantua/REPORTS/PDO/JO%20Pacific%20Decadal%20Oscillation%20rev.pdf
N. Sidorenkov I.R.G. Wilson A.I. Kchlystov (2010) Synchronizations of the geophysical processes and asymmetries in the solar motion about the Solar System’s barycentre. EPSC Abstracts Vol. 5, EPSC2010-21, 2010 European Planetary Science Congress 2010.


![etb58j[1]](http://wattsupwiththat.files.wordpress.com/2011/01/etb58j1.gif?resize=430%2C317)







I can add something to this. Normal Guassian noise (the type we learn about in school/university) is the sum of a large number of small random perturbations from an average, so e.g. the surface level of a layer of sand laid on a flat substrate is Guassian.
There is however another kind of noise, which is called pink or 1/f noise. This is typical of a system which contains a large number of substates and which randomly changes between state. Typical examples are the flow of electrons through a material with channels which randomly open and close. Another is the flow of water along a stream.
Now, if the world consists of a large number of phenomena exist for (very) long periods changing between states and individually increase/decrease the global temperature, when they change, then what you would expect is a 1/f type noise.
This seems to fit very well with the above article.
The implication is that we should see 1/f noise (which we do) in the climate signal. This has several implications:
1. The longer the period you are looking at, the larger the noise. Or to put it in GW terms, if you measure the variation in climate using a short period, you will not have a good estimate for the amount the climate varies over longer periods.
2. Because the signal contains so much long term variation, it contains random components that look like long term change, so it is very easy to confuse e.g. manmade change on the climate with (large) long term random fluctuations.
3. The fun bit …. if you look at enough small sections of a 1/f signal, you will find one that closely resembles the total signal! So, e.g. if you look at the section 1910-1945, you’ll find roughly the same appearance and number of major up/downs as the total modern climate signal. Obviously the size of the peaks and troughs are smaller on a smaller section, and no two will exactly match, but a fun game if you have time is to try and find howmany small sections of the global temperature graph have the same appearance as the total … and see how small it goes!! (it has fractal-like properties!)
Very interesting article, thank you!
Chaotic oscillation is the correct way of describing the periodic changes of states within the planetary weather system (“climate” is a characteristic regional pattern of weather conditions; this term cannot be, in all seriousness, applied to global patterns).
It is obvious that any consequences of the human activity are but a minor factor within this interplay of cosmic forces (solar activity, cosmic rays, magnetic field variations, volcanic activity, biological feedback, water vapor atmospheric content and resulting changes of temperature, etc.).
Any attempt to predict a weather system behavior by modeling linear relationships, applying the textbook Boltzmann’s formula and regarding the Earth’s biosphere as the proverbial “black body” (which is, in essence, the IPCC approach) is futile.
The majority of climatologists are grasping this simplistic last straw because they lack required imagination, mathematical skills and, generally, any clear understanding of their subject. What they understand very clearly, however, is how to pull the wool over politicians’ eyes to get more grants and financing.
The root problem of the AGW hysteria is the mercurial human nature itself: moral and mental weakness of the majority of the people in general, their readiness to lie and turn away when their well-being and popularity are at stake.
I’m attracted by the smell of a way around Leif’s hypersensitivity objection to the sun as the forcer.
==============
Fascinating.
I’ve long suspected harmonic resonances at work on the Earth, amplifying input well beyond the apparent level of forcing. Not just Svensmark’s cloud cover changes but other factors as well. Thanks for the reference to Sidorenkov et al, looks most interesting. I’d like to see Erl Happ’s work tying in with your ideas too.
There’s also a strange resonance of synchronicity I often experience here which keeps drawing me back to WUWT. I’ve just been working on El Nino myself. I found this great little video – oversimplified, sure, origins still not explained, but it helps me visualize.
I heard that some weeks/months prior to El Nino, there is a correlation with increased seismic activity – lost that link for the mo. And many now know that seismic activity is often forewarned with electrical changes – perhaps this is what animals sense. Lastly, I’ve been trying to hunt down work I saw a while back that shows the 1998 El Nino as a quantum shifter of temperature, linked to cyclical solar activity. Anyone know where I can find this? Interesting that the 1998 temperature spike is closely abutted by troughs either side – support for the idea of resonance.
I asked ‘Bob’ the same question about trade winds and downwelling back in August of 2009- pretty much got the same answer. Go Bob!
These textures are like 0ld friends. They are similar to certain rock textures, as observed by John Elliston, a former Director of Exploration for a company in which I was Chief Geochemist. My copy of the many relevant images is not for circulation, but it is described here from the University of Tasmania:
“The Origin of Rocks and Mineral Deposits
The Origin of Rocks and Mineral Deposits: is the first comprehensive application of modern colloid science to define the properties and behaviour of the ancient high-energy sedimentary particles from which crustal rocks and mineral deposits were formed.
This classic pioneering work, compiled by world leaders in surface chemistry and the earth sciences over many years, is based on the current physical chemistry of small particle systems and the interactions between charged sediment particles and ions in the pore fluids surrounding them. It has been found that existing problematic observations relating to ore deposits and the formation of rocks are simply resolved by using the principles more recently developed in colloid science.” (more) at
http://fcms.its.utas.edu.au/scieng/codes/cpage.asp?lCpageID=38
It is hard to distil the 706 pages and 756 colour photos into a few sentences. In rock formation in hydrated systems, the chemistry & physics of colloids have been under-researched. There are illustrated processes that lead for example to Liesegang banding, which can then be preserved through solidification of the gel, making it amenable to study permanently. There are many more processes than Liesegang banding that refect systems out of equilibrium that are diffusion controlled (at least to a degree) and where there are opposing forces giving more than one stability well with respect to, for example, distance of separation of particles. There is a lovely test-tube example of banding of gold precipitated from hydrated gold chloride in colloidal silica, with various concentrations of reducing agents gently poured on top of the colloid and allowed to diffuse. (ref Hatschek & Simon 1912, Gels in Relation to Ore Deposition, Trans. Inst. Min. Metall., 21, 451-479). However, the rock genesis and metamorphism work sits side by side with the discussion above, in a different sub-discipline of science. We predated chaos theory and butterfly wings and concentrated on documenting and explaining. I have no difficulty putting John’s explanations into the more recent arcane world of Lorenz attractors as I understand them. While the pictures convey a likeness to the repetition of the BX reaction above, I’d exercise some caution before drawing parallels with ocean heat circulation; but then I’d be happy to see it all work in a unified theory.
Phil Salmon: Many thanks for the repeated references.
A couple of notes: In the second paragraph below your Figure 6, you wrote, “Conversely, during an el Nino cycle, upwelling is slowed or interrupted, resulting proximally in increased solar heating of more static, less mixed surface water in the Pacific east.”
During an El Nino, warmer-than-normal water sloshes from the western tropical Pacific to the east. Convection and cloud cover accompany the warm water and travel from west to east. This means there is less downward shortwave radiation (solar heating) in the east, (but more in the west). Just a clarification that should not impact your post.
You’ve used Pacific Decadal Oscillation (PDO) but not in the classical sense associated with the JISAO description and data. If you were to use Pacific Decadal Variability (PDV) instead, you would avoid any confusion on the parts of your readers.
Regards
Thanks Phil.
I studied unforced/forced non-linear dynamical systems as part of my (recent) maths degree, and can follow your arguments. At the superficial level anyway, need time to think about it. I’ll come back in a couple of days to see what critiques there are from the more knowledgeable.
Off Topic: Mind boggling press stupidity:
http://www.telegraph.co.uk/science/space/8275530/Second-sun-on-its-way.html
‘Second sun’ on its way
The Earth could find itself with a ‘second sun’ for a period of weeks later this year when one of the night sky’s most luminous stars explodes, scientists have claimed.
Will this disturb weather patterns? Will the radiation cause mass sunburn? When will it happen?
Fortunately, then tell us when:
Brad Carter, senior lecturer of physics at the University of southern Queensland in Australia, said the explosion could take place before the end of the year – or indeed at any point over the next million years.
Good post and line of thought.
One observation, I saw no mention of salinity, which is a important factor in the Thermohaline Circulation;
http://en.wikipedia.org/wiki/Thermohaline_circulation
http://oceanmotion.org/html/impact/conveyor.htm
and its circulation patterns:
http://en.wikipedia.org/wiki/File:Conveyor_belt.svg
http://www.whoi.edu/page.do?pid=12455&tid=441&cid=47170&ct=61&article=20727
http://www.john-daly.com/polar/flows.jpg
This map shows where cold dense ocean water is sinking;
http://www.thewe.cc/thewei/&/&/bbc12/gulf_stream.gif
this one shows where heat is released to the atmosphere
http://www.windows2universe.org/earth/Water/images/thermohaline_circulation_conveyor_belt_big.gif
Now take a look at this Global Sea Surface Temperature – 12 Month Animation;
http://www7320.nrlssc.navy.mil/global_ncom/anims/glb/sst12m.gif
and note tentacles/tendrils of cold water that begin dancing across the Equatorial Pacific in May as the La Nina takes hold. Now look in the same location and timeframe on this Global Sea Surface Salinity – 12 Month Animation;
http://www7320.nrlssc.navy.mil/global_ncom/anims/glb/sss12m.gif
and note that you can still see the essence of the same tentacles/tendrils.
New cooling predictions from Joe Bastardi—pointing to the PDO and weather patterns never seen before—hinting a solar connection:
http://www.accuweather.com/video/756131056001/bastardi-a-la-nina-that-is-k.asp?channel=vbbastaj
How about “tippy/wobbly/bouncy”?
“prima facie” is more apt.
One might indeed! See you later, oscillator!
What a fascinating read! I wont sully the discussion by asking any questions–and I have many!–but will simply thank Phil profusely for expanding the territory. I have always been intrigued by chaos theory, and Phil’s exploration of this “angle” is most illuminating.
Cheers!
Phil,
Science seemed to have forgotten we are under pressure for water to be exist in liquid form so it holds energy.
Also the planet rotates beside oscillating and being round generating opposing actions in both hemispheres.
This is a helpful post. I’m a sort of wholistic thinker and need overarching concepts to actually understand a given part of the world. Willis Eichenbach’s posts here help me when it comes to climate sensitivity and I think this post will serve similarly when it comes to thinking about long-term oscillatory activity. Thanks much!
I was always fascinated by the butterfly theory and in my musings I found a parallel analogy – that of the grain of sand in the oyster; the source of irritation and disturbance which generated a response in the surrounding tissue and became the nucleous of the pearl.
It is not inconceivable that local disturbances can escalate and become self sustaining, for instance tornados. I was once working on scaffold in a courtyard and saw a ‘dust devil’ 15 feet high and no more than an inch in diameter. Something in the configuration of buildings around us triggered that event. Perhaps they are incredibly common and it was merely the presence of the dust that revealed its passage, because it was not particularly or distinctively loud.
A glider pilot once told me that after launch, on still days he would head for a large farm complex, the vast acerage of shiny hot tin roof created updrafts which he was able to ride thousands of feet into the clear air above the empty green countryside.
Large entities which might be expected to display stable or static climate conditions at certain times of the year namely Siberia, Antarctica, the equatorial oceans, the equatorial landmass and Australia, are subject, at their intersections, to recognizable weather patterns, but when you introduce unpredictable (and not yet understood) factors like: Ocean Currents, solar/cosmic influences, rotational wobbles, volcanic activity, deforestation, urbanization….and who knows maybe even synthetic gases, aerosols, particulates etc etc…. it seems the one thing you can be sure about is that you can be sure of nothing, prediction is impossible.
But it did occur to me that if you wanted to conduct a butterfly effect type experiment that Antarctica would be the place to do it Go down there into the pristine wastes where it’s always bitterly cold and burn say 400,000 tons of fuel a year for thirty years, release the heat into the atmosphere, see what spins out….maybe southern ocean cyclones?
No hang about, isn’t that’s what’s actually happening? All those bases, research stations, ships, cruises, flights, snowmobiles… they’re injecting vast chunks of heat into the frigid wastes…could that be the grain of sand in the oyster…the nucleous of climate change?
They do say that the very act of looking at a thing changes it. And the quantum guys tell me that you can’t measure a darned thing down there, is it a wave or a particle, is it here or over there?
In conclusion it seems to me quite possible that local disturbances can resonate and cause weather patterns, obvious in the case of say…mountains.
It also appears that any attempts to measure ‘scientifically’ the chaotic swirls and fluctuations of the atmosphere are doomed to failure.
As a techician I can assure you that you can take at least three different temperature readings inside your own fridge!
This has the ring of reality to it. I caution those who see the Sun as a variable entity. That is input prior to reaching our outer atmospheric layers. Another plausible variable is that leaky, sometimes reflecting sometimes inviting, atmosphere which is then recharged by the relatively constant solar irradiation. That leaky atmosphere can itself be a BZ reaction and may be seen at the outer edge of our atmosphere when viewing OLR parameters. Furthermore, the entire depth of our atmosphere is not well sampled (especially at the outer edge), and certainly not for a long enough period of time in terms of temperature, and CO2 and other gasses, including ozone.
Rather it seems the ENSO being a linear oscillator of the Sun-Earth EM relation:
http://www.vukcevic.talktalk.net/MF.htm
Chaos being only in the minds of confused and lost beholders.
Great post! Looking for relatively prime numbers for beat frequencies within the possible forcings might be a way of homing in on quasi-periodic forcings.
Long, long ago I worked on a measurement system to demonstrate the reality of the Green and Callen, Fluctuation Dissipation Theorem, Phys. Rev. 83, 1951, linking microscopic fluctuations to the macroscopic relaxation function. If one were to view the varied forcings to the Earth’s climate system as microscopic drivers for the quasi-periodic oscillations, then the result is the macroscopic relaxations seen in ENSO, PDO, etc. The change in the behavior of these over time is the change in the exponential parameters of the relaxations. What the actual parameters are would be an exercise left to the reader 😉
There’s a much less obscure example of a nonlinear oscillator, much easier to observe and experiment on. The human heart. Each beat depends on just the right set of conditions; the next beat is never guaranteed like the next stroke of a pendulum.
You can observe a raised baseline by increasing your anxiety or blood pressure, or by hard exercise. The relaxation side of each beat doesn’t fall back to the default, so the amplitude gets smaller and the frequency gets faster.
BTW: Time to revisit Prof.Giorgio Piccardi’s work:
http://www.rexresearch.com/piccardi/piccardi.htm
Take a look at a chart of the past 450,000 of reconstructed global temperatures (Al Gore’s infamous chart will do nicely). Then take a look at the pattern of the BZ nonlinear oscillation chart presented in this article. It you flip the BZ chart upside down and eliminate the overall decline in amplitude with time, you will see a pattern almost identical to the global temperature chart. The temperature chart shows five almost identical cycles in which temperature slowly falls to a lower limit and then abruptly climbs back up to an upper limit. If that isn’t a bounded chaotic system at work, I’ve never seen one. That chart also tells you we are almost certainly now on the back side of the next slippery slope into an next Ice Age.
Just a thought – If man could influence the Peruvian deep cold upwelling – amplifying it to help form a La Nina, or dampening in to provoke an El Nino – then it seems it would change local climates.
Please keep all researchers and scientists away from the Peruvian coast – not a good place for large-scale experimentation! I’d hate for someone to drop a few hundred tons of salt into the ocean off of the Peruvian coast to see what would happen!
One thing I remember about Lyapunov stability in post grad NL dynamics was that even if you cannot find a Lyapunov candidate (proof of global stability), that does not mean that the system is unstable.
I second the ‘interesting’ and ‘fascinating’ compliments.
The mathematician David Garcia, (“Casting Paradox out of Cantor’s Paradise”) in an effort to cram into me a greater understanding of things chaotic, was clear on the difference between being chaotic and being completely unpredictable. Phil’s parsing of the meaning was helpful and should not be forgotton as the analysis unfolds.
Garcia’s view was that what looks like chaos is only a lower level of order. If one scales up or down something that looks very tidy and ‘mathematical’ it may suddenly appear to be chaotic to someone who does not understand the order(s) that drive it.
Thus we have the word ‘ergodic’ to describe systems that, like climate, appear to be chaotic when viewed in ignorance but which exhibit many predictable ‘self-correcting’ macro features.
The Free Dictionary Sez:
“Adj. 1. ergodic – positive recurrent aperiodic state of stochastic systems; tending in probability to a limiting form that is independent of the initial conditions.”
Trasnslation: however you start or perturb the system, you usually end up with pretty much the same result.
With reference to the climate, my understanding is it means ‘specifically unpredictable at any time or place, but generally predictable as to limits, given parameters A-Z’.
There is a great deal of prima facie evidence that the climate is chaotic and a good deal more that it is ergodic, i.e. essentially predictable.
People seem latch onto the word ‘chaotic’, over-react and infer it means ‘un-understandable’. Contrapuntally some scientists of less philosophical bent assume that all systems are inherently understandable of there is enough information processed on a large enough computer. The third way is that things can be driven by chaotic events and give generally predictable results.
David’s ‘orders of order’ approach is better. As one observes at smaller and smaller scales, drivers start to appear chaotic. Underlying this apparent chaos is a lower level or order, which if examined ever more closely, exhibits chaotic appearances at its roots, which further ingestigation will reveal is really the manifestation of a lower level of order, and so on.
The example given, the BZ reaction, is ergodic. No particular molecule is specifically predictable at any given moment, but the system as a whole, being ergodic, can be described without having each and every atom positioned and its states known.
Physicists will happily tell you they already think like that because that is the way of the ultra-small world. Fine. Now scale it up. Suppose there are very large things like the planet’s climate that have components which are still very large and look chaotic. That is also fine, and true, but not the whole story.
As Phil has shown above, appearing chaotic at a large scale does not rule out its being ergodic at an even larger scale.
This is so much better than “settled science”.
It may be interesting if you also study the fractal dimension of that figures
Lucy has long suspected harmonic resonances; Geoff has made practical use of rock textures which now seem to illustrate the points made in this posting.
On the 1st of June 1565, Andres Urdaneta, charged with finding a sailable route from the Phillippines to Mexico and suspecting a “gyre” of wind and current in the Pacific like the one already known in the Atlantic, sailed north from Cebu, caught the easterlies and arrived in Acapulco on the 8th of October. The Pacific became a “Spanish lake” for 250 years. The log books of the galleons must contain a history of ENSO.
Wave form analysis should be a useful tool in studying the rates of inter-dependent, competing processes.
polistra says:
January 25, 2011 at 6:36 am
Here, again, the ruler is….Do you know what Circadian rhythms are all about?
Could you say why your heart is inclined to one side?. See, everything is out there, except our intelligence?
Great essay Phil. I plotted the HadCRUT delta t’s here, which look amazingly like your figure 7 (a).
The idea of the positive feedback loop that you describe is useful for demonstrating how an instability of the system might arise.
But it does not really explain the oscillations.
An interesting mechanism that generates oscillations is negative feedback, combined with a time delay.
A good example of this is the temperature in the shower. At first the water is cold so you turn it up. It’s still cold so you turn it up some more. Eventually the hot water gets through and then it’s too hot so you turn it down a bit, but because of the delay with the water travelling down the pipe there’s no immediate effect so you turn it down some more, and so on.
A bit of googling finds a paper by C Wang “On the ENSO mechanisms” that talks about this delayed-negative-feedback mechnism for the oscillation.
Bravo! Amazing post.
I would only add the Dansgaard-Oeschger events and the AMO to the list of these potential nonlinear oscillators.
But wow, thanks for this…much food for thought…a feast!
jack morrow says:
January 25, 2011 at 7:10 am
This is so much better than “settled science”.
Wouldn’t it be better to say, instead, it is surprisingly “unsettled”, as far as “post-normal-scientists” are unable to grasp, by far much more simple, universal laws.
They say it’s cool…and as unpredictable as a southern seas’ hip waving dancing, in order to justify Jerome Ravetz’ s “Precautionary principle”, which translated means: you’ll gonna pay more for everything buddy!…..just because WE are the ones!
Delineating chaos?
It’s given me too much to think about while I’m at work…….I’ll re-read when I get home, but thanks. Good post.
This is a great post! Thanks.
Climate Science is much to important for leaving it to the Climate Scientists that is in “AGW mode”.
Their minds are sort of frozen it time. It happened back around 1970.
It is much like music; You like the music that was popular when you were a teenager.
Nonlinear biomass albedo feedback
Biomass provides further complex nonlinear feedback mechanisms through albedo, humidity, clouds, and CO2.
As the Sahara moistens/dries out, biomass grows/recedes, with corresponding impacts on ground albedo, humidity, and cloud albedo. Those factors in turn change the atmospheric and ocean climatic feedbacks.
The annual northern hemisphere biomass growth/die off provides a clear signal in the global CO2 concentration.
Ocean biomass similarly changes the absorptivity/albedo of the ocean, with corresponding changes in temperature, humidity, clouds and CO2. On ocean productivity:
As one example of these complex interactions, Rising ocean temperature reduces planckton’s CO2 absorption
So, how goes the modeling of the suns cycles, some chance they are very long.
Ah, but there is that word, so small, yet so much of a chance it is important.
One thought along the lines of the periodic forcing on the ENSO system involved the North Atlantic down welling. The currently warm North Atlantic decreases the overall down welling of very cold water to the subsurface currents. It takes about 2,000 years for this cold water to then rise up in the Pacific ocean.
Variation in each of the three major locations of cold water downwelling (Norway, Greenland and Antarctic) could be part of the periodic forcing 1,000-2,000 years from now.
Such an long term feedback oscillation would certainly make long term forecasting of the ENSO difficult, but such a long term feedback is certainly possible.
Any period of strong deep water current creation would put a “wave” of increased cold water in the pipe. The reverse decreased “wave” would be happening now, especially from the North Atlantic near Greenland.
Proving such a long term feedback loop would certainly be a start at gaining the proper perspective on the Earth’s climate system.
John Kehr
Great article!
I don’t think one can get very far with understanding weather / climate systems without bumping up against chaos theory and its components along the way.
What I’ve read about it so far left me feeling that the authors were just making it up as they go along, like Elliot Waves in the financial markets, but this article puts a lot of the stuff into perspective.
It’s nice to see the work that Bob Tisdale has done to date reinforced, and there’s also some good insights here in their own right.
Thank you Phil, and thank you Anthony
Rather OT, but these words from Matthias Bertram, quoted by Phil Salmon above, sound almost like a description of the defining principle of living matter: “exporting entropy”!
Spherical harmonics?
http://en.wikipedia.org/wiki/File:Spherical_harmonics.png
http://en.wikipedia.org/wiki/Spherical_harmonics
great post – in the top five for WUWT!
The next task is to organize the proxy data across the Pacific to characterize the attractors better. ( There is a lot of data for fisheries in the Eastern Pacific going back several thousands of years. )
Thank you for this amazing article, Phil!
It is another beautiful instance of how WUWT is like a online university – so thank you, Anthony, as well.
I leave the mathematical comments to those who know way more about this than I do – but the visual connection you drew between Bob Tisdale’s animated temperature charts and the Belousov-Zhabotinsky oscillations underlines for me that scientists can find such apparently unconnected similarities – and, if they’re good, start enquiring from there.
It’s the ‘hm … now I wonder …’ moment we hopefully all had at one stage or another. And thus new questions get asked and new relationships can be discovered.
That is what drew me to science, that is what I love about it.
So – thanks again, everybody!
I’ve been interested in chaos theory since reading Mandlebrot’s excellent book on the subject. My initial reaction was one of amazement that these patterns can form. One of the simplest is an arithmetic iteration where you can select different ‘forcings’ by changing the coefficient. The result are a series of numbers that repeat, but here’s the interesting bit – when the forcing is small you get 2 numbers, essentially a bifurcation. As you increase it you get more and more different numbers that all repeat like a mathematical pattern.
That said, I despair when climate scientists scratch their heads trying to find variations in forcings to account for climate changes, when chaos theory shows that you can have changes with a constant forcing. I would bet that the PDO and AMO are manifestations of strange attractors which don’t require changes in external forcings to account for them. The next question is can we go further and assign the 900 year warming/cooling periods to a strange attactor operating over even longer timescales?
I think this presentation has the potential to advance our understanding considerably. Thanks Phil, and plaudits for the detail and references you have brought to the story – one big job! There seem to be several cycles, from lunar through sunspot to longer term. You (and the PDO) relate mainly to the 60 years cycle but there is also the Jose cycle (179 years) that seems fairly regular, and the deep grand minimum (DGM) solar cycle (364 years?), and probably a near 1100 year cycle. Any way, addressing the weak and strong forcings. when the 60 and 179 year cycle are in phase at maxima or minima, there should be a strong forcing. When the DGM is there also there should be a very strong forcing. This is probably what happened during the Maunder Minimum, which was also at the bottom of the 1100 year cycle. Unfortunately, we don’t know what El Ninos and La Ninas were like back then. It is not unlikely that we are now going into near simultaneous bottoms of the 60 year, Jose and DGM cycles reaching max. cold about 2035-2040, (I’m with Joe Bastardi on the prolonged cooling), but nearer the top than the bottom of the 1100 year cycle, so not like the Maunder. However, compared to the 1976-2006 half cycle, we may be in for an 80 year long cool period, with the 1930s being seriously cold. See http://www.agwnot.blogspot.com/ for a more speculative take.
One more point – turn Fig 1B upside down and it is reminiscent of the last several 100k years of glacial/interglacial oscillations.
Thanks for a very interesting read. Great post and comments.
As usual some very clever people here.
No doubt Prof Paul Nurse will comment later.
Good post another wow moment
I’m not very good with names but a russian scientist discovered this oscillante/pattern process accidently and was (as usual) laughed out of court. He finally committed suicide. It was during the cold war so the info never got out. Turin kicked it off through his study of animal skin patterning eg Giraffe and Zebra. Turin actually defined some equations which when run in a computer showed the same oscillante patterns. He too was eventually driven to suicide and this work died with him. The russian and Turin were of the same era but never knew of each other’s work.
Re: jtom says:
January 25, 2011 at 6:53 am
“Please keep all researchers and scientists away from the Peruvian coast – not a good place for large-scale experimentation! I’d hate for someone to drop a few hundred tons of salt into the ocean off of the Peruvian coast to see what would happen!”
If you’d ever been involved in a really big, government funded, large-scale experiment, you wouldn’t worry about this one. By the time they’d overrun their entire budget several times over, you might find one lonely dump-truck load of salt sitting on the Peruvian beach, but none in the ocean. The combined weight of the attendant, published research papers would outweigh that forlorn little pile of salt.
APACHEWHOKNOWS sorry, but the handle reminds me of another way to forecast climate:
It’s late fall and the Indians on a remote reservation in South Dakota asked their new chief if the coming winter was going to be cold or mild.
Since he was a chief in a modern society, he had never been taught the old secrets. When he looked at the sky, he couldn’t tell what the winter was going to be like.
Nevertheless, to be on the safe side, he told his tribe that the winter was indeed going to be cold and that the members of the village should collect firewood to be prepared.
But, being a practical leader, after several days, he got an idea. He went to the phone booth, called the National Weather Service and asked, ‘Is the coming winter going to be cold?’
‘It looks like this winter is going to be quite cold,’ the meteorologist at the weather service responded.
So the chief went back to his people and told them to collect even more firewood in order to be prepared.
A week later, he called the National Weather Service again. ‘Does it still look like it is going to be a very cold winter?’
‘Yes,’ the man at National Weather Service again replied, ‘it’s going to be a very cold winter.’
The chief again went back to his people and ordered them to collect every scrap of firewood they could find.
Two weeks later, the chief called the National Weather Service again. ‘Are you absolutely sure that the winter is going to be very cold?’
‘Absolutely,’ the man replied. ‘It’s looking more and more like it is going to be one of the coldest winters we’ve ever seen.’
‘How can you be so sure?’ the chief asked.
The weatherman replied, ‘The Indians are collecting a shitload of firewood’
I think that to invoke chaos might be just the same as giving up,it is just chaos.the patterns of enso/pdo are interesting and it will be important to see how they develop with world temperatures in the coming years with regard to co2 concentration in the atmosphere and solar activity.
Bravo Antony. That’s exactly along the lines I was suggesting
In the global circulation patterns you will find the greatest strange attractor to be the Moon and its combination of tidal forces felt on the Earth, from the further modulation of solar electromagnetic effects, by the tidal and gravitational inner actions of the inner planets, at a period known as the Saros cycle of 18.03 years. (minus 27.3 days to get an even number [240] of cycles of the 27.3 day pattern of the magnetic rotation of the sun that drives the moon’s declinational position on the ecliptic in sync.)
IF you take three past cycles of this period and over lay the effects on the global circulation you will see three repeating patterns that are about ~80% predictive of the conditions of the next cycle. Which I think shows there is a predictable effect of the repeating drivers of the ocean oscillations, once you realize it is the moon, and look at the forces at work, watch animations of the GOES satellites showing the passage of the moon over lines of thunderstorms, surges in growth in hurricane intensity, most noticeable in their early formations.
In fact I have taken the past weather data for the USA and presented the composite maps as forecasts for the past three years and the next three years. The forecast for today [generated with a three year lead time], looks about like the daily total composite radar.
IF this cyclic repeating pattern of weather can forecast the next cycle (Today) now can you not think that there is something else than CO2 to look at? Lot more details in the research section of the site.
Murray Duffin says:
January 25, 2011 at 10:33 am
One more point – turn Fig 1B upside down and it is reminiscent of the last several 100k years of glacial/interglacial oscillations.
My thoughts exactly! Interesting times we live in.
I have a question about the ENSO cycle that is fueled by thinking about the recent post on the trends of the last 10-12 years, but that thread is exhausted so I’ll post the question here, and hope it’s meaningful.
My understanding of the ENSO cycle is that in many respects the underlying physics is the opposite of what seems to be the case. In other words, during a La Nina event, although the surface ocean temps cool dramatically and this leads to cooling of global atmospheric temperatures, what is actually going on is that the tropical sun is warming the surface waters and evaporating them, leading to higher saline content and a sinking of these warmer yet heavier waters into a subsurface zone that stays there for years. So the La Nina event is actually a “warming event”, from the ocean’s point of view, even if it appears to be cooling event.
Likewise, the El Nino warming events are actually a cooling process from the ocean’s point of view, in that the warmer, sunken heat from the La Nina event finally surfaces and produces higher than normal surface temps which then heat up the atmosphere until the heat is finally dissipated. Hence, the atmospheric warming is actually part of a cooling event, and this cycle then leads back to another La Nina event that produces cooling of the atmosphere, but warming of the ocean beneath the surface.
So my question is about how this process works over many cycles to either warm or cool the general climate. I’m curious as to whether the huge 1998 El Nino was as much responsible for the climate moving to a higher temperature level as the longer La Nina event that followed it. And also, if in some respects it would lower temps for the La Nina events to become less powerful or at least shorter in duration, so that less heat becomes stored in the sub-surface ocean to emerge later as a surface warming event.
Basically, I’m asking for more detail on how this system actually works during a general climate cooling cycle. Some say that stronger La Nina events will lead to a cooling climate, but shouldn’t the opposite be the case in the long run? I guess I’m a little confused as to how this works, and what to look for as a sign of a cooling climate cycle ahead.
Maybe we should be using some kind of speech recognition software to find out what language nature is using and what she is trying to tell us. Our present climate models are not Rosetta stones.
Great article!
I just hope this doesn’t drag too many dancing off into never land. I have never viewed the earth’s climate system as chaotic. Now “infinitely complex”, that I buy. Chaos as I read has no limits but this world has all kinds of limits, it is limited by diffusibility, thermal conductivity, inertia, momentum, acceleration, specific heats, and on and on and on. But can you see very similar effects within the climate, absolutely. The visuals in this article are fantastic.
But I have to still to feel that what we see is hundreds of coupled equations of cause and effect, many times interconnected and recursive across three or more cause and effect links and all having limits placed on them by physics, the physical limits, to how fast they can proceed in reality and these loops within the graph (mathematical graph that is with nodes and links) that makes it appear chaotic with endless patterns. That’s just my view.
I have to say though that mathematics in the realm of chaos may very well give us the best approximations that mimic these processes and should be pursued. It may be the only real way we can even approach a mathematical solution for in reality it is simply too complex for computers today, we can only approximate.
But still, this was a great article Phil. Opens your mind.
In the discussion about forcing and whether or not the period was weakly or strongly locked there was an implicit assumption that the forcing was periodic. However it not impossible (and indeed quite likely) that the forcing itself is only weakly periodic. The world weather system is probably best described as a series of linked chaotic oscillators.
Good stuff. Will need some time to digest.
polistra says: January 25, 2011 at 6:36 am “There’s a much less obscure example of a nonlinear oscillator, much easier to observe and experiment on. The human heart. ”
For some years I’ve had a mental image of climate fluctuations not just as a heart, but as a body, which has other repetitive cycles such as respiration. Each can, in theory, be varied independent of the other, but OTOH some factors like exertion can cause both to change together. Then there are other variables like adrenalin production, the ATP cycle .. probably the list is long. The difficulty is to isolate the behaviour of one pulsating element from the confounding effects of the others, which can sometimes give the appearance of a resonance (hence records get set).
The BZ example with changing colours remins me of two effects, which we can use here by example of easy things for chemists, being pH and oxidation state. I’m not at all saying these are the actuals, just examples. Both pH and degree of oxidation can be changed (in theory) independently. Both can change the colour of solutions. But they can also act together. When they act together, I think of the predator-prey mathematics, which in some circumstances might tip a happy pH out and put in a happy oxidation state. Then vice versa. Hence the oscillation.
This is a verbal description to help understand the way things appear. I do not pretend that it is verifiable by easy mathematics.
Another topic above is self-replication. There is a lovely example from nature, the “broc-cauli” or Brassica romanesque. The whole resembles the shape of its parts, which are placed in a non-random order. The parts of a sub-part resemble a sub-part, and so on until botanical noise takes over and the detail is lost.
It’s worth a look at http://en.wikipedia.org/wiki/Romanesco_broccoli
I sometimes think not all La Ninas are true La Ninas but merely a cooling of the tropical pacific waters following an El Nino event.
The graphic above of the 1998-9 La Nina(Fig 4) shows the tropical waters cooling FROM the WEST.
The current La Nina emerged from the EAST and travelled WEST as we’d expect would happen with cool upwelling waters along the Peruvian coast.
The current La Nina is also accompanied by much cooler sub-surface waters, up to 4DegC according to the Oz BoM
Looking at the sea level chart on the WUWT ENSO page the 98-9 La Nina associated sea level drop wasn’t exceptional, the lower limit was still higher than the 1997 lower limit.
However, the current sea level drop associated with this La Nina is more substantial and still dropping.
These lead me to believe that not all La Ninas are true La Ninas even though the indices may suggest they are.
There’ll be a clue in the changing lengths of the PDO cycle from around 30-60 years, and the distribution of Los Ninos and Las Ninas therein, with the sun somehow forcing, whether it be magnetically, electrically, with albedo functions or with cosmic rays or Erl’s sultry ultryviolet ones. I still think the stability of these two flipped phenomena must ameliorate the hypersensitivity which might accrue from whatever solar mechanisms are most active.
=========
This is a nice, graphical layman’s introduction to the labyrinth of nonlinear, equilibrium-seeking systems. The idea of ENSO as a nolinear oscillator, of course, has been bandied about for many years. What makes ENSO so fascinating, however, is that the idea does not pan out dynamically without specifying a forcing of the subdecadal oscillations that persistently characterize the phenomenon, which is a leading indicator for global temperatures in that spectral range. What really drives ENSO thus is as much a mystery at present (up through Dijkstra’s 2005 monograph) as ever.
It is far easier to determine what does NOT. Certainly Milankovitch cycles, measured in tens of thousands of years, can be ruled out; thousand-order harmonics make no sense on physical grounds. Thermodynamics at terrestrial temperatures has not demonstrated any resonance, eliminating strong subharmonics from consideration. The multidecadal signal components of ENSO3.4 are, at any rate, minor in magnitude and virtually incoherent with global temperatures. Thermohaline circulation is not a factor in the iconic upwelling off the coast of Peru, which is driven by wind-stresses rather than density. And true positive feedback–as opposed to energy recirculation, with which it it often confused–runs afoul of Lyapunov stabilty. Thus we are left with speculation based on qualitative similarities of some features of time series, rather than with quantitative science.
Thank you all, I have read the article and the posts a couple of times. I will never understand the math but I like the questions and the fact that they lead to more questions which may increase our understanding of what is going on. I have a question to add. Does anyone understand the ocean circulation in three dimensions? I see a lot about gyres and connection with the winds. I see people talking about upwelling and down welling but I also know that the old “conveyor belt” theory was shown to be be misunderstood once neutral buoyancy floats were used to track the deep currents and they were found to be diffuse (ignoring the complexity and probable errors in the tracking system). Basically I see a lot of assumptions being made as you can’t start off from first principles. You need a starting point to create a hypothesis, but how do you know the hypothesis is correct? We are learning that so much of what were taught in University and in business was based on flawed research. Yet things worked. I recall feeling really good about getting 90% on one of my differential equation and vector analysis exams … until I thought about it and realized that if 10% of the bridges one of my fellow engineers designed fell down, this would not be good. Bridges need to stand up 100% of the time. (They don’t, but that is another story.)
It took me hours to read, re-read and think about the last few posts here.
A lot of good thoughts and I suspect in 30 or 40 years we will have a much better understanding of how our world works. In the mean time, we will keep applying reasonable safety factors to make sure those bridges you drive over stand up, even though we may not always know why.
A bientot.
Great article.
I got the impression that Mr. Watts is a little suspect of “chaos” as a branch of anything scientific, and I tend to agree. Chaos is an anthropomorphic construct
of a situation that we either are too stupid to understand or don’t have all the facts on, or both. I doubt that God ever uses the word.
“However beyond an intriguing qualitative visual similarity, what basis is there for proposing that the ENSO could constitute the same type of nonlinear oscillator as the BZ reaction?…”
Probably none.
It’s an interesting article.
It has crossed my mind that ENSO and other ocean “oscillations” might be chaotic. It has provably occurred to others.
However these assertions should be checked
———
1. The global circulation models (GCMs) are essentially linear.
2. That presumably is why they generally fail to reproduce the ENSO and PDO.
3. (If they show any nonlinear behaviour it is probably more by accident than design.)
I suspect they are not correct.
PaulM says:
January 25, 2011 at 7:28 am
The idea of the positive feedback loop that you describe is useful for demonstrating how an instability of the system might arise.
But it does not really explain the oscillations.
An interesting mechanism that generates oscillations is negative feedback, combined with a time delay.
Requires both negative and positive feedback with a time delay.
If you look at the annual rainfall for Sydney Australia, you will see a very chaotic pattern.
There are large spikes upwards every 20, 40 or 60 years or so.
In between the rainfall declines in a zigzag pattern.
The long term trend since 1859 has been flat (R squared 0.0001).
There are two basic chaotic patterns, according to Hurst.
Sydney rain is chaotic of the type – “mean reversion” as opposed to “random walking”.
That is typified by a generally spiky shape – one year up, the next down.
(Hurst number close to zero, on a zero to one scale, 0.5 being Brownian motion).
In Australia, annual maximum average temperature tends to vary with rainfall, except when boosted by UHI.
Sydney is a prime example.
stephen richards says:
January 25, 2011 at 11:43 am
I’m not very good with names but a russian scientist discovered this oscillante/pattern process accidently and was (as usual) laughed out of court. He finally committed suicide. It was during the cold war so the info never got out. Turin kicked it off through his study of animal skin patterning eg Giraffe and Zebra. Turin actually defined some equations which when run in a computer showed the same oscillante patterns. He too was eventually driven to suicide and this work died with him. The russian and Turin were of the same era but never knew of each other’s work.
That was Turing of course, Prigogine saw one of Turing’s lectures on the topic and it has been said that he owed his ’77 Nobel to Turing. Turing’s work didn’t die with him I teach his reaction-diffusion mechanisms in one of my classes for example.
Phil. says:
January 25, 2011 at 10:51 pm
PaulM says:
January 25, 2011 at 7:28 am
Nope, sorry.
http://www.electronics-tutorials.ws/oscillator/oscillators.html
Note that “in-phase” feedback with a plus is the same as “out of phase” feedback with a minus.
Mark
Indeed, indeed! One tires of reading qvetches about how small are the TSI changes, how noisy the GCR/temperature link, etc. But there’s something happening here …
One of Joe’s more interesting segments evah! Note also that he sez this La Nina’s second year is likely to be howlin’ cold — and then the subsequent El Ninos get even colder (centered on SE USA).
Ted Turner will be wimpering in Atlanta. Judith won’t be too happy, either!
This is all quite superb thinking and pattern-spotting.
As for a label, how about the NEPS acronym: “Non-Equilibrium/nonlinear Pattern Systems”?
Puts me in mind of some of the “Constructal Law” thinking. Even the IEEE is getting in on it:
http://www.constructal.org/img/ieee_comp_and_pack_cover_fig8.png
Of course writing this :
A note on reading the literature on chaos and non-equilibrium pattern dynamics. Only pay minimal attention to the text and even less to the maths. Just look at the pictures.
in a post dedicated in non linear dynamics is not a good beginning and is bound to lead to misconceptions .
The pictures of a tenis ball and of the sun look strikingly similar yet there is no nuclear fusion going on in the tenis ball 🙂
In summary I would say :
1) Yes , ENSO and all pseudo periodical climatic structures are chaotic
2) No , this has nothing to do at all with the Lorenz or Rossler attractor
To develop the arguments it is necessary to use and understand some mathematical concepts . Sorry but it is not more possible to understand non linear dynamics without maths than to understand quantum mechanics without maths .
1)
To the first argument , there is this paper (chosen among dozens of papers dealing with the same matter) : http://www.environment.harvard.edu/docs/faculty_pubs/tziperman_chaos.pdf
Basically the authors conclude : An analysis of a time series from an ENSO prediction model is consistent with the low-order chaos mechanism
The term to be stressed is the low-order and deserves some development .
The temporal chaos theory , non linear dynamics , low-order chaos (all these terms are synonymous) studies the time evolution of a system in a low-dimensional phase space .
The phase space is a space where the system states are represented by a point whose coordinates are the dynamical variables . So it is an abstract structure which has nothing to do with the usual space we all know .
For instance the Lorenz system has 3 independent variables so its phase space has the dimension of 3 (it is just a coincidence that it is the same dimension like the usual space) .
The phase space of ENSO (see linked paper) has a dimension smaller than 8 what means that the number of independent variables driving its dynamics is smaller than 8 hence the term “low dimensional chaos” even if its dimension is much greater than the Lorenz system .
Caveat : the chaos theory allows to estimate how long a time series must be to get a robust estimate of the dimension of the phase space as well as of the attractors (if they exist) .
The 100 years of data for ENSO is shorter than the necessary length so the estimation is not very robust . It is a strong suggestion but not a certainty . We will need a couple of centuries more of data to get a robust answer .
2)
Why ENSO , even if it is chaotic what it is with a high probability , has nothing to do with Lorenz or any other popular attractor ?
Well an attractor is a subspace of the phase space . So it is something that you will never see because it doesn’t happen in the ordinary space .
The dimension of the Lorenz attractor is a number between 1 and 2 .
So it is more than a “curve” but less than a “surface” .
That’s why it is called fractal or strange .
Moreover all these attractors strange or not , happen in a finite dimensional phase space as already explained in 1) above .
But what is the phase space of any real oceanic oscillation ?
Well as this oscillation is an evolution of a spatial structure in time , or in other words an evolution of the field f(x,y,z,t) , the phase space is infinite dimensional .
It is easy to understand intuitively why – there is an infinity of points (x,y,z) and each of these points oscillates .
The spatial structure known as ENSO is the spatial result of an interaction of an infinity of oscillators (one in each point) .
This is called spatio-temporal chaos and is completely different from the temporal (Lorenzian) chaos .
More specifically there are no attractors in spatio-temporal chaos (how could one define or make a “picture” of an infinite dimensional structure ?) . Also almost none of the results of the temporal chaos theory transport to the spatio-temporal domain .
That’s why the Lorenz attractor , a child of finite dimensional dynamics dependent on time only has nothing to do with ENSO , a child of infinite dimensional spatio-temporal chaos .
Those who have followed the arguments as far as here will certainly be able now to point out an apparent contradiction between what I wrote in 1 and what I wrote in 2 .
Indeed in 1 I have written that ENSO was a low dimensional temporal chaos while in 2 I have written that ENSO was an infinite dimensional spatio-temporal chaos which had nothing to do with temporal chaos .
As the explanation of why this is not really a contradiction allows a rather deep insight in the spatio-temporal chaos , I will do it right away .
We have seen that the main difficulty of spatio-temporal chaos is its infinite dimensionality due to the dependence on spatial coordinates .
The ordinary temporal chaos theory can only deal with finite dimensional phase spaces .
So clearly one can try to get a finite phase space dimension by discretizing the continuous space .
By cutting up the space in a finite number of grids and nodes , the number of oscillators becomes now finite (instead of an infinite number of points we get a finite number of nodes) and hence the phase space is now finite too .
The good old temporal chaos theory can now be applied on this new system of N coupled oscillators .
And what one hopes is that this approximation will give results that will not be too far from the results that would be given by a true spatio-temporal chaos theory which doesn’t exist yet and won’t probably exist for decades .
This paper : http://amath.colorado.edu/faculty/juanga/Papers/PhysRevLett_96_254103.pdf shows how it works in reality .
So now you also understand what the authors of the paper in 1 really did – they discretized the space .
Admittedly they discretized it rather dramatically because they reduced this huge thousands km by thousands km area to a single number , namely the average sea surface temperature which then depends only on time and no more on space .
So if one admits that this single number still contains traces of the real infinite dimensional spatio-temporal chaos , one may look for them with classical temporal chaos tools .
It is similar to an even more dramatical discretization that all climate “scientists” do when they reduce the area of the whole Earth to a single number – average global temperature .
However if somebody said that this extreme discretization is a rather brutal way to rape the subtle spatially correlated data and that it could potentially destroy the important signals , I would have to agree .
Thanks for all the positive and helpful feedback and criticism. Makes the enterprise seem worthwhile. No time now to address all the issues, just a random sample:
Mike Haseler says:
January 25, 2011 at 3:24 am
Your point about 1/f noise and its fractal nature is useful. One of the characteristics of a nonequilibrium pattern system is what is called “log-log” power law distribution – which amounts to what you explained – it looks similar in the large scale as the small scale. The book “Deep Simplicity” by John Gribben, Random House NY, explains this well.
Murray Duffin says:
January 25, 2011 at 10:29 am
Thanks for your suggestions about possible forcing periodicities.
Bob Tisdale says:
January 25, 2011 at 3:54 am
The “sloshing” of warm west Pacific water eastwards in an el Nino is presumably linked to the weakened trade winds – so my overall approximate scheme survives? Thanks for the clarification about PDO and PDV, I had seen the terms but was not clear what PDV was.
PaulM says:
January 25, 2011 at 7:28 am
Yes negative feedback is an important aspect of nonlinear systems. It goes alternatively by the names of dissipation or friction or damping. This “friction” indeed generated emergent complex pattern, while a dominance of positive only feedback tends to establish monotonous regular oscillation. So negative and positive feedback are in a sort of balance. Someone correctly mentioned the heartbeat as an example of a nonlinear oscillator. This is one dominated by positive feedbacks, thus – fortunately for most of us – it is regular (I wouldnt like to experience an ECG like the ENSO time plot!) Matthias Bertram in his thesis goes on to study the Pt-catalysed oxidation of CO as an example of the role of feedback – if you download his thesis from the link provided (8MB) and read this section it should be helpful. Thanks.
wayne says:
January 25, 2011 at 2:34 pm
Thanks for the positive comments. I tried to explain in the intro that it was not chaos per se but the border region before chaos where the nonlinear complex pattern formation emerges.
TomVonk says:
January 26, 2011 at 4:30 am
This is exactly the expert input I was hoping to attract – even if critical. OK the ENSO attractor is multidimensional, fractal and thus strange. However presumably one can choose how many dimensions to look at and study. If one chooses just 2-3 then maybe a Lorenz attractor can be an approximation or starting point.
Thanks again for all responses, I’ll return soon when I have time,
Phil Salmon
(“phlogiston”)
This makes iceages and other extreme events more understandable. So much change with so little drivers. I’ve always had trouble understanding how such large changes can occure. We need more discussion down this path.
Thank you for this fascinating and important article. It really does seem clear that the current Climate is determined by which attractor the weather is orbiting right now, and the future Climate by which other attractor the weather will shift to next. It also seems really clear there are two groups of attractors – Glacial and Inter-glacial. It also seems clear that Climate models developed without this insight will not be useful predictors of Climate, and further it is entirely possible that no model will be useful in that way.
TomVonk says:
January 26, 2011 at 4:30 am
“It is similar to an even more dramatical discretization that all climate “scientists” do when they reduce the area of the whole Earth to a single number – average global temperature .
However if somebody said that this extreme discretization is a rather brutal way to rape the subtle spatially correlated data and that it could potentially destroy the important signals , I would have to agree .”
It is not only brutal, but senseless. In studying the cross-regional coherence of the multidecadal signal components of temperature series, I find not only diminution with distance, but occasional phase-reversals as well as rather abrupt curtailments. This is consistent with the widely-noted inconsistent global effects of ENSO. GST is indeed an unscientific way of characterizing the chaotic thermalization and flux of solar energy through the climate system.
Fascinating post. Thank you for your time and effort in putting it together. Well done!
Anthony –
I was going to post this as a comment on your excellent ENSO piece, but the darned thing grew too big and I thought I’d send it here instead. Apologies if this is outside what you intended your email for.
To begin:
Anthony –
To be honest, I would have thought all this is pretty obvious. I had not heard of B-Z reactions, but it is clear that this oscillation from a one state to another state occurs. Thanks for giving me a name for it.
I’ve been asking here for quite a while if anyone could point me to ANY explanation of what causes the ENSO oscillations. Every online source just talks about ENSO as if it is a primary forcing/causative agent, and none of them talk about what causes IT.
Your and Bob’s description here is essentially what I was trying to put into words, without me knowing of the existence of the B-Z reaction. I could see in Bob’s graphics of the ENSO exactly what you described. But you two are able put it all in scientific terms and with a higher level of understanding.
To me talking about “averages” in a dynamic system is massively oversimplifying the system, dumbing it all down. Converging all that is going on at one moment into one temperature data point is ludicrous for understanding because “the devil is in the details” – i.e., the more local events/effects/values. I have always seen Standard Deviation as the two averages that together can be combined to make up an overall average, but the real goodies are in the high and low and what oscillations are going on around those two values. That seems to be essentially what the B-Z reaction deals with – the oscillations around two states, the wings of the Lorenz “attractor” – the higher SD and the lower SD. For some reason this seems obvious.
And in my questioning of the ENSO’s cause, my mind – like yours and Bob’s – went to upwellings of deep cold waters and some mechanism in the system that allowed the upwellings to occur in an oscillatory manner. And, conversely, to “put a lid on it.” The heat – or lack of it – for El Niño and La Niña – had to come from somewhere, and the only source of heat/cold was down below. Thus it had to either be a separate heat/cold source that itself was oscillating, or it had to be a submerging of heat/cold that was oscillating. (I toyed with the idea of heat input from sea vents, but then I would have to explain why the output of those oscillated, and there just isn’t anything known about them at the present. But they are adding heat to the system, and the amount is not known at present. I presently doubt this amount is significant, but will keep an eye on it.)
I looked at ENSO as a resonance – that the system was going in and out of resonance. Audible resonance and mechanical/vibratory resonance – if too much energy is being put into the system – will overshoot and drop out of resonance, dropping the state to chaos and back the starting point again (more or less). I do not know the names for any of it, but it happens. When the resonance occurs each time, it is as if the system organizes momentarily, but the overloading of input energy means it can’t maintain that state for long.
I am very pleased that you and Bob have gone in this direction (as if you cared specifically for my vote!…LOL). I believe there is a paper in this for you two.
I am also very happy to see you mention the PDO in this, too, because IMHO it is a longer-period version of the same kind of system. I would suggest that rather than being the wings of the Lorenz “butterfly” attractor, that it might stand alone. I suggest this because it is possible that at the latitudes of the PDO the energy input is also present – but of a lower magnitude. This would suggest longer periods of oscillation, which is what we see. Also, the Mid-Latitude Cells might be the direct output mechanism for the PDO as opposed to the Hadley Cells and the Intertropical Convergence Zone with ENSO. I believe the two B-Z systems can be somewhat independent.
…As a last mention, I would suggest a look at the very similar effects of “cymatics” which is the study of sound vibrations and the patterns they form on Chladni plates – thin vibrating surfaces. They look VERY MUCH like Bertram’s patterns. And I believe the two are related. Slight variations in sound frequencies or energy input make quite a change in the patterns, similar to the forced samples of Bertram. Light and sound are all EM frequencies, after all. Thus far cymatics has not looked at the effects in a dynamic system, however. That would open up all kinds of new avenues of exploration. (There are also implications for atomic theory and possibly even cosmological theory, IMHO.) My understanding is that it all has to do with local energy states and nodes. It might be worth noting that the patterns in cymatics tend to “stay put,” with only brief transition states. The “system” wants, it seems, to be at some more organized state. This might well be an important feature – that chaos isn’t necessarily the norm. Weather – the small-scale version of climate – seems to always actually be more or less organized, with highs and lows and trade winds, etc. A starting point: http://tiny.cc/2f0nw.
Looking at averages, like climatologists do, is missing the dynamism in the system, trying to simplify it – apparently because that is all the level they can deal with at our present stage of knowledge and present capacity to understand complexity. I can’t blame them for wanting to, to see what it tells them – but then they should acknowledge that it is probably oversimplifying things and that we shouldn’t read too much into the “averages.” Averaging water things down. That should be obvious. But it is the exact details of what is going on that allows us to move forward in our understanding. Averages can’t do that.
Sorry for the length of this comment…
TomVonk says:
January 26, 2011 at 4:30 am
Of course writing this :
“A note on reading the literature on chaos and non-equilibrium pattern dynamics. Only pay minimal attention to the text and even less to the maths. Just look at the pictures.”
in a post dedicated in non linear dynamics is not a good beginning and is bound to lead to misconceptions .
Yes I was asking for trouble to add that paragraph, probably a mistake. In my case I don’t have much choice – as a biologist most of the maths in papers on nonlinear dynamics is beyond me. But I dont let this stop me reading the papers. I try to qualitatively understand the main features of the systems being described. One of the points of my article was to promote some more engagement between the field of nonlinear “chaotic” system dynamics and mathematics, and climate / oceanographic research. The consensus here and your view also is that the ENSO is indeed some kind of nonlinear oscillator. What is needed is for those knowledgable about the analysis of attractors and nonlinear oscillators to do some work with (e.g.) the ENSO and characterise it accurately, for instance as I suggested in the paper, finding the Lyapunov exponents.
I do feel there is in scientific research too much of “you in your small corner and I in mine”. Getting interdisciplinary engagement means people trying to get past technical jargon and maths and, even if they understand less than 50% of a paper in an alien discipline, still try to get something from it.
In summary I would say :
1) Yes , ENSO and all pseudo periodical climatic structures are chaotic
2) No , this has nothing to do at all with the Lorenz or Rossler attractor
To develop the arguments it is necessary to use and understand some mathematical concepts . Sorry but it is not more possible to understand non linear dynamics without maths than to understand quantum mechanics without maths .
As shown by Bob Tisdale (referenced in the article) the ENSO is characterised by alternating periods predominantly favouring the warming el Nino evens and cooling La Nina events. Such segregation into two phase space domains looks like a torn Lorenz type attractor. Note that there are many variations of each attractor type such as the Lorenz and Roessler – I included in the article a Roessler attractor that was torn and looked very much like a Lorenz. As for dimensionality, you could look at as many variables as you like, but the normal practice in the case of ENSO (see Bob Tisdale’s postings) is just two dimensions, time, and the sea surface temperature for a defined region of the equatorial Pacific (e.g. Nino 3.4). Looking just at this would allow someting like a Lorenz or Roessler to operate. But I defer to your greater knowledge about the mathematical nature of attractors.
To the first argument , there is this paper (chosen among dozens of papers dealing with the same matter) :
http://www.environment.harvard.edu/docs/faculty_pubs/tziperman_chaos.pdf
Basically the authors conclude : An analysis of a time series from an ENSO prediction model is consistent with the low-order chaos mechanism. The term to be stressed is the low-order and deserves some development. The temporal chaos theory , non linear dynamics , low-order chaos (all these terms are synonymous) studies the time evolution of a system in a low-dimensional phase space .
If so many authors have studied the chaos structure of ENSO and found it to be a “low order chaos mechanism”, then why do Mantua et al. (2002) who review data on palaeo-records of the PDO, (finding that its wavelength varies from 50-70 years) conclude that the causes of the PDO are unknown?
http://www.atmos.washington.edu/~mantua/REPORTS/PDO/JO%20Pacific%20Decadal%20Oscillation%20rev.pdf
This is an example of the disconnect between disciplines that I was trying to address. The field of nonlinear chaos knows about nonlinear oscillators, and has studied ENSO. Some match-making is needed here.
Why by the way does your whole posting not include the word oscillator? The hypothesis I advanced concerned a specific well characterised system, the nonlinear oscillator operating in a reaction-diffusion system, of which the BZ reaction is the reference example.
Caveat : the chaos theory allows to estimate how long a time series must be to get a robust estimate of the dimension of the phase space as well as of the attractors (if they exist) .
The 100 years of data for ENSO is shorter than the necessary length so the estimation is not very robust . It is a strong suggestion but not a certainty . We will need a couple of centuries more of data to get a robust answer .
Yes indeed, more time is needed with good data to characterise the ENSO, and climate variation in general. There is a paper on “Topological characterisation of spatio-temporal chaos:
http://math.fau.edu/kalies/papers/tcstc.pdf
which shows a relation between a nonlinear dynamic time plot and a corresponding chaos topology map. What would be perhaps appropriate here would be to apply such an approach to take for instance a time plot of ENSO (e.g. Nino 3.4) and convert it into a chaos topology map. This might illucidate the nature of the attractors. (A similar approach could also be taken to something like the Vostok and other ice cores of the last few glacial-interglacial cycles.)
2)
Why ENSO , even if it is chaotic what it is with a high probability , has nothing to do with Lorenz or any other popular attractor ?
Well an attractor is a subspace of the phase space . So it is something that you will never see because it doesn’t happen in the ordinary space .
The dimension of the Lorenz attractor is a number between 1 and 2 .
So it is more than a “curve” but less than a “surface” .
That’s why it is called fractal or strange .
Moreover all these attractors strange or not , happen in a finite dimensional phase space as already explained in 1) above .
But what is the phase space of any real oceanic oscillation ?
Well as this oscillation is an evolution of a spatial structure in time , or in other words an evolution of the field f(x,y,z,t) , the phase space is infinite dimensional .
It is easy to understand intuitively why – there is an infinity of points (x,y,z) and each of these points oscillates .
The spatial structure known as ENSO is the spatial result of an interaction of an infinity of oscillators (one in each point) .
This is called spatio-temporal chaos and is completely different from the temporal (Lorenzian) chaos .
More specifically there are no attractors in spatio-temporal chaos (how could one define or make a “picture” of an infinite dimensional structure ?) . Also almost none of the results of the temporal chaos theory transport to the spatio-temporal domain .
That’s why the Lorenz attractor , a child of finite dimensional dynamics dependent on time only has nothing to do with ENSO , a child of infinite dimensional spatio-temporal chaos .
I made the point in the introduction to the paper that the term “chaos” is an incorrect generalisation of the systems we are looking at, i.e. the BZ reaction and ENSO. Pure chaos is turbulent and not rich in emergent pattern. However it is the transient region where Hopf bifurcation begins where emergent pattern formation occurs. We are talking here about spontaneous pattern formation in a non-equilibrium dissipative sysem. This is not chaos.
It makes no sense to consider every molecule of water in the equatorial Pacific as an independent player and with a dimension to itself in the phase space. Sea water is liquid, not gaseous. Even in the atmosphere with the trade winds that are integral to the ENSO system, air atoms and molecules are influenced by their neighbors. We talk about ocean currents and atmospheric winds, not just about independent water and air molecules.
ENSO is not turbulence. Again turbulence is chaos and we are not interested in chaos here. ENSO has a repeating spatiotemporal structure (call it discretised if you like), the large tongue of alternatively cold or warm water at the eastern equatorial Pacific. It resembles the alternating and repeating 2-phase patterns of the BZ reactor, but not chaotic turbulence. It is a function of other discretised entities, Peruvian coast upwelling (as part of the oceanic thermo-haline circulation – THC – system of deep currents) and the equatorial trade winds – both entities comprising more than one molecule. Of course we deal with discretised entities because that is how they behave in the real world.
Once we recognise discretised elements operating in the ocean and atmosphere, such as periodic upwelling in a certain restricted region and an alternating wind patter in a restricted region, then this reduces the number of dimensions of our phase space to a much more manageable number. I disagree with your conclusion that the ENSO is “a child of infinite dimensional spatio-temporal chaos”.
I do agree that discretising the sea surface temperature – or troposphere temperature – on a much larger scale and over the whole world is a “brutal” generalisation that misses most or all of the important detail and the operation of independent systems. But we can recognise particular oceanic or atmospheric entities operating approximately as discreet entities.
@phlogiston:
Modeling/analyzing this doesn’t need to include the entire globe, IMHO.
I don’t know enough about the maths to contribute anything, but in terms of concept, I can see quite a bit of all of this.
Most of the time I disagree that ocean currents are created by winds, which is what I keep reading is what the oceanographers say. But if there is one region where I might agree, it would be there where ENSO happens, along the Equator in the Pacific Ocean, where the N & S Hadley cells might push the water toward the Equator before the winds go vertical in the Intertropical Convergence Zone. That would tend to recycle heat back to the Equator, in both the atmosphere and hydrosphere.
In terms of ENSO, this is a starting point for the weather systems in both the northern and southern hemispheres, iwhich to my mind simplifies the problem to be analyzed. It seems enlarging the analysis to the entire globe wouldn’t add anything to the study of it. I am a mechanical designer. Looked at as a driveR-vs-driveN system, I would only look at the driveN part of the system only to see what its needs are on the output end. I wouldn’t look even beyond the Pacific Mid-Latitude cells if I was analyzing this. It is not necessary to include anything beyond that. The Hadley cells-cum-IVZ is the entire system except for bleed-through to the Mid-Latitudes cell. The mid-latitudes are not demanding the heat energy output, although they accept it gladly, and take that heat energy off the hands of the Hadley cells in heat transfer.
So it seems that the system to be looked at is a lot less than the entire globe. ENSO is about as independent as you can get in looking at global climate systems. It is one end of the chain of heat energy events, and that is far simpler than if it were in the middle of the chain of events.
Now, the PDO is a different story in that respect. But in studying ENSO’s special case a lot should be able to be learned that would then apply to the PDO in its middle-of-the-chain position. And that position should be part of the reason why its oscillating frequency is so much lower, because of greater dissipation/blending of the heat being carried poleward, acting like a shock absorber in the system. The incoming heat from the Sun being less dense should be the main factor: lower solar W/m^2 would seem to mean a slower cycle time. Neither of the two factors would seem to contribute to quicker cycling, IMHO.
phlogiston says:
January 27, 2011 at 2:01 am
It is understandable that, as a biologist, you would seek holistic, non-mathematical explanations of physical phenomena such as ENSO and be satisfied with qualitative similarities. But physical science is much more demanding than that. It requires a detailed specification of the sources of energy and a rigorous determination of the effects produced thereby. That is what is meant by the term “dynamical mechanism.” Neither Tom Vonk, who looks at physics from the theoretical quantum-level upward, or a geophysicist like myself taking a meso- to global scale view of ENSO, finds your speculation credible. It is not a matter of compartamentalization of science into narrow disciplines that do not communicate with one another. Some odeas are just plainly inapplicable on both theoretical and empirical grounds. Purely phenomenolgical treatments of data, such as Bob Tisdale does superbly, may provide a good qualitative description, but they do not constitute bona fide physics.
It is at the analytic level that many of the connections you make simply fail. Despite fledgling attempts at modelling the variation of equatorial thermocline depth as low-order chaos, what drives the temperature variations seen in Nino3.4 has never been adequately explained. Nor has any physical connection between ENSO and the PDO ever been established. And THC is by definition the density-driven, as opposed to the enrmously mre energetic wind-driven, component of ocean currents; it does NOT drive upwelling or the mixing in the surface layer. I won’t touch on other miscomprehensions here. Suffice to say that the lapses are as glaring as would be my speculations on unsolved problems of biology.
I have 2 questions for Phil Salmon:
1) Do you believe that strange nonchaotic attractors play no role in terrestrial climate?
2) Do you believe that mathematical “proofs” that terrestrial climate is chaotic are based on tenable assumptions?
sky wrote, “In studying the cross-regional coherence of the multidecadal signal components of temperature series, I find not only diminution with distance, but occasional phase-reversals as well as rather abrupt curtailments.”
And what of interannual timescales?
TomVonk wrote, “More specifically there are no attractors in spatio-temporal chaos (how could one define or make a “picture” of an infinite dimensional structure ?) . “
Was this a slip?
sky says:
January 27, 2011 at 2:08 pm
phlogiston says:
January 27, 2011 at 2:01 am
It is understandable that, as a biologist, you would seek holistic, non-mathematical explanations of physical phenomena such as ENSO and be satisfied with qualitative similarities. But physical science is much more demanding than that. It requires a detailed specification of the sources of energy and a rigorous determination of the effects produced thereby. That is what is meant by the term “dynamical mechanism.” Neither Tom Vonk, who looks at physics from the theoretical quantum-level upward, or a geophysicist like myself taking a meso- to global scale view of ENSO, finds your speculation credible. It is not a matter of compartamentalization of science into narrow disciplines that do not communicate with one another. Some ideas are just plainly inapplicable on both theoretical and empirical grounds. Purely phenomenolgical treatments of data, such as Bob Tisdale does superbly, may provide a good qualitative description, but they do not constitute bona fide physics.
There is more in common between climate (the integrated ocean and atmosphere dynamics) and biology than you think. Its all very well for the “exact” sciences to look down their noses at biology – perhaps a consolation for the fact that there is much more money in the biosciences 🙂 . Both biological and climate processes are characterised by nonequilibrium pattern phenomena, and “bottom up” physical and mathematical analysis of climate that ignores such phenomena will only be exact in the sense of being exactly wrong.
I do not seek “non-mathematical” explanations, the maths of nonlinear dynamics is well established – all I seek to do is identify the processes at work – for instance proposing a common pattern mechanism (the nonlinear oscillator) between the BZ reactor and the ENSO – and leave the detailed maths to others. I have some experience in this field of nonlinear / nonequilibrium dynamics and have published in the peer reviewed literature on the subject.
Nor am I “satisfied with similarities”, Tom’s comparison of the sun to a tennis ball was funny but unfair. I stated in the article that similarity alone was insufficient, and went on to set out the conditions that the ENSO would have to satisfy to allow the operation of a BZ reaction-like nonlinear oscillator: a far-from-equilibrium condition, an open dissipative energy throughput and an excitable or reactive medium. I gave reasons and evidence that those conditions were satisfied. At the outset I made the clear distinction between non-linear pattern formation at the border of chaos, and full-blown chaos itself. Tom overlooked this distinction and tried to categorise ENSO as actual chaos (phase space tending to infinite dimensions) with which I disagreed.
Your advocacy of reductionism and disparaging use of the term “phenomenological” raise the important underlying issue of reductionism versus a heirarchical approach. (You use the word “holistic” tries to liken this to mystical new age like thinking). Reductionism gets you no-where in biology. It may not be stated out loud but practicing biologists realise that they are largely confined to speculative guesses based on phenomenological observations. Some systems such as molecular genetics allow the illusion of exactness but integrated up to the organism level, the predictiveness decays fast. Why else has an exponential increase in resources for molecular genetic research by pharmaceutical companies been accompanied by a drying up of drug candidate pipelines? Because the message has still to get through that reductionistic bottom-up biology does not work.
The problem (one of the problems) with reductionism is that it leads to denial of the real world. Calling an observation “phenomenological” is a form of denial. Something is observed, but “the models dont predict it” so the observation is denied. It is linked to argumentam ad ignorantium. We cant comprehend an observed phenomenon on the basis of our current understanding so we deny the existence of the phenomenon. Like the long resistance to the hypothesis of continental drift. Or the geologist Lyell, author of uniformitarian geology, instinctively rejecting Agassi’s claims to have evidence for former ice ages – on the basis that no mechanism could be envisioned for the climate fluctuating from colder to warmer and back.
In complex systems such as biology and climate it is not difficult to cast doubt on a complex phenomenon, by using obscurantist tactics and demanding complete and tidy, linear mathematical explanations prematurely. CAGW is a deeply reductionist body of theory, its bottom-up mechanism is the Arrhenius CO2 story, and the real world and climate are forced to fit the theory. Observations that contradict it are subject to obscurantist attacks and derided as “phenomenological” in denial of observed fact.
It is at the analytic level that many of the connections you make simply fail. Despite fledgling attempts at modelling the variation of equatorial thermocline depth as low-order chaos, what drives the temperature variations seen in Nino3.4 has never been adequately explained. Nor has any physical connection between ENSO and the PDO ever been established. And THC is by definition the density-driven, as opposed to the enrmously mre energetic wind-driven, component of ocean currents; it does NOT drive upwelling or the mixing in the surface layer. I won’t touch on other miscomprehensions here. Suffice to say that the lapses are as glaring as would be my speculations on unsolved problems of biology.
In the context of the BZ reactor, what do you mean by the analytic level? The dynamics and attractors of this system are well understood mathematically, and in the “Brusselator” they are accurately simulated. There is no need for bottom up simulation of atomic interactions. Just understanding of the nature of the non-equilibrium nonlinear pattern phenomena.
It is a reductionist oversimplification to say “the THC is driven by density only” or that “upwelling has nothing to do with THC”. I demonstrated in the article how upwelling and surface winds can be linked in a positive feedback. If we understand the system as an excitable medium with potential for positive feedbacks then it becomes redundant to talk about what drives what, what comes first the chicken or the egg.
“Nor has any physical connection between ENSO and the PDO ever been established.” A perfect example of reductionist arrogance. Bob Tisdale – the arch phenomenologician – demonstrates clearly the PDO and PDV being linked to the ENSO, but you deny this observation on the basis of an a priori demand for a complete finished physical explanation. This is flawed epistemology. To return to the biomedical / pharmaceutical analogy: some medicines like bisphosphonate drugs for osteoporosis for example are effective for a range of bone diseases and have been the standard treatment for decades. But the biology of how they work is incompletely understood – new aspects of the mechanisms are still being found. A drug industry demanding reductionist explanations for drug efficacy in advance, would have no medicines.
The recognition of non-equilibrium pattern phenomena requires a step back from the complacency of reductionist bottom-up thinking. An integrated understanding of phenomena in complex systems allowing for emergent patterns should not be derided as “holistic” or phenomenological. A non-linear attractor is just as real as an electron or a photon.
Feet2theFire says:
January 27, 2011 at 12:25 pm
@phlogiston:
So it seems that the system to be looked at is a lot less than the entire globe. ENSO is about as independent as you can get in looking at global climate systems. It is one end of the chain of heat energy events, and that is far simpler than if it were in the middle of the chain of events.
Thanks for your engineer’s perspective, this apparent independence of the ENSO makes it a good system to study. For instance as a nonlinear oscillator.
because of greater dissipation/blending of the heat being carried poleward, acting like a shock absorber in the system.
Indeed dissipation (or “friction” or “damping”) are recognised as necessary elements of a nonlinear dynamic system and tend to favour complex patterns and attractors – by contrast a nonlinear oscillator dominated by positive feedbacks without damping becomes regular and monotonic, like the cardiac cycle.
Paul Vaughan says:
January 27, 2011 at 10:21 pm
I have 2 questions for Phil Salmon:
1) Do you believe that strange nonchaotic attractors play no role in terrestrial climate?
This sounds like a trick question. I deliberately focused on the ENSO system as a convenient model. The term chaotic is ambiguous for reasons already discussed. The appearence of ENSO oscillation alternating between el Nino dominated and La Nina dominated multidecadal regimes – documented by Bob Tisdale – led to the proposal of a torn Lorenz-like attractor. (Providing we can convincingly limit the system variables and phase-space dimensions to 2-3 only.)
2) Do you believe that mathematical “proofs” that terrestrial climate is chaotic are based on tenable assumptions?
I’m not really qualified to answer this – sorry for the cop-out! I was hoping that someone like you might take up a challenge like this.
Thinking out loud….
The mention in this post of “butterfly” brought to mind the second thing that Maunder is famous for (after the Maunder Minimum), and that is his butterfly pattern of sunspots. Sunspots do not occur at the solar equator nor close to the poles. And they also seem to be unequally distributed north or south in each sunspot cycle. Their distribution is not a whole lot different than the phase space displacement of a Lorentz attractor as shown in Figure 7 (b).
This suggests a limiting mechanism for sunspots. Among other things, I wonder if anyone has looked at the sequence of sunspots, if they alternate N-S or if they come in N groupings and then S groupings. But they do start out at higher latitudes and then the pattern works its way equator-ward over the life of each cycle.
All this seems to parallel the Lorentz attractor pattern, which may mean sunspots are a non-linear oscillation – perhaps even an oscillation within an oscillating pattern.
All this is based on similarities and speculation as to what is going on. There does not seem to be any explanation for the Maunder butterfly pattern. It is just accepted as the way things are, without understanding of the whys of it.
It would be interesting – if these are both BZR patterns – if ENSO’s manifestation was ON the equator and the Sun’s manifestation is in the mid-latitudes. On the other hand, (still speculating) perhaps the real thing going on on the Sun is actually on the equator but it is causing visual “symptoms” away from the equator. In that regard, perhaps internally the Sun has some equivalents to Hadley cells that transport heat (EM?) energy away from the equator. (Which would imply there is an internal ICZ as well…) I don’t know jack about solar mechanisms but have been reading up on sunspots, so my knowledge is piecemeal.
And BTW, I love the phrase in this post, “…the fine scale oscillation itself oscillates over a longer time period between higher and lower values of the phase space parameter…” This is how I see SDs in general, and in this Lorentz attractor it displays this idea magnificently.
Phil, have you reviewed the literature (which goes back decades) on modeling ENSO as a nonlinear oscillator? (recent example: Warren White at Scripps)
Clarification: I’m not suggesting this will be either a fruitful exercise or a constructive use of time, but there are bases to be covered (& perhaps courtesies to be paid) before suggesting a “new” approach.
I believe you have misunderstood sky’s comments, but you are absolutely correct in asserting that ignorance of scale in the study of spatiotemporal pattern & process is (on ethics alone) a condemnable failure. Disciplines like landscape ecology & advanced physical geography, out of sheer necessity in grappling with pervasively rich & thick complexity, attained enlightenment on extent decades ago, but my impression is that such an awakening has not yet occurred (or at least has not yet matured) in disciplines that have traditionally focused narrowly & rigidly on only grain (which is enough to get the job done when investigating relatively simple phenomena). Fortunately there are some bright mainstream lights like Franklin Schwing, who appear to be slowly but surely developing a handle on the nature of multiscale spatiotemporal variation, so perhaps (at least we can hope) there will be more widespread awareness of the spatiotemporal version of Simpson’s Paradox in the not so distant future.
@phlogistin said Januay 28, 3:01pm:
I got a good chuckle in reading the first of this, because my mind went exactly to uniformitarianism and Lyell and Agassiz – and then that is exactly where you took it. Then I laughed out loud. Uniformitarianism is based on denying phenomena. Its very premise is that “only what we see today could ever have happened in the past.” The operative word there is “see.” In you saying “we cant [sic] comprehend” you are in essence talking about seeing. Blinders exist in all of us – what we chose not to see, we simply can’t comprehend, or even apprehend.
I do like your points to sky about reductionism and phenomenology. Building up from iota is theoretically a good way to approach science, but grasping the context, the framework, the phenomena is of primary importance. Stem cells – what is it that allows them to become different cells? There is some pattern, some resonance, or (at the risk of sounding New Age) some gestalt/holistic construct that must inform the infinitesimals. There is something in flocks of birds and schools of fish that makes them move as if one body. Yes, the parts are important, too, and must be studied – but not to the exclusion of the bigger picture. Yet models must be built from the reductionist POV – the code insists on it. But how those subroutines fit together is the crux of making the models parallel the empirical world.
Sorry for my generalist/interdisciplanary-leaning dogma there, but I had to voice my agreement. Quantification and qualification in science both have their places. It doesn’t seem like any of the non-math/non-hard sciences have 100% understanding that. Modelers for sure don’t. Bottom-up science has nearly infinite paths upward from that bottom, and the chances of them choosing the correct path to an understanding of the whole is not good, to say the least. There has to be an idea of the target and the ability to recognize when the results are balderdash, and the humility to say, “Oops!”
Paul Vaughan says:
January 28, 2011 at 8:52 am
Phil, have you reviewed the literature (which goes back decades) on modeling ENSO as a nonlinear oscillator? (recent example: Warren White at Scripps)
I am certainly not the first to draw the obvious conclusion that climatic systems such as ENSO behave like nonlinear far-from-equilibrium pattern systems. You are right it would have been better to have mentioned some other such studies, e.g. Lockwood 2001:
http://onlinelibrary.wiley.com/doi/10.1002/joc.630/pdf
J. Lockwood, “Abrupt and sudden climatic transitions and fluctuations: a review” (
Int. J. Climatol. 21: 1153–1179, 2001) in which he actually refers to the BZ reaction and draws an analogy to climate systems:
“For example, the Belousov–Zhabotinsky reaction in inorganic chemistry …
Because the movement from one stable state to another, as the distance from equilibrium increases, depends on universal numerical features rather than the actual
mechanisms involved, it is not surprising that some of the curves look similar to climatological time series.”
Another is by A. Mary Selvam 2003, “The Dynamics of Deterministic Chaos in Numerical Weather Prediction Models “:
http://arxiv.org/ftp/physics/papers/0310/0310034.pdf
in which the author suggests the ENSO might be linked to “semi permanent dominant eddies (limit cycles) in the atmosphere boundary layer”, with the 5 year ENSO periodicity representing 40-50 days (the period of atmospheric general circulation oscillation) squared.
I believe you have misunderstood sky’s comments
If so then I apologise.
I agree with your comments about heirarchical levels of organisation, I read some years ago “The Cosmic Blueprint” by Paul Davies which also articulated these arguments nicely.
Its just possible that eventually climate science and the aftermath of AGW could be the trigger for more general acceptance over many scientific disciplines of, as you put it, “multiscale spatiotemporal variation” and a challenge to the dominance of reductionism.
Feet2theFire says:
January 28, 2011 at 8:24 am
Thinking out loud….
What you are suggesting about the space and time pattern of sun spots sounds like a “limit cycle”, a repeating pattern that “shakes down” out of infinite possibilites in a non-equilibrium pattern system.
http://en.wikipedia.org/wiki/Limit-cycle
Your biological analogies are persuasive. It reminds me of a passage in “Deep Simplicity” by John Gribben, where he talks about limit cycles. Apparently a sort of “chaotic network” with chaotic transmission between multiple nodes will converge to cycle between only a small subset of the nodes – the “limit cycle”. In one experimental example, 30,000 light bulbs (virtual or real) are so linked, and the resultant limit cycle was about 250 nodes only. The significance? There are about 30,000 genes in the human body, and the number of cell (tissue) types is 256.
Oh – that brings up post number 100 – you narcissist!!
Paul Vaughan says:
January 27, 2011 at 10:25 pm
To avoid aliasing, I deal mostly with data decimated to yearly, rather than monthly, averages. Thus I have little to say about interannual variability, which is at Nyquist. The subdecadal variations are quite region-specfic; they do not cohere well beyond several hundred kilometers.
phlogiston says:
January 28, 2011 at 3:01 am
Your philosophical ruminations about “arrogant reductionism” are neither here nor there. The great leaps forward in biology in the last several decades were made by physicists such as Bronowski and many others at Salk Institute, looking at biological processes at the molecular level. As mentioned earlier, however, that is not the scale at which geophycisists work. Our goal likewise is to understand the workings of the integral system. I, in particular, who is perpetually testing theoretical expectations against measuremets would be the last one to ignore the implications of field data. But the standard of proof is far more rigorous than just the qualitative similarity of certain features of synthesized index time series. Quantifications of the theoretical expectations need to be tested against the measurements.
I don’t think Bob Tisdale would claim to have discovered any true DYNAMICAL relationship between ENSO and PDO. He provides a phenomenological explanation of a connection, but not one that allows any determination of the energy levels and strength of coupling in the distinct oscillations. And when the similarity of time-series depends on the arbitrary offset in the NINO3.4 index, the scientific credibility suffers.
The whole topic of nonlinear oscillators is fascinating, but best left for another venue. Have a good weekend.
phlogiston;
The existence of “emergent properties” is pretty hard to deny. Observe the long struggle to link the atomic structure of H2O to its many unique characteristics. Complexity has its own logic.
Reductionism’s demand on itself would have to be that all chemistry and structure etc. should be predictable from the properties of subatomic particles — strings, maybe? Good luck with that.
Reductionism vs. holism is a false dichotomy. The term “hierarchy theory” is misleading for those who do not differentiate between grain & extent. For example, a beetle’s ecosystem is not a human’s ecosystem, even if the beetle is perched on the human. Such misunderstandings are inevitable not only in cross-disciplinary communication, but also within disciplines.
I would be curious to hear sometime (in the weeks & months ahead) how sky, who is very careful about temporal aliasing, avoids (or more likely attempts to avoid) issues with spatial aliasing in spatiotemporally nonstationary contexts.
Organization (and along with it Simpson’s Paradox) is just a form of nonrandom aliasing, so it is people like sky who can rigorously carry the ball to the end zone following insightful data exploration (which should absolutely not be confused with statistical inference). [Note that sky is not deriding data exploration – quite the contrary.]
–
Phil, like Erl Happ you are a talented writer, but I have one request:
If you write more articles, please consider (for your busy audience’s sake) keeping them much more succinct. Thank you for considering this request.
Best Regards.
Yes, I had found the Wiki article about limit cycles, from looking up Hopf bifurcations. All the math is over my head, but I believe I got the implications of the limit cycles. Even the Hopf bifurcations seemed to tie in with the upwelling water in the eastern Pacific.
Hopf bifurcation was described as
If one looks at the thermocline perhaps as the “fixed point” and the complex plane being the sea surface, then what might be happening is that the thermocline may be breaking (moving across) the sea surface, and since the thermocline is such a distinct entity/discontinuity, when it drops below the surface the eastern Pacific immediately shifts modes. All because of the interplay of upwelling and other forces/currents/winds pushing and pulling at each other. In this case, the cause of the El Niño has itself a cause, which is of course, linked back to the Hadley cells and the ICZ.
The balancing act is an oscillation, not a single fixed state. The real question must be why climatologists wouldn’t already be aware that this is a normal occurrence in a dynamic system such as the climate, normal enough that it should have been one of the first things they looked for.
…With the one PDO phase change that originally was called the Great Climate Change of 1976-1977, it should have been seen in the 1980s and 1990s that a BZR oscillation was going on. Or suspected it, anyway. The ENSO is even more clear. Seriously, if I’d known the BZR thing existed, I would have been yelling it out long ago. That doesn’t mean it is the definitive answer, but it was sure a hypothesis that should have been thrown into the mix to be falsified or not. And with the ENSO climate effect and then the PDO one, too, it seems to be the best explanation – at least from a semi-lay POV.
I have 3 questions for Feet2theFire:
1) Have you reviewed the literature (which goes back decades) on modeling ENSO as a nonlinear oscillator? (recent example: Warren White at Scripps)
2) Do you believe that mathematical “proofs” that terrestrial climate is chaotic are based on tenable assumptions?
3) Do you believe that strange nonchaotic attractors play no role in terrestrial climate?
Feet2theFire says:
January 29, 2011 at 8:08 am
If one looks at the thermocline perhaps as the “fixed point” and the complex plane being the sea surface, then what might be happening is that the thermocline may be breaking (moving across) the sea surface, and since the thermocline is such a distinct entity/discontinuity, when it drops below the surface the eastern Pacific immediately shifts modes. All because of the interplay of upwelling and other forces/currents/winds pushing and pulling at each other. In this case, the cause of the El Niño has itself a cause, which is of course, linked back to the Hadley cells and the ICZ.
This looks like it could be a starting point for going from a hand-waving analogy of BZR-ENSO and discussion of pre-requisite conditions, to a testable model. I mentioned that the BZR is readily simulated by computer, the “Brusselator” is a well known example. One aspect of the upwelling that I focused on is that is certain places and times it might become self-accelerating, e.g. upwelling cold water might influence trade winds in such a way as to drive further upwelling, connecting a positive feedback. The inverse in the case of el Nino – weakened upwelling would self-limit further by the same trade winds link. This would qualify the upwelling region as an excitable medium, a pre-condition for a BZ style nonlinear oscillator.
It should be possible to obtain more data on the behaviour of the thermocline in that region and other Bob Tisdale type meteorological data on the ENSO to have the basis of a testable model.
The balancing act is an oscillation, not a single fixed state. The real question must be why climatologists wouldn’t already be aware that this is a normal occurrence in a dynamic system such as the climate, normal enough that it should have been one of the first things they looked for.
…With the one PDO phase change that originally was called the Great Climate Change of 1976-1977, it should have been seen in the 1980s and 1990s that a BZR oscillation was going on. Or suspected it, anyway. The ENSO is even more clear. Seriously, if I’d known the BZR thing existed, I would have been yelling it out long ago. That doesn’t mean it is the definitive answer, but it was sure a hypothesis that should have been thrown into the mix to be falsified or not. And with the ENSO climate effect and then the PDO one, too, it seems to be the best explanation – at least from a semi-lay POV.
There have been a few published papers which mention the BZ reaction and ENSO in the same paper, speculating that ENSO might be a nonlinear oscillator (indeed an obvious enough proposition) and mentioning the BZ reaction as one of the best studied exampes of an experimental nonlinear oscillator in a chemical reaction-diffusion system. I mentioned above in reply to Paul Vaughan a paper by Lockwood back in 2001 where he wrote:
“For example, the Belousov–Zhabotinsky reaction in inorganic chemistry …
Because the movement from one stable state to another, as the distance from equilibrium increases, depends on universal numerical features rather than the actual mechanisms involved, it is not surprising that some of the curves look similar to climatological time series.”
http://onlinelibrary.wiley.com/doi/10.1002/joc.630/pdf
J. Lockwood, “Abrupt and sudden climatic transitions and fluctuations: a review” (
Int. J. Climatol. 21: 1153–1179, 2001).
However the BZ-ENSO link has indeed been very marginal to the ENSO discussion and I am sure you are far from alone among even scientists studying the ENSO professionally, in being previously unaware of the BZ reaction. Much of the mainstream discussion of ENSO ignores the non-linear oscillator paradigm.
This is the point about fences between scientific disciplines and parochialism. Scientists publish in densely technical code specifically to exclude outsiders, to the detriment of science as a whole.
More gate-crashing is needed!
@Paul Vaughn –
Answers for you:
1) Have you reviewed the literature (which goes back decades) on modeling ENSO as a nonlinear oscillator? (recent example: Warren White at Scripps)
Ans: No. Although I’ve read a whole lot. Maths are generally over my head. This article is the first I’ve run across that addresses nonlinear oscillators at all. Literally, I’ve been looking for years for some cause of El Niño. Online searches have been useless – hit after hit of what ENSO affects, and nothing on the other side of the equation.
2) Do you believe that mathematical “proofs” that terrestrial climate is chaotic are based on tenable assumptions?
Ans: Two responses. First, I think if there were mathematical proofs – in quotes or not – the models would do a better job, so no on that account. Second, chaos is something I know little about and haven’t the time or background to get into. I am not even sure chaos is quite applicable. Just because something is too complicated for our present ability to study doesn’t mean it has to be chaotic. Third, what their assumptions are, I have no clue.
3) Do you believe that strange nonchaotic attractors play no role in terrestrial climate?
Ans: The maths are over my head, but the implications of what I am reading only just now are fascinating me. As much as I can glean from them. I only just heard of attractors of any kind, much less be able to distinguish one from another.
Thanks for the questions, but they are over my head, to be honest with you. That doesn’t mean I can’t grasp some of the principles behind what is happening. Since the level of connecting all of the maths to climate seem not to have gotten anyone complete understanding of climate, I assume some of their underlying concepts are, indeed, untenable. Which ones? I think that is why I am trying to grasp this all in the first place. I have a fairly adept spatial visualization capacity, and I can envision some of what is going on. I guess I am similar to the generalist ancient Greeks who tried to explain everything conceptually. If someone throws math at me, I will ask what principles are behind it and what they believe it implies. That is my level. Again thanks for asking.
Feet2theFire, Thanks for your response. A simple example of a strange nonchaotic attractor: Tides. Russian scientists have suggested something a little more complicated for terrestrial climate, but that story is for another day…
Cheers.
@phlogistin –
I have an impression it would more directly affect the ICZ’s convection, rather than the tradewinds. I see the trade winds begging the inflow before the air reaches the equator, therefore being on the last leg of the Hadley cell loop of air. The first thing affected would seem to be the ICZ. Basically there are two upwellings – one in the ocean and one in the troposphere. Or not. No?
Basically, the thermocline dropping below the surface would be a brake on the ICZ, by cutting off one of its two inflows of heat energy.
In a dynamic system, I just don’t see equilibrium being a single energy state. It is much more likely to be either some randomness within two boundaries or some sort of oscillation.
From a geographical perspective:
In the equatorial Pacific off Peru/Ecuador, the convection that uplifts the cold water – convection is a low-intensity force. (This is one reason why I argue elsewhere against its being a driving force in the THC.) It would seem this is relatively easily overcome by incoming trade-wind-pushed warmer surface waters from the surrounding region just to the north, over the top of the cold plume, effectively capping it. There is normal a great deal of heat energy off the Central American/Mexican coast, which happens to be the birthing place of many of the Pacific hurricanes. (Having spent time in SW Mexico, I pay attention to their weather systems.) There are seemingly always plumes of heated atmosphere there (though, ironically, not at the moment). It doesn’t seem that very much of it would need to move south to cap off the cold plume.
(One question might be why this happens in the Pacific and not in the Atlantic off the west cost of Guinea. My first intuition on this is that the shape of the African coast blocks the southern flow just north of the Equator, pushing the equator-ward water to the west and disrupting what in the Pacific is a more clean, unhindered system. In looking at the currents, the Equatorial Counter Current and the Benguela Current more or less run head-on into each other near the SW corner of the bulge of Africa. The coast there has to be contributing mightily to the inability of the cold Benguela Current having a bigger effect. Off South America, the Equatorial Counter Current has a free flow path to the coast instead of being pinched off as the Atlantic one is. The pinching off makes the Atlantic one that is more chaotic. It would also seem to stretch the cold plume out to the west and diffuse it over that whole distance, moderating its extreme.)
In my mind oscillating is an organized mechanism. I would think that, in effect, makes it the opposite of chaos. Lack of geographic complications in the Pacific would seem to suggest why we have a Pacific ENSO and not an Atlantic one. (I don’t see the AMO as the same thing.) Organization and oscillation are cleaner in the Pacific – once a regime begins to take hold, it has less to disrupt its growing until it reaches its own feedback from overshooting. This, I suppose is when the cold plume’s convection cannot be held down anymore by the intrusive warm cap from the north.
I am probably looking at all this too simplistically, but it is just incredible to me that people havn’t see this mechanism as the probable cause of El Niño.
@Paul Vaughn –
“Russian scientists have suggested something a little more complicated for terrestrial climate…”
Any links you’d want to point me to?