By Christopher Monckton of Brenchley
I am most grateful to Mr Stokes for his interesting recent posting in which he explains what he sees as the difference between official climatology’s implementation of feedback in deriving climate sensitivity and the approach taken by my co-authors and me.
The sheer quantity of the comments on these mathematical and physical discussions is an indication that getting down and dirty among the equations is of more than passing interest to the readership.
Let me begin this response to Mr Stokes by setting out, in round numbers and in the simplest possible terms, the difference between official climatology’s conclusion that feedback triples the direct or reference warming from greenhouse gases and our conclusion that, with remarkably little error, one can safely ignore feedback altogether in calculating equilibrium sensitivities.
In the CMIP5 models, the latest generation for which ensemble results have been published, the mean reference sensitivity to doubled CO2 – that is, the amount of warming that would occur in response to a doubling of the atmospheric concentration of CO2 if no temperature feedbacks were operating or if they were net-zero – is 1.05 Kelvin (based on Andrews 2012).
It is also currently thought (rightly or wrongly) that that value is very close to exact: the uncertainty is only 10% either way. Therefore, ad argumentum, we shall accept as canonical the fact that reference sensitivity to doubled CO2 before accounting for feedback is 1.05 K.
However, the same models give a mean Charney sensitivity – that is, the amount of warming that will occur after all sensitivity-altering temperature feedbacks have acted and the climate system has returned to equilibrium – of 3.35 K per CO2 doubling (based on Andrews, op. cit.).
From these two canonical values, we know that official climatology reckons that the feedback response to doubled CO2 is 3.35 – 1.05, or a whopping 2.3 K, in response to a mere 1.05 K reference sensitivity. Recall that feedback represents the entire difference between reference sensitivity (before feedback) and equilibrium sensitivity (after feedback).
If official climatology were right, then the system-gain factor, which is the ratio of equilibrium to reference sensitivity, would be 3.35 / 1.05, or 3.2. Official climatology actually imagines that feedbacks multiply any directly-forced warming 3.2 times over.
Where does official climatology get this massive multiple 3.2 from? Here’s how. The emission temperature of the Earth is usually taken as about 255 K, and the reference sensitivity to the naturally-occurring, noncondensing greenhouse gases present in 1850 is taken as about 10 K (see e.g. Lacis+ 2010) so that the reference temperature in 1850 – the temperature that would have prevailed in the absence of feedback – is 265 K.
However, the measured temperature in 1850 was 287.5 K (HadCRUT4), and that was an equilibrium temperature (there would be no trend during the following 80 years). The difference between the emission temperature of 255 K and the measured temperature of 287.5 K in 1850 is 32.5 K. Divide the equilibrium sensitivity of 32.5 K by the reference sensitivity of 10 K and you get 3.25 – more or less exactly the system-gain factor that official climatology takes as its midrange estimate.
Thus, to IPCC et hoc genus omne, feedback is the big enchilada. It is imagined to account for between two-thirds and (in the sillier extremist papers, up to nine-tenths) of total global warming.
In official climatology, feedback not only accounts for up to 90% of total warming but also for up to 90% of the uncertainty in how much warming there will be. How settled is “settled science”, when after 40 years and trillions spent, the modelers still cannot constrain that vast interval? IPCC’s lower bound is 1.5 K Charney sensitivity; the CMIP5 models’ upper bound is 4.7 K. The usual suspects have no idea how much warming there is going to be.
My co-authors and I beg to differ. Feedback is not the big enchilada. Official climatology has – as far as we can discover – entirely neglected a central truth. That truth is that whatever feedback processes are present in the climate at any given moment must necessarily respond not merely to changes in the pre-existing temperature: they must respond to the entire reference temperature obtaining at that moment, specifically including the emission temperature that would be present even in the absence of any non-condensing greenhouse gases or of any feedbacks.
To see why this must be so, consider the following simple block diagram:
In the block diagram, emission temperature comes in at top left. Then (following the arrows) the reference sensitivities that occur over time, first natural and then anthropogenic, are successively added to it. Then the reference temperature, the sum of all these, passes to the input/output node and thence infinitely round and round the feedback loop, where the separately-powered feedback block (powered by the retention in the atmosphere of radiation that would, without feedback, have passed harmlessly out to space) adds a smidgin to the signal on each pass. The output signal is equilibrium temperature after feedback has acted.
Your mission, should you choose to accept it, is to try to find a respectable explanation for official climatology’s notion that the feedback loop, which receives as its input signal the entire reference temperature, can somehow magically decide that it will respond only to the perturbations of that reference temperature caused by the presence of natural and then also of anthropogenic noncondensing greenhouse gases, and yet that it will not also respond at all to the emission temperature, two orders of magnitude greater than the sensitivities.
No doubt one could devise an electronic circuit that would perform that feat. But the climate is not a circuit. The feedbacks that were present in 1850 must perforce have acted not only upon the greenhouse warming to that date but also upon the emission temperature that was there before any noncondensing greenhouse gases had made their presence felt.
Here, then, is the corrected calculation. The reference temperature in 1850, before feedback, was 265 K. In that year the equilibrium temperature, after feedback, was 287.5 K. So the system-gain factor that applied in 1850 was 287.5 / 265, or 1.085, about a third of climatology’s 3.2.
Now, if we multiply the 1.05 K reference sensitivity to doubled CO2 by the corrected system-gain factor 1.085, we get a Charney sensitivity not of 3.35 K, as official climatology does, but of just 1.15 K.
Ah, you may say, but perhaps the curve of equilibrium temperature as a response to reference temperature is nonlinear. Maybe it is, but it cannot be very nonlinear. Why not? Because the reference temperature in 1850 was more than 92% of equilibrium temperature.
Now, Mr Stokes’ article is correct as far as it goes. His central point is that if you are starting from an equilibrium, such as that which obtained in 1850, you don’t need to know how that equilibrium occurred: you can work out the system-gain factor simply as the ratio of equilibrium sensitivity to reference sensitivity in any period later than that equilibrium, rather than as the ratio of equilibrium temperature to reference temperature at the time of equilibrium.
So let’s do it climatology’s way, using official climatology’s own data to 2011, the year to which the figures were brought up to date in time for IPCC’s 2013 Fifth Assessment Report.
The net anthropogenic forcing from 1850 to 2011 was about 2.5 Watts per square meter. However, the heat capacity of the ocean introduces a delay in the equilibrium response. This delay is reflected in a radiative imbalance, thought to have been about 0.6 Watts per square meter to 2010 (Smith+ 2015).
Taking Smith as correct ad argumentum, climatology’s period system-gain factor derivable from the data for 1850-2011 is simply the ratio of 2.5 to (2.5 – 0.6), i.e. 1.315 (see Lewis & Curry 2018 for the equations). Then Charney sensitivity would be 1.315 x 1.05, or just 1.4 K, not the 3.35 K that official climatology would currently have us imagine.
Notice how much closer to our estimate 1.15 K is that real-world 1.4 K Charney sensitivity, based on official climatology’s own estimates of actual anthropogenic forcing and radiative imbalance, than it is to climatology’s midrange estimate 3.35 K.
Why is our estimate of midrange Charney sensitivity so very much closer to what is inferred from official, published estimates of forcing and radiative imbalance than official climatology’s midrange estimate?
The reason is that, unlike official climatology, we use all the available information, and specifically the information about the respective magnitudes, in 1850, of the reference temperature (265 K) and of the feedback response (22.5 K). The sum of these two was the observed surface equilibrium temperature in 1850.
Official climatology, which simply does not realize that feedbacks necessarily respond to the entire reference temperature that obtains at a given moment, is left with no choice but to throw that vital information away. Here is Mr Stokes doing that quite specifically:
“It is wrong to include variables from the original state equation [i.e., in 1850]. One reason is that they have been accounted for already in the balance of the state before perturbation. They don’t need to be balanced again. The other is that they aren’t proportional to the perturbation, so the results would make no sense. In the limit of small perturbation, you still have a big reference temperature term that won’t go away. No balance could be achieved.”
Now, Mr Stokes is quite right to say that there was a temperature equilibrium in 1850 and that, therefore, at that time the surface temperature of 287.5 K already included the various variables, i.e. the 255 K emission temperature, the 10 K reference sensitivity to the naturally-occurring noncondensing greenhouse gases present in 1850 and the 22.5 K feedback response to the 265 K reference temperature.
He is also right to say these variables “do not need to be balanced again”. But, and this is crucial, they do need to be taken into account in deriving the corrected system-gain factor of 287.5 / 265 and, from that, the corrected Charney sensitivity.
Climatology overlooks these values because it is unaware that at any given moment (such as 1850) feedbacks respond to the entire reference temperature that prevails at that time. Like Luther, they can do no other.
Mr Stokes is also right to say that the variables – in which I think he includes the feedback response – are “not proportional to the perturbation”. Here, he makes precisely our point. The feedback response in 1850 was, of course, necessarily and ineluctably proportional to the entire 265 K reference temperature, which is the sum of the 255 K emission temperature and the 10 K reference sensitivity to the natural forcings present in that year.
But climatology, in effect, takes the entire feedback response in 1850 to have been proportional solely to the 10 K natural perturbation of reference temperature. And there is its mistake. That is why its estimate of Charney sensitivity – and of all equilibrium sensitivities – is three times too big. It has, in effect, allocated to greenhouse gases the large feedback response that arises simply because the Sun is shining.
Yes, one can derive the system-gain factor as the ratio of sensitivities, just as we can derive it as the ratio of absolute temperatures. But the former approach, that of official climatology, is subject to vast uncertainty, while our approach, using those vital data from 1850 that climatology has for so long ignored in its sensitivity calculations, provides an interval of Charney sensitivities that is both accurate and well constrained.
To derive equilibrium temperature, one needs to know the reference temperature and either the feedback response or the system-gain factor. But we don’t know and cannot by any rational means determine how big the feedback response is by counting up the individual feedbacks, as climatology currently tries to do, because it is feedbacks that are the near-exclusive cause of the uncertainty in official climatology’s global-warming predictions.
No feedback can be quantified by direct measurement. Nor can any form of observation, however well-resolved, meticulous and honest, allow us to distinguish reliably, and quantitatively, between different individual feedbacks, or even between feedbacks and the forcings that engendered them.
Climatology cannot calculate Charney sensitivity reliably, because, though it knows that the reference sensitivity to doubled CO2 is 1.05 K, it cannot know the value of the feedbacks and it does not know the system-gain factor. It does not know this vital quantity because it has thrown away the information available at the one point – before any significant anthropogenic intervention – for which the data are quite well constrained, and from which it can be directly derived: i.e., 1850.
The data for 1850 are quite well constrained precisely because the entire equilibrium and reference temperatures in that year exceed by two orders of magnitude the tiny equilibrium and reference sensitivities that are the basis of climatology’s so-far-failed attempts to constrain the system-gain factor and hence the likely magnitude of future global warming.
We know quite reliably what the system-gain factor was in 1850. We also know that it is not going to be a whole lot different in 2100 from its value of 287.5 / 265, or 1.085, in 1850.
Why do we know this? Because the industrial-era anthropogenic reference sensitivity of just 0.75 K from 1850 to 2011 was so very small compared with the 265 K reference temperature already present in 1850. The climate has simply not changed enough to engender a major shift in the feedback regime that obtained in that year.
Even if such a major shift were to have occurred, the additional feedbacks would have responded not merely to our perturbation of emission temperature but to the entire reference temperature, including emission temperature. For one thing, the Great Pause of almost 19 years in global temperature up to 2015 could not possibly have occurred.
Therefore, we can be reasonably confident that Charney sensitivity – i.e. equilibrium sensitivity to doubled CO2 compared with 2011 – is not going to be very much different from 1.15 K. In fact, our professor of statistics, having gone through all the numbers in the most meticulous detail, has calculated that the corrected 95% confidence interval of Charney sensitivity is 1.09 to 1.23 K, an interval of just one-seventh of a Kelvin. Compare that with the 3.2 K interval of official Charney sensitivities, which range from 1.5 to 4.7 K.
Notice that we are only able to calculate the Charney sensitivity correctly because we already knew the system-gain factor. We knew it because we were able to derive it from the data that official climatology throws away because it does not know feedbacks respond to the entire reference temperature and not only to arbitrarily-chosen reference sensitivities.
Mr Stokes talks of the 255 K reference temperature in 1850 “not going away”. Precisely: it was then present, as was the additional 10 K in warming forced by the presence of the naturally-occurring noncondensing greenhouse gases in that year. Because it was present, it should have been taken into account. But it was not taken into account.
Since we know from theory, and from the block diagram, and from the test rig built by one of our co-authors, and from the more sophisticated rig built and operated for us by a government laboratory, that the feedbacks that were present in 1850 perforce acted upon the entire reference temperature that was present in that year, we can instantly and quite safely derive from that year’s data the system-gain factor and hence Charney sensitivity.
No need for vast, costly general-circulation models, if all you want to know is how much warming we may cause.
No need to know the value of any individual feedback.
Remarkably, no need even to take feedback into account in the calculation: the undershoot in Charney sensitivity that arises by ignoring feedback altogether is little more than a tenth of a Kelvin.
In our submission, this really is Game Over.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.
Since we seem to be having commentators with quite different perspectives on what feedback means and how it applies, I suppose I can try for some insight here, and support a certain way of looking at the matter with a couple of quick web links?
Basically, I am taking the view that Lord Monckton has the whole matter of feedback *and* it’s plausible relevance to the most usefully idealized climate models *correct*. So the implication is that Nick Stokes and some others, call them “climate conventional theorists”, are either getting it wrong, or else they are applying a more or less odd or eclectic view of the basic idea of feedback (at least at those times when the conventional climatists deem that feedback is a useful concept, which strangely enough, they don’t always seem to). The thing to note here, right away, is that feedback is, in itself a “large” topic, easy for even experts to misapply or make over complicated, if they aren’t careful! I myself am layman enough to mess things up quite easily, I’m sure, so I’m not here to critique Mr. Stokes or anyone else line by line exactly.
What I want to do here is, I only want to throw in a couple of relevant Control Theory web references, just put a couple of examples into this discussion, to help illustrate the basics of how feedbacks ought to work (at least in any regular DC amplifier or DC regulator kind of scenario).
Now my initial “kick off”, or inspiration for digging out a couple of web links on this, was my reading of Stokes vs. Monckton back a bit in the current discussion. This was when Lord Monckton was supporting his idea by referencing the success of his op-amp based test rig for feedback (using voltage as the analog for earth average temperature). Mr. Stokes then said, in essence, that instead of using *that* sort of DC level feedback, or DC gain rig as a model, modellers should instead be using calculus for “deducing rates of change” (said rates of change would be amplified and/or integrated so as to give more of a “slope boost” effect to the idea of feedback as such)? Note that “slope boost” is my term here, not Stokes’ (I am honestly struggling, trying to visualize what he means).
Thus, I refer to Web Link #1 (of 2 links):
https://www.maplesoft.com/content/EngineeringFundamentals/11/MapleDocument_11/Block%20Diagrams,%20Feedback%20and%20Transient%20Response%20Specifications.pdf
The above is a primer on “Block Diagrams, Feedback and Transient Response .. ” for understanding how to model such things on Maplesoft math software. The thing to notice here is that right away they give a couple of block diagrams, one for a “household heating system”, then a very slightly more generalized version of the same thing, the ” System plant” block feedback diagram. This is then followed by a still more abstract “Fig. 3: Block diagram with feedback” diagram. So they are going carefully “step by step” on the abstraction, you see, like “techno nerd” babytalk (I really like that, myself).
The thing is, if you follow the diagrams and the bits of math below, you wind up at a “Fig. 8: Equivalent system diagram”, where the situation is very much as Lord M. would have the idea of feedback working all along! The only distinction is that the formula here is the one for negative feedback as opposed to positive (a very minor distinction, if you like, you can just change the sign in the denominator and that will give you the positive feedback version of things, i.e., just by flipping the ‘+” sign in the denominator over to a ‘-‘ you can get the positive feedback formula). So since the initial example being used here is a heating system, you have the temperature reference going *in*, the “heating system modified” temperature coming *out*, with no special amplification of slopes as such, or anything like that.
Now if the above reference isn’t quite technical enough, I will also offer the following,
Web Link #2 of 2:
http://www.ti.com/lit/an/slva947/slva947.pdf
My link number 2, above, is an interesting description of a certain kind of voltage regulator device (Texas Instruments device, the paper here gets quite technical on frequency response and how the device can be stable despite having *positive* feedback on some frequencies and *negative* feedback on others). Note carefully the technicality here, that even though the device operates on DC levels and is, in fact, a DC voltage regulator, the use of AC test signals is still considered vital for proving that the gadget as such is stable!
The reason they are so careful about testing at different frequencies, is that even a system whose whole intent is to modulate DC (i.e., it’s not a signal amplifer in the radio or audio amp sense), even *there* it is important that the gadget should not go wild in some way when it is switched on, or when there is some other transient change. Transients imply frequency components, *then* you have to consider those separately if you want stability, and *so* maybe this is where you get some of the confusion that we’re seeing?
The simpler discussion in this TI paper is really about the two kinds of feedback, positive and negative, being *not much different* at low feedback values (and therefore stable at low values of feedback factor)! Why, that just sounds a *lot* like the point that Christopher Monckton has been making all along, about low feedback being what it takes to have a stable system!
So make of this what you will, all, the above is about as “feedback theory” as I am likely to want to get, for now anyway.
Mr Blenkinsop has been uncommonly diligent in chasing down primers on feedback theory that are available on the web. I am delighted, but not surprised, that these references seem to support our stance. I am not surprised because we get our feedback theory not from me (I am no expert) but from a tenured professor of control theory, a man of more than usual ability and determination, together with not one but two experienced, hands-on control engineers, one of whom built and ran our test rig, and an eminent scientist at a national laboratory who also built and ran a test rig for us. It is of course possible that all of us could be wrong, but consider the following facts:
1. The world is warming at only one-third of the officially-predicted medium-term rate.
2. Two-thirds of the warming predicted by official climatology comes from feedbacks.
3. The error we have identified, once corrected, leaves very little influence for feedback: one can ignore it altogether without much error in deriving equilibrium sensitivities.
4. The direct warming to be expected in the absence of any feedback and the direct warming that has been observed since 1850 are more or less identical.
This coherence of several lines of evidence suggests at least the possibility that we may be on to something. If we are right, that is the end of the climate scare.
“The above is a primer on “Block Diagrams, Feedback and Transient Response .. ””
It’s right there in the title – transient response. It does not include things that do not change. If you look at fig 4, it starts with a differencer, where you subtract the output from the reference signal to get the error signal. It is that difference which is then passed through the feedback apparatus to tell the plant what change it should make. The only thing that enters the loop is the difference. Eq 4 (with Fig 7) spells that out very explicitly. Lord M is trying to smuggle something past the differencer.
If you read further, you might get excited where it introduces K, which it calls the DC gain. But it isn’t amplifying an unchanging input. Instead it is the response to a step change as an input signal.
AS for Fig 8, that actually merely writes down Laplace transforms. But a Laplace transform is inherently of a transient signal; it can’t deal with one that never changes. It integrates only forward from a zero time; the quantity (integrand) before that was zero. The Laplace transform of 1 is actually the Laplace transform of a step change at t=0.
Well, OK, so in mentioning “K … the DC gain”, you’ve made my point, and in the graph in the article immediately following the heading “DC Gain, K” this graph clearly shows that the system output approaches the steady state (or DC) gain as the time variable approaches infinity (of course the practical amount of time for a system to settle to steady state will be something less than infinity).
So, the basic feedback formula doesn’t just apply to AC Laplace domain calculations, it also applies to long term steady state output levels as well, in any continuous feedback situation (where the system steadily feeds back some part of the output level). Heck, they even define the practical timing or Settling Time in terms of the DC (steady state) output value (therefore necessarily factoring in the K factor as such, everything is defined using that). To quote the Settling Time definition given:
“The settling time is defined as the time after which the output is within a specified band around the steady state value.
The specified band is usually plus or minus 1% or plus or minus 5% of the steady state value.”
“So, the basic feedback formula doesn’t just apply to AC Laplace domain calculations, it also applies to long term steady state output levels as well”
No, it doesn’t. A step change is not a steady state. It is a change. It is a difference between a before and after state. But Lord M’s emission temperature always has been and will be. He doesn’t take the difference of before and after.
He could. It would actually be valid to include emission temperature on that basis. But the difference is zero.
But mainly you haven’t dealt with the key ingredient in your control diagrams. It is the initial differencer. The system explicitly computes, and amplifies with feedback, the error signal. The difference between before and after. It does not feed back the state.
Aren’t we in danger of confusing or conflating about three somewhat different issues here, even if all three issues come from essentially the same block diagram?
For instance the Mathsoft primer I referenced talks about a “home heating system” as it’s initial example, but the concept pictured isn’t like any real home heating system I ever saw (not when it comes right down to it)!
I mean, the block diagrams there are of continuously controlled flow systems,
so there is no mercury switch, no furnace lighting up, no running for a while, shutting down again, etc.
I submit that in a *continuous flow* version of a heating system, there would be no actual “difference detector”,so nothing like a mercury switch banging on in response to a “zero difference”, and no “error detection” in that sense. At least I think there won’t be anything very meaningful as “error” in the time domain anyway!
So, what I’m saying, I think there’s a potential confusion between on/off type systems, and also a confusing conflation of terminologies.
I don’t know the history of referring to combined inputs as “error”, but maybe that is only helpful when looking at the Laplace domain, or AC response as such?
To see what I mean here, imagine something that *is* patently a continuous flow controller, such as, say, an old fashioned centrifugal ball governor on a steam engine.
The ball governor controls a valve, with the opening of the valve directly driven by the result you want to get out of this machine, i.e., the valve is closed or the valve inlet narrowed directly according to the speed in rpm’s of the engine drive shaft.
Further, let’s say it is a given that the shaft speed is proportional to the steam flow rate through the valve, so if you cut down on the steam flow by 10 per cent, the shaft is sure to turn at only 90 percent of the rpm’s you had originally.
Now in this situation, we may not be happy with just letting the steam through from our boiler direct into the piston chamber – ?
If, say, a nominal calculation says we’ve got 5 kilograms per second of flow available, for 1000 rpm on the shaft, but for some reason we think that might cause problems?
So, we go ahead, put the governor in place, and set the linkages involved so that we have a shaft speed signal feedback fraction (negative feedback) of 0.20, or 20 percent.
Nothing tricky about that, right, we could do that?
The (very simplistic) implication here is that we’ve now limited the flow to 4 kilos per second, and we’ve limited the speed to 800 rpm.
All this hopefully with an advantage in greater stability, such as not allowing the boiler to go cold through expelling too much steam!
Now, the point that must not be missed here is that we *are dealing with a live system, an energetic flow system, so control theory has to cut in here, telling us that the engine will react and actually produce more output than the most simple minded physics scaling would have said!
The block gain on this situation is, I believe, 1/1.2, so the system will end up running at 83 percent of the nominal “straight through” capacity. so the output is 833 rpm,
not 800 rpm as I scaled it initially!
My point is, what does this have to do with making the ‘plus’ versus the ‘minus’ on a block diagram input into a “difference error”?
In this example you’ve got 1000 rpm on the “plus” of the summation element going in, then you’ve got (nominally) 200 rpm on the ‘minus’ of the summation, followed by 833 rpm output!
This most basic result is a steady state or “DC” output in principle — it has nothing to do with trying to subtract one thousand from one thousand to get zero, or whatever.
Now, I just know someone is going to say that I’ve violated a conservation law somehow, so I’m going to finish up by quickly pointing out that the “feedback fraction” is specified as 0.2 here, so we are only subtracting *0.2 times* the 833 ending output (i.e., we are subtracting only 167 rpm off the 1000 rpm that we count as reference signal input). So the signals in this example *do* balance, and again, we’re *never* trying to subtract 1000 from 1000 !
Mr Blenkinsop will find the regulation mechanism he seeks in the fact that where a radiative imbalance occurs it is in due course resolved by an increase in temperature, which restores the balance.
Mr Stokes continues to have difficulty in admitting what the simplest of test rigs would demonstrate – namely, that the feedback block present at any given moment will perforce modify the entire signal that has entered the summative input-output node of the feedback loop. Elementary control theory establishes that this is the case; the elementary equations of control theory demonstrate that it is the case; and test rigs built both by a co-author and by a government laboratory demonstrate that it is the case.
“test rigs built both by a co-author and by a government laboratory demonstrate that it is the case”
We keep hearing this, when other arguments fail, but never get to see what the rig even is or does, let alone how it can possibly demonstrate what is claimed.
Oh, I think we know generally what it is, and I’m sure it will indeed demonstrate that—at least according to some interpretation of Lord Monckton’s awkward phrasing—that “the feedback block present at any given moment will perforce modify the entire signal that has entered the summative input-output node of the feedback loop.”
But it will also demonstrate the validity of Mr. Stokes approach to calculating the output by perturbations.
Both things can be true.
The test apparatus demonstrated many things, not the least of which was that feedback responds not merely to some arbitrarily-selected fraction of the reference temperature but to the entire reference temperature, in which the largest element is the 255 K emission temperature.
As the head posting states, one can do climate-sensitivity calculations either by using sensitivities or by using absolute temperatures. But if one uses the former, as official climatology does, even a small uncertainty in the value of the sensitivities entails a large uncertainty in their ratio, the system-gain factor, while using the latter, which are two orders of magnitude greater than the former, even quite large uncertainties in the value of the temperatures entails only a small uncertainty in their ratio, the corrected system-gain factor. As Bill Rostron has pointed out earlier in this thread, using absolute tempeatures – which is of course permissible, contrary to the impression Mr Stokes has been giving – increases the signal-to-noise ratio considerably, and that makes reliable derivation and constraint of equilibrium sensitivities a whole lot easier.
Here is the weakness of both the Lord Monckton and Stokes analysis:
Why should the 255+32.5K reference condtion be treated as invariant? While indeed there is data to show the condtion to be steady (or more likely steady state) over an 80 year period of time, that is not the same as invariant.
That assumption needs to examined quite closely. If one assumes the reference condition to be invariant (and thus decoupled from post 1850 changes in climate conditions of solar radiation, atmospheric gases, ocean temperatures, etc.), then whatever calculation of the system gain is solely attributed to the proposed transfer function (CO₂ in the current work) elements. This simplification is rather hard to swallow regardless of how one goes about calibrating the transfer function.
Consequently, the argument that the feedback contribution is small falls short of being totally convincing because one can mathematically postulate that elements of the feedback transfer function are working to suppress atmospheric warming (some kind of global thermal moderator) resulting in a net slight feedback signal. Consequently, the thermal forcing of green house gases is massively deadly, but for now the planetary climate machine is holding back the tide.
One can correctly point-out that the T/CO₂ relationship is exhibiting an agreeably low system gain factor over the intervening years. That’s dandy, but one can then counter that we’re reaching the limits of what the global thermal moderator can stand and we’re nearing the tipping point. You argue that the system must be linear because of the disproportinate contribution of the reference signal. I cannot disprove that argument, but one can equally argue that the end of that linearity approaches. Anything here sound regretably familiar?
Why I consider your proposed proof to fall short of convincing is as follows. All the parties have chosen to simplfy a complex system with many factors (or state variables in control-speak) to an input reference condition and a CO₂ forcing transfer function. One then calibrates that multi-variable transfer function from that output/input ratio. That could be correct. It could be incorrect. The mathematical pitfall is considered observability and controlability in state-variable control analysis (The Broom Balancer is considered the classic state variable control problem.) In short, one may not be able to predict (observe) or influence (control) a multi-variable system based on a reduced set of inputs and/or outputs. The problem become more peculiar if one considers sampled-data system (z-transform math) versus analogue data signals (Laplace transforms). Since the majority of the historical data is either daily averages or hourly readings, we’re embracing sampled-data analysis.
Thus, while I appreciate your effort and acknowledge that you have put your finger on a problem with the prior analysis, you cannot quite reach your proof as a more appropriate calibration of a flawed approach is still flawed.
Master of the Obvious
I quite like your observability point. Because if you are right, you are saying the enhanced greenhouse effect cannot observed (in the sense that we cannot confirm all of the relevant state variables) and therefore the scientific argument faces an intractable problem in providing relevant measurements to construct a supportable link to CO2 as a cause of warming.
And by extension, you have destroyed your suggestion that “the thermal forcing of green house gases is massively deadly, but for now the planetary climate machine is holding back the tide”. And certainly no way to assert “one can then counter that we’re reaching the limits of what the global thermal moderator can stand and we’re nearing the tipping point”.
Likewise, I quite like your consequential controllability argument as the unobservable state variables (according to your position) will frustrate any case to manage human emissions of CO2 in order to deliver some desired outcome with respect to future average temperatures (a measure which lacks physical meaning).
Why should we assume the elements of the transfer function are small? I can offer two reasons. The first is to assume the atmospheric climate system is passive (it has no energy supply to call upon in order to amplify any of its variables) and open loop gain must therefore be less than unity. The second (which supports the first) is to observe that the climate is a stable system and this is also a characteristic of the same open loop gain.
If you think the climate will reach some tipping point (amplification of any of its variables), you must argue that it will behave as an active system (has an energy source which will support amplification of the relevant variables) and show that this behaviour accords with conservation of energy.
“Jordan June 9, 2019 at 1:44 pm
If you think the climate will reach some tipping point (amplification of any of its variables), you must argue that it will behave as an active system (has an energy source which will support amplification of the relevant variables) and show that this behaviour accords with conservation of energy.”
I am not any good with words however, this perfectly explains the point I have been trying to make for sometime (Not always at WUWT). So, thank you Jordan. Where does the extra energy come from is my point?
The Sun you i***t!
If we wanted to heat the Earth up dramatically, all we would have to do would be to eliminate all the ice and all the clouds, to lower the albedo. Oh, that’s quite hard I suppose. But that is where the extra energy comes from, by not reflecting it back to space.
See – owe to Rich
Except you have overlooked angle of incidence. Its cold at the poles because incident sunlight is non existent for half the year, and the angle of incidence has its greatest impact at the solstice when the Earth’s tilt is at 23 degrees.
To evaluate the ice albedo feedback, you have to focus your attention at the edge of the ice. As the ice retreats, the incident power of sunlight declines because the Earth is not a flat object, but the exposed surface radiate outward into the hemisphere above it at “local temperature”. This is a process which must cease at the point where the (reducing) incoming solar power can no longer melt any more ice. It is a saturated process (zero gain). Things are a bit more complicated than this because of the seasonal variation, but that’s just detail.
The reason why there is ice at the poles is simply because there is no incoming sunlight there. Ice albedo feedback only exists in the imagination of people who have nothing better to worry about.
The Sun, NOT CO2 and positive feed-backs?
Thanks!
If you read the posts by the resident solar expert, he says there isn’t enough energy to do that.
Patrick MJD: yes, the Sun, but via positive feedbacks from melting ice and (supposedly) increasing water vapour.
Jordan: I agree that the picture is complicated by angles of incidence, but right now the Sun is 23 degrees above the North Pole, which is the same as at midday in London in mid February. I can assure you that even with the air temperature around freezing, the Sun at that angle has plenty of power to melt snow and ice. Currently that pole has ice, but if it should ever be ice free there will be more absorption of sunlight.
You talk about the edge of the ice, and there the Antarctic is more important because the edge is at lower latitudes than in the Arctic.
The Antar
“See – owe to Rich June 11, 2019 at 1:35 am”
Where are these feedbacks? Where is the extra energy?
If there were such a feedback, there would be linear warming (Due to CO2 increase and “warming”). There isn’t.
Just for clarity, I am not arguing for this point; rather, arguing that utilizing transfer function mathematics will not settle the question in either direction. I’m going to presume that you meant “one” where the comment addressed “you”.
The energy source can be postulated to be the sun; thus, under (admittedly questionable) assumptions of feedback gain, it could achieve the results proposed by some. I do not discount the arguments that experience suggests the thermal regulator to be more robust such that we’re unlikely to “tip” over the edge into a thermal runaway based on greenhouse gases. If I were the betting type, that is where I would place my money.
However, Lord Monckton decried the lack of meaningful peer review of his work. He is now certainly getting it. Consequently, I will challenge his methods so he may improve his arguments. A combination of “open loop”, “passive” and (in Lord Monckton’s words) “typically near-invariant” are nice arguments and perhaps even the close to reality; but, it is not proof of reality (as science rarely achieves that exalted pinnacle).
The work raises very salient questions about the nature of the transfer function climate models and their calibration. However, there is a limit to how far the argument can be taken. In particular, one cannot argue that since the net feedback signal is low, that the contributing signals are also low. That is a non-sequitur. Examination of even a single state-variable model can have large terms in the feedback transfer function that subsequently net near-zero. In the more likely multi-state-variable case, the math of observability renders discering the behavior of the state variables from the limited selection of input/output data rather doubtful.
Now, do I believe that the individual terms are massively high and we’re all living on the edge? I do not for the reason that such a system would be (in my experience) rather twitchy and unstable. While the planet has exhibited variation in climate behavior on a long-term time scale, it has not shown the behavior of a high-gain system with under-damped response.
However, if one is trying to argue by examination of transfer function models that there is no boogy-man lurking out there just around the CO2 corner, then the argument fails as one (not necessarily me) can arrange the transfer functions to fit any narrative one cares to concoct. Does that exercise make the assertion correct? Certainly not; however, the climate debate has not been a bastion of clear logic and consistent argument.
So, if I were refereeing this paper, I would recomend it for publication with some comments back to the editor about the feedback assertion. It meets the criteria of raising good questions about the prior art and has well-constructed arguments. I would suggest being more clear about postulating the low feedback condition as being based on an examination of individual contributors and some analysis of the damping behavior of historical climate/temperature data. Preponderance of evidence is not proof, but it can be good argument.
“Master of the obvious” has not, perhaps, understood that the term “invariant” is not applicable to single points on a curve, such as that which obtained in 1850, where reference temperature (before accounting for feedback) was 265 K and equilibrium temperature was observed to be 287.5 K. The ratio of these two values, 287.5 / 265, was the system-gain factor applicable at that moment.
The question is whether the curve of the system-gain factor over time is invariant or nearly so. Official climatology describes the climate-sensitivity parameter, which encompasses the influences of forcings and of feedbacks, as “typically near-invariant”. Since we accept all of official climatology except what we can disprove, we accept that the climate-sensitivity parameter, and therefore the curve of the system-gain factor over time, to be invariant or nearly so.
But our paper also examines all of the sensitivity-altering feedbacks in detail, concluding that none of them could, under anything like modern conditions, give rise to a pronouncedly invariant response curve. Put simply, all sensitivity-altering feedbacks self-cancel except that of water vapor.
By the Clausius-Clapeyron relation, specific humidity – the atmospheric burden of water vapor – is supposed to increase near-exponentially at about 7% per Kelvin (Wentz+ 2007) as the space occupied by the atmosphere warms. However, two considerations prevent the water vapor feedback from being anything like as strong as 7% per Kelvin. First, the temperature response to the water-vapor feedback forcing is approximately logarithmic, roughly canceling the exponentiality of the increase in specific humidity. Secondly, the specific humidity is not increasing at all in the crucial tropical mid-troposphere: it is declining, contrary to the predictions of all the models.
Therefore, there is no good reason in atmospheric physics to expect a strongly nonlinear temperature response due to feedback. And that is why official climatology’s system-gain factors both for the preindustrial era to 1850 and for a subsequent doubling of CO2 concentration work out at about 3.2. This, at least, is consistent with the statement in IPCC (2001, ch. 6.1) that the climate-sensitivity parameter is “a typically near-invariant parameter”.
What official climatology has not appreciated is that, once one takes into account the undeniable fact that such feedback processes as subsist in the climate at a given moment must act upon the entire temperature obtaining at that moment, and not merely to some arbitrarily-specified small fraction of that temperature, it is in fact predicting such wildly-exaggerated warming as to be strongly nonlinear, directly contrary to its finding that the climate-sensitivity parameter is “typically near-invariant”.
Since there are good physical reasons to suppose that the climate-sensitivity parameter is indeed near-invariant, the system-gain factor over the geologically minuscule period from 1850 to a doubling of CO2 concentration compared with 2011 is scarcely going to change much. That is why we are reasonably confident that Charney sensitivity is not 3.35 K, as imagined by the CMIP5 models, but only 1.15 K, ending the climate “crisis”. That “crisis” arose solely from official climatology’s elementary error of physics in not appeciating that feedbacks act upon the entire reference signal they find, and not merely upon some fraction thereof.
I will agree that you make many good arguments for that case; however, a preponderance of evidence does not disprove an assertion that a CO2 menance lurks in the near future.
The models presented are of the form:
T(lots_of_stuff@1850) + T(much_less_stuff@since 1850) = T(@today)
Run a system gain calculation of T/CO2 and one now has the greatest menance to human survival since the Black Death. I reject that construct for the following reasons:
(1) By tucking much of the climate mechanisms into the 1850 reference signal results in a model with all positive gain (post 1850) and no balancing negative gain. Such a supposition is dubious.
(2) If one adopts the supposition that our climatic system has mechanisms to both capture heat (least we have moon-like temperatures at night) and ultimately loose that heat (as the sun sends more everyday), then the post-1850 transfer function should feature at least a good sub-set of the mechanisms present in the 1850 reference signal. The narrow choice of mechanisms in the post 1850 signal is doubtful.
Consequently, I reject the T_reference invarance on first principals as I find the inherient assumptions indefensible. The proper form of the transfer function should be:
T(still_lots_of_stuff@today) + T(much_less_stuff@today) = T(@today).
You make arguments for the near invariance of the 1850 reference signal so that the model can be simplied to the previous form. Not an unreasonable approach. You offer analysis of various candidate mechanisms. But, you invoke Wentz et al., note the variation between predicted water vapor (based on equilibrium of a reversible, closed system) and observations while passing lightly over the mechanisms responsible for the variance.
I agree with the analysis that solar radiance is the main signal input and should be properly accounted in the calibration. Bravo. However, your assertion that the climate system must be linear does not hold-up. You offer much evidence and analysis, but can you definitely account for why atmospheric moisture is almost never in equilbrium with the liquid state (per Clausius-Clapeyron)? If those mechanisms have slipped your dragnet, then what else have you missed?
All the reasons that a climate feedback model fails to convice me of the CO2 menance still apply to your model. So, I can’t go that last step with you. Your preponderance of evidence makes a strong case, but I part company with reverse engineering a transfer function to predict individual elements (including CO2 effect). As I detailed for Jordan (vide supra), the math can be conveniently (and improperly) construed to fit whatever narrative one cares to propose.
You have certainly cut the menance down to size. You make some good arguments for a stable climatic system which I believe to be a more fruitful narrative than trying to disprove things that go bump in the night. My suggestion is be ruthless on what you can prove/disprove and pick defensible positions.
“Master of the Obvious” appears very confused. Though I have patiently explained to him that describing a signal at a single moment as “near-invariant” is inappropriate (the signal is what it is), he continues as though this had not been explained to him.
He says I “make arguments for the near-invariance of the 1850 reference signal”. I do no such thing. I assert that the reference temperature in 1850 was about 265 K.
Official climatology asserts that the climate-sensitivity parameter – the quantum of warming to be expected at equilibrium per unit radiative forcing – is “a typically near-invariant parameter”. If “Master of the Obvious” considers that it is not near-invariant, then his quarrel is not with us but with official climatology. He should direct his concerns to the Secretariat of the IPCC, which will give him short shrift.
“Official climatology asserts that the climate-sensitivity parameter – the quantum of warming to be expected at equilibrium per unit radiative forcing – is “a typically near-invariant parameter”.”
To be honest, I have no idea what this is supposed to mean.
If it is saying that climate sensitivity is stationary, it could just say it in those well-understood terms.
Or if the phrase “invariant” means something other than “stationary”, could you please just tell me what you are trying to say.
If my comments rankle due to my attempt to pin-down your claims, I do ask your forebearance but offer no apology. In your postings, you claimed to have “ended the ‘crisis'” and that it is “game over”. As many have noted, extrodinary claims require extrodinary proof. I applaud you for having stepped into the arena, but you are the one who set the bar quite high.
This forum will offer you the fairest hearing you’ll get. One need only look at the treatment consciencious workers like Kidd and Pielke received for a preview of what lies ahead.
I will offer an apology if I have become confused. As I both read and write dense technical documents and am also quite versant professionally in thermodynamics, equilibrium and transfer function mathematics (both s- and z-domain), I will politely suggest that some editting could facilitate readers of varying levels of experience in understanding your arguments. I have often found my own writing wonderfully clear. I rely heavily on outside review and editing to make sure my arguments are actually clear, cogent and (where achievable) concise.
Here is the source of the confusion:
You also previously wrote:
If you postulate near-invariance from 1850 onwards, then the refernence condition should also be near-invariant. If I have construed your concepts incorrectly, then some clarification would be useful.
The 1850 reference temperature is a resonable estimate based on physical principals. I have no argument with that. However, that reference temperature is inheriently valid for calcuations concerning other signals only in 1850. The moment one utilizes that value in a calculation involving a signal from another time period (as in over a time interval), an implicit assumption of invariance has been embraced. Might be a good approximation, might not. in either case, it is yours to defend. I do sincerely apologize if I was unclear.
However, please anticipate that any deficiency or even legitimate disagreement with any one argument/assertion will be mercilessly exploited in attempt to invalidate all of your arguments. Highly unfair and unscientific? You bet, but it’s the order of the day.
In short, be your own harshest critic. If you pass on that opportunity, there are many volunteers who will gladly step into that role. You should be able to slice and dice my questions and not merely assert that I don’t get it. Yes, it is a tall order.
In response to “Master of the Obvious”, who praises himself for the clarity of his technical writing, I am not as incautious as to make the same claim for my own technical writing, because technical writing is difficult. It may be helpful if I explain that the system-gain factor is simply the ratio of equilibrium temperature (after feedback has acted) to reference temperature (before feedback acts) at a given moment.
Therefore, if the system-gain factor is near-invariant over time, as official climatology finds it is (and in this I do not disagree), then it is the ratio that is near-invariant. There is nothing to stop the reference temperature from increasing over time, provided that the equilibrium temperature correspondingly increases so as to leave the ratio of equilibrium to reference temperature near-invariant.
The reference temperature in 1850 was 265 K or thereby. It was the value at that point in time. “Master of the Obvious” had previously written that I was not correct in stating that the reference temperature on that date was near-invariant. But I had written no such thing: for a value at a particular time is what it is, and the term “near-invariant” is simply not applicable to it at all.
The reference temperature in 2011 exceeded the reference temperature in 1850 by 0.75 K, and the reference temperature in response to a doubling of CO2 concentration compared with 1850 would add another 1.05 K to the reference temperature. But the system-gain factor, being near-invariant, will remain at or close to the ratio of equilibrium to reference temperature as it was in 1850: i.e., 287.5 /265, or 1.085.
Simple climate sensitivity equations based on data
Climate sensitivity is the warming from two times CO2. Only one basic parameter is needed: The temperature response factor, K, estimated from data.
Basic relationship: Surface temperature rise from CO2 follows a log function of CO2 ppm changes.
Tr = Klog(C2/C1)
Where Tr = the global temperature rise over a time period.
C1 and C2 are the CO2 ppm values at the beginning and end of the period.
Solving for K gives: K = Tr/log(C2/C1)
And climate sensitivity, CS = KLog(2)
Example
Christopher Monckton, et. al, published a paper in the 2015 Science China Press titled. “Why models run hot: results from an irreducibly simple climate model”. Using the temperature vs. time plot on page 2, Fig. 1, of the paper for the years from 1990 to 2015 shows a temperature rise of 0.34 C. Average CO2 ppm for these years is reported from Mauna Lao data are 354 and 401 ppm.
Using the above equations, we get:
Temperature response factor, K = 0.34/log(401/354) = 2.727
Climate sensitivity = 2.727 x log(2) = 1.89 C
Much less than the IPCC 4.5 value.
Using other sources of temperature dates give the following:
Dates Temp Rise C C1 ppm C2 ppm K = Tr/log(C2/C1) CS = Klog(2)
1880 to 1944 0.24 283 310 2.63 1.82
1944 to 2014 0.65 310 399 2.58 1.79
1880 to 2014 0.94 283 399 2.74 1.89
Average – – – 2.65 1.83
Of course, the above must assume the temperature data is correct and temperature increases are all due to CO2. The reduction of the temperature slope due to ocean heat storage is mostly gone in about 20 years depending on the depth of the mixing layer.
Note: The above is taken from part of a submission to this a website that was not used.
“Much less than the IPCC 4.5 value.”
That is the upper extreme. The IPCC range is 1.5 to 4.5, so this estimate is within it. But it is also right outside of Lord M’s 1.09 to 1.23 range (calculated by a professor of statistics).
My estimates, based on data, include the urban heat effect that some feel is significant and other factors that I have no way of knowing. So my estimates could be high. But still much less that what most of the dire predictions are based on. This is coupled with estimates that assume all emission increases end up as more CO2 rather than much being absorbed, further increasing estimates of future warming.
That is a completely different approach to Lord Monckton’s, and it has its merits. Its demerits, however, are first the choice of endpoints, second the assumption that all other things are equal, and third that it gives Transient Climate Response which is generally thought to be less than Equilibrium Climate Sensitivity.
Despite all that, I agree that your data support an ECS of below 2.5K.
Note my last sentence: “The reduction of the temperature slope due to ocean heat storage is mostly gone in about 20 years depending on the depth of the mixing layer.”
In other words, the transient and equilibrium temperature responses are now basically equal for rates of temperature increases.
The primary difference in transient and equilibrium temperature responses to a doubling of CO2 (a step function) is the delay because of heat absorption on the oceans. And any positive feedback will increase this delay. However, the temperature data usually taken is the rate of warming, such as degrees/decade. This value trends to be constant with an exponential increase of CO2 combined with a log response of temperature to CO2 content (a ramp function of temperature vs. time). I have done modeling with both step and ramp functions of input heat forcing to the ocean and heat loss to the atmosphere with a typical mixing layer of 50 meters (a large heat capacitor) and a variable number mixing layers down to 1000 meters, each layer with a thermal resistance and heat capacity that together cause delay and attenuation of the heat absorption.
When the heat input ramp begins, the temperature rise rate after about 20 years is nearly the same as if there was no heat absorbed by the ocean. Since the ramp of CO2 increase is now at least 60 years old, the transient and equilibrium temperature responses for rate of temperature increases are nearly the same for a constant rate of CO2 increase.
To Richard P.:
“”All warming due to CO2” – as assumption! This is important. Because it is a wrong assumption. The warming is a result of Earth orbital oscillations.
See: http://www.knowledgeminer.eu/climate-papers.html, Climate Recognition Paper part 8, 1600-2050.
Furthermore: The climate sensitivity value was developped by Schneider and Maas. This value is entirely
wrong, based on physical grounds. See G. Kramm and G.Gerlich, explained in detail.
As all warming is wrongly attributed to CO2, then, logically, it is waste of time calculating further into this assumed sensitivity direction.
I think this is estimating TCR, not ECS.
The IPCC says that TCR is likely to be between 1°C and 2.5°C, so your estimates are pretty much in the center of that range.
https://longhairedmusings.wordpress.com/2019/06/11/political-cartoons/
A Blast From the Past American Thinker 2009
November 27, 2009
Politics and Greenhouse Gases
By John McLaughlin
And Lord Monckton’s St Pauls Blockbuster.
Claes Johnson remains for me the leading voice on the Climate Modelling question along with Geoffrey Glassman.
https://claesjohnson.blogspot.com/2011/01/greenhouse-effect-debate.html
MÅNDAG 31 JANUARI 2011
Greenhouse Effect Debate
Judy Curry has opened a debate on the book Slaying the Sky Dragon: Death of the Greenhouse Gas Theory, focussing on my two chapters
Computational Blackbody Radiation
Climate Thermodynamics
I look forward to a hopefully constructive lively discussion. Science does not thrive under dead
silence. In particular, I hope that Spencer, Lord Monckton, Lindzen and other leading skeptics will give the debate some attention.
My perspective is mathematical including both mathematical modeling and computation. I believe that physics must be expressed in mathematical terms, typically as differential equations, to have a precise meaning, and that understanding physics basically boils down to understanding mathematical models of different physical real phenomena, in the spirit of Dijkstra.
I give different presentations of the underlying idea of computation of finite precision in posts on thermodynamics, blackbody radiation, greenhouse effect and climate on this blog and in My Book of Knols and under “books” on my home page.
I repeat that I do not say “that there is no greenhouse effect” since the “greenhouse effect” is not well described in the literature. So anyone preparing to accuse me of “denying the greenhouse effect” should also prepare to tell me what sort of “greenhouse effect” I am supposed to deny. “Greenhouse effect denier” has the same value as “climate change denier”.
What I am saying is that there is no backradiation, because that would correspond to an unstable physical phenomenon, as unstable and unphysical as “backdiffusion” or “backconduction”.
What I am saying is that radiation alone without thermodynamics cannot tell anything meaningful about climate. A no-feedback sensitivity of + 1 C is just a formality or definition without any connection to reality, as non-informative as the statement that there are 100 centimeters on a meter, with its nature of definition signified by the message that it is “unassailable”. Anything “unassailable” is a definition and a definition carries no information about reality. This is important to understand for both CO2 alarmists and skeptics, since CO2 alarmism starts with the basic postulate of a no-feedback climate sensitivity of + 1 C, which is then jacked up to + 3 C by positive feedback. Without the + 1 to start from, CO2 alarmism has to start feedbacks from 0, which is a completely open game with not even the sign being known.
Review of the debate after 83 comments Jan 31:
None of the big skeptics has had anything to say. Only Judy Curry who agrees that something is wrong with the Kiehl-Trenberth energy budget, but does not want to tell what.
Of course Monckton and Spencer do not want to answer any of my questions, or Lindzen…
If you are a skeptic then you pose questions, and of course do not answer any, just like a professional journalist or Freudian therapist. But scientists need to answer questions.
Mostly confusing remarks as if my message has not be absorbed at all. Absorbitivity = 0.
The “greenhouse effect” is strong and healthy science, although the equations are missing.
Judy Curry clarifies and says that the KT budget with backradiation is basically correct.
Summary of my position Febr 1:
Radiative heat transfer is carried by electromagnetic waves described by Maxwell’s equations. The starting point of a scientific discussion of radiation should better start with Maxwell’s equations than with some simplistic ad hoc model like the ones typically referred to in climate science with ad hoc invented “back radiation” of heat energy. If there is anything like “backradiation” it must be possible to find it in Maxwell’s wave equations. In my analysis I use a version of Maxwell’s wave equations and show that there is no backradiation, because that would correspond to an unstable phenomenon and unstable physics does not persist over time.
Climate results from thermodynamics with radiative forcing, and radiation alone cannot tell anything of real significance, such as the effect of changing the atmospheric radiative properties a little: It is not clear if more clouds orwater vapour will cause global cooling or warming, or the effect of a small change of CO2. Climate CO2 alarmism is based on a postulate of a climate sensitivity of + 1 C which is a formality without known real significance.
I welcome specific comments on these two points.
This appears to be yet another tiresome attempt to flog the dead horse “There is no greenhouse effect”. Time and time again it is explained to those who flog that dead horse that the greenhouse effect does not, repeat not, repeat not operate by way of back-radiation. It operates at the quantum level when a photon in one of the absorption bands of CO2 interacts with a CO2 molecule. The collision induces a quantum oscillation in the bending vibrational mode of the molecule (which, due to the disposition of its atoms, does not in itself possess a dipole moment), and that oscillation is by definition heat.
As Professor Christopher Essex puts it, it is like switching on trillions of tiny radiators, which emit heat in all directions. By processes that are near-exclusively non-radiative – e.g. subsidence and precipitation – the heat from some of these collisions is transferred throughout the atmosphere. Maundering on about “back-radiation” is, therefore, off the point.
It is also off topic. Here, we are considering not the directly-forced warming but the consequential feedbacks.
Saturation of the CO2 reflection bands by water vapor destroys the whole exercise. A saturated system has zero gain (or very close to zero).
In response to Mr Simon, the saturation only obtains at or near the surface. Higher up, where the atmosphere is drier, there is no saturation. However, in the tropical mid-troposphere, where the bulk of the warming caused by the water-vapor feedback is supposed to originate, there has been a decline, rather than the predicted strong increase, in specific humidity, greatly reducing the impact of the imagined (and largely imaginary) water vapor feedback.
A lot has already been discussed but I’ll add my few observations.
First, I can usually best any typical warmist but when I come to this site I can find some who I would have difficulty arguing with, Nick being one of them.
So I was intrigued when I saw his post and read it. I got lost quickly as I’ve never had calculus but this is what I surmised from the article: All things that go into temperature outside of CO2 can be considered “noise” or a set of variables that don’t matter much. And so a linear equation can be used to show that if CO2 increases so does the temperature.
That is what Nick’s post boiled down to me. And as having studied astronomy and having some science background I felt this was a very simplistic view that doesn’t account for any other variables such as the sun. I want to thank Christopher Monckton as I was at least able to follow the logic of his thought. I have been a skeptic for a long time, since the change from global cooling to warming I realized they had no idea of what they were talking about. Then following the subject for years and reading that, during the period when they were saying our ice cap was shrinking it was also noted that the ice cap on Mars was shrinking, hmmm, maybe it has nothing to do with CO2 I thought but maybe the sun? Then reading about ice core samples that showed CO2 PPM in the 3000-5000 ranges during periods where it was estimated were colder than current, hmmm, maybe CO2 has little to do with our temperature, maybe it is more driven by solar radiation?
Anyway, I want to thank both Nick and Christopher for the lively back and forth as I enjoy reading this site even if the math and science goes beyond my understanding. 🙂
Many thanks to Mr Capricci for his kind comments. Unfortunately, feedback theory is not at all easy to understand, which is why – in our submission – climate science has gotten it so wrong for so long. It will be good to get proper peer review of our paper, so that we can see who is right. And I hope that, now it is becoming known that the police are beginning to take an interest in those aspects of the global-warming case that are fraudulent, those who have by their action or inaction perpetrated and perpetuated the fraud will think twice and thrice before continuing to do so.
Lord Monckton is correct to identify a big error in climatology’s treatment of feedbacks.
However the next step is to realise that feedbacks in a dissipative open chaotic system lead to complex oscillatory behaviour. As Lorenz showed in 1961 (Deterministic Nonperiodic Flow).
Miskolczi grasped this, that the atmosphere chaotically selfregulates and overall radiative balance is maintained regardless of small increases in trace gasses.
Miskolczi’s analysis based on actual radiosonde atmospheric data, showed that at present CO2 concentrations, the radiative warming effect is saturated, because the atmospheric heat engine is always striving to maximize the dissipation of surface heat into space. In the present circumstance, any additional input of heat produces a reaction of additional evaporation or convection to restore the energy balance. Radiative equilibrium is not disturbed, as shown by the stability of the optical depth in the upper troposphere.
Miskolczi’s insigt means that the land-sea surface heats the atmosphere only by evaporation, conduction, and subsequent convection, not by radiation. The layer of air in contact with the surface is in radiative equilibrium, so that warming and cooling of the surface is matched by the immediate air. The land-sea surface does not cool by radiation to the atmosphere, nor is it warmed by “back-radiation.”
Above the surface-air boundary, heat exchanges between layers of air do include radiative activity, and at the TOA it is all radiation into space. The dissipative-nonlinear climate system makes regulatory adjustment to compensate for changes in CO2 with changes in humidity and clouds, in order to most efficiently convert short wave incoming solar energy, into long wave outgoing energy. With warming and cooling periods, the proportions of H20 and CO2 at the TOA have fluctuated, but the combined optical depth has been stable over the last 60 years.
Mr Salmon has rightly identified the key evidence for Miskolczi’s case, which is that the optical depth – as far as we can measure it – has remained stable, when theory dictates that it should decrease with warming. However, it is difficult to prove Miskolczi’s case due to uncertainties in measurement. That is why we have adopted the theoretical approach of demonstrating that official climatology has incorrectly defined temperature feedback, and that, in consequence, the global warming predicted by the models is thrice what is occurring, and thrice what the corrected theoretical approach would lead us to expect.
Thanks, that’s a helpful clarification. Are people still making radiosonde measurements in an attempt to confirm or disprove Miskolczi?
BTW I attended a Prep School near Bath, UK called Monkton Combe Junior School, in Combe Down. Is your title linked to that Monkton, or a different one (containing a “c”)?
Much of my above post was quoted from:
https://rclutz.wordpress.com/2017/05/17/the-curious-case-of-dr-miskolczi/
https://claesjohnson.blogspot.com/2013/11/standard-calculus-as-ill-posed-unstable.html
Standard Calculus as Ill-Posed Unstable Backward Magic
Jacques Hadamard (1865-1963) was a gentle man with strong opinions on mathematics.
Previous posts on the Fundamental Theorem of Calculus have exposed two approaches to the connection between primitive function/integral x(t), derivative Dx=dxdt and integrand v(t) connected by the equations:
Dx(t)=v(t)
x(t)=∫t0v(s)ds.
In the standard approach as presented in e.g. the standard text book Calculus: A Complete Course by Adams and Essex, the integral x(t) as an area under the graph t→v(t) is the primary given object and the proof of the Fundamental Theorem consists of showing that x(t) satisfies the differential equation Dx=v.
https://claesjohnson.blogspot.com/2013/11/standard-calculus-as-ill-posed-unstable.html
Claes always seemed to have rather a good point with this.
https://claesjohnson.blogspot.com/2013/11/standard-calculus-as-ill-posed-unstable.html
Standard Calculus as Ill-Posed Unstable Backward Magic
Jacques Hadamard (1865-1963) was a gentle man with strong opinions on mathematics.
Previous posts on the Fundamental Theorem of Calculus have exposed two approaches to the connection between primitive function/integral x(t), derivative Dx=dxdt and integrand v(t) connected by the equations:
Dx(t)=v(t)
x(t)=∫t0v(s)ds.
In the standard approach as presented in e.g. the standard text book Calculus: A Complete Course by Adams and Essex, the integral x(t) as an area under the graph t→v(t) is the primary given object and the proof of the Fundamental Theorem consists of showing that x(t) satisfies the differential equation Dx=v.
https://claesjohnson.blogspot.com/2013/11/standard-calculus-as-ill-posed-unstable.html
Claes always seemed to have rather a good point with this.
Certainty about uncertainties
What of the uncertainties in our result? Some of the official input values on which we have relied are subject to quite wide error margins. However, because our mid-range estimate of Charney sensitivity is low, occurring at the left-hand end of the rectangular-hyperbolic curve of Charney sensitivities in response to various values of the feedback fraction, the interval of plausible sensitivities is nothing like as broad as the official interval, which I shall now demonstrate to be a hilarious fiction.
clip_image004
The Charney report of 1979, echoed by several IPCC Assessment Reports, gives a Charney-sensitivity interval 3.0 [1.5, 4.5] K. The 2013 Fifth Assessment Report retains the bounds but no longer dares to state the mid-range estimate, for a reason that I shall now reveal.
is it only me that sees Claes observation to the general Mathematics and the specifics in Image oo4 above?
Milord,
In response to Paramenter, I don’t suppose it will be as easy as all that. Official climatology simply does not realize that the feedback processes present at any moment must respond not merely to some small and arbitrarily-defined fraction of the reference signal but to the entire signal […]
Sooner or later they start to realise that. This truth will be also leaking into the public domain, even without formal article published (this blog may plays small role in this). I know that getting your article publish will be a mammoth task. We’re dealing with determined and ruthless defenders of the party line. I’m afraid some of them share Pilate worldview (‘what is the truth?’) what won’t make things easier. Still, good to know that you’re pursuing!
Dear Lord Monckton,
I see that you defend well your analysis of feedback and climate sensitivity, showing that in official climatology their calculations were done with numerous errors.
I hope that you succeed in this undertaking and that a revision of official numbers will be the result of your efforts.
I therefore understand that you leave the question whether climate sensitivity does exist or not aside and rather concentrate onto the errors in official sensitivity and feedback calculations.
This post should, however, also be taken as opportunity to point to additional directions in research.
According to Gerlich, Kramm et. al., the climate sensitivity is based onto the formula proposed by Schneider and Maas, and this formula is plainly wrong. And therefore all subsequent calculations with a wrong root MUST therefore also be wrong, and even increase in wrongness. And there is no such thing as an accumulation of “wrong” to make one “right”, no matter the amount of calculations done with 10, 30, 50% wrongness subtracted or added.
To my research: Earth orbital perturbations in decadal/centennial size, which can eactly be calculated, are the true cause of the the temperature increase in the past. The low point was in 1610, with the Sun-Earth distance largest at the both ends of the minor [not major! axis, which is constant], therefore the coldest decades in the 17. century. The high temperature peak will be 439 years later, at 2049, with the shortest Sun-Earth distance at both ends of the minor axis of the Earth orbit. And the temperature increase since the 17. century is exactly in size what the orbital values demand. Therefore, there is NO place for CO2 and NO warming effects caused by CO2. All warming is entirely covered by the Earth orbital perturbations.
At the moment, we are entering a warming temperature plateau for the next 30 years until the peak in 2049, with an average temperature level of 0.25 – 0.30 C above the 30 year running mean. See for yourself: The temperatures in the coming years will remain plateau and not increase.
The literature see http://www.knowledgeminer.eu/climate-papers.html,
Climate pattern recognition,PART 8, also PART 1-7 for covering the entire Holocene.
The scientific temperature calculations are given in a separate booklet.
best regards JS.
I’m not going to respond to Lord Monckton’s most-recent distortion of what I’ve said. But for the sake of any lurkers I’ll make one observation.
A recent addition to his arguments for near linearity is the IPCC’s statement that certain parameters are “nearly invariant.” But that statement neither intentionally nor accidentally implies linearity. The IPCC was merely saying that the temperature a given model says is caused by a given increment of forcing seems not to depend on whether that forcing increment results from a change in, say, albedo instead of greenhouse-gas concentration. Furthermore, the IPCC was probably focusing only on small forcing increments that occur in a global-average-surface temperature regime within a few degrees of those that prevail now.
Independently of whether that was its focus, though, there’s no reason to interpret “nearly invariant” as meaning that all modes’ common incremental response could not be very different at much lower temperatures; as I explained to him before, invariance is orthogonal to linearity. Lord Monckton’s failure to grasp this concept, which at least as to time invariance is among control-systems theory’s most basic, shows yet again how woefully unqualified he is to pontificate as he endlessly does about that discipline.
I might add in passing that this isn’t his first invariance problem. In his execrable paper “Why Models Run Hot: Results from an Irreducibly Simple Climate Model” the central equation’s fundamental error was to treat a time-invariant system that has memory as though it were a memoryless time-variant system. So far as I can tell he’s learned nothing in the four years since.
Joe,
I say with the greatest respect that I would strongly recommend that you tone down the personal content. While I can sympathise with the frustration you are feeling, and I recognise that some/many of your responses are reactive, your venting your frustration in intemperate personal insults serves no useful purpose. Please think about what you are trying to achieve. The anger in your posts positively inhibits your ability to convince any readers of the validity of your views – and I do accept the validity of most of your mathematical arguments – and it only serves to evoke a bad response from Lord Monckton. (Please don’t tell me you believe that you have just cause. That is really not the issue.)
I would also invite you to consider the likelihood that Lord Monckton is honestly presenting his beliefs, and that the biggest problem is that you are talking past each other using quite different languages which just happen to look like English.
On a different point, as a result of your comment about “Why models Run Hot…”, I took a look at the paper for the first time. Yes, you are correct that the paper is founded on a memoryless model (which is difficult to support). It requires a convolution or superposition formulation to calculate transient temperatures from the arbitrary forcing series used as input, and not a rescaling of a linear relationship between forcing and temperature – which I understand to be your main point. Secondly, the “transience fraction” has to do a lot of work to try to make the linear relationship between temperature and forcing look like the convolution solution. In particular, it is not just a function of time and total feedback; it is a strong function of ocean heat capacity and the rate of heat exchange with the deep ocean – which are not parameterised in the base equations and which were not investigated in the text. Thirdly, I can see no benefit in expressing the total feedback as a gain term. The authors would have got the same results, all else being equal, if they had just left the total feedback term in their base Eq 1, without expressing it as a factor of a reference feedback. However, this third point did give me what I hope is insight into where Lord Monckton is coming from and how he got to where he is. I may yet be able to change his paradigm.
“I would also invite you to consider the likelihood that Lord Monckton is honestly presenting his beliefs.”
Believe me, I have considered that possibility. And I think that to a degree he actually does believe he knows what he’s talking about. He would be far from the only person who honestly thinks his talent for rapidly regurgitating facts is the same as being good at understanding their implications. Moreover, I’ll admit that I’m not as innately patient with such people as I wish I were.
Still, in most contexts I make an honest, and I believe usually successful, attempt to combat that impatience by regularly calling to mind Max Ehrmann’s advice that we “listen to others, even the dull and the ignorant; they too have their story.” Indeed, for years I attempted despite Lord Monckton’s vitriol to nudge him gently toward more-rational views—to the extent that it was remarked upon at the time: https://wattsupwiththat.com/2013/11/21/on-co2-residence-times-the-chicken-or-the-egg/#comment-1142100.
But he has evaded and mischaracterized my arguments so consistently for so long that there’s no chance he’s being honest in his arguments. A few examples of how evasive and deceptive his responses have been are found at https://wattsupwiththat.com/2015/03/16/where-the-complex-climate-models-go-wrong/ and https://wattsupwiththat.com/2015/04/05/a-reply-to-born-how-to-represent-temperature-feedbacks-in-a-simple-model/.
Despite that I might have persisted in biting my tongue if there weren’t another factor. It has become apparent that at this site there are very few people who, like you and Greg, can comprehend much about feedback. Indeed, few seem to have patience with even a single algebraic equation, much less calculus or differential equations (which, fortunately, haven’t come into play here).
So the majority of this site’s readers are completely vulnerable to being swayed by atmospherics. Many are accordingly being badly misled; some have offered Lord Monckton financial support. Since objective facts and incontrovertible math therefore have little effect, the best I can do for them is express how outrageously wrong his theory is and hope that the scales fall from the eyes of one or two readers at least.
I appreciate your thoughts. And in your position I might have thought the same thing—had my experience with him had not been so extensive and so uniformly unedifying. (If I recall, in fact, I myself may once have suggested overlooking his lack of courtesy.)
Under the circumstances, though, I think I’ll continue to be plain about his evasiveness, dishonesty, and lack of knowledge.
Sorry to break this to you Joe but nothing that you or anyone that you know has ever written on climate feedbacks is worth the paper it’s printed on or the thumb-ATP consumed posting it. It all assumes linearity and equilibrium. The climate is a nonlinear far from equilibrium system. In such a system the role and effect of feedbacks is fundamentally different. Negative feedbacks exert friction and cause complex emergent pattern. Positive feedbacks cause collapse of such patterns and monotonic oscillations. Consider their role for example in the monotonic oscillation of Cepheid variable stars.
Everything written on climate dynamics that is not built on the understanding that it is a dissipative periodically forced nonlinear chaotic system is irrelevant fiction. Probably a few million years of wasted human effort. A good point to go back to would be Ilya Prigogine’s nonlinear thermodynamics, and then, if you have the stomach for it, Miskolczi.
Sorry folks, you all are wrong! Why? Because the Earth orbit perturbations are entirely omitted in
proposed calculations. The Earth´s flight around the Sun is a screw-type, spiral advance on its
elliptic path, which means that Earth constantly deviates to either left, right, above and below
the calculated elliptic path. And this shortens and lengthens on decadal and centennial scale the
distance Sun-Earth, thus increasing and decreasing temperatures on Earth. And this on significant
scale, see temp increase from the 17 to the 21st century (here: distance shortening).
And this temperature increase caused by distance shortening is by collution kept under the table, in in order
to attribute the observed warming to atmospheric feedbacks and sensitivities, on which you
all waste your time trying to derive a correct calculation approach, which is futile because of
omission of major climate variables od the Earths flight,
More on this, see http://www.Climate Pattern Recognition, part 8 and also 1, here empirically
derived over 10,000 years of the entire Holocene.
f
In response to Mr Seifert, there are many things wrong with official climatology’s approach, but the focus of the head posting was on just one of these things: the incorrect definition of temperature feedback in official climatology.
If Mr Seifert can refer me to peer-reviewed papers in respected astronomical journals quantifying the influence on terrestrial temperature of the Milankovich cycles – and specifically the variations in the eccentricity of the Earth’s orbit, which seem to be his present focus – I should be most grateful.
From my recollection, though, the Milonkovic cycles operate on timescales of thousands of years: therefore, they are not good for explaining the short-term temperature fluctuations with which we are at present concerned.
Dear Lord Monckton,
the literature question was just explained by me as a separate comment, instead of
a reply comment within the Salmon comment.
And, as I read your questions once more over: The osculating Earth orbital flight has nothing to do with eccentricity changes. Eccentricity of the orbit is uninteresting for the osculating Earth flight advance, because eccentricity changes are millenium- scale thus too small for a centennialscale and do not affect the spiral orbital flight.
Joe
I went too far in my language in the above post which I regret. I sometimes over-react when someone I admire is attacked.
However I strongly believe there is an issue here which goes beyond the climate and CO2 debate. It’s about how the global scientific community has absorbed – or failed to absorb – the discoveries and new theoretic paradigm of chaos and nonlinearity. For various reasons many fields of research have ignored chaos and nonlinear dynamics, to their detriment.
Imagine the following.
the scientific community superficially accept discoveries by Galileo, Kepler et al., that the earth is not static and orbits the sun. However, despite this, researchers continue to work on epicycles and a geocentric model of astronomy.
Or that the discovery of chemical elements and Mendeleev’s periodic table is accepted; but that there is no pause in research into alchemy and the attempts via physical and chemical methods – with a little sorcery added – to transmute lead into gold.
Or alternatively, while the proof of former ice ages, by Agassis and others, and the discovery by geology of rock strata showing the age of earth to be billions of years, are accepted, there is no interruption in research into Noah’s flood as a cause of present day geography.
Something similar to this has happened in regard to the discoveries by Mandelbrot, Turing, Feigenbaum, Lorenz and many others concerning the role of chaos and edge-of-chaos nonlinear pattern formation in many natural processes as well as living organisms. Superficial acceptance is given to these discoveries. But fields of research such as climate, whose complex systems are grounded on such chaos-related phenomena, are proceeding as if chaos and nonlinearity did not exist. Only a few restricted fields such as chemical engineering and population ecology actually accept chaos and nonlinear dynamics at the heart, not the periphery, of what they are studying.
Feedbacks are fundamental to spontaneous nonlinear pattern formation in a far-from-equilibrium system. And the paradigm and body of theory of dynamic feedbacks is totally different for such quasi-chaotic systems compared to linear systems at equilibrium. This affects how we interpret feedbacks in the chaotically churning atmosphere-ocean climate system.
I get the feeling that science as a whole exerts a continual selection, perhaps unknowingly, where they confine their efforts to linear and equilibrium approximations of complex systems and choose research projects where they don’t have to invoke chaos/nonlinear dynamics. And often chaotic theory is wrongly excluded where it is at the heart of how a particular system behaves.
Part of this is linked to a separation of mathematics and physics, politically and culturally, that took place during the 20th century. This is described nicely in James Gleik’s book “Chaos”.
For example, if there had been a proper appreciation of chaotic dynamics in the climate system, especially the ocean, then the correlation of rising temperature and rising CO2 in the 20th century would not have been uncritically accepted as proof of CO2 forcing of climate. The concept of the null hypothesis together with an understanding of chaotic ocean dynamics, might have prompted a much more serious evaluation of whether the 20th century climate oscillations were not of the same natural kind that have always been continually happening, unrelated to CO2.
Mr Born imagines that IPCC’s account of the near-invariance of the climate-sensitivity parameter, and, therefore, of the system-gain factor and the feedback fraction does not also encompass near-linearity in the response function. However, the approximate value of that parameter is stated as about 0.5 Watts per square meter per Kelvin, which would not make a whole lot of sense if the parameter were to vary significantly over time.
Exegesis of the inspissate holy books of IPeCaC is far from easy, so the approach we took was to take forcings and temperature changes every decade in the two growth scenarios – RCP6.0 and 8.5 – and calculate therefrom the feedback fractions for successive 30-year periods fro 2010-2040 to 2070-2100. The feedback fractions varied only from 0.41 to 0.55. From this it follows that official climatology does indeed expect the response function to be near-linear, as one would deduce from the fact that the climate-sensitivity parameter is near-invariant.
“… and calculate therefrom the feedback fractions for successive 30-year periods fro 2010-2040 to 2070-2100. From this it follows that official climatology does indeed expect the response function to be near-linear, as one would deduce from the fact that the climate-sensitivity parameter is near-invariant.”
But isn’t there a difference between expecting something to be near-linear over a range of a few degrees, and being near linear from 0 – 265K?
In response to Bellman, we have assumed that emission temperature is 255 K (our calculations lead us to suspect it is actually more like 276 K once Hoelder’s inequalities between integrals have been allowed for). We have also taken 10 K as the directly-forced warming from the noncondensing greenhouse gases present in 1850. Therefore, the reference temperature in that year – i.e., the temperature that would then have obtained in the absence of temperature feedback – was 265 K. However, the observed equilibrium temperature was 287.5 K. The entire difference between these two values is attributable to feedback.
Official climatology imagines that the entire 22.5 K feedback response in 1850 was driven by the 10 K warming forced noncondensing greenhouse gases, and that none of it was driven by the 255 K emission temperature (which, once one allows for Hoelder’s inequalities between integrals, is actually more like 276 K).
The simplest approach is to recognize that the ratio of equilibrium to reference temperature in 1850 was incontrovertibly 287.5 / 265, or 1.085. We need not concern ourselves with what might have happened at 0 K, for two reasons: first, the values of reference and equilibrium temperature in 1850 are known and quite well constrained, so we know what the system-gain factor was in that year; and secondly, at 0 K temperature the feedback response would also be 0 K, for that is a characteristic of feedback response curves, for rather obvious reasons.
The feedbacks present in 1850 operated in proportion to the respective contributions to reference temperature of emission temperature and of the warming forced by the pre-industrial noncondensing greenhouse gases.
Now, since the climate-sensitivity parameter is near-invariant, it follows that the curve of the equilibrium-temperature response function is near-linear. From that, we infer – legitimately – that the equilibrium sensitivity to doubled CO2 will be the product of the reference sensitivity thereto, which is 1.05 K, and the system-gain factor 1.085 that obtained in 1850. The system-gain factor will not have changed much since then.
We calibrated that result in two ways. First, we noted that the industrial-era net anthropogenic forcing to 2011 was about 2.5 Watts per square meter and the radiative imbalance due to the large heat capacity of the ocean was about 0.6 Watts per square meter. The system-gain factor in 2011, on the basis of these published estimates, is simply 2.5 / (2.5 – 0.6), or 1.316, quite close to our 1.085 and not at all close to official climatology’s imagined 3.2.
Then we calculated the system-gain factors for successive 30-year periods from 2010-2040 to 2070-2100, based on predicted RCP6.0 and RCP8.5 forcings and temperature responses. The typical value was around 2.0, implying Charney sensitivity of about 2.1 K, which is right at the bottom of the CMIP5 interval.
All of these considerations rule out the high sensitivities on which the current genocidal climate mitigation policies are based.
Thanks for the reply. For the sake of your figures might I suggest you don’t have to repeat all your calculations for each response.
My question was about why your assumption of a linear relationship between feedback processes over a range from 0K to 256K, and I don’t think you really address that issue beyond repeating that assertion.
So you have two points, (0,0) and (265, 287.5) and can fit an infinite number of curves through those points. But you assert that only near-linear curves are valid.
To me, with no specialist knowledge, it just seems unlikely that feedback processes would follow a simple curve, let alone a straight line.
You are again asserting that feedback operated “in proportion”, without explaining why.
Again, an assertion that the climate-sensitivity is near-invariant. As I originally asked, why assume that near-invariant over a range of a few K, under real world conditions, must mean near-invariant between 0K and 255K?
Why not?
I find it difficult to believe that the various feedback processes would behave in the same way at say 100K, as they do at 256K.
I can’t say if this is correct, but the fact that by 2011 you’ve quadrupled the feedback value doesn’t suggest it’s near-linear.
But 2.1 K is well outside your ECS interval of [1.09, 1.23].
In response to Bellman, it should now be clear 1) that the system-gain factor in 1850 was 1.085; 2) that the feedbacks then present, which acted upon the entire reference temperature, acted proportionately at that moment, so that close to 22 K of the feedback response to reference temperature was response to the 255 K emission temperature, and less than 1 K was response to the preindustrial greenhouse-gas warming of 10 K (this is an elementary consequence of the fact that the feedback loop responds to the entire reference temperature); 3) that, on the generous assumption that IPCC’s midrange estimate of net anthropogenic radiative forcing to 2011 was 2.5 Watts per square meter, and that the radiative imbalance was as much as 0.6, the implicit system-gain factor was only 1.316, closer to our 1.085 than to the predicted midrange estimate 3.35 K in the CMIP5 ensemble; 4) that IPCC considers the climate-sensitivity parameter to be near-invariant, which necessarily implies that the equilibrium-sensitivity response function is near-linear; 5) that IPCC’s exaggerated predictions of 21st-century warming demonstrate a very near-linear evolution of the system-gain factor; 6) that even those exaggerated predictions only imply a 2.1 K Charney sensitivity, at the very bottom end of the CMIP5 predicted range, though the system-gain factor cannot have been as high as 2 because the equilibrium temperature in 2011 would then have been greater than 530 K, which it was not; 7) that it does not matter what happened at 0 K or 100 K, because we know what happened at 265 K, and official climatology assumes that the evolution of the response function since then is near-linear; 8) that the system-gain factor for 2011 cannot have have as high as the 1.316 implicit in IPCC’s midrange estimate of net anthropogenic forcing to that year because 1.316 times the reference temperature of 265.75 K in 2011 is approaching 350 K, and the Earth is nothing like that hot.
This is the nub of the problem. I, and others who have raised the problem before, think it does matter what would have happened at 100K. Your argument for a feedback of 0.085K for each K rise in reference temperature is based on averaging the warming caused by feedbacks in 1850 by the entire 256K of reference temperature. This makes the implicit assumption that the feedback responses are identical across all temperatures from 0K on.
If in reality there would not be 8.5K of feedback warming with a reference temperature of 100K, then it follows the average is not meaningful across the temperature spectrum and you cannot deduce from it how much feedback response there will be when going from say 265K to 266K.
As you demonstrate in points 6 and 8, the assumption of a linear feedback response for all temperatures leads to absurdities. Much more plausible to my mind to accept that the feedback response at 265K is different to the average.
Bellman has not, perhaps, understood that, since the usual value of the emission temperature that would have obtained in the absence of any feedback is 255 K, and the usual value of the warming occasioned by the presence of the preindustrial noncondensing greenhouse gases to 1850 is 10 K (giving a reference or pre-feedback temperature of 265 K in 1850), and since the equilibrium temperature in 1850 was measured as 287.5 K, it follows that in 1850 the ratio of equilibrium to reference temperature – the system-gain factor – was 287.5 / 265, or 1.085. No ifs, no buts, no maybes: that’s what it was.
The only way to dispute that fact is to assert that 255 K, 10 K and 287.5 K are incorrect values. If they are accepted as correct, than the system-gain factor was 1.085.
Next, it is necessary to address the question whether the system-gain factor is likely to prove invariant over the next two or three degrees of global warming. The answer is Yes, because official climatology finds the climate-sensitivity parameter to be near-invariant (see IPCC 2007 ch. 6 passim, or notice that the ratio of predicted transient warming to predicted net anthropogenic radiative forcing in the RCP6.0 and 8.5 scenarios for 30-year or 60-year periods throughout the 21st century from 2010-2100 is near-invariant), from which it necessarily follows that the system-gain factor is near-invariant.
Accordingly, Charney sensitivity is simply the product of the 1.05 K reference sensitivity to doubled CO2 and the system-gain factor 1.085, giving 1.15 K, or thereby.
It simply does not matter what might have happened at 0 K or 100 K or 200 K or some other arbitrarily-chosen value <255 K. What we are concerned with are the feedback processes that obtained from 1850 onward, in the industrial era. All that is necessary to establish Charney sensitivity is knowledge of the well-constrained values of reference and equilibrium temperatures in 1850 and knowledge of the 1.05 K reference sensitivity to doubled CO2, whereupon Charney sensitivity is equal to 1.05 x 287.5 / 265, or about 1.15 K. And that's a wrap.
If it doesn’t matter how feedback processes respond below 255K, then what’s the point of your 287.5 / 265 formula? You are claiming you can predict how feedbacks will respond to post 1850 warming by taking an average over all temperature responses from 0K to 265K, and assuming the same average increase will happen over the next few degrees increase. If you accept that feedback processes might not have caused a proportionate response at 100K then why would you assume an increase from 265K to 266K will be equal to the average?
And as I said at the start, even if the system-gain factor is invariant over the next two or three degrees, it does not follow that it is the same as the factor from 0K to 256K.
I think you mean IPCC 2001, but no matter. As I keep saying I doubt the IPCC means that the parameter is near constant for all radiative forcings, rather than the range of forcings that the earth will actually experience.They also explain that the value is only used for a first order estimation. It seems strange to insist on the idea that
must be invariant for all time and temperatures, whilst insisting it doesn’t matter what it’s real value would be below 255K.
Bellman asks: If it doesn’t matter how feedback processes respond below the emission temperature of 255 K, then what’s the point of deriving the system-gain factor that converts reference temperatures (before feedback acts) to equilibrium temperatures (after feedback has acted and the climate has resettled to equilibrium) as the ratio of the 287.5 K observed equilibrium temperature in 1850 to the reference temperature of 265 K that obtained that year?
The trivial answer to Bellman’s question is that, since the reference temperature in 1850 was 10 K above the 255 K emission temperature (the 10 K being reference sensitivity to the presence of the preindustrial noncondensing greenhouse gases), it was not a temperature below 255 K.
A more detailed answer is that Bellman has not, perhaps, understood (and, in this, he stands alongside the whole of official climatology) that the system-gain factor A – the ratio of equilibrium temperature E to reference temperature R – is not, repeat not, the secant slope of the curve of the equilibrium-temperature response function E(R). It is simply the ratio of E to R at a given moment of interest.
Because this error is so widespread, the long version of our paper actually takes the trouble to prove what we might legitimately have simply left as a matter of definition. Briefly, the proof consists in demonstrating that the system-gain factor A is equal to 1 / (1 – f), where f is the feedback fraction (i.e., the fraction of E represented by the feedback response b), and then in formally demonstrating that, since the signal passes around the feedback loop an infinite number of times, multiplying itself by f each time, the system-gain factor A is the sum of the infinite convergent geometric series {f^0 + f^1 +f^2 + … + f^infinity} under the convergence criterion | f | < 1. Now, the sum of that power series is 1 / (1 – f). The proof that this is the case long predates the dismal science of climatology: it is, in fact, the oldest of all the proofs of the sums of infinite geometric series. However, climatologists are not necessarily familiar with the elements of number theory, which is why one of my co-authors asked me to prove the sum of the series. Once I had proven it, another co-author then asked why the proof was so detailed. I explained that the detail was necessary to establish the proposition rigorously.
Once it is accepted – as in our submission it must be accepted – that A = 1 / (1 – f), it follows that, if for any year in the modern era we know the well-constrained values of E and R, as we do for 1850, we may at once derive the system-gain factor A that then obtained: A is simply E/R.
What is more, if we also know that the climate-sensitivity parameter (the ratio of period equilibrium sensitivity to net period anthropogenic forcing for any given period in the industrial era) is near-invariant, without error we may state that A is the system-gain factor that will apply – say – to a CO2 doubling compared with 2011, the year to which sensitivity-relevant data for IPCC (2013) were brought up to date.
That consideration answers Bellman's next point. He says it does not follow that, just because the system-gain factor A is invariant over the next two or three degrees' warming, A will be the same as "the factor from 0 K to 265 K". The point here is that A is not, repeat not, repeat not, the secant slope of the curve of E(R). It is not even the point slope of that curve either. It is simply the ratio of E to R at any point of interest on the curve – in the present instance, in 1850. We know the equilibrium temperature was then 287.5 K because we measured it. We know that the reference temperature was the sum of the 255 K emission temperature and the 10 K reference sensitivity to the pre-industrial noncondensing greenhouse gases. So we know their ratio. In 1850, that ratio was, as a matter of fact, 1.085, or very close thereto.
Finally, Bellman says he doubts whether IPCC, in ch. 6.1 of its 2001 Third Assessment Report (I apologize for having inadvertently referred to the 2007 report when I meant 2001 in my earlier reply), meant that the climate-sensitivity parameter is near-constant for all radiative forcings, rather than for the range of forcings that the Earth will actually experience. If he will read the chapter carefully, he will find that it is both. The chapter is indeed principally concerned with demonstrating the utility of the concept of radiative forcing: however, an approximate value 0.5 is given for the system-gain factor. It is also true that IPCC cites some authors who say that in some circumstances and for some forcings the climate-sensitivity parameter may not necessarily be close to invariant. So we tested the values of reference sensitivity to net projected anthropogenic forcings against those of projected transient sensitivities in IPCC's Fifth Assessment Report (2013) and found that, for successive 30-year and 60-year periods in the 21st century, the system-gain factor was indeed remarkably near-invariant. In addition, we examined each of the sensitivity-relevant temperature feedbacks individually, including the Planck "feedback" that has caused some commenters here a good deal of difficulty, and found no reason to imagine that any of these feedbacks – most notably the water-vapor feedback – would be at all likely to contribute to an appreciably nonlinear feedback response.
Bellman says: "It seems stange to insist on the idea that the climate-sensitivity parameter must be invariant for all time and temperatures while insisting it does not matter what its real value would be below 255 K. Here, he may have failed to recall that, since official climatology has hitherto unwisely confined its analysis to reference and equilibrium sensitivities to net anthropogenic forcings rather than to entire reference temperatures, when it talks of the near-invariance of the climate-sensitivity parameter it is talking only of the industrial era, and not of any period before 1850. And, as we have explained. we, too, are only concerning ourselves with the period from 1850 onward: we are not, repeat not, repeat not, repeating official climatology's mistake in assuming that the system-gain factor is the secant-slope of some segment of the equilibrium-temperature response curve E(R).
It is quite possible – though not at all easy to demonstrate – that the system-gain factor that would obtain in the absence of the pre-industrial noncondensing greenhouse gases and, therefore, purely in response to the 255 K emission temperature is quite close to that which has obtained since 1850. The reason is that at 255 K approximately one-third of the dayside of the Earth would be ice-free, allowing all of the sensitivity-altering feedbacks listed in IPCC (2013) to operate. The water-vapor feedback would be somewhat less than at present, but the ice-albedo feedback would be quite a bit greater than at present. It is also possible that the evolution of E(R) follows an epidemic curve, and that we are now approaching the asymptote.
Be that as it may, for present purposes it is necessary for us to demonstrate no more than that the system-gain factor A in 1850 was 1.085, that official climatology, both in theory and in its modeled predictions, treats it as near-invariant, and that it considers the reference sensitivity to doubled CO2 to be 1.05 K. From these facts, it follows that the midrange estimate of Charney sensitivity – equilibrium sensitivity to doubled CO2 – is 1.15 K.
If Bellman considers that official climatology ought not to have relied upon a near-invariant climate-sensitivity parameter in its derivation of the equilibrium-sensitivity response curve shown in its 2013 report, he should address his concerns not to me but to the IPCC Secretariat. Our approach has been to adopt all of official climatology except what we can demonstrate to be erroneous. Our investigations of the question of nonlinearity, which were detailed and time-consuming, have led us to conclude that official climatology is right to treat the climate-sensitivity parameter as near-invariant, from which it follows that the system-gain factor will also be near-invariant.
And this consideration answers Bellman's next point, which is that even if the A
The last part-sentence of my reply to Bellman, “And this consideration … “, should be delete.
Regardless of how you derived the system-gain factor, you still require the function to be near-linear back to 0K. If not it’s strange how much time you’ve devoted to claiming that the curve of the response function must be near-linear and pass through (0,0).
Your claim is that the feedback loop responds to all emission temperatures, not just to increases, so the question is do you regard the feedback fraction to be constant over all temperatures?
If yes then it requires E(R) to be linear. If not you cannot assume that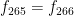
, and in that case you cannot use the results from 1850 to determine ECS.
You only need small changes in the actual feedback fraction to get very different rates of warming, so however correct you derivation might be mathematically, I don’t see how it can be useful in calculating true climate sensitivity.
Suppose hypothetically that temperatures in the real world did rise by 3.5K after a doubling of CO2, so that at some point in the future reference temperature was 266.05K and equilibrium temperature was 291K. Your argument would be that the system gain factor would be 291 / 266.05 = 1.094. By your logic Charney sensitivity would then be 1.15K, despite the fact that observations show 3.5K warming.
Bellman asks whether we require the equilibrium-temperature response function to be near-linear across all temperatures. The answer is that we do not require it to be anything. However, since official climatology finds the climate-sensitivity parameter to be near-linear across the interval of interest, in the industrial era, so that the system-gain factor is also near-linear across that interval, after much investigation we agree with official climatology on that point.
The advantage of our method is that it makes use of information discarded by official climatology in its derivation of equilibrium sensitivities: namely, the information that the system-gain factor expressed as the ratio of entire equilibrium to reference temperatures in 1850 was only 1.085, and not the 3.25 implicit in official climatology’s method.
Bellman’s example, like all such examples that have been presented here, entails a manifest and physically-impossible contradiction. He posits official climatology’s midrange Charney and reference sensitivities respectively as 3.5 and 1.05 K. The implication is that the feedback response is the difference between these two values: i.e., 2.45 K. But then, using official climatology’s method, the feedback fraction – the ratio of the feedback response to equilibrium sensitivity – will be 2.45 / 3.5, or 0.7. Yet the feedback fraction in 1850 was only 0.08. By what physical process does he imagine that a mere doubling of CO2 concentration will engender a feedback fraction an order of magnitude greater than that which obtained in 1850?
As to the observations about the IPCC reports, I suppose the question I should ask is why are you referring to a 20 year old report as “official climatology”? AR5 makes no mention of the climate sensitivity parameter as being near-invariant or linear as far as I can see.
Again, how can “official climatology” treat the system-gain factor as near-invariant when by your own definition “official climatology” doesn’t understand the system-gain factor. The climate sensitivity parameter that TAR describes as near-invariant is not the same thing as your system-gain factor.
This matters because a small change to the near-invariant climate sensitivity parameter will have a proportionate effect on the climate sensitivity, but the same change to your parameter will result in a huge change to climate sensitivity.
Bellman:
Well said; you put it better than I did. For anyone who can follow a logical argument, your explanation should be the end of Lord Monckton’s theory.
Let me just add, though, that the cause of my morbid fascination isn’t that Lord Monckton nonetheless remains unpersuaded; we encounter folks all the time who display no reasoning ability. No, the thing that’s remarkable to me is how many of this site’s visitors are swayed by an argument so bereft of logic–even though many have physical-science backgrounds.
I’ve speculated that much of the reason is his use of ambiguous formulations and idiosyncratic terminology; they mask his lack of logic. Although they make it inconvenient for people to really follow what he’s saying, readers just assume his conclusions follow from the welter of background facts that readers often recognize as true.
As you’ve discovered, they don’t.
I don’t posit anything. I was trying to provide a simple example that illustrates the problem with your derivation of sensitivity. The same logic that says that it’s physically impossible for there to be 3.5K of warming after doubling of CO2 would also have to conclude that the response has to be linear since 0K.
You’re comparing two different derivations of the feedback fraction, one of which you think is completely wrong and wonder why they are different. Applying your own derivation of the feedback fraction, the value in 1850 was 0.078, after my hypothetical 3.5K rise the fraction would be 0.086. An increase of about 10%, you could almost say near-invariant.
Bellman might like to explain in what respects he considers IPCC reports not to be official climatology. And, as I have explained to him before, the Fifth Assessment Report (2013) treats the climate-sensitivity parameter – the ratio of equilibrium sensitivity to radiative forcing – as near-invariant, as one may deduce from the evolution of the published values for the RCP6.0 and 8.5 scenarios (the other two scenarios find sensitivity low, as we do).
Bellman asks how official climatology treats the system-gain factor as near-invariant, when by our definition it does not understand the system-gain factor. He is perhaps unaware that if the system-gain factor is near-invariant the values derived by our method using entire temperatures and by official climatology using sensitivities only will be near-identical.
He also says that the climate-sensitivity parameter is not the same thing as the system-gain factor. He has not, however, spotted that if the climate-sensitivity parameter as defined above is near-invariant then official climatology’s system-gain factor must also be near-invariant, whereupon our system-gain factor will be near-invariant a fortiori because it is the ratio of temperatures that exceed by two orders of magnitude the sensitivities whose ratio is official climatology’s system-gain factor.
Bellman says that a small change to the near-invariant climate sensitivity parameter will have a proportionate effect on climate sensitivity as derived by official climatology, but the same small change to our system-gain factor will result in a huge change to climate sensitivity. So let us do the math. We know that the system-gain factor at the equilibrium in 1850, derived by our method as the ratio of the entire equilibrium to reference temperatures in that year, was 1.085. We also know that, since the system was then in equilibrium, official climatology’s system-gain factor was also 1.085.
Now, official climatology says that the midrange net industrial-era anthropogenic radiative forcing to 2011 was 2.5 Watts per square meter, or thereby, and that in 2010 there subsisted a radiative imbalance of 0.6 Watts per square meter, implying that climatology’s period system-gain factor was 2.5 / (2.5 – 0.6), or 1.316, implying a feedback fraction 0.240, three times the 0.078 that obtained in 1850.
What, then, is our system-gain factor for 2011 under these circumstances? It is (287.5+1.0) / (265+0.75), or 1.0856, barely changed since 1850. However, there is no plausible physical process by which climatology’s period system-gain factor could be anything like as much as thrice the system-gain factor that prevailed at the equilibrium in 1850, and such a result would also fall foul of official climatology’s current understanding that the climate-sensitivity parameter, and therefore both climatology’s and our system-gain factors, is near-invariant.
And even if, per impossibile, official climatology’s midrange period system-gain factor 1.316 were correct, Charney sensitivity would be only 1.316 times the 1.05 K reference sensitivity to doubled CO2 – i.e., less than 1.4 K, a result a great deal closer to our 1.15 K than to the CMIP5 models’ midrange 3.35 K.
A further clarification for Bellman: where the climate-sensitivity parameter is near-invariant, the values of the system-gain factor expressed as the ratio of entire equilibrium to reference temperatures and the proxy system-gain factor expressed as the secant-slope between two moments of interest [the secant slope is only equal to the system-gain factor where the curve is precisely linear] will not only be near-invariant, as explained in my earlier answer: they will also be near-identical.
I presume, “official climatology” means the most up-to-date science on the subject. Therefore the IPCC report from 203 is more “official” than one from 20 years ago.
I see nothing to suggest the climate-sensitivity parameter to be near-invariant in AR5 – most of the chapter is explaining the complexity of forcings and feedbacks, and suggests that feedbacks respond differently to different forcings.
The fact that you say two of the scenarios show lower sensitivity than the other two would suggest to me that the parameter is not invariant.
You say that if the climate-sensitivity parameter being constant would imply that the system-gain factor must be constant. This is only true if it is constant for all temperatures back to 0K. Say, hypothetically there were no feedbacks until forcings were equal to 250K, and then where near-invariant for all forcings above this. The IPCC’s climate sensitivity parameter would be invariant, but your system-gain factor would be increasing as the forcings increased.
I’m not sure what your point was with all the math at the end. It seems to confirm my point that local climate sensitivity is sensitive to very small changes in your definition of system-gain, but then you just say it’s impossible. You again seem to be comparing official climatology’s definition of feedback with your own and saying the fact that a feedback based on local changes is larger than the own based on your definition proves that the official one is impossible.
Bellman may like to investigate the ratios of output to reference sensitivity on the RCP6.0 and 8.5 scenarios, which – though he may perhaps not have realized this – were not in AR3 but in AR5, IPCC’s latest assessment report. The system-gain factors that are thus derivable are near-identical in both scenarios, and change very little over time.
I do not require the curve of the equilibrium-temperature response function to be near-linear all the way to zero Kelvin. That may or may not be the case. All I need to demonstrate is that, in 1850, the system-gain factor derived as the ratio of equilibrium to reference temperatures was 1.085; that official climatology’s secant-slope proxy for the system-gain factor is near-invariant; that, therefore, our system-gain factor is near-invariant a fortiori, and that, in consequence, Charney sensitivity is 1.085 times the 1.05 K reference sensitivity to doubled CO2: i.e., 1.15 K or thereby.
Recall that official climatology’s secant-slope proxy for the system-gain factor is obtained via a localized linearization in the form of a leading-order Taylor-series expansion. If one centers the linearization about 1850, then one has no need to concern oneself about what might have happened if the Sun were not shining and the preindustrial greenhouse gases were not present. All we are concerned with are modern conditions.
Bellman’s suggestion that “You only need small changes in the actual feedback fraction to get very different rates of warming, so however correct you derivation might be mathematically, I don’t see how it can be useful in calculating true climate sensitivity” is only true for feedback fractions >0.3, for the curve of equilibrium-temperature response to feedback fractions is a rectangular hyperbola with its singularity at f = 1.0. That is the reason why some of the sillier extremist papers on climate sensitivity find it possible for Charney sensitivity to reach 10 K. However, since we know that the system-gain factor in 1850 was 1.085, it follows that the feedback fraction is 1 – 1 / 1.085, or only 0.078.
The point here, illustrated by the math at the end of my previous response to Bellman, is that, since the system-gain factor is near-invariant, the curve of the response function is near-linear. Therefore, the proxy system-gain factor used by official climatology is, in 1850, just about identical to our system-gain factor. Now, climatology’s system-gain factor may grow by, say, 15% over the period 1850 to 2011 (though there is no particular reason to suppose that it will), but the corresponding growth in our system-gain factor will be negligible, because the entire temperatures of which our system-gain factor is the ratio exceed the tiny sensitivities posited by official climatology by two orders of magnitude.
And I disagree, so we are back to square one.
Firstly, though you say here you don’t require it to be near linear, but your head post says “Ah, you may say, but perhaps the curve of equilibrium temperature as a response to reference temperature is nonlinear. Maybe it is, but it cannot be very nonlinear.”, and you say the same and the end of this comment – ” since the system-gain factor is near-invariant, the curve of the response function is near-linear.”. So I’m still puzzled whether you think the response curve is near-liear or not, and why you keep emphasizing the near-linearity of it when you don’t require it.
Secondly, if you accept the feedback factor might have been different, possibly much lower, below 255K, you have to accept it is increasing at a relatively fast rate after 255K. You simply cannot predict what the feedback factor will mean for future warming based on the factor in 1850, unless you assume a very near-invariant value.
And there’s your big mistake – that last statement does not follow at all from the first two, let alone a fortiori.
Your complaint was that modern climatology forgot the sun was shining, which I take to mean they start their calculations at a point where the sun is shining – say 255K. You insist that you have to consider the whole range of temperatures. So your feedback fraction acts on 265K of temperature, which includes the 255K when the sun wasn’t shining.
If, say for the sake of argument, there were no feedbacks until the sun started shining, your definition still effectively spreads the feedback fraction across the whole range of temperature starting at absolute zero.
I think this argument should be obvious, but lets spell out what happens in the hypothetical scenario of feedbacks only operating when temperatures are above 255K. At 0K there are zero feedbacks – your system gain factor tends to 1. At 255K there are zero feedbacks, and your system gain factor is still 1. When the refence temperature is 265K the actual temperature is 287.5K. Your system gain factor is 287.5 / 265 = 1.085.
Now suppose the “official” version is correct and the climate sensitivity parameter is near-invariant. They only calculate the parameter as a delta, so the parameter is (287.5 – 255) / (265 – 255) = 32.5 / 10 = 3.25.
So now what happens when the reference temperature rises to 266K? The “official” version says there will be a 1 degree rise that has to be multiplied by the near-invariant climate sensitivity parameter of 3.25, given around 3.25 degrees of total warming. By contrast your prediction is that at 266K reference temperature the actual temperature becomes
, that is 1.085 degrees of warming. But if the official parameter is correct the temperature is 287.5 + 3.25 = 290.75K, and your system gain factor becomes 290.75 / 266 = 1.093.
Hence an invariant climate sensitivity parameter does not imply an invariant system gain factor.
I’m not sure if you are following my point – I’m sorry if I wasn’t clear. It’s true that small changes to the feedback fraction will only result in small changes to the system gain factor, but my point is small changes to the system gain factor will result in big temperature changes. This follows simply from the fact that any system gain has to be multiped by the absolute temperature. As absolute temperature are two orders of magnitude bigger than the temperature changes we are interested in it follows that a small change in the feedback fraction or system gain factor will have a large effect on the temperature change. Every 0.01 added to the system gain factor will be adding 2.6K to the temperature.
You should understand this, because you make the same point in the head posting and even at the end of this current comment, when you say
Bellman says that if the curve of the equilibrium-temperature response function is near-linear across the interval of interest – i.e., from 1850 via 2011 to a CO2 doubling compared with 2011 – it must be near-linear all the way from zero Kelvin. He does not, however, adduce any argument in support of this proposition. I have already explained to him that official climatology’s climate-sensitivity parameter, and hence the system-gain factor, is near-invariant across the interval of interest, so that the response curve is near-linear across that interval.
Bellman thinks that if the system-gain factor was much lower below than above the 255 K emission temperature than above it, we must accept that it is increasing at a relatively fast rate above 255 K. Yet, as I have explained to him, we know what the system-gain factor was in 1850, so we do not know at what rate it was rising.
Bellman says one cannot predict what the system-gain factor will mean for future warming based on the factor in 1850, unless one assumes a near-invariant value. Official climatology, however, assumes and states just that, and we have accepted its finding.
Bellman disagrees with my statement that if in 1850 the system-gain factor was 1.085 and if official climatology’s secant-slope proxy for the system-gain factor is near-invariant, it follows that our system-gain factor is near-invariant a fortiori. The reason why this statement is self-evidently true is that at the equilibrium temperature in 1850 the two system-gain factors – ours and official climatology’s – were identical. If, therefore, official climatology’s system-gain factor were to rise by, say 15% compared with 1850 by 2100, then our system-gain factor would rise by a far lesser percentage because entire temperatures exceed official climatology’s sensitivities by two orders of magnitude.
Bellman says we insist we must consider the whole range of temperatures. No: we say that the system-gain factor acts on 265 K of temperature, which includes the 255K emission temperature that would obtain in the absence of any forcings or feedbacks, merely because the Sun is shining.
Bellman imagines that if there were no feedbacks until the sun started shining, our definition effectively spreads the system-gain factor across the whole range of temperature starting at absolute zero. No: all we say is that the feedback processes present in the atmosphere in 1850 were bound to act on the entire reference temperature then obtaining. That statement says nothing about what might have been: what the feedbacks respond to is the temperature they find at a particular moment.
Bellman says that, since at 0 K there are zero feedbacks, ur system gain factor tends to 1. No: it is undefined.
Bellman says that at 255 K there are zero feedbacks. However, I have on repeated occasions explained that, to first order, one-third of the dayside of the Earth would be open water at 255 K, wherefore all of the sensitivity-altering feedbacks listed by IPCC would be operating.
Bellman says that official climatology’s system-gain factor is only calculated as a delta, so the parameter is (287.5 – 255) / (265 – 255) = 32.5 / 10 = 3.25, and so that when the temperature rises to 265.75 K there will be a 0.75 K reference sensitivity that must be multiplied by 3.25, giving 2.45 K equilibrium sensitivity. But the midrange equilibrium sensitivity to the 0.75 K warming from 1850-2011 is 0.75 x 2.5 / (2.5 06) = 1.00 K, not 2.45 K. The system-gain factor 3.25 is far too large because official climatology makes Bellman’s mistake of assuming that at the 255 K emission temperature there are no feedbacks in operation.
Bellman imagines that, though small changes to the feedback fraction will only result in small changes to the system gain factor, small changes to the system gain factor will result in big temperature changes. He has not understood that it is climatology’s system-gain factor that is near-invariant, changing the equilibrium sensitivity by a smallish fraction, and accordingly changing the equilibrium temperature by a very much smaller fraction, which is why our system-gain factor barely changes when official climatology’s system-gain factor changes.
If I said that, I wasn’t speaking clearly. It’s been my contention that a curve can be near linear across the interval of interest, but not very linear back to 0K. I rather thought it was your argument that any curve meeting the points (0, 0) and (265, 287.5) must be near linear. For example in a comment above you state:
There you are saying even an exponential function must be near linear all the way from zero Kelvin. (Incidentally you are not describing an exponential function there but a monomial, and your derivation of an exponent cannot be correct as you cannot have ln(0).)
You need to explain to me why the two system-gain factors are identical in 1850. I note a comment above where talk about a proxy system-gain factor as being the gradient between two points of interest, but I’m completely lost as to why this must be the same as your system-gain factor.
I’m probably not making myself clear. When I say you consider the whole range of temperatures I’m simply stating what you do when you derive the system-gain factor with respect to the absolute temperature – this inevitably means considering all the temperature resulting from the sun shining.
I’m not sure how your definition could do anything else. There are 22.5K of feedbacks in your scenario and you divide them by the absolute temperature 265K. I am not saying that this means that actual feedback response would be proportionate at all sub 255K temperatures – on the contrary I’m suggesting they won’t be. I expect feedbacks don’t really kick in until much warmer temperatures, but if they do your definition which requires feedbacks to respond to the entire reference temperature is not going to be very useful.
Yes, I meant to say that. That’s why I meant it would trend to 1, unfortunately I mistyped this as “tend”.
No, I said if hypothetically there were no feedbacks at 255K. It was a thought experiment to demonstrate the difference between your system-gain factor and the IPCC’s climate sensitivity parameter, and to demonstrate that near-invariance in one does not imply near-invariance in the other.
However, even if you are correct that the feedback fraction was a strong at 255K as it was at 265K, you still have to decide if there wasn’t some magical point below which feedbacks were either non-existent or at least much smaller than they now are. Either the function E(R) is near-linear or it isn’t.
Lord Monckton,
In light of the exchange we had upthread and my perusal of your paper “Why models run hot, results from an irreducibly simple climate model”, I think that at last I might have some insight into the source of some of your misconceptions. I was particularly struck by something which appeared in Figure 3 of that paper, which you or a co- author had referenced as having been “adapted” from an AR5 figure. Someone (you, perhaps?) had written in the textual subtitle for the figure:-
“The Planck value shown as a ‘‘feedback’’ is not a true feedback, but a part of the climatic reference system.”
I am 97% certain that this was an addition by you or one of your co-authors, rather than anything in the IPCC report, since the IPCC, as well as every climate scientist I know, explicitly recognises Planck as one of the atmospheric feedbacks.
Your comment raises some interesting questions. Does the Planck feedback actually know that it is not a member of the feedback club? Did the other members actually advise it that it was no longer a member? I ask this because it continues to turn up for membership meetings. And who decided on its appointment to the Climatic Reference Council (CRC)? Can any of the other members of the atmospheric feedbacks join the CRC? Who gets to decide?
I will return to these questions shortly, but first I want to show you a magic trick.
Any screaming capitals below are for emphasis only.
In my post upthread, I set out the (conventional) derivation of the linear feedback equation. I will continue to use the same variable names and definitions, but will eventually convert them into the form used by Roe 2009 with which you are obviously familiar so that you can confirm that changing the definitions of the constants has no impact on the results or inferences.
The solution of the linear feedback equation for a constant step-forcing at infinite time yields:-
T-T0 = F/lambda (i)
where lambda = the total feedback (including the Planck response) Not Controversial.
If we partition the total feedback into just two parts – the Planck response and “other”, we can write:-
T-T0 = F/{lambda(Planck) + lambda(other)} (ii)
Note that the variable T here is NOT a transient temperature; it is the equilibrium temperature achieved at infinite time in response to the constant step-forcing F.
I will set T-T0 equal to ΔTall, defined as the expected change in temperature from the previous equilibrium state at T0 to the new equilibrium state induced by a flux forcing, F.
We now obtain:-
ΔTall = F/{lambda(Planck) + lambda(other)} (iii)
The following are just mathematical re-arrangements of (iii) in slow motion.
{lambda(Planck) + lambda(other)}xΔTall = F
lambda(Planck)xΔTall = F – lambda(other)xΔTall
ΔTall = 1/lambda(Planck) x (F – lambda(other)xΔTall) (iv)
You see what I did there? I ask you to note that Eq (iv) looks remarkably like a temperature to temperature feedback! Moreover, if we expand the brackets, we see that the first term = F/lambda(Planck), which is the change in temperature at infinite time for a system which only has Planck as a feedback. [ Let me convert the variables (actually constants) to those used by Roe 2009. The ruleset that I offered previously was:-
“set my F = ΔRf from Roe
set my lambda(Planck) = 1/λ0 from Roe (Yes, he uses an inverted form)
set my lambda(other) = -c1 from Roe (His sign convention for non-Planck feedbacks is different from mine ”
Equation (iv) then becomes:-
ΔTall = λ0 x (ΔRf +c1xΔTall) (v) ]
Yep. You can verify that this equation is identical to Eq 4 in Roe 2009, which I suspect has sourced much of your paradigm.
But now consider what I have just done with this magic trick. I have taken a mathematical IDENTITY, Equation (iii), which represents the equilibrium temperature solution (at infinite time) to the EBM or “linear feedback equation” in this instance, and solely by re-arranging the expression, I have magically produced what looks like a temperature feedback to temperature – still translated always via a net flux feedback, you might note. In so doing, we have now promoted the Planck-only temperature response at equilibrium into being a member of your Climate Reference Council, and taken it out of the feedback member’s enclosure. It looks like an input before feedback. Does this imply that this is then a physical input? In fact, does it imply that it is any type of input signal to the climate system? We started with an identity and we must end with an identity barring algebraic error. This expression comes from a stopped clock which is correct not twice a day but only once – at the equilibrium state.
Now let us consider the question of membership of the Climate Reference Council.
If I repartition lambda(other) into its constituent parts, then it might look something like:-
lambda(other) = lambda(LapseRate) + lambda(WV) + lambda(surface albedo) + lambda(clouds)
So now consider what happens if instead of choosing to separate out lambda(Planck) in the above magic trick, I separate out lambda(Planck) plus lambda(LapseRate). When modified Eq (iv) has similar form except that we have now promoted lambda(LapseRate) into being a member of the Climate Reference Council, and it has lost its membership of the feedback club. The “input temperature signal” has now become F/(lambda(Planck) + lambda(LapseRate)). Is this now the new physical input to the system? How can you have these two inputs to the system at the same time if they represent physical inputs?
Earlier, in response to my assertion that there were no direct feedbacks to temperature in conventional climate science, only “temperature-dependent feedbacks to net flux”, you wrote:-
” In the climate, the input signal is the 255 K emission temperature. Would that signal itself engender a feedback response, in the absence of any noncondensing greenhouse gases?
The answer is Yes. …
With respect, therefore, Kribaez is wrong to state, in capitals at that, that the feedback response to the input temperature signal DOES NOT EXIST. It does exist, in physical reality.”
OK, then let us consider in a bit more detail your chosen reference input temperature signal – which you have defined in line with Roe as the theoretical response of the system to just the Planck response. Using my nomenclature, AT EQUILIBRIUM this is :-
ΔTplanck = F/lambda(Planck) (vi)
ΔTplanck, like ΔTall refers to a change in temperature from the previous equilibrium state to the present theoretical equilibrium state, the latter being under the assumption that only Planck feedback is operating.
In Roe nomenclature, Eq (vi) can be restated as ΔTplanck = Fxλ0 (vii)
Mathematically, I can trivially take the ratio of ΔTall/ΔTplanck to yield an amplification or gain. It yields the same as Roe’s result or your own.
I would first ask you to note that (a) ALL OF THE MATHS ABOVE RELATE TO A CHANGE FROM ONE EQUILIBRIUM CONDITION TO ANOTHER FORCED BY A FLUX FORCING ; THEY HAVE NOTHING TO DO WITH ANY DYNAMIC SYSTEM (b) the only reference temperature which is actually real is the previous equilibrium temperature, T0 (C) I can arbitrarily change the “input reference signal” without changing the physical system in any way; does that sound like a physical signal or an abstraction? (d) The only signal actually seen by the climate is the (real) temperature field. How does the climate know how to find your physical underlying reference signal which it is supposed to be responding to?
You are, I’m afraid, hunting a snark, but you need to convince yourself of that.
Krib
All the feedbacks (they are legion) in the earth’s climate operate in an open dissipative system which is chaotic-nonlinear, and in such a system, it is the feedbacks, specifically the interplay between the positive (excitability) and negative (friction) ones which determine the nature of the emergent spontaneous pattern formation by which the system as a whole exports entropy.
All your equations assume linearity. And equilibrium. They are thus irrelevant. Climate is nonlinear and always far from equilibrium.
It is because the climate is a far-from-equilibrium system that Monckton is right and you are wrong. There can be no component of feedback that operates on “departure from equilibrium” only, because there is no equilibrium. Feedbacks operate at all points in the multi-dimensional phase space and probabilistic landscape.
Phil,
You have read the first page of a book and then jumped to the last page without reading any of the pages in between. I explained upthread that the GCMs and the EBMs (which is what Lord Monckton’s formulation derives from) both already do apply feedbacks to the entire temperature.
That is already a given. The comment that you are responding to is my attempt to get Lord Monckton to convince himself that the input signal on which he is basing his calculations is not physical and not an input signal at all. At any point in time, the climate system can only see one input signal and that is the actual temperature expressed in absolute terms. Lord Monckton believes that it is responding in a physical way to some mystical underlying temperature signal. The formulation above that you are responding to so negatively is actually the basis for Lord Monckton’s assertion of the existence of a physical reference input signal based on the Planck response alone. I am merely trying to show that it cannot possibly exist as a physical input and that his reference signal which derives from Roe 2009 is actually an arbitrary choice.
Kribaez,
Not disagreeing on anything, and I treat Planck as a feedback, but just an observation.
The closed-loop gain is often written
CG=OG/(1+f*OG)
where OG is the openloop gain and f could be a sum of feedback coefficients. That could be written
CG=1/(1/OG+f)
Then you could say that 1/OG is also a member of the club. It behaves just like another member of the f club.
This has practical consequences, which I was thinking of when I wrote my feedback article. I used a finite gain transistor rather than an op amp. An op amp with feedback could have emulated the transistor. Then the feedback would have entered the arithmetic in exactly the place of 1/OG.
Climate analogies are usually like that. The emulation could either be an infinite OG with Planck feedback, or a finite OG based on Planck. Both ways work. In the latter case, Planck is not in the club.
Nick,
The main point I was trying to make is that the choice of “reference system” here is essentially arbitrary. My main aim is to get Lord Monckton to recognise that the reference system response is not a physical input; he has repeated several times that he believes that it is. In your universe, you are recognising (at least) that it is a choice made by the analyst – a mathematical abstraction.
The subsidiary point is that this CG calculation so far at least is only justified to work between two equilibrium states, and is abstracted from a known result. It cannot generate that result. It is ironic that, on the one hand, Lord Monckton has claimed several times that Official Climatology does not recognise absolute temperatures, when in reality both GCMs and EBMs use real (absolute) temperatures as state variables, and, on the other hand, the derivation of the CG can be shown to be only legitimate for a ratio of temperature increments measured between two Equilibrium states.
As an aside, you wrote:- “The emulation could either be an infinite OG with Planck feedback, or a finite OG based on Planck. Both ways work.” While I understand your comment in the context of the choice of a reference response, I invite you to try running either approach on a dynamic (i.e. transient) dataset, and you will find that neither approach works, or at least not without a reverse calculation after solving the EBM equations. To emulate an arbitrary forcing series (i.e. real life), a superposition or convolution approach is required. Temperature-dependent feedbacks all actuate net flux changes, which can take centuries to millenia to stabilise even for a fixed step-forcing. Prior to that, these “gains” are functions of time and ocean model characteristics, notably heat capacities and heatflow characterisation. This probably explains why nobody has tried to use a Control Box for dynamic emulation in CliSci.
Kribaez is of course correct that one can treat the Planck parameter as either a feedback or a part of the reference system. The caption complained of was unsatisfactorily worded. However, we agree with Roe that it matters to treat it as part of the reference system. Over the interval of interest, from 1850 via 2011 to a CO2 doubling compared with 2011, the Planck parameter (expressed as the Schlesinger ratio) does not change significantly, so the point is largely moot.
And of course one can do feedback calculations between one equilibrium state and the next, using the secant slope of the response function as a proxy for the system-gain factor. If one had a sufficiently perfect knowledge of the magnitudes and interactions of the various forcings and feedbacks, that would of course be preferable in a sufficiently nonlinear response curve.
However, climatology regards the response curve as near-linear, in which event the position in 1850, for instance, is of more than passing interest. The emission temperature before allowing for any forcing or feedback is 255 K, and the reference sensitivity (before accounting for any feedback) to the noncondensing greenhouse gases present in 1850 is 10 K. Of the 287.5 K equilibrium temperature in 1850, 265 K would, therefore, have obtained in the absence of temperature feedback. The remaining 22.5 K is attributable to feedback.
Climatology imagines that the whole of that 22.5 K arises in response to the warming forced by the presence of the preindustrial noncondensing greenhouse gases. However, in the absence of those gases a third of the dayside of the Earth would be open water, and all the sensitivity-altering feedbacks now in operation would be operating. Climatology takes no account of the consequent (and large) feedback response, instead attributing all of it to the preindustrial noncondensers.
Lord Monckton,
Thank you for this. It demonstrates some advance in your thinking, I hope.
Can we now agree on the following facts:-
a) “Atmospheric Feedbacks” in GCMs and EBMs are all temperature-dependent feedbacks to net flux. There are no direct feedbacks to an “input” temperature anywhere in the real system.
b) The feedbacks in GCMs and EBMs translate into the partial derivatives of TOA flux with respect to temperature at the absolute temperature prevailing at that time.
c) The choice of temperature response to Planck alone as a reference against which to quantify a temperature amplification or gain is a discretionary choice of the analyst. It is not founded on a physical input.
d) The derivation of amplification or gain outlined in Roe 2009, based on (c) above applies strictly between two equilibrium points.
If we can clear the above deadwood out of the way, then we can take a forensic trip backwards in time and in temperature to consider different ways of viewing your assumed equilibrium state in 1850. If, on the other hand, you are still resistant to any of the above, then please highlight which of them you do not accept.
In response to Kribaez, I have no particular interest in how the models currently arrive at their estimates of equilibrium sensitivity to radiative forcing, since those models have for 40 years failed utterly to constrain the very broad interval of Charney sensitivities first published in 1979. The models do not explicitly represent feedbacks at all. But, whatever they are doing, our result shows they must be doing it wrong.
It is official climatology that denominates temperature feedbacks in Watts per square meter per Kelvin of the temperature change that arises from a direct radiative forcing (i.e., per Kelvin of the reference sensitivity). Our approach is to accept all of official climatology except what we can disprove. Since official climatology, supported explicitly by Roe (2009), accordingly treats the Planck sensitivity parameter as part of the reference system so that the reference sensitivity to radiative forcings can be calculated, we have adopted official climatology’s approach in this respect. Therefore, if Kribaez wishes to argue with that methodology, his argument is not with us but with official climatology and he should address his concern to the IPCC Secretariat.
We have at no time cited Roe (2009) as authority for our result. We can find no paper in climatology that acknowledges the fact that any feedback processes operating at a given moment must respond not solely to the reference sensitivity but to the entire reference temperature. Our experiments at a national laboratory left us in no doubt about this fact, which is also self-evident in the governing equations of control theory, which are set out and formally proven in the long version of our paper.
To establish that midrange Charney sensitivity is 1.15 K, all we need to do is to establish three propositions.
First, that the reference sensitivity to doubled CO2 is 1.05 K. We do this with data from Andrews+ (2012).
Secondly, that the system-gain factor in 1850, derived as the ratio of the 287.5 K equilibrium temperature to the 265 K reference temperature then obtaining, is 1.085.
Thirdly, that official climatology regards the climate-sensitivity parameter as near-invariant (IPCC, 2007, ch. 6) and, therefore, that the curve of the equilibrium-temperature response function E(R) is near-linear. We modeled various nonlinear curves, all of which produced impossible contradictions. We also derived the system-gain factor 2.5 / (2.5 – 0.6) = 1.316 as the system-gain factor implicit in the finding in IPCC (2013) that there had been about 2.5 Watts per square meter of net anthropogenic radiative forcing to 2011 and that to the previous year there had been a radiative imbalance of 0.6 Watts per square meter (Smith 2015). And we carried out further tests on both the RCP6.0 and the RCP8.5 datasets to establish that the ratio of transient sensitivity to net anthropogenic forcing over successive 30-year and 60-year periods from 2010-2100 is near-invariant.
If these three propositions are agreed – as, in our submission, they must be – then midrange Charney sensitivity is 1.05 x 1.085, or 1.15 K.
Lord Monckton,
“The models do not explicitly represent feedbacks at all. But, whatever they are doing, our result shows they must be doing it wrong.”
The GCMs do not have feedbacks as inputs, but they do simulate a feedback process to net flux; net flux is calculated on the then-current state-variables (which includes the absolute temperature field), which are updated every time-step. Post hoc evaluations of atmospheric feedbacks seek to estimate the rate of change of net flux with respect to surface temperature. The EBMs, on the other hand, explicitly represent feedbacks to net flux. In both instances, the calculations are based on absolute temperatures. There are numerous genuine reasons why GCMs are running hot and why they should not be deemed fit to inform decision-making. Your explanation is not one of them. Post hoc ergo propter hoc fallacy.
Your propositions which “must be accepted”:-
“First, that the reference sensitivity to doubled CO2 is 1.05 K. We do this with data from Andrews+ (2012). ” The more generally accepted median estimate is a little higher, but OK, accepted ad argumentum.
“Secondly, that the system-gain factor in 1850, derived as the ratio of the 287.5 K equilibrium temperature to the 265 K reference temperature then obtaining, is 1.085. ” There is no “reference temperature” without your defining one as a mathematical abstraction. At the aggregate level you are working at, there is an average surface temperature and there is an average emission temperature or brightness temperature, which can be back-calculated from S-B. If you would take the trouble to understand that the feedbacks are not “temperature feedbacks” but “temperature-dependent feeedbacks to net flux”, then you would understand more clearly why it makes little sense to attempt to partition an absolute temperature.
“Thirdly, that official climatology regards the climate-sensitivity parameter as near-invariant (IPCC, 2007, ch. 6) and, therefore, that the curve of the equilibrium-temperature response function E(R) is near-linear. ” While it may be valid to assume that feedbacks are invariant if we are considering only small changes to temperature and climatology, it is patently and demonstrably invalid to assume that they remain invariant over very large temperature ranges or when you start playing with major changes in the climatology. I invite you to try calculating the surface temperature and the feedback values if you eliminate clouds and water vapour from your construct climatology.
” We also derived the system-gain factor 2.5 / (2.5 – 0.6) = 1.316 as the system-gain factor implicit in the finding in IPCC (2013) that there had been about 2.5 Watts per square meter of net anthropogenic radiative forcing to 2011 and that to the previous year there had been a radiative imbalance of 0.6 Watts per square meter (Smith 2015). ”
Your description of this 1.316 value as a “system gain factor” is different from your other uses of the term. This value, as you calculate it, is (unambiguously) an estimate of the ratio of temperature change to equilibrium divided by a single point estimate of transient temperature change (evaluated in 2011), under the assumption that the total forcing level is held constant at its 2011 value and that a constant linear feedback is in operation. It may be compared directly with the estimate from Lewis and Curry which can be found here:- https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=13&cad=rja&uact=8&ved=2ahUKEwiBhLqVgvXiAhWGTcAKHWEDCtEQFjAMegQIBhAC&url=https%3A%2F%2Fniclewis.files.wordpress.com%2F2014%2F09%2Flewiscurry_ar5-energy-budget-climate-sensitivity_clim-dyn2014_accepted-reformatted-edited.pdf&usg=AOvVaw2xGESkvk_ppHwtK4DxuxPp
The equivalent value from Lewis and Curry is 1.98/(1.98 – 0.36) = 1.22 (dimensionless)
Note that your estimate is higher than L&C because you assumed that 1850 was in equilibrium, whereas L&C accounted for change from non-zero initial forcing and heat uptake levels.
L&C used an estimate of temperature change of 0.71K from base period (1859-1882) to final period (1985-2011). From the L&C values, you can obtain:-
Projected change to equilibrium temperature at Forcing of 1.98 W/m2/K = 1.22*0.71 = 0.87K
Projected change to equilibrium temperature for a 2xCO2 forcing of 3.7
= 1.22*0.71*3.7/1.98 = 1.62K for a doubling of CO2. (L&C actually report a median value of 1.64K ECS for a doubling of CO2. )
Now let us repeat the calculation for your values.
I will use the same estimate of temperature change as in L&C i.e. 0.71K
Projected change to equilibrium temperature at 2011 Forcing of 2.5 W/m2/K = 1.316*0.71 = 0.93 K
Projected change to equilibrium temperature for a 2xCO2 forcing of 3.7
= 1.316*0.71*3.7/2.5 = 1.38K for a doubling of CO2.
Your estimated midrange Charney sensitivity is 1.15K. So, if I accept one of the three propositions you suggest must be agreed, it is incompatible with the other two. You may think that this difference is small, but given that the assumptive basis is identical, the key question from a forensic point of view is: why is this difference there at all?
Let us re-do the calculation a different way. We will do it forwards from 1850.
Your idiosyncratically-defined reference temperature is 265K. You define the (constant) Planck response as 1.05K/W/m2 to equilibrium. For your estimated forcing of 2.5 W/m2, your reference temperature therefore achieves, at the new equilibrium, a value of
265 + 1.05*2.5 = 267.6k. Given that your estimated ratio of surface temperature equilibrium to reference temperature equilibrium of 1.085 is “invariant”, then we can now estimate your new surface temperature equilibrium value from the new reference temperature value using this ratio. We obtain for the new surface equilibrium temperature (all feedbacks) 1.085 * 267.6 = 290.4K. Since your previous 1850 equilibrium temperature was 287.5K, then this represents a change of (290.4-287.5) or 2.9K . This equilibrium, however, using your data, relates to a forcing of (only) 2.5 W/m^2. To project this to a doubling of CO2 at 3.7W/m2 forcing, we need to scale this up by 3.7/2.5, which yields your new estimate of ECS for a doubling of CO2 of 4.25K. Whoops! Even you must see that this is not consistent with the 1.38K ECS you derive from the incremental calculation based on your chosen values.
First, Kribaez says that my explanation of the agreed fact that the models are predicting twice or thrice the warming that is occurring – i.e., that the models’ error lies in their implementation of feedback – is an instance of the post hoc ergo propter hoc fallacy. It is no such thing. Official climatology, all of whose tenets we accept ad argumentum except to the extent that we can demonstrate that they are false, says that the uncertainty in the directly-forced warming from CO2 is 10% – i.e., plus or minus about 0.l K. Yet the uncertainty in the equilibrium warming is plus or minus about 1.5-1.6 K. From these values, it is inescapable that the only part of the calculation in which a large enough error to account for the large overshoot in predicted against observed temperatures is the feedback part.
Next, Kribaez says he accepts ad argumentum that the CMIP5 models’ mean reference sensitivity to doubled CO2 is 1.05 K: yet, a few paragraphs later, he presents a calculation implying that it is 0.71 x 3.7 / 1.98, or 1.33 K.
Then Kribaez repeats that there is no physical meaning to our statement that in 1850 the reference temperature – i.e., the temperature that would have obtained that year in the absence of feedback – was the sum of the 255 K emission temperature and the 10 K reference sensitivity to the preindustrial noncondensing greenhouse gases. He says these values are “idiosyncratic”, when in fact they are warranted in the peer-reviewed journals. Here, as so often, his dispute is not with us but with official climatology, whose tenets in this respect we have accepted ad argumentum.
In the same vein, he jibs at our description of temperature feedbacks as “temperature feedbacks”. Again, his quarrel is not with us but with official climatology, which describes temperature feedbacks as “temperature feedbacks”. For good measure, it denominates them and lists them in Watts per square meter per Kelvin of the reference sensitivity (not a change in flux density, but a temperature change) to which they are responding. It is a truism that the reference sensitivity is itself driven by a forcing – i.e., a change in flux density, but, given the near-invariance of the Planck parameter over the period of interest, calculation on the basis of fluxes only will not in itself give a result that differs from a result obtained by doing things official climatology’s way in this respect.
He then says it makes no sense to partition an absolute temperature. Here again he is at odds with official climatology, which partitions the absolute temperature that would prevail at equilibrium after a perturbation into a) the reference temperature before feedback has acted and b) the feedback response. Likewise, control theory partitions the output signal into the reference signal and the feedback response. And it is perfectly permissible to partition the reference signal into the input signal and as many subsequent perturbations as may have occurred at the moment of interest.
He says there is no such thing as a reference temperature. Here his quarrel is not only with official climatology but also with control theory and, for good measure, with elementary logic. He accepts that in the absence of temperature feedback the reference sensitivity to doubled CO2 – and the reference sensitivity is a change in temperature – is about 1.05 K. He accepts that after accounting for temperature feedback the equilibrium sensitivity to doubled CO2 – and the equilibrium sensitivity is also a change in temperature – has a value higher than 1.05 K. From this it follows that he accepts that the difference between the equilibrium and reference sensitivities – also a change in temperature – is the feedback response. By the same token, there is an entire reference temperature in, say, 1850: that reference temperature is the sum of the emission temperature that would obtain without forcing or feedback and the reference sensitivity to the preindustrial noncondensing greenhouse gases. In effect, Kribaez is trying to say there is no such thing as a feedback response: for if there is one it is inescapable that the equilibrium temperature (or sensitivity) will comprise the sum of the reference temperature (or sensitivity) and the feedback response.
Next, Kribaez quibbles about our derivation of the (excessive) system-gain factor derivable from official climatology’s estimate that there had been 2.5 Watts per square meter of net anthropogenic radiative forcing to 2011, at which time there also subsisted a radiative imbalance of 0.6 Watts per square meter. The system-gain factor thus derived (which is not ours but that of IPCC) is simply 2.5 / (2.5 – 0.6), or 1.316.
But Kribaez says that Lewis & Curry 2018 (who used data and timescales that differed somewhat from those of IPCC 2013) found the period reference sensitivity since was 0.71 K (IPCC data implies 0.75 K); that the secant-slope system-gain factor was 1.22 (IPCC data implies 1.32); that period equilibrium sensitivity was 0.87 K (IPCC data implies 1.00 K); and that Charney sensitivity was 1.62 K (IPCC data implies 1.40 K). Therefore, there is not much difference between L&C’s result and the result derivable from IPCC data.
Next, Kribaez asks why the secant-slope system-gain factor derivable from IPCC data to 2011 differs from our system-gain factor. It would be much more apposite to ask why the system-gain factor derivable from IPCC data or from L&C 2018 is so close to our system-gain factor and so far from the models’ midrange system-gain factor.
Nevertheless, it is easy to answer his question. There is very little uncertainty as to the value of our system-gain factor, since it is derived from two well-constrained quantities that obtained in 1850. There is considerably greater uncertainty as to the secant-slope proxy system-gain factor derivable from IPCC forcings and from official climatology’s estimate of the radiative imbalance from 1850-2011, because there is uncertainty as to the magnitude of the net anthropogenic forcing and still more uncertainty as to the magnitude of the radiative imbalance, and because – as I have tried to explain to Kribaez before – the sensitivities whose ratio is official climatology’s secant-slope proxy for the system-gain factor are smaller than the entire temperatures whose ratio is our system-gain factor by two orders of magnitude: therefore, even small uncertainties in those sensitivities entail a large uncertainty in the secant-slope system-gain factor, while even large uncertainties in entire temperatures entail a small uncertainty in our system-gain factor.
Next, Kribaez says we define the Planck response as 1.05 K to equilibrium. No: as we have repeatedly stated, we have taken the mean of the values from the 15 CMIP5 models given in Andrews 2012, and we have taken the 1.05 K value as near-invariant because, across the interval of interest, from 1850 via 2011 to a CO2 doubling compared with 2011, the Schlesinger ratio, a good approximation for the Planck parameter (see Schlesinger 1985) is near-perfectly invariant.
Kribaez then performs a calculation forward from 1850 that appears erroneous. The correct calculation is as follows: The reference temperature owing to the Sun shining is 255 K; the reference sensitivity to the preindustrial noncondensing greenhouse gases is 10 K; the reference sensitivity to the industrial-era anthropogenic noncondensing greenhouse gases to 2011 is 0.75 K; and the reference sensitivity to a CO2 doubling compared with 2011 is 1.05 K. Therefore, the reference temperature at the moment of CO2 doubling compared with 2011 is the sum of these four values: i.e., 266.8 K. Since the system-gain factor is near-invariant at 1.085, the equilibrium temperature at the moment of CO2 doubling compared with the 2011 concentration is about 289.6 K, compared with 287.5 K in 1850. This approximately 2.1 K warming is the sum of the 1 K equilibrium sensitivity to the industrial-era noncondensing greenhouse gases from 1850 to 2011 and the 1.15 K equilibrium sensitivity to doubled CO2 thereafter.
But I am most grateful to Kribaez for the trouble he is taking. It is very difficult for any one person to hold in mind all the various branches of science upon which our result depends, which is why I have an army of co-authors and pre-submission reviewers at my back. And I am always happy to try to explain what we are up to, and to listen carefully to any concerns that may be raised.
Dear Lord Monckton,
You asked me about astronomical literature on the influence of the Earth orbit onto the terrestrial climate.
At first: ALL text connected with Milankovitch are Cycles on the scale of minimum 19,000 to maximum 100,000 years. Therefore NOT relevant for ANY climate changes on Earth on decadal and centennial scale, therefore: Lets forget everything connected with Milankovitch to explain global warming and global cooling on centennial scale, and the recent global warming, which occurred since the 17th century.
We therefore have to focus onto Earth orbital features and their annual/decadal/centennial variations.
To the literature: There is a literature scarcity on this astronomical matter, because astronomists for quite some time look into the depths of the universe and there is no new papers about the old, long explored Earth orbit around the Sun. All astronomers know the orbital basics: The Earth advance is NOT like an airplane advance, but screws around this advance line in a spiral fashion. In fact, a lot of advances in space are spiral movements, as the solar system spirals forward in space, as the planets spiral around the Sun, as does Earth, the Moon spirals around Earth in its daily flight line and even new lanched satellites start to spiral in their flight around Earth, which has to be compensated, for instance in GPS data. The spiralling flight is called an “osculating forward movement” – with deviations from the flight line to the left/right/up/down….. therefore the stars in large distance “jump up and down”, as so-called “osculating elements”, jumping along the up-down movement of Earth depending on its spiral position. This is general astronomical knowledge. The authors for the earth orbital osculating flight is Isaak Newton (he fought long with Leibniz on the shape and number of osculations – Leibniz counted five) and then Carl Gauss, he tried to derive a formula for the Earth´s flight, observed the sky 4 years, could not complete the formula and invented the Least Squares Method based on his astronomical measurements. Exact details and calculations you will find in my booklet: J.S.: Das Ende der globalen Erwärmung, Berechnung des Klimawandels” – have it machine translated, all relevant orbital features are understandably explained, this saves you quite a lot of time to comprehend the orbital subject, new to almost everyone.
Also see: http://www.Climate Patter Recognition, Part 8, and Part 1, the orbital movement is derived empirically out of GISP2 temperature variations over the entire Holocene, the calculation method is explained. Here you can see that global Earth temperature is a product of the Sun-Earth distance. The Climate Pattern Recognition series needed 8 parts, for analyzing each and every temperature spike since 8,500 BC, thus over 10,000 years.
The Earth orbital data is all known in JPL Pasadena, but kept under table, because they are NASA GISS and
orbital data, which clearly MUST have an effect on the Earth temperature is kept out of public observations.
And if none mentions the Earth orbit, then all climate forcings “are atmospherical” and the climate scientists may say: ALL forcing belongs to manmade CO2, BECAUSE WE DO NOT KNOW OF ANY OTHER FORCING since 1850. And thats what they need, keeping the orbit out of public focus andthat is what they colluded on in 2006 in preparation of AR4-
Any questions welcome on weltklima at gmail.point com
It appears that there is no peer-reviewed paper establishing what Mr Seifert says. Without it, his theory will not be easily accepted.
Dear Lord Monckton,
I reckon that there is astronomical literature covering the details and osculations of the Earth orbit somewhere, because these are no secrets on this and the osculation data is used in the JPL star positioning programs….
The measurements, carried out by Issak Newton himself, which I employed in my texts, should suffice to provide a lot credibility, much more than in todays climate science peer/pal warmist reviewed papers.
No-one would doubt the greatest mathematicien of the world.
The measurements are given in Newtons major solar system calculation book.
General details of the orbit I took from encyclopedias, which I found in the London British Library.
To: “Not easily accepted”: The Earth orbital path and Issak Newton´s measurements would by endorsed by any knowledgable astronomer.
Sufficient is the fact that orbital perpetuations exist due to the spiral flight shape, causing deviations from the elliptical flight line. And those, therefore, must be INCLUDED in climate forcing calculations, as well as resulting climatic effects, caused by increasing/decreasing the distances Sun-Earth, increasing/decreasing global temperatures.
To abate the doubt, I recommend a consultation of a knowledgable astronomer concerning the osculating spiral flight of Earth: He will agree, and therefore flight path deviations/perturbations exist, with resulting climatic effects.
Solar System 2.0 – the helical model
https://www.youtube.com/watch?v=mvgaxQGPg7I
CRITIC/INSTRUCTOR – RHYS TAYLOR
Here we have the rare individual who is both a scientist, critic and yet not above being an educator/instructor. Mr. Smith and Mr. Plait could learn much from Mr. Taylor (post-doctorate in astrophysics).
Mr. Taylor wrote a few articles here, here and here. What sets him off from Mr. Plait and Mr. Smith is two-fold:
He understands that DjSadhu’s first couple of videos have scientific errors, yet the basicpremise of the solar system moving through space in a helical motion is for the most part correct.
He takes a constructive win-win approach and works in a positive manner with DjSadhu to fix the errors in an attempt to produce a more accurate video than the original two.
https://longhairedmusings.wordpress.com/2017/09/07/social-conditioning-and-conventional-pieties-conspiracy-hypothesis-theory-crime-statecrimesagainstdemocracy-scads-conspiracy-of-context/
J.Seifert,
Nicola Scafetta has been trying for many years to convince people that climate oscillations are caused by orbital effects. Like you, he points to the coincidence of certain celestial/orbital frequencies with climate cycle frequencies. You might find it interesting to Google some of his publications.
His views have received only limited acceptance, and that is largely, I believe, because of his inability to propose a credible physical mechanism to relate climate effects to planetary influence. I believe that there does exist a possible mechanism, (as I explained somewhere up-thread in response to a comment from Tonyb about the correlation between winds and temperatures), but at the moment this exists as a poorly quantifiable hypothesis.
I would also note that NASA JPL a few years ago were working on a similar hypothesis – wind variation arising from induced changes in atmospheric angular momentum. However, they were postulating that the external torque which was controlling changes in angular velocity of the surface of the Earth was exerted by inertial changes in Earth’s liquid core. Again, you might find it interesting to Google some of their findings.
To kribaez:
I read all the Scafetta literature. He dedicates himself to the influence/effects/interactions of the OTHER solar planetary orbits onto Earth. Now a new paper is out, trying to prove that sunspot cycles are caused by planetary orbiting.
Myself, I am not on this line, only the Earth orbit and its detailed perturbations, which can be recognized in the Earth´s climate, are my focus. Those effects are numbers larger than effects of other planets onto Earth.
You can check my papers: http://www.climate pattern recognition, Part 8 and Part1 are the most important.
J Seifert,
Your lonk takes me to a digital farming site with no pointers to your articles.
https://rwer.wordpress.com/2019/06/15/atmospheric-co2-concentration-year-1-to-2018/
This Bed Wetting post appeared in my feed from “The Real Economics Blog”, Its an interesting read often with some good articles on the “Dismal Science”, It took your Good Name in Vain, and I had to point out the Absurd Axis employed by the Bed Wetting Graff (Brian Cox).
June 16, 2019 at 1:30 pm
Monckton is a Lord of the British Realm, he does not sit in the now Re constituted House of Lords, that does not make him an Imposter.
Secondly Regarding Monckton’s paper on the errors in basic Climate modelling his Status as a British Peer of the realm has nothing to do with the mathematics of modelling feedbacks.
Finally, perhaps William Happer or Freeman Dyson will tick more of your boxes for an appropriate expert qualified opinion.
https://www.youtube.com/watch?v=YKBwoO8DOPw
A Good Frolly video, there that should do it.
I asked Mr Seifert for peer-reviewed and published evidence of the effect of orbital variability on the Earth’s climate. All he has offered is peer-reviewed and published evidence of the Earth’s orbital characteristics. I am already familiar with that. I do not need it: I need the peer-reviewed and published evidence of the effect of those orbital variations on variations in global mean surface temperature.
However, all of this is off topic. The present focus is on the influence of temperature feedbacks on global temperature.
Dear Lord Monckton,
The effect of Earth orbital oscillations can clearly be detected and proven in global annual temperatures on a weekly scale. A paper on this will abate the talk of a CO2-effect and the talk of climate being chaotic only and nothing can be revealed, which is a meme of those who understand nothing.
I aim at publishing it peer reviewed over 2020. So you just need to wait and I will inform you on the progress in this matter in time.The orbital topic was on my backburner because I am dedicated to reveal the climatic effects of meteor impacts on Earth, which is at present my major concern. See my papers. For this reason, the “orbit paper delay”..
On looking at the astronomical tables, it is not clear to me that the variability in the Sun-Earth distance over the past century has any correlation with the variability in global mean surface temperature. There is, however, a correlation between the quantum of sunlight reaching the ground and variability in regional mean surface temperature. But there appears to be no correlation between global warming and the variability in the extent of global (and particularly tropical) cloud cover that governs the quantum of sunlight reaching the surface.
In any event, all of this is off topic. Here, we are discussing the magnitude of the feedback response to radiative forcings.
Dear Lord Monckton,
Let us agree on this: If not all variables are included, and major variables are missing then all calculations with the remaining, uncomplete variables must be faulty. I am sure we agree on that, and that is why I insist on my approach.
Secondly, to “looking at tables”. An eye-balling needs the additional background of the
matter, particularly when not generally known.
Lets then leave the astronomical topic aside for now. once my peer-reviewed paper is at hand, I will inform you in time. I thank you for your appreciated time and conversation.
Best regards, J.S,
Let us return to the topic at hand: temperature feedback.