The title question often appears during discussions of global surface temperatures. That is, GISS, Hadley Centre and NCDC only present their global land+ocean surface temperatures products as anomalies. The questions is: why don’t they produce the global surface temperature products in absolute form?
In this post, I’ve included the answers provided by the three suppliers. I’ll also discuss sea surface temperature data and a land surface air temperature reanalysis which are presented in absolute form. And I’ll include a chapter that has appeared in my books that shows why, when using monthly data, it’s easier to use anomalies.
Back to global temperature products:
GISS EXPLANATION
GISS on their webpage here states:
Anomalies and Absolute Temperatures
Our analysis concerns only temperature anomalies, not absolute temperature. Temperature anomalies are computed relative to the base period 1951-1980. The reason to work with anomalies, rather than absolute temperature is that absolute temperature varies markedly in short distances, while monthly or annual temperature anomalies are representative of a much larger region. Indeed, we have shown (Hansen and Lebedeff, 1987) that temperature anomalies are strongly correlated out to distances of the order of 1000 km. For a more detailed discussion, see The Elusive Absolute Surface Air Temperature.
UKMO-HADLEY CENTRE EXPLANATION
The UKMO-Hadley Centre answers that question…and why they use 1961-1990 as their base period for anomalies on their webpage here.
Why are the temperatures expressed as anomalies from 1961-90?
Stations on land are at different elevations, and different countries measure average monthly temperatures using different methods and formulae. To avoid biases that could result from these problems, monthly average temperatures are reduced to anomalies from the period with best coverage (1961-90). For stations to be used, an estimate of the base period average must be calculated. Because many stations do not have complete records for the 1961-90 period several methods have been developed to estimate 1961-90 averages from neighbouring records or using other sources of data (see more discussion on this and other points in Jones et al. 2012). Over the oceans, where observations are generally made from mobile platforms, it is impossible to assemble long series of actual temperatures for fixed points. However it is possible to interpolate historical data to create spatially complete reference climatologies (averages for 1961-90) so that individual observations can be compared with a local normal for the given day of the year (more discussion in Kennedy et al. 2011).
It is possible to develop an absolute temperature series for any area selected, using the absolute file, and then add this to a regional average in anomalies calculated from the gridded data. If for example a regional average is required, users should calculate a time series in anomalies, then average the absolute file for the same region then add the average derived to each of the values in the time series. Do NOT add the absolute values to every grid box in each monthly field and then calculate large-scale averages.
NCDC EXPLANATION
Also see the NCDC FAQ webpage here. They state:
Absolute estimates of global average surface temperature are difficult to compile for several reasons. Some regions have few temperature measurement stations (e.g., the Sahara Desert) and interpolation must be made over large, data-sparse regions. In mountainous areas, most observations come from the inhabited valleys, so the effect of elevation on a region’s average temperature must be considered as well. For example, a summer month over an area may be cooler than average, both at a mountain top and in a nearby valley, but the absolute temperatures will be quite different at the two locations. The use of anomalies in this case will show that temperatures for both locations were below average.
Using reference values computed on smaller [more local] scales over the same time period establishes a baseline from which anomalies are calculated. This effectively normalizes the data so they can be compared and combined to more accurately represent temperature patterns with respect to what is normal for different places within a region.
For these reasons, large-area summaries incorporate anomalies, not the temperature itself. Anomalies more accurately describe climate variability over larger areas than absolute temperatures do, and they give a frame of reference that allows more meaningful comparisons between locations and more accurate calculations of temperature trends.
SURFACE TEMPERATURE DATASETS AND A REANALYSIS THAT ARE AVAILABLE IN ABSOLUTE FORM
Most sea surface temperature datasets are available in absolute form. These include:
- the Reynolds OI.v2 SST data from NOAA
- the NOAA reconstruction ERSST
- the Hadley Centre reconstruction HADISST
- and the source data for the reconstructions ICOADS
The Hadley Centre’s HADSST3, which is used in the HADCRUT4 product, is only produced in absolute form, however. And I believe Kaplan SST was also only available in anomaly form.
With the exception of Kaplan SST, all of those datasets are available to download through the KNMI Climate Explorer Monthly Observations webpage. Scroll down to SST and select a dataset. For further information about the use of the KNMI Climate Explorer see the posts Very Basic Introduction To The KNMI Climate Explorer and Step-By-Step Instructions for Creating a Climate-Related Model-Data Comparison Graph.
GHCN-CAMS is a reanalysis of land surface air temperatures and it is presented in absolute form. It must be kept in mind, though, that a reanalysis is not “raw” data; it is the output of a climate model that uses data as inputs. GHCN-CAMS is also available through the KNMI Climate Explorer and identified as “1948-now: CPC GHCN/CAMS t2m analysis (land)”. I first presented it in the post Absolute Land Surface Temperature Reanalysis back in 2010.
WHY WE NORMALLY PRESENT ANOMALIES
The following is “Chapter 2.1 – The Use of Temperature and Precipitation Anomalies” from my book Climate Models Fail. There was a similar chapter in my book Who Turned on the Heat?
[Start of Chapter 2.1 – The Use of Temperature and Precipitation Anomalies]
With rare exceptions, the surface temperature, precipitation, and sea ice area data and model outputs in this book are presented as anomalies, not as absolutes. To see why anomalies are used, take a look at global surface temperature in absolute form. Figure 2-1 shows monthly global surface temperatures from January, 1950 to October, 2011. As you can see, there are wide seasonal swings in global surface temperatures every year.
The three producers of global surface temperature datasets are the NASA GISS (Goddard Institute for Space Studies), the NCDC (NOAA National Climatic Data Center), and the United Kingdom’s National Weather Service known as the UKMO (UK Met Office). Those global surface temperature products are only available in anomaly form. As a result, to create Figure 2-1, I needed to combine land and sea surface temperature datasets that are available in absolute form. I used GHCN+CAMS land surface air temperature data from NOAA and the HADISST Sea Surface Temperature data from the UK Met Office Hadley Centre. Land covers about 30% of the Earth’s surface, so the data in Figure 2-1 is a weighted average of land surface temperature data (30%) and sea surface temperature data (70%).
When looking at absolute surface temperatures (Figure 2-1), it’s really difficult to determine if there are changes in global surface temperatures from one year to the next; the annual cycle is so large that it limits one’s ability to see when there are changes. And note that the variations in the annual minimums do not always coincide with the variations in the maximums. You can see that the temperatures have warmed, but you can’t determine the changes from month to month or year to year.
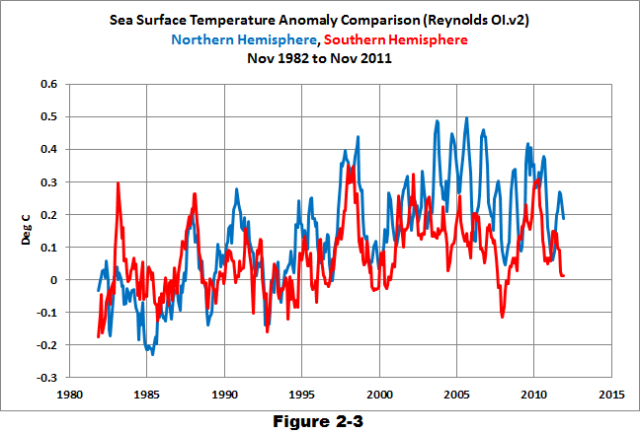
Take the example of comparing the surface temperatures of the Northern and Southern Hemispheres using the satellite-era sea surface temperatures in Figure 2-2. The seasonal signals in the data from the two hemispheres oppose each other. When the Northern Hemisphere is warming as winter changes to summer, the Southern Hemisphere is cooling because it’s going from summer to winter at the same time. Those two datasets are 180 degrees out of phase.
After converting that data to anomalies (Figure 2-3), the two datasets are easier to compare.
Returning to the global land-plus-sea surface temperature data, once you convert the same data to anomalies, as was done in Figure 2-4, you can see that there are significant changes in global surface temperatures that aren’t related to the annual seasonal cycle. The upward spikes every couple of years are caused by El Niño events. Most of the downward spikes are caused by La Niña events. (I discuss El Niño and La Niña events a number of times in this book. They are parts of a very interesting process that nature created.) Some of the drops in temperature are caused by the aerosols ejected from explosive volcanic eruptions. Those aerosols reduce the amount of sunlight that reaches the surface of the Earth, cooling it temporarily. Temperatures rebound over the next few years as volcanic aerosols dissipate.
HOW TO CALCULATE ANOMALIES
For those who are interested: To convert the absolute surface temperatures shown in Figure 2-1 into the anomalies presented in Figure 2-4, you must first choose a reference period. The reference period is often referred to as the “base years.” I use the base years of 1950 to 2010 for this example.
The process: First, determine average temperatures for each month during the reference period. That is, average all the surface temperatures for all the Januaries from 1950 to 2010. Do the same thing for all the Februaries, Marches, and so on, through the Decembers during the reference period; each month is averaged separately. Those are the reference temperatures. Second, determine the anomalies, which are calculated as the differences between the reference temperatures and the temperatures for a given month. That is, to determine the January, 1950 temperature anomaly, subtract the average January surface temperature from the January, 1950 value. Because the January, 1950 surface temperature was below the average temperature of the reference period, the anomaly has a negative value. If it had been higher than the reference-period average, the anomaly would have been positive. The process continues as February, 1950 is compared to the reference-period average temperature for Februaries. Then March, 1950 is compared to the reference-period average temperature for Marches, and so on, through the last month of the data, which in this example was October 2011. It’s easy to create a spreadsheet to do this, but, thankfully, data sources like the KNMI Climate Explorer website do all of those calculations for you, so you can save a few steps.
CHAPTER 2.1 SUMMARY
Anomalies are used instead of absolutes because anomalies remove most of the large seasonal cycles inherent in the temperature, precipitation, and sea ice area data and model outputs. Using anomalies makes it easier to see the monthly and annual variations and makes comparing data and model outputs on a single graph much easier.
[End of Chapter 2.1 from Climate Models Fail]
There are a good number of other introductory discussions in my ebooks, for those who are new to the topic of global warming and climate change. See the Tables of Contents included in the free previews to Climate Models Fail here and Who Turned on the Heat? here.



Steve Mosher is unwittingly letting the cat out of the bag with the discussion (actually ridiculing) the concept of raw data. It’s not raw data, it’s the “first report”, and like any “report” it’s subject to editing by the higher ups. Well, they’ve been repeatedly caught editing the first reports. That’s the basis for all of the changes in previously reported temperatures.
Today, when Steve can just look at his WUWT wall weather station, it’s easy for him to imagine that 100, 150, and 200 years ago people didn’t take data acquisition seriously. After all, having to go outside in the cold/rain/snow/ice/heat to read a temperature is such a bother, better to just fake it. Clearly the weather monitoring stations weren’t manned by postal workers, only they do things in in-climate weather.
Adjusting data is bogus. Take a dataset, copy it, and adjust away, but leave the original dataset alone! Don’t even ask me about miracle filtering…
Interesting that the average annual surface temp of Death Valley and the South Pole, averaged together, is 11.2 deg F, but I would not want to live in either place. Supposedly Mercury has both the highest and lowest surface temperatures in the solar system (excluding the gas giants for which we do not know if there are surfaces) which might lead one to think this might result in excellent temperatures around the terminator. How usefull are averages? Like for the the man that drowned in the river with average depth of 6 inches.
Anyway the real question is :
“Why ARE Global Surface Temperature Data Produced ?”
Temperature is an intensive property that souldn’t be summed up nor averaged, and that cannot be “global”.
What should be used is heat content. Energy.
“markx says:
January 27, 2014 at 5:14 am
Nick Boyce says: January 26, 2014 at 10:09 pm
NOAA/NCDC continues to publish “The climate of 1997″ …. http://www.ncdc.noaa.gov/oa/climate/research/1997/climate97.html ….. this document states categorically,
“For 1997, land and ocean temperatures averaged three quarters of a degree Fahrenheit (F) (0.42 degrees Celsius (C)) above normal. (Normal is defined by the mean temperature, 61.7 degrees F (16.5 degrees C), for the 30 years 1961-90).”
Can someone (Steve Mosher perhaps?) please explain what has changed in the last decades that has apparently resulted in some recent revision downwards of these earlier “global mean temperatures”.
I have an explanation which is untestable by any empirical means, and is therefore highly unscientific in the Popperian sense, but here goes nonetheless.
Having trawled through the internet in search of the “highest global surface temperature ever recorded”, I think that the 1997 global surface temperature of 16.92°C is the highest GST which anyone has ever dared to publish. If global warming were to continue after 1997, then annual GSTs would have to be greater than 16.92°C, and if NOAA/NCDC were to claim that the GST of 2005, for example, were noticably greater than 16.92, some people at RSS and UAH might suggest that this is very implausible.
http://www.drroyspencer.com/2013/04/a-simple-model-of-global-average-surface-temperature/
So, NCDC sneakily, surreptitiously, and artificially reduced GSTs precisely in order raise them again forthwith, so as to give the appeareance of continuous and unabated global warming. Unfortunately, or fortunately, whichever way you wish to look at it, NOAA/NCDC omitted to remove “The climate of 1997” from public view, and it is plain for all to see, that any estimates of GSTs published by NOAA/NCDC are highly suspect, to put it mildly.
There is another point which I have mentioned more than once before. NASA’s “The elusive absolute air temperature” is one of the most subversive documents in climatology, and everyone interested in the subject should read it.
http://data.giss.nasa.gov/gistemp/abs_temp.html
Amongst other things, this document entails, that nobody has even come close to measuring the GST of the entire earth between 1961 and 1990, or any other interval for that matter. Therefore, nobody can prove beyond reasonable doubt, that 16.5°C or 14°C is, or is not, the average GST between 1961 and 1990. In which case, anyone can assert, without fear of empirical refutation, that 16.5°C or 14°C is the average GST between 1961 and 1990. Per “The elusive absolute surface air temperature”, both figures are guesstimates based on very scanty data. “The elusive absolute surface air temperature” entails that the entire global surface temperature record is a castle in the air.
John Finn says:
“You appear to be confused between LIA and MWP. Easily done – they both have 3 alpha characters.”
John, try to relax. Lay down and meditate. When you are fully relaxed, try to understand this concept:
Current excavations are uncovering Viking settlements on Greenland that have been frozen in permafrost for close to 800 years. They are just now re-appearing due to the planet’s current warming cycle.
Do you understand what that means?
It means that the planet was warmer during the MWP. Warmer than now, John.
There is extensive evidence supporting the fact that the MWP was warmer. As more settlements thaw out, we add those to the current mountain of empirical evidence showing that the MWP was pretty warm [but not as warm as prior warm cycles during the Holocene].
I think even you can understand that concept, John — if you’re fully relaxed, and not hyperventilating over the global warming scare.
===================================
Typhoon says to Steven Mosher
“Another assertion. Evidence?”
Steven doesn’t do evidence. He’s a computer model guy. ☺
OK, make that Kelvin with vertical range fitting.
I spend most days wading in economic data, and this reminds me of the “seasonally adjusted” dispute… and various other disputes over “proper” unemployment rates and price indices.
Take for instance ATTM, the temperatures in the Midwest (single digits) or Denver Colorado even (twenties) due to the latest ‘polar vortex’ and compare with West coast LA area (sixties) … correlation?
Ya … do you mean over time? In the sense that they will ‘track’ (a fixed offset)? This would also seem to be problematic, as, the temperature maxima in the Midwest is bound to exceed that of the LA basin seasonally therefore there is no ‘fixed offset’ and therefore no ‘tracking’ ….
.
The instrumental temperature record shows fluctuations of the temperature of the global land and ocean surface. This data is collected from several thousand meteorological stations, Antarctic research stations and satellite observations of sea-surface temperature. The longest-running temperature record is the Central England temperature data series, that starts in 1659. The longest-running quasi-global record starts in 1850.
Chuck Nolan says: “Bob, are you telling us that James Hansen said using anomalies is a good thing to do so we’re doing it?”
Nope, I presented the reasons why GISS, UKMO and NCDC say they supply data in anomalies. And I illustrated how using anomalies removes much of the seasonal cycle. That’s all.
Kip Hansen says: “Mr. Tisdale ==> This still doesn’t answer the question : “’When all is said and done, when all the averaging and adding in and taking out is done, why isn’t the global Average, or US Average Land, or Monthly Average Sea Surface, or any of them simply given, at least to the public, in °C?…'”
Even if GISS, UKMO, NCDC presented the data in absolutes, they and the media would still be making claims that it was the “4th hottest on record”, so I don’t know what you’d gain.
I think things are made unnecessarily complicated by using anomalies and by performing adjustments of the data set.
The hypothesis is that air temperature (K) measured close to ground, averaged around the globe and averaged over a suitable time period has a positive and significant correlation with level of CO2 (ppmCO2) in the atmosphere. If we assume that the dependency is linear around a working point:
Global average Temperature (K) = Constant (K) + CO2 level (ppmCO2) *Sensitivity (K/ppmCO2)
The importance of the measurements and the time series in the data set used to test the hypothesis is that:
– No new measurement points are added to the data set
– No measurement points are removed from the data set
– The measurements does not drift during the period used to test the hypothesis
– The time series for each measurement has a constant interval
– The integrity of the data set is undoubted
As long as the CO2 level is monotonously increasing at a constant rate the only thing you should have to do to test the hypothesis is to:
– Calculate the average of all measurements in the time series in the data set for a suitable averaging period
– Use a calculation tool to calculate the correlation between average temperature K and CO2 level in ppm
– Check if the correlation is positive and significant
The absolute level is not important at all to test the hypothesis as what we are looking for is the rate of change in temperature ( K/ppmCO2 ). In the same manner there is no reason to complicate the issue and bring in uncertainty by introducing anomaly. It is a good practice to stick to international units to avoid wasting effort on uncertainty about and discussion related to units.
You cannot add information by interpolating between points of measurement. So there is no point in interpolating.
The importance of the scale in a figure is that is is suitable for a visual impression about standard deviation of the average temperature and correlation between temperature and CO2 level.
I would be happy to se data sets with proper integrity. 🙂
Anomalization of time-series data is nothing more than the removal of an
ESTIMATED time-average of the data. While intended to put the variations of
all time-series on the same datum level, the critical question is: how
accurately can that be accomplished when data records are of different,
often non-overlapping, short lengths and do not display the same
variability or the same systematic biases? Despite various ad hoc
“homogenization” schemes, that question remains largely unresolved by
aggregate averaging of anomalies in producing various temperature indices.
The situation is scarcely improved by resorting to the conceptual model of
data = regional average + constant local offset + white noise. Clearly, only
the left-hand side is known–and only over irregular intervals. Furthermore,
the spatial extent of a “region” is undetermined. Although dynamic
programming may be used to obtain most-likely ESTIMATES of the regional
average when the station separation is small enough to ensure high
coherence, the technique becomes very misleading in the opposite case. “Kriging”
across climate zones cannot be relied upon to fill gaps in geographic coverage.
In both cases, what is obtained is a statistical melange of inadequately
short data records combined through blithe PRESUMPTION in piecemeal
manufacture of long-term “climate” series. As recognized by “DHF”, what is
sufficient for a global view of temperature changes is a geographically
representative set of intact, vetted station-records of UNIFORMLY LONG
duration. Their absolute average may be off significantly from the real
global average, but the VARIATIONS are free from manufacturing defects.
Sadly, index-makers seem more concerned with claiming high numbers of data
inputs than with the scientific integrity of their product.
DHF says: January 28, 2014 at 10:51 am
“The hypothesis is that air temperature (K) measured close to ground, averaged around the globe and averaged over a suitable time period has a positive and significant correlation with level of CO2 (ppmCO2) in the atmosphere.”
That’s not what is being discussed here. It’s just measuring the global temperature anomaly. Scientists don’t usually do the test you describe; dependence on CO2 is more complicated – history-dependent, for a start. That’s why GCMs are used.
1sky1 says: January 28, 2014 at 4:37 pm
“Anomalization of time-series data is nothing more than the removal of an
ESTIMATED time-average of the data. While intended to put the variations of
all time-series on the same datum level, the critical question is: how
accurately can that be accomplished when data records are of different,
often non-overlapping, short lengths and do not display the same
variability or the same systematic biases?”
Another critical question is, how accurate does it have to be. The objective is to get different stations onto the same datum level to reduce dependence on how sampling is done. If anomalization get’s 90% of the way, it is worth doing.
Hansen looked at your question thirty years ago. He didn’t produce anomalies for individual stations, and index orgs do not generally publish these. Instead he built up anomalies for grid cells, where there was more collective information over a reference period (for him, 1951-80).
“The situation is scarcely improved by resorting to the conceptual model of
data = regional average + constant local offset + white noise.”
That’s what I do with TempLS (offsets month-dependent). “regional average” is actually what you are looking for. Of course the remainder isn’t really white noise; it contains various residual biases etc. If these could be better characterised, they would go into the model.
“what is sufficient for a global view of temperature changes is a geographically representative set of intact, vetted station-records of UNIFORMLY LONG duration”
We have to work with the historic data available. In fact, I’ve been looking at ways of trading numbers for duration quality here.
Does not the use of anomalies under report the absolute variance, giving the false impression that natural variability is much less than it actually is?
Nick Stokes says: January 28, 2014 at 5:24 pm
“That’s not what is being discussed here. It’s just measuring the global temperature anomaly.”
What you intend to use your measurand for has an impact on your choice of measurand. You need a very good reason to deviate from presenting your measurand in another unit than prescribed by ISO 80000 Quantity and units. (International System of Units). Because if you do, you will with certainty end up in having a discussion about it.
Further, if you are interested in the uncertainty of your measurand you should observe the ISO guide 98-3 “Guide to the expression of uncertainty in measurement”. This Guide is primarily concerned with the expression of uncertainty in the measurement of a well-defined physical quantity — the measurand — that can be characterized by an essentially unique value. If the phenomenon of interest can be represented only as a distribution of values or is dependent on one or more parameters, such as time, then the measurands required for its description are the set of quantities describing that distribution or that dependence.
Any operation you perform on your measurands will add uncertainty.
I have not read all that is said above. However, I wonder why people always talk about surface temperatures. I think it would be more scientific to talk about the heat content (in Joules) of the atmosphere + oceans, which would really tell how much the Earth is gaining – or losing – solar energy. Of course the surface temperature, the measurement of which is always more or less biased (on purpose or not) tells something about the current living conditions for the majority of the biosphere, but that can change quickly. I´m afraid the heat content may be too difficult to estimate at present.
Paul Vaughan says:
January 26, 2014 at 9:00 am
“@ur momisugly RichardLH
I wonder if you’re familiar with Marcia Wyatt’s application of MSSA?
http://www.wyattonearth.net/home.html
Marcia bundles everything into a ‘Stadium Wave’ (~60 year multivariate wave):
http://www.wyattonearth.net/originalresearchstadiumwave.html”
Sorry I was traveling for the last few days.
Yes, Figs 7 though 10 in the Curry & Wyatt Stadium Wave paper clearly show 58-60 Year patterns in the data.
http://curryja.files.wordpress.com/2013/10/stadium-wave.pdf
Figs from Curry & Wyatt
http://i29.photobucket.com/albums/c274/richardlinsleyhood/StadiumWaveFig7_zps47c1bc73.png
http://i29.photobucket.com/albums/c274/richardlinsleyhood/StadiumWaveFig8_zps888a9a96.png
http://i29.photobucket.com/albums/c274/richardlinsleyhood/StadiumWaveFig9_zpsf3c705a6.png
http://i29.photobucket.com/albums/c274/richardlinsleyhood/StadiumWaveFig10_zps366be8ef.png
Fig from Wyatt & Peters 2012
http://i29.photobucket.com/albums/c274/richardlinsleyhood/WyattandPeters2012_zpse2e75309.png
REPLY TO BOB TISDALE’S REPLY ==> “Even if GISS, UKMO, NCDC presented the data in absolutes, they and the media would still be making claims that it was the “4th hottest on record”, so I don’t know what you’d gain.”
Maybe, just maybe, a little bit of sanity, Bob. NASA gives, for children, a simple average temperature for the Earth at about 15°C and tells them that this is a requirement for Earth-type planets everywhere. In the USA, children are trained to convert this to about 60°F, which most consider a bit chilly — sweater weather.
By junior high school (or now Middle School in many places) children learn that because the poles are very cold and the tropics continually in the upper 20s°C (80s°F), they can be comfortable in their American cities most of the year.
The smart kids are somehow not threatened by hearing that the higher northern latitudes alone are warming a few degrees C. Some people want them to be — so they keep pushing these plus so many little partial degrees on wide spread graphs — sharp looking rises.
If we (people like you and I, Bob) are going to talk and write about and around Climate Change and Global Warming, then let’s use real language and real numbers that the common people can understand and apply in their day to day lives. Let the snobs say gnash their teeth, rant and say we don’t understand because we don’t speak the sacred secret language. Speak the truth and the devil take them, I say.
See my little, somewhat stupid essay on sea level rise in NY City, published just the other day, as an example.
Nick Stokes says: January 28, 2014 at 5:24 pm
“Scientists don’t usually do the test you describe; dependence on CO2 is more complicated – history-dependent, for a start. That’s why GCMs are used.”
By “Scientists don’t usually do the test you describe” I understand that you mean climate scientists do not do the test I describe. I would expect that scientists in general normally do check for correlation between dependent and independent variables in their data sets.
“Formally, dependence refers to any situation in which random variables do not satisfy a mathematical condition of probabilistic independence. In loose usage, correlation can refer to any departure of two or more random variables from independence, but technically it refers to any of several more specialized types of relationship between mean values.”
A Global Circulation Model is a model or theory subject for test. It is neither a test nor a demonstration of dependency in itself.
Nick Stokes:
Putting data on the same datum level reduces dependence only upon WHERE, not HOW, measurements are made. It does nothing to reduce the often striking discrepancies between neighboring station-records. Nor can there be “more collective information” in a grid-cell than that produced by available INTACT records over the reference period. Despite what Hansen does, anomalies for INCOMPLETE data records cannot be “built up” without tacitly ASSUMING their complete spatial homogeneity–and high coherence to boot. I learned forty-some years ago that real-world anomalies do not satisfy such presumptions!
P.S. Your sparse-sampling estimate of “global average anomaly” differs very materially from what I’ve obtained using nearly intact century-long station records in conjunction with knowledge of climate zones and of robust signal detection methods.
1sky1 says:
January 29, 2014 at 5:45 pm
“P.S. Your sparse-sampling estimate of “global average anomaly” differs very materially from what I’ve obtained using nearly intact century-long station records in conjunction with knowledge of climate zones and of robust signal detection methods.”
Indeed. I think that Nyquist summed it up rather well. You can just measure the deltas in the points you sample without trying to ‘guess’ the wave shape in between as well.
Statistically you get a better answer.
“The average temperature of the ocean surface waters is about 17 degrees Celsius (62.6 degrees Fahrenheit).”
http://www.windows2universe.org/earth/Water/temp.html
So real average temperature of Earth is 17 C.
But if want include land and you think average ocean and land is 15 or 14 C.
What is average land temperature?
If 70% of earth surface is has average 17 C what does the temperature of land
area have to be to make it average land and sea of 15 C.
So, 10 area of 15 is 150. 7 areas of 17 is 119. So 31 divided by 3 is 10.3 C
If 14 C it’s 10 area of 140. And land has average of 7 C.
So land causes the average global temperature to be cooler,
And land also cools the ocean. Or Ocean warms land.
But suppose land has average elevation of 2000 meters.
And suppose that land as average temperature of 10 C.
If adjust for elevation, if ocean is 17 C, 2000 meters above it
at lapse rate of 6.5 is 4 C . So land would 10 C compared to
ocean being 4 C. So land would warmer than ocean.
In that situation land would not cool ocean- I doubt would warm ocean buy much,
but it should cool ocean. Or ocean should not warm the land which at 2000 meters
elevation.
“The mean height of land above sea level is 840 m.”- wiki
So at 6.5 lapse that’s 5.46 C. Or if you could [and it’s dumb] use this
ocean compared to land is 17 C minus 5.46 or 11.54 compared 15 C world average
of land being 10.3 C. So ocean would not warm land by much. But we know
ocean mostly warms coastal area [tend to be low elevation]. But one could extend this
to interior region which are low elevation.
But such things only “work” on broad sense.
If earth were completely covered with water it seem it’s average temperature would
be around 17 C, maybe a bit more, maybe even less. It’s seems South America
due to higher elevation and being warmer it could be land mass that warms.
But anyhow if one planet ocean covered it’s average temperature would higher
than 15 C
Or better… “The Beauty of Anomalies… How to Create the Illusion of Warming by Cooling the Past”
Last absolute figures I came across printed were:
Trenberth-Fasullo-Kiehl’s last report was 60.71°F (15.95 Celsius).
288.15 K (15.15 Celsius) seems to be a good median for today’s mean.