By Christopher Monckton of Brenchley
I am most grateful to Mr Stokes for his interesting recent posting in which he explains what he sees as the difference between official climatology’s implementation of feedback in deriving climate sensitivity and the approach taken by my co-authors and me.
The sheer quantity of the comments on these mathematical and physical discussions is an indication that getting down and dirty among the equations is of more than passing interest to the readership.
Let me begin this response to Mr Stokes by setting out, in round numbers and in the simplest possible terms, the difference between official climatology’s conclusion that feedback triples the direct or reference warming from greenhouse gases and our conclusion that, with remarkably little error, one can safely ignore feedback altogether in calculating equilibrium sensitivities.
In the CMIP5 models, the latest generation for which ensemble results have been published, the mean reference sensitivity to doubled CO2 – that is, the amount of warming that would occur in response to a doubling of the atmospheric concentration of CO2 if no temperature feedbacks were operating or if they were net-zero – is 1.05 Kelvin (based on Andrews 2012).
It is also currently thought (rightly or wrongly) that that value is very close to exact: the uncertainty is only 10% either way. Therefore, ad argumentum, we shall accept as canonical the fact that reference sensitivity to doubled CO2 before accounting for feedback is 1.05 K.
However, the same models give a mean Charney sensitivity – that is, the amount of warming that will occur after all sensitivity-altering temperature feedbacks have acted and the climate system has returned to equilibrium – of 3.35 K per CO2 doubling (based on Andrews, op. cit.).
From these two canonical values, we know that official climatology reckons that the feedback response to doubled CO2 is 3.35 – 1.05, or a whopping 2.3 K, in response to a mere 1.05 K reference sensitivity. Recall that feedback represents the entire difference between reference sensitivity (before feedback) and equilibrium sensitivity (after feedback).
If official climatology were right, then the system-gain factor, which is the ratio of equilibrium to reference sensitivity, would be 3.35 / 1.05, or 3.2. Official climatology actually imagines that feedbacks multiply any directly-forced warming 3.2 times over.
Where does official climatology get this massive multiple 3.2 from? Here’s how. The emission temperature of the Earth is usually taken as about 255 K, and the reference sensitivity to the naturally-occurring, noncondensing greenhouse gases present in 1850 is taken as about 10 K (see e.g. Lacis+ 2010) so that the reference temperature in 1850 – the temperature that would have prevailed in the absence of feedback – is 265 K.
However, the measured temperature in 1850 was 287.5 K (HadCRUT4), and that was an equilibrium temperature (there would be no trend during the following 80 years). The difference between the emission temperature of 255 K and the measured temperature of 287.5 K in 1850 is 32.5 K. Divide the equilibrium sensitivity of 32.5 K by the reference sensitivity of 10 K and you get 3.25 – more or less exactly the system-gain factor that official climatology takes as its midrange estimate.
Thus, to IPCC et hoc genus omne, feedback is the big enchilada. It is imagined to account for between two-thirds and (in the sillier extremist papers, up to nine-tenths) of total global warming.
In official climatology, feedback not only accounts for up to 90% of total warming but also for up to 90% of the uncertainty in how much warming there will be. How settled is “settled science”, when after 40 years and trillions spent, the modelers still cannot constrain that vast interval? IPCC’s lower bound is 1.5 K Charney sensitivity; the CMIP5 models’ upper bound is 4.7 K. The usual suspects have no idea how much warming there is going to be.
My co-authors and I beg to differ. Feedback is not the big enchilada. Official climatology has – as far as we can discover – entirely neglected a central truth. That truth is that whatever feedback processes are present in the climate at any given moment must necessarily respond not merely to changes in the pre-existing temperature: they must respond to the entire reference temperature obtaining at that moment, specifically including the emission temperature that would be present even in the absence of any non-condensing greenhouse gases or of any feedbacks.
To see why this must be so, consider the following simple block diagram:

In the block diagram, emission temperature comes in at top left. Then (following the arrows) the reference sensitivities that occur over time, first natural and then anthropogenic, are successively added to it. Then the reference temperature, the sum of all these, passes to the input/output node and thence infinitely round and round the feedback loop, where the separately-powered feedback block (powered by the retention in the atmosphere of radiation that would, without feedback, have passed harmlessly out to space) adds a smidgin to the signal on each pass. The output signal is equilibrium temperature after feedback has acted.
Your mission, should you choose to accept it, is to try to find a respectable explanation for official climatology’s notion that the feedback loop, which receives as its input signal the entire reference temperature, can somehow magically decide that it will respond only to the perturbations of that reference temperature caused by the presence of natural and then also of anthropogenic noncondensing greenhouse gases, and yet that it will not also respond at all to the emission temperature, two orders of magnitude greater than the sensitivities.
No doubt one could devise an electronic circuit that would perform that feat. But the climate is not a circuit. The feedbacks that were present in 1850 must perforce have acted not only upon the greenhouse warming to that date but also upon the emission temperature that was there before any noncondensing greenhouse gases had made their presence felt.
Here, then, is the corrected calculation. The reference temperature in 1850, before feedback, was 265 K. In that year the equilibrium temperature, after feedback, was 287.5 K. So the system-gain factor that applied in 1850 was 287.5 / 265, or 1.085, about a third of climatology’s 3.2.
Now, if we multiply the 1.05 K reference sensitivity to doubled CO2 by the corrected system-gain factor 1.085, we get a Charney sensitivity not of 3.35 K, as official climatology does, but of just 1.15 K.
Ah, you may say, but perhaps the curve of equilibrium temperature as a response to reference temperature is nonlinear. Maybe it is, but it cannot be very nonlinear. Why not? Because the reference temperature in 1850 was more than 92% of equilibrium temperature.
Now, Mr Stokes’ article is correct as far as it goes. His central point is that if you are starting from an equilibrium, such as that which obtained in 1850, you don’t need to know how that equilibrium occurred: you can work out the system-gain factor simply as the ratio of equilibrium sensitivity to reference sensitivity in any period later than that equilibrium, rather than as the ratio of equilibrium temperature to reference temperature at the time of equilibrium.
So let’s do it climatology’s way, using official climatology’s own data to 2011, the year to which the figures were brought up to date in time for IPCC’s 2013 Fifth Assessment Report.
The net anthropogenic forcing from 1850 to 2011 was about 2.5 Watts per square meter. However, the heat capacity of the ocean introduces a delay in the equilibrium response. This delay is reflected in a radiative imbalance, thought to have been about 0.6 Watts per square meter to 2010 (Smith+ 2015).
Taking Smith as correct ad argumentum, climatology’s period system-gain factor derivable from the data for 1850-2011 is simply the ratio of 2.5 to (2.5 – 0.6), i.e. 1.315 (see Lewis & Curry 2018 for the equations). Then Charney sensitivity would be 1.315 x 1.05, or just 1.4 K, not the 3.35 K that official climatology would currently have us imagine.
Notice how much closer to our estimate 1.15 K is that real-world 1.4 K Charney sensitivity, based on official climatology’s own estimates of actual anthropogenic forcing and radiative imbalance, than it is to climatology’s midrange estimate 3.35 K.
Why is our estimate of midrange Charney sensitivity so very much closer to what is inferred from official, published estimates of forcing and radiative imbalance than official climatology’s midrange estimate?
The reason is that, unlike official climatology, we use all the available information, and specifically the information about the respective magnitudes, in 1850, of the reference temperature (265 K) and of the feedback response (22.5 K). The sum of these two was the observed surface equilibrium temperature in 1850.
Official climatology, which simply does not realize that feedbacks necessarily respond to the entire reference temperature that obtains at a given moment, is left with no choice but to throw that vital information away. Here is Mr Stokes doing that quite specifically:
“It is wrong to include variables from the original state equation [i.e., in 1850]. One reason is that they have been accounted for already in the balance of the state before perturbation. They don’t need to be balanced again. The other is that they aren’t proportional to the perturbation, so the results would make no sense. In the limit of small perturbation, you still have a big reference temperature term that won’t go away. No balance could be achieved.”
Now, Mr Stokes is quite right to say that there was a temperature equilibrium in 1850 and that, therefore, at that time the surface temperature of 287.5 K already included the various variables, i.e. the 255 K emission temperature, the 10 K reference sensitivity to the naturally-occurring noncondensing greenhouse gases present in 1850 and the 22.5 K feedback response to the 265 K reference temperature.
He is also right to say these variables “do not need to be balanced again”. But, and this is crucial, they do need to be taken into account in deriving the corrected system-gain factor of 287.5 / 265 and, from that, the corrected Charney sensitivity.
Climatology overlooks these values because it is unaware that at any given moment (such as 1850) feedbacks respond to the entire reference temperature that prevails at that time. Like Luther, they can do no other.
Mr Stokes is also right to say that the variables – in which I think he includes the feedback response – are “not proportional to the perturbation”. Here, he makes precisely our point. The feedback response in 1850 was, of course, necessarily and ineluctably proportional to the entire 265 K reference temperature, which is the sum of the 255 K emission temperature and the 10 K reference sensitivity to the natural forcings present in that year.
But climatology, in effect, takes the entire feedback response in 1850 to have been proportional solely to the 10 K natural perturbation of reference temperature. And there is its mistake. That is why its estimate of Charney sensitivity – and of all equilibrium sensitivities – is three times too big. It has, in effect, allocated to greenhouse gases the large feedback response that arises simply because the Sun is shining.
Yes, one can derive the system-gain factor as the ratio of sensitivities, just as we can derive it as the ratio of absolute temperatures. But the former approach, that of official climatology, is subject to vast uncertainty, while our approach, using those vital data from 1850 that climatology has for so long ignored in its sensitivity calculations, provides an interval of Charney sensitivities that is both accurate and well constrained.
To derive equilibrium temperature, one needs to know the reference temperature and either the feedback response or the system-gain factor. But we don’t know and cannot by any rational means determine how big the feedback response is by counting up the individual feedbacks, as climatology currently tries to do, because it is feedbacks that are the near-exclusive cause of the uncertainty in official climatology’s global-warming predictions.
No feedback can be quantified by direct measurement. Nor can any form of observation, however well-resolved, meticulous and honest, allow us to distinguish reliably, and quantitatively, between different individual feedbacks, or even between feedbacks and the forcings that engendered them.
Climatology cannot calculate Charney sensitivity reliably, because, though it knows that the reference sensitivity to doubled CO2 is 1.05 K, it cannot know the value of the feedbacks and it does not know the system-gain factor. It does not know this vital quantity because it has thrown away the information available at the one point – before any significant anthropogenic intervention – for which the data are quite well constrained, and from which it can be directly derived: i.e., 1850.
The data for 1850 are quite well constrained precisely because the entire equilibrium and reference temperatures in that year exceed by two orders of magnitude the tiny equilibrium and reference sensitivities that are the basis of climatology’s so-far-failed attempts to constrain the system-gain factor and hence the likely magnitude of future global warming.
We know quite reliably what the system-gain factor was in 1850. We also know that it is not going to be a whole lot different in 2100 from its value of 287.5 / 265, or 1.085, in 1850.
Why do we know this? Because the industrial-era anthropogenic reference sensitivity of just 0.75 K from 1850 to 2011 was so very small compared with the 265 K reference temperature already present in 1850. The climate has simply not changed enough to engender a major shift in the feedback regime that obtained in that year.
Even if such a major shift were to have occurred, the additional feedbacks would have responded not merely to our perturbation of emission temperature but to the entire reference temperature, including emission temperature. For one thing, the Great Pause of almost 19 years in global temperature up to 2015 could not possibly have occurred.
Therefore, we can be reasonably confident that Charney sensitivity – i.e. equilibrium sensitivity to doubled CO2 compared with 2011 – is not going to be very much different from 1.15 K. In fact, our professor of statistics, having gone through all the numbers in the most meticulous detail, has calculated that the corrected 95% confidence interval of Charney sensitivity is 1.09 to 1.23 K, an interval of just one-seventh of a Kelvin. Compare that with the 3.2 K interval of official Charney sensitivities, which range from 1.5 to 4.7 K.
Notice that we are only able to calculate the Charney sensitivity correctly because we already knew the system-gain factor. We knew it because we were able to derive it from the data that official climatology throws away because it does not know feedbacks respond to the entire reference temperature and not only to arbitrarily-chosen reference sensitivities.
Mr Stokes talks of the 255 K reference temperature in 1850 “not going away”. Precisely: it was then present, as was the additional 10 K in warming forced by the presence of the naturally-occurring noncondensing greenhouse gases in that year. Because it was present, it should have been taken into account. But it was not taken into account.
Since we know from theory, and from the block diagram, and from the test rig built by one of our co-authors, and from the more sophisticated rig built and operated for us by a government laboratory, that the feedbacks that were present in 1850 perforce acted upon the entire reference temperature that was present in that year, we can instantly and quite safely derive from that year’s data the system-gain factor and hence Charney sensitivity.
No need for vast, costly general-circulation models, if all you want to know is how much warming we may cause.
No need to know the value of any individual feedback.
Remarkably, no need even to take feedback into account in the calculation: the undershoot in Charney sensitivity that arises by ignoring feedback altogether is little more than a tenth of a Kelvin.
In our submission, this really is Game Over.

Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.

In the CMIP5 models, the latest generation for which ensemble results have been published, the mean reference sensitivity to doubled CO2 – that is, the amount of warming that would occur in response to a doubling of the atmospheric concentration of CO2 if no temperature feedbacks were operating or if they were net-zero – is 1.05 Kelvin (based on Andrews 2012).
It is also currently thought (rightly or wrongly) that that value is very close to exact: the uncertainty is only 10% either way. Therefore, ad argumentum, we shall accept as canonical the fact that reference sensitivity to doubled CO2 before accounting for feedback is 1.05 K.
Two points:
“official climatology’s notion that the feedback loop, which receives as its input signal the entire reference temperature, can somehow magically decide that it will respond only to the perturbations of that reference temperature”
The feedback loop doesn’t decide. You decide, because you have chosen to analyse the differences between two states – say 1850 and now. This is then linearised so that the difference between states is set to a linear variation of the differences between variables – standard calculus as I described. In that environment of differences, you develop gains and feedback coefficients based on ratios of differences.
“Mr Stokes talks of the 255 K reference temperature in 1850 “not going away”. Precisely: it was then present…”
It was then present; it is now present. So it does not belong among the differences which are the material for perturbation analysis that yield gain and feedback. And if you try to include it, the arithmetic will treat it as a difference; in the case between its value and zero, and it becomes very large. Not only that, but it is insensitive to how close the states are. With a small or larger difference, you can work out gain and feedback in ratio. But if, no matter how small the difference, you add in the entire reference temperature, the ratios become meaningless.
Let me illustrate with the beginning point of most calculus classes. You have a function f(x), just of 1 variable now. And you consider the effect of adding a small amount h to x. Newton says that the ratio
(f(x+h)-f(x))/h
tends to a constant – the derivative, also called rate or gradient. The ratio of differences.
But then what happens if someone says that some part of f(x) (the state) should be added into the numerator. The ratio doesn’t tend to a constant any more, because the addendum was not proportional. It tends to infinity. And since most applications of calculus are made short of but near the limit, that is a big error.
I used the common math terminology of zero order and first order. Here f(x) is zero order. The difference f(x+h)-f(x) is first order in h. You can analyse first order terms in ratio – Newton’s derivatives. But you must keep them separate from the zero order terms.
Precisely to avoid complications such as that which Mr Stokes attempts to advance, we built a test rig and found, not at all to our surprise, that the feedbacks present in the feedback block will act upon the entire reference temperature, and not merely upon some arbitrarily-selected fraction thereof.
The head posting explicitly accepts that one can attempt to derive the system-gain factor as the ratio of equilibrium to reference sensitivities rather than as the ratio of entire equilibrium to reference temperatures. But that approach has not proven effective, because there is so much uncertainty as to the value of the individual temperature feedbacks, to say nothing of the uncertainty as to the interactions between them, and between them and the forcings.
Given that our test rig shows very clearly that feedbacks respond to the entire reference temperature, no amount of sophistry will demonstrate that they do not. Mr Stokes, in failing to concede that such feedbacks as are present at a given moment will necessarily respond to the entire reference temperature present at that moment, is at odds with control theory.
“we built a test rig”
Well, I don’t believe you can overturn climate science by building a test rig, but even less do I accept that you can overturn calculus. You are deducing rates of change (gain, feedback coefficients) by differencing things that became different because of the change, and taking ratios. Or should be. If you put in quantities themselves, rather than the amount they changed, then the rate calculation will treat them as if they changed from zero in one step. And the answer returned will be a very high rate indeed, and not approaching a limit with small change.
First of all, our test rig, and that constructed and operated under conditions of strict ambient-temperature control by a national laboratory, did not “overturn climate science”. It demonstrated that control theory is correct to find that the feedbacks operating in a dynamical system at any given moment must respond to the entire reference signal then obtaining, and not solely to a small and arbitrarily-chosen fraction thereof.
Nick Stokes –
“In that environment of differences, you develop gains and feedback coefficients based on ratios of differences.”
Those items must be consistent with what came before, though. If your gains and coefficients, applied to an earlier era, would produce results that are not in evidence in later data, then your estimates of these values are wrong.
Temperature is not proportional to energy when the vast amount of water on the Earth must be taken into account. It takes substantially more energy to change water from 0 degrees to 1 degree than from 1 degree to 2 degrees. It takes even more energy to vaporize the water. https://www.britannica.com/science/latent-heat
This is easily proven by dropping an ice cube into a cup of warm water. The ice cube with much less volume than the water can easily cool the warm water down. As long as there are huge masses of ice at the poles, it will require an enormous change in energy input to change temperatures significantly.
The temperature changes that are seen are mostly caused by water currents moving warm water from the tropics to the poles and cold water back. The poles can quickly cool any warm water with only minimal ice melt. If less warm water makes its way to the poles, “average” temperatures can rise only because there are more non-polar temperature readings are used in calculating the average. This is seen in the temperature spikes caused by El Nino events. The total energy entering and leaving the Earth hasn’t changed, just it’s effect on local thermometers used to calculate an “average” temperature that has changed.
CM’s approach to the problem is very similar to Salby’s analysis to the evolution of CO2 in the atmosphere and the conclusion that the Bern model is not physical because it removes CO2 when there is none left. See
(https://edberry.com/blog/climate-physics/agw-hypothesis/what-is-really-behind-the-increase-in-atmospheric-co2/) at 58 min. If the problem is correctly framed the analysis can be decisive without quantifying things outside the frame. If the problem is framed poorly quantification of unobserved factors is necessary and the analysis becomes a guess.
Here is what bothers me so much on this quote, from Nick Stokes article:
“However, the measured temperature in 1850 was 287.5 K (HadCRUT4), and that was an equilibrium temperature (there would be no trend during the following 80 years). The difference between the emission temperature of 255 K and the measured temperature of 287.5 K in 1850 is 32.5 K. Divide the equilibrium sensitivity of 32.5 K by the reference sensitivity of 10 K and you get 3.25 – more or less exactly the system-gain factor that official climatology takes as its midrange estimate.”
That 1850 number is built on minimal data that covers maybe <1% of the planets surface, the rest of the world including 99.99% of the ocean water has ZERO temperature data to draw from
This makes for a wild guess on what the temperature really was for that year. Too little data points with 99% of Southern Hemisphere without any data at all.
Here is a post I made yesterday on this very point:
http://www.politicalforum.com/index.php?threads/uncertainty-in-early-temp-records.551859/page-2#post-1070649639
There are TWO NOAA charts for year 1900, showing how little of the planets surface have any daily temperature stations on it. Now imagine that 1850, with far less than that.
“this quote, from Nick Stokes article”
It’s actually a quote from Lord M’s article. I’m getting lambasted for what is his choice of 1850. But I don’t disagree with it. On this point, it seems it is Lord M and I against the world.
In response to sunsettommy, the HadCRUT4 dataset, unlike most other datasets, takes care to publish not only the midrange estimate but also the 2-sigma (i.e., 95%) confidence interval, which, for 1850, was less than one-third of a Kelvin either side of the midrange estimate. That variability is too little to influence calculations based upon absolute reference and emission temperatures in 1850.
The core point of disagreement is whether or not CO2 feedback is proportional to average temperature T in degrees Kelvin. Can someone please point us to a list of feedback mechanisms so that we can assess that they are all proportional to T ?
I now understand Stokes’ argument to be: “we know that temperature was stable at 287.5 K; so feedback must go to zero at 287.5 deg K.” This certainly seems to suggest a non-linearity? Or am I missing something?
In response to boffin77, test apparatus constructed by one of my co-authors, and a further and more sophisticated apparatus built by a national laboratory, confirmed beyond all doubt that such feedback processes as subsist in a dynamical system at any given moment must perforce respond, at that moment, to the entire reference signal then obtaining, and not merely to some small and arbitrarily-chosen fraction of that reference signal. There is no doubt whatever about this. it is inherent in the equations, and, strictly speaking, did not need to be empirically verified, but we empirically verified it anyway, with a well designed experiment by a co-author and then with another well-designed experiment from a national laboratory.
Thanks for the quick reply. I agree completely (always have) that “such feedback processes as subsist in a dynamical system at any given moment must perforce respond, at that moment, to the entire reference signal.”
My concern is that linear control systems with positive feedback don’t reach equilibrium. (Many of us know this from ancient school assemblies where the gain on the microphone was turned up too high and the room was immediately filled with an ear-splitting shriek.) In your simplified diagram (above) the “feedback fraction” [f_t] might be better written as [f * delta(t)] to indicate that the impact of feedback is very small over very short times, and grows with time. The fact that the impact is linear with time is an assumption you and I are making, not a requirement. Obviously, delta(t) = t – (t-1) and f will have units of inverse years.
Given R(t-1) = temperature at time (t-1), the temperature at some new time t (which you call [E_t]) can be calculated as follows:
E_t = R(t-1) / ( 1 – f * delta(t) ).
This gives us what we expected: E_t gets larger as delta(t) gets positively larger.
A key observation is that there is no equilibrium temperature under this model; T(t) will always rise with time t. I’m not sure why your diagram suggest it will reach equilibrium.
I will add that I don’t think this is the correct model – runaway temperature feedback would have killed us all eons ago. However it might be an adequate model for estimating climate sensitivity, as you have done.
Stokes? I’m trying to keep mouth shut in order to just appear stupid.
It is not clear why Boffin77 imagines that “linear control systems with positive feedback don’t reach equilibrium”. Of course they do, provided that the feedback fraction is well below unity. Just build a test rig and you can find this out. That’s what we did. Or you can just work the equations.
Of course, some of the sillier extremist papers, predicting up to 11 K warming per CO2 doubling, are in effect assuming feedback fractions dangerously close to unity. But it was the observation that these absurdly high feedback fractions would lead to an instability not observed in the real world that led us to carry out our research in the first place.
Well I admit it has been many years since I designed control systems, but I did (long ago) build some that demonstrated what positive feedback does – and we all ducked for cover and pulled the plug.
My analysis of the simplest case (the case where reference temperature Rt is constant) can be summarized non-mathematically as follows: Rt is being augmented by a feedback that gets larger with each passing year (such is the nature of positive feedback applied to a constant input). Your model is so admirably simple that nothing more needs to be said.
Alarmists seem to think this will actually happen, but if it can happen now it must have happened in the past, in which case we would not be here to talk about it. Ergo it will not actually happen. Rather there must be, for example:
– negative feedbacks that kick in at some temperature. or
– non-linearities in the CO2 feedback.
– or maybe the whole CO2 positive-feedback myth is inaccurate (and I know it is not your invention)
I appreciate your educated and innovative and original approach to the investigation.
Boffin77 is incorrect to summarize by saying that reference temperature is augmented by a feedback that gets larger with each passing year, and wrong to suggest that such is the nature of a positive feedback applied to a constant input.
He neglects to take account of the fact that a feedback is merely a radiative forcing whose magnitude is proportional to the temperature change driven by an original, direct forcing. Just like the direct forcing, the indirect forcing arising from temperature feedback is resolved by an increase in temperature, which restores radiative equilibrium.
Well these new comments make sense, though I can’t really match them up against the original diagram and text. So I’ll just say “thank you” for your patient replies to my comments, and best wishes for your radical critique of climate science.
In response to Boffin77, the block diagram in the head posting is standard fare. But one can only really understand how it works if one also has a grasp of the underlying mathematics. Briefly, the system-gain factor is equal to the reciprocal of (1 minus the feedback fraction), provided that the absolute value of the feedback fraction is less than 1. The reason why this is so goes back to the very first formal demonstration of the sum of an infinite convergent geometric series, some hundreds of years ago.
Consider the block diagram. As the signal passes infinitely around the feedback loop, passing through the feedback block each time, an infinite series of successive powers of the feedback fraction arises. The sum of that series is 1 / (1 – f). In the long version of our paper that has been submitted to a journal, we have included the formal demonstration that this is the case, precisely to address the concerns of reviewers who might not otherwise realize that net-positive feedback does not necessarily entail a runaway response. Provided that the feedback fraction is safely below unity, there will be no runaway response.
In practice, the feedback fraction (the fraction of equilibrium temperature represented by the feedback response) must be below 0.3, for otherwise the formidable stability of the temperature regime on Earth would be impossible. But official climatology imagines it must be about 0.6, and might even be very close to unity in some of the sillier, extremist papers, which is why it has been unable to constrain equilibrium sensitivity.
The curve of 1 / (1 – f) is rectangular-hyperbolic, so that as f approaches unity the equilibrium sensitivity approaches infinity. It was our realization that this is the case that led us to begin examining what climatology was doing wrong.
So, mathematically what is the sensitivity to a 38% increase in CO2? In 1850 CO2 was 300ppm and it is currently 415ppm. We have 169 years of observational evidence to work with. What does it tell us?
In response to artimms, it is implicit in the CMIP5 midrange estimates that reference sensitivity to a change in CO2 concentration is the Planck parameter 0.31 times the forcing coefficient 4.85 times the natural logarithm of the proportionate change in concentration. Thus, the reference sensitivity to a 38% increase in CO2 concentration is 4.85 x 0.31 x ln(1.38), or 0.5 K.
Or one could take the entire net anthropogenic forcing of 2.5 Watts per square meter from 1850-2011. The reference sensitivity is then 2.5 times the Planck parameter: i.e., 0.75 K (which, coincidentally, is the actual least-squares linear regression trend on the HadCRUT4 temperature data from 1850-2011.
To find out what the equilibrium sensitivity to the 2.5 Watts per square meter net period anthropogenic forcing would be were it not for a radiative imbalance of 0.6 Watts per square meter to 2010 (Smith+ 2015), one simply multiplies the 0.75 K directly-forced anthropogenic reference warming by 2.5 / (2.5 – 0.6), which means there should have been an equilibrium warming of 1 K by 2011, were it not for the time delay occasioned by the vast heat capacity of the oceans.
The factor 2.5 / (2.5 – 0.6) is the period system-gain factor. But it is only 1.3, and not official climatology’s 3.2 – another sign that official climatology’s estimates of equilibrium sensitivity are about three times too big.
“Taking Smith as correct ad argumentum, climatology’s period system-gain factor derivable from the data for 1850-2011 is simply the ratio of 2.5 to (2.5 – 0.6)”
That isn’t a gain. It is just saying that of the forcing, as proportion went into the sea. It is a correction that you might make to a gain for the shortfall from equilibrium. But it isn’t the gain.
Mr Stokes is wrong – or very largely so. The purpose of the radiative imbalance (it seems first to have been introduced to the literature by James Hansen in 2006 or thereby) is to correct for the timelag in the equilibrium-temperature response to radiative forcings and consequential feedbacks.
The equilibrium sensitivity is derived from the sum of the direct forcings and the consequential forcings driven by temperature feedbacks (which are expressed as forcings denominated in Watts per square meter per Kelvin of the reference temperature, or sensitivity, that engendered the feedback response).
Broadly speaking, the warming consequent upon the sum of the direct and feedback forcings is proportional to the magnitude of that sum, wherefore it follows that the ratio of the direct forcing to the difference between that forcing and the radiative imbalance is (or is very close to) the system-gain factor.
It is of interest to note that,as Monckton states ,the feed back to CO2 is so small as to be immeasurable. It will be a surprise to most readers to see that the IPCC Summary for Policy Makers agrees with him see: https://climatesense-norpag.blogspot.com/2017/02/the-coming-cooling-usefully-accurate_17.html
“Various approaches to improve the precision of multi-model projections have been explored, but there is still no agreed strategy for weighting the projections from different models based on their historical performance so that there is no direct means of translating quantitative measures of past performance into confident statements about fidelity of future climate projections. The use of a multi-model ensemble in the IPCC assessment reports is an attempt to characterize the impact of parameterization uncertainty on climate change predictions. The shortcomings in the modeling methods, and in the resulting estimates of confidence levels, make no allowance for these uncertainties in the models. In fact, the average of a multi-model ensemble has no physical correlate in the real world.
The IPCC AR4 SPM report section 8.6 deals with forcing, feedbacks and climate sensitivity. It recognizes the shortcomings of the models. Section 8.6.4 concludes in paragraph 4 (4): “Moreover it is not yet clear which tests are critical for constraining the future projections, consequently a set of model metrics that might be used to narrow the range of plausible climate change feedbacks and climate sensitivity has yet to be developed”
What could be clearer? The IPCC itself said in 2007 that it doesn’t even know what metrics to put into the models to test their reliability. That is, it doesn’t know what future temperatures will be and therefore can’t calculate the climate sensitivity to CO2. This also begs a further question of what erroneous assumptions (e.g., that CO2 is the main climate driver) went into the “plausible” models to be tested any way. The IPCC itself has now recognized this uncertainty in estimating CS – the AR5 SPM says in Footnote 16 page 16 (5): “No best estimate for equilibrium climate sensitivity can now be given because of a lack of agreement on values across assessed lines of evidence and studies.” Paradoxically the claim is still made that the UNFCCC Agenda 21 actions can dial up a desired temperature by controlling CO2 levels. This is cognitive dissonance so extreme as to be irrational. There is no empirical evidence which requires that anthropogenic CO2 has any significant effect on global temperatures.
The climate model forecasts, on which the entire Catastrophic Anthropogenic Global Warming meme rests, are structured with no regard to the natural 60+/- year and, more importantly, 1,000 year periodicities that are so obvious in the temperature record. The modelers approach is simply a scientific disaster and lacks even average commonsense. It is exactly like taking the temperature trend from, say, February to July and projecting it ahead linearly for 20 years beyond an inversion point. The models are generally back-tuned for less than 150 years when the relevant time scale is millennial. The radiative forcings shown in Fig. 1 reflect the past assumptions. The IPCC future temperature projections depend in addition on the Representative Concentration Pathways (RCPs) chosen for analysis. The RCPs depend on highly speculative scenarios, principally population and energy source and price forecasts, dreamt up by sundry sources. The cost/benefit analysis of actions taken to limit CO2 levels depends on the discount rate used and allowances made, if any, for the positive future positive economic effects of CO2 production on agriculture and of fossil fuel based energy production. The structural uncertainties inherent in this phase of the temperature projections are clearly so large, especially when added to the uncertainties of the science already discussed, that the outcomes provide no basis for action or even rational discussion by government policymakers. The IPCC range of ECS estimates reflects merely the predilections of the modellers – a classic case of “Weapons of Math Destruction” (6).
” … What could be clearer? The IPCC itself said in 2007 that it doesn’t even know what metrics to put into the models to test their reliability. That is, it doesn’t know what future temperatures will be and therefore can’t calculate the climate sensitivity to CO2. … ”
>>
Not to mention that such physical ‘testing’ would be non-helpful, when the testing time-scale is of the order of millennia.
It’s thus not merely a “known unknown” but for practical purposes it’s an unknowable unknown, (unless you have a time-machine, and we don’t, but if we did we would already know when the next glacial commences, and intervening trend … plus have a record of the WX noise).
This is the mother-of-all fool’s errands, but thank you for pointing out some within the IPCC’s publications agree with that.
It is of interest to note that ,as Monckton says ,the effect of anthropogenic CO2 is too small to be measurable. Most readers will be surprised to learn that the IPCC Summaries for Policy Makers agree with him. See
https://climatesense-norpag.blogspot.com/2017/02/the-coming-cooling-usefully-accurate_17.html
“………The IPCC AR4 SPM report section 8.6 deals with forcing, feedbacks and climate sensitivity. It recognizes the shortcomings of the models. Section 8.6.4 concludes in paragraph 4 (4): “Moreover it is not yet clear which tests are critical for constraining the future projections, consequently a set of model metrics that might be used to narrow the range of plausible climate change feedbacks and climate sensitivity has yet to be developed”
What could be clearer? The IPCC itself said in 2007 that it doesn’t even know what metrics to put into the models to test their reliability. That is, it doesn’t know what future temperatures will be and therefore can’t calculate the climate sensitivity to CO2. This also begs a further question of what erroneous assumptions (e.g., that CO2 is the main climate driver) went into the “plausible” models to be tested any way. The IPCC itself has now recognized this uncertainty in estimating CS – the AR5 SPM says in Footnote 16 page 16 (5): “No best estimate for equilibrium climate sensitivity can now be given because of a lack of agreement on values across assessed lines of evidence and studies.” Paradoxically the claim is still made that the UNFCCC Agenda 21 actions can dial up a desired temperature by controlling CO2 levels. This is cognitive dissonance so extreme as to be irrational. There is no empirical evidence which requires that anthropogenic CO2 has any significant effect on global temperatures. ………….Harrison and Stainforth 2009 say (7): “Reductionism argues that deterministic approaches to science and positivist views of causation are the appropriate methodologies for exploring complex, multivariate systems where the behavior of a complex system can be deduced from the fundamental reductionist understanding. Rather, large complex systems may be better understood, and perhaps only understood, in terms of observed, emergent behavior. The practical implication is that there exist system behaviors and structures that are not amenable to explanation or prediction by reductionist methodologies. The search for objective constraints with which to reduce the uncertainty in regional predictions has proven elusive. The problem of equifinality ……. that different model structures and different parameter sets of a model can produce similar observed behavior of the system under study – has rarely been addressed.” A new forecasting paradigm is required.
W.Elsasser addresses the limits of that reductionist paradigm, for biology.
A Form of Logic Suited for Biology
Walter M. Elsasser Department of Earth and Planetary Sciences The Johns Hopkins University Baltimore, Maryland http://www.nap.edu/readingroom/books/biomems/welsasser.htm
The complexity of almost any living organism is beyond comprehension with a positivist approach. Still on a (discreet) continuum it might be possible to classify planetary climates. Zeller and Nikolev’s atmospheric pressure continuum points to another view.
tony b and guy pearse discussed rapid cooling stops and starts in northern hemisphere temperatures -MWP, LIA and even current Arctic warming.
Could the reason be Dansgaard-Oeschger events? Here is how I understand the causes of Arctic temperatures going up and down.
Warm Gulf Stream waters flow upward past Greenland and Norway into the Arctic Ocean and under the sea ice;
This warm saline water is found below cold saline covered by fresh water and in turn insulated by sea ice;
Interestingly the cold periods last about 1000 years and the warm cycles a few decades defining D-O events;
During the last Ice Age, Greenland’s average temperatures dramatically rose on average every 1500 years by 10°C (+/- 5°C) in a just matter of one or two decades, and then more gradually cooled;
The cause of abrupt warming was the sudden removal of insulating sea ice that allowed ventilation of heat previously stored in the Arctic;
70% of the D-O events occurred in times of CO2 indicating it not to be a factor in warming;
When sea ice prevents heat ventilation, the inflow of warm and dense Atlantic water continues to store heat in the subsurface layers;
The warm Atlantic water becomes more buoyant, upwells and melts the insulating ice cover; and,
The loss of an insulating ice cover allows for the transfer of heat to the atmosphere causing a dramatic rise in surface temperatures to begin a D-O warm phase.
Other studies show the Arctic Ocean has cooled since the early 1990’s and continues to cool as it seeks equilibrium with the atmosphere while transferring heat
As quickly as the Arctic warmed occurred, cooling could be as abrupt and rapid returning to its normal cold state. The wobbly jet stream which has brought wide swings in weather would likely settle down and stabilize as the Arctic cools.
Any opposition to these understandings?
Keith
I obtained Hubert lambs records of wind direction back to around 1500 and tried to bring it up to date and then compared it to my reconstruction of CET back to 1540 . There is a close match most times showing how climate is affected by the direction of prevailing winds .
Generally in this part of the world westerlies aRe warming, easterlies cold in winter and warm in summer etc. there was a preponderance of cold easterlies in the LIA and a surfeit of westerlies during the warm eras.
our local abbey made windows smaller in the 1170’s as the climate cooled and the warm westerlies became much less common. Curiously the coldest eras also seem to be the wettest and stormiest which does not follow the general understanding that a warm atmosphere can contain more moisture
The weather systems are driven by the meandering jet streams so rapid change from a cold to a warm state and back again seems to be the norm, but with protracted periods when winds from one direction or other predominate .
So not disputing your comments and all we need is a few million in grants to carry out some more research
Tonyb
TonyB
There have been recent papers confirming Arctic heat ingress by wind. My own study of high latitude areas with high monthly temperature anomalies confirmed wind direction change.
Regatds
tonyb and Martin Cropp both make good points about the influence of variability in wind direction on global mean surface temperatures. There are many such variable influences, such as the relative frequencies of el Nino and la Nina, for instance (and that, too, is partly influenced by wind direction).
“confirming Arctic heat ingress by wind”
Is that just air heading up be cooled? Does it also imply cold air coming down be warmed?
Tonyb,
That is extremely interesting. A very common unstated-but-implicit assumption in climate science is that energy can only enter or leave the climate system via radiative transfer. Some models do take into account some small geothermal effect as well, but generally it is assumed that all other methods of energy transfer in and out are negligible and can be safely ignored.
One of the largely ignored mechanisms for transfer of energy is kinetic and heat energy addition/subtraction arising from momentum change. The “solid” Earth changes its axial rotation rate on a cyclic basis with periodicities ranging across all observable time scales from days to lunar cycle (weeks) to biannual to annual to multidecadal to multicentury. Measurements of the LOD (Length of Day which is inversely proportional to angular velocity) date back to the 17th century albeit with poor precision until the 20th century. Empirical Mode Decomposition or Fourier analysis of LOD records show identical frequency content to EMD or Fourier applied to the GMST series for multiannual periodicities. As the solid Earth spins faster or slower there is a frictional torque between the solid Earth and the hydrosphere and atmosphere which changes their angular momentum. Some of the variation is undoubtedly expliquable in terms of reditribution of surface masses. If there is no external driver for the variation in solid Earth angular velocity then we expect via conservation of angular momentum to see a clear correlation of Atmospheric Angular Momentum (AAM) and LOD, and indeed we do see a very strong correlation over periods of less than seven years. There is now general agreement that most of the changes in LOD on time scales from weeks to a few years are excited by changes in AAM – and vice versa. The atmosphere exchanges angular momentum with the solid Earth as expected. Because of the massive difference in moment of inertia, a very small change in LOD translates into a big change in AAM. This AAM to LOD correlation however shows a clear long-wavelength drift when longer periods are considered, which makes it highly likely that the solid Earth variation is subject to some “external” driver. “External” here means external to the climate system, so it could be a torque associated with variation in Earth’s liquid core or it could be external-to-Earth driven by orbital mechanics. Whatever the root cause, it has the effect of adding and subtracting about 4 x 10^22 joules of KE to the atmosphere every 60 years or so (full amplitude).
Independently, there is also very strong evidence to suggest that the quasi-60 years cycles are forced cycles rather than any oscillation of ocean heat distribution. This comes from the relative phasing of net flux and temperature. If these cycles were caused by natural oscillations of heat distribution we would expect the temperature oscillation to be pi radians out of phase with the net flux oscillation; i.e. maximum surface temperature should yield maximum outgoing flux or cooling and minimum surface temperatures should encourage maximum incoming flux or warming. To the extent that we can estimate net flux phasing (from ocean heat estimates or from sea level rates historically) it does NOT exhibit this phasing. Instead, it shows a phasing which is entirely compatible with externally forced heating ( i.e. less than pi/2 phase separation) .
So, in summary, we have a fairly substantial oscillation which is (a) probably externally forced and (b) of a magnitude which is too large to be explained by exchange of angular momentum as a sole cause and (c) cannot be explained by the current basket of external radiative drivers. We can add to this that the period between 1980 and 2000 during the most recent warm phase of the 60-year oscillation was driven by SW heating largely attributed to a major change in cloud albedo.
The most dominant effect of the oscillation in LOD is its effect on the wind stress tensor. Primarily, it either strengthens or weakens the main east to west trade winds. This then changes both cloud fraction and distribution (which provides the missing energy in the net flux oscillation via SW). This also controls the likelihood of relative strength and frequency of ENSO events. In conclusion, I think that there is an oscillatory external torque, probably driven by orbital mechanics, which is responsible for the 60 year oscillation aka stadium wave via control of winds. The “missing” energy in this oscillation is determined by a parallel induced change in cloud fraction and distribution. Your observations fit into this hypothesis quite comfortably.
” … As quickly as the Arctic warmed occurred, cooling could be as abrupt and rapid returning to its normal cold state. The wobbly jet stream which has brought wide swings in weather would likely settle down and stabilize as the Arctic cools. Any opposition to these understandings? … ‘
>>
That’s not what we see even via the annual seasonal change, colder season phase equates to faster and deeper jetstream flows that become closer to the equator as peak of cold approaches, and greater latitudinal excursion ‘wobble’ in general. So I see little reason to expect a general cooling phase to become more settled in time. In fact, such seems to correlate with greater storminess and variability.
Keith, my point was more that the descent from the MWP, which was much like the present warm period, to the cold depths of LIA occurred naturally without a connection to CO2, or any atmospheric drivers.
Essentially, this is strong evidence that natural variations are the first order drivers of climate and that CO2 is at best a third order effect after water which is the source of multiple large effects: radiative; phase change enthalpies; convective heat transfer, albedo change from clouds, massive heat sink of the oceans, their heat transfer in ocean currents…
Christopher Monckton,
Very interesting work and I agree with others that your explanation in this post is the best yet.
However, I have trouble understanding how the global mean surface air temperature could ever be at a steady “equilibrium” because it is constantly changing. For instance, there is an annual cycle in the global mean surface air temperature of about 4K, ranging from about 276K to about 285K to 289K (12C to 15C) in recent years as can be seen here:
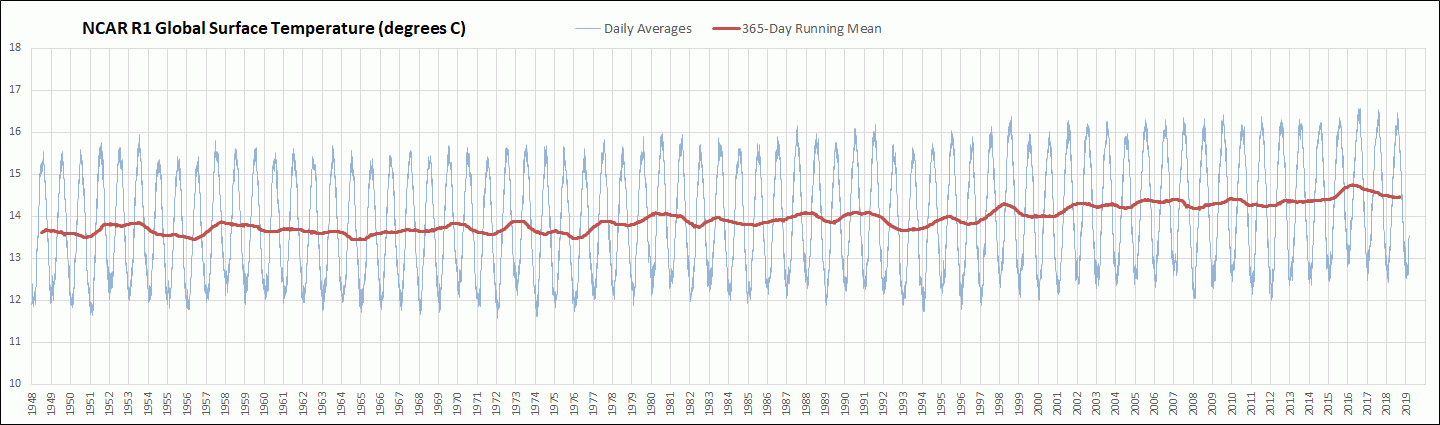
And over longer time periods, our best proxies indicate more substantial variations of the annual average global mean surface air temperature in the past, as can be seen here:
https://oz4caster.wordpress.com/paleo-climate/
Maybe we could say “quasi-equilibrium” for an annual average?
Oops … should be “ranging from about 285K to 289K (12C to 16C)” …
“your explanation in this post is the best yet”
It makes one think clear that before took some delving:
“Here, then, is the corrected calculation. The reference temperature in 1850, before feedback, was 265 K. In that year the equilibrium temperature, after feedback, was 287.5 K. So the system-gain factor that applied in 1850 was 287.5 / 265, or 1.085, about a third of climatology’s 3.2.”
That is indeed the basic arithmetic, and since that 1.085 factor is the ratio of two absolute temperatures in the climate ball park, it has to be close to 1, what ever observations or anything else say.
But it isn’t justified here. In the first of this recent series it was, in a way. A function E(R) was defined, where E is actual surface temperature, and R is an imputed temperature that would exist without feedbacks. Now that does give a way forward; the sensitivity ECS could be written as response to forcing F:
ECS = dE/dF = dE/dR dR/dF.
But in the arithmetic here, dE/dR has been replaced by E/R. Joe Born has been focussing on that. Then why?
The earlier paper did try to justify it by fitting various functions E(R) – linear, exponential etc. It didn’t make much difference, so let’s look at linear. The common requirement was that E(R) had to pass through (0,0) – ie E(0)=0. That is, 0K.
But this is totally unphysical. For a start, air liquefies at about 80K. But you can’t sensibly extrapolate the properties of the atmosphere below about 200K. But it’s worse than that.
E is not actually a function of R. They are related through the varying values of GHG. When GHGs go to zero, E and R both stand at about 255K. They can’t meaningfully go any lower, because there are no more GHGs to be removed. You certainly can’t say that there would be constant slope down to 0K.
So if you want to make a gross linear approx, the point to relate to is (255,255), not (0,0). But that would be a gross approximation indeed. Even if you could reliably impute R over that range, the behaviour of the atmosphere changes radically. We are talking about snowball earth, after all. But if you did make that gross approx, the ratio would be something like
(288-255)/(265-255)
or about 3.3. Right in the IPCC range.
Thanks Nick. I appreciate your insight.
Do you have any thoughts on global mean surface air temperature “equilibrium”?
Bryan,
“Do you have any thoughts on global mean surface air temperature “equilibrium”?”
They would be considering at least an annual average, so that gets rid of the seasonal cycle. It hardly matters whether the system actually sat at equilibrium in 1850. You could have an amplifier sitting in a telecom network which is never at equilibrium. That doesn’t affect its ability to function as a linear amplifier. The key thing is that, over some range of perturbations, differences in states relate linearly to differences in state variables. If you imagine the results of a two variable system graphed, they would lie on a line, which is all that you need. The intercept at zero x (whatever you consider x) would be the notional equilibrium point, but it doesn’t matter whether you have data exactly there.
People have odd ideas about Lord M’s starting point of 1850. It isn’t supposed to be a particularly perfect period. It is just one state; the present is another, and you can use differences between them to estimate rates. Both ends with have fluctuations due to cause other than the variables you are relating (noise). The criterion for choice are that you have a good period of separation, so that the differences you think are due to cause are large relative to the noise. On the other side, the start should not be so long ago that information is poor, and it should not create differences so large that the linear approximation is in doubt. Some might think 1850 fails the first – OK, choose a later period. Of course, the other criterion is that you should expect the cause that you are analysing should have been operating during the period. There is no point in including periods when it wasn’t; it will just add noise without information.
Nick thanks, your discussion makes good sense to me. It’s human nature to want to simplify problems in order to better address them and many times simplistic approaches that are not very accurate can work well enough for many purposes. My concern about climate science is that the numerous complex, chaotic, and interacting perturbations of varying magnitudes and durations that influence climate change introduce so much “noise” in the system that it is nearly impossible to accurately isolate the effect of a single perturbation like CO2, both for diagnostic and predictive purposes.
I strongly suspect that many modelers are far too overconfident in their models, whether they be very simplistic or very complicated models. Until these models are validated with decades of future observations, I see little reason to have much confidence in them. At this point, they are little more than speculation. Because of all the parameterizations involved in the more complicated models, I suspect much iterative tweaking will be needed over many decades of comparing results to observations. Even then, because of the extreme complexity of the climate system, I have serious doubts that the current models will ever have enough skill to engender much confidence in their decadal to century scale predictive capabilities, especially on regional or local scales that are more important to most people. However, considering how much modeling has improved over the last 30 years, there could easily be unforeseen modifications that will improve model skill as has happened with short-term weather modeling. For that reason, I support both weather and climate modeling efforts, but strongly caution against unwarranted premature confidence.
Mr Stokes imagines, incorrectly, that at the emission temperature of 255 K there are no feedbacks. Perhaps he would care to calculate the temperature at the ocean surface directly beneath the zenith point, and think again. Or he may like to read Merlis+ (2010).
He continues to fail to acknowledge that the feedback processes that were present in 1850 perforce responded to the entire temperature then prevalent, and not to some arbitrary and minuscule fraction thereof. In this, our professor of control theory is entirely clear: feedbacks respond to the entire reference signal, and not merely to some small fraction thereof.
“Mr Stokes imagines, incorrectly, that at the emission temperature of 255 K there are no feedbacks.”
There are no GHG feedback fluxes, because there are no non-condensing GHGs. 255K is defined as the temperature when they have been removed. You’re trying to create the smile without the cat. In Lacis’ model I think there is still some water vapor at 255K. But it can’t provide feedback to GHG which aren’t there. And the wv certainly won’t be there at 200K.
In response to Mr Stokes, it is self-evident that there were no feedback responses to pre-industrial noncondensing greenhouse gases when there were no such gases in the atmosphere and the reference temperature comprised the 255 K emission temperature alone. However, that emission temperature on its own engendered a substantial temperature feedback response to precisely the same sensitivity-altering feedbacks as IPCC lists as driving the feedback response to the greenhouse gases.
We have not at any stage suggested what Mr Stokes here implies we have suggested: namely that when there no greenhouse gases there was nevertheless a feedback response to the greenhouse gases.
And, since the emission temperature is 255 K (actually, it’s probably about 10 K above that, once one has allowed for Hoelder’s inequalities between integrals, because one-third of the dayside would be open ocean), our current draft does not concern itself with what might have been the case if the Earth’s temperature were as low as 200 K.
“We have not at any stage suggested what Mr Stokes here implies we have suggested: namely that when there no greenhouse gases there was nevertheless a feedback response to the greenhouse gases.”
Implies? Implies? From just the previous comment:
“Mr Stokes imagines, incorrectly, that at the emission temperature of 255 K there are no feedbacks”
“our current draft does not concern itself with what might have been the case if the Earth’s temperature were as low as 200 K.”
The summary, from just a few days ago, was based heavily on the proposition that the E(R) function, of surface temperature vs imputed temperature without feedback, passed through (0,0), ie absolute zero 0K. That is the basis for expressing the gain as a ratio of absolute temperatures.
In fact the lowest it can reach by reducing GHGs is a point near 255K where there are no GHGs and no feedback. And at that point E=R=255. And if you extend linearly to that point, you get a system gain, and hence sensitivity, of about 3K/doubling.
I don’t profess to know what magnitude any feedback at 255 K may have, but as a matter of theory I see no reason for your implied assumption that no greenhouse gas means no feedback.
Let’s return to the physically more evocative feedback formulation —which Lord Monckton changed to his by replacing
—which Lord Monckton changed to his by replacing 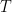 with
with 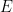 ,
, 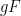 with
with  , and
, and 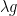 with
with  . (Note here that I’m using the whole quantities rather than perturbation. That makes the use of a single forcing variable and addition problematic, but we’ll ignore that.) A temperature change initially resulting from a forcing
. (Note here that I’m using the whole quantities rather than perturbation. That makes the use of a single forcing variable and addition problematic, but we’ll ignore that.) A temperature change initially resulting from a forcing 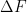 that represents, say, a dimming of the sun might have knock-on effects such as an albedo increase that further changes
that represents, say, a dimming of the sun might have knock-on effects such as an albedo increase that further changes 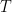 .
.
The feedback coefficient ‘s value would reflect that temperature-caused albedo change. If you accept the possibility of such knock-on effects but don’t consider them feedback, then it seems to me your disagreement with Lord Monckton on that issue is merely semantic.
‘s value would reflect that temperature-caused albedo change. If you accept the possibility of such knock-on effects but don’t consider them feedback, then it seems to me your disagreement with Lord Monckton on that issue is merely semantic.
Obviously, though, that albedo feedback’s magnitude is unlikely to be the same as, say, water-vapor or lapse-rate feedback’s at a higher temperature in the presence of greenhouses, so it is not unreasonable to entertain the notion that the feedback coefficient is highly dependent on temperature
is highly dependent on temperature 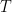 and thus, contrary to what Lord Monckton thinks is dictated by feedback theory, that
and thus, contrary to what Lord Monckton thinks is dictated by feedback theory, that  is highly dependent on
is highly dependent on 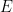 :
: 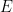 is a significantly nonlinear function of
is a significantly nonlinear function of  .
.
I hasten to add that I have no idea whether the function actually is very nonlinear. But nothing in feedback theory rules that possibility out; a feedback-amplifier circuit could be built to model it.
“I see no reason for your implied assumption that no greenhouse gas means no feedback”
I said there was no GHG feedback flux. It could of course be possible to have a feedback to some other heat source. But you can’t have feedback to GHG that aren’t there.
The relevance is to Lord M’s function E(R), which you have been looking at. E is the surface temperature; R the temperature you would have with GHG forcing but no GHG feedback. As you remove GHG (in a thought experiment) the temperature drops until at 255K, they have all gone. E is then the temperature in the absence of GHG feedback (there are no GHGs). So E=R. The E(R) curve passes through that point.
I don’t endorse Lord M’s practice of using the difference between such a point and present as the gradient for sensitivity purposes. I agree with you that it should be the local gradient at present climate. But if you do, then the system gain is (288-255)/(265-255)=3.3. Multiply by 1.05 to get the sensitivity.
Contrary to what I surmised, Mr. Stokes’ use of feedback seems to differ substantively from Lord Monckton’s, not merely semantically:
If I’m interpreting that correctly, Mr. Stokes doesn’t look upon as what the temperature would be without any feedback to temperature at all. His version seems instead to include feedback to the entire temperature except the portion for which CO2 forcing is responsible. In contrast, Lord Monckton does seem to define
as what the temperature would be without any feedback to temperature at all. His version seems instead to include feedback to the entire temperature except the portion for which CO2 forcing is responsible. In contrast, Lord Monckton does seem to define  as excluding all feedback whatsoever.
as excluding all feedback whatsoever.
That substantive difference manifests itself in Mr. Stokes’ following statement:
That is, the two 255 K values imply that Mr. Stokes sees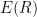 as passing through
as passing through 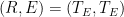 ; there’s no CO2 forcing at the emission temperature
; there’s no CO2 forcing at the emission temperature  , so
, so 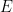 has to equal
has to equal  at that point.
at that point.
But emission temperature is based on today’s albedo and clouds, not on what they would be if the surface temperature equaled the emission temperature. This implies that, although Mr. Stokes’ version of excludes some feedback, it includes any feedback that may occur at low temperatures through, say, the albedo-change mechanism.
excludes some feedback, it includes any feedback that may occur at low temperatures through, say, the albedo-change mechanism.
Since Lord Monckton’s version excludes all feedback, on the other hand,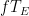 is non-zero and makes the
is non-zero and makes the 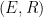 curve pass instead through some
curve pass instead through some  . That puts the emission-temperature point to the left of where Mr. Stokes puts it, and Lord Monckton no doubt imagines it’s near the line from the origin to the
. That puts the emission-temperature point to the left of where Mr. Stokes puts it, and Lord Monckton no doubt imagines it’s near the line from the origin to the  point that represents 1850’s conditions. If it is, then the resultant ECS estimate is much less than the one Mr. Stokes made for the sake of argument.
point that represents 1850’s conditions. If it is, then the resultant ECS estimate is much less than the one Mr. Stokes made for the sake of argument.
So, as a high-ECS-value partisan, Mr. Stokes would seem to provide some support for Lord Monckton’s argument that in the view of “climatology” feedback “will not respond at all to the emission temperature.”
I’m afraid I overstated that. It’s not that Mr. Stokes believes there’s no feedback at all below the emission temperature. It’s merely that he ignored it in applying the hypothetical technique for the sake of argument.
“Contrary to what I surmised, Mr. Stokes’ use of feedback seems to differ substantively from Lord Monckton’s, not merely semantically:”
I don’t think so. But it actually doesn’t matter. This whole discussion, based on what Lord M mostly says he does, has been totally off the beam relative to what he actually does, which is summarised in the post above:
“Here, then, is the corrected calculation. The reference temperature in 1850, before feedback, was 265 K. In that year the equilibrium temperature, after feedback, was 287.5 K. So the system-gain factor that applied in 1850 was 287.5 / 265, or 1.085, about a third of climatology’s 3.2.
Now, if we multiply the 1.05 K reference sensitivity to doubled CO2 by the corrected system-gain factor 1.085, we get a Charney sensitivity not of 3.35 K, as official climatology does, but of just 1.15 K.”
Two major things:
1. There isn’t actually a feedback calculation at all, with or without emission temperature. If you think there is, then what is the feedback coefficient f?
2. Nothing depends on the difference between 1850 and present. Only 1850 is used. The answer would be basically the same if only present were used (or 1950 etc).
So back to basics. F is a forcing due to non-condensable GHG, expressed as equivalent CO2 in doublings (ie log_2(CO2)). E is surface temperature. The target is
CS = dE/dF
He introduces another quantity R, and writes, from calculus
CS = dE/dR dR/dF
and calls dE/dR system gain, and gets dR/dF from “official climatology” (OC) who get it from Soden and Held. And there is a generally agreed value of 1.05, which he used.
So what is R? He uses the OC value, so it is whatever OC says it is. And that is the response to F that would occur without feedbacks. That is, feedback to F. Whenever you say feedback, it always has to be feedback to a defined signal.
So then it is a matter of estimating dE/dR. In his first post of a week ago, he set out a lot of curve fitting options for the function E(R). He took Lacis’ estimate for present (E=287.5, R=265) as one point and he took E=0, R=0 as the other. A linear fit gives the ratio 287.5 / 265 cited here.
But as I’ve objected above, 0K is nonsense here, and Lord M then said he didn’t do it (but he did). And I’ve said that a proper second point is E=R=255K. It could rather be Lacis’ 243K, resulting from progressively removing GHG. But the point is that at some temperature there, all non-condensable GHG’s have been removed. R is defined as the temperature you would have in the absence of feedback to those GHGs. No GHGs – no feedback. So at that point, certainly, E=R.
And so if you put that into the linear fit, you would get not (287.5-0)/(265-0)=1.085, but
(287.5-255)/(265-255)=3.25 as the system gain (a bit less if you use Lacis’ 243). That gives an ECS in the upper part of the IPCC range.
Mr Stokes continues to perpetrate elementary errors.
1. Mr Stokes maintains that at the emission temperature of 255 K, in the absence of any noncondensing greenhouse gases, there would be no feedbacks – i.e., that the reference or pre-feedback emission temperature R_0 and the equilibrium or post-feedback temperature E_0 would be equal at 255 K. However, there would in fact be a large feedback, since one-third of the dayside (to first order) would be open ocean. Therefore, E_0 would be greater than R_0. Mr Stokes, like official climatology, fails to take account of that feedback to emission temperature – or, rather, he misallocates it to the preindustrial greenhouse gases.
2. Mr Stokes seems to think that the calculations in the head posting (one of which he himself copies without acknowledgement and presents as a feedback calculation), are not feedback calculations. He may perhaps be unfamiliar with control theory and, therefore, unaware of the relationship between the system-gain factor and the feedback factor. Any textbook of control theory will enlighten him.
3. Mr Stokes imagines that, because air becomes solid at well above 0 K, I am not permitted to point out that zero temperature entails zero feedback response. Again, any textbook of control theory will enlighten him. In the absence of an input signal or of any pre-feedback perturbation of that signal – in other words, if no signal enters the feedback loop by way of the summative input-output node – there will be a zero feedback response. One does not need to know anything about the state of a theoretically-impossible climate at 0 K to know that that is the case. Therefore, if one imagines that the equilibrium-temperature response function E(R) is exponential, one can derive the exponent from the point (0,0), which applies to all curves of temperature response to the action of feedback, and (265, 287.5), the quite well constrained values of reference and equilibrium sensitivity in 1850. The exponent is 1.0146 or thereby, which gives a curve that is vanishingly different from linear.
4. In repeating (albeit without attribution) my calculation of official climatology’s system-gain factor 3.25 derivable from the position in 1850, Mr Stokes perpetrates the same mistake as official climatology itself: he assigns all of the feedback response to emission temperature to the preindustrial greenhouse gases – or, rather, he states that there would be no feedback response to emission temperature in the absence of greenhouse gases. A careful reading of the admittedly inspissate paper by Lacis+ (2010) would draw his attention to the fact that even they find a feedback response of about 10 K to emission temperature.
5. Mr Stokes continues to fail to acknowledge the self-evident truth that the feedback processes that subsist in a dynamical object at any given moment must, at that moment, respond to the entire reference signal then obtaining. And he continues to fail to explain why he considers that truth not to be a truth. Since it is a truth, it follows that the 22.5 K feedback response, the difference between the reference temperature of (255 + 10) = 265 K and the observed equilibrium temperature of 287.5 K in 1850, is a feedback response not, as he tries to suggest, solely to the 10 K reference sensitivity to the preindustrial noncondensing greenhouse gases but to the entire reference temperature. Thus, 255/265 of that 22.5 K, i.e., 21.65 K, is feedback response to emission temperature, and only 0.85 K is feedback response to the 10 K reference sensitivity to the preindustrial noncondensers. Note that we do not need to know what the feedback response to emission temperature was in the absence of the noncondensing greenhouse gases: all we need to know is that not only the warming of 10 K forced by their presence but also the emission temperature was present in 1850 and that, therefore, at that time the feedbacks then present had to respond to both parts of the signal, and to respond proportionately to each part thereof.
6. Mr Stokes imagines that deriving the system-gain factor as the ratio of sensitivities is preferable to deriving it as the ratio of entire reference signals. Of course, if we knew that the response curve was appreciably nonlinear (when in fact climatology finds it to be nearly linear), and if we had a sufficiently perfect knowledge either of the magnitudes of all sensitivity-altering feedbacks or of the system-gain factor, it would be best to concentrate on the most recent sensitivities: that goes without saying. However, the fact that the interval of Charney sensitivities has not budged for 40 years and is absurdly broad should have suggested to Mr Stokes’ mind, as it has to ours, that it is necessary to use the entire temperatures because they exceed the reference temperatures by two orders of magnitude and thus provide the opportunity to increase the signal-to-noise ratio dramatically.
Mr Born continues to state the blindingly obvious – that, if one divorces a feedback calculation from any physical reality whatsoever, one can imagine any shape one wants for the response curve. However, as I have several times pointed out to him, we are not doing calculations in vacuo. The head posting demonstrates that official climatology regards – and treats – the climate-sensitivity parameter as near-invariant: calculations done on the basis of its error show that the system-gain factor in 1850 was 3.25 and the mean system-gain factor in response to doubled CO2 compared with today, as imagined by the CMIP5 ensemble (Andrews+ 2012), is 3.2. Looks pretty darn near-linear to me. Of course, the moment one corrects official climatology’s error in defining temperature feedback one observes an apparently extravagant nonlinearity if one takes official climatology’s interval of Charney sensitivities as canonical. But that nonlinearity is not only inconsistent with official climatology’s understanding that the climate-sensitivity parameter (and, therefore, the system-gain factor) is near-linear, but also inconsistent with physical reality. A careful examination of each of the sensitivity-altering temperature feedbacks shows that there is no physical basis for assuming the highly nonlinear equilibrium-temperature response curve imagined by Mr Born.
“In repeating (albeit without attribution)”
How could the attribution be clearer? I said:
“what he actually does, which is summarised in the post above:…”
and quoted the words from it, in italics with quotation marks, as is my custom. If that isn’t clear, the authorship is unmistakeable by style.
I’ll respond to other matters somewhat out of sequence:
“Mr Stokes seems to think that the calculations in the head posting … are not feedback calculations”
Yes, and I gave the test. If it is a feedback calculation, what is the feedback factor? Where is it derived?
“A careful reading of the admittedly inspissate paper by Lacis+ (2010) would draw his attention to the fact that even they find a feedback response of about 10 K to emission temperature.”
Lacis did an experiment with GISS Model E in which he removed all noncondensing GHGs, and followed events. After about 30 years, the surface temperature dropped to 265K and stayed there. Lacis didn’t make there a feedback attribution – GCMs do not deal with feedback, so you can’t experiment with removing it, only the gases. But arguing in reverse, one can say that the rise from 265K to 288K (putting the GHGs back) was due to the effect of both the GHGs directly and their feedbacks. You would probably wish to argue that the residual 10K is a feedback to emission temperature, but it makes no sense. 10K is simply the amount of warming relative to 255K that is created by the remaining water vapor when the non-condensing GHGs have been removed.
In fact, Lacis et al wrote a more expansive paper in Tellus B, 2013 in which they do do feedback attribution (but not with GCM), see esp sec 6.6.
“Therefore, E_0 would be greater than R_0. “
In that “fraudulent practices” post of a week ago, in the section starting System Gain, it gives a value for R₀:
“in 1850, R₀ + ΔR₀ = 265K, and ΔR₀ = 10K”.
Clearly, there it is said that R₀ = 255K and that is with GHGs removed. The surface temperature E₀ with all GHGs (including water) removed is the emission temperature; E₀ = 255K.
“Mr Stokes imagines that, because air becomes solid at well above 0 K, I am not permitted to point out that zero temperature entails zero feedback response.”
What you actually say is that at R=0K, E=0K, and you use this as one of two fitting points for an inferred E(R) function, from which the CS was derived. Assuming that the function still applies after the atmosphere has solidified is, well, courageous. But even worse, it isn’t clear how the variables could even be defined there, or indeed how E(R) even makes sense as a functional relationship at any level. R is the notional limit after removing all non-condensing GHGs. So the addition of GHG since 1850 doesn’t change it, although it changes E. The removal process would just take them away the added GHG and still get down to 265K. I can’t see how it could actually take any other value. Certainly not values below 255K, when all GHGs have gone.
“Therefore, E_0 would be greater than R_0. “
In your “fraudulent practices” post of a week ago, in the section starting System Gain, it gives a value for R₀:
“in 1850, R₀ + ΔR₀ = 265K, and ΔR₀ = 10K”.
Clearly, there it is said that R₀ = 255K and that is with GHGs removed. The surface temperature E₀ with all GHGs (including water) removed is the emission temperature; E₀ = 255K.
“Mr Stokes continues to fail to acknowledge the self-evident truth that the feedback processes that subsist in a dynamical object at any given moment must, at that moment, respond to the entire reference signal then obtaining.”
Well, we’ve been through it many times. But again, amplification and feedback respond to proportionately to perturbation. The factor is called gain. You work out the output response by differencing the state variables. You can include constant factors like emission temperature if you really insist. But you must difference them as you do with other variables. And that, of course, yields zero.
At least two commenters have sought to present a standard control diagram showing the whole state as input. An example is here. But in each case, as I point out, the very first thing done to that state is that it is passed into a differencer, which forms the difference with the output. What actually goes around the loop is not the state, but the error signal. Standard control terminology. That is the difference between the states. Anything that is constant between them will go to zero.
“because they exceed the reference temperatures by two orders of magnitude and thus provide the opportunity to increase the signal-to-noise ratio dramatically”
Well, you could add in the temperature of the sun. That would be even more dramatic. And just as devoid of meaning. Sensitivity represents the ratio of the change in one thing to the change in the other. If you add in something like emission temperature, it treats it as a change from zero, which of course is not what happened.
Sensitivities are, well, sensitive. No use trying to eradicate noise.
Lord Monckton says he’s trained in formal logic, yet he seems congenitally incapable of following a logical argument.
He contended that the E(R) curve couldn’t be very nonlinear, because it passes through (R, E) = (265 K, 287.5 K) (and, implicitly, through (0 K, 0 K)). (“[T]he curve of equilibrium temperature as a response to reference temperature . . . cannot be very nonlinear . . . [b]ecause the reference temperature [265 K] in 1850 was more than 92% of equilibrium temperature [287.5 K].”) So I showed him what shouldn’t have required demonstration: that a nearly cubic (and thus highly nonlinear) function could indeed pass through those points.
First he denied that it could, then he falsely attributed a dreamed-up ratio to it, and now he runs away from his own test for function nonlinearity by saying I’ve shown only that “one can imagine any shape one wants for the response curve” if “one divorces a feedback calculation from any physical reality whatsoever.” He just throws random assertions against the wall in the hope that one will stick. But they rarely do.
Among the other bases of his “mathematical proof” that E(R) is nearly linear is his notion of surpassing silliness that near linearity is established if the change in its average slope (“system gain factor”) is small over a small domain increment. Again, my simple power relationship demonstrated what should have been obvious without it: even a highly nonlinear function’s average slope needn’t change much over a small domain increment.
Another basis is his nutty contention that, by referring to the small-signal equation’s feedback coefficient as a “near-invariant,” climatologists intended to say that E is a nearly linear function of R. Not only is such an interpretation inconsistent with the sensitivity he admits they estimate, but it would be wildly at odds with the way invariant is ordinarily used in control-systems contexts; in control systems the concept of invariance is typically orthogonal to that of linearity.
I’m tempted use Lord Monckton’s own words and say that “any textbook of control theory will enlighten him” on this point. But in view of how woefully he misinterpreted Hendrik Bode’s work I doubt that he’d get much from consulting an authoritative text.
Any lurker who thinks I’m judging Lord Monckton too harshly may be interested in reviewing how we got here. Lord Monckton now espouses applying to climate an equilibrium feedback equation seen more often in electronics and control systems. But that hasn’t always been his position.
In publicity for a paper that he previously wrote about climate feedback he instead called it a “rogue equation.” In that paper he criticized the equation’s use in climate, saying of the closed-loop-gain-vs.-loop-gain hyperbola it produces that “in electronic circuits, the singularity at , where the voltage transits from the positive to the negative rail, has a physical meaning: in the climate, it has none.” The truth is that the hyperbola’s fourth-quadrant portion to which he thereby referred has nothing to do with a circuit’s “[transiting] from the positive to the negative rail.”
, where the voltage transits from the positive to the negative rail, has a physical meaning: in the climate, it has none.” The truth is that the hyperbola’s fourth-quadrant portion to which he thereby referred has nothing to do with a circuit’s “[transiting] from the positive to the negative rail.”
I explained that to him, but rather than availing himself of an explanation from someone who’d begun studying the discipline half a century ago, he publicly disputed it. Without acknowledgement, though, he quietly dropped that “rogue equation” position—which he had previously propounded with just as much seeming authority as that with which he now characterizes (his misunderstanding of) that equation as universally applicable.
Although he has now reversed his position he failed to comprehend my explanation’s implications; he now interprets that hyperbola’s fourth-quadrant portion as implying global cooling. Common sense tells us it implies no such thing, of course; if some positive feedback increases equilibrium temperature, more of it won’t do just the opposite. But common sense doesn’t seem to affect him.
Now, he often invokes the authority of his “eminent”—albeit suspiciously absent—co-authors. But some of them were no doubt co-authors of that previous paper, too. And, although the previous paper’s central equation was a clear, fundamental error in linear-systems theory, none of those co-authors has so far as I’m aware retracted any aspect. So his co-authors’ authority doesn’t impress me.
By my count this site has run something like ten of Lord Monckton’s head posts about his theory, and each one misled readers who lack the math and control-systems knowledge to see through it. Now, I can’t seriously fault the site’s personnel for failing to see how egregiously wrong that theory is; no one’s born knowing this stuff. But you’d think they’d have started to wonder after a claimed discovery that high sensitivity estimates have been based on “a fundamental error of physics” had persisted in attracting no support from any of the better-regarded skeptics.
Mr Stokes continues to double down on the elementary errors he makes.
1. He says that he had cited me in italics on the following point from official climatology’s method:
“So if you put that into the linear fit, you would get not
(287.5-0)/(265-0)=1.085,
but
(287.5-255)/(265-255)=3.25
as the system gain (a bit less if you use Lacis’ 243). That gives an ECS in the upper part of the IPCC range.”
In fact, Mr Stokes had not put that quotation in italics: instead, he had presented it as though he were revealing something new. More importantly, he has failed to grasp the main point, which is that, since using climatology’s method as above gives a preindustrial system-gain factor 3.25 and since using the CMIP5 models’ estimated reference and equilibrium responses to doubled CO2 gives a predicted future system-gain factor 3.2, climatology indeed regards the climate-sensitivity parameter as near-linear, wherefore one may do the sensitivity calculation either climatology’s way using sensitivities or our way using the entire equilibrium and reference temperatures, and there will be very little difference in the answer either way – always provided that one has sufficient information to perform both calculations. But one does not have sufficient information to perform the calculation climatology’s way, since the uncertainties in the sensitivities on which it relies are so large in relation to the sensitivities themselves.
2. Mr Stokes continues to fail to admit the truth that the feedbacks that subsist in the climate at any given moment must perforce respond to the entire reference temperature then present. That being the case, one can use the well constrained entire reference and equilibrium temperatures in 1850 as the necessary information to derive a far more reliable estimate of Charney sensitivity than if one uses the sensitivities, which are two orders of magnitude smaller. He seeks to argue that in an electronic circuit the input state is passed into a differencer and that what passes into the feedback loop is not the entire reference state but the error signal. But we are not dealing with an electronic circuit (though it was by reference to electronic circuits that the mathematics of feedback was first developed): we are dealing with the climate. Is Mr Stokes seriously seeking to maintain that, in 1850, the feedbacks then present were not responding to the entire reference temperature of 265 K? If he is, then perhaps he should approach a national laboratory, as we did, to build a test rig and see what happens. What happens is exactly what the equations predict will happen: the feedback processes will, like it or not, respond to the entire reference temperature.
Mr Stokes
3. Mr Stokes continues to pretend that he does not understand the relationship between the system-gain factor and the feedback fraction, so that he can maintain his silly pretence that the calculations we are discussing are not feedback calculations. Of course they are.
4. Mr Stokes continues to pretend that in the absence of noncondensing greenhouse gases equilibrium temperature would be identical to reference temperature. This would not, however, be the case, because in the absence of the non-condensers about a third (to first order) of the dayside surface would be open water, so that water-vapor, cloud and (at that stage most importantly) ice-albedo feedbacks would be in operation. Even without noncondensers, therefore, there would be a substantial feedback response to emission temperature, wherefore E_0 would be almost 22 K greater than R_0.
5. Mr Stokes continues to pretend that, because air becomes solid at well above 0 Kelvin, one cannot safely draw the conclusion that the feedback response to 0 Kelvin would be 0 Kelvin. That pretence is nonsense.
6. Mr Stokes introduces a new and fatuous error: the suggestion that one might as well introduce the temperature of the Sun into the calculation. If he were to read any textbook of elementary celestial physics, he would learn that what is relevant to us here is the total incoming solar irradiance, which, owing to the distance of the Earth from the Sun, is more than somewhat smaller than the temperature of the Sun itself.
7. Mr Stokes says it is “no use trying to eradicate noise”. If he will read an elementary textbook of control he will come to appreciate the advantage of increasing the signal-to-noise ratio, which our approach achieves.
Then there is Mr Born. He continues to fail to understand that if a) the reference temperature in 1850 was 92% of the equilibrium temperature in that year and b) the climate-sensitivity parameter (which encompasses inter alia the effect of feedback) is near-linear, then functions such as his lead to spectacular and unphysical contradictions.
His equivocation as to the meaning of “nonlinear” does not impress.
Monckton of Brenchley,
Could you give the full formula for this exponential function, and explain how you derived a unique formula from two data points?
Bellman’s implicit objection is correct, of course: exponentials through those points are not unique.
But one possible exponential through (0 K, 0 K) and (265 K, 287.5 K) is , where
, where  and
and 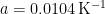 . That curve additionally passes through (266.05 K, 290.89 K) and thereby implies an ECS of 3.38 K.
. That curve additionally passes through (266.05 K, 290.89 K) and thereby implies an ECS of 3.38 K.
That’s one objection.
But I also suspect he’s not using an exponential function at all. I think he’s got a monomial, , which would explain why he thinks it is almost linear.
, which would explain why he thinks it is almost linear.
Bellman:
Ah, yes, you’re probably right; I had previously pointed out to him that a relationship of the general form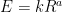 , which I had provided him at https://wattsupwiththat.com/2019/06/05/the-moral-case-for-honest-and-competent-climate-science/#comment-2717450, is not an exponential, but I guess he’s a slow learner. (Technically, of course, his relationship needs a coefficient
, which I had provided him at https://wattsupwiththat.com/2019/06/05/the-moral-case-for-honest-and-competent-climate-science/#comment-2717450, is not an exponential, but I guess he’s a slow learner. (Technically, of course, his relationship needs a coefficient 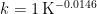 .)
.)
When GHGs go to zero, E and R both stand at about 255K.
And that’s precisely where you go wrong. What makes you think think that there are no feedback effects unless there are greenhouse gases? You’re assuming your result.
In response to Bryan-oz4caster, in a multivariate dynamical system such as the climate, there is no such thing as a true equilibrium. However, if we are considering simply one variable – global mean surface temperature – we may look for a longish period during which, whatever the year-to-year fluctuations, the least-squares linear-regression trend is zero. For 80 years after 1850, the trend was zero. Therefore, it is respectable to take the temperature in 1850 as having been an equilibrium temperature.
Of course, one should also allow for the uncertainty in that temperature measurement – but it was, if I remember correctly, only about 0.4 K either side of the midrange observation.
Lord Monckton keeps repeating the same illogical arguments:
That challenge has a false premise. Nothing in “official climatology” requires that “the feedback loop, which receives as its input signal the entire reference temperature . . . magically decide that it will respond only to the perturbations of that reference temperature caused by the presence of natural and then also of anthropogenic noncondensing greenhouse gases, and yet that it will not also respond at all to the emission temperature.”
In particular, the high “system gain factor” that Lord Monckton attributes to “official climatology’s” estimate imposes no such requirement. To see this, consider the following equilibrium equation for a hypothetical correspondence between an “equilibrium temperature” resulting from feedback in accordance with a feedback factor
resulting from feedback in accordance with a feedback factor  and the “reference temperature”
and the “reference temperature”  that would have prevailed in the feedback’s absence:
that would have prevailed in the feedback’s absence:
That equation says operates on the entire reference temperature. Here we’ve made
operates on the entire reference temperature. Here we’ve made  depend on temperature, as we would expect it to. If we pick, say, the following nonlinear dependence:
depend on temperature, as we would expect it to. If we pick, say, the following nonlinear dependence:
where and
and  , then—even though, again, the feedback factor operates on the entire reference temperature—we get the “system gain factor” 3.2 that Lord Monckton says “official climatology” produces. So nothing about that high a value implies that the feedback doesn’t operate on the emission temperature.
, then—even though, again, the feedback factor operates on the entire reference temperature—we get the “system gain factor” 3.2 that Lord Monckton says “official climatology” produces. So nothing about that high a value implies that the feedback doesn’t operate on the emission temperature.
That doesn’t follow; the above-defined feedback-factor dependence does indeed cause a very nonlinear curve of equilibrium temperature as a response to reference temperature; it’s nearly cubic. Yet in that curve the ratio of 1850’s reference temperature 265 K to the corresponding equilibrium temperature 287.5 K. is 92%, which Lord Monckton implies is too high for a very nonlinear curve.
Now, you may not think the real-life relationship is that nonlinear. Fine, neither do I. But Lord Monckton has not proven it isn’t. And he certainly hasn’t provided a “mathematical proof” that “official climatology” made a “grave error” in applying feedback theory.
Our mathematical model must mirror the real world, and not the other way round.
If the model does not match, pitch it and start over.
Thanks Joe, I think this paragraph shows where CoB is going.
So he seems to have missed the word noncondensing, ie water vapour : the most important GHG.
He then goes on to compare calculations of the mean temperature calculated will all other GHG with actual recorded temperatures and cries : GOTCHA !
His tortuous attempts at explaining what Nick Stokes explained so simply implies that either he does not understand it himself ( 90% confidence ) or he is simply trying to mislead and obfuscating to the point hardly anyone can follow it in an attempt to look learned and “baffle them with science”.
Greg may not, perhaps, appreciate that official climatology distinguishes between the noncondensing greenhouse gases, which, if their concentrations change, drive radiative forcings and the condensing greenhouse gas (water vapor), which, if its concentration changes, is responding to the change in temperature caused by the forcings from the noncondensing greenhouse gsaes.
Since our approach is to adopt all of official climatology except what we can demonstrate to be false, we have adopted official climatology’s distinction between what is a forcing and what is a feedback consequential upon the warming caused by the forcing.
Greg also seems unfamiliar with the notion of verifying a theoretical result empirically. Well, he’d better get over it: that, like it or not, is how science is done.
Mr Born, having been called out on his ridiculous function, merely repeats it. On his own admission, his function suggests that the feedback fraction in response to greenhouse-gas warming exceeds the feedback fraction in response to emission temperature by 1000%, spectacularly contrary not only to all that we know of feedbacks in the climate but also to official climatology’s view that the climate-sensitivity parameter, which embodies the entire action of feedback on temperature, is “a typically near-linear parameter”.
It is only if one assumes that there is no feedback response to emission temperature that climatology’s system-gain factor gives a near-linear feedback response: i.e., in 1850 the equilibrium sensitivity of 32.5 K is about 3.2 times the reference sensitivity of 10 K, and in response to doubled CO2 the CMIP5 models’ midrange estimate is that the 3.35 K equilibrium sensitivity is about 3.2 times the 1.15 K reference sensitivity. The system gain factor is about 3.2 in both cases.
It is only when one realizes that feedbacks in fact respond to the entire reference temperature and that, therefore, even in the absence of the naturally-occurring greenhouse gases the 255 K emission temperature itself induced a feedback that it becomes possible to realize that, though official climatology thinks it is treating feedback response as approximately linear it is in fact treating it – inadvertently – as so wildly nonlinear as to give rise to a readily-demonstrable contradiction whenever one assumes that any point on its interval of equilibrium sensitivities is correct.
As our own illustration in the head posting demonstrated, the equilibrium warming of 1.4 K per CO2 doubling that is to be expected on the basis of the IPCC’s midrange estimate of net anthrogenic forcing to 2011 and official climatology’s estimate of the radiative imbalance to 2010 (Smit+ 2015) is in very much the same ballpark as our own estimate of 1.15 K, but falls a very long way short of the CMIP5 models’ imagined 3.35 K Charney sensitivity.
Climatology has erred, and that is why it has not appreciated that, as Mr Born has noticed, its Charney-sensitivity estimates imply an extravagant nonlinearity in the equilibrium-temperature response curve that is wholly unwarranted in physical reality.
Priceless. I point out that Lord Monckton made three demonstrably false statements in a single comment, and he says I’m the one who’s been “called out.”
Look, this is really simple. The conclusion of “climatology,” as Lord Moncton calls it, is that the equilibrium temperature with feedback is a very nonlinear function of what it would be without feedback. And despite all the logorrhea he uses to mask it, Lord Monckton’s “proof” boils down to little more than his bald assertion that the function can’t be very nonlinear.
What’s his argument? The demonstrably false proposition that no function whose values are those he claims for the year 1850 could be very nonlinear:
Yet he knew that argument was invalid when he made it, because only three days before, at https://wattsupwiththat.com/2019/06/05/the-moral-case-for-honest-and-competent-climate-science/#comment-2717128, I had showed him by example that a very nonlinear E(R) curve could indeed exhibit those values.
But his response to that explanation was to make three demonstrably false statements: (1) that the E(R) curve I described was “exponential,” (2) that it had a y-intercept of 38 instead of the necessary zero, and (3) that its “feedback fraction f in response to greenhouse gases would be greater than the feedback fraction in response to emission temperature by a factor exceeding 80.”
But substituting my example feedback-fraction expression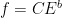 into the relationship
into the relationship  implies the function’s form is
implies the function’s form is 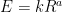 , where a, b, C, and k are all constants: contrary to what Lord Monkton said, E is a power of R, not an exponential. Lord Monckton just seemed to say whatever came to mind, with no concern for whether it was true. But it didn’t matter, because his fanboys couldn’t tell the difference.
, where a, b, C, and k are all constants: contrary to what Lord Monkton said, E is a power of R, not an exponential. Lord Monckton just seemed to say whatever came to mind, with no concern for whether it was true. But it didn’t matter, because his fanboys couldn’t tell the difference.
And a power function clearly passes through the origin, so, again, despite what Lord Monckton said the function’s y-intercept is 0, not greater than 38. Lord Monckton just said whatever came to mind, with no concern for whether it was true. Because his fanboys couldn’t tell the difference.
Moreover, by simply placing that function on a spreadsheet, anyone could have obtained the following values
and seen that the ratio 0.0854/0.0074 of f’s doubled-CO2 value to its emission-temperature value is only 11.5. So, when Lord Monckton said that the “feedback fraction f in response to greenhouse gases would be greater than the feedback fraction in response to emission temperature by a factor exceeding 80,” his statement was again demonstrably false.
Three objectively, demonstrably, mathematically false statements in a single comment. That’s the way he operates: he just says whatever comes to mind, without regard to its truth, which his fanboys seem unable to recognize.
And when I explained his errors to him, did he thank me for setting him straight? He did not. Instead he just denied: “On no evidence, the Born Liar maintains that the feedback-fraction ratio for Charney sensitivity of 3.35 K is 11 and not 80.” No evidence? The evidence was the incontrovertible math right in front of him. But his fanboys don’t do math, apparently, so he could make that claim with impunity.
Now that he’s quietly discarded his ratio = 80 factoid in the face of my explanation, he presents the 11.5 value I showed him as though I’d made a grudging admission of some important point instead of having demonstrated that yet another of his pointless statements is erroneous: “On his own admission, his function suggests that the feedback fraction in response to greenhouse-gas warming exceeds the feedback fraction in response to emission temperature by 1000%.” The feedback fraction increased by 1000%? Of course it did; that’s just another way of saying the function is very nonlinear.
So his whole theory boils down to his saying that the relationship can’t be very nonlinear because, well—then it would be very nonlinear. He’s saying climatology is wrong because it’s wrong. Apparently that’s what passes for reasoning in Lord Monckton’s circles.
Mr Born, in his increasing desperation to prove us wrong, continues to plug his dog of a function that entails a feedback fraction in response to greenhouse warming that is 11 times the feedback fraction in response to emission temperature in the absence of greenhouse gases. There is no physical basis for any such 1000% increase in the feedback fraction. And, however much he wrestles with the absurd over-predictions of official climatology, he will find that all of them lead to contradictions as absurd as his.
As I have pointed out to him before, official climatology regards the climate-sensitivity parameter as “typically near-invariant”. Mr Born’s silly function is manifestly and egregiously at odds with that finding.
Finally, he falsely asserts that I had said his function produces a feedback-fraction ratio of 80. No, I had said my illustrative exponential function had produced that ratio. He had written that “the example” had produced a ratio of 11, but he had written so confusingly that it was not clear he was talking of his example rather than mine.
Be that as it may, official climatology regards the climate-sensitivity parameter and, therefore, the feedback fraction, as near-invariant, and it is demonstrable that – if one replicates official climatology’s error in failing to take account of the fact that feedback responds not only to some arbitrarily-chosen fraction of the reference temperature but to the entire reference temperature obtaining at a given moment – official climatology is indeed assuming the feedback fraction to be near-invariant. Let us do the math.
The reference sensitivity to the pre-industrial greenhouse gases was 10 K or thereby. The equilibrium sensitivity was 287.5 – 255, or 32.5 K. The ratio of the equilibrium sensitivity to the reference sensitivity was thus about 3.25.
The reference and equilibrium sensitivities in response to doubled CO2 concentration in the CMIP5 models are 1.05 K and 3.35 K respectively. The ratio of the equilibrium sensitivity to the reference sensitivity is thus predicted to be about 3.2 – not a whole lot different from the 3.25 that obtained in the pre-industrial era.
That is how we know official climatology means what it says when it says the climate-sensitivity parameter is “typically near-invariant”.
However, official climatology has not realized that feedback responds to the entire reference temperature. So the correct calculation for the preindustrial era is that the ratio of equilibrium to reference sensitivity was 287.5 / (255 + 10), or 1.085. But that is about a third of official climatology’s predicted midrange ratio 3.2.
One should not jump, as Mr Born so eagerly does, into assuming that official climatology considers the climate-sensitivity parameter to be extravagantly nonlinear after all. The apparent nonlinearity arises from its fundamental error in defining temperature feedback.
Joe Born,
The two points that you have been focused on (extrapolation from the origin vs use of local gradient and the lack of any general requirement for a feedback factor to be independent of the signal on which it operates) are well made. However, I can’t help thinking that the various hypothetical examples you are using to illustrate your maths points are by accident actually reinforcing one of the most egregious errors which Lord Monckton is making here – namely his assumption that there exists a feedback to temperature of an input temperature signal. This DOES NOT EXIST in climate science, either in the GCMs or in analytic application of energy balance models (EBMs). The feedbacks of most interest here are temperature-dependent feedbacks to net flux. There is no mechanism whereby a temperature input can induce any further change in temperature via feedback other than via a change in state-variables which then induces a change in net flux which then causes heating or cooling.
This distinction is important. The input to this process is a flux forcing – a forced and sustained change in either incoming or outgoing flux – NOT a change in temperature. If a temperature perturbation is introduced into a system at steady-state by an internal redistribution of heat (eg an El Nino event) the feedbacks TO NET FLUX work to restore the flux balance and return the transient temperature to the same equilibrium temperature as before. The system equilibrium temperature remains unchanged throughout this process even though the transient temperature is varying. The equilibrium temperature cannot be changed without a forced change in either the incoming or the outgoing flux.
Energy balance over a time period says that
Energy accumulated = Energy entering – Energy leaving
Differentiating the statement of energy balance (and dividing by global area to convert power to flux density), we obtain the instantaneous flux balance at TOA – expressed as an equation in surface temperature rather than brightness temperature: –
Net Flux, N (positive downwards) = Incoming Flux – Outgoing Flux (1)
Let us assume that we have a system in quasi steady-state in 1850 at time t= 0 and surface temperature, T0, which corresponds to the equilibrium surface temperature at that time. N must be equal to zero at t= 0 for steady-state. We now consider a forced constant step-change, F, to the incoming flux (positive downwards by convention).
At time t, the incoming flux is equal to {Incoming flux at time t=0 + F} and the outgoing flux is equal to R(T) where T is the surface temperature at time t, and R is the temperature-dependent restorative flux. (As an aside, note that this restorative flux is a function of absolute temperature at this stage.)
Eq (1) simply becomes N(t) = {Incoming flux at time t = 0} + F – R(T) (2)
We don’t know the exact form of R(T) but we can perform a Taylor series expansion about the point T = T0. This yields:-
R(T) = R(T0) + R'(T0) x (T – T0) + R”(T0) x (T – T0)^2 + higher order terms
For small perturbations from T0, it is common but not compulsory to use just the first order approximation. Substituting this into Eq 2 yields:-
N(t) = {Incoming flux at time t = 0} + F – { R(T0) + R'(T0) x (T – T0)} (3)
We now note that at steady state at time t = 0, the incoming flux at time t=0 was equal to R(T0), the outgoing flux at time t = 0 . So we can write:-
N(t) = F – R'(T0) x (T – T0) (4)
Eq 4 is commonly called the “linear feedback equation”. R'(T0) is a constant in the above derivation, and it is positive, since it is dominated by the Planck response; i.e. the outgoing flux increases as temperature increases. The feedback to net flux is (therefore) unconditionally negative. If however you were to start at a different equilibrium temperature to derive Eq 4, R'(T0) would assume a very different value. If we assume that the only feedback in operation is the so-called “Planck response”, we can estimate its value by equating incoming radiation from Sol with outgoing radiation from Stefan-Boltzman and then consider the derivative of outgoing radiation with respect to temperature change. This yields a value of around 3.3 W/m^2/K – the Planck response. If the rest of the climatology is kept exactly the same, but we wish to consider a different equilibrium temperature, then this derivative term varies in proportion with the temperature derivative of Stefan-Boltzmann. In other words, it varies as the cube of the equilibrium temperature. So the point you make above about there being no justification for the assumption of constant feedback over a temperature range is completely correct. My main issue with your examples is that they give the impression that you have accepted Lord Monckton’s story that climate science recognises (or is founded on) a temperature feedback to temperature input as opposed to its recognition of a temperature-dependent feedback to net flux.
We can eliminate N(t) from Eq 4 by postulating an ocean–heating model. In the simplest example – a single body model – we can replace N(t) with C dT/dt, the rate of energy gain with time, where C represents the heat capacity of the single body expressed in watt-years/m^2/k. I invite you to compare the form of the equations which you are using as examples against this new form of Eq 4. In this new form of Eq 4, it is the rate of change of temperature which receives the effect of feedback to net flux. Since we expect net flux to control the rate of heat gain, this seems eminently reasonable. In summary, and knowing that I am repeating myself, there is no direct feedback of temperature to temperature.
Let us then briefly visit the question of the “gain associated with feedbacks”. This is not a gain associated with an input signal, as Lord Monckton wishes to treat it. It is a theoretical amplification factor expressed as the ratio of the predicted theoretical (non-physical) equilibrium temperature from all feedbacks relative to the predicted theoretical (non-physical) equilibrium temperature from just the Planck feedback, when both are predicted with the same flux forcing. The denominator is not an input signal to the numerator in any physical way.
From Eq 4, the transient temperature must head for equilibrium temperature as t -> infinity and N(t) -> 0. As N(t) -> 0, we see that T -> F/ R'(T0)
If we say that for the Planck response alone, R'(T0) = lambda(Planck)
and that for the total feedback, R'(T0) = lambda(Planck) + lambda(other)
then we see that the ratio of equilibrium temperature for all feedbacks to equilibrium temperature for Planck alone is just
Amplification = lambda(Planck) / {lambda(Planck) + lambda(other))
I have no problem with someone deciding to call this a “gain”. I do have a problem with someone declaring that they can prove the above basic maths is incorrect by declaring that it is based on the abuse of a control theory that it neither uses nor needs to use.
You’re absolutely correct about the “input temperature” and the risk that I’m reinforcing Lord Monckton’s misconception. Moreover, I’ll confess that I omitted any caveat even though I thought of that risk almost every time I commented on the subject.
In my (partial) defense, though, I’m sure that commenters (maybe including me) brought that problem up more than once over a year ago, when Lord Monckton first unveiled his theory on this site. Since then, most of the knowledgeable commenters have drifted away in the face of Lord Monckton’s dishonest argumentation, and we now see mostly Monckton fanboys. So I’ve tried to make my comments as simple as possible.
Also, complications arise from my attempt to give as fair a reading as possible to his contention that “whatever feedback processes are present in the climate at any given moment must necessarily respond not merely to changes in the pre-existing temperature: they must respond to the entire reference temperature obtaining at that moment.” As usual, his formulation is too vague to restrict itself to one interpretation. Rather than find fault with it, though, I’ve attempted to accord it a construction that is actually true.
As I say, though, that causes complications. Surface temperature, for instance, ends up not being a single-valued function of forcing. Also, as we depart from small perturbations I feel increasingly queasy about combining the various forcings additively. So any treatment even nodding at rigor would demand more math tolerance of the reader than I’ve observed in this site’s regulars.
Still, your criticism hasn’t be made often enough, so I’m glad you took the opportunity to make it now.
In response to Kribaez, one may derive the system-gain factor either as a secant slope, as climatology does, or simply as the ratio of equilibrium to reference sensitivities at a particular moment. The disadvantage of climatology’s approach is not, repeat not, that it is wrong, but that it is not useful: the very broad interval of equilibrium sensitivities to doubled CO2 concentration has not proven constrainable for 40 years.
What is wrong is official climatology’s definition of feedback, which fails to encompass the fact that any feedback processes present in the climate at a given moment will respond not merely to changes in the input signal but also to the input signal itself. In the climate, the input signal is the 255 K emission temperature. Would that signal itself engender a feedback response, in the absence of any noncondensing greenhouse gases?
The answer is Yes. Elementary calculations on annuli about the zenith point demonstrate that one-third of the dayside surface (to first order) would be ice-free, so that ice-albedo, water vapor and cloud feedbacks would operate.
At present, however, as the head posting demonstrates, official climatology effectively misallocates all or most of the feedback response to emission temperature and attributes it to the naturally-occurring, noncondensing greenhouse gases that were present in 1850.
With respect, therefore, Kribaez is wrong to state, in capitals at that, that the feedback response to the input temperature signal DOES NOT EXIST. It does exist, in physical reality. Just calculate the surface temperature at the zenith point in the absence of the noncondensing greenhouse gases, and the matter will become clearer.
Kribaez maintains, in bold face, that the feedbacks of most interest are temperature-dependent feedbacks to net flux. He adds that “the input to this process is a flux foriing – a forced and sustained change in either incoming or outgoing flux – NOT a change in temperature.” However, in climatology feedbacks are denominated in Watts per square meter per Kelvin of the reference temperature (or, doing it climatology’s way, the reference sensitivity) that engendered them.
His consideration of the Planck parameter as a feedback is one way of looking at it, but Roe (2009) prefers to treat that parameter as part of the reference system, expressing it in Kelvin per Watt per square meter rather than as though it were a feedback in Watts per square meter per Kelvin. Over the interval of interest – i.e., from 1850 via 2011 to a CO2 doubling compared with 2011 – the Planck parameter is near-invariant.
Kribaez says I have told a “story that climate science recognises (or is founded on) a temperature feedback to temperature input as opposed to its recognition of a temperature-dependent feedback to net flux”. Surely I have made it plain enough that climate science does not at present define temperature feedback as responding, at any given moment, to the entire temperature then obtaining as well as to some arbitrarily-chosen fraction thereof.
He ends by suggesting, in effect, that we ought not to be saying that the mathematical approach taken by official climatology in attempting to derive the system-gain factor from sensitivities rather than from entire temperatures is incorrect. But we do not say it is incorrect: merely that it is not useful. If it were useful, after 40 years and trillions spent, it would surely have been possible to constrain the interval of equilibrium sensitivities, but it has not been possible. It turns out to be more useful to derive the system-gain factor from the well-constrained reference and equilibrium temperatures that obtained in 1850. But climatology cannot do that, because its definition of feedback is defective in that it does not recognize that feedbacks respond to the entire temperature they find, specifically including emission temperature, to which, like it or not, there is a large feedback response.
Mr Born continues to write in a characteristically malevolent, dishonest and bad-tempered fashion, adding heat but no light to the discussion.
He professes to find it difficult to understand my statement that “whatever feedback processes are present in the climate at any given moment must necessarily respond not merely to changes in the pre-existing temperature: they must respond to the entire reference temperature obtaining at that moment.”
Since nomenclature in feedback theory is not standardized, I shall clarify matters for Mr Born. The sensitivity-altering feedback processes present in the climate, which were acting in the absence of the noncondensing greenhouse gases and also act in their presence, are the water-vapor/lapse-rate, surface-albedo and cloud feedbacks. Broadly speaking, in official climatology’s understanding, all feedbacks except the water-vapor feedback self-cancel.
The reference temperature at any given moment is the sum of the input temperature (emission temperature) and all subsequent perturbations thereof up to that moment.
The feedback processes, being temperature-dependent (which is why they are called “temperature feedbacks” and are denominated in Watts per square meter per Kelvin of the reference temperature that engenders the feedback response to them) respond to the entire reference temperature.
Though one can build an electronic feedback amplifier circuit with a differencer to permit the feedback loop to respond only to the perturbations of the input signal, in the climate there is no such differencer: the feedbacks, therefore, respond to the entire reference temperature.
Mr Born is concerned about whether one should combine radiative forcings additively if one departs from small perturbations. But we know what the system-gain factor was in 1850, and all subsequent perturbations are small perturbations. In any event, we have simply adopted official climatology’s estimates of net radiative forcing in the industrial era: we have not combined them additively. And we have adopted official climatology’s estimate of reference sensitivity to doubled CO2.
In general, we have followed an Occam’s-razor approach: essentia non sunt multiplicanda praeter necessitatem. Once it is recognized that feedbacks, being temperature-dependent, respond to the entire reference temperature and not merely to some arbitrary fraction thereof, and that reference temperature in 1850 was more than 92% of equilibrium temperature that year, and that the climate-sensitivity parameter is near-invariant, the derivation and constraint of equilibrium sensitivities becomes quite straightforward.
Lord Monckton,
You should note that you can readily map from my equations to those of Roe 2009 with a simple change of variable definitions. [To confirm that my “gain” is entirely compatible with Roe’s, just redefine my variables as follows:-
set my F = ΔRf from Roe
set my lambda(Planck) = 1/λ0 from Roe (Yes, he uses an inverted form)
set my lambda(other) = -c1 from Roe (His sign convention for non-Planck feedbacks is different from mine ]
His Equation 4 – which is the only thing that looks like a temperature feedback to temperature input – is actually just a re-statement and rearrangement of the equilibrium temperature for all feedbacks i.e. ΔT = F/(lambda(Planck) + lambda(other)) using my variables, and leads to exactly the same “amplification” which I defined above. But note that I did not use Control Theory in any shape or form to arrive at estimates of climate sensitivity. Nor did I need Control Theory to define the “amplification”. As I have said before, it is very difficult to abuse Control Theory when it is neither used nor necessary.
It is also worth noting that Roe’s work is looking strictly at a change in temperature from one equilibrium state to another, not transient temperatures. The change of state is brought about by a flux forcing, not a temperature input. Moreover, the only physical feedback in his equations is temperature-dependent feedback to net flux, a point which he himself makes several times.
“The major feedbacks in the climate system are well known: For example,
a positive radiative forcing such as that due to an increase in CO2 tends to increase temperatures, which tends to increase water vapor, which, in turn, produces a perturbation in the downwelling longwave radiation that amplifies the original forcing… When a feedback process is included in the system, the radiative perturbation to the system gets an additional nudge (either positive or negative) that is a function of the system response. The simplest representation is that this radiative nudge is linearly proportional to the system response, c1ΔT, where c1 is a constant…”
The “amplification” which I define above and which is identical to that found by Roe is NOT the gain of a physical system driven by temperature input, as my derivation should demonstrate if you follow it carefully. There is only a temperature-dependent feedback to net flux arising as the result of a forced perturbation to net flux, something that Roe and I are apparently agreed on.
On a second point, you wrote:-
” Surely I have made it plain enough that climate science does not at present define temperature feedback as responding, at any given moment, to the entire temperature then obtaining as well as to some arbitrarily-chosen fraction thereof.”
There are a number of ways of arriving at Eq (4) in my post above, the linear feedback equation. I chose to show this particular method specifically to demonstrate the point that the feedbacks in EBMs use the absolute temperature as the relevant state variable, and not the incremental temperature – despite any appearances to the contrary. The restorative flux in my derivation, R(T), is by definition the outgoing flux at the absolute temperature T. If we apply a Taylor series expansion about the equilibrium temperature T0, then the full Taylor series expansion reproduces R(T) exactly; there is no estimation. The only approximation I then made was to drop higher order terms and use the first order approximation R(T) = R(T0) + R'(T0) (T-T0) . Note that this is STILL an estimate of the restorative flux at the absolute temperature, not incremental temperature. The fact that R(T0) can subsequently be eliminated does not mean that only incremental temperatures have been or are being considered! What it is actually telling us is that for a calculation of the temperature-dependent feedback to net flux, the most important thing to know is the local rate of change of the restorative flux (i.e. in the vicinity of T0) with respect to temperature change, which seems eminently reasonable. And although R'(T0) may be assumed to be constant for small perturbations from today’s temperatures, it would certainly have to be replaced if one wanted to initialise a model with a very different absolute temperature or if a very large temperature range was to be modelled.
The AOGCMs, on the other hand, work strictly on absolute temperature field which is updated like all state variables at the end of every time-step. So both EBMs and AOGCMs do recognise absolute temperatures for estimation of feedbacks. It is certainly true that they do not recognise your “reference temperature” approach, but on the basis of the above, I can still not see any good reason or justification for trying to partition an equilibrium temperature as you wish to do, since the reference temperature you seek is at best a mathematical construct and not a driver of feedback in a physical sense. And if such good reason exists, it still seems to me to be an impossible task to do unambiguously, given that you have to “make a planet’s climatology” by assumption.
Lastly, the fact that AOGCMs run hot, over-estimate climate sensitivity and still exhibit a very wide range of sensitivites says that they are not useful as predictors but does not per se provide any evidential support for your methodology. This is a post hoc ergo propter hoc fallacy.
Erratum:-
In my response to Joe Born above, I derived the linear feedback equation typically used in EBMs. However, one of the paragraphs reflects the fact that I forgot my own variable definition in the text, which is never a great idea. Specifically, I frgot briefly that I was using T to denote an absolute temperature rather than a change in temperature.
The original paragraph read:-
“From Eq 4, the transient temperature must head for equilibrium temperature as t -> infinity and N(t) -> 0. As N(t) -> 0, we see that T -> F/ R'(T0)
If we say that for the Planck response alone, R'(T0) = lambda(Planck)
and that for the total feedback, R'(T0) = lambda(Planck) + lambda(other)
then we see that the ratio of equilibrium temperature for all feedbacks to equilibrium temperature for Planck alone is just
Amplification = lambda(Planck) / {lambda(Planck) + lambda(other))”
This should have read:-
“From Eq 4, the transient temperature must head for equilibrium temperature as t -> infinity and N(t) -> 0. As N(t) -> 0, we see that T-T0 -> F/ R'(T0)
If we say that for the Planck response alone, R'(T0) = lambda(Planck)
and that for the total feedback, R'(T0) = lambda(Planck) + lambda(other)
then we see that the ratio of temperature change to equilibrium temperature for all feedbacks divided by temperature change to equilibrium temperature for Planck alone is just
Amplification = lambda(Planck) / {lambda(Planck) + lambda(other))”
In all subsequent discussion, including the comparison with Roe 2009, the maths is correct and compatible with this textual correction.
Mea culpa. (It is amusingly strange how much Latin appears in responses to Lord Monckton.)
In response to Kribaez, I do not disagree with him that one may represent the Planck “feedback” as a true feedback. However, as Roe (2009) points out, it is more useful to treat it as part of the reference system, for then it can be used to derive both reference sensitivities and feedback responses. Nothing injurious to our result turns on this point.
Dear Lord Monckton,
it grieves me to see your valuable time wasted with those climate sensitivity assessments…..
This sensitivity value is an entire hoax value, please check the authors Gerhard Gerlich and Gerhard Kramm (today in Fairbanks).
Today a Willis article is out, setting the sensitivity to only 0.38 C for CO2 doubling, please check this article.
….. Let me explain the following: All those atmospheric sensitivity “calculations” contain the major error that they neglect/negate/omit/ignore decadal and centennial Earth orbit variations or orbital perturbations.
[This has nothing to do with Milankovitch ,which is multi-millenial stuff (19-100 thou. years).]
The warming since 1850, in fact, since the 17. century, is clearly due to variations in the Earth orbit, which were clearly and unrefutably calculated.
Those orbital perturbations must be, and therefore are ignored on purpose, by all those atmospherical “experts”, because their entire calculations DEPEND on that all warming BELONGS to atmospherical/tropospherical “variables” and that orbital variables are kept constant by the method of ignoring them.
If you do not get into the orbital perturbations theme, you will not be able to resolve global warming and make an accurate forecast.
If you are able to understand/computer translate German, the perturbation literature is:
Joachim Seifert: Das Ende der globalen Erwärmung, Berechnung des Klimawandels” (2010)
….otherwise see http://www.knowledgeminer.eu/climate-papers.html and in this case “Climate pattern Recognition,Part 8, 1600 – 2050 and part 1 to understand the orbital perturbation cycle development.
JS.
Mr Seifert may not have noticed that the approach we are taking is to accept ad argumentum all of official climatology except what we can formally demonstrate to be false. When I say “demonstrate” I mean “prove formally by logic and beyond doubt”.
Therefore, solely for the sake of argument, we accept – and in the head posting we explicitly state that we accept – that the reference sensitivity to doubled CO2 (i.e., the sensitivity before accounting for any temperature feedback) is 1.05 K. We think it possible that reference sensitivity is less than 1.05 K, but we cannot prove it and nor, with the best will in the world, can Mr Eschenbach or anyone else, given the present state of climate science.
So we go with the official value because we cannot disprove it and do not propose to waste anyone’s time trying. Instead, we are able to demonstrate that official climatology, but not realizing that the feedback processes that existed in the climate in 1850 must have responded not only to the 10 K reference warming from greenhouse gases but also to the 255 K pre-existing emission temperature caused by the fact that the Sun is shining, has denied itself the opportunity to obtain quite a reliable and well-constrained value of equilibrium sensitivity to doubled CO2.
The point is that we can prove what we assert, and we can confirm it not only by experimentation on a co-author’s test apparatus but also on the test apparatus constructed for us by a scientist at a government laboratory (who was promoted shortly thereafter, thanks to the quality of his work).
We have also confirmed our result by performing calculations based on ten distinct, authoritative, published estimates of net anthropogenic radiative forcing over various periods.
The kind of monkeying about that we have endured at the hands of reviewers to date is not acceptable and will no longer be tolerated. We are going to get our work properly reviewed. if the reviews find genuine defects, then that will be that. At least we tried. But if not, make no mistake about it – this is the end of the global warming scare. Climatology’s error is a large one. And millions are dying every year in consequence. The deaths have to stop, so we have to get the science right, notwithstanding the attempts of numerous vested interests to stop us.
Dear Lord Monckton,
thank you for your kind reply! I appreciate your work, your fight for truth in science, actions in many parts of the world – I read all articles of yours, as soon as they come up at Anthonys. You are one of the major good players in climate science.
However, the fact still remains that the Profs. Gerhard Gerlich and Gerhard Kramm entirely rebutted the climate sensitivity concept (just google), a scientific swindle, revealed in their detailed physical calculations.
The other fact is that the climate sensitivity concept ignores all Earth orbital perturbations, which in reality cause climate warming and climate cooling, due to their varying of distances between Sun and Earth.
Remaining within the atmosphere with whatever atmospherical concept and sensitivities, excludes the
true Earth orbital climate drivers, variables, that govern the climate on Earth.
In response to Mr Seifert, official climatology has not accepted that Gerlich and Tscheuschner, or Gerlich and Dlugi, have proven that there is no such thing as climate sensitivity. And our approach is to focus the discussion on the topic of the head posting, which is feedback, and, therefore, to accept all of official climatology except what we can demonstrate to be false.
We can demonstrate that official climatology’s definition of feedback is erroneous. That, and that alone, is the focus of the head posting. If, per impossibile, there were no greenhouse effect, then our conclusion that global warming will be small, slow, harmless and net-beneficial is demonstrated a fortiori.
This is the literaturee,please take a look:
r. rer. nat. Gerhard Kramm
Research Associate Professor of Meteorology (ret.)
Fairbanks, Alaska, USA
URL: http://engineeringmeteorologyconsulting.com/
New:
Mölders, N., Kramm, G., 2018: Climatology of Air Quality in Arctic Cities—Inventory and Assessment. Open Journal of Air Pollution, 7, 48-93 (http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=82999).
Kramm, G., Dlugi, R., Mölders, N., 2017: Using Earth’s Moon as a testbed for quantifying the effect of the terrestrial atmosphere. Natural Science, 9, 251-288 (http://www.scirp.org/Journal/PaperDownload.aspx?paperID=78836).
Textbook:
Mölders, N., Kramm, G., 2014: Lectures in Meteorology. Springer Ingternational, (https://www.springer.com/us/book/9783319021430
I repeat that the focus of the head posting is not on arguing whether or not there is a greenhouse effect, but on discussing the feedback response to radiative forcings. Discussion of whether there is a greenhouse effect is off topic.
As a layman with limited math ability, would the following analogy be correct?
Water from various sources is combined and then fed into a heater and the output water is hotter Than the input temperature. If we then feed some of the output back to the input, it would have a heating action on the entirety of the input water temperature.
If we change the temperature of one of the input water sources, the feedback can still only effect the combined water temperature. If by some magical process, the feedback only effected the comment of water that changed temperature, It would soon mix in with the rest of the water.
Not sure if this is relevant, but in the above analogy, the amount of feedback can be regulated with a valve in the feedback line and so the feedback can be made variable.
Is the above anology correct?
Peter’s analogy is almost correct. What we are saying is that if water from various sources is combined, the warmth of all of that water, and not just of some small, arbitrarily-chosen fraction thereof, is what is fed to the feedback loop. The magnitude of the feedback response, therefore, is determined not merely by the small fraction but by the entire body of water.
>>
” … But we don’t know and cannot by any rational means determine how big the feedback response is by counting up the individual feedbacks, as climatology currently tries to do, because it is feedbacks that are the near-exclusive cause of the uncertainty in official climatology’s global-warming predictions. …”
>>
>>
” … Why do we know this? Because the industrial-era anthropogenic reference sensitivity of just 0.75 K from 1850 to 2011 was so very small compared with the 265 K reference temperature already present in 1850. The climate has simply not changed enough to engender a major shift in the feedback regime that obtained in that year. Even if such a major shift were to have occurred, the additional feedbacks would have responded not merely to our perturbation of emission temperature but to the entire reference temperature, including emission temperature. For one thing, the Great Pause of almost 19 years in global temperature up to 2015 could not possibly have occurred. … ”
>>
>>
” … Compare that with the 3.2 K interval of official Charney sensitivities, which range from 1.5 to 4.7 K. …”,
>>
* Hence why the models run hotter than reality (and also do not account for a ‘hiatus’ occurring … ‘forcing’ apparently lacks the vital ingredient of a force vector).
>>
” … We knew it because we were able to derive it from the data that official climatology throws away because it does not know feedbacks respond to the entire reference temperature and not only to arbitrarily-chosen reference sensitivities. …”
>>
* In which case, how does a real-world hiatus even occur? The models don’t do hiatus, but the real world does. So even the prevailing feedbacks that should have occurred didn’t respond as “expected” in the real world.
So how the heck can current models and “expected” future climate evolution behavior be useful for generating conclusions for policy implementations and with massive global economic and social implications?
I don’t see anything ‘settled’ here, and it isn’t science either, as reality is the test of that, and the models consistently fail that test, yet we’re supposed to intellectually genuflect to this assertion that this is ‘scientific’, let alone that it’s a ‘settled science’?
Elaborate garbage in still equates to detailed useless garbage coming out.
What we are left with, at present, is another cyclic multi-decadal warming in recent decades, just like numerous other temporary warmings before it, and the absence of any anthropogenic differentiation of this multi-decadal warming from all of the other prior warmings, coolings and past approximations to a ‘hiatus’ condition interval, between such cyclic trend oscillations.
Hence no detectable climate-change signal or even irregularity is present today (especially once you discount the corrupt endless adjustments and interpolation practices of systematic data corruption by ideologically undermined an apparently anti-scientific weather agencies).
Same-Same.
In other words, ” … Remarkably, no need even to take feedback into account in the calculation: the undershoot in Charney sensitivity that arises by ignoring feedback altogether is little more than a tenth of a Kelvin. …”.
Time for a pitifully childish humanity to get over its imaginary scary-monster under the collective united nations bed.
And time for this writhing Medusa of what now passes for some sort of variety of ‘Climatology’, to have its head cut off before it can do more harm .
And thank you Lord Monckton for coming back with such a damning reply to this prevailing ‘climate-sciencey-ness’ complacency, that’s so evident in the obvious need to constantly fudge the sensitivity, but to still get it completely out of whack with observed reality, even then.
The ardent stubborn ‘belief’ is thus demonstrably a discontinuity in a ‘sensitivity’ that’s not actually physically present.
That’s not science, it’s ignorance claiming ‘victory’, via style over substance, to make a nothing look like it’s something.
As we say here, “Pull the other leg”, which was once something one did to make the person swimming around in front of you to image a shark may have bit their foot. When they don’t buy it, it is time to pull on the other leg even harder. And it seems we’ve all had our legs repeatedly over-extended by this ridiculous style-over-substance routine of the UN IPCC jiggery-pokery machine and the mass-media’s fish-‘n-chip wrapper production over-capacity.
Well said but the bewildering irony with the jiggery-pokery machine is it’s the surplus value of fossil fuels that has fostered and fed the monstrous style over substance edifice and yet they want to chop off the very hand that feeds it. That will be their undoing as the feedback effects are swift acting and obvious. Democratic majority trumps elite consensus any day.
I am grateful to WXCycles and to Observa for their kind comments. We shall persist in our research until either we are published or we are given proper scientific reviews, by reviewers who have actually read our paper and are willing to review it and can demonstrate in their reviews that we are incorrect. That is how science is supposed to work. Is it really unreasonable for us to ask for that?
If, for instance, there is a fundamental and obvious error in our work, a competent reviewer expert in the field will be able to demonstrate the error in a few lines, and to the entire satisfaction of my expert colleagues. If not, then that is the end of the global warming scare.
“It is wrong to include variables from the original state equation. One reason is that the have been accounted for already in the balance of the state before perturbation.”
I can’t follow the math from either side. Take a balance sheet. That’s 1850. An income statement from that point on, makes no reference to that balance sheet. (This is a simplification.) You need to track inputs and outputs to get an income statement. You don’t say, we lost money, but look at the beginning balance sheet from 1850. That’s a distraction. We aren’t interested in the beginning or ending balance sheets as much as we are the income statement. The income statements drive the various balance sheets from different dates. Not the other way around. (This is a simplification.)
Balance sheets are still important. If you have a lot of money, you can lose money for a long time. The thermal mass of all the oceans are like a huge amount of cash on a balance sheet. Which means you can add a lot of CO2 before those change a lot. So, we should give the correct amount of weight to each thing. The balance sheets and the income statements.
Yes, that is a reasonable analogy. If you think of total growth of wealth, you might include capital appreciation. Value of asset after, compared with before. All these go into a rate of change (income) statement.
But you would put in the difference of asset values. What Lord M is doing, in effect, is adding total asset values in as income.
No Lord M is saying the interest rate return applies to the total retained capital, the base plus retaining earnings.
No, Lord M. is saying that the annual interest return on investment applies to the total capital, which is the base capital plus retained earnings. That is after all how an investment yielding 10% annually doubles in 7 years not 10.
So where is the interest rate in his calc?
See Willis post about measuring temperature against total surface flux absorbed. He ended up with a increase of 0.38C for a 3.7 W/m^2 because of CO2 doubling. Because clouds are 85% of the DWIR , this is the reason why the 0.38C is so low. The CO2 ppm in 1850 was 285ppm . That means at present day of 413ppm there is a difference of 128ppm which represents only a 45 % increase.
Therefore we have with the 5.35 Ln 2((CO2b-CO2a)/CO2a)) formula we obtain 1.66 W/m^2 . Now because of Holders inequality we cannot simply plug this into the Stefan_Boltzmann equation . Even if we did the increase in temperature would be no different from 1K. We are a long way from doubling CO2.
Let us take the old 1974 produced NCAR graph of temperature for 1870 (I strongly suspect that the NASA graph has been doctored twice, once in 2000 and again 18 years later). The NCAR graph shows 1870 as 0.2 warmer than 1882. However that was northern hemisphere only.
In any case for 1970 it shows 0.12 warm anomaly whereas the NASA graph shows 0. Because UAH shows 0.4 for 2019 that would mean only a difference of 0.28 from NCAR in 1970 to UAH today. Going backward on the NCAR graph to the start of 1870 we get 0.2 as per the above , so comparing that to UAH we get only a 0.2 C increase in 150 years. Since we have had only a 128ppm increase since 1850, that would explain the small increase of 0.4 from 1882 to now or the even smaller increase of 0.2C from 1870 to now. Since the LIA ended in 1850 I suspect that from 1850 to 1870 it was all warming , so let us say that 1850 temperature was probably close to the 1882 temperature which represents a total of 0.4C increase for 170 years. That is more in line with the 128 ppm increase since that time, if CO2 is the cause of warming (which I doubt anyway). So the 0.8C which the IPCC comes up with is double the increase in temperature which is all based on a faulty NASA temperature graph. The NCAR graph that was produced in 1974 had no agenda and can be believed. https://twitter.com/ATomalty/status/1136879230074130432
I got stuck on your first calculation. Why use a difference in the numerator?
If the doubled-CO2 forcing increase is given by and the pre-industrial and current CO2 concentrations are given by
and the pre-industrial and current CO2 concentrations are given by 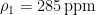 and
and  , I would have thought the current forcing would be given by
, I would have thought the current forcing would be given by 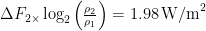 . Note that this formula yields
. Note that this formula yields  , as expected, for doubled CO2, i.e., for
, as expected, for doubled CO2, i.e., for  .
.
Still, I’m not sure it makes much difference—except to a reader trying to follow the math.
Hi Joel,
As a person that struggles with math. I am trying to follow the math. Even when most of it goes over may head. I still push the understanding peanut ahead, a bit at least. If we’re not following the math? Using it to make a prediction. What are we doing?
Though I find Monckton’s presentation Byzantine and confused, I think his manuscript should get published or at least refused with well documented and objective reasons. Not “because I don’t like what it implies” rejection.
That way it can be refuted thoroughly and officially if there is anything wrong with it.
That is the way peer review and scientific discussion is supposed to work.
I strongly suspect those reviewers who have rejected it so far were not able to follow it either and rejected out of ignorance they did not want to admit.
I agree with your general view, but you may be optimistic about the “refuted thoroughly” part. His writing is so impressionistic and his terminology so idiosyncratic that he can respond to any interpretation the critic gives by contending that he actually meant something else.
Moreover, reviewer quality is an issue. I was appalled at how superficial the Richardson et al. rebuttal to his “irreducibly simple model” paper was; it missed the fundamental linear-systems error in the paper’s central equation, namely, that it purported to calculate a system’s response as the product of its stimulus and its step response. Similarly, Judith Curry hosted a Rud Istvan piece that pronounced the math “impeccable.” Yet simply applying Lord Moncton’s “simple model” to the historical numbers in the IPCCs Representative Concentration Pathways would have demonstrated how erroneous it is.
This is basic, fundamental stuff that every undergraduate electrical-engineering major should have mastered by the time he graduated, but even among the commenters here who profess to be EEs there are many who seem unable to grasp such concepts.
In response to Greg, unfortunately most people find control theory Byzantine and confused. If we argue it with equations, people say there are too many equations. If we simplify the equations, people say there are too few equations. If we use practically no equations at all and explain the main points in the simplest English, as in the current head posting, those who genuinely want to understand us will say – as many kindly have – that the exposition is clear. But there will always be those who simply lack the necessary background expertise to comprehend the point being made, and there are those who very much want us to fail, for various reasons, especially if we are right.
Mr Born is, regrettably, in the last category. He continues, with increasing desperation, to fire off a scatter-gun farrago of nonsense dressed up as though it meant something, and professes to substitute his zero qualifications and expertise in control theory for that of our tenured professor int he subject. He attempts to provide detailed criticism of a paper he has not even read, and refuses even to look up references demonstrating that what he says is nonsense, on the aprioristic ground that because I have cited the references I must have misunderstood them.
I agree with Greg that our paper should now be subjected to proper peer review, rather than the pathetic and flagrantly dishonest pantomime to which it has been subjected so far. I have some reason to hope that we shall now get a proper review. If not, the police will be watching.
In response to Greg, unfortunately most people find control theory Byzantine and confused. If we argue it with equations, people say there are too many equations. If we simplify the equations, people say there are too few equations.
I reckon two versions should be prepared: one formal and exact (as I’m sure in your submitted paper) and second ‘for dummies’, in order to facilitate dissemination of this precious knowledge. So at least folks with different technical backgrounds may access and evaluate those finding by themselves.
In response to Paramenter, the formal version of our paper has indeed been submitted, and we have received the usual automated acknowledgement. A simpler account is in the head posting.
Milord,
In response to Paramenter, the formal version of our paper has indeed been submitted, and we have received the usual automated acknowledgement.
Good stuff! All the best in this errand. Hopefully soon we will hear glorious and victorious announcement that the paper has been published. I’m sure it will draw lots of attention.
In response to Paramenter, I don’t suppose it will be as easy as all that. Official climatology simply does not realize that the feedback processes present at any moment must respond not merely to some small and arbitrarily-defined fraction of the reference signal but to the entire signal, which of course includes the 255 K emission temperature as well as the 10 K reference sensitivity to the preindustrial noncondensing greenhouse gases present in the atmosphere in 1850. Reviewers tend to be shocked by this suggestion, so we have had to provide a lengthy and tedious formal demonstration of the obvious. But, like one or two here, even with formal and unassailable proof – for the theory of feedback was established almost a century ago, and we couldn’t have gotten to the Moon without getting it right – the reviewers and editors can be expected to wriggle like stuck pigs, and duck and dive and dodge and weave. In the end, though, the truth will out.
This whole exposition seems hopelessly muddled. What Monckton calls “reference sensitivity to doubled CO2” is literally the result of feedback – the outgoing radiation of the surface is intercepted by GHGs and “fed back'” to the Earth. This is textbook feedback, but Monckton’s analysis doesn’t treat it as such; he somehow interprets this physical feedback process as an open-loop gain, i.e. gain without feedback. Ironically, the “feedback” equations given in the post are what mathematically should result in his assumed 1.05K base sensitivity. Adding more GHGs just increases the value of the feedback fraction by intercepting more radiation that would otherwise escape to space and re-radiating it downward towards the surface.
What “Monckton calls “feedback” (and I don’t blame him for this since this is what climate scientists inappropriately call it) is just a loose analogy to feedback, but not true feedback. It is not properly modeled by the equations and drawings he gives. For example, Monckton states that “whatever feedback processes are present in the climate at any given moment must necessarily respond not merely to changes in the pre-existing temperature: they must respond to the entire reference temperature obtaining at that moment.” The first problem with this statement is that what Monckton considers “feedback” is not “present in the climate at any given moment.” Consider, for example, the hypothesis that methane released from permafrost present in certain locations of the world will act as a feedback mechanism. Obviously, this feedback is only triggered once those particular locations have risen to the temperature where they start thawing; in the distant past, if temperatures were much cooler, incremental warming would not trigger this proposed feedback. Hence, it is not “present at any given moment.”
The second problem is that physically, temperature cannot act as a feedback; it’s radiation that is emitted, and is therefore what has to fed back to become an input. Temperature is just a state variable, it can’t be moved around and “fed back.” What climate scientists call “feedback” does not reroute a portion of an output and turn it into an input; it’s always some other natural process with hypothesized intermediate steps, like receiving radiation as an input, which warms snow and ice, which melts, which causes more radiation to be absorbed, and so forth. But ice melting to increase the Earth’s albedo is not a feedback process because no output (outgoing radiation) is being directly rerouted to become an input (more radiation). It’s the input that drives this entire process, not the output. The equations Monckton cites therefore do not mathematically describe the way that this physical process (ice melting) operates.
A principal problem in many of these expositions, including your comment here, and indeed my comment here, is using English where mathematics is needed. One needs unambiguously defined variables with values. To be fair, Lord Monckton does sometimes do that.
Your first paragraph points out the need to elucidate “feedback”. Radiative back scattering from CO2 is generally not thought of as a feedback, but a principal forcing from CO2. “Feedback” is usually taken to refer to the various effects of consequent changes to H2O: if absolute humidity increases then water vapour GHG effect increases, and if ice melts then the albedo decreases, leading to Earth absorbing more warming rays of the Sun.
I agree with your comment that temperature cannot feed back on itself. Bear in mind though, that LM only assumes that because mainstream climate claptrap does, and he wants to prove them wrong at their own game. I mentioned in a comment below that I have a model of T = f(F), F=g(T), where T is absolute temperature, F is radiative forcing, and f and g are functions. f() is a standard function, and g() includes all the normal forcings plus H2O feedbacks. I can do quite neat things with these equations, and get a wide range of sensitivities (S) to doubled CO2, dependent on the gradient g'(T). A 2004 paper on the annual variation of g allows me to extrapolate to get S = 2.1K (higher than Monckton, lower than IPCC). The validity of the extrapolation is the greatest concern.
I can locally (in the mathematical sense) turn these into a linear feedback, but that is pretty irrelevant.
“I agree with your comment that temperature cannot feed back on itself. Bear in mind though, that LM only assumes that because mainstream climate claptrap does,”
Eh!
No “mainstrean” science doesn’t assume anything of the sort!
In fact it beyond illogical to think that an equilibrium (ref temp) can have a feedback.
Quite obviously it cannot, else the climate would be forever under a forcing that would be acting to move it away from that equilibrium.
A deltaT caused by a deltaF is what creates feedback.
The classics educated/journalist snake-oil seller’s torchured writing and specious replies have sold many bottles of the said oil to gullible people.
Look up Potholer54 (Peter Hadfield) videos, or his failure to answer his rebuttals of the efficacy of the snake-oil he markets on this very website.
Mr Banton, having been outed, now at last publishes here under his own name rather than under a furtive pseudonym. But he is as poisonously intemperate as ever. He resorts to the usual climate-Communist device of not dealing with the subject at hand but instead referring readers to another climate Communist’s ill-informed and profoundly prejudiced comments on matters entirely separate from the current discussion. That is the argumentum ad hominem, which has no place in true science but is widely adopted on the climate-Communist hard Left.
He appears unaware that official climatology denominates feedback in Watts per square meter of the reference temperature (or sensitivity) that engendered it. The hint is in the name “temperature feedback”.
It’s absolutely true that Moncton’s analysis simply follows the nomenclature that climate scientists use. But my point is that, regardless of the terminology used, the mathematical calculations he uses don’t match the physical behavior of the system. Even though radiative capture and emission from CO2 is called forcing instead of feedback, in reality it acts as textbook feedback, and if you’re going to model it you have to treat it as it is – as feedback. Similarly, the things climate scientists call “feedback” cannot be accurately modeled by the equations Monckton uses because these processes do not involve directly feeding an output back to add to the input. Climate scientists just call them “feedback” because they believe that they are mechanisms other than CO2 by which some warming begets more warming and so forth.
Kurt’s insistence that direct forcings from changes in the concentration of greenhouse gases is at odds with official climatology, and he should take the matter up with the IPCC and not with me. The focus of the present paper is not on the direct forcings but upon official climatology’s overstatement of the consequential forcings that are known as feedbacks.
In reply to Kurt, our concept is by no means muddled. Understanding it, though, does require some knowledge of elementary methods in climatology. If one adds greenhouse gases to the atmosphere, one inhibits outgoing radiation and turns on the gas molecules so that they oscillate at the quantum level in their respective vibrational modes (with CO2 it is the bending mode), and that oscillation is, by definition, heat. This, therefore, is treated (and appropriately treated) by climatology as a forcing.
Then various changes occur as a result of the fact that the space occupied by the atmosphere has become warmer in consequence of the forcing. These changes are appropriately treated as temperature feedbacks – in other words, they are denominated in Watts per square meter per Kelvin of reference temperature (if one does things our way) or of reference sensitivity (if one does things climatology’s way). It is a true feedback, for the mathematics of feedback is applicable mutatis mutandis to any dynamical system moderated by feedback. The climate is one such system.
Kurt is perhaps not aware that the principal sensitivity-altering feedbacks, the ones that IPCC and the CMIP5 models use as the basis for converting reference sensitivity (sensitivity before accounting for feedback) to equilibrium sensitivity (sensitivity after allowing for feedback) are all short-acting – on timescales typically of hours, days, weeks or months – years at most. The only feedback that actually matters (because, broadly speaking, all others self-cancel) is the water vapor feedback. That feedback operates on a timescale of hours to days. So time-delay is not, after all, an issue as far as the feedbacks are concerned.
However, one must cautiously allow for the fact that not all of the warming we engender will come through as sensible heat in the atmosphere, owing to the time-delay caused by the very large heat capacity of the oceans. We allow appropriately for this time-delay by taking account of the estimated radiative imbalance that was thought to subsist in 2010 (Smith+ 2015), as explained in the head posting.
Contrary to what Kurt imagines, temperature can and does act as a feedback, which is precisely why feedbacks are denominated in Watts per square meter per Kelvin of the directly-forced reference temperature (or sensitivity) that engendered them. Feedbacks are, in effect, additional forcings whose magnitude is proportional to the reference temperature (or sensitivity).
Again contrary to what Kurt imagines, the surface albedo feedback is indeed a feedback in official climatology’s understanding. If he wishes to argue against its being a feedback, his quarrel is not with me but with the IPCC. We don’t mind either way, because IPCC considers that, at midrange estimates, all feedbacks other than that of water vapor self-cancel, so the point is moot.
I certainly do not fault you for adopting climatology’s “feedback” terminology. In this respect, you pretty much have to take what you are given. But I made two main points in my post above, only one of which you seem to be responding to. Your mathematical analysis uses textbook engineering feedback expressions to try to model the Earth’s response to GHG emissions. But these models and equations physically represent only the process that occurs when GHGs intercept outgoing radiation and send half of what is intercepted back to the surface. Rather than mathematically treating this process as “feedback” (which it is) your exposition treats it as the “gain” of the climate system absent feedback. Granted, climate scientists do not refer to this process as “feedback” but this is irrelevant to my point, which is that your mathematics does not match the physical process you are modeling.
The flip side of this same error is that you are using textbook feedback analysis to describe processes that in the real world don’t act the way your math describes. This has nothing to do with a time lag; even if the process were instantaneous, for example, melting ice to increase albedo is not a feedback process – it physically operates entirely as a result of the input radiation. Climate scientists call this “feedback” as a loose analogy, but that does not mean that it is appropriate to mathematically express it using the equations you do.
As far as temperature ostensibly being feedback, temperature is a state variable that characterizes the heat content and thermal capacity of a specific material. Temperature can’t be moved around or “fed back.” A temperature determines the amount an object radiates and that radiation can be fed back towards the object, but I don’t see how the mathematical expressions you use are going to be applicable with temperatures as an input signal and as a feedback signal.
In response to Kurt, my original reply had in fact described, in some detail, the reasons why official climatology treats the forcings from changes in greenhouse-gas concentrations as forcings and the consequential forcings that arise from the temperature change engendered by the original forcings as feedbacks.
if Kurt wishes to argue the toss on these definitions, his argument lies not with me but with the IPCC secretariat as the mouthpiece of official climatology. Our approach is to accept all of official climatology except what we can demonstrate to be false. Kurt’s attempt to define radiative forcings from changes in greenhouse-gas concentrations is idiosyncratic and inconsistent with official climatology: therefore, it is a distraction from the focus of our paper, which is exclusively on that fraction of predicted global warming that is contributed by what official climatology defines as feedback.
Although I have studied and criticized this linear feedback stuff for the sake of argument, a year ago I derived a model wherein feeback is a function of temperature which is a function of forcing (which includes feedback). This is very incestuous, i.e. one gets an implicit equation rather than an explicit one. Nevertheless it can be solved numerically and sensitivity derived algebraically. The bottom line is that sensitivity depends on the gradient of H2O feedback relative to CO2 forcing.
But I’ll need to get it published to get any traction, I suppose!
Rich.
To paraphrase Feynman, if the theory disagrees with the data, the theory is wrong.
….. no problem, they’ll adjust the data to fit the theory.
The Sun started out only 70% as luminous as it is now 4.6 billion years ago. Despite that, there have been liquid oceans and life on Earth for about 4 billion years. There may be positive feedback over short temperature ranges, but in the LONG run, feedbacks are consistently large and negative. Else the oceans and life wouldn’t have lasted for 4 billion years.
The Sun started out only 70% as luminous as it is now 4.6 billion years ago. Despite that fact, there have been liquid oceans and life on Earth for 4 billion years.
There may be positive or zero feedback over short timescales and temperature ranges, but in the LONG run, feedback must be both large and negative to maintain those oceans and life over long periods. I suspect that most of the feedback comes from water in all of its phases.
In response to Mr McIntyre, in IPCC’s understanding all feedbacks other than that of water vapor self-cancel, so he is right that most of the feedback comes from water vapor. But that feedback is not reliably quantifiable by observation: nor can it be derived by any theoretical method. It is really guesswork. That is why we took an approach that did not require knowledge of the magnitude of any individual feedback.
I am reminded of a Gary Larson cartoon where scientists in white lab coats stand in front of a chalkboard full of equations while engaged in a heated debate over a mathematical model of the elephant.
Anyway, back in 2010, I asked Dr. Dimitri Koutsoyiannis (‘A Random Walk on Water’) if it might be possible to directly observe and characterize the postulated water vapor feedback mechanism in real time while it is operating in the earth’s atmosphere, using instrumentation systems and data collection systems designed specifically for that purpose.
Paraphrasing Dr. Koutsoyiannis’ response, this is what he said:
Owing to the magnitude of the problem, it is not possible at the current state of science to do these kinds of direct, real-time observations. Proof of the existence of the postulated feedback mechanism can only be gathered inferentially through a complicated process of examining and analyzing other lines of evidence.
My question is this:
If we can’t observe the feedback mechanism directly — assuming it actually exists — then what specifically are those other lines of evidence needed to inferentially characterize and quantify the postulated mechanism? What would a comprehensive list of these other lines of evidence look like?
Moreover, how should these other lines of evidence, whatever the comprehensive list contains, be assembled and organized so that a knowledge base is available for reference and citation by each opposing side of the debate?
A caveat to my question:
Be careful what you ask for. If they choose to do so, whoever controls the knowledge base can also control the progress and outcome of the debate through selective choice of the information and the data the knowledge base contains. In other words, let the buyer beware.
In response to Beta Blocker, our method requires no knowledge of the magnitude of any individual feedback. The system-gain factor is at or very close to the available equilibrium and reference temperatures in 1850: i.e., 287.5 / 265, or 1.085. That system-gain factor embodies the entire influence of feedback on reference temperature.
There is no reliable method of deriving the value of any temperature feedback by measurement. The uncertainties are too great.
Lord Monckton, so far you have not replied to Anthony Banton’s comment on my own. I hope you will, because I think you are better placed to set the picture straight than I am.
CO2rich should refer to my comment in response to the characteristically discourteous contribution from the dreadful Mr Banton, who, as usual, brings more heat than light, more prejudice than knowledge, more fiction than fact to the discussion.