Guest Post by Willis Eschenbach [note new Update at the end, and new Figs. 4-6]
In climate science, linearity is the order of the day. The global climate models are all based around the idea that in the long run, when we calculate the global temperature everything else averages out, and we’re left with the claim that the change in temperature is equal to the climate sensitivity times the change in forcing. Mathematically, this is:
∆T = lambda ∆F
where T is global average surface temperature, F is the net top-of-atmosphere (TOA) forcing (radiation imbalance), and lambda is called the “climate sensitivity”.
In other words, the idea is that the change in temperature is a linear function of the change in TOA forcing. I doubt it greatly myself, I don’t think the world is that simple, but assuming linearity makes the calculations so simple that people can’t seem to break away from it.
Now, of course people know it’s not really linear … but when I point that out, often the claim is made that it’s close enough to linear over the range of interest that we can assume linearity with little error.
So to see if the relationships really are linear, I thought I’d use the CERES satellite data to compare the surface temperature T and the TOA forcing F. Figure 1 shows that graph:
 Figure 1. Land only, forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude. Note that there is little land from 50S to 65S. Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. Click graphics to enlarge.
Figure 1. Land only, forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude. Note that there is little land from 50S to 65S. Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. Click graphics to enlarge.
As you can see, far from being linear, the relationship between TOA forcing and surface temperature is all over the place. At the lowest temperatures, they are inversely correlated. In the middle there’s a clear trend … but then at the highest temperatures, they decouple from each other, and there is little correlation of any kind.
The situation is somewhat simpler over the ocean, although even there we find large variations:
 Figure 2. Ocean only, net forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude.
Figure 2. Ocean only, net forcing F (TOA radiation imbalance) versus Temperature T, on a 1° x 1° grid. Colors indicate latitude.
While the changes are not as extreme as those on land, the relationship is still far from linear. In particular, note how the top part of the data slopes further and further to the right with increasing forcing. This is a clear indication that as the temperature rises, the climate sensitivity decreases. It takes more and more energy to gain another degree of temperature, and so at the upper right the curve levels off.
At the warmest end, there is a pretty hard limit to the surface temperature of the ocean at just over 30°C. (In passing, I note that there also appears to be a pretty hard limit on the land surface air temperature, at about the same level, around 30°C. Curiously, this land temperature is achieved at annual average TOA radiation imbalances ranging from -50 W/m2 up to 50 W/m2.)
Now, what I’ve shown above are the annual average values. In addition to those, however, we are interested in lambda, the climate sensitivity which those figures don’t show. According to the IPCC, the equilibrium climate sensitivity (ECS) is somewhere in the range of 1.5 to 4.5 °C for each doubling of CO2. Now, there are a several kinds of sensitivities, among them monthly, decadal, and equilibrium climate sensitivities.
Monthly sensitivity
Monthly climate sensitivity is what happens when the TOA forcing imbalance in a given 1°x1° gridcell goes from say plus fifty W/m2 one month (adding energy), to minus fifty W/m2 the next month (losing energy). Of course this causes a corresponding difference in the temperature of the two months. The monthly climate sensitivity is how much the temperature changes for a given change in the TOA forcing.
But the land and the oceans can’t change temperature immediately. There is a lag in the process. So monthly climate sensitivity is the smallest of the three, because the temperatures haven’t had time to change. Figure 3 shows the monthly climate sensitivities based on the CERES monthly data.
 Figure 3. The monthly climate sensitivity.
Figure 3. The monthly climate sensitivity.
As you might expect, the ocean temperatures change less from a given change in forcing than do the land temperatures. This is because of the ocean’s greater thermal mass which is in play at all timescales, along with the higher specific heat of water versus soil, as well as the greater evaporation over the ocean.
Decadal Sensitivity
Decadal sensitivity, also called transient climate response (TCR), is the response we see on the scale of decades. Of course, it is larger than the monthly sensitivity. If the system could respond instantaneously to forcing changes, the decadal sensitivity would be the same as the monthly sensitivity. But because of the lag, the monthly sensitivity is smaller. Since the larger the lag, the smaller the temperature change, we can use the amount of the lag to calculate the TCR from the monthly climate response. The lag over the land averages 0.85 months, and over the ocean it is longer at 2.0 months. For the land, the TCR averages about 1.6 times the monthly climate sensitivity. The ocean adjustment for TCR is larger, of course, since the lag is longer. Ocean TCR is averages about 2.8 times the monthly ocean climate sensitivity. See the Notes below for the calculation method.
Figure 4 shows what happens when we put the lag information together with the monthly climate sensitivity. It shows, for each gridcell, the decadal climate sensitivity, or transient climate response (TCR). It is expressed in degrees C per doubling of CO2 (which is the same as degrees per a forcing increase of 3.7 W/m2). The TCR shown in Figure 4 includes the adjustment for the lag, on a gridcell-by-gridcell basis.
 Figure 4. Transient climate response (TCR). This is calculated by taking the monthly climate sensitivity for each gridcell, and multiplying it by the lag factor calculated for that gridcell. [NOTE: This Figure, and the values derived from it, are now updated from the original post. The effect of the change is to reduce the estimated transient and equilibrium sensitivity. See the Update at the end of the post for details.]
Figure 4. Transient climate response (TCR). This is calculated by taking the monthly climate sensitivity for each gridcell, and multiplying it by the lag factor calculated for that gridcell. [NOTE: This Figure, and the values derived from it, are now updated from the original post. The effect of the change is to reduce the estimated transient and equilibrium sensitivity. See the Update at the end of the post for details.]
Now, there are a variety of interesting things about Figure 3. One is that once the lag is taken into account, some of the difference between the climate sensitivity of the ocean and the land disappears, and some is changed. This is particularly evident in the southern hemisphere, compare Southern Africa or Australia in Figures 3 and 4.
Also, you can see, water once again rules. Once we remove the effect of the lags, the drier areas are clearly defined, and they are the places with the greatest sensitivity to changes in TOA radiative forcing. This makes sense because there is little water to evaporate, so most of the energy goes into heating the system. Wetter tropical areas, on the other hand, respond much more like the ocean, with less sensitivity to a given change in TOA forcing.
Equilibrium Sensitivity
Equilibrium sensitivity (ECS), the longest-term kind of sensitivity, is what would theoretically happen once all of the various heat reservoirs reach their equilibrium temperature. According to the study by Otto using actual observations, for the past 50 years the ECR has stayed steady at about 130% of the TCR. The study by Forster, on the other hand, showed that the 19 climate models studied gave an ECR which ranged from 110% to 240% of the TCR, with an average of 180% … go figure.
This lets us calculate global average sensitivity. If we use the model percentages to estimate the equilibrium climate sensitivity (ECS) from the TCR, that gives an ECS of from 0.14 * 1.1 to 0.14 *2.4. This implies an equilibrium climate sensitivity in the range of 0.2°C to 0.3°C per doubling of CO2, with a most likely value (per the models) of 0.25°C per doubling. If we use the 130% estimate from the Otto study, we get a very similar result, .14 * 1.3 = 0.2°C per doubling. (NOTE: these values are reduced from the original calculations. See the Update at the end of the post for details.]
This is small enough to be lost in the noise of our particularly noisy climate system.
A final comment on linearity. Remember that we started out with the following claim, that the change in temperature is equal to the change in forcing times a constant called the “climate sensitivity”. Mathematically that is
∆T = lambda ∆F
I have long held that this is a totally inadequate representation, in part because I say that lambda itself, the climate sensitivity, is not a constant. Instead, it is a function of T. However, as usual … we cannot assume linearity in any form. Figure 5 shows a scatterplot of the TCR (the decadal climate sensitivity) versus surface temperature.
 Figure 5. Transient climate response versus the average annual temperature, land only. Note that the TCR only rarely goes below zero. The greatest response is in Antarctica (dark red).
Figure 5. Transient climate response versus the average annual temperature, land only. Note that the TCR only rarely goes below zero. The greatest response is in Antarctica (dark red).
Here, we see the decoupling of the temperature and the TCR at the highest temperatures. Note also how few gridcells are warmer than 30°C. As you can see, while there is clearly a drop in the TCR (sensitivity) with increasing temperature, the relationship is far from linear. And looking at the ocean data is even more curious. Figure 6 shows the same relationship as Figure 5. Note the different scales in both the X and Y directions.
 Figure 6. As in Figure 5, except for the ocean instead of the land. Note the scales differ from those of Figure 5.
Figure 6. As in Figure 5, except for the ocean instead of the land. Note the scales differ from those of Figure 5.
Gotta love the climate system, endlessly complex. The ocean shows a totally different pattern than that of the land. First, by and large the transient climate response of the global ocean is less than a tenth of a degree C per doubling of CO2 (global mean = 0.08°C/2xCO2). And contrary to my expectations, below about 20°C, there is very little sign of any drop in the TCR with temperature as we see in the land in Figure 5. And above about 25°C there is a clear and fast dropoff, with a number of areas (including the “Pacific Warm Pool”) showing negative climate responses.
I also see in passing that the 30°C limit on the temperatures observed in the open ocean occurs at the point where the TCR=0 …
What do I conclude from all of this? Well, I’m not sure what it all means. A few things are clear. My first conclusion is that the idea that the temperature is a linear function of the forcing is not supported by the observations. The relationship is far from linear, and cannot be simply approximated.
Next, the estimates of the ECS arising from this observational study range from 0.2°C to 0.5°C per doubling of CO2. This is well below the estimate of the Intergovernmental Panel on Climate Change … but then what do you expect from government work?
Finally, the decoupling of the variables at the warm end of the spectrum of gridcells is a clear sign of the active temperature regulation system at work.
Bottom line? The climate isn’t linear, never was … and succumbing to the fatal lure of assumed linearity has set the field of climate science back by decades.
Anyhow, I’ve been looking at this stuff for too long. I’m gonna post it, my eyeballs are glazing over. My best regards to everyone,
w.
NOTES
LAG CALCULATIONS
I used the Lissajous figures of the interaction between the monthly averages of the TOA forcing and the surface temperature response to determine the lag.
 Figure N1. Formula for calculating the phase angle from the Lissajous figure.
Figure N1. Formula for calculating the phase angle from the Lissajous figure.
This lets me calculate the phase angle between forcing and temperature. I always work in degrees, old habit. I then calculate the multiplier, which is:
Multiplier = 1/exp(phase_angle°/360°/-.159)
The derivation of this formula is given in my post here. [NOTE: per the update at the end, I’m no longer using this formula.]
To investigate the shape of the response of the surface temperature to the TOA forcing imbalance, I use what I call “scribble plots”. I use random colors, and I draw the Lissajous figures for each gridcell along a given line of latitude. For example, here are the scribble plots for the land for every ten degrees from eighty north down to the equator.
Figure N2. Scribble plots for the northern hemisphere, TOA forcing vs surface temperature.
And here are the scribble plots from 20°N to 20°S:
Figure N3. Scribble plots for the tropics, TOA forcing vs surface temperature.
As you can see, the areas near the equator have a much smaller response to a given change in forcing than do the extratropical and polar areas.
DATA AND CODE
Land temperatures from here.
CERES datafile requisition site
CERES datafile (zip, 58 MByte)
sea temperatures from here.
R code is here … you may need eyebeach, it’s not pretty.
All data in one 156 Mb file here, in R format (saved using the R instruction “save()”)
[UPDATE] Part of the beauty of writing for the web is that my errors don’t last long. From the comments, Joe Born identifies a problem:
Joe Born says:
December 19, 2013 at 5:37 am
My last question may have been a little obscure. I guess what I’m really asking is what model you’re using to obtain your multiplier.
Joe, you always ask the best questions. Upon investigation, I see that my previous analysis of the effect of the lags was incorrect.
What I did to check my previous results was what I should have done, to drive a standard lagging incremental formula with a sinusoidal forcing:
R[t] = R[t-1] + (F[t] – F[t-1]) * (1 – timefactor) + (R[t-1] – R[t-2]) * timefactor
where t is time, F is some sinusoidal forcing, R is response, timefactor = e ^ (-1/tau), and tau is the time constant.
Then I measured the actual drop in amplitude and plotted it against the phase angle of the lag. By examination, this was found to be an extremely good fit to
Amplitude as % of original = 1 – e ^ (-.189/phi)
where phi is the phase angle of the lag, from 0 to 1. (The phase angle is the lag divided by the cycle length.)
The spreadsheet showing my calculations is here.
My thanks to Joe for the identification of the error. I’ve replaced the erroneous figures, Figure 4-6. For Figs. 5 and 6 the changes were not very visible. They were a bit more visible in Figure 4, so I’ve retained the original version of Figure 4 below.
NOTE: THE FIGURE BELOW CONTAINS AN ERROR AND IS RETAINED FOR COMPARISON VALUE ONLY!! 
NOTE: THE FIGURE ABOVE CONTAINS AN ERROR AND IS RETAINED FOR COMPARISON VALUE ONLY!!


I suspect that Willis is a lot closer to understanding the climate than a lot of these so called climate scientists are.
Next, the estimates of the ECS arising from this observational study range from 0.2°C to 0.5°C per doubling of CO2.
==========
Wow! Great work. Wondered where you’d been hiding. The color graphics are a fantastic aid to visualizing the complexity. This lower ECS estimate make much more sense and explains the “pause” much better than the climate models.
Another excellent analysis, Willis. We pay gobs of bucks to support super computer number crunching to get results I could get with a slipstick and y=mx+b? Have Decitrig, will compute.
Bottom line? The climate isn’t linear, never was … and succumbing to the fatal lure of assumed linearity has set the field of climate science back by decades.
=============
It has the advantage of allowing a whole generation of climate scientists to tackle really hard science questions armed with nothing more than liberal arts degrees.
Excellent post Willis! Of course anyone who spends a little time thinking about it would realize that trying to model complex systems with a linear model is not going to work. It explains perfectly why they fail so monstrously.
v/r,
David Riser
When I saw
I was reminded that during my Engineering studies, where I learnt (a little) computer programming. That was in the 1970’s when one still had to be “clever” to use computers and get reasonable answers to complicated questions; within a limited time.
Anyways; I’d observed that almost all the “constants” in formulae with which I was dealing, were only “constant” over a short range of conditions.
An example of this is the treatments of Young’s Modulus (E) is a linear approximation of the elasticity of a material over a limited range. For most engineering purposes, a constant is good enough as the design is well within the elastic range in most applications and dimensional variability (the ability to make stuff to the exact dimensions of the design) and material variability tend to, in most cases, swamp any “error” of using the constant for E. Using a constant is also quicker for checking stuff by hand.
But if you need to be really accurate in predicting deflection under stress, or your design approaches plasticity, then you must also consider stress vectors in magnitude, the material’s bulk modulus and other obvious factors such as temperature.
It puzzled a few of my tutors as to why I made E a function of stress in my programming assignments. I had to draw a stress-strain curve to explain. The difference in results is small, and the effort to “completely” define the function is huge.
I was discouraged from doing it the right way after a while because they thought it a waste of time even when my E() function as a place-holder, returned a constant regardless of the value of input parameters. The “waste” of programming time was a minute or two. And the documentation value was immense.
When I looked into some (a lot) of the GCM and other modelling code (mis)used by the catastrophists, It was clear that the models would never be able to produce realistic results as they had fundamentally variable parameters as constants. There was no possibility to introduce coupling and confounding factors. In the systems being modelled, it does matter that that parameter varies “only” a few percent because an iterative finite element analysis will accummulate those errors.
The climate-sensitivity parameter lambda does not take a fixed value either by place or by time. The IPCC takes its value as beginning at 0.31 Kelvin per Watt per square meter, as 0.44 after 100 years, as 0.5 over 200 years, and 0.88 over 3500 years. The curve is similar to the top left quadrant of an ellipse. It is anything but linear.
The key question is whether any value as high as 0.88 for lambda is justifiable. To obtain so high a value, the models assume that temperature feedbacks are so strongly net-positive as to triple the small direct warming from CO2, which is not much more than 1 K per doubling. Suddenly that becomes 3.26 K thanks to imagined net-positive temperature feedbacks. However, the mutual-amplification function that all of the models use is defective in that it is based on an equation from process engineering that has a physical meaning in an electronic circuit but has no physical meaning in the real climate unless one introduces a damping term. But any plausible value for a damping term would divide the IPCC’s central estimate of climate sensitivity by at least 4.
So don’t worry too much about linearity, for lambda is a Humpty-Dumpty variable: it can take any value that is likely to keep the climate scare going.
Willis,
As usual, I understood at least some of it. However, how anyone can claim that almost anything in nature, including its fauna, is linear, is beyond me. From quarks to black matter the universe is a wave. Representing a wave with a linear “anything” is almost willful misrepresentation. Like you said, it is easier to make things linear. What I mostly noticed though was the actual amount of data that disappears when using a linear function. Being a bit of a cynic, could that be the reason?
Do climate models “assume” the linear equation, or is that equation used (ex post facto) to back out a bulk lamda value based on the models derived forcings and its temperature output? My understanding would be that lamda is NOT a fixed parameter, rather something that can be derived and compared afterwords.
I’ve been pondering a “degrees of surface T per W/m^” over ocean by month by latitude as a way to show something similar. That the degrees per W/m^2 are all over the place. I think this may make that unnecessary. Nicely done.
I think you will find that Willis has shown in a previous post that the models can be reduced to a liner approximation as they all have different forcings matched with different lamda that when graphed effectively reduces all their effort to a simple liner equation, hence the starting point of this post.
If Present Trends Continue….. you can predict anything by selecting the measurement period
IIRC Idso got a ECS of 0.4 deg C for doubling of CO2 years ago in his “natural experiments”.
I like the scribble plots. I think they may be a new art form.
Yeah I’ve always had a problem with ‘assumed linearity’. I’m entirely with you on this, assumed linearity is one of the major flaws in current climate research.
One of the best examples I can think of illustrating non-linearity, which I came across in my university days and which has intrigued me ever since, is the way iron behaves in stars. From memory, as a star burns up elements during its lifetime, all the elements prior to iron behave in a more or less linear fashion during nuclear fusion, until the star starts to use up the iron in its mass. Iron just doesn’t want to behave like the others. The linear trend breaks down spectacularly, and causes a supernova, which totally destroys the star (depending on its mass). So much for a linear trend within stellar processes.
Most scientists assume linearity out of a combination of laziness and ignorance about the real world. Non-linearity is much harder to predict because the exact position of inflection points and changes in trend/rates may be unknown, meaning non linear discoveries in science usually come well after assumed linearity. (There is also a political element which I won’t go into here, as a major part of social planning assumes the human benefits of ‘evenness’ over units of space and time, which is the same sort of assumption as ‘linearity’).
In my field of mineral exploration non-linearity underpins much of the research. The distribution of mineral concentration in the earth’s crust is very non-linear, both in terms of spatial extent and in terms of time. Often one simply cannot use linear models to analyse it, yet I find that many academics and public service scientists often assume linearity in the way they conduct their research and make public policy, and this is also partly the reason that mineral exploration is largely left to the private sector; there are simply too many public policy analysts who want to ‘arrange’ the minerals evenly across the landscape, where in most cases this is simply not how they occur in nature. They are unevenly distributed, their position is often unknown or uncertain, and this also creates unevenness in social wealth and ultimately society. And this sort of unevenness in a likewise fashion with other fields, permeates right through to the stockmarket, and ultimately to wealth between individuals, cultures, and nations. Non linearity is built into the economic system, from the foundation of the raw materials that underpin economies, and is also at least partly the sort of reason that central and social planning often fails. It is difficult to tell this to various politicians and ideologues, but it is often the first mistake they make when making major policy decisions.
Bernd Felsche says: “…When I looked into some (a lot) of the GCM and other modelling code (mis)used by the catastrophists, It was clear that the models would never be able to produce realistic results as they had fundamentally variable parameters as constants. There was no possibility to introduce coupling and confounding factors. In the systems being modelled, it does matter that that parameter varies “only” a few percent because an iterative finite element analysis will accumulate those errors.”
I was added to a project back in the 60’s where they were deriving material physical properties at temperatures of about 5,000°F from measurements on very small specimens. Certain materials gave negative thermal conductivities. Something was clearly wrong. It remained a mystery until, over dinner one night, I had an “AHA moment.” The early research team, to save apparatus costs, had assumed linearity over the shortest specimen dimension, so short that any deviation from linearity was assumed similarly “small.” During finite element analysis, however, that erroneous profile smeared itself throughout the relaxation network, inverting the temperature distribution at the very center of those specimens. After running the program, the hot side became the cold side and vice versa.
This shows the Tower of Babel principle: Any computer program whose complexity exceeds the ability of any human to grasp the calculations in their entirety is doomed to mysterious failures, as is any program which has been dumbed down via simple-minded assumptions to match the ability of its creators.
Elegant Willis. Thanks for your work. Your scatter-grams are great. The flattening of some of the color’s curve at 30° is reminiscent of a log curve. But the impact of combinations? of effects are driving things in different directions. For example the cyan, 0-30°N. Latt. in figure 2 has something akin to a refraction pattern in a negative response at 12°-28°C SSTs, but scattered in a positive response with a lower limit at .1°C per W/m^2.
In climate as in the study of many natural systems, nonlinearity = enlightenment.
Those “scribble plots” look like Lorenz attractors.
Willis has nicely demonstrated the essence of nonlinearity which is that as a system e.g. an atmospheric or ocean system evolves or changes it changes the controlling parameters of that system in real time as it does so. Those parameters e.g. lambda are not fixed or linear.
Or as James Gleik put it in his book “Chaos”: “Nonlinearity means that the act of playing the game has a way of changing the rules”.
These graphs seem to indicate on a quick look, that the climate has a thermostat type effect such that far from being linear, there are limits to how hot or how cold the climate system will go.
For instance, on the hot side of things, does heat create more clouds, limiting the increase of heat as the clouds reflect more radiation? I’m not sure what the effect is on the cold side of things. That’s the direction that can get a bit “runaway” in my mind. Get cold, get ice, reflect more radiation, get colder, etc.
We have a history of the cold side running away with things in the Earth’s long history. But we seem to have some hard limits to how hot things can get.
Willis,
Thank you, I have tried and tried to bring out the point many times that treating climate sensitivity as a constant is wrong, wrong, wrong, and that as temperature rises climate sensitivity falls, to a point at which at about 30 degrees C over water it becomes 0. The gain of the system is inversely related to temperature. Taking up Monckton’s point, this is analogous in engineering to an amplifier approaching saturation. At some point increasing the drive or feedback can’t increase the output because the energy available has been exhausted. It has been my contention for some time that climate is being held in such a narrow range by saturation effects, that is Lamda being an inverse function of temperature. If this is the case (and it almost certainly is) then Climate Sensitivity is irrelevant.
It’s important however to consider physical mechanisms though. In the climate the energy isn’t limited by the power source exactly, it’s limited by the instability of evaporating too much water in one place, and the dew point in the atmosphere causing condensation. So as our “Drive” goes up, we reach a threshold – dare I say a tipping point, where there is too much water to be held in solution at a given temperature and it precipitates as clouds. That then causes the Input power from the sun to fall until the gain reaches zero (the system is saturated). This is very Non linear behaviour it rapidly onsets at particular humidity, temperature and air pressures. As average temperature rises, the region near the equator that this happens will expand, reducing the average gain across the planet. Ultimately – Venus earth is more like Miami earth, cosy and warm with Maxes around 30 and mins around 20, just like in the tropics.
WIllis,
The other problem is that lamda is also a Complex Number. The idea that feedbacks in the climate can be treated as a single lumped SCALAR is just naive in the extreme. I wanted to write a paper on that but need to find someone to help with the math. (I’m not sure how to deal with the non linearities). The only solution that allows any sort of positive feedback but is as stable as our climate is one that is approaching saturation and inherently non-linear
On the other hand such high transient sensitivity in the presence of obvious saturation means that in the past ice ages weather should have been very unstable, high gain should have lead to greater instability, but it didn’t. This probably means the gain is nothing like they say either, and that we have saturation occuring AND lower gain.
Totally off topic, but I’ve been told David Appell, after being banned here for his nonsense, brags of sneaking back under several aliases to continue his nonsensical harassment of the climate realists who post here. He apparently admitted to doing this on the following thread: http://dailycaller.com/2013/12/18/reddit-bans-comments-from-global-warming-skeptics/#comment-1169709832
I swear I’m not a fan boy. Just a big fan. I love the way you find some aspect of science, look at it, turn it upside down, study it and then come up with a plan to crunch some numbers to support what you figured out. Good to see you back.
PS – /sarc on/ With oceans as energy buffers that vary how they take up or give off energy, the feedbacks, the time constants, convection, radiations, humidity, latent heat of vaporization, and condensation, clouds, wind, pressure. They all add up to a neat linear system that won’t ever change unless we add CO2.
Mario Lento says:
December 18, 2013 at 9:48 pm
Thanks, Mario, but actually the process is much less directed than you imagine. What I do is more like play. I just graph up various combinations of variables, and think about them, and then graph up some more combinations, and consider how I might change my graphs to give more insight into some aspect or other …
After looking at lots and lots of graphs, if I’m lucky I can start to get some idea of what might be happening … but that’s never guaranteed.
In other words, it’s amateur science, which means science done for fun and the love of the game rather than for money. I just mess around with the variables until something interesting pops up.
Regards,
w.
0.2°C to 0.5°C per doubling of CO2? Uh-oh, I’m not sure that’s enough to hold back the next glaciation 🙁
Willis: Great to see you back, i pray your health is improving daily. Great post, illustrates the non-linearity much better than I have seen before, and for land and oceans.
I often chuckle when I remember the old saying I heard somewhere in the 60’s but don’t remember where. It is. “Constants aren’t and variables won’t”.
Good health to you.
” Net TOA radiation is calculated as downwelling solar less reflected solar less upwelling longwave radiation. ”
My understanding is that the error in satellite measurement of these two quantities is too great to permit their difference to be calculated meaningfully. So, presumably some Climate Science “forcing” results were used here, rather than genuine data. Is that a fair assumption?
This once again goes to demonstrate the time proven adage of “nature always abhors a straight line”.
I was so impressed by the logic of this article that I was really hoping for some alarmist criticism to see if anyone could try and undermine Willis’ logic. There has been none so far.
As it stands, and assuming the conclusions are correct, then it is one of the most important articles ever written on climate science, totally destroying the foundations of climate alarmism.
The temperature sensitivity of 0.2°C to 0.5°C for a doubling of CO2 levels is, as you say, lies within the boundaries of statistical noise.
So if we could return to the year 1900 and could somehow strip out the effects of natural climate cycles, UHI, agriculture, irrigation, plus cherry picking and homogenisation of historical data, by how much would the Earth’s temperature have risen today?
The answer: Not a lot and much less than the usually quoted figure of 0.7°C.
The cost of climate alarmism is apparently approaching $1.0 billion per day, so you can rely on the fact the contents of Willis’ article will be ignored and/or condemned and/or ridiculed by the Climate Establishment. Nothing can be allowed to derail the Global Waming Gravy Train.
Beautiful pics !
A few thoughts. Neg slope tails in land record may not be too important in total energy if area is considered.
I’m surprised there’s not more change in slope in oceans near tropics but by eye it’s a least a factor of 3 or 4 which is huge. Fitting central area, poles and tropics to get relative figures may be useful.
If I wanted Lissajous figures I’d be interested in the NH oceans. There is a whole ‘tube’ of loops that look very regular there like a tunnel of breaking surf, it would be interesting to isolate them and see what the storey is.
Not too convinced by the lag formula approach based on a pure harmonic. I’d suggest lag regression plots or just plotting different lags and see how flat you can get the loops. They are not round by you can compromise.
See examples I posted on Euan Mearns’ site:
http://euanmearns.com/uk-temperatures-since-1956-physical-models-and-interpretation-of-temperature-change/#comment-266
http://climategrog.wordpress.com/?attachment_id=638
regards.
I agree with Lord Monkton. The IPCC has never claimed linearity. They have always said that the “forcing” (hate that term – there’s no “force” involved) is itself dependent on the concentration of CO2 in the atmosphere. At some point the levels of CO2 in the atmosphere reach a saturation point and have no further impact. Some scientists have claimed that the 17 year pause might indicate we have already reached the effective saturation point of CO2 in the atmosphere.
The models are effectively “piecewise linear” with the linear equation only being relevent to the concentration we have at any given time (normally the present).
As you know, I dispute the models entirely. I claim that the theory of CO2 based warming supposes that an IR emitter can add energy to another IR emitter and normally we would never model a system that way since it would allow a system to “pull itself up by its own bootstraps” to a higher level of overall energy in direct contradiction of the law of conservation of energy. That is to say, in its simplest form the greenhouse gas theory implies a greenhouse gas would make a planet warmer, causing it to emit more energy, making the greenhouse gas more energetic, causing it to emit more energy, making the planet more energetic so on ad infinitum. This is not possible. We avoid the same difficulty in radio frequency calculations by assuming the radio transmitter does not receive any energy from nearby radio transmitters, even though in principle you would expect that a radio transmitter would indeed receive energy from other radio transmitters.
We always have to ignore the possibility that two emitters of energy can absorb energy from each other, not matter how tempting it might be to speculate that this is what must be happening, because it will always lead us to a model that contradcits the conservation of energy law.
A fair bit of this is above my pay rate but if you fire heated gas from a paint stripping gun at the surface of water, the water temperature will not rise indicating that surface tension blocks physical heat. Water accepts radiation but not “heat”. Would that have anything to do with it.
The problem is that the only bit of surface IR energy comprising OLR is in the ‘atmospheric window’. The H2O IR (defined as its spectral temperature) comes from -1.5 deg C, about 2.6 km in temperate zones, and the CO2 IR mainly comes from the lower stratosphere.
This is because for equal surface and local air temperature, there is zero net surface IR emission in self-absorbed GHG bands, standard radiative physics.
The concept of surface forcing is unscientific and irrelevant: for Climate Alchemy to become a Science, it has to junk forcing.
I like this work by Willis and in the end I think we are all going to find that the limiting factor for ocean heat content at a given level of insolation (after accounting for internal ocean circulations) is atmospheric pressure on the ocean surface.
And ocean heat content controls air heat content on a watery world.
Of course, that brings us full circle back to atmospheric mass and gravity leaving the radiative characteristics of GHGs nowhere in comparison.
In my comment above change the first sentence to ‘The problem is that the only bit of surfaceIR energy’
[Fixed – w.]
stephen wilde says:
December 19, 2013 at 2:23 am
Its feedbacks like that which give rise to the nonlinearity.
“The lag over the land averages 0.85 months, and over the ocean it is longer at 2.0 months.”
Yes, so you are still dealing with annual sensitivity, not decadal.
First temperature can only be accurately taken when a body is in thermal equilibrium. The earth never is!!!!!!!!! So how can we accurately find an average temperature???
Secondly the assumed TOA solar input is assumed to be 340W/m2 by the IPCC. With this poor energy input the water cycle would not work!!! Actual solar input is 1370W/m2 which averages to 500W/m2 onto the SUNLIT hemisphere which is enough to have a water cycle. This is reality not some model built to suit a crappy theory.
As always I stand in awe of your ability to visualize the mountains of data.
There’s a detail I don’t understand, though. The formula for the multiplier comes from diffusion through a depth. In particular, it uses the relative amplitude at the depth that gives the phase lag you observed. I’m having trouble understanding why that quantity is relevant in this context. A particular difficulty is that in diffusion the phase lag can exceed 2 pi, whereas I don’t see how that would happen for the radiation / surface-temperature relationship.
Could you elaborate a little on how the one relationship is relevant to the other?
Aw come on. Take that first diagram, invert it a la Mickey Mann, twist it around in the best tradition of the Global Warmmongering twisters and behold! A hockey stick.
Very interesting, presentation, looking at the numbers in different ways. I certainly like how clearly the oceans limit at 32C. I actually dove in water that warm in Darwin Bay, Australia. Now I’m off to shovel the snow of the driveway.
I find this very convincing.
Why? Because it is based on real data, reflects more accurately what we are actually seeing, is much closer to what basics physics says should happen, and Willis doesn’t get another grant or academic posting based on slanting the results and hiding the data.
“We always have to ignore the possibility that two emitters of energy can absorb energy from each other, not matter how tempting it might be to speculate that this is what must be happening, because it will always lead us to a model that contradcits the conservation of energy law.”
Not quite. Two RF emitters near each other will indeed absorb energy from each other and output energy on a new frequency. This is called inter-modulation and is a big problem at some locations. Now, is the total RF energy changed? I strongly doubt it, but I don’t know for sure.
Figure 1. reminds me on HR diagram, see :
http://en.wikipedia.org/wiki/H-R_Diagram
Can you please plot logT- LogF graph?
You can call it than Eschenbach- Štritof (to much sch or Š) or Willis- Nikki diagram. 🙂
Willis says: So to see if the relationships really are linear, I thought I’d use the CERES satellite data …
Unfortunately, that first graph doesn’t tell you anything about the linearity of sensitivity. What it tells you is that convection carries lots of energy from the equator to the poles.
Consider Antarctica – the red dots. There is a net negative radiation imbalance, so more radiative energy is leaving than arriving each year. On an annual basis, this means that roughly equal amounts of OTHER energy must be arriving, which would be air and water currents. Similarly, the areas near the equator have a positive value, meaning large amounts of energy are being carried away by convection.
The “hook” in the red data does NOT tell us that as the forcing increases, the temperature will decrease in that region. It simply tells us that convection carries a lot of energy to the coasts of Antarctica but not so much to the interior.
Without digging into the details of your calculations, I wonder if convection may be confounding some of your other calculations.
My last question may have been a little obscure. I guess what I’m really asking is what model you’re using to obtain your multiplier.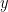 is related to the stimulus
is related to the stimulus  as follows:
as follows:

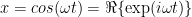 ,
,
 .
.



 . It isn’t, of course. You seem instead to have chosen a model in which the response is that of a semi-infinite slab at some depth. Since I don’t see why you base responses at the surface to responses at various depths, though, I suspect that not all is as it seems.
. It isn’t, of course. You seem instead to have chosen a model in which the response is that of a semi-infinite slab at some depth. Since I don’t see why you base responses at the surface to responses at various depths, though, I suspect that not all is as it seems.
Suppose, for example, that according to your model the response
and the stimulus is sinusoidal:
then, since the system is (gasp) linear, we know that the response is given by
Plugging that into the system equation gives:
So your multiplier would have been
I know I’ve just gotten hung up on a detail, but I’ll appreciate any answer you have time for.
Willis: “But the land and the oceans can’t change temperature immediately. There is a lag in the process. So monthly climate sensitivity is the smallest of the three, because the temperatures haven’t had time to change.”
No, it would be more appropriate to compare delta_d/dt(SST) to delta_Rad , the fast response is mostly orthogonal ie rate of change.
The response to the ‘lambda’ relaxation equation is neither purely in-phase nor orthogonal but a sliding mix of the two which varies with frequency, so you really can’t just plot SST-Rad and start drawing simplistic conclusions. and defining “monthly” sensitivities.
http://climategrog.wordpress.com/?attachment_id=399
However, if you can estimate the lag for a particular frequency range, or the ratio of in-phase and orthogonal components that make up the temp response , that could give an estimation of tau and hence lambda.
Do that separately for tropics and temperate zones and it put numbers on the degree of regulation provided by your governor.
Just an idea.
Joe, you seem familiar with this stuff. Do you see any flaws in what I linked there?
http://climategrog.wordpress.com/?attachment_id=399
Thanks Willis, for this inspiring approach – I wish I had your graphing capabilities!
and to reply to Martin A – yes, you are right to finger the TOA imbalance ‘data’…..its resolution is about 5 watts per square metre with a consistent excess of that value over zero…..and the modellers are looking for 0.5 to 1 watt excess as their expectation. So – the ‘data’ is ‘constrained’ to use NASA’s phrase, by the ocean heat content data. As Bob Tisdale will tell you, the OHC data is not accurate either and – guess what? It is adjusted in ‘re-analysis’ to reflect the expected excess from the TOA!!!! I think this is what is called a circular argument! It doesn’t seem to worry the modellers at all.
If the IPCC don’t claim linearity how do they justify simple scalar number (3) as their feedback multiplier, when this multiplier is clearly inversely related to temperature. Surely the question must then be, how quickly does gain fall as temperature rises, as this will have a critical effect on ultimate equilibrium temperature rise for a doubling of CO2
Thanks Willis; A superb post!
Your illustrations make clear lambda is a chimera at best. Again proof that it is not possible to model Earth’s climate with the little physical knowledge that we have now.
And then to conduct “experiments” where these models supply the “data” is criminal.
My guess is that if you looked at two slabs of ocean at plus and minus 60 degrees latitude over the course of years you would see a pair of race track ‘8’s, where you have to pump more energy into the ocean in spring and less in the fall, to achieve the same temperature.
Thanks for another another thought-provoking view of the big picture, Willis.
I have what I hope will be a constructive suggestion. I think your graphs in this article could be more informative if you used the absolute value of latitude instead of latitude. The color differences between the polar regions seem to track each, and fewer colors would make them simpler to read. Of course this would squash out some of the information distinguishing land vs sea differences between the northern vs southern hemispheres. Or maybe you do a both charts, and the difference between them would show something about those land / sea differences?
There is also the assumption that all types of forcing can be simply converted into watts. I don’t think so. Solar shortwave directly heats the surface, which gets much hotter on sunny days of the same air temperature (go ahead, put you hand on your car in the sun vs shade in Texas). This high surface temperature both leads to more longwave radiation (which is a 4th power of temperature function) and to more evaporation. In contrast, the greenhouse effect of water vapor keeps the air warm at night (or not in a desert, leading to very cold nights). This explains (in my view) why the main effect of GHG in recent decades has been warming of nighttime minima rather than daytime maxima. The rise in station records (and divergence between station and satellite data) is mainly due to the (min+max)/2 artifice of computing a daily value.
Greg: “Joe, you seem familiar with this stuff.”
I hope I haven’t misrepresented myself. I’m no scientist, just a retired lawyer who’s (mis?)remembered isolated facts that experts told me over the years. Without going through your linked page in detail, though, I’d say it uses the same math I did above.
Thank you, John! As always, Prof. Eschenbach is ‘way ahead of the pack on that concept as well. Please see: http://wattsupwiththat.com/2009/06/14/the-thermostat-hypothesis/
Willis, fascinating work. It goes again to my belief that regionalism dominates the “global” record, that what we have rammed down our throats is (my term) Computational Reality, not Representational Reality, i.e. “facts” about the world that are derived from 100% correct mathematical methods of taking numbers apart and putting them together again, but not facts that give a correct description of what is going on in the world in which people live. Kudos.
Something sparked at your comment about temps not above 30*C:
In the spirit of Computational vs Representational Reality, I wondered about temperature distributions. Instead of a map of the world, if we were to look at frequency plots of temperature of the world as an annual stat, how would that look for the highs and lows at a planetary level?
The theory of CAGW has the hot areas getting beastly hot in the future, frying the planet, right? If we were to look at annual top 5*C level and didn’t see any top-end change or percentage of total change, we’d be inclined to believe that the “hotter” world was less cold, not more hot.
More regionalism, not globalism.
To me, the bottom line is that CO2 “climate sensitivity” is a fudge factor that has no physical relationship. Try doing your plots substituting ln(CO2) for SST(skin surface temperature). I expect atmospheric concentrations to be a lagging function of energy embalance. We know it follows temperature.
Willis
Great data graphing, discussion, and giving us new ways to examine, explore and understand what is happening.
On lags, suggest exploring lags of 90 deg (Pi/2) on the annual and Schwab solar cycles.
i.e. 3 month lag for the annual and 2.75 year lag for the ~11 year solar cycle.
You may also find it useful to explore the integral of the fluxes.
See Key evidence for the accumulative model of high solar influence on global temperature David R.B. Stockwell, August 23, 2011
It seems this ‘linearity’ stuff is just another name for extrapolation science.
Nature does not do straight lines.
Those who do must practice unnatural science, or psuedo-science as it is more usually known.
David L. Hagen says: Great data graphing, discussion, and giving us new ways to examine, explore and understand what is happening. On lags, suggest exploring lags of 90 deg (Pi/2) on the annual and Schwab solar cycles.
You cannot really look at a fixed in a system with so many different things going. Unless there is one massively over-riding variation (like the annual one).
If you think there is 90 deg lag you need to differentiate (or integrate) one of the variables. In fact you need to study both , which is what this was about:
http://climategrog.wordpress.com/?attachment_id=399
Mr. Eschenbach… I’m writing to confirm that your first graph is accurate and spot-on. It’s obvious because if you rotate it 180 degrees, it show a definite hockey stick. Thanks for bringing it to my attention. I’m using it for my next peer reviewed study on tempurature proxies.
Signed: Michael E Mann.
lgl says:
December 19, 2013 at 2:47 am
Thanks, lgl. In fact, I’m using the lag to remove the effect of the annual cycle, which reveals the longer term (decadal or TCR) values.
w.
As I see it the real issue is not linearity per se. It is something more basic; the assumption that there is a simple deterministic relationship between forcing and temperature anomalies. This is possible only if natural variability is insignificant on time scales of decades to centuries so that changes in temperature over those time scales must be direct responses to forcing. I am not convinced that this is the case.
Tim Folkerts says:
December 19, 2013 at 5:31 am
Say what? No matter what is moving the results away from linearity, the end result is that temperature is NOT linearly related to TOA forcing.
All you’ve done is identified one of the many reasons the relationship is NOT linear. So while your claim that “convection carries lots of energy from the equator to the poles” is certainly true, it doesn’t follow from that fact that we can say that the relationship is linear.
w.
Thank you again.
What is “eyebeach”?
What is the full reference to “the study by Otto”?
Can you quickly summarize how the grid-specific TCRs were estimated? were the calculated from GCMs? (not necessary if described in “the study by Otto”.)
Just out of curiosity, have you saved your many posts in .doc or .pdf formats for easy reference and downloading?
To clarify, I have started doing this myself by copying and pasting. Today’s is called TOATEMPNonlinearity20131219.doc; it’s in the Eschenbach\wuwt folder. The hot links in your post are hot links in the doc, and the figures copy nicely. I am always a little suspicious of transcribing errors. I think that “The collected climate writings of Willis Eschenbach” would make a nice addition to the Springer series” on climate, should it interest you to collect them..
When I do a drag and drop on the first graphic I get a bunch of chinese characters….???????????
Willis, my point is that the first graph is not expected to be linear. The linear behavior (if it indeed turns out to be linear) would be related to the GLOBAL CHANGE in temperature as a function of a global FORCING CHANGE. The fact that the graph is not a straight line tells us NOTHING about ∆T = lambda ∆F Your first graph shows how temperature and forcing are related as you change position, rather than how temperature and forcing are related as you change time.
If anything, you should plot the CHANGE in temperature of each grid point during the year vs the CHANGE in radiative forcing for the year. Some thing like “the grid cell at 42N, 99E averaged 2 W/m^2 more radiation than last year (∆F) and warmed up 0.7 C (∆T) since last year”. That would give you the ‘climate sensitivity’ for that point for that year (0.35 C/(W/m^2) in that case). I think THAT plot would be interesting to see (more interesting than Graph 1) — there should be a lot of scatter but also a general positive slope (ie areas with less radiation than last year should cool; areas with more radiation than the previous year should warm).
I think that is much closer to the graphs you plotted later (but it is not completely clear to me how you did the later graphs). This also seem like an easy way to get the longer-term changes. Take the temperature change for a given cell from Jan 2003 to Jan 2013. Find the radiative imbalance over that time. Divide the two. There’s the decade climate sensitivity for that cell.
Stoat has some commentary on all of this.
http://scienceblogs.com/stoat/
Stoat’s commentary here:
http://scienceblogs.com/stoat/
The work of J Eggert seems to indicate that any forcing from CO2 is also limited.
It appears to be logarithmic below about 280ppm, then FLAT above that.
http://johneggert.files.wordpress.com/2010/09/agw-an-alternate-look-part-1-details1.pdf
To use audio parlance.. its like having a compressor with a hard limiter set.
Now as the CO2 concentration is not uniform around the globe (in both time and location), there may still be areas where some increase in forcing is still possible, but as the general level of forcing increases, there are less and less places with concentration of less than 280ppm for less and less part of the day, until eventually, no more extra forcing is possible.
Thanks Willis, I’ve added your ECS estimate to a compilation of 9 others, averaging out to an ECS of ~0.45, right in line with your mean estimate of 0.4 C
http://hockeyschtick.blogspot.com/2013/12/observations-show-ipcc-exaggerates.html
Joe Born says:
December 19, 2013 at 5:37 am
Joe, you always ask the best questions. Upon investigation, I see that my analysis of the effect of the lags was incorrect.
What I did to check my previous results was what I should have done, to drive a standard lagging incremental formula with a sinusoidal forcing:
R[t] = R[t-1] + (F[t] – F[t-1]) * (1 – timefactor) + (R[t-1] – R[t-2]) * timefactor
where t is time, F is some sinusoidal forcing, R is response, timefactor = e ^ (-1/tau), and tau is the time constant.
Then I measured the actual drop in amplitude and plotted it against the phase angle of the lag. By examination, this was found to be an extremely good fit to
Amplitude as % of original = 1 – e ^ (-.189/phi)
where phi is the phase angle of the lag, from 0 to 1. (The phase angle is the lag divided by the cycle length.)
The spreadsheet showing my calculations is here.
I’ll redo the calculations shortly. It won’t make a lot of difference. The main effect will be to reduce the multiplication factor due to the lag. This in turn will reduce the estimate of the overall sensitivity, and also increase the land/ocean difference.
Thanks as always for finding my mistakes, that’s how we move forwards. I’ll redo the graphics and change the text to reflect the proper calculations.
w.
stephen wilde says:
” is atmospheric pressure on the ocean surface.”…………………………
“Of course, that brings us full circle back to atmospheric mass and gravity leaving the radiative characteristics of GHGs nowhere in comparison.”
many thumbs up, stephen !! (if we had thumbs on this forum)
Nice work, Willis. You quickly demonstrated the lack of linear response between forcing and temperature and laid bare another aspect of the ineptitude of modern climate science.
The cyclical, oscillating nature of the scribble plots reminds me of those tracing in sand by pendulums.
The scatter plots could be paintings by elephants.
I noted in one comment that you had been ill. I hope this is all over with and nice to see you back with your heretical and artistic presentations of data. I wonder why we don’t see more of this compelling type of presentation from other quarters – did you invent this type of graph?
I noted your figures of ECS of land 0.37, NH O.17, SH 0.08 and ocean 0.03 and global 0.12. I did a weighted calc of these using ocean as 70% of globe, 87.5% of NH as land (at 0.37) and12.5% ocean and the same type of calc for SH and global and arrived at: calc global 0.13, NH 0.13, SH 0.03. Not bad. It seems that the land is reasonably homogeneous, as is the ocean. Maybe ice accounts for some of the differences.
Finally, that 31 C is so firm and appears in the darndest places. It is a constant like the freezing point and boiling point of water at sea leve. One should be able to identify this as a solid physical metric somehow – wouldn’t an equation expressing this as a law be nice? It’s in there somewhere.
tjfolkerts says:
December 19, 2013 at 11:39 am
Thanks, Tim. The data is there. Plot it as you wish. I’ve shown certain relationships. However, there are many more to explore.
w.
Your plots have made me curious about how the TOA difference appears in the output of the models (assuming they provide that). It would be an interesting validation to see if the models replicate the pattern that you’ve identified. Obviously, models that don’t are not valid representations of the earth. If they can’t match that profile then their physics is wrong. Especially if they can’t replicate the 30 deg cutoff that you show. That would seem to be a better comparison than global temperature.
Hope your recovery is proceeding well.
Gary Pearse said:
“Finally, that 31 C is so firm and appears in the darndest places. It is a constant like the freezing point and boiling point of water at sea level”.
Interestingly all three are pressure related.
http://www.animations.physics.unsw.edu.au/jw/freezing-point-depression-boiling-point-elevation.htm
just not a lot in the case of the freezing point because the volume of ice is not a lot different from the volume of water.
“because the volume occupied by a kilogram of liquid is not much different from that occupied by a kilogram of solid, this effect is very small unless the pressures are very large. For most substances, the freezing point rises, though only very slightly, with increased pressure.
Water is one of the very rare substances that expands upon freezing (which is why ice floats). Consequently, its melting temperature falls very slightly if pressure is increased. ”
Which brings us back to my contention that atmospheric pressure on the ocean surfaces determines the energy content that the oceans can hold at a given level of insolation (subject to internal ocean circulation).
http://www.newclimatemodel.com/the-setting-and-maintaining-of-earths-equilibrium-temperature/
The mass and gravity issue just won’t go away.
Temperature (heat) IS electric potential at WORK . One of the first things we learnt was to blow on our food, Why? Its all about how fast the electron moves around the molecule or solid .
Tjfolkerts, while the first graph might not be expected to be linear, it does show the relationship between Lambda and temperature pretty well and it shows lambda is inversely related to temperature, gain falls with temperature. The IPCC is therefore wrong say there is a system gain of 3, clearly effects of a doubling of CO2 get smaller and smaller, not only because the log term, but also because the gain falls, to the point that at 30 odd degrees any amount of energy causes no warming. Nobody ever talks about the doubling after this one.
I have to say this is obvious if you think about it, little stock is made from the fact that the gain, that is predominately evaporation feedbacks, are also logarithmic, the energy available for trapping/scattering, is always limited and you have to deal with law of diminishing returns as any of these gases rise. this tells me that Lamda has a log term in it somewhere, probably in the denominator
This suggest a discussion a I had with Will Kinimonth some time back has some merit. The conclusion of that was that climate change would behave like moving latitude toward the equator. Temperature will become less extreme, with lower maximums and higher minimums, with minimums rising more than maximums, New York becomes like Miami. So those of you New Yorkers who are catastrophists, but want to move to Miami, don’t bother, just wait it out.
Mr. Eschenbach:
Thanks for taking time to respond. Unfortunately, my ineptitude at quickly reverse-engineering spreadsheets has resulted in your having cast pearls before swine.
Still, I hope to try again when time permits.
Well here we go again.
I don’t know how many times we have been told that “””…CLIMATE SENSITIVITY…”””” is the increase in mean global (near) surface Temperature for a doubling of atmospheric CO2 abundance.
That after all, is the slope of the claimed logarithmic connection between CO2 and Temperature.
The solar physicists keep telling us there has been NO statistically significant change in TSI in recorded history, so how can top of atmosphere flux change ?
Could someone point us to the official SI definition of “Climate Sensitivity” Please.
On a related subject, some time back I developed a simple analog of carbon dioxide’s ability to intercept and scatter individual infrared photons as they leave the surface and pass through the troposphere, based on Nasif Nahle’s calculations of mean free photon path. Running this for a few hours gives a graphable series relating CO2 concentration to percentage of photons prevented from escaping to the stratosphere or beyond. The results show a good correlation to the theory, in that the relationship is logarithmic, with 90% of the maximum possible effect being achieved with only 30ppm CO2 at sea level pressure.
Bear in mind I’m no climate scientist, though I have studied physics. I daresay this overly simple model does not include all of the factors in the real atmosphere, and might even contain a few errors. It does clearly show the logarithmic behaviour of the greenhouse effect, though, and achieves this from first principles without any ‘adjustments’ being required.
http://iwrconsultancy.co.uk/climate/photon.png
george e. smith says:
December 19, 2013 at 3:00 pm
“The solar physicists keep telling us there has been NO statistically significant change in TSI in recorded history, so how can top of atmosphere flux change ?”
George: While the variation in radiative flux density from the sun is very small, on the order of +/-0.1% IIRC, the change in the percentage of this shortwave radiation reflected, mostly due to changes in cloud cover, and snow/ice surface cover, can be a lot larger. Similarly, the changes in longwave radiation from the earth at TOA can vary quite significantly due to temperature changes, humidity changes, and cloud cover changes. These variations are what the CERES satellites are monitoring.
george e. smith says:
December 19, 2013 at 3:00 pm
George, there are a few things at work. First, we’re talking about the solar flux that is available gridcell by gridcell … consider the gridcells right by one of the poles as example of the extreme variations in solar flux.
Next, the earth is not always the same distance from the sun, which makes an annual difference of (from memory) about 28 W/m2.
Next, the TOA flux is not just the solar radiation. It is the solar minus the upwelling longwave and the reflected shortwave. Both of these later variables change constantly.
As a result, the Net TOA imbalance varies both in space for a given time, and in time for a given location.
w.
Sensitivity is the global response willis. The assumption is that if you average the forcing globally, and average the response globally that it will be linear over the temperature of interest and time period of interest. The temperature of interest is roughly 12C to 18C. we are currently at 15C.
Steven Mosher says:
December 19, 2013 at 8:58 pm
Not sure what your point is here, Steven. Global sensitivity is the global response. Local sensitivity is the local response. Are you saying that globally averaging a wildly non-linear system somehow makes it linear?
w.
“The solar physicists keep telling us there has been NO statistically significant change in TSI in recorded history, so how can top of atmosphere flux change ?”
Well whatever they conclude about TSI the effect on surface temperature is there
http://climategrog.wordpress.com/?attachment_id=748
So rather than saying there can be no significant effect from the sun “because TSI is almost constant” someone needs look at something other than TSI, or explore what mechanism is amplifying TSI variations.
For the last 30 years they’ve been insisting it’s irrelevant, since the “pause” it suddenly becomes polite to talk about it, though they still try to ignore the fact that if it (partly) explains the “pause” it (partly) explains the late 20th. c. warming too.
Oh, dear. We won’t mention that.
Alan Robertson says: The cyclical, oscillating nature of the scribble plots reminds me of those tracing in sand by pendulums.
It’s quite analogous. Two oscillations of same period that are out of phase. In fact there is a very small difference in freq with the pendulum if the two amplitudes are different since there is a slightly non-linear relationship between freq and amplitude. That is what makes the pattern interesting as the two shift.
However, climate is not quite that simple The phase relation changes with season that’s why the shapes are not elliptic. You can get an average value of the lag from a lag-correlation plot. This would be preferable to Willis’ formula based on a clean harmonic pendulum like, oscillation.
http://climategrog.wordpress.com/?attachment_id=645
That is the usual way of estimating a phase relationship.
Willis-
Very interesting post. Thank you for your efforts.
I think the y axis labels in Figures 5 and 6 are not correct. The figure title says Degrees C per doubled CO2, but the y axis is labeled Degrees C per Watts/m^2. The figure title appears to be consistent with your text descriptions of the figures.
[Fixed, thanks. -w.]
tjfolkerts says:
December 19, 2013 at 11:39 am
If anything, you should plot the CHANGE in temperature of each grid point during the year vs the CHANGE in radiative forcing for the year.
====
Indeed. As I also posted:
Greg says:
December 19, 2013 at 5:48 am
Willis: “But the land and the oceans can’t change temperature immediately. There is a lag in the process. So monthly climate sensitivity is the smallest of the three, because the temperatures haven’t had time to change.”
No, it would be more appropriate to compare delta_d/dt(SST) to delta_Rad , the fast response is mostly orthogonal ie rate of change.
====
The fact is it’s neither one nor the other but a sliding mix of the two. http://climategrog.wordpress.com/?attachment_id=399
The monthly in-phase change will be small but the monthly (and shorter) dT/dt will be large. By the time you are looking at decades the dT/dt will be small and the response will be mainly the in-phase term.
All that is entirely consistent with a linear relaxation process , so I don’t see the bee in Willis’ bonnet being particularly satisfied with what he’s shown here.
This is very analogous to the on-going discussions of out-gassing. MacRae, Humlum etc have shown the fast orthogonal response, this is only one step to determining the long term result.
This is why there is all the talk of TCS and ECS. We are seeing some intermediary mix that is getting called TCS. I don’t think that one value is sufficient to even guess at ECS. You need a much fuller understanding of the process than one reading of a mix of the two.
“Multiplier = 1/exp(phase_angle°/360°/-.159)
The derivation of this formula is given in my post here.”
Say What?
So you are using tautochrones relationship for a diffusive process in the ground and applying it to the ocean surface well-mixed layer, with non linear feedbacks like tropical storm governor. with a whole climate system sitting on it that means the surface temp is determined by a hundred things , not of which are diffusive.
I’m in the uncomfortable position of having to agree with stoat-face on this one.
http://scienceblogs.com/stoat/
“The fatal lure of making stuff up”
Get a grip Willis. You are capable of better. This is frankly a crock. (And you don’t have the excuse of working for the government.).
Mods, if you can tell me what is that text is causing it to stick in moderation , I will do my best to avoid the repeating offence in the future.
Willis: If you haven’t realized it, you have discovered clouds (and to a lesser extent, humidity). Clouds reflect incoming SWR, which usually creates a negative radiative imbalance. Clouds also block outgoing LWR from below and radiate outgoing LWR from their top surface, so the altitude of clouds has a big influence on the radiative imbalance they create. High cold cirrus clouds can radiate so little LWR to space that they create a positive imbalance (warming). The temperature of the surface below has no impact on the radiative imbalance in cloudy areas because all of the action takes place at the top surface of the cloud. The cloudy portion of the planet therefore creates perturbs the relationship between surface temperature and TOA imbalance and the biggest perturbation occurs in the tropics where surface radiates most strongly the height of the clouds tops varies the most. (The coldest place in the atmosphere is often at the tropopause above the ITCZ – where the surface is warmest.)
At some wavelengths, humidity also blocks outgoing LWR. Actually it absorbs and re-emits it, and the temperature at the altitude from which the photons that escape to space are emitted determines the outgoing flux. For the most part humidity varies strongly with temperature, but the relative humidity is low in the downward leg of the Hadley cell and near the poles.
Fewer than 10% of the photons emitted by the surface escape directly to space, so there is no reason to expect the TOA LWR flux to correlate perfectly with surface temperature. The TOA LWR flux depends on the temperature in the atmosphere where the photons that escape to space are emitted. The more GHG’s (including water vapor) in the atmosphere, the higher the “characteristic emission level” (and temperature drops an average of 6.5 degC with every kilometer of altitude).
What matters is whether there is a linear relationship between the mean global temperature and forcing. Due to the asymmetric distribution of land, the planet as a whole warms from about 290.5 degC during winter in the NH to 294 degC in the summer. This gives us a 3.5 degC deltaT to work. The results are fairly linear. “Assessment of radiative feedback in climate models using satellite observations of annual flux variation”
http://www.pnas.org/content/early/2013/04/23/1216174110.abstract
Greg says:
December 19, 2013 at 10:49 pm
No, I’m not. Re-read the update at the end of the head post.
w.
Frank says:
December 19, 2013 at 11:05 pm
Frank, if you haven’t realized it, you haven’t discovered humility … giving me a lecture as though I’ve never heard of clouds? Get a grip, my friend.
w.
Ok Willis, I’ll check out the update. Sorry I did not see you’d changed it.
The spreadsheet you put on dropbox does not display because it seems to contain lots of refs to a local file. Could you check it is an independent file ?
“%08myfunctions1.xla’#dsin”
is that something that can be corrected by and edit or does it need some defs from another file?
Willis Eschenbach: “Then I measured the actual drop in amplitude”
That’s where my difficulty with the spreadsheet lay: the values in Sheet 2’s Q column seem to have been generated by a digitizer or something, but I don’t know where “actual” comes from.
Looking at the scribble plots , I doubt the validity of this method of assessing lag. Lag-regression seems more appropriate.
Once you have a lag, how this relates to all the different frequencies involved is complex. I suspect this is a far worse approximation than linearity. In fact I don’t see where the approximation that is being made is clearly stated.
Accepting that Willis has now dropped back to the linear relaxation equation as the base for the lag, and assuming one unique tau is enough at least to have a guess, it still comes down to a whole range of frequency dependant contributions , each at some different balance of it’s phase relationship.
http://climategrog.wordpress.com/?attachment_id=399
So is the current method here just focussing on the ‘dominant’ periodicity having the most effect on the Lissagous scribble plots?
It seems dangerous using that to estimate the decadal from the monthly. At least until it is more clearly defined why this will produce the declared result.
Greg: “The spreadsheet you put on dropbox does not display because it seems to contain lots of refs to a local file.”
Just replace his …dsin(x) with sin(x/180*pi())
Frank says:
December 19, 2013 at 11:05 pm
… Fewer than 10% of the photons emitted by the surface escape directly to space, …
———————————-
I don’t think I’ve heard that before. Not exactly the “atmospheric window” and “GHG interception wavelengths” explanation. The window is supposed to be huge, not 10%.
Which makes the argument “How does energy move in and out of the Earth system”. Take it down to the photon level, collisional energy exchange level and include time. Because that is the level it operates at. Climate theory operates many levels above that and probably misses all the important processes.
Willis-
Your Figure 5 is extremely interesting. In my opinion, it demonstrates that water vapor feedback overall is strongly negative. Over land at very low temperatures, the climate sensitivity approaches 1 C per CO2 doubling, which is the no-feedback value. There is very little water vapor at these temperatures. As temperature increases, the atmospheric water vapor absolute concentrations generally increase, and climate sensitivity drops asymptotically towards the values over the oceans shown in Figure 6.
“I don’t think I’ve heard that before. ”
The whole argument is mistaken. It is true that straight CO2 lines are totally saturated. The supposed logarithmic dependency now is due to spectral line broadening, specifically collision broadening.
His calculation is probably correct as far as it goes but misses the reason for the broadening.
Thanks Joe, that fixed it. Now we just need to know what col Q is !
I have not checked this through the maths but that curve in the spread sheet looks a lot like my graph’s A = S/(1+(ωτ)^2) , where S is tau/(heat capacity of mixed layer)
http://climategrog.wordpress.com/?attachment_id=399
Col Q must come from the data but not sure exactly what it is.
This may be getting somewhere but I still say it needs to combine delta_T and d/dt(delta_T) to get the correct response to the linear relaxation model.
The full response is:
A * forcing – Aτ * d/dt(forcing) + Aωτ * transient
(The transitory term can be ignored in the real data, it is model spin-up.)
It seems like Willis is currently looking at the first term since he’s only examining the in-phase response. My tau will be similar in magnitude to the lag, so there is a strong chance monthly changes will be neither clearly in-phase of clearly orthogonal, We need to take account of both or justify that one is negligible since we are not in the cross-over regime.
This has the potential to provide a method to evaluate independent sensitivity for different latitude bands, That would be informative.
Question is, if Rad goes up by say 0.5W/m2 and stays there how long will it take the mixed layer to stabilise? My gut feel is 3 or 4 months at least, that gives tau of the order of a month. If the major variation here is the annual cycle (probably with strong 6 months in tropics) , omega = 0.5 or 1 per month.
Thus omega.tau is of similar size and we are bang in the zone of the cross-over where T and dT/dt are about equal. That means Willis’ current estimations could be off by a factor of 2 or 3 but I have not worked out in which direction yet.
It may account for his figures being so far off every other estimation. 0.3 * 3 would be getting near the low end of the range that other are ready to conceive of (assuming the correction goes that way ).
oops, just remembered , omega in those equations in not in radians, it’s straight frequency but it needs to be established if this reaction is in cross-over for the annual cycle. Since that seems to be what the derived lag is related to.
Willis,
Take a function and perturb it by a small enough amount and it will appear to respond in a linear fashion. Only as the perturbation becomes llarger does one start to see the nonlinearity.
cba says:
December 21, 2013 at 7:15 am
Thanks, cba. I’m well aware of that, but it doesn’t apply here. If things were only perturbed a small amount, you would be right. But look at Figure 1. The size of the “perturbation” in the natural system goes from -60°C to plus 30°C, and it’s more than that if we look on a daily basis. As a result, any assumption of normality is suspect, the perturbation in natural systems is often far from small.
Regards,
w.
Curt says:
December 19, 2013 at 5:40 pm
george e. smith says:
December 19, 2013 at 3:00 pm
“The solar physicists keep telling us there has been NO statistically significant change in TSI in recorded history, so how can top of atmosphere flux change ?”
George: While the variation in radiative flux density from the sun is very small, on the order of +/-0.1% IIRC, the change in the percentage of this shortwave radiation reflected, mostly due to changes in cloud cover, and snow/ice surface cover, can be a lot larger. Similarly, the changes in longwave radiation from the earth at TOA can vary quite significantly due to temperature changes, humidity changes, and cloud cover changes. These variations are what the CERES satellites are monitoring.
Willis Eschenbach says:
December 19, 2013 at 5:53 pm
george e. smith says:
December 19, 2013 at 3:00 pm
“The solar physicists keep telling us there has been NO statistically significant change in TSI in recorded history, so how can top of atmosphere flux change ?”
George, there are a few things at work. First, we’re talking about the solar flux that is available gridcell by gridcell … consider the gridcells right by one of the poles as example of the extreme variations in solar flux.
Next, the earth is not always the same distance from the sun, which makes an annual difference of (from memory) about 28 W/m2.
Next, the TOA flux is not just the solar radiation. It is the solar minus the upwelling longwave and the reflected shortwave. Both of these later variables change constantly.
As a result, the Net TOA imbalance varies both in space for a given time, and in time for a given location.
w………..””””””””
Well I didn’t come down with the last shower. I do know that the earth sun distance changes throughout the year, and I do know that the sun’s radiance changes about 0.1% p-p over the solar cycle. All of those factors are averaged out in the published value for TSI, which was about 1362 Watts per square meter, the last time, I recall NASA/NOAA stating a recommended value. It is that averaged best value that they tell us hasn’t changed perceptibly. Well when I went to school the value was 1353 W/m^2, but that was based on balloon and rocket borne measures, in the upper atmosphere. But TSI is not affected by clouds. Absorption by the oceans is, and loss of outgoing IR is; and we have no ground level global monitoring of surface tsi, so there is no reliable surface energy absorption. Satellite cloud measurements, don’t tell you what radiation reaches the ground, and the satellites don’t give you full 4pi global 24hour continuous cloud measurement. Clouds come and go while a satellite crosses the sky, but the lost surface radiant energy happens in real time, and isn’t properly Nyquist sampled by any means. I have about zero confidence, that anybody knows what cloud influence on earth’s radiant energy balance is.