Guest Post by Willis Eschenbach
Since we’ve been discussing smoothing in datasets, I thought I’d repost something that Steve McIntyre had graciously allowed me to post on his amazing blog ClimateAudit back in 2008.
—————————————————————————————–
Data Smoothing and Spurious Correlation
Allan Macrae has posted an interesting study at ICECAP. In the study he argues that the changes in temperature (tropospheric and surface) precede the changes in atmospheric CO2 by nine months. Thus, he says, CO2 cannot be the source of the changes in temperature, because it follows those changes.
Being a curious and generally disbelieving sort of fellow, I thought I’d take a look to see if his claims were true. I got the three datasets (CO2, tropospheric, and surface temperatures), and I have posted them up here. These show the actual data, not the month-to-month changes.
In the Macrae study, he used smoothed datasets (12 month average) of the month-to-month change in temperature (∆T) and CO2 (∆CO2) to establish the lag between the change in CO2 and temperature . Accordingly, I did the same. [My initial graph of the raw and smoothed data is shown above as Figure 1, I repeat it here with the original caption.]
Figure 1. Cross-correlations of raw and 12-month smoothed UAH MSU Lower Tropospheric Temperature change (∆T) and Mauna Loa CO2 change (∆CO2). Smoothing is done with a Gaussian average, with a “Full Width to Half Maximum” (FWHM) width of 12 months (brown line). Red line is correlation of raw unsmoothed data (referred to as a “0 month average”). Black circle shows peak correlation.
At first glance, this seemed to confirm his study. The smoothed datasets do indeed have a strong correlation of about 0.6 with a lag of nine months (indicated by the black circle). However, I didn’t like the looks of the averaged data. The cycle looked artificial. And more to the point, I didn’t see anything resembling a correlation at a lag of nine months in the unsmoothed data.
Normally, if there is indeed a correlation that involves a lag, the unsmoothed data will show that correlation, although it will usually be stronger when it is smoothed. In addition, there will be a correlation on either side of the peak which is somewhat smaller than at the peak. So if there is a peak at say 9 months in the unsmoothed data, there will be positive (but smaller) correlations at 8 and 10 months. However, in this case, with the unsmoothed data there is a negative correlation for 7, 8, and 9 months lag.
Now Steve McIntyre has posted somewhere about how averaging can actually create spurious correlations (although my google-fu was not strong enough to find it). I suspected that the correlation between these datasets was spurious, so I decided to look at different smoothing lengths. These look like this:
Figure 2. Cross-correlations of raw and smoothed UAH MSU Lower Tropospheric Temperature change (∆T) and Mauna Loa CO2 change (∆CO2). Smoothing is done with a Gaussian average, with a “Full Width to Half Maximum” (FWHM) width as given in the legend. Black circles shows peak correlation for various smoothing widths. As above, a “0 month” average shows the lagged correlations of the raw data itself.
Note what happens as the smoothing filter width is increased. What start out as separate tiny peaks at about 3-5 and 11-14 months end up being combined into a single large peak at around nine months. Note also how the lag of the peak correlation changes as the smoothing window is widened. It starts with a lag of about 4 months (purple and blue 2 month and 6 month smoothing lines). As the smoothing window increases, the lag increases as well, all the way up to 17 months for the 48 month smoothing. Which one is correct, if any?
To investigate what happens with random noise, I constructed a pair of series with similar autoregressions, and I looked at the lagged correlations. The original dataset is positively autocorrelated (sometimes called “red” noise). In general, the change (∆T or ∆CO2) in a positively autocorrelated dataset is negatively autocorrelated (sometimes called “blue noise”). Since the data under investigation is blue, I used blue random noise with the same negative autocorrelation for my test of random data. However, the exact choice is immaterial to the smoothing issue.
This was my first result using random data:
Figure 3. Cross-correlations of raw and smoothed random (blue noise) datasets. Smoothing is done with a Gaussian average, with a “Full Width to Half Maximum” (FWHM) width as given in the legend. Black circles show peak correlations for various smoothings.
Note that as the smoothing window increases in width, we see the same kind of changes we saw in the temperature/CO2 comparison. There appears to be a correlation between the smoothed random series, with a lag of about 7 months. In addition, as the smoothing window widens, the maximum point is pushed over, until it occurs at a lag which does not show any correlation in the raw data.
After making the first graph of the effect of smoothing width on random blue noise, I noticed that the curves were still rising on the right. So I graphed the correlations out to 60 months. This is the result:
Figure 4. Rescaling of Figure 3, showing the effect of lags out to 60 months.
Note how, once again, the smoothing (even for as short a period as six months, green line) converts a non-descript region (say lag +30 to +60, right part of the graph) into a high correlation region, by the lumping together of individual peaks. Remember, this was just random blue noise, none of these are represent real lagged relationships despite the high correlation.
My general conclusion from all of this is to avoid looking for lagged correlations in smoothed datasets, they’ll lie to you. I was surprised by the creation of apparent, but totally spurious, lagged correlations when the data is smoothed.
And for the $64,000 question … is the correlation found in the Macrae study valid, or spurious? I truly don’t know, although I strongly suspect that it is spurious. But how can we tell?
My best to everyone,
w.
Try wayback machine: http://web.archive.org/web/20041230090904/http://www.john-daly.com/
Try the internet archive: http://web.archive.org/web/20041230090904/http://www.john-daly.com/
Correlation is not
causationcorrelation. Thanks, WillisThis has some similarities to an essay I wrote a few years ago when the first BEST results were made public. I was concerned by the large correlation coefficients between temperatures at large station separations, the graph is in the following.
It started off with a bit of geostatistics, a sub-discipline that I think needs more examination for context in climate work. It deals a lot with lagged data and correlations.
For simplicity, I started with a single station and then lagged various blocks of Temperature data from daily to monthly to annual, separating Tmax from Tmin, showing that at this station (Melbourne BoM Central) they had different behaviour.
A four-part series was intended, but the first part (here) drifted off because there was too much noise in the data.
I’d really appreciate some feedback as I know Willis would also, because as you take these concepts further they end up interacting with procedures like gridding, interpolating, contouring, map making etc. I think that we have a current case in Australia where maps showing Australia temperature as a whole have some bad looks about them and some headlines that might not be supportable.
I will have to learn R program. I started with machine language in 1969.
http://www.geoffstuff.com/GHS%20on%20chasing%20R%2c%20extended.pdf
Willis – I always enjoy your contributions. Particular thanks this time for noting the exemplar of McIntyre to thoroughness and the gentlemanly art of polite disagreement.
Both of you have the gift of droll wit, pointed irony, and damnation with faint praise.
From my geological perspective, I can only say that “Because the world has not gone to ruin in the past, it is highly unlikely to do so in the future. Any belief to the contrary is an arrogance of human influence.”
This post leaves me with more questions than answers & my gut says something is wrong with the calculations here , although not enough information is provided to tear this apart.
“Since the data under investigation is blue”. Is it really ? Did you look at the power spectrum & did it have increasing power density with increasing frequency? Very few signals in nature have this characteristic. This would surprise me, but since the original data sets & their associated power spectra aren’t present, I really can’t say if this is right or not (this is critical to the rest of the thoughts below). So, I would love to see a plot of the original raw data & it’s power spectra if you could add those to this post – that would certainly help clarify things. Next, is this the character of both the CO2 signal & the temp signal vs time ( That would be even more surprising !! ).
All that being said, if the data has a blue characteristic to it, a gausian filter will hammer the data. Remember that a gausian filter is basically a high cut / low pass filter . If the data is blue, then most of the energy is in the higher frequencies , so if we run a gausian filter over the data, we will remove most of the energy from the data (and that’s likely where the signal is – the rest may be just noise). So, again, looking at the original datasets, filtered & unfiltered would be instructive & useful. If the data is blue, the filtered data is going to look like a very lazy & very flat signal compared to the unfiltered signal – is that in fact the case ? As described , it should be – since most of the energy (amplitude) was in the higher frequencies – which you filtered out – so the remaining signal has very little amplitude of all & may only be the noise component of the dataset.
Which bring us to the next point – a proper cross-correlation of signals pre-conditions the signal by dividing through by the mean, but the mean has now been completely changed by the filtering. Just because you are getting a strong cross-correlation peak with the filtered data doesn’t mean anything now – as again, if the data is blue, you have basically removed the majority of the energy from the signal – all it is saying is that there is some sort of correlation in the low frequencies, which supposedly don’t have much energy in them to start with – it could just be showing you some non-random noise in the datasets .
Again, the way this is all presented, it leaves me with a whole lot more questions than answers. A re-post showing all the intermediate steps, with datasets vs time, associated power spectra, filtered data sets & spectra & ultimately the cross-correlations, both filtered & unfiltered would be a lot more instructive & would help answer your question :
” … is the correlation found in the Macrae study valid, or spurious? ”
I don’t think you even need to do the random data set if you can set forth the above plots – it should be pretty obvious whether it is valid or not & exactly what the physical meaning of the cross-correlations are (both filtered & unfiltered).
BTW, thanks for the tip on R – I will be looking into that!
Willis,
About a week ago I noticed John Daly’s site was suspended. I inquired at Jo Nova’s site and she said it had been down for about a week already at that time. John’s wife passed away last year. So it may be down permanently. Jo inquired of someone in the area who is trying to get more information, but she hadn’t heard back. I’m with you, it would be a shame to have John’s site gone permanently, but John passed in 2004 and eventually all good things come to an end.
“Since then I’ve learned… several dialects of Basic including… Assembly Language…”
I truly hope there was an editing problem here. Actually, probably should say “… and several others including Basic… Assembly Language…”
[Thanks, clarified I think. -w.]
Who let John Daly become suspended?
nice.
for those wanting to learn R. get Rstudio.
subscribe to the R list.
Domain Name: JOHN-DALY.COM
Registrar: DNC HOLDINGS, INC.
Whois Server: whois.directnic.com
Referral URL: http://www.directnic.com
Name Server: DNS1.HRNOC.NET
Name Server: DNS2.HRNOC.NET
Status: clientDeleteProhibited
Status: clientTransferProhibited
Status: clientUpdateProhibited
Updated Date: 18-jul-2009
Creation Date: 06-apr-2001
Expiration Date: 06-apr-2014
>>> Last update of whois database: Sun, 31 Mar 2013 04:07:23 UTC <<<
NOTICE: The expiration date displayed in this record is the date the
registrar's sponsorship of the domain name registration in the registry is
currently set to expire. This date does not necessarily reflect the expiration
date of the domain name registrant's agreement with the sponsoring
registrar. Users may consult the sponsoring registrar's Whois database to
view the registrar's reported date of expiration for this registration.
TERMS OF USE: You are not authorized to access or query our Whois
database through the use of electronic processes that are high-volume and
automated except as reasonably necessary to register domain names or
modify existing registrations; the Data in VeriSign Global Registry
Services' ("VeriSign") Whois database is provided by VeriSign for
information purposes only, and to assist persons in obtaining information
about or related to a domain name registration record. VeriSign does not
guarantee its accuracy. By submitting a Whois query, you agree to abide
by the following terms of use: You agree that you may use this Data only
for lawful purposes and that under no circumstances will you use this Data
to: (1) allow, enable, or otherwise support the transmission of mass
unsolicited, commercial advertising or solicitations via e-mail, telephone,
or facsimile; or (2) enable high volume, automated, electronic processes
that apply to VeriSign (or its computer systems). The compilation,
repackaging, dissemination or other use of this Data is expressly
prohibited without the prior written consent of VeriSign. You agree not to
use electronic processes that are automated and high-volume to access or
query the Whois database except as reasonably necessary to register
domain names or modify existing registrations. VeriSign reserves the right
to restrict your access to the Whois database in its sole discretion to ensure
operational stability. VeriSign may restrict or terminate your access to the
Whois database for failure to abide by these terms of use. VeriSign
reserves the right to modify these terms at any time.
The Registry database contains ONLY .COM, .NET, .EDU domains and
Registrars.Registration and WHOIS Service provided by Directnic.com
DNC Holdings, Inc. provides the data in the directNIC.com Registrar WHOIS
database for informational purposes only. The information may only be
used to assist in obtaining information about a domain name's registration
record. The use of this data for any other purpose without prior written
consent by DNC Holdings, Inc. is expressly forbidden.
By submitting a WHOIS query, you agree to all the terms and limitations
herein and that you will use this data only for lawful purposes. You also
agree that under no circumstances will you use this data to:
(a) allow, enable, or otherwise support the transmission by email,
telephone, or facsimile of mass, unsolicited, commercial advertising or
solicitations, including, but not limited to, spam, to entities other than
the data recipient's own existing customers;
(b) enable high volume, automated, electronic processes that send queries
or data to the systems of any Registry Operator or ICANN-accredited
registrar or
(c) enable any automated or robotic processes to collect or compile data
for any purpose, including data mining.
DNC Holdings makes this information available "as is", and provides no guarantee
or warranty as to its accuracy.
Registrant:
Jerry Brennan
5 Craigmoor Terrace
Danbury, CT 06810
US
203 743 7899
Domain Name: JOHN-DALY.COM
Administrative Contact:
Brennan, Jerry brennan@john-daly.com
5 Craigmoor Terrace
Danbury, CT 06810
US
203 743 7899
Technical Contact:
Brennan, Jerry brennan@john-daly.com
5 Craigmoor Terrace
Danbury, CT 06810
US
203 743 7899
Record last updated 03-20-2004 08:22:50 PM
Record expires on 04-06-2014
Record created on 04-06-2001
Domain servers in listed order:
DNS1.HRNOC.NET 216.120.225.19
DNS2.HRNOC.NET 216.120.238.254
The compilation, repackaging, dissemination, or other use of this WHOIS
data is expressly prohibited without the prior written consent of
DNC Holdings, Inc.
DNC Holdings reserves the right to terminate your access to its WHOIS
database in its sole discretion, including without limitation, for
excessive querying of the database or for failure to otherwise abide by
this policy.
DNC Holdings reserves the right to modify these terms at any time.
NOTE: THE WHOIS DATABASE IS A CONTACT DATABASE ONLY.
LACK OF A DOMAIN RECORD DOES NOT SIGNIFY DOMAIN AVAILABILITY.
” Fortran, LISP/LOGO, C, C++, several dialects of Basic including Visual Basic, Pascal, Hypertalk, Datacom, Assembly Language, VectorScript, and a couple of the Mathematica languages. ”
But no LabView; that, my friend, (LV) represents a paradigm shift …
BTW, for those interested Mathics (*1) a Mathematica look-alike “is a free, general-purpose computer algebra system featuring Mathematica-compatible syntax and functions”
Mathics also offers an online calc engine, then there is Wolfram Alpha (*2), a “computational knowledge or answer engine developed by Wolfram Research”
*1 – http://www.mathics.org/
*2 – http://www.wolframalpha.com/
.
Thanks, Willis. Most instructive.
And thanks for the “R” plug. I’ll add:
An Introduction to Statistics – R Tutorial: http://www.r-tutor.com/
The Blackboard » Learning R: http://rankexploits.com/musings/category/statistics/learning-r/
I believe William Briggs, professional statistician, counsels against smoothing data. Here is the link to his blog on this subject. http://wmbriggs.com/blog/?p=195
I have an idea why the smoothed data shows a correlation and a lag, and
the unsmoothed does not.
There are annual cycles in global temperature and in CO2 level. The
annual cycle in global temperature comes from the northern hemisphere
having more land and less water than the southern hemisphere, and so
the northern hemisphere has greater seasonal variation in temperature.
Global troposphere temperature probably peaks in August, when the
northern hemisphere as a whole (land and sea, including temporarily
ice-covered sea) is hottest. Or a little after northern hemisphere land
temperature or maybe surface temperature peaks – the surface warms the
troposphere, so the troposphere lags the surface – or at least lags land.
Also, seasons on northern hemisphere extratropical land affects that
land’s production and capture of CO2. CO2 tends to peak in May, just
before northern hemisphere vegetation gets busiest at converting CO2
to biomass.
As for lack of correlation in the unsmoothed data: I suspect the
unsmoothed data has its variations mainly short-term noisy or noise-like
ones that the smoothing removes. I suspect that a spectrum analysis of
the temperature and CO2 datasets will show most of the “AC content”
being at frequencies high enough for the smoothing to largely remove.
And the short term (few months or less) noise items and “noise-
resembling signals” in one dataset are unlikely to have much all-same-
lag correlation with each other, if any at all.
I thought that’s a pretty old rule: never analyze smoothed data. When you average over
data points, you are causing correlation between each point and the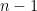 
others it was averaged with.
Steven Mosher says:
March 30, 2013 at 9:11 pm
Thanks, Mosh. Since I’d not heard of either one, let me add the links:
Rstudio I just took a look at that, very, very impressive. I’m migrating, at least I think so …
R list
I wasn’t clear which list you referred to, as the cite says there are four of them.
Regards, appreciated,
w.
I think that the breadth of features and ease of use of R can make it *too* simple for modelers and data analysts to achieve glib results from methods which they have not adequately analyzed.
The technology should perhaps be harder and more conducive to requiring careful thought about what is being done at each step.
Something like Haskell, which is a pure functional language and therefore very unforgiving of sloppy work, would be my preference.
_Jim says:
March 30, 2013 at 9:14 pm
True ‘dat … I played with it a little, never could afford the modules. I did like the paradigm, though. That kind of visual building-block programming was used as well in a database whose name now escapes me.
w.
Readers might want to follow with these:
“Do not smooth times series, you hockey puck!”
3 in a series by William M. Briggs
Number I:
http://wmbriggs.com/blog/?p=195
Number II:
http://wmbriggs.com/blog/?p=86
Number III:
http://wmbriggs.com/blog/?p=735
I just realized something else: Looking at smoothings of more than a year,
the correlation time increases with smoothing time. I suspect the reason here
is that for longer term smoothing, annual cycles are smoothed out.
When smoothing is Gaussian with FWHM of 9-12 months, CO2 lag is
seasonal. With longer term smoothing, the lag could increase due to the
smoothing causing the correlation to concentrate more on longer term
correlations, such as with more lag when the (non-constant) positive
feedbacks are greater.
Something else I noticed: The correlation curves for smoothing by 2 to 24
months appear to me to have a fair amount of symmetry about zero both
horizontally and vertically. I would expect seasonal variations to have a pair
of correlation peaks, one leading and one lagging, 1 year apart – showing
1-year periodicity, rather than symmetry about the origin (zero-zero point).
Or, am I missing something? Perhaps, temperature anomalies lasting a
few months to a year have an effect on production and decomposition of
biomass, causing biomass short-term-accumulated-decomposition to lag
upward temperature anomalies by almost a year.
Something else I noted: Figure 4 shows positive correlation running high
in longer correlation periods, when the two correlated datasets are random
samples of “blue noise”. Is not “blue noise” something biased to higher
frequency spectral content? If random samples repeat positive correlation
towards longer of periods of correlation, then I question the correlation
method. Does the correlation method intrinsically have a bias to indicate
positive correlation – even (and especially) if for long lag periods and higher
frequency noise spectral content? Since Fig. 4 shows mostly positive
correlation over all of the frequencies being considered, I would suspect the
smoothing method to have a bias to show positive correlation, especially at
frequencies among the lower frequency ones being considered.
By any chance, does the smoothing method use RMS calculations for
smoothing when calculations of averages instead of RMS could be what
shows a type of random noise to be random?
An interesting read on smoothing data:
http://wmbriggs.com/blog/?p=195
Slightly OT, but after reading this post I checked John Daly’s Wikipedia entry. What a shambles.
He gets less than this week’s reality TV nobody, and looking at the history of amendments, his entry has been a battleground for years even though he died in 2004.
I suppose that it’s a backhanded compliment (the Supreme Censor Connolly has been involved), but it’s just another reminder that Wiki is really useful for checking episode guides for your favourite TV show, but utterly unreliable when it comes to anything that is contested.
Just saw this:
http://www.dailymail.co.uk/news/article-2301757/Governments-climate-watchdog-launches-astonishing-attack-Mail-Sunday–revealing-global-warming-science-wrong.html
“The empire strikes back”?????
Shameless commercial plug – do read my little essay about 4 posts down from the top, because it raises similar outcomes but without smoothing. It simply uses averaging, as in making days into weeks. And the process constructs artefacts from numbers. And people make the mistakes daily.
I learned Algol on the great god Burroughs B5500 back in 1967. Hollerith cards, overnight batch processing. The advanced Computer Science majors were using a new high-level language called BASIC.
@Willis: You’ll probably want to subscribe to -help and -announce.
cheers,
gary
For muti-varaible correlation use the software “formulize” available on http://www.nutonian.com (for free for limited dataset, in earlier times it was totally free).
You can get amazing results as for example this: http://climate.mr-int.ch/NotesImages/Correlation_1.png which correlates observed monthly temperature anomalies (HADCRUT3) with Atlantic Multi Decadal Oscillations (AMO), El Niño-La Niña, transmitted solar radiation (which reveals volcanic eruptions almost as a Dirac impulse), CO2 atmospheric concentration, and solar spots. Caution: correlation does not necessarily imply causation!
wrt the delay from temperature to CO2:
There is a lot of noise in data for both temperature and CO2. However, the 1998 El Nino shows up quite clearly –
http://members.westnet.com.au/jonas1/CO2FocusOn1998.jpg
Temperature is RSS TLT Tropics Ocean for the given date.
CO2s are as at the given date, averaged over various stations in each of the 5 given regions, minus the same value as at 12 months earlier.
The delay from temperature to CO21 is clearly visible. Interestingly, there isn’t a large difference in travel times.
It’s easier to see if the CO2 data is smoothed –
http://members.westnet.com.au/jonas1/CO2FocusOn1998Smoothed.jpg
Is it OK to use smoothed data for this? It looks OK in this example, but as W shows, it’s best to check carefully, and to do proper calcs on the unsmoothed data if you’re using it for anything other than just seeing what it looks like.
PS. Tropic temperature is scaled in the 2 graphs for easy visual comparison. It isn’t smoothed.
Additional note to my previous post at 1:01 am: no smoothing was made prior to the correlation. But the Hadley dataset is anyway the result of data massaging to calculate global averages etc.
johanna says: March 31, 2013 at 12:09 am
Slightly OT, but after reading this post I checked John Daly’s Wikipedia entry. What a shambles.
____________________________
So why not update it? Unfortunately, I don’t know enough about him to do it myself, but surely someone here can tidy it up and explain things a bit more.
.
Willis, what you have discovered by this study is that “smoothers” don’t smooth they corrupt.
Maybe you should have used a filter instead.
I say this because those who are using a “smoother” usually don’t even realise they are using a filter. They just want the data to look “smoother”. If they realised they needed to low pass filter the data, they would realise they needed to design a filter or chose a filter based of some criterion. That would force them to decide what the criterion was and chose a filter that satisfies it.
Sadly, most times they just smooth and end up with crap.
This is one of my all biggest time gripes about climate science, that they can not get beyond runny mean “smoothers”.
You have not shown that you should not filter data, what you have shown is that runny means are a crap filter. . That’s why I call them runny mean filters. You use them and end up with crap everywhere.
The frequency response of the rectangular window used in a running mean is the sync function. It has a zero ( the bit you want to filter out is bang on ) at pi and a negative lobe that peaks at pi*1.3317 ( tan(x)=x at 1.3771*pi if you were wondering ) .
This means that it lets through stuff you imagined you “smoothed” away . Not only that but it inverts it !!
Now guess what? 12 / 1.3317 = 8.97 BINGO
Your nine month correlation is right in the hole.
Now have a look at the data and the light 2m “smoother” There is a peak either side and a negative around 8 months !! It is that 8m negative peak that is getting trough the 12m smoother and being inverted.
Not only have you let through something you intended to remove , you turned it upside down and made a negative correlation into a positive one.
So Allan Macrae may (or may not) have found true correlation but if he did it was probably negated.
There was a similar article that got some applause here a while called something like “Don’t smooth , you hockey puck” in which the author made similar claims similarly based SOLEY on problems of runny means. He totally failed to realise it was not whether you filter but waht filter you choose. But there again he was talking about “smoothers” so probably had not even realised the difference.
I emailed him explaining all this and got a polite but dismissive one word reply: “thanks”.
I really ought to right this up formally and post it somewhere.
Bottom line: don’t smooth, filter. And if you don’t know how to filter either find out or get a job as a climate scientist 😉
BTW there is +ve correlation in CO2 at about 3m though 0.1 looks a bit low in terms of 95% confidence.
Of course the other problem is that he’s also starting with monthly averages , which are themselves sub-sampled running means of 30 days. That’s two more data distortions, the mean and then sub sampling without a proper anti-alias filter.
With a method like that you’d be better flipping a coin. There’s a better chance of getting the right answer.
And I kid you not, this is par for the course in climatology.
Nice discussion of sawtooth CO2 @ the end of that old thread.
========================
FWIW, I think the fact that temperature leads CO2 jumps out of the data.
Look here http://www.robles-thome.talktalk.net/carbontemp.pdf
This is just two charts: the twelve month change in atmospheric Carbon, and the twelve month change in temperature (HADCRUT3). These are the very noisy faint lines. The thick lines are the 12 month moving averages of each of these separately. Without doing any correlations, what leads what is very clear. My best fit is that temperature leads carbon by about 7 months.
There are no smoothed series being correlated here, so can be no spurious correlations. I’ll read the article again more slowly to see if it shows some errors in my analysis.
In addition to the numbers, there is of course a good reason why temperature should lead CO2: the gas is less soluble in warmer water, so higher temp is (eventually) more CO2.
The CO2 vs temperature lags are interesting.
But let’s remember CO2 has a seasonal cycle (which varies from location to location). It is tied to the vegetation growth and decay cycles which vary across the planet. It also moves across the planet with large-scale winds which also vary in time. CO2 also has a long-term exponentially increasing trend which should be taken into account.
Temperature, as well, has a seasonal cycle which varies from location to location. Normally we deal with anomalies that are adjusted for the known seasonal patterns but both of these series have seasonal cycles which are offset from each.
It’s hard to say CO2 lags X months behind Temperature changes without properly accounting for all these time series patterns properly.
If you are smoothing either of them improperly compared to their true seasonal and underlying increasing/decreasing trends, your X will not be the true one.
The Dangers of smoothing. (And if you are a climate scientist, a fabulous Opportunity to mislead, which is why nearly every climate science paper uses smoothed data ONLY. Reminds one of a recent Marcott and a recent Hansen paper).
RStudio is a step forward but Eclipse with the StatET add-on is more advanced. For example, multiple plot windows; ability to view multiple sections of code simultaneously; source code debugging with breakpoints; and views of variable space. Really great if you’re combining R with other languages such as C or Perl or Java. They can all be handled under Eclipse with appropriate add-ons.
Matt Briggs has a number of posts on the dangers inherent in smoothing, particularly when combined with prediction.
http://wmbriggs.com/blog/?s=smoothing&x=0&y=0
or just go to wmbriggs.com and search for “smoothing” if the above doesn’t work.
Silver Ralph says:
March 31, 2013 at 1:40 am
johanna says: March 31, 2013 at 12:09 am
Slightly OT, but after reading this post I checked John Daly’s Wikipedia entry. What a shambles.
____________________________
So why not update it? Unfortunately, I don’t know enough about him to do it myself, but surely someone here can tidy it up and explain things a bit more.
———————-
Ralph, people have been trying to do that for nearly a decade. That is my point.
Any attempt to write an objective account of John Daly’s work would immediately be jumped all over by the resident “rapid response team” on wikipedia.
I absolutely agree that someone who is young and wakeful and interested enough should take up the task. It is a worthy project.
As I am older, and need to husband my energy to what will get results (the 80/20 rule), this one is not for me. But, I will never forgive the bastards who sent, received, and subsequently acquiesced to (by silence) that awful email where they cheered John Daly’s death. That includes those who saw the first round of released emails, when it appeared, and said nothing.
Sorry, don’t have the reference at hand, but it is well known to Anthony and long term readers of WUWT.
MODS: I am willing to consider a hosting option for John Daly’s data mine.
Crispin
I was taught to smooth data only prior to display for human consumption, all previous steps and calculation were performed on unfiltered data.
After all, the unknown signal we are looking for is in the original data, careless filtering/smoothing can lose or change these signals.
In its infancy, smoothing of brainwave patterns was also fraught with complications and could result in lost peaks that were valuable in calculating stimulus onset to peak and peak to peak measures. Worse, an industry standard was not set early on so it was difficult to compare results across studies completed by different labs. Climate science is still in its infancy and is hardly making gains to become anything other than an infant.
I’d be happy to host it. I lease a dedicated Linux server and have plenty of space and bandwidth. No idea who I’d need to contact, so if anyone knows, my email is alberts dot jeff at gmail dot com.
Greg Goodman says:
March 31, 2013 at 2:21 am
“The frequency response of the rectangular window used in a running mean is the sync function. It has a zero ( the bit you want to filter out is bang on ) at pi and a negative lobe that peaks at pi*1.3317 ( tan(x)=x at 1.3771*pi if you were wondering ) .
This means that it lets through stuff you imagined you “smoothed” away . Not only that but it inverts it !!
Now guess what? 12 / 1.3317 = 8.97 BINGO
Your nine month correlation is right in the hole.”
————————————————————————————
I think you may be onto something here however, Willis states he used a gausian filter , implying a gausian operator / gauasian weights were applied in the smoothing, which would get rid of the sync function / ringing / bleeding issues associated with a square wave operator. Your assumption is that he basically used a square wave (no weights ) in calculating the smoothing. Now, based on Willis’ results & your analysis, I think you might be on to something – that the actual filtering was a square wave & not a gausian filter as stated. So, once again, this raises more questions & increases my suspicion there is something fundamentally wrong with the calculations presented here as there are many inconsistencies. None of it really makes sense as presented. I would add to my list of what I would like to see the filter operator & it’s associated power spectrum.
Answering the question of “… is the correlation found in the Macrae study valid, or spurious?” should not be a very hard question to answer – it just needs a different analysis – plots of the raw data , the filter operator(s), the filtered data, the spectra of all of the above & the then cross-correlations of both filtered & unfiltered data – if you could look at all of those together, anyone with some signal analysis background ought to be able to look the plots & answer the question, quickly & definitively.
Greg Goodman says:
March 31, 2013 at 2:21 am”
Yours is an intriguing comment. Anyone that can include crap, Bingo, and π in a few lines of text deserves a crack at a full-blown post. Set yourself down and have a go at getting your runny means and filtered points properly sorted out. I’ll suggest having a couple of others (Willis, Geoff S., ?) review it before posting. Why not ask Anthony if this would work for him, insofar as this is his site?
As somebody involved professionally in the analysis of time series for over a decade can I make a few points:
1, smoothing is of NO VALUE unless it is used to create a forecast; I don’t care what the “smooth trend” of past data is — the past data is the best presentation of the past data.
2, never-ever compute an auto-correlation function or cross-correlation function from data to which a process that induces auto-correlation has already been applied (i.e. from a smooth). The random errors of independent and identically distributed data are computable (or bootstrappable), and so the difference of your ACF or CCF from that expected for IID noise processes is also computable. Once you start throwing ad-hoc filters into the data, who knows how those errors are going to behave. Remember the window size of your filter is a degree of freedom that is being adjusted — are you using the standard error of that in your induced error covariance matrix?
3, there are so many ad-hoc smoothing windows thrown around because the make the data look “nice” to the analyst (see #1 above) that it makes one cringe.
Time series analysis was studied extensively by several excellent English statisticians. Kendall, Box and Jenkins made huge contributions. The Box-Jenkins book is really a gem. If you want to do any time-series analysis please read at least that — or Hamilton, for a more modern treatment. The Akiake Information Criterion (AICc) is an excellent tool to tune up Box-Jenkins style models to find the best approximating model for in-sample data. This is based upon very well defined information theoretic analysis of the estimation process.
When you don’t know what the underlying structure is, yes. If you do, however, then there’s nothing wrong with the practice.
Exactly.
Mark
gary turner says:
March 31, 2013 at 12:55 am
Thanks, Gary, noted. Also thanks again to Mosh, Rstudio is awesome.
w.
RERT says:
March 31, 2013 at 2:57 am
FWIW, I think the fact that temperature leads CO2 jumps out of the data.
Look here http://www.robles-thome.talktalk.net/carbontemp.pdf
This is just two charts: the twelve month change in atmospheric Carbon, and the twelve month change in temperature (HADCRUT3). These are the very noisy faint lines. The thick lines are the 12 month moving averages of each of these separately. Without doing any correlations, what leads what is very clear. My best fit is that temperature leads carbon by about 7 months.
What’s clear from that plot is that by the arbitrary shift of the CO2 axis by about -0.3% you’ve given the impression that the linear increase in CO2 independent of T doesn’t exist! What your graph actually shows is that CO2 increases steadily independently of temperature with a superimposed modulation due to temperature. As far as the lag is concerned, you don’t say whether your data is global or not, but if so there’s a problem due to the differences between the hemispheres, Arctic showing intra-annual fluctuations of ~10ppm, Mauna Loa ~5ppm, S Pole ~0ppm
Geoff L: ”
I think you may be onto something here however, Willis states he used a gausian filter , implying a gausian operator / gauasian weights were applied in the smoothing”
Willis (article): “In the Macrae study, he used smoothed datasets (12 month average) of the month-to-month change in temperature (∆T) and CO2 (∆CO2) to establish the lag between the change in CO2 and temperature . Accordingly, I did the same. ”
I read this to mean “running 12 month average” since he is clearly still working with monthly data , not annual data, as would be the case if it was (12 month average) as stated by Willis.
However, he does state later it was done with gaussian filters. So it appears that he was calling his 12m FWHM gaussian which would be an average over 72 months of data a “12 month average”. At least that’s the best I can make of it.
None of that goes against what I said about the problems with running means in general.
What would seem rather odd with what is reported of the McRae study is why anyone would look for a lag correlation of less than 12 months in data that they have tried to remove variations of less than twelve months from.
Jon says:
March 30, 2013 at 9:08 pm
> Who let John Daly become suspended?
His wife was keeping the site up in his memory, but from what I can glean so far, apparently she died last year and stopped paying the account fees. The domain name was maintained by someone else, and he seems to have disappeared fairly recently. The domain is paid through this year.
I expect that his site will appear, but possibly at a different URL. I and others are on the issue.
Mike Jonas says:
March 31, 2013 at 1:10 am
That’s a fascinating chart, Mike, thanks for the link. It’s an interesting analysis I’m not sure what it means, but I like it.
My interpretation is somewhat different from yours. I wrote a piece a few months ago called “The Tao of El Nino” The peak you show above in the air temperature reflects the initial El Nino stage of the El Nino/La Nina pump.
Once the tropical ocean heats up, the pump kicks in and moves that warm tropical water first westward across the Pacific, and then polewards, both north and south.
Of course, this process takes some time … and I suspect that the lag you show above between CO2 and temperature is the result of that process, rather than some delayed cause-effect lag.
I take a somewhat more middle position on this question than does William Briggs, whose opinion I respect greatly.
I smooth stuff all the time. But as you quote me as advising above, it’s good to be very cautious.
In particular, as the good Briggs advises, don’t use smoothed series for anything but display—that is to say, don’t utilize them as input to other transformations like say a lagged correlation analysis, as McCrae did, and as I did above to illustrate the problem.
But yes, I do use smooths, just as I use averages … and I’m not fond of using averages either. You may have noticed that much of my results of say the TAO buoys or the like are displays of the actual raw data.
w.
Greg Goodman says:
March 31, 2013 at 2:21 am
OK, so in your world a smoother IS NOT a filter.
(And as an aside, since I was studying the effect of what McRae had done, I used what he used, duh …)
OK, so in your world a smoother IS a filter, just not a very good filter.
Come back when you make up your mind. Until then, such an opening invites me to stop reading, and I did. Why should I listen to a man who says a smoother is not a filter and then turns around and says it is a filter?
w.
Jeff L says:
March 31, 2013 at 8:40 am
Jeff, thanks for pointing out the obvious problems with Greg Goodman’s analysis before I got there.
I used a Gaussian filter, with the specified FWHM, as detailed in the captions. Why is there any question about this?
And as to your final point, whether the problem was square wave filtering, since the problem appears (above) with Gaussian filtering, it is clearly NOT a problem associated with square wave filtering (although square wave might give the same or similar results to Gaussian, I didn’t investigate that).
w.
John F. Hultquist says:
March 31, 2013 at 9:44 am
I agree with you, John, I thought his post included crap, but mainly because he failed to notice that I was using a Gaussian rather than a square-wave filter …
w.
Willis, two things that I want to thank you for in this marvelous post: 1) You showed yourself totally unbiased (your letting the chips fall where they may as one has come to expect of you) – many sceptics may have, perhaps liked to see proven that Temperature leads CO2 but you didn’t give them satisfaction. 2) The best part: your post generated a flurry of evaluation and insight into the whys of the spuriousness of the method from very savvy practitioners ( Jeff L says: March 30, 2013 at 8:58 pm; Donald L. Klipstein says:March 30, 2013 at 10:47 pm; Greg Goodman says: March 31, 2013 at 2:21 am [his “Now guess what? 12 / 1.3317 = 8.97 BINGO” is a thesis in itself]; Bill Illis says: March 31, 2013 at 4:04 am [ Bill shows us that numerical “data” itself is at least one step removed from data in its native habitat – a geologist’s way of looking at things is the raw “derivative” before integration.]; apologies for some I missed out; and of course links to Briggs and others on the subject of smoothing.
I’ve used statistics as a geologist and engineer over many decades but, from what I see here, I’ve operated at a very low level. I think this post should be an introduction to a series of posts by the scary guys I have listed above. It would also be particularly interesting to have a theme of the use and misuse of statistics in climate science (or maybe not – I’d like all climate scientists to read it, too). It should even be the theme of a special conference and publication for use of statistical methods by scientists and engineers. No wonder the “consensus” has found itself in troubled waters of late. Bravo all of you.
John Daly’s site MUST be maintained!
I would have thought that Heartland would want to investigate and rescue it, if no one else….
FrozenOut says:
March 31, 2013 at 10:20 am
I appreciate your comments and that you work in the field.
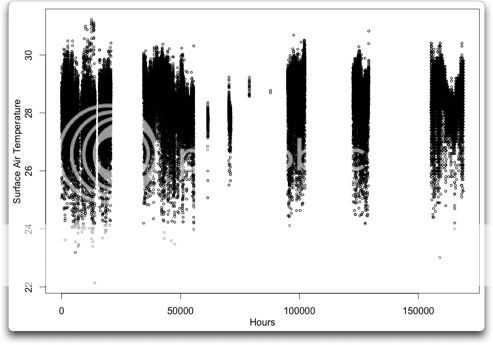
However, what I do is present BOTH the past data AND a smoothed version of the data. See the difference between Hansen’s and my presentations here for an example of what I mean.
And in those conditions, proper smoothing can have great value in allowing for and supporting the proper interpretation of the past data. I said “proper smoothing”, because Hansen’s smoothing is ridiculously improper.
If the data is noisy, or if there is a lot of data, it may not even be understandable without some kind of smoothing to make sense out of what is happening.
As to your claim that “the past data is the best presentation of the past data”, that assumes that data has some innate “presentation”. It has no such thing. We actively choose HOW to present that data. The presentation may involve separating it by time, as a time series. Or it may involve presenting it all as a “box and whiskers” plot or a “violin” plot of the shape of the distribution of the data. There is literally no end to the ways we can present past data.
I would say that the past data itself is the best INITIAL presentation of the past data, and that beyond that, there’s lots of other presentations (including smoothing and a variety of measurements of central tendency) that can further our understanding of that past data. Here’s an example. This is air temperature versus time for one of the TAO buoys:
I’d agree with you, Frozen, that that is the best initial presentation. And it is certainly the one that I always start with.
However, if that were overlaid, not replaced but overlaid with a smoothed version of the same data, I hold that the person reading the graph can learn more than just from the raw data itself.
All the best,
w.
Willis:
http://www.amazon.com/Handbook-Probability-Statistics-Richard-Burlington/dp/0070090300/ref=sr_1_1?s=books&ie=UTF8&qid=1364762591&sr=1-1&keywords=Handbook+of+Probability+and+Statistics+with+Tables
By this book! It is the most useful book on Statistics I’ve EVER come across. Gives you the REAL formulas, the applications, and the history/utility.
$3 and $5 shipping, USED…
Trust me, you are SO SHARP this will “complete your rapiere set” and you’ll cut the opposition (weak minded as they are) to ribbons with this!
Hello MODS, my comment seems to have become frozen between to Willis responses with the “awaiting moderation” still there.
Gary Pearse says:
Your comment is awaiting moderation.
March 31, 2013 at 1:11 pm
Willis says “[..] the El Nino/La Nina pump[..] moves that warm tropical water [..] this process takes some time … and I suspect that the lag you show above between CO2 and temperature is the result of that process, rather than some delayed cause-effect lag.” (http://wattsupwiththat.com/2013/03/30/the-pitfalls-of-data-smoothing/#comment-1262107)
Here’s my take: Before the warm water rises it contains just as much CO2 as the surface water. It can do this because it is at higher pressure. On reaching the surface, it releases CO2. That CO2 then travels across the planet giving the time delay shown in the graph. The air, with its CO2, travels faster than the ocean currents.
The connection between TLT tropical ocean temperature and CO2 is visible over the satellite period, not just at the 1998 El Nino, but there is quite a lot of noise and the delay isn’t constant (presumably because air currents vary).
This is elementary signal processing. irrespective of the computational language.
I would suggest that you study the underlting mathematics of filtering and correlation (see; Bendat & Piersiol ” Random Data” or Hayes “Statistical Signal Processing” ) rather than presenting empirical results.
John Daly’s site is back up and running.
http://www.john-daly.com/
Maybe someone should help the family keep the site open and even consider updating it to the present time?
Willis, look for a seasonal correlation between Mauna Loa and Northern hemisphere temperatures. CO2 rises through the winter, peaks in early spring, then declines though the summer. Here’s some Southern hemisphere CO2 data: http://www.esrl.noaa.gov/gmd/dv/data/index.php?site=smo
*sarc* So, you can see, increased CO2 leads to hemispheric warming in the spring.
Also, the decline in CO2 brings on winter.
/sarc
HI Willis,
I thought we settled this matter in my favour in 2008 – that dCO2/dt correlated with temperature, and CO2 lagged temperature by abut 9 months. I am looking for the correspondence – I recall the key points were on ClimateAudit.
As I recall, Matt Briggs avoided the alleged pitfales of “data smoothing” and still came up with a similar concousion, althouh the resolution using his methodology was no better than 12 months.
Incidentally, several parties have now “discovered” the same phenomenon (dCo2/dt, CO2 lags temperature), namely Murry Salby, among others.
Here is Murry Salby’s address to the Sydney Institute in 2011.
Here is a more recent presentation to the Sydney Institute by Salby:
Here is what I have found so far in emailsr.
From: Willis Eschenbach [mailto:willis@solomon.com.sb]
Sent: May-11-08 9:29 PM
To: Allan Macrae
Subject: Re: CARBON DIOXIDE IS NOT THE PRIMARY CAUSE OF GLOBAL WARMING: THE FUTURE CANNOT CAUSE THE PAST
Hey, Allan, good to hear from you.
The problem that I see with both your paper and the Kuo paper has to do with causation. Due to our “common sense” real world experience, we tend to assume that causation only goes one direction — the sun coming up causes the day to be light, but increasing light doesn’t cause the sun to rise.
But let’s look at another climate phenomenon, tropical cumulus clouds. The onset, type, and number of these is determined by (inter alia) the local surface temperature. But the local surface temperature, in turn, is determined by (inter alia again) the onset, type, and number of clouds. Clearly, causation in this cases is running in both directions. This situation is not uncommon in complex systems.
As a result, it may not be possible to say unequivocally that A causes B. This is particularly true when we may be dealing with different temporal scales. For example, it seems pretty clear that in the short term, increasing temperature causes the CO2 to increase. However, this does not prevent increasing CO2 from increasing temperature in the longer term. Both processes may be going on simultaneously at different time scales.
It is good, however, to find the Kuo et al. paper, which supports your claim that in the short term temperature leads CO2.
My best to you,
w.
PS – there is an interesting anecdote about causation which applies here. In a town, there are two clocks, we’ll call them by the imaginative names “Clock A” and “Clock B”. Clock B runs right on time, but Clock A is five minutes fast. So, every hour, Clock A strikes, and then five minutes later, Clock B strikes.
The question therefore arises … does Clock A cause Clock B to strike? I mean, every time Clock A strikes, five minutes later, Clock B strikes.
Or, to relate it to the subject under discussion … does the temperature rise cause the following CO2 rise? I mean, every time temperature rises, five months later the CO2 rises …
PPS – Kuo finds a five month lag, whereas you find a nine month lag. Have you determined why this difference exists, and what it means?
________________________________________
on 11/5/08 7:06 PM, Allan MacRae at firsst@shaw.ca wrote:
Hi Willis,
Please see the attached paper by Kuo et al.
Coherence established between atmospheric carbon dioxide and global temperature
ref. Kuo C, Lindberg C & Thomson DJ, Nature 343, 709 – 714 (22 February 1990)
Its summary says;
The hypothesis that the increase in atmospheric carbon dioxide is related to observable changes in the climate is tested using modern methods of time-series analysis. The results confirm that average global temperature is increasing, and that temperature and atmospheric carbon dioxide are significantly correlated over the past thirty years. Changes in carbon dioxide content lag those in temperature by five months.
I suggest that Kuo et al reaches similar conclusions to my paper published at:
http://icecap.us/index.php/go/joes-blog/carbon_dioxide_in_not_the_primary_cause_of_global_warming_the_future_can_no/
Best regards, Allan
Tuesday, February 05, 2008
Carbon Dioxide in Not the Primary Cause of Global Warming: The Future Can Not Cause the Past
Paper by Allan M.R. MacRae, Calgary Alberta Canada
Despite continuing increases in atmospheric CO2, no significant global warming occurred in the last decade, as confirmed by both Surface Temperature and satellite measurements in the Lower Troposphere. Contrary to IPCC fears of catastrophic anthropogenic global warming, Earth may now be entering another natural cooling trend. Earth Surface Temperature warmed approximately 0.7 degrees Celsius from ~1910 to ~1945, cooled ~0.4 C from ~1945 to ~1975, warmed ~0.6 C from ~1975 to 1997, and has not warmed significantly from 1997 to 2007.
CO2 emissions due to human activity rose gradually from the onset of the Industrial Revolution, reaching ~1 billion tonnes per year (expressed as carbon) by 1945, and then accelerated to ~9 billion tonnes per year by 2007. Since ~1945 when CO2 emissions accelerated, Earth experienced ~22 years of warming, and ~40 years of either cooling or absence of warming.
The IPCC’s position that increased CO2 is the primary cause of global warming is not supported by the temperature data. In fact, strong evidence exists that disproves the IPCC’s scientific position. This UPDATED paper and Excel spreadsheet show that variations in atmospheric CO2 concentration lag (occur after) variations in Earth’s Surface Temperature by ~9 months. The IPCC states that increasing atmospheric CO2 is the primary cause of global warming – in effect, the IPCC states that the future is causing the past. The IPCC’s core scientific conclusion is illogical and false.
There is strong correlation among three parameters: Surface Temperature (“ST”), Lower Troposphere Temperature (“LT”) and the rate of change with time of atmospheric CO2 (“dCO2/dt”). For the time period of this analysis, variations in ST lead (occur before) variations in both LT and dCO2/dt, by ~1 month. The integral of dCO2/dt is the atmospheric concentration of CO2 (“CO2”).
I figured out the content provider for john-daly.com and contacted them a stateside operation in New York. The support person stuck with working on Easter unsuspended the account while we figure what to do with it. I will refrain from saying http://john-daly.com/ has arisen. 🙂
REPLY: Excellent work Ric! – Anthony
REPLY: Let me add my congratulations as well, nicely done. The combined power of the WUWT folks is awesome. -w.
Still looking for the key correspondence. Sorry about all the typos in my previous message.
Also see Keeling et al (1995):
http://climateaudit.org/2008/02/12/data-smoothing-and-spurious-correlation/#comments
Allan MacRae
Posted May 12, 2008 at 5:57 PM
Interannual extremes in the rate of rise of atmospheric carbon dioxide since 1980
C. D. Keellng*, T. P. Whorf*, M. Wahlen* & J. van der Plicht†
* Scripps Institution of Oceanography, La Jolla, California 92093-0220, USA
† Center for Isotopic Research, University of Groningen, 9747 AG Groningen, The Netherlands
Nature, Vo. 375, 22 June 1995
OBSERVATIONS of atmospheric C02 concentrations at Mauna Loa, Hawaii, and at the South Pole over the past four decades show an approximate proportionality between the rising atmospheric concentrations and industrial C02 emissions. This proportionality, which is most apparent during the first 20 years of the records, was disturbed in the 1980s by a disproportionately high rate of rise of atmospheric CO2, followed after 1988 by a pronounced slowing down of the growth rate. To probe the causes of these changes, we examine here the changes expected from the variations in the rates of industrial CO2 emissions over this time, and also from influences of climate such as EI Niño events. We use the 13C/12Cratio of atmospheric CO2 to distinguish the effects of interannual variations in biospheric and oceanic sources and sinks of carbon. We propose that the recent disproportionate rise and fall in CO2 growth rate were caused mainly by interannual variations in global air temperature (which altered both the terrestrial biospheric and the oceanic carbon sinks), and possibly also by precipitation. We suggest that the anomalous climate-induced rise in CO2 was partially masked by a slowing down in the growth rate of fossil-fuel combustion, and that the latter then exaggerated the subsequent climate-induced fall.
An unexpected slowing in the rate of rise of atmospheric CO2 appeared recently in measurements of CO2 made at Mauna Loa Observatory, Hawaii and the South Pole…
In summary, the slowing down of the rate of rise of atmospheric CO2 from 1989 to 1993, seen in our data and confirmed by other measurements6,15, is partially explained (about 30% according to Fig. Ie) by the reduction in growth rate of industrial CO2 emissions that occurred after 1979. We further propose that arming of surface water in advance of this slowdown caused
an anomalous rise in atmospheric CO2, accentuating the subsequent slowdown, while the terrestrial biosphere, perhaps by sequestering carbon in a delayed response to the same warming, caused most of the slowdown itself…
… We point out, in closing, that the unprecedented steep decline in the atmospheric CO2 anomaly ended late in 1993 (see Fig. Ie). Neither the onset nor the termination was predictable. Environmental factors appear to have imposed larger changes on the rate of rise of atmospheric CO2 than did changes in fossil fuel combustion rates, suggesting uncertainty in projecting
future increases in atmospheric CO2 solely on the basis of anticipated rates of industrial activity.
Sorry – I’m tired of looking – Anyway, here is a note from Ken Gregory:
I really lost my intense interest in this subject several years ago since I have no time to pursue it.
http://climateaudit.org/2008/02/12/data-smoothing-and-spurious-correlation/#comments
Ken Gregory
Posted Feb 16, 2008 at 5:55 PM
The third paragraph of Willis Eschenbach original post of February 12 says:
“In the MacRae study, he used smoothed datasets (12 month average) of the month-to-month change in temperature (∆T) and CO2 (∆CO2) to establish the lag between the change in CO2 and temperature . Accordingly, I did the same.”
This is false. Allan MacRae never calculated any month-to-month change in either temperature or CO2 or ∆CO2.
The temperature curves are all 12 month averages of the detrended temperatures.
The CO2 curve is the 12 month average of the detrended CO2 concentration.
The ∆CO2/yr curve is the 12 month change of the 12 month average of the detrended CO2 concentration.
I suggest the original post should be corrected.
It seems that Willis confused detrending with taking a derivative. Note that all the temperature curves in the paper are labeled LT or ST, not delta LT and delta ST. Detrending temperature is just plotting the difference between temperature and the temperature trend line, effectively rotating the graph to change the best fit slope to zero, so the detrended best fit line is now horizontal at 0 Celsius.
In post number 125, Willis correctly says that Allan compared ∆CO2 to Temp, rather that ∆Temp.
Willis then says “I cannot say from this that there is any lead or lag. Which is what I would expect rather than a several month lag, the globe reacts quickly.”
Of course, Allan’s analysis also shows that there is no significant lag between ∆CO2 and Temp, so Willis and Allan agree on this point. But why does Wilis say “rather than a several month lag”? Nobody every suggested that there was a lag of ∆CO2 of several months!
Allan’s analysis shows a lag of 9 months of CO2 wrt temperature, but no significant lag of ∆CO2 to Temperature.
Here is a more recent paper (2012) that reaches similar conclusions. Please note the conclusion:
“Changes in global atmospheric CO2 are lagging about 9 months behind changes in global lower troposphere temperature.”
I thank Richard Courtney for drawing my attention to the Kuo and Keeling papers some months after I published on icecap.us
I did have the prior benefit of several (excellent imo) papers by Jan Veizer et al.
I recall I did considerable work on this question in 2008 and did not change my conclusion then, and see no reason to do so now.
However, I think this subject is a little more complicated than my frazzled brain can handle today.
Happy Easter everyone, and
Best to all, Allan
http://wattsupwiththat.com/2012/08/30/important-paper-strongly-suggests-man-made-co2-is-not-the-driver-of-global-warming/
Important paper strongly suggests man-made CO2 is not the driver of global warming
Posted on August 30, 2012 by Anthony Watts
Fig. 1. Monthly global atmospheric CO2 (NOOA; green), monthly global sea surface temperature (HadSST2; blue stippled) and monthly global surface air temperature (HadCRUT3; red), since January 1980. Last month shown is December 2011.
Reposted from the Hockey Schtick, as I’m out of time and on the road.- Anthony
An important new paper published today in Global and Planetary Changefinds that changes in CO2 follow rather than lead global air surface temperature and that “CO2 released from use of fossil fuels have little influence on the observed changes in the amount of atmospheric CO2” The paper finds the “overall global temperature change sequence of events appears to be from 1) the ocean surface to 2) the land surface to 3) the lower troposphere,” in other words, the opposite of claims by global warming alarmists that CO2 in the atmosphere drives land and ocean temperatures. Instead, just as in the ice cores, CO2 levels are found to be a lagging effect ocean warming, not significantly related to man-made emissions, and not the driver of warming. Prior research has shown infrared radiation from greenhouse gases is incapable of warming the oceans, only shortwave radiation from the Sun is capable of penetrating and heating the oceans and thereby driving global surface temperatures.
The highlights of the paper are:
► The overall global temperature change sequence of events appears to be from 1) the ocean surface to 2) the land surface to 3) the lower troposphere.
► Changes in global atmospheric CO2 are lagging about 11–12 months behind changes in global sea surface temperature.
► Changes in global atmospheric CO2 are lagging 9.5-10 months behind changes in global air surface temperature.
► Changes in global atmospheric CO2 are lagging about 9 months behind changes in global lower troposphere temperature.
► Changes in ocean temperatures appear to explain a substantial part of the observed changes in atmospheric CO2 since January 1980.
► CO2 released from use of fossil fuels have little influence on the observed changes in the amount of atmospheric CO2, and changes in atmospheric CO2 are not tracking changes in human emissions.
The paper:
The phase relation between atmospheric carbon dioxide and global temperature
Ole Humluma, b,
Kjell Stordahlc,
Jan-Erik Solheimd
a Department of Geosciences, University of Oslo, P.O. Box 1047 Blindern, N-0316 Oslo, Norway
b Department of Geology, University Centre in Svalbard (UNIS), P.O. Box 156, N-9171 Longyearbyen, Svalbard, Norway
c Telenor Norway, Finance, N-1331 Fornebu, Norway
d Department of Physics and Technology, University of Tromsø, N-9037 Tromsø, Norway
________________________________________
Abstract
Using data series on atmospheric carbon dioxide and global temperatures we investigate the phase relation (leads/lags) between these for the period January 1980 to December 2011. Ice cores show atmospheric CO2 variations to lag behind atmospheric temperature changes on a century to millennium scale, but modern temperature is expected to lag changes in atmospheric CO2, as the atmospheric temperature increase since about 1975 generally is assumed to be caused by the modern increase in CO2. In our analysis we use eight well-known datasets; 1) globally averaged well-mixed marine boundary layer CO2 data, 2) HadCRUT3 surface air temperature data, 3) GISS surface air temperature data, 4) NCDC surface air temperature data, 5) HadSST2 sea surface data, 6) UAH lower troposphere temperature data series, 7) CDIAC data on release of anthropogene CO2, and 8) GWP data on volcanic eruptions. Annual cycles are present in all datasets except 7) and 8), and to remove the influence of these we analyze 12-month averaged data. We find a high degree of co-variation between all data series except 7) and 8), but with changes in CO2 always lagging changes in temperature. The maximum positive correlation between CO2 and temperature is found for CO2 lagging 11–12 months in relation to global sea surface temperature, 9.5-10 months to global surface air temperature, and about 9 months to global lower troposphere temperature. The correlation between changes in ocean temperatures and atmospheric CO2 is high, but do not explain all observed changes.
Allan MacRae says:
March 31, 2013 at 5:59 pm
Hi, Allan, glad to hear from you. Thanks for posting the correspondence, I lost my old emails in a crash a while back. I don’t recall Brigg’s work in this regard, but that means little after this much time, lots of water under the bridge since then, so you may well be right that it was settled in your favor. I took no position on that question, either then or now.
Instead, my point in this posting was the issue of spurious trends introduced by smoothing, not the particulars of your analysis which (as you point out above) may well be correct.
For those interested, the earlier discussion is here on ClimateAudit. There is a bunch of good stuff from Allan there.
Regards,
w.
RCS says:
March 31, 2013 at 3:59 pm
Another man who is all hat and no cattle … we pay little attention to such pompous sanctimonious lectures here, RCS. If you think you can do better, then grab the dataset and demonstrate your method to us. What I have presented here is a method for empirical determination of the relative strength of various methods for a given natural dataset (which may be far from normally distributed).
You claim to have a better way for smoothing the end-points of a given block of non-normal data? Fine. Show us your results. So far all you are is another in a long list, one more random anonymous internet popup with a big mouth and grandiose unverifiable claims.
w.
I have no difficulty accessing http://www.john-daly.com/
I have noticed that many on RealScience cannot access some NASA sites – especially http://pubs.giss.nasa.gov/docs/1988/1988_Hansen_etal.pdf
Again I have no problem with this.
I’m in Australia and I suspect you may be having your IP addresses blocked/censored.
SkepticalScience block my IP address – an easy workaround is via a proxy server but I no longer bother as such childish censorship displays a lack of any real science.
It would be interesting to know if some form of IP blocking/censorship is occurring !
Allan MacRae quotes, from a paper by Humlum et al:- ““CO2 released from use of fossil fuels have little influence on the observed changes in the amount of atmospheric CO2”“.
I have worked on the data and am satisfied that the above statement is incorrect. I am working on getting my calcs up to publication standard, which will take a while.
As far as I can tell, Humlum et al in their paper have compared short(ish)-term CO2 fluctuations with temperature, and have found a good correlation, and then have assumed that other factors are minor. However, CO2 changes driven by temperature follow quite a strong pattern which is easily seen, but man-made CO2 is pumped out at a relatively steady rate and therefore does not show up very well in short-term fluctuations. Looking at the effect of CO2 on temperature, the ‘consensus’ science is that high concentrations of CO2 affect temperature fairly streadily over quite long periods of time, ie. the temperature changes driven by CO2 would show little variability, so they too would be difficult to pick up in a study such as that by Humlum et al.
Other possible problems with the paper are
(a) the use of annual change in temperature, when actual temperature would be more relevant. The point is that the rate of atmospheric CO2 absorption or emission by the ocean is driven by temperature, not by how much the temperature differs from last year’s temperature.
(b) the use of annual change in man-made CO2 emissions, when actual emissions would be more relevant. All of the man-made emissions enter the atmosphere and therefore contribute to the change in atmospheric CO2 – not just the amount of CO2 emission which is different to last year’s emission.
HI Willis,
Here is Matt Briggs work.
http://wmbriggs.com/blog/?p=122
Best, Allan
Thank you Ric – great work on John Daly’s site.
I cannot recall the person’s name, but when John died someone took over management of his site and deleted some (many?) published papers, including one of more of my own, because they were allegedly copyright by newspapers or journals.
I protested that I owned all of my published articles since I had never accepted payment for any of them, but to no avail.
In any case, you may find John’s site somewhat depleted.
Allan MacRae says:
March 31, 2013 at 9:14 pm
First, you can’t really examine causality mathematically. You can examine Granger causality. Granger causality measures exactly what Matt is discussing, whether CO2 predicts temperature rise or vice-versa.
Next, in Granger causality there are four possible scenarios.
1). CO2 Granger-causes Temperature
2). Temperature Granger-causes CO2
3). Neither one Granger-causes the other.
4). CO2 Granger-causes Temperature —AND— Temperature Granger-causes CO2
Matt Briggs admits above that he “ignores the very real possibility” that each one Granger-causes the other … the problem is, I’ve done the analysis. The answer that I got was Number 4), that each one Granger-causes the other one. And that’s the one he ignores.
Finally, Matt’s conclusion is:
I would hardly call that a ringing endorsement of the idea that temperature changes cause CO2 changes 9 months later.
However, I intend to take another look at this, always new ideas and new datasets. Thanks for the push.
My best to you,
w.
Willis,
You asked me to show you what happens when you smooth real data using a Fourier method. Here is your UAH data. You can compare the original to 3 month and 12 month smoothed versions. Used R fft.
Time UAH UAH_3m UAH_12m
1979 -0.08 -0.008539224 -0.004108392
1979.08 0.05 0.001612929 -0.008500194
1979.17 -0.09 -0.003505892 -0.007833117
1979.25 -0.05 -0.037399051 -0.002801893
1979.33 -0.11 -0.04411988 0.005382925
1979.42 -0.06 -0.010358059 0.015363334
1979.5 0.06 0.027467731 0.02596757
1979.58 0.05 0.035534778 0.036426131
1979.67 0.07 0.047906606 0.046427538
1979.75 0.18 0.1002987 0.056018996
1979.83 0.24 0.111512434 0.065399103
1979.92 0.04 0.05729056 0.07467573
1980 0.15 0.059295181 0.083666377
1980.08 0.17 0.097500129 0.091801484
1980.17 0.08 0.068134228 0.098159222
1980.25 0.19 0.073608283 0.101622776
1980.33 0.25 0.154716442 0.101118341
1980.42 0.26 0.138009658 0.095872253
1980.5 0.1 0.042036078 0.085622971
1980.58 0.01 0.033513045 0.070737562
1980.67 0.13 0.063171411 0.052207687
1980.75 0.08 0.046366718 0.031529483
1980.83 0.02 0.027382731 0.010497033
1980.92 -0.01 -0.003469599 -0.009045598
1981 -0.13 -0.05458334 -0.025446277
1981.08 -0.14 -0.059952362 -0.037442264
1981.17 -0.08 -0.033014287 -0.044291027
1981.25 -0.06 -0.019244334 -0.045829816
1981.33 -0.02 -0.00786738 -0.042472645
1981.42 -0.09 -0.022762758 -0.035159026
1981.5 -0.11 -0.064752878 -0.025266516
1981.58 -0.17 -0.061034807 -0.01449179
1981.67 -0.03 -0.01059729 -0.004697239
1981.75 0.06 0.029047263 0.00228282
1981.83 0.03 0.04141028 0.004877085
1981.92 0.04 0.01312394 0.002040458
1982 -0.1 -0.037208206 -0.006486312
1982.08 -0.14 -0.052833261 -0.019970345
1982.17 -0.09 -0.050530566 -0.036593442
1982.25 -0.15 -0.057918495 -0.053527216
1982.33 -0.1 -0.036594655 -0.067210024
1982.42 0 -0.007612419 -0.073821857
1982.5 -0.1 -0.0251548 -0.069907281
1982.58 -0.12 -0.053150569 -0.053052181
1982.67 -0.11 -0.067678627 -0.022489248
1982.75 -0.26 -0.080284081 0.020499939
1982.83 0.04 -0.019058447 0.072496306
1982.92 0.19 0.142730891 0.128228101
1983 0.58 0.275704913 0.18121919
1983.08 0.58 0.30870024 0.224714983
1983.17 0.6 0.300739452 0.25273525
1983.25 0.47 0.258859023 0.261064556
1983.33 0.39 0.178114066 0.247989978
1983.42 0.22 0.150642807 0.214634787
1983.5 0.41 0.180501318 0.164809977
1983.58 0.19 0.134618412 0.10439851
1983.67 0.09 0.025461752 0.040380583
1983.75 -0.1 -0.017423268 -0.020318301
1983.83 -0.08 -0.047901454 -0.071937642
1983.92 -0.34 -0.155206865 -0.110740149
1984 -0.44 -0.209054099 -0.135459843
1984.08 -0.26 -0.124996617 -0.147267714
1984.17 -0.11 -0.049295701 -0.149282752
1984.25 -0.19 -0.076307351 -0.145748927
1984.33 -0.28 -0.139065626 -0.141063684
1984.42 -0.35 -0.175867018 -0.138866796
1984.5 -0.44 -0.175522427 -0.141375546
1984.58 -0.24 -0.169715304 -0.149089408
1984.67 -0.54 -0.196444501 -0.160899687
1984.75 -0.35 -0.219666637 -0.17454778
1984.83 -0.5 -0.210891237 -0.187300779
1984.92 -0.39 -0.193214843 -0.196671852
1985 -0.28 -0.143383562 -0.201013557
1985.08 -0.25 -0.090642384 -0.199853214
1985.17 -0.22 -0.136570089 -0.193909386
1985.25 -0.51 -0.209296927 -0.184809556
1985.33 -0.36 -0.197384789 -0.174601169
1985.42 -0.43 -0.205516742 -0.165194151
1985.5 -0.59 -0.257160512 -0.157882398
1985.58 -0.33 -0.204867631 -0.153063669
1985.67 -0.34 -0.116593715 -0.15021999
1985.75 -0.24 -0.131340683 -0.148149653
1985.83 -0.26 -0.132093733 -0.145375589
1985.92 -0.2 -0.062452903 -0.14061026
1986 -0.11 -0.073389226 -0.133145234
1986.08 -0.35 -0.154521136 -0.123056871
1986.17 -0.33 -0.154132216 -0.111171324
1986.25 -0.18 -0.08827268 -0.098798632
1986.33 -0.17 -0.071074766 -0.087309358
1986.42 -0.22 -0.108884238 -0.077671381
1986.5 -0.29 -0.118131279 -0.0700775
1986.58 -0.1 -0.072504037 -0.063772877
1986.67 -0.18 -0.048220315 -0.05714053
1986.75 -0.11 -0.064121747 -0.048036112
1986.83 -0.08 -0.039024939 -0.034297189
1986.92 -0.02 0.023499683 -0.014304373
1987 0.15 0.064196666 0.012545574
1987.08 0.2 0.100602866 0.045576365
1987.17 0.13 0.114145871 0.082850777
1987.25 0.24 0.071204166 0.121474902
1987.33 0.03 0.072221703 0.158121279
1987.42 0.35 0.161994422 0.189649371
1987.5 0.43 0.218564188 0.213676844
1987.58 0.37 0.208539132 0.228966315
1987.67 0.42 0.214241289 0.235537245
1987.75 0.52 0.251837623 0.234480477
1987.83 0.5 0.291134304 0.227526798
1987.92 0.62 0.287670661 0.216482591
1988 0.4 0.218580162 0.202679488
1988.08 0.28 0.170911136 0.186582551
1988.17 0.44 0.176220126 0.167662897
1988.25 0.09 0.121093935 0.144575239
1988.33 0.15 0.022267104 0.115604281
1988.42 -0.09 0.000905258 0.079274964
1988.5 0.03 0.016195098 0.034977134
1988.58 0.05 0.020118108 -0.016553758
1988.67 0.03 0.039619585 -0.073029233
1988.75 -0.07 -0.028613624 -0.130742556
1988.83 -0.4 -0.206958319 -0.185036977
1988.92 -0.64 -0.288475298 -0.231021999
1989 -0.52 -0.264874215 -0.264394328
1989.08 -0.62 -0.30806891 -0.282194366
1989.17 -0.74 -0.337704931 -0.283341049
1989.25 -0.49 -0.26281105 -0.268834462
1989.33 -0.5 -0.227048763 -0.241585769
1989.42 -0.48 -0.22846577 -0.205911552
1989.5 -0.29 -0.150500646 -0.166797106
1989.58 -0.23 -0.091316052 -0.129076236
1989.67 -0.19 -0.097618412 -0.096685154
1989.75 -0.14 -0.049984781 -0.072124691
1989.83 0.01 -0.005817707 -0.056215273
1989.92 -0.2 -0.061277952 -0.048165396
1990 -0.17 -0.110038428 -0.045911617
1990.08 -0.27 -0.102587896 -0.04663977
1990.17 -0.17 -0.079946411 -0.04737239
1990.25 -0.01 -0.013474499 -0.045508998
1990.33 0 0.037042589 -0.039230608
1990.42 0.03 -0.004440867 -0.027719063
1990.5 -0.12 -0.03026285 -0.011184775
1990.58 0.01 -0.001532182 0.009267084
1990.67 -0.03 0.006704662 0.031879289
1990.75 0.1 0.046872033 0.054535321
1990.83 0.19 0.109078801 0.07505149
1990.92 0.15 0.090721899 0.091434591
1991 0.2 0.088070493 0.102089649
1991.08 0.2 0.134378689 0.105975862
1991.17 0.16 0.070874825 0.102714012
1991.25 -0.01 0.004049484 0.092645485
1991.33 0.14 0.092924141 0.076835079
1991.42 0.29 0.138680077 0.057002678
1991.5 0.13 0.072096464 0.035368049
1991.58 0.05 0.059697961 0.014402099
1991.67 0.1 0.01501111 -0.003503232
1991.75 -0.32 -0.108773023 -0.016409601
1991.83 -0.18 -0.104887008 -0.023191172
1991.92 -0.07 -0.028557026 -0.023803456
1992 -0.13 -0.036729023 -0.019389822
1992.08 0.03 0.002028652 -0.012174714
1992.17 0.13 0.085877716 -0.005131198
1992.25 0.1 0.054799812 -0.001459142
1992.33 -0.02 0.004866796 -0.003958139
1992.42 0.01 -0.006639456 -0.014414004
1992.5 -0.27 -0.089520515 -0.033129028
1992.58 -0.22 -0.146432677 -0.058708706
1992.67 -0.3 -0.10162643 -0.088172561
1992.75 -0.17 -0.101854461 -0.117392186
1992.83 -0.3 -0.129648732 -0.141789264
1992.92 -0.21 -0.102411232 -0.157166107
1993 -0.3 -0.132959943 -0.160505791
1993.08 -0.39 -0.199477742 -0.150577771
1993.17 -0.35 -0.153005361 -0.128219838
1993.25 -0.13 -0.063678281 -0.096231914
1993.33 -0.05 -0.018274402 -0.058897664
1993.42 0.02 0.02699991 -0.021228369
1993.5 0.04 0.020199025 0.011917901
1993.58 -0.15 -0.064503633 0.036663629
1993.67 -0.19 -0.078251665 0.050721728
1993.75 0.08 0.030667082 0.053674226
1993.83 0.2 0.133240695 0.046880584
1993.92 0.32 0.141768093 0.033057851
1994 0.08 0.072994946 0.015643959
1994.08 -0.01 -0.01458152 -0.001903554
1994.17 -0.16 -0.06164302 -0.016717269
1994.25 -0.13 -0.056992449 -0.02691508
1994.33 -0.09 -0.044898105 -0.031718716
1994.42 -0.16 -0.054019932 -0.03130616
1994.5 -0.05 -0.041857399 -0.026474364
1994.58 -0.07 0.004466785 -0.018231189
1994.67 0.04 -0.002332096 -0.007444326
1994.75 -0.15 -0.041987995 0.005351446
1994.83 0.07 0.030366654 0.019941017
1994.92 0.26 0.140545623 0.036228281
1995 0.18 0.104307787 0.053926891
1995.08 0.05 0.023679644 0.072258818
1995.17 0.05 0.048339892 0.089780967
1995.25 0.2 0.084860144 0.104428263
1995.33 0.07 0.078988053 0.113801713
1995.42 0.26 0.096150372 0.115657424
1995.5 0.14 0.11597382 0.108486937
1995.58 0.25 0.114322758 0.092038858
1995.67 0.22 0.115184883 0.067629287
1995.75 0.12 0.086816777 0.038127084
1995.83 0.04 0.010913884 0.007572071
1995.92 -0.17 -0.071150561 -0.019526478
1996 -0.24 -0.103667472 -0.039079173
1996.08 -0.09 -0.047335732 -0.048303493
1996.17 0 0.011410818 -0.046402321
1996.25 -0.09 -0.0267085 -0.034860821
1996.33 -0.08 -0.049557025 -0.017264639
1996.42 -0.04 0.008550891 0.001354073
1996.5 0.05 0.014922697 0.015528932
1996.58 -0.07 -0.00792167 0.020529729
1996.67 0.1 0.040345949 0.013446565
1996.75 0.05 0.046189761 -0.006047569
1996.83 -0.09 -0.034926517 -0.03542911
1996.92 -0.16 -0.089818784 -0.069623018
1997 -0.32 -0.125100082 -0.101821654
1997.08 -0.29 -0.152346654 -0.124666935
1997.17 -0.27 -0.136624874 -0.131563414
1997.25 -0.38 -0.142797947 -0.117864634
1997.33 -0.15 -0.120512092 -0.081705216
1997.42 -0.04 0.040153405 -0.024329202
1997.5 0.42 0.180297304 0.050127504
1997.58 0.31 0.190158231 0.135330792
1997.67 0.43 0.201554277 0.223756878
1997.75 0.36 0.208525415 0.307803117
1997.83 0.42 0.207542664 0.380786687
1997.92 0.73 0.366317232 0.437661898
1998 1.08 0.575609721 0.475365531
1998.08 1.25 0.598366938 0.492790955
1998.17 1.04 0.554248257 0.490472911
1998.25 1.09 0.549054854 0.470116946
1998.33 0.91 0.449945986 0.434119762
1998.42 0.54 0.296215288 0.385199413
1998.5 0.45 0.226724119 0.326197782
1998.58 0.41 0.204014524 0.260049682
1998.67 0.3 0.180487157 0.189853404
1998.75 0.35 0.15735462 0.118943374
1998.83 0.14 0.103784813 0.050866244
1998.92 0.07 0.021387215 -0.010803473
1999 -0.18 -0.063537266 -0.062813738
1999.08 -0.22 -0.112132688 -0.102692123
1999.17 -0.22 -0.099708867 -0.129199203
1999.25 -0.26 -0.11654271 -0.142645807
1999.33 -0.39 -0.191000579 -0.144957913
1999.42 -0.39 -0.187892081 -0.139425235
1999.5 -0.28 -0.124472968 -0.130145837
1999.58 -0.26 -0.126801274 -0.121259946
1999.67 -0.28 -0.133857277 -0.116129921
1999.75 -0.24 -0.10247343 -0.116651635
1999.83 -0.21 -0.102803097 -0.122865577
1999.92 -0.22 -0.105692672 -0.132975102
2000 -0.28 -0.117875658 -0.143787559
2000.08 -0.37 -0.187849037 -0.151492915
2000.17 -0.39 -0.188177147 -0.152609085
2000.25 -0.24 -0.096551078 -0.144875467
2000.33 -0.17 -0.091470219 -0.127879789
2000.42 -0.29 -0.135640578 -0.103259563
2000.5 -0.26 -0.105194511 -0.074416317
2000.58 -0.13 -0.077247938 -0.045796107
2000.67 -0.15 -0.056582623 -0.021895839
2000.75 0.02 0.022737488 -0.006225574
2000.83 0.12 0.0656018 -0.000473807
2000.92 0.07 0.024547777 -0.004080314
2001 -0.18 -0.033309872 -0.014328168
2001.08 -0.05 -0.076990522 -0.02694441
2001.17 -0.2 -0.047699548 -0.03707665
2001.25 0.04 0.021113789 -0.040420033
2001.33 -0.02 -0.023297894 -0.034228931
2001.42 -0.23 -0.083232133 -0.017970812
2001.5 -0.01 0.006897479 0.006538164
2001.58 0.21 0.076856806 0.035554224
2001.67 -0.06 0.032608399 0.064288908
2001.75 0.2 0.060970662 0.088046707
2001.83 0.21 0.142600301 0.103346361
2001.92 0.26 0.123623769 0.108755393
2002 0.12 0.080455154 0.105233374
2002.08 0.19 0.092327213 0.095895582
2002.17 0.17 0.09469414 0.085247749
2002.25 0.1 0.079235608 0.078071129
2002.33 0.24 0.086374909 0.078224126
2002.42 0.12 0.117479715 0.087650528
2002.5 0.34 0.142222547 0.105838633
2002.58 0.19 0.118509976 0.129870272
2002.67 0.14 0.079350038 0.15505861
2002.75 0.19 0.099018491 0.176031854
2002.83 0.3 0.162100956 0.188010627
2002.92 0.45 0.225339891 0.187976332
2003 0.46 0.259352804 0.175449034
2003.08 0.48 0.218289399 0.15268201
2003.17 0.22 0.142112591 0.124215697
2003.25 0.17 0.095537426 0.095884616
2003.33 0.13 0.041274088 0.073501372
2003.42 -0.11 0.001273274 0.061520932
2003.5 0.13 0.036083502 0.061997103
2003.58 0.09 0.062904575 0.074078775
2003.67 0.07 0.061566385 0.094170796
2003.75 0.29 0.125182587 0.116731567
2003.83 0.31 0.183475415 0.13553208
2003.92 0.31 0.161481827 0.14509345
2004 0.32 0.155415837 0.141976958
2004.08 0.27 0.164552188 0.1256322
2004.17 0.27 0.121178996 0.098607825
2004.25 0.09 0.072859339 0.066072608
2004.33 0.03 0.013857437 0.034749397
2004.42 -0.13 -0.064491272 0.011495386
2004.5 -0.18 -0.050778639 0.001839769
2004.58 0.12 0.021097038 0.008797107
2004.67 -0.05 0.032304022 0.032211004
2004.75 0.18 0.064980974 0.0687634
2004.83 0.26 0.15214421 0.112637767
2004.92 0.35 0.180039879 0.156683149
2005 0.37 0.204132685 0.193821856
2005.08 0.62 0.291234476 0.218398814
2005.17 0.49 0.292656441 0.227193289
2005.25 0.39 0.168743346 0.219896666
2005.33 0.12 0.084883558 0.198982487
2005.42 0.17 0.099370989 0.169028269
2005.5 0.28 0.127816237 0.135662655
2005.58 0.16 0.114743146 0.104381719
2005.67 0.21 0.087724971 0.079491302
2005.75 0.13 0.097313313 0.063388207
2005.83 0.25 0.115383197 0.056305015
2005.92 0.17 0.099056248 0.056533469
2006 0.15 0.097887502 0.061035947
2006.08 0.27 0.11039506 0.066276891
2006.17 -0.01 0.044404628 0.069071962
2006.25 -0.08 -0.063949318 0.067266729
2006.33 -0.2 -0.077127023 0.060112133
2006.42 0.02 0.021245698 0.048284875
2006.5 0.25 0.122827269 0.033586499
2006.58 0.21 0.125823781 0.018425021
2006.67 0.1 0.043815494 0.005222204
Thank you W.
I did my PhD in a signal processing laboratory and have used it professionally for much of my career.
In a nutshell, the cross correlation function is the inverse Fourier Transform (or discrete inverse FT if one is using sampled data) of the cross-power spectrum. It is easy to show that when you filter a signal and perform a correlation, you are multiplying the cross-spectrum by the squared amplitude response of the filter. This has the obvious effect of introducing serial correlation into the inverse transformed record because it constrains the frequency of the correlation function. The ACF of an ideal random signal is an impulse at T=0, because it has a uniform power spectrum. When high frequencies in the power spectrum are eliminated, low frequency oscillations are generated in the correlation function after inverse transformation, i.e.: serial correlation is generated. The degree of additional correlation is calculable from the filter frequency response.
To put this another way, the filtered signals are the result of a convolution between the raw signals and the impulse response of the filter. In a purely random signal, in which, by definition, each sample is uncorrelated. If one imagines a 3 point, non recursive, filter with an impulse response of 0.5, 1.0, 0.5 it is clear that any sample in the output is dependent on the the original sample and its neighbours, so introducing serial correlation into the signal.
I agree that “R” allows one to do quite complex calculations with the minimum of effort. What is important, when using such packages, is that one understands the results one has obtained.
I’m sorry that I omitted one important aspect of your question that relates to basic signal processing. A real sampled record, as opposed to an analytical record, has very important features that relate to its Fourier Transform. The Fourier Transform of a real sequence does not exist. The reason for this is that the limits of integration of the FT extend between + and – infinity and therefore one has to assume that a real signal is one of infinite duration multiplied by finite length window. This is important because it shows that a real record can only be represented by a discrete Fourier Series, not its transform.
While this might seem an abstract point, it is actually very important because all correlations can be calculated via (discrete) Fouriier Transforms and this allows analysis of what happens at the end of signals. Given that one has a record, one can establish the discrete Fourier Series of that record, which allows efficient filtering and correlation. The problem is that one is actually creating an infinite series that repeats with a period determined by the length of the initial record. In principle, one can calculate the first point in the repeat of the record from the last point in the record by a Taylor’s series expansion, but in practice, unless the signal in question is an exact harmonic of the sampling record length, one will not be able to do so. This means that signal is discontinuous at its ends. In practice, this is overcome by using a tapering “window” to remove the discontinuity and also by extending the record by at least its length with zeros. This gives an approximation to the underlying signal by allows consistent manipulations such as filtering or correlation.
Thus the problem of start-up and finishing transients are well recognised and leads to the rule of thumb that one should only use, at most, one third of a record to establish correlation.
Phil –
The data is Mauna Loa. Because the base plot is annual increments, the seasonal movement is essentially irrelevant. No-one is suggesting that all of the CO2 movement is caused solely by temperature change, simply that temperature change has a manifest influence on the CO2 level, and leads it by several months. There is no attempt to hide anything by changing the scales, which in anycase has no bearing on the above point.
Cheers,
re running mean: Allan’s paper does not explicitly say how he did the averaging but does not use the word gaussian anywhere. It does explicitly mention “all Running Means” , “no Running Means” in all graph titles. So I have to assume that is clearly what he was using.
I was confused in my initial comment by Willis referring to a 12 month average when apparently this meant a gaussian FWHM (two sigma width) 12m filter which as a 3 sigma filter would need 36m window (correcting my ealier 72m which I’d calculated for 12m sigma not 12m FWHM). I’d already acknowledged that confusion so no need to continue on that.
http://climateaudit.org/2008/02/12/data-smoothing-and-spurious-correlation/#comment-136804
Allan MacRae:
LT data: http://www.atmos.uah.edu/data/msu/t2lt/tltglhmam_5.2
ST data: http://www.cru.uea.ac.uk/cru/data/temperature/hadcrut3gl.txt
The main problem I see here (aside the use of RM) is that both these are “anomally” data sets . That means they have had the annual “seasonal” pattern from some period (usually 1960-90 or similar) removed.
hadCRUT* has hadSST* as the major shareholder. The convoluted processing used to calculate the “climatology” that is subtracted to create the “anomaly” makes notable changes to frequency content as I showed here and discussed with John Kennedy in comments:
http://judithcurry.com/2012/03/15/on-the-adjustments-to-the-hadsst3-data-set-2
That would support Allan’s comments about the reliability of surface temps in the CA thread.
Surely this sort of thing needs to be done _actual_ temperatures and data with the least amount of processing.
I would suggest that untampered ICOADS SST data may be a better choice if looking for short term correlations.
The final comment by Ray Tomes at CA, that the 9m maybe phase shift of differentiation seems pertinent. It would seem from Allans’s paper (I also looked at this relationship a few years back too) that it is d/dt (CO2) that is affected by temperature rather than CO2 level. For CO2 conc there is a short term correlation with lag but a strong underlying rise.
Allen has detrended CO2 conc which is a crude high-pass filter. This makes the short term correlation visible in CO2.
There is a fairly obvious oscillatory component as Ray points out and that explains the lag.
Out gassing is caused by the temperature deviation from the current “equilibrium” state of the water that supports the current absorbed concentration.
The strong similarity that Allan shows in ST and d/dt CO2 is quite striking and seems to account for a large part of the variation in the two. This would suggest that the dominant factor is oceanic out-gassing. At least on the sub-decadal time-scale studied.
It does not support the idea of CO2 causing temp change. In essence, it seems Allan’s conclusions are basically correct.
Bill Illis –
As in my answer to Phil, I’m taking the percentage 12-month change in Mauna Loa CO2 ppm, not seasonally adjusted. There is no obvious reason to believe those numbers should have a seasonal signal. The temperature data is the 12 month change in the HADCRUT3 global temperature anomaly. The key point is that if you take incremental CO2, and smooth it, and incremental temperature, and smooth it (both by taking 12 month averages), I contend that the fact that Temperature leads CO2 is manifest. Not that it’s the only or even major cause of change, but it is a major driver of the volatility in CO2 changes.
This isn’t an enviromentalist scam. In fact, the relationship in reverse of that expected for ‘global warming’ I suspect is giving some a propaganda-hernia. The only thing I would comment is that this clearly points to a positive feedback on CO2 itself, rather than temperature.
BTW, apologies if you followed my link early on, when the graph was devoid of scales and titles. Here it is again, for other completer-finisher types:
http://www.robles-thome.talktalk.net/carbontemp.pdf
I cannot see how Figure 3, as it stands, can be correct general case. Clearly there will be a random phase shift in the cross-spectrum which will be exagerated with low pass filtering. However, there there should be a systematic time delay in the cross-correlation between two random signals. The mean time shift should be 0.
Is Figure 3 the mean of many trials? If so, I suspect that the results have been miscalculated. If it is a single trial, it shows one case of a time shift with one particular data and does show a general case..
This has implications for the statistics of the phase shift. If the statistics of the underlying process is known, the limits of the time shift is calculable.
This is a manifestation of a fundamental problem in climate statistics. We only have 1 record of temperature and any other variable. Normally, when one uses the statistical methods discussed here, one uses ensemble statistics – which is not possible. However, if one is looking for short delays only, one can segment the record, obtain the ensemble power spectra and hence perform the corellations. In this case, only a modest increase in accuracy will be obtained, but one will get a better idea of the variability.
I am sorry, Mr Eschenbach, if my initial comment upset you. However, I do think that this post shows signal processing or statistical skill. If, as you request, you want me to show how to do this better, I would be delighted to write a post on signal correlation from a signal processors perspective.
Sorry, that should read in line 3: “there should NOT be a systematic time delay”
RCS: “I would be delighted to write a post on signal correlation from a signal processors perspective.”
That would be very valuable.
I’m sure Anthony would be willing to publish something like that.
@ Greg Goodman Sure, send it along.
OK, If Anthony would like me to, I can write a post about how correlation, convolution, Fourier transforms, filtering and degrees of freedom etc fit together.
@RCS sure, go for it. Write it in MS Word with embedded graphs, and then leave a note in “submit a story” and I’ll send you an email to send the entire essay to.
Here’s a plot I did in 2010 investigating similarly to Allen MacRae:
http://climategrog.wordpress.com/?attachment_id=207
my gauss3 is a gaussian with sigma=3 months , equivalent of FWHM=6 months in Willis’ notation.
Note the phase lags 0.05 year that I used to best align ERSST with the other two. Y-axis shifts of 0.23 and 0.26 are immaterial.
Volcano dates are not supposed to prove anything , it was an exploratory plot an I wanted to see whether anything was visible.
The fact that CO2 significantly steps away from SST around 1987 is interesting. Having closely matched before hand this change merits a closer look.
PS diff3 was differential (rate of change) of CO2. Taken over three points.
Anthony Watts says:
April 1, 2013 at 9:23 am
“@RCS sure, go for it. Write it in MS Word with embedded graphs,”
This is what sets thinking sceptics apart from the “commited”. Sceptics roll up their sleeves and using sharp tools, take apart the facile “creations of the “decided” folks. This stuff would be censored in Real Climate and like quarters, robbing them of the magnificent education available. When one only lets ideas in that agree with one’s own, there may be a lot of comfort but there’s zero education. I suspect that WUWT, CA, and other analytical sceptic blogs get frequent quiet visits by the hockey team. Steve McIntyre notes that CA was not referenced in the turnaround taken by Marcott et al. This harkens back to Gergis et al. After being demolished by CA, Gergis makes an “independent” discovery of his paper’s terminal deficiencies the next day – no “thank you Steve” forthcoming. The surfacestations project set off a round of station closures, new deployments, and a snarky, premature paper attempting to marginalize the project. Oh there is no thanks from that quarter. Worse, the consensus’s mediocre “work” has cost us a trillion or two and sceptics who have brought real science to the subject are basically unfunded.
“…and sceptics who have brought real science to the subject are basically unfunded.”
You’re kidding, right? Hasn’t Hearthand forwarded your regular check from Koch Bros and Exxon Mobil this month? I know I got mine. 😉
Matt Briggs says:
“Two broad hypotheses are advanced: (Hypothesis 1) As more CO2 is added to the air, through radiative effects, the temperature later rises; and (Hypothesis 2) As temperature increases, through ocean-chemical and biological effects, CO2 is later added to the atmosphere.”
“All I am confident of saying is, conditional on this data and its limitations etc., that Hypothesis 2 is more probable than Hypothesis 1, but I won’t say how much more probable.”
Willis Eschenbach says: March 31, 2013 at 11:26 pm
I would hardly call that a ringing endorsement of the idea that temperature changes cause CO2 changes 9 months later.
Hi Willis,
I think I must have been smarter when I did this work – now, it just makes my head hurt. 🙂
As I recall, Matt Briggs’ conclusion is limited by his analytical method, which only examined integer multiples of 1-year lags. He then concluded that “CO2 lags temperature” is more probable than “temperature lags CO2”. I recall he found the best indication of this probability at a one-year lag.
This is all from memory and may all be crap – it’s late and I’ve been working all day.
Best personal regards, Allan
Greg Goodman says: April 1, 2013 at 3:19 am
re running mean: Allan’s paper does not explicitly say how he did the averaging but does not use the word gaussian anywhere. It does explicitly mention “all Running Means” , “no Running Means” in all graph titles. So I have to assume that is clearly what he was using.
HI Greg,
There should be a spreadsheet of all calcs available for download at
http://icecap.us/index.php/go/joes-blog/carbon_dioxide_in_not_the_primary_cause_of_global_warming_the_future_can_no
Try
http://icecap.us/images/uploads/CO2vsTMacRaeFig5b.xls
Best, Allan
Thanks, Alan. As I mentioned, I’m still not clear if what you found was real or not, nor was that my point. I just wanted to show the difficulties with the smoothing of data before you do further analyses.
Best to you,
w.
Hi Willis, a Mathematica news tag led me here. It’s a very powerful system, and worth the money (for a home license if you’re not being bankrolled!). Did you know that the latest version has R integration? So you can run R code and display results in Mathematica? That way you needn’t throw away all that hard earned knowledge of yours.
Allan MacRae says “As I recall, Matt Briggs’ conclusion is limited by his analytical method, which only examined integer multiples of 1-year lags. He then concluded that “CO2 lags temperature” is more probable than “temperature lags CO2”. I recall he found the best indication of this probability at a one-year lag.
This is all from memory and may all be crap … ”
Just looking at unsmoothed monthly data, it’s pretty clear that CO2 lags temperature:
http://members.westnet.com.au/jonas1/deltaCO2vsTemp.JPG
The graph shows y-o-y CO2 change and temperature (NB. scaled), with CO2 change shifted back in time 6 months. ie, CO2 changes usually lag temperature by 6-12 months.
But that’s not the whole story. The annual changes in temperature are high enough to make the resultant CO2 change show up above the noise, and that’s visible in the graph. But percentage-wise, CO2 from fossil fuels doesn’t vary much y-o-y. For its effect on CO2, and for CO2’s effect on temperature,you have to look elsewhere, or look differently.
Pete says:
April 3, 2013 at 12:55 am (Edit)
Hey, Pete, thanks. I have Mathematica and I do use it. I can program it in two of the four languages it understands … but like I said, the learning curve is so steep it gives me nosebleed.
Plus (and more important) it’s way expensive for your average guy, I got mine from my work. But if I do the same work in R, anyone can replicate it.
Thanks for the tip about displaying R results in Mathematica … but since an upgrade to do that will likely be more money than I’m willing to spend, I’ll just putter along.
w.
Mike Jonas says:
April 3, 2013 at 2:37 am (Edit)
Thanks, Mike. Unfortunately, you’re just looking at an artifact created by comparing today’s temperature to a 12-month change in temperature. To see the effect, try graphing the temperature versus the 12 month change in the temperature in the same manner …
w.
Willis says “Unfortunately, you’re just looking at an artifact created by comparing today’s temperature to a 12-month change in temperature. To see the effect, try graphing the temperature versus the 12 month change in the temperature in the same manner …”
Presumably you mean that by looking at 12-month change in CO2 I am effectively looking at 12-month change in temperature. I disagree, and the reason is very important to this whole temperature-CO2 thing…..
The temperature-CO2 relationship is a bit surprising. When I first started looking at temperature and CO2 data, I rather naturally plotted temperature change against CO2 change. Then Frank Lansner pointed to the correlation between CO2 change and temperature (not temperature change). It took me a long time before the penny dropped …
… as I explained in an earlier comment (http://wattsupwiththat.com/2013/03/30/the-pitfalls-of-data-smoothing/#comment-1262333), “Other possible problems with the paper are [] the use of annual change in temperature, when actual temperature would be more relevant. The point is that the rate of atmospheric CO2 absorption or emission by the ocean is driven by temperature, not by how much the temperature differs from last year’s temperature.“.
In simple terms, the rather small CO2 change caused by last year’s temperature has no effect on the subsequent rate of CO2 absorption/emission by the ocean. In other words, today’s temperature drives the rate of CO2 absorption/emission by the ocean, unaffected by anything that last year’s temperature did. The y-o-y change in CO2 reflects that rate.
My argument only applies in a world in which a relatively steady stream of man-made CO2 is maintaining a high ocean-atmosphere imbalance. Without the man-made CO2, the relationship between CO2 change and temperature would be weaker, and the relationship between CO2 change and temperature change would be stronger.
It’s counter-intuitive, but by plotting temperature, not temperature change, against CO2 change, I’m matching the relevant two variables.
So it isn’t an artefact. And as I pointed out in the same comment, y-o-y CO2 changes relate to man-made CO2 emissions, not to changes in man-made emisssions.
Hi again Willis,
I re-examined the plots in the Excel spreadsheet at
http://icecap.us/images/uploads/CO2vsTMacRaeFig5b.xls
and recall that I ran Figures 5, 6, 7, and 8 all without running means, and added Figure 5b (to address your question at that time).
I think that without running means, the stated relationship between dCO2/dt and Temperature and the 9-month lag of Temperature after CO2 still hold true, although they are less beautiful than with running means.
Anyone who wants to review the math can do so through the spreadsheet.
I do not think the relationship that I alleged to exist is an artifact of the mathematical technique, although I obviously welcome anyone using a better approach. The challenge is to deal with the seasonal “sawtooth” oscillation in the CO2 data in a manner that is valid.
Of course, the temperature data is itself not actually temperature, but is a temperature anomaly created in order to deal with another seasonal oscillation.
Regarding the suggestion from several parties that fossil fuel emissions drive CO2, I did considerable work on this premise at the time and could not find the relationships that others allege to exist. The so-called “mass balance” argument has been ongoing between Richard Courtney and Ferdinand Engelbeen for over a decade. I lean towards Richard’s view, although I respect both gentlemen.
I have also participated in this debate. I concluded at the time, based on limited Salt Lake City data, that it appeared that manmade CO2 emissions were captured close to the source at that locality, at least during the growing season. The absence of any “rush-hour” spikes in CO2 concentrations was surprising.
Best, Allan
.
Hi Willis and Allan Macrae
I looked at the auto-correlation of dCO2 in the linked data. As well as the obvious peaks at 0,+/- 12, +/- 24… months, there are lesser but significant peaks at +/- 3, +/- 15, +/- 27,,, and at +/- 9, +/- 21…
I then looked at the monthly averages of dCO2 (ie current CO2 level – previous month’s CO2 level). The figures for January and October are literally hundreds of times greater than those for the other months (essentially the figures for those 2 months are always positive and “big” while the other months are smaller and, more importantly, vary in sign). The 9 month gap between January and October obviously accounts for the other peaks in the auto-correlation of dCO2.
I’ve used the data you link to and have been able to replicate your results so I don’t think anything is wrong there.
I wonder whether the original data are correct and, if so, what could be the mechanism which makes net CO2 emissions so much greater in January and October.
BTW, I’m not sure whether the date labels in the data correspond to the beginning or end of the relevant month so “January” may be “December” and “October” may be “September”.
BTBTW, I don’t know whether this 9/3 monthly gap between dCO2 peaks could account for the apparent similarly lagged correlation between dCO2 and dT. At first sight I can’t see how it could, but maybe I’m missing something obvious.
Simon Anthony
Clarification:
When I wrote: “I then looked at the monthly averages of dCO2 (ie current CO2 level – previous month’s CO2 level).” what I meant was that I looked at the average (taken over the years in the date set) for each month of the difference between that month’s CO2 level and the previous month’s.
Simon Anthony
Addendum: The absence of any “rush-hour” spikes in urban CO2 concentrations was surprising.
When I first pointed out this relationship (dCO2/dt varies with T and T lags CO2 by 9 months), it was deemed incorrect.
Then it was accepted as valid by some on the warmist side of this debate, but dismissed as a “feedback”.
This “feedback argument” appears to be a “cargo cult” rationalization, derived as follows:
“We KNOW that CO2 drives Temperature, therefore it MUST BE a feedback.”
More below from 2009:
__________________
http://wattsupwiththat.com/2009/01/21/antarctica-warming-an-evolution-of-viewpoint/#comment-77000
Time is limited so I can only provide some more general answers to your questions:
My paper was posted Jan.31/08 with a spreadsheet at
http://icecap.us/index.php/go/joes-blog/carbon_dioxide_in_not_the_primary_cause_of_global_warming_the_future_can_no/
The paper is located at
http://icecap.us/images/uploads/CO2vsTMacRae.pdf
The relevant spreadsheet is
http://icecap.us/images/uploads/CO2vsTMacRaeFig5b.xls
There are many correlations calculated in the spreadsheet.
In my Figure 1 and 2, global dCO2/dt closely coincides with global Lower Tropospheric Temperature LT and Surface Temperature ST. I believe that the temperature and CO2 datasets are collected completely independently, and yet there is this clear correlation.
After publishing this paper, I also demonstrated the same correlation with different datasets – using Mauna Loa CO2 and Hadcrut3 ST going back to 1958. More recently I examined the close correlation of LT measurements taken by satellite and those taken by radiosonde.
Further, I found (actually I was given by Richard Courtney) earlier papers by Kuo (1990) and Keeling (1995) that discussed the delay of CO2 after temperature, although neither appeared to notice the even closer correlation of dCO2/dt with temperature. This correlation is noted in my Figures 3 and 4.
See also Roy Spencer’s (U of Alabama, Huntsville) take on this subject at
http://wattsupwiththat.wordpress.com/2008/01/25/double-whammy-friday-roy-spencer-on-how-oceans-are-driving-co2/
and
http://wattsupwiththat.wordpress.com/2008/01/28/spencer-pt2-more-co2-peculiarities-the-c13c12-isotope-ratio/
This subject has generated much discussion among serious scientists, and this discussion continues. Almost no one doubts the dCO2/dt versus LT (and ST) correlation. Some go so far as to say that humankind is not even the primary cause of the current increase in atmospheric CO2 – that it is natural. Others rely on a “material balance argument” (mass balance argument) to refute this claim – I think these would be in the majority. I am an agnostic on this question, to date.
The warmist side also has also noted this ~9 month delay, but try to explain it as a “feedback effect” – this argument seems more consistent with AGW religious dogma than with science (“ASSUMING AGW is true, then it MUST be feedback”). 🙂
It is interesting to note, however, that the natural seasonal variation in atmospheric CO2 ranges up to ~16ppm in the far North, whereas the annual increase in atmospheric CO2 is only ~2ppm. This reality tends to weaken the “material balance argument”. This seasonal ‘sawtooth” of CO2 is primarily driven by the Northern Hemisphere landmass, which is much greater in area than that of the Southern Hemisphere. CO2 falls during the NH summer due primarily to land-based photosynthesis, and rises in the late fall, winter and early spring as biomass degrades.
There is also likely to be significant CO2 solution and exsolution from the oceans.
See the excellent animation at http://svs.gsfc.nasa.gov/vis/a000000/a003500/a003562/carbonDioxideSequence2002_2008_at15fps.mp4
It is also interesting to note that the detailed signals we derive from the data show that CO2 lags temperature at all time scales, from the 9 month delay for ~ENSO cycles to the 600 year delay inferred in the ice core data for much longer cycles.
Regards, Allan
The overwhelming importance of the changes in CO2 from Dec to Jan and from Sep to Oct in the data can be seen by taking the CO2 measurement at the start of the data (Jan 1979), adding the changes in CO2 for only Dec-Jan and Sep-Oct for all successive years and comparing with the final measurement (Sep 2006).
Start measurement is 336.67, final measurement is 381.55. The result from adding just those 2 months’ additions to the start figure is 381.47.
It seems as though 10 months of the year make no net difference to CO2 levels. That seems unlikely.
I looked up Mauno Loa CO2 data here… ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_mm_mlo.txt
The numbers are different from those linked by Willis in the original post. That might not matter (there may have been later minor adjustments) but, more significantly, they don’t show the strange concentration of CO2 changes in 2 months. It seems possible that the data linked to by Willis might have some errors.
Allan MacRae says:
April 4, 2013 at 6:57 am
Addendum: The absence of any “rush-hour” spikes in urban CO2 concentrations was surprising.
Indeed it is, take a look at this paper which indicates otherwise:
http://www.ars.usda.gov/SP2UserFiles/ad_hoc/12755100FullTextPublicationspdf/Publications/sookim/ElevatedAtmosphericCO2ConcentrationandTemperatureAcrossanUrbanRuralTransect.pdf
Willis Eschenbach says:
April 3, 2013 at 9:53 am
Thanks, Mike. Unfortunately, you’re just looking at an artifact created by comparing today’s temperature to a 12-month change in temperature. To see the effect, try graphing the temperature versus the 12 month change in the temperature in the same manner …
Willis, the CO2 concentration has to be modulated by the temperature since the natural fluxes of CO2 are functions of inter alia temperature, due to Henry’s Law, temperature sensitivity of photosynthesis etc.
The balance equation for the atmosphere takes the form:
dCO2/dT= fossil fuel combustion+(Natural sources-sinks)= F+So(T)-Si(T)= F+ΔS(T)
Observations show that dCO2/dT≅F/2 over the course of a year, therefore ΔS(T)≅-F/2 so natural sinks exceed natural sources and about half the fossil fuel emissions are sequestered.
So the overall growth of CO2 is a steady annual increase due to fossil fuel emissions with superimposed fluctuations due to ΔS(T). I’m sure that the short term lags are due to the hemispheric differences, the seasonal change is mostly due to NH seasons with very little SH coupled with atmospheric transport. For those non-believers in mass balance equations I suggest a conversation with a Chem engineer (or an accountant for that matter)!
Hi Willis and Allan MacRae
If you replace the CO2 data linked to by Willis with the monthly Mauna Loa data from this site… ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_mm_mlo.txt … and then look at the correlation between the monthly changes in CO2 and the monthly temp changes (from Willis’s data) – not the smoothed versions, just the differences – then you find that there’s a “clean” peak at 4 months and at annual intervals before and after. This is in contrast to the same correlation using Willis’s data for CO2 which has no such peaks. However, although it’s clean, the peak height is quite low (no higher than the “random” peaks generated by Willis’s data).
The smoothed data (with a 12 month filter) has a peak at 8 months and at annual intervals before and after.
If you replace the “real” CO2 data with simulated numbers with an increment equal to the average change over the real data set, perturbed by a random amount up to +/- the standard deviation of “real” dCO2 data, you find that the correlation of the unsmoothed data goes away. However, for the 12 month smoothed data, you usually (ie for different random number sets) find peaks of about the same size as those in Willis’s first chart, although their location varies.
I haven’t worked through the maths but it seems likely you’ll get misleading results if you average data over 12 months – which effectively smooths away structure of shorter time intervals – and then look for correlations at less than 12 months displacement (9 months in Willis’s example above).
These and earlier observations suggest the following:
– The CO2 data linked to by Willis seems to have some problems; I don’t know the source of the data but the dominance of just 2 months in determining CO2 levels seems wrong;
– The peaks in the smoothed correlation function are likely to be spurious if the peak’s displacement is less than the smoothing interval;
– The “real” unsmoothed Mauna Loa data does seem to have a peak in the correlation with temp changes at a 4-month displacement. It’s low but “clean” and, as such peaks aren’t present with simulated data, it may be that it’s a genuine effect rather than an artifact of the methods or an accident of the data.
Simon Anthony
Allan MacRae April 4, 2013 at 7:21 am “When I first pointed out this relationship (dCO2/dt varies with T and T lags CO2 by 9 months), it was deemed incorrect.” – do you mean “CO2 lags T by 9 months”?
Phil. says “So the overall growth of CO2 is a steady annual increase due to fossil fuel emissions with superimposed fluctuations due to ΔS(T).”
Thanks for putting it so concisely. I am quite sure that your explanation is correct, but I have struggled to explain it as clearly.
Simon Anthony says “The overwhelming importance of the changes in CO2 from Dec to Jan and from Sep to Oct in the data can be seen by […].
It seems as though 10 months of the year make no net difference to CO2 levels. That seems unlikely.”
If I understand you correctly, the effect you refer to could be obtained from any data with a regular cycle.
http://members.westnet.com.au/jonas1/CO2Profile.jpg
Mike Jonas says:
If I understand you correctly, the effect you refer to could be obtained from any data with a regular cycle.
Although the data are annually cyclic, they aren’t “any data with a regular cycle”. This particular annual cycle has the months of January and October always positive while the others are ~randomly distributed about zero. The data seem to be wrong – other data showing supposedly the same measurements have an annual cycle which is more like a sine wave – but I don’t know where Willis got them from. It’s a long time since he made the original post so he may not now be able to trace the source.
Simon Anthony – OK, I see what you mean.
Hi Willis and Allan MacRae
Another way to see that the 9-month lagged relationship between dT and dCO2 is likely to be spurious is that, if genuine, you’d expect to see further, successively smaller, peaks in the correlation at annual intervals. There are no such peaks.
Mike Jonas says:
April 4, 2013 at 1:16 pm
Allan MacRae April 4, 2013 at 7:21 am “When I first pointed out this relationship (dCO2/dt varies with T and T lags CO2 by 9 months), it was deemed incorrect.” – do you mean “CO2 lags T by 9 months”?
Answer – Yes – my apologies – blame it on absence of coffee – thanks, Allan
Phil. says:
April 4, 2013 at 8:58 am
Allan MacRae says:
April 4, 2013 at 6:57 am
Addendum: The absence of any “rush-hour” spikes in urban CO2 concentrations was surprising.
Indeed it is, take a look at this paper which indicates otherwise:
http://www.ars.usda.gov/SP2UserFiles/ad_hoc/12755100FullTextPublicationspdf/Publications/sookim/ElevatedAtmosphericCO2ConcentrationandTemperatureAcrossanUrbanRuralTransect.pdf
Thank you Phil .
But please look at Fig. 2 in your http://www.ars…. paper. (God – who does these acronyms in the USA – it’s almost as bad as PNAS)
Yes, CO2 concentrations are higher in urban areas than in rural areas as stated in the paper, no surprise there –
BUT atmospheric CO2 concentrations plummet starting at about 7am daily.
That was my earlier point. At the time of peak morning CO2 emissions from power plants and the morning rush hour, CO2 concentrations drop. Obviously, photosynthesis is the dominant factor and “excess” CO2 appears to be trapped at the source. However, I suppose one could argue that atm. CO2 would drop even more if it were not for emissions from power plants and cars.
Warning – no coffee yet today.
Phil. says: April 4, 2013 at 9:33 am
“For those non-believers in mass balance equations I suggest a conversation with a Chem engineer (or an accountant for that matter)!”
Phil – Kindly Google the discussions between Ferdinand Engelbeen and Richard Courtney here and on ClimateAudit. It’ s a bit more complicated than you think, imo.
But it is possible that you are almost correct…
to Phil 2:
http://wattsupwiththat.com/2012/04/19/what-you-mean-we-arent-controlling-the-climate/
to Phil 3:
http://wattsupwiththat.com/2011/08/05/the-emily-litella-moment-for-climate-science-and-co2/
http://wattsupwiththat.com/2011/08/05/the-emily-litella-moment-for-climate-science-and-co2/#comment-713773
AllanMRMacRae says: August 7, 2011 at 5:09 am
Hi Ferdinand,
I hope you are well, and am enjoying once again your longstanding dialogue with Richard Courtney.
I think you raise some very interesting points, particularly in the quantification of certain factors.
I wonder if some of these questions can be explained by at least two, and possibly more, time lags of CO2 AFTER temperature change. We think we know there is an ~~800 year “long cycle” lag of CO2 after temperature from the ice core data, and also a ~9-month “short-cycle” lag as derived from modern data. If I recall correctly, the dear, late Ernst Beck also postulated another such “intermediate-cycle” lag, and it may still become apparent, even if it takes more than ~5 years to manifest itself.
However, with sincere respect, I don’t agree with your “material balance argument”. I think it is incorrect because it inherently assumes the climate-CO2 system is static, but it is highly dynamic, and the relatively small humanmade fraction of total CO2 flux is insignificant in this huge system, as it continues to chase equilibrium into eternity.
Best personal regards, Allan
http://wattsupwiththat.com/2012/08/30/important-paper-strongly-suggests-man-made-co2-is-not-the-driver-of-global-warming/#comment-1070493
Here is an interesting article about Japanese satellite results, at
http://chiefio.wordpress.com/2011/10/31/japanese-satellites-say-3rd-world-owes-co2-reparations-to-the-west/
Japanese Satellites say 3rd World Owes CO2 Reparations to The West
Posted on 31 October 2011
[excerpt]
“ It seems that the Japanese have a nice tool on orbit and set out to figure out who was a “maker” and who was a “taker” in the CO2 production / consumption game. Seems they found out that CO2 was largely net absorbed in the industrialized ‘west’ and net created in the ’3rd world’. “
See also Murry Salby’s video at time 10:38 – the major global CO2 sources are NOT in industrial areas – they are in equatorial areas where deforestation is rampant.
As I’ve posted to Ferdinand Engelbeen in the past:
“Variations in biomass (e.g. deforestation and reforestation) may be the huge variable that would make your mass balance equation work better.”
As Richard Courtney ably summarizes above:
“The unresolved issues are
(a) what is the equilibrium state of the carbon cycle?
(b) how does the equilibrium state of the carbon cycle vary?
(c) what causes the equilibrium state of the carbon cycle to vary?
(d) does the anthropogenic CO2 emission induce the equilibrium state of the carbon cycle to vary discernibly?”
To summarize:
This is an important scientific debate about the carbon cycle and the primary sources of increasing atmospheric CO2. It is entirely possible, some say it is probable, that increasing atmospheric CO2 is NOT primarily caused by the burning of fossil fuels, others say it IS, and the scientific debate goes on.
To be clear, however, the only significant apparent impact of increasing atmospheric CO2 is beneficial, because CO2 is a plant food.
The claim that increasing CO2 is causing catastrophic global warming is being falsified by these facts:
– there has been no net global warming for 10 to 15 years, despite increasing atmospheric CO2;
– predictions of catastrophic global warming are the result of deeply flawed climate computer models that are inconsistent with actual observations;
– the leading proponents of catastrophic global warming hysteria have been shown in the Climategate emails to be dishonest.
A decade ago, we wrote:
“Climate science does not support the theory of catastrophic human-made global warming – the alleged warming crisis does not exist.”
Since then there has been NO net global warming.
Also a decade ago, I (we) predicted global cooling would commence by 2020 to 2030. When this cooling does occur, many of these scientific questions will be answered.
In the meantime, society should reject the claims of the global warming alarmists, because they have a demonstrated track record of being wrong in ALL their major climate alarmist predictions.
In science, such an utter failure on one’s predictive track record is a fair and objective measure of the falsification of one’s hypotheses.
Repeating, from 2002, with ten more years of confirming data:
“Climate science does not support the theory of catastrophic human-made global warming – the alleged warming crisis does not exist.”
Allan MacRae says:
April 6, 2013 at 8:41 pm
Phil. says: April 4, 2013 at 9:33 am
“For those non-believers in mass balance equations I suggest a conversation with a Chem engineer (or an accountant for that matter)!”
Phil – Kindly Google the discussions between Ferdinand Engelbeen and Richard Courtney here and on ClimateAudit. It’ s a bit more complicated than you think, imo.
But it is possible that you are almost correct…
It can be more complicated but the rate of change will always equal the difference between total sources and total sinks! You can break down the terms to give more detail but that will always be true.
So yes I am correct, thank you.
However, with sincere respect, I don’t agree with your “material balance argument”. I think it is incorrect because it inherently assumes the climate-CO2 system is static,
No it does not, if it did dCO2/dt would be zero, sources and sinks can both be functions of temperature as I explicitly stated (and also of time of course)!
Now Euro-Nutcases are Burning Vast Tracts of Forest as so called Biomass, in the name of saving the environment by burning it. It’s a bit like Bombing for Peace. In some
countries, such as Poland and Finland, wood meets more than 80% of renewable-energy
demand. So much wood is burned that Construction board companies have gone bust by the cartload. Read more at URL enviromental-lunacy.notlong.com – Economist Mag.
Phil – I still do not like the Mass Balance argument that attributes increases in atmospheric CO2 to the burning of coal, oil and natural gas, but another possibility is that increasing atmospheric CO2 is not primarily due to the aforementioned fossil fuel burning but rather primarily due to deforestation. Here is some evidence:
From above:
“ It seems that the Japanese have a nice tool on orbit and set out to figure out who was a “maker” and who was a “taker” in the CO2 production / consumption game. Seems they found out that CO2 was largely net absorbed in the industrialized ‘west’ and net created in the ’3rd world’. “
See also Murry Salby’s video at time 10:38 – the major global CO2 sources are NOT in industrial areas – they are in equatorial areas where deforestation is rampant.