 By Christopher Monckton of Brenchley
By Christopher Monckton of Brenchley
The monthly satellite lower-troposphere temperature anomaly from Remote Sensing Systems, Inc., is now available.
Taking the least-squares linear-regression trend on this dataset (the bright blue horizontal line through the dark blue data), there has now been no global warming – at all – for 17 years 5 months.
Would readers like to make a projection of how many mainstream media outlets will report this surely not uninteresting fact?
It shows that the Hiatus hernia for true believers in the New Religion continues.
My own prediction is that the number of media reporting 17 years 5 months without any global warming will be approximately equal to the number of general-circulation models that predicted such a long Pause notwithstanding ever-rising CO2 concentration.
Print out the graph as a postcard and send it to the editor of a newspaper near you that has shut down democratic debate by announcing that it will refuse to print any letters at all from “climate deniers”.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.

If he would like to say how many scientists the task would need, and how long it would take, and how much it would cost, it might be possible to find funding for the project.
One “scientist” (or one halfway decent statistician), three or four months, and a living in the meantime. As I understand it, the data is all there and openly accessible, although collecting it on a single workstation and organizing it for the analysis might take some time. But three or four months would be to do a really good job — to do the preliminary work and then use THAT to do a meta-analysis of some of the other questions dodged in AR5 chapter 9, like the reasonably precise extent that common parentage in climate models affects their bias, like doing a run-weighted analysis of the MME. If the perturbed parameter ensemble (PPE) data for the different models are readily available on a per-model basis, it is just a matter of taking the actual data and comparing the integrated amount of time the model spends above or below the actual data.
That’s why I made the null hypothesis explicit. I do this all the time in random number generator testing. The null hypothesis there is This is a perfect random number generator. One then uses the supposedly perfect RNG to generate a statistical result with a known distribution and mean. If the result the RNG produces is very, very improbable in terms of that known distribution and mean, the RNG can reasonably be said to fail the test and falsify the null hypothesis. That doesn’t prove that it really is a bad generator — “p happens”, in the words of George Marsaglia, one of the past masters of RNG testing — but it certainly doesn’t give one confidence that it is a good generator and at some value of p we become virtually certain that the generator is not a good generator.
Given PPE data, the process is almost identical. If a model is used to generate (say) 100 possible future trajectories for global mean surface temperature from a given starting point, and over time those trajectories spend 99% of their collective time warmer than the actual temperature, then one can state that if the null hypothesis is correct, the probability of getting the actual trajectory (given this perfect model) is no greater than 1%. Only it is actually going to be much lower than this, if none of the trajectories (as will usually be the case) have even a median performance that matches the actual trajectory. Again, one can easily transform this into terms anyone can understand. Either we have been very, very lucky not to have warmed the way the models predict, or else the models are wrong, one model at a time.
Ordinarily in science, we assume that what nature does is the most probable outcome, not the least probable outcome. It is very, very difficult to assert that the Earth should have warmed because a model that has never been properly validated outside of its training set predicted warming that did not occur. It is far more reasonable to assert that this is strong evidence that the model is incorrect.
I think it would take very little time indeed to sort models out according to three general categories: a) Models that are egregiously wrong. AR5 implicitly acknowledges that they are there in section 9.2.2.3, when it asserts that it is “challenging” to know how to make quantitative predictions based on the MME mean when it incorporates failed models. That does not, however, prevent them from doing so anyway. b) Models that are probably wrong. p does, indeed, happen, but almost all of the models have a poor p-value. Indeed, one would expect that at least a few models would have decent p-values on the basis of pure data dredging, given so many models to pull results from. Models that have p-values under 0.1 should at the very least be suspect, and I’d be tempted to make the cut-off even higher given the purely monotonic direction of failure of all of the models, suggesting a common error in them. c) Models that at least could be right. Indeed, it would be lovely to rank the models in terms of how accurately the model in question predicted the actual temperature, how deeply embedded the actual temperature trajectory is in its PPPE runs. A good model would be one where roughly half of the runs were above the observed temperature and half below and I rather doubt that any models make that grade, but it could be that there are models that produce a respectable number of climate trajectories that show little to no warming, especially if they match other features that one might reasonably expect a climate model to reproduce, such as the correct variance around some mean smoothed trajectory, the right autocorrelation times (the duration and sharpness of temperature fluctuations), as well as things like Pielke’s article on a different thread discusses, failure to accurately predict gross measures like regional distribution of rainfall, storm frequency and violence, tropospheric warming.
This preliminary, rapid analysis might motivate a deeper analysis if GCMs predominantly fail the PPE test — as one rather expects — on the basis of some set of common features or shared lineage. Here one would apply the entire apparatus intended to correct for data dredging — given 36 distinct strands of spaghetti to choose from in AR5 figure 9.8a, one actually has to be more stringent in assessing model success or failure compared to reality. One would expect even bad models to sometimes produce decent p-values given enough opportunities, after all. Studying the pattern of failure might motivate the rejection of entire model families even when one or two members are nominally within some arbitrary cut-off But this sort of thing would be icing on the cake compared to the primary job of cleaning up AR5’s statistics section.
Once this sorting is done, one could do the following very interesting thing. Observe the systematic variation of the MME weighted sub-average of member models as one smoothly increases the cut-off PPE p-value from 0 (include them all, no matter how bad) to the inclusion of the single best model in the lot in terms of straddling the actual observational data. This would be a map of weighted estimated climate sensitivity as a function of the observational accuracy of the models, and would clearly identify a probable range for the actual climate sensitivity subject to the sole assumption that the actual climate trajectory is probable rather than improbable. This process would substantially and immediately lower the most probable value of the climate sensitivity by eliminating the crap GCMs that are included, as far as I can tell, for the sole purpose of propping the MME equally weighted global mean surface temperature estimate up so that it continues to predict “catastrophic” warming by 2100 in the face of data that (to say the least) does not support that conclusion. It would also make it quite clear, in an easily understandable way, that the residual MME mean estimate would almost certainly be an upper bound, not in any sense a Gaussian mean, of the eventual climate sensitivity.
Finally, it would make it appallingly clear that it is time to go back to the drawing board, something that is obvious by looking at the past behavior (hindcasting) in figure 9.8a as well. I simply do not see how any reasonable person could look at figure 9.8a’s performance and not reject CMIP5 en masse until models are built that can do much, much better. Here is a single metric that doesn’t require a rocket scientist or Ph.D. statistician to evaluate. Compare the CMIP5 MME mean (red line) to HADCRUT4 (black line). The red line is below the black line for an eyeballed total of roughly 25 years out of the nearly 155 years represented on the curve. Hell, I’d go to thirty. And this includes the training set!
Oh, my, god. How anyone has the balls to actually put this figure into a report as evidence that the models are working is beyond me.
Let me put it this way. Suppose that both curves are actually drawn by taking some underlying smooth curve that represents what we might call the “climate set point” around which the climate is oscillating, and then adding delta correlated, exponentially smeared noise (that is, make it bounce around the true mean behavor with bounces that are roughly in agreement with the observed amplitude and widths of variations from this mean behavior. What is the probability that one of the curves would be spend 5/6ths of its time above or below the other? Guestimating the number of autocorrelation-separated samples in this to be at least 30 (five years is a reasonable measure of the feature persistence in HADCRUT4) that’s ballpark the odds of flipping a coin 30 times and getting 5 heads. Plugging that into a handy-dandy online calculator for the binomial distribution here:
http://stattrek.com/online-calculator/binomial.aspx
we see that the probability of getting five heads or fewer in 30 trials is roughly 0.000162. This is a crude, but quite reasonable upper bound estimate of the p-value for the following null hypothesis:
The CMIP5 MME mean is an accurate measure of the true climate within the bounds of natural variability.
Upper bound because the trials above contain the training interval! Because this ignores the two spans of forty and fifteen years outside of the training interval when the MME mean is always greater than HADCRUT4.
In the modelling business we call this sort of p-value failing validation! There isn’t the slightest bit of doubt in this. The actual p-value, corrected for this and that and done properly, is probably order of 0.000001 — one in a million. We may not know how models in CMIP5 fail, or which models in CMIP5 fail, but we know from figure 9.8a alone that the CMIP5 MME mean itself fails to describe the climate variation of the last 155 years with near certainty. A trained monkey armed with a coin to flip to go up or down according to some simple rules around the smoothed behavior of HADCRUT4 could do better than the CMIP5 MME mean. It would actually be as likely to produce mean temperatures lower than the observed ones as ones above them.
The sad thing is that all of the rules these claims egregiously violate are well known in statistics. They are standard operating procedure in building models in e.g. economics, simply because anybody that tries to build a simple economic/market model that validated on the training data would rapidly be described by a single word.
Broke.
rgb
I have mentioned before that the greenhouse effect on planet Earth (33c) is accounted for incorrectly. The reason being only the atmosphere is taken into account and not the energy content of the oceans. The greenhouse affect also doesn’t explain the difference in temperature between both poles. How can we calculate what greenhouse effect the ocean has compared to the atmosphere?
This is not so difficult as it sounds because we can compare the temperature difference between the poles. In theory if both poles were oceans then during winter and summer they would both measure similar temperatures. If both poles were continents then during winter and summer they would also measure similar temperatures.
The advantage we have is that this is not the case and one pole is ocean and the other land. The difference in temperature between the two is how much the greenhouse effect of the ocean is having compared the two. The atmosphere is similar above both poles, so should have similar atmospheric greenhouse effect. Therefore the difference in temperature is mainly down to just the ocean greenhouse effect in the Arctic. If the greenhouse effect was only down to the atmosphere then temperatures at both poles would be similar.
This is only an estimate, but the difference in winter between both poles is about 30 c. The difference between both poles in summer is also about 30 c. Therefore this concludes that 30 c of 33c total greenhouse affect is exclusively down to the ocean heat content. The rest of the atmospheric greenhouse gases including water vapor and CO2 only account for 3 c. This would be a controversial observation, but if true would improve the understanding of climate science.
This value would also explain why some planets are colder near the surface when compared to Earth. The value when taking into account yearly variation and more accurate regional variation though, would likely be lower than 30 c .
Professor Brown has sold me on his proposal. Now we move to what the Whitehall mandarins call “the modalities”, or what Margaret Thatcher, more bluntly, called “names, dear, names!” Who is going to do this?
First step: if Professor Brown is willing, perhaps he would assemble the outline he has given in his various posts above into a clear brief that a competent statistician would understand, and email it to me with an indication of whether he is willing to supervise the project if I can find someone qualified to take it on. The output, presumably, would be a devastating paper for publication not in a climate journal – where the barriers against the truth are formidable – but in a leading journal of statistics.
Assuming that the result is as the Professor expects – and the Mk. 1 eyeball suggests that his is a hypothesis well worth testing – the final step would be to arrange for the lead authors of the modeling chapters in the next IPCC report to be thoroughly briefed. One more nail in the already well-studded coffin of Thermageddon.
First step: if Professor Brown is willing, perhaps he would assemble the outline he has given in his various posts above into a clear brief that a competent statistician would understand, and email it to me with an indication of whether he is willing to supervise the project if I can find someone qualified to take it on. The output, presumably, would be a devastating paper for publication not in a climate journal – where the barriers against the truth are formidable – but in a leading journal of statistics.
I would sort of be willing — that is, willing with some caveats. The first problem is my time commitments. Here is a short list of my current activities:
a) Co-teaching introductory mechanics (96 students) in a new experimental format.
b) Co-teaching introductory electricity and magnetism (270 students) in a new but slightly different experimental format.
c) Participating in one “established” startup company doing predictive modelling and other high end statistical work of which I am a co-founder and in which I have a substantial interest. And I use the term participating already with a grain of salt as I’ve been too busy to do more than pay lip service to actual activity on its behalf for months now.
d) Preparing to co-found a brand new startup company providing a key security service for websites as a primary contributor to the core security technology and algorithm. This might or might not involve me writing a patent application over the next month, which I’ve done several times now and is enormously time consuming with its stilted language and need for carefully constrained statements.
e) Finishing/refining the two textbooks, two associated review guides, one novel, and one philosophical work (Axioms) that I am working on, where there is some urgency about the first four items as they are in active use by students at Duke and elsewhere.
f) Supporting at least dieharder, the aforementioned RNG tester. I’m way behind in bugfix requests, but this is the lowest priority task in the list, sadly, in spite of the fact that a lot of people use the tool and more would use it if I ever had the time to add planned improvements, additional tests, and so on that I have in mind.
g) Trying to support a marriage to a woman I love and who works harder than I do (she’s a physician), three sons with two in college and one trying to start a family on a shoestring, and a couple of rascally vagrant dogs, all of whom not unreasonably make demands on my time when I’m not totally committed to one task or another above.
And somewhere in there is writing long posts on WUWT as a hobby of sorts, trying to police the science and make up my own mind about what is properly “known” in climate science, what is sheer speculation and fancy, and what the most ethical course of action is for myself, at least, in the ongoing debate.
You can see my problem, I hope. If all I were divorced and living alone, teaching a single course, basking on the coast living on a substantial income from companies that were no longer starting up, with all of my offspring well-launched I would have already done the work I outlined above, as climate science is indeed my “hobby” to the extent that it generates no income but intrigues me and is clearly one of the more important issues of the day. Happily in some ways, sadly in others, I am not retired and single and free to do whatever I damn well please — yet. So if I’m to supervise anyone in doing the work, they have to be a self-starter and not an idiot when it comes to e.g. using R or other tools to do statistics, finding and downloading data sets, as well as the general ideas underlying Bayesian reasoning and hypothesis testing, at least. I simply don’t have time to teach someone this stuff — it would be faster to do it all myself and I don’t have time to do THAT.
Does this make sense? I’m not trying to wuss out — I am seriously overcommitted in my time well out into the indefinite future barring one of my companies being bought out and transforming me into the idle rich overnight, and I very much doubt that will happen this year in either current case although I do have some hopes for next year and the year after. So my expected time commitment would have to be at most an hour or two a week, maybe, and at that I’d pretty much have to not write on WUWT in the meantime (sigh).
That might be enough. As I said, 9.8a speaks for itself, even without pegging on the last two years to further extend the divergence of the predicted from the realized. But the really interesting possibility is fixing the multimodel “ensemble” by eliminating the cruft through simple statistical analysis and comparison to the real world data. This is to some extent contingent on being able to obtain PPEs per model. I Do Not Know how easy this will be — there is one figure in AR5 that I recall that shows a single collection of PPEs for one of the models, so I’m certain the data is out there for SOME of them, but I’m not at all certain about all. Steve M. probably knows if he doesn’t already archive it.
rgb
That’ll be a wrap from me, folks.
I would rather “verify” any theory or “model” trying to calculate the heat budget and radiation theory for ANY planet-sized rotating body in this solar system be able to first provide an accurate year-long stable radiation-surface temperature map for two stable bodies near the sun with no atmosphere.
If the proposed model can produce stable multi-years-long temperature plots at all latitudes of the Moon and Mercury, THEN maybe it can be expected to start explaining the extra and very difficult physics of the planets with collapsible atmospheres but NO water: Venus, Mars, Uranus, Neptune.
get those “right” then we can begin discussing the difficult ones: Jupiter (way too hot due to ????), Earth, and Saturn.
Sure, it is not glorious and glamorous to discuss moon dust and lunar seas and lunar mountain albedo and dust heat capacity. But. A VALID and working radiation-heat-exchange model must be able to do those simple, static things first.
And no, the WUWT article which ran a wire up the outside of a cylinder did not rebut it because the wire also develops a temperature gradient which prevents perpetual energy circulation.
My article, and I cry foul. The temperature gradients inside the wire — which can be a thick, well-insulated, excellent thermal conductor like a square meter bar of silver in a double insulated vacuum, it’s a gedanken experiment so we don’t have to actually pay for it — will not match the temperature gradient inside the cylinder because it is a much better conductor of heat.
Your problem is that you are confounding temperature and heat. The heat equation is straightforward. Depending on the TEMPERATURE of the ends, heat will flow through the wire from the hotter bottom to the colder top, because heat flows in materials from a higher temperature to a lower one, period. Which itself is pure statistical mechanical diffusion of available energy into the degrees of freedom of the rod’s atomic/molecular constituents. If you assert that gravitation can maintain a thermal equilibrium thermal gradient in a sealed fluid, in spite of the fact that this is a classic example of Maxwell’s Demon and that it can be directly proven in both stat mech and thermo that thermal equilibrium is isothermal in precisely this case, there is no question that thermal equilibrium for the e.g. silver “wire” is isothermal, gravitational gradient or not.
So when you place an isothermal wire at an intermediate temperature in contact with the hot bottom and cold top of your column (assuming that this ends up being equilibrium, which it won’t other than transiently) there is absolutely no doubt that heat will flow out of the bottom and into the top of your column — the temperatures are different at the point of contact. There is also no doubt that a thermal gradient will be maintained across the rod. The problem is, this thermal gradient violates the second law of thermodynamics because it can only be maintained by heat flow.
Heat flow satisfies the moral equivalent of “Ohm’s Law” in this case — a thermal gradient in the rod requires a heat “current” driven by a temperature difference. You cannot have a thermally conductive rod in thermal equilibrium with a temperature gradient, and the only way to have a temperature gradient is in direct association with heat flow.
I’m surprised that you would get this wrong. You assert that you understand that one proposed mechanism for the surplus heat emitted by Jupiter is that it is still gravitationally contracting (which releases heat/kinetic energy as the gravitational potential energy of the system slowly decreases). You point out, correctly, that if a planet has a large rocky core and comparatively shallow atmosphere — as do Mercury, Venus, Earth, Mars and arguably Uranus (although what we don’t know about the structure of the gas giants outweighs what we know by a substantial margin) plus the larger moons with atmospheres — there is no ongoing gravitational collapse, and if anything a slow top of atmosphere outgassing with a very slight cooling effect as a tiny slice of Maxwell-Boltzmann distributed molecular temperatures have escape energy and are headed in the right direction there. Surely you understand that for a static gas in thermal equilibrium, neighboring vertical slices are in direct thermal contact and that there is no relative mass transport between them, so there is no net heating from downward directed molecules unbalanced by net cooling from upward directed molecules in a stationary density gradient and mere conduction/diffusion/radiation will maintain identical temperatures on both sides of the interface.
Thermal equilibrium is isothermal, period. Gravity does not act as a Maxwell Demon, sorting out faster moving molecules so that they only exist in perpetuity at the bottom of a thermally isolated fluid while leaving behind the slower moving molecules at the top. Any proposed mechanism that requires no input of free energy that spontaneously sorts a molecular reservoir into distinct temperatures as a supposedly equilibrium state violates the second law of thermodynamics and can be used to build perpetual motion machines of the second kind. This is kiddy thermo. The grown-up stat mech involves looking at detailed balance between adjacent parcels of the material at supposedly distinct temperatures with an appropriate choice for e.g. canonical distribution, where it is merely probable that energy will be transferred from the higher temperature reservoir to the lower one until detailed balance is satisfied. Either way, no, the wire does not build up a thermal gradient that stops heat transfer, heat transfer must accompany any thermal gradient in the wire.
rgb
I’ve done it all for you in thousands of hours of study and thinking about how the laws of physics apply to planetary atmospheres, surfaces, crusts, mantles and cores.
I’ve put in my own hours, thank you. This is not helpful in the specific context of doing a defensible statistical analysis of CMIP5. Also, I am enormously skeptical about any work that asserts that the DALR is the result of anything but convection in an open system, given that this is how it is properly derived in a treatment of the Navier-Stokes equation, although there are semi-heuristic treatments like the one in Caballero that examine only uplifting or downfalling parcels. The DALR is a dynamic feature of an open, driven fluid systems, not something that is maintained in by gravity functioning as a Maxwell Demon.
Whenever this sort of thing is proposed, I cannot help but connect the dots and conclude that the proposer is seeking some sort of physical mechanism that would permit them to claim that there is no such thing as the greenhouse effect, that surface temperature is maintained “by gravity” in some sort of stationary way. It is often accompanied by the assertion that CO_2 is a cooling gas and other idiocy. I sincerely hope that you are not yet another “dragonslayer” in disguise, as this is the sort of thing that runs rampant amongst them, especially when “distinguished” 19th century physics is invoked (pretending that Gibbs and the entire 20th century progression of stat mech never happened, that quantum mechanics is irrelevant, etc.) and above all, when the laws of thermodynamics are invoked by individuals that clearly do not understand them.
If you are indeed a “physicist”, then surely you understand Maxwell’s Demon, detailed balance, have taken a credible course in statistical mechanics (and several in thermodynamics), have studied graduate-level electrodynamics and quantum theory, have taken courses in partial differential equations, complex variables, advanced calculus, and so on and hence should no better than to invoke gravity as a Demon. If you have done all of these things but somehow missed that part, I suggest that you do a web search or literature search, as I was able to find online derivations presented as parts of ordinary undergrad classes in thermo that covered it without much difficulty — you don’t even need to go back to your textbooks to try to find it (as it might well have been omitted from any given textbook). You might also review the heat equation as you seem to have a serious misunderstanding about the connection between a thermal gradient and heat flow through a homogeneous medium in a non-equilibrium dynamic energy transfer.
If you are in fact a dragonslayer, then to the best of my experience there is little or no hope for you. I have yet to find a single slayer that takes instruction in physics well, or is even willing to openly debate the physics with the use of actual equations and derivations following from clear statements of physical law.
rgb
rgbatduke @ur momisugly February 10, 2014 at 8:00 am
I’ve searched with combinations of ‘wattsupwiththat wire cylinder rgbatduke rgb’, and although I pull up interesting material, your silver wire stratified cyclinder gedunken article doesn’t seem to be among the results.
Can you suggest any additional specific terms I can use to help pull up your piece? Or is a link available? Thanks!
tc
It was in response to a proposal by Nikolov and Zeller (IIRC) and another person named Jelbring that the DALR was a static feature of true thermal equilibrium in a gravitational field (Jelbring more than N&Z) so that surface temperature strictly depended on fluid pressure. I pointed out in threads on multiple blogs that thermodynamic equilibrium is isothermal, gravitational field or not, and finally wrote a top article demonstrating in a fairly simple way that one could build a perpetual motion machine of the second kind if in fact gravity acted like a Maxwell Demon so that the bottom of an adiabatically insulated fluid column in a gravitational field was warmer than the top in stable thermodynamic equilibrium.
Since then, people periodically revisit it and assert without any actual support that my argument is wrong without ever (of course) being able to prove it or refute it algebraically from some sort of first principles. I’ve had people actually claim that heat flow itself is subject to gravity and flows more easily downhill than uphill (which of course is the absurdity that is at the heart of this, as one way or another that is the consequence of non-isothermal equilibrium).
In actual fact, the DALR is derived by considering the convective motion of approximately adiabatically isolated fluid parcels up and down in a gravitational field, something that only happens if the fluid is being driven by thermal asymmetry into convective flow in an open system that is differentially heated. The heating need not be at the bottom vs cooling at the top, although that is certainly the simplest example; for a planet or moon heating at the equator and cooling at the poles is sufficient to cause a bulk convective transport sufficient to maintain a troposphere with a DALR and a stratosphere. To put it another way, if one placed a heated plate on the ceiling of your well-insulated room on one side and a cold plate on the ceiling of your well insulated room on the other side, the cold plate would increase the density of fluid locally, which would then sink, displacing warmer fluid beneath, and being replaced by fluid from the side while the hot plate would heat air in contact with it, reducing its density and maintaining it at the ceiling. In time a convective roll would develop that sinks on the cold half of the room and rises on the warm half of the room. Of course it would be much simpler to put the hot plate on the ground (as it effectively is on the Earth with its visible-light transparent atmosphere) and the cold plate at the top of the troposphere where the atmosphere radiatively cools in the LWIR, and of course in a real planet one has to still throw in equatorial/polar asymmetry and substantial lateral asymmetry and latent heat and phase transitions in water and even more stuff.
This is all part of the Big Question — how do asymmetrically heated and cooled fluids in open complex systems self-organize to transport the energy? What are the emergent structures, and how do things like their transport efficiency vary with the non-equilibrium state? These are really difficult questions, and cannot be answered with trivial linear models as the self-organized structures themselves are highly nonlinear, highly variable and have their own rules that cannot easily or meaningfully be reduced to the microscopic level. Fluid dynamics in an an open system with the complexity of the Earth is very, very complicated; arguably the most difficult problem in physics. There is nothing shameful in the fact that we cannot yet solve it, although there is something wrong with claiming that we have solved it at a precision sufficient to justify the mortgage of human civilization for the next century on the basis of its predictions when manifestly we have not.
The WUWT article is here:
http://wattsupwiththat.com/2012/01/24/refutation-of-stable-thermal-equilibrium-lapse-rates/
It’s one of the only articles I actually have written for WUWT, although periodically a thread comment gets elevated to become a comment.
rgb
Ted Clayton says:
February 10, 2014 at 9:07 am
It’s here
rgbatduke @ur momisugly February 10, 2014 at 10:16 am
Thank you for the background & context, and the link!
It sounds not that far from having an apparatus in it. With equations.
This might be implemented … cloud chamber, heat pipe, thermocouple/diode, amp … or use them as model-elements.
tc
Electric sail could send probe to explore Uranus
A probe to Uranus ranks high & is being considered at several agencies.
A high level of activity at Answers in Genesis and in the wider Creationism community, seeking to use the irregularities of Uranus as a challenge to planetary evolution, may be helping raise the profile of this mission.
Data & facts on Uranus are fairly close at hand.
per Fritz.
“””””……Anyhow my eye says it curves down, just like my eyebrows.
Eyes are notorious for their abilities to find trends where none exists. You could easily test it in Excel with a second order fit…….””””””
Eyes (and ears) also have an uncanny ability to see “information” that sometimes defies analytical discovery.
For example, a two year old child can easily distinguish a tree; ANY tree, from a telephone pole (the AT&T “tree”).
Try locating some software on the web (any software) that can do likewise.
Now the rugrat, may get stumped (pun intended) by the Baja desert “boojum tree”, but then lots of humans aren’t sure its a tree, and not maybe a cactus.
But in self defense, I DID query, whether some formal analysis might put numbers, where my eye simply sees a pattern; (even if none really exists) in this case.
george e. smith says @ur momisugly February 10, 2014 at 2:35 pm
It’s a Boundary layer effects and Heat and mass transfer issue, isn’t it?
rgbatduke says:
February 9, 2014 at 1:59 pm
Indeed, one would expect that at least a few models would have decent p-values on the basis of pure data dredging, given so many models to pull results from.
———————————————————————————
Your posts enlighten all of us, and your clear understandable wording simplifies the complex, so that even a full amateur such as myself can follow the thought stream. Your arguments have a keen edge to them.
I have explained in this comment (and in more detail in my book) why thermodynamic equilibrium in a gravitational field is not an isothermal state. , and it is this lapse rate that you claim is stable thermodynamic equilibrium, one that will be maintained in a completely isolated fluid column.
, and it is this lapse rate that you claim is stable thermodynamic equilibrium, one that will be maintained in a completely isolated fluid column.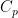 here is not a constant — it is the heat capacity of the fluid in question — different fluids, different densities, different heat capacity. A monoatomic fluid and diatomic fluid and molecular fluid with many degrees of freedom will all have different heat capacities, as will any one of these kinds of fluids as their density is changed. The point being — the lapse rate is not a constant!
here is not a constant — it is the heat capacity of the fluid in question — different fluids, different densities, different heat capacity. A monoatomic fluid and diatomic fluid and molecular fluid with many degrees of freedom will all have different heat capacities, as will any one of these kinds of fluids as their density is changed. The point being — the lapse rate is not a constant!
Explained in detail is utterly meaningless. Have you done a stat mech computation that demonstrates this? Of course not. Words don’t count in physical theory. Equations and derivations from established physical laws do.
You are also pretending that both Venus and Uranus have adiabatically isolated static atmospheres, as thermodynamic equilibrium naturally contains no driven motion or heat absorption or dissipation. I would have to state that both of these things are observationally false. They are open systems as you implicitly acknowledge when you talk about temperature variation, and are not in anything like thermal equilibrium.
Finally, I note that you carefully avoid addressing my recapitulated proof that if an actual adiabatically isolated fluid column in a gravitational field had a true thermodynamic equilibrium with a thermal lapse rate that varied with the density, it would violate the second law of thermodynamics. Let me once again refute you in a way that you cannot possibly blind yourself to.
The DALR (established by convection, not equilibrium processes, but never mind) is
However, you seem to not have realized that
Now imagine the scenario I clearly lay out in my refutation of any possibility that the lapse rate describes thermodynamic equilibrium in the article linked above. We mentally build not one but a dozen adiabatically insulated columns. We fill each of them with a different fluid at a different density and wait a long time so we end up (according to you!) with a dozen different thermodynamic equilibrium lapse rates in then different columns, which all have the same height.
Now, I’m certain that you recall the zeroth law of thermodynamics, because it is the one that defines thermodynamic equilibrium and permits us to define and measure temperature. What exactly do you think will happen when you establish a thermal connection between the tops and bottoms of the adiabatic columns you have built? The tops and bottoms will be at different temperatures! Heat will flow!
When, exactly, will it stop flowing?
If this is too abstruse for you, imagine connecting the top and bottom of each column with an identical well-insulated silver rod. You have asserted — incorrectly — that the silver rod will somehow also have a thermal lapse rate because it is in a gravitational field so that heat will stop flowing, in spite of the fact that there is ample empirical evidence that no such thing will occur. But even if it does, the lapse rate will not match all of the dozen fluid columns and the properties of the silver could not possibly lead to the same lapse rate as any of the columns — it is Dulong-Petit (an incompressible solid) not a molecular fluid with highly variable density and structurally variable degrees of freedom!
So once again, heat will flow in perpetuity because you have built a perpetual motion machine of the second kind with your assertions.
Normal people, especially if they are in fact physicists (which at this point I very much have to say that I doubt) know better than to assert processes that violate the second law. Indeed, to quote Eddington:
If someone points out to you that your pet theory of the universe is in disagreement with Maxwell’s equations—then so much the worse for Maxwell’s equations. If it is found to be contradicted by observation—well these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.
Please collapse.
rgb
rgbatduke 7:37am: “What exactly do you think will happen when you establish a thermal connection between the tops and bottoms of the adiabatic columns you have built?”
Once connected, the two systems are 1 system again, an adiabatic thermal universe of their own. Entropy will increase to the maximum possible value. At that exact point (ideal & exact T(z) determined by relevant Poisson eqn.), heat will stop flowing – thermodynamic equilibrium will once again be achieved isentropic, non-isothermal by a small percent in a gravity field. There is no PPM. 2nd law is observed. See Dr. Bohren’s 1998 text sec. 4.4 for the mathematical proof. The Verkley et. al. 2004 paper we discussed before shows a great, concise mathematical explanation/extension proof using 1st and 2nd law with the calculus required.
Once connected, the two systems are 1 system again, an adiabatic thermal universe of their own. Entropy will increase to the maximum possible value. At that exact point (ideal & exact T(z) determined by relevant Poisson eqn.), heat will stop flowing – thermodynamic equilibrium will once again be achieved isentropic, non-isothermal by a small percent in a gravity field. There is no PPM. 2nd law is observed. See Dr. Bohren’s 1998 text sec. 4.4 for the mathematical proof. The Verkley et. al. 2004 paper we discussed before shows a great, concise mathematical explanation/extension proof using 1st and 2nd law with the calculus required.
Are you mad, sir? Next you’ll be telling me that if I take a column of gas at equilibrium, attach a hot reservoir to the bottom known to the gas only by the temperature maintained on a plate there and a cold reservoir to the top known to the gas only by the temperature maintained on the plate there that no heat will be flowing in the new “equilibrium” that establishes itself. Because that’s just what you just told me.
A hint, sir. There are many itsy bitsy coarse grained differential chunks — parcels — of fluid in the gas column. Not one of them “knows” or interacts with any of the other chunks outside of its nearest neighbors — there are no long range interactions. Each such parcel of matter — including the matter bounding the container — obeys entirely simple rules concerning the need for detailed balance in equilibrium. What that means practically is that the zeroth law of thermodynamics must be satisfied — the one that defines the state of equilibrium.
This law is defined for each and every parcel interacting only with its immediate neighbors. The zeroth law for equilibrium requires detailed balance of energy flow across the boundary of each parcel. Locally, without question, if you increase or decrease the temperature on one side of a boundary surface, energy will diffuse across that surface until the temperature change is eliminated. It is that property that defines temperature — two reservoirs in equilibrium with a third must be in equilibrium with each other.
The thermodynamic equilibrium of an isolated gas column is a property of that column. It is the state whereby detailed balance is maintained between all neighboring parcels. It is the state that the entire system will spontaneously evolve to, if left alone with no energy inputs from the outside world. If you increase the temperature on the boundary of the bottom parcels, you disequilibrate them. Heat will flow into the system at the bottom, and start to migrate up through the gas column to try to bring the entire system into equilibrium with the new temperature. Because (as I hope is perfectly obvious) the temperature of the entire column whether or not you believe in a stable lapse rate is a monotonic function of the temperature maintained at any point on the boundary of the fluid, the only possible response to putting a surface at a higher temperature on the bottom of the column is for the entire column to increase its temperature (over time) until detailed balance is once again maintained. Note well that “increase temperature” means that heat will flow in at that bottom plate and diffuse upward through the entire column until it is once again in equilibrium at a new, higher, temperature.
Of course, if you put a plate in at the top of the column that is colder (in temperature) than the prior equilibrium temperature, the entire system will attempt to come into equilibrium with that colder temperature. The entire column would monotonically shift its equilibrium temperature, or temperature distribution as you erroneously prefer, down. Energy would flow out of the entire system at the top until detailed balance was once again maintained and the energy that goes out through this surface is once again on average equal to the energy that come in.
There is absolutely nothing special about the bottom or top, or vertical or horizontal in this. If you place a boundary anywhere on the container wall and maintain a temperature there, heat will flow until the entire container (with or without a lapse) is in thermal equilibrium with that temperature. That’s what thermal equilibrium means.
The problem arises the second you put in two such plates. Equilibrium is a property of the unforced fluid. If you warm or cool one such plate, you have absolutely no freedom to independently choose the temperature of the second plate — you cannot have two temperature distributions that constitute equilibrium because (recall from above) we’ve already established that parcel to parcel, detailed balance determines the temperature difference between parcels at equilibrium and nothing else. Heat will not flow between the neighboring parcels only when the correct temperature difference is maintained between them. I (and every other book on thermodynamics ever published) hold that the temperature difference when heat no longer flows is zero, but even if you want it to be non-zero, it can’t have two or more values as it is a local property of the fluid.
Consequently, when you put two plates in, one at the top and one at the bottom, and maintain a higher (than the original equilibrium) temperature on one and a lower temperature on the other, heat will flow and never stop flowing as long as the temperature differential is maintained. Of course you know this perfectly well (at least, I hope you do!) because there are some really simple limits here such as heating a bottom plate to 1000 K and maintaining the top plate at 3 K. Are you going to try to assert that this is an “equilibrium” state of the fluid and that no heat will flow through the fluid from the hot plate to the cold plate? Of course not.
So exactly what temperature difference will constitute thermal equilibrium, the state where there is no heat flow through the fluid? Remember that the fluid in the column has no knowledge of the process that maintains the temperatures of the two plates. On the other side of those plates there could be heaters and refrigerators, or there could be a second gas column that spontaneously creates a different lapse based temperature difference, there could be a thermal superconductor that maintains a zero temperature difference between the top and bottom plate that is too cold for your imaginary stable lapse at the bottom, too warm for it at the top. The gas column itself doesn’t know — it just knows about the temperatures of the plates, and knows that if those two plates are not at precisely the temperatures that constitute the equilibrium temperatures of the gas column, heat will flow between the two plates. If one connects two columns with different equilibrium temperatures at the point of connection, heat will flow forever because there is no common state that can be called equilibrium in which no heat flow! If there were, the thermodynamic equilibrium of each gas column would not be unique, would it?
What is the correct thermal equilibrium of the gas column? We can already see it as the limit of the examples given above. If we place a thermal superconductor inside the fluid column, there is no question that the top and bottom of the superconductor will be at the same temperature, always. The only possible way the fluid could be in equilibrium with this superconductor is if it, too, were at the same temperature throughout. There are not two thermal equilibrium states of this fluid, as thermal equilibrium is established locally on the basis of detailed balance and you cannot simultaneously tell me that detailed balance has a higher temperature by some however tiny amount on the lower of two neighboring parcels and that detailed balance is also satisfied by those two parcels having the same temperature.
All of this is precisely analogous to what one gets when considering resistance, potential difference, and current flow in loops, by the way. Equipotential is equipotential. For absolutely identical reasons, one cannot assert that charged particles in motion get a “gravity assist” so that they have a greater equilibrium potential difference across one medium than they do across another medium, because if one then connects the two media in parallel current will flow forever violating all sorts of important laws.
Fortunately, this condition — thermal equilibrium means “at the same temperature” also satisfies all of the laws of thermodynamics. No heat flow in equilibrium? Check. Two reservoirs in equilibrium with a third in equilibrium with each other? Check. First Law? Check. Second Law? Check.
I mean, seriously dude — suppose you have a thermometer stuck into the bottom of your fluid at the bottom while the whole shebang comes into equilibrium. You then remove it and move it to the top and poke it in there. The whole point of the zeroth law is that that thermometer must be in equilibrium when you poke it in at the top, but its temperature didn’t change as you carried it reversibly slowly uphill. If its temperature is different — and of course it will be different if there is a stable lapse rate — than heat will flow from the thermometer and the entropy of the entire system will increase, demonstrating that no your system was not at maximum entropy in its previous state.
rgb
You have not proved this. I have proved the opposite. Isothermal conditions have unbalanced energy potentials (because of the additional mean gravitational potential energy at the top) and so they are not the state of maximum entropy as described in the Second Law.
So you are saying that if you lift a sealed, adiabatically isolated container of gas up 10 km, its temperature will change according to the lapse rate.
The problem, sir, is obvious.
They are also demonstrably not in the state of maximum entropy. That’s the whole point of connecting the top and bottom of your supposedly maximum entropy fluid by a good conductor of heat. Heat will flow because it is not in maximum entropy — you have a thermal gradient that is just begging to be equilibrated by transferring heat from the higher temperature to the lower temperature, a process that macroscopically, without doubt, increases entropy. You actually have to come up with a glib explanation for why this entropy increase does not occur, since gravity is a conservative force and is net neutral in all energy exchanges from the top of the fluid to the bottom, and the fluid is a conductive medium perfectly capable of moving heat from the bottom to the top.
I just don’t get it. All of this is perfectly obvious. Also, there are numerous books that derive the DALR, which is not a “thermal equilibrium” or “thermodynamic equilibrium” condition either one, it is a condition established by the vertical convective motion of the gas. You cannot just redefine the language of physics to suit yourself, by the way — everybody knows that “thermodynamics” is a misnomer, but everybody also understands perfectly well what it means and that it does not apply to open system dynamics per se, hence the phrase “non-equilibrium thermodynamics”.
If you want to say that planetary atmospheres will generally establish a lapse rate, that is just fine with me. I agree. However that lapse rate is not therma-whatever equilibrium any more than a rod between two thermal reservoirs is in thermal equilibrium. Heat is being actively transported throughout the system, both in the rod and in the planetary atmospheres. If one takes an isolated column of fluid and waits for it to stop moving and equilibrate, therma-whatever equilibrium is isothermal, period, because it is absolutely trivial to show a) any other state is not, in fact, maximum entropy because the transfer of energy from the higher to the lower temperatures increases entropy; b) if one connects the two supposedly equilibrated regions with a heat engine, one has a perpetual motion machine of the second kind, as one might expect since you have violated the second law with your assertion of therma-whatever equilibrium.
The problem with this is that suddenly you aren’t contributing to the discussion at all any more. The DALR has been derived and reasonably well understood for a long time. So are its variations with things like humidity. Its role as one of the legs upon which the greenhouse effect is built is reasonably well understood — the greenhouse effect would produce warming in a pure single layer model, sure, but the real thing in a real atmosphere is vastly more complex because the real atmosphere is not a single layer with ideal properties, it is a complex entity with substantial circulation that maintains a lapse rate that varies substantially with humidity and local conditions, such that the radiative temperature of the top of the troposphere where it becomes transparent to LWIR is much cooler than the surface temperature and is not identical to the temperature that one might expect from a “perfect” single layer model even with the approximately correct mean absorptivities.
I personally generally recommend that people such as yourself consider reading e.g. Caballero’s lecture notes on atmospheric physics available here:
http://people.su.se/~rcaba/index.php?view=teaching
In particular, note his entire chapter 2. This is all pretty straightforward stuff, and note well that it involves moving air parcels — it does not assert, nor would it be correct to assert, that it describes thermodynamic equilibrium. Note well that considering the DALR and scale height in the context of planetary atmospheres is often assigned as homework in atmospheric physics courses. What, exactly, are you contributing to this that isn’t well-known, more correctly derived without all of the assertions of second-law-violating “equilibrium”, derived with consideration of the actual chemistry of the atmosphere in question (e.g. wet air lapse rates)? Would that be “nothing”?
Finally, even Caballero’s treatment isn’t quite “right” — it is semi-heuristic. The proper way to derive the DALR is to consider the Navier-Stokes equation itself. This derivation is in books on the advanced physics of planetary atmospheres, but I failed to bookmark the one I did find online that contained it and so I cannot give you a link. I’m guessing it is in several, however, so if you search I’m sure you will find. Navier-Stokes, of course, is not at all about equilibrium thermodynamics, it is about transport processes, both bulk fluid and heat/energy, usually driven by temperature/pressure differences.
rgb
[DALR = Downward ? ??? Lapse Rate? Longwave Radiation? Mod]
DALR = Dry Adiabatic Lapse Rate
http://climateaudit101.wikispot.org/Glossary_of_Acronyms
VERY HANDY Steve McIntyre List
rgbatduke 7:46am: “Are you mad, sir?”
No, I seldom get mad at confused but inquisitive students that want to improve. I only get mad at my tags that fail, let’s hope these work out. Thanks for your response. This 7:46am response shows you have not yet read up on the basic proofs in the cites I provided. My statements at 9:25am the day before are proven beyond reasonable doubts in the cites I gave using 1st principles and a bit of calculus. There is at least one step in the calculus checking that may need a visit to your math dept. but that is always a good thing to do.
If you want to contribute to developing an understanding of the FLAT 17+ years in near surface and lower troposphere mean global temperature observations in the face of ever increasing infrared-active gas ppm shown in top post, you must first end your confusion and master the basic science (the adiabatic columns). This is easily done by traipsing over to the library and checking out Dr. Bohren’s 1998 text and having the pre-req.s to read thru the proof of my 9:25am statements in sec. 4.4 (don’t just take the word of an anonymous poster on the internet). You will have to re-read it a couple times, it is idealized, exact, concise, you are smart and the work is physically correct so you will eventually come around to writing the right stuff on the basics.
As I would do for any critical, informed student visiting during my office hours, I will give some hints on why you have been marked down on exams and homework assignments in the past. I will not do the fix-up work for you, that is up to you if you want to apply yourself to advancing the science. Here goes; assume you just marched into my office and announced yes, you want to apply yourself to further study.
1) You announce but: “The zeroth law for equilibrium requires detailed balance of energy flow across the boundary of each parcel.”
Dr. Bohren discusses this and shows why you are wrong.
Hint: the zeroth is applicable to three thermodynamic systems. Research assignment: The adiabatic tall column of interest is how many thermodynamic systems? Once the adiabatic two are connected, how many adiabatic systems remain? Come back when you have a cite with your answer about whether zeroth is applicable. You are confused, as Dr. Bohren writes, by conduction in solids. Solid enthalpy is the same as gas enthalpy except a term is assumed to be so small as to be justly ignored in a solid. What term is that exactly? Hint: It cannot be ignored in the study of gas enthalpy in the pursuit of understanding adiabatic thermodynamic equilibrium in a tall m^2 column of standard air.
2) You counter: “If you increase the temperature on the boundary of the bottom parcels, you disequilibrate them…..heat will flow until the entire container…”
Hint: read up on the term “adiabatic”. Return when you can explain that term in your own words and why this statement of yours is irrelevant.
3) You complain I have not read every other book: “I (and every other book on thermodynamics ever published) hold that the temperature difference when heat no longer flows is zero, but even if you want it to be non-zero, it can’t have two or more values as it is a local property of the fluid.”
Again, you were marked down because you confuse conduction (and enthalpy) in solids with conduction (and enthalpy) in fluids and gases and plasmas. This is nothing to be ashamed over, many, if not all, students are in this position entering Dr. Bohren’s classes as he writes and have to be first unlearned of gibberish then re-learned in the right stuff of science.
4) You have to re-ask: “So exactly what temperature difference will constitute thermal equilibrium, the state where there is no heat flow through the fluid?
Dr. Bohren points out in the literature that the T(z) difference in the tall adiabatic column at max. entropy that will constitute thermodynamic equilibrium is the relevant Poisson eqn. (ref. eqn. 4.149 p. 166). If you run the numbers from earth surface to tropopause, find a temperature ( z) difference of a small percent (not constant).
5) You ask: “If one connects two columns with different equilibrium temperatures at the point of connection, heat will flow forever because there is no common state that can be called equilibrium in which no heat flow! If there were, the thermodynamic equilibrium of each gas column would not be unique, would it?”
Hint: Figure out your best answer to 3) above and re-examine these questions. Return during office hours when you have thought this through without confusion.
6) You ask repeatedly as if the answer was not already in the literature: “What is the correct thermal equilibrium of the gas column?”
Hint: This allows me to judge you have not completed the classroom assigned reading assignments. Get back to me when you have answered your own question by digging thru Bohren 1998 sec. 4.4 assigned in class above.
7) You state: “Fortunately, this condition — thermal equilibrium means “at the same temperature” also satisfies all of the laws of thermodynamics. No heat flow in equilibrium? Check. Two reservoirs in equilibrium with a third in equilibrium with each other? Check. First Law? Check. Second Law? Check.”
Hint: Think about when this is actually true. Giving it away hint: Think about when there is no external gravity field applied. Thermodynamic equilibrium at max. entropy with an external gravity field applied is proven in the literature to be not at the same temperature(z). By using fundamental correct, testable, observable-in-the-wild physics, see Bohren 1998 sec. 4.4 including his cites.
8) You conclude: “If its temperature is different — and of course it will be different if there is a stable lapse rate — than heat will flow from the thermometer and the entropy of the entire system will increase, demonstrating that no your system was not at maximum entropy in its previous state.”
Hint: This shows you have attended class, done a little study already. What happened to the adiabatic system max. entropy point as soon as you poked in the thermometers? Think what the (adiabatic) thermometers would show had they been in the system as it came to thermodynamic equilibrium. Think about the Poisson eqn. T(z) 4.149 p. 166 in Bohren 1998. Then let’s have another office hour session chat; this one was fun and allowed me to actually practice the art of teaching. I appreciate that.
A few further ideas on lapse rate and steady state. A steady temperature gradient in a conducting medium generates entropy at a rate k(1/T dT/dx)^2 per unit vol. This also works pretty well if conductivity k is a turbulent conductivity. If the gradient is in steady state, something must be removing that entropy.
That needs a heat pump, which is provided by air motion. Wind, but it’s the vertical component that is effective. That pumps heat against the gradient (if below the DALR). Of course there is no global entropy loss; the energy comes from the kinetic energy of the wind, which was generated from the atmospheric heat engine. Heat engines necessarily create entropy.
“I suggest that this discussion be combined with that on the more recent thread about the models.”
I don’t thing so. You can’t even keep your own ‘comment-spaghetti’ straight. 😉
Trick and I are correct in stating that a new equilibrium state will evolve for the complete system…
…in which energy is actively flowing from point to point, so that it is not, in fact, an equilibribium state.
There ain’t no such thing as a free lunch. Seriously. If you think that it is possible to build a perpetual motion machine of either the first or the second kind, you are wrong at such a deep level that there is probably no correcting you. Feel free to think that it is possible, but sorry, it isn’t.
And Trick, explain to me how thermal equilibrium (defined as a state where heat does not flow) depends on the boundary conditions of a system, again?
rgb