Guest Post by Reed Coray
On Dec. 6, 2011 12:12 am Lord Monckton posted a comment on a thread entitled Monckton on sensitivity training at Durban that appeared on this blog on Dec. 5, 2011. In that comment he wrote:
“First, it is not difficult to calculate that the Earth’s characteristic-emission temperature is 255 K. That is the temperature that would obtain at the surface in the absence of any greenhouse gases in the atmosphere. Since today’s surface temperature is 288 K, the presence as opposed to absence of all the greenhouse gases causes a warming of 33 K”.
Since I’m not sure what the definition of the “Earth’s characteristic-emission temperature” is, I can’t disagree with his claim that its value is 255 K. However, I can and do disagree with his claim that 255 K is “the temperature that would obtain at the surface in the absence of any greenhouse gases in the atmosphere”.
When computing the Earth’s surface temperature difference in “the presence as opposed to the absence of all greenhouse gases”, (i) two temperatures (A and B) must be measured/estimated and (ii) the difference in those temperatures computed. The first temperature, A, is the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases. The second temperature, B, is the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only–i.e., an atmosphere that contains non-greenhouse gases but is devoid of greenhouse gases.
For temperature A almost everyone uses a “measured average” of temperatures over the surface of the Earth. Although issues may exist regarding the algorithm used to compute a “measured average” Earth surface temperature, for the purposes of this discussion I’ll ignore all such issues and accept the value of 288 K as the value of temperature A (the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases).
Thus, we are left with coming up with a way to measure/estimate temperature B (the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only). We can’t directly measure B because we can’t remove greenhouse gases from the Earth’s atmosphere. This means we must use an algorithm (a model) to estimate B. I believe the algorithm most commonly used to compute the 255 K temperature estimate of B does NOT correspond to a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only”. As will be evident by my description (see below) of the commonly used algorithm, if anything that algorithm is more representative of a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases” than it is representative of a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only.”
If I am correct, then the use of 255 K in the computation of the Earth surface temperature difference with and without greenhouse gases is invalid.
Although there are many algorithms that can potentially lead to a 255 K temperature estimate of B, I now present the algorithm that I believe is most commonly used, and discuss why that algorithm does NOT represent “the temperature of the Earth’s surface in the presence of an atmosphere that is devoid of greenhouse gases”. I believe the algorithm described below represents the fundamental equation of radiative transfer for the Earth/Sun system assuming (a) an Earth absorption albedo of 0.3, and (b) an Earth emissivity of 1.
(1) The “effective temperature” of the Sun [i.e., the temperature of a sun-size spherical blackbody for which the radiated electromagnetic power (a) is representative of the total solar radiated power, and (b) has a power spectral density similar to the solar power spectral density] is approximately 5,778 K.
(2) For a spherical blackbody of radius 6.96×10^8 meters (the approximate radius of the sun) at a uniform surface temperature of 5,778 K, (a) the total radiated power is approximately 3.85×10^26 Watts, and (b) the radiated power density at a distance of 1.5×10^11 meters from the center of the blackbody (the approximate distance between the center of the Sun and the center of the Earth) is approximately 1,367 Watts per square meter.
(3) If the center of a sphere of radius 6.44×10^6 meters (the approximate radius of the Earth) is placed at a distance of 1.5×10^11 meters from the center of the Sun, to a good approximation the “effective absorbing area” of that sphere for blackbody radiation from the Sun is 1.3×10^14 square meters; and hence the solar power incident on the effective absorbing area of the sphere of radius 6.44×10^6 meters is approximately 1.78×10^17 Watts (1.3×10^14 square meters x 1,367 Watts per square meter).
(4) If the sphere of radius 6.44×10^6 meters absorbs electromagnetic energy with an “effective absorption albedo” of 0.3, then the solar power absorbed by the sphere is 1.25×10^17 Watts [1.78×10^17 Watts x (1 – 0.3)].
(5) A spherical blackbody (i.e., a spherical body whose surface radiates like a surface having an emissivity of 1) of radius 6.44×10^6 meters and at a temperature 254.87 K (hereafter rounded to 255 K) will radiate energy at the approximate rate of 1.25×10^17 Watts.
(6) If independent of the direction of energy incident on a sphere, the surface temperature of the sphere at any instant in time is everywhere the same, then the sphere possesses the property of perfect-thermal-conduction. Thus, for (a) an inert (no internal thermal energy source) perfect-thermal-conduction spherical body of radius 6.44×10^6 meters and uniform surface temperature 255 K whose center is placed at a distance of 1.5×10^11 meters from the center of an active (internal thermal energy source) spherical blackbody of radius 6.96×10^8 meters and uniform surface temperature 5,778 K, and (b) the inert perfect-thermal-conduction spherical body (i) absorbs electromagnetic energy with an effective absorption albedo of 0.3, and (ii) radiates electromagnetic energy with an emissivity of 1 then the perfect-thermal-conduction inert spherical body at temperature 255 K will be in radiation rate equilibrium with the active spherical blackbody at temperature 5,778 K. If the phrase “inert perfect-thermal-conduction spherical body of radius 6.44×10^6 meters” is replaced with the word “Earth,” and the phrase ” active spherical blackbody of radius 6.96×10^8 meters and uniform surface temperature 5,778 K” is replaced with the word “Sun”, it can be concluded that: If (a) an “Earth” at temperature 255 K is placed at a distance of 1.5×10^11 meters from the “Sun” and (b) the “Earth” (i) absorbs electromagnetic energy with an effective absorption albedo of 0.3, and (ii) radiates energy with an emissivity of 1, then the “Earth” will be in radiation rate equilibrium with the “Sun.” For the above conditions, the temperature of the “Earth” in radiation rate equilibrium with the “Sun” will be 255 K.
This completes the algorithm that I believe is commonly used to arrive at an “Earth’s characteristic-emission temperature” of 255 K, and hence is used to compute the 33 K temperature difference.
Even ignoring the facts that (1) it is incorrect to use the “average surface temperature” when computing radiation energy loss from a surface, and (2) in the presence of an atmosphere, (a) the blackbody radiation formula may not apply, and (b) blackbody radiation from the surface of the Earth is not the only mechanism for Earth energy loss to space (the atmosphere even without greenhouse gases will be heated by conduction from the Earth surface and both conduction and convection will cause that thermal energy to be distributed throughout the atmosphere, and the heated atmosphere will also radiate energy to space), the problem with using the 255 K temperature computed above to determine the difference between the Earth’s temperature with and without greenhouse gases is that the effective Earth absorption albedo of 0.3 used to generate the 255 K temperature is in part (mainly?) due to clouds in the atmosphere, and atmospheric clouds are created from water vapor, which is a greenhouse gas.
Thus an effective absorption albedo of 0.3 is based on the presence of a greenhouse gas–water vapor. It is illogical to compute a difference between two temperatures both of whose values are based on the presence of greenhouse gases and then claim that temperature difference represents the temperature difference with and without greenhouse gases. Without water vapor, there won’t be any clouds as we know them. Without clouds, the effective absorption albedo of the Earth will likely not be 0.3, and hence without the greenhouse gas water vapor, the Earth’s surface temperature in the absence of greenhouse gases is likely to be something other than 255 K. Thus, the 255 K “Earth characteristic-emission temperature” as computed using the algorithm above is NOT relevant to a discussion of the Earth surface temperature difference for an atmosphere that does and an atmosphere that does not contain greenhouse gases. Only if 0.3 is the effective absorption albedo of the Earth in the presence of an atmosphere devoid of all greenhouse gases is it fair to claim the presence of greenhouse gases increases the temperature of the Earth by 33 K.
Because clouds reflect a significant amount of incoming solar power, without water vapor I believe the effective absorption albedo of the Earth will be less than 0.3. If true, then more of the Sun’s energy will be absorbed by an Earth whose atmosphere is devoid of greenhouse gases than by an Earth whose atmosphere contains clouds formed from the greenhouse gas water vapor. This implies a higher Earth surface temperature in the absence of water vapor than the “Earth’s characteristic-emission temperature of 255 K”.
For an effective absorption albedo of 0, the temperature of the Earth in radiation rate equilibrium with the Sun will be approximately 278.64 K (hereafter rounded to 279 K). If this value is used as the Earth temperature in the presence of an atmosphere devoid of greenhouse gases, then it can be argued that the presence of greenhouse gases introduces a warming of approximately 9 K (288 Kelvin minus 279 K).
In summation, using the simplified arguments that I believe are also used to arrive at the 33 K temperature difference (i.e., assumed perfect-thermal-conduction Earth, blackbody Earth emission, greybody Earth absorption with an effective absorption albedo between 0 and 0.3, and ignoring atmospheric radiation to space for an Earth atmosphere devoid of greenhouse gases), I conclude the presence of greenhouse gases in the Earth’s atmosphere increases the Earth’s temperature by somewhere between 9 K and 33 K. Thus, I believe the claim that the presence of atmospheric greenhouse gases increases the temperature of the Earth by 33 K is based on an argument that has little relevance to the Earth’s temperature in the presence of an atmosphere devoid of greenhouse gases; and hence at best is misleading and at worst incorrect.
Note: Upon first publication – the guest author Reed Coray was accidentally and unintentionally omitted.
Dave Springer says………..
…No one knows exactly what the earth’s average albedo really is. Climate models use values which differ by as much as 0.07 from one to another. Speaking in W/m^2 that 0.07 uncertainty is 7% of some 200 Watts per square meter or about 14 W/m2. The net effect of all anthropogenic forcings is claimed to be around 2.5W/m2 so in essence this means that uncertainty in natural albedo forcing is about 6 times greater than anthropogenic forcing. In other words, the models are operating in the dark (so to speak) with uncertainties far greater than the anthropogenic factor they are trying to calculate…
—————————————————————————————————————————
…. Yep, that has been my opinion for this whole debate on AGW and the purported catastrophic effects to the Earths climate. Like Dave I consider that the noise of natural climate variation to be wholly overwhelming of any anthropogenic effect on the climate system, and real observations seem to bear this out…… It is only within the unnatural computer models of the Earths climate system that the AGW hypothesis continues to exist.
The confounding effects of the natural world defeat any simplistic climate model or math equations
Greenhouse gasses increase the Earth’s outgoing radiation budget. Remove them from the atmosphere and the remaining theremal sources: black-body and thermally radiating gasses (NGHGs) must increase their radiative output to compensate for this loss. As thermally radiative sources they can only do this through an increase in temperature. Hence:
GREENHOUSE GASSES CAUSE ABSOLUTE GLOBAL COOLING.
And lots of it.
It is so mind cringingly obvious and yet the sceptics continually support the warmist myths by denying the obvious: If GHGs are better radiating gasses than other radiative sources they increase the radiative output of the Earth and therefore cool the planet. Likewise remove the atmosphere entirely and all thermally radiation would have to be emitted by the surface so the temperature would rise much higher.
To put it another way: RADIATORS COOL THE SOURCE.
Otherwise we would have no central heating.
Get cool. Think..
I think there are a few essential elements missing in this generation of the null hypothesis,
1: The standard no-atmosphere “black body” model uses temperature of the surface, whereas the global temperature is the atmospheric temperature at 1.5 meters above the surface. Think about that
2: Non radiating gasses cannot lose their heat by radiation, only conduction and convection and there is only the earth surface to conduct heat to. Nothing can be emitted to the atmosphere.
3: There is no negative convection.
This is how I wrapped the null hypothesis up in UKww:
“The null hypothesis is usually describing the situation which would it make different from the actual -or alternative- hypothesis. It’s used mostly in statistics, I think, but why not try and see what happens if we apply it to the GHG hypothesis.
We read all over internet that the black body temperature of the Earth would have been -18C, but the actual average temperature is +15C; consequently this 33 degrees difference is supposed to be the greenhouse effect. But is this true?
Is the blackbody situation the “null hypothesis”? I don’t think so. The black body calculation assumes a sphere with a constant flux of light energy, uniformely distributed over the surface, using the Stefan Boltzman equation to derive it’s temperature like this.
But the earth is nowhere near a blackbody and if we want to really look at the null hypothesis, we would have to look at an earth without greenhouse effect, but still with an (inert) atmosphere and still rotating in 24 hrs, with seasons and all.
Now instead of using an average steady state solar radiation, we need to realize that we have the diurnal cycle with max insolation radiation at noon and no radiation incoming when the sun is below the horizon. So during daytime the earth surface warms up and much more than the according the average radiation. Equilibrium temperature at the equator in a steady state with the sun in zenith, using the full incoming 1365 w/m2 (albedo 30%) would be 360K or 87C. This follows from applying the Stephan Boltzman equation for the spot directly under the sun, instead of a uniformely distributed radiation.
So this much higher temperature of the earth surface is transmitted via conduction to the lowermost boundary layer of the atmosphere. This heated air gets is less dense, and it becomes buoyant so it rises up; Convection, the very basics of meteorology. So at daytime the atmosphere receives thermal energy of the earth. How can it lose this energy again? Remember we are in the null hypothesis, no radiation, no greenhouse effect, so the inert atmosphere cannot lose the energy by radiation.
Now, at night time the Earth does not receive radiation energy from the sun but it radiates energy out and cools quickly, obviously much more quickly in the null hypothesis even than with the greenhouse effect, which would have directed (“reflects”) some radiation back to earth. Now the cooler earth also cools the boundary layer of the atmosphere by conduction again, however there is no negative convection as the cool air gets more dense and tends to stay put; the inversion; also very basic meteorology. So despite the cooling of the earth, the missing radiation from the atmosphere prevents it from cooling at night and the next day more conducted energy is convected into the atmosphere, that stays there again.
Obviously we have an unbalance. And equilibrium can only be reached, maybe after thousands of years, when the convection at daytime has reduced so much to balance heat loss at night time via conduction back to the surface. For that the lower level atmosphere needs to be at the same temperature / density than the boundary layer would reach due to the conduction of heat from the surface.
Conclusion, in the null hypothesis, without greenhouse effect, the average temperature of the lower atmosphere would be considerably higher than the black body temperature of the surface. How much I don’t know. But the main point is that a certain portian of the temperature difference between black body and actual atmospheric temperature is not due to greenhouse effect but to the inability of the inert atmosphere to cool down by radiation. “
@Andre says:
December 27, 2011 at 1:58 am
At last, somebody on the right track.
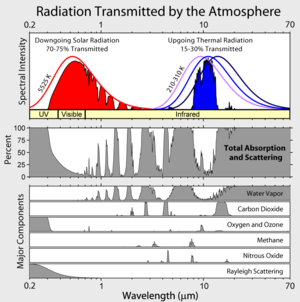
I think there is at least one (potentially major) error in this whole atmospheric transmission mess-up. There not TWO (Transmission vs. “Absorption AND Scattering”) but THREE (wavelength dependent) components for each atmospheric component:
1. Transmission
2. Absorption (and Re-Emission!)
3. Reflectance (“Scattering”)
I think Climate Science has an oversimplified model of this mess-up by putting Absorption and Scattering together.
Baa Humbug says:
December 26, 2011 at 8:24 pm
Myrrh says:
December 26, 2011 at 5:50 pm
Does anyone have access to this paper? http://www.agu.org/pubs/crossref/2011/2010JD015343.shtml
A precis of results would be appreciated..
Will this do?
http://www.gewex.org/BSRN/BSRN-11_presentations/Tues-wacker.pdf
============================
Many thanks! I wondered how the science had progressed from its beginnings:
I am sorry to disagree with the famous Lord but the theory of GHG’s violates the laws of thermodynamics.
The BB radiated temperature calculated is incorrect because the earth is not a black body. the nobel Lord has completely forgotten the small fact that the atmosphere generates heat through adiabatic compression, rather like a diesel engine increases its cylinder temperature to the diesel oil combustion temperature of 250C by compressing the internal gasses. Refrigerators work by the same process. Using the combined gas laws will produce the required temperature at the earth’s surface. Venus, with a surface pressure of 90 atmospheres generates 480C or 750K by the same process and the high surface pressure is due to the heave CO2 atmosphere. It is interesting to note that in the Jovian atmosphere, without any greenhouse gasses present, generates a similar temperature to earth at the 1000mb level.
The GHG theory relies on these gasses to be IR reactive. But are they? The rerun of Gore’s experiment by Anthony Watts in which two identical containers with air in one and a CO2 rich mixture in the second were heated by light. Anthony got no temperature rise in his CO2 enriched container above that of the air filled container. Both remained at similar temperatures. He repeated this experiment several times without any greenhouse effect. The rigerous way Anthony carried out this experiment should have got people thinking harder about this discredited GHG theory.
A moments thought will show that if a molecule of CO2 is preferentially heated it will immediately share this heat with its surroundings. It cannot do anything else. It cannot ‘store it’ because the 2nd law must hold true. Any heated volume of gas in the atmosphere will convect due to density changes and convecting air in the atmosphere must expand and loose heat due to adiabatic expansion. The gas will very soon be cooler than the surface so cannot re-radiate heat to the surface, heat can only flow by whatever means from hot to cold as the laws of thermodynamics dictate. Also as confirmation the so called heat anomaly in the mid troposphere as predicted by the theory of GHG’s cannot be found. Why? because the theory is WRONG.
Andre says:
December 27, 2011 at 1:58 am
Finally someone able to do some logical thinking.
For interest:
In the words of Dr. Evil … magma … the earth is hardly a cold rock in space …
I don’t know why you are arguing about this. I have it on good authority that the science is settled.
http://www.financialpost.com/story.html?id=c47c1209-233b-412c-b6d1-5c755457a8af
/sarc
Ned Nikolov says:
December 26, 2011 at 3:36 pm
///////////////////////////////////////
Dr Nikolov
#
On the assumption that we are heading towards an ice age, what process according to your theory, explains such a change in temperature?
Richard Verney wrote: “Two problems. First, the length of the lunar day. Eg., what would be the average temperature of the moon if a lunar day was only one hour rather than about 27;5 days? ”
A while back, I wrote a simulation model of what the Earth surface temperature would look like if it had no atmosphere, and spun on its axis once an hour. The mean temperature is the same as with a 24 hour rotation period, but there’s less variation around it.
Henry@Stephen Fisher Wilde
http://wattsupwiththat.com/2011/12/21/ben-santers-damage-control-on-uah-global-temperature-data/#comment-843410
Henry@Dave Springer
http://wattsupwiththat.com/2011/12/21/ben-santers-damage-control-on-uah-global-temperature-data/#comment-843405
http://wattsupwiththat.com/2011/12/21/ben-santers-damage-control-on-uah-global-temperature-data/#comment-843407
http://wattsupwiththat.com/2011/12/21/ben-santers-damage-control-on-uah-global-temperature-data/#comment-843557
>>
D. Cohen says:
December 26, 2011 at 3:35 am
I just looked up the average surface temperature of the moon.
<<
All the comments about the Moon’s surface temperature are essentially comparing apples to oranges. The temperature usually quoted for the Earth’s surface is really the Surface Air Temperature or SAT. This is a value measured about two meters ABOVE the Earth’s surface–not the actual Earth’s surface. (Climatologists and climate modelers seem to confuse the two.) The Moon has no atmosphere, so there can be no SAT. The Moon’s surface temperature is the actual surface temperature.
I’ve been to beaches where the sand burns my feet. If I wear sandals to insulate my feet from the hot surface, I find that the corresponding air temperature is quite pleasant.
Jim
I like Dr. Nikolov’s presentation. I believe it is the same concept as has been put forward by several others, most notably, Postma and Huffman. The argument against it has always been that the air pressure can do no additional work once it stabilizes. However, I think another comment above is important. Without gravity the atmosphere would expand and lose its thermal energy. Gravity prevents this and hence keeps the gas molecules in close contact. This continued kinetic action must have some affect on temperature.
However, the fact is GHGs do radiate and absorb thermal heat. So, it seems they still need to be looked at more formally than I saw in Nikolov’s presentation. I don’t think asserting they are “completely counterbalanced” is sufficient. Do they block heat (through absorption) or do they cool the planet (through emission). I’m starting to lean towards the latter.
Re: surface moisture effects:
“Soil Moisture–Atmosphere Interactions during the 2003 European Summer Heat Wave”
http://www.iac.ethz.ch/people/fischeer/docs/fischer_et_al_2007c.pdf
(etc):
http://journals.ametsoc.org/doi/abs/10.1175/2011JCLI3523.1
http://www.lmd.ens.fr/dandrea/i1520-0442-22-18-4747.pdf
http://www.nature.com/ngeo/journal/v3/n10/full/ngeo950.html
****
John Marshall says:
December 27, 2011 at 3:39 am
The BB radiated temperature calculated is incorrect because the earth is not a black body. the nobel Lord has completely forgotten the small fact that the atmosphere generates heat through adiabatic compression, rather like a diesel engine increases its cylinder temperature to the diesel oil combustion temperature of 250C by compressing the internal gasses.
****
Yes but since the atmospheric mass is fixed, any compression (downward movement) in a local area must be countered by an equal decompression somewhere else, so the net effect is zero. Obviously, some regional areas are warmed by compression, like Chinook winds just east of the Rockies in NA, but other regions must experience counteracting decompression (upward movement).
The 33C temperature difference with/without greenhouse gases is simply a Gedankenexperiment (http://en.wikipedia.org/wiki/Thought_experiment), exploring the potential consequences of a change, what happens if a single variable is modified – and in this case _with all other things held to be unchanging_.
Now, if we could experimentally remove all greenhouse gases, the end resulting temperature of the Earth would not be 33C colder, because that would kick in all kinds of other changes: missing clouds reducing albedo, glaciers increasing albedo, vegetation changes, changes in the lapse rate due to modified atmospheric energy, etc. Some of these changes would make the Earth warmer, some would make it colder.
But – the greenhouse gas contribution to current temperatures is 33C. That’s just spectroscopy, shown both by computations from numerically integrating over the depth of the atmosphere and measurements of the outgoing IR spectrum. The IR emissivity of ground and water is ~0.98 (98% as efficient as a pure blackbody), while the IR emissivity of the Earth to space through our greenhouse-gas containing atmosphere is ~0.612. An IR emissivity of 0.98 would allow the Earth radiate energy equal to incoming sunlight at ~-18C, while the emissivity of 0.612 means a temperature of ~15C is required.
And again, that’s just spectroscopy.
Secondary changes which would occur in a “real-world” removal of greenhouse gases, positive or negative, don’t change the GHG contribution to current temperatures – because those secondary changes are additional contributions +/-.
John Marshall says:
December 27, 2011 at 3:39 am
I am sorry to disagree with the famous Lord but the theory of GHG’s violates the laws of thermodynamics.
So you disagree with Lord Monkton? Well John, if you learn some basic physics your opinion may count for something, but until then your misconceptions of the 2nd Law of Thermodynamics and pressure causing heat don’t carry much weight.
For instance, the car in my garage has pressurised tyres. Do you think the tyres are hotter than the rest of the car?
Bomber_the_Cat says:
December 27, 2011 at 8:35 am:
“For instance, the car in my garage has pressurised tyres. Do you think the tyres are hotter than the rest of the car?”..
How about the charge temp in the cylinder at the top of the compression stroke as JM indicated?
Not sure what your argument is, but if it is re: compression and atmospheric temps check this:
http://pds-atmospheres.nmsu.edu/education_and_outreach/encyclopedia/adiabatic_lapse_rate.htm
KR says:
“Now, if we could experimentally remove all greenhouse gases, the end resulting temperature of the Earth would not be 33C colder.”
In this he agrees with the vast majority of posters who notice that the bogus calculation requires an Earth system albedo of 0.3.
Any realistic estimate of the real Earth system without greenhouse gases would be less that 0.1
Making the greenhouse effect less than 16K
However he then goes on to say
“But – the greenhouse gas contribution to current temperatures is 33C.”
So even though the theory is bogus we refuse to change the value!!!
“That’s just spectroscopy, shown both by computations from numerically integrating over the depth of the atmosphere and measurements of the outgoing IR spectrum. ”
This is just another layer of subterfuge used by CGW advocates like KR.
Only by incorrectly calibrating instruments so as to arrive at the 33K figure.
Instrument makers acknowledge that there is circular reasoning involved in radiation measurement.
You can calibrate the instruments to agree with your initial assumptions – what does that prove?
By defending the indefensible the adherents of the greenhouse theory are increasingly being seen as rather odd.
I think the number being referenced may have been made by making a few very simple assumptions that avoid all complex details about the surface of the Earth.
1. The Earth is characterized by a single temperature.
2. The total black body energy radiated at that temperature over the entire spherical surface of the earth is equal to the energy received from the sun on its disk shaped cross-section.
beng says:
December 27, 2011 at 8:12 am
“Yes but since the atmospheric mass is fixed, any compression (downward movement) in a local area must be countered by an equal decompression somewhere else, so the net effect is zero. Obviously, some regional areas are warmed by compression, like Chinook winds just east of the Rockies in NA, but other regions must experience counteracting decompression (upward movement).”
How about as you move up and down vertically in the atmosphere? Is pressure constant? Is any decrease in pressure accompanied by an increase elsewhere? Think of getting in a submarine and descending in the sea – does the hull experience a change in pressure loading?…
It is the vertical pressure gradient which supports the temperature lapse rate. Check the link above for bomber_the_cat.
Frank Davis says:
December 27, 2011 at 6:29 am
//////////////////////////////
Frank
Thanks for the link. I have not yet read your paper but will definitely do so. I am not surprised by your summary. The position with respect to the Earth would be different if the speed of rotation was very much slower, may be measured in decades rather than in a day. The thermal capacity of the oceans stores the energy received during the day and releases it during the night. It smoothes the energy budget. However, for the thermal reservoirs to work, obviously they must not freeze (since in that condition they reflect most of the incoming solar energy) and this requires that solar inpout is regularly received (as in the case of the Earth every 12 hours).
The point with the moon is that it has no such thermal reservoirs. If it did, the diurnal differences would not be as stark. Since the moon does not have these thermal reservoirs, there is little to smooth the diurnal range since the rocky surface does not get heated to a significant depth. Lacking the thermal reservoirs the only other way to obtain diurnal smoothing would be a fast rotation. In my post, I suggested a rotation of once an hour, I have not done the calculations and it may be that the day would need to be even shorter than that!