Guest Post by Reed Coray
On Dec. 6, 2011 12:12 am Lord Monckton posted a comment on a thread entitled Monckton on sensitivity training at Durban that appeared on this blog on Dec. 5, 2011. In that comment he wrote:
“First, it is not difficult to calculate that the Earth’s characteristic-emission temperature is 255 K. That is the temperature that would obtain at the surface in the absence of any greenhouse gases in the atmosphere. Since today’s surface temperature is 288 K, the presence as opposed to absence of all the greenhouse gases causes a warming of 33 K”.
Since I’m not sure what the definition of the “Earth’s characteristic-emission temperature” is, I can’t disagree with his claim that its value is 255 K. However, I can and do disagree with his claim that 255 K is “the temperature that would obtain at the surface in the absence of any greenhouse gases in the atmosphere”.
When computing the Earth’s surface temperature difference in “the presence as opposed to the absence of all greenhouse gases”, (i) two temperatures (A and B) must be measured/estimated and (ii) the difference in those temperatures computed. The first temperature, A, is the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases. The second temperature, B, is the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only–i.e., an atmosphere that contains non-greenhouse gases but is devoid of greenhouse gases.
For temperature A almost everyone uses a “measured average” of temperatures over the surface of the Earth. Although issues may exist regarding the algorithm used to compute a “measured average” Earth surface temperature, for the purposes of this discussion I’ll ignore all such issues and accept the value of 288 K as the value of temperature A (the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases).
Thus, we are left with coming up with a way to measure/estimate temperature B (the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only). We can’t directly measure B because we can’t remove greenhouse gases from the Earth’s atmosphere. This means we must use an algorithm (a model) to estimate B. I believe the algorithm most commonly used to compute the 255 K temperature estimate of B does NOT correspond to a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only”. As will be evident by my description (see below) of the commonly used algorithm, if anything that algorithm is more representative of a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains both greenhouse gases and non-greenhouse gases” than it is representative of a model of “the temperature of the Earth’s surface in the presence of an atmosphere that contains non-greenhouse gases only.”
If I am correct, then the use of 255 K in the computation of the Earth surface temperature difference with and without greenhouse gases is invalid.
Although there are many algorithms that can potentially lead to a 255 K temperature estimate of B, I now present the algorithm that I believe is most commonly used, and discuss why that algorithm does NOT represent “the temperature of the Earth’s surface in the presence of an atmosphere that is devoid of greenhouse gases”. I believe the algorithm described below represents the fundamental equation of radiative transfer for the Earth/Sun system assuming (a) an Earth absorption albedo of 0.3, and (b) an Earth emissivity of 1.
(1) The “effective temperature” of the Sun [i.e., the temperature of a sun-size spherical blackbody for which the radiated electromagnetic power (a) is representative of the total solar radiated power, and (b) has a power spectral density similar to the solar power spectral density] is approximately 5,778 K.
(2) For a spherical blackbody of radius 6.96×10^8 meters (the approximate radius of the sun) at a uniform surface temperature of 5,778 K, (a) the total radiated power is approximately 3.85×10^26 Watts, and (b) the radiated power density at a distance of 1.5×10^11 meters from the center of the blackbody (the approximate distance between the center of the Sun and the center of the Earth) is approximately 1,367 Watts per square meter.
(3) If the center of a sphere of radius 6.44×10^6 meters (the approximate radius of the Earth) is placed at a distance of 1.5×10^11 meters from the center of the Sun, to a good approximation the “effective absorbing area” of that sphere for blackbody radiation from the Sun is 1.3×10^14 square meters; and hence the solar power incident on the effective absorbing area of the sphere of radius 6.44×10^6 meters is approximately 1.78×10^17 Watts (1.3×10^14 square meters x 1,367 Watts per square meter).
(4) If the sphere of radius 6.44×10^6 meters absorbs electromagnetic energy with an “effective absorption albedo” of 0.3, then the solar power absorbed by the sphere is 1.25×10^17 Watts [1.78×10^17 Watts x (1 – 0.3)].
(5) A spherical blackbody (i.e., a spherical body whose surface radiates like a surface having an emissivity of 1) of radius 6.44×10^6 meters and at a temperature 254.87 K (hereafter rounded to 255 K) will radiate energy at the approximate rate of 1.25×10^17 Watts.
(6) If independent of the direction of energy incident on a sphere, the surface temperature of the sphere at any instant in time is everywhere the same, then the sphere possesses the property of perfect-thermal-conduction. Thus, for (a) an inert (no internal thermal energy source) perfect-thermal-conduction spherical body of radius 6.44×10^6 meters and uniform surface temperature 255 K whose center is placed at a distance of 1.5×10^11 meters from the center of an active (internal thermal energy source) spherical blackbody of radius 6.96×10^8 meters and uniform surface temperature 5,778 K, and (b) the inert perfect-thermal-conduction spherical body (i) absorbs electromagnetic energy with an effective absorption albedo of 0.3, and (ii) radiates electromagnetic energy with an emissivity of 1 then the perfect-thermal-conduction inert spherical body at temperature 255 K will be in radiation rate equilibrium with the active spherical blackbody at temperature 5,778 K. If the phrase “inert perfect-thermal-conduction spherical body of radius 6.44×10^6 meters” is replaced with the word “Earth,” and the phrase ” active spherical blackbody of radius 6.96×10^8 meters and uniform surface temperature 5,778 K” is replaced with the word “Sun”, it can be concluded that: If (a) an “Earth” at temperature 255 K is placed at a distance of 1.5×10^11 meters from the “Sun” and (b) the “Earth” (i) absorbs electromagnetic energy with an effective absorption albedo of 0.3, and (ii) radiates energy with an emissivity of 1, then the “Earth” will be in radiation rate equilibrium with the “Sun.” For the above conditions, the temperature of the “Earth” in radiation rate equilibrium with the “Sun” will be 255 K.
This completes the algorithm that I believe is commonly used to arrive at an “Earth’s characteristic-emission temperature” of 255 K, and hence is used to compute the 33 K temperature difference.
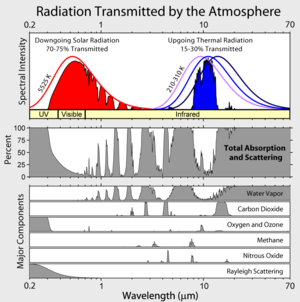
Even ignoring the facts that (1) it is incorrect to use the “average surface temperature” when computing radiation energy loss from a surface, and (2) in the presence of an atmosphere, (a) the blackbody radiation formula may not apply, and (b) blackbody radiation from the surface of the Earth is not the only mechanism for Earth energy loss to space (the atmosphere even without greenhouse gases will be heated by conduction from the Earth surface and both conduction and convection will cause that thermal energy to be distributed throughout the atmosphere, and the heated atmosphere will also radiate energy to space), the problem with using the 255 K temperature computed above to determine the difference between the Earth’s temperature with and without greenhouse gases is that the effective Earth absorption albedo of 0.3 used to generate the 255 K temperature is in part (mainly?) due to clouds in the atmosphere, and atmospheric clouds are created from water vapor, which is a greenhouse gas.
Thus an effective absorption albedo of 0.3 is based on the presence of a greenhouse gas–water vapor. It is illogical to compute a difference between two temperatures both of whose values are based on the presence of greenhouse gases and then claim that temperature difference represents the temperature difference with and without greenhouse gases. Without water vapor, there won’t be any clouds as we know them. Without clouds, the effective absorption albedo of the Earth will likely not be 0.3, and hence without the greenhouse gas water vapor, the Earth’s surface temperature in the absence of greenhouse gases is likely to be something other than 255 K. Thus, the 255 K “Earth characteristic-emission temperature” as computed using the algorithm above is NOT relevant to a discussion of the Earth surface temperature difference for an atmosphere that does and an atmosphere that does not contain greenhouse gases. Only if 0.3 is the effective absorption albedo of the Earth in the presence of an atmosphere devoid of all greenhouse gases is it fair to claim the presence of greenhouse gases increases the temperature of the Earth by 33 K.
Because clouds reflect a significant amount of incoming solar power, without water vapor I believe the effective absorption albedo of the Earth will be less than 0.3. If true, then more of the Sun’s energy will be absorbed by an Earth whose atmosphere is devoid of greenhouse gases than by an Earth whose atmosphere contains clouds formed from the greenhouse gas water vapor. This implies a higher Earth surface temperature in the absence of water vapor than the “Earth’s characteristic-emission temperature of 255 K”.
For an effective absorption albedo of 0, the temperature of the Earth in radiation rate equilibrium with the Sun will be approximately 278.64 K (hereafter rounded to 279 K). If this value is used as the Earth temperature in the presence of an atmosphere devoid of greenhouse gases, then it can be argued that the presence of greenhouse gases introduces a warming of approximately 9 K (288 Kelvin minus 279 K).
In summation, using the simplified arguments that I believe are also used to arrive at the 33 K temperature difference (i.e., assumed perfect-thermal-conduction Earth, blackbody Earth emission, greybody Earth absorption with an effective absorption albedo between 0 and 0.3, and ignoring atmospheric radiation to space for an Earth atmosphere devoid of greenhouse gases), I conclude the presence of greenhouse gases in the Earth’s atmosphere increases the Earth’s temperature by somewhere between 9 K and 33 K. Thus, I believe the claim that the presence of atmospheric greenhouse gases increases the temperature of the Earth by 33 K is based on an argument that has little relevance to the Earth’s temperature in the presence of an atmosphere devoid of greenhouse gases; and hence at best is misleading and at worst incorrect.
Note: Upon first publication – the guest author Reed Coray was accidentally and unintentionally omitted.
The classic mistake or “trick” is to calculate the outgoing radiation from earth surface.
As if GHG and cloud does not exist.
Do the math from middle of atmosphere: 50% of atmosphere weight is 500 Mb equal to 5500 meter altitude. Lapse rate for humid atmosphere are about 6 C/1000 meter or for 5500m …… “Ta da”……..33 C colder than on earth surface. Such a coincidence. Not.
The atmospheric window is just that, a small wavelength window where just some radiation escape from earth surface direct to space. Most of outgoing radiation are radiated from the atmosphere.
For an average temperature are an average altitude and by that an average radiation balance just making sense.
By the way, change in UV radiation from the sun alter atmosphere height, that is changing the 500mb altitude, which will change the average surface temperature.
“the effective Earth absorption albedo of 0.3 used to generate the 255 K temperature is in part (mainly?) due to clouds in the atmosphere, and atmospheric clouds are created from water vapor, which is a greenhouse gas.”
A sticky wicket indeed. The earth and moon are made of the same stuff. The moon has an albedo of ~0.15 which is what the earth would be without an atmosphere. The ocean has an albedo of ~0.00 which makes it a lot darker than the moon. But the ocean can’t exist without an atmosphere to keep it from boiling away. And you can’t have a liquid ocean and an atmosphere without clouds. Clouds have an albedo of ~0.80 and then the combination of all these things gives the planet an albedo in the range of ~0.35 which varies interannually by an unknowm but presumably small amount in the range of +-0.03.
No one knows exactly what the earth’s average albedo really is. Climate models use values which differ by as much as 0.07 from one to another. Speaking in W/m^2 that 0.07 uncertainty is 7% of some 200 Watts per square meter or about 14 W/m2. The net effect of all anthropogenic forcings is claimed to be around 2.5W/m2 so in essence this means that uncertainty in natural albedo forcing is about 6 times greater than anthropogenic forcing. In other words, the models are operating in the dark (so to speak) with uncertainties far greater than the anthropogenic factor they are trying to calculate. Albedo in the climate models is a proverbial fudge factor that is adjusted by the model maker to whatever value gives the best result in conjuction with all the other assumptions and variables. If these models weren’t being considered with more credibility than instruments (if observations disagree with models it is presumed the observations must be wrong!) this would be material for late night talk show comedy skits.
The writeup is wrong on the two major points. PeterF made the first one, that if there is no greenhouse effect, the atmosphere will not radiate much to space (there would be a small amount from aerosols and very weak diatomic gas effects, but not significant). The second point is the albedo effect. Oceans and clouds have effects, but if no greenhouse effect were present, the clouds (and water vapor) would not be present. The albedo would then be due to ground level absorption. It does not matter if there are oceans or not if the assumption of equivalent albedo is assumed to be the same, as long as no clouds or water vapor is present. The only effect of oceans is storage and distribution, and long term averages would be the same as if no oceans were present. Lord Monckton is correct as far as his statements are made. Get over it.
What about a “leaking condenser”,where the atmosphere, being the dielectric, short circuits during lightning storms (and also during tornadoes, etc.)?
This implies a higher Earth surface temperature in the absence of water vapor than the “Earth’s characteristic-emission temperature of 255 K”.
“For an effective absorption albedo of 0, the temperature of the Earth in radiation rate equilibrium with the Sun will be approximately 278.64 K (hereafter rounded to 279 K). If this value is used as the Earth temperature in the presence of an atmosphere devoid of greenhouse gases, then it can be argued that the presence of greenhouse gases introduces a warming of approximately 9 K (288 Kelvin minus 279 K).”
Bingo. The ocean has an albedo of effectively 0 and it covers 70% of the surface. The rocks have an effective albedo of 0.15, same as the moon, which is (believe it or not) about the same as weathered asphalt. The moon is a much darker color than one might guess by looking at it because it is contrasted against the inky blackness of space. If it had the albedo of a cloud or snow it would be blinding to look at it.
Anyhow, the albedo of the earth sans greenhouse gases would be around 0.05 instead of .035 which would make it quite a bit warmer than 255K on average.
Technically however, clouds aren’t greenhouse gases. They are composed of liquid water droplets. Water is highly reflective at high angles of incidence so unlike the surface of the ocean with presents a low angle of incidence to sunlight except near the poles and near sundown &* sunset when it doesn’t really matter because solar power is very weak then anyhow, clouds are liquid water in a highly reflective configuration.
It’s tough to imagine how clouds would form without atmospheric water vapor but to be fair one must point out that clouds aren’t composed of water vapor.
Don’t we already have a close by object with no atmosphere? What’s the surface temp on the moon? Can that not be used an an example?
“The Earth is a water world and cannot be likened to a rocky world. As far as I understand matters BB calculations do not work properly for the moon nor for any of the planets in the solar system and the Earth (due to its watery nature) is far more complicated.”
That makes sense. Then it begs the question, that as the earth rotates and continents interupt the water absorbtion, then less heat is captured. Correct? Then that begs the question, was then the differences in climate (ie no winters prior to this ice age) caused by the configuration of the continents? Less exposed land the warmer the planet became? Shallow seas means more life (our oil today), which changes the climate as well.
I don’t think the climate modelers are even close to how the planet works.
Complicating all this even more is rotation rate. The *measured* average temperature of the moon’s surface is 250K. Its albedo is much lower than the earth’s so by that empirical yardstick the earth should be colder than the moon. However, the blackbody calculation for the earth presumes that it is rotating fast enough for day/night temperature difference to be erased. But it does rotate and does have a diurnal temperature difference. Sans atmosphere the difference would be nearly as great as on the moon (which is a couple of hundred degrees K). Because heat is lost faster when temperature is higher this makes the real-life rotating body colder than the blackbody calculation would produce. Thus we have the circumstance where the earth’s moon with an albedo of 0.15 and a 28 day rotation period has a measured average temperature of 250K and a theoretical earth at albedo 0.30 spinning infinitely fast would be 5K warmer even though the theoretical earth absorbs 15% less energy.
There are so many confounding factors that the 33K figure bandied about for an earth without greenhouse gases is completely untrustworthy and without merit. I use that figure solely for the sake of argument because it isn’t necessary to dispute it in order to show the hideous flaws in computer climate models.
But this is still a great OP as it does point out a very flawed assumption bandied about by CAGW fraudsters as some kind of basic fact that is beyond dispute. Little of what they claim is beyond dispute.
PeterF says:
December 26, 2011 at 5:26 am
““… and the heated atmosphere will also radiate energy to space)”
No, it won’t. When you start with the assumption that there are no greenhouse gases in the atmosphere, then the remaining gases (oxygen and nitrogen in this case) will neither absorb nor radiate in the relevant micrometer range, and hence can’t radiate energy to space. They are not a blackbody.”
So O2 and N2 will keep their energy forever even if in the vacuum of space, as they can’t radiate anything? I don’t think that’s how it works. Would be an interesting energy storage if it worked.
http://www.americanthinker.com/2010/02/the_hidden_flaw_in_greenhouse.html
Now, of course O2 and N2 don’t have the absorption/emission bands in the LWIR range that CO2 or H2O have but that surely doesn’t stop them from having SOME emissivity.
Is there a substance with zero emissivity? Only at 0 K.
“real substances have an emissivity between zero and one (0 <ε< 1)."
http://www.learnthermo.com/T1-tutorial/ch04/lesson-B/pg22.php
Infrared radiation can’t heat gases (atmosphere), so where is warming effect?
jrwakefield says:
December 26, 2011 at 6:57 am
Don’t we already have a close by object with no atmosphere? What’s the surface temp on the moon? Can that not be used an an example?
__________________________
250K degrees.
Everything concerning the fictitious 33°C greenhouse gases effect has been definitively explained and rebutted by Gerlich & Tscheuschner (2009) in “Falsi fication Of The Atmospheric CO2 Greenhouse E ffects Within The Frame Of Physics” (http://arxiv.org/abs/0707.1161)
This value comes from a wrong use of the Stefan-Boltzmann law (flux imposing local temperature, which is wrong) involving an over simplified planet model (no atmosphere, infinite conductivity, no rotation). The real temperature would be -129°C.
Therefore, this -18°C has no meaning at all.
I do not understand why there is still a debate here.
Leonard Weinstein says:
December 26, 2011 at 6:32 am
“The writeup is wrong on the two major points. PeterF made the first one, that if there is no greenhouse effect, the atmosphere will not radiate much to space (there would be a small amount from aerosols and very weak diatomic gas effects, but not significant). The second point is the albedo effect. Oceans and clouds have effects, but if no greenhouse effect were present, the clouds (and water vapor) would not be present. The albedo would then be due to ground level absorption. It does not matter if there are oceans or not if the assumption of equivalent albedo is assumed to be the same, as long as no clouds or water vapor is present. The only effect of oceans is storage and distribution, and long term averages would be the same as if no oceans were present. Lord Monckton is correct as far as his statements are made. Get over it.”
No, you’re wrong. The ocean has an effective albedo near zero and it radiates very little. Look up any ocean heat budget study in the literature and you will discover that the ocean loses most of its heat by evaporation not radiation. Land surfaces radiate. Water evaporates. Write that down. Land has an albedo of 0.15. Water has an albedo of 0.00. Write that down too. The go figure out your errors. Monckton is full of crap which is no surprise. He’s a legend in his own mind and has a goodly number of shallow-thinking sycophants such as yourself who worship him simply because he’s on the same side of the debate as you are.
This subject has been pretty well beaten to death by “Science of Doom”. Leonard Weinstein and DeWitt Payne were two of the folks who made the most sense there.
PeterF says:
December 26, 2011 at 5:26 am
“… and the heated atmosphere will also radiate energy to space)”
No, it won’t. When you start with the assumption that there are no greenhouse gases in the atmosphere, then the remaining gases (oxygen and nitrogen in this case) will neither absorb nor radiate in the relevant micrometer range, and hence can’t radiate energy to space. They are not a blackbody.
>>>
Sorry PeterF but your statement is not strictly correct. Have you never seen the oxygen radiation in lower frequency spectra? You are saying there are no vibrational lines in oxygen and nitrogen in mid-IR but all matter above zero Kelvin, even gases, though weakly, and primarily at microwave frequencies, do radiate electromagnetic wave energy away due to electron accelerations in the gas molecules interactions with each other.
However, a lone isolated molecule of oxygen or nitrogen in the void of space will do exactly as you said, never radiate at all, zero.
One paper I read about a year ago, listed on HITRAN site of I believe nitrogen-argon interaction continuum at about wavenumber 400/cm and lower.
If you have problems with this, give me a link to a radiometry scientific paper proving this otherwise.
PeterF says:
December 26, 2011 at 5:26 am
“… and the heated atmosphere will also radiate energy to space)”
No, it won’t. When you start with the assumption that there are no greenhouse gases in the atmosphere, then the remaining gases (oxygen and nitrogen in this case) will neither absorb nor radiate in the relevant micrometer range, and hence can’t radiate energy to space.>>>
Yes it will. The absorptive/radiative spectrum for Oxygen and NO2 is right in the graphic in the article. It may not be as pronounced as water vapour and CO2, but it isn’t zero either. Further, the atmosphere contains plenty of dust which will absorb and radiate depending on the composition of the dust, but more than likely in a very broad spectrum.
To the author of this post: It is strange that with all that Monckton got wrong in that post (as was well-explained by some of us in the comments therein) you have chosen to attack the one thing that he got right. As davidmhoffer points out, the calculation of the 255 K number is for an atmosphere without a greenhouse effect, not an atmosphere without greenhouse gases. So, the correct calculation to do is to keep the Earth system albedo constant … Or, in other words, to ask, “Given that the Earth system (earth + atmosphere) absorbs 240 W/m^2, how warm could its surface possibly be if there were not a greenhouse effect?” And, the answer is that it could only be about 255 K at most.
BenAW: Your notions don’t even obey energy conservation. You are running yourself in circles getting confused about averages. I suggest you work in terms of total power in and out and then you will hopefully understand why your argument is nonsense.
Richard M says:
December 26, 2011 at 5:52 am
” think were on the right track here. First, we need to consider the Earth with no oceans and an atmosphere just like the current one without GHGs. Then, we need to add back in the oceans but still keep the GHGs out of the atmosphere. Yes, I realize this is unphysical, but I think in doing those calculations we could learn a lot.”
What you get is a snowball earth. We already have something very similar to that condition to look at in the geologic column. The vast majority of the atmospheric greenhouse effect is from water vapor. On a snowball earth most of the water vapor is frozen out of the atmosphere and the ocean is effectively removed from the equation be being covered with permanent sea ice.
The earth with an atmosphere but no ocean would be a frozen wasteland. Without greenhouse gases it would be colder but not much colder so long as a liquid ocean covered most of the surface. Where non-condensing greenhouse gases are very important is in a snowball earth episode. On a snowball earth volcanoes continue to spew CO2 and dark ashes. On a snowball there are no CO2 sinks so CO2 keeps building up in the atmosphere. Ashes also accumulate as some float so when ice surfaces partially melt in the summer it concentrates the ash on the surface making it darker and darker. After millions of years of that a tipping point is reached. So non-condensing greenhouse gases are the kindling which ignites the water cycle. Once the water cycle is ignited it keeps the earth unfrozen (most of the time) and is self-regulating through cloud formation which caps the maximum temperature preventing a runaway greenhouse. It’s quite elegant and works so well that for most of the earth’s history, even though the sun has increased its output 10% over geologic time, the earth stays warm and green from pole to pole. Episodes where there is permanent ice cover at the poles are rare. If anything right now the big climate danger lurking around the corner is the end of the Holocene Interglacial period and unless one finds hunting wooly mammoths over frozen tundra to be a good way to earn a living then we should welcome what little additional warming that anthropogenic greenhouse gases can give us and be concerned about what happens when we no longer have a way of fluffing up the earth’s temperature enough to maybe avoid the return of mile-thick glaciers as far south as New York City.
snip – both you and Dave Springer need to take your arguments elsewhere – I’m sick of this moderating this war between you two – Anthony
Why do you only consider radiation? The GHG-less atmosphere will receive energy by conduction. Since the atmosphere has low emissivity that heat will not be radiated away quickly as it can be with GHGs. However, once it gets warm enough it will start conducting heat back to the surface. Where is this equilibrium point? Is it 255 K and if so, why?
I’ll admit I don’t have any training in this area so maybe there is a simple explanation. I’ve never seen it though and can’t help feeling this could a positive feedback situation where the Earth would heat up.
Dave Springer said:
“On a snowball earth most of the water vapor is frozen out of the atmosphere and the ocean is effectively removed from the equation by being covered with permanent sea ice.”
How could that happen when solar shortwave continues to be received into the oceans from equator poleward ? It is that which maintains our liquid oceans and not non condensing GHGs.
Removing non condensing GHGs would actually INCREASE such solar input to the oceans because it would no longer be absorbed by those gases on the way down through the atmosphere and thereby be converted from solar shortwave which DOES penetrate the ocean surface to infrared longwavewhich DOES NOT penetrate the ocean surface.
On that basis non condensing GHGS result in a COLDER oceanic equilibrium temperature for a given level of solar input to the system than would otherwise have been the case.
Only the energy content of the air is raised by non condensing GHGs but that extra energy is all in latent form and serves only to speed up the water cycle.
In contrast the energy content of the oceans is actually lowered.
However the total system energy content for the system as a whole in response to a given solar energy input remains pretty much unchanged because the atmospheric Greenhouse Effect is many magnitudes smaller than the Oceanic Hot Water Bottle Effect.
@Stephen Fisher Wilde
I just read your treatise:
http://climaterealists.com/attachments/ftp/TheSettingAndMaintainingOfEarth.pdf
I had no idea you were a member of the Royal Meteorlogical Society!
I swear by all that is Holy and my mother’s eyes too that I hadn’t read your treatise before arriving at the same conclusions.
The only caveat I would add to it is that the earth isn’t entirely covered by ocean so there is still some validity in the atmospheric greenhouse effect particularly at the surface of the rocks where we live and work. On average the ocean is the big kahuna but on average we live in continental interiors far enough removed from the ocean so that we experience some warming due to greenhouse gases. That warming though simply isn’t enough to throw the entire system into a catastrophic tailspin. Perhaps it might be enough, given the greatest effect is in higher latitudes over continental interiors, that it can extend the Holocene Interglacial through the peak of the Milankovitch cycle without glaciation getting the upper hand this time. In point of fact I’m very hard pressed to come up with anything at all in the way of negative consequences from much higher atmospheric CO2 level. The earth is pretty much green from pole to pole when it is far higher and unless one actually likes barren rocks and ice one should ardently adore the prospect of more CO2.
Dave Springer;
Adding insult to injury the ocean doesn’t absorb any significant energy from downwelling infrared from greenhouse gases because the LWIR energy is completely absorbed in a skin layer just a few micrometers deep which doesn’t mix downwards but rather evaporates and carries the LWIR energy immediately away as latent heat of vaporization.>>>
This would be true of still water with no impurities. In windy or rainy conditions, the surface tension layer doesn’t exist for the most part as the surface must be relatively still for a period of 5 to 7 seconds before the skin layer reforms. Ocean surfaces subjected to wind are covered about 15% in sea foam or more. Sea water also containe silt, algae and other impurities which are brought to the surface by turbulence and which are good absorbers in the IR spectrum.
First, I think the entire model is flat wrong. (From American Thinker) Certified Consulting Meteorologist Joseph D’Aleo and computer expert E. Michael Smith appeared together on KUSI TV [Video] to discuss the Climategate — American Style scandal they had discovered. This time out, the alleged perpetrators are the National Oceanic and Atmospheric Administration (NOAA) and the NASA Goddard Institute for Space Studies (GISS).
Perhaps the key point discovered by Smith was that by 1990, NOAA had deleted from its datasets
all but 1,500 of the 6,000 thermometers in service around the globe. For example, Canada’s reporting stations dropped from 496 in 1989 to 44 in 1991, with the percentage of stations at lower elevations tripling while the numbers of those at higher elevations dropped to one. That’s right: As Smith wrote in his blog, they left “one thermometer for everything north of LAT 65.” And that one resides in a place called Eureka, which has been described as “The Garden Spot of the Arctic” due to its unusually moderate summers.
Overall, U.S. online stations have dropped from a peak of 1,850 in 1963 to a low of 136 as of 2007. In his blog, Smith wittily observed that “the Thermometer Langoliers have eaten 9/10 of the thermometers in the USA[,] including all the cold ones in California.” But he was deadly serious after comparing current to previous versions of USHCN data and discovering that this “selection bias” creates a +0.6°C warming in U.S. temperature history.
Willis Eschenbach’s WUWT essay, “The smoking gun at Darwin Zero,” and it plots GHCN Raw versus homogeneity-adjusted temperature data at Darwin International Airport in Australia is another excellent article outlining huge problems with “averaging” temperatures with mostly fake data. Furthermore, Smith cited boatloads of problems and errors he found in the Fortran code “adjustments” written to accomplish this task, ranging from hot airport stations being mismarked as “rural” to the “correction” having the wrong sign (+/-) and therefore increasing when it meant to decrease or vice-versa.
The real chicanery begins in the next phase, wherein the planet is flattened and stretched onto an 8,000-box grid, into which the time series are converted to a series of anomalies (degree variances from the baseline). Now, you might wonder just how one manages to fill 8,000 boxes using 1,500 stations.
Here’s NASA’s solution:
For each grid box, the stations within that grid box and also any station within 1200km of the center of that box are combined using the reference station method.
Even on paper, the design flaws inherent in such a process should be glaringly obvious.
Is there a reason why the author, who refers to him/herself as “I”, continues to remain unknown?